- Champalimaud Neuroscience Programme, Champalimaud Centre for the Unknown, Lisbon, Portugal
Mapping tissue microstructure accurately and noninvasively is one of the frontiers of biomedical imaging. Diffusion Magnetic Resonance Imaging (MRI) is at the forefront of such efforts, as it is capable of reporting on microscopic structures orders of magnitude smaller than the voxel size by probing restricted diffusion. Double Diffusion Encoding (DDE) and Double Oscillating Diffusion Encoding (DODE) in particular, are highly promising for their ability to report on microscopic fractional anisotropy (μFA), a measure of the pore anisotropy in its own eigenframe, irrespective of orientation distribution. However, the underlying correlates of μFA have insofar not been studied. Here, we extract μFA from DDE and DODE measurements at ultrahigh magnetic field of 16.4T with the goal of probing fixed rat spinal cord microstructure. We further endeavor to correlate μFA with Myelin Water Fraction (MWF) derived from multiexponential T2 relaxometry, as well as with literature-based spatially varying axon diameter. In addition, a simple new method is presented for extracting unbiased μFA from three measurements at different b-values. Our findings reveal strong anticorrelations between μFA (derived from DODE) and axon diameter in the distinct spinal cord tracts; a moderate correlation was also observed between μFA derived from DODE and MWF. These findings suggest that axonal membranes strongly modulate μFA, which—owing to its robustness toward orientation dispersion effects—reflects axon diameter much better than its typical FA counterpart. μFA varied when measured via oscillating or blocked gradients, suggesting selective probing of different parallel path lengths and providing insight into how those modulate μFA metrics. Our findings thus shed light into the underlying microstructural correlates of μFA and are promising for future interpretations of this metric in health and disease.
Introduction
Diffusion Magnetic Resonance Imaging (MRI) has become a mainstay of contemporary microstructural imaging in biomedical applications. Diffusion MRI can provide rich information on the sample's microstructure by interrogating micron-scale dimensions within millimeter-scale voxels [1]. In the hierarchical scaling of dimensions in biological systems, the micron-scale is fortuitously a characteristic length scale of many (sub)cellular structures of interest, such as axons, dendrites or cell bodies, which cannot be accessed using routine spatial resolutions in MRI. Most diffusion MRI methods utilize variants of Stejskal and Tanner's [2] Single Diffusion Encoding (SDE) technique [3], which probes diffusion using a single diffusion epoch spanned by diffusion-sensitizing gradient waveforms. The flexibility of SDE in terms of parameter space led to numerous variants [4], as well as diffusion models [5, 6], that have been devised to probe different aspects of the microstructure. For example, Diffusion Tensor Imaging (DTI) models diffusion using a single tensor [7, 8] under the assumption of (time-dependent) Gaussian diffusion, and the tensor's rotationally invariant properties can then report on diffusion anisotropy and parallel/perpendicular diffusivities. Other methods, such as q-space imaging [9, 10] or diffusion spectrum imaging [11] utilize Fourier relationships between the diffusion propagator and signal decay with the q-value (where is the wavevector, γ is the gyromagnetic ratio, δ represents the gradient duration, and |G| is the gradient amplitude) to extract information on pore size or orientation distributions, respectively. Diffusion time- and/or frequency-dependence can also provide much insight into the restricting geometry by probing the way in which the diffusion path is modulated with time and/or the diffusion spectrum, respectively [12–19]. Furthermore, more advanced biophysical modeling has been recently put forth to characterize specific microstructural components such as neurite density [20, 21], or water fractions tentatively associated with axons in white matter [19] from specific acquisition schemes. Such SDE methods have been widely useful in neuroscience [22] and biomedical applications, typically targeting longitudinal processes such as stroke, learning, or chronic disease progression [1].
One interesting metric that can be probed by diffusion is the microscopic diffusion anisotropy (μA) [23–25], from which its normalized counterpart – the microscopic fractional anisotropy (μFA) – can be derived. μFA defines a single compartment's anisotropy in its own eigenframe [26], e.g., for a sphere μFA = 0 while for an infinite cylinder μFA can approach 1. However, in practice, the MRI signal will always originate from an ensemble, thereby making it necessary to account for orientation dispersion within the ensemble [27]. In systems comprising coherently-aligned anisotropic objects where orientation dispersion is ideally zero, μFA would be equivalent to the fractional anisotropy (FA) derived from DTI. However, in conventional SDE methods, when orientation dispersion is significant, estimated FA values typically do not represent the true anisotropy, or μFA, as they are conflated with orientation dispersion [28, 29]. For example, in ideal randomly oriented infinite cylinders, the averaging of anisotropic compartments results in FA = 0, which—without a-priori knowledge or extensive modeling—would suggest that the microscopic geometry is spherical.
In recent years, the Double Diffusion Encoding (DDE) methodology (Figure 1) has been gaining increasing attention for its potential to refine and identify microstructural aspects not so easily probed by SDE [25, 30]. Unlike SDE, DDE probes diffusion correlations using—as its name suggests—two diffusion encoding periods, spanned by two independent gradient wavevectors, which are separated by a mixing time (τm). Comparing q-space-like signal decays using parallel and perpendicular relative gradient orientations, Cheng and Cory have been able to measure the sizes of randomly oriented elongated (anisotropic) yeast cells, and distinguish them from spherical cells [24]. Similarly, Callaghan and Komlosh have shown that diffusivities extracted from parallel vs. perpendicular DDE experiments could provide insight into μFA in randomly oriented liquid crystals characterized by Gaussian diffusion [23]. Such measurements provided the first clues that μFA (termed using many divergent terms [3]) could be recovered from DDE irrespective of orientation dispersion.
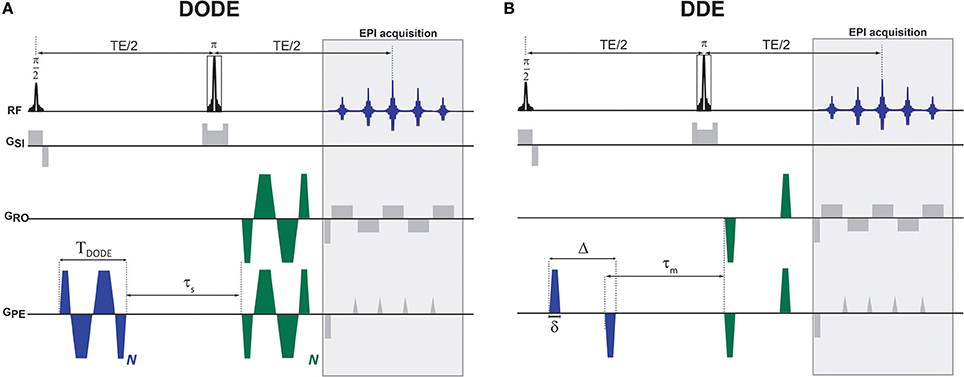
Figure 1. Diffusion MRI pulse sequences used in this study. (A) DODE and (B) DDE weightings were overlaid on a basic SE-EPI sequence. The diffusion gradient orientations are independent and can vary in any of the axes, the particular instantiation here represents one particular case where G1 is oriented along the PE axis and G2 is at an angle in the PE-RO plane. Other than the relative orientations that varied, identical waveforms were used for the two diffusion encodings.
Mitra [25], and later Özarlsan [31] derived exact solutions for DDE signals, and have identified the importance of the mixing time in decoupling μA from other effects. In the short mixing time regime, interesting diffusion-diffraction phenomena can be produced [32–36], and angular dependencies can provide insight into pore sizes as shown experimentally first by Koch and Finsterbusch [37, 38] and then by others [39–41]; however, by analyzing the displacement correlation tensor [42], the short τm angular DDE experiment aiming to measure compartment sizes was found by Jespersen to be equivalent to a time-dependent SDE experiment [43]. By contrast, in the long mixing time regime, the second order term in the displacement correlation tensor, from which sizes are measured, is decoupled from μA, making its measurement much less complicated [25, 31]. The ability to measure accurate μA values was validated in Shemesh et al. [34] and its importance was shown in biological systems such as ex-vivo neural tissues [44], yeast cells [45], and preclinical in-vivo experiments [46], where the orientational variance of the measurements was highlighted. Lawrenz et al. have proposed rotationally invariant schemes for mapping an index of μA [47, 48], and Jespersen et al. subsequently generalized rotationally invariant DDE measurements up to 5th order (in q-values) via a measurement scheme termed DDE 5-design [26]. Numerous promising studies have also been performed on human scanners [37, 38, 48–51], suggesting quite promising potential for disentangling μFA from the underlying orientation dispersion. Additional recent experiments have even extended the DDE methodology toward MR spectroscopy, aiming to impart specificity toward specific cell populations via cellular-specific metabolites [52, 53].
As alluded to above, the diffusion process in biological tissues is highly time-dependent, and thus the filter with which the diffusion experiment is performed can be important. Oscillating Diffusion Encoding (ODE) experiments [14, 54, 55] have been widely used in SDE to enhance contrast in neural tissue, likely since they access shorter diffusion time than could be reached using pulsed-gradient-spin-echo methods [56]. Additionally, ODE has been shown to be highly beneficial for mapping axonal sizes in rat spinal cord [57, 58] as well as for contrasting malignancy in tissues [59, 60]. More recently, the DDE framework was extended toward accommodation of oscillating gradients, termed Double Oscillating Diffusion Encoding (DODE, Figure 1A), first in theory [61], and more recently, in experiment [62]. Importantly, DODE enables the time/frequency-dependence of μFA to be studied. Furthermore, DODE sequences reach the long mixing time regimes much more easily than their DDE counterparts, thereby making the experiments less mixing-time dependent [61], and, as a result, offering the benefit of reduced echo times. This property is likely due to the mixing beginning already from the first gradient pair, and accumulating over the entire gradient waveform. Such DODE experiments were recently reported for the first time in the ex-vivo mouse brain, and μFA maps derived from DODE indeed showed richer contrast than those of their DDE-derived counterparts [62].
Many studies have investigated the underlying microstructural correlates of FA, mainly in white matter (for a classical review, the reader is referred to Beaulieu [63]). It is clear that although myelin strongly modulates FA, it is not necessary for detection of anisotropy in biological systems. Axonal membranes, for example, can impede the diffusion processes with orientational preference and thus can contribute to FA. However, in most studies attempting to investigate the origins of restriction in tissues, orientation dispersion was conflated with SDE-driven metrics; an interesting question is therefore whether μFA, which should not suffer from orientation dispersion effects, could be associated with microstructural features to different extents than FA. The goal of this study was therefore to investigate how μFA and FA correlate underlying microstructural features such as myelin water fraction (MWF) or axonal diameters. As well, we aimed to investigate whether these parameters are differently correlated, and to qualitatively assess the importance of orientation dispersion, especially in the white matter. The final goal of this study was to determine whether μFA is modulated when different length scales are probed via DODE and DDE sequences. A well-characterized system, namely, fixed spinal cord—which has been extensively used in the past to study diffusion [15, 58, 64–66] or relaxation [67–70] microstructural correlates—was used for these investigations. Our findings demonstrate interesting differences in correlations between μFA and FA and MWF, as well as with the a-priori known axonal sizes in white matter, when measured using DODE or DDE. Interesting findings in gray matter tissues are also presented. Implications for D(O)DE contrasts and future routes for investigations of the origin of μFA in neural tissue, are discussed.
Theory
Most DDE-MRI studies up to date have used only a single b-value to extract μFA. However, very recently, Ianus et al. showed that for most plausible microstructural scenarios, μFA obtained in such a way can be highly biased due to neglecting the higher-order terms in the signal decay [62]. Ianus et al. proposed to more accurately estimate μFA in both DDE and DODE methodologies by performing D(O)DE experiments at multiple b-values, and fitting both μA (from which μFA is then calculated) and the higher-order term via polynomial fits. That is, the D(O)DE signal decay at long mixing times can be expanded with b-value as:
where are the diffusion tensor eigenvalues, S‖ and S⊥ represent the D(O)DE signals acquired using parallel and perpendicular gradients, respectively, and P3 contains the higher-order terms up to third order (even higher-order terms are neglected). Ianus et al. showed that polynomial fitting can be used to estimate μA2 and P3 from Equation 1. When the mean diffusivity (MD) is additionally measured at lower b-values (e.g., from fitting a tensor to the 12 parallel orientations in the 5-design), μFA can be directly calculated from Eq. 2:
Although polynomial fitting probably yields more accurate estimates of μA2, it should be noted that ideally, many b-value shells would be required for robust fitting. An alternative approach would be to acquire a much more minimalistic dataset and still be able to quantify μA2 and P3. Setting , Eq. 1 can be rewritten for two different b-values b1 and b2:
It is then straightforward to show that from two measurements at different b-values, μA2 can be directly obtained from
which can then be plugged into Equation 2 to obtain μFA directly. Note that we use the tilde to distinguish the extracted from the real μA2. This approach for accurate μFA extraction thus requires, in principle, only two measurements, one at low b-value, from which MD and would be obtained, and another at higher b-value, where would be obtained. However, since at low b-values required for accurate estimation of MD, may be very small and comparable to noise levels, it is more appropriate to acquire and at somewhat higher b-values (where the b2 terms are more dominant) and perform a separate, third acquisition for extracting MD at lower b-values. This 3-shell approach was thus preferred in this study.
Materials and Methods
This study was carried out in accordance with the recommendations of the directive 2010/63/EU of the European Parliament of the Council, authorized by the Champalimaud Centre for the Unknown's Animal Welfare Body, and approved by the national competent authority (Direcção Geral de Alimentação e Veterinária, DGAV).
Specimen Preparation
Spinal cord specimens were obtained from adult male Wistar rats (N = 2) weighing ~300 gr. The rats underwent standard transcardial perfusion under deep pentobarbital anesthesia. Cervical spinal cords were extracted, washed in PBS, and kept in 4% paraformaldehyde (PFA) for 24 h at 4°C. The samples were then placed in freshly prepared phosphate buffer saline (PBS) for at least 48 h prior to MRI experiments. The samples were cut to ~1 cm segments and placed in a 5 mm NMR tube filled with fluorinert (Sigma Aldrich, Lisbon, Pt).
MRI Experiments
All MRI experiments were performed on a vertical 16.4T (700 MHz 1H frequency) Aeon Ascend scanner (Bruker, Karlsruhe, Germany) interfaced with a Bruker AVANCE IIIHD console. A Micro5 probe equipped with a 5 mm birdcage coil for transmit and receive functions and a gradient system capable of producing amplitudes of up to 3T/m isotropically was used. The sample was kept at a constant temperature of 23°C throughout the experiments by means of air flow, and the samples were allowed to equilibrate with the surrounding temperature for at least 4 h before acquiring any diffusion or relaxation experiments.
All diffusion sequences were written in-house and were based on an Echo Planar Imaging (EPI) readout. For both DODE and DDE, the same acquisition parameters were used, namely, two-shot and double-sampled EPI with a readout bandwidth of 555.555 kHz, Field of View (FOV) of 6 × 4 mm2 and in-plane matrix size of 120 × 80, leading to an isotropic in-plane resolution of 50 × 50 μm2. The slice thickness was 500 μm, and TR/TE = 2,500/52 ms. For both DODE and DDE acquisitions, Jespersen's 5-design sampling scheme [26] was used for the diffusion weighted images, and, additionally, eight images with zero b-value were acquired, such that the total number of images acquired in a given scan was 80. For both DODE and DDE, three separate acquisitions were performed with different b-values, namely, 2b = 1.2, 2.4 and 3.0 ms/μm2 (where the factor of 2 reflects the accumulated diffusion weighting along the two diffusion epochs). The specific b-values were chosen based on signal-to-noise and contrast considerations: on the one hand, they have to be sufficiently low such that even higher-order terms do not contribute, but on the other hand, they have to be high enough for μFA contrast to be detectable. The lowest b-value scans were acquired with 12 averages, while the other two b-value shells were acquired with 32 averages each. The DODE diffusion parameters were: TDODE = 13 ms, N = 5, τs = 2 ms. The DDE diffusion parameters were Δ/δ = 12/1 ms, τm = 12 ms, see Figure 1 for definitions of the parameters.
Additional experiments were performed for mapping myelin water fraction. Those consisted of a Carr-Purcell-Meiboom-Gill (CPMG)-based acquisition performed using a modified pulse multi-slice-multi-echo (MSME) sequence. The same slice was acquired as in the diffusion images with identical in-plane resolution and FOV. The acquisition bandwidth for the pulse sequence was 100 kHz, and the pulses used for slice-selective excitation and refocusing had durations of 1.16 ms (Shinnar-Le-Roux design) and 50 μs (Gaussian shape), respectively. The respective bandwidths of the excitation and refocusing pulses were 3625 and 32,100 Hz, respectively, such that the refocusing pulse provided complete refocusing on the entire slice. The ΔTE that could be achieved using these parameters was 2.85 ms, and 96 echoes were acquired from 2.85 to 273.6 ms. The repetition time was 2500 ms and two averages were acquired.
Diffusion Data Preprocessing
All preprocessing and analyses were performed using MatLab® (The MathWorks, Inc., Natick, Massachusetts, United States). Raw images were registered using an implementation of Guizar-Sicairos et al. [71] found in https://goo.gl/3bGU8b. The images were then denoised using Veraart's method based on Marchenko-Pastur distributions in Principal Component Analysis of redundant data [72]. Gibbs unringing was performed using Kellner's method [73] implemented in Matlab. Finally, the denoised and unrung images were very slightly smoothed using a [2 2] median filter.
Relaxation Data Preprocessing
The preprocessing steps for the relaxation data were identical to the diffusion data preprocessing steps, except for an additional step in the very beginning of the pipeline whereby the magnitude data was converted to real data using Eichner's method [74]. All steps listed above including denoising, unringing and median filter smoothing were then executed in sequence.
Diffusion Data Analysis
The first analysis step for D(O)DE data was to fit the diffusion tensor. Diffusivities were computed using a simple linear fitting of S‖ data acquired at the lowest b-value experiments followed by diagonalization and extraction of the diffusion tensor eignevalues and eigenvectors. The mean diffusivity and fractional anisotropy were then calculated from the tensor eigenvalues as and , where λi represent the tensor eigenvalues.
The second step in the analysis was to use the data from the two higher b-values to extract μFA. First, was extracted directly from Eq. 4; the mean diffusivity estimate was then used along with the extracted to obtain μFA via Equation 2.
Relaxation Data Analysis
Following the preprocessing steps listed above, the filtered relaxation data were subject to a voxelwise inverse Laplace Transform (iLT) using 150 T2 components log-spaced between 2.1 and 328.3 ms. The T2 spectra were smoothed by minimum-curvature constraint as in Dula et al. [75] and extended phase graph analysis was performed to account for any inhomogeneity and ensuing stimulated echoes [76]. The myelin water fraction (MWF) was computed from each spectrum as the fraction of signal originating from components with peak T2 smaller than 17 ms. ROIs were drawn manually on the raw data closely following Dula et al. [75], and the ROI data underwent the same analysis using the mean signal decay in each ROI.
Statistical Analysis
Gray matter and white matter masks were created by thresholding MWF maps with MWF < 0.22 for gray matter and MWF > 0.25 for white matter. The histograms in Figure 4 were then generated for each metric/method using Matlab's histogram function which automatically selects the bin width to represent the underlying distribution in the most accurate way. Parameter means and standard deviations are reported in the text and Tables.
Correlation analyses between different diffusion metrics were performed using automatic outlier rejection (Grubbs test for outliers) followed by calculation of Spearman's ρ (μFA and FA data from all methods were not normally distributed). An analysis of variance (ANOVA) was performed to compare μFA and FA arising from DODE and DDE methods, with post-hoc Bonferroni tests corrected for multiple comparisons.
To correlate MWF with μFA or FA extracted from the different methods, the diffusion maps were registered to the MWF using Matlab's imregister function using a multimodal configuration, initial radius of 1e-5, maximum number of iterations = 1,000, and allowing for affine transformations due to the small differences in image geometry arising from EPI-based (diffusion) and line-by-line (relaxation) acquisitions.
When linear fits are presented (Figure 8), Matlab's robustfit function was used to extract the coefficients.
Results
Diffusion data quality can be appraised in Figure 2, which plots representative raw data from one of the spinal cords, obtained from experiments with zero b-value (Figure 2A), parallel (Figure 2B), and perpendicular (Figure 2C) diffusion orientations at the highest b-value used in this study. Before denoising, the worst-case signal to noise ratio (SNR)—measured at the highest b-value and with significant diffusion weighting gradients in the direction parallel to the spinal cord's principal axis—was ~20 in white matter. The middle column in Figure 2 shows the corresponding preprocessed data and the ensuing enhancement of image quality from denoising and Gibbs unringing (Figures 2D–F). Figures 2G–I show the result of subtracting raw and denoised images. The lack of structure in the subtracted images suggest that indeed only noise was removed and that no significant signal components were lost during denoising [72]. The SNR of the preprocessed images was enhanced by a factor of ~2.
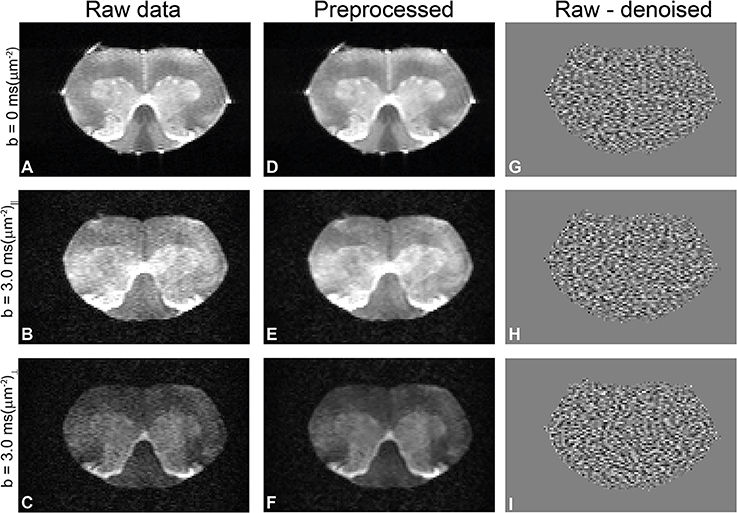
Figure 2. Quality of diffusion MRI data and preprocessing in a representative spinal cord. (A–C) Raw data with zero b-value, parallel, and perpendicular waveforms acquired at the highest b-value, respectively. In this particular direction, the perpendicular waveform had more significant components along the spinal cord principal axis and thus show greater attenuation. (D–F) Results of preprocessing the data in A–C (denoising and Gibbs unringing). Notice how the noise is highly reduced in the preprocessed images without adverse effects to image quality. (G–I) Subtraction of denoised and raw data, showing only noise and thus demonstrating that no significant signal components were removed during Marchenko-Pastur PCA denoising.
To assess the different maps obtained in this study, representative μFA and FA maps derived from DODE as well as DDE experiments (hereafter referred to as μFADODE and μFADDE or FADODE and FADDE, respectively) are shown in Figure 3. Several interesting qualitative features can be highlighted from these images: (1) both μFADODE and μFADDE maps (Figures 3A,C) have higher values than their FADODE and FADDE counterparts (Figures 3B,D) in white matter, as well as in gray matter; (2) μFADDE is higher and less tract-specific when compared with μFADODE (for approximate definitions of tract locations and spinal cord anatomy, the reader is referred to Figure 3E); (3) μFADDE appears quite homogeneous in the WM while μFADODE shows more variation within WM; (4) similarly, FADDE is more homogeneous in white matter compared with FADODE, which shows a greater variance in different tracts. To provide a more quantitative view on these features, Figure 4 plots histograms of μFA and FA in white matter and gray matter (c.f. Figures 4A,B for the ROI masks). In white matter, μFADODE is higher than its FADODE counterpart (Figure 4C), while in gray matter, μFADODE is distributed at much higher values compared to FADODE (Figure 4D). Similar trends were observed for DDE but with μFA or FA shifted toward somewhat higher values (Figures 4E,F).
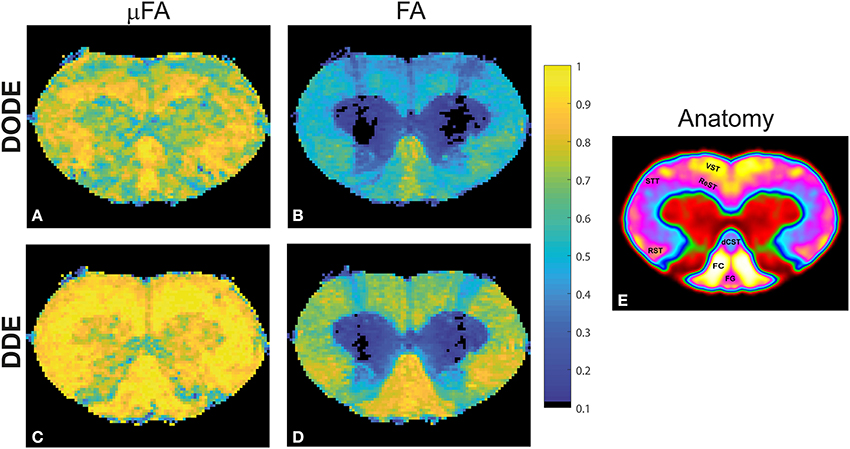
Figure 3. Parameter maps for a representative spinal cord. (A) μFADODE; (B) FADODE; (C) μFADDE; (D) FADDE. Notice the differences in contrast both in white and in gray matter tissues both between metrics and between sequences. Most notably, μFA is higher than FA and DDE-driven metrics are higher than DODE-driven metrics, especially in white matter. (E) Anatomy of the spinal cord for reference, displayed over a smoothed false-color image of the cervical segment. The gray matter is shown in red and green, while the tracts are highlighted on the left side of the cord.
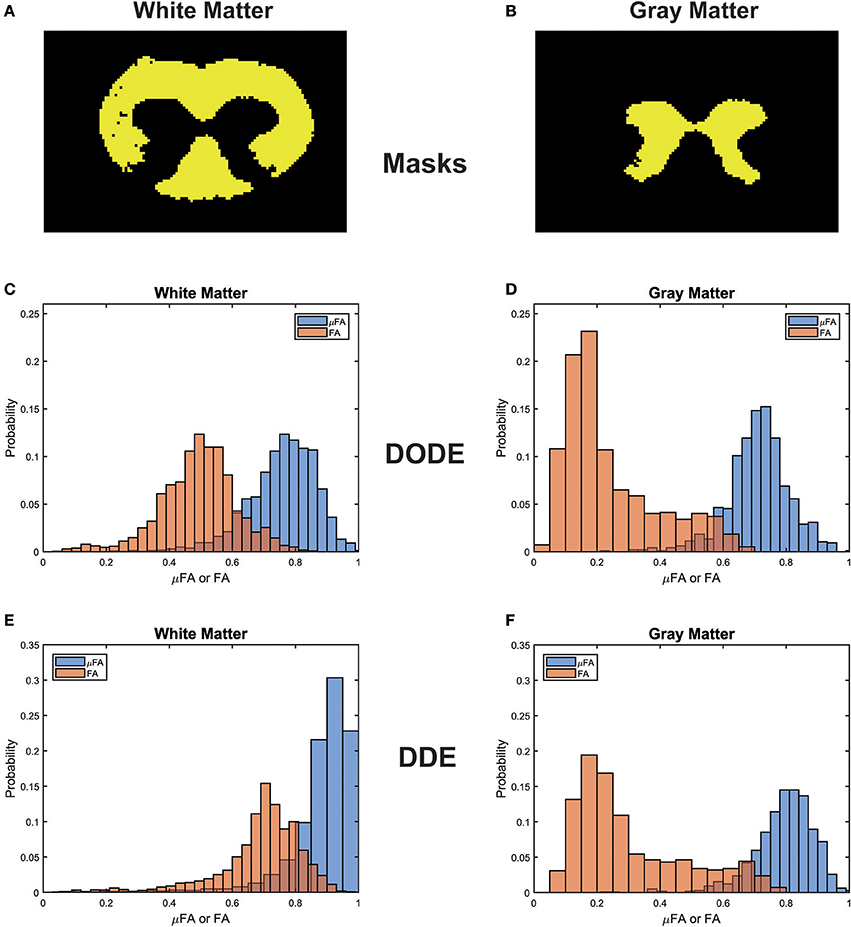
Figure 4. Histogram distributions of the different metrics in white matter and gray matter. (A,B) Masks for the white and gray matter tissues, respectively. (C,D) μFADODE and FADODE for white and gray matter. (E,F) μFADDE and FADDE for white and gray matter. Notice the different distributions in white matter for both DODE- and DDE-driven metrics, as well as the higher μFA as compared to FA in all tissues.
It is also interesting to compare differences between methods within the same tissue type (e.g., comparing same-color distributions down the columns of Figure 4). μFADODE is clearly lower and more widely distributed compared with μFADDE in white matter. In gray matter, μFADDE is high, while μFADODE is somewhat smaller. Another interesting finding in gray matter, is that FADODE and FADDE values are only slightly different. The means and standard deviations of μFA and FA for each method are tabulated in Table 1.

Table 1. White matter and gray matter microscopic and fractional anisotropies, along with their spearman correlation coefficient and significance.
A statistical analysis of these data is given in Figure 5, which presents box plots of the data. A one-way ANOVA revealed that in each tissue type (e.g., white matter or gray matter), all four metrics are highly statistically significantly different from each other (corrected p < 1e-12, post-hoc Bonferroni test). However, it should be noted that although the metrics are different, they are not completely uncorrelated. Table 1 reports Spearman's ρ and its significance levels when comparing μFA and FA (extracted by the same method) in each ROI. While μFADODE and FADODE are correlated in white matter (Spearman's ρ = ~0.41), μFADDE and FADDE metrics are only weakly correlated (Spearman's ρ = ~0.19). In gray matter, the correlations between μFA and FA were weak for both methods and (Spearman's ρ = 0.22 and −0.10 for DODE and DDE, respectively). Note that although outlier rejection was used, in all cases < ~1% of the data were identified as outliers and rejected.
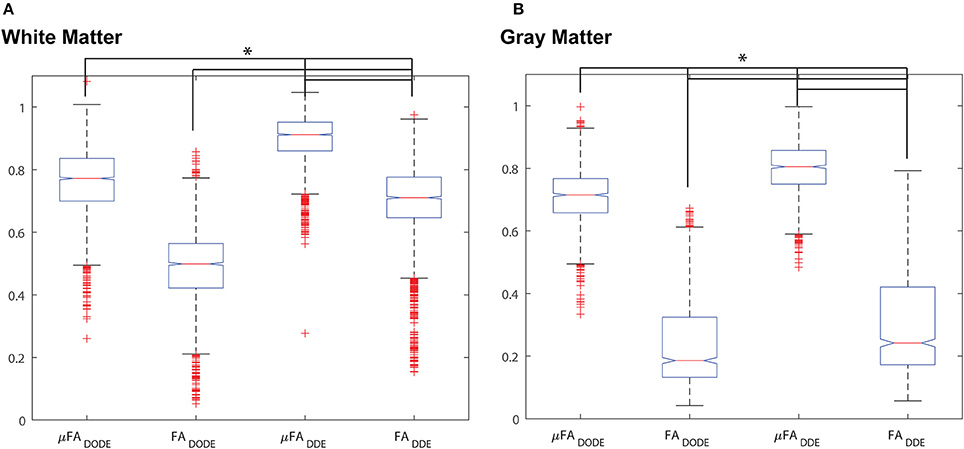
Figure 5. Box-and-whisker plots of the different metrics. (A) White matter analysis. (B) Gray matter analysis. *p < 10−12 between all pairs from ANOVA with Bonferroni post-hoc comparison and corrected for multiple comparisons.
To establish whether and how myelin modulates the anisotropy metrics, Carr-Purcell-Meiboom-Gill (CPMG) MRI experiments were performed on the same slice with the same resolution as the diffusion experiments. To assess the quality of the data, Figures 6A,B show the preprocessed data at short and very short TE of 2.9 ms and very long TE of 142.5 ms, respectively, in a representative spinal cord. Even at the very long TE, the SNR remains very high, especially after denoising. Denoising and unringing procedures were validated and found to have no negative impact on the quality of T2 fitting procedure (data not shown), while improving the fits significantly. Figure 6C shows ROIs drawn in the major tracts of the spinal cord, while Figures 6D,E show the T2 decays (with the ordinate drawn in log scale) and the resultant T2 spectra (with the abscissa drawn in linear scale), respectively. The decays in white matter are clearly non-linear, and the myelin water can be seen as an early peak in the T2 spectrum with its peak T2 around ~10 ms.
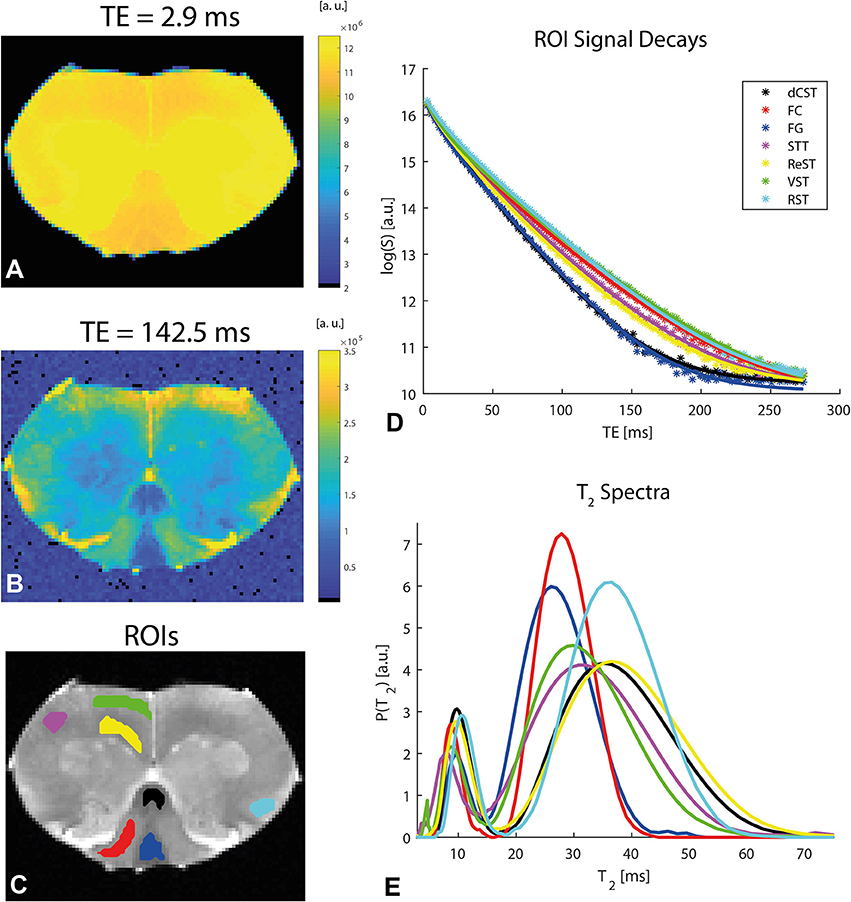
Figure 6. Relaxation data and analysis in a representative spinal cord. (A,B) Preprocessed data at short and long TEs, respectively, reveal excellent SNR. (C) ROI definitions. (D) Mean ROI signal decays with TE (symbols) along with their respective fits (solid lines). N.b. the log scale in the ordinate. (E) T2 spectra (plotted in log scale in the abscissa) extracted from an iLT fit to the ROI data. The myelin water is associated with the peak corresponding to shorter T2 values. The ROI colors in (C) correspond to the color of the plots in (D,E).
A representative myelin water fraction (MWF) map arising from pixel-by-pixel quantification of the spectra is shown in Figure 7A. Note the sharp contrast between the different tracts in MWF: for example, the dCST shows the lowest MWF (MWF~0.30) while VST and FC exhibit the highest MWF (MWF~0.45). Scatter plots between MWF and μFA or FA in white matter are shown in Figure 7 for DODE (Figure 7B) and DDE (Figure 7C), respectively. Table 2 summarizes the correlation coefficients and associated statistics. A moderate anticorrelation between MWF and μFADODE is observed in the white matter (Spearman's ρ = ~ −0.36), while FADODE did not correlate with MWF in a statistically significant manner. The DDE counterparts μFADDE and FADDE exhibited weak anti-correlation and correlation, respectively. Figures 7D,E show similar plots as described above, but for gray matter. Notably, correlations between MWF and FADODE, as well as FADDE were very weak and their statistical significance not very high; on the contrary, μFADODE was found to correlate somewhat with MWF, while μFADDE correlated moderately with MWF, with very high statistical significance (c.f. Table 2).
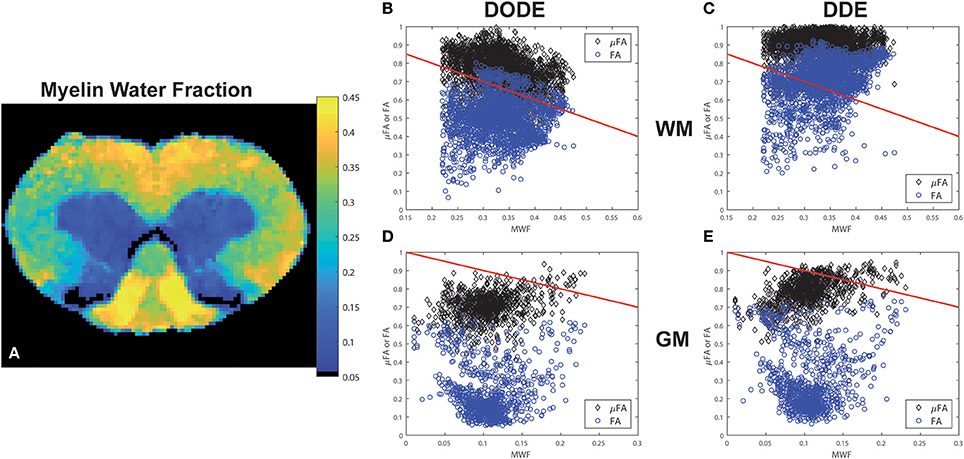
Figure 7. Myelin Water Fraction (MWF) and its correlations with diffusion-derived metrics. (A) MWF from a representative spinal cord, showing excellent contrast between the white matter and gray matter as well as within most white matter tracts. (B–E) Correlations between DODE and DDE metrics with MWF in white and gray matter tissues. Blue circles represent FA whereas black diamonds represent μFA. Red lines represent−1*identity to guide the eye.
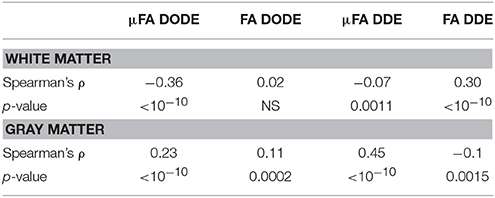
Table 2. Statistical analysis of correlations between (μ)FA and myelin water fraction in white matter and gray matter.
Finally, the correlation of the mean μFA in the different tracts with literature regional averaged axon diameter was assessed. Figures 8A,B plot mean μFA and FA against the axon diameters reported in Dula et al. [75] for the different spinal cord tracts. These data, along with the values tabulated in Table 3, demonstrate that μFADODE exhibits very strong anticorrelation with axon diameters (Spearman's ρ = −0.96, p = 0.0028). All other metrics are not significantly correlated with axon diameter.
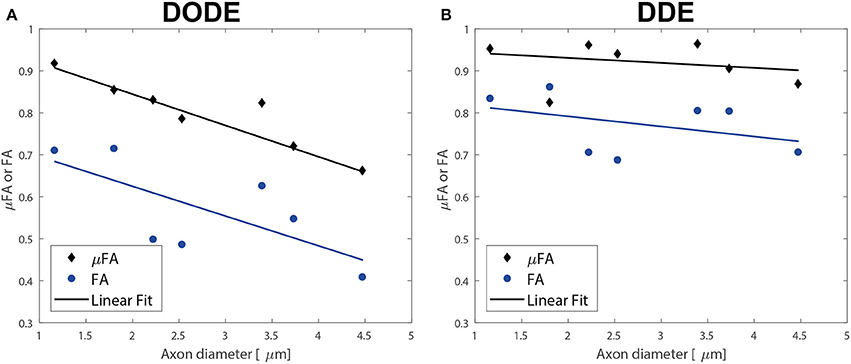
Figure 8. Correlations of diffusion metrics with literature-based average axon diameters in the different white matter tracts. (A) Correlations of metrics derived from DODE. (B) Correlations derived from DDE. The best linear regressions to the experimental data are also given as solid lines. Note the excellent inverse agreement between μFADODE and axon diameter, which also had a very high anticorrelation coefficient of ρ ~−0.96 while all other metrics did not show significant correlations.
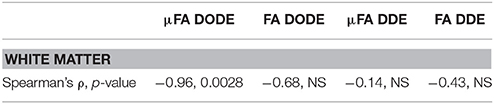
Table 3. Statistical analysis of correlations between (μ)FA and literature-based average axon diameter (extracted from Dula et al. 75) in the rat spinal cord.
Discussion
μFA has been recently gaining increasing attention as a potentially useful source of contrast in microstructural MRI due to its ability to disentangle anisotropy from orientation dispersion. Methods other than D(O)DE, targeting μFA such as tailoring b-tensor shapes are emerging, with many potential applications [77–80]. However, such methods may be confounded by time-dependent diffusion effects [27, 81–83], whereas D(O)DE at long mixing times naturally avoids these confounds [43]. It is therefore imperative to investigate how μFA may be correlated with underlying microstructural features such as axon dimensions and myelin, much like the early studies aiming to understand the sources for FA [63, 67, 84, 85]. In general, perhaps the most significant findings of prior studies on FA (conducted nearly invariably with SDE) were that (1) anisotropy in white matter depends on axonal membranes; and (2) the presence of myelin can further modulate FA metrics [63]. The application of oscillating gradients has also been shown to generate more contrast and more accurate estimations of small dimensions as compared to long diffusion time experiments, presumably due to the more efficient probing of smaller dimensions via the shorter diffusion times [58, 86, 87].
The present study aimed to investigate how μFA differs from FA in terms of correlations with myelin water and axonal diameters, and to compare those metrics when measured with DDE or DODE sequences. We first focus attention to our results arising from white matter tissue. Notably, μFA was always larger than FA (Figures 3–5 and Table 2), in agreement with previous DDE experiments in fixed tissues [26] and in-vivo [88]. Since the μFA and FA metrics were extracted from the same acquisition, it is unlikely that other effects such as exchange or relaxation contributed to μFA > FA. Thus, our finding supports the notion that that orientation dispersion is significant even in highly structured tissues, such as spinal cord white matter. This is in excellent agreement with a recent study of SDE-derived diffusion tensor and kurtosis time-dependencies which also pointed to the same conclusion in pig spinal cord [15], as well as with histological studies attempting to measure the dispersion directly in white matter [89]. It is difficult to draw conclusions on whether the orientation dispersion arises within intra- or extra-axonal spaces (or both), or, whether undulations [90] or passing collateral fibers [91] can contribute to these observations. Performing similar spectroscopic measurements utilizing cell-specific markers such as NAA or mI [52, 53], or performing much more extensive time/frequency/b-value-dependent measurements on water [19, 59, 92], or on metabolites [93, 94] may further assist in addressing this question in the future.
Another interesting aspect when comparing μFA with FA in white matter, is that the two metrics are only moderately correlated when measured with DODE, and very weakly correlated when measured with DDE (c.f. Table 1). This finding suggests that when diffusion is encoded using oscillating gradients, spins experience less orientation dispersion than when they are probed using block gradients, since μFA would be perfectly correlated (and identical) to FA for perfectly aligned fibers. Hence, our findings point to specific length scales for orientation dispersion that are probed differently using the different sequences.
Next, we consider the relationships between myelin and μFA. Akin to its FA counterpart–μFA is ambiguous in that a compartment with length “L” and radius “R” can give rise to the same μFA as a compartment with length 2L and radius 2R. The axial path length could be restricted due to nodes of Ranvier, non-ideal cylindrical structure, varicosities, etc. However, if the path length parallel to the (assumingly) ellipsoids is constant, then one could predict that when larger amounts of myelin surround an axon, the μFA will be smaller as the restriction will increase in the perpendicular direction. However, in our study, a moderate negative correlation was observed between MWF and μFADODE in white matter (Figure 7 and Table 2). This can be explained by considering the dependence of MWF and axon diameter via the g-ratio [95]: the larger the axon, the thicker the myelin around it in (healthy) mammalian white matter [96]. Hence, the negative correlation between μFADODE and MWF would reflect indirectly the approximately constant g-ratio in healthy tissue, rather than enhanced restriction. Interestingly, μFADDE showed a much weaker, yet still negative correlation with MWF. Since the microstructure has not changed between measurements, this likely reflects that DODE and DDE probe different path lengths parallel to the spinal cord's major axis: the larger the diffusion time, the longer path will be probed in the unrestricted dimension, and thence the μFA will be larger and less reflective of axon diameter or, by proxy, its myelin thickness. FADDE showed a small positive correlation with MWF, which perhaps reflects the ambiguity of probing restriction and orientation distribution at the same time. Extracellular space contributions again cannot be neglected here, but for coherently aligned systems the arguments are similar as one could potentially treat the space between densely packed axons as potentially even more restricted than the intra-axonal space itself [45]. It is also worth mentioning that MWF extracted from multiexponential T2 measurements, as performed in this study, have been shown in the past to reflect microstructural metrics such as axon size and myelin thickness very faithfully in white matter [67, 75, 97].
Our most striking findings in this study, perhaps, is that μFADODE showed an extremely high, and statistically significant, negative correlation with axon diameters reported by Dula et al. [75] and Harkins et al. [98] for the different tracts (Table 3). This observation lends further credence to the explanation above: the finite parallel length scale probed by DODE makes the measurement strongly dependent on the perpendicular restriction, which in this case is reflected through axon sizes. Although the axon diameters were obtained from literature, it is worth stressing that axon diameter dependence in healthy spinal cords is highly reproducible and that the tracts analyzed were obtained from very similar cervical slices as in Dula et al. [75]. Such a strong correlation is also highly unlikely to be obtained randomly. It is very interesting to also note that all other metrics did not correlate in a statistically significant fashion with axon diameters: μFADDE likely due to its probing of longer parallel lengths, and the FA from both methods due to its inherent conflation or restriction with orientation dispersion.
In the spinal cord gray matter, very low FADODE and FADDE values were measured, suggesting a much lower degree of restriction compared to white matter diffusion. However, the μFADODE and μFADDE metrics in gray matter were still very high in the gray matter. In fact, the values reported in Table 1 also reflect and . Combined with the low FA values in the gray matter, our findings suggest that a significant component of gray matter tissue experiences restricted diffusion but with a large degree of orientation dispersion. This finding is also in good agreement with previous literature demonstrating significant angular DDE modulations in ex-vivo gray matter [44, 45]. Further studies are needed to establish which underlying biological components give rise to such high μFA in gray matter, but dendrites, astrocyte branches, and nonmyelinated or myelinated axons traversing gray matter could be suspected [93, 99]. Time-dependent or spectroscopic experiments on metabolites could provide insight into such questions in the future.
Several limitations can be identified in this study. First, we have introduced a new way of measuring harnessing the 5-design acquisition at two b-values to reduce the recently-reported bias in μA2 estimation due to higher order terms. Our new method is likely inferior to a sampling of a large range of b-values and the ensuing polynomial fitting as done in Ianus et al. [62]. However, the advantage of the current approach is that it manages to avoid a prohibitively long experiment duration. Future studies will identify the accuracy and precision of the method proposed above vis-à-vis the ground-truth, and attempt to find optimal b-values for measuring as accurately and with as little bias as possible. Second, to compute μFA, we executed a third measurement at lower b-value to extract MD, which is then input into Eq. 2 along with . However, MD itself may be conflated with higher-order terms, as pointed out recently by Chuhutin et al. [100]; in this study, this issue was not accounted for, and may induce minor biases in the measurements of μFA. Better estimation of MD could probably be performed by sampling one or more low b-values and fitting kurtosis and MD at the same time from spherically averaged data. In addition, we have not explored the impact of specific b-value selection. At too low b-values, the difference in the log signals is very small, while at higher b-values, even higher-order terms may come into play. Third, the sample size was quite small (N = 2 spinal cords, only a single slice per cord), such that the variability across animals was not very well sampled. However, it is worth noting that the results were actually very consistent between both spinal cords: the mean μFA and FA, for both DODE and DDE, varied <10% between the cords (both in gray and white matter tissues), and the MWF varied <6% between the tissues. Although this consistency is promising for the robustness of the approach, the small number of samples renders this study perhaps more exploratory. Fourth, the experiments were performed at a relatively long TE of 52 ms. Given that the MWF was associated with T2 < 20 ms and that the other water T2s were distributed between ~20 and 60 ms, the diffusion experiments can be considered completely filtered for (directly contributing) myelin water, as 0.005. Exchange between myelin water and intra/extra-axonal water is likely to occur, which may also confound the measurements, although it should be noted that at least for conventional DODE MRI, the relatively long TE is nearly unavoidable due to the necessity of non-negligible diffusion gradient waveform durations. Double-stimulated-echo approaches [101, 102] would thus be nearly impossible to execute for DODE, even before considering the significant SNR reduction associated with such sequences, (1/2)N, where N is the number of stimulated echoes. Finally, a histological study was not here performed, and the study relies on literature reports of correlations between MRI-derived MWF and myelin thickness and the values for axon diameters. Future studies can expand the findings here and perform more direct correlations with histology, although it should be pointed out that big differences in these parameters are unlikely to be observed for healthy tissues. In addition, it would be fruitful to modulate the microstructure actively and to observe how μFA varies, e.g., using genetic mutations that alter myelin content. All these highly interesting avenues will be pursued in the future, but the present study provides the first steps in this direction.
Conclusions
This study investigated the microstructural correlates of μFA and FA using high resolution D(O)DE experiments in fixed spinal cords at 16.4 T. Our results indicate very strong anticorrelations of μFADODE with axon size, and moderate anticorrelations of μFADODE with MWF, whereas μFADDE, FADODE and FADDE correlate to a much lesser or no extent with those microstructural features. These findings shed light on the mechanisms of restriction in spinal cord white matter when investigate without conflation by orientation dispersion. The correlations of μFADODE with axon diameters and myelin water fraction are thus promising for future investigations of longitudinal variations in these properties, e.g., in disease or with learning.
Author Contributions
NS designed the study, collected and analyzed data, and wrote the paper.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This study was funded in part by the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement No. 679058-DIRECT-fMRI). The author would like to thank Prof. Sune N. Jespersen and Mr. Jonas Lynge Olesen (Aarhus University) for providing the codes for denoising and Gibbs unringing, as well as for many insightful discussions. The author also thanks Dr. Daniel Nunes for extracting the tissues used in this study, Dr. Andrada Ianus and Ms. Teresa Serradas Duarte for providing parts of code used in the analyses performed here, and Prof. Mark D. Does from Vanderbilt University for the REMMI pulse sequence and its analysis tools, that were supported through grant number NIH EB019980.
References
1. Johansen-Berg H, Behrens T. (2009). Diffusion MRI: From Quantitative Measurement to in Vivo Neuroanatomy. San Diego, CA: Academic Press.
2. Stejskal EO, Tanner JE. Spin diffusion measurements: spin echoes in the presence of a time-dependent field. J Chem Phys. (1965) 42:288–92. doi: 10.1063/1.1695690
3. Shemesh N, Jespersen SN, Alexander DC, Cohen Y, Drobnjak I, Dyrby TB, et al. Conventions and nomenclature for double diffusion encoding NMR and MRI. Magn Reson Med. (2016) 75: 82–7. doi: 10.1002/mrm.25901
4. Grebenkov DS. NMR survey of reflected Brownian motion. Rev Mod Phys. (2007) 79:1077–137. doi: 10.1103/RevModPhys.79.1077
5. Assaf Y, Alexander DC, Jones DK, Bizzi A, Behrens TEJ, Clark CA, et al. The CONNECT project: combining macro- and micro-structure. Neuroimage (2013) 80:273–82. doi: 10.1016/j.neuroimage.2013.05.055
6. Panagiotaki E, Schneider T, Siow B, Hall MG, Lythgoe MF, Alexander DC. Compartment models of the diffusion MR signal in brain white matter: a taxonomy and comparison. Neuroimage (2012) 59:2241–54. doi: 10.1016/j.neuroimage.2011.09.081
7. Basser PJ, Jones DK. Diffusion-tensor MRI: theory, experimental design and data analysis-A technical review. NMR Biomed. (2002) 15:456–67. doi: 10.1002/nbm.783
8. Mori S, Zhang J. Principles of diffusion tensor imaging and its applications to basic neuroscience research. Neuron (2006) 51:527–39. doi: 10.1016/j.neuron.2006.08.012
9. Callaghan PT, Coy A, MacGowan D, Packer KJ, Zelaya FO. Diffraction-like effects in NMR diffusion studies of fluids in porous solids. Nature (1991) 351:467–69. doi: 10.1038/351467a0
10. Cohen Y, Assaf Y. High b-value q-space analyzed diffusion-weighted MRS and MRI in neuronal tissues-A technical review. NMR Biomed. (2002) 15:516–42. doi: 10.1002/nbm.778
11. Wedeen VJ, Hagmann P, Tseng WYI, Reese TG, Weisskoff RM. Mapping complex tissue architecture with diffusion spectrum magnetic resonance imaging. Magn Reson Med. (2005) 54:1377–386. doi: 10.1002/mrm.20642
12. Clark CA, Hedehus M, Moseley ME. Diffusion time dependence of the apparent diffusion tensor in healthy human brain and white matter disease. Magn Reson Med. (2001) 45:1126–9. doi: 10.1002/mrm.1149
13. Fieremans E, Burcaw LM, Lee HH, Lemberskiy G, Veraart J, Novikov DS. In vivo observation and biophysical interpretation of time-dependent diffusion in human white matter. Neuroimage (2016) 129:414–27. doi: 10.1016/j.neuroimage.2016.01.018
14. Gore JC, Xu J, Colvin DC, Yankeelov TE, Parsons EC, Does MD. Characterization of tissue structure at varying length scales using temporal diffusion spectroscopy. NMR Biomed. (2010) 23:745–56. doi: 10.1002/nbm.1531
15. Jespersen SN, Olesen JL, Hansen B, Shemesh N. Diffusion time dependence of microstructural parameters in fixed spinal cord. Neuroimage (2017). doi: 10.1016/j.neuroimage.2017.08.039. [Epub ahead of print].
16. Latour LL, Svoboda K, Mitra PP, Sotak CH. Time-dependent diffusion of water in a biological model system. Proc Natl Acad Sci USA. (1994) 91:1229–33. doi: 10.1073/pnas.91.4.1229
17. Novikov DS, Fieremans E, Jensen JH, Helpern JA. Random walks with barriers. Nat Phys. (2011) 7:508–14. doi: 10.1038/nphys1936
18. Stepišnik J, Lasič S, Mohorič A, Serša I, Sepe A. Spectral characterization of diffusion in porous media by the modulated gradient spin echo with CPMG sequence. J Magn Reson. (2006) 182:195–9. doi: 10.1016/j.jmr.2006.06.023
19. Veraart J, Fieremans E, Novikov DS. Universal power-law scaling of water diffusion in human brain defines what we see with MRI. arXiv (2016). 1–8.
20. Jespersen SN, Kroenke CD, Østergaard L, Ackerman JJH, Yablonskiy DA. Modeling dendrite density from magnetic resonance diffusion measurements. Neuroimage (2007) 34:1473–86. doi: 10.1016/j.neuroimage.2006.10.037
21. Jespersen SN, Bjarkam CR, Nyengaard JR, Chakravarty MM, Hansen B, Vosegaard T, et al. Neurite density from magnetic resonance diffusion measurements at ultrahigh field: comparison with light microscopy and electron microscopy. Neuroimage (2010) 49:205–16. doi: 10.1016/j.neuroimage.2009.08.053
22. Zatorre RJ, Fields RD, Johansen-Berg H. Plasticity in gray and white: neuroimaging changes in brain structure during learning. Nat Neurosci. (2012) 15:528–36. doi: 10.1038/nn.3045
23. Callaghan PT, Komlosh ME. Locally anisotropic motion in a macroscopically isotropic system: displacement correlations measured using double pulsed gradient spin-echo NMR. Magn Reson Chem. (2002) 40:15–9. doi: 10.1002/mrc.1122
24. Cheng Y, Cory DG. Multiple scattering by NMR. J Am Chem Soc. (1999) 121:7935–6. doi: 10.1021/ja9843324
25. Mitra PP. Multiple wave-vector extensions of the NMR pulsed-field-gradient spin-echo diffusion measurement. Phys Rev B. (1995) 51:15074–8. doi: 10.1103/PhysRevB.51.15074
26. Jespersen SN, Lundell H, Sønderby CK, Dyrby TB. Orientationally invariant metrics of apparent compartment eccentricity from double pulsed field gradient diffusion experiments. NMR Biomed. (2013) 26:1647–62. doi: 10.1002/nbm.2999
27. Jespersen SN, Olesen JL, Ianu A, Shemesh N. (2017b). Anisotropy in “isotropic diffusion ”measurements due to nongaussian diffusion. arXiv 1–22.
28. Mollink J, Kleinnijenhuis M, Cappellen van Walsum AM, van Sotiropoulos SN, Cottaar M, Mirfin C, et al. Evaluating fibre orientation dispersion in white matter: comparison of diffusion MRI, histology and polarized light imaging. Neuroimage (2017) 157:561–74. doi: 10.1016/j.neuroimage.2017.06.001
29. Reisert M, Kellner E, Dhital B, Hennig J, Kiselev VG. Disentangling micro from mesostructure by diffusion MRI: a bayesian approach. Neuroimage (2017) 147:964–75. doi: 10.1016/j.neuroimage.2016.09.058
30. Cory DG, Garroway AN, Miller J. Applications of Spin Transport as a probe of local geometry. Polym Preprints. (1990) 31:149.
31. Özarslan E. Compartment shape anisotropy (CSA) revealed by double pulsed field gradient MR. J Magn Reson. (2009) 199:56–67. doi: 10.1016/j.jmr.2009.04.002
32. Laun FB, Kuder TA, Semmler W, Stieltjes B. Determination of the defining boundary in nuclear magnetic resonance diffusion experiments. Phys Rev Lett. (2011) 107:2–5. doi: 10.1103/PhysRevLett.107.048102
33. Laun FB, Kuder TA, Wetscherek A, Stieltjes B, Semmler W. NMR-based diffusion pore imaging. Phys Rev E. (2012) 86:021906. doi: 10.1103/PhysRevE.86.021906
34. Shemesh N, Özarslan E, Adiri T, Basser PJ, Cohen Y. Noninvasive bipolar double-pulsed-field-gradient NMR reveals signatures for pore size and shape in polydisperse, randomly oriented, inhomogeneous porous media. J. Chem. Phys. (2010) 133:044705. doi: 10.1063/1.3454131
35. Shemesh N, Özarslan E, Basser PJ, Cohen Y. Detecting diffusion-diffraction patterns in size distribution phantoms using double-pulsed field gradient NMR: theory and experiments. J Chem Phys. (2010) 132:034703. doi: 10.1063/1.3285299
36. Shemesh N, Westin CF, Cohen Y. Magnetic resonance imaging by synergistic diffusion-diffraction patterns. Phys Rev Lett. (2012) 108:058103. doi: 10.1103/PhysRevLett.108.058103
37. Koch MA, Finsterbusch J. Compartment size estimation with double wave vector diffusion-weighted imaging. Magn Reson Med. (2008) 60:90–101. doi: 10.1002/mrm.21514
38. Koch MA, Finsterbusch J. Towards compartment size estimation in vivo based on double wave vector diffusion weighting. NMR Biomed. (2011) 24:1422–32. doi: 10.1002/nbm.1711
39. Komlosh ME, Özarslan E, Lizak MJ, Horkay F, Schram V, Shemesh N, et al. Pore diameter mapping using double pulsed-field gradient MRI and its validation using a novel glass capillary array phantom. J Magn Reson. (2011) 208:128–35. doi: 10.1016/j.jmr.2010.10.014
40. Morozov D, Bar L, Sochen N, Cohen Y. Microstructural information from angular double-pulsed-field-gradient NMR: from model systems to nerves. Magn Reson Med. (2015) 74:25–32. doi: 10.1002/mrm.25371
41. Shemesh N, Özarslan E, Basser PJ, Cohen Y. Measuring small compartmental dimensions with low-q angular double-PGSE NMR: the effect of experimental parameters on signal decay. J Magn Reson. (2009) 198:15–23. doi: 10.1016/j.jmr.2009.01.004
42. Nørhøj Jespersen S, Buhl N. The displacement correlation tensor: microstructure, ensemble anisotropy and curving fibers. J Magn Reson. (2011) 208:34–43. doi: 10.1016/j.jmr.2010.10.003
43. Jespersen SN. Equivalence of double and single wave vector diffusion contrast at low diffusion weighting. NMR Biomed. (2012) 25:813–18. doi: 10.1002/nbm.1808
44. Shemesh N, Cohen Y. Microscopic and compartment shape anisotropies in gray and white matter revealed by angular bipolar double-PFG MR. Magn Reson Med. (2011) 65:1216–27. doi: 10.1002/mrm.22738
45. Shemesh N, Adiri T, Cohen Y. Probing microscopic architecture of opaque heterogeneous systems using double-pulsed-field-gradient NMR. J Am Chem Soc. (2011) 133:6028–35. doi: 10.1021/ja200303h
46. Shemesh N, Barazany D, Sadan O, Bar L, Zur Y, Barhum Y, et al. Mapping apparent eccentricity and residual ensemble anisotropy in the gray matter using angular double-pulsed-field-gradient MRI. Magn Reson Med. (2012) 68:794–806. doi: 10.1002/mrm.23300
47. Lawrenz M, Koch MA, Finsterbusch J. A tensor model and measures of microscopic anisotropy for double-wave-vector diffusion-weighting experiments with long mixing times. J Magn Reson. (2010) 202:43–56. doi: 10.1016/j.jmr.2009.09.015
48. Lawrenz M, Finsterbusch J. Mapping measures of microscopic diffusion anisotropy in human brain white matter in vivo with double-wave-vector diffusion-weighted imaging. Magn Reson Med. (2015) 73:773–83. doi: 10.1002/mrm.25140
49. Avram AV, Özarslan E, Sarlls JE, Basser PJ. In vivo detection of microscopic anisotropy using quadruple pulsed-field gradient (qPFG) diffusion MRI on a clinical scanner. Neuroimage (2013) 64:229–39. doi: 10.1016/j.neuroimage.2012.08.048
50. Ulloa P, Wottschel V, Koch MA. Studying the extracellular contribution to the double wave vector diffusion-weighted signal. Curr Dir Biomed Eng. (2015) 1:240–4. doi: 10.1515/cdbme-2015-0060
51. Finsterbusch J. Annual Reports on NMR Spectroscopy. Multiple-Wave-Vector Diffusion-Weighted NMR. 1st ed. Elsevier Ltd. (2011) 72:225–99.
52. Shemesh N, Rosenberg JT, Dumez JN, Muniz JA, Grant SC, Frydman L. Metabolic properties in stroked rats revealed by relaxation-enhanced magnetic resonance spectroscopy at ultrahigh fields. Nat Commun. (2014) 5:1–8. doi: 10.1038/ncomms5958
53. Shemesh N, Rosenberg JT, Dumez J.-N., Grant SC, Frydman L. Distinguishing neuronal from astrocytic subcellular microstructures using in vivo double diffusion encoded 1H MRS at 21.1 T. PLoS ONE (2017) 12:e0185232. doi: 10.1371/journal.pone.0185232
54. Does MD, Parsons EC, Gore JC. Oscillating gradient measurements of water diffusion in normal and globally ischemic rat brain. Magn Reson Med. (2003) 49:206–15. doi: 10.1002/mrm.10385
55. Stepišnik J. Time-dependent self-diffusion by NMR spin-echo. Phys B Phys Condens Matter (1993) 183:343–50. doi: 10.1016/0921-4526(93)90124-O
56. Drobnjak I, Zhang H, Ianuş A, Kaden E, Alexander DC. PGSE, OGSE, sensitivity to axon diameter in diffusion MRI: insight from a simulation study. Magn Reson Med. (2016) 75:688–700. doi: 10.1002/mrm.25631
57. Xu J, Does MD, Gore JC. Quantitative characterization of tissue microstructure with temporal diffusion spectroscopy. J Magn Reson. (2009) 200:189–97. doi: 10.1016/j.jmr.2009.06.022
58. Xu J, Li H, Harkins KD, Jiang X, Xie J, Kang H, et al. Mapping mean axon diameter and axonal volume fraction by MRI using temporal diffusion spectroscopy. Neuroimage (2014) 103:10–9. doi: 10.1016/j.neuroimage.2014.09.006
59. Reynaud O, Winters KV, Hoang DM, Wadghiri YZ, Novikov DS, Kim SG. Surface-to-volume ratio mapping of tumor microstructure using oscillating gradient diffusion weighted imaging. Magn Reson Med. (2016) 76:237–47. doi: 10.1002/mrm.25865
60. Xu J, Li K, Smith RA, Waterton JC, Zhao P, Chen H, et al. Characterizing tumor response to chemotherapy at various length scales using temporal diffusion spectroscopy. PLoS ONE (2012) 7:e41714. doi: 10.1371/journal.pone.0041714
61. Ianuş A, Shemesh N, Alexander DC, Drobnjak I. Double oscillating diffusion encoding and sensitivity to microscopic anisotropy. Magn Reson Med. (2017) 78:550–64. doi: 10.1002/mrm.26393
62. Ianuş A, Jespersen SN, Serradas T, Alexander DC. (2017). Accurate Estimation of Microscopic Diffusion Anisotropy and its Time Dependence in the Mouse Brain. arxiv.
63. Beaulieu C. The basis of anisotropic water diffusion in the nervous system-A technical review. NMR Biomed. (2002) 15:435–55. doi: 10.1002/nbm.782
64. Klawiter EC, Schmidt RE, Trinkaus K, Liang HF, Budde MD, Naismith RT, et al. Radial diffusivity predicts demyelination in ex vivo multiple sclerosis spinal cords. Neuroimage (2011) 55:1454–60. doi: 10.1016/j.neuroimage.2011.01.007
65. Komlosh ME, Lizak MJ, Horkay F, Freidlin RZ, Basser PJ. Observation of microscopic diffusion anisotropy in the spinal cord using double-pulsed gradient spin echo MRI. Magn Reson Med. (2008) 59:803–09. doi: 10.1002/mrm.21528
66. Schwartz ED, Cooper ET, Chin C.-L., Wehrli S, Tessler A, Hackney DB. Ex vivo evaluation of ADC values within spinal cord white matter tracts. AJNR. Am J Neuroradiol. (2005) 26:390–7.
67. Kozlowski P, Liu J, Yung AC, Tetzlaff W. High-resolution myelin water measurements in rat spinal cord. Magn Reson Med. (2008) 59:796–802. doi: 10.1002/mrm.21527
68. Kozlowski P, Raj D, Liu J, Lam C, Yung AC, Tetzlaff W. Characterizing white matter damage in rat spinal cord with quantitative mri and histology. J Neurotrauma (2008) 25:653–76. doi: 10.1089/neu.2007.0462
69. Nunes D, Cruz TL, Jespersen SN, Shemesh N. Mapping axonal density and average diameter using non-monotonic time-dependent gradient-echo MRI. J Magn Reson. (2017) 277:117–30. doi: 10.1016/j.jmr.2017.02.017
70. Wilhelm MJ, Ong HH, Wehrli SL, Li C, Tsai P.-H., Hackney DB, et al. Direct magnetic resonance detection of myelin and prospects for quantitative imaging of myelin density. Proc Natl Acad Sci USA. (2012) 109:9605–10. doi: 10.1073/pnas.1115107109
71. Guizar-Sicairos M, Thurman ST, Fienup JR. Efficient subpixel image registration algorithms. Opt Let. (2008) 33:156. doi: 10.1364/OL.33.000156
72. Veraart J, Novikov DS, Christiaens D, Ades-aron B, Sijbers J, Fieremans E. Denoising of diffusion MRI using random matrix theory. Neuroimage (2016). 142:394–406. doi: 10.1016/j.neuroimage.2016.08.016
73. Kellner E, Dhital B, Kiselev VG, Reisert M. Gibbs-ringing artifact removal based on local subvoxel-shifts. Magn Reson Med. (2016) 76:1574–81. doi: 10.1002/mrm.26054
74. Eichner C, Cauley SF, Cohen-Adad J, Möller HE, Turner R, Setsompop K, et al. Real diffusion-weighted MRI enabling true signal averaging and increased diffusion contrast. Neuroimage (2015) 122:373–84. doi: 10.1016/j.neuroimage.2015.07.074
75. Dula AN, Gochberg DF, Valentine HL, Valentine WM, Does MD. Multiexponential T2, magnetization transfer, and Quantitative histology in white matter tracts of rat spinal cord. Magn Reson Med. (2010) 63:902–09. doi: 10.1002/mrm.22267
76. Prasloski T, Mädler B, Xiang QS, MacKay A, Jones C. Applications of stimulated echo correction to multicomponent T2analysis. Magn Reson Med. (2012) 67:1803–14. doi: 10.1002/mrm.23157
77. De Almeida Martins JP, Topgaard D. Two-dimensional correlation of isotropic and directional diffusion using NMR. Phys Rev Lett. (2016) 116:1–6. doi: 10.1103/PhysRevLett.116.087601
78. Lasič S, Szczepankiewicz F, Eriksson S, Nilsson M, Topgaard D. Microanisotropy imaging: quantification of microscopic diffusion anisotropy and orientational order parameter by diffusion MRI with magic-angle spinning of the q-vector. Front Phys. (2014) 2:11. doi: 10.3389/fphy.2014.00011
79. Szczepankiewicz F, Lasič S, van Westen D, Sundgren PC, Englund E, Westin CF, et al. Quantification of microscopic diffusion anisotropy disentangles effects of orientation dispersion from microstructure: applications in healthy volunteers and in brain tumors. Neuroimage (2015) 104:241–52. doi: 10.1016/j.neuroimage.2014.09.057
80. Westin CF, Knutsson H, Pasternak O, Szczepankiewicz F, Özarslan E, van Westen D, et al. Q-space trajectory imaging for multidimensional diffusion MRI of the human brain. Neuroimage (2016) 135:345–62. doi: 10.1016/j.neuroimage.2016.02.039
81. De Swiet TM, Mitra PP. Possible systematic errors in single-shot measurements of the trace of the diffusion tensor. J Magn Reson Ser B (1996) 111:15–22. doi: 10.1006/jmrb.1996.0055
82. Vellmer S, Edelhoff D, Suter D, Maximov II. Anisotropic diffusion phantoms based on microcapillaries. J Magn Reson. (2017) 279:1–10. doi: 10.1016/j.jmr.2017.04.002
83. Vellmer S, Stirnberg R, Edelhoff D, Suter D, Stöcker T, Maximov II. Comparative analysis of isotropic diffusion weighted imaging sequences. J Magn Reson. (2017) 275:137–47. doi: 10.1016/j.jmr.2016.12.011
84. Mädler B, Drabycz SA, Kolind SH, Whittall KP, MacKay AL. Is diffusion anisotropy an accurate monitor of myelination? Correlation of multicomponent T2 relaxation and diffusion tensor anisotropy in human brain. Magn Reson Imaging (2008) 26:874–88. doi: 10.1016/j.mri.2008.01.047
85. West KL, Kelm ND, Carson RP, Does MD. A revised model for estimating g-ratio from MRI. Neuroimage (2016) 125:1155–8. doi: 10.1016/j.neuroimage.2015.08.017
86. Álvarez GA, Shemesh N, Frydman L. Coherent dynamical recoupling of diffusion-driven decoherence in magnetic resonance. Phys Rev Lett. (2013) 111:080404. doi: 10.1103/PhysRevLett.111.080404
87. Jiang X, Li H, Xie J, Zhao P, Gore JC, Xu J. Quantification of cell size using temporal diffusion spectroscopy. Magn Reson Med. (2016) 75:1076–85. doi: 10.1002/mrm.25684
88. Lawrenz M, Brassen S, Finsterbusch J. Microscopic diffusion anisotropy in the human brain: age-related changes. Neuroimage (2016) 141:313–25. doi: 10.1016/j.neuroimage.2016.07.031
89. Leergaard TB, White NS, De Crespigny A, Bolstad I, Dandapos Arceuil H, Bjaalie JG, et al. Quantitative histological validation of diffusion MRI fiber orientation distributions in the rat brain. PLoS ONE (2010) 5:e8595. doi: 10.1371/journal.pone.0008595
90. Nilsson M, Lätt J, Ståhlberg F, van Westen D, Hagslätt H. The importance of axonal undulation in diffusion MR measurements: a monte carlo simulation study. NMR Biomed. (2012) 25:795–805. doi: 10.1002/nbm.1795
91. Lundell H, Nielsen JB, Ptito M, Dyrby TB. Distribution of collateral fibers in the monkey cervical spinal cord detected with diffusion-weighted magnetic resonance imaging. Neuroimage (2011) 56:923–29. doi: 10.1016/j.neuroimage.2011.02.043
92. Papaioannou A, Novikov DS, Fieremans E, Boutis GS. Observation of structural universality in disordered systems using bulk diffusion measurement. Phys Rev E (2017) 96:61101. doi: 10.1103/PhysRevE.96.061101
93. Palombo M, Ligneul C, Najac C, Le Douce J, Flament J, Escartin C, et al. New paradigm to assess brain cell morphology by diffusion-weighted MR spectroscopy in vivo. Proc Natl Acad Sci USA. (2016) 113:6671–6. doi: 10.1073/pnas.1504327113
94. Valette J, Ligneul C, Marchadour C, Najac C, Palombo M. Brain metabolite diffusion from ultra-short to ultra-long time scales: what do we learn, where should we go? Front Neurosci. (2018) 12:2. doi: 10.3389/fnins.2018.00002
95. Guy J, Ellis EA, Kelley K, Hope GM. Spectra of G ratio, myelin sheath thickness, and axon and fiber diameter in the guinea pig optic nerve. J Comp Neurol. (1989) 287:446–54. doi: 10.1002/cne.902870404
96. Innocenti GM. Development and evolution. Two determinants of cortical connectivity. Prog Brain Res. (2011) 189:65–75. doi: 10.1016/B978-0-444-53884-0.00018-X
97. MacKay A, Laule C, Vavasour I, Bjarnason T, Kolind S, Mädler B. Insights into brain microstructure from the T2 distribution. Magn Reson Imaging (2006) 24:515–25. doi: 10.1016/j.mri.2005.12.037
98. Harkins KD, Xu J, Dula AN, Li K, Valentine WM, Gochberg DF, et al. The microstructural correlates of T1 in white matter. Magn Reson Med. (2016) 75:1341–5. doi: 10.1002/mrm.25709
99. Palombo M, Shemesh N, Ronen I, Valette J. (2017). Insights into brain microstructure from in vivo DW-MRS. Neuroimage doi: 10.1016/j.neuroimage.2017.11.028. [Epub ahead of print].
100. Chuhutin A, Hansen B, Jespersen SN. Precision and accuracy of diffusion kurtosis estimation and the influence of b-value selection. NMR Biomed. (2017) 30:1–14. doi: 10.1002/nbm.3777
101. Jerschow A, Muller N. Suppression of convection artifacts in stimulated-echo diffusion experiments. Double-stimulated-echo experiments. J Magn Reson. (1997) 375:372–5.
Keywords: microscopic anisotropy, MRI, microstructure, diffusion MRI, myelin water fraction, spinal cord, axon diameter
Citation: Shemesh N (2018) Axon Diameters and Myelin Content Modulate Microscopic Fractional Anisotropy at Short Diffusion Times in Fixed Rat Spinal Cord. Front. Phys. 6:49. doi: 10.3389/fphy.2018.00049
Received: 22 December 2017; Accepted: 07 May 2018;
Published: 08 June 2018.
Edited by:
Julien Valette, Commissariat à l'Energie Atomique et aux Energies Alternatives (CEA), FranceReviewed by:
Pascal Sati, National Institutes of Health (NIH), United StatesTim B. Dyrby, Copenhagen University Hospital, Denmark
Copyright © 2018 Shemesh. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Noam Shemesh, bm9hbS5zaGVtZXNoQG5ldXJvLmZjaGFtcGFsaW1hdWQub3Jn
 Noam Shemesh
Noam Shemesh