- 1Digital Image Processing Lab, Center for Medical Physics and Biomedical Engineering, Medical University of Vienna, Vienna, Austria
- 2University Clinic for Radiotherapy and Radiation Biology, Medical University of Vienna, Vienna, Austria
With the introduction of computers in medical imaging, which were popularized with the presentation of Hounsfield's ground-breaking work in 1971, numerical image reconstruction and analysis of medical images became a vital part of medical imaging research. While mathematical aspects of reconstruction dominated research in the beginning, a growing body of literature attests to the progress made over the past 30 years in image fusion. This article describes the historical development of non-deformable software-based image co-registration and it's role in the context of hybrid imaging and provides an outlook on future developments.
Introduction
The advent of computed tomography (CT) [1–3] can be considered a milestone in medical imaging, not only due to its undisputed value for diagnostic radiology but also for introducing computers as an integral part of medical imaging. What started as a comparatively simple exercise in solving large sets of linear equations soon evolved into a broadened research effort driven by mathematicians, computer scientists and physicists to further refine the reconstruction of a novel type of medical image data, the three-dimensional (3D) volume dataset. Shortly after the introduction of the first CT scanner, transverse motion of the patient during scanning was introduced [4], thus, providing a correlate of human anatomy in 3D chunks of data where the well-known image element of digital images, the pixel, was replaced by its 3D counterpart, the voxel. Even earlier, nuclear medicine, which was made a “visual” discipline of medicine by the invention of the Anger camera [5] in the late 1950s also became a 3D-image source when single photon emission tomography (SPECT) [6] and positron emission tomography (PET) was developed [7]. Together with the introduction of magnetic resonance imaging (MRI) around the same time [8–10], the spectrum of widely applied 3D modalities was completed. From that moment on, the fusion of different 3D information on mobility and density of certain nuclei, such as protons in MRI, the chemical properties of tissue, such as in CT, and patients metabolism, such as in nuclear medicine became a desire.
The problem of multimodal image registration in general lies in the determination of a patient-related coordinate system in which all image data from different modalities have a common frame of reference. In general, this is not the case as the coordinate system of the volume is defined by the tomography unit itself. Still, combined imaging systems, such as PET/CT [11] and PET/MR [12] are well established, and other combinations such as MR/CT [13] are currently being conceived. Also, multiple protocols acquired with the patient in a consistent position, such as fMRI and MR spectroscopy image data fall into this category. In addition, combinations with therapeutic devices, for instance linear accelerators (LINACs) used in radiotherapy with cone-beam CT [14] and MRI systems [15] are also considered. Establishing a common frame of reference between image data and a patient-related coordinate system is necessary in these cases as well. Furthermore, ultrasound (US) imaging must not be forgotten in this context as it plays a vital role in image-guided biopsies. The purpose of this article is to give an overview of mathematical image fusion methods within the context of multimodal imaging.
The Development of Paradigms for Medical Image Co-registration
All image registration methods rely on the same principle. They assume the image data (often called the base and match image IBase and IMatch) to be positioned in a common frame of reference. By iterative comparison of image features at the same position in this reference frame, it is possible to design a merit function that is optimized for a variation of spatial transform parameters. These parameters are the three Euler angles and the three possible degrees of freedom in translation. A combination of the corresponding rotation matrices and a translation operator results in a transformation matrix V = TRxRyRz, where T is a translation matrix in homogeneous coordinates [16] and Ri are the respective rotation matrices. The order of single transformations is of course subject to convention; for rotation, it is also worth mentioning that a more convenient and useful parameterization of the rotation group is given in unit quaternions. Once an optimum is found by varying six degrees-of-freedom in rotation and translation, the match image is moved to the appropriate position, presenting patient specific image data at the same location (Figure 1). Usually, the image area where the comparison of image element gray values takes places is confined to a common overlap, which makes many image fusion algorithms dependent of an appropriate initial guess of the registration matrix V. The merit function which is to be optimized with respect to the transfomation parameters applied to the image Imatch, can be derived from the position of known markers, point clouds indentified in both image data sets, or from intrinsic image element intensities.
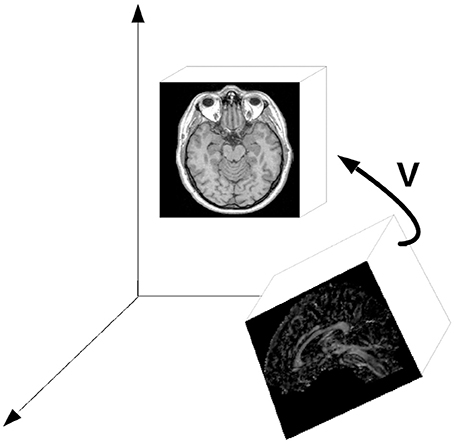
Figure 1. The general principle of image registration; a spatial transform V—basically a combination of three-dimensional rotation and translation—is iteratively determined by comparing features in both image datasets (referred to as base and match images in the text). The important issue is the fact that the comparison of image element coordinates in a common frame of reference.
Marker-Based Methods
The most straightforward and often most precise and failsafe method for finding common features in different datasets or in a dataset and the patient located in a device is to use artificial landmarks or fiducial markers. A hallmark in this technology was the introduction of the Leksell-frame in neurosurgery [17]. The field of neurosurgery, where the patient is often immobilized by means of a Mayfield clamp, was also an early adopter of patient-to-image registration for registration of a surgical microscope [18] or for fusion of functional data such as SPECT with anatomical data derived from MRI [19–21].
Markers can be stickers attached to the patients, skin or per- and subcutaneous screws (e.g., in cranio-and maxillofacial surgery [22]), removable attachments [23] and implanted structures such as gold markers in fractionated prostate radiotherapy and related fields [24, 25]. The latter markers are often located by means of additional imaging such as B-mode ultrasound (US) [24] or X-ray [26]. Technically, registration based on fiducial markers is performed by minimizing the Euclidean distance between paired point sets coordinates [27, 28], thus, resulting in the aforementioned six parameters of rigid body motion. To date, fiducial-marker based registration is widespread—especially in therapeutic interventions—but it bears the disadvantage of being clinically elaborate and invasive. For the field of multi-modal imaging, soon other techniques were about to be developed.
It has to be mentioned that anatomical landmarks which can be localized with sufficient accuracy (for instance foramina in the facial skeleton) can also be utilized as fiducial markers. In many retrospective studies, this is the only way to assess registration accuracy of, for instance, an image-guided procedure. A potential risk here lies in the fact that this process is dependent on the accuracy of landmark localization. Sometimes, point-to-point registration of anatomical landmarks is also used to initialize a registration process.
In summary, fiducial marker based registration is generally robust and accurate if a reproducible marker position is ensured. On the downside, it is invasive and cannot be applied in retrospective studies. An example is found in Birkfellner et al. [22] where miniature titanium screws placed under the oral mucosa preoperatively were used to register a high-resolution CT to a position sensor rigidly attached to the patient's facial skeleton in image-guided oral implant placement (Figure 2).
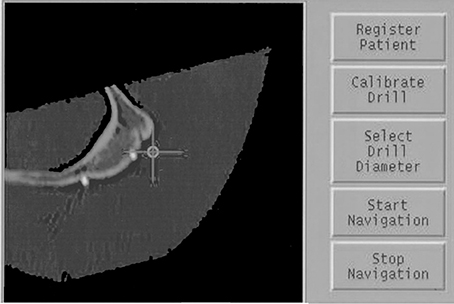
Figure 2. A screenshot of fiducial markers attached to a cadaver heads zygoma. In this case, miniature titanium screws (2 mm overall length, 2 mm head diameter) were inserted prior to the CT scan. Localization of these fiducial markers using an optical tracking system allowed for precise registration for image-guided maxillofacial surgery. The crosshair is determined by measuring the 3D-location of a surgical probe. The multiplanar reformatted CT slice shows two titanium markers located on the zygomatic bone.
Surface– and Gradient Based Methods
Early efforts that go beyond simple patent-fixation approaches, such as the aforementioned Leksell frame are closely related to therapeutic applications and CT-MR image fusion. One milestone of modern image fusion was certainly the “Head-and-Hat” algorithm [29, 30] for merging multimodal image data; here, unordered sets of surface point data from segmented volume data are iteratively matched by finding a rigid-body transform—again expressed as an algebraic matrix defined by six parameters of rotation and translation in 3D space [16]—as a result of an iterative numerical optimization procedure.
Today, this method is known by a refined form, referred to as the Iterative Closest Point (ICP) algorithm, which was presented in 1992 [31]. Again, it is interesting to see the link between multimodal image fusion—the application this method was intended for in Levin et al. [29]—and image-guided therapy, where ICP is still a mainstay when it comes to merging physical coordinate systems such as a stereotactic fixation device or a LINAC to the coordinate system of a volume image [32–43]. In the latter case, surface points can either be manually digitized by using a 3D input device [40] or by optical or other non-invasive technologies such as A-mode US [34, 35, 37, 41, 42].
While these image registration methods using surface matching are straightforward and computationally inexpensive (which is less of an argument nowadays compared to the computing power available one or two decades ago), there are also considerable drawbacks. Above all, the exact determination of contoured image data requires segmentation, an error prone process often including manual interaction. Furthermore, the surface used for matching is a critical component as, for instance, a spherical surface offers less information content on unique spatial landmarks compared to a complex-shaped manifold, such as the human face.
Surface-based methods turned out to be advantageous over fiducial marker based methods as they are usually not highly invasive; on the other hand, segmentation of body surfaces—a sometimes error-prone process—is necessary, and dedicated hardware for surface digitization is required.
Around the same time, a similar method was presented based on deriving a parameterization of sudden intensity changes in image data. In short, rapid changes in gray values in an image are considered edges. These can be derived by computing a local total differential of the image; in order to understand this concept, an image has to be understood as a discrete mathematical function. The gray value in an image element is determined by a physical measurement (e.g., the linear attenuation of X-rays), and it is considered the dependent variable for a pair or triplet of independent variables, the location of the pixels or voxels. By computing finite differences, it is possible to determine a gradient vector for the image, and the length of this gradient vector gives the amount of change in the image. A large gradient is associated with an edge. A number of edge detection algorithms is known in image processing, with all of them being essentially based on the same principle. A popular method for computing image gradients is the Sobel filter [43].
In medicine, it was the desire to merge the coordinate systems of image data and a physical device that promoted the development of image fusion techniques. For repeated patient positioning in fractionated radiotherapy, Gilhuijs and van Herk presented a method called chamfer matching [44]. Here, an X-ray image derived from the planning CT data, the simulator image or digitally rendered radiograph (DRR) [45–47] is compared to a low-contrast electronic portal image (EPI), a projection of attenuation coefficients of photons produced by the LINAC [48, 49]. The EPI is produced using photons at an energy of approximately 6 MeV. Therefore, the contrast is very low compared to conventional radiographs taken with photons in an energy range of typically 90–120 keV. Still, image edges from cortical bone can be identified in an EPI, and this information can be used for further image registration.
The chamfer matching algorithm relies on the identification of image edges in both the EPI and the DRR. Both edge images undergo segmentation by a simple threshold, producing binary black-and-white images. One of the images also undergoes a morphological operation—dilation- and a distance transform [16], which encodes the distance of a white (non-zero) image element to the closest black (zero) image element. The product of gray values of both images becomes a maximum when the two images coincide. While edge-based methods can be very sensitive, they usually do not show very favorable numerical convergence behavior; in other words, the images have to be pre-registered in a rather precise manner in order to gain a usable result. This is a reasonable challenge for clinical applications, but could become more difficult for the serial automated registration of large numbers of datasets.
In summary, image registration based on surface and image edges is a straightforward approach, especially for therapeutic applications, and has found wide acceptance in a whole lot of commercially available solutions. It also has another important intrinsic property—image edges, above all surfaces of organs or the skeleton—are visible in a variety of modalities; in cases where it is possible to identify common surfaces or edges, these methods are intrinsically multi-modal. Therefore, they can also be applied to multimodal image-to-image registration. More general, these methods are termed feature-based registration methods as sudden changes in image brightness are considered features in the sense of computer vision terminology. These are to be covered in the following sections.
Intensity-Based Image Registration
While the previous sections highlighted the close connection of patient-to-image registration and multimodal image fusion, the registration of multiple datasets, either from the same individual or a collective of individuals, is an important topic in clinical research, for instance in therapy assessment or multicentric studies. While the development of hybrid imaging devices is an ongoing process, offline registration of datasets will therefore stay an important tool for clinical applications of multimodal imaging.
Early efforts were reported when MRI became a second mainstay for tomographic imaging aside from CT in the late 1980's. While marker-based methods were continuously used [50], statistical measures, such as the cross correlation coefficient became increasingly important. The general principle of intensity-based image registration is of course again the comparison of image element intensities in a common frame of reference. Gray values at the same location from both the base and match image are considered statistically distributed random variables. In an iterative process, a spatial transform is applied to the match image until an optimal correlation of these variables is achieved. Such methods were reported in computer vision for a variety of problems and solutions relying on correlation were presented both in the spatial and the Fourier-domain [51, 52]. An interesting example of an early registration effort can be found in a classical textbook on digital image processing [53]; here, the base and match image are segmented to binary shapes, and for each image, the resulting distribution of black and white pixels is considered a scatterplot. A principal component analysis—a well-known method for decorrelation of random variables from statistics—is subsequently applied in order to align the shapes to the main coordinate axes. An early review from 1993 [54] lists some of these efforts; however, the intrinsic three-dimensional nature of medical images soon rendered more specific methods necessary.
As soon as 1998, a thorough review and classification scheme for medical image registration was published [55]. In this work, not only an excellent overview of the technical developments during the first decade where multimodal image fusion became a topic is given, but also the proposed classification scheme is still valid; in general, this scheme involved the dimensionality (e.g., 2D vs. 3D data), the nature of the information used for registration (extrinsic markers or features, intrinsic information such as image intensities, or non-image based methods such as the knowledge of the relative position of imaging modalities as used in hybrid imaging machines), the nature of the transformation between the base and matching images (rigid transformation, additional inclusion of local degrees-of-freedom for compensation of deformations, and additional use of projective degrees-of-freedom) and information on the modalities involved. Furthermore, registration subjects (images from the same subject, intersubject registration and registration to atlases) need to be distinguished.
While the solutions for intersubject registration and atlases or statistical shape models [56–58] gained considerable interest, the major breakthrough for intensity based registration was the definition of a similarity measure that is suited for intermodal image data. Previous approaches, such as the aforementioned gradient-based methods suffer from problematic numerical convergence. Simple statistical measures such as cross correlation or rank correlation [59, 60] cannot be applied to multimodal image data where a linear or monotonous relationship between image intensities is unavailable. A straightforward example for a non-monotonous relationship between voxel intensities is the comparison of CT and MR—both cortical bone and air are usually black in MR, which, for air, is definitely not the case in CT.
The major breakthrough for multimodal image co-registration was the introduction of Shannons entropy [61] in image fusion. While the information theoretic approach of Shannon, derived from Boltzmanns entropy definition in statistical physics, was not originally defined for image data, it led to the development of similarity functions based on mutual information. Shannons entropy H is given as:
where I(x,y,z) is an image with voxel coordinates (x,y,z)T and P(I) is the probability distribution—the histogram—of the image intensities for a given image element. Zero values are usually omitted. For comparing two images, Shannons entropy gives a measure of disorder in a joint histogram P(IBase, IMatch), where the occurrence of similar gray values at the same image element position in IBase and IMatch is recorded in a two-dimensional occurrence statistic [62–67]. Figure 3 illustrates the appearance of a joint histogram of two images of different origin (CT and MRI) and the effect of relative misregistration. Generally speaking—the larger the number of occupied bins with small counts, the higher the disorder. As already mentioned it is also necessary to start with a gross estimate of the registration in order to define the domain of image elements where the evaluation of the single and joint histograms is to take place. This development paved the way for multimodal image registration as a valuable clinical tool in a plethora of applications and has to some extent become the standard method for image fusion with a plethora of publications.
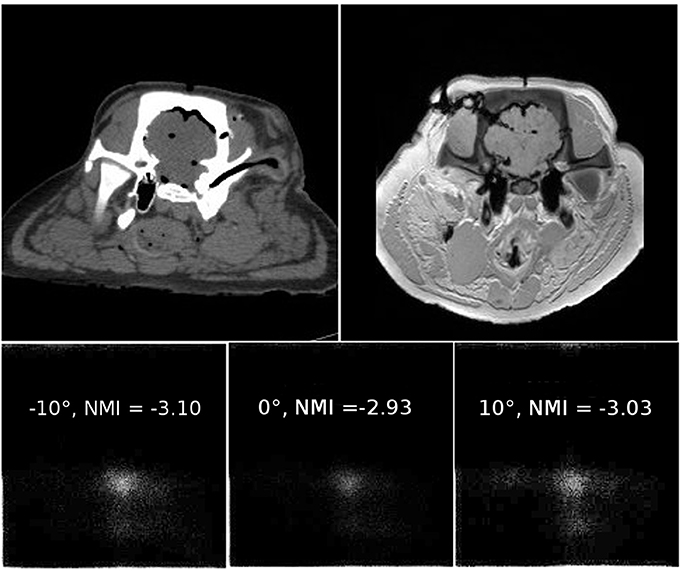
Figure 3. An example of joint histograms and related normalized mutual information values. The two upper images show roughly co-registered slices of a porcine cadaver specimen plus additional soft tissue deformation which was not accounted for. The left image was taken using a 64 slice CT, and the right image is a T1-weighted image from a clinical 3 T scanner. Details on the image dataset can be found in Pawiro et al. [68]. The MR image was rotated by 10° clockwise, and the resulting joint histogram is shown in the lower left corner of the illustration. Joint histograms are counting statistics where the occurrence of a gray value at the same image element position in the two images under comparison is logged; the abscissa indicates bin locations for all possible gray values in the first image, often referred to as IBase–the base image. The ordinate holds bins for all gray values of the second image to be matched—IMatch. The more bins occupied with low total counts, the bigger the entropy in the joint histogram. Normalized mutual information reaches a maximum of −2.93 when the relative rotation of the images is 0°. For relative rotation of ±10°, visual inspection shows that more bins are obviously occupied, leading to a higher entropy in the histogram. The dataset is available from https://midas3.kitware.com/midas/community/3.
However, pitfalls still exist, as there is no absolute optimum for this type of similarity measure—the numerical value of Shannons entropy does neither provide an indication whether the registration process was successful, nor does it indicate the quality of the result. It is also necessary to emphasize that as of today, Shannons entropy is not widely used directly, but a derived quantity, normalized mutual information (NMI), has become the standard for multimodal image registration. A merit function MNMI to be optimized numerically is given as:
where H(IBase) and H(IMatch) are the entropies of the single images to be compared and H(IBase, IMatch) is the entropy for the joint histogram. A potential problem of the method lies in the fact that it depends on a dense population of the joint histogram; two-dimensional images or images with little contrast will give a very sparse population of the joint histogram, therefore leading to insufficient gradients for the optimization process. Figures 4, 5 show the user interface of a research grade software for image fusion using mutual information metrics [69].
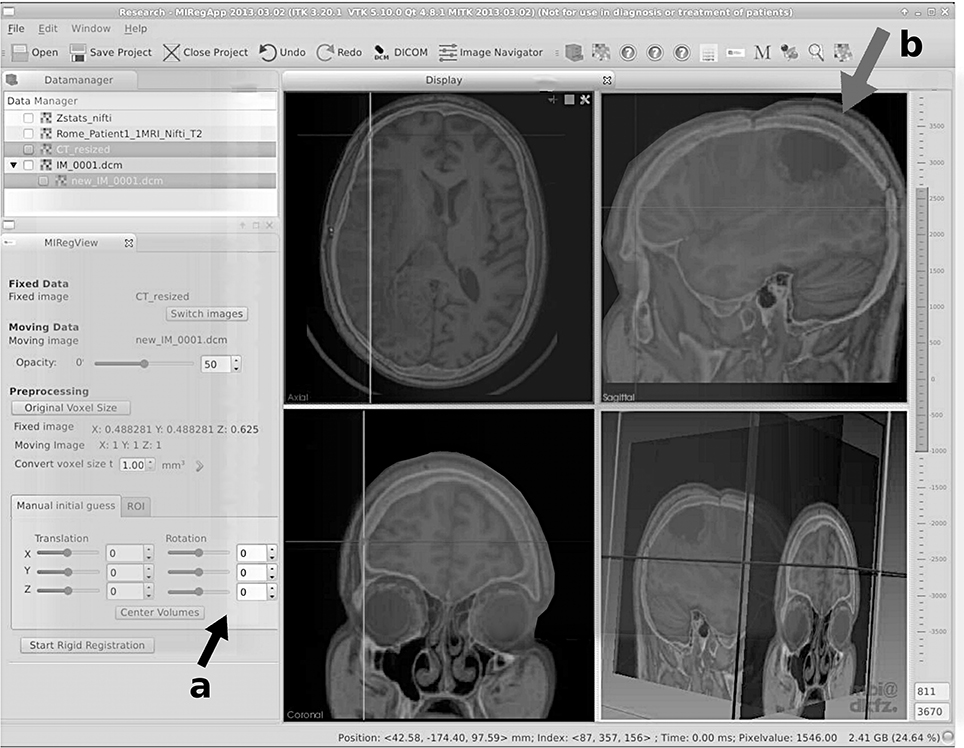
Figure 4. User interface of a modern research grade image fusion software for merging CT and MRI data using normalized mutual information. Here, a fusion of CT and T2-weighted MRI of a neurological case is shown. Aside from rough manual positioning (see the user interface elements, indicated with arrow a), the process is automatic. In this case, a neurological tumor is seen in the upper right fused image (indicated by arrow b). Deformation due to a neurosurgical intervention is obvious, still the algorithm is capable of coping with these deviations for this case of rigid registration. This software was developed in the course of FP7-PEOPLE-2011-ITN “SUMMER—Software for the Use of Multi-Modality images in External Radiotherapy” funded by the European Commission. More details on the software are provided in Aselmaa et al. [69].
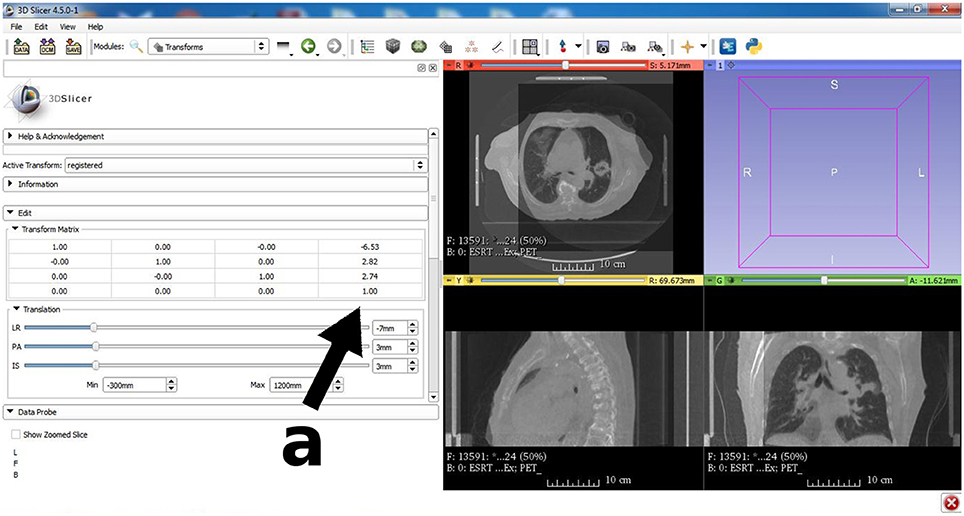
Figure 5. An important image processing tool for the research community is 3D Slicer (www.slicer.org). The image registration module is similar to Figure 4, but here a fusion of a diagnostic CT is shown together with a cone-beam CT acquired prior to radiation therapy treatment. Fusion of diagnostic grade CT for radiation therapy planning and low quality pre-fraction CBCT is a widespread application in routine quality control for fractionated radiotherapy despite the fact that patient specific molds and other fixation measures are taken. A closer look at the transformation matrix (see arrow a) reveals that no correction with respect to rotation was necessary, but a spatial translation by (−6.5, 2.8, 2.7)T mm had to be carried out to ensure that the target region is aligned with the treatment plan.
In summary, the advantages of intensity-based multi-modal registration algorithms are evident; however, sparse histogram population and low image depth can lead to a merit function that is hard to optimize numerically due to the presence of many local optima. Even with the wide availability of intensity-based image registration tools, the most important limitation of the method is still the availability of corresponding structures in the respective datasets. Registration of high-resolution data from morphological modalities like CT and MR or—with certain limitations—US is generally feasible [70–73], but severe limitations become eminent when moving to co-registration of anatomical and functional data. While registration of MR and tomographic data from nuclear medicine (PET or SPECT) for neurological purposes is reported to be successful for decades [19, 20, 54, 74, 75], the same statement cannot be made for other regions of the body. Here, the number of common features is too small to guarantee an accurate result where the registration error is in the range of the image resolution. With the advent of hybrid imaging modalities like PET/CT and PET/MR, a more robust and reliable clinical solution for this problem became available. However, with PET/CT it is possible to achieve robust registration of PET and MR by applying an intensity-based registration to the CT-part of the PET/CT dataset. Multi-dimensional image registration.
A special case is the intensity-based registration of image data, which were derived using the same principle but with different imaging geometry. The most important case is 2D/3D image registration of digitally rendered radiographs (DRRs) and X-ray images taken with a known projection geometry [68, 76–82]. This is widely used in image-guided surgery and image-guided radiotherapy. One or more DRRs are iteratively compared to radiographs which are usually taken prior to or during an intervention; while early efforts suffered from the high computational load connected to the iterative DRR-generation, the advent of general purpose computing on graphics processor units (GPGPU) [47, 83–85] boosted this application as a valuable tool, especially for patient positioning in radiotherapy [84, 86–89]. Figure 6 shows a screenshot from such a program for 2D/3D registration of projective images—the software and its underlying mechanism is described in more detail in Spoerk et al. [83], Gendrin et al. [84], Furtado et al. [87], Li et al. [88].
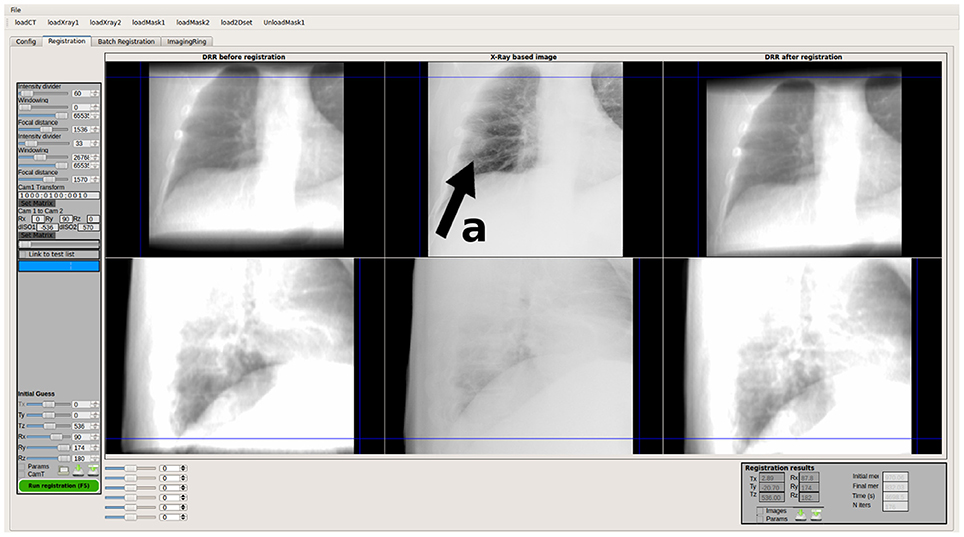
Figure 6. User interface of FIRE, a research grade software for real-time 2D/3D image registration in fractionated external radiation therapy. The position of the patient as well as intrafractional tumor motion—in this case caused by lung motion—is measured using simulated digitally rendered radiographs and calibrated X-ray and electronic portal imaging data. The upper row represents the x-ray data from the LINAC mounted digital x-ray source (the tumor is indicated by arrow a in this case), and the lower row shows a comparison of an artificial x-ray image rendered from CT compared to a low-contrast electronic portal image taken with the therapy beam itself.
Another important 2D/3D registration method is the fusion of single slices to a complete volume dataset of the same patient [90–95]—this is generally referred to as slice-to-volume registration. The application here is either a modality that acquires a single slice in a fixed position while the patient is, for instance, breathing. In the case of CT, such an imaging mode is called Fluoro CT-mode; it has applications in interventional radiology, where biopsies are taken under CT surveillance. Slice-to-volume registration is of some help here as the co-registration of a volume featuring contrast enhancement can aid in localization of the biopsy target site. Other modalities that acquire single slices are histology [96], Cine-MR [97] and conventional ultrasound [98, 99]. It has to be said that multi-dimensional image registration is not multi-modal image fusion in a strict sense—yet the difference in image dimensionality makes it a special case worth mentioning.
In principle, 2D/3D registration has a huge advantage—it is usually non-invasive if markers are avoided, and it can be fully automated. However, the sparse information in 2D data makes the optimization process a delicate operation, and gross misregistrations can occur.
Deformable Registration
Another important topic in image fusion in general is deformable image co-registration [100], a method to compensate for inter- and intra-specimen specific morphological differences. In general, deformable registration is typically intensity-based and a deformation model adds additional degrees-of freedom. In the context of multimodal imaging, the relevance of deformable registration is limited as these methods will most likely stay in the domain of pure algorithmic applications from a current perspective. Still it is emerging as a powerful tool in image-guided and adaptive radiotherapy for compensation of organ motion and handling of anatomical changes in the course of treatment [101–108].
Registration Validation
Finally, a topic that applies to both hybrid imaging and image registration is the question of registration accuracy validation. In hybrid imaging, this might apply to quality control routine applications and resolution of anatomical detail; for PET/CT, this might be necessary if image fusion errors are encountered after maintenance since the relative positioning of the PET and CT image data is not automatic but given in a specific DICOM tag in some systems. If this value is not properly set, misregistration might occur in PET/CT or even in SPECT/CT [109, 110]. For PET/MR, local field in homogeneities might lead to a local change in the image metric that leads to misregistration.
In image registration, the most important application for validation measures is the assessment of the clinical relevance of registration outcome. An image registration algorithm producing irreproducable or too inaccurate results does not provide any patient benefit. As stated earlier, the residual value of the similarity measure is not necessarily a reasonable quantity in this case since it is possible that no absolute minimum can be defined like in the case of normalized mutual information. Therefore, target registration error (TRE) was estimated as the most important measure for assessing registration quality [111, 112]. The term was originally applied to marker-based registration but found general application; in short, the TRE is defined as the average or maximum euclidean distance of unique and well-defined landmarks whose position was not subject to the registration effort itself. These markers are either defined as anatomical landmarks, or as fiducial markers excluded from the registration process, for instance by masking their position in the images. The number of registration accuracy studies is immeasurable—what is, however, important in such a process is the use of standardized image datasets, which were published for a number of anatomical entities and registration methods [65, 66, 68, 82, 113, 114]. It is to be noted that recent efforts aim at automatic TRE estimation by automated localization of feature points [115, 116]; these methods stem from computer vision [117, 118], and their role in image registration is not yet fully clear. In general, it has to be stated that despite the considerable research efforts that went into the subject, a final visual assessment by an expert is inevitable in clinical decision making [119]. Awareness of potential misregistration—even in fully hybrid imaging systems—is therefore an absolute necessity for all diagnostic decisions based on hybrid image data.
Conclusions
We tried to give an overview of both the historical and technical development of image registration algorithms; in total, it can be said that invasive methods using implanted fiducial markers provide utmost robustness and accuracy and will be of importance for image-guided and robotic procedures for the future. Gradient-based methods using surface digitization suffer mainly from numerical robustness as the convergence range for solving the optimization problem is limited, but provide a non-invasive alternative if a good initial guess is available, for instance for patient repositioning in image-guided radiotherapy. Intensity-based registration of patient pose and pre-interventional image data—this field is mainly dominated by 2D/3D registration—is probably the most advanced method for co-registration in image-guided therapy but suffers from additional imaging dose and also problematic numerical stability.
The methods for image-intensity based co-registration of multi-modal features compete directly with hybrid imaging devices—we dare to state that the fusion of nuclear medicine data and morphological imaging such as MR or CT is superior when using hybrid imaging, whereas the co-registration of time series, deformable registration or, in general, fusion of morphological data from different modalities will remain field where numerical methods excel.
The latter application field—fusion of data from different time points and modalities—deserves special mentioning and discussion; as the statistical analysis of image data becomes a more and more important topic—just consider the recent interest in “Big Data” and “Deep Learning” in medicine [120, 121]—the utilization of different images of the same patient in this context is a central issue. The de-facto standard for storage of medical images—DICOM [122]—is of limited usability here as its basic structure stems from the computing requirements of the last century. While enhancements and additions were made for this standard, it is hard to imagine from a practical point of view that large amounts of multi-modal image data for a big population can be stored and handled in this way. What is a challenge for medical informatics is the definition of a new standard for digital image storage format that allows for comparison of patient-specific co-registered image data over a large range of individuals. In such a setup, the further development of robust and clinically applicable image registration methods will be an integral part.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Hounsfield GN. Computerized transverse axial scanning (tomography). 1. Description of system. Br J Radiol. (1973) 46:1016–22. doi: 10.1259/0007-1285-46-552-1016
2. Ambrose J. Computerized transverse axial scanning (tomography). 2. Clinical application. Br J Radiol. (1973) 46:1023–47. doi: 10.1259/0007-1285-46-552-1023
3. Perry BJ, Bridges C. Computerized transverse axial scanning (tomography). 3. Radiation dose considerations. Br J Radiol. (1973) 46:1048–51. doi: 10.1259/0007-1285-46-552-1048
4. Ledley RS, Di Chiro G, Luessenhop AJ, Twigg HL. Computerized transaxial x-ray tomography of the human body. Science (1974) 186:207–12. doi: 10.1126/science.186.4160.207
6. Kuhl DE, Hale J, Eaton WL. Transmission scanning: a useful adjunct to conventional emission scanning for accurately keying isotope deposition to radiographic anatomy. Radiology (1966) 87:278–84 doi: 10.1148/87.2.278
7. Ter-Pogossian MM, Phelps ME, Hoffman EJ, Mullani NA. A positron-emission transaxial tomograph for nuclear imaging (PETT). Radiology (1975) 114:89–98. doi: 10.1148/114.1.89
8. Damadian R. Tumor detection by nuclear magnetic resonance. Science (1971) 171:1151–3. doi: 10.1126/science.171.3976.1151
9. Lauterbur PC. Progress in n.m.r. zeugmatography imaging. Philos Trans R Soc Lond B Biol Sci. (1980) 289:483–7. doi: 10.1098/rstb.1980.0066
10. Mansfield P, Maudsley AA. Line scan proton spin imaging in biological structures by NMR. Phys Med Biol. (1976) 21:847–52. doi: 10.1088/0031-9155/21/5/013
11. Kinahan PE, Townsend DW, Beyer T, Sashin D. Attenuation correction for a combined 3D PET/CT scanner. Med Phys. (1998) 25:2046–53. doi: 10.1118/1.598392
12. Judenhofer MS, Catana C, Swann BK, Siegel SB, Jung WI, Nutt RE, et al. PET/MR images acquired with a compact MR-compatible PET detector in a 7-T magnet. Radiology (2007) 244:807–14. doi: 10.1148/radiol.2443061756
13. Wang G, Kalra M, Murugan V, Xi Y, Gjesteby L, Getzin M, et al. Vision 20/20: Simultaneous CT-MRI-Next chapter of multimodality imaging. Med Phys. (2015) 42:5879–89. doi: 10.1118/1.4929559
14. Oelfke U, Tücking T, Nill S, Seeber A, Hesse B, Huber P, et al. Linac-integrated kV-cone beam CT: technical features and first applications. Med Dosim. (2006) 31:62–70. doi: 10.1016/j.meddos.2005.12.008
15. Lagendijk JJ, Raaymakers BW, Raaijmakers AJ, Overweg J, Brown KJ, Kerkhof EM, et al. MRI/linac integration. Radiother Oncol. (2008) 86:25–9. doi: 10.1016/j.radonc.2007.10.034
16. Birkfellner W. Medical Image Processing – A Basic Course. Boca Raton, FL: Taylor & Francis (2014).
17. Leksell L. A stereotaxic apparatus for intracerebral surgery. Acta. Chir. Scand. (1949) 99:229–33.
18. Roberts DW, Strohbehn JW, Hatch JF, Murray W, Kettenberger H. A frameless stereotaxic integration of computerized tomographic imaging and the operating microscope. J Neurosurg. (1986) 65:545–9. doi: 10.3171/jns.1986.65.4.0545
19. Lehmann ED, Hawkes DJ, Hill DL, Bird CF, Robinson GP, Colchester AC, et al. Computer-aided interpretation of SPECT images of the brain using an MRI-derived 3D neuro-anatomical atlas. Med Inform (Lond). (1991) 16:151–66. doi: 10.3109/14639239109012124
20. Turkington TG, Jaszczak RJ, Pelizzari CA, Harris CC, MacFall JR, Hoffman JM, et al. Accuracy of registration of PET, SPECT and MR images of a brain phantom. J Nucl Med. (1993) 34:1587–94.
21. Maurer CR Jr, Fitzpatrick JM, Wang MY, Galloway RL Jr, Maciunas RJ, Allen GS. Registration of head volume images using implantable fiducial markers. IEEE Trans Med Imaging. (1997) 16:447–62. doi: 10.1109/42.611354
22. Birkfellner W, Solar P, Gahleitner A, Huber K, Kainberger F, Kettenbach J, et al. In vitro assessment of a registration protocol for image guided implant dentistry. Clin Oral Implants Res. (2001) 12:69–78. doi: 10.1034/j.1600-0501.2001.012001069.x
23. Martin A, Bale RJ, Vogele M, Gunkel AR, Thumfart WF, Freysinger W. Vogele-Bale-Hohner mouthpiece: registration device for frameless stereotactic surgery. Radiology (1998) 208:261–5. doi: 10.1148/radiology.208.1.9646822
24. Jones D, Christopherson DA, Washington JT, Hafermann MD, Rieke JW, Travaglini JJ, et al. A frameless method for stereotactic radiotherapy. Br J Radiol. (1993) 66:1142–50. doi: 10.1259/0007-1285-66-792-1142
25. Nederveen A, Lagendijk J, Hofman P. Detection of fiducial gold markers for automatic on-line megavoltage position verification using a marker extraction kernel (MEK). Int J Radiat Oncol Biol Phys. (2000) 47:1435–42. doi: 10.1016/S0360-3016(00)00523-X
26. Shimizu S, Shirato H, Kitamura K, Shinohara N, Harabayashi T, Tsukamoto T, et al. Use of an implanted marker and real-time tracking of the marker for the positioning of prostate and bladder cancers. Int J Radiat Oncol Biol Phys. (2000) 48:1591–7. doi: 10.1016/S0360-3016(00)00809-9
27. Arun KS, Huang TS, Blostein SD. Least-squares fitting of two 3-d point sets. IEEE Trans Pattern Anal Mach Intell. (1987) 9:698–700. doi: 10.1109/TPAMI.1987.4767965
28. Horn BKP. Closed-form solution of absolute orientation using unit quaternions. J Opt Soc A (1987) 4:629–42. doi: 10.1364/JOSAA.4.000629
29. Levin DN, Pelizzari CA, Chen GT, Chen CT, Cooper MD. Retrospective geometric correlation of MR, CT, and PET images. Radiology (1988) 169:817–23. doi: 10.1148/radiology.169.3.3263666
30. Pelizzari CA, Chen GT, Spelbring DR, Weichselbaum RR, Chen CT. Accurate three-dimensional registration of CT, PET, and/or MR images of the brain. J Comput Assist Tomogr. (1989) 13:20–6. doi: 10.1097/00004728-198901000-00004
31. Besl PJ, McKay ND. A method for registration of 3-D shapes. IEEE Trans Patt Anal Mach Intell. (1992) 14:239–56. doi: 10.1109/34.121791
32. Maurer CR, Aboutanos GB, Dawant BM, Maciunas RJ, Fitzpatrick JM. Registration of 3-D images using weighted geometrical features. IEEE Trans Med Imaging. (1996) 15:836–49. doi: 10.1109/42.544501
33. Cuchet E, Knoplioch J, Dormont D, Marsault C. Registration in neurosurgery and neuroradiotherapy applications. J Image Guid Surg. (1995) 1:198–207. doi: 10.1002/(SICI)1522-712X(1995)1:4<198::AID-IGS2>3.0.CO;2-5
34. Miga MI, Sinha TK, Cash DM, Galloway RL, Weil RJ. Cortical surface registration for image-guided neurosurgery using laser-range scanning. IEEE Trans Med Imaging (2003) 22:973–85. doi: 10.1109/TMI.2003.815868
35. Heger S, Mumme T, Sellei R, De La Fuente M, Wirtz DC, Radermacher K. A-mode ultrasound-based intra-femoral bone cement detection and 3D reconstruction in RTHR. Comput Aided Surg. (2007) 12:168–75. doi: 10.3109/10929080701336132
36. Tsai CL, Li CY, Yang G, Lin KS. The edge-driven dual-bootstrap iterative closest point algorithm for registration of multimodal fluorescein angiogram sequence. IEEE Trans Med Imaging. (2010) 29:636–49. doi: 10.1109/TMI.2009.2030324
37. Clements LW, Chapman WC, Dawant BM, Galloway RL Jr, Miga MI. Robustsurface registration using salient anatomical features for image-guided liver surgery: algorithm and validation. Med Phys. (2008) 35:2528–40. doi: 10.1118/1.2911920
38. Maier-Hein L, Franz AM, dos Santos TR, Schmidt M, Fangerau M, Meinzer HP, et al. Convergent iterative closest-point algorithm to accomodate anisotropic and inhomogenous localization error. IEEE Trans Pattern Anal Mach Intell. (2012) 34:1520–32. doi: 10.1109/TPAMI.2011.248
39. Yang J, Li H, Campbell D, Jia Y. Go-ICP: a globally optimal solution to 3D ICP point-set registration. IEEE Trans Pattern Anal Mach Intell. (2016) 38:2241–54. doi: 10.1109/TPAMI.2015.2513405
40. Sipos EP, Tebo SA, Zinreich SJ, Long DM, Brem H. In vivo accuracy testing and clinical experience with the ISG Viewing Wand. Neurosurgery (1996) 39:194–202 doi: 10.1097/00006123-199607000-00048
41. Colchester AC, Zhao J, Holton-Tainter KS, Henri CJ, Maitland N, Roberts PT, et al. Development and preliminary evaluation of VISLAN, a surgical planning and guidance system using intra-operative video imaging. Med Image Anal. (1996) 1:73–90. doi: 10.1016/S1361-8415(01)80006-2
42. Liu W, Cheung Y, Sabouri P, Arai TJ, Sawant A, Ruan D. A continuous surface reconstruction method on point cloud captured from a 3D surface photogrammetry system. Med Phys. (2015) 42:6564–71. doi: 10.1118/1.4933196
44. Gilhuijs KG, van Herk M. Automatic on-line inspection of patient setup in radiation therapy using digital portal images. Med Phys. (1993) 20:667–77. doi: 10.1118/1.597016
45. Weinhous MS, Li Z, Holman M. The selection of portal aperture using interactively displayed Beam's Eye Sections. Int J Radiat Oncol Biol Phys. (1992) 22:1089–92. doi: 10.1016/0360-3016(92)90813-W
46. Galvin JM, Sims C, Dominiak G, Cooper JS. The use of digitally reconstructed radiographs for three-dimensional treatment planning and CT-simulation. Int J Radiat Oncol Biol Phys. (1995) 31:935–42. doi: 10.1016/0360-3016(94)00503-6
47. Spoerk J, Bergmann H, Wanschitz F, Dong S, Birkfellner W. Fast DRR splat rendering using common consumer graphics hardware. Med Phys. (2007) 34:4302–8. doi: 10.1118/1.2789500
48. Lam KS, Partowmah M, Lam WC. An on-line electronic portal imaging system for external beam radiotherapy. Br J Radiol. (1986) 59:1007–13. doi: 10.1259/0007-1285-59-706-1007
49. Meertens H, van Herk M, Bijhold J, Bartelink H. First clinical experience with a newly developed electronic portal imaging device. Int J Radiat Oncol Biol Phys. (1990) 18:1173–81. doi: 10.1016/0360-3016(90)90455-S
50. Hill DL, Hawkes DJ, Crossman JE, Gleeson MJ, Cox TC, Bracey EE, et al. Registration of MR and CT images for skull base surgery using point-like anatomical features. Br J Radiol. (1991) 64:1030–5. doi: 10.1259/0007-1285-64-767-1030
51. Alliney S, Morandi C. Digital image registration using projections. IEEE Trans Pattern Anal Mach Intell. (1986) 8:222–33. doi: 10.1109/TPAMI.1986.4767775
52. De Castro E, Morandi C. Registration of translated and rotated images using finite Fourier transforms. IEEE Trans Pattern Anal Mach Intell. (1987) 9:700–3. doi: 10.1109/TPAMI.1987.4767966
54. Toga AW, Banerjee PK. Registration revisited. J Neurosci Methods (1993) 48:1–13. doi: 10.1016/S0165-0270(05)80002-0
55. Maintz JB, Viergever MA. A survey of medical image registration. Med Image Anal. (1998) 2:1–36. doi: 10.1016/S1361-8415(01)80026-8
56. Cootes TF, Taylor CJ. Anatomical statistical models and their role in feature extraction. Br J Radiol. (2004) 77:S133–9. doi: 10.1259/bjr/20343922
57. Twining CJ, Cootes T, Marsland S, Petrovic V, Schestowitz R, Taylor CJ. A unified information-theoretic approach to groupwise non-rigid registration and model building. Inf Process Med Imaging. (2005) 19:1–14. doi: 10.1007/11505730_1
58. Heimann T, Meinzer HP. Statistical shape models for 3D medical image segmentation: a review. Med Image Anal. (2009) 13:543–63. doi: 10.1016/j.media.2009.05.004
59. Birkfellner W, Stock M, Figl M, Gendrin C, Hummel J, Dong S, et al. Stochastic rank correlation: a robust merit function for 2D/3D registration of image data obtained at different energies. Med Phys. (2009) 36:3420–8. doi: 10.1118/1.3157111
60. Figl M, Bloch C, Gendrin C, Weber C, Pawiro SA, Hummel J, et al. Efficient implementation of the rank correlation merit function for 2D/3D registration. Phys Med Biol. (2010) 55:N465–71. doi: 10.1088/0031-9155/55/19/N01
61. Shannon CE. A mathematical theory of communication. Bell Syst Tech J. (1948) 27:379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x
62. Maes F, Collignon A, Vandermeulen D, Marchal G, Suetens P. Multimodality image registration by maximization of mutual information. IEEE Trans Med Imaging. (1997) 16:187–98. doi: 10.1109/42.563664
63. Wells WM III, Viola P, Atsumi H, Nakajima S, Kikinis R. Multi-modal volume registration by maximization of mutual information. Med Image Anal. (1996) 1:35–51. doi: 10.1016/S1361-8415(01)80004-9
64. Studholme C, Hill DL, Hawkes DJ. Automated three-dimensional registration of magnetic resonance and positron emission tomography brain images by multiresolution optimization of voxel similarity measures. Med Phys. (1997) 24:25–35. doi: 10.1118/1.598130
65. West J, Fitzpatrick JM, Wang MY, Dawant BM, Maurer CR Jr, Kessler RM, et al. Comparison and evaluation of retrospective intermodality brain image registration techniques. J Comput Assist Tomogr. (1997) 21:554–66. doi: 10.1097/00004728-199707000-00007
66. Risholm P, Golby AJ, Wells W III. Multimodal image registration for preoperative planning and image-guided neurosurgical procedures. Neurosurg Clin N Am. (2011) 22:197–206. doi: 10.1016/j.nec.2010.12.001
67. Knops ZF, Maintz JB, Viergever MA, Pluim JP. Normalized mutual information based registration using k-means clustering and shading correction. Med Image Anal. (2006) 10:432–9. doi: 10.1016/j.media.2005.03.009
68. Pawiro SA, Markelj P, Pernus F, Gendrin C, Figl M, Weber C, et al. Validation for 2D/3D registration. I: a new gold standard data set. Med Phys. (2011) 38:1481–90. doi: 10.1118/1.3553402
69. Aselmaa A, van Herk M, Laprie A, Nestle U, Götz I, Wiedenmann N, et al. Using a contextualized sensemaking model for interaction design: a case study of tumor contouring. J Biomed Inform. (2017) 65:145–58. doi: 10.1016/j.jbi.2016.12.001
70. Blackall JM, Penney GP, King AP, Hawkes DJ. Alignment of sparse freehand 3-D ultrasound with preoperative images of the liver using models of respiratory motion and deformation. IEEE Trans Med Imaging. (2005) 24:1405–16. doi: 10.1109/TMI.2005.856751
71. Huang X, Moore J, Guiraudon G, Jones DL, Bainbridge D, Ren J, et al. Dynamic 2D ultrasound and 3D CT image registration of the beating heart. IEEE Trans Med Imaging. (2009) 28:1179–89. doi: 10.1109/TMI.2008.2011557
72. Kaar M, Figl M, Hoffmann R, Birkfellner W, Stock M, Georg D, et al. Automatic patient alignment system using 3D ultrasound. Med Phys. (2013) 40:041714. doi: 10.1118/1.4795129
73. Hoffmann R, Kaar M, Bathia A, Bathia A, Lampret A, Birkfellner W, et al. A navigation system for flexible endoscopes using abdominal 3D ultrasound. Phys Med Biol. (2014) 59:5545–58. doi: 10.1088/0031-9155/59/18/5545
74. Woods RP, Mazziotta JC, Cherry SR. MRI-PET registration with automated algorithm. J Comput Assist Tomogr. (1993) 17:536–46. doi: 10.1097/00004728-199307000-00004
75. Ardekani BA, Braun M, Hutton BF, Kanno I, Iida H. A fully automatic multimodality image registration algorithm. J Comput Assist Tomogr. (1995) 19:615–23. doi: 10.1097/00004728-199507000-00022
76. Markelj P, TomaŽevič D, Likar B, Pernuš F. A review of 3D/2D registration methods for image-guided interventions. Med Image Anal. (2012) 16:642–61. doi: 10.1016/j.media.2010.03.005
77. Lemieux L, Jagoe R, Fish DR, Kitchen ND, Thomas DG. A patient-to-computed-tomography image registration method based on digitally reconstructed radiographs. Med Phys. (1994) 21:1749–60. doi: 10.1118/1.597276
78. Tomazevic D, Likar B, Slivnik T, Pernus F. 3-D/2-D registration of CT and MR to X-ray images. IEEE Trans Med Imaging. (2003) 22:1407–16. doi: 10.1109/TMI.2003.819277
79. Hipwell JH, Penney GP, McLaughlin RA, Rhode K, Summers P, Cox TC, et al. Intensity-based 2-D-3-D registration of cerebral angiograms. IEEE Trans Med Imaging (2003) 22:1417–26. doi: 10.1109/TMI.2003.819283
80. Penney GP, Weese J, Little JA, Desmedt P, Hill DL, Hawkes DJ. A comparison of similarity measures for use in 2-D-3-D medical image registration. IEEE Trans Med Imaging. (1998) 17:586–95. doi: 10.1109/42.730403
81. van de Kraats EB, Penney GP, Tomazevic D, van Walsum T, Niessen WJ. Standardized evaluation methodology for 2-D-3-D registration. IEEE Trans Med Imaging. (2005) 24:1177–89. doi: 10.1109/TMI.2005.853240
82. Gendrin C, Markelj P, Pawiro SA, Spoerk J, Bloch C, Weber C, et al. Validation for 2D/3D registration. II: the comparison of intensity- and gradient-based merit functions using a new gold standard data set. Med Phys. (2011) 38:1491–502. doi: 10.1118/1.3553403
83. Spoerk J, Gendrin C, Weber C, Figl M, Pawiro SA, Furtado H, et al. High-performance GPU-based rendering for real-time, rigid 2D/3D-image registration and motion prediction in radiation oncology. Z Med Phys. (2012) 22:13–20. doi: 10.1016/j.zemedi.2011.06.002
84. Gendrin C, Furtado H, Weber C, Bloch C, Figl M, Pawiro SA, et al. Monitoring tumor motion by real time 2D/3D registration during radiotherapy. Radiother Oncol. (2012) 102:274–80. doi: 10.1016/j.radonc.2011.07.031
85. Hatt CR, Speidel MA, Raval AN. Real-time pose estimation of devices from x-ray images: application to x-ray/echo registration for cardiac interventions. Med Image Anal. (2016) 34:101–8. doi: 10.1016/j.media.2016.04.008
86. Künzler T, Grezdo J, Bogner J, Birkfellner W, Georg D. Registration of DRRs and portal images for verification of stereotactic body radiotherapy: a feasibility study in lung cancer treatment. Phys Med Biol. (2007) 52:2157–70. doi: 10.1088/0031-9155/52/8/008
87. Furtado H, Steiner E, Stock M, Georg D, Birkfellner W. Real-time 2D/3D registration using kV-MV image pairs for tumor motion tracking in image guided radiotherapy. Acta Oncol. (2013) 52:1464–71. doi: 10.3109/0284186X.2013.814152
88. Li G, Yang TJ, Furtado H, Birkfellner W, Ballangrud Å, Powell SN, et al. Clinical assessment of 2D/3D registration accuracy in 4 major anatomic sites using on-board 2D kilovoltage images for 6D patient setup. Technol Cancer Res Treat. (2015) 14:305–14. doi: 10.1177/1533034614547454
89. Shirato H, Shimizu S, Kitamura K, Onimaru R. Organ motion in image-guided radiotherapy: lessons from real-time tumor-tracking radiotherapy. Int J Clin Oncol. (2007) 12:8–16. doi: 10.1007/s10147-006-0633-y
90. Ferrante E, Paragios N. Slice-to-volume medical image registration: a survey. Med Image Anal. (2017) 39:101–123. doi: 10.1016/j.media.2017.04.010
91. Kim B, Boes JL, Bland PH, Chenevert TL, Meyer CR. Motion correction in fMRI via registration of individual slices into an anatomical volume. Magn Reson Med. (1999) 41:964–72. doi: 10.1002/(SICI)1522-2594(199905)41:5<964::AID-MRM16>3.0.CO;2-D
92. Fei B, Duerk JL, Boll DT, Lewin JS, Wilson DL. Slice-to-volume registration and its potential application to interventional MRI-guided radio-frequency thermal ablation of prostate cancer. IEEE Trans Med Imaging. (2003) 22:515–25. doi: 10.1109/TMI.2003.809078
93. Birkfellner W, Figl M, Kettenbach J, Hummel J, Homolka P, Schernthaner R, et al. Rigid 2D/3D slice-to-volume registration and its application on fluoroscopic CT images. Med Phys. (2007) 34:246–55. doi: 10.1118/1.2401661
94. Frühwald L, Kettenbach J, Figl M, Hummel J, Bergmann H, Birkfellner W. A comparative study on manual and automatic slice-to-volume registration of CT images. Eur Radiol. (2009) 19:2647–53. doi: 10.1007/s00330-009-1452-0
95. Bagci U, Bai L. Automatic best reference slice selection for smooth volume reconstruction of a mouse brain from histological images. IEEE Trans Med Imaging (2010) 29:1688–96. doi: 10.1109/TMI.2010.2050594
96. Goubran M, Crukley C, de Ribaupierre S, Peters TM, Khan AR. Image registration of ex-vivo MRI to sparsely sectioned histology of hippocampal and neocortical temporal lobe specimens. Neuroimage (2013) 83:770–81. doi: 10.1016/j.neuroimage.2013.07.053
97. Seregni M, Paganelli C, Summers P, Bellomi M, Baroni G, Riboldi M. A hybrid image registration and matching framework for real-time motion tracking in MRI-guided radiotherapy. IEEE Trans Biomed Eng. (2018) 65:131–9. doi: 10.1109/TBME.2017.2696361
98. Ferrante E, Fecamp V, Paragios N. Slice-to-volume deformable registration: efficient one-shot consensus between plane selection and in-plane deformation. Int J Comput Assist Radiol Surg. (2015) 10:791–800. doi: 10.1007/s11548-015-1205-2
99. Hummel J, Figl M, Bax M, Bergmann H, Birkfellner W. 2D/3D registration of endoscopic ultrasound to CT volume data. Phys Med Biol. (2008) 53:4303–16. doi: 10.1088/0031-9155/53/16/006
100. Sotiras A, Davatzikos C, Paragios N. Deformable medical image registration: a survey. IEEE Trans Med Imaging (2013) 32:1153–90. doi: 10.1109/TMI.2013.2265603
101. Christensen GE, Carlson B, Chao KS, Yin P, Grigsby PW, Nguyen K, et al. Image-based dose planning of intracavitary brachytherapy: registration of serial-imaging studies using deformable anatomic templates. Int J Radiat Oncol Biol Phys. (2001) 51:227–43. doi: 10.1016/S0360-3016(01)01667-4
102. Truong MT, Kovalchuk N. Radiotherapy planning. PET Clin. (2015) 10:279–96. doi: 10.1016/j.cpet.2014.12.010
103. Brock KK, Mutic S, McNutt TR, Li H, Kessler ML. Use of image registration and fusion algorithms and techniques in radiotherapy: report of the AAPM Radiation Therapy Committee Task Group No. 132. Med Phys. (2017) 44:e43–76. doi: 10.1002/mp.12256
104. Landry G, Nijhuis R, Dedes G, Handrack J, Thieke C, Janssens G, et al. (2015). Investigating CT to CBCT image registration for head and neck proton therapy as a tool for daily dose recalculation. Med Phys. 42:1354–66. doi: 10.1118/1.4908223
105. Schlachter M, Fechter T, Jurisic M, Schimek-Jasch T, Oehlke O, Adebahr S, et al. Visualization of deformable image registration quality using local image dissimilarity. IEEE Trans Med Imaging. (2016) 35:2319–28. doi: 10.1109/TMI.2016.2560942
106. Fabri D, Zambrano V, Bhatia A, Furtado H, Bergmann H, Stock M, et al. A quantitative comparison of the performance of three deformable registration algorithms in radiotherapy. Z Med Phys. (2013) 23:279–90. doi: 10.1016/j.zemedi.2013.07.006
107. Eiland RB, Maare C, Sjöström D, Samsøe E, Behrens CF. Dosimetric and geometric evaluation of the use of deformable image registration in adaptive intensity-modulated radiotherapy for head-and-neck cancer. J Radiat Res. (2014) 55:1002–8. doi: 10.1093/jrr/rru044
108. Keszei AP, Berkels B, Deserno TM. Survey of non-rigid registration tools in medicine. J Digit Imaging (2017) 30:102–16. doi: 10.1007/s10278-016-9915-8
109. Thomas MD, Bailey DL, Livieratos L. (2005). A dual modality approach to quantitative quality control in emission tomography. Phys Med Biol. 50:N187–94. doi: 10.1088/0031-9155/50/15/N03
110. Pietrzyk U, Herzog H. Does PET/MR in human brain imaging provide optimal co-registration? A critical reflection. Magn Reson Mater Phys. (2013) 26:137–47. doi: 10.1007/s10334-012-0359-y
111. Fitzpatrick JM, West JB, Maurer CR Jr. Predicting error in rigid-body point-based registration. IEEE Trans Med Imaging. (1998) 17:694–702. doi: 10.1109/42.736021
112. Fitzpatrick JM, West JB. (2001). The distribution of target registration error in rigid-body point-based registration. IEEE Trans Med Imaging. 20:917–27. doi: 10.1109/42.952729
113. Castillo R, Castillo E, Fuentes D, Ahmad M, Wood AM, Ludwig MS, et al. A reference dataset for deformable image registration spatial accuracy evaluation using the COPDgene study archive. Phys Med Biol. (2013) 58:2861–77. doi: 10.1088/0031-9155/58/9/2861
114. Madan H, Pernuš F, Likar B, Špiclin Ž. A framework for automatic creation of gold-standard rigid 3D-2D registration datasets. Int J Comput Assist Radiol Surg. (2017) 12:263–75. doi: 10.1007/s11548-016-1482-4
115. Hauler F, Furtado H, Jurisic M, Polanec SH, Spick C, Laprie A, et al. Automatic quantification of multi-modal rigid registration accuracy using feature detectors. Phys Med Biol. (2016) 61:5198–214. doi: 10.1088/0031-9155/61/14/5198
116. Paganelli C, Peroni M, Riboldi M, Sharp GC, Ciardo D, Alterio D, et al. Scale invariant feature transform in adaptive radiation therapy: a tool for deformable image registration assessment and re-planning indication. Phys Med Biol. (2013) 58:287–99. doi: 10.1088/0031-9155/58/2/287
117. Lowe DG. Object recognition from local scale-invariant features Int. J. Comput Vis. (2004) 60:91–110. doi: 10.1023/B:VISI.0000029664.99615.94
118. Bay H, Ess A, Tuytelaars T, Van Gool L. Speeded-up robust features (SURF). Comput Vis Image Underst. (2008) 110:346–59. doi: 10.1016/j.cviu.2007.09.014
119. Pietrzyk U, Herholz K, Schuster A, Stockhausen H-M, Lucht H, Heiss W-D. Clinical applications of registration and fusion of multimodality brain images from PET, SPECT, CT and MRI. Eur J Radiol (1996) 21:174–82.
120. Litjens G, Kooi T, Bejnordi BE, Setio AAA, Ciompi F, Ghafoorian M, et al. A survey on deep learning in medical image analysis. Med Image Anal. (2017) 42:60–88. doi: 10.1016/j.media.2017.07.005
121. Shen D, Wu G, Suk HI. Deep learning in medical image analysis. Annu Rev Biomed Eng. (2017) 19:221–48. doi: 10.1146/annurev-bioeng-071516-044442
Keywords: multi-modal imaging, image registration, 2D/3D registration, image guided therapy, medical image processing
Citation: Birkfellner W, Figl M, Furtado H, Renner A, Hatamikia S and Hummel J (2018) Multi-Modality Imaging: A Software Fusion and Image-Guided Therapy Perspective. Front. Phys. 6:66. doi: 10.3389/fphy.2018.00066
Received: 17 January 2018; Accepted: 13 June 2018;
Published: 17 July 2018.
Edited by:
Zhen Cheng, Stanford University, United StatesReviewed by:
Uwe Pietrzyk, Forschungszentrum Jülich, GermanyDavid Mayerich, University of Houston, United States
Copyright © 2018 Birkfellner, Figl, Furtado, Renner, Hatamikia and Hummel. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wolfgang Birkfellner, d29sZmdhbmcuYmlya2ZlbGxuZXJAbWVkdW5pd2llbi5hYy5hdA==
 Wolfgang Birkfellner
Wolfgang Birkfellner Michael Figl1
Michael Figl1 Sepideh Hatamikia
Sepideh Hatamikia