- Theory of Polymers and Soft Matter, Department of Applied Physics, Eindhoven University of Technology, Eindhoven, Netherlands
Understanding the physics of glass formation remains one of the major unsolved challenges of condensed matter science. As a material solidifies into a glass, it exhibits a spectacular slowdown of the dynamics upon cooling or compression, but at the same time undergoes only minute structural changes. Among the numerous theories put forward to rationalize this complex behavior, Mode-Coupling Theory (MCT) stands out as a unique framework that provides a fully first-principles-based description of glass phenomenology. This review outlines the key physical ingredients of MCT, its predictions, successes, and failures, as well as recent improvements of the theory. We also discuss the extension and application of MCT to the emerging field of non-equilibrium active soft matter.
1. Introduction to the Physics of Glass Formation
Glasses are solid materials that lack any long-range structural order, representing a state of matter that lies somewhere in between a crystalline solid and a disordered liquid. The most common pathway toward a glassy state is by rapidly cooling a liquid to below its melting point–thus entering the so-called supercooled regime–, until the liquid's viscosity η simply becomes so large that it stops flowing on any practical time scale [1–3]. The operational definition of the glass transition temperature Tg is the point where the viscosity exceeds a value of 1012 Pa.s or the structural relaxation time τ exceeds 100 s, but most glasses in our everyday lives have a viscosity that is still orders of magnitude higher [4]. Aside from common applications such as window panes and household items, amorphous solids can be found in, e.g., phase-change memory devices, pharmaceutical compounds, optical fibers, and wearable electronics, and there is compelling evidence that even living cells employ glass-like behavior to regulate intra- and intercellular processes [5–11]. Curiously, most of the water in the universe is also believed to exist in the glassy state [12].
Given the vast abundance and importance of glasses, it may come as a surprise that we still understand very little about them. In fact, after decades of intense research, there is still no consensus on which physical mechanisms underlie the process of glass formation. Unraveling the nature of the glassy state ranks among the “most compelling puzzles and questions facing scientists today” [13], and Nobel laureate Philip Anderson even called it “the deepest and most interesting unsolved problem in solid-state theory” [14]. What makes the glass transition so notoriously difficult to understand? At the heart of the problem lies the fact that a vitrifying material exhibits a spectacular growth of viscosity (or relaxation time) upon cooling or compression, but at the same time undergoes only minute structural changes. Thus, at the molecular level, the structure of a glass is almost indistinguishable from that of a normal liquid (as probed by, e.g., the radial distribution function or the static structure factor), yet their viscosities differ by at least fifteen (!) orders of magnitude. This is unlike any conventional thermodynamic phase transition, such as the liquid-to-crystal transition, which is marked by the appearance of long-range, periodic structural order (Figure 1). Nonetheless, it is not unimaginable that some kind of “amorphous order” emerges during vitrification, albeit in a far less obvious way than in the crystallization example. A popular hypothesis is that the subtle microstructural changes observed in supercooled liquids might somehow contain a “hidden” growing (and possibly diverging) length scale that accompanies the transition from liquid to amorphous solid, and indeed a large ongoing effort is devoted to identifying such a length scale [15–17].
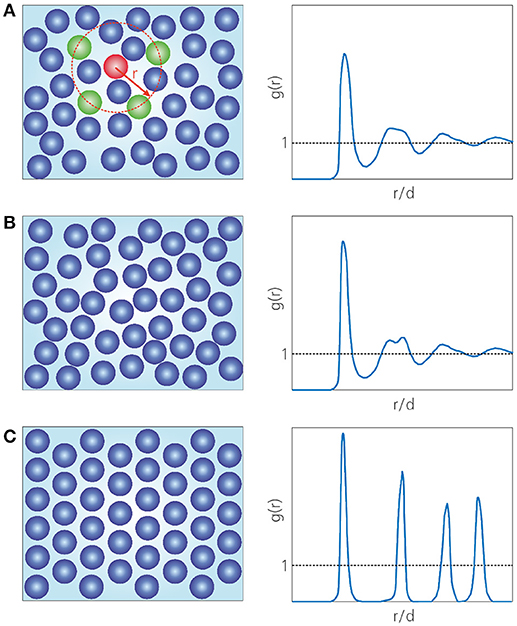
Figure 1. Schematic picture of the structure of (A) a normal liquid, (B) an amorphous solid, i.e., a glass, and (C) a crystalline solid. The first panel highlights four (green) particles which are separated by a distance r from a (red) reference particle. The right panels illustrate the corresponding radial distribution functions g(r), which describe the probability of finding a particle a distance r away from any reference particle, relative to the ideal-gas case. The first peak in g(r) represents the first solvation shell at r ≈ 1d, where d is the particle diameter. The dashed black lines indicate the ideal-gas result g(r) = 1.
Another major unresolved piece of the glass puzzle is that not all materials vitrify in the same manner. More specifically, the viscosity growth as a function of inverse temperature can differ significantly from one material to another. These differences are captured in an empirical property called “fragility” [1, 18, 19], which characterizes the slope of the viscosity with temperature as a material approaches the glass transition (Figure 2). Materials such as silica fall in the class of “strong” glass formers, exhibiting an Arrhenius-type (exponential) viscosity growth upon cooling, while “fragile” materials have a viscosity that increases faster than an Arrhenius law. It is widely believed that a thorough understanding of the mechanisms underlying fragility will be key to achieving a universal description of the glass transition, but no theory to date has been able to predict a material's degree of fragility from the sole knowledge of its microscopic structure [20].
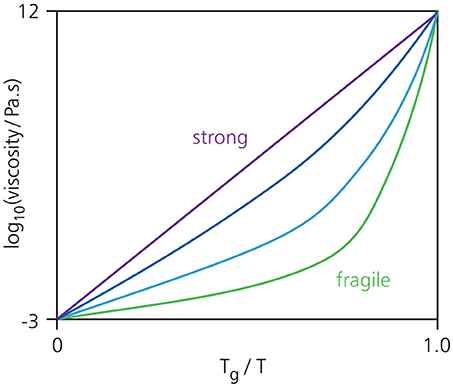
Figure 2. Typical fragility plot, showing the logarithm of the viscosity as a function of inverse temperature 1/T, normalized with respect to the glass transition temperature Tg. A viscosity of 10−3 Pa.s corresponds to a normal liquid, while a value of 1012 Pa.s defines a glassy solid. So-called strong glass formers such as silica exhibit an Arrhenius-type growth of the viscosity upon cooling, while fragile glass formers such as o-terphenyl show a much steeper temperature dependence close to Tg. Many materials, including colloidal hard spheres and confluent cells, fall in between these two extremes.
While the viscosity already gives an important clue about the complex behavior of glass-forming materials, the most detailed information is contained in the microscopic relaxation dynamics, and this will also be the focus of the remainder of this review. A common probe of such dynamics is the time-dependent density-density correlation function or so-called intermediate scattering function, F(k, t), which probes correlations in particle density fluctuations over a certain wavenumber k and over a time interval t [21]. Simply put, F(k, t) measures to what extent the instantaneous molecular configuration of a material will resemble the new configuration a time t later; the wavenumber k designates the inverse length scale over which this resemblance is measured. By choosing k as approximately one inverse particle diameter, F(k, t) will thus probe the relaxation dynamics at the molecular level, while the limit k → 0 describes the macroscopic dynamics. We note that the characteristic relaxation time τ associated with F(k, t) is also a measure for the viscosity (with the shear modulus as the proportionality factor [4]), and hence F(k, t) also provides a means to quantify e.g. the fragility.
The behavior of F(k, t) upon cooling thus reveals how the microscopic relaxation dynamics changes during the vitrification process [22, 23] (Figure 3). In a normal high-temperature liquid, F(k, t) will decay to zero in a rapid and simple exponential fashion, since the particles can move around easily and therefore quickly lose track of their initial positions. At temperatures in the supercooled regime, however, F(k, t) shows a more complex multi-step relaxation pattern (also see Figure 7): at intermediate times (the so-called β-relaxation regime), a plateau develops during which F(k, t) remains constant, indicating the transient freezing of particles; only at sufficiently long times will the correlation function fully decay to zero. Notably, this final decorrelation process (so-called α-relaxation) is not a simple exponential decay, as in a normal liquid, but rather a more slowly decaying, “stretched” exponential behavior of the form exp(−t/τ)β, with 0 < β < 1. As the temperature decreases toward the glass transition temperature, the plateau in F(k, t) will extend to increasingly long times, until it finally exceeds the entire time window of observation. Thus, at the glass transition, F(k, t) fails to decorrelate on any practical time scale–implying that particles always stay reasonably close to their initial positions–, marking the onset of solidity. The final value of the intermediate scattering function, , is known as the non-ergodicity parameter [25], and is often used as the order parameter for the glass transition: f(k) = 0 corresponds to the liquid state, and f(k) > 0 indicates a solid (Figure 3D).
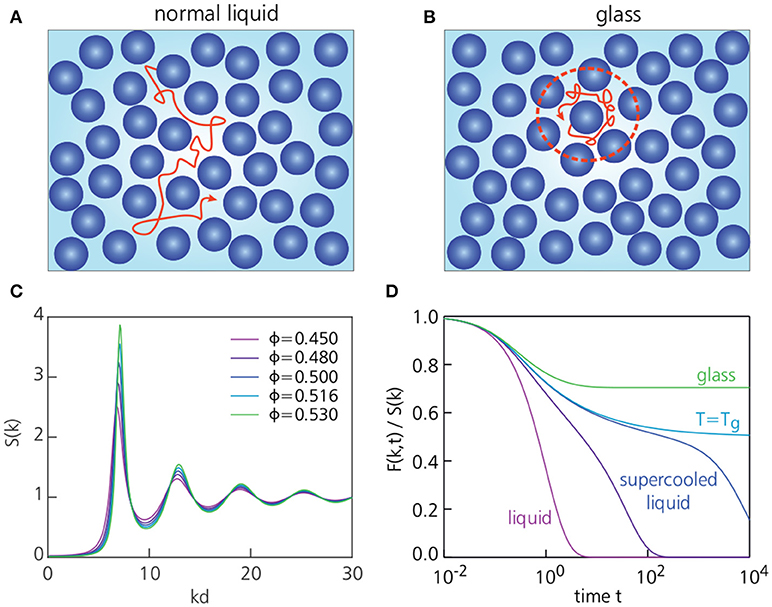
Figure 3. Schematic picture of the structure and dynamics in a normal liquid, supercooled liquid, and glass. (A,B) depict a typical trajectory of a particle in the normal liquid phase and glassy phase, respectively. In the glassy state, particles become trapped in a cage formed by their neighbors. The dashed red line indicates the typical size of a cage, with a radius of approximately one particle diameter d. (C) Shows the static structure factors S(k) for a glass-forming system of hard spheres for several packing fractions ϕ, calculated using the Percus-Yevick approximation. The main peak position of S(k) corresponds to a wavenumber of approximately one inverse particle diameter, k ≈ 2π/d. Within MCT, the glass transition for this system takes place at ϕc = 0.516 [24]. (D) Shows typical intermediate scattering functions F(k, t) as a function of time for k ≈ 2π/d. As the temperature is decreased or the packing fraction is increased, the system becomes more glassy and F(k, t) decays more slowly.
There are several other aspects in the dynamics of supercooled liquids that differ markedly from those seen in ordinary liquids, including the emergence of dynamic heterogeneity [26–29] and the breakdown of the Stokes-Einstein relation [30, 31]. Dynamic heterogeneity refers to the fact that structural relaxation does not take place uniformly throughout the entire material–as in a normal liquid–, but rather in clusters of collectively rearranging particles, while the rest of the supercooled liquid remains temporarily frozen (Figure 4). The appearance of such mobile domains will vary both in space and in time, thus giving rise to non-trivial spatiotemporal fluctuations that become more pronounced as the glass transition is approached. Dynamic heterogeneity cannot be seen in F(k, t) itself, but rather in the fluctuations of F(k, t) among different particle trajectories [32, 33]. These fluctuations are encoded in the so-called dynamic susceptibility χ4(t), whose peak height is a measure for the size of the cooperatively rearranging regions. As a material is supercooled, a growing χ4(t) thus indicates a growing dynamic length scale associated with vitrification, but a true divergence of this length scale–as expected for typical critical phenomena–has not yet been observed [17]. A related puzzling phenomenon concerns the Stokes-Einstein equation, which states that the viscosity (or relaxation time), diffusion constant D, and temperature of a liquid are related as Dη/T = constant. This ratio holds generally for normal liquids, but in the supercooled regime the viscosity increase tends to be stronger than the diffusion-constant decrease. This breakdown of Stokes-Einstein behavior is widely believed to be a manifestation of dynamic heterogeneity, but the fundamental origins of both phenomena remain poorly understood.
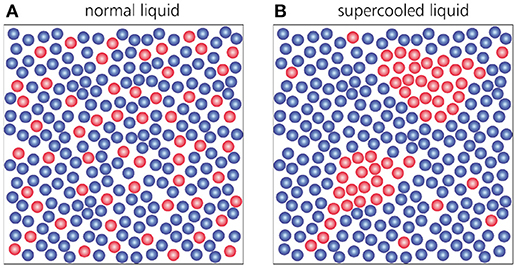
Figure 4. Illustration of dynamic heterogeneity in supercooled liquids. The red-colored particles represent mobile particles that have moved further than a certain distance Δr during a time interval Δt, while blue-colored particles represent particles that have moved less than this distance in the same time interval. In the normal liquid phase (A), particle motion occurs rather homogeneously across the entire sample. Conversely, in a supercooled liquid (B), particle motion occurs heterogeneously in clusters of collectively moving particles, and the appearance of such mobile clusters fluctuates both in space and in time. The figure is based on Weeks et al. [26].
Finally, we mention another hallmark of glassy dynamics that is rather general for out-of-equilibrium systems, namely aging [2, 20, 23, 34, 35]. Aging implies that the behavior of a material depends explicitly on its age, i.e., the structural and dynamical properties may slowly change as time progresses. These changes are commonly a manifestation of the material's gradual approach to an equilibrium state. In the supercooled phase, such aging effects are usually observed after a (small) temperature quench, but vanish after a sufficiently long equilibration time. Indeed, “properly equilibrated” supercooled liquids that are cooled sufficiently slowly (such that there is ample time for the material to undergo full structural relaxation at a given temperature) behave as ordinary equilibrium liquids in the sense that, e.g., ergodicity and the fluctuation-dissipation theorem hold. Within the glass state, however, ergodicity is broken and the relaxation time to reach equilibrium exceeds–by definition–any practical time scale. Hence, a glass can be regarded as a supercooled liquid that has fallen out of equilibrium, and its properties depend explicitly on its history. There is a large body of literature devoted to aging effects in glasses (see e.g. Ref.[2] and references therein), but here we only briefly mention that physical aging within the glassy state is generally associated with the material's tendency to reach a lower-energy state that–eventually–will correspond to a deeply supercooled (quasi-equilibrium) liquid phase at a temperature below the original Tg. Whether the equilibrium supercooled liquid branch terminates at a low but finite temperature, the so-called Kauzmann temperature TK (TK < Tg), remains a matter of debate.
In this review, we focus on one of several theories that seeks to describe the above complex phenomenology of glass-forming materials, namely Mode-Coupling Theory (MCT) [36, 37]. This theory was first put forward by Götze and coworkers in the 1980s [24, 38], and is one of the few frameworks of glassy dynamics that is based entirely on first principles, starting from the exact microscopic picture of a correlated liquid. A somewhat related and more recent theory, the Self-Consistent Generalized Langevin Equation (SCGLE) approximation [39], will also briefly be discussed. We outline the key physical ingredients and sketch of the MCT derivation, its predictions, successes, and failures, as well as recent improvements and extensions of the theory. Part of this work is based on the review by Reichman and Charbonneau [22], which also contains a full derivation of the MCT equations, and the review by Szamel [40]; For a detailed discussion of the original theory, including an extensive treatment of the involved mathematics, we refer to the seminal work of Götze [36]. For an overview of the many other existing theories of glass formation, such as free volume theory, Adam-Gibbs theory, Random First Order Transition (RFOT) theory, dynamic facilitation and kinetically constrained models, energy landscape approaches, and geometric frustration, see e.g. Refs.[2, 15, 20, 41–43]. A discussion of these alternative theories falls outside the scope of the present work; here we only mention that, of all the other existing frameworks, RFOT theory is directly related to MCT at high temperatures, but is further augmented with thermodynamic, Adam-Gibbs-like concepts at low temperatures.
2. Derivation of the MCT Equations
2.1. Preliminaries
As already noted in the introduction, MCT provides a purely first-principles route toward the description of glassy behavior, making it a unique theory that does not rely on any phenomenological assumptions. Explicitly, MCT aims to predict the full microscopic relaxation dynamics of a glass-forming material–as a function of time, wavenumber, temperature, and density–, using only knowledge of static, time-independent properties as input. Aside from constants such as the system's temperature and density, the main theory input is the average microscopic structure of the material. The simplest experimental measure of the latter is the static structure factor S(k), which can be obtained directly from scattering experiments. This structure function is related to the radial distribution function g(r) (Figure 1) through a Fourier transform [21, 44], and thus probes–in Fourier space–the likelihood of finding a particle at a certain distance r~2π/k away from any other particle (Figure 3D). Formally S(k) is also equivalent to F(k, t = 0). It must be noted that MCT also admits more intricate three-particle correlation functions as additional structural input, but–with the exception of network-forming fluids [45, 46]–the sole knowledge of S(k) generally suffices. Importantly, it is through these structural metrics that MCT knows about the chemical composition of the material under study. That is, the theory is able to distinguish between, say, a glass-forming fluid of silica or Lennard-Jones particles only through their differences in (wavevector-dependent) structure.
In the standard formulation of MCT, the theory seeks to predict the full dynamics of the intermediate scattering function F(k, t) of a given material, starting with the exact equation of motion for F(k, t). Below we sketch the derivation of this equation, followed by a discussion of the various MCT approximations made to solve it. Briefly, the derivation will amount to an exact integro-differential equation for F(k, t) (Equation 10) that is governed by an even more complicated time-dependent correlation (“memory”) function. MCT makes the ad hoc assumption that the latter memory function can be approximated as a product of F(k, t) functions, thus yielding a closed, self-consistent equation (see Figure 5). As described in section 2.3, the final MCT equation (Equation 12) is reminiscent of a damped harmonic oscillator, but with a time-dependent damping term that ultimately produces the dramatic dynamic slowdown in supercooled liquids.
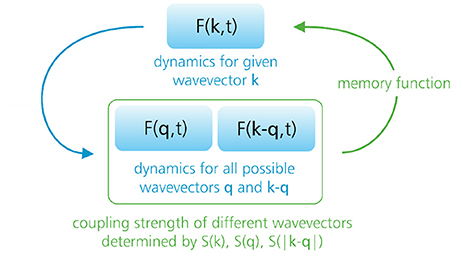
Figure 5. Sketch of the MCT equations. The theory seeks to predict the full dynamics of the intermediate scattering function F(k, t) for all possible wavevectors k and all times t. The exact F(k, t) dynamics is governed by a memory function that, within standard MCT, is approximated as a product of two intermediate scattering functions that probe density correlations at different wavevectors q and k − q. The couplings among the different wavevectors {k, q, k − q} are determined by the so-called vertices, which depend explicitly on the static structure factor. Hence, the static structure factor must be given as input to the theory, and dynamical information is given as output.
Let us first define our variables of interest, namely the collective density modes,
where N denotes the total number of particles and rj(t) is the position of particle j at time t. The real-space density ρ(r, t) thus simply measures where all particles are located at a given point in time, and ρ(k, t) is the corresponding Fourier transform for wavevector k. The intermediate scattering function F(k, t) probes the time-dependent correlations between these collective density modes,
where the brackets denote a canonical ensemble average. At time t = 0, this correlation function reduces to the static structure factor,
which thus contains information on the static density distribution of the material, i.e., the average microscopic structure. Note that in an isotropic material, such as a powder or a “simple” fluid, both S(k) and F(k, t) depend only on the magnitude of the wavector, k = |k|, but in e.g. the presence of an external field the full wavevector dependence should be considered [47].
2.2. Mori-Zwanzig Projection Formalism
In order to obtain an exact equation of motion for F(k, t), we make use of the so-called Mori-Zwanzig projection formalism [48, 49]. The basic idea behind this formalism is to divide the entire universe into two mutually orthogonal subspaces: one containing the variables of interest, and one simply containing “everything else.” The goal is to describe how the dynamics of the relevant variables evolves over time, in the presence of all other “non-interesting” variables. Physically, this idea relies on a separation of time scales in the dynamics, whereby the fast variables are integrated out. Here we will focus mainly on molecular glass-forming fluids, in which case the variables of interest are the collective density modes of Equation (1) and their associated current modes
where the dots denote time derivatives. Note that in general there is no simple recipe for deciding which variables are “relevant”; typically we focus on quasi-conserved or “slow” variables that show some non-trivial time-dependence (unlike strictly conserved variables that are constant), but which do not fluctuate too fast either, so as not to be confused with noise. From Equation (4), it is easy to see that in the limit k → 0, corresponding to very large length scales, the current will vanish and consequently the macroscopic density is strictly conserved. On smaller length scales, however, i.e., k > 0, the local density will fluctuate as particles move around, and it is these fluctuations–and their time-dependent correlations–that we seek to probe in F(k, t) and predict with MCT.
For convenience we will organize the variables ρ(k, t) and j(k, t) into a two-component vector A, which thus spans our subspace of interest:
Importantly, in this notation, time-dependent correlation functions may now be identified simply as scalar products between such vector elements, e.g., , where we have used the standard bra-ket notation with the asterisk representing the complex conjugate. We define the full matrix of all possible scalar products as C(t), with matrix elements
Note that the first matrix element C11(t) equals NF(k, t), and C21(t) = (N/i)(dF(k, t)/dt). Furthermore, in analogy to ordinary projections in vector space, we can now use these scalar products to define a projection operator as
where the sums run over all possible matrix elements. The projection of some vector C onto A is then given by . Such a projection essentially extracts all the “slow” or “relevant” character (defined through A) from an arbitrary variable C, leaving the remaining part of C orthogonal to A. It is easy to show that and , i.e., the projection of A onto itself returns A. This projection formalism, introduced by Zwanzig and Mori, thus establishes a link between dynamic variables and standard vector algebra. Without any loss of generality, it will enable us to separate the full dynamical behavior of our system into two contributions: i) the dynamics evolving in the “slow” subspace spanned by A(0), and ii) the dynamics due to all remaining “fast” variables, obtained simply by projecting out all the slow A-character from the full dynamics.
Let us now look explicitly at the time-dependent dynamics of a glass-forming supercooled liquid. For classical fluids that obeys Newton's equation of motion, the time evolution of A(t) can always be formally written as
where is the so-called Liouvillian operator. The definition of can be found in (e.g., [22]), but here we will not be concerned with its explicit form; it suffices to know that this operator governs the full dynamics of our variables of interest. Note that for colloidal glass-forming systems undergoing Brownian rather than Newtonian motion, a similar equation applies when considering only the density modes in A and replacing the Liouvillian by the so-called Smoluchowski operator [50].
While Equation (8) is formally exact, it does not necessarily yield any new physical insight into the complex time-dependent dynamics of supercooled liquids. Instead, we can rewrite this equation through a somewhat lengthy derivation (involving the insertion of the unit matrix operator and separating the time-evolution operator into a “slow” component and its orthogonal part) in the following form [22]:
For the matrix of correlation functions C(t) we similarly find
Here, Ω is the so-called frequency matrix (the name will become apparent later on), which captures the part of the time derivative of A that remains in the slow subspace as time evolves, K(s) is a time-dependent memory function, and f(t) is the “fast” fluctuating force, which is defined as . That is, f(t) is obtained by first removing all the “slow” character from the time derivative of A using the complementary projection operator , and is subsequently propagated in time in the “fast” subspace orthogonal to A. The memory function K(t) is given by the time-autocorrelation function of this fluctuating force; physically, K(t) represents a dissipative term that ultimately breaks the conservation of A. In other words, K(t) and f(t) embody how our slow variable A–which at time t = 0 lives strictly in the slow subspace–will gradually evolve under the influence of the rest of the universe, e.g. in the presence of “fast” variables such as thermal noise. Note that in arriving at Equation (10), we have used that 〈A(0)|f(t)〉 = 0 by construction. Importantly, Equations (9) and (10), which are known as the generalized Langevin equation and memory equation, respectively, are both exact.
2.3. Mode-Coupling Theory Approximations
By Equation (10), the difficulty of predicting the full time-dependent dynamics of F(k, t) is now deferred to the the question of how the memory function K(t) evolves with time. In general, there is no rigorous solution for this equation, and hence approximations must be made. The main idea behind MCT is to approximate K(t) in “the simplest non-trivial way” using a two-step approach:
1. Approximate the memory function as a four-point density correlation function. First, using the density modes as the main physical variables of interest, the fluctuating force f(t) is projected onto a new basis of products of two density modes, ρ(k1, t)ρ(k2, t), where k1 and k2 run over all possible wavevectors relevant to our system. Physically, this projection is motivated by the fact that for particles interacting through an arbitrary pair potential, such products of densities emerge naturally in the expression for the fluctuating force [22]. This may seem rather counterintuitive at first, since the fluctuating force is a fast variable while density modes are slow by definition, but it can be shown by Fourier transformation that, for an n-body interaction potential, f(t) always contains products of n density modes [41]. In the standard MCT formulation, it is assumed that the pair densities dominate the fluctuating force entirely, but higher-order generalizations with projections onto an n-density-mode basis have also been considered [51, 52]. Mathematically, the projection onto pair densities also corresponds to the first non-vanishing component in density space, i.e., “the simplest non-vanishing term,” since a projection onto a single density mode would always give zero by construction [36]. Overall, this approximation brings the memory function K(t), which is the time-correlation function of f(t), into the form of a four-point density correlation function:
with the time-propagation operator acting in the fast subspace.
2. Factorize four-point correlation functions into two-point correlation functions. Second, the (unknown) four-point correlation functions in K(t) are further simplified by factorizing them into a product of two two-point correlation functions and . At the same time, the operator is replaced by the normal operator , since the single density modes ρ(k1, t) and ρ(k2, t), which start out in the slow subspace, would otherwise give a zero contribution. It is important to note that this factorization is an ad hoc approximation that is not necessarily motivated by any physical insight; rather, it merely serves to produce a “simple” memory function that is not trivially zero. Nonetheless, it can be shown that the factorization is exact for so-called Gaussian variables [53], but density modes in general do not behave as such.
After the second approximation is made, we may then realize that the factorized two-point density correlation functions are, in fact, equal to NF(ki, t) by virtue of Equation (2). Thus, our full equation of motion for the intermediate scattering function F(k, t) is now governed by a memory function containing precisely the same function, but for many different wavenumbers. After explicitly working out all the expressions for the frequency matrix Ω and the (approximate) memory function K(t), and concentrating on the lower left corner of the correlation matrix C21(t) in Equation (10), we finally arrive at the full MCT equation [22]:
with the memory function given by
Here, kB is the Boltzmann constant, m is the particle mass, ρ is the bulk density, and the factors
are referred to as vertices, with c(k) = ρ−1[1 − 1/S(k)] denoting the direct correlation function [21]. These vertices represent the strength of the coupling between different density modes at wavevectors q and k − q. In arriving at this equation, we have also assumed that S(k) contains all the relevant microscopic structural information (using the so-called convolution approximation [22, 23, 54]), but in general the vertices may also contain higher-order, triplet-density correlations [45, 55]. Equation (12) is a closed, self-consistent equation, and is subject to the boundary conditions F(k, 0)/S(k) = 1 and Ḟ(k, 0) = 0.
Let us briefly compare this MCT result with the equation of motion for a one-dimensional damped harmonic oscillator: ẍ + ω2x + 2ζωẋ = 0, where ω is the frequency of the undamped oscillator and ζ is the damping coefficient. It can be seen that the MCT equation is rather similar, with x(t)~F(k, t) and playing the role of ω2. Hence, the Ω matrix is referred to as the frequency matrix. The damping coefficient, on the other hand, appears in the MCT equation in the form of the memory function KMCT(t) (note the first derivative of F(k, t) in the integrand). Consequently, we may interpret the memory function as a generalized, time-dependent damping, which will ultimately cause the dynamical slowdown in F(k, t) [23].
To make the comparison with a damped harmonic oscillator more explicit, let us first drop all wavevector dependence in the MCT equations and write x(t) = F(k, t) and , so that the MCT equation of motion becomes . Such simplified, k-independent MCT equations are known as schematic MCT models [24, 38]. We may now write the schematic memory function as , with a denoting a damping factor that represents the effective strength of the vertices at a given temperature. Note that if the memory function would be a simple delta-function aδ(t), the schematic MCT equation would reduce to a damped harmonic oscillator with a = 2ζω. The fact that the true (schematic) MCT memory function contains the non-linear product x2(t) instead of a simple delta-function, however, has important consequences for the dynamics and gives rise to a strong feedback effect that is absent in an ordinary damped oscillator. Figure 6 shows the solutions x(t) for a one-dimensional damped harmonic oscillator and for the schematic MCT model as a function of time for different damping factors a. It may be seen that, as the damping a is increased, the harmonic oscillator undergoes only a moderate change in the dynamics, while the MCT solution develops a plateau and exhibits an orders-of-magnitude dynamical slowdown. At a critical damping value of ac = 4, the schematic MCT model predicts an ergodicity-breaking transition such that the function x(t) fails to decay to zero on any time scale–i.e., a glass has formed. Increasing the damping further (a > 4) brings the system more deeply in the glass phase. The full wavevector-dependent MCT equation predicts a similar scenario, in which the memory function constitutes a non-linear dynamical feedback mechanism (with the damping strength implicitly controlled by small changes in the static structure factor as the temperature is decreased), though of course the explicit coupling of density modes at different wavevectors leads to richer (and more complicated) behavior than that predicted by schematic MCT (see section 3). Despite the simplicity of schematic MCT models, it is now well established that many predictions of schematic MCT–which can often be derived analytically (see [38])–are also preserved in the full wavevector-dependent version, and hence schematic MCT approaches remain widely used to gain better insight into the phenomenology of glassy materials.
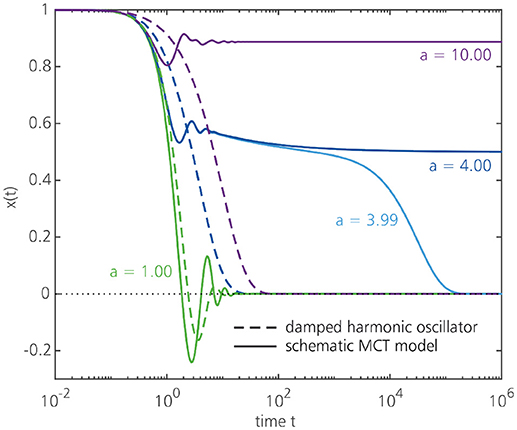
Figure 6. Solutions x(t) for a damped harmonic oscillator, ẍ(t) + ω2x(t) + aẋ(t) = 0 (dashed lines), and for a schematic MCT equation, (solid lines), with ω2 = 1 and a = 2ζω. Note the logarithmic scale for the time axis. As the damping a is increased, the MCT solution exhibits a highly non-linear slowdown and becomes non-ergodic for damping values a ≥ 4, signaling the formation of a glass. For the damped harmonic oscillator, the solutions for a = 3.99 and a = 4 are indistinguishable on the scale of this figure.
While analytic solutions of the full wavevector-dependent MCT equation generally do not exist, it is always possible to solve the equation numerically, namely by iteratively making an ansatz for F(k, t) for all k, subsequently constructing the memory function, and updating F(k, t) until convergence is reached. See Fuchs et al. [56] and Flenner and Szamel ([57], appendix) for a detailed discussion of the numerical algorithm to solve the MCT equations. We also note that for systems undergoing Brownian instead of Newtonian dynamics, in which case the Liouvillian should be replaced by the Smoluchowski operator, MCT yields an identical equation (with kBT/m being replaced by the diffusion constant D) [58]; however, the origin of this similarity is subtle and rather non-trivial. Moreover, it has also been shown that this equation applies reasonably well to glass-forming polymer chains [59], suggesting that MCT captures at least some degree of universal dynamical behavior. Finally, we note that MCT-based equations have also been formulated for, e.g., the self-part of the intermediate scattering function (i.e., the density correlation function for a single particle j) [24], the shear relaxation function [60], the dynamics under shear flow [61] and in confinement [62–64], microrheology studies [65, 66], fluids composed of anisotropic particles [67], and multi-component glass-forming systems [57, 60, 68]. In case of the latter, the MCT equations can be derived in a similar manner as above, except that the density modes (and their corresponding currents) are replaced by their partial analogs ρxi(k, t), where xi labels a particle species. For an M-component system, the MCT equations (Equations 12, 13) will then amount to an M×M matrix equation that explicitly couples the partial intermediate scattering functions and partial structure factors for all species. These MCT extensions and variations, however, will not further be discussed in this review.
As a final note, we mention that an alternative and more recent first-principles-based theory has been formulated that is somewhat related to MCT, namely the Self-Consistent Generalized Langevin Equation approximation [39]. This SCGLE theory also starts from the exact generalized Langevin equation (Equation 9), but employs different and somewhat simpler approximations to obtain a self-consistent equation for the dynamics. Instead of projecting the fluctuating force onto pair density modes, the main assumptions of SCGLE theory are a Vineyard-like approximate relation between the memory function of F(k, t) and the memory function of the self part Fs(k, t), and a Gaussian-like approximation for the memory function of Fs(k, t) that relates its dynamics to the Brownian motion of individual particles [39]. Overall, SCGLE theory also amounts to a closed, self-consistent dynamical equation that requires only simple static properties as input. An important advantage is that the SCGLE theory can be readily extended to account for non-equilibrium aging effects, such that the dynamics depends explicitly on the waiting time or age of the material [69–72]. This is to be contrasted with standard MCT, which in its standard form applies only to stationary (quasi-)equilibrium systems and consequently cannot make any predictions of aging phenomena; the extension of MCT to non-equilibrium aging systems is technically rather involved [73]. The SCGLE equations have also been extended to multi-component systems [74, 75] and to non-spherical particles [76, 77], and are generally somewhat simpler to use than the MCT equations. For a more detailed discussion of SCGLE theory [see [39, 72]] and references therein.
3. Mode-Coupling Theory Predictions
The microscopic MCT equation, Equation (12), can be solved for any glass-forming material at a given bulk density ρ and temperature T once the corresponding static structure factor S(k) = S(k; ρ, T) is known. Thus, MCT predicts the full microscopic dynamics given only time-independent information as input. In order to describe the entire vitrification process from liquid to glass, one typically measures S(k) for a series of temperatures or densities, and performs a separate MCT calculation for every relevant temperature and density. In this section, we summarize the main successes and failures of such MCT predictions.
3.1. Successes
Despite the various approximations made in MCT, the theory gives a remarkable set of accuracte predictions. Firstly, MCT is indeed capable of predicting a glass transition, which is non-trivial considering that the static structure factor S(k)–the main theory input–changes only very weakly upon vitrification (Figure 3C). As mentioned earlier, the relaxation time of the predicted F(k, t) is used as an indicator for the glassiness: at the glass transition, the relaxation time diverges and F(k, t) fails to decay to zero on any time scale. The corresponding non-ergodicity parameter f(k) is also often in good quantitative agreement with the results of computer simulations and experiments (see, e.g., [68, 78]).
Mathematically, MCT's ability to predict a glass follows from the non-linearity of the equation (by virtue of the product of two F(k, t) functions in the memory function), which renders the theory very sensitive to any small change in structural input. This non-linearity leads to a feedback mechanism that ultimately drives the dramatic dynamical slowdown: upon cooling, S(k) will become slightly larger at certain wavevectors, causing the vertices to increase as well. Consequently, the memory function will become larger and produce a stronger damping for F(k, t). The resulting slower intermediate scattering function will further strengthen the memory function, slowing down the dynamics even more. This non-linear feedback effect explains at least qualititatively why the relaxation dynamics can change so dramatically upon only small changes in the structure and temperature [23].
A related success of MCT is its prediction of the cage effect as a microscopic mechanism for vitrification (Figures 3, 7). Caging refers to the fact that, in a supercooled liquid, particles become (transiently) trapped in local cages formed by their neighboring particles, which in turn are trapped in their respective cages, preventing them from moving around as in a normal liquid. This is the molecular origin of the β-relaxation regime, which is manifested as a plateau in F(k, t). As long as the material is on the supercooled-liquid side of the transition, the particles will eventually manage to escape their cages, but at and below the glass transition, the cage effect keeps them trapped indefinitely. The only motion in the glassy state then corresponds to a vibrational or rattling motion of the particles within their confining cages. More mathematically, the cage effect emerges from MCT by considering that the most prominent change in S(k) upon supercooling occurs at the main peak at wavenumber k0, corresponding to length scales of approximately one particle diameter. As a consequence, the first intermediate scattering function that falls out of equilibrium at the glass transition is F(k0, t), which in turn drives the freezing on all other wavevectors. Notably, within MCT, the dominant structural length scale governing vitrification thus remains on the order of only one particle diameter, in stark contrast with conventional critical phenomena that are usually accompanied by diverging, macroscopic length scales. However, as will be described in section 4.3, recent work suggests that a diverging length scale also emerges within an extended (“inhomogeneous”) version of MCT that is related to the dynamic susceptibility χ4(t).
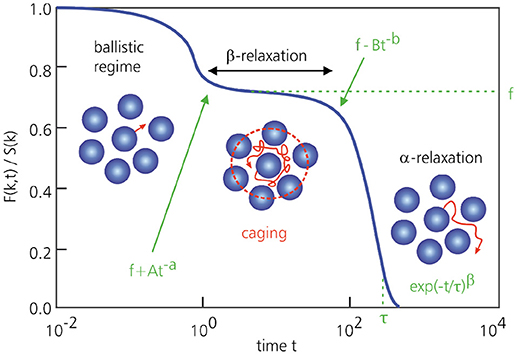
Figure 7. Typical MCT prediction for F(k, t) of a supercooled liquid as a function of time, for a wavenumber k = k0 that corresponds to the first peak of the static structure factor. At very short times, particles undergo ballistic motion. At intermediate times, particles become transiently trapped in cages (β-relaxation) and F(k, t) correspondingly remains approximately constant. Only at sufficiently long times will particles break free and full relaxation takes place (α-relaxation).
Regardless of the molecular details of the material, which are contained in S(k), MCT also makes several general predictions for the relaxation dynamics [22, 23, 36, 38]. Firstly, MCT predicts that close to the glass transition temperature Tc, the relaxation time F(k, t) will always diverge as a power law, . Such a functional form is often in good agreement with experiments and simulations in the mildly supercooled regime (using γ as a fit parameter), but generally breaks down closer to the experimental glass transition [see [79]]. We will return to this point in the next subsection. Furthermore, MCT predicts that the onset and decay of the β-relaxation regime, i.e., the plateau in F(k, t) at intermediate times, are described by power laws of the form F(k, t) ~ f + At−a and f − Btb, respectively, where f is the (constant) plateau height (Figure 7). Sufficiently close to Tc, the MCT exponents a and b are related as Γ(1 − a)2/Γ(1 − 2a) = Γ(1 + b)2/Γ(1 + 2b), where Γ denotes the Gamma function. This is an entirely non-trivial and remarkable prediction that is fully consistent with experiments and simulations. For the α-relaxation regime, i.e., the final decay of F(k, t) on the liquid side of the transition, MCT predicts a stretched exponential of the form exp(−t/τ)β, with 0 < β ≤ 1 (Figure 7). This is again in excellent agreement with experimental and simulation data, and physically arises from the coupling of multiple density-mode relaxation channels over different length scales, each relaxing on its own time scale. Another success of MCT that has been verified experimentally is its prediction of a time-temperature superposition principle, such that , where is a master function and τ(T) is the α-relaxation time.
Among the other celebrated results of MCT, we mention here its qualitative prediction of complex reentrant effects in sticky hard spheres (particles with a hard repulsive core and short-ranged attractions) [80] and ultrasoft repulsive particles [81], which exhibit glass-fluid-glass and fluid-glass-fluid phases upon a monotonic increase in attraction stength and density, respectively. In the case of sticky hard spheres, MCT has also provided a qualitative explanation for the existence of the two distinct glass phases in terms of different dominant length scales [80]. Furthermore, the schematic version of MCT [24, 38], which is obtained by ignoring all wavevector dependence in Equation (12), is rigorously exact for certain classes of spin-glass models with queched disorder (so-called p-spin spherical spin glasses), pointing toward a possible deep connection between systems with quenched and self-generated disorder. For a more extensive overview of MCT results, we refer the reader to Kob[23], and especially Götze [36].
3.2. Failures
Even though MCT successfully predicts a glass transition, its most notable failure is that the predicted glass transition temperature Tc occurs at much higher temperatures than the true experimental value Tg. Thus, the static structure factor for which MCT predicts a glassy state corresponds in reality to only a mildy supercooled liquid. In practice, the MCT predictions are often rescaled such that Tc coincides with Tg [68], but even with such a relative comparison, MCT generally fails to accurate describe the dynamics in the deeply supercooled regime. This discrepancy is attributed to MCT's lack of ergodicity-restoring relaxation mechanisms that keep the experimental system in the liquid phase well below Tc (Figure 8). Such mechanisms are generally referred to as activated dynamics, and are commonly identified with particles “hopping” out of their local cages to resist freezing [82]. MCT fails to account for such hopping motion and thus strongly overestimates the degree of caging–a feature that is believed to arise from its so-called mean-field nature. In practice, the predicted MCT transition at Tc is therefore interpreted as a crossover point where the dynamics changes into an activated form [83]. In section 4, we will return to this point and address recent efforts to incorporate activated dynamics directly into the theory. We note that activated dynamics may also be incorporated via, e.g., the Random First Order Transition theory, which is a spin-glass-inspired framework that merges MCT with thermodynamics-based concepts [84, 85]. A description of RFOT falls outside the scope of the present work, but we refer the interested reader to [e.g.,[43, 83, 86]] for a recent overview.
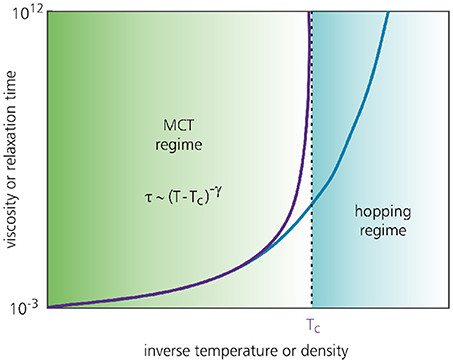
Figure 8. Typical MCT prediction (purple curve) and simulation result (blue curve) for the dynamical slowdown of a glass-forming material as a function of the control parameter. MCT generally predicts that the viscosity or relaxation time grows as a power law and diverges at the glass transition temperature Tc or critical packing fraction ϕc. In reality, a material tends to remain in the supercooled-liquid phase at temperatures well below Tc (or packing fractions above ϕc), which is attributed to so-called activated or hopping dynamics missing in standard MCT. The figure is based on Charbonneau et al. [82].
As mentioner earlier, MCT's prediction of a power-law divergence of the relaxation time also breaks down in most experimental and simulated glass-forming systems. More generally, the fact that MCT always yields a power law, regardless of the molecular composition of the material, also implies that MCT has essentially no notion of the concept of fragility. At best, an MCT power law may correctly describe the relaxation dynamics of fragile glass formers, but strong glass formers exhibit a fundamentally different, Arrhenius-type growth of the relaxation time. Indeed, an accurate (first-principles) prediction of the fragility of a material on the sole basis of its microscopic structure remains a major open challenge in the field [20]. Nonetheless, we note that MCT can predict other properties of strong glass formers rather accurately, such as the wavevector-dependent non-ergodicity parameter in the glassy phase [45].
MCT is also generally unable to account for the breakdown of the Stokes-Einstein relation in the deeply supercooled regime. This is again attributed to the inherent mean-field character of the theory and the absence of activated hopping dynamics [82]. Moreover, in its standard formulation, MCT does not offer an explanation for the emergence of dynamic heterogeneity, since MCT only predicts a single F(k, t) for a given wavevector, density, and temperature, and hence does not give access to correlations in the fluctuations of F(k, t). However, as discussed in section 4.3, an extension of the theory does allow for the calculation of a quantity related to the dynamic susceptibility χ4(t) and a corresponding growing (and ultimately diverging) correlation length scale. Furthermore, despite its mean-field character, it was recently shown that MCT does not become exact in the mean-field limit of infinite dimensions for a system composed of hard spheres [87–89], making it difficult to rationalize the set of standard-MCT approximations in a simple physical manner. Moreover, MCT assumes that the material is in (quasi-)equilibrium, and consequently fails to account for non-equilibrium aging and protocol-dependent history effects. The afore-mentioned SCGLE theory does allow for explicit aging predictions [72], and hence it constitutes an attractive alternative to MCT in this regard. Finally, since MCT (like SCGLE) is a purely dynamical theory, it cannot make any statements about thermodynamic properties such as the entropy. The latter is believed to also play an important role in the process of glass formation, and in particular may point toward an underlying thermodynamic transition that in practice is masked by the dynamic transition. Nonetheless, it is possible that MCT is implicitly aware of at least some changes in thermodynamic properties through changes in the static structure factor [90, 91].
4. Going Beyond Standard Mode-Coupling Theory
Since standard MCT is not exact, as exemplified by the drawbacks and failures discussed in the previous section, various attempts have been made in the last few decades to improve the theory's predictive power for glassy dynamics. Below we will summarize the most notable efforts to remedy at least some of MCT's problems, including the formulation of “Extended” MCT (EMCT) and “Generalized” MCT (GMCT) to incorporate activated dynamics mechanisms, the potential of GMCT to account for fragility and dynamic heterogeneity, and the formulation of “Inhomogeneous” MCT (IMCT) to predict dynamic susceptibilities. Finally, we also briefly discuss recent generalizations of MCT to a new class of soft condensed-matter systems referred to as active matter. Such active materials are composed of particles that can undergo autonomous motion through the consumption of energy, and are now emerging as a new paradigm to understand collective behavior seen in many living systems. The recent realization that active particles can also vitrify into a glassy state has spurred the formulation of various MCT frameworks for active matter, the development of which will be reviewed in section 4.4.
4.1. “Extended” Mode-Coupling Theory: Incorporating Couplings to Currents
The first attempts to remove the spurious MCT transition at Tc were proposed by Das and Mazenko in 1986 [92] and by Götze and Sjögren in 1987 [93], only a few years after the original formulation of standard MCT [24, 38]. Das and Mazenko employed a field-theoretic description, commonly referred to as fluctuating nonlinear hydrodynamics, while Götze and Sjögren used a projection-based formalism to improve the theory in the temperature regime near and below Tc. Both approaches amount to a perturbative treatment of nonlinear couplings to certain current modes that are neglected in the standard formulation of MCT, and which cut off the sharp MCT transition such that the strict divergence of the relaxation time at Tc is removed. This “rounding off” of the MCT transition was interpreted as a mechanism for activated or hopping dynamics that would keep the material ergodic, i.e., in the supercooled liquid phase, below Tc. The 2004 review by Das [37] provides an extensive overview of this line of EMCT research.
However, more recent theoretical studies have argued on general physical grounds that the invoked couplings to currents in EMCT cannot provide a satisfactory explanation of activated dynamics, since these couplings should always become negligible close to a glass transition [94]. Moreover, Andreanov et al. [95] suggested that the fluctuating nonlinear hydrodynamics approach employs an incorrect treatment of time-reversal symmetry. Another argument that casts doubt on the general applicability of EMCT is the fact that experimental and numerical simulation studies have unambiguously established that materials obeying Newtonian and Brownian (stochastic) dynamics exhibit the same deviations from standard-MCT behavior, despite their differences in microscopic dynamical details. This suggests that the physical mechanisms governing activated behavior below Tc have a universal origin in both molecular (Newtonian) fluids and colloidal (Brownian) systems. Since the current modes introduced in EMCT cannot be properly defined in Brownian systems [40], the proposed EMCT mechanism may thus only apply to materials undergoing Newtonian dynamics. Hence, it appears likely that EMCT cannot offer a rigorous, universal remedy for the lack of ergodicity-restoring activated dynamics within the standard MCT framework.
4.2. “Generalized” Mode-Coupling Theory: Toward an Exact Equation for the Memory Function
An alternative route to rigorously improve MCT was put forward by Szamel in 2003 [96]. This approach, referred to as Generalized MCT or GMCT, seeks to systematically avoid the second main approximation of standard MCT, i.e., the uncontrolled factorization of the four-point density correlations appearing in the memory function. To this end, a new and formally exact equation of motion is developed for the four-point correlation functions themselves (again by applying the Mori-Zwanzig projection formalism of section 2.2, this time using the basis of pair densities ρ(k1, t)ρ(k2, t) as the “relevant” variables). The new equation is governed by another memory function that, to leading order, is controlled by six-point density correlation functions, which in turn are dominated by eight-point correlations, etc. Hence, by repeatedly developing a new equation of motion for the new memory function, a hierarchy of coupled equations emerges, in which the uncontrolled factorization approximation may be applied at an arbitrary level to close the set of equations. This GMCT scheme thus allows, in principle, for a systematic delay of the closure approximation and, notably, remains based entirely on first principles (see Figure 9).

Figure 9. (A) Graphical illustration of the GMCT hierarchy. GMCT seeks to systematically avoid the uncontrolled MCT factorization approximation by developing a new, and formally exact, equation of motion for the unknown memory function. This equation in turn is governed by a new memory function, which is controlled by another memory function, etc. Standard MCT corresponds to the lowest-order (self-consistent) closure of this hierarchy. (B) Microscopic GMCT predictions for F(k, t) [97] compared to numerical data obtained from computer simulations [68] for a system of quasi-hard spheres at packing fraction ϕ = 0.570 and wavenumber kd = 7.4. These results indicate that the GMCT hierarchy apparently converges and that the theory becomes more quantitatively accurate as the closure level is increased. The figure is adapted from Janssen and Reichman [97] with permission.
Szamel [96] and Wu and Cao [98] showed that GMCT hierarchies factorized at the level of six- and eight-point correlation functions, respectively, indeed bring the predicted glass transition density systematically closer to the empirical value for a system of colloidal hard spheres. More recent work [97] also established that the full time-dependent microscopic dynamics for a quasi-hard-sphere glass former is systematically improved by GMCT. In fact, fit-parameter-free third-order GMCT calculations could achieve full quantitative agreement for F(k, t) up to the moderately supercooled regime, at densities where standard MCT would already predict a spurious glass transition [97]. Furthermore, within a simplified schematic (wavevector-independent) GMCT model, Mayer et al.[99] showed analytically that the sharp MCT glass transition can be completely removed when avoiding the closure approximation altogether, i.e., when applying infinite-order GMCT. Even though all GMCT studies to date still rely on several approximations–including the neglect of “projected” dynamics in the memory functions (section 2.3) and the factorization of all static correlation functions into products of S(k)'s–, the good agreement so far with computer simulations and experiments, as well as the apparent convergent behavior of the hierarchy [100], suggest that GMCT offers a promising first-principles path toward systematic MCT improvement. In particular, it appears that higher-order GMCT captures at least some aspects of activated dynamics to keep the material ergodic at temperatures below Tc, consistent with empirical observations. Importantly, we note that GMCT is applicable to both Newtonian and Brownian systems, and therefore also holds the potential to offer a more universal picture of glassy dynamics.
In addition to accounting for some kind of ergodicity-restoring processes below Tc, GMCT might also provide a suitable framework to describe fragility. The work of Mayer et al.[99] revealed that, within their particular schematic model, infinite-order GMCT predicts an exponential growth of the relaxation time, fundamentally distinct from the fragile power-law behavior of standard MCT. In later studies, we demonstrated that other schematic GMCT models may also give rise to other functional forms of relaxation-time growth, ranging from fragile super-Arrhenius to strong (sub-)Arrhenius behavior, depending on the choice of schematic parameters [101]. Although these simplified GMCT models inherently lack any wavevector dependence, and therefore cannot make detailed predictions for any structural glass former with a realistic S(k), they suggest that higher-order GMCT has at least the mathematical flexibility to account for different fragilities. This is notably different from standard MCT, which is mathematically only capable of predicting power-law growth close to the transition. It remains to be tested whether the fully microscopic (wavevector-dependent) version of GMCT will indeed be able to account for different degrees of fragility, given solely the static structure factors S(k) (and possibly higher-order static correlation functions) of strong and fragile materials as input. It might be tempting to assume that, with increasing closure level, the GMCT predictions should become more accurate, but let us reiterate that the current formulation of GMCT still relies on several approximations, and it is still unclear how the remaining assumptions ultimately affect the dynamics.
Finally, we note that by construction, higher-order GMCT also makes microscopic predictions for the (approximate) dynamics of unfactorized four-point density correlations [97]. Although these functions are not exactly equivalent to the dynamic susceptibility χ4(t), they should nonetheless be able to provide insight into dynamic heterogeneities, since they essentially describe particle correlations over two points in time and at least two points in space. Hence, GMCT may also offer a suitable starting point to study dynamic heterogeneity, as well as the breakdown of the Stokes-Einstein relation in supercooled liquids, from a strictly first-principles perspective. We expect this avenue of research to be explored in the coming years.
4.3. “Inhomogeneous” Mode-Coupling Theory: A Measure for Dynamic Heterogeneity
As noted earlier, standard MCT seeks to describe the “average” F(k, t) for a given set of wavevectors and system parameters, but does not give immediate access to the fluctuations of F(k, t) that are encoded in the dynamic susceptibility χ4(t) [33]. Hence, standard MCT cannot make direct predictions about dynamically heterogeneous behavior, which is generally revealed as a growing peak in χ4(t). There is, however, an indirect way to extract a dynamic susceptibility from MCT by incorporating an external field into the theory–a framework referred to as Inhomogeneous MCT or IMCT. The idea of IMCT is to measure the dynamic response of the intermediate scattering function F(k, t) to changes in the external field; this response amounts to a three-point dynamic density correlation function χ3(t). The IMCT study of Biroli et al.[47] argues that the induced fluctuations by the external field are intimately related to the spontaneous fluctuations described by χ4(t), and hence the susceptibility χ3(t) should behave in a similar manner as the four-point function χ4(t).
Biroli et al. found that χ3(t) grows upon approaching the dynamical MCT transition, and in fact diverges at the critical temperature Tc. Furthermore, a correlation length ξ could be defined–a measure, perhaps, for the size of cooperatively rearranging particles in the supercooled regime–, that grows as with a critical exponent of ν = 1/4. Notably, IMCT also predicts that this length scale governs both the α- and β-relaxation regimes. This suggests that the traditional picture of caging in the β-regime, commonly interpreted as the rattling of particles in local cages formed by their nearest neighbors (see 3.1), is actually more subtle; rather, IMCT implies that these cages become more and more collective as the MCT transition is approached. However, it should be noted that the predictions of IMCT are not generally in quantitative agreement with empirical results. For example, numerical simulations for a model glass former composed of Lennard-Jones particles indicate a growth of ξ (extracted from the numerical χ4(t)) with a fitted exponent of ν ≈ 0.5, and suggest that the length scale predicted by IMCT does not necessarily describe the true size of the correlated spatial domains relevant in real glass-forming materials [102]. On the other hand, simulations for another model glass former (the so-called Gaussian core model, which is believed to behave more as a mean-field system) have revealed that the predicted IMCT scaling of χ3(t) is in good quantitative agreement with the numerical χ4(t) [103], implying that IMCT constitutes at least in some sense a suitable mean-field framework for glassy dynamics. The question to what extent, and under which conditions, IMCT can offer an accurate description of dynamic heterogeneity, and how the IMCT predictions relate to, e.g., the four-point dynamic correlations emerging from GMCT, still remains to be established.
4.4. Mode-Coupling Theories for Active Matter
We end this review with a very recent development in the field, namely the study of active matter. Active materials consist of particles that can convert energy into autonomous motion, rendering them out of thermodynamic equilibrium at the single-particle level [104]. Such particle activity can lead to rich self-organizing behavior, as exemplified in nature by, e.g., the collective motion of living cells and the flocking of birds. During the last decade, numerous synthetic active systems have also become available [105], spurring the development of theoretical approaches to describe the emergent behavior in these non-equilibrium materials. In particular, it was found that dense active matter can also exhibit properties of supercooled liquids and vitrifying colloidal suspensions [6, 8, 10, 11, 106–114], including slow structural relaxation, dynamic heterogeneity, varying degrees of fragility, and the ultimate formation of a kinetically arrested, amorphous solid state.
Here we briefly discuss recent extensions of standard MCT to describe the glassy dynamics in active materials. Since many synthetic active particles are composed of colloids undergoing active Brownian motion, all active versions of MCT to date are based on the Smoluchowski formalism for Brownian systems, rather than the Newtonian description for molecular fluids discussed in section 2. We note, however, that continuum descriptions of active matter, such as those for active liquid crystals, are usually derived from Newtonian-based fluid mechanics [104].
The first MCT approach to active glasses was presented by Farage and Brader in 2014 [115]. In this work, they considered so-called active Brownian particles (ABPs) that move with a constant self-propulsion speed in a random direction, subject to translational and rotational Brownian motion. The authors assumed that a single, non-interacting ABP behaves effectively as a passive colloid, but with a higher effective diffusion constant. This approximation was subsequently used to derive an effective Smoluchowski operator for the collective dynamics of a dense ensemble of active particles. In essence, this effective-diffusion approach amounts to the removal of explicit rotational degrees of freedom. The resulting MCT approach yields a modified version of Equation (12), in which both the frequency term and the memory function acquire an activity-dependent prefactor. The main outcome of this MCT study is that the addition of particle activity can soften (i.e., decrease the non-ergodicity parameter) and eventually melt a passive glass, and shift the glass transition toward higher densities. These findings are also in qualitative agreement with computer simulations of a similar active material composed of self-propelling Brownian hard particles [107, 108]. The MCT approach of Farage and Brader was later also extended by Ding et al.[116] to mixtures of active and passive particles.
A different and more extensive active-matter study was performed by Szamel et al. [110, 117]. Here, the authors modeled active particles by an Ornstein-Uhlenbeck stochastic process, characterized by an effective temperature that quantifies the strength of the active forces, and a persistence time that describes the duration of persistent self-propelled motion. In this model, particle motion is thus described as a persistent random walk. Within their framework, the self-propulsion is first integrated out before applying the projection-operator method and MCT-like approximation; this approach essentially assumes that particle positions evolve on a time scale much larger than the time scale needed for reorientation of the activity direction, somewhat akin to the effective-diffusion assumption of Farage and Brader [115]. An important difference between the active MCT of Szamel et al. and previous MCT studies is that not only the static structure factor–i.e., static correlations between particle positions–should be given as input to the theory, but also static correlations between particle velocities. Contrary to the behavior of ABPs, it was found that the incorporation of activity can both enhance and suppress glass formation: for small persistence times, the active fluid relaxes faster than a passive system at the same effective temperature, but for large persistent times the active material becomes more glass-like compared to the passive reference system. This non-monotonic dependence of the relaxation time was observed both in the MCT analysis and in computer simulations, and was attributed to the competition between increasing velocity correlations (which speed up the dynamics) and increasing structural correlations (which slow down the dynamics) [110]. For sufficiently large persistence times, it was found that the fitted MCT glass transition temperature increases monotonically with increasing persistence time, suggesting that–at least within this active-matter model–vitrification occurs more easily as the material becomes more active. An MCT-based scaling analysis for this type of active-matter system was later performed by Nandi and Gov [118].
Feng and Hou [119] subsequently studied a quasi-equilibrium thermal version of the active Ornstein-Uhlenbeck model of Szamel and co-workers, which additionally accounts for thermal translational noise. Their MCT derivation differs from the approach taken by Szamel [117], however: it is valid only for sufficiently small persistence times (since it relies on a perturbative expansion), and does not require explicit velocity correlation functions to be given as input. Rather, their active-MCT dynamics is governed by an averaged diffusion constant and a non-trivial steady-state structure function S2(k), which both depend on the effective temperature and density of the system, as well as on the persistence time of the active particles. The coefficient and S2(k) should both be given as additional input to the theory in order to predict F(k, t). It was found that the critical density at which the glass transition takes place shifts to larger values with increasing magnitude of the self-propulsion force or effective temperature, and that the critical effective glass temperature increases with the persistence time. In the limit of a vanishing persistence time, the theory naturally yields the expected result for a simple passive Brownian system [119].
Very recently, Liluashvili, et al. [120] formulated the first MCT for ABPs in which both the translational and rotational degrees of freedom are treated on an equal footing. That is, rather than seeking to reduce the active material to a near-equilibrium system, the rotational degrees of freedom governing the reorientation of the active forces are now explicitly coupled to the translational motion. This approach thus avoids the effective-diffusion assumption (which in principle may be valid only at low densities and sufficiently long times), and the resulting dynamics now also depends non-trivially on the rotational diffusion constant. The only required material-dependent input for this active MCT is the passive-equilibrium static structure factor. An important outcome of this study is the three-dimensional fluid-glass phase diagram for hard ABPs as a function of packing fraction, self-propulsion speed, and rotational diffusion constant. It was shown that this surface cannot be collapsed onto a single line in the two-dimensional plane, highlighting the importance of treating the rotational degrees of freedom explicitly. Indeed, depending on the density of the active material, separate regimes could be identified that are dominated either by translational or reorientational motion. As in the study of Farage and Brader [115], and in agreement with computer simulations [107, 108], it was also found that activity generally makes hard-sphere systems more fluid-like and consequently shifts the glass transition to higher packing fractions. Notably, this active fluidization effect grows monotonously with increasing persistence time or inverse rotational diffusion constant, in contrast with the findings of Szamel and co-workers [110]. This difference is attributed to the absence of thermal Brownian noise in the model of Szamel et al.; in the limit of infinitely large persistence (vanishing rotational diffusion), active particles can block themselves and produce a glassy state, while the finite thermal diffusive motion in ABPs will make such blocking ineffective [120].
Finally, we mention another class of non-equilibrium materials that is closely related to active fluids, namely driven granular matter. Such systems can be realized experimentally by placing granular particles on, e.g., an air-fluidized or vibrating bed. Kranz, Sperl, and Zippelius [121–123] developed an MCT for driven granular spheres, focusing on the role of energy dissipation (due to inelastic particle collisions) on the dynamics. In their work, the “activity” is modeled by a driving amplitude that gives rise to random particle kicks and that implicitly sets an effective kinetic temperature; a coefficient of restitution ϵ is introduced to account for dissipative particle collisions. The resulting MCT equations are similar to Equation (12), except for an explicit ϵ-dependent prefactor in the frequency term and memory function. It was found that the critical glass transition systematically shifts to higher densities as the dissipation increases (decreasing ϵ). Furthermore, the increasing dissipation was found to have three noticeable effects in the non-ergodicity parameter at and above the glass transition density: i) correlations at small wave numbers are enhanced, ii) oscillations reflecting the local structure become less pronounced, and iii) the localization length (measured by the inverse of the width of the non-ergodicity-parameter peak) decreases. The last finding is a consequence of the glass transition taking place at a higher density.
5. Conclusions and Outlook
This review has sought to provide a brief overview of the main phenomenology of glassy dynamics, and of its theoretical description using Mode-Coupling Theory–arguably the most successful theory of the glass transition that is based entirely on first principles. We have focused mainly on the behavior of the density correlation function F(k, t) as a probe of the microscopic dynamics associated with vitrification. In the normal liquid phase, this correlation function rapidly decays to zero, but at the glass transition it fails to decay on any practical time scale, marking the onset of rigidity and providing an order parameter for the transition. Upon approaching the glass transition temperature, several complex features become visible in the dynamics, such as a transient plateau and stretched exponential behavior in F(k, t), a breakdown of the Stokes-Einstein relation, and the emergence of dynamical heterogeneity–the latter being associated with increasingly large fluctuations in F(k, t). Remarkably, during the process of glass formation, the microscopic structure of the material, as probed by e.g., the radial distribution function g(r) or static structure factor S(k), undergoes only very minor changes, yet the viscosity and dynamic relaxation time increase by many orders of magnitude. It is this seemingly paradoxical discrepancy between structure and dynamics that makes the glass transition a notoriously difficult problem in theoretical physics.
MCT offers a first-principles-based framework to account for at least some aspects of glassy dynamics. Its starting point is the exact equation of motion for F(k, t); through a series of (partly uncontrolled) approximations, MCT subsequently provides a self-consistent equation for F(k, t) that can be solved numerically using only the static structure factor as input. As such, the theory makes a set of detailed predictions for the full microscopic relaxation dynamics of a glass-forming material as a function of time, wavevector, temperature, and density, on the sole basis of simple structural information. Among its notable successes is the qualitative prediction of a glass transition, a physically intuitive picture for glass formation in terms of the cage effect, and the correct prediction of several highly non-trivial scaling behaviors in F(k, t). However, MCT is generally not quantitatively accurate, and cannot account properly for the concept of fragility, the violation of the Stokes-Einstein relation, and the emergence of dynamic heterogeneity.
The shortcomings of MCT might be remedied using (first-principles-based) extensions of the theory, such as Generalized MCT and Inhomogeneous MCT. The first studies in this direction show that GMCT can indeed offer a more quantitative description of the F(k, t) dynamics and can potentially describe fragility, while IMCT offers a framework to qualitatively account for dynamic heterogeneity. However, GMCT still relies on several approximations such as the neglect of certain wavevector-dependent density correlations, and IMCT provides–just like standard MCT–only a mean-field description of glassy dynamics. Hence, more work will be needed to establish how successful these theoretical approaches are in ultimately achieving a fully correct first-principles description of glassy dynamics.
A more recent addition to the palette of Mode-Coupling theories involves the study of non-equilibrium active matter. In the last few years, several MCT frameworks have been developed to describe glassy dynamics in active materials that are composed of self-propelled particles. Not only can these theories offer new insight into the behavior of dense assemblies of synthetic active colloids, but they might also shed new light on glassy and jamming phenomena in living cell tissues. Similar to how standard MCT has shaped our understanding of passive glass-forming materials over the last few decades, it can be expected that active MCT will also contribute to our understanding of disordered active and living materials from a statistical-physics-based and purely first-principles perspective.
In conclusion, despite the fact that Mode-Coupling Theory is not exact, it does provide a suitable–and in some cases remarkably accurate–foundation for the study of glassy dynamics in amorphous materials. The theory also offers ample opportunity for new research aimed toward a complete and ultimately rigorously exact description of the glass transition, as well as for the study of emergent new classes of materials such as active matter. We expect future work to be directed toward these exciting avenues of research.
Author Contributions
The author confirms being the sole contributor of this work and approved it for publication.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
It is a pleasure to thank David Reichman, Grzegorz Szamel, Jürgen Horbach, Thomas Voigtmann, Hartmut Löwen, Matthias Fuchs, Jörg Baschnagel, Jean Farago, Atsushi Ikeda, Peter Mayer, and Till Kranz for many interesting and enlightening discussions.
References
1. Debenedetti P, Stillinger F. Supercooled liquids and the glass transition. Nature (2001) 410:259–67. doi: 10.1038/35065704
2. Berthier L, Biroli G. Theoretical perspective on the glass transition and amorphous materials. Rev Mod Phys. (2011) 83:587–645. doi: 10.1103/RevModPhys.83.587
3. Biroli G, Garrahan JP. Perspective: the glass transition. J Chem Phys. (2013) 138:12A301. doi: 10.1063/1.4795539
5. Zhou EH, Trepat X, Park CY, Lenormand G, Oliver MN, Mijailovich SM, et al. Universal behavior of the osmotically compressed cell and its analogy to the colloidal glass transition. Proc Natl Acad Sci USA. (2009) 106:10632–7. doi: 10.1073/pnas.0901462106
6. Angelini TE, Hannezo E, Trepat X, Marquez M, Fredberg JJ, Weitz DA. Glass-like dynamics of collective cell migration. Proc Natl Acad Sci USA. (2011) 108:4714–9. doi: 10.1073/pnas.1010059108
7. Schötz E-M, Lanio M, Talbot JA, Manning ML. Glassy dynamics in three-dimensional embryonic tissues. J R Soc Interface (2013) 10:20130726
8. Sadati M, Nourhani A, Fredberg JJ, Taheri Qazvini N. Glass-like dynamics in the cell and in cellular collectives. Wiley Interdiscip Rev Syst Biol Med. (2014) 6:137–49. doi: 10.1002/wsbm.1258
9. Parry BR, Surovtsev IV, Cabeen MT, O'Hern CS, Dufresne ER, Jacobs-Wagner C. The bacterial cytoplasm has glass-like properties and is fluidized by metabolic activity. Cell (2014) 156:183–94. doi: 10.1016/j.cell.2013.11.028
10. Bi D, Lopez JH, Schwarz JM, Manning ML. A density-independent rigidity transition in biological tissues. Nat Phys. (2015) 11:1074. doi: 10.1038/NPHYS3471
11. Bi D, Yang X, Marchetti MC, Manning ML. Motility-driven glass and jamming transitions in biological tissues. Phys Rev X (2016) 6:021011. doi: 10.1103/PhysRevX.6.021011
12. Debenedetti PG, Stanley HE. Supercooled and glassy water. Phys Today (2003) 56:40. doi: 10.1063/1.1595053
15. Royall CP, Williams SR. The role of local structure in dynamical arrest. Phys Rep. (2015) 560:1–75. doi: 10.1016/j.physrep.2014.11.004
16. Karmakar S, Dasgupta C, Sastry S. Length scales in glass-forming liquids and related systems: a review. Rep Prog Phys. (2016) 79:016601. doi: 10.1088/0034-4885/79/1/016601
17. Albert S, Bauer T, Michl M, Biroli G, Bouchaud J-P, Loidl A, et al. Fifth-order susceptibility unveils growth of thermodynamic amorphous order in glass-formers. Science (2016) 352:1308–11. doi: 10.1126/science.aaf3182
18. Angell CA. Formation of glasses from liquids and biopolymers. Science (1995) 267:1924–35. doi: 10.1126/science.267.5206.1924
19. Xia X, Wolynes PG. Fragilities of liquids predicted from the random first order transition theory of glasses. Proc Natl Acad Sci USA. (2000) 97:2990–4. doi: 10.1073/PNAS.97.7.2990
20. Tarjus G. An overview of the theories of the glass transition. In: Berthier L, Biroli G, Bouchaud JP, Cipelletti L, van Saarloos W, editors. Dynamical Heterogeneities in Glasses, Colloids, and Granular Media. Oxford: Oxford University Press (2011). p. 39–67.
22. Reichman DR, Charbonneau P. Mode-coupling theory. J Stat Mech Theor Exp. (2005) 2005:P05013. doi: 10.1088/1742-5468/2005/05/P05013
23. Kob W. Supercooled liquids, the glass transition, and computer simulations. In: Barrat J-L, Feigelman MV, Kurchan J, Dalibard J. editors. Les Houches 2002 Summer School Session LXXVII: Slow Relaxations Nonequilibrium Dynamics in Condensed Matter. Berlin: Springer-Verlag (2002). p. 199–269.
24. Bengtzelius U, Götze W, Sjölander A. Dynamics of supercooled liquids and the glass transition. J Phys C Solid State Phys. (1984) 17:5915–34. doi: 10.1088/0022-3719/17/33/005
25. van Megen W, Underwood SM, Pusey PN. Nonergodicity parameters of colloidal glasses. Phys Rev Lett. (1991) 67:1586–9. doi: 10.1103/PhysRevLett.67.1586
26. Weeks ER, Crocker JC, Levitt AC, Schofield A, Weitz DA. Three-dimensional direct imaging of structural relaxation near the colloidal glass transition. Science (2000) 287:5453.
27. Kegel WK, van Blaaderen A. Direct observation of dynamical heterogeneities in colloidal hard-sphere suspensions. Science (2000) 287:290–3. doi: 10.1126/science.287.5451.290
28. Ediger MD. Spatially heterogeneous dynamics in supercooled liquids. Annu Rev Phys Chem. (2000) 51:99–128. doi: 10.1146/annurev.physchem.51.1.99
29. Berthier L. Dynamic heterogeneity in amorphous materials. Physics (2011) 4:7. doi: 10.1103/Physics.4.42
30. Tarjus G, Kivelson D. Breakdown of the Stokes–Einstein relation in supercooled liquids. J Chem Phys. (1995) 103:3071–3. doi: 10.1063/1.470495
31. Shi Z, Debenedetti PG, Stillinger FH. Relaxation processes in liquids: variations on a theme by Stokes and Einstein. J Chem Phys. (2013) 138:12A526. doi: 10.1063/1.4775741
32. Lačević N, Starr FW, Schrøder TB, Glotzer SC. Spatially heterogeneous dynamics investigated via a time-dependent four-point density correlation function. J Chem Phys. (2003) 119:7372–87. doi: 10.1063/1.1605094
33. Biroli G, Bouchaud J-P. Diverging length scale and upper critical dimension in the Mode-Coupling Theory of the glass transition. Europhys Lett. (2004) 67:21–27. doi: 10.1209/epl/i2004-10044-6
34. Struik CEL. Physical Aging in Amorphous Polymers and Other Materials. Ph.D. thesis, Technische Hogeschool Delft (1977).
35. Berthier L, Biroli G. A statistical mechanics perspective on glasses and aging. In: Meyers RE, editor. Encyclopedia of Complexity and Systems Science. (Springer) (2009). p. 4209–4240. Available online at: https://www.springer.com/gp/book/9780387758886
36. Götze W. Complex dynamics of glass-forming liquids: A Mode-Coupling Theory. Oxford, UK: Oxford University Press (2009).
37. Das SP. (2004). Mode-coupling theory and the glass transition in supercooled liquids. Rev Mod Phys. 76:785. doi: 10.1103/RevModPhys.76.785
39. Yeomans-Reyna L, Chávez-Rojo MA, Ramírez-González PE, Juárez-Maldonado R, Chávez-Páez M, Medina-Noyola M. Dynamic arrest within the self-consistent generalized Langevin equation of colloid dynamics. Phys Rev E (2007) 76:041504. doi: 10.1103/PhysRevE.76.041504
40. Szamel G. Mode-coupling theory and beyond: a diagrammatic approach (2013) 2013:012J01. doi: 10.1093/ptep/pts036
41. Schilling R. Theories of the structural glass transition. In: Radons G, Just W, Häussler P, editors. Collective Dynamics of Nonlinear and Disordered Systems Heidelberg: Springer (2005). p. 171–202.
42. Langer JS. Theories of glass formation and the glass transition. Rep Prog Phys. (2014) 77:042501. doi: 10.1088/0034-4885/77/4/042501
43. Lubchenko V, Wolynes PG. Theory of structural glasses and supercooled liquids. Annu Rev Phys Chem. (2007) 58:235–66. doi: 10.1146/annurev.physchem.58.032806.104653
45. Sciortino F, Kob W. Debye-waller factor of liquid silica: theory and simulation. Phys Rev Lett. (2001) 86:648–51. doi: 10.1103/PhysRevLett.86.648
46. Coslovich D. Static triplet correlations in glass-forming liquids: A molecular dynamics study. J Chem Phys. (2013) 138:12A539. doi: 10.1063/1.4773355
47. Biroli G, Bouchaud J-P, Miyazaki K, Reichman DR. Inhomogeneous Mode-Coupling Theory and Growing Dynamic Length in Supercooled Liquids. Phys Rev Lett. (2006) 97:195701. doi: 10.1103/PhysRevLett.97.195701
48. Zwanzig R. Memory effects in irreversible thermodynamics. Phys Rev. (1961) 124:983–992. doi: 10.1103/PhysRev.124.983
49. Mori H. Transport, collective motion, and Brownian Motion. Prog Theor Phys. (1965) 33:423–55. doi: 10.1143/PTP.33.423
50. Nägele G. On the dynamics and structure of charge-stabilized suspensions. Phys Rep. (1996) 272:215–372. doi: 10.1016/0370-1573(95)00078-X
51. Schofield J, Lim R, Oppenheim I. Mode coupling and generalized hydrodynamics. Physica A (1992) 89:181.
52. van Zon R, Schofield J. Mode-coupling theory for multiple-point and multiple-time correlation functions. Phys Rev E (2001) 65:011106. doi: 10.1103/PhysRevE.65.011106
53. Zaccarelli E, Foffi G, Sciortino F, Tartaglia P, Dawson KA. Gaussian density fluctuations and mode coupling theory for supercooled liquids. EPL (2001) 55:157–63. doi: 10.1209/epl/i2001-00395-x
54. Jackson HW, Feenberg E. Energy spectrum of elementary excitations in Helium II. Rev Mod Phys (1962) 34:686–93. doi: 10.1103/RevModPhys.34.686
55. Berthier L, Tarjus G. Nonperturbative effect of attractive forces in viscous liquids. Phys Rev Lett. (2009) 103:170601. doi: 10.1103/PhysRevLett.103.170601
56. Fuchs M, Götze W, Hofacker I, Latz A. Comments on the alpha-peak shapes for relaxation in supercooled liquids. J Phys Condens Matter (1991) 3:5047–71. doi: 10.1088/0953-8984/3/26/022
57. Flenner E, Szamel G. Relaxation in a glassy binary mixture: comparison of the mode-coupling theory to a Brownian dynamics simulation. Phys Rev E (2005) 72:031508. doi: 10.1103/PhysRevE.72.031508
58. Szamel G, Löwen H. Mode-coupling theory of the glass transition in colloidal systems. Phys Rev A (1991) 44:8215–9. doi: 10.1103/PhysRevA.44.8215
59. Chong S-H, Aichele M, Meyer H, Fuchs M, Baschnagel J. Structural and conformational dynamics of supercooled polymer melts: insights from first-principles theory and simulations. Phys Rev E (2007) 76:051806. doi: 10.1103/PhysRevE.76.051806
60. Nägele G, Bergenholtz J. Linear viscoelasticity of colloidal mixtures. J Chem Phys. (1998) 108:9893. doi: 10.1063/1.476428
61. Fuchs M, Cates ME. A mode coupling theory for Brownian particles in homogeneous steady shear flow. J Rheol. (2009) 53:957. doi: 10.1122/1.3119084
62. Lang S, Boan V, Oettel M, Hajnal D, Franosch T, Schilling R. Glass transition in confined geometry. Phys Rev Lett. (2010) 105:125701. doi: 10.1103/PhysRevLett.105.125701
63. Mandal S, Lang S, Gross M, Oettel M, Raabe D, Franosch T, et al. Multiple reentrant glass transitions in confined hard-sphere glasses. Nat Commun. (2014) 5:4435. doi: 10.1038/ncomms5435
64. Franosch T, Lang S, Schilling R. Fluids in extreme confinement. Phys Rev Lett. (2012) 109:240601. doi: 10.1103/PhysRevLett.109.240601
65. Gazuz I, Puertas AM, Voigtmann T, Fuchs M. Active and nonlinear microrheology in dense colloidal suspensions. Phys Rev Lett. (2009) 102:248302. doi: 10.1103/PhysRevLett.102.248302
66. Puertas AM, Voigtmann T. Microrheology of colloidal systems. J Phys Condens Matter (2014) 26:243101. doi: 10.1088/0953-8984/26/24/243101
67. Schilling R, Scheidsteger T. Mode coupling approach to the ideal glass transition of molecular liquids: linear molecules. Phys Rev E (1997) 56:2932–49. doi: 10.1103/PhysRevE.56.2932
68. Weysser F, Puertas AM, Fuchs M, Voigtmann T. Structural relaxation of polydisperse hard spheres: comparison of the mode-coupling theory to a Langevin dynamics simulation. Phys Rev E (2010) 82:011504. doi: 10.1103/PhysRevE.82.011504
69. Ramírez-González P, Medina-Noyola M. General nonequilibrium theory of colloid dynamics. Phys Rev E (2010) 82:061503. doi: 10.1103/PhysRevE.82.061503
70. Ramírez-González P, Medina-Noyola M. Aging of a homogeneously quenched colloidal glass-forming liquid. Phys Rev E (2010) 82:061504. doi: 10.1103/PhysRevE.82.061504
71. Sánchez-Díaz LE, Ramírez-González P, Medina-Noyola M. Equilibration and aging of dense soft-sphere glass-forming liquids. Phys Rev E (2013) 87:052306. doi: 10.1103/PhysRevE.87.052306
72. Mendoza-Méndez P, Lázaro-Lázaro E, Sánchez-Díaz LE, Ramírez-González PE, Pérez-Ángel G, Medina-Noyola M. Crossover from equilibration to aging: nonequilibrium theory versus simulations. Phys Rev E (2017) 96:022608. doi: 10.1103/PhysRevE.96.022608
73. Latz A. Non-equilibrium mode-coupling theory for supercooled liquids and glasses. J Phys Condens Matter (2000) 12:6353–63. doi: 10.1088/0953-8984/12/29/307
74. Juárez-Maldonado R, Medina-Noyola M. Theory of dynamic arrest in colloidal mixtures. Phys Rev E (2008) 77:051503. doi: 10.1103/PhysRevE.77.051503
75. Sánchez-Díaz LE, Lázaro-Lázaro E, Olais-Govea JM, Medina-Noyola M. Non-equilibrium dynamics of glass-forming liquid mixtures. J Chem Phys. (2014) 140:234501. doi: 10.1063/1.4882356
76. Elizondo-Aguilera LF, Zubieta Rico PF, Ruiz-Estrada H, Alarcón-Waess O. Self-consistent generalized Langevin-equation theory for liquids of nonspherically interacting particles. Phys Rev E(2014) 90:052301. doi: 10.1103/PhysRevE.90.052301
77. Cortés-Morales EC, Elizondo-Aguilera LF, Medina-Noyola M. Equilibration and aging of liquids of non-spherically interacting particles. J Phys Chem B (2016) 120:7975. doi: 10.1021/ACS.JPCB.6B04635
78. Kob W, Nauroth M, Sciortino F. Quantitative tests of mode-coupling theory for fragile and strong glass formers. J Non Cryst Solids (2002) 307–310:181–7. doi: 10.1016/S0022-3093(02)01457-6
79. Brambilla G, El Masri D, Pierno M, Berthier L, Cipelletti L, Petekidis G, et al. Probing the equilibrium dynamics of colloidal hard spheres above the mode-coupling glass transition. Phys Rev Lett. (2009) 102:085703. doi: 10.1103/PhysRevLett.102.085703
80. Pham KN, Puertas AM, Bergenholtz J, Egelhaaf SU, Moussad A, Pusey PN, et al. Multiple glassy states in a simple model system. Science (2002) 296:104–6. doi: 10.1126/science.1068238
81. Berthier L, Moreno AJ, Szamel G. Increasing the density melts ultrasoft colloidal glasses. Phys Rev E (2010) 82:060501. doi: 10.1103/PhysRevE.82.060501
82. Charbonneau P, Jin Y, Parisi G, Zamponi F. (2014). Hopping and the Stokes–Einstein relation breakdown in simple glass formers. Proc Natl Acad Sci USA. 111:15025. doi: 10.1073/pnas.1417182111
83. Biroli G, Bouchaud J-P. The random first-order transition theory of glasses: a critical assessment. arXiv:0912.2542 (2009).
84. Kirkpatrick TR, Thirumalai D. Dynamics of the structural glass transition and the p-Spin-Interaction Spin-Glass Model. Phys Rev Lett. (1987) 58:2091–2094. doi: 10.1103/PhysRevLett.58.2091
85. Kirkpatrick TR, Wolynes PG. Connections between some kinetic and equilibrium theories of the glass transition. Phys Rev A (1987) 35:3072–80. doi: 10.1103/PhysRevA.35.3072
86. Kirkpatrick TR, Thirumalai D. Random First Order Theory concepts in Biology and Condensed Matter physics. arXiv:1412.5017 (2014).
87. Ikeda A, Miyazaki K. Mode-coupling theory as a mean-field description of the Glass transition. Phys Rev Lett. (2010) 104:255704. doi: 10.1103/PhysRevLett.104.255704
88. Schmid B, Schilling R. Glass transition of hard spheres in high dimensions. Phys Rev E (2010) 81:041502. doi: 10.1103/PhysRevE.81.041502
89. Maimbourg T, Kurchan J, Zamponi F. Solution of the dynamics of liquids in the large-dimensional limit. Phys Rev Lett. (2016) 116:015902. doi: 10.1103/PhysRevLett.116.015902
90. Banerjee A, Sengupta S, Sastry S, Bhattacharyya SM. Role of structure and entropy in determining differences in dynamics for glass formers with different interaction potentials. Phys Rev Lett. (2014) 113:225701. doi: 10.1103/PhysRevLett.113.225701
91. Nandi MK, Banerjee A, Sengupta S, Sastry S, Bhattacharyya SM. Unraveling the success and failure of mode coupling theory from consideration of entropy. J Chem Phys (2015) 143:174504. doi: 10.1063/1.4934986
92. Das SP, Mazenko GF. Fluctuating nonlinear hydrodynamics and the liquid-glass transition. Phys Rev A (1986) 34:2265–82. doi: 10.1103/PhysRevA.34.2265
93. Götze W, Sjögren L. The glass transition singularity. Z Phys B (1987) 65:415–27. doi: 10.1007/BF01303763
94. Cates ME, Ramaswamy S. Do current-density nonlinearities cut off the glass transition? Phys Rev Lett. (2006) 96:135701. doi: 10.1103/PhysRevLett.96.135701
95. Andreanov A, Biroli G, Lefèvre A. Dynamical field theory for glass-forming liquids, self-consistent resummations and time-reversal symmetry. J Stat Mech (2006) 2006:P07008. doi: 10.1088/1742-5468/2006/07/P07008
96. Szamel G. Colloidal Glass Transition: beyond mode-coupling theory. Phys Rev Lett. (2003) 90:228301. doi: 10.1103/PhysRevLett.90.228301
97. Janssen LMC, Reichman DR. Microscopic dynamics of supercooled liquids from first principles. Phys Rev Lett. (2015) 115:205701. doi: 10.1103/PhysRevLett.115.205701
98. Wu J, Cao J. High-order mode-coupling theory for the colloidal glass transition. Phys Rev Lett. (2005) 95:078301. doi: 10.1103/PhysRevLett.95.078301
99. Mayer P, Miyazaki K, Reichman DR. Cooperativity beyond caging: generalized mode-coupling theory. Phys Rev Lett. (2006) 97:095702. doi: 10.1103/PhysRevLett.97.095702
100. Janssen LMC, Mayer P, Reichman DR. Generalized mode-coupling theory of the glass transition: schematic results at finite and infinite order. J Stat Mech Theor Exp. (2016) 2016:054049. doi: 10.1088/1742-5468/2016/05/054049
101. Janssen LMC, Mayer P, Reichman DR. Relaxation patterns in supercooled liquids from generalized mode-coupling theory. Phys Rev E (2014) 90:052306. doi: 10.1103/PhysRevE.90.052306
102. Karmakar S, Dasgupta C, Sastry S. Growing length and time scales in glass-forming liquids. Proc Natl Acad Sci USA. (2009) 106:3675. doi: 10.1073/pnas.0811082106
103. Coslovich D, Ikeda A, Miyazaki K. Mean-field dynamic criticality and geometric transition in the Gaussian core model. Phys Rev E (2016) 93:042602. doi: 10.1103/PhysRevE.93.042602
104. Marchetti MC, Joanny JF, Ramaswamy S, Liverpool TB, Prost J, Rao M, et al. Hydrodynamics of soft active matter. Rev Mod Phys. (2013) 85:1143–89. doi: 10.1103/RevModPhys.85.1143
105. Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G, Volpe G. Active brownian particles in complex and crowded environments. Rev Mod Phys. (2016) 88:045006
106. Henkes S, Fily Y, Marchetti MC. Active jamming: self-propelled soft particles at high density. Phys Rev E (2011) 84:040301. doi: 10.1103/PhysRevE.84.040301
107. Ni R, Cohen Stuart MA, Dijkstra M. Pushing the glass transition towards random close packing using self-propelled hard spheres. Nat Commun. (2013) 4:789–845. doi: 10.1038/ncomms3704
108. Berthier L. Nonequilibrium glassy dynamics of self-propelled hard disks. Phys Rev Lett. (2014) 112:220602. doi: 10.1103/PhysRevLett.112.220602
109. Pilkiewicz KR, Eaves JD. Reentrance in an active glass mixture. Soft Matter (2014) 10:7495–501. doi: 10.1039/C4SM01177E
110. Szamel G, Flenner E, Berthier L. Glassy dynamics of athermal self-propelled particles: computer simulations and a nonequilibrium microscopic theory. Phys Rev E (2015) 91:062304. doi: 10.1103/PhysRevE.91.062304
111. Delarue M, Hartung J, Schreck C, Gniewek P, Hu L, Herminghaus S, et al. Self-driven jamming in growing microbial populations. Nat. Phys. (2016) 12:762–6. doi: 10.1038/nphys3741
112. Yazdi A, Sperl M. Glassy dynamics of Brownian particles with velocity-dependent friction. Phys Rev E (2016) 94:032602. doi: 10.1103/PhysRevE.94.032602
113. Berthier L, Flenner E, Szamel G. How active forces influence nonequilibrium glass transitions. New J Phys. (2017) 19:125006. doi: 10.1088/1367-2630/aa914e
114. Janssen LMC, Kaiser A, Löwen H. Aging and rejuvenation of active matter under topological constraints. Sci Rep. (2017) 7:5667. doi: 10.1038/s41598-017-05569-6
116. Ding H, Feng M, Jiang H, Hou Z. Nonequilibrium glass transition in mixtures of active-passive particles. arXiv:1506.02754 (2015).
117. Szamel G. Theory for the dynamics of dense systems of athermal self-propelled particles. Phys Rev E (2016) 93:012603. doi: 10.1103/PhysRevE.93.012603
118. Nandi SK, Gov NS. Nonequilibrium mode-coupling theory for dense active systems of self-propelled particles. Soft Matter (2017) 13:7609. doi: 10.1039/c7sm01648d
119. Feng M, Hou Z. Mode coupling theory for nonequilibrium glassy dynamics of thermal self-propelled particles. Soft Matter (2017) 13:4464. doi: 10.1039/c7sm00852j
120. Liluashvili A, Onody J, Voigtmann T. Mode-coupling theory for active Brownian Particles. Phys Rev E (2017) 96:062608.
121. Kranz WT, Sperl M, Zippelius A. Glass transition for driven granular fluids. Phys Rev Lett. (2010) 104:225701. doi: 10.1103/PhysRevLett.104.225701
122. Sperl M, Kranz WT, Zippelius A. Single-particle dynamics in dense granular fluids under driving. EPL (2012) 98:28001.
Keywords: mode-coupling theory, glass transition, molecular hydrodynamics, liquid structure, amorphous solids, supercooled liquids, colloids, active matter
Citation: Janssen LMC (2018) Mode-Coupling Theory of the Glass Transition: A Primer. Front. Phys. 6:97. doi: 10.3389/fphy.2018.00097
Received: 01 June 2018; Accepted: 17 August 2018;
Published: 02 October 2018.
Edited by:
Jennifer Lynn Ross, University of Massachusetts Amherst, United StatesReviewed by:
Ramon Castañeda-Priego, Universidad de Guanajuato, MexicoJ. M. Schwarz, Syracuse University, United States
Copyright © 2018 Janssen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Liesbeth M. C. Janssen, bC5tLmMuamFuc3NlbkB0dWUubmw=
 Liesbeth M. C. Janssen
Liesbeth M. C. Janssen