Linear Viscoelastic Responses: The Prony Decomposition Naturally Leads Into the Caputo-Fabrizio Fractional Operator

Nothing is done in a vacuum; we must all stand on our forefathers to better ourselves and the world around us.

(Sir Isaac Newton, in his letter to rival Robert Hooke in 1676)

Science is built up of facts, as a house is built of stones; but an accumulation of facts is no more a science than a heap of stones is a house.

(Henri Poincare)

1. Introduction

This article addresses the physical background of modeling of dissipative phenomena, precisely response functions such as stress-strain relationships in the framework of the linear viscoelasticity and their reasonable relationships to the Caputo-Fabrizio fractional operator [1] via the Prony (Dirichlet series) series decomposition [2].

The appearance of the new definition of fractional derivatives with non-singular kernels was provoked by needs to model dissipative transport processes in many new materials appearing in modern technologies [1]. Recently the main achievements, especially results related to diffusion problems, were analyzed Hristov in [3] and we will avoid the thorough browsing and comments of published results (see also the rich list of reference in Hristov [3]). In the context of diffusion problems it was demonstrated that the Caputo-Fabrizio operator appears naturally in diffusion models [3, 4] when the flux-gradient relationship is expressed by a Jeffrey relaxation kernel and the Maxwell-Cattaneo concept of flux.

At the same time the Caputo-Fabrizio fractional operator was criticized [5–7] with points of view based on the classical fractional calculus with singular power-law memory kernel and with examples from the signal processing [6] and to some extent touching formal rheological relationship [5]. Despite the mathematical exactness of the counterexamples they do not focus the attention on the physical basis leading to exponential memory kernels. As a matter of fact, we need a clear answer what really this new operator models and how it appears in the modeling of physical problems, despite the fact that some properties known from the classical fractional calculus, such as the index law [6] , are not satisfied.

1.1. Motivation of This Study

The analysis done here and the principle task are oriented to modeling of viscoelastic constitutive relationships in terms of Caputo-Fabrizio operator naturally appearing through Prony series decomposition [2] of stress relaxation functions and not obeying power-law behaviors. That is, we focus on viscoelastic materials with dynamics which cannot be modeled with the classical fractional derivatives of Riemann-Liouville and Caputo [8].

This introduction avoids huge citations of works on Caputo-Fabrizio operators since without understanding of the physical background and the logic of its appearance any analysis of models created by formalistic fractionalization (see the comments in Hristov et al. [3]) is unproductive. Moreover, to the author personal experience as editor many manuscripts devoted to applications of the Caputo-Fabrizio derivative in formalistically fractionalized existing models are directly rejected by the reviewers with motivations based of the opinions in the criticizing articles [5–7]. This situation resembles that in the Catch 22 movie without perspective for escape. The existing situation is a consequence of some main reasons: (1) The Caputo-Fabrizio operator does not hold some properties such as the semi-groups, which are existing with the classical fractional derivatives with singular kernels, the strange form of the associated fractional integral and these issues cast doubts when it is applied inadequately (in blind manner) to various functions in a manner known from the integer-order calculus. (2) The formalistic approach by simple replacements of integer or fractional order (with singular kernels) derivatives with the Caputo-Fabrizio operator in existing models without taking into account the physics behind. (3) Last but not least, the human factor of author's rivaling which is dividing the scientific society into competing groups rejecting the achievements of each other. All these elements of the current situation create a discouraging atmosphere and disbelieve that this new fractional operator really cannot model natural phenomena and actually stops the further research, generally among the young researchers highly aspiring publications of submitted manuscripts.

The deep physics behind the fractional operator with exponential kernel (and the author's long time experience in science) motivated this study and the efforts are oriented to show that the existing knowledge and models, as well as techniques of data treatment, in the framework of linear viscoelasticity, lead naturally to formulation of the Caputo-Fabrizio fractional operator. This is in the context of the Sir Isaac Newton quote at the beginning of the article: the steps ahead on the shoulder of existing facts and results on the road to creations of new information are natural ways and actually the exciting moments in the beautiful journey in the world of science.

1.2. Aim and Paper Organization

This article is organized as follows: section 3 presents briefly the main properties of the Caputo-Fabrizio operator that will be used further in the analysis of the viscoelastic problems. Section 3 addresses the constitutive equations of viscoelasticity based on the Boltzmann superposition principle [9] and fading memory approach incorporated the hereditary stress and strain integrals. The principle problems of the quality and choice of the response function are discussed and the main properties requited are outlined in section 3.3. The interconversion of relaxation and creep response functions is discussed in section 4: the linear and non-linear scale-invariant (power-law) (related to application of Riemann-Liouville and responses are analyzed. Section 5 focuses on decompositions of experimental response functions by Prony series leading to discrete spectra and the related interconversions by examples with single term, two-terms and multi-term responses of exponential type, as well as interconversion of relaxation and creep compliance expressed as Prony series. Section 6 demonstrates how the constitutive equations (based on the Maxwell model) can be expressed in terms of the Caputo-Fabrizio fractional operator. The subsection 6.3 demonstrates that approximation of the response function by Bessel functions (of Maxwell-like materials) of first kind and expressed as infinite Dirichlet series naturally leads to incorporation of the Caputo-Fabrizio operator in the constitutive equations. Section 7 demodulates briefly how constitutive relationship (following the idea of Bagley and Torvik) with two fractional operators of Caputo-Fabrizio (of different orders) can be formulated.

2. Caputo -Fabrizio Operator

2.1. Definition

The Caputo -Fabrizio operator is defined as [1]

$\begin{array}{cc}{}_{cf}{D}_t^{\alpha }f\left(t\right)=\frac{M\left(\alpha \right)}{1-\alpha }{\displaystyle \underset{0}{\overset{t}{\int }}\exp \left[-\frac{\alpha \left(t-s\right)}{1-\alpha }\right]}\frac{df\left(s\right)}{dt}ds,0<\alpha <1\hfill & (1)\end{array}$

In Equation (1) M(α) is a normalization function such that M(0) = M(1) = 1. This definition is of Caputo-type because there is a convolution of the derivative df(t)/dt. The explanations in [1] relate the development of Equation (1) to the classical Caputo derivative [8] by mechanistic replacements of the singular kernel (by a non-singular exponential kernel) and the normalization function (see the explanations in Hristov [3].

From Equation (1) it follows that if f(t) = C = const., then ${}_{cf}{D}_t^{\alpha }C=0$ as in the classical Caputo derivative [8]. Actually, Equation (1) is a convolution of f(t) and the convolution operator K [1]

$\begin{array}{cc}K=\exp \left[-\frac{\alpha }{1-\alpha }\left(t-s\right)\right]\frac{d}{ds}\hfill & (2)\end{array}$

The integration by parts in Equation (1) results in an alternative form Caputo et al. [10]

$\begin{array}{cc}{}_{cf}^c{D}_t^{\alpha }=\frac{1}{1-\alpha }f\left(t\right)-\frac{\alpha }{1-\alpha }{\displaystyle \underset{a}{\overset{t}{\int }}f\left(s\right)}\exp \left[-\frac{\alpha \left(t-s\right)}{1-\alpha }\right]ds,t>a\hfill & (3)\end{array}$

Futher, the integer order differentiation of ${}_{cf}^c{D}_t^{\alpha }$follows the rule [1]

$\begin{array}{cc}{}_{cf}^c{D}_t^{\left(\alpha +n\right)}f\left(t\right){=}_{cf}^c{D}_t^{\alpha }\left(D_t^{\left(n\right)}f\left(t\right)\right),n>0,\alpha \in \left[0,1\right]\hfill & (4)\end{array}$

The associated fractional integral is Hristov [3] and Losada and Nieto [11]

$\begin{array}{cc}{}_{cf}^c{D}_t^{\left(\alpha +n\right)}f\left(t\right){=}_{cf}^c{D}_t^{\alpha }\left(D_t^{\left(n\right)}f\left(t\right)\right),n>0,\alpha \in \left[0,1\right]\hfill & (5)\end{array}$

With the assumption that M(α) = 1 used by Caputo and Fabrizio [1, 10]. The second definition of Losada and Nieto [11] is

$\begin{array}{cc}{}_{cf}{D}_t^{\alpha }f\left(t\right)=\frac{1}{1-\alpha }{\displaystyle \underset{0}{\overset{t}{\int }}\exp \left[-\frac{\alpha \left(t-s\right)}{1-\alpha }\right]}\frac{df\left(s\right)}{dt}ds\hfill & (6)\end{array}$

Hereafter we will use the definition (Equation 6).

2.2. Laplace Transform

The Laplace transform of ${}_{CF}{D}_t^{\alpha }$ with a = 0 has the following Laplace transform L_T given with p variable [1] taking into account the general rule of Laplace transform of a convolution, namely

$\begin{array}{cc}{L}_T\left[{}_{cf}^c{D}_t^{\alpha }f\left(t\right)\right]=\frac{1}{1-\alpha }{L}_T\left[f\left(t\right)\right]L_T\left[\exp \left(-\frac{\alpha }{1-\alpha }t\right)\right]\hfill & (7)\end{array}$

Hence,

$\begin{array}{cc}{L}_T\left[{}_{cf}^c{D}_t^{\alpha }f\left(t\right)\right]=\frac{p{L}_T\left[f\left(t\right)-f\left(0\right)\right]}{p+\alpha \left(1-p\right)}\hfill & (8)\end{array}$

2.3. Fractional Derivative of Elementary and Transcendental Functions

Linear function f(t) = Ct [1]

$\begin{array}{l}{}_{cf}^c{D}_t^{\alpha }\left[Ct\right]=\frac{1}{1-\alpha }{\displaystyle \underset{0}{\overset{t}{\int }}C\exp \left[-\frac{\alpha }{1-\alpha }\left(t-s\right)\right]}\\ ds=\frac{C}{\alpha }\left[1-\exp \left(-\frac{\alpha }{1-\alpha }t\right)\right],0<\alpha \le 1& (9)\end{array}$

Power-Law function f(t) = Ct^β [3, 12].

For f(t) = Ct^β and β > 0 the fractional derivative ${}_{cf}^c{D}_t^{\alpha }\left[C{t}^{\beta }\right]$ is

$\begin{array}{cc}{}_{cf}^c{D}_t^{\alpha }{t}^{\beta }=\left(C\beta t^{\beta -1}\right)\frac{1}{\alpha }\left[1-\exp \left(-\frac{\alpha }{1-\alpha }\right)t\right]\hfill & (10)\end{array}$

For α = 1 the expression (Equation 10) reduces to the classical (integer-order) result Cβt^β−1.

Exponential function f(t) = exp(βt) [3, 12]

$\begin{array}{cc}{}_{cf}^c{D}_t^{\alpha }\exp \left(\beta t\right)=\frac{\beta \exp \left(\beta t\right)-\exp \left(-At\right)}{\beta +\alpha \left(1-\beta \right)},A=\frac{\alpha }{1-\alpha }\hfill & (11)\end{array}$

For α → 1 the second exponential term in the nominator of Equation (11) goes to zero and therefore $\underset{\alpha \to 1}{\underbrace{{}_{cf}^c{D}_t^{\alpha }\exp \left(\beta t\right)}}\to \beta \exp \left(\beta t\right)$.

For β < 0 we have

$\begin{array}{cc}{}_{cf}^c{D}_t^{\alpha }\exp \left(-\beta t\right)=\frac{-\beta \exp \left(-\beta t\right)+\exp (-At)}{A-\beta }\hfill & (12)\end{array}$

For α → 1 the second exponential term in the nominator of Equation (12) goes to zero and therefore $\underset{\alpha \to 1}{\underbrace{{}_{cf}^c{D}_t^{\alpha }\exp \left(-\beta t\right)}}\to -\beta \exp \left(-\beta t\right)$.

2.4. Caputo-Fabrizio Fractional Operator: Determination of the Fractional Parameter

In the Caputo-Fabrizio operator there is formal ambiguity because the stretched time is multiplied by a dimensional factor α/(1 − α) which should have a dimension s⁻¹. This contradicts the definition of the fractional order (parameter) because physically α is dimensionless. The answer given in [3, 13] resolved the problem by nondimesionalization of the exponential function by help of characteristic time scale of the relaxation process t₀ (the maximum time of the experiment in the sense of the rheological tests discussed here) , namely

$\begin{array}{cc}\exp \frac{\left(t-s\right)}{\tau }=\exp \frac{\left(t/t_0-s/t_0\right)}{\tau /t_0}=\exp \frac{\left(\overline{t}-\overline{s}\right)}{\overline{\tau }}\hfill & (13)\end{array}$

The nondimensalization does not change the meaning of the exponential relaxation function but avoid any doubts about the definition of the fractional order α as [3, 13].

$\begin{array}{cc}\frac{1-\alpha }{\alpha }=\frac{\tau }{t_0}\Rightarrow \alpha =\frac{1}{1+\tau /t_0}\hfill & (14)\end{array}$

and relates it to data that can be really recovered from experimental data, such the relaxation and retardation times (see the sequel)

The relationship (Equation 14) says that for τ/t₀ = 1 we get α = 1/2. Further, depending on the ratio τ/t₀ we may have fractional orders roughly arranged in two groups [14]: a) when 0 ≤ τ/t₀ ≤ 1 we have fractional orders α ∈ [0.5, 1.0] and the relaxation time τ is shorter than the macroscopic process observation time t₀, and b) 1 ≤ τ/t₀ < ∞ the fractional orders are α∈(0, 0.5] since the relaxation time τ is larger than the macroscopic process observation time t₀. Qualitatively, for τ/t₀ < 1 the relaxations could be considered as fast (rapid) relaxations, while τ/t₀>1 is related to slow relaxations (see in Hristov [14] the comments of numerical values of Prony decomposition and relaxation times)

Last to this point, but not least, as it was commented in Hristov [14], the ratio τ/t₀ is not integer and expressing the memory kernel as $exp\left[-\beta (\bar{t}-\bar{s})\right]$ where $\beta ={(\tau /t_0)}^{-1}=\alpha /(1-\alpha )$ we get a fractional operator. Therefore, the memory kernel of the Caputo-Fabrizio operator is controlled by a non-integer parameter in the context of what is needed to say that this operator is fractional, despite the fact that it does not repeat exactly the properties of the Classical Riemann-Liouville and Caputo derivatives.

3. Constitutive Equations of Viscoelasticity: Fading Memory Approach

3.1. Boltzmann Superposition Principle and Fading Memory Concept

The fading memory concept relating the flux to its gradient, for simple materials [15–17], is expressed by the following relation relating the flux and the gradient , namely

$\begin{array}{cc}j\left(x,t\right)=-D_0\nabla C\left(x,t\right)-D^{\prime }{\displaystyle \underset{-\infty }{\overset{t}{\int }}R}\left(t-\tau \right)\nabla C\left(x,\tau \right)d\tau \hfill & (15)\end{array}$

This definition is actually the Boltzmann linear superposition functional (Equation 16))

$\begin{array}{cc}\phi \left(x,t\right)=m\left[v_x\left(x,t\right)\right]+\lambda {\displaystyle \underset{0}{\overset{t}{\int }}R\left(t,\tau \right)}{v}_x\left(\tau \right)d\tau \hfill & (16)\end{array}$

relating the present state of the flux to its history [9, 16–18] through the influence function (memory kernel) R(t, z) during the time interval defined by τ. In Equation (16) m and λ are transport coefficients (diffusivities) with real physical meanings as it will be demonstrated in the sequel.

The memory function could be unbounded and scale invariant such as R(t, τ) = t^−μ with integration singularity at or bounded and not scale invariant such as R(t, τ) = e^−t/τ (see the analysis in Hristov [14] and the comments further in this article).

3.2. Stress-Strain Viscoelasticity Response and Hereditary Integral Construction and Response Functions

The linear theory of elasticity [19] (chapter 1) considers the stress in a sheared solid body as a quantity proportional to the shear, while in the liquids the shearing stresses are proportional to the rate of shear . Most solid materials, for example polymers, compromising both effects are called viscoelastic. When a slab of solid material under a shearing motion caused by a step change in the stress load applied to it (Heaviside unit step function H₀(t)) exhibits a strain (in one dimension) [19] (chapter 1)

$\begin{array}{cc}\epsilon \left(t\right)={\epsilon }_0{H}_0\left(t\right)\hfill & (17)\end{array}$

With perfect elastic behavior of the body [19] σ(t) = σ₀H₀(t) for t > 0. On the contrary, in an ideal viscous fluid the stress is infinite and for t > 0 and the strain is ε(t) = (σ₀/η)t, thus introducing the coefficient of viscosity η. Real materials do not shear with infinite speeds that is the reason of the concept of a finite relaxation time τ [19]. Precisely, in solids the stresses attain finite values for long times. In contrast, in viscous fluids the stresses approach zero.

The task of this study addresses the functional representations of the viscoelastic material responses, that is : 1) the stress relaxation function R(k, t), that is the stress history due to a shear step of size ε, and 2) the creep function C(t) (shear history) due to unit stress σ applied. In the linear viscoelastic theory [19] the responses can be approximated as R(ε, t) = G(t)ε + O(ε³) and C(σ, t) = J(t)σ + O(σ³), thus defining the linear stress relaxation modulus G(t) and the linear creep compliance J(t). The common mechanistic models explaining the behavior of viscoelastic materials utilize linear springs and dashpots coming from the Maxwell interpretation [20–22] and modeling the pure elastic behavior and the pure viscous state, correspondingly.

Superposition of single-step material responses results in functional relationships of stress and strain in the linear viscoelasticity concept [19] incorporating the a time lag in G(t) and J(t) through hereditary stress (Equation 18) and creep integrals (Equation 19), namely

$\begin{array}{cc}\sigma \left(t\right)={\displaystyle \underset{0}{\overset{t}{\int }}G\left(t-s\right)}d\epsilon \left(s\right)\hfill & (18)\end{array}$

$\begin{array}{cc}\epsilon \left(t\right)={\displaystyle \underset{0}{\overset{t}{\int }}J\left(t-s\right)}d\sigma \left(s\right)\hfill & (19)\end{array}$

Both σ(t) a and ε(t) are causal functions and therefore the lower terminals in Equations (18, 19) are set at t = 0.

Applying the fading memory concept [9, 20] it is possible to relate the instantaneous responses G_∞ and J_∞ corresponding to equilibrium states (for long times) when the effects of memory terms (convolution integrals) fade out, namely

$\begin{array}{cc}\sigma \left(t\right)=G_{\infty }+{\displaystyle \underset{0}{\overset{t}{\int }}G\left(t-s\right)}d\epsilon \left(s\right)\hfill & (20)\end{array}$

$\begin{array}{cc}ϵ\left(t\right)=J_{\infty }-{\displaystyle \underset{0}{\overset{t}{\int }}J\left(t-s\right)}d\sigma \left(s\right)\hfill & (21)\end{array}$

3.3. Response Function: General Properties and Requirements

For a linear isotropic viscoelastic body exerting uniaxial stress the Boltzmann superposition principle formulates the constitutive equation relating the strain responses by help of the following hereditary integral [23]

$\begin{array}{cc}\sigma \left(t\right)={\displaystyle \underset{0}{\overset{t}{\int }}G\left(t-s\right)}\frac{d\epsilon \left(s\right)}{d\tau }ds\hfill & (22)\end{array}$

The relaxation function G(t) should decrease monotonically and account for short and long-time strains, thus the condition (Equation 23) should be obeyed [24–26]

$\begin{array}{cc}{\left(-1\right)}^n\frac{{\partial }^n}{\partial t^n}G\left(t\right)\ge 0,n=1,2,\mathrm{...}\hfill & (23)\end{array}$

Coleman and Noll, in their article on foundation principles of linear viscoelasticity [27], point out that there is no universal approach in definition of unique relaxation function R(s) [the fading memory R(s) in Equation (15) its is equivalent to G(s) in Equation (22) . Despite this, two principle features are required to be obeyed by R(s):

1) R(s) is defined for 0 ≤ s < ∞ and R(s) > 0, and

2) R(s) decays monotonically to zero for large s , that is ${lim}_{s\to \infty }{s}^{r}R(s)=0$.

Boltzmann (1874) in [9] (see also [14, 27]) suggested two memory functions widely applied so far, namely

a) Generalized power-law memory function R(s) = s^r(s+1)^−μ of order r when r < μ. For r = 0 the memory function R(s) is unbounded (singular) at t₀₊ and this scale invariant kernel forms the constructions of the classical fractional integrals and derivatives [8].

b) Ordinary memory kernel , bounded at t₀₊ as exponential function e^−βs , which is not invariant with respect to the time scale. The definition of Caputo-Fabrizio fractional operator utilizes this memory kernel.

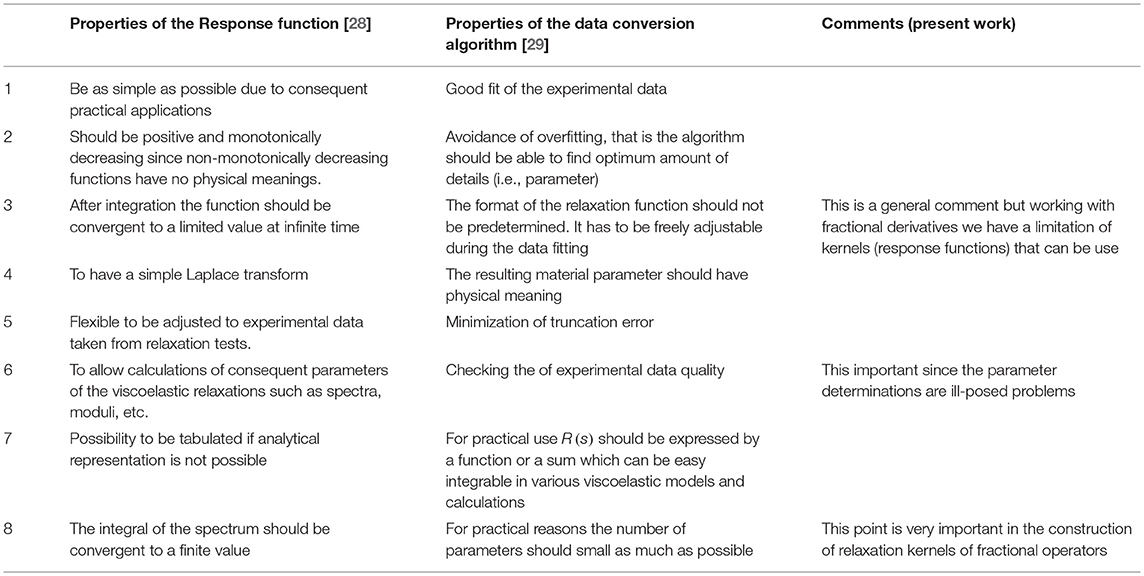
The adequate mathematical structure in the construction of the relaxation (memory) function is the main problem that should be resolved in the modeling of viscoelastic responses. Generally, the relaxation function should adequately describe the natural process and therefore its structure should be tested (defined)by a data conversion algorithm (by fitting experimental data). Despite this intuitive and to greater extent logical approach the response function should satisfy some requirement defined in Garbarski [28] and Winter [29], and summarized in Table 1; with some author's comments related to application of fractional operators in the viscoelastic constitutive equations. Further, in the response of viscoelastic material to strain excitation, the stress relaxation spectrum (relaxation modulus) provides complete information concerning the time-dependent part of the material response. In the opposite situation, with materials undergoing stress excitations the retardation spectra (the compliances) [30] provide the required information. Hence, if the spectra are known it is possible to calculate the response of any excitation [20].

TABLE 1

Table 1. Response function desired properties.

Besides, the thermodynamic theory of linear viscoelastic materials was developed extensively in the sixties of the last century [31]. In this context, the second law of thermodynamics yields severe restrictions on the constitutive properties [32–34]. This problem is beyond the scope of the present analysis but we may say that when the constitutive equation (Equation 20) contains exponential kernel it is compatible to second law of thermodynamics [34].

The principle relaxation functions used and the applicability of the aforementioned requirements will be analyzed next.

4. Interconversion of Relaxation and Creep: Problem and Power-law Responses

4.1. Interconversion Problem

In the linear viscoelastic materials the relationships between the creep compliance J(t) and the relaxation response G(t) are expressed as convolution integrals in accordance with the Boltzmann superposition principle [9] (see Equations 20, 21)

With the Laplace transforms of Equations (20, 21) we get equivalent relationships in the p-space (p is the transform variable)

$\begin{array}{cc}\sigma \left(p\right)=pG\left(p\right)\epsilon \left(p\right),\epsilon \left(p\right)=pJ\left(p\right)\sigma \left(p\right)\hfill & (24)\end{array}$

Hence, we may recast Equation (24) as

$\begin{array}{cc}\frac{\sigma \left(p\right)}{\epsilon \left(p\right)}=pG\left(p\right),\frac{\sigma \left(p\right)}{\epsilon \left(p\right)}=\frac{1}{pJ\left(p\right)}\hfill & (25)\end{array}$

Equating the right-hand sides of Equation (25) we get an implicit fundamental relationship

$\begin{array}{cc}G\left(p\right)J\left(p\right)=\frac{1}{p^2}\Rightarrow J\left(t-s\right)G\left(t\right)={\displaystyle \underset{o}{\overset{t}{\int }}G\left(t-s\right)J\left(s\right)ds}=t\hfill & (26)\end{array}$

with the constraints that

$\begin{array}{cc}G\left(t_{0^{+}}\right)J\left(t_{0^{+}}\right)=G\left(t\to \infty \right)J\left(t\to \infty \right)\hfill & (27)\end{array}$

Explicit form of Equation (26) can be obtained if the analytical forms of either G(t) orJ(t) is known. Examples of interconversion related to power-law and exponential memory kernels are discussed in the sequel.

4.2. Scale-Invariant (Power-Law) Response

4.2.1. Physical Preliminaries Related to the Power-Law Response

Relatively short-time relaxation history modeled by time-dependent power-law can be observed in the time evolution of G(t) from zero to the end of the time of observation t₀ [19]: commonly at the beginning of the relaxation process (short times) and along the long tail (long times). The power law is scale-invariant. Materials exhibiting such behavior are called power-law viscoelastic materials [35–42] and can be easily detected by the linear behaviors of J(t) ~ t^p and G(t) ~ t^−p in logarithmic scales [43]. Actually, we have to memorize that this type of relaxation was modeled in the article of Caputo (1967) where the construction of the Caputo derivative was conceived [44]. The power-law functional relationships of the relaxation and the compliance, actually are the reasons to recognize the integral and derivatives of the classical fractional calculus [8] as adequate modeling tools since they are based on the same type of kernels [39, 42, 45], known also as weak singular kernels. As commented by Tschoegl [20] the scaling relationship G(t) ~ t^−p is a fractional version of the Trouton law $\sigma (t)=\eta \stackrel{·}{\epsilon }(t)$. Here, we have to mention that Metzler et al. [39] discussing relaxations of filled /polymers stated that non-exponential (non-Debay) relaxation implies memory (Sic!). We may consider this declarative opinion (the results of Glockle and Nonnemacher [46]) as adequate to the situation in the 90s of the last century, when fractional calculus was only related to power-law kernels [47].

Moreover, as a valuable analysis showing when the power-law is the adequate response function we refer to Chapter 5 of Findley et al. [48] where it is clearly demonstrated that for many materials the power-law response function t^μ with μ < 0.5 [48] is a good short-time approximation for materials such as plastics, metals and concrete. For short-time loading the creep of many different rigid plastics with sufficient accuracy can be presented as linear power-law $\epsilon ={\epsilon }_0+{\epsilon }_{+}{t}^{\mu }$, where μ is stress-independent and nearly temperature-independent, too. The same approach following from the linear approximation approach of Pipkin [19] is commented in 3.2 . In this case the corresponding retardation spectrum is Findley et al. [48]

$\begin{array}{cc}\phi \left(t\right)\equiv \frac{\mu }{\Gamma \left(1-\mu \right)}{t}^{\mu -1}\equiv t^{-\alpha },0<\alpha =1-p<1\hfill & (28)\end{array}$

The function (Equation 28) may be considered as continuum spectrum of material retardation times proportional to t^−α . From this position, the step from Equation (28) toward modeling of the relaxation processes by the classical Riemann-Liouville derivative is straightforward. In this context, Bagley and Torvik [49] using (Equation 28) demonstrated that following constitutive equation holds

$\begin{array}{cc}\sigma \left(t\right)=G_1{}^{RL}{D}_t^{\alpha }\left[k\left(t\right)\right]=\frac{G_1}{\Gamma \left(1-\alpha \right)}\frac{d}{dt}{\displaystyle \underset{0}{\overset{t}{\int }}\frac{k\left(t-s\right)}{{\alpha }^k}ds},t>0\hfill & (29)\end{array}$

After application of the Leibniz rule to Equation (29) the result is

$\begin{array}{cc}\sigma \left(t\right)=\frac{1}{\Gamma \left(1-\alpha \right)}{\displaystyle \underset{0}{\overset{t}{\int }}\frac{G_1}{t^{\alpha }}\frac{dk\left(t-s\right)}{dt}ds}+G\left(t\right)k\left(0\right)\hfill & (30)\end{array}$

For ε(0) = 0, since no strain at t = 0 exists we get

$\begin{array}{cc}\sigma \left(t\right)=\frac{1}{\Gamma \left(1-\alpha \right)}{\displaystyle \underset{0}{\overset{t}{\int }}\frac{G_1}{{\left(t-s\right)}^{\alpha }}\frac{dk\left(s\right)}{ds}ds}=G_1{}^{RL}{D}_t^{\alpha }k\left(t\right),t>0\hfill & (31)\end{array}$

Then, for G₁ = G₀ = const. the stress relaxation modulus G(t) and the creep compliance J(t) are

$\begin{array}{cc}G\left(t\right)=\frac{G_1}{\Gamma \left(1-\alpha \right)}{t}^{-\alpha },J\left(t\right)=\frac{1}{G_1}\frac{1}{\Gamma \left(1-\alpha \right)}{t}^{\alpha }\hfill & (32)\end{array}$

4.2.2. Example 1. Interconversion of Power-Law Relaxation and Creep: Linear Case

Here, we consider again the power-law response in the context of the response function interconversion and in the sense of the relationships (Equations 26, 27). With G(t) = At^−μ , where A is a data fitting coefficient and 0 < μ < 1 , the Laplace transform in Equation (26) provides a power-law creep (Equation 33) compliance [50]

$\begin{array}{cc}G\left(t\right)=\frac{G_1}{\Gamma \left(1-\alpha \right)}{t}^{-\alpha },J\left(t\right)=\frac{1}{G_1}\frac{1}{\Gamma \left(1-\alpha \right)}{t}^{\alpha }\hfill & (33)\end{array}$

Following Hanyga, neither experimental nor theoretical reasons lead to the assumption that the creep rate function and the stress relaxation function are bounded and regular at t = 0 [26]. The same point of view is valid for the unbounded kernels singular at t = 0 [14]. In the seminal study of Boltzmann [9] the value of α = 1 was suggested. The condition 0 < α < 1 comes from the fact that for α > 1 we get an infinite propagation speed [26]. Actually, the idea to apply fractional calculus, as is demonstrated by the model developed in the foundation studies of Scott-Blair [51–53] and Bagley and Torvik [49] comes from the experimental (empirical) findings of Nutting [54, 55]: precisely, for some viscoelastic materials the power-law relationship [ε(t)/Const] ~ σⁿt^α is satisfied. Consequently, we may obtain (Equation 32).

Since the power-law relaxation is not the main problem discussed in this work, at the end of this point, we refer to the study of Carillo and Giorgi [56] (section 4 in this chapter) where it is clearly demonstrated that the response of the material may be for short-time or as long tail (for long times) modeled by time-dependent power-law function. Here, we may repeat again (see the comments in Hristov [14], too) that, if the power-law is not exhibited by the material response functions then it is inadequate to apply the power-law memory kernels.

4.2.3. Example 2.Interconversion of Power-Law Relaxation and Creep: Non-linear Case

If the material exhibits a non-linear viscoelastic behavior, for instance, as commented by Lakes et al. [50], that is

$\begin{array}{l}\sigma \left(t\right)={\displaystyle \underset{0}{\overset{t}{\int }}G\left[\left(t-s\right),\epsilon \left(s\right)\right]}\frac{d\epsilon }{ds}ds,\\ \epsilon \left(t\right)={\displaystyle \underset{0}{\overset{t}{\int }}J\left[\left(t-s\right),\sigma \left(s\right)\right]}\frac{d\sigma }{ds}ds& (34)\end{array}$

The relaxation function G(t, ε) can be expressed as a sum of products, precisely sum of products of functions of time and functions of strain, that is Lakes and Vanderby [50] G(t, ε) = G_t(t)g(ε) . Assuming no interaction between the steps (immediate and delayed Heaviside steps) strains in the summation series and may write [50]

$\begin{array}{cc}{\sigma }_c=\epsilon \left(0\right)G\left(t,s\right)+{\displaystyle \sum _{i=0}^N\Delta {\epsilon }_{i}G\left(t-t_i,\epsilon \right)}\hfill & (35)\end{array}$

Consequently, the creep compliance is

$\begin{array}{cc}1=J\left(0\right)G\left(t,\epsilon \right)+{\displaystyle \underset{0}{\overset{t}{\int }}G\left[\left(t-s\right),\epsilon \left(s\right)\right]}\frac{dJ\left(s\right)}{ds}ds\hfill & (36)\end{array}$

and for the linear case we will obtain the relationship (Equation 26).

To have explicit form of these relationships, if we assume a power-law approximation in time [50] J(σ, t) = A(σ)t^μ, that is $J(\sigma ,t)=(g_1+g_2\sigma +g_3{\sigma }^2+\dots )t^{\mu }$, then we get

$\begin{array}{cc}1=J\left(0\right)G\left(t,\epsilon \right)+{\displaystyle \underset{0}{\overset{t}{\int }}G\left[\left(t-s\right),\epsilon \left(s\right)\right]}\frac{dJ\left(s\right)}{ds}ds\hfill & (37)\end{array}$

$\begin{array}{cc}G\left(t,\epsilon \right)=\left[f_1{t}^{-\mu }+f_2\epsilon \left(t\right)t^{-2\mu }+f_3{t}^{-3\mu }\right]\hfill & (38)\end{array}$

The nonlinear material exhibits a relaxation response which contains a sum of power-law terms, as given in equation (Equation 38) (see more comments in Lakes and Vanderby [50]).

Hereafter, non-linear behavior generally related to temperature-dependent and aging viscoelastic materials will not be discussed since the principle task of the present analysis is to show the correct origin and the physical background leading to the formulation of the Caputo-Fabrizio fractional operator.

5. Interconversion of Non Power-law Relaxation and Creep

5.1. Non Power-Law Response: Relaxation Curve Approximation

The selection of approximation function which would fit the experimental points depends on the type of materials and would be established by simple trial error process. In this context, two principle issues arise when experimental data for linear viscoelastic materials should be treated [57]: (1) Appropriate relaxation curve approximation and (2) interconversion problem. The experimental data are commonly taken in the time-domain (or frequency-domain) tests. Now, we stress the attention on discrete spectrum approximation by Prony series [2] where the condition for the monotonicity of the functions (see the sequel) is satisfied.

5.2. Discrete Relaxation Spectrum by Prony Series Decompositions and Relevant Interconversions

Unlike the linear elasticity, where the material functions are related algebraically, the relationships in the linear viscoelasticity are time-dependent, as already was demonstrated in the previous section of the article. One known method is to find the unknown functions G(t) and J(t) by fitting the data points by a known function. However, when the focus is on the adequate construction of a fractional operator with a memory kernel obeying all mandatory conditions imposed on it, then the choice of approximating function is highly restricted. If the power-law is not the adequate choice then a series approximation is the more suitable solution. Since we address the construction of the Caputo-Fabrizio operator, thus it is natural to tackle data fitting by series of exponential terms (matching the function of the desired memory kernel) known as Prony series (also as Dirichlet series [58]).

5.2.1. Prony Series Decompositions

The viscoelastic relaxation function can be expressed by a discrete relaxation spectrum through a decomposition as a Prony series g_P(t)with N^ϕ terms [25, 59–64] with rate constants β_i, namely

$\begin{array}{cc}{g}_P\left(t\right)=g_{\infty }+{\displaystyle \sum _{i=1}^{N^{\varphi }}{g}_i}{e}^{-{\beta }_{i}t}=g_{\infty }+{\displaystyle \sum _{i=1}^{N^{\varphi }}{g}_i}{e}^{-\frac{t}{{\tau }_i}},{\beta }_i=\frac{1}{{\tau }_i}\ge 0\hfill & (39)\end{array}$

or through normalized weights (amplitudes or normalized relaxation moduli) λ_i [21, 59] as

$\begin{array}{cc}\frac{g_P\left(t\right)}{g_{\infty }}=1+{\displaystyle \sum _{i=1}^{N^{\varphi }}{\lambda }_{gi}}\left(e^{-{\beta }_{i}t}-1\right),{\lambda }_{gi}=\frac{g_i}{g_{\infty }}\hfill & (40)\end{array}$

In Equations (39, 40) the parameters g_∞ and g_i are equilibrium (at large times) values and the relaxation moduli (stiffness), respectively, are constrained according to Brinson and Brinson [21]

$\begin{array}{cc}{g}_{\infty }+{\displaystyle \sum _1^{N^{\varphi }}{g}_i}=1\hfill & (41)\end{array}$

The Prony series components have spectral strength g_i and relaxation time τ_i. This is the so-called discrete Prony series representation known also as discrete relaxation spectrum [20, 65–69]. Besides, the series approximation (Equation 39) may be substituted in formulation of the materials law such as Maxwell, Kelvin Voigt, etc. The relaxation time τ_i associated with the i_th element is related to the characteristic time of the spring-damper (dashpot) element and can be defined as the ratio of the viscosity over the elastic modulus, that is τ_i = g_i/λ_i [68].

The first derivative of the Prony series (Equation 42) for t = 0 is finite, a fact irrespective of the number of terms used in the approximation.

$\begin{array}{cc}\frac{d\varphi }{dt}=\frac{d}{dt}{\displaystyle \sum _{i=1}^{N^{\varphi }}{g}_i{e}^{-{\beta }_{i}t}}\hfill & (42)\end{array}$

As commented by Bradshaw and Brinson [57], an exact solution of interconversion problem is possible if the known function is approximated by Prony series where all coefficients are positive [using the forms (Equation 39, 40) ] and the basic interconversion relationship (Equation 26) is satisfied. In this case, by applying Laplace transform solutions, the resulting Prony series are analytically exact [70–73].

The Prony series approximations lead to the generalized Maxwell viscoelastic body (known also as Maxwell-Wiechert model) with N^ϕ spring-dashpot elements in parallel. The Prony series decompositions are applicable to any viscoelastic models through their time-dependent shear and bulk moduli [74–76]. For a deep thermodynamic analysis of such type of materials termed viscoelastic solids of exponential type (VESET) we refer to works of Fabrizio et al. [32, 33].

A common step in approximation by the truncated exponential sums is the definition of preliminary stipulated decay rates β_i , in a logarithmic scale that is , for N_ϕ = 4 , for instance β_1…4 = 100, 10, 1, 0.1 [77]. This approach, is useful because the corresponding fractional parameters in the α_i in this case can be easily calculated (see further Equation 65) as α_1…4 = 0.009, 0.09, 0.5, 0.9, respectively. Alternatively, fixing the points (in normal or logarithmic scale) t_i along the time axis we may define the corresponding β_i = 1/τ_i.

The parameter estimation is important and the first step was done in the seminal work of Prony (1795) [2] and several algorithms have been developed among them: graphically by log−log plots [78, 79], least squares method [80–82], nonlinear optimization methods [83], genetic based algorithm [84], from the continuous relaxation time spectrum [68, 72], logarithm equidistant distribution of relaxation times (known as R- method) [68, 77, 85], quasi-linearization for multi-exponential decay curves fitting [86], etc.

The number of the exponential terms in Equation (39) depends on the accuracy of data fitting. Commonly fourth-order Prony series fit adequately the stress-relaxation data in cases of non-linear viscoelastic behaviors [62, 87–93], while long-term relaxation tests need 10-15 terms [76, 85, 94–100]. In general, the problem corresponds to identifications of the kernel of an integral Fredholm equation which, actually, is ill-posed problem [68, 101–103] requiring Tikhonov regularization [104]. Comments on the required terms in the Prony decomposition are available in [14].

5.3. Examples of Interconversions With Exponential Terms

5.3.1. Example 3. Interconversion of a Single Exponential Model [105]

For a single exponential model (the Maxwell model) the relaxation and creep functions are

$\begin{array}{cc}{G}_1=1+g_1\exp \left(-\frac{t}{{\tau }_1}\right)\hfill & (43)\end{array}$

$\begin{array}{cc}{J}_1=1-j_1\exp \left(-\frac{t}{{\lambda }_1}\right)\hfill & (44)\end{array}$

The condition (Equation 27) is automatically satisfied, while for t = 0 in (Equation 43) (and taking into account ;Equation 27) the results is

$\begin{array}{cc}{G}_1\left(0\right)J_1\left(0\right)=\left(1+g_1\right)\left(1-j_1\right)=1\hfill & (45)\end{array}$

The Laplace transforms of (Equations 43, 44) lead to an equation that should be solved

$\begin{array}{cc}\left[\left(1+g_1\right)\left(1-j_1\right)-1\right]p^2+\left[\frac{g_1}{{\lambda }_1}-\frac{j_1}{{\tau }_1}\right]p=0\hfill & (46)\end{array}$

Since (Equation 46) should be satisfied for all p it follows that τ₁ = j₁λ₁ and this condition with (Equation 46) leads to Anderssen et al. [105]

5.3.1.1. Interconversion from relaxation to creep

$\begin{array}{cc}{j}_1=\frac{g_1}{1+g_1},{\lambda }_1={\tau }_1\left(1+g_1\right)\hfill & (47)\end{array}$

5.3.1.2. Interconversion from creep to relaxation

$\begin{array}{cc}{g}_1=\frac{j_1}{1-j_1},{\tau }_1={\lambda }_1\left(1-j_1\right)\hfill & (48)\end{array}$

More details related to the sensitivities and relative errors of these two interconversions are available in Anderssen et al. [105]

5.3.2. Example 4. Interconversion of a Double Exponential Model [105]

In this case the relaxation and creep functions are

$\begin{array}{cc}{G}_2\left(t\right)=1+g_1\exp \left(-\frac{t}{{\tau }_1}\right)+g_2\exp \left(-\frac{t}{{\tau }_2}\right)\hfill & (49)\end{array}$

$\begin{array}{cc}{J}_2\left(t\right)=1-j_1\exp \left(-\frac{t}{{\lambda }_1}\right)+j_2\exp \left(-\frac{t}{{\lambda }_2}\right)\hfill & (50)\end{array}$

The values of the relaxation times τ_i are zeros of

$\begin{array}{cc}\frac{1}{\tau }+\frac{j_1}{\left(\tau -{\lambda }_1\right)}+\frac{j_2}{\left(\tau -{\lambda }_2\right)}=0& \left(51\right)\end{array}$

and consequently

$\begin{array}{cc}{\tau }_1{\tau }_2=K{\lambda }_1{\lambda }_2,K=\frac{1}{1+j_1+j_2}<1& \left(52\right)\end{array}$

5.3.3. Example 5. Interconversion of Multi-Term Exponential Model [105]

By Prony decomposition the relaxation and creep functions can be generally presented through discrete spectra as Anderssen et al. [105]

$\begin{array}{cc}{G}_N\left(t\right)=G_{\infty }+{\displaystyle \sum _{i=1}^N{g}_i}\exp \left(-\frac{t}{{\tau }_i}\right),g_i\ge 0\hfill & \left(53\right)\end{array}$

$\begin{array}{cc}{J}_N\left(t\right)=J_{\infty }-{\displaystyle \sum _{i=1}^N{j}_i}\exp \left(-\frac{t}{{\lambda }_i}\right),j_i\ge 0\hfill & \left(54\right)\end{array}$

The inverse times, that is the relaxation times τ_i and the retardation times λ_i satisfy

$\begin{array}{cc}0<{\tau }_1<{\tau }_2<\mathrm{...}{\tau }_N,0<{\lambda }_1<{\lambda }_2<\mathrm{...}{\lambda }_N\hfill & \left(55\right)\end{array}$

The advantage of this (Prony decomposition) approach is that the monotonicity is automatically satisfied [105]

The attempts to solve (Equation 26) address many approaches for either J(t) or G(t) depending on the experimental data available [30, 106–109]

Now we recall that the Caputo-Fabrizio fractional operator [1, 3, 4, 110, 10] uses an exponential kernel matching the basic element of the Prony series.

5.3.4. Example 6. Interconversion of Prony Series of Relaxation and Creep

With Prony decomposition of the relaxation spectrum, the next step is to determine the creep modulus (compliance) J(t). The interconversion equation (Equation 56) simple gives [22, 70, 71, 105, 111, 112].

$\begin{array}{cc}\left[G\left(t\right)\ast J\left(t\right)\right]={\displaystyle \underset{0}{\overset{t}{\int }}G\left(t-s\right)}J\left(s\right)ds=\left[J\left(t\right)\ast G\left(t\right)\right]=t\hfill & \left(56\right)\end{array}$

As a rule in the rheological studies, the discrete exponential models for G(t) and J(t), corresponding to associated relaxation and creep spectra H(τ) and L(τ) [105] (as sums of delta functions ) are used that assures the monotonic behavior automatically and we have

$\begin{array}{cc}G\left(t\right)=G\left(\infty \right)+{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\frac{t}{\tau }\right)}\frac{H\left(\tau \right)}{\tau }d\tau ,H\left(\tau \right)\ge 0\hfill & \left(57\right)\end{array}$

$\begin{array}{cc}J\left(t\right)=J\left(0\right)+{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\frac{t}{\tau }\right)}\frac{L\left(\tau \right)}{\tau }\hfill & \\ d\tau =J\left(\infty \right)-{\displaystyle \underset{0}{\overset{\infty }{\int }}\exp \left(-\frac{t}{\tau }\right)}\frac{L\left(\tau \right)}{\tau }d\tau & \left(58\right)\end{array}$

The constraint imposed [70, 105] by (Equations 26, 27) (see also Equation 56) allows H(τ) to be defined as function of L(τ) and vice versa. We will skip this general problem solved in [105] and to some extent demonstrated by Example 3 and 4, and will focus the attention on the discrete approximation of the relaxation (and compliance) spectra by Prony series.

The Prony series approximation of the stress relaxation (in a normalized form) is

$\begin{array}{cc}{G}_N\left(t\right)=g_0+{\displaystyle \sum _{i=1}^N{g}_i}\exp \left(-\frac{t}{{\tau }_i}\right),g_0>0,g_i\ge 0,{\tau }_i\ge 0\hfill & \left(59\right)\end{array}$

The corresponding form of J(t) is

$\begin{array}{cc}{J}_N\left(t\right)=j_0-{\displaystyle \sum _{i=1}^N{j}_i}\exp \left(-\frac{t}{{\lambda }_i}\right),j_0>0,j_i\ge 0,{\lambda }_i\ge 0\hfill & \left(60\right)\end{array}$

The inverse times, that is the relaxation times τ_i and the retardation times λ_i satisfy the inequalities (Equation 55). The attempts to solve (Equation 56) address many approaches for either J(t) or G(t) depending on the type of experimental data available [30, 106–109].

6. Caputo-Fabrizio Operator in the Constitutive Viscoelastic Equations

6.1. Relaxation Function in Terms of Caputo-Fabrizio Operator

Thus, applying the Prony approximation of the relaxation curve and substituting (Equation 61) in the convolution integral (Equation 22) the following approximation is obtained [14, 113]

$\begin{array}{cc}\sigma ={\displaystyle \underset{0}{\overset{t}{\int }}{E}_i}\exp \left(-\frac{t-s}{{\tau }_i}\right)\frac{d\epsilon }{ds}ds\hfill & \left(61\right)\end{array}$

Since we operate with a Prony series, that is with a finite sum of exponentials, then the inversion of the summation and the integral yields [113]

$\begin{array}{cc}\sigma \left(t\right)={\displaystyle \underset{0}{\overset{t}{\int }}{\displaystyle \sum _{i=0}^N{E}_i}}{e}^{-\frac{\left(t-s\right)}{{\tau }_i}}\frac{d\epsilon }{ds}ds={\displaystyle \sum _{i=0}^N{E}_i}\left[{\displaystyle \underset{0}{\overset{t}{\int }}{e}^{-\frac{\left(t-s\right)}{{\tau }_i}}\frac{d\epsilon }{ds}ds}\right]\hfill & \left(62\right)\end{array}$

Thus, the memory effect from the convolution integral can be easy incorporated in each term of the Prony series [99],namely

$\begin{array}{cc}\sigma \left(t\right)={\displaystyle \sum _{i=0}^N{E}_i{k}_i\left(t\right)},k_i\left(t\right)={\displaystyle \underset{0}{\overset{t}{\int }}{e}^{-\frac{\left(t-s\right)}{{\tau }_i}}\frac{d\epsilon }{ds}ds}\hfill & \left(63\right)\end{array}$

The finite sum of N+1 terms σ_i(t) leads directly to the generalized Maxwell model, that is at any time t we have

$\begin{array}{cc}{\sigma }_i\left(t\right)=E_i{k}_i\left(t\right)\hfill & \left(64\right)\end{array}$

σ_i(t) is a product of the spring modulus E_i and its current strain k_i(t), which to some extent could be considered as a hidden material variable. The clear physical meaning of this result is that the strain k_i(t) at a given time t is expressed as convolution integral with an exponential kernel [14]. Therefore, the model parameters that should be defined, following the approximation of the right-hand side of (Equation 62), are [14, 113] : the single separate spring stiffness E₀ and the spring stiffness E_i as well as the relaxations time τ_i of each i^−th Maxwell element.

6.2. Relationships of the Relaxation Time Spectrum and Fractional Order Spectrum

As it was mentioned at the beginning, the fractional parameter α is related to the dimensionless relation time as α = 1/(1 − τ/t₀). Since we have a spectrum of relaxation times τ_i, then the spectrum of the fractional orders (parameters) is

$\begin{array}{cc}{\alpha }_i=\frac{1}{1-{\tau }_i/t_0}\hfill & \left(65\right)\end{array}$

Therefore, k_i(t) can be expressed in a form related to the construction of the Caputo-Fabrizio operator, namely

$\begin{array}{cc}\begin{array}{l}{k}_i\left(t\right)=\left(1-{\alpha }_i\right)\left[\frac{1}{1-{\alpha }_i}{\displaystyle \underset{0}{\overset{t}{\int }}{e}^{-\frac{{\alpha }_1}{1-{\alpha }_i}\left(\overline{t}-\overline{s}\right)}\frac{d\epsilon }{d\overline{s}}d\overline{s}}\right]\\ =\left(1-{\alpha }_i\right)D_t^{{\alpha }_i}\epsilon \left(t\right)\end{array}\hfill & \left(66\right)\end{array}$

6.2.1. Stress Relaxation in Terms of Caputo-Fabrizio Operator

Thus, the constitutive equation of the stress relaxation can be presented as Hristov [14]

$\begin{array}{cc}\sigma \left(t\right)={\displaystyle \sum _{i=0}^N{E}_i\left(1-{\alpha }_i\right)D_t^{{\alpha }_i}\epsilon \left(t\right)}\hfill & \left(67\right)\end{array}$

Now, we turn on the determination of the spectrum of fractional orders α_i = τ_i/t₀ . From experimental data fittings there are a limited number of numerical values of relaxation times τ_i. Now, the principle problem at issue is the determination of the characteristic time t₀. Since the experiments last limited times then we may assume that t₀ equal the elapsed time t_e of the experiments. The literature data concerning Prony decompositions reveal (see the analysis in [14]) that the relaxation times form two groups (see the comments at the begging when the fractional order determination of the Caputo-Fabrizio operators was commented):: (1) relaxation times less then the elapsed time τ_i < t_e ⇒ τ_i/t_e ≤ 1 and (2) relaxation time greater than the elapsed time τ_i > t_e ⇒ τ_i/t_e ≥ 1 .

Consequently, addressing the fractional orders α_i we have: i) fast relaxations for α_i ∈ [0.5−1) corresponding to τ_i/t_e ≤ 1 and ii) slow relaxations for α_i ∈ (0−0.5] when τ_i/t_e ≥ 1. Numerical examples supporting this estimates are reported in Hristov [14]

6.2.2. Creep Compliance in Terms of Caputo-Fabrizio Operator

By analogy of the stress relaxation expression in terms of Caputo-Fabrizio derivative, we may transform the Prony series decomposed compliance (Equation 54) as

$\begin{array}{cc}\begin{array}{l}{J}_N\left(t-s\right)={\displaystyle \sum _{i=0}^N{j}_i}\exp \left(-\frac{t-s}{{\lambda }_i}\right)\\ ={\displaystyle \sum _{i=0}^N{j}_i}\left\{\exp \left[-\frac{{\beta }_i}{1-{\beta }_i}\left(\overline{t}-\overline{s}\right)\right]\right\},\\ {\overline{\lambda }}_i=\frac{{\lambda }_i}{t_0}=\frac{1-{\beta }_i}{{\beta }_i}\end{array}\hfill & \left(68\right)\end{array}$

where ${\bar{\lambda }}_i={\lambda }_i/t_0$ are the scaled (dimensionless) retardation times.

Hence, with the construction of the convolution integral describing the strain history we have

$\begin{array}{cc}\begin{array}{l}{\displaystyle \underset{0}{\overset{t}{\int }}J\left(t-s\right)}\frac{d\sigma }{dt}\Rightarrow {\displaystyle \underset{0}{\overset{t}{\int }}{\displaystyle \sum _{i=0}^N{j}_i}\left\{\exp \left[-\frac{{\beta }_i}{1-{\beta }_i}\left(\overline{t}-\overline{s}\right)\right]\right\}}\frac{d\sigma \left(\overline{s}\right)}{}\\ d\overline{s}d\overline{s}={\displaystyle \sum _{i=0}^N{j}_i}{c}_i\left(t\right)\end{array}\hfill & \left(69\right)\end{array}$

$\begin{array}{cc}{c}_i\left(t\right)={\displaystyle \underset{0}{\overset{t}{\int }}\exp \left[-\frac{{\beta }_i}{1-{\beta }_i}\left(\overline{t}-\overline{s}\right)\right]\frac{d\sigma \left(\overline{s}\right)}{d\overline{s}}d\overline{s}}\hfill & \left(70\right)\end{array}$

Thus, the strain history is

$\begin{array}{cc}\epsilon \left(t-s\right)={\displaystyle \sum _{i=1}^N{j}_i}\left(1-{\beta }_i\right)\left[\frac{1}{1-\beta }{c}_i\left(t\right)\right]={\displaystyle \sum _{i=1}^N{j}_i}\left(1-{\beta }_i\right)D_t^{\beta }\sigma \left(t\right)\hfill & \left(71\right)\end{array}$

Then, the strain can be expressed as

$\begin{array}{cc}\epsilon \left(t\right)=J_{\infty }-{\displaystyle \sum _{i=1}^N{j}_i\left(1-{\beta }_i\right)}{c}_i\left(t\right)=J_{\infty }-{\displaystyle \sum _{i=1}^N{j}_i\left(1-{\beta }_i\right)}{D}_t^{{\beta }_i}\sigma \left(s\right)\hfill & \left(72\right)\end{array}$

where

$\begin{array}{cc}{D}_t^{{\beta }_i}\sigma \left(s\right)=\left\{\frac{1}{\left(1-{\beta }_i\right)}{\displaystyle \underset{0}{\overset{t}{\int }}\exp \left[-\frac{{\beta }_i}{1-{\beta }_i}\left(t-s\right)\right]}\right\}\frac{d\sigma \left(s\right)}{ds}\hfill & \left(73\right)\end{array}$

Therefore,(Equation 73) defines a Caputo-Fabrizio operators with respect to σ(t) and the fractional order β_i is related to the scaled retardation time ${\bar{\lambda }}_i$ ( from the spectrum) as

$\begin{array}{cc}{\beta }_i=\frac{1}{1+{\lambda }_i/t_0}\hfill & \left(74\right)\end{array}$

6.3. Description of Maxwell-Type Viscoelastic Media With Material Responses Modeled by Bessel Functions in Terms of Caputo-Fabrizio Operators

In the last two years (2016-2017) an interesting approach was developed by the group around Professor Mainardi [114–119] which could be considered as attempts to generalize the relaxation functions in the linear viscoelastic models, an approach also investigated in Colombaro et al. [120] and Guisti and Colombaro [121]. The main idea comes from the possibility to represent the relaxation function in a viscoelastic Maxwell-type body by infinite discrete spectrum with times related to the zeros of Bessel functions of the first kind [118, 119]. Here we will present some key points of these studies,in the context of the ideas developed in this article, that is to show the incorporation of the Caputo-Fabrizio operators in the relaxation functions expressed as infinite Dirichlet series (or infinite Prony series as the authors of these studies defined them).

The analysis developed in Colombaro et al. [114], Colombaro et al. [115], Colombaro and Guisti [116], Colombaro et al. [117], Guisti and Mainardi [118], and Guisti and Mainardi [119] is based on the power series representation of the modified Bessel function of the fist kind as Abramowitz and Stegun [122]

$\begin{array}{cc}{I}_{\nu }\left(z\right)={\left(\frac{z}{2}\right)}^{\nu }{\displaystyle \sum _{k=0}^{\infty }\frac{1}{k!\Gamma \left(\nu +k+1\right)}}{\left(\frac{z}{2}\right)}^{2k}\hfill & \left(75\right)\end{array}$

with an asymptotic representation

$\begin{array}{cc}{I}_{\nu }\left(z\right)~\frac{e^z}{\sqrt{2\pi }}\frac{1}{\sqrt{z}},\left|z\right|\to \infty ,\left|\arg z\right|<\frac{\pi }{2}\hfill & \left(76\right)\end{array}$

Now, if the function F_ν(t) has a Laplace transform [118]

$\begin{array}{cc}\overline{F}\left(s\right)=\frac{2\left(\nu +1\right)}{s\sqrt{s}}\frac{I_{\nu +1}\left(\sqrt{s}\right)}{I_{\nu }\left(\sqrt{s}\right)}\hfill & \left(77\right)\end{array}$

It can be presented in the time domain as Guisti and Mainardi [118]

$\begin{array}{cc}{F}_{\nu }\left(t\right)=1-4\left(\nu +1\right){\displaystyle \sum _{n=1}^{\infty }\frac{\exp \left(-j_{\nu ,n}^{2}t\right)}{j_{\nu ,n}^2}},t>0\hfill & \left(78\right)\end{array}$

which is an expression as Dirichlet series, locally integrable, positive and increasing function for t > 0 [118], that is

$\begin{array}{cc}{F}_{\nu }\left(t\right)~4\left(\nu +1\right)\frac{\sqrt{t}}{\sqrt{\pi }},t>0^{+}\hfill & \left(79\right)\end{array}$

because for s → ∞ from Equation (77) we have

$\begin{array}{cc}{\overline{F}}_{\nu }\left(s\right)~2\left(\nu +1\right)s^{-\frac{3}{2}},\mathrm{Re}\left\{s\right\}\to +\infty \hfill & \left(80\right)\end{array}$

If the ${\bar{F}}_{\nu }(s)$ is considered as a part of the Laplace transformation of the relaxation memory function Φ_ν(t) ( here we use the original notations as that used in Guisti and Mainardi [118]), that is ${\bar{\Phi }}_{\nu }(s)=s{\bar{F}}_{\nu }(s)$ , we have

$\begin{array}{cc}{\overline{\Phi }}_{\nu }\left(s\right)=s{\overline{F}}_{\nu }\left(s\right)=\frac{2\left(\nu +1\right)}{\sqrt{s}}\frac{I_{\nu +1}\left(\sqrt{s}\right)}{I_{\nu }\left(\sqrt{s}\right)},\nu >-1\hfill & \left(81\right)\end{array}$

In the time domain the relaxation function Φ_ν(t) is [recall equation (Equation 78)]

$\begin{array}{cc}{\Phi }_{\nu }\left(t\right)=\frac{d{F}_{\nu }\left(t\right)}{dt}=4\left(\nu +1\right){\displaystyle \sum _{n=1}^{\infty }\exp \left(-j_{\nu ,n}^{2}t\right)}\hfill & \left(82\right)\end{array}$

Now, let us turn on to the interconversion problem. From $\sigma (s)=s{Ḡ}_{\nu }(s)\bar{\epsilon }(s)$ as it is suggested [118] that

$\begin{array}{cc}\sigma \left(s\right)=s{\overline{G}}_{\nu }\left(s\right)\overline{\epsilon }\left(s\right)=1-{\overline{\Phi }}_{\nu }\left(s\right)\overline{\epsilon }\left(s\right)\hfill & \left(83\right)\end{array}$

In the time domain the relaxation modulus G(t) is

$\begin{array}{cc}G\left(t\right)=1-{\displaystyle \underset{0}{\overset{t}{\int }}{\Phi }_{\nu }\left(\tau \right)}d\tau =1-4\left(\nu +1\right){\displaystyle \sum _{n=1}^{\infty }\frac{\exp \left(-j_{\nu ,n}^{2}t\right)}{j_{\nu ,n}^2}}\hfill & \left(84\right)\end{array}$

Skipping details in calculation, the creep memory function denoted as $\overline{\text{Ψ}}(s)$ in the Laplace domain is Colombaro et al. [114], Colombaro and Guisti [116], and Guisti and Mainardi [119]

$\begin{array}{cc}\overline{\Psi }\left(s\right)=\frac{2\left(\nu +1\right)}{\sqrt{s}}\frac{I_{\nu +1}\left(\sqrt{s}\right)}{I_{\nu +2}\left(\sqrt{s}\right)},\nu >-1\hfill & \left(85\right)\end{array}$

and

$\begin{array}{cc}1+\overline{\Psi }\left(s\right)=\frac{1}{1-\overline{\Phi }\left(s\right)}\hfill & \left(86\right)\end{array}$

which follows from the interconversion relationships.

For further deep reading in this elegant mathematical studies we refer to Colombaro et al. [114], Colombaro and Guisti [116], Colombaro et al. [117], Guisti and Mainardi [118], and Guisti and Mainardi [119] where it is was demonstrated that the asymptotic behaviors of the viscoelastic responses in the so-called Bessel medium are (precisely in Colombaro et al. [114])

$\begin{array}{cc}\begin{array}{l}{\Phi }_{\nu }(t)\propto \frac{2(\nu +1)}{\sqrt{\pi }}{t}^{-1/2},t\to 0\\ {\Phi }_{\nu }(t)\propto 4(\nu +1)exp(0-j_{\nu ,1}^{2}t),t\to \infty \end{array}\hfill & \left(87\right)\end{array}$

$\begin{array}{cc}\begin{array}{l}{\Psi }_{\nu }(t)\propto \frac{2(\nu +1)}{\sqrt{\pi }}{t}^{-1/2},t\to 0\\ {\Psi }_{\nu }\propto 4(\nu +1)(\nu +2),t\to \infty \end{array}\hfill & \left(88\right)\end{array}$

which actually follows from Equation (79).

The main idea to use a relaxation function expressed by modified Bessel functions of first kind comes from the possibility to calculate the sum of the infinite series of reciprocal positive zeros of the Bessel functions J_ν [118], namely

$\begin{array}{cc}{S}_{\nu }={\displaystyle \sum _{n=1}^{\infty }\frac{1}{j_{\nu ,n}^2}}=\frac{1}{4\left(\nu +1\right)},\nu >-1\hfill & \left(89\right)\end{array}$

With (Equation 89) the relaxation modulus becomes [118]

$\begin{array}{cc}G\left(t\right)=4\left(\nu +1\right){\displaystyle \sum _{n=1}^{\infty }\frac{\exp \left(-j_{\nu ,n}^{2}t\right)}{j_{\nu ,n}^2}}\hfill & \left(90\right)\end{array}$

Hence, the relaxation modulus is represented as an infinite Dirichlet series which are absolutely converging, which actually represent a discrete spectrum where the stiffness of the n^th element (spring-dashpot) is

${}_B{E}_n=\left(1/j_{\nu ,n}^2\right)$

(the prefix B means Bessel) and the relaxation times are ${\tau }_n=1/j_{\nu ,n}^2$ . That is, in the context of the analysis done in this study, we have

$\begin{array}{cc}G\left(t\right)=4\left(\nu +1\right){\displaystyle \sum _{n=1}^{\infty }{}_B{E}_n\exp \left(-\frac{t}{{\tau }_n}\right)}\hfill & \left(91\right)\end{array}$

Therefore, we get an expression in terms of an infinite sum of exponential functions, as in the Prony approximations, but now the relaxation times are defined by the zeros of the Bessel function. If a time scale t₀ of modeled relaxation process exists, then n^th dimensionless relaxation time is 0 < τ_n/t₀ ≤ 1, as it was demonstrated several times with the Prony series. Now, let us consider that τ_n/t₀ = (1 − β_n)/β_n ,where 0 < β < 1 and then we may re-write (Equation 91) as

$\begin{array}{cc}G\left(t\right)=4\left(\nu +1\right){\displaystyle \sum _{n=1}^{\infty }{}_B{E}_n\exp \left(-\frac{{\beta }_n}{1-{\beta }_n}\overline{t}\right)},0<\overline{t}=t/t_0<1\hfill & \left(92\right)\end{array}$

Then, the construction the convolution integral of the stress relaxation with G(t) yields

$\begin{array}{cc}\begin{array}{l}\sigma \left(t\right)={\displaystyle \underset{0}{\overset{t}{\int }}G\left(t-s\right)\frac{d\epsilon \left(s\right)}{ds}ds}\\ ={\displaystyle \underset{0}{\overset{t}{\int }}4\left(\nu +1\right){\displaystyle \sum _{n=1}^{\infty }{}_B{E}_n\exp \left[-\frac{{\beta }_n}{1-{\beta }_n}\left(\overline{t}-\overline{s}\right)\right]}}\frac{d\epsilon \left(s\right)}{ds}ds\end{array}\hfill & \left(93\right)\end{array}$

Interchanging the orders of the summation and the integral in equation (Equation 93) , we get

$\begin{array}{cc}\sigma \left(t\right)=4\left(\nu +1\right){\displaystyle \sum _{n=1}^{\infty }{}_B{E}_n{\displaystyle \underset{0}{\overset{t}{\int }}\exp \left[-\frac{\beta }{1-\beta }\left(\overline{t}-\overline{s}\right)\right]}\frac{d\epsilon \left(s\right)}{ds}d}s\hfill & \left(94\right)\end{array}$

Further, the step toward incorporation of the Caputo-Fabrizio operator is straightforward, namely

$\begin{array}{cc}\begin{array}{l}\sigma \left(t\right)=4\left(\nu +1\right){\displaystyle \sum _{n=1}^{\infty }{}_B}{E}_n\left(1-{\beta }_n\right)\\ \left\{\frac{1}{1-{\beta }_n}{\displaystyle \underset{0}{\overset{t}{\int }}\exp \left[-\frac{{\beta }_n}{1-{\beta }_n}\left(\overline{t}-\overline{s}\right)\right]\frac{d\epsilon \left(s\right)}{ds}ds}\right\}\end{array}\hfill & \left(95\right)\end{array}$

or in a compact form as

$\begin{array}{cc}\begin{array}{l}\sigma \left(t\right)=4\left(\nu +1\right){\displaystyle \sum _{n=1}^{\infty }{}_B{E}_n{\left(1-{\beta }_n\right)}_B{D}_t^{{\beta }_n}\left[\epsilon \left(t\right)\right]},\\ {\beta }_n=\frac{1}{1-{\tau }_n/t_0},{\tau }_n=1/j_{\nu ,n}^2\end{array}\hfill & \left(96\right)\end{array}$

with the condition

$\begin{array}{cc}\sigma \left(t\right)=4\left(\nu +1\right){\displaystyle \sum _{n=1}^{\infty }{}_B{E}_n\left(1-{\beta }_n\right)}=1\hfill & \left(97\right)\end{array}$

Here ${}_B{D}_t^{{\beta }_n}(•)$ denotes a Caputo-Fabrizio fractional operator with a fractional order β_n based on the positive zeros of J_v.

Now, the naturally question coming to mind is: How this result can be applied to real data related to the stress relaxation and creep compliance of real viscoelastic materials? Unfortunately, no answers to this question exist in all works dealing with so-called Bessel media [114–119]. The first problem immediately appearing is: how the relaxation times ${\tau }_n=1/j_{\nu ,n}^2$ can be related to the real data? As mentioned in several points of this article, the relaxation times corresponds to measurements taken at equidistantly distributed (in normal scale or logarithmic scale) points along the time axis. How, this real approach could be related to the zeros of the Bessel function is a question still remaining open. The second problem comes from the impossibility to work with infinite sum in (Equations 90 , 95 , and 97) . Actually, all computer simulations should use finite number of terms that immediately leads to truncated Dirichlet series obeying the condition (Equation 97). This immediately, transforms the approximation of the relaxation function to approximation through Prony series, but the first problem formulated above, still remains unanswered.

Actually, the approximation by Prony series or infinite Dirichlet series, generally speaking, is an approach considering approximations of Non-Debye responses (relaxations) by superpositions of sub-processes (as Debye relaxations) with different relaxation times (an approach widely applied in the relaxation processes in glass transitions [123], for instance).

7. Final Comments

The ideas and results developed in this work focused on the new fractional operator conceived in [1, 10] (2015) naturally appearing when we stayed on the shoulders of two classical results: the Prony series (1795) [2] and the Boltzmann superposition principle (1864) [9].

It was demonstrated that in many cases there are viscoelastic materials which experimental behaviors exhibit strong departures from the power-law. In such cases it is natural to rise the questions about the adequate modeling of the dynamic processes in such media and to ask for new fractional operators. This is, actually, the same question raised by Bagley and Torvik [49, 124] who in case of power-law media suggested the constitutive relationship

$\begin{array}{cc}\sigma \left(t\right)=E_0\epsilon \left(t\right)+E_1·D_t^{\mu }\left[\epsilon \left(t\right)\right],0<\mu <1\hfill & \left(98\right)\end{array}$

Following Bagley and Torvik [49, 124] for a homogeneous viscoelastic materials the constitutive equation is

$\begin{array}{cc}\sigma \left(t\right)+{\displaystyle \sum _{m=1}^N{b}_m{D}^{{\beta }_m}\sigma =E_0}\epsilon \left(t\right)+{\displaystyle \sum _{n=1}^N{E}_n{D}^{{\alpha }_m}\epsilon \left(t\right)}\hfill & \left(99\right)\end{array}$

In (Equation 99) the derivatives have power-law kernels (Riemann-Liouville derivatives), which for N = 1 (one-term series of fractional derivatives) results in the simple expression

$\begin{array}{cc}\sigma \left(t\right)+b{D}^{\beta }\sigma \left(t\right)=E_0\epsilon \left(t\right)+E_1{D}^{\alpha }\epsilon \left(t\right)\hfill & \left(100\right)\end{array}$

containing two fractional derivatives with different orders.

This article does not focus on development of different viscoelastic models based on the Caputo-Fabrizio fractional operator since this is out of its scope and draws new problems to be resolved. Despite this, if the kernels in the convolution integrals departure from the power-law we may consider a similar (formally) constitutive equation, namely

$\begin{array}{cc}\sigma \left(t\right)+{\displaystyle \sum _{i=1}^N{b}_i\left[{}^{CF}{D}^{\beta i}\sigma \right]=E_0}\epsilon \left(t\right)+{\displaystyle \sum _{i=1}^N{E}_i\left[{}^{CF}{D}^{{\alpha }_i}\epsilon \left(t\right)\right]}\hfill & \left(101\right)\end{array}$

where, following the main idea of the Prony decompositions of the relaxation and the compliance, the series of fractional order of both sides of the equation have equal numbers of terms. Following [20, 107] the retardation times λ_i are satisfying the conditions

$\begin{array}{cc}{\tau }_1<{\lambda }_1<\mathrm{....}<{\tau }_i<{\lambda }_i<\mathrm{...}{\tau }_N<{\lambda }_N\hfill & \left(102\right)\end{array}$

Therefore, from α_i = 1/(1+τ_i/t₀) and β_i = 1/(1+λ_i/t₀) it follows from Equation (102) that the fractional orders should satisfy the inequalities

$\begin{array}{cc}0<{\beta }_1<{\alpha }_1<\mathrm{...}<{\beta }_i<{\alpha }_i<\mathrm{...}<{\beta }_N<{\alpha }_N<1\hfill & \left(103\right)\end{array}$

The example of Renardy [125] (see also [26] and [14]), related to polymer rheology, reveals that a discrete relaxation spectrum with accumulation point at zero behaves as a power-law for short times, namely

$\begin{array}{cc}{\displaystyle \sum _{i=0}^{\infty }e}xp(-i^{\gamma }\xi )\to t^{-\frac{1}{\gamma }},t\to 0,\gamma >1\hfill & \left(104\right)\end{array}$

Thus, in the asymptotic case (for t → 0 ) we may expect that the model (Equation 101) would converge to the model (Equation 100).

If we suggest only, for example, that N = 1, which actually is a departure of the main idea of Prony series, we have

$\begin{array}{cc}\sigma \left(t\right)+b^{CF}{D}^{\beta }\sigma =E_0\epsilon \left(t\right)+E_1{}^{CF}{D}^{\alpha }\epsilon \left(t\right),1>\beta >\alpha >0\hfill & \left(105\right)\end{array}$

This equation contains two fractional derivatives of different orders as in Equation (100). For instance, fractional viscoelastic models containing fractional derivatives and operators of two different order are thoroughly analyzed in Rossikhin and Shitikova [126] and Rossikhin and Shitikova [127] in the light of power-law materials. All these formal similarities and dissimilarities provoke new ideas that should be resolved.

To recapitulate, actually, we demonstrated that the Caputo-Fabrizio fractional operator naturally appears in the constitutive viscoelastic equations based on hereditary integrals when the material responses do not match the power-law. Moreover, it plays the same role as the fractional operators (derivatives) based on power-law memory kernels when they are inapplicable. At this moment the task of this study is accomplished and a lot of future works would be developed starting from results obtained here.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Caputo M, Fabrizio M. A new definition of fractional derivative without singular kernel. Progr Fract Differ Appl. (2015) 1:73–85. doi: 10.12785/pfda/010201

CrossRef Full Text | Google Scholar

2. de Prony GR. Essai experimentale at analitique. J Ecole Polytech. (1795) 1:24–76.

3. Hristov J. Derivatives with non-singular kernels: from the Caputo-Fabrizio definition and beyond: Appraising analysis with emphasis on diffusion models. In: Frontiers in Fractional Calculus, 2017 , Bhalekar S, editor. Sharjah: Bentham Science Publishers. (2017). pp. 269–342

Google Scholar

4. Hristov J. Transient heat diffusion with a non-singular fading memory: from the cattaneo constitutive equation with Jeffrey's kernel to the caputo-fabrizio time-fractional derivative. Thermal Sci. (2016) 20:765–70. doi: 10.2298/TSCI160112019H

CrossRef Full Text | Google Scholar

5. Guisti A. A comment on some new definitions of fractional derivative. Nonlinear Dyn. (2018) 93:1757–63. doi: 10.1007/s11071-018-4289-8

CrossRef Full Text | Google Scholar

6. Ortigueira MD, Machado JAT. A critical analysis of the Caputo–Fabrizio operator. Commun Nonlinear Sci Numer Simul. (2018) 59:608–11. doi: 10.1016/j.cnsns.2017.12.001

CrossRef Full Text | Google Scholar

7. Tarasov VE. No nonlocality. No fractional derivative. Commun. Nonlinear Sci. Numer. Simul. (2018) 62:157–63. doi: 10.1016/j.cnsns.2018.02.019

CrossRef Full Text | Google Scholar

8. Podlubny I. Fractional Differential Equations. New York, NY: Academic Press (1999).

Google Scholar

9. Boltzmann L. Zur Theorie der Elastischen Nachwirkung. Sitzungsber Akad Wiss Wien Mathem Naturwiss. (1874) 70:275–300.

10. Caputo M, Fabrizio M. Applications of new time and spatial fractional derivatives with exponential kernels. Progr Fract Differ Appl. (2016) 2:1–11. doi: 10.18576/pfda/020101

CrossRef Full Text | Google Scholar

11. Losada J, Nieto JJ. Properties of a new fractional derivative without singular kernel. Progr Fract Differ Appl. (2015) 1:87–92. doi: 10.12785/pfda/010202

CrossRef Full Text | Google Scholar

12. Hristov J. The non-linear Dodson diffusion equation: Approximate solutions and beyond with formalistic fractionalization. Math Natural Sci. (2017) 1:1–7. doi: 10.22436/mns.01.01.01

CrossRef Full Text | Google Scholar

13. Hristov J. Derivation of fractional Dodson's equation and beyond: Transient mass diffusion with a non-singular memory and exponentially fading-out diffusivity. Progr Fract Differ Appl. (2017) 3: 255–70. doi: 10.18576/pfda/030402

CrossRef Full Text | Google Scholar

14. Hristov J. Response functions in linear viscoelastic constitutive equations and related fractional operators. Math Model Natur Phenomena. doi: 10.1051/mmnp/2018067

CrossRef Full Text

15. Storm ML. Heat conduction in simple metals. J Appl Phys. (1951) 22:940–51. doi: 10.1063/1.1700076

CrossRef Full Text | Google Scholar

16. Gurtin ME. On the thermodynamics of materials with memory. Arch Rational Mech Anal. (1968) 28:40–50. doi: 10.1007/BF00281562

CrossRef Full Text | Google Scholar

17. Miller RK. An integrodifferential equation for rigid heat conductors with memory. J Math Anal Appl. (1978) 66:313–32. doi: 10.1016/0022-247X(78)90234-2

CrossRef Full Text | Google Scholar

18. Nunciato JW. On heat conduction in materials with memory. Q Appl Math. (1971) 29:187–273.

Google Scholar

19. Pipkin AC. Lectures on Viscoelasticity Theory, 2nd Edn., Berlin: Sprimger-Verlag (1972).

Google Scholar

20. Tschoegl NW. The Phenomenological Theory of Linear Viscoelastic Behaviour: An Introduction. New York, NY: Springer–Verlag (1989).

Google Scholar

21. Brinson H, Brinson L Polymer Engineering Science and Viscoelasticity. New York, NY: Springer (2008).

Google Scholar

22. Ferry JD. Viscoelastic Properties of Polymers. New York, NY: Wiley (1980).

Google Scholar

23. Markovitz H. Boltzmann and the beginning of rheology. Trans Soc Rheol. (1977) 21:384–98. doi: 10.1122/1.549444

CrossRef Full Text | Google Scholar

24. Ciambella J, Paolone A, Vidoli S. A comparison of nonlinear integral-based viscoelastic models through compression tests on filled rubber. Mech Mater. (2010) 42:932–44. doi: 10.1016/j.mechmat.2010.07.007

CrossRef Full Text | Google Scholar

25. Ciambella J, Paolone A, Vidoli S. Identification of the viscoelastic properties of soft materials at low frequencies: Performance, ill-conditioning and extrapolation capabilities of fractional and exponential models. J Mech Behav Biomed Mater. (2014) 37:286–98. doi: 10.1016/j.jmbbm.2014.05.031

CrossRef Full Text | Google Scholar

26. Hanyga A. Wave propagation in media with singular memory. Math Comp Modell. (2001) 34:1399–421. doi: 10.1016/S0895-7177(01)00137-6

CrossRef Full Text | Google Scholar

27. Coleman B, Noll W. Foundations of linear Viscoelasticity. Rev Modern Phys. (1961) 33:239–49. doi: 10.1103/RevModPhys.33.239

CrossRef Full Text | Google Scholar

28. Garbarski J. The application of an exponentially-type function for the modeling of viscoelasticity of solid polymers. Polymer Eng Sci. (1992) 32:107–14. doi: 10.1002/pen.760320206

CrossRef Full Text | Google Scholar

29. Winter HH. Analysis of dynamic mechanical data L inversion into relaxation time spectrum and consistency check. J Nonnewtonian Fluid Mech. (1997) 68:225–39. doi: 10.1016/S0377-0257(96)01512-1

CrossRef Full Text | Google Scholar

30. Emri I, Tschoegl NW. Determination of mechanical spectra from experimental data. Int J Solids Struct. (1995) 32:817–26. doi: 10.1016/0020-7683(94)00162-P

CrossRef Full Text | Google Scholar

31. Day WA. The Thermodynamic Theory of Simple Materials With Fading Memory. Berlin: Springer (1972).

Google Scholar

32. Fabrzio M, Giorgi C, Naso MG. Viscoelastic Solids of Exponential type. 1. Minimal representations and Contralability. Meccanica (2004) 39:531–46. doi: 10.1007/s11012-003-6437-5

CrossRef Full Text | Google Scholar

33. Fabrzio M, Giorgi C, Naso MG. Viscoelastic Solids of Exponential type. 2. Free energies . Stability and attractors. Meccanica (2004) 39:547–61. doi: 10.1007/s11012-003-9400-6

CrossRef Full Text | Google Scholar

34. Fabrizio M, Morro A. Thermodynamic restrictions on relaxation functions in linear viscoelasticity. Mech Res Commun. (1985) 12:101–5. doi: 10.1016/0093-6413(85)90077-1

CrossRef Full Text | Google Scholar

35. Crook RA, Letton A. The viscoelastic behaviour of notched glassy polymers. Eng Fracture Mech. (1993) 44:167–73.

Google Scholar

36. Jaishankar A, McKinley GH. A fractional K-BKZ constitutive formulation for describing the nonlinear theology of multiscale complex fluids. J Rheol. (2014) 58:1751–88. doi: 10.1122/1.4892114

CrossRef Full Text | Google Scholar

37. Jozwiak B, Orczykowska M, Dziubinski M. Fractionalgeneralization of maxell and Kelvin-Voight models for biopolymer characterization. PLoS ONE (2015) 10:e0143090. doi: 10.1371./journal.pone.0143090

CrossRef Full Text | Google Scholar

38. Meral FC, Roston TJ, Magin R. Fractional calculus in viscoelasticity: an experimental study Commun Nonlinear Sci Numer Simulat. (2010) 15:939–45. doi: 10.1016/j.cnsns.2009.05.004

CrossRef Full Text | Google Scholar

39. Metzler R, Schick W, Kilian H-G, Nonnenmacher TF. Relaxation in filled polymers: a fractional calculus approach. J Chem Phys. (1995) 103:7180–6. doi: 10.1063/1.470346

CrossRef Full Text | Google Scholar

40. Song KW, Kuk HY, Chamg GS. Rheology of concentrated xanthan gum solutions: oscillatory shear flow behaviour. Korea Austr Rheol J. (2006) 18:18–24.

41. Wyatt NB, Liberatore MW. Rheology and viscosity scaling of polyelectrolyte xanthan gum. J Appl Polymer Sci. (2010) 114:4076–84. doi: 10.1002/app.31093

CrossRef Full Text | Google Scholar

42. Schiessel H, Metzler R, Blumen A, Nonnenmacher TF. Generalized viscoelastic models: their fractional equations with solutions. J Phys A Math Gen. (1995) 28:6567–84. doi: 10.1088/0305-4470/28/23/012

CrossRef Full Text | Google Scholar

43. Papagiannnopoulos A, Sotiropoulos K, Pispas S. Particle tracking microrheology of the power-law viscoelasticity of xantan solution. Food Hydrocolloids (2016) 61:201–10. doi: 10.1016/j.foodhyd.2016.05.020

CrossRef Full Text | Google Scholar

44. Caputo M. Linear models of dissipation whose Q is almost frequency independent-II. Geophys J R Astr Soc. (1967) 13:529–39. doi: 10.1111/j.1365-246X.1967.tb02303.x

CrossRef Full Text | Google Scholar

45. Mainardi F. Fractional Calculus and Waves in Linear Viscoelasticity. London-Singapore: Imperial College Press and World Scienific (2010).

46. Glockle WG, Nonnemacher TF. Fractional relaxation and the time-temperature superposition principle. Rheol Acta (1994) 33:337–43. doi: 10.1007/BF00366960

CrossRef Full Text | Google Scholar

47. Padovan J, Guo Y. General response of viscoelastic systems modelled by fractional operators. J Franklin Inst. (1988) 325:247–75. doi: 10.1016/0016-0032(88)90086-5

CrossRef Full Text | Google Scholar

48. Findley WN, Lai JS, Onaran K Creep and Relaxation of Nonlinear Viscoelastic Materials. New York, NY: North-Holland Pub (1974).

Google Scholar

49. Bagley RL, Torvik PJ. On the fractional Calculus model of viscoelastic behavior. J Rheol. (1986) 30:133–55. doi: 10.1122/1.549887

CrossRef Full Text | Google Scholar

50. Lakes RS, Vanderby R. Interrelation of creep and relaxation: a modelling approach for ligaments. J Biomech Eng. (1999) 121:612–5. doi: 10.1115/1.2800861

CrossRef Full Text | Google Scholar

51. Scott-Blair GW, Reiner M. The rheological law underlying the Nutting equation. Appl Sci Res. (1951) A2:225–34. doi: 10.1007/BF00411984

CrossRef Full Text | Google Scholar

52. Scott-Blair GW. A model to describe the flow curves of concentrated suspensions of spherical particles. Rheol Acta(1965) 6:201–3. doi: 10.1007/BF01976435

CrossRef Full Text | Google Scholar

53. Scott-Blair GW. Mathematics and rheology. Rheol Acta (1972) 11:237–40. doi: 10.1007/BF01993026

CrossRef Full Text | Google Scholar

54. Nutting PG. A new general law of deformation. J Franklin Inst. (1921) 191:679–85. doi: 10.1016/S0016-0032(21)90171-6

CrossRef Full Text | Google Scholar

55. Nutting PG. Deformation in relation to time, pressure and temperature. J Franklin Inst. (1946) 242:449–58. doi: 10.1016/0016-0032(46)90636-9

CrossRef Full Text | Google Scholar

56. Carillo S, Giorgi C. Non-classical memory kernels in linear viscoelasticity. In: Viscoelastic and Viscoplastic Materials, Mohamed Fathy El-Amin editor. Split: IntechOpen (2016). p. 295–331. doi: 10.5772/64251

CrossRef Full Text | Google Scholar

57. Bradshaw RD, Brinson LC. A sing control method for fitting and interconverting material functions for linear viscoelastic solids. Mech Time Depend Mater. (1997) 1:85–108. doi: 10.1023/A:1009772018066

CrossRef Full Text | Google Scholar

58. Mandelbrot S. Dirichlet Series. Principle and Methods. Dordrecht: D. Reidel Publ. Co. (1972).

Google Scholar

59. Czyz JA, Szyszkowski W. An effective method for non-linear viscoelastic structural analysis. Comput Struct. (1990) 37:637–46. doi: 10.1016/0045-7949(90)90096-K

CrossRef Full Text | Google Scholar

60. Cristensen RM. Theory of Viscoelasticity. An introduction. New York, NY: Academic Press (1982).

Google Scholar

61. Bilston LE, Liu Z, Phan-Thien N. Linear viscoelastic properties of bovine brain tissue in shear. Bioreology (1997) 34:377–85.

PubMed Abstract | Google Scholar

62. Phillips A, Pankaj P, May F, Taylor K, Howie C, Usmani A. Constitutive models for impacted morsellised cortico-cancelous bone. Biomateials (2006) 27:2162–70. doi: 10.1016/j.biomaterials.2005.10.034

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Ravikumar N, Noble C, Cramphorn E, Taylor ZA. A short constitutive model for ballistic gelatine at surgical strain rates. J Mech Behav Biomed Mater. (2015) 47:87–94. doi: 10.1016/j.jmbbm.2015.03.011

CrossRef Full Text | Google Scholar

64. Londono JG, Berger-Vergioat L, Waisman H. A Prony series type viscoelastic solid coupled with continuous damage law for polar ice modeling. Mech Mater. (2016) 98:81–97. doi: 10.1016/j.mechmat.2016.04.002

CrossRef Full Text | Google Scholar

65. Babaei B, Davarian A, Pryse KM, Elson EL, Genin GM. Efficient and optimized identification of generalized viscoelastic relaxation spectra. J Mech Behav Biomed Mater. (2016) 55:32–41. doi: 10.1016/j.jmbbm.2015.10.008

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Mauro JC, Mauro YZ. On the Prony representation of stretched exponential relaxation. Phys A (2018) 506:75–87. doi: 10.1016/j.physa.2018.04.047

CrossRef Full Text | Google Scholar

67. McGrum NG, Buckley CP, Bucknall CB. Principles of Polymer Engineering. 2nd Edn. Oxford: Oxford Science Publications (2003).

68. Jaloha D, Constantinescu A, Neviere R. Revisiting the identification of the generalized Maxwell models from experimental results. Int J Solids Struct. (2015) 67–68: 169–81. doi: 10.1016/j.ijsolstr.2015.04.018

CrossRef Full Text | Google Scholar

69. Sun Y, Chen J, Huang B. Characterization of asphalt concrete linear viscoelastic behaviour utilizing the Havriliak-Negami complex modulus model. Constr Build Mater. (2015) 99:226–34. doi: 10.1016/j.conbuildmat.2015.09.016

CrossRef Full Text | Google Scholar

70. Gross B., Mathematical Structure of the Theories of Viscoelasticity. Paris: Hermann (1953)

71. Gross B. Distribution functions in linear viscoelastic theory. J Appl Phys. (1987) 62:2763–70. doi: 10.1063/1.339404

CrossRef Full Text | Google Scholar

72. Baumgaertel M, Winter H. Interrelation between continuous and discrete relaxation time spectra. J Non Newtonian Fluid Mech. (1992) 44:15–36. doi: 10.1016/0377-0257(92)80043-W

CrossRef Full Text | Google Scholar

73. Mead DW. Numerical interconversion of linear viscoelastic functions. J Rheol. (1994) 38: 1769–95. doi: 10.1122/1.550526

CrossRef Full Text | Google Scholar

74. Fernandez P, Lamela Rey RM, Fenandez Canteli A. Viscoelastic characterisation of the temporomandibular joint disc in bovines. Strain (2011) 47:188–93. doi: 10.1111/j.1475-1305.2008.00502.x

CrossRef Full Text | Google Scholar

75. Prieto-Munoz P, Yin H, Testa R. Mechaniscs of an adhesive anchor system subjected to a pullout load, II: viscoelastic analysis. J Struc Eng. (2013) 140:04013053. doi: 10.1061/(ASCE)ST.1943-541X.0000822

CrossRef Full Text | Google Scholar

76. Shou Z, Chen F, Yin H. Self-heating of a polymeric particulate composite under mechanical excitations. Mech Mater. (2018) 117:116–25. doi: 10.1016/j.mechmat.2017.11.003

CrossRef Full Text | Google Scholar

77. Laksari K, Shafieian M, Darvish K. Constitutive model for brain tissue under finite compression. J Biomech. (2012) 45:642–6. doi: 10.1016/j.jbiomech.2011.12.023

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Choi ST, Lee SR, Earmme YY. Flat indentation of viscoelastic polymer film on a rigid substrate. Acta Mater. (2008) 56:5377–87. doi: 10.1016/j.actamat.2008.07.030

CrossRef Full Text | Google Scholar

79. Schapery RA. Viscoelastic behavior and analysis of composite materials. In: Mechanics of Composite Materials, Vol. 2, Sendeckyi GP editor. New York, NY: Academic Press (1974). p. 85–169.

80. Fajman P, Seinoja J. A simplified approach to time-dependent subsoil-structure interaction. Comput. Struct. (2007) 85:1514–23. doi: 10.1016/j.compstruc.2007.01.024

CrossRef Full Text | Google Scholar

81. Tayeb A, Arfaoui M, Zine A, Hamdi A, Benabdallah J, Ichchou M. On the non-linear viscoelastic behaviour of rubber-like materials: constitutive description and identification Int J Mech Sci. (2017) 130:437–47. doi: 10.1016/j.ijmecsci.2017.06.032

CrossRef Full Text | Google Scholar

82. Vandenberghe E, Choucharina S, Luca S, De Ketelaere B, De Baerdemaeker J, Claes J. Spatio-temporal gradients of dry matter content and fundamental material parameters of Gouda cheese. J Food Eng. (2014) 142:31–48. doi: 10.1016/j.jfoodeng.2014.05.019

CrossRef Full Text | Google Scholar

83. Hill SA. The analytic representation of viscoelastic material properties using optimization techniques. NASA TM-108394, February, 199, (1993).

84. Mitra S, Mitra A. A genetic algorithms based techniques for computing the nonlinear least squares estimates of parameters of sum of exponential model. Expert Syst Appl. (2012) 39: 6370–9. doi: 10.1016/j.eswa.2011.12.033

CrossRef Full Text | Google Scholar

85. Huang AW, Lu CH, Wu SC, Vinci RP, Brown WL, Lin MT. Viscoelastic mechanical properties measurement of thin AL and Al-Mg films using bulge testing. Thin Solid Films (2016) 618:2–7. doi: 10.1016/j.tsf.2016.03.064

CrossRef Full Text | Google Scholar

86. Enderlein J, Erdmann R. Fast fitting of multi-exponential decay curves. Optics Commun. (1997) 134:371–8. doi: 10.1016/S0030-4018(96)00384-7

CrossRef Full Text | Google Scholar

87. DeHoff PH, Barrett AA, Lee RB, Anusavice KJ. Thermal compatibility of dental ceramic system using cylindrical an spherical geometries. Dental Mater. (2008) 24:744–52. doi: 10.1016/j.dental.2007.08.008

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Drozdov A. A constitutive models for nonlinear viscoelastic media. Int J Solids Struct. (1997) 34:2685–707. doi: 10.1016/S0020-7683(96)00178-3

CrossRef Full Text | Google Scholar

89. Andrews SHJ, Rattner JB, Shrive NG, Ronsky JL. Swelling significantly affects the material properties of the menisci in compression. J Biomech. (2015) 48:1485–9. doi: 10.1016/j.jbiomech.2015.02.001

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Kosa A, Berezvai S. Visco-hyperelastic characterization of polymeric foam materials. Mater Today Proc. (2016) 3:1003–8. doi: 10.1016/j.matpr.2016.03.037

CrossRef Full Text | Google Scholar

91. Lin RC. On a nonlinear viscoelastic material law at finite strain for polymers. Mech Res Commun. (2001) 28:365–72. doi: 10.1016/S0093-6413(01)00185-9

CrossRef Full Text | Google Scholar

92. Liu F, Li C, Liu S, Genin GM, Huang G, Lu TJ, Xu F. Effects of viscoelasticity on skin pain sensation. Theor Appl Mech Lett. (2012) 5:222–6. doi: 10.1016/j.taml.2015.11.002

CrossRef Full Text | Google Scholar

93. Sliker LJ, Ciuti G, Rentschler M, Menxciasi A. Frictional resistance model for tissue-capsule endoscope sliding contact in the gastrointenstinal tract. Tribol Int. (2016) 2012:472–84. doi: 10.1016/j.triboint.2016.06.003

CrossRef Full Text | Google Scholar

94. Cui T, Lin CW, Chien CH, Chao YJ, Van Zee JW. Service life estimation of liquid silicone rubber seals in polymer electrolyte membrane fuel cell environments. J Power Sources (2011) 196:1216–21. doi: 10.1016/j.jpowsour.2010.08.075

CrossRef Full Text | Google Scholar

95. Drozdov A Finite Elasticity and Viscoelasticity. Singapore: World Scientific (1996).

Google Scholar

96. Lai J, Bakker A. Analysis of the non-linear creep of high-density polyethylene. Polymer(1995) 36:93–9.

Google Scholar

97. Pelayo F, Lamela-Rey M, Minuz-Calvente M, Lopez-Aenlle M, Alvarez-Vasquez A. Study of the time-temperature behaviour of PVB: Application of laminated glass elements. Thin Walled Struct.(2017) 119:324–31. doi: 10.1016/j.tws.2017.06.030

CrossRef Full Text | Google Scholar

98. Schneider J, Hilcken J, Aronen A, Karvinen R, Olesen JF, Nielsen J. Stress relaxation in tempered glass caused by hear soak testing. Eng Struct. (2016) 122:42–9. doi: 10.1016/j.engstruct.2016.04.024

CrossRef Full Text | Google Scholar

99. Sheng W, Alcorn R, Lewis A. A new method for radiation forces for floating platforms in waves. Ocean Eng. (2015) 105:43–53. doi: 10.1016/j.oceaneng.2015.06.023

CrossRef Full Text | Google Scholar

100. Troyer KL, Estep DJ, Puttliz ChM. Viscoelasticity effects during loading play an integral role in soft tissue mechanics. Acta Biomater. (2012) 8:240–3. doi: 10.1016/j.actbio.2011.07.035

CrossRef Full Text | Google Scholar

101. Lavrentiev M Some ill-Posed Problems of Mathematical Physics. Berlin: Springer (1967).

Google Scholar

102. Hansen PC. Numerical tools for analysis and solution of Fredholm integral equations of the first kind. Inverse Prob. (1992) 8:849–72. doi: 10.1088/0266-5611/8/6/005

CrossRef Full Text | Google Scholar

103. Honerkamp J. Ill-posed problems in rheology. Rheol Acta (1989) 28:363–71. doi: 10.1007/BF01336803

CrossRef Full Text | Google Scholar

104. Honerkamp J, Weese J. Determination of the relaxation spectrum by a regularization method. Macromolecules (1989) 22:4372–7. doi: 10.1021/ma00201a036

CrossRef Full Text | Google Scholar

105. Anderssen RS, Davies AR, de Hoog FR. On the interconversion integral equation for relaxation and creep. ANZIAM J. (2007) 48:346–63. doi: 10.21914/anziamj.v48i0.64

CrossRef Full Text | Google Scholar

106. Park SW, Schapery RA. Methods of Interconversion between linear viscoelastic material functions from single experiment. Int J Solids Sruct. (1999) 36:1653–75. doi: 10.1016/S0020-7683(98)00055-9

CrossRef Full Text | Google Scholar

107. Luk-Cyr J, Crochon T, li C, Levesque M. Interconversion of linearly viscoelastic material functions expressed as Prony series: a closure. Mech Time Depend Mater (2013) 17:53–82. doi: 10.1007/s11043-012-9176-y

CrossRef Full Text | Google Scholar

108. Plazek DJ, Echeverria I. Do not cry for me Charlie Brown, or with compliance comes comprehension. J Rheol. (2000) 44:931–41. doi: 10.1122/1.551117

CrossRef Full Text | Google Scholar

109. Hopkins IL, Hamming RW. On creep and relaxation. J Appl Phys. (1957) 28:906–9. doi: 10.1063/1.1722885

CrossRef Full Text | Google Scholar

110. Hristov J. Steady-state heat conduction in a medium with spatial non-singular fading memory: derivation of caputo-fabrizio space-fractional derivative with Jeffrey's kernel and analytical solutions. Thermal Sci. (2017) 21:827–39. doi: 10.2298/TSCI160229115H

CrossRef Full Text | Google Scholar

111. Loy RJ, de Hoog FR, Anderssen RS. Interconversion of Prony series for relaxation and creep. J Rheol. (2015) 59:1261–70. doi: 10.1122/1.4929398

CrossRef Full Text | Google Scholar

112. Loy RJ, Aderssen RS. Interconversion relationships for completely monotone functions. SIAM J Math Anal. (2014) 46:2008–13. doi: 10.1137/120891988

CrossRef Full Text | Google Scholar

113. Canestrati F, Stimilli A, Bahia HA, Virgili A. Pseudo-variables method to calculate HMA relaxation modulus through low-temperature induced stress and strain. Mater Design (2015) 76:141–9. doi: 10.1016/j.matdes.2015.03.063

CrossRef Full Text | Google Scholar

114. Colombaro I, Guisti A, Mainardi F. A class of linear viscoelastic models based on Bessel functtions Meccanica (2017) 52:825–32. doi: 10.1007/s11012-016-0456-5

CrossRef Full Text | Google Scholar

115. Colombaro I, Guisti A, Mainardi F. On the propagation of transient waves in a viscoelastic Bessel medium Z Angew Math Phys. (2017) 62:2017. doi: 10.1007/s00033-017-0808-6

CrossRef Full Text | Google Scholar

116. Colombaro I, Guisti A. Bessel models of linear viscoelasticity. Int J Theor Appl. Mech. (2018) 3:26–31.

Google Scholar

117. Colombaro I, Guisti A, Mainardi F. A one parameter class of fractionalMaxwell-like models. Appl Math Comp Sci AIP Conf Proc. (2017) 1836:020003. doi: 10.1063/1.4981943

CrossRef Full Text | Google Scholar

118. Guisti A, Mainardi F. On infinite series concerning zeros of Bessel functions of the first kind. Eur Phys J Plus(2016) 131:206. doi: 10.1140/ep.jp/i2016-16206-4

CrossRef Full Text | Google Scholar

119. Guisti A, Mainardi F. A dynamic viscoelastic analogy for fluid-filled elastic tubes . Meccanica (2016) 51:2321–30. doi: 10.1007/s11012-016-0376-4

CrossRef Full Text | Google Scholar

120. Colombaro I, Guisti A, Vitali S. Storage and dissipation of energy in Prabhakar viscoelasticity. Mathematics 2018 6:15. doi: 10.3390/math6020015

CrossRef Full Text

121. Guisti A, Colombaro I. Prabhakar-like fractional viscoelasticity. Comm Nonlinear Sci Numer Simulat. (2018) 56:138–43. doi: 10.1016/j.cnsns.2017.08.002

CrossRef Full Text | Google Scholar

122. Abramowitz M, Stegun IA Handbook of Mathematical Functions. New York, NY: Dover (1965).

Google Scholar

123. Hunt A. Non-Debye relaxation and the glass transition. J Non Crystal Solids (1993) 160:183–227.

Google Scholar

124. Bagley RL, Torvik J. Fractional calculus – a different approach to the analysis of viscoelastically damped structures. AIAA J. (1983) 21:741–8. doi: 10.2514/3.8142

CrossRef Full Text | Google Scholar

125. Renardy M. Some remarks on the propagation and non-propagation of discontinuities in linear viscoelastic liquids. Rheol Acta (1982) 21:251–4. doi: 10.1007/BF01515713

CrossRef Full Text | Google Scholar

126. Rossikhin YuA, Shitikova M. Analysis of viscoelastic rod dynamics via models involving fractional derivatives or operators of different orders. Shock Vibration Digest (2004) 36:3–26. doi: 10.1177/0583102404039131

CrossRef Full Text | Google Scholar

127. Rossikhin YuA, Shitikova M. Comparative analysis of viscoelastic models involving fractional derivatives of different orders. Frac Calc Appl Anal. (2007) 10:111–21.

Google Scholar