- 1Faculty of Exact and Natural Science, Mar del Plata Institute for Physics Research, UNMdP, CONICET, National University of Mar del Plata, Mar del Plata, Argentina
- 2Faculty of Engineering, Universidad Atlántida Argentina, Mar del Plata, Argentina
- 3Center for Neuroscience, Swammerdam Institute for Life Sciences, University of Amsterdam, Amsterdam, Netherlands
- 4Institute for Cross-Disciplinary Physics and Complex Systems, UIB, CSIC, University of the Balearic Islands, Palma de Mallorca, Spain
Energy landscapes are a highly useful aid for the understanding of dynamical systems, and a particularly valuable tool for their analysis. For a broad class of rate neural-network models of relevance in neuroscience, we derive a global Lyapunov function which provides an energy landscape without any symmetry constraint. This newly obtained “nonequilibrium potential” (NEP)—the first one obtained for a model of neural circuits—predicts with high accuracy the outcomes of the dynamics in the globally stable cases studied here. Common features of the models in this class are bistability—with implications for working memory and slow neural oscillations—and population bursts, associated with signal detection in neuroscience. Instead, limit cycles are not found for the conditions in which the NEP is defined. Their nonexistence can be proven by resorting to the Bendixson–Dulac theorem, at least when the NEP remains positive and in the (also generic) singular limit of these models. This NEP constitutes a powerful tool to understand average neural network dynamics from a more formal standpoint, and will also be of help in the description of large heterogeneous neural networks.
1. Introduction
The analysis of dissipative, autonomous1 dynamic flows (especially high-dimensional ones) can be greatly simplified, if a function can be constructed to provide an “energy landscape” to the problem. Note that only in very few cases can a nonlinear dynamical system be analytically solved; for instance, if the system itself is a quadratic form, one can use the Wei–Norman (Lie-algebraic) method to reduce it to a linear one (see e.g., [1]). Energy landscapes not only help visualize the systems' phase space and its structural changes as parameters are varied, but allow predicting the rates of activated processes [2–4]. Some fields that benefit from the energy landscape approach are optimization problems [5], neural networks [6], protein folding [7], cell nets [8], gene regulatory networks [9, 10], ecology [11], and evolution [12].
For continuous-time flows, the possibility of this “Lyapunov function”—with its distinctive property outside the attractors—was suggested in the context of the general stability problem of dynamical systems [13] and in a sense, it adds a quantitative dimension to the qualitative theory of differential equations. The linearization of the flow around its attractors always provides such a function, but its validity breaks down well inside their own basin. Instead, finding a global Lyapunov function is not an easy problem2. If only the information of the (deterministic) dynamical system is to be used, this function can be found for the so-called “gradient flows”—purely irrotational flows in 3D, exact (longitudinal) forms in any dimensionality. But since for general relaxational flows (having nontrivial Helmholtz–Hodge decomposition) the integrability conditions are not automatically met, some more information is needed.
A hint of what information is needed comes from recalling that dynamical systems are models and as such, they leave aside a multitude of degrees of freedom—deemed irrelevant to the model, but nonetheless coupled to the “system.” A useful framework to deal with them is the one set forward by Langevin [15], which makes the dynamical flow into a stochastic process (thus nonautonomous, albeit driven by a stationary “white noise” process).
What Graham and his collaborators [16, 17] realized more than 30 years ago is that even in the deterministic limit, this space enlargement can eventually help meet the integrability conditions. Given an initial state xi of a (continuous-time, dissipative, autonomous) dynamic flow ẋ = f (x), its conditional probability density function (pdf) P(x, t|xi, 0) when submitted to a (Gaussian, centered) white noise ξ(t) with variance γ, namely3
obeys the Fokker–Planck equation (FPE)
in terms of the “drift” D(1) = f (x) and “diffusion” D(2) = γ Kramers–Moyal coefficients [18–20]. Being the flow nonautonomous but dissipative, one can expect generically situations of statistical energy balance in which the pdf becomes stationary, ∂tPst(x) = 0, thus independent of the initial state. Then by defining , it is immediate to find .
For an n–component dynamic flow submitted to m ≤ n (Gaussian, uncorrelated, centered) white noises ξi(t) with common variance γ,
(σ is an n × m constant matrix) the nonequilibrium potential (NEP) has been thus defined [16] as
That implies , which replaced into the stationary n–variable FPE ∇·[f(x)Pst(x) − γQ∇Pst(x)] = 0 (with Q : = σσT = QT) yields in the the equation
from which Φ(x) can in principle be found. In an attractor's basin, asymptotic stability imposes D : = det Q > 0. In fact, for m = n (restriction adopted hereafter) it is D = (det σ)2, which in turn requires σ to be nonsingular. Using Equation (2),
for γ → 0. Hence, Φ(x) is a Lyapunov function for the deterministic dynamics.
Equation (2) has the structure of a Hamilton–Jacobi equation. This trouble can be circumvented if we can decompose f(x) = d(x) + r(x), with d(x) : = −Q∇Φ the dissipative part of f(x)4. Then Equation (2) reads rT(x)∇Φ = 0, and r(x) is the conservative part of f(x). Note that d(x) is still irrotational (in the sense of the Helmholtz decomposition) but is not an exact form (the Hodge decomposition is made in the enlarged space).
For n = 2 we may write r(x) = κ Ω∇Φ, with Ω the N = 1 symplectic matrix. Hence f(x) = −(Q − κΩ)∇Φ, with det(Q − κΩ) = D + κ2 > 0, and thus
For arbitrary real σij we can parameterize
and define (note that the condition D > 0 imposes α2 ≠ α1). Then
and Equation (3) reads
(∂k is a shorthand for ∂/∂xk). If a set {λ1, λ2, λ, κ} can be found such that Φ(x) fulfills the integrability condition ∂2∂1Φ = ∂1∂2Φ, then a NEP exists. Early successful examples are the complex Ginzburg–Landau equation (CGLE) [21, 22] and the FitzHugh–Nagumo (FHN) model [23, 24]5. This scheme has been later reformulated [29], extended [30], and exploited in many interesting cases [6–12].
The goal of this work is to show that a NEP exists for a broad class of rate models of neural networks, of the type proposed by Wilson and Cowan [31]. The Wilson–Cowan model has been used to model many different dynamics, brain areas, and neural-network structures in the brain. Therefore, the derivation of a NEP has potential implications for many problems in computational neuroscience. Section 2 is devoted to an analysis of the model and variations of section 3, to the derivation of the NEP in some of the cases studied in section 2, which are of high relevance in neuroscience. Section 4 undertakes a thorough discussion of our findings, and section 5 collects our conclusions.
2. The Wilson–Cowan Model
Elucidating the architecture and dynamics of the neocortex is of utmost importance in neuroscience. But despite ongoing titanic efforts like the Human Brain Project or the BRAIN initiative, we are still very far from that goal. Given that the dynamics of single typical neurons has been relatively well described (in some cases even by analytical means), a fundamental approach can be practiced for small neural circuits. This means describing them as networks of excitable elements (neurons) connected by links (synapses), and solving the network dynamics by hybrid (analytical-numerical) techniques. However, the time employed in the analytical solution has poor scaling with size. Hence, this approach becomes unworkable for more than a few recurrently interconnected neurons, and one has to rely only on numerical simulations.
Fortunately—as evidenced since long ago by the existence (as in a medium) of wavelike excitations—the huge connectivity of the neocortex enables coarse-grained or mean-field descriptions, which provide more concise and relevant information to understand the mesoscopic dynamics of the system6. Frequently obtained via mean-field techniques and commonly referred to as rate models or neural mass models, coarse-grained reductions have been widely used in the theoretical study of neural systems [31, 33–35]. In particular, the one proposed by Wilson and Cowan [31] has proved to be very useful in describing the macroscopic dynamics of neural circuits. This level of description is able to capture many of the dynamical features associated with several cognitive and behavioral phenomena, such as working memory [33, 36] or perceptual decision making [35, 37]. It is also possible to use a rate model approach to study the dynamics of networks constituted by heterogeneous neurons [38, 39], thus recovering part of the complexity lost in the averaging. Disposing of an “energy function” (not restricted to symmetric couplings) for rate-level dynamics of neural networks would be a major added advantage.
The Wilson–Cowan model describes the evolution of competing populations x1, x2 of excitatory and inhibitory neurons, respectively. The model is defined by [31]
where x1 and x2 represent the coarse-grained activity of an excitatory and an inhibitory neural population, respectively, and the monotonically increasing (sigmoidal) response functions
are such that sk(0) = 0, and range from for ik → −∞ to for ik → ∞. So the first crucial observation about the model is that it is asymptotically linear.
The currents ik are in turn linearly related to the xk:
All the parameters are real and moreover, the jkl are positive (j11 and j22 are recurrent interactions, j12 and j21 are cross-population interactions). The above definitions are such that for M = 0, x = 0 is a stable fixed point. To avoid confusions in the following, note that det J = −(j11j22 − j12j21).
Wilson and Cowan [31] found interesting features as e.g., staircases of bistable regimes and limit cycles. A thorough analysis of the model's bifurcation structure has been undertaken in Borisyuk and Kirillov [40]. The authors create a two-parameter structural portrait by fixing all the parameters but μ1 and j21 and find that the μ1−j21 plane turns out to be partitioned into several regions by:
• a fold point bifurcation curve (the number of fixed points changes by two when crossed),
• an Andronov–Hopf bifurcation curve (separates regions with stable and unstable foci),
• a saddle separatrix loop (a limit cycle on one side, none on the other), and
• a double limit cycle curve (the number of limit cycles changes by two).
The uncoupled case (j12 = j21 = 0) is clearly a gradient system, with potential
where i1 = j11x1 + μ1 and i2 = −j22x2 + μ2. Functions Fk differ only in the values of their parameters. Their functional expression, involving polylogs, is uninteresting besides being complicated. Much more insight is obtained by observing the global features:
• for ik → −∞, Equation (4) become ,
• for ik → ∞, .
So it seems interesting to look at them in the limit βk → ∞ (k = 1, 2),
θ(x) being Heaviside's unit step function. Unfortunately, neither Equation (4) nor their singular limit fulfill the above mentioned integrability condition.
In practice however, the names of Wilson and Cowan are associated to the broader class of rate models. In the following we shall show that the model defined by
does admit a NEP—for any functional forms of the nonlinear single-variable functions sk(ik)7—provided global stability is assured.
3. Nonequilibrium Potential
For the model defined by Equation (6), it is . The condition ∂2∂1Φ = ∂1∂2Φ, namely
boils down to
(and these in turn to j21 j11 τ1 λ1 = j12 j22 τ2 λ2) so that λ2, λ and κ can be expressed in terms of λ1, which sets the global scale of Φ(x):
Since r(x) = κ Ω∇Φ, τ1 = τ2 suffices to render the flow purely dissipative (albeit not gradient). From this, a good choice is . In summary,
and Equation (3) becomes
Integrating Equation (7) over any path from x = 0, yields
4. Theoretical Analysis
The first—crucial—observation is that being sk(ik) sigmoidal functions, Equation (8) is at most quadratic. Global stability thus imposes detJ < 0, i.e., j11j22 > j12j21. But note that matrix J also determines the paraboloid's cross section8.
If the form in the first term of Equation (8) could be straightforwardly factored out, then one could tell what its section is by watching whether the factors are real or complex. A more systematic approach is to reduce xTAx to canonical form by a similarity transformation that involves the normalized eigenvectors of A. Then the inverse squared lengths of the principal axes are the eigenvalues of A. Since the jkl are positive and detJ < 0, the second term is lesser than the first and the cross section is definitely elliptic. Although global stability rules out detJ > 0, we can conclude that the instability proceeds through a pitchfork (codimension one) bifurcation along the minor principal axis (because of the double role of detJ), not a Hopf (codimension two) one.
For the remaining terms, we note that Equation (7) can be written as and recall that sk(ik) have sigmoidal shape. So at large |x|, the component will tend to different constants—according to the signs of ik—so the asymptotic contribution of these terms will be piecewise linear, namely a collection of half planes.
The reduction to the uncoupled case can be safely done by writing j12 = ϵ and j21 = αϵ:
To first order as ϵ → 0, one retrieves
so by choosing and ,
A popular choice—that can be cast in the form of Equation (5)—is , βk > 0, for which9
Its βk → ∞ limit, νkθ(ik) with
highlights the cores of the response functions while keeping the global landscape10.
As a check of Equation (8), we show in the next subsections the mechanism whereby Equation (6) can sustain bistability.
4.1. Analytically, for Steplike Response Function sk(ik): = νkθ(ik)
• For μk < 0 (k = 1, 2), there is no question that x = 0 is a fixed point (we may call it the “off” node); Equation (8) reduces to its first term and Φ(0) = 0.
• By suitably choosing the half planes—taking advantage of the relative sign in the numerator of the second term in Equation (8)—another fixed point (the “on” node) can be induced11 if (JN)k > −μk, k = 1, 2 (namely j11ν1−j12ν2 > −μ1, j21ν1 − j22ν2 > − μ2) with
If μ1 is varied (as in [31, 40]), equistability is achieved for
The intersection of the cores of the sk(ik)12 is a (singular in this limit) saddle point. Figure 1B illustrates this situation for the parameters quoted in the caption (the choice obeys to the fact that global stability makes condition j21ν1 −j22 ν2 > −μ2 rather stringent).
• As μk → 0, k = 1, 2, this saddle point moves toward the “off” node. After a (direct) saddle-node bifurcation, only the “on” node at xk = νk remains, since conditions (JN)k > −μk, k = 1, 2 are better satisfied, see Figure 1A.
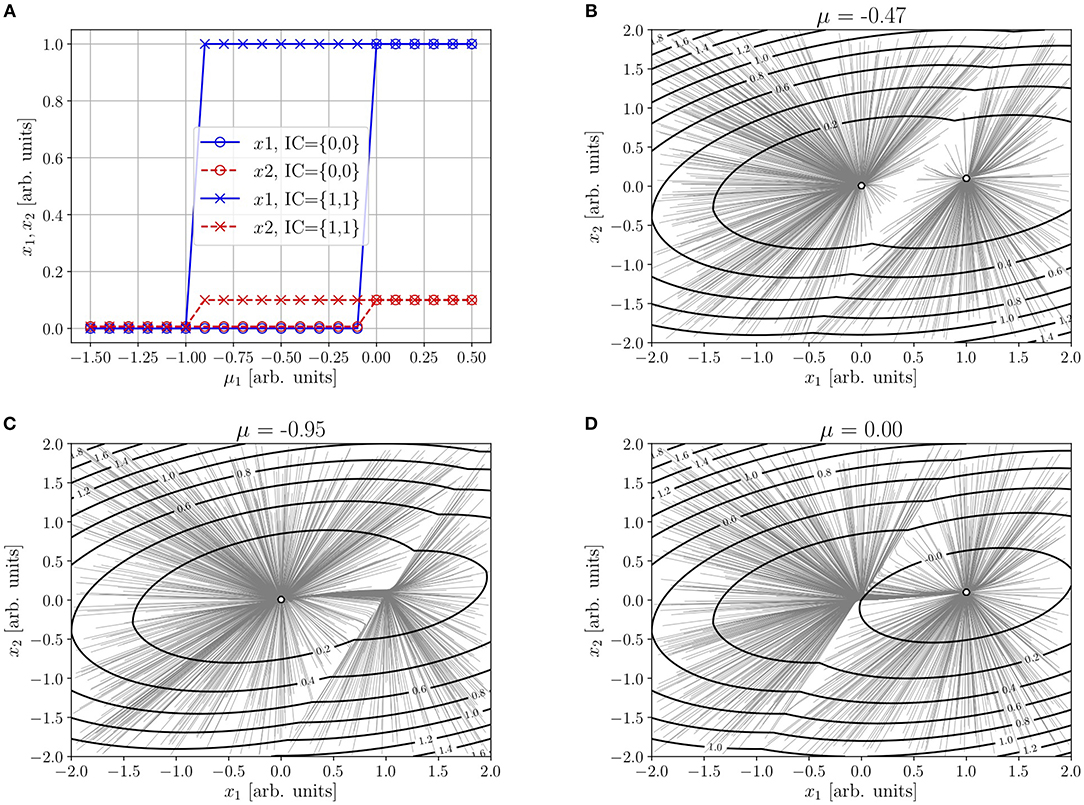
Figure 1. Illustration of the analytical results in section 4.1, for ρ = 1, τ1 = τ2 = 1, μ2 = −0.01, ν1 = 1, ν2 = 0.1, j11 = 1, j22 = 0.5, j12 = 0.5, j21 = 0.1. (A) Abscissas (solid line) and ordinates (dashed line) of the “off” (circle) and “on” (cross) nodes of Equation (6) with sk(ik): = νkθ(ik), as functions of μ1. Trajectories from random initial conditions and contour plot of the NEP—Equation (8), with Sk(ik)−Sk(μk) given by Equation (10)—in the equistable case given by Equation (11) (B), and near the “off” (C) and “on” (D) saddle-node bifurcations.
If there is room for some spreading of the core, as seen in Figures 1B–D, the former result remains valid for whatever analytical form of the response functions. In such a case, the saddle point will be analytical.
In the singular limit sk(ik) : = νkθ(ik) we deal with in this subsection, we can prove rigorously the nonexistence of limit cycles (at least for large μk < 0, k = 1, 2). The Bendixson–Dulac theorem states that if there exists a function Φ(x) (called the Dulac function) such that div(Φf) has the same sign almost everywhere13 in a simply connected region of the plane, then the plane autonomous system has no nonconstant periodic solutions lying entirely within the region. Because of Equation (2),
Clearly, divf < 0 almost everywhere [i.e., except at the cores of the sk(ik)]. For μk < 0 (k = 1, 2) and large, Φ(x) will be essentially the quadratic form in the first term of Equation (8), so it meets the conditions to be a Dulac function in a simply connected region of the plane.
4.2. Numerically, For a (More) Realistic Example
For the integrable version (r1 = r2 = 0) of Equations (4)–(5), it is
(recall that μ = i(x = 0)). Here, because of the condition sk(0) = 0, the “off” node will move as μ1 is varied. Figure 2 considers the integrable version of Figures 4 and 5 in [31] (the only ones for which det J < 0). The parameters specified by the authors are j11 = 12, j12 = 4, j21 = 13, j22 = 11, β1 = 1.2, , β2 = 1, , μ2 = 0. The values of τ1 and τ2 (as well as ν1 and ν2, not specified by the authors) have been chosen as 1 throughout14.
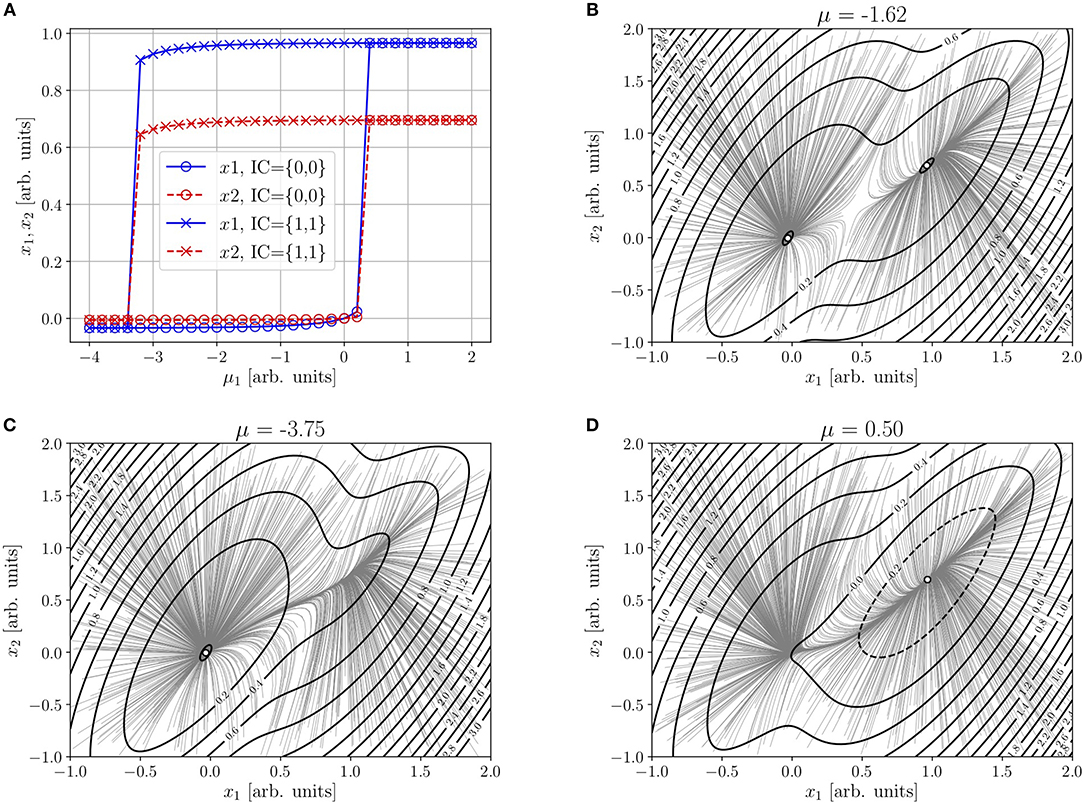
Figure 2. (A) Abscissas (solid line) and ordinates (dashed line) of the “off” (circle) and “on” (cross) nodes of Equations (4)–(5) (with r1 = r2 = 0) as functions of μ1. (B) Trajectories from random initial conditions and contour plot of the NEP—Equation (8), with Sk(ik)−Sk(μk) given by Equation (12)—near the equistable case μ1 = −1.7 (B), and near the “off” (C), and “on” (D) saddle-node bifurcations. Remaining parameters: ρ = 1, τ1 = τ2 = 1, ν1 = ν2 = 1, μ2 = 0, j11 = 12, j12 = 4, j21 = 13, j22 = 11, β1 = 1.2, , β2 = 1, and .
Frame (a), as well as the trajectories from random initial conditions (uniform distribution) in frames (b)–(d), of Figures 1, 2 are the result of a 4th order Runge–Kutta integration of Equation (6), after 100,000,000 iterations with Δt = 10−4. In the contour plots of Φ(x) of frames (b)–(d) of Figure 2, Sk(ik) − Sk(μk) is given by Equation (12). Even though the details differ between Figures 1, 2, the structural picture (in particular, the inverse-direct saddle-node mechanism) remains the same.
5. Different Relaxation Times
When τ1 ≠ τ2, then
and d(x) = f(x) − r(x). However Φ(x) can remain the same, as far as τ1τ2 does not change. So whereas the contour plots of the NEP in Figure 3 reproduce those of Figures 2C,D, the displayed set of trajectories (from random initial conditions within suitably selected tiny patches) have r(x)≠0 and consequently, many of them perform a large excursion toward the attractor.
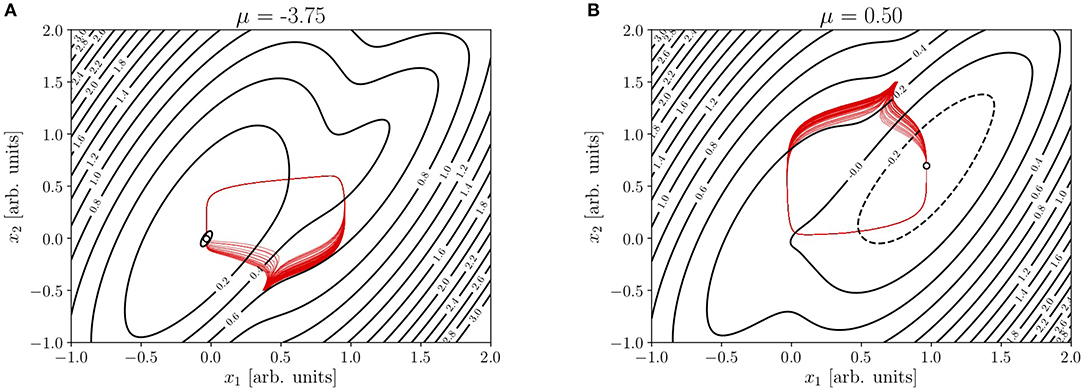
Figure 3. (A,B) Contour plot of the NEP in Figures 2C,D, together with trajectories (in red) from random initial conditions within suitably selected tiny patches. Parameters: ρ = 1, τ1 = 0.5, τ2 = 2, ν1 = ν2 = 1, μ2 = 0, j11 = 12, j12 = 4, j21 = 13, j22 = 11, β1 = 1.2, , β2 = 1, and .
Excitable events such as those described here by the NEP, in which the activity of excitatory neurons in the population shows a sharp peak, are known in the computational neuroscience literature as “population bursts.” These are brief events of high excitatory activity in the neural system being modeled. In neural network models composed of interconnected spiking neurons, they reflect a sudden rise in spiking activity at the level of the whole population (or a significant part of it), in such a way that a high proportion of neurons in the network fire at least one action potential during a short time window. Spiking neurons participating in the population burst are therefore transiently synchronized. In spite of not being able to properly capture synchronous phenomena, the Wilson–Cowan model may capture this phenomenon as a transient peak of activity that is later shut down by inhibition. But for more realistic models, additional biophysical mechanisms (such as actual spiking dynamics, refractory period of neurons or short-term adaptation) have to be considered since they are likely involved in population bursts on real neural systems [41]. Population bursts have several computational uses; for example, they can be used to transmit temporally precise information to other brain areas, even in the presence of noise or heterogeneity [38].
6. Conclusions
Rate- (also called neural mass-) models have been a useful approach to neural networks for half a century. Today, their simplicity (not short of comprehensivity) makes them ideal to fulfill the node dynamics in, for instance, connectome-based brain networks. So the availability of an “energy function” for rate models is expected to be welcome news.
Dynamical systems of the form given by Equation (6) admit a NEP regardless of the functional forms of the nonlinear single-variable functions sk(ik). Throughout this work, the latter are assumed to have the same functional form, of sigmoidal shape. But neither condition is necessary to satisfy the integrability condition.
A crucial observation about rate models—even the one put forward by Wilson and Cowan [31], and given by Equations (4)–(5)—is that they are asymptotically linear, so their eventual NEP can be at most quadratic. Then in principle, global stability rules out some coupling configurations. Obviously, this requirement can be relaxed if the rate model fulfills the node dynamics of a neural network, for what matters in that case is the network's global stability.
The here obtained NEP provides a more quantitative intuition on the phenomenon of bistability, that has been naturally found in real neural systems. Neural bistability underlies e.g., the persistent activity which is commonly found in neurons of the prefrontal cortex, a mechanism that is thought to maintain information during working memory tasks [36, 42]. In the presence of neural noise and other adaptation mechanisms, bistability is also a useful hypothesis to explain slow irregular dynamics or “up” and “down” dynamics, also observed across cortex and modeled using bistable dynamics [43–45].
Our results open the door to considering the calculation of nonequilibrium potentials of rate-based neural network models, and in particular considering the implications of different biologically realistic dynamics in such potentials. One interesting possibility is to consider in our model the effect of short-term synaptic plasticity effects. Short-term plasticity has been shown to impact computational properties of neural systems, such as their signal detection abilities [46–48], their pattern storage capacity [49, 50], or the statistics of neural bistable dynamics [44, 45]. We would expect, for example, that changes in the ability of neural systems to detect weak signals due to short-term plasticity could be reflected in changes in the nonequilibrium potential landscape, making population bursts easier to be triggered by weak stimuli. Changes in the statistics of neural bistable dynamics, or ‘up-down' transitions, could be reflected in swifts of the dwells in the landscape, and also on the statistics of real experimental data.
Finally, it is worth mentioning that the here obtained NEP—valid as argued for generic transfer functions sk(ik)—opens the door to the potential use of more generic rate models in the field of artificial neural networks and deep learning. By identifying the NEP with the cost function to be minimized, gradient descent algorithms can be used to train networks of generic Wilson–Cowan units for different tasks. This implies that more realistic and less computationally expensive neural population models can be trained and used for behavioral tasks, a topic that has gathered attention recently [51, 52].
Author Contributions
All the listed authors have made substantial and direct intellectual contribution to this work, and approve its publication. In particular, JM proposed the idea, contributed preliminary analytical calculations, and provided key information from the field of neuroscience.
Funding
RD acknowledges support from UNMdP http://dx.doi.org/10.13039/501100007070, under Grant 15/E779–EXA826/17. NM acknowledges a Doctoral Fellowship from CONICET http://dx.doi.org/10.13039/501100002923.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
JM thanks warmly A. Longtin for his support during the early stages of this work. ID and HW thank, respectively, IFIMAR and IFISC for their hospitality. NM thanks HW and IFISC for their hospitality during his research visit.
Footnotes
1. ^The framework can also be applied to nonautonomous flows, as far as their explicit time-dependence can be regarded as slow in comparison with the relaxation times toward the system's attractors (adiabatic approximation).
2. ^By this we mean that we know no systematic methods other than the one we describe here. Of course, there is always room for heuristically finding a global Lyapunov function for some systems, even those containing dynamical variables that exert feedback control (see e.g.,[14]).
3. ^We follow the usual notation in physics, which strictly means dx = f(x)dt + dW(t) in terms of the Wiener process . Note that dx−dW(t) is still a (deterministic) dynamic flow, which implies some kind of connection in the x−W bundle (but not the one of gauge theory).
4. ^Had we written ẋ = f(x) + σξ(t) for n = 1, then
5. ^The knowledge of a NEP for FHN units has greatly simplified the dynamical analysis of reaction–diffusion [2–4] and network [25–27] FHN models, as well as the study of stochastic resonance in some extended systems [3, 28].
6. ^Note that the usually large connectivity of general networks already enables mean-field descriptions (see e.g.,[32]). But the connectivity of the neocortex is overwhelmingly larger than that.
7. ^With our mind in neurophysiology applications, we shall assume sk(ik) to have the same functional form, of sigmoidal shape. But neither condition is necessary to satisfy the integrability condition.
8. ^Incidentally, note that .
9. ^Using sk(ik): = tanhik, Tsodyks et al. have reported a paradoxical increase in x1 as a result of an increase in μ2. Unfortunately, this occurs for det J > 0. What we can assure is that there is a saddle point involved.
10. ^For μk ≠ 0, Equation (10) can be arrived at from Equation (9) given that for βk → ∞, . Once Equation (10) is obtained, one can let μk → 0.
11. ^(through an inverse saddle-node bifurcation at the “on” location: in one variable, resets the slope to zero at x = a).
12. ^(located at the solution of Jx+M = 0)
13. ^Everywhere except possibly in a set of measure 0.
14. ^This has the additional advantage that the flow is purely dissipative, facilitating dynamical conclusions from the landscape.
References
1. Shang Y. Analytical solution for an in-host viral infection model with time-inhomogeneous rates. Acta Phys Pol B (2015) 46:1567–77. doi: 10.5506/APhysPolB.46.1567
2. Wio HS. Nonequilibrium potential in reaction–diffusion systems. in: Garrido P, Marro J, editors. 4th Granada Seminar in Computational Physics. Dordrecht: Springer (1997). p. 135–93.
3. Wio HS, Deza RR. Aspects of stochastic resonance in reaction–diffusion systems: the nonequilibrium-potential approach. Eur Phys J Special Topics (2007) 146:111–26. doi: 10.1140/epjst/e2007-00173-0
4. Wio HS, Deza RR, López JM. An Introduction to Stochastic Processes and Nonequilibrium Statistical Physics, revised edition. Singapore: World Scientific (2012).
5. Kirkpatrick S, Gelatt CD, Vecchi MP. Optimization by simulated annealing. Science (1983) 220:671–80. doi: 10.1126/science.220.4598.671
6. Yan H, Zhao L, Hu L, Wang X, Wang E, Wang J. Nonequilibrium landscape theory of neural networks. Proc Natl Acad Sci USA (2013) 110:E4185–94. doi: 10.1073/pnas.1310692110
7. Wang J, Oliveira RJ, Chu X, Whitford PC, Chahine J, Han W, et al. Topography of funneled landscapes determines the thermodynamics and kinetics of protein folding. Proc Natl Acad Sci USA (2012) 109:15763–8. doi: 10.1073/pnas.1212842109
8. Wang J, Huang B, Xia X, Sun Z. Funneled landscape leads to robustness of cell networks: yeast cell cycle. PLoS Comput Biol. (2006) 2:e147. doi: 10.1371/journal.pcbi.0020147
9. Kim KY, Wang J. Potential energy landscape and robustness of a gene regulatory network: toggle switch. PLoS Comput Biol. (2007) 3:e60. doi: 10.1371/journal.pcbi.0030060
10. Wang J, Xu L, Wang E, Huang S. The potential landscape of genetic circuits imposes the arrow of time in stem cell differentiation. Biophys J. (2010) 99:29–39. doi: 10.1016/j.bpj.2010.03.058
11. Li C, Wang E, Wang J. Potential landscape and probabilistic flux of a predator prey network. PLoS Comput Biol. (2011) 6:e17888. doi: 10.1371/journal.pone.0017888
12. Zhang F, Xu L, Zhang K, Wang E, Wang J. The potential and flux landscape theory of evolution. J Chem Phys. (2012) 137:065102. doi: 10.1063/1.4734305
13. Lyapunov AM. The General Problem of the Stability of Motion (in russian). Kharkiv: Mathematical Society of Kharkov (1892). English transl.: Int. J. Control (1992) 55:531–772.
14. Shang Y. Global stability of disease-free equilibria in a two-group SI model with feedback control. Nonlin Anal. (2015) 20:501–8. doi: 10.15388/NA.2015.4.3
16. Graham R. Weak noise limit and nonequilibrium potentials of dissipative dynamical systems. In: Tirapegui E, Villarroel D, editors. Instabilities and Nonequilibrium Structures. Dordrecht: Reidel (1987). p. 271–90.
17. Graham R, Tél T. Steady-state ensemble for the complex Ginzburg–Landau equation with weak noise. Phys Rev A (1990) 42:4661. doi: 10.1103/PhysRevA.42.4661
18. Risken H. The Fokker-Planck Equation: Methods of solution and applications. 2nd ed. Berlin: Springer (1996).
19. Gardiner CW. Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences. Berlin: Springer (2004).
21. Descalzi O, Graham R. Gradient expansion of the nonequilibrium potential for the supercritical Ginzburg–Landau equation. Phys Lett A (1992) 170:84. doi: 10.1016/0375-9601(92)90777-J
22. Montagne R, Hernández-García E, San Miguel M. Numerical study of a Lyapunov functional for the complex Ginzburg–Landau equation. Physica D (1996) 96:47. doi: 10.1016/0167-2789(96)00013-9
23. Izús GG, Deza RR, Wio HS. Exact nonequilibrium potential for the FitzHugh–Nagumo model in the excitable and bistable regimes. Phys Rev E (1998) 58:93–8. doi: 10.1103/PhysRevE.58.93
24. Izús GG, Deza RR, Wio HS. Critical slowing-down in the FitzHugh–Nagumo model: a non-equilibrium potential approach. Comp Phys Comm. (1999) 121–122:406–7. doi: 10.1016/S0010-4655(99)00368-9
25. Izús GG, Sánchez AD, Deza RR. Noise-driven synchronization of a FitzHugh–Nagumo ring with phase-repulsive coupling: a perspective from the system's nonequilibrium potential. Physica A (2009) 388:967–76. doi: 10.1016/j.physa.2008.11.031
26. Sánchez AD, Izús GG. Nonequilibrium potential for arbitrary-connected networks of FitzHugh–Nagumo elements. Physica A (2010) 389:1931–44. doi: 10.1016/j.physa.2010.01.013
27. Sánchez AD, Izús GG, dell'Erba MG, Deza RR. A reduced gradient description of stochastic-resonant spatiotemporal patterns in a FitzHugh–Nagumo ring with electric inhibitory coupling. Phys Lett A (2014) 378:1579–83. doi: 10.1016/j.physleta.2014.03.048
28. Wio HS, Von Haeften B, Bouzat S. Stochastic resonance in spatially extended systems: the role of far from equilibrium potentials. Physica A (2002) 306:140–56. doi: 10.1016/S0378-4371(02)00493-4
29. Ao P. Potential in stochastic differential equations: novel construction. J Phys A (2004) 37:L25–30. doi: 10.1088/0305-4470/37/3/L01
30. Wu W, Wang J. Landscape framework and global stability for stochastic reaction diffusion and general spatially extended systems with intrinsic fluctuations. J Phys Chem B (2013) 117:12908–34. doi: 10.1021/jp402064y
31. Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J. (1972) 12:1–24. doi: 10.1016/S0006-3495(72)86068-5
32. Shang Y. Impact of self-healing capability on network robustness. Phys Rev E (2015) 91:042804. doi: 10.1103/PhysRevE.91.042804
33. Amit DJ, Brunel N. Model of global spontaneous activity and local structured activity during delay periods in the cerebral cortex. Cereb Cortex (1997) 7:237–52. doi: 10.1093/cercor/7.3.237
34. Brunel N. Dynamics of sparsely connected networks of excitatory and inhibitory spiking neurons. J Comp Neurosci. (2000) 8:183–208. doi: 10.1023/A:1008925309027
35. Wong K, Wang XJ. A recurrent network mechanism of time integration in perceptual decisions. J Neurosci. (2006) 26:1314–28. doi: 10.1523/JNEUROSCI.3733-05.2006
36. Wang XJ. Synaptic reverberation underlying mnemonic persistent activity. Trends Neurosci. (2001) 24:455–63. doi: 10.1016/S0166-2236(00)01868-3
37. Wang XJ. Probabilistic decision making by slow reverberation in cortical circuits. Neuron (2002) 36:955–68. doi: 10.1016/S0896-6273(02)01092-9
38. Mejías JF, Longtin A. Optimal heterogeneity for coding in spiking neural networks. Phys Rev Lett. (2012) 108:228102. doi: 10.1103/PhysRevLett.108.228102
39. Mejías JF, Longtin A. Differential effects of excitatory and inhibitory heterogeneity on the gain and asynchronous state of sparse cortical networks. Front Comput Neurosci. (2014) 8:107. doi: 10.3389/fncom.2014.00107
40. Borisyuk RM, Kirillov AB. Bifurcation analysis of a neural network model. Biol Cybern. (1992) 66:319–25. doi: 10.1007/BF00203668
41. Tsodyks M, Uziel A, Markram H. Synchrony generation in recurrent networks with frequency-dependent synapses. J Neurosci. (2000) 20:RC50. doi: 10.1523/JNEUROSCI.20-01-j0003.2000
42. Funahashi S, Bruce CJ, Goldman-Rakic PS. Mnemonic coding of visual space in the monkey's dorsolateral prefrontal cortex. J Neurophysiol. (1989) 61:331–49. doi: 10.1152/jn.1989.61.2.331
43. McCormick DA. Neuronal networks: flip-flops in the brain. Curr Biol. (2005) 15:R294–6. doi: 10.1016/j.cub.2005.04.009
44. Holcman D, Tsodyks M. The emergence of up and down states in cortical networks. PLoS Comput Biol. (2006) 2:174–81. doi: 10.1371/journal.pcbi.0020023
45. Mejías JF, Kappen HJ, Torres JJ. Irregular dynamics in up and down cortical states. PLoS ONE (2010) 5:e13651. doi: 10.1371/journal.pone.0013651
46. Mejías JF, Torres JJ. The role of synaptic facilitation in spike coincidence detection. J Comput Neurosci. (2008) 24:222–34. doi: 10.1007/s10827-007-0052-8
47. Mejías JF, Torres JJ. Emergence of resonances in neural systems: the interplay between adaptive threshold and short-term synaptic plasticity. PLoS ONE (2011) 6:e17255. doi: 10.1371/journal.pone.0017255
48. Torres JJ, Marro J, Mejías JF. Can intrinsic noise induce various resonant peaks? New J Phys. (2011) 13:053014. doi: 10.1088/1367-2630/13/5/053014
49. Mejías JF, Torres JJ. Maximum memory capacity on neural networks with short-term synaptic depression and facilitation. Neural Comput. (2009) 21:851–71. doi: 10.1162/neco.2008.02-08-719
50. Mejías JF, Hernández-Gómez B, Torres JJ. Short-term synaptic facilitation improves information retrieval in noisy neural networks. Europhys Lett. (2012) 97:48008. doi: 10.1209/0295-5075/97/48008
51. Mante V, Sussillo D, Shenoy KV, Newsome WT. Context-dependent computation by recurrent dynamics in prefrontal cortex. Nature (London). (2013) 503:78–84. doi: 10.1038/nature12742
Keywords: nonequilibrium potential, energy landscape, neural networks, bistability, firing rate dynamics
Citation: Deza RR, Deza I, Martínez N, Mejías JF and Wio HS (2019) A Nonequilibrium-Potential Approach to Competition in Neural Populations. Front. Phys. 6:154. doi: 10.3389/fphy.2018.00154
Received: 05 May 2018; Accepted: 17 December 2018;
Published: 10 January 2019.
Edited by:
Manuel Asorey, Universidad de Zaragoza, SpainReviewed by:
Fernando Montani, Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), ArgentinaYilun Shang, Northumbria University, United Kingdom
Copyright © 2019 Deza, Deza, Martínez, Mejías and Wio. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Roberto R. Deza, ZGV6YUBtZHAuZWR1LmFy
 Roberto R. Deza
Roberto R. Deza Ignacio Deza1,2
Ignacio Deza1,2 Jorge F. Mejías
Jorge F. Mejías Horacio S. Wio
Horacio S. Wio