Weak Quasielastic Hyperon Production Leading to Pions in the Antineutrino-Nucleus Reactions

1. Introduction

A simultaneous knowledge of the neutrino and antineutrino cross sections in the same energy region for the nuclear targets is highly desirable in order to understand the systematics relevant for the analyses of various neutrino oscillation experiments being done in search of CP violation in the leptonic sector and in the determination of neutrino mass hierarchy [1–7]. Experimentally there are many results available in the cross section measurements for the various weak processes induced by the neutrinos in nuclei in the sub-GeV and few-GeV energy region [8–11]. There are very few measurements reported for the processes induced by the antineutrinos in the same energy region specially around $E_{{\bar{\nu }}_{\mu }}\approx 1$ GeV [8, 12]. Theoretically, however, there exists quite a few calculations for the antineutrino-nucleus cross sections and some of them have been incorporated in most of the neutrino event generators like GENIE [13], NEUT [14], NuWro [15] and GiBUU [16]. In this energy region of antineutrinos, $E_{{\bar{\nu }}_{\mu }}\approx 0.5-1.2$ GeV, the most important processes contributing to the nuclear cross sections are the quasielastic (QE) scattering and the inelastic scattering where the excitation of Δ resonance is the dominant process contributing to the single pion production (CC1π). There is some contribution from the excitation of higher resonances and very little contribution from the deep inelastic scattering (DIS) [17–21].

It is well known that the cross sections for the various weak processes induced by the neutrinos and antineutrinos differ by the sign of the interference terms between the vector and the axial vector currents making the antineutrino cross sections smaller and fall faster with Q² as compared to the neutrino cross sections [22–27]. There is another difference between the neutrino and antineutrino induced processes on the nucleon and the nuclear targets which has not been adequately emphasized in the context of the discussion of the systematics in the neutrino oscillation experiments. This difference arises due to the phenomenological ΔS = ΔQ rule implicit in the standard model (SM) in the charged current sector which allows the quasielastic production of hyperons on nucleons induced by the antineutrinos, i.e., ${\bar{\nu }}_l+N\to l^{+}+Y;N=n\mathrm{\text{ or }}p,Y=\Lambda ,{\Sigma }^0\mathrm{\text{or}}{\Sigma }^{-}$, but not with the neutrinos i.e., ${\nu }_l+N\cancel{\to }{l}^{-}+Y$. The hyperon production process is Cabibbo suppressed and its cross section is generally small as compared to the quasielastic or Δ production in the ΔS = 0 sector. However, in the lower energy region of the antineutrinos i.e., $E_{{\bar{\nu }}_{\mu }}<<1$ GeV where the production of Δ resonance is kinematically inhibited due to a higher threshold for the Δ production as compared to Λ production, the hyperon production cross section may not be too small. These hyperons dominantly decay into π⁻ and π^o and give additional contribution to the pion production induced by the antineutrinos from the nucleon and the nuclear targets.

Since π⁻ and π^o are the largest misidentified background for the ${\bar{\nu }}_{\mu }$ disappearance and ${\bar{\nu }}_e$ appearance channels in the present neutrino oscillation experiments with the antineutrino beams, the hyperon production becomes an important process to be considered in the accelerator experiments specially at T2K [8], MicroBooNE [9], MiniBooNE [10, 12] and NOνA [28], where the antineutrino energies are in the sub-GeV energy region. Moreover, these experiments are being done using nuclear targets like ¹²C, ¹⁶O, ⁴⁰Ar, etc., where the pion production cross sections through the Δ excitations are considerably suppressed due to the nuclear medium effect (NME) and the final state interaction (FSI) effect [17, 18]. On the other hand, the pions arising from the hyperons are expected to be less affected by these effects due to the fact that the hyperon decay widths are highly suppressed in the nuclear medium making them live longer and travel through most of the nuclear medium before they decay [29, 30]. Therefore, the two effects discussed above i.e., the lower threshold energy of the hyperon production and near absence of the FSI for the pions coming from the hyperon decay compensate for the ${tan}^2{\theta }_c$ suppression as compared to the pions coming from the Δ production. This makes these processes important in the context of oscillation experiments with antineutrino beams in the sub-GeV energy region.

Notwithstanding the importance of the hyperon production in the context of present day oscillation experiments with the accelerator antineutrino beams at lower energies, the study of these processes is important in their own right as these processes give us an opportunity to understand the weak interactions at higher energies in the ΔS = 1 sector through the study of the nucleon-hyperon transition form factors at higher energy and Q². The information about these form factors is obtained through the analysis of semileptonic hyperon decays which is limited to very low Q² [31–33]. It is for this reason that the work in the quasielastic production of hyperons induced by the antineutrino was started more than 50 years back and many theoretical papers have reported results for the cross section and the polarization of the hyperons in the literature [34–55] which have been summarized in the early works of Marshak et al. [56], Llewellyn Smith [57], and Pais [58]. Experimentally, however, there are very few attempts made where the quasielastic production of Λ, Σ⁰, Σ⁻ have been studied, like at CERN [59–61], BNL [62], FNAL [63, 64] and SKAT [65]. A summary of all the experimental results on the energy dependence of the total cross sections on the hyperon production and its comparison with the theoretical calculations has been given by Kuzmin and Naumov [66] and Rafi Alam et al. [67]. With the availability of the high intensity antineutrino beams at JPARC¹ and FNAL² and the advances made in the detector technology, the feasibility of studying the quasielastic production of hyperons and their polarizations have been explored in many theoretical calculations [66, 68–84]. Experimentally, while the MINERνA [85] collaboration has included the study of quasielastic production of hyperons in its future plans, some other collaborations are also considering the feasibility of making such measurements³.

In this review, we have attempted to give an overview of the present and the earlier works done in the study of the quasielastic production of hyperons induced by the antineutrinos from the nucleon [78] and the nuclear targets [80] and its implications for the pion production [50, 67] relevant for the analysis of the oscillation experiments being done with the antineutrino beams in the sub-GeV energy region. Specifically, we describe the energy and the Q² dependence of the production cross section and polarizations of Λ, Σ⁰ and Σ⁻ hyperons in the quasielastic reactions on the nucleon and the nuclear targets like ¹²C, ¹⁶O, ⁴⁰Ar, and ²⁰⁸Pb. In view of the future experiments to be done with the antineutrino beams in the medium energy region of few GeV, it is useful to review the current status of the theoretical and experimental work on this subject.

We also take into account the nuclear medium effects on the production cross section of hyperons in a local density approximation [67, 80]. The effect of the final state interaction of the hyperons on the production cross section and its Q² dependence arising due to the strong interactions in the presence of the nucleons in the nuclear medium leading to elastic and charge exchange reactions like ΣN → ΛN and ΛN → ΣN is also taken into account in a simple model [49]. The effect of the second class current with or without the presence of T-invariance [78, 79] on the total and the differential cross sections, and the Q² dependence of the polarization components of the hyperons have also been presented.

These hyperons decay into pions through the different Y → Nπ decay modes and contribute to the pion production cross sections induced by the antineutrinos which is in addition to the pion production cross section through the excitation of Δ⁰ and Δ⁻ resonances. Keeping in mind the present and future (anti)neutrino experiments being done with the accelerator (anti)neutrinos at T2K, MicroBooNE, MiniBooNE, NOνA, MINERνA and DUNE, as well as the atmospheric (anti)neutrino experiments being planned in this energy region, we have also presented some new results on the pion production in the kinematic region of these experiments based on the formalism discussed here in brief in sections 2 and 3.

In section 2, we describe in brief the formalism for calculating the cross sections and the polarization components of the Λ, Σ⁰ and Σ⁻ hyperons produced in the quasielastic reactions of the antineutrinos from the nucleons in the presence of the second class currents. We also reproduce the essential formalism for the excitation of Δ in this section and describe the process of pion production from the hyperon (Y) and Δ decay. We describe in section 3 the effect of the nuclear medium on the Δ and the hyperon productions, and in section 4 final state interactions of the hyperons in the nuclear medium and the final state interactions on the production of pions as a result of the Δ excitations. In section 5, we present our results and finally in section 6 conclude the findings.

2. Formalism

2.1. Hyperon Production Off the Free Nucleon

2.1.1. Matrix Element and Form Factors

The transition matrix element for the processes,

$\begin{array}{ll}{\bar{\nu }}_{\mu }\left(k\right)+p\left(p\right)\to {\mu }^{+}\left(k^{\prime }\right)+\Lambda \left(p^{\prime }\right),& \left(1\right)\end{array}$

$\begin{array}{ll}{\bar{\nu }}_{\mu }\left(k\right)+p\left(p\right)\to {\mu }^{+}\left(k^{\prime }\right)+{\Sigma }^0\left(p^{\prime }\right),& \left(2\right)\end{array}$

$\begin{array}{ll}{\bar{\nu }}_{\mu }\left(k\right)+n\left(p\right)\to {\mu }^{+}\left(k^{\prime }\right)+{\Sigma }^{-}\left(p^{\prime }\right),& \left(3\right)\end{array}$

shown in Figure 1A, may be written as

$\begin{array}{ll}{M}=\frac{G_F}{\sqrt{2}}sin{\theta }_c{l}^{\mu }{J}_{\mu },& \left(4\right)\end{array}$

where the quantities in the brackets represent the four momenta of the corresponding particles, G_F is the Fermi coupling constant and θ_c is the Cabibbo mixing angle.

FIGURE 1

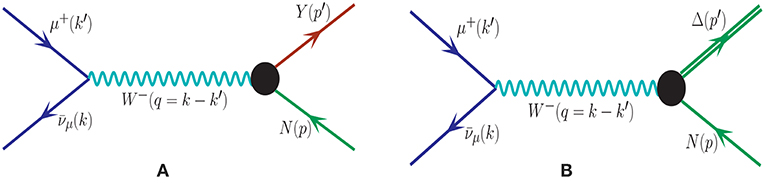
Figure 1. Feynman diagram for the processes (A) ${\bar{\nu }}_{\mu }\left(k\right)+N\left(p\right)\to {\mu }^{+}\left(k^{\prime }\right)+Y\left(p^{\prime }\right)$ (left) and (B) ${\bar{\nu }}_{\mu }\left(k\right)+N\left(p\right)\to {\mu }^{+}\left(k^{\prime }\right)+\Delta \left(p^{\prime }\right)$ (right). The quantities in the bracket represent four momenta of the corresponding particles. N stands for a n or p, Y may be a Λ or Σ⁰ or Σ⁻ and the Δ may be a Δ⁰ or Δ⁻ depending upon the initial nucleon state.

The leptonic current l^μ is given by

$\begin{array}{ll}{l}^{\mu }=ū\left(k^{\prime }\right){\gamma }^{\mu }\left(1+{\gamma }_5\right)u\left(k\right),& \left(5\right)\end{array}$

and the hadronic current J_μ is expressed as:

$\begin{array}{ll}{J}_{\mu }=ū\left(p^{\prime }\right){\Gamma }_{\mu }u\left(p\right)& \left(6\right)\end{array}$

with

$\begin{array}{ll}{\Gamma }_{\mu }=V_{\mu }-A_{\mu }.& \left(7\right)\end{array}$

The vector (V_μ) and the axial vector (A_μ) currents are given by [78]:

$\begin{array}{l}\langle Y(p^{\prime })\left|V_{\mu }\right|N(p)\rangle =\overline{u}(p^{\prime })[{\gamma }_{\mu }{f}_1^{NY}(Q^2)+i{\sigma }_{\mu \nu }\frac{q^{\nu }}{M+M^{\prime }}{f}_2^{NY}(Q^2)\\ +\frac{2q_{\mu }}{M+M^{\prime }}{f}_3^{NY}(Q^2)]u(p),& \left(8\right)\end{array}$

and

$\begin{array}{l}\langle Y(p^{\prime })\left|A_{\mu }\right|N(p)\rangle =\overline{u}(p^{\prime })[{\gamma }_{\mu }{\gamma }_5{g}_1^{NY}(Q^2)+i{\sigma }_{\mu \nu }\frac{q^{\nu }}{M+M^{\prime }}{\gamma }_5{g}_2^{NY}(Q^2)\\ +\frac{2q_{\mu }}{M+M^{\prime }}{g}_3^{NY}(Q^2){\gamma }_5]u(p),& \left(9\right)\end{array}$

which may be rewritten as

$\begin{array}{l}\langle Y\left(p^{\prime }\right)\left|A_{\mu }\right|N\left(p\right)\rangle =ū\left(p^{\prime }\right)[{\gamma }_{\mu }{\gamma }_5{g}_1^{NY}\left(Q^2\right)\\ +\left(\frac{{\Delta }_M}{M+M^{\prime }}{\gamma }_{\mu }{\gamma }_5-\frac{p_{\mu }+p_{\mu }^{\prime }}{M+M^{\prime }}{\gamma }_5\right)g_2^{NY}\left(Q^2\right)\\ +\frac{2q_{\mu }}{M+M^{\prime }}{g}_3^{NY}\left(Q^2\right){\gamma }_5]u\left(p\right),& \left(10\right)\end{array}$

where Y(= Λ, Σ⁰and Σ⁻) represents a hyperon, ${\Delta }_M=M^{\prime }-M$ with M and M′ being the masses of the initial nucleon and the final hyperon. $q_{\mu }\left(=k_{\mu }-k_{\mu }^{\prime }=p_{\mu }^{\prime }-p_{\mu }\right)$ is the four momentum transfer with Q² = − q², Q² ≥ 0. $f_1^{NY}\left(Q^2\right)$, $f_2^{NY}\left(Q^2\right)$ and $f_3^{NY}\left(Q^2\right)$ are the vector, weak magnetic and induced scalar form factors and $g_1^{NY}\left(Q^2\right)$, $g_2^{NY}\left(Q^2\right)$, and $g_3^{NY}\left(Q^2\right)$ are the axial vector, induced tensor (or weak electric) and induced pseudoscalar form factors, respectively.

The six form factors $f_i^{NY}\left(Q^2\right)$ and $g_i^{NY}\left(Q^2\right)\left(i=1-3\right)$ are determined using the following assumptions about the symmetry properties of the weak vector (V) and axial vector (A) currents in the SM. Under the assumption of the SU(3) symmetry, the initial and the final baryons as well as the weak V and A currents belong to the octet (8) representation, each form factor $f_i^{NY}\left(Q^2\right)$ and $g_i^{NY}\left(Q^2\right)$ occurring in the definition of the transition form factors defined in Equations (8, 10) can be written in terms of the two functions D(Q²) and F(Q²) corresponding to the symmetric octet (8^S) and antisymmetric octet (8^A) couplings of the octets of the vector and the axial vector currents to the octets of the initial and the final baryons. Specifically, we write

$\begin{array}{ll}{f}_i^{NY}\left(Q^2\right)=a{F}_i^V\left(Q^2\right)+b{D}_i^V\left(Q^2\right),& \left(11\right)\end{array}$

$\begin{array}{ll}{g}_i^{NY}\left(Q^2\right)=a{F}_i^A\left(Q^2\right)+b{D}_i^A\left(Q^2\right),& \left(12\right)\end{array}$

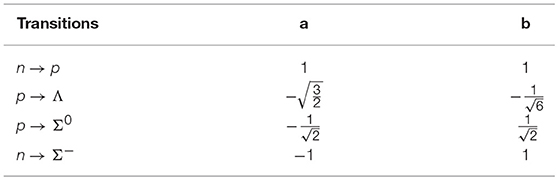
where a and b are the SU(3) Clebsch-Gordan coefficients given in Table 1 for the reactions shown in Equations (1–3). $F_i^V\left(Q^2\right)\left(D_i^V\left(Q^2\right)\right)$ and $F_i^A\left(Q^2\right)\left(D_i^A\left(Q^2\right)\right);\left(i=1,2\right)$, are the couplings corresponding to the antisymmetric (symmetric) couplings of the vector and the axial vector currents.

TABLE 1

Table 1. Values of the coefficients a and b given in Equations (11),(12).

For the determination of the N − Y transition form factors, we take the following considerations into account:

a) The assumption of the conserved vector current (CVC) hypothesis leads to $f_3^{NY}\left(Q^2\right)=0$ and the two vector form factors viz. $f_1^{NY}\left(Q^2\right)$ and $f_2^{NY}\left(Q^2\right)$ are determined in terms of the electromagnetic form factors of the nucleon, i.e., $f_1^N\left(Q^2\right)$ and $f_2^N\left(Q^2\right),N=\left(p,n\right)$ as

$\begin{array}{ll}{f}_{1,2}^{p\Lambda }\left(Q^2\right)=-\sqrt{\frac{3}{2}}{f}_{1,2}^p\left(Q^2\right),& \left(13\right)\end{array}$

$\begin{array}{ll}{f}_{1,2}^{n{\Sigma }^{-}}\left(Q^2\right)=-\left[f_{1,2}^p\left(Q^2\right)+2f_{1,2}^n\left(Q^2\right)\right],& \left(14\right)\end{array}$

$\begin{array}{ll}{f}_{1,2}^{p{\Sigma }^0}\left(Q^2\right)=-\frac{1}{\sqrt{2}}\left[f_{1,2}^p\left(Q^2\right)+2f_{1,2}^n\left(Q^2\right)\right].& \left(15\right)\end{array}$

The electromagnetic form factors $f_{1,2}^p\left(Q^2\right)$ and $f_{1,2}^n\left(Q^2\right)$ are expressed in terms of the Sachs electric and magnetic form factors $G_E^{p,n}\left(Q^2\right)$ and $G_M^{p,n}\left(Q^2\right)$ of the nucleons as

$\begin{array}{ll}{f}_1^{p,n}\left(Q^2\right)={\left(1+\frac{Q^2}{4M^2}\right)}^{-1}\left[G_E^{p,n}\left(Q^2\right)+\frac{Q^2}{4M^2}{G}_M^{p,n}\left(Q^2\right)\right],& \left(16\right)\end{array}$

$\begin{array}{ll}{f}_2^{p,n}\left(Q^2\right)={\left(1+\frac{Q^2}{4M^2}\right)}^{-1}\left[G_M^{p,n}\left(Q^2\right)-G_E^{p,n}\left(Q^2\right)\right].& \left(17\right)\end{array}$

For $G_E^{p,n}\left(Q^2\right)$ and $G_M^{p,n}\left(Q^2\right)$ various parameterizations are available in the literature and in our numerical calculations, we have used the parameterization given by Bradford et al. [86].

b) The axial vector form factors $g_1^{NY}\left(Q^2\right)$ and $g_2^{NY}\left(Q^2\right)$ are determined from Equation (12) in terms of the two functions $F_{1,2}^A\left(Q^2\right)$ and $D_{1,2}^A\left(Q^2\right)$. $g_{1,2}^{p\Lambda }\left(Q^2\right)$, $g_{1,2}^{p{\Sigma }^0}\left(Q^2\right)$ and $g_{1,2}^{n{\Sigma }^{-}}\left(Q^2\right)$ are rewritten in terms of $g_{1,2}^{pn}\left(Q^2\right)$ and $x_{1,2}\left(Q^2\right)=\frac{F_{1,2}^A\left(Q^2\right)}{F_{1,2}^A\left(Q^2\right)+D_{1,2}^A\left(Q^2\right)}$ as

$\begin{array}{ll}{g}_{1,2}^{p\Lambda }\left(Q^2\right)=-\frac{1}{\sqrt{6}}\left(1+2x_{1,2}\right)g_{1,2}^{np}\left(Q^2\right),& \left(18\right)\end{array}$

$\begin{array}{ll}{g}_{1,2}^{n{\Sigma }^{-}}\left(Q^2\right)=\left(1-2x_{1,2}\right)g_{1,2}^{np}\left(Q^2\right),& \left(19\right)\end{array}$

$\begin{array}{ll}{g}_{1,2}^{p{\Sigma }^0}\left(Q^2\right)=\frac{1}{\sqrt{2}}\left(1-2x_{1,2}\right)g_{1,2}^{np}\left(Q^2\right).& \left(20\right)\end{array}$

We further assume that $F_{1,2}^A\left(Q^2\right)$ and $D_{1,2}^A\left(Q^2\right)$ have the same Q² dependence, such that $x_{1,2}\left(Q^2\right)$ become constant given by $x_{1,2}\left(Q^2\right)=x_{1,2}=\frac{F_{1,2}^A\left(0\right)}{F_{1,2}^A\left(0\right)+D_{1,2}^A\left(0\right)}$.

c) For the axial vector form factor $g_1^{pn}\left(Q^2\right)$, a dipole parameterization has been used:

$\begin{array}{ll}{g}_1^{pn}\left(Q^2\right)=g_A\left(0\right){\left(1+\frac{Q^2}{M_A^2}\right)}^{-2},& \left(21\right)\end{array}$

where M_A is the axial dipole mass and g_A(0) is the axial charge. For the numerical calculations, we have used the world average value of M_A = 1.026 GeV. g_A(0) and x₁ are taken to be 1.2723 and 0.364, respectively, as determined from the experimental data on the β−decay of neutron and the semileptonic decay of hyperons.

d) The induced tensor form factor $g_2^{pn}\left(Q^2\right)$ is taken to be of the dipole form, i.e.,

$\begin{array}{ll}{g}_2^{pn}\left(Q^2\right)=g_2^{pn}\left(0\right){\left(1+\frac{Q^2}{M_2^2}\right)}^{-2}.& \left(22\right)\end{array}$

There is limited experimental information about $g_2^{pn}\left(Q^2\right)$ which is obtained from the analysis of the weak processes made for the search of G-noninvariance assuming T-invariance which implies $g_2^{pn}\left(0\right)$ to be real. A purely imaginary value of $g_2^{pn}\left(0\right)$ implies T-violation [87]. In the numerical calculations we have taken real as well as imaginary values, with |g₂(0)| varying in the range 0−3 [78].

e) The pseudoscalar form factor $g_3^{NY}\left(Q^2\right)$ is proportional to the lepton mass and the contribution is small in the case of antineutrino scattering with muon antineutrinos. However, in the numerical calculations, we have taken the following expression given by Nambu [88] using the generalized GT relation.

$\begin{array}{ll}{g}_3^{NY}\left(Q^2\right)=\frac{{\left(M+M^{\prime }\right)}^2}{2\left(m_K^2+Q^2\right)}{g}_1^{NY}\left(Q^2\right),& \left(23\right)\end{array}$

where m_K is the mass of the kaon.

2.1.2. Cross Section

The general expression of the differential cross section corresponding to the processes (1), (2), and (3), in the rest frame of the initial nucleon, is written as:

$\begin{array}{l}d\sigma =\frac{1}{{\left(2\pi \right)}^2}\frac{1}{4E_{{\bar{\nu }}_{\mu }}M}{\delta }^4\left(k+p-k^{\prime }-p^{\prime }\right)\frac{d^3{k}^{\prime }}{2E_{k^{\prime }}}\frac{d^3{p}^{\prime }}{2E_{p^{\prime }}}\\ {\displaystyle \overline{\sum }}{\displaystyle \sum }|{M}{|}^2,& \left(24\right)\end{array}$

where the transition matrix element squared is expressed as:

$\begin{array}{ll}{\displaystyle \overline{\sum }}{\displaystyle \sum }|{M}{|}^2=\frac{G_F^{2}si{n}^2{\theta }_c}{2}{{L}}_{\mu \nu }{{J}}^{\mu \nu }& \left(25\right)\end{array}$

The leptonic (${L}$_μν) and the hadronic (${J}$^μν) tensors are given by

$\begin{array}{ll}{{L}}^{\mu \nu }=\text{ Tr}\left[{\gamma }^{\mu }\left(1+{\gamma }_5\right)\Lambda \left(k\right){\gamma }^{\nu }\left(1+{\gamma }_5\right)\Lambda \left(k^{\prime }\right)\right],& \left(26\right)\end{array}$

$\begin{array}{ll}{{J}}_{\mu \nu }=\frac{1}{2}\text{Tr}\left[\Lambda \left(p^{\prime }\right)J_{\mu }\Lambda \left(p\right){\tilde{J}}_{\nu }\right],& \left(27\right)\end{array}$

with Λ(p) = ($\cancel{p}$ + M), Λ(p′) = ($\cancel{p}$′ + M′), Λ(k) = $\cancel{k}$, $\Lambda (k^{\prime })=({\cancel{k}}^{\prime }+m_{\mu })$, ${\tilde{J}}_{\nu }={\gamma }^0{J}_{\nu }^{†}{\gamma }^0$ and J_μ is defined in Equation (6).

Using the above definitions, the Q² distribution is written as

$\begin{array}{ll}\frac{d\sigma }{d{Q}^2}=\frac{G_F^{2}si{n}^2{\theta }_c}{16\pi M^2{E_{{\bar{\nu }}_{\mu }}}^2}N\left(Q^2\right),& \left(28\right)\end{array}$

where the expression of N(Q²) is given in the Appendix-I of Fatima et al. [78].

2.1.3. Polarization of the Hyperon

Using the covariant density matrix formalism, the polarization 4-vector (ξ^τ) of the hyperon produced in the reactions given in Equations (1–3) is written as [89]:

$\begin{array}{ll}{\xi }^{\tau }=\left(g^{\tau \sigma }-\frac{p^{\prime \tau }{p}^{\prime \sigma }}{{M^{\prime }}^2}\right)\frac{{{L}}^{\alpha \beta }\text{Tr}\left[{\gamma }_{\sigma }{\gamma }_5\Lambda \left(p^{\prime }\right)J_{\alpha }\Lambda \left(p\right){\tilde{J}}_{\beta }\right]}{{{L}}^{\alpha \beta }\text{Tr}\left[\Lambda \left(p^{\prime }\right)J_{\alpha }\Lambda \left(p\right){\tilde{J}}_{\beta }\right]}.& \left(29\right)\end{array}$

One may write the polarization vector $\overrightarrow{\xi }$ in terms of the three orthogonal vectors ê_i (i = L, P, T), i.e.,

$\begin{array}{ll}\overrightarrow{\xi }={\xi }_L{ê}_L+{\xi }_P{ê}_P+{\xi }_T{ê}_T,& \left(30\right)\end{array}$

where ê_L, ê_P and ê_T are chosen to be the set of orthogonal unit vectors corresponding to the longitudinal, perpendicular and transverse directions with respect to the momentum of the hyperon, depicted in Figure 2, and are written as

$\begin{array}{ll}{\widehat{e}}_L=\frac{{\overrightarrow{p}}^{\prime }}{|{\overrightarrow{p}}^{\prime }|},{\widehat{e}}_P={\widehat{e}}_L\times {\widehat{e}}_T,{ê}_T=\frac{{\overrightarrow{p}}^{\prime }\times \overrightarrow{k}}{|{\overrightarrow{p}}^{\prime }\times \overrightarrow{k}|}.& \left(31\right)\end{array}$

The longitudinal, perpendicular and transverse components of the polarization vector ${\overrightarrow{\xi }}_{L,P,T}\left(Q^2\right)$ using Equations (30, 31) may be written as:

$\begin{array}{ll}{\xi }_{L,P,T}\left(Q^2\right)=\overrightarrow{\xi }·{ê}_{L,P,T}.& \left(32\right)\end{array}$

FIGURE 2

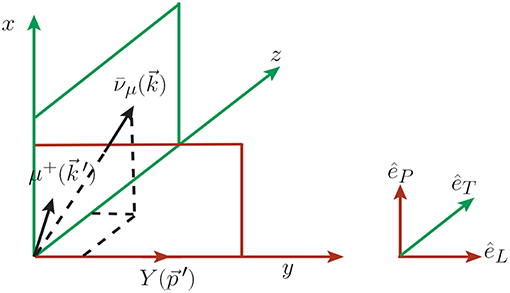
Figure 2. Polarization observables of the hyperon. ê_L, ê_P, and ê_T represent the orthogonal unit vectors corresponding to the longitudinal, perpendicular, and transverse directions with respect to the momentum of the final hadron.

In the rest frame of the initial nucleon, the polarization vector $\overrightarrow{\xi }$ is expressed as

$\begin{array}{ll}\overrightarrow{\xi }=A\left(Q^2\right)\overrightarrow{k}+B\left(Q^2\right){\overrightarrow{p}}^{\prime }+C\left(Q^2\right)M\left(\overrightarrow{k}\times {\overrightarrow{p}}^{\prime }\right)& \left(33\right)\end{array}$

and is explicitly calculated using Equation (29). The expressions for the coefficients A(Q²), B(Q²), and C(Q²) are given in the Appendix-I of Fatima et al. [78].

The longitudinal ($P_L(Q^2)$), perpendicular ($P_P(Q^2)$) and transverse ($P_T(Q^2)$) components of the polarization vector in the rest frame of the final hyperon are obtained by performing a Lorentz boost and are written as Fatima et al. [78]:

$\begin{array}{ll}{P}_L\left(Q^2\right)=\frac{M^{\prime }}{E^{\prime }}{\xi }_L\left(Q^2\right),P_P\left(Q^2\right)={\xi }_P\left(Q^2\right),P_T\left(Q^2\right)={\xi }_T\left(Q^2\right).& \left(34\right)\end{array}$

The expressions for $P_L\left(Q^2\right)$, $P_P\left(Q^2\right)$ and $P_T\left(Q^2\right)$ are then obtained using Equations (31–33) in Equation (34) and are expressed as

$\begin{array}{ll}{P}_L(Q^2)=\frac{M^{\prime }}{E^{\prime }}\frac{A\left(Q^2\right)\overrightarrow{k}·{\widehat{p}}^{\prime }+B\left(Q^2\right)|{\overrightarrow{p}}^{\prime }|}{N\left(Q^2\right)},& \left(35\right)\end{array}$

$\begin{array}{ll}{P}_P\left(Q^2\right)=\frac{A\left(Q^2\right)[{\left(\overrightarrow{k}.{\widehat{p}}^{\prime }\right)}^2-|\overrightarrow{k}{|}^2]}{N\left(Q^2\right)|{\widehat{p}}^{\prime }\times \overrightarrow{k}|},& \left(36\right)\end{array}$

$\begin{array}{ll}{P}_T\left(Q^2\right)=\frac{C\left(Q^2\right)M|{\overrightarrow{p}}^{\prime }|[{\left(\overrightarrow{k}.{\widehat{p}}^{\prime }\right)}^2-|\overrightarrow{k}{|}^2]}{N\left(Q^2\right)|{\widehat{p}}^{\prime }\times \overrightarrow{k}|}.& \left(37\right)\end{array}$

If the T-invariance is assumed then all the vector and the axial vector form factors are real and the expression for C(Q²) vanishes which implies that the transverse component of polarization, $P_T\left(Q^2\right)$ perpendicular to the production plane, vanishes.

2.2. Δ Production Off the Free Nucleon

In the intermediate energy region of about 0.5−1 GeV, the antineutrino induced reactions on a nucleon is dominated by the Δ excitation, presented in Figure 1B and is given by:

$\begin{array}{ll}{\bar{\nu }}_{\mu }\left(k\right)+n\left(p\right)\to {\mu }^{+}\left(k^{\prime }\right)+{\Delta }^{-}\left(p^{\prime }\right),& \left(38\right)\end{array}$

$\begin{array}{ll}{\bar{\nu }}_{\mu }\left(k\right)+p\left(p\right)\to {\mu }^{+}\left(k^{\prime }\right)+{\Delta }^0\left(p^{\prime }\right),& \left(39\right)\end{array}$

and the matrix element for the antineutrino induced charged current process on the free neutron is written as [26]:

$\begin{array}{ll}T=\sqrt{3}\frac{G_F}{\sqrt{2}}cos{\theta }_c{l}_{\mu }{J}^{\mu },& \left(40\right)\end{array}$

where the leptonic current l_μ is defined in Equation (5) and the hadronic current J^μ is given by

$\begin{array}{ll}{J}^{\mu }={\overline{\psi }}_{\alpha }\left(p^{\prime }\right)O^{\alpha \mu }u\left(p\right).& \left(41\right)\end{array}$

In the above expression, ${\psi }_{\alpha }\left(p^{\prime }\right)$ is the Rarita Schwinger spinor for the Δ of momentum p′ and u(p) is the Dirac spinor for the nucleon of momentum p. O^αμ is the N − Δ transition operator which is the sum of the vector ($O_V^{\alpha \mu }$) and the axial vector ($O_A^{\alpha \mu }$) pieces, and the operators $O_V^{\alpha \mu }$ and $O_A^{\alpha \mu }$ are given by:

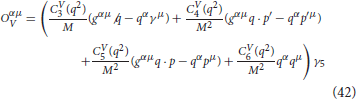
and

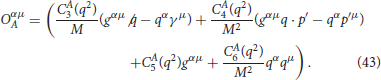
A similar expression for J^μ is used for the Δ⁰ excitation from the proton target without a factor of $\sqrt{3}$ in Equation (40). Here q(= p′ − p = k − k′) is the momentum transfer, Q²(= − q²) is the momentum transfer square and M is the mass of the nucleon. $C_i^V\left(i=3-6\right)$ are the vector and $C_i^A\left(i=3-6\right)$ are the axial vector transition form factors which have been taken from Lalakulich et al. [90].

The differential scattering cross section for the reactions given in Equations (38, 39) is given by Akbar et al. [71], Alvarez-Ruso et al. [91], Singh et al. [92]:

$\begin{array}{ll}\frac{d^2\sigma }{d{E}_{k^{\prime }}d{\Omega }_{k^{\prime }}}=\frac{1}{64{\pi }^3}\frac{1}{M{M}_{\Delta }}\frac{|{\overrightarrow{k}}^{\prime }|}{E_k}\frac{\frac{\Gamma \left(W\right)}{2}}{{\left(W-M_{\Delta }\right)}^2+\frac{{\Gamma }^2\left(W\right)}{4}}|T{|}^2,& \left(44\right)\end{array}$

where M_Δ is the mass of Δ resonance, Γ is the Delta decay width, W is the center of mass energy i.e., $W=\sqrt{{\left(p+q\right)}^2}$ and

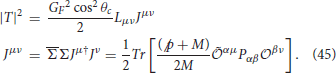
In the above expression L_μν is given by Equation (26), ${\tilde{{O}}}^{\alpha \mu }={\gamma }^0{{{O}}^{\alpha \mu }}^{†}{\gamma }^0$, ${{O}}^{\alpha \mu }=O_V^{\alpha \mu }+O_A^{\alpha \mu }$ and P^μν is the spin $\frac{3}{2}$ projection operator defined as

$P^{\mu \nu }={\displaystyle \sum _{spins}}{\psi }^{\mu }{\overline{\psi }}^{\nu }$

and is given by:

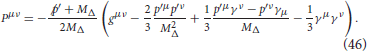
In Equation (44), the Delta decay width Γ is taken to be an energy dependent P-wave decay width given by Oset and Salcedo [93]:

$\begin{array}{ll}\Gamma \left(W\right)=\frac{1}{6\pi }{\left(\frac{f_{\pi N\Delta }}{m_{\pi }}\right)}^2\frac{M}{W}|{\overrightarrow{q}}_{cm}{|}^3\Theta \left(W-M-m_{\pi }\right),& \left(47\right)\end{array}$

where f_πNΔ is the πNΔ coupling constant taken as 2.12 for numerical calculations and $\left|{\overrightarrow{q}}_{cm}\right|$ is defined as

$|{\overrightarrow{q}}_{cm}|=\frac{\sqrt{{\left(W^2-m_{\pi }^2-M^2\right)}^2-4m_{\pi }^2{M}^2}}{2W}.$

The step function Θ in Equation (47) denotes the fact that the width is zero for the invariant masses below the Nπ threshold, $\left|{\overrightarrow{q}}_{cm}\right|$ is the pion momentum in the rest frame of the resonance.

2.3. Pion Production From the Hyperons and Δ

The basic reactions for the charged current antineutrino induced one pion production off the nucleon N, arising from a hyperon in the final state are given by,

$\begin{array}{l}{\bar{\nu }}_l+p\to l^{+}+\Lambda \\ \searrow n+{\pi }^o\left[35.8\%\right]\\ \searrow p+{\pi }^{-}\left[63.9\%\right]& \left(48\right)\end{array}$

$\begin{array}{l}{\bar{\nu }}_l+p\to l^{+}+{\Sigma }^0\\ \searrow \gamma +\Lambda \left[100\%\right]\\ \searrow n+{\pi }^o\left[35.8\%\right]\\ \searrow p+{\pi }^{-}\left[63.9\%\right]& \left(49\right)\end{array}$

$\begin{array}{l}{\bar{\nu }}_l+n\to l^{+}+{\Sigma }^{-}\\ \searrow n+{\pi }^{-},\left[99.85\%\right]& \left(50\right)\end{array}$

where the quantities in the square brackets represent the branching ratios of the respective decay modes.

The basic reactions for the charged current neutrino and antineutrino induced one pion production off the nucleon N (proton or neutron) through the production of Δ are:

$\begin{array}{l}{\nu }_l+p\to l^{-}+{\Delta }^{++}\\ \searrow p+{\pi }^{+}\left[1\right],& \left(51\right)\end{array}$

$\begin{array}{l}{\nu }_l+n\to l^{-}+{\Delta }^{+},\\ \searrow p+{\pi }^o,\left[\sqrt{\frac{2}{3}}\right]\\ \searrow n+{\pi }^{+},\left[\sqrt{\frac{1}{3}}\right]& \left(52\right)\end{array}$

$\begin{array}{l}{\bar{\nu }}_l+p\to l^{+}+{\Delta }^0,\\ \searrow p+{\pi }^{-},\left[\sqrt{\frac{1}{3}}\right]\\ \searrow n+{\pi }^o,\left[\sqrt{\frac{2}{3}}\right]& \left(53\right)\end{array}$

$\begin{array}{l}{\bar{\nu }}_l+n\to l^{+}+{\Delta }^{-},\\ \searrow n+{\pi }^{-},\left[1\right]& \left(54\right)\end{array}$

where the quantities in the square brackets represent the respective Clebsch-Gordan coefficients for Δ → Nπ channel.

3. Nuclear Medium Effects

3.1. Hyperons Produced Inside the Nucleus

When the reactions shown in Equations (48–50) take place on nucleons which are bound in the nucleus, Fermi motion and Pauli blocking effects of initial nucleons are considered. In the present work the Fermi motion effects are calculated in a local Fermi gas model (LFGM), and the cross section is evaluated as a function of local Fermi momentum p_F(r) and integrated over the whole nucleus. The incoming antineutrino interacts with the nucleon moving inside the nucleus of density ρ_N(r) such that the differential scattering cross section inside the nucleus is expressed in terms of the differential scattering cross section for an antineutrino scattering from a free nucleon (Equation 28) as

$\begin{array}{ll}\frac{d\sigma }{d{Q}^2}=2{\displaystyle \int }{d}^{3}r{\displaystyle \int }\frac{d^{3}p}{{\left(2\pi \right)}^3}{n}_N\left(p,r\right){\left[\frac{d\sigma }{d{Q}^2}\right]}_{\bar{\nu }N},& \left(55\right)\end{array}$

where n_N(p, r) is the occupation number of the nucleon. n_N(p, r) = 1 for p ≤ p_FN(r) and is equal to zero for p > p_FN(r), where p_FN(r) is the Fermi momentum of the nucleon and is given as:

$p_F{}_p(r)={\left(3{\pi }^2{\rho }_p(r)\right)}^{\frac{1}{3}};p_F{}_n(r)={\left(3{\pi }^2{\rho }_n(r)\right)}^{\frac{1}{3}},$

with ρ_p(r) and ρ_n(r) are, respectively, the proton and the neutron densities inside the nucleus and are, in turn, expressed in terms of the nuclear density ρ(r) as

$\begin{array}{l}{\rho }_p\left(r\right)\to \frac{Z}{A}\rho \left(r\right);{\rho }_n\left(r\right)\to \frac{A-Z}{A}\rho \left(r\right).\end{array}$

In the above expression, ρ(r) is determined in the electron scattering experiments for the different nuclei [94].

The produced hyperons are further affected by the FSI within the nucleus through the hyperon-nucleon elastic processes like ΛN → ΛN, ΣN → ΣN, etc. and the charge exchange scattering processes like Λ+n → Σ⁻ +p, Λ+n → Σ⁰ +n, Σ⁻ +p → Λ+n, Σ⁻ +p → Σ⁰ +n, etc. Because of such types of interaction in the nucleus, the probability of Λ or Σ production changes and has been taken into account by using the prescription given in Singh and Vicente Vacas [49].

3.2. Delta Produced Inside the Nucleus

When an antineutrino interacts with a nucleon (Equation 38) inside a nuclear target, nuclear medium effects come into play like Fermi motion, Pauli blocking, etc. The produced Δs have no such constraints in the production channel but their decay is inhibited by the Pauli blocking of the final nucleons. Also, there are other disappearance channels open for Δs through particle hole excitations and this leads to the modification in the mass and width of the propagator defined in Equation (47).

To take into account the nuclear medium effects, we have evaluated the cross section using the local density approximation, following the same procedure as mentioned in section-3.1, and the differential scattering cross section for the reactions given in Equations (38, 39) is defined as :

$\begin{array}{l}{\frac{d^2\sigma }{d{E}_{k^{\prime }}d{\Omega }_{k^{\prime }}}|}_{\bar{\nu }A}={\displaystyle \int }{d}^{3}r\frac{1}{64{\pi }^3}\frac{1}{M{M}_{\Delta }}\frac{|{\overrightarrow{k}}^{\prime }|}{E_k}\frac{\left(\frac{\tilde{\Gamma }\left(W\right)}{2}-Im{\Sigma }_{\Delta }\right)}{{\left(W-M_{\Delta }-Re{\Sigma }_{\Delta }\right)}^2+{\left(\frac{\tilde{\Gamma }\left(W\right)}{2}-Im{\Sigma }_{\Delta }\right)}^2}\\ \left({\rho }_n\left(r\right)+\frac{1}{3}{\rho }_p\left(r\right)\right)|T{|}^2.& \left(56\right)\end{array}$

In the nuclear medium the properties of Δ like its mass and decay width Γ to be used in Equation (47) are modified due to the nuclear medium effect which have been discussed in detail in Oset and Salcedo [93], Garcia Recio et al. [95] and the modifications are given by

$\begin{array}{ll}\frac{\Gamma }{2}\to \frac{\tilde{\Gamma }}{2}-Im{\Sigma }_{\Delta }\mathrm{\text{and }}{M}_{\Delta }\to {\tilde{M}}_{\Delta }=M_{\Delta }+Re{\Sigma }_{\Delta }.& \left(57\right)\end{array}$

The expressions of ReΣ_Δ and ImΣ_Δ are given in Oset and Salcedo [93].

4. Final State Interaction Effect

4.1. Pions Produced Inside the Nucleus

4.1.1. Delta Production

When the reactions, given in Equations (51–54) take place inside the nucleus, the pions may be produced in two ways, through the coherent channel and the incoherent channel. If the target nucleus stays in the ground state and does not loose its identity, giving all the transferred energy in the reaction to the outgoing pion, then the pion production process is called coherent pion production otherwise if the nucleus can be excited and/or broken up then it leads to the incoherent production of pions. The contribution of coherent pion production has been found to be < 2−3% at the antineutrino energies of the present interest [18, 19], and is not discussed here. We have not considered the contributions from the nonresonant background terms and higher resonances like P₁₁(1440), S₁₁(1535), etc.

The transition amplitude for an incoherent pion production process is written as Sajjad Athar et al. [26]:

$\begin{array}{ll}{{M}}_{fi}=\sqrt{3}\frac{G_F}{\sqrt{2}}\frac{f_{\pi N\Delta }}{m_{\pi }}cos{\theta }_cū\left(p^{\prime }\right)k_{\pi }^{\sigma }{P}_{\mu \nu }{{O}}^{\lambda \alpha }u\left(p\right)l_{\alpha },& \left(58\right)\end{array}$

where the symbols have the same meaning as in section-2.2.

Starting with the general expression for the differential scattering cross section in the lab frame

$\begin{array}{l}d\sigma =\frac{1}{2E_{{\bar{\nu }}_{\mu }}2E_N{\left(2\pi \right)}^5}\frac{d{\overrightarrow{k}}^{\prime }}{\left(2E_l\right)}\frac{d{{\overrightarrow{p}}_N}^{\prime }}{\left(2E_N^{\prime }\right)}\frac{d{\overrightarrow{k}}_{\pi }}{\left(2E_{\pi }\right)}{\delta }^4\\ \left(k+p_N-k^{\prime }-p_N^{\prime }-k_{\pi }\right){\displaystyle \sum ^{-}}{\displaystyle \sum }|{{M}}_{fi}{|}^2,\end{array}$

and using the local density approximation, following the same procedure as mentioned in section-3.1, we may write

$\begin{array}{ll}{\left(\frac{d\sigma }{d{Q}^{2}dcos{\theta }_{\pi }}\right)}_{\bar{\nu }A}={\displaystyle \int }d\overrightarrow{r}{\rho }_n\left(r\right){\left(\frac{d\sigma }{d{Q}^{2}dcos{\theta }_{\pi }}\right)}_{\bar{\nu }N}& \left(59\right)\end{array}$

which gives

$\begin{array}{r}{\left(\frac{d\sigma }{d{Q}^{2}dcos{\theta }_{\pi }}\right)}_{\bar{\nu }A}=2{\displaystyle \int }{d}^{3}r{\displaystyle \sum _{N=n,p}}\frac{d^3{p}_N}{{\left(2\pi \right)}^3}{\Theta }_1\left(E_F^N\left(r\right)-E_N\right)\\ {\Theta }_2\left(E_N+q_0-E_{\pi }-E_F^{N^{\prime }}\left(r\right)\right)\\ \times {\left(\frac{d\sigma }{d{Q}^{2}dcos{\theta }_{\pi }}\right)}_{\bar{\nu }N},& \left(60\right)\end{array}$

where q₀ is the energy transferred to the target particle. Using

$d^3{p}_N=\left|{\overrightarrow{p}}_N{|}^{2}d\right|{\overrightarrow{p}}_N|dcos{\theta }_{N}d{\varphi }_N,$

$E_N=\sqrt{|{\overrightarrow{p}}_N{|}^2+M^2};\overrightarrow{k}+{\overrightarrow{p}}_N={\overrightarrow{k}}^{\prime }+{\overrightarrow{p}}_N^{\prime }+{\overrightarrow{p}}_{\pi },$

and

$E_N^{\prime }=\sqrt{|{\overrightarrow{p}}_N^{\prime }{|}^2+M^2}=\sqrt{|\overrightarrow{q}-{\overrightarrow{p}}_{\pi }+{\overrightarrow{p}}_N{|}^2+M^2}.$

Equation (60) may also be written as

$\begin{array}{r}{\left(\frac{d\sigma }{d{Q}^{2}dcos{\theta }_{\pi }}\right)}_{\bar{\nu }A}=\frac{1}{{\left(4\pi \right)}^5}{\displaystyle {\int }_{r_{min}}^{r_{max}}}{\rho }_N\left(r\right)d\overrightarrow{r}{\displaystyle {\int }_{{k^{\prime }}_{min}}^{{k^{\prime }}_{max}}}d{k}^{\prime }{\displaystyle {\int }_0^{2\pi }}\\ d{\varphi }_{\pi }\frac{\pi |{\overrightarrow{k}}^{\prime }||{\overrightarrow{k}}_{\pi }|}{M{E}_{\bar{\nu }}^2{E}_l}\frac{1}{E_p^{\prime }+E_{\pi }\left(1-\frac{|\overrightarrow{q}|}{|{\overrightarrow{k}}_{\pi }|}cos{\theta }_{\pi }\right)}\\ \times {\displaystyle \overline{\sum }}{\displaystyle \sum }|{{M}}_{fi}{|}^2,& \left(61\right)\end{array}$

where ρ_N(r) is the nucleon density defined in terms of nuclear density ρ(r). In a nucleus, the contributions to π⁻ and π^o productions come from the neutron and proton targets. These are taken into account using the Clebsch-Gordan coefficients written in Equations (51–54). The total production cross section for π⁻ and π^o from a nucleus can be written by replacing ρ_N as

$\begin{array}{l}{\rho }_N\left(r\right)={\rho }_n\left(r\right)+\frac{1}{9}{\rho }_p\left(r\right)\mathrm{\text{for }}{\pi }^{-}\mathrm{\text{ production}},\end{array}$

$\begin{array}{ll}{\rho }_N\left(r\right)=\frac{2}{9}\left[{\rho }_n\left(r\right)+{\rho }_p\left(r\right)\right]\mathrm{\text{for }}{\pi }^o\mathrm{\text{ production}}.& \left(62\right)\end{array}$

The pions produced in these processes inside the nucleus may re-scatter or may produce more pions or may get absorbed while coming out from the final nucleus. We have taken the results of Vicente Vacas et al. [96] for the final state interaction of pions which is calculated in an eikonal approximation using probabilities per unit length as the basic input. The details are given Vicente Vacas et al. [96].

4.1.2. Hyperon Production

The pions produced as a result of hyperon decays are shown in Equations (48–50). However, when the hyperons are produced in a nuclear medium, some of them disappear through the hyperon-nucleon interaction processes like YN → NN, though it is suppressed due to nuclear effects [29, 30]. The pionic modes of hyperons are Pauli blocked as the momentum of the nucleons available in these decays is considerably below the Fermi level of energy for most nuclei leading to a long lifetime for the hyperons in the nuclear medium [29, 30]. Therefore, the hyperons which survive the YN → NN decay in the medium live long enough to travel the nuclear medium and decay outside the nucleus. In view of this we have assumed no final state interaction of the produced pions with the nucleons inside the nuclear medium. In a realistic situation, all the hyperons produced in these reactions will not survive in the nucleus, and the pions coming from the decay of hyperons will undergo FSI [49]. A quantitative analysis of the hyperon disappearance through the YN → NN interaction and the pions having FSI effect, will require a dynamic nuclear model to estimate the nonmesonic and mesonic decay of the hyperons in a nucleus which is beyond the scope of the present work. Our results in the following section, therefore, represent an upper limit on the production of pions arising due to the production of hyperons.

5. Results and Discussion

In this section, we first present a review of the old experimental results on the total cross sections and their Q² dependence in the case of hyperon production from CERN on Freon [60] and Propane [59, 61], FNAL on Neon [63, 64], SKAT on Freon [65], and BNL on H₂ [62] and compare them with the theoretical results. We also present the experimental results on the Lambda hyperon polarizations from CERN [61] and compare them with the most recent theoretical calculations [80]. The theoretical calculations used for making comparisons with the experimental results are done for the nucleon targets assuming the nuclear medium effects in hyperon production to be small at the energies relevant for these experiments [49, 61]. The results have also been presented for the total cross sections and their Q² dependence for nuclear targets like ¹²C, ¹⁶O, ⁴⁰Ar and ²⁰⁸Pb with and without the nuclear medium (NME) and final state interaction (FSI) effects. The results have also been presented for the longitudinal ($P_L\left(Q^2\right)$), perpendicular ($P_P\left(Q^2\right)$) and transverse ($P_T\left(Q^2\right)$) components of the polarization vector of the hyperon in the presence of the second class currents with and without T-invariance by taking the numerical values of g₂(0) to be real and imaginary, respectively.

The following points describe the inputs used for the numerical calculations which have been done to obtain these results:

1. For the hyperon production cross section off the free nucleon target, we have integrated over Q² in Equation (28) and obtained the results for the total scattering cross section. For the Δ production cross section off the free nucleon target in the charged current neutrino and antineutrino induced reactions, we have used Equation (44) and integrated over the final lepton kinematical variables.

2. In the presence of nuclear medium effects the expression of the cross sections given in Equations (55, 56), respectively for the Y production and the Δ production, have been used. In the case of hyperon production FSI arising due to the quasielastic and charge exchange hyperon nucleon scattering has been taken into account as described in section-3.1.

3. For the pion production cross section from the hyperons, we have used the same expression (Equation 55) with the hyperon-nucleon interaction. For the pions arising from the Δ decay with NME+FSI, we have used Equation (61) with the pion FSI effect as described in section-4.1.1. Therefore, FSI effect in the case of pion production from the hyperons is different from the FSI effect for the pion production from the Δ i.e., there is no pion absorption in the case of hyperons giving rise to pions, whereas there is pion absorption inside the nucleus when Δs give rise to pions.

4. We have used ${\rho }_{\mathrm{\text{p}}}\left(r\right)=\frac{Z}{A}\rho \left(r\right)$ for the proton density, and ${\rho }_{\mathrm{\text{n}}}\left(r\right)=\frac{A-Z}{A}\rho \left(r\right)$ for the neutron density, where ρ(r) is nuclear density taken as 3-parameter Fermi density for ¹²C, ¹⁶O, ⁴⁰Ar and ²⁰⁸Pb given by:

$\rho \left(r\right)=\frac{{\rho }_0\left(1+w\frac{r^2}{c^2}\right)}{\left(1+exp\left(\frac{r-c}{z}\right)\right)},$

with the density parameters c = 2.355 fm, z = 0.5224 fm and w = −0.149 for ¹²C, c = 2.608 fm, z = 0.513 fm and w = −0.051 for ¹⁶O, c = 3.73 fm, z = 0.62 fm and w = −0.19 for ⁴⁰Ar and c = 6.624 fm, z = 0.549 fm and w = 0 for ²⁰⁸Pb and have been taken from De Jager et al. [94].

5. The results for the longitudinal ($P_L\left(Q^2\right)$), perpendicular ($P_P\left(Q^2\right)$) and transverse ($P_T\left(Q^2\right)$) components of the polarization of the Λ hyperon have been obtained using Equations (35–37) respectively in the presence of second class currents with and without T-invariance. For the axial vector form factors, the expressions used in Equations (18–20) for $g_1^{NY}\left(Q^2\right)$ and $g_2^{NY}\left(Q^2\right)$ have been used while the parameterization of BBBA05 for the nucleon form factors as they appear in Equations (13–15) for $f_1^{NY}\left(Q^2\right)$ and $f_2^{NY}\left(Q^2\right)$ have been used. For the pseudoscalar form factor $g_3^{NY}\left(Q^2\right)$, Nambu's parameterization given in Equation (23) has been used.

6. We have also presented the results for the flux averaged cross section and the polarization observables in order to compare our results with the experimental results. For this, we have integrated the differential cross section dσ/dQ² and polarization observables $P_L\left(Q^2\right)$ and $P_P\left(Q^2\right)$ over $E_{{\bar{\nu }}_{{}_{\mu }}}$ and Q² distributions to obtain the total cross section 〈σ〉 defined as:

$\begin{array}{ll}\langle \sigma \rangle =\frac{{\int }_{E_{th}}^{E_{max}}{\int }_{Q_{min}^2}^{Q_{max}^2}\frac{d\sigma }{d{Q}^2}d{Q}^2\Phi (E_{{\bar{\nu }}_{{}_{\mu }}})d{E}_{{\bar{\nu }}_{{}_{\mu }}}}{{\int }_{E_{min}}^{E_{max}}\Phi (E_{{\bar{\nu }}_{{}_{\mu }}})d{E}_{{\bar{\nu }}_{{}_{\mu }}}}& \left(63\right)\end{array}$

and components of hyperon polarization 〈P_{L, P}〉 defined as:

$\begin{array}{ll}\langle P_{L,P}\rangle =\frac{1}{\langle \sigma \rangle }{\displaystyle {\int }_{E_{th}}^{E_{max}}}{\displaystyle {\int }_{Q_{min}^2}^{Q_{max}^2}}{P}_{L,P}(Q^2,E_{{\bar{\nu }}_{{}_{\mu }}})\frac{d\sigma }{d{Q}^2}d{Q}^2\Phi (E_{{\bar{\nu }}_{{}_{\mu }}})d{E}_{{\bar{\nu }}_{{}_{\mu }}}.& \left(64\right)\end{array}$

5.1. Hyperon and Delta Productions From Free Nucleons

5.1.1. Hyperon Production

In Figure 3, we have presented the results for the hyperon production cross sections from the free nucleons presented in Equations (1–3) as a function of antineutrino energies. These results are presented for the Λ, Σ⁻ and Σ⁰ cross sections at the two values of M_A viz. M_A = 1.026 GeV and 1.2 GeV. We find that in this region there is very little dependence of M_A on the cross section in the case of Σ⁻ and Σ⁰ production, while in the case of Λ production, the cross section increases with energy and the increase is about 5% at $E_{{\bar{\nu }}_{\mu }}=1$ GeV. In the case of free nucleon, the cross sections for ${\bar{\nu }}_{\mu }+n\to {\mu }^{+}+{\Sigma }^{-}$ and ${\bar{\nu }}_{\mu }+p\to {\mu }^{+}+{\Sigma }^0$ are related by a simple relation i.e., $\sigma \left({\bar{\nu }}_{\mu }p\to {\mu }^{+}{\Sigma }^0\right)=\frac{1}{2}\sigma \left({\bar{\nu }}_{\mu }n\to {\mu }^{+}{\Sigma }^{-}\right)$, while no Σ⁺ is produced off the free nucleon target due to ΔS ≠ ΔQ rule. A comparison is made with available experimental results from CERN [59–61], BNL [62], FNAL [63, 64] and SKAT [65] experiments as well as with the theoretical calculations performed by Wu et al.[84] and Finjord and Ravndal [55] using quark model and the calculations performed by Erriquez et al. [61], Brunner et al.[65] and Kuzmin and Naumov [68] based on the prediction from Cabibbo theory. A reasonable agreement with the experimental results can be seen.

FIGURE 3

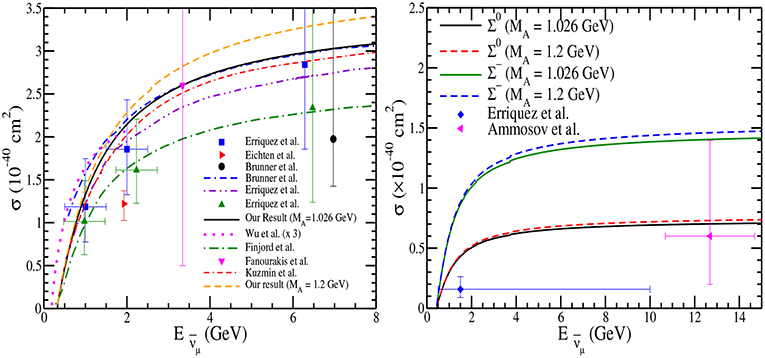
Figure 3. σ vs. $E_{{\bar{\nu }}_{\mu }}$ for the Λ production (left), Σ⁰ and Σ⁻ production (right) cross sections. Solid (dashed) line represents the result using M_A = 1.026 (1.2) GeV. Experimental results for the process ${\bar{\nu }}_{\mu }p\to {\mu }^{+}\Lambda$ (triangle right [60], triangle up [59], square [61], triangle down($\sigma =2.6_{-2.1}^{+5.9}\times 10^{-40}c{m}^2$) [62], circle [65]) and for the process ${\bar{\nu }}_{\mu }p\to {\mu }^{+}{\Sigma }^0$ (diamond [59]) are shown with error bars. Theoretical curves are of Kuzmin and Naumov [68](double dashed-dotted line), Brunner et al. [65](dashed line), Erriquez et al. [61](dashed-double dotted line) obtained using Cabibbo theory with axial vector dipole mass as 0.999, 1.1, and 1 GeV, respectively, while the results of Wu et al. [84](dotted line) and Finjord and Ravndal [55](dashed dotted line) are obtained using quark model.

In Figure 4, the results are presented for the differential cross section (dσ/dQ²) as a function of Q² for the Λ and Σ⁻ produced in the final state at the different antineutrino energies viz. $E_{{\bar{\nu }}_{\mu }}=0.5$ GeV, 0.75 GeV and 1 GeV at the two values of M_A viz. M_A = 1.026 GeV and 1.2 GeV. One may notice that the Q²-distribution is not much sensitive to the choice of M_A.

FIGURE 4

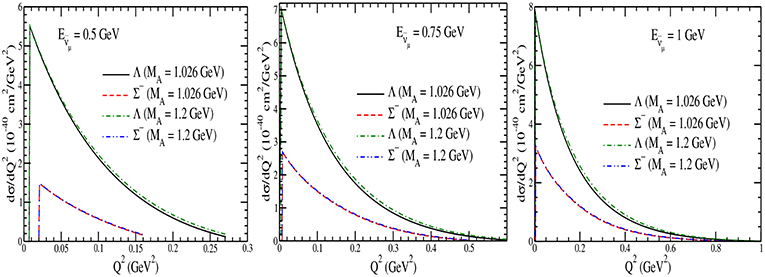
Figure 4. dσ/dQ² vs. Q² for the hyperon production cross sections at different antineutrino energies viz. $E_{{\bar{\nu }}_{\mu }}=0.5$ GeV (left), 0.75 GeV (middle), and 1 GeV (right). Lines and points have the same meaning as in Figure 3.

In Figure 5, we have presented the comparison of present results for the Q² distribution with the results given in Figure 3 of [63]. Solid line represents the present results using M_A = 1 GeV, dashed-dotted line represents the present results obtained using Equation (12) of [63] and the data points are taken from Ammosov et al. [63]. We have multiplied our results with an arbitrary factor of 7 in order to compare our result with the experimental data points.

FIGURE 5

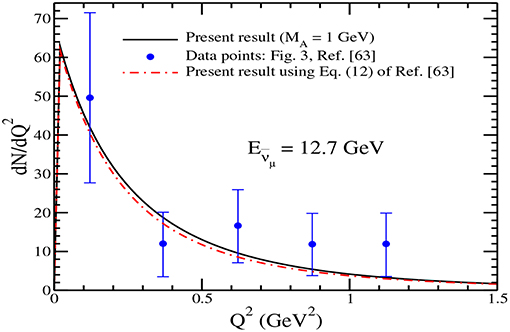
Figure 5. Comparison of present results for the Q² distribution with the results given in Figure 3 of Ammosov et al. [63]. Solid line represents the present results using M_A = 1 GeV, dashed-dotted line represents the present results obtained using Equation (12) of Ammosov et al. [63] and the data points are taken from Ammosov et al. [63].

In order to compare with the experimental results of CERN experiment [61], we have performed the numerical calculations for the flux averaged cross section 〈σ〉, longitudinal 〈P_L〉 and perpendicular 〈P_P〉 polarization components relevant for the antineutrino flux of SPS antineutrino beam of Gargamelle experiment at CERN [97] and present our results in Table 2. The results are compared with the available experimental results from CERN [59–61] experiment and the theoretical results quoted by Erriquez et al. [61].

TABLE 2

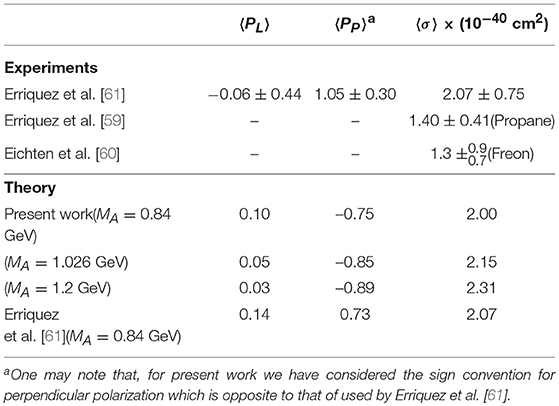
Table 2. Flux averaged cross section 〈σ〉(using Equation 63), longitudinal 〈P_L〉 and perpendicular 〈P_P〉 components of polarization(using Equation 64) are given for the process ${\bar{\nu }}_{\mu }p\to {\mu }^{+}\Lambda$.

Experimentally, one may get information about the polarization of hyperons through the structure of the angular distribution of the pions, which are produced by the hyperon decay via. Y → Nπ. The observation of the components of the polarization provide an alternative method to determine the axial dipole mass, M_A, nature of the second class current (whether with or without TRI) and the pseudoscalar form factor independent of the total and the differential scattering cross sections. Moreover, the experimental observation of the transverse component of polarization can be used to study the physics of T-violation. In Figure 6, we have made an attempt to explore the possibility of determining the pseudoscalar form factor $g_3^{NY}\left(Q^2\right)$ in |ΔS| = 1 sector and studied the sensitivity of the Q²-dependence on the polarization components $P_L\left(Q^2\right)$, $P_P\left(Q^2\right)$ and $P_T\left(Q^2\right)$ using the expression of Nambu [88] in Equation (23) for the process ${\bar{\nu }}_{\mu }p\to {\mu }^{+}\Lambda$ at $E_{{\bar{\nu }}_{{}_{\mu }}}$=0.4 and 0.7 GeV. We see that at $E_{{\bar{\nu }}_{{}_{\mu }}}=0.4$ GeV, $P_L\left(Q^2\right)$, $P_P\left(Q^2\right)$ and $P_T\left(Q^2\right)$ are sensitive to $g_3^{NY}\left(Q^2\right)$, but with the increase in energy the results obtained with and without $g_3^{NY}\left(Q^2\right)$ are almost the same. It seems, therefore, possible in principle, to determine the pseudoscalar form factor in the Λ polarization measurements at lower antineutrino energies. The total cross section σ and the differential cross section dσ/dQ² are not found to be very sensitive to the values of $g_3^{NY}\left(Q^2\right)$ and are not shown here [80].

FIGURE 6

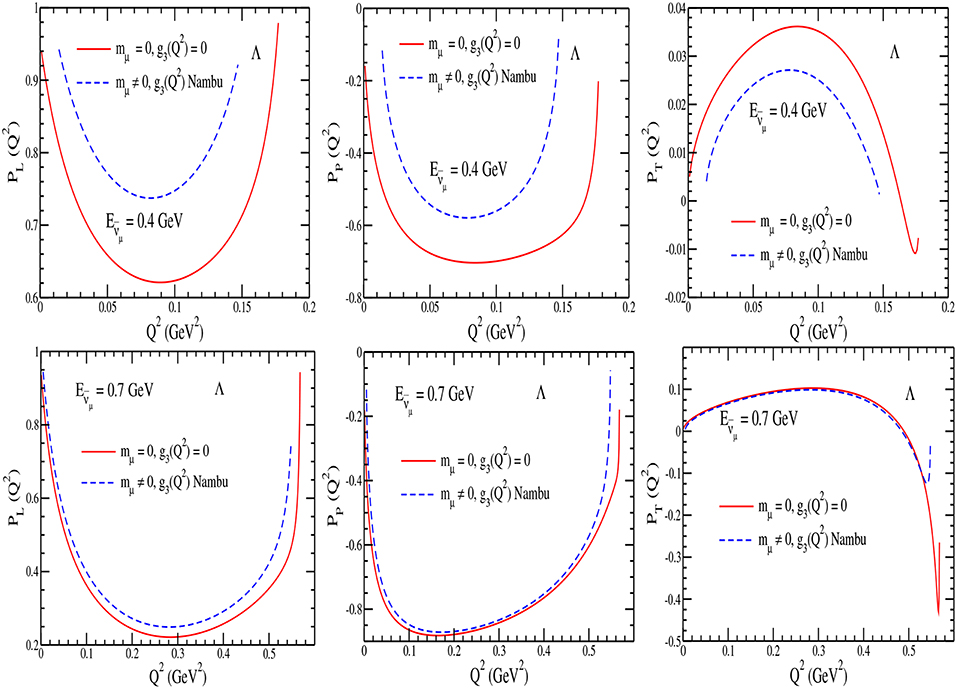
Figure 6. $P_L\left(Q^2\right)$ (left), $P_P\left(Q^2\right)$ (middle), and $P_T\left(Q^2\right)$ (right) for the process ${\bar{\nu }}_{\mu }+p\to {\mu }^{+}+\Lambda$ at $E_{{\bar{\nu }}_{\mu }}=0.4$ GeV (upper) and 0.7 GeV (lower) with $m_{\mu }=0,g_3\left(Q^2\right)$ = 0 (solid line) and m_μ ≠ 0 and $g_3\left(Q^2\right)$ given by Nambu (dashed line).

For the reaction ${\bar{\nu }}_{\mu }+p\to {\mu }^{+}+\Lambda$, we have also studied the dependence of the polarization components on the second class currents with T-invariance and showed the results for $P_L\left(Q^2\right)$ and $P_P\left(Q^2\right)$ as a function of Q² in Figure 7. These results are presented for the polarization components using the second class current form factor in the presence of T invariance i.e., using the real values of $g_2^{np}\left(0\right)=g_2^R\left(0\right)=$ 0, ±1 and ±3 and M₂ = M_A in Equation (22) at the different values of $E_{{\bar{\nu }}_{\mu }}=$ 0.4 and 0.7 GeV. We find that $P_L\left(Q^2\right)$ shows large variations as we change $\left|g_2^R\left(0\right)\right|$ from 0 to 3 at high antineutrino energies, $E_{{\bar{\nu }}_{\mu }}$ (say 0.7 GeV) in comparison to the lower energies (say 0.4 GeV). For example, in the peak region of Q², the difference is 80% at E_νμ = 0.7 GeV and it is 20% at E_νμ = 0.4 GeV as $g_2^R\left(0\right)$ is changed from 0 to 3. In the case of $P_P\left(Q^2\right)$ also, the Q² dependence is quite strong and similar to $P_L\left(Q^2\right)$.

FIGURE 7

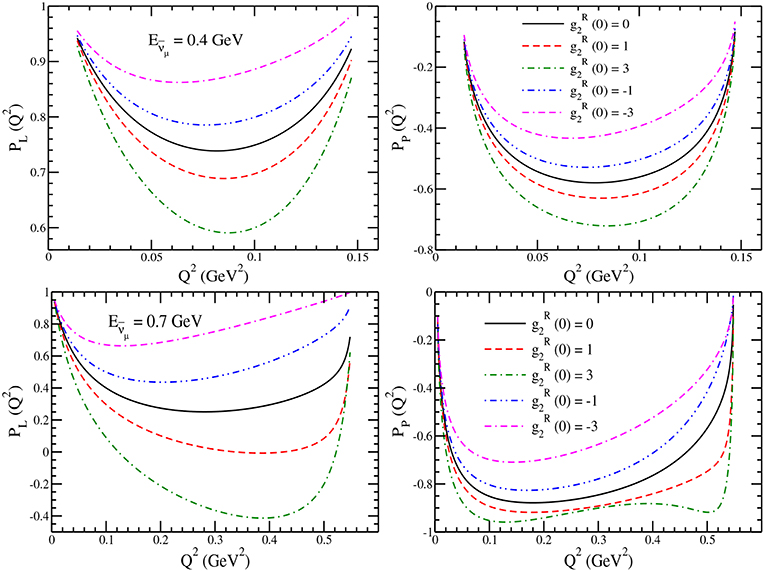
Figure 7. $P_L\left(Q^2\right)$ (left) and $P_P\left(Q^2\right)$ (right) for the process ${\bar{\nu }}_{\mu }+p\to {\mu }^{+}+\Lambda$ at $E_{{\bar{\nu }}_{\mu }}=0.4$ GeV (upper) and 0.7 GeV (lower) with $g_2^R\left(0\right)=$ 0 (solid line), 1 (dashed line), 3 (dash-dotted line), −1 (dash-double-dotted line), and −3 (double-dash-dotted line).

In Figure 8, the results are presented for $P_L\left(Q^2\right)$, $P_P\left(Q^2\right)$ and $P_T\left(Q^2\right)$ as a function of Q² in the presence of the second class current without T-invariance, using the imaginary values of the induced tensor form factor i.e., $g_2^{np}\left(0\right)=i{g}_2^I\left(0\right)$, where (0) = 0, 1 and 3, at the different values of $E_{{\bar{\nu }}_{\mu }}=$ 0.4 and 0.7 GeV. We see that while $P_L\left(Q^2\right)$ is less sensitive to $g_2^I\left(0\right)$ at $E_{{\bar{\nu }}_{\mu }}$ in the range 0.4−0.7 GeV. $P_P\left(Q^2\right)$ is almost insensitive to $g_2^I\left(0\right)$ at the lower $E_{{\bar{\nu }}_{\mu }}$, say at $E_{{\bar{\nu }}_{\mu }}=$ 0.4 GeV. However, at higher antineutrino energies, say at $E_{{\bar{\nu }}_{\mu }}=$ 0.7 GeV, $P_P\left(Q^2\right)$ is sensitive to $g_2^I\left(0\right)$. Moreover, $P_T\left(Q^2\right)$ is sensitive to $g_2^I\left(0\right)$ at all antineutrino energies. $P_T\left(Q^2\right)$ shows 8% and 25% variations at Q² = 0.08, and 0.25 GeV² at $E_{{\bar{\nu }}_{\mu }}=$ 0.4 and 0.7 GeV, respectively, when $g_2^I\left(0\right)$ is varied from 0 to 3.

FIGURE 8

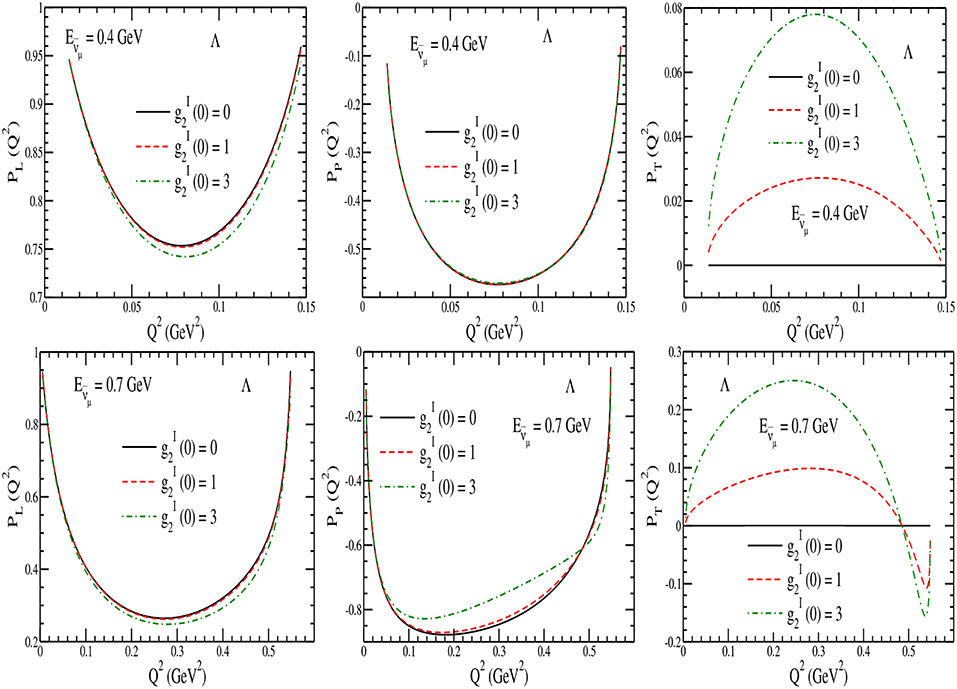
Figure 8. $P_L\left(Q^2\right)$ (left), $P_P\left(Q^2\right)$ (middle), and $P_T\left(Q^2\right)$ (right) for the process ${\bar{\nu }}_{\mu }+p\to {\mu }^{+}+\Lambda$ at $E_{{\bar{\nu }}_{\mu }}=0.4$ GeV (upper) and 0.7 GeV (lower) with $g_2^I\left(0\right)=$ 0 (solid line), 1 (dashed line), and 3 (dash-dotted line).

5.1.2. Δ Production

The results for the Δ production cross sections are presented in Figure 9 for ν_μ and ${\bar{\nu }}_{{}_{\mu }}$ induced processes off the free nucleon target. For ν_μ induced reaction, the leptonic current in Equation (5) will read as $l_{\mu }=ū\left(k^{\prime }\right){\gamma }_{\mu }\left(1-{\gamma }_5\right)u\left(k\right)$. In the case of Δ production, the cross sections are inhibited by the threshold effect at lower energies, and there is almost no cross section until $E_{{\bar{\nu }}_{\mu }}$ = 0.4 GeV. In Figure 10, the results for dσ/dQ² are presented for the Δs produced in the final state at the different (anti)neutrino energies viz. $E_{{\nu }_{\mu },{\bar{\nu }}_{{}_{\mu }}}$ = 0.5, 0.75 and 1 GeV. The total cross section and its energy dependence as well as the Q² dependence have been discussed elsewhere in literature [24, 26, 50, 67, 92].

FIGURE 9

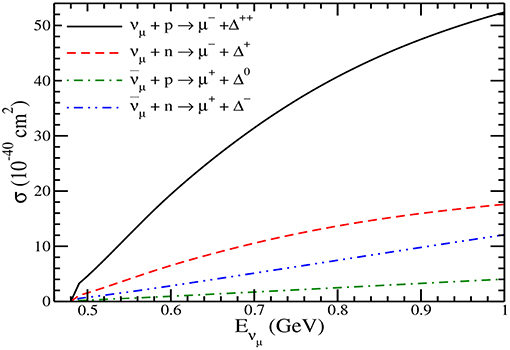
Figure 9. σ vs. E_νμ for the Delta production cross sections. Solid line represents the result for Δ⁺⁺ production cross section, dashed line represents the result for Δ⁺ cross section, dash-dotted line represents the result for Δ⁰ production and the dash-double-dotted line represents the result for the Δ⁻ production cross section.

FIGURE 10

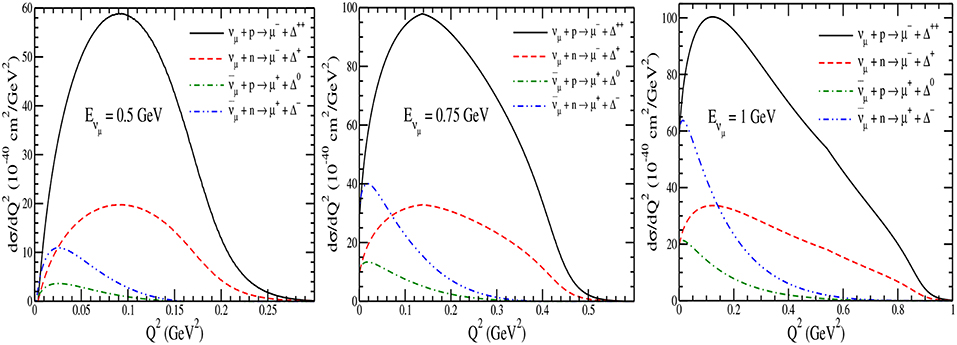
Figure 10. dσ/dQ² vs. Q² for the Δ production cross sections at the different antineutrino energies viz. E_νμ = 0.5 GeV (left), 0.75 GeV (middle), and 1 GeV (right). Lines and points have the same meaning as in Figure 9.

5.2. Hyperon and Delta Production From Nuclei

In Figure 11, we have presented the results for σ vs $E_{{\bar{\nu }}_{\mu }}$, for the Δ⁰ produced off the proton bound in various nuclear targets like ¹²C, ¹⁶O, ⁴⁰Ar and ²⁰⁸Pb with and without the NMEs. It may be noticed that the NMEs due to the modification of the Δ properties in nuclei reduce the cross section. In the case of lighter nuclei like ¹²C and ¹⁶O, this reduction is about ~ 35% at $E_{{\bar{\nu }}_{{}_{\mu }}}$=1 GeV. The reduction in the cross section increases with the increase in the nuclear mass number and decreases with the increase in energy. For example, it becomes ~ 40% and 50% in ⁴⁰Ar and ²⁰⁸Pb, respectively at $E_{{\bar{\nu }}_{{}_{\mu }}}=1$ GeV. We find that the NMEs due to Pauli blocking and Fermi motion effects, in the case of hyperons in the final state, are negligibly small and therefore we have not discussed these effects and the results of the cross sections are almost the same as for the free hyperon case (Figure 3). Moreover, when the hyperon-nucleon interaction i.e., the FSI effect in the hyperon production, is taken into account the overall change in the hyperon production cross section is very small. These results are used to obtain the ratio of total hyperon to Δ production cross sections i.e., $\frac{{\sigma }_Y}{{\sigma }_{\Delta }}$ which have been shown in the inset of these figures. It may be noticed that due to the threshold effect initially the hyperon production cross section dominates and with the increase in energy the ratio reduces. Due to the substantial reduction in the cross section for the Δ production, the ratio increases when NME is taken into account in comparison to the free case. Moreover, this ratio is larger in heavy nuclei like ²⁰⁸Pb as NME increases with the nucleon number.

FIGURE 11

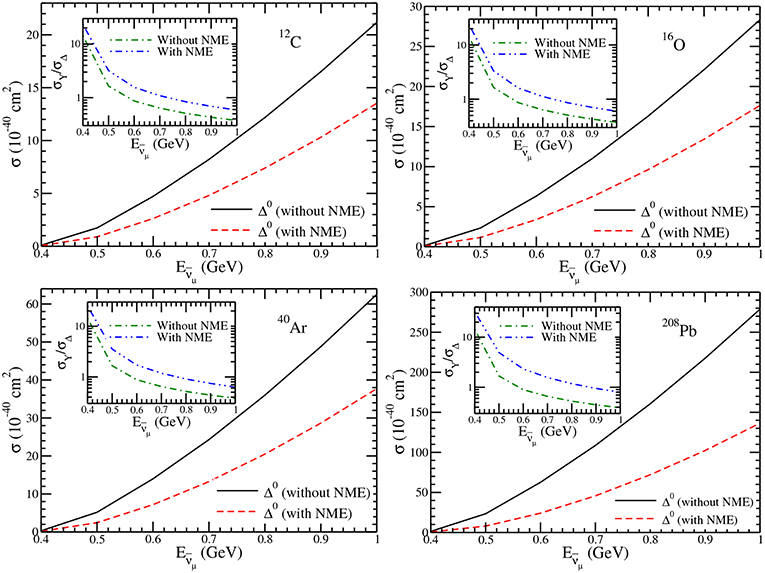
Figure 11. σ vs. $E_{{\bar{\nu }}_{\mu }}$ for the Δ⁰ production cross sections without (solid line) and with (dashed line) NME for the various nuclear targets. Ratio, ${\sigma }_Y/{\sigma }_{{\Delta }^0}$ vs. $E_{{\bar{\nu }}_{\mu }}$ without (dash-dotted line) and with (dash-double-dotted) NME for the various nuclear targets are presented in the inset.

5.3. Pion Production

In this section the results are presented for the π⁻ and π^o productions respectively in the nuclei like ¹²C, ¹⁶O, ⁴⁰Ar and ²⁰⁸Pb. We give a preview of our main results for π⁻ and π^o productions before they are presented in detail in Figures 12–15 and Figures 16–19, for each case. These results are shown for the cross sections obtained without and with NME+FSI effect for the pion production arising due to the Λ production, total hyperon(Y) production and the Δ production. In the case of hyperon production, NMEs in the production process as well as the FSI due to hyperon-nucleon interactions have been taken into account. Moreover, we do not include the FSI of pions within the nuclear medium which are produced as a result of hyperon decays. This is because the decay width of pionic decay modes of hyperons is highly suppressed in the nuclear medium. Due to which these hyperons live long enough to pass through the nucleus and decay outside the nuclear medium. Thus, the produced pions are less affected by the strong interaction of nuclear field. This is not the case with the pion produced through strong decays of Δ, as they are further suppressed by the strong absorption of pions in the nuclear medium. Therefore, in the low energy region the Cabibbo suppression in the case of pion production through hyperons get compensated by the threshold suppression as well as by the strong pion absorption effects in the case of the pions produced through the Delta excitation. On the other hand, FSI due to Σ − N and Λ − N interactions in various channels tend to increase the Λ production cross section and decrease the Σ⁻ production cross section, which is mainly a threshold effect. The quantitative increase (decrease) in Λ(Σ) yield due to FSI increases with the increase in the nucleon number. The interaction of hyperons with the nucleons bound inside the nucleus, separately affect Σ⁻ and Σ⁰ productions and the relation $\sigma \left({\bar{\nu }}_{\mu }+p\to {\mu }^{+}+{\Sigma }^0\right)=\frac{1}{2}\sigma \left({\bar{\nu }}_{\mu }+n\to {\mu }^{+}+{\Sigma }^{-}\right)$ which holds for the free case, does not hold for the case of nuclear targets. We must point out that although Σ⁺ is not produced from a free nucleon but can be produced through the final state interactions like Λp → Σ⁺n and Σ⁰p → Σ⁺n, albeit the contributions would be small.

FIGURE 12

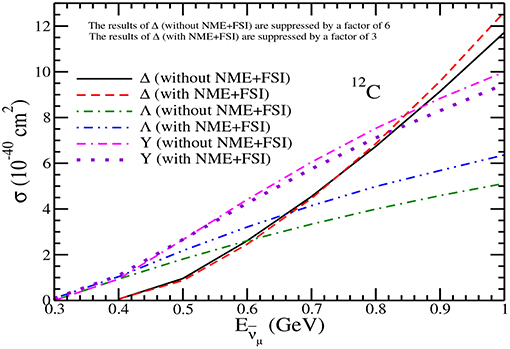
Figure 12. Results for the charged current π⁻ production in ¹²C with and without NME+FSI. The results are presented for the pion production from the Δ, Λ, and total hyperon Y(= Λ + Σ) with and without NME+FSI. Notice that the results of Δ without NME+FSI are suppressed by a factor of 6 and the results with NME+FSI are suppressed by a factor of 3 to bring them on the same scale.

FIGURE 13

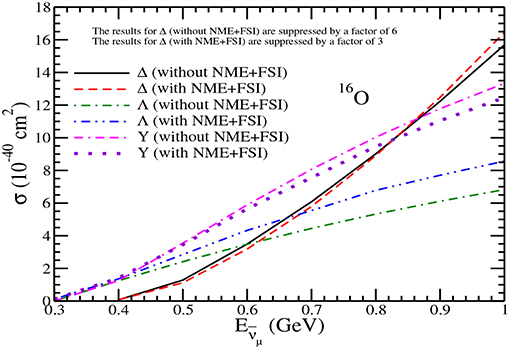
Figure 13. Results for π⁻ production in ¹⁶O. Lines and points have the same meaning as in Figure 12.

FIGURE 14

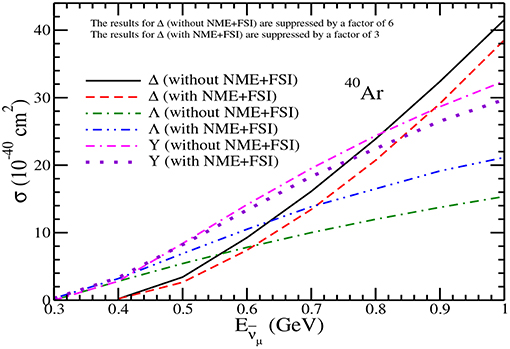
Figure 14. Results for π⁻ production in ⁴⁰Ar. Lines and points have the same meaning as in Figure 12.

FIGURE 15

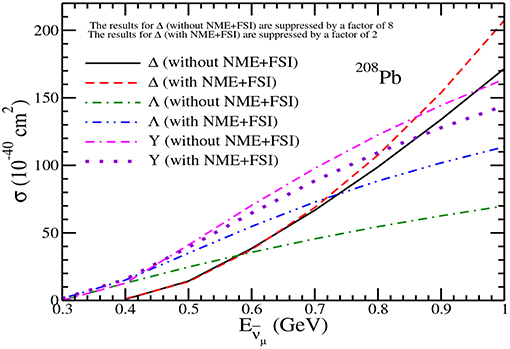
Figure 15. Results for π⁻ production in ²⁰⁸Pb. Lines and points have the same meaning as in Figure 12. Notice that the results of Δ without NME+FSI are suppressed by a factor of 8 and the results with NME+FSI are suppressed by a factor of 2 to bring them on the same scale.

FIGURE 16

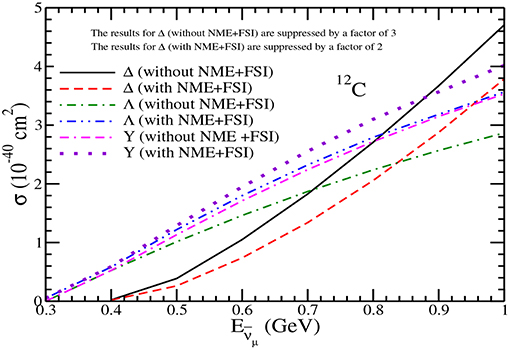
Figure 16. Results for the charged current π^o production in ¹²C with and without NME+FSI. The results are presented for the pion production from Δ, Λ, and total hyperon Y = Λ + Σ with and without NME+FSI. Notice that the results of Δ without NME+FSI are suppressed by a factor of 3 and the results with NME+FSI are suppressed by a factor of 2.

FIGURE 17

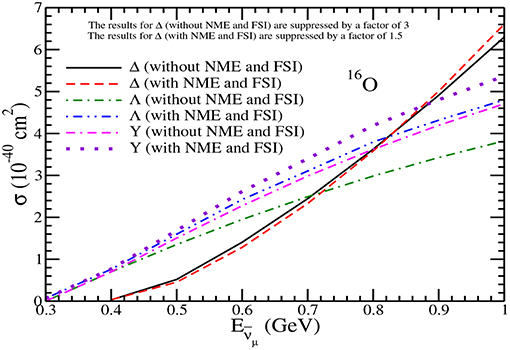
Figure 17. Results for π^o production in ¹⁶O. Lines and points have the same meaning as in Figure 16. Notice that the results of Δ without NME+FSI are suppressed by a factor of 3 and the results with NME+FSI are suppressed by a factor of 1.5.

FIGURE 18

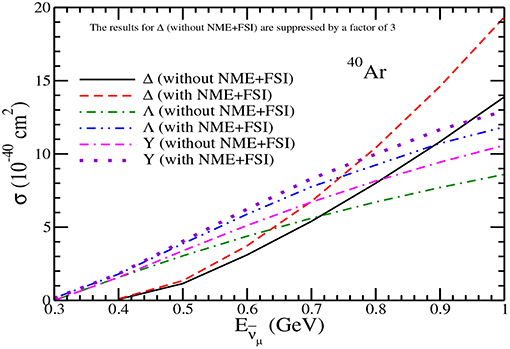
Figure 18. Results for π^o production in ⁴⁰Ar. Lines and points have the same meaning as in Figure 16. Notice that the results of Δ without NME+FSI are suppressed by a factor of 3.

FIGURE 19

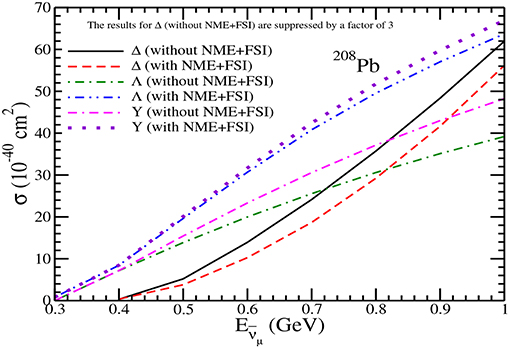
Figure 19. Results for π^o production in ²⁰⁸Pb. Lines and points have the same meaning as in Figure 16. Notice that the results of Δ without NME+FSI are suppressed by a factor of 3.

Using the results of σ, we have obtained the results for the ratio of hyperon to Delta production cross sections, with and without NME+FSI, for π⁻ as well as π^o productions for all the nuclear targets considered here by defining

${R_N=\frac{\sigma \left(Y\to N\pi \right)}{\sigma \left(\Delta \to N\pi \right)}|}_{\text{without NME }+\text{ FSI effects}}\left(65\right)$

and

${R_A=\frac{\sigma \left(Y\to N\pi \right)}{\sigma \left(\Delta \to N\pi \right)}|}_{\text{with NME }+\text{ FSI effects}}.\left(66\right)$

This ratio directly tells us the enhancement of the ratio R_A due to NME+FSI with the increase in the mass number of the nuclear targets as the pions getting produced through the Δ-resonant channel undergo a suppression due to NME+FSI effect, while the pions getting produced from the hyperons (all the interactions taken together i.e., Λ as well as Σ contributions) have comparatively small NME+FSI effect.

In Figures 12, 13, we have presented the results for the total scattering cross section σ vs $E_{{\bar{\nu }}_{\mu }}$, for ${\bar{\nu }}_{\mu }$ scattering off the nucleon in ¹²C and ¹⁶O nuclear targets giving rise to π⁻. The results are presented for the pion production from Δ, Λ and Y with and without NME and FSI. In the case of hyperon production for ¹²C, the effect of FSI due to Y−N interaction increases the Λ production cross section from the free case by about 23−24% for $E_{{\bar{\nu }}_{\mu }}=0.6-1$ GeV, while the change in the total hyperon production cross section results in a decrease in the cross section due to the FSI effect which is about 3−5% at these energies. We find that in the case of pions produced through Δ excitations, NME+FSI lead to a reduction of around 50% in the π⁻ production for the antineutrino energies 0.6 $<E_{{\bar{\nu }}_{\mu }}<$ 1GeV. This results in the change in the ratio of R_N (Equation 65) from 0.28 and 0.14 respectively at $E_{{\bar{\nu }}_{\mu }}$=0.6 and 1GeV to R_A (Equation 66) → 0.58 and 0.25 at these energies. In the case of ¹⁶O nuclear target the observations are similar to what has been discussed above in the case of ¹²C nuclear target.

In Figure 14, we have presented the results for σ vs $E_{{\bar{\nu }}_{\mu }}$, for ${\bar{\nu }}_{\mu }$ scattering off ⁴⁰Ar nuclear target. In the case of Λ production, the effect of FSI leads to an increase in the cross section by about 34−38% for $E_{{\bar{\nu }}_{\mu }}=0.6-1$ GeV, however, the overall change in the π⁻ production from the hyperons results in a net reduction in the cross section from the free case, which is about 6−8% at these energies. In the case of pions produced through Δ excitations, NME+FSI leads to a reduction of around 55−60% in the π⁻ production for the antineutrino energies 0.6 $\le E_{{\bar{\nu }}_{\mu }}\le$ 1 GeV, and the reduction is less at higher energies. This results in the change in the ratio of R_N from 0.25 and 0.13 respectively at $E_{{\bar{\nu }}_{\mu }}=0.6$ and 1 GeV to R_A, 0.6 and 0.26 at the corresponding energies.

In the case of heavy nuclear target like ²⁰⁸Pb, the change in the cross section due to NME+FSI is quite large and the results for σ vs $E_{{\bar{\nu }}_{\mu }}$, for ${\bar{\nu }}_{\mu }$ scattering off the nucleon in ²⁰⁸Pb nuclear target are shown in Figure 15. For example, the reduction in the cross section due to NME+FSI when a Δ is produced as the resonant state, is about 75% at $E_{{\bar{\nu }}_{\mu }}=$ 0.6 GeV and 70% at $E_{{\bar{\nu }}_{\mu }}=$ 1 GeV from the cross sections calculated without the medium effect. The enhancement in the Λ production cross section is about 55−60% at these energies. While the overall change in the π⁻ production from the hyperons results in a net reduction which is about 8−12%. This results in the change in the ratio of R_N from 0.23 and 0.12 respectively at $E_{{\bar{\nu }}_{\mu }}=0.6$ and 1 GeV to R_A → 0.86 and 0.35, respectively.

In Figures 16–19, we have presented the results for the total scattering cross section σ vs $E_{{\bar{\nu }}_{\mu }}$, for ${\bar{\nu }}_{\mu }$ scattering off nucleon in ¹²C, ¹⁶O, ⁴⁰Ar and ²⁰⁸Pb nuclear targets giving rise to π^o. These results are presented for the pion production from Δ, Λ and Y with and without NME+FSI. In the case of π^o arising due to hyperon decay, the contribution comes from the Λ and Σ⁰ decay, while there is no contribution from Σ⁻. Due to the FSI effect there is substantial increase in the Λ production cross section and reduction in the Σ⁰ production cross section from the free case, which leads to an overall increase in the π^o production. Therefore, unlike the π⁻ production where there is overall reduction, in the case of π^o production there is an increase in the cross section which is about 13−14% in ¹²C and ¹⁶O, 22−23% in ⁴⁰Ar and 26−38% in ²⁰⁸Pb for $E_{{\bar{\nu }}_{\mu }}$ = 0.6 to 1 GeV. The different Clebsch-Gordan coefficients for Δ (in Equations 51–54) and the branching ratios for the hyperons (in Equations 48–50) give a different ratios of R_N and R_A. This results in the change in the ratio of R_N from 0.58 and 0.26 respectively at $E_{{\bar{\nu }}_{\mu }}=$ 0.6 and 1 GeV to R_A → 1.3 and 0.5 in ¹²C and ¹⁶O, from 0.55 and 0.25 respectively at $E_{{\bar{\nu }}_{\mu }}=0.6$ and 1 GeV to 1.68 and 0.66 in ⁴⁰Ar, and from 0.56 and 0.26 respectively at $E_{{\bar{\nu }}_{\mu }}=0.6$ and 1 GeV to 3 and 1.2 in ²⁰⁸Pb. Thus, in the case of π^o production, there is significant increase in Y → Nπ to Δ → Nπ ratio when NME+FSI are taken into account specially in the case of heavier nuclear targets.

In Figure 20, we have presented the results for the ν_μ induced π⁺ and π^o productions and ${\bar{\nu }}_{\mu }$ induced π⁻ and π^o productions. For ν_μ induced reactions, the leptonic current in Equation (5) will read as $l_{\mu }=ū\left(k^{\prime }\right){\gamma }^{\mu }\left(1-{\gamma }_5\right)u\left(k\right)$ and the expression of ρ_N(r) in Equation (62) will become ${\rho }_N\left(r\right)={\rho }_p\left(r\right)+\frac{1}{9}{\rho }_n\left(r\right)$. These results are shown for ¹²C, ¹⁶O, ⁴⁰Ar and ²⁰⁸Pb with NME+FSI. For ν_μ scattering, the contribution to the pions is coming from Δ only, while for ${\bar{\nu }}_{\mu }$ scattering the contribution to the pions is coming from the Δ as well the hyperons. Though in the case of the pions produced through the hyperon production, there is an overall suppression by a factor of sin${}^2{\theta }_c$ but these are kinematically favored as the Λ production starts around $E_{{\bar{\nu }}_{\mu }}$ = 250 MeV, while Σ⁻ and Σ⁰ production start around $E_{{\bar{\nu }}_{\mu }}$ = 325 MeV, and there is overall no NME effect on the total hyperon production and no FSI effect on the outgoing pions, whereas the reduction is quite significant for the pions arising from the Δs.

FIGURE 20

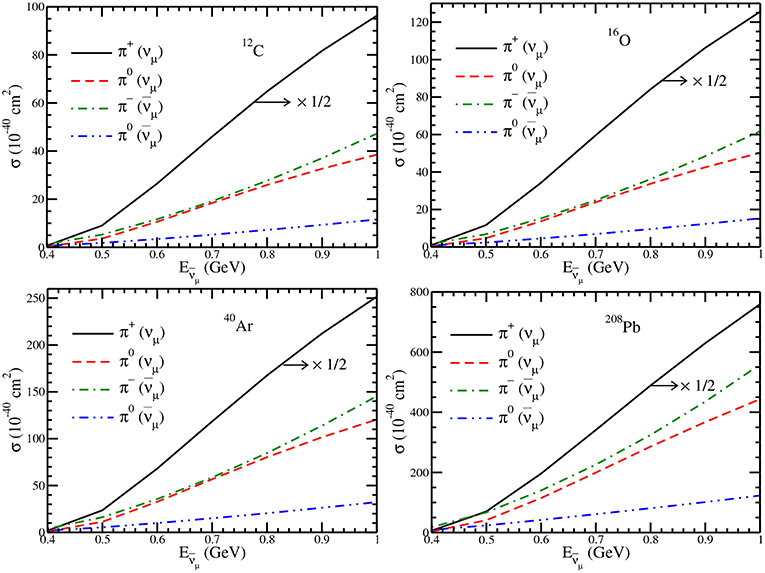
Figure 20. Results for the ν_μ induced π⁺ and π^o production cross sections and ${\bar{\nu }}_{\mu }$ induced π⁻ and π^o production cross sections. For ν_μ scattering the contribution to the pions is coming from the Δ only, while for ${\bar{\nu }}_{\mu }$ scattering the contribution to the pions is coming from the Δ as well as the hyperons. The results are presented for ¹²C, ¹⁶O, ⁴⁰Ar, and ²⁰⁸Pb with NME+FSI. Notice that π⁺ production cross section has been reduced by half to bring it on the same scale.

In Figures 21–24, we have presented the results for the Q² distribution i.e., $\frac{d\sigma }{d{Q}^2}$ vs Q² in ¹²C, ¹⁶O, ⁴⁰Ar and ²⁰⁸Pb nuclear targets with NME+FSI at the different incident antineutrino energies viz. $E_{{\bar{\nu }}_{\mu }}=0.5$ GeV, 0.75 GeV and 1 GeV. These results are presented for the π⁻ contribution from the Δs and the hyperons. It may be observed that at low $E_{{\bar{\nu }}_{\mu }}$, π⁻ has significant contribution from the hyperons, like at $E_{{\bar{\nu }}_{\mu }}=0.5$ GeV, in the peak region of Q², hyperons contribute ~ 40% in ¹²C, ¹⁶O and ⁴⁰Ar and 50% in ²⁰⁸Pb of the total π⁻ production, while with the increase in energy the contribution from the hyperons decreases, for example, at $E_{{\bar{\nu }}_{\mu }}=1$ GeV hyperons contribute 16% in ¹²C, ¹⁶O and ⁴⁰Ar and 24% in ²⁰⁸Pb. The peak region of Q² for the hyperons shifts toward the lower Q² than the Δs. In the case of π^o(not shown here), the results are similar except that the contributions from the hyperons dominate at lower energies in all the nuclear targets in comparison to the Δ contributions and the dominance increases with the increase in the nuclear mass number.

FIGURE 21

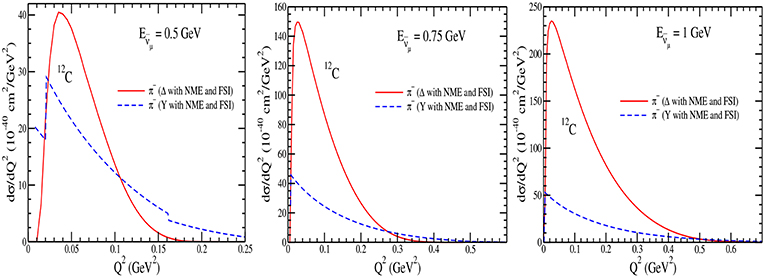
Figure 21. $\frac{d\sigma }{d{Q}^2}$ vs Q² at $E_{{\bar{\nu }}_{\mu }}=0.5$ GeV (left), 0.75 GeV (middle), and 1 GeV (right) for the ${\bar{\nu }}_{\mu }$ induced process in ¹²C nuclear target with NME+FSI. The results are shown for the π⁻ contribution from the Δ (solid line) and from the hyperons (dashed line).

FIGURE 22

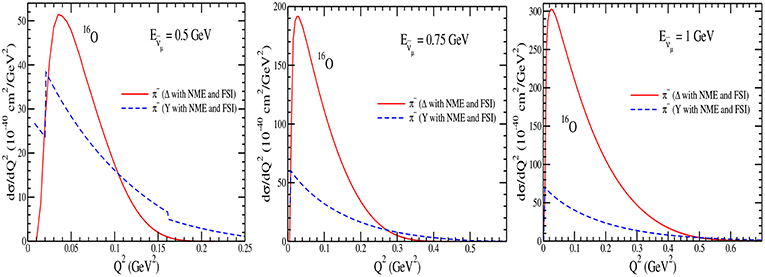
Figure 22. $\frac{d\sigma }{d{Q}^2}$ vs. Q² at $E_{{\bar{\nu }}_{\mu }}=0.5$ GeV (left), 0.75GeV (middle), and 1GeV (right) in ¹⁶O. Lines and points have the same meaning as in Figure 21.

FIGURE 23

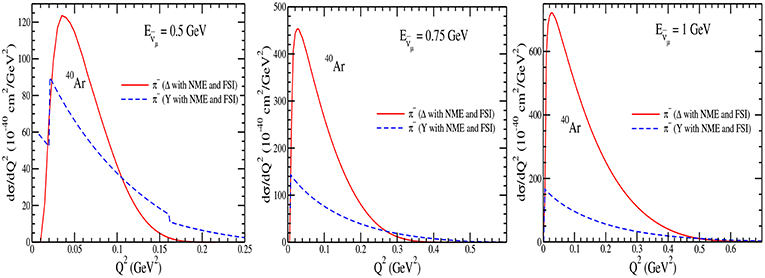
Figure 23. $\frac{d\sigma }{d{Q}^2}$ vs Q² at $E_{{\bar{\nu }}_{\mu }}=0.5$ GeV (left), 0.75GeV (middle), and 1GeV (right) in ⁴⁰Ar. Lines and points have the same meaning as in Figure 21.

FIGURE 24

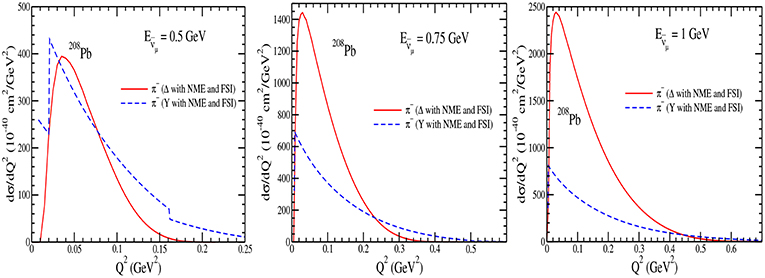
Figure 24. $\frac{d\sigma }{d{Q}^2}$ vs Q² at $E_{{\bar{\nu }}_{\mu }}=0.5$ GeV (left), 0.75GeV (middle), and 1GeV (right) in ²⁰⁸Pb. Lines and points have the same meaning as in Figure 21.

6. Summary and Conclusions

In this work, we have presented a review of the theoretical and experimental work done on the quasielatic production of hyperons induced by antineutrinos which was started more than 50 years ago soon after the V−A theory of weak interactions was extended to the strangeness sector by Cabibbo [41] using SU(3) symmetry properties of the weak hadronic currents. The experimental results on the total cross sections and their Q² dependence available from the older experiments at CERN [59–61], FNAL[63, 64], SKAT [65] and BNL [62] and the results on Lambda hyperon polarizations from CERN [61] are compared with the most recent theoretical results [79, 80].

In view of the future experiments proposed with the antineutrinos at the accelerator and atmospheric antineutrino experiments in the medium energy region of few GeV on the nuclear targets like ¹²C, ¹⁶O, ⁴⁰Ar and ²⁰⁸Pb. We have also presented a summary of the recent theoretical works on the total cross sections, polarization components and their Q² dependence corresponding to many energies relevant for these experiments. These results may be useful in determining the axial vector transition form factor in the strangeness sector specially for the pseudoscalar form factor and the form factor corresponding to the second class currents with and without T-invariance and test the validity of various symmetry properties of the weak hadronic currents. We have also studied the contribution of hyperons produced in these reactions toward the $\bar{\nu }$ induced pion production cross sections in the neutrino oscillation experiments being done at T2K, MINERνA, DUNE, SUPER-K and HYPER-K.

We summarize our results in the following:

(A) In the case of the nucleon targets:

(i) The hyperon production is generally Cabibbo suppressed as compared to the Δ production but in the low energy region of $E_{{\bar{\nu }}_{\mu }}<0.6$ GeV it could be comparable to the Δ production due to the threshold effects.

(ii) (a) The Q² distributions are sensitive to the pseudoscalar form factor at lower antineutrino energies.

(b) The longitudinal $P_L\left(Q^2\right)$ as well as the perpendicular $P_P\left(Q^2\right)$ components of the hyperon polarization are sensitive to the pseudoscalar form factor $g_3\left(Q^2\right)$ specially at lower energies.

(iii) In the presence of the second class currents with T-invariance:

(a) The Q² distribution is not much sensitive to the presence of the second class current until its coupling strength $g_2^R\left(0\right)$ becomes large i.e., $\left|g_2^R\left(0\right)\right|>1$.

(b) The longitudinal component of the polarization $P_L\left(Q^2\right)$ is positive at lower antineutrino energies and becomes negative at higher energies for the values of $g_2^R\left(0\right)$ taken to be positive and large i.e., $g_2^R\left(0\right)>1$.

(c) The perpendicular component of the polarization $P_P\left(Q^2\right)$ is negative for all the values of $g_2^R\left(0\right)$ taken to be positive or negative in the energy range of the present interest.

(iv) In the presence of the second class currents without T-invariance:

(a) The Q² distribution is not much sensitive to the second class current unless $g_2^I\left(0\right)>1$.

(b) The transverse component of the polarization $P_T\left(Q^2\right)$ is nonvanishing and it increases with $g_2^I\left(0\right)$. It changes sign when the sign of $g_2^I\left(0\right)$ is reversed and the absolute value of $P_T\left(Q^2\right)$ increases with the increase in the energy.

(c) The longitudinal($P_L(Q^2)$) and the perpendicular ($P_P(Q^2)$) components of the polarization are not very sensitive to the choice of $g_2^I\left(0\right)$.

(B) In the case of the nuclear targets:

(i) The effect of NME and FSI is to increase the production of Λ-hyperon and to decrease the production of Σ-hyperons in the nuclear medium due to charge exchange processes like Σ N → Λ N and Λ N → Σ N, but the total hyperon production remains the same.

(ii) In the case of the Δ production cross sections, the NME+FSI effect reduces the cross section significantly. This reduction in the cross section increases with the increase in mass number, for example, at $E_{{\bar{\nu }}_{\mu }}=1$ GeV in the case of ¹²C, ¹⁶O and ⁴⁰Ar, the reduction in the cross section is in the range of 40−50% which becomes 70% in the case of ²⁰⁸Pb.

(iii) The reduction due to NME+FSI effects in the case of pions obtained from Δ excitation is large enough to compensate for Cabibbo suppression of pions produced through the hyperon decay specially in the low energy region. Because of this, the pion production from the hyperons is comparable to the pion production from the Δ excitation up to the antineutrino energies of about 0.5 GeV for π⁻ production and 0.65 GeV for π^o production.

(iv) The ratio of pions produced through Y and Δ excitations in nuclei increases with the mass number due to the final state interactions of the pions as the pions coming from the Δ decays are suppressed due to FSI as compared to the pions coming from the hyperons. This ratio decreases with the increase in the antineutrino energies.

(v) We have also presented the numerical results for dσ/dQ² in the various nuclear targets like ¹²C, ¹⁶O, ⁴⁰Ar and ²⁰⁸Pb at the different antineutrino energies.

Thus, to conclude, the contribution of hyperon production to the π⁻ and π^o productions induced by the antineutrinos on the nuclear targets is important specially in the sub-GeV energy region.

Author Contributions

MSA discussed the possible topics which are of topical interest with SKS and decided that Weak quasielastic hyperon production leading to pions in the antineutrino-nucleus reactions would be the most appropriate one as several experiments in the few GeV energy region using antineutrino beam are being performed. The calculations have been performed by AF and MSA. The introduction and the results and discussion part have been written by SKS and MSA together.

Funding

MSA and SKS are thankful to Department of Science and Technology (DST), Government of India for providing financial assistance under Grant No. EMR/2016/002285.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^http://j-parc.jp/index-e.html

2. ^http://www.fnal.gov/

3. ^http://www.dunescience.org/

References

1. Abe K, Adam J, Aihara H, Akiri T, Andreopoulos C, Aoki S, et al. [T2K Collaboration]. Neutrino oscillation physics potential of the T2K experiment. PTEP (2015) 2015:043C01. doi: 10.1093/ptep/ptv031

CrossRef Full Text | Google Scholar

2. Paley JM. [NOνA and LBNE Collaborations]. The search for CP violation and the determination of the neutrino mass hierarchy in NOνA and LBNE. PoS ICHEP (2013) 2012:393. doi: 10.22323/1.174.0393

CrossRef Full Text | Google Scholar

3. Acero MA, Adamson P, Aliaga L, Alion T, Allakhverdian V, Anfimov N, et al. [NOνA Collaboration]. New constraints on oscillation parameters from νe appearance and νμ disappearance in the NOνA experiment. Phys Rev D (2018) 98:032012. doi: 10.1103/PhysRevD.98.032012

CrossRef Full Text | Google Scholar

4. Abe K, Aihara H, Andreopoulos C, Anghel I, Ariga A, Ariga T, et al. [Hyper-Kamiokande Proto-Collaboration]. Physics potential of a long-baseline neutrino oscillation experiment using a J-PARC neutrino beam and Hyper-Kamiokande. PTEP (2015) 2015:053C02. doi: 10.1093/ptep/ptv061

CrossRef Full Text | Google Scholar

5. Acciarri R, Acero MA, Adamowski M, Adams C, Adamson P, Adhikari S, et al. [DUNE Collaboration]. Long-Baseline Neutrino Facility (LBNF) and Deep Underground Neutrino Experiment (DUNE) : Conceptual Design Report, Volume 4 The DUNE Detectors at LBNF. arXiv:1601.02984 [physics.ins-det].

6. Galymov V. [LAGUNA-LBNO Consortium]. The LAGUNA-LBNO neutrino observatory in Europe. Nucl Part Phys Proc. (2016) 273–75:1854–60. doi: 10.1016/j.nuclphysbps.2015.09.299

CrossRef Full Text | Google Scholar

7. Goodman M. The deep underground neutrino experiment. Adv High Energy Phys. (2015) 2015:256351. doi: 10.1155/2015/256351

CrossRef Full Text | Google Scholar

8. Abe K, Amey J, Andreopoulos C, Antonova M, Aoki S, Ariga A, et al. [T2K Collaboration]. Measurement of ${\bar{\nu }}_{\mu }$ and νμ charged current inclusive cross sections and their ratio with the T2K off-axis near detector. Phys Rev D (2017) 96:052001. doi: 10.1103/PhysRevD.96.052001

CrossRef Full Text | Google Scholar

9. Tsai YT. [MicroBooNE Collaboration]. MicroBooNE and its cross section measurement. arXiv:1705.07800 [hep-ex].

10. Aguilar-Arevalo AA, Anderson CE, Bazarko AO, Brice SJ, Brown BC, Bugel L, et al. [MiniBooNE Collaboration]. Measurement of neutrino-induced charged-current charged pion production cross sections on mineral oil at Eν~ 1 GeV. Phys Rev D (2011) 83:052007. doi: 10.1103/PhysRevD.83.052007

CrossRef Full Text | Google Scholar

11. Mariani C. [SciBooNE Collaboration]. Neutrino cross section measurements at SciBooNE. J Phys Conf Ser. (2013) 408:012038. doi: 10.1088/1742-6596/408/1/012038

CrossRef Full Text | Google Scholar

12. Aguilar-Arevalo AA, Brown BC, Bugel L, Cheng G, Church ED, Conrad JM, et al. [MiniBooNE Collaboration]. Measurement of the antineutrino neutral-current elastic differential cross section. Phys Rev D (2015) 91:012004. doi: 10.1103/PhysRevD.91.012004

CrossRef Full Text | Google Scholar

13. Andreopoulos C, Bell A, Bhattacharya D, Cavanna F, Dobson J, Dytman S, et al. The GENIE neutrino Monte carlo generator. Nucl Instrum Meth A (2010) 614:87. doi: 10.1016/j.nima.2009.12.009

CrossRef Full Text | Google Scholar

14. Hayato Y. A neutrino interaction simulation program library NEUT. Acta Phys Polon B (2009) 40:2477.

Google Scholar

15. Golan T, Juszczak C, Sobczyk JT. Final state interactions effects in neutrino-nucleus interactions. Phys Rev C (2012) 86:015505. doi: 10.1103/PhysRevC.86.015505

CrossRef Full Text | Google Scholar

16. Buss O, Gaitanos T, Gallmeister K, van Hees H, Kaskulov M, Lalakulich O, et al. Transport-theoretical description of nuclear reactions. Phys Rept. (2012) 512:1. doi: 10.1016/j.physrep.2011.12.001

CrossRef Full Text | Google Scholar

17. Alvarez-Ruso L, Sajjad Athar M, Barbaro MB, Cherdack D, Christy ME, Coloma P, et al. NuSTEC White Paper: status and challenges of neutrino–nucleus scattering. Prog Part Nucl Phys. (2018) 100:1–68. doi: 10.1016/j.ppnp.2018.01.006

CrossRef Full Text | Google Scholar

18. Katori T, Martini M. Neutrino-nucleus cross sections for oscillation experiments. J Phys G (2018) 45:013001. doi: 10.1088/1361-6471/aa8bf7

CrossRef Full Text | Google Scholar

19. Alvarez-Ruso L, Hayato Y, Nieves J. Progress and open questions in the physics of neutrino cross sections at intermediate energies. New J Phys. (2014) 16:075015. doi: 10.1088/1367-2630/16/7/075015

CrossRef Full Text | Google Scholar

20. Formaggio JA, Zeller GP. From eV to EeV: neutrino cross sections across energy scales. Rev Mod Phys. (2012) 84:1307. doi: 10.1103/RevModPhys.84.1307

CrossRef Full Text | Google Scholar

21. Morfin JG, Nieves J, Sobczyk JT. Recent developments in neutrino/antineutrino - nucleus interactions. Adv High Energy Phys. (2012) 2012:934597. doi: 10.1155/2012/934597

CrossRef Full Text | Google Scholar

22. Rafi Alam M, Sajjad Athar M, Chauhan S, Singh SK. Weak charged and neutral current induced one pion production off the nucleon. Int J Mod Phys E (2016) 25:1650010. doi: 10.1142/S0218301316500105

CrossRef Full Text | Google Scholar

23. Akbar F, Rafi Alam M, Sajjad Athar M, Chauhan S, Singh SK, Zaidi F. Electron and Muon production cross-sections in quasielastic am, M, Sajjad Athar, M, Chauhan, S, Singh, SK, and Zaidi, F Electron and Muon production cross-sections in quasielastic $\nu \left(\bar{\nu }\right)$-Nucleus scattering for Eν < 1GeV. Int J Mod Phys E (2015) 24:1550079. doi: 10.1142/S0218301315500792

CrossRef Full Text | Google Scholar

24. Ahmad S, Sajjad Athar M, Singh SK. Neutrino induced charged current 1 π+ production at intermediate energies. Phys Rev D (2006) 74:073008. doi: 10.1103/PhysRevD.74.073008

CrossRef Full Text | Google Scholar

25. Singh SK, Sajjad Athar M, Ahmad S. Nuclear effects in neutrino induced coherent pion production at K2K and MiniBooNE. Phys Rev Lett. (2006) 96:241801. doi: 10.1103/PhysRevLett.96.241801

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Sajjad Athar M, Ahmad S, Singh SK. Charged current anti-neutrino reactions from 12C at MiniBooNE energies. Phys Rev D (2007) 75:093003. doi: 10.1103/PhysRevD.75.093003

CrossRef Full Text | Google Scholar

27. Hernandez E, Nieves J, Valverde M. Weak pion production off the nucleon. Phys Rev D (2007) 76:033005. doi: 10.1103/PhysRevD.76.033005

CrossRef Full Text | Google Scholar

28. Adamson P, Ader C, Andrews M, Anfimov N, Anghel I, Arms K, et al. [NOνA Collaboration]. First measurement of muon-neutrino disappearance in NOνA. Phys Rev D (2016) 93:051104. doi: 10.1103/PhysRevD.93.051104

CrossRef Full Text | Google Scholar

29. Holstein BR. Weak Interactions in Nuclei. Princeton, NJ: Princeton University Press (1990).

Google Scholar

30. Oset E, Fernandez de Cordoba P, Salcedo LL, Brockmann R. Decay modes of Σ and Λ hypernuclei. Phys Rep. (1990) 188:79. doi: 10.1016/0370-1573(90)90091-F

CrossRef Full Text | Google Scholar

31. Cabibbo N, Swallow EC, Winston R. Semileptonic hyperon decays. Ann Rev Nucl Part Sci. (2003) 53:39. doi: 10.1146/annurev.nucl.53.013103.155258

CrossRef Full Text | Google Scholar

32. Gaillard JM, Sauvage G. Hyperon beta decays. Ann Rev Nucl Part Sci. (1984) 34:351. doi: 10.1146/annurev.ns.34.120184.002031

CrossRef Full Text | Google Scholar

33. Garcia A, Kielanowski P. Lecture Notes in Physics, Vol. 222. Berlin: Springer (1985).

Google Scholar

34. Henley EM. Parity and time-reversal invariance in nuclear physics. Ann Rev Nucl Part Sci. (1969) 19:367. doi: 10.1146/annurev.ns.19.120169.002055

CrossRef Full Text | Google Scholar

35. Cannata F, Leonardi R, Strocchi F. T-violation effects and final-state interactions. II. photoproduction, electroproduction, and neutrino-induced production of a single pion. Phys Rev D (1970) 1:191. doi: 10.1103/PhysRevD.1.191

CrossRef Full Text | Google Scholar

36. De Rujula A, De Rafael E. Unitarity bounds to T odd correlations in neutrino reactions. Phys Lett. (1970) 32B:495. doi: 10.1016/0370-2693(70)90394-1

CrossRef Full Text | Google Scholar

37. Adler SL. Polarization effects in high-energy weak interactions. Nuovo Cimento (1963) 30:1020. doi: 10.1007/BF02828811

CrossRef Full Text | Google Scholar

38. Berman SM, Veltman M. Transverse muon polarization in neutrino induced interactions as a test for time reversal violation. Phys Lett. (1964) 12:275. doi: 10.1016/0031-9163(64)91102-3

CrossRef Full Text | Google Scholar

39. Fujii A, Yamaguchi Y. Transverse nucleon polarization in elastic lepton production by high energy neutrino. Prog Theor Phys. (1965) 33:552. doi: 10.1143/PTP.33.552

CrossRef Full Text | Google Scholar

40. Fujii A, Yamaguchi Y. Nucleon polarization in elastic lepton or antilepton production by high-energy neutrino or antineutrino. Nuovo Cimento (1966) 43:325. doi: 10.1007/BF02752861

CrossRef Full Text | Google Scholar

41. Cabibbo N. Possibility of large CP and T violation in weak interactions. Phys Lett. (1964) 12:137. doi: 10.1016/0031-9163(64)91138-2

CrossRef Full Text | Google Scholar

42. Glashow SL. Model of weak interactions with CP violation. Phys Rev Lett. (1965) 14:35. doi: 10.1103/PhysRevLett.14.35

CrossRef Full Text | Google Scholar

43. Okamura H. Second class currents in high energy neutrino reactions. Prog Theor Phys. (1971) 45:1707. doi: 10.1143/PTP.45.1707

CrossRef Full Text | Google Scholar

44. Ketley IJ. Form factors and polarization effects in neutrino-induced interactions. Nuovo Cimento (1965) 38:302. doi: 10.1007/BF02750459

CrossRef Full Text | Google Scholar

45. Egardt L. Polarization of hyperons in the reaction ν+N → Y+l. Nuovo Cimento (1963) 29:954. doi: 10.1007/BF02827957

CrossRef Full Text | Google Scholar

46. Block MM. Future experiments in neutrino physics. In: Zichichi A, editor. Symmetries in Elementary Particle Physics. New York, NY: Academic Press (1965) p. 341–59.

Google Scholar

47. Block M. Neutrino physics. NAL Summer Study (1968) 1:215.

Google Scholar

48. Cabibbo N, Chilton F. Hyperon production by neutrinos in an SU3 model. Phys Rev. (1965) 137:B1628. doi: 10.1103/PhysRev.137.B1628

CrossRef Full Text | Google Scholar

49. Singh SK, Vicente Vacas MJ. Weak quasi-elastic production of hyperons. Phys Rev D (2006) 74:053009. doi: 10.1103/PhysRevD.74.053009

CrossRef Full Text | Google Scholar

50. Rafi Alam M, Sajjad Athar M, Chauhan S, Singh SK. Quasielastic hyperon production in ${\bar{\nu }}_{\mu }$-nucleus interactions. J Phys G (2015) 42:055107. doi: 10.1088/0954-3899/42/5/055107

CrossRef Full Text | Google Scholar

51. Cabibbo N. Unitary symmetry and leptonic decays. Phys Rev Lett. (1963) 10:531. doi: 10.1103/PhysRevLett.10.531

CrossRef Full Text | Google Scholar

52. Block MM. Neutrino interactions and a unitary universal model. Phys Rev Lett. (1964) 12:262. doi: 10.1103/PhysRevLett.12.262

CrossRef Full Text | Google Scholar

53. Chilton F. Cross-section for hyperon production by neutrinos. Nuovo Cim. (1964) 31:447. doi: 10.1007/BF02733649

CrossRef Full Text | Google Scholar

54. Sirlin A. Cabibbo's theory and neutrino-induced reactions. Nuovo Cim. (1965) 37:137. doi: 10.1007/BF02734702

CrossRef Full Text | Google Scholar

55. Finjord J, Ravndal F. Weak production of strange resonances in a relativistic quark model. Nucl Phys B (1976) 106:228. doi: 10.1016/0550-3213(76)90379-5

CrossRef Full Text | Google Scholar

56. Marshak RE, Riazuddin Ryan CP. Theory of Weak Interactions in Particle Physics. New York, NY: Wiley-Interscience (1969).

Google Scholar

57. Llewellyn Smith CH. Neutrino reactions at accelerator energies. Phys Rept. (1972) 3:261. doi: 10.1016/0370-1573(72)90010-5

CrossRef Full Text | Google Scholar

58. Pais A. Weak interactions at high energies. Ann Phys. (1971) 63:361. doi: 10.1016/0003-4916(71)90018-2

CrossRef Full Text | Google Scholar

59. Erriquez O, Fogli Muciaccia MT, Natali S, Nuzzo S, Halsteinslid A, Myklebost K, et al., Strange particle production by anti-neutrinos. Phys Lett B (1977) 70:383. doi: 10.1016/0370-2693(77)90683-9

CrossRef Full Text

60. Eichten T, Faissner H, Kabe S, Krenz W, Von Krogh J, Morfin J, et al. Observation of 'Elastic' hyperon production by anti-neutrinos. Phys Lett B (1972) 40:593. doi: 10.1016/0370-2693(72)90490-X

CrossRef Full Text | Google Scholar

61. Erriquez O, Fogli-Muciaccia MT, Natali S, Nuzzo S, Halsteinslid A, Jarlskog C, et al. Production of strange particles in anti-neutrino interactions at the CERN PS. Nucl Phys B (1978) 140:123. doi: 10.1016/0550-3213(78)90316-4

CrossRef Full Text | Google Scholar

62. Fanourakis G, Resvanis LK, Grammatikakis G, Tsilimigras P, Vayaki A, Camerini U, et al. Study of low-energy antineutrino interactions on protons. Phys Rev D (1980) 21:562. doi: 10.1103/PhysRevD.21.562

CrossRef Full Text | Google Scholar

63. Ammosov VV, Gapienko VA, Gapienko GS, Denisov AG, Klyukhin VI, Koreshev VI, et al. Neutral strange particle exclusive production in charged current high-energy anti-neutrino interactions. Z Phys C (1987) 36:377. doi: 10.1007/BF01573931

CrossRef Full Text | Google Scholar

64. Ammosov VV, Asratian AE, Gapienko VA, Gapienko GS, Gorichev PA, Denisov AG, et al., Quasielastic production Of lambda hyperon in anti-neutrino interactions at high-energies. JETP Lett (1986) 43:716.

65. Brunner J, Grabosch HJ, Kaufmann HH, Nahnhauer R, Nowak S, Schlenstedt S, et al. [SKAT Collaboration]. Quasielastic nucleon and hyperon production by neutrinos and anti-neutrinos with energies below 30-GeV. Z Phys C (1990) 45:551. doi: 10.1007/BF01556267

CrossRef Full Text | Google Scholar

66. Kuzmin KS, Lyubushkin VV, Naumov VA. Lepton polarization in neutrino nucleon interactions. Mod Phys Lett A (2004) 19:2815. doi: 10.1142/S0217732304016172

CrossRef Full Text | Google Scholar

67. Rafi Alam M, Chauhan S, Sajjad Athar M, Singh SK. ${\bar{\nu }}_l$induced pion production from nuclei at ~ 1 GeV. Phys Rev D (2013) 88:077301. doi: 10.1103/PhysRevD.88.077301

CrossRef Full Text | Google Scholar

68. Kuzmin KS, Naumov VA. Axial mass in reactions of quasielastic antineutrino-nucleon scattering with strange hyperon production. Phys Atom Nucl. (2009) 72:1501. doi: 10.1134/S1063778809090105

CrossRef Full Text | Google Scholar

69. Bilenky SM, Christova E. Polarization of the final nucleon in quasi-elastic neutrino scattering and the axial form factor of the nucleon. J Phys G (2013) 40:075004. doi: 10.1088/0954-3899/40/7/075004

CrossRef Full Text | Google Scholar

70. Bilenky SM, Christova E. On the polarization of the final nucleon in NC elastic ${\nu }_{\mu }\left({\bar{\nu }}_{\mu }\right)-N$ scattering. Phys Part Nucl Lett. (2013) 10:651. doi: 10.1134/S154747711307011X

CrossRef Full Text | Google Scholar

71. Akbar F, Sajjad Athar M, Fatima A, Singh SK. Weak quasielastic electroproduction of hyperons with polarization observables. Eur Phys J A (2017) 53:154. doi: 10.1140/epja/i2017-12340-4

CrossRef Full Text | Google Scholar

72. Graczyk KM, Kowal BE. Polarization transfer in weak pion production off the nucleon. Phys Rev D (2018) 97:013001. doi: 10.1103/PhysRevD.97.013001

CrossRef Full Text | Google Scholar

73. Kuzmin KS, Lyubushkin VV, Naumov VA. Polarization of tau leptons produced in quasielastic neutrino nucleon scattering. Mod Phys Lett A (2004) 19:2919. doi: 10.1142/S0217732304016184

CrossRef Full Text | Google Scholar

74. Graczyk KM. Tau polarization in charge current neutrino-nucleon deep inelastic scattering. Nucl Phys Proc Suppl. (2005) 139:150. doi: 10.1016/j.nuclphysbps.2004.11.230

CrossRef Full Text | Google Scholar

75. Hagiwara K, Mawatari K, Yokoya H. Polarization effects in tau production by neutrino. Nucl Phys Proc Suppl (2005) 139:140. doi: 10.1016/j.nuclphysbps.2004.11.201

CrossRef Full Text | Google Scholar

76. Graczyk KM. Tau polarization in quasielastic charged-current neutrino(antineutrino)-nucleus scattering. Nucl Phys A (2005) 748:313. doi: 10.1016/j.nuclphysa.2004.10.029

CrossRef Full Text | Google Scholar

77. Valverde M, Amaro JE, Nieves J, Maieron C. Nuclear effects on lepton polarization in charged-current quasielastic neutrino scattering. Phys Lett B (2006) 642:218. doi: 10.1016/j.physletb.2006.08.087

CrossRef Full Text | Google Scholar

78. Fatima A, Sajjad Athar M, Singh SK. Second class currents and T violation in quasielastic neutrino and antineutrino scattering from nucleons. Phys Rev D (2018) 98:033005. doi: 10.1103/PhysRevD.98.033005

CrossRef Full Text | Google Scholar

79. Fatima A, Sajjad Athar M, Singh SK. Polarization observables and T-noninvariance in the weak charged current induced electron proton scattering. Eur Phys J A (2018) 54:95. doi: 10.1140/epja/i2018-12534-2

CrossRef Full Text | Google Scholar

80. Akbar F, Rafi Alam M, Sajjad Athar M, Singh SK. Quasielastic production of polarized hyperons in antineutrino–nucleon reactions. Phys Rev D (2016) 94:114031. doi: 10.1103/PhysRevD.94.114031

CrossRef Full Text | Google Scholar

81. Mintz SL. The weak production of Λ particles in electron proton scattering and the contributions of the interference terms. J Phys G (2004) 30:565. doi: 10.1088/0954-3899/30/5/002

CrossRef Full Text | Google Scholar

82. Mintz SL, Barnett MA. Weak production of Λ particles near threshold in electron proton scattering. Phys Rev D (2002) 66:117501. doi: 10.1103/PhysRevD.66.117501

CrossRef Full Text | Google Scholar

83. Mintz SL. The weak electroproduction of Σ0 in electron proton scattering. Nucl Phys A (2001) 690:711. doi: 10.1016/S0375-9474(01)00364-5

CrossRef Full Text | Google Scholar

84. Wu JJ, Zou BS. Hyperon production from neutrino–nucleon reaction. Few Body Syst. (2015) 56:165. doi: 10.1007/s00601-015-0973-0

CrossRef Full Text | Google Scholar

85. Drakoulakos D, Stamoulis P, Tzanakos G, Zois M, Casper D, Paschos E, et al. [MINERνA Collaboration]. Proposal to Perform a High-Statistics Neutrino Scattering Experiment Using a Fine-Grained Detector in the NuMI Beam. hep-ex/0405002.

86. Bradford R, Bodek A, Budd HS, Arrington J. A New parameterization of the nucleon elastic form factors. Nucl Phys Proc Suppl. (2006) 159:127. doi: 10.1016/j.nuclphysbps.2006.08.028

CrossRef Full Text | Google Scholar

87. Weinberg S. Charge symmetry of weak interactions. Phys Rev. (1958) 112:1375. doi: 10.1103/PhysRev.112.1375

CrossRef Full Text | Google Scholar

88. Nambu Y. Axial vector current conservation in weak interactions. Phys Rev Lett. (1960) 4:380. doi: 10.1103/PhysRevLett.4.380

CrossRef Full Text | Google Scholar

89. Bilenky SM. Basics of Introduction to Feynman Diagrams and Electroweak Interactions Physics. Singapore: Editions Frontieres (1994).

Google Scholar

90. Lalakulich O, Paschos EA, Piranishvili G. Resonance production by neutrinos: The Second resonance region. Phys Rev D (2006) 74:014009. doi: 10.1103/PhysRevD.74.014009

CrossRef Full Text | Google Scholar

91. Alvarez-Ruso L, Singh SK, Vicente Vacas MJ. νd → μ−Δ++n reaction and axial vector N−Δ coupling. Phys Rev C (1999) 59:3386. doi: 10.1103/PhysRevC.59.3386

CrossRef Full Text | Google Scholar

92. Singh SK, Vicente Vacas MJ, Oset E. Nuclear effects in neutrino production of Δ at intermediate energies. Phys Lett B (1998) 416:23. Erratum: [Phys Lett B 423:428 (1998)]. doi: 10.1016/S0370-2693(97)01325-7

CrossRef Full Text | Google Scholar

93. Oset E, Salcedo LL. “Δ self energy in nuclear matter. Nucl Phys A (1987) 468:631.

Google Scholar

94. De Jager CW, De Vries H, De Vries C. Nuclear charge and magnetization density distribution parameters from elastic electron scattering. Atom Data Nucl Data Tabl. (1974) 14:479. Erratum: [Atom Data Nucl Data Tabl 16:580 (1975)]. doi: 10.1016/S0092-640X(74)80002-1

CrossRef Full Text | Google Scholar

95. Garcia Recio C, Oset E, Salcedo LL, Strottman D, Lopez MJ. Pion nucleus elastic scattering in the microscopic local Δ hole model. Nucl Phys A (1991) 526:685.

Google Scholar

96. Vicente Vacas MJ, Khankhasaev MK, Mashnik SG. Inclusive Pion Double Charge Exchange Above .5-GeV. nucl-th/9412023. M. J. Vicente Vacas, Private Communication.

97. Armenise N, Erriquez O, Fogli Muciaccia MT, Nuzzo S, Ruggieri F, Halsteinslid A, et al. Charged current elastic anti-neutrino interactions in propane. Nucl Phys B (1979) 152:365.

Google Scholar