TDHF Theory and Its Extensions for the Multinucleon Transfer Reaction: A Mini Review

1. Introduction

Multinucleon transfer (MNT) reactions may be a promising means to produce yet-unknown, neutron-rich unstable nuclei, whose production is difficult by other methods. This possibility makes the study of MNT both fascinating and important. For instance, besides the fundamental interest in nuclear structures such as shell evolution [1] and shape transitions [2, 3], properties of extremely neutron-rich nuclei are crucial to fully understanding the detailed scenario of r-process nucleosynthesis [4]. Needless to say, the historic detection of gravitational waves from a merger of two neutron stars, GW170817 [5], together with radiation from a short γ-ray burst, GRB 170817A [6], followed by a kilonova [7] makes it a timely and imperative task to unveil inherent properties of the nuclei far away from stability. Furthermore, the superheavy nuclei produced so far are neutron-deficient ones, and the predicted island of stability has not yet been reached [8, 9]. The production of neutron-rich superheavy nuclei in the island is highly desired, as it would provide a new stringent constraint for microscopic theories. Therefore, the study of MNT reactions is listed as one of the key subjects at the current and future RI beam facilities, such as RIBF (RIKEN, Japan) [10], HIRFL-CSR and HIAF (IMP, China)¹, RAON (RISP, Korea) [11], DRIB (FLNR, Russia)², SPIRAL2 (GANIL, France) [12], FAIR (GSI, Germany)³, SPES (INFN, Italy)⁴, FRIB (MSU, USA) [13], and so on.

This review briefly digests recent advances of microscopic reaction theories to stimulate new ideas for the future study of MNT reactions. In section 2, the theoretical framework of TDHF is succinctly recalled. In section 3, the current status of the MNT study with TDHF is given. In section 4, recent advances of theoretical approaches are outlined, along with a discussion on possible future applications. The article is concluded in section 5. The readers are intended to refer to other articles in this Research Topic for discussions on experimental as well as other theoretical studies.

2. The TDHF Theory

The TDHF theory was first proposed by Dirac [14] and its application to nuclear physics started in the 1970s [15–22]. The TDHF theory can be formally derived based on the time-dependent variational principle (various derivations can be found in a recent review [23]). In TDHF, the wave function is a Slater determinant for all times, and the Pauli principle is thus automatically ensured. The TDHF equations read as follows:

$\begin{array}{cc}i\hslash \frac{\partial {\varphi }_i(r\sigma q,t)}{\partial t}=\widehat{h}[\rho (t)]{\varphi }_i(r\sigma q,t),& (1)\end{array}$

where ϕ_i(rσq, t) is the single-particle wave function of ith nucleon at position r with spin σ and isospin q. $ĥ\left[\rho (t)\right]=\frac{\delta E}{\delta \rho }$ is the single-particle Hamiltonian with ρ being the one-body density. E[ρ] is the total energy, which may be regarded as an energy density functional (EDF) in the context of time-dependent density functional theory (TDDFT)⁵ [27–31]. The EDF is constructed so as to reproduce static properties of finite nuclei in a wide mass region and also the basic nuclear matter properties (see e.g., [32–35] and references therein). There is no adjustable parameter in TDHF, once an EDF is given. The non-linearity arises because ĥ[ρ(t)] contains the mean-field potential which depends on densities generated by all the nucleons, e.g., $\rho (r,t)=\sum _{i,\sigma ,q}|{\varphi }_i(r\sigma q,t){|}^2$. Such non-linear couplings between single-particle and collective degrees of freedom give rise to the so-called one-body dissipation mechanism (known as wall-and-window formulas [36]). Note that as is evident from a derivation of TDHF from the lowest order truncation of the Bogoliubov-Born-Green-Kirkwood-Yvon (BBGKY) hierarchy [23], where two-body correlations are neglected, two-body dissipations associated with nucleon-nucleon collisions are absent in TDHF. They are, however, expected to play a minor role at low energy due to the Pauli exclusion principle.

TDHF is notably versatile—by changing initial condition, external potential, boundary condition, etc., one can study a wide variety of phenomena: not only collective excitations in the linear response regime [37–46], where TDHF is formally equivalent to the random phase approximation (RPA), but also induced fission [47–52], dynamics of exotic configurations like α-chain structure [53], toroidal nucleus [54, 55], nuclear pasta formation [56–59], as well as heavy-ion reactions, such as nucleon transfer [60–74], quasifission (QF) [75–87], and fusion [88–104], and so on (see [22, 23, 26, 31, 105, 106], for review papers).

In the case of heavy-ion reactions, the initial wave function is composed of projectile and target nuclei in their ground state, which is obtained by self-consistently solving the static Hartree-Fock equations [iℏ∂/∂t → ε_i in Equation 1]. Those wave functions are placed in a computational box, with a sufficiently large relative distance, boosted with a proper relative momentum. The time evolution according to Equation (1) then allows us to follow reaction dynamics in real space and real time. As the theory deals with the single-particle wave functions of nucleons, not only dynamic effects such as nucleon transfer and internal excitations, but also structural effects such as static/dynamic shell effects and shape evolution are naturally incorporated into the description. Spin-orbit coupling is known to play an important role in energy dissipation processes in heavy-ion reactions [107–110]. The effects of the tensor term on nuclear dynamics were also investigated recently [101, 111–114]. TDHF enables us to study rich and complex physics of low-energy heavy-ion reactions from nucleonic degrees of freedom.

3. TDHF Theory for Multinucleon Transfer Reactions

3.1. Multinucleon Transfer Reactions

The MNT reaction may be regarded as a non-equilibrium quantum transport process of nucleons during a collision. With the help of the particle-number projection technique [64], transfer probabilities can be deduced from a TDHF wave function after collision. In Sekizawa and Yabana [65, 66], a range of reactions at energies around the Coulomb barrier were studied within TDHF, for which precise experimental data are available [115–118]. Those reactions are characterized by different neutron-to-proton ratios, N/Z, and charge product, Z_PZ_T. TDHF identified two distinct transfer mechanisms: (1) a fast isospin equilibration process and (2) transfer of many nucleons associated with dynamics of neck formation and its breaking. The neck breaking dynamics emerge at small impact parameters, especially in reactions with a large Z_PZ_T (≳ 1,600). The latter may be regarded as a precursor to QF, where the system starts evolving toward the mass equilibrium. Comparisons with measured cross sections showed that TDHF works fairly well in accuracy comparable to other model predictions. However, effects of secondary neutron evaporation become substantial, when many protons are transferred. Combining TDHF with a statistical compound-nucleus deexcitation model, GEMINI++ [119], it became possible to compute production cross sections after secondary deexcitation processes. With the method, dubbed TDHF+GEMINI, it was shown that the inclusion of deexcitation effects substantially improves agreement with the experimental data [72] (see Figures 1A,B). (For more details, see, e.g., [69, 72]).

FIGURE 1

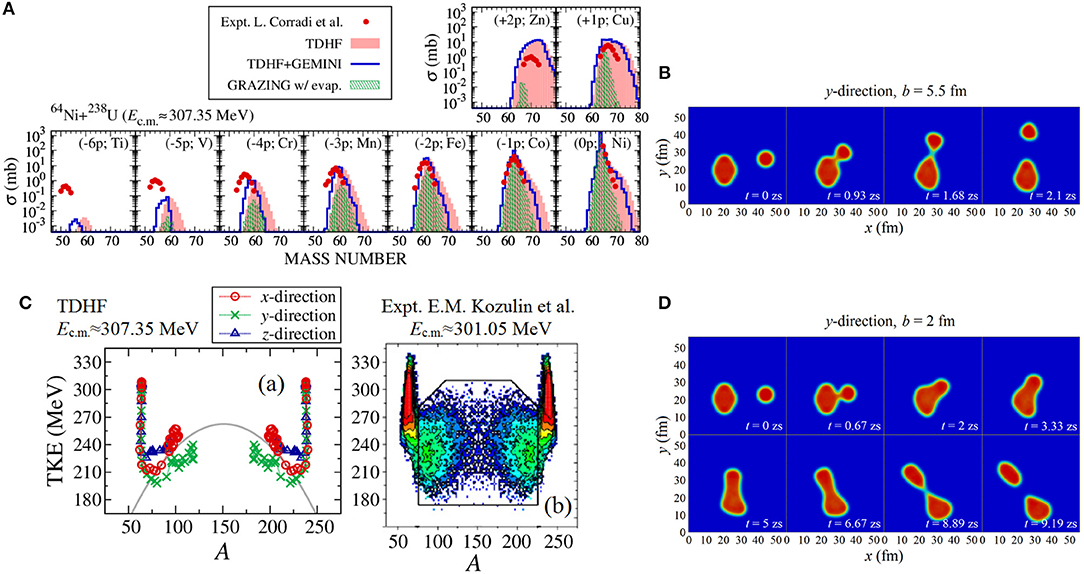
Figure 1. Results of TDHF calculations for the ⁶⁴Ni+²³⁸U reaction at E_c.m. ≈ 307 MeV are shown as an illustrative example. (A) Production cross sections for various proton transfer channels [indicated by (±xp), where plus (minus) sign corresponds to transfer from ²³⁸U to ⁶⁴Ni (vise versa)] as a function of the mass number of the reaction products. Red points are the experimental data [120], red-filled histograms are cross sections for primary products by TDHF [70], and blue histograms are cross sections for secondary products by TDHF+GEMINI [72]. For comparison, cross sections by a semi-classical model, GRAZING⁶, including neutron evaporation effects, are also shown by green shaded histograms. (B) This picture exhibits the time evolution of the density in the reaction plane in a peripheral collision (b = 5.5 fm), where MNT processes shown in (A) take place. Elapsed time in the simulation is indicated in zeptoseconds (1 zs = 10⁻²¹ s). (C) Correlation between the total kinetic energy (TKE) and the mass number A of the outgoing fragments. The left figure (a) shows results of TDHF calculations [70], while the right figure (b) shows the experimental data [121]. (D) Same as (B), but for a smaller impact parameter (b =2 fm), where QF processes shown in (C) take place. In the figure, x-, y-, and z-direction indicate the orientation of deformed ²³⁸U [70]. In this way, TDHF can describe both peripheral and damped collisions in a unified way. Figures were reprinted from Sekizawa and Yabana [70] and Sekizawa [72].

The description is still, however, not perfect, especially for channels where both neutrons and protons are removed. It would be improved when one includes missing one-body fluctuations into the description (cf. section 4.2). Nevertheless, TDHF may be used, taking advantage of its non-empirical nature, to explore the optimal or novel reaction mechanism for producing new neutron-rich unstable nuclei, at least qualitatively. Recently, other groups have also implemented TDHF+GEMINI: e.g. production of N = 126 neutron-rich nuclei was investigated for the ¹³²Sn+²⁰⁸Pb reaction [122].

3.2. Quasifission Processes

To synthesize the heaviest elements and also to explore the predicted island of stability, it is crucial to establish deep understanding of the main competitive process, the quasifission. The QF process is characterized by a large amount of mass transfer, full energy dissipation, and a long contact time (typically several to tens of zeptoseconds). The characteristic observables of QF are correlations between fragment masses with scattering angles, known as mass-angle distribution (MAD), or with the total kinetic energy (TKE) of outgoing fragments, sometimes called mass-energy distribution (MED) (see e.g., [121, 123–126]). In recent applications of TDHF, it has been shown that TDHF can quantitatively describe main QF dynamics, consistent with experimental observations [70, 78, 80, 81] (see Figures 1C,D). An intriguing indication is that in collisions involving an actinide nucleus, TKE becomes larger (smaller energy dissipation) for tip collisions as compared to side collisions [70, 84], perhaps due to shell effects of ²⁰⁸Pb [127]. This may be in contrast to the naive consideration, where one expects a compact shape at scission for side collisions, which would result in larger TKE for side collisions.

The revival of interest in the MNT reaction was initiated by the seminal work by Zagrebaev and Greiner [128–137]. In their work, the importance of shell effects in MNT processes was emphasized. For example, in the ²³⁸U+²⁴⁸Cm reaction, ²³⁸U tends to evolve toward doubly-magic ²⁰⁸Pb, giving the rest of the 30 nucleons to the heavier partner, resulting in the production of transcurium nuclei as primary reaction products. The latter process is called inverse (anti-symmetrizing) QF (IQF), since the ordinary QF drives the system toward the mass equilibrium. Clearly, it is essential to correctly include static and dynamic effects of nuclear shells to describe IQF. The IQF was also observed in TDHF. In Kedziora and Simenel [76], a typical “tip-on-side" orientation in collisions of two actinide nuclei, ²³²Th+²⁵⁰Cf, was found to result in IQF, where about 15 nucleons in the tip of ²³²Th were transferred to the side of ²⁵⁰Cf. Another type of IQF was reported in Sekizawa [73], where complex surface vibration modes are induced in tip collisions of ²³⁸U+¹²⁴Sn at energies well above the Coulomb barrier, which resulted in an abrupt development of a neck, forming a smaller subsystem, leading to transfer of around 27 nucleons from ¹²⁴Sn to ²³⁸U.

An important message here is that those IQF processes emerge as a main reaction outcome in TDHF. Since larger effects of fluctuations and correlations, that give rise to a wider fragment mass distribution, are expected in such damped collisions [105, 138–140], novel IQF processes may pave new pathways to unexplored territories in the nuclear chat far away from stability.

4. New Techniques and Extensions

4.1. Extraction of Macroscopic Physical Ingredients

The potential energy surface in a colliding nuclear system is often a key ingredient in phenomenological approaches. With the constrained Hartree-Fock technique [141], one can compute the adiabatic potential energy in a composite system. However, it differs, in general, from the potential in the entrance channel of a collision, where incident-energy-dependent dynamic effects come into play. Such a dynamic potential should be derived from microscopic theories, e.g., TDHF, where dynamic effects such as shape deformation (or necking), nucleon transfer, and inelastic excitations through the one-body dissipation mechanism are naturally taken into account. A method named dissipative-dynamics TDHF (DD-TDHF) [82, 142, 143] allows us to extract from TDHF not only a dynamic potential, but also a friction coefficient, based on a mapping of TDHF trajectories onto a set of classical equations of motion. Density-constrained TDHF (DC-TDHF) [88] is another way to extract a potential. In the latter approach, the density distribution obtained from TDHF is used as a constraint for Hartree-Fock calculations, leading to an adiabatic potential along the TDHF dynamical trajectory (see e.g., [53, 89–101], for various applications). Energy dependence as well as transition from dynamic to adiabatic potentials may be important as well. Later, the idea of the density constraint was also applied to extract a bare (without density distortion) potential taking full account of the Pauli exclusion principle, which is named density-constrained frozen Hartree-Fock (DC-FHF) [144]. Such a bare potential can be applied to, e.g., coupled-channel calculations for fusion reactions [145, 146]. Indeed, such a connection was established, where excitation energies of low-lying collective excitations were also determined by TDHF [147]. This is a remarkable example of building a bridge between elaborated macroscopic or phenomenological frameworks and those rooted with microscopic degrees of freedom, that may enhance predictability of the former.

4.2. Balian-Vénéroni Variational Principle and TDRPA

While there are, of course, limitations inherent in TDHF (e.g., the absence of many-body correlations, deterministic nature as well as spurious cross-channel couplings due to the single mean-field description [141]), some of them can nowadays be overcome with extended approaches. One such approach can be obtained from the variational principle of Balian and Vénéroni [148, 149]. The Balian-Vénéroni variational principle enables us to control the variational space according to not only the state in the Schrödinger picture, but also to the observable in the Heisenberg picture. For instance, a variation optimized for a Slater determinant and a one-body observable derives the TDHF equations [105]. By extending the variational space for fluctuations of a one-body observable, one obtains a formula that includes effects of one-body fluctuations on top of the TDHF mean-field trajectory, which may be regarded as time-dependent RPA (TDRPA). It has recently been shown that the description of the width of fragment mass distributions in deep-inelastic collisions, which is severely underestimated in TDHF [17, 18, 150], is substantially improved [151, 152], or even quantitatively agrees with experimental data [153], in TDRPA. It implies that one-body dissipation and fluctuations described by TDHF and TDRPA, respectively, are the predominant mechanisms in deep-inelastic collisions. Here, caution is required: the TDRPA formula in the present form can only be applied to symmetric reactions [153]. To overcome this difficulty, one may extend the derivation based on the Balian-Vénéroni variational principle to include higher-order corrections, or derive a formula generalized for asymmetric reactions from, e.g., the stochastic mean-field (SMF) theory [154, 155], from which one can derive the TDRPA formula in the small fluctuation limit [154]. Note that effects of two-body correlations were also indicated by the time-dependent density-matrix (TDDM) approach [156–160].

4.3. Stochastic Extensions

Another limitation of TDHF lies in its deterministic nature. To correctly describe abundant reaction outcomes as observed experimentally, one may need to introduce quantal, collisional, or thermal fluctuations that induce bifurcations of dynamics, leading to, in the end, minor processes apart from the TDHF mean-field trajectory. In the SMF approach, extensively developed by Ayik and his coworkers [138–140, 154, 155, 161–169], initial fluctuations are introduced in a stochastic manner, which gives rise to an ensemble of final states after dynamic evolutions. For the MNT study, the SMF description can be cast into the Fokker-Planck equations, where transport (drift and diffusion) coefficients are determined by the single-particle orbitals in TDHF. In Yilmaz et al. [169], the SMF approach was also applied to the Ni+Ni reaction, showing quantitative agreement with experimental data [153], comparable to TDRPA. Recently, Bulgac et al. [170] proposed another way to introduce stochasticity by means of external potentials which are random in both space and time. The method was applied to describe induced fission processes, with a simplified orbital-free approach, getting a sufficient width of the fission fragment mass distribution [170]. Further applications of those approaches may be promising for exploring optimal reactions, especially for producing the most exotic isotopes, where correct description of rare processes may be essential.

4.4. Inclusion of Pairing

Despite the known importance of pairing in nuclear structure studies, the effect of pairing on nuclear reaction dynamics has rarely been investigated thus far. While the BCS approximation has been employed to date [171–174], inclusion of dynamic effects of pairing became possible only quite recently with top-tier supercomputers. One may naively expect that pairing in the nucleus is so fragile and it would only affect tunneling phenomena below the Coulomb barrier, where clear effects of nucleon-nucleon correlations were indeed observed experimentally [62, 175–177]. To the contrary, Magierski et al. [178–180] found unexpectedly large effects associated with the relative phase (or gauge angles) of colliding superfluid nuclei on the reaction outcomes, such as TKE and fusion cross section. In this context, experimental fusion cross sections were analyzed, which indicates fusion barrier width may be increased by the superfluid effect [181]. In the work by Magierski et al., a local formulation of superfluid TDDFT, known as time-dependent superfluid local density approximation (TDSLDA) (see e.g., [182–185]), was employed, which is formally similar to the time-dependent Hartree-Fock-Bogoliubov (TDHFB) approach [141]. The TDSLDA has been extensively developed by Bulgac and his coworkers, which was successfully applied to the unitary Fermi gas [186–191], finite nuclei [178, 192–196], as well as interiors of neutron stars [197]. Hashimoto has developed a Gogny TDHFB code that works with a 2D harmonic oscillator and 1D-Lagrange-mesh hybrid basis [198], which could be applied for head-on collisions [199, 200]. Qualitatively, the same effects of the relative phase as reported in Magierski et al. [178] were observed with their code. We have just entered a new era in which dynamic effects of pairing can be fully incorporated with microscopic nuclear dynamics studies. With the aforementioned sophisticated approaches with the usage of top-tier supercomputers, the dynamic effects of pairing in MNT and QF processes will be unveiled in the near future.

4.5. Remarks on Other Theoretical Approaches

There are many models that have been developed so far for the study of MNT, such as the semi-classical model, like GRAZING [201– 205]⁴,⁷ or CWKB [116–118, 206], the dinuclear system (DNS) model [207–221], the improved quantum molecular dynamics (ImQMD) model [222–225], and the Langevin model [128–137, 226, 227]. There are pros and cons in each of those approaches. For instance, on the one hand, the semi-classical model can describe successive transfer processes at peripheral collisions, while on the other hand it misses deep-inelastic components at small impact parameters. In contrast, the DNS model is capable of describing the dynamic evolution of a composite system, according to a master equation with a potential energy (including shell effects) for mass asymmetry and deformation of the subsystem, that gives rise to a probability distribution for massive nucleon transfer as well as fusion. By construction, however, the latter model assumes a formation of a “di-nucleus” in a potential pocket, and thus it misses (quasi)elastic components at large impact parameters. A simple addition of those model predictions, DNS+GRAZING, was considered in the literature [228, 229]. The ImQMD model is applicable for both peripheral and damped collisions. By taking into account stochastic nucleon-nucleon collisions, it provides distributions of observables accumulated in a number of simulations. To the author's knowledge, however, the spin-orbit interaction has been neglected in ImQMD, which prevents a proper description of shell effects in MNT and QF processes. The elaborated Langevin model [226] may be promising in describing complex processes of MNT, QF and fusion, in a unified way. The model contains, however, various parameters that have to be tuned carefully to reproduce available experimental data [226].

A possible future task is to non-empirically determine model ingredients based on microscopic theories: potential energy surface with respect to an arbitrary set of variables, drift, diffusion, and friction coefficients, etc., can be derived from the microscopic approaches, which may lead to, e.g., kind of a TDHF+Langevin approach.

5. Summary and Prospect

Production of neutron-rich heavy nuclei is listed as one of the high-priority subjects of nuclear science today. In this contribution, recent advances in the MNT study, especially those based on microscopic dynamic theories, have been briefly reviewed. The traditional TDHF approach has shown remarkable successes in describing a variety of phenomena in nuclear systems. It has been shown that TDHF is capable of describing the main reaction channels, not only MNT processes in peripheral collisions but also deep-inelastic and QF processes in damped collisions, positioning it as a good starting point for building a fully microscopic theory for low-energy heavy-ion reactions. Moreover, the inclusion of one-body fluctuations significantly improves quantitative agreements of the width of fragment mass distributions with experimental data. With the use of top-tier supercomputers, studies of dynamic effects of pairing have just been started. One of the great advantages of microscopic approaches is their non-empirical nature—one may explore novel pathways toward the dreamed-of production of yet-unknown neutron-rich nuclei. Another possible future direction is to use microscopic approaches to determine phenomenological parameters in other theoretical models. It may be the time to combine knowledge obtained with different approaches to construct the most reliable framework to lead future experiments to the successful production of extremely neutron-rich nuclei, the farthest from the continent of stability.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author acknowledges P. D. Stevenson, J. A. Maruhn, C. Simenel, Lu Guo, and A. S. Umar for careful reading of the manuscript and for providing valuable comments on this article.

Footnotes

1. ^http://english.imp.cas.cn/Home2017/

2. ^http://flerovlab.jinr.ru/flnr/dribs.html

3. ^https://fair-center.eu/

4. ^https://web.infn.it/spes/

5. ^Here a local EDF (like Skyrme) has been assumed, which makes the TDHF Equation (1) local in space, as it is currently used in most practical applications. In general, $E=\int {E}(r)dr$ is composed of various local densities, $\overrightarrow{\xi }\equiv \left\{\rho ,\tau ,\dots \right\}$, and the TDHF Equation (1) should read: $i\hslash \frac{\partial {\varphi }_i(r\sigma q,t)}{\partial t}=\int \sum _k\frac{\delta {E}[\overrightarrow{\xi }(r^{\prime },t)]}{\delta {\xi }_k(r^{\prime },t)}\frac{\delta {\xi }_k(r^{\prime },t)}{\delta {\varphi }_i^{*}(r\sigma q,t)}d{r}^{\prime }=\sum _{{\sigma }^{\prime }}{ĥ}_{\sigma {\sigma }^{\prime }}^{(q)}(r,t){\varphi }_i(r{\sigma }^{\prime }q,t)$. In such a case, the single-particle Hamiltonian can have spin dependence as well as differential operators (for the explicit form, see, e.g., [24–26]).

6. ^Website of Nuclear Reactions Video (NRV) Project. Available online at: http://nrv.jinr.ru/nrv/webnrv/grazing/

7. ^http://personalpages.to.infn.it/~nanni/grazing/

References

1. Otsuka T, Gade A, Sorlin O, Suzuki T, Utsuno Y. Evolution of nuclear structure in exotic nuclei and nuclear forces. arXiv:1805.06501 [nucl-th]. (2018).

Google Scholar

2. Cejnar P, Jolie J, Casten RF. Quantum phase transitions in the shapes of atomic nuclei. Rev Mod Phys. (2010) 82:2155. doi: 10.1103/RevModPhys.82.2155

CrossRef Full Text | Google Scholar

3. Heyde K, Wood JL. Shape coexistence in atomic nuclei. Rev Mod Phys. (2011) 83:1467. doi: 10.1103/RevModPhys.83.1467

CrossRef Full Text | Google Scholar

4. Cowan JJ, Sneden C, Lawler JE, Aprahamian A, Wiescher M, Langanke K, et al. Making the heaviest elements in the Universe: a review of the rapid neutron capture process. arXiv:1901.01410 [astro-ph.HE]. (2019).

Google Scholar

5. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C. GW170817: observation of gravitational waves from a binary neutron star inspiral. Phys Rev Lett. (2017) 119:161101. doi: 10.1103/PhysRevLett.119.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C. Gravitational waves and gamma-rays from a binary neutron star merger: GW170817 and GRB 170817A. Astrophys J Lett. (2017) 848:L13. doi: 10.3847/2041-8213/aa920c

CrossRef Full Text | Google Scholar

7. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C. Estimating contribution of dynamical ejecta in the Kilonova associated with GW170817. Astrophys J Lett. (2017) 850:L39. doi: 10.3847/2041-8213/aa9478

CrossRef Full Text | Google Scholar

8. Hofmann S, Münzenberg G. The discovery of the heaviest elements, Rev Mod Phys. (2000) 72:733. doi: 10.1103/RevModPhys.72.733

CrossRef Full Text | Google Scholar

9. Oganessian YT, Sobiczewski A, Ter-Akopian GM. Superheavy nuclei: from predictions to discovery. Phys Scr. (2017) 92:023003. doi: 10.1088/1402-4896/aa53c1

CrossRef Full Text | Google Scholar

10. Sakurai H. Nuclear physics with RI Beam Factory. Front Phys. (2018) 13:132111. doi: 10.1007/s11467-018-0849-0

CrossRef Full Text | Google Scholar

11. Shin T, Kang BH, Kim GD, Kim YJ, Kwon YK, Park YH, et al. Rare isotope production and experimental systems of RAON. New Phys. (2016) 66:1500. doi: 10.3938/NPSM.66.1500

CrossRef Full Text | Google Scholar

12. Gales S. SPIRAL2 at GANIL: a world leading ISOL facility at the dawn of the next decade. Prog Part Nucl Phys. (2007) 59:22. doi: 10.1016/j.ppnp.2006.12.021

CrossRef Full Text | Google Scholar

13. Abel EP, Avilov M, Ayres V, Birnbaum E, Bollen G, Bonito G. Isotope harvesting at FRIB: additional opportunities for scientific discovery. arXiv:1812.03984 [nucl-th]. (2018).

Google Scholar

14. Dirac PAM. Note on exchange phenomena in the thomas atom. Proc Camb Philos Soc. (1930) 26:376. doi: 10.1017/S0305004100016108

CrossRef Full Text | Google Scholar

15. Bonche P, Koonin S, Negele JW. One-dimensional nuclear dynamics in the time-dependent Hartree-Fock approximation. Phys Rev C. (1976) 13:1226. doi: 10.1103/PhysRevC.13.1226

CrossRef Full Text | Google Scholar

16. Cusson RY, Smith RK, Maruhn JA. Time-dependent Hartree-Fock calculation of the reaction ¹⁶O+¹⁶O in three dimensions. Phys Rev Lett. (1976) 36:1166. doi: 10.1103/PhysRevLett.36.1166

CrossRef Full Text | Google Scholar

17. Koonin SE, Davies KTR, Maruhn-Rezwani V, Feldmeier H, Krieger SJ, Negele JW. Time-dependent Hartree-Fock calculations for ¹⁶O+¹⁶O and ⁴⁰Ca+⁴⁰Ca reactions. Phys Rev C. (1977) 15:1359. doi: 10.1103/PhysRevC.15.1359

CrossRef Full Text | Google Scholar

18. Davies KTR, Maruhn-Rezwani V, Koonin SE, Negele JW. Test of the time-dependent mean-field theory in Kr-induced strongly damped collisions. Phys Rev Lett. (1978) 41:632. doi: 10.1103/PhysRevLett.41.632

CrossRef Full Text | Google Scholar

19. Flocard H, Koonin SE, Weiss MS, Three-dimensional time-dependent Hartree-Fock calculations: application to ¹⁶O+¹⁶O collisions. Phys Rev C. (1978) 17:1682. doi: 10.1103/PhysRevC.17.1682

CrossRef Full Text

20. Krieger SJ, Davies KTR, Time-dependent Hartree-Fock calculations of fusion cross sections for the reactions ¹⁶O+¹⁶O and ⁴⁰Ca+⁴⁰Ca. Phys Rev C. (1978) 18:2567. doi: 10.1103/PhysRevC.18.2567

CrossRef Full Text

21. Davies KTR, Sandhya Devi KR, Strayer MR. Time-dependent Hartree-Fock calculations of ⁸⁶Kr+¹³⁹La at E_lab=505, 610, and 710 MeV. Phys Rev C. (1979) 20:1372. doi: 10.1103/PhysRevC.20.1372

CrossRef Full Text | Google Scholar

22. Negele JW. The mean-field theory of nuclear structure and dynamics. Rev Mod Phys. (1982) 54:913. doi: 10.1103/RevModPhys.54.913

CrossRef Full Text | Google Scholar

23. Simenel C, Umar AS. Heavy-ion collisions and fission dynamics with the time-dependent Hartree-Fock theory and its extensions. Prog Part Nucl Phys. (2018) 103:19. doi: 10.1016/j.ppnp.2018.07.002

CrossRef Full Text | Google Scholar

24. Engel YM, Brink DM, Goeke K, Krieger SJ, Vautherin D. Time-dependent hartree-fock theory with Skyrme's interaction. Nucl Phys. (1975) A249:215. doi: 10.1016/0375-9474(75)90184-0

CrossRef Full Text | Google Scholar

25. Dobaczewski J, Dudek J. Time-odd components in the mean field of rotating superdeformed nuclei. Phys Rev C. (1995) 52:1827. doi: 10.1103/PhysRevC.52.1827

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Stevenson PD, Barton MC. Low-energy heavy-ion reactions and the Skyrme effective interaction. Prog Part Nucl Phys. (2019) 104:142. doi: 10.1016/j.ppnp.2018.09.002

CrossRef Full Text | Google Scholar

27. Hohenberg P, Kohn W. Inhomogeneous electron gas. Phys Rev. (1964) 136:B864. doi: 10.1103/PhysRev.136.B864

CrossRef Full Text | Google Scholar

28. Kohn W, Sham LJ. Self-consistent equations including exchange and correlation effects. Phys Rev. (1965) 140:A1133. doi: 10.1103/PhysRev.140.A1133

CrossRef Full Text | Google Scholar

29. Runge E, Gross EKU. Density-functional theory for time-dependent systems. Phys Rev Lett. (1984) 52:997. doi: 10.1103/PhysRevLett.52.997

CrossRef Full Text | Google Scholar

30. van Leeuwen R. Mapping from densities to potentials in time-dependent density-functional theory. Phys Rev Lett. (1999) 82:3863. doi: 10.1103/PhysRevLett.82.3863

CrossRef Full Text | Google Scholar

31. Nakatsukasa T, Matsuyanagi K, Matsuo M, Yabana K. Time-dependent density-functional description of nuclear dynamics. Rev Mod Phys. (2016) 88:045004. doi: 10.1103/RevModPhys.88.045004

CrossRef Full Text | Google Scholar

32. Bender M, Heenen PH, Reinhard PG. Self-consistent mean-field models for nuclear structure. Rev Mod Phys. (2003) 75:121. doi: 10.1103/RevModPhys.75.121

CrossRef Full Text | Google Scholar

33. Kortelainen M, McDonnell J, Nazarewicz W, Reinhard PG, Sarich J, Schunck N, et al. Nuclear energy density optimization: large deformations. Phys Rev C. (2012) 85:024304. doi: 10.1103/PhysRevC.85.024304

CrossRef Full Text | Google Scholar

34. Kortelainen M, McDonnell J, Nazarewicz W, Olsen E, Reinhard PG, Sarich J, et al. Nuclear energy density optimization: shell structure. Phys Rev C. (2014) 89:054314. doi: 10.1103/PhysRevC.89.054314

CrossRef Full Text | Google Scholar

35. Bulgac A, Forbes MM, Jin S, Perez RN, Schunck N. Minimal nuclear energy density functional. Phys Rev C. (2018) 97:044313. doi: 10.1103/PhysRevC.97.044313

CrossRef Full Text | Google Scholar

36. Blocki J, Boneh Y, Nix JR, Randrup J, Robel M, Sierk AJ, et al. One-body dissipation and the super-viscidity of nuclei. Ann Phys. (1978) 113:330. doi: 10.1016/0003-4916(78)90208-7

CrossRef Full Text | Google Scholar

37. Nakatsukasa T, Yabana K. Liner response theory in the continuum for deformed nuclei: Green's function vs time-dependent Hartree-Fock with the absorbing boundary condition. Phys Rev C. (2005) 71:024301. doi: 10.1103/PhysRevC.71.024301

CrossRef Full Text | Google Scholar

38. Umar AS, Oberacker VE. Time-dependent response calculations of nuclear resonances. Phys Rev C. (2005) 71:034314. doi: 10.1103/PhysRevC.71.034314

CrossRef Full Text | Google Scholar

39. Maruhn JA, Reinhard PG, Stevenson PD, Rikovska Stone J, Strayer MR. Dipole giant resonances in deformed heavy nuclei. Phys Rev C. (2005) 71:064328. doi: 10.1103/PhysRevC.71.064328

CrossRef Full Text | Google Scholar

40. Ebata S, Nakatsukasa T, Inakura T, Yoshida K, Hashimoto Y, Yabana K. Canonical-basis time-dependent Hartree-Fock-Bogoliubov theory and linear-response calculations. Phys Rev C. (2010) 82:034306. doi: 10.1103/PhysRevC.82.034306

CrossRef Full Text | Google Scholar

41. Fracasso S, Suckling EB, Stevenson PD. Unrestricted Skyrme-tensor time-dependent Hartree-Fock model and its application to the nuclear response from spherical to triaxial nuclei. Phys Rev C. (2012) 86:044303. doi: 10.1103/PhysRevC.86.044303

CrossRef Full Text | Google Scholar

42. Pardi CI, Stevenson PD. Continuum time-dependent Hartree-Fock method for giant resonances in spherical nuclei. Phys Rev C. (2013) 87:014330. doi: 10.1103/PhysRevC.87.014330

CrossRef Full Text | Google Scholar

43. Scamps G, Lacroix D. Systematics of isovector and isoscalar giant quadrupole resonances in normal and superfluid spherical nuclei. Phys Rev C. (2013) 88:044310. doi: 10.1103/PhysRevC.88.044310

CrossRef Full Text | Google Scholar

44. Scamps G, Lacroix D. Systematic study of isovector and isoscalar giant quadrupole resonances in normal and superfluid deformed nuclei. Phys Rev C. (2014) 89:034314. doi: 10.1103/PhysRevC.89.034314

CrossRef Full Text | Google Scholar

45. Ebata S, Nakatsukasa T, Inakura T. Systematic investigation of low-lying dipole modes using the canonical-basis time-dependent Hartree-Fock-Bogoliubov theory. Phys Rev C. (2014) 90:024303. doi: 10.1103/PhysRevC.90.024303

CrossRef Full Text | Google Scholar

46. Ebata S, Nakatsukasa T, Inakura T. Systematic investigation of low-lying dipole modes using the canonical-basis time-dependent Hartree-Fock-Bogoliubov theory. Phys Rev C. (2015) 92:049902. doi: 10.1103/PhysRevC.92.049902

CrossRef Full Text | Google Scholar

47. Simenel C, Umar AS. Formation and dynamics of fission fragments. Phys Rev C. (2014) 89:031601(R). doi: 10.1103/PhysRevC.89.031601

CrossRef Full Text | Google Scholar

48. Scamps G, Simenel C, Lacroix D. Superfluid dynamics of ²⁵⁸Fm fission. Phys Rev C. (2015) 92:011602(R). doi: 10.1103/PhysRevC.92.011602

CrossRef Full Text | Google Scholar

49. Tanimura Y, Lacroix D, Scamps G. Collective aspects deduced from time-dependent microscopic mean-field with pairing: application to the fission process. Phys Rev C. (2015) 92:034601. doi: 10.1103/PhysRevC.92.034601

CrossRef Full Text | Google Scholar

50. Goddard P, Stevenson P, Rios A. Fission dynamics within time-dependent Hartree-Fock: deformation-induced fission. Phys Rev C. (2015) 92:054610. doi: 10.1103/PhysRevC.92.054610

CrossRef Full Text | Google Scholar

51. Goddard P, Stevenson P, Rios A. Fission dynamics within time-dependent Hartree-Fock. II. Boost-induced fission. Phys Rev C. (2016) 93:014620. doi: 10.1103/PhysRevC.93.014620

CrossRef Full Text | Google Scholar

52. Scamps G, Simenel C. Impact of pear-shaped fission fragments on mass-asymmetric fission in actinides. Nature. (2018) 564:382. doi: 10.1038/s41586-018-0780-0

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Umar AS, Maruhn JA, Itagaki N, Oberacker VE. Microscopic study of the triple-α reaction. Phys Rev Lett. (2010) 104:212503. doi: 10.1103/PhysRevLett.104.212503

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Ichikawa T, Matsuyanagi K, Maruhn JA, Itagaki N. Pure collective precession motion of a high-spin torus isomer. Phys Rev C. (2014) 89:011305(R). doi: 10.1103/PhysRevC.89.011305

CrossRef Full Text | Google Scholar

55. Ichikawa T, Matsuyanagi K, Maruhn JA, Itagaki N. High-spin torus isomers and their precession motions. Phys Rev C. (2014) 90:034314. doi: 10.1103/PhysRevC.90.034314

CrossRef Full Text | Google Scholar

56. Schuetrumpf B, Klatt MA, Iida K, Maruhn JA, Mecke K, Reinhard PG. Time-dependent Hartree-Fock approach to nuclear “pasta” at finite temperature. Phys Rev C. (2013) 87:055805. doi: 10.1103/PhysRevC.87.055805

CrossRef Full Text | Google Scholar

57. Schuetrumpf B, Iida K, Maruhn JA, Reinhard PG. Nuclear “pasta matter” for different proton fractions. Phys Rev C. (2014) 90:055802. doi: 10.1103/PhysRevC.90.055802

CrossRef Full Text | Google Scholar

58. Schuetrumpf B, Klatt MA, Iida K, Schröder-Turk GE, Maruhn JA, Mecke K, et al. Appearance of the single gyroid network phase in “nuclear pasta” matter. Phys Rev C. (2015) 91:025801. doi: 10.1103/PhysRevC.91.025801

CrossRef Full Text | Google Scholar

59. Schuetrumpf B, Nazarewicz W. Twist-averaged boundary conditions for nuclear pasta Hartree-Fock calculations. Phys Rev C. (2015) 92:045806. doi: 10.1103/PhysRevC.92.045806

CrossRef Full Text | Google Scholar

60. Umar AS, Oberacker VE, Maruhn JA. Neutron transfer dynamics and doorway to fusion in time-dependent Hartree-Fock theory. Eur Phys J A. (2008) 37:245. doi: 10.1140/epja/i2008-10614-6

CrossRef Full Text | Google Scholar

61. Iwata Y, Otsuka T, Maruhn JA, Itagaki N. Suppression of charge equilibration leading to the synthesis of exotic nuclei. Phys Rev Lett. (2010) 104:252501. doi: 10.1103/PhysRevLett.104.252501

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Evers M, Dasgupta M, Hinde DJ, Luong DH, Rafiei R, du Rietz R, et al. Cluster transfer in the reaction ¹⁶O+²⁰⁸Pb at energies well below the fusion barrier: a possible doorway to energy dissipation. Phys Rev C. (2011) 84:054614. doi: 10.1103/PhysRevC.84.054614

CrossRef Full Text | Google Scholar

63. Umar AS, Simenel C, Ye W. Transport properties of isospin asymmetric nuclear matter using the time-dependent Hartree-Fock method. Phys Rev C. (2017) 96:024625. doi: 10.1103/PhysRevC.96.024625

CrossRef Full Text | Google Scholar

64. Simenel C. Particle transfer reactions with the time-dependent Hartree-Fock theory using a particle number projection technique. Phys Rev Lett. (2010) 105:192701. doi: 10.1103/PhysRevLett.105.192701

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Sekizawa K, Yabana K. Time-dependent Hartree-Fock calculations for multinucleon transfer processes in ^{40, 48}Ca+¹²⁴Sn, ⁴⁰Ca+²⁰⁸Pb, and ⁵⁸Ni+²⁰⁸Pb reactions. Phys Rev C. (2013) 88:014614. doi: 10.1103/PhysRevC.88.014614

CrossRef Full Text | Google Scholar

66. Sekizawa K, Yabana K. Time-dependent Hartree-Fock calculations for multinucleon transfer processes in ^{40, 48}Ca+¹²⁴Sn, ⁴⁰Ca+²⁰⁸Pb, and ⁵⁸Ni+²⁰⁸Pb reactions. Phys Rev C. (2016) 93:029902(E). doi: 10.1103/PhysRevC.93.029902

CrossRef Full Text | Google Scholar

67. Sekizawa K, Yabana K. Particle-number projection method in time-dependent Hartree-Fock theory. Phys Rev C. (2014) 90:064614. doi: 10.1103/PhysRevC.90.064614

CrossRef Full Text | Google Scholar

68. Sonika Roy BJ, Parmar A, Pal UK, Kumawat H, Jha V, et al. Multinucleon transfer study in ²⁰⁶Pb(¹⁸O, x) at energies above the Coulomb barrier. Phys Rev C. (2015) 92:024603. doi: 10.1103/PhysRevC.92.024603

CrossRef Full Text | Google Scholar

69. Sekizawa K, Yabana K. Multinucleon transfer reaction in time-dependent Hartree-Fock theory. arXiv:1511.08322 [nucl-th]. (2015).

Google Scholar

70. Sekizawa K, Yabana K. Time-dependent Hartree-Fock calculations for multinucleon transfer and quasifission processes in the ⁶⁴Ni+²³⁸U reaction. Phys Rev C. (2016) 93:054616. doi: 10.1103/PhysRevC.93.054616

CrossRef Full Text | Google Scholar

71. Sekizawa K, Heinz S. Quasifission dynamics and stability of superheavy systems. Acta Phys Pol B Proc Suppl. (2017) 10:225. doi: 10.5506/APhysPolBSupp.10.225

CrossRef Full Text | Google Scholar

72. Sekizawa K. Microscopic description of production cross sections including deexcitation effects. Phys Rev C. (2017) 96:014615. doi: 10.1103/PhysRevC.96.014615

CrossRef Full Text | Google Scholar

73. Sekizawa K. Enhanced nucleon transfer in tip collisions of ¹²⁴Sn+²³⁸U. Phys Rev C. (2017) 96:041601(R). doi: 10.1103/PhysRevC.96.041601

CrossRef Full Text | Google Scholar

74. Roy BJ, Sawant Y, Patwari P, Santra S, Pal A, Kundu A, et al. Deep-inelastic multinucleon transfer processes in the ¹⁶O+²⁷Al reaction. Phys Rev C. (2018) 97:034603. doi: 10.1103/PhysRevC.97.034603

CrossRef Full Text | Google Scholar

75. Golabek C, Simenel C. Collision dynamics of two ²³⁸U atomic nuclei. Phys Rev Lett. (2009) 103:042701. doi: 10.1103/PhysRevLett.103.042701

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Kedziora DJ, Simenel C. New inverse quasifission mechanism to produce neutron-rich transfermium nuclei. Phys Rev C. (2010) 81:044613. doi: 10.1103/PhysRevC.81.044613

CrossRef Full Text | Google Scholar

77. Simenel C, Hinde DJ, du Rietz R, Dasgupta M, Evers M, Lin CJ, et al. Influence of entrance-channel magicity and isospin on quasi-fission. Phys Lett. (2012) B710:607. doi: 10.1016/j.physletb.2012.03.063

CrossRef Full Text | Google Scholar

78. Wakhle A, Simenel C, Hinde DJ, Dasgupta M, Evers M, Luong DH, et al. Interplay between quantum shells and orientation in quasifission. Phys Rev Lett. (2014) 113:182502. doi: 10.1103/PhysRevLett.113.182502

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Oberacker VE, Umar AS, Simenel C. Dissipative dynamics in quasifission. Phys Rev C. (2014) 90:054605. doi: 10.1103/PhysRevC.90.054605

CrossRef Full Text | Google Scholar

80. Umar AS, Oberacker VE. Time-dependent HF approach to SHE dynamics. Nucl Phys. (2015) A944:238. doi: 10.1016/j.nuclphysa.2015.02.011

CrossRef Full Text | Google Scholar

81. Hammerton K, Kohley Z, Hinde DJ, Dasgupta M, Wakhle A, Williams E, et al. Reduced quasifission competition in fusion reactions forming neutron-rich heavy elements. Phys Rev C. (2015) 91:041602(R). doi: 10.1103/PhysRevC.91.041602

CrossRef Full Text | Google Scholar

82. Washiyama K. Microscopic analysis of fusion hindrance in heavy nuclear systems. Phys Rev C. (2015) 91:064607. doi: 10.1103/PhysRevC.91.064607

CrossRef Full Text | Google Scholar

83. Umar AS, Oberacker VE, Simenel C. Shape evolution and collective dynamics of quasifission in the time-dependent Hartree-Fock approach. Phys Rev C. (2015) 92:024621. doi: 10.1103/PhysRevC.92.024621

CrossRef Full Text | Google Scholar

84. Umar AS, Oberacker VE, Simenel C. Fusion and quasifission dynamics in the reactions ⁴⁸Ca+²⁴⁹Bk and ⁵⁰Ti+²⁴⁹Bk using a time-dependent Hartree-Fock approach. Phys Rev C. (2016) 94:024605. doi: 10.1103/PhysRevC.94.024605

CrossRef Full Text | Google Scholar

85. Yu C, Guo L. Angular momentum dependence of quasifission dynamics in the reaction ⁴⁸Ca+²⁴⁴Pu. Sci China Phys Mech Astron. (2017) 60:092011. doi: 10.1007/s11433-017-9063-3

CrossRef Full Text | Google Scholar

86. Guo L, Shen C, Yu C, Wu Z. Isotopic trends of quasifission and fusion-fission in the reactions ⁴⁸Ca+^{239, 244}Pu. Phys Rev C. (2018) 98:064609. doi: 10.1103/PhysRevC.98.064609

CrossRef Full Text | Google Scholar

87. Zheng H, Burrello S, Colonna M, Lacroix D, Scamps G. Connecting the nuclear equation of state to the interplay between fusion and quasifission processes in low-energy nuclear reactions. Phys Rev C. (2018) 98:024622. doi: 10.1103/PhysRevC.98.024622

CrossRef Full Text | Google Scholar

88. Umar AS, Oberacker VE. Heavy-ion interaction potential deduced from density-constrained time-dependent Hartree-Fock calculation. Phys Rev C. (2006) 74:021601(R). doi: 10.1103/PhysRevC.74.021601

CrossRef Full Text | Google Scholar

89. Umar AS, Oberacker VE, Maruhn JA, Reinhard PG. Microscopic calculation of precompound excitation energies for heavy-ion collisions. Phys Rev C. 80:041601(R) (2009).

Google Scholar

90. Umar AS, Oberacker VE, Maruhn JA, Reinhard PG. Entrance channel dynamics of hot and cold fusion reactions leading to superheavy elements. Phys Rev C. (2010) 81:064607. doi: 10.1103/PhysRevC.81.064607

CrossRef Full Text | Google Scholar

91. Oberacker VE, Umar AS, Maruhn JA, Reinhard PG. Microscopic study of the ^{132, 124}Sn+⁹⁶Zr reactions: dynamic excitation energy, energy-dependent heavy-ion potential, and capture cross section. Phys Rev C. (2010) 82:034603. doi: 10.1103/PhysRevC.82.034603

CrossRef Full Text | Google Scholar

92. Umar AS, Oberacker VE, Maruhn JA, Reinhard PG. Microscopic composition of ion-ion interaction potentials. Phys Rev C. (2012) 85:017602. doi: 10.1103/PhysRevC.85.017602

CrossRef Full Text | Google Scholar

93. Oberacker VE, Umar AS, Maruhn JA, Reinhard PG. Dynamic microscopic study of pre-equilibrium giant resonance excitation and fusion in the reactions ¹³²Sn+⁴⁸Ca and ¹²⁴Sn+⁴⁰Ca. Phys Rev C. (2012) 85:034609. doi: 10.1103/PhysRevC.85.034609

CrossRef Full Text | Google Scholar

94. Keser R, Umar AS, Oberacker VE. Microscopic study of Ca + Ca fusion. Phys Rev C. (2012) 85:044606. doi: 10.1103/PhysRevC.85.044606

CrossRef Full Text | Google Scholar

95. Oberacker VE, Umar AS. Microscopic analysis of sub-barrier fusion enhancement in ¹³²Sn+⁴⁰Ca versus ¹³²Sn+⁴⁸Ca. Phys Rev C. (2013) 87:034611. doi: 10.1103/PhysRevC.87.034611

CrossRef Full Text | Google Scholar

96. Simenel C, Keser R, Umar AS, Oberacker VE. Microscopic study of ¹⁶O+¹⁶O fusion. Phys Rev C. (2013) 88:024617. doi: 10.1103/PhysRevC.88.024617

CrossRef Full Text | Google Scholar

97. Umar AS, Simenel C, Oberacker VE. Energy dependence of potential barriers and its effect on fusion cross sections. Phys Rev C. 89:034611 (2014). doi: 10.1103/PhysRevC.89.034611

CrossRef Full Text | Google Scholar

98. Steinbach TK, Vadas J, Schmidt J, Haycraft C, Hudan S, deSouza RT, et al. Sub-barrier enhancement of fusion as compared to a microscopic method in ¹⁸O+¹²C. Phys Rev C. (2014) 90:041603(R). doi: 10.1103/PhysRevC.90.041603

CrossRef Full Text | Google Scholar

99. Reinhard PG, Umar AS, Stevenson PD, Piekarewicz J, Oberacker VE, Maruhn JA. Sensitivity of the fusion cross section to the density dependence of the symmetry energy. Phys Rev C. (2016) 93:044618. doi: 10.1103/PhysRevC.93.044618

CrossRef Full Text | Google Scholar

100. Godbey K, Umar AS, Simenel C. Dependence of fusion on isospin dynamics. Phys Rev C. (2017) 95:011601(R). doi: 10.1103/PhysRevC.95.011601

CrossRef Full Text | Google Scholar

101. Guo L, Godbey K, Umar AS. Influence of the tensor force on the microscopic heavy-ion interaction potential. Phys Rev C. (2018) 98:064607. doi: 10.1103/PhysRevC.98.064607

CrossRef Full Text | Google Scholar

102. Simenel C, Chomaz Ph, de France G. Fusion process studied with a preequilibrium giant dipole resonance in time-dependent Hartree-Fock theory. Phys Rev C. (2007) 76:024609. doi: 10.1103/PhysRevC.76.024609

CrossRef Full Text | Google Scholar

103. Bourgin D, Simenel C, Courtin S, Haas F. Microscopic study of ⁴⁰Ca+^{58, 64}Ni fusion reactions. Phys Rev C. (2016) 93:034604. doi: 10.1103/PhysRevC.93.034604

CrossRef Full Text | Google Scholar

104. Vo-Phuoc K, Simenel C, Simpson EC. Dynamical effects in fusion with exotic nuclei. Phys Rev C. (2016) 94:024612. doi: 10.1103/PhysRevC.94.024612

CrossRef Full Text | Google Scholar

105. Simenel C. Nuclear quantum many-body dynamics. Eur Phys J A. (2012) 48:152. doi: 10.1140/epja/i2012-12152-0

CrossRef Full Text | Google Scholar

106. Nakatsukasa T. Density functional approaches to collective phenomena in nuclei: time-dependent density functional theory for perturbative and non-perturbative nuclear dynamics. Prog Theor Exp Phys. (2012) 2012:01A207. doi: 10.1093/ptep/pts016

CrossRef Full Text | Google Scholar

107. Umar AS, Strayer MR, Reinhard PG. Resolution of the fusion window anomaly in heavy-ion collisions. Phys Rev Lett. (1986) 56:2793. doi: 10.1103/PhysRevLett.56.2793

PubMed Abstract | CrossRef Full Text | Google Scholar

108. Reinhard PG, Umar AS, Davies KTR, Strayer MR, Lee SJ. Dissipation and forces in time-dependent Hartree-Fock calculations. Phys Rev C. (1988) 37:1026. doi: 10.1103/PhysRevC.37.1026

PubMed Abstract | CrossRef Full Text | Google Scholar

109. Umar AS, Strayer MR, Reinhard PG, Davies KTR, Lee SJ. Spin-orbit force in time-dependent Hartree-Fock calculations of heavy-ion collisions. Phys Rev C. (1989) 40:706. doi: 10.1103/PhysRevC.40.706

PubMed Abstract | CrossRef Full Text | Google Scholar

110. Dai GF, Guo L, Zhao EG, Zhou SG. Dissipation dynamics and spin-orbit force in time-dependent Hartree-Fock theory. Phys Rev C. (2014) 90:044609. doi: 10.1103/PhysRevC.90.044609

CrossRef Full Text | Google Scholar

111. Iwata Y, Maruhn JA. Enhanced spin-current tensor contribution in collision dynamics. Phys Rev C. (2011) 84:014616. doi: 10.1103/PhysRevC.84.014616

CrossRef Full Text | Google Scholar

112. Dai DF, Guo L, Zhao EG, Zhou SG. Effect of tensor force on dissipation dynamics in time-dependent Hartree-Fock theory. Sci China Phys Mech Astron. (2014) 57:1618. doi: 10.1007/s11433-014-5536-8

CrossRef Full Text | Google Scholar

113. Stevenson PD, Suckling EB, Fracasso S, Barton MC, Umar AS. Skyrme tensor force in heavy ion collisions. Phys Rev C. (2016) 93:054617. doi: 10.1103/PhysRevC.93.054617

CrossRef Full Text | Google Scholar

114. Guo L, Simenel C, Shi L, Yu C. The role of tensor force in heavy-ion fusion dynamics. Phys Lett. (2018) B782:401. doi: 10.1016/j.physletb.2018.05.066

CrossRef Full Text | Google Scholar

115. Corradi L, He JH, Ackermann D, Stefanini AM, Pisent A, Beghini S, et al. Multinucleon transfer reactions in ⁴⁰Ca+¹²⁴Sn. Phys Rev C. (1996) 54:201. doi: 10.1103/PhysRevC.54.201

PubMed Abstract | CrossRef Full Text | Google Scholar

116. Corradi L, Stefanini AM, He JH, Beghini S, Montagnoli G, Scarlassara F, et al. Evidence of complex degrees of freedom in multinucleon transfer reactions of ⁴⁸Ca+¹²⁴Sn. Phys Rev C. (1997) 56:938. doi: 10.1103/PhysRevC.56.938

CrossRef Full Text | Google Scholar

117. Corradi L, Vinodkumar AM, Stefanini AM, Fioretto E, Prete G, Beghini S, et al. Light and heavy transfer products in 58Ni+208Pb at the Coulomb barrier. Phys Rev C. (2002) 66:024606. doi: 10.1103/PhysRevC.66.024606

CrossRef Full Text | Google Scholar

118. Szilner S, Corradi L, Pollarolo G, Beghini S, Behera BR, Fioretto E, et al. Multinucleon transfer processes in 40Ca+208Pb. Phys Rev C. (2005) 71:044610. doi: 10.1103/PhysRevC.71.044610

CrossRef Full Text | Google Scholar

119. Charity RJ. GEMINI: a code to simulate the decay of a compound nucleus by a series of binary decays. In: Joint ICTP-AIEA Advanced Workshop on Model Codes for Spallation Reactions. Vienna: IAEA (2008). p. 139.

Google Scholar

120. Corradi L, Stefanini AM, Lin CJ, Beghini S, Montagnoli G, Scarlassara F, et al. Multinucleon transfer processes in ⁶⁴Ni+²³⁸U. Phys Rev C. (1999) 59:261. doi: 10.1103/PhysRevC.59.261

CrossRef Full Text | Google Scholar

121. Kozulin EM, Knyazheva GN, Itkis IM, Itkis MG, Bogachev AA, Krupa L, et al. Investigation of the reaction ⁶⁴Ni+²³⁸U being an option of synthesizing element 120. Phys Lett B. (2010) 686:227. doi: 10.1016/j.physletb.2010.02.041

CrossRef Full Text | Google Scholar

122. Jiang X, Wang N. Production mechanism of neutron-rich nuclei around N = 126 in the multi-nucleon transfer reaction ¹³²Sn+²⁰⁸Pb. Chin Phys C. (2018) 42:104105. doi: 10.1088/1674-1137/42/10/104105

CrossRef Full Text | Google Scholar

123. Tōke JT, Bock R, Dai GX, Gobbi A, Gralla S, Hildenbrand KD, et al. Quasi-fission - The mass-drift mode in heavy-ion reactions. Nucl Phys. (1985) A440:327.

Google Scholar

124. Bock R, Chu YT, Dakowski M, Gobbi A, Grosse E, Olmi A, et al. Dynamics of the fusion process. Nucl Phys. (1982) A388:334.

Google Scholar

125. du Rietz R, Hinde DJ, Dasgupta M, Thomas RG, Gasques LR, Evers M, et al. Predominant time scales in fission processes in reactions of S, Ti, and Ni with W: zeptosecond versus attosecond. Phys Rev Lett. (2011) 106:052701. doi: 10.1103/PhysRevLett.106.052701

PubMed Abstract | CrossRef Full Text | Google Scholar

126. du Rietz R, Williams E, Hinde DJ, Dasgupta M, Evers M, Lin CJ, et al. Mapping quasifission characteristics and timescales in heavy element formation reactions. Phys Rev C. (2013) 88:054618. doi: 10.1103/PhysRevC.88.054618

CrossRef Full Text | Google Scholar

127. Morjean M, Hinde DJ, Simenel C, Jeung DY, Airiau M, Cook KJ, et al. Evidence for the role of proton shell closure in quasifission reactions from X-Ray fluorescence of mass-identified fragments. Phys Rev Lett. (2017) 119:222502. doi: 10.1103/PhysRevLett.119.222502

PubMed Abstract | CrossRef Full Text | Google Scholar

128. Zagrebaev V, Greiner W. Unified consideration of deep inelastic, quasi-fission and fusion-fission phenomena. J Phys G Nucl Part Phys. (2005) 31:825. doi: 10.1088/0954-3899/31/7/024

CrossRef Full Text | Google Scholar

129. Zagrebaev VI, Oganessian YT, Itkis MG, Greiner W. Superheavy nuclei and quasi-atoms produced in collisions of transuranium ions. Phys Rev C. (2006) 73:031602(R). doi: 10.1103/PhysRevC.73.031602

CrossRef Full Text | Google Scholar

130. Zagrebaev V, Greiner W. Shell effects in damped collisions: a new way to superheavies. J Phys G Nucl Part Phys. (2007) 34:2265. doi: 10.1088/0954-3899/34/11/004

CrossRef Full Text | Google Scholar

131. Zagrebaev V, Greiner W. Low-energy collisions of heavy nuclei: dynamics of sticking, mass transfer and fusion. J Phys G Nucl Part Phys. (2007) 34:1. doi: 10.1088/0954-3899/34/1/001

CrossRef Full Text | Google Scholar

132. Zagrebaev V, Greiner W. Production of new heavy isotopes in low-energy multinucleon transfer reactions. Phys Rev Lett. (2008) 101:122701. doi: 10.1103/PhysRevLett.101.122701

PubMed Abstract | CrossRef Full Text | Google Scholar

133. Zagrebaev V, Greiner W. Synthesis of superheavy nuclei: a search for new production reactions. Phys Rev C. (2008) 78:034610. doi: 10.1103/PhysRevC.78.034610

CrossRef Full Text | Google Scholar

134. Zagrebaev VI, Greiner W. Production of heavy and superheavy neutron-rich nuclei in transfer reactions. Phys Rev C. (2011) 83:044618. doi: 10.1103/PhysRevC.83.044618

CrossRef Full Text | Google Scholar

135. Zagrebaev VI, Greiner W. Production of heavy trans-target nuclei in multinucleon transfer reactions. Phys Rev C. (2013) 87:034608. doi: 10.1103/PhysRevC.87.034608

CrossRef Full Text | Google Scholar

136. Zagrebaev VI, Fornal B, Leoni S, Greiner W. Formation of light exotic nuclei in low-energy multinucleon transfer reactions. Phys Rev C. (2014) 89:054608. doi: 10.1103/PhysRevC.89.054608

CrossRef Full Text | Google Scholar

137. Zagrebaev VI, Greiner W. Cross sections for the production of superheavy nuclei. Nucl Phys. (2015) A944:257. doi: 10.1016/j.nuclphysa.2015.02.010

CrossRef Full Text | Google Scholar

138. Ayik S, Yilmaz B, Yilmaz O. Multinucleon exchange in quasifission reactions. Phys Rev C. (2015) 92:064615. doi: 10.1103/PhysRevC.92.064615

CrossRef Full Text | Google Scholar

139. Ayik S, Yilmaz B, Yilmaz O, Umar AS, Turan G. Multi-nucleon transfer in central collisions of ²³⁸U+²³⁸U. Phys Rev C. (2017) 96:024611. doi: 10.1103/PhysRevC.96.024611

CrossRef Full Text | Google Scholar

140. Ayik S, Yilmaz B, Yilmaz O, Umar AS. Quantal diffusion description of multinucleon transfers in heavy-ion collisions. Phys Rev C. (2018) 97:054618. doi: 10.1103/PhysRevC.97.054618

CrossRef Full Text | Google Scholar

141. Ring P, Schuck P. The Nuclear Many-Body Problem. Berlin; Heidelberg: Springer-Verlag (1980). doi: 10.1007/978-3-642-61852-9

CrossRef Full Text | Google Scholar

142. Washiyama K, Lacroix D. Energy dependence of the nucleus-nucleus potential close to the Coulomb barrier. Phys Rev C. (2008) 78:024610. doi: 10.1103/PhysRevC.78.024610

CrossRef Full Text | Google Scholar

143. Washiyama K, Lacroix D, Ayik S. One-body energy dissipation in fusion reactions from mean-field theory. Phys Rev C. (2009) 79:024609. doi: 10.1103/PhysRevC.79.024609

CrossRef Full Text | Google Scholar

144. Simenel C, Umar AS, Godbey K, Dasgupta M, Hinde DJ. How the Pauli exclusion principle affects fusion of atomic nuclei. Phys Rev C. (2017) 95:031601(R). doi: 10.1103/PhysRevC.95.031601

CrossRef Full Text | Google Scholar

145. Hagino K, Rowley N, Kruppa AT. A program for coupled-channels calculations with all order couplings for heavy-ion fusion reactions. Comput Phys Commun. (1999) 123:143. doi: 10.1016/S0010-4655(99)00243-X

CrossRef Full Text | Google Scholar

146. Hagino K, Takigawa N. Subbarrier fusion reactions and many-particle quantum tunneling. Prog Theor Phys. (2012) 128:1061. doi: 10.1143/PTP.128.1061

CrossRef Full Text | Google Scholar

147. Simenel C, Dasgupta M, Hinde DJ, Williams E. Microscopic approach to coupled-channels effects on fusion. Phys Rev C. (2013) 88:064604. doi: 10.1103/PhysRevC.88.064604

CrossRef Full Text | Google Scholar

148. Balian R, Vénéroni M. Time-dependent variational principle for predicting the expectation value of an observable. Phys Rev Lett. (1981) 47:1353. doi: 10.1103/PhysRevLett.47.1353

CrossRef Full Text | Google Scholar

149. Balian R, Vénéroni M. Time-dependent variational principle for predicting the expectation value of an observable. Phys Rev Lett. (1981) 47:1765. doi: 10.1103/PhysRevLett.47.1765.3

CrossRef Full Text | Google Scholar

150. Dasso CH, Døssing T, Pauli HC. On the mass distribution in Time-Dependent Hartree-Fock calculations of heavy-ion collisions. Z Phys A. (1979) 289:395. doi: 10.1007/BF01409391

CrossRef Full Text | Google Scholar

151. Broomfield JMA, Stevenson PD. Mass distributions beyond TDHF. AIP Conf Proc. (2009) 1098:133. doi: 10.1063/1.3108767

CrossRef Full Text | Google Scholar

152. Simenel C. Particle-number fluctuations and correlations in transfer reactions obtained using the Balian-Vénéroni variational principle. Phys Rev Lett. (2011) 106:112502. doi: 10.1103/PhysRevLett.106.112502

PubMed Abstract | CrossRef Full Text | Google Scholar

153. Williams E, Sekizawa K, Hinde DJ, Simenel C, Dasgupta M, Carter IP, et al. Exploring zeptosecond quantum equilibration dynamics: from deep-inelastic to fusion-fission outcomes in ⁵⁸Ni+⁶⁰Ni reactions. Phys Rev Lett. (2018) 120:022501. doi: 10.1103/PhysRevLett.120.022501

CrossRef Full Text | Google Scholar

154. Ayik S. A stochastic mean-field approach for nuclear dynamics. Phys Lett. (2008) B658:174. doi: 10.1016/j.physletb.2007.09.072

CrossRef Full Text | Google Scholar

155. Lacroix D, Ayik S. Stochastic quantum dynamics beyond mean field. Eur Phys J A. (2014) 50:95. doi: 10.1140/epja/i2014-14095-8

CrossRef Full Text | Google Scholar

156. Shun-jin W, Cassing W. Explicit treatment of N-body correlations within a density-matrix formalism. Ann Phys (NY). (1985) 159:328. doi: 10.1016/0003-4916(85)90116-2

CrossRef Full Text | Google Scholar

157. Gong M, Tohyama M. Application of a time-dependent density-matrix formalism. Z Phys A. (1990) 335:153. doi: 10.1007/BF01294470

CrossRef Full Text | Google Scholar

158. Tohyama M, Umar AS. Fusion window problem in time-dependent Hartree-Fock theory revisited. Phys Rev C. (2002) 65:037601. doi: 10.1103/PhysRevC.65.037601

CrossRef Full Text | Google Scholar

159. Tohyama M, Umar AS. Two-body dissipation effects on the synthesis of superheavy elements. Phys Rev C. (2016) 93:034607. doi: 10.1103/PhysRevC.93.034607

CrossRef Full Text | Google Scholar

160. Wen K, Barton MC, Rios A, Stevenson PD. Two-body dissipation effect in nuclear fusion reactions. Phys Rev C. (2018) 98:014603. doi: 10.1103/PhysRevC.98.014603

CrossRef Full Text | Google Scholar

161. Ayik S, Washiyama K, Lacroix D. Fluctuation and dissipation dynamics in fusion reactions from a stochastic mean-field approach. Phys Rev C. (2009) 79:054606. doi: 10.1103/PhysRevC.79.054606

CrossRef Full Text | Google Scholar

162. Washiyama K, Ayik S, Lacroix D. Mass dispersion in transfer reactions with a stochastic mean-field theory. Phys Rev C. (2009) 80:031602(R). doi: 10.1103/PhysRevC.80.031602

CrossRef Full Text | Google Scholar

163. Yilmaz B, Ayik S, Lacroix D, Washiyama K. Nucleon exchange mechanism in heavy-ion collisions at near-barrier energies. Phys Rev C. (2011) 83:064615. doi: 10.1103/PhysRevC.83.064615

CrossRef Full Text | Google Scholar

164. Yilmaz B, Ayik S, Lacroix D, Yilmaz O. Nucleon exchange in heavy-ion collisions within a stochastic mean-field approach. Phys Rev C. (2014) 90:024613. doi: 10.1103/PhysRevC.90.024613

CrossRef Full Text | Google Scholar

165. Ayik S, Yilmaz O, Yilmaz B, Umar AS, Gokalp A, Turan G, Lacroix D. Quantal description of nucleon exchange in a stochastic mean-field approach. Phys Rev C. (2015) 91:054601. doi: 10.1103/PhysRevC.91.054601

CrossRef Full Text | Google Scholar

166. Ayik S, Yilmaz O, Yilmaz B, Umar AS. Quantal nucleon diffusion: central collisions of symmetric nuclei. Phys Rev C. (2016) 94:044624. doi: 10.1103/PhysRevC.94.044624

CrossRef Full Text | Google Scholar

167. Tanimura Y, Lacroix D, Ayik S. Microscopic phase-space exploration modeling of 258Fm spontaneous fission. Phys Rev Lett. (2017) 118:152501. doi: 10.1103/PhysRevLett.118.152501

CrossRef Full Text | Google Scholar

168. Tanimura Y, Lacroix D, Ayik S. Microscopic phase-space exploration modeling of 258Fm spontaneous fission. Phys Rev Lett. (2018) 121:059902(E). doi: 10.1103/PhysRevLett.121.059902

CrossRef Full Text | Google Scholar

169. Yilmaz B, Ayik S, Yilmaz O, Umar AS. Multinucleon transfer in ⁵⁸Ni+⁶⁰Ni and ⁶⁰Ni+⁶⁰Ni in a stochastic mean-field approach. Phys Rev C. (2018) 98:034604. doi: 10.1103/PhysRevC.98.034604

CrossRef Full Text | Google Scholar

170. Bulgac A, Jin S, Stetcu I. Unitary evolution with fluctuations and dissipation. arXiv:1805.08908 [nucl-th]. (2018).

Google Scholar

171. Scamps G, Lacroix D, Bertsch GF, Washiyama K. Pairing dynamics in particle transport. Phys Rev C. (2012) 85:034328. doi: 10.1103/PhysRevC.85.034328

CrossRef Full Text | Google Scholar

172. Scamps G, Lacroix D. Effect of pairing on one- and two-nucleon transfer below the Coulomb barrier: a time-dependent microscopic description. Phys Rev C. (2013) 87:014605. doi: 10.1103/PhysRevC.87.014605

CrossRef Full Text | Google Scholar

173. Ebata S, Nakatsukasa T. Pairing effects in nuclear fusion reaction. JPS Conf Proc. (2014) 1:013038. doi: 10.7566/JPSCP.1.013038

CrossRef Full Text | Google Scholar

174. Ebata S, Nakatsukasa T. Repulsive aspects of pairing correlation in nuclear fusion reaction. JPS Conf Proc. (2015) 6:020056. doi: 10.7566/JPSCP.6.020056

CrossRef Full Text | Google Scholar

175. Corradi L, Szilner S, Pollarolo G, Colo G, Mason P, Farnea E. Single and pair neutron transfers at sub-barrier energies. Phys Rev C. (2011) 84:034603. doi: 10.1103/PhysRevC.84.034603

CrossRef Full Text | Google Scholar

176. Montanari D, Corradi L, Szilner S, Pollarolo G, Fioretto E, Montagnoli G. Neutron pair transfer in ⁶⁰Ni+¹¹⁶Sn far below the coulomb barrier. Phys Rev Lett. (2014) 113:052501. doi: 10.1103/PhysRevLett.113.052501

CrossRef Full Text | Google Scholar

177. Montanari D, Corradi L, Szilner S, Pollarolo G, Goasduff A, Mijatović T. Pair neutron transfer in ⁶⁰Ni+¹¹⁶Sn probed via γ-particle coincidences. Phys Rev C. (2016) 93:054623. doi: 10.1103/PhysRevC.93.054623

CrossRef Full Text | Google Scholar

178. Magierski P, Sekizawa K, Wlazłowski G. Novel role of superfluidity in low-energy nuclear reactions. Phys Rev Lett. (2017) 119:042501. doi: 10.1103/PhysRevLett.119.042501

PubMed Abstract | CrossRef Full Text | Google Scholar

179. Sekizawa K, Magierski P, Wlazłowski G. Solitonic excitations in collisions of superfluid nuclei. Proc Sci. (2017) 214. doi: 10.22323/1.281.0214

CrossRef Full Text | Google Scholar

180. Sekizawa K, Wlazłowski G, Magierski P. Solitonic excitations in collisions of superfluid nuclei: a qualitatively new phenomenon distinct from the Josephson effect. EPJ Web Conf. (2017) 163:00051. doi: 10.1051/epjconf/201716300051

CrossRef Full Text | Google Scholar

181. Scamps G. Examining empirical evidence of the effect of superfluidity on the fusion barrier. Phys Rev C. (2018) 97:044611. doi: 10.1103/PhysRevC.97.044611

CrossRef Full Text | Google Scholar

182. Bulgac A, Magierski P, Forbes MM. The unitary fermi gas: from Monte Carlo to density functionals. In: Zwerger W, editor. BCS-BEC Crossover and the Unitary Fermi Gas. Lecture Notes in Physics. Heidelberg: Springer (2012). p. 305–73.

Google Scholar

183. Bulgac A. Time-dependent density functional theory and real-time dynamics of fermi superfluids. Ann Rev Nucl Part Sci. (2013) 63:97. doi: 10.1146/annurev-nucl-102212-170631

CrossRef Full Text | Google Scholar

184. Magierski P. Nuclear reactions and superfluid time dependent density functional theory. arXiv:1606.02225 [nucl-th]. (2016).

Google Scholar

185. Magierski P, Grineviciute J, Sekizawa K. Pairing dynamics and time-dependent density functional theory. Acta Phys Pol B. (2018) 49:281. doi: 10.5506/APhysPolB.49.281

CrossRef Full Text | Google Scholar

186. Bulgac A, Yoon S. Large amplitude dynamics of the pairing correlations in a unitary fermi gas. Phys Rev Lett. (2009) 102:085302. doi: 10.1103/PhysRevLett.102.085302

PubMed Abstract | CrossRef Full Text | Google Scholar

187. Bulgac A, Luo YL, Magierski P, Roche KJ, Yu Y. Real-time dynamics of quantized vortices in a unitary fermi superfluid. Science. (2011) 332:1288. doi: 10.1126/science.1201968

PubMed Abstract | CrossRef Full Text | Google Scholar

188. Bulgac A, Luo YL, Roche KJ. Quantum shock waves and domain walls in the real-time dynamics of a superfluid unitary fermi gas. Phys Rev Lett. (2012) 108:150401. doi: 10.1103/PhysRevLett.108.150401

PubMed Abstract | CrossRef Full Text | Google Scholar

189. Wlazłowski G, Sekizawa K, Marchwiany M, Magierski P. Suppressed solitonic cascade in spin-imbalanced superfluid fermi gas. Phys Rev Lett. (2018) 120:253002. doi: 10.1103/PhysRevLett.120.253002

PubMed Abstract | CrossRef Full Text | Google Scholar

190. Bulgac A, Forbes MM, Kelley MM, Roche KJ, Wlazłowski G. Quantized superfluid vortex rings in the unitary fermi gas. Phys Rev Lett. (2014) 112:025301. doi: 10.1103/PhysRevLett.112.025301

PubMed Abstract | CrossRef Full Text | Google Scholar

191. Wlazłowski G, Bulgac A, Forbes MM, Roche KJ. Life cycle of superfluid vortices and quantum turbulence in the unitary Fermi gas. Phys Rev A. (2015) 91:031602(R). doi: 10.1103/PhysRevA.91.031602

CrossRef Full Text | Google Scholar

192. Stetcu I, Bulgac A, Magierski P, Roche KJ. Isovector giant dipole resonance from the 3D time-dependent density functional theory for superfluid nuclei. Phys Rev C. (2011) 84:051309(R). doi: 10.1103/PhysRevC.84.051309

CrossRef Full Text | Google Scholar

193. Stetcu I, Bertulani C, Bulgac A, Magierski P, Roche KJ. Relativistic coulomb excitation within time dependent superfluid local density approximation. Phys Rev Lett. (2015) 114:012701. doi: 10.1103/PhysRevLett.114.012701

PubMed Abstract | CrossRef Full Text | Google Scholar

194. Bulgac A, Magierski P, Roche KJ, Stetcu I. Induced fission of ²⁴⁰Pu within a real-time microscopic framework. Phys Rev Lett. (2016) 116:122504. doi: 10.1103/PhysRevLett.116.122504

CrossRef Full Text | Google Scholar

195. Bulgac A, Jin S, Roche KJ, Schunck N, Stetcu I. Fission Dynamics. arXiv:1806.00694 [nucl-th] (2018).

196. Stetcu I, Bulgac A, Jin S, Roche KJ, Schunck N. Real Time Description of Fission. arXiv:1810.04024 [nucl-th]. (2018).

197. Wlazłowski G, Sekizawa K, Magierski P, Bulgac A, Forbes MM. Vortex pinning and dynamics in the neutron star crust. Phys Rev Lett. (2016) 117:232701. doi: 10.1103/PhysRevLett.117.232701

PubMed Abstract | CrossRef Full Text | Google Scholar

198. Hashimoto Y. Time-dependent Hartree-Fock-Bogoliubov calculations using a Lagrange mesh with the Gogny interaction. Phys Rev C. (2013) 88:034307. doi: 10.1103/PhysRevC.88.034307

CrossRef Full Text | Google Scholar

199. Hashimoto Y, Scamps G. Gauge angle dependence in time-dependent Hartree-Fock-Bogoliubov calculations of ²⁰O+²⁰O head-on collisions with the Gogny interaction. Phys Rev C. (2016) 94:014610. doi: 10.1103/PhysRevC.94.014610

CrossRef Full Text | Google Scholar

200. Scamps G, Hashimoto Y. Transfer probabilities for the reactions ^{14, 20}O+²⁰O in terms of multiple time-dependent Hartree-Fock-Bogoliubov trajectories. Phys Rev C. (2017) 96:031602(R).

Google Scholar

201. Winther A. Grazing reactions in collisions between heavy nuclei. Nucl Phys. (1994) A572:191. doi: 10.1016/0375-9474(94)90430-8

CrossRef Full Text | Google Scholar

202. Winther A. Dissipation, polarization and fluctuation in grazing heavy-ion collisions and the boundary to the chaotic regime. Nucl Phys. (1995) A594:203. doi: 10.1016/0375-9474(95)00374-A

CrossRef Full Text | Google Scholar

203. Dasso CH, Pollarolo G, Winther A. Systematics of isotope production with radioactive beams. Phys Rev Lett. (1994) 73:1907. doi: 10.1103/PhysRevLett.73.1907

PubMed Abstract | CrossRef Full Text | Google Scholar

204. Dasso CH, Pollarolo G, Winther A. Particle evaporation following multinucleon transfer processes with radioactive beams. Phys Rev C. (1995) 52:2264. doi: 10.1103/PhysRevC.52.2264

PubMed Abstract | CrossRef Full Text | Google Scholar

205. Yanez R, Loveland W. Predicting the production of neutron-rich heavy nuclei in multinucleon transfer reactions using a semi-classical model including evaporation and fission competition, GRAZING-F. Phys Rev C. (2015) 91:044608.

Google Scholar

206. Vigezzi E, Winther A. On the application of complex trajectories to direct heavy-ion reactions. Ann Phys. (1989) 192:432. doi: 10.1016/0003-4916(89)90145-0

CrossRef Full Text | Google Scholar

207. Adamian GG, Antonenko NV, Zubov AS. Production of unknown transactinides in asymmetry-exit-channel quasifission reactions. Phys Rev C. (2005) 71:034603. doi: 10.1103/PhysRevC.71.034603

CrossRef Full Text | Google Scholar

208. Penionzhkevich YE, Adamian GG, Antonenko NV. Towards neutron drip line via transfer-type reactions. Phys Lett. (2005) B621:119. doi: 10.1016/j.physletb.2005.05.085

CrossRef Full Text | Google Scholar

209. Penionzhkevich YE, Adamian GG, Antonenko NV. Production of neutron-rich Ca isotopes in transfer-type reactions. Eur Phys J A. (2006) 27:187. doi: 10.1140/epja/i2005-10252-6

CrossRef Full Text | Google Scholar

210. Feng ZQ, Jin GM, Li JQ. Production of heavy isotopes in transfer reactions by collisions of ²³⁸U+²³⁸U. Phys Rev C. (2009) 80:067601. doi: 10.1103/PhysRevC.80.067601

CrossRef Full Text | Google Scholar

211. Adamian GG, Antonenko NV, Sargsyan VV, Scheid W. Possibility of production of neutron-rich Zn and Ge isotopes in multinucleon transfer reactions at low energies. Phys Rev C. (2010) 81:024604. doi: 10.1103/PhysRevC.81.024604

CrossRef Full Text | Google Scholar

212. Adamian GG, Antonenko NV, Sargsyan VV, Scheid W. Predicted yields of new neutron-rich isotopes of nuclei with Z = 64–80 in the multinucleon transfer reaction ⁴⁸Ca+²³⁸U. Phys Rev C. (2010) 81:057602. doi: 10.1103/PhysRevC.81.057602

CrossRef Full Text | Google Scholar

213. Adamian GG, Antonenko NV, Lacroix D. Production of neutron-rich Ca, Sn, and Xe isotopes in transfer-type reactions with radioactive beams. Phys Rev C. (2010) 82:064611. doi: 10.1103/PhysRevC.82.064611

CrossRef Full Text | Google Scholar

214. Mun MH, Adamian GG, Antonenko NV, Oh Y, Kim Y. Production cross section of neutron-rich isotopes with radioactive and stable beams. Phys Rev C. (2014) 89:034622. doi: 10.1103/PhysRevC.89.034622

CrossRef Full Text | Google Scholar

215. Mun MH, Adamian GG, Antonenko NV, Oh Y, Kim Y. Toward neutron-rich nuclei via transfer reactions with stable and radioactive beams. Phys Rev C. (2015) 91:054610. doi: 10.1103/PhysRevC.91.054610

CrossRef Full Text | Google Scholar

216. Zhu L, Feng ZQ, Zhang FS. Production of heavy neutron-rich nuclei in transfer reactions within the dinuclear system model. J Phys G Nucl Part Phys. (2015) 42:085102. doi: 10.1088/0954-3899/42/8/085102

CrossRef Full Text | Google Scholar

217. Zhu L, Su J, Xie WJ, Zhang FS. Production of neutron-rich transcalifornium nuclei in ²³⁸U-induced transfer reactions. Phys Rev C. (2016) 94:054606. doi: 10.1103/PhysRevC.94.054606

CrossRef Full Text | Google Scholar

218. Feng ZQ. Production of neutron-rich isotopes around N = 126 in multinucleon transfer reactions. Phys Rev C. (2017) 95:024615. doi: 10.1103/PhysRevC.95.024615

CrossRef Full Text | Google Scholar

219. Zhu L, Su J, Xie WJ, Zhang FS. Theoretical study on production of heavy neutron-rich isotopes around the N = 126 shell closure in radioactive beam induced transfer reactions. Phys Lett. (2017) B767:437. doi: 10.1016/j.physletb.2017.01.082

CrossRef Full Text | Google Scholar

220. Li C, Wen P, Li J, Zhang G, Li B, Zhang FS. Production of heavy neutron-rich nuclei with radioactive beams in multinucleon transfer reactions. Nucl Sci Tech. (2017) 28:110. doi: 10.1007/s41365-017-0266-z

CrossRef Full Text | Google Scholar

221. Zhu L, Zhang FS, Wen PW, Su J, Xie WJ. Production of neutron-rich nuclei with Z = 60–73 in reactions induced by Xe isotopes. Phys Rev C. (2017) 96:024606. doi: 10.1103/PhysRevC.96.024606

CrossRef Full Text | Google Scholar

222. Zhao K, Li Z, Wang N, Zhang Y, Li Q, Wang Y, Wu X. Production mechanism of neutron-rich transuranium nuclei in ²³⁸U+²³⁸U collisions at near-barrier energies. Phys Rev C. (2015) 92:024613. doi: 10.1103/PhysRevC.92.024613

CrossRef Full Text | Google Scholar

223. Li C, Zhang F, Li J, Zhu L, Tian J, Wang N, et al. Multinucleon transfer in the ¹³⁶Xe+²⁰⁸Pb reaction. Phys Rev C. (2016) 93:014618. doi: 10.1103/PhysRevC.93.014618

CrossRef Full Text | Google Scholar

224. Wang N, Guo L. New neutron-rich isotope production in ¹⁵⁴Sm+¹⁶⁰Gd. Phys Lett. (2016) B760:236. doi: 10.1016/j.physletb.2016.06.073

CrossRef Full Text | Google Scholar

225. Zhao K, Li Z, Zhang Y, Wang N, Li Q, Shen C, et al. Production of unknown neutron-rich isotopes in ²³⁸U+²³⁸U collisions at near-barrier energy. Phys Rev C. (2016) 94:024601. doi: 10.1103/PhysRevC.94.024601

CrossRef Full Text | Google Scholar

226. Karpov AV, Saiko VV. Modeling near-barrier collisions of heavy ions based on a Langevin-type approach. Phys Rev C. (2017) 96:024618. doi: 10.1103/PhysRevC.96.024618

CrossRef Full Text | Google Scholar

227. Saiko V, Karpov A. Analysis of multinucleon transfer reactions involving spherical and statically deformed nuclei using a Langevin-type approach. Phys Rev C. (2019) 99:014613. doi: 10.1103/PhysRevC.99.014613

CrossRef Full Text | Google Scholar

228. Welsh T, Loveland W, Yanez R, Barrett JS, McCutchan EA, Sonzogni AA, et al. Modeling multi-nucleon transfer in symmetric collisions of massive nuclei. Phys Lett. (2017) B771:119. doi: 10.1016/j.physletb.2017.05.044

CrossRef Full Text | Google Scholar

229. Wen PW, Li C, Zhu L, Lin CJ, Zhang FS. Mechanism of multinucleon transfer reaction based on the GRAZING model and DNS model. J Phys G Nucl Part Phys. (2017) 44:115101. doi: 10.1088/1361-6471/aa8b07

CrossRef Full Text | Google Scholar