Nuclear Matrix Elements for β and ββ Decays and Quenching of the Weak Coupling gA in QRPA

Nuclear matrix elements (NMEs) for double beta decays (DBDs) are crucial for studying neutrino mass and neutrino properties of particle physics interest. The major components of the DBD NMEs are axial-vector NMEs associated with spin isospin transition operators. In this work it is discussed how absolute values for the NMEs are reduced (quenched) with respect to those for the model NMEs. The reduction is discussed in terms of the renormalized (quenched) axial-vector coupling $g_A^{eff}$ in unit of g_A for free nucleon. Recent experimental studies at RCNP on single and double β NMEs relevant to DBDs are briefly discussed. The axial-vector single β NMEs are shown to be reduced by the renormalization (quenching factor) factor $g_A^{eff}/g_A\approx$ 0.5–0.6 with respect to the QRPA (Quasi particle Random Phase Approximation) model NMEs due to non-nucleonic and nuclear medium effects which are not explicitly included in the model. Two-neutrino axial-vector DBD NMEs are reduced much with respect to the QP (Quasi Particle) NMEs, and are reproduced by the FSQP (Fermi Surface Quasi Particle) model NMEs. Impact of the reduction of the axial-vector NMEs on the DBD NMEs and the DBD experiments is briefly discussed.

1. Introduction

Nuclear matrix elements (NMEs) are crucial for neutrino studies by neutrinoless double beta decays (DBDs). The neutrino effective mass and other properties of the weak interaction beyond the standard electro-weak model are derived from the experimental DBD rate by using the NME. The NME is necessary to design the DBD detector since the DBD isotope mass needed for given neutrino-mass sensitivity is proportional to the forth power of the NME. Recent works on the DBD experiments and the NMEs are given in reviews and references therein in Ejiri [1], Avignone et al. [2], Vergados et al. [3], Sakyaan [4], and Vergados et al. [5]. The NMEs are discussed in reviews and references therein [6–12]. In the previous reviews, we discussed various DBD mechanisms and various nuclear model NMEs [1, 3, 12].

The present report aims to discuss briefly recent experimental studies of the single β and double β NMEs at RCNP (Research Center for Nuclear Physics) Osaka University and to compare them with QRPA NMEs and others. In fact there are several mechanisms for neutrinoless DBD. They are the light Majorana ν-mass, the heavy Majorana ν-mass, the right-handed weak current, the SUSY particle, and others, as discussed in details in review articles [1–3]. Here we concentrate our discussions to NMEs for the light ν-mass mechanism of current interest. The DBD rate is conventionally given by using the inverse of the halflife $T_{1/2}^{0\nu }$,

$\begin{array}{ll}{\left[T_{1/2}^{0\nu }\right]}^{-1}=g_A^4{G}^{0\nu }\left|M^{0\nu }{|}^2\right|m_{\nu }/m_e{|}^2,& (1)\end{array}$

where g_A =1.27 is the axial-vector weak coupling for free nucleon in units of the Fermi coupling g_V, G^0ν is the phase space factor, M^0ν is the NME for the light Majorana mass term, m_ν is the effective light Majorana mass and m_e is the electron mass. The phase space factor is discussed in Vergados et al. [3], Suhonen and Civitarese [7], Stoica and Mirea [13], and Mirea et al. [14]. The effective mass is given as $m_{\nu }=\sum _i{a}_i{m}_i$ with m_i and a_i being the ith mass eigen value and the ith mixing-coefficient including the mixing phase as given in DBD reviews [1–3].

The DBD transition rate is proportional to the nuclear response defined by the square of the absolute value of the NME. So hereafter we mainly discuss the absolute value for the NME. The current interest is the reduction of the absolute NMEs with respect to the values by theoretical models due to various effects which are not explicitly included in the model calculations. We thus discuss reductions of the NMEs for single beta decays and two neutrino DBDs, and then discuss possible reduction of the NMEs for neutrinoless DBDs relevant to neutrino mass studies [1, 3, 12]. In the present work, we mainly compare experimental NMEs with QRPA model NMEs, which are widely used for β and ββ NMEs in medium heavy nuclei of current interests. Actually many calculations on DBD NMEs have been made by using various kinds of nuclear models as given in reviews [7, 9, 12].

The theoretical DBD NME is expressed as

$\begin{array}{ll}{M}^{0\nu }=M^{0\nu }(GT)+M^{0\nu }(T)+M^{0\nu }(F),& (2)\end{array}$

where M^0ν(GT), M^0ν(T) and M^0ν(F) are axial-vector (Gamow-Teller GT), tensor (T), and vector (Fermi F) NMEs, respectively. Among them the axial-vector one is the major component according to theoretical calculations [3, 7, 12]. The GT T and F NMEs are discussed in section 5. Actually the vector one plays some role since the axial-vector one is much reduced as discussed later in section 4.

The axial-vector and tensor NMEs of M^0ν(GT) and M^0ν(T) are associated with spin isospin operators. Thus they are much modified in the nucleus from the simple quasi-particle (QP) NME by all kinds of nucleonic and non-nucleonic correlations due to the strong spin isospin nuclear interactions, and also by nuclear medium effects. The GT NME is expressed as

$\begin{array}{ll}{M}^{0\nu }(GT)={\displaystyle \sum _k}<t_{\pm }\sigma (h_{GT}(r_{12}{E}_k)t_{\pm }\sigma )>,& (3)\end{array}$

where t_± is the isospin operator, σ is the spin operator, r₁₂ is the distance between the nucleons 1 and 2, E_k is the intermediate state energy, and h_GT(r₁₂E_k) is the neutrino potential [1, 3]. We mainly discuss the axial-vector NME in the present work. The axial-vector NME is expressed conventionally as

$\begin{array}{ll}{M}^{0\nu }(GT)={(\frac{g_A^{eff}}{g_A})}^2{M}_M^{0\nu }(GT),& (4)\end{array}$

where $g_A^{eff}/g_A$ is the effective axial-vector coupling in units of the coupling g_A and $M_M^{0\nu }(GT)$ is the GT model NME without the quenching (renormalization) effect.

The renormalization (quenching) factor $g_A^{eff}/g_A$ is introduced to incorporate such nucleonic and non-nucleonic correlations and nuclear medium effects that are not explicitly included in the model NME. It manifests as the reduction of the actual NME from the model NME. Actually the renormalization (quenching) factor $g_A^{eff}/g_A$ is as small as 0.4–0.7 depending on the model used to evaluate the GT NME [12]. It is of great interest to study experimentally and theoretically the factor $g_A^{eff}/g_A$ and the model NME $M_{GT}^{0\nu }$. At present there are no experimental ways to get directly the DBD NMEs M^0ν unless one knows the neutrinoless DBD rate and the effective neutrino mass.

The DBD NME is given by the sum of the NMEs M^0ν(i) via the i-th intermediate state and M^0ν(i) is associated with the single β^± NMEs via the i-th intermediate state. The axial single β^± NME is given as $M^{\pm }(GT)=(g_A^{eff}/g_A)M_M^{\pm }(GT)$, where $M_M^{\pm }(GT)$ is the model GT NME. Accordingly experimental and theoretical studies of the single β^±-NMEs are interesting to help evaluate the DBD NMEs.

Two-neutrino DBD NME M^2ν is derived experimentally from the measured 2ν DBD rate. It is given by the sum of the products of single β^± GT NMEs via the intermediate GT state with the energy denominator. Then the M^2ν NME is used to give information on the GT NMEs M^0ν(GT) [1, 3, 15].

Axial-vector nuclear responses B(α) are derived experimentally from transition rates for single β-decays and electron captures (ECs). They are also derived from cross-sections for charge exchange reactions (CERs) [1, 3, 12]. Here α stands for the axial transition mode, α = GT, SD, HD being Gamow-Teller, spin-dipole, and hexa-decapole transitions. Then the axial-vector NME M(α) (absolute value) is derived from the experimental responses as [1, 3]

$\begin{array}{ll}\left|M(\alpha )\right|={(2J+1)}^{-1/2}B{(\alpha )}^{1/2},& (5)\end{array}$

where J is the initial state spin and B(α) is the reduced width. The axial-vector transition operator is given as [1, 3]

$\begin{array}{ll}T(\alpha )=t^{\pm }{i}^L{\left[\sigma \times r^L{Y}_L\right]}_J,& (6)\end{array}$

where t^± and σ are isospin and spin, r is the radius and Y_L is the spherical harmonics with rank L, and the orbital and total angular momenta are L = 0, J = 1 for α = GT, L = 1, J = 2 for α = SD and L = 3, J = 4 for α = HD.

2. Experimental Probes for GT, SD, and HD NMEs

Axial-vector NMEs M(GT) and M(SD) are studied experimentally by using weak interaction, EM (electro magnetic) interaction and nuclear interaction probes as schematically illustrated in Figure 1. Single β/EC decays, muon capture reactions and nuclear CERs have been extensively used to study the neutrino nuclear responses and the NMEs. They are discussed in DBD review articles [1, 3, 12]. The decay and transition schemes are shown in Figure 2. The DBD via the light Majorana-neutrino exchange is also shown schematically in Figure 2.

FIGURE 1

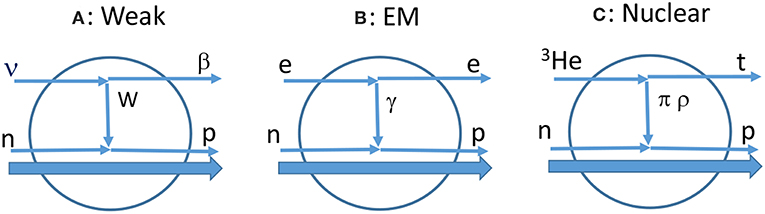
Figure 1. Experimental probes for neutrino nuclear responses. (A) Weak probe. (B) EM probe. (C) Nuclear CER probe.

FIGURE 2

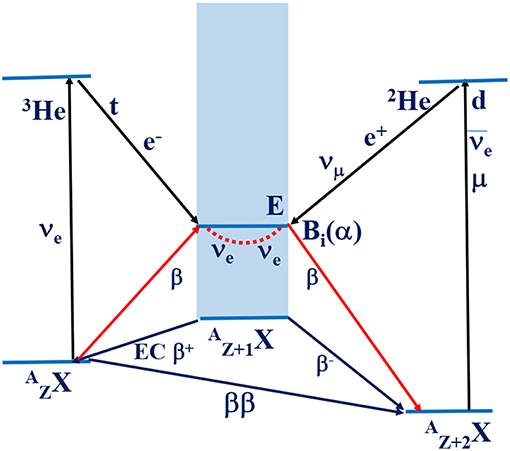
Figure 2. Schematic transition diagrams for β^± decays and EC, neutrino and antineutrino interactions, muon capture reaction of (μ, ν_μ), nuclear CERs of (³He,t) and (d,²He) and neutrinoless DBD via a light Majorana neutrino [12].

Weak interaction probes include single β^± decays and ECs, neutrino CC (charged current) and NC (neutral current) interactions and muon capture reactions. The β decays and ECs are mainly for ground state transitions. Axial-vector GT and SD NMEs are studied by single β/EC rates for allowed GT and unique first forbidden β-decays. Neutrino interactions require huge flux neutrinos and multi-ton scale detectors because of the extremely small cross section. Neutrino CERs are of potential interest for future experiments. Muon capture reactions are used to study β⁺-side axial-vector GT and SD NMEs and vector NMEs [12, 16, 17].

EM probes provide isovector NMEs corresponding to CC weak responses. Then photo nuclear reactions via IAS (isobaric analog state) are used to get the weak NMEs analogous to the EM NMEs [9, 12].

Nuclear CERs with angular-momentum transfers of ΔL, ΔJ = 0,1 and 1,2 provide GT and SD responses in a wide excitation region. In particular high energy-resolution (³He,t) CERs have been extensively studied at RCNP Osaka to measure GT and SD responses for DBD nuclei [1, 9, 12].

3. GT SD and HD NMEs and Renormalization (Quenching) Factors

3.1. GT and SD Responses for Low-Lying States and Giant Resonances

Axial-vector responses show unique features characteristic of the spin isospin responses. The GT and SD responses for the DBD nuclei are measured by the high energy-resolution (³He,t) CERs with the incident particle ³He and the outgoing particle t [1] at RCNP, as given in review articles [1, 3, 9, 12] and also in the recent work [18]. The CER energy spectrum for ¹³⁰Te [19] is shown in Figure 3.

FIGURE 3

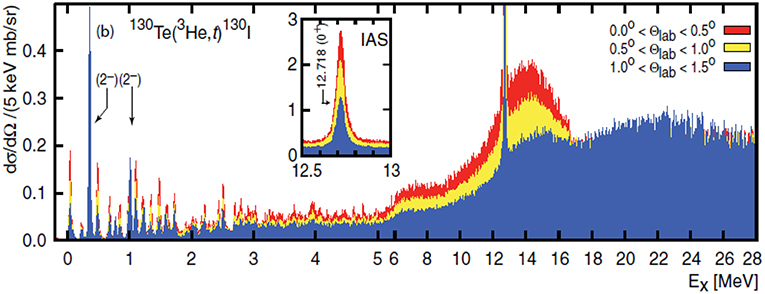
Figure 3. Energy spectrum of the (³He,t) CER on ¹³⁰Te at several angles from 0° to 1.5°. The spectrum at each angle is folded on top of each other.

Several GT and SD states are clearly observed at the low excitation region of E = 0-3 MeV, and broad GT and SD giant resonances (GRs) are excited strongly at the high excitation region of E = 15–30 MeV. The low-lying GT and SD states are simple QP GT and SD states. Here QP is the single particle modified by the pairing correlation. The responses B(GT) and B(SD) are more than an order of magnitude smaller than the single QP responses. On the other hand the responses for the high-lying GRs are more than an order of magnitude larger than the single QP responses. Thus the axial-vector (spin isospin) responses at the low-lying QP states are pushed up to the GR region by the strong repulsive spin isospin interactions to form the spin isospin GRs, which are the coherent sum of many QP excitations.

We note in Figure 3 the sharp state IAS excited strongly by the F (Fermi)-type interaction. This is the isospin GR and the F response is the sum rule limit of B(F) = N−Z with N, Z being the neutron and proton numbers. Because of the good isospin symmetry, all the F strengths are concentrated into the sharp IAS. On the other hand, the spin isospin symmetry is not quite good, and the GT and SD resonances are broad and some GT and SD strengths remain at the low-excitation region.

Single β^± GT, SD and F NMEs for DBD nuclei are derived from the CER cross sections [3, 12, 15]. The spin dipole (SD) NMEs are found to be proportional to the FSQP (Fermi Surface Quasi Particle) NMEs [18], as shown in Figure 4. Here it is noted that experimental NMEs derived from β-decay and EC rates are based on the experimental half lives and are accurate within 1%, while experimental NMEs derived from CERs are based on the CER cross sections calibrated by referring to the known β/EC rates for neighboring states/nuclei and are consistent within 5% [9, 12].

FIGURE 4

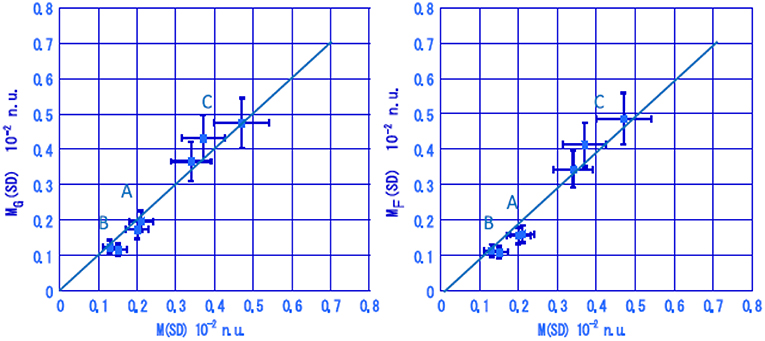
Figure 4. Spin dipole (SD) NMEs obtained from the (³He,t) CER cross sections are plotted against the FSQP model SD NMEs for DBD nuclei. (Left Panel) SD NMEs derived by referring to the GT NMEs. (Right Panel) SD NMEs derived by referring to the F NMEs. A, B, and C are the NMEs for the nuclei with the mass A = 76 and 82, 96 and 100, and 128, 130 and 136. See Ejiri and Frekers [18].

3.2. GT SD and HD NMEs

Single β^± GT and SD NMEs M(α) with α = GT and SD in the DBD mass region of A = 70-140 are obtained from the observed transition rate [20]. The initial and final states involved are low-lying QP states (mostly ground states), and thus the transitions discussed are mostly simple QP transitions between quasineutron and quasiproton.

The QP NME M_QP(α) for the single QP transition is expressed in terms of the single particle NME M_SP(α) and the pairing factor P_np as [6, 21, 22]

$\begin{array}{ll}{M}_{QP}(\alpha )=P_{np}{M}_{SP}(\alpha ),& (7)\end{array}$

where the paring factor is expressed in terms of the occupation and vacancy amplitudes for the QPs ( quasiproton and quasineutron) in the initial and final orbits. The paring factor depends on the neutron and proton configurations at the Fermi surface, and thus stands for the QP configurations at the nuclear surface.

The values M_EX(GT) and M_EX(SD) for the experimental GT and SD NMEs are reduced with respect to M_QP(GT) and M_QP(SD) as discussed in Ejiri [9], Ejiri and Suhonen [21], and Ejiri et al. [22]. Actually the quasineutron and quasiproton in nuclei are modified in nuclei, and thus the actual axial-vector NMEs are reduced much with respect to the simple QP NMEs due to such nucleonic and non-nucleonic correlations and nuclear medium effects that are not explicitly included in the QP model.

The QP transition between the initial and final nuclei are given as

$\begin{array}{ll}{\text{Q}}_{\text{i}}(\text{n}){\text{C}}_{\text{i}}(\text{X})\leftrightarrow {\text{Q}}_{\text{f}}(\text{p}){\text{C}}_{\text{f}}(\text{X}),& (8)\end{array}$

where Q_i(n) and C_i(X) are the initial quasineutron and the initial core nucleus and Q_f(p) and C_f(X) are the final quasiproton and the final core. Then it is noted that Q_i(n) and Q_f(p) with their meson clouds are much modified in the initial and final nuclei and the Q_i(X) and C_f(X) are also modified from the initial to the final nuclei due to all kinds of nuclear correlations and nuclear medium effects. The deformation is likely different between the initial and final nuclei.

So we introduce the effective reduction coefficient k(α) to incorporate these modification effects on the QP NMEs [6, 9, 21, 22].

$\begin{array}{ll}{M}_{EX}(\alpha )=k(\alpha )M_{QP}(\alpha ),& (9)\end{array}$

where α = GT and SD. The experimental GT and SD NMEs are found to be reduced by the coefficients k(GT) ≈0.23 and k(SD) ≈ 0.2, as shown in Figure 5 [21, 22]. A possible reduction of the M1 moment in a nucleus is discussed in terms of the isobar effect [23]. The renormalization (quenching) of the axial-vector weak coupling is discussed theoretically [24].

FIGURE 5

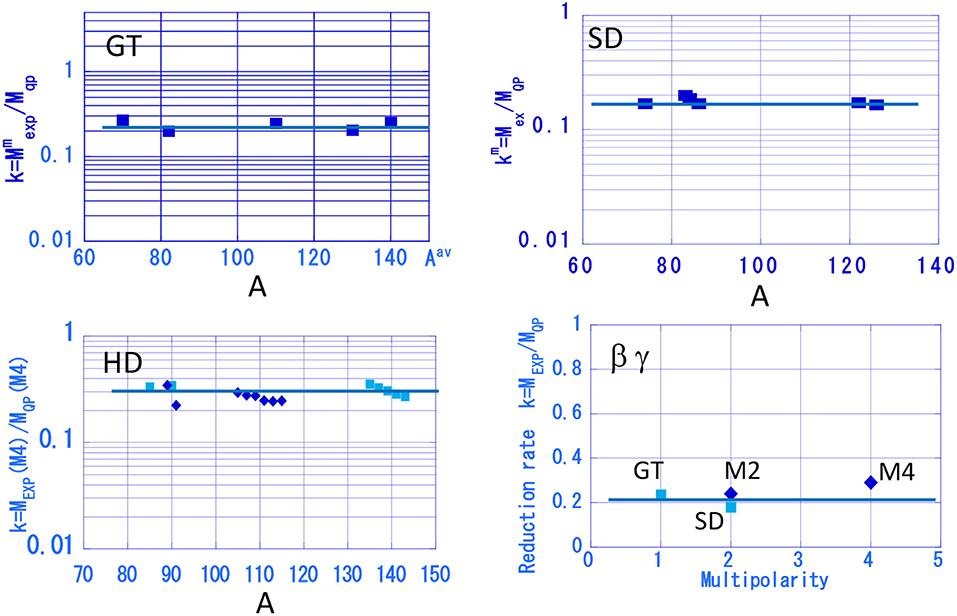
Figure 5. The reduction coefficients for single GT, SD, and HD NMEs with respect to the QP NMEs are plotted against the mass number A in panels GT, SD, and HD. The average reduction coefficients for β and γ decays are given against the multipolarity in panel βγ.

Higher multipole β-γ transitions are not well studied experimentally except HD (M4) γ transitions. The M4 NMEs are mainly the isovector ones, which are analogous to the unique third forbidden β NMEs with L = 3 and J = 4. The observed NMEs are also reduced with respect to the QP NMEs [25] with the reduction coefficient k(HD) ≈0.3 as shown in Figure 5.

The reduction coefficients k(α) for α = GT, SD, HD transitions in medium heavy nuclei are around 0.25. These reductions have been discussed in 1960–1970 in terms of the effective coupling constant g^eff/g in Ejiri and Fujita [6] and Ejiri [9].

The nucleonic spin isospin correlations push up the axial-vector strengths to the axial-vector GRs at the higher excitation region, and reduce NMEs for low-lying states. The nucleonic spin isospin correlations are included in QRPA (Quasi particle Random Phase Approximation) with adequate spin isospin interactions. Then the QRPA, QP and the experimental NMEs are expressed as

$\begin{array}{ll}{M}_{QR}(\alpha )=k_{\tau \sigma }(\alpha )M_{QP}(\alpha ).& (10)\end{array}$

$\begin{array}{ll}{M}_{EX}(\alpha )=k_{NM}(\alpha )M_{QR}(\alpha ),& (11)\end{array}$

where the subscripts QR, QP, and EX are for the QRPA, quasiparticle and experimental NMEs, k_τσ(α) is the reduction coefficient due to the nucleonic isospin spin (τσ) correlation, and k_NM(α) is the reduction coefficient due to non-nucleonic and nuclear medium effects (NM) that are not explicitly included in the QRPA, see Ejiri and Fujita [6], Ejiri and Suhonen [21], and Ejiri et al. [22]. The former effect is incorporated in QRPA with the appropriate nucleonic spin isospin interactions, while the latter effect is alternatively expressed as the effective axial-vector coupling $g_A^{eff}$ in units of the free one g_A as discussed in Vergados et al. [3], Ejiri et al. [12], Ejiri and Suhonen [21], and Ejiri et al. [22] and references therein. The reduction coefficient with respect to the QP NME is given as k(α) = k_τσ(α) × k_NM(α).

The $M_i^{\pm }$ is renormalized by k ≈ 0.2−0.3 and k_NM ≈ 0.5−0.6 with respect to the QP and QRPA NMEs. Likewise the axial vector M^0ν(GT) for neutrinoless DBD is considered to be renormalized by the coefficient k² ≈ 0.04 - 0.09 and $k_{NM}^2\approx 0.25$ - 0.36 with respect to the QP and QRPA DBD NMEs since the axial single β NMEs for GT, SD, and other multi polarities involved in the DBD are renormalized [6, 9].

3.3. Momentum Dependence of the Axial Vector Coupling

The weak coupling for the momentum transfer q is usually expressed by using the dipole approximation,

$\begin{array}{ll}{g}_{\text{W}}=\frac{g_{\text{W}}^0}{(1+q^2/M_{\text{W}}^2){}^2},& (12)\end{array}$

where $g_{\text{W}}^0$ is the weak coupling strength at zero momentum transfer (q² = 0), and M_W is the weak mass parameter, respectively. For the vector (W = V) and axial vector (W = A) mass parameters one usually takes M_V = 840 MeV and M_A ~ 1GeV [26–28] coming from the accelerator-neutrino scattering. In the present momentum region of q ≈20–100 MeV/c, the q dependence yields an effect of 2% on g_W. Thus one may assume constant g_W in the present momentum region. Then it is interesting to see if the axial-vector NMEs show some q dependence in the region of 1–100 MeV/c [12, 15].

The (³He,t) CERs on DBD nuclei were used to study the q dependence of the NMEs. In case of the RCNP beam energy of E = 0.42 GeV, the differential cross sections in the medium momentum region of q≈ 20–100 MeV/c are measured by observing the angular distribution of t over θ = 0–4 deg.

The differential cross section for the emitted triton is derived as a function of the momentum transfer q from the observed angular distributions [19]. The CER cross section for the i-th final state is expressed as

$\begin{array}{ll}\frac{d{\sigma }_i}{d\Omega }=K_i(\alpha )F_i(\alpha ,q)J_i{(\alpha )}^2{\kappa }^{eff}{(q)}^2{B}_i(\alpha ),& (13)\end{array}$

where K_i(α) and J_i(α) with α = F, GT, and SD are the kinematic factor and the volume integral of the interaction, respectively. The volume integral is usually calibrated so as to reproduce experimental NMEs with q ≈0 for other states with NMEs known from β/EC rates. The uncertainty of this expression at the q ≈0 is of the order of 5% or less for simple QP states of the present interest. The kinematic q-dependence is given by the DWBA (Distorted Wave Born Approximation) F_i(α, q). The q-dependent response is effectively expressed as κ^eff(q)² B_i(α) with B_i(α) being the nuclear response at q = 0. The coefficient k^eff(q) stands for the effective q-dependent coupling.

The F, GT, and SD NMEs at the momentum region of q = 30–100 MeV/c are found to be same as the NMEs at q ≈0. The GT and SD NMEs at q ≈0 for DBD and other medium-heavy nuclei are experimentally available from β/EC data. They are reduced with respect to the QRPA NMEs by the coefficient k_NM(0) ≈0.5–0.6 at the β/EC point of q ≈0 [21, 22]. Thus the axial-vector weak coupling is considered to be renormalized (quenched) by the coefficient k_NM(q) ≈0.5–0.6 in the wide momentum region of q = 0–120 MeV/c, which is the region of the neutrinoless DBDs and medium-energy supernova neutrinos.

4. Neutrinoless and Two-Neutrino DBD NMEs

The neutrinoless DBD NME is reduced much according to the reduction of the axial-vector NME, depending on the relative weight of the axial-vector components of M^0ν(GT) and M^0ν(T) with respect to the vector component of M^0ν(F) as given in Equation (4). Then the neutrinoless DBD model NME is expressed conventionally as

$\begin{array}{ll}{M}_M^{0\nu }=\left[M_M^{0\nu }(GT)+M_M^{0\nu }(T)\right]+{[\frac{g_V}{g_A^{eff}}]}^2{M}_M^{0\nu }(F),& (14)\end{array}$

where $M_M^{0\nu }$ is the model NME calculated by the nuclear model and $g_A^{eff}$ is the effective axial-vector coupling to incorporate the renormalization (quenching) effect due to the non-nucleonic and nuclear medium effects that are not included in the model NMEs of $M_M^{0\nu }(GT)+M_M^{0\nu }(T)$. Here the vector NME $M_M^{0\nu }(F)$ is assumed to be given by the model vector NME. Then the neutrinoless NME is given by the sum of GT and T NMEs with the renormalized (quenched) axial-vector coupling and the model NME of $M_M^{0\nu }(F)$,

$\begin{array}{ll}{M}^{0\nu }={[\frac{g_A^{eff}}{g_A}]}^2\left[M_M^{0\nu }(GT)+M_M^{0\nu }(T)\right]+{[\frac{g_V}{g_A}]}^2{M}_M^{0\nu }(F),& (15)\end{array}$

where $g_A^{eff}/g_A$ is the renormalization factor for the axial-vector single β NME. It is around 0.5-0.6 in case of the QRPA model NMEs. The tensor NME itself is very small, and we assume the same $g_A^{eff}/g_A$ for both the GT and T NMEs in Equation (15). Actually several axial vector NMEs with L = 0, 1, 2, 3, 4, 5 are involved, and the renormalization factors depend to some extent on the multipolarity L [9, 21, 22, 25]. Exactly speaking the renormailzation factor is also depends on individual states. Thus the coefficient $g_A^{eff}$ in Equation (15) is a kind of effective value to represent the common nuclear core effect, and the individual nuclear surface effects are considered to be taken into account by the model NMEs.

In case of the QRPA calculation for ⁷⁶Ge, the model NMEs are $M_{QR}^{0\nu }(GT)$ = 5.4, $M_{QR}^{0\nu }(T)$ = - 0.36 and $M_{QR}^{0\nu }(F)$ = 1.76 [29]. The values for M^0ν are plotted as a function of the renormalization (quenching) factor $k_{NM}=(g_A^{eff}/g_A)$ in Figure 6. It is interesting to note that the value for M^0ν decreases rapidly and becomes nearly the value of M(F) ≈1.1 as k_NM decreases from 1 to 0. At the reduction factor of k_NM ≈0.6, the axial-vector NMEs are reduced to 1/3 of the values at k_NM ≈1.0, while the value for M^0ν is reduced to 1/2 of the NME without the quenching.

FIGURE 6

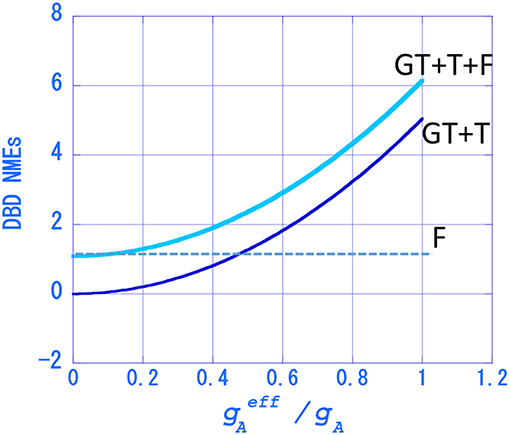
Figure 6. Neutrinoless NME as a function of the renormalization (quenching) factor of $g_A^{eff}/g_A$. Thick line: M^0ν. Thin line: ${(g_A^{eff}/g_A)}^2(M_{QR}^{0\nu }(GT)+M_{QR}^{0\nu }(T))$. Dotted line: ${(g_V/g_A)}^2{M}_{QR}^{0\nu }(F)$.

The two-neutrino NMEs M^2ν is given by the sum of the products of the β⁻ and β⁺ NMEs as

$\begin{array}{ll}{M}^{2\nu }={\displaystyle \sum _i}\frac{M_i^{-}{M}_i^{+}}{{\Delta }_i},& (16)\end{array}$

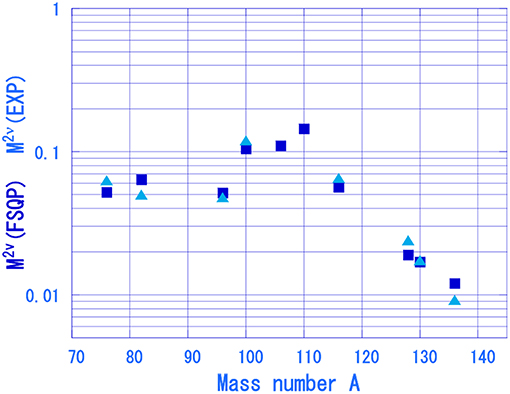
where $M_i^{\pm }$ is the single β^± NME for the i-th intermediate GT state and Δ_i is the energy denominator. On the basis of FSQP [1, 12, 30–32], the single QP intermediate states at the Fermi surface (low-lying states) are considered. The number of the FSQP GT states are i = 1–4, depending on the shell orbits. The β^± NME for the ith QP state is expressed as $M_i^{\pm }=k^{\pm }{M}_{QPi}^{\pm }$, where k^± is the renormalization factor, and $M_{QPi}^{\pm }$ is the QP NMEs for the ith state. The QP NME and Δ_i are derived from a simple QP model, while k^± is from the experimental β^± and CER data. Since k^± stands for the nuclear core effect, the same k^± value is used for all QP states in the same nucleus [12, 30]. The FSQP NME reproduces well the observed 2ν DBD NME as shown in Figure 7.

FIGURE 7

Figure 7. Two neutrino DBD NMEs M^2ν [3, 12]. Triangles: experimental NMEs. Squares: FSQP NMEs.

The FSQP NMEs for two-neutrino ββ NMEs are semi-empirical NMRs based on thel β^± NMEs with the experimental κ^±(GT). The coefficients κ^±(GT) are around 0.25 with respect to QP and around 0.5–0.6 with respect to QRPA, being consistent with the single β^±/EC GT values [21]. Thus the two-neutrino NMEs are quenched by 0.06 and 0,3 with respect to QP and QRPA ones. The good agreement of the FSQP NMEs with the experimental ones shows that the two-neutrino ββ NMEs are given by using the β^± NMEs for low-lying QP states. Theoretical discussions on the quenching factors for two-neutrino and neutrinoless ββ are given in Suhonen [24].

5. Concluding Remarks

Nuclear matrix elements M^0ν for neutrinoless DBDs are crucial for studying neutrino masses and neutrino properties from experimental DBD rates, once observed. The axial-vector NME M^0ν(GT) is the major component of the DBD NME. Recent experimental studies of axial-vector NMEs for single β-decays, CER cross-sections and two-neutrino DBDs are briefly discussed. They are associated with the axial-vector DBD NME M^0ν(GT) and thus are used to help understand and evaluate the DBD NME M^0ν. The present discussions are summarized as follows.

i. Single GT SD and HD NMEs for simple QP transitions are given as M(α) = k(α)M_QP(α) with α = GT, SD. HD. They are reduced more or less by the reduction factor k(α) ≈0.25 with respect to the QP NMEs due to nucleonic correlations, non-nucleonic correlations and nuclear medium effects, which are not included in the simple QP model. The SD NME is one of the major components of M^0ν.

ii. In case of QRPA model NMEs, the nucleonic spin-isospin and other correlations are incorporated by QRPA with adequate spin isospin interactions. Then the NMEs are expressed as M(α) = k_NM(α)M_QR(α), where M_QR(α) with α = GT, SD and HD are the QRPA NME and k_NM(α) is the reduction (quenching) factor due to such non-nucleonic and nuclear medium effects that are not explicitly included in the QRPA model. The value for the reduction factor is around 0.5–0.6 for the simple GT, SD, HQ QP-transitions in medium heavy nuclei. The reduction (quenching) factor is conventionally expresses as $k_{NM}(\alpha )=g_A^{eff}/g_A$ where $g_A^{eff}$ and g_A are the effective and free axial weak couplings. The factor is $g_A^{eff}/g_A\approx$0.5–0.6 for the axial vector β^± in case of QRPA model NMEs. Thus the two-neutrino DBD NME, which is product of the axial-vector GT single β^± NMEs, is reduced by around 0.3 (square of 0.5–0.6), in consistent with experimental data.

iii. The GT and SD reduction coefficients are studied in a wide momentum region of q = 1−120 MeV/c, which is the momentum involved in neutrinoless DBD. The reduction (quenching) factors remain similar to those at the single β ones with q ≈0. Thus the quenching factor for the axial-vector component of the neutrinoless ββ NME is ${\kappa }_{NM}^2$ = ($g_A^{eff}/g_A{)}^2\approx$0.3 in case of the QRPA model NME.

iv. Then the neutrinoless DBD NME, which is the sum of the axial-vector and vector components, may be reduced by the renormalization (quenching) factor of k² ≈ 0.5, depending on the vector coupling NME, with respect to the QRPA NME $M_{QR}^{0\nu }$.

v. Muon capture reactions provide low-multipolarity NMEs in the momentum region of the neutrinoless DBD. It is also very interesting to study CC NMEs by using the intense neutrino beam at SNS and J-PARC.

vi. Theoretical studies of single-β and DBD NMEs, in particular accurate theoretical calculations for the renormalization (quenching) factor and the model NMEs including all non-nucleonic and nuclear medium effects, and appropriate ab-initio calculations are strongly encouraged.

vii. The reduction of the neutrinoless DBD NME by a factor around 1/2 suggests the reduction of the rate by 1/4 with respect to the QRPA rate. Then the required DBD-isotope mass for the DBD detector may be larger by an order of magnitude than the mass without the reduction (quenching).

The renormalization (quenching) factors of the NMEs relevant to DBD transitions are briefly discussed so far. They are very important in general for neutrino studies in nuclei and also very interesting for nuclear structure studies and nuclear reaction reactions [33]. Actually, the renormalization factor depends to some extent on the multipolarity L, the individual nuclear orbits and on the QRPA model parameters, as discussed in reviews [3, 9, 12] and references therein. Further experimental and theoretical studies of the quenching factor are encouraged to investigate relevant neutrino properties and nuclear structures from view points of particle astro and nuclear physics.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Ejiri H. Double beta decays and neutrino masses. J Phys Soc Jpn. (2005) 74:2101–27. doi: 10.1143/JPSJ.74.2101

CrossRef Full Text | Google Scholar

2. Avignone F, Elliott S, Engel J. Double beta decay, Majorana neutrino, and neutrino mass. Rev Mod Phys. (2008) 80:481–516. doi: 10.1103/RevModPhys.80.481

CrossRef Full Text | Google Scholar

3. Vergados J, Ejiri H, Šimkovic F. Theory of neutrinoless double-beta decay. Rep Prog Phys. (2012) 75:106301. doi: 10.1088/0034-4885/75/10/106301

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Sakyaan R. Two-neutrino double beta decay. Ann Rev Nucl Part Sci. (2013) 63:503–29. doi: 10.1146/annurev-nucl-102711-094904

CrossRef Full Text | Google Scholar

5. Vergados J, Ejiri H, Šimkovic F. Neutrinoless double beta decay and neutrino mass. Int J Mod Phys E. (2016) 25:1630007. doi: 10.1142/S0218301316300071

CrossRef Full Text | Google Scholar

6. Ejiri H, Fujita JI. Effective coupling constants for beta and gamma transitions in medium and heavy nuclei. Phys Rep. (1978) 38:85–131. doi: 10.1016/0370-1573(78)90138-2

CrossRef Full Text | Google Scholar

7. Suhonen J, Civitarese O. Weak interaction and nuclear structure aspect of nuclear double beta decay. Phys Rep. (1998) 300:123–214. doi: 10.1016/S0370-1573(97)00087-2

CrossRef Full Text | Google Scholar

8. Faessler A, Šimkovic F. Double beta decay. J Phys G. (1998) 24:2139–78. doi: 10.1088/0954-3899/24/12/001

CrossRef Full Text | Google Scholar

9. Ejiri H. Nuclear spin isospin responses for low-energy neutrinos. Phys Rep. (2000) 338:265–351. doi: 10.1016/S0370-1573(00)00044-2

CrossRef Full Text | Google Scholar

10. Suhonen J, Civitarese O. Review of the properties of the 0νβ⁻β⁻ nuclear matrix elements. J Phys G Nucl Part Phys. (2012) 39:124005. doi: 10.1088/0954-3899/39/12/124005

CrossRef Full Text | Google Scholar

11. Engel J, Menendez J. Status and future of nuclear matrix elements for neutrinoless double beta decay: a review. Rep Prog Phys. (2017) 60:046301. doi: 10.1088/1361-6633/aa5bc5

CrossRef Full Text | Google Scholar

12. Ejiri H, Suhonen J, Zuber K. Neutrino-nuclear responses for astro-neutrinos, single beta decays and double beta decays. Phys Rep. (2019). doi: 10.1016/j-physrep.2018.12.001 [Epub ahead of print].

CrossRef Full Text | Google Scholar

13. Stoica S, Mirea M. New calculations for phase space factors involved in double-beta decay. Phys Rev C. (2013) 88:037303. doi: 10.1103/PhysRevC.88.037303

CrossRef Full Text | Google Scholar

14. Mirea M, Pahomi T, Stoica S. Values of the phase space factors involved in double beta decay. Romanian Rep Phys. (2015) 67:872–89.

Google Scholar

15. Ejiri H. Experimental studies of neutrino nuclear responses and nuclear structures for neutrino physics, CNNP2017, Catania. J Phys. (2018) 1056:012019. doi: 10.1088/1742-6596/1056/1/02019

CrossRef Full Text | Google Scholar

16. Measday DF. The nuclear physics of muon capture. Phys Rep. (2001) 354:243–409. doi: 10.1016/S0370-1573(01)00012-6

CrossRef Full Text | Google Scholar

17. Hashim IH, Ejiri H, Shima T, Takahisa K, Sato A, Kuno Y, et al. Muon capture reaction on ¹⁰⁰Mo to study nuclear responses for double-β decays and neutrinos of astrophysics origins. Phys Rev C. (2018) 97:014617. doi: 10.1103/PhysRevC.97.014617

CrossRef Full Text | Google Scholar

18. Ejiri H, Frekers D. Spin dipole matrix elements for double beta decay nuclei by charge-exchange reactions. J Phys G Nucl Part Phys. (2016) 43:11LT01. doi: 10.1088/0954-3899/43/11/11LT01

CrossRef Full Text | Google Scholar

19. Puppe P, Lennarz, Adachi T, Akimune H, Ejiri H, Frekers D, et al. High resolution (³He,t) experiment on the double-β decaying nuclei ¹²⁸Te and ¹³⁰Te. Phys Rev C. (2012) 86:044603. doi: 10.1103/PhysRevC.86.044603

CrossRef Full Text | Google Scholar

20. Firestone RB, Frank Chu SY, Baglin CM editor. Table of Isotopes, 8th ed. Hoboken, NJ: Wiley-Interscience Publication (1999).

21. Ejiri H, Suhonen J. GT neutrino-nuclear responses for double beta decays and astro neutrinos. J Phys G. (2015) 42:055201. doi: 10.1088/0954-3899/42/5/055201

CrossRef Full Text | Google Scholar

22. Ejiri H, Soukouti N, Suhonen J. Spin-dipole nuclear matrix elements for double beta decays and astro-neutrinos. Phys Lett B. (2014) 729:27–32. doi: 10.1016/j.physletb.2013.12.051

CrossRef Full Text | Google Scholar

23. Bohr A, Mottelson B. Nuclear Structure, Vol. II. New York, NY: Benjamin (1975).

24. Suhonen J. Impact of the quenching of g_A on the sensitivity of 0νββ experiments. Phys Rev C. (2017) 96:05501. doi: 10.1103/PhysRevC.96.055501

CrossRef Full Text | Google Scholar

25. Jokiniemi L, Suhonen J, Ejiri H. Magnetic hexadecapole γ transitions and neutrino-nuclear responses in medium-heavy nuclei. Adv High Energy Phys. (2016) 2016:8417598. doi: 10.1155/2016/8417598

CrossRef Full Text | Google Scholar

26. Bodek A, Avvakumov S, Bradford R, Budd H. Vector and axial nucleon form factors: a duality constrained parametrization. Eur Phys J C. (2008) 53:349–54. doi: 10.1140/epjc/s10052-007-0491-4

CrossRef Full Text | Google Scholar

27. Bhattacharya B, Hill RJ, Paz G. Model-independent determination of the axial mass parameter in quasielastic neutrino-nucleus scattering. Phys Rev D. (2011) 84:073006. doi: 10.1103/PhysRevD.84.073006

CrossRef Full Text | Google Scholar

28. Amaro JE, Arriola ER. Axial-vector dominance predictions in quasielastic neutrino-nucleus scattering. Phys Rev D (2016) 93:053002. doi: 10.1103/PhysRevD.93.053002

CrossRef Full Text | Google Scholar

29. Jokiniemi L, Ejiri H, Frekers D, Suhonen J. Neutrinoless ββ nuclear matrix elements using isovector spin-dipole J^π = 2⁻ data. Phys Rev C. (2018) 98:024608. doi: 10.1103/PhysRevC.98.024608

CrossRef Full Text | Google Scholar

30. Ejiri H. Experimental nuclear matrix elements for two neutrino double beta decays and single beta decays. J Phys Soc Jpn. (2009) 78:074201. doi: 10.1143/JPSJ.78.074201

CrossRef Full Text | Google Scholar

31. Ejiri H. Nuclear matrix element for two neutrino double beta decay from ¹³⁶Xe. J Phys Soc Jpn Lett. (2012) 81:033201. doi: 10.1143/JPSJ.81.033201

CrossRef Full Text | Google Scholar

32. Ejiri H. Fermi surface quasi particle model nuclear matrix elements for two neutrino double beta decays. J Phys G Nucl Part Phys. (2017) 44:115201. doi: 10.1088/1361-6471/aa8a1f

CrossRef Full Text | Google Scholar

33. Kay BP, Schiffer JP, Freeman SJ. Quenching of cross sections in nucleon transfer reactions. Phys Rev Lett. (2013) 111:042502. doi: 10.1103/PhysRevLett.111.042502

PubMed Abstract | CrossRef Full Text | Google Scholar