- 1Department of Mathematics, Science Faculty, Firat University, Elazig, Turkey
- 2Department of Mathematics, Science Faculty, Federal University Dutse, Jigawa, Nigeria
- 3Department of Mathematics, Faculty of Arts and Sciences, Cankaya University, Ankara, Turkey
- 4Institute of Space Sciences, Magurele, Romania
This research obtains some new optical soliton solutions with beta derivative for Chen-Lee-Liu equation (CLL) in optical fibers. Three integration schemes which are Ricatti-Bernoulli (RB) sub-ODE, generalized Bernoulli (GB) sub-ODE and generalized tanh (GT) methods are applied to reach such solutions. The constraints conditions for the existence of soliton solutions are reported. The solutions are obtained using newly introduced fractional derivative called beta derivative. Numerical simulations of some of the obtained solutions are illustrated.
1. Introduction
Nonlinearity has been very attractive area of study whose vitality have been thought of by considering a heavy-amplitude wave motions determined in several areas starting from fluids and plasmas to solid state, chemical biological systems among others. Owing to this, solitons have been one of the most mesmerizing viewpoint in nonlinear phisical aspect. A philosophical balance of nonlinearity and dispersion are the major essence for the presence of solitonic concept [1]. Several studies on soliton and other results for the multiple traveling wave solutions of nonlinear partial differential equations can be seen in Miller and Ross [2], Podlubny [3], Oldham and Spanier [4], and Kiryakova [5]. Monopulse water wave is the first soliton reported in El-Sayed and Gaber [6]. Optical solitons has also brought about mathematical insight and innovation of the various mechanism for their analytical and numerical solutions [7–23].
2. Beta Derivative
The idea of the effect of memory has been an issue for quite a long time in the community of modeling. Naturally, the classical models are not convenient to admit this memory [24–26]. A lot of authors have proposed that the effect of the memory could be fully explained by fractional derivatives [27–30]. In Khalil et al. [31], Khalil introduced a new definition of derivative called “conformable derivative,” this derivative satisfied some conventional characteristics, for instance, the chain rule. Atangana in Atangana et al. [32] analyzed some characteristics of this derivative, thereby proving some related theorems and proposing a new definitions. An exciting research that has a great relationship with this operator are stated in Cenesiz et al. [33], He et al. [34], Abdeljawad [35], Chung [36], and Cenesiz and Kurt [37]. Recently, Atangana in [38] introduced the “beta-derivative.” The newly introduced derivatives satisfies a lot of characteristics that have been considered as limitation for the fractional derivatives and is used to model some physical problems. These derivatives may not be seen as fractional derivative but can be considered to be a natural extension of the classical derivative [31]. The beta-derivative is defined as Atangana et al. [38].
Beta derivative has the following properties
1.
2.
for any constant c,
3.
4.
Considering , h → 0 when ϵ → 0, therefore we have
with
where l is a constant.
5.
The proofs of the above beta properties were plainly presented in [29].
3. Governing Equation
Here, we consider the evolution of a slowly varying envelope u as modeled by a family of the CLL equation of the form [30]:
where u(x, t) is the normalized electric-field envelope, and are beta derivatives [29]. The coefficient of the constant a is group velocity dispersion, the coefficient of b is the Bohm potential that is explored in chiral solitons with quantum Hall effect.
It is imperative to know that many equations in nonlinear sciences contain an empirical parameters. These parameters can be investigated through establishing an exact solutions thereby designing an experiments to generate a convenient conditions that could determine these parameters. Thus, generating an exact traveling wave solutions is becoming more mesmerizing in nonlinear sciences [31–37].
The aim of current work is to establish optical soliton solutions by via three different analytical methods which are RB method [35], GB method [36] and GT method [37].
4. Mathematical Analysis
To solve Equation (9), the starting step is
u(x, t) represent the shape of the pulse so that
and the phase component is given by
where k denotes the soliton frequency, w is the wave number of the soliton, θ0(ξ) is an extra phase function depending on the variable ξ, υ indicates the speed of the soliton. Substituting (10) into (9), and isolating the real and imaginary parts, we obtain the following
and
where , , , and . In order to solve the equation above, we use the ansatz of the form
where z1, z2 are the nonlinear and constant chirp parameters, respectively to be found. Using Equation (15) in Equation (14), we obtain two algebraic equations that define the chirp parameters
Inserting Equation (16) along with Equation (15) into Equation (14) gives
where
Applying the balancing principle in Equation (17) gives which is not closed form. In order to obtain closed form solutions, we use the transformation
in Equation (17) to obtain
Applying the balancing principle in Equation (20) gives n = 1.
5. Applications
In this section, we apply three integration schemes to attain optical solitons for the underlying equation.
5.1. Application of RB sub-ODE Method
This section will apply RB sub-ODE method [39] to obtain soliton solutions for Equation (9). Assuming that the solution of Equation (20) is the solution of the RB equation
where a1, b1, c1 and M are constants and will be found later. Substituting Equation (21) into Equation (20) we have
Setting m = 0, we obtain
Setting each coefficients of Ui(i = 0, 2, 3, 4) to zero, we have
Solving Equation (24), we obtain
Result 1 , , c1 = 0.
Case 1. When M ≠ 1, b1 ≠ 0, c1 = 0, we get the following algebraic solution
Case 2. When M ≠ 1, , we have the following singular periodic solutions
provided that B3 > 0.
Case 3. When M ≠ 1, , we obtain the following dark optical and singular optical soliton solutions, respectively
provided that B3 > 0.
Case 4. When M ≠ 1, , we acquire the following algebraic solution
5.2. Application for GB Sub-ODE Method
This section will apply GB Sub-ODE method to produce optical soliton solutions for Equation (9). According to GB method [40], Equation (20) has the solution given as
where a0 and a1 are unknown constants and Φ(ξ) satisfies the Ricatti equation
where μ is a non-zero constant. Inserting Equation (31) along with Equation (32) into the Equation (20), we get
Collecting the coefficients Φi(i = 0, 1, 2, 3, 4), we obtain
Solving Equation (34), we obtain
Result 1. λμ ≠ 0, , . This results yield the following dark optical and singular optical soliton solutions, respectively
5.3. Application for GT Method
This section will apply GB Sub-ODE method to produce optical soliton solutions for Equation (9). According to GB method [41], Equation (20) has the solution given as
where a0 and a1 are unknown constants and Φ(ξ) satisfies the Ricatti equation
where μ is a non-zero constant. Inserting Equation (37) along with Equation (38) into the Equation (20), we get
Collecting the coefficients Φi(i = 0, 1, 2, 3, 4), we obtain
Solving Equation (40), we obtain
Result 1. , . If C < 0, this results yield the following dark optical and singular optical soliton solutions, respectively.
and
If C > 0, this results yield the following dark optical and singular optical soliton solutions, respectively.
and
6. Results and Discussion
The RB sub-ODE, GB Sub-ODE and GT integration schemes are employed to establish optical and other solitons for the Chen-Lee-Liu equation in optical fibers. Dark, singular and albegraic solutions are constructed successfully. The RB sub-ODE scheme provided dark soliton (Equation 28), singular soliton (Equation 29), trigonometric solutions (Equations 26, 27), algebraic solutions (Equations 25,30). The GB Sub-ODE scheme provided dark and singular optical solitons reported in Equations (35) and (36), respectively. The GT scheme provided similar solution as RB sub-ODE that is dark, singular and trigonometric solutions reported in Equations (41–44), respectively. The GB sub-ODE scheme could not provide the algebraic solutions and trigonometric solutions in comparison with RB sub-ODE and GT schemes. Moreover, the GT schemes could not provide the algebraic solutions as provided by RB sub-ODE. The following paragraph will give some explanations for the obtained results.
Dark optical soliton explains the solitary waves with smaller intensity than the background, the singular soliton solutions depict a solitary wave possessing discontinuous derivatives; an instance of such solitary waves are compactions, which possess a finite (compact) support, and peakons, whose peaks possess a discontinuous first derivative. These kinds of solitary waves are of extreme important owing to their efficiency and of course flexibility in the long-distance optical communication.
It worth noting that optical fibers are thin long strands of ultra-pure glass or plastic such that a light can be transmitted from one end to another without much attenuation or loss. In order to have a clear vision on the affect of parameters to the transmission of solitons, we consider the following investigation:
Suppose that α ∈ ℂ, then the solutions reported in Equations (28), (29), (35), (36), (41), and (42) will turn to periodic wave solutions with singularity. This shows that when α ∈ ℂ, the long distance light transmission through the optical materials will automatically be affected or lost owing to the smaller attenuation. The plain understanding for the physical features and mechanisms to the reported solutions by suitable choice of the parameter values are shown through 2D and 3D. The perspective view and the propagation pattern of the wave along the x-axis of the obtained dark optical solitons appeared in (28), (35), (41), singular optical solitons appeared in Equations (29), (36), and (42), trigonometric solutions appeared in Equations (25), (26), (43), and (44) can be seen in the 3D and 2D plots in Figures 1–3.
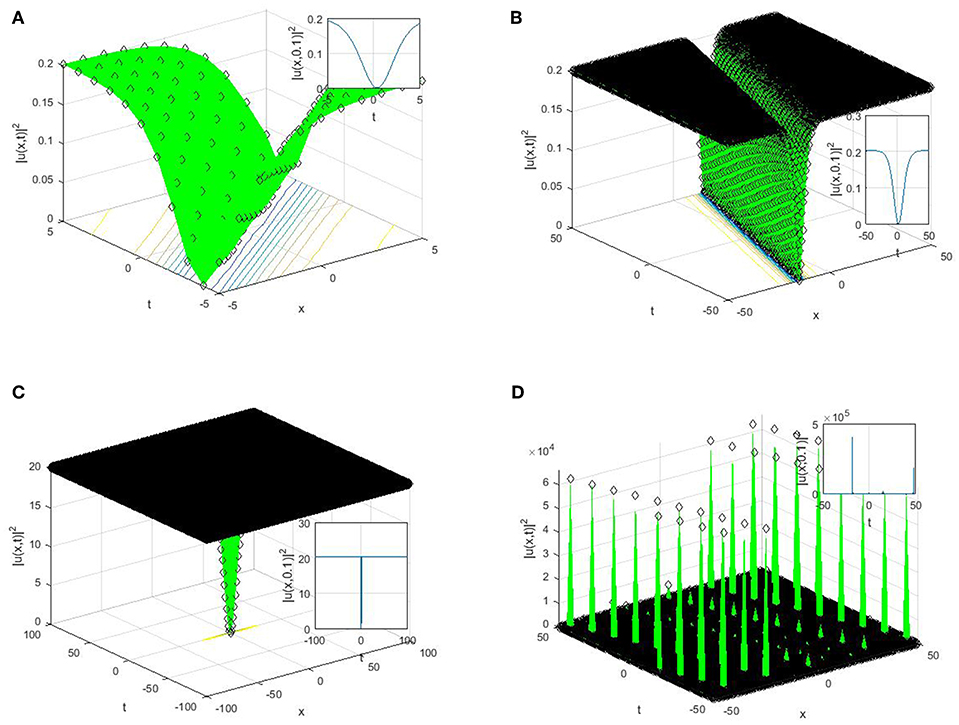
Figure 1. Some physical features of the obtained solutions a = k = w = C = 0.9, μ = 1.2, λ = 1.5, b = 1.7, α = 0.3, υ = 0.3. (A) 3 and 2 dimensional plots for (29). (B) 3 and 2 dimensional plots for (28). (C) 3 and 2 dimensional plots for (26). (D) 3 and 2 dimensional plots for (27).
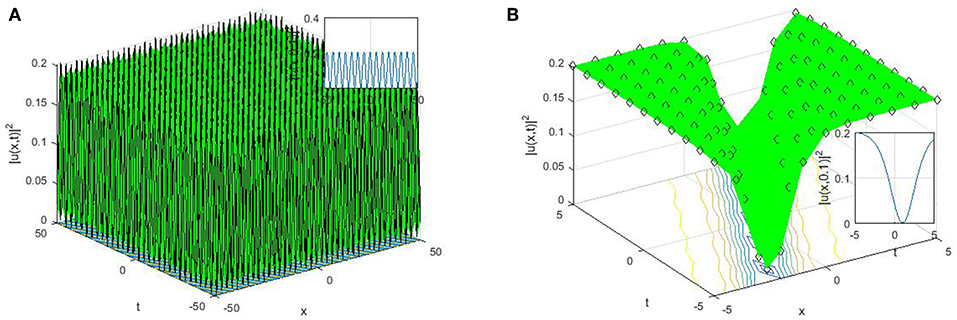
Figure 2. Some physical features of the obtained solutions with the parameter values a = k = w = C = 1.9, μ = 1.2, λ = 1.5, b = 1.7, α = 0.3, υ = 0.3. (A) 3 and 2 dimensional plots for (36). (B) 3 and 2 dimensional plots for (35).
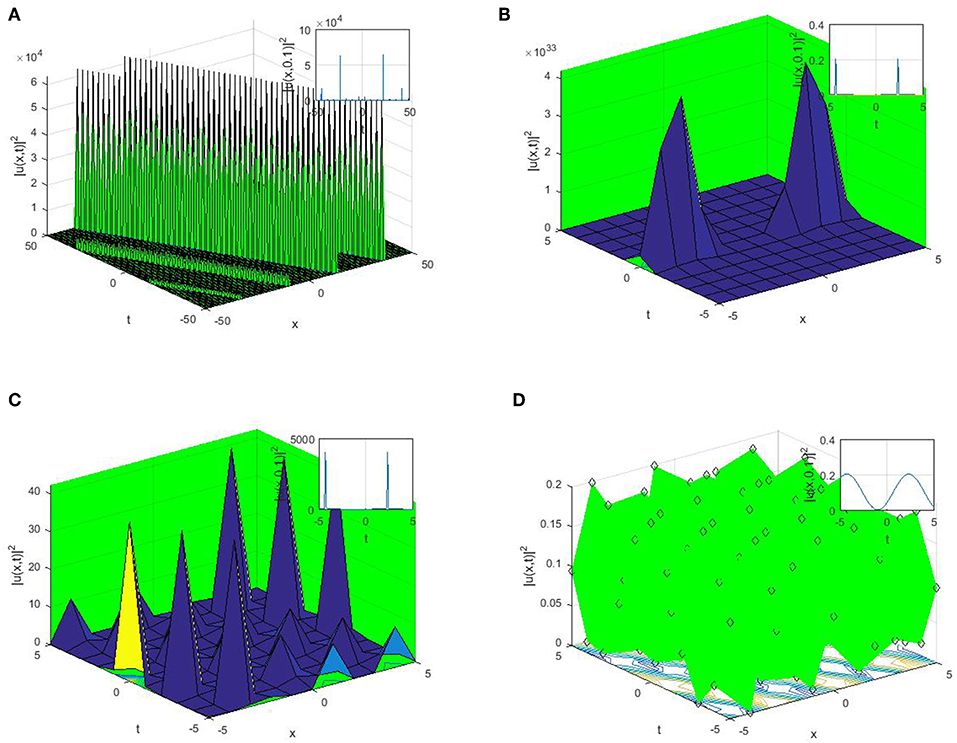
Figure 3. Some physical features of the obtained solutions with the parameter values a = k = w = 1.2, C = −1, μ = 2.2, λ = 2.5, b = 1.7, α = 0.3, υ = 0.3. (A) 3 and 2 dimensional plots for (41). (B) 3 and 2 dimensional plots for (42). (C) 3 and 2 dimensional plots for (43). (D) 3 and 2 dimensional plots for (44).
7. Conclusion
This research obtained some new optical soliton solutions with beta derivative for CLL in optical fibers. Three integration schemes which are RB sub-ODE, GB sub-ODE and GT are applied to reach such solutions. The constraints conditions for the existence of soliton solutions are reported. The solutions are obtained using newly introduced fractional derivative called beta derivative. Numerical simulations of some of the obtained solutions are illustrated.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
2. Miller KS, Ross B. An Introduction to the Fractional Calculus and Fractional Differential Equations. New York, NY: Wiley (1993).
5. Kiryakova V. Generalised Fractional Calculus and Applications. Pitman Research Notes in Mathematics Series, Vol. 301. Harlow: Longman Science & Technical (1994).
6. El-Sayed AMA, Gaber M. The adomian decomposition method for solving partial differential equations of fractal order in finite domains. Phys Lett A. (2006) 359:175–82. doi: 10.1016/j.physleta.2006.06.024
7. Kumar D, Hosseini K, Samadani F. The sine-Gordon expansion method to look for the traveling wave solutions of the Tzitzeica type equations in nonlinear optics. Optik. (2017) 149:439–46. doi: 10.1016/j.ijleo.2017.09.066
8. Atangana A, Alkahtani BT. Analysis of non-homogenous heat model with new trend of derivative with fractional order. Chaos Solit Fractals. (2016) 89:566–71. doi: 10.1016/j.chaos.2016.03.027
9. Atangana A, Alkahtani BST. Analysis of the Keller-Segel model with a fractional derivative without singular kernel. Entropy. (2015) 17:4439–53. doi: 10.3390/e17064439
10. Atangana A. A novel model for the lassa hemorrhagic fever: deathly disease for pregnant women. Neural Comput Appl. (2015) 26:1895–903. doi: 10.1007/s00521-015-1860-9
11. Hashemi MS. Group analysis and exact solutions of the time fractional Fokker-Planck equation. Phys A. (2015) 417:141–9. doi: 10.1016/j.physa.2014.09.043
12. Gazizov RK, Ibragimov NH, Lukashchuk SY. Nonlinear self-adjointness, conservation laws and exact solutions of time-fractional Kompaneets equations. Commun Nonlinear Sci Numer Simul. (2014) 23:153–63. doi: 10.1016/j.cnsns.2014.11.010
13. Lukashchuk SY. Conservation laws for time-fractional sub-diffusion and diffusion-wave equations. Nonlinear Dyn. (2015) 80:791–802. doi: 10.1007/s11071-015-1906-7
14. Hosseini K, Ansari R. New exact solutions of nonlinear conformable time-fractional Boussinesq equations using the modified Kudryashov method. Waves Random Complex Media. (2017) 27:628–36. doi: 10.1080/17455030.2017.1296983
15. Hosseini K, Bekir A, Ansari R. New exact solutions of the conformable time-fractional Cahn-Allen and Cahn-Hilliard equations using the modified Kudryashov method. Optik. (2017) 132:203–9. doi: 10.1016/j.ijleo.2016.12.032
16. Abdel-Gawad HI, Tantawy M, Inc M, Yusuf A. On multi-fusion solitons induced by inelastic collision for quasi-periodic propagation with nonlinear refractive index and stability analysis. Modern Phys Lett B. (2018) 32:1850353. doi: 10.1142/S0217984918503530
17. Qureshi S, Yusuf A, Shaikh AA, Inc M, Baleanu D. Fractional modeling of blood ethanol concentration system with real data application. Chaos. (2019) 29:013143. doi: 10.1063/1.5082907
18. Ghanbari B, Inc M, Yusuf A, Bayram M. Exact optical Solitons of Radhakrishnan-Kundu-Lakshmanan equation with Kerr law nonlinearity. Modern Phys Lett. B (2019) 33:1950061. doi: 10.1142/S0217984919500611
19. Ghanbari B, Yusuf A, Inc M, Baleanu D. The new exact solitary wave solutions and stability analysis for the (2+1)-dimensional Zakharov-Kuznetsov equation. Adv Diff Equat. (2019) 2019:49. doi: 10.1186/s13662-019-1964-0
20. Liu X, Triki H, Zhou Q, Mirzazadeh M, Lu W, Biswas A, et al. Generation and control of multiple solitons under the influence of parameters. Nonlinear Dyn. (2018) 95:143–50. doi: 10.1007/s11071-018-4556-8
21. Yu W, Zhou Q, Mirzazadeh M, Lu W, Biswas A. Phase shift, amplification, oscillation and attenuation of solitons in nonlinear optics. J Adv Res. (2019) 15:69–76. doi: 10.1016/j.jare.2018.09.001
22. Liu W, Zhang Y, Triki H, Mirzazadeh M. Interactions properties of solitonics in inhomogeneous optical fibers. Nonlinear Dyn. (2019) 94:557–63. doi: 10.1007/s11071-018-4582-6
23. Zhang Y, Yang C, Yu W, Mirzazadeh M, Zhou Q. Interactions of vector anti-dark solitons for the coupled nonlinear Schrodinger equation in inhomogeneous fibers. Nonlinear Dyn. (2018) 94:1351–60. doi: 10.1007/s11071-018-4428-2
24. Podlubny I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of TheirSolution and Some of Their Applications. New York, NY: Academic Press (1998). p. 198.
26. Singh J, Kumar D, Al Qurashi M, Baleanu D. A new fractional model for giving up smoking dynamics. Adv Differ Equ. (2017) 2017:88. doi: 10.1186/s13662-017-1139-9
27. Caputo M, Mainardi F. A new dissipation model based on memory mechanism. Pure Appl Geophys. (1971) 91:134–47. doi: 10.1007/BF00879562
28. Caputo M, Fabricio M. A new definition of fractional derivative without singular kernel. Prog Fract Differ Appl. (2015) 1:73–85.
29. Atangana A, Baleanu D. New fractional derivatives with nonlocal and non-singular kernel. Theory and application to heat transfer model. Therm Sci. (2016) 20:763–9. doi: 10.2298/TSCI160111018A
30. Atangana A, Secer A. A note on fractional order derivatives and table of fractional derivatives of some special functions. Abstr Appl Anal. (2013) 2013:279681. doi: 10.1155/2013/279681
31. Khalil R, Al Horani M, Yousef A, Sababheh M. A new definition of fractional derivative. J Comput Appl Math. (2014) 264:65–70. doi: 10.1016/j.cam.2014.01.002
32. Atangana A, Baleanu D, Alsaedi A. New properties of conformable derivative. Open Math. (2015) 13:1–10. doi: 10.1515/math-2015-0081
33. Cenesiz Y, Baleanu D, Kurt A, Tasbozan O. New exact solutions of Burgers' type equations with conformable derivative. Waves Random Complex Media. (2016) 1:1–14. doi: 10.1080/17455030.2016.1205237
34. He S, Sun K, Mei X, Yan B, Xu S. Numerical analysis of a fractional-order chaotic system based on conformable fractional-order derivative. Eur Phys J Plus. (2017) 132:36.
35. Abdeljawad T. On conformable fractional calculus. J Comput Appl Math. (2015) 279:57–66. doi: 10.1140/epjp/i2017-11306-3
36. Chung WS. Fractional newton mechanics with conformable fractional derivative, J Comput Appl Math. (2015) 290:150–8. doi: 10.1016/j.cam.2015.04.049
37. Cenesiz Y, Kurt A. The new solution of time fractional wave equation with conformable fractional derivative definition. J New Theor. (2015) 7:79–85.
38. Atangana A, Baleanu D, Alsaedi A. Analysis of time-fractional Hunter-Saxton equation: a model of neumatic liquid crystal. Open Phys. (2016) 14:145–149 doi: 10.1515/phys-2016-0010
39. Yang XF, Deng ZC, Wei Y. Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its application. Adv Diff Equat. (2015) 2015:117. doi: 10.1186/s13662-015-0452-4
40. Salam MA, Uddin MS, Dey P. Generalized bernoulli sub-ODE method and its applications.Ann Pure Appl Math. (2015) 10:1–6.
Keywords: CLL, RB sub-ODE, GB sub-ODE, GT methods, beta derivative
Citation: Yusuf A, Inc M, Aliyu AI and Baleanu D (2019) Optical Solitons Possessing Beta Derivative of the Chen-Lee-Liu Equation in Optical Fibers. Front. Phys. 7:34. doi: 10.3389/fphy.2019.00034
Received: 10 September 2018; Accepted: 26 February 2019;
Published: 20 March 2019.
Edited by:
Jos Fernando Cariñena, Universidad de Zaragoza, SpainReviewed by:
Guo-Cheng Wu, Neijiang Normal University, ChinaMohammad Mirzazadeh, University of Guilan, Iran
Copyright © 2019 Yusuf, Inc, Aliyu and Baleanu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Abdullahi Yusuf, eXVzdWZhYmR1bGxhaGlAZnVkLmVkdS5uZw==
 Abdullahi Yusuf
Abdullahi Yusuf Mustafa Inc1
Mustafa Inc1 Aliyu Isa Aliyu
Aliyu Isa Aliyu Dumitru Baleanu
Dumitru Baleanu