Laser-Wakefield Electron Beams as Drivers of High-Quality Positron Beams and Inverse-Compton-Scattered Photon Beams

1. Introduction

Since their first realization in the 1930s, conventional particle accelerators such as cyclotrons and linacs have experienced a fast-paced development and have become vital components in laboratories and industries working in a broad range of diverse areas. Typical applications of these accelerators include particle colliders, generation of radio-isotopes, cancer therapy, and generation of high-quality and bright photon beams. However, despite their reliability and high-performance, conventional accelerators present a number of fundamental shortcomings. Arguably, the most limiting factor in this technology is the maximum accelerating field that can be sustained by these machines, due to the dielectric breakdown of their solid-state components. Typically, this is of the order of tens of MV/m, demanding km-scale accelerating structures if energies per particle of the order of tens or hundreds of GeV are sought. Alternative accelerating schemes are currently being actively researched, in order to establish if more compact and generally less expensive accelerators can be built in the near future. One of the most promising schemes identified in this area is the so-called laser wakefield acceleration (LWFA).

LWFA was originally proposed in 1979 by Tajima and Dawson [1], who suggested using the large electric fields that can be sustained by a laser-generated plasma to accelerate particles [2–4]. The unavailability of high-power femtosecond laser pulses limited the initial experimental application of this pioneering theoretical proposal to sparse and indirect cases, exploiting, for instance, Plasma Beat Wave Acceleration [5], Self-Modulated Laser Wakefield Acceleration [6, 7], or Resonant Laser Wakefield Acceleration [8]. The full experimental realization of the original proposal by Tajima and Dawson was only achieved after the development of TeraWatt-class, femtosecond-scale laser systems (see, for instance [2–4]). Since then, LWFA accelerators have spread world-wide, with continuous developments being reported in the efficiency and performance of this technique. It is beyond the scope of this article to discuss the rich physics behind this acceleration mechanisms and we refer the interested reader to dedicated reviews available in the literature (See, for instance [9, 10]).

Generally speaking though, LWFA can be triggered by the propagation of an intense laser pulse through a gaseous medium. Under optimum conditions, the laser ionizes the gas and ponderomotively expels electrons from its main propagation axis, toward regions of lower laser intensity. On short time scales, one can assume the ions to remain immobile, resulting in the creation of strong and quasi-electrostatic charge-separation fields. After the laser has propagated through the gas, the electrons are then called backed on-axis, creating electron plasma waves with quasi-electrostatic fields with a strong longitudinal accelerating component. Different regimes have been theoretically proposed and experimentally tested, but it will suffice here to say that appealing electron beam characteristics have been already experimentally achieved using this mechanism. Electron beams with durations as short as a few femtosecond are now routinely generated [11]. Moreover, external guiding recently allowed reaching energies of up to 8 GeV from a cm-scale accelerator [12]. Due to the relatively large bandwidth of these beams, different groups are studying the mechanisms leading to the injection of electrons into the accelerating structure, such as shock injection and down-ramp injection [13, 14], which have been shown to produce high-quality beams with bandwidths as low as ΔE/E = 0.4%, tuneable energy in the range 200−600MeV and sub-mrad divergence [13]. The ultra-low emittance of these beams has already enabled studying their injection in secondary laser-driven stages, which has been observed at modest energies, with a charge transfer of ~3.5% [15].

These continuously improving characteristics have excited significant interest in the use of these electron beams to generate secondary sources, such as photon and positron beams. In the present manuscript we present a brief overview of recent developments in this area. Even though other mechanisms for photon and positron generation from a laser-driven electron beam have been proposed and are actively studied, we will focus our attention here only on Inverse Compton Scattering and quantum cascades in solid targets, respectively. The remainder of the article is structured as follows: the current state-of-the-art of inverse-Compton-scattered photon sources from LWFA electron beams is discussed in section 2, whilst experimental results on the generation of positron beams from LWFA electrons interacting with a solid target are discussed in section 3. Finally, concluding remarks are given in section 4.

2. Compton X-ray Sources

The development of high energy γ-ray sources is of paramount importance for a diverse range of applications. These extend from radiotherapy and oncology based on photon irradiation [16, 17] to active interrogation of nuclear material and shipping containers [18] for security purposes. Moreover, high frequency radiation has been found to lead to nuclear resonance fluorescence [19] as well as photo-induced fission [20]. In addition to these applications of interest in industry, the value of these sources from the scientific point of view is also extremely attractive. Besides the potential interest for laboratory astrophysics [21], inverse-Compton-scattering (ICS) from an ultra-relativistic electron beam is an ideally suited mechanism to probe strong field quantum electrodynamics [22]. Thanks to a significant Doppler shift of the laser radiation, an ultra-relativistic electron can experience, in its own rest frame, an electric field that is close to, or even exceeding, the critical field of quantum electrodynamics, or Schwinger field (Es = 1.38 × 10¹⁸ V/m). High-field quantum electrodynamic phenomena such as Breit-Wheeler pair production [23], elastic photon-photon scattering [24], quantum radiation reaction [25–27], and vacuum breakdown [28] can then be triggered and precisely studied, with preliminary experimental results already obtained using this setup [29, 30].

High energy photons can be mainly obtained via two mechanisms: radioactive sources or accelerating charges. In the latter case, the properties of the generated radiation are mostly dictated by the specific acceleration of the charge, an electron for definiteness. Arguably, the simplest mechanism to reproduce in the laboratory is bremsstrahlung, whereby the radiation is generated during the scattering of an ultra-relativistic electron beam as it propagates through a high-Z solid target [31–33]. This mechanism produces broad-band photon spectra with their maximum energy coincident with that of the primary electron beam. It is thus relatively simple to produce high-energy γ-ray beams but it is virtually impossible to produce narrow-band beams, an important pre-requisite for many industrial applications. Moreover, the scattering processes inside the material significantly broaden the divergence and source size of the photon beam, resulting in a relatively low peak brilliance. Gas harmonics [34, 35], betatron [36–39], laser-thin foil irradiation [40, 41], synchrotron radiation [42], and free electron lasers [43, 44] also constitute viable sources of high energy photons. However, the photon maximum energy at which these methods operate is typically in the sub-MeV range. Similarly, betatron radiation, i.e., the radiation produced within the accelerating plasma cavity due to transverse oscillations of the accelerated electrons, can produce high-brightness and coherent photon beams [36, 45]. However, they usually present broad-band spectra and have typical energies per photon in the range of 10s of keV.

On the other hand, ICS is able to produce photon energies up to tens of MeV [30, 46, 47], with ~μm source size, low divergence, and brilliances exceeding 10¹⁹ photons s⁻¹ mm⁻² mrad⁻² × 0.1% bandwidth. These properties, together with the intrinsic tuneability in energy of these sources, make them appealing for practical applications especially in nuclear physics and several experimental results have been recently reported in this area [30, 34, 46–54]. A summary of the typical energy and peak brilliance achievable by different photon sources is depicted in Figure 1, showing how ICS is uniquely suited to provide, simultaneously, multi-MeV energy per photon and a high peak brilliance. Due to these appealing properties, we will focus here only on this photon generation mechanism and refer the reader to other reviews available in the literature for a more in-depth discussion of alternative mechanisms (see for instance [60] and [10]).

FIGURE 1

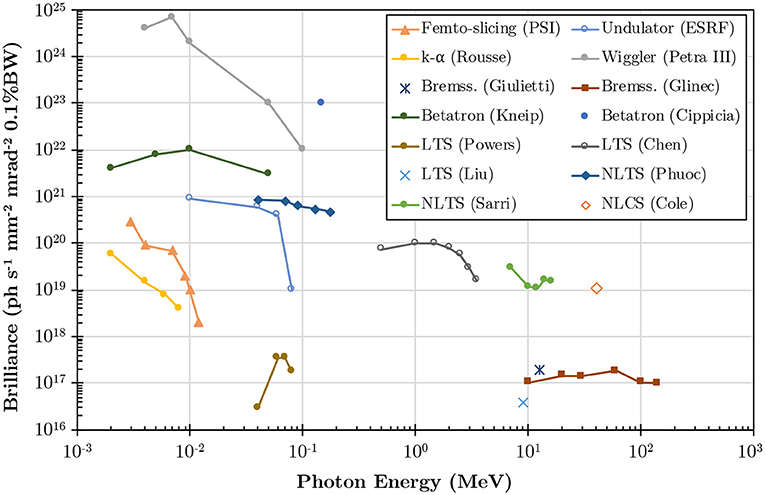
Figure 1. Typical ranges of achievable brilliance and energy per photon of experimentally demonstrated X-Ray and γ-ray sources. Femto-Slicing at PSI [55]; Undulator source at ESRF [56]; K-α emission by Rousse et al. [57]; Wiggler source at Petra III [58]; Bremsstrahlung by Glinec et al. [31], and Giulietti et al. [32]; Betatron by Kneip et al. [45], and Cipiccia et al. [59]; Linear Thomson Scattering (LTS) by Powers et al. [50], Chen et al. [51], and Liu et al. [52]; Non-Linear Thomson Scattering (NLTS) by Phuoc et al. [48]. and Sarri et al. [47]; Non-Linear Compton Scattering (NLCS) by Cole et al. [30].

Existing Compton scattering facilities have conventional accelerators at the core of their operation. While they constitute reliable, tuneable and efficient means of seeding Compton facilities, conventional accelerators are not only large scale, but also expensive machines to shield and operate. The relative long duration of the photon beams generated also limits the peak brilliance achievable and the temporal resolution of probing schemes based on this technology. Examples of such facilities include the HIGS facility at Duke University [61], the Accelerator Test Facility at Lawrence Berkeley National Laboratory [62] and the TREX/MEGA-Ray facility [63, 64], to name a few.

The all-optical alternative to the generation of Compton scattered photons poses the advantage that the Compton pulse duration is mainly dictated by the pulse length of the particle beam [53], due to the relativistic compression of the laser pulse in the rest reference frame of the particle. In LWFA, the typical bunch duration of an electron beam can be down to a few tens of fs [9] Moreover, practical advantages of all-optical ICS sources include the compact nature of laser laboratories, the relatively low running cost, and the wide degree of tuneability that they guarantee. Petawatt-class facilities with the capability to perform high-energy ICS experiments include Astra-Gemini [65], HERCULES [66], the BELLA laser [67], and CoReLS [68]. Moreover, the capabilities of all-optical Compton sources will be extended by upcoming facilities in the multi-petawatt regime, including the Extreme Light Infrastructure (ELI) [69, 70] and Vulcan 20PW [71]. It must be noted, however, that aside from peak scattering laser intensity, the seed electron beam quality is of prime importance.

In the following section, a brief description of the main properties of all-optical ICS photon sources is presented.

2.1. All-Optical Generation of Compton X-ray Sources

Thomson scattering can be described as the elastic scattering of a photon by a free charged particle (an electron, for definiteness), with Compton loosely denoting the inelastic counterpart. Traditionally, both Compton and Thomson scattering refer to processes in which an electron gains energy from the photon, whereas Inverse Compton and Inverse Thomson scattering are the terms employed for those interactions in which the photon gains energy from a high-energy particle.

The physics governing the dynamics of electrons scattering in a high intensity electromagnetic field and the subsequent radiation emitted closely resembles the nature of conventional undulators. The same physics can be described if the period of the undulator is replaced by half of the wavelength of the scattering laser and the undulator strength (commonly denoted as K) is replaced by the dimensionless laser intensity a₀ = eE_L/m_eω_L where e and m_e are the electron charge and mass respectively and E_L and ω_L are the peak electric field and frequency of the laser, respectively (see [60] and references therein for further details).

For the purpose of the following discussion, there are two regimes of interest, namely the linear regime (a₀ ≪ 1), known as the “undulator” regime, and the non-linear regime (a₀ ≥ 1), known as the “wiggler” regime. The linear/non-linear nomenclature arises from the number of photons absorbed per electron (N_γ) in a formation length. In the linear regime (a₀ ≪ 1), electrons will mainly absorb up to a single photon (N_γ ~ 1), while for high-intensity lasers (a₀ ≫ 1), the number of photons absorbed by a single electron scales up to $N_{\gamma }~a_0^3$. The theoretical study of the multi-photon variant of Compton Scattering has been active since the mid-twentieth century (see Di Piazza et al. [22] and references therein). Multiple experimental campaigns have observed these effects [54], and noticed the effects on both induced radiation [46] and spectrum of the primary electron beam [29, 30].

To characterize the different regimes of operation of Compton experiments, it is useful to define the energy (ℏω_X) and number (N_X) of produced photons per laser cycle. These may be expressed as [60]

$\{\begin{array}{c}{N}_X~1.5\times {10}^{-2}{a}_0^2{a}_0\ll 1\\ N_X~3.38\times {10}^{-2}{a}_0{a}_0\ge 1& (1)\end{array}$

$\begin{array}{rc}\hslash {\omega }_X~\frac{4{\gamma }_e^2\hslash {\omega }_L{N}_{\gamma }}{1+{({\gamma }_e\theta )}^2+\frac{a_0^2}{2}+2\frac{N_{\gamma }\chi }{a_0}}& (2)\end{array}$

where the laser and produced radiation are denoted by the subscripts L, and X, respectively; θ corresponds to the angle of emission, γ_e is the electron Lorentz factor, and χ is the quantum invariant parameter. This latter parameter is defined as the ratio of the peak electric field in the electron reference frame and the Schwinger field [22], and it indicates the importance of quantum effects in the interaction in question. For a plane wave, the quantum invariant parameter can be expressed as $\chi ~3\times 10^{-6}\left[1-cos(\phi )\right]{\gamma }_e{a}_0$, where φ is the angle between the direction of propagation of the electron and laser beams (e.g., φ = π for counter-propagating experiments). For χ ≪ 1 quantum effects may be neglected, whereas quantum effects must be taken into account to fully determine the dynamics of the seed electron and produced radiation beams when χ ≃ 1. Considering the semi-classical (χ ≪ 1) interaction of two counter-propagating electron and laser beams, the energy of the photons emitted on axis from Equation 2 scales as $E_X\propto {\gamma }_e^2$ in the linear regime (a₀ ≪ 1), and $E_X\propto {\gamma }_e^2{a}_0$ in the non-linear regime (a₀ ≥ 1) [60].

As given by Equations 1, 2, the energy and flux of the X-ray beam can be enhanced by entering the non-linear regime; i.e., by increasing the intensity of the laser. However, despite these more favorable scalings, the bandwidth of the emitted radiation also increases with a₀ [72]:

$\begin{array}{rc}\frac{\Delta {\omega }_X}{{\omega }_X}~\sqrt[]{{\left(\frac{a_0^2}{2}\right)}^2+{\left(\frac{\Delta {\omega }_L}{{\omega }_L}\right)}^2+{\left(\frac{2\Delta {\gamma }_e}{{\gamma }_e}\right)}^2}& (3)\end{array}$

where Δω_L and Δγ_e are the bandwidth of the scattering laser and electron spectrum, respectively. An increase in the bandwidth of the generated radiation contributes to the reduction of the quality of the photon beam for applications. In the non-linear regime, a non-negligible bandwidth is obtained even in the ideal approximation of a perfectly monochromatic electron beam (Δγ_e → 0), suggesting that it is an unavoidable by-product of the multi-photon absorption involved in these high-intensity electron-laser interactions. A possible solution of the non-linear spectral broadening for a₀ > 1 has been presented in recent theoretical work [72–75], which shows how a suitable chirping of the laser pulse can minimize the broadening of the generated radiation, effectively forcing an electron to emit at a constant frequency throughout its transit through the laser envelope. To the knowledge of the authors, this technique has not been experimentally demonstrated yet, but it is worth noticing that, if successfully applied, it could reduce the spectral broadening of the emitted radiation to ideally be only a function of the bandwidth of the electron beam: Δω_X/ω_X ≈ 2Δγ_e/γ_e.

2.2. Experimental Observations of Compton Radiation in All-Optical Configurations

In an all-optical scenario, several ICS experimental campaigns have been carried out in the past few years. In the linear regime (a₀ ≪ 1), maximum energies from ~10 KeV to ~1 MeV and low bandwidths have been reported by various groups (see e.g., [50–53]). In particular, peak brilliances in excess of 10²⁰ photons s⁻¹ mm⁻² mrad⁻² × 0.1% BW have been reported in this regime by Chen et al. [51].

Experiments in the non-linear regime, however, have pushed the boundaries of peak energy while maintaining similar brilliance performance. Where brilliances of 10²¹ photons s⁻¹ mm⁻² mrad⁻² × 0.1% bandwidth were reported by Phuoc et al. [48], the barrier of high brilliance at high energies was overcome by Sarri et al. [47], who reported photon beams in the multi-MeV regime via an a₀ ~ 2 interaction while maintaining a brilliance exceeding 5 × 10¹⁹ photons s⁻¹ mm⁻² mrad⁻² × 0.1% bandwidth. Since then, more experiments have been carried out which have pushed the boundaries of peak energy even further to reach the multi-tens of MeV regime [30, 46] by carrying out interactions at a₀ ~ 10. Notably, some of these experiments have also observed the onset of quantum effects in the interaction [29, 30].

Multi-photon effects play a vital role in these experiments, as first observed experimentally by Bula et al. [54], where these effects were indirectly inferred from the photon spectrum observed. However, multiple photon interactions contribute not only to the energy of the outgoing radiation, but also to the divergence of the beam. In the interaction of a linearly polarized laser with a particle beam, the divergence of Compton radiation along the polarization direction (θ_i) is proportional to a₀/γ, whereas the divergence in the direction perpendicular to the polarization direction (θ_o) is proportional to 1/γ [60]. In the ideal case of a non-divergent electron beam, the ratio θ_i/θ_o would simply give a direct measurment of the peak dimensionless intensity of the laser at interaction, as originally proposed in Har-Shemes and Di Piazza [76]. However, the finite divergence of the electron beam changes the distribution, as shown in Figure 2 for an electron beam with a 10 mrad divergence [46]. This effect serves anyway as a useful tool to estimate the peak intensity of a laser beam in focus.

FIGURE 2

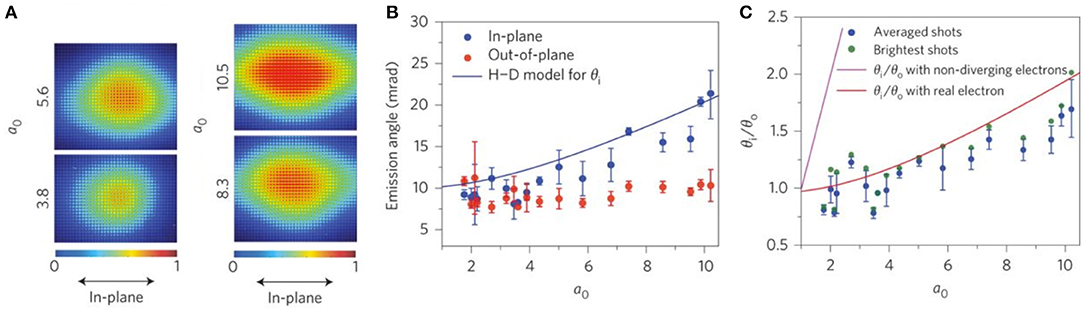
Figure 2. Effect of the intensity of the scattering laser on the divergence of Compton radiation. Sub-figure (A) shows the increase in divergence along the scattering beam polarization direction with intensity. Sub-figure (B) shows the agreement of the H-D model[76] with the observed divergence change. Sub-figure (C) illustrates how the intensity may be inferred when taking into account a non-diverging electron beam vs. the experimentally attained 10 mrad beam. Figure obtained and modified from Yan et al. [46], with permission from Springer Nature.

2.3. Prospects

As mentioned in the previous paragraphs, a brilliant source of multi-MeV narrow-band photon beams is of extreme interest for a wide range of applications in fields as diverse as industry, nuclear physics, medicine, and fundamental science. These beams are achievable with inverse Compton scattering of an ultra-relativistic electron beam in the field of an intense laser. LWFA electron beams present some unique characteristics, such as their inherent ultra-short duration and intrinsic synchronization with high-power lasers. However, active research is ongoing in order to solve some of the most pressing problems for LWFA electron beams, namely the almost intrinsic shot-to-shot fluctuations, and the non-negligible divergence and bandwidth. A summary of typical limitations in LWFA beams affecting ICS experiments is presented in Samarin et al. [77]. Improving the quality of LWFA beams in these respects is important not only for ICS but virtually for any other application of these beams, such as seeding free electron lasers.

One can also envisage a hybrid configuration, whereby the electron beam is provided by a radio-frequency accelerator and the scattering field is provided by a high-power laser. This scheme has the advantage of currently providing more favorable electron beam characteristics, and several schemes are currently being proposed around the world, including the Extreme Light Infrastructure Nuclear Pillar [78], FACET-II [79] (following a scheme already used in [54]), HIBEF [80], and EuPRAXIA [81].

Another limitation of all-optical Compton sources is their current repetition rate. Even if the peak brilliance of these photon sources is extremely high, the low repetition rate (usually at the Hz or sub-Hz level) implies that the average brilliance is relatively modest. The problem of designing high-repetition rate and high-power laser system is a pressing one also for many other applications of high-power lasers. For example, generating 10 or 100 Hz high-power lasers for particle acceleration is included as a main development requirement in the US accelerator roadmap [82] and in the UK laser-wakefield acceleration roadmap [83]. As an example, a current active project, DiPOLE [84], has recently demonstrated stable operation of a 10 J femtosecond laser at a 10 Hz level.

3. Laser-Based Positron Generation

The laser-driven generation of high-quality positron beams has attracted significant attention following the developments in high-power lasers and their intrinsic importance in a wide range of fields, including high-energy physics (HEP), material science, and laboratory astrophysics. However, different applications present largely different requirements in terms of the positron source, particularly regarding the energy of the positrons.

High-energy positron beams are required in high-energy physics experiments, predominantly in electron-positron colliders. In conventional colliders, an electron beam is accelerated to ultra-relativistic energies in a LINAC, which is used to initiate an electromagnetic cascade inside a high-Z converter in order to generate the positron beam (see section 3.1). These positrons are then injected into storage rings before being further accelerated to the final collision energies in a synchrotron-like accelerator. However, the large energies required in HEP experiments, in conjunction with the relatively low accelerating field in conventional accelerators (limited to tens of MV/m), result in the need for increasingly large and expensive machines. For example, the current center-of-mass energy record in an electron-positron collider belongs to the recently dismissed LEP at CERN, reaching up to 209 GeV using a 27 km-radius synchrotron accelerator. The current proposals for the next generation of electron-positron colliders study the use of state-of-the-art LINACs to reach TeV-level center-of-mass energies, with an extension >30 km.

Material science applications typically require positron sources of significantly lower energy, in the sub-MeV level. In the positron annihilation lifetime spectroscopy (PALS) technique, low energy positrons impinge onto a sample. As the positrons lose their energy and recombine with electrons in the material, two 511 keV photons are emitted, producing a signal that can be collected using scintillators. However, if a defect in the crystal lattice exists in the region where the positron has thermalised, the positron is likely to be diffused and trapped due to the lower energy of the defect compared to the surrounding lattice. As a result, the internal properties of the material can be characterized in terms of the positron lifetime inside the material, by measuring the time of arrival of the emitted photons. Traditionally, PALS studies have been performed using the β⁺ decay of ²²Na: ²²Na → ²²Ne*+e${}^{+}+{\nu }_e{\to }^{22}$Ne+γ+e${}^{+}+{\nu }_e$. The lifetime of the excited Ne is 3.7 ps, and the emitted photon is used as a zero-time reference to measure the lifetime of the emitted positron in the material. Despite the interest in using PALS to characterize micro-fractures inside materials, its applicability has been limited by the long exposure times and fixed energy of the β⁺ decay. A long exposure time prevents characterization of defects in kinetic processes and the low energy of these decays has limited the PALS study to materials only a few microns in thickness. An ultra-short and tuneable positron beam can solve these shortcomings, allowing for increased use in the material science community.

In terms of positron generation using lasers, the field is currently following two distinct lines, depending on the type of plasma the laser interacts with. In the context of this overview, we will focus on the indirect generation of positrons, in which the laser interacts with an underdense plasma (gas) in order to accelerate a high-quality electron beam, which is subsequently used to generate the positron beam. Alternatively, a direct scheme for the generation of positrons is also being actively studied [85–87]. However, this is beyond the scope of this overview, and it is only mentioned here for completeness. In this latter case, the laser is directly focused onto a solid target, where it interacts with an overdense plasma. As a result of this interaction, a fast electron population is driven into the bulk of the target. During this propagation, and depending on the target thickness and material, the electron can be scattered by the material's nuclei emitting high-energy photons, which in turn decay into an electron-positron pair (see section 3.1). The positron beams obtained in this case typically exhibit a high overall charge, with relatively modest energies (few tens of MeV), high divergence (hundreds of mrad), and relatively long durations (from picoseconds to nanoseconds). Some recent results for positron generation from solid targets are summarized in Table 1. A more thorough comparison between a direct and indirect laser-driven generation of positrons can be found in Sarri et al. [88].

TABLE 1

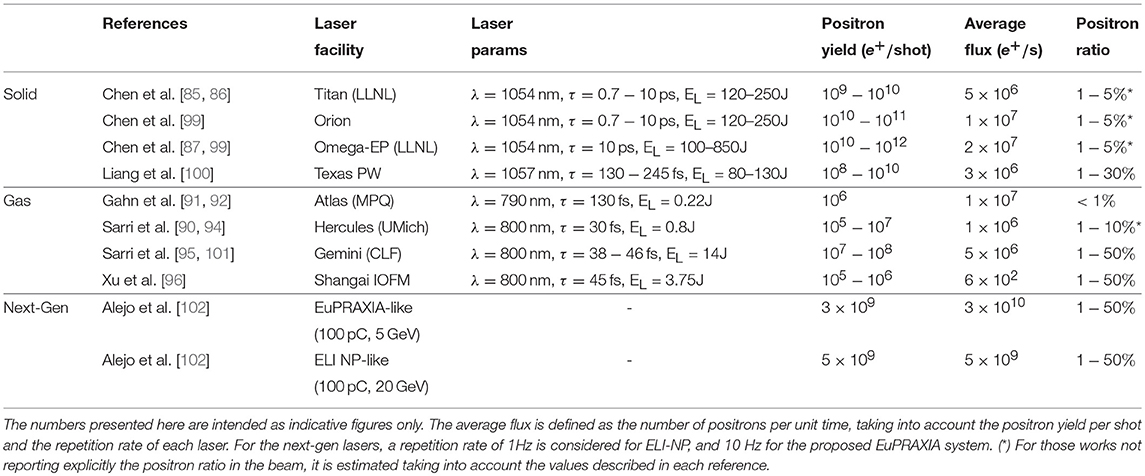
Table 1. Summary of results for laser-driven positron generation [adapted from Gorlova et al. [98], with data from Chen et al. [85], Chen et al. [86], Chen et al. [99], Chen et al. [87], Liang et al. [100], Gahn et al. [91], Gahn et al. [92], Sarri et al. [90], Sarri et al. [94], Sarri et al. [95], Sarri et al. [101], Xu et al. [96], and Alejo et al. [102]].

In the following sections, the current status of positron generation using LWFA electron beams will be presented. Initially, the process by which these positrons are typically generated will be introduced, followed by an overview of the experimental results reported in the literature. The prospects of the field and the applications following the ongoing development in laser science will be discussed in section 3.3.

3.1. Positron Production in QED Cascades

The propagation of ultra-relativistic electrons through a high-Z converter can result in the generation of a positron beam, mainly via two mechanisms, namely the trident process and the Bethe-Heitler process. In the trident process, an e⁻e⁺ pair is directly produced during the propagation of an electron through the nuclear field, mediated by the emission of a virtual photon. Alternatively, the Bethe-Heitler process is a two-step mechanism, in which an electron emits a real high-energy photon via bremsstrahlung, which subsequently decays in an e⁻e⁺ pair during its propagation in the field of a nucleus. Both the Trident and the Bethe-Heitler mechanisms have a cross-section proportional to (Z²ρd/A)n [89], where Z and A are the atomic and mass numbers of the converter material, ρ is its density, and d its thickness. The value of n depends on the mechanism, being n = 1 for Trident and n = 2 for Bethe-Heitler. Therefore, for sufficiently thick converters, such as those typically employed in positron generation from ultra-relativistic electrons, Bethe-Heitler accounts for the majority of the positrons produced, with the Trident yield being limited to a few percent at most.

Furthermore, for sufficiently thick targets, the generated electron and positrons can in turn produce additional high-energy photons via bremsstrahlung, resulting in a multi-step cascade. A useful parameter to define in this context is the radiation length (L_rad), which quantifies the average length an electron/positron (photon) needs to propagate through the converter before emitting a photon (decaying in a pair). For an order-of magnitude estimate of L_rad, we can assume here to be in the total-screening regime. By including Coulomb corrections, the radiation length is approximately given by $L_{rad}~1/(4\alpha {(Z\alpha )}^{2}n{\lambda }_C^2{L}_0)$, where α is the fine structure constant, Z is the atomic number, n is de atomic density, λ_C is the Compton wavelength, and $L_0=log(183Z^{-1/3})-f(Z\alpha )$, being $f(x)=\sum _{a=1}^{\infty }{x}^2/a(a^2+x^2)$. The number of electrons (f₋), positrons(f₊), and gammas (f_γ) depending on the target thickness (d) can be approximated by,

$\begin{array}{l}\frac{\partial f_{\pm }}{\partial \delta }=-{\displaystyle {\int }_0^{1}d}v{\psi }_{rad}(v)\left[f_{\pm }(E,\delta )-\frac{1}{1-v}{f}_{\pm }\left(\frac{E}{1-v},\delta \right)\right]\\ +{\displaystyle {\int }_0^1\frac{dv}{v}}{\psi }_{pair}(v)f_{\gamma }\left(\frac{E}{v},\delta \right),& (4)\end{array}$

$\begin{array}{rcll}\frac{\partial f_{\gamma }}{\partial \delta }& =& {\displaystyle {\int }_0^1}\frac{dv}{v}{\psi }_{rad}(v)\left[f_{-}\left(\frac{E}{v},\delta \right)+f_{+}\left(\frac{E}{v},\delta \right)\right]-{\mu }_0{f}_{\gamma }(E,\delta ),& (5)\end{array}$

where δ = d/L_rad is the target thickness in radiation length units, μ₀ = (7−3b)/9, being b = 1/18log(183/Z^1/3), and the functions ψ_rad(v) and ψ_pair(v) are related to the cross-section of bremsstrahlung and pair photo-production, and are given by

$\begin{array}{rc}{\psi }_{rad}(v)=\frac{1}{v}\left[1+{(1-v)}^2-(1-v)\left(\frac{2}{3}-2b\right)\right],& (6)\end{array}$

$\begin{array}{rc}{\psi }_{pair}(v)=v^2+{(1-v)}^2+v(1-v)\left(\frac{2}{3}-2b\right).& (7)\end{array}$

For these equations to be valid, we neglect low-energy scattering and absorption mechanisms, such as Compton scattering and ionization.

The calculated number of electrons and positrons (E > 120MeV) generated from the interaction of an electron beam with a converter, depending on the converter thickness, is shown in Figure 3A. It can be seen that the number of positron peaks for a converter thickness of 2L_rad. For much thicker converter targets, one can also eventually reach neutrality in the leptonic beam. The dependence of the fraction of positrons in the leptonic beam on the converter thickness is shown in Figure 3B, showing that neutrality is reached for converters thicker than 5L_rad.

FIGURE 3

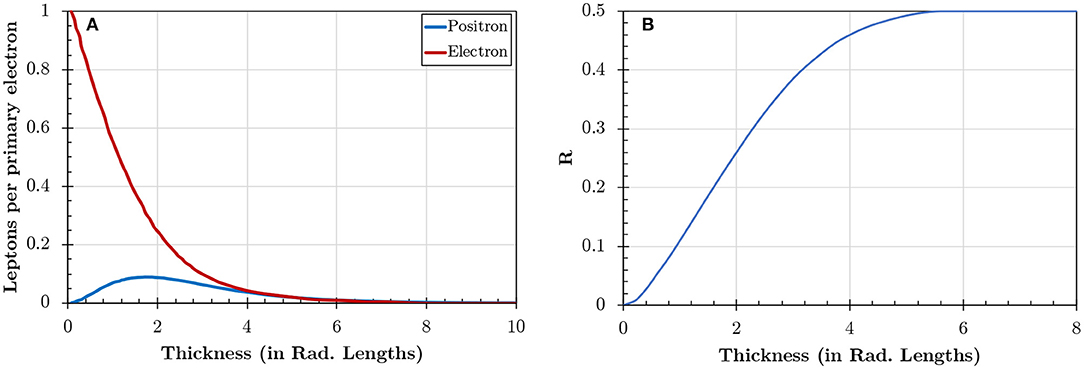
Figure 3. Positron generation from a quantum cascade depending on the converter thickness (Data from Sarri et al. [90]). (A) Calculated number of ultra-relativistic (E > 120MeV) leptons leaving the converter, normalized to the number of electrons in the parent beam. (B) Fraction of positrons in the leptonic jet ($R=N_{e^{+}}/(N_{e^{+}}+N_{e^{-}})$. The beam neutrality is first achieved for a converter thickness of ~5L_rad.

3.2. Experimental Results

Pioneering work on positron generation using laser-driven electrons was first reported by Gahn et al. [91, 92], following theoretical studies by Shkolinov and Kaplan [93]. In their work, a low-power (1.7TW) laser was focused onto a gas jet, where an electron beam was accelerated to energies up to ~12MeV, albeit the acceleration mechanism was direct laser acceleration instead of LWFA. These electrons were made to collide a 2-mm-thick Pb slab in order to generate bursts of positrons. By placing the converter inside a collimator to reduce the noise, a few tens of positrons were detected in a narrow energy bin (ΔE = 0.16 MeV at E = 2 MeV) and reduced solid angle (ΔΩ = 7.0 msr). The measured positron yield could be scaled considering the full spectrum, obtaining a total of ~2 × 10⁷e⁺/pulse, corresponding to an activity of 2 × 10⁸Bq.

As 100+ TW laser systems became available, different groups started working on the generation of positrons, either from the interaction of the laser with solid targets, in which suprathermal electrons driven at the front surface undergo the Bethe-Heitler process inside the bulk of the target, or from wakefield-driven electrons propagating through high-Z converters. In the latter scenario, different experiments have deployed similar experimental configurations to fully characterize the positron beam, rather than a narrow spectral bin, as shown in Figure 4a. In a nutshell, the laser propagates through an underdense plasma, leading to wakefield acceleration of electrons to ultra-relativistic energies. The electron beam impinges onto a secondary high-Z solid converter, were positrons are generated mainly via the Bethe-Heitler mechanism. Finally, the electron-positron beam is characterized using a magnetic spectrometer, which typically incorporate either image plates or scintillating screens as detectors. It should be noted that, as a result of the propagation of the electrons through the converter, a bright γ ray beam is also generated. In such harsh radiation environment, the positron signal can be obscured by the background. In order to mitigate this effect, different experiments have also deployed different types of shielding and collimators in front of the spectrometer in order to reduce the background levels. Notwithstanding the use of shielding, the characterization of the positron beam can be extremely challenging, which can be eased by increasing the charge of the parent electron beam. Williams et al. [97] found that, depending on the experimental configuration, charges as high as 100pC could be necessary in order to directly observe the positron beam. A summary of recent results for positron generation from LWFA-driven electrons is shown in Table 1.

FIGURE 4

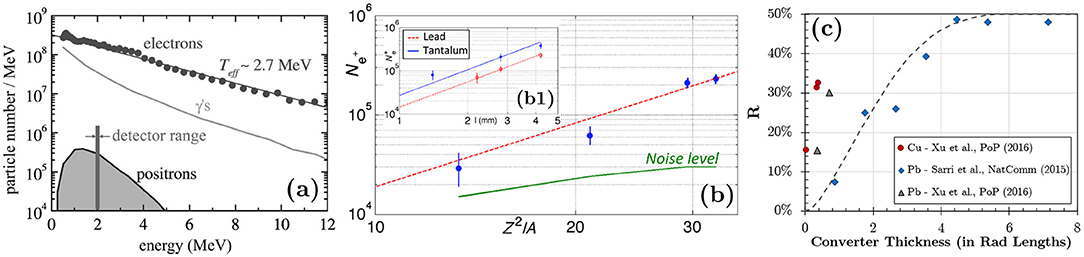
Figure 4. Experimental measurements of positron generation using laser-driven electrons. (a) Electron, positron and gamma spectra observed from a low power (1.7 TW) laser (Image taken from Gahn et al. [91], with permission from AIP Publishing). (b) Scaling of the positron yield with the converter thickness (l) and with Z²/A (Image taken from Ref. [94], with permission from APS). The quadratic scaling with those parameters indicates that the main positron generation mechanism is the Bethe-Heitler. (c) Scaling of the ratio of positrons in the leptonic beam depending on the thickness of the converter (Image adapted from Sarri et al. [95], including data from Xu et al. [96]). Quasi-neutral beams have been observed for converters of thickness >~5L_rad.

In 2013, Sarri et al. reported results on the generation of an ultra-relativistic positron beam using electrons driven by a 30TW laser [90, 94]. In the experiment, the Hercules laser (Michigan, USA) was focused (I ≃ 6 × 10¹⁸W cm−2, a₀≃1.7) onto a 97.5%-He/2.5%-N₂ gas mix, with an electron density of 9 × 10¹⁸cm⁻³. A reproducible electron beam was obtained, exhibiting a peak energy of ~200MeV, divergence of 2.5mrad, and a charge of 50pC for the electrons of energy >80MeV. This beam interacted with high-Z converters of different materials (Ta, Sn, Pb, and Cu) and thicknesses (ranging between 1.6 and 6.7 mm). Positron yields up to 4 × 10⁵ for positrons of energy >90MeV were measured, which corresponds to a total (full spectrum) of 3.5 × 10⁷ positrons/shot, as inferred considering matched Monte-Carlo simulations. By comparing the dependence of the positron yield on the converter material and thickness, a scaling given by $N_{e^{+}}\propto {(d{Z}^2/A)}^{2.1\pm 0.1}$ was obtained, where d is the converter thickness, and Z and A are the atomic and mass numbers, respectively, as shown in Figure 4b. The quadratic scaling confirms that, for the converter thickness considered in the experiment, the Bethe-Heitler mechanism significantly dominated the positron production over the Trident process.

Following the results using a table-top laser, Sarri et al. reported results on positron generation using ASTRA-GEMINI [95, 101], a PW-class laser at the Central Laser Facility (UK). In that case, the laser (15J, 42fs) was focused using an F/20 parabola, reaching an intensity in the focus of 3 × 10¹⁹W cm−2 (a₀ ≃ 3.7), which interacted with a plasma density $n_e=6.0\times 10^{18}$cm⁻³ produced by a gas jet. A reproducible electron beam was produced from the interaction, with maximum energy of ~600MeV and overall charge ~0.3nC (1.9 × 10⁹e⁻/shot). A positron beam was generated from the interaction of the electron beam with a secondary Pb converter of variable thickness. The maximum measured positron yield was ~1 × 10⁸e⁺/shot, obtained from a converter thickness of d = 1cm, which corresponds to a thickness of two radiation lengths ($L_{rad}^{Pb}\simeq 0.5$cm), as expected for the Bethe-Heitler process, and confirmed numerically and theoretically by Wu et al. [103].

Furthermore, thanks to the high energy and charge contained in the parent electron beam, thicker converters could be tested, reaching several radiation lengths. As the converter thickness is increased, a boost in the ratio of positrons in the beam $R=N_{e^{+}}/(N_{e^{+}}+N_{e^{-}})$ is observed, saturating to a 50−50% for sufficiently thick targets (d ≥ 5L_rad), as shown in Figure 4c. This corresponds to the first observation of a purely neutral electron-positron beam in a laboratory, with a yield of 2 × 10⁷leptons/shot. The short duration of this beam, in conjunction with the reduced source size and low divergence, enable the production of high-density electron-positron beams, $n_e\simeq 1.8\times 10^{16}\mathrm{\text{cm}}-3$, which opened up the possibility of studying the dynamics of neutral electron-positron plasmas in the laboratory, of interest in astrophysical scenarios, such as gamma ray bursts.

Due to the interest in spreading the study of neutral electron-positron beams, Xu et al. have analyzed the possibility of generating such beams using more modest laser systems (sub-100 TW rather than PW-class) [96]. In their experiment,the focused the laser (I≃3.5 × 10¹⁹W cm−2, a₀≃4.0) onto gas mix from a gas-jet, producing an electron density of $n_e\simeq 3.8\times 10^{20}\mathrm{\text{cm}}-3$. The electron beam generated from the interaction was optimized in terms of the charge contained in the beam, producing a yield of 1.23nC ($n_e~7.7\times 10^9$), exhibiting an exponential-like spectrum extending up to ~40MeV. By placing thin (2mm) Pb or Cu converters in the path, a yield of 3.5 × 10⁸ positrons/shot is estimated to be generated, with a divergence of ${\theta }_{e^{+}}~11.5deg$, mainly given by the initial divergence of the parent electron beam (${\theta }_{e^{-}}~11deg$). By further increasing the converter thickness to 20 mm of Cu, a quasi-neutral (R~48%, see Figure 4c) electron-positron beam was observed, albeit with a lower leptonic density than in Sarri et al. [95].

3.3. Prospects

The laser-driven generation of positrons is being actively developed, driven by its broad range of applications. Currently, the main focus is in optimizing the positron generation both using currently-available laser systems, as well as with the prospects offered by the upcoming laser facilities. Yan et al. have performed extensive numerical work to simulate and optimize the positron generation [104–106]. In their work, consisting of a combination of Particle-In-Cell and Monte-Carlo simulations, they investigated the electron acceleration and subsequent use for positron generation using a 100TW laser. A yield of up to 1.9 × 10¹⁰ positrons/shot was produced with small divergence (10deg), high energy (k_BT ~ 67.2MeV) and short pulse duration (1.7ps), which represents an increase of two orders of magnitude with respect to the experimental results using a laser of similar characteristics [96].

The large positron yields and interesting properties of those beams suggest that table-top laser systems can be used to generate positron beams of interest in material science. As explained in section 3, PALS is capable of probing materials in a nondestructive manner to study the atomic-scale structure. Thanks to the high intensity and short duration of the laser-driven positron beams, these sources have been suggested as an alternative to the use of radioactive source, with advantages in terms of time resolution, lower exposure times, and the possibility of probing deeper into materials by selecting a higher energy region of the positron spectrum [96]. Gorlova et al. have recently reported a study on the use of laser-driven positron beams at the International Laser Centre at the Moscow State University [98]. Considering the electron beams generated using the ~2TW, 10Hz system, a positron flux of 10⁴−10⁶s⁻¹ of positrons of energy below 10 MeV was estimated. This flux can be significantly boosted by orders of magnitude considering commercially available, tens of TW, table-top lasers, already making laser-driven positron sources an interesting alternative to the conventional sources.

Despite the large positron yield and properties of those beams, interesting for applications in material science, their properties need further improvement before being used in fields such as high energy physics and colliders. For this reason, the properties of positron beams expected from the upcoming multi-PW laser facilities have been numerically studied [102, 103]. Considering the multi-GeV electron beams expected from these facilities, Alejo et al. have shown that ultra-short positron beams can be used as injector for a future multi-stage, plasma-based positron accelerator [102] (see Table 1). The characteristics of the positron beams are shown not only to depend on the energy of the parent electron beam, with greater positron fluxes and improved characteristics for higher energy electron beams, but also present a strong dependence on the energy of the positrons. In that way, positrons with higher energies exhibit more appealing properties, such as lower emittance, shorter pulse direction, smaller source size and reduced divergence. However, these improved characteristics are obtained at the expense of lower number of positrons at the high energy end of the spectrum. A compromise is required between having improved beam properties while ensuring a significant charge in the positron beam. In particular, considering a 5GeV, 100pC electron beam, such as those proposed by the EuPRAXIA project or expected from ELI, up to 5 × 10⁶ positrons can be generated in a narrow energy band (1.00±0.05GeV), with a normalized emittance of 190πmm mrad. These values are already compatible with a further injection in secondary acceleration stages and to perform proof-of-principle studies of novel acceleration schemes. By injecting the positron beam into secondary plasma stages, quasi-monoenergetic positron beams can be produced and accelerated using all-optical configurations [107].

Finally, the other main application of positron beams is in the field of laboratory astrophysics. Alongside interesting developments to use stellarators to produce and confine electron-positron plasmas, such as the APEX experiment at the Positron Accumulation Experiment [108, 109], the unique features of laser-driven positron sources have made them an appealing alternative to study electron-positron plasmas in astrophysical scenarios. Although work has been done to produce neutral beams using solid targets [100], most effort has been put in producing highly-energetic, neutral beams using wakefield-driven electron beams [95, 96, 101].

The first observation of collective behavior of an electron-positron plasma has been recently reported by Warwick et al. [110] and Warwick et al. [111]. In this work, a neutral electron-positron beam was propagated through a low-density background plasma, resulting in the growth of a current-driven instability and the generation of strong magnetic fields (≥1T). An indispensable condition for the growth of such instabilities was found to be the neutrality of the beam, with no observable magnetic field appearing for a fraction of positrons in the beam (R) below 40%. It should be noted that, for the experimental conditions reported, the oblique instability should be dominant, as shown by Shukla et al. [112]. The observation of a purely-transverse filamentation instability is explained in terms of the beam longitudinal size. The generated electron-positron beam was longitudinally shorter than its skin depth, thus avoiding the growth of collective effects along the longitudinal direction. Further studies on the evolution and saturation of the instability would be of great interest for the direct analogy to lepton-dominated astrophysical jets. Of particular interest is the study of pair-shocks along the propagation of the jet, after saturation of the filamentation instability, which has been speculated as a possible origin for the production of gamma-ray bursts and may be studied in upcoming laser facilities [99]. Such facilities may also enable the study of the propagation of lower temperature electron-positron plasmas into a background plasma, predicted to generated bipolar electric fields capable of accelerating ions in unmagnetised ambient plasmas, such as the inter-galactic medium [113, 114].

4. Conclusions

In the present paper, the current status in the generation of secondary sources of radiation using LWFA-driven electron beams has been shown, focusing in the generation of x-ray beams via Compton scattering, and positron beams via the Bethe-Heitler mechanism. Inverse Compton scattering using laser-driven electron beams has been shown to produce high-quality X-ray beams, with the highest brilliances reported for MeV photon sources. Positron beams can be generated from the interaction of an electron beam with a solid, high-Z converter, via the Bethe-Heitler mechanism. An overview of the experimental results reported in the literature has been presented, showing that ultra-short, high-charge, high-quality positron beams can be generated using currently-available laser systems, as well as being capable of producing neutral electron-positron beams of interest in astrophysical scenarios. The ongoing developments in the laser technology will allow to further improve the characteristics of these sources, allowing for their widespread use in industrial applications.

Data Availability

All the data to which this article refers are either published in scientific journals or otherwise available online.

Author Contributions

AA, GMS, JW, and GS equally contributed to writing the article. The final version of the manuscript was collated by AA and finally checked by GS.

Funding

This work has been supported by EPSRC (grant No. EP/N027175/1 and EP/P010059/1).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Tajima T, Dawson JM. Laser electron accelerator. Phys Rev Lett. (1979) 43:267. doi: 10.1103/PhysRevLett.43.267

CrossRef Full Text

2. Mangles SP, Murphy C, Najmudin Z, Thomas AGR, Collier J, Dangor AE, et al. Monoenergetic beams of relativistic electrons from intense laser–plasma interactions. Nature. (2004) 431:535. doi: 10.1038/nature02939

PubMed Abstract | CrossRef Full Text

3. Faure J, Glinec Y, Pukhov A, Kiselev S, Gordienko S, Lefebvre E, et al. A laser–plasma accelerator producing monoenergetic electron beams. Nature. (2004) 431:541. doi: 10.1038/nature02963

PubMed Abstract | CrossRef Full Text

4. Geddes C, Toth C, Van Tilborg J, Esarey E, Schroeder C, Bruhwiler D, et al. High-quality electron beams from a laser wakefield accelerator using plasma-channel guiding. Nature. (2004) 431:538. doi: 10.1038/nature02900

PubMed Abstract | CrossRef Full Text

5. Clayton C, Marsh K, Dyson A, Everett M, Lal A, Leemans W, et al. Ultrahigh-gradient acceleration of injected electrons by laser-excited relativistic electron plasma waves. Phys Rev. Lett. (1993) 70:37. doi: 10.1103/PhysRevLett.70.37

CrossRef Full Text

6. Modena A, Najmudin Z, Dangor A, Clayton C, Marsh K, Joshi C, et al. Electron acceleration from the breaking of relativistic plasma waves. Nature. (1995) 377:606. doi: 10.1038/377606a0

CrossRef Full Text

7. Leemans W, Catravas P, Esarey E, Geddes C, Toth C, Trines R, et al. Electron-yield enhancement in a laser-wakefield accelerator driven by asymmetric laser pulses. Phys Rev Lett. (2002) 89:174802. doi: 10.1103/PhysRevLett.89.174802

PubMed Abstract | CrossRef Full Text

8. Umstadter D, Esarey E, Kim J. Nonlinear plasma waves resonantly driven by optimized laser pulse trains. Phys Rev Lett. (1994) 72:1224. doi: 10.1103/PhysRevLett.72.1224

PubMed Abstract | CrossRef Full Text

9. Esarey E, Schroeder C, Leemans W. Physics of laser-driven plasma-based electron accelerators. Rev Modern Phys. (2009) 81:1229. doi: 10.1103/RevModPhys.81.1229

CrossRef Full Text

10. Albert F, Thomas A. Applications of laser wakefield accelerator-based light sources. Plasma Phys Control Fusion. (2016) 58:103001. doi: 10.1088/0741-3335/58/10/103001

CrossRef Full Text

11. Lundh O, Lim J, Rechatin C, Ammoura L, Ben-Ismail A, Davoine X, et al. Few femtosecond, few kiloampere electron bunch produced by a laser–plasma accelerator. Nat Phys. (2011) 7:219. doi: 10.1038/nphys1872

CrossRef Full Text

12. Gonsalves AJ, Nakamura K, Daniels J, Benedetti C, Pieronek C, de Raadt TCH, et al. Petawatt laser guiding and electron beam acceleration to 8 GeV in a laser-heated capillary discharge waveguide. Phys Rev Lett. (2019) 122:084801. doi: 10.1103/PhysRevLett.122.084801

CrossRef Full Text

13. Wang W, Li W, Liu J, Zhang Z, Qi R, Yu C, et al. High-brightness high-energy electron beams from a laser wakefield accelerator via energy chirp control. Phys Rev Lett. (2016) 117:124801. doi: 10.1103/PhysRevLett.117.124801

PubMed Abstract | CrossRef Full Text

14. Buck A, Wenz J, Xu J, Khrennikov K, Schmid K, Heigoldt M, et al. Shock-front injector for high-quality laser-plasma acceleration. Phys Rev Lett. (2013) 110:185006. doi: 10.1103/PhysRevLett.110.185006

PubMed Abstract | CrossRef Full Text

15. Steinke S, Van Tilborg J, Benedetti C, Geddes C, Schroeder C, Daniels J, et al. Multistage coupling of independent laser-plasma accelerators. Nature. (2016) 530:190. doi: 10.1038/nature16525

PubMed Abstract | CrossRef Full Text

16. Podgorsak EB. Radiation Oncology Physics. Vienna: International Atomic Energy Agency (2005). p. 123–271.

PubMed Abstract

17. Lawrence TS, Ten Haken RK, Giaccia A. Principles of radiation oncology. In: Cancer: Principles and Practice of Oncology, 8th ed. Philadelphia, PA: Lippincott Williams and Wilkins (2008).

18. Runkle RC, Chichester DL, Thompson SJ. Rattling nucleons: New developments in active interrogation of special nuclear material. Nuclear Instrum Methods Phys Res A (2012) 663:75–95. doi: 10.1016/j.nima.2011.09.052

CrossRef Full Text

19. Pruet J, McNabb D, Hagmann C, Hartemann F, Barty C. Detecting clandestine material with nuclear resonance fluorescence. J Appl Phys. (2006) 99:123102. doi: 10.1063/1.2202005

CrossRef Full Text

20. Baldwin G, Klaiber G. Photo-fission in heavy elements. Phys Rev. (1947) 71:3. doi: 10.1103/PhysRev.71.3

CrossRef Full Text

21. Longair MS. High Energy Astrophysics. Cambridge: Cambridge University Press (2011).

22. Di Piazza A, Müller C, Hatsagortsyan K, Keitel C. Extremely high-intensity laser interactions with fundamental quantum systems. Rev Modern Phys. (2012) 84:1177. doi: 10.1103/RevModPhys.84.1177

CrossRef Full Text

23. Breit G, Wheeler JA. Collision of two light quanta. Phys Rev. (1934) 46:1087. doi: 10.1103/PhysRev.46.1087

CrossRef Full Text

24. Lundström E, Brodin G, Lundin J, Marklund M, Bingham R, Collier J, et al. Using high-power lasers for detection of elastic photon-photon scattering. Phys Rev Lett. (2006) 96:083602. doi: 10.1103/PhysRevLett.96.083602

PubMed Abstract | CrossRef Full Text

25. Di Piazza A, Hatsagortsyan K, Keitel CH. Quantum radiation reaction effects in multiphoton compton scattering. Phys Rev Lett. (2010) 105:220403. doi: 10.1103/PhysRevLett.105.220403

PubMed Abstract | CrossRef Full Text

26. Thomas A, Ridgers C, Bulanov S, Griffin B, Mangles S. Strong radiation-damping effects in a gamma-ray source generated by the interaction of a high-intensity laser with a wakefield-accelerated electron beam. Phys Rev X. (2012) 2:041004. doi: 10.1103/PhysRevX.2.041004

CrossRef Full Text

27. Blackburn T, Ridgers CP, Kirk JG, Bell A. Quantum radiation reaction in laser–electron-beam collisions. Phys Rev Lett. (2014) 112:015001. doi: 10.1103/PhysRevLett.112.015001

PubMed Abstract | CrossRef Full Text

28. Popov VS. Schwinger mechanism of electron-positron pair production by the field of optical and X-ray lasers in vacuum. J Exp Theor Phys Lett. (2001) 74:133–8. doi: 10.1134/1.1410216

CrossRef Full Text

29. Poder K, Tamburini M, Sarri G, Di Piazza A, Kuschel S, Baird C, et al. Experimental signatures of the quantum nature of radiation reaction in the field of an ultraintense laser. Phys Rev X. (2018) 8:031004. doi: 10.1103/PhysRevX.8.031004

CrossRef Full Text

30. Cole J, Behm K, Gerstmayr E, Blackburn T, Wood J, Baird C, et al. Experimental evidence of radiation reaction in the collision of a high-intensity laser pulse with a laser-wakefield accelerated electron beam. Phys Rev X. (2018) 8:011020. doi: 10.1103/PhysRevX.8.011020

CrossRef Full Text

31. Glinec Y, Faure J, Le Dain L, Darbon S, Hosokai T, Santos J, et al. High-resolution γ-ray radiography produced by a laser-plasma driven electron source. Phys Rev Lett. (2005) 94:025003. doi: 10.1103/PhysRevLett.94.025003

PubMed Abstract | CrossRef Full Text

32. Giulietti A, Bourgeois N, Ceccotti T, Davoine X, Dobosz S, D'Oliveira P, et al. Intense γ-ray source in the giant-dipole-resonance range driven by 10-TW laser pulses. Phys Rev Lett. (2008) 101:105002. doi: 10.1103/PhysRevLett.101.105002

PubMed Abstract | CrossRef Full Text

33. Schumaker W, Sarri G, Vargas M, Zhao Z, Behm K, Chvykov V, et al. Measurements of high-energy radiation generation from laser-wakefield accelerated electron beams. Phys Plasmas. (2014) 21:056704. doi: 10.1063/1.4875336

CrossRef Full Text

34. Chen Sy, Maksimchuk A, Umstadter D. Experimental observation of relativistic nonlinear Thomson scattering. Nature. (1998) 396:653. doi: 10.1038/25303

CrossRef Full Text

35. Phuoc KT, Rousse A, Pittman M, Rousseau JP, Malka V, Fritzler S, et al. X-ray radiation from nonlinear Thomson scattering of an intense femtosecond laser on relativistic electrons in a helium plasma. Phys Rev Lett. (2003) 91:195001. doi: 10.1103/PhysRevLett.91.195001

CrossRef Full Text

36. Rousse A, Phuoc KT, Shah R, Pukhov A, Lefebvre E, Malka V, et al. Production of a keV X-ray beam from synchrotron radiation in relativistic laser-plasma interaction. Phys Rev Lett. (2004) 93:135005. doi: 10.1103/PhysRevLett.93.135005

PubMed Abstract | CrossRef Full Text

37. Kneip S, McGuffey C, Dollar F, Bloom M, Chvykov V, Kalintchenko G, et al. X-ray phase contrast imaging of biological specimens with femtosecond pulses of betatron radiation from a compact laser plasma wakefield accelerator. Appl Phys Lett. (2011) 99:093701. doi: 10.1063/1.3627216

CrossRef Full Text

38. Cole J, Wood J, Lopes N, Poder K, Abel R, Alatabi S, et al. Laser-wakefield accelerators as hard x-ray sources for 3D medical imaging of human bone. Sci Rep. (2015) 5:13244. doi: 10.1038/srep13244

PubMed Abstract | CrossRef Full Text

39. Cole JM, Symes DR, Lopes NC, Wood JC, Poder K, Alatabi S, et al. High-resolution CT of a mouse embryo using a compact laser-driven X-ray betatron source. Proc Natl Acad Sci USA. (2018) 115:6335–40. doi: 10.1073/pnas.1802314115

CrossRef Full Text

40. Murnane MM, Kapteyn HC, Rosen MD, Falcone RW. Ultrafast x-ray pulses from laser-produced plasmas. Science. (1991) 251:531–6. doi: 10.1126/science.251.4993.531

PubMed Abstract | CrossRef Full Text

41. Kmetec J, Gordon C III, Macklin J, Lemoff B, Brown G, Harris S. MeV x-ray generation with a femtosecond laser. Phys Rev Lett. (1992) 68:1527. doi: 10.1103/PhysRevLett.68.1527

PubMed Abstract | CrossRef Full Text

42. Sokolov AA, Ternov IM. Synchrotron Radiation (Russian title: Sinkhrotronnoie Izluchenie). Nauka editors. Moscow: Akademia Nauk SSSR, Moskovskoie Obshchestvo Ispytatelei Prirody. Sektsia Fiziki (1966).

43. Deacon DA, Elias L, Madey JM, Ramian G, Schwettman H, Smith TI. First operation of a free-electron laser. Phys Rev Lett. (1977) 38:892. doi: 10.1103/PhysRevLett.38.892

CrossRef Full Text

44. Emma P, Akre R, Arthur J, Bionta R, Bostedt C, Bozek J, et al. First lasing and operation of an ångstrom-wavelength free-electron laser. Nat Photonics. (2010) 4:641. doi: 10.1038/nphoton.2010.176

CrossRef Full Text

45. Kneip S, McGuffey C, Martins J, Martins S, Bellei C, Chvykov V, et al. Bright spatially coherent synchrotron X-rays from a table-top source. Nat Phys. (2010) 6:980. doi: 10.1038/nphys1789

CrossRef Full Text

46. Yan W, Fruhling C, Golovin G, Haden D, Luo J, Zhang P, et al. High-order multiphoton Thomson scattering. Nat Photonics. (2017) 11:514. doi: 10.1038/nphoton.2017.100

CrossRef Full Text

47. Sarri G, Corvan D, Schumaker W, Cole J, Di Piazza A, Ahmed H, et al. Ultrahigh brilliance multi-MeV γ-ray beams from nonlinear relativistic Thomson scattering. Phys Rev Lett. (2014) 113:224801. doi: 10.1103/PhysRevLett.113.224801

PubMed Abstract | CrossRef Full Text

48. Phuoc KT, Corde S, Thaury C, Malka V, Tafzi A, Goddet JP, et al. All-optical Compton gamma-ray source. Nat Photonics. (2012) 6:308. doi: 10.1038/nphoton.2012.82

CrossRef Full Text

49. Kaneyasu T, Takabayashi Y, Iwasaki Y, Koda S. Generation of laser Compton gamma-rays in the SAGA light source storage ring. Nuclear Instrum Methods Phys Res A. (2011) 659:30–5. doi: 10.1016/j.nima.2011.08.047

CrossRef Full Text

50. Powers ND, Ghebregziabher I, Golovin G, Liu C, Chen S, Banerjee S, et al. Quasi-monoenergetic and tunable X-rays from a laser-driven Compton light source. Nat Photonics. (2014) 8:28. doi: 10.1038/nphoton.2013.314

CrossRef Full Text

51. Chen S, Powers N, Ghebregziabher I, Maharjan C, Liu C, Golovin G, et al. MeV-energy X rays from inverse Compton scattering with laser-wakefield accelerated electrons. Phys Rev Lett. (2013) 110:155003. doi: 10.1103/PhysRevLett.110.155003

PubMed Abstract | CrossRef Full Text

52. Liu C, Golovin G, Chen S, Zhang J, Zhao B, Haden D, et al. Generation of 9 MeV γ-rays by all-laser-driven Compton scattering with second-harmonic laser light. Opt Lett. (2014) 39:4132–5. doi: 10.1364/OL.39.004132

PubMed Abstract | CrossRef Full Text

53. Khrennikov K, Wenz J, Buck A, Xu J, Heigoldt M, Veisz L, et al. Tunable all-optical quasimonochromatic Thomson X-ray source in the nonlinear regime. Phys Rev Lett. (2015) 114:195003. doi: 10.1103/PhysRevLett.114.195003

PubMed Abstract | CrossRef Full Text

54. Bula C, McDonald K, Prebys E, Bamber C, Boege S, Kotseroglou T, et al. Observation of nonlinear effects in Compton scattering. Phys Rev Lett. (1996) 76:3116. doi: 10.1103/PhysRevLett.76.3116

PubMed Abstract | CrossRef Full Text

55. Beaud P, Johnson S, Streun A, Abela R, Abramsohn D, Grolimund D, et al. Spatiotemporal stability of a femtosecond hard–X-ray undulator source studied by control of coherent optical phonons. Phys Rev Lett. (2007) 99:174801. doi: 10.1103/PhysRevLett.99.174801

PubMed Abstract | CrossRef Full Text

56. Elleaume P, Ropert A. The ultimate hard X-ray storage-ring-based light source. Nuclear Instrum Methods Phys Res A (2003) 500:18–24. doi: 10.1016/S0168-9002(03)00737-X

CrossRef Full Text

57. Rousse A, Audebert P, Geindre JP, Fallies F, Gauthier JC, Mysyrowicz A, et al. Efficient Kα x-ray source from femtosecond laser-produced plasmas. Phys Rev E. (1994) 50:2200. doi: 10.1103/PhysRevE.50.2200

CrossRef Full Text

58. Altarelli M, Brinkmann R, Chergui M, Decking W, Dobson B, Düsterer S, et al. The European x-ray Free-Electron Laser. Technical Design Report, DESY (2006).

PubMed Abstract

59. Cipiccia S, Islam MR, Ersfeld B, Shanks RP, Brunetti E, Vieux G, et al. Gamma-rays from harmonically resonant betatron oscillations in a plasma wake. Nat Phys. (2011) 7:867. doi: 10.1038/nphys2090

CrossRef Full Text

60. Corde S, Phuoc KT, Lambert G, Fitour R, Malka V, Rousse A, et al. Femtosecond x rays from laser-plasma accelerators. Rev Modern Phys. (2013) 85:1. doi: 10.1103/RevModPhys.85.1

CrossRef Full Text

61. Carman TS, Scarlett C, Schreiber E, Roberson N, Weller H. Production of Gamma-Rays for Nuclear Physics Using the Duke Free-Electron-Laser Facility. Triangle Universities Nuclear Laboratory (1994).

62. Schoenlein RW, Leemans W, Chin A, Volfbeyn P, Glover T, Balling P, et al. Femtosecond X-ray pulses at 0.4 Å generated by 90 Thomson scattering: a tool for probing the structural dynamics of materials. Science. (1996) 274:236–8. doi: 10.1126/science.274.5285.236

CrossRef Full Text

63. Gibson D, Albert F, Anderson S, Betts S, Messerly M, Phan H, et al. Design and operation of a tunable MeV-level Compton-scattering-based γ-ray source. Phys Rev Spec Top. (2010) 13:070703. doi: 10.1103/PhysRevSTAB.13.070703

CrossRef Full Text

64. Albert F, Anderson S, Gibson D, Hagmann C, Johnson M, Messerly M, et al. Characterization and applications of a tunable, laser-based, MeV-class Compton-scattering γ-ray source. Phys Rev Spec Top. (2010) 13:070704. doi: 10.1103/PhysRevSTAB.13.070704

CrossRef Full Text

65. Hooker C, Collier J, Chekhlov O, Clarke R, Divall E, Ertel K, et al. The Astra Gemini project–A dual-beam petawatt Ti: Sapphire laser system. J Phys IV. (2006) 133:673–7. doi: 10.1051/jp4:2006133135

CrossRef Full Text

66. Yanovsky V, Chvykov V, Kalinchenko G, Rousseau P, Planchon T, Matsuoka T, et al. Ultra-high intensity-300-TW laser at 0.1 Hz repetition rate. Opt Express. (2008) 16:2109–14. doi: 10.1364/OE.16.002109

PubMed Abstract | CrossRef Full Text

67. Leemans W, Daniels J, Deshmukh A, Gonsalves A, Magana A, Mao H, et al. Bella laser and operations. In: Proceedings of PAC2013, Pasadena, CA (2013). p. 1097–100.

68. Sung JH, Lee SK, Yu TJ, Jeong TM, Lee J. 0.1 Hz 1.0 PW Ti: sapphire laser. Opt Lett. (2010) 35:3021–3. doi: 10.1364/OL.35.003021

PubMed Abstract | CrossRef Full Text

69. Habs D, Tajima T, Zamfir V. Extreme light infrastructure–nuclear physics (ELI–NP): new horizons for photon physics in Europe. Nuclear Phys News. (2011) 21:23–9. doi: 10.1080/10619127.2010.529741

CrossRef Full Text

70. Zamfir N. Extreme Light Infrastructure–Nuclear Physics (ELI-NP) European Research Centre. In: EPJ Web of Conferences. Vol. 66. Prague: EDP Sciences (2014). p. 11043.

71. Lyachev A, Chekhlov O, Collier J, Hancock S, Holligan P, Hernandez-Gomez C, et al. Development of the Joule Level Amplification Stage for the Phase 1 of the Vulcan 10 PW OPCPA project. CLF Annual Report (2007).

72. Rykovanov S, Geddes C, Vay J, Schroeder C, Esarey E, Leemans W. Quasi-monoenergetic femtosecond photon sources from Thomson Scattering using laser plasma accelerators and plasma channels. J Phys B. (2014) 47:234013. doi: 10.1088/0953-4075/47/23/234013

CrossRef Full Text

73. Rykovanov S, Geddes C, Schroeder C, Esarey E, Leemans W. Controlling the spectral shape of nonlinear Thomson scattering with proper laser chirping. Phys Rev Accel Beams. (2016) 19:030701. doi: 10.1103/PhysRevAccelBeams.19.030701

CrossRef Full Text

74. Ghebregziabher I, Shadwick BA, Umstadter D. Spectral bandwidth reduction of Thomson scattered light by pulse chirping. Phys Rev Spec Top. (2013) 16:030705. doi: 10.1103/PhysRevSTAB.16.030705

CrossRef Full Text

75. Seipt D, Rykovanov S, Surzhykov A, Fritzsche S. Narrowband inverse Compton scattering x-ray sources at high laser intensities. Phys Rev A. (2015) 91:033402. doi: 10.1103/PhysRevA.91.033402

CrossRef Full Text

76. Har-Shemesh O, Di Piazza A. Peak intensity measurement of relativistic lasers via nonlinear Thomson scattering. Opt Lett. (2012) 37:1352–4. doi: 10.1364/OL.37.001352

PubMed Abstract | CrossRef Full Text

77. Samarin G, Zepf M, Sarri G. Radiation reaction studies in an all-optical set-up: experimental limitations. J Modern Opt. (2017) 65:1362. doi: 10.1080/09500340.2017.1353655

CrossRef Full Text

78. Turcu I, Murphy C, Negoita F, Stutman D, Zepf M, Schreiber J, et al. High field physics and QED experiments at ELI-NP. Rom Rep Phys. (2016) 68:S145.

79. SLAC-R-1072. FACET-II Technical Design Report. US Department of Energy (2016).

80. Cowan Thomas and Hibef Collaboration. Status of the proposed helmholtz international beamline for extreme fields (HIBEF) at the European XFEL. In: APS Meeting Abstracts. Denver, CO (2013).

81. Walker PA, Alesini P, Alexandrova A, Anania MP, Andreev N, Andriyash I, et al. Horizon 2020 EuPRAXIA design study. J Phys Conf Ser. (2017) 874:012029. doi: 10.1088/1742-6596/874/1/012029

CrossRef Full Text

82. Advanced Accelerator Development Strategy Report. DOE Advanced Accelerator Concepts Research Roadmap Workshop. Washington, DC: USDOE Office of Science (2016).

83. PWASC. UK Roadmap for Plasma Wakefield Accelerator Research 2018-2050. UK Plasma Wakefield Accelerator Steering Committee (PWASC) (2018).

84. Banerjee S, Ertel K, Mason PD, Phillips PJ, De Vido M, Smith JM, et al. DiPOLE: a 10 J, 10 Hz cryogenic gas cooled multi-slab nanosecond Yb: YAG laser. Opt Express. (2015) 23:19542–51. doi: 10.1364/OE.23.019542

PubMed Abstract | CrossRef Full Text

85. Chen H, Wilks SC, Bonlie JD, Liang EP, Myatt J, Price DF, et al. Relativistic positron creation using ultraintense short pulse lasers. Phys Rev Lett. (2009) 102:105001. doi: 10.1103/PhysRevLett.102.105001

PubMed Abstract | CrossRef Full Text

86. Chen H, Wilks S, Bonlie J, Chen S, Cone K, Elberson L, et al. Making relativistic positrons using ultraintense short pulse lasers. Phys Plasmas. (2009) 16:105001. doi: 10.1063/1.3271355

CrossRef Full Text

87. Chen H, Wilks S, Meyerhofer D, Bonlie J, Chen C, Chen S, et al. Relativistic quasimonoenergetic positron jets from intense laser-solid interactions. Phys Rev Lett. (2010) 105:015003. doi: 10.1103/PhysRevLett.105.015003

PubMed Abstract | CrossRef Full Text

88. Sarri G, Dieckmann ME, Kourakis I, Di Piazza A, Reville B, Keitel CH, et al. Overview of laser-driven generation of electron-positron beams. J Plasma Phys. (2015) 81:455810401. doi: 10.1017/S002237781500046X

CrossRef Full Text

89. Williams G, Barnak D, Fiksel G, Hazi A, Kerr S, Krauland C, et al. Target material dependence of positron generation from high intensity laser-matter interactions. Phys Plasmas. (2016) 23:123109. doi: 10.1063/1.4971235

CrossRef Full Text

90. Sarri G, Schumaker W, Di Piazza A, Poder K, Cole J, Vargas M, et al. Laser-driven generation of collimated ultra-relativistic positron beams. Plasma Phys Control Fusion. (2013) 55:124017. doi: 10.1088/0741-3335/55/12/124017

CrossRef Full Text

91. Gahn C, Tsakiris G, Pretzler G, Witte K, Delfin C, Wahlström CG, et al. Generating positrons with femtosecond-laser pulses. Appl Phys Lett. (2000) 77:2662–4. doi: 10.1063/1.1319526

CrossRef Full Text

92. Gahn C, Tsakiris G, Pretzler G, Witte K, Thirolf P, Habs D, et al. Generation of MeV electrons and positrons with femtosecond pulses from a table-top laser system. Phys plasmas. (2002) 9:987–99. doi: 10.1063/1.1446879

CrossRef Full Text

93. Shkolnikov P, Kaplan A, Pukhov A, Meyer-ter Vehn J. Positron and gamma-photon production and nuclear reactions in cascade processes initiated by a sub-terawatt femtosecond laser. Appl phys Lett. (1997) 71:3471–3. doi: 10.1063/1.120362

CrossRef Full Text

94. Sarri G, Schumaker W, Di Piazza A, Vargas M, Dromey B, Dieckmann ME, et al. Table-top laser-based source of femtosecond, collimated, ultrarelativistic positron beams. Phys Rev Lett. (2013) 110:255002. doi: 10.1103/PhysRevLett.110.255002

PubMed Abstract | CrossRef Full Text

95. Sarri G, Poder K, Cole J, Schumaker W, Di Piazza A, Reville B, et al. Generation of neutral and high-density electron–positron pair plasmas in the laboratory. Nat Commun. (2015) 6:6747. doi: 10.1038/ncomms7747

PubMed Abstract | CrossRef Full Text

96. Xu T, Shen B, Xu J, Li S, Yu Y, Li J, et al. Ultrashort megaelectronvolt positron beam generation based on laser-accelerated electrons. Phys Plasmas. (2016) 23:033109. doi: 10.1063/1.4943280

CrossRef Full Text

97. Williams G, Pollock B, Albert F, Park J, Chen H. Positron generation using laser-wakefield electron sources. Phys Plasmas. (2015) 22:093115. doi: 10.1063/1.4931044

CrossRef Full Text

98. Gorlova DA, Nedorezov VG, Ivanov KA, Savel'ev AB, Turinge AA, Tsymbalov IN. On the possibility of generating low-energy positrons on accelerators of electrons with a beam energy of a few MeV and on terawatt lasers. Quantum Electron. (2017) 47:522. doi: 10.1070/QEL16328

CrossRef Full Text

99. Chen H, Fiuza F, Link A, Hazi A, Hill M, Hoarty D, et al. Scaling the yield of laser-driven electron-positron jets to laboratory astrophysical applications. Phys Rev Lett. (2015) 114:215001. doi: 10.1103/PhysRevLett.114.215001

PubMed Abstract | CrossRef Full Text

100. Liang E, Clarke T, Henderson A, Fu W, Lo W, Taylor D, et al. High e+/e- ratio dense pair creation with 10 21 W. cm- 2 Laser irradiating solid targets. Sci Rep. (2015) 5:13968. doi: 10.1038/srep13968

PubMed Abstract | CrossRef Full Text

101. Sarri G, Warwick J, Schumaker W, Poder K, Cole J, Doria D, et al. Spectral and spatial characterisation of laser-driven positron beams. Plasma Phys Control Fusion. (2016) 59:014015. doi: 10.1088/0741-3335/59/1/014015

CrossRef Full Text

102. Alejo A, Walczak R, Sarri G. Laser-driven high-quality positron sources as possible injectors for plasma-based accelerators. Sci. Rep. (in press). doi: 10.1038/s41598-019-41650-y

PubMed Abstract | CrossRef Full Text

103. Wu Y, Han D, Zhang T, Dong K, Zhu B, Yan Y, et al. Optimization of positrons generation based on laser wakefield electron acceleration. Phys Rev Accel Beams. (2016) 19:081303. doi: 10.1103/PhysRevAccelBeams.19.081303

CrossRef Full Text

104. Yan Y, Dong K, Wu Y, Zhang B, Yao Z, Gu Y. Numerical simulation study of positron production by intense laser-accelerated electrons. Phys Plasmas. (2013) 20:103106. doi: 10.1063/1.4824107

CrossRef Full Text

105. Yan Y, Zhang B, Wu Y, Dong K, Yao Z, Gu Y. Comparison of direct and indirect positron-generation by an ultra-intense femtosecond laser. Phys Plasmas. (2013) 20:103114. doi: 10.1063/1.4826219

CrossRef Full Text

106. Yan Y, Wu Y, Dong K, Zhang B, Zhao Z, Yao Z, et al. Simulation study of indirect positron generation by an ultra-short laser. Eur Phys J D. (2014) 68:4. doi: 10.1140/epjd/e2013-40473-x

CrossRef Full Text

107. Sahai AA. Quasimonoenergetic laser plasma positron accelerator using particle-shower plasma-wave interactions. Phys Rev Accel Beams. (2018) 21:081301. doi: 10.1103/PhysRevAccelBeams.21.081301

CrossRef Full Text

108. Pedersen TS, Boozer A, Dorland W, Kremer J, Schmitt R. Prospects for the creation of positron–electron plasmas in a non-neutral stellarator. J Phys B. (2003) 36:1029. doi: 10.1088/0953-4075/36/5/322

CrossRef Full Text

109. Pedersen TS, Danielson J, Hugenschmidt C, Marx G, Sarasola X, Schauer F, et al. Plans for the creation and studies of electron–positron plasmas in a stellarator. New J Phys. (2012) 14:035010. doi: 10.1088/1367-2630/14/3/035010

CrossRef Full Text

110. Warwick J, Dzelzainis T, Dieckmann ME, Schumaker W, Doria D, Romagnani L, et al. Experimental observation of a current-driven instability in a neutral electron-positron beam. Phys Rev Lett. (2017) 119:185002. doi: 10.1103/PhysRevLett.119.185002

PubMed Abstract | CrossRef Full Text

111. Warwick J, Alejo A, Dzelzainis T, Schumaker W, Doria D, Romagnani L, et al. General features of experiments on the dynamics of laser-driven electron–positron beams. Nuclear Instrum Methods Phys Res A. (2018) 909:95–101. doi: 10.1016/j.nima.2018.02.054

CrossRef Full Text

112. Shukla N, Vieira J, Muggli P, Sarri G, Fonseca R, Silva L. Conditions for the onset of the current filamentation instability in the laboratory. J Plasma Phys. (2018) 84:14. doi: 10.1017/S0022377818000314

CrossRef Full Text

113. Dieckmann ME, Alejo A, Sarri G. Expansion of a mildly relativistic hot pair cloud into an electron-proton plasma. Phys Plasmas. (2018) 25:062122. doi: 10.1063/1.5036954

CrossRef Full Text

114. Dieckmann ME, Alejo A, Sarri G, Folini D, Walder R. One-dimensional thermal pressure-driven expansion of a pair cloud into an electron-proton plasma. Phys Plasmas. (2018) 25:064502. doi: 10.1063/1.5026568

CrossRef Full Text