- 1Donostia International Physics Center, San Sebastian, Spain
- 2Ikerbasque, Bilbao, Spain
This article reviews the application of high pressure gaseous xenon time projection chambers to neutrinoless double beta decay experiments. First, the fundamentals of the technology and the historical development of the field are discussed. Then, the state of the art is presented, including the prospects for the next generation of experiments with masses in the ton scale range.
1. Introduction
The invention of the time projection chamber (TPC) [1] revolutionized the imaging of charged particles in gaseous detectors. More than four decades after its introduction, the TPC is still one of the most used detectors in particle physics.
Over the last decade, xenon TPCs have emerged as powerful tools for the study of rare events, in particular concerning dark matter and neutrinoless double decay (ββ0ν) searches. Their principle of operation is the same as for all TPCs: charged radiation ionizes the fluid and the ionization electrons are drifted under the action of an electric field to sensitive image planes, where their transverse position information (X,Y) is collected. Their arrival times (relative to the start-of-the-event time, or t0) are then translated to longitudinal positions, Z, through their average drift velocity. Yet the application of TPCs to ββ0ν searches has its own peculiarities. In this case xenon is not only the sensitive medium, but also the target where the decays occur. Since the sensitivity of the search is proportional to the target mass, the apparatus needs to be as large and compact as possible, leading to either high pressure gaseous xenon (HPXe) or liquid xenon (LXe) TPCs. Furthermore, the energy of the decay is relatively low (the end-point of the decay Xe → Ba++ + 2e−, Qββ, is 2458 keV [2]) and thus the tracks left by the two electrons can be rather short for HPXe detectors (of the order of 15 cm for electrons with Qββ energies at 15 bar) or even point-like objects for LXe chambers. In both cases the TPCs act as calorimeters, measuring the total energy of the products and identifying the interaction vertex in a well-defined fiducial volume thanks to the availability of a mechanism to signal t0, namely the VUV scintillation emitted by xenon as a response to ionizing radiation. In addition, a HPXe TPC provides a topological signature, thanks to its ability to image the electron tracks.
In this review we discuss the fundamentals, state of the art and potential for the next generation of experiments searching for neutrinoless double beta decay processes with high pressure xenon TPCs. A more general discussion encompassing the various TPCs used for rare event searches can be found in Gonzalez-Diaz et al. [3].
Neutrinoless double beta decay is a hypothetical, very slow radioactive process in which two neutrons undergo β-decay simultaneously and without the emission of neutrinos, (Z, A) → (Z + 2, A) + 2 e−. An unambiguous observation of this process would establish that neutrinos are Majorana particles [4], identical to their antiparticles, with deep implications in physics and cosmology [5].
The simplest mechanism to mediate such a transition is the virtual exchange of light Majorana neutrinos. Assuming this exchange to be dominant at low energies, the half-life of ββ0ν can be written as:
where G0ν is a phase-space integral for the emission of two electrons, M0ν is the nuclear matrix element (NME) of the transition, and mββ is the effective Majorana mass of the electron neutrino, defined in terms of the neutrino mass eigenstates (mi) and the elements of the neutrino mixing matrix [6].
The signal of a neutrinoless double beta decay is a peak in the kinetic energy spectrum of the two electrons emitted in the process, therefore an experiment with discovery potential requires excellent energy resolution and sufficient background rejection power to eliminate events with an energy very close to Qββ. Over the last decade, several ββ0ν experiments, with masses in the range of few tens to few hundreds of kilograms, have pushed the sensitivity to the half-life of ββ0ν processes by more than one order of magnitude using three different isotopes. Four of these experiments (GERDA [7], EXO [8], KamLAND-Zen [9, 10], and CUORE [11]) have recently published the results of their analysis. The best limit on the lifetime of a ββ0ν isotope was obtained by KamLAND-Zen [9, 10]), corresponding to > 1.07 × 1026 yr for the ββ0ν decay of 136Xe. The GERDA experiment has recently published a limit > 0.8 × 1026 yr for the ββ0ν decay of 76Ge.
The goal of the “next generation” of xenon-based experiments is to improve the sensitivity to by at least one order of magnitude, to more than 1027 yr, or less than 20 meV in mββ. If the neutrino mass ordering is inverted (e.g., , where and mi, i = 1, 3 denotes the mass of the three neutrino mass eigenstates), reaching such a sensitivity on mββ would result in a discovery if the neutrino is a Majorana particle. In the case of a normal ordering () a statistical analysis [12] suggests that the probability of discovery would be rather large, around 50%.
Reaching a sensitivity of 1027 yr in the half-life requires larger exposures (the product of fiducial mass M and observation time t), and thus larger detectors than those of the current generation. The number of events observed in a detector containing a mass M of a ββ0ν decaying isotope of atomic weight W and taking data over a period of time t is related with through:
where NA is the Avogadro number and ϵ the detector efficiency. In the absence of background, the observation of a single event would determine the existence of the process and measure the value of . For example, if = 1027 year, the observation of one event in one year in a detector with 30% efficiency would require a mass of 1 tonne.
In the presence of backgrounds, however, the sensitivity to will scale like (where N is the number of observed events) rather than scaling like 1/N as in the case of a background-free experiment. Consequently, the sensitivity to improves with rather than with Mt. Alas, equation 1 dictates that the sensitivity to the physical parameter (the effective neutrino mass mββ) goes with the square root of the half-life, and thus each order of magnitude of improvement in the latter brings in only a three factor improvement in the former. In an experiment where backgrounds need to be subtracted, on the other hand, one needs an increase of two orders of magnitude in the exposure Mt to improve one order of magnitude in . It follows that the next generation of ββ0ν experiments must feature target masses in the tonne-range, while aiming to reduce backgrounds to virtually zero.
Among all the ββ decay isotopes where ββ0ν processes could occur, 136Xe is the cheapest and easiest to obtain. Furthermore, xenon is a noble gas that can be dissolved in liquid scintillator (the approach of KamLAND-Zen, from an original idea by Raghavan [13]) or used to build TPCs. The EXO collaboration has pioneered the LXe technology, while the NEXT program [14] is leading the development of the HPXe technology.
When compared with the other xenon-based experiments, the HPXe technology has the advantage of very good intrinsic energy resolution and the availability of a topological signature (the observation of the two electrons characteristic of the ββ0ν decay) that permits a very low background count in the region of interest (ROI) near Qββ. The main disadvantage is a relatively lower selection efficiency, of the order of 30%, mostly due to the losses of events that radiate bremsstrahlung photons and to the cost of imposing topological recognition. Although not as compact as LXe TPCs, at sufficiently large pressures (e.g.,15 bar) a HPXe of relatively modest size (about 10 m3 of volume) can host masses in the ton scale. Furthermore, the possibility of tagging the Ba++ nuclei produced in the ββ0ν decay of xenon, as pointed out originally by Moe [15], opens up the possibility of background-free searches for xenon-based TPCs.
This review is organized as follows. Fundamentals are discussed in section 2. A quick historical review of the field is presented in section 3. Section 4 is devoted to the NEXT program. In section 5 the AXEL and PANDA-X-III proposals are described. Section 6 describes the on-going efforts in barium tagging in HPXe detectors. An outlook is presented in section 7.
2. Fundamentals
2.1. Operational Parameters of a HPXe TPC: Pressure, Temperature and Density
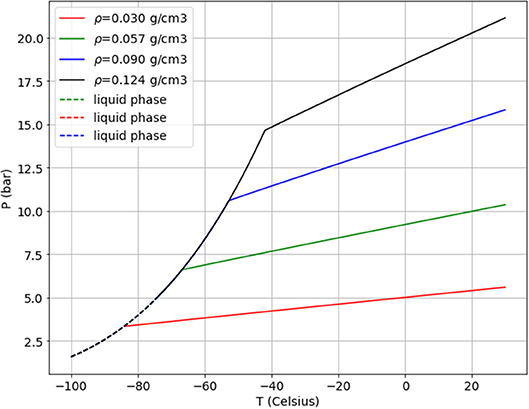
So far, HPXe detectors have operated at ambient temperature with pressures varying between 5 bar—St.Gotthard TPC [16]— and 20 bar—NEXT-DBDM prototype [17]. The NEXT-White detector [18] is currently taking data at 10 bar. In practice, at standard temperature, the operational pressure for ton-scale detectors will be in the range 10 bar to 20 bar. Given the density of xenon gas at a pressure of 1 bar and temperature of 300 K (5.761 kg m−3), a HPXe TPC of 10 m3 operating at 10 bar would contain a target mass of near 600 kg (1.2 ton at 20 bar). The detector dimensions are large (3.2 m length by 3 m diameter) but technically feasible. On the other hand, the NEXT demonstrators (NEXT-DEMO, NEXT-DBDM and NEXT-White) have shown excellent energy resolution and a powerful topological signature in this pressure range.
However, pressure can be traded with temperature, as illustrated in Figure 1, which shows the four isochoric (constant density) curves corresponding to pressures of 5, 10, 15, and 20 bar (at a temperature of 20 °C). An interesting possibility would be cooling the detector to temperatures near the liquefaction point (e.g., −70 °C for a density of 0.057 g cm−3). The advantages of operating at low temperatures will be discussed in section 4.
2.2. Ionization
When a charged particle propagates through a noble gas, the Coulomb interaction with the atoms results in ionization of the medium, releasing on average electron-ion pairs and Nex excited atoms. Sub-excitation electrons, (e.g., free electrons with a kinetic energy lower than the energy of the first excited level) are also produced. This can be expressed as [19]:
where E is the energy deposited in the medium in the form of ionization, excitation, and sub-excitation electrons; Ni is the number of electron-ion pairs produced at an average energy deposition Ei, Nex is the number of excited atoms produced at an average energy deposition Eex and ϵ is the average kinetic energy of sub-excitation electrons. Then the expected number of electrons produced for an energy deposition E is:
where WI is the average energy required to produce one electron-ion pair. In xenon gas WI = 21.9 eV [19]. A ββ0ν event of energy 2458 keV results, therefore, in the average production of 112 237 electron-ion pairs. In a HPXe TPC a moderate electric field will drift the electrons toward the anode and the ions toward the cathode, minimizing recombination.
2.3. Scintillation
The propagation of a charged particle in a noble gas also results in the emission of VUV scintillation light (with an average wavelength of 172 nm in xenon). Defining Ws as the average energy needed in the creation of one primary scintillation photon, the average number of scintillation photons produced when a particle releases its energy E in the gas is:
The NEXT collaboration has measured the value of Ws in xenon gas to be [20]:
This measurement was carried out using pressures of 1, 2, and 3 bar and a reduced electric drift field of 2 V/cm/torr. Thus a ββ0ν event will release on average 32, 342 photons. Since light production is isotropic, only a small fraction of the produced photons, Ω (typically of the order of a small %) can be collected. Measurement of the primary scintillation, however, is crucial for a ββ0ν detector, as it signals t0. A measurement of t0 is essential to fiducialize the events and remove the large rate of background events that accumulate at the electrodes as well as to correct for charge losses occurring during charge drift. Without such corrections, the performance of the detector both in terms of background rate and resolution is seriously compromised.
2.4. Electron and Ion Diffusion
As the ionization electrons (and the positive ions) drift toward the anode (cathode) under the action of the electric field, they interact with the noble gas atoms, resulting in both longitudinal and transverse diffusion.
Defining as the density of electrons per unit volume, DL(T) as the longitudinal (transverse) diffusion coefficient(s), vd as the drift velocity and η as the attachment coefficient one can write:
where the formula applies far from the TPC boundaries [3]. Here x′, y′, z′ and t denote position and time measured typically at the charge collection plane (the anode), and (x, y, z, t0) refer to the initial position and time of the ionization cloud, e.g., the interaction point, assumed to be point-like and containing electrons. The solution in Equation (7) is an asymmetric Gaussian cloud that broadens and loses carriers as it goes on. Arbitrary track topologies can be propagated directly by superposition of such solutions. Choosing z = 0 as the coordinate of the amplification plane, and assuming that all charge arrives at a fixed time t-t0 ≃ z/vd, Equation (7) simplifies to:
where . As it turns out, the electrons produced in a ββ0ν decay produce extended tracks in a HPXe detector. One can still make use of Equation (8) making the approximation that the track consists of a superposition of point-like energy depositions that arrive at successive times to the anode.
Diffusion in pure xenon is large, with , and , where L is the drift length in meters. As a consequence, the ionization electrons produced by tracks located at relatively long distances from the anode will have spread considerably both in the longitudinal and transverse coordinates, and the resulting reconstructed image of the track will be consequently blurred. This undesirable effect can be limited by using mixtures that add a quencher capable of cooling the diffusion electrons, therefore reducing the diffusion.
2.5. Electron Lifetime
As primary electrons drift to the anode, some of them will be absorbed by impurities in the gas. This results in the so-called “electron lifetime”:
Thus, if the initial number of drift electrons is n0 (at t0), the number n reaching the anode at time t will be:
The main cause of attachment in large TPCs is related to the presence of O2 [21]. For a given fraction of oxygen concentration, fO2, the lifetime is inversely proportional to both the square of the pressure, P, and . The only realistic way to achieve the necessary purity levels is through material selection and continuous recirculation and purification, to minimize the factor fO2. The dependence on 1/P2 is also a major constraint for the operational pressure. In pure xenon, the drift velocity is 1 mm μs−1, and thus 1 ms is required to drift 1 m. The drift length of a next-generation HPXe detector with a mass in the ton scale will be in the range 1 m to 3 m. An electron lifetime in the range 10–30 ms would translate in a 10% charge loss at the maximum drift length. This energy loss can be computed event by event, if t0 is known, and therefore a correction can be applied, with a residual relative error on the energy equal to the relative error on the determination of the lifetime. Thus, a relative error of 5% in the determination of the lifetime would translate into a residual of 0.5%, which is of the same order of the practical intrinsic resolution in an electroluminescent HPXe TPC (see section 4). Thus, long lifetimes and precise lifetime corrections (which imply a precise measurement of t0) are a must for a HPXe TPC aiming for the best energy resolution. Without t0 the fluctuations in energy introduced by attachment at the large drift distances become very large.
2.6. Intrinsic Energy Resolution in Xenon
Excellent energy resolution is a crucial ingredient for a ββ0ν experiment. Indeed, physics allows such resolution to be attained in a gaseous xenon TPC. However, those very same physics processes limit the resolution in a liquid xenon TPC. This is clearly seen in Figure 2, reproduced from Bolotnikov and Ramsey [22]. The resolutions displayed were extracted from the photo-conversion peak of the 662 keV gamma ray from the 137Cs isotope. Only the ionization signal was detected. A striking feature in Figure 2 is the apparent transition at density ρt ~ 0.55 g/cm3. Below this density, the energy resolution is approximately constant:
For densities greater than ρt, energy resolution deteriorates rapidly, approaching a plateau at LXe density.
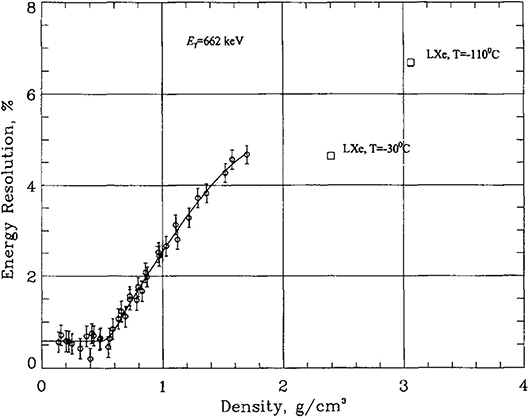
Figure 2. The energy resolution (FWHM) is shown for 137Cs 662 keV gamma rays, as a function of xenon density, for the ionization signal only. Reproduced from Bolotnikov and Ramsey [22].
The most plausible explanation underlying this strange behavior is the appearance, as density increases, of two-phase xenon ([23] and references therein). In contrast, given the xenon critical density, the intrinsic resolution in the gas phase is very good up to pressures in the vicinity of 50 bar. Extrapolating the observed relative resolution in Figure 2 as to the 136Xe Q-value (Qββ), allows one to predict the intrinsic energy resolution in xenon gas at the region of interest for ββ0ν searches to be δE/E = 3 × 10−3FWHM.
Based on ionization signals only, the above energy resolution reflects an order of magnitude of improvement relative to liquid xenon. For densities less than ρt, the measured energy resolution in Figure 2 matches the prediction based on Fano's theory [24]. The Fano factor F reflects a constraint, for a fixed energy deposited, on the fluctuations in energy partition between excitation and the ionization yield NI. For electrons depositing a fixed energy E, the rms fluctuations σI in the total number of free electrons NI can be expressed as For pure gaseous xenon (GXe) various measurements [23] show that FGXe = 0.15 ± 0.02. In liquid xenon (LXe), however, the anomalously large fluctuations in the partitioning of energy to ionization produce an anomalous Fano factor of FLXe ~ 20, larger than the one corresponding to xenon gas by about two orders of magnitude. The EXO Collaboration has demonstrated that a better energy resolution (3.86% FWHM) can be obtained in liquid xenon, combining scintillation and ionization signals, since they are anticorrelated [25, 26]. However, this value is still much larger than the intrinsic resolution of gaseous xenon.
2.7. Electroluminescence
2.7.1. The Gas Proportional Scintillation Chamber
The principle of a Gas Proportional Scintillation Chamber (GPSC) is the following [27]. A GPSC is a chamber filled with a noble gas. An X-ray enters through the chamber window and is absorbed in a region of weak electric field (> 0.8 kV cm−1 bar−1) known as the drift region. The ionization electrons drift under such a field to a region of a moderately high electric field (around 3 kV cm−1 bar−1), the so-called scintillation or EL region. There, each electron is accelerated so that it excites, but does not ionize, the gas atoms/molecules. The excited atoms decay, emitting UV light (the so-called secondary scintillation), which is detected by photosensors. The intensity of the secondary scintillation light is at least two orders of magnitude higher than that of the primary scintillation. However, since the secondary scintillation is produced while the electrons drift, its latency is much longer than that of the primary scintillation, and its rise time is much longer (up to hundreds of μs for ββ0ν events, compared to a few ns). For properly chosen electric field strengths and EL region spatial widths, the number nph of secondary scintillation photons produced by a single primary electron is nearly constant and can reach values of the order of one thousand photons per electron. The average total number, Nt, of secondary scintillation photons produced by an interaction is then Nt = nph · NI (where NI is the number of primary ionization electrons); that is, the photosensor signal amplitude is nearly proportional to E.
What made GPSCs extraordinarily attractive was their improved energy resolution compared with conventional Proportional Chambers (PC). In a PC, the primary electrons are left to drift toward a strong electric field region, usually in the vicinity of a small diameter (typically 25 μm) anode wire. In this region, electrons engage in ionizing collisions that lead to an avalanche with an average multiplication gain M of the order of 103 to 104. If M is not too large, space charge effects can be neglected, and the average number of electrons at the end of the avalanche, Na = M · NI, is also proportional to the energy E of the absorbed radiation. However, for PC detectors, there are fluctuations not only in NI but also in M. For GPSCs, since the gain is achieved through a scintillation process with almost no fluctuations, only fluctuations in NI and in the photosensor need to be considered, and a better energy resolution can be achieved.
2.7.2. Electroluminescent Yield
A detailed Monte Carlo study of the energy resolution that can be achieved in a high pressure xenon TPC with electroluminescent amplification (HPXe-EL TPC) as a function of the EL yield was performed in Oliveira et al. [28]. The study obtained a formula for the the reduced electroluminescence yield, , as a function of the reduced electric field, .
where the reduced electroluminescence yield is defined as the number of photons emitted per primary electron and per unit of drift length divided by the pressure of the gas, and E/p is expressed in kV cm−1bar−1.
The formula was found to be in good agreement with experimental data measured at 1 bar [29].
2.7.3. Energy Resolution in an EL TPC
One of the desirable features of a HPXe-EL TPC is its excellent intrinsic energy resolution due to the small value of the Fano factor in gaseous xenon and to the small fluctuations of the EL yield. Following Oliveira et al. [28], the resolution RE (FWHM) of a HPXe-EL TPC can be written as:
In Equation (14) the factor corresponds to the relation between the FWHM and the standard deviation σ, of a given probability distribution (). The first term of the expression is related to fluctuations in the number of primary charges created per event, Ne, the second to fluctuations in the number of EL photons produced per primary electron, NEL, the third reflects the variations in the number of photoelectrons extracted to the photosensor (e.g., PMTs, SiPMs) per decay, Nep, and the fourth the distribution in the photosensor single electron pulse height, Gq.
The primary charge fluctuations are described by the Fano factor, . The fluctuations associated with the electroluminescence production are described by the parameter J, defined as the relative variance in the number of emitted VUV photons per primary electron, . The conversion of VUV photons into photoelectrons follows a Poisson distribution, and thus . The fluctuations in the photoelectron multiplication gain can be described by [28], a conservative upper bound both for PMTs and SiPMs. Taking into account the previous relation, Equation (14) can be rewritten as:
The first term in Equation (15), R(Fano), corresponds to the intrinsic resolution in xenon, the second term, R(EL), to the resolution associated to fluctuations in electroluminescence and the third, R(EP), to fluctuations in the number of photoelectrons produced in the photosensor plane per ββ0ν decay, , which can be obtained as:
where k is the fraction of EL photons produced per ββ0ν decay that gives rise to the production of a photoelectron.
Figure 3 shows the simulation of EL yield and energy resolution, RE as a function of the reduced electric field of a HPXe-EL TPC operating at 15 bar for the energy corresponding to Qββ(2458 keV). The values of the EL width (relevant for the yield) and of k (relevant for the resolution) correspond to those of the NEXT-100 detector. Notice that R(Fano) is constant, R(EL) is essentially negligible and R(EP) improves quickly with the reduced field E/P. A typical value of operation for E/P is such that R(Fano) = R(EL) (E/P ~ 2). The combined resolution at this value is around 0.5% FWHM and the yield around 500 photons per electron. Increasing E/P results in very little improvement in resolution.
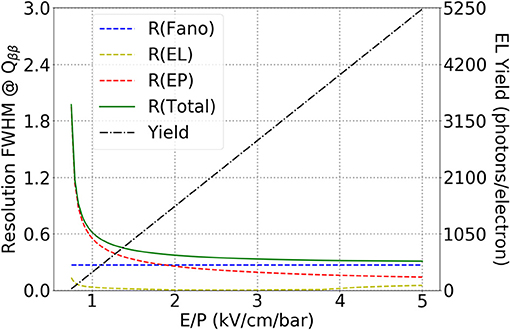
Figure 3. Energy resolution terms and EL yield characteristic of a HPXe-EL TPC as a function of the reduced electric field for an EL gap of 6 mm a value of k ~ 0.016 and a pressure of 15 bar.
2.8. Avalanche Multiplication in HPXe Applied to ββ0ν Searches
The use of avalanche multiplication in HPXe detectors searching for ββ0ν processes presents two distinct problems. First, the fluctuation in the gain, G, is considerably larger than F in gas proportional counters involving avalanche multiplication and thus becomes the dominant term in the resolution. Second, electron multiplication in pure xenon is difficult due to the fact that VUV scintillation light, copiously produced in the multiplication process, ejects electrons from the metallic surfaces defining the electrodes. Those electrons, in turn, ionize the gas to the point of breakdown.
The use of quenchers, on the other hand, suppresses the primary scintillation light and has a heavy cost in terms of energy resolution and particle identification (without primary scintillation it is not possible to define t0). Two approaches have been considered to solve this problem: a) the use of a “magic gas,” capable of absorbing the VUV light emitted by xenon and re-emitting it at a more manageable wavelength (e.g., in the visible region), without introducing extra fluctuations, and b) the use of micro-pattern devices, such as Micromegas or GEMs, whose confined geometrical structure makes them capable, a priori, of operating at high pressure without quenchers.
This second possibility was explored in Balan et al. [30]. While Micromegas were found, indeed, robust enough to allow operation in pure xenon and at high pressures, their resolution was measured to degrade with increased pressure. It was found that the resolution attainable at Qββ by micro-bulk micromegas at 10 bar would be 3%, to be compared with that of 0.4% found in Fernandes et al. [20] using electroluminescence. Both measurements were carried out with very small setups, in close-to-ideal conditions, and therefore can be taken as reflecting the intrinsic performance of the devices under study.
No magic gas capable of re-emitting xenon scintillation light at longer wavelengths has been found so far. Penning mixtures have been tried as a part of the R&D of the NEXT collaboration, as will be further described in section 4.
2.9. Topological Signature
Another major advantage of gas relative to liquid—and in general relative to high density calorimeters—is the ability to exploit the topological signature of a ββ0ν event, that is the capability to image the tracks left in the gas by the two electrons produced in the ββ0ν decay. At 15 bar the track length of the electrons is of the order of 15 cm and can easily be reconstructed in a HPXe TPC. Such a topological signature is not available in LXe detectors, due to the high density of the liquid phase—in fact, most other experimental techniques are based on high density calorimeters, none of which can reconstruct the electron trajectories.
An electron propagating in high density xenon ionizes the medium and results in a random trajectory due to large multiple scattering. Delta rays and bremsstrahlung photons are emitted along the trajectory, as is shown in Figure 4. Even with a detector capable of reconstructing perfectly the electron trajectory, the track would still be twisted and diffuse due to multiple scattering and the emission of delta rays and photons. Diffusion will further blur the “electron picture.”
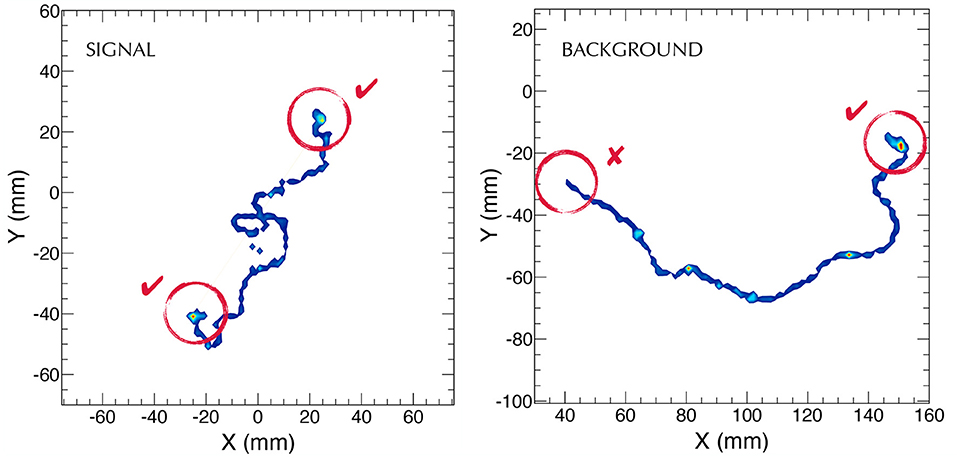
Figure 4. The left panel shows two electrons emitted in a ββ0ν decay propagating in HPXe with perfect track reconstruction; the right panel shows a single background electron produced by a photoelectric interaction from a 214Bi gamma of energy very close to Qββ. While the energy of the background electron could enter the ROI, the two topologies are different. A ββ0ν event results in two electrons which are ended in two areas of denser energy depositions as the electron deposits suddenly its energy near the end-of-the-ionization path (Bragg peak). In the case of a background electron there is only a single area of higher energy density. Figure from Martín-Albo et al. [31].
There are some differences between a background electron with energy near Qββ and a “double electron” event emitted by a ββ0ν decay where the Qββ energy is shared between the two electrons. Naively one could expect to be able to distinguish the emission vertex, but this is not possible due to multiple scattering. A lower number of “satellite photons” (e.g., photons deposited in the chamber and not associated to the electron track, due to bremsstrahlung radiation) are expected for signal with respect to the background, due to the fact that the background electron has on average twice the energy of the signal electrons and radiates considerably more. Also, the initial trajectory of the background electron is less twisted than that of the double electrons, since multiple scattering is inversely proportional to the momentum. However, the more powerful “smoking gun” separating signal from background is the energy deposited at the end of the electron trajectory. Electrons moving through xenon gas lose energy at an approximately fixed rate until they become non-relativistic. At the end of the trajectory the 1/v2 rise of the energy loss (where v is the speed of the particle) leads to a significant energy deposition in a compact region, which can be referred to as a ‘blob.’ The two electrons produced in double beta decay events appear as a single continuous trajectory with a blob at each end. Background events from single electrons (photoelectric or Compton interactions of gammas), however, typically leave a single continuous track with only one blob.
Plotting the energy of each blob reveals a clear separation between signal and background event. The left panel of Figure 5 shows the case for background electrons, while the right plot shows the case for signal. In the first case, the energy of the lower energy blob is much smaller than the energy of the higher energy blob, and in the second case both are roughly the same. A cut requiring that the energy of both blobs is larger than about 250 keV separates very effectively single and double electrons.
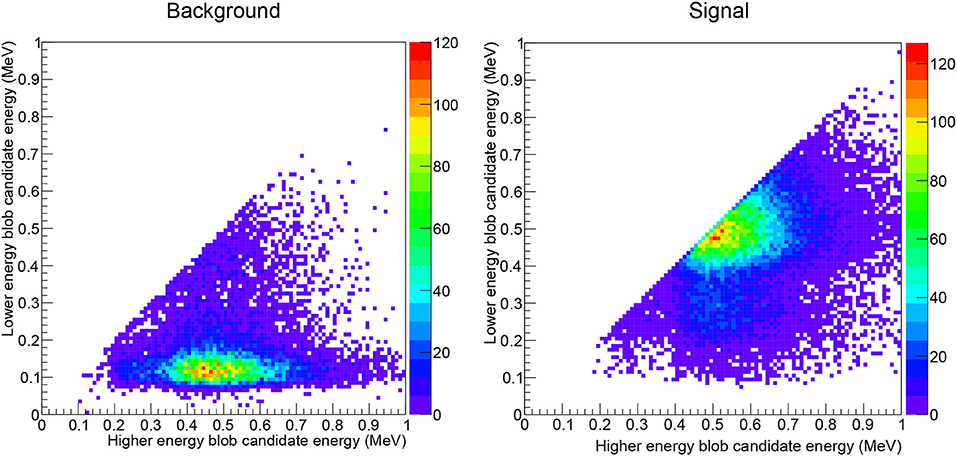
Figure 5. The left panel shows the energy of the blob of lower energy vs. the energy of the blob of higher energy for a background electron propagating in a HPXe TPC—perfect track reconstruction. The right plot shows the same distribution referred to two electrons produced in a ββ0ν propagating under the same conditions. In the first case the energy of the lower energy blob is much smaller than the energy of the higher energy blob, in the second case both are roughly the same.
3. The Development of the HPXe and HPXe-EL Technology for ββ0ν Searches
The first proposal to search for ββ0ν decays using 136Xe was published in 1976 [32] (an even earlier paper by the same authors dates back to 1961 [33]). The proposed technology was a self-triggered cloud chamber filled with a mixture of xenon and helium, with helium being the permanent gas of the chamber and xenon acting as condensable vapor. Electroluminescence was proposed to trigger the chamber and to measure the energy of the particles. The setup included an electric field, to produce electroluminescence and clear the ionization, and a magnetic field whose role was to bend the tracks, and thus separate single electrons arising from backgrounds from double electrons arising from ββ decays. Thus, remarkably, two of the major assets of the HPXe-EL technology (e.g., energy resolution thanks to proportional amplification of the ionization signal and a topological signature to distinguish two electrons from backgrounds) were exploited in this pioneer work.
The concept of the gas proportional scintillation counter (GPSC), discussed in section 2.7.1, dates back to 1967 [27]. In 1975 the notion of the GPSC was combined with that of a TPC, resulting in the Scintillation Drift Chamber (SDC) [34]. A proposal to build a HPXe-EL TPC was made in 1983 [35] (see also [36]). A large SDC with 19 PMTs [37] demonstrated excellent energy resolution at high pressure (9 bar) for high energy X-rays, consistently extrapolating to 0.5% FWHM at Qββ.
And yet, the early attempts to search for ββ0ν processes with high pressure xenon chambers were not based on electroluminescence. The first such attempt was a small ionization chamber (with a mass of 627 g) operating at a pressure of 3 MPa (30 bar) built at the Baksan neutrino observatory [38]. The resolution achieved by this early apparatus (2.7% FWHM at Qββ) was, in fact, better than that attained by subsequent detectors based on multiplication gain. The setup, however, had large 222Rn contamination, due to radon emanating from the purification getters. The Baksan experiment managed to set a first limit of 5.5 × 1019 yr on the lifetime of the ββ0ν decay for 136Xe.
At about the same time, a multi-element proportional chamber, operating at 10 bar and with a mass of around 4 kg was built by Fiorini and collaborators—the so-called “Milano experiment”—[39]. The resolution achieved was 4.2% FWHM at Qββ. The setup was operated at the LNGS laboratory with natural xenon and with xenon enriched at 64% in the isotope 136Xe. The detector was able to perform a crude reconstruction of the event topology that allowed for the separation between “single cluster events” (e.g., single or double electrons with no satellite energy depositions) and “multiple cluster events” (e.g., background events where additional energy deposition was identified). However, the reconstruction could not separate between single and double electrons. The main sources of background were high energy gammas coming from the natural radioactive decay chains of the nuclei concentrated mainly in the steel wires making up the cells as well as the titanium vessel. The background counting rates were (5.1 ± 0.3) × 10−3 counts/keV/hour for the enriched xenon sample. The best sensitivity achieved was 1.2 × 1022 yr (at 95% CL) in the lifetime of the ββ0ν decay for 136Xe [40, 41]. The experiment did not observe the ββ2ν mode, setting a limit of 1.6 × 1020 yr at the 95%CL [41].
The Gotthard TPC (GTPC) was built in 1987 [16]. It was a 300 l HPXe detector, built with radiopure materials and operating at a pressure of 5 bar in the St. Gotthard Tunnel Underground Laboratory. The experiment used xenon enriched at 62.5% with the isotope 136Xe. Ionization was read by charge amplification in a wire plane and the transverse position was determined by XY strips. Being a TPC, the longitudinal position was determined by the arrival time of the ionization charge.
In order to quench the VUV light, the GTPC used a mixture that contained 5% of methane. As a consequence, the TPC lacked the information on the start time of the event (t0) and could not use a fiducial veto on the tracks along the Z coordinate. The lack of t0 was a major limitation of this pioneer experiment, since one of the most important backgrounds in a HPXe TPC is the decay:
Due to 222Rn contamination, there is a steady-state concentration of 214Bi in the cathode. In a HPXe TPC with t0 the bismuth decay described in Equation (17) can be vetoed by requiring a fiducial cut on Z. In the absence of t0 this background becomes dominant, although it can be partially vetoed by looking for a delayed coincidence with an alpha particle due to the decay:
The energy resolution of the GTPC was 6.6% FWHM at Qββ. This was much worse than the intrinsic resolution expected in xenon. The reasons for the degraded performance were the fluctuations in avalanche gain, and the quenching of the scintillation by the gas mixture, which introduced an irreducible additional fluctuation.
A first search for ββ0ν events was published in 1991 [42], followed by an improved result in 1998 [43]. The total exposure of the experiment was 12 843 h, corresponding to about 1.5 yr. The experiment set a limit of 4.4 × 1023 yr in the lifetime of the ββ0ν decay mode of 136Xe and a limit of 0.72 × 1022 yr in the ββ2ν mode.
The GTPC was the first detector to demonstrate the topological signature available to a (high pressure) gas TPC. A peculiarity of the experimental technique was that the scan of candidates was done visually. The efficiency and rejection power of the procedure was evaluated by mixing Monte Carlo events with real data. A 68% acceptance for double electrons and a rejection power of 96.5% for single electrons was found. This performance is similar to the best results obtained by the NEXT and PANDA-III-X collaborations using deep neural networks, as will be discussed in sections 4 and 5.
The dominant source of background in the GTPC were electrons emanating from the cathode that could not be rejected due to the lack of t0. Still, the background rate at the ROI of the detector was 0.01counts/(keV · kg · y), the lowest among all the ββ0ν searches of the time.
The original proposal for the EXO detector, published in 19991, presented a large version of the GTPC. Like the former, it used multiplication gain to read the ionization, substituting the wire-pad arrangement by micro-pattern structures (GEMs). Operation at a pressure of 5 bar was assumed. PMTs placed in the barrel region were used to read the primary scintillation and thus measure t0. In addition, a system of lasers to tag the Ba++ ion produced in the ββ0ν decay of 136Xe on the fly was envisioned.
The EXO design assumed that the xenon would be mixed with another gas capable of quenching the xenon VUV light (so that the detector could be operated in the regime of charge multiplication without breaking the gas) and at the same time capable of neutralizing one of the positive charges of the Ba++ ion, so that tagging based on laser-induced resonance excitation of Ba+ could be used. At the same time, this gas should be able to cool the drifting electrons, reducing diffusion, and re-emit in the visible region, so that t0 could be measured. Alas, such a “magic gas” was found neither by EXO nor by extensive R&D conducted later by NEXT (see section 4).
To summarize, the GPSC was invented in 1965 and electroluminescence was proposed as early as 1975 for a ββ0ν detector. However, the Baksan, Milano and Gotthard experiments were all based on electron multiplication for the readout of the ionization. None of these experiments had good energy resolution, but the Gotthard TPC demonstrated a powerful topological signature and achieved a very good background rate in the ROI (for the time), in spite of the lack of t0 which was responsible for most of its background rate. The original EXO proposal also considered avalanche gain as the choice option and later switched to liquid xenon.
The possibility of using a HPXe-EL TPC for ββ0ν searches was resurrected in 2009 [44] and adopted as the baseline solution by the NEXT collaboration in its Letter of Intent [45]. The choice of an asymmetric HPXe-EL TPC with an energy plane based on PMTs for energy measurement and a tracking plane based on SiPMs was established in the NEXT conceptual design report [46] and further developed in the technical design report (TDR) [47]
4. The NEXT Program
The Neutrino Experiment with a Xenon TPC (NEXT) is an experimental program developing the technology of high-pressure xenon gas Time Projection Chambers (TPCs) with electroluminescent amplification for neutrinoless double beta decay searches (ββ0ν).
The first phase of the program included the construction, commissioning and operation of two prototypes, called NEXT-DBDM and NEXT-DEMO (with masses around 1 kg). The NEXT-White2 detector, containing 5 kg of xenon, implements the second phase of the program. NEXT-White has been running successfully since October 2016 at the Laboratorio Subterráneo de Canfranc (LSC), Spain.
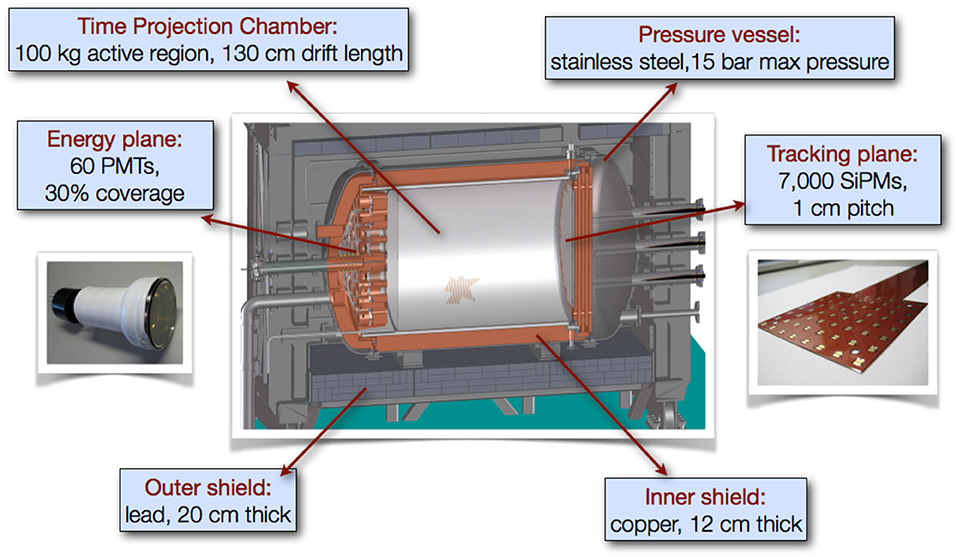
NEXT-100 constitutes the third phase of the program. It is a radiopure detector deploying 100 kg of xenon at 15 bar and scaling up NEXT-White by slightly more than 2:1 in both the longitudinal and the radial dimensions. In addition to a physics potential competitive with the best current experiments in the field, NEXT-100 can be considered as a large-scale demonstrator of the suitability of the HPXe-EL technology for detector masses in the ton-scale.
The fourth envisioned phase of the program is called NEXT-2.0, a detector that will multiply the mass of NEXT-100 by a factor of 5 while reducing NEXT-100 background in the ROI by at least one order of magnitude, thanks to the combination of an improved topological signature and a reduced radioactive budget. Furthermore, NEXT-2.0 could implement Ba++-tagging based in single-molecule fluorescence imaging (SMFI) (see section 6). The importance of SMFI Ba++-tagging cannot be overemphasized, since it would permit a background-free experiment at the ton scale leading to a full exploration of the Inverse Hierarchy (IH) and beyond, with a high probability of discovery.
4.1. The DEMO and DBDM Prototypes
The NEXT prototypes were the first HPXe-EL chambers built since the pioneer Gotthard TPC experiment discussed in section 3. NEXT-DBDM was instrumented with a single energy plane made of an array of 19 Hamamatsu R7378A 1” photomultipliers capable of operating up to 20 bar pressure. The detector geometry was designed to minimize the dependence of light collection on position. Without a light sensor array near the EL region, precise tracking information was not available and only coarse average position could be obtained using the PMT array light pattern. That was sufficient, nonetheless, to fiducialize events within regions of the TPC with uniform light collection efficiencies.
Figure 6 shows the most important result obtained with DBDM. The energy resolution was measured with xenon X-rays and with a radioactive 137Cs source, at pressures of 10 and 15 bar. The results obtained approached the intrinsic resolution that could be achieved in xenon (see discussion in section 2.7.3), extrapolating to 0.5% FWHM at Qββ3.
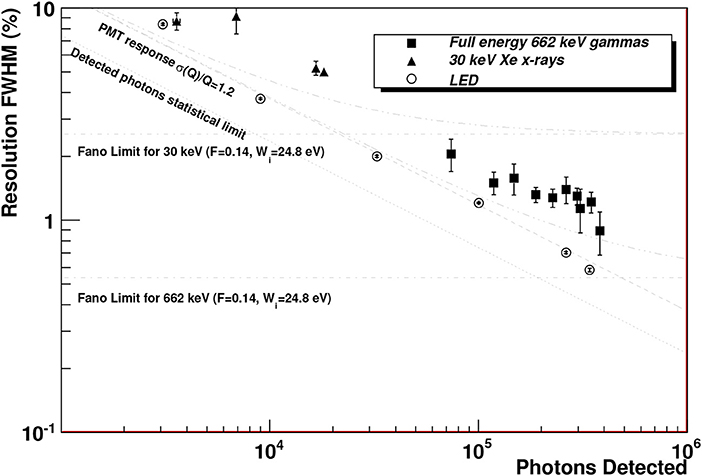
Figure 6. Energy resolution measured by NEXT-DBDM: Data points show the measured energy resolution for 662 keV gammas (squares), ~ 30 keV xenon X-rays (triangles) and LED light pulses (circles) as a function of the number of detected photons. The expected resolution including the intrinsic Fano factor, the statistical fluctuations on the number of detected photons and the PMT charge measurement variance are shown for X-rays (dot dot dashed) and for 662 keV gammas (dot dot dot dashed). Resolutions for the 662 keV peak were obtained from 15 bar data runs while X-ray resolutions were obtained from 10 bar runs. Figure from Álvarez et al. [17].
NEXT-DEMO was a larger-scale prototype of NEXT-100. The pressure vessel had a length of 60 cm and a diameter of 30 cm. The vessel could withstand a pressure of up to 15 bar but was normally operated at 10 bar. The energy plane was instrumented with 19 Hamamatsu R7378A PMTs (the same model as those used in DBDM) and a tracking plane made of 256 Hamamatsu silicon photomultipliers (SiPMs). The detector operated for several years, demonstrating: (a) excellent operational stability, with no leaks and very few sparks; (b) good energy resolution; (c) electron reconstruction using the SiPM tracking plane; (d) excellent electron drift lifetime, of the order of 10 ms [17, 48–51].
Figure 7 shows the first demonstration of topological signature in an HPXe-EL TPC. The left panel corresponds to single electrons due to photoelectric interactions of the 511 keV gamma emitted in 22Na decays. The right panel corresponds to tracks selected in the double escape peak of 208Tl and thus it is enriched in “double electrons” (pairs electron-positron). The plots show clearly the difference between “electron-like” and “double-electron like” events, which can be easily separated with a cut on the energy of the lower-energy blob as extensively discussed in Ferrario et al. [52].
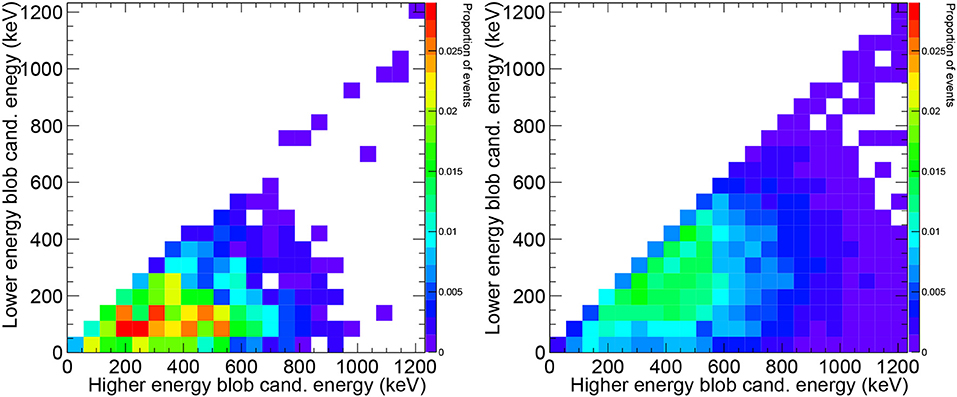
Figure 7. Energy distribution of the blobs at the end-point of single electrons coming from 22NA decays (Left) and tracks (mostly electron-positron pairs) coming from the 208Tl double escape peak (Right). Figure from Ferrario et al. [52].
4.2. The NEXT-White Detector
The NEXT-White apparatus [18] has roughly the same dimensions as the Gotthard TPC experiment and is currently the world's largest HPXe-EL TPC. The detector operates inside a pressure vessel fabricated with a radiopure titanium alloy, 316Ti[53]. The pressure vessel sits on a seismic table and is surrounded by a lead shield (the lead castle). Since a long electron lifetime is a must, the xenon circulates and is purified in a gas system described in great detail in Monrabal et al. [18]. An electron lifetime larger than 5 ms has been demonstrated to affect very little the energy resolution in NEW. This means that for NEXT-100, an electron lifetime of roughly 10 ms is required. The whole setup sits on top of a tramex platform elevated over the ground at Hall-A, in the LSC.
Figure 8 shows the NEXT-White detector and a selection of its main subsystems. The TPC is, in essence, a scaled-down version (2:1) of the NEXT-100 TPC, and its construction and operation have been essential to guide the design of the latter. It has a length of 664.5 mm and a diameter of 454 mm. The field cage body is a High Density Polyethylene (HDPE) cylindrical shell of 21 mm thickness. The inner part of the field cage body is machined to produce grooves, where radiopure copper rings are inserted (Figure 8a). The drift field is created by applying a voltage difference between the cathode and the gate through high voltage feedthroughs (Figure 8c). The field transports ionization electrons to the anode where they are amplified. The drift length is (530.3 ± 2.0) mm, and the drift voltage is 400 V cm−1.

Figure 8. Left: the NEXT-White detector at the LSC. Right: a selection of the main subsystems of NEXT-White: (a) the field cage; (b) the anode plate; (c) high voltage feedthrough; (d) energy plane; (e) PMTs used in the energy plane; (f) tracking plane; (g) kapton boards composing the tracking plane.
The amplification or electroluminescent region is the most delicate part of the detector, given the requirements for a high and yet very uniform electric field. The anode is defined by a Poly-Ethylenedioxythiophene (PEDOT) surface coated over a fused silica plate of 522 mm diameter and 3 mm thickness (Figure 8b). The entire region is mounted on top of the tracking plane to ensure its flatness and is only connected to the rest of the field cage when closing the detector. A thin layer of Tetraphenyl Butadiene (TPB), commonly used in noble gases detectors to shift VUV light to the visible spectrum is vacuum-deposited on top of the PEDOT. The EL gap is 6 mm wide.
The measurement of the event energy as well as the detection of the primary scintillation signal that determines the t0 of the event is performed by the NEXT-White energy plane (EP), shown in Figure 8d. The Hamamatsu R11410-10 PMTs (Figure 8e) are chosen for their low radioactivity ((0.37 ± 0.08) mBq unit−1 in 214Bi) [54] and good performance. Since they cannot withstand high pressure they are protected from the main gas volume by a radiopure copper plate, 120 mm thick, which also acts as shielding against external radiation. The PMTs are coupled to the xenon gas volume through 12 sapphire windows welded to a radiopure copper frame that seals against the copper plate. The windows are coated with PEDOT in order to define a ground while at the same time avoiding sharp electric field components near the PMT windows. A thin layer of TPB is vacuum-deposited on top of the PEDOT.
The tracking function in NEXT-White is performed by a plane holding a sparse matrix of SiPMs. The sensors have a size of 1 mm and are placed at a pitch of 10 mm. The tracking plane is placed 2 mm behind the end of the quartz plate that defines the anode with a total distance to the center of the EL region of 8 mm. The sensors are SensL C series model MicroFC-10035-SMT-GP with 35 μm cell size and a dark count of less than 100 kHz at room temperature. The cell's size is sufficient to guarantee good linearity and to avoid saturation in the expected operating regime (~ 250 pes μs−1). The SiPMs are distributed in 28 boards (DICE boards) with 8 x 8 pixels each for a total of 1792 sensors (Figure 8g). The DICE boards are mounted on a 120 mm thick copper plate intended to shield against external radiation. The material used for the DICE boards is a low-radioactivity kapton printed circuit with a flexible pigtail that passes through the copper, where it is connected to another kapton cable that brings the signal up to the feed-through. Each DICE has a temperature sensor to monitor the temperature of the gas and SiPMs and also a blue LED to allow calibration of the PMTs at the opposite end of the detector. The NEXT-White tracking plane (Figure 8f) is currently the only large system deploying SiPMs as light pixels in the world.
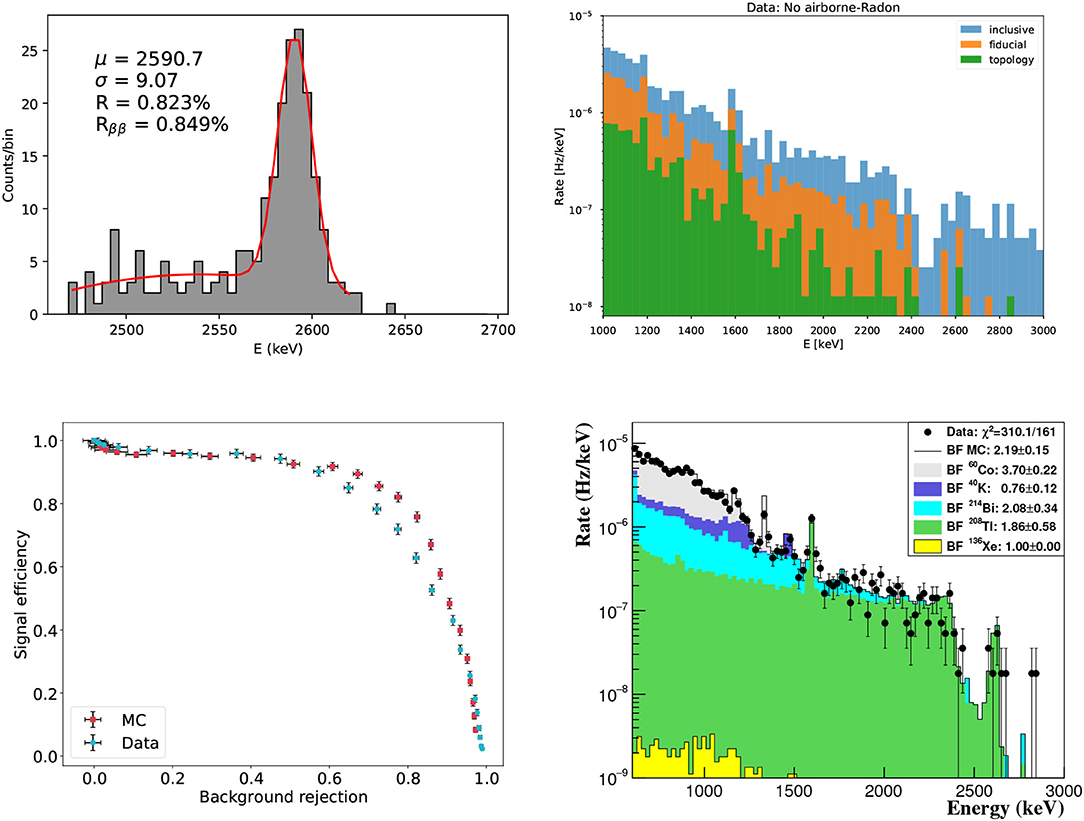
The detector operated with normal xenon during 7 months in 2017 at a pressure of 7 bar (Run II) and during 9 months in 2018 at a pressure of 10 bar (Run IV). Run V, with enriched xenon, has started in early 2019. Operation in Run II established a procedure to calibrate the detector with krypton decays [55] and provided initial measurements of energy resolution [56], electron drift parameters such as drift velocity, transversal and longitudinal diffusion [57] and a measurement of the impact of 222Rn in the radioactive budget, which was found to be small [58]. In addition, the performance of the topological signal was measured using dedicated calibration runs with a 228Th radioactive source. Figure 9 shows a selection of preliminary results, including resolution obtained at high energy fitting the 208Tl photopeak, which extrapolates to 0.85% FWHM at Qββ (top-left); rate (in Hz/keV) of background events as a function of energy after 41.5 days of low background run, for three different event selections (top-right); signal efficiency vs. background acceptance for the topological signature (bottom-left); and fiducial background energy spectra, showing good agreement between data and Monte Carlo (bottom-right).
Run IV has demonstrated excellent operational stability and a long electron lifetime, which in turn translates to improved resolution. Furthermore, the background rate of the detector has been reduced by a factor of 4 with respect to Run II, thanks to operation in a radon-free atmosphere and enhanced external shielding. Preliminary results indicate good agreement between the measured data and the Monte Carlo background model, with an average rate of 2 mHz.
4.3. The NEXT-100 Detector
The NEXT-100 apparatus is shown schematically in Figure 10. The fiducial region is a cylinder with a diameter of 1,050 mm and a length of 1,300 mm (1.27 m3 fiducial volume), holding a mass of 97 kg of xenon gas enriched at 90 % in 136Xeand operating at 15 bar. The energy plane (EP) features 60 PMTs. The tracking plane (TP) presents an array of 5,600 SiPMs. NEXT-100 is essentially a 2:1 scaled up version of NEXT-White.
The combination of excellent energy resolution and background rejection provided by the topological signature results in a very low background rate of 4.5 × 10−4 counts/kg/keV/yr [31]. The projected background in the ROI for NEXT-100 is 0.7 counts/yr, with the leading background sources being the PMTs and the substrates of the SiPMs as illustrated in Figure 11. The overall efficiency of the detector is 32%. NEXT-100 is scheduled to begin operations in 2020. NEXT-100 will reach a sensitivity of 1 × 1026 yr in after an exposure of 500 kg yr. Although this is the same sensitivity achieved by KamLAND-Zen, the capability of NEXT-100 to provide a nearly background-free experiment at the 100 kg scale, and the potential (discussed below) to improve its radioactive budget, resolution and topological signature so that background-free experiments at the ton scale are also possible, is the strongest asset of the experiment.
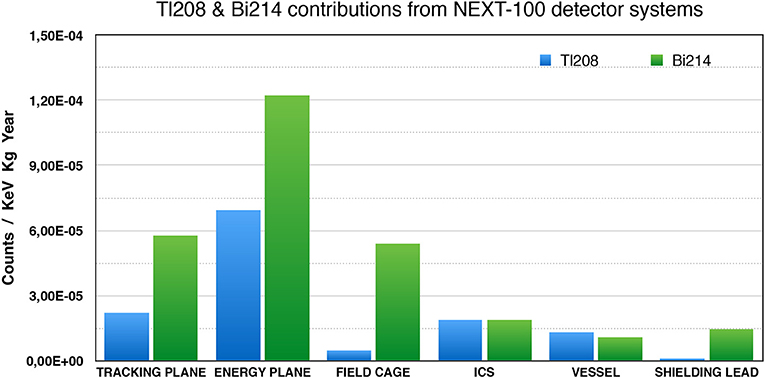
Figure 11. NEXT-100 background budget after selection. Figure from Muñoz Vidal [59].
4.4. Exploring the Inverted Hierarchy With NEXT-2.0
As discussed in the introduction, exploring the inverse hierarchy (IH) requires detectors with large masses (in the range of one ton) which should be ideally background-free. The detrimental effects of the presence of background are illustrated in Figure 12, which shows the sensitivity to mββ (using a reasonable set of nuclear matrix elements) of a fully efficient 136Xe experiment as a function of exposure, for different background rates. A fiducial exposure of almost 1.5 t yr (corresponding to an actual exposure of 5 t yr, when accounting for an efficiency of the order of 30%) is required for a full exploration of the inverse hierarchy for 0.1 events of background or less. The exposure increases to 2 t yr (6.6 t yr) for <1 events of background and degrades rapidly for larger backgrounds.
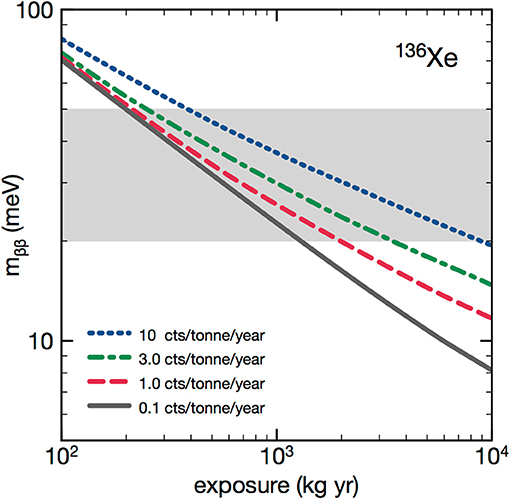
Figure 12. Sensitivity to mββ of a fully efficient 136Xe experiment as a function of the exposure, for different background rates [60].
The HPXe-EL technology can be scaled up to multi-tonne target masses while keeping extremely low levels of background by introducing several new technological advancements [14], including: (a) the replacement of PMTs (which are the leading source of background in NEXT-100) with SiPMs, which are intrinsically radiopure, resistant to pressure and able to provide better light collection; (b) operation of the detector at 175 K, not far from the gas triple point. Operation in this regime has two marked advantages: (i) it reduces the dark count rate of the SiPMs by a large factor (see, for instance, Figure 25, in reference [61]) and (ii) it permits operation at a lower pressure than NEXT-100 (15 bar at 293 K) for the same gas density, as shown in Figure 1. Reducing the pressure, in turn, simplifies the construction of future larger detectors; (c) operation of the detector with a low diffusion mixture, for example a 0.85/0.15 xenon/helium mixture [21], which reduces the large transverse diffusion of natural xenon gas from to , resulting in sharper reconstructed images for the electron trajectories and improving the performance of the topological signature [62]—other possible mixtures have been investigated in Henriques et al. [63].
The improvement of the topological signature in the low diffusion regime is illustrated in Figure 13. The left panel shows the three projections of a reconstructed Monte Carlo electron in the case of high diffusion (top display) and low diffusion (bottom display). For the large transverse diffusion of natural xenon (~ 10 mm, where L is the length drifted by the electrons), the optimal size of the x, y, z “voxels”, making up the reconstructed track is 10 × 10 × 5 mm3—for smaller voxels, the large diffusion results in disconnected tracks. For the smaller transverse diffusion of a 0.85/0.15 xenon/helium mixture, (~2 mm/) the track can then be reconstructed with much smaller voxels, 2 × 2 × 2 mm3. The right panel of Figure 13 shows the expected efficiency vs. rejection power of the topological cut separating single and double electrons for high diffusion (solid line, large voxels) and low diffusion (dashed line, small voxels). The figure of merit shown in the figure maximizes at an efficiency close to 70% in both cases, but the background accepted is 6.6% for high diffusion and 2.5% for low diffusion. Thus, a reduction by a factor of 2.6 in background is achieved.
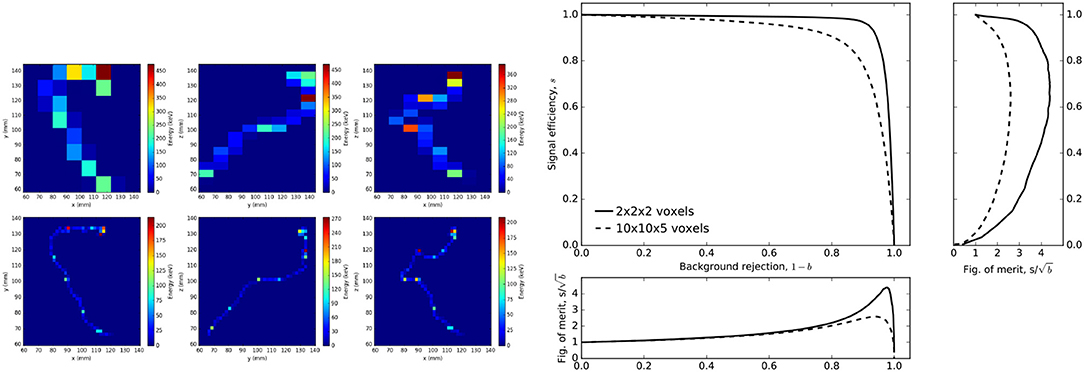
Figure 13. (Left) The three projections of a reconstructed Monte Carlo electron in NEXT-100 (top panels) and NEXT-2.0 (bottom panels). (Right) Signal efficiency vs. background rejection provided by the topological signature in both detectors. See text for details. Reproduced from Renner et al. [62].
The NEXT collaboration is planning a future detector, provisionally called NEXT-2.0, that will incorporate all of the above improvements while deploying masses in the ton scale. If the tantalizing possibility of tagging the Ba++ ion is confirmed, NEXT-2.0 could incorporate a Ba++ tagging system. The target background of NEXT-2.0 is <1 events t−1 yr−1, allowing the experiment to reach a sensitivity of 1 × 1027 yr in with an exposure of 5.0 t yr. This performance would improve the current state of the art by a factor of 10, opening the possibility for a discovery. With Ba++-tagging, NEXT-2.0 would be a truly background-free experiment, capable of exploring even further (or faster) the physical parameter space. Importantly, all the crucial technology improvements for NEXT-2.0 can be demonstrated by suitable upgrades to the NEXT-100 detector, which would permit testing each of the crucial steps leading to the ton-scale technology, namely cool gas operation, SiPM as energy sensors, low diffusion mixtures and barium tagging.
4.5. HPXe TPCs Based on Electron Multiplication: the NEXT-MM Prototype
Although the baseline of the NEXT program is electroluminescence, a vigorous R&D was conducted to assess the performance and potential of a HPXe TPC based on electron multiplication [64, 65]. As extensively discussed in this report, the use of avalanche gain to amplify the ionization signal implies a cost in energy resolution with respect to electroluminescence. Such a cost could, in principle, be compensated by other factors.
One of them is radiopurity. Micropattern structures such as micromegas are very light and can be manufactured with radiopure components (e.g., copper, kapton), thus offering a very radiopure readout system. Yet, the same applies to readouts based on SiPMs [66]. Indeed, as discussed above, the main source of internal background in the NEXT-White and NEXT-100 detectors is the PMTs in the energy plane. However, getting rid of the PMTs is not easy, since they are needed to detect primary scintillation and thus provide a measurement of t0. Indeed, the current trend in underground experiments both searching for dark matter and for ββ0ν decays is replacing the PMTs with SiPMs, mounted on ultra-pure substrates [61, 67]. Such a sensor arrangement will likely be as radiopure or more radiopure than micro-pattern-based readout planes.
The use of micromegas alone does not provide a way to measure t0 and therefore one would need to revert to an asymmetric TPC, perhaps considering a detector that uses a plane of SiPMs behind the cathode to read primary scintillation and a micromegas-based readout located in the anode that would provide the event energy and topology. This solution has the same drawback already mentioned when discussing the early EXO proposal. One needs to build a large energy plane anyway, which could measure the energy with far better resolution than the solution being adopted.
A second reason to consider a micro-pattern device readout is the possibility to combine a very fine pitch (e.g., finely pixelized micro-bulk micromegas) with a low diffusion gas mixture in order to improve the topological signature. In order to keep t0 such a low diffusion mixture also needs to shift the xenon VUV light to the visible or near UV spectrum, since the performance of micromegas in pure xenon deteriorates at high pressure, as discussed in section 2.
In Gonzalez-Diaz et al. [64] and Álvarez et al. [65], the NEXT collaboration investigated the possibility that a mixture of xenon with Trimethylamine (TMA) could reduce electron diffusion while simultaneously displaying the Penning effect and scintillation. Furthermore, TMA could also provide charge neutralization of Ba++ to Ba+, as needed for some Ba-tagging schemes (see section 6).
The studies were carried out with a medium-size HPXe TPC called NEXT-MM, of dimensions similar to NEXT-DEMO (73 L). The detector was instrumented with a large microbulk-Micromegas readout plane [65], covering an area of 700 cm2 and comprising 1,152 pixels of 8 × 8 mm2.
The main results of those studies, using a mixture containing 2.2% of TMA and operating at 10 bar were as follows:
1. The use of TMA allowed stable operation of the micromegas-based system at high pressure.
2. TMA quenches the primary VUV xenon scintillation light even in very small concentrations. On the other hand, TMA scintillation was observed above 250 nm at the level of 100 photons per MeV in Nakajima et al. [68]. In another study [69], TMA scintillation was not observed and a limit on re-emission with regard to the primary VUV light of 0.3% was set. The conclusion is that in xenon-TMA mixtures it is not possible to use scintillation to measure t0.
3. The use of TMA reduced by a large factor both the longitudinal and transverse diffusion with regard to pure xenon. The measured values of at 1 bar ranged between 340 and 649 depending of the value of the reduced electric field, a reduction by a factor of 2-3 with regard to pure xenon. The measured value of the transverse diffusion was , that is a factor of 10 with regard to pure xenon.
4. The energy resolution (FWHM) ultimately achieved on the full fiducial volume was 14.6% at 30 keV, with contributions from the limited S/N, sampling frequency and non-uniformity of the readout plane explaining the deterioration with respect to results obtained earlier in small setups (9%).
5. The calorimetric response to 511 keV and 1275 keV electron tracks extrapolated to Qββ gives energy resolutions varying from 3.2% FWHM (for the best sector) to 3.9% FWHM in the full TPC.
6. Due to the very low electron diffusion measured for the mixture (at the scale of 1 mm for 1 m drift), and the ease of increasing the readout granularity, the technology offers the possibility of mm-accurate true-3D reconstruction of MeV-electron tracks on large detection volumes and at high pressure. Unfortunately, the lack of a source of double electrons in the system prevented a full study characterizing the topological signature in this device similar to those carried out in NEXT-DEMO and NEXT-White.
In conclusion, this R&D confirmed both the advantages—excellent track reconstruction due to reduced diffusion—and disadvantages—worse energy resolution—of using electron amplification, known since the pioneer work of the Gotthard TPC. The fact that TMA does not behave as a “magical gas” (its scintillation cannot be used to measure t0) excludes its use for a future ton-scale experiment, unless alternative ways of measuring t0 are found.
5. Other HPXe proposals
5.1. AXEL
AXEL is an R&D lead by the U. of Kyoto, in Japan. The envisioned AXEL detector is almost identical to the NEXT design. Both are HPXe-EL TPCs, with an energy plane (AXEL assumes PMTs, as in the NEXT-100 detector) and a tracking plane based on SiPMs. In the AXEL concept, however, the SiPMs are VUV sensitive and provide a measurement of the energy of the event in addition to a reconstruction of the topological signal. Rather than an open EL region, AXEL introduces the concept of an Electroluminescence Light Collection Cell (ELCC), shown in Figure 14. The ELCC consists of an anode plate, a supporting PTFE plate, a mesh and a plane of VUV SiPMs. The anode plate and PTFE have holes aligned with the SiPMs and define a cell structure. By applying high voltage between the anode plate and the mesh, ionized electrons are collected into the cells along the lines of electric field, and generate EL photons, which are detected by the SiPMs cell by cell. Because the EL region is contained in each cell, a measurement of the energy with this arrangement has a milder dependence on event position than in the case of the open grid used by NEXT. Notice, however, that the energy of the event in NEXT is measured with the PMT plane, while in AXEL the same PMT plane is only used to detect the primary scintillation light and thus measure t0. This is due to the fact that the ELCC does not produce enough backward-going light, since only the photons moving along the narrow channel defined by the cell escape the structure, while all the others are absorbed.
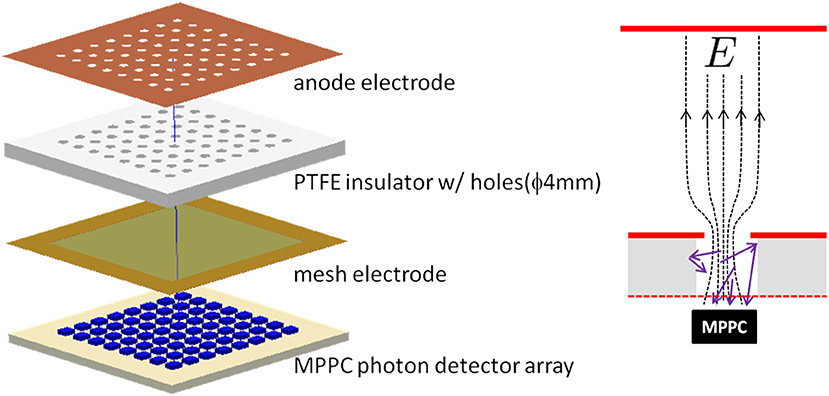
Figure 14. The ELCC concept. Figure from Nakamura et al. [70].
A small prototype has been developed by the AXEL collaboration. The detector is 6 cm long and has a diameter of 10 cm. The ELCC plane has 64 3 × 3 Hamamatsu SiPMs arranged in a 8 × 8 matrix and placed at 7.7 mm pitch. Two VUV sensitive PMTs, capable of operating up to 10 bar pressure, provide t0. The detector has operated at a pressure of 4 bar and has been calibrated with low energy X-rays produced by a 57Co source.
The energy resolution was measured using the xenon X-rays [71] (of energies 29.8 keV, 33 keV) as well as the photoelectric and escape peak from the 57Co source (energies of 122 keV, 92 keV). The energy resolution as a function of the peak energy was fitted to the simple statistical model and also to a function of the form , which described better the data. The extrapolation to Qββ was 0.85% FWHM using the law, and 2.03% FWHM using the law with an additional constant term.
Thus, in terms of energy resolution, the ELCC does not appear to provide an improvement over the open grid used by NEXT (notice that the NEXT-White detector measures krypton X-rays, of energy 41.5 keV, with a resolution of 3.86 ± 0.01% FWHM in the central region of the detector, which extrapolates to 0.5% FWHM at Qββ, to be compared with 4% obtained by the AXEL prototype for the 122 keV gamma, which extrapolates to 0.9% at Qββ.). On the other hand PMTs are still needed to measure t0 and those PMTs could measure the energy with better resolution than AXEL has achieved so far. It remains to be seen if the ELCC yields improvements in the topological signal. So far, the energies investigated by AXEL are too small to produce significant tracks.
On the other hand, the AXEL R&D addresses two important points. One is the need to build very large EL structures for future ton-scale detectors. In that respect, the modular nature of the ELCC appears, a priori, well suited to scale up to large dimensions. The second point is the interest in measuring the energy at the anode, if the cathode is to be used, in a future experiment for Ba++ tagging. However, the ELCC provides only a partial solution, since AXEL still needs to instrument the cathode with PMTs to measure t0. Further progress is to be expected from the larger prototype that the AXEL group plans to build in the near future.
5.2. PandaX-III
The PandaX-III collaboration [72] has proposed the construction of a detector which is essentially a large-scale version of the NEXT-MM prototype discussed in section 4, that is, a HPXe TPC based on electron amplification with a micromegas-based readout and a xenon-TMA mixture. The main arguments for this technological choice are the reduction of background associated with the PMT energy plane and the expected enhancement of the topological signature.
The performance of the topological signature expected in the detector has been quantified with Monte Carlo studies. A selection efficiency of 59% for signal with a rejection of the background at the level of 97% is found using a blob-search analysis. The results improve when using deep neural networks, which result in an 80% signal efficiency and 98% background rejection [73]. This result is comparable with that obtained by NEXT using low diffusion mixtures (70% signal efficiency, 97.5% background rejection). Indeed, both the PANDAX-III and the NEXT studies using DNNs show that the separation between single and double electrons in dense xenon gas reaches an intrinsic limit where about 2% of the background events imitate the signature of signal events, even assuming perfect reconstruction. These are events where multiple scattering or bremsstrahlung in single, energetic electrons, “fake” an energetic blob at the beginning of the electron track.
The parameters of the first PANDAX-III module are described in [73]. The expected energy resolution (3% at Qββ) is consistent with the best results obtained by NEXT-MM. The efficiency (35%) is typical of a HPXe TPC with track reconstruction and also consistent with that found by the NEXT detectors.
Comparing PANDAX-III with the GTPC, we notice that both detectors are rather similar, in particular concerning the performance of the topological signature, since both operate in the low diffusion regime (recall from section 3 the excellent performance of the topological signal of GTPC). On the other hand, the energy resolution of the GTPC was roughly a factor of two worse than that projected by PANDAX-III, and none of the two detectors had t0, thus one expects a similar background level associated with radon degassing at the cathode. Yet, the SGTPC measured a background rate of 10−2counts/(keV · kg · y), which is a factor of 100 worse than the projected background level of PANDAX-III (10−4counts/(keV · kg · y)). A naive expectation in terms of energy resolution would be a factor of two improvement. This suggests that the background rate estimation of PANDAX-III may be somewhat optimistic.
6. Barium Tagging in a HPXe TPC
It has long been recognized that the detection of single barium ions emanating from the decay of 136Xe, when combined with a Gaussian energy resolution better than 2% FWHM—needed to reject ββ2ν events which also produce barium ions—could enable a background-free ββ0ν experiment, since no conventional radioactive process can produce a barium ion in the xenon gas.
A method to tag barium in a HPXe TPC was proposed in 2000 [74], following the idea pointed out in Moe [75] of using laser-induced fluorescence to tag the presence of a Ba+ ion in xenon gas.
The level structure of the Ba+ ion shows a strong 493 nm allowed transition, and therefore ground-state ions can be optically excited to the state from where they have substantial branching ratio (30%) to decay into the metastable state. A Ba+ ion confined in a radio frequency trap can then be illuminated with suitable lasers to induce fluorescence. Specific Ba+ detection is achieved by exciting the system back into the state with 650 nm radiation and observing the blue photon from the decay to the ground state (70% branching ratio). This transition has a spontaneous lifetime of 8 ns and radiates 6 × 107 photons/s.
While the technique has been established by atomic physicists since 1978 the application of it to a ββ0ν experiment in a large HPXe TPC presents many formidable problems. The method proposed in Danilov et al. [74] assumed that the ion position in the TPC could be located in flight and illuminated with a pair of lasers tuned to the appropriate frequencies and simultaneously steered to the place where the ββ0ν candidate event was found. This is far from easy in a large HPXe TPC such as those foreseen for the next generation of neutrinoless double beta experiments. Additional complications were the detection of the fluorescence and the Doppler broadening of the transition line width at high pressure. Finally, barium resulting from double beta decay is initially highly ionized due to the disruptive departure of the two energetic electrons from the nucleus [76]. Rapid capture of electrons from neutral xenon is expected to reduce this charge state to Ba++, which may then be further neutralized through electron-ion recombination. Unlike in liquid xenon, where recombination is frequent and the barium daughters are distributed across charge states [77], recombination in the gas phase is minimal [? ], and thus Ba++ is the expected outcome. Thus, an additional transfer gas needs to be added to xenon, capable of transferring Ba++ to Ba+. TEA has been demonstrated to do the job [78] and similar gases such as TMA will probably also work. On the other hand, those very same gases quench the scintillation signal and thus the event cannot be located in the longitudinal coordinate. This fact alone makes the prospect for in situ tagging very dim.
Since 2000, the R&D effort in barium-tagging has branched into two main lines, both within the EXO Collaboration. Tagging in liquid xenon [79]—not discussed in this report—and tagging in high-pressure gas with two main approaches: (a) extracting the Ba++ ion to a secondary detection volume via funneling and (b) tagging the Ba++ ion in a suitable detector located in the cathode.
In fact, the approaches are not incompatible. The key notion proposed in Brunner et al. [80] is to develop an RF ion-funnel to extract the Ba++ from the high pressure detector. If this is achieved, the detection of the ion could proceed via guiding it to a quadrupole trap and using laser-induced fluorescence or any other method. In particular, the ion could be guided to a Ba++ ion detector. On the other hand, the very same RF-carpets proposed for funneling the ion outside the HPXe can be used to guide it to a small region in the cathode itself, where it can be detected. Both approaches (in situ vs. extraction) have their cons and pros and both need still considerable R&D (much of it synergic) to establish their feasibility.
Yet, tagging “in situ” without lasers requires a new detection technique. Such a technique, based in Single Molecule Fluorescence Imaging (SMFI), was proposed in Nygren et al. [81].
SMFI is a technique invented by physicists and developed by biochemists that enables single-molecule sensitive, super-resolution microscopy. Among the applications of SMFI are the sensing of individual ions [82], demonstrated in various environments, including inside living cells [83]. In SMFI, a thin layer containing potentially fluorescent molecules is repeatedly illuminated with a laser at frequencies in the blue or near-ultraviolet range. The response of the molecules depends on whether they have captured a specific ion—for example, Ca++ which is of great interest in neurological applications given its role as neurotransmitter channel—or not. Chelated molecules (molecules that have captured an ion) fluoresce strongly, while un-chelated (ion-free) molecules respond very weakly. Image-intensified CCD cameras are used to detect single photons and precisely identify and localize single molecules.
The NEXT collaboration is pursuing a program of R&D to tag the barium ion using SMFI techniques. Since the Ba++ energy in high pressure gas is thermal, and charge exchange with xenon is highly energetically disfavored, the Ba++ state is expected to persist through drift to the anode plane. For this reason, and because barium and calcium are congeners, dyes which have been developed for Ca++ sensitivity for biochemistry applications provide a promising path toward barium tagging in HPXe. In Jones et al. [84] the properties of two such dyes, Fluo-3 and Fluo-4 were explored. In the presence of Ba++ excitation at 488 nm yielded strong emission peaking around 525 nm, demonstrating the potential of these dyes to serve as barium tagging agents.
A convincing proof-of-concept was carried out by the NEXT collaboration in McDonald et al. [85]. The experiment managed to resolve individual Ba++ ions on a scanning surface using an SMFI-based sensor.
The SMFI sensor concept uses a thin quartz plate with surface-bound fluorescent indicators continuously illuminated with excitation light and monitored by an EM-CCD camera. It is anticipated that such a sensor would form the basis for a Ba++ detection system in HPXe, with ions delivered to a few ~1 mm 2 sensing surfaces, first via drift to the cathode and then transversely by RF-carpet [86], a method already demonstrated at large scales [87], and for barium transport in HPXe [80] as discussed above.
To demonstrate single Ba++ the proof-of-concept imaged individual near-surface Ba++ ions from dilute barium salt solutions using total internal reflection fluorescence (TIRF) microscopy [88]. The fluorophores used as detectors were fixed at the sensor surface. This emulates the conditions in a HPXe TPC detector, where the ions will drift to the sensor plate and adhere to fluorophores immobilized there.
The hallmark of single molecule fluorescence is a sudden discrete photo-bleaching transition [89]. This occurs when the fluorophore transitions from a fluorescent to a non-fluorescent state, usually via interaction with reactive oxygen species [90]. This discrete transition signifies the presence of a single fluor, rather than a site with multiple fluors contributing. The 375 s scan time is significantly longer than the typical photo-bleaching time of Fluo-3 at this laser power [90], so the majority of spots are observed to bleach in our samples. A typical near-surface fluorescence trajectory is shown in Figure 15. In summary, the NEXT proof of concept shows that SMFI can be used to resolve individual Ba++ ions at surfaces via TIRF microscopy. Ba++ ions have been detected above a background of free residual ions at 12.9σ statistical significance, with individual ions spatially resolved and observed to exhibit single-step photo-bleaching trajectories characteristic of single molecules.
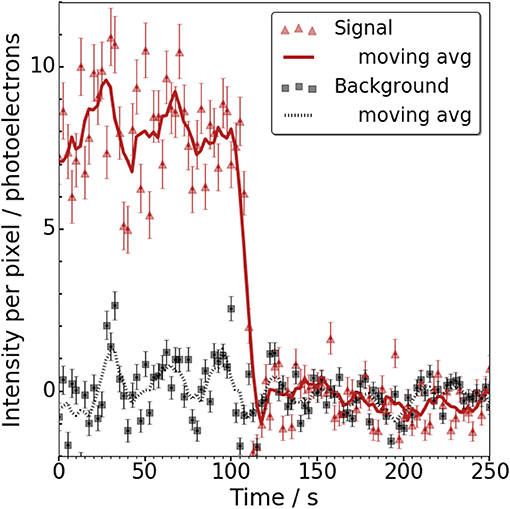
Figure 15. Fluorescence trajectory for one candidate in a barium-spiked sample. “Signal” shows the average activity in 5 × 5 pixels centered on the local maximum. “Background” shows the average in the 56 surrounding. The single step photo-bleach is characteristic of single molecule fluorescence. Figure from McDonald et al. [85].
An SMFI sensor in a future HPXe TPC will differ from the apparatus described here in a few key ways. First, the fluorophores will be surface-tethered and not embedded in a thick sample. Thus, only near-surface bright spots are expected, and offline separation from the deeper background fluors will not be necessary. Second, the target signature will be the appearance of a new candidate over a pre-characterized background, coincident in a spatiotemporal region with a ββ0ν candidate in the TPC. In this case, only the ability to resolve the appearance of a new ion is important, and the spatial localization of individual ion candidates demonstrated here shows that many can be recorded on the same sensor before saturation. Third, the micro-environment around the Fluor will be different, being immobilized on a dry surface rather than within a PVA matrix, and this may modify chelation and fluorescence properties of the Fluor. Finally, the extent to which photo-bleaching will be active in a clean HPXe environment is unknown. Thus, there is still a long and uncertain R&D road ahead before barium tagging can be successfully implemented in a HPXe detector searching for ββ0ν decays.
7. Outlook
The Time Projection Chamber (TPC), invented by D. Nygren in 1975, revolutionized the imaging of charged particles in gaseous detectors. This article has presented a review of the application of high-pressure xenon (HPXe) TPCs to the search for neutrinoless double beta decay (ββ0ν) processes. This field has been active for more than half a century, but its importance has been re-asserted with the discovery of neutrino oscillations and the implication that neutrinos have mass. Massive neutrinos could be Majorana particles, identical to their own antiparticles, a fact that would be unambiguously proven if ββ0ν processes are observed.
The simplest mechanism to mediate ββ0ν decays (the exchange of a light neutrino) provides a rationale to evaluate the state-of-the-art and prospects of the field. The current generation of ββ0ν experiments have explored half-lives in the vicinity of 1026 yr, corresponding to effective neutrino masses—in the case of xenon and for the most favorable nuclear matrix element—in the vicinity of 60 meV. The next generation of experiments aims to reach half-lives of at least 1027 yr and thus explore effective neutrino masses of up to 20 meV, with a significant probability of a discovery.
To be sensitive to ββ0ν half-lives in the range of 1027 yr and more, it is necessary that the next-generation experiments deploy exposures in the range of up to 10 ton·yr, and a background rate in the ROI as close to zero as possible. This tremendous challenge all but forces a paradigm shift in the experimental techniques of the field.
High-pressure xenon TPCs offer one of the most attractive approaches to address such a daunting challenge thanks to the combination of: (a) excellent energy resolution; (b) the availability of a robust topological signature that allows full fiducialization of the events, identification of satellite clusters (signaling Compton scatters and other background processes); and the capability to separate single (background) from double (signal) electrons. HPXe TPCs can be built with ultra-pure materials and are scalable to large masses. On top of that, the possibility to tag the daughter Ba++ ion produced in the decay Xe → Ba++ + 2e−(+2ν), may provide a way to build truly background-free experiments.
The use of xenon for ββ0ν searches was proposed as early as 1961, and the realization that electroluminescence (EL) was a promising way to achieve excellent energy resolution dates from 1975 (as part of the first detector proposal, a bubble chamber), and was revisited in 1983. However, the first generation of HPXe detectors (the Baksan and Milano experiments) did not use EL but electron amplification. The first true HPXe time projection chamber—the Gotthard TPC—was also based on avalanche gain, and used a mixture of 0.95-0.05 Xe/CH4 to stabilize the gas, which quenched the primary scintillation (thus the detector had to make do without t0) and resulted in mediocre energy resolution (~ 7% at Qββ). However, the GTPC also demonstrated the robust topological signal available to the technology and boasted the lowest background rate level (10−2counts(keV · kg · y)) of its time.
And yet, after the GTPC the technology was frozen for two decades until it was resurrected again by the NEXT experiment, which incorporated D. Nygren's proposal to build an EL TPC, along with technological solutions developed by J. White and one of the authors of this review (JJGC). The NEXT program has built two large prototypes and a detector of the size of the GTPC (NEXT-White), which is currently taking data at the Canfranc Underground Laboratory and has already shown excellent energy resolution (1% FWHM at Qββ) and a robust topological signal, along with a well understood background model. The NEXT-100 detector, currently in the early phases of construction (scheduled to start data taking in 2020), can achieve a sensitivity competitive with the best experiments of the current generation while at the same time demonstrating the potential of the technology for a background-free experiment.
Two other projects are proposing HPXe TPCs for ββ0ν searches. One is AXEL, in Japan, which has so far developed a small prototype in which the interesting concept of the Electroluminescence Light Collection Cell (ELCC) is explored. The other is PANDAX-III, which proposes what is essentially a large-scale version of the GTPC, using Micromegas (rather than wires and pads) for readout, and TMA (rather than CH4) as quencher. As it was the case with GTPC, PANDAX-III is expected to feature an excellent topological signature but has the double handicap of a mediocre resolution (3–4 % FWHM according to the R&D measurements done in the context of the NEXT collaboration) and lack of t0.
This review has also summarized the state-of-the-art of Ba++ tagging in gaseous HPXe detectors. R&D has been conducted on this front by the EXO collaboration (which is also studying Ba++ tagging in liquid and solid xenon) and by NEXT. The EXO-gas collaboration has studied the possibility to extract the Ba++ ion from the main chamber through funneling, while NEXT is studying the potential of applying Single Molecular Fluorescence Imaging, SMFI (also proposed by Dave Nygren), to barium tagging with very promising initial results.
In summary it appears that the HPXe technology, in particular using electroluminescence and barium tagging, can assert itself as one of the major possibilities for the next generation of ββ0νẽxperiments.
Author Contributions
JG-C has defined the structure of the paper and he has been in charge of the writing process. FM has been in charge of a review of the historical part and the technical description for the different processes inside the TPC. PF has reviewed the latest information about topological description. All three authors have contributed to the final revision of the paper.
Funding
This research work has been supported by the European Research Council (ERC) under the Advanced Grant 339787-NEXT the Ministerio de Economía y Competitividad of Spain under grants FIS2014-53371-C04, and the GVA of Spain under grants PROMETEO/2016/120 and SEJI/2017/011.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We gratefully acknowledge the privilege of working and learning from Dave Nygren, and the late James White. We would also like to acknowledge José Ángel Hernando, Michel Sorel, Pau Novella, Joaquim dos Santos, Lior Arazi, and our colleagues of the NEXT collaboration for many fruitful discussions. We also acknowledge Oliviero Cremonesi and Alexander Barabash for their kind input on the historical development of the HPXe technology. Finally, we would like to thank Josh Renner for the thorough reading of the final manuscript.
Footnotes
1. ^available online at https://www-project.slac.stanford.edu/exo/docs/white_v5.pdf
2. ^Named after the late Prof. James White, a pioneer of the technique and a crucial scientist for the experiment.
3. ^For all energy extrapolations in this report we use, unless otherwise stated, the simple statistical 1/ dependence.
References
1. Nygren DR. The time projection chamber: a new 4 pi detector for charged particles. eConf. (1974) C740805:58.
2. Redshaw M, Wingfield E, McDaniel J, Myers EG. Mass and double-beta-decay Q value of Xe-136. Phys Rev Lett. (2007) 98:053003. doi: 10.1103/PhysRevLett.98.053003
3. Gonzalez-Diaz D, Monrabal F, Murphy S. Gaseous and dual-phase time projection chambers for imaging rare processes. Nucl Instrum Meth. (2018) A878:200–55. doi: 10.1016/j.nima.2017.09.024
4. Majorana E. Theory of the symmetry of electrons and positrons. Nuovo Cim. (1937) 14:171–84. doi: 10.1007/BF02961314
5. Fukugita M, Yanagida T. Baryogenesis without grand unification. Phys Lett B. (1986) 174:45–7. doi: 10.1016/0370-2693(86)91126-3
6. Gómez Cadenas JJ, Martín-Albo J, Mezzetto M, Monrabal F, Sorel M. The search for neutrinoless double beta decay. Riv Nuovo Cim. (2012) 35:29–98. doi: 10.1393/ncr/i2012-10074-9
7. Agostini M, Bakalyarov AM, Balata M, Barabanov I, Baudis L, Bauer C, et al. Improved limit on neutrinoless double-β decay of 76Ge from GERDA phase II. Phys Rev Lett. (2018) 120:132503. doi: 10.1103/PhysRevLett.120.132503
8. Albert JB, Anton G, Badhrees I, Barbeau PS, Bayerlein R, Beck D, et al. Search for neutrinoless double-beta decay with the upgraded EXO-200 detector. Phys Rev Lett. (2018) 120:072701. doi: 10.1103/PhysRevLett.120.072701
9. Gando A, Gando Y, Hachiya T, Hayashi A, Hayashida S, Ikeda H, et al. Search for majorana neutrinos near the inverted mass hierarchy region with KamLAND-Zen. Phys Rev Lett. (2016) 117:082503. doi: 10.1103/PhysRevLett.117.082503
10. Gando A, Gando Y, Hachiya T, Hayashi A, Hayashida S, Ikeda H, et al. Publisher's Note: search for majorana neutrinos near the inverted mass hierarchy region with KamLAND-Zen. Phys Rev Lett. (2016) 117:109903. doi: 10.1103/PhysRevLett.117.109903
11. Alduino C, Alfonso K, Andreotti E, Arnaboldi C, Avignone FT III, Azzolini O, et al. First results from CUORE: a search for lepton number violation via 0νββ decay of 130Te. Phys Rev Lett. (2018) 120:132501. doi: 10.1103/PhysRevLett.120.132501
12. Agostini M, Benato G, Detwiler J. Discovery probability of next-generation neutrinoless double-β decay experiments. Phys Rev. (2017) D96:053001. doi: 10.1103/PhysRevD.96.053001
13. Raghavan RS. New approach to the search for neutrinoless double beta decay. Phys Rev Lett. (1993) 72:1411–14. doi: 10.1103/PhysRevLett.72.1411
14. Gomez-Cadenas JJ. Status of NEXT and prospects for a future Next Array apparatUS with improved CApAbilities (NAUSICAA). PoS. (2018) 307:32. doi: 10.22323/1.307.0032
15. Moe MK. New approach to the detection of neutrinoless double-beta decay. Phys Rev C. (1991) 44:931–34
16. Iqbal MZ, Henrikson HE, Mitchell LW, O'Callaghan BMG, Thomas J, Wong HT. Design and construction of a high pressure xenon time projection chamber. Nucl Instrum Meth. (1987) A259:459–65. doi: 10.1016/0168-9002(87)90827-8
17. Álvarez V, Borges FIGM, Cárcel S, Castel J, Cebrián S, Cervera A, et al. Near-intrinsic energy resolution for 30 to 662 keV gamma rays in a high pressure xenon electroluminescent TPC. Nucl Instrum Meth. (2012) A708:101–14. doi: 10.1016/j.nima.2012.12.123
18. Monrabal F, Gómez-Cadenas JJ, Toledo JF, Álvarez V, Benlloch-Rodríguez JM, Cárcel S, et al. The next white (NEW) detector. arXiv: 180402409 (2018).
19. Aprile E, Doke T. Liquid xenon detectors for particle physics and astrophysics. Rev Mod Phys. (2010) 82:2053–97. doi: 10.1103/RevModPhys.82.2053
20. Fernandes LMP, Freitasa EDC, Ballb M, Gómez-Cadenasb JJ, MonteiroaCMB Yahlali N, et al. Primary and secondary scintillation measurements in a xenon Gas Proportional Scintillation Counter. JINST. (2010) 5:P09006. doi: 10.1088/1748-0221/5/09/P09006
21. Felkai R, Monrabal F, Gonzalez-Díaz D, Sorel M, López-March N, Gómez-Cadenas JJ, et al. Helium-Xenon mixtures to improve topological signature in high pressure gas Xenon TPCs. Nucl Instrum Meth. (2018) A905:82–90. doi: 10.1016/j.nima.2018.07.013
22. Bolotnikov A, Ramsey B. The spectroscopic properties of high-pressure xenon. Nucl Inst Meth. (1997) A396:360–70. doi: 10.1016/S0168-9002(97)00784-5
23. Nygren D. Optimal detectors for WIMP and 0νββ searches: identical high-pressure xenon gas TPCs? Nucl Instrum Meth. (2007) A581:632–42. doi: 10.1016/j.nima.2007.07.062
24. Fano U. Ionization Yield of Radiations. II. The Fluctuations of the Number of Ions. Phys Rev. (1947) 72:26–9. doi: 10.1103/PhysRev.72.26
25. Conti E, DeVoe R, Gratta G, Koffas T, Waldman S, Wodin J, et al. Correlated fluctuations between luminescence and ionization in liquid xenon. Phys Rev B. (2003) 68:054201. doi: 10.1103/PhysRevB.68.054201
26. Albert JB, Auty DJ, Barbeau PS, Beauchamp E, Beck D, Belov V, et al. Search for Majorana neutrinos with the first two years of EXO-200 data. Nature. (2014) 510:229–34. doi: 10.1038/nature13432
27. Conde CAN, Policarpo AJPL. A gas proportional scintillation counter. Nucl Instr Meth. (1967) 53:7–12. doi: 10.1016/0029-554X(67)91323-7
28. Oliveira CAB, Sorel M, Martin-Albo J, Gomez-Cadenas JJ, Ferreira AL, Veloso JFCA. Energy resolution studies for NEXT. JINST. (2011) 6:P05007. doi: 10.1088/1748-0221/6/05/P05007
29. Monteiro CMB, Fernandes LMP, Lopes JAM, Coelho LCC, Veloso JFCA, dos Santos JMF, et al. Secondary scintillation yield in pure xenon. J Instrument. (2007) 2:P05001. doi: 10.1088/1748-0221/2/05/P05001
30. Balan C, Freitas EDC, Papaevangelou T, Giomataris I, da Luz HN, Monteiro CMB, et al. Micromegas operation in high pressure xenon: charge and scintillation readout. JINST. (2011) 6:P02006. doi: 10.1088/1748-0221/6/02/P02006
31. Martín-Albo J, et al. Sensitivity of NEXT-100 to neutrinoless double beta decay. JHEP. (2016) 5:159. doi: 10.1007/JHEP05(2016)159
32. De'Munari GM, Mambriani G. A cloud chamber triggered by the electroluminescence of its He+Xe filling mixture: a new instrument for investigating double beta-decay. Nuovo Cimento. (1976) 33A:299–308. doi: 10.1007/BF02734407
34. Charpak G, Majewski S, Sauli F. The scintillating drift chamber: a new tool for high accuracy, very high rate particle localization. Nucl Instr Meth. (1975) 126:381. doi: 10.1016/0029-554X(75)90701-6
36. Barabash AS, Novikov VM, M OB. High pressure ionization chamber designed to search for 2β decay of 136Xe. Nucl Instr Meth. (1991) 300:77. doi: 10.1016/0168-9002(91)90708-X
37. Bolozdynya A, Egorov V, Koutchenkov A, Safronov G, Smirnov G, Medved S, et al. A high pressure xenon self-triggered scintillation drift chamber with 3D sensitivity in the range of 20-140 keV deposited energy. Nuc Inst Meth. (1997) A385:225. doi: 10.1016/S0168-9002(96)01035-2
38. Barabash AS, Golubev AA, Kazachenko OV, Kuzminov VV, Lobashev VM, Novikov VM, et al. Low background installation for the 136Xe double beta decay experiment. Nucl Instrum Methods. (1986) B17:450–1. doi: 10.1016/0168-583X(86)90183-7
40. Alessandrello A, Bellotti E, Camin D, Cremonesi O, Fiorini E, Liguori C, et al. Multielement proportional chamber for 136Xe ββ decay. Nucl Instrum Meth. (1986) A252:227–33. doi: 10.1016/0168-9002(86)91181-2
41. Bellotti E, Cremonesi O, Fiorini E, Gervasio G, Liguori C, Ragazzi S, et al. A search for lepton number nonconservation in double beta decay of 136Xe. Phys Lett. (1989) B221:209–15. doi: 10.1016/0370-2693(89)91500-1
42. Wong HT, Boehm F, Fisher P, Gabathuler K, Henrikson HE, Imel DA, et al. First 0 nu halflife limit from the Gotthard xenon time projection chamber. J Phys. (1991) G17:S165-72. doi: 10.1088/0954-3899/17/S/017
43. Luscher R, et al. Search for ββ decay in Xe-136: new results from the Gotthard experiment. Phys Lett B. (1998) 434:407–14. doi: 10.1016/S0370-2693(98)00906-X
44. Nygren D. High-pressure xenon gas electroluminescent TPC for 0−ν ββ-decay search. NuclInstrumMeth. (2009) A603:337–48. doi: 10.1016/j.nima.2009.01.222
46. Álvarez V, et al. The NEXT-100 experiment for neutrinoless double beta decay searches (Conceptual Design Report). (2011).
47. Álvarez V, Borges FIGM, Cárcel S, Carmona JM, Castel J, Catalá JM, et al. NEXT-100 technical design report (TDR): executive summary. JINST. (2012) 7:T06001. doi: 10.1088/1748-0221/7/06/T06001
48. Álvarez V, Borges FIGM, Cárcel S, Castel J, Cebrián S, Cervera A, et al. Initial results of NEXT-DEMO, a large-scale prototype of the NEXT-100 experiment. JINST. (2013) 8:P04002. doi: 10.1088/1748-0221/8/04/P04002
49. Álvarez V, Borges FIGM, Cárcel S, Cebrián S, Cervera A, Conde CAN, et al. Ionization and scintillation response of high-pressure xenon gas to alpha particles. JINST. (2013) 1305:P05025. doi: 10.1088/1748-0221/8/05/P05025
50. Álvarez V, Borges FIGM, Cárcel S, Cebrián S, Cervera A, Conde CAN, et al. Operation and first results of the NEXT-DEMO prototype using a silicon photomultiplier tracking array. JINST. (2013) 8:P09011. doi: 10.1088/1748-0221/8/09/P09011
51. Lorca D, Martín-Albo J, Laing A, Ferrario P, Gómez-Cadenas JJ, Álvarez V, et al. Characterisation of NEXT-DEMO using xenon Kα X-rays. JINST. (2014) 9:P10007. doi: 10.1088/1748-0221/9/10/P10007
52. Ferrario P, Laing A, López-March N, Gómez-Cadenas JJ, Álvarez V, Azevedo CDR, et al. First proof of topological signature in the high pressure xenon gas TPC with electroluminescence amplification for the NEXT experiment. JHEP. (2016) 1:104.
53. Álvarez V, Bandac I, Bettini A, Borges FIGM, Carcel S, Castel J, et al. Radiopurity control in the NEXT-100 double beta decay experiment: procedures and initial measurements. JINST. (2012) 8:T01002. doi: 10.1088/1748-0221/8/01/T01002
54. Cebrián S, Pérez J, Bandac I, Labarga L, Álvarez V, Azevedo CDR, et al. Radiopurity assessment of the energy readout for the NEXT double beta decay experiment. JINST. (2017) 12:T08003. doi: 10.1088/1748-0221/12/08/T08003
55. Martínez-Lema G, Hernando Morata JA, Palmeiro B, Botas A, Ferrario P, Monrabal F, et al. Calibration of the NEXT-White detector using 83mKr decays. JINST. (2018) 13:P10014. doi: 10.1088/1748-0221/13/10/P10014
56. Renner J, Ferrario P, Martínez-Lema G, Monrabal F, Para A, Gómez-Cadenas JJ, et al. Initial results on energy resolution of the NEXT-White detector. JINST. (2018) 13:P10020.
57. Simón A, Felkai R, Martínez-Lema G, Monrabal F, González-Díaz D, Sorel M, et al. Electron drift properties in high pressure gaseous xenon. JINST. (2018) 13:P07013. doi: 10.1088/1748-0221/13/07/P07013
58. Novella P, et al. Measurement of radon-induced backgrounds in the NEXT double beta decay experiment. JHEP. (2018) 10:112. doi: 10.1007/JHEP10(2018)112
59. Muñoz Vidal J. The NEXT Path to Neutrino Inverse Hierarchy. Universitat de València, Valencia (2018). Available online at: http://roderic.uv.es/handle/10550/66537
60. Martín-Albo J. The NEXT experiment for neutrinoless double beta decay searches. Valencia U., IFIC (2015). Available online at: http://roderic.uv.es/handle/10550/41728
61. Aalseth CE, Acerbi F, Agnes P, Albuquerque IFM, Alexander T, Alici A. DarkSide-20k: a 20 tonne two-phase LAr TPC for direct dark matter detection at LNGS. Eur Phys J Plus. (2018) 133:131. doi: 10.1140/epjp/i2018-11973-4
62. Renner J, Farbin A, Muñoz Vidal J, Benlloch-Rodriguez JM, Botas A, Ferrario P, et al. Background rejection in NEXT using deep neural networks. JINST. (2017) 12:T01004. doi: 10.1088/1748-0221/12/01/T01004
63. Henriques CAO, Monteiro CMB, González-Díaz D, Azevedo CDR, Freitas EDC, Mano RDP, et al. Electroluminescence TPCs at the thermal diffusion limitreference. JHEP. (2019) 27. doi: 10.1007/JHEP01(2019)27
64. Gonzalez-Diaz D, et al. Accurate γ and MeV-electron track reconstruction with an ultra-low diffusion Xenon/TMA TPC at 10 atm. Nucl Instrum Meth. (2015) A804:8–24. doi: 10.1016/j.nima.2015.08.033
65. Álvarez V, et al. Characterization of a medium size Xe/TMA TPC instrumented with microbulk Micromegas, using low-energy γ-rays. JINST. (2014) 9:C04015.
66. Cebrián S, et al. Radiopurity assessment of the tracking readout for the NEXT double beta decay experiment. JINST. (2015) 10:P05006. doi: 10.1088/1748-0221/10/05/P05006
67. Rethmeier C. Characterization of VUV sensitive SiPMs for nEXO. J Instrument. (2016) 11:C03002. doi: 10.1088/1748-0221/11/03/C03002
68. Nakajima Y, Goldschmidt A, Matis HS, Nygren D, Oliveira C, Renner J. Measurement of scintillation and ionization yield with high-pressure gaseous mixtures of Xe and TMA for improved neutrinoless double beta decay and dark matter searches. J Phys Conf Ser. (2015) 650:012012. doi: 10.1088/1742-6596/650/1/012012
69. Trindade AMF, Escada J, Cortez AFV, Borges FIGM, Santos FP, Adams C, et al. Study of the loss of xenon scintillation in xenon-trimethylamine mixtures. Nucl Inst Meth. (2018) 905:23.
70. Nakamura K, Ichikawa AK, Nakaya T, Minamino A, Ban S, Yanagita S, et al. AXEL-a high pressure xenon gas TPC for neutrinoless double beta decay search. Nucl Instrum Meth. (2017) A845:394–7. doi: 10.1016/j.nima.2016.06.083
71. Ban S. AXEL: neutrinoless double beta decay search with a high pressure xenon gas Time Projection Chamber. J Phys Conf Ser. (2017) 888:012233. doi: 10.1088/1742-6596/888/1/012233
72. Chen X, et al. PandaX-III: searching for neutrinoless double beta decay with high pressure136Xe gas time projection chambers. Sci China Phys Mech Astron. (2017) 60:061011. doi: 10.1007/s11433-017-9028-0
73. Han K. PandaX-III: searching for neutrinoless double beta decay with high pressure gaseous time projection chambers. In: 15th International Conference on Topics in Astroparticle and Underground Physics (TAUP 2017) July 24-28, 2017. Sudbury, ON (2017).
74. Danilov M, et al. Detection of very small neutrino masses in double beta decay using laser tagging. Phys Lett. (2000) B480:12–8. doi: 10.1016/S0370-2693(00)00404-4
75. Moe MK. New approach to the detection of neutrinoless double beta decay. Phys Rev. (1991) C44:931–4.
76. Green AES. Single electron shakeoff probability following the beta decay of krypton. Phys Rev. (1957) 107:1646–50. doi: 10.1103/PhysRev.107.1646
77. Albert JB, Auty DJ, Barbeau PS, Beck D, Belov V, Breidenbach M, et al. Measurements of the ion fraction and mobility of α- and β- decay products in liquid xenon using the EXO-200 detector. Phys Rev. (2015) C92:045504. doi: 10.1103/PhysRevC.92.045504
78. Sinclair D, et al. Prospects for barium tagging in gaseous xenon. J Phys Conf Ser. (2011) 309:012005. doi: 10.1088/1742-6596/309/1/012005
79. Mong B, et al. Spectroscopy of Ba and Ba+ deposits in solid xenon for barium tagging in nEXO. Phys Rev. (2015) A91:022505. doi: 10.1103/PhysRevA.91.022505
80. Brunner T, et al. An RF-only ion-funnel for extraction from high-pressure gases. Int J Mass Spectr. (2015) 379:110–20. doi: 10.1016/j.ijms.2015.01.003
81. Nygren DR. The biochemistry of 136Xe; 2014. In: 7th International Symposium on Large TPCs for Low-Energy Rare Event Detection. Available online at: https://indico.cern.ch/event/340656/contributions/1737337/attachments/668439/918718/Nygren_-_Biochemistry_of_Xe136.pdf
82. Lu Y, Paige MF. An ensemble and single-molecule fluorescence spectroscopy investigation of calcium green 1, a calcium-ion sensor. J Fluorescence. (2007) 17:739–48. doi: 10.1007/s10895-007-0185-1
83. Stuurman N, Vale R. Imaging Single Molecules Using Total Internal Reflection Fluorescence Microscopy. Cold Spring Harbor, NY: Cold Spring Harbor Laboratory Press (2006).
84. Jones BJP, McDonald AD, Nygren DR. Single molecule fluorescence imaging as a technique for barium tagging in neutrinoless double beta decay. JINST. (2016) 11:P12011.
85. McDonald AD, et al. Demonstration of single barium ion sensitivity for neutrinoless double beta decay using single molecule fluorescence imaging. Phys Rev Lett. (2018) 120:132504. doi: 10.1103/PhysRevLett.120.132504
86. Arai F, Wada M, Sonoda T, Ito Y, Schury P, Mita H. Investigation of the ion surfing transport method with a circular rf carpet. Int J Mass Spectr. (2014) 362:56–8. doi: 10.1016/j.ijms.2014.01.005
87. Gehring AE, Brodeur M, Bollen G, Morrissey DJ, Schwarz S. Research and development of ion surfing {RF} carpets for the cyclotron gas stopper at the {NSCL}. Nucl Instrum Methods Phys Res Sect B Beam Interact Mater Atoms. (2016) 376:221–4. doi: 10.1016/j.nimb.2016.02.012
88. Burghardt TP. Measuring incidence angle for through-the-objective total internal reflection fluorescence microscopy. J Biomed Opt. (2012) 17:126007. doi: 10.1117/1.JBO.17.12.126007
89. Habuchi S, Ando R, Dedecker P, Verheijen W, Mizuno H, Miyawaki A, et al. Reversible single-molecule photoswitching in the GFP-like fluorescent protein Dronpa. Proc Natl Acad Sci USA. (2005) 102:9511–6. doi: 10.1073/pnas.0500489102
Keywords: xenon, neutrinos, electroluminescence, resolution, topology, barium tagging, SMFI
Citation: Gomez-Cadenas JJ, Monrabal Capilla F and Ferrario P (2019) High Pressure Gas Xenon TPCs for Double Beta Decay Searches. Front. Phys. 7:51. doi: 10.3389/fphy.2019.00051
Received: 09 December 2018; Accepted: 19 March 2019;
Published: 16 April 2019.
Edited by:
Alexander S. Barabash, Institute for Theoretical and Experimental Physics, RussiaReviewed by:
Andrea Pocar, University of Massachusetts Amherst, United StatesAnnarita Margiotta, University of Bologna, Italy
Copyright © 2019 Gomez-Cadenas, Monrabal Capilla and Ferrario. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Juan J. Gomez-Cadenas, ampnb21lemNhZGVuYXNAZGlwYy5vcmc=
 Juan J. Gomez-Cadenas1,2*
Juan J. Gomez-Cadenas1,2* Francesc Monrabal Capilla
Francesc Monrabal Capilla Paola Ferrario
Paola Ferrario