The Top-Quark Mass: Challenges in Definition and Determination

1. Introduction

The mass of the top quark is a fundamental parameter of the Standard Model, since it enters in the electroweak precision tests [1] and constrained the mass of the Higgs boson even before its discovery at the LHC. It plays a role in Higgs inflation model (see [2, 3] for some recent work on the subject), while the property of the electroweak vacuum to lie on the boundary between stability and metastability regimes [4] does depend on the actual values and definitions of top and Higgs masses used in the computation¹. Also, in the determination of the lifetime of the Universe, undertaken in Andreassen et al. [5], part of the uncertainty is related to the top-quark mass.

In such calculations, one typically assumes that the measured top-quark mass, whose current world average reads m_t = [173.34 ± 0.27(stat)±0.71(syst)] GeV [6], corresponds to the pole mass and eventually adds errors of the order of few hundreds MeV to account for possible deviations from this identification. For instance, possible changes of the central value or of the uncertainty on m_t may affect the results in Degrassi et al. [4], to the point of even moving the vacuum position inside the stability or instability regions. It is therefore of paramount importance determining m_t at the LHC with the highest possible precision, estimating reliably all sources of uncertainty and eventually interpreting the results in terms of field-theory mass definitions.

More generally, the top-quark mass is determined by comparing experimental data with theory predictions, so that the measured mass has to be identified with the parameter m_t employed in the calculations. From the viewpoint of the techniques used in the extraction, one usually labels as “standard measurements” those relying on the direct reconstruction of the top-decay products by means of the template, matrix-element or ideogram methods, and as “alternative measurements” the top-mass determinations which use suitably defined observables, such as total production cross section or peaks/endpoints of differential distributions. It is remarkable noticing that, up to now, such classes of mass determinations have never been combined.

From the theory side, as most top-mass extractions use Monte Carlo shower codes, one traditionally defines “Monte Carlo mass” the quantity which is determined. On the other hand, one refers to pole- or $\overline{\text{MS}}$-mass extraction whenever a measurement is compared with a fixed-order, possibly resummed QCD calculation employing a given field-theory mass definition. The distinction between Monte Carlo and well-posed mass definitions like the pole mass has been the core of several discussions within the top-quark physics community, as we have authors trying to quantify the discrepancy between such masses, finding results of the order of a few hundreds of MeV [7–11] and others who instead present arguments against the classification of some measurements as Monte Carlo mass determinations [12, 13] and try to interpret them still as pole-mass extractions, with an uncertainty which depends on the specific measurement strategy and details of the event generation. Furthermore, as will be discussed later, even the so-called pole or $\overline{\text{MS}}$ mass determinations are not completely Monte Carlo independent, since the evaluation of the experimental acceptance depends, though quite mildly, on the shower code which is employed and on the implemented mass parameter.

Another issue that was often used to argue against the employment of the pole mass has been the infrared renormalon ambiguity [14, 15], namely the factorial growth of the coefficients of the expansion in powers of the strong coupling of the heavy-quark self energy, whenever it is expressed in terms of the pole mass. However, recent work on this topic [16, 17] showed that, using the 4-loop relation between pole and (renormalon-free) $\overline{\text{MS}}$ masses [18], the renormalon ambiguity is actually of the order at most of 250 MeV, hence smaller than the current error on the top mass. Furthermore, although the projections for the future high-energy and high-luminosity runs of the LHC aim at even lower uncertainties, it should always be reminded that the top quark is an unstable particle with a width of the order of 1 GeV which, as long as it is included in the computation, acts as a cutoff for radiation off top quarks².

In the following, I shall give an overview of the up-to-date top-mass determinations and, above all, I will try to stress the main points of the existing controversies concerning mass definitions and interpretation of the LHC measurements, as well as the sources of theory uncertainty. In section 2 I shall review the heavy-quark mass definitions; in section 3 I will discuss the renormalon ambiguity; in section 4 the main strategies to measure the top mass will be presented. The interpretation of the measurements and the theoretical uncertainties will be investigated in section 5, while section 6 will contain some final remarks.

2. Top-Quark Mass Definitions

Heavy-quark mass definitions are related to how one subtracts the ultraviolet divergences in the renormalized heavy-quark self energy Σ^R. Higher-order corrections to the self energy are typically calculated in dimensional regularization, with d = 4−2ϵ dimensions. At one loop in QCD, for a heavy quark with four-momentum p and bare mass m₀, the renormalized self energy reads:

$\begin{array}{l}{\Sigma }^R(m_0,p,\mu )=\frac{i{\alpha }_S}{4\pi }\{\left[\frac{1}{ϵ}-\gamma +\ln 4\pi +A(m_0,p,\mu )\right]\cancel{p}\\ -\left[4\left(\frac{1}{ϵ}-\gamma +\ln 4\pi \right)+B(m_0,p,\mu )\right]m_0\}\\ +i[(Z_2-1)\cancel{p}-(Z_2{Z}_m-1)m_0]+\mathcal{O}({\alpha }_S^2),& (1)\end{array}$

where Z₂ and Z_m are the wave-function and mass renormalization constants, respectively, γ = 0.577216… the Euler–Mascheroni constant and μ is the renormalization scale³. The functions A and B in Equation (1) depend on p, m₀ and μ and are independent of ϵ. The bare heavy-quark propagator is $S^0(p)=i/(\cancel{p}-m_0)$, while the renormalized S^R reads, in terms of the renormalized self energy:

$\begin{array}{ll}{S}^R(p,\mu )=\frac{i}{\cancel{p}-m_0-i{\Sigma }^R(m_0,p,\mu )}.& (2)\end{array}$

The on-shell renormalization scheme, leading to the pole mass, is defined so that the self energy and its partial derivative with respect to /p vanish whenever /p = 0:

$\begin{array}{ll}\begin{array}{c}{\Sigma }^R{\left|{ }_{\cancel{p}=0}=0 ; \frac{\partial {\Sigma }^R}{\partial /\cancel{p}}\right|}_{\cancel{p}=0}=0.\end{array}& (3)\end{array}$

The minimal-subtraction $(\overline{\text{MS}})$ scheme is indeed typical of dimensional regularization and fixes Z₂ and Z_m in order to subtract just the contributions $~\frac{1}{ϵ}-\gamma +ln4\pi$ in Equation (1)⁴.

Since pole and $\overline{\text{MS}}$ masses are the most popular top-mass schemes, hereafter I will devote some discussion on such definitions. In the on-shell (o.s.) and $\overline{\text{MS}}$ schemes S^R(p) can then be expressed in terms of pole and $\overline{\text{MS}}$ masses, respectively, as follows:

$\begin{array}{lll}{S}_{\text{o}.\text{s}.}^R(p)& \simeq & \frac{i}{\cancel{p}-m_{\text{pole}}},\\ S_{\overline{\text{MS}}}^R(p,\mu )& \simeq & \frac{i}{\cancel{p}-m_{\overline{\text{MS}}}(\mu )-(A-B)m_{\overline{\text{MS}}}(\mu )}.& (4)\end{array}$

From Equation (4), one can learn that m_pole is still the pole of the propagator, even after the renormalization procedure, which is in agreement with the intuitive notion of the mass of a free particle, whereas $m_{\overline{\text{MS}}}(\mu )$ may be quite far from the pole. Also, unlike the pole mass, the $\overline{\text{MS}}$ mass depends on the renormalization scale μ. The relation between top-quark pole (m_{t, pole}) and $\overline{\text{MS}}$ (${\bar{m}}_t({\bar{m}}_t)$) masses was calculated up to four loops in Marquard et al. [18] and reads:

$\begin{array}{l}{m}_{t,\text{pole}}={\overline{m}}_t({\overline{m}}_t)[1+0.4244 {\alpha }_S+0.8345 {\alpha }_S^2+2.375 {\alpha }_S^3\\ +(8.615\pm 0.017) {\alpha }_S^4+\mathcal{O}({\alpha }_S^5)]\\ =[163.508+7.529+1.606+0.496+(0.195\pm 0.0004)]\\ \text{ GeV}.& (5)\end{array}$

The last term in Equation (5) yields an uncertainty of about 200 MeV on the pole-$\overline{\text{MS}}$ conversion. Beyond four loops, one can find in Kataev and Molokoedov [20] the dependence of the five- and six-loop corrections to the pole-$\overline{\text{MS}}$ relation on the number of light flavors.

As discussed in the introduction, higher-order corrections to the self energy, when expressed in terms of the pole mass, lead to infrared renormalons [14], namely the factorial growth of the coefficients of ${\alpha }_S^n$: we shall discuss recent calculations on renormalons in the next section. For the time being, I just point out that the $\overline{\text{MS}}$ mass is renormalon-free and it is therefore a so-called short-distance mass, well defined in the infrared regime. However, differently from the pole mass, it is not a suitable mass definition at threshold, as it exhibits corrections ${({\alpha }_S/v)}^k$, v being the top velocity, that are large in the threshold limit v → 0. On the contrary, the $\overline{\text{MS}}$ mass is appropriate to describe processes far from threshold, i.e., at scales Q ≫ m_t for top quarks, since, by setting the renormalization scale μ ≃ Q, one is capable of resumming large logarithms $ln(Q^2/m_t^2)$ in the mass definition itself. As will be highlighted in the next section, Equation (5), relating the pole mass to the renormalon-free $\overline{\text{MS}}$ one, can be used as a starting point to evaluate the renormalon ambiguity in the top pole mass.

Another mass definition, which has been employed especially in the framework of Soft Collinear Effective Theory (SCET), is the so-called MSR mass, which was introduced to interpolate between pole and $\overline{\text{MS}}$ masses [7]. Such a mass, labeled as $m_t^{\text{MSR}}(R,\mu )$ for top quarks, besides the renormalization scale μ, depends on an extra scale R, in such a way that:

$\begin{array}{lll}{m}_t^{\text{MSR}}(R)& \to & m_{t,pole}\text{ for }R\to 0\text{ and }{m}_t^{\text{MSR}}(R)\to {\bar{m}}_t({\bar{m}}_t)\text{ for}\\ \hfill R& \to & {\bar{m}}_t({\bar{m}}_t).& (6)\end{array}$

The MSR mass can be related to any other mass definitions, such as the pole mass, by means of a counterterm like:

$\begin{array}{ll}{m}_{t,pole}=m_t^{\text{MSR}}(R,\mu )+\delta m_t(R,\mu ),& (7)\end{array}$

where the μ-dependence of m^MSR(R, μ) follows renormalization group equations. As will be argued in the following, the MSR mass has often been adopted in the literature to connect the top-mass measurements with well-defined top-mass definitions, with $R~{O}(1\text{ GeV})$.

For the sake of generality, although the present review will be mostly devoted to hadron-collider top-mass determinations, I wish to remind some other top mass definitions which are often employed in analyses on the m_t extraction at future lepton colliders. In fact, physical observables at threshold, such the $t\bar{t}$ cross section in e⁺e⁻ collisions at $\sqrt{s}\simeq 2m_t$, require suitable mass schemes. One of such definitions is the 1S mass, defined as half the mass of a fictitious Υ(1S) resonance, made up of a bound $t\bar{t}$ state [21]:

$\begin{array}{ll}{m}_{t,1\text{S}}=\frac{1}{2}\left\{m\left[{\rm Y}(1\text{S})\right]\right\}.& (8)\end{array}$

The 1S mass reads, in terms of the pole mass (Hoang et al. [22]):

$\begin{array}{ll}{m}_{t,1\text{S}}=m_{t,\text{pole}}\left(1-{\Delta }^{\text{LL}}-{\Delta }^{\text{NLL}}-{\Delta }^{\text{NNLL}}\right).& (9)\end{array}$

The explicit expression of the Δ terms can be found in Hoang et al. [22], where the threshold $e^{+}{e}^{-}\to t\bar{t}$ cross section was computed in the next-to-next-to-leading logarithmic approximation, and the superscripts LL, NLL and NNLL refer to the resummation of large logarithms of the top velocity v, which are large in the regime v ~ α_S ≪ 1 and α_Sln v ~ 1.

The potential-subtracted (PS) mass is instead constructed in terms of the $t\bar{t}$ Coulomb potential, in such a way that contributions below a factorization scale μ_F are subtracted off, as to suppress renormalons [23]:

$\begin{array}{ll}{m}_{\text{PS}}({\mu }_F)=m_{\text{pole}}-\frac{1}{2}{\displaystyle {\int }_{\left|q\right|<{\mu }_F}}\frac{d^{3}q}{{(2\pi )}^3}Ṽ(q).& (10)\end{array}$

In Equation (10) Ṽ(q) is the transform in momentum space of the $t\bar{t}$ Coulomb potential. The PS mass is a threshold mass too, particularly suitable to deal with $t\bar{t}$ production at energies slightly above 2m_t. The relation between PS and pole top-quark masses is given by the following equation [24]:

$\begin{array}{ll}{m}_{t,PS}({\mu }_F)=m_{t,\text{pole}}-\frac{4}{3\pi }{\alpha }_S({\mu }_F){\mu }_F+{O}({\alpha }_S^2).& (11)\end{array}$

More recently, the theoretical error on the possible extraction of 1S and PS masses in e⁺e⁻ collisions just above the $t\bar{t}$ threshold was estimated. In detail, by using a NNLL threshold resummation of the ratio $R=\sigma (e^{+}{e}^{-}\to t\bar{t})/\sigma (e^{+}{e}^{-}\to {\mu }^{+}{\mu }^{-})$, the 1S mass can be extracted with an uncertainty about 40 MeV [25], whereas, by employing a fixed-order NNNLO calculation, the PS mass can be determined with an error below 50 MeV [26]. It will be of course desirable to combine such fixed-order and resummed computations to possibly decrease further such an uncertainty.

Another threshold mass definition is the renormalon-subtracted (RS) mass, which removes from the pole mass the pure renormalon contribution [27]. The RS mass was determined in Pineda [27] after constructing its Borel transform and reads, in terms of the pole mass:

$\begin{array}{ll}{m}_{t,RS}=m_{t,pole}-{\displaystyle \sum _{n=0}^{\infty }}{N}_m{\mu }_F{\alpha }_S^{n+1}({\mu }_F){\displaystyle \sum _{k=0}^{\infty }}{c}_k\frac{\Gamma (n+1+b-k)}{\Gamma (1+b-k)},& (12)\end{array}$

where the expression for the coefficients N_m and c_k are given in Pineda [27] and b can be expressed in terms of the QCD β-function as $b={\beta }_1/(2{\beta }_0^2)$. Potential-, renormalon-subtracted and 1S top-quark masses were related to the $\overline{\text{MS}}$ mass in Marquard et al. [18] with four-loop accuracy in the conversion. The uncertainty in the conversion was gauged about 7, 11 and 23 11 MeV for PS, RS and 1S masses, respectively.

Finally, the so-called kinetic mass was defined in Bigi et al. [28] for the purpose of improving the convergence of the perturbative expansion of the semileptonic B-meson decay width. It was constructed by subtracting from the pole mass the HQET (Heavy Quark Effective Theory) matrix elements, denoted by $\bar{\Lambda }(\mu )$ in Bigi et al. [28], expressing the shift between pole and meson masses. The kinetic bottom-quark mass reads, up to terms suppressed as the inverse of the quark/meson mass:

$\begin{array}{ll}{m}_{b,kin}({\mu }_F)=m_B-\bar{\Lambda }({\mu }_F)+{O}\left(\frac{1}{m_B}\right).& (13)\end{array}$

In Hoang et al. [24], the kinetic mass was generalized to $t\bar{t}$ bound states, obtaining the following expansion in terms of the pole mass:

$\begin{array}{ll}{m}_{t,\text{kin}}({\mu }_F)=m_{t,\text{pole}}-\frac{16}{9\pi }{\alpha }_S({\mu }_F){\mu }_F+{O}({\alpha }_S^2).& (14)\end{array}$

As underlined before, the 1S, PS, and RS masses are threshold masses which, unlike the pole mass, do not exhibit the renormalon ambiguity. Recent calculations aimed at estimating the renormalon uncertainty in the pole mass will be the topic of next section.

3. The Renormalon Ambiguity in the Top Mass

Problems with the renormalized heavy-quark self energy, when expressed in terms of the pole mass, were first understood in Beneke and Braun [14] and Beneke [15]. In fact, after including higher-order contributions in the strong coupling constant, the renormalized heavy-quark self energy exhibits the following expansion in powers of α_S:

$\begin{array}{ll}{\Sigma }^R(m_{\text{pole}},m_{\text{pole}})\approx m_{\text{pole}}{\displaystyle \sum _n}{\alpha }_S^{n+1}{(2b_0)}^{n}n!,& (15)\end{array}$

where b₀ is first β-function coefficient entering in the $\overline{\text{MS}}$ strong coupling constant⁵. From Equation (15), one learns that the coefficients of the expansion grow like n! at order ${\alpha }_S^{n+1}$.

After re-expressing α_S in terms of the β function and of the QCD scale Λ, and inserting Σ^R in the on-shell propagator as in Equation (4), one will get a correction to the pole mass:

$\begin{array}{ll}\Delta m_{\text{pole}}\simeq {O}(\Lambda ),& (16)\end{array}$

which is the renowned renormalon ambiguity in m_pole, i.e., an uncertainty of the order of the QCD scale in the pole-mass definition. This result can be related to the fact that a quark is not a free parton, but has to be confined into a hadron: in fact, one can prove that the renormalon uncertainty is due to the gluon self coupling, while it is not present when dealing with leptons. Therefore, the pole mass behaves like a physical mass for electrons or muons, whereas for heavy quarks it is not a short-distance mass, because of infrared renormalon effects, and one should choose on a case-by-case basis whether the pole mass or other definitions are adequate to describe a given physical process.

In order to quantify the renormalon ambiguity in the pole mass, one can employ the relation between pole and $\overline{\text{MS}}$ masses, relying on the fact that the $\overline{\text{MS}}$ mass is unaffected by renormalons. Equation (5) can be parametrized to all orders as in Beneke et al. [16]:

$\begin{array}{ll}{m}_{\text{pole}}=\bar{m}({\mu }_m)\left[1+{\displaystyle \sum _{n=1}^{\infty }}{c}_n(\mu ,{\mu }_m,\bar{m}({\mu }_m)){\alpha }_S^n(\mu )\right],& (17)\end{array}$

with $\bar{m}({\mu }_m)$ being the $\overline{\text{MS}}$ mass at some scale μ_m and μ the renormalization scale at which the strong coupling is evaluated. The dominant renormalon divergence implies that the coefficients c_n in the asymptotic expansion have to satisfy the following relation at large n:

$\begin{array}{ll}{c}_n(\mu ,{\mu }_m,m({\mu }_m))\to N\frac{\mu }{m({\mu }_m)}{c}_n^{\text{as}}\text{ for }n\to \infty .& (18)\end{array}$

The expression for the asymptotic coefficients $c_n^{\text{as}}$ can be found in Beneke et al. [16] and is consistent with the fact that the renormalon factorial growth is due to the low-momentum region in the higher-order loop corrections to the heavy-quark self energy. The calculation of the normalization coefficient N is non trivial: in Beneke et al. [16] N was extracted after fitting the third- and fourth-order coefficient in the exact four-loop $\overline{\text{MS}}$-pole mass conversion and amounts to N ≃ 0.976… for N_C = 3 number of colors.

Furthermore, an alternative and possibly better method to deal with factorially divergent series consists in using the Borel transform, which, for a function f(α_S) reads:

$\begin{array}{ll}f({\alpha }_S)={\displaystyle \sum _{n=0}^{\infty }}{c}_n{\alpha }_S^{n+1};B\left[f\right](t)={\displaystyle \sum _{n=0}^{\infty }}{c}_n\frac{t^n}{n!},& (19)\end{array}$

which implies

$\begin{array}{ll}f({\alpha }_S)={\displaystyle {\int }_0^{\infty }}{e}^{-t/{\alpha }_S}B\left[f\right](t).& (20)\end{array}$

The evaluation of the Borel integral in Equation (20) depends on a prescription: one typically takes its principal value and, following the so-called “Im/Pi” method, the uncertainty is estimated as the modulus of the imaginary part, arising from the integration above and below the singular cuts in the complex plane, divided by π. In fact, in Beneke et al. [16] the asymptotic expansion of the pole mass with respect to the $\overline{\text{MS}}$ one was computed as an inverse Borel transform, by using the Im/Pi method for the error, considering only three light flavors and accounting for charm and bottom masses. The final result is that the leading renormalon ambiguity amounts to about 110 MeV for top as well as bottom and charm pole masses.

A different strategy to gauge the renormalon ambiguity was instead tackled in Hoang et al. [17], where the MSR mass m_MSR(R) was used. In the relation between m_pole and m_MSR(R),

$\begin{array}{ll}{m}_{\text{pole}}=m_{\text{MSR}}(R)+R{\displaystyle \sum _{n=1}^{\infty }}{a}_n{\left[\frac{{\alpha }_S(R)}{4\pi }\right]}^n,& (21)\end{array}$

the scale R is set to the $\overline{\text{MS}}$ top mass $m_t({\bar{m}}_t)$ and the series in Equation (21) is truncated at some fixed order n. A value n_min is determined in such a way to minimize the difference Δ(n) = m_pole(n)−m_pole(n−1) and a number f slightly above unity is defined. The set {n}_f is thus constructed in such a way that Δ(n) ≤ fΔ(n_min): the midpoint of m_pole(n) within {n}_f is then chosen as the central value and half of the variation range of m_pole(n) as an estimate of the ambiguity, accounting for the running of the renormalization scale as well. After observing that the results depend on f rather mildly, in Hoang et al. [17] f = 5/4 was chosen, yielding an ambiguity about 253 MeV in the pole mass. Both in Beneke et al. [16] and Hoang et al. [17], some thorough discussion is devoted to the inclusion of charm and bottom masses. The results of 110 and 253 MeV would go down to 70 [16] and 180 [17] MeV if one treated charm and bottom quarks as massless. Some attempts to relate the different methods adopted in Beneke et al. [16] and Hoang et al. [17] were made in Nason [13]. In fact, the result in Beneke et al. [16] can be obtained even following the method in Hoang et al. [17], but taking as central value half the sum of all Δ(n) and setting f = 1+1/(4π) in the uncertainty evaluation.

In the following, no strong statement supporting the calculation in Beneke et al. [16] or Hoang et al. [17] will be made. I just wish to point out that, on the one hand, as long as the uncertainties in the top-mass measurement stay around 500 GeV, both renormalon determinations are smaller and should not play any role in supporting the use of a given mass definition. This may not be the case if, in future perspective, one ideally aims at precisions about 200–300 MeV. However, as will be underlined when dealing with Monte Carlo modeling and theoretical errors, recent implementations of top production and decay in shower codes include width effects [29], in such a way that the top width, about 1.4 GeV and well above the energy range of both renormalon estimates, acts as a cutoff for the radiation off top quarks ⁶. Of course, if one considers observables relying on top decays (t→bW), the b-quark is allowed to emit soft radiation down to the shower cutoff and, in principle, in quantities depending on b-jets one may have to deal with renormalons.

A careful exploration of renormalon effects in observables depending on the top mass was carried out in Ferrario Ravasio et al. [30]. The authors found that the $\overline{\text{MS}}$ mass is a better definition for quantities like the total $t\bar{t}$ cross section, while using the pole mass would lead to a linear renormalon and an ambiguity of ${O}(100\text{ MeV})$ on the m_t extraction. Indications in favor of such a short-distance mass were also given whenever final-state jets are reconstructed using algorithms with a large jet radius R. As for the reconstructed top mass from, e.g., the b-jet+W invariant mass, in the pole-mass scheme a linear renormalon correction is present, whose coefficient is nevertheless pretty small if one employs a large R in the b-jet definition. Finally, leptonic observables exhibit a linear renormalon with both mass definitions, as long as one works in the narrow-width approximation. On the contrary, there are no linear renormalons if one adopts a a short-distance mass and includes the finite top width.

4. Top-Quark Mass Extraction at LHC

Top-quark mass determinations at hadron colliders are classified as standard or alternative measurements and, according to the decay modes of the two W's in top decays, as measurements in the dilepton, lepton+jet or all-hadronic channels. Standard top-mass analyses are based on the direct reconstruction of top-decay final states and compare observables, such as the b-jet+lepton invariant- mass distribution, with the predictions yielded by the Monte Carlo codes. So-called alternative measurements use instead other observables, such as total/differential cross sections or distribution peaks/endpoints. Since, as will be detailed in the following, Monte Carlo codes are of paramount importance for most top-mass analyses, I shall first sketch their main features, and then review the experimental methods to extract m_t.

4.1. Monte Carlo Generators for Top Physics

The last couple of decades has seen a tremendous progress in the implementation of Monte Carlo event generators, besides the reknowned general-purpose HERWIG [31, 32] and PYTHIA [33, 34], in such a way that several reliable programs are currently available for the top-mass analyses. On the one hand, strategies to match NLO calculations with parton showers were developed, on the other one a number of so-called matrix-element generators were released. In fact, matrix-element generators simulate multi-leg amplitudes and are interfaced to HERWIG or PYTHIA for shower and hadronization: besides top-quark signals, they are very useful to simulate backgrounds with high jet multiplicities, such as W/Z+n jets, which would be poorly described by HERWIG or PYTHIA for n > 1.

Regarding top phenomenology, standard Monte Carlo programs simulate both top production and decays using leading order (LO) matrix elements, multi-parton emission in the soft or collinear limit and the interference between top-production and decay stages is neglected (narrow-width approximation). HERWIG parton showers satisfy angular ordering [35, 36], with the latest version even allowing the option of dipole-like evolution [37]; PYTHIA cascades are instead ordered in transverse momentum⁷. Matrix-element corrections to parton showers are implemented for top decays [38, 39], but not for production, and the total production cross section and top-decay width are still calculated at LO. Hadronization is included by adopting the cluster model [40], based on color pre-confinement, in HERWIG and the string model [41] in PYTHIA. The underlying event used to be described assuming soft collisions between the proton spectators and tuning the model parameters to minimum-bias events at small transverse momentum. Nevertheless, all modern codes implement it through multiple scatterings strongly ordered in transverse momentum: the underlying event is thus a secondary collision, whose transverse momentum is much lower than the primary hard scattering [42, 43].

Among the new generation of Monte Carlo programs, SHERPA [44] can also be considered a multi-purpose code, in the light of the wide spectrum of processes which it is capable of simulating. In detail, matrix elements are computed by means of the AMEGIC++ [45] and COMIX [46] codes, while the interface to one-loop generators, implemented along the lines of [47], allows one to include NLO QCD and possibly electroweak corrections. Parton showers are then accounted for according to the dipole formalism developed in Catani and Seymour [48], underlying event and hadronization follow the multiple-scattering and cluster models in PYTHIA and HERWIG, respectively.

For the purpose of the matching of NLO matrix elements and multi-parton cascades, NLO+shower programs, such as MadGraph5_aMC@NLO [49, 50] and POWHEG [51], implement NLO hard-scattering amplitudes, but still depend on HERWIG and PYTHIA for parton cascades and non-perturbative phenomena. The earlier versions of such NLO+shower algorithms only included NLO corrections to $t\bar{t}$ production, while (LO) top decays and hadronization were still handled in the parton shower approximation. The later implementation of POWHEG [29] includes in the $b\bar{b}4\ell$ code both top production and decay at NLO, accounting for the interference between top production and decay stages, as well as non-resonant contributions leading to $(W^{+}b)(W^{-}\bar{b})$ final states⁸. As for MadGraph5_aMC@NLO, strictly speaking, top decays are still at LO, however spin correlations are included through the MadSpin package [53] and, as discussed in Frederix et al. [54], they account for a significant part of the NLO corrections. For the purpose of HERWIG, it has its own implementation of NLO+shower merging/matching [55, 56], working for top-quark production and decay in the narrow-width approximation [57].

Regarding matrix-element generators, suitable codes to describe top-quark signals and backgrounds are, among others, ALPGEN [58], MCFM [59], CalcHEP [60], HELAC [61], and WHIZARD [62]. In particular, ALPGEN and CalcHEP simulate multi-parton final states at LO and can be interfaced to HERWIG or PYTHIA for shower and hadronization. HELAC and WHIZARD have been lately provided with NLO corrections [63, 64] and matching to shower and hadronization codes as well. MCFM is a NLO parton-level Monte Carlo code: top production and decay are handled at NLO, in the narrow-width approximation.

Before concluding this subsection, it is worthwhile saying a few words on the precision of the predictions yielded by Monte Carlo codes. As observed before, parton showers simulate multiple radiation in the soft or collinear approximation and, in general, the accuracy of a prediction depends on the specific observable under investigation. Although total cross sections and widths are (N)LO, for most quantities Monte Carlo predictions are equivalent to leading-logarithmic resummations, i.e., they resum double soft and collinear logarithms, and include some classes of subleading logarithms, i.e., only soft- or collinear-enhanced⁹. Catani et al. [66] even proved that, in Deep Inelastic Scattering and Drell–Yan processes at large values of the Bjorken x, the HERWIG algorithm is capable of capturing all next-to-leading logarithms, i.e., all single logarithms, enhanced for soft or collinear emission, as long as one rescales the QCD scale Λ to a Monte Carlo value, labeled Λ_MC. ¹⁰

4.2. Standard and Alternative Top-Mass Measurements

In this subsection I shall briefly present the main strategies to measure the top mass at hadron colliders in $t\bar{t}$ events, taking particular care about the analyses carried out at the LHC.

4.2.1. Direct Reconstruction Methods

Strategies based on the direct reconstruction of the top-decay products, namely the template, matrix-element and ideogram methods, have been traditionally classified as standard top-mass determinations. As for ATLAS, the most up-to-dated measurements are given at 8 TeV and 19.7 fb⁻¹ in Aaboud et al. [67–69] for dilepton, lepton+jets and all-hadronic modes, respectively. Regarding CMS, at the moment even results at $\sqrt{s}=13$ TeV and ${L}=35.9$ fb⁻¹ are available and are reported in Sirunyan et al. [70] (dileptons), [71] (lepton+jets) and [72] (all hadrons). Regarding these analyses and summing in quadrature systematic and statistical errors, CMS quotes uncertainties about 0.73 GeV for dileptons, 0.62 GeV for leptons+jets and 0.61 GeV for the all-hadron channel. As for ATLAS, the uncertainties are 0.84 GeV (dileptons), 0.91 GeV (lepton+jets) and 0.73 GeV (all jets). The standard top-mass measurements have been the basis to determine the world average [6], already presented in the introduction, which, after summing statistical and systematic errors in quadrature, yields an overall uncertainty about 800 MeV. Work toward an updated world average is currently under way. The LHC collaborations have nevertheless released their own combined measurements using 7 and 8 TeV data together: details on such studies can be found in Aaboud et al. [69] and Khachatryan et al. [73] for ATLAS and CMS, respectively. Both analyses yield a total error about 0.5 GeV, hence an overall precision on the top mass around 0.3%. Figure 1 summarizes the state of the art on top-mass measurements carried out at the LHC, including the world average, as well as ATLAS and CMS combinations.

FIGURE 1

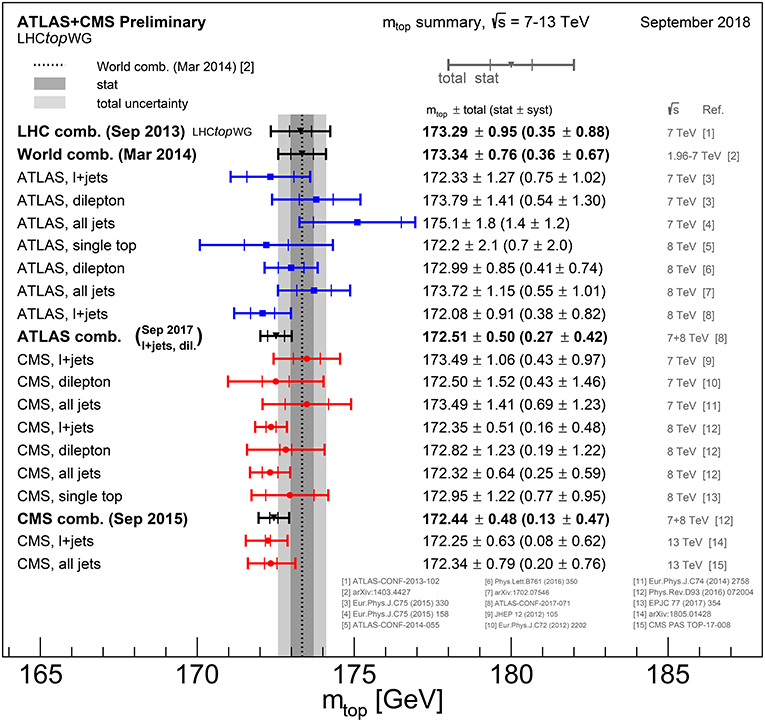
Figure 1. Summary of the top-mass analyses at the LHC, accounting for the world average and the ATLAS and CMS combinations as well.

As discussed in the introduction, since the standard m_t-reconstruction methods rely on the use of Monte Carlo generators, such measurements are usually quoted as “Monte Carlo mass” and much debate has been taking place on whether the extracted mass can be related to any well-posed definition, with some calculable uncertainty, such as the pole mass. The ongoing discussion on the theoretical interpretation of the measured top mass will be the main topic of next session. Before moving to this issue, it is worthwhile reviewing the so-called “alternative” strategies, making use of total/differential cross sections, endpoints or other kinematic properties of $t\bar{t}$ final states.

4.2.2. Total and Differential $t\bar{t}$ Cross Section

The total $t\bar{t}$ cross section was calculated in QCD in the NNLO+NNLL approximation in Czakon et al. [74] ¹¹ and was used to determine m_t by ATLAS in Aad et al. [75] (7 and 8 TeV data) and by CMS in Khachatryan et al. [76] (7 and 8 TeV) and Sirunyan et al. [77] (13 TeV). Since the calculation in Czakon et al. [74] employed the pole mass definition, the results in Khachatryan et al. [73], Aad et al. [75], and Sirunyan et al. [77] are quoted as pole mass measurements. Although to some extent this is mostly correct, it should always be reminded that even those analyses are not completely independent of the shower generator, and therefore of its mass parameter, which is still used to evaluate the acceptance. Nevertheless, it was proved that such a sensitivity is rather mild. Overall, the errors in Aad et al. [75], Khachatryan et al. et al. [76], and Sirunyan et al. [77] are larger than those in the standard methods, as they are about 2.5 GeV; however, they are expected to decrease thanks to the higher statistics foreseen in the LHC future runs. After the computation of the total cross section, even differential distributions were calculated at NNLO in Czakon et al. [78], still using the top pole mass: this computation was used by the D0 Collaboration [79] to extract the top mass at the Tevatron accelerator, namely $\sqrt{s}=1.96$ TeV and ${L}=9.7{\text{fb}}^{-1}$. The error on this measurement is about 2.5 GeV, hence competitive with those obtained at the LHC from the total production cross section.

Dowling and Moch [80] explored the extraction of the top mass by using the NNLO total $t\bar{t}$ cross section and NLO differential distributions, such as transverse momentum, rapidity and $t\bar{t}$ invariant mass, expressed in terms of pole and $\overline{\text{MS}}$ masses. Overall, Dowling and Moch [80] found that using the running mass yields a milder scale dependence of such observables; nevertheless, implementing the full NNLO differential cross section or the four-loop pole-$\overline{\text{MS}}$ mass conversion, along the lines of Czakon et al. [78] and Marquard et al. [18], respectively, will be obviously very useful to shed light on the scale dependence.

Still on the $t\bar{t}$ total cross section, it is worthwhile pointing out the recent work carried out to merge NNLO QCD and NLO electroweak corrections in Czakon et al. [81]. Such a computation was then used to predict the top-quark charge asymmetry at Tevatron and LHC and the electroweak corrections exhibited a remarkable impact, say about 20%, on the forward-backward asymmetry. It will be clearly very interesting determining the top pole mass from differential distributions, along the lines of [79], including electroweak contributions as well.

4.2.3. $t\bar{t}j$ Cross Section

The top mass was also extracted from the measurement of the $t\bar{t}+1$ jet cross section, which has a stronger sensitive to m_t than the inclusive $t\bar{t}$ rate. In Alioli et al. [82], the NLO $t\bar{t}j$ cross section was calculated using POWHEG and its pole mass implementation, matched to PYTHIA. Detector and shower/hadronization effects were unfolded in order to recover the pure NLO $t\bar{t}j$ cross section. From the experimental viewpoint, the approach proposed in Alioli et al. [82] was followed in Aad et al. [83] by ATLAS (7 TeV and 5 fb⁻¹) and by CMS in Collaboration [84] (8 TeV and 19.7 fb⁻¹). The error on m_t extracted from the $t\bar{t}j$ cross section is slightly smaller than from the inclusive $t\bar{t}$ one, but still much above the direct-reconstruction measurements. Such mass determinations are referred to as pole mass measurements, since this is the mass definition employed by POWHEG, while the PYTHIA mass parameter used in the parton shower has a mild effect in the determination of the acceptance. Fuster et al. [85] used the running $\overline{\text{MS}}$ top mass in the calculation of the NLO $t\bar{t}j$ rate and, after comparing with the cross section measurements, obtained results which are, within the errors, in agreement with the pole mass yielded by the approach in Alioli et al. [82].

Other so-called alternative methods to reconstruct m_t rely on the kinematic properties of top-decay final states: since they are based on the comparison with Monte Carlo predictions, the measured m_t has to be identified with the mass parameter in the shower code. Overall, such techniques yield uncertainties in the mass about the order of magnitude of those relying on the total cross section, say about 1 GeV or above.

4.2.4. Peak of the b-Jet Energy Spectrum

It was observed that the peak of the b-jet energy in top decay at LO is independent of the boost from the top to the laboratory frame, as well as of the production mechanism [86]. The CMS Collaboration did measure the top mass from the b-jet energy peak data at 8 TeV and 19.7 fb⁻¹ [87], by using POWHEG and MadGraph to simulate top production and decay, and PYTHIA for parton shower, hadronization and underlying event. The resulting uncertainties are 1.17 GeV (statistics) and 2.66 GeV (systematics).

4.2.5. m_bℓ, m_bℓν and Stranverse Mass m_T2

The b-jet+lepton invariant-mass (m_bℓ) spectrum was used by CMS to reconstruct m_t in the dilepton channel in CMS Collaboration [88], at 8 TeV and 19.7 fb⁻¹. The data were compared with the MadGraph+PYTHIA simulation, yielding a measurement consistent with the world average and an uncertainty about 1.3 GeV. In CMS Collaboration [88], for the sake of comparison, even the NLO code MCFM was used to predict the m_bℓ distribution. More recently, in Sirunyan et al. [89] CMS extracted m_t even from the so-called stransverse mass m_T2 [90] and from m_bℓν, which accounts for the neutrino missing transverse momentum as well. The sensitivity of these observables to m_t yields an uncertainty about 180 MeV (statistics) and 900 MeV (systematics).

4.2.6. Endpoint Method

Another method to measure m_t consists of using the endpoints of distributions sensitive to m_t, namely the endpoints of m_bℓ, μ_bb and μ_ℓℓ, where b is a b-flavored jet, and μ_bb and μ_ℓℓ generalizations of the $b\bar{b}$ and ℓ⁺ℓ⁻ invariant masses in the dilepton channel, as described in Chatrchyan et al. [91] (CMS, 7 TeV and 5 fb⁻¹). Since b-flavored jets can be calibrated directly from data, the endpoint strategy is claimed to minimize the Monte Carlo error on m_t, which is mostly due to color reconnection, namely the formation of a B hadron by combining a b quark in t decay with an antiquark from $\bar{t}$ decay or initial-state radiation. Constraining the neutrino and W masses to their world-average values, this method leads to uncertainties about 900 MeV (statistics) and 2 GeV (systematics).

4.2.7. Leptonic Observables

Purely leptonic observables in the dilepton channel, such as the Mellin moments of lepton energies or transverse momenta, were proposed to measure m_t, since in this way one can escape the actual reconstruction of the top quarks [92]. However, this method still yields uncertainties due to hadronization, production mechanism, Lorentz boost from the top to the laboratory frame, as well as missing higher-order corrections. Preliminary analyses have been carried out in CMS Collaboration [93] (CMS, based on LO MadGraph) and Aaboud et al. [68] (ATLAS, based on the MCFM NLO parton-level code [94]) using data at 8 TeV and 19.7 fb⁻¹ and are expected to be improved by matching NLO amplitudes with shower/hadronization generators. For the time being, the uncertainties quoted in Collaboration [93] are 1.1 GeV (statistics), 0.5 GeV (experimental systematics) and 2.5–3.1 GeV (theoretical systematics), whereas in Aaboud et al. [68] they read 0.9, 0.8, and 1.2 GeV, respectively. CMS Collaboration [93] also quotes an uncertainty ${ }_{-0.0}^{+0.8}\text{ GeV}$ due to the description of the top-quark transverse momentum. In fact, previous CMS analyses had displayed a mismodeling of the top p_T simulated by MadGraph+PYTHIA, and therefore CMS Collaboration [93] reweighted the transverse momentum to match the measured one.

4.2.8. J/ψ Method

Final states with J/ψ mesons were exploited by the CMS Collaboration in Khachatryan et al. [95] to measure m_t, using data collected at 8 TeV and a luminosity about 19.7 fb⁻¹. In this work, one explores t→bW processes where b-flavored hadrons decay into states containing a J/ψ, the J/ψ decays according to J/ψ → μ⁺μ⁻ pair and the W bosons undergo the leptonic transition W → ℓν. The top mass is then extracted by fitting the invariant mass distributions m_μμ or m_J/ψℓ, as well as the transverse momentum of the J/ψ. The analysis was carried out by using the MadGraph code, interfaced with PYTHIA, while, for the sake of estimating the theoretical error, POWHEG and SHERPA were employed as well. Overall, the statistical uncertainty in the investigation [95] amounts to 3 GeV, while the systematic error to 0.9 GeV. The conclusion of Khachatryan et al. [95] is that, since the systematic uncertainties are of different origin from those entering in the measurements based on direct reconstruction and given the higher statistics which are foreseen, the J/ψ method should ultimately be worth to be included in the combination with the extractions from matrix-element or template strategies.

4.2.9. Final-State Charged Particles

A novel technique was presented by the CMS Collaboration in Khachatryan et al. [96], where m_t is measured by exploiting the kinematic properties of final-state charged particles. The observable used in this analysis is the mass m_svℓ of the secondary vertex-lepton system, namely the invariant mass of a system made of the charged lepton in W decays and charged hadrons in a jet originating from a common secondary vertex. Using only charged particles, in fact, reduces the overall acceptance uncertainty, whereas this method is obviously dependent on the modeling of top decays and bottom hadronization. The investigation was undertaken using MadGraph+PYTHIA to simulate the signal, POWHEG and SHERPA to estimate the uncertainty due to the matrix-element generation and hadronization, respectively. The final error on the measurement of m_t from charged particles is then 200 MeV (statistics) and ${ }_{-0.97}^{+1.58}$ GeV (systematics), by using data sets of 8 TeV collisions and a luminosity of 19.7 fb⁻¹.

4.2.10. Perspectives at High Luminosity

The perspectives for the top-mass determination at High Luminosity (HL) LHC were debated in Azzi et al. [97], where the HL-LHC will collide protons at 14 TeV and accumulate an integrated luminosity of 3,000 fb⁻¹. In the report [97] the ATLAS Collaboration presented a projection for the accuracy on m_t using samples of events in the lepton+jets mode and J/ψ → μ⁺μ⁻ decays in the final state, along the lines of CERN [98]. The expected statistical and systematic uncertanties amount to 0.14 and 0.48, GeV respectively. As for CMS, the potentials for the top-mass extraction at HL-LHC are detailed in CERN [99] and summarized in Figure 2: one can learn that all uncertainties will tremendously decrease at HL-LHC. In particular, one expects an error which ranges from about 0.2 GeV (0.1%) for direct reconstruction in the lepton+jets channel to 1.2 GeV (0.7%) from the total $t\bar{t}$ NNLO cross section. It is remarkable that the uncertainty from J/ψ final states will go down to about 0.6 TeV (0.35%).

FIGURE 2

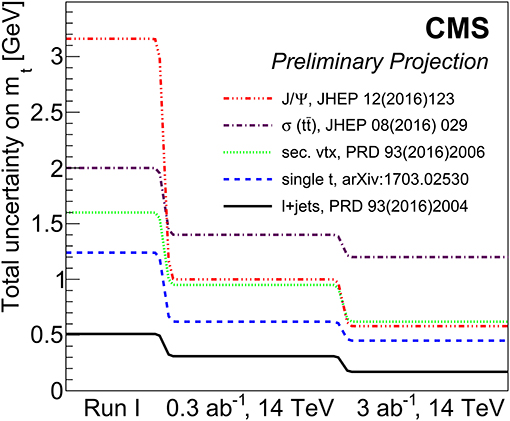
Figure 2. Projections of the uncertainty on the top-mass determination for different strategies, according to the CMS Collaboration, as a function of the integrated luminosity at HL-LHC.

5. Interpretation of the Top-Mass Measurements and Theoretical Uncertainties

The nature of the reconstructed top-quark mass and its possible relations with field-theory mass definitions has lately become the topic of a very lively debate (see, e.g., the reviews in Nason [13], Hoang [100], and Corcella [101]). I shall first overview the main issues concerning the m_t interpretation and then discuss the dominant sources of theoretical uncertainty.

5.1. Measured Mass Ad Theoretical Definitions

The discussion on the identification of the measured quantity is mostly based on the claim that Monte Carlo codes are LO, while well-posed field-theory mass definitions need at least a NLO computation. Although it is certainly true that, referring to standard codes, total cross sections are LO, event shapes and differential distributions go well beyond LO and account for a resummation of enhanced logarithms. NLO+shower codes like POWHEG and MC@NLO yield NLO total cross sections, adopting the top pole mass in the computation, while the differential spectra rely on the shower approximation and on the modeling of hadronization and underlying event. Nevertheless, it is indeed cumbersome interpreting the reconstructed top mass in terms of theoretical definitions or, in other words, scrutinizing all possible sources of uncertainties which may prevent such an identification. As far as this controversy is concerned, one can basically follow two mainstream viewpoints.

On the one hand, there are authors [7–11] who claim that the measured quantity cannot be directly associated with any field-theory mass definition and therefore one must stick to the notion of Monte Carlo mass. Along this point of view, much work has been undertaken in order to relate the Monte Carlo mass to definitions like the pole mass: the quoted discrepancies between Monte Carlo and pole masses have through the years ranged from few hundreds MeV to, in the most extreme case, almost 1 GeV. If this were indeed the case, it would be an uncertainty comparable or even larger than the current errors on the directly reconstructed top mass. On the other hand, we have authors [12, 13] who instead argue against the use of the Monte Carlo mass and claim that, under given circumstances, the reconstructed mass should actually mimic the pole mass. According to this viewpoint, instead of constructing other mass definitions to properly interpret the measurements, the effort should rather be devoted to carefully estimate the theoretical uncertainties, of both perturbative and non-perturbative nature, in the identification of the measured quantity with the pole mass. In the following, I will briefly review the work carried out in this respect.

As far as I know, the pioneering work on relating the measured mass to the pole mass was carried out in Fleming et al. [7] and Hoang and Stewart [8]. First, Fleming et al. [7] defined, for the case study of $e^{+}{e}^{-}\to t\bar{t}$ collisions, the SCET (MSR-like) short-distance jet mass m_J(μ), associated with the collinear jet function and corresponding to the MSR mass at a scale about the top width, i.e., R = Γ_t. Then, m_J(μ) was related to the pole mass by means of the following equation:

$\begin{array}{ll}{m}_J(\mu )=m_{\text{pole}}-\frac{{\alpha }_S(\mu )C_F{\Gamma }_t}{\pi }\left(ln\frac{\mu }{{\Gamma }_t}+\frac{3}{2}\right)+{O}({\alpha }_S^2).& (22)\end{array}$

Setting, e.g., μ ≃ 1 GeV, then the jet mass differs from the pole mass by about 200 MeV at ${O}({\alpha }_S)$. It is also remarkable that the correction is of order ${O}({\alpha }_S{\Gamma }_t)$, which confirms the intuition that the top width has to play a role in the uncertainty in the measured mass. Later on, Hoang and Stewart [8] did define a Monte Carlo mass and, relying on the standard shower implementations, stated that the extracted top mass could be interpreted as the jet mass evaluated at a scale of the order of the shower cutoff Q₀, i.e., $m_t^{\text{MC}}\simeq m_t^{\text{MSR}}(Q_0)$. Hoang and Stewart [8] set $Q_0=(3_{-2}^{+6})$ GeV and $m_t^{\text{MSR}}(Q_0)$ to the value of the (Tevatron-based) top-mass world average at that time, and got a consistent value of the $\overline{\text{MS}}$ mass ${\bar{m}}_t({\bar{m}}_t)$, by using renormalization group evolution equations.

More recently, Butenschoen et al. [9] compared PYTHIA with a SCET computation in the NLO approximation, resumming soft- and collinear-enhanced contributions to NLL or even NNLL accuracy. As in Hoang and Stewart [8], the SCET resummed calculation employed the MSR mass $m_t^{\text{MSR}}(R)$, with R~Γ_t and $m_t^{\text{MSR}}(R)\to m_{t,pole}$ for R → 0. The PYTHIA mass parameter was then calibrated to reproduce the SCET prediction for the 2-jettiness τ₂, after running the code for several center-of-mass energies and a few values of the top mass. The result of Butenschoen et al. [9] is that the PYTHIA mass is consistent, within the errors, with the MSR mass evaluated at a scale of 1 GeV. Using instead the pole mass in the computation yields a shift with respect to the PYTHIA m_t about 600–900 MeV, according to whether the Monte Carlo results are compared with a NLL or NNLL resummation. The work in Butenschoen et al. [9] was extended to pp collisions in Hoang et al. [10], where the extraction of m_t from boosted top jets with light soft-drop grooming was proposed¹². By comparing the NLL resummation for the groomed top-jet mass with PYTHIA, the pole mass was found about 400–700 MeV below the calibrated Monte Carlo mass, depending on the energy of the pp collision and non-perturbative parameters contained in the resummation. Still on this subject, Hoang et al. [11] explores the dependence of m_t on the parton shower cutoff, referring to the HERWIG 7 angular-ordered cascade. By working in the quasi-collinear limit, with boosted massive quarks in the NLL approximation, the authors of Hoang et al. [11] stated that the mass parameter in a Monte Carlo code should be identified with a cutoff-dependent, coherent-branching (CB) mass, labeled as $m_t^{\text{CB}}(Q_0)$. Such a coherent-branching mass is a low-scale short-distance mass, free from renormalon corrections, related to the pole mass by a relation like:

$\begin{array}{ll}{m}_{t,{\mathrm{\text{CB}}}^{({\mathit{\text{Q}}}_0)}}=m_{t,pole}-\frac{2}{3}{\alpha }_S(Q_0)Q_0+{O}({\alpha }_S^2{Q}_0).& (23)\end{array}$

Expressing in Equation (23) α_S in terms of the Monte Carlo QCD scale Λ_MC defined in Catani et al. [66] and setting Q₀ = 1.25 GeV, like the shower cutoff of HERWIG 7, the shift between pole and CB masses amounts to about 500 MeV. Using instead the standard $\overline{\text{MS}}$ scheme for α_S yields a discrepancy of the order of 300 MeV. Concerning the calibration of the Monte Carlo mass parameter, another approach was suggested in Kieseler et al. [103]: one measures an observable, e.g., a total or differential cross section, ignoring anything on the event generation, and, by comparing the data with the simulation, calibrates both observable and m_t. The finding of Kieseler et al. [103] is that, given the current precision on the inclusive $t\bar{t}$ rate, the uncertainty on this calibration is roughly 2 GeV.

As anticipated above, other authors, such as Nason [12, 13], claim that it is not really necessary to introduce the Monte Carlo mass concept to interpret measurements relying on final-state direct reconstruction. The starting point is the observation that, in the narrow-width approximation and assuming that one is able to catch all final-state radiation, the invariant mass of top-decay products in t→bWX, X being some extra radiation off top and bottom quarks, should mimic the on-shell top mass, i.e., the pole mass. Effects due to the top final width, parton emission which is not included in the reconstruction, contamination from initial-state radiation and non-perturbative phenomena, such as color reconnection or underlying event, clearly spoil the direct identification of the invariant mass of top-decay final states with the pole mass. However, in the perspective of Nason [12, 13] rather than a genuine shift of the measured mass with respect to the pole mass, such effects are seen as uncertainties, of either perturbative or non-perturbative nature, in the identification of the extracted mass as pole mass.

Although such approaches may sound pretty different, work toward a possible compromize was carried out in Azzi et al. [97], in such a way to guide the top-quark community and avoid confusion or statements claiming a sort of ignorance on the nature of the measured top-quark mass. Though starting from different perspectives, all those papers agree that the measured m_t can be connected to the pole mass by means of a relation like:

$\begin{array}{ll}{m}_t=m_{t,pole}+\delta m_t\pm \Delta m_t,& (24)\end{array}$

where δm_t is a possible shift between measured and pole masses and Δm_t is an uncertainty. According to Nason [12, 13], which basically discourage the use of the concept of Monte Carlo mass, the extracted mass through top-decay final-state reconstruction mimics the pole mass, up to some computable uncertainty. In this approach δm_t ≃ 0, while Δm_t is a theoretical (Monte Carlo based) error that, in measurements employing event generators, should be estimated, e.g., varying shower/hadronization parameters, confronting different models (cluster and string models for hadronization are a typical example) or changing the analysis details (for final-state jets, increasing/decreasing the jet radius leads to accounting for more or less gluon radiation). In the view of Nason [12, 13], the uncertainty Δm_t in the identification of the measurements with the pole mass should be of the order of the hadronization scale, i.e., ${O}(\Lambda )$. On the contrary, in the work carried out in Hoang and Stewart [8], Butenschoen et al. [9], Hoang et al. [10], and Hoang et al. [11] m_t is labeled as Monte Carlo mass and δm_t is an actual discrepancy with respect to the pole mass, typically about ${O}\left[Q_0{\alpha }_S(Q_0)\right]$ as in Equation (23), while Δm_t is still an uncertainty, which one can estimate by varying the parameters or options in the codes and computations employed in the comparison.

Therefore, the disagreement among most authors of the relevant literature on the interpretation of the top-mass measurement is conceptually relevant, but in practice concerns whether one should calculate an actual discrepancy δm_t or not, as well as the meaning of Δm_t and its numerical magnitude. In Hoang and Stewart [8], Butenschoen et al. [9], Hoang et al. [10], and Hoang et al. [11] different values for δm_t and Δm_t have been quoted, which is reasonable, since, as also advocated in Nason [12] for the purpose of the uncertainty, any possible relation between the pole mass and the measured quantity has to depend on the observable which is used to extract m_t, on the details of the analysis, such as the imposed cuts, the energy of the collider and whether it runs, e.g., e⁺e⁻ or pp modes. Moreover, since such determinations are based on a comparison between Monte Carlo results with resummed calculations, with m_t being a tunable parameter, δm_t and Δm_t also depend on the accuracy of the resummations, e.g., NLL or NNLL. As discussed above, δm_t is about 200 MeV in Hoang and Stewart [8], in the range 600-900 MeV in Butenschoen et al. [9], 400–700 MeV in Hoang et al. [10] and 300–500 MeV in Hoang et al. [11]. The uncertainty Δm_t in the relation of Equation (24) was estimated to be roughly 250 MeV in Hoang et al. [11] and 280–380 MeV in Butenschoen et al. [9]. Nason [12, 13] do not contain an explicit calculation of Δm_t, but rather propose a method to compute it, e.g., by varying Monte Carlo perturbative and non-perturbative parameters or, in a POWHEG-like implementation, switching NLO and width effects on or off. Of course, it will be very interesting to follow such an approach and compare the results with the numbers obtained in Hoang and Stewart [8], Butenschoen et al. [9], Hoang et al. [10], and Hoang et al. [11]. One may already guess that, since Nason [12, 13] do not account for any explicit discrepancy δm_t, one may likely get a larger uncertainty Δm_t when following this approach. Furthermore, it will be crucial understanding how much, for a given observable, any shift/uncertainty of the measured mass with respect to the pole mass depends on the specific shower code and, e.g., one finds an impact of the late implementation of NLO corrections and width effects along the lines of [29].

5.2. Theoretical Uncertainties in the Top Mass Determination

For the sake of a precise determination of the top-quark mass, a reliable estimate of the theoretical error is of paramount importance. In the top-mass world-average extraction, i.e., The ATLAS et al. [6], based on the so-called standard measurements, the overall theory uncertainty accounts for about 540 MeV of the total 710 MeV systematics. In particular, The ATLAS et al. [6] distinguishes the contributions due to Monte Carlo generators, radiation effects, color reconnection and parton distribution functions (PDFs).

The Monte Carlo systematics is due to the differences in the implementation of parton showers, matrix-element matching, width effects, hadronization and underlying event in the various programs available to describe top-quark production and decay. There is no unique way to estimate this uncertainty, though, and each collaboration even follows different prescription according to the analysis. One can either compare two different generators, which are considered appropriate for a given analysis and have been properly tuned to some data sets, or choose one single code and explore how its predictions fare with respect to variations of its parameters. For example, in The ATLAS et al. [6] CDF compares HERWIG and PYTHIA, while D0 uses ALPGEN+PYTHIA and ALPGEN+HERWIG; both Tevatron experiments use MC@NLO to gauge the overall impact of NLO corrections. At the LHC, ATLAS compares MC@NLO with POWHEG for the NLO contributions and PYTHIA with HERWIG for shower and hadronization; CMS instead confronts LO MadGraph with NLO POWHEG.

The radiation uncertainty gauges the effect of initial- and final-state radiation on the top mass and is typically obtained by varying in suitable ranges the relevant parameters in the parton-shower generators. Concerning PDFs, there are distinct strategies to evaluate the induced error on m_t in the different experiments, although using two different sets or a given set but with different parametrizations are common trends. More generally, the choice of the PDF set in analyses based on event generators has also been the topic of several discussions: as pointed out before, although Monte Carlo codes yield LO or NLO total cross sections, differential spectra go beyond such approximations and include the resummation of classes of enhanced logarithmic terms. An attempt to propose some improved sets of parton distribution functions for standard parton shower generators was presented in Sherstnev and Thorne [104].

Among the sources of theoretical uncertainty and possible shifts between measured and pole masses, color reconnection should deserve some special attention. In fact, it accounts for about 310 MeV in the world average presented in The ATLAS et al. [6]. Also, the very fact that, for example, a bottom quark in top decay (t→bW) can be color-connected to an initial-state antiquark does not have its counterpart in e⁺e⁻ annihilation and therefore its modeling in Monte Carlo event generators may need retuning at hadron colliders. Investigations on the impact of color reconnection on m_t were undertaken in Argyropoulos and Sjöstrand [105] and Corcella [106], in the frameworks of PYTHIA and HERWIG, respectively. In particular, Corcella [106] addresses this issue by simulating fictitious top-flavored hadrons T in HERWIG and comparing final-state distributions, such as the BW invariant mass, with standard $t\bar{t}$ events. In fact, in the top-hadron case, assuming T decays according to the spectator model, the b quark is forced to connect its color with the spectator or with antiquarks in its own shower, namely b→bg, followed by $g\to q\bar{q}$, and color reconnection is suppressed. The analysis in Corcella [106] is still ongoing and, in future perspectives, it may also serve to address the error on the identification of the measured mass with the pole mass. In fact, in the event samples simulated in Corcella [106] the Monte Carlo (HERWIG) mass is the mass of a heavy hadron, which can be related to any definition of the heavy-quark (top for T mesons) mass definition by means of lattice, potential models or Non Relativistic QCD. In Argyropoulos and Sjöstrand [105], color reconnection is instead investigated within the Lund string model, tuned to charged-particle multiplicity or transverse-momentum data. Several possible models for color reconnection were investigated and the yielded uncertainty on the top mass varied between 200 and 500 MeV, depending on the chosen framework.

Another non-perturbative phenomenon which plays a role in the theoretical error is bottom-quark fragmentation, i.e., the hadronization of bottom quarks in top decays into b-flavored mesons or baryons. The usual way to deal with it consists in tuning the Monte Carlo fragmentation parameters to precise $e^{+}{e}^{-}\to b\bar{b}$ data and then using the best parametrizations to describe bottom-quark hadronization in top decays. This approach was followed, e.g., in Corcella and Drollinger [107] and Corcella and Mescia [108], where data from DELPHI [109] SLD [110], OPAL [111] and ALEPH [112] were employed to tune the parameters of HERWIG [31] and PYTHIA [33]. In particular, Corcella and Mescia [108] used such a tuning to predict the B-hadron+lepton invariant mass m_Bℓ in $t\bar{t}$ events at LHC. A possible extraction of m_t using this observable exhibited a large discrepancy between the two event generators, which was explained as due to the different quality of the e⁺e⁻ fits, with HERWIG being only marginally consistent with the data. More recent modeling and fits, such as the so-called Monash [113] or A14 [114], or using the dipole-like shower implementation in Cormier et al. [57] are expected to give a better description of bottom fragmentation in top decays. Investigations on the uncertainties using these implementations are currently in progress; it will be very interesting, in particular, exploring bottom-quark fragmentation by using NLO+shower codes, such as POWHEG and aMC@NLO, interfaced to HERWIG or PYTHIA. In fact, it is mandatory to understand whether the Monte Carlo default parameterizations or tunings like those in Skands et al. [113] and Collaboration [114] work well at the LHC even when the hard scattering is at NLO, or one would rather need to refit the Monte Carlo parameters. In general, although the approach followed in Corcella and Mescia [108] relies on the universality of the hadronization transition, it is not absolutely guaranteed that models which reproduce e⁺e⁻ data work equally well in a colored environment like $t\bar{t}$ events at the LHC, where initial-state radiation, color reconnection and underlying event play a role. Therefore, tuning shower and hadronization parameters to LHC data should become a ultimate goal.

From this viewpoint, more recently, Corcella et al. [115] reconsidered the issue of the dependence of m_t on Monte Carlo parameters, suggesting a possible in-situ calibration of the shower codes using top events in the dilepton channel, and taking particular care about observables sensitive to b-fragmentation in top decays. In particular, Corcella et al. [115] extended the work in Corcella and Mescia [108] exploring top-decay observables in terms of B-hadrons, instead of b-jets, so that one should deal with fragmentation uncertainties, rather than with the jet-energy scale. For instance, if 〈O〉 is the average value of a given observable O and θ a generic generator parameter, then one can write the following relations:

$\begin{array}{ll}\frac{d{m}_t}{m_t}={\Delta }_O^m\frac{d\langle O\rangle }{\langle O\rangle };\frac{d\langle O\rangle }{\langle O\rangle }={\Delta }_{\theta }^O\frac{d\theta }{\theta }\Rightarrow \frac{d{m}_t}{m_t}={\Delta }_{\theta }^m\frac{d\theta }{\theta },& (25)\end{array}$

where we defined ${\Delta }_{\theta }^m={\Delta }_O^m{\Delta }_{\theta }^O$. Therefore, if one aims at, e.g., an error of 500 MeV on m_t, namely dm_t/dm_t < 0.003, one should also have ${\Delta }_{\theta }^m(d\theta /\theta )<0.003$. Corcella et al. [115] then identifies some so-called calibration observables, which depend on the shower/hadronization parameters but are rather insensitive to the top mass. Examples of such quantities are, e.g., the ratios of B-hadron to b-jet (b) transverse momenta p_{T, B}/p_{T, b}, of invariant masses $m_{B\bar{B}}/m_{b\bar{b}}$ ($\bar{b}$ being a jet containing a $\bar{B}$ hadron), the azimuthal separations and invariant opening angles $\Delta \varphi (b\bar{b})$, $\Delta \varphi (B\bar{B})$, $\Delta R(b\bar{b})$, $\Delta R(B\bar{B})$¹³. Then, imagining that one could ideally tune the parameters to measurements of the calibration observables, other quantities can be explored to extract m_t, such as the B-hadron energy and transverse momentum E_B and p_{T, B}, or the invariant masses m_Bℓ, $m_{\ell \bar{\ell }}$ and $m_{B\bar{B}\ell \bar{\ell }}$. The conclusion of this exploration is that, in order to achieve a 0.3% precision on the top mass, one needs to determine the strong coupling constant at 1% accuracy and other parameters, such as the shower cutoff, the gluon and quark effective masses or the hadronization parameters at 10%. Overall, Corcella et al. [115] proposes a method to tune directly Monte Carlo generators to data from top events at the LHC, which, whenever top-production data were to become precise enough, should be preferable to the use of fits to e⁺e⁻ data, in such a way to avoid all uncertainties and ambiguities in the application of e⁺e⁻-based fits to hadron collisions.

6. Conclusions

I discussed some challenging issues regarding the determination and interpretation of the top quark mass at hadron colliders. I reviewed the main top mass definitions, pointing out their most notable features and taking particular care about the pole and $\overline{\text{MS}}$ masses. I described recent calculations for the purpose of the renormalon ambiguity in the pole mass in the infrared regime, yielding uncertainties about 100–250 MeV, which, for the time being, are below the current error on the top mass. Also, such estimates are well below the top-width energy scale, about 1.4 GeV.

The most relevant features of Monte Carlo codes for top-quark phenomenology were then presented, stressing the late implementation of NLO corrections and interference effects between top-production and decay phases. Even the standard shower codes are nevertheless beyond LO in the differential distributions which account for classes of enhanced soft/collnear logarithms to all orders.

The main experimental methods to measure the top mass were discussed, pointing out the differences among the so-called standard and alternative measurements and the magnitude of the quoted uncertainties. For the time being, although the alternative measurements provide an excellent ground to reconstruct m_t using the kinematic properties of the final states and, in some cases, they are even capable of minimizing the impact of the chosen Monte Carlo generator, the standard methods are still those which yield the lowest uncertainty. This will also be the case in the future LHC runs, albeit the higher statistics are expected to decrease the errors in the alternative strategies too.

Much space was then devoted to the present debate on the interpretation of the measurements and whether one should relate the extracted m_t to some alternative mass definition or rather express it in terms of the pole mass, up to some uncertainty. A common features of both attitudes is nonetheless that there is no universal relation between the measured mass and any field-theory definition, but it depends on the considered observable and on the type of Monte Carlo shower code or QCD calculation which is employed in the comparison. There have been many investigations to relate the measured m_t to short-distance masses by comparing Monte Carlo predictions with SCET resummed computations: the obtained shift with respect to the pole mass was eventually derived and is of the order of a few hundreds of MeV, depending on the specific analysis and accuracy of the calculation. On the other hand, work is in progress to explore the sources of errors which, on the top of the theoretical systematics, affect the straightforward identification of the top mass in direct-reconstruction analyses as a pole mass, such as color reconnection. Although the starting point of such approaches are conceptually different, a compromize can be reached and it will be very appealing applying the ongoing work on color-reconnection and bottom-fragmentation uncertainties to the interpretation of the top-mass measurements in terms of well-defined field-theory quantities.

Finally, referring in particular to the world-average analysis, the contributions to the quoted theoretical error were debated, along with the current work aimed at obtaining even more reliable estimates of such uncertainties. Furthermore, it was discussed the possibility to use top-quark events and suitable calibration observables to fit Monte Carlo parameters, which will probably be the way to follow in future perspectives, once the data become precise enough to compete with e⁺e⁻ experiments for the purpose of the tuning of event generators.

In summary, top-quark phenomenology at the LHC, especially in the high-luminosity perspective, has become precision physics and the smallness of the current and foreseen uncertainties in the top-mass measurement are a clear example of such a level of accuracy. However, for the sake of a robust and reliable top-mass determination, much work is still necessary, in order to understand better and possibly reduce the sources of uncertainties. In particular, progress in Monte Carlo studies and QCD calculations for top production and decay, as well as in theoretical work concerning top-mass definitions, should definitely be encouraged. As pointed out many times in this review, investigations along these lines are already in progress, in such a way that one can feel confident that the theoretical and experimental efforts will eventually converge to match the precisions which are expected in the future LHC runs and ultimately at HL-LHC.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I acknowledge discussions with André Hoang and Paolo Nason, co-authors of the top-mass section in Azzi et al. [97], on the interpretation of the top-mass measurements.

Footnotes

1. ^Strictly speaking the stability of the electroweak vacuum also depends on whether there is New Physics up to the Planck scale or not. Degrassi et al. [4] assumes that the Standard Model is valid up to the Planck scale; other alternatives are discussed in Branchina et al. [3].

2. ^The latest Particle Data Group [19] quotes a top width ${\Gamma }_t=(1.41_{-0.15}^{+0.19})$ GeV.

3. ^In d dimensions, the coupling g_S, related to α_S via ${\alpha }_S=g_S^2/(4\pi )$, gets mass dimension ϵ, i.e., $g_S\to g_s{\mu }_r^{ϵ}$, μ_r being a regularization scale. After adding suitable counter-terms, Σ^R is eventually expressed in terms of the renormalization scale μ.

4. ^Alternatively to working in d dimensions, one can use a mass regularization scheme, giving the gluon a fictitious mass λ. The renormalized self energy with a gluon mass λ can be obtained from Equation (1) by means of the replacement: $1/ϵ-\gamma +ln\left[(4\pi {\mu }^2)/m_0^2\right]\to ln({\lambda }^2/m_0^2)$.

5. ^We recall that, e.g., at LO in the $\overline{\text{MS}}$ scheme, it is ${\alpha }_S(Q^2)=1/\left[b_{0}ln(Q^2/{\Lambda }^2)\right]$, Λ being the QCD scale. For Q²~Λ² one hits the well-known Landau pole and perturbative QCD can no longer be applied.

6. ^This would not be the case in codes or calculations which instead neglect width effects and interference between top-production and decay phases. In this case, even top quarks are capable of radiating down to the infrared cutoff.

7. ^The old PYTHIA 6 code also implements virtuality ordering, with the option to veto non-angular-ordered emissions.

8. ^See also Heinrich et al. [52] for an independent investigation of NLO and top-width effects on the top-mass determination.

9. ^A notable exception is given by leading non-global logarithms, sensitive to a limited portion of the phase space, which, as discussed in Banfi et al. [65], are partially accounted for by the angular-ordered showers of HERWIG, while they are mostly absent in virtuality- or transverse-momentum-ordered PYTHIA.

10. ^With respect to Λ in the $\overline{\text{MS}}$ scheme it is Λ_MC = Λexp[K/(4πb₀)], with $K=N_C(67/18-{\pi }^2/6)-5N_f/9$, with N_C and N_f being the number of colors and active flavors, respectively.

11. ^At NNLO the $t\bar{t}$ cross section is ${O}({\alpha }_S^4)$, whereas the threshold logarithms which are resummed in Czakon et al. [74] are $~{\alpha }_S^n{\left[{ln}^m(1-z)/(1-z)\right]}_{+}$, with $z=m_t^2/ŝ$, ŝ being the partonic center-of-mass energy and m ≤ 2n−1.

12. ^Soft-drop grooming is a jet-substructure technique, which recursively removes soft wide-angle radiation from a jet. See [102] for details.

13. ^For two particles at Δϕ and Δη distances in azimuth and rapidity, the invariant opening angle is defined as $\Delta R=\sqrt{{(\Delta \varphi )}^2+{(\Delta \eta )}^2}$.

References

1. Baak M, Cúth J, Haller J, Hoecker A, Kogler R, Mönig K, et al. The global electroweak fit at NNLO and prospects for the LHC and ILC. Eur Phys J. (2014) C74:3046. doi: 10.1140/epjc/s10052-014-3046-5

CrossRef Full Text | Google Scholar

2. Masina I, Notari A. Standard model false vacuum inflation: correlating the tensor-to-scalar ratio to the top quark and Higgs boson masses. Phys Rev Lett. (2012) 108:191302. doi: 10.1103/PhysRevLett.108.191302

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Branchina V, Messina E, Platania A. Top mass determination, Higgs inflation, and vacuum stability. J High Energy Phys. (2014) 9:182. doi: 10.1007/JHEP09(2014)182

CrossRef Full Text | Google Scholar

4. Degrassi G, Di Vita S, Elias-Miro J, Espinosa JR, Giudice GF, Isidori G, et al. Higgs mass and vacuum stability in the Standard Model at NNLO. J High Energy Phys. (2012) 8:098. doi: 10.1007/JHEP08(2012)098

CrossRef Full Text | Google Scholar

5. Andreassen A, Frost W, Schwartz MD. Scale invariant instantons and the complete lifetime of the standard model. Phys Rev. (2018) D97:056006. doi: 10.1103/PhysRevD.97.056006

CrossRef Full Text | Google Scholar

6. The ATLAS, CDF, CMS, D0 Collaborations. First combination of Tevatron and LHC measurements of the top-quark mass. arXiv:1403.4427.

7. Fleming S, Hoang AH, Mantry S, Stewart IW. Jets from massive unstable particles: top-mass determination. Phys Rev. (2008) D77:074010. doi: 10.1103/PHYSREVD.77.074010

CrossRef Full Text | Google Scholar

8. Hoang AH, Stewart IW. Top mass measurements from jets and the tevatron top-quark mass. Nucl Phys Proc Suppl. (2008) 185:220–6. doi: 10.1016/j.nuclphysbps.2008.10.028

CrossRef Full Text | Google Scholar

9. Butenschoen M, Dehnadi B, Hoang AH, Mateu V, Preisser M, Stewart IW. Top quark mass calibration for Monte Carlo event generators. Phys Rev Lett. (2016) 117:232001. doi: 10.1103/PhysRevLett.117.232001

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Hoang AH, Mantry S, Pathak A, Stewart IW. Extracting a Short Distance Top Mass with Light Grooming. arXiv:1708.02586 (2017).

Google Scholar

11. Hoang AH, Plätzer S, Samitz D. On the cutoff dependence of the quark mass parameter in angular ordered parton showers. J High Energy Phys. (2018) 10:200. doi: 10.1007/JHEP10(2018)200

CrossRef Full Text | Google Scholar

12. Nason P. Theory summary. PoS. (2016) arXiv:1602.00443. doi: 10.22323/1.257.0056

CrossRef Full Text | Google Scholar

13. Nason P. The top mass in hadronic collisions. In: Levy A, Forte S, Ridolfi G, editors. From my Vast Repertoire: Guido Altarelli's Legacy. Singapore: World Scientific (2019). p. 123–51.

Google Scholar

14. Beneke M, Braun VM. Heavy quark effective theory beyond perturbation theory: Renormalons, the pole mass and the residual mass term. Nucl Phys. (1994) B426:301–43. doi: 10.1016/0550-3213(94)90314-X

CrossRef Full Text | Google Scholar

15. Beneke M. More on ambiguities in the pole mass. Phys Lett. (1995) B344:341–7. doi: 10.1016/0370-2693(94)01505-7

CrossRef Full Text | Google Scholar

16. Beneke M, Marquard P, Nason P, Steinhauser M. On the ultimate uncertainty of the top quark pole mass. Phys Lett. (2017) B775:63–70. doi: 10.1016/j.physletb.2017.10.054

CrossRef Full Text | Google Scholar

17. Hoang AH, Lepenik C, Preisser M. On the light massive flavor dependence of the large order asymptotic behavior and the ambiguity of the pole mass. J High Energy Phys. (2017) 9:099. doi: 10.1007/JHEP09(2017)099

CrossRef Full Text | Google Scholar

18. Marquard P, Smirnov AV, Smirnov VA, Steinhauser M. Quark mass relations to four-loop order in perturbative QCD. Phys Rev Lett. (2015) 114:142002. doi: 10.1103/PhysRevLett.114.142002

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Tanabashi M, Nagoya U, Nagoya KMI. Review of particle physics. Phys Rev. (2018) D98:030001. doi: 10.1103/PhysRevD.98.030001

CrossRef Full Text | Google Scholar

20. Kataev AL, Molokoedov VS. Dependence of five- and six-loop estimated QCD corrections to the relation between pole and running masses of heavy quarks on the number of light flavors. JETP Lett. (2018) 108:777–82. doi: 10.1134/S0021364018240050

CrossRef Full Text | Google Scholar

21. Hoang AH, Teubner T. Top quark pair production close to threshold: top mass, width and momentum distribution. Phys Rev. (1999) D60:114027.

Google Scholar

22. Hoang AH, Manohar AV, Stewart IW, Teubner T. The threshold $t\bar{t}$ cross-section at NNLL order. Phys Rev. (2002) D65:014014. doi: 10.1103/PhysRevD.65.014014

CrossRef Full Text | Google Scholar

23. Beneke M. A Quark mass definition adequate for threshold problems. Phys Lett. (1998) B434:115–25. doi: 10.1016/S0370-2693(98)00741-2

CrossRef Full Text | Google Scholar

24. Hoang AH, Melnikov K, Teubner T, Yelkhovsky A, Yakovlev O, Beneke M, et al. Top - anti-top pair production close to threshold: synopsis of recent NNLO results. Eur Phys Jdirect. (2000) 2:3. doi: 10.1007/s1010500c0003

CrossRef Full Text | Google Scholar

25. Hoang AH, Stahlhofen M. The top-antitop threshold at the ILC: NNLL QCD uncertainties. J High Energy Phys. (2014) 5:121. doi: 10.1007/JHEP05(2014)121

CrossRef Full Text | Google Scholar

26. Beneke M, Kiyo Y, Marquard P, Penin A, Piclum J, Steinhauser M. Next-to-next-to-next-to-leading order QCD prediction for the top antitop S-wave pair production cross section near threshold in e⁺e⁻ annihilation. Phys Rev Lett. (2015) 115:192001. doi: 10.1103/PhysRevLett.115.192001

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Pineda A. Determination of the bottom quark mass from the Υ(1S) system. J High Energy Phys. (2001) 6:022. doi: 10.1088/1126-6708/2001/06/022

CrossRef Full Text | Google Scholar

28. Bigi Y II, Shifman MA, Uraltsev N, Vainshtein AI. High power n of m_b in beauty widths and n = 5 → ∞ limit. Phys Rev. (1997) D56:4017–30.

Google Scholar

29. Jezo T, Lindert JM, Nason P, Oleari C, Pozzorini S. An NLO+PS generator for $t\bar{t}$ and Wt production and decay including non-resonant and interference effects. Eur Phys J. (2016) C76:691. doi: 10.1140/epjc/s10052-016-4538-2

CrossRef Full Text | Google Scholar

30. Ferrario Ravasio S, Nason P, Oleari C. All-orders behaviour and renormalons in top-mass observables. J High Energy Phys. (2018). 2018:203. doi: 10.1007/JHEP01(2019)203

CrossRef Full Text | Google Scholar

31. Corcella G, Knowles IG, Marchesini G, Moretti S, Odagiri K, Richardson P, et al. HERWIG 6: an event generator for hadron emission reactions with interfering gluons (including supersymmetric processes). J High Energy Phys. (2001) 1:010. doi: 10.1088/1126-6708/2001/01/010

CrossRef Full Text | Google Scholar

32. Bellm J, Gieseke S, Grellscheid D, Plätzer S, Rauch M, Reuschle C, et al. Herwig 7.0/Herwig++ 3.0 release note. Eur Phys J. (2016) C76:196. doi: 10.1140/epjc/s10052-016-4018-8

CrossRef Full Text | Google Scholar

33. Sjostrand T, Mrenna S, Skands PZ. PYTHIA 6.4 physics and manual. J High Energy Phys. (2006) 5:026. doi: 10.1088/1126-6708/2006/05/026

CrossRef Full Text | Google Scholar

34. Sjöstrand T, Ask S, Christiansen JR, Corke R, Desai N, Ilten P, et al. An introduction to PYTHIA 8.2. Comput Phys Commun. (2015) 191:159–77. doi: 10.1016/j.cpc.2015.01.024

CrossRef Full Text | Google Scholar

35. Marchesini G, Webber BR. Simulation of QCD jets including soft gluon interference. Nucl Phys. (1984) B238:1–29. doi: 10.1016/0550-3213(84)90463-2

CrossRef Full Text | Google Scholar

36. Gieseke S, Stephens P, Webber B. New formalism for QCD parton showers. J High Energy Phys. (2003) 12:045. doi: 10.1088/1126-6708/2003/12/045

CrossRef Full Text | Google Scholar

37. Plätzer S, Gieseke S. Dipole showers and automated NLO matching in Herwig++. Eur Phys J. (2012) C72:2187. doi: 10.1140/epjc/s10052-012-2187-7

CrossRef Full Text | Google Scholar

38. Corcella G, Seymour MH. Matrix element corrections to parton shower simulations of heavy quark decay. Phys Lett. (1998) B442:417–26.

Google Scholar

39. Norrbin E, Sjostrand T. QCD radiation off heavy particles. Nucl Phys. (2001) B603:297–342. doi: 10.1016/S0550-3213(01)00099-2

CrossRef Full Text | Google Scholar

40. Webber BR. A QCD model for jet fragmentation including soft gluon interference. Nucl Phys. (1984) B238:492–528.

Google Scholar

41. Andersson B, Gustafson G, Ingelman G, Sjostrand T. Parton fragmentation and string dynamics. Phys Rept. (1983) 97:31–145.

Google Scholar

42. Butterworth JM, Forshaw JR, Seymour MH. Multiparton interactions in photoproduction at HERA. Z Phys. (1996) C72:637–46.

Google Scholar

43. Sjostrand T, Skands PZ. Multiple interactions and the structure of beam remnants. J High Energy Phys. (2004) 3:053. doi: 10.1088/1126-6708/2004/03/053

CrossRef Full Text | Google Scholar

44. Gleisberg T, Hoeche S, Krauss F, Schonherr M, Schumann S, Siegert F, et al. Event generation with SHERPA 1.1. J High Energy Phys. (2009) 2:007. doi: 10.1088/1126-6708/2009/02/007

CrossRef Full Text | Google Scholar

45. Krauss F, Kuhn R, Soff G. AMEGIC++ 1.0: a Matrix element generator in C++. J High Energy Phys. (200) 2:044. doi: 10.1088/1126-6708/2002/02/044

CrossRef Full Text

46. Gleisberg T, Hoeche S. Comix, a new matrix element generator. J High Energy Phys. (2008) 12:039. doi: 10.1088/1126-6708/2008/12/039

CrossRef Full Text | Google Scholar

47. Binoth T, Boudjema F, Dissertori G, Lazopoulos A, Denner A, Dittmaier S, et al. A Proposal for a standard interface between Monte Carlo tools and one-loop programs. Comput Phys Commun. (2010) 181:1612–22. doi: 10.1016/j.cpc.2010.05.016

CrossRef Full Text | Google Scholar

48. Catani S, Seymour MH. The Dipole formalism for the calculation of QCD jet cross-sections at next-to-leading order. Phys Lett. (1996) B378:287–301. doi: 10.1016/0370-2693(96)00425-X

CrossRef Full Text | Google Scholar

49. Frixione S, Webber BR. Matching NLO QCD computations and parton shower simulations. J High Energy Phys. (2002) 6:029. doi: 10.1088/1126-6708/2002/06/029

CrossRef Full Text | Google Scholar

50. Alwall J, Frederix R, Frixione S, Hirschi V, Maltoni F, Mattelaer O, et al. The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations. J High Energy Phys. (2014) 7:079. doi: 10.1007/JHEP07(2014)079

CrossRef Full Text | Google Scholar

51. Alioli S, Nason P, Oleari C, Re E. A general framework for implementing NLO calculations in shower Monte Carlo programs: the POWHEG BOX. J High Energy Phys. (2010) 6:043. doi: 10.1007/JHEP06(2010)043

CrossRef Full Text | Google Scholar

52. Heinrich G, Maier A, Nisius R, Schlenk J, Schulze M, Scyboz L, et al. NLO and off-shell effects in top quark mass determinations. J High Energy Phys. (2017). 2017: 129. doi: 10.1007/JHEP07(2018)129

CrossRef Full Text | Google Scholar

53. Artoisenet P, Frederix R, Mattelaer O, Rietkerk R. Automatic spin-entangled decays of heavy resonances in Monte Carlo simulations. J High Energy Phys. (2013) 3:015. doi: 10.1007/JHEP03(2013)015

CrossRef Full Text | Google Scholar

54. Frederix R, Frixione S, Papanastasiou AS, Prestel S, Torrielli P. Off-shell single-top production at NLO matched to parton showers. J High Energy Phys. (2016) 6:027. doi: 10.1007/JHEP06(2016)027

CrossRef Full Text | Google Scholar

55. Plätzer S. Controlling inclusive cross sections in parton shower + matrix element merging. J High Energy Phys. (2013) 08:114. doi: 10.1007/JHEP08(2013)114

CrossRef Full Text | Google Scholar

56. Bellm J, Gieseke S, Plätzer S. Merging NLO multi-jet calculations with improved unitarization. Eur Phys J. (2018) C78:244. doi: 10.1140/epjc/s10052-018-5723-2

CrossRef Full Text | Google Scholar

57. Cormier K, Plätzer S, Reuschle C, Richardson P, Webster S. Parton shower and matching uncertainties in top quark pair production with Herwig 7. (2018).

Google Scholar

58. Mangano ML, Moretti M, Piccinini F, Pittau R, Polosa AD. ALPGEN, a generator for hard multiparton processes in hadronic collisions. J High Energy Phys. (2003) 7:001. doi: 10.1088/1126-6708/2003/07/001

CrossRef Full Text | Google Scholar

59. Campbell JM, Ellis RK. MCFM for the Tevatron and the LHC. Nucl Phys Proc Suppl. (2010) 205-6:10–5. doi: 10.1016/j.nuclphysbps.2010.08.011

CrossRef Full Text | Google Scholar

60. Belyaev A, Christensen ND, Pukhov A. CalcHEP 3.4 for collider physics within and beyond the Standard Model. Comput Phys Commun. (2013) 184:1729–69. doi: 10.1016/j.cpc.2013.01.014

CrossRef Full Text | Google Scholar

61. Kanaki A, Papadopoulos CG. HELAC: a Package to compute electroweak helicity amplitudes. Comput Phys Commun. (2000) 132:306–15. doi: 10.1016/S0010-4655(00)00151-X

CrossRef Full Text | Google Scholar

62. Kilian W, Ohl T, Reuter J. WHIZARD: simulating multi-particle processes at LHC and ILC. Eur Phys J. (2011) C71:1742. doi: 10.1140/epjc/s10052-011-1742-y

CrossRef Full Text | Google Scholar

63. Bevilacqua G, Czakon M, Garzelli MV, van Hameren A, Kardos A, Papadopoulos CG, et al. HELAC-NLO. Comput. Phys. Commun. (2013) 184: 986–97. doi: 10.1016/j.cpc.2012.10.033

CrossRef Full Text | Google Scholar

64. Weiss C, Chokoufe Nejad B, Kilian W, Reuter J. Automated NLO QCD corrections with WHIZARD. PoS. (2015) EPS-HEP2015:466. doi: 10.22323/1.234.0466

CrossRef Full Text | Google Scholar

65. Banfi A, Corcella G, Dasgupta M. Angular ordering and parton showers for non-global QCD observables. J High Energy Phys. (2007) 3:050. doi: 10.1088/1126-6708/2007/03/050

CrossRef Full Text | Google Scholar

66. Catani S, Webber BR, Marchesini G. QCD coherent branching and semiinclusive processes at large x. Nucl Phys. (1991) B349:635–54. doi: 10.1016/0550-3213(91)90390-J

CrossRef Full Text | Google Scholar

67. Aaboud M, Aad G, Abbott B, Abdallah J, Abdinov O, Abeloos B, et al. Measurement of the top quark mass in the $t\bar{t}\to$ dilepton channel from $\sqrt{s}=8$ TeV ATLAS data. Phys Lett. (2016) B761:350–71. doi: 10.1016/j.physletb.2016.08.042

CrossRef Full Text | Google Scholar

68. Aaboud M, Aad G, Abbott B, Abdallah J, Abdinov O, Abeloos B, et al. Top-quark mass measurement in the all-hadronic $t\overline{t}$ decay channel at $\sqrt{s}=8$ TeV with the ATLAS detector. J High Energy Phys. (2017) 9:118. doi: 10.1007/JHEP09(2017)118

CrossRef Full Text | Google Scholar

69. Aaboud M, Aad G, Abbott B, Abdallah J, Abdinov O, Abeloos B, et al. Measurement of the top quark mass in the $t\bar{t}\to$ lepton+jets channel from $\sqrt{s}=8$ TeV ATLAS data and combination with previous results. Eur Phys J. (2018) C79:290. doi: 10.1140/epjc/s10052-019-6757-9

CrossRef Full Text | Google Scholar

70. Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Asilar E, Bergauer T, et al. Measurement of the $t\bar{t}$ production cross section, the top quark mass, and the strong coupling constant using dilepton events in pp collisions at $\sqrt{s}=$ 13 TeV. (2018).

Google Scholar

71. Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Asilar E, Bergauer T, et al. Measurement of the top quark mass with lepton+jets final states using pp collisions at $\sqrt{s}=13\text{TeV}$. Eur Phys J. (2018) C78:891. doi: 10.1140/epjc/s10052-018-6332-9

CrossRef Full Text | Google Scholar

72. Sirunyan AM, Tumasyan A, Adam W, Ambrogi F, Asilar E, Bergauer T, et al. Measurement of the top quark mass in the all-jets final state at $\sqrt{s}=$ 13 TeV and combination with the lepton+jets channel. Eur Phys J. (2018). doi: 10.1140/epjc/s10052-019-6788-2

CrossRef Full Text | Google Scholar

73. Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Aşılar E, Bergauer T. Measurement of the top quark mass using proton-proton data at $\sqrt{s}$ = 7 and 8 TeV. Phys Rev D. (2016) D93:072004. doi: 10.1103/PhysRevD.93.072004

CrossRef Full Text | Google Scholar

74. Czakon M, Fiedler P, Mitov A. Total Top-Quark pair-production cross section at hadron colliders through $O({\alpha }_S^4)$. Phys Rev Lett. (2013) 110:252004. doi: 10.1103/PhysRevLett.110.252004

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Aad G, Abbott B, Abdallah J, Abdel Khalek S, Abdinov O, Aben R. Measurement of the $t\bar{t}$ production cross-section using eμ events with b-tagged jets in pp collisions at $\sqrt{s}$ = 7 and 8 TeV with the ATLAS detector. Eur Phys J. (2014) C74:3109. doi: 10.1140/epjc/s10052-014-3109-7

CrossRef Full Text | Google Scholar

76. Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Aşılar E, Bergauer T. Measurement of the $t\bar{t}$ production cross section in the eμ channel in proton-proton collisions at $\sqrt{s}=$ 7 and 8 TeV. J High Energy Phys. (2016) 1608:029. doi: 10.1007/JHEP08(2016)029

CrossRef Full Text | Google Scholar

77. Sirunyan AM, et al. Measurement of the $t\bar{t}$ production cross section using events with one lepton and at least one jet in pp collisions at $\sqrt{s}$ = 13 TeV. J High Energy Phys. (2017) 2017:51. doi: 10.1007/JHEP09(2017)051

CrossRef Full Text | Google Scholar

78. Czakon M, Heymes D, Mitov A. High-precision differential predictions for top-quark pairs at the LHC. Phys Rev Lett. (2016) 116:082003. doi: 10.1103/PhysRevLett.116.082003

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Czakon M, Fiedler P, Heymes D, Mitov A. Measurement of the Pole Mass of the Top Quark using Differential $t\bar{t}$ Cross Sections in $p\bar{p}$ Collisions at $\sqrt{s}$ = 1.96 TeV (2016). Available online at: http://lss.fnal.gov/archive/2016/conf/fermilab-conf-16-383-ppd.pdf.

80. Dowling M, Moch SO. Differential distributions for top-quark hadro-production with a running mass. Eur Phys J. (2014) C74:3167. doi: 10.1140/epjc/s10052-014-3167-x

CrossRef Full Text | Google Scholar

81. Czakon M, Heymes D, Mitov A, Pagani D, Tsinikos I, Zaro M. Top-pair production at the LHC through NNLO QCD and NLO EW. J High Energy Phys. (2017) 10:186. doi: 10.1007/JHEP10(2017)186

CrossRef Full Text | Google Scholar

82. Alioli S, Fernandez P, Fuster J, Irles A, Moch SO, Uwer P, et al. A new observable to measure the top-quark mass at hadron colliders. Eur Phys J. (2013) C73:2438. doi: 10.1140/epjc/s10052-013-2438-2

CrossRef Full Text | Google Scholar

83. Aad G, et al. Determination of the top-quark pole mass using $t\overline{t}$ + 1-jet events collected with the ATLAS experiment in 7 TeV pp collisions. JHEP. (2015) 10:121. doi: 10.1007/JHEP10(2015)121

CrossRef Full Text | Google Scholar

84. Collaboration C. Determination of the normalised invariant mass distribution of $t\bar{t}+$jet and extraction of the top quark mass (2016).

Google Scholar

85. Fuster J, Irles A, Melini D, Uwer P, Vos M. Extracting the top-quark running mass using $t\bar{t}+1-jet$ events produced at the Large Hadron Collider. Eur Phys J. (2017) C77:794. doi: 10.1140/epjc/s10052-017-5354-z

CrossRef Full Text | Google Scholar

86. Agashe K, Franceschini R, Kim D, Schulze M. Top quark mass determination from the energy peaks of b-jets and B-hadrons at NLO QCD. Eur Phys J. (2016) C76:636. doi: 10.1140/epjc/s10052-016-4494-x

CrossRef Full Text | Google Scholar

87. CMS Collaboration. Measurement of the Top-Quark Mass from Thebjet Energy Spectrum. (2015). CMS-PAS-TOP-15-002.

88. CMS Collaboration. Determination of the top-Quark Massfrom the m_lb Distribution in Dileptonic $t\bar{t}$ Events at $\sqrt{s}=8$ TeV. (2014), CMS-PAS-TOP-14-014.

89. Sirunyan AM, Tumasyan A, Adam W, Aşilar E, Bergauer T, Brandstetter J. Measurement of the top quark mass in the dileptonic $t\bar{t}$ decay channel using the mass observables M_bℓ, M_T2, and M_bℓν in pp collisions at $\sqrt{s}=8$ TeV. Phys Rev. (2017) D96:032002. doi: 10.1103/PhysRevD.96.032002

CrossRef Full Text | Google Scholar

90. Lester CG, Summers DJ. Measuring masses of semiinvisibly decaying particles pair produced at hadron colliders. Phys Lett. (1999) B463:99–103. doi: 10.1016/S0370-2693(99)00945-4

CrossRef Full Text | Google Scholar

91. Chatrchyan S, et al. Measurement of masses in the $t\bar{t}$ system by kinematic endpoints in pp collisions at $\sqrt{s}$ = 7 TeV. Eur Phys J. (2013) C73:2494. doi: 10.1140/epjc/s10052-013-2494-7

CrossRef Full Text | Google Scholar

92. Frixione S, Mitov A. Determination of the top quark mass from leptonic observables. J High Energy Phys. (2014) 2014:012. doi: 10.1007/JHEP09(2014)012

CrossRef Full Text | Google Scholar

93. CMS Collaboration. Determination of the top Quark Mass from Leptonic Observables Using eμ+jets Final States Selected in Proton-Proton Collisions at $\sqrt{s}=8$ TeV. (2016), CMS-PAS-TOP-16-002.

94. Campbell JM, Ellis RK, Giele WT. A multi-threaded version of MCFM. Eur Phys J. (2015) C75:246. doi: 10.1140/epjc/s10052-015-3461-2

CrossRef Full Text | Google Scholar

95. Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Aşılar E, Bergauer T. Measurement of the mass of the top quark in decays with a J/ψ meson in pp collisions at 8 TeV. J High Energy Phys. (2016) 12:123. doi: 10.1007/JHEP12(2016)123

CrossRef Full Text | Google Scholar

96. Khachatryan V, et al. Measurement of the top quark mass using charged particles in pp collisions at $\sqrt{s}=8$ TeV. Phys Rev. (2016) D93:092006. doi: 10.1103/PhysRevD.93.092006

CrossRef Full Text | Google Scholar

97. Azzi P, et al. Standard model physics at the HL-LHC and HE-LHC. (2019).

Google Scholar

98. The ATLAS collaboration. Prospects for measurement of the top quark mass using $t\bar{t}$ events with J/ψ → μ⁺μ⁻ decays with the upgraded ATLAS detector at the High Luminosity LHC.

99. CERN. ECFA 2016: Prospects for Selected Standard Model Measurements With the CMS Experiment at the High-Luminosity LHC. Geneva: CERN. Available online at: https://cds.cern.ch/record/2262606.

100. Hoang AH. The top mass: interpretation and theoretical uncertainties. In: Proceedings, 7th International Workshop on Top Quark Physics (TOP2014). (2014) (Cannes).

Google Scholar

101. Corcella G. Interpretation of top-quark mass measurements: a theory overview. In: 8th International Workshop on Top Quark Physics (TOP2015) - Session 10: Top Mass and Combinations. (2015). doi: 10.22323/1.257.0037

CrossRef Full Text | Google Scholar

102. Larkoski AJ, Marzani S, Soyez G, Thaler J. Soft drop. J High Energy Phys. (2014) 05:146. doi: 10.1007/JHEP05(2014)146

CrossRef Full Text | Google Scholar

103. Kieseler J, Lipka K, Moch SO. Calibration of the top-quark monte carlo mass. Phys Rev Lett. (2016) 116:162001. doi: 10.1103/PhysRevLett.116.162001

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Sherstnev A, Thorne RS. Parton distributions for LO generators. Eur Phys J. (2008) C55:553–75. doi: 10.1140/epjc/s10052-008-0610-x

CrossRef Full Text | Google Scholar

105. Argyropoulos S, Sjöstrand T. Effects of color reconnection on $t\bar{t}$ final states at the LHC. J High Energy Phys. (2014) 11:043. doi: 10.1007/JHEP11(2014)043

CrossRef Full Text | Google Scholar

106. Corcella G. Hadronization systematics and top mass reconstruction. EPJ Web Conf. (2014) 80:00019. doi: 10.1051/epjconf/20148000019

CrossRef Full Text | Google Scholar

107. Corcella G, Drollinger V. Bottom-quark fragmentation: Comparing results from tuned event generators and resummed calculations. Nucl Phys. (2005) B730:82–102. doi: 10.1016/j.nuclphysb.2005.09.030

CrossRef Full Text | Google Scholar

108. Corcella G, Mescia F. A phenomenological study of bottom quark fragmentation in top quark decay. Eur Phys J. (2010) C65:171–80.

Google Scholar

109. Abreu P, et al. Tuning and test of fragmentation models based on identified particles and precision event shape data. Z Phys. (1996) C73:11–60.

Google Scholar

110. Abe K, Abe K, Abe T, Adam I, Akimoto H, Aston D. Precise measurement of the b quark fragmentation function in Z⁰ boson decays. Phys Rev Lett. (2000) 84:4300–4. doi: 10.1103/PhysRevLett.84.4300

CrossRef Full Text | Google Scholar

111. Abbiendi G, Ainsley C, Akesson PF, Alexander G, Allison J, Amaral P. Inclusive analysis of the b quark fragmentation function in Z decays at LEP. Eur Phys J. (2003) C29:463–78. doi: 10.1140/epjc/s2003-01229-x

CrossRef Full Text | Google Scholar

112. Heister A, Schael S, Barate R, De Bonis I, Decamp D, Goy C. Study of the fragmentation of b quarks into B mesons at the Z peak. Phys Lett. (2001) B512:30–48. doi: 10.1016/S0370-2693(01)00690-6

CrossRef Full Text | Google Scholar

113. Skands P, Carrazza S, Rojo J. Tuning PYTHIA 8.1: the Monash 2013 Tune. Eur Phys J. (2014) C74:3024. doi: 10.1140/epjc/s10052-014-3024-y

CrossRef Full Text | Google Scholar

114. Collaboration A. ATLAS pythia 8 Tunes to 7 TeV data. (2014).

Google Scholar

115. Corcella G, Franceschini R, Kim D. Fragmentation Uncertainties in Hadronic Observables for Top-quark Mass Measurements. Nucl Phys. (2018) B929:485–526. doi: 10.1016/j.nuclphysb.2018.02.012

CrossRef Full Text | Google Scholar