- 1Department of Physics, University of Lucknow, Lucknow, India
- 2Department of Physics, Babasaheb Bhimrao Ambedkar University, Lucknow, India
- 3Department of Physics, Bundelkhand University, Jhansi, India
- 4Department of Physics, Indian Institute of Technology, Rupnagar, India
Employing the projected-Hartree-Fock-Bogoliubov (PHFB) approach, nuclear transition matrix elements (NTMEs) have been calculated to study the three complementary modes of β−β− decay, namely two neutrino β−β− (2νβ−β−) decay, neutrinoless β−β− (0νβ−β−) decay within mass mechanism and Majoron accompanied 0νβ−β− (0νβ−β−χ) decay. Reliability of HFB wave functions generated with four different parametrizations of the pairing plus multipolar type of effective two-body interaction has been ascertained by comparing a number of nuclear observables with the available experimental data. Specifically, the calculated NTMEs M(2ν) of 2νβ−β− decay have been compared with the observed data. Effects due to different parametrizations of effective two-body interactions, form factors and short-range correlations have been studied. It has also been observed that deformation plays a crucial role in the nuclear structure aspects of 0νβ−β− decay. Uncertainties in NTMEs calculated with wave functions generated with four different parametrizations of the pairing plus multipolar type of effective two-body interaction, dipole form factor and three different parametrizations of Jastrow type of short-range correlations within mechanisms involving light Majorana neutrinos, heavy Majorana neutrinos, sterile neutrinos and Majorons have been statistically estimated.
1. Introduction
The story of neutrinos as well as weak interaction is rather checkered and quite exciting due to their enigmatic nature. Presently, a number of projects, namely 48Ca (CANDLES), 76Ge (GERDA, MAJORANA, LEGEND), 82Se (SuperNEMO, Lucifer), 100Mo (MOON, AMoRE), 116Cd (COBRA), 130Te (CUORE, CUPID, SNO+), 136Xe (XMASS, EXO, KamLAND-Zen, NEXT), 150Nd (SNO++, SuperNEMO, DCBA/MTD) are dedicated (already designed/planned) [1, 2] to observe the possible occurrence of neutrinoless double beta (0νββ) decay for establishing the Majorana nature of neutrinos. In addition, information on the lepton number violation, possible hierarchies in the neutrino mass spectrum, the origin of neutrino mass and CP violation in the leptonic sector can be inferred [3, 4]. Over the past years, the four experimentally distinguishable modes ββ decay, namely two neutrino double beta (2νββ) decay, neutrinoless double beta (0νββ) decay, single Majoron accompanied neutrinoless double beta (0νββϕ) and double Majoron accompanied neutrinoless double beta (0νββϕϕ) decay have been studied extensively both experimentally [1, 2] and theoretically [3, 4].
The possible occurrence of 0νββ decay has been investigated within a number of mechanisms, namely the exchange of light as well as heavy neutrinos, and the right handed currents in the left-right symmetric model (LRSM), the exchange of sleptons, neutralinos, squarks, and gluinos in the Rp-violating minimal super symmetric standard model, existence of heavy sterile neutrinos, Majoron models, compositeness, the exchange of leptoquarks, and extradimensional scenarios. Arguably, the observation of 0νββ decay due to any mechanism would imply the Majorana nature of neutrinos/sneutrinos [5, 6]. The main objective of the nuclear structure calculations is to provide reliable nuclear transition matrix elements (NTMEs) for extracting gauge theoretical parameters with minimum uncertainty.
In the conventional nuclear models, there are three basic ingredients, namely the model space, the single particle energies (SPEs) and the effective two body interaction. Usually, they are chosen on the basis of practical considerations albeit a consistent procedure is available for their choice. Due to the rare nature of nuclear ββ decay, strongly suppressed channels play a crucial role in the evolution of NTMEs and hence, NTMEs are quite sensitive to the details of wave functions of the parent, intermediate and daughter nuclei. Remarkably, the observed suppression of M(2ν) was first explained in the quasiparticle random phase approximation (QRPA) approach [7, 8]. Over the years, the QRPA as well as its extensions [9–11], and QRPA with isospin restoration [12] have emerged as the most successful models. In spite of the impressive success of shell-model approach [13–26], presently available numerical facilities highly limit its application to the description of medium and heavy mass nuclei.
In deformed QRPA formalism, the effect of suppression of NTMEs for the 2νβ−β− as well as 0νβ−β− decay due to different deformations of parent and daughter nuclei has been reported in Rodríguez et al. [27], Simkovic et al. [28], Pacearescu et al. [29], Yousef et al. [30], and Fang et al. [31]. In the shell model [16–18], the effect of deformation on the NTMEs has been investigated and it has been shown that the NTMEs are the largest for equal deformation of parent and daughter nuclei. Proper consideration of nuclear deformation in the evaluation of NTMEs has resulted in the implementation of deformed QRPA [32–36], projected Hartree-Fock-Bogoliubov (PHFB) model [37–39], energy density functional (EDF) approach [40], covariant density functional theory (CDFT) [41, 42], and interacting boson model (IBM) [43–46] with isospin restoration [47]. By adjusting the free parameters of the models, the observed half-lives of 2νβ−β− decay have been reproduced in all models. However, different predictions are obtained for other observables. Specifically, the calculated NTMEs M(0ν) differ by a factor of 2–3.
In the theoretical study of decay, three different approaches have been adopted sofar to estimate the uncertainties in NTMEs. The spread between all the calculated NTMEs for a particular ββ emitter [48] has been translated to theoretical uncertainty by estimating the average and standard deviation of NTMEs [49, 50]. As a model independent approach to check the accuracy of NTMEs, the ratios of calculated NTMEs-squared have been compared with the ratios of observed half-lives [51]. With the consideration of two models, namely QRPA and RQRPA, three sets of basis states and three realistic two-body effective interactions based on the charge dependent Bonn, Argonne, and Nijmen potentials, theoretical uncertainties have been estimated by Rodin et al. [52]. Interestingly, the results of QRPA and RQRPA are not only close but the variances are also substantially smaller than the average values. Further, the approach of Rodin et al. [52] has been preferred in Hyvärinen et al. [53] following an extensive analysis by Suhonen [54] and Rodin et al. [55]. In addition, uncertainties in NTMEs due to short range correlations (SRC) have been estimated using the unitary correlation operator method (UCOM) [56, 57], self-consistent coupled cluster method (CCM) [58] and PHFB approach [38]. Recently, it has been suggested by Engel [59] that the systematic errors can be reduced by including all physics known to be important in the error analysis following Reference [60].
In addition to successfully reproducing experimental data on the yrast spectra, reduced B(E2 : 0+ → 2+) transition probabilities, quadrupole moments Q(2+), gyromagnetic factors g(2+), the PHFB approach was employed to study the effect of deformation on the 0+ → 0+ [61] and the 0+ → 2+ [62] transitions of 2νβ−β− decay in 100Mo. In conjunction with the summation method [63–65], the PHFB model has already been applied to study the 0+ → 0+ [66, 67] and 0+ → 2+ transition [68] of 2νβ−β− decay of nuclei in the mass range 90 ≤ A ≤ 150 as well as 2νe+ββ decay modes of 96Ru, 102Pd, 106Cd and 108Cd isotopes [69, 70]. The effects of nuclear deformation inhibiting 2νββ decay [67, 71], 0νβ−β− decay [72] and 0νe+ββ modes [73, 74] in the Majorana neutrino mass mechanism have been reported. The influence of hexadecapolar interaction on the ββ decay matrix elements has also been analyzed [75].
Uncertainties in NTMEs calculated with the PHFB approach using four different parametrizations of a nuclear Hamiltonian and three different short-range correlations, was first performed for the 0νβ−β− decay in the light Majorana neutrino mass mechanism [37]. Including pseudoscalar and weak magnetism terms in the nucleonic current, uncertainties in the NTMEs of 0νβ−β− decay have been estimated in the mechanisms involving light Majorana neutrinos, sterile neutrinos, classical Majorons [38], heavy Majorana neutrinos [39], and new Majorons [76]. In Rath et al. [38], no difference has been observed in the effects due to finite size of nucleons (FNS) either by employing dipole form factors or form factors taking the structure of nucleons into account. In addition, uncertainties in the NTMEs of 0νe+β+β+ modes [74] due to the exchange of light and heavy Majorana neutrinos have been reported.
2. Reliability of HFB Wave Functions
With the assumption that the nucleus consists of non-relativistic point nucleons and neglecting many-nucleon forces, the conventional nuclear many-body Hamiltonian H in an appropriate model space M is given by
where the effective two-body interaction Veff is usually derived from nucleon-nucleon force by the use of Brandow's linked cluster diagram expansion [77] and the energy dependence of the Veff can be eliminated by Kuo's folded diagram expansion [78]. Usually, the “realistic interactions” obtained from the above theoretical procedure are not quite successful in reproducing spectroscopic properties of nuclei. Hence, “empirical effective interactions” and “schematic effective interactions” are used quite often in reproducing the observed spectroscopic data [79, 80]. An effective operator Oeff is also to be defined such that the same observable are obtained in a finite dimensional model space M as reproduced by a bare operator O acting in an infinite dimensional Hilbert space. The problems associated with the numerical implementation of such effective operators in perturbative approach have been discussed by Haxton and Lau [81].
In the HFB theory [82], the HF field and the pairing interaction are treated simultaneously and on equal footing. Further, the particle coordinates are transformed to quasiparticle coordinates through general Bogoliubov transformation
such that the interaction between quasiparticles is relatively weak. Essentially, the Hamiltonian H is expressed as
where H0 is the energy of the quasiparticle vacuum, Hqp is the elementary quasiparticle excitations and Hqp−qp is a weak interaction between the quasiparticles. In the HFB theory, the interaction between the quasiparticles is usually neglected and the Hamiltonian H is approximated by independent quasiparticle Hamiltonian. In TDHFB and QRPA, the effects of quasiparticle interaction are included to certain extent.
In the PHFB model, a state with good angular momentum J is obtained from the HFB intrinsic state |Φ0〉 using the standard projection technique [83].
The axially symmetric HFB intrinsic state |Φ0〉 with K = 0 can be formulated as
where the creation operators and are given by
with
and N is a normalization constant.
In Rath et al. [37], Chandra et al. [66], Singh et al. [67], and Chandra et al. [75], the model space, SPE's, parameters of pairing plus multipolar type of effective two-body interaction have already been discussed. Specifically, the wave functions are obtained by minimizing the expectation value of the effective Hamiltonian consisting of single particle Hamiltonian Hsp, and pairing V(P) plus multipolar (quadrupole-quadrupole V(QQ) and hexadecapole-hexadecapole V(HH) parts) type of effective two-body interaction [75]
In the V(QQ), the strengths of proton-proton, neutron-neutron and proton-neutron interactions are denoted by χ2pp, χ2nn and χ2pn, respectively. By reproducing the experimental excitation energy either by taking χ2pp = χ2nn and varying χ2pn or by considering χ2pp = χ2nn = χ2pn/2 and adjusting the three parameters together, two different parameterizations of V(QQ), namely PQQ1 and PQQ2 [75] were obtained. Additional consideration of the hexadecapolar V(HH) part of the effective interaction provided two more parametrizations, namely PQQHH1 and PQQHH2 [37].
In Rath et al. [37] and Chandra et al. [75], the reliability of wave functions generated with four different parametrizations of the effective two-body interaction, namely PQQ1, PQQHH1, PQQ2, and PQQHH2 has been established by comparing the theoretically calculated results for a number of spectroscopic properties, namely the yrast spectra, reduced B(E2:0+ → 2+) transition probabilities, deformation parameters β2, quadrupole moments Q(2+) and g-factors g(2+) of 94, 96Zr, 94, 96, 100Mo, 100Ru, 110Pd, 110Cd, 128, 130Te, 128, 130Xe, 150Nd, and 150Sm isotopes with the available experimental data.
By adjusting the strength parameter χ2pn or χ2pp, the experimental excitation energies [84] have been reproduced to about 98% accuracy. With respect to PQQ1 interaction, the maximum change in excitation energies and is about 8 and 31%, respectively [66, 67]. The reduced B(E2:0+ → 2+) transition probabilities, deformation parameters β2, static quadrupole moments Q(2+) and gyromagnetic factors g(2+) differ by about 20%, 10% (except for 94Zr and PQQ2 interaction), 27 and 12% (except for 94, 96Zr and PQQ2 interaction), respectively, and there is an overall agreement between the theoretically calculated and experimentally observed data [85, 86]. Employing wave functions generated with the above mentioned four parametrizations of effective two-body interaction, the calculated [75] and experimental deformation parameters β2 [85] of parent and daughter nuclei involved in the ββ decay of 94, 96Zr, 100Mo, 110Pd, 128, 130Te, and 150Nd isotopes have been presented in Table 1. Interestingly, the experimentally observed deformation parameters β2 have been well reproduced.
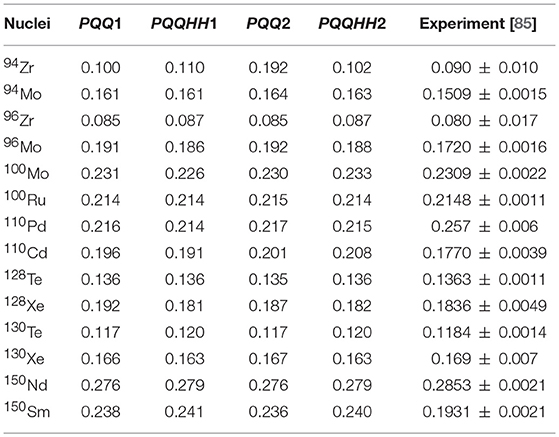
Table 1. Theoretically calculated deformation parameters β2 of nuclei participating in ββ decay with PQQ1, PQQ2, PQQHH1, and PQQHH2 parametrizations of effective two-body interaction along with experimental recommended values [85].
3. Two Neutrino Double Beta Decay
Incorporating the summation method [63–65], the PHFB model has already been applied to study the 0+ → 0+ [66, 67] and 0+ → 2+ [68] transitions of 2νβ−β− decay. The inverse half-life for the 0 transition of the decay can be written as
and the integrated kinematical factor has been calculated with good accuracy employing the exact Dirac wave functions in conjunction with finite nuclear size and screening effects [87–89]. Further, the model dependent NTME M(2ν)(J+) is defined as
where
Further, and are the initial, final and virtual intermediate states, respectively. By performing the summation over intermediate states using the summation method [63–65], the NTME is written as
with Δβ(k) = ε(nπ, lπ, jπ)−ε(nν, lν, jν). Notably, this expression is same as reported by Hirsch et al. [90].
In the energy denominator, the difference in single particle energies Δβ(k) of protons in the intermediate nucleus and neutrons in the parent nucleus is mainly due to the difference in Coulomb energies. Hence
where the Coulomb energy difference ΔC is given by Bohr and Mottelson [91].
Presently, each proton-neutron excitation is treated according to its spin-flip or non–spin-flip nature and the spin-orbit splitting is explicitly included in the energy denominator. Hence, the use of summation method goes beyond the closure approximation and previously employed summation method in the pseudo SU(3) model [90, 92].
In the PHFB model, the NTMEs corresponding to a transition operator (k = 2ν or 0ν) for the 0 transition of β−β− decay are obtained using
In Chandra et al. [66] and Singh et al. [67], the required expressions to evaluate amplitudes (uim, vim) and expansion coefficients Cij, m of axially symmetric HFB intrinsic state |Φ0〉 with K = 0, nJ, n(Z, N), (Z+2, N−2)(θ), fZ, N and FZ, N(θ) have been presented.
In Table 2, the theoretically calculated NTMEs M(2ν)(0+) using wave functions generated with PQQ1, PQQ2, PQQHH1 and PQQHH2 parameterizations of effective two-body interaction, along with their averages (gA = 1.2701) and recommended values of Barabash [93] have been displayed. With different parametrizations, the theoretically calculated NTMEs M(2ν) for the 0+ → 0+ transition change up to approximately 11% except 94Zr, 128, 130Te, and 150Nd isotopes, for which the changes are approximately 42, 21, 26, and 18%, respectively.
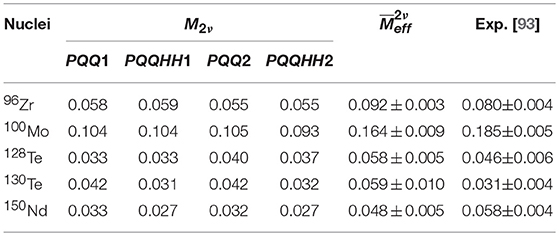
Table 2. Theoretically calculated NTMEs M(2ν) with four different parametrizations of the effective two-body interaction along with experimental recommended values [93].
With the observation that the inclusion of deformation in the mean field can suppress the NTMEs M(2ν)(2+) calculated employing pnQRPA by about a factor of 341 [94], the 0+ → 2+ transition of 2νβ−β− decay has been studied in the PHFB approach [68]. With respect to NTMEs M(2ν) (2+) calculated using pnQRPA, the average NTMEs (2+) estimated employing the PHFB model are further reduced by a factor between 1 and 150 corresponding to 96Zr and 128Te isotopes, respectively. Further, the compiled theoretical and experimental results [68] suggest that the observation of the 0+ → 2+ transition of 2νβ−β− decay may be possible in 96Zr, 100Mo, 110Pd, 130Te and 150Nd isotopes.
4. Neutrinoless Double Beta Decay
In the left-right symmetric model [95–97], the possible mechanisms of decay, namely the exchange of left and right handed Majorana neutrinos, involve strangeness conserving left handed and right handed charged currents. The detailed theoretical formalism required to study the decay was developed in Doi and Kotani [95, 96], Haxton and Stephenson [98], and Tomoda [99] with the assumption that in the charged current weak processes, the vector and axial vector parts of the current-current interaction give dominant contribution and under the assumption of zero mass neutrinos, the other terms being proportional to the lepton mass squared are negligible. With the inclusion of pseudoscalar and weak magnetism terms in the nucleonic current, it has been shown by Šimkovic et al. [100] that the contribution of the pseudoscalar term is equivalent to a modification of the axial vector current due to Goldberger-Treiman PCAC relation and greater than the vector current. In the standard mass mechanism, the contributions of pseudoscalar and weak magnetism terms of the recoil current can change the NTMEs M(0ν) up to about 30% in the QRPA [100, 101], 20% in the ISM [16, 17] and 15% in the IBM [43]. The change in M(0N) is quite substantial. Presently, the calculation of NTMEs of decay within mechanisms involving light Majorana neutrinos, heavy Majorana neutrinos, sterile neutrinos and Majorons has been discussed.
4.1. Light Majorana Neutrino Mass Mechanism
In the mechanism involving light Majorana neutrino mass, the half-life for the 0+ → 0+ transition of decay is given by [100, 101]
where
Incorporating the exact Dirac wave functions, finite nuclear size and screening effects, the phase space factors have been calculated recently to good accuracy [87, 88, 102] and in the closure approximation, the NTME M(0ν) is defined as
with
The neutrino potentials associated with Fermi, Gamow-Teller (GT) and tensor operators are given by
where fα(qrnm) = j0(qrnm) and fα(qrnm) = j2(qrnm) for α = Fermi/GT and tensor potentials, respectively. The effects due to FNS have been incorporated through two different parametrizations of the form factors, namely dipole form factor and an alternative parametrization of and with the consideration of internal structure of protons and neutrons [103]. The details about these form factors and form factor related functions hF(q), hGT(q) and hT(q) have been given in Rath et al. [38].
4.2. Heavy Majorana Neutrino Mass Mechanism
In order to ascertain the dominant mechanism contributing to 0νβ−β− decay [104–106], there has been an increased interest recently to calculate reliable NTMEs for 0νβ−β− decay due to the exchange of heavy Majorana neutrinos. Due to the exchange of heavy Majorana neutrinos between nucleons having finite size, the half-life for the 0+ → 0+ transition of 0νβ−β− decay is given by
where mp is the proton mass and
In the closure approximation, the NTMEs M(0N) are of the form [32, 58, 107]
The short ranged neutrino potentials due to the exchange of heavy Majorana neutrinos are given by
with fFh(qrnm) = fGTh(qrnm) = j0(qrnm) and fTh(qrnm) = j2(qrnm). The details regarding the hF(q), hGT(q) and hT(q) are given in Rath et al. [39].
4.3. Mechanism Involving Sterile Neutrinos
The indication of conversion in the short base line experiments [108, 109] has been explained with 0.2 eV < Δm2 < 2 eV and 10−3 < sin22θ < 4.10−2. The short base line oscillation [110–112] is also supported by recent results of the reactor fluxes. All these observations, if confirmed, would imply the existence of more than three massive neutrinos [113]. Further, it has already been shown that the mixing of a light sterile neutrino (mass ≪ 1 eV) with a much heavier sterile neutrino (mass ≫ 1 GeV) would result in observable signals in current ββ decay experiments [114]. In addition, other interesting alternative scenarios are also possible [115, 116].
With the consideration of the exchange of a Majorana neutrino between two nucleons, the contribution of the sterile νh neutrino to the half-life for the 0+ → 0+ transition of decay [116] is given by
where Ueh is the νh − νe mixing matrix element and the NTME is written as
In Equation (25), the neutrino potentials are of the form
and the expressions for are given in Rath et al. [38]. In the limits mh → 0, and mh → large, NTMEs and , respectively.
4.4. Majoron Accompanied Neutrinoless Double Decay
The proposed nine classical [117–121] and new Majoron models [114, 122–124] may be distinguished as single Majoron emitting 0νββϕ decay and double Majoron emitting 0νββϕϕ decay modes. Over the past decades, experimental studies devoted to 0νββχ decay have provided stringent limits on the Majoron coupling constant < g > ~10−5 and information on the sensitivities of the ongoing experiments to different new Majoron models [125, 126]. In the QRPA [127] and PHFB [76] approach, the observability of nine Majoron models has been investigated theoretically.
The half-life for the 0+ → 0+ transition of decay is written by
The symbol χ denotes modes involving single Majoron ϕ or two Majorons ϕϕ and the index m = 2 and 4 for the and 0νβ−β−ϕϕ decay modes, respectively. Further, the index α indicates different Majoron models as given in Table 3. The phase space factors have been calculated to good accuracy by Kotila et al. [128]. In the same Table 3, NTMEs corresponding to different Majoron models are also presented. In the closure approximation, the NTMEs are defined as
where NTMEs of the classical Majoron models and NTMEs M(0ν) of the light Majorana neutrino mass mechanism are identical. Retaining only the central part of the recoil term in following Hirsch et al. [127], the neutrino potentials and required for the calculation of the other two matrix elements and , respectively, are defined as
and all the details about the required parameters have been given in Rath et al. [76]. The qualitative dependence of different neutrino potentials and on momentum transfer q is of different nature. In contrast to the neutrino potential , is quite singular in nature. In the evolution of , the contributions from low momentum q are crucial and the accuracy of the calculated NTMEs is quite uncertain. In accordance with Hirsch et al. [127], the magnitudes of are uncertain by about one order magnitude.

Table 3. Different Majoron models according to Bamert et al. [114].
5. Nuclear Structure Aspects of Transition Matrix Elements
In addition to the spin-isospin dependence as in case of , the NTMEs for 0νββ decay are momentum dependent. In the evaluation of reliable NTMEs, the FNS, SRC and the renormalized value of axial vector coupling constant gA [47, 129–132] play a decisive role. Employing two different parametrizations of the form factors, namely dipole form factor and an alternative parametrization with the consideration of internal structure of protons and neutrons [38], it has been shown that the difference in NTMEs due to these different form factors is almost negligible. Presently, we consider the calculation of NTMEs with dipole form factor only.
Due to the exchange of ρ and ω mesons, the repulsive nucleon-nucleon potentials result in SRC, which has been incorporated through phenomenological Jastrow type of correlations with Miller-Spencer parametrization [133]. In addition, the use of effective transition operator [134], the exchange of ω-meson [135], UCOM [32, 56, 57] and the self-consistent CCM [58] have also been considered. In the self-consistent CCM [58], effects of Argonne and CD-Bonn two nucleon potentials have been parametrized by Jastrow type of correlations within a few percent accuracy. Explicitly,
where a = 1.1, 1.59 and 1.52 fm−2, b = 0.68, 1.45 and 1.88 fm−2 and c = 1.0, 0.92 and 0.46 for Miller-Spencer parametrization, CD-Bonn and Argonne V18 NN potentials, denoted as SRC1, SRC2 and SRC3, respectively.
In order to estimate theoretical uncertainties in NTMEs statistically, sets of twelve NTMEs M(0ν), M(0N), , , , and for the decay of 94, 96Zr, 100Mo, 110Pd, 128, 130Te, and 150Nd isotopes have been calculated with the consideration of four different parametrizations of effective two-body interaction, dipole form factor (FNS) and three different parametrizations of the Jastrow type of SRC (FNS+SRC) using Equation (16).
5.1. Effects Due to FNS and SRC
In Table 4, the relative changes (in %) in NTMEs M(0ν), M(0N), , and calculated with four different parametrizations of the effective two-body interaction due to the inclusion of FNS, FNS+SRC (FNS+SRC1, FNS+SRC2, and FNS + SRC3) have been presented. Considering as point nucleon case, the NTMEs M(0ν) are reduced by about 18–23% in the case of FNS. With the addition of SRC1, SRC2, and SRC3, the NTMEs M(0ν) are further reduced by 12–17%, 1.0–2.0%, and 2.4–3.0% approximately relative to the FNS case. Due to FNS, the maximum change in the values of are in between 13 and 16%. With the inclusion of SRC, the NTMEs change by about 12–15%, less than 1% and 3–4% due to SRC1, SRC2, and SRC3, respectively. It is noteworthy that the NTMEs change negligibly due to FNS and SRC.
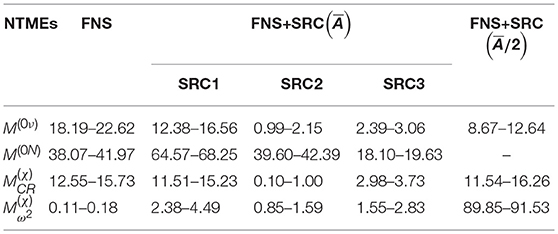
Table 4. Relative changes (in %) in NTMEs M(0ν), M(0N), , and calculated with four different parametrizations of the effective two-body interaction due to the inclusion of FNS, FNS+SRC (FNS+SRC1, FNS+SRC2, and FNS + SRC3), and average energy denominator .
It is observed [39] that the Fermi matrix element MFh = MFh−VV contributes about 20% to the total NTME. Due to the inclusion of the pseudoscalar and weak magnetism terms in the hadronic currents, the Gamow-Teller matrix element is noticeably modified. The absolute value of MGT−AA is increased by MGT−PP and the contribution of MGT−AP is significant with an opposite sign. The contribution of MGT−MM is quite small and with the inclusion of SRC, a change of sign is noticed. The contribution of tensor matrix elements is less that 2%. With the consideration of SRC, the Fermi and GT matrix elements change significantly and the tensor matrix element is the least affected. With respect to the point nucleon case, the NTMEs are reduced by about 40% due to FNS. Due to SRC1, the NTMEs are reduced to about one third of its original value and the other two parameterizations of the SRC, namely SRC2 and SRC3, have a sizable effect, albeit much smaller than SRC1.
5.2. Validity of Closure Approximation
In order to test the validity of closure approximation, the NTMEs are calculated for in the energy denominator and the changes in NTMEs due to four different parametrizations of the effective two-body interaction and three different parameterizations of SRC are given in Table 4. In the case of light Majorana neutrino exchange, the relative change in NTMEs M(0ν), by changing the energy denominator to instead of is in between 8.7–12.6%. In the Majoron accompanied 0νβ−β−χ decay, the relative changes in NTMEs due to the use of instead of in the energy denominator is at the most about 16.0%. As the is reduced by a factor of 2, the NTMEs , however, change appreciably. It may be mentioned that the structure of neutrino potentials associated with different matrix elements is reflected in the observed sensitivities of different NTMEs to the magnitudes of .
5.3. Effects Due to PQQ1, PQQHH1, PQQ2, and PQQHH2 Parametrizations
The evaluated NTMEs M(0ν) of considered nuclei but for 128Te with PQQ1 and PQQ2 parameterizations are quite close and with the inclusion of the hexadecapolar term, they are reduced in magnitude, depending specifically on the structure of nuclei. With respect to PQQ1, the maximum variation in M(0ν) due to the PQQHH1, PQQ2, and PQQHH2 parameterizations lies between 20–25% [38]. Due to PQQHH1, PQQ2, and PQQHH2 parametrizations, the maximum variations in M(0N) with reference to PQQ1 interaction, are about 24, 18, and 26%, respectively [39]. With respect to PQQ1 parametrization, NTMEs and due to other three parametrizations change up to 25 and 34%.
5.4. Radial Evolutions of NTMEs
The best possible way of studying the role of the FNS and SRC is to display the radial evolution of NTMEs defined by [32]
By studying the radial evolution of NTMEs M(0ν) due to the exchange of light Majorana neutrino, it has been shown in the QRPA [32] and ISM [18] that the magnitude of M(0ν) for all nuclei undergoing decay exhibits a maximum at about the internucleon distance r ≈ 1 fm, and the contributions of decaying pairs coupled to J = 0 and J > 0 almost cancel out beyond r ≈ 3 fm. Within the PHFB approach, similar observations on the radial evolution of NTMEs M(0ν) due to the exchange of light [38] Majorana neutrinos have also been reported.
In Figure 1, the radial distributions of C(0ν), C(0N), , and of 130Te nuclei with the PQQ1 parameterization of the effective two body interaction in four cases, namely FNS, FNS+SRC1, FNS+SRC2 and FNS+SRC3 have been plotted. As noticed, the distribution of C(0ν) are peaked at r = 1.0 fm for FNS and the peak is shifted to 1.25 fm with the addition of SRC1 and SRC2. With the inclusion of SRC3, the position of the peak remains, however, unchanged at r = 1.0 fm. The distribution of in the case of FNS is peaked at r = 1.0 fm and with the addition of SRC1, the peak shifts to 1.4 fm. The position of the peak with the inclusion of SRC2 and SRC3, is however, changed to r = 1.2 fm. Although, the radial distributions of C(0ν) and extend up to about 10 fm, the radial evolutions of M(0ν) and result from distributions of C(0ν) and up to 3 fm. The distributions are oscillating in nature with decreasing amplitudes, albeit, the first peak is similar to the distributions of NTMEs M(0ν) and . The total distribution extending up to 15 fm contributes to the evolution of matrix element .
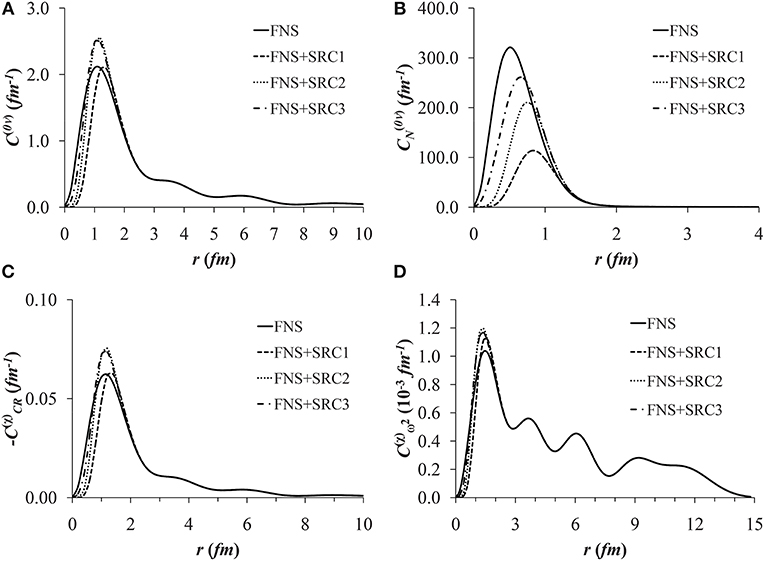
Figure 1. Radial dependence of (A) C(0ν)(r), (B) , (C) , and (D) for the 0νβ−β− and 0νβ−β−χ decay modes of 130Te isotope.
With the exchange of heavy Majorana neutrino, the distribution in the case of FNS is peaked at r≈0.5 fm and the peak shifts to about 0.8 fm with the addition of SRC1 and SRC2. With SRC3, the position of peak is shifted to 0.7 fm. In the evolution of matrix element M(0N), the total distribution extending up to 2 fm contributes. Remarkably, the above observations regarding the radial distributions of C(0ν), C(0N), , and remain valid in the cases of PQQ2, PQQHH1, and PQQHH2 parametrizations for all considered seven nuclei, namely 94, 96Zr, 100Mo, 110Pd, 128, 130Te, and 150Nd isotopes.
5.5. Deformation Effects
In Auerbach et al. [136, 137] and Troltenier et al. [138], an inverse correlation between the GT strength and quadrupole moment has been reported. Using a quasiparticle Tamm-Dancoff approximation (TDA) based on deformed Hartree-Fock (DHF) calculations with Skyrme interactions [139], a deformed self consistent HF+RPA method with Skyrme type interactions [140–142], the effect of deformation on the distribution of the GT and β decay properties have been studied. The comparison between the experimental GT strength distribution B(GT) and the results of QRPA calculations was implemented as a novel method of deducing the deformation of N = Z nucleus 76Sr [143].
In the PHFB model [66, 67, 69, 70, 72], the effect of deformation on the NTMEs of ββ decay has been studied and the role of quadrupolar correlations has also been investigated. The quenching of NTMEs seems to be closely related with the explicit inclusion of deformation effects, which are absent in the other models. Out of several possibilities, the quadrupole moment of the intrinsic state and quadrupole deformation parameter β2 have been taken as a quantitative measure of the deformation. The variation of the , β2, and M(K) with respect to the change in strength of QQ interaction ζqq has been investigated in order to understand the role of deformation on the NTMEs M(K) [66, 67, 72].
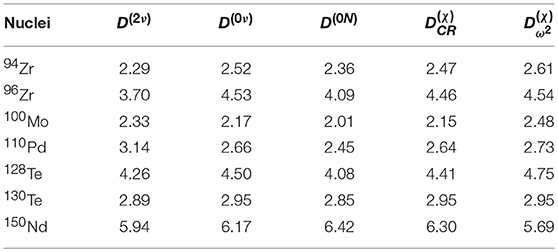
It is noticed that there is an anticorrelation between the deformation parameter and the NTMEs M(K) in general. The effect of deformation on M(K) is quantified by the quantity D(K) defined as the ratio of M(K) at zero deformation (ζqq = 0) and full deformation (ζqq = 1) and is given by [72, 73]
In Table 5, the values of deformation ratios D(2ν), D(0ν), D(0N), and are presented for 94, 96Zr, 100Mo, 110Pd, 128, 130Te, and 150Nd nuclei. Owing to deformation effects, the NTMEs M(2ν), M(0ν), M(0N), , and are suppressed by factor of about 2–6 in the mass range 90 ≤ A ≤ 150, and the deformation ratios are independent of underlying mechanisms. Although the results are presented for PQQ1 parametrization with SRC1, the deformation ratios are independent of used SRC.
5.6. Uncertainties in NTMEs
Employing sets of twelve NTMEs M(K) calculated for 94, 96Zr, 100Mo, 110Pd, 128, 130Te, and 150Nd isotopes, averages and variances have been statistically estimated using
and
By evaluating the same mean and standard deviations for eight NTMEs calculated using SRC2 and SRC3 parameterizations, the role of Miller-Spencer parameterization of Jastrow type of SRC has been ascertained. In Table 6, the estimated averages , , , and along with their respective variances , , , and for 94, 96Zr, 100Mo, 110Pd, 128, 130Te, and 150Nd isotopes have been presented. The calculated NTMEs due to exchange of light Majorana neutrino as well as heavy Majorana neutrino within PHFB model have been compared with the results of other models in Table 7.
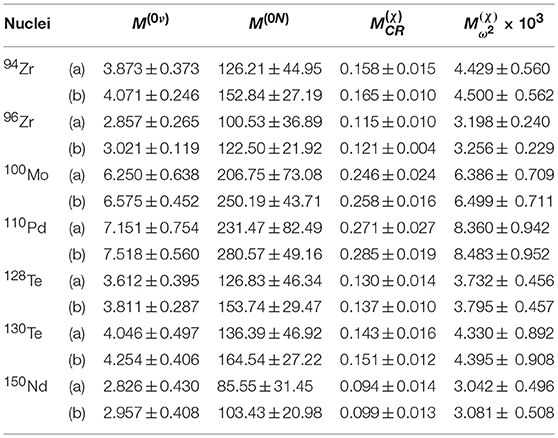
Table 6. Average values of NTMEs , , , and for 94, 96Zr, 100Mo, 110Pd, 128, 130Te, and 150Nd isotopes (a) with and (b) without SRC1 [39, 76].
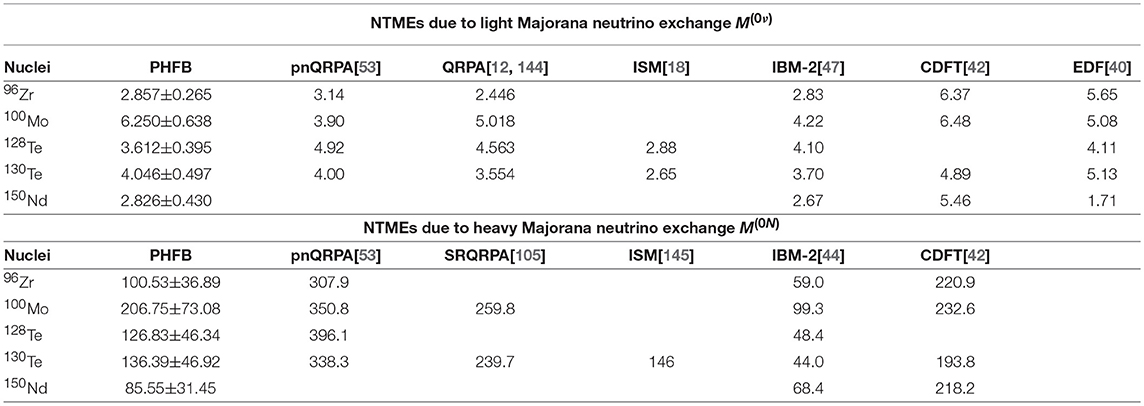
Table 7. Comparison of NTMEs due to light Majorana neutrino exchange M(0ν) and heavy Majorana neutrino exchange M(0N) calculated within PHFB model (case (a)) for 96Zr, 100Mo, 128, 130Te, and 150Nd isotopes with those of other models.
In general, the uncertainties displayed in Table 7, are of the order of 10%. In the case of 130Te and 150Nd isotopes, the uncertainties are about 12 and 15%, respectively. Exclusion of NTMEs due to SRC1 in the statistical analysis reduce the uncertainties by 1.5–5%. Without (with) SRC1, estimated uncertainties are about 4–14% (9–15%). Due to the identical form of corresponding operators, the uncertainties in both the NTMEs and are of the same order. Uncertainties in NTMEs exhibit a negligible dependence on SRC and are about 7.0–21% (7.5–21%) without (with) SRC1. Estimated uncertainties in average NTMEs for the decay of 94, 96Zr, 100Mo, 110Pd, 128, 130Te and 150Nd isotopes are about 35%. With the exclusion of NTMEs due to SRC1, uncertainties in NTMEs are reduced to about 16–20%. Without (with) SRC1, uncertainties in are about 4% (9%)–20% (36%) depending on the considered mass of the sterile neutrinos [38].
5.7. Nuclear Sensitivities
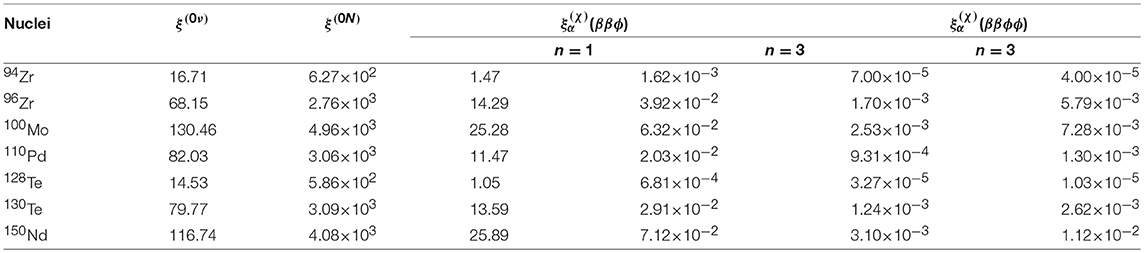
The nuclear sensitivity ξ(K) is related to the sensitivity of effective parameter of underlying mechanism and has been defined by [100]
with an arbitrary normalization factor 108 so that the nuclear sensitivities turn out to be order of unity. In Table 8, the nuclear sensitivities ξ(K), with K = 0ν, 0N, ξ(χ)(ββϕ), ξ(χ)(ββϕϕ) for the decay of 94, 96Zr, 100Mo, 110Pd, 128, 130Te, and 150Nd isotopes are presented. It is observed that the nuclear sensitivities for 0νβ−β− decay of 100Mo, 150Nd, 130Te, 110Pd, 96Zr, 94Zr, and 128Te isotopes are in the decreasing order of their magnitudes. However, the nuclear sensitivities ξ(χ) for the decay of 150Nd, 100Mo, 96Zr, 130Te, 110Pd, 94Zr, and 128Te isotopes are in the decreasing order of their magnitudes. In comparison with new Majoron models, the nuclear sensitivities of the promising nuclei for the classical Majoron models are larger by about a factor of 103−4. Remarkably, the nuclear sensitivities ξ(K) of different nuclei are mode dependent.
5.8. Extraction of Gauge Theoretical Parameters
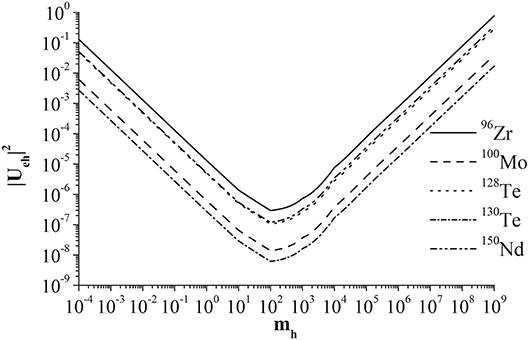
Limits on the effective mass of light Majorana neutrino 〈mν〉, effective mass of heavy Majorana neutrino 〈MN〉, the νh−νe mixing matrix element Ueh, and effective Majoron-neutrino coupling constants 〈gα〉 have been extracted from the largest observed limits on half-lives of decay of 94, 96Zr, 98, 100Mo, 128, 130Te, and 150Nd isotopes and given in Table 9. In Table 10, the effective parameters 〈mν〉, 〈MN〉, and 〈gα〉 in classical and new Majoron models have been presented. In the case of 130Te nuclei, the most stringent limits on 〈mν〉 and 〈MN〉 are < 0.17 eV and >1.12 × 108 GeV, respectively. Within classical Majoron model, the most stringent extracted limit on is obtained for 100Mo isotope. As the NTMEs and phase space factors of the new Majoron models are smaller than those of classical Majoron models, the extracted limits on 〈gα〉 of new Majoron models are large by a factor of 104−5 than those of classical Majoron models. In Figure 2, the extracted limits on the νh−νe mixing matrix element Ueh from the largest observed limits on the half-lives of 0νβ−β− decay are displayed. In comparison to laboratory experiments, astrophysical and cosmological observations [156, 157], the extracted limits on the νh−νe mixing matrix element Ueh span a wider region of νh mass mh and are comparable to the limits obtained in Blennow et al. [158].

Table 9. Experimentally observed half-lives , (yr) and (yr) of 94Zr, 96Zr, 100Mo, 110Pd 128, 130Te, and 150Nd isotopes.
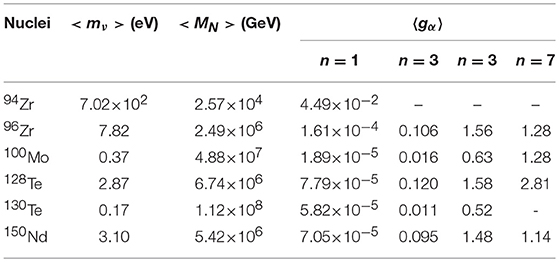
Table 10. Extracted effective light Majorana mass < mν>, effective heavy Majorana mass < MN>, effective Majoron-neutrino couplings 〈gα〉.
As the sensitivities of the ongoing double-β decay experiments juxtaposed with the new Majoron models are quite weak, a comparison between the expected half lives of 94, 96Zr, 100Mo, 128, 130Te, and 150Nd isotopes within classical and new Majoron models is of experimental interest. In Table 11, the predicted half-lives for spectral indices n = 1, 3 of and n = 3, 7 of 0νβ−β−ϕϕ decay modes with and gA = 1.254 are presented. In addition, the predicted half-lives of decay of 94, 96Zr, 100Mo, 110Pd, 128, 130Te, and 150Nd isotopes are also given for 〈mν〉 = 50 meV. The smallest and largest predicted half-lives correspond to 150Nd and 128Te isotopes, respectively. It is noticed that the predicted half-lives of classical Majoron models for the potential nuclei are within the reach of planned experiments and in the near future, no observable decay signal of new Majoron models can be detected.
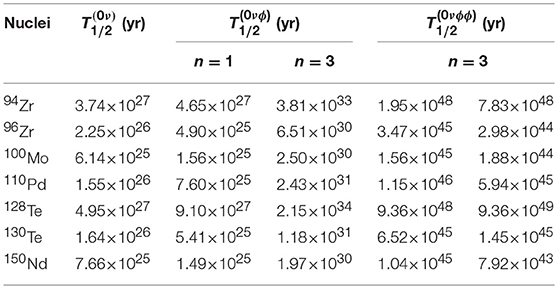
Table 11. Predicted half-lives , (yr) and (yr) of 94Zr, 96Zr, 100Mo, 110Pd 128, 130Te, and 150Nd isotopes with mν = 0.05 eV and 〈g〉 = 10−6.
6. Conclusions
In the PHFB model, sets of four HFB intrinsic wave functions have been generated with four different parameterizations of pairing plus multipole effective two body interaction. These sets of four HFB intrinsic wave functions reasonably reproduced the observed spectroscopic properties, namely the yrast spectra, deformation parameters β2 (the reduced B(E2:0+ → 2+) transition probabilities), static quadrupole moments Q(2+), g-factors g(2+) of participating nuclei in decay, and the NTMEs M2ν [66, 67]. With the consideration of three different parameterizations of Jastrow type of SRC, sets of twelve NTMEs have been calculated using dipole form factor to study the 0νβ−β− decay of 94, 96Zr, 100Mo, 110Pd, 128, 130Te, and 150Nd isotopes within mechanisms involving light as well as heavy Majorana neutrino, sterile neutrinos, and Majorons.
By using in place of , relative changes in NTMEs M(0ν) and are less than 16%, and the NTMEs vary by a factor of 2. Due to FNS and SRC, changes in NTMEs M(0ν) and are below 23 and 17%, respectively, and NTMEs remain almost unchanged. In the case of heavy Majorana neutrino exchange, the NTMEs M(0N) are reduced by about 38–42% due to FNS and with the addition of SRC1, SRC2 and SRC3, NTMEs are further reduced by 65–68%, 40–42%, and 18–20%, respectively. Due to deformation, the NTMEs M(0ν), M(0N), , and change by a factor of 2–6.
With (without) SRC1, estimated uncertainties and are about 8–15% (4–13%) and 9–15% (4–14%), respectively. Uncertainties in NTMEs exhibit a negligible dependence on SRC and are about 7.0–21% (7.5–21%) without (with) SRC1. Further, uncertainties in NTMEs are about 35% and by excluding NTMEs due to SRC1 corresponding to Miller-Spencer parametrization of Jastrow type of SRC, the maximum uncertainty is reduced to less than 20%. In the case of sterile neutrinos, the uncertainties in NTMEs without (with) SRC1 are in between 4–20% (8–36%) depending on the considered mass of the sterile neutrinos.
The nuclear sensitivities ξ(χ) for new Majoron models are smaller by 3 to 4 order of magnitudes than those of classical Majoron models. The study of sensitivities of considered nuclei suggests that to extract the effective mass of light Majorana neutrino 〈mν〉, 100Mo is the preferred isotope and 150Nd is the favorable isotope to extract the 〈gM〉. Thus, the sensitivities of different nuclei are mode dependent. The best limit on the effective neutrino mass 〈mν〉 < 0.17 eV is obtained from the observed limit on the half-live > 1.5 × 1025 yr of decay of 130Te isotope [151]. Using average NTMEs , the extracted stringent limit on the effective heavy Majorana neutrino mass 〈MN〉 from available limits on experimental half-lives is >1.12 × 108 GeV for 130Te isotope. It has been observed that in comparison to laboratory experiments, astrophysical and cosmological observations, the extracted limits on the sterile neutrino νh−νe mixing matrix element Ueh extend over a wider region of mass mh. In the case of 100Mo isotope, one obtains the best limit on the classical Majoron-neutrino coupling constant 〈gM〉 < 1.89 × 10−5. Extracted effective Majoron-neutrino coupling constants 〈gα〉 for new Majoron models are 3–4 order of magnitude larger than those of classical Majoron models. The calculated half lives for < g> = 10−6 suggest that although in the ongoing/planned ββ experiments, the classical Majoron accompanied 0νβ−β−ϕ decay might be observed, it would be very difficult to observe the Majoron accompanied 0νβ−β−χ decay within new Majoron models in the near future.
Author Contributions
PRat substantial contributions to the conception or design of the work; or the acquisition, analysis, or interpretation of data for the work. RC drafting the work and analysis of data for the work. KC revising it critically for important intellectual content. PRai revising it critically for important intellectual content.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank all our collaborators, especially Dr. J. G. Hirsch, for providing valuable suggestions through his active participation over the years. This work has been partially supported by DST-SERB, India (Grant No. SR/FTP/PS-085/2011), DST-SERB (Grant No. SB/S2/HEP-007/2013), the Council of Scientific and Industrial Research (CSIR), India (Sanction No. 03(1216)/12/EMR-II), and the Indo-Italian Collaboration DST-MAE project via Grant No. INT/Italy/P-7/2012 (ER).
References
1. Barabash AS. Main features of detectors and isotopes to investigate double beta decay with increased sensitivity. Int J Mod Phys A. (2018) 33:1843001. doi: 10.1142/S0217751X18430017
2. Dell'Oro S, Marcocci S, Viel M, Vissani F. Neutrinoless Double Beta Decay: 2015 Review. Adv High Energy Phys. (2016) 2016:2162659. doi: 10.1155/2016/2162659
3. Vergados JD, Ejiri H, Šimkovic F. Neutrinoless double beta decay and neutrino mass. Int. J. Mod Phys E. (2016) 25:1630007. doi: 10.1142/S0218301316300071
4. Vergados JD, Ejiri H. Theory of neutrinoless double-beta decay. Rep Prog Phys. (2012) 75:106301. doi: 10.1088/0034-4885/75/10/106301
5. Schechter J, Valle JWF. Neutrinoless double-β decay in SU(2) × U(1) theories. Phys Rev D. (1982) 25:2951. doi: 10.1103/PhysRevD.25.2951
6. Hirsch M, Klapdor-Kleingrothaus HV, Kovalenko SG. B-L-violating masses in softly broken supersymmetry. Phys Lett B. (1997) 398:311–4. doi: 10.1016/S0370-2693(97)00234-7
7. Vogel P, Zirnbauer MR. Suppression of the two-neutrino double-beta decay by nuclear-structure effects. Phys Rev Lett. (1986) 57:3148–51. doi: 10.1103/PhysRevLett.57.3148
8. Civitarese O, Faessler A, Tomoda T. Suppression of the two-neutrino double β decay. Phys Lett B. (1987) 194:11–4. doi: 10.1016/0370-2693(87)90760-X
9. Suhonen J, Civitarese O. Weak-interaction and nuclear-structure aspects of nuclear double beta decay. Phys Rep. (1998) 300:123–214.
10. Faessler A, Šimkovic F. Double beta decay. J Phys G. (1998) 24:2139. doi: 10.1088/0954-3899/24/12/001
11. Engel J, Menéndez J. Status and future of nuclear matrix elements for neutrinoless double-beta decay: a review. Rep Prog Phys. (2017) 80:046301. doi: 10.1088/1361-6633/aa5bc5
12. Šimkovic F, Rodin V, Faessler A, Vogel P. 0νββ and 2νββ nuclear matrix elements, quasiparticle random-phase approximation, and isospin symmetry restoration. Phys Rev C. (2013) 87:045501. doi: 10.1103/PhysRevC.87.045501
13. Caurier E, Poves A, Zuker AP. A full 0hω description of the 2νββ decay of 48Ca Phys Lett B. (1990) 252:13–17. doi: 10.1016/0370-2693(90)91071-I
14. Caurier E, Nowacki F, Poves A, Retamosa J. Shell model studies of the double beta decays of 76Ge, 82Se, and 136Xe. Phys Rev Lett. (1996) 77:1954. doi: 10.1103/PhysRevLett.77.1954
15. Horoi M, Neacsu N. Shell model study of the neutrinoless double beta decays. Nucl Phys A. (1999) 654:973c–6c. doi: 10.1016/S0375-9474(00)88583-8
16. Caurier E, Menéndez J, Nowacki F, Poves A. Influence of pairing on the nuclear matrix elements of the neutrinoless ββ decays. Phys Rev Lett. (2008) 100:052503. doi: 10.1103/PhysRevLett.100.052503
17. Caurier E, Nowacki F, Poves A. Nuclear-structure aspects of the neutrinoless ββ -decays. Eur Phys J A. (2008) 36:195–200. doi: 10.1140/epja/i2007-10527-x
18. Menéndez J, Poves A, Caurier E, Nowacki F. Disassembling the nuclear matrix elements of the neutrinoless ββ decay. Nucl Phys A. (2009) 818:139–51. doi: 10.1016/j.nuclphysa.2008.12.005
19. Brown BA, Horoi M, Sen'kov RA. Nuclear structure aspects of neutrinoless double-β decay. Phys Rev Lett. (2014) 113:262501. doi: 10.1103/PhysRevLett.113.262501
20. Neacsu A, Horoi M. Shell model studies of the 130Te neutrinoless double-β decay. Phys Rev C. (2015) 91:024309. doi: 10.1103/PhysRevC.91.024309
21. Horoi M, Brown BA. Shell-model analysis of the 136Xe double beta decay nuclear matrix elements. Phys Rev Lett. (2013) 110:222502. doi: 10.1103/PhysRevLett.110.222502
22. Horoi M, Stoica S. Shell model analysis of the neutrinoless double-β decay of 48Ca. Phys Rev C. (2010) 81:024321. doi: 10.1103/PhysRevC.81.024321
23. Brown BA, Fang DL, Horoi M. Evaluation of the theoretical nuclear matrix elements for ββ decay of 76Ge. Phys Rev C. (2015) 92:041301(R). doi: 10.1103/PhysRevC.92.041301
24. Sen'kov RA, Horoi M. Shell-model calculation of neutrinoless double-β decay of 76Ge. Phys Rev C. (2016) 93:044334. doi: 10.1103/PhysRevC.93.044334
25. Sen'kov RA, Horoi M. Accurate shell-model nuclear matrix elements for neutrinoless double-β decay. Phys Rev C. (2014) 90:051301(R). doi: 10.1103/PhysRevC.90.051301
26. Sen'kov RA, Horoi M, Brown BA. Neutrinoless double-β decay of 82Se in the shell model: beyond the closure approximation. Phys Rev C. (2014) 89:054304. doi: 10.1103/PhysRevC.89.054304
27. Rodríguez RA, Sarriguren P, Moya de Guerra E, Pacearescu L, Faessler A, Šimkovic F. Deformed quasiparticle random phase approximation formalism for single- and two-neutrino double β decay. Phys Rev C. (2004) 70:064309. doi: 10.1103/PhysRevC.70.064309
28. Šimkovic F, Pacearescu L, Faessler A. Two-neutrino double beta decay of 76Ge within deformed QRPA. Nucl Phys A. (2004) 733:321–50. doi: 10.1016/j.nuclphysa.2004.01.002
29. Pacearescu L, Faessler A, Šimkovic F. Nuclear deformation and the double-beta decay. Phys At Nucl. (2004) 67:1210–5. doi: 10.1134/1.1772462
30. Yousef MS, Rodin V, Faessler A, Šimkovic F. Two-neutrino double β decay of deformed nuclei within the quasiparticle random-phase approximation with a realistic interaction. Phys. Rev. C. (2009) 79:014314. doi: 10.1103/PhysRevC.79.014314
31. Fang DL, Faessler A, Šimkovic F. 0νββ-decay nuclear matrix element for light and heavy neutrino mass mechanisms from deformed quasiparticle random-phase approximation calculations for 76Ge, 82Se, 130Te, 136Xe, and 150Nd with isospin restoration. Phys. Rev. C. (2018) 97:045503. doi: 10.1103/PhysRevC.97.045503
32. Šimkovic F, Faessler A, Rodin V, Vogel P, Engel J. Anatomy of the 0νββ nuclear matrix elements. Phys Rev C. (2008) 77:045503. doi: 10.1103/PhysRevC.77.045503
33. Faessler A, Rodin V, Šimkovic F. Nuclear matrix elements for neutrinoless double-beta decay and double-electron capture. J Phys G. (2012) 39:124006. doi: 10.1088/0954-3899/39/12/124006
34. Fang DL, Faessler A, Rodin V, Šimkovic F. Neutrinoless double-β decay of deformed nuclei within quasiparticle random-phase approximation with a realistic interaction. Phys Rev C. (2011) 83:034320. doi: 10.1103/PhysRevC.83.034320
35. Fang DL, Faessler A, Rodin V, Šimkovic F. Neutrinoless double-β decay of 150Nd accounting for deformation. Phys Rev C. (2010) 82:051301(R). doi: 10.1103/PhysRevC.82.051301
36. Mustonen MT, Engel J. Large-scale calculations of the double-β decay of 76Ge, 130Te, 136Xe, and 150Nd in the deformed self-consistent Skyrme quasiparticle random-phase approximation. Phys Rev C. (2013) 87:064302. doi: 10.1103/PhysRevC.87.064302
37. Rath PK, Chandra R, Chaturvedi K, Raina PK, Hirsch JG. Uncertainties in nuclear transition matrix elements for neutrinoless ββ decay within the PHFB model.Phys Rev C. (2010) 82:064310. doi: 10.1063/1.3671043
38. Rath PK, Chandra R, Chaturvedi K, Lohani P, Raina PK, Hirsch JG. Neutrinoless ββ decay transition matrix elements within mechanisms involving light Majorana neutrinos, classical Majorons and sterile neutrinos. Phys Rev C. (2013) 88:064322. doi: 10.1103/PhysRevC.88.064322
39. Rath PK, Chandra R, Raina PK, Chaturvedi K, Hirsch JG. Uncertainties in nuclear transition matrix elements for neutrinoless ββ decay: the heavy Majorana neutrino mass mechanism. Phys Rev C. (2012) 85:014308. doi: 10.1103/PhysRevC.85.014308
40. Rodríguez TR, Pinedo GM. Energy density functional study of nuclear matrix elements for neutrinoless ββ decay. Phys Rev Lett. (2010) 105:252503. doi: 10.1103/PhysRevLett.105.252503
41. Yao JM, Song LS, Hagino K, Ring P, Meng J. Systematic study of nuclear matrix elements in neutrinoless double-β decay with a beyond-mean-field covariant density functional theory. Phys Rev C. (2015) 91:024316. doi: 10.1103/PhysRevC.91.024316
42. Song LS, Yao JM, Ring P, Meng J. Nuclear matrix element of neutrinoless double-β decay: relativity and short-range correlations. Phys Rev C. (2017) 95:024305. doi: 10.1103/PhysRevC.95.024305
43. Barea J, Iachello F. Neutrinoless double-β decay in the microscopic interacting boson model. Phys Rev C. (2009) 79:044301. doi: 10.1103/PhysRevC.79.044301
44. Barea J, Kotila J, Iachello F. Nuclear matrix elements for double-β decay. Phys Rev C. (2013) 87:014315. doi: 10.1103/PhysRevC.87.014315
45. Iachello F, Barea J, Kotila J. Advances in the theory of 0νββ decay. AIP Conf Proc. (2011) 1417:62. doi: 10.1063/1.3671038
46. Iachello F, Barea J. Advances in the theory of 0νββ decay. Nucl Phys B Proc Suppl. (2011) 217:5–8. doi: 10.1016/j.nuclphysbps.2011.04.055
47. Barea J, Kotila J, Iachello F. 0νββ and 2νββ nuclear matrix elements in the interacting boson model with isospin restoration. Phys Rev C. (2015) 91:034304. doi: 10.1103/PhysRevC.91.034304
48. Vogel P. Double beta decay: theory, experiment, and implications. In: Caldwell OD, editor. Current Aspects of Neutrino Physics. Berlin; Heidelberg: Springer (2001). p. 177. arXiv:nucl-th/0005020. doi: 10.1007/978-3-662-04597-8_8
49. Bahcall JN, Murayama H, Garay CP. What can we learn from neutrinoless double beta decay experiments? Phys Rev D. (2004) 70:033012. doi: 10.1103/PhysRevD.70.033012
50. Avignone FT III, King GS III, Zdesenko Yu G. Next generation double-beta decay experiments: metrics for their evaluation. New J Phys. (2005) 7:6. doi: 10.1088/1367-2630/7/1/006
51. Bilenky SM, Grifols JA. The possible test of the calculations of nuclear matrix elements of the (ββ)0ν-decay. Phys Lett B. (2002) 550:154–9. doi: 10.1016/S0370-2693(02)02978-7
52. Rodin VA, Faessler A, Šimkovic F, Vogel P. Uncertainty in the 0νββ decay nuclear matrix elements. Phys Rev C. (2003) 68:044302. doi: 10.1103/PhysRevC.68.044302
53. Hyvärinen J, Suhonen J. Nuclear matrix elements for 0νββ decays with light or heavy Majorana-neutrino exchange. Phys Rev C. (2015) 91:024613. doi: 10.1103/PhysRevC.91.024613
54. Suhonen J. Nuclear matrix elements of ββ decay from β-decay data. Phys Lett B. (2005) 607:87–95. doi: 10.1016/j.physletb.2004.12.048
55. Rodin VA, Faessler A, Šimkovic F, Vogel P. Assessment of uncertainties in QRPA 0νββ-decay nuclear matrix elements. Nucl Phys A. (2006)766:107–31. Erratum to: Assessment of uncertainties in QRPA 0νββ-decay nuclear matrix elements. [Nucl. Phys. A 766 (2006) 107] (2007) 793:213–5. doi: 10.1016/j.nuclphysa.2007.06.014
56. Kortelainen M, Suhonen J. Nuclear matrix elements of 0νββ decay with improved short-range correlations. Phys Rev C. (2007) 76:024315. doi: 10.1103/PhysRevC.76.024315
57. Kortelainen M, Civitarese O, Suhonen J, Toivanen J. Short-range correlations and neutrinoless double beta decay. Phys Lett B. (2007) 647:128–32. doi: 10.1016/j.physletb.2007.01.054
58. Šimkovic F, Faessler A, Müther H, Rodin V, Stauf M. 0νββ-decay nuclear matrix elements with self-consistent short-range correlations. Phys Rev C. (2009) 79:055501. doi: 10.1103/PhysRevC.79.055501
59. Engel J. Uncertainties in nuclear matrix elements for neutrinoless double-beta decay. J Phys G. (2015) 42:034017. doi: 10.1088/0954-3899/42/3/034017
60. Dobaczewski J, Nazarewicz W, Reinhard P. Error estimates of theoretical models: a guide. J Phys G. (2015) 41:074001. doi: 10.1088/0954-3899/41/7/074001
61. Dixit BM, Rath PK, Raina PK. Deformation effect on the double Gamow-Teller matrix element of 100Mo for the 0+ → 0 + transition. Phys Rev C. (2002) 65:034311. Erratum: Deformation effect on the double Gamow-Teller matrix element of 100Mo for the 0+ → 0+ transition [Phys. Rev. C 65, 034311 (2002)] Phys Rev C. (2003) 67:059901E. doi: 10.1103/PhysRevC.67.059901
62. Chaturvedi K, Dixit BM, Rath PK, Raina PK. Two neutrino double β decay of 100Mo to the 2+ excited state of 100Ru. Phys Rev C. (2003) 67:064317. doi: 10.1103/PhysRevC.67.064317
63. Civitarese O, Suhonen J. Use of summation methods in the calculation of nuclear double beta decay processes. Phys Rev C. (1993) 47:2410. doi: 10.1103/PhysRevC.47.2410
64. Civitarese O, Suhonen J. Two-neutrino double-beta decay to excited one- and two-phonon states. Nucl Phys A. (1994) 575:251–68. doi: 10.1016/0375-9474(94)90188-0
65. Civitarese O, Suhonen J. Is the single-state dominance realized in double β decay transitions? Phys Rev C. (1998) 58:1535. doi: 10.1103/PhysRevC.58.1535
66. Chandra R, Singh J, Rath PK, Raina PK, Hirsch JG. Two-neutrino double- β decay of 94 ≤ A ≤ 110 nuclei for the 0+ → 0+ transition. Eur Phys J A. (2005) 23:223–34. doi: 10.1140/epja/i2004-10087-7
67. Singh S, Chandra R, Rath PK, Raina PK, Hirsch JG. Nuclear deformation and the two-neutrino double-β decay in 124, 126Xe,128, 130Te,130, 132Ba and 150Nd isotopes. Eur Phys J A. (2007) 33:375–81. doi: 10.1140/epja/i2007-10481-7
68. Singh YK, Chandra R, Raina PK, Rath PK. Two neutrino double-β decay of 94 ≤ A ≤ 150 nuclei for the 0+ → 2+ transition. Eur Phys J A. (2017) 53:244–8. doi: 10.1140/epja/i2017-12445-8
69. Raina PK, Shukla A, Singh S, Rath PK, Hirsch JG. The 0+ → 0+ positron double-β decay with emission of two neutrinos in the nuclei 96Ru, 102Pd, 106Cd and 108Cd. Eur Phys J A. (2006) 28:27–35. doi: 10.1140/epja/i2005-10280-2
70. Shukla A, Raina PK, Chandra R, Rath PK, Hirsch JG. Two-neutrino positron double-beta decay of 106Cd for the 0+ → 0+ transition. Eur Phys J A. (2005) 23:235–42. doi: 10.1140/epja/i2004-10084-x
71. Rath PK, Chandra R, Singh S, Raina PK, Hirsch JG. Quadrupolar correlations and deformation effect on two-neutrino ϵβ+and ϵϵ modes of 156Dy isotope. J Phys G. (2010) 37:055108. doi: 10.1088/0954-3899/37/5/055108
72. Chaturvedi K, Chandra R, Rath PK, Raina PK, Hirsch JG. Nuclear deformation and neutrinoless double-β decay of 94, 96Zr, 98, 100Mo, 104Ru, 110Pd, 128, 130Te, and 150Nd nuclei within a mechanism involving neutrino mass. Phys Rev C. (2008) 78:054302. doi: 10.1103/PhysRevC.78.054302
73. Rath PK, Chandra R, Chaturvedi K, Raina PK, Hirsch JG. Deformation effects and neutrinoless positron ββ decay of 96Ru,102Pd,106Cd,124Xe,130Ba, and 156Dy isotopes within a mechanism involving Majorana neutrino mass. Phys Rev C. (2009) 80:044303. doi: 10.1103/PhysRevC.80.044303
74. Rath PK, Chandra R, Chaturvedi K, Lohani P, Raina PK, Hirsch JG. Uncertainties in nuclear transition matrix elements for β+β+and ϵβ+modes of neutrinoless positron double-β decay within the projected Hartree-Fock-Bogoliubov model. Phys Rev C. (2013) 87:014301. doi: 10.1103/PhysRevC.87.014301
75. Chandra R, Chaturvedi K, Rath PK, Raina PK, Hirsch JG. Multipolar correlations and deformation effect on nuclear transition matrix elements of double-β decay. Europhys Lett. (2009) 86:32001. doi: 10.1209/0295-5075/86/32001
76. Rath PK, Chandra R, Chaturvedi K, Lohani P, Raina PK. Nuclear transition matrix elements for Majoron-accompanied neutrinoless double-β decay within a projected-Hartree-Fock-Bogoliubov model. Phys Rev C. (2016) 93:024314. doi: 10.1103/PhysRevC.93.024314
77. Brandow BH. Linked-cluster expansions for the nuclear many-body problem. Rev Mod Phys. (1967) 39:771. doi: 10.1103/RevModPhys.39.771
78. Jensen MH, Kuo TTS, Osnes E. Realistic effective interactions for nuclear systems. Phys Rep. (1995) 261:125. doi: 10.1016/0370-1573(95)00012-6
79. Brussard PJ, Glaudemans PWM. Shell-Model Applications in Nuclear Spectroscopy. Amsterdam: North-Holland (1977).
80. Caurier E, Pinedo GM, Nowacki F, Poves A, Zuker AP. The shell model as a unified view of nuclear structure. Rev Mod Phys. (2005) 77:427–88. doi: 10.1103/RevModPhys.77.427
81. Haxton WC, Lau T. The canonical nuclear many-body problem as an effective theory. Nucl Phys A. (2001) 690:15–28. doi: 10.1016/S0375-9474(01)00927-7
82. Goodman AL. Hartree-Fock-Bogoliubov theory with applications to nuclei. In: Negele JW, Voget E, editors. Advances in Nuclear Physics, Vol. 11. New York, NY: Plenum (1979). p. 263.
83. Onishi N, Yoshida S. Generator coordinate method applied to nuclei in the transition region. Nucl Phys. (1966) 80:367–76. doi: 10.1016/0029-5582(66)90096-4
84. Sakai M. Quasi-bands in even-even nuclei. At Data Nucl Data Tables. (1984) 31:399–432. doi: 10.1016/0092-640X(84)90010-X
85. Raman S, Nestor CW Jr, Tikkanen P. Transition Probability from the ground to the first-excited 2+ state of even-even nuclides. At Data Nucl Data Tables. (2001) 78:1–128. doi: 10.1006/adnd.2001.0858
86. Raghavan P. Table of nuclear moments. At Data Nucl Data Tables. (1989) 42:189–291. doi: 10.1016/0092-640X(89)90008-9
87. Kotila J, Iachello F. Phase-space factors for double-β decay Phys Rev C. (2012) 85:034316. doi: 10.1103/PhysRevC.85.034316
88. Stoica S, Mirea M. New calculations for phase space factors involved in double-β decay. Phys Rev C. (2013) 88:037303. doi: 10.1103/PhysRevC.88.037303
89. Pahomi TE, Neacsu A, Mirea M, Stoica S. Phase space calculations for beta- beta- decays to final excited 2+1 states. Roman Rep Phys. (2014) 66:370.
90. Hirsch JG, Castaños O, Hess PO, Civitarese O. Double-beta decay to excited states in 150Nd. Nucl Phys A. (1995) 589:445–59. doi: 10.1016/0375-9474(95)00090-N
92. Hirsch JG, Castanos O, Hess PO, Civitarese O. Double-beta decay of 100Mo: the deformed limit. Phys Rev C. (1995) 51:2252. doi: 10.1103/PhysRevC.51.2252
93. Barabash AS. Average and recommended half-life values for two-neutrino double beta decay. Nucl Phys A. (2015) 935:52–64. doi: 10.1016/j.nuclphysa.2015.01.001
94. Raduta AA, Raduta CM. Double beta decay to the first 2+ state within a boson expansion formalism with a projected spherical single particle basis. Phys Lett B. (2007) 647:265–70. doi: 10.1016/j.physletb.2007.02.007
95. Doi M, Kotani T, Takasugi E. Double beta decay and majorana neutrino. Prog Theor Phys Suppl. (1985) 83:1–175. doi: 10.1143/PTPS.83.1
96. Doi M, Kotani T. Neutrinoless modes of double beta decay. Prog Theor Phys. (1993) 89:139–59. doi: 10.1143/PTP.89.139
97. Hirsch M. Klapdor-Kleingrothaus HV and Panella O. Double beta decay in left-right symmetric models. Phys Lett B. (1996) 374:7–12. doi: 10.1016/0370-2693(96)00185-2
98. Haxton WC, Stephenson GJ. Double beta decay. Jr Prog Part Nucl Phys. (1984) 12:409–79. doi: 10.1016/0146-6410(84)90006-1
100. Šimkovic F, Pantis G, Vergados JD, Faessler A. Additional nucleon current contributions to neutrinoless double β decay. Phys Rev C. (1999) 60:055502. doi: 10.1103/PhysRevC.60.055502
101. Vergados JD. The neutrinoless double beta decay from a modern perspective. Phys Rep. (2002) 361:1–56. doi: 10.1016/S0370-1573(01)00068-0
102. Štefánik D, Dvornický R, Šimkovic F, Vogel P. Reexamining the light neutrino exchange mechanism of the 0νββ decay with left- and right-handed leptonic and hadronic currents. Phys Rev C. (2015) 92:055502. doi: 10.1103/PhysRevC.92.055502
104. Šimkovic F, Vergados JD, Faessler A. Few active mechanisms of the 0νββ decay and effective mass of Majorana neutrinos. Phys Rev D. (2010) 82:113015. doi: 10.1103/PhysRevD.82.113015
105. Faessler A, Meroni A, Petcov ST, Šimkovic F, Vergados J. Uncovering multiple CP nonconserving mechanisms of (ββ)0ν decay. Phys Rev D. (2011) 83:113003. doi: 10.1103/PhysRevD.83.113003
106. Tello V, Nemevsek M, Nesti F, Senjanovic G, Vissani F. Left-right symmetry: from the LHC to neutrinoless double beta decay. Phys Rev Lett. (2011) 106:151801. doi: 10.1103/PhysRevLett.106.151801
107. Šimkovic F, Nowak M, Kaminski WA, Raduta AA, Faessler A. Neutrinoless double beta decay of 76Ge,82Se,100Mo, and 136Xe to excited 0+ states. Phys Rev C. (2001) 64:035501. doi: 10.1103/PhysRevC.64.035501
108. Aguilar A, Auerbach LB, Burman RL, Caldwell DO, Church ED, Cochran AK, et al. Evidence for neutrino oscillations from the observation of appearance in a beam. Phys Rev D. (2001) 64:112007. doi: 10.1103/PhysRevD.64.112007
109. Aguilar-Arevalo AA, Anderson CE, Brice SJ, Brown BC, Bugel L, Conrad JM, et al. Event Excess in the MiniBooNE Search for Oscillations. Phys Rev Lett. (2010) 105:181801. doi: 10.1103/PhysRevLett.105.181801
110. Mention G, Fechner ÂM, Lasserre ÂTh, Mueller  ThA, Lhuillier ÂD, Cribier ÂM, et al. Reactor antineutrino anomaly. Phys Rev D. (2011) 83:073006. doi: 10.1103/PhysRevD.83.073006
111. Mueller ThA, Lhuillier D, Fallot M, Letourneau A, Cormon S, Fechner M, et al. Improved predictions of reactor antineutrino spectra. Phys Rev C. (2011) 83:054615. doi: 10.1103/PhysRevC.83.054615
112. Huber P. Determination of antineutrino spectra from nuclear reactors. Phys Rev C. (2011) 84:024617. doi: 10.1103/PhysRevC.84.024617
113. Giunti C, Laveder M. Short-baseLine electron neutrino disappearance. Nucl Phys B Proc Suppl. (2011) 217:193–5. doi: 10.1016/j.nuclphysbps.2011.04.098
114. Bamert P, Burgess CP, Mohapatra RN. Multi-majoron modes for neutrinoless double-beta decay. Nucl Phys B. (1995) 449:25–48. doi: 10.1016/0550-3213(95)00273-U
115. Pilaftsis A. Astrophysical and terrestrial constraints on singlet Majoron models. Phys Rev D. (1994) 49:2398. doi: 10.1103/PhysRevD.49.2398
116. Beneš P, Faessler A, Kovalenko A, Šimkovic F. Sterile neutrinos in neutrinoless double beta decay. Phys Rev D. (2005) 71:077901. doi: 10.1103/PhysRevD.71.077901
117. Chikashige Y, Mohapatra RN, Peccei RD. Spontaneously broken lepton number and cosmological constraints on the neutrino mass spectrum. Phys Rev Lett. (1980) 45:1926. doi: 10.1103/PhysRevLett.45.1926.2
118. Chikashige Y, Mohapatra RN, Peccei RD. Are there real goldstone bosons associated with broken lepton number? Phys Lett B. (1981) 98:265–8. doi: 10.1016/0370-2693(81)90011-3
119. Gelmini GB, Roncadelli M. Left-handed neutrino mass scale and spontaneously broken lepton number. Phys Lett B. (1981) 99:411–5. doi: 10.1016/0370-2693(81)90559-1
120. Georgi HM, Glashow SL, Nussinov S. Unconventional model of neutrino masses. Nucl Phys B. (1981) 193:297–316. doi: 10.1016/0550-3213(81)90336-9
121. Aulakh CS, Mohapatra RN. The neutrino as the supersymmetric partner of the majoron. Phys Lett B. (1982) 119:136–40. doi: 10.1016/0370-2693(82)90262-3
122. Burgess CP, Cline JM. Majorons without majorana masses and neutrinoless double beta decay. Phys Lett B. (1993) 298:141. doi: 10.1016/0370-2693(93)91720-8
123. Burgess CP, Cline JM. New class of Majoron-emitting double-β decays. Phys Rev D. (1994) 49:5925. doi: 10.1103/PhysRevD.49.5925
124. Carone CD. Double beta decay with vector majorons. Phys Lett B. (1993) 308:85–8. doi: 10.1016/0370-2693(93)90605-H
125. Barabash AS. Double beta decay experiments. Phys At Nucl. (2010) 73:162. doi: 10.1134/S1063778810010187
126. IV International Pontecorvo Neutrino Physics School, Ukraine Sepetember 26-October 6. Alushta (2010).
127. Hirsch M, Klapdor-Kleingrothaus HV, Kovalenko SG, Päs H. On the observability of Majoron emitting double beta decays. Phys Lett B. (1996) 372:8–14. doi: 10.1016/0370-2693(96)00038-X
128. Kotila J, Barea J, Iachello F. Phase-space factors and half-life predictions for Majoron-emitting β−β− decay. Phys Rev C. (2015) 91:064310. doi: 10.1103/PhysRevC.91.064310
129. Menéndez J, Gazit D, Schwenk A. Chiral two-body currents in nuclei: gamow-teller transitions and neutrinoless double-beta decay. Phys Rev Lett. (2011) 107:062501. doi: 10.1103/PhysRevLett.107.062501
130. Suhonen J, Civitarese O. Probing the quenching of gA by single and double beta decays. Phys Lett B. (2013) 725:153–7. doi: 10.1016/j.physletb.2013.06.042
131. Engel J, Šimkovic F, Vogel P. Chiral two-body currents and neutrinoless double-β decay in the quasiparticle random-phase approximation. Phys Rev C. (2014) 89:064308. doi: 10.1103/PhysRevC.89.064308
132. Suhonen J. Value of the axial-vector coupling strength in β and ββ decays: a review. Front Phys. (2017) 5:55. doi: 10.3389/fphy.2017.00055
133. Miller GA, Spencer JE. A survey of pion charge-exchange reactions with nuclei. Ann Phys. (1976) 100:562–606. doi: 10.1016/0003-4916(76)90073-7
134. Wu HF, Song HQ, Kuo TTS, Cheng WK, Strottman D. Majorana neutrino and Lepton-Number non-conservation in 48Ca nuclear double beta decay. Phys Lett B. (1985) 162:227–32. doi: 10.1016/0370-2693(85)90911-6
135. Hirsch JG, Castaños O, Hess PO. Neutrinoless double beta decay in heavy deformed nuclei. Nucl Phys A. (1995) 582:124–40.
136. Auerbach N, Zheng DC, Zamick L, Brown BA. Correlation between the quenching of total GT+ strength and the increase of E2 strength. Phys Lett B. (1993) 304:17. doi: 10.1016/0370-2693(93)91392-Z
137. Auerbach N, Bertsch GF, Brown BA, Zhao L. β+ Gamow-teller strength in nuclei. Nucl Phys A. (1993) 556:190–200. doi: 10.1016/0375-9474(93)90347-Z
138. Troltenier D, Draayer JP, Hirsch JG. Correlations between the quadrupole deformation, B(E2; 01 → 21) value, and total GT+ strength. Nucl Phys A. (1996) 601:89–102. doi: 10.1016/0375-9474(96)00092-9
139. Frisk F, Hamamoto I, Zhang XZ. Gamow-teller β+ decay of deformed nuclei near the proton drip line. Phys Rev C. (1995) 52:2468. doi: 10.1103/PhysRevC.52.2468
140. Sarriguren P, Moya de Guerra E, Escuderos A, Carrizo AC. β decay and shape isomerism in 74Kr. Nucl Phys A. (1998) 635:55–85. doi: 10.1016/S0375-9474(98)00158-4
141. Sarriguren P, Moya de Guerra E, Escuderos A. Shapes and β−decay in proton rich Ge, Se, Kr and Sr isotopes. Nucl Phys A. (1999) 658:13–44. doi: 10.1016/S0375-9474(99)00346-2
142. Sarriguren P, Moya de Guerra E, Escuderos A. Spin–isospin excitations and β+/EC half-lives of medium-mass deformed nuclei. Nucl Phys A. (2001) 691:631–48. doi: 10.1016/S0375-9474(01)00565-6
143. Nacher E, et al. Deformation of the N=Z Nucleus 76Sr using β-Decay Studies. Phys Rev Lett. (2004) 92:232501. doi: 10.1103/PhysRevLett.92.232501
144. Šimkovic F, Štefánik D, Dvornický R. The λ Mechanism of the 0νββ-Decay. Front Phys. (2017) 5:57. doi: 10.3389/fphy.2017.00057
145. Menéndez J. Neutrinoless ββ decay mediated by the exchange of light and heavy neutrinos: the role of nuclear structure correlations. J Phys G. (2018) 45:014003. doi: 10.1088/1361-6471/aa9bd4
147. Argyriades J, Arnold R, Augier C, Baker J, Barabash AS, Basharina-Freshville A, et al. Measurement of the two neutrino double beta decay half-life of Zr−96 with the NEMO-3 detector. Nucl Phys A. (2010) 847:168–79.
148. Arnold R, Augier C, Baker JD, Barabash AS, Basharina-Freshville A, Blondel S, et al. Results of the search for neutrinoless double β decay in100Mo with the NEMO-3 experiment. Phys Rev D. (2015) 92:072011. doi: 10.1103/PhysRevD.92.072011
149. Arnold R, Augier C, Baker J, Barabash AS, Brudanin V, Caffrey AJ, et al. Limits on different majoron decay modes of 100Mo and 82Se for neutrinoless double beta decays in the NEMO-3 experiment. Nucl Phys A. (2006) 765:483–94. doi: 10.1016/j.nuclphysa.2005.11.015
150. Winter RG. A search for double beta-decay in palladium. Phys Rev. (1952) 85:687. doi: 10.1103/PhysRev.85.687
151. Alduino C, et al. First results from CUORE: a search for lepton number violation via 0νββ decay of 130Te. Phys Rev Lett. (2018) 120:132501.
152. Arnold R, Augier C, Baker J, Barabash AS, Basharina-Freshville A, Blondel S, et al. Measurement of the ββ decay half-life of 130Te with the NEMO-3 detector. Phys Rev Lett. (2011) 107:062504. doi: 10.1103/PhysRevLett.107.062504
153. Arnaboldi C, Brofferio C, Bucci C, Capelli S, Cremonesi O, Fiorini E, et al. A calorimetric search on double beta decay of 130Te. Phys Lett B. (2003) 557:167–75. doi: 10.1016/S0370-2693(03)00212-0
154. Arnold R, Augier C, Baker JD, Barabash AS, Basharina-Freshville A, Blondel S, et al. Measurement of the 2νββ decay half-life of 150Nd and a search for 0νββ decay processes with the full exposure from the NEMO-3 detector. Phys Rev D. (2016) 94:072003.
155. Argyriades J, Arnold R, Augier C, Baker J, Barabash AS, Basharina-Freshville A, et al. Measurement of the double β decay half-life of 150Nd and search for neutrinoless decay modes with the NEMO-3 detector. Phys Rev C. (2009) 80:032501(R). doi: 10.1103/PhysRevC.80.032501
156. Dolgov AD, Hansen SH, Raffelt G, Semikoz DV. Heavy sterile neutrinos: bounds from big-bang nucleosynthesis and SN 1987A. Nucl Phys B. (2000)590:562. doi: 10.1016/S0550-3213(00)00566-6
157. Dolgov AD, Hansen SH, Raffelt G, Semikoz DV. Cosmological and astrophysical bounds on a heavy sterile neutrino and the KARMEN anomaly. Nucl Phys B. (2000) 580:331–51. doi: 10.1016/S0550-3213(00)00203-0
Keywords: double beta decay, nuclear transition matrix elements, Majoron models, short range correlations, Majorana neutrino mass
Citation: Rath PK, Chandra R, Chaturvedi K and Raina PK (2019) Nuclear Transition Matrix Elements for Double-β Decay Within PHFB Model. Front. Phys. 7:64. doi: 10.3389/fphy.2019.00064
Received: 05 December 2018; Accepted: 15 April 2019;
Published: 07 May 2019.
Edited by:
Alexander S. Barabash, Institute for Theoretical and Experimental Physics, RussiaReviewed by:
Fedor Simkovic, Comenius University, SlovakiaJonathan Engel, University of North Carolina at Chapel Hill, United States
Copyright © 2019 Rath, Chandra, Chaturvedi and Raina. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ramesh Chandra, cmFtZXNoLmx1cGh5QGdtYWlsLmNvbQ==
 P. K. Rath1
P. K. Rath1 Ramesh Chandra
Ramesh Chandra P. K. Raina
P. K. Raina