- Katedra Fizyki Teoretycznej i Informatyki Kwantowej, Politechnika Gdańska, Gdańsk, Poland
Young's double-slit experiment [1] requires two waves produced simultaneously at two different points in space. In quantum mechanics the waves correspond to a single quantum object, even as complex as a big molecule. An interference is present as long as one cannot tell for sure which slit is chosen by the object. The more we know about the path, the worse the interference. In the paper we show that quantum mechanics allows for a dual version of the phenomenon: self-interference of waves propagating through a single slit but at different moments of time. The effect occurs for time-independent Hamiltonians and thus should not be confused with Moshinsky-type time-domain interference [2], a consequence of active modulation of parameters of the system (oscillating mirrors, chopped beams, time-dependent apertures, moving gratings, etc.). The discussed phenomenon is counterintuitive even for those who are trained in entangled-state quantum interferometry. For example, the more we know about the trajectory in space, the better the interference. Exactly solvable models lead to formulas deceptively similar to those from a Youngian analysis. The models are finite dimensional, with interaction terms based on two-qubit CNOT quantum gates. The effect is generic and should be observable in a large variety of experimental configurations. Moreover, there are reasons to believe that this new type of quantum interference was in fact already observed in atomic interferometry almost three decades ago, but was misinterpreted and thus rejected as an artifact of unknown origin.
1. Introduction
The idea of time-domain interferometry can be traced back to the seminal paper by Moshinsky [2] on diffraction in time. Since then, the issue was both theoretically and experimentally investigated by a number of authors. With apparently no exception, all the examples discussed in the literature were based on time-dependent Hamiltonians (a time-dependent magnetic field [3], a periodically opened grating [4], a moving grating [5], a moving mirror [6, 7], laser-controlled windows of short duration [8]). Different combinations of interference in space and time were also discussed [9]. A review of the first five decades of research in the field can be found in Paulus and Bauer [10].
In what follows, I discuss a new quantum interferometric phenomenon, in some respects similar to interference in time. Its manifestations can be confused with Young's double-slit interference. They may be at the heart of a controversy raised by an experiment performed almost three decades ago.
In 1991–1992 the atom interferometer group from Univeristé Paris-Nord reported observation of an optical phenomenon that resembled a Young-type self-interference of photons spontaneously emitted from a multi-peaked atomic center-of-mass wave packet [11, 12]. The result suggested that a single-atom wave packet can play a role of a multi-point coherent source of light. The effect was weak but clearly visible, with small error bars, and reappeared in various configurations of the experiment (Figure 1).
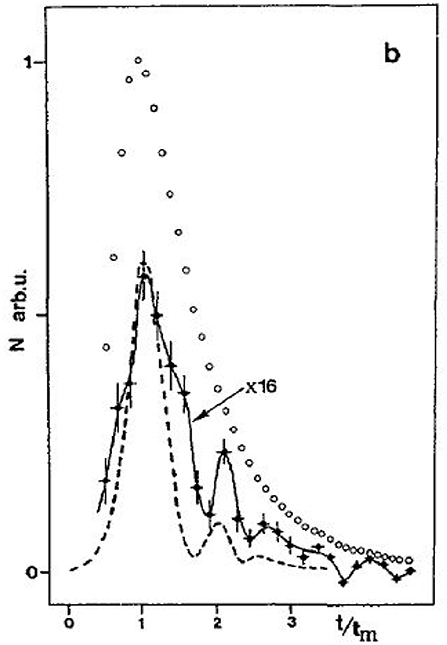
Figure 1. An example of the data from Robert et al. [12]. Intensity of the emitted radiation as a function of time of flight t (in units of the most probable time of flight tm). The dashed line is an analogous prediction for an appropriate Young-type single-photon experiment.
However, there was a fundamental problem with the data. In principle, after (or before) having detected a photon one could perform a direct measurement of the atomic position, revealing location of the source at the moment of emission, and thus destroying the interference. Accordingly, this was not a typical Young experiment, but rather its which-way version [13–15]. What one expects is a radiation typical of several incoherent sources of light. An atomic wave packet of the form α|1〉 + βeiϕ|2〉 should emit light whose intensity contains contributions proportional to |α|2 and |β|2, but Youngian terms involving cos ϕ should be absent. Quantum optical analysis of spontaneous emission from extended wave packets did not support the data either [16–21]. The extensive review [22] on optics and atomic interferometry did not even mention the effect.
Yet, the plot from Figure 1 is very disturbing for a theorist. Is it possible that we overlook something? Is the analogy to which-way measurements as superficial as the one to Young's double slits? And indeed, we will see that the analogy to which-way experiments may be misleading. Examples will be given of exactly solvable quantum mechanical models inheriting all the basic physical properties of the Paris experiment, but leading to predictions that may be easily confused with Young's interference. The discussed phenomenon is counterintuitive even for those who are trained in entangled-state interferometry. One of its possible interpretations is in terms of an interference of fields emitted from the same point in space but at different moments of time. The emitted radiation may contain contributions proportional to cos ϕ, even though the initial atomic state is α|1〉 + βeiϕ|2〉.
In order to understand the problem let us have a look at Figure 2 describing the conceptual structure of standard theoretical papers (an exception is [23, 30]). The analyzed radiation pattern is obtained under the assumption that at t = 0 the spontaneous emission is ‘turned on’ in a position independent way, but the experiment was closer to the scheme from Figure 3. A beam of hydrogen atoms was prepared in a metastable 2s1/2 internal state in such a way that its center-of-mass wave function consisted of three well separated (by 120 or 240 nm) peaks. The atoms moved with average velocity 10 km/s toward a region of 40 V/cm static electric field. Stark mixing 2s1/2 ↔ 2p1/2 followed by spontaneous emission 2p1/2 → 1s1/2 of Lyman-α 121.6 nm photons was induced in the interaction zone. The observed dependence of intensity of radiation on the shape of the atomic wave function was compared with an analogous prediction for the Young experiment, where instead of a multi-peaked source one took a multi-hole obstacle. The resulting intensity curves were qualitatively similar.
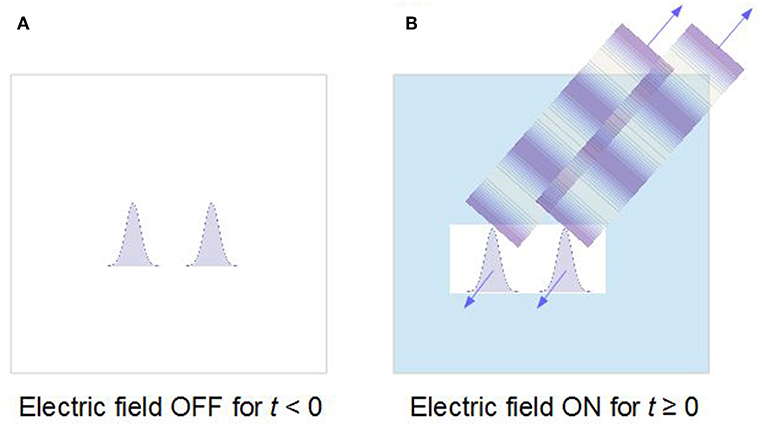
Figure 2. Standard configuration analyzed in the literature. (A) When the external field is absent, the atom remains in a long-lived, not radiating state. (B) At t = 0 the electric field is turned on, simultaneously at all points occupied by the wave-packet. The atomic state becomes short-lived and decays by spontaneous emission. The act of emission changes atomic center-of-mass momentum via a recoil, creating an entangled atom-photon state. Tracing out the atomic degrees of freedom one obtains a mixed state of a single photon, with incoherent contributions from both atomic peaks. Spectrum of the emitted radiation is modified only by Doppler shifts, statistically distributed in accordance with the probability density of atomic center-of-mass momenta.
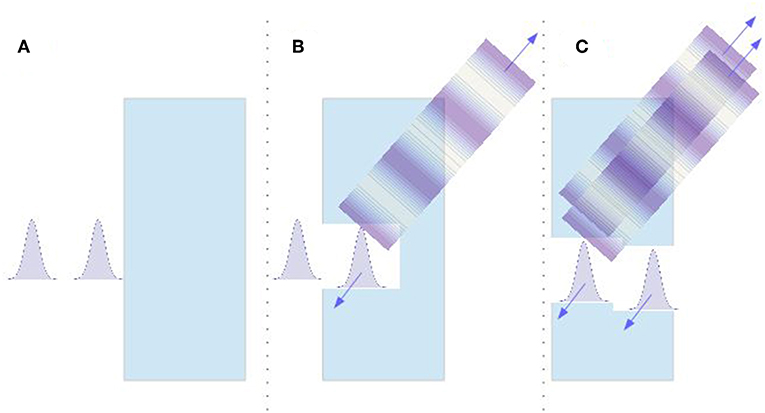
Figure 3. Configuration closer to the Paris experiment. (A) A two-peaked center of mass wave packet propagates toward the region of non-zero electric field. At this stage the internal state of the atom is long-lived and there is no radiation. (B) Different parts of the wave packet couple to the external field in a position dependent way. (C) In principle, one can observe interference of photons emitted from the same point in space, but at different moments of time. Here standard intuitions from entangled-state interferometry fail, and an exact quantum mechanical solution is needed.
The authors of Robert et al. [12] were well aware of the theoretical difficulties one will encounter in a realistic modeling of their experiment. They wrote: “In conclusion it seems that an interference phenomenon characterized by a wavelength close to the Lyman α one does occur in the optical emission. The theoretical interpretation of this experiment is a priori rather difficult, not only because of the emission process itself but also because of the complexity of the present induced emission process (2s-2p transition in a profile of electric field combined with the 2p-1s transition).”
An early attempt of including non-simultaneity of excitation in a Weisskopf-Wigner approach can be found in Czachor and You [23, 30], but the results were difficult to interpret due to a large number of uncontrollable approximations. The problem is so fundamental that it would be imprudent to base conclusions on approximate results. Let us note, however, that the essence of quantum self-interference can be discussed already in a two-dimensional Hilbert space. The main counterargument against the very possibility of self-interference in a which-way experiment can be formulated with only two qubits, hence in four dimensions. In spite of low dimensionality, the available formal structures are there rich enough for proof-of-principle conclusive arguments. So, it is best to follow an analogous strategy. Striping the problem of unnecessary details we have to maintain certain physical characteristics:
1. The position state outside of the interaction zone should be a superposition of at least two orthogonal states, |1〉 and |2〉.
2. While the system is outside of the interaction zone the field should be in a vacuum state |0〉, and the internal state of the system should be excited |+〉.
3. One should be able to distinguish between states inside and outside of the interaction zone, so there must exist at least one position state |3〉, corresponding to the region of space where spontaneous emission occurs. This state has to be orthogonal to both |1〉 and |2〉.
4. The system should be able to propagate into the interaction zone, so its free Hamiltonian must be nontrivial.
5. The emitted state of light should be orthogonal to the vacuum, but a single radiated state |k〉 = |1〉 is enough. Moreover, the reduction of the radiated degree of freedom to a single state effectively means that the state is monochromatic and thus its coherence time 1/Δω is infinite. For this reason, the time of detection provides no information about the moment of emission. The emitted particle can be bosonic, fermionic, or whatever, since identical formal problems occur if one replaces spontaneous emission by ionization, or by any other kind of unitarity-preserving interaction.
6. The act of spontaneous emission should change the atomic state by recoil. The realistic case
can be replaced by
since the pair |+, 3〉, |−, 3〉, is as orthogonal as |+, P〉, |−, P − k〉, and it is the orthogonality of the two states that counts in the formal argument. Their exact mathematical representation is irrelevant.
7. Total Hamiltonian should be time independent, to avoid confusion with time-domain interferometry, based on time dependent Hamiltonians.
8. The emitted states should involve exclusively single particles, to avoid confusion with intensity interferometry, based on Hanbury-Brown–Twiss effect [24, 25].
9. The dynamics of the whole atom-field system must be unitary and exactly solvable.
A Hilbert space that satisfies all these postulates is at least 12-dimensional. The question is: Can the probability of finding |k〉 = |1〉 depend on cos ϕ, if the initial state of the whole system is ? The answer is in the affirmative. The effect may look like a Youngian interference but its physical meaning is different. The result is generic and should be observable in a large variety of quantum systems.
2. Finite-State Analog of a Longitudinal Stern-Gerlach Interferometer
Consider a system (“an atom”) whose center of mass can occupy one of the three positions, X1, X2, or X3, corresponding to the following three eigenstates of the discrete center-of-mass position operator , as shown in Figure 4,
Let the two “photon” states (a vacuum or a single particle) be represented by a qubit,
The atom is two-level,
For simplicity we assume that in the absence of interactions the two internal atomic states have the same energy, so that we can ignore their contribution to the free Hamiltonian (for a justification of this assumption in the context of atomic interferometry see [26]). As required, the Hilbert space is 2 × 2 × 3 = 12 dimensional, with the basis
Let an “electric field” evaluated at the center-of-mass position satisfy . An internal “dipole moment” is . The interaction term is taken in the usual form
where the leftmost σx is the operator that creates or annihilates photons, and we do not assume a rotating wave approximation. One can also write the interaction term as
where the leftmost σx is treated as the dipole moment, and
is the field operator Ê(X) = σx ⊗ E(X) evaluated at the center-of-mass position operator . All operators are independent of time since we work in the Schrödinger picture and the system is closed. An act of emission or absorption of a photon is always accompanied by a change |±〉 → |∓〉 of an internal atomic state. An entanglement we will obtain in such a toy model is an analog of the entanglement in momentum space.
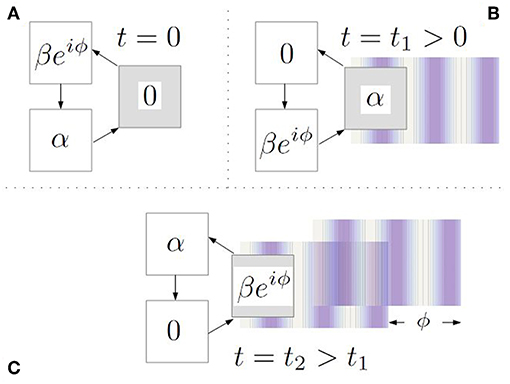
Figure 4. An intuitive picture of a three-state analog of a longitudinal Stern-Gerlach interferometer. The interaction is controlled by position X3 (the gray square). The free evolution performs an anticlockwise rotation. (A) At t = 0 the system is prepared in a two-peaked superposition of center-of-mass positions X1 and X2, located outside of the interaction zone. (B) At t = t1 a half of the wave packet is already in the interaction zone and emits a photon. (C) At t = t2 the first half of the wave packet has already left the interaction region, but now the second half interacts with the field. In spite of its idealization, the picture correctly describes the structure of an exact quantum mechanical prediction.
In quantum information terminology the interaction term is a two-qubit NOT gate controlled by the center-of-mass position. The free Hamiltonian is chosen in a form of a generator of rotations in three dimensions, with the rotation axis parallel to (1, 1, 1),
The free evolution operator is thus a rotation in position space around (1, 1, 1) with frequency ,
with . In order to visualize the free dynamics consider t = T/3. Then
The rotation is counterclockwise, as in Figure 4. In particular, the initial superposition , prepared in the region where E(X) = 0, would propagate through the interaction zone as follows,
T is here an analog of the time of flight employed in the experiment.
This would be the case of a free evolution. However, when the interaction at X3 occurs, the dynamics becomes much more interesting. The full evolution U(t) = e−iΩt is generated by
In the basis |n, ±, j〉 the Hamiltonian is represented by the matrix
A general state |Ψ〉 and the initial condition |Ψ(0)〉 are in this basis given by
(α, β, ϕ are assumed to be real). With this initial condition the problem is effectively six dimensional. It can be further simplified by bringing Ω to a block-diagonal form by means of V which diagonalizes . So, let W = V ⊗ V ⊗ 𝕀3. Then
where
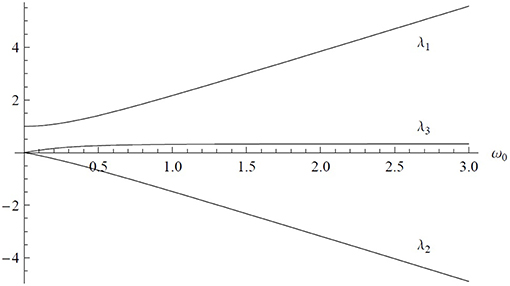
The above model is exactly solvable for any ω0 and ω1. Let us choose the units of frequency so that ω1 = 1. Normalized eigenvectors of Ω+ = Ω+(ω0) then read
where λ is one of the three eigenvalues (Figure 5),
The results for Ω− are obtained from
Unfortunately, I have not managed to find a value of ω0 that would make the size of the explicit form of |Ψ(t)〉 reasonably compact (still, see the next two Sections). So, let us illustrate the prediction for ω0 = ω1 = 1. The solution |Ψ(t)〉 = e−iΩt|Ψ(0)〉 has six vanishing components, Ψ(t)0−1 = Ψ(t)0−2 = Ψ(t)0−3 = Ψ(t)1+1 = Ψ(t)1+2 = Ψ(t)1+3 = 0. The probability of emitting a photon has a Youngian form,
and is plotted in Figure 6, for , as a function of both ϕ and t. The functions A(t) B(t), C(t) from Equation (24) are plotted in Figure 7.
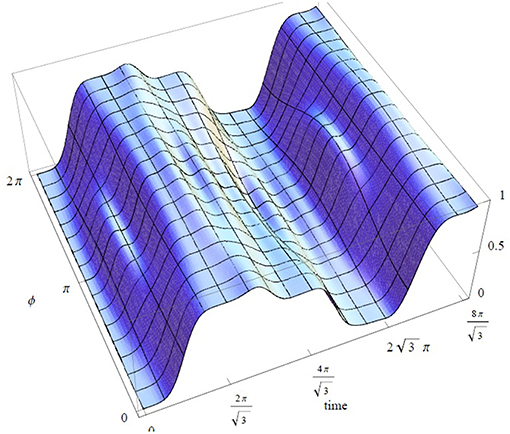
Figure 6. Probability (Equation 23) as a function of time t and the center-of-mass phase ϕ, for , ω0 = ω1 = 1. The dependence on ϕ is nontrivial and has the same periodicity as the atomic center-of-mass phase, similarly to a Youngian interference pattern. However, both atomic peaks arrive through the same path, and the self-interfering photons are emitted from the same point in space.
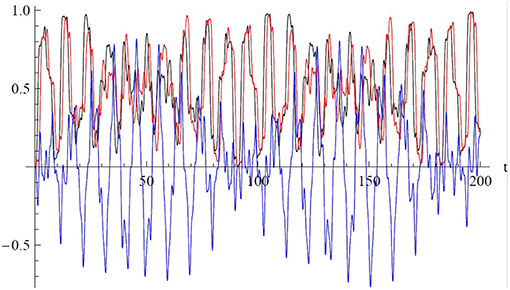
Figure 7. The three time-dependent functions occurring in Equation (24) for 0 ≤ t ≤ 200: A(t) (black), B(t) (red), C(t) (blue). The blue curve is a measure of self-interference in time.
Let us note that our model has been simplified to its extremes, so that it is clear that the presence of cos ϕ is not a consequence of a Young interference of fields emitted from two different points in space — the emission here is restricted to a single point X3. It makes no sense to analyze the experiment in terms of which-way measurements either — the center-of-mass wave packet arrives through a single path. The dependence on ϕ is present as well if one restricts the dynamics to one single cycle of evolution, for in Figure 6, so that each of the peaks occurs in the interaction zone only once.
3. Finite-State Analog of a Combined Longitudinal/Transverse Stern-Gerlach Interferometer
The next example is a toy model of two two-peaked wave packets interfering at the interaction zone. This is an analog of an experiment where one first splits the atomic wave packet by a beam splitter, and then at each of the resulting paths one creates a longitudinal superposition. So effectively, we have here an analog of a four-peak single-atom wave packet. In the model, we first observe an interference of |1〉 arriving at X3 clockwise with |2〉 arriving anticlockwise; then |2〉 arriving clockwise interferes with |1〉 arriving anticlockwise. Self-interference occurs here in both space and time. This can be achieved by taking the free Hamiltonian in the form
In spite of a cosmetic change in the free Hamiltonian, the model is mathematically more tractable than the previous one, so a compact form of a solution can be explicitly written. The free field evolution operator in position space is no longer a rotation, but a superposition of two opposite rotations:
A single cycle of the free dynamics is T = 2π/(3ω0). Taking the same interaction and initial condition as in the previous section, and choosing the same parameters in the Hamiltonian, ω0 = ω1 = 1, we find the solution of ,
The explicit form of the Hamiltonian is
Probability (Equation 23) now has the form
with f(t) independent of ϕ. The emission is completely blocked for , ϕ = π.
4. The Case of a Two-Peaked Source of Radiation
It the previous two examples the interaction was controlled by X3, so the source of radiation was located at a single point in space. Let us now consider the case of four positions: X1 and X2 playing the same role as before, and X3 and X4 controlling the interaction. The dimension of the Hilbert space is 2 × 2 × 4 = 16. The example will show that the structure of radiation may involve coherent superpositions of contributions arriving from different atomic peaks. In this concrete example we will see that expressions proportional to cos ϕ cancel each other, although they reappear if one postselects the part of data which is correlated with a single peak. The effect is again exactly opposite to what one might expect on the basis of entanglement-in-space intuitions.
The 16-dimensional Hilbert space is spanned by |n〉 ⊗ |s〉 ⊗ |Xj〉, n = 0, 1, s = ±, j = 1, 2, 3, 4. The free Hamiltonian is a 4-dimensional generalization of the example from the previous section,
The interaction part is again a two-qubit NOT gate, but controlled by X3 or X4,
In matrix form the total Hamiltonian reads
Diagonalizing σx we can bring Ω to a block-diagonal form consisting of four 4 × 4 blocks. The eigenvalues of Ω are
where all the eight combinations of pluses and minuses occur, and each eigenvalue is twice degenerate. In order to make the solution as readable as possible we take ω0 = 2, ω1 = 3. The initial condition is again a vacuum times a superposition of excited atomic states located at X1 and X2,
The solution of reads explicitly
where Okl and Ikl are time dependent functions defined by the above formula. Now, since
the probability of detecting a photon at time t,
is independent of ϕ. However, probabilities of detecting a photon at time t, under the condition that the atom was detected at X3 (or X4, respectively) are
Both probabilities depend on ϕ. The coherence is lost when we do not have the information about the place of emission, but is regained if we know from which peak the photon has arrived. The behavior is completely counterintuitive if one thinks in the categories of the MIT “coherence lost and regained” experiment [14].
5. Can We Literally See the Atomic Phase?
Young's self-interference is “double-slit but single-time.” Self-interference we have discussed is “single-slit but double-time.” The models are simplified but exactly solvable, a fact guaranteeing that Youngian terms are not artifacts of some approximation. However, it is clear that the similarity to the Young effect is superficial and misleading. The effect is generic and should be observable in various experimental configurations. For example, the static electric field employed in Miniatura et al. [11] and Robert et al. [12] could be replaced by a laser beam [14, 27, 28]. In principle, one should be able to literally see the matter-wave matter-wave phase by incarnating it into the phase of an emitted radiation.
The effect is predicted on the basis of exact solutions of Schrödinger equations for toy-model but physically meaningful Hamiltonians. We can safely claim the phenomenon exists in Nature, still bearing in mind that the models are oversimplified. We have proved the principle, but it would be premature to claim we have explained the data. Our theoretical prediction shows that single particles emitted from a single point in space can produce self-interference that may be confused with Youngian two-slit fringes. This is obviously similar to the reported phenomenon, but there are differences as well. For example, the observed interference was direction dependent, whereas what we describe does not depend on direction. A second peculiarity of Figure 1 is an apparent presence of twice as many peaks as in the reference double slit curve. This type of doubling, with unchanged photon wavelength, may be a signature of a two-photon interference [29]. It is therefore possible in principle that detectors sometimes detect single photons from a two-photon pair. But what could be the origin of such a pair is in this concrete experimental arrangement unclear. We have shown that the effect is possible even in a single-particle scenario, but it probably has an n-particle analog.
The next step would be to perform realistic quantum electrodynamics calculations for scattering of two-peaked center-of-mass atomic wave packets on localized static electric fields. Simultaneously, one should think of performing an alternative experiment, directly aimed at confirmation of the effect. Some work remains to be done.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This research goes back to my postdoc at MIT, 1994-95, and at that time it was funded by the Fulbright Commission. The publication costs have been covered by Gdańsk University of Technology.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
It is a great pleasure to thank Kazimierz Rza̧żewski for the original inspiration, and David E. Pritchard for hospitality and patience during my stay in his lab during those memorable years. I gratefully acknowledge the support I obtained from members of MIT and Paris-Nord atom interferometer groups. Special thanks to Li You for intensive collaboration. The work was partly funded by the Fulbright Commission.
References
1. Young T. The bakerian lecture. Experiments and calculations relative to physical optics. Phil Trans R Soc Lond. (1804) 94:1–16. doi: 10.1098/rstl.1804.0001
3. Badurek G, Rauch H, Tuppinger D. Neutron interferometric double-resonance experiment. Phys Rev A. (1986) 34:2600–8. doi: 10.1103/PhysRevA.34.2600
4. Hils Th, Felber J, Gähler R, Gläser W, Golub R, Habicht K, et al. Matter-wave optics in the time domain: Results of a cold-neutron experiment. Phys Rev A. (1998) 58:4784–90. doi: 10.1103/PhysRevA.58.4784
5. Balashov SN, Bondarenko IV, Frank AI, Geltenbort P, Høghøj P, Kulin GV, et al. Diffraction of ultracold neutrons on a moving grating and neutron focusing in time. Physica B. (2004) 350:246–9. doi: 10.1016/j.physb.2004.04.038
6. Arndt M, Szriftgiser P, Dalibard J, Steane AM. Atom optics in the time domain. Phys Rev A. (1996) 53:3369–78. doi: 10.1103/PhysRevA.53.3369
7. Szriftgiser P, Guéry-Odelin D, Arndt M, Dalibard J. Atomic diffraction and interference using temporal slits. Phys Rev Lett. (1996) 77:4–7. doi: 10.1103/PhysRevLett.77.4
8. Lindner F, Schaetzel MG, Walther H, Baltuska A, Goulielmakis E, Krausz F, et al. Attosecond double-slit experiment. Phys Rev Lett. (2005) 95:040401. doi: 10.1103/PhysRevLett.95.040401
9. Bruckner Č, Zeilinger A. Diffraction of matter waves in space and in time. Phys Rev A. (1997) 56:3804–2824. doi: 10.1103/PhysRevA.56.3804
10. Paulus GG, Bauer D. Double-slit in the time domain. Lect Notes Phys. (2009) 789:303–39. doi: 10.1007/978-3-642-03174-8_11
11. Miniatura ch, Perales F, Vassilev G, Reinhardt J, Robert J, Baudon J. A longitudinal Stern-Gerlach interferometer: the ‘beaded’ atom. J Physique II. (1991) 1:425–36. doi: 10.1051/jp2:1991177
12. Robert J, Ch. Miniatura, Gorceix O, Le Boiteux S, Lorent V, Reinhardt J, et al. Atomic quantum phase studies with a longitudinal Stern-Gerlach interferometer. J Physique II. (1992) 2:601–4. doi: 10.1051/jp2:1992155
13. Wootters WK, Zurek WH. Complementarity in the double-slit experiment: quantum nonseparability and a quantitative statement of Bohr's principle. Phys Rev D. (1979) 19:473–84. doi: 10.1103/PhysRevD.19.473
14. Chapman MS, Hammond TD, Lenef A, Schmiedmayer J, Rubenstein RA, Smith E, et al. Photon scattering from atoms in an atom interferometer: coherence lost and regained. Phys Rev Lett. (1995) 75:3783–7. doi: 10.1103/PhysRevLett.75.3783
15. Englert B-G. Fringe visibility and which-way information: an inequality. Phys Rev Lett. (1996) 77:2154. doi: 10.1103/PhysRevLett.77.2154
16. Rza̧żewski K, Żakowicz W. Spontaneous emission from an extended wavepacket. J Phys B. (1992) 25:L319–22. doi: 10.1088/0953-4075/25/13/001
17. Steuernagel O, Paul H. Spontaneous emission from an extended wave packet: field correlations. Phys Rev A. (1996) 53:2983–5. doi: 10.1103/PhysRevA.53.2983
18. Chan KW, Law CK, Eberly JH. Quantum entanglement in photon-atom scattering. Phys Rev A. (2003) 68:022110. doi: 10.1103/PhysRevA.68.022110
19. Fedorov MV, Efremov MA, Kazakov AE, Chan KW, Law CK, Eberly JH. Spontaneous emission of a photon: wave-packet structures and atom-photon entanglement. Phys Rev A. (2005) 72:032110. doi: 10.1103/PhysRevA.72.032110
20. Guo R, Guo H. Momentum entanglement and disentanglement between an atom and a photon. Phys Rev A. (2007) 76:012112. doi: 10.1103/PhysRevA.76.012112
21. de Melo e Souza R, Impens F, Maia Neto PA. Decoherence by spontaneous emission: a single-atom analog of superradiance. Phys Rev A. (2016) 94:062114. doi: 10.1103/PhysRevA.94.062114
22. Cronin D, Schmiedmayer J, Pritchard DE. Optics and interferometry with atoms and molecules. Rev Mod Phys. (2009) 81:1051–129. doi: 10.1103/RevModPhys.81.1051
23. Czachor M, You L. Nonsimultaneous spontaneous emission from atomic wave packets. In: Eberly JH, Mandel L, Wolf E, editors. it Coherence and Quantum Optics VII. New York, NY: Plenum Press (1996). p. 719–20.
24. Gyulassy M, Kauffmann S.K, Wilson LW. Pion interferometry of nuclear collisions. Theory I. Phys Rev C. (1979) 20:2267–92. doi: 10.1103/PhysRevC.20.2267
25. Florkowski W. Phenomenology of Ultra-Relativistic Heavy-Ion Collisions. Singapore: World Scientific (2010). doi: 10.1142/7396
26. Marzlin K-P, Sanders BC, Knight PL. Complementarity and uncertainty relations for matter-wave interferometry. Phys Rev A. (2009) 78:062107. doi: 10.1103/PhysRevA.78.062107
27. Pfau T, Spälter S, Kurtsiefer C, Ekstrom CR, Mlynek J. Loss of spatial coherence by a single spontaneous emission. Phys Rev Lett. (1994) 73:1223–6. doi: 10.1103/PhysRevLett.73.1223
28. Kurtsiefer C, Dross O, Voigt D, Ekstrom CR, Pfau T, Mlynek J. Observation of correlated atom-photon pairs on the single-particle level. Phys Rev A. (1997) 55:R2539–42. doi: 10.1103/PhysRevA.55.R2539
29. Dopfer B, Kwiat PG, Weinfurter H, Zeilinger A, Horne MA. Brillouin scattering and dynamical diffraction of entangled photon pairs. Phys Rev A. (1995) 52:R2531–4. doi: 10.1103/PhysRevA.52.R2531
Keywords: quantum interferometers, CNOT gate, entanglement, which-way information, spontaneous emission and dephasing
Citation: Czachor M (2019) Swapping Space for Time: An Alternative to Time-Domain Interferometry. Front. Phys. 7:79. doi: 10.3389/fphy.2019.00079
Received: 05 February 2019; Accepted: 06 May 2019;
Published: 29 May 2019.
Edited by:
Adam Miranowicz, Adam Mickiewicz University in Poznań, PolandReviewed by:
Jan Mostowski, Polish Academy of Sciences, PolandAdrian Paul Flitney, The University of Melbourne, Australia
Ievgen Arkhipov, Palacký University, Olomouc, Czechia
Copyright © 2019 Czachor. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Marek Czachor, bWN6YWNob3JAcGcuZWR1LnBs
 Marek Czachor
Marek Czachor