Mini Review on Vector-Like Leptonic Dark Matter, Neutrino Mass, and Collider Signatures

1. Introduction

The existence of dark matter (DM) in a large scale (> a few kpc) has been proven irrefutably by various astrophysical observations. The prime among them are galaxy rotation curves [1, 2], gravitational lensing [3], and large scale structure of the Universe. See for a review [4, 5]. In the recent years the satellite borne experiments like Wilkinson Microwave Anisotropy Probe (WMAP) [6] and PLANCK [7, 8] precisely determined the relic abundance of DM by measuring the temperature fluctuation in the cosmic microwave background radiation (CMBR). All the above said evidences of DM emerge via gravitational interaction in astrophysical environments, which make a challenge to probe the existence of DM in a terrestrial laboratory where density of DM is feeble.

Alternatively one can explore other elementary properties of DM which can be probed at an earth based laboratory. In fact, one can assign a weak interaction property to DM through which it can be thermalized in the early Universe at a temperature above its mass scale. As the temperature falls due to adiabatic expansion of the Universe, the DM gets decoupled from the thermal bath below its mass scale. As a result the ratio: n_DM/s, where s is the entropy density, remains constant and is precisely measured by PLANCK in terms of ${\Omega }_{\text{DM}}{h}^2=0.1186\pm 0.0020$ [7, 8].

The particle nature of DM, apart from relic abundance, is completely unknown. In particular, the mass, spin, and interaction apart from gravity, etc. This leads to huge uncertainty in search of DM. Despite this, many experiments are currently operational, that uses direct, indirect and collider search methods. Xenon-100 [9], LUX [10], Xenon-1T [11, 12], PANDA [13] are some of the direct DM search experiments which are looking for signature of DM via nuclear scattering, while PAMELA [14, 15], AMS-2 [16], Fermi gamma ray space telescope [17], IceCube [18, 19], etc., are some of the indirect DM search experiments which are looking for signature of DM in the sky. The search of DM is also going on at collider experiments like large Hadron Collider (LHC) [20–22]. Except some excess in the antiparticle flux in the indirect search data, direct and collider searches for DM has produced null observation so far. This in turn put a strong bound on the DM mass and coupling with which it can interact to the visible sector of the universe.

After the Higgs discovery in 2012 at CERN LHC, the standard model (SM) seems to be complete. However, it is found that none of the particles in SM can be a candidate of DM, which is required to be stable on cosmological time scale. While neutrinos in SM are stable, but their relic density is far less than the required DM abundance and is also disfavored from the structure formation. Moreover, neutrinos are massless within the SM. A tiny but non-zero neutrino mass generation requires the SM to be extended. This opens up the possibility of exploring new models of DM, while explaining non-zero masses for neutrinos in the same framework and thus predict a measurable alternation to DM phenomenology, which can be examined in some of the above said experiments.

In this review we explore the possibility of leptonic DM and non-zero neutrino masses [23] in a framework beyond the SM. The simplest leptonic DM can arise by augmenting the SM with an additional singlet fermion [24–42] χ, stabilized by a ${{Z}}_2$ symmetry. However, unless we assume the presence of an additional scalar singlet, which acquires vacuum expectation value (vev) and thus mixes with SM Higgs, the lepton singlet DM cannot possess renormalizable interaction with visible sector. The next possibility is to introduce a vector-like leptonic doublet: N = (N⁰ N⁻)^T, which is also odd under the ${{Z}}_2$ symmetry. The annihilation cross-section of such fermions are large due to Z mediation and correct relic density can only be achieved at a very high DM mass. However, the combination of singlet χ with the doublet vector-like lepton N provides a good candidate of DM [43–52], which has been discussed in details here. We discuss the phenomenological constraints on model parameters and then elucidate the allowed parameter space of such models from relic density and direct detection constraints. We also indicate collider search strategies for such DM. It turns out that the displaced vertex of the charged fermion: N^± [also called next to lightest stable particle (NLSP)] is a natural signature of such DM model.

In an attempt to address neutrino mass generation in the same framework, we further add a scalar triplet Δ of hypercharge 2 and study the consequences [53]. In particular, after electro weak symmetry breaking (EWSB), the triplet scalar acquires an induced vacuum expectation value (vev) which give rise sub-eV Majorana masses to light neutrinos through the Type II Seesaw mechanism [54–60]. The scalar triplet also generates a Majorana mass for the neutral component of the vector-like lepton doublet: N⁰, which constitutes a minor component of the DM. Due to Majorana mass of DM, the Z mediated elastic scattering with nucleon is forbidden [61–65]. As a result, the model survives from the stringent direct search bound. In absence of scalar triplet, the singlet-doublet DM is allowed to have only a tiny fraction of doublet component (sin θ ≤ 0.1) to evade direct search bound. In this limit, due to large contribution from the singlet component, the annihilation cross section of the DM becomes smaller than what it requires to achieve correct relic density. To make it up for correct relic density, the DM additionally requires to co-annihilate with its charged and heavy neutral companions and therefore requires small mass difference (Δm ~ 10 GeV) with charged companion or NLSP. However, in presence of the scalar triplet, we show that both the singlet-doublet mixing (sin θ) and the mass difference with NLSP (Δm) can be relaxed and larger parameter space is available for correct relic density and being compatible with the latest direct detection bounds. Moreover, the scalar triplet aid observability of hadronically quiet leptonic final states at LHC while one may also confirm/rule-out the model through displaced vertex of NLSP, a characteristic signature of the model in relic density and direct search allowed parameter space.

The paper is arranged as follows. In section 2, we briefly discuss about a vector-like singlet leptonic DM. In section 3, we discuss the viable parameter space of a vector-like inert doublet lepton DM. It is shown that an inert lepton doublet DM alone is ruled out due to large Z-mediated elastic scattering with the nucleus. However, in presence of a scalar triplet of hyper charge-2, the inert lepton doublet DM can be reinstated in a limited parameter space, which we discuss in section 4. Moreover in section 4, we discuss how the scalar triplet can give rise non-zero masses to active neutrinos via type-II seesaw [54–60]. In section 5 we discuss how an appropriate combination of singlet and doublet vector like leptons can give rise a nice possibility of DM in a wide range of parameter space. A triplet extension of singlet-doublet leptonic DM is further discussed in section 6. We discuss collider signature of singlet-doublet leptonic DM in presence of a scalar triplet in section 7 and conclude in section 8. We provide some vertices of inert lepton doublet (ILD) DM in presence of scalar triplet in Appendix A.

2. Vector-Like Leptonic Singlet Dark Matter

A simplest possibility to explain DM content of the present Universe is to augment the SM by adding a vector-like singlet lepton χ. The stability of χ can be ensured by imposing an additional discrete Z₂ symmetry, under which χ is odd while all other particles are even. In fact, a singlet DM has been discussed extensively in the literature [24–42]. Here we briefly recapitulate the main features to show the allowed parameter space by observed relic density and latest constraint from direct detection experiments.

The Lagrangian describing the singlet leptonic DM χ can be given as:

$\begin{array}{ll}{L}=\overline{\chi }(i{\gamma }^{\mu }{\partial }_{\mu }-m_{\chi })\chi -\frac{1}{\Lambda }{(H}^{†}H-\frac{v^2}{2})\overline{\chi }\chi .& (1)\end{array}$

Notice that the Lagrangian introduces two new parameters: DM mass, m_χ and the new physics scale Λ connecting DM to the SM through effective dimension five operator, on which the DM phenomenology depends. In the early Universe, χ freezes out via the interaction $\overline{\chi }\chi \to \text{SM}$ particles to give rise a net relic density that we observe today. We use micrOmegas [66] to calculate the relic density as well as spin independent elastic cross-section with nucleon of χ. In Figure 1, we show relic abundance (left-panel) and spin independent direct detection (SIDD) cross section (right panel) as a function of DM mass (m_χ) for different values Λ ~ {500 − 4000} GeV ¹. We observe that the constraint on SIDD cross section favors large values of Λ, while large Λ values yield over abundance of DM. We also note in the right panel Figure 1, that the SIDD cross section is very less sensitive to DM mass. This is because the direct search cross-section is proportional to the effective DM-nucleon reduced mass square (${\mu }_r=\frac{m_N{m}_{\chi }}{m_N+m_{\chi }}$) (see Equations 58, 59), where m_N < m_χ yields a mild dependence on DM mass. This feature is observed in rest of the analysis as well.

FIGURE 1

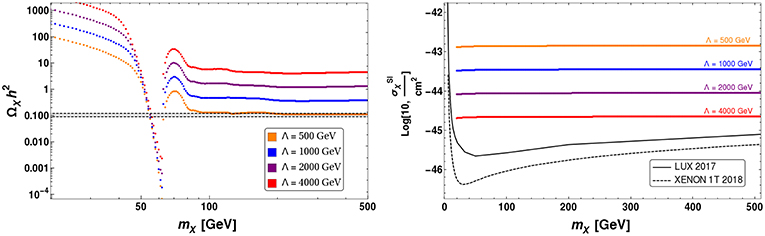
Figure 1. (Left) Relic density as a function of singlet DM mass, m_χ for different values of Λ mentioned in the figure inset. (Right) SI DD cross-section vs. DM mass, m_χ for different values of Λ.

Therefore, a singlet leptonic DM alone is almost ruled out. However, the dark sector of the Universe may not be simple as in the case of singlet leptonic DM. In the following we discuss a few more models with larger number of parameters, yet predictive. We end this section by noting that one can think of a pseudoscalar propagator to yield an effective DM-SM interaction of the form $(\bar{\chi }{\gamma }_5\chi )(H^{†}H)/\Lambda$. In this case, the relic density and direct search cross-sections become velocity dependent (see for example in Ghorbani [67]). Please also see section 5 below Equation (35) for more details.

3. Inert Lepton Doublet Dark Matter

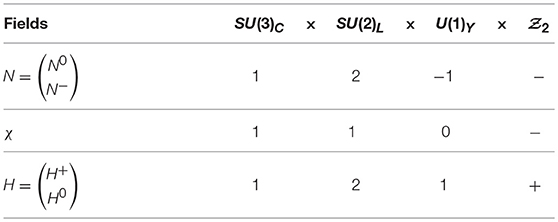
Let us assume that the dark sector is composed of a vector-like lepton doublet: N = (N⁰ N⁻)^T, which is odd under an extended ${{Z}}_2$ symmetry [hence called inert lepton doublet (ILD)], while all the Standard Model (SM) fields are even. As a result the neutral component of the ILD N is stable. The quantum numbers of dark sector fields and that of SM Higgs under the SM gauge group, augmented by a ${{Z}}_2$ symmetry, are given in Table 1. We will check if N⁰ can be a viable candidate of DM with correct relic abundance while satisfying the direct detection constraints from the null observation at various terrestrial laboratories.

TABLE 1

Table 1. Quantum numbers of additional dark sector fermion and SM Higgs under ${G}\equiv SU{(3)}_C\times SU{(2)}_L\times U{(1)}_Y\times {{Z}}_2$.

The Lagrangian of the model is given as:

$\begin{array}{ll}{{L}}^{IL}=\overline{N}[i{\gamma }^{\mu }({\partial }_{\mu }-ig\frac{{\sigma }^a}{2}{W}_{\mu }^a-i{g}^{\prime }\frac{Y}{2}{B}_{\mu })-m_N]N.& (2)\end{array}$

Thus the only new parameter introduced in the above Lagrangian is the mass of N, i.e., m_N. Expanding the covariant derivative of the above Lagrangian ${{L}}^{IL}$, we get the interaction terms of N⁰ and N^± with the SM gauge bosons as:

$\begin{array}{l}{{L}}_{int}^{IL}=\overline{N}i{\gamma }^{\mu }(-ig\frac{{\sigma }^a}{2}{W}_{\mu }^a+i\frac{g^{\prime }}{2}{B}_{\mu })N\\ =\left(\frac{e_0}{2sin{\theta }_{W}cos{\theta }_W}\right)\overline{N^0}{\gamma }^{\mu }{Z}_{\mu }{N}^0+\frac{e_0}{\sqrt{2}sin{\theta }_W}\overline{N^0}{\gamma }^{\mu }{W}_{\mu }^{+}{N}^{-}\\ +\frac{e_0}{\sqrt{2}sin{\theta }_W}{N}^{+}{\gamma }^{\mu }{W}_{\mu }^{-}{N}^0-e_0{N}^{+}{\gamma }^{\mu }{A}_{\mu }{N}^{-}\\ -\left(\frac{e_0}{2sin{\theta }_{W}cos{\theta }_W}\right)cos2{\theta }_W{N}^{+}{\gamma }^{\mu }{Z}_{\mu }{N}^{-}.& (3)\end{array}$

where g = e₀/sin θ_W and $g^{\prime }=e_0/cos{\theta }_W$ with e₀ being the electromagnetic coupling constant and θ_W being the Weinberg angle.

Since N is a doublet under SU(2)_L, it can contribute to invisible Z-decay width if its mass is <45 GeV which is strongly constrained. Therefore, in our analysis we will assume m_N > 45 GeV.

3.1. Relic Abundance of ILD Dark Matter

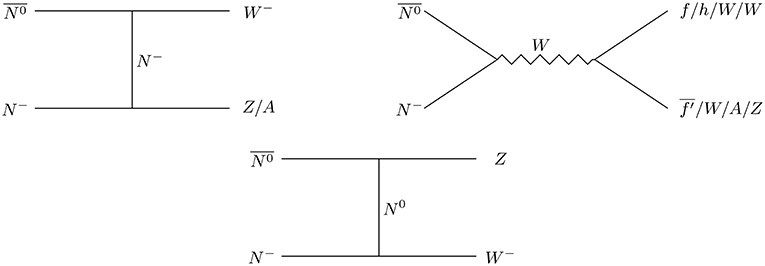
The number changing annihilation and co-annihilation processes which control freeze-out and hence relic density of DM N⁰ are shown in Figures 2–4.

FIGURE 2

Figure 2. Annihilation of ILD DM to SM particles.

FIGURE 3

Figure 3. Annihilation of charged partner of ILD DM to SM particles which contributes as co-annihilation with ILD DM.

FIGURE 4

Figure 4. Co-annihilation processes of DM N⁰ with its charged partner N^± to SM particles.

To estimate the relic density of DM in this framework one needs to solve the relevant Boltzmann equation:

$\begin{array}{l}\frac{d{n}_{N^0}}{dt}+3H{n}_{N^0}=-{\langle \sigma v\rangle }_{N^0\overline{N^0}\to SMSM}(n_{N^0}^2-{n_{N^0}^{eq}}^2)\\ -{\langle \sigma v\rangle }_{N^0{N}^{\pm }\to SMSM}(n_{N^0}{n}_{N^{\pm }}-n_{N^0}^{eq}{n}_{N^{\pm }}^{eq}).& (4)\end{array}$

To find the relic density of ILD DM, here we adopted micrOmegas [66] and implemented the model in it. Notice that the relic density of DM is mainly controlled by DM mass, m_N and SM gauged couplings. Since SM gauge couplings are fixed, the only relevant parameter which controls the relic density is the DM mass, m_N. The behavior of relic density with DM mass shown in Figure 5 along with correct relic density bound which is shown in gray patch. Note here that a sharp drop around DM mass m_N ~ m_h/2 due to Higgs resonance. From Figure 5 we can see that the DM mass around m_N ~ 1 TeV only satisfy current relic density bound. For heavier mass of N⁰ we get over abundance of DM (due to small cross section), while for lighter mass of N⁰ we get under abundance of DM (due to large cross-section).

FIGURE 5

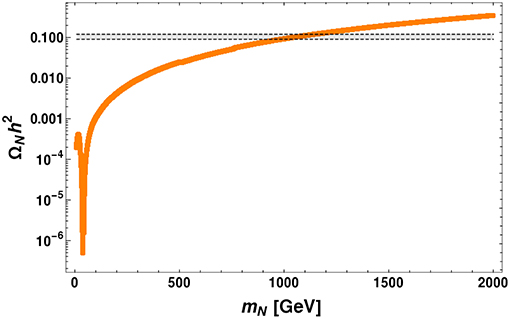
Figure 5. Variation of relic density of DM N⁰ with mass m_N. The gray patch corresponds to relic density allowed limit from PLANCK: 0.1166 ≤ Ωh² ≤ 0.1206.

3.2. Direct Search Constraint on ILD Dark Matter

In a direct detection experiment, the DM N⁰ scatters with the nucleon through t-channel Z mediated diagram, as shown schematically in the left panel of Figure 6. Like relic density we obtain the DM-nucleon cross-section using micrOmegas [66]. Since $\overline{N^0}{N}^{0}Z$ interaction is coming from SM gauge coupling and which is large, so the outcome of spin independent direct detection (SIDD) cross section becomes large. The SIDD cross-section in this case is plotted with DM mass, m_N, which is shown in orange colored patch in right panel of Figure 6. The green patch in this Figure 6 indicates relic density allowed mass range in the same plane. LUX 2017 [10] and XENON 1T [11, 12] direct detection limits are also plotted in the same figure (right panel of Figure 6). Thus we see that an ILD DM is completely ruled out by direct detection bound. However, as we discuss in section 4 the ILD DM can be resurrected in presence of a scalar triplet of hyper charge 2. Moreover, the scalar triplet will generate sub-eV masses of active neutrinos through type-II seesaw.

FIGURE 6

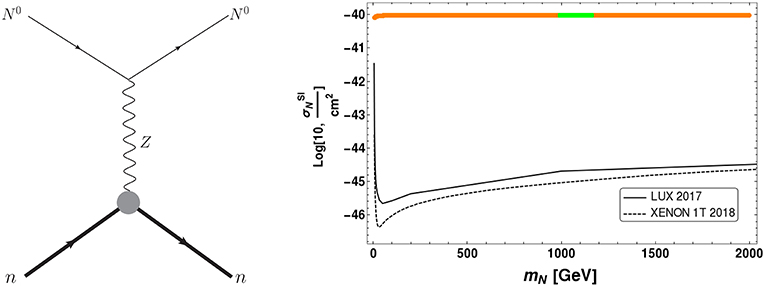
Figure 6. Left: Feynman diagram for direct detection (DD) of DM, N⁰. Right: Spin independent(SI) DM-nucleon cross-section is plotted in $m_N-{\sigma }_N^{SI}$ plane. Relic density allowed DM mass region is indicated here by green patch.

4. Triplet Extension of the ILD Dark Matter

We now extend the ILD dark matter model with a scalar triplet, Δ (Y_Δ = 2) which is even under the discrete ${{Z}}_2$ symmetry. The Lagrangian of this extended sector is given as:

$\begin{array}{ll}{{L}}^{II}=\text{Tr}\left[{(D_{\mu }\Delta )}^{†}(D^{\mu }\Delta )\right]-V(H,\Delta )+{{L}}_{\text{Yuk}}^{II},& (5)\end{array}$

where the covariant derivative is defined as

$\begin{array}{l}{D}_{\mu }\Delta ={\partial }_{\mu }\Delta -ig[\frac{{\sigma }^a}{2}{W}_{\mu }^a,\Delta ]-i{g}^{\prime }\frac{Y_{\Delta }}{2}{B}_{\mu }\Delta \end{array}$

and in the adjoint representation the triplet Δ can be expressed in a 2 × 2 matrix form: $\Delta =\left(\begin{array}{cc}\frac{H^{+}}{\sqrt{2}}& H^{++}\\ {\delta }^0& -\frac{H^{+}}{\sqrt{2}}\end{array}\right)$.

Similarly the scalar doublet H can be written in component form as:

$\begin{array}{ll}H=\left(\begin{array}{c}{\varphi }^{+}\\ {\varphi }^0\end{array}\right).& (6)\end{array}$

The modified scalar potential including Δ and H can be given as:

$\begin{array}{ll}\begin{array}{l}V(H,\Delta )=-{\mu }_H^2(H^{†}H)+\frac{{\lambda }_H}{4}{(H^{†}H)}^2+M_{\Delta }^2\text{Tr}[{\Delta }^{†}\Delta ]\hfill \\ +{\lambda }_1(H^{†}H)\text{Tr}[{\Delta }^{†}\Delta ]+{\lambda }_2{(\text{Tr}[{\Delta }^{†}\Delta ])}^2\hfill \\ +{\lambda }_3\text{Tr}[{({\Delta }^{†}\Delta )}^2]+{\lambda }_4{H}^{†}\Delta {\Delta }^{†}H\hfill \\ +[\mu (H^{T}i{\sigma }^2{\Delta }^{†}H)+\text{h}.\text{c}.],\hfill \end{array}& (7)\end{array}$

where we assume that $M_{\Delta }^2$ is positive. So the scalar triplet Δ does not acquire any vev. However, it acquires an induced vev after EW phase transition. The vevs of the scalar fields are given by:

$\begin{array}{ll}\langle \Delta \rangle =\left(\begin{array}{cc}0& 0\\ v_t/\sqrt{2}& 0\end{array}\right)\text{ and }\langle H\rangle =\left(\begin{array}{c}0\\ v/\sqrt{2}\end{array}\right).& (8)\end{array}$

Since the addition of a scalar triplet can modify the ρ parameter, whose observed value: ρ = 1.00037±0.00023 [68], does not differ much from SM prediction: ρ = 1, so we have a constraint on the vev v_t as:

$\begin{array}{ll}{v}_t\le 3.64\text{GeV}.& (9)\end{array}$

On the other hand electroweak symmetry breaking gives $\sqrt{v^2+2v_t^2}=246\text{GeV}$. This implies that v_t << v.

Now minimizing the scalar potential, V(H, Δ) (in Equation 7) we get:

$\begin{array}{ll}\begin{array}{l}{M}_{\Delta }^2=\frac{2\mu v^2-\sqrt{2}({\lambda }_1+{\lambda }_4)v^2{v}_t-2\sqrt{2}({\lambda }_2+{\lambda }_3)v_t^3}{2\sqrt{2}{v}_t},\hfill \\ {\mu }_H^2=\frac{{\lambda }_H{v}^2}{4}+\frac{({\lambda }_1+{\lambda }_4)v_t^2}{2}-\sqrt{2}\mu v_t.\hfill \end{array}& (10)\end{array}$

In the limit v_t << v, from Equation (10) we get the vevs,

$\begin{array}{ll}{v}_t=\frac{\mu v^2}{M_{\Delta }^2+({\lambda }_1+{\lambda }_4)v^2/2} \text{and} v\approx \frac{2{\mu }_H}{\sqrt{{\lambda }_H}}.& (11)\end{array}$

In presence of the scalar triplet Δ, the Yukawa interactions in Equation (5) are given by:

$\begin{array}{ll}{{L}}_{Yuk}^{II}=\frac{1}{\sqrt{2}}[{(f_L)}_{\alpha \beta }\overline{L_{\alpha }^c}i{\sigma }^2\Delta L_{\beta }+f_N\overline{N^c}i{\sigma }^2\Delta N+h.c.],& (12)\end{array}$

where L is the SM lepton doublet and α, β denote family indices. The Yukawa interactions importantly inherit the source of neutrino masses (first term in square bracket) and DM-SM interactions (second term in square bracket).

4.1. Scalar Doublet-Triplet Mixing

The quantum fluctuations around the minimum of scalar potential, V(H, Δ) can be given as:

$\begin{array}{ll}\Delta =\left(\begin{array}{cc}\frac{H^{+}}{\sqrt{2}}& H^{++}\\ \frac{v_t+h_t+i{A}^0}{\sqrt{2}}& -\frac{H^{+}}{\sqrt{2}}\end{array}\right)\text{ and }H=\left(\begin{array}{c}0\\ \frac{v+h}{\sqrt{2}}\end{array}\right).& (13)\end{array}$

Thus the scalar sector constitute two CP-even Higgses: h and h_t, one CP-odd Higgs: A⁰, one singly charged scalar: H^± and one doubly charged scalar: H^±±. In the limit v_t << v, the mass matrix of the CP-even Higgses: h and h_t, is given by:

$\begin{array}{ll}{{M}}^2=\left(\begin{array}{cc}{m}_h^2& -\sqrt{2}\mu v\\ \\ -\sqrt{2}\mu v& m_T^2\end{array}\right),& (14)\end{array}$

where $m_h^2\approx {\lambda }_H{v}^2/2$ and $m_T^2=\mu v^2/\sqrt{2}{v}_t$. Diagonalizing the above mass matrix we get two neutral physical Higgses: H₁ and H₂:

$\begin{array}{ll}{H}_1=cos\alpha h+sin\alpha h_t,H_2=-sin\alpha h+cos\alpha h_t,& (15)\end{array}$

where H₁ is the standard model like Higgs and H₂ is the triplet like scalar. The corresponding mass eigenvalues are m_H1 (SM like Higgs) and m_H2 (triplet like scalar) are given by:

$\begin{array}{l}{m}_{H_1}^2\approx m_h^2-\frac{{(\mu v/\sqrt{2})}^2}{m_T^2-m_h^2},\\ m_{H_2}^2\approx m_T^2+\frac{{(\mu v/\sqrt{2})}^2}{m_T^2-m_h^2}.& (16)\end{array}$

The mixing angle is given by

$\begin{array}{ll}tan2\alpha =\frac{-\sqrt{2}\mu v}{(m_T^2-m_h^2)}.& (17)\end{array}$

From Equations (9, 11, 17) we see that there exist an upper bound on the mixing angle

$\begin{array}{ll}sin\alpha <0.02\left(\frac{174\text{ GeV}}{v}\right)\left(\frac{1}{1-0.39\frac{{(m_h/125\text{ GeV})}^2}{{(m_T/200\text{ GeV})}^2}}\right).& (18)\end{array}$

We also get a constraint on sin α from SM Higgs phenomenology, since the mixing can change the strength of the Higgs coupling to different SM particles. See for example [69, 70], in which the global fit yields a constraint on mixing angle sin α ≲ 0.5, which is much larger than the above constraint obtained using ρ parameter.

From Equation (7), all the couplings λ_H, λ₁, λ₂, λ₃, λ₄ and μ can be expressed in terms of physical scalar masses: m_H1, m_H2, $m_{H^{\pm }}$, $m_{H^{\pm \pm }}$, $m_{A^0}$ and the vevs v and v_t as Arhrib et al. [71] :

$\begin{array}{l}{\lambda }_H=\frac{2}{v^2}(m_{H_1}^2{cos}^2\alpha +m_{H_2}^2{sin}^2\alpha ),\\ {\lambda }_1=\frac{4m_{H^{\pm }}^2}{v^2+4v_t^2}-\frac{2m_{A^0}^2}{v^2+4v_t^2}+\frac{sin2\alpha }{2v_{t}v}(m_{H_1}^2-m_{H_2}^2),\\ {\lambda }_2=\frac{1}{v_t^2}\left[\frac{1}{2}\right(m_{H_1}^2{sin}^2\alpha +m_{H_2}^2{cos}^2\alpha )+\frac{v^2}{2(v^2+4v_t^2)}{m}_{A^0}^2\\ -\frac{2v^2}{v^2+4v_t^2}{m}_{H^{\pm }}^2+m_{H^{\pm \pm }}^2],\\ {\lambda }_3=\frac{1}{v_t^2}[\frac{2v^2}{v^2+2v_t^2}{m}_{H^{\pm }}^2-\frac{v^2}{v^2+4v_t^2}{m}_{A^0}^2-m_{H^{\pm \pm }}^2],\\ {\lambda }_4=\frac{4m_{A^0}^2}{v^2+4v_t^2}-\frac{4m_{H^{\pm }}^2}{v^2+2v_t^2},\\ \mu =\frac{\sqrt{2}{v}_t}{v^2+4v_t^2}{m}_{A^0}^2.& (19)\end{array}$

where $m_{A^0}$ is the mass of pseudo scalar. It is important to note that the quartic couplings λ₂ and λ₃ are inversely proportional to the triplet vev v_t which has important consequences for dark matter relic abundance that we discuss in section 4.4.

4.2. Non-zero Neutrino Masses

The coupling of scalar triplet Δ to SM lepton and Higgs doublet combinely break the lepton number by two units as given in Equation (12). As a result the ΔL_αL_β coupling yields Majorana masses to three flavors of active neutrinos as Magg and Wetterich [54], Lazarides et al. [55], Mohapatra and Senjanovic [56], Ma and Sarkar [57], Konetschny and Kummer [58], Schechter and Valle [59], Cheng and Li [60]:

$\begin{array}{ll}{(M_{\nu })}_{\alpha \beta }=\sqrt{2}{(f_L)}_{\alpha \beta }\langle \Delta \rangle \approx {(f_L)}_{\alpha \beta }\frac{-\mu v^2}{\sqrt{2}{M}_{\Delta }^2}.& (20)\end{array}$

Assuming $\mu \simeq M_{\Delta }\simeq {O}(10^{13})$ GeV, we can explain neutrino masses of order 1eV with a coupling strength f_L ≃ 1. However, the scale of M_Δ can be brought down to ~ TeV by taking the coupling to be much smaller $f_L\simeq 10^{-11}$, and indeed represents a bit of fine tuning in the neutrino sector.

To get the neutrino mass eigen values, the above mass matrix can be diagonalized by the usual U_PMNS matrix as :

$\begin{array}{ll}{M}_{\nu }=U_{\text{PMNS}}{M}_{\nu }^{diag}{U}_{\text{PMNS}}^T,& (21)\end{array}$

where U_PMNS is given by

$\begin{array}{l}{U}_{\text{P}MNS}=\\ \left(\begin{array}{ccc}{c}_{12}{c}_{13}& s_{12}{c}_{13}& s_{13}{e}^{-i{\delta }_{13}}\\ -s_{12}{c}_{23}-c_{12}{s}_{23}{s}_{13}{e}^{i{\delta }_{13}}& c_{12}{c}_{23}-s_{12}{s}_{23}{s}_{13}{e}^{i{\delta }_{13}}& s_{23}{c}_{13}\\ s_{12}{s}_{23}-c_{12}{c}_{23}{s}_{13}{e}^{i{\delta }_{13}}& -c_{12}{s}_{23}-s_{12}{c}_{23}{s}_{13}{e}^{i{\delta }_{13}}& c_{23}{c}_{13}\end{array}\right).U_{ph},& (22)\end{array}$

with c_ij, s_ij stand for cos θ_ij and sin θ_ij respectively and U_ph is given by

$\begin{array}{ll}{U}_{ph}=\text{Diag }(e^{-i{\gamma }_1},e^{-i{\gamma }_2},1).& (23)\end{array}$

Where γ₁, γ₂ are two Majorana phases. The diagonal matrix $M_{\nu }^{diag}$ = Diag (m₁, m₂, m₃) with diagonal entries are the mass eigen values for the neutrinos. The current neutrino oscillation data at 3σ confidence level give the constraint on mixing angles [68] :

$\begin{array}{l}0.259<{sin}^2{\theta }_{12}<0.359,0.374<{sin}^2{\theta }_{23}<0.628,0.0176\\ <{sin}^2{\theta }_{13}<0.0295.& (24)\end{array}$

However little information is available about the CP violating Dirac phase δ as well as the Majorana phases. Although the absolute mass of neutrinos is not measured yet, the mass square differences have already been measured to a good degree of accuracy :

$\begin{array}{l}\Delta m_0^2\equiv m_2^2-m_1^2=(6.99-8.18)\times 10^{-5}\text{e}{\text{V}}^2\\ |\Delta m_{\text{atm}}^2|\equiv |m_3^2-m_1^2|=(2.23-2.61)\times 10^{-3}\text{e}{\text{V}}^2.& (25)\end{array}$

One of the main issues of neutrino physics lies in the sign of the atmospheric mass square difference $|\Delta m_{\text{atm}}^2|\equiv |m_3^2-m_1^2|$, which is still unknown. This yields two possibilities: normal hierarchy (NH) (m₁ < m₂ < m₃) or inverted hierarchy (IH) (m₃ < m₁ < m₂). Another possibility, yet allowed, is to have a degenerate (DG) neutrino mass spectrum (m₁ ~ m₂ ~ m₃). Assuming that the neutrinos are Majorana, the mass matrix can be written as:

$\begin{array}{ll}{M}_{\nu }=\left(\begin{array}{ccc}a& b& c\\ b& d& e\\ c& e& f\end{array}\right).& (26)\end{array}$

Using equations (21), (22), (24) and (25), we can estimate the unknown parameters in neutrino mass matrix of Equation (26). To estimate the parameters in NH, we use the best fit values of the oscillation parameters. For a typical value of the lightest neutrino mass of m₁ = 0.0001 eV, we get the mass parameters (in eV) as :

$\begin{array}{l}a=0.003833,b=0.00759,c=0.002691,\\ d=0.023865,e=0.02083,f=0.03038.& (27)\end{array}$

Similarly for IH case, choosing the lightest neutrino mass m₃ = 0.001 eV, we get the mass parameters (in eV) as :

$\begin{array}{l}a=0.0484,b=-0.00459,c=-0.00573,\\ d=0.02893,e=-0.02366,f=0.02303.& (28)\end{array}$

In both the cases, we put the Dirac and Majorana phases to be zero for simplicity.

The analysis of neutrino mass is more indicative here than being exhaustive. This is essentially to build the connection between the dark sector and neutrino sector advocated in the model set up. One can easily perform a scan over the mass matrix parameters to obtain correct ranges of the neutrino observables, and that of course lies in the vicinity of the aforementioned values. But, we do not aim to elaborate that in this draft. We have not also adhered to a specific lepton mixing matrix pattern (say tri-bi-maximal mixing) coming from a defined underlying flavor symmetry (say A₄), which will be able to correlate different parameters of the mass matrix.

The mass of the scalar triplet can also be brought down to TeV scale by choosing appropriate Yukawa coupling as explained before. If the triplet mass is order of a few hundreds of GeV, then it can give interesting dilepton signals in the collider. See for example, [72–78] for a detailed discussion regarding the dilepton signatures of the scalar triplet at collider.

4.3. Pseudo-Dirac Nature of ILD Dark Matter

From Equation (12) we see that the vev of Δ induces a Majorana mass to N⁰ which is given by:

$\begin{array}{ll}m=\sqrt{2}{f}_N\langle \Delta \rangle \approx f_N\frac{-\mu v^2}{\sqrt{2}{M}_{\Delta }^2}.& (29)\end{array}$

Thus the N⁰ has a large Dirac mass M_N (as in Equation 2) and a small Majorana mass m as shown in the above Equation (29). Therefore, we get a mass matrix in the basis $\left\{N_L^0,{(N_R^0)}^c\right\}$ as:

$\begin{array}{ll}{M}=\left(\begin{array}{cc}m& M_N\\ M_N& m\end{array}\right).& (30)\end{array}$

Thus the Majorana mass m splits the Dirac spinor N⁰ into two pseudo-Dirac states $N_{1,2}^0$ with mass eigenvalues M_N ± m. The mass splitting between the two pseudo-Dirac states $N_{1,2}^0$ is given by

$\begin{array}{ll}\delta m=2m=2\sqrt{2}{f}_N\langle \Delta \rangle .& (31)\end{array}$

Note that δm << M_N from the estimate of induced vev of the triplet and hence does not play any role in the relic abundance calculation. However, the sub-GeV order mass splitting plays a crucial role in direct detection by forbidding the Z-boson mediated DM-nucleon elastic scattering. Now from Equations (20, 29) we see that the ratio:

$\begin{array}{ll}R=\frac{(M_{\nu })}{m}=\frac{f_L}{f_N}\lesssim 10^{-5},& (32)\end{array}$

where we assume M_ν ~ 1 eV and m ~ 100 keV. Here the mass splitting between the two states $N_1^0$ and $N_2^0$ is chosen to be ${O}$(100) keV in order to forbid the Z-mediated inelastic scattering with the nucleons in direct detection. Thus, we see that the ratio R ≲ 10⁻⁵ is heavily fine tuned. In other words, the scalar triplet strongly decay to ILD dark matter, while its decay to SM leptons is suppressed.

4.4. Effect of Scalar Triplet on Relic Abundance of ILD Dark Matter

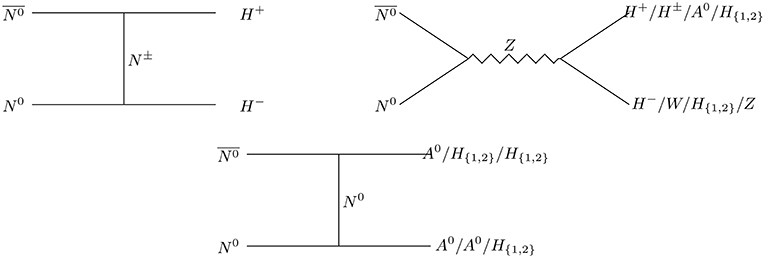
In presence of a scalar triplet, when the DM mass is larger than the triplet mass, a few additional annihilation and co-annihilation channels open up as shown in Figures 7–10 in addition to the previously mentioned Feynman diagrams given in Figures 2–4. These additional channels also play a key role in number changing processes of DM, N⁰ to yield a modified freeze-out abundance. We numerically calculate relic density of N⁰ DM once again by implementing the model in the code micrOmegas [66]. The parameter space, in comparison to the ILD dark matter alone, is enhanced due to the additional coupling of N⁰ with Δ. In particular, the new parameters are: triplet scalar masses $m_{H_2},m_{A^0},m_{H^{\pm }},m_{H^{\pm \pm }}$, vev of scalar triplet v_t, coupling of scalar triplet with ILD dark matter N⁰, i.e., f_N, scalar doublet-triplet mixing sin α.

FIGURE 7

Figure 7. Additional annihilation $N^0\overline{N^0}$, in presence of scalar triplet.

FIGURE 8

Figure 8. Dominant annihilation ($N^0\overline{{(N^0)}^c}$) and co-annihilation ($N^{-}\overline{{(N^0)}^c},N^{-}\overline{{(N^{-})}^c}$) processes of ILD DM (N⁰) to scalar triplet in final states.

FIGURE 9

Figure 9. Co-annihilation channels of ILD DM (N⁰), with charged fermions N⁻ in presence of scalar triplet.

FIGURE 10

Figure 10. Co-annihilation processes involving only charged partner of ILD DM, N^± in presence of scalar triplet.

To understand the effect of the triplet scalar on relic density of ILD DM, we show in Figure 11 the variation of relic density as a function of DM mass (m_N) with different choices of triplet vev (v_t) while keeping a fixed f_N and sin α. In the left panel of Figure 11 we choose the scalar doublet-triplet mixing to be sin α = 0.001 while in the right-panel of Figure 11 we choose sin α = 0.1. In both cases we set the physical CP even, CP odd and charged triplet scalar masses respectively at $m_{H_2}=280,m_{A^0}=280,m_{H^{\pm }}=300$ and $m_{H^{\pm \pm }}=310$ GeV and f_N = 0.1. We note that there is a resonance drop near m_N ~ m_Z/2 as usual for Z mediated s-channel diagrams. Additionally we find that near m_N ~ 280 GeV (which is the mass of H₂), relic density drops suddenly because of new annihilation processes NN → ΔΔ start to contribute (see diagrams in Figures 7–10). With larger triplet vev v_t ~ GeV, the effect of annihilation to scalar triplet becomes subdued. This can be understood as follows. First of all, we see that the quartic couplings involving the triplet, as given in Equation (19), are inversely proportional to the triplet vev (v_t). In a typical annihilation process: $N^{-}\overline{{N^{-}}^c}\to H^{-}{H}^{-}$, mediated by H⁻⁻, the vertex H⁻⁻H⁻H⁻ is proportional to $\sqrt{2}{v}_t{\lambda }_3~1/v_t$, which diminishes with larger v_t. On the other hand, let us consider the process: $N^0\overline{{N^0}^c}\to H^{++}{H}^{--}$, which has a significant contribution to the total relic density. This process is mediated by H₁ and H₂. In small sin α limit, the H₁ mediated diagram is vanishingly small as the $N^0\overline{N^0}{H}_1~sin\alpha$. So, H₂ mediation dominates here. However, the vertex involving $H_2{H}^{++}{H}^{--}$ is proportional to (2 cos α λ₂v_t − sin αλ₁v_d). One can see that for small v_t, the first term is negligible, while for a larger v_t, the first term becomes comparable to that of the second one and has a cancelation. This cancelation therefore decreases the annihilation cross-section to the chosen final state. Such a phenomena is also present for co-annihilation processes like $N^{-}\overline{{N^{-}}^c}\to H^{--}{H}_2$ etc., where the vertices involve a combination of λ₁, and λ₂. On the other hand, for smaller values of triplet vev (v_t ~ 0.01 GeV), there is a larger drop in relic density due to the additional annihilation channels (to the triplet scalars as mentioned). Therefore, the DM N⁰ achieves correct relic density for larger DM mass m_N (as compared to that of the case in absence of triplet). Moreover, we set f_N = 0.1 in both cases. It is straightforward to see that annihilation to the triplet final states are proportional to f_N. Therefore, with larger f_N, the drop in relic density in the vicinity of triplet scalar mass decreases even further. In summary, the presence of scalar triplet shifts the relic density of ILD DM to a higher DM mass region which crucially depends on the choice of the triplet vev as well as ΔNN coupling f_N.

FIGURE 11

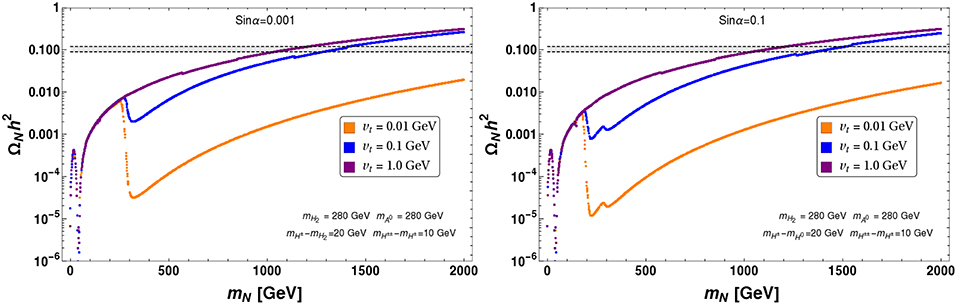
Figure 11. Relic density vs. m_N plot for different choices triplet vev, v_t, keeping sin α = 0.001 (left) and sin α = 0.1 (right). Others parameters are mentioned in the figure. The gray patch indicates relic density bounds. In both cases we set f_N = 0.1.

An important conclusion about ILD dark matter is that the mass of DM (m_N) is around 1 TeV which satisfies the observed relic abundance. This implies the mass of N⁻, the charged partner of N⁰, is about 1 TeV as well. However, the electroweak correction induces a small mass splitting between N⁰ and N⁻ to be around 162 MeV. Therefore, N⁻ can give rise a displaced vertex signature through the 3-body decay $N^{-}\to N^0{\ell }^{-}\overline{{\nu }_{\ell }}$ [79]. But the main drawback is that the production cross-section of N^± of mass ~ TeV is highly suppressed at LHC as this can only be possible through Drell-Yan. Therefore, in section 5 we discuss a more predictive model by enlarging the dark sector with an additional singlet fermion χ.

4.5. Effect of Salar Triplet on Direct Detection of ILD Dark Matter

As discussed in section 3.2, the ILD dark matter alone is ruled out due to large Z-mediated elastic scattering with nucleus. However, it can be reinstated in presence of the scalar triplet, which not only forbids the Z-mediated elastic scattering [61–65] but also provides a new portal for the detection of ILD dark matter via the doublet-triplet mixing as we discuss below.

The interaction of DM with the Z boson with the kinetic term is given as

$\begin{array}{ll}{{L}}_{Z-DM}\supset i\overline{N^0}\left({\gamma }^{\mu }{\partial }_{\mu }-i{g}_Z{\gamma }^{\mu }{Z}_{\mu }\right)N^0,& (33)\end{array}$

where $i{g}_Z=\frac{g}{2cos{\theta }_W}$. After the symmetry breaking the scalar triplet Δ gets an induced vev and hence gives Majorana mass to the ILD dark matter N₀ as shown in Equation (29). The presence of such Majorana mass term splits the Dirac DM state into two real Majorana states $N_1^0$ and $N_2^0$ with a mass splitting of δm as discussed in section 4.3. Now we rewrite the Lagrangian involving DM-Z interaction in terms of the new Majorana states as:

$\begin{array}{ll}{{L}}_{\text{Z}-\text{DM}}\supset \overline{N_1^0}i{\gamma }^{\mu }{\partial }_{\mu }{N}_1^0+\overline{N_2^0}i{\gamma }^{\mu }{\partial }_{\mu }{N}_2^0-i{g}_z\overline{N_1^0}{\gamma }^{\mu }{N}_2^0{Z}_{\mu }.& (34)\end{array}$

We can see that the dominant gauge interaction becomes off-diagonal. The absence of diagonal interaction term for the DM-Z vertex leads to the vanishing contribution to elastic scattering of the DM with the nucleus. However, there could be an inelastic scattering through Z mediation, which is suppressed if the mass splitting between two states is of the order ${O}$(100) keV or less. But the Yukawa term involving DM and Δ is still diagonal in the new basis and hence can lead to elastic scattering through a mixing between the doublet-triplet Higgs. Assuming $N_1^0$ to be the lightest among the two Majorana states, hence being the DM, the relevant diagram for the elastic scattering is shown in Figure 12.

FIGURE 12

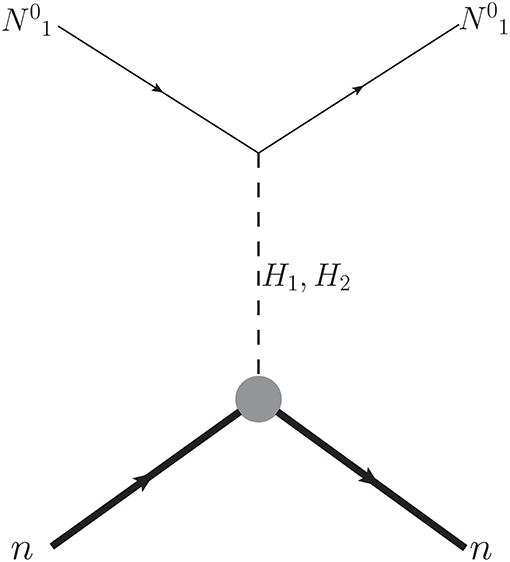
Figure 12. Elastic scattering of the ILD DM(N⁰) with the nucleon through scalar mediation due to doublet triplet mixing.

The direct detection cross-section mainly depends on m_H2, f_N and sin α. We have plotted the spin independent direct detection cross-section as a function of the DM mass $m_{N_1^0}$ in Figure 13. Keeping m_H2 = 280 GeV (Solid) and m_H2 = 600 GeV (Dashed) fixed, we have shown the cross-section for three different values {f_N = 0.01, 0.1, 1} in Red, Blue, and Green color, respectively. Since there is a relative negative sign between the two amplitudes, the destructive interference is more for m_H2 comparable to SM Higgs. Hence cross section for m_H2 = 280 GeV turns out to be smaller than m_H2 = 600 GeV. But if we increase the mass of m_H2 to TeV scale then H₂ mediated process will be suppressed due to the large mass in the propagator and only H₁ mediated process will contribute. The direct search cross-section increases with larger Yukawa coupling f_N from 0.01 to 1 and can be is easily seen from the Figure 13. Since the DM couples dominantly to the triplet scalar, the more the mixing angle (sin α), the more is the cross-section which can be clearly seen from the left and right panel of Figure 13. But all these cross-sections are well below the present experimental bound of LUX and Xenon-1T. Note that the relic density allowed parameter space of ILD DM in presence of a scalar triplet live in a very high DM mass region ~ TeV with moderate f_N and Higgs data unambiguously indicates that the mixing angle (sin α) should be kept small, as we have shown in Figure 13. Therefore, the ILD becomes a viable DM candidate in the presence of a triplet scalar allowed by both relic density and direct search constraints.

FIGURE 13

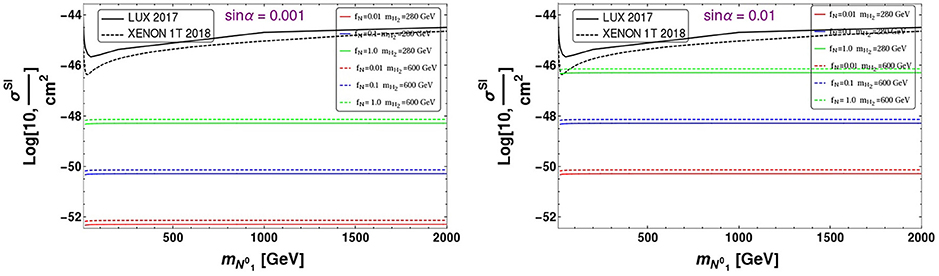
Figure 13. SI direct detection cross-section σ^SI as a function of DM mass $m_{N_1^0}$ for sin α = 0.001 (Left) and sin α = 0.01 (Right). Different choices of the coupling {f_N = 0.01, 0.1, 1} are shown in Red, Blue, and Green color, respectively. Dashed and solid lines corresponds to different values of the heavy Higgs m_H2 = 600, 280 GeVs, respectively. The bound from LUX 2017 and XENON1T 2018 are shown.

5. Singlet-Doublet Leptonic Dark Matter

Now let us assume that the dark sector is composed of two vector like leptons : a doublet, N = (N⁰ N⁻)^Tand a singlet χ, which are odd under an extended ${{Z}}_2$ symmetry while all the Standard Model (SM) fields are even. As a result the lightest odd particle in the dark sector is stable and behave as a candidate of DM. The quantum numbers of dark sector fields and that of SM Higgs under the SM gauge group, augmented by a ${{Z}}_2$ symmetry, are given in Table 2.

TABLE 2

Table 2. Quantum numbers of additional dark sector fermions and that of Higgs under ${G}\equiv SU{(3)}_C\times SU{(2)}_L\times U{(1)}_Y\times {{Z}}_2$.

The Lagrangian of the model can be given as follows:

$\begin{array}{l}{{L}}^{VF}=\overline{N}[i{\gamma }^{\mu }({\partial }_{\mu }-ig\frac{{\sigma }^a}{2}{W}_{\mu }^a-i{g}^{\prime }\frac{Y}{2}{B}_{\mu })-m_N]N\\ +\overline{\chi }(i{\gamma }^{\mu }{\partial }_{\mu }-m_{\chi })\chi -(Y_1\overline{N}\tilde{H}\chi +h.c).& (35)\end{array}$

Note that here we have assumed to have a CP conserving interaction between the additional vector like fermion to the SM Higgs. One may also think of a coupling $-(Y_1\overline{N}{\gamma }_5\tilde{H}\chi +h.c)$ that will violate CP. Now, it is a bit intriguing to think of such interactions before the debate on the SM Higgs to be a scalar or a pseudoscalar is settled. The outcome of such an interaction will alter the subsequent phenomenology significantly. For example, it is known that advocating a pseudoscalar (S) interaction to a vector like DM (ψ), for example, with a term like $-yS\bar{\psi }{\gamma }_5\psi$ indicates that DM-nucleon scattering becomes velocity dependent and therefore reduces the direct search constraint significantly to allow the model live in a larger allowed parameter space. However, the Yukawa interaction term itself ($-yS\bar{\psi }{\gamma }_5\psi$) do not violate parity as S is assumed to be pseudoscalar by itself (see for example in Ghorbani [67]).

After Electroweak symmetry breaking (EWSB) the SM Higgs acquires a vacuum expectation value v. The quantum field around the vacuum can be given as: $H={\left(\begin{array}{cc}0& \frac{1}{\sqrt{2}}(v+h)\end{array}\right)}^T$where v = 246 GeV. The presence of the Yukawa term: $Y_1\overline{N}\tilde{H}\chi$ term in the Lagrangian (Equation 35), arises an admixture between N⁰ and χ. The bare mass terms of the vector like fermions in ${{L}}^{VF}$ then take the following form:

$\begin{array}{l}-{{L}}_{mass}^{VF}=m_N\overline{N^0}{N}^0+m_N{N}^{+}{N}^{-}+m_{\chi }\overline{\chi }\chi +\frac{Y_{1}v}{\sqrt{2}}\overline{N^0}\chi \\ +\frac{Y_{1}v}{\sqrt{2}}\overline{\chi }{N}^0\\ =\overline{(\begin{array}{cc}\chi & N^0\end{array})}\left(\begin{array}{cc}{m}_{\chi }& \frac{Y_{1}v}{\sqrt{2}}\\ \frac{Y_{1}v}{\sqrt{2}}& m_N\end{array}\right)\left(\begin{array}{c}\chi \\ N^0\end{array}\right)+m_N{N}^{+}{N}^{-}.& (36)\end{array}$

The unphysical basis, (χ N⁰)^T is related to physical basis, ${(\begin{array}{cc}{N}_1& N_2\end{array})}^T$ through the following unitary transformation:

$\begin{array}{ll}\left(\begin{array}{c}\chi \\ N^0\end{array}\right)={U}\left(\begin{array}{c}{N}_1\\ N_2\end{array}\right)=\left(\begin{array}{cc}cos\theta & -sin\theta \\ sin\theta & cos\theta \end{array}\right)\left(\begin{array}{c}{N}_1\\ N_2\end{array}\right),& (37)\end{array}$

where the mixing angle

$\begin{array}{ll}tan2\theta =-\frac{\sqrt{2}{Y}_{1}v}{m_N-m_{\chi }}.& (38)\end{array}$

The mass eigenvalues of the physical states N₁ and N₂ are respectively given by:

$\begin{array}{l}{m}_{N_1}=m_{\chi }{cos}^2\theta +m_N{sin}^2\theta +\frac{Y_{1}v}{\sqrt{2}}sin2\theta \\ m_{N_2}=m_{\chi }{sin}^2\theta +m_N{cos}^2\theta -\frac{Y_{1}v}{\sqrt{2}}sin2\theta & (39)\end{array}$

For small sin θ (sin θ → 0) limit, m_N1 and m_N2 can be further expressed as:

$\begin{array}{l}{m}_{N_1}\simeq m_{\chi }+\frac{Y_{1}v}{\sqrt{2}}sin2\theta \equiv m_{\chi }-\frac{{(Y_{1}v)}^2}{(m_N-m_{\chi })},\\ m_{N_2}\simeq m_N-\frac{Y_{1}v}{\sqrt{2}}sin2\theta \equiv m_N+\frac{{(Y_{1}v)}^2}{(m_N-m_{\chi })}.& (40)\end{array}$

Here we have considered $Y_{1}v/\sqrt{2}\ll m_{\chi }<m_N$. Hence m_N1 < m_N2. Therefore, N₁ becomes the stable DM candidate. From Equations (38, 39), one can write :

$\begin{array}{l}{Y}_1=-\frac{\Delta msin2\theta }{\sqrt{2}v},\\ m_N=m_{N_1}{sin}^2\theta +m_{N_2}{cos}^2\theta .& (41)\end{array}$

where Δm = m_N2 − m_N1² is the mass difference between the two mass eigenstates and m_N is the mass of electrically charged component of vector like fermion doublet N⁻.

Therefore, one can express interaction terms of ${{L}}^{VF}$ in mass basis of N₁ and N₂ as

$\begin{array}{l}{{L}}_{int}^{VF}=\left(\frac{e_0}{2sin{\theta }_{W}cos{\theta }_W}\right)[{sin}^2\theta \overline{N_1}{\gamma }^{\mu }{Z}_{\mu }{N}_1+{cos}^2\theta \overline{N_2}{\gamma }^{\mu }{Z}_{\mu }{N}_2\\ +sin\theta cos\theta (\overline{N_1}{\gamma }^{\mu }{Z}_{\mu }{N}_2+\overline{N_2}{\gamma }^{\mu }{Z}_{\mu }{N}_1)]\\ +\frac{e_0}{\sqrt{2}sin{\theta }_W}sin\theta \overline{N_1}{\gamma }^{\mu }{W}_{\mu }^{+}{N}^{-}+\frac{e_0}{\sqrt{2}sin{\theta }_W}cos\theta \overline{N_2}{\gamma }^{\mu }{W}_{\mu }^{+}{N}^{-}\\ +\frac{e_0}{\sqrt{2}sin{\theta }_W}sin\theta N^{+}{\gamma }^{\mu }{W}_{\mu }^{-}{N}_1+\frac{e_0}{\sqrt{2}sin{\theta }_W}cos\theta N^{+}{\gamma }^{\mu }{W}_{\mu }^{-}{N}_2\\ -\left(\frac{e_0}{2sin{\theta }_{W}cos{\theta }_W}\right)cos2{\theta }_W{N}^{+}{\gamma }^{\mu }{Z}_{\mu }{N}^{-}-e_0{N}^{+}{\gamma }^{\mu }{A}_{\mu }{N}^{-}\\ -\frac{Y_1}{\sqrt{2}}h[sin2\theta (\overline{N_1}{N}_1-\overline{N_2}{N}_2)+cos2\theta (\overline{N_1}{N}_2+\overline{N_2}{N}_1)]& (42)\end{array}$

The relevant DM phenomenology of the model then mainly depend on following three independent parameters :

$\begin{array}{ll}\left\{m_{N_1},\Delta m,sin\theta \right\}& (43)\end{array}$

5.1. Constraints on the Model Parameters

The model parameters are not totally free from theoretical and experimental bounds. Here we would like to discuss briefly the constraints coming from Perturbativity, invisible decay widths of Z and H, and corrections to electroweak parameters.

• Perturbativity: The upper limit of perturbativity bound on quartic and Yukawa couplings of the model are given by,

$\begin{array}{ll}\left|Y_1\right|<\sqrt{4\pi }.& (44)\end{array}$

• Invisible decay width of Higgs: If the mass of DM is below m_h/2, then Higgs can decay to two invisible particles in final state and will yield invisible decay width. Recent Large Hadron Collider (LHC) data put strong constraint on the invisible branching fraction of Higgs to be Br(h → inv) ≤ 0.24 [80–82], which can be expressed as:

$\begin{array}{ll}\frac{\Gamma (h\to inv.)}{\Gamma (h\to SM)+\Gamma (h\to inv.)}\le 0.24,& (45)\end{array}$

where Γ(h → SM) = 4.2 MeV for Higgs mass m_h = 125.09 GeV, obtained from recent measured LHC data [68]. Therefore, the invisible Higgs decay width is given by

$\begin{array}{ll}\Gamma (h\to inv.)\le 1.32\text{ MeV},& (46)\end{array}$

where

$\begin{array}{l}\Gamma (h\to inv.)=\Gamma (h\to \overline{N_1}{N}_1).\\ =\frac{1}{16\pi }{\displaystyle (Y_{1}sin2\theta {)}^2}{m}_h{\displaystyle (1-\frac{4m_{N_1}^2}{m_h^2}{)}^{\frac{3}{2}}}\Theta (m_h-2m_{N_1}),& (47)\end{array}$

where the step function Θ(m_h − 2m_N1) = 1 if m_N1 ≤ m_h/2 and is 0 if m_N1 > m_h/2. The decay width of Higgs to DM is proportional to $Y_1=-\frac{\Delta msin2\theta }{\sqrt{2}v}$. Therefore, it depends on the mass splitting with NLSP (Δm) as well as on the doublet singlet mixing (sin θ). The invisible Higgs decay constraint on the model for m_N1 < m_h/2 is shown in Figure 14, where we have shown the exclusion in M_N1 − sin θ plane for different choices of Δm ranging from 10 GeV to 500 GeV. The inner side of the contour is excluded. This essentially shows that with large Δm ~ 500 GeV, essentially all of m_N1 ≤ m_h/2 is excluded, while for a small Δm ~ 10 GeV, the constraint is milder due to less Higgs decay width and excludes only regions for DM masses M_N1 ≤ 30 GeV within sin θ ~ {0.6 − 0.8}. Therefore, even in m_N1 ≤ m_h/2 region, if Δm and sin θ are small, which turns out to be the case for satisfying relic density and direct search as we demonstrate later, then are allowed by the Higgs invisible decay constraint.

• Invisible decay width of Z: If the masses of dark sector particles are below m_Z/2, then Z can decay to dark sector particles leading to an increase of Z-decay width. However, from current observation, invisible decay width of Z boson is strongly bounded. The upper limit on invisible Z-decay width is given by Patrignani et al. [68]:

$\begin{array}{ll}\Gamma (Z\to inv.)=499.0\pm 1.5\text{ MeV},& (48)\end{array}$

where the decay of Z to N₁ DM is given as:

$\begin{array}{l}\Gamma (Z\to \overline{N_1}{N}_1)=\frac{1}{48\pi }{\displaystyle (\frac{g{sin}^2\theta }{cos{\theta }_W}{)}^2{m}_Z}(1+\frac{2m_{N_1}^2}{m_Z^2})\\ \sqrt{1-\frac{4m_{N_1}^2}{m_Z^2}}\Theta (m_Z-2m_{N_1}).& (49)\end{array}$

FIGURE 14

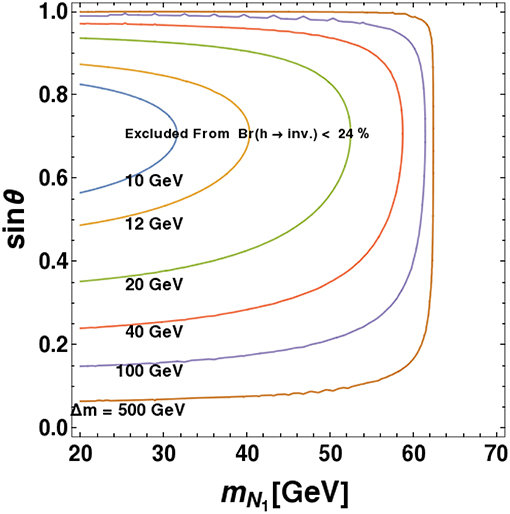
Figure 14. Constraints from Higgs invisible decay width is shown in m_N1 − sin θ plane. Here each contour line correspond to different value of Δm depicted in the figure. Inner region of each contour line excluded from Higgs invisible decay width, Γ(h → inv.) ≤ 1.32 MeV for a particular value of Δm.

The Z− invisible decay does not play a crucial role in small sin θ regions, which are required for the DM to achieve correct relic density, thus allowing almost all of the M_N1 ≤ m_Z/2 parameter space of the model.

5.2. Corrections to the Electroweak Precision Parameters

Addition of a vector like fermion doublet to the SM gives correction to the electroweak precision test parameters S, T and U[83–86]. The values of these parameters are tightly constrained by experiments. The new observed parameters are infect four in number Ŝ, $\widehat{T}$, W and Y [87], where the Ŝ, $\widehat{T}$ are related to Peskin-Takeuchi parameters S, T as $Ŝ=\alpha S/4{sin}^2{\theta }_w$, $\widehat{T}=\alpha T$, while W and Y are two new set of parameters. The measured values of these parameters at LEP-I and LEP-II put a lower bound on the mass scale of vector like fermions. The result of a global fit of the parameters is presented in the Table 3 for a light Higgs [87]³.

TABLE 3

Table 3. Global fit for the electroweak precision parameters taken from reference [87].

In the present scenario, we have a vector like doublet and a singlet fermion field are added to the SM. But the physical states are a charged fermion N⁻, and two singlet doublet mixed neutral fermions N₁ (dominant singlet component) and N₂ (dominant doublet component). Therefore, the contribution to the precision parameters also depends on the mixing angle sin θ. The expression for Ŝ in terms m_N1, m_N2, m_N and sin θ of is given as Cynolter and Lendvai [88]:

$\begin{array}{ll}\begin{array}{l}\widehat{S}=\frac{g^2}{16{\pi }^2}[\frac{1}{3}\{\ln \left(\frac{{\mu }_{ew}^2}{m_N^2}\right)-{\cos }^4\theta \ln \left(\frac{{\mu }_{ew}^2}{m_{N_2}^2}\right)\hfill \\ -{\sin }^4\theta \ln \left(\frac{{\mu }_{ew}^2}{m_{N_1}^2}\right)\}-2{\sin }^2\theta {\cos }^2\theta \{\ln \left(\frac{{\mu }_{ew}^2}{m_{N_1}{m}_{N_2}}\right)\hfill \\ +\frac{m_{N_1}^4-8m_{N_1}^2{m}_{N_2}^2+m_{N_2}^4}{9{(m_{N_1}^2-m_{N_2}^2)}^2}\hfill \\ +\frac{(m_{N_1}^2+m_{N_2}^2)(m_{N_1}^4-4m_{N_1}^2{m}_{N_2}^2+m_{N_2}^4)}{6{(m_{N_1}^2-m_{N_2}^2)}^3}\ln \left(\frac{m_{N_2}^2}{m_{N_1}^2}\right)\hfill \\ +\frac{m_{N_1}{m}_{N_2}(m_{N_1}^2+m_{N_2}^2)}{2{(m_{N_1}^2-m_{N_2}^2)}^2}+\frac{m_{N_1}^3{m}_{N_2}^3}{{(m_{N_1}^2-m_{N_2}^2)}^3}\ln \left(\frac{m_{N_2}^2}{m_{N_1}^2}\right)\}]\hfill \end{array}& (50)\end{array}$

where μ_ew is at the EW scale.

In the left panel of Figure 15, we have plotted Ŝ as a function of m_N2 keeping m_N1 = 200 GeV for different values of the mixing angle. In the right panel, we have shown the allowed values of Ŝ in the plane of m_N2 − m_N vs. m_N2 for sin θ = 0.05 (Green Color), sin θ = 0.1 (Red color) and sin θ = 0.2 (Maroon color). We observed that Ŝ does not put strong constraints on m_N1 and m_N2. Moreover, small values of sin θ allows a small mass splitting between N₂ and N⁻ which relaxes the constraint on $\widehat{T}$ parameter as we discuss below. The expression for $\widehat{T}$ is given as Cynolter and Lendvai [88]:

$\begin{array}{ll}\begin{array}{l}\widehat{T}=\frac{g^2}{16{\pi }^2{M}_W^2}[2{\sin }^2\theta {\cos }^2\theta \Pi (m_{N_1},m_{N_2},0)\hfill \\ -2{\cos }^2\theta \Pi (m_N,m_{N_2},0)-2{\sin }^2\theta \Pi (m_N,m_{N_1},0)]\hfill \end{array}& (51)\end{array}$

where Π(a, b, 0) is given by:

$\begin{array}{ll}\begin{array}{l}\Pi (a,b,0)=-\frac{1}{2}(M_a^2+M_b^2)\left(\text{Div}+\ln \left(\frac{{\mu }_{ew}^2}{M_a{M}_b}\right)\right)\hfill \\ -\frac{1}{4}(M_a^2+M_b^2)-\frac{(M_a^4+M_b^4)}{4(M_a^2-M_b^2)}\ln \frac{M_b^2}{M_a^2}\hfill \\ +M_a{M}_b\{\text{Div}+\ln \left(\frac{{\mu }_{ew}^2}{M_a{M}_b}\right)+1\hfill \\ +\frac{(M_a^2+M_b^2)}{2(M_a^2-M_b^2)}\ln \frac{M_b^2}{M_a^2}\}\hfill \end{array}& (52)\end{array}$

with Div $=\frac{1}{ϵ}+\text{ln}4\pi -{\gamma }_{ϵ}$ contains the divergent term in dimensional regularization method. From the left panel of Figure 16 we see that for sin θ < 0.05 we don't get strong constraints on m_N2 and m_N1. Moreover, small values of sin θ restricts the value of m_N2 − m_N to be less than a GeV. As a result large m_N2 values are also allowed. Near m_N2 ≈ m_N, $\widehat{T}$ vanishes as expected. The value of Y and W are usually suppressed by the masses of new fermions. Since the allowed masses of N₁, N₂ and N^± are above 100 GeV by the relic density constraint (to be discussed later), so Y and W are naturally suppressed.

FIGURE 15

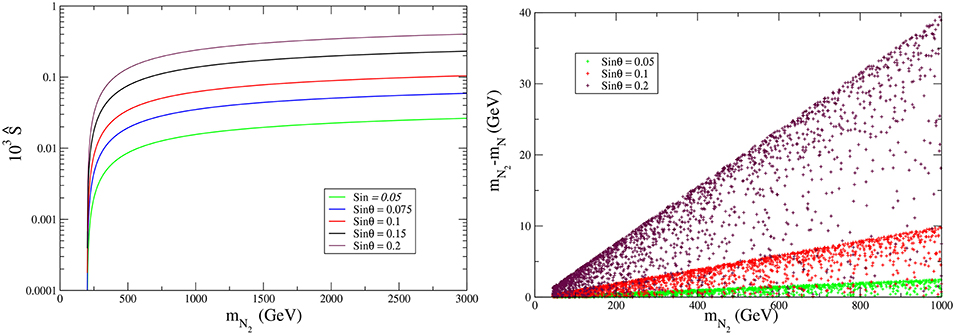
Figure 15. In the left panel, Ŝ is shown as a function of m_N2 for m_N1 = 200 GeV and sinθ = 0.05 (Green color), sinθ = 0.075 (Blue color), sinθ = 0.1 (Red color), sinθ = 0.15 (Black color), and sinθ = 0.2 (Maroon color). In the right panel, allowed values of Ŝ is plotted in m_N2 − m_N vs. m_N2 plane for sin θ = 0.05 (Green Color), sinθ = 0.1 (Red color), and sinθ = 0.2 (Maroon color).

FIGURE 16

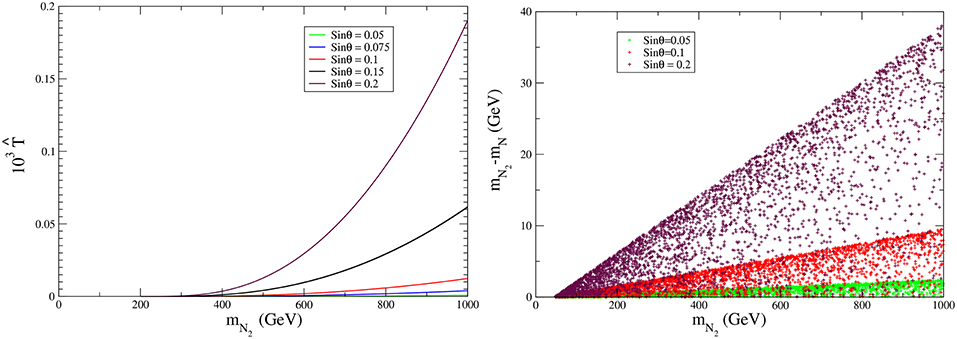
Figure 16. In the left panel, $\widehat{T}$ is shown as a function of m_N2 for m_N1 = 200 GeV and sinθ = 0.05 (Green color), sinθ = 0.075 (Blue color), sinθ = 0.1 (Red color), sinθ = 0.15 (Black color), and sinθ = 0.2 (Maroon color). In the right panel, allowed values of $\widehat{T}$ is plotted in m_N2 − m_N vs. m_N2 plane for sin θ = 0.05 (Green color), sin θ = 0.1 (Red color), and sinθ = 0.2 (Maroon color).

5.3. Relic Density of Singlet-Doublet Leptonic Dark Matter

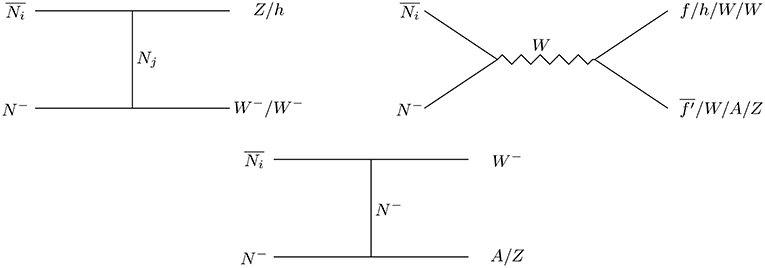
As stated earlier, the lightest stable physical state N₁ is the DM, which is an admixture of a singlet vector-like fermion (χ) and the neutral component of a vector-like fermionic doublet (N). Due to presence of mass hierarchy between dark sector particles $N_1,N_2\text{ and }{N}^{-}$, the lightest component N₁ not only annihilate with itself but also co-annihilate with N₂ and N⁻ to yield a net a relic density. The relevant diagrams are shown in Figures 17–19.

FIGURE 17

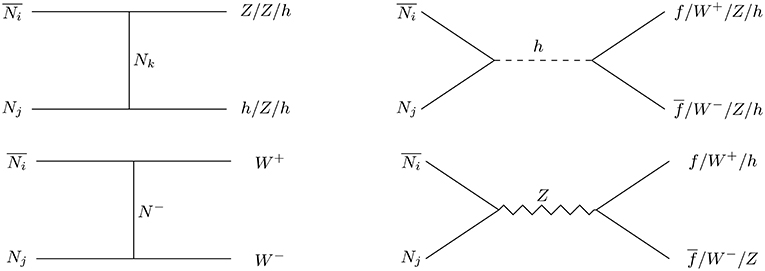
Figure 17. Annihilation (i = j) and co-annihilation (i ≠ j) of vector-like fermion DM. Here (i, j = 1, 2).

FIGURE 18

Figure 18. Co-annihilation process of N_i (i = 1, 2) with the charge component N⁻ to SM particles.

FIGURE 19

Figure 19. Co-annihilation process of charged fermions N^± to SM particles in final states.

We assume all the heavier particles: $N_{2}and{N}^{-}$ in the dark sector ultimately decay to lightest stable particle N₁. So in this scenario one can write the Boltzmann equation in terms of total number density $n=n_{N_1}+n_{N_2}+n_{N^{\pm }}$ as

$\begin{array}{ll}\frac{dn}{dt}+3Hn=-{\langle \sigma v\rangle }_{eff}(n^2-n_{eq}^2),& (53)\end{array}$

where

$\begin{array}{l}{\langle \sigma v\rangle }_{eff}=\frac{g_1^2}{g_{eff}^2}{\langle \sigma v\rangle }_{\overline{N_1}{N}_1}+\frac{2g_1{g}_2}{g_{eff}^2}{\langle \sigma v\rangle }_{\overline{N_1}{N}_2}{\displaystyle (1+\frac{\Delta m}{m_{N_1}}{)}^{\frac{3}{2}}}{e}^{-x\frac{\Delta m}{m_{N_1}}}\\ +\frac{2g_1{g}_3}{g_{eff}^2}{\langle \sigma v\rangle }_{\overline{N_1}{N}^{-}}{\displaystyle (1+\frac{\Delta m}{m_{N_1}}{)}^{\frac{3}{2}}}{e}^{-x\frac{\Delta m}{m_{N_1}}}\\ +\frac{2g_2{g}_3}{g_{eff}^2}{\langle \sigma v\rangle }_{\overline{N_2}{N}^{-}}{\displaystyle (1+\frac{\Delta m}{m_{N_1}}{)}^3}{e}^{-2x\frac{\Delta m}{m_{N_1}}}\\ +\frac{g_2^2}{g_{eff}^2}{\langle \sigma v\rangle }_{\overline{N_2}{N}_2}{\displaystyle (1+\frac{\Delta m}{m_{N_1}}{)}^3}{e}^{-2x\frac{\Delta m}{m_{N_1}}}\\ +\frac{g_3^2}{g_{eff}^2}{\langle \sigma v\rangle }_{N^{+}{N}^{-}}{\displaystyle (1+\frac{\Delta m}{m_{N_1}}{)}^3}{e}^{-2x\frac{\Delta m}{m_{N_1}}}.& (54)\end{array}$

In above equation, g_eff, defined as effective degrees of freedom, which is given by

$\begin{array}{ll}{g}_{eff}=g_1+g_2{\displaystyle (1+\frac{\Delta m}{m_{N_1}}{)}^{\frac{3}{2}}}{e}^{-x\frac{\Delta m}{m_{N_1}}}+g_3{\displaystyle (1+\frac{\Delta m}{m_{N_1}}{)}^{\frac{3}{2}}}{e}^{-x\frac{\Delta m}{m_{N_1}}},& (55)\end{array}$

where g₁, g₂ and g₃ are the degrees of freedom of $N_1,N_{2}and{N}^{-}$, respectively and $x=x_f=\frac{m_{N_1}}{T_f}$, where T_f is the freeze out temperature. Then the relic density of the N₁ DM can be given by Griest and Seckel [89], Chatterjee and Sahu [90], and Patra et al. [91]

$\begin{array}{ll}{\Omega }_{N_1}{h}^2=\frac{1.09\times 10^9\text{Ge}{\text{V}}^{-1}}{g_{\star }^{1/2}{M}_{PL}}\frac{1}{J(x_f)},& (56)\end{array}$

where J(x_f) is given by

$\begin{array}{ll}J(x_f)={\displaystyle {\int }_{x_f}^{\infty }}\frac{{\langle \sigma \left|v\right|\rangle }_{eff}}{x^2}dx.& (57)\end{array}$

We note here that the freeze-out abundance of N₁ DM is controlled by the annihilation and co-annihilation channels as shown in Figures 17–19. Therefore, the important parameters which decide the relic abundance of N₁ are mass of DM (m_N1), the mass splitting (Δm) between the DM and the next-to-lightest stable particle (NLSP) and the singlet-doublet mixing angle sin θ. Here we use MicrOmega [66] to calculate the relic density of N₁ DM.

Variation of relic density of N₁ DM is shown in Figure 20 as a function of its mass, for a fixed Δm = 10 − 100 GeV (in left and right panels of Figure 20, respectively) and different choices of mixing angle sin θ. We note that the annihilation cross-section increases with sin θ, due to larger SU(2) component, resulting in smaller relic density. The resonance drop at m_Z/2 and at m_h/2 is observed due to s-channel Z and H mediated contributions to relic abundance. Another important feature of Figure 20 is that when Δm is small, relic density is smaller due to large co-annihilation contribution (less Boltzmann suppression followed from Equation 54). This feature can also be corroborated from Figure 21, where we have shown relic density as a function of DM mass by keeping a fixed range of sin θ and chosen different possible Δm. Alternatively in Figure 21, we have shown relic density as a function of DM mass by keeping a fixed range of Δm, while varying sin θ. We see from the left panel of Figure 21 that for small Δm co-annihilation dominates and hence the effect of sin θ on relic abundance is quite negligible. On the other hand, from the right panel of Figure 21, we see that for large Δm, where co-annihilation is suppressed, the effect of sin θ on relic abundance is clearly visible. For small sin θ, the effective annihilation cross-section is small which leads to large relic abundance, while for large sin θ the relic abundance is small provided that the Δm is big enough to avoid co-annihilation contributions.

FIGURE 20

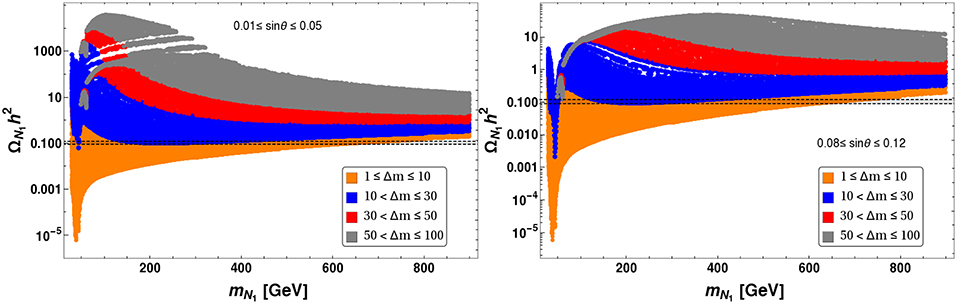
Figure 20. Variation of relic density with DM mass m_N1 keeping fixed range of sin θ: 0.01 ≤ sin θ ≤ 0.05 (left panel) and 0.08 ≤ sin θ ≤ 0.12 (right panel). The different color patches corresponds to different Δm region : 1 ≤ Δm(inGeV) ≤ 10 (Orange), 10 < Δm(inGeV) ≤ 30 (Blue), 30 < Δm(inGeV) ≤ 50 (Red) and 50 < Δm(inGeV) ≤ 100 (Gray). Correct relic density, 0.1166 ≤ Ωh² ≤ 0.1206 is shown by black dashed line. All the masses are in GeVs.

FIGURE 21

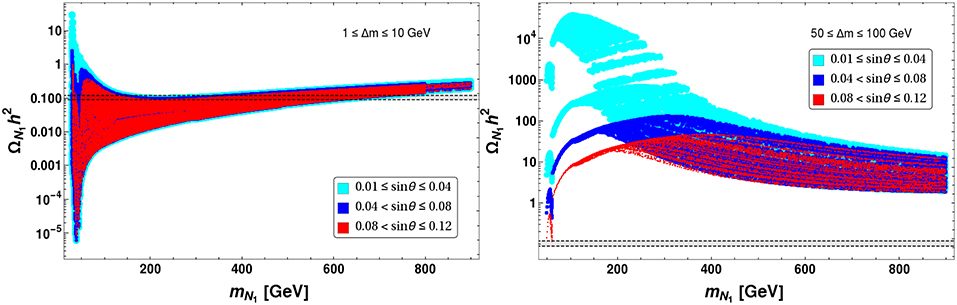
Figure 21. Variation of relic density with DM mass m_N1 keeping fixed region of Δm: 1 ≤ Δm ≤ 10 GeV (left panel) and 50 ≤ Δm ≤ 100 GeV (right panel). The different color patches are corresponding to different sin θ region : 0.01 ≤ sin θ ≤ 0.04 (Cyan), 0.04 < sin θ ≤ 0.08 (Blue), 0.08 < sin θ ≤ 0.12 (Red). Correct relic density, 0.1166 ≤ Ωh² ≤ 0.1206 is shown by black dashed line. All the masses are in GeVs.

From Figure 22, we see that for a wide range of singlet-doublet mixing (sin θ), we can get correct relic abundance in the plane of m_N1 vs. Δm. Different ranges of sin θ are indicted by different color codes. To understand our result, we divide the plane of m_N1 vs. Δm into two regions: (i) the bottom portion with small Δm, where Δm decreases with larger mass of N₁, (ii) the top portion with larger mass splitting Δm, where Δm increases slowly with larger DM mass m_N1. In the former case, for a given range of sin θ, the annihilation cross-section decreases for large mass of N₁. Therefore, we need more co-annihilation contribution to compensate, which requires Δm to decrease. This also imply that the region below to each colored zone is under abundant (small Δm implying large co-annihilation for a given mass of N₁), while the region above is over abundant (large Δm implying small co-annihilation for a given mass of N₁). To understand the allowed parameter space in region (ii), we first note that co-annihilation contribution is much smaller here due to large Δm, so the annihilation processes effectively contribute to relic density. Now, let us recall that the Yukawa coupling Y ∝ Δm sin θ. Therefore, for a given sin θ, larger Δm can lead to larger Y and therefore larger annihilation cross-section to yield under abundance, which can only be tamed down to correct relic density by having a larger DM mass. Hence in case-(ii), the region above to each colored zone (allowed region of correct relic density) is under abundant, while the region below to each colored zone is over abundant. Thus, the over and under abundant regions of both cases (i) and (ii) are consistent with each other.

FIGURE 22

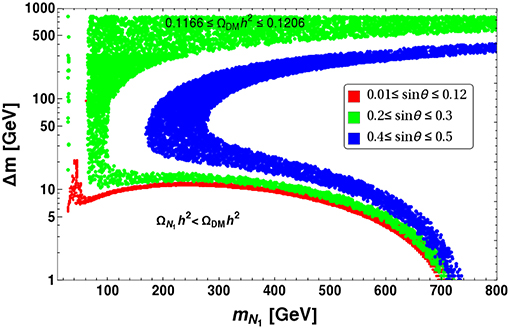
Figure 22. Relic density allowed region are shown in m_N1 − Δm plane for different range of range of sin θ: {0.01 − 0.12} (Red), {0.2 − 0.03} (Green), and {0.4 − 0.5} (Blue).

5.4. Constraints on Parameters From Direct Search of Singlet-Doublet Leptonic Dark Matter

Let us now turn to constraints on parameters from direct search of N₁ DM in terrestrial laboratories. Due to singlet-doublet mixing, the N₁ DM in direct search experiments can scatter off the target nucleus via Z and Higgs mediated processes as shown by the Feynman graphs in Figure 23. The cross-section per nucleon for Z-boson mediation is given by Goodman and Witten [92] and Essig [93]

$\begin{array}{ll}{\sigma }_{\text{SI}}^Z=\frac{1}{\pi A^2}{\mu }_r^2|{M}{|}^2& (58)\end{array}$

where A is the mass number of the target nucleus, μ_r = M₁m_n/(M₁ + m_n) ≈ m_n is the reduced mass, m_n is the mass of nucleon (proton or neutron) and ${M}$ is the amplitude for Z-boson mediated DM-nucleon cross-section given by

$\begin{array}{ll}{M}=\sqrt{2}{G}_F\left[\tilde{Z}(f_p/f_n)+(A-\tilde{Z})\right]f_n{sin}^2\theta ,& (59)\end{array}$

where f_p and f_n are the interaction strengths (including hadronic uncertainties) of DM with proton and neutron, respectively and $\tilde{Z}$ is the atomic number of the target nucleus. On the other hand, the spin-independent DM-nucleon cross-section per nucleon mediated via the exchange of SM Higgs is given by:

$\begin{array}{ll}{\sigma }_{\text{SI}}^h=\frac{1}{\pi A^2}{\mu }_r^2{\left[Z{f}_p+(A-Z)f_n\right]}^2& (60)\end{array}$

where the effective interaction strengths of DM with proton and neutron are given by:

$\begin{array}{ll}{f}_{p,n}={\displaystyle \sum _{q=u,d,s}}{f}_{Tq}^{(p.n)}{\alpha }_q\frac{m_{(p,n)}}{m_q}+\frac{2}{27}{f}_{TG}^{(p,n)}{\displaystyle \sum _{q=c,t,b}}{\alpha }_q\frac{m_{p.n}}{m_q}& (61)\end{array}$

with

$\begin{array}{ll}{\alpha }_q=\frac{Ysin2\theta }{M_h^2}\left(\frac{m_q}{v}\right).& (62)\end{array}$

In Equation (61), the different coupling strengths between DM and light quarks are given by Bertone et al. [4] $f_{Tu}^{(p)}=0.020\pm 0.004$, $f_{Td}^{(p)}=0.026\pm 0.005$, $f_{Ts}^{(p)}=0.118\pm 0.062$, $f_{Tu}^{(n)}=0.014\pm 0.004$, $f_{Td}^{(n)}=0.036\pm 0.008$, $f_{Ts}^{(n)}=0.118\pm 0.062$. The coupling of DM with the gluons in target nuclei is parameterized by

$\begin{array}{ll}{f}_{TG}^{(p,n)}=1-{\displaystyle \sum _{q=u,,d,s}}{f}_{Tq}^{(p,n)}.& (63)\end{array}$

Thus from Equations (60–63) the spin-independent DM-nucleon cross-section is given to be:

$\begin{array}{ll}\begin{array}{l}{\sigma }_{\text{SI}}^h=\frac{4}{\pi A^2}{\mu }_r^2\frac{Y^2{\sin }^{2}2\theta }{M_h^4}[\frac{m_p}{v}\left(f_{Tu}^p+f_{Td}^p+f_{Ts}^p+\frac{2}{9}{f}_{TG}^p\right)\hfill \\ {+\frac{m_n}{v}\left(f_{Tu}^n+f_{Td}^n+f_{Ts}^n+\frac{2}{9}{f}_{TG}^n\right)]}^2.\hfill \end{array}& (64)\end{array}$

In the above equation the only unknown quantity is Y or sin2θ which can be constrained by requiring that ${\sigma }_{\text{SI}}^h$ is less than the current DM-nucleon cross-sections.

FIGURE 23

Figure 23. Feynman diagrams of SI direct detection of singlet-doublet N₁ DM.

Now we make a combined analysis by taking both Z and H mediated diagrams taken into account together. In Figure 24, we show the spin-independent cross-section for N₁ DM within its mass range m_N1:1 − 1000 GeV. The plot is obtained by varying sin θ within {0.001 − 0.12} with sin θ = {0.001 − 0.01} (Cyan), sin θ = {0.01 − 0.04} (Blue), sin θ = {0.04 − 0.08} (Red), sin θ = {0.08 − 0.12} (Green). It clearly shows that the larger is sin θ, the stronger is the interaction strength (through larger contribution from Z mediation) and hence the larger is the DM-nucleon cross-section. Hence, it turns out that direct search experiments constraints sin θ to a large extent. For example, we see that sin θ ≤ 0.04, for the DM mass m_N1 > 300 GeV. The effect of Δm on DM-nucleon cross-section is less. However, we note that Δm plays a dominant role in the relic abundance of DM. Approximately, sin θ ≤ 0.05 (Blue points) are allowed for most of the parameter space except for smaller DM masses. Cyan points indicate sin θ < 0.01. The discrete bands correspond to specific values of sin θ chosen for the scan and essentially one can consider the whole region together to fall into this category which evidently have sensitivity close to neutrino floor. Note here, the scanned points in Figure 24, do not satisfy relic abundance.

FIGURE 24

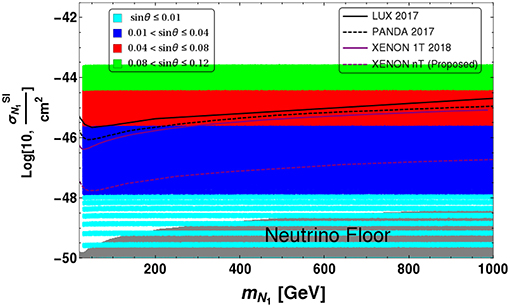
Figure 24. Spin independent direct detection cross-section σ^SI as a function of DM mass m_N1 for different range of sin θ: {0.001 − 0.01} (Cyan),{0.01 − 0.04} (Blue), {0.04 − 0.08} (red), and {0.08 − 0.12} (Green). The direct search limits from LUX, PANDA, XENON1T are shown while that of the future sensitivity of XENONnT is also indicated.

Now let us turn to the parameter space, simultaneously allowed by observed relic density and latest constraints from direct DM search experiments, such as Xenon-1T. In Figure 25, we have shown the allowed parameter space again in m_N1− Δm plane. We see that null observation from direct search crucially tames down the relic density allowed parameter space to sin θ < 0.05 (Purple). Figure 25 also shows that large singlet-doublet mixing, i.e., sin θ ≳ 0.05, allowed by correct relic density, is no more allowed by direct search limit in accordance with Figure 24.

FIGURE 25

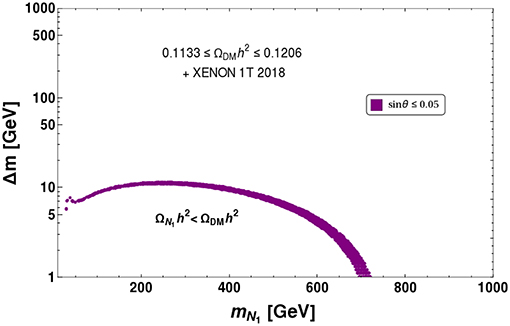
Figure 25. Relic density and direct detection (XENON 1T 2018) allowed parameter space plotted in m_N1 − Δm plane.

We finally summarize the DM analysis of singlet doublet case here. The model offers an interesting phenomenology to exploit singlet-doublet mixing (sin θ) in accordance with DM mass (m_N1) and the splitting with charged fermion content (Δm) to yield a large available parameter space for correct relic density. However, due to Z-mediated process contributing to direct detection of singlet-doublet leptonic dark matter, a stringent constraint on sin θ ≤ 0.05 arises. This leads the DM to be allowed only in small Δm region (as in Figure 25) to achieve correct relic density through co-annihilation processes. However, this constraint can be relaxed in presence of a scalar triplet as we discuss below. Moreover, the triplet can also give rise Majorana masses to light neutrinos (see section 4.2) through type-II seesaw to address DM and neutrinos in the same framework.

6. Triplet Extension of Singlet-Doublet Leptonic Dark Matter

6.1. Pseudo-Dirac Nature of Singlet-Doublet Leptonic Dark Matter

As discussed in section 5, the DM is assumed to be $N_1=cos\theta \chi +sin\theta N^0$ with a Dirac mass m_N1. However, from Equation (12) we see that the vev of Δ induces a Majorana mass to N₁ due to singlet-doublet mixing and is given by:

$\begin{array}{ll}{m}_1=\sqrt{2}{f}_N{sin}^2\theta \langle \Delta \rangle \approx f_N{sin}^2\theta \frac{-\mu v^2}{\sqrt{2}{M}_{\Delta }^2}.& (65)\end{array}$

Thus the N⁰ has a large Dirac mass m_N1 and a small Majorana mass m as shown in the above Equation (65). Therefore, we get a mass matrix in the basis $\left\{N_{1L},{(N_{1R})}^c\right\}$ as:

$\begin{array}{ll}{M}=\left(\begin{array}{cc}{m}_1& m_{N_1}\\ m_{N_1}& m_1\end{array}\right).& (66)\end{array}$

Thus the Majorana mass m splits the Dirac spinor N₁ into two pseudo-Dirac states ψ_1,2 with mass eigenvalues m_N1 ± m. The mass splitting between the two pseudo-Dirac states ψ_1,2 is given by

$\begin{array}{ll}\delta m_1=2m_1=2\sqrt{2}{f}_N{sin}^2\theta \langle \Delta \rangle .& (67)\end{array}$

Note that δm₁ << m_N1 from the estimate of induced vev of the triplet and hence does not play any role in the relic abundance calculation. However, the sub-GeV order mass splitting plays a crucial role in direct detection by forbidding the Z-boson mediated DM-nucleon elastic scattering. Now from Equations (20, 65) we see that the ratio:

$\begin{array}{ll}R=\frac{M_{\nu }}{m_1}=\frac{f_L}{f_N{sin}^2\theta }.& (68)\end{array}$

Thus we see that for R ~ 10⁻⁵ the ratio, $f_L/f_N~10^{-3}$ if we assume sin θ = 0.1, which is much larger than the singlet-doublet mixing being used in section 5.4.

6.2. Effect of Scalar Triplet on Relic Abundance and Direct Search of Singlet-Doublet Dark Matter

We already have noted the diagrams that are present due to the addition of a scalar triplet for the ILD DM to freeze-out (see section 4.4). The main features of having an additional scalar triplet in the singlet-doublet DM model is very similar to what we have discussed before in case of ILD DM. The additional freedom that we have in case of singlet-doublet leptonic DM is to play with the mixing parameter sin θ and Δm.

Let us first study relic density as a function of DM mass in presence of scalar triplet. This is shown in Figure 26, where we choose two fixed values of Δm = 10, 200 GeV in left and right panel, respectively for a scalar triplet mass around 280 GeV. Different possible ranges of sin θ are shown by different color codes. The main feature is again to see a drop in relic density near the value of the triplet mass, where the additional annihilation channel to the scalar triplet reduces relic density significantly. For small Δm, co-annihilation channels play an important part and therefore different mixing angles do not affect relic density significantly (compare left and right panel figures). Also due to large co-annihilation for small Δm as in the left panel, the relic density turns out to be much smaller than the right panel figure where Δm is large and do not offer the co-annihilation channels to be operative. An additional resonance drop at half of the triplet scalar mass is observed here (~ 140 GeV) due to s-channel triplet mediated processes.

FIGURE 26

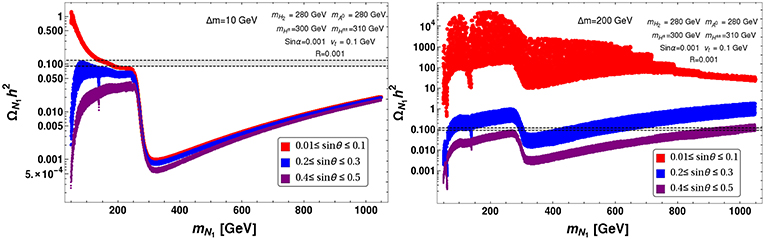
Figure 26. Variation of relic density with DM mass m_N1 keeping fixed region of Δm: Δm = 10 GeV (left panel) and Δm = 200 GeV (right panel) in presence of scalar triplet. Different color patches correspond to different sin θ region : 0.01 ≤ sin θ ≤ 0.1 (Red), 0.2 < sin θ ≤ 0.3 (Blue), 0.4 < sin θ ≤ 0.5 (Purple). Correct relic density, 0.1166 ≤ Ωh² ≤ 0.1206 is shown by black dashed line. All the masses are in GeVs.

A similar plot is shown in Figure 27 with larger value of the scalar triplet mass ~ 1000 GeV. Obviously the features from Figure 26, is mostly retained where the drop in relic density is observed around ~ 1000 GeV and the drop is also smaller than what we had for smaller triplet mass.

FIGURE 27

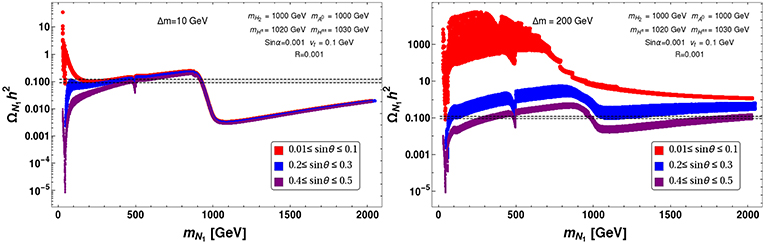
Figure 27. Variation of relic density with DM mass m_N1 keeping fixed region of Δm: Δm = 10 GeV (left panel) and Δm = 200 GeV (right panel) for heavy scalar triplet mass, m_H2 = 1000 GeV. Different color patches correspond to different sin θ region : 0.01 ≤ sin θ ≤ 0.1 (Red), 0.2 < sin θ ≤ 0.3 (Blue), 0.4 < sin θ ≤ 0.5 (Purple). Correct relic density, 0.1166 ≤ Ωh² ≤ 0.1206 is shown by black dashed line. All the masses are in GeVs.

Relic density allowed parameter space of the model in m_N1 − Δm plane is shown in left panel of Figure 28. The bottom part of the allowed parameter space is again due to co-annihilation. For small sin θ ~ 0.1 (red points), this is the only allowed parameter space except the resonance at the extreme left hand side. For larger sin θ, the resonance drops of doublet and triplet scalars also yield correct relic density. There is an under-abundant region when the triplet channel opens up, which is then reduced with larger DM mass. Therefore, it ends up with two different patches (both for blue and purple points) to be allowed below and above the scalar triplet mass. The direct search constraint in presence of scalar triplet thankfully omits the Z mediated diagram due to the pseudo-Dirac splitting and allows a larger sin θ ~ 0.3. However, in addition to the Yukawa coupling (Y) initiated SM Higgs mediation, there is an added contribution from the heavy Higgs due to the doublet triplet mixing. We have already seen before that the effect of the additional contribution to direct search cross-section is small in the small sin α limit with a moderate choice of f_N. Therefore, we have omitted such contributions in generating the direct search allowed parameter space of the model as shown in the right panel of Figure 28. This again depicts that the model in presence of scalar triplet earns more freedom in relaxing Δm and sin θ to some extent.

FIGURE 28

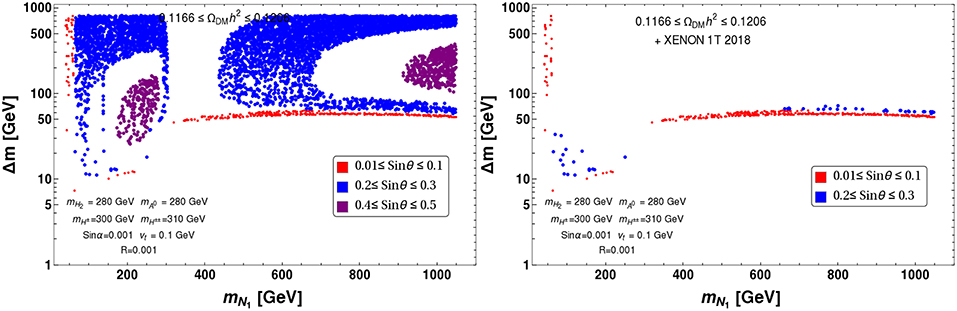
Figure 28. Relic density (left panel) and both relic density and direct search (XENON 1T 2018) (right panel) allowed parameter space plotted in m_N1 − Δm plane with different range of sin θ : 0.01 ≤ sin θ ≤ 0.1 (Red), 0.2 < sin θ ≤ 0.3 (Blue), 0.4 < sin θ ≤ 0.5 (Purple).

7. Collider Signatures

Finally, we discuss the collider signature of the model, which can be subdivided into two categories: (i) Displaced vertex signature and (ii) Excess in leptonic final states.

7.1. Displaced Vertex Signature

In the small sin θ limit, the charged inert fermion can show a displaced vertex signature. If the mass difference between the N⁻ and N₁ is greater than W⁻ mass then N⁻ can decay via a two body process. But if the mass difference is smaller than M_W, then N⁻ can decay via three body process say $N^{-}\to N_1{l}^{-}\overline{{\nu }_l}$. The three body decay width is given as Bhattacharya et al. [53]:

$\begin{array}{ll}\Gamma =\frac{G_F^{2}si{n}^2\theta }{24{\pi }^3}{m}_N^{5}I& (69)\end{array}$

where G_F is the Fermi coupling constant and I is given as:

$\begin{array}{l}I=\frac{1}{4}{\lambda }^{1/2}(1,a^2,b^2)F_1(a,b)+6F_2(a,b)ln\\ \left(\frac{2a}{1+a^2-b^2-{\lambda }^{1/2}(1,a^2,b^2)}\right).& (70)\end{array}$

In the above Equation F₁(a, b) and F₂(a, b) are two polynomials of a = m_N1/m_N and b = m_ℓ/m_N, where m_ℓ is the charged lepton mass. Up to ${O}$(b²), these two polynomials are given by

$\begin{array}{ll}\begin{array}{l}{F}_1(a,b)=(a^6-2a^5-7a^4(1+b^2)+10a^3(b^2-2)\hfill \\ +a^2(12b^2-7)+(3b^2-1))\hfill \\ F_2(a,b)=\left(a^5+a^4+a^3(1-2b^2)\right).\hfill \end{array}& (71)\end{array}$

In Equation (70), ${\lambda }^{1/2}=\sqrt{1+a^4+b^4-2a^2-2b^2-2a^2{b}^2}$ defines the phase space. In the limit b = m_ℓ/m_N → 1 − a = δM/m_N, λ^1/2 goes to zero and hence I → 0. The life time of N⁻ is then given by τ ≡ Γ⁻¹. We take the freeze out temperature of DM to be T_f = m_N1/20. Since the DM freezes out during radiation dominated era, the corresponding time of DM freeze-out is given by :

$\begin{array}{ll}{t}_f=0.301g_{\star }^{-1/2}\frac{m_{\text{pl}}}{T_f^2},& (72)\end{array}$

where g_* is the effective massless degrees of freedom at a temperature T_f and m_pl is the Planck mass. Demanding that N⁻ should decay before the DM freezes out (i.e., τ ≲ t_f) we get

$\begin{array}{l}sin\theta \gtrsim 1.1789\times 10^{-5}{\left(\frac{1.375\times 10^{-5}}{I}\right)}^{1/2}{\left(\frac{200\text{GeV}}{m_N}\right)}^{5/2}\\ {\left(\frac{g_{\star }}{106.75}\right)}^{1/4}\left(\frac{m_{N_1}}{180\text{GeV}}\right).& (73)\end{array}$

The lower bound on the mixing angle depends on the mass of N⁻ and N₁. For a typical value of m_N = 200 GeV, m_N1 = 180 GeV, we get sin θ ≳ 1.17 × 10⁻⁵. Since τ is inversely proportional to $m_N^5$, larger the mass, smaller will be the lower bound on the mixing angle.

To explore more whether we can get the relic abundance and displaced vertex simultaneously, we have shown in Figure 29 relic abundance as a function of DM mass keeping the mass splitting ΔM ≤ 50 GeV and sin θ = 10⁻⁴. In this small mixing angle limit there are coannihilation channels (see Figure 19) which are independent of sin θ contributes to relic density. We choose the set of points which are giving us the correct relic density and tried to find the displaced vertex value. We have plotted in the right panel of Figure 29 displaced vertex (Γ⁻¹) as a function of m_N. We can see that in the large mass of m_N, the displaced vertex is very small as expected as Γ⁻¹ decreases with increase in mass. For larger mixing angles displaced vertex is suppressed. Again sin θ cannot be arbitrarily small as shown in Equation (73), so Γ⁻¹ will not be very large.

FIGURE 29

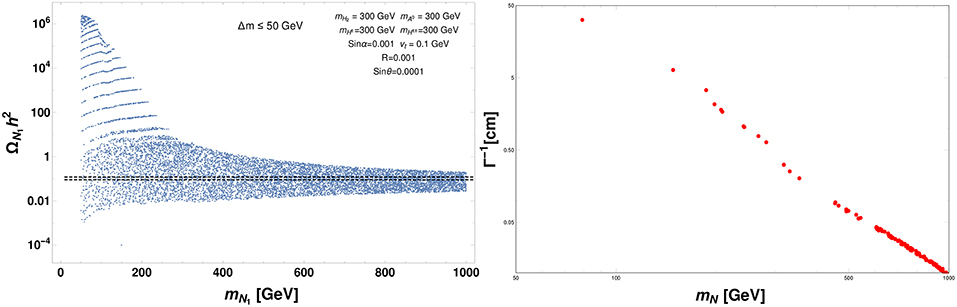
Figure 29. Variation of relic density with DM mass m_N1 keeping fixed Δm ≤ 50 GeV (left panel). Black dashed lines correspond to measured value of relic density by PLANCK. Displaced vertex (Γ⁻¹) is plotted as a function of m_N (right panel). For the displaced vertex we choose the set of parameters satisfying relic density from the left panel figure.

7.2. Hadronically Quiet Dilepton Signature

Since our proposed scenario have one vector like leptonic doublet, there is a possibility of producing charge partner pair of the doublet (N⁺ N⁻) at proton collider (LHC). The decay of N^± further produce leptonic final states through on-shell/off-shell W^± mediator to yield opposite sign dilepton plus missing energy as is shown in Figure 30. Obviously, W can decay to jets as well, to yield single lepton plus two jets and missing energy signature or that of four jets plus missing energy signature. But, LHC being a QCD machine, the jet rich final states are prone to very heavy SM background and cannot be segregated from that of the signal. We therefore refrain from calculating the other two possibilities here. A detailed analysis of collider signature of this model will be addressed in Barman et al. [94].

FIGURE 30

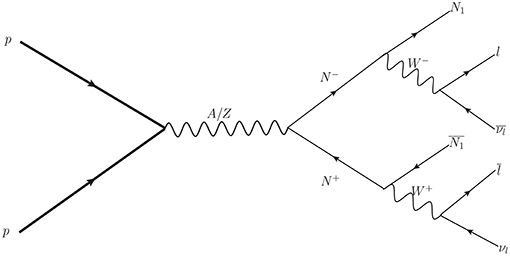
Figure 30. Feynman diagram for producing hadronically quiet opposite sign dilepton plus missing energy (${\ell }^{+}{\ell }^{-}+({\cancel{E}}_T)$) signal events at LHC.

Doublet-singlet fermion DM in absence or in presence of scalar triplet do not distinguish to yield a different final state from that of ${\ell }^{+}{\ell }^{-}+({\cancel{E}}_T)$ shown in Figure 30. However, there is an important distinction that we discuss briefly here. N⁺ N⁻ production cross-section depends on the charge lepton masses and nothing else, leptonic decay branching fraction is also fixed. However, the splitting between DM (N⁰) and its charged partner (N^±) ($\Delta m=m_{N^{\pm }}-m_{N^0}$) is seen in the missing energy distribution. The signal can only be segregated from that of the SM background when the splitting is large and it falls within the heaps of SM background when Δm is small. This feature can distinguish between the two cases of singlet doublet DM in presence and in absence of scalar triplet. To illustrate, we choose two benchmark points from two scenarios: i) doublet singlet leptonic DM (BP1) in absence of scalar triplet and ii) doublet singlet leptonic DM in presence of triplet (BP2), shown in Table 4. For BP1, we see that Δm = 10 GeV, has to be very small because relic density and direct search (XENON 1T 2018) put strong constraint on Δm (≤ 12 GeV). On the other hand, presence of triplet in this scenario can relax the situation to some extent, and one may choose large Δm ~ 150 GeV for low DM mass (~ 50 GeV) and obey both relic density and direct search constraint, as indicated in BP2. Again, we note here, that such a low DM mass is still allowed by the Invisible Higgs data due to small sin θ that we have taken here.

TABLE 4

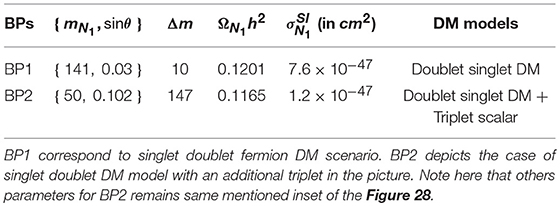
Table 4. DM mass, sin θ, $\Delta m=m_{N^{\pm }}-m_{N_1}$, relic density, and SI direct search cross-sections of two benchmark points are mentioned for collider study.

To study the collider signature of the model, we first implemented the model in FeynRule [95]. To generate events files, we used Madgraph [96] and further passed to Pythia [97] for analysis. We have imposed further selection cuts on leptons (ℓ = e, μ) and jets as follows to mimic the actual collider environment:

• Lepton isolation: Leptons are the main constituent of the signal. We impose transverse momentum cut of p_T > 20 GeV, pseudorapidity of |η| < 2.5 and separation cut ΔR ≥ 0.2 for separating from other leptons. Additionally, ΔR ≥ 0.4 is required to separate the leptons from jets. The definition of separation in azimuthal-pseudorapidity plane is $\Delta R=\sqrt{{(\Delta \eta )}^2+{(\Delta \varphi )}^2}$.

• Jet formation and identification is performed in Pythia. We use cone-algorithm and impose that the jet initiator parton must have p_T ≥ 20 GeV and forms a jet within a cone of ΔR ≤ 0.4. Jets are required to be defined for our events as to have zero jets.

Using above basic cuts, we have studied hadronically quite opposite signed dilepton final states :

$\begin{array}{l}\text{Signal}:: {\ell }^{\text{+}}{\ell }^{-}\text{+}({\cancel{E}}_{\text{T}}): \text{p} \text{p}\to {\text{N}}^{+} {\text{N}}^{-},({\text{N}}^{-}\to {\ell }^{-} \overline{{\nu }_{\ell }} {\text{N}}_1),\hfill \\ (N^{+}\to {\ell }^{+} {\nu }_{\ell } \overline{N_1}),\text{ w}here \ell =e,\mu .\hfill \end{array}$

The distribution of signal events with respect to missing Energy ($\cancel{E}$_T), invariant mass of OSD (m_ℓℓ) and effective momentum (H_T) is shown in Figure 31, respectively top left, top right and bottom panel. We see that each of the distribution becomes flatter and the peak is shifted to higher energy value with larger Δm. As we have already mentioned that SM background yields a very similar distribution to that of BP1 and therefore cannot be segregated from small Δm cases. For details of background estimate and distribution, see for example, [98]. Without further selection cuts, the signals constitute a very tiny fraction of hadronically quiet dilepton channel at LHC. To reduce SM background, further selection cuts must be employed:

• m_ℓℓ < |m_z − 15| and m_ℓℓ > |m_z + 15|,

• H_T > 100, 200 GeV,

• $\cancel{E}$_T > 100, 200 GeV.

FIGURE 31

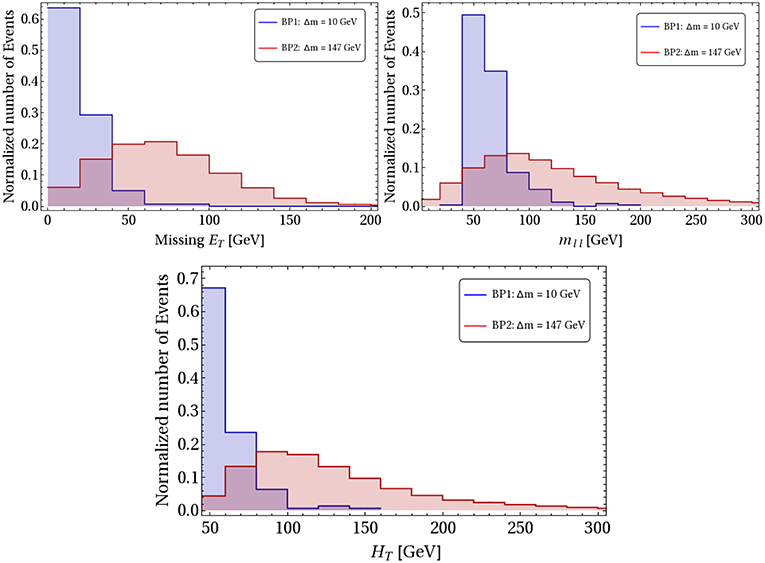
Figure 31. Missing energy ($\cancel{E}$_T), invariant mass of dilepton (m_ℓℓ), and transverse mass (H_T) distributions of the hadronically quite dilepton signal events (${\ell }^{+}{\ell }^{-}+{\cancel{E}}_T$) for C.O.M. energy, $\sqrt{s}=14\text{ TeV}$ at LHC.

We see that the signal events for BP1, after such a cut is reduced significantly, while for BP2, we are still left with moderately large number of events as shown in Table 5.

TABLE 5

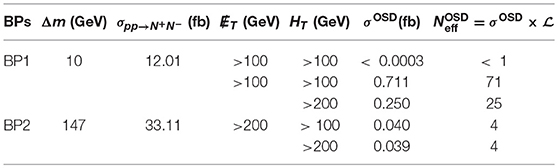
Table 5. Signal events for above mentioned benchmark points with $\sqrt{s}$ = 14 TeV at the LHC for the luminosity ${L}=100f{b}^{-1}$ after $\cancel{E}$_T, H_T and m_ℓℓ cuts.

To summarize, we point out that singlet-doublet fermion DM can possibly yield a displaced vertex signature out of the charged fermion decay, thanks to small mass splitting and small sin θ, while due to the same reason, seeing an excess in leptonic final state will be difficult. On the other hand, the model where singlet-doublet fermion DM is extended with a scalar triplet satisfy relic density and direct search with a larger mass splitting between the DM and charged companion which allows such a case to yield a lepton excess to be probed at LHC, but the displaced vertex signature may get subdued due to this. The complementarity of the two cases will be elaborated in Barman et al. [94]. We also note that scalar triplet extension do not allow the fermion DM to have any mass to also accommodate large Δm. This is only possible in the vicinity of Higgs resonance. We can however, earn a freedom on choosing a large Δm at any fermion mass value in the presence of a second DM component and see a lepton signal excess as has been pointed out in Barman et al. [94].

8. Conclusions and Future Directions

Vector like leptons stabilized by a symmetry, provide a simple solution to DM problem of the universe. The relic density allowed parameter space provide a wide class of phenomenological implications to be explored in DM direct search experiments and in collider searches through signal excess or displaced vertex. In this article, we have provided a thorough analysis of different possible models in such a category. The results have been illustrated with parameter space scans, taking into account the constraints coming from non-observation of DM in present direct search data, constraints from electroweak precision tests, vacuum stability, invisible decay widths of Higgs and Z etc., to see the allowed region where the model(s) can be probed in upcoming experiments.

We first reviewed the possibility of vector-like leptonic singlet χ, doublet N and their combination χ − N as viable candidates of DM. First we discussed about a vector-like singlet leptonic DM χ. In this case, the DM can only couple to visible sector through non-renormalizable dimension-5 operator $\overline{\chi }\chi H^{†}H/\Lambda$, where Λ denotes a new physics (NP) scale. We find relic density allowed parameter space of the model requires Λ to be 500 GeV or less for DM mass ranging between 100 GeV to 500 GeV. However, the direct search cross-section for such Λ is much larger than the constraints obtained from XENON1T data. Therefore, a singlet lepton is almost ruled out being a viable candidate of DM.

We then discussed the possibility of neutral component of a vector-like inert lepton doublet (ILD) N⁰ to be a viable DM candidate. Since the doublet has only gauge interaction, the correct relic abundance can be obtained only at heavy DM mass around ~ TeV. Again, the doublet DM suffers a stringent constraint from Z-mediated elastic scattering at direct search experiments. The relic density allowed parameter space therefore lies way above than the XENON1T bound of not observing a DM in direct search experiment. Therefore, an ILD DM alone is already ruled out. However, we showed that in presence of a scalar triplet, an ILD DM can be reinstated by forbidding the Z-mediated elastic scattering with the nucleons thanks to pseudo Dirac splitting. Due to additional interaction of ILD in presence of a scalar triplet, the mass of ILD DM is pushed to a higher side to achieve correct relic density. Moreover, the scalar triplet mixes with the SM doublet Higgs and paves a path for detecting the ILD DM at terrestrial laboratories. The presence of scalar triplet also yield a non-zero neutrino mass to three flavors of active neutrinos which are required by oscillation data. However, we noticed that the parameter space of an ILD DM is very limited to a very high mass due to its gauge coupling.

We then searched for a combination of singlet χ and neutral component of doublet N = (N⁻, N⁰) being a viable candidate of DM. This is possible if both of the fermion fields possess same Z₂ symmetry. They mix after electroweak symmetry breaking. In fact, we found that the appropriate combination of a singlet-doublet can be a viable DM candidate in a large parameter space spanning DM mass between Z resonance to ~ 700 GeV. The singlet-doublet mixing plays a key role in deciding the relic abundance of DM as well as detecting it in terrestrial laboratories. In fact, we found that a large singlet component admixture with a small doublet component is an appropriate combination to be a viable candidate for DM, particularly to meet direct search bounds (sin θ ≤ 0.05). However, it is difficult for a DM with large singlet component to yield correct relic density due to small annihilation cross-section. Therefore, it has to depend heavily on co-annihilation to make up the small annihilation cross section, which in turn requires a small mass difference between the DM N₁ and its partners $N^{\pm },N_2$. In particular, if the mixing angle is very small (around sin θ ~ 10⁻⁴), the decay of NLSP ($N^{-}\to N_1+l^{-}+{\bar{\nu }}_l$) gives a measurable displaced vertex signature at LHC, aided by a small mass difference of N⁻ with the DM (N₁). However, this typical feature makes it difficult to identify any signal excess from production of the NLSP at LHC.

The situation becomes more interesting in presence of a scalar triplet. The latter, not only enhances the allowed parameter space of singlet-doublet mixed DM (by allowing a larger mixing sin θ ≲ 0.2 and also a larger mass splitting between NLSP and DM), but also generates masses to three flavors active neutrinos via type-II seesaw. Presence of scalar triplet may also pave the path to discover this model through hadronically quiet dilepton channel at LHC. We would also like to add here that if the DM (singlet-doublet admixture) including the SM particles are charged under an additional flavor symmetry, say A₄, then non-zero value of θ₁₃ can be obtained from the flavor charge of DM, which has been elaborated in Bhattacharya et al. [99, 100].

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Basabendu Barman for helpful discussions. SB would like to acknowledge the support from DST-INSPIRE faculty grant IFA-13-PH-57 at IIT Guwahati. PG also like to thank MHRD, Government of India for research fellowship.

Footnotes

1. ^The scale Λ is a priori unknown and should be validated from experimental constraints. In effective theory consideration, we ensure that m_χ < Λ.

2. ^We would like to remind the readers that N₁ and N₂ are not same as $N_1^0$ and $N_2^0$. N_{1, 2} are the physical eigenstates arising out of the singlet (χ) doublet (N) admixture. Here, N₁ is the DM while N₂ is the NLSP. Where as, $N_1^0$ and $N_2^0$ are the two pseudo Dirac states that emerge from the neutral component (N⁰) of the vector-like lepton doublet (N) due to the majorana mass term acquired by N⁰ in presence of the scalar triplet Δ.

3. ^The value Ŝ, $\widehat{T}$, W and Y are obtained using a Higgs mass m_h = 115 GeV. However, we now know that the SM Higgs mass is 125 GeV. Therefore, the value of Ŝ, $\widehat{T}$, W and Y are expected to change. But this effect is nullified by the small values of sin θ.

References

1. Zwicky F. Die Rotverschiebung von extragalaktischen Nebeln. Helv Phys Acta. (1933) 6:110–27. [Gen Rel Grav. (2009) 41:207].

Google Scholar

2. Rubin VC, Ford Jr WK. Rotation of the Andromeda Nebula from a spectroscopic survey of emission regions. Astrophys J. (1970) 159:379.

Google Scholar

3. Clowe D, Bradac M, Gonzalez AH, Markevitch M, Randall SW, Jones C, et al. A direct empirical proof of the existence of dark matter. Astrophys J. (2006) 648:L109–13. doi: 10.1086/508162

CrossRef Full Text | Google Scholar

4. Bertone G, Hooper D, Silk J. Particle dark matter: evidence, candidates and constraints. Phys Rept. (2005) 405:279–390. doi: 10.1016/j.physrep.2004.08.031

CrossRef Full Text | Google Scholar

5. Jungman G, Kamionkowski M, Griest K. Supersymmetric dark matter. Phys Rept. (1996) 267:195–373.

Google Scholar

6. Hinshaw G, Larson D, Komatsu E, Spergel DN, Bennett CL, Dunkley J, et al. WMAP Collaboration. Nine-year Wilkinson Microwave Anisotropy Probe (WMAP) observations: cosmological parameter results. Astrophys J Suppl. (2013) 208:19. doi: 10.1088/0067-0049/208/2/19

CrossRef Full Text | Google Scholar

7. Ade PAR, Aghanim N, Armitage-Caplan C, Arnaud M, Ashdown M, Atrio-Barandela F, et al. Planck Collaboration. Planck 2013 results. XVI. Cosmological parameters. Astron Astrophys. (2014) 571:A16. doi: 10.1051/0004-6361/201321591

CrossRef Full Text | Google Scholar

8. Aghanim N, Akrami Y, Ashdown M, Aumont J, Baccigalupi C, Ballardini M, et al. Planck collaboration. Planck 2013 results. VI. Cosmological parameters. arXiv: 1807.06209 (2018).

Google Scholar

9. Aprile E, Alfonsi M, Arisaka K, Arneodo F, Balan C, Baudis L, et al. XENON100 Collaboration. Dark matter results From 225 live days of XENON100 data. Phys Rev Lett. (2012) 109:181301. doi: 10.1103/PhysRevLett.109.181301

CrossRef Full Text | Google Scholar

10. Akerib DS, Alsum S, Arajo HM, Bai X, Bailey AJ, Balajthy J, et al. LUX Collaboration. Limits on spin-dependent WIMP-nucleon cross section obtained from the complete LUX exposure. Phys Rev Lett. (2017) 118:251302. doi: 10.1103/PhysRevLett.118.251302

CrossRef Full Text | Google Scholar

11. Aprile E, Aalbers J, Agostini F, Alfonsi M, Althueser L, Amaro FD, et al. XENON Collaboration. Physics reach of the XENON1T dark matter experiment. JCAP. (2016) 1604:027. doi: 10.1088/1475-7516/2016/04/027

CrossRef Full Text | Google Scholar

12. Aprile E, Aalbers J, Agostini F, Alfonsi M, Althueser L, Amaro FD, et al. XENON Collaboration. Dark matter search results from a one ton-year exposure of XENON1T. Phys Rev Lett. (2018) 121:111302. doi: 10.1103/PhysRevLett.121.111302

CrossRef Full Text | Google Scholar

13. Cui X, Abdukerim A, Chen W, Chen X, Chen Y, Dong B, et al. PandaX-II Collaboration. Dark matter results from 54-ton-day exposure of PandaX-II experiment. Phys Rev Lett. (2017) 119:181302. doi: 10.1103/PhysRevLett.119.181302

CrossRef Full Text | Google Scholar

14. Adriani O, Barbarino GC, Bazilevskaya GA, Bellotti R, Bianco A, Boezio M, et al. PAMELA Collaboration. Cosmic-ray positron energy spectrum measured by PAMELA. Phys Rev Lett. (2013) 111:081102. doi: 10.1103/PhysRevLett.111.081102

CrossRef Full Text | Google Scholar

15. Adriani O, Barbarino GC, Bazilevskaya GA, Bellotti R, Bianco A, Boezio M, et al. PAMELA Collaboration. The cosmic-ray electron flux measured by the PAMELA experiment between 1 and 625 GeV. Phys Rev Lett. (2011) 106:201101. doi: 10.1103/PhysRevLett.106.201101

CrossRef Full Text | Google Scholar

16. Corti C, AMS Collaboration. The cosmic ray electron and positron spectra measured by AMS-02. arXiv:1402.0437 (2014).

Google Scholar

17. Atwood WB, Abdo AA, Ackermann M, Althouse W, Anderson B, Axelsson M, et al. Fermi-LAT Collaboration. The large area telescope on the Fermi gamma-ray space telescope mission. Astrophys J. (2009) 697:1071. doi: 10.1088/0004-637X/697/2/1071

CrossRef Full Text | Google Scholar

18. Aartsen MG, Ackermann M, Adams J, Aguilar JA, Ahlers M, Ahrens M, et al. IceCube Collaboration. Search for neutrinos from dark matter self-annihilations in the center of the milky way with 3 years of IceCube/DeepCore. Eur Phys J C. (2017) 77:627. doi: 10.1140/epjc/s10052-017-5213-y

CrossRef Full Text | Google Scholar

19. Aartsen MG, Ackermann M, Adams J, Aguilar JA, Ahlers M, Ahrens M, et al. IceCube Collaboration. Search for neutrinos from decaying dark matter with IceCube. Eur Phys J C. (2018) 78:831. doi: 10.1140/epjc/s10052-018-6273-3

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Aaboud M, ATLAS Collaboration. Search for dark matter at $\sqrt{s}=13$ TeV in final states containing an energetic photon and large missing transverse momentum with the ATLAS detector. Eur Phys J C. (2017) 77:393. doi: 10.1140/epjc/s10052-017-4965-8

CrossRef Full Text | Google Scholar

21. Burns DR. A Collider Search for Dark Matter Produced in Association With a Higgs Boson With the CMS Detector at the 13 TeV LHC. CERN-THESIS-2017-048. Davis, CA: University of California.

Google Scholar

22. Kopecky AC. A Search for Dark Matter in the Monophoton Final State at CMS. CERN-THESIS-2012-265.

Google Scholar

23. Fukuda S, Fukuda Y, Ishitsuka M, Itow Y, Kajita T, Kameda J, et al. Super-Kamiokande Collaboration. Constraints on neutrino oscillations using 1258 days of Super-Kamiokande solar neutrino data. Phys Rev Lett. (2001) 86:5656–60. doi: 10.1103/PhysRevLett.86.5656

CrossRef Full Text | Google Scholar

24. Kim YG, Lee KY. The minimal model of fermionic dark matter. Phys Rev D. (2007) 75:115012. doi: 10.1103/PhysRevD.75.115012

CrossRef Full Text | Google Scholar

25. Kim YG, Lee KY, Shin S. Singlet fermionic dark matter. JHEP. (2008) 0805:100. doi: 10.1088/1126-6708/2008/05/100

CrossRef Full Text | Google Scholar

26. Pospelov M, Ritz A, Voloshin MB. Secluded WIMP dark matter. Phys Lett B. (2008) 662:53. doi: 10.1016/j.physletb.2008.02.052

CrossRef Full Text | Google Scholar

27. Kim YG, Shin S. Singlet fermionic dark matter explains DAMA signal. JHEP. (2009) 0905:036. doi: 10.1088/1126-6708/2009/05/036

CrossRef Full Text | Google Scholar

28. Heo JH. Minimal dirac fermionic dark matter with nonzero magnetic dipole moment. Phys Lett B (2010) 693:255. doi: 10.1016/j.physletb.2010.08.035

CrossRef Full Text | Google Scholar

29. Cao QH, Chen CR, Li CS, Zhang H. Effective dark matter model: relic density, CDMS II, Fermi LAT and LHC. JHEP. (2011) 1108:018. doi: 10.1007/JHEP08(2011)018

CrossRef Full Text | Google Scholar

30. Lopez-Honorez L, Schwetz T, Zupan J. Higgs portal, fermionic dark matter, and a Standard Model like Higgs at 125 GeV. Phys Lett B. (2012) 716:179. doi: 10.1016/j.physletb.2012.07.017

CrossRef Full Text | Google Scholar

31. Ettefaghi MM, Moazzemi R. Annihilation of singlet fermionic dark matter into two photons. JCAP. (2013) 1302:048. doi: 10.1088/1475-7516/2013/02/048

CrossRef Full Text | Google Scholar

32. Fairbairn M, Hogan R. Singlet fermionic dark matter and the electroweak phase transition. JHEP. (2013) 1309:022. doi: 10.1007/JHEP09(2013)022

CrossRef Full Text | Google Scholar

33. Esch S, Klasen M, Yaguna CE. Detection prospects of singlet fermionic dark matter. Phys Rev D (2013) 88:075017. doi: 10.1103/PhysRevD.88.075017

CrossRef Full Text | Google Scholar

34. Dutta Banik A, Majumdar D. Extension of minimal fermionic dark matter model: a study with Two Higgs doublet model. Eur Phys J C. (2015) 75:364. doi: 10.1140/epjc/s10052-015-3589-0

CrossRef Full Text | Google Scholar

35. Fedderke MA, Chen JY, Kolb EW, Wang LT. The fermionic dark matter Higgs portal: an effective field theory approach. JHEP. (2014) 1408:122. doi: 10.1007/JHEP08(2014)122

CrossRef Full Text | Google Scholar

36. Bagherian Z, Ettefaghi MM, Haghgouyan Z, Moazzemi R. A new parameter space study of the fermionic cold dark matter model. JCAP. (2014) 1410:033. doi: 10.1088/1475-7516/2014/10/033

CrossRef Full Text | Google Scholar

37. Kim YG, Lee KY, Park CB, Shin S. Secluded singlet fermionic dark matter driven by the Fermi gamma-ray excess. Phys Rev D. (2016) 93:075023. doi: 10.1103/PhysRevD.93.075023

CrossRef Full Text | Google Scholar

38. Ettefaghi M, Moazzemi R. Analyzing of singlet fermionic dark matter via the updated direct detection data. Eur Phys J C. (2017) 77:343. doi: 10.1140/epjc/s10052-017-4894-6

CrossRef Full Text | Google Scholar

39. Kim YG, Lee KY, Nam SH. Singlet fermionic dark matter with Veltman conditions. Phys Lett B. (2018) 782:316. doi: 10.1016/j.physletb.2018.05.044

CrossRef Full Text | Google Scholar

40. McDonald J, Sahu N. Z(2)-Singlino dark matter in a portal-like extension of the minimal supersymmetric standard model. JCAP. (2008) 0806:026. doi: 10.1088/1475-7516/2008/06/026

CrossRef Full Text | Google Scholar

41. McDonald J, Sahu N. KeV warm dark matter via the supersymmetric Higgs portal. Phys Rev D. (2009) 79:103523. doi: 10.1103/PhysRevD.79.103523

CrossRef Full Text | Google Scholar

42. Sahu N, Sarkar U. Extended Zee model for neutrino mass, leptogenesis and sterile neutrino like dark matter. Phys Rev D. (2008) 78:115013. doi: 10.1103/PhysRevD.78.115013

CrossRef Full Text | Google Scholar

43. Arkani-Hamed N, Dimopoulos S, Kachru S. Predictive Landscapes and New Physics at a TeV. arXiv:hep-th/0501082 (2005).

Google Scholar

44. Mahbubani R, Senatore L. The minimal model for dark matter and unification. Phys Rev D. (2006) 73:043510. doi: 10.1103/PhysRevD.73.043510

CrossRef Full Text | Google Scholar

45. Eramo FD. Dark matter and Higgs boson physics. Phys Rev D. (2007) 76:083522. doi: 10.1103/PhysRevD.76.083522

CrossRef Full Text | Google Scholar

46. Enberg R, Fox PJ, Hall LJ, Papaioannou AY, Papucci M. LHC and dark matter signals of improved naturalness. JHEP. (2007) 0711:014. doi: 10.1088/1126-6708/2007/11/014

CrossRef Full Text | Google Scholar

47. Cohen T, Kearney J, Pierce A, Tucker-Smith D. Singlet-doublet dark matter. Phys Rev D. (2012) 85:075003. doi: 10.1103/PhysRevD.85.075003

CrossRef Full Text | Google Scholar

48. Cheung C, Sanford D. Simplified models of mixed dark matter. JCAP. (2014) 1402:011. doi: 10.1088/1475-7516/2014/02/011

CrossRef Full Text | Google Scholar

49. Restrepo D, Rivera A, Sánchez-Peláez M, Zapata O, Tangarife W. Radiative neutrino masses in the singlet-doublet fermion dark matter model with scalar singlets. Phys Rev D. (2015) 92:013005. doi: 10.1103/PhysRevD.92.013005

CrossRef Full Text | Google Scholar

50. Calibbi L, Mariotti A, Tziveloglou P. Singlet-doublet model: dark matter searches and LHC constraints. arXiv:1505.03867 (2015).

Google Scholar

51. Cynolter G, Kovacs J, Lendvai E. Doublet-singlet model and unitarity. Mod Phys Lett A. (2015) 31:1650013. doi: 10.1142/S0217732316500139

CrossRef Full Text | Google Scholar

52. Bhattacharya S, Sahoo N, Sahu N. Minimal vectorlike leptonic dark matter and signatures at the LHC. Phys Rev D. (2016) 93:115040. doi: 10.1103/PhysRevD.93.115040

CrossRef Full Text | Google Scholar

53. Bhattacharya S, Sahoo N, Sahu N. Singlet-doublet fermionic dark matter, neutrino mass and collider signatures. Phys Rev D. (2017) 96:035010. doi: 10.1103/PhysRevD.96.035010

CrossRef Full Text | Google Scholar

54. Magg M, Wetterich C. Neutrino mass problem and gauge hierarchy. Phys Lett. (1980) 94B:61. doi: 10.1016/0370-2693(80)90825-4

CrossRef Full Text | Google Scholar

55. Lazarides G, Shafi Q, Wetterich C. Proton lifetime and fermion masses in an SO(10) model. Nucl Phys B. (1981) 181:287. doi: 10.1016/0550-3213(81)90354-0

CrossRef Full Text | Google Scholar

56. Mohapatra RN, Senjanovic G. Neutrino masses and mixings in gauge models with spontaneous parity violation. Phys Rev D. (1981) 23:165. doi: 10.1103/PhysRevD.23.165

CrossRef Full Text | Google Scholar

57. Ma E, Sarkar U. Neutrino masses and leptogenesis with heavy Higgs triplets. Phys Rev Lett. (1998) 80:5716. doi: 10.1103/PhysRevLett.80.5716

CrossRef Full Text | Google Scholar

58. Konetschny W, Kummer W. Nonconservation of total lepton number with scalar bosons. Phys Lett. (1977) 70B:433. doi: 10.1016/0370-2693(77)90407-5;

CrossRef Full Text | Google Scholar

59. Schechter J, Valle JWF. Neutrino masses in SU(2) x U(1) theories. Phys Rev D. (1980) 22:2227. doi: 10.1103/PhysRevD.22.2227

CrossRef Full Text | Google Scholar

60. Cheng TP, Li LF. Neutrino masses, mixings and oscillations in SU(2) x U(1) models of electroweak interactions. Phys Rev D. (1980) 22:2860. doi: 10.1103/PhysRevD.22.2860

CrossRef Full Text | Google Scholar

61. Tucker-Smith D, Weiner N. Inelastic dark matter. Phys Rev D. (2001) 64:043502. doi: 10.1103/PhysRevD.64.043502

CrossRef Full Text | Google Scholar

62. Cui Y, Morrissey DE, Poland D, Randall L. Candidates for inelastic dark matter. JHEP. (2009) 0905:076. doi: 10.1088/1126-6708/2009/05/076

CrossRef Full Text | Google Scholar

63. Arina C, Sahu N. Asymmetric inelastic inert doublet dark matter from triplet scalar leptogenesis. Nucl Phys B. (2012) 854:666. doi: 10.1016/j.nuclphysb.2011.09.014

CrossRef Full Text | Google Scholar

64. Arina C, Gong JO, Sahu N. Unifying darko-lepto-genesis with scalar triplet inflation. Nucl Phys B. (2012) 865:430. doi: 10.1016/j.nuclphysb.2012.07.029

CrossRef Full Text | Google Scholar

65. Arina C, Mohapatra RN, Sahu N. Co-genesis of matter and dark matter with vector-like fourth generation leptons. Phys Lett B. (2013) 720:130. doi: 10.1016/j.physletb.2013.01.059

CrossRef Full Text | Google Scholar

66. Belanger G, Boudjema F, Pukhov A, Semenov A. Dark matter direct detection rate in a generic model with micrOMEGAs 2.2. Comput Phys Commun. (2009) 180:747. doi: 10.1016/j.cpc.2008.11.019

CrossRef Full Text | Google Scholar

67. Ghorbani K. Fermionic dark matter with pseudo-scalar Yukawa interaction. JCAP. (2015) 1501:015. doi: 10.1088/1475-7516/2015/01/015

CrossRef Full Text | Google Scholar

68. Patrignani C, Agashe K, Aielli G, Amsler C, Antonelli M, Asner DM, et al. Particle Data Group. Review of particle physics. Chin Phys C. (2016) 40:100001. doi: 10.1088/1674-1137/40/10/100001

CrossRef Full Text | Google Scholar

69. Cheung K, Ko P, Lee JS, Tseng PY. Bounds on Higgs-Portal models from the LHC Higgs data. JHEP. (2015) 1510:057. doi: 10.1007/JHEP10(2015)057

CrossRef Full Text | Google Scholar

70. Hartling K, Kumar K, Logan HE. Indirect constraints on the Georgi-Machacek model and implications for Higgs boson couplings. Phys Rev D. (2015) 91:015013. doi: 10.1103/PhysRevD.91.015013

CrossRef Full Text | Google Scholar

71. Arhrib A, Benbrik R, Chabab M, Moultaka G, Peyranere MC, Rahili L, et al. The Higgs potential in the type II seesaw model. Phys Rev D. (2011) 84:095005. doi: 10.1103/PhysRevD.84.095005

CrossRef Full Text | Google Scholar

72. Akeroyd AG, Aoki M, Sugiyama H. Probing majorana phases and neutrino mass spectrum in the Higgs triplet model at the CERN LHC. Phys Rev D. (2008) 77:075010. doi: 10.1103/PhysRevD.77.075010

CrossRef Full Text | Google Scholar

73. Garayoa J, Schwetz T. Neutrino mass hierarchy and Majorana CP phases within the Higgs triplet model at the LHC. JHEP. (2008) 0803:009. doi: 10.1088/1126-6708/2008/03/009

CrossRef Full Text | Google Scholar

74. Chun EJ, Lee KY, Park SC. Testing Higgs triplet model and neutrino mass patterns. Phys Lett B. (2003) 566:142. doi: 10.1016/S0370-2693(03)00770-6

CrossRef Full Text | Google Scholar

75. Kadastik M, Raidal M, Rebane L. Direct determination of neutrino mass parameters at future colliders. Phys Rev D. (2008) 77:115023. doi: 10.1103/PhysRevD.77.115023

CrossRef Full Text | Google Scholar

76. Fileviez Perez P, Han T, Huang GY, Li T, Wang K. Neutrino masses and the CERN LHC: testing type II seesaw. Phys Rev D. (2008) 78:015018. doi: 10.1103/PhysRevD.78.015018

CrossRef Full Text | Google Scholar

77. Majee SK, Sahu N. Dilepton signal of a type-II seesaw at CERN LHC: reveals a TeV scale B-L symmetry. Phys Rev D. (2010) 82:053007. doi: 10.1103/PhysRevD.82.053007

CrossRef Full Text | Google Scholar

78. McDonald J, Sahu N, Sarkar U. Type-II seesaw at collider, lepton asymmetry and singlet scalar dark matter. JCAP. (2008) 0804:037. doi: 10.1088/1475-7516/2008/04/03

CrossRef Full Text | Google Scholar

79. Thomas SD, Wells JD. Phenomenology of massive vectorlike doublet leptons. Phys Rev Lett. (1998) 81:34. doi: 10.1103/PhysRevLett.81.34

CrossRef Full Text | Google Scholar

80. Aad G, ATLAS Collaboration. Search for invisible decays of a Higgs boson using vector-boson fusion in pp collisions at $\sqrt{s}=8$ TeV with the ATLAS detector. JHEP. (2016) 1601:172. doi: 10.1007/JHEP01(2016)172

CrossRef Full Text | Google Scholar

81. Baek S, Ko P, Park WI. Invisible Higgs decay width vs. dark matter direct detection cross section in Higgs portal dark matter models. Phys Rev D. (2014) 90:055014. doi: 10.1103/PhysRevD.90.055014

CrossRef Full Text | Google Scholar

82. Djouadi A, Lebedev O, Mambrini Y, Quevillon J. Implications of LHC searches for Higgs–portal dark matter. Phys Lett B. (2012) 709:65. doi: 10.1016/j.physletb.2012.01.062;

CrossRef Full Text | Google Scholar

83. Peskin ME, Takeuchi T. Estimation of oblique electroweak corrections. Phys Rev D. (1992) 46:381–409.

PubMed Abstract | Google Scholar

84. Lavoura L, Silva JP. The oblique corrections from vector–like singlet and doublet quarks. Phys Rev D. (1993) 47:2046–57.

Google Scholar

85. del Aguila F, de Blas J, Perez-Victoria M. Effects of new leptons in electroweak precision data. Phys Rev D. (2008) 78:013010. doi: 10.1103/PhysRevD.78.013010

CrossRef Full Text | Google Scholar

86. Erler J, Langacker P. Precision constraints on extra fermion generations. Phys Rev Lett. (2010) 105:031801. doi: 10.1103/PhysRevLett.105.031801

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Barbieri R, Pomarol A, Rattazzi R, Strumia A. Electroweak symmetry breaking after LEP-1 and LEP-2. Nucl Phys B. (2004) 703:127. doi: 10.1016/j.nuclphysb.2004.10.014

CrossRef Full Text | Google Scholar

88. Cynolter G, Lendvai E. Electroweak precision constraints on vector-like fermions. Eur Phys J C. (2008) 58:463. doi: 10.1140/epjc/s10052-008-0771-7

CrossRef Full Text | Google Scholar

89. Griest K, Seckel D. Three exceptions in the calculation of relic abundances. Phys Rev D. (1991) 43:3191.

PubMed Abstract | Google Scholar

90. Chatterjee A, Sahu N. Resurrecting L-type sneutrino dark matter in light of neutrino masses and LUX data. Phys Rev D. (2014) 90:095021. doi: 10.1103/PhysRevD.90.095021

CrossRef Full Text | Google Scholar

91. Patra S, Sahoo N, Sahu N. Dipolar dark matter in light of the 3.5 keV x-ray line, neutrino mass, and LUX data. Phys Rev D. (2015) 91:115013. doi: 10.1103/PhysRevD.91.115013

CrossRef Full Text | Google Scholar

92. Goodman MW, Witten E. Detectability of certain dark matter candidates. Phys Rev D. (1985) 31:3059.

PubMed Abstract | Google Scholar

93. Essig R. Direct detection of non-chiral dark matter. Phys Rev D. (2008) 78:015004. doi: 10.1103/PhysRevD.78.015004

CrossRef Full Text | Google Scholar

94. Barman B, Bhattacharya S, Ghosh P, Kadam S, Sahu N. Fermion dark matter with scalar triplet at direct and collider searches. arXiv:1902.01217(2019).

Google Scholar

95. Alloul A, Christensen ND, Degrande C, Duhr C, Fuks B. FeynRules 2.0—a complete toolbox for tree-level phenomenology. Comput Phys Commun. (2014) 185:2250. doi: 10.1016/j.cpc.2014.04.012

CrossRef Full Text | Google Scholar

96. Alwall J, Herquet M, Maltoni F, Mattelaer O, Stelzer T. MadGraph 5: going beyond. JHEP. (2011) 1106:128. doi: 10.1007/JHEP06(2011)128

CrossRef Full Text

97. Sjostrand T, Mrenna S, Skands PZ. PYTHIA 6.4 physics and manual. JHEP. (2006) 0605:026. doi: 10.1088/1126-6708/2006/05/026

CrossRef Full Text

98. Bhattacharya S, Ghosh P, Sahu N. Multipartite dark matter with scalars, fermions and signatures at LHC. JHEP. (2019) 1902:059. doi: 10.1007/JHEP02(2019)059

CrossRef Full Text | Google Scholar

99. Bhattacharya S, Karmakar B, Sahu N, Sil A. Flavor origin of dark matter and its relation with leptonic nonzero θ₁₃ and Dirac CP phase δ. JHEP. (2017) 1705:068. doi: 10.1007/JHEP05(2017)068

CrossRef Full Text | Google Scholar

100. Bhattacharya S, Karmakar B, Sahu N, Sil A. Unifying the flavor origin of dark matter with leptonic nonzero θ₁₃. Phys Rev D. (2016) 93:115041. doi: 10.1103/PhysRevD.93.115041

CrossRef Full Text | Google Scholar

Appendix A: Couplings of ILD Dark Matter With Scalar Triplets and SM Particles

Trilinear vertices involving ILD and triplet Scalar:

$\begin{array}{rrr}\overline{{(N^{-})}^c}{N}^{-}{H}^{++}& :& \sqrt{2}{f}_N\\ \overline{{(N^{-})}^c}{N}^0{H}^{+}& :& f_N\\ \overline{{(N^0)}^c}{N}^0{H}_1& :& -sin\alpha f_N\\ \overline{{(N^0)}^c}{N}^0{H}_2& :& -cos\alpha f_N\\ \overline{{(N^0)}^c}{N}^0{A}^0& :& -i{f}_N& (\mathrm{A1})\end{array}$

Trilinear vertices involving triplet scalars:

$\begin{array}{l}{H}^{++}{H}^{-}{H}^{-}:\sqrt{2}{v}_t{\lambda }_3\propto 1/v_t\\ H^{++}{H}^{--}{H}_2:-(2cos\alpha v_t{\lambda }_2-sin\alpha v{\lambda }_1)\\ {\displaystyle \underset{}{\overset{sin\alpha \to 0}{\to }}}-2v_t{\lambda }_2\propto 1/v_t\\ H^{++}{H}^{--}{H}_1:-(cos\alpha v{\lambda }_1+2sin\alpha v_t{\lambda }_2)& (\mathrm{A2})\end{array}$

Trilinear vertices involving ILD and SM particles:

$\begin{array}{rrr}\overline{N^0}{N}^{-}{W}^{+}& :& \frac{e_0}{\sqrt{2}sin{\theta }_W}{\gamma }^{\mu }\\ N^{-}{N}^{+}Z& :& -\frac{e_0}{sin2{\theta }_W}cos2{\theta }_W{\gamma }^{\mu }\\ N^{-}{N}^{+}A& :& -e_0{\gamma }^{\mu }\\ \overline{N^0}{N}^{0}Z& :& \frac{e_0}{sin2{\theta }_W}{\gamma }^{\mu }& (\mathrm{A3})\end{array}$