Abstract
The purpose of this paper is three-fold. First, we present a discretization process to obtain numerical solutions of a conformable fractional-order system with delays. Second, we extend the classical Bertrand duopoly game with integer delays to that with fractional delays. Third, we extend the game based on ordinary differential derivative to that based on conformable fractional-order derivative. Finally, we analyze the local stability, Hopf bifurcation, and chaos of the proposed game model.
1. Introduction
Bifurcation and chaos [1] are frequent phenomena in various scientific fields including economics. By analyzing bifurcation and chaos, we can reveal its evolutionary mechanism to control proposed systems [2–4]. Delay is another common phenomenon which usually occurs in various economic systems, such as the discrete duopoly game with integer delays [5–13], the monopoly with integer delay and bounded rationality [14, 15], the continuous time Cournot duopoly with integer delays [16, 17], the continuous Bertrand duopoly with integer delay [18, 19]. Naturally, we will consider what the Bertrand duopoly game with fractional delays should be.
As a natural extension of a classical ordinary differential equation, the fractional derivative is a derivative of arbitrary order, real or complex [20–28]. Similarly we also want to extend the integer delay to arbitrary delay, integer or fractional, real or complex. Thus the continuous time Bertrand duopoly game with fractional delay and conformable derivative would have stronger ability to represent complex problems than the corresponding game with integer delay and derivative.In other words, the fractional delay can also be conceived as a kind of conformable fractional delay.
Although researchers proposed various fractional operators, such as Riemann-Liouville, Caputo, and Grunwald-Letnikov [29–33], widely used in many fields including economics, physics, and engineering [34–38], these definitions of operators satisfy two characteristics: one is that they must be non-integer in form, and the other is that they must be non-local in essence. But non-locality is a double-edged sword. It has the advantage of long memory, but it also has the disadvantage of not satisfying the classical differential operator, such as the chain rule. The conformable operator is conceived as a natural extension of the classical differential operator [39–45], whose most important properties hold, such as the chain rule [21, 22, 46]. Certainly, the conformable derivative is only a kind of local definition of fractional derivative and is non-integer in form, but it has no non-locality. In fact, there are two opposing viewpoints about the definitions of fractional derivatives: one is two above-mentioned characteristics must hold simultaneously, but the other is the first characteristic is the key of the fractional derivative. The later opinion means that a derivative is fractional derivative only if the first characteristic holds. We will support the later opinion in this paper. The conformable operator has recently occurred in many scientific fields [23–27, 40, 47–50]. In this paper, we will introduce the conformable fractional-order derivative to the continuous time Bertrand duopoly game with integer delays. Thus we can obtain a conformable Bertrand duopoly game with fractional delay.
After we propose the continuous time Bertrand duopoly game with fractional delay and conformable derivative, we need suitable approaches to obtain its solutions. Though there are several schemes to solve a conformable fractional-order system without any delay [40, 41, 45, 50–72], they are not suitable for conformable system with fractional delays. Mohammadnezhad et al. [73] employed conformable Euler's method to obtain approximation solutions of conformable fractional differential equations. Inspired by the discretization process for other derivatives [74–78], we will present a simple discretization process for a conformable system with fractional delays. Our proposed method well coincides with the conformable Euler method [73]. Using the proposed discretization scheme, we will detect the stability, Hopf bifurcations, and chaotic attractors of the continuous time Bertrand duopoly game with fractional delay and conformable derivative.
The remainder of this paper is organized as follows. In section 2, we show preliminaries of conformable calculus and stability conditions of a discrete system. In section 3, we propose a discretization process for conformable systems with fractional delays. In section 4, we present a continuous time Bertrand duopoly game with fractional delays and conformable derivative. In section 5, we analyze Nash equilibrium points, local stabilities, and Hopf bifurcation in the game model. In section 6, we employ 0-1 test algorithm to detect chaotic attractors. This paper concludes with a summary in section 7.
2. Preliminaries
Definition 1.(See [22])
For a function f : [t0, ∞) → ℝ, its left conformable fractional derivative starting from t0of order α ∈ (0, 1) is defined by
in which the function f is called as α-differentiable.
Definition 2.(See [22])
For a function f : [t0, ∞) → ℝ, its left conformable fractional integral starting from t0of order α ∈ (0, 1) is defined by
where the integral is the usual Riemann improper integral.
Lemma 1.(See [22])
Suppose the derivative order α ∈ (0, 1) and the function f is α-differentiable at a point t0 > 0, then the left conformable fractional derivative satisfies:
Lemma 2.(Conformable fractional power series expansion) [22] Given an infinitely α−differentiable function f : [0, ∞) → ℝ, α ∈ (0, 1], f has the following conformable fractional power series expansion at a neighborhood of a point t0:
wheredenotes the application of the conformable fractional derivative n times.
Consider the following discrete dynamical system:
where X = (x1, x2, ··· , xn), and F = (f1, f2, ··· , fn) is C2 from ℝn to ℝn. Let Xeq be a fixed point of system (4), and λ1, λ2, ··· , λn be eigenvalues of Jacobian matrix . Then we can obtain the following characteristic polynomial of J(Xeq)
Lemma 3.(See [79]).
(i) If all the eigenvalues λiof J(Xeq) have |λi| < 1, then the periodic orbitis attracting.
(ii) If one eigenvalue λi0of J(Xeq) has |λi0| > 1, then the periodic orbitis unstable.
(iii) If all the eigenvalues λiof J(Xeq) have |λi| > 1, then the periodic orbitis repelling.
3. Discretization Process of Conformable Fractional Systems With Delays
Theorem 1.(Conformable delay discretization by piecewise constant approximation)
Consider the following conformable fractional-order delay system
we obtain the following discretization of Equation (6)
where xndenotes xn(tn), , tn = nh, n = 0, 1, ··· , N.
Proof: By drawing on the discretization process proposed by Raheem and Salman [74], El-Sayed et al. [75], El-Sayed et al. [76], Agarwal et al. [77], and El-Sayed et al. [78], we discretize the fractional-order delay Equation (6) with piecewise constant approximation as follows
By using Lemma 1, we rewrite Equation (8) as follows.
which leads to
We apply the step method presented in Kartal and Gurcan [59], El-Sayed et al. [76], and El-Sayed et al. [78] for discretizing Equation (9) with piecewise constant approximation as follows
(i) Let n = 0, then t ∈ [0, h), we rewrite Equation (9) as follows
and the solution of Equation (10) is given by
(ii) Let n = 1, then t ∈ [h, 2h), we rewrite Equation (9) as follows
and the solution of Equation (11) is given by
(iii) By repeating the above process, we obtain the following solution of Equation (9)
Let t → (n + 1)h, we deduce the the following discretization
that is
It is proved.
Remark 1.The presented conformable discretization process is well line with the conformable Euler's method proposed by Mohammadnezhad et al. [73].
Theorem 2.The conformable delay discretization process in Theorem 1 is convergent.
Proof: According to Lemma 2 and the conformable Euler's method [73], we obtain the following conformable fractional power series expansion:
where 0 < θn < 1 and .
So the conformable delay discretization process is convergent when step size h is small enough.
4. Modeling
4.1. A Continuous Time Bertrand Duopoly Game With Fractional Delays and Conformable Derivative
Assume that each firm decides on a different product pricing strategy in a duopoly market, in which pi(t) indicates the i-th firm's price during time period t ∈ Z+, qi(t) represents the i-th firm's supply during time period t ∈ Z+, and qi and pi satisfies the common linear inverse demand function as follows.
where ai and b are positive constants. ai denotes the i-th firm's constant reservation price in the product market. b denotes supply margin effects on its price from itself and its rival. Suppose i-th firm's marginal costs is equal to ci, which is also a positive constant, as follows
Then the i-th firm's profit is
Thus we can obtain the i−th firm's marginal profit with respect to pi as follows
As we know, the higher a firm's marginal profit is, the greater its price adjustment range is. In other words, the a firm's price growth rate is proportional to its marginal profit . We get the gradient adjustment process of price as follows
where vi > 0 represents the i−th firm's price adjustment speed.
Inspired by Matsumoto et al. [15] who regarded the marginal profit as a delayed value, we rewrite Equation (17) with delay τ as follows
We can regard the conformable fractional-order derivative as a natural extension of the integer order form. Thus, we introduce the conformable derivative to Equation (18) and obtain the following Bertrand duopoly game with αi-order conformable derivative and fractional delay:
where α ∈ (0, 1], di = ai − ci, τ ≥ 0 denotes a fractional delay.
Remark 2.When α = 1, Equation (19) degenerates to Equation (18).
Remark 3.When α = 1 and τ = 0, Equation (19) degenerates to Equation (17).
4.2. Discretization Process
According to Theorem 1, we employ piecewise constant approximation to discretize the game model (18) as follows
Remark 4. If τ = mh, and m is integer, then we rewrite the game model (20) as follows
In the following, we only study the case m = 1. Then we rewrite the game model (21) as follows
5. Local Stability, Hopf Bifurcation, and Chaos
5.1. Local Stability
Fixed points of system (22) satisfy
By algebraic computation, we obtain the following fixed points: E1 = (0, 0, 0, 0), , , and E4 = (pe1, pe2, pe1, pe2), where , . There are some economic information as follows:
(i) At the first fixed point E1, no firm can gain anything by production if its opponent stops production.
(ii) At the second fixed point E2, stoping production is the best strategy for firm 1 if is the output strategy of firm 2, and vice versa.
(iii) At the third fixed point E3, stoping production is the best strategy for firm 2 if firm 1 adopts its output strategy , and vice versa.
(iv) At the fourth fixed point E4, firm 1 cannot obtain extra benefit from deviating unilaterally from its equilibrium output strategy if firm 2 adopts its equilibrium output strategy , and vice versa.
Points E1, E2, and E3 are all bounded equilibria [80]. Thus, we only study the stability of non-bounded equilibrium point E4.
We obtain the following Jacobian matrix of system (23) evaluated at the fourth fixed point E4:
The characteristic equation of Jacobian matrix (24) is
where
According to Jury stability criterion, we directly obtain the following proposition for system (22).
Proposition 1.The fixed point E4is locally asymptotically stable if the following stability constraints holds simultaneously: W(1) > 0, W(−1) > 0, |w4| < 1, , |k1| < k2, where
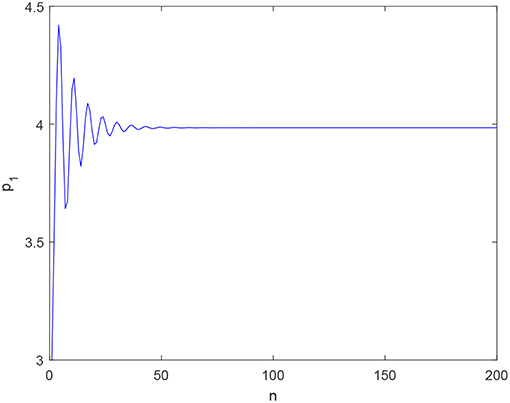
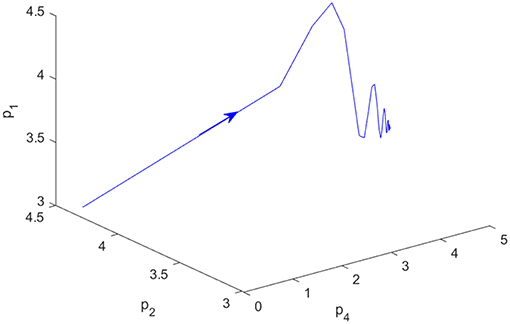
Set h = 0.01, d1 = 8, d2 = 6, b = 0.01, v1 = 0.05, v2 = 0.01, α = 0.2. We can obtain E1 = (0, 0, 0, 0), E2 = (0, 3, 0, 3), E3 = (4, 0, 4, 0), and E4 = (3.99, 2.98, 3.99, 2.98). Obviously, Proposition 1 holds, i.e., system (22) is stable, as shown in Figures 1, 2. As time goes on with α = 0.2, Figure 1 demonstrates outputs of firm 1 trend to an invariant value, and Figure 2 demonstrates system (22) convergences to a fixed point. Figures 1, 2 mutually validate the existence of fixed points E4 in system (22).
Figure 1
Figure 2
5.2. Hopf Bifurcation
According to the explicit criterion of Hopf bifurcation [81], we directly obtain the following theorem:
Theorem 3.In system (22), a Hopf bifurcation occurs at α = α*if the following conditions (H1)-(H3) hold:
(H1) Eigenvalue assignmentW(1) > 0, W(−1) > 0,
(H2)Transversality condition
(H3) Nonresonance condition cos(2π/m) ≠ ψ or resonance condition cos(2π/m) = ψ, where m = 3, 4, 5, ··· and.
where
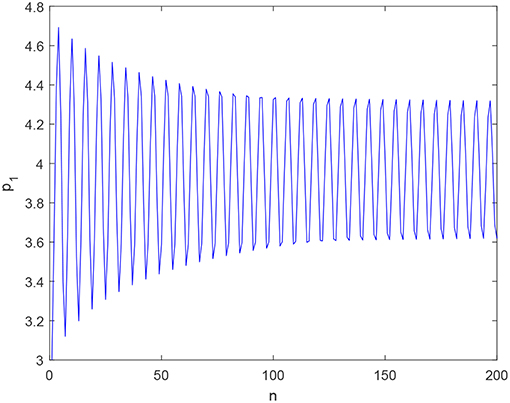
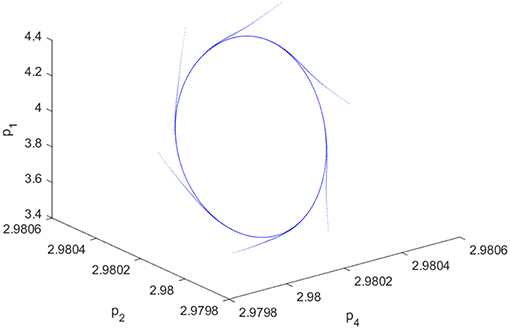
If h = 0.01, d1 = 8, d2 = 6, b = 0.01, v1 = 0.05, v2 = 0.01, a Hopf bifurcation will occur at α* = 0.1767. When we adopt a small perturbation Δα = 0.0007, a sufficiently small positive real number, i.e. α = α* + Δα = 0.176, system (22) has a stable closed invariant curve around the fixed point E4, as shown in Figures 3, 4. As time goes on with α = 0.1767, Figure 3 demonstrates outputs of firm 1 trend to periodic fluctuation, and Figure 4 demonstrates system (22) convergences to an invariant closed curve. Figures 3, 4 mutually validate the existence of Hopf bifurcation in system (22).
Figure 3
Figure 4
6. 0-1 Test for Chaos
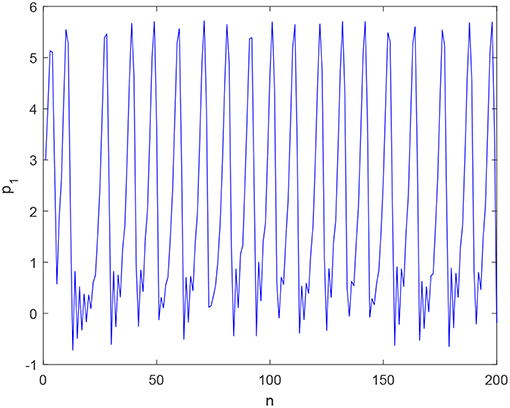
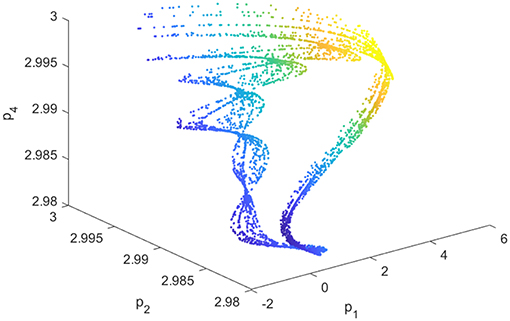
When h = 0.01, d1 = 8, d2 = 6, b = 0.01, v1 = 0.05, v2 = 0.01, α = 0.2, system (22) is chaotic, as shown in Figures 5, 6. Figure 5 shows that the time series of p1 irregularly evolutes with time. Figure 6 shows that a chaotic attractor exists in system (22).
Figure 5
Figure 6
Following the 0-1 test algorithm [82–89], we sample 10,000 data points from p1(n) and set a random number satisfies (μ(n), ν(n)), as follows
We obtain the 0-1 test value K for chaos as follows:
where ξ = (1, 2, 3, …, round(N/10)), Δ = (Dc(1), Dc(2), …, Dc(round(N/10))), the covariance is defined with vectors ξ, Δ of length m by
and
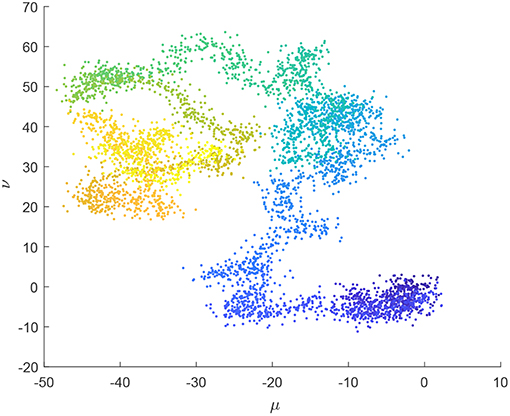
For system (22) with α = 0.137, we obtain K = 0.9977 and plot a phase portrait in (μ, ν)-plane whose trajectories in the (μ, ν)−plane are Brownian-like, which indicate it is chaotic, as shown Figure 7.
Figure 7
As time goes on with α = 0.137, Figure 5 demonstrates outputs of firm 1 trend to irregular vibration, and Figure 6 demonstrates system (22) has chaotic attractors in (p1, p2, p4)-plane, and Figure 7 demonstrates the motion trajectories of system (22) are Brownian-like in (μ, ν)-plane. Figures 5–7 mutually validate the existence of chaos in system (22).
7. Conclusion
Introducing conformable derivative to a classical continuous Bertrand duopoly game with integer delays, we present a generalized game model with delays, named a continuous time Bertrand duopoly game with fractional delay and conformable derivative. We design a discretization process for conformable systems with fractional delays. Utilizing the proposed discretization process, we obtain a simplified model and get its solutions. At last, we examine the local stability, Hopf bifurcation, and chaos of the game model.
There are some future research directions that deserve our attention. We can apply the modeling approach and discretization process to other scientific researches, such as conformable partial differential equations with delays [90–94], conformable differential games with delays [95]. In addition, we can also develop other discretization methods for conformable system with specific characteristics, such as stochastic, fuzzy, pulse factors.
Statements
Data availability statement
All datasets generated for this study are included in the manuscript and/or the supplementary files.
Author contributions
BX and LG: conceptualization. BX, WP, and LG: methodology. BX and WP: software. BX and LG: validation. BX: formal analysis. BX and WP: writing-original draft preparation. BX and LG: writing-review and editing. BX and WP: visualization. BX: supervision, project administration, and funding acquisition.
Funding
This work is supported partly by Natural Science Foundation of Shandong Province (Grant No. ZR2016FM26), National Social Science Foundation of China (Grant No.16FJY008), and National Natural Science Foundation of China (Grant No.11801060).
Acknowledgments
The authors would like to express many thanks to referees for their time and efforts in reviewing this manuscript. Their helpful comments and constructive suggestions greatly improved this manuscript.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The reviewer ZW declared a shared affiliation, with no collaboration, with the authors BX, WP to the handling editor at time of review.
References
1.
WeiZZhuBYangJPercMSlavinecM. Bifurcation analysis of two disc dynamos with viscous friction and multiple time delays. Appl Math Comput. (2019) 347:265–81. 10.1016/j.amc.2018.10.090
2.
RajagopalKKarthikeyanADuraisamyP. Hyperchaotic chameleon: fractional order FPGA implementation. Complexity. (2017) 2017:8979408. 10.1155/2017/8979408
3.
MouJSunKWangHRuanJ. Characteristic analysis of fractional-order 4D hyperchaotic memristive circuit. Math Prob Eng. (2017) 2017:2313768. 10.1155/2017/2313768
4.
El-SayedANourHElsaidAMatoukAElsonbatyA. Dynamical behaviors, circuit realization, chaos control, and synchronization of a new fractional order hyperchaotic system. Appl Math Model. (2016) 40:3516–34. 10.1016/j.apm.2015.10.010
5.
HowroydTRussellA. Cournot oligopoly models with time delays. J Math Econ. (1984) 13:97–103. 10.1016/0304-4068(84)90009-0
6.
MatsumotoASzidarovszkyF. Nonlinear Cournot duopoly with implementation delays. Chaos Soliton Fract. (2015) 79:157–65. 10.1016/j.chaos.2015.05.010
7.
MatsumotoASzidarovszkyFYoshidaH. Dynamics in linear Cournot duopolies with two time delays. Comput Econ. (2011) 38:311. 10.1007/s10614-011-9295-6
8.
ElsadanyAMatoukA. Dynamic Cournot duopoly game with delay. J Complex Sys. (2014) 2014:384843. 10.1155/2014/384843
9.
ChenWWangW. Global exponential stability of Cournot duopolies with delays. Comput Econ. (2016) 48:147–54. 10.1007/s10614-015-9503-x
10.
PecoraNSodiniM. A heterogenous Cournot duopoly with delay dynamics: Hopf bifurcations and stability switching curves. Commun Nonlinear Sci Numer Simul. (2018) 58:36–46. 10.1016/j.cnsns.2017.06.015
11.
BignamiFAgliariA. Chaotic dynamics in a three-dimensional map with separate third iterate: the case of Cournot duopoly with delayed expectations. Chaos Soliton Fract. (2018) 110:216–225. 10.1016/j.chaos.2018.03.023
12.
AskarSSAlnowibetK. Cooperation versus noncooperation: Cournot duopolistic game based on delay and time-dependent parameters. Chaos Soliton Fract. (2016) 91:580–4. 10.1016/j.chaos.2016.08.004
13.
FantiL. An observable delay game with unionised managerial firms. Scottish J Polit Econ. (2017) 64:50–69. 10.1111/sjpe.12117
14.
MatsumotoASzidarovszkyF. Nonlinear delay monopoly with bounded rationality. Chaos Soliton Fract. (2006) 28:507–19. 10.1016/j.chaos.2012.01.005
15.
MatsumotoAChiarellaCSzidarovszkyF. Dynamic monopoly with bounded continuously distributed delay. Chaos Soliton Fract. (2013) 47:66–72. 10.1016/j.chaos.2012.12.003
16.
GoriLGuerriniLSodiniM. A continuous time Cournot duopoly with delays. Chaos Soliton Fract. (2015) 79:166–77. 10.1016/j.chaos.2015.01.020
17.
BrianzoniSCampisiGGuerriniL. A continuous-time heterogeneous duopoly model with delays. Decis Econ Finan. (2018) 41:259–75. 10.1007/s10203-018-0227-y
18.
MaJSiF. Complex dynamics of a continuous Bertrand duopoly game model with two-stage delay. Entropy. (2016) 18:266. 10.3390/e18070266
19.
GuerriniL. Complex dynamics of a continuous Bertrand duopoly game model with delay. Appl Math Sci. (2017) 11:1077–81. 10.12988/ams.2017.7269
20.
XinBPengWKwonY. Modeling, discretization, and hyperchaos detection of conformable derivative approach to a financial system with market confidence and ethics risk. Adv Differ Equat. (2019) 2019:138. 10.1186/s13662-019-2074-8
21.
KhalilRHoraniMAYousefASababhehM. A new definition of fractional derivative. J Comput Appl Math. (2014) 264:65–70. 10.1016/j.cam.2014.01.002
22.
AbdeljawadT. On conformable fractional calculus. J Comput Appl Math. (2015) 279:57–66. 10.1016/j.cam.2014.10.016
23.
AcanOFiratOKeskinY. Conformable variational iteration method, conformable fractional reduced differential transform method and conformable homotopy analysis method for non-linear fractional partial differential equations. Wave Rand Complex Media. (2018). 10.1080/17455030.2018.1502485. [Epub ahead of print].
24.
AttiaRAMLuDMAKhaterM. Chaos and relativistic energy-momentum of the nonlinear time fractional duffing equation. Math Comput Appl. (2019) 24:10. 10.3390/mca24010010
25.
Dynamic cobweb models with conformable fractional derivatives. Nonlinear Anal Hybrid Syst. (2019) 32:157–67. 10.1016/j.nahs.2018.09.004
26.
TarasovVE. No nonlocality. No fractional derivative. Commun Nonlinear Sci Numer Simul. (2018) 62:157–63. 10.1016/j.cnsns.2018.02.019
27.
RosalesJJGodínezFABandaVValenciaGH. Analysis of the Drude model in view of the conformable derivative. Optik. (2019) 178:1010–5. 10.1016/j.ijleo.2018.10.079
28.
BaleanuDJajarmiAAsadJ. Classical and fractional aspects of two coupled pendulums. Roman Rep Phys. (2019) 71:103.
29.
ZhengRJiangX. Spectral methods for the time-fractional Navier–Stokes equation. Appl Math Lett. (2019) 91:194–200. 10.1016/j.aml.2018.12.018
30.
YangXQiHJiangX. Numerical analysis for electroosmotic flow of fractional Maxwell fluids. Appl Math Lett. (2018) 78:1–8. 10.1016/j.aml.2017.10.012
31.
WangFChenDZhangXWuY. Finite-time stability of a class of nonlinear fractional-order system with the discrete time delay. Int J Syst Sci. (2017) 48:984–93. 10.1080/00207721.2016.1226985
32.
WuGCBaleanuDHuangLL. Novel Mittag-Leffler stability of linear fractional delay difference equations with impulse. Appl Math Lett. (2018) 82:71–8. 10.1016/j.aml.2018.02.004
33.
WuGCBaleanuDLuoWH. Analysis of fractional non-linear diffusion behaviors based on Adomian polynomials. Therm Sci. (2017) 21:813–7. 10.2298/TSCI160416301W
34.
KumarDSinghJBaleanuDRathoreS. Analysis of a fractional model of the Ambartsumian equation. Euro Phys J Plus. (2018) 133:259. 10.1140/epjp/i2018-12081-3
35.
SinghJKumarDBaleanuDRathoreS. An efficient numerical algorithm for the fractional Drinfeld–Sokolov–Wilson equation. Appl Math Comput. (2018) 335:12–24. 10.1016/j.amc.2018.04.025
36.
KumarDAgarwalRPSinghJ. A modified numerical scheme and convergence analysis for fractional model of Lienard's equation. J Comput Appl Math. (2018) 339:405–13. 10.1016/j.cam.2017.03.011
37.
KumarDTchierFSinghJBaleanuD. An efficient computational technique for fractal vehicular traffic flow. Entropy. (2018) 20:259. 10.3390/e20040259
38.
HajipourMJajarmiABaleanuDSunH. On an accurate discretization of a variable-order fractional reaction-diffusion equation. Commun Nonlinear Sci Numer Simul. (2019) 69:119–33. 10.1016/j.cnsns.2018.09.004
39.
Morales-DelgadoVGómez-AguilarJEscobar-JiménezRTaneco-HernándezM. Fractional conformable derivatives of Liouville–Caputo type with low-fractionality. Phys A. (2018) 503:424–38. 10.1016/j.physa.2018.03.018
40.
PérezJGómez-AguilarJBaleanuDTchierF. Chaotic attractors with fractional conformable derivatives in the Liouville–Caputo sense and its dynamical behaviors. Entropy. (2018) 20:384. 10.3390/e20050384
41.
Yépez-MartínezHGómez-AguilarJAtanganaA. First integral method for non-linear differential equations with conformable derivative. Math Model Nat Phenom. (2018) 13:14. 10.1051/mmnp/2018012
42.
EslamiMKhodadadFSNazariFRezazadehH. The first integral method applied to the Bogoyavlenskii equations by means of conformable fractional derivative. Opt Quant Electron. (2017) 49:391. 10.1007/s11082-017-1224-z
43.
RezazadehHKorkmazAEslamiMVahidiJAsghariR. Traveling wave solution of conformable fractional generalized reaction Duffing model by generalized projective Riccati equation method. Opt Quant Electron. (2018) 50:150. 10.1007/s11082-018-1416-1
44.
EslamiM. Exact traveling wave solutions to the fractional coupled nonlinear Schrodinger equations. Appl Math Comput. (2016) 285:141–8. 10.1016/j.amc.2016.03.032
45.
KhodadadFSNazariFEslamiMRezazadehH. Soliton solutions of the conformable fractional Zakharov–Kuznetsov equation with dual-power law nonlinearity. Opt Quant Electron. (2017) 49:384. 10.1007/s11082-017-1225-y
46.
AbdeljawadTAl-MdallalQMJaradF. Fractional logistic models in the frame of fractional operators generated by conformable derivatives. Chaos Soliton Fract. (2019) 119:94–101. 10.1016/j.chaos.2018.12.015
47.
AkbulutAKaplanM. Auxiliary equation method for time-fractional differential equations with conformable derivative. Comput Math Appl. (2017) 75:876–82. 10.1016/j.camwa.2017.10.016
48.
RezazadehHKhodadadFSManafianJ. New structure for exact solutions of nonlinear time fractional Sharma-Tasso-Olver equation via conformable fractional derivative. Appl Appl Math. (2017) 12:405–14.
49.
KorkmazA. Explicit exact solutions to some one-dimensional conformable time fractional equations. Wave Rand Complex Media. (2019) 29:124–37. 10.1080/17455030.2017.1416702
50.
HeSBanerjeeSYanB. Chaos and symbol complexity in a conformable fractional-order memcapacitor system. Complexity. (2018) 2018:1–15. 10.1155/2018/4140762
51.
EslamiMRezazadehH. The first integral method for Wu-Zhang system with conformable time-fractional derivative. Calcolo. (2016) 53:475–85. 10.1007/s10092-015-0158-8
52.
IlieMBiazarJAyatiZ. The first integral method for solving some conformable fractional differential equations. Opt Quant Electron. (2018) 50:55. 10.1007/s11082-017-1307-x
53.
HosseiniKBekirAAnsariR. New exact solutions of the conformable time-fractional Cahn–Allen and Cahn–Hilliard equations using the modified Kudryashov method. Optik. (2017) 132:203–9. 10.1016/j.ijleo.2016.12.032
54.
ÜnalEGökdoǧanA. Solution of conformable fractional ordinary differential equations via differential transform method. Optik. (2017) 128:264–73. 10.1016/j.ijleo.2016.10.031
55.
KumarDSeadawyARJoardarAK. Modified Kudryashov method via new exact solutions for some conformable fractional differential equations arising in mathematical biology. Chin J Phys. (2018) 56:75–85. 10.1016/j.cjph.2017.11.020
56.
SrivastavaHMGünerhanH. Analytical and approximate solutions of fractional-order susceptible-infected-recovered epidemic model of childhood disease. Math Meth Appl Sci. (2019) 42:935–41. 10.1002/mma.5396
57.
KaplanM. Applications of two reliable methods for solving a nonlinear conformable time-fractional equation. Opt Quant Electron. (2017) 49:312. 10.1007/s11082-017-1151-z
58.
YavuzMÖzdemirN. A different approach to the European option pricing model with new fractional operator. Math Model Nat Phenom. (2018) 13:12. 10.1051/mmnp/2018009
59.
KartalSGurcanF. Discretization of conformable fractional differential equations by a piecewise constant approximation. Int J Comput Math. (2018) 10.1080/00207160.2018.1536782. [Epub ahead of print].
60.
IyiolaOSTasbozanOKurtAÇenesizY. On the analytical solutions of the system of conformable time-fractional Robertson equations with 1-D diffusion. Chaos Soliton Fract. (2017) 94:1–7. 10.1016/j.chaos.2016.11.003
61.
RuanJSunKMouJHeSZhangL. Fractional-order simplest memristor-based chaotic circuit with new derivative. Euro Phys J Plus. (2018) 133:3. 10.1140/epjp/i2018-11828-0
62.
HeSSunKMeiXYanBXuS. Numerical analysis of a fractional-order chaotic system based on conformable fractional-order derivative. Euro Phys J Plus. (2017) 132:36. 10.1140/epjp/i2017-11306-3
63.
YokuşA. Comparison of Caputo and conformable derivatives for time-fractional Korteweg-de Vries equation via the finite difference method. Int J Modern Phys B. (2018) 32:1850365. 10.1142/S0217979218503654
64.
RezazadehHZiabaryBP. Sub-equation method for the conformable fractional generalized kuramoto sivashinsky equation. Comput Res Prog Appl Sci Eng. (2016) 2:106–9.
65.
ZhongWWangL. Basic theory of initial value problems of conformable fractional differential equations. Adv Differ Equat. (2018) 2018:321. 10.1186/s13662-018-1778-5
66.
TayyanBASakkaAH. Lie symmetry analysis of some conformable fractional partial differential equations. Arab J Math. (2018). 10.1007/s40065-018-0230-8. [Epub ahead of print].
67.
Çerdik YaslanH. Numerical solution of the conformable space-time fractional wave equation. Chin J Phys. (2018) 56:2916–25. 10.1016/j.cjph.2018.09.026
68.
KurtAÇenesizYTasbozanO. On the solution of Burgers' equation with the new fractional derivative. Cent Euro J Phys. (2015) 13:355–60. 10.1515/phys-2015-0045
69.
KhalilRAbu-ShaabH. Solution of some conformable fractional equations. Int J Pure Appl Math. (2015) 103:667–673. 10.12732/ijpam.v103i4.6
70.
LiuSWangHLiXLiH. The extremal iteration solution to a coupled system of nonlinear conformable fractional differential equations. J Nonlinear Sci Appl. (2017) 10:5082–9. 10.22436/jnsa.010.09.44
71.
ÇenesizYKurtA. The solutions of time and space conformable fractional heat equations with conformable Fourier transform. Acta Univ Sapient Math. (2015) 7:130–40. 10.1515/ausm-2015-0009
72.
Morales-DelgadoVGómez-AguilarJTaneco-HernandezM. Analytical solutions of electrical circuits described by fractional conformable derivatives in Liouville-Caputo sense. AEU-Int J Elect Commun. (2018) 85:108–17. 10.1016/j.aeue.2017.12.031
73.
MohammadnezhadVEslamiMRezazadehH. Stability analysis of linear conformable fractional differential equations system with time delays. Bol Soc Paran Math. (2020) 38:159–71. 10.5269/bspm.v38i6.37010
74.
RaheemZFESalmanSM. On a discretization process of fractional-order Logistic differential equation. J Egypt Math Soc. (2014) 22:407–12. 10.1016/j.joems.2013.09.001
75.
El-SayedAMEl-RaheemZFSalmanSM. Discretization of forced Duffing system with fractional-order damping. Adv Differ Equat. (2014) 2014:66. 10.1186/1687-1847-2014-66
76.
El-SayedAMEl-RaheemZFSalmanSM. On a discretization process of fractional-order Riccati differential equation. Fract Calc Appl Anal. (2013) 4:251–9.
77.
AgarwalRPEl-SayedAMASalmanSM. Fractional-order Chua's system: discretization, bifurcation and chaos. Adv Differ Equat. (2013) 2013:320. 10.1186/1687-1847-2013-320
78.
El-SayedAMSalmanSMElabdNA. On a fractional-order delay Mackey-Glass equation. Adv Differ Equat. (2016) 2016:137. 10.1186/s13662-016-0863-x
79.
RobinsonRC. An Introduction to Dynamical Systems: Continuous and Discrete, Vol. 19. Upper Saddle River, NJ: American Mathematical Society (2012).
80.
BischiGINaimzadaA. Global analysis of a dynamic duopoly game with bounded rationality. Adv Dyn Game Appl. (2000) 5:361. 10.1007/978-1-4612-1336-9_20
81.
WenG. Criterion to identify Hopf bifurcations in maps of arbitrary dimension. Phys Rev E. (2005) 72:26201. 10.1103/PhysRevE.72.026201
82.
GottwaldGAMelbourneI. On the implementation of the 0-1 test for chaos. SIAM J Appl Dyn Syst. (2009) 8:129–45. 10.1137/080718851
83.
GottwaldGAMelbourneI. On the validity of the 0-1 test for chaos. Nonlinearity. (2009) 22:1367–82. 10.1088/0951-7715/22/6/006
84.
FalconerIGottwaldGAMelbourneIWormnesK. Application of the 0-1 test for chaos to experimental data. SIAM J Appl Dyn Syst. (2007) 6:395–402. 10.1137/060672571
85.
XinBLiY. 0-1 test for chaos in a fractional order financial system with investment incentive. Abst Appl Anal. (2013) 2013:876298. 10.1155/2013/876298
86.
Belaire-FranchJ. Exchange rates expectations and chaotic dynamics: a replication study. Economics. (2018) 12:2018–37. 10.5018/economics-ejournal.ja.2018-37
87.
YuanLZhengSAlamZ. Dynamics analysis and cryptographic application of fractional Logistic map. Nonlinear Dyn. (2019) 96:1–22. 10.1007/s11071-019-04810-3
88.
Munoz-PachecoJZambrano-SerranoEVolosCJafariSKengneJRajagopalK. A new fractional-order chaotic system with different families of hidden and self-excited attractors. Entropy. (2018) 20:564. 10.3390/e20080564
89.
BaoBCWuPYBaoHXuQChenM. Numerical and experimental confirmations of quasi-periodic behavior and chaotic bursting in third-order autonomous memristive oscillator. Chaos Soliton Fract. (2018) 106:161–70. 10.1016/j.chaos.2017.11.025
90.
Yépez-MartínezHGómez-AguilarJ. Fractional sub-equation method for Hirota–Satsuma-coupled equation and coupled mKdV equation using the Atangana's conformable derivative. Wave Rand Complex Media. (2018). 10.1080/17455030.2018.1464233. [Epub ahead of print].
91.
Yépez-MartínezHGómez-AguilarJBaleanuD. Beta-derivative and sub-equation method applied to the optical solitons in medium with parabolic law nonlinearity and higher order dispersion. Optik. (2018) 155:357–65. 10.1016/j.ijleo.2017.10.104
92.
EslamiMMirzazadehM. First integral method to look for exact solutions of a variety of Boussinesq-like equations. Ocean Eng. (2014) 83:133–7. 10.1016/j.oceaneng.2014.02.026
93.
EslamiM. Solutions for space–time fractional (2+ 1)-dimensional dispersive long wave equations. Iran J Sci Tech Trans A Sci. (2017) 41:1027–32. 10.1007/s40995-017-0320-z
94.
EslamiMRezazadehHRezazadehMMosaviSS. Exact solutions to the space–time fractional Schrödinger–Hirota equation and the space–time modified KdV–Zakharov–Kuznetsov equation. Opt Quant Electron. (2017) 49:279. 10.1007/s11082-017-1112-6
95.
XinBSunM. A differential oligopoly game for optimal production planning and water savings. Eur J Oper Res. (2018) 269:206–17. 10.1016/j.ejor.2017.07.016
Summary
Keywords
conformable calculus, fractional-order Bertrand game, fractional delay, Hopf bifurcation, 0-1 test for chaos
Citation
Xin B, Peng W and Guerrini L (2019) A Continuous Time Bertrand Duopoly Game With Fractional Delay and Conformable Derivative: Modeling, Discretization Process, Hopf Bifurcation, and Chaos. Front. Phys. 7:84. doi: 10.3389/fphy.2019.00084
Received
11 April 2019
Accepted
16 May 2019
Published
04 June 2019
Volume
7 - 2019
Edited by
Carla M. A. Pinto, Instituto Superior de Engenharia do Porto (ISEP), Portugal
Reviewed by
Devendra Kumar, University of Rajasthan, India; Zhen Wang, Shandong University of Science and Technology, China; Amin Jajarmi, University of Bojnord, Iran; Mostafa Eslami, University of Mazandaran, Iran; Francisco Gomez, Centro Nacional de Investigación y Desarrollo Tecnológico, Mexico
Updates
Copyright
© 2019 Xin, Peng and Guerrini.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Baogui Xin xin@tju.edu.cn
This article was submitted to Mathematical Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.