Effect of Grain Boundary on Diffusion of P in Alpha-Fe: A Molecular Dynamics Study

Introduction

Typically, structural materials in the nuclear industry are polycrystalline materials having pre-existent structural impurities. The grain boundaries (GBs) substantially influence mechanical properties of polycrystalline materials [1]. A small concentration of any impurity can modify the GBs diffusion rate during crystal growth [2, 3]. Hence, understanding the behavior of impurities and their interaction with the lattice defects and the grain boundaries has become crucial for designing a better engineering material [4–8].

The diffusion phenomenon of the defects and solute elements around the GBs has long been an area of intrigue for the researchers due to its impact on various mechanical properties, such as; corrosion resistance, and embrittlement [9]. The tempered embrittlement and radiation embrittlement has been observed in steel during rapid cooling from higher temperature and irradiation [10]. Phosphorus is one of the major impurity amongst the embrittlement species in steel [10–12]. The Phosphorus grain boundary segregation plays an important role in the intergranular embrittlement of the reactor pressure vessel (RPV), especially under irradiation enhancing diffusion [11, 13]. The embrittlement is instigated due to the shift of Ductile-to-Brittle Transition Temperature (DBTT) to higher temperatures, resulting in the decrease of the GB cohesion. It is proportional to the Phosphorus coverage at the GBs [14]. The Phosphorus diffusion has also been observed at the obstacle-matrix interfaces in poly crystals [15]. A GB is the interface between two oriented crystallites. Hence, their lattice mismatch can result in the expansion of interface between the grains, creating free volume [16]. Thus, the GBs can act as the preferential sites for a secondary phase particle and can possibly help in the diffusion of impurities like; P segregation in steel [17].

The atomistic simulations have revealed that self-interstitial atoms in α-Fe have favorable <110> dumbbell configuration. They have a slightly low energy migration pathway toward the nearest <111> directions, having a lower migration barrier than the vacancy-P pairs [18]. For Fe-P mixed dumbbell, a similar stable <110> dumbbell configuration and migration pathway has been observed [15]. Hurchand et al. reported that the three <100> symmetric tilt grain boundaries relaxed with two EAM potentials, showed that the P atoms preferentially segregate into the free volume of the GBs planes [19]. If the vacancy mechanism is not available, a substitutional P atom will capture a self-interstitial dumbbell, transiting from the low mobile state into a mixed Fe-P dumbbell. This reaction promotes the mobility of P even under the low temperature irradiation [20]. The authors have also reported the transition from Fe-P dumbbell to tetrahedral interstitial [20, 21].

Although, numerous experimental and atomistic simulations have already been performed on the Phosphorus diffusion in the GBs of alpha-Fe, their trapping effect mechanism has not been considered frequently [9, 10, 12, 14, 15, 19, 22, 23]. Henceforth, it is of great significance to research and explore the fundamental mechanism of the P segregation in the GBs [19, 24]. Since, the analysis and interpretation of atomic disorder in the GBs is difficult to obtain experimentally, it can only be understood by MD simulations [25].

In this study, six symmetric tilt grain boundaries models (STGBs) are created to investigate the effect of the GB on the diffusion of P atom. A Fe-P mixed dumbbell is placed near/far away from the GB center, allowing the free diffusion at different temperatures. The reason behind the trapping effect of the GB has also been discussed.

Simulation and Methods Details

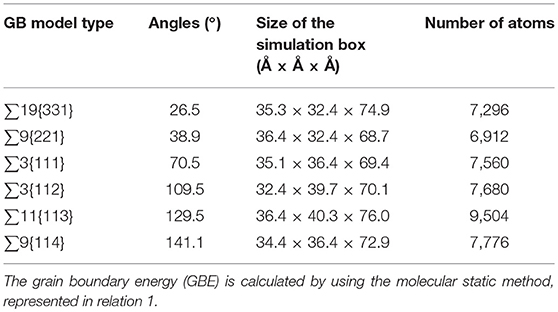
The six <110> STGBs models are created by using GBstudio [26] with the periodic boundaries in three dimensions. The |A|B| type bi-crystal cells having at least 34 Å between the two GBs, in order to eliminate any interaction between them. Here | denotes the grain boundary. The GB model type, size of the simulation box and the number of atoms in each model, have been displayed in Table 1.

$\begin{array}{ll}\gamma =\frac{(E_{GB}-n{E}_{coh})}{2A}& (1)\end{array}$

where E_GB is the total energy of the GB model, nE_coh is the total energy of the model without GB, A is the GB area, n is the number of atoms, which is identical for the GB model and the single crystal model [16]. A Fe-P mixed dumbbell is created at different sites and it is allowed to diffuse freely at different temperatures. NVT simulations were performed, where a standard Noose-Hoover thermostat is used to control the temperature [27]. The configuration of Fe-P mixed dumbbell can be found in references such as Domain and Becquart [15]. The diffusion simulations are conducted at different temperatures from 400 to 1,000 K, having 100 K as an interval for up to 2 ns. Three initial sites 5, 7, and 10 Å have been chosen to evaluate the trapping strength of the GBs. The trajectories of P have been recorded during the diffusion and are further used to analyze the migration process. The Mean-Squared Displacement (MSD) is also derived from the trajectories every 2 ps during the diffusion. The slope of the MSD vs. time is proportional to the diffusion coefficient of the diffusing atom. Since, there is only one P atom in a model, taking its average would not be useful. However, the squared displacement from its reference position is beneficial for analyzing the diffusion behavior.

TABLE 1

Table 1. Characteristics of <110> STGB models.

In order to investigate the trapping effect of the GBs, formation energy E_f of Fe-P dumbbell and substitutional P are calculated, based on the formula derived by Tschopp et al. [28].

$\begin{array}{ll}{\text{E}}_{\text{f}}={\text{E}}_{\text{tot}}-{\text{E}}_{\text{GB}}-{\text{E}}_{\text{p}}& (2)\end{array}$

where E_tot is the total energy of the GB structure with a Fe-P dumbbell inside, E_GB is the total energy of the GB defect free configuration, and E_p is the cohesive energy of P, which is −3.4 eV [15].

To calculate the formation energy of Fe-P dumbbell as a function of distance from the GB, amongst the several layers of atoms in its neighborhood (up to 18 Å away from the GB center), one Fe atom is selected and paired with one P atom to form a dumbbell at each desired position.

The saddle point searching algorithm, like Nudged Elastic Band (NEB) is widely used to search the possible migration paths and energy barriers, where calculations at initial and final states are required as inputs [29]. In our cases, the NEB method is used to calculate the Fe-P dumbbell diffusion energy barriers at different positions around the GB in the ∑3{112} model. In the presence of the GB trapping effects, energy barriers of the diffusion away and toward the GB are always non-symmetrical. Therefore, we have calculated the barriers toward both diffusion directions. Furthermore, the trapping effect as a function of distance from the GB center has also been revealed by evaluating the variation of the diffusion barrier with distance. Three parallel tests have been conducted in order to obtain the average values and standard deviations.

All of the simulations and calculations are performed using the classical molecular dynamics code LAMMPS developed by Plimpton [30]. The Finnis-Sinclair type EAM interatomic potential, developed by Ackland et al. [31] has been employed. It is extensively used for the dilute Fe-P models since, it is in good agreement with DFT calculations [32]. A time step of 2 fs is used in the diffusion simulations in accordance with the Verlet integration method. For the atomic visualization OVITO has been used [33].

Results and Discussion

Structure and Energies of the GBs

After creating the GB models, the GBE is calculated and compared with the reference [28]. The GB structure model is widely used to predict the GB property [6, 24, 34]. The basic concept is that a GB can be designated as a combination of building blocks or structural units (SUs), and the combination and sequence of the SUs are representative for the GB properties. The six STGB models with their structural units are shown in Figure 1.

FIGURE 1

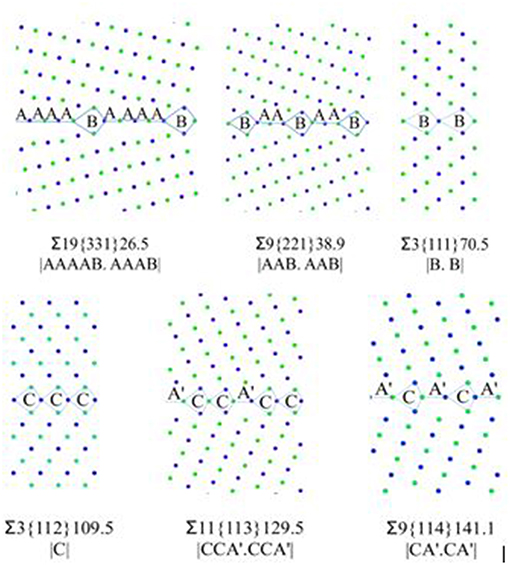
Figure 1. <110> STGB structures with structural units notations. Green and blue colors denote atoms on different (110) planes.

In this study, ∑3{111} and ∑3{112} are the delimiting boundaries having SUs as “B” and “C,” respectively. ∑19{331} and ∑9{221} are composed of “A” and “B” SUs, while, ∑11{113} and ∑9{114} are composed of “C” and “À” SUs [34]. The two ∑3 STGBs are more “favored” and possess high symmetry at the GB planes. For example, the structure of ∑9{221} GB is composed of both “A” and “B” SUs in 2:1 ratio, which can be described as |AAB.AAB|. In this notation, “A” and “B” are the repeating cells of the grain boundary. A favored boundary consists of an adjoining sequence of the units for only one type and those units are then defined to be in their ideal (undistorted) state, as defined by Sutton and Vitek [24]. This difference in the GB structure can be one of the reasons for the different trapping strength among the six models. The following formation energy discussion would provide different point of views.

Table 2 shows the calculation results of the six models. ∑3{112} model has the lowest γ at around 0.3 J/m², the others are between 1.3 and 1.4 J/m². The values and trend are comparable with other authors [24, 35]. The Fe-P dumbbells in all the models have been trapped by the GBs regardless of the temperature and the starting positions, which are 5, 7, and 10 Å or further away from the GB center. After analyzing the atomic configuration, it has been observed that the trapped Fe-P dumbbell dissociates into substitutional P near the GB. It is difficult for substitutional P to diffuse even in the bulk. As for ∑3{111} and ∑3{112}, the GBs show very weak trapping effect, regardless of the temperature and starting position.

TABLE 2

Table 2. Parameters for six models and their corresponding behavior.

The GB width shown in Table 2 has been defined as the region, where the average potential energy of the atoms has diverged more than 0.2% from the cohesive energy of one Fe atom in a defect free lattice [19]. It is noted that ∑3{112} has the narrowest GB width. However, all of the substitutional P atoms stop diffusing outside the GB area. Therefore, the GB width has nothing to do with the diffusion of P atoms, as the narrowest GBs of ∑3{112} and ∑9{114}, the diffusion has shown entirely different results.

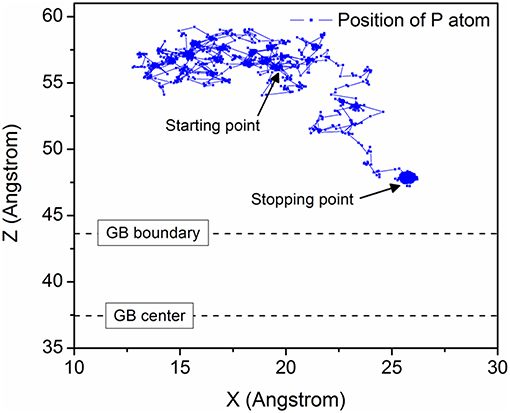
Figure 2 shows the diffusion trajectories of P in the model ∑19{331} at 600 K. The starting point is almost 20 Å away from the GB center and free migration has been observed at the beginning. After about 1 ns, as evident from Figure 2, P atom is diffused at the GB boundary and finally stops outside the GB area, even before ~4 Å along Z axis. All the models have displayed a similar kind of trapping behavior.

FIGURE 2

Figure 2. P atom trajectory in X-Z plane of model ∑19{331} at 600 K.

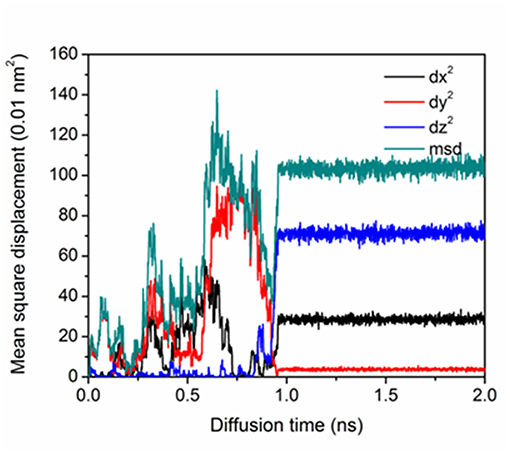
Figure 3 shows the mean square displacement of P atom corresponding to Figure 2. It is noted that before 1 ns, the Fe-P dumbbell migration was random and in the 3-dimensional directions. The P atom dissociates from one dumbbell leaving the paired Fe going back to the lattice site. Another nearest <110> Fe-P dumbbell appears accompanying a rotation to a different plane, which is similar to SIA migration in the pure Fe [6]. At ~1 ns, components of dx and dz increase, corresponding to the diffusion at the GB boundary in Figure 3. The plateau after 1 ns represents the transition of interstitial P to substitutional P at the stopping point which is evident by the visual inspection.

FIGURE 3

Figure 3. MSD as a function of diffusion time of P atom in model ∑19{331} at 600 K.

Influence of the GBs on Formation Energies

Since, local atomic configuration at the GBs contributes in formation of point defects like; dumbbell type interstitials and vacancies, it is significant for understanding defect-trapping behavior at the GBs. In this section, the substitutional P and dumbbell Fe-P formation energies have been examined as a function of distance from the GBs. For the plots in Figure 4, all the grain boundaries are initially centered at 0 Å, so that the formation energies become symmetrical.

FIGURE 4

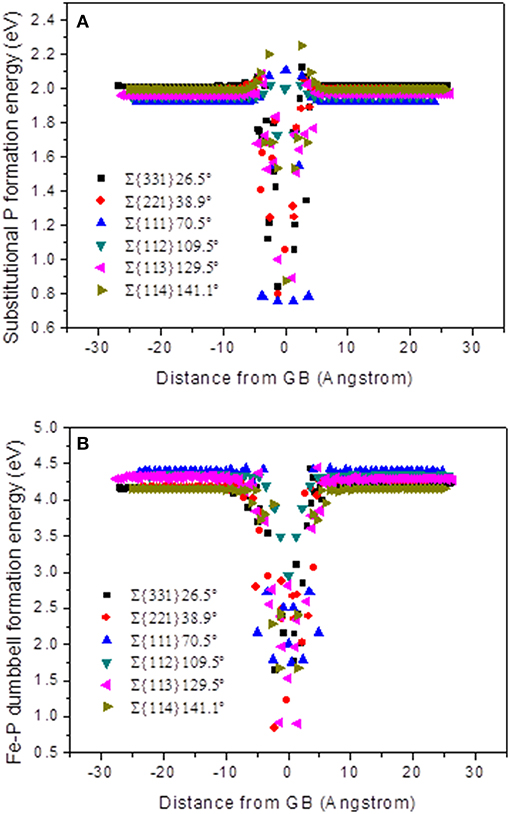
Figure 4. Formation energy as a function of distance from the center of the GB for all STGBs. (A) Substitutional P formation energy and (B) Fe-P mixed dumbbell formation energy.

In Figure 4A, the majority of substitutional P formation energy near the boundary has higher values than the bulk values, and it appears like shoulders. It can be seen that the formation energies at the center of the GB with the substitutional P atoms are much lower than the bulk values, which means it is more stable in the GB area for substitutional P. In Figure 4B, it can be seen that the formation energy is far from the GB corresponding to that in the bulk, which is in the range of 4.1~4.4 eV being higher than that of 3.5 eV of Fe-Fe SIA, as reported by Tschopp et al. [34].

The Formation energy of Fe-P dumbbell at the GBs is lower than in the bulk, which means higher binding energy exists at the GBs. Therefore, there is an energetic driving force present for the interstitials and substitutional P atoms to segregate at the GBs [36]. Furthermore, the formation energy of Fe-P dumbbell is higher than that of substitutional P, which means that the latter is more stable in the area of the GB. This is consistent with the observation of the transition from the former to the latter configuration, just before the diffusion stops.

As for ∑3{111}70.5° and ∑3{112}109.5°, the difference between the minimum formation energy at the GB center and in the bulk is lower than the other models. This could be an explanation for the weak trapping effect of these two GBs. While, the formation energies approach the bulk values between 5 to 8 Å away from the GB center, no obvious difference can be seen among the six models. Consequently, demonstrating that the length scale of absorption effect has no difference. It is evident in all the cases discussed here.

In the present study, the initial state is a <110> Fe-P dumbbell, and the final state is a nearest <110> Fe-P dumbbell being a step away, along the <111> direction. For the diffusion at the GB in the initial state, the P atom sits at a place far from the GB. In the final state, the P sits near the GB and vice versa for diffusion away from the GB. The atomic configurations for the diffusion away from the GB of Fe-P mixed dumbbell in the model ∑3 {112}109.5° is shown in Figure 5. The corresponding diffusion energy barriers are obtained by performing the NEB calculations that have been shown in Figure 6.

FIGURE 5

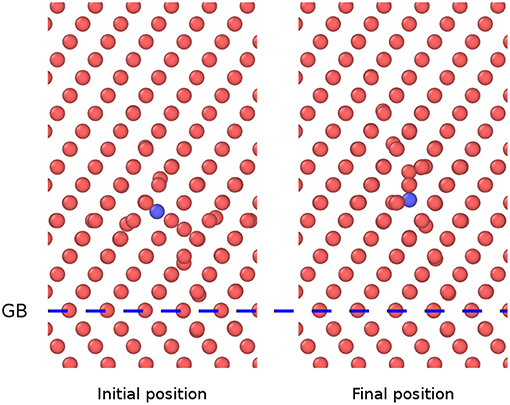
Figure 5. Atomic configuration of Fe-P mixed dumbbell in the model ∑3{112}109.5°, showing initial and final states before and after diffusion away from the GB (The blue spheres denote P atoms and the red ones denote Fe atoms).

FIGURE 6

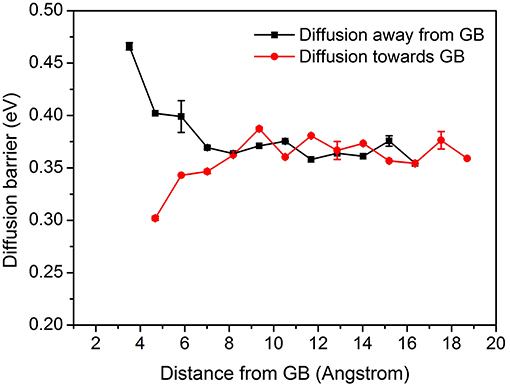
Figure 6. Diffusion energy barrier of ∑3{112}109.5° model as a function of distance from the GB, including diffusion away and toward the GB (Error bars denote the standard deviations).

Figure 6, displays diffusion energy barrier of the model ∑3{112}109.5° as a function of distance from the GB, with error bars denoting the standard deviations. It can be observed in Figure 6, that the GB shows trapping effect, demonstrating that the energy barrier for the diffusion toward the GB is lower than that in the bulk and the energy barrier for diffusion away from the GB has an opposite tendency. Due to the lattice mismatch toward the GB center, the NEB cannot be carried out there. The lowest and highest energy barrier obtained at around 5 Å from the GB center is 0.3 and 0.47 eV, respectively. It concludes that the diffusion toward the GB is easier as compared to the diffusion away from the GB. At ~8 Å, both barriers tend to be the same as that of the bulk, proving the saturation of trapping effects. Only a few deviations have been observed. Figure 6 shows the plot for the diffusion energy barrier as a function of distance from the GB for ∑3{112}109.5° model.

Conclusion

This study concludes STGBs structure impact on the diffusion behavior of the Fe-P mixed dumbbell. The high Σ STGBs, trap Fe-P dumbbell even outside the GB area. While, the two “favored” low Σ STGBs have shown significantly weak trapping effect. It has been proven by the formation energy of the Fe-P dumbbell near the GB that the two favored GBs have lower sink strength. Thus, the NEB results have confirmed the trapping effect of the GBs. In short, this study offers an atomistic framework for comprehending the P diffusion in alpha-Fe at the GBs.

Data Availability

The datasets for this manuscript are not publicly available because the data used to support the findings and more details of this study are available from the corresponding author on request. Requests to access the datasets should be directed to wangqingyu@hrbeu.edu.cn.

Author Contributions

All the authors contributed substantially in simulation and preparation of the manuscript. MA drafted the manuscript and assisted in MD simulations and formation energy calculations. SL did NEB calculations. MZ corrected initial draft. YZ proofread and corrected the manuscript. QW designed and guided overall activity.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

MA would like to extend his gratitude toward Chinese Scholarship Council (CSC) and College of Nuclear Science and Technology, Harbin Engineering University for their International Scholarship Program and immense academic support. QW acknowledges support from National Natural Science Foundation of China (grant no. 11505037) and Fundamental Research Funds for Central Universities (grant no. HEUCFJ171502 and 3072019CF1502).

Abbreviations

EAM, Embedded Atom Method; MD, Molecular Dynamics; LAMMPS, Large-scale Atomic/Molecular Massively Parallel Simulator; GB, Grain boundaries; NEB, Nudged Elastic Band.

References

1. Jingliang W. Grain boundaries in bcc-Fe: a density-functional theory and tight-binding study. Model Simul Mater Sci Eng. (2018) 26:025008. doi: 10.1088/1361-651X/aa9f81

CrossRef Full Text | Google Scholar

2. Mendelev MI, Srolovitz DJ. Grain-boundary migration in the presence of diffusing impurities: simulations and analytical models. Philos Mag A. (2001) 81:2243–69. doi: 10.1080/01418610108217146

CrossRef Full Text | Google Scholar

3. Spitaler J, Estreicher SK. Perspectives on the theory of defects. Front Mater. (2018) 5:70. doi: 10.3389/fmats.2018.00070

CrossRef Full Text | Google Scholar

4. Bhatia MA, Groh S, Solanki KN. Atomic-scale investigation of point defects and hydrogen-solute atmospheres on the edge dislocation mobility in alpha iron. J Appl Phys. (2014) 116:64302. doi: 10.1063/1.4892630

CrossRef Full Text | Google Scholar

5. Bhatia MA, Solanki KN. Energetics of vacancy segregation to symmetric tilt grain boundaries in hexagonal closed pack materials. J Appl Phys. (2013) 114:244309. doi: 10.1063/1.4858401

CrossRef Full Text | Google Scholar

6. Han J, Vitek V, Srolovitz DJ. The grain-boundary structural unit model redux. Acta Mater. (2017) 133:186–99. doi: 10.1016/j.actamat.2017.05.002

CrossRef Full Text | Google Scholar

7. Rajagopalan M, Tschopp MA, Solanki KN. Grain boundary segregation of interstitial and substitutional impurity atoms in alpha-iron. JOM. (2014) 66:129–38. doi: 10.1007/s11837-013-0807-9

CrossRef Full Text | Google Scholar

8. Yamaguchi M. First-principles study on the grain boundary embrittlement of metals by solute segregation: part I. iron (Fe)-solute (B, C, P, and S) systems. Metall Mater Trans A. (2011) 42:319–29. doi: 10.1007/s11661-010-0381-5

CrossRef Full Text | Google Scholar

9. Lidiard AB. The migration of phosphorus in ferritic iron alloys under irradiation. Philos Mag A. (1999) 79:1493–506. doi: 10.1080/01418619908210374

CrossRef Full Text | Google Scholar

10. Ebihara KI, Suzudo T. Atomistic simulation of phosphorus segregation to Σ3 (111) symmetrical tilt grain boundary in α-iron. Model Simul Mater Sci Eng. (2018) 26:065005. doi: 10.1088/1361-651X/aace6a

CrossRef Full Text | Google Scholar

11. Ebihara K, Suzudo T, Yamaguchi M. Modeling of phosphorus transport by interstitial dumbbell in α – iron using first-principles-based kinetic Monte Carlo. Mat Trans. (2017) 58:26–32. doi: 10.2320/matertrans.ML201602

CrossRef Full Text | Google Scholar

12. Solanki KN, Tschopp MA, Bhatia MA, Rhodes NR. Atomistic investigation of the role of grain boundary structure on hydrogen segregation and embrittlement in α-Fe. Metall Mat Trans A. (2013) 44:1365–75. doi: 10.1007/s11661-012-1430-z

CrossRef Full Text | Google Scholar

13. Lejček P, Všianská M, Šob M. Recent trends and open questions in grain boundary segregation. J Mater Res. (2018) 33:2647–60. doi: 10.1557/jmr.2018.230

CrossRef Full Text | Google Scholar

14. Barashev AV. Segregation of phosphorus atoms to grain boundaries in ferritic steels under neutron irradiation. Philos Mag Lett. (2002) 82:323–32. doi: 10.1080/09500830210135021

CrossRef Full Text | Google Scholar

15. Domain C, Becquart CS. Diffusion of phosphorus in α-Fe: an ab initio study. Phys Rev B. (2005) 71:214109. doi: 10.1103/PhysRevB.71.214109

CrossRef Full Text | Google Scholar

16. Uesugi T, Higashi K. First-principles calculation of grain boundary energy and grain boundary excess free volume in aluminum: role of grain boundary elastic energy. J Mater Sci. (2011) 46:4199–205. doi: 10.1007/s10853-011-5305-2

CrossRef Full Text | Google Scholar

17. Terentyev D, He X, Serra A, Kuriplach J. Structure and strength of 〈 1 0〉 tilt grain boundaries in bcc Fe: an atomistic study. Comput Mater Sci. (2010) 49:419–29. doi: 10.1016/j.commatsci.2010.05.033

CrossRef Full Text | Google Scholar

18. Fu CC, Torre JD, Willaime F, Bocquet JL, Barbu A. Multiscale modelling of defect kinetics in irradiated iron. Nat Mater. (2005) 4:68–74. doi: 10.1038/nmat1286

CrossRef Full Text | Google Scholar

19. Hurchand H, Kenny SD, Smith R. The interaction of P atoms and radiation defects with grain boundaries in an α-Fe matrix. Nucl Instruments Methods Phys Res B. (2005) 228:146–50. doi: 10.1016/j.nimb.2004.10.037

CrossRef Full Text | Google Scholar

20. Vasiliev AA, Rybin VV, Zisman AA. The nature of the phosphorus atom mobility in bcc iron irradiated at low temperatures. J Nucl Mater. (1996) 231:249–53. doi: 10.1016/0022-3115(96)00201-2

CrossRef Full Text | Google Scholar

21. Gordon SMJ, Hurchand H, Kenny SD, Smith R. Diffusion of radiation damage in Fe-P systems. Nucl Instruments Methods Phys Res Sect B Beam Interact with Mater Atoms. (2005) 228:131–6. doi: 10.1016/j.nimb.2004.10.034

CrossRef Full Text | Google Scholar

22. Martino SFD, Faulkner RG, Smith R. Modelling radiation damage effects on a bcc iron lattice containing phosphorous impurity atoms near symmetrical tilt boundaries. J Nucl Mater. (2011) 417:1058–62. doi: 10.1016/j.jnucmat.2011.01.086

CrossRef Full Text | Google Scholar

23. Kim JI, Pak JH, Park K-S, Jang JH, Suh D-W, Bhadeshia HKDH. Segregation of phosphorus to ferrite grain boundaries during transformation in an Fe-P alloy. Int J Mater Res. (2014) 105:1166–72. doi: 10.3139/146.111129

CrossRef Full Text | Google Scholar

24. Sutton AP, Vitek V. On the structure of tilt grain boundaries in cubic metals I. Symmetrical Tilt Boundaries Phil Trans R Soc A. (1983) 309:1–36. doi: 10.1098/rsta.1983.0020

CrossRef Full Text | Google Scholar

25. Chen D, Wang J, Chen T, Shao L. Defect annihilation at grain boundaries in alpha-Fe. Sci Rep. (2013) 3:1450. doi: 10.1038/srep01450

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Ogawa H. GBstudio: a builder software on periodic models of CSL boundaries for molecular simulation. Mater Trans. (2006) 47:2706–10. doi: 10.2320/matertrans.47.2706

CrossRef Full Text | Google Scholar

27. Evans DJ, Holian BL. The Nose-Hoover thermostat. J Chem Phys. (1985) 83:4069–74. doi: 10.1063/1.449071

CrossRef Full Text | Google Scholar

28. Tschopp MA, Gao F, Yang L, Solanki KN. Binding energetics of substitutional and interstitial helium and di-helium defects with grain boundary structure in α-Fe. J Appl Phys. (2014) 115:033503. doi: 10.1063/1.4861719

CrossRef Full Text | Google Scholar

29. Baibuz E, Vigonski S, Lahtinen J, Zhao J, Jansson V, Zadin V, et al. Migration barriers for surface diffusion on a rigid lattice: challenges and solutions. Comput Mater Sci. (2018) 146:287–302. doi: 10.1016/j.commatsci.2017.12.054

CrossRef Full Text | Google Scholar

30. Plimpton S. Fast parallel algorithms for short–range molecular dynamics. J Comput Phys. (1995) 117:1–19. doi: 10.1006/jcph.1995.1039

CrossRef Full Text | Google Scholar

31. Ackland GJ, Mendelev MI, Srolovitz DJ, Han S, Barashev AV. Development of an interatomic potential for phosphorus impurities in α-iron. J Phys Condens Matter. (2004) 16:S2629–42. doi: 10.1088/0953-8984/16/27/003

CrossRef Full Text | Google Scholar

32. Malerba L, Marinica MC, Anento N, Björkas C, Nguyen H, Domain C, et al. Comparison of empirical interatomic potentials for iron applied to radiation damage studies. J Nucl Mater. (2010) 406:19–38. doi: 10.1016/j.jnucmat.2010.05.017

CrossRef Full Text | Google Scholar

33. Stukowski A. Visualization and analysis of atomistic simulation data with OVITO-the open visualization tool. Model Simul Mater Sci Eng. (2010) 18:015012. doi: 10.1088/0965-0393/18/1/015012

CrossRef Full Text | Google Scholar

34. Tschopp MA, Solanki KN, Gao F, Sun X, Khaleel MA, Horstemeyer MF. Probing grain boundary sink strength at the nanoscale: energetics and length scales of vacancy and interstitial absorption by grain boundaries in α-Fe. Phys Rev B - Condens Matter Mater Phys. (2012) 85:1–21. doi: 10.1103/PhysRevB.85.064108

CrossRef Full Text | Google Scholar

35. Shibuta Y, Takamoto S, Suzuki T. A molecular dynamics study of the energy and structure of the symmetric tilt boundary of iron. ISIJ Int. (2008) 48:1582–91. doi: 10.2355/isijinternational.48.1582

CrossRef Full Text | Google Scholar

36. Tschopp MA, Horstemeyer MF, Gao F, Sun X, Khaleel M. Energetic driving force for preferential binding of self-interstitial atoms to Fe grain boundaries over vacancies. Scr Mater. (2011) 64:908–11. doi: 10.1016/j.scriptamat.2011.01.031

CrossRef Full Text | Google Scholar