Resonance Energy Transfer: From Fundamental Theory to Recent Applications

Resonance energy transfer (RET), the transport of electronic energy from one atom or molecule to another, has significant importance to a number of diverse areas of science. Since the pioneering experiments on RET by Cario and Franck in 1922, the theoretical understanding of the process has been continually refined. This review presents a historical account of the post-Förster outlook on RET, based on quantum electrodynamics, up to the present-day viewpoint. It is through this quantum framework that the short-range, R⁻⁶ distance dependence of Förster theory was unified with the long-range, radiative transfer governed by the inverse-square law. Crucial to the theoretical knowledge of RET is the electric dipole-electric dipole coupling tensor; we outline its mathematical derivation with a view to explaining some key physical concepts of RET. The higher order interactions that involve magnetic dipoles and electric quadrupoles are also discussed. To conclude, a survey is provided on the latest research, which includes transfer between nanomaterials, enhancement due to surface plasmons, possibilities outside the usual ultraviolet or visible range and RET within a cavity.

Introduction and the Early Years of RET

Resonance energy transfer (RET, also known as fluorescence resonance energy transfer, FRET, or electronic energy transfer, EET) is an optical process, in which the excess energy of an excited molecule—usually called the donor—is transferred to an acceptor molecule [1–4]; as depicted schematically in Figure 1. Fundamentally, RET involves two types of elementary particles: electrons and photons. In RET, all the electrons (including the dynamically active electrons) are bound to the nuclei of the molecules, and typically reside in their valence molecular orbitals. As such, the individual electrons do not migrate between molecules during the transfer process, since the molecular orbitals (the wavefunctions) do not overlap, but instead move between individual electronic states within the molecules. This is fundamentally different to the ultra-short-range Dexter energy transfer, where electrons do in fact migrate between molecules via covalent chemical bonds [5]. In RET, on relaxation of the electron to a lower energy electronic state in the donor, the excess energy is transported to the acceptor in the form of the emitted virtual photon—this transfer is facilitated by dipole-dipole couplings between the molecules. In fact, photons play two distinct roles toward the process: one as the mediator of donor-acceptor transfer, and the other as an external energy source that promotes donor valence electrons into an electronic excited state, via an absorption process prior to RET.

FIGURE 1

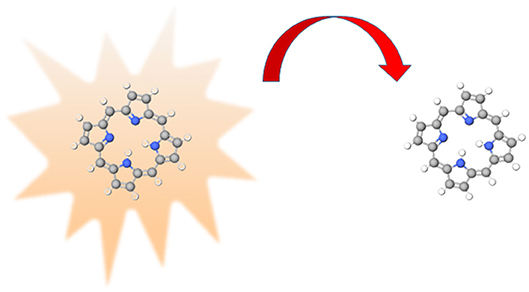
Figure 1. Representation of energy transfer, the excited donor (on the left-hand side) transfers energy, represented by the red arrow, to the acceptor (on the right).

In 1922, the pioneering work of Cario and Franck enabled the earliest observation of RET [6–8]. Their spectroscopy experiment involved the illumination of a mixture of mercury and thallium vapors at a wavelength absorbed only by the mercury; the fluorescence spectra that results show frequencies lines that can only be due to thallium. In 1927, the Nobel laureate J. Perrin provided the first theoretical explanation [9]: he recognized that energy could be transferred from an excited molecule to a nearby-unexcited molecule via dipole interactions. Five years later, his son F. Perrin developed a more accurate theory of RET [10] based on Kallman and London's results [11]. Extending the works of both Perrins, Förster developed an improved theoretical treatment of RET [12–14]. Förster found that energy transfer, through dipole coupling between molecules, mostly depends on two important quantities: spectral overlap and intermolecular distance. He discovered the now famous R⁻⁶ distance-dependence law for the rate of resonance energy transfer in the short-range. Much later, in 1965, this distance dependence predicted by Förster was verified [15]. This led to the “spectroscopic ruler” by Stryer and Haugland [16, 17], a useful technique to measure the proximity of chromophores and conformational change in macromolecules using RET. The next section, which is more technical than the rest of the article, details the history of RET based on quantum electrodynamics (QED); it can be safely skipped by readers more interested in the current understanding of RET.

Historical Role of Quantum Electrodynamics in RET

The Success of QED

Quantum electrodynamics is a rigorous and accurate theory—which is completely verifiable by experiment [18]—that describes the interaction of electromagnetic radiation with matter. This quantum field approach differs to other theories in that the whole system is quantized, i.e., both matter and radiation are treated quantum mechanically. QED provides additional physical insights compared to classical and semi-classical electrodynamics, which treats electromagnetic radiation only as a non-quantized wave. For example, the wave-particle duality of light is uniquely portrayed within QED but not semi-classical theories. However, despite their deficiencies, classical and semi-classical theories can still be useful since, often, they are easier to implement analytically and more economic computationally.

The first major QED publication is credited to Dirac who, in 1927, wrote a description of light emission and absorption that incorporated both quantum theory and special relativity [19]; this depiction later became known as the relativistic form of QED, which is used in systems that contain fast moving electrons. Three years later Dirac completed his classic book “The Principles of Quantum Mechanics” [20] in which, among other exceptional works, he derived a relativistic generalization of the Schrödinger equation. However, for elementary physical quantities such as the mass and charge of particles, calculations using this early form of QED produce diverging results. In the late 1940s, this problem was resolved (by renormalization) leading to a complete form of QED developed independently by Feynman [21–25], Schwinger [26–29], and Tomonaga [30, 31]—all three procedures were unified by Dyson [32].

The ability of QED to provide novel predictions is monumental, but its quantitative successes are even more impressive. In particular, the theory accurately predicts the electronic g-factor of the free electron to 12 decimal places. In Bohr magneton units, the most precise measurement of g/2 is 1.00115965218073(28) [33]; QED has a predicted value of 1.00115965218203(27) [34]. In addition, there are other staggering quantitative successes. For example, the numerical calculation of Lamb shift splitting of the 2S_1/2 and 2P_1/2 energy levels in molecular hydrogen predicts 1,057,838(6) kHz [35], which is highly accurate compared to the experimental value of 1,057,839(12) kHz [36]. QED also provides a number of predictions that are unobtainable by semi-classical theory. These include forecasts of spontaneous decay and the Casimir-Polder forces, a deviation from London forces for long-range intermolecular interactions [37–41].

Non-relativistic QED: A Theoretical Framework for RET

An individual RET process, which arises after excitation of the donor, involves light emission at one molecule and light absorption at the other. Such light-molecule interactions are best described by QED. This means that the quantum properties and the retardation effects of the mediating light, which leads to the concept of a photon, is directly incorporated into the calculations. Therefore, in terms of this framework, it is natural to describe RET in terms of photon creation and annihilation events. Namely, the creation of a photon at the excited donor and a photon annihilation at the unexcited acceptor. Mathematically, these couplings are represented as off-diagonal matrix elements of the interaction Hamiltonian. A full quantum description is usually necessary to describe the RET process over all distances, this is because the electronic energy is not transferred instantaneously as assumed by the classical and semi-classical descriptions (although retardation effects are sometimes provided in such frameworks [42]). The transfer of energy between molecules occurs via the exchange of a virtual photon, which has increasingly real (transverse) characteristics as the intermolecular separation grows; this is discussed, in more detail, in section Physical Interpretation of the RET Coupling Tensor. The term virtual being indicative of the fact that the photon is reabsorbed before its properties, such as wavelength, take on physical significance. The dipole of each molecule is also correctly described as a transition dipole moment, connecting two non-degenerate energy states of the molecule.

Since RET involves slow moving electrons, bound within the valence states of the molecules, the non-relativistic variant of QED (as opposed to relativistic or Lorenz gauge QED) is used. The theory that underpins the quantum description of RET is the Power-Zienau-Woolley formalism of molecular (or non-relativistic) QED [43–48], which utilizes the Coulomb gauge, $\nabla ·\overrightarrow{A}=0$, where $\overrightarrow{A}$ is the vector potential and the fields of the mediating photons can be naturally deconstructed into longitudinal and transverse components. The longitudinal components, with respect to the displacement vector $\overrightarrow{R}$, are associated with the scalar potential and have a particular affinity for coupling molecular transition moments in the near-zone, where the donor-acceptor pair are close together. In regions far from the source (i.e., distant from the donor) the wave-vector $\overrightarrow{k}$ and $\overrightarrow{R}$ are essentially collinear and the scalar potential approaches zero. In this case, the transverse part of the field dominates the coupling of the transition dipole moments of individual molecules [49]. This has important implications for the spatial and temporal dynamics of excitons within molecular aggregates [50, 51]; namely, transition dipole moment pairs that are collinear to each other and collinear to the displacement vector are coupled by the longitudinal components of the field only.

The QED model of RET is traceable to the 1966 paper by Avery, which extended the Perrin and Förster theory of RET by replacing the Coulomb interaction with the relativistic Breit interaction [52]. Although Avery did not explicitly include the effects of the mediating photon, in terms of the creation and annihilation field operators, he nevertheless made a direct connection between RET and spontaneous emission. Moreover, he determined the R⁻² dependence on the transfer rate in the far-zone. He concluded that investigating RET from the point-of-view of the ‘direct action’ formulation of QED, devised by Wheeler and Feynman [53], would be ‘extremely interesting’. Soon afterwards, in the same year, the Avery work was enhanced by a more formal and rigorous quantum theoretical outlook provided by Gomberoff and Power [54].

RET Coupling Tensor: The Quest for Its Correct Form

In the early 1980s there were a number of RET studies by Thirunamachandran, in collaboration with Power and Craig, which give valuable insights into the physical connections between the near- and far-zone mechanisms of RET. In 1983, Power and Thirunamachandran published three seminal papers on QED theory [55–57]. Here they consider the problem within the Heisenberg formalism, via the time evolution of operators associated with both electron fields and Maxwell fields. In the third paper of the series, they derive an expression for the time dependent evolution of the RET quantum amplitude as;

$\begin{array}{l}{c}_{fi}(t)=\frac{1}{\hslash c}{\mu }_i^{0p}(D){\mu }_j^{q0}(A)(-{\nabla }^2{\delta }_{ij}+{\nabla }_i{\nabla }_j)\\ \times \frac{1}{\pi R}{\displaystyle \underset{-\infty }{\overset{+\infty }{\int }}}sin(kR)\left[\frac{e^{ict(k_A-k_D)}-1}{(k_A-k_D)(k-k_D)}+\frac{e^{ict(k_A-k)}-1}{(k-k_A)(k-k_D)}\right]dk,& (1)\end{array}$

where μ_k(X) is the transition dipole moment of molecule X along the k^th canonical coordinate and R is the distance between the two molecules. The transfer occurs from an excited molecule D to molecule A, initially in its ground state. Subscripts i and j represent Cartesian components with the usual tensor summation convention being employed [58]. The transition dipole moments elements are ${\mu }_i^{0p}(D)$ and ${\mu }_j^{q0}(A)$; where molecule D is initially in state p, and the final state of molecule A is q. Integration is over all possible wave-vectors (denoted by k) of the mediating photon. In this work, the rapidly oscillating terms were dropped, to leave only two terms instead of the usual four; vide infra, Equation (6). The terms k_D and k_A represent the wave-vectors resonant with a transition of molecules D and A, respectively. Power and Thirunamachandran did not explicitly describe how the singularities in Equation (1) were dealt with mathematically, but they show that the final expression conforms to the correct distance dependencies in the appropriate limits.

Around the same time, Thirunamachandran and Craig considered resonance coupling between molecules “where one was in an excited state,” within the dipole approximation (the term ‘resonance energy transfer’ was not used in this work). They initially published the work as an extended paper [59], and expanded upon it in their widely known book [45]. They consider two identical molecules and calculate the interaction of the excited system D with the unexcited system A. Firstly, they considered calculations that ignored retardation effects and any time explicit dependencies. The calculated electric field at A, produced by the oscillating dipole at D, produces an energy change of;

$\begin{array}{ll}\Delta E={(4\pi {\epsilon }_0)}^{-1}{R}^{-3}{\mu }_i^{0p}(D){\mu }_j^{q0}(A)\left({\delta }_{ij}-3{\widehat{R}}_i{\widehat{R}}_j\right).& (2)\end{array}$

The final term is an orientational factor that modulates the magnitude of the energy difference based on the relative dipole orientations of the molecules. Through the inclusion of retardation effects, Equation (2) becomes;

$\begin{array}{l}\Delta E={(4\pi {\epsilon }_0)}^{-1}{\mu }_i^{0p}(D){\mu }_j^{q0}(A)e^{i\overrightarrow{k}·\overrightarrow{R}}\\ \times \left\{k^2{R}^{-1}\frac{coskR}{R}\left({\delta }_{ij}-{\widehat{R}}_i{\widehat{R}}_j\right)-\left(\frac{coskR}{R^3}+\frac{ksinkR}{R^2}\right)\left({\delta }_{ij}-3{\widehat{R}}_i{\widehat{R}}_j\right)\right\}.& (3)\end{array}$

Retardation effects give rise to the appearance of a phase factor, ${\mathrm{\text{e}}}^{i\overrightarrow{k}·\overrightarrow{R}}$, as well as two other distance dependencies, namely, R⁻¹ and R⁻².

The authors then calculated the fully retarded matrix element in tensor-form and show that it is the same as expression (Equation 3). The calculation formally involves summing over all photon wave-vectors connecting the initial and final states. In practice, this summation involves using a box quantization technique to transform the problem to an integral in momentum space. The solution can be found by contour integration, in a way analogous to that in which Green's functions solutions are found in quantum scattering problems [60]. For identical molecules, the final matrix element (or quantum amplitude) in tensorial form is:

$\begin{array}{l}{M}_{fi}^{ }={\mu }_i^{0n}(D)V_{ij}(k,\overrightarrow{R}){\mu }_j^{m0}(A),\end{array}$

where;

$\begin{array}{l}{V}_{ij}\left(k,\overrightarrow{R}\right)=\frac{1}{4\pi {\epsilon }_0{R}^3}[\left({\delta }_{ij}-3{\widehat{R}}_i{\widehat{R}}_j\right)\left(\cos kR+kR\sin kR\right)\\ -\left({\delta }_{ij}-{\widehat{R}}_i{\widehat{R}}_j\right)\left(k^2{R}^2\cos kR\right)].& (4)\end{array}$

In light of the subsequent analysis shown later, it is important to note that the interaction tensor V_ij, derived in this early work, is purely the real part of the full expression. In deriving Equation (4), four different contours could be chosen around the two poles (the singularities), leading to different results. The contour they chose ensures a correct outgoing-wave solution, although there is no a priori mathematical basis for this choice.

Further advances were achieved by Andrews and co-workers who proved a direct relationship between radiationless and radiative RET [61–63]. Although all three regimes of RET—i.e., the R⁻², R⁻⁴, and R⁻⁶ dependencies on the rate—were mathematically predicted in the original derivations, Andrews et al. were the first to comment upon the relevance of the intermediate-zone contribution, which has a R⁻⁴ dependence. This term dominates at critical distances; that is, when the distance separating the molecules is in the order of the reduced wavelength, $ƛ=\frac{\lambda }{2\pi }$, of the mediating photon (i.e., R ~ƛ). Inclusion of all three distance-dependencies in one rate equation is known as the unified theory of RET. The particulars of which are provided in section Physical Interpretation of the RET Coupling Tensor.

Initially Andrews and Sherborne [61], reconsidered the problem in the Schrödinger representation, where they derived the electric dipole-electric dipole tensor without the need of “outgoing wave” arguments of scattering theory [59]. Starting from the second-order expression for the time-dependent probability amplitude for energy transfer, they inserted all intermediate states to obtain a rather complicated looking expression (not reproduced here). As detailed in the original paper, the integral of the expression gives rise to four different Green's functions, and hence four choices of contour. The fact that four terms arise is attributed to the forward and reverse transfer processes. They showed that the choice of contour was not unique, with each giving different expressions for $V_{ij}(k,\overrightarrow{R})$. Interestingly, they found that these new contours introduced imaginary terms into $V_{ij}(k,\overrightarrow{R})$, i.e., those not included in the derivations of the earlier work by Thirunamachandran and Craig. By choosing the contour that appeared to be the “most acceptable,” they derived the coupling matrix element to be of the form (corrected later by Daniels et al. [63] and modifying the indexing here for better comparison with the expressions above):

$\begin{array}{ll}{V}_{ij}(k,\overrightarrow{R})={\sigma }_{ij}(k,\overrightarrow{R})+i{\tau }_{ij}(k,\overrightarrow{R}),& (5)\end{array}$

where,

$\begin{array}{l}{\sigma }_{ij}\left(k,\overrightarrow{R}\right)=\frac{1}{4\pi {\epsilon }_0{R}^3}[\left({\delta }_{ij}-3{\widehat{R}}_i{\widehat{R}}_j\right)\left(\cos kR+kR\sin kR\right)\\ -\left({\delta }_{ij}-{\widehat{R}}_i{\widehat{R}}_j\right)\left(k^2{R}^2\cos kR\right)],\\ {\tau }_{ij}\left(k,\overrightarrow{R}\right)=\frac{1}{4\pi {\epsilon }_0{R}^3}[\left({\delta }_{ij}-3{\widehat{R}}_i{\widehat{R}}_j\right)\left(\sin kR-kR\cos kR\right)\\ -\left({\delta }_{ij}-{\widehat{R}}_i{\widehat{R}}_j\right)\left(k^2{R}^2\sin kR\right)],\end{array}$

in which σ_ij is the expression given in Equation (4). This derivation eliminates the need for physical arguments based on quantum scattering theory used in the earlier work. It, nevertheless, did require careful consideration of the correct contour with which to apply Cauchy's residue theorem for solving the integral. In later work, Andrews and Juzeliunas applied an alternative method of contour integration, whereby they infinitesimally displaced the problematic poles away from the real axis [64]. The idea being that the imaginary addenda shifted the poles to enable integration around a closed contour along the real axis. The approach gave results in agreement with those of Andrews and Sherborne's favored choice of contour. Thus, this study removes the need to choose a contour; however, artificial displacements of the poles, including the choice of direction of displacement on the complex plane, must be made.

In 2003, Daniels et al. re-examined the problem and avoided the uncertainties of the contour integration entirely by solving the Green's function using judicious substitutions within the integrals. Namely, when the Green's function is expressed as a sum of two integrals, so that;

$\begin{array}{ll}G(k,R)={\displaystyle \underset{0}{\overset{\infty }{\int }}}\frac{sinpR}{R(k-p)}dp+{\displaystyle \underset{0}{\overset{\infty }{\int }}}\frac{sinpR}{R(-k-p)}dp,& (6)\end{array}$

substitutions of the form t = pR − kR and s = pR + kR for the first and second integral, respectively, give an expression in which terms are oscillatory, but convergent. The authors solved these integrals by expressing them as series expansions (in the form of special functions) to get a result, analogous to Equation (5), in the form:

$\begin{array}{l}{\sigma }_{ij}\left(k,\overrightarrow{R}\right)=\frac{1}{4\pi {\epsilon }_0{R}^3}\{\left(\cos kR+kR\sin kR\right)\left[{\delta }_{ij}-3{\widehat{R}}_i{\widehat{R}}_j\right]\\ -k^2{R}^2\cos kR\left[{\delta }_{ij}-{\widehat{R}}_i{\widehat{R}}_j\right]\}\\ {\tau }_{ij}^{\pm }\left(k,\overrightarrow{R}\right)=\frac{1}{4\pi {\epsilon }_0{R}^3}\{\mp \left(\sin kR-kR\cos kR\right)\left[{\delta }_{ij}-3{\widehat{R}}_i{\widehat{R}}_j\right]\\ \pm k^2{R}^2\sin kR\left[{\delta }_{ij}-{\widehat{R}}_i{\widehat{R}}_j\right]\}.& (7)\end{array}$

Here, on comparing with the earlier expressions, the only difference is a choice of sign for the imaginary term τ_ij. The authors suggested that the ambiguity of sign for this term signifies that $V_{ij}^{\pm }(k,\overrightarrow{R})$ describes both incoming and outgoing waves, accommodating thereby both time-ordered (Feynman) diagrams, as a complete quantum description should. However, the authors stress that it is unimportant which sign to ascribe to a particular process (photon absorption or emission), as only the modulus squared of the matrix element is physically measureable and, hence, using either sign on τ_ij provides an identical result for all calculations relevant to experiment. Jenkins et al. wrote a follow-up paper that analyzed the importance of each Feynman diagram, called time-ordered pathways, to the overall RET rate. They discovered that both pathways have equal contribution when the two molecules are close together; however, one pathway begins to dominate as the molecules are moved further apart [65].

In 2016, Grinter and Jones re-derived expression (7) using a spherical wave description of the mediating photon, via vector spherical harmonics [66]. All previous derivations employed a plane-wave description of the mediating photon. One advantage of the spherical wave approach is that multipole contributions are more concretely defined in terms of the angular momentum quantum numbers l and m. Furthermore, the work involved the development of an approach complementary to the plane wave methods, giving additional insight into orientational aspects of RET and forming a natural setting for the decomposition of fields into transverse and longitudinal components. In 2018, a comprehensive review of the spherical wave approach was published [67]. In the plane-wave method, defined in terms of the position vector $\overrightarrow{r}$, the oscillating part of the field is expanded as;

$\begin{array}{ll}{\overrightarrow{e}}_{1n}{\text{e}}^{i\overrightarrow{k}·\overrightarrow{r}}={\overrightarrow{e}}_{1n}\left[1+i\overrightarrow{k}·\overrightarrow{r}+\frac{{\left(i\overrightarrow{k}·\overrightarrow{r}\right)}^2}{2!}+\frac{{\left(i\overrightarrow{k}·\overrightarrow{r}\right)}^3}{3!}+\dots \right].& (8)\end{array}$

where the first term relates to the electric dipole, the second to the magnetic dipole and the electric quadrupole, and so on. In the spherical wave description, the expansion is written as;

$\begin{array}{ll}{\text{e}}^{i\overrightarrow{k}·\overrightarrow{r}}={\displaystyle \sum _l}{i}^l(2l+1)j_l(kr)P_l(cos\vartheta ).& (9)\end{array}$

where j_l(kr) are Bessel functions and P_l(cosϑ) are Legendre polynomials. The spherical wave description consequently attributes radiation emerging from specific pure multipole sources to specific angular momentum quantum numbers, thereby separating different multipole contributions that are of the same order.

Additionally, derivation of the RET matrix element using spherical waves eliminates the need to perform contour integration and, therefore, select the physically correct solutions. The arbitrary choice of sign, which can be seen in the imaginary part (τ_ij) of Equation (7), does not appear in the spherical wave analysis. The R dependence can be expressed in terms of Hankel functions of the first kind, i.e., $h_l^{(1)}(kR)=j_l(kR)+i{n}_l(kR)$ for outgoing waves, while Hankel functions of the second kind, i.e., $h_l^{(2)}(kR)=j_l(kR)-i{n}_l(kR)$ describe incoming waves. The ambiguous sign in Equation (7) was interpreted to mean that both incoming and outgoing waves are required to calculate the quantum amplitude of the process (i.e., photon absorption and emission). In the spherical wave approach, the incoming and outgoing waves emerge naturally and can be linked directly to one or other of the signs in the imaginary part of Equation (7), up to the phase factor exp(±iωt).

In a separate study, Grinter and Jones also analyzed the transfer of angular momentum between multipoles using a spherical description of the mediating photon [68]. Although it has been known for some time that coupling between multipoles of different order can be non-zero [69–74], this work showed that RET between multipoles of different order is formally allowed. This is because the isotropy of space is broken during an individual transfer event, even though one may expect the process to be forbidden on the grounds of the violation of the conservation of angular momentum. For example, in the case of electric dipole-electric quadruple (E1-E2) transfer, two units of angular momentum are lost from the electronic state of a quadrupole emitter (the donor), whereas the dipole acceptor only takes up one quantum of electronic angular momentum. The above analyses indicate that treating the mediating photon of an RET process in terms of spherical waves may be valuable in some applications, particularly in the case of multipolar QED. A discussion on higher-order considerations, such as these, is found in section Higher Order RET.

RET Based on Quantum Electrodynamics

Derivation of the RET Coupling Tensor

In order to understand any optical process within the framework of QED, a matrix element (or quantum amplitude) that links the initial and final states is required. In the case of RET between two molecules, the initial state is the donor, D, in an excited state and an acceptor, A, in the ground state. In the final state, the acceptor molecule is in an excited state and the donor molecule is in its ground state. Photophysically, this can be simply understood as;

$\begin{array}{ll}{D}^{*}+A\to D+A^{*},& (10)\end{array}$

where, in this type of chemical expression, the asterisk denotes the molecule in an electronically excited state.

The usual starting point for any QED analysis is the illustration of the process by Feynman diagrams [23], thereby aiding construction of the matrix element by defining all of the intermediate system states. Feynman diagrams are graphical descriptions of electronic and photonic processes with a time frame that moves upwards. Resonance energy transfer between two molecules, in isolation, involves two Feynman diagrams—as shown in Figure 2. Here, examining the left-hand diagram, the initial system state has the donor in excited state n and the acceptor in the ground state, labeled 0 (the red section). Moving up the time axis, a photon is created from the excited donor to provide an intermediate system state, in which both molecules are in the ground state and a photon is present (the black section). Higher up the diagram this photon is annihilated at the donor and, thus, excites it to state m (the blue section). The diagram on the right-hand side is legitimate, albeit counter-intuitive. In this case, the intermediate system state represents both molecules simultaneously in their excited states in the presence of the mediating photon—meaning that conservation of energy is clearly violated. However, this is fully justifiable within the constraints of the energy-time uncertainty principles.

FIGURE 2

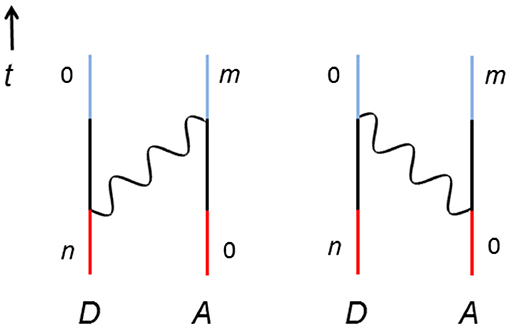
Figure 2. Two time-orderings for RET between a donor (D) and an acceptor (A). The vertical lines denote the two molecules, wavy lines are the photons, n and m represents the excited state of D and A, respectively, and 0 is their ground state; time, t, increases up the graph. Red, black, and blue lines represent the initial, intermediate, and final system state.

These diagrams (which represent the two pathways of RET) involve two light-molecule interactions: one at the donor and the other at the acceptor. This is indicative of second-order perturbation theory, which we examine below, as the minimal level of theory necessary to describe RET. The total Hamiltonian for RET between neutral molecules, in multipolar form, is written as;

$\begin{array}{ll}H=H_{\text{mol}}(D)+H_{\text{mol}}(A)+H_{\text{rad}}+H_{int}(D)+H_{int}(A).& (11)\end{array}$

Here, the first two terms correspond to the molecular Hamiltonians of the donor and acceptor H_mol(X) ; X = D, A, which are usually the non-relativistic Born-Oppenheimer molecular Hamiltonian. The third term is the radiation Hamiltonian, H_rad, not seen in semi-classical theory; this is typically defined in terms of the electric and magnetic field operators and/or the auxiliary field operator, $\overrightarrow{a}(\overrightarrow{R},t)$ [45, 75]. Although these three Hamiltonians are important for describing the light-matter system in its entirety, they play no explicit role in the derivation of the matrix element for RET. The key parts of the Hamiltonian for RET are the interaction terms H_int(X) ; X = D, A. These two terms represent the interaction between each molecule and the electromagnetic field; they are perturbative in nature because the light-molecule interactions of RET is weak compared to the large Columbic energies of the molecules. The eigenstates of the interaction Hamiltonian are constructed with the tensor product of molecule and radiation states. Of particular note is that no interaction term between the donor and acceptor exists in Equation (11), unlike in semi-classical formalisms. The QED description of RET is, therefore, a genuinely full quantum theory, whereby the transfer of energy between an excited donor to an unexcited acceptor is via the electromagnetic field; direct Coulombic interactions between the two molecules do not arise in this multipolar form of the Hamiltonian [55].

Using the electric dipole approximation, in which only the transition electric dipole (E1) of each molecule are considered, the interaction Hamiltonian is written as;

$\begin{array}{ll}{H}_{int}=-{\epsilon }_0^{-1}\overrightarrow{\mu }(D)·{\overrightarrow{d}}^{\perp }({\overrightarrow{R}}_D)-{\epsilon }_0^{-1}\overrightarrow{\mu }(A)·{\overrightarrow{d}}^{\perp }({\overrightarrow{R}}_A),& (12)\end{array}$

where $\overrightarrow{\mu }(X)$ is the dipole operator of molecule X at position ${\overrightarrow{R}}_X$ (it is usually presumed that the donor is positioned at the origin); ε₀ is the permittivity of free space. The displacement electric field operator, ${\overrightarrow{d}}^{\perp }({\overrightarrow{R}}_X)$, can be written in terms of a mode expansion;

$\begin{array}{l}{\overrightarrow{d}}^{\perp }\left({\overrightarrow{R}}_X\right)=i{{\displaystyle \sum _{\overrightarrow{p},\lambda }\left(\frac{\hslash cp{\epsilon }_0}{2V}\right)}}^{\frac{1}{2}}\{{\overrightarrow{e}}^{(\lambda )}\left(\overrightarrow{p}\right)a^{(\lambda )}\left(\overrightarrow{p}\right){\text{e}}^{i\overrightarrow{p}·{\overrightarrow{R}}_X}\\ -{\overrightarrow{e}}^{*(\lambda )}\left(\overrightarrow{p}\right)a^{†(\lambda )}\left(\overrightarrow{p}\right){\text{e}}^{-i\overrightarrow{p}·{\overrightarrow{R}}_X}\}.& (13)\end{array}$

Here, c is the speed of light in a vacuum, ${\overrightarrow{e}}^{(\lambda )}(\overrightarrow{p})$ defines the polarization of the mediating photon (the asterisk denoting its complex conjugate), $a^{(\lambda )}(\overrightarrow{p})$ and $a^{†(\lambda )}(\overrightarrow{p})$ are the annihilation and creation operators, respectively, for a photon of wave-vector $\overrightarrow{p}$ and polarization λ. In the pre-exponential factor, V represents the volume used in the box quantization procedure that enables fields to be defined in terms of operators, as required by QED. The second-order perturbative term, which is the leading term in the matrix element for RET, is explicitly written (in terms of Dirac brackets) as;

$\begin{array}{ll}{M}_{fi}^{ }=\frac{\langle f\left|H_{\text{int}}\right|I_1\rangle \langle I_1\left|H_{\text{int}}\right|i\rangle }{E_i-E_{I_1}}+\frac{\langle f\left|H_{\text{int}}\right|I_2\rangle \langle I_2\left|H_{\text{int}}\right|i\rangle }{E_i-E_{I_2}}.& (14)\end{array}$

From Figure 2, we easily identify the key system states (which is a combination of the two molecular states and the radiation state). These are the initial state $|i\rangle =|E_D^n,E_A^0;0\left(\overrightarrow{p},\text{λ}\right)\rangle$ (donor excited, acceptor unexcited and no photon), the final state $|f\rangle =|E_D^0,E_A^m;0\left(\overrightarrow{p},\text{λ}\right)\rangle$ (donor unexcited, acceptor excited and no photon) and the two possible intermediate states, $|I_1\rangle =|E_D^0,E_A^0;1\left(\overrightarrow{p},\text{λ}\right)\rangle$ (donor and acceptor unexcited and one photon) and $|I_2\rangle =|E_D^n,E_A^m;1\left(\overrightarrow{p},\text{λ}\right)\rangle$ (donor and acceptor excited and one photon). The radiation states, often referred to as number or Fock states, have eigenvalues that are occupation numbers of the quantized electromagnetic field, i.e., the number of photons in the system. The creation and annihilation operators act on the relevant radiation states via $a^{†}{ }^{(\text{λ})}(\overrightarrow{p})|0(\overrightarrow{p},\lambda )\rangle =1|1(\overrightarrow{p},\text{λ})\rangle$ and $a^{(\text{λ})}(\overrightarrow{p})|1(\overrightarrow{p},\lambda )\rangle =1|0(\overrightarrow{p},\text{λ})\rangle$. The commutator involving these two operators is given by the relationship $\left[a^{(\lambda )}(\overrightarrow{p}),{a^{†}}^{({\lambda }^{\prime })}({\overrightarrow{p}}^{\prime })\right]={(8{\pi }^{3}V)}^{-1}{\delta }^3(\overrightarrow{p}-{\overrightarrow{p}}^{\prime }){\delta }_{\lambda {\lambda }^{\prime }}$, where $\delta (\overrightarrow{p}-{\overrightarrow{p}}^{\prime })$ is a Dirac delta function and ${\delta }_{\lambda {\lambda }^{\prime }}$ is a Kronecker delta [76].

Equipped with these state expressions, the interaction Hamiltonian of Equation (12) and the energies of each state in Table 1 (note that the initial and final states have the same energy, since conservation of energy has to be restored after a miniscule amount of time), an expression for the RET matrix element can be found. For illustrative purposes, we explicitly calculate just one of the Dirac brackets, namely 〈I₁|H_int|i〉; which is the initial bracket, since it is convention to move from right to left in these equations. Explicitly, it is written as;

$\begin{array}{l}\langle I_1|H_{\mathrm{int}}|i\rangle =\langle E_D^0,E_A^0;1\left(\overrightarrow{p},\text{λ}\right)|-{\epsilon }_0^{-1}\overrightarrow{\mu }\left(D\right)·d^{\perp }\left({\overrightarrow{R}}_D\right)\\ -{\epsilon }_0^{-1}\overrightarrow{\mu }\left(A\right)·{\overrightarrow{d}}^{\perp }\left({\overrightarrow{R}}_A\right)|E_D^n,E_A^0;0\left(\overrightarrow{p},\text{λ}\right)\rangle .& (15)\end{array}$

This represents the creation of a photon when the excited donor relaxes (the acceptor is unchanged, as denoted by the same superscript on both E_A) and, hence, dipole operators acting on the acceptor molecular state and the annihilation operator (within d^⊥) on the radiation state are zero due to orthonormality. Therefore, Equation (15) is simplified to;

$\begin{array}{ll}\langle I_1\left|H_{int}\right|i\rangle =-{\epsilon }_0^{-1}\langle E_D^0\left|\overrightarrow{\mu }(D)\right|E_D^n\rangle \langle 1(\overrightarrow{p},\lambda )\left|{\overrightarrow{d}}^{\perp }({\overrightarrow{R}}_D)\right|0(\overrightarrow{p},\lambda )\rangle .& (16)\end{array}$

The solution of which, on insertion of Equation (13), is expressed concisely as;

$\begin{array}{ll}\langle I_1\left|H_{int}\right|i\rangle =i{{\displaystyle \sum _{\overrightarrow{p},\lambda }}\left(\frac{\hslash cp{\epsilon }_0}{2V}\right)}^{\frac{1}{2}}{e}_i^{{ }^{*(\lambda )}}(\overrightarrow{p}){\mu }_i^{0n}(D){\text{e}}^{-i\overrightarrow{p}·{\overrightarrow{R}}_D},& (17)\end{array}$

with the i^th component of the transition dipole moment written as;

$\begin{array}{ll}{\mu }_i^{0n}(D)=\langle E_D^0\left|{\mu }_i(D)\right|E_D^n\rangle .& (18)\end{array}$

Following a similar procedure for the other three Dirac brackets, and finding the energy denominators for each term of Equation (14), the full expression for the RET process is given as;

$\begin{array}{l}{M}_{fi}={\displaystyle \sum _{\overrightarrow{p},\lambda }\left(\frac{\hslash cp}{2{\epsilon }_{0}V}\right)e_i^{*\left(\text{λ}\right)}\left(\overrightarrow{p}\right)e_j^{\left(\text{λ}\right)}\left(\overrightarrow{p}\right)\{{\mu }_i^{0n}\left(D\right){\mu }_j^{m0}\left(A\right)\frac{{\text{e}}^{i\overrightarrow{p}·\overrightarrow{R}}}{E_{n0}-\hslash cp}}\\ +{\mu }_j^{0n}\left(D\right){\mu }_i^{m0}\left(A\right)\frac{{\text{e}}^{-i\overrightarrow{p}·\overrightarrow{R}}}{-E_{n0}-\hslash cp}\}.& (19)\end{array}$

In order to determine a final result for the RET matrix element, we use the cosine rule to rewrite the summation over of polarizations as;

$\begin{array}{ll}{\displaystyle \sum _{\lambda }}{e}_i^{*(\lambda )}(\overrightarrow{p})e_j^{(\lambda )}(\overrightarrow{p})={\delta }_{ij}-{\widehat{p}}_i{\widehat{p}}_j,& (20)\end{array}$

where δ_ij is the Kronecker delta and a caret denotes a unit vector, and convert the inverse of the quantization volume to an integral in momentum space;

$\begin{array}{ll}\frac{1}{V}{\displaystyle \sum _{\overrightarrow{p}}}\to \int \frac{d^3\overrightarrow{p}}{{(2\pi )}^3}.& (21)\end{array}$

The quantum amplitude then becomes an integral of the form;

$\begin{array}{l}{M}_{fi}^{ }=\frac{1}{2{\epsilon }_0}{\mu }_i^{0n}(D){\mu }_j^{m0}(A)\int \frac{p}{k^2-p^2}({\delta }_{ij}-{\widehat{p}}_i{\widehat{p}}_j)\\ \times \left\{k\left({\text{e}}^{i\overrightarrow{p}·\overrightarrow{R}}-{\text{e}}^{-i\overrightarrow{p}·\overrightarrow{R}}\right)+p\left({\text{e}}^{i\overrightarrow{p}·\overrightarrow{R}}\text{+}{\text{e}}^{-i\overrightarrow{p}·\overrightarrow{R}}\right)\right\}\frac{d^3\overrightarrow{p}}{{(2\pi )}^3},& (22)\end{array}$

where hck is the energy transferred from D to A. As outlined in the subsequent section, this integral has been solved analytically using various vector calculus techniques. Omitting the long and intricate derivation based on special functions [63], the matrix element for RET—including the retarded electric dipole-electric dipole (E1-E1) coupling tensor, denoted as V_ij—is obtained as;

$\begin{array}{llll}{M}_{fi}^{ }& =& {\mu }_i^{0n}(D)V_{ij}(k,\overrightarrow{R}){\mu }_j^{m0}(A),& (23)\end{array}$

$\begin{array}{l}{V}_{ij}(k,\overrightarrow{R})=\frac{e^{ikR}}{4\pi {\epsilon }_0{R}^3}\{\left(1-ikR\right)\left({\delta }_{ij}-3{\widehat{R}}_i{\widehat{R}}_j\right)\\ -{\left(kR\right)}^2\left({\delta }_{ij}-{\widehat{R}}_i{\widehat{R}}_j\right)\}& (24)\end{array}$

A more in-depth analysis of the derivation of the E1-E1 coupling tensor, V_ij, and the transfer rate of RET (an outline of which follows)—without providing all of the intricate specifics—is delivered by Salam in his recent review [77].

TABLE 1

Table 1. All the system states and their associated energies for RET.

Physical Interpretation of the RET Coupling Tensor

The physical observable derived from the V_ij tensor, via the matrix element, is the transfer rate of RET, symbolized by Γ. This rate is demined from the Fermi rule [78]: $\Gamma =2\pi /\hslash {\left|M_{fi}\right|}^2{\rho }_f$, where ρ_f is the density of acceptor final states. Assuming a system of two freely tumbling molecules, meaning that a rotational average is applied [79], the following is found;

$\begin{array}{ll}\Gamma ~\frac{1}{9}{\left|\overrightarrow{\mu }(D)\right|}^2{\left|\overrightarrow{\mu }(A)\right|}^2\text{A}(k,R).& (25)\end{array}$

where the E1-E1 transfer function, A(k, R), is defined by Andrews [62];

$\begin{array}{l}A(k,R)=V_{ij}^{ }(k,\overrightarrow{R})V_{ij}^{*}(k,\overrightarrow{R})\\ =\frac{2}{{(4\pi {\epsilon }_0{R}^3)}^2}\left\{3+{(kR)}^2+{(kR)}^4\right\}.& (26)\end{array}$

In contrast to Förster coupling, the QED form of the electronic coupling has a complicated distance dependence, which underscores the unification of the radiationless and radiative transfer mechanisms. Whereas, the semi-classical Förster theory predicts only an R⁻⁶ dependence [80], the QED rate expression of Equation (26) contains three distance dependencies: R⁻², R⁻⁴, and R⁻⁶. This signifies three distinct regimes that dominate in the long-, intermediate- and short-range, respectively.

The different regimes of RET are most readily understood in terms of the mediating photon [49]. As outlined in section Non-relativistic QED: A Theoretical Framework for RET, the photon is said to have real characteristics—i.e., it has a large transverse component w.r.t. $\overrightarrow{R}$—when the separation of the donor and acceptor exceeds its reduced wavelength (i.e., R ≫ ƛ). Meaning that, since the mediating photon is always transverse w.r.t. its wave-vector $\overrightarrow{p}$, the photons (emitted in all directions by D) that are annihilated at A in the long-range are the ones where $\overrightarrow{p}$ is essentially co-linear with $\overrightarrow{R}$. Conversely, if R is significantly less than the reduced wavelength the photon is fully virtual, meaning that retardation effects are not present. That is, it does not have well-defined physical characteristics, such as momentum. This arises because, due to the uncertainty principle, the position of the mediating photon is “smeared out” in the short-range so that $\overrightarrow{p}$ may no longer be co-linear with $\overrightarrow{R}$—therefore, there is a longitudinal component to the photon w.r.t. $\overrightarrow{R}$. The two limiting cases of RET are, hence, often referred to as radiationless (virtual photon) and radiative (real) transfer—in the past, until the unified theory, they were usually considered to be two completely separate and distinct mechanisms. Since all three terms of Equation (26) are non-zero in RET (or, at least, the short-range term always exists), it is justifiable to say that all photons are virtual in nature [49, 81]. This means that a notional “real” photon—which is transverse w.r.t both $\overrightarrow{p}$ and $\overrightarrow{R}$—does not exist, because these two vectors are never exactly collinear due to the uncertainty principle.

To summarize, long-range (or far-zone) energy transfer has an inverse-square, R⁻², dependence on the rate, and short-range (or near-zone or Förster) transfer has the well-known R⁻⁶ dependence. That leaves the intermediate zone, which was not previously identified until Andrews's work [62], where the distance separating the molecules is of the same order as the reduced wavelength of the mediating photon; this region has an R⁻⁴ dependence. Our expressions have assumed dynamic coupling between the transition dipole moments of the donor and acceptor, for cases of static dipole couplings (in which k = 0) only the first term of Equation (26) applies.

Higher Order RET

Often the electric dipole approximation is employed for studies on RET, which means that only E1-E1 coupling is considered. However, the coupling of the electric dipole of a molecule with the magnetic dipole (M1) or electric quadrupole (E2) of the other can be important [82], for example, in chirality-sensitive RET [77, 83–86]. E1-M1 and E1-E2 couplings are, in general, of similar magnitude but are roughly 150 times smaller than E1-E1 interactions; other multipoles are even smaller and almost never utilized in RET analyses.

The derivation of the matrix element for E1-M1 coupling, with use of special functions, is provided elsewhere [63]. The final result is given by;

$\begin{array}{ll}{M}_{fi}^{\text{E1-M1}}=\left\{{\mu }_i^{0m}(D)\frac{m_j^{n0}(A)}{c}+\frac{m_j^{0m}(D)}{c}{\mu }_i^{n0}(A)\right\}{U}_{ij}^{ }(k,\overrightarrow{R}),& (27)\end{array}$

which features the transition magnetic dipole, m_j, and the E1-M1 tensor, $U_{ij}^{ }(k,\overrightarrow{R})$, with the latter explicitly expressed as;

$\begin{array}{ll}{U}_{ij}^{ }(k,\overrightarrow{R})=\frac{{\text{e}}^{-ikR}}{4\pi {\epsilon }_0}{\epsilon }_{ijk}\frac{{\widehat{R}}_k}{R^3}(-ikR+k^2{R}^2),& (28)\end{array}$

where ε_ijk is the Levi-Civita symbol. Following a rotational average [79], the rate of RET based on this type of coupling is;

$\begin{array}{l}{\Gamma }^{\prime }~\frac{\text{B}\left(k,R\right)}{9c^2}\{{\left|\overrightarrow{\mu }\left(D\right)\right|}^2{\left|\overrightarrow{m}\left(A\right)\right|}^2+{\left|\overrightarrow{\mu }\left(A\right)\right|}^2{\left|\overrightarrow{m}\left(D\right)\right|}^2\\ -2\mathrm{Re}\left|\overrightarrow{\mu }\left(D\right)·{\overrightarrow{m}}^{*}\left(D\right)\right|\left|{\overrightarrow{\mu }}^{*}\left(A\right)·\overrightarrow{m}\left(A\right)\right|\}.& (29)\end{array}$

where the E1-M1 transfer function, B(k, R), is written as;

$\begin{array}{ll}\text{B}(k,R)=U_{ij}^{ }(k,\overrightarrow{R})U_{ij}^{*}(k,\overrightarrow{R})=\frac{2}{{(4\pi {\epsilon }_0{R}^3)}^2}(k^2{R}^2+k^4{R}^4).& (30)\end{array}$

Comparing Equations (26) with (30), i.e., the A and B functions, it is clear that the first term (the R⁻⁶ dependent term) is missing in E1-M1 coupling. Physically, this means that the photons that mediate E1-M1 interactions have real characteristics, i.e., they are never fully virtual. However, in contrast to a commonly held view, E1-M1 coupling is not exclusively related to radiative energy transfer since a short-range R⁻⁴ term also exists. The lack of the R⁻⁶ term also tells us that static electric and magnetic dipoles (in which k = 0) do not interact, since all the other terms involve k.

The matrix element for E1-E2 interactions is determined as [69, 71];

$\begin{array}{ll}{M}_{fi}^{\text{E1-E2}}=\left\{{\mu }_i^{ }(D)Q_{jk}^{ }(A)-Q_{jk}^{ }(D){\mu }_i^{ }(A)\right\}{V}_{i(jk)}^{\pm }(k,\overrightarrow{R}),& (31)\end{array}$

where the E1-E2 tensor, $V_{i(jk)}^{\pm }(k,\overrightarrow{R})$, is expressed by;

$\begin{array}{l}{V}_{i\left(jk\right)}(k,\overrightarrow{R})=\frac{{\text{e}}^{\text{i}kR}}{4\pi {\epsilon }_0{R}^4}\{\left(-3+3\text{i}kR+k^2{R}^2\right)({\delta }_{ij}{\widehat{R}}_k+{\delta }_{jk}{\widehat{R}}_i\\ +{\delta }_{ki}{\widehat{R}}_j-5{\widehat{R}}_i{\widehat{R}}_j{\widehat{R}}_k)+\left(k^2{R}^2-i{k}^3{R}^3\right)(\frac{1}{2}\left({\delta }_{ij}{\widehat{R}}_k+{\delta }_{ik}{\widehat{R}}_j\right)\\ -{\widehat{R}}_i{\widehat{R}}_j{\widehat{R}}_k)\}.& (32)\end{array}$

This expression is the -jk index symmetry form of the tensor, which is justified since it contracts with the index-symmetric electric quadrupole, Q_jk. After a rotational average, the corresponding rate is obtained as;

$\begin{array}{l}{\Gamma }^{″}~\frac{\text{C}\left(K,R\right)}{15}\{{\left|\overrightarrow{\mu }\left(D\right)\right|}^2{Q}_{\lambda \mu }\left(A\right)Q_{\lambda \mu }^{\ast }\left(A\right)\\ +{\left|\overrightarrow{\mu }\left(A\right)\right|}^2{Q}_{\lambda \mu }\left(D\right)Q_{\lambda \mu }^{\ast }\left(D\right)\},& (33)\end{array}$

where C(k, R) is found as;

$\begin{array}{l}\text{C}(K,R)=V_{i(jk)}^{ }(k,\overrightarrow{R})V_{i(jk)}^{*}(k,\overrightarrow{R})\\ =\frac{1}{{(4\pi {\epsilon }_0{R}^4)}^2}\left\{90+18k^2{R}^2+3k^4{R}^4+k^6{R}^6\right\}.& (34)\end{array}$

Examining this expression, we see that E1-E2 coupling has four terms with the distance dependencies R⁻², R⁻⁴, R⁻⁶, and R⁻⁸ (rather than the three of E1-E1 interactions). The new radiationless (R⁻⁸) term dominates in the near-zone, as predicted by Dexter [5], while the usual inverse-square distance dependence of radiative transfer dictates the far-zone. The presence of these terms (and the distinctive middle terms) in a single expression again signifies that they are the two extremes of a unified theory. Since the first term does not depend on k, we determine that static electric dipole and quadrupoles can interact.

Effects of a Bridging Molecule

Recent theoretical work, based on QED in the electric dipole approximation, is an analysis on the effects of a third molecule, M, on RET [87–91]. In this sub-section, we touch upon the case where M bridges the energy transfer between D and A—a Feynman diagram of which is provided in Figure 3. This is the DMA configuration; the other cases (DAM and MDA), in which the molecules are interchanged, have also been investigated. The matrix element for DMA, delivered from fourth-order perturbation theory, is given by;

$\begin{array}{ll}{M}_{fi}^{DMA}={\mu }_i^{0n}(D)V_{ij}(k,{\overrightarrow{R}}_{DM}){\alpha }_{jk}^{00}(M)V_{kl}(k,{\overrightarrow{R}}_{MA}){\mu }_l^{m0}(A),& (35)\end{array}$

where ${\alpha }_{jk}^{00}(M)$ is the polarizability tensor that arises because two light-molecule interactions occur at the third molecule (which begins and ends in its ground state, as denoted by the superscript 00) and two couplings tensors are used since two energy transfer steps occur. Using the Fermi rule, the leading term in the physically observable rate (that includes the third body) is the quantum interference, i.e., the cross-term, that involves multiplication of Equations (23) and (35) so that [88];

$\begin{array}{l}{M}_{fi}^{DMA}{M}_{fi}^{*DA}={\mu }_i^{0n}(D)V_{ij}(k,{\overrightarrow{R}}_{DM}){\alpha }_{jk}^{00}(M)V_{kl}(k,{\overrightarrow{R}}_{MA})\\ \times {\mu }_l^{m0}(A){\mu }_p^{0n}(D)V_{pq}^{*}(k,\overrightarrow{R}){\mu }_q^{m0}(A).& (36)\end{array}$

This is the rate that dominates if energy transfer between D and A is forbidden, for example, due to symmetry selection rules or when the dipole moments of D and A are both orthogonal with each other and their displacement vector, $\overrightarrow{R}$. In this scenario, the mediator M facilitates the RET that would not occur otherwise [89]. A recent review by Salam provides a more comprehensive analysis on the role of a third body in RET [77].

FIGURE 3

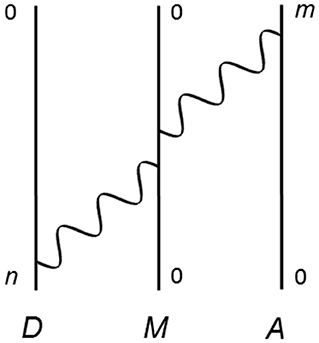
Figure 3. One of 24 possible time-orderings for RET mediated by a third molecule, M, acting as a bridge between donor D and acceptor A. Energy is transferred from D to A, and M begins and ends in its ground state.

Recent RET Research

Nanomaterials for Energy Transfer

While the generic term “molecule” has been used throughout this manuscript, other materials can be used in RET such as atoms, chromophores, particles and, more recently, carbon nanotubes [92–96] and quantum dots (QDs). In 1996, first observation of energy transfer between the latter was achieved with cadmium selenide (CdSe) QDs [97] and similar compounds followed; for example, cadmium telluride (CdTe) [98] and lead sulfide (PbS) [99] QDs. In experiments, quantum dots are attractive because they can be much brighter, and contain greater photostability, than typical organic chromophores [100, 101]. Hence, QDs have become important in bio-inspired RET-based applications [102, 103], such as nanosensors [104–111] and photodynamic therapy [112, 113]. In terms of theory, it has been determined that RET between quantum dots and nanotubes can be modeled using dipole-dipole couplings [90, 114–119]. For more on the experiments and theory of RET in nanomaterials, Liu and Qiu provide an excellent review on recent advances [120].

While quantum dots are suggested as artificial antennas in synthetic light-harvesting materials [111, 121], research on such systems usually involve multi-chromophore macromolecules. One type of which are known as dendrimers; from its periphery to core, these branch-like structures comprise decreasing number of chromophores [122–130]. They work on the principle that photons are absorbed at the periphery and the excitation energy is funneled to a central reaction center via multiple RET steps; an example of this is shown in Figure 4. A significant amount of theory has been published on this multi-chromophore transfer mechanism [131–140]. Toward the center of the dendrimer, where the number of chromophores is decreased, there is a possibility that two excited donors will be in the vicinity of an acceptor. In this case, another RET mechanism, known as energy pooling [141–143], becomes possible. This process is illustrated in Figure 5 and can be written, in terms of photophysics, as;

$\begin{array}{l}{D}^{*}+D^{*}+A\to D+D+A^{**},\end{array}$

where the double asterisk denotes that the acceptor is doubly excited, i.e., the acceptor is promoted to an excited state that requires the excitation energies of the sum of the two donors. This contrasts to the process known as energy transfer up-conversion [144, 145], which has the same initial condition but excitation is transferred from one donor to the other—so that one of the donors is doubly excited—and the third molecule is not involved. The matrix element for energy pooling has an analogous form to Equation (35); the only difference is that the superscript m0 on A (which is now a donor) becomes 0n and the superscript 00 on M (now the acceptor) becomes s0, where s signifies a doubly excited molecule. In recent years, Lusk et al. have demonstrated energy pooling experimentally [146] and discovered, among other advances, that the efficiency of energy pooling can be improved within a cavity [147–149]. Lately, moreover, they have studied the time-inverse mechanism of energy pooling, known as quantum cutting, which involves the excitation on A transferring to both D molecules [150].

FIGURE 4

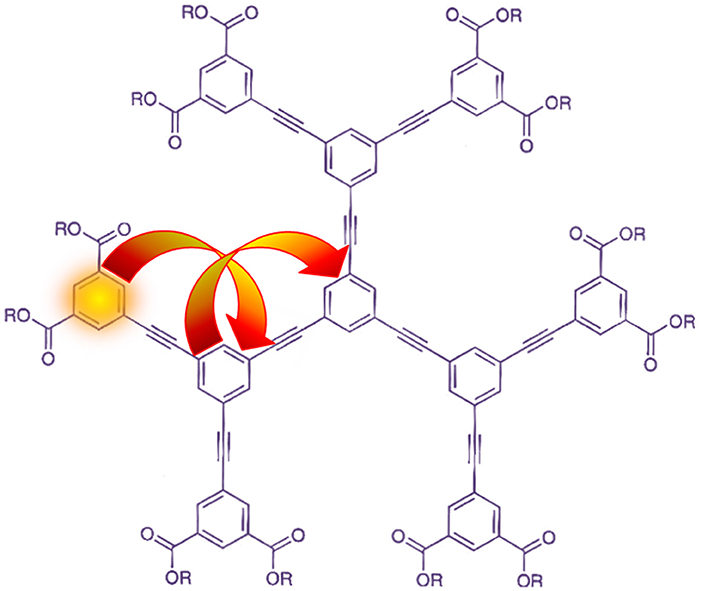
Figure 4. Two-step RET in a second-generation phenylacetylene dendrimer. This schematic depicts initial electronic excitation at a peripheral phenyl group, which acts as a donor of energy to a neighboring inner-ring chromophore; this acceptor then becomes a donor of energy to the phenaline core. Original image appeared in Bradshaw and Andrews [131].

FIGURE 5

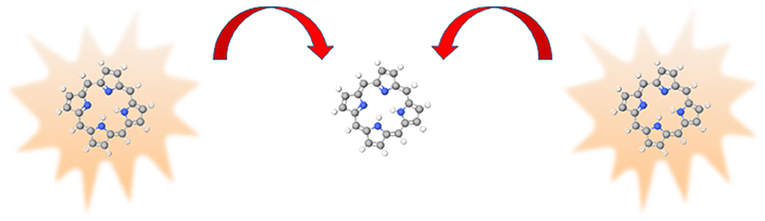
Figure 5. Representation of energy pooling, the two excited donors (on the left- and right-hand side) transfer energy, represented by the red arrows, to the acceptor (in the center).

Another double-excitation mechanism is two-photon RET [151, 152], which involves the absorption of two photons at the donor and the transfer of the resulting excitation to the acceptor. The matrix element of this process is identical to Equation (23), except the superscript on D is 0s rather than 0n. Since the incident light in two-photon RET is lower in energy compared to RET, photo-destruction of living tissue can be circumvented. Therefore, biological applications of this process have arisen, including photodynamic therapy [153–160] and bioimaging [155, 160–163].

Plasmon-Based RET

The quest for control of light-energy at the nanoscale has led to some very interesting studies, from both an experimental and a theoretical point-of-view, that often involve RET coupling between molecules near a surface plasmon [164–194]—the latter, basically, acting as a bridging material for the energy transfer. Plasmons are the collective excitations of conduction electrons by light, which generally reside in a confined metallic structure. By coupling plasmonic materials to RET chromophores, a substantial amount of energy transfer can occur over significantly larger separations than the RET between conventional materials—up to distances approaching the optical wavelength. The effects of a surrounding nanophotonic environment, such as a surface plasmon, on RET is an ongoing debate [189, 195].

In 2011, Pustovit and Shahbazyan developed a classical theory of plasmon-assisted RET that involves an isotropic complex polarizability [196]. Their model, which maintains an energy balance between transfer, dissipation and radiation, analyses the geometry of a plasmon-RET system—with a focus on distance and orientational effects—by providing numerical results. This mechanism shows that plasmon-assisted RET will dominate the usual non-radiative (Förster) transfer, even in the near-zone. While a comparable study predicts, over hundreds of nanometres, an enhanced rate by a factor of 10⁶ [197]. These forecast improvements now have experimental verification. For example, Wenger et al. demonstrate enhanced transfer between donor-acceptor pairs confined to a gold “nanoapparatus”; they endorse a six-fold increase in the rate of RET over 13 nm [198].

In the years that followed, other innovative studies on plasmon RET have arisen. An experimental study by Zhao et al. showed that the efficiency of RET can be controlled by the plasmonic wavelength [199]. Remarkably, they discovered that RET can be turned off and on by tuning the plasmon spectrum with the donor emission and acceptor absorption peaks, respectively. Related theory develops the concept of a “generalized spectral overlap,” whereby the rate of plasmon RET is not just dependent on the overlap integral of the donor emission and acceptor absorption spectra (as follows from Förster theory), but includes a plasmonic contribution from an electromagnetic coupling factor [200, 201]. Other experimental work, which is analogous to the effects of a bridging molecule that is discussed earlier [89], use plasmonic nanoantennas to enable E1-E1 RET that is otherwise forbidden by geometry [202].

Bershike et al. explain, by comparing model and experimental data, enhanced coupling between a nanoscale metal and a light emitting dipole [203]. They employ a complex dielectric function that indicates an R⁻⁴ distance dependence (ranging from 0.945 to 8.25 nm) between the fluorescent molecule and the gold nanoparticle surface. Similar to this study, Bradley and co-workers provide an investigation, which employs a Green's tensor analysis of Mie theory, that again show plasmon RET can display an R⁻⁴ dependence [204]. These results are consistent with numerical predictions, based on QED, that intermediate-zone RET dominates at these separation distances [51].

Energy Transfer at Non-optical Frequencies

Resonance energy transfer usually occurs in the ultraviolet or visible range of the electromagnetic spectrum, which is comparable to the energy required for electronic transitions in molecules etc. Recently, however, energy transfer involving either a much lower or higher frequency range has gained traction. An outline on which now follows.

At the lower end, in the infrared range, transfer of vibrational energy can arise between excited (donor) and unexcited (acceptor) oscillating bonds on adjacent molecules. Applications include the observation of local orientational order in liquids [205] and, analogous to the spectroscopic ruler in RET, a measure of intermolecular distances at the sub-nanoscale in the condensed phase [206, 207]. This type of transfer is especially prevalent between water molecules, due to the strong dipole-dipole interactions between the O–H stretch vibrations [208–210]. It has been determined that, with some modifications, that Förster theory can be valid at these light frequencies [211]. Energy transfer at even lower frequencies, namely in the microwave range, is the subject of a very recent paper by Wenger et al. [212]. In this work, the energy transfer is enhanced by positioning the donor and acceptor pair within a cavity.

At the higher end is interatomic and intermolecular Coulombic decay (collectively ICD), a process that involves the x-ray range of the spectrum. First predicted in 1997 [213], and experimentally verified 6 years later [214], ICD is a process in which photoionization of one atom or molecule can lead to remote photoionization of another atom or molecule via the exchange of a high energy photon. In terms of fundamental theory, ICD is now understood to be equivalent to Förster transfer (although ICD involves much more complex prior and posterior processes)—since the mechanism is driven by dipole-dipole coupling with the characteristic R⁻⁶ distance dependence. Nevertheless, there is a major fundamental difference between RET and ICD. Namely, as explained previously, the former typically involves only valence electrons whereas ICD is initiated by an intra-atomic (or intra-molecular) decay process; a high-energy transition, in which a donor valence electron relaxes to the core shell resulting in promotion of an acceptor valence electron to the continuum, i.e., acceptor ionization. This means that an ionization cross-section will feature instead of the absorption cross-section of Förster transfer.

A prototypical example is the photo-ionization of a neon dimer (Ne₂) via 2S-electron emission from one of its atoms. This results in the relaxation of a valence 2P-electron into the formed vacancy and, consequently, a high-energy photon is released. Following absorption of this light by the neighboring atom, a 2P-electron is ejected from it [215, 216]. The interaction of the two newly charged ions causes a Coulomb explosion, i.e., the fragmentation of the dimer. For clarity, the whole mechanism is illustrated in Figure 6. ICD is typically ultra-short-range, in which (just like Dexter transfer) wavefunction overlap occurs; hence, terms relating to electron correlation and exchange will contribute. Moreover, since ICD involves electron relaxation from a valence shell to the core shell in the donor, account of the Auger effect is required. This competing mechanism occurs because the energy generated from the relaxation could be transferred to another electron within the donor (and, thus, ejecting it), so energy in the form of a photon would not reach the acceptor. Therefore, for an accurate theoretical description of ICD, a detailed interpretation of the Auger effect along with electron correlation and exchange is required. This is achieved by considering direct and exchange Coulomb integrals for the decay rate. An overview of this is provided by Jahnke in his recent review [217].

FIGURE 6

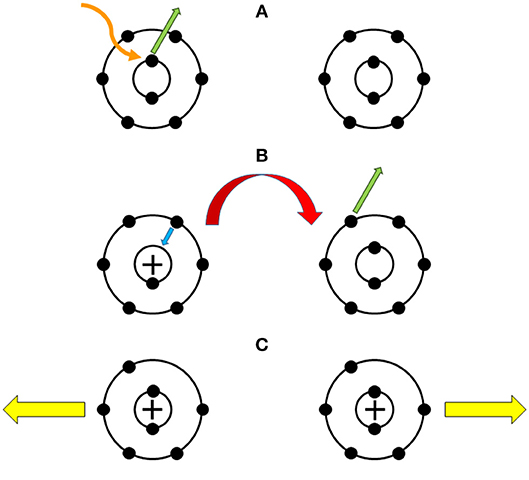
Figure 6. (A) Photoionization of a neon dimer, via ejection of an inner shell electron from an atom (green arrow), due to incident x-ray radiation (orange wavy line). (B) Interatomic Coulombic decay: an outer electron relaxes into the vacancy (blue arrow) and, consequently, photo-ionization of the other atom occurs due to energy transfer between the atoms (red arrow). (C) The newly charged atoms (plus signs) repel each other (yellow arrows), which results in destruction of the neon dimer.

Since the pioneering studies on diatomic systems, there have been a number of experimental and theoretical investigations into ICD that involve different materials, including clusters of atoms and molecules [218], quantum dots [219, 220], and quantum wells [221]. Although ICD has considerable theoretical interest, there is evidence of its practical importance to biological chemistry; in particular, in the understanding of a DNA repair mechanism provided by the enzymes known as photolyases [222, 223]. The theoretical developments of ICD often mirror those already established in RET—such as the effects of retardation, dielectric environments, a third body and virtual photons [224, 225]. Clearly, more research in this exciting emerging field is required, with much still to learn in terms of its fundamental theory and applications.

RET in Cavities

It can be challenging to elucidate fundamental processes experimentally, particularly because RET often occurs in natural biological systems and ‘energy materials’ in the condensed phase. Necessarily involving a level of phenomenological modeling, their simulation can be tremendously complicated. Associated research, especially in connection to the field of biology, has been covered in a numerous recent reviews [226–246]. Cavity quantum electrodynamics (cQED) works on the principle that electronic species are restricted to small volumes (usually bounded by mirrors in one or more dimensions) so that the electromagnetic field is tuned to specific quantized modes and the quantum nature of the light becomes more apparent compared to the free field. In terms of mathematical formulation, the arbitrary quantization volume, V, of Equation (19) is simply replaced by the dimensions of the cavity. Early applications of cQED revealed an understanding of the fundamental light-matter interactions in atoms, quantum dots and similar materials [247–252].

More recently cQED has been applied to chemical substances, such as organic dyes, and connected to phenomena such as RET [253]. The main advantage of studying these cavity-based schemes is that experimentalists are able to control the electromagnetic radiation at the quantum level, while simultaneously reducing interference with the surroundings to a significant extent. This allows for the explicit study of polariton modes (sometimes called hybrid states in this context), which is typically difficult in the condensed phase because of the rapid decoherence that derives from system coupling with a continuum of environmental modes. For example, in 2012, Ebbesen and co-workers experimentally showed that the photophysical properties of light-induced chemical reactions can be influenced by cavity fields, which can modify the chemical reaction landscape [254]. In another study, the same research group cleverly showed how to alter the reaction rates of chemical reactions by coupling molecular vibrations to infrared cavity modes [255].

Since experiments with negligible amount of decoherence are now conceivable, there is increasing interest in the effects of polariton modes on energy transfer within a cavity. In 2015, for instance, a couple of theoretical studies indicated that “exciton conductance” could be considerably enhanced, by orders of magnitude, when organic materials are coupled to cavity modes [256, 257]. Experimental verification of this amplified energy transfer soon followed [258–260]. Attempts to better understand polariton-assisted RET are increasingly prevalent. In 2018, Du et al. developed a “polariton-assisted remote energy transfer” model to explain how enhanced RET is mediated by vibrational relaxation in an optical microcavity [261]. While earlier this year, Schäfer et al. proposed that energy transfer could be drastically affected by a modification of the vacuum fluctuations in the cavity. In this research, they make a connection to Förster and Dexter transfer, and account for the often-disregarded Coulomb and self-polarization interactions. Interestingly, they predict that photonic degrees of freedom give rise to electron-electron correlations over large distances in the cavity [262]. What we do know for sure is that cavity RET is a representative example of the strong coupling regime; an excellent recent review on such strong light-matter interactions is provided by Börjesson et al. [263].

Discussion

Today it is nearly 100 years since the discovery of RET and, remarkably, the 71 year-old Förster theory that describes this transfer is still widely utilized. This model has provided us with the famous R⁻⁶ distance dependence on the rate between donor and acceptor molecules. Following these earlier times, from the 1960s until the late 1980s, significant theoretical developments based on fundamental quantum electrodynamics has been applied to two-center RET. This has culminated into the unified theory of RET, which links the short-range (near-zone) process of Förster with a long-range (far-zone), R⁻² dependent transfer consistent with Coulomb's Law. It also predicts a R⁻⁴ dependence in the intermediate region, where the distance between the molecules approximately equals the reduced wavelength of the mediating virtual photon. The latter could be said to have increasingly real characteristics in this range. Although not detailed in this review, further work in the 1990s predicted that optically active molecules in the condensed phase could also have a R⁻³ and a R⁻⁵ distance dependence, which become significant when the imaginary part of the refractive index is especially large [264, 265]. Soon afterwards, a QED description for the rate of RET in the presence of dispersing and absorbing material bodies of arbitrary shapes was provided [266]. In the twenty-first century, among other advances, quantum theory has helped us understand the role of mediators in energy transfer (i.e., 3- and 4-body RET) and the rederivations of the RET coupling tensor has provided new physical insights.

In the last 10 years, research into RET has moved into many exciting directions—too numerous to cover in detail in a single review. For example, the enhancement and control of long-range, super-Coulombic RET in hyperbolic metamaterials is shown [267, 268] and the influence of epsilon-and-mu-near-zero waveguide super-coupling on RET is considered [269]. Moreover, many research groups continue to unravel the nature of energy transfer within biological photosynthesis, with a special focus on the understanding of the roles that molecular vibrations may play in facilitating the process. There are also enormous efforts to develop “energy materials” that may enable new technologies, which include those focused on solar energy harvesting. Materials based on surface plasmons have shown great promise, especially in its connection to the huge enhancements of RET efficiency. Research groups are also working on RET in both the non-optical regions of the electromagnetic spectrum and within optical cavities. In all of these exciting areas of research, new experiments and theory need continued development. The theory of QED, while the most precise theory we know for light-matter interactions, assumes non-dissipative closed systems and that the electrons are localized to the molecules. Consequently, in its current formulation, microscopic QED is not directly applicable to the investigation of surface plasmons (delocalized excitons) or the process of decoherence, which occurs because the system is open to the environment. While semi-classical theories can address these questions in a limited way, the continued development of macroscopic QED [270] is desirable for accurate portrayals of such processes.

Author Contributions

GJ and DB equally wrote and edited the final manuscript. The figures and table are produced by them.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We are grateful for many helpful comments from Professor David Andrews, Dr. Kayn Forbes and Dr. Stefan Buhmann. We would also like to thank the reviewers for their constructive comments.

References

1. van der Meer BW, Coker G, Chen SYS. Resonance Energy Transfer: Theory and Data. New York, NY: VCH (1994).

Google Scholar

2. Andrews DL, Demidov AA. Resonance Energy Transfer. Chichester: Wiley (1999).

Google Scholar

3. May V. Charge and Energy Transfer Dynamics in Molecular Systems. Hoboken, NJ: John Wiley and Sons (2008).

Google Scholar

4. Medintz I, Hildebrandt N. Förster Resonance Energy Transfer: From Theory to Applications. Weinheim: Wiley-VCH (2013).

Google Scholar

5. Dexter DL. A theory of sensitized luminescence in solids. J Chem Phys. (1953) 21:836–50. doi: 10.1063/1.1699044

CrossRef Full Text | Google Scholar

6. Franck J. Einige aus der theorie von Klein und Bosseland zu ziehende folgerungen über fluoreszenz, photochemische prozesse und die elektronenemission glühender körper. Z Phys. (1922) 9:259–6. doi: 10.1007/bf01326976

CrossRef Full Text | Google Scholar

7. Carlo G. Über Entstehung wahrer Lichtabsorption und scheinbare Koppelung von Quantensprüngen. Z Phys. (1922) 10:185–99. doi: 10.1007/bf01332559

CrossRef Full Text | Google Scholar

8. Cario G, Franck J. Über zerlegung von Wasserstoffmolekülen durch angeregte Quecksilberatome. Z Phys. (1922) 11:161–6. doi: 10.1007/bf01328410

CrossRef Full Text | Google Scholar

9. Perrin J. Fluorescence et induction moléculaire par résonance. C R Acad Sci. (1927) 184:1097–100.

Google Scholar

10. Perrin F. Théorie quantique des transferts d'activation entre molécules de même espèce. Cas des solutions fluorescentes. Ann Phys. (1932) 10:283–14. doi: 10.1051/anphys/193210170283

CrossRef Full Text | Google Scholar

11. Kallmann H, London F. Über quantenmechanische energieübertragung zwischen atomaren systemen. Z. Phys. Chem. (1929) 2B:207–43 doi: 10.1515/zpch-1929-0214

CrossRef Full Text | Google Scholar

12. Förster T. Energiewanderung und fluoreszenz. Naturwissenschaften. (1946) 33:166–75. doi: 10.1007/bf00585226

CrossRef Full Text | Google Scholar

13. Förster T. Zwischenmolekulare energiewanderung und fluoreszenz. Ann Phys. (1948) 437:55–75. doi: 10.1002/andp.19484370105

CrossRef Full Text | Google Scholar

14. Förster T. 10th Spiers Memorial Lecture. Transfer mechanisms of electronic excitation. Discuss. Faraday Soc. (1959) 27:7–17. doi: 10.1039/DF9592700007

CrossRef Full Text | Google Scholar

15. Latt SA, Cheung HT, Blout ER. Energy transfer. A system with relatively fixed donor-acceptor separation. J Am Chem Soc. (1965) 87:995–1003. doi: 10.1021/ja01083a011

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Stryer L, Haugland RP. Energy transfer: a spectroscopic ruler. Proc Natl Acad Sci USA. (1967) 58:719–26. doi: 10.1073/pnas.58.2.719

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Sahoo H. Förster resonance energy transfer – A spectroscopic nanoruler: principle and applications. J Photochem Photobiol C. (2011) 12:20–30. doi: 10.1016/j.jphotochemrev.2011.05.001

CrossRef Full Text | Google Scholar

18. Ruggenthaler M, Tancogne-Dejean N, Flick J, Appel H, Rubio A. From a quantum-electrodynamical light–matter description to novel spectroscopies. Nat Rev Chem. (2018) 2:0118. doi: 10.1038/s41570-018-0118

CrossRef Full Text | Google Scholar

19. Dirac PAM. The quantum theory of the emission and absorption of radiation. Proc R Soc A. (1927) 114:243–65. doi: 10.1098/rspa.1927.0039

CrossRef Full Text | Google Scholar

20. Dirac PAM. The Principles of Quantum Mechanics. 4th ed. Oxford: Clarendon Press (1981).

Google Scholar

21. Feynman RP. Relativistic cut-off for quantum electrodynamics. Phys Rev. (1948) 74:1430–8. doi: 10.1103/PhysRev.74.1430

CrossRef Full Text | Google Scholar

22. Feynman RP. The theory of positrons. Phys. Rev. (1949) 76:749–59. doi: 10.1103/PhysRev.76.749

CrossRef Full Text | Google Scholar

23. Feynman RP. Space-time approach to quantum electrodynamics. Phys Rev. (1949) 76:769–89. doi: 10.1103/PhysRev.76.769

CrossRef Full Text | Google Scholar

24. Feynman RP. Mathematical formulation of the quantum theory of electromagnetic interaction. Phys Rev. (1950) 80:440–57. doi: 10.1103/PhysRev.80.440

CrossRef Full Text | Google Scholar

25. Feynman RP. An operator calculus having applications in quantum electrodynamics. Phys Rev. (1951) 84:108–28. doi: 10.1103/PhysRev.84.108

CrossRef Full Text | Google Scholar

26. Schwinger J. On quantum-electrodynamics and the magnetic moment of the electron. Phys Rev. (1948) 73:416–7. doi: 10.1103/PhysRev.73.416

CrossRef Full Text | Google Scholar

27. Schwinger J. Quantum electrodynamics. I. A covariant formulation. Phys Rev. (1948) 74:1439–61. doi: 10.1103/PhysRev.74.1439

CrossRef Full Text | Google Scholar

28. Schwinger J. Quantum electrodynamics. II. Vacuum polarization and self-energy. Phys Rev. (1949) 75:651–79. doi: 10.1103/PhysRev.75.651

CrossRef Full Text | Google Scholar

29. Schwinger J. Quantum electrodynamics. III. The electromagnetic properties of the electron-radiative corrections to scattering. Phys Rev. (1949) 76:790–817. doi: 10.1103/PhysRev.76.790

CrossRef Full Text | Google Scholar

30. Tomonaga SI, Oppenheimer JR. On infinite field reactions in quantum field theory. Phys Rev. (1948) 74:224–5. doi: 10.1103/PhysRev.74.224

CrossRef Full Text | Google Scholar

31. Tomonaga SI. Development of quantum electrodynamics. Science. (1966) 154:864–8. doi: 10.1126/science.154.3751.864

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Dyson FJ. The radiation theories of Tomonaga, Schwinger, and Feynman. Phys Rev. (1949) 75:486–502. doi: 10.1103/PhysRev.75.486

CrossRef Full Text | Google Scholar

33. Hanneke D, Fogwell Hoogerheide S, Gabrielse G. Cavity control of a single-electron quantum cyclotron: Measuring the electron magnetic moment. Phys Rev A. (2011) 83:052122. doi: 10.1103/PhysRevA.83.052122

CrossRef Full Text | Google Scholar

34. Aoyama T, Kinoshita T, Nio M. Revised and improved value of the QED tenth-order electron anomalous magnetic moment. Phys Rev D. (2018) 97:036001. doi: 10.1103/PhysRevD.97.036001

CrossRef Full Text | Google Scholar

35. Pachucki K. Complete two-loop binding correction to the Lamb shift. Phys Rev Lett. (1994) 72:3154–7. doi: 10.1103/PhysRevLett.72.3154

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Hagley EW, Pipkin FM. Separated oscillatory field measurement of hydrogen 2S_1/2-2P_3/2 fine structure interval. Phys Rev Lett. (1994) 72:1172–5. doi: 10.1103/PhysRevLett.72.1172

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Casimir HBG, Polder D. The influence of retardation on the London-van der Waals forces. Phys Rev. (1948) 73:360–72. doi: 10.1103/PhysRev.73.360

CrossRef Full Text | Google Scholar

38. Buhmann SY, Knöll L, Welsch DG, Dung HT. Casimir-Polder forces: a nonperturbative approach. Phys Rev A. (2004) 70:052117. doi: 10.1103/PhysRevA.70.052117

CrossRef Full Text | Google Scholar

39. Przybytek M, Jeziorski B, Cencek W, Komasa J, Mehl JB, Szalewicz K. Onset of Casimir-Polder retardation in a long-range molecular quantum state. Phys Rev Lett. (2012) 108:183201. doi: 10.1103/PhysRevLett.108.183201

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Salam A. Non-Relativistic QED Theory of the van der Waals Dispersion Interaction. Cham: Springer (2016).

Google Scholar

41. Passante R. Dispersion interactions between neutral atoms and the quantum electrodynamical vacuum. Symmetry. (2018) 10:735. doi: 10.3390/sym10120735

CrossRef Full Text | Google Scholar

42. Jackson JD. Classical Electrodynamics. New York, NY: Wiley (1975).

Google Scholar

43. Power EA, Zienau S. Coulomb gauge in non-relativistic quantum electrodynamics and the shape of spectral lines. Philos Trans R Soc A. (1959) 251:427–54. doi: 10.1098/rsta.1959.0008

CrossRef Full Text | Google Scholar

44. Woolley R. Molecular quantum electrodynamics. Proc R Soc A. (1971) 321:557–2. doi: 10.1098/rspa.1971.0049

CrossRef Full Text | Google Scholar

45. Craig DP, Thirunamachandran T. Molecular Quantum Electrodynamics: An Introduction to Radiation-Molecule Interactions. Mineola, NY: Dover Publications (1998).

Google Scholar

46. Salam A. Molecular quantum electrodynamics in the Heisenberg picture: a field theoretic viewpoint. Int Rev Phys Chem. (2008) 27:405–48. doi: 10.1080/01442350802045206

CrossRef Full Text | Google Scholar

47. Salam A. Molecular Quantum Electrodynamics. Long-Range Intermolecular Interactions. Hoboken, NJ: Wiley (2010).

Google Scholar

48. Andrews DL, Jones GA, Salam A, Woolley RG. Quantum Hamiltonians for optical interactions. J Chem Phys. (2018) 148:040901. doi: 10.1063/1.5018399

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Andrews DL, Bradshaw DS. Virtual photons, dipole fields and energy transfer: a quantum electrodynamical approach. Eur J Phys. (2004) 25:845–58. doi: 10.1088/0143-0807/25/6/017

CrossRef Full Text | Google Scholar

50. Lock MPE, Andrews DL, Jones GA. On the nature of long range electronic coupling in a medium: distance and orientational dependence for chromophores in molecular aggregates. J Chem Phys. (2014) 140:044103. doi: 10.1063/1.4861695

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Frost JE, Jones GA. A quantum dynamical comparison of the electronic couplings derived from quantum electrodynamics and Förster theory: application to 2D molecular aggregates. New J Phys. (2014) 16:113067. doi: 10.1088/1367-2630/16/11/113067

CrossRef Full Text | Google Scholar

52. Avery JS. The retarded dipole-dipole interaction in exciton theory. Proc Phys Soc. (1966) 89:677–82. doi: 10.1088/0370-1328/89/3/321

CrossRef Full Text | Google Scholar

53. Wheeler JA, Feynman RP. Classical electrodynamics in terms of direct interparticle action. Rev. Mod. Phys. (1949) 21:425–33. doi: 10.1103/RevModPhys.21.425

CrossRef Full Text | Google Scholar

54. Gomberoff L, Power EA. The resonance transfer of excitation. Proc Phys Soc. (1966) 88:281–4. doi: 10.1088/0370-1328/88/2/302

CrossRef Full Text | Google Scholar

55. Power EA, Thirunamachandran T. Quantum electrodynamics with nonrelativistic sources. I. Transformation to the multipolar formalism for second-quantized electron and Maxwell interacting fields. Phys Rev A. (1983) 28:2649–62. doi: 10.1103/PhysRevA.28.2649

CrossRef Full Text | Google Scholar

56. Power EA, Thirunamachandran T. Quantum electrodynamics with nonrelativistic sources. II. Maxwell fields in the vicinity of a molecule. Phys Rev A. (1983) 28:2663–70. doi: 10.1103/PhysRevA.28.2663

CrossRef Full Text | Google Scholar

57. Power EA, Thirunamachandran T. Quantum electrodynamics with nonrelativistic sources. III. Intermolecular interactions. Phys Rev A. (1983) 28:2671–5. doi: 10.1103/PhysRevA.28.2671

CrossRef Full Text | Google Scholar

58. Einstein A. Die Grundlage der allgemeinen relativitätstheorie. Ann Phys. (1916) 354:769–822. doi: 10.1002/andp.19163540702

CrossRef Full Text | Google Scholar

59. Craig DP, Thirunamachandran T. Radiation-molecule interactions in chemical physics. Adv Quant Chem. (1982) 16:97–160. doi: 10.1016/S0065-3276(08)60352-4

CrossRef Full Text | Google Scholar

60. Newton RG. Scattering Theory of Waves and Particles. New York, NY; Heidelberg; Berlin: Springer-Verlag (2013).

Google Scholar

61. Andrews DL, Sherborne BS. Resonant excitation transfer: a quantum electrodynamical study. J Chem Phys. (1987) 86:4011–7. doi: 10.1063/1.451910

CrossRef Full Text | Google Scholar

62. Andrews DL. A unified theory of radiative and radiationless molecular energy transfer. Chem Phys. (1989) 135:195–201. doi: 10.1016/0301-0104(89)87019-3

CrossRef Full Text | Google Scholar

63. Daniels GJ, Jenkins RD, Bradshaw DS, Andrews DL. Resonance energy transfer: the unified theory revisited. J Chem Phys. (2003) 119:2264–74. doi: 10.1063/1.1579677

CrossRef Full Text | Google Scholar

64. Andrews DL, Juzeliunas. G. Intermolecular energy transfer: retardation effects. J Chem Phys. (1992) 96:6606–12. doi: 10.1063/1.462599

CrossRef Full Text | Google Scholar

65. Jenkins RD, Daniels GJ, Andrews DL. Quantum pathways for resonance energy transfer. J Chem Phys. (2004) 120:11442–8. doi: 10.1063/1.1742697

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Grinter R, Jones GA. Resonance energy transfer: the unified theory via vector spherical harmonics. J Chem Phys. (2016) 145:074107. doi: 10.1063/1.4960732

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Jones GA, Grinter R. The plane- and spherical-wave descriptions of electromagnetic radiation: a comparison and discussion of their relative merits. Eur J Phys. (2018) 39:053001. doi: 10.1088/1361-6404/aac366

CrossRef Full Text | Google Scholar

68. Grinter R, Jones GA. Interpreting angular momentum transfer between electromagnetic multipoles using vector spherical harmonics. Opt Lett. (2018) 43:367–70. doi: 10.1364/OL.43.000367

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Scholes GD, Andrews DL. Damping and higher multipole effects in the quantum electrodynamical model for electronic energy transfer in the condensed phase. J Chem Phys. (1997) 107:5374–84. doi: 10.1063/1.475145

CrossRef Full Text | Google Scholar

70. Salam A. Resonant transfer of excitation between two molecules using Maxwell fields. J Chem Phys. (2005) 122:044113. doi: 10.1063/1.1827596

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Salam A. A general formula for the rate of resonant transfer of energy between two electric multipole moments of arbitrary order using molecular quantum electrodynamics. J Chem Phys. (2005) 122:044112. doi: 10.1063/1.1830430

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Andrews DL. On the conveyance of angular momentum in electronic energy transfer. Phys Chem Chem Phys. (2010) 12:7409–17. doi: 10.1039/c002313m

PubMed Abstract | CrossRef Full Text | Google Scholar

73. Andrews DL. Optical angular momentum: multipole transitions and photonics. Phys Rev A. (2010) 81:033825. doi: 10.1103/PhysRevA.81.033825

CrossRef Full Text | Google Scholar

74. Rice EM, Bradshaw DS, Saadi K, Andrews DL. Identifying the development in phase and amplitude of dipole and multipole radiation. Eur J Phys. (2012) 33:345–58. doi: 10.1088/0143-0807/33/2/345

CrossRef Full Text | Google Scholar

75. Loudon R. The Quantum Theory of Light. Oxford: Oxford University Press (2000).

Google Scholar

76. Andrews DL, Forbes KA. Quantum features in the orthogonality of optical modes for structured and plane-wave light. Opt Lett. (2018) 43:3249–52. doi: 10.1364/OL.43.003249

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Salam A. The unified theory of resonance energy transfer according to molecular quantum electrodynamics. Atoms. (2018) 6:56. doi: 10.3390/atoms6040056

CrossRef Full Text | Google Scholar

78. Fermi E. Nuclear Physics. Chicago, IL: University of Chicago Press (1950).

Google Scholar

79. Andrews DL, Thirunamachandran T. On three-dimensional rotational averages. J Chem Phys. (1977) 67:5026–33. doi: 10.1063/1.434725

CrossRef Full Text | Google Scholar

80. Förster T. Mechanisms of energy transfer. In: Florkin M and Stotz EH, editors. Comprehensive Biochemistry. Amsterdam: Elsevier (1967). p. 61–80.

Google Scholar

81. Andrews DL, Bradshaw DS. The role of virtual photons in nanoscale photonics. Ann Phys. (2014) 526:173–86. doi: 10.1002/andp.201300219

CrossRef Full Text | Google Scholar

82. Nasiri Avanaki K, Ding W, Schatz GC. Resonance energy transfer in arbitrary media: Beyond the point dipole approximation. J Phys Chem C. (2018) 122:29445–56. doi: 10.1021/acs.jpcc.8b07407

CrossRef Full Text | Google Scholar

83. Craig DP, Power EA, Thirunamachandran T. The interaction of optically active molecules. Proc R Soc A. (1971) 322:165–79. doi: 10.1098/rspa.1971.0061

CrossRef Full Text | Google Scholar

84. Craig D, Thirunamachandran T. Chiral discrimination in molecular excitation transfer. J Chem Phys. (1998) 109:1259–63. doi: 10.1063/1.476676

CrossRef Full Text | Google Scholar

85. Rodriguez JJ, Salam A. Effect of medium chirality on the rate of resonance energy transfer. J Phys Chem B. (2010) 115:5183–90. doi: 10.1021/jp105715z

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Andrews DL. Chirality in fluorescence and energy transfer. Methods Appl Fluoresc. (2019) 7:032001. doi: 10.1088/2050-6120/ab10f0

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Salam A. Mediation of resonance energy transfer by a third molecule. J Chem Phys. (2012) 136:014509. doi: 10.1063/1.3673779

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Andrews DL, Ford JS. Resonance energy transfer: influence of neighboring matter absorbing in the wavelength region of the acceptor. J Chem Phys. (2013) 139:014107. doi: 10.1063/1.4811793

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Ford JS, Andrews DL. Geometrical effects on resonance energy transfer between orthogonally-oriented chromophores, mediated by a nearby polarisable molecule. Chem Phys Lett. (2014) 591:88–92. doi: 10.1016/j.cplett.2013.11.002

CrossRef Full Text | Google Scholar

90. Weeraddana D, Premaratne M, Andrews DL. Direct and third-body mediated resonance energy transfer in dimensionally constrained nanostructures. Phys Rev B. (2015) 92:035128. doi: 10.1103/PhysRevB.92.035128

CrossRef Full Text | Google Scholar

91. Salam A. Near-zone mediation of RET by one and two proximal particles. J Phys Chem A. (2019) 123:2853–60. doi: 10.1021/acs.jpca.9b00827

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Qian H, Georgi C, Anderson N, Green AA, Hersam MC, Novotny L, Hartschuh A. Exciton energy transfer in pairs of single-walled carbon nanotubes. Nano Lett. (2008) 8:1363–7. doi: 10.1021/nl080048r

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Lefebvre J, Finnie P. Photoluminescence and Förster resonance energy transfer in elemental bundles of single-walled carbon nanotubes. J Phys Chem C. (2009) 113:7536–40. doi: 10.1021/jp810892z

CrossRef Full Text | Google Scholar

94. Wong CY, Curutchet C, Tretiak S, Scholes GD. Ideal dipole approximation fails to predict electronic coupling and energy transfer between semiconducting single-wall carbon nanotubes. J Chem Phys. (2009) 130:081104. doi: 10.1063/1.3088846

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Mehlenbacher RD, McDonough TJ, Grechko M, Wu MY, Arnold MS, Zanni MT. Energy transfer pathways in semiconducting carbon nanotubes revealed using two-dimensional white-light spectroscopy. Nat Commun. (2015) 6:6732. doi: 10.1038/ncomms7732

PubMed Abstract | CrossRef Full Text | Google Scholar

96. Davoody AH, Karimi F, Arnold MS, Knezevic I. Theory of exciton energy transfer in carbon nanotube composites. J Phys Chem C. (2016) 120:16354–66. doi: 10.1021/acs.jpcc.6b04050

CrossRef Full Text | Google Scholar

97. Kagan CR, Murray CB, Nirmal M, Bawendi MG. Electronic energy transfer in CdSe quantum dot solids. Phys Rev Lett. (1996) 76:1517–20. doi: 10.1103/PhysRevLett.76.1517

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Koole R, Liljeroth P, de Mello Donegá C, Vanmaekelbergh D, Meijerink A. Electronic coupling and exciton energy transfer in CdTe quantum-dot molecules. J Am Chem Soc. (2006) 128:10436–41. doi: 10.1021/ja061608w

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Clark SW, Harbold JM, Wise FW. Resonant energy transfer in PbS quantum dots. J Phys Chem C. (2007) 111:7302–5. doi: 10.1021/jp0713561

CrossRef Full Text | Google Scholar

100. Bruchez M, Moronne M, Gin P, Weiss S, Alivisatos AP. Semiconductor nanocrystals as fluorescent biological labels. Science. (1998) 281:2013–6. doi: 10.1126/science.281.5385.2013

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Chan WCW, Nie S. Quantum dot bioconjugates for ultrasensitive nonisotopic detection. Science. (1998) 281:2016–8. doi: 10.1126/science.281.5385.2016

PubMed Abstract | CrossRef Full Text | Google Scholar

102. Clapp AR, Medintz IL, Mattoussi H. Förster resonance energy transfer investigations using quantum-dot fluorophores. ChemPhysChem. (2006) 7:47–57. doi: 10.1002/cphc.200500217

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Medintz IL, Mattoussi H. Quantum dot-based resonance energy transfer and its growing application in biology. Phys Chem Chem Phys. (2009) 11:17–45. doi: 10.1039/B813919A

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Willard DM, Van Orden A. Resonant energy-transfer sensor. Nat Mater. (2003) 2:575–6. doi: 10.1038/nmat972

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Sapsford KE, Granek J, Deschamps JR, Boeneman K, Blanco-Canosa JB, Dawson PE, et al. Monitoring botulinum neurotoxin A activity with peptide-functionalized quantum dot resonance energy transfer sensors. ACS Nano. (2011) 5:2687–99. doi: 10.1021/nn102997b

PubMed Abstract | CrossRef Full Text | Google Scholar

106. Algar WR, Ancona MG, Malanoski AP, Susumu K, Medintz IL. Assembly of a concentric Förster resonance energy transfer relay on a quantum dot scaffold: Characterization and application to multiplexed protease sensing. ACS Nano. (2012) 6:11044–58. doi: 10.1021/nn304736j

PubMed Abstract | CrossRef Full Text | Google Scholar

107. Chou KF, Dennis AM. Förster resonance energy transfer between quantum dot donors and quantum dot acceptors. Sensors. (2015) 15:13288–325. doi: 10.3390/s150613288

PubMed Abstract | CrossRef Full Text | Google Scholar

108. Qiu X, Hildebrandt N. Rapid and multiplexed microRNA diagnostic assay using quantum dot-based Förster resonance energy transfer. ACS Nano. (2015) 9:8449–57. doi: 10.1021/acsnano.5b03364

PubMed Abstract | CrossRef Full Text | Google Scholar

109. Stanisavljevic M, Krizkova S, Vaculovicova M, Kizek R, Adam V. Quantum dots-fluorescence resonance energy transfer-based nanosensors and their application. Biosens Bioelectron. (2015) 74:562–74. doi: 10.1016/j.bios.2015.06.076

PubMed Abstract | CrossRef Full Text | Google Scholar

110. Shi J, Tian F, Lyu J, Yang M. Nanoparticle based fluorescence resonance energy transfer (FRET) for biosensing applications. J Mater Chem B. (2015) 3:6989–7005. doi: 10.1039/C5TB00885A

CrossRef Full Text | Google Scholar

111. Hildebrandt N, Spillmann CM, Algar WR, Pons T, Stewart MH, Oh E, et al. Energy transfer with semiconductor quantum dot bioconjugates: a versatile platform for biosensing, energy harvesting, and other developing applications. Chem Rev. (2017) 117:536–711. doi: 10.1021/acs.chemrev.6b00030

PubMed Abstract | CrossRef Full Text | Google Scholar

112. Samia ACS, Dayal S, Burda C. Quantum dot-based energy transfer: Perspectives and potential for applications in photodynamic therapy. Photochem Photobiol. (2006) 82:617–25. doi: 10.1562/2005-05-11-ir-525

PubMed Abstract | CrossRef Full Text | Google Scholar

113. Li L, Zhao JF, Won N, Jin H, Kim S, Chen JY. Quantum dot-aluminum phthalocyanine conjugates perform photodynamic reactions to kill cancer cells via fluorescence resonance energy transfer. Nanoscale Res Lett. (2012) 7:386. doi: 10.1186/1556-276x-7-386

PubMed Abstract | CrossRef Full Text | Google Scholar

114. Scholes GD, Andrews DL. Resonance energy transfer and quantum dots. Phys Rev B. (2005) 72:125331. doi: 10.1103/PhysRevB.72.125331

CrossRef Full Text | Google Scholar

115. Allan G, Delerue C. Energy transfer between semiconductor nanocrystals: validity of Förster's theory. Phys Rev B. (2007) 75:195311. doi: 10.1103/PhysRevB.75.195311

CrossRef Full Text | Google Scholar

116. Curutchet C, Franceschetti A, Zunger A, Scholes GD. Examining Förster energy transfer for semiconductor nanocrystalline quantum dot donors and acceptors. J Phys Chem C. (2008) 112:13336–41. doi: 10.1021/jp805682m

CrossRef Full Text | Google Scholar

117. Weeraddana D, Premaratne M, Gunapala SD, Andrews DL. Quantum electrodynamical theory of high-efficiency excitation energy transfer in laser-driven nanostructure systems. Phys Rev B. (2016) 94:085133. doi: 10.1103/PhysRevB.94.085133

CrossRef Full Text | Google Scholar

118. Weeraddana D, Premaratne M, Andrews DL. Quantum electrodynamics of resonance energy transfer in nanowire systems. Phys Rev B. (2016) 93:075151. doi: 10.1103/PhysRevB.93.075151

CrossRef Full Text | Google Scholar

119. Moroz P, Royo Romero L, Zamkov M. Colloidal semiconductor nanocrystals in energy transfer reactions. Chem Commun. (2019) 55:3033–48. doi: 10.1039/C9CC00162J

PubMed Abstract | CrossRef Full Text | Google Scholar

120. Liu X, Qiu J. Recent advances in energy transfer in bulk and nanoscale luminescent materials: from spectroscopy to applications. Chem Soc Rev. (2015) 44:8714–46. doi: 10.1039/C5CS00067J

PubMed Abstract | CrossRef Full Text | Google Scholar

121. Nabiev I, Rakovich A, Sukhanova A, Lukashev E, Zagidullin V, Pachenko V, et al. Fluorescent quantum dots as artificial antennas for enhanced light harvesting and energy transfer to photosynthetic reaction centers. Angew Chem Int Ed. (2010) 49:7217–21. doi: 10.1002/anie.201003067

PubMed Abstract | CrossRef Full Text | Google Scholar

122. Adronov A, Fréchet JMJ. Light-harvesting dendrimers. Chem Commun. (2000):1701–10. doi: 10.1039/B005993P

PubMed Abstract | CrossRef Full Text | Google Scholar

123. Balzani V, Ceroni P, Maestri M, Vicinelli V. Light-harvesting dendrimers. Curr Opin Chem Biol. (2003) 7:657–65. doi: 10.1016/j.cbpa.2003.10.001

PubMed Abstract | CrossRef Full Text | Google Scholar

124. Nantalaksakul A, Reddy DR, Bardeen CJ, Thayumanavan S. Light harvesting dendrimers. Photosynth Res. (2006) 87:133–50. doi: 10.1007/s11120-005-8387-3

PubMed Abstract | CrossRef Full Text | Google Scholar

125. Ziessel R, Ulrich G, Haefele A, Harriman A. An artificial light-harvesting array constructed from multiple bodipy dyes. J Am Chem Soc. (2013) 135:11330–44. doi: 10.1021/ja4049306

PubMed Abstract | CrossRef Full Text | Google Scholar

126. Zhang X, Zeng Y, Yu T, Chen J, Yang G, Li Y. Advances in photofunctional dendrimers for solar energy conversion. J Phys Chem Lett. (2014) 5:2340–50. doi: 10.1021/jz5007862

PubMed Abstract | CrossRef Full Text | Google Scholar

127. Pan SJ, Ma DD, Liu JS, Chen KZ, Zhang TT, Peng YR. Benzophenone and zinc(II) phthalocyanine dichromophores-labeled poly (aryl ether) dendrimer: synthesis, characterization and photoinduced energy transfer. J Coord Chem. (2016) 69:618–27. doi: 10.1080/00958972.2015.1131271

CrossRef Full Text | Google Scholar

128. Zou Q, Liu K, Abbas M, Yan X. Peptide-modulated self-assembly of chromophores toward biomimetic light-harvesting nanoarchitectonics. Adv Mater. (2016) 28:1031–43. doi: 10.1002/adma.201502454

PubMed Abstract | CrossRef Full Text | Google Scholar

129. Nelson T, Fernandez-Alberti S, Roitberg AE, Tretiak S. Electronic delocalization, vibrational dynamics, and energy transfer in organic chromophores. J Phys Chem Lett. (2017) 8:3020–31. doi: 10.1021/acs.jpclett.7b00790

PubMed Abstract | CrossRef Full Text | Google Scholar

130. Viswanath V, Santhakumar K. Perspectives on dendritic architectures and their biological applications: from core to cell. J Photochem Photobiol. (2017) 173:61–83. doi: 10.1016/j.jphotobiol.2017.05.023

PubMed Abstract | CrossRef Full Text | Google Scholar

131. Bradshaw DS, Andrews DL. Mechanisms of light energy harvesting in dendrimers and hyperbranched polymers. Polymers. (2011) 3:2053–77. doi: 10.3390/polym3042053

CrossRef Full Text | Google Scholar

132. Jenkins RD, Andrews DL. Multichromophore excitons and resonance energy transfer: molecular quantum electrodynamics. J Chem Phys. (2003) 118:3470–9. doi: 10.1063/1.1538611

CrossRef Full Text | Google Scholar

133. Andrews DL, Bradshaw DS. Optically nonlinear energy transfer in light-harvesting dendrimers. J Chem Phys. (2004) 121:2445–54. doi: 10.1063/1.1769354

PubMed Abstract | CrossRef Full Text | Google Scholar

134. Andrews DL, Li SP, Rodríguez J, Slota J. Development of the energy flow in light-harvesting dendrimers. J Chem Phys. (2007) 127:134902. doi: 10.1063/1.2785175

PubMed Abstract | CrossRef Full Text | Google Scholar

135. May V. Beyond the Förster theory of excitation energy transfer: importance of higher-order processes in supramolecular antenna systems. Dalton Trans. (2009):10086–105. doi: 10.1039/B908567J

PubMed Abstract | CrossRef Full Text | Google Scholar

136. Olaya-Castro A, Scholes GD. Energy transfer from Förster-Dexter theory to quantum coherent light-harvesting. Int Rev Phys Chem. (2011) 30:49–77. doi: 10.1080/0144235x.2010.537060

CrossRef Full Text | Google Scholar

137. Jang S. Theory of multichromophoric coherent resonance energy transfer: A polaronic quantum master equation approach. J Chem Phys. (2011) 135:034105. doi: 10.1063/1.3608914

PubMed Abstract | CrossRef Full Text | Google Scholar

138. Schröter M, Ivanov SD, Schulze J, Polyutov SP, Yan Y, Pullerits T, et al. Exciton-vibrational coupling in the dynamics and spectroscopy of Frenkel excitons in molecular aggregates. Phys Rep. (2015) 567:1–78. doi: 10.1016/j.physrep.2014.12.001

CrossRef Full Text | Google Scholar

139. Freixas VM, Ondarse-Alvarez D, Tretiak S, Makhov DV, Shalashilin DV, Fernandez-Alberti S. Photoinduced non-adiabatic energy transfer pathways in dendrimer building blocks. J Chem Phys. (2019) 150:124301. doi: 10.1063/1.5086680

PubMed Abstract | CrossRef Full Text | Google Scholar

140. Workineh ZG. Effect of surface functionalization on the structural properties of single dendrimers: Monte Carlo simulation study. Comput Mater Sci. (2019) 168:40–7. doi: 10.1016/j.commatsci.2019.05.061

CrossRef Full Text | Google Scholar

141. Jenkins RD, Andrews DL. Three-center systems for energy pooling: Quantum electrodynamical theory. J Phys Chem A. (1998) 102:10834–42. doi: 10.1021/jp983071h

CrossRef Full Text | Google Scholar

142. Andrews DL, Curutchet C, Scholes GD. Resonance energy transfer: Beyond the limits. Laser Photon Rev. (2011) 5:114–23. doi: 10.1002/lpor.201000004

CrossRef Full Text | Google Scholar

143. Steer RP. Electronic energy pooling in organic systems: a cross-disciplinary tutorial review. Can J Chem. (2017) 95:1025–40. doi: 10.1139/cjc-2017-0369

CrossRef Full Text | Google Scholar

144. Zhang C, Sun L, Zhang Y, Yan C. Rare earth upconversion nanophosphors: synthesis, functionalization and application as biolabels and energy transfer donors. J Rare Earth. (2010) 28:807–19. doi: 10.1016/S1002-0721(09)60206-4

CrossRef Full Text | Google Scholar

145. Dong H, Sun LD, Yan CH. Energy transfer in lanthanide upconversion studies for extended optical applications. Chem Soc Rev. (2015) 44:1608–34. doi: 10.1039/C4CS00188E

PubMed Abstract | CrossRef Full Text | Google Scholar

146. Weingarten DH, LaCount MD, van de Lagemaat J, Rumbles G, Lusk MT, Shaheen SE. Experimental demonstration of photon upconversion via cooperative energy pooling. Nat Commun. (2017) 8:14808. doi: 10.1038/ncomms14808

PubMed Abstract | CrossRef Full Text | Google Scholar

147. LaCount MD, Weingarten D, Hu N, Shaheen SE, van de Lagemaat J, Rumbles G, et al. Energy pooling upconversion in organic molecular systems. J Phys Chem A. (2015) 119:4009–16. doi: 10.1021/acs.jpca.5b00509

PubMed Abstract | CrossRef Full Text | Google Scholar

148. LaCount MD, Lusk MT. Electric dipole coupling in optical cavities and its implications for energy transfer, up-conversion, and pooling. Phys Rev A. (2016) 93:063811. doi: 10.1103/PhysRevA.93.063811

CrossRef Full Text | Google Scholar

149. LaCount MD, Lusk MT. Improved energy pooling efficiency through inhibited spontaneous emission. J Phys Chem C. (2017) 121:8335–44. doi: 10.1021/acs.jpcc.7b01693

CrossRef Full Text | Google Scholar

150. LaCount MD, Lusk MT. Quantum cutting using organic molecules. Phys Chem Chem Phys. (2019) 21:7814–21. doi: 10.1039/C9CP00329K

PubMed Abstract | CrossRef Full Text | Google Scholar

151. Allcock P, Andrews DL. Two-photon fluorescence: resonance energy transfer. J Chem Phys. (1998) 108:3089–95. doi: 10.1063/1.475706

CrossRef Full Text | Google Scholar

152. Bradshaw DS, Andrews DL. Competing mechanisms for energy transfer in two-photon absorbing systems. Chem Phys Lett. (2006) 430:191–4. doi: 10.1016/j.cplett.2006.08.116

CrossRef Full Text | Google Scholar

153. Dichtel WR, Serin JM, Edder C, Fréchet JMJ, Matuszewski M, Tan LS, et al. Singlet oxygen generation via two-photon excited FRET. J Am Chem Soc. (2004) 126:5380–1. doi: 10.1021/ja031647x

PubMed Abstract | CrossRef Full Text | Google Scholar

154. Oar MA, Serin JM, Dichtel WR, Fréchet JMJ, Ohulchanskyy TY, Prasad PN. Photosensitization of singlet oxygen via two-photon-excited fluorescence resonance energy transfer in a water-soluble dendrimer. Chem Mater. (2005) 17:2267–75. doi: 10.1021/cm047825i

CrossRef Full Text | Google Scholar

155. Tian N, Xu QH. Enhanced two-photon excitation fluorescence by fluorescence resonance energy transfer using conjugated polymers. Adv Mater. (2007) 19:1988–91. doi: 10.1002/adma.200700654

CrossRef Full Text | Google Scholar

156. Cheng SH, Hsieh CC, Chen NT, Chu CH, Huang CM, Chou PT, et al. Well-defined mesoporous nanostructure modulates three-dimensional interface energy transfer for two-photon activated photodynamic therapy. Nano Today. (2011) 6:552–63. doi: 10.1016/j.nantod.2011.10.003

CrossRef Full Text | Google Scholar

157. Ngen EJ, Xiao L, Rajaputra P, Yan X, You Y. Enhanced singlet oxygen generation from a porphyrin–rhodamine B dyad by two-photon excitation through resonance energy transfer. Photochem Photobiol. (2013) 89:841–8. doi: 10.1111/php.12071

PubMed Abstract | CrossRef Full Text | Google Scholar

158. Chen NT, Tang KC, Chung MF, Cheng SH, Huang CM, Chu CH, et al. Enhanced plasmonic resonance energy transfer in mesoporous silica-encased gold nanorod for two-photon-activated photodynamic therapy. Theranostics. (2014) 4:798–807. doi: 10.7150/thno.8934

PubMed Abstract | CrossRef Full Text | Google Scholar

159. Drozdek S, Szeremeta J, Lamch L, Nyk M, Samoc M, Wilk KA. Two-photon induced fluorescence energy transfer in polymeric nanocapsules containing CdSe_xS_1−x/ZnS core/shell quantum dots and zinc(II) phthalocyanine. J Phys Chem C. (2016) 120:15460–70. doi: 10.1021/acs.jpcc.6b04301

CrossRef Full Text | Google Scholar

160. Zhu M, Zhang J, Zhou Y, Xing P, Gong L, Su C, et al. Two-photon excited FRET dyads for lysosome-targeted imaging and photodynamic therapy. Inorg Chem. (2018) 57:11537–42. doi: 10.1021/acs.inorgchem.8b01581

PubMed Abstract | CrossRef Full Text | Google Scholar

161. Kim S, Huang H, Pudavar HE, Cui Y, Prasad PN. Intraparticle energy transfer and fluorescence photoconversion in nanoparticles: an optical highlighter nanoprobe for two-photon bioimaging. Chem Mater. (2007) 19:5650–6. doi: 10.1021/cm071273x

CrossRef Full Text | Google Scholar

162. Acosta Y, Zhang Q, Rahaman A, Ouellet H, Xiao C, Sun J, Li C. Imaging cytosolic translocation of Mycobacteria with two-photon fluorescence resonance energy transfer microscopy. Biomed Opt Express. (2014) 5:3990–4001. doi: 10.1364/BOE.5.003990

PubMed Abstract | CrossRef Full Text | Google Scholar

163. He T, Chen R, Lim ZB, Rajwar D, Ma L, Wang Y, et al. Efficient energy transfer under two-photon excitation in a 3D, supramolecular, Zn(II)-coordinated, self-assembled organic network. Adv Opt Mater. (2014) 2:40–7. doi: 10.1002/adom.201300407

CrossRef Full Text | Google Scholar

164. Choi Y, Park Y, Kang T, Lee LP. Selective and sensitive detection of metal ions by plasmonic resonance energy transfer-based nanospectroscopy. Nat Nanotechnol. (2009) 4:742. doi: 10.1038/nnano.2009.258

PubMed Abstract | CrossRef Full Text | Google Scholar

165. Martín-Cano D, Martín-Moreno L, García-Vidal FJ, Moreno E. Resonance energy transfer and superradiance mediated by plasmonic nanowaveguides. Nano Lett. (2010) 10:3129–34. doi: 10.1021/nl101876f

PubMed Abstract | CrossRef Full Text | Google Scholar

166. Faessler V, Hrelescu C, Lutich AA, Osinkina L, Mayilo S, Jäckel F, et al. Accelerating fluorescence resonance energy transfer with plasmonic nanoresonators. Chem Phys Lett. (2011) 508:67–70. doi: 10.1016/j.cplett.2011.03.088

CrossRef Full Text | Google Scholar

167. Vincent R, Carminati R. Magneto-optical control of Förster energy transfer. Phys Rev B. (2011) 83:165426. doi: 10.1103/PhysRevB.83.165426

CrossRef Full Text | Google Scholar

168. Cushing SK, Li J, Meng F, Senty TR, Suri S, Zhi M, et al. Photocatalytic activity enhanced by plasmonic resonant energy transfer from metal to semiconductor. J Am Chem Soc. (2012) 134:15033–41. doi: 10.1021/ja305603t

PubMed Abstract | CrossRef Full Text | Google Scholar

169. Gonzaga-Galeana JA, Zurita-Sánchez JR. A revisitation of the Förster energy transfer near a metallic spherical nanoparticle: (1) Efficiency enhancement or reduction? (2) The control of the Förster radius of the unbounded medium. (3) The impact of the local density of states. J Chem Phys. (2013) 139:244302. doi: 10.1063/1.4847875

PubMed Abstract | CrossRef Full Text | Google Scholar

170. Schleifenbaum F, Kern AM, Konrad A, Meixner AJ. Dynamic control of Förster energy transfer in a photonic environment. Phys Chem Chem Phys. (2014) 16:12812–7. doi: 10.1039/C4CP01306A

PubMed Abstract | CrossRef Full Text | Google Scholar

171. Li J, Cushing SK, Meng F, Senty TR, Bristow AD, Wu N. Plasmon-induced resonance energy transfer for solar energy conversion. Nat Photonics. (2015) 9:601. doi: 10.1038/nphoton.2015.142

CrossRef Full Text | Google Scholar

172. Ghenuche P, Mivelle M, de Torres J, Moparthi SB, Rigneault H, Van Hulst NF, et al. Matching nanoantenna field confinement to FRET distances enhances Förster energy transfer rates. Nano Lett. (2015) 15:6193–201. doi: 10.1021/acs.nanolett.5b02535

PubMed Abstract | CrossRef Full Text | Google Scholar

173. Konrad A, Metzger M, Kern AM, Brecht M, Meixner AJ. Controlling the dynamics of Förster resonance energy transfer inside a tunable sub-wavelength Fabry–Pérot-resonator. Nanoscale. (2015) 7:10204–9. doi: 10.1039/C5NR02027A

PubMed Abstract | CrossRef Full Text | Google Scholar

174. Tumkur TU, Kitur JK, Bonner CE, Poddubny AN, Narimanov EE, Noginov MA. Control of Förster energy transfer in the vicinity of metallic surfaces and hyperbolic metamaterials. Faraday Discuss. (2015) 178:395–412. doi: 10.1039/C4FD00184B

PubMed Abstract | CrossRef Full Text | Google Scholar

175. Bidault S, Devilez A, Ghenuche P, Stout B, Bonod N, Wenger J. Competition between Förster resonance energy transfer and donor photodynamics in plasmonic dimer nanoantennas. ACS Photonics. (2016) 3:895–903. doi: 10.1021/acsphotonics.6b00148

CrossRef Full Text | Google Scholar

176. de Torres J, Ferrand P, Colas des Francs G, Wenger J. Coupling emitters and silver nanowires to achieve long-range plasmon-mediated fluorescence energy transfer. ACS Nano. (2016) 10:3968–76. doi: 10.1021/acsnano.6b00287

PubMed Abstract | CrossRef Full Text | Google Scholar

177. Poudel A, Chen X, Ratner MA. Enhancement of resonant energy transfer due to an evanescent wave from the metal. J Phys Chem Lett. (2016) 7:955–60. doi: 10.1021/acs.jpclett.6b00119

PubMed Abstract | CrossRef Full Text | Google Scholar

178. Marocico CA, Zhang X, Bradley AL. A theoretical investigation of the influence of gold nanosphere size on the decay and energy transfer rates and efficiencies of quantum emitters. J Chem Phys. (2016) 144:024108. doi: 10.1063/1.4939206

PubMed Abstract | CrossRef Full Text | Google Scholar

179. Wubs M, Vos WL. Förster resonance energy transfer rate in any dielectric nanophotonic medium with weak dispersion. New J Phys. (2016) 18:053037. doi: 10.1088/1367-2630/18/5/053037

CrossRef Full Text | Google Scholar

180. Higgins LJ, Marocico CA, Karanikolas VD, Bell AP, Gough JJ, Murphy GP, et al. Influence of plasmonic array geometry on energy transfer from a quantum well to a quantum dot layer. Nanoscale. (2016) 8:18170–9. doi: 10.1039/C6NR05990B

PubMed Abstract | CrossRef Full Text | Google Scholar

181. Bujak Ł, Ishii T, Sharma DK, Hirata S, Vacha M. Selective turn-on and modulation of resonant energy transfer in single plasmonic hybrid nanostructures. Nanoscale. (2017) 9:1511–9. doi: 10.1039/C6NR08740J

PubMed Abstract | CrossRef Full Text | Google Scholar

182. Murphy GP, Gough JJ, Higgins LJ, Karanikolas VD, Wilson KM, Garcia Coindreau JA, et al. Ag colloids and arrays for plasmonic non-radiative energy transfer from quantum dots to a quantum well. Nanotechnology. (2017) 28:115401. doi: 10.1088/1361-6528/aa5b67

PubMed Abstract | CrossRef Full Text | Google Scholar

183. Steele JM, Ramnarace CM, Farner WR. Controlling FRET enhancement using plasmon modes on gold nanogratings. J Phys Chem C. (2017) 121:22353–60. doi: 10.1021/acs.jpcc.7b07317

CrossRef Full Text | Google Scholar

184. Akulov K, Bochman D, Golombek A, Schwartz T. Long-distance resonant energy transfer mediated by hybrid plasmonic-photonic modes. J Phys Chem C. (2018) 122:15853–60. doi: 10.1021/acs.jpcc.8b03030

CrossRef Full Text | Google Scholar

185. Asgar H, Jacob L, Hoang TB. Fast spontaneous emission and high Förster resonance energy transfer rate in hybrid organic/inorganic plasmonic nanostructures. J Appl Phys. (2018) 124:103105. doi: 10.1063/1.5052350

CrossRef Full Text | Google Scholar

186. Eldabagh N, Micek M, DePrince AE, Foley JJ. Resonance energy transfer mediated by metal-dielectric composite nanostructures. J Phys Chem C. (2018) 122:18256–65. doi: 10.1021/acs.jpcc.8b04419

CrossRef Full Text | Google Scholar

187. Glaeske M, Juergensen S, Gabrielli L, Menna E, Mancin F, Gatti T, et al. PhysicaPlasmon-assisted energy transfer in hybrid nanosystems. Phys Status Solidi Rapid Res. Lett. (2018) 12:1800508. doi: 10.1002/pssr.201800508

CrossRef Full Text | Google Scholar

188. Hu J, Wu M, Jiang L, Zhong Z, Zhou Z, Rujiralai T, et al. Combining gold nanoparticle antennas with single-molecule fluorescence resonance energy transfer (smFRET) to study DNA hairpin dynamics. Nanoscale. (2018) 10:6611–9. doi: 10.1039/C7NR08397A

PubMed Abstract | CrossRef Full Text | Google Scholar

189. Roth DJ, Nasir ME, Ginzburg P, Wang P, Le Marois A, Suhling K, et al. Förster resonance energy transfer inside hyperbolic metamaterials. ACS Photonics. (2018) 5:4594–603. doi: 10.1021/acsphotonics.8b01083

CrossRef Full Text | Google Scholar

190. Wu JS, Lin YC, Sheu YL, Hsu LY. Characteristic distance of resonance energy transfer coupled with surface plasmon polaritons. J Phys Chem Lett. (2018) 9:7032–9. doi: 10.1021/acs.jpclett.8b03429

PubMed Abstract | CrossRef Full Text | Google Scholar

191. Zurita-Sánchez JR, Méndez-Villanueva J. Förster energy transfer in the vicinity of two metallic nanospheres (dimer). Plasmonics. (2018) 13:873–83. doi: 10.1007/s11468-017-0583-4

CrossRef Full Text | Google Scholar

192. Olivo J, Zapata-Rodríguez CJ, Cuevas M. Spatial modulation of the electromagnetic energy transfer by excitation of graphene waveguide surface plasmons. J Opt. (2019) 21:045002. doi: 10.1088/2040-8986/ab0ab9

CrossRef Full Text | Google Scholar

193. Bohlen J, Cuartero-González Á, Pibiri E, Ruhlandt D, Fernández-Domínguez AI, Tinnefeld P, et al. Plasmon-assisted Förster resonance energy transfer at the single-molecule level in the moderate quenching regime. Nanoscale. (2019) 11:7674–81. doi: 10.1039/C9NR01204D

PubMed Abstract | CrossRef Full Text | Google Scholar

194. Wang Y, Li H, Zhu W, He F, Huang Y, Chong R, et al. Plasmon-mediated nonradiative energy transfer from a conjugated polymer to a plane of graphene-nanodot-supported silver nanoparticles: an insight into characteristic distance. Nanoscale. (2019) 11:6737–46. doi: 10.1039/C8NR09576K

PubMed Abstract | CrossRef Full Text | Google Scholar

195. Cortes CL, Jacob Z. Fundamental figures of merit for engineering Förster resonance energy transfer. Opt Express. (2018) 26:19371–87. doi: 10.1364/OE.26.019371

PubMed Abstract | CrossRef Full Text | Google Scholar

196. Pustovit VN, Shahbazyan TV. Resonance energy transfer near metal nanostructures mediated by surface plasmons. Phys Rev B. (2011) 83:085427. doi: 10.1103/PhysRevB.83.085427

CrossRef Full Text | Google Scholar

197. Ding W, Hsu LY, Schatz GC. Plasmon-coupled resonance energy transfer: a real-time electrodynamics approach. J Chem Phys. (2017) 146:064109. doi: 10.1063/1.4975815

PubMed Abstract | CrossRef Full Text | Google Scholar

198. Ghenuche P, de Torres J, Moparthi SB, Grigoriev V, Wenger J. Nanophotonic enhancement of the Förster resonance energy-transfer rate with single nanoapertures. Nano Lett. (2014) 14:4707–14. doi: 10.1021/nl5018145

PubMed Abstract | CrossRef Full Text | Google Scholar

199. Zhao L, Ming T, Shao L, Chen H, Wang J. Plasmon-controlled Förster resonance energy transfer. J Phys Chem C. (2012) 116:8287–96. doi: 10.1021/jp300916a

CrossRef Full Text | Google Scholar

200. Hsu LY, Ding W, Schatz GC. Plasmon-coupled resonance energy transfer. J Phys Chem Lett. (2017) 8:2357–67. doi: 10.1021/acs.jpclett.7b00526

PubMed Abstract | CrossRef Full Text | Google Scholar

201. Ding W, Hsu LY, Heaps CW, Schatz GC. Plasmon-coupled resonance energy transfer II: Exploring the peaks and dips in the electromagnetic coupling factor. J Phys Chem C. (2018) 122:22650–9. doi: 10.1021/acs.jpcc.8b07210

CrossRef Full Text | Google Scholar

202. de Torres J, Mivelle M, Moparthi SB, Rigneault H, Van Hulst NF, García-Parajó MF, et al. Plasmonic nanoantennas enable forbidden Förster dipole-dipole energy transfer and enhance the FRET efficiency. Nano Lett. (2016) 16:6222–30. doi: 10.1021/acs.nanolett.6b02470

PubMed Abstract | CrossRef Full Text | Google Scholar

203. Breshike CJ, Riskowski RA, Strouse GF. Leaving Förster resonance energy transfer behind: Nanometal surface energy transfer predicts the size-enhanced energy coupling between a metal nanoparticle and an emitting dipole. J Phys Chem C. (2013) 117:23942–9. doi: 10.1021/jp407259r

CrossRef Full Text | Google Scholar

204. Zhang X, Marocico CA, Lunz M, Gerard VA, Gun'ko YK, Lesnyak V, et al. Experimental and theoretical investigation of the distance dependence of localized surface plasmon coupled Förster resonance energy transfer. ACS Nano. (2014) 8:1273–83. doi: 10.1021/nn406530m

PubMed Abstract | CrossRef Full Text | Google Scholar

205. Panman MR, Shaw DJ, Ensing B, Woutersen S. Local orientational order in liquids revealed by resonant vibrational energy transfer. Phys Rev Lett. (2014) 113:207801. doi: 10.1103/PhysRevLett.113.207801

PubMed Abstract | CrossRef Full Text | Google Scholar

206. Chen H, Wen X, Li J, Zheng J. Molecular distances determined with resonant vibrational energy transfers. J Phys Chem A. (2014) 118:2463–9. doi: 10.1021/jp500586h

PubMed Abstract | CrossRef Full Text | Google Scholar

207. Chen H, Bian H, Li J, Wen X, Zhang Q, Zhuang W, et al. Vibrational energy transfer: An angstrom molecular ruler in studies of ion pairing and clustering in aqueous solutions. J Phys Chem B. (2015) 119:4333–49. doi: 10.1021/jp512320a

PubMed Abstract | CrossRef Full Text | Google Scholar

208. Piatkowski L, Eisenthal KB, Bakker HJ. Ultrafast intermolecular energy transfer in heavy water. Phys Chem Chem Phys. (2009) 11:9033–8. doi: 10.1039/B908975F

PubMed Abstract | CrossRef Full Text | Google Scholar

209. Zhang Z, Piatkowski L, Bakker HJ, Bonn M. Ultrafast vibrational energy transfer at the water/air interface revealed by two-dimensional surface vibrational spectroscopy. Nat Chem. (2011) 3:888. doi: 10.1038/nchem.1158

PubMed Abstract | CrossRef Full Text | Google Scholar

210. Piatkowski L, de Heij J, Bakker HJ. Probing the distribution of water molecules hydrating lipid membranes with ultrafast Förster vibrational energy transfer. J Phys Chem B. (2013) 117:1367–77. doi: 10.1021/jp310602v

PubMed Abstract | CrossRef Full Text | Google Scholar

211. Yang M, Li F, Skinner JL. Vibrational energy transfer and anisotropy decay in liquid water: Is the Förster model valid? J Chem Phys. (2011) 135:164505. doi: 10.1063/1.3655894

PubMed Abstract | CrossRef Full Text | Google Scholar

212. Rustomji K, Dubois M, Kuhlmey B, de Sterke CM, Enoch S, Abdeddaim R, et al. Direct imaging of the energy-transfer enhancement between two dipoles in a photonic cavity. Phys Rev X. (2019) 9:011041. doi: 10.1103/PhysRevX.9.011041

CrossRef Full Text | Google Scholar

213. Cederbaum LS, Zobeley J, Tarantelli F. Giant intermolecular decay and fragmentation of clusters. Phys Rev Lett. (1997) 79:4778–81. doi: 10.1103/PhysRevLett.79.4778

CrossRef Full Text | Google Scholar

214. Marburger S, Kugeler O, Hergenhahn U, Möller T. Experimental evidence for interatomic coulombic decay in Ne clusters. Phys Rev Lett. (2003) 90:203401. doi: 10.1103/PhysRevLett.90.203401

PubMed Abstract | CrossRef Full Text | Google Scholar

215. Santra R, Zobeley J, Cederbaum LS, Moiseyev N. Interatomic coulombic decay in van der Waals clusters and impact of nuclear motion. Phys Rev Lett. (2000) 85:4490-4493. doi: 10.1103/PhysRevLett.85.4490

PubMed Abstract | CrossRef Full Text | Google Scholar

216. Scheit S, Cederbaum LS, Meyer HD. Time-dependent interplay between electron emission and fragmentation in the interatomic Coulombic decay. J Chem Phys. (2003) 118:2092–107. doi: 10.1063/1.1531996

CrossRef Full Text | Google Scholar

217. Jahnke T. Interatomic and intermolecular Coulombic decay: the coming of age story. J Phys B. (2015) 48:082001. doi: 10.1088/0953-4075/48/8/082001

CrossRef Full Text | Google Scholar

218. Fasshauer E. Non-nearest neighbour ICD in clusters. New J Phys. (2016) 18:043028. doi: 10.1088/1367-2630/18/4/043028

CrossRef Full Text | Google Scholar

219. Dolbundalchok P, Peláez D, Aziz EF, Bande A. Geometrical control of the interatomic coulombic decay process in quantum dots for infrared photodetectors. J Comput Chem. (2016) 37:2249–59. doi: 10.1002/jcc.24410

PubMed Abstract | CrossRef Full Text | Google Scholar

220. Haller A, Chiang YC, Menger M, Aziz EF, Bande A. Strong field control of the interatomic Coulombic decay process in quantum dots. Chem Phys. (2017) 482:135-145. doi: 10.1016/j.chemphys.2016.09.020

CrossRef Full Text | Google Scholar

221. Goldzak T, Gantz L, Gilary I, Bahir G, Moiseyev N. Vertical currents due to interatomic Coulombic decay in experiments with two coupled quantum wells. Phys Rev B. (2016) 93:045310. doi: 10.1103/PhysRevB.93.045310

CrossRef Full Text | Google Scholar

222. Dreuw A, Faraji S. A quantum chemical perspective on (6-4) photolesion repair by photolyases. Phys Chem Chem Phys. (2013) 15:19957–69. doi: 10.1039/C3CP53313A

PubMed Abstract | CrossRef Full Text | Google Scholar

223. Harbach PHP, Schneider M, Faraji S, Dreuw A. Intermolecular coulombic decay in biology: the initial electron detachment from FADH⁻ in DNA photolyases. J Phys Chem Lett. (2013) 4:943–9. doi: 10.1021/jz400104h

PubMed Abstract | CrossRef Full Text | Google Scholar

224. Hemmerich JL, Bennett R, Buhmann SY. The influence of retardation and dielectric environments on interatomic Coulombic decay. Nat Commun. (2018) 9:2934. doi: 10.1038/s41467-018-05091-x

PubMed Abstract | CrossRef Full Text | Google Scholar

225. Bennett R, Votavová P, Kolorenč P, Miteva T, Sisourat N, Buhmann SY. Virtual photon approximation for three-body interatomic coulombic decay. Phys Rev Lett. (2019) 122:153401. doi: 10.1103/PhysRevLett.122.153401

PubMed Abstract | CrossRef Full Text | Google Scholar

226. Beljonne D, Curutchet C, Scholes GD, Silbey RJ. Beyond Förster resonance energy transfer in biological and nanoscale systems. J Phys Chem B. (2009) 113:6583–99. doi: 10.1021/jp900708f

PubMed Abstract | CrossRef Full Text | Google Scholar

227. Xia Z, Rao J. Biosensing and imaging based on bioluminescence resonance energy transfer. Curr Opin Biotechnol. (2009) 20:37–44. doi: 10.1016/j.copbio.2009.01.001

PubMed Abstract | CrossRef Full Text | Google Scholar

228. Ling J, Huang CZ. Energy transfer with gold nanoparticles for analytical applications in the fields of biochemical and pharmaceutical sciences. Anal Methods. (2010) 2:1439–47. doi: 10.1039/C0AY00452A

CrossRef Full Text | Google Scholar

229. Scholes GD, Fleming GR, Olaya-Castro A, van Grondelle R. Lessons from nature about solar light harvesting. Nat Chem. (2011) 3:763–74. doi: 10.1038/nchem.1145

PubMed Abstract | CrossRef Full Text | Google Scholar

230. Sener M, Strümpfer J, Hsin J, Chandler D, Scheuring S, Hunter CN, et al. Förster energy transfer theory as reflected in the structures of photosynthetic light-harvesting systems. Chem Phys Chem. (2011) 12:518–31. doi: 10.1002/cphc.201000944

PubMed Abstract | CrossRef Full Text | Google Scholar

231. Chen NT, Cheng SH, Liu CP, Souris JS, Chen CT, Mou CY, et al. Recent advances in nanoparticle-based Förster resonance energy transfer for biosensing, molecular imaging and drug release profiling. Int J Mol Sci. (2012) 13:16598–623. doi: 10.3390/ijms131216598

PubMed Abstract | CrossRef Full Text | Google Scholar

232. Lohse MJ, Nuber S, Hoffmann C. Fluorescence/bioluminescence resonance energy transfer techniques to study G-protein-coupled receptor activation and signaling. Pharmacol Rev. (2012) 64:299–336. doi: 10.1124/pr.110.004309

PubMed Abstract | CrossRef Full Text | Google Scholar

233. Yang J, Yoon MC, Yoo H, Kim P, Kim D. Excitation energy transfer in multiporphyrin arrays with cyclic architectures: towards artificial light-harvesting antenna complexes. Chem Soc Rev. (2012) 41:4808–26. doi: 10.1039/C2CS35022J

PubMed Abstract | CrossRef Full Text | Google Scholar

234. Zadran S, Standley S, Wong K, Otiniano E, Amighi A, Baudry M. Fluorescence resonance energy transfer (FRET)-based biosensors: visualizing cellular dynamics and bioenergetics. Appl Microbiol Biotechnol. (2012) 96:895–902. doi: 10.1007/s00253-012-4449-6

PubMed Abstract | CrossRef Full Text | Google Scholar

235. Fassioli F, Dinshaw R, Arpin PC, Scholes GD. Photosynthetic light harvesting: excitons and coherence. J R Soc Interface. (2014) 11:20130901. doi: 10.1098/rsif.2013.0901

PubMed Abstract | CrossRef Full Text | Google Scholar

236. Chenu A, Scholes GD. Coherence in energy transfer and photosynthesis. Annu Rev Phys Chem. (2015) 66:69–96. doi: 10.1146/annurev-physchem-040214-121713

PubMed Abstract | CrossRef Full Text | Google Scholar

237. Peng HQ, Niu LY, Chen YZ, Wu LZ, Tung CH, Yang QZ. Biological applications of supramolecular assemblies designed for excitation energy transfer. Chem Rev. (2015) 115:7502–42. doi: 10.1021/cr5007057

PubMed Abstract | CrossRef Full Text | Google Scholar

238. Brédas JL, Sargent EH, Scholes GD. Photovoltaic concepts inspired by coherence effects in photosynthetic systems. Nat Mater. (2016) 16:35–44. doi: 10.1038/nmat4767

PubMed Abstract | CrossRef Full Text | Google Scholar

239. Jiang Y, McNeill J. Light-harvesting and amplified energy transfer in conjugated polymer nanoparticles. Chem Rev. (2017) 117:838–59. doi: 10.1021/acs.chemrev.6b00419

PubMed Abstract | CrossRef Full Text | Google Scholar

240. Mirkovic T, Ostroumov EE, Anna JM, van Grondelle R, Govindjee, Scholes GD. Light absorption and energy transfer in the antenna complexes of photosynthetic organisms. Chem Rev. (2017) 117:249–93. doi: 10.1021/acs.chemrev.6b00002

PubMed Abstract | CrossRef Full Text | Google Scholar

241. Scholes GD, Fleming GR, Chen LX, Aspuru-Guzik A, Buchleitner A, Coker DF, et al. Using coherence to enhance function in chemical and biophysical systems. Nature. (2017) 543:647. doi: 10.1038/nature21425

PubMed Abstract | CrossRef Full Text | Google Scholar

242. Su Q, Feng W, Yang D, Li F. Resonance energy transfer in upconversion nanoplatforms for selective biodetection. Acc Chem Res. (2017) 50:32–40. doi: 10.1021/acs.accounts.6b00382

PubMed Abstract | CrossRef Full Text | Google Scholar

243. Jumper CC, Rafiq S, Wang S, Scholes GD. From coherent to vibronic light harvesting in photosynthesis. Curr Opin Chem Biol. (2018) 47:39–46. doi: 10.1016/j.cbpa.2018.07.023

PubMed Abstract | CrossRef Full Text | Google Scholar

244. Lerner E, Cordes T, Ingargiola A, Alhadid Y, Chung S, Michalet X, et al. Toward dynamic structural biology: two decades of single-molecule Förster resonance energy transfer. Science. (2018) 359:eaan1133. doi: 10.1126/science.aan1133

PubMed Abstract | CrossRef Full Text | Google Scholar

245. El Khamlichi C, Reverchon-Assadi F, Hervouet-Coste N, Blot L, Reiter E, Morisset-Lopez S. Bioluminescence resonance energy transfer as a method to study protein-protein interactions: application to G-protein coupled receptor biology. Molecules. (2019) 24:E537. doi: 10.3390/molecules24030537

PubMed Abstract | CrossRef Full Text | Google Scholar

246. Cupellini L, Corbella M, Mennucci B, Curutchet C. Electronic energy transfer in biomacromolecules. WIREs Comput Mol Sci. (2019) 9:e1392. doi: 10.1002/wcms.1392

CrossRef Full Text | Google Scholar

247. Power EA, Thirunamachandran T. Quantum electrodynamics in a cavity. Phys Rev A. (1982) 25:2473–84. doi: 10.1103/PhysRevA.25.2473

CrossRef Full Text | Google Scholar

248. Mabuchi H, Doherty AC. Cavity quantum electrodynamics: coherence in context. Science. (2002) 298:1372–7. doi: 10.1126/science.1078446

PubMed Abstract | CrossRef Full Text | Google Scholar

249. Miller R, Northup TE, Birnbaum KM, Boca A, Boozer AD, Kimble HJ. Trapped atoms in cavity QED: coupling quantized light and matter. J Phys B. (2005) 38:S551–65. doi: 10.1088/0953-4075/38/9/007

CrossRef Full Text | Google Scholar

250. Walther H, Varcoe BTH, Englert BG, Becker T. Cavity quantum electrodynamics. Rep Prog Phys. (2006) 69:1325–82. doi: 10.1088/0034-4885/69/5/r02

CrossRef Full Text | Google Scholar

251. Hohenester U. Cavity quantum electrodynamics with semiconductor quantum dots: role of phonon-assisted cavity feeding. Phys Rev B. (2010) 81:155303. doi: 10.1103/PhysRevB.81.155303

CrossRef Full Text | Google Scholar

252. Chang DE, Jiang L, Gorshkov AV, Kimble HJ. Cavity QED with atomic mirrors. New J Phys. (2012) 14:063003. doi: 10.1088/1367-2630/14/6/063003

CrossRef Full Text | Google Scholar

253. Andrew P, Barnes WL. Förster energy transfer in an optical microcavity. Science. (2000) 290:785–8. doi: 10.1126/science.290.5492.785

PubMed Abstract | CrossRef Full Text | Google Scholar

254. Hutchison JA, Schwartz T, Genet C, Devaux E, Ebbesen TW. Modifying chemical landscapes by coupling to vacuum fields. Angew Chem Int Ed. (2012) 51:1592–6. doi: 10.1002/anie.201107033

PubMed Abstract | CrossRef Full Text | Google Scholar

255. Thomas A, George J, Shalabney A, Dryzhakov M, Varma SJ, Moran J, et al. Ground-state chemical reactivity under vibrational coupling to the vacuum electromagnetic field. Angew Chem Int Ed. (2016) 55:11462–6. doi: 10.1002/anie.201605504

PubMed Abstract | CrossRef Full Text | Google Scholar

256. Feist J, Garcia-Vidal FJ. Extraordinary exciton conductance induced by strong coupling. Phys Rev Lett. (2015) 114:196402. doi: 10.1103/PhysRevLett.114.196402

PubMed Abstract | CrossRef Full Text | Google Scholar

257. Schachenmayer J, Genes C, Tignone E, Pupillo G. Cavity-enhanced transport of excitons. Phys Rev Lett. (2015) 114:196403. doi: 10.1103/PhysRevLett.114.196403

PubMed Abstract | CrossRef Full Text | Google Scholar

258. Zhong X, Chervy T, Wang S, George J, Thomas A, Hutchison JA, et al. Non-radiative energy transfer mediated by hybrid light-matter states. Angew Chem Int Ed. (2016) 55:6202–6. doi: 10.1002/anie.201600428

PubMed Abstract | CrossRef Full Text | Google Scholar

259. Zhong X, Chervy T, Zhang L, Thomas A, George J, Genet C, et al. Energy transfer between spatially separated entangled molecules. Angew Chem Int Ed. (2017) 56:9034–8. doi: 10.1002/anie.201703539

PubMed Abstract | CrossRef Full Text | Google Scholar

260. Georgiou K, Michetti P, Gai L, Cavazzini M, Shen Z, Lidzey DG. Control over energy transfer between fluorescent BODIPY dyes in a strongly coupled microcavity. ACS Photonics. (2018) 5:258–66. doi: 10.1021/acsphotonics.7b01002

CrossRef Full Text | Google Scholar

261. Du M, Martínez-Martínez LA, Ribeiro RF, Hu Z, Menon VM, Yuen-Zhou J. Theory for polariton-assisted remote energy transfer. Chem Sci. (2018) 9:6659–69. doi: 10.1039/C8SC00171E

PubMed Abstract | CrossRef Full Text | Google Scholar

262. Schäfer C, Ruggenthaler M, Appel H, Rubio A. Modification of excitation and charge transfer in cavity quantum-electrodynamical chemistry. Proc Natl Acad Sci USA. (2019) 116:4883–92. doi: 10.1073/pnas.1814178116

PubMed Abstract | CrossRef Full Text | Google Scholar

263. Hertzog M, Wang M, Mony J, Börjesson K. Strong light–matter interactions: a new direction within chemistry. Chem Soc Rev. (2019) 48:937–61. doi: 10.1039/C8CS00193F

PubMed Abstract | CrossRef Full Text | Google Scholar

264. Juzeliunas G, Andrews DL. Quantum electrodynamics of resonant energy-transfer in condensed matter. Phys Rev B. (1994) 49:8751–63. doi: 10.1103/PhysRevB.49.8751

PubMed Abstract | CrossRef Full Text | Google Scholar

265. Juzeliunas G, Andrews DL. Quantum electrodynamics of resonant energy-transfer in condensed matter. II. dynamical aspects. Phys Rev B. (1994) 50:13371–8. doi: 10.1103/PhysRevB.50.13371

PubMed Abstract | CrossRef Full Text | Google Scholar

266. Dung HT, Knöll L, Welsch DG. Intermolecular energy transfer in the presence of dispersing and absorbing media. Phys Rev A. (2002) 65:043813. doi: 10.1103/PhysRevA.65.043813

CrossRef Full Text | Google Scholar

267. Cortes CL, Jacob Z. Super-Coulombic atom–atom interactions in hyperbolic media. Nat Commun. (2017) 8:14144. doi: 10.1038/ncomms14144

PubMed Abstract | CrossRef Full Text | Google Scholar

268. Newman WD, Cortes CL, Afshar A, Cadien K, Meldrum A, Fedosejevs R, et al. Observation of long-range dipole-dipole interactions in hyperbolic metamaterials. Sci Adv. (2018) 4:eaar5278. doi: 10.1126/sciadv.aar5278

PubMed Abstract | CrossRef Full Text | Google Scholar

269. Mahmoud AM, Liberal I, Engheta N. Dipole-dipole interactions mediated by epsilon-and-mu-near-zero waveguide supercoupling. Opt Mater Express. (2017) 7:415–24. doi: 10.1364/OME.7.000415

CrossRef Full Text | Google Scholar

270. Scheel S, Buhmann S. Macroscopic quantum electrodynamics-concepts and applications. Acta Phys Slov. (2008) 58:675–809. doi: 10.2478/v10155-010-0092-x

CrossRef Full Text | Google Scholar