Variation of Elastic Energy Shows Reliable Signal of Upcoming Catastrophic Failure

1. Introduction

Accurate prediction of upcoming catastrophic failure events has important and far-reaching consequences. It is a central problem in material science in connection with the durability of composite materials under external stress [1–5]. The same problem exists at a large scale (field-scale) associated with mine and cave collapses, landslides, snow avalanches and the onset of earthquakes due to plate movements [6, 7]. In medical science, understanding fracturing of human bones exposed to a sudden stress is an important research area [8]. These phenomena belong to the class of phenomena called stress-induced fracturing, where initially micro-fractures are produced here and there in the system and at some point, due to gradual stress increase, a major fracture develops through coalescence of micro-fractures and the whole system collapses (catastrophic event). Such stress-induced failures occur also in very different domains—for example, in breakdown of social relationships and mental health [9, 10].

The central question is—when does the catastrophic failure occur? Is there any prior signature that can tell us whether catastrophic failure is imminent? The inherent heterogeneities of the systems and the stress redistribution mechanisms (inhomogeneous in most cases) make things complicated and a concrete theory of the prediction schemes, even in model systems, is still lacking.

In this article, we address this problem (prediction of catastrophic events) in the Fiber Bundle Model (FBM) which has been used as a standard model [11–14] for fracturing in composite materials under external stress. We will show theoretically that in the Equal-Load-Sharing (ELS) model: (1) At the catastrophic failure point, the elastic energy is always larger than the damage energy. (2) The elastic energy variation shows a distinct peak before the catastrophic failure point and this is a universal feature, i.e., it does not depend on the threshold distribution of the elements in the system. (3) The energy release during final catastrophic event is much bigger than the elastic energy stored in the system at the failure point. Our numerical results show perfect agreement with the theoretical estimates.

We organize our article as follows: After the brief introduction (section 1), we define the elastic energy and the damage energy in the Fiber Bundle Model in section 2. In sections 3 and 4 we calculate the elastic and damage energies of the model in terms of strain or extension. In several subsections of sections 3 and 4 we explore the theoretical calculations for power-law type and Weibull type distribution of fiber thresholds. Simulation results are presented and numerical results are compared with the theoretical estimates in these sections. We present a general analysis of elastic energy variations and existence of an elastic-energy maximum in section 5. In section 6 we identify the warning sign of catatrophic failure by locating the inflection point. Here, in addition to uniform and Weibull distributions, we choose a mixed threshold distribution and present the numerical results, based on Monte Carlo simulation, to confirm the universality of the behavior in the ELS models. Finally, we keep some discussions in section 7.

2. The Fiber Bundle Model

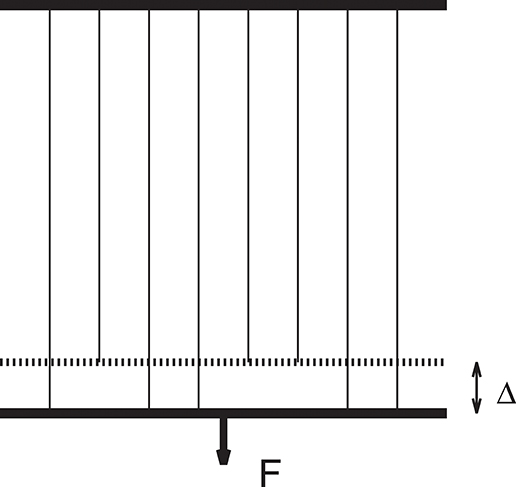
The fiber bundle model consists of N parallel fibers placed between two solid clamps (Figure 1). Each fiber responds linearly with a force f to a stretch or extension Δ,

$\begin{array}{ll}f=\kappa \Delta ,& (1)\end{array}$

where κ is the spring constant. κ is the same for all fibers. Each fiber has a threshold x assigned to it. If the stretch Δ exceeds this threshold, the fiber fails irreversibly. When the clamps are stiff, load will be redistributed equally on the surviving fibers and this is called the equal-load-sharing (ELS) scheme. Throughout this article we work with ELS models only.

FIGURE 1

Figure 1. The fiber bundle model.

The fiber thresholds are drawn from a probability density p(x). The corresponding cumulative probability is:

$\begin{array}{ll}P(x)={\displaystyle {\int }_0^x}d{x}^{\prime }p(x^{\prime }).& (2)\end{array}$

When the fiber bundle is loaded, the fibers fail according to their thresholds, the weaker before the stronger. Suppose that n fibers have failed. At a stretch Δ, the fiber bundle carries a force:

$\begin{array}{ll}F=\kappa (N-n)\Delta =N\kappa (1-d)\Delta ,& (3)\end{array}$

where we have defined the damage:

$\begin{array}{ll}d=\frac{n}{N}.& (4)\end{array}$

When N is large enough, d may be treated as a continuous parameter.

We will now assume that the stretch Δ is our control parameter. We can construct the energy budget according to continuous damage mechanics [1, 15]. Clearly, when we stretch the bundle with external force, work is done on the system. At a stretch Δ and damage d, the elastic energy stored by the surviving fibers is:

$\begin{array}{ll}{E}^e(\Delta ,d)=\frac{N\kappa }{2}{\Delta }^2(1-d).& (5)\end{array}$

The damage energy of the failed fibers is given by:

$\begin{array}{ll}{E}^d(d)=\frac{N\kappa }{2}{\displaystyle {\int }_0^d}d\delta {\left[P^{-1}(\delta )\right]}^2.& (6)\end{array}$

The total energy at stretch Δ and damage d is, then:

$\begin{array}{ll}E(\Delta ,d)=E^e(\Delta ,d)+E^d(d).& (7)\end{array}$

3. Elastic Energy and Damage Energy at the Failure Point

We are going to analyze the energy relations when the bundle is in equilibrium. We know that there is a certain value, Δ = Δ_c, beyond which catastrophic failure occurs and the system collapses completely. We are particularly interested in what happens at the failure point. Is there a universal relation between elastic energy and damage energy at the failure point?

When N is large, we can reframe (Equations 5, 6) and express the energies in terms of external stretch (or extension) Δ as:

$\begin{array}{ll}{E}^e(\Delta )=\frac{N\kappa }{2}{\Delta }^2\left(1-P(\Delta )\right).& (8)\end{array}$

and

$\begin{array}{ll}{E}^d(\Delta )=\frac{N\kappa }{2}{\displaystyle {\int }_0^{\Delta }}dx\left[p(x)x^2\right].& (9)\end{array}$

The force on the bundle at a stretch Δ can be written as:

$\begin{array}{ll}F=\kappa (N-n)\Delta =N\kappa (1-P(\Delta ))\Delta .& (10)\end{array}$

The force must have a maximum at the failure point Δ_c, therefore setting dF(Δ)/dΔ = 0 we get:

$\begin{array}{ll}1-{\Delta }_{c}p({\Delta }_c)-P({\Delta }_c)=0.& (11)\end{array}$

3.1. Uniform Threshold Distribution

We start with the simplest threshold distribution: the uniform distribution, which is well-known in fiber bundle research [14]. For a uniform fiber threshold distribution within the range (0, 1), p(x) = 1 and P(x) = x. Therefore we get, from Equation (11),

$\begin{array}{ll}{\Delta }_c=\frac{1}{2}.& (12)\end{array}$

Now putting Δ_c = 1/2 in Equations (8, 9), we get:

$\begin{array}{ll}{E}^e({\Delta }_c)=\frac{N\kappa }{16},& (13)\end{array}$

and

$\begin{array}{ll}{E}^d({\Delta }_c)=\frac{N\kappa }{2}{\displaystyle {\int }_0^{1/2}}dx\left[x^2\right]=\frac{N\kappa }{48}.& (14)\end{array}$

Therefore, the ratio between damage energy and elastic energy at the failure point (Δ_c) is:

$\begin{array}{ll}\frac{E^d({\Delta }_c)}{E^e({\Delta }_c)}=\frac{1}{3}.& (15)\end{array}$

3.2. Power-Law Type Threshold Distribution

Now we move to a general power law type fiber threshold distributions within the range (0, 1),

$\begin{array}{ll}p(x)=(1+\alpha )x^{\alpha }.& (16)\end{array}$

The cumulative distribution takes the form:

$\begin{array}{ll}P(x)={\displaystyle {\int }_0^x}p(y)dy=x^{1+\alpha }.& (17)\end{array}$

We insert the expressions for p(x) and P(x) into Equation (11) and find the critical extention:

$\begin{array}{ll}{\Delta }_c={\left(\frac{1}{2+\alpha }\right)}^{\frac{1}{1+\alpha }}.& (18)\end{array}$

We can calculate the elastic energy and damage energy at the failure point Δ_c:

$\begin{array}{l}{E}^e({\Delta }_c)=\frac{N\kappa }{2}{\Delta }_c^2(1-P({\Delta }_c))\\ =\frac{N\kappa }{2}{\Delta }_c^2(1-{\Delta }_c^{1+\alpha }),& (19)\end{array}$

and

$\begin{array}{l}{E}^d({\Delta }_c)=\frac{N\kappa }{2}{\displaystyle {\int }_0^{{\Delta }_c}}dx\left[p(x)x^2\right]\\ =\frac{N\kappa }{2}\frac{1+\alpha }{3+\alpha }{\Delta }_c^{3+\alpha }.& (20)\end{array}$

Plugging in the value of Δ_c (Equation 18) into the above equations for elastic energy and damage energy we end up with the following relation:

$\begin{array}{ll}\frac{E^d({\Delta }_c)}{E^e({\Delta }_c)}=\frac{1}{3+\alpha }.& (21)\end{array}$

Clearly, the ratio depends on the power factor α (Figure 2). When α = 0, the threshold distribution reduces to a uniform distribution and we immediately go back to Equation (15).

FIGURE 2

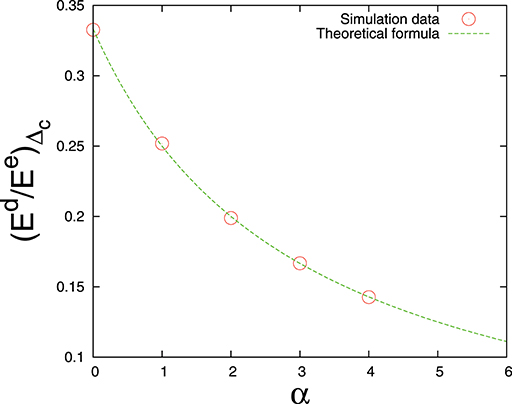
Figure 2. Ratio between damage energy and elastic energy at the failure point Δ_c vs. power law exponent α. Single bundle with N = 10⁷ fibers. Dashed line is the theoretical estimate (Equation 21).

3.3. Energy Balance

It is easy to show that the work done on the system up to the failure point Δ_c is equal to the sum of the energies E^e and E^d. The total work done on the system can be calculated as:

$\begin{array}{ll}W({\Delta }_c)={\displaystyle {\int }_0^{{\Delta }_c}}d\Delta F(\Delta ).& (22)\end{array}$

Inserting the expression for F(Δ) into the integral we get, for a general power law type distribution,

$\begin{array}{ll}W({\Delta }_c)=Nk{\Delta }_c^2\left[\frac{1}{2}-\frac{{\Delta }_c^{1+\alpha }}{3+\alpha }\right],& (23)\end{array}$

which is the total of elastic energy and damage energy, W = E^e + E^d (see Equations 19, 20). In fact, the energy conservation here is analogous to the one in thermodynamics.

3.4. Energy Release During the Final Catastrophic Avalanche

It is known that when the extension exceeds the critical value Δ_c, the whole bundle collapses via a single avalanche called the final or catastrophic avalanche [14]. Can we calculate how much energy will be released in this final avalanche? It must be equal to the total damage energy of the fibers between threshold values Δ_c and the upper cutoff level of the fiber thresholds for the distribution in question.

We calculate the damage energy of the final avalanche for power-law type distributions as

$\begin{array}{l}{E}_{final}^d=\frac{N\kappa }{2}{\displaystyle {\int }_{{\Delta }_c}^1}d\delta \left[p(\delta ){\delta }^2\right]\\ =\frac{N\kappa }{2}\frac{(1+\alpha )}{(3+\alpha )}(1-{\Delta }_c^{3+\alpha }).& (24)\end{array}$

It is important to find out whether the damage energy for the catastrophic avalanche has a universal relation with the elastic or damage energies at the failure point. As already mentioned, the bundle has stable (equilibrium) states up to Δ ≤ Δ_c. Therefore, if we correlate the final avalanche energy with E^e or E^d values at Δ_c, we can predict the catastrophic power of the final avalanche.

Comparing the expressions for $E_{{\Delta }_c}^e$, $E_{{\Delta }_c}^d$ and $E_{final}^d$ we can write the following relation:

$\begin{array}{ll}\frac{E_{final}^d}{E_{{\Delta }_c}^d}=\left[{(2+\alpha )}^{\frac{3+\alpha }{1+\alpha }}-1\right].& (25)\end{array}$

As $E_{{\Delta }_c}^e=(3+\alpha )E_{{\Delta }_c}^d$, we can easily get the other relation:

$\begin{array}{ll}\frac{E_{final}^d}{E_{{\Delta }_c}^e}=\frac{1}{3+\alpha }\left[{(2+\alpha )}^{\frac{3+\alpha }{1+\alpha }}-1\right].& (26)\end{array}$

We can get the last relation (Equation 26) by comparing expressions (Equations 24 and 19) directly. These theoretical estimates are compared with numerical simulation results in Figures 3, 4.

FIGURE 3

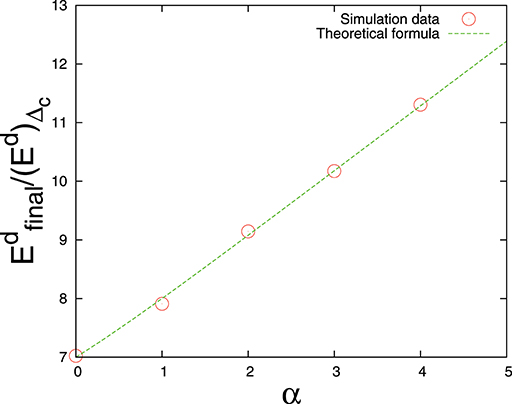
Figure 3. Ratio between damage energy of final catastrophic avalanche and damage energy at the failure point Δ_c vs. power law exponent α. Single bundle with N = 10⁷ fibers. Solid line is the theoretical estimate (Equation 25).

FIGURE 4

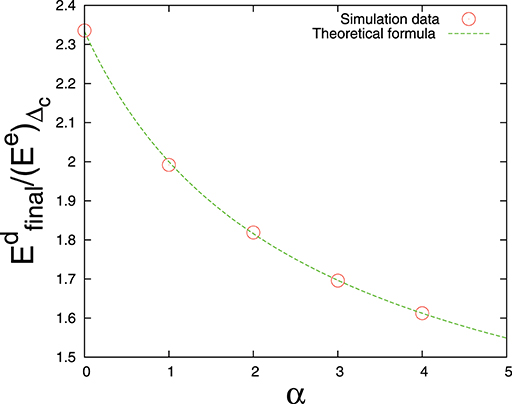
Figure 4. Ratio between damage energy of final catastrophic avalanche and elastic energy at the failure point Δ_c vs. power law exponent α. Single bundle with N = 10⁷ fibers. The dashed line is the theoretical estimate (Equation 26).

Now, if we put α = 0, we get these energy relations for uniform fiber threshold distribution:

$\begin{array}{ll}\frac{E_{final}^d}{E_{{\Delta }_c}^d}=\left[{(2)}^3-1\right]=7.& (27)\end{array}$

And

$\begin{array}{ll}\frac{E_{final}^d}{E_{{\Delta }_c}^e}=\frac{1}{3}\left[{(2)}^3-1\right]=\frac{7}{3}.& (28)\end{array}$

That means the energy release during final catastrophic avalanche is much bigger than the the elastic energy stored in the system just before failure (final stable state when Δ = Δ_c).

It is commonly believed that during catastrophic events like earthquakes, landslides, dam collapses etc., the accumulated elastic energy releases through avalanches [6, 7]. We observe a different scenario in this simple fiber bundle model where the system is doing work during the catastrophic failure phase as the external force is still acting on the bundle. As a result, the energy release (during catastrophic failure event) becomes much bigger than the elastic energy stored at the final stable phase.

4. Energy-Analysis for Weibull Distribution of Thresholds

We now consider the Weibull distribution, which has been used widely in material science [14]. The cumulative Weibull distribution has a form:

$\begin{array}{ll}P(x)=1-exp(-x^k),& (29)\end{array}$

where k is the Weibull index. Therefore the probability density takes the form:

$\begin{array}{ll}p(x)=k{x}^{k-1}exp(-x^k).& (30)\end{array}$

As the force has a maximum at the failure point Δ_c, inserting P(x) and p(x) values in expression (Equation 11) we get:

$\begin{array}{ll}exp(-{\Delta }_c^k)-{\Delta }_{c}k{\Delta }_c^{k-1}exp(-{\Delta }_c^k)=0.& (31)\end{array}$

From the above equation we can easily calculate the critical extension value as:

$\begin{array}{ll}{\Delta }_c=k^{-1/k}.& (32)\end{array}$

The elastic energy at the critical extension Δ_c is:

$\begin{array}{l}{E}^e({\Delta }_c)=\frac{N\kappa }{2}{\Delta }_c^2(1-P({\Delta }_c))\\ =\frac{N\kappa }{2}{\Delta }_c^{2}exp(-{\Delta }_c^k),& (33)\end{array}$

and the damage energy is:

$\begin{array}{l}{E}^d({\Delta }_c)=\frac{N\kappa }{2}{\displaystyle {\int }_0^{{\Delta }_c}}d\delta \left[p(\delta ){\delta }^2\right]\\ =\frac{N\kappa }{2}{\displaystyle {\int }_0^{{\Delta }_c}}d\delta k\left[exp(-{\delta }^k){\delta }^{k+1}\right].& (34)\end{array}$

Putting,

$\begin{array}{ll}{\delta }^k=u,& (35)\end{array}$

we get:

$\begin{array}{ll}{E}^d({\Delta }_c)=\frac{N\kappa }{2}{\displaystyle {\int }_0^{{\Delta }_c^k}}du\left[exp(-u)u^{2/k}\right].& (36)\end{array}$

This integral is exactly calculable for k = 1 and k = 2.

4.1. Weibull Distribution With k = 1

For Weibull index k = 1, Δ_c = 1 and the damage energy expression at the failure point takes the form:

$\begin{array}{ll}{E}^d({\Delta }_c)=\frac{N\kappa }{2}{\displaystyle {\int }_0^1}duexp(-u)u^2.& (37)\end{array}$

Using integration by parts we arrive at the result:

$\begin{array}{ll}{E}^d({\Delta }_c=1)=\frac{N\kappa }{2}(2-5e^{-1}).& (38)\end{array}$

We get the elastic energy at the failure point directly by putting k = 1 in Equation (33),

$\begin{array}{ll}{E}^e({\Delta }_c=1)=\frac{N\kappa }{2e};& (39)\end{array}$

Therefore, the ratio between damage and elastic energies at the failure point for Weibull distribution with k = 1 is:

$\begin{array}{ll}\frac{E^d({\Delta }_c)}{E^e({\Delta }_c)}=2e-5.& (40)\end{array}$

In Figure 5, we have shown numerical results of the variation of elastic and damage energies with strain for Weibull distribution (with k = 1). The theoretical estimates of the ratio between damage and elastic energies at the failure point are compared with numerical results in Figure 6.

FIGURE 5

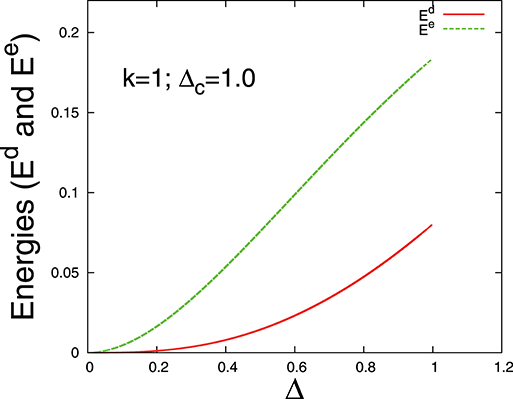
Figure 5. Damage energy and elastic energy vs. extension Δ (up to the failure point Δ_c) for Weibull distribution of thresholds with Weibull index k = 1. The simulation data (solid lines) are for a single bundle with N = 10⁷ fibers.

FIGURE 6

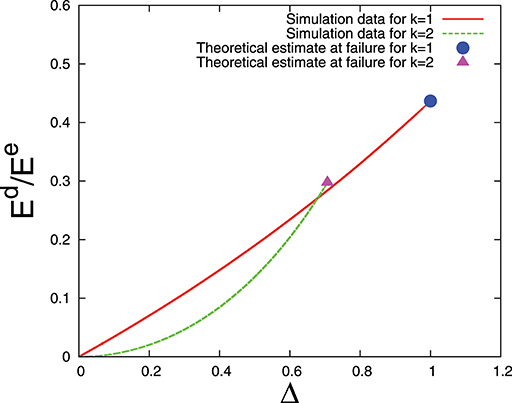
Figure 6. Ratio between damage energy and elastic energy vs. extension Δ (up to the failure point Δ_c) for a fiber bundle with Weibull distribution of thresholds. In simulation, we used a single bundle with N = 10⁷ fibers. Circle and triangle are the theoretical estimates (Equations 40, 44) for the ratios at the failure point Δ_c.

4.2. Weibull Distribution With k = 2

For Weibull index k = 2, ${\Delta }_c=1/\sqrt{2}$ and the damage energy expression at the failure point is:

$\begin{array}{ll}{E}^d({\Delta }_c)=\frac{N\kappa }{2}{\displaystyle {\int }_0^{1/2}}duexp(-u)u.& (41)\end{array}$

Again, using integration by parts we arrive at the result:

$\begin{array}{ll}{E}^d({\Delta }_c=1/\sqrt{2})=\frac{N\kappa }{2}\left(1-\frac{3}{2\sqrt{e}}\right).& (42)\end{array}$

We get the elastic energy at the failure point directly by putting k = 2 in Equation (33):

$\begin{array}{ll}{E}^e({\Delta }_c=1/\sqrt{2})=\frac{N\kappa }{2}\frac{1}{2\sqrt{e}}.& (43)\end{array}$

Therefore, the ratio between damage and elastic energies at the failure point for Weibull distribution with k = 2 is:

$\begin{array}{ll}\frac{E^d({\Delta }_c)}{E^e({\Delta }_c)}=2\left(\sqrt{e}-\frac{3}{2}\right).& (44)\end{array}$

The theoretical estimates of the ratio between damage and elastic energies at the failure point is compared with numerical results in Figure 6. In Appendix A, we give a general argument that elastic energy will be always bigger than damage energy at the critical (failure) point.

5. Elastic Energy Maximum

There are two distinct phases of the system: A stable phase for 0 < Δ ≤ Δ_c and an unstable phase for Δ > Δ_c. If we plot the elastic energy and damage energy vs. Δ, we see that damage energy always increases with Δ but elastic energy has a maximum at a particular value of Δ, let us call it Δ_m. Can we calculate the exact value of Δ_m for a given threshold distribution? Is it somehow connected to Δ_c? In this section we are going to answer these questions.

We recall the elastic energy expression (Equation 8). If we differentiate the elastic energy with respect to the extension Δ, we get:

$\begin{array}{ll}\frac{d{E}^e(\Delta )}{d\Delta }=\frac{N\kappa }{2}\left[2\Delta (1-P(\Delta ))-{\Delta }^{2}p(\Delta )\right],& (45)\end{array}$

Which is 0 at Δ_m, with:

$\begin{array}{ll}{\Delta }_m=\frac{2(1-P({\Delta }_m))}{p({\Delta }_m)}.& (46)\end{array}$

If we consider a general power law type distribution p(x) = (1 + α)x^α, within (0, 1), we can write:

$\begin{array}{ll}{\Delta }_m={\left[\frac{2}{3+\alpha }\right]}^{\frac{1}{1+\alpha }}={\Delta }_c{\left[\frac{2(2+\alpha )}{3+\alpha }\right]}^{\frac{1}{1+\alpha }}>{\Delta }_c.& (47)\end{array}$

For Weibull distribution P(x) = 1−exp(−x^k), we can write:

$\begin{array}{ll}{\Delta }_m={\left[\frac{2}{k}\right]}^{\frac{1}{k}}={\Delta }_c{2}^{\frac{1}{k}}>{\Delta }_c.& (48)\end{array}$

Therefore we can conclude that Δ_m is bigger than Δ_c, i.e., elastic energy shows a maximum in the unstable phase (Figures 7, 8). A more general treatment for the relation between Δ_m and Δ_c is given in the Appendix B.

FIGURE 7

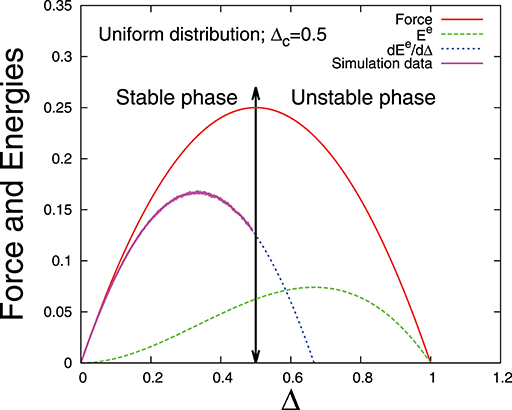
Figure 7. Force and elastic energies vs. extension Δ for fiber bundles with uniform distribution of thresholds: Comparison with simulation data for a single bundle with N = 10⁷ fibers.

FIGURE 8

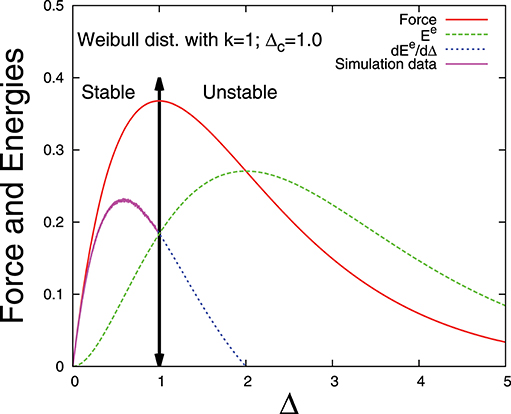
Figure 8. Force and elastic energies vs. extension Δ for fiber bundles with Weibull distribution of thresholds: Comparison with simulation data for a single bundle with N = 10⁷ fibers.

6. Elastic Energy Inflection Point: The Warning Sign of Catastrophic Failure

Are there any prior indications of the catastrophic failure (complete failure) of a bundle under stress? In the fiber bundle model, although the elastic energy has a maximum, it appears after the critical extension value, i.e., in the unstable phase of the system. Therefore it can not help us to predict the catastrophic failure point of the system.

However, if we plot dE^e/dΔ, the change of elastic energy with the change of extension value Δ, we see that dE^e/dΔ has a maximum and, most importantly, this maximum appears before the critical extension value Δ_c (Figures 7, 8). In this section we calculate the particular value of Δ at which dE^e/dΔ has a maximum. Let us call this Δ value Δ_max. We will also see whether there is a relation between Δ_max and Δ_c.

6.1. Theoretical Analysis

We recall the expression for the derivative of elastic energy with respect to strain of extension (Equation 45). Taking derivative of the equation, we get:

$\begin{array}{ll}\frac{d^2{E}^e(\Delta )}{d{\Delta }^2}=\frac{N\kappa }{2}\left[2(1-P(\Delta ))-4\Delta p(\Delta )-{\Delta }^2{p}^{\prime }(\Delta )\right].& (49)\end{array}$

Setting d²E^e(Δ)/dΔ² = 0 at Δ = Δ_max we get for a general power law type distribution:

$\begin{array}{ll}{\Delta }_{max}={\left[\frac{2}{(3+\alpha )(2+\alpha )}\right]}^{\frac{1}{1+\alpha }}={\Delta }_c{\left[\frac{2}{3+\alpha }\right]}^{\frac{1}{1+\alpha }}.& (50)\end{array}$

This expression confirms that Δ_max < Δ_c for α ≥ 0. For a Weibull distribution with index k, we can write:

$\begin{array}{ll}\frac{d^2{E}^e(\Delta )}{d{\Delta }^2}=\frac{N\kappa }{2}\left[k^2{\Delta }^{2k}-(k^2+3k){\Delta }^k+2\right]exp(-{\Delta }^k).& (51)\end{array}$

The solution (of d²E^e(Δ)/dΔ² = 0) with (−) sign is the acceptable solution for the maximum. Hence,

$\begin{array}{l}{\Delta }_{max}={\left[\frac{(k+3)-\sqrt{{(k+3)}^2-8}}{2k}\right]}^{\frac{1}{k}}\\ ={\Delta }_c{\left[\frac{(k+3)-\sqrt{{(k+3)}^2-8}}{2}\right]}^{\frac{1}{k}}\\ <{\Delta }_c,& (52)\end{array}$

since,

$\begin{array}{ll}{\left[\frac{(k+3)-\sqrt{{(k+3)}^2-8}}{2}\right]}^{1/k}<1\forall k>0.& (53)\end{array}$

From Equations (50) and (52) we see that the relation between Δ_max and Δ_c depends on the threshold distributions and we can express Δ_c in terms of Δ_max with a prefactor as:

$\begin{array}{ll}{\Delta }_c=G(\alpha ){\Delta }_{max},& (54)\end{array}$

for power-law type distributions and

$\begin{array}{ll}{\Delta }_c=H(k){\Delta }_{max},& (55)\end{array}$

for Weibull distributions. Now can we find a reasonable approximation for the prefactor that is useful for more than one threshold distributions? An intuitive first choice is the result for the uniform distribution with α = 0 gives Δ_c = 1.5Δ_max. This is a good approximation for α close to 0, as expected, but not for very large α values. This prediction is also exact for a Weibull distribution with k ≃ 2. If k is noticeably smaller, then the prediction 1.5Δ_max is smaller than the true failure point Δ_c. In this case the estimate errs on the side of caution, and the bundle can withstand more than the estimate predicts. A better choice would be to set a prediction-window (1.2 to 1.5) for the prefactor G(α), H(k). Then it can cover a wide range of α and k values (see Figure 9). Overall, such a prediction-window for the failure point works well when the threshold distribution does not vary too much with Δ. If we have prior information about the threshold distribution in the system (i.e., range of k or α values), it is possible to narrow down the prediction window and this is consistent with the common philosophy—extra information helps to develop a better prediction scheme.

FIGURE 9

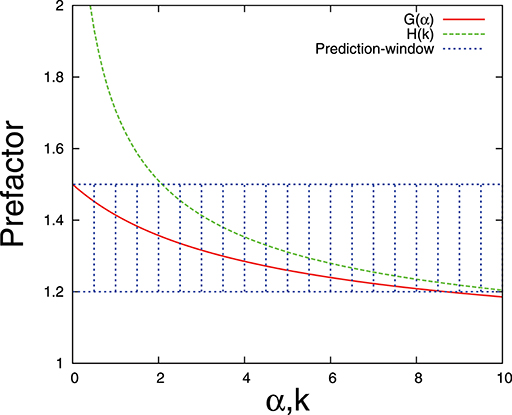
Figure 9. The prefactor (Equations 54, 55) vs. α, k values of the fiber threshold distributions and the suggested prediction-window.

A more general argument is given in Appendix C for the relation between Δ_max and Δ_c.

6.2. Comparison With Simulation Data

In Figures 7, 8 we compare the simulation results with the theoretical estimates. The simulations are done for a single bundle with large number (N = 10⁷) of fibers and the agreement is convincing. We have used Monte Carlo technique to generate uncorrelated fiber thresholds that follow a particular statistical distributions (uniform and Weibull distributions). It is obvious that in simulations we can measure energy values in the stable phase only.

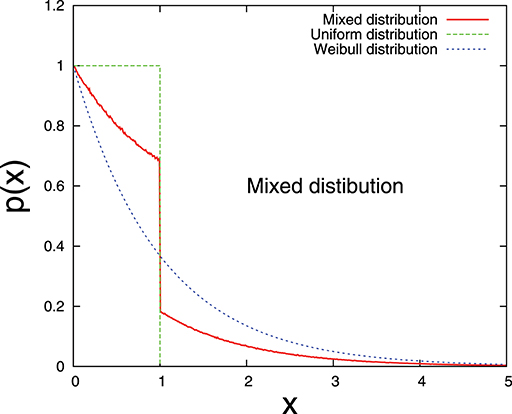
6.3. Simulation Results for a Mixed Threshold Distribution

Now we choose a mixed fiber threshold distribution. Can we see similar signature (maximum of dE^e/dΔ appears before Δ_c) as we have seen in previous section? The chosen distribution is a mixture of uniform distribution and Weibull distribution (k = 1) which is shown in Figure 10. We assign strength thresholds to N/2 fibers from a uniform distribution and to N/2 fibers from a Weibull distribution. The simulation result (Figure 11) reveals that dE^e/dΔ has a maximum which appears before the failure point Δ_c and Δ_max is somewhere in between the respective Δ_max values for uniform and Weibull threshold distributions—as expected intuitively. If we express the Δ_c value in terms of Δ_max, the prefactor is well inside the prediction-window, shown in Figure 9.

FIGURE 10

Figure 10. A mixture of uniform and Weibull (k = 1) distributions.

FIGURE 11

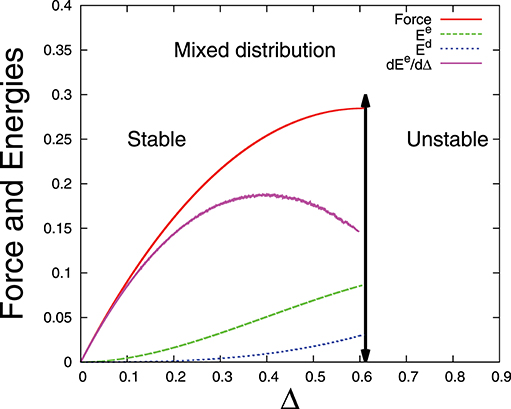
Figure 11. Force and elastic energies vs. extension Δ for a fiber bundle (10⁷ fibers) with a mixed distribution of thresholds.

7. Discussions

The Fiber Bundle Model has been used as a standard model for studying stress-induced fracturing in composite materials. In the Equal-Load-Sharing version of the model, all intact fibers share the load equally. In this work we have chosen the ELS models and we have studied the energy budget of the model for the entire failure process, starting from intact bundle up to the catastrophic failure point where the bundle collapses completely. Following the standard definition of elastic and damage energies from continuous damage mechanics framework, we have calculated the energy relations at the failure points for different types of fiber threshold distributions (power law type and Weibull type). At the critical or catastrophic failure point, the elastic energy is always larger than the total damage energy. Another important observation is that the elastic energy variation has a distinct peak before the catastrophic failure point. Also, the energy-release during final catastrophic event is much bigger than the elastic energy stored in the system at the failure point (see section 3 and section 4). Our simulation results on a single bundle with large numbers (10⁷) of fibers, show perfect agreement with the theoretical estimates. We have chosen a single bundle, keeping in mind that for prediction purposes it is important and necessary that the warning sign can be seen in a single sample.

These observations can form the basis of a prediction scheme by finding the correlation between the position (strain or stretch level) of elastic energy variation peak and the actual failure point. The main concern is to find a direct relation between the elastic energy inflection point (Δ_max) and the failure point (Δ_c). We found that Δ_c and Δ_max are related through a prefactor that depends on the exponent of the threshold distribution. Then we tried to find a window of the prefactor (Equations 54 and 55) that can cover a wide range of threshold distributions (Figure 9) so that we can express the failure point in terms of energy inflection point, i.e., Δ_c = prefactor · Δ_max and the approximate prefactor window is 1.2 to 1.5 (Figure 9). Moreover, it is also possible to predict the size (energy release) of the final catastrophic event by measuring the stored elastic energy of the system at the failure point.

Our observations in this work have already opened up some scientific questions and challenges: what happens for Local-Load-Sharing (LLS) models [16]? Does the elastic energy variation show similar peaks before the catastrophic failure point? Can we measure and analyze the elastic energy during a rock-fracturing test in terms of the applied strain?

During rock-fracturing experiments [17–20], one can measure axial stress (force), axial and radial strain directly through strain gauges. Amount of damage can be recorded via acoustic emissions (AE) in terms of number of events (micro cracks) and the energy of the events. Clearly, total acoustic energy is the amount of damage energy in the system. It is possible to calculate the amount of work done on the system from applied force and effective strain value. Therefore, the difference between total work done and the damage energy (accumulated acoustic energy) will be the elastic energy of the system. Once we plot the elastic energy vs. strain curve, it is straight forward to estimate the elastic energy growth rate by measuring the slope of the curve at different strain points.

Our next article will resolve some of these issues –we are now working on energy budget of LLS models.

Data Availability

The datasets generated in this study are available on request to the corresponding author.

Author Contributions

SP: theory, simulation, data analysis, and plotting. JK: theory (Appendix part). AH: theory. Equal contributions in discussions and writing the article.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was partly supported by the Research Council of Norway through its Centers of Excellence funding scheme, project number 262644.

References

1. Krajcinovic D. Damage mechanics. Amsterdam: Elsevier (1996).

Google Scholar

2. Henkel M, Hinrichsen H, Lubeck S, Pleimling M. Non-equilibrium Phase Transitions vol. 1. Berlin: Springer (2008).

Google Scholar

3. Bonamy D, Bouchaud E. Failure of heterogeneous materials: a dynamic phase transition? Phys Rep. (2011) 498:1–44. doi: 10.1016/j.physrep.2010.07.006

CrossRef Full Text | Google Scholar

4. Abaimov SG. Statistical Physics of Non-thermal Phase Transitions. Heidelberg: Springer Verlag (2015).

Google Scholar

5. Berthier E. Quasi-brittle failure of heterogeneous materials: damage statistics and localization (Thesis). Université Pierre et Marie Curie, Paris, France (2015).

Google Scholar

6. Chakrabarti BK, Benguigui LG. Statistical Physics of Fracture and Breakdown in Disordered Solids. Oxford: Oxford University Press (1997).

Google Scholar

7. Biswas S, Ray P, Chakrabarti BK. Statistical Physics of Fracture, Breakdown, and Earthquake. Berlin: Wiley-VCH (2015).

Google Scholar

8. Villa P, Mahieu E. Breakage patterns of human long bones. J Hum Evol. (1991) 21:27–48.

Google Scholar

9. Etzion D. Moderating effect of social support on the stress-burnout relationship. J App Psych. (1984) 69:615–22.

PubMed Abstract | Google Scholar

10. Ramirez AJ, Graham J, Richards MA, Cull A, Gregory WM. Mental health of hospital consultants: the effect of stress and satisfaction at work. Lancet (1996) 347:724–28.

Google Scholar

11. Peirce FT. Tensile tests for cottom yarns. “The weakest link" theorems on the strength of long and composite specimens. J Text Ind. (1926) 17:355.

Google Scholar

12. Daniels HE. The statistical theory of the strength of bundles of threads. Proc Roy Soc Ser A. (1945) 183:243.

Google Scholar

13. Pradhan S, Hansen A, Chakrabarti BK. Failure processes in elastic fiber bundles. Rev Mod Phys. (2010) 82:499. doi: 10.1103/RevModPhys.82.499

CrossRef Full Text | Google Scholar

14. Hansen A, Hemmer PC, Pradhan S. The fiber bundle model: Modeling Failure in Materials. Berlin: Wiley-VCH (2015).

Google Scholar

15. Pradhan S, Hansen A, Ray P. A renormalization group procedure for fiber bundle models. Front Phys. (2018) 6:65. doi: 10.3389/fphy.2018.00065

CrossRef Full Text | Google Scholar

16. Harlow DG, Phoenix SL. Approximations for the strength distribution and size effects in an idealized lattice model of material breakdown. J Mech Phys Sol. (1991) 39:173–200.

Google Scholar

17. Pradhan S, Stroisz A, Fjar E, Stenebraten J, Lund H, Sonstebo E. Stress-induced fracturing of reservoir rocks: acoustic monitoring and mCT image analysis. Rock Mech Rock Eng. (2015) 48:2529–40. doi: 10.1007/s00603-015-0853-4

CrossRef Full Text | Google Scholar

18. Baud P, Meredith PG. Damage accumulation during triaxial creep of darley dale sandstone from pore volumetry and acoustic emission. Int J Rock Mech Min Sci. (1997) 34:3–4.

Google Scholar

19. Holcomb DJ, Stone CM Costin LS. Combining Acoustic Emission Locations and Microcrack Damage Model to Study Development of Damage in Brittle Materials. Rotterdam: Rock Mechanics Contributions and Challaenges, Hustrulid and Johnson (1990).

Google Scholar

20. Amitrano D. Rupture by damage accumulation in rocks. Int J Fract. (2006) 139:369–81. doi: 10.1007/s10704-006-0053-z

CrossRef Full Text | Google Scholar

Appendix

As stated in section 2, the elastic energy in the system at extension Δ is:

$\begin{array}{ll}{E}^e(\Delta )=\frac{N\kappa }{2}{\Delta }^2(1-P(\Delta )),& (56)\end{array}$

where P(Δ) is the cumulative probability distribution of the fiber thresholds. The force per fiber σ = F/N required to continue the breaking process at a given extension Δ is:

$\begin{array}{ll}\sigma (\Delta )=\kappa \Delta (1-P(\Delta ))& (57)\end{array}$

The critical extension Δ_c where the bundle collapses is hence given by:

$\begin{array}{ll}0={\frac{d\sigma }{d\Delta }|}_{{\Delta }_c}=\kappa (1-P({\Delta }_c)-{\Delta }_{c}p({\Delta }_c)).& (58)\end{array}$

A. Elastic vs. Damage Energy at the Critical Point

Numerical data seems to suggest that E^e > E^d at the critical point for most threshold distributions. Let us try to prove this analytically by investigating the difference between elastic and damage energy:

$\begin{array}{l}{E}_{diff}(\Delta )=E^e(\Delta )-E^d(\Delta )\\ =\frac{N\kappa }{2}\left[{\Delta }^2(1-P(\Delta ))-{\displaystyle {\int }_0^{\Delta }}dx{x}^{2}p(x)\right].& (59)\end{array}$

The derivative of this energy difference is:

$\begin{array}{l}\frac{d{E}_{diff}}{d\Delta }=\frac{N\kappa }{2}\left[2\Delta (1-P(\Delta ))-{\Delta }^{2}p(\Delta )-{\Delta }^{2}p(\Delta )\right]\\ =N\kappa \Delta \left[1-P(\Delta )-\Delta p(\Delta )\right]& (60)\\ =N\Delta \frac{d\sigma }{d\Delta }.\end{array}$

We can now express the energy difference in terms of the forces acting on the fiber bundle. We integrate this expression to find:

$\begin{array}{l}{E}_{diff}(\Delta )={\displaystyle {\int }_0^{\Delta }}dx\frac{d{E}_{diff}}{dx}=N{\displaystyle {\int }_0^{\Delta }}dxx\frac{d\sigma }{dx}\\ =N\left[\Delta \sigma (\Delta )-{\displaystyle {\int }_0^{\Delta }}dx\sigma (x)\right]& (61)\end{array}$

by partial integration. In particular, this gives the result:

$\begin{array}{ll}{E}_{diff}({\Delta }_c)=N\left[{\Delta }_c{\sigma }_c-{\displaystyle {\int }_0^{{\Delta }_c}}dx\sigma (x)\right]& (62)\end{array}$

at the critical point. Since σ_c = max σ(Δ), we see that E_diff(Δ_c) > 0 for all threshold distributions. The only exception possible is a threshold distribution with a constant force σ(Δ) = σ_c. But this results in a lower cut-off Δ₀ = Δ_c > 0 (for the threshold distribution to be normalizable), and then $E^e({\Delta }_c)>E^d({\Delta }_c)=0$.

B. Elastic Energy Maximum Point

First, rewrite (Equation 3) as:

$\begin{array}{ll}1=g({\Delta }_c)\equiv \frac{1-P({\Delta }_c)}{{\Delta }_{c}p({\Delta }_c)}.& (63)\end{array}$

This definition of g(Δ) will be useful in the following derivations. The maximum of the elastic energy is found at an extension Δ_m, which is given by:

$\begin{array}{ll}0={\frac{d{E}^e}{d\Delta }|}_{{\Delta }_m}\propto 2{\Delta }_m(1-P({\Delta }_m))-{\Delta }_m^{2}p({\Delta }_m),& (64)\end{array}$

i.e.,

$\begin{array}{ll}\frac{1}{2}=\frac{1-P({\Delta }_m)}{{\Delta }_{m}p({\Delta }_m)}=g({\Delta }_m).& (65)\end{array}$

Comparing this expression to Equation (8) allows us to find a relation between Δ_c and Δ_m. We investigate the function g(Δ):

$\begin{array}{l}g(\Delta )=\frac{1-P(\Delta )}{\Delta p(\Delta )}=\frac{1-P(\Delta )}{1-P(\Delta )-\frac{d\sigma }{d\Delta }}\\ =\{\begin{array}{l}<1\text{for}\frac{\text{d}\sigma }{\text{d}\Delta }<0\\ >1\text{for}\frac{\text{d}\sigma }{\text{d}\Delta }>0\end{array}.& (66)\end{array}$

It is clear from Equation (12) that for a threshold distribution with only a single maximum in the load curve, g(Δ_m) = 1/2 must occur in the unstable phase, i.e., Δ_m > Δ_c.

C. Elastic Energy Inflection Point

The elastic energy maximum occurs after the critical point and is hence unsuitable as a predictor for failure. But what about the maximum of the derivative of the elastic energy, the inflection point Δ_max? As stated in the section 6:

$\begin{array}{ll}\frac{d^2{E}^e}{d{\Delta }^2}\propto 2(1-P(\Delta ))-4\Delta p(\Delta )-{\Delta }^2{p}^{\prime }(\Delta ).& (67)\end{array}$

Setting this second derivative to zero and rearranging terms gives the equation:

$\begin{array}{ll}2(1-P({\Delta }_{max}))-4{\Delta }_{max}p({\Delta }_{max})={\Delta }_{max}^2{p}^{\prime }({\Delta }_{max}).& (68)\end{array}$

To investigate the relation between Δ_max and Δ_c, we combine this with the relations dσ/dΔ = 1 − P(Δ) − Δp(Δ) and d²σ/dΔ² = − 2p(Δ) − Δp′(Δ) evaluated at Δ_max to get:

$\begin{array}{ll}{\frac{d\sigma }{d\Delta }|}_{{\Delta }_{max}}=-\frac{{\Delta }_{max}}{2}{\frac{d^2\sigma }{d{\Delta }^2}|}_{{\Delta }_{max}}.& (69)\end{array}$

Let's once again assume that we are working with a threshold distribution that has only a single maximum in its load curve. Then dσ/dΔ > 0 corresponds to the stable phase and dσ/dΔ <0 corresponds to the unstable phase. We see that any threshold distribution with d²σ/dΔ² < − 2/Δ · dσ/dΔ everywhere in the unstable phase must have Δ_max in the stable phase, i.e., Δ_max < Δ_c.

This is a general (but weak) condition that is sufficient, but not necessary, for Δ_max < Δ_c.