Kinematic Collisionless Relaxation of Ions in Supercritical Shocks

Gedalin, Michael

doi:10.3389/fphy.2019.00114

ORIGINAL RESEARCH article

Front. Phys., 14 August 2019

Sec. Space Physics

Volume 7 - 2019 | https://doi.org/10.3389/fphy.2019.00114

This article is part of the Research Topic Collisionless Shock Research: Current State and Perspectives View all 4 articles

Kinematic Collisionless Relaxation of Ions in Supercritical Shocks

$\nMichael Gedalin$ Michael Gedalin^*

Department of Physics, Ben Gurion University of the Negev, Beer-Sheva, Israel

We show that kinematic collisionless relaxation in the macroscopic electric and magnetic fields plays the main role in the formation of the downstream ion distributions in a super-critical shock with ion reflection present. It is done by comparison of a theoretically predicted magnetic profile with the magnetic profile of a shocks observed by MMS mission. It is shown that pressure balance remains the main constraint for the shock stability.

1. Introduction

Collisionless shocks are one of the most fundamental phenomena in plasmas and one of the most efficient accelerators of charged particles in the visible Universe. The large variety processes, leading to the energy redistribution by a shock, occurs at a larger variety of the spatial scales. Yet, the outcome of all these processes depends crucially on the narrow shock transition where the incident upstream flow brakes down. The only place where the structure of this transitions can be explored via in situ measurements is the heliosphere. At least a part of the heliosphere is accessible to a fleet of scientific spacecraft, the sizes of which are much smaller than the transition width to allow local measurements of the magnetic and electric fields and particle distributions as well. In the heliospheric conditions all known shocks are magnetized, that is, magnetic field plays the decisive role in the shock formation and properties. The magnetic field jump serves at the major signature of the shock front. Despite vast improvement of the quality of particle and electric field measurements, the magnetic field measurements remain by far the best by precision and resolution. It is therefore natural that in most cases magnetic observations not only are used to describe the shock structure but also for comparison of theory and observations, even if the theoretically predicted magnetic profile is a result of particle dynamics.

In an ideal MHD a shock is a discontinuity [1]. Real shock have finite width. Dissipative MHD predicts that the shock width is determined by the corresponding dissipative coefficients [2–4]. Up to the critical Mach number, depending on the shock angle and upstream pressure, a shock can be maintained by resistivity or resistivity with thermal conductivity in the so-called subcritical regime. Super-critical dissipative MHD shocks require viscosity [4]. Subcritical shocks are expected to have a monotonically increasing magnetic profile, while super-critical shocks rely on ion reflection and become non-monotonic. In the post-MHD two-fluid theory shocks possess dispersive profiles with upstream oscillations ahead of the main magnetic field jump (ramp) [5]. Yet, dissipation is needed to have these oscillations damp farther from the shock. Downstream oscillations of the magnetic field also require dissipation which is inserted by hand in all theses approaches.

Real observed shocks, even subcritical ones, rarely have monotonic profiles [6–13]. Moreover, the shock width is smaller than the upstream ion convective gyroradius, so that the ion behavior inside the transition region is essentially kinetic and hydrodynamics is no longer a useful approach since the equation of motion is not known a priori. For a long while it was believed that overshoots of the downstream magnetic field are signatures of super-criticality, that is, of ion reflection [14–17], and are produced by reflected ions [10, 12, 14, 18–21]. Observations of a very low-Mach number subcritical shock with an overshoot followed by a trail of coherent magnetic oscillations, spatially periodic at the ion dynamical scale [22], have shown that ion motion in the macroscopic electric and magnetic fields of the shock front plays the main role in the formation of the magnetic profile. Similar oscillations have been observed at many other shocks [23, 24]. It appeared that ions begin to gyrate coherently upon crossing the shock front, which causes spatially periodic oscillations of ion pressure downstream. In a steady shock the sum of the magnetic pressure and plasma pressure should be constant throughout the shock, which means that oscillations of ion pressure would cause oscillations of the magnetic field in the opposite phase. The pressure oscillations gradually damp out because of the gyrophase mixing and gyrotropization of the downstream ion distribution. The whole process, named kinematic collisionless relaxation, was shown theoretically [22, 25–27], numerically [25, 28], and observationally [29, 30] to be responsible for the downstream magnetic field profiles of low-Mach number shocks. It was used theoretically to predict the shapes of observed shocks with unprecedented precision [30]. Until recently, it was believed that the kinematic collisionless relaxation cannot be observed in super-critical shocks, even if it plays there a significant role (which was also casted a doubt upon). Yet, there are no differences between sub- and super-critical shocks from the point of view of equations of motion for ions. Therefore, it is unreasonable to expect that the major effect suddenly disappears upon crossing a borderline. The objective of the present paper is to check whether main features of a super-critical shock with substantial ion reflection can be explained by kinematic collisionless relaxation. In this approach we choose an observed quasi-perpendicular shock with high resolution measurements of the magnetic field and clear presence of a reflected ion population. We identify the features of magnetic profile which we expect to be related to ion gyration. We perform an advanced test particle analysis (ATPA) [31] in a simple model shock front with a limited number of basic parameters similar to those of the observed shock: the shock angle θ_Bn, the magnetic compression B_d/B_u, and the upstream kinetic-to-magnetic pressure ratios β_i and β_e. ATPA allows to determine the magnetic field profile which would be consistent with the ion distributions formed in this shock. Comparison of the features of the ATPA predicted magnetic profile with the observed one will show what can be attributed to the mechanism of the kinematic collisionless relaxation. The model fields are taken one-dimensional and stationary so that waves and time-dependence of the profile are not included. If a major feature/mechanism is missing in the analysis then comparison of the derived magnetic field with the observed one will fail, that is, they will be essentially different.

2. The Observed Shock

We have chosen an intetplanetary super-critical shock observed by MMS on 2018-01-08 [32]. All spacecraft observed the same transition so that one can conclude that the shock was reasonably planar and steady. In what follows we shall use the magnetic profile measured by MMS-3. The shock crossing occurred at 06:41:11 UT. The shock profile is plotted over the ion spectrogram is shown in Figure 1.

FIGURE 1

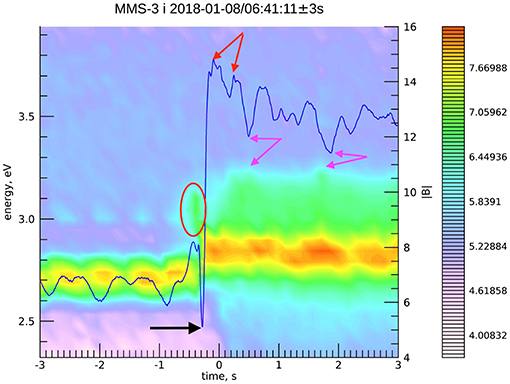
Figure 1. Quasi-perpendicular shock crossing by MMS-3 at 2018-01-08/06:41:11. The magnetic profile is shown in the background of the ion spectrogram (log of energy).

Reflected ions are clearly seen in the spectrogram. In the downstream part pressure oscillations can be also seen which anti-correlate with the magnetic field. The shock is a quite typical supercritical quasi-perpendicular shock with B_d/B_u ≈ 2. The shock angle is estimated as $θ_{B n} \approx 7 0^{∙}$ , while the ion kinetic-to-magnetic pressure ratio is β_i ≈ 0.35. The forthcoming analysis will also use β_e ≈ 1.2. These parameters are taken from Table 1 in [32] where the ion temperature is inferred from Wind measurements.

We identify the following features which we may be possibly related to ion dynamics in the macroscopic fields of the shock front: (a) the reflected ions ahead of the ramp (shown by the orange oval), (b) the overshoot behind the ramp which is the strongest magnetic peak and the decreasing subsequent peaks (red arrows), and (c) the magnetic depression just ahead of the ramp (black arrow). The magenta arrows show the positions where the anti-correlation of the ion distribution and the magnetic field can be seen by eye. The magnetic oscillations do not exhibit clean spatial periodicity and monotonic damping as in laminar shocks [22, 30].

3. The Analysis

We perform advanced test particle analysis of the shock. Namely, we start with a model shock profile in the form

\begin{array}{l} B_{z} = B_{u} sin θ_{B n} [1 + \frac{R - 1}{2} (1 + tanh \frac{3 x}{D})] & (1) \end{array}

with B_x = B_ucosθ_Bn, B_y∝dB_z/dx, and E_x∝dB_z/dx, and $R = \sqrt{{(B_{d} / B_{u})}^{2} - {cos}^{2} θ_{B n}} / sin θ_{B n}$ . The coefficients of proportionality for B_y and E_x are constrained by the chosen values of the normal incidence frame cross-shock potential s_NIF and the de Hoffman-Teller potential s_HT [21, 33, 34]. Initially Maxwellian distributed (in the upstream plasma frame) ions with $v_{T} = \sqrt{β_{i} / 2} / M$ were traced in the model fields. Here M is the Alfvenic Mach number. Ion motion was found to be not sensitive to the latter which was kept s_HT = 0.1 in the subsequent analysis. The magnetic field is further derived from the condition

\begin{array}{l} p_{e} + p_{i, x x} + \frac{B^{2}}{8 π} = const & (2) \end{array}

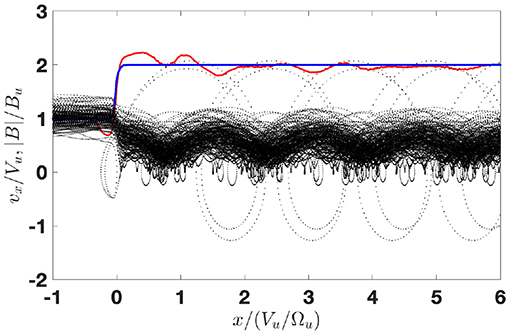
where the ion pressure was determined numerically from the numerically found ion distribution and for the electron pressure the polytropic equation of state $p_{e} / n^{5 / 3}$ was used, together with the quasineutrality. The derived magnetic field is the one which is predicted by the theory. The parameters M, s_NIF, and D were varied for adjustment until the asymptotic predicted field be equal to the model downstream value. Figure 2 shows the initial model magnetic field (blue line) and the predicted magnetic field magnitude obtained from (2) (red line). The parameters of this run are: the Alfvenic Mach number M = 2.8, the cross-shock potential s_NIF = 0.55, and the ramp width D = 0.4(c/ω_pi), where c/ω_pi is the ion inertial length. Variation of the parameters within 5% of these values gave similar results. This set is chosen as a representative one. We note that for the chosen angle and β the corresponding fast magnetosonic Mach number is M_f ≈ 1.83 which is rather close to the value M_g ≈ 1.9 estimated by Cohen et al. [32]. The coordinate is normalized on the upstream ion convective gyroradius r_g = V_u/Ω_u, where V_u is the upstream plasma speed in NIF and Ω_u = eB_u/m_ic is the upstream gyrofrequency. The magnetic field is normalized on B_u. The basic features of the magnetic field, as identified above, are clearly caught by the calculation: there is a clear overshoot with subsequently decreasing oscillations of the magnetic field at the downstream side of the profile and a magnetic dip just ahead of the ramp. Figure 3 shows orbits of 1% of ions randomly chosen from the initial Maxwellian. The velocities are normalized on V_u. The reflected ions are clearly seen as well as the competing contributions of the directly transmitted and reflected ions into downstream ion pressure and the resulting effect of the magnetic field. Figure 4 shows the ion distribution in the v_x − v_y plane accumulated in the spatial region of the width of 0.5(V_u/Ω_u) just upstream of the middle of the ramp. The reflected ions are clearly seen as a distinct population. The maximum density of reflected ions is about 10% of the upstream density and is achieved at the magnetic depression as was predicted earlier [31] and can be seen in Figure 1.

FIGURE 2

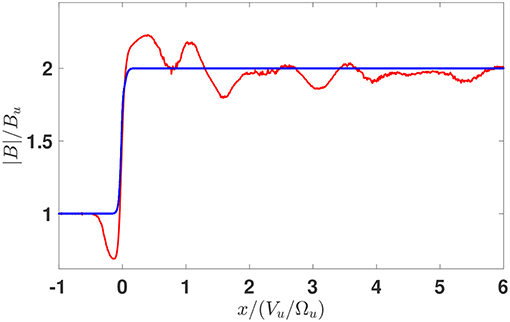
Figure 2. The model magnetic field (blue) and the predicted magnetic field (red). The adjusted parameters are: M = 2.8, s_NIF = 0.55, and D = 0.4(c/ω_pi).

FIGURE 3

Figure 3. Ion orbits represented as x vs. v_x, with the magnetic profile on the background.

FIGURE 4

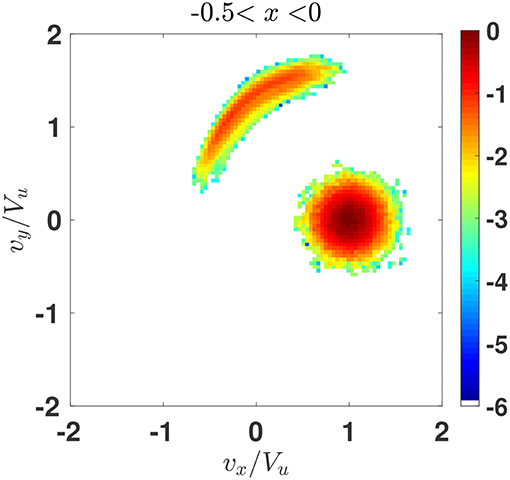
Figure 4. Ion distribution projected on the plane v_x − v_y, accumulated in the spatial region of the width of 0.5r_g toward upstream from the middle of the ramp.

4. Discussion and Conclusions

Obviously, ATPA cannot reproduce exactly the observed shock profile. Supercritical shocks are not exactly planar and time-independent and ion dynamics should be affected by deviations from planarity and time-dependent fields. Moreover, even if the shock were exactly one-dimensional and stationary, the measurements are not precise and the shock parameters are known only approximately. In addition, our knowledge of the detailed shape of the fields inside the shock is far from being complete. Therefore, it does not make sense to try to exactly fit the predicted profile to the observed one, and this certainly was not the objective. However, it is reasonable to check what major features of the magnetic profile can be explained by theory. By comparing theoretical predictions with an observed interplanetary super-critical shock we have shown that the overshoot with subsequent damping oscillations, even not spatially periodic, as well as the magnetic dip just ahead of the ramp, appear naturally due to the gyration of the directly transmitted and reflected ions in the macroscopic fields of the shock front. The role of time-dependent fields and/or non-planarity is secondary: they may affect the amplitude of the oscillations, the peak-to-peak distance, and the damping rate (gyrotropization) but only mildly. The very existence of the above mentioned features is due to the kinematic collisionless relaxation. At this stage we do not have quantitative predictions of the overshoot amplitude or spatial parameters. This will require additional study as well as the issue of the increasing importance of the time-dependent features with the increase of the Mach number.

Data Availability

The MMS data was retrieved and processed using the SPEDAS software [35].

Author Contributions

The whole study and writing is done by MG.

Funding

This study was supported in part by the Israel Science Foundation (Grant No. 368/14).

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. de Hoffmann F, Teller E. Magneto-hydrodynamic shocks. Phys Rev. (1950) 80:692–703. doi: 10.1103/PhysRev.80.692