Non-locality in Granular Flow: Phenomenology and Modeling Approaches

This paper reviews the emergence of non-local flow phenomena in granular materials and discusses a range of models that have been proposed to integrate an intrinsic length-scale into granular rheology. The frameworks discussed include micro-polar modeling, kinetic theory, three particular order-parameter-based models, and strongly non-local integral-based models. An extensive commentary is included discussing the current capabilities of these existing models as well as their implementational ease, physical motivation, and breadth of predictive ability.

1. Introduction

Let us define a local rheology as a constitutive model whose well-developed strain-rate response depends only on the stress and no higher-gradients of kinematic quantities or stress. Such models include relations between the stress tensor and the tensors of strain and/or strain-rate and state variables evolving locally within each material element. In granular flow modeling, local models can provide qualitative and sometimes quantitative predictions for flows and stresses [1–13]. However, it is now widely accepted that such models lack robustness in their ability to predict all flow phenomena and, in many cases, predictions of local models disagree with experiments by nontrivial amounts [14–19]. This is true even though such models predict uniform flows well, such as steady simple shearing. It is the fact that these models succeed in homogeneous cases but break down in the presence of spatial inhomogeneity that the origin of this difference can be attributed to a non-local effect. In such models, a microscopic length-scale emerges on dimensional grounds. In the case of granular media, it is evident that the mean grain size d provides this microscopic length unit, and the observed length-scale of non-local effects should be some multiple of d.

2. Commonly Observed Manifestations of Non-locality in Granular Flows

There are a few particular manifestations of non-locality in granular flow that bear mentioning as canonical examples. All of these effects are evident in systems of the simplest grains—round, stiff, frictional particles, with a restitution coefficient.

First, there is the class of problems wherein the size of shear features is influenced by the grain size, not just the size scale of stress gradients.

• In geometries with wall-located shear bands at steady state, such as flow in an annular couette cell, the shear stress decays gradually toward zero as one moves away from the rapid zone near the inner wall. Therefore, any local concept of a yield stress would predict that the velocity field should vanish in some extended domain outside the main shear band. However, slow, creeping flow is seen throughout the entire geometry. The velocity field has an exponential-type decay moving away from the rapid flow zone, with decay length governed by the grain size [20–23].

• A similar phenomena is observed in steady flow geometries where the zone of flow is not concentrated near walls, such as silo flows [24–27], split-bottom couette flows [16, 28], or sub-surface flows in heaps/rotating-drums [19, 29]. In these cases, despite the fact that there are spatial zones where the stress varies below what a local model may predict to be the yield stress, non-zero flow is observed everywhere. In triaxial compression of a highly packed column of grains, an unsteady flow case, a shear-band of grain-size-dependent width emerges within the sample to mitigate the boundary displacement [30, 31].

Another non-local effect is connected to the reverse problem—rather than material flowing even though the stress seems too small, there are cases where material does not flow even though the stress appears to be above the yield limit. In these cases, non-locality makes thinner domains act stronger. There are two common examples of this effect.

• In silos, hoppers, and hourglasses, it is common experience that the nozzle arch-jams when the opening size is on the order of a few d [26, 32–34]. The critical opening size plays a key role in models that predict silo outflow rates such as the seminal Beverloo correlation [33]. However, local continuum models cannot capture this effect. Nozzle jamming requires an intrinsic length-scale in order to give a critical opening size.

• In flows down rough inclined surfaces, classical understanding gives an angle of repose characteristic of the material; material flows until the tilt is reduced below this angle. However, as layers get thinner it is observed that the repose angle is not constant; it is thickness dependent with thinner layers acting stronger [14, 35, 36]. This effect is often described inversely through the function H_stop(θ)/d, which maps tilt angles to the critical thickness H_stop at which such a flow would arrest.

The third non-local effect we discuss is the “secondary rheology,” where flow somewhere causes the rest of the domain to lose its yield stress. This more recently studied non-local effect can be seen in tests where a constant-force probe is placed in approximately rigid subdomains of a flowing collection of grains. For example:

• A heavy ball that is placed on the surface of a cup of grains will sit on the free surface after some mild sinkage [37, 38]. However, if any part of the cup's boundary is moved—such as by replacing the bottom of the cup with a rotating turn-table—the ball will sink even though the material near it is otherwise quiescent. This is true even if the free surface of the grains is far from the moving bottom boundary of the container. The notion that perturbations from a boundary cause rheological changes away has been observed as well in suspensions of fine particles [39].

• In annular shear of a granular media, the material far from the rotating wall appears to be still. However, if a probe is placed in this part of the domain and a constant force applied to it, it is observed to move through the material even as the force on the probe shrinks to zero [18]. When the rotation of the inner wall stops, the same probe only moves if the force on it exceeds a critical value; i.e., the yield stress is “restored” once the far-away boundary stops moving.

3. Non-local Modeling Approaches

Below is a non-exhaustive summary of non-local granular flow models with a brief description of the model assumptions and how the length-scale is introduced. The discussion is limited to models that address (at least) steady-state flow behavior.

3.1. Cosserat Continuum

One of the most straightforward and oldest ways to introduce a size-scale is to presume the continuum is a “micropolar” or “Cosserat” continuum [40–43]. In such models it is assumed that a body posseses not just a stress field σ and velocity field v but also a couple-stress field M and intrinsic spin field ω (see Figure 1). Like a standard continuum, on any internal surface with outward normal n the force per area (traction) on the surface is given by σn. However, Cosserat material elements are presumed to also have a non-vanishing torque-per-area given by Mn. As a result, while standard continua satisfy torque balance as long as one imposes σ = σ^T, a Cosserat continuum requires an additional, non-trivial differential equation for angular momentum balance invoking the divergence of the tensor M, possible asymmetry in σ, and the rate-of-change of ω. It is understood that ω represents the spin of the individual microscopic components of the media, which can differ from the vorticity, ∇ × v, which measures the spin of a collection of those components as seen from following their center-of-mass velocities. An intrinsic length-scale arises in such models when imposing a constitutive relation, in our case a yield criterion—since the couple-stress and stress differ by a unit of length, a yield criterion mixing these two fields requires a length-scale [44].

FIGURE 1

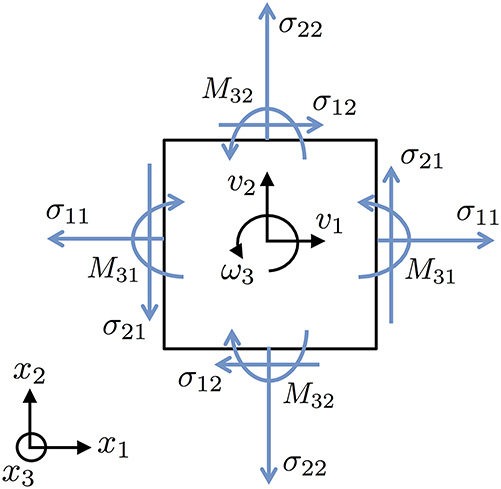
Figure 1. Primary fields in a Cosserat continuum (in-plane components shown). Note that σ₂₁ may differ from σ₁₂, ω may differ from ∇ × v, and the couple stress tensor components M_ij admit surface moment down to the continuum scale.

The motivation to connect Cosserat continuum assumptions to granular media stems from the clear possibility that the microscopic components are the grains themselves, and that their individual spins give rise to ω. Thus, the needed length-scale is some multiple of the grain size d. One might visualize a “rolling resistance” mechanism, where couple-stress per d governs the onset of rolling, which blends with sliding to produce a joint yield condition.

3.2. Kinetic Theory

The kinetic theory of gases has a well-known extension to the case of granular media, which ultimately brings a dependence on granular temperature (given microscopically by particle velocity fluctuations) into the granular constitutive relations [45–49]. While it may at first seem odd to describe a thermal flow model as non-local, note that it passes our definition from the introduction—by letting the rheology depend on the temperature field, the length-scale controlling the spread in temperature, a multiple of d, can now influence the flow field.

Unlike an ideal gas, granular media lose energy every collision. Thus, energy balance can be expressed via

$\frac{\rho }{2}Ṫ=2\eta {\dot{ϵ}}_{ij}{\dot{ϵ}}_{ij}+\frac{\partial }{\partial x_j}K\frac{\partial T}{\partial x_j}-\Gamma$

where, up to prefactors involving packing fraction and restitution, the viscosity η and conductivity K are $~d\sqrt{T}$, and the dissipation rate Γ is $~\frac{1}{d}{T}^{3/2}$. At steady state the temperature field finds a distribution whereby the thermal energy generated by the work term (the first on the right side) is diffused by the conduction term (second on the right side), and reduced by the dissipation term (last term). Therefore, thanks to the non-vanishing conductivity K, non-locality emerges through a self-heating process; work done deforming a material element somewhere produces heat that spreads to material nearby and changes its rheology (see Figure 2). As will be seen in the upcoming sections, this notion that fluctuations spread into neighboring material and alter the flow rule is important in a variety of non-local theories.

FIGURE 2

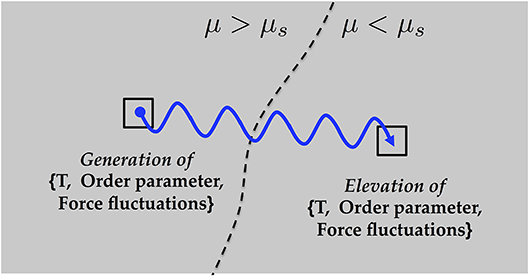
Figure 2. The basic “self-heating” picture common to many recent non-local models [50–53]. Zones whose stress ratio μ are beneath the local friction coefficient μ_s can be made to flow in inhomogeneous stress environments by diffusive passage of a state field (e.g., temperature, order-parameter, force-fluctuations) sourced in higher stress media nearby, which spreads over some grain-size dependent correlation length. The influx elevates the value of the state field in the low-stress media, which reduces its flow resistance and allows flow to occur. The newly “heated” material then “heats” neighboring material triggering a cascade that causes all material to flow.

3.3. Order Parameter Models

Some models append a scalar order parameter to the system of equations, which indicates how “fluid-like” the material is. The idea to use an order parameter is connected to the notion that the transition from solid to flowing is a type of phase change. The order-parameter is presumed to obey a diffusion-like equation and its value affects the rheology, thereby imbuing a length-scale into the flow. While these features are similar to kinetic theory, different order-parameter models differ on what precise variable is diffusing and what its diffusion equation looks like.

3.3.1. Partial Fluidization Theory

One of the first granular models of this type was the partial fluidization theory of Aranson and Tsimring [50, 54] and Volfson et al. [55]. Their order parameter, ρ, varies from 1 (solid) to 0 (fluid). In its common usage, the material's viscosity is presumed to obey η_f/(1 − ρ) so that the viscosity diverges as the material becomes solid and reverts to a (constant) fluid-like viscosity η_f when ρ goes to zero. The order parameter is assumed to participate in a free-energy functional $F~\int \frac{l}{2}|\nabla \rho {|}^2+f(\rho ,\sigma )dV$ and its evolution is obtained assuming purely dissipative dynamics, $\dot{\rho }=\delta F/\delta \rho$. The evolution equation that emerges looks like a basic diffusion equation but with a source term given by the choice of f. Their suggested choice of f gives the final result:

$\begin{array}{ll}\tau \frac{D\rho }{Dt}=l^2{\nabla }^2\rho +\rho (1-\rho )(\rho -\delta )& (1)\end{array}$

where δ ≡ (μ − μ_d)/(μ_s − μ_d). The constants μ_s and μ_d represent static and dynamic friction coefficients, respectively, and μ is the ratio of local shear stress to pressure. The cubic nature of the source term causes stability switches that give rise to frictional hysteresis. By setting l ~ d, the equation forces an inherent grain-size dependent length-scale into the model's flow predictions, and causes flow stability to be size-sensitive, giving rise to size-dependent flow start/stoppage.

3.3.2. Non-local Granular Fluidity

The Non-local Granular Fluidity (NGF) model is a more recent approach, developed by the author and coworkers (primarily Henann and Koval) [51, 56, 57]. Inspired by a similar model for emulsions [58, 59], the NGF model presumes a scalar-valued order-parameter-like field called the granular fluidity, g, whose value ranges from zero to infinity. Whereas, the fluidity in the emulsion flow model operates as an inverse-viscosity-like field in their flow rule, the granular fluidity g enters the flow rule through $\dot{\gamma }=g\mu$ and hence may be interpreted as a pressure-weighted inverse viscosity field. The fluidity field, in steady flow, is then posited to obey

$\begin{array}{ll}g=g_{loc}(\mu ,P)+{\xi }^2{\nabla }^{2}g,\text{where }\xi =A\frac{d}{\sqrt{|\mu -{\mu }_s|}}.& (2)\end{array}$

The diverging of the correlation length, ξ, where μ = μ_s has been shown directly in simulations [51, 56] and experiments [23], with A an order-one material constant. The function g_loc is what the fluidity would be if the rheology were local. The local rheology, obtained in uniform simple shearing, is the μ(I) rheology [1], where the stress ratio μ = τ/P is given by the normalized shear rate $I=\dot{\gamma }\sqrt{d^2{\rho }_s/P}$. The fluidity at a point is then viewed as having a contribution from local effects (g_loc) and a non-local contribution due to “disturbances” from neighboring material (ξ²∇²g). Out of the many choices of “flow variable”/“load variable” one could choose for the role of fluidity, $g=\dot{\gamma }/\mu$ was initially selected for practical reasons as it was the only one that produced quantitative flow predictions for a range of data from several different flow geometries [51, 56]. This choice gained additional support when it was shown that g has a clear kinematic meaning as a function of particle velocity fluctuations and packing fraction; other possible fluidity definitions do not [52]. This suggests the fluidity field measures the degree of fluctuation-based activation in the material. Parameter studies indicate the NGF model is robust to material changes—varying particle properties such as surface friction affects the parameters, including A, but the model itself maintains its accuracy [60]. The model has been extended into a transient form that evolves g over time, which can be used to model the smaller-is-stronger effect as an instability process [57, 61]. The more primitive transient form can be justified thermomechanically under the virtual power principle with g as an energetic order parameter [61].

3.3.3. I-gradient Model

Shortly after the NGF model, an alternative model for steady-state non-local flow was proposed in Bouzid et al. [62, 63]. The proposed form is a more direct non-local expansion of the μ(I) rheology:

$\begin{array}{ll}\mu =\mu (I)(1-\nu {\nabla }^{2}I/I).& (3)\end{array}$

The above does not propose an independent order parameter with its own equation, but rather treats I itself as a fluidity-type field within a gradient expansion of the flow rule. If an İ term were added to account for unsteady cases (like in [64]), the model would claim direct diffusion of the I field. For constant ν ~ d², the form above has the primary feature that effective friction μ is reduced when neighboring material is flowing faster, and increased when neighboring material flows slower. In doing so, the model can, by design, replicate the effect of creeping flow beneath the local yield criterion, μ_s, as well as rate independence of the non-local response due to the scaling of ∇²I by 1/I. Like NGF, the model replicates the effect of a diverging length-scale about μ_s.

3.4. Integral Equation Approaches

While the previous models produce non-locality by letting a rheological variable obey an additional PDE, non-locality can also be achieved through an integral equation, which describes the flow response at a point in terms of influences coming from surrounding material finite distances away. In simplified 1D, these “strongly non-local” models generally take the form

$\begin{array}{ll}\dot{\gamma }(x)={\displaystyle {\int }_H}F(\dot{\gamma }(x^{\prime }),\sigma (x^{\prime }),x^{\prime },\dot{\gamma }(x),\sigma (x),x)\frac{1}{d}\text{d}{x}^{\prime }& (4)\end{array}$

where H can be the entire domain, or be limited to a horizon a finite distance away. It is well known that one can Taylor expand in x′ under the integral and integrate through to obtain an approximate model in the form of a PDE.

One model of the strongly non-local type is the self-activation model of Pouliquen and Forterre [53], in which the function F is selected to represent the product of the frequency of fluctuations emitted from position x′ and the probability that a fluctuation from x′ will result in a forward vs. backward shear event at x. Another strongly non-local model is the recent model of Nott [65], in which the integral is a weighted spatial convolution of what the local flow-rate formula would give in the surrounding media. A strongly non-local eddy-viscosity-type model has also been written [66], in which the shear-rate has a contribution from redistribution of vorticity occurring through the geometry. The corresponding PDE approximation of this model takes a form similar to an order-parameter model [66, 67].

4. Commentary

All models discussed could be evaluated based on three criteria: (i) ease of implementation, (ii) physical motivation, and (iii) breadth of predictive capability. Below, we summarize where each model stands, and conversely where models need further understanding.

On issue (i), clearly, PDE's are simpler to solve than integral equations. Kinetic theory, partial fluidization, and NGF propose one additional PDE involving one new state variable. These can be solved numerically using the finite-element method (see for example, the implementation in [68]) and sometimes analytically in unidirectional flow cases [44, 54, 57, 62, 69]. Based on its mathematical form, it is not clear what the difficulty of numerical integration of the I−gradient model would be in arbitrary cases. However, the fact that it requires no new state variables and is a straightforward extension of μ(I) is a plus. Another issue is that of (Hadamard) well-posedness, which determines if small wavelength flow perturbations grow unboundedly in the linear regime, an issue known to arise for basic local models [70, 71]. Hadamard unstable models may lack existence of a solution, and/or have grid-size dependent or unstable numerical solutions. It is known that gradient corrections have the potential to resolve the ill-posedness [72]. It has been directly shown that NGF and certain strongly non-local models [65] are Hadamard well-posed, while the I−gradient model has been proven Hadamard ill-posed [73].

On issue (ii), kinetic theory and Cosserat continua have a strong microscopic basis, with their additional PDE's representing energy balance and moment balance, respectively. The physics of the boundary conditions are, hence, fairly clear in these models. While derived for dilute systems, the kinetic theory has gone through a number of recent enhancements to bring it closer to representing dense media [74, 75]. With Cosserat theory, to this author's knowledge, stress asymmetry, couple stresses, and spin-differences are notably small in tests of simple particles excluding cases of non-negligible rolling resistance or directly wall-adjacent behavior [15, 76, 77]. The partial fluidization and NGF models have each identified (post-facto) kinematic observables that match the behavior of their hypothesized order parameter, i.e., static contact fraction for partial fluidization [55], and weighted velocity fluctuations for NGF [52]. The full physical meaning of these models' phenomenological PDE's is not understood, and selection of boundary conditions can be unclear. That said, NGF has been shown to follow a virtual power principle, which aids in boundary condition selection [61]. The I-gradient model does not require a new state variable, though it is also conceivable, in cases of high ∇²I, that the model produces negative μ values, violating non-negative dissipation. Strongly non-local models have the benefit of absolving the question of boundary conditions [65]. Moreover, the strongly non-local self-activation model is obtained entirely from statistical and mechanical propositions at the small scale.

On issue (iii), the extent to which the different models have been tested varies quite a bit. NGF, with its own dedicated numerical solver [68], has been validated in the most geometries and conditions [78]. The NGF and the I−gradient models have each shown quantitative agreement with non-local creep in multiple 2D experiments [23, 51, 62], capturing proper flow spreading and the emergence of rate-independence. NGF also produces quantitative predictions in 3D cases such as flows in split-bottom cells [56] and wall-bounded heap flows [79]. It also captures smaller-is-stronger phenomenology in multiple geometries including H_stop [57, 69], as well as all features of secondary rheology [80] including the effect's direction sensitivity [81]. Partial fluidization captures these different phenomena to a qualitative level [50], and additionally is equipped to model stick-slip and start-stop differences due to the inclusion of hysteresis (although our understanding of the form for frictional hysteresis is evolving [82]). The strongly non-local self-activation model has matched an experimental H_stop curve and produces reasonable non-local flow-spreading [53]. Cosserat and kinetic theories produce non-local flow spreading as well [44, 83], and certain kinetic theories can also produce an H_stop effect [84]. It is not clear if these predictions are quantitative across many geometries. Similarly, the strongly non-local plasticity model of Nott [65] possesses qualitative elements of non-local flow spreading.

In closing, to those interested in new model development, it should be emphasized that the universe of non-local models is not unconstrained. The reader is directed to Gurtin et al. [85] and Maugin [42] for a review of the constraints of thermodynamic consistency and existing modeling formalisms.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author graciously acknowledges useful discussions with Prof. David L. Henann of Brown University. The author acknowledges grant CBET-1253228 CAREER for multiple years of support on this research topic.

References

1. da Cruz F, Emam S, Prochnow M, Roux JN, Chevoir F. Rheophysics of dense granular materials: discrete simulation of plane shear flows. Phys Rev E. (2005) 72:021309. doi: 10.1103/PhysRevE.72.021309

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Jop P, Forterre Y, Pouliquen O. A constitutive law for dense granular flows. Nature. (2006) 441:727. doi: 10.1038/nature04801

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Staron L, Lagrée PY, Popinet S. Continuum simulation of the discharge of the granular silo. Eur Phys J E. (2014) 37:5. doi: 10.1140/epje/i2014-14005-6

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Kamrin K. Nonlinear elasto-plastic model for dense granular flow. Int J Plastic. (2010) 26:167–88. doi: 10.1016/j.ijplas.2009.06.007

CrossRef Full Text | Google Scholar

5. Dunatunga S, Kamrin K. Continuum modeling of projectile impact and penetration in dry granular media. J Mech Phys Solids. (2017) 100:45–60. doi: 10.1016/j.jmps.2016.12.002

CrossRef Full Text | Google Scholar

6. Schofield A, Wroth C. Critical State Soil Mechanics. London: McGraw-Hill (1968).

Google Scholar

7. Anand L, Gu C. Granular materials: constitutive equations and strain localization. J Mech Phys Solids. (2000) 28:1701. doi: 10.1016/S0022-5096(99)00066-6

CrossRef Full Text | Google Scholar

8. Lagrée PY, Staron L, Popinet S. The granular column collapse as a continuum: validity of a two-dimensional Navier–Stokes model with a μ (I)-rheology. J Fluid Mechan. (2011) 686:378–408. doi: 10.1017/jfm.2011.335

CrossRef Full Text | Google Scholar

9. Forterre Y. Kapiza waves as a test for three-dimensional granular flow rheology. J Fluid Mechan. (2006) 563:123–32. doi: 10.1017/S0022112006001509

CrossRef Full Text | Google Scholar

10. Dunatunga S, Kamrin K. Continuum modelling and simulation of granular flows through their many phases. J Fluid Mechan. (2015) 779:483–513. doi: 10.1017/jfm.2015.383

CrossRef Full Text | Google Scholar

11. Nemat-Nasser S, Zhang J. Constitutive relations for cohesionless frictional granular materials. Int J Plastic. (2002) 18:531–47. doi: 10.1016/S0749-6419(01)00008-0

CrossRef Full Text | Google Scholar

12. Gao Z, Zhao J. Strain localization and fabric evolution in sand. Int J Solids Struct. (2013) 50:3634–48. doi: 10.1016/j.ijsolstr.2013.07.005

CrossRef Full Text | Google Scholar

13. Sun J, Sundaresan S. A constitutive model with microstructure evolution for flow of rate-independent granular materials. J Fluid Mechan. (2011) 682:590–616. doi: 10.1017/jfm.2011.251

CrossRef Full Text | Google Scholar

14. Pouliquen O. Scaling laws in granular flows down rough inclined planes. Phys Fluids. (1999) 11:542. doi: 10.1063/1.869928

CrossRef Full Text | Google Scholar

15. Koval G, Roux JN, Corfdir A, Chevoir F. Annular shear of cohesionless granular materials: from the inertial to quasistatic regime. Phys Rev E. (2009) 79:021306. doi: 10.1103/PhysRevE.79.021306

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Fenistein D, van Hecke M. Wide shear zones in granular bulk flow. Nature. (2003) 425:256. doi: 10.1038/425256a

PubMed Abstract | CrossRef Full Text | Google Scholar

17. MiDi G. On dense granular flows. Eur Phys J E. (2004) 14:341–65. doi: 10.1140/epje/i2003-10153-0

CrossRef Full Text | Google Scholar

18. Reddy K, Forterre Y, Pouliquen O. Evidence of mechanically activated processes in slow granular flows. Phy Rev Lett. (2011) 106:108301. doi: 10.1103/PhysRevLett.106.108301

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Komatsu TS, Inagaki S, Nakagawa N, Nasuno S. Creep motion in a granular pile exhibiting steady surface flow. Phys Rev Lett. (2001) 86:1757. doi: 10.1103/PhysRevLett.86.1757

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Mueth DM. Measurements of particle dynamics in slow, dense granular Couette flow. Phys Rev E. (2003) 67:011304. doi: 10.1103/PhysRevE.67.011304

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Bocquet L, Losert W, Schalk D, Lubensky T, Gollub J. Granular shear flow dynamics and forces: experiment and continuum theory. Phys Rev E. (2001) 65:011307. doi: 10.1103/PhysRevE.65.011307

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Chambon G, Schmittbuhl J, Corfdir A, Vilotte JP, Roux S. Shear with comminution of a granular material: microscopic deformations outside the shear band. Phys Rev E. (2003) 68:011304. doi: 10.1103/PhysRevE.68.011304

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Tang Z, Brzinski TA, Shearer M, Daniels KE. Nonlocal rheology of dense granular flow in annular shear experiments. Soft Matter. (2018) 14:3040–8. doi: 10.1039/C8SM00047F

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Mullins J. Experimental evidence for the stochastic theory of particle flow under gravity. Powder Technol. (1974) 9:29–37. doi: 10.1016/0032-5910(74)80006-9

CrossRef Full Text | Google Scholar

25. Nedderman R, Tüzün U. A kinematic model for the flow of granular materials. Powder Technol. (1979) 22:243–53. doi: 10.1016/0032-5910(79)80030-3

CrossRef Full Text | Google Scholar

26. Choi J, Kudrolli A, Bazant MZ. Velocity profile of gravity-driven dense granular flow. J Phys Condens Matter. (2005) 17:S2533–48. doi: 10.1088/0953-8984/17/24/011

CrossRef Full Text | Google Scholar

27. Rycroft CH, Grest GS, Landry JW, Bazant MZ. Analysis of granular flow in a pebble-bed nuclear reactor. Phys Rev E. (2006) 74:021306. doi: 10.1103/PhysRevE.74.021306

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Depken M, van Saarloos W, van Hecke M. Continuum approach to wide shear zones in quasistatic granular matter. Phys Rev E. (2006) 73:031302. doi: 10.1103/PhysRevE.73.031302

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Bonamy D, Daviaud F, Laurent L. Experimental study of granular surface flows via a fast camera: a continuous description. Phys Fluids. (2002) 14:1666–73. doi: 10.1063/1.1459720

CrossRef Full Text | Google Scholar

30. Han C, Drescher A. Shear bands in biaxial tests on dry coarse sand. Soils Foundat. (1993) 33:118–32. doi: 10.3208/sandf1972.33.118

CrossRef Full Text | Google Scholar

31. Gu X, Huang M, Qian J. Discrete element modeling of shear band in granular materials. Theor Appl Fracture Mechan. (2014) 72:37–49. doi: 10.1016/j.tafmec.2014.06.008

CrossRef Full Text | Google Scholar

32. Zuriguel I, Parisi DR, Hidalgo RC, Lozano C, Janda A, Gago PA, et al. Clogging transition of many-particle systems flowing through bottlenecks. Sci Rep. (2014) 4:7324. doi: 10.1038/srep07324

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Beverloo WA, Leniger HA, de Velde JV. The flow of granular solids through orifices. Chem Eng Sci. (1961) 15:260–9. doi: 10.1016/0009-2509(61)85030-6

CrossRef Full Text | Google Scholar

34. Sheldon HG, Durian DJ. Granular discharge and clogging for tilted hoppers. Granular Matter. (2010) 12:579–85. doi: 10.1007/s10035-010-0198-3

CrossRef Full Text | Google Scholar

35. Silbert LE, Ertaş D, Grest GS, Halsey TC, Levine D, Plimpton SJ. Granular flow down an inclined plane: Bagnold scaling and rheology. Phys Rev E. (2001) 64:051302. doi: 10.1103/PhysRevE.64.051302

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Silbert LE, Landry JW, Grest GS. Granular flow down a rough inclined plane: transition between thin and thick piles. Phys Fluids. (2003) 15:1–10. doi: 10.1063/1.1521719

CrossRef Full Text | Google Scholar

37. Nichol K, Zanin A, Bastien R, Wandersman E, van Hecke M. Flow-induced agitations create a granular fluid. Phys Rev Lett. (2010) 104:078302. doi: 10.1103/PhysRevLett.104.078302

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Wandersman E, Van Hecke M. Nonlocal granular rheology: role of pressure and anisotropy. EPL. (2014) 105:24002. doi: 10.1209/0295-5075/105/24002

CrossRef Full Text | Google Scholar

39. Lin NY, Ness C, Cates ME, Sun J, Cohen I. Tunable shear thickening in suspensions. Proc Natl Acad Sci USA. (2016) 113:10774–8. doi: 10.1073/pnas.1608348113

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Cosserat E, Cosserat F. Deformable Bodies. Scientific Library a Hermann and Sons (1909).

Google Scholar

41. Eringen AC. Theory of micropolar fluids. J Mathemat Mechan. (1966) 16:1–18. doi: 10.1512/iumj.1967.16.16001

CrossRef Full Text | Google Scholar

42. Maugin GA. Non-Classical Continuum Mechanics. Singapore: Springer (2017).

Google Scholar

43. De Borst R. Simulation of strain localization: a reappraisal of the Cosserat continuum. Eng Comput. (1991) 8:317–32. doi: 10.1108/eb023842

CrossRef Full Text | Google Scholar

44. Mohan LS, Rao KK, Nott PR. A frictional Cosserat model for the slow shearing of granular materials. J Fluid Mechan. (2002) 457:377–409. doi: 10.1017/S0022112002007796

CrossRef Full Text | Google Scholar

45. Haff P. Grain flow as a fluid-mechanical phenomenon. J Fluid Mechan. (1983) 134:401–30. doi: 10.1017/S0022112083003419

CrossRef Full Text | Google Scholar

46. Jenkins JT, Savage SB. A theory for the rapid flow of identical, smooth, nearly elastic particles. J Fluid Mech. (1983) 130:187–202. doi: 10.1017/S0022112083001044

CrossRef Full Text | Google Scholar

47. Lun C, Savage S, Jeffrey D, Chepurniy N. Kinetic theories for granular flow: inelastic particles in Couette flow and slightly inelastic particles in a general flowfield. J Fluid Mech. (1984) 140:223–56. doi: 10.1017/S0022112084000586

CrossRef Full Text | Google Scholar

48. Garzó V, Dufty J. Dense fluid transport for inelastic hard spheres. Phys Rev E. (1999) 59(5 Pt B):5895–911. doi: 10.1103/PhysRevE.59.5895

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Brilliantov NV, Pöschel T. Kinetic Theory of Granular Gases. Oxford: Oxford University Press (2010).

Google Scholar

50. Aranson IS, Tsimring LS. Continuum description of avalanches in granular media. Phys Rev E. (2001) 64:020301. doi: 10.1103/PhysRevE.64.020301

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Kamrin K, Koval G. Nonlocal constitutive relation for steady granular flow. Phys Rev Lett. (2012) 108:178301. doi: 10.1103/PhysRevLett.108.178301

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Zhang Q, Kamrin K. Microscopic description of the granular fluidity field in nonlocal flow modeling. Phys Rev Lett. (2017) 118:058001. doi: 10.1103/PhysRevLett.118.058001

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Pouliquen O, Forterre Y. A non-local rheology for dense granular flows. Philos Trans R Soc Lond A. (2009) 367:5091–107. doi: 10.1098/rsta.2009.0171

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Aranson IS, Tsimring LS. Continuum theory of partially fluidized granular flows. Phys Rev E. (2002) 65:061303. doi: 10.1103/PhysRevE.65.061303

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Volfson D, Tsimring LS, Aranson IS. Order parameter description of stationary partially fluidized shear granular flows. Phys Rev Lett. (2003) 90:254301. doi: 10.1103/PhysRevLett.90.254301

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Henann DL, Kamrin K. A predictive, size-dependent continuum model for dense granular flows. Proc Natl Acad Sci USA. (2013) 110:6730–5. doi: 10.1073/pnas.1219153110

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Kamrin K, Henann DL. Nonlocal modeling of granular flows down inclines. Soft Matter. (2015) 11:179–85. doi: 10.1039/C4SM01838A

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Goyon J, Colin A, Ovarlez G, Ajdari A, Bocquet L. Spatial cooperativity in soft glassy flows. Nature. (2008) 454:84–7. doi: 10.1038/nature07026

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Bocquet L, Colin A, Ajdari A. Kinetic theory of plastic flow in soft glassy materials. Phys Rev Lett. (2009) 103:036001. doi: 10.1103/PhysRevLett.103.036001

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Kamrin K, Koval G. Effect of particle surface friction on nonlocal constitutive behavior of flowing granular media. Comp Part Mech. (2014) 1:169–76. doi: 10.1007/s40571-014-0018-3

CrossRef Full Text | Google Scholar

61. Henann DL, Kamrin K. Continuum thermomechanics of the nonlocal granular rheology. Int J Plastic. (2014) 60:145–62. doi: 10.1016/j.ijplas.2014.05.002

CrossRef Full Text | Google Scholar

62. Bouzid M, Trulsson M, Claudin P, Clément E, Andreotti B. Nonlocal rheology of granular flows across yield conditions. Phys Rev Lett. (2013) 111:238301. doi: 10.1103/PhysRevLett.111.238301

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Bouzid M, Izzet A, Trulsson M, Clément E, Claudin P, Andreotti B. Non-local rheology in dense granular flows. Eur Phys J E. (2015) 38:1–15. doi: 10.1140/epje/i2015-15125-1

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Lee Kl, Yang FL. Relaxation-type nonlocal inertial-number rheology for dry granular flows. Phys Rev E. (2017) 96:062909. doi: 10.1103/PhysRevE.96.062909

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Nott PR. A non-local plasticity theory for slow granular flows. In: EPJ Web of Conferences. Vol. 140. Montpellier: EDP Sciences (2017). p. 11015.

Google Scholar

66. Kharel P, Rognon P. Partial jamming and non-locality in dense granular flows. In: EPJ Web of Conferences. Vol. 140. Montpellier: EDP Sciences (2017). p. 03060.

Google Scholar

67. Rognon PG, Miller T, Metzger B, Einav I. Long-range wall perturbations in dense granular flows. J Fluid Mech. (2015) 764:171–92. doi: 10.1017/jfm.2014.707

CrossRef Full Text | Google Scholar

68. Henann DL, Kamrin K. A finite element implementation of the nonlocal granular rheology. Int J Numer Meth Engng. (2016) 108:273–302. doi: 10.1002/nme.5213

CrossRef Full Text | Google Scholar

69. Liu D, Henann DL. Size-dependence of the flow threshold in dense granular materials. Soft Matter. (2018) 14:5294–305. doi: 10.1039/C8SM00843D

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Schaeffer DG. Instability in the evolution equations describing incompressible granular flow. J Different Equat. (1987) 66:19–50. doi: 10.1016/0022-0396(87)90038-6

CrossRef Full Text | Google Scholar

71. Barker T, Schaeffer DG, Bohórquez P, Gray J. Well-posed and ill-posed behaviour of the μ(I)-rheology for granular flow. J Fluid Mech. (2015) 779:794–818. doi: 10.1017/jfm.2015.412

CrossRef Full Text | Google Scholar

72. Goddard J, Lee J. On the stability of the μ (I) rheology for granular flow. J Fluid Mech. (2017) 833:302–31. doi: 10.1017/jfm.2017.651

CrossRef Full Text | Google Scholar

73. Li S, Henann DL. Material stability and instability in non-local continuum models for dense granular materials. J Fluid Mech. (2019) 871:799–830. doi: 10.1017/jfm.2019.311

CrossRef Full Text | Google Scholar

74. Jenkins JT, Berzi D. Dense inclined flows of inelastic spheres: tests of an extension of kinetic theory. Granular Matter. (2010) 12:151–8. doi: 10.1007/s10035-010-0169-8

CrossRef Full Text | Google Scholar

75. Berzi D. Extended kinetic theory applied to dense, granular, simple shear flows. Acta Mech. (2014) 225:2191–8. doi: 10.1007/s00707-014-1125-1

CrossRef Full Text | Google Scholar

76. Campbell CS. Boundary interactions for two-dimensional granular flows. Part 1. Flat boundaries, asymmetric stresses and couple stresses. J Fluid Mech. (1993) 247:111–36. doi: 10.1017/S0022112093000400

CrossRef Full Text | Google Scholar

77. Luding S. From DEM simulations towards a continuum theory of granular matter. Powders Grains. (2001) 1:141–148.

Google Scholar

78. Kamrin K. Quantitative rheological model for granular materials: the importance of particle size. In: Andreoni W, Yip S, editors. Handbook of Materials Modeling: Applications: Current and Emerging Materials. Cham: Springer (2018). p. 1–24.

Google Scholar

79. Liu D, Henann DL. Non-local continuum modelling of steady, dense granular heap flows. J Fluid Mech. (2017) 831:212–27. doi: 10.1017/jfm.2017.554

CrossRef Full Text | Google Scholar

80. Henann DL, Kamrin K. Continuum modeling of secondary rheology in dense granular materials. Phys Rev Lett. (2014) 113:178001. doi: 10.1103/PhysRevLett.113.178001

PubMed Abstract | CrossRef Full Text | Google Scholar

81. Henann D, Liu D, Kamrin K. Continuum modeling of secondary rheology in slow granular flows. Bull Am Phys Soc. (2019) 60.

Google Scholar

82. DeGiuli E, Wyart M. Friction law and hysteresis in granular materials. Proc Natl Acad Sci USA. (2017) 114:9284–9. doi: 10.1073/pnas.1706105114

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Berzi D, Jenkins JT. Dense, inhomogeneous shearing flows of spheres. In: EPJ Web of Conferences. vol. 140. Montpellier: EDP Sciences (2017). p. 11006.

Google Scholar

84. Kumaran V. Dense granular flow down an inclined plane: from kinetic theory to granular dynamics. J Fluid Mech. (2008) 599:121–68. doi: 10.1017/S002211200700002X

CrossRef Full Text | Google Scholar

85. Gurtin ME, Fried E, Anand L. The Mechanics and Thermodynamics of Continua. Cambridge: Cambridge University Press (2010).

Google Scholar