- 1Department of Mathematics and Physics, Roma Tre University, Rome, Italy
- 2BCAM–Basque Center for Applied Mathematics, Bilbao, Spain
- 3ISTI-CNR, Institute of Information Science and Technologies “A. Faedo”, Pisa, Italy
- 4Ikerbasque–Basque Foundation for Science, Bilbao, Spain
Normal or Brownian diffusion is historically identified by the linear growth in time of the variance and by a Gaussian shape of the displacement distribution. Processes departing from the at least one of the above conditions defines anomalous diffusion, thus a nonlinear growth in time of the variance and/or a non-Gaussian displacement distribution. Motivated by the idea that anomalous diffusion emerges from standard diffusion when it occurs in a complex medium, we discuss a number of anomalous diffusion models for strongly heterogeneous systems. These models are based on Gaussian processes and characterized by a population of scales, population that takes into account the medium heterogeneity. In particular, we discuss diffusion processes whose probability density function solves space- and time-fractional diffusion equations through a proper population of time-scales or a proper population of length-scales. The considered modeling approaches are: the continuous time random walk, the generalized gray Brownian motion, and the time-subordinated process. The results show that the same fractional diffusion follows from different populations when different Gaussian processes are considered. The different populations have the common feature of a large spreading in the scale values, related to power-law decay in the distribution of population itself. This suggests the key role of medium properties, embodied in the population of scales, in the determination of the proper stochastic process underlying the given heterogeneous medium.
1. Introduction
Normal diffusion has been widely investigated by means of different modeling approaches, such as:
conservation of mass, constitutive laws, random walks based on central limit theorem (CLT), stochastic models, i.e., Wiener process, Langevin equation, Fokker–Planck equation, and other Markovian Master equations [1–3]. The adjective normal highlights that a Gaussian-based process is considered.
However, many natural phenomena show a diffusive behavior that cannot be modeled by classical methods based on the CLT or linear and/or local constitutive laws. This is a ubiquitous observation in life sciences, soft condensed matter, geophysics and ecology, among others. These phenomena are generally labeled with the term anomalous diffusion in order to distinguish them from normal diffusion. In this last case, when assumptions of the CLT are satisfied, i.e., independence of random variables and finiteness of variances, the mean square displacement (MSD) of diffusing particles increases linearly in time. Conversely, departures from the CLT determine the emergence of anomalous diffusion. There are numerous experimental measurements in which the MSD scales with a non-linear power-law in time. These processes are successfully modeled through Fractional Calculus (see, e.g., [4–6]), so that the corresponding processes are referred to as Fractional Diffusion [7–16].
Anomalous diffusion is ubiquitously observed in many complex systems, ranging from turbulence [17, 18], plasma physics [19, 20] to soft matter, e.g., the cell cytoplasm, membrane, and nucleus [21–30] and neuro-physiological systems [31, 32]. In particular, the analysis of highly accurate data of single particle tracking (SPT), which are nowadays available thanks to the great instrumental advancement in fluorescence-based microscopy [33], has allowed to reveal the clear emergence of anomalous diffusion in many biological systems [27, 34–37].
As a consequence, the debate on the understanding of the most suitable microscopic model explaining the observed statistical features of SPT has taken momentum in the scientific community. The emergence of long-range correlations and anomalous diffusion asks for stochastic models departing from the classical Brownian motion based on the Gaussian-Wiener process and the standard random walk [1, 3]. At first, the main debate has been focused on whether the best stochastic approach should be one based on time-continuous trajectories, i.e., fractional Brownian motion (FBM), or to discontinuous trajectories characterized by jump events, i.e., continuous time random walk (CTRW) (see, e.g., [38] for a short discussion). However, both stochastic models, FBM and CTRW, do not describe the observed features of the SPT data. As a consequence, this implies that the above two minimal models (FBM and CTRW) do not take into account some microscopic dynamics affecting the particle motion and determining the emergence of long-range correlations, anomalous diffusion, non-Gaussian power-law distributions, ergodicity breaking, and aging [38].
For this reason, the scientific community is now focusing on the role of the system's heterogeneity, which was at first neglected in the above mentioned modeling approaches. Superstatistics [39–43] is probably the first model where heterogeneity is taken into account through a time modulation of a fast relaxing variable by a slow, adiabatic, variable. Many authors follow the main idea of superstatistics, developing stochastic models that try to go beyond superstatistics itself. This is obtained by developing an explicit stochastic dynamics for the adiabatic modulating variables characterizing the superstatistical models [44, 45]. Along this line, an interesting approach is the recently proposed diffusing diffusivity model (DDM) [46–50]. Approaches similar to superstatistics have also been proposed to model the inter-event times in point processes [51–54], which describe the intermittent events at the basis of event-driven diffusion processes, e.g., CTRWs where the inter-event time distribution is modulated by an external perturbation [41, 54, 55].
Other authors follow a somewhat different approach based on random-scaled Gaussian processes (RSGPs) [38, 56–59], which are physically based on a recently proposed model where inter-particle heterogeneity is explicity described through a population of scales characterizing the dynamical parameters of particle diffusive motion. This modeling approach has been denoted as heterogeneous ensemble of Brownian particles (HEBP) and has been developed on the basis of a Langevin model [57–59]. The HEBP model is then based on the Gaussian-Wiener process and, thus, on trajectories that are strongly continuous in the stochastic sense [60], while anomalous diffusion emerge as a consequence of heterogeneity. Fractional diffusion can be also interpreted as a consequence of complex heterogeneity in the underlying medium, where a classical diffusion takes place for the single particle. According to this approach, fractional diffusion emerges from the population of scales characterizing the medium. Interestingly, for a given stationary Gaussian process, the displacement distribution is uniquely related to the distribution of scales in the considered population. Thus, the observed diffusion properties can be used to guess the properties of the underlying diffusing medium.
All the above mentioned stochastic models where fractional diffusion follows from medium heterogeneity are essentially based on processes with continuous trajectories. Conversely, sudden transition events play a crucial role in the diffusing dynamics in many complex systems. Further, the role of microscopic models with smooth trajectories (Gaussian-based processes) and of event-based models with discontinuous trajectories in biological diffusion is not yet clear.
For this reason, we here propose, discuss, and review different models based on different Gaussian processes, whose parameters are characterized by a population of time or length scales. These models include stochastic processes with both time-continuous single particle trajectories and discontinuous trajectories with crucial jump events. We show that proper choices of the populations lead to space- or time-fractional diffusion. In this paper we propose and discuss a further development of the Master thesis by FDT [61].
The paper is organized as follows. In section 6 we propose and discuss two different Markovian CTRWs with population of time or length scales. In sections 3 and 4 we discuss RSGPs and subordination processes, respectively. Finally, in section 5 we give a brief discussion and draw some conclusions.
2. Continuous Time Random Walk (CTRW)
2.1. The Approach of Continuous Time Random Walk to Study Diffusion Processes
2.1.1. Basic Formulation of the CTRW
For the purposes of the present paper we briefly report some fundamentals on the CTRW. It is well-known that the CTRW is a successful approach to study diffusion processes. It considers the trajectories of discrete particles within a discrete space, according to the original formulation [7, 62, 63], or within a continuous underlying space, according to more recent studies [64, 65].
The trajectory of each particle is considered to be governed by the joint probability density function (PDF) φ(δr, δt) of making a jump of length δr in the time interval δt. If the particle is located in r′ at time t′ and the position r is the particle position after a inter-event time (IET) δt, then: r = r′ + δr, and t = t′ + δt. The times t and t′ are occurrence times of crucial jump events. In the basic theory of CTRW, these events are mutually independent and, thus, the IETs are statistically independent random variables whose features are described in the framework of renewal theory [51–54]. The marginal jump PDF λ(δr) and the marginal waiting-time PDF ψ(τ) are, respectively
The integral is the probability that at least one step is made (0, τ) [64, 66]. Therefore, the probability that a given waiting time between two consecutive jumps is greater or equal to τ is:
and upon differentiation: [64, 66]
Following Klafter et al. [62], the PDF η(r, t) for a particle to arriving in r in the time interval from t to t + δt is
where the initial condition is stated at t = 0 in r = 0. Hence, the PDF for a particle to be in r at time t is [62, 63]
Finally, by using (4), the PDF p(r, t) is given by the following integral equation [62]
2.1.2. The Uncoupled Case and the Memory Effects
The simplest case of the CTRW modeling is the uncoupled case, i.e., the case when the jumps and the waiting times are statistically independent and it holds φ(δr, τ) = λ(δr)ψ(τ). In this case Equation (6) can be re-arranged as [7]
For our purposes we rewrite Equation (7) in the Fourier–Laplace domain. The standard Laplace and Fourier transforms for sufficiently well-behaved functions are, respectively
Then the Laplace transform of formula (6) is
Now, after Fourier transform, we have that the Fourier–Laplace transform of the solution of (6) is
and then, after re-arrangement, the above equation becomes
According to Mainardi et al. [64], formula (11) can be written in the alternative form
where
After Fourier–Laplace anti-transforming, relation (12) gives
where it is evident the memory effect due to the auxiliary function Φ(τ).
2.1.3. The Markovian CTRW Model
A Markovian model is obtained from (14) when Φ(τ) = δ(τ). This implies that and, from the second equality in (13), it holds and Ψ(τ) = ψ(τ). The functions Ψ(τ) and ψ(τ) are related by (3), then a CTRW model is Markovian if
and the resulting Markovian master equation is
On the contrary, when Ψ(τ) is not an exponential function the resulting CTRW model is non-Markovian.
2.2. Markovian CTRW Model With a Population of Time-Scales
Let the functions λn(δr) and ψn(τ) be the n-fold convolutions of the jump and of the waiting-time PDFs, respectively. The most general solution of (6) can be written as [63, 65]
where P(n, t) is the probability of n jumps occurring up to time t:
In particular, since Ψ(τ) is, by definition, the probability that the particle remains fixed (0, τ), then it holds ψ0(τ) = δ(τ) and [63]
Let us consider a heterogeneous condition. Hence, for any Markovian trajectory, the waiting-time τ is scaled by a proper timescale T. This timescale is taken to be a random variable following a proper distribution. In particular, the survival probability Ψ(τ) for each single Markovian trajectory is:
where the index M has been added to remark that it is the survival probability corresponding to the Markovian case. In this case the random walk goes on according to the standard iteration procedure with the same meaning for the symbols, but the random waiting time τ is driven by the rescaled PDF ψ(τ). The characteristic function of the particle PDF turns out to be
where pM(r, t) refers to the Markovian PDF, and f(T/T0, t)/T0 is the distribution of the random timescale T such that and T0 is the effective observed timescale. The single timescale case is recovered when f(T/T0, t)/T0 = δ(T − T0).
Hence, by Fourier inversion and by using formula (17) for the Markovian PDF pM(r, t), it follows
To conclude, the combination of (17) and (22) gives
and setting n = 0 it holds the following
Let hereinafter be T0 = 1 for simplicity. In their pioneering work [7], derived the following fundamental result:
if the survival probability Ψ(τ) is a function of the Mittag–Leffler type, i.e.
the particle PDF p(r; t) solves the time-fractional diffusion equation, i.e., equation (A.1) with α = 2. Therefore, from (24) and (25) it follows that, for any T-distribution f(T, t) such that the following integral holds
the resulting process is a time-fractional diffusion process.
In particular, in the stationary case there is a unique the time-scale distribution, i.e., f(T, t) = fS(T). In fact, it is well-known that it holds [6]
where
and, by comparing of (26) and (27), the stationary timescale distribution fS(T) turns out to be [67]
It is worth noting that the Kβ, defined in (28), is the fundamental solution of the space-time fractional diffusion equation (A.1) when space and time fractional orders of derivation are equal each other and equal to β and when the asymmetry parameter assumes the extremal value, in which case the distribution has support solely on the positive real axis [11]. This case is also known as neutral diffusion [68, 69]. In the Markovian limit, i.e., β = 1, it holds and a single timescale follows.
Concerning the waiting time PDF ψ(t), we observe that, from formula (24) for the survival probability Ψ(t) and from (3), we have
By the fact that the involved functions are the exponential function ΨM and the normalized distribution fS(T), the following equality holds
Finally, we can write the rescaled PDF ψ(t) as.
2.3. Markovian CTRW Model With a Population of Length-Scales
In this section we consider the case of a Markovian CTRW model with a population of length-scales. Hence, the space variable r is scaled by a proper distributed length-scale ℓ and the ratio r/ℓ is a distributed variable because ℓ is a distributed variable. The characteristic function of the particle PDF turns out to be
where pG(r, t) is the PDF of the Gaussian CTRW model and q(ℓ/ℓ0)/ℓ0 is the distribution of the length-scale ℓ such that
and ℓ0 is the effective observed length-scale. The case with a single length-scale is recovered when q(ℓ/ℓ0)/ℓ0 = δ(ℓ − ℓ0). Hereinafter we consider ℓ0 = 1.
Let the jump PDF be
where Λ(r − r′) is the cumulative distribution function of jumps, then we have
where q(ℓ) is the distribution of the length-scale and is the cumulative distribution function of Gaussian jumps. Assuming q(ℓ) such that is integrable and differentiable and it holds , with g(ℓ) integrable, then we have
The PDF p(r; t) of the process under consideration results to be
Now, we want to find an explicit formula for q(ℓ) and we proceed considering the Fourier transform of the above equation, i.e.,
or analogously
Reminding that in the Markovian case the survival probability is and the waiting time PDF ψ(t) = e−t, Equation (40) becomes
and the following relation holds
Considering Equation (11) in the Markovian case (that is β = 1), we have
and after Laplace anti-transforming we obtain
that is the general expression for . Since from the proprieties of characteristic functions, then also , i.e.,
Hence, the above general representation of shows that is a characteristic function for all t ∈ ℝ+ and k ∈ ℝ because it holds
The explicit expression of can also be obtained. We know that the Gaussian density for jumps λG comes from an unbiased random walk in one-dimension. In this random walk, a particle starts from the origin and, at each time step Δt, makes a jump ±Δx to the left or the right with equal probability. We call Ph,n the probability that the particle will be in point x = hσG at the time t = nΔt. In this simple case we have
assuming P0,0 = 1. The characteristic function for this binomial formulation is
that n even becomes
Finally, the characteristic function turns out to be.
2.3.1. Comparison With the Green Function of the Space-Fractional Diffusion Equation
We recall that the Fourier transform of the Lévy stable density that solves the space-fractional diffusion equation, i.e., Equation (A.1) with β = 1, is
If we compare the above relation with Equation (50), we obtain also the following consistent pair and q(ℓ):
Moreover, this choice is consistent also with the proprieties of unitary initial value for the characteristic function and of normalization for the PDF, i.e.,
and
In general for k ∈ ℝ it holds
In the limit |k| ≪ 1 the characteristic function results to be
Then, for |k| ≪ 1, it holds
Hence the characteristic function of the considered process is a Lévy stable density, that is the fundamental solution of the space-fractional diffusion equation. To conclude, since a characteristic function corresponds to a unique distribution and vice versa, in the considered limit (k ≪ 1) the PDF p(r − r′; t) is a Lévy stable density.
3. Randomly-Scaled Gaussian Processes
Let us denote a randomly-scaled Gaussian process (RSGP) as a stochastic process defined by the product of a Gaussian process times a non-negative random variable. In general, the one-point one-time PDF is not sufficient to characterize a stochastic process. There are infinitely many stochastic processes that follow the same one-dimensional distribution and, thus, solve the same Cauchy problem for the associated diffusion/master equation describing the time evolution of the PDF. However, in RSGPs, this indeterminacy is solved by the choice of the Gaussian process that is fully characterized for given first and second moments.
In this paper we consider a special class of RSGPs called generalized gray Brownian motion (ggBm), that is defined by using the fractional Brownian motion as Gaussian process [70–75]. For other form of randomly-scaled Gaussian process we refer the reader to Sliusarenko et al. [59]. Hence, we consider the following class of processes:
where BH(t) is the fBm process with Hurst exponent 0 < H < 1, and then with power law variance t2H.
The application of this approach to fractional diffusion is based on the correspondence of the PDFs resulting from the product of two independent random variables with the PDFs resulting from the integral representation formula (A.10).
Let define Z1 and Z2 as two real independent random variables: z1 ∈ ℝ and . The associated PDFs are p1(z1) and p2(z2), respectively. Let Z be the random variable obtained by the product of Z1 and , i.e., . Denoting with p(z) the PDF of Z, it results:
Comparing the above formula with the integral representation formula (A.10), and applying the change of variables z = xt−γω and λ = τt−ω, the integral representation (71) is recovered from (59) by setting:
Then, by identifying functions and parameters as
formula (59) reduces to the integral formula (A.10) for the symmetric space-time fractional diffusion equation. In terms of random variables it follows that [56]
hence it holds
Since p1(z1) ≡ G(z1), Z1 is a Gaussian random variable. Consequently, the variable is Gaussian with variance proportional to t2β/α. Hence, we chose the fBm with 0 < H = β/α < 1 as a Gaussian process with consistent power law variance. Furthermore, the random variable Z2 = Λα/2,β is distributed according to . Finally, we have the process
where is an independent constant non-negative random variable distributed according to the PDF , λ ≥ 0, that is a special case of (A.7). The process defined above is the solution of the space-time fractional diffusion Equation (A.1) in the symmetric case. This means that the one-time one-point PDF of Xα,β(t) is the fundamental solution of Equation (A.1) in the symmetric case, namely the PDF defined in (A.10).
The space-fractional diffusion is recovered when β = 1, in fact by using formula (A.7) with t = 1, we have
Here we are interested in the distribution of then, by normalization condition, the PDF of ℓ results to be
Analogously, the time-fractional diffusion is recovered when α = 2, in fact by using formula (A.7) with t = 1, we have
and the corresponding PDF of ℓ is
4. Time-Subordination for Gaussian Processes
Another approach proposed to model the emergence of fractional and, more in general, anomalous diffusion in complex media is the time-subordination of a otherwise standard diffusion process (see, e.g., [15, 76, 77]). Even when the time-subordination procedure is applied to a Gaussian process, the PDF of the resulting process is no longer Gaussian, and the particle MSD has a non-linear time dependence. Let Y(τ), τ > 0, be a stochastic process. Time-subordination is defined by the following expression:
Thus, time-subordination follows from the randomization of the time clock in a stochastic process Y(τ), i.e., by using a new clock τ = Q(t), being Q(t) a random process with non-negative increments. The resulting process Y(Q(t)) is said to be subordinated to Y(τ). This is called the parent process, while Q(t) is called the directing process, so that it is said that Y(τ) it is directed by Q(t) [78].
In diffusion processes, the parameter τ is named operational time. The process t = t(τ), which is the inverse of τ = Q(t), is called the leading process [15, 79]. It is worth noting that, in general, X(t) is non-Markovian, even when the parent process Y(τ) is Markovian. At the macroscopic level, i.e., in terms of the particle PDF, the subordination process X(t) is described by the following expression:
where p(x; t) is the PDF of X(t), ψ(x; τ) the PDF of Y(τ) and φ(τ; t) the PDF of Q(t). In the following, the PDFs are self-similar, i.e., have a scaling property. Similarly to the approaches previously described, we introduce a population of time-scales T with distribution function f(T) for the subordinated process Y(τ). Then parameter τ is now determined by the process Q(t/T).
By comparing (71) and (A.10) we have
Hence, the integral representation (71) turns out to be
In the case of space-fractional diffusion, from formula (A.11) we observe that the scaling property gives Q(t/T) = (t/T)1/α, and f(T) results to be
Analogously, in the case of time-fractional diffusion, from formula (A.12) we observe that the scaling property gives Q(t/T) = (t/T)β, and f(T) results to be
5. Conclusions
In this paper we studied a framework for explaining the emergence of anomalous diffusion in media characterized by random structures. In particular, we considered three different modeling approaches based on Gaussian processes but displaying a population of scales. The main idea is that the deviation from Gaussianity is indeed an indirect estimation of the population of the scales that characterize the medium where the diffusion takes place. We discussed the cases of space- and time-fractional diffusion through the CTRW, the ggBm and time-subordinated process.
The introduction of a population of scales significantly affects the particle PDF. The same fractional diffusion follows from different populations of scales when different Gaussian processes are considered. This suggests that the same macroscopic fractional process can be experimentally observed in different systems displaying different populations of scales and, consequently, driven by different underlying mesoscopic Gaussian processes. In Figures 1, 2 we give a synthetic picture of the three processes here described, all leading to the macroscopic space- or time-fractional diffusion equations.
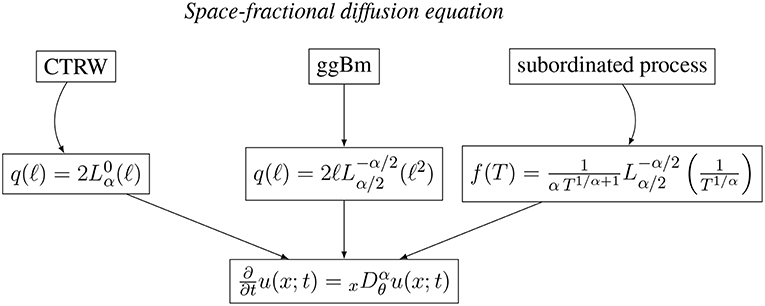
Figure 1. Schematic picture of the three stochastic processes in heterogenous media leading to the same space-fractional diffusion equation for the 1-point 1-time PDF.
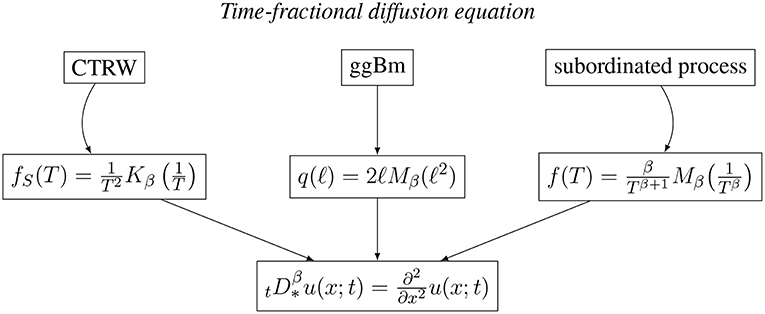
Figure 2. Schematic picture of the three stochastic processes in heterogenous media leading to the same time-fractional diffusion equation for the 1-point 1-time PDF.
When a macroscopic fractional process is experimentally observed, the simultaneous measurement of the population of scales embodies a selection criterion for the corresponding mesoscopic (and maybe not experimentally detectable) underlying Gaussian process. The same holds in the other way round, when a macroscopic fractional process is experimentally observed in place of a specific Gaussian process theoretically and/or experimentally expected, and then the deviation from Gaussianity embodies an indirect measurement of the population of the scales.
In general, this framework can be adopted for studying the presence and the characterization of impurities, as well as of obstacles, in a given complex medium. These results highlight the key role of the properties of the medium, embodied by the population of the scales, in the determination of the proper stochastic process for a given medium. The present research and our final claim aim to analyze and provide an explanation to the role and the effects of the system's configuration (environment plus particles) on the emergence of deviations from Gaussianity. In this respect, the present results add a contribution to similar existing literature concerning, for example, the dependence on system's configuration of the emergence of nonextensive statistical mechanics in confined granular media [80], or the emergence of processes modeled by fractional linear diffusion or by integer non-linear diffusion accordingly to different settings of CTRW simulations [81].
Data Availability
All datasets generated for this study are included in the manuscript and the Supplementary Files.
Author Contributions
GP, PP, FD, and RS discussed the main ideas and took care of the text. The research presented in this paper and, in particular, the mathematical derivation of the models has been carried out at BCAM, Bilbao, and was developed by FD for his Master Thesis in Mathematics, Roma Tre University, under the supervision of GP and RS. GP wrote the Appendix in Supplementary Material.
Funding
This research was supported by the Basque Government through the BERC 2014–2017 and BERC 2018–2021 programs, and by the Spanish Ministry of Economy and Competitiveness MINECO through BCAM Severo Ochoa excellence accreditations SEV-2013-0323 and SEV-2017-0718 and through project MTM2016-76016-R MIP.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors would like to acknowledge Francesco Mainardi for his motivating attitude to the scientific research and his positive example to human relations that are at the basis of this collaborative research.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2019.00123/full#supplementary-material
References
2. Risken H. The Fokker-Planck Equation. Methods of Solution and Applications. 2nd Edn. Berlin; Heidelberg: Springer-Verlag (1989).
3. Gardiner CW. Handbook of Stochastic Methods for Physics, Chemistry and the Natural Sciences. 2nd Edn. Berlin; Heidelberg: Springer-Verlag (1990).
4. Sneddon IN. The Use of Operators of Fractional Integration in Applied Mathematics. Warszawa: RWN - Polish Science Publishers (1979).
5. Samko SG, Kilbas AA, Marichev OI. Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach Science Publishers (1993). Philadelphia, PA: Reprinted 2002 by Taylor & Francis Books Ltd, London.
6. Mainardi F. Fractional Calculus and Waves in Linear Viscoelasticity. London: Imperial College Press (2010).
7. Hilfer R, Anton L. Fractional master equations and fractal time random walks. Phys Rev E. (1995) 51:R848–51. doi: 10.1103/PhysRevE.51.R848
8. Mainardi F. Fractional relaxation-oscillation and fractional diffusion-wave phenomena. Chaos Solit Fract. (1996) 7:1461–77. doi: 10.1016/0960-0779(95)00125-5
9. Klafter J, Lim SC, Metzler R. Fractional Dynamics: Recent Advances. Singapore: World Scientific (2011).
10. Metzler R, Klafter J. The random walk's guide to anomalous diffusion: a fractional dynamics approach. Phys Rep. (2000) 339:1–77. doi: 10.1016/S0370-1573(00)00070-3
11. Mainardi F, Luchko Y, Pagnini G. The fundamental solution of the space-time fractional diffusion equation. Fract Calc Appl Anal. (2001) 4:153–92.
12. Mainardi F, Pagnini G. The Wright functions as solutions of the time-fractional diffusion equations. Appl Math Comput. (2003) 141:51–62. doi: 10.1016/S0096-3003(02)00320-X
13. Mainardi F, Pagnini G, Saxena RK. Fox H functions in fractional diffusion. J Comput Appl Math. (2005) 178:321–1. doi: 10.1016/j.cam.2004.08.006
14. Mainardi F, Pagnini G. The role of the Fox–Wright functions in fractional sub-diffusion of distributed order. J Comput Appl Math. (2007) 207:245–57. doi: 10.1016/j.cam.2006.10.014
15. Gorenflo R, Mainardi F. Subordination pathways to fractional diffusion. Eur Phys J. (2011) 193:119–32. doi: 10.1140/epjst/e2011-01386-2
16. Paradisi P. Fractional calculus in statistical physics: the case of time fractional diffusion equation. Comm Appl Ind Math. (2015) 6:e530. doi: 10.1685/journal.caim.530
17. Paradisi P, Cesari R, Donateo A, Contini D, Allegrini P. Scaling laws of diffusion and time intermittency generated by coherent structures in atmospheric turbulence. Nonlinear Proc Geoph. (2012) 19:113–26. doi: 10.5194/npg-19-113-2012
18. Paradisi P, Cesari R, Donateo A, Contini D, Allegrini P. Diffusion scaling in event-driven random walks: an application to turbulence. Rep Math Phys. (2012) 70:205–20. doi: 10.1016/S0034-4877(12)60040-8
19. del Castillo-Negrete D. Fractional diffusion in plasma turbulence. Phys Plasmas. (2004) 11:3854–64. doi: 10.1063/1.1767097
20. del Castillo-Negrete D, Carreras BA, Lynch VE. Nondiffusive transport in plasma turbulence: a fractional diffusion approach. Phys Rev Lett. (2005) 94:065003. doi: 10.1103/PhysRevLett.94.065003
21. Tolić-Nørrelykke IM, Munteanu EL, Thon G, Odderhede L, Berg-Sørensen K. Anomalous diffusion in living yeast cells. Phys Rev Lett. (2004) 93:078102. doi: 10.1103/PhysRevLett.93.078102
22. Golding I, Cox EC. Physical nature of bacterial cytoplasm. Phys Rev Lett. (2006) 96:098102. doi: 10.1103/PhysRevLett.96.098102
23. Bronstein I, Israel Y, Kepten E, Mai S, Shav-Tal Y, Barkai E, et al. Transient anomalous diffusion of telomeres in the nucleus of mammalian cells. Phys Rev Lett. (2009) 103:018102. doi: 10.1103/PhysRevLett.103.018102
24. Zaid IM, Lomholt MA, Metzler R. How subdiffusion changes the kinetics of binding to a surface. Biophys J. (2009) 97:710–21. doi: 10.1016/j.bpj.2009.05.022
25. Gal N, Lechtman-Goldstein D, Weihs D. Particle tracking in living cells: a review of the mean square displacement method and beyond. Rheol Acta. (2013) 52:425–3. doi: 10.1007/s00397-013-0694-6
26. Javer A, Kuwada NJ, Long Z, Benza VG, Dorfman KD, Wiggins PA, et al. Persistent super-diffusive motion of Escherichia coli chromosomal loci. Nat Commun. (2014) 5:3854. doi: 10.1038/ncomms4854
27. Metzler R, Jeon JH, Cherstvy AG. Non–Brownian diffusion in lipid membranes: experiments and simulations. Biochim Biophys Acta. (2016) 1858:2451–67. doi: 10.1016/j.bbamem.2016.01.022
28. Pöschke P, Sokolov IM, Nepomnyashchy AA, Zaks MA. Anomalous transport in cellular flows: the role of initial conditions and aging. Phys Rev E. (2016) 94:032128. doi: 10.1103/PhysRevE.94.032128
29. Stadler L, Weiss M. Non-equilibrium forces drive the anomalous diffusion of telomeres in the nucleus of mammalian cells. New J Phys. (2017) 19:113048. doi: 10.1088/1367-2630/aa8fe1
30. Pierro MD, Potoyan DA, Wolynes PG, Onuchic JN. Anomalous diffusion, spatial coherence, and viscoelasticity from the energy landscape of human chromosomes. Proc Natl Acad Sci USA. (2018) 115:7753–8. doi: 10.1073/pnas.1806297115
31. Allegrini P, Paradisi P, Menicucci D, Laurino M, Piarulli A, et al. Self-organized dynamical complexity in human wakefulness and sleep: different critical brain-activity feedback for conscious and unconscious states. Phys Rev E. (2015) 92:032808. doi: 10.1103/PhysRevE.92.032808
32. Paradisi P, Allegrini P. Intermittency-driven complexity in signal processing. In: Barbieri R, Scilingo EP, Valenza G, editors. Complexity and Nonlinearity in Cardiovascular Signals. Cham: Springer (2017). p. 161–96.
33. Manzo C, Garcia-Parajo MF. A review of progress in single particle tracking: from methods to biophysical insights. Rep Progr Phys. (2015) 78:124601. doi: 10.1088/0034-4885/78/12/124601
34. Burov S, Jeon JH, Metzler R, Barkai E. Single particle tracking in systems showing anomalous diffusion: the role of weak ergodicity breaking. Phys Chem Chem Phys. (2011) 13:1800–2. doi: 10.1039/c0cp01879a
35. Javanainen M, Hammaren H, Monticelli L, Jeon JH, Miettinen MS, Martinez-Seara H, et al. Anomalous and normal diffusion of proteins and lipids in crowded lipid membranes. Faraday Discuss. (2012) 161:397–417. doi: 10.1039/C2FD20085F
36. Metzler R, Jeon JH, Cherstvy AG, Barkai E. Anomalous diffusion models and their properties: non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys Chem Chem Phys. (2014) 16:24128. doi: 10.1039/C4CP03465A
37. Jeon JH, Javanainen M, Martinez-Seara H, Metzler R, Vattulainen I. Protein crowding in lipid bilayers gives rise to non-Gaussian anomalous lateral diffusion of phospholipids and proteins. Phys Rev X. (2016) 6:021006. doi: 10.1103/PhysRevX.6.021006
38. Molina-García D, Minh Pham T, Paradisi P, Manzo C, Pagnini G. Fractional kinetics emerging from ergodicity breaking in random media. Phys Rev E. (2016) 94:052147. doi: 10.1103/PhysRevE.94.052147
39. Beck C. Dynamical foundations of nonextensive statistical mechanics. Phys Rev Lett. (2001) 87:180601. doi: 10.1103/PhysRevLett.87.180601
40. Beck C, Cohen EGD. Superstatistics. Phys A. (2003) 322:267–75. doi: 10.1016/S0378-4371(03)00019-0
41. Allegrini P, Barbi F, Grigolini P, Paradisi P. Renewal, modulation, and superstatistics in times series. Phys Rev E Stat Nonlin Soft Matter Phys. (2006) 73(4 Pt 2):046136. doi: 10.1103/PhysRevE.73.046136
42. Paradisi P, Cesari R, Grigolini P. Superstatistics and renewal critical events. Cent Eur J Phys. (2009) 7:421–31. doi: 10.2478/s11534-009-0069-x
43. Van Der Straeten E, Beck C. Superstatistical fluctuations in time series: applications to share-price dynamics and turbulence. Phys Rev E. (2009) 80:036108. doi: 10.1103/PhysRevE.80.036108
44. Massignan P, Manzo C, Torreno-Pina J, García-Parajo M, Lewenstein M, Lapeyre G Jr. Nonergodic subdiffusion from Brownian motion in an inhomogeneous medium. Phys Rev Lett. (2014) 112:150603. doi: 10.1103/PhysRevLett.112.150603
45. Manzo C, Torreno-Pina JA, Massignan P, Lapeyre GJ, Lewenstein M, Garcia–Parajo MF. Weak ergodicity breaking of receptor motion in living cells stemming from random diffusivity. Phys Rev X. (2015) 5:011021. doi: 10.1103/PhysRevX.5.011021
46. Chubynsky MV, Slater GW. Diffusing diffusivity: a model for anomalous, yet brownian, diffusion. Phys Rev Lett. (2014) 113:098302. doi: 10.1103/PhysRevLett.113.098302
47. Chechkin AV, Seno F, Metzler R, Sokolov IM. Brownian yet non-Gaussian diffusion: from superstatistics to subordination of diffusing diffusivities. Phys Rev X. (2017) 7:021002. doi: 10.1103/PhysRevX.7.021002
48. Jain R, Sebastian KL. Diffusing diffusivity: a new derivation and comparison with simulations. J Chem Sci. (2017) 129:929–37. doi: 10.1007/s12039-017-1308-0
49. Lanoiselée Y, Grebenkov DS. A model of non-Gaussian diffusion in heterogeneous media. J Phys A Math Theor. (2018) 51:145602. doi: 10.1088/1751-8121/aab15f
50. Sposini V, Chechkin AV, Seno F, Pagnini G, Metzler R. Random diffusivity from stochastic equations: comparison of two models for Brownian yet non-Gaussian diffusion. New J Phys. (2018) 20:043044. doi: 10.1088/1367-2630/aab696
52. Bianco S, Grigolini P, Paradisi P. A fluctuating environment as a source of periodic modulation. Chem Phys Lett. (2007) 438:336–40. doi: 10.1016/j.cplett.2007.03.013
53. Paradisi P, Grigolini P, Bianco S, Akin OC. Renewal aging in non-homogeneous Poisson processes with periodic rate modulation. Int J Bif Chaos. (2008) 18:2681–91. doi: 10.1142/S0218127408021890
54. Akin OC, Paradisi P, Grigolini P. Perturbation-induced emergence of Poisson-like behavior in non-Poisson systems. J Stat Mech Theory Exp. (2009) 2009:P01013. doi: 10.1088/1742-5468/2009/01/P01013
55. Akin OC, Paradisi P, Grigolini P. Periodic trend and fluctuations: the case of strong correlation. Phys A. (2006) 371:157–70. doi: 10.1016/j.physa.2006.04.054
56. Pagnini G, Paradisi P. A stochastic solution with Gaussian stationary increments of the symmetric space-time fractional diffusion equation. Fract Calc Appl Anal. (2016) 19:408–40. doi: 10.1515/fca-2016-0022
57. Vitali S, Sposini V, Sliusarenko O, Paradisi P, Castellani G, Pagnini G. Langevin equation in complex media and anomalous diffusion. J R Soc Interface. (2018) 15:20180282. doi: 10.1098/rsif.2018.0282
58. D′Ovidio M, Vitali S, Sposini V, Sliusarenko O, Paradisi P, Castellani G, et al. Centre-of-mass like superposition of Ornstein-Uhlenbeck processes: a pathway to non-autonomous stochastic differential equations and to fractional diffusion. Fract Calc Appl Anal. (2018) 21:1420–35. doi: 10.1515/fca-2018-0074
59. Sliusarenko OY, Vitali S, Sposini V, Paradisi P, Chechkin A, Castellani G, et al. Finite-energy Lévy-type motion through heterogeneous ensemble of Brownian particles. J Phys A. (2019) 52:095601. doi: 10.1088/1751-8121/aafe90
60. Kloeden PE, Platen E. Numerical solution of Stochastic Differential Equations. Springer-Verlag (1992).
61. Di Tullio F. Fractional diffusion in random media on the basis of Gaussian stochastic processes. Master Thesis in Mathematics, University of Roma Tre, Rome, Italy (2016).
62. Klafter J, Blumen A, Shlesinger MF. Stochastic pathway to anomalous diffusion. Phys Rev A. (1987) 35:3081–5. doi: 10.1103/PhysRevA.35.3081
63. Montroll EW, Weiss GH. Random walks on lattices. II. J Math Phys. (1965) 6:167–81. doi: 10.1063/1.1704269
64. Mainardi F, Raberto M, Gorenflo R, Scalas E. Fractional calculus and continuous-time finance II: the waiting-time distribution. Phys A. (2000) 287:468–81. doi: 10.1016/S0378-4371(00)00386-1
65. Scalas E, Gorenflo R, Mainardi F. Uncoupled continuous-time random walks: solution and limiting behavior of the master equation. Phys Rev E. (2004) 69:011107. doi: 10.1103/PhysRevE.69.011107
66. Scalas E, Gorenflo R, Mainardi F. Fractional calculus and continuous-time finance. Phys A. (2000) 284:376–84. doi: 10.1016/S0378-4371(00)00255-7
67. Pagnini G. Short note on the emergence of fractional kinetics. Phys A. (2014) 409:29–34. doi: 10.1016/j.physa.2014.03.079
68. Metzler R, Nonnenmacher TF. Space- and time-fractional diffusion and wave equations, fractional Fokker-Planck equations, and physical motivation. Chem Phys. (2002) 284:67–90. doi: 10.1016/S0301-0104(02)00537-2
69. Luchko Y. Models of the neutral-fractional anomalous diffusion and their analysis. AIP Conf Proc. (2012) 1493:626–32. doi: 10.1063/1.4765552
70. Mura A, Taqqu MS, Mainardi F. Non-Markovian diffusion equations and processes: analysis and simulations. Phys A. (2008) 387:5033–64. doi: 10.1016/j.physa.2008.04.035
71. Mura A, Pagnini G. Characterizations and simulations of a class of stochastic processes to model anomalous diffusion. J Phys A Math Theor. (2008) 41:285003. doi: 10.1088/1751-8113/41/28/285003
72. Mura A, Mainardi F. A class of self-similar stochastic processes with stationary increments to model anomalous diffusion in physics. Integr Transf Spec F. (2009) 20:185–98. doi: 10.1080/10652460802567517
73. Pagnini G, Mura A, Mainardi F. Generalized fractional master equation for self-similar stochastic processes modelling anomalous diffusion. Int J Stoch Anal. (2012) 2012:427383. doi: 10.1155/2012/427383
74. Pagnini G, Mura A, Mainardi F. Two-particle anomalous diffusion: probability density functions and self-similar stochastic processes. Philos Trans R Soc A. (2013) 371:20120154. doi: 10.1098/rsta.2012.0154
75. Pagnini G. Erdélyi–Kober fractional diffusion. Fract Calc Appl Anal. (2012) 15:117–27. doi: 10.2478/s13540-012-0008-1
76. Mainardi F, Pagnini G, Gorenflo R. Mellin transform and subordination laws in fractional diffusion processes. Fract Calc Appl Anal. (2003) 6:441–59.
77. Mainardi F, Pagnini G, Gorenflo R. Mellin convolution for subordinated stable processes. J Math Sci. (2006) 132:637–42. doi: 10.1007/s10958-006-0008-y
78. Feller W. An Introduction to Probability Theory and its Applications, Vol. 2. 2nd Edn. New York, NY: Wiley (1971).
79. Gorenflo R, Mainardi F. Parametric subordination in fractional diffusion processes. In: Klafter J, Lim SC, Metzler R, editors. Fractional Dynamics. Recent Advances. Singapore: World Scientific (2012). p. 227–61.
80. Combe G, Richefeu V, Stasiak M, Atman APF. Experimental validation of a nonextensive scaling law in confined granular media. Phys Rev Lett. (2015) 115:238301. doi: 10.1103/PhysRevLett.115.238301
81. Pereira APP, Fernandes JP, Atman APF, Acebal JL. Parameter calibration between models and simulations: connecting linear and non-linear descriptions of anomalous diffusion. Phys A. (2018) 509:369–82. doi: 10.1016/j.physa.2018.06.025
82. Mainardi F, Mura A, Pagnini G. The M-Wright function in time-fractional diffusion processes: a tutorial survey. Int J Differ Equat. (2010) 2010:104505. doi: 10.1155/2010/104505
83. Mainardi F, Mura A, Pagnini G. The functions of the Wright type in fractional calculus. Lect Notes Semin Interdisc Matemat. (2010) 9:111–28.
84. Cahoy DO. On the parametrization of the M-Wright function. Far East J Theor Stat. (2011) 34:155–64.
85. Cahoy DO. Estimation and simulation for the M-Wright function. Commun Stat-Theor M. (2012) 41:1466–77. doi: 10.1080/03610926.2010.543299
86. Cahoy DO. Moment estimators for the two-parameter M-Wright distribution. Comput Stat. (2012) 27:487–97. doi: 10.1007/s00180-011-0269-x
87. Pagnini G. The M-Wright function as a generalization of the Gaussian density for fractional diffusion processes. Fract Calc Appl Anal. (2013) 16:436–53. doi: 10.2478/s13540-013-0027-6
Keywords: anomalous diffusion, fractional diffusion, complex medium, Gaussian process, heterogeneity, continuous time random walk, generalized gray Brownian motion, time-subordinated process
Citation: Di Tullio F, Paradisi P, Spigler R and Pagnini G (2019) Gaussian Processes in Complex Media: New Vistas on Anomalous Diffusion. Front. Phys. 7:123. doi: 10.3389/fphy.2019.00123
Received: 01 June 2019; Accepted: 14 August 2019;
Published: 06 September 2019.
Edited by:
Carlos Mejía-Monasterio, Polytechnic University of Madrid, SpainReviewed by:
Marcin Magdziarz, Wroclaw University of Science and Technology, PolandAllbens Picardi Faria Atman, Federal Center for Technological Education of Minas Gerais, Brazil
Copyright © 2019 Di Tullio, Paradisi, Spigler and Pagnini. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gianni Pagnini, Z3BhZ25pbmlAYmNhbWF0aC5vcmc=
 Francesco Di Tullio
Francesco Di Tullio Paolo Paradisi
Paolo Paradisi Renato Spigler
Renato Spigler Gianni Pagnini
Gianni Pagnini