- 1Department of Mathematics, Science Faculty, Firat University, Elazig, Turkey
- 2Department of Mathematics, Science Faculty, Federal University Dutse, Jigawa, Nigeria
- 3Cankaya University, Department of Mathematics, Ankara, Turkey
- 4Institute of Space Sciences, Bucharest, Romania
This paper studies optical solitons with M-truncated and beta derivatives (BD) for the Complex Ginzburg-Landau equation (CGLE) with Kerr Law nonlinearity. Two well-known integration schemes which are generalized tanh method (GTM) and generalized Bernoulli sub-ODE method (GBM) are utilized to extract such optical soliton solutions. For the successful existence of the solutions, the constraints conditions have been presented. The discussion for the physical features of the obtained solutions is reported.
1. Introduction
Nonlinearity has been potent field of research and its vitality is thought of through a sweer-amplitude wave oscillation analyzed in numerous fields from plasmas and fluids to biological and chemical phenomenon, solid state, to mention a few. Therefore, the most captivating viewpoint in nonlinear physical phenomenon are solitons. The availability of solitonic concepts are due to the philosophical balance of dispersion and nonlinearity [1]. A lot of researches on solitons and associated aspects of solitary wave (SW) solutions for example monopulse water wave which depict the first soliton can be found in Miller and Ross [2], Podlubny [3], Oldham [4], Kiryakova [5], and El-Sayed and Gaber [6]. Moreover, various mathematical insight and modeling can be interpreted through optical solitons for their numerical and analytical structures of the numerous mechanism. These stimulated many engineers and scientists to focus on the establishments of solitons with optical structures with the help of various integration schemes [7–38].
For quite a long time, the effect of memory is an idea that has been of great concern in the locality of modeling. Genuinely, the integer systems are not conveniently addressing this memory effect [39–41]. Many researchers have presented that, one can get to know more on the memory effect through non-integer operators [42–45]. An extension to integer order systems such as conformable [46], beta [47], and M-derivatives [48] have also been introduced and they play a vital role in modeling physical systems. These extension to integer order systems satisfy a lot of characteristics that were not satisfied before and it can be employed to model several physical phenomenon. In this study, we establish new optical solitons for the governing equation with M-truncated and beta derivatives with the aid of two well-known method. The M-truncated and beta derivatives are defined in the following subsections, respectively.
1.1. Truncated M-Fractional Derivative
We define the truncated Mittag-Leffler function of one parameter by
Truncated M-fractional derivative (TMD) is a fractional derivative that has been introduced in Sousa and de Oliveira [48]. This derivative has expunged the obstacles with the existing derivatives. It is defined in the following definition.
Definition 1.1. Assume that f : (0, ∞) → ℝ, the TMD of f with order γ exhibited is given by
for τ > 0, and iEβγ ∈ (0, 1), β > 0 is a truncated Mittag-Leffler function of one parameter, as defined in (1). Note that, if f is γ-differentiable in some open interval (0, a), a > 0, and . Then we attain
Theorem 1.1. Surmise that f : (0, ∞) → ℝ is γ−differentiable for τ0 > 0, with γ ∈ (0, 1], β > 0, then f is continuous at τ0.
Theorem 1.2. Let 0 < γ ≤ 1, β > 0, a, b ∈ ℝ, f, g, γ-differentiable, at a point τ > 0. Then
• , a, b ∈ ℝ
• , μ ∈ ℝ
• ,
• ,
• If f is differentiable, then ,
• , for f differentiable at g.
1.2. Beta Derivative
The beta derivative can be stated by [49]
along with the properties as comes next
1.
2.
for any c depicting a constant,
3.
4.
Considering , h → 0 when ϵ → 0, therefore we have
with
where l is a constant.
5.
The arrangements of the paper is as follows: In section 2 the governing equation has been presented. In section 3, applications have been reported, whereas section 4 provides the discussion of the obtained results along with their physical features. Finally, concluding remark is given in section 5.
2. Governing Equation
The CGLE equation [50, 51] in the sense of M-truncated derivative is given by:
whereas in the sense of beta derivative is given by
where , , and , depicts M-truncated and beta derivatives, respectively. 0 < γ ≤ 1, describing the order of the fractional derivatives and a, b, δ, B, and A are real constants.
In Equations (12) and (13), 𝔽 ∈ ℝ, and the complex function and its smoothness is necessary to be possessed 𝔽(|u|2)u : ℂ → ℂ. Consider ℂ to be a two-dimensional linear space ℝ2, and that 𝔽(|u|2)u is k times continuously differentiable, so that
2.1. Mathematical Analysis
To solve Equations (12) and (13), the beginning step is as come next
the shape of the pulse is represented by u(η, τ) so that in the sense of M-truncated derivatives we have
and
and in the sense of beta derivative we have
and
where w is the wave number of the soliton, k denotes the soliton frequency, υ indicates the speed of the soliton, ϕ(η, τ) is the phase component, θ0(ξ) depicts an additional phase function depending on ξ. Plugging (15) and (17) into (12) and (13), respectively, and decomposing the real and imaginary parts, one attains
and
Equation (20) denotes the soliton velocity. Setting δ = 2B in Equation (19) yields.
2.2. Kerr Law
This law has got its origin through the reality that a light wave in an optical fiber heads to responses by a nonlinear patterns from non-harmonic motion of electrons bound in molecules, brought externally by an electric field. Although the responses by nonlinear terms are seriously low, over a long distance of propagation, the effects standstill in numerous patterns measuring in terms of light wavelength. This law is given by , therefore Equation (21) becomes.
3. Applications
This section will utilize the GT and GB sub-ODE methods to provide optical solitons for the governing equation with beta-derivative.
3.1. Application for GTM
According to GTM [52], Equation (22) has possessed the solution as comes next
with a0 and a1 depicting an unknown constants and Φ(ξ) holds for the Ricatti equation
with μ a non-zero constant. Plugging Equation (23) together with Equation (24) in Equation (22), one reaches
Collecting the terms in Φi(i = 0, 1, 2, 3), one attains
Solving Equation (26), we obtain
Result 1. , A = −4Bk2 − w, a0 = 0, b ≠ 0, . If C < 0, we attain
If C > 0, we acquire
Result 2. 2C + k2 ≠ 0, , a0 = 0, b ≠ 0, . If C < 0, we have
If C > 0, we attain
where ξ and ϕ(η, τ) are defined by (15) and (16) for M-truncated derivative solutions and by (17) and (18) for beta derivative solutions.
3.2. Application for GBM
This section will apply GBM for Equations (12) and (13). According to GB sub-ODE method [53], Equation (22) has possessed the solution as comes next
with a0 and a1 representing an unknown constants and Φ(ξ) holds for the Ricatti equation
with μ a non-zero constant. Plugging Equation (36) together with Equation (35) in Equation (22), one attains
Collecting the terms in Φi(i = 0, 1, 2, 3), one obtains
Solving Equation (38), we reaches
Result 1. , A = −2Bλ2 − w, b ≠ 0, , λ(a − 4B) ≠ 0, . We obtain
or
Result 2. 2k2 − λ2 ≠ 0, , b ≠ 0, , . We acquire
or
where ξ and ϕ(x, t) are defined by (15) and (16) for M-truncated derivative solutions and by (17) and (18) for beta derivative solutions.
4. Discussion
The M-truncated and beta-derivatives have been successfully utilized to reach optical solitons for the underlying equation. This has been achieved by utilizing two potent integration schemes which are GTM and GBM. Singular-dark, dark and singular-periodic solutions have been reported. The GTM has provided dark optical soliton (DOS) (27) and (31), singular optical soliton (28) and (32), optical singular periodic (29), (30), (33), and (34). The GBM has provided optical dark solitons reported in (39) and (41), optical singular solitons reported in (40) and (42).
Solitary waves (SW) with mitigating intensity than the background can be interpreted by DOS [49]. SW with discontinuous derivative can be depicted by singular solitons [54, 55]. These sorts of SW are potent as a results of efficiency and applicability they possessed optical communications of a long distance. Optical fibers can be considered as a thin lengthy strands of pure-ultra glass so that an electromagnetic radiations can be communicated without any mitigation from one point to the next [56].
5. Conclusion
In this research, we have applied the well-known M-truncated and beta derivatives to reach the optical solitons for the governing equation with Kerr Law nonlinearity. Two techniques which GTM and GBM have been used to attain such solutions. For the successful existence of the solutions, the constraints conditions have been presented. The discussion for the physical features of the obtained solutions are have been reported. The explicit behavior for the obtained results by suitable choice of the parameter values have been presented in the presented Figures 1–3. The effects of the γ, β-M-truncated derivative and γ-beta derivative have influenced the behavior of the solutions. The obtained solutions are new and novel and can be of great potent in explaining physical systems in nonlinear optics.
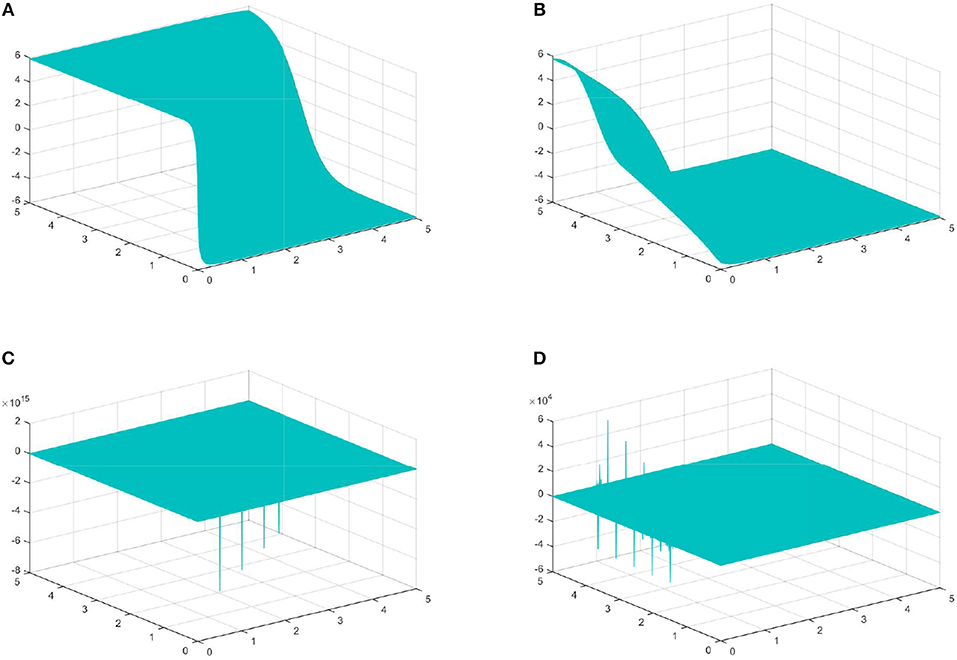
Figure 1. Physical features with suitable values of the parameters. (A) M-truncated with γ = 0.5, β = 0.9 for (27). (B) Beta with γ = 0.5 for (27). (C) M-truncated with γ = 0.5, β = 0.9 for (28). (D) Beta with γ = 0.5, β = 0.9 for (27).
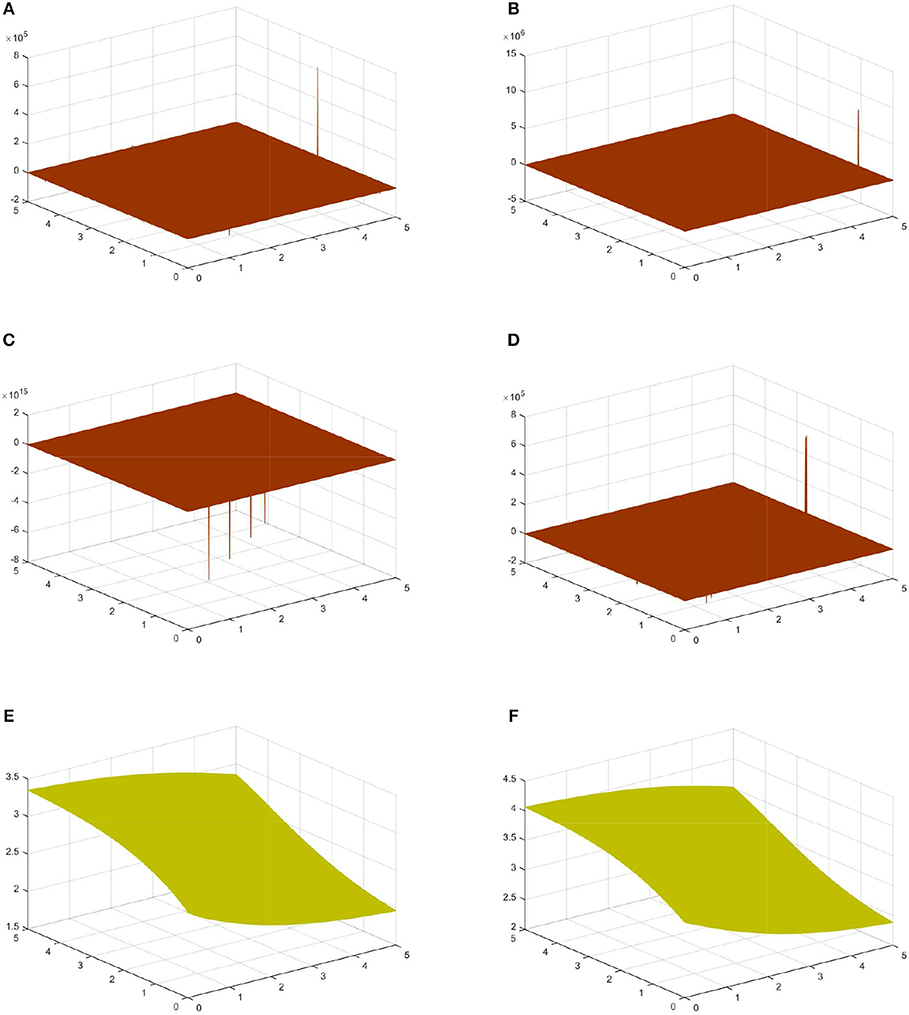
Figure 2. Physical features with suitable values of the parameters. (A) M-truncated with γ = 0.5, β = 0.9 for (29). (B) Beta with γ = 0.5 for (29). (C) M-truncated with γ = 0.5, β = 0.9 for (30). (D) Beta with γ = 0.5, β = 0.9 for (30). (E) M-truncated with γ = 0.85, β = 0.76 for (39). (F) Beta with γ = 0.85 for (39).
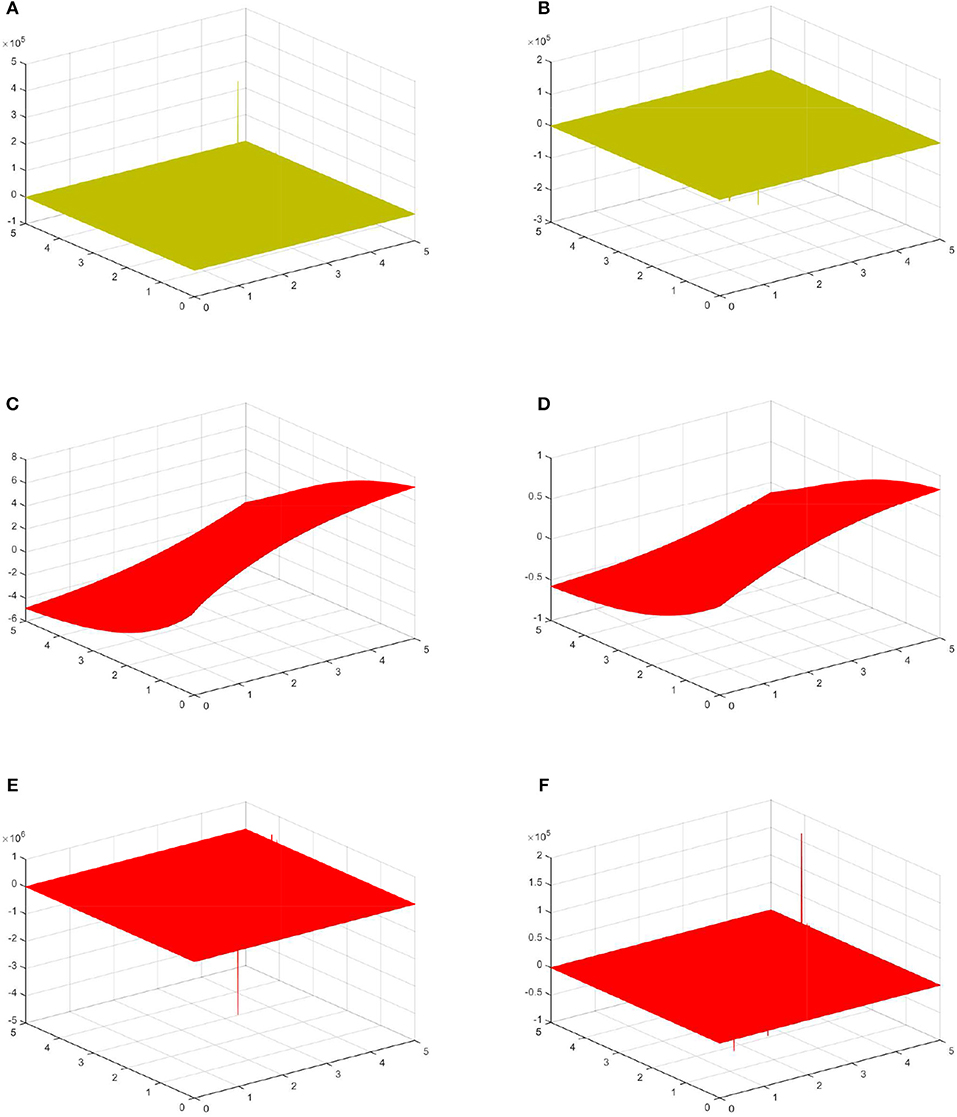
Figure 3. Physical features with suitable values of the parameters. (A) M-truncated with γ = 0.85, β = 0.76 for (40). (B) Beta with γ = 0.85, β = 0.9 for (40). (C) M-truncated with γ = 0.85, β = 0.76 for (41). (D) Beta with γ = 0.85 for (41). (E) M-truncated with γ = 0.85, β = 0.76 for (42). (F) Beta with γ = 0.85, β = 0.9 for (42).
Data Availability
All datasets generated for this study are included in the manuscript and the supplementary files.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor is currently organizing a Research Topic with one of the authors DB, and confirms the absence of any other collaboration.
References
2. Miller KS, Ross B. An Introduction to the Fractional Calculus and Fractional Differential Equations. New York, NY: Wiley (1993).
5. Bas E, Ozarslan R. Real world applications of fractional models by Atangana-Baleanu fractional derivative. Chaos Solitons Fractals. (2018) 116:121–5. doi: 10.1016/j.chaos.2018.09.019
6. El-Sayed AMA, Gaber M. The Adomian decomposition method for solving partial differential equations of fractal order in finite domains. Phys Lett A. (2006) 359:175–82. doi: 10.1016/j.physleta.2006.06.024
7. Mirzazadeh M, Eslami M, Biswas A. Dispersive optical solitons by Kudryashov's method. Optik. (2014) 125:6874–80. doi: 10.1016/j.ijleo.2014.02.044
8. Nazarzadeh A, Eslami M, Mirzazadeh M. Exact solutions of some nonlinear partial differential equations using functional variable method. Pramana. (2013) 81:225–36. doi: 10.1007/s12043-013-0565-9
9. Osman MS, Korkmaz A, Rezazadeh H, Mirzazadeh M, Eslami M, Zhou Q. The unified method for conformable time fractional Schrodinger equation with perturbation terms. Chin J Phys. (2018) 56:2500–6. doi: 10.1016/j.cjph.2018.06.009
10. Ghanbari B, Yusuf A, Inc M. Dark optical solitons and modulation instability analysis of nonlinear Schrodinger equation with higher order dispersion and cubic-quintic nonlinearity. J Coupled Syst Multiscale Dyn. (2018) 6:217–27. doi: 10.1166/jcsmd.2018.1160
11. Qureshi S, Yusuf A, Shaikh AA, Inc M, Baleanu D. Fractional modeling of blood ethanol concentration system with real data application. Chaos (2019) 29:013143. doi: 10.1063/1.5082907
12. Qureshi S, Yusuf A. Modeling chickenpox disease with fractional derivatives: from caputo to atangana-baleanu. Chaos Solit Fract. (2019) 122:111–8. doi: 10.1016/j.chaos.2019.03.020
13. Qureshi S, Yusuf A. Fractional derivatives applied to MSEIR problems: comparative study with real world data. Eur Phys J Plus. (2019) 134:171. doi: 10.1140/epjp/i2019-12661-7
14. Younas B, Younis M, Ahmed MO, Rizvi STR. Exact optical solitons in (n + 1)-dimensions under anti-cubic law of nonlinearity. Optik. (2018) 156:479–86. doi: 10.1016/j.ijleo.2017.11.148
15. Tariq KU, Younis M, Rizvi STR. Optical solitons in monomode fibers with higher order nonlinear Schrodinger equation. Optik. (2018) 154:360–71. doi: 10.1016/j.ijleo.2017.10.035
16. Ashraf R, Ahmad MO, Younis M, Tariq KU, Rizvi STR. Dipole and combo solitons in DWDM systems. Optik. (2018) 158:1073–9. doi: 10.1016/j.ijleo.2017.12.201
17. Inc M, Abdel-Gawad HI, Tantawy M, Yusuf A. On multiple soliton similariton-pair solutions, conservation laws via multiplier and stability analysis for the Whitham-Broer-Kaup equations inweakly dispersive media. Math Meth Appl Sci. (2019) 42:2455–64. doi: 10.1002/mma.5521
18. Nawaz B, Rizvi STR, Ali K, Younis M. Optical soliton for perturbed nonlinear fractional Schrodinger equation by extended trial function method. Opt Quant Electr. (2018) 50:204. doi: 10.1007/s11082-018-1468-2
19. Yusuf A, Inc M, Baleau D. Optical solitons possessing beta derivative of the Chen-Lee-Liu equation in optical fibers. Front. Phys. (2019) 7:34. doi: 10.3389/fphy.2019.00034
20. Abdel-Gawad HI, Tantawy M, Inc M, Yusuf A. On multi-fusion solitons induced by inelastic collision for quasi-periodic propagation with nonlinear refractive index and stability analysis. Mod Phys Lett B. (2018) 32:1850353. doi: 10.1142/S0217984918503530
21. Ghanbari B, Yusuf A, Inc M, Baleanu D. The new exact solitary wave solutions and stability analysis for the (2+1)-dimensional Zakharov-Kuznetsov equation. Adv Diff Equat. (2019) 2019:49. doi: 10.1186/s13662-019-1964-0
22. Eslami M, Neirameh A. New exact solutions for higher order nonlinear Schrodinger equation in optical fibers. Opt Quant Electr. (2018) 50:47. doi: 10.1007/s11082-017-1310-2
23. Eslami M, Mirzazadeh M. Optical solitons with Biswas Milovic equation for power law and dual-power law nonlinearities. Nonlin Dyn. (2016) 83:731–8. doi: 10.1007/s11071-015-2361-1
24. Eslami M, Rezazadeh H. The first integral method for Wu Zhang system with conformable time-fractional derivative. Calcolo. (2016) 53:475–85. doi: 10.1007/s10092-015-0158-8
25. Khodadad FS, Nazari F, Eslami M, Rezazadeh H. Soliton solutions of the conformable fractional Zakharov Kuznetsov equation with dual-power law nonlinearity. Opt Quant Electr. (2017) 49:384. doi: 10.1007/s11082-017-1225-y
26. Eslami M, Mirzazadeh M. First integral method to look for exact solutions of a variety of Boussinesq-like equations. Ocean Eng. (2014) 83:133–7. doi: 10.1016/j.oceaneng.2014.02.026
27. Biswas A, Mirzazadeh M, Eslami M, Milovic D, Belic M. Solitons in optical metamaterials by functional variable method and first integral approach. Frequenz. (2014) 68:525–30. doi: 10.1515/freq-2014-0050
28. Ekici M, Mirzazadeh M, Eslami M. Solitons and other solutions to Boussinesq equation with power law nonlinearity and dual dispersion. Nonlin Dyn. (2016) 84:669–76. doi: 10.1007/s11071-015-2515-1
29. Mirzazadeh M, Eslami M, Biswas A. 1-Soliton solution of KdV6 equation. Nonlin Dyn. (2015) 80:387–96. doi: 10.1007/s11071-014-1876-1
30. Rezazadeh H, Korkmaz A, Eslami M, Vahidi J, Asghari R. Traveling wave solution of conformable fractional generalized reaction Duffing model by generalized projective Riccati equation method. Opt Quant Electr. (2018) 50:150. doi: 10.1007/s11082-018-1416-1
31. Zhou Q, Ekici M, Sonmezoglu A, Mirzazadeh M, Eslami M. Optical solitons with Biswas Milovic equation by extended trial equation method. Nonlin Dyn. (2016) 84:1883-900. doi: 10.1007/s11071-016-2613-8
32. Eslami M. Trial solution technique to chiral nonlinear Schrodinger's equation in (1+ 2)-dimensions. Nonlin Dyn. (2016) 85:813–6. doi: 10.1007/s11071-016-2724-2
33. Mirzazadeh M, Eslami M, Zerrad E, Mahmood MF, Biswas A, Belic M. Optical solitons in nonlinear directional couplers by sine cosine function method and Bernoulli's equation approach. Nonlin Dyn. (2015) 81:1933–49. doi: 10.1007/s11071-015-2117-y
34. Neirameh A, Eslami M. An analytical method for finding exact solitary wave solutions ofthe coupled (2 1)-dimensional Painlev Burgers equation. Sci Iran. (2017) 24:715–26. doi: 10.24200/sci.2017.4056
35. Neirameh A, Eslami M. New travelling wave solutions for plasma model of extended K-dV equation. Afrika Matematika. (2019) 30:335–44. doi: 10.1007/s13370-018-00651-2
36. Mirzazadeh M, Eslami M, Biswas A. Soliton solutions of the generalized Klein Gordon equation by using G' G-expansion method. Comput Appl Math. (2014) 33:831–9. doi: 10.1007/s40314-013-0098-3
37. Eslami M. Solutions for Space Time Fractional (2+ 1)-Dimensional Dispersive Long Wave Equations. Iran J Sci Technol Trans A. (2017) 41:1027–32. doi: 10.1007/s40995-017-0320-z
38. Eslami M, Rezazadeh H, Rezazadeh M, Mosavi SS. Exact solutions to the space time fractional Schrdinger Hirota equation and the space time modified KDV Zakharov Kuznetsov equation. Opt Quant Electron. (2017) 49:279. doi: 10.1007/s11082-017-1112-6
39. Podlubny I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of TheirSolution and Some of Their Applications. New York, NY: Academic Press (1998). p. 198.
41. Singh J, Kumar D, Al Qurashi M, Baleanu D. A new fractional model for giving up smoking dynamics. Adv Differ Equ. (2017) 2017:88. doi: 10.1186/s13662-017-1139-9
42. Caputo M, Mainardi F. A new dissipation model based on memory mechanism. Pure Appl. Geophys. (1971) 91:134–47. doi: 10.1007/BF00879562
43. Bas E, Acay B, Ozarslan R. Fractional models with singular and non-singular kernels for energy efficient buildings. Chaos. (2019) 29:023110. doi: 10.1063/1.5082390
44. Atangana A, Baleanu D. New fractional derivatives with nonlocal and non-singular kernel. Theory Appl Heat Transfer Model Therm Sci. (2016) 20:763–9. doi: 10.2298/TSCI160111018A
45. Atangana A, Secer A. A note on fractional order derivatives and table of fractional derivatives of some special functions. Abstr Appl Anal. (2013) 2013:279681. doi: 10.1155/2013/279681
46. Khalil R, Al Horani M, Yousef A, Sababheh M. A new definition of fractional derivative. J Comput Appl Math. (2014) 264:65–70. doi: 10.1016/j.cam.2014.01.002
47. Acay B, Bas E, Abdeljawad T. Non-local fractional calculus from different viewpoint generated by truncated M-derivative. J Comput Appl Math. (2019) 366:112410. doi: 10.1016/j.cam.2019.112410
48. Sousa JVDC, de Oliveira EC. A new truncated M-fractional derivative type unifying some fractional derivative types with classical properties. Int J Anal Appl. (2018) 16:83–96.
49. Scott AC. Encyclopedia of Nonlinear Science. New York, NY: Routledge, Taylor and Francis Group (2005).
50. Mirzazadeh M, Ekici M, Sonmezoglu A, Eslami M, Zhou Q, Kara AH, et al. Optical solitons with complex Ginzburg-Landau equation. Nonlin Dyn. (2016) 85:1979–2016. doi: 10.1007/s11071-016-2810-5
51. Shwetanshumala S. Temporal 1-soliton solution of the complex Ginzburg-Landau equation with power law nonlinearity. Prog Electromagn Res Lett. (2009) 96:1–7. doi: 10.2528/PIER09073108
52. Tian B, Gao YT. On the generalized Tanh method for the (2+1)-dimensional breaking soliton equation. Modern Phys Lett A. (1995) 10:2937–41. doi: 10.1142/S0217732395003070
53. Inc M, Yusuf A, Isa AI, Baleanu D. Dark and singular optical solitons for the conformable space-time nonlinear Schrodinger equation with Kerr and power law nonlinearity. Optik. (2018) 162:65–75. doi: 10.1016/j.ijleo.2018.02.085
54. Rosenau P, Hyman JM, Staley M. Multidimensional compactons. Phys Rev Lett. (2007) 98:024101. doi: 10.1103/PhysRevLett.98.024101
Keywords: complex Ginzburg-Landau equation, generalized tanh method, generalized Bernoulli sub-ODE method, beta derivative, optical solitons
Citation: Yusuf A, Inc M and Baleanu D (2019) Optical Solitons With M-Truncated and Beta Derivatives in Nonlinear Optics. Front. Phys. 7:126. doi: 10.3389/fphy.2019.00126
Received: 15 April 2019; Accepted: 21 August 2019;
Published: 04 September 2019.
Edited by:
Alex Hansen, Norwegian University of Science and Technology, NorwayReviewed by:
Mostafa Eslami, University of Mazandaran, IranHaci Mehmet Baskonus, Harran University, Turkey
Copyright © 2019 Yusuf, Inc and Baleanu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Abdullahi Yusuf, eXVzdWZhYmR1bGxhaGlAZnVkLmVkdS5uZw==
 Abdullahi Yusuf
Abdullahi Yusuf Mustafa Inc
Mustafa Inc Dumitru Baleanu
Dumitru Baleanu