The Multiple Point Principle and Extended Higgs Sectors

1. Introduction

It is widely believed that investigations of the Higgs boson and the resulting breaking of Electroweak Symmetry provide the best opportunity for finding new physics beyond the Standard Model (SM). In part, this is because the Higgs boson is the most recently discovered fundamental particle [1], and investigations of its properties are still underway (though so far no significant deviation from the SM has been observed [2–5]). This view is reinforced by the required relative smallness of the Higgs boson mass and its related hierarchy problem. Since the SM Higgs boson mass is unprotected by any symmetries, it should have large quantum corrections of magnitude comparable to the scale of new physics. To restore a physical Higgs mass of order the Electroweak scale one must fine-tune to ensure the unnatural cancelation of the bare Higgs mass with its corrections. Provided there is new physics of some type beyond the SM (a reasonable assumption, given its large number of problems and omissions) this is a genuine and very real issue that must be addressed.

The combined ATLAS and CMS value of the Higgs mass [2], m_h = 125.09 ± 0.23GeV, raises further questions. This is a challenging value for both supersymmetry and composite Higgs models, requiring a significant tuning of parameters or a non-minimal field content [6–8], making it difficult to motivate any particular models and unclear which direction to head next. However, this particular mass has another reason for being peculiar—it is just the right value to allow the Higgs potential to be metastable at high energies [6].

As usual for a parameter of a Quantum Field Theory, the Higgs quartic coupling λ evolves with energy according to the Renormalization Group (RG) and is pulled downwards at higher energies by the large top-quark mass. If it were to run to negative values the potential may become unstable and the correct pattern of Electroweak Symmetry breaking is lost. Indeed, requiring absolute stability of the vacuum up to the Planck scale M_Pl, i.e., λ(M_Pl) ≥ 0, places a limit on the top mass [6],

$\begin{array}{ll}{m}_t<171.36\pm 0.46\text{ GeV},& (1)\end{array}$

which is in tension with the current experimental value by about 2.6 σ. Figure 1A shows the quartic coupling dependence on renormalization scale μ, and the 3 σ uncertainties that arise from the uncertainties in the top-quark mass m_t and the strong coupling constant α_s. The quartic coupling turns negative at an energy scale of μ ~ 10¹⁰ GeV, though a stable potential is not ruled out due to the uncertainties. However, a very small negative value is not a catastrophe, since the vacuum may still be metastable with a lifetime much longer than the age of the universe. That nature should choose this metastable vacuum is intriguing. Why does the quartic coupling become so very nearly zero right at the Planck scale?

FIGURE 1

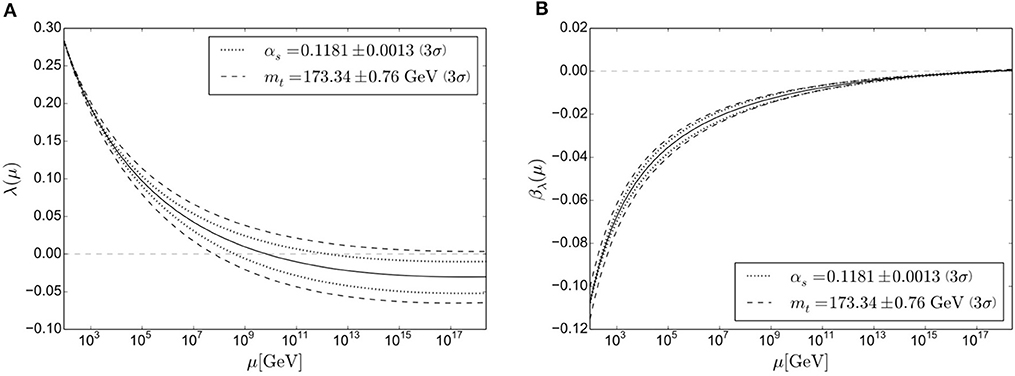
Figure 1. (A) Three-loop running of the SM Higgs quartic coupling λ and (B) its β function with 3 σ uncertainties from the top pole mass m_t (dashed) and the strong coupling constant α_s (dotted). These plots originally appeared in McDowall and Miller [9].

We may gain further insight by examining the beta-function of the quartic coupling, shown in Figure 1B. As indicated already in Figure 1A, the running of λ flattens out at high energies, i.e., β_λ(M_Pl) ≈ 0 too. We stress that in the SM this is not an ultraviolet fixed-point since λ would continue to evolve if we increased the energy further. However, if some new physics theory takes over above the Planck scale, then the SM running becomes irrelevant and we must instead consult the new theory. If this new theory sets λ = β_λ = 0 at the Planck scale we may recover a low energy phenomenology very similar to what we observe, modulo the slight deviation in the Higgs mass.

In this article, we will review one proposed high scale possibility, the Multiple Point Principle (MPP) [10]. Although this is not compatible with the SM running, it provides a Higgs mass prediction that is curiously close to the measured value. We will then examine several theories with extended Higgs sectors to see if they alter the running sufficiently to provide the correct Higgs mass. For recent investigations of alternative high scale boundary conditions at M_Pl (see for example [11–16]).

2. The Multiple Point Principle in the SM

The Multiple Point Principle (MPP) asserts that nature chooses the Higgs potential parameters so that different phases of electroweak symmetry breaking may coexist. This is analagous to how ice, water and vapor may coexist for specific values of temperature and pressure near water's triple-point. Since the two phases must be energetically comparable in order to coexist, this means that the potential should have at least two degenerate vacua, that is an additional vacuum degenerate with the usual Electroweak vacuum.

The authors of this principle argue in Froggatt and Nielsen [10] that this is rather natural if we consider extensive variables constrained by some new physics theory at high energies, as long as the system has a rather strong first order phase transition. Again we may use the analogy of water and note that slush (in which ice and liquid water coexist) is present for a (relatively) wide range of extensive variables (in this case temperature and pressure) due to the existence of a first order phase transition. Returning to the Higgs potential, a possible extensive quantity could be 〈|ϕ|²〉. If this were set by some new physics theory at the Planck scale with a strong first order phase transition, it would be rather likely to find $\langle |\varphi {|}^2\rangle ~M_{\text{Pl}}^2$, leading to a second degenerate vacuum at the Planck Scale. In essence, this principle is relying on a rather flat distribution of extensive parameter space set at the Planck scale matching to a rather peaked distribution of intensive parameters (i.e., the usual Higgs potential parameters) due to a strong first-order phase transition, which in turn leads to a second degenerate vacuum [17].

We should note that what this Planck scale theory could be is still unknown, and Froggatt and Nielsen [10] makes no attempt to describe one, using only general principles to support the assertion. Also, we note that this provides no explanation of why the Planck scale is so much bigger than the electroweak scale. Nevertheless, the constraints on the Higgs parameters does provide a prediction of the Higgs boson mass that can be compared with experiment, and we further note that this prediction was first made long before the Higgs boson discovery.

The one-loop Coleman-Weinberg effective potential [18] can be written,

$\begin{array}{ll}{V}_{\text{eff}}=-{\mu }^2(\mu ){\varphi }^2+\frac{1}{4}\lambda (\mu ){\varphi }^4(\mu )+\frac{1}{16{\pi }^2}{V}_1,& (2)\end{array}$

where V₁ takes the schematic form $V_1~{\varphi }^{2}log({\varphi }^2/{\mu }^2)$. For a more explicit form see, for example, Jegerlehner et al. [19]. We see that at one-loop, in addition to the new logarithmic contribution, the parameters μ and λ become energy dependent. For low field values (and low energies) this reproduces the usual “wine-bottle” potential of the Higgs mechanism, but for higher field values, the logarithm pulls the potential back down. Eventually the ϕ⁴ terms becomes dominant and the potential will remain stable at the Planck scale if λ(M_Pl) > 0. However, the additional structure causes a second minimum very close to the Planck scale. This is schematically depicted in Figure 2. In the SM, taking the measured central values of the Higgs potential parameters, the second vacuum is of slightly lower energy than the Electroweak vacuum, causing the potential to be metastable. The MPP posits that the two minima should be degenerate.

FIGURE 2

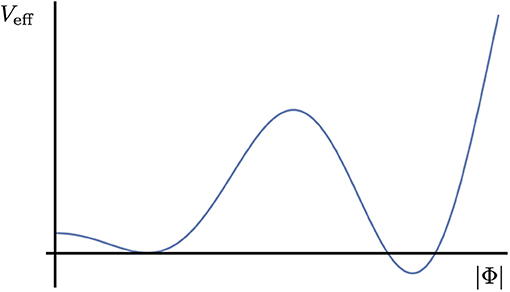
Figure 2. A schematic depiction of the one-loop effective potential in the SM. This is intended only to present a general picture of the minima and is not to scale.

For high field values the effective potential is dominated by its quadratic term, $V_{\text{eff}}\approx \lambda (\mu ){\varphi }^4$, so the second minima at the Planck scale requires

$\begin{array}{ll}{\frac{d{V}_{\text{eff}}}{d\varphi }|}_{\varphi =M_{\text{Pl}}}\approx \lambda (\mu ){\varphi }^3+\frac{1}{4}{\beta }_{\lambda }(\mu ){\varphi }^4=0.& (3)\end{array}$

We see that the MPP is satisfied if λ(M_Pl) = β_λ(M_Pl) = 0.

Applying this boundary condition, the MPP hypothesis gave an early prediction [10] of the Higgs mass m_h = 135 ± 9 GeV, which is remarkably good considering it was made 17 years before the discovery of the Higgs boson, and they simultaneously predicted the top-quark mass (finding 173 ± 5GeV) in the same year it was discovered. A more recent calculation using the measured top-quark mass and newer determinations of e.g., α_s, gave m_h = 129 ± 1.5 GeV [6]. Although this is slightly too high to be compatible with our by now very accurate Higgs mass measurement, it is still rather remarkable.

Figure 3A shows contours corresponding to the boundary conditions λ(M_Pl) = 0 and β_λ (M_Pl) = 0 in the m_h − m_t plane, and we see that a slightly heavier Higgs is needed for both conditions to be satisfied. These contours are calculated using three-loop SM RG equations; the Higgs mass is calculated to two-loop order, while the top mass additionally contains three-loop QCD corrections. This plot is in agreement with the similar plot in Degrassi et al. [11], but we used a different value of the uncertainty in the strong coupling constant α_s(M_Z) = 0.1181 ± 0.0013 to reflect more recent estimates [20]. We also use the reduced Planck scale $M_{\text{Pl}}=2.4\times 10^{18}$GeV as our scale at which these boundary conditions are set. Figure 3A shows that λ(M_Pl) = 0 can be satisfied with an acceptable value of m_h for a top mass 171GeV ≲ m_t ≲ 174GeV, and although the corresponding value of β _λ(M_Pl) is not zero, it is extremely small.

FIGURE 3

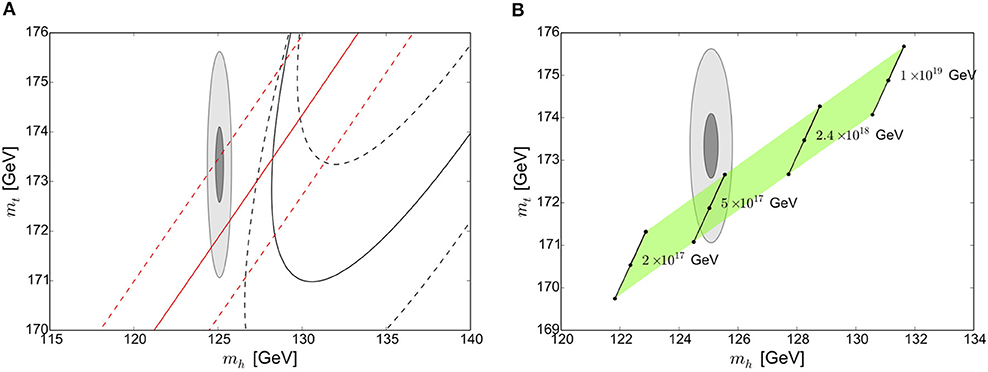
Figure 3. (A) λ (M_Pl) = 0 (red) and β_λ (M_Pl) = 0 (black) contours in the m_h − m_t plane. The dashed lines show 3 σ variations in α_s(M_Z) = 0.1181 ± 0.0013. (B) Mass values that satisfy both boundary conditions at various UV scales. The green region corresponds to a 1 σ uncertainty in α_s. Ellipses show the experimentally allowed values of m_t and m_h with 1 σ (dark gray) and 3 σ (light gray) uncertainty. These plots originally appeared in McDowall and Miller [9].

Note that we have required that these boundary conditions be satisfied at M_Pl, but if the theory that dictates the appearance of a second minimum were to become active at a lower energy scale, these boundary conditions would need to be altered. Figure 3B shows the m_h − m_t plane with points that satisfy both boundary conditions λ = β_λ = 0 simultaneously at different UV scales. The green region corresponds to a 1 σ uncertainty in α_s. We see it is possible to obtain a Higgs mass that is within experimental limits by applying these boundary conditions at approximately 5 × 10¹⁷ GeV. It's interesting to note that this is a scale of importance in string scenarios (see e.g., [21, 22]).

As one approaches the Planck Scale, one might expect gravity to become significant and contribute to the RGE running of couplings. The study of these effects has caused some confusion in the literature. An initial calculation of the effect on the running of gauge couplings [23], using a quantized Einstein-Hilbert action as an effective field theory below the Planck scale, showed that this alters the gauge couplings sufficiently to render them asymptotically free. However, this calculation was disputed [24, 25] on the grounds that the derived result is gauge-dependent and therefore unreliable; a calculation performed with a different gauge choice (the harmonic gauge) instead revealed the contributions to be exactly zero. A recalculation was then done using the gauge-invariant background field method [26, 27] and found a result in support of the original claim that the gauge coupling is rendered asymptotically free, though with a modified β-function. Also see He et al. [28] and Daum et al. [29] for alternative calculations. Calculations have also been performed to asses the affect on the quartic Higgs self-coupling relevant to the MPP [30, 31]. These two calculations disagree on the sign of the gravitational contributions to Yukawa couplings, but the corrections to the predicted Higgs mass are small; they predict a Higgs mass of “approximately 130 GeV” and “≳131.5 GeV,” neither of which are differing very far from the earlier prediction of 129 ± 1.5 GeV [6] and remain incompatible with the SM. See also Branchina et al. [32] for a discussion of the effect on the electroweak vacuum of Planck suppressed operators.

3. A Real Singlet Extension

The simplest extension to the Higgs sector is to include an extra real singlet S, with potential,

$\begin{array}{ll}V(\Phi ,S)={\mu }^2{\Phi }^{†}\Phi +m_S^2{S}^2+\lambda {\left({\Phi }^{†}\Phi \right)}^2+{\lambda }_S{S}^4+k_2{\Phi }^{†}\Phi S^2,& (4)\end{array}$

where a Z₂ symmetry, under which the new scalar is odd, has been used to eliminate terms odd in S [see [33] for a discussion of this model]. During electroweak symmetry breaking, the real singlet field can acquire a non-zero vacuum expectation value (vev) v_S alongside the SM Higgs. The usual Higgs scalar may then mix with the new singlet, though this mixing should not be too strong if we want to avoid LHC constraints. The singlet mass m_S is fixed by the tadpole equation minimizing the potential, analagous to the fixing of μ using the vev v. This leaves the parameters λ, λ_S, k₂, and v_S. We refer to this as the “broken phase.” Alternatively, if the new scalar does not acquire a vev (i.e., v_S = 0) the tadpole equation becomes trivial and cannot be used to remove m_S. Therefore we have parameters λ, λ_S, k₂, and m_S. Now the scalars do not mix, and the new scalar may be a Dark Matter candidate, so we refer to this as the “Dark Matter phase.”

This real singlet model has been investigated in the context of the MPP in Haba et al. [34–36], Hamada et al. [37], and Kawana [38, 39], with varying results. Haba et al.[34] investigated the model in the Dark Matter phase for the MPP as well as the Veltman condition [40]. They found that both boundary conditions could be accommodated (separately) with a 126 GeV Higgs boson, while simultaneously providing the correct DM relic density. An alternative approach was taken in Haba et al. [35, 36] where the MPP was instead imposed on the real singlet model with the addition of an extra right-handed neutrino. Again, the MPP could be made compatible with a 126 GeV Higgs boson provided the scalar mass fell between approximately 850–1,400 GeV and the right-handed neutrino remained very heavy (of order 10¹⁴ GeV). The MPP can instead be imposed at the “string scale” of 10¹⁷ GeV in order to facilitate Higgs inflation, which results in somewhat lighter DM at around 400 − 470 GeV [37]. Kawana [38] includes three additional right-handed neutrinos (one for each generation) at 10¹³ GeV and instead of fixing the MPP condition at M_Pl allows the boundary condition energy scale to shift, insisting only that λ = β_λ = 0 at a single scale. Similarly to the other analyses this finds the DM mass must be of order 770–1,050 GeV. Finally, Kawana [39] investigates a gauged B-L model, and claim that this can accommodate an MPP condition applied at 10¹⁷ GeV, as well as Higgs inflation, by tuning the coupling of the Higgs boson to the new scalar.

We see that applying the Planck scale MPP to the real singlet model requires λ = λ_S = k₂ = β_λ = β_λS = β_k2 = 0. However, this constraint will immediately decouple the new scalar state, and the couplings will not be regenerated by renormalization group running. In other words we revert back to the SM. This seems a serious barrier to the MPP, but is not quite as bad as it appears. Firstly, the MPP itself is somewhat imprecise—the strong first order phase transition made the particular choice of parameters more likely but some wriggle-room in these parameters is not unreasonable. (How much wriggle-room is appropriate depends on the UV theory of course.) Furthermore, our calculations themselves are imprecise and include uncertainties. We truncate our β-functions at two-loops and apply approximations to find the MPP solutions themselves. Therefore, it is more appropriate to ask if the MPP constraints can be approximately applied, i.e., λ, λ_S, k₂, β_λ, β_λS, and β_k2 should be “small.”

To investigate if small parameters are compatible with the low energy observations we fix all the quartic scalar couplings at M_Pl. We perform a scan over Planck scale parameters, allowing λ, λ_S, and |κ₂| to vary between 0 and 1. We also allow v_S or m_S to vary between zero and 2TeV in the broken or Dark Matter phases, respectively. We use SARAH 4.12.2 [41] to calculate the two-loop β functions as well as the mass matrices, tadpole equations, vertices and loop corrections we need to calculate mass spectra at low energies; and FlexibleSUSY 2.0.1 [42–45] is used to build the spectrum generator needed to get the mass spectrum for each point.

Valid parameter choices must result in a vacuum that is bounded from below up to M_Pl, so we also require, at all scales, the vacuum stability conditions,

$\begin{array}{ll}\lambda ,{\lambda }_S\ge 0,\sqrt{\lambda {\lambda }_S}+k_2\ge 0.& (5)\end{array}$

We also require dimensionless couplings remain perturbative up to M_Pl, so,

$\begin{array}{ll}\lambda ,{\lambda }_S,k_2\le \sqrt{4\pi }.& (6)\end{array}$

We further check vacuum stability using Vevacious [46] which minimizes the one-loop effective potential and checks that it is indeed the global minimum. We also require that one of the two scalars of the model is a valid SM Higgs, with mass in the range 124.7 GeV ≤ m_h,H ≤ 127.1 GeV. We allow for a wider range of Higgs masses than the experimental uncertainty as an estimate of the theoretical uncertainty associated with the calculation of the mass spectrum.

These constraints already invalidate much of the parameter space, but we must also apply experimental constraints from the LHC, LEP, and Tevatron to ensure they are phenomenologically viable. To this end, we employ HiggsBounds [47] and HiggsSignals [48], and further use sHDECAY [49–51] to calculate the total widths and branching ratios for each parameter choice.

In the Dark Matter phase we must also include constraints from the dark matter, using micrOMEGAS [52] to calculate the relic density to compare with the combined WMAP [53] and Planck [54] result,

$\begin{array}{ll}\Omega h^2=0.1199\pm 0.0027.& (7)\end{array}$

A point is excluded if the calculated relic density is greater than Ωh² + 3 σ to ensure that a DM candidate does not overclose the universe, but we allow for the possibility that there may be some other contributions to the relic density which we are not taking into account. We also include constraints from dark matter direct detection that place limits on the spin independent cross section of weakly interacting massive particles (WIMPs) on nucleons. The strongest of those constraints comes from the LUX experiment [55].

We present the results of the analysis of the broken phase in Figure 4, where we see lots of parameter choices pass the theoretical and experimental constraints, although only a few of these obey the MPP criterion of the quartic couplings being small. We are interested in points that fall in the lower left corner of Figures 4A–C as well as those to the left in Figure 4D. To further aid in the discrimination of small values we have colored red those points for which β_λ < 0.0009, β_λS < 0.019, and β_k2 < 0.0045, which is an estimate of the truncation error in their high scale values as estimated by the difference between the one and two loop Renormalization Group running.

FIGURE 4

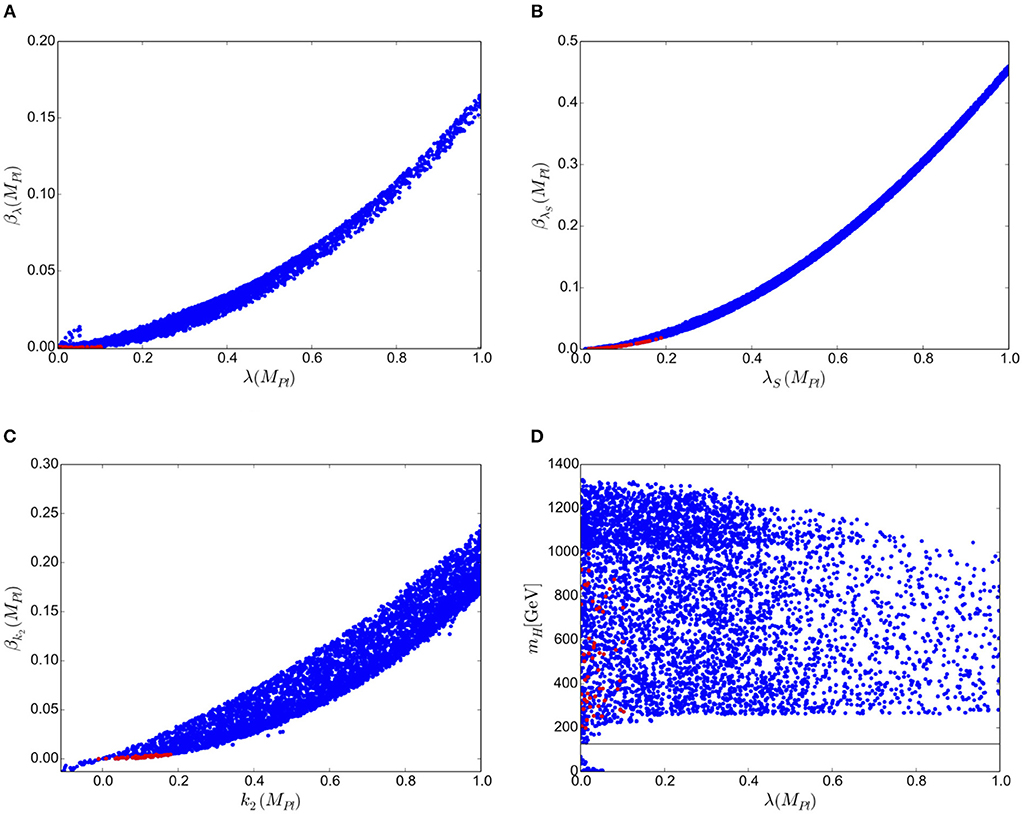
Figure 4. Values of (A) λ(M_Pl), (B) λ_S(M_Pl) and (C) λ(M_Pl) compared to their respective β-functions in the broken phase. All points pass theoretical and experimental constraints. Red points further obey β_λ < 0.0009, β_λS < 0.019, β_k2 < 0.0045 at M_Pl. Also shown (D) is the mass of the additional Higgs for values of λ(M_Pl).

These reasonably numerous red points indicate parameter choices for which there is indeed a second approximately degenerate vacuum at the Planck scale, that provide the correct Higgs boson mass and conform to all low energy observations. This remarkable result need not have been the case. Unfortunately we have also lost predictive power. The SM Higgs mass is fixed by our constraints, so not a prediction and the new Higgs mass can take on a rather wide range of values between 200GeV and 2TeV.

It is much more difficult to accommodate the MPP in the Dark Matter phase, as can bee seen in Figure 5, which is in part due to the extra constraint from Dark Matter which considerably reduces the acceptable points. We do see parameter choices that evade all constraints with very small values of the β-functions (red points) but these often have rather large values of the quartic couplings. This is especially true for κ₂ but is also true, to a lesser degree, for λ.

FIGURE 5

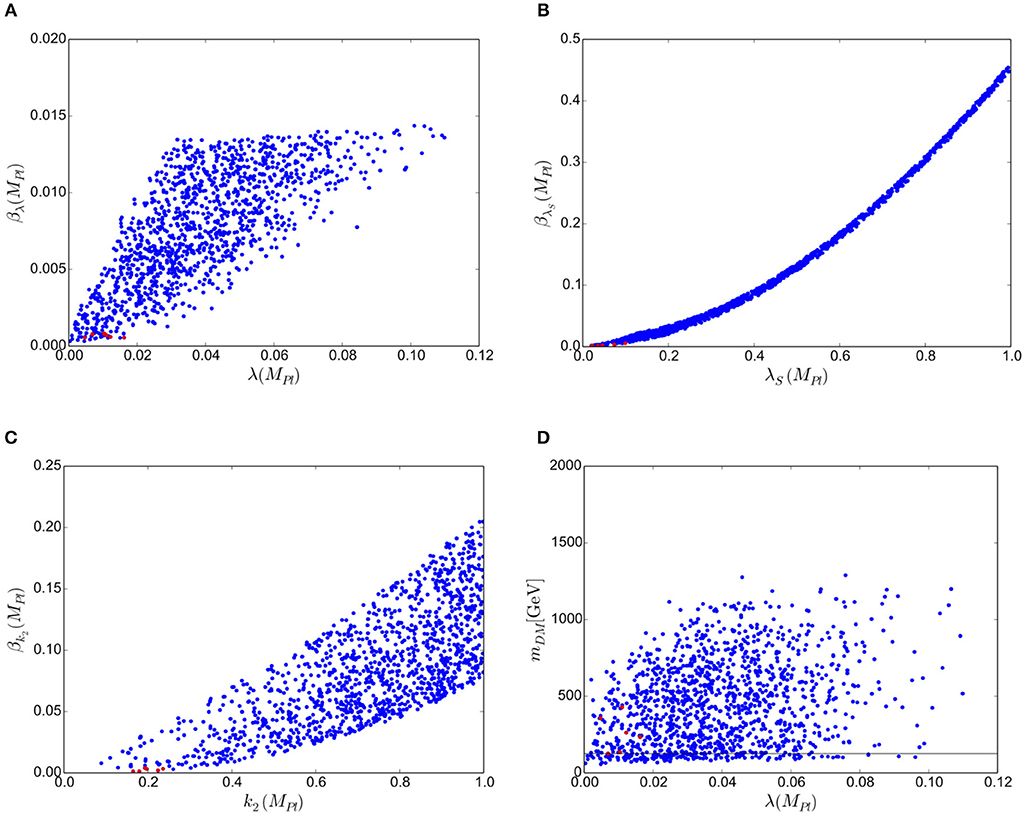
Figure 5. Values of (A) λ(M_Pl), (B) λ_S(M_Pl) and (C) λ(M_Pl) compared to their respective β-functions in the Dark Matter phase. All points pass theoretical and experimental constraints. Red points further obey β_λ < 0.0009, β_λS < 0.019, β_k2 < 0.0045 at M_Pl. Also shown (D) is the mass of the additional scalar for values of λ(M_Pl).

4. A Complex Singlet Extension

We may complicate the model only slightly be promoting our new singlet to a complex field, 𝕊 = S₁ + iS₂, and consider a potential of the form [33, 50, 56–60]

$\begin{array}{lll}V& =& \frac{{\mu }^2}{2}{H}^{†}H+\frac{\lambda }{4}{\left(H^{†}H\right)}^2+\frac{\delta }{2}\left(H^{†}H\right)|\text{𝕊}{|}^2+\frac{b_2}{2}|\text{𝕊}{|}^2\\ & +& \frac{d_2}{4}|\text{𝕊}{|}^4+\left(\frac{b_1}{4}{\text{𝕊}}^2+a_1\text{𝕊}+c.c\right).& (8)\end{array}$

For computational convenience we define

$\begin{array}{ll}{b}_{\pm }=\frac{1}{2}(b_2\pm b_1),& (9)\end{array}$

which function as the (squared) masses if the model is recast as two real scalar fields. The complex singlet field may acquire a non-zero vev for its real, and possibly imaginary, part. If both real and imaginary parts acquire non-zero vevs,

$\begin{array}{ll}\text{𝕊}=\frac{1}{\sqrt{2}}\left[v_{s_1}+s_1+i\left(v_{s_2}+s_2\right)\right],& (10)\end{array}$

we again call this the “broken phase” following our earlier nomenclature (introduced in [59]). Therefore, in addition to the bilinear terms μ² and b_± which are fixed via the electroweak vacuum minimization conditions, the model is described by

$\begin{array}{ll}\lambda ,d_2,\delta ,v_{s_1},v_{s_2},a_1.& (11)\end{array}$

In this phase, all three scalar field fluctuations h, s₁ and s₂ mix.

In contrast, if the vev of the imaginary part remains zero, the second electroweak vacuum minimization condition (for S₂) is trivial and b₋ becomes a free parameter. In this case the input parameters are

$\begin{array}{ll}\lambda ,d_2,\delta ,v_{s_1},b_{-},a_1.& (12)\end{array}$

Now we find ourselves in the “dark matter phase,” where mixing is allowed between h and the real part of the complex singlet field s₁. The imaginary part s₂ does not mix and is a dark matter candidate kept stable by the symmetry S₂ → −S₂.

The numerical analysis of this model follows closely with that of the real singlet extension discussed above. We scan over λ, d₂, and δ, allowing them to vary between 0 and 0.5; v_s1 and v_s2, if present, are allowed to take values up to 2TeV; b₋ has dimension mass² and is allowed to range to 10⁵GeV². Finally a₁, with dimension mass³ and is allowed up to 10⁸ GeV³.

We make use of SARAH and FlexibleSUSY again (though slightly older versions, 4.9.3 and 1.6.1, respectively). Constraints on vacuum stability and perturbativity are again applied; in this case stability requires [58]

$\begin{array}{ll}\lambda ,d_2\ge 0,\delta +\sqrt{\lambda d_2}\ge 0.& (13)\end{array}$

The global minimum is ensured with Vevacious. Finally, we allowed the same Higgs mass range as before and apply experimental constraints using HiggsBounds, and HiggsSignals [48], and sHDECAY. MicrOMEGAS is used to provide constraints from Dark Matter in the Dark Matter phase. For further details of this analysis (see [9]).

We are in principle interested in the high scale constraints λ = β_λ = 0, d₂ = β_d2 = 0 and δ = β_δ = 0. However, similar to the real scalar case, we note that setting δ to zero at M_Pl decouples the extra scalars from the SM, and since β_δ = 0 for this choice, δ remains zero at all scales and the new scalars are unobservable. We are therefore forced to only consider δ “small.” The situation for d₂ is slightly more subtle—for non-zero values of δ, we cannot set d₂ exactly to zero at M_Pl since it is immediately driven negative by RG running and the vacuum destabilizes according to (13). So again, we are forced to only consider d₂ “small” at the Planck scale and indeed must keep it large enough at M_Pl to stop it running negative. Fortunately this is not too onerous, and stability is still viable with d₂ as small as 0.005 at the Planck scale, but it is not really clear how large we should permit this to be and still regard the MPP as “approximately valid.”

In the broken phase, we now have three neutral scalars that mix. One must provide the SM Higgs, while we will call the other two m_hLight and m_hHeavy. Obviously m_hLight < m_hHeavy, but that h_Light may still be heavier than the SM-like Higgs, or correspondingly h_Heavy may be lighter. We note that these new states may be considerably lighter than the discovered Higgs mass as long as the component from the doublet is not too large, leaving it relatively decoupled.

This time we will look first at surviving scenarios in the m_hLight − m_hHeavy plane, with small values of λ and β_λ at the high scale. In Figure 6A we see scenarios that survive all theoretical and experimental constraints. For clarity of the plot, we restrict our points to those with λ < 0.067 and β_λ,δ,d2 < 0.05 at M_Pl. Points shown in red have been further restricted to have exceptionally small values of β_λ < 0.00005, which is the appropriate truncation error arising from the RG running. Corresponding restrictions on β_δ and β_d2 would be β_δ < 0.00025 and β_d2 < 0.001, but unfortunately we find if we apply these then no points survive.

FIGURE 6

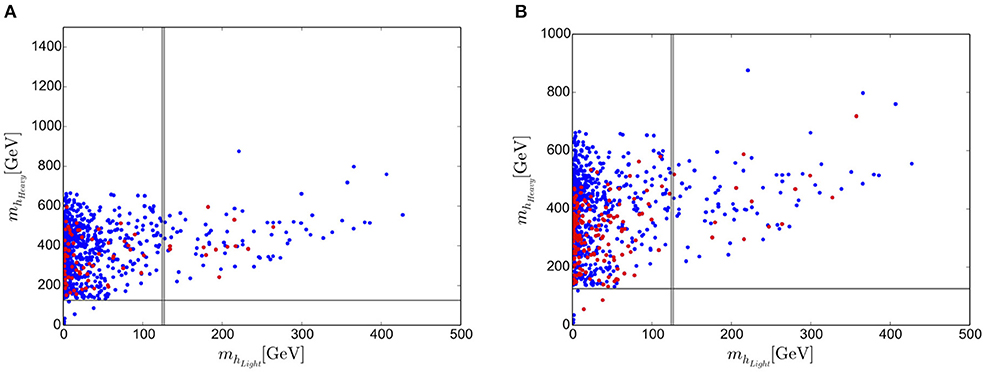
Figure 6. Values of m_hLight and m_hHeavy in the broken phase. All points obey λ < 0.067 and β_λ,δ,d2 < 0.05 at M_Pl. The gray bands highlight the SM Higgs mass range. (A) Red points obey the more restrictive condition β_λ < 0.00005. (B) Red points obey β_λ < 0.0005, β_δ < 0.0025 and β_d2 < 0.01. These plots originally appeared in McDowall and Miller [9].

However, we are reluctant to declare the MPP incompatible with the complex singlet extension. These restrictions on the β-functions are exceedingly severe and may be too strong. Without knowing the form of the UV completion, we don't know the size of any possible threshold corrections that might arise was we approach the Planck scale, so really don't know how much deviation from zero we should allow in our boundary conditions. To allow some extra slack, we can somewhat arbitrarily relax our boundary condition β-function cut-offs to ten times the truncation error. We now find some points survive and plot these in Figure 6B. Notice that a small number of points survive that have the SM Higgs as the heaviest of the three scalars.

In the dark matter phase only two of the three scalars are allowed to mix, with the third becoming a dark matter candidate. We call the non-SM-like Higgs h_New whilst the DM scalar is h_DM. Figure 7A examines these extra scalar masses when we restrict λ and β_λ to be consistent with zero. Again, for clarity of the plot, we show only points with β_λ < 0.05 in blue before demonstrating the effect of the constraint β_λ < 0.00005 in red. It is interesting to note that no points with m_hNew < m_hSM survive the stronger constraint on β_λ, and the majority of the points that do survive have almost degenerate masses of m_hNew and m_hDM. The tree level masses of m_hNew (m_hDM) have a linear dependence on a₁ (b₋) which appears to dominate when both of the additional scalars are heavier than the SM Higgs.

FIGURE 7

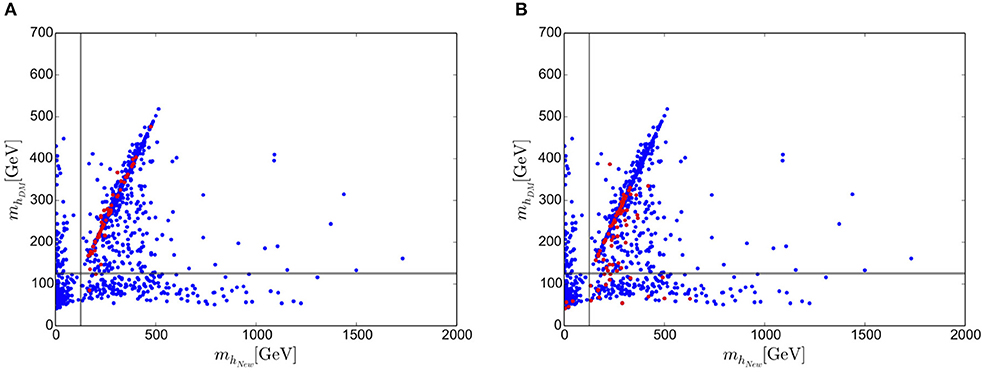
Figure 7. Values of m_hLight and m_hHeavy in the DM phase. All points obey λ < 0.067 and β_λ,δ,d2 < 0.05 at M_Pl. The gray bands highlight the SM Higgs mass range. (A) Red points obey the more restrictive condition β_λ < 0.00005. (B) Red points obey β_λ < 0.0005, β_δ < 0.0025 and β_d2 < 0.01. These plots originally appeared in McDowall and Miller [9].

Figure 7A might suggest that small values of the β functions at the Planck scale correlates with a small mass difference Δm = |m_hNew − m_hDM|. However, while 80% of the points that pass through the constraint λ < 0.067, β_λ < 0.00005 result in Δm < 40 GeV, so do 67% of the points that don't. This tendency toward degeneracy is a feature of all of the points that satisfy the theoretical constraints. These points exhibit small values of the soft U(1) breaking parameters a₁ and b₁, forcing a small Δm [50]. It is interesting to note that many points in the degenerate mass region can completely account for the dark matter relic density. The degeneracy opens up co-annihilation channels involving both m_hDM and m_hNew that enter the relic density calculation [61, 62]. These new channels help bring down the relic density to within the 3 σ range.

As in the broken phase, no DM phase points survive when the severe truncation error cut-offs are applied simultaneously with the experimental constraints. However, we see scenarios survive if we relax the constraints by a factor of 10. These scenarios are shown in Figure 7B.

5. The Two Higgs Doublet Model

Finally we will examine models with two Higgs doublets to see if they are compatible with the MPP. The most general potential of the Two Higgs Doublet Model (2HDM) (see [63] for a useful review) is,

$\begin{array}{ll}V(H_1,H_2)& =m_{11}^2{H}_1^{†}{H}_1+m_{22}^2{H}_2^{†}{H}_2-\left(m_{12}^2{H}_1^{†}{H}_2+c.c\right)\\ & +{\lambda }_1{\left(H_1^{†}{H}_1\right)}^2+{\lambda }_2{\left(H_2^{†}{H}_2\right)}^2+{\lambda }_3\left(H_1^{†}{H}_1\right)\left(H_2^{†}{H}_2\right)\\ & +{\lambda }_4\left(H_1^{†}{H}_2\right)\left(H_2^{†}{H}_1\right)+(\frac{{\lambda }_5}{2}{\left(H_1^{†}{H}_2\right)}^2\\ & +{\lambda }_6\left(H_1^{†}{H}_1\right)\left(H_1^{†}{H}_2\right)+{\lambda }_7\left(H_2^{†}{H}_2\right)\left(H_1^{†}{H}_2\right)+c.c),& (14)\end{array}$

where the two Higgs-doublets themselves are given by,

$\begin{array}{ll}{H}_n=\left(\begin{array}{c}{\chi }_n^{+}\\ \left(H_n^0+i{A}_n^0\right)/\sqrt{2}\end{array}\right),n=1,2.& (15)\end{array}$

The parameters $m_{11}^2$, $m_{22}^2$ and λ_{1, 2, 3, 4} are real, whilst $m_{12}^2$ and λ_{5, 6, 7} can in principle be complex and induce CP violation. During electroweak symmetry breaking the neutral components of the Higgs fields, $H_n^0$, develop vacuum expectation values (vevs) $\langle H_n^0\rangle =v_n/\sqrt{2}$. The relationship to the SM vev $v=\sqrt{v_1^2+v_2^2}=246\text{GeV}$ is determined by the Fermi constant but the ratio of the vevs, tanβ = v₂/v₁, is a free parameter. The physical scalar sector of the model includes two neutral scalar Higgs h and H, a pseudoscalar Higgs A and the charged Higgs H^±.

It's clear that the 2HDM potential is considerably more complicated than its Standard Model counterpart, so it's common to employ additional global symmetries to increase the predictivity of the model. There are only six possible types of global symmetry that have a distinctive effect on the potential [64, 65]. The 2HDM has been considered for suitability of the MPP in Froggatt et al. [66, 68–70], Laperashvili [67], and McDowall and Miller [71], though all but the last of these predate the Higgs discovery so could not be confronted with the measured Higgs mass. Froggatt et al. [70] is notable in that it shows that the MPP itself may be used as a mechanism for suppressing CP-violation and Flavor Changing Neutral Currents (FCNCs).

In McDowall and Miller [71] we took the more usual route of implementing a ℤ₂ symmetry to forbid FCNCs by allowing only one type of fermion to couple to one Higgs doublet. This requirement sets λ₆, λ₇ and m₁₂ to zero. Following McDowall and Miller [71]'s treatment, we may then softly break this ℤ₂ by re-introducing a (real) non-zero m₁₂. We will restrict ourselves to a Type-II model where up-type quarks and leptons couple to the first Higgs-doublet and down-type quarks to the second Higgs-doublet, though we note that the most significant effect of the Yukawa sector comes from which doublet the top-quark couples to, so results for other 2HDM Yukawa assignments would be very similar to those for Type-II.

For each parameter point the model is described by the bilinear terms m₁₁ and m₂₂, which are replaced by M_Z and tanβ by applying the electroweak vacuum minimization conditions, as well as the additional input parameters, m₁₂ and λ_i(M_Pl) with i = 1…5. As previously we use SARAH to calculate the two-loop β functions, which are used by FlexibleSUSY to run the couplings between M_Z and M_Pl.

We also consider a simpler model, the Inert Doublet Model (IDM), where we introduce an additional unbroken ℤ₂ symmetry, under which the new doublet has odd parity but all other fields are even (see [72] for a useful review). The scalar sector now consists of the SM Higgs field H and an inert doublet Φ, with mixing between the two forbidden by the new symmetry. The inert doublet does not couple to any of the SM fields and does not gain a vacuum expectation value.

The potential is,

$\begin{array}{lll}V(H,\Phi )& =& m_{11}^2{H}^{†}H+m_{22}^2{\Phi }^{†}\Phi +{\lambda }_1{\left(H^{†}H\right)}^2+{\lambda }_2{\left({\Phi }^{†}\Phi \right)}^2\\ & & +{\lambda }_3\left(H^{†}H\right)\left({\Phi }^{†}\Phi \right)+{\lambda }_4\left(H^{†}\Phi \right)\left({\Phi }^{†}H\right)\\ & +& \left(\frac{{\lambda }_5}{2}{\left(H^{†}\Phi \right)}^2+c.c\right).& (16)\end{array}$

Once again the quartic coupling can have complex values, but we will focus on the real-valued case. Note that now the mixing term proportional to $m_{12}^2$ is absent. During electroweak symmetry breaking the neutral component of the SM Higgs doublet acquires a vacuum expectation value v = 246GeV. The neutral Higgs h corresponds to the SM Higgs boson whilst H, A, and H^± are inert scalars. The lightest of these is stable thanks to the ℤ₂ symmetry and, assuming it is one of the neutral scalars H or A, it is a potential Dark Matter (DM) candidate [73, 74].

As in the previous case, the mass term associated with the SM Higgs doublet $m_{11}^2$ is fixed via the electroweak minimization conditions, but now we don't have a second vev to fix $m_{22}^2$, which must remain an input. Our input parameters are therefore m₂₂ and λ_i(M_Pl) with i = 1…5. As in the Type-II model, we use SARAH and FlexibleSUSY to calculate the mass spectrum and to run couplings between the low and high scales of interest.

Valid points in our parameter space scan must be perturbative up to the Planck scale. For the Higgs quartic couplings this requires them to satisfy ${\lambda }_i<\sqrt{4\pi }$ up to M_Pl. We require points that are bounded from below at all scales up to M_Pl [75]. To that end we check if the boundedness conditions [63],

$\begin{array}{lll}\hfill {\lambda }_1,{\lambda }_2& >& 0,\\ \hfill {\lambda }_3& >& -2\sqrt{{\lambda }_1{\lambda }_2},\\ \hfill {\lambda }_3+{\lambda }_4-\left|{\lambda }_5\right|& >& -2\sqrt{{\lambda }_1{\lambda }_2},& (17)\end{array}$

are met at all scales [76, 77].

The goal for the MPP is to have an additional minimum at M_Pl, degenerate with the electroweak minimum,. This is naively satisfied if all of the quartic couplings are zero at M_Pl, i.e., λ_i = 0, i = 1…5. However, the RG running of λ₁ and λ₂ results in an unstable vacuum configuration [66–69]. It is also possible for degenerate vacua to exist within the 2HDM if we relax the condition λ_i = 0. Specifically, by allowing λ₁, λ₂, λ₃, and λ₄ to be non-zero at M_Pl, the following conditions [66] are consistent with the implementation of the MPP at M_Pl;

$\begin{array}{lll}\hfill {\lambda }_5(M_{\text{Pl}})& =& 0\\ \hfill {\lambda }_4(M_{\text{Pl}})& <& 0\\ \hfill \tilde{\lambda }(M_{\text{Pl}})=\sqrt{{\lambda }_1{\lambda }_2}+{\lambda }_3+\text{min}(0,{\lambda }_4)& =& 0\\ \hfill {\beta }_{\tilde{\lambda }}(M_{\text{Pl}})& =& 0.& (18)\end{array}$

To investigate whether these MPP conditions in the Type-II 2HDM are consistent with the current experimental constraints on the SM Higgs mass m_h and the top-quark mass m_t, we generated points in the parameter space, applying the theoretical constraint of vacuum stability at all scales. Figure 8A shows an example of the running of λ₁, λ₂ and $\tilde{\lambda }$ for a point that results in experimentally valid values of the SM Higgs mass and the top-quark mass, and is also consistent with the MPP conditions of (18). Vacuum stability requires that all of these couplings remain greater than zero at all scales, but the negative running of $\tilde{\lambda }$ pulls it to negative values.

FIGURE 8

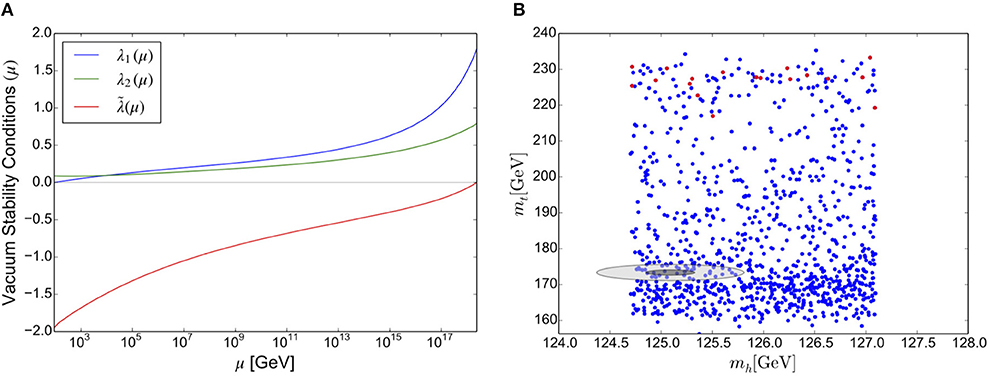
Figure 8. (A) Example running of λ₁, λ₂, and $\tilde{\lambda }$ for a point that provides valid masses for the SM Higgs and the top quark in the Type-II Two Higgs Doublet Model. Boundedness from below and vacuum stability requires that all three couplings are positive at all scales. (B) Results of our Multiple Point Principle scan in the m_h − m_t plane of the Type-II Two Higgs Doublet Model. The blue points provide valid SM higgs masses whilst the red points also pass the vacuum stability conditions at all scales. The ellipses show the experimentally allowed values of m_t and m_h at 1 σ (dark gray) and 3 σ (light gray) uncertainty. These plots originally appeared in McDowall and Miller [71].

Figure 8B shows an investigation of the m_h − m_t plane, where we temporarily suspend vacuum stability to demonstrate the effect. We see plenty of valid points in blue, where vacuum stability is not required. However, the points that satisfy the vacuum stability conditions, highlighted in red, have larger values of the top Yukawa y_t which positively contribute to the running of the quartic couplings. The larger required y_t corresponds to a top mass in the range 220 ≲ m_t ≲ 230GeV which is not compatible with current experimental bounds on the top-quark mass.

These MPP constraints also apply to the Inert Doublet Model. We examined the IDM parameter space as we did for the Type-II 2HDM, applying the MPP conditions at M_Pl and requiring valid points to be stable up to the Planck scale and to have a SM Higgs candidate.

Figure 9 shows the running of the quartic couplings λ₁, λ₂, and $\tilde{\lambda }$ for an example point in our scan that provided a valid SM Higgs and top mass. As in the Type-II model, a stable vacuum requires all three of these couplings to be positive at all scales. Clearly this point fails our vacuum stability test, and unfortunately it is representative of the other points in our scan. We found no points that could simultaneously satisfy the constraints of perturbativity, vacuum stability and the requirement of a realistic SM mass spectrum. Specifically, there are points that provide valid SM Higgs and top masses, but all of these points fail the condition $\tilde{\lambda }>0$. In fact, we found no points that could satisfy the MPP conditions outlined in (18) that remained stable up to the Planck scale, regardless of their Higgs or top masses. This therefore suggests that the multiple point principle cannot be implemented successfully in the Inert Doublet Model.

FIGURE 9

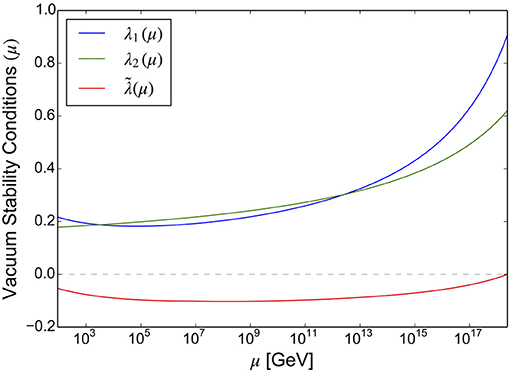
Figure 9. Example running of λ₁, λ₂, and $\tilde{\lambda }$ for a point that provides valid masses for the SM Higgs and the top quark in the Inert Doublet Model. Boundedness from below and vacuum stability requires that all three couplings are positive at all scales. This plot originally appeared in McDowall and Miller [71].

6. More Exotic Models

The MPP has also been applied to several other models of new physics, of varying degrees of complexity. For example, Hamada and Kawana [78] consider one of the more minimal extensions by including either a Majorana fermion triplet or a real scalar triplet, and in both cases were able to find good agreement with the MPP by keeping the new states rather heavy (of order 10¹⁶ GeV for the fermion triplet and slightly higher for the scalar).

Bennett et al. [79] studies what the authors term an “anti-GUT” within the context of the SM. This is a model where each generation comes with a full complement of the SM gauge groups, augmented with an additional local U(1), so that the full group (at high energies) is [SU(3) × U(2) × U(1)]³ × U(1). The resulting Higgs mass prediction is 139 ± 16 GeV, though the uncertainty in this prediction would no doubt be significantly reduced with more modern inputs, and they also find reasonable agreement with the SM Yukawa couplings.

Another proposed alternative is to mix a fundamental scalar with the scalar bound states of a new strongly interacting gauge symmetry [80]. This allows for the dynamical generation of the Higgs mass, with a classically scale invariant theory satisfying the MPP condition. They predict new scalar states at approximately 300 GeV as well as a new gauge boson coupling to the SM fermions.

The MPP may also be used to constrain theories with extra dimensions. Hamada and Shiu [81] examines the SM compactified at high scales onto S¹ and T¹, additionally applying the MPP. They find this constrains the neutrinos in the model to have Dirac masses, with the lightest of order 1−10 meV. This would prevent neutrinoless double-beta decay and have interesting cosmological consequences.

An more exotic suggestion comes from the original authors of the MPP: the existence of a bound state made of six top-quarks and six anti-top-quarks [82–87]. They postulate a new phase different from and degenerate with the standard electroweak Higgs phase, caused by the condensation of this new top-anti-top bound state. They claim this bound state arises from the exchange of Higgs bosons due to the large top Yukawa coupling. Therefore the MPP is extended to insist on not just two, but three degenerate vacua: two at low energies and one at the Planck scale. The authors also claim that the extra energy density of this new bound state provides a solution for the cosmological constant problem.

7. Summary and Conclusions

The measured value of the Higgs boson mass implies that, if the SM is true to high scales, the Higgs quartic coupling and its β-function are intriguingly close to zero at the Planck scale. Indeed, their values imply that the SM vacuum is metastable, with a slightly deeper vacuum at the Planck scale.

One suggested explanation for this is the Multiple Point Principle. By considering extensive variables, nature tends to choose Higgs parameters so that different phases of Electroweak symmetry breaking may coexist. This predicts a second degenerate vacuum at the Planck scale, rather similar to that implied by the Higgs measurements. An analysis of the MPP in the SM provides a prediction of the Higgs mass, m_h = 129 ± 1.5Gev which is slightly above the measured value. It is therefore interesting to ask how extensions to the SM might change this picture, especially since we do expect new physics to appear well before the Planck scale. In this paper, we have reviewed the compatibility of the MPP with simple Higgs sector extensions, considering both extra scalars and doublets.

We began our review of extended models by considering an additional real scalar field, in both the broken and Dark Matter phases. We had to weaken the MPP constraints somewhat in order to prevent the extra states from decoupling, but found promising results. These real scalar extensions were both compatible with the (relaxed) MPP, though working scenarios in the Dark Matter case were rare due to the additional Dark Matter constraints. Unfortunately the MPP didn't prove very predictive because it left us with a wide range of allowed additional scalar masses.

The next extension we considered was an extra complex singlet, where again we had to relax the MPP condition in order to prevent decoupling. We also found that we were unable to keep the parameter d₂ very small at the Planck scale since it tended to run negative, destabilizing the vacuum. Furthermore, our constraints setting the β-functions for the Higgs parameters to zero could not all be accommodated simultaneously while keeping viable low energy phenomenology. However, relaxing these constraints somewhat did again yield scenarios that are stable, evade experimental constraints, have the correct Higgs mass, and in the Dark Matter phase, provide the correct relic density.

Finally we investigated the Type-II Two Higgs Doublet Model and the Inert Doublet Model. Models with a second Higgs doublet have much more flexibility in their scalar potential, which one might expect gives them more freedom to accommodate the boundary conditions of the MPP. However, we found that both the Type-II 2HDM and the IDM cannot satisfy the conditions required at the Planck scale by the MPP. Specifically, we found no points in either model's parameter space that was consistent with the MPP whilst also having a valid SM Higgs, an experimentally acceptable top quark mass, and a stable vacuum. In the Type-II case we found that a stable vacuum would require a top mass on the order of 230GeV, whilst in the Inert case we found no points at all that could meet our theoretical requirements. The results of our analysis would suggest that the Multiple Point Principle is not compatible with the Two Higgs Doublet Models that we investigated.

In general it seems rather difficult to accommodate an exact MPP in any of these models. There are several possible explanations for this. Firstly the MPP conditions may only hold approximately. The original conjecture that there should be a second degenerate vacuum at the Planck scale was itself based on general arguments, and may be realized with some slight modifications. Indeed, one might expect threshold corrections for the new theory to become significant as we approach the Planck scale, slightly modifying the RG running. Secondly, we do expect new physics before the Planck scale to solve the many deficiencies of the SM. It could be that this new physics alters the Higgs running sufficiently to allow the MPP to hold more exactly. It would be interesting to examine the SM Higgs sector with alternative additions, such as vector-like fermions. Finally, the literature thus far has entirely neglected finite temperature effects in the study of the MPP. Such effects could very well alter the vacuum structure.

Ultimately the question remains, is the peculiar behavior of the SM Higgs potential at the Planck scale a coincidence or a sign of new physics?

Author Contributions

The text of this review was written by DM. The research itself was performed jointly by DM and JM, with DM taking a lead role as supervisor.

Funding

DM acknowledges partial support from the STFC grants ST/L000446/1 and ST/P000746/1.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to thank Peter Athron for invaluable help with FlexibleSUSY; as well as Karl Nordstrom, António Morais, and David Sutherland for useful discussions.

References

1. Aad G, Abajyan T, Abbott B, Abdallah J, Abdel Khalek S, Abdelalim AA, et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys Lett. (2012) B716:1–29. doi: 10.1016/j.physletb.2012.08.020

CrossRef Full Text | Google Scholar

2. Aad G, Abbott B, Abdallah J, Abdinov O, Aben R, Abolins M, et al. Combined measurement of the Higgs Boson Mass in pp collisions at $\sqrt{s}=7$ and 8 TeV with the ATLAS and CMS experiments. Phys Rev Lett. (2015) 114:191803. doi: 10.1103/PhysRevLett.114.191803

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Bergauer T, Dragicevic M, et al. Constraints on the spin-parity and anomalous HVV couplings of the Higgs boson in proton collisions at 7 and 8 TeV. Phys Rev D. (2015) 92:012004. doi: 10.1103/PhysRevD.92.012004

CrossRef Full Text | Google Scholar

4. Khachatryan V, Sirunyan AM, Tumasyan A, Adam W, Bergauer T, Dragicevic M, et al. Precise determination of the mass of the Higgs boson and tests of compatibility of its couplings with the standard model predictions using proton collisions at 7 and 8 TeV. Eur Phys J C. (2015) 75:212. doi: 10.1140/epjc/s10052-015-3351-7

CrossRef Full Text | Google Scholar

5. Aad G, Abbott B, Abdallah J, Abdinov O, Aben R, Abolins M, et al. Measurements of the Higgs boson production and decay rates and coupling strengths using pp collision data at $\sqrt{s}=7$ and 8 TeV in the ATLAS experiment. Eur Phys J C. (2016) 76:6. doi: 10.1140/epjc/s10052-015-3769-y

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Buttazzo D, Degrassi G, Giardino PP, Giudice GF, Sala F, Salvio A, et al. Investigating the near-criticality of the Higgs boson. J High Energy Phys. (2013) 12:089. doi: 10.1007/JHEP12(2013)089

CrossRef Full Text | Google Scholar

7. Craig N. The state of supersymmetry after run I of the LHC. arXiv: 1309.0528 [Preprint] (2013).

Google Scholar

8. Ross GG, Schmidt-Hoberg K, Staub F. Revisiting fine-tuning in the MSSM. J High Energy Phys. (2017) 03:021. doi: 10.1007/JHEP03(2017)021

CrossRef Full Text | Google Scholar

9. McDowall J, Miller DJ. High scale boundary conditions with an additional complex singlet. Phys Rev D. (2018) 97:115042. doi: 10.1103/PhysRevD.97.115042

CrossRef Full Text | Google Scholar

10. Froggatt CD, Nielsen HB. Standard model criticality prediction: top mass 173 +- 5-GeV and Higgs mass 135 +- 9-GeV. Phys Lett B. (1996) 368:96–102. doi: 10.1016/0370-2693(95)01480-2

CrossRef Full Text | Google Scholar

11. Degrassi G, Di Vita S, Elias-Miro J, Espinosa JR, Giudice GF, Isidori G, et al. Higgs mass and vacuum stability in the standard model at NNLO. J High Energy Phys. (2012) 08:098. doi: 10.1007/JHEP08(2012)098

CrossRef Full Text | Google Scholar

12. Holthausen M, Lim KS, Lindner M. Planck scale Boundary Conditions and the Higgs Mass. J High Energy Phys. (2012) 02:037. doi: 10.1007/JHEP02(2012)037

CrossRef Full Text | Google Scholar

13. Iacobellis G, Masina I. Stationary configurations of the Standard Model Higgs potential: electroweak stability and rising inflection point. Phys Rev D. (2016) 94:073005. doi: 10.1103/PhysRevD.94.073005

CrossRef Full Text | Google Scholar

14. Eichhorn A, Scherer MM. Planck scale, Higgs mass, and scalar dark matter. Phys Rev D. (2014) 90:025023. doi: 10.1103/PhysRevD.90.025023

CrossRef Full Text | Google Scholar

15. Khan N, Rakshit S. Study of electroweak vacuum metastability with a singlet scalar dark matter. Phys Rev D. (2014) 90:113008. doi: 10.1103/PhysRevD.90.113008

CrossRef Full Text | Google Scholar

16. Helmboldt AJ, Humbert P, Lindner M, Smirnov J. Minimal conformal extensions of the Higgs sector. J High Energy Phys. (2017) 07:113. doi: 10.1007/JHEP07(2017)113

CrossRef Full Text | Google Scholar

17. Bennett DL. Multiple point criticality, nonlocality, and fine tuning in fundamental physics: predictions for gauge coupling constants gives alpha**−1 = 136.8 +− 9. arXiv:hep-ph/9607341 [Preprint] (1996).

Google Scholar

18. Coleman SR, Weinberg EJ. Radiative corrections as the origin of spontaneous symmetry breaking. Phys Rev D. (1973) 7:1888–910. doi: 10.1103/PhysRevD.7.1888

CrossRef Full Text | Google Scholar

19. Jegerlehner F, Kalmykov MYu, Kniehl BA. Self-consistence of the Standard Model via the renormalization group analysis. J Phys Conf Ser. (2015) 608:012074. doi: 10.1088/1742-6596/608/1/012074

CrossRef Full Text | Google Scholar

20. Bethke S, Dissertori G, Salam GP. Particle Data Group Review on Quantum Chromodynamics (2015). Available online at: http://pdg.lbl.gov/2015/reviews/rpp2015-rev-qcd.pdf

21. Ginsparg PH. Gauge and gravitational couplings in four-dimensional string theories. Phys Lett B. (1987) 197:139–43. doi: 10.1016/0370-2693(87)90357-1

CrossRef Full Text | Google Scholar

22. Witten E. Strong coupling expansion of Calabi-Yau compactification. Nucl Phys B. (1996) 471:135–58. doi: 10.1016/0550-3213(96)00190-3

CrossRef Full Text | Google Scholar

23. Robinson SP, Wilczek F. Gravitational correction to running of gauge couplings. Phys Rev Lett. (2006) 96:231601. doi: 10.1103/PhysRevLett.96.231601

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Pietrykowski AR. Gauge dependence of gravitational correction to running of gauge couplings. Phys Rev Lett. (2007) 98:061801. doi: 10.1103/PhysRevLett.98.061801

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Toms DJ. Quantum gravity and charge renormalization. Phys Rev D. (2007) 76:045015. doi: 10.1103/PhysRevD.76.045015

CrossRef Full Text | Google Scholar

26. Toms DJ. Quantum gravitational contributions to quantum electrodynamics. Nature. (2010) 468:56–9. doi: 10.1038/nature09506

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Mackay PT, Toms DJ. Quantum gravity and scalar fields. Phys Lett B. (2010) 684:251–5. doi: 10.1016/j.physletb.2009.12.032

CrossRef Full Text | Google Scholar

28. He HJ, Wang XF, Xianyu ZZ. Gauge-invariant quantum gravity corrections to gauge couplings via Vilkovisky-DeWitt method and gravity assisted gauge unification. Phys Rev D. (2011) 83:125014. doi: 10.1103/PhysRevD.83.125014

CrossRef Full Text | Google Scholar

29. Daum JE, Harst U, Reuter M. Running gauge coupling in asymptotically safe quantum gravity. J High Energy Phys. (2010) 01:084. doi: 10.1007/JHEP01(2010)084

CrossRef Full Text | Google Scholar

30. Haba N, Kaneta K, Takahashi R, Yamaguchi Y. Gravitational effects on vanishing Higgs potential at the Planck scale. Phys Rev D. (2015) 91:016004. doi: 10.1103/PhysRevD.91.016004

CrossRef Full Text | Google Scholar

31. Wang F, Liu GL, Wu K. Bounds on higgs and top quark masses from the other degenerate vacua near the planck scale with gravitational contributions. Sci China Phys Mech Astron. (2018) 61:091011. doi: 10.1007/s11433-017-9179-1

CrossRef Full Text | Google Scholar

32. Branchina V, Contino F, Pilaftsis A. Protecting the stability of the electroweak vacuum from Planck-scale gravitational effects. Phys Rev D. (2018) 98:075001. doi: 10.1103/PhysRevD.98.075001

CrossRef Full Text | Google Scholar

33. Robens T, Stefaniak T. Status of the Higgs singlet extension of the standard model after LHC Run 1. Eur Phys J C. (2015) 75:104. doi: 10.1140/epjc/s10052-015-3323-y

CrossRef Full Text | Google Scholar

34. Haba N, Kaneta K, Takahashi R. Planck scale boundary conditions in the standard model with singlet scalar dark matter. J High Energy Phys. (2014) 04:029. doi: 10.1007/JHEP04(2014)029

CrossRef Full Text | Google Scholar

35. Haba N, Ishida H, Kaneta K, Takahashi R. Vanishing Higgs potential at the Planck scale in a singlet extension of the standard model. Phys Rev D. (2014) 90:036006. doi: 10.1103/PhysRevD.90.036006

CrossRef Full Text | Google Scholar

36. Haba N, Ishida H, Okada N, Yamaguchi Y. Multiple-point principle with a scalar singlet extension of the Standard Model. PTEP. (2017) 2017:013B03. doi: 10.1093/ptep/ptw186

CrossRef Full Text | Google Scholar

37. Hamada Y, Kawai H, Oda Ky. Predictions on mass of Higgs portal scalar dark matter from Higgs inflation and flat potential. J High Energy Phys. (2014) 07:026. doi: 10.1007/JHEP07(2014)026

CrossRef Full Text | Google Scholar

38. Kawana K. Multiple point principle of the standard model with scalar singlet dark matter and right handed neutrinos. PTEP. (2015) 2015:023B04. doi: 10.1093/ptep/ptv006

CrossRef Full Text | Google Scholar

39. Kawana K. Multiple point principle of the gauged B-L model. In: 2nd Toyama International Workshop on Higgs as a Probe of New Physics (HPNP2015), Japan, February 11–15, 2015. Toyama (2015).

Google Scholar

40. Veltman MJG. The infrared - ultraviolet connection. Acta Phys Polon B. (1981) 12:437.

41. Staub F. SARAH 4: a tool for (not only SUSY) model builders. Comput Phys Commun. (2014) 185:1773–90. doi: 10.1016/j.cpc.2014.02.018

CrossRef Full Text | Google Scholar

42. Athron P, Bach M, Harries D, Kwasnitza T, Park JH, Stöckinger D, et al. FlexibleSUSY 2.0: extensions to investigate the phenomenology of SUSY and non-SUSY models. Comput Phys Commun. (2018) 230:145–217. doi: 10.1016/j.cpc.2018.04.016

CrossRef Full Text | Google Scholar

43. Athron P, Park Jh, Stockinger D, Voigt A. FlexibleSUSY - A spectrum generator generator for supersymmetric models. Comput Phys Commun. (2015) 190:139–72. doi: 10.1016/j.cpc.2014.12.020

CrossRef Full Text | Google Scholar

44. Allanach BC. SOFTSUSY: a program for calculating supersymmetric spectra. Comput Phys Commun. (2002) 143:305–31. doi: 10.1016/S0010-4655(01)00460-X

CrossRef Full Text | Google Scholar

45. Allanach BC, Athron P, Tunstall LC, Voigt A, Williams AG. Next-to-minimal SOFTSUSY. Comput Phys Commun. (2014) 185:2322–39. doi: 10.1016/j.cpc.2014.04.015

CrossRef Full Text | Google Scholar

46. Camargo-Molina JE, O'Leary B, Porod W, Staub F. Vevacious: a tool for finding the global minima Of one-loop effective potentials with many scalars. Eur Phys J C. (2013) 73:2588. doi: 10.1140/epjc/s10052-013-2588-2

CrossRef Full Text | Google Scholar

47. Bechtle P, Brein O, Heinemeyer S, Stal O, Stefaniak T, Weiglein G, et al. HiggsBounds−4: improved tests of extended higgs sectors against exclusion bounds from LEP, the tevatron and the LHC. Eur Phys J C. (2014) 74:2693. doi: 10.1140/epjc/s10052-013-2693-2

CrossRef Full Text | Google Scholar

48. Bechtle P, Heinemeyer S, Stal O, Stefaniak T, Weiglein G. HiggsSignals: confronting arbitrary Higgs sectors with measurements at the Tevatron and the LHC. Eur Phys J C. (2014) 74:2711. doi: 10.1140/epjc/s10052-013-2711-4

CrossRef Full Text | Google Scholar

49. Costa R, Mühlleitner M, Sampaio MOP, Santos R. Singlet extensions of the standard model at LHC run 2: benchmarks and comparison with the NMSSM. J High Energy Phys. (2016) 06:034. doi: 10.1007/JHEP06(2016)034

CrossRef Full Text | Google Scholar

50. Coimbra R, Sampaio MOP, Santos R. ScannerS: constraining the phase diagram of a complex scalar singlet at the LHC. Eur Phys J C. (2013) 73:2428. doi: 10.1140/epjc/s10052-013-2428-4

CrossRef Full Text | Google Scholar

51. Butterworth JM, Arbey A, Basso L, Belov S, Bharucha A, Braam F, et al. The tools and Monte Carlo working group summary report from the Les Houches 2009 workshop on TeV colliders. In: Physics at TeV Colliders. Proceedings, 6th Workshop, dedicated to Thomas Binoth, June 8–26, 2009. Les Houches (2010). Available online at: https://inspirehep.net/record/848006

Google Scholar

52. Bélanger G, Boudjema F, Pukhov A, Semenov A. micrOMEGAs4.1: two dark matter candidates. Comput Phys Commun. (2015) 192:322–9. doi: 10.1016/j.cpc.2015.03.003

CrossRef Full Text | Google Scholar

53. Hinshaw G, Larson D, Komatsu E, Spergel DN, Bennett CL, Dunkley J, et al. Nine-year Wilkinson microwave anisotropy probe (WMAP) observations: cosmological parameter results. Astrophys J Suppl. (2013) 208:19. doi: 10.1088/0067-0049/208/2/19

CrossRef Full Text | Google Scholar

54. Ade PAR, Aghanim N, Arnaud M, Ashdown M, Aumont J, Baccigalupi C, et al. Planck 2015 results. XIII. Cosmological parameters. Astron Astrophys. (2016) 594:A13. doi: 10.1051/0004-6361/201525830

CrossRef Full Text | Google Scholar

55. Akerib DS, Alsum S, Araújo HM, Bai X, Bailey AJ, Balajthy J, et al. Results from a search for dark matter in the complete LUX exposure. Phys Rev Lett. (2017) 118:021303. doi: 10.1103/PhysRevLett.118.021303

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Barger V, Langacker P, McCaskey M, Ramsey-Musolf M, Shaughnessy G. Complex singlet extension of the standard model. Phys Rev D. (2009) 79:015018. doi: 10.1103/PhysRevD.79.015018

CrossRef Full Text | Google Scholar

57. Barger V, McCaskey M, Shaughnessy G. Complex scalar dark matter vis-à-vis CoGeNT, DAMA/LIBRA and XENON100. Phys Rev D. (2010) 82:035019. doi: 10.1103/PhysRevD.82.035019

CrossRef Full Text | Google Scholar

58. Gonderinger M, Lim H, Ramsey-Musolf MJ. Complex scalar singlet dark matter: vacuum stability and phenomenology. Phys Rev D. (2012) 86:043511. doi: 10.1103/PhysRevD.86.043511

CrossRef Full Text | Google Scholar

59. Costa R, Morais AP, Sampaio MOP, Santos R. Two-loop stability of a complex singlet extended Standard Model. Phys Rev D. (2015) 92:025024. doi: 10.1103/PhysRevD.92.025024

CrossRef Full Text | Google Scholar

60. Muhlleitner M, Sampaio MOP, Santos R, Wittbrodt J. Phenomenological comparison of models with extended Higgs sectors. J. High Energ. Phys. (2017) 2017:132. doi: 10.1007/JHEP08(2017)132

CrossRef Full Text | Google Scholar

61. Baker MJ, Brod J, El Hedri S, Kaminska A, Kopp J, Liu J, et al. The coannihilation codex. J High Energy Phys. (2015) 12:120. doi: 10.1007/JHEP12(2015)120

CrossRef Full Text | Google Scholar

62. Ghorbani K, Ghorbani H. Scalar split WIMPs in future direct detection experiments. Phys Rev D. (2016) 93:055012. doi: 10.1103/PhysRevD.93.055012

CrossRef Full Text | Google Scholar

63. Branco GC, Ferreira PM, Lavoura L, Rebelo MN, Sher M, Silva JP. Theory and phenomenology of two-Higgs-doublet models. Phys Rept. (2012) 516:1–102. doi: 10.1016/j.physrep.2012.02.002

CrossRef Full Text | Google Scholar

64. Ivanov IP. Minkowski space structure of the Higgs potential in 2HDM. Phys Rev D. (2007) 75:035001. [Erratum: Phys. Rev. D76, 039902(2007)]. doi: 10.1103/PhysRevD.76.039902

CrossRef Full Text | Google Scholar

65. Ferreira P, Haber HE, Santos E. Preserving the validity of the Two-Higgs Doublet Model up to the Planck scale. Phys Rev D. (2015) 92:033003. doi: 10.1103/PhysRevD.92.033003

CrossRef Full Text | Google Scholar

66. Froggatt CD, Laperashvili LV, Nevzorov RB, Nielsen HB, Sher M. The two Higgs doublet model and the multiple point principle. In: Bled Workshops in Physics. Vol. 5 (2004). p. 28–39.

Google Scholar

67. Laperashvili LV. The Multiple point principle and Higgs bosons. Phys Part Nucl. (2005) 36:S38–40.

Google Scholar

68. Froggatt CD, Laperashvili L, Nevzorov R, Nielsen HB, Sher M. Implementation of the multiple point principle in the two-Higgs doublet model of type II. Phys Rev D. (2006) 73:095005. doi: 10.1103/PhysRevD.73.095005

CrossRef Full Text | Google Scholar

69. Froggatt CD, Nevzorov R, Nielsen HB, Thompson D. Fixed point scenario in the Two Higgs Doublet Model inspired by degenerate vacua. Phys Lett B. (2007) 657:95–102. doi: 10.1016/j.physletb.2007.10.010

CrossRef Full Text | Google Scholar

70. Froggatt CD, Nevzorov R, Nielsen HB. Multiple point principle as a mechanism for the suppression of FCNC and CP-violation phenomena in the 2HDM. In: SUSY 2007 Proceedings, 15th International Conference on Supersymmetry and Unification of Fundamental Interactions, July 26 - August 1, 2007, Karlsruhe, Germany (2007). p. 710–3. Available online at: http://inspirehep.net/record/792568

Google Scholar

71. McDowall J, Miller DJ. High scale boundary conditions in models with two higgs doublets. Phys Rev D. (2019) 100:015018. doi: 10.1103/PhysRevD.100.015018

CrossRef Full Text

72. Ilnicka A, Krawczyk M, Robens T. Inert doublet model in light of LHC Run I and astrophysical data. Phys Rev D. (2016) 93:055026. doi: 10.1103/PhysRevD.93.055026

CrossRef Full Text | Google Scholar

73. Datta A, Ganguly N, Khan N, Rakshit S. Exploring collider signatures of the inert Higgs doublet model. Phys Rev D. (2017) 95:015017. doi: 10.1103/PhysRevD.95.015017

CrossRef Full Text | Google Scholar

74. Khan N, Rakshit S. Constraints on inert dark matter from the metastability of the electroweak vacuum. Phys Rev D. (2015) 92:055006. doi: 10.1103/PhysRevD.92.055006

CrossRef Full Text | Google Scholar

75. Chowdhury D, Eberhardt O. Global fits of the two-loop renormalized Two-Higgs-Doublet model with soft Z₂ breaking. J High Energy Phys. (2015) 11:052. doi: 10.1007/JHEP11(2015)052

CrossRef Full Text | Google Scholar

76. Sher M. Electroweak Higgs potentials and vacuum stability. Phys Rept. (1989) 179:273–418. doi: 10.1016/0370-1573(89)90061-6

CrossRef Full Text | Google Scholar

77. Chataignier L, Prokopec T, Schmidt MG, Swiezewska B. Single-scale renormalisation group improvement of multi-scale effective potentials. J High Energy Phys. (2018) 03:014. doi: 10.1007/JHEP03(2018)014

CrossRef Full Text | Google Scholar

78. Hamada Y, Kawana K. Vanishing Higgs potential in minimal dark matter models. Phys Lett B. (2015) 751:164–70. doi: 10.1016/j.physletb.2015.10.006

CrossRef Full Text | Google Scholar

79. Bennett DL, Nielsen HB, Froggatt CD. Standard model parameters from the multiple point principle and anti-GUT. In: Recent developments in nonperturbative quantum field theory. Proceedings, APCTP-ICTP Joint International Conference, Seoul, May 26-30, 1997 (1997). p. 362–93.

Google Scholar

80. Haba N, Yamada T. Multiple-point principle realized with strong dynamics. Phys Rev D. (2017) 95:115015. doi: 10.1103/PhysRevD.95.115015

CrossRef Full Text | Google Scholar

81. Hamada Y, Shiu G. Weak gravity conjecture, multiple point principle and the standard model landscape. J High Energy Phys. (2017) 11:043. doi: 10.1007/JHEP11(2017)043

CrossRef Full Text | Google Scholar

82. Froggatt CD, Laperashvili LV, Nielsen HB. The fundamental-weak scale hierarchy in the standard model. Phys Atom Nucl. (2006) 69:67–80. doi: 10.1134/S1063778806010108

CrossRef Full Text | Google Scholar

83. Froggatt CD, Nielsen HB, Laperashvili LV. Hierarchy-problem and a bound state of 6 t and 6 anti-t. Int J Mod Phys A. (2005) 20:1268–75. doi: 10.1142/S0217751X0502416X

CrossRef Full Text | Google Scholar

84. Das CR, Froggatt CD, Laperashvili LV, Nielsen HB. New bound states of heavy quarks at LHC and tevatron. Int J Mod Phys A. (2011) 26:2503–21. doi: 10.1142/S0217751X11053420

CrossRef Full Text | Google Scholar

85. Laperashvili LV, Nielsen HB, Das CR. New results at LHC confirming the vacuum stability and multiple point principle. Int J Mod Phys A. (2016) 31:1650029. doi: 10.1142/S0217751X16500299

CrossRef Full Text | Google Scholar

86. Laperashvili LV, Nielsen HB, Froggatt CD, Sidharth BG, Das CR. New resonances at LHC are possible. Multiple point principle and new bound states in the standard model. arXiv:1703.01757 [Preprint] (2017).

Google Scholar

87. Nielsen HFB, Bennett DL, Das CR, Froggatt CD, Laperashvili LV. F(750), we miss you as a bound state of 6 top and 6 antitop quarks, multiple point principle. PoS. (2017) CORFU2016:050. doi: 10.22323/1.292.0050

CrossRef Full Text | Google Scholar