- 1School of Quantitative Sciences, Universiti Utara Malaysia, Sintok, Malaysia
- 2Department of Mathematics, Faculty of Science, University of Sargodha, Sargodha, Pakistan
- 3Higher Education Department (HED) Punjab, Lahore, Pakistan
- 4Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam
- 5Department of Mathematics, College of Science Al-Zulfi, Majmaah University, Al Majmaah, Saudi Arabia
- 6Department of Teacher Training in Electrical Engineering, Faculty of Technical Education, Renewable Energy Research Centre, King Mongkut's University of Technology North Bangkok, Bang Sue, Thailand
- 7Department of Mathematics, College of Arts and Sciences, Prince Sattam bin Abdulaziz University, Wadi Al Dawasir, Saudi Arabia
In this article, the effects of a Casson Nanofluid boundary layer flow, over an inclined extending surface with Soret and Dufour, is scrutinized. The model used in this study is based on the Buongiorno model of the thermal efficiencies of the fluid flows in the presence of Brownian motion and thermophoresis properties. The non-linear problem for Casson Nanofluid flow over an inclined channel is modeled to gain knowledge on the heat and mass exchange phenomenon, by considering important flow parameters of the intensified boundary layer. The governing non-linear partial differential equations are changed to non-linear ordinary differential equations and are afterward illustrated numerically by the Keller-Box scheme. A comparison of the established results, if the incorporated effects are lacking, is performed with the available outcomes of Khan and Pop [1] and recognized in a nice settlement. Numerical and graphical results are also presented in tables and graphs.
Introduction
In recent times, nanofluid has accomplished an incredible position among scientists because of its dynamic thermal performance and notable potential in the number of heat transfers without any pressure drops. Nanofluid is a formula of various nanoparticles, containing Al2O3, Cu, CuO, in a base liquid, for example, oil, water, ethylene glycol, and so forth. It is investigated through examination that the thermal conductivity of base fluid is usually not exactly the same as the nanofluid Choi and Eastman [2]. Nanofluid is used as a working fluid (base fluid) due to its high thermal conductivity. Buongiorno [3] examined the causes that perform a key job in the advancement of nanofluid's thermal conductivity. He perceived that the Brownian movement and thermophoresis effects in conventional fluid play an important role to enhance the thermal conductivity of the fluid. Nield and Kuznetsov [4] considered the result of thermophoresis and Brownian movement on the boundary layer stream. The steady flow of nanofluid on an extending sheet was examined by Khan and Pop [1]. Anwar et al. [5] presented the Brownian movement and thermophoresis impact on the heat and mass exchange of nanofluids over a non-linear extending sheet. Suriyakumar and Devi [6] examined the nanofluid flow over a slanted sheet. Ziaei-Rad et al. [7] investigated a similar solution of nanofluid stream on a slanted surface. Thumma et al. [8] discussed the nanofluid flow on a slanted plate by incorporating the heat source. Govindarajan [9] discussed the flow of nanofluid over a slanted sheet by incorporating a non-uniform temperature. Khan et al. [10] illustrated the heat and mass transfer of MHD Jeffery nanofluid flow over an inclined sheet. Nanofluid flow with radiation effects on a slanted surface was examined by Chakraborty [11]. Recently, different scholars investigated the nanofluid flow on different models, as some of them are given in references [12–18].
The investigation of boundary layer flow and heat exchange on a stretching surface has been considered by various experts due to its immense mechanical and designing applications in the field of industry, and engineering, for example, strengthening and tinning of copper wires, assembling plastic and elastic sheets, non-stop cooling and fiber turning, expulsion of polymer, wire drawing, food processing, and paper, and so forth. Boundary layer flow on a steady surface was first investigated by Sakiadis [19]. Additionally, Crane [20] considered the closed structure solution of boundary layer flow on an extending sheet. Ali et al. [21] investigated the conjugate effects of heat and mass exchange on MHD free convection flow over an inclined plate. Ramesh et al. [22] investigated the boundary layer flow over the slanted sheet with convective boundaries. MHD free convection dissipative fluid stream past over an inclined sheet was investigated by Malik [23]. The boundary layer flow on a slanted sheet through convective boundaries was discussed by Ramesh et al. [24]. Griffiths [25] investigated the non-Newtonian boundary layer flow over a slanted sheet. Soret and Dufour effect over a slanted plate was discussed by Pal and Mondal [26]. Pandya and Shukla [27] investigated the unsteady MHD flow over a slanted surface by taking viscous dissipations. Thermal radiation impacts are important in solar plants [28].
In 1959, Casson offered the Casson fluid model for the flow of viscoelastic liquids. Casson fluid is a shear thinning fluid which should have zero viscosity at an infinite rate of shear and infinite viscosity at zero rates of shear, yielding stress under which no flow takes place. Some examples of Casson fluid are, honey, jelly, sauce, soup etc. [29] Ali et al. [30] examined the Casson fluid flow on a slanted sheet by incorporating the Soret-Dufour effects. Manideep et al. [31] studied the Casson fluid flow on vertically inclined sheets. Shamshuddin et al. [32] numerically investigated the effect of chemical reaction on Casson fluid flow on a slanted plate. Casson fluid flow over a slanted plate calculated by Vijayaragavan and Kavitha [33]. Prasad et al. [34] investigated the Casson fluid flow over an inclined sheet by considering the hall current. Jain and Parmar [35] studied the inclined Casson fluid flow on a permeable sheet. Sailaja et al. [36] studied the Casson fluid flow on a vertical sheet by incorporating the angle effect. Rawi et al. [37] discussed the Casson fluid flow over a slanted sheet by considering nanoparticles. Rauju et al. [38] discussed the Casson fluid flow on a vertically slanted sheet. The Casson fluid model is more compatible with blood flow simulation [39, 40].
Persuaded by the above referred literature review, and due to the growing needs of non-Newtonian nanofluid flows in industry and engineering areas, the present work focuses on the Casson nanofluid flow over a non-linear inclined stretching surface with Soret and Dufour effects. Casson nanofluid is more helpful for cooling and friction reducing agents compared to Newtonian based nanofluid flow [15]. To the best of the author's knowledge, the solution of the Casson nanofluid flow over a non-linear inclined stretching surface with radiation, as well as Soret and Dufour effects with the Keller-Box method, has not yet been reported. The model under consideration is newly developed from Khan and Pop [1] and results obtained from the current study are new. In this work, we found that the Dufour effect reduces the Nusselt and Sherwood number due to Soret impact. A non-linear form of radiative heat exchange also enhances the fluid temperature. This study is very useful in nuclear reactors, MHD generators, and in geothermal energy. In the future, it can be extended on an exponentially inclined stretching surface.
Problem Formulation
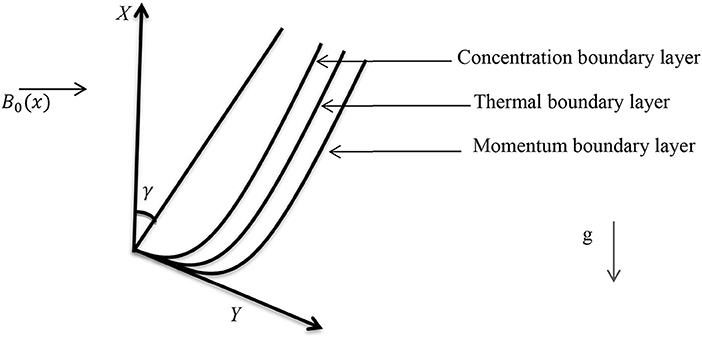
A steady, two-dimensional boundary layer flow of Casson Nano fluid over a non-linear slanted extending surface on angle γ is considered. The extending and free stream velocities are taken as, and u∞(x) = 0. Where, “x” is the coordinate dignified in the direction of the extending surface with “a” supposed constant. An external transverse magnetic field is assumed normal to the flow path. The Brownian motion and thermophoresis effects are considered. The temperature T and Nano particle fraction C at the wall take the constant values Tw and Cw, while the ambient forms for the nanofluid mass and temperature fractions C∞ and T∞ are accomplished as y approaches to immensity, as shown in Figure 1.
The flow equations for this study [1] are given by:
Here, the Rosseland approximation (for radiation flux) is defined as:
Where, σ* is the Stefan-Boltzmann constant and k* is the mean absorption coefficient. It is assumed that the temperature difference between the free steam T∞ and local temperature T is small enough, expanding T4 in Taylor series about T∞ and neglecting higher order terms for:
Using Equations (5) and (6) the Equation (3) converts into:
Where u and v are the velocity components in the x and y directions, respectively, g is the acceleration due to gravity, B0 is the uniform magnetic field strength, σ is the electrical conductivity, u is the viscosity, δf is the density of the base fluid, δp is the density of the nanoparticle, β is the Casson parameter, βt is the coefficient of thermal expansion, βc is the coefficient of concentration expansion, DB is the Brownian diffusion coefficient and DT is the thermophoresis diffusion coefficient, k is the thermal conductivity, (δc)p is the heat capacitance of the nanoparticles, (δc)f is the heat capacitance of the base fluid, is the thermal diffusivity parameter, is the ratio between the effective heat capacity of the nanoparticle and heat capacity of the fluid.
The subjected boundary conditions are:
The non-linear partial differential equations are reduced into non-linear ordinary differential equations. For that purpose, the stream function ψ = ψ(x, y) is defined as:
continuity (Equation 1) is satisfied identically.
The similarity transformations are defined as:
On substituting (Equation 7), system of Equations (2), (3), and (7) reduce to the following non-linear ordinary differential equations:
Where,
Here, primes denote the differentiation with respect to η, λ Buoyancy parameter, δ Solutal buoyancy parameter, M is the magnetic parameter called Hartmann number, ν is the kinematic viscosity of the liquid, Pr denotes the Prandtl number, Le denotes the Lewis number, Nb denotes the Brownian motion parameter, Nt indicates thermophoresis parameter, and N is the radiation parameter.
The corresponding boundary conditions are transformed to:
The skin friction, Sherwood number and Nusselt number for the present problem are defined as:
Where,
The associated expressions of dimensionless reduced Nusselt number −θ′(0), reduced Sherwood number −ϕ′(0), and skin friction coefficient Cfx are defined as
Where, is the local Reynolds number.
The converted non-linear differential (Equations 9–12) with the boundary conditions (14) are elucidated by the Keller box scheme consisting of the steps; finite-differences technique, Newton's scheme, and the block elimination process clearly explained by Anwar et al. [41]. This method has been extensively applied and it looks to be the most flexible compared to common techniques. It has been presented as much quicker, easier to program, more efficient and easier to practice. Currently, there are many alternative techniques to solve such types of problems [42].
Results and Discussion
This portion of study manages the calculated results of converted non-linear ordinary differential (Equations 8–10) with boundary conditions (12) elucidated via Killer-box method. Concerning numerical results of physical parameters, including Brownian motion parameter Nb, radiation parameter N, thermophoresis parameter Nt, magnetic factor M, buoyancy factor λ, solutal buoyancy factor δ, inclination factor γ, Prandtl number Pr, Lewis number Le, Dufour effect Df, Soret effect Sr, non-linear stretching parameter m, and Casson fluid parameter β, several figures and tables are prepared. In Table 1, in the deficiency of Dufour effect Df, Soret effect Sr, buoyancy parameter λ, solutal buoyancy constraint δ, magnetic factor M, radiation parameter N and non-linear stretching parameter ‘m' K with γ = 90° when Casson parameter β → ∞ produces a reduced Nusselt number −θ′(0), the reduced Sherwood number −ϕ′(0) equate with existing outcomes of Khan and Pop [1]. The consequences establishes a brilliant settlement. The effects of −θ′(0), −ϕ′(0), and Cfx(0), against changed values of involved physical parameters Nb, Nt, M, β, λ, δ, γ, m, Le, Df, Sr, N, and Pr are shown in Table 2. From Table 2 is can be clearly seen that −θ′(0) declines for growing values of Nb,Nt, M,Le, Df, m, γ, β, N, and increases with enhancing numerical values of λ, δ, Sr, and Pr. Moreover, it is perceived that −ϕ′(0) enhanced with the larger values of Nb, λ, δ, Nt, Le, N, Pr, Df, and drops for bigger values of M, m, β, Sr, and γ. Physically, the thermal boundary layer thickness enhances, as the Brownian parameter Nb increases impacting a large extent of the fluid. Moreover, for large values of thermophoresis effects, the Nusselt number decreases and the Sherwood number increases because, the thermal boundary layer becomes thicker due to deeper diffusion penetration into the fluid. On the other hand, Cfx(0) rises with the growing values of Nb, Le, M, β, Pr, γ, m, Df, and drops with the higher values of, λ, δ, Nt, N, and Sr. The current results are novel and show the impact of the buoyancy parameter, solutal buoyancy parameter and inclination parameter impacts on the driven flow in the presence of Soret and Dufour effects on power-law fluid which is currently unavailable in the literature.
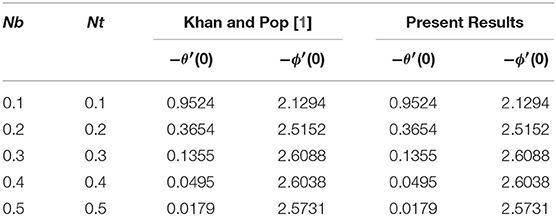
Table 1. Comparison of the reduced Nusselt number −θ′(0) and the reduced Sherwood number −θ′(0) when M, N = 0, β → ∞, δ, Sr, Df, λ = 0, m = 1, Pr = Le = 10 and γ = 90°.
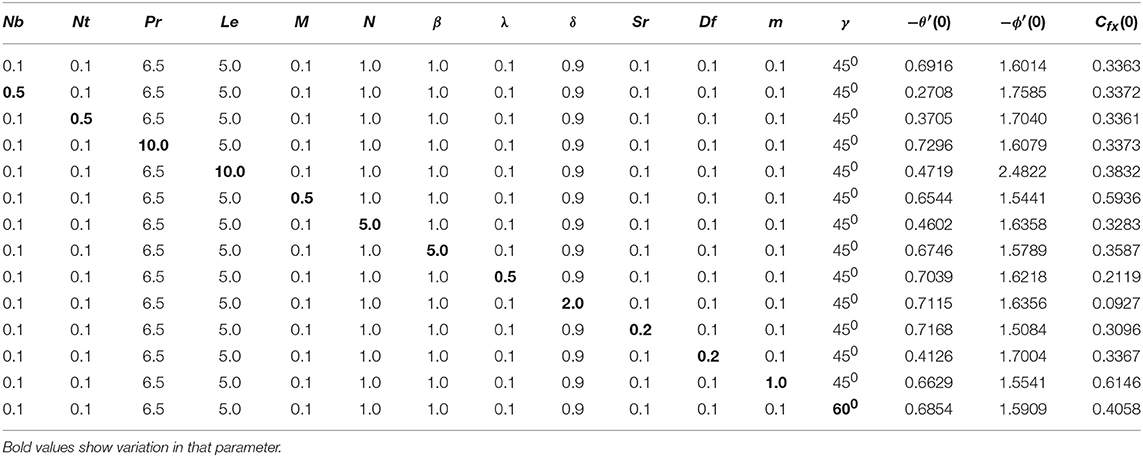
Table 2. Values of the reduced Nusselt number −θ′(0), the Sherwood number −ϕ′(0) and the Skin-friction coefficient Cfx(0).
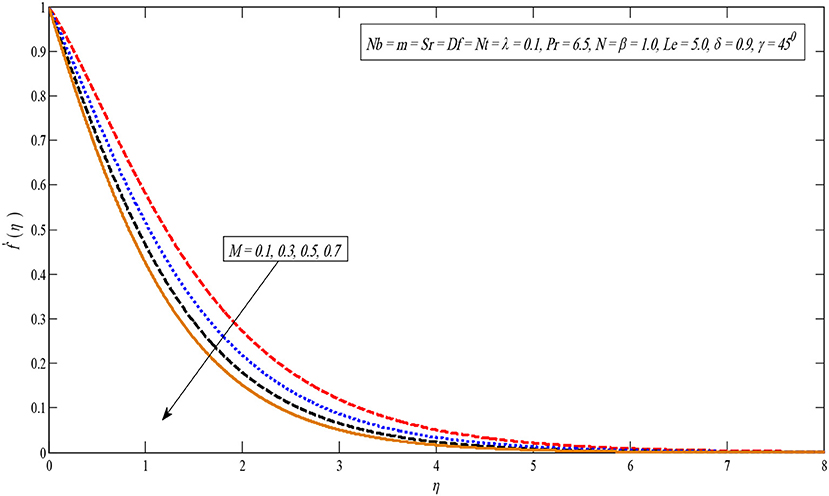
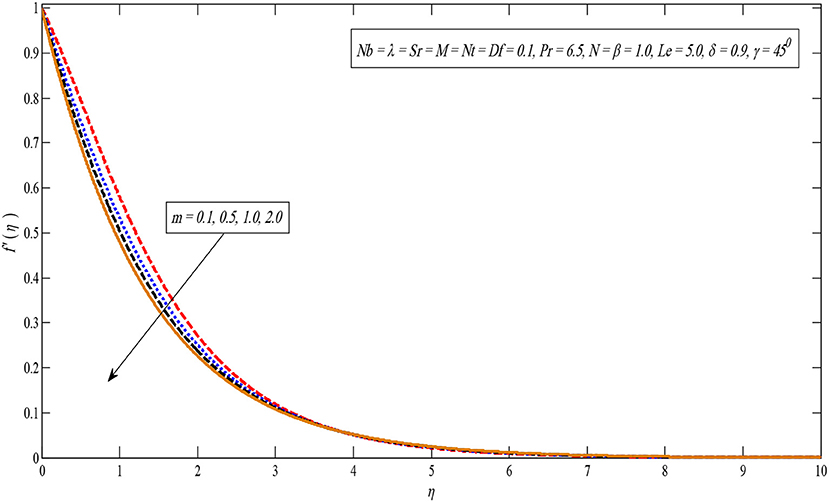
An image of the effect of factor M on velocity profile is portrayed in Figure 2. According to Figure 2, by improving the constraint M, the velocity outline reduces. Since the magnetic field produces Lorentz force, by slowing down the speed of the liquid. On the other hand, the velocity profile slows down for large values of the non-linear stretching parameter m, shown in Figure 3. Physically, the momentum boundary layer thickness reduces for higher values of m.
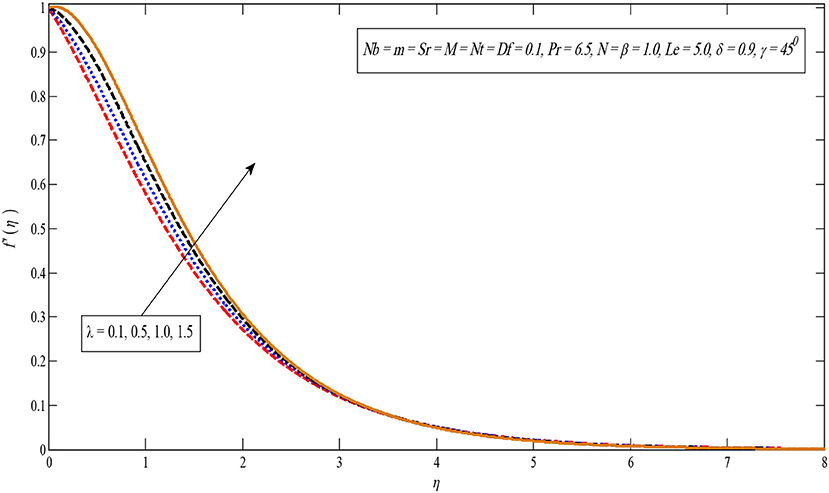
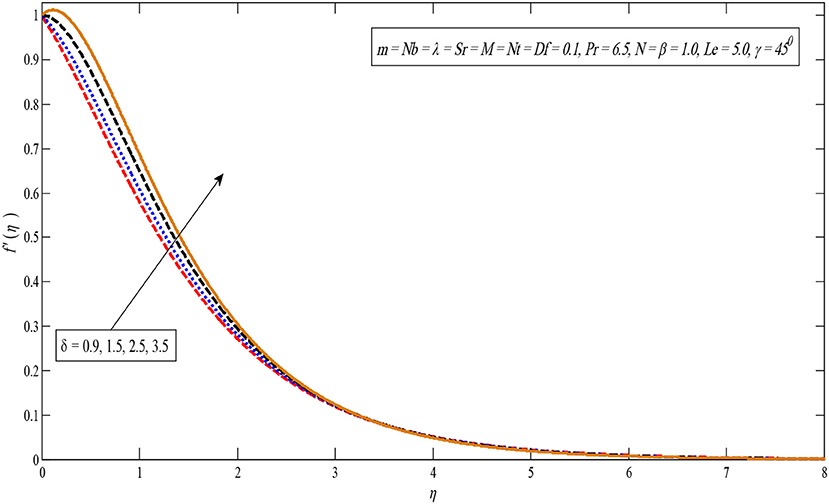
The impact of the buoyancy factor is shown in Figure 4. It is observed that the velocity profile rises by improving the buoyancy limit. It is due to the fact that buoyancy effect increases the strength of the fluid flow whereby the boundary layer thickness and velocity enhances. Figure 5 indicates that the velocity outline increases by enhancing the solutal buoyancy factor. Physically, the buoyancy parameter reduces the viscous forces whereby the velocity upturns. In addition, the opposite impact can be seen in temperature and concentration profiles for large values of δ.
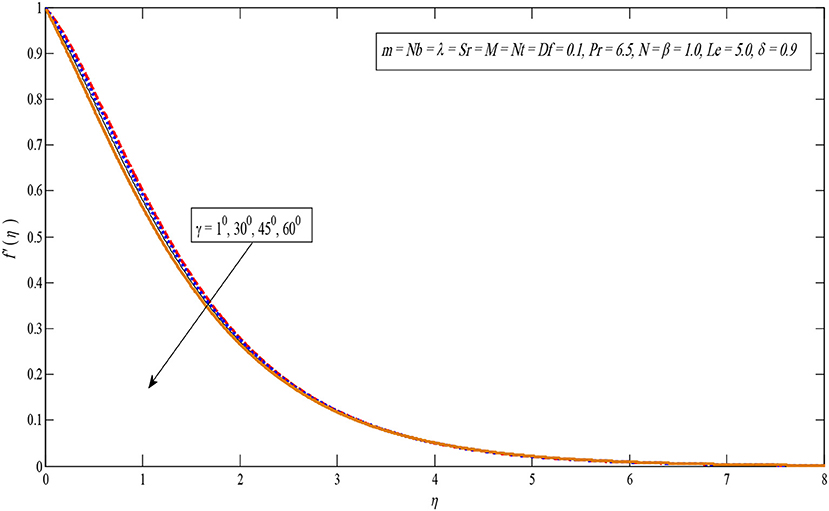
Figure 6 interprets the significance of inclination factor γ on the velocity outline. It is perceived in Figure 6 that the velocity outline runs down by enhancing the values of γ. Moreover, the circumstances indicate that the maximum gravitational force acts on flow in the case of γ = 0, because in this state the sheet will be vertical. On the other hand, for γ = 900, the sheet will be horizontal which causes the decline in velocity profile as the power of the bouncy forces drop.
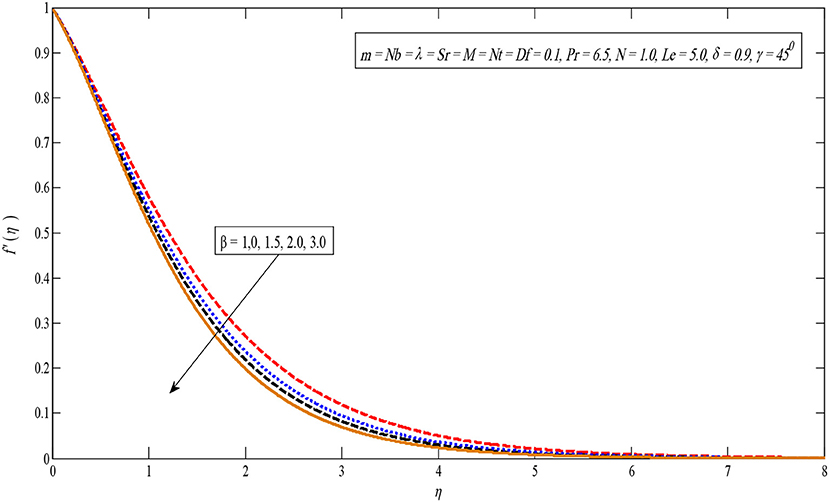
The effect of the Casson parameter on the velocity parameter is presented in Figure 7. It is observed that for large values of the Casson parameter, the velocity profile decreases. The reason behind this behavior is that by increasing the values of the Casson parameter, β increases the fluid viscosity i.e., reducing the yield stress. Therefore, the momentum boundary layer thickness reduces [43].
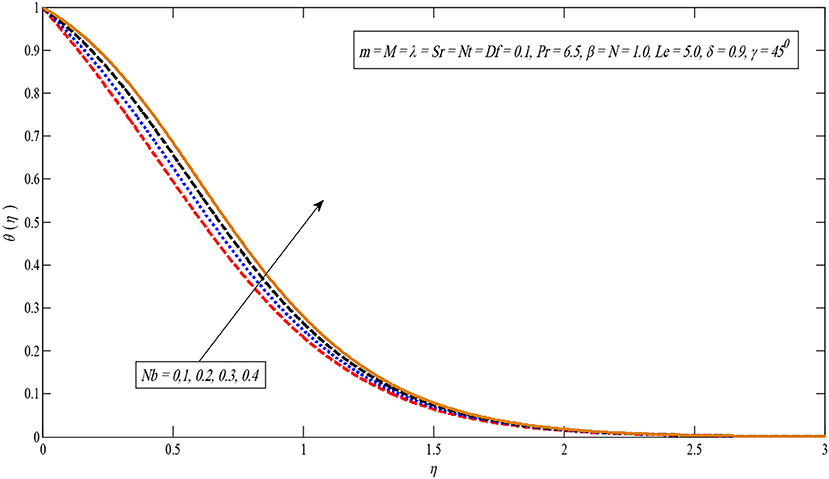
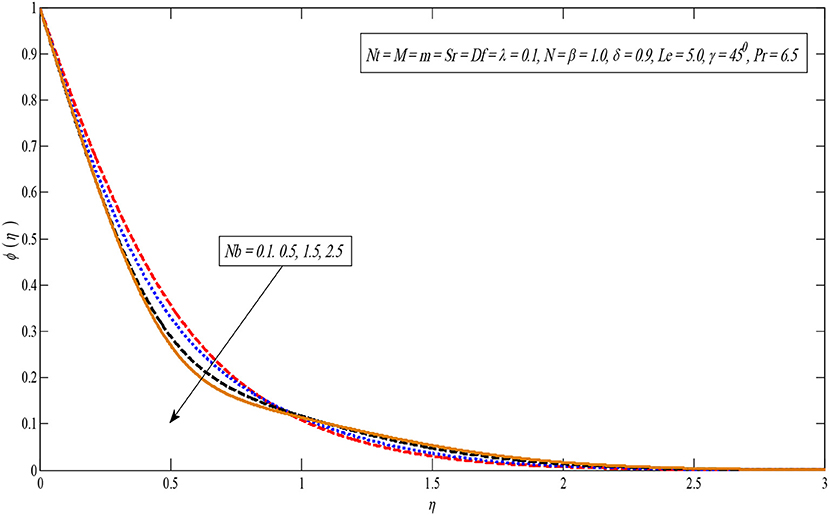
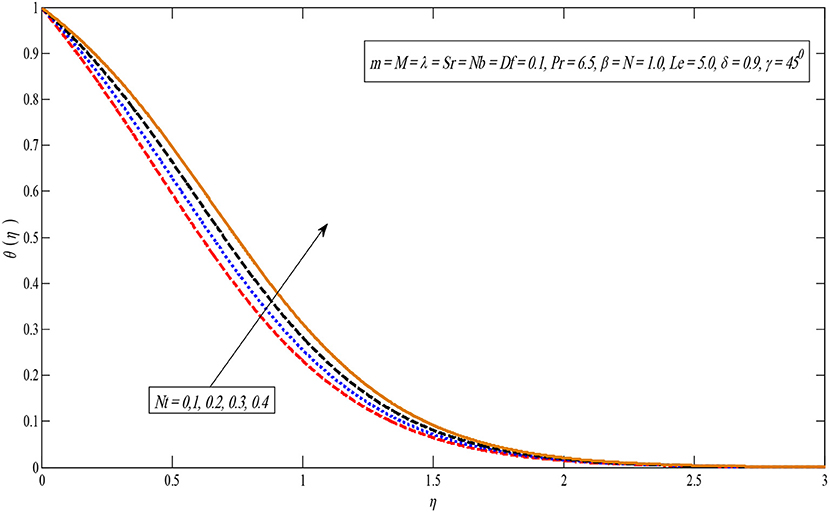
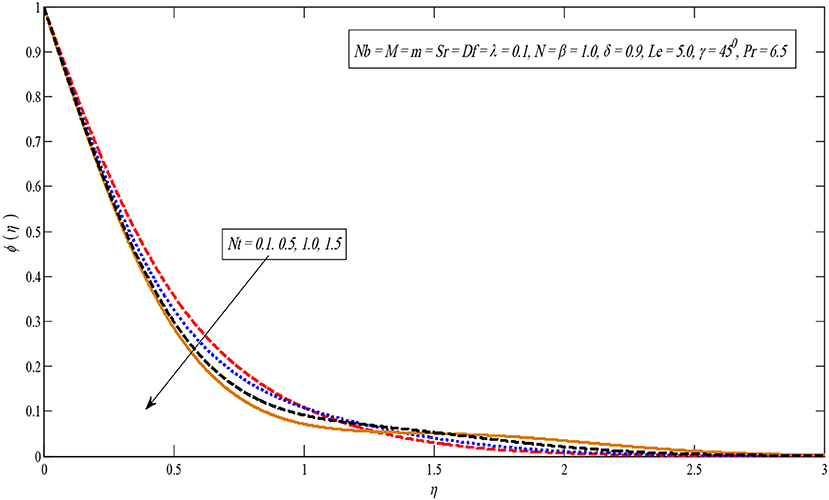
Figures 8, 9 show the effect of the Brownian motion on the temperature and concentration profiles, respectively. The temperature sketch enlarges on enlarging Nb; on the other hand, concentration distribution enlightens a dissimilar style. Physically, the boundary layer heats up due to the development in the Brownian motion which is inclined to transport nanoparticles from the extending sheet to the motionless liquid. Therefore, the absorption nanoparticle lessens. Figures 10, 11 present temperature and concentration profiles for altered values of thermophoresis parameters Nt. It is perceived that both temperature and concentration contours upsurge by growing the thermophoresis parameter because thermophoresis causes the small particles to compel away from a warm surface to the cold one.
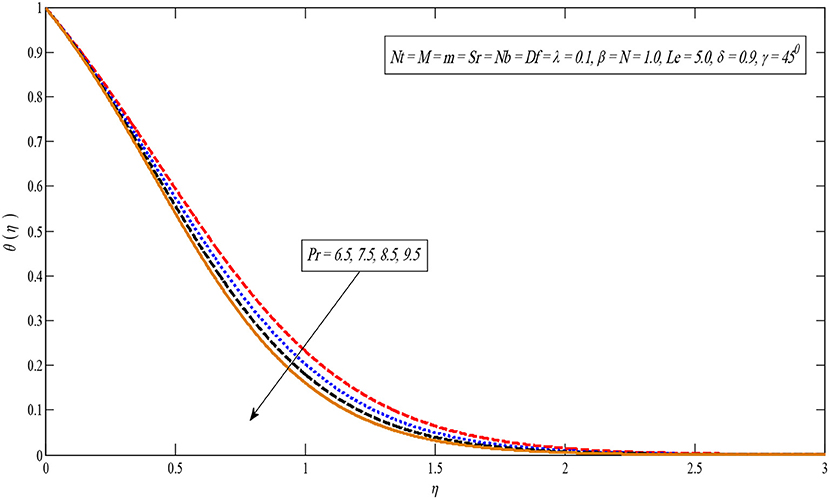
Figure 12 reveals that by growing the values of the Prandtl number parameter Pr, the temperature profile drops because the thermal boundary layer viscosity declines when growing the Prandtl number Pr. In short an upturn in the Prandtl number Pr means a deliberate amount of thermal dispersion.
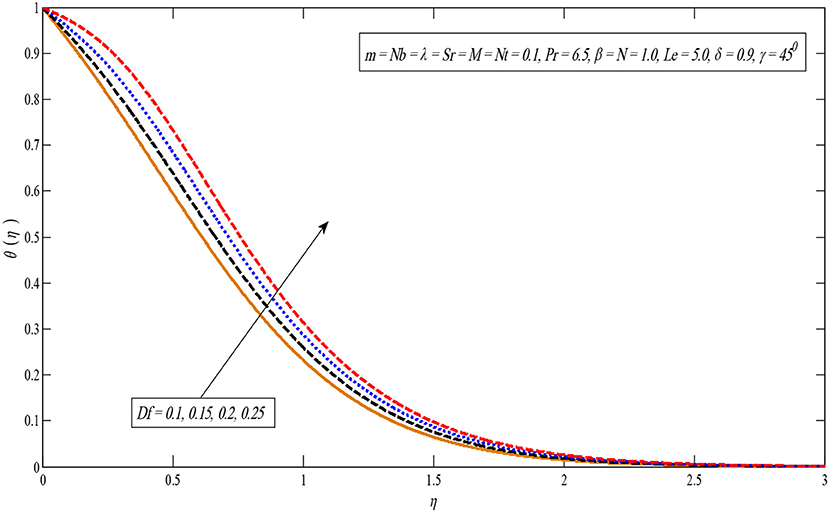
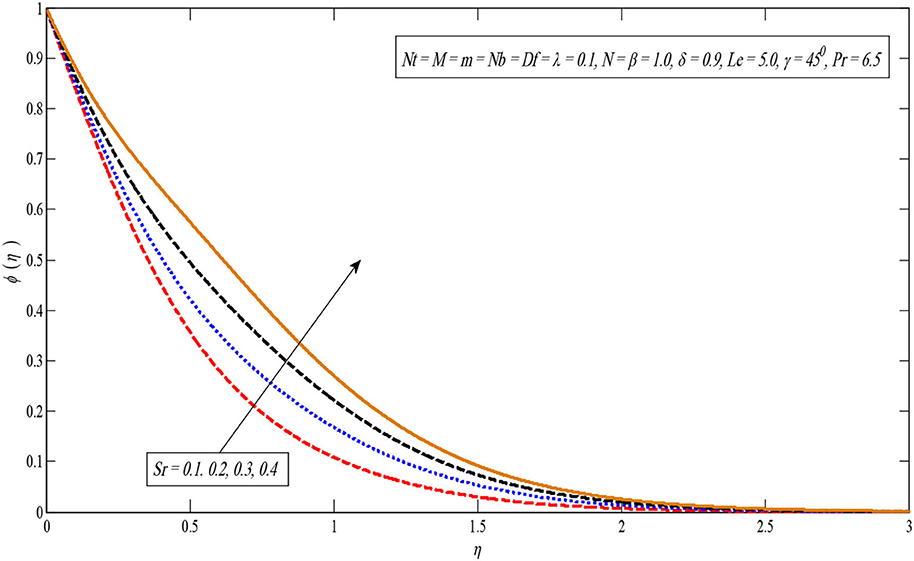
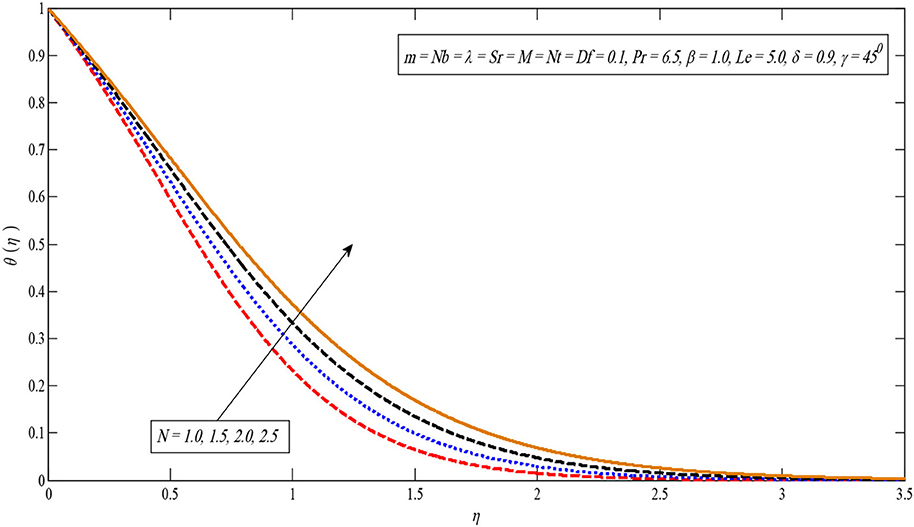
Figure 13 shows that the temperature profile becomes large for larger values in parameter Df. This can be justified as an increase in the Dufour parameter, causing an increase in the concentration gradient, resulting in a mass diffusion taking place more rapidly. In this way, the rate of energy transfer related to the particles becomes higher. That is why the temperature profiles enhance. The impact of the Soret number on the concentration profile is observed similar to the impact of the Dufour number on the temperature profile. As parameter Sr increases, the concentration profile increases as displayed in Figure 14. Additionally, Figure 15 indicates a temperature profile enhanced for large values of N.
Conclusions
This study explored the heat and mass exchange of Casson nanofluid flow over a non-linear slanted extending sheet. The numerical results are successfully obtained via the Keller-Box method and are finally performed with the resulting outcomes of already published work [1]. The main findings of the current study are summarized as:
• The velocity outline decreases by enhancing the inclination parameter.
• An increment in Casson fluid factor declines the velocity profile.
• Improving the buoyancy and solutal buoyancy parameters cause an enhancement in the velocity profile.
• Temperature profile upturns when increasing the radiation factor.
• Dufour effect causes the enhancement in the temperature profile.
• Mass diffusion and energy of the fluid upturns by enhancing the Brownian motion factor.
• The thermophoresis factor increases the temperature profile and decreases the concentration profile.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
The formulation was done by KR and MA. Similarity transformation was done by MM. Problem solved by IK and SA. Results plotted and discussed by PT and KN. All authors equally contributed in writing this manuscript.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author (SA) would like to thank the Deanship of Scientific Research (DSR) Majmaah University for supporting this work.
References
1. Khan WA, Pop I. Boundary-layer flow of a nanofluid past a stretching sheet. Int J Heat Mass Trans. (2010) 53:2477–83. doi: 10.1016/j.ijheatmasstransfer.2010.01.032
2. Choi SUS, Eastman JA. Enhancing thermal conductivity of fluids with nanoparticle. Mater Sci. (1995) 231:99–105
3. Buongiorno J. Convective transport in nanofluids. J Heat Transf. (2006) 128:240–50. doi: 10.1115/1.2150834
4. Nield DA, Kuznetsov AV. The Cheng–Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid. Int J Heat Mass Transf. (2009) 52:5792–5. doi: 10.1016/j.ijheatmasstransfer.2009.07.024
5. Anwar MI, Khan I, Sharidan S, Salleh MZ. Conjugate effects of heat and mass transfer of nanofluids over a nonlinear stretching sheet. Int J Phys Sci. (2012) 7:4081–92. doi: 10.5897/IJPS12.358
6. Suriyakumar P, Devi SPA. Effects of suction and internal heat generation on hydromagnetic mixed convective nanofluid flow over an inclined stretching plate. Eur J Adv Eng Technol. (2015) 2:51–8.
7. Ziaei-Rad M, Kasaeipoor A, Rashidi MM, Lorenzini G. A similarity solution for mixed-convection boundary layer nanofluid flow on an inclined permeable surface. J Therm Sci Eng Appl. (2017) 9:021015 doi: 10.1115/1.4035733
8. Thumma T, Bég OA, Sheri SR. Finite element computation of magnetohydrodynamic nanofluid convection from an oscillating inclined plate with radiative flux, heat source and variable temperature effects. Proc Inst Mech Eng Part N J Nanomater Nanoeng Nanosyst. (2017) 231:179–94. doi: 10.1177/2397791417731452
9. Govindarajan A. Radiative fluid flow of a nanofluid over an inclined plate with non-uniform surface temperature. J Phys Conf. (2018) 1000:012173. doi: 10.1088/1742-6596/1000/1/012173
10. Khan M, Shahid A, Malik MY, Salahuddin T. Thermal and concentration diffusion in Jeffery nanofluid flow over an inclined stretching sheet: a generalized Fourier's and Fick's perspective. J Mol Liquids. (2018) 251:7–14. doi: 10.1016/j.molliq.2017.12.001
11. Chakraborty T, Das K, Kundu PK. Ag-water nanofluid flow over an inclined porous plate embedded in a non-Darcy porous medium due to solar radiation. J Mech Sci Technol. (2017) 31:2443–9. doi: 10.1007/s12206-017-0442-4
12. Bhatti MM, Abbas T, Rashidi MM. Effects of thermal radiation and electromagnetohydrodynamics on viscous nanofluid through a Riga plate. Multidiscipline Model Mater Struct. (2016) 12:605–18. doi: 10.1108/MMMS-07-2016-0029
13. Bhatti MM, Mishra SR, Abbas T, Rashidi MM. A mathematical model of MHD nanofluid flow having gyrotactic microorganisms with thermal radiation and chemical reaction effects. Neural Comput Appl. (2018) 30:1237–49. doi: 10.1007/s00521-016-2768-8
14. Hussanan A, Khan I, Gorji MR, Khan WA. CNT S-water–based nanofluid over a stretching sheet. BioNanoScience. (2019) 9:21–9. doi: 10.1007/s12668-018-0592-6
15. Souayeh B, Reddy MG, Sreenivasulu P, Poornima T, Rahimi-Gorji M, Alarifi IM. Comparative analysis on non-linear radiative heat transfer on MHD Casson nanofluid past a thin needle. J Mol Liquids. (2019) 284:163–74. doi: 10.1016/j.molliq.2019.03.151
16. Ma Y, Mohebbi R, Rashidi MM, Yang Z. Study of nanofluid forced convection heat transfer in a bent channel by means of lattice Boltzmann method. Phys Fluids. (2018) 30:032001. doi: 10.1063/1.5022060
17. Makulati N, Kasaeipoor A, Rashidi MM. Numerical study of natural convection of a water–alumina nanofluid in inclined C-shaped enclosures under the effect of magnetic field. Adv Powder Technol. (2016) 27:661–72. doi: 10.1016/j.apt.2016.02.020
18. Bhatti MM, Abbas T, Rashidi MM. Entropy generation as a practical tool of optimisation for non-Newtonian nanofluid flow through a permeable stretching surface using SLM. J Comput Design Eng. (2017) 4:21–8. doi: 10.1016/j.jcde.2016.08.004
19. Sakiadis BC. Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J. (1961) 7:26–8. doi: 10.1002/aic.690070108
20. Crane LJ. Flow past a stretching plate. Z Angew Mathematik Physik. (1970) 21:645–7. doi: 10.1007/BF01587695
21. Ali M, Alim MDA, Alam MS. Heat transfer boundary layer flow past an inclined stretching sheet in the presence of magnetic field. Int J Adv Res Technol. (2014) 3:34–40.
22. Ramesh GK, Gireesha BJ, Bagewadi CS. Heat transfer in MHD dusty boundary layer flow over an inclined stretching sheet with non-uniform heat source/sink. Adv Math Phys. (2012) 2012:657805. doi: 10.1155/2012/657805
23. Malik MY. effects of second order chemical reaction on MHD free convection dissipative fluid flow past an inclined porous surface by way of heat generation : a lie group analysis 1 introduction 2 flow analysis. (2016) 45:35–45. doi: 10.18576/isl/050201
24. Ramesh GK, Chamkha AJ, Gireesha BJ. Boundary layer flow past an inclined stationary/moving flat plate with convective boundary condition. Afrika Matematika. (2016) 27:87–95. doi: 10.1007/s13370-015-0323-x
25. Griffiths PT. Stability of the shear-thinning boundary-layer flow over a flat inclined plate. Proc R Soc A Math Phys Eng Sci. (2017) 473:20170350. doi: 10.1098/rspa.2017.0350
26. Pal D, Mondal H. Influence of Soret-Dufour and thermophoresis on hydromagnetic mixed convection heat and mass transfer over an inclined flat plate with non-uniform heat source/sink and chemical reaction. Int J Comput Methods Eng Sci Mech. (2018) 19:49–60. doi: 10.1080/15502287.2018.1430073
27. Pandya N, Shukla AK. Soret-Dufour and radiation effect on unsteady MHD flow over an inclined porous plate embedded in porous medium with viscous dissipation. Int J Adv Appl Math Mech. (2014) 2:107–19.
28. Qing J, Bhatti M, Abbas M, Rashidi M, Ali M. Entropy generation on MHD Casson nanofluid flow over a porous stretching/shrinking surface. Entropy. (2016) 18:123. doi: 10.3390/e18040123
29. Bhatti MM, Abbas MA, Rashidi MM. Entropy generation for peristaltic blood flow with casson model and consideration of magnetohydrodynamics effects. Walail J Sci Techn. (2016) 14:451–61.
30. Ali M, Aruna G, Raju RS. MHD boundary layer casson fluid flow over a vertically inclined plate: grid study and convergence analysis of finite element technique. J Nanofluids. (2018) 7:1195–207. doi: 10.1166/jon.2018.1541
31. Manideep P, Raju RS, Rao TS N, Reddy GJ. Unsteady MHD free convection flow of casson fluid over an inclined vertical plate embedded in a porous media. In: AIP Conference Proceedings. Bikaneer: AIP Publishing. (2018). p. 140038. doi: 10.1063/1.5033213
32. Shamshuddin MD, Mishra SR, Thumma T. Chemically reacting radiative casson fluid over an inclined porous plate: a numerical study. In: Numerical Heat Transfer and Fluid Flow. Singapore: Springer. (2019) p. 469–479. doi: 10.1007/978-981-13-1903-7_54
33. Vijayaragavan R, Kavitha MA. Heat and mass transfer in unsteady MHD casson fluid flow past an inclined plate with thermal radiation and heat source/sink. Res J Eng Techn. (2018) 9:214–33. doi: 10.5958/2321-581X.2018.00030.2
34. Prasad DK, Chaitanya GK, Raju RS. Role of casson fluid on MHD natural convective flow towards vertically inclined plate with hall current. In: AIP Conference Proceedings. Bikaneer: AIP Publishing. (2018). p. 140073. doi: 10.1063/1.5033248
35. Jain S, Parmar A. Multiple slip effects on inclined MHD Casson fluid flow over a permeable stretching surface and a melting surface. Int J Heat Techn. (2018) 36:585–94. doi: 10.18280/ijht.360222
36. Sailaja SV, Shanker B, Raju RS. Finite element analysis of magneto-hydrodynamic casson fluid flow past a vertical plate with the impact of angle of inclination. J Nanofluids. (2018) 7:383–95. doi: 10.1166/jon.2018.1456
37. Rawi NA, Ilias MR, Lim YJ, Isa ZM, Shafie S. Unsteady mixed convection flow of Casson fluid past an inclined stretching sheet in the presence of nanoparticles. In: Journal of Physics: Conference Series. Kuantan: IOP Publishing. (2017) p. 012048. doi: 10.1088/1742-6596/890/1/012048
38. Raju RS, Reddy BM, Reddy GJ. Finite element solutions of free convective Casson fluid flow past a vertically inclined plate submitted in magnetic field in presence of heat and mass transfer. Int J Comput Methods Eng Sci Mechan. (2017) 18:250–65. doi: 10.1080/15502287.2017.1339139
39. Rashidi MM, Yang Z, Bhatti MM, Abbas MA. Heat and mass transfer analysis on MHD blood flow of Casson fluid model due to peristaltic wave. Therm Sci. (2018) 22:2439–48. doi: 10.2298/TSCI160102287R
40. Abbas MA, Bai YQ, Rashidi MM, Bhatti MM. Application of drug delivery in magnetohydrodynamics peristaltic blood flow of nanofluid in a non-uniform channel. J Mechan Med Biol. (2016) 16:1650052. doi: 10.1142/S0219519416500524
41. Anwar MI, Shafie S, Hayat T, Shehzad SA, Salleh MZ. Numerical study for MHD stagnation-point flow of a micropolar nanofluid towards a stretching sheet. J Braz Soc Mechan Sci Eng. (2017) 39:89–100. doi: 10.1007/s40430-016-0610-y
42. Kumar D, Singh J, Purohit SD, Swroop R. A hybrid analytical algorithm for nonlinear fractional wave-like equations. Math Model Nat Phenom. (2019) 14:304. doi: 10.1051/mmnp/2018063
Keywords: casson nanofluid, MHD, power law fluid, soret effect, dufour effect, inclined surface
Citation: Rafique K, Anwar MI, Misiran M, Khan I, Alharbi SO, Thounthong P and Nisar KS (2019) Numerical Solution of Casson Nanofluid Flow Over a Non-linear Inclined Surface With Soret and Dufour Effects by Keller-Box Method. Front. Phys. 7:139. doi: 10.3389/fphy.2019.00139
Received: 08 July 2019; Accepted: 06 September 2019;
Published: 11 October 2019.
Edited by:
Muhammad Mubashir Bhatti, Shanghai University, ChinaReviewed by:
Devendra Kumar, University of Rajasthan, IndiaMohammad Rahimi Gorji, Ghent University, Belgium
Mohammad Mehdi Rashidi, Tongji University, China
Copyright © 2019 Rafique, Anwar, Misiran, Khan, Alharbi, Thounthong and Nisar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ilyas Khan, aWx5YXNraGFuQHRkdHUuZWR1LnZu
 Khuram Rafique1
Khuram Rafique1