Application of Raman and Brillouin Scattering Phenomena in Distributed Optical Fiber Sensing

We present a review of the basic operating principles and measurement schemes of standalone and hybrid distributed optical fiber sensors based on Raman and Brillouin scattering phenomena. Such sensors have been attracting a great deal of attention due to the wide industrial applications they offer, ranging from energy to oil and gas, transportation and structural health monitoring. In distributed sensors, the optical fiber itself acts as a sensing element providing unique measurement capabilities in terms of sensing distance, spatial resolution and number of sensing points. The most common configuration exploits optical time domain reflectometry, in which optical pulses are sent along the sensing fiber and the backscattered light is detected and processed to extract physical parameters affecting its intensity, frequency, phase, polarization or spectral content. Raman and Brillouin scattering effects allow the distributed measurement of temperature and strain over tens of kilometers with meter-scale spatial resolution. The measurement is immune to electromagnetic interference, suitable for harsh environments and highly attractive whenever large industrial plants and infrastructures have to be continuously monitored to prevent critical events such as leakages in pipelines, fire in tunnels as well as structural problems in large infrastructures like bridges and rail tracks. We discuss the basic sensing mechanisms based on Raman and Brillouin scattering effects used in distributed measurements, followed by configurations commonly used in optical fiber sensors. Hybrid configurations which combine Raman and Brillouin-based sensing for simultaneous strain and temperature measurements over the same fiber using shared resources will also be addressed. We will also discuss advanced techniques based on pulse coding used to overcome the tradeoff between sensing distance and spatial resolution affecting both types of sensors, thereby allowing measurements over tens of kilometers with meter-scale spatial resolution, and address recent advances in measurement schemes employing the two scattering phenomena.

Introduction: Optical Fiber Sensors and Scattering Phenomena

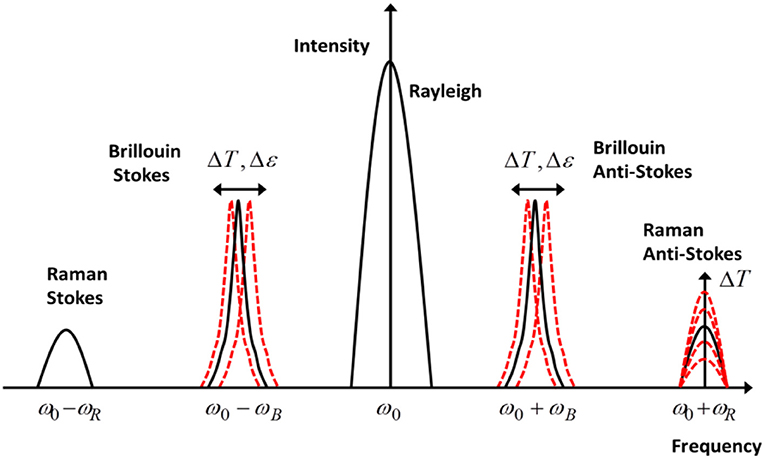
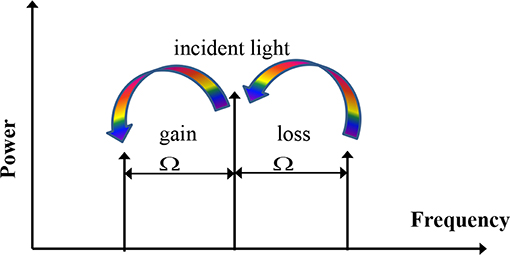
Optical fiber sensors (OFS) have some inherent advantages with respect to electronic sensors. Using the fiber as both the transducer and the transmitter of the data makes it possible to probe over long distances in a distributed manner. In addition, each sensing point does not require electrical energy supply, and the signals are intrinsically immune to electromagnetic interference. While early use of optical fibers in measurements involved simple loss characterizations, later applications involved more precise measurement of specific parameters such as strain, temperature and vibration [1]. Today, OFS systems constitute a ubiquitous technology widely used in measuring environmental parameters or the presence of chemicals, with key applications in, among others, the oil & gas, transportation and structural health monitoring sectors [2]. Commonly used OFS are broadly categorized into discrete/point and distributed sensors. Discrete OFS enable measurement at a single point and are mainly based on Fiber Bragg Gratings (FBGs), which exhibit reflectivity whose center wavelength varies with strain/temperature. A number of them can also be inscribed along the same fiber to make quasi-distributed measurements using wavelength or time division multiplexing techniques [3]. Recently, ultra-weak FBGs (UWFBGs) have also been used, whereby 100s of gratings with very low reflectivity are inscribed on the same fiber, resulting in a significantly lower cumulative loss suitable for long distance sensing [4]. Distributed OFS (DOFS), on the other hand, enable simultaneous measurements at multiple locations along a sensing fiber, and typically employ scattering phenomena. As light propagates through the fiber, it interacts with the constituent material and gets backscattered. Part of the backscattered signal has some particular intensity or spectral properties which depend on local stimuli applied to the environment in the vicinity of the fiber, and enable measurement of external parameters such as strain, vibration, temperature, current, magnetic field, etc., at multiple locations. The most commonly used scattering phenomena in DOFS are Rayleigh Backscattering (RBS), Spontaneous Raman Scattering (SpRS), Spontaneous Brillouin Scattering (SpBS), and Stimulated Brillouin Scattering (SBS) whose spectra are illustrated in Figure 1.

FIGURE 1

Figure 1. Scattering phenomena used in DOFS.

As shown, the RBS has a component at the incident signal spectrum while SpBS, SBS, and SpRS have ones at lower (Stokes) and upper (anti-Stokes) frequency shifts with respect to the incident signal. In the following sections, the theoretical background of SpRS, SpBS, and SBS phenomena and their applications in OFS will be presented in more detail, followed by some advanced schemes using these phenomena and recent trends of research in this area.

Spontaneous Raman Scattering

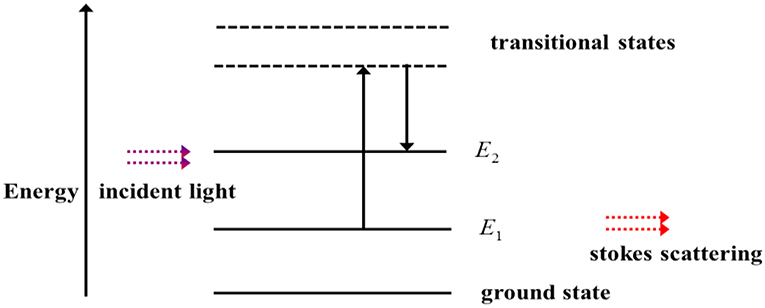
Spontaneous Raman Scattering is an inelastic scattering phenomenon, resulting from the interaction of light with the vibrational or rotational modes of molecules in the transmitting medium [5]. In the process, energy is transferred between the energy levels of the molecules constituting a material and the incident light [6]. This is more clearly depicted in Figure 2, which shows the energy diagram in Raman interactions where light with angular frequency of ω passes through a material where molecules have an initial energy of E_1.

FIGURE 2

Figure 2. Schematic of energy states in Raman Stokes scattering.

As energy is transferred from the light to the vibrational modes of the material, the molecules go to transitional virtual states, which are not stable energy states. When the molecules transit to another state E₂, the differential energy is absorbed by the material and hence the scattered Stokes wave with angular frequency ω_s has energy less than that of the incident light by an amount given by [6]:

$\begin{array}{ll}\Delta E=\hslash (\omega -{\omega }_s)& (1)\end{array}$

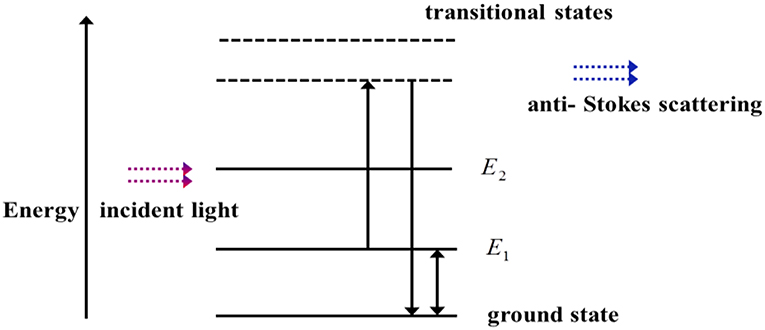
where $\hslash {=}^h{/}_{2\pi }$, and h = 6.62607004 ×10⁻³⁴ m² kg/s is Planck's constant. The equivalent interactions for the Raman anti-Stokes case is shown in Figure 3. In this case, first, upon an incident light with frequency of ω, the vibrational/rotational states of the material are transferred from E₁ to a transitional state, and then back to the ground state_. The energy difference between the two levels, which will be transferred to the incident light, results in anti-Stokes light with angular frequency of ω_AS, with a difference in energy given by [6]:

$\begin{array}{ll}\Delta E=\hslash ({\omega }_{AS}-\omega )& (2)\end{array}$

In the special case of the Raman scattering in a glass fiber, the Raman signal is located in a very wide band centered at ~13 THz from the input light, which corresponds to a shift of ~100 nm at 1,550 nm wavelength.

FIGURE 3

Figure 3. Schematic of energy states in Raman anti-Stokes scattering.

Spontaneous Brillouin Scattering

Brillouin scattering occurs due to the interaction of light with the sound waves or the acoustic phonons of a material. The SpBS phenomenon can be understood by considering the wave vector diagram shown in Figure 4A [7], which depicts the interaction between an incident and scattered light which respectively have wave vectors k and k′. The incident light interacts with the sound wave in the material which is represented by a vector q. As shown in Figure 4B, the magnitude of the sound wave vector for a generic scattering direction of ϕ will be given by [7]:

$\begin{array}{ll}{\left|q\right|}^2={\left|k\right|}^2+{\left|k^{\prime }\right|}^2-2\left|k\right|\left|k^{\prime }\right|\cos \varphi & (3)\end{array}$

Assuming the frequency of the sound wave is much smaller than that of light [7], which will be justified later, the energy conservation allows the approximation|k| ≅ |k′|, and considering the trigonometric identity 1 − cosϕ = 2sin²(ϕ/2), we obtain:

$\begin{array}{ll}{\left|q\right|}^2=2{\left|k\right|}^2\times 2{\sin }^2(\varphi /2),\left|q\right|=2\left|k\right|\sin (\varphi /2).& (4)\end{array}$

To obtain the frequency of the sound wave, it is possible to employ the dispersion relation for the sound wave which connects its velocity and angular frequency Ω [8]:

$\begin{array}{ll}\Omega =q.\upsilon =2\left|k\right|\upsilon \sin (\varphi /2)=2n\omega \frac{\upsilon }{c}\sin \varphi /2,& (5)\end{array}$

where n is the phase refractive index. It can be seen from (5) that the Stokes shift has a sinusoidal dependence on the scattering wave vector angle and hence, there is no scattering in the forward direction, where ϕ = 0, while being non-zero for all other directions. Since light propagates in the longitudinal direction in the fiber, this in turn means that Brillouin scattering in an optical fiber is essentially Brillouin backscattering. The maximum value happens for ϕ = π, for which the frequency will have ${\Omega }_{s-max}=2n\frac{\upsilon }{c}\omega$. For typical values of the parameters in a singlemode silica fiber, the speed of sound υ = 5,960 m/s, group index n = 1.5, λ = 1,550 nm, the maximum frequency shift due to Brillouin scattering can be calculated as [9]:

$\begin{array}{ll}\Delta v_{B-\max }=\frac{{\Omega }_{s-\max }}{2\pi }=\frac{2\times n\times \upsilon }{\lambda f\times 2\pi }\times 2\pi f=\frac{2n\upsilon }{\lambda }~11.536GHz& (6)\end{array}$

The anti-Stokes counterpart of the aforementioned process has a vector schematically described in Figure 5A. In this case, as energy is transferred from the soundwave to the incident light, the scattered light has a wave vector component which is the summation of the wave vectors of the incident light and acoustic wave. As per the dispersion relation, the frequency of the scattered light will be the sum of the two waves.

FIGURE 4

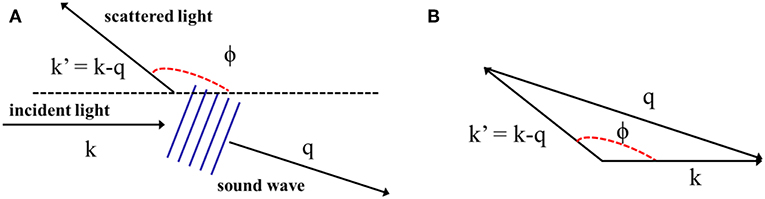
Figure 4. (A) Schematic of Brillouin Stokes scattering. (B) Wave vector diagram showing interaction of incident light and sound wave.

FIGURE 5

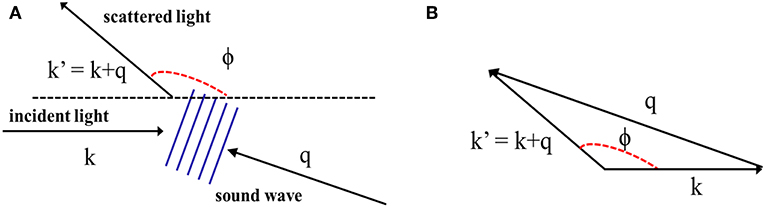
Figure 5. (A) Brillouin anti-Stokes scattering of light from an acoustic wave. (B) Wave vector diagram for anti-Stokes component of Brillouin scattering.

As shown in the schematic in Figure 5B, the scattered wave vector will be given by k' = k + q and the frequency will be ω′ = ω + Ω, where ω and Ω are the angular frequencies of the two waves related to the wave vectors via each other's dispersion relations. The magnitude of q will now be given by [7]:

$\begin{array}{ll}{\left|q\right|}^2={\left|k\right|}^2+{\left|k^{\prime }\right|}^2+2\left|k\right|\left|k^{\prime }\right|\cos \varphi .& (7)\end{array}$

Using the previous property |k| ≅ |k′|and inserting this in (7), the anti-Stokes frequency is also given by:

$\begin{array}{ll}{\Omega }_{AS}=2n\omega \frac{\upsilon }{c}\sin \varphi /2& (8)\end{array}$

Hence, for singlemode silica fibers, the frequency shift due to the anti-stokes light is also the same as Ω ~11.536 GHz at 1,550 nm. Note that, like any other medium, the soundwave propagating in an optical fiber inevitably undergoes damping. This results in the scattering in any direction to have a certain bandwidth. The bandwidth of the Brillouin scattering can be given by [7]:

$\begin{array}{ll}\delta \omega =4{\Gamma }^{\prime }\frac{w^2}{n^2}{c}^2{\sin }^2(\varphi /2)& (9)\end{array}$

In (9), Γ′ represents the damping parameter of the acoustic wave, which gives a measure of the decay of the oscillations in a system. Note that, the Stokes and anti-Stokes components of Brillouin scattering signal have spectra which are symmetric and have similar bandwidth. Since they also have equal shifts in the two directions as shown in (5) and (8), the two components are located symmetrically at the two sides of the spectrum of the incident light, which is also depicted in Figure 1.

Stimulated Brillouin Scattering

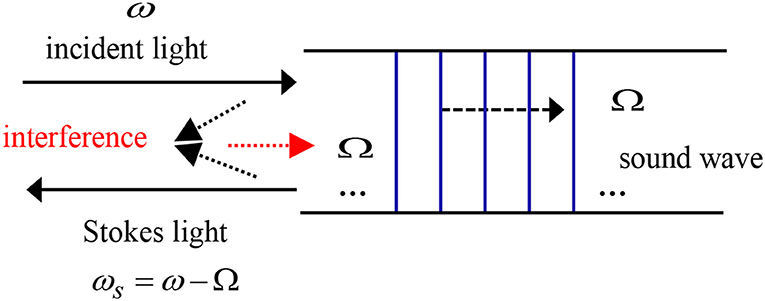
Stimulated Brillouin scattering takes place when the intensity of the incident light is high enough to result in a change in the density of the material through a mechanism known as electrostriction, whereby the material becomes denser in places where the gradient of the optical intensity is high. This mechanism is exploited in optical amplification as well as optical fiber sensing. When light with time varying electric field E passes through a medium, the change in the material density ρ is proportional to the dot product of the field and is given by [7]:

$\begin{array}{ll}\Delta \rho =\frac{1}{2}{\epsilon }_0\rho C{\gamma }_e\langle \tilde{E}·\tilde{E}\rangle ,& (10)\end{array}$

Where C = 1/K, is the compressibility with K being the bulk modulus, and γ_e the electrostrictive constant. To obtain a quantitative expression for the wave interactions in SBS, we consider the induced (i.e., stimulated) scattering from a seed Stokes signal via electrostriction, assuming a counter-propagating signal and Stokes waves in a generic medium such as an optical fiber, as shown in Figure 6.

FIGURE 6

Figure 6. Counter-propagating waves in a medium interacting through electrostriction.

For the general case in which the wave vector for the incident light is k and that of the counter-propagating Stokes wave is k_s, since the sound wave is enhanced by the interaction between the Stokes and incident light waves, its wave vector will be:

$\begin{array}{ll}{q}_B=k-k_s,\left|q_B\right|=\left|k\right|+\left|k_s\right|,& (11)\end{array}$

where vector sum in the calculation of the magnitude is made considering that the two waves are counter-propagating in the medium. Considering the angular frequency of an acoustic wave having velocity υ, Ω_B = |q_B|υ and inserting this in equation (11), while using dispersion relations for the signal |k| = nω/c and corresponding expression for the Stokes wave ω = ω_s + Ω, the acoustic wave will have angular frequency given by [8, 9]:

$\begin{array}{ll}{\Omega }_B=\frac{\upsilon }{c/n}\left({\omega }_s+{\Omega }_B+{\omega }_s\right)=\frac{\upsilon }{c/n}(2{\omega }_s+{\Omega }_B)& (12)\end{array}$

Equation (12) can be further expanded and solved, using the aforementioned dispersion relations to obtain an expression for the Brillouin frequency shift:

$\begin{array}{ll}{\Omega }_B=\frac{\frac{2\upsilon }{c/n}{\omega }_s}{1+\frac{\upsilon }{c/n}}& (13)\end{array}$

Note that for light waves typically used in optical fibers, the velocity of the acoustic wave is significantly small with respect to c/n. Hence, from the expression in (13), a good approximation to the Brillouin frequency shift can be ${\Omega }_B=\frac{2\upsilon }{c/n}{\omega }_s$.

The diagram in Figure 7 shows transfer of energy to and from the incident light and the two symmetric components. If the component at a higher frequency has an intensity of I_AS and the incident signal has an intensity of I_si, it can be shown that it will transfer energy to the pump along the longitudinal direction z with its intensity given by [7]:

$\begin{array}{ll}{I}_{AS}=I_{AS}(0)e^{(-g{I}_{si}z)}.& (14)\end{array}$

In (14) g is the Brillouin gain:

$\begin{array}{ll}g=g_0\frac{({\Gamma }_B/2)}{{({\Omega }_B-\Omega )}^2+{({\Gamma }_B/2)}^2},& (15)\end{array}$

where ${\Gamma }_B=\frac{1}{{\tau }_p}=q^2{\Gamma }^{\prime }$ is the Brillion line width, with τ_p and Γ′ being the acoustic phonon life time and the damping factor, while q is the velocity of the acoustic wave and g_o is a material dependent constant.

FIGURE 7

Figure 7. SBS interaction showing transfer of energy to and from the incident light.

Mechanisms of Measurement in DOFS Based on Brillouin and Raman Scattering in Time Domain

In this section, we describe how each of the three scattering phenomena discussed in the previous section can be used in a sensing scheme for distributed measurement of a certain physical parameter in an optical fiber in time domain. In DOFS based on time domain, typically a pulse of laser light is used to probe the sensing fiber. Since the speed of light in the fiber is known, the relative time delay of the backscattering signal from a reference instant is used to locate the response from each specific point along the fiber, thereby constructing a spatial trace of the backscattering signal, which will then be further processed to extract a specific parameter at any desired location.

Raman Distributed Temperature Sensing (RDTS)

Distributed measurement of temperature using SpRS is made possible due to the fact that the intensity of the anti-Stokes scattering optical fibers is dependent on the ambient temperature in the vicinity of the fiber. Since the Stokes component is only slightly dependent on the local temperature T at each spatial point z, the ratio between the two is given by [10]:

$\begin{array}{ll}R(z)=\frac{I_{AS}}{I_S}={\left(\frac{{\lambda }_S}{{\lambda }_{AS}}\right)}^4{e}^{\raisebox{1ex}{$-\Delta E$}\!\left/ \!\raisebox{-1ex}{${}_{k_{B}T}$}\right.\text{}}={\left(\frac{{\lambda }_S}{{\lambda }_{AS}}\right)}^4{e}^{\raisebox{1ex}{$-\hslash {\Omega }_R$}\!\left/ \!\raisebox{-1ex}{${}_{k_{B}T}$}\right.\text{ }}.& (16)\end{array}$

where Ω_R is the Raman frequency shift and ΔE = −ℏΩ_R is the energy difference between the incident and scattered light. The dependence of the ratio between the Stokes and anti-Stokes components on temperature comes from the population levels of the excited vibrational modes of the glass in thermodynamic equilibrium. The anti-Stokes process requires a pre-existing optical phonon, which is more likely to occur at higher temperatures. Specifically, the phonons in the different vibrational energy states follow Boltzman's distribution with temperature and the ratio of the anti-Stokes to Stokes intensities scales exponentially with temperature. The dependence on temperature is more for the anti-Stokes component compared to the Stokes one since the relative sensitivities $\epsilon =\frac{1}{I}\frac{dI}{dT}$ of the two are, respectively, 0.83% K^−f and 0.096% K^−a for typical silica-based glass at room temperature [11].

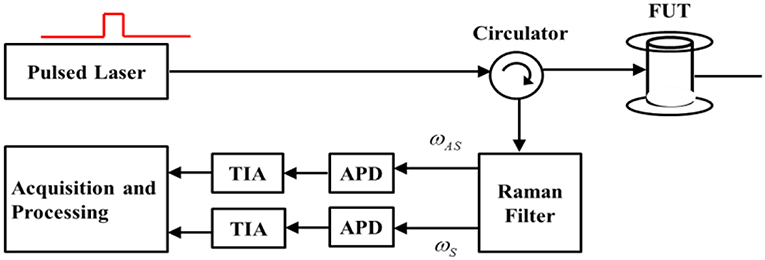
The use of SpRS for measurement of distributed temperature in time domain is known as Raman Distributed Temperature Sensing (RDTS), and its basic schematic is shown in Figure 8. Light from a pulsed laser is sent into the sensing fiber through a circulator and Raman filter with output at the Stokes and anti-Stokes lights is used to separate the two components of the backscattered light, which are detected using Avalanche Photodiodes (APDs), amplified using the Trans-impendence Amplifiers (TIAs) and acquired for further processing.

FIGURE 8

Figure 8. Schematic of a basic RDTS.

To account for the wavelength-dependent factor, the ratio in (20) is made at a reference temperature T_ref, and a reference ratio is made to yield:

$\begin{array}{ll}\frac{R(T)}{R(T_{ref})}=\frac{e^{\raisebox{1ex}{$-h{\omega }_R$}\!\left/ \!\raisebox{-1ex}{${}_{k_{B}T}$}\right.\text{ }}}{e^{\raisebox{1ex}{$-h{\omega }_R$}\!\left/ \!\raisebox{-1ex}{$k_B{T}_{ref}$}\right.}}=e^{-h{\omega }_R\left[\frac{1}{k_{B}T}-\frac{1}{k_B{T}_{ref}}\right]}.& (17)\end{array}$

Subsequently, (17) is rearranged to make distributed temperature measurement at each point along the fiber:

$\begin{array}{ll}T={\left\{\frac{1}{T_{ref}}-\frac{k_B}{h{\nu }_R}\ln \frac{R(T)}{R(T_{ref})}\right\}}^{-1}.& (18)\end{array}$

Brillouin Optical Time Domain Reflectometry (BOTDR)

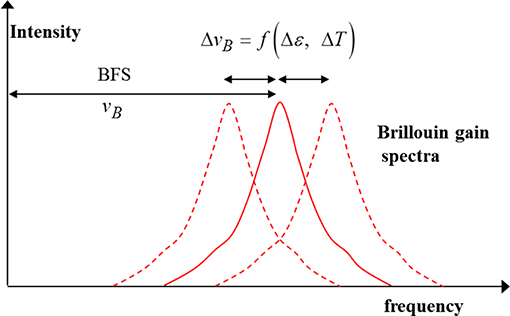
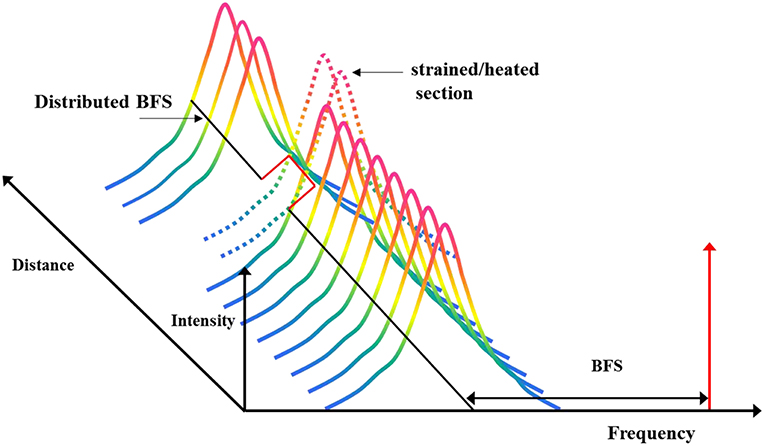
Measurement based on spontaneous Brillouin scattering hinges on the dependence of the Brillouin Gain Spectrum (BGS) on presence of heating or expansion of the fiber. Specifically, the frequency offset between the peak of the BGS and that of the spectrum of the incident light, also known as the Brillouin Frequency Shift (BFS), is linearly dependent on the strain or temperature at each point of the fiber, as shown in Figure 9. Hence, distributed measurement with this technique boils down to determining the distributed BFS along the fiber.

FIGURE 9

Figure 9. Measurement of frequency shift in Brillouin scattering based sensing.

For a change in longitudinal strain Δε and that of temperature ΔT, the BFS has the form:

$\begin{array}{ll}\Delta {\nu }_B(\Delta \epsilon ,\Delta T)=C_{\epsilon }\Delta \epsilon +C_T\Delta T,& (19)\end{array}$

where the parameters C_ε and C_T are the strain and temperature coefficients of the specific fiber. They have typical values of ~0.05MHz/με and ~1MHz/°C for standard singlemode silica fibers at 1,550 nm.

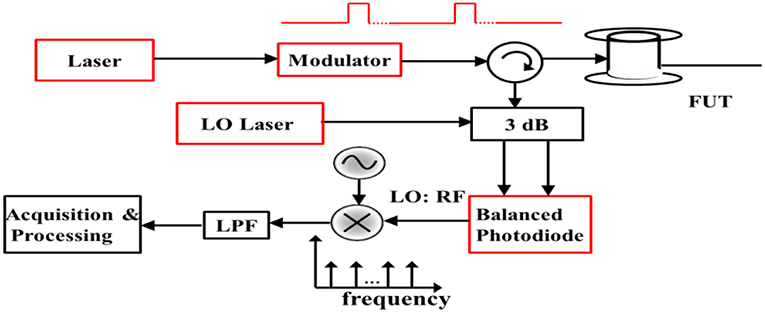
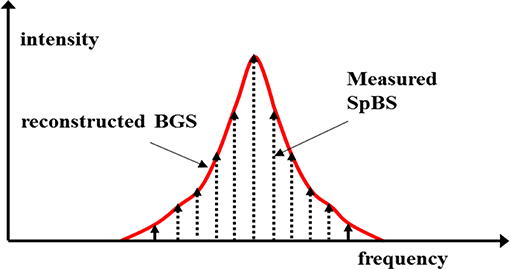
A simple schematic for measurement using the BOTDR technique is shown in Figure 10. As shown, the CW signal from a narrowband laser is gated into optical pulses using an intensity modulator. The pulses are then sent into the Fiber Under Test (FUT) through the three-port circulator. The backscattering from the fiber at the return port of the circulator at the Stokes frequency is then allowed to beat with a local oscillator through a 3 dB coupler and detected using the balanced photodiode. The resulting beating is mixed with an RF local oscillator whose frequency is scanned across the possible range of the BGS in subsequent measurements. The LPF is used to remove high frequency components. The schematic shown in Figure 11 shows the scanning of the frequency of the mixer to reconstruct the plot of the BGS.

FIGURE 10

Figure 10. Schematic of a simple BOTDR sensor for measurement of distributed strain/temperature.

FIGURE 11

Figure 11. Scanning of the frequency of the RF mixer to reconstruct the Brillouin Gain Spectrum.

Brillouin Optical Time Domain Analysis (BOTDA)

The basic mechanism of sensing using the BOTDA involves pump and probe signals which are applied at the two ends of the sensing fiber. As these signals counter-propagate and interact through electrostriction, energy is transferred from the pump to the probe via SBS. As shown in a basic schematic given in Figure 12, first a CW light from a single narrowband laser is allowed to pass through a coupler, which feeds the input light in two paths: an upper one constituting the path for the pulsed pump and the lower one for the CW probe.

FIGURE 12

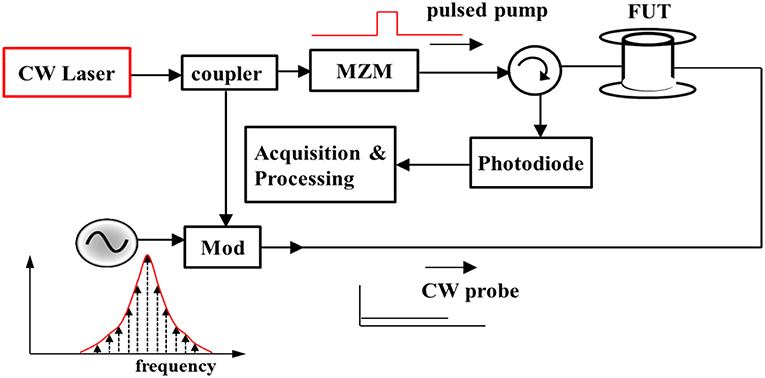
Figure 12. Schematic of a simple BOTDA configuration showing counter-propagating pump and probe powers.

The pulsed light is generated using a Mach-Zehnder Modulator (MZM) which acts as an intensity modulator and forms the pump which is fed to the sensing fiber through an optical circulator. The other part of the CW light is modulated with a sinusoidal RF signal at the Brillouin shift and will act as the CW probe, which is sent into the other end of the fiber. After proper bandpass filtering of the SBS signal at the Stokes frequency, the resulting trace is detected using a photodiode followed by a digital acquisition and processing block. The frequency of the CW probe, which has a nominal frequency with offset at the BGS shift of a singlemode fiber at around 11 GHz, is swept with respect to the center frequency of the pump.

The measurement mechanism involved in BOTDA is depicted in Figure 13, where the BGS of the fiber is determined for the whole fiber and the resulting plot becomes a three-dimensional plot of intensity vs. frequency for each spatial location along the fiber with a resolution determined by the pulse width. The distributed BFS is then calculated and exhibits an offset for any section which is either strained or heated.

FIGURE 13

Figure 13. Measurement in BOTDA showing reconstruction of distributed BGS.

Note that RDTS allows distributed temperature measurements without any cross-sensitivity with other parameters such as strain, while Brillouin-based sensors suffer from cross-sensitivity of temperature and strain which require other techniques to resolve. These include hybrid Raman/BOTDA schemes or hybrid Raman/BOTDR configurations. In addition, while simple RDTS involves an intensity-based measurement in which methods to account for non-local intensity changes are needed, Brillouin-based measurements are solely based on wavelength shift. As can be seen from Figures 10, 12, a key difference between BOTDA and BOTDR schemes is that the former requires both ends of the fiber as opposed to the latter in which one end suffices. It is worth noting that some RDTS schemes which address time-varying wavelength-dependent losses involve loop configurations requiring both ends of the fiber [12, 13]. Thanks to advanced schemes which include differential pulse pair, BOTDA is able to offer more spatially resolved temperature measurements compared to RDTS.

Advanced Schemes in Raman and Brillouin Distributed Sensing

Note that the scheme presented in Figure 12 is a simplified version and practical schemes contain more components which enable high-SNR measurements using advanced techniques and configurations of the pump in RDTS and pump/and probe light in BOTDA. There are also others addressing issues such as cross-sensitivity between temperature and strain and speed enhancement in BOTDA.

SNR Improvement in RDTS and BOTDA Using Optical Pulse Coding

In conventional distributed sensors, only a single pulse is sent into the sensing fiber. However, in BOTDA or RDTS measurements, shorter pulses which enable spatially resolved measurements have less energy and vice versa. The peak power of the pulse can be increased for a higher energy but there is a threshold of power levels before the onset of other detrimental non-linear effects in long distance sensing. This entails a tradeoff between spatial resolution and sensing distance which needs resolving using advanced techniques. Detrimental non-linear effects include modulation instability and forward stimulated Raman scattering. In addition, there is also pump depletion, which ensues due to gradual power transfer from the higher frequency wave to the lower one along the fiber resulting in measurement errors due to a reduction in the pump power (in a gain configuration) at long distances [14].

One of the methods to resolve the resolution-distance tradeoff is the use of optical pulse coding. In this technique, instead of sending a single pulse per measurement round, a given pattern of pulses is sent within a single round-trip-time (RTT) as shown in the schematic given in Figure 14, where τ is the bit duration given by RTT/N, N being the length of the pattern, also known as a codeword. The resulting response will be a superposition of the delayed responses. The pulse patterns could be linearly combinational codes (e.g., Simplex codes) [15], or complementary correlation ones such as Golay codes. When the fiber is probed with a simplex codeword, the resulting response is equivalent to a matrix multiplication involving a simplex Matrix S_M representing the presence and absence of a pulse by either a 1 or a 0, respectively. If η_i(t) for i = [1, 2] represents the response of the signal for a given combination of the pulse, and y_i(t) = y(t-iτ) is the delayed response with e_i(t) being the error associated with each measurement, the matrix multiplication representing such a response can be written as:

$\begin{array}{ll}\left(\begin{array}{c}{\eta }_1(t)\\ {\eta }_2(t)\\ {\eta }_3(t)\end{array}\right)=\left(\begin{array}{ccc}1& 0& 1\\ 0& 1& 1\\ 1& 1& 0\end{array}\right)\left(\begin{array}{c}{y}_1(t)\\ y_2(t)\\ y_3(t)\end{array}\right)+\left(\begin{array}{c}{e}_1(t)\\ e_2(t)\\ e_3(t)\end{array}\right).& (20)\end{array}$

Subsequently, the equivalent of the single pulse can be obtained from this sum by using an inverse matrix multiplication operation. The same can be done for a generic case of a codeword having a simplex matrix S_M of length M and it can be shown that for a simplex coded word of size M, the gain in SNR when using pulse coding when compared to a single pulse, also known as the coding gain, is given by [16]:

$\begin{array}{ll}{G}_{coding}=\frac{M+1}{2\sqrt{M}}.& (21)\end{array}$

In complementary Golay correlation coding, first conceived by Naseem et al. [17] and Golay [18], each sequence in the set is such that the number of pairs of like elements with any separation in one sequence is the same as the number of pairs of unlike elements in another. Formally, a complementary correlation Golay code of sequence A and B with respective elements a_i and b_i, each of length L, must ensure that the respective autocorrelation functions c_i and d_i, given by [18]:

$\begin{array}{ll}{c}_i={\displaystyle \sum _{i=1}^{i=L-j}{a}_i}{a}_{i+j},d_i={\displaystyle \sum _{j=1}^{i=L-j}{b}_i}{b}_{i+j}& (22)\end{array}$

are such that:

$\begin{array}{ll}{c}_0+d_0=2n,c_j+d_j=0,j\ne 0.& (23)\end{array}$

where the expression in [19] is also commonly denoted by a delta function. Golay complementary codes are bipolar and, for use in optical systems which are unipolar, they must be represented in an equivalent form. This is typically done by defining the elements in each sequence corresponding to “1”s and “−1”s as A₁ = (1+A)/2, A₂ = (1−A)/2, and B₁ = (1+B)/2, B₂ = (1−B)/2 [17]. Note that the coding gain with respect to a single pulse when using unipolar Golay sequence is given by $G=\sqrt{L/4}$. Among others, Golay coding has been used to suppress the impact of pump depletion in BOTDA with a coding gain $G=\sqrt{L}$, with a more enhanced scheme based on three-tone bipolar Golay code offering increased robustness against this non-linear effect [20].

FIGURE 14

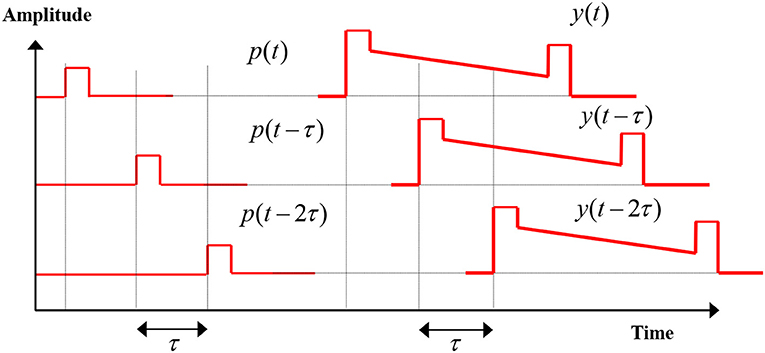
Figure 14. Schematic of individual pulses with varying delays at multiples of the bit-duration τ and their corresponding responses.

Hence, the use of optical pulse coding results in an SNR enhancement in the measurement with a given pulse width at low power levels, and hence enables more accurate measurements at long distances with meter-scale spatial resolution. A number of pulse coding schemes have been demonstrated in advanced BOTDA configurations [21, 22] and a representative scheme is shown in Figure 15 [21]. First, light from a narrowband Distributed Feedback (DFB) laser is coupled into two branches using a 30:70 coupler which results in the probe in the upper arm and the pump in the lower one. In the probe branch, the Mach-Zhender Modulator (MZM) is modulated with a sinusoidal signal whose frequency is scanned in steps of a few MHz. After amplification with an Erbium-Doped Fiber Amplifier (EDFA) and using a Variable Optical Attenuator (VOA) to adjust the power, a polarization scrambler is used to depolarize the light, and an isolator blocks light coming from the probe side.

FIGURE 15

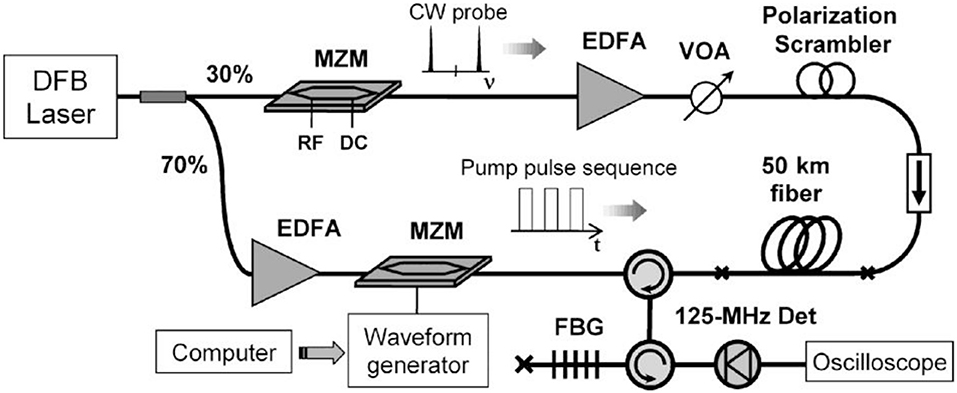
Figure 15. Experimental setup of a BOTDA sensor using coding for distributed temperature measurements [21].

On the lower branch of the pump, the light is first amplified and fed to an MZM which is used to generate the pulses. The high-peak power pulses are then sent through the circulator into a FUT comprised of 50-km standard single-mode fiber at the end of which a 1-m segment is heated. At the receiver, the backscattered signal is filtered using a combination of an FBG and circulator and the resulting traces are detected using a simple pin photoreceiver which feeds the data acquisition system composed of an oscilloscope. Then, subsequent post-processing is applied to reconstruct the BGS via a curve fitting algorithm for each point along the fiber. The technique is used to experimentally demonstrate distributed measurement at a spatial resolution of 1 m, with a temperature/strain accuracy of 2.2°C/44 με at 50 km.

Note that differences in the power levels of consecutive pulses can lower the accuracy of the measurement in coding at long distances [23]. The linear superposition of the contribution of the backscattering from long pulses could also be lost as successive pulses encounter a probe wave front which has been amplified by previous ones, resulting in the sensitivity of the pump depletion to the amplification of the wave font by previous pulses in the sequence [24]. In addition, use of long coded sequences has been demonstrated to lower the threshold of amplified spontaneous Brillouin scattering in the fiber. Techniques such as linearization using logarithmic processing of the probe response [25] allow maintaining superposition with coding while probe dithering has been demonstrated to address the limitations of pump depletion and lowered amplified spontaneous scattering threshold due to coding [24].

Pulse Coding in RDTS and Addressing Cross-Sensitivity Between Strain and Temperature in BOTDA Using Hybrid Measurements

The application of optical pulse coding has also been extended to RDTS configurations. One such demonstration includes the use of low-repetition rate cyclic coding [19] and the experimental setup is depicted in Figure 16. As shown, first light from a pulsed narrowband laser is modulated using an Acousto-optic Modulator (AOM) driven with a pulse pattern generator before being sent into the FUT composed of a 26-km SMF using a Raman filter, which also separates the Stoke and anti-Stokes components of the Raman backscattering signal. The signal in each branch is then detected using an avalanche photodiode (APD), and acquired using FPGA-controlled analog to digital converter. This is followed by post-processing to extract the temperature from the two components. A 71-bit cyclic simplex coding is shown to result in a dynamic range enhancement of 6 dB, enabling fast measurement of temperature (within 30 s, as opposed to few minutes in other systems) with a resolution of 3°C at 26 km, with a spatial resolution of 1 m.

FIGURE 16

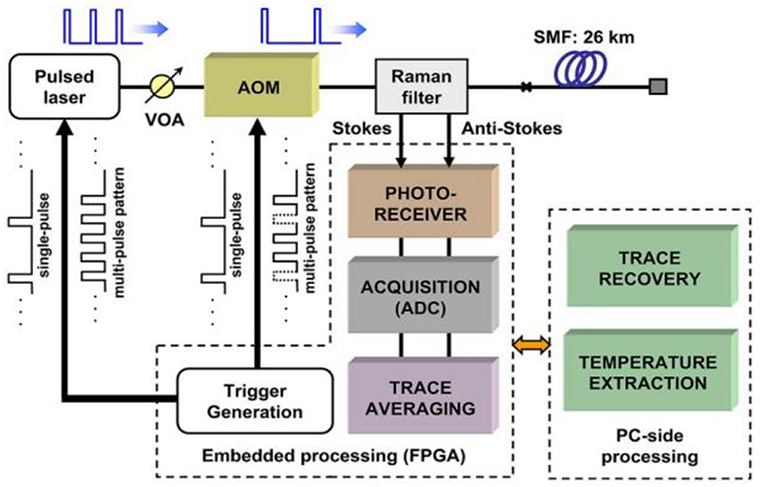
Figure 16. An RDTS with enhanced performance using cyclic simplex coding [19].

Note that one of the critical issues hampering the long-term stability of RDTS systems is the variation of Wavelength-Dependent Losses (WDL) with time due to various environmental factors. One way to address this issue is by using a loop configuration in which the geometric mean of the ratio of the backscattering intensities in the forward and backward directions is used to mitigate detrimental effects of WDL in reducing the accuracy of temperature measurements [19]. A method which uses two light sources at different emission wavelength is also demonstrated, whereby the anti-Stokes backscattering of one source spectrally overlaps with the incident light from the other and cancels out non-identical attenuations caused by wavelength differences between Stokes and anti-Stokes components [26]. An alternative scheme addresses WDL without the need for additional source employing a mirror at the end of the fiber which generates an anti-Stokes wave canceling out the effect of local attenuation [27]. There is also a more robust method to correct WDL via the measurement of anti-Stokes component alone in which the data processing is simplified by avoiding correction of the differential group velocity between the two Raman components [19]. There are also investigations of other advanced standalone BOTDA schemes for fast measurements using slope-assisted BOTDA [28], adaptive filtering [29], high spatial resolution using a Differential Pulse-Pair (DPP-BOTDA) [30], and dynamic Brillouin gratings (DBG), which have applications in birefringence measurement and all-optical processing [31].

Note that BOTDA suffers from cross-sensitivity between temperature and strain as shown in equation (19). Various configurations have so far been proposed and demonstrated to discriminate between of the effects of the change in BFS due to strain and temperature. Among others, a hybrid sensing scheme combining BOTDA in a loss configuration and SpRS requiring two separate lasers for the two scattering phenomena has been proposed [32], but it does not allow concurrent measurements as the source has to be used alternatively. A method for complete discrimination of strain and temperature based on a polarization maintaining fiber [33], and distributed measurement of Brillouin frequency shift and birefringence at short distances has been demonstrated [34] as well as one for simultaneous measurement of the Rayleigh and SpBS components [35]. Another investigation involved the study of fibers with multiple acoustic modes for simultaneous strain and temperature measurements [36]. A hybrid scheme involving the combination of the SpRS and SpBS has also been proposed but is limited by the SpBS intensity having low strain dependence in long distance sensing [37]. A technique based on microwave coherent detection of SpBS intensity and frequency shift has also been proposed [38], where measurement accuracy is affected by low strain dependence of the SpRS intensity. It is worth noting that methods using hybrid techniques or birefringence allow better discrimination compared to others, for instance ones using different acoustic optical or acoustic modes, since they involve higher decoupling between the variations of BFS due to temperature and strain.

Hybrid schemes combining RDTS and BOTDA using a single source and sensing fiber have also been used to address this issue and optical pulse coding has been used to provide SNR improvement in both schemes [39, 40]. Among others, a hybrid Raman/BOTDA for simultaneous measurement of strain and temperature has been demonstrated using cyclic coding [41, 42]. The hybrid configuration, which is shown in Figure 17, is the same as the one in Figure 15, except that a Raman filter separates the Stokes and anti-Stokes signal of the SpRS at the receiver, which are detected by APDs, and the remaining signal containing the SBS signal is detected using a pin photodiode. Using a 511-bit cyclic code enables measurement at a temperature resolution of ~3.4°C, which also addresses the cross-sensitivity, yielding a strain resolution of 80 με at the end of a 10-km fiber with a spatial resolution of 1 m.

FIGURE 17

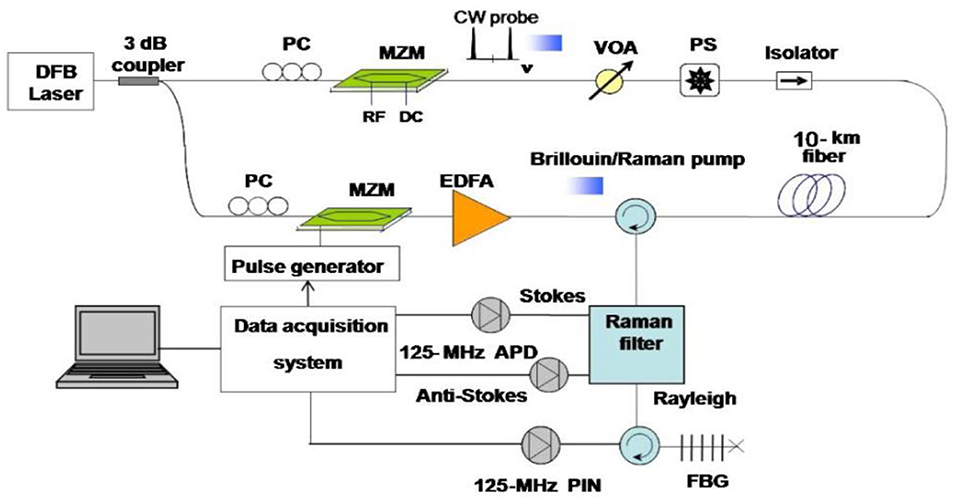
Figure 17. Hybrid Raman/BOTDA sensor based on cyclic coding [41].

Recent Advances and Trends in Raman and Brillouin Distributed Sensing in Time Domain

Recently, there have been new investigations of distributed fiber optic sensing based on Raman and Brillouin Scattering. Studies on distributed measurement schemes exploiting spontaneous Raman scattering include ultra-high temperature sensing in harsh environments operating in the range from room temperature to 1,400°C for saphire optical fiber albeit at the commercially available length of only 2 m with a spatial resolution of 0.2 mm [43]. Future studies are expected to address longer measurement ranges. The study of label-free distributed hydrogen sensing has also been demonstrated using stimulated Raman Scattering in hollow-core photonic crystal fibers (HC-PCF) [44]. The use of HC-PCF entails higher threshold for other detrimental non-linear effects while allowing faster measurements compared to Brilloiun-based sensing which involves static frequency scanning. The investigation opens a new trend in multi-point gas or liquid sensing with high sensitivity and selectivity suitable for environmental monitoring and biomedical applications. Another study has also been made in the use of multimode fiber for simultaneous measurement of liquid temperature via the ratio of the Raman Stokes and anti-Stokes components and refractive index using the Fresnel reflection of the forward-scattered Raman Stokes signal from the fiber [45]. A mechanism for early warning for fire prediction in a long-range RDTS system has been proposed and demonstrated using first and second order moving average methods, resulting in the prediction of temperature trends in advance of 43 sec [46]. Owing to the large amount of data involved in long distances, such systems can benefit from further investigations in more robust prediction algorithms, including the use of AI and big data storage and processing services.

Though advanced BOTDA configurations allow spatially resolved measurements at long distances, the rather low dynamic performance of the measurements owing to the required sweeping to construct the BGS has still remained a key limitation. Improvements in the sensing scheme which included sweep-free and slope-assisted [47] configurations resulted in relatively faster measurements but distributed measurements at long distances are still limited in speed, and such techniques require complex setups. A recent scheme avoids the need for conventional scanning via the use of the backscattering signal itself in a closed-loop tracking of the evolution of the BFS across the fiber, and is reported to offer a significant reduction in measurement time scale compared to standard BOTDA [48]. On the other hand, Phase-sensitive OTDR (ϕ-OTDR), which is based on coherent Rayleigh scattering [2], is becoming more attractive in this regard as it offers high-frequency acoustic and ultrasonic sensing with capability to measure vibrations of up to 10s of kHz along few kilometers, with dynamic performance near the limit set by the sensing distance or even exceeding it [49]. It is also worth noting that ϕ-OTDR enables measurement of distributed temperature with very small resolution values at fractions of kelvin [50]. Such temperature profiling using ϕ-OTDR has also been optimized for enhanced dynamic range with more sensitivity at high temperature change values by being coupled with BOTDA in a multicore fiber in a scheme which harnesses the temperature resolution performance of ϕ-OTDR and the high-temperature sensitivity of BOTDA [51].

Recent study on BOTDA schemes include investigation of design rules for optimization of BOTDA based on unipolar pulse coding schemes [52], as well as hybrid coding schemes combining unipolar Golay coding with differential-pulse pair which enable spatially resolved measurements with enhanced speed and SNR [53]. A comparative investigation of BFS measurement techniques has also been made and the Lorentzian cross-correlation technique has been proven to provide more accurate fitting compared to others [54]. Another notable effort to mitigate the issue of curve-fitting time in BOTDA sensing is the use of a support vector machine (SVM) combined with a hardware accelerator based on Field-Programmable Gate Arrays (FPGA) to construct the BGS [55]. The method offers the construction of 96,100 gain spectra along a 38.44-km fiber only in 0.46 s suggesting potentials for methods with enhanced speed and power efficiency compared to implementations with a single processor. A technique for BFS reconstruction based on Feed-forward Neural Networks (FNN) has also been proposed and demonstrated to offer more efficient measurements compared to curve fitting methods opening doors for implementations exploiting machine learning algorithms [56]. In addition, discrimination of distributed strain and temperature by employing the excitation of acoustic modes which appear in multiple peaks of the BGS in a single mode fiber has been demonstrated [57], proving the potential for exploiting multiple acoustic, as opposed to optical, modes for measurement. Finally, a technique offering athermal distributed strain sensing has been demonstrated by heavily doping silica fibers in Germanium (98-mol. %), providing a new way of making temperature-independent strain measurement in BOTDA [58].

Conclusions

Optical fiber sensors are becoming ubiquitous and their market share is expected to continue its growth. Some of the advantages compared to alternative technologies make them the only choice in certain applications, for instance in those requiring long-range monitoring. In this paper, we have reviewed the physics of Raman and Brillouin scattering, which can be exploited for making distributed sensors for strain and temperature profiles. We also showed representative schemes of fiber-optic sensing systems and techniques to improve their performance in addition to recent advances and trends in distributed sensing based on Raman and Brillouin scattering in time domain. While some of these ideas are already part of commercial products, others will probably be developed very soon, which proves that this area is now undergoing optimum conditions for the combination of academic research and industrial development.

Author Contributions

YM, CO, and FD have contributed to the organization and writing of this article.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Muanenda Y. Recent advances in distributed acoustic sensing based on phase-sensitive optical time domain reflectometry. J Sens. (2018) 2018:3897873. doi: 10.1155/2018/3897873

CrossRef Full Text | Google Scholar

2. Muanenda Y, Oton CJ, Faralli S, Di Pasquale F. A ϕ-OTDR sensor for high-frequency distributed vibration measurements with minimal post-processing. In: 19th Italian National Conference on Photonic Technologies (Fotonica 2017). Padua (2017). p. 1–4.

Google Scholar

3. Kersey AD, Berkoff TA, Morey WW. Multiplexed fiber Bragg grating strain-sensor system with a fiber Fabry–Perot wavelength filter. Opt Lett. (1993) 18:1370–2. doi: 10.1364/OL.18.001370

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Muanenda Y, Faralli S, Oton CJ, Cheng C, Yang M, Di Pasquale F. Dynamic phase extraction in high-SNR DAS based on UWFBGs without phase unwrapping using scalable homodyne demodulation in direct detection. Opt Express. (2019) 27:10644–58. doi: 10.1364/OE.27.010644

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Raman CV. A new radiation. Indian J Phys. (1928) 2:387–98.

Google Scholar

6. Farahani MA, Gogolla T. Spontaneous Raman scattering in optical fibers with modulated probe light for distributed temperature Raman remote sensing. J Lightwave Technol. (1999) 17:1379–91. doi: 10.1109/50.779159

CrossRef Full Text | Google Scholar

7. Boyd RW. Nonlinear Optics. 3rd ed. New York, NY: Academic Press (2008).

Google Scholar

8. Agrawal GP. Nonlinear Fiber Optics. 4th ed. San Diego, CA: Academic Press (2007).

Google Scholar

9. Agrawal GP. Fiber-Optic Communication Systems. 3rd ed. New York, NY: John Wiley & Sons (2002).

Google Scholar

10. Bao X, Chen L. Recent progress in distributed fiber optic sensors. Sensors. (2012) 12:8601–39. doi: 10.3390/s120708601

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Hartog AH. An Introduction to Distributed Optical Fiber Sensors. Boca Raton, FL: CRC Press (2017).

Google Scholar

12. Fernandez AF, Rodeghiero P, Brichard B, Berghmans F, Hartog AH, Hughes P, et al. Radiation-tolerant raman distributed temperature monitoring system for large nuclear infrastructures. IEEE Trans. Nucl. Sci. (2005) 52:2689–94. doi: 10.1109/TNS.2005.860736

CrossRef Full Text | Google Scholar

13. Soto MA, Signorini A, Nannipieri T, Faralli S, Bolognini G, Di Pasquale F. Impact of loss variations on double-ended distributed temperature sensors based on raman anti-stokes signal only. J Lightwave Technol. (2012) 30:1215–22. doi: 10.1109/JLT.2011.2174966

CrossRef Full Text | Google Scholar

14. Thévenaz L, Mafang SF, Lin J. Effect of pulse depletion in a Brillouin optical time-domain analysis system. Opt Express. (2013) 21:14017–35. doi: 10.1364/OE.21.014017

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Taki M, Muanenda Y, Oton CJ, Nannipieri T, Signorini A, Di Pasquale F. Cyclic pulse coding for fast BOTDA fiber sensors. Opt Lett. (2013) 38:2877–80. doi: 10.1364/OL.38.002877

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Lee D, Yoon H, Kim P, Park J, Park N. Optimization of SNR improvement in the noncoherent OTDR based on simplex codes. J Lightwave Technol. (2006) 24:322–8. doi: 10.1109/JLT.2005.859437

CrossRef Full Text | Google Scholar

17. Naseem A, Mehmood H, Muhammad SS, Abbas SA. Composite coding scheme for OTDR SNR enhancement. In: Proceedings of the 11th International Conference on Telecommunications. Graz. (2011). p. 321–4.

Google Scholar

18. Golay M. Complementary series. IRE Trans Inf Theory. (1961) 7:82–7. doi: 10.1109/TIT.1961.1057620

CrossRef Full Text | Google Scholar

19. Soto MA, Nannipieri T, Signorini A, Lazzeri A, Baronti F, Roncella R, et al. Raman-based distributed temperature sensor with 1 m spatial resolution over 26 km SMF using low-repetition-rate cyclic pulse coding. Opt Lett. (2011) 36:2557–9. doi: 10.1364/OL.36.002557

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Yang Z, Soto MA, Thévenaz L. Increasing robustness of bipolar pulse coding in Brillouin distributed fiber sensors. Opt Express. (2016) 24:586–97. doi: 10.1364/OE.24.000586

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Marcelo Soto A, Bolognini G, Di Pasquale F, Thévenaz L. Simplex-coded BOTDA fiber sensor with 1 m spatial resolution over a 50 km range. Opt Lett. (2010) 35:259–61. doi: 10.1364/OL.35.000259

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Muanenda YS, Taki M, Di Pasquale F. Fast brillouin optical time domain analysis sensor based on adaptive linear prediction and cyclic pulse coding. In Frontiers in Optics 2014, OSA Technical Digest (Optical Society of America), Paper FTu4B.5. Tucson. (2014). doi: 10.1364/FIO.2014.FTu4B.5

CrossRef Full Text | Google Scholar

23. Le Floch S, Sauser F, Llera M, Soto MA, Thevenaz L. Colour simplex coding for Brillouin distributed sensors. In: Proceedings of Fifth European Workshop on Optical Fibre Sensors. Vol. 8794, Kraków. (2013). doi: 10.1117/12.2025795

CrossRef Full Text | Google Scholar

24. Iribas H, Loayssa A, Sauser F, Llera M, Le Floch S. Cyclic coding for Brillouin optical time-domain analyzers using probe dithering. Opt Express. (2017) 25:8787–800. doi: 10.1364/OE.25.008787

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Mariñelarena J, Iribas H, Loayssa A. Pulse coding linearization for Brillouin optical time-domain analysis sensors. Opt Lett. (2018) 43:5607–10. doi: 10.1364/OL.43.005607

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Suh K, Lee C. Auto-correction method for differential attenuation in a fiber-optic distributed-temperature sensor. Opt Lett. (2008) 33:1845–7. doi: 10.1364/OL.33.001845

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Hwang D, Yoon DJ, Kwon IB, Seo DC, Chung Y. Novel auto-correction method in a fiber-optic distributed-temperature sensor using reflected anti-Stokes Raman scattering. Opt Express. (2010) 18:9747–54. doi: 10.1364/OE.18.009747

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Peled Y, Motil A, Yaron L, Tur M. Slope-assisted fast distributed sensing in optical fibers with arbitrary Brillouin profile. Opt Express. (2011) 19:19845–54. doi: 10.1364/OE.19.019845

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Muanenda Y, Taki M, Di Pasquale F. Long-range accelerated BOTDA sensor using adaptive linear prediction and cyclic coding. Opt Lett. (2014) 39:5411–4. doi: 10.1364/OL.39.005411

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Liang H, Li W, Linze N, Chen L, Bao X. High-resolution DPP-BOTDA over 50 km LEAF using returnto-zero coded pulses. Opt Lett. (2010) 35:1503–5. doi: 10.1364/OL.35.001503

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Song KY, Zou W, He Z, Hotate K. All-optical dynamic grating generation based on Brillouin scattering in polarization-maintaining fiber. Opt Lett. (2008) 33:926–9. doi: 10.1117/12.786181

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Brown K, Brown A, Colpitts B. Combined Raman and Brillouin scattering sensor for simultaneous high-resolution measurement of temperature and strain. In: Proc. SPIE 6167, Smart Structures and Materials 2006: Smart Sensor Monitoring Systems and Applications. Vol. 616716, San Diego, CA. (2006).

Google Scholar

33. Zou W, He Z, Hotate K. Complete discrimination of strain and temperature using Brillouin frequency shift and birefringence in a polarization-maintaining fiber. Opt Exp. (2009) 17:1248–55. doi: 10.1364/OE.17.001248

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Cao Z, Ji X, Wang R, Zhang Z, Shui T, Xu F, et al. Compact fiber sensor with high spatial resolution for simultaneous strain and temperature measurement. IEEE Sens J. (2013) 13:1447–51. doi: 10.1109/JSEN.2012.2237092

CrossRef Full Text | Google Scholar

35. Kishida K, Li CH, Nichiguchi K, Yamauchi Y, Tsuda T. Hybrid Brillouin-Rayleigh distributed sensing system. In: Proceedings of SPIE 8421, OFS2012, 22nd International Conference on Optical Fiber Sensors. Vol. 84212G, Beijing. (2012).

Google Scholar

36. Alahbabi MN, Cho YT, Newson TP. Comparison between standard SMF and nonzero dispersion shifted fibre LEAF for long range simultaneous temperature and strain measurements. In: Proceedings of SPIE 5502, Second European Workshop on Optical Fibre Sensors. Vol. 484, Santander. (2004).

Google Scholar

37. Alahbabi MN, Cho YT, Newson TP. Simultaneous temperature and strain measurement with combined spontaneous Raman and Brillouin scattering. Opt Lett. (2005) 30:1276–8. doi: 10.1364/OL.30.001276

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Maughan SM, Huai Kee H, Newson TP. Simultaneous distributed fibre temperature and strain sensor using microwave coherent detection of spontaneous Brillouin backscatter. Meas Sci Technol. (2001) 12:834–42. doi: 10.1088/0957-0233/12/7/315

CrossRef Full Text | Google Scholar

39. Taki M, Muanenda YS, Toccafondo I, Signorini A, Nannipieri T, Pasquale FD. Optimized hybrid Raman/Fast-BOTDA sensor for temperature and strain measurements in large infrastructures. IEEE Sens J. (2014) 14:4297–304. doi: 10.1109/JSEN.2014.2328374

CrossRef Full Text | Google Scholar

40. Taki M, Muanenda Y, Nannipieri T, Signorini A, Oton CJ, Di Pasquale F. Advanced coding techniques for long-range Raman/BOTDA distributed strain and temperature measurements. In: Optical Fiber Communication Conference, OSA Technical Digest, Paper W3I.3, Los Angeles, CA. (2015).

Google Scholar

41. Taki M, Signorini A, Oton CJ, Nannipieri T, Di Pasquale F. Hybrid Raman/Brillouin-optical-time-domain-analysis-distributed optical fiber sensors based on cyclic pulse coding. Opt Lett. (2013) 38:4162–5. doi: 10.1364/OL.38.004162

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Muanenda Y, Taki M, Toccafondo I, Signorini A, Nannipieri T, Oton CJ, et al. Cyclic pulse coding for hybrid fast BOTDA/Raman sensor. In: Proc. SPIE 9157, 23rd International Conference on Optical Fibre Sensors. Vol. 91575L, Santander. (2014).

Google Scholar

43. Liu B, Buric MP, Chorpening BT, Yu Z, Homa DS, Pickrell GR, et al. Design and implementation of distributed ultra-high temperature sensing system with a single crystal fiber. J Lightwave Technol. (2018) 36:5511–20. doi: 10.1109/JLT.2018.2874395

CrossRef Full Text | Google Scholar

44. Yang F, Zhao Y, Qi Y, Tan Y, Ho HL, Jin W. Label-free distributed hydrogen sensing with stimulated Raman scattering in hollow-core fibers. In: 26th International Conference on Optical Fiber Sensors, OSA Technical Digest (Optical Society of America, 2018), Paper TuE4, Lausanne. doi: 10.1364/OFS.2018.TuE4

CrossRef Full Text | Google Scholar

45. Wang D, Cheng B, Jin B, Wang Y, Zhang M, Liu X, et al. Remote simultaneous measurement of liquid temperature and refractive index using fiber-optic spontaneous Raman scattering. IEEE Sens J. (2019) 1–1. doi: 10.1109/JSEN.2019.2930108

CrossRef Full Text | Google Scholar

46. Li J, Yan B, Zhang M, Zhang J, Jin B, Wang Y, et al. Long-range raman distributed fiber temperature sensor with early warning model for fire detection and prevention. IEEE Sens J. (2019) 19:3711–7. doi: 10.1109/JSEN.2019.2895735

CrossRef Full Text | Google Scholar

47. Zhou D, Dong Y, Wang B, Jiang T, Ba D, Xu P, et al. Slope-assisted BOTDA based on vector SBS and frequency-agile technique for wide-strain-range dynamic measurements. Opt Express. (2017) 25:1889–902. doi: 10.1364/OE.25.001889

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Yang Z, Soto MA, Chow DM, Ray P, Thévenaz L. Brillouin distributed optical fiber sensor based on a closed-loop configuration. J Lightwave Technol. (2018) 36:1239–48. doi: 10.1109/JLT.2017.2786084

CrossRef Full Text | Google Scholar

49. Chen D, Liu Q, Fan X, He Z. Distributed fiber-optic acoustic sensor with enhanced response bandwidth and high signal-to-noise ratio. J Lightwave Technol. (2017) 35:2037–43. doi: 10.1109/JLT.2017.2657640

CrossRef Full Text | Google Scholar

50. Koyamada Y, Imahama M, Kubota K, Hogari K. Fiber-optic distributed strain and temperature sensing with very high measure and resolution over long range using coherent OTDR. J Lightwave Technol. (2009) 27:1142–6. doi: 10.1109/JLT.2008.928957

CrossRef Full Text | Google Scholar

51. Dang Y, Zhao Z, Tang M, Zhao C, Gan L, Fu S, et al. Towards large dynamic range and ultrahigh measurement resolution in distributed fiber sensing based on multicore fiber. Opt Express. (2017) 25:20183. doi: 10.1364/OE.25.020183

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Yang Z, Li Z, Zaslawski S, Thévenaz L, Soto MA. Design rules for optimizing unipolar coded Brillouin optical time-domain analyzers. Opt Express. (2018) 26:16505–23. doi: 10.1364/OE.26.016505

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Li Z, Yang Z, Yan L, Soto MA, Thévenaz L. Hybrid coding scheme for Brillouin optical time-domain analysis based on Golay and Differential Pulses. In: 26th International Conference on Optical Fiber Sensors, OSA Technical Digest (Optical Society of America, 2018), Paper WF27, Lausanne.

Google Scholar

54. Haneef S, Yang Z, Thévenaz L, Venkitesh D, Srinivasan B. Performance analysis of frequency shift estimation techniques in Brillouin distributed fiber sensors. Opt Express. (2018) 26:14661–77. doi: 10.1364/OE.26.014661

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Wu H, Wang H, Shu C, Choy C, Lu C. Brillouin optical time domain analyzer fiber sensor based on FPGA accelerated support vector regression. In: 2019 Optical Fiber Communications Conference and Exhibition (OFC). San Diego, CA (2019). p. 1–3.

Google Scholar

56. Liang Y, Jiang J, Chen Y, Zhu R, Lu C, Wang Z. Optimized feedforward neural network training for efficient Brillouin frequency shift retrieval in fiber. IEEE Access. (2019) 7:68034–42. doi: 10.1109/ACCESS.2019.2919138

CrossRef Full Text | Google Scholar

57. Xing C, Ke C, Guo Z, Yang K, Wang H, Zhong Y, et al. Distributed multi-parameter sensing utilizing Brillouin frequency shifts contributed by multiple acoustic modes in SSMF. Opt Express. (2018) 26:28793–807. doi: 10.1364/OE.26.028793

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Deroh M, Sylvestre T, Chretien J, Maillotte H, Kibler B, Beugnot J-C. Towards athermal Brillouin strain sensing based on heavily germania-doped core optical fibers. APL Photonics. (2019) 4:030801. doi: 10.1063/1.5085640

CrossRef Full Text | Google Scholar