- 1Center of Excellence in Theoretical and Computational Science (TaCS-CoE), SCL 802 Fixed Point Laboratory, King Mongkut's University of Technology Thonburi (KMUTT), Bangkok, Thailand
- 2KMUTT Fixed Point Research Laboratory, SCL 802 Fixed Point Laboratory, Department of Mathematics, Faculty of Science, King Mongkut's University of Technology Thonburi (KMUTT), Bangkok, Thailand
- 3KMUTT-Fixed Point Theory and Applications Research Group, Theoretical and Computational Science Center (TaCS), Faculty of Science, King Mongkut's University of Technology Thonburi (KMUTT), Bangkok, Thailand
- 4Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, Taiwan
- 5Department of Mathematics, Abdul Wali Khan University Mardan, Mardan, Pakistan
- 6Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah, Saudi Arabia
- 7Renewable Energy Research Centre, Department of Teacher Training in Electrical Engineering, Faculty of Technical Education, King Mongkut's University of Technology North Bangkok, Bangkok, Thailand
The steady non-isothermal convective heat transfer in magnetohydrodynamic micropolar fluid flow over a non-linear extending wall is examined. The fluid flow is treated with strong magnetic field. The influence of magnetic field, Hall current, and couple stress are mainly focused in this work. The fluid flow problem is solved analytically. The impact of developing dimensionless parameters on primary, secondary, and angular velocity components and temperature profile are determined through graphs. The primary velocity component has reduced throughout the flow study. The greater magnetic parameter, Hall parameter and couple stress parameter have increased the secondary velocity component while the local Grashof number has reduced the secondary velocity component. The greater magnetic parameter and Hall parameter have reduced the angular velocity component. The greater magnetic parameter has increased the temperature profile while the Hall parameter and local Grashof number have decreased the temperature profile. The impact of developing dimensionless parameters on skin friction coefficient and local Nusselt number are determined through Tables.
Introduction
The flow of non-Newtonian fluids has plentiful importance in industries and modern technology. Recently, the couple stress fluid among non-Newtonian fluid has acquired the exceptional position due to the spin field in the fluid. The elementary concept of couple stress was established by Stokes [1]. Khan et al. [2] deliberated the suggested model of couple stress fluid in a uniformly porous stretching channel. The axial velocity function heightens while the radial velocity function declines for escalating couple stress. The couple stress effect on heat transfer in four different nanofluids flows was determined by Farooq et al. [3]. Srinivasacharya et al. [4] explored the couple stress fluid flow. They originate that the couple stress parameter diminishes the fluid velocity and temperature while heightens the concentration. Ramzan et al. [5] deliberated the couple stress fluid flow over extending sheet. It is found that velocity profiles along both directions are declined with the escalation in couple stress parameter. Also the fluid temperature escalated with viscous dissipation effect. Hayat et al. [6] determined the heat transmission rate in the couple stress flow over extending surface and originate that the heat transfer intensifies with the rising estimations of the couple stress. Over an extending sheet, the couple stress fluid flow was determined by Turkyilmazoglu [7]. It is concluded that over a stretching sheet the couple stress gives double solution while over shrinking sheet it gives triple solution. The unsteady couple stress fluid flow was determined by Awad et al. [8]. Here, the fluid velocity and temperature decline with heightened couple stress. Sreenadh et al. [9] examined the fluid flow with couple stress impact. Hayat et al. [10] analyzed the mass transfer in couple stress fluid with chemical reaction. Khan et al. [11] scrutinized the incompressible and unsteady couple stress fluid flow considering three dimensional cylindrical polar coordinate systems. Hayat et al. [12] measured the flow of couple stress nanofluid with convective conditions. The fluid temperature and concentration are increased with escalating couple stress parameter. The dissipation influence on couple stress nanofluid flow was determined by Ramzan [13]. The magnetic field impact on couple stress nanofluid flow was determined by Hayat et al. [14]. In this article, the authors determined that temperature of fluid flow up surged with the large estimation of couple stress parameter. With Cattaneo-Chritov heat flux Hayat et al. [15] deliberated the flow of couple stress nanofluid flow. They found that the velocity components are increased while the temperature is decreased with the couple stress parameter. Umavathi et al. [16] deliberated the laminar flow of couple stress fluid and heat transmission considering horizontal plates. Umavathi et al. [17] scrutinized the fluid flow with couple stress impact in between two infinite porous walls. They concluded that the fluid velocity and temperature are reduced in the boundary layer regime. Srinivasacharyulu et al. [18] observed the couple stress fluids flow over stretching walls. Zueco et al. [19] inspected the couple stress nanofluid in a rigid channel. Zakaria [20] deliberated the couple stress fluid under magnetic field impact. Ellahi et al. [21] determined the couple stress blood flow under the impact of activation energy and chemical reaction.
In recent times, the researchers have got interest in megnetohydrodynamic (MHD) owing to plentiful applications in industrial, engineering, and medical devices. Rudolf et al. [22] briefly reviewed the properties of magnetic field in the universe. The MHD nanofluid flow with chemical reaction was deliberated by Hayat et al. [23]. The fluid flow velocity is reduced with higher estimation of magnetic field, and temperature escalated with chemical reactions and Dufour influences. The heat transmission in the flow of MHD nanofluid over unsteady extending sheet was observed by Lin et al. [24]. The fluid flow velocity is reduced with heightens in magnetic field while the temperature of the fluid escalated. The heat transfer in the flow of MHD incompressible second-grade nanofluid was deliberated by Ramesh et al. [25]. The MHD nanofluid flow in a symmetric channel was probed by Reddy et al. [26]. The elementary study of micropolar fluid was introduced by Eringen [27]. Bég et al. [28] presented the applications of micropolar fluid flow. Uddin et al. [29] probed the MHD micropolar fluid with Hall effect. Here, interesting results are concluded. The velocity of the fluid heightens with the escalation in magnetic field while the temperature of the fluid reduces with higher estimation of magnetic field (i.e. M>2). Khan et al. [30] determined the radiation and inertial coefficient influences on the flow of nanofluid. The higher inertial coefficient, porosity parameter, and coupling parameter reduce the fluid velocity and the temperature heightens with the escalation in thermal radiation. Dawar et al. [31] deliberated the unsteady MHD nanofluid with viscous dissipation effect. Here, the authors originate that the fluid flow velocity reduces with escalation in magnetic field and the fluid flow temperature reduces with viscous dissipation impacts. Kumam et al. [32] probed the MHD Casson nanofluid flow. Shah et al. [33] deliberated the flow of MHD thin film fluid with radiation impact. The MHD Casson nanofluid flow in a cylindrical tube was considered by Ali et al. [34]. The nanofluid flow with Hall effect was studied by Shah et al. [35]. The MHD nanofluid flow with magnetic and electric fields, and Hall impacts was determined by Shah et al. [36]. Kumar et al. [37] investigated the MHD nanofluid with magnetic and heat sink/source impacts. Temple et al. [38] scrutinized the nanoparticles of ferromagnetic for their size and magnetic properties. Ellahi et al. [39] examined the MHD nanofluid flow with thermal conductivity. Asadollahi et al. [40] deliberated the phase change of a fluid in a square microchannel. The most relevant and new studied studies can be reads in Ellahi et al. [41–43], Bhatti et al. [44], Ameen et al. [45], Vo et al. [46], Ahmad et al. [47], Sheikholeslami et al. [48], Ali et al. [49], and Ullah et al. [50].
In view of the above mentioned literature survey, the authors are in position to examine the three-dimensional MHD micropolar fluid flow over an extending wall with couple stress, Hall current and viscous dissipation influences. Section of Problem Formulation agrees with problem formulation. In the section of Solution by HAM, the recommended model is solved by HAM. Results section includes the results of the problem and the section of Discussion of the problem is presented independently. The final observations are obtainable in the section of Conclusion.
Problem Formulation
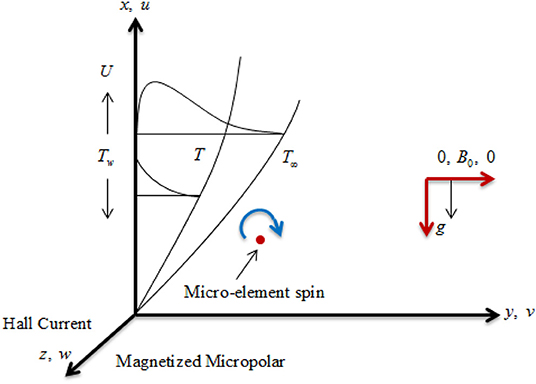
We assume the incompressible, steady, and electrically conducting couple stressed flow of micropolar fluid and heat transfer in the near wall zone of MHD Hall generator. The wall is considered as non-linearly stretching and concerned with x−direction (as shown in Figure 1). The magnetic field B0 is functional in y−axis. In the presence of magnetic field, the Hall current influences the electrically conducting fluid. The flow of fluid develops to 3D due to the Hall current, which increases the force in z−direction. All properties of fluid are considered constant and isotropic.
The principal equations for the fluid flow can be written as [27, 28]:
with
Here, the positive n indicates the acceleration of the wall and negative n indicates the deceleration of wall form the origin whereas n = 0 is the case for stationary wall, u, vandw are the velocity components, N is the micro-rotation, T denotes the fluid temperature, and are the currents along x− and z−directions correspondingly, also electrical conductivity-σ, fluid viscosity-μe, applied uniform magnetic field-B0, Hall parameter-m, couple stress viscosity-ν′, = cosα where α indicates the angle between the magnetic field and the transverse plane to the plate, thermal expansion volumetric coefficient-β, kinematic viscosity-ν, fluid density-ρ, Eringen vortex viscosity-K2, thermal conductivity-κ, Eringen spin gradient viscosity-G1, specific heat-cp, γ, and A-constants.
To transform the coordinate system to a non-dimensional one and this is achieved readily via non-similar transformations, simultaneously eliminating one of the independent variables and reducing the PDEs into ODEs, the following transformation variables are defined.
The transformed equations are defined as:
with transformed boundary conditions:
Here, symbolizes the Grashof number, characterizes the Hartmann number in which is the scaled magnetic field strength, represents the micro-rotation parameter, m Hall parameter, represents the dimensionless couple stress parameter, γ indicates the non-isothermal power-law index, characterizes the material parameter, embodies the Prandtl number, epitomizes the Eckert number, and n represents the non-linear wall geometric parameter.
For primary and secondary velocity components, the skin frication are defined as:
Using Equation (7), the skin fraction coefficients for primary and secondary velocities are reduced as:
The Nusselt number is specified by:
Solution by HAM
To solve the Equations (8)–(11) using boundary conditions (12), we proceed HAM with the following manners.
Initial gausses
Linear operators
with the following properties:
where si(i = 1 − 9) are arbitrary constants.
The consequential non-linear operators Nf, Ng, Nh, and Nθ are specified as:
The zeroth-order problems from Equations (8)–(11) are:
The equivalent boundary conditions are:
When Θ = 0 and Θ = 1 we have:
By Taylor's series expansion f(ξ; Θ), g(ξ; Θ), h(ξ; Θ), and θ(ξ; Θ) can be written as:
where
The secondary constraints ħf, ħg, ħh and ħθ are nominated in such a way that the series (31) converges at Θ = 1, changing Θ = 1 in Equation (31), we get:
The qth−order problem satisfies the following:
The equivalent boundary conditions are:
Here,
where,
Results
Electrically conducting steady non-isothermal convective heat transfer in magnetohydrodynamic micropolar fluid flow over a non-linear extending wall is examined. Modeled equations are solved analytically through HAM. The impact of obtained important parameters M, Gr, m, and K on the fluid flow behavior are displayed in Figures 2–15.
Discussion
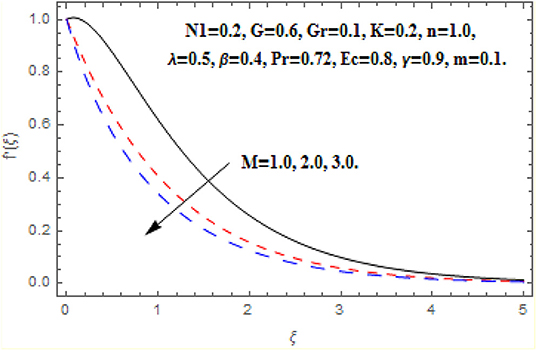
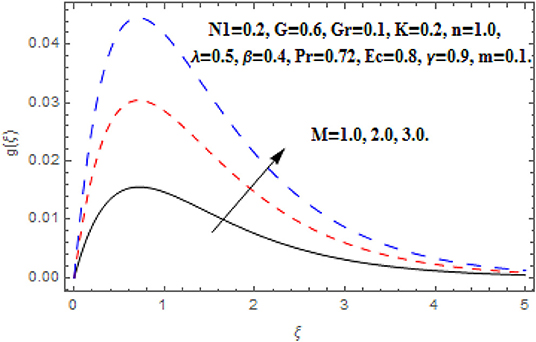
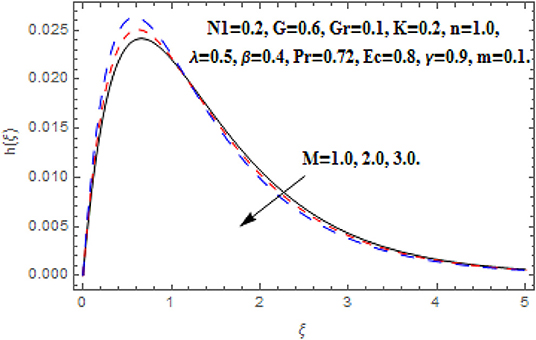
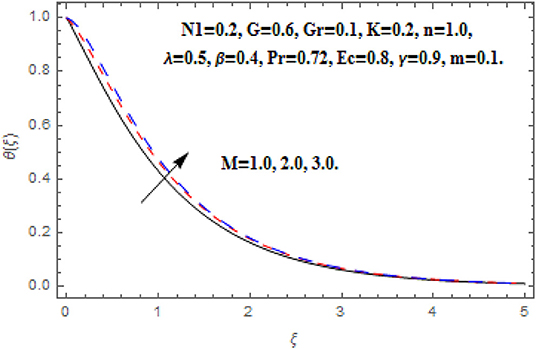
In this section we have discussed the effects of obtained parameter which are shown graphically and numerically through tables. The greater Hartmann number strongly reduced the primary and angular velocity profile owing to the Lorentz drag force components as appear in Equations (8) and (9). The components are negative and positive and thus inhibit the fluid flow. According to the secondary Lorentz drag force is truthfully positive and is assistive to secondary momentum development when the magnetic field is positive. These impacts are depicted in Figures 2, 4. The opposite impacts of M on secondary velocity and temperature functions are depicted in Figures 3, 5. It is perceived that the strong magnetic field has direct relationship with the secondary velocity and temperature functions. Against the magnetic field, the upsurge in temperature function is an attribute to the dissipation in kinetic energy consumed in dragging the micropolar. In addition, the temperature is always supreme at the wall.
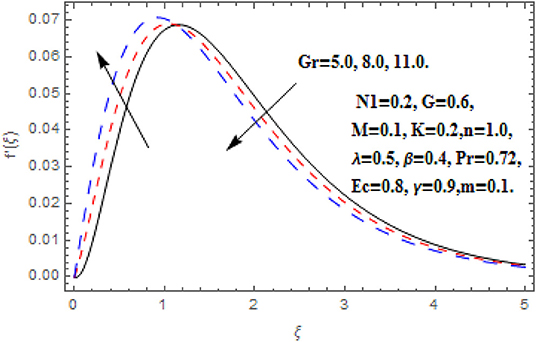
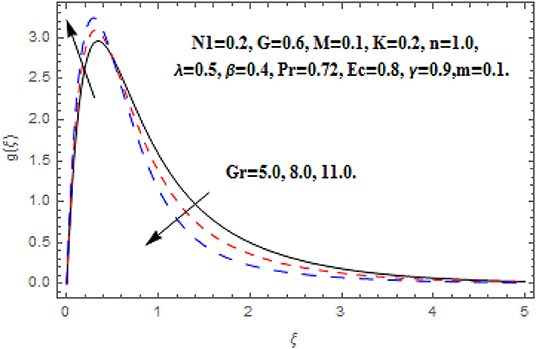
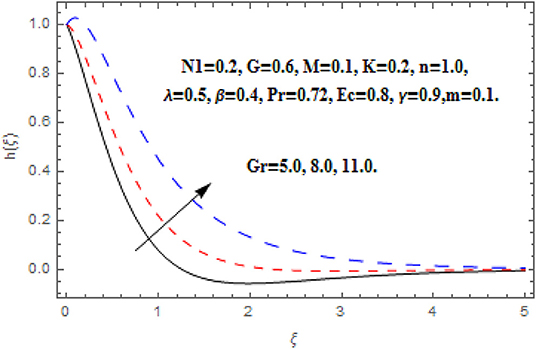
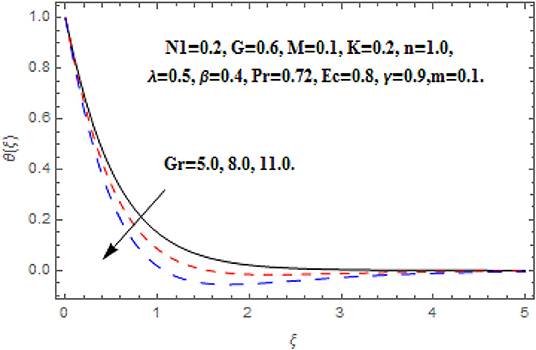
Figures 6–9 display the consequence of Gr on f′(ξ), g (ξ), h (ξ), and θ(ξ). The influence of Gr on f′(ξ) is portrayed in Figure 6. Here, the velocity heightens with the acceleration in Grashof number near the wall. However, the free convention current deteriorates at a critical distance from the wall which conserved into the free stream. A similar impact of Grashof number secondary velocity can be seen in Figure 7. Near the wall the fluid flow escalates with greater Grashof number but thereafter a deceleration started after some critical distance. Furthermore, the greater proportion of the region is observed for secondary velocity in comparison of primary velocity. Figure 8 reveals the consequence of Gr on h (ξ). The angular velocity heightens via Grashof number. A very quick growing behavior in the whole boundary layer regime is observed in the angular velocity. Figure 9 reveals the impact of Gr on θ(ξ). The intensifying Grashof number shrinks the boundary layer thickness, consequently the decline in temperature function is depicted.
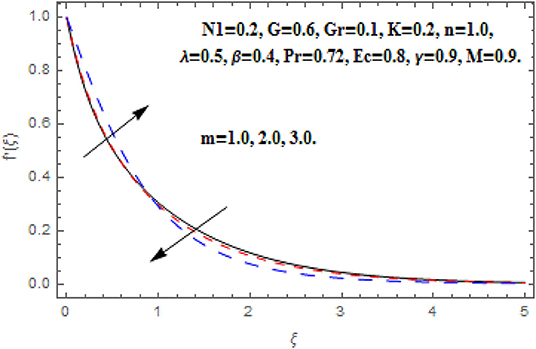
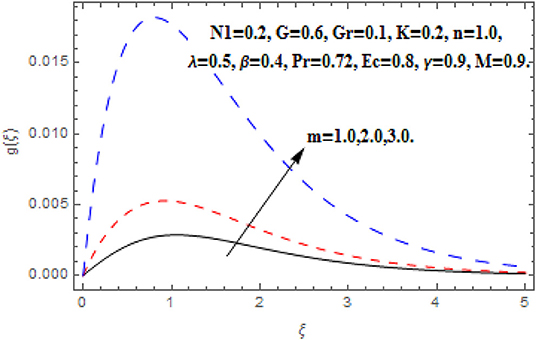
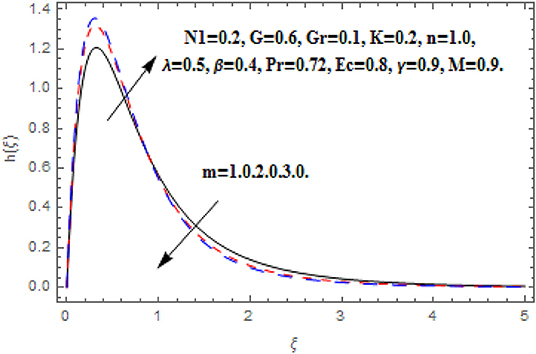
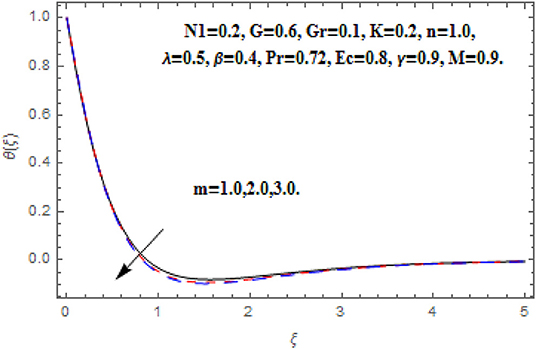
Figures 10–13 reveal the impact m on f′(ξ), g (ξ), h (ξ), and θ(ξ). Figure 10 reveals the impact of m on f′(ξ). Acceleration in m escalates the f′(ξ) in the neighborhood of the wall. Further toward the free stream, after some critical points the primary velocity function reduces. The drag force moderates which produce acceleration in f′(ξ) and in conclusion f′(ξ) diminishes. Figure 11 reveals the impact of m on g (ξ). Acceleration in m escalates the g (ξ) throughout the fluid flow. The Hall term in Equation (9) is effectively positive for positive magnetic field parameter. This assists to support the cross flow and demonstrates in significant cross flow spurt. Figure 12 reveals the impact of m on h (ξ). The Hall current parameter shows dual behavior in the flow of fluid. An enhancement in h (ξ) is perceived nearer to the wall and then deceleration to the flow stream is observed at some critical points. Generally, nevertheless the Hall current emboldens the rotary motions of microelements. Figure 13 reveals the impact of m on θ(ξ). The temperature function is regularly inhibited with Hall current parameter. Here, the decline in thickness of the boundary layer is perceived.
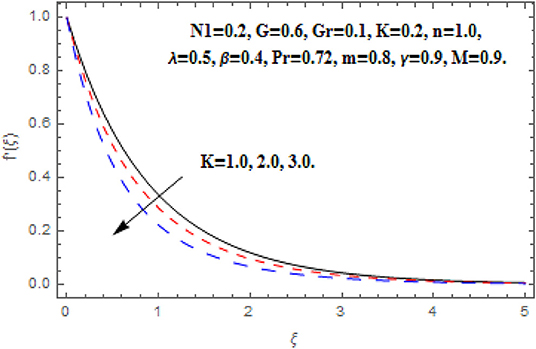
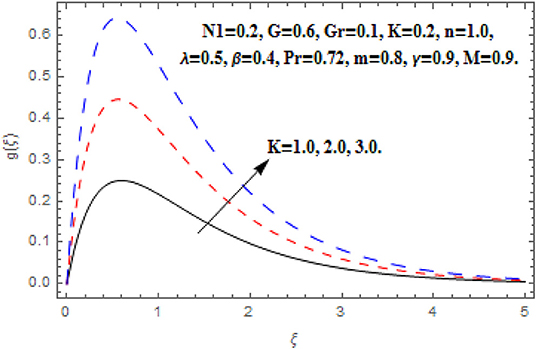
Figures 14, 15 reveal the impact of K on f′(ξ), g (ξ), h (ξ), and θ(ξ). At the point when an extra force added to the fluid which contradicts the fluid stream, this resistance makes a couple forces thus a couple stresses are persuaded in the fluid. This sort of fluid is recognized as couple stress fluid. Generally, the couple stress parameter and couple stress viscosity parameter n′ has direct relationship. The growing couple stress parameter leads the fluid to be more viscous which reduces the fluid flow. Therefore, the escalation approximations of couple stress parameter reduced the primary and secondary velocity as shown in Figures 14, 15. Additionally, the couples stress parameter is associated with the fluid motion. Therefore, it has no impact on temperature function.
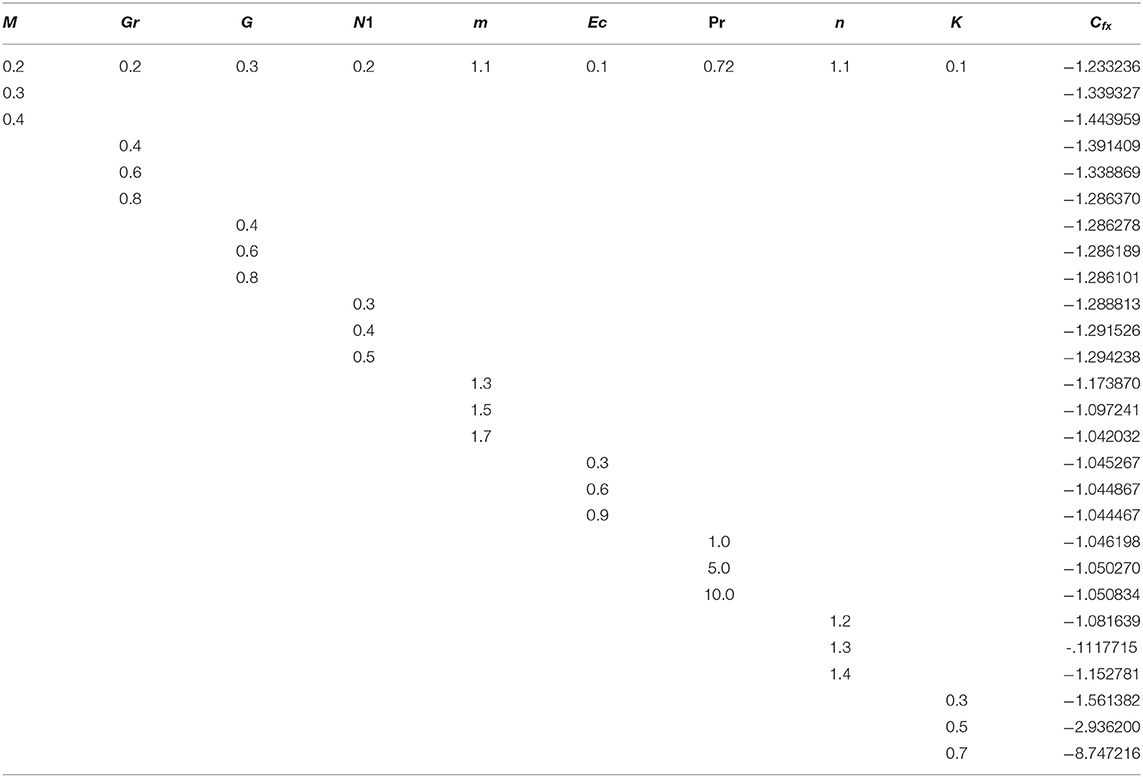
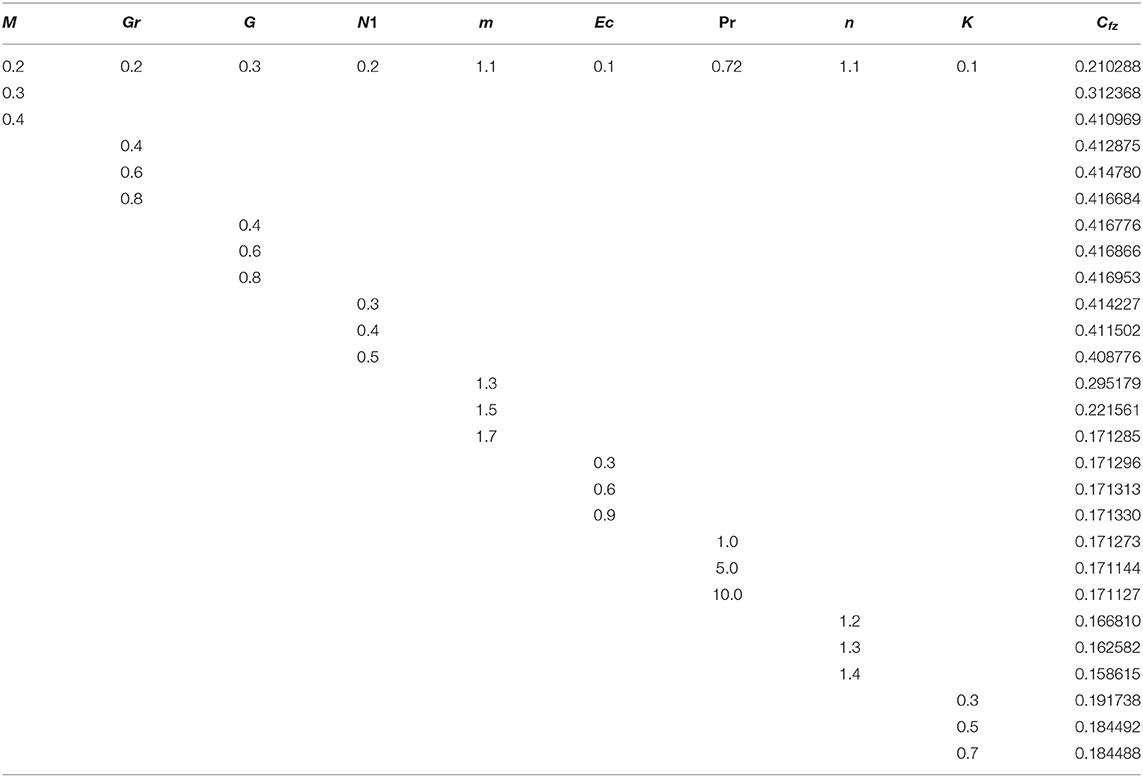
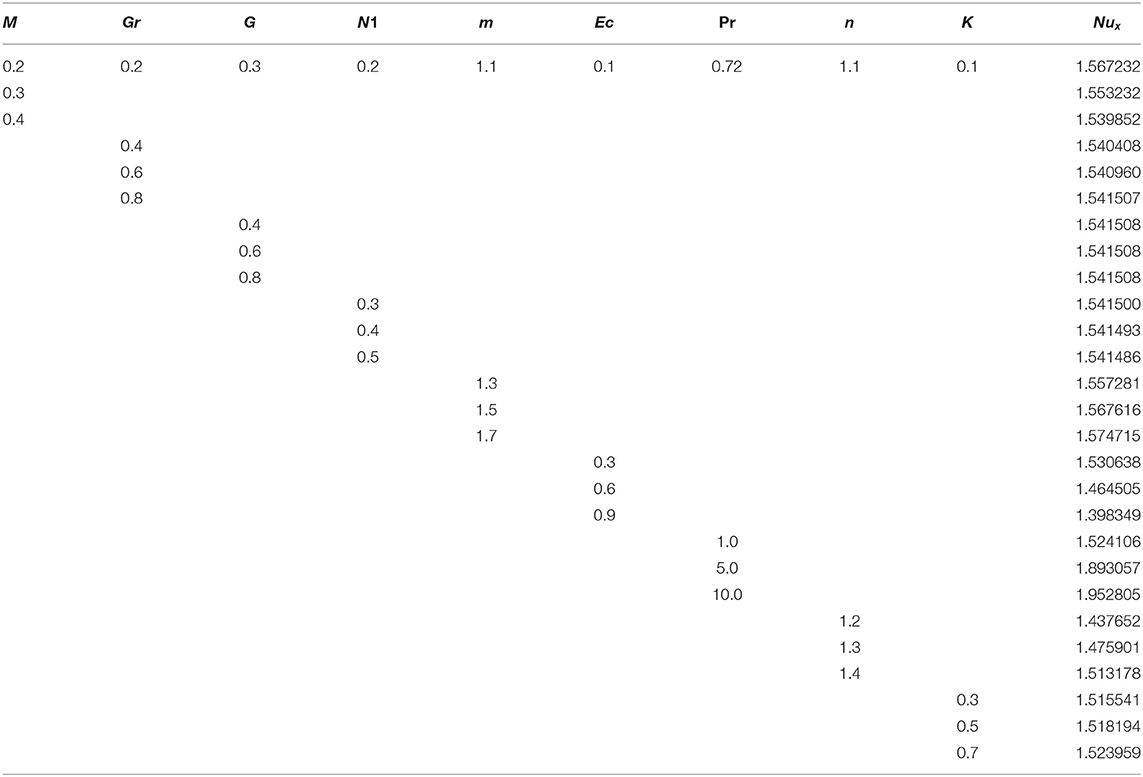
Tables 1–3 are displayed to observe the impact of embedded parameters on velocities and temperature profiles. The impact M, Gr, G, N1, m, Ec, Pr, n, and K on Cfx and Cfz are shown in Tables 1, 2. The rising value of M, N1, n, and K augmented the skin friction along x-axis Cfx where Gr, G, and m have opposite impact on the skin friction along x-axis Cfx. The higher value of M, Gr, G, and Ec augmented skin friction along z-axis Cfz where, m, N1, n, and K reduces the skin friction along z-axis Cfz. The influence of M, Gr, N1, m, Ec, Pr, n, and K on heat flux Nux are presented in Table 3. The greater value of Gr, m, Pr, n, and K augmented the heat flux Nux while, remaining parameter reduces the heat flux Nux. It should be noted that G has no impact on Nux.
Conclusion
In the current paper, the MHD micropolar boundary layer flow and heat transfer over a non-linear extending sheet infused by a strong magnetic field with couple stress, viscous dissipation and Hall impact have been determined.
The final observations are:
• The primary velocity reduces with greater magnetic parameter, local Grashof number, Hall parameter and couples stress parameter.
• The secondary velocity increases with greater magnetic parameter, Hall parameter and couple stress parameter.
• The secondary velocity decreases with greater local Grashof number.
• The angular velocity reduces with greater magnetic parameter and Hall parameter.
• The angular velocity increases with greater local Grashof number.
• The temperature profile increases with greater magnetic parameter.
• The temperature profile increases with greater Hall parameter and local Grashof number.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
ZS and PK developed the numerical method and led the manuscript preparation. AD contributed to the code development and to the article preparation. EA and PT contributed to the analysis and discussion of the results.
Funding
This research was funded by the Center of Excellence in Theoretical and Computational Science (TaCS-CoE), KMUTT under Grant KMUTNB-61-GOV-A-0.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by the research program International Research Common Laboratory in cooperation under Renewable Energy Research Centre (RERC)—King Mongkut's University of Technology North Bangkok (KMUTNB), Center of Excellence in Theoretical and Computational Science (TaCS-CoE)—King Mongkut's University of Technology Thonburi (KMUTT), and Groupe de Recherche en Energie Electrique de Nancy (GREEN)—Université de Lorraine (UL) under Grant KMUTNB-61-GOV-A-01.
References
2. Khan NA, Mahmood A, Ara A. Approximate solution of couple stress fluid with expanding or contracting porous channel. Eng Comput. (2013) 30:399–408. doi: 10.1108/02644401311314358
3. Farooq M, Islam S, Haroon T. Heat transfer analysis of the couple stress fluid between two parallel plates. Heat Trans Res. (2011) 42:737–80. doi: 10.1615/HeatTransRes.2012000996
4. Srinivasacharya D, Kaladhar K. Mixed convection flow of couple stress fluid in a non-darcy porous medium with Soret and Dufour effects. J Appl Sci Eng. (2012) 15:415–22.
5. Ramzan M, Farooq M, Alsaedi A, Hayat T. MHD three-dimensional flow of couple stress fluid with Newtonian heating. Eur Phys J Plus. (2013) 128:49. doi: 10.1140/epjp/i2013-13049-5
6. Hayat T, Mustafa M, Iqbal Z, Alsaedi A. Stagnation-point flow of couple stress fluid with melting heat transfer. Appl Math Mech. (2013) 34:167–76. doi: 10.1007/s10483-013-1661-9
7. Turkyilmazoglu M. Exact solutions for two-dimensional laminar flow over a continuously stretching or shrinking sheet in an electrically conducting quiescent couple stress fluid. Int J Heat Mass Transfer. (2014) 72:1–8. doi: 10.1016/j.ijheatmasstransfer.2014.01.009
8. Awad F, Haroun NAH, Sibanda P, Khumalo M. On couple stress effects on unsteady nanofluid flow over stretching surfaces with vanishing nanoparticle flux at the wall. J Appl Fluid Mech. (2016) 9:1937–44. doi: 10.18869/acadpub.jafm.68.235.24940
9. Sreenadh S, Kishore SN, Srinivas ANS, Reddy RH. MHD free convection flow of couple stress fluid in a vertical porous layer. Adv Appl Sci Res. (2011) 2:215–22.
10. Hayat T, Awais M, Safdar A, Hendi AA. Unsteady three dimensional flow of couple stress fluid over a stretching surface with chemical reaction. Nonlin Analy Mod. Cont. (2012) 17:47–59. doi: 10.15388/NA.17.1.14077
11. Khan NA, Aziz S, Khan NA. Numerical simulation for the unsteady MHD flow and heat transfer of couple stress fluid over a rotating disk. PLoS ONE. (2014) 9:e95423. doi: 10.1371/journal.pone.0095423
12. Hayat T, Aziz A, Muhammad T, Ahmad B. Influence of magnetic field in three-dimensional flow of couple stress nanofluid over a nonlinearly stretching surface with convective condition. PLoS ONE. (2015) 10:e0145332. doi: 10.1371/journal.pone.0145332
13. Ramzan M. Influence of Newtonian heating on three dimensional MHD flow of couple stress nanofluid with viscous dissipation and joule heating. PLoS ONE. (2015) 10:e0124699. doi: 10.1371/journal.pone.0124699
14. Hayat T, Muhammad T, Shehzad SA, Alsaedi A. Simultaneous effects of magnetic field and convective condition in three dimensional flow of couple stress nanofluid with heat generation/absorption. J Braz Soc Mech Sci Eng. (2017) 39:1165–76. doi: 10.1007/s40430-016-0632-5
15. Hayat T, Muhammad T, Alsaedi A. On three-dimensional flow of couple stress fluid with Cattaneo–Christov heat flux. Chin J Phys. (2017) 55:930–8. doi: 10.1016/j.cjph.2017.03.003
16. Umavathi JC, Chamkha AJ, Manjula MH, Al-Mudhaf A. Flow and heat transfer of a couple-stress fluid sandwiched between viscous fluid layers. Can J Phys. (2005) 83:705–20. doi: 10.1139/p05-032
17. Umavathi JC, Malashetty MS. Oberbeck convection flow of a couple stress fluid through a vertical porous stratum. Int J Nonlin Mech. (1999) 34:1037–45. doi: 10.1016/S0020-7462(98)00074-2
18. Srinivasacharyulu N, Odelu O. Flow and heat transfer of couple stress fluid in a porous channel with expanding and contracting walls. Int Commun Heat Mass Transfer. (2009) 36:180–5. doi: 10.1016/j.icheatmasstransfer.2008.10.005
19. Zueco J, Beg OA. Network numerical simulation applied to pulsatile non-Newtonian flow through a channel with couple stress and wall mass flux effects. Int J Appl Math Mech. (2009) 5:1–16.
20. Zakaria M. Hydromagnetic fluctuating flow of a couple stress fluid through a porous medium. Korean J Comput Appl Math. (2002) 10:175–91. doi: 10.1007/BF02936216
21. Ellahi R, Zeeshan A, Hussain F, Asadollahi A. Peristaltic blood flow of couple stress fluid suspended with nanoparticles under the influence of chemical reaction and activation energy, Symmetry. (2019) 11:276. doi: 10.3390/sym11020276
22. Rudolf AT, Baumjohann W, Balogh. A. The strongest magnetic fields in the universe: how strong can they become? Front Phys. (2014) 2:59. doi: 10.3389/fphy.2014.00059
23. Hayat T, Iqbal R, Tanveer A, Alsaed A. Soret and Dufour effects in MHD peristalsis of pseudoplastic nanofluid with chemical reaction. J Mol Liq. (2016) 220:693–706. doi: 10.1016/j.molliq.2016.04.123
24. Lin Y, Zheng L, Zhang X, Chen G. MHD pseudo-plastic nanofluids unsteady flow and heat transfer in a finite thin film over stretching sheet with internal heat generation. Int J Heat Mass Transf. (2015) 84:903–11. doi: 10.1016/j.ijheatmasstransfer.2015.01.099
25. Ramesh K, Devakar M. The influence of heat transfer on peristaltic transport of MHD second grade fluid through porous medium in a vertical asymmetric channel. J Appl Fluid Mech. (2015) 8:351–65. doi: 10.18869/acadpub.jafm.67.222.23471
26. Reddy MG, Reddy KV. Influence of Joule heating on MHD peristaltic flow of a nanofluid with compliant walls. Process Eng. (2015) 127:1002–9. doi: 10.1016/j.proeng.2015.11.449
27. Eringen AC. Theory of micropolar fluids. J Math Mech. (1966) 16:1–18. doi: 10.1512/iumj.1967.16.16001
28. Bég AO, Bhargava R, Rashidi MM. Numerical Simulation in Micropolar Fluid Dynamics. Saarbrücken: Lap Lambert Academic Publishing GmbH KG (2011).
29. Uddin Z, Kumar M. Hall and ion-slip effect on MHD boundary layer flow of a micro polar fluid past a wedge. Sci Iran. (2013) 20:467–76. doi: 10.1016/j.scient.2013.02.013
30. Khan A, Shah Z, Islam S, Dawar A, Bonyah E, Ullah H, Khan A. Darcy-Forchheimer flow of MHD CNTs nanofluid radiative thermal behaviour and convective non uniform heat source/sink in the rotating frame with microstructure and inertial characteristics, AIP Adv. (2018) 8:125024. doi: 10.1063/1.5066223
31. Dawar A, Shah Z, Khan W, Idrees M, Islam S. Unsteady squeezing flow of magnetohydrodynamic carbon nanotube nanofluid in rotating channels with entropy generation and viscous dissipation. Adv Mech Eng. (2019) 11:1–18. doi: 10.1177/1687814018823100
32. Kumam P, Shah Z, Dawar A, Rasheed HU, Islam S. Entropy Generation in MHD radiative flow of CNTs casson nanofluid in rotating channels with heat source/sink. Math Problems Eng. (2019) 2019:9158093. doi: 10.1155/2019/9158093
33. Shah Z, Dawar A, Kumam P, Khan W, Islam S. Impact of nonlinear thermal radiation on MHD nanofluid thin film flow over a horizontally rotating disk. Appl. Sci. (2019) 9:1533. doi: 10.3390/app9081533
34. Ali F, Sheikh NA, Khan I, Saqib M. Magnetic field effect on blood flow of Casson fluid in axisymmetric cylindrical tube: a fractional model. J Magn Magn Mater. (2017) 423:327–36. doi: 10.1016/j.jmmm.2016.09.125
35. Shah Z, Dawar A, Alzahrani EO, Kumam P, Khan A, Islam S. Hall effect on couple stress 3D nanofluid flow over an exponentially stretched surface with Cattaneo Christov Heat Flux Mode. IEEE Access. (2019) 7: 64844–55. doi: 10.1109/ACCESS.2019.2916162
36. Shah Z, Islam S, Gul T, Bonyah E, Altaf Khan M. The electrical MHD and Hall current impact on micropolar nanofluid flow between rotating parallel plates. Results Phys. (2018) 9:1201–14. doi: 10.1016/j.rinp.2018.01.064
37. Kumar KA, Reddy JV, Sugunamma V, Sandeep N. Simultaneous solutions for MHD flow of williamson fluid over a curved sheet with nonuniform heat source/sink. Heat Transfer Res. (2019) 50:581–603. doi: 10.1615/HeatTransRes.2018025939
38. Temple RC, Mihai AP, Arena DA, Marrows CH. Ensemble magnetic behavior of interacting CoFe nanoparticles. Front Phys. (2015) 3:52. doi: 10.3389/fphy.2015.00052
39. Ellahi R, Zeeshan A, Shehzad N, Alamri SZ. Structural impact of Kerosene-Al2O3 nanoliquid on MHD Poiseuille flow with variable thermal conductivity: application of cooling process. J Mol Liquids. (2018) 264:607–15. doi: 10.1016/j.molliq.2018.05.103
40. Asadollahi A, Rashidi S, Esfahani JA, Ellahi R. Simulating phase change during the droplet deformation and impact on a wet surface in a square microchannel: An application of oil drops collision. Eur Phys J Plus. (2018) 133:306. doi: 10.1140/epjp/i2018-12135-6
41. Ellahi R, Alamri SZ, Basit A, Majeed A. Effects of MHD and slip on heat transfer boundary layer flow over a moving plate based on specific entropy generation. J Taibah Univ Sci. (2018) 12:476–82. doi: 10.1080/16583655.2018.1483795
42. Ellahi R, Bhatti M, Pop I. Effects of hall and ion slip on MHD peristaltic flow of Jeffrey fluid in a non-uniform rectangular duct. Int J Num Methods Heat Fluid Flow. (2016) 26:1802–20. doi: 10.1108/HFF-02-2015-0045
43. Ellahi R, Sait SM, Shehzad N, Mobin N. Numerical simulation and mathematical modeling of electro-osmotic couette–poiseuille flow of MHD power-law nanofluid with entropy generation. Symmetry. (2019) 11:1038. doi: 10.3390/sym11081038
44. Bhatti MM, Zeeshan A, Ellahi R, Shit GC. Mathematical modeling of heat and mass transfer effects on MHD peristaltic propulsion of two-phase flow through a Darcy-Brinkman-Forchheimer Porous medium. Adv Powder Technol. (2018) 29:1189–97. doi: 10.1016/j.apt.2018.02.010
45. Ameen I, Shah Z, Islam S, Nasir S, Khan W, Kumam P, Thounthong P. Hall and Ion-Slip Effect on CNTS nanofluid over a porous extending surface through heat generation and absorption. Entropy. (2019) 21:801. doi: 10.3390/e21080801
46. Vo DD, Shah Z, Sheikholeslami M, Shafee A, Nguyen TK. Numerical investigation of MHD nanomaterial convective migration and heat transfer within a sinusoidal porous cavity. Phys. Scr. (2019) 94:115225. doi: 10.1088/1402-4896/ab2ced
47. Ahmad MW, Kumam P, Shah Z, Farooq AA, Nawaz R, Dawar A, et al. Darcy–Forchheimer MHD Couple Stress 3D nanofluid over an exponentially stretching sheet through cattaneo–christov convective heat flux with zero nanoparticles mass flux conditions. Entropy. (2019) 21:867. doi: 10.3390/e21090867
48. Sheikholeslami M, Shah Z, Shafee A, Khan I, Tlili I. Uniform magnetic force impact on water based nanofluid thermal behavior in a porous enclosure with ellipse shaped obstacle. Sci Rep. (2019) 9:1196. doi: 10.1038/s41598-018-37964-y
49. Ali AY, Ali Y, Kumam P, Babar K, Ahmed A, Shah Z. Flow of a nanofluid and heat transfer in channel with contractingexpanding walls. IEEE Access. (2019) 7:102427–36. doi: 10.1109/ACCESS.2019.2928030
Keywords: hall MHD generator system, convective heat transfer, magnetohydrodynamic, micropolar fluid, couple stress, hall current, HAM
Citation: Shah Z, Kumam P, Dawar A, Alzahrani EO and Thounthong P (2019) Study of the Couple Stress Convective Micropolar Fluid Flow in a Hall MHD Generator System. Front. Phys. 7:171. doi: 10.3389/fphy.2019.00171
Received: 25 August 2019; Accepted: 16 October 2019;
Published: 05 November 2019.
Edited by:
Muhammad Mubashir Bhatti, Shanghai University, ChinaReviewed by:
R. Ellahi, University of California, Riverside, United StatesArash Asadollahi, Southern Illinois University Carbondale, United States
Copyright © 2019 Shah, Kumam, Dawar, Alzahrani and Thounthong. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zahir Shah, emFoaXIuc2hhQGttdXR0LmFjLnRo; Poom Kumam, cG9vbWt1bWFtQGttdXR0LmFjLnRo
 Zahir Shah
Zahir Shah Poom Kumam
Poom Kumam Abdullah Dawar
Abdullah Dawar Ebraheem O. Alzahrani6
Ebraheem O. Alzahrani6