- Instituto de Física Corpuscular, CSIC-Universitat de València, Valencia, Spain
The discovery of a non-zero rate for a lepton flavor violating decay mode of the Higgs boson would definitely be an indication of New Physics. We review the prospects for such signal in Two Higgs Doublet Models, in particular for Higgs boson decays into τμ final states. We will show that this scenario contains all the necessary ingredients to provide large flavor violating rates and still be compatible with the stringent limits from direct searches and low-energy flavor experiments.
1. Introduction
The discovery of the Higgs boson in 2012 at the LHC by the ATLAS and CMS collaborations constitutes a historical milestone for particle physics and another brilliant triumph for the Standard Model (SM). With this long-awaited completion of the SM particle spectrum, it stands as one of the most successful theories ever built, providing precise predictions for a wide range of particle physics phenomena, in good agreement with a large amount of experimental results at low and high energies.
Despite this remarkable success, many fundamental questions remain unanswered in the SM. The list is long and contains experimental observations that cannot be addressed in the SM and theoretical issues that cannot be fully understood in its context. It includes the origin of neutrino masses, the nature of dark matter, the conservation of CP in the strong interactions or the reason for the replication of fermion generations, to mention a few. These open problems clearly call for an extension of the SM with new states, presumably present at high energies, and/or new dynamics.
New Physics (NP) may manifest in the form of Higgs boson properties different from those predicted by the SM. For this reason, it is crucial to look for deviations in the Higgs couplings to fermions and gauge bosons and the Higgs boson total decay width or the existence of new Higgs decay channels. In particular, new degrees of freedom coupling to the SM leptons and the Higgs boson could induce non-zero lepton flavor violating (LFV) Higgs boson decays, such as h → ℓiℓj with i ≠ j, indeed a common feature in many models with extended scalar or lepton sectors. The observation of these processes, strictly forbidden in the SM, would provide a clear hint of NP at work.
Higgs lepton flavor violating (HLFV) signatures face many indirect constraints, since most of the NP scenarios that lead to them modify other Higgs properties as well, some already experimentally determined to lie close to the SM prediction. Moreover, HLFV signatures typically come along with other LFV processes, such as the ℓi → ℓjγ radiative decays. While model-independent studies [1–6] have shown that large HLFV rates are in principle compatible with the existing experimental constraints, this is not generally the case in specific models. In fact, most models predict HLFV rates below the current LHC sensitivity. In contrast, the Two Higgs Doublet Model (2HDM) [7, 8] has been shown to be able to accommodate large h → ℓiℓj branching ratios [9], clearly within the reach of the ATLAS and CMS detectors.
This minireview focuses on HLFV in the 2HDM. Several pioneer works already addressed HLFV in the pre-LHC era [10–18], and many have revisited the subject in the context of the 2HDM [19–21] or in other contexts [22–28] after the LHC has started delivering data. In fact, early results by the CMS collaboration hinted at a non-zero h → τμ branching ratio [29], and this raised a considerable attention in the community, leading to many works [9, 30–91]. We will first follow some general model-independent arguments that identify the 2HDM as a scenario with potentially large HLFV signatures and later highlight some selected phenomenological results on HLFV in the 2HDM. Even though the theoretical discussion will be general and not concentrate on any particular combination of lepton flavors, we will focus on τμ LFV in the phenomenological discussion.
The rest of the manuscript is structured as follows. In section 2 the current experimental bounds for the rates of several LFV processes, including h → ℓiℓj, are briefly discussed. Section 3 contains general model-independent considerations, while section 4 argues that a type-III 2HDM may accommodate sizable h → ℓiℓj branching ratios and makes this point explicitly after introducing our 2HDM notation and conventions. Finally, we comment on some 2HDM scenarios that generate neutrino masses and may lead to large HLFV rates in section 5 and conclude in section 6.
2. Experimental Status
A remarkable effort has been devoted to the search for LFV in processes involving charged leptons, resulting in impressive bounds in some channels. This has been particularly well motivated after the discovery of neutrino flavor oscillations, which imply that charged lepton flavor violating processes must exist, although perhaps with low rates.
In what concerns HLFV, the ATLAS and CMS collaborations have searched for h → ℓiℓj, setting limits for the corresponding branching ratios in the 10−5 − 10−3 ballpark, as shown in Table 11. The CMS limit on BR(h → μe) has been obtained using TeV data, whereas the rest of ATLAS and CMS limits have been updated including TeV data. Dedicated strategies can in principle improve these limits substantially with future LHC data [3], in particular in the 14 TeV HL-LHC phase [63]. Furthermore, HLFV can also be searched for at e+e− colliders, which offer a very clean environment, perfectly suited for the exploration of the Higgs boson properties. As shown by several analyses [63, 66, 86, 87], the planned future e+e− facilities (CEPC, FCC-ee, and ILC) can probe HLFV branching ratios as low as 10−5 − 10−4, improving on the current LHC limits by about one order of magnitude for channels involving the τ lepton.
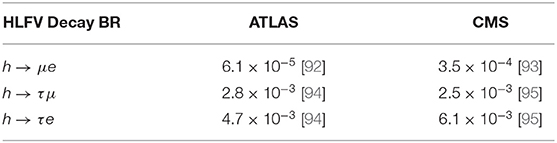
Table 1. Experimental 95 % C.L. upper bounds on HLFV branching ratios from the ATLAS and CMS collaborations.
The NP degrees of freedom and interactions leading to h → ℓiℓj also generate other LFV processes, such as ℓi → ℓjγ. Since these are subject to much stronger experimental bounds, they tend to be crucial constraints in most specific models and must be considered in any phenomenological study on HLFV decays. Table 2 collects the current bounds and future sensitivities for several LFV processes of interest. Muon LFV observables have the best experimental limits due to the existence of high-intensity muon beams, while the branching ratios for tau LFV decays are bound to be below ~10−8. The most constraining processes in many models are the ℓi → ℓjγ radiative decays. The MEG collaboration has established the strong limit BR(μ → eγ) < 4.2 · 10−13, a bound that will be improved by about an order of magnitude in the MEG-II phase [97]. Regarding the ℓi → ℓjℓkℓk 3-body decays, the μ → eee branching ratio sensitivity is expected to be improved by four orders of magnitude by the Mu3e experiment [101]. Finally, the most spectacular progress in the search for LFV are expected in μ − e conversion experiments, which are also expected to improve the current limits for different nuclei by several orders of magnitude [104, 106, 107]. See Calibbi and Signorelli [108] for an experimental and theoretical review of the current situation in charged lepton flavor violation experiments.
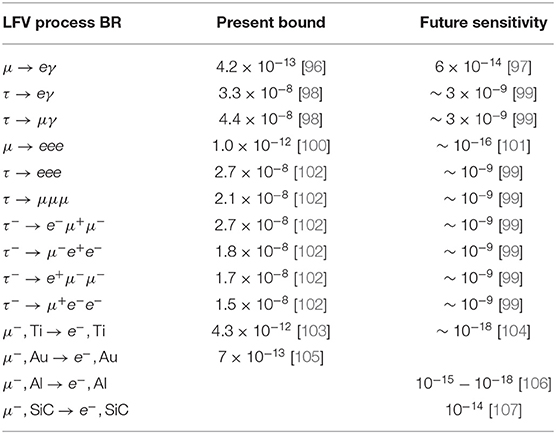
Table 2. Current experimental bounds and future sensitivities for several LFV observables of interest.
3. Model-Independent Considerations
In order to explore HLFV in a model-independent way, it proves convenient to adopt an approach based on Effectively Field Theory (EFT). This is particularly well motivated due to lack of NP signals at the LHC, which arguably implies that any new particles responsible for HLFV would lie clearly above the electroweak scale. We will now continue along the lines of Herrero-Garcia et al. [72]2.
In addition to canonical kinetic terms, the SM Lagrangian contains the Yukawa terms for the leptons
where
denote the SM lepton SU(2)L doublets and singlets and Higgs doublet, respectively, and we give the representation under the SM gauge group SU(3)c × SU(2)L × U(1)Y. Γe is a 3 × 3 complex matrix that can be taken to be diagonal without loss of generality. Therefore, the three lepton flavors are exactly conserved in the SM, which then possesses a Gf = U(1)e × U(1)μ × U(1)τ global flavor symmetry3.
The flavor symmetry Gf gets generally broken in the presence of NP. This can be generically parametrized by means of non-renormalizable gauge-invariant operators of dimension d > 4 that encode the LFV effects induced by unknown heavy states,
Here Λ is the scale of NP, of the order of the masses of the states whose decoupling induces the dimension-d operator Qi, and Ci the associated Wilson coefficient. There are many of such LFV operators. However, the only dimension-six operator giving rise to Higgs LFV is Qeφ, defined as
This operator was first highlighted in the context of HLFV in Harnik et al. [3], later denoted the Yukawa operator in Herrero-Garcia et al. [72] and is one of the operators in the Warsaw basis of the Standard Model Effective Field Theory [110]4. Any additional gauge-invariant dimension-six operator leading to HLFV can be shown to be redundant, and therefore reducible to Qeφ by using equations of motion, Fierz transformations or other field redefinitions [3]. Therefore, all HLFV effects are encoded (at least in scenarios leading to NP contributions of dimension six) by Qeφ.
After electroweak symmetry breaking, the SM Yukawa term in Equation (1) and the NP contribution encoded in Qeφ add up to
where
is the 3 × 3 charged lepton mass matrix and
are the Higgs boson couplings to a pair of charged leptons. We have used the decomposition , with h the physical Higgs boson with a mass mh ≃ 125 GeV, G0 the Goldstone boson that constitutes the longitudinal component of the massive Z-boson and v ≃ 246 GeV the electroweak vacuum expectation value (VEV). It is clear that, in general, the matrices and are not diagonal in the same basis. In fact, in the mass basis, defined by
the Higgs boson couplings to charged leptons read
While the first term in Equation (8) is proportional to the charged lepton masses, the second one can in general contain off-diagonal entries and induce HLFV processes. In particular, this piece leads to the h → ℓiℓj decays, with i ≠ j. One finds
where Γh (≃ 4 MeV in the SM) is the total Higgs boson decay width.
So far, we only discussed the Qeφ operator, which induces the HLFV decays h → ℓiℓj we are interested in. However, in a complete ultraviolet theory other operators will be generated as well. In particular, operators that give rise to other LFV processes, such as ℓi → ℓjγ, with much stronger experimental bounds. At dimension six, two gauge-invariant operators of this type exist [110],
where τI, with I = 1, 2, 3, are the Pauli matrices. At low energies, these two operators are matched to the dimension-five photonic dipole operator5
which is directly responsible for the ℓi → ℓjγ radiative LFV decays. Defining the contribution of to the low-energy effective Lagrangian as
where Leγ is its Wilson coefficient, the resulting branching ratios are
with mi and Γi the mass and total decay width of the charged lepton ℓi, respectively.
Any theory that induces Qeφ will also generate , since these operators transform in the same way under flavor and chiral symmetries [33] and mix under renormalization group evolution [113]. Therefore, one cannot simply get rid of the latter. However, different NP scenarios predict a different balance between the Ceφ and Leγ Wilson coefficients, and this is what determines the magnitude of the allowed HLFV effects in a specific model. Let us consider an example to illustrate this connection: a model inducing predominantly (QeB)12 at the high-energy scale Λ. In this case the operator (Qeφ)12 gets induced due to renormalization group running while is obtained after matching at the electroweak scale. Since the HLFV operator is induced by operator mixing effects, the resulting coefficient is suppressed and one expects the relation , which clearly precludes the observation of the HLFV decay. More generally, in models with Leγ ~ Ceφ or Leγ > Ceφ, as in the example we just considered, the strong constraints derived from the non-observation of ℓi → ℓjγ would imply tiny HLFV rates. In contrast, models predicting Leγ ≪ Ceφ may accommodate sizable HLFV effects. As we will see in section 4.1, the 2HDM is one of such models.
4. HLFV in the 2HDM
We now concentrate on the 2HDM. First, in section 4.1 we particularize the previous model-independent discussion to the case of a 2HDM in order to motivate this model as the perfect scenario to obtain large HLFV rates. Section 4.2 will introduce our notation and conventions for the 2HDM. Finally, we will concentrate on τμ flavor violation, discuss τ → μγ in the 2HDM in section 4.3 and show some selected phenomenological results on h → τμ in the 2HDM in section 4.4.
4.1. EFT Motivation
A NP model with a second scalar SU(2)L doublet would induce the Qeφ operator, as shown in Figure 1. This is one of the possible topologies contributing to the HLFV operator, as discussed in great detail in Herrero-Garcia et al. [72]. The scalar Φ must be an SU(2)L doublet for the diagram to be gauge invariant, and would be identified with a second Higgs doublet in a 2HDM. Moreover, it should be noticed that this topology requires both scalar doublets to couple to leptons. The Φ coupling is clearly shown, and φ was already assumed to couple to leptons, see Equation (1). For this reason, the 2HDM behind the generation of this topology would be a type-III 2HDM, in which both Higgs doublets are allowed to couple to leptons in a general way6.
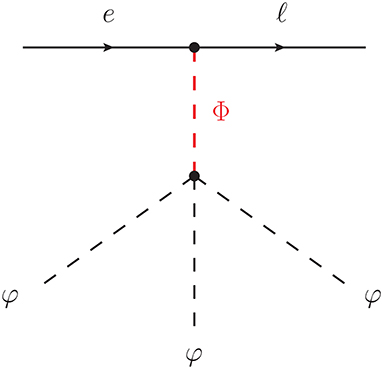
Figure 1. 2HDM ultraviolet completion of the Qeφ operator. Here Φ is a heavy new scalar SU(2)L doublet. See Herrero-Garcia et al. [72] for details.
We note that Qeφ is generated at tree-level in this scenario, thus enhancing the Wilson coefficient Ceφ. We expect
where λ and yΦ are the quartic scalar and Yukawa couplings involved in the topology shown in Figure 1 and mΦ the Φ scalar mass term. Next, we consider the generation of . This operator can be generated by attaching one of the external φ lines in Figure 1 to a charged lepton line and then adding the photon. There are, however, three effects that suppress the generation of this operator in the 2HDM:
• The operator gets induced at the 1-loop level.
• Closing the loop by attaching the φ line to the charged lepton line introduces a charged lepton mass insertion.
• The operator requires a chirality flip, which in a SM extension with only new scalar fields (such as the 2HDM) implies an additional charged lepton mass insertion.
These considerations allow us to estimate
This estimate is known to be very poor due to the presence of several additional contributions in a complete 2HDM, as we will show in section 4.4. Nevertheless, it serves as a good motivation to consider this scenario as potentially promising in what concerns HLFV, since the required hierarchy between Ceφ and Leγ is naturally obtained.
4.2. 2HDM: Model Basics
In the following, we consider the general 2HDM, usually referred to as type-III 2HDM, and denote the two Higgs doublets as φ1 and φ2. In contrast to other variants of the 2HDM, no distinction between the two Higgs doublets is introduced. This has two consequences for our discussion. First, both φ1 and φ2 are allowed to couple to all fermion species, and in particular to leptons, a fundamental ingredient for the generation of HLFV effects, see section 4.1. And second, one can perform arbitrary U(2) basis transformations in {φ1, φ2} space, without any impact on physical observables. This freedom can be used to go to a specific basis in which only one Higgs doublet acquires a VEV, the so-called Higgs basis [117–119]. In this basis, the scalar potential of the model is given by7
and the Higgs doublets can be decomposed as
Here , and A are neutral scalars, H+ is a charged scalar and G+ and G0 are Goldstone bosons. Assuming CP conservation, the CP-even states and do not mix with the CP-odd state A, which is a physical mass eigenstate. and are related to the mass eigenstates h and H (with mh < mH) as
where sβ−α ≡ sin(β − α), cβ − α ≡ cos(β − α) and β − α is a physical mixing angle. The lightest CP-even state, h, is identified with the Higgs boson discovered at the LHC. With these definitions at hand, one can derive several relations between the potential parameters and the physical Higgs masses [120],
Let us now discuss the Yukawa interactions of the model. Again, we use the freedom to choose specific weak bases. In the Higgs basis for the scalar doublets and the mass basis for the fermions, the Yukawa Lagrangian can be written as
Here we denote , with a = 1, 2, and define the diagonal matrices and . K is the CKM matrix and ρu, d, e are general 3 × 3 complex matrices in flavor space, which in the following will be assumed to be Hermitian for simplicity. Using Equations (17) and (18), and expanding in SU(2)L indices, the leptonic part of Equation (24) can be rewritten as
where U is the PMNS matrix. This expression allows us to extract the couplings of the neutral scalars of the model to leptons. By following the same steps with the quarks, one finds the general expressions
where f = u, d, e. He have introduced sf = +1 for down-type quarks and charged leptons and sf = −1 for up-type quarks. Equation (26) must be compared to the general expression in Equation (8). Again, the first term is diagonal, whereas the second may contain off-diagonal entries. We therefore conclude that the ρe matrix is the source of the HLFV processes that we are about to discuss.
Finally, the neutral scalar couplings to a pair of gauge bosons are fully dictated by the gauge symmetry. One has
and the couplings to a pair of Z-bosons follow the same proporcionalities.
4.3. τ → μγ in the 2HDM
Given the strong experimental bounds on μe flavor violating processes, we will concentrate on τ LFV. In particular, we will consider τμ LFV, and therefore discuss h → τμ and the related τ → μγ. The h → τμ HLFV decay is the main focus of this manuscript and we show some phemenological results in section 4.4. However, in order to assess the observability of this process, one must take into account the strong constraint coming from BR(τ → μγ), which we now proceed to evaluate in the 2HDM.
The τ → μγ radiative decay is induced by the dipole operator defined by Equations (11) and (12). It proves convenient to define the form factors AL and AR as
Since we assume the matrix ρ to be Hermitian, |ghτμ| = |ghμτ|, which implies |AL| = |AR| ≡ |A|. We just need to determine the most relevant contributions to the form factor A in the 2HDM.
It is well known that in the 2HDM 2-loop contributions to ℓi → ℓjγ may easily dominate over 1-loop ones [121]. The reason is easy to understand. Dipole transitions require a chirality flip. In a 1-loop diagram with a virtual scalar in the loop, two chirality flips take place in the Yukawa vertices, and therefore one more is required in the fermion propagator, giving a total of three. This largely suppresses the loop amplitude, which explains why 2-loop diagrams with only one chirality flip can be dominant even if one pays the extra loop suppression factor of 1/(16π2). In particular, 2-loop Barr-Zee diagrams [122] can easily dominate if the involved scalar fields have large couplings to the virtual fermions or bosons running in the loops. Taking all these ingredients into account, the authors of Davidson and Grenier [19] identified three main contributions to τ → μγ in the type-III 2HDM:
• 1-loop diagrams with neutral Higgs bosons and charged leptons in the loop
• 2-loop Barr-Zee diagrams with an internal photon and a third generation quark
• 2-loop Barr-Zee diagrams with an internal photon and a W-boson
These contributions were computed in Chang et al. [123] and are shown in Figure 2. One can write
where the different contributions were computed by Davidson and Grenier [19] and are given explicitly in Appendix. Armed with these expressions we are ready to explore the HLFV phenomenology of the type-III 2HDM.
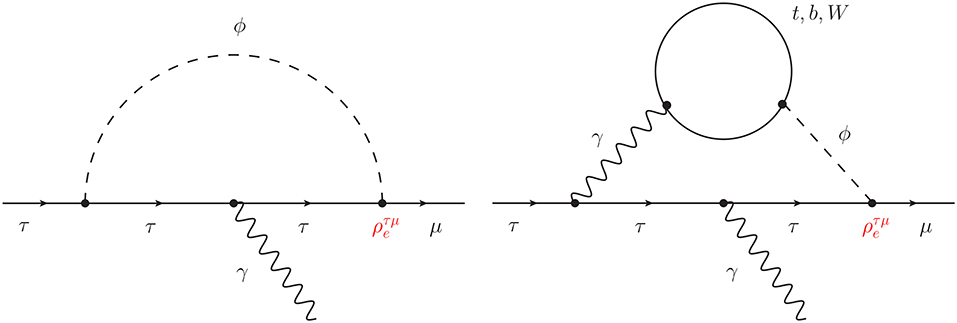
Figure 2. Most important contributions to τ → μγ in the 2HDM. Here ϕ = h, H, A. To the left, 1-loop diagrams with neutral Higgs bosons and charged leptons in the loop. To the right, 2-loop Barr-Zee diagrams with an internal photon and a third generation quark or a W-boson. The LFV vertex proportional to is explicitly indicated.
4.4. HLFV Phenomenology
Following Aristizabal Sierra and Vicente [9], we show now some phenomenological results on HLFV in the type-III 2HDM. We refer to Crivellin et al. [31], Omura et al. [34], Crivellin et al. [42], Botella et al. [46], Liu et al. [47], Benbrik et al. [53], Bizot et al. [56], Herrero-Garcia et al. [72], Wang et al. [76], Tobe [78], Qin et al. [87], Babu and Jana [89], and Sher and Thrasher [124] for additional HLFV phenomenological studies in the 2HDM.
First, we must make an observation about the type-III 2HDM. As already explained, in this version of the 2HDM one can apply rotations in Higgs space that modify the Higgs VEVs. For this reason, the usual ratio of VEVs tan β is not uniquely defined. Given that we are mainly interested in tau flavor violation, we define [120]
We note that tan βτ is the physical ratio between the tau Yukawa coupling and , which would correspond to the usual tan β in the Type-II 2HDM.
Let us now discuss our parameter choices. The results presented here are based on a random scan of the parameter space, taking the parameter ranges,
These are based on the following considerations and experimental constraints:
• It proves convenient to use as input the scalar masses, rather than the scalar potential parameters. These should nevertheless be computed to make sure that they never exceed the perturbative limit of 4π. The Λ1, Λ2, Λ4, Λ5 and Λ6 parameters can be computed by means of Equations (19)–(23). The remaining Λ parameters do not have any impact on the observables studied here, but they can be chosen by demanding that the scalar potential is bounded from below [125– 127].
• A small mass difference is required by electroweak precision data. In particular, larger values could potentially lead to a T oblique parameter value outside the 1σ range determined by Baak et al. [128], T ∈ [−0.03, 0.19].
• The lower limit on sin(β − α) is motivated by the fact that the observed Higgs boson has SM-like couplings to fermions and gauge bosons. Lower values of sin(β − α) could potentially induce deviations, see Equations (26) and (29), in tension with the experimental results. In our analysis we consider the CMS measurements presented in CMS Collaboration [129] and require that the signal strengths for , defined as μ = (σ × BR) / (σ × BR)SM, are within the CMS 1 σ ranges [129]. For the determination of the Higgs production cross-section we assume gluon fusion.
• The lower limit on is motivated by flavor physics (mainly B physics, see for instance [130]).
Finally, our scan also fixes mh = 125.1 GeV [131]. In what concerns the Yukawa matrices, and in order to reduce the number of free parameters, we will consider specific textures for the ρ matrices. Inspired by the Cheng-Sher ansatz [132], we express ρe as
By construction, κττ = 1. However, the other entries of the κ matrix are free parameters. In particular, is the relevant parameter giving rise to the h → τμ and τ → μγ decays. In our random scan we will take 0.1 < |κτμ| < 3.0. For the quark ρ matrices we assume the usual Type-II textures
This ansatz is particularly convenient since it ensures compatibility with the (already constraining) experimental bounds on the Higgs boson couplings to quarks. Furthermore, it can be regarded as a departure beyond the popular Type-II 2HDM, with the only deviation in the τμ coupling [133]8.
After these preliminaries, we are ready to show some results on h → τμ. Figure 3 shows BR(h → τμ) as a function of BR(τ → μγ). The vertical lines shown in this figure correspond to the current experimental bound BR(τ → μγ) < 4.4 × 10−8 [98] and the expected sensitivity of the Belle-II experiment, of about ~ 10−9 [99]. The horizontal line corresponds to the limit BR(h → τμ) < 0.0025, set by the CMS collaboration [95]. As can be seen from this figure, the correlation between these two observables is not exact, and this can be traced back to the different contributions to τ → μγ, which might even cancel in some cases. We find that, in general, the dominant contribution to the τ → μγ amplitude comes from 2-loop Barr-Zee diagrams with internal W bosons, although the other contributions typically play a relevant role as well.
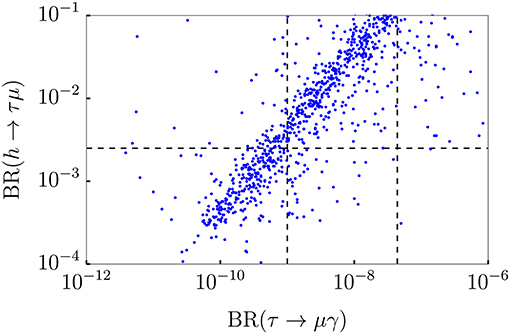
Figure 3. BR(h → τμ) as a function of BR(τ → μγ) in the type-III 2HDM. The parameters are fixed as explained in the text. The vertical lines correspond to the current bound BR(τ → μγ) < 4.4 × 10−8 [98] and the expected Belle-II sensitivity, estimated to be ~ 10−9 [99]. Finally, the horizontal line indicates the limit by the CMS collaboration BR(h → τμ) < 0.0025 [95].
The main qualitative message that one can extract from Figure 3 is that the type-III 2HDM can induce h → τμ rates close to the current bound while being in agreement with all experimental constraints. All LFV observables increase with κτμ, and in some regions of the parameter space they can be close to their current experimental limits, explicitly shown in Figure 3. These regions are characterized by tan βτ ≳ 2, sin(β − α) ~ 0.9 and κτμ ≳ 0.1.
Finally, some additional comments are in order. A Higgs doublet with μτ LFV couplings can also address the long-standing muon g − 2 anomaly. This was studied in relation to the LFV decay h → τμ in Aristizabal Sierra and Vicente [9], Davidson and Grenier [19], Omura et al. [34], Liu et al. [47], Benbrik et al. [53], Altmannshofer et al. [70], Wang et al. [76], and Crivellin et al. [130] and very recently in Iguro et al. [134] and Wang and Zhang [135]. It could also be linked to the popular b → s [31, 48] or b→c [42] anomalies observed in B-meson decays or be a crucial ingredient for lepton-flavored electroweak baryogenesis [80]. In fact, the type-III 2HDM with generic Yukawa couplings has a very rich flavor phenomenology, see Crivellin et al. [130]. The analogous quark flavor violating decay h → bs was studied in Crivellin et al. [136]. It is also remarkable that the 2HDM with a BGL symmetry [137–139] can also lead to large h → τμ branching ratios, strongly correlated with other flavor observables, as shown in Botella et al. [46]. Here we concentrated on the 2HDM. For HLFV studies in other multi-Higgs doublet models see the interesting works [140–143].
5. 2HDMs, Neutrino Masses and HLFV
Neutrino flavor oscillations constitute the only existing experimental proof of LFV. Since these are sourced by non-zero neutrino masses and mixings, it is interesting to discuss their possible connection to HLFV [72, 79].
First, one should notice that while the existence of non-zero neutrino masses and mixings implies the violation of lepton flavor, the observation of lepton flavor violating processes does not require neutrinos to be massive. In fact, there are many examples of the latter, the 2HDM being the simplest one. Indeed, in the model presented in section 4.2, the most general 2HDM, neutrino masses are exactly zero but processes such as ℓi → ℓjγ or h → ℓiℓj are perfectly possible. Similarly, neutrino masses vanish in the Minimal Supersymmetric Standard Model, but LFV processes are indeed induced if the slepton soft mass contain off-diagonal entries. Other examples are also known, see for instance [144].
There are, however, many neutrino mass models that require the introduction of a second Higgs doublet, and these may potentially lead to an interesting connection between the generation of neutrino masses and HLFV. One of the most popular examples of this link is the Zee model [145], a setup that induces neutrino masses at the 1-loop level9. This model can actually be regarded as an extension of the general 2HDM with the addition of a singly-charged scalar,
If both lepton doublets couple to leptons, as in the type-III 2HDM, the simultaneous presence of the Yukawa term and the trilinear scalar potential term breaks lepton number in two units, thus inducing Majorana neutrino masses. Therefore, the model contains all the ingredients to induce neutrino masses and observable HLFV rates. Interestingly, these two consequences of the Zee model are connected in a non-trivial way. Assuming for simplicity feμ = 0, neglecting the electron mass compared to the muon and tau masses, and keeping the term proportional to the muon mass in the (3,3) element to get three massive neutrinos, the neutrino mass matrix is given by Herrero-García et al. [83]
where A is a dimensionless combination of model parameters, containing the corresponding loop function, s2δ ∝ μ quantifies the mixing in the charged scalar sector and we denote sβτ = sin βτ. The ρe matrix was introduced in Equation (24). We see that in order to accommodate the measured leptonic mixing angles (see for instance the global fit [147]) both and must be different from zero. Therefore, the Zee model leads to correlations between the leptonic mixing angles and the h → τμ and h → τe rates. These can be used to set a lower limit on the HLFV rates [83]. For instance, one finds
for normal (inverted) neutrino mass ordering. We refer to Herrero-García et al. [83], where a detailed exploration of the parameter space of the Zee model is performed, concluding that the model can accommodate large HLFV rates, even exceeding the current bounds. Similar findings were recently found in Nomura et al. [91], where a Zee model supplemented with a flavor-dependent U(1) symmetry was considered.
There are other neutrino mass models including a second Higgs doublet. For instance, in left-right symmetric models [148–152] one usually introduces a scalar field that is a doublet of both SU(2)L and SU(2)R. This bidoublet can be denoted by Σ and decomposed as
The scalar representation Σ has two gauge invariant Yukawa couplings to leptons and can be regarded at energies below the SU(2)R breaking scale as a pair of SU(2)L doublets. However, these setups cannot be identified with a type-III 2HDM since the left-right symmetry require the two lepton Yukawa matrices to be Hermitian, thus strongly restricting the allowed parameter space. Furthermore, current limits on quark flavor violation require the second CP-even mass eigenstate, H, to have a large mass, mH ≳ 25 TeV [153], suppressing all HLFV effects. Therefore, the minimal left-right models would have to be enlarged with additional scalar fields in order to be able to provide large HLFV rates [72].
6. Summary and Discussion
In this mini-review we have discussed Higgs lepton flavor violating decays, such as h → ℓiℓj, in the context of the general 2HDM. After motivating this scenario with some model-independent considerations, we have explicitly shown that the 2HDM can indeed allow for large HLFV rates while being in perfect agreement with the experimental constraints at low and high energies. A possible connection to the mechanism behind the generation of neutrino masses is also discussed.
The 2HDM must face many stringent constraints in order to generate large HLFV rates. The first tension comes from existing measurements of the Higgs boson couplings to fermions and gauge bosons, which already place bounds on the parameter that controls the mixing between the two CP-even scalars in the model, sin(β − α). This must necessarily deviate from 1 in order to allow for non-standard Higgs decays, but not too much in order to be in agreement with the constraints on the Higgs boson couplings. The dipole transitions ℓi → ℓjγ also set very strong limits on the LFV parameters, and these cannot be avoided by any flavor symmetry. However, the associated operators turn out to be suppressed in the 2HDM compared to the operators leading to HLFV, thus increasing the chances to have observable effects of the latter. Taking all these constraints into account, as well as those from electroweak precision data or direct LHC searches, we find that the 2HDM can accommodate HLFV rates arbitrarily close to the current limits, hence making them a very attractive way to search for NP.
The determination of the properties of the recently discovered Higgs boson is among the current priorities for the particle physics community. The increasingly precise measurements of the Higgs couplings and decay rates might eventually reveal a deviation from the SM expectations and hint toward the existence of NP. In particular, the search for HLFV has just started. A positive signal could shed light on questions as central as the flavor puzzle or the fundamental nature of electroweak symmetry breaking.
Author Contributions
The author declares that he contributed to the design and implementation of the research, to the analysis of the results and to the writing of the manuscript.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
I am very grateful to my collaborators in the subjects discussed in this review. In particular, I thank Diego Aristizábal Sierra for many long and enjoyable discussions on Higgs lepton flavor violating decays. I also thank Luca Fiorini for drawing my attention to updated results on h → ℓiℓj by the ATLAS collaboration. I acknowledge financial support from the Spanish grants SEV-2014-0398 and FPA2017-85216-P (AEI/FEDER, UE) and SEJI/2018/033 (Generalitat Valenciana) and the Spanish Red Consolider MultiDark FPA2017-90566-REDC.
Footnotes
1. ^We define .
2. ^See also the comprehensive reference Doršner et al. [33] for a similar reasoning in a multi-Higgs EFT that further strengthens the case for potentially large HLFV effects in the 2HDM.
3. ^The global flavor symmetry of the SM is known to be broken since the experimental observation of neutrino flavor oscillations. Therefore, the NP behind the generation of neutrino masses must necessarily violate Gf and induce LFV processes such as ℓi → ℓjγ and h → ℓiℓj. The resulting rates in some specific models are too low to be observed in any foreseeable experiment. For instance, in the SM minimally extended with Dirac neutrino masses one expects tiny LFV branching ratios, as low as BR(μ → eγ) ~ 10−55 [109] or BR(h → τμ) ~ 10−56 [72]. However, this is not a generic expectation, since these rates get hugely enhanced in most NP scenarios. We refer to section 5 for more details about the connection between HLFV and neutrino masses.
4. ^In what concerns effective operators, we follow the notation of DsixTools [111].
5. ^Explicit expressions for the tree-level matching can be found in Jenkins et al. [112].
6. ^This excludes more popular versions of the 2HDM. In particular it excludes 2HDMs with natural flavor conservation [114, 115], like the type-II 2HDM included in supersymmetric models. We refer to Branco et al. [116] for a comprehensive review of the 2HDM and all its variants.
7. ^We follow the conventions of Davidson and Haber [120], with a slightly different notation.
8. ^A modified Cheng-Sher ansatz was recently proposed in Babu and Jana [89] in order to suppress all Higgs-mediated flavor effects.
9. ^See Cai et al. [146] for a comprehensive review of radiative neutrino mass models and their phenomenology.
References
1. Goudelis A, Lebedev O, Park JH. Higgs-induced lepton flavor violation. Phys Lett B. (2012) 707:369–74. doi: 10.1016/j.physletb.2011.12.059
2. Blankenburg G, Ellis J, Isidori G. Flavour-changing decays of a 125 GeV Higgs-like particle. Phys. Lett B. (2012) 712:386–90. doi: 10.1016/j.physletb.2012.05.007
3. Harnik R, Kopp J, Zupan J. Flavor violating Higgs decays. J High Energy Phys. (2013) 3:26. doi: 10.1007/JHEP03(2013)026
4. Dery A, Efrati A, Hochberg Y, Nir Y. What if BR(h → μμ) ? J High Energy Phys. (2013) 5:39. doi: 10.1007/JHEP05(2013)039
5. Celis A, Cirigliano V, Passemar E. Lepton flavor violation in the Higgs sector and the role of hadronic τ-lepton decays. Phys Rev D. (2014) 89:013008. doi: 10.1103/PhysRevD.89.013008
6. Dery A, Efrati A, Nir Y, Soreq Y, Susič V. Model building for flavor changing Higgs couplings. Phys Rev D. (2014) 90:115022. doi: 10.1103/PhysRevD.90.115022
7. Lee TD. A theory of spontaneous T violation. Phys Rev D. (1973) 8:1226–39. doi: 10.1103/PhysRevD.8.1226
8. Branco GC. Spontaneous CP nonconservation and natural flavor conservation: a minimal model. Phys Rev D. (1980) 22:2901. doi: 10.1103/PhysRevD.22.2901
9. Aristizabal Sierra D, Vicente A. Explaining the CMS Higgs flavor violating decay excess. Phys Rev D. (2014) 90:115004. doi: 10.1103/PhysRevD.90.115004
10. Pilaftsis A. Lepton flavor nonconservation in H0 decays. Phys Lett B. (1992) 285:68–74. doi: 10.1016/0370-2693(92)91301-O
11. Diaz-Cruz JL, Toscano JJ. Lepton flavor violating decays of Higgs bosons beyond the standard model. Phys Rev D. (2000) 62:116005. doi: 10.1103/PhysRevD.62.116005
12. Sher M. Scalar mediated FCNC at the first muon collider. Phys Lett B. (2000) 487:151–4. doi: 10.1016/S0370-2693(00)00789-9
13. Diaz-Cruz JL. A More flavored Higgs boson in supersymmetric models. J High Energy Phys. (2003) 5:36. doi: 10.1088/1126-6708/2003/05/036
14. Brignole A, Rossi A. Lepton flavor violating decays of supersymmetric Higgs bosons. Phys Lett B. (2003) 566:217–25. doi: 10.1016/S0370-2693(03)00837-2
15. Diaz-Cruz JL, Noriega-Papaqui R, Rosado A. Mass matrix ansatz and lepton flavor violation in the THDM-III. Phys Rev D. (2004) 69:095002. doi: 10.1103/PhysRevD.69.095002
16. Kanemura S, Matsuda K, Ota T, Shindou T, Takasugi E, Tsumura K. Search for lepton flavor violation in the Higgs boson decay at a linear collider. Phys Lett B. (2004) 599:83–91. doi: 10.1016/j.physletb.2004.08.024
17. Arganda E, Curiel AM, Herrero MJ, Temes D. Lepton flavor violating Higgs boson decays from massive seesaw neutrinos. Phys Rev D. (2005) 71:035011. doi: 10.1103/PhysRevD.71.035011
18. Parry JK. Lepton flavor violating Higgs boson decays, τ → μγ and in the constrained MSSM+NR with large tan beta. Nucl Phys B. (2007) 760:38–63. doi: 10.1016/j.nuclphysb.2006.10.011
19. Davidson S, Grenier GJ. Lepton flavour violating Higgs and tau to mu gamma. Phys Rev D. (2010) 81:095016. doi: 10.1103/PhysRevD.81.095016
20. Dery A, Efrati A, Hiller G, Hochberg Y, Nir Y. Higgs couplings to fermions: 2HDM with MFV. J High Energy Phys. (2013) 8:6. doi: 10.1007/JHEP08(2013)006
21. Kopp J, Nardecchia M. Flavor and CP violation in Higgs decays. J High Energy Phys. (2014) 10:156. doi: 10.1007/JHEP10(2014)156
22. Diaz-Cruz JL, Ghosh DK, Moretti S. Lepton flavour violating heavy higgs decays within the nuMSSM and their detection at the LHC. Phys Lett B. (2009) 679:376–81. doi: 10.1016/j.physletb.2009.07.065
23. Giang PT, Hue LT, Huong DT, Long HN. Lepton-flavor violating decays of neutral Higgs to Muon and Tauon in supersymmetric economical 3-3-1 model. Nucl Phys B. (2012) 864:85–112. doi: 10.1016/j.nuclphysb.2012.06.008
24. Arhrib A, Cheng Y, Kong OCW. Higgs to mu tau decay in supersymmetry without R-parity. EPL. (2013) 101:31003. doi: 10.1209/0295-5075/101/31003
25. Arhrib A, Cheng Y, Kong OCW. Comprehensive analysis on lepton flavor violating Higgs boson to μ∓τ± decay in supersymmetry without R parity. Phys Rev D. (2013) 87:015025. doi: 10.1103/PhysRevD.87.015025
26. Arana-Catania M, Arganda E, Herrero MJ. Non-decoupling SUSY in LFV Higgs decays: a window to new physics at the LHC. J High Energy Phys. (2013) 9:160. doi: 10.1007/JHEP09(2013)160
27. Falkowski A, Straub DM, Vicente A. Vector-like leptons: Higgs decays and collider phenomenology. J High Energy Phys. (2014) 5:92. doi: 10.1007/JHEP05(2014)092
28. Arganda E, Herrero MJ, Marcano X, Weiland C. Imprints of massive inverse seesaw model neutrinos in lepton flavor violating Higgs boson decays. Phys Rev D. (2015) 91:015001. doi: 10.1103/PhysRevD.91.015001
29. CMS Collaboration. Search for Lepton-Flavour-violating decays of the Higgs boson. Phys Lett B. (2015) 749:337–62. doi: 10.1016/j.physletb.2015.07.053
30. Heeck J, Holthausen M, Rodejohann W, Shimizu Y. Higgs → μτ in Abelian and non-Abelian flavor symmetry models. Nucl Phys B. (2015) 896:281–310. doi: 10.1016/j.nuclphysb.2015.04.025
31. Crivellin A, D'Ambrosio G, Heeck J. Explaining h → μ±τ∓, B→K*μ+μ− and B→Kμ+μ−/B→Ke+e− in a two-Higgs-doublet model with gauged Lμ−Lτ. Phys Rev Lett. (2015) 114:151801. doi: 10.1103/PhysRevLett.114.151801
32. de Lima L, Machado CS, Matheus RD, do Prado LAF. Higgs flavor violation as a signal to discriminate models. J High Energy Phys. (2015) 11:74. doi: 10.1007/JHEP11(2015)074
33. Doršner I, Fajfer S, Greljo A, Kamenik JF, Košnik N, Nišandžic I. New physics models facing lepton flavor violating higgs decays at the percent level. J High Energy Phys. (2015) 6:108. doi: 10.1007/JHEP06(2015)108
34. Omura Y, Senaha E, Tobe K. Lepton-flavor-violating Higgs decay h → μτ and muon anomalous magnetic moment in a general two Higgs doublet model. J High Energy Phys. (2015) 5:28. doi: 10.1007/JHEP05(2015)028
35. Vicente A. Lepton flavor violation beyond the MSSM. Adv High Energy Phys. (2015) 2015:686572. doi: 10.1155/2015/686572
36. Das D, Kundu A. Two hidden scalars around 125 GeV and h → μτ. Phys Rev D. (2015) 92:015009. doi: 10.1103/PhysRevD.92.015009
37. Yue CX, Pang C, Guo YC. Lepton flavor violating Higgs couplings and single production of the Higgs boson via eγ collision. J Phys G. (2015) 42:075003. doi: 10.1088/0954-3899/42/7/075003
38. Bhattacherjee B, Chakraborty S, Mukherjee S. Lepton flavour violating decay of 125 GeV Higgs boson to μτ channel and excess in . Mod Phys Lett A. 31 (2016) 30:1650174. doi: 10.1142/S0217732316501741
39. Kobayashi T, Omura Y, Takayama F, Yasuhara D. Study of lepton flavor violation in flavor symmetric models for lepton sector. J High Energy Phys. (2015) 10:42. doi: 10.1007/JHEP10(2015)042
40. Mao YN, Zhu SH. Higgs boson-μ-τ coupling at high and low energy colliders. Phys Rev D. (2016) 93:035014. doi: 10.1103/PhysRevD.93.035014
41. He XG, Tandean J, Zheng YJ. Higgs decay h → μτ with minimal flavor violation. J High Energy Phys. (2015) 9:93. doi: 10.1007/JHEP09(2015)093
42. Crivellin A, Heeck J, Stoffer P. A perturbed lepton-specific two-Higgs-doublet model facing experimental hints for physics beyond the Standard Model. Phys Rev Lett. (2016) 116:081801. doi: 10.1103/PhysRevLett.116.081801
43. Altmannshofer W, Gori S, Kagan AL, Silvestrini L, Zupan J. Uncovering mass generation through Higgs flavor violation. Phys Rev D. (2016) 93:031301. doi: 10.1103/PhysRevD.93.031301
44. Cheung K, Keung WY, Tseng PY. Leptoquark induced rare decay amplitudes h → τ∓μ± and τ → μγ. Phys Rev D. (2016) 93:015010. doi: 10.1103/PhysRevD.93.015010
45. Arganda E, Herrero MJ, Marcano X, Weiland C. Enhancement of the lepton flavor violating Higgs boson decay rates from SUSY loops in the inverse seesaw model. Phys Rev D. (2016) 93:055010. doi: 10.1103/PhysRevD.93.055010
46. Botella FJ, Branco GC, Nebot M, Rebelo MN. Flavour changing higgs couplings in a class of two higgs doublet models. Eur Phys J C. (2016) 76:161. doi: 10.1140/epjc/s10052-016-3993-0
47. Liu X, Bian L, Li XQ, Shu J. Type-III two Higgs doublet model plus a pseudoscalar confronted with h → μτ, muon g−2 and dark matter. Nucl Phys B. (2016) 909:507–24. doi: 10.1016/j.nuclphysb.2016.05.027
48. Huang W, Tang YL. Flavor anomalies at the LHC and the R-parity violating supersymmetric model extended with vectorlike particles. Phys Rev D. (2015) 92:094015. doi: 10.1103/PhysRevD.92.094015
49. Baek S, Nishiwaki K. Leptoquark explanation of h → μτ and muon (g−2). Phys Rev D. (2016) 93:015002. doi: 10.1103/PhysRevD.93.015002
50. Baek S, Kang ZF. Naturally large radiative lepton flavor violating higgs decay mediated by lepton-flavored dark matter. J High Energy Phys. (2016) 3:106. doi: 10.1007/JHEP03(2016)106
51. Arganda E, Herrero MJ, Morales R, Szynkman A. Analysis of the h, H, A → τμ decays induced from SUSY loops within the Mass Insertion Approximation. J High Energy Phys. (2016) 3:55. doi: 10.1007/JHEP03(2016)055
52. Aloni D, Nir Y, Stamou E. Large BR(h → τμ) in the MSSM? J High Energy Phys. (2016) 4:162. doi: 10.1007/JHEP04(2016)162
53. Benbrik R, Chen CH, Nomura T. , ΔAμ, τ → (3μ, μγ) in generic two-Higgs-doublet models. Phys Rev D. (2016) 93:095004. doi: 10.1103/PhysRevD.93.095004
54. Zhang HB, Feng TF, Zhao SM, Yan YL, Sun F. 125 GeV Higgs decay with lepton flavor violation in the μνSSM. Chin Phys C. (2017) 41:043106. doi: 10.1088/1674-1137/41/4/043106
55. Hue LT, Long HN, Thuc TT, Phong Nguyen T. Lepton flavor violating decays of Standard-Model-like Higgs in 3-3-1 model with neutral lepton. Nucl Phys B. (2016) 907:37–76. doi: 10.1016/j.nuclphysb.2016.03.034
56. Bizot N, Davidson S, Frigerio M, Kneur JL. Two Higgs doublets to explain the excesses pp → γγ(750 GeV) and h → τ±μ∓. J High Energy Phys. (2016) 3:73. doi: 10.1007/JHEP03(2016)073
57. Buschmann M, Kopp J, Liu J, Wang XP. New Signatures of Flavor Violating Higgs Couplings. J High Energy Phys. (2016) 6:149. doi: 10.1007/JHEP06(2016)149
58. Han XF, Wang L, Yang JM. An extension of two-Higgs-doublet model and the excesses of 750 GeV diphoton, muon g-2 and h → μτ. Phys Lett B. (2016) 757:537–47. doi: 10.1016/j.physletb.2016.04.036
59. Chang CF, Chang CHV, Nugroho CS, Yuan TC. Lepton flavor violating decays of neutral higgses in extended mirror fermion model. Nucl Phys B. (2016) 910:293–308. doi: 10.1016/j.nuclphysb.2016.07.009
60. Bélusca-Maïto H, Falkowski A. On the exotic Higgs decays in effective field theory. Eur Phys J C. (2016) 76:514. doi: 10.1140/epjc/s10052-016-4362-8
61. Chen CH, Nomura T. Bounds on LFV Higgs decays in a vector-like lepton model and searching for doubly charged leptons at the LHC. Eur Phys J C. (2016) 76:353. doi: 10.1140/epjc/s10052-016-4197-3
62. Alvarado C, Capdevilla RM, Delgado A, Martin A. Minimal models of loop-induced lepton flavor violation in Higgs boson decays. Phys Rev D. (2016) 94:075010. doi: 10.1103/PhysRevD.94.075010
63. Banerjee S, Bhattacherjee B, Mitra M, Spannowsky M. The lepton flavour violating Higgs decays at the HL-LHC and the ILC. J High Energy Phys. (2016) 7:59. doi: 10.1007/JHEP07(2016)059
64. Hayreter A, He XG, Valencia G. CP violation in h → ττ and LFV h → μτ. Phys Lett B. (2016) 760:175–7. doi: 10.1016/j.physletb.2016.06.066
65. Huitu K, Keus V, Koivunen N, Lebedev O. Higgs-flavon mixing and h → μτ. J High Energy Phys. (2016) 5:26. doi: 10.1007/JHEP05(2016)026
66. Chakraborty I, Datta A, Kundu A. Lepton flavor violating Higgs boson decay h → μτ at the ILC. J Phys G. (2016) 43:125001. doi: 10.1088/0954-3899/43/12/125001
67. Lami A, Roig P. H → ℓℓ′ in the simplest little Higgs model. Phys Rev D. (2016) 94:056001. doi: 10.1103/PhysRevD.94.056001
68. Thuc TT, Hue LT, Long HN, Nguyen TP. Lepton flavor violating decay of SM-like Higgs boson in a radiative neutrino mass model. Phys Rev D. (2016) 93:115026. doi: 10.1103/PhysRevD.93.115026
69. Baek S, Nomura T, Okada H. An explanation of one-loop induced h → μτ decay. Phys Lett B. (2016) 759:91–8. doi: 10.1016/j.physletb.2016.05.055
70. Altmannshofer W, Carena M, Crivellin A. Lμ−Lτ theory of Higgs flavor violation and (g−2)μ. Phys Rev D. (2016) 94:095026. doi: 10.1103/PhysRevD.94.095026
71. Baek S, Tandean J. Flavor-changing Higgs decays in grand unification with minimal flavor violation. Eur Phys J C. (2016) 76:673. doi: 10.1140/epjc/s10052-016-4486-x
72. Herrero-Garcia J, Rius N, Santamaria A. Higgs lepton flavour violation: UV completions and connection to neutrino masses. J High Energy Phys. (2016) 11:84. doi: 10.1007/JHEP11(2016)084
73. Phan KH, Hung HT, Hue LT. One-loop contributions to neutral Higgs decay h → μτ. PTEP. (2016) 2016:113B03. doi: 10.1093/ptep/ptw158
74. Hammad A, Khalil S, Un CS. Large BR(h → τμ) in Supersymmetric Models. Phys Rev D. (2017) 95:055028. doi: 10.1103/PhysRevD.95.055028
75. Demidov SV, Sobolev IV. Lepton flavor-violating decays of the Higgs boson from sgoldstino mixing. J High Energy Phys. (2016) 8:30. doi: 10.1007/JHEP08(2016)030
76. Wang L, Yang S, Han XF. h → μτ and muon g-2 in the alignment limit of two-Higgs-doublet model. Nucl Phys B. (2017) 919:123–41. doi: 10.1016/j.nuclphysb.2017.03.013
77. Di Iura A, Herrero-Garcia J, Meloni D. Phenomenology of SU(5) low-energy realizations: the diphoton excess and Higgs flavor violation. Nucl Phys B. (2016) 911:388–424. doi: 10.1016/j.nuclphysb.2016.08.005
78. Tobe K. Michel parameters for τ decays in a general two Higgs doublet model with μ−τ flavor violation. J High Energy Phys. (2016) 10:114. doi: 10.1007/JHEP10(2016)114
79. Aoki M, Kanemura S, Sakurai K, Sugiyama H. Testing neutrino mass generation mechanisms from the lepton flavor violating decay of the Higgs boson. Phys Lett B. (2016) 763:352–7. doi: 10.1016/j.physletb.2016.10.055
80. Guo HK, Li YY, Liu T, Ramsey-Musolf M, Shu J. Lepton-flavored electroweak baryogenesis. Phys Rev D. (2017) 96:115034. doi: 10.1103/PhysRevD.96.115034
81. Choudhury D, Kundu A, Nandi S, Patra SK. Unified resolution of the R(D) and R(D*) anomalies and the lepton flavor violating decay h → μτ. Phys Rev D. (2017) 95:035021. doi: 10.1103/PhysRevD.95.035021
82. Arganda E, Herrero MJ, Marcano X, Morales R, Szynkman A. Effective lepton flavor violating Hℓiℓj vertex from right-handed neutrinos within the mass insertion approximation. Phys Rev D. (2017) 95:095029. doi: 10.1103/PhysRevD.95.095029
83. Herrero-García J, Ohlsson T, Riad S, Wirén J. Full parameter scan of the Zee model: exploring Higgs lepton flavor violation. J High Energy Phys. (2017) 4:130. doi: 10.1007/JHEP04(2017)130
84. Thao NH, Hue LT, Hung HT, Xuan NT. Lepton flavor violating Higgs boson decays in seesaw models: new discussions. Nucl Phys B. (2017) 921:159–80. doi: 10.1016/j.nuclphysb.2017.05.014
85. Chamorro-Solano S, Moyotl A, Pérez MA. Lepton flavor changing Higgs Boson decays in a Two Higgs Doublet Model with a fourth generation of fermions. J Phys G. (2018) 45:075003. doi: 10.1088/1361-6471/aac458
86. Chakraborty I, Mondal S, Mukhopadhyaya B. Lepton flavor violating Higgs boson decay at e+e− colliders. Phys Rev D. (2017) 96:115020. doi: 10.1103/PhysRevD.96.115020
87. Qin Q, Li Q, Lü CD, Yu FS, Zhou SH. Charged lepton flavor violating Higgs decays at future e+e− colliders. Eur Phys J C. (2018) 78:835. doi: 10.1140/epjc/s10052-018-6298-7
88. Nguyen TP, Le TT, Hong TT, Hue LT. Decay of standard model-like Higgs boson h → μτ in a 3-3-1 model with inverse seesaw neutrino masses. Phys Rev D. (2018) 97:073003. doi: 10.1103/PhysRevD.97.073003
89. Babu KS, Jana S. Enhanced di-higgs production in the two higgs doublet model. J High Energy Phys. (2019) 2:193. doi: 10.1007/JHEP02(2019)193
90. Hou WS, Jain R, Kao C, Kohda M, McCoy B, Soni A. Flavor changing heavy Higgs interactions with leptons at hadron colliders. Phys Lett B. (2019) 795:371–8. doi: 10.1016/j.physletb.2019.06.044
91. Nomura T, Yagyu K. Zee Model with flavor dependent global U(1) symmetry (2019). arXiv[Preprint]. arXiv:1905.11568.
92. ATLAS Collaboration. Search for the decays of the Higgs boson H→ee and H→eμ in pp collisions at = 13 TeV with the ATLAS detector. ATLAS-CONF-2019-037 (2019).
93. CMS Collaboration. Search for lepton flavour violating decays of the Higgs boson to eτ and eμ in proton-proton collisions at 8 TeV. Phys Lett B. (2016) 763:472–500. doi: 10.1016/j.physletb.2016.09.062
94. ATLAS Collaboration. Searches for lepton-flavour-violating decays of the Higgs boson in TeV pp collisions with the ATLAS detector. arXiv[Preprint]. arXiv:1907.06131.
95. CMS Collaboration. Search for lepton flavour violating decays of the Higgs boson to μτ and eτ in proton-proton collisions at 13 TeV. J High Energy Phys. (2018) 6:1. doi: 10.1007/JHEP06(2018)001
96. MEG Collaboration. Search for the lepton flavour violating decay μ+→e+γ with the full dataset of the MEG experiment. Eur Phys J C. (2016) 76:434.
97. Baldini AM, Cei F, Cerri C, Dussoni S, Galli L, Grassi M. MEG upgrade proposal (2013). arXiv[Preprint]. arXiv:1301.7225.
98. BaBar Collaboration. Searches for Lepton Flavor Violation in the Decays τ±→e±γ and τ± → μ±γ. Phys Rev Lett. (2010) 104:021802. doi: 10.1103/PhysRevLett.104.021802
99. Aushev T, Bartel W, Bondar A, Brodzicka J, Browder TE, Chang P, et al. Physics at super B factory. arXiv[Preprint]. arXiv:1002.5012.
101. Blondel A, Bravar A, Pohl M, Bachmann S, Berger N, Kiehn M, et al. Research proposal for an experiment to search for the decay μ → eee (2013). arXiv[Preprint]. arXiv:1301.6113.
102. Hayasaka K, Inami K, Miyazaki Y. Search for lepton flavor violating Tau decays into three leptons with 719 million produced Tau+Tau- pairs. Phys Lett B. (2010) 687:139–43. doi: 10.1016/j.physletb.2010.03.037
103. SINDRUM II Collaboration. Test of lepton flavor conservation in μ → e conversion on titanium. Phys Lett B. (1993) 317:631–6.
104. The PRIME Working Group Collaboration. Search for the μ → e Conversion Process at an Ultimate Sensitivity of the Order of 10−18 With Prism. Available online at: http://www-ps.kek.jp/jhf-np/LOIlist/pdf/L25.pdf
105. SINDRUM II Collaboration, Bertl WH, Hermes EA, Kurz G, Kozlowski T, Kuth J, et al. A Search for muon to electron conversion in muonic gold. Eur Phys J C. (2006) 47:337–46. doi: 10.1140/epjc/s2006-02582-x
106. Mu2e Collaboration. The Mu2e experiment at Fermilab: a search for lepton flavor violation. Nucl Part Phys Proc. (2017) 285–286:3–7. doi: 10.1016/j.nuclphysbps.2017.03.002
107. DeeMe Collaboration. DeeMe experiment - An experimental search for a mu-e conversion reaction at J-PARC MLF. Nucl Phys Proc Suppl. (2014) 248–250:52–7. doi: 10.1016/j.nuclphysbps.2014.02.010
108. Calibbi L, Signorelli G. Charged lepton flavour violation: an experimental and theoretical introduction. Riv Nuovo Cim. (2018) 41:71–174. doi: 10.1393/ncr/i2018-10144-0
109. Petcov ST. The Processes μ → eγ, μ → eeē, ν′ → νγ in the Weinberg-Salam Model with Neutrino Mixing. Sov J Nucl Phys. (1977) 25:340.
110. Grzadkowski B, Iskrzynski M, Misiak M, Rosiek J. Dimension-six terms in the standard model lagrangian. J High Energy Phys. (2010) 10:85. doi: 10.1007/JHEP10(2010)085
111. Celis A, Fuentes-Martin J, Vicente A, Virto J. DsixTools: the standard model effective field theory toolkit. Eur Phys J C. (2017) 77:405. doi: 10.1140/epjc/s10052-017-4967-6
112. Jenkins EE, Manohar AV, Stoffer P. Low-energy effective field theory below the electroweak scale: operators and matching. J High Energy Phys. (2018) 3:16. doi: 10.1007/JHEP03(2018)016
113. Alonso R, Jenkins EE, Manohar AV, Trott M. Renormalization Group Evolution of the Standard Model Dimension Six Operators III: gauge Coupling Dependence and Phenomenology. J High Energy Phys. (2014) 4:159. doi: 10.1007/JHEP04(2014)159
114. Glashow SL, Weinberg S. Natural conservation laws for neutral currents. Phys Rev D. (1977) 15:1958. doi: 10.1103/PhysRevD.15.1958
115. Paschos EA. Diagonal neutral currents. Phys Rev D. (1977) 15:1966. doi: 10.1103/PhysRevD.15.1966
116. Branco GC, Ferreira PM, Lavoura L, Rebelo MN, Sher M, Silva JP. Theory and phenomenology of two-Higgs-doublet models. Phys Rept. (2012) 516:1–102. doi: 10.1016/j.physrep.2012.02.002
117. Georgi H, Nanopoulos DV. Suppression of flavor changing effects from neutral spinless meson exchange in gauge theories. Phys Lett. (1979) 82B:95–6. doi: 10.1016/0370-2693(79)90433-7
118. Donoghue JF, Li LF. Properties of charged higgs bosons. Phys Rev D. (1979) 19:945. doi: 10.1103/PhysRevD.19.945
119. Botella FJ, Silva JP. Jarlskog - like invariants for theories with scalars and fermions. Phys Rev D. (1995) 51:3870–5. doi: 10.1103/PhysRevD.51.3870
120. Davidson S, Haber HE. Basis-independent methods for the two-Higgs-doublet model. Phys Rev D. (2005) 72:035004. doi: 10.1103/PhysRevD.72.035004
121. Bjorken JD, Lane KD, Weinberg S. The Decay μ → eγ in models with neutral heavy leptons. Phys Rev D. (1977) 16:1474. doi: 10.1103/PhysRevD.16.1474
122. Barr SM, Zee A. Electric Dipole Moment of the Electron and of the Neutron. Phys Rev Lett. (1990) 65:21–4. doi: 10.1103/PhysRevLett.65.21
123. Chang D, Hou WS, Keung WY. Two loop contributions of flavor changing neutral Higgs bosons to μ → eγ. Phys Rev D. (1993) 48:217–24. doi: 10.1103/PhysRevD.48.217
124. Sher M, Thrasher K. Flavor changing leptonic decays of heavy higgs bosons. Phys Rev D. (2016) 93:055021. doi: 10.1103/PhysRevD.93.055021
125. Ivanov IP. Minkowski space structure of the Higgs potential in 2HDM. Phys Rev D. (2007) 75:035001. doi: 10.1103/PhysRevD.75.035001
126. Ivanov IP. Minkowski space structure of the Higgs potential in 2HDM. II. Minima, symmetries, and topology. Phys Rev D. (2008) 77:015017. doi: 10.1103/PhysRevD.77.015017
127. Ferreira PM, Jones DRT. Bounds on scalar masses in two Higgs doublet models. J High Energy Phys. (2009) 8:69. doi: 10.1088/1126-6708/2009/08/069
128. Baak M, Goebel M, Haller J, Hoecker A, Kennedy D, Kogler R, et al. The electroweak fit of the standard model after the discovery of a New Boson at the LHC. Eur Phys J C. (2012) 72:2205. doi: 10.1140/epjc/s10052-012-2205-9
129. CMS Collaboration. Precise Determination of the Mass of the Higgs Boson and Studies of the Compatibility of Its Couplings With the Standard Model. Tech. Rep. CMS-PAS-HIG-14-009, CERN, Geneva (2014). Available online at: https://cds.cern.ch/record/1728249
130. Crivellin A, Kokulu A, Greub C. Flavor-phenomenology of two-Higgs-doublet models with generic Yukawa structure. Phys Rev D. (2013) 87:094031. doi: 10.1103/PhysRevD.87.094031
131. Particle Data Group Collaboration. Review of particle physics. Phys Rev D. (2018) 98:030001. doi: 10.1103/PhysRevD.98.030001
132. Cheng TP, Sher M. Mass matrix ansatz and flavor nonconservation in models with multiple higgs doublets. Phys Rev D. (1987) 35:3484. doi: 10.1103/PhysRevD.35.3484
133. Kanemura S, Ota T, Tsumura K. Lepton flavor violation in Higgs boson decays under the rare tau decay results. Phys Rev D. (2006) 73:016006. doi: 10.1103/PhysRevD.73.016006
134. Iguro S, Omura Y, Takeuchi M. Testing the 2HDM explanation of the muon g-2 anomaly at the LHC (2019). arXiv[Preprint]. arXiv:1907.09845.
135. Wang L, Zhang Y. A μ-τ-philic Higgs doublet confronted with the muon g-2, τ decays and LHC data (2019). arXiv[Preprint]. arXiv:1908.03755.
136. Crivellin A, Heeck J, Müller D. Large h→bs in generic two-Higgs-doublet models. Phys Rev D. (2018) 97:035008. doi: 10.1103/PhysRevD.97.035008
137. Branco GC, Grimus W, Lavoura L. Relating the scalar flavor changing neutral couplings to the CKM matrix. Phys Lett B. (1996) 380:119–26. doi: 10.1016/0370-2693(96)00494-7
138. Botella FJ, Branco GC, Rebelo MN. Minimal flavour violation and multi-Higgs models. Phys Lett B. (2010) 687:194–200. doi: 10.1016/j.physletb.2010.03.014
139. Botella FJ, Branco GC, Nebot M, Rebelo MN. Two-Higgs leptonic minimal flavour violation. J High Energy Phys. (2011) 10:37. doi: 10.1007/JHEP10(2011)037
140. Bhattacharyya G, Leser P, Päs H. Exotic Higgs boson decay modes as a harbinger of S3 flavor symmetry. Phys Rev D. (2011) 83:011701. doi: 10.1103/PhysRevD.83.011701
141. Bhattacharyya G, Leser P, Päs H. Novel signatures of the Higgs sector from S3 flavor symmetry. Phys Rev D. (2012) 86:036009. doi: 10.1103/PhysRevD.86.036009
142. Arroyo-Ureña MA, Diaz-Cruz JL, Díaz E, Orduz-Ducuara JA. Flavor violating Higgs signals in the Texturized Two-Higgs Doublet Model (THDM-Tx). Chin Phys C. (2016) 40:123103. doi: 10.1088/1674-1137/40/12/123103
143. Campos MD, Cárcamo Hernández AE, Päs H, Schumacher E. Higgs → μτ as an indication for S4 flavor symmetry. Phys Rev D. (2015) 91:116011. doi: 10.1103/PhysRevD.91.116011
144. Bernabeu J, Santamaria A, Vidal J, Mendez A, Valle JWF. Lepton flavor nonconservation at high-energies in a superstring inspired standard model. Phys Lett B. (1987) 187:303–8. doi: 10.1016/0370-2693(87)91100-2
145. Zee A. A theory of lepton number violation, neutrino majorana mass, and oscillation. Phys Lett. (1980) 93B:389. Erratum: Phys. Lett. 95B:461. doi: 10.1016/0370-2693(80)90349-4
146. Cai Y, Herrero-García J, Schmidt MA, Vicente A, Volkas RR. From the trees to the forest: a review of radiative neutrino mass models. Front. Phys. (2017) 5:63. doi: 10.3389/fphy.2017.00063
147. de Salas PF, Forero DV, Ternes CA, Tortola M, Valle JWF. Status of neutrino oscillations 2018: 3σ hint for normal mass ordering and improved CP sensitivity. Phys Lett B. (2018) 782:633–40. doi: 10.1016/j.physletb.2018.06.019
148. Pati JC, Salam A. Lepton number as the fourth color. Phys Rev D. (1974) 10:275–89. Erratum: Phys Rev D. 11:703. doi: 10.1103/PhysRevD.10.275
149. Mohapatra RN, Pati JC. A natural left-right symmetry. Phys Rev D. (1975) 11:2558. doi: 10.1103/PhysRevD.11.2558
150. Senjanovic G, Mohapatra RN. Exact left-right symmetry and spontaneous violation of parity. Phys Rev D. (1975) 12:1502. doi: 10.1103/PhysRevD.12.1502
151. Mohapatra RN, Senjanovic G. Neutrino mass and spontaneous parity nonconservation. Phys Rev Lett. (1980) 44:912. doi: 10.1103/PhysRevLett.44.912
152. Mohapatra RN, Senjanovic G. Neutrino masses and mixings in gauge models with spontaneous parity violation. Phys Rev D. (1981) 23:165. doi: 10.1103/PhysRevD.23.165
153. Zhang Y, An H, Ji X, Mohapatra RN. General CP violation in minimal left-right symmetric model and constraints on the right-handed scale. Nucl Phys B. (2008) 802:247–79. doi: 10.1016/j.nuclphysb.2008.05.019
Appendix
Contributions to τ → μγ in the Type-III 2HDM
The most relevant 1- and 2-loop contributions to τ → μγ in the type-III 2HDM were computed in Davidson and Grenier [19]. Splitting the form factor A as in Equation (33), these are given by
Here ϕ = h, H, A and f = t, b and we have defined the ratios
In the derivation of these contributions, the charged lepton masses have been neglected whenever possible. The expressions for the and CϕWW couplings are given in section 4.2. Finally, the loop functions introduced in the previous expressions are given by Chang et al. [123]
Keywords: Higgs boson, lepton flavor violating decays, beyond the standard model, two Higgs doublet models, effective field theory
Citation: Vicente A (2019) Higgs Lepton Flavor Violating Decays in Two Higgs Doublet Models. Front. Phys. 7:174. doi: 10.3389/fphy.2019.00174
Received: 21 August 2019; Accepted: 17 October 2019;
Published: 05 November 2019.
Edited by:
Ernesto Arganda, Instituto de Física La Plata, ArgentinaReviewed by:
Frank Franz Deppisch, University College London, United KingdomSayantan Choudhury, Max-Planck-Institut für Gravitationsphysik, Germany
Copyright © 2019 Vicente. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Avelino Vicente, YXZlbGluby52aWNlbnRlQGlmaWMudXYuZXM=
 Avelino Vicente
Avelino Vicente