Self-Adjoint Extension Approach for Singular Hamiltonians in (2 + 1) Dimensions

In this work, we review two methods used to approach singular Hamiltonians in (2 + 1) dimensions. Both methods are based on the self-adjoint extension approach. It is very common to find singular Hamiltonians in quantum mechanics, especially in quantum systems in the presence of topological defects, which are usually modeled by point interactions. In general, it is possible to apply some kind of regularization procedure, as the vanishing of the wave function at the location of the singularity, ensuring that the wave function is square-integrable and then can be associated with a physical state. However, a study based on the self-adjoint extension approach can lead to more general boundary conditions that still gives acceptable physical states. We exemplify the methods by exploring the bound and scattering scenarios of a spin 1/2 charged particle with an anomalous magnetic moment in the Aharonov-Bohm potential in the conical space.

1. Introduction

Singular and pathological Hamiltonians are quite common in quantum mechanics and already have a long history [1]. Probably, the first work to deal with δ-like singularities was in the Kronig-Penny model [2] for the description of the band energy in solid-state physics. Since then, point interactions have been of great interest in various branches of physics for their relevance as solvable models [3]. For instance, in the famous Aharonov-Bohm (AB) effect [4] of spin-1/2 particles [5–7] a two-dimensional δ function appears as the mathematical description of the Zeeman interaction between the spin and the magnetic flux tube [8, 9]. The presence of this δ function cannot be discarded when the electron spin is taken into account and it leads to changes in the scattering amplitude and cross-section [6]. This question can also be understood in connection with the quantum mechanics of a particle in a δ function potential in one dimension. When we wish to solve the problem for bound states, it is well-known that such a function guarantees at least one bound state [10, 11], and this property is maintained when studying the quantum mechanics of other physical systems in the presence of external magnetic fields. The inclusion of the spin element in the approach of the AB problem allows us to establish an exact equivalence with another well-known effect in the literature, namely the Aharonov-Casher (AC) effect [12]. In the AC effect, a spin-1/2 neutral particle with a magnetic moment is placed in an electric field generated by an infinitely long, an infinitesimally thin line of charge. The interaction term involving the particle spin with the electric field in the AC Hamiltonian is proportional to the δ function. Some works in the literature state that point interaction does not affect the scattering cross-section [13]. However, as in the spin-1/2 particle AB problem, the solution of the equation of motion via the self-adjoint extension in the spin-1/2 neutral particle AC problem reveals that the presence of the δ function changes the scattering phase shift and consequently the S-matrix [14, 15].

The study of physical systems with singular Hamiltonians appears in various contexts of physics. In reference [16], the discrete spectrum of a massive particle trapped in an infinitely long cylinder with two attractive delta-interactions in the cosmic string spacetime is studied. The authors showed that the physical effects due to the cosmic string background are similar to those of the AB effect in quantum mechanics. This is verified when the cosmic string determines a deviation on the trajectory of a particle, despite the locally flat character of the manifold. In reference [17], the one-dimensional spinless Salpeter Hamiltonian with finitely many Dirac delta potentials was solved using the heat kernel techniques and self-adjoint extension method. As in the case involving a single δ potential, the model requires a renormalization to be made. They investigated the problem in the context of bound states and showed that the ground state energy is bounded from below. Besides, they also showed that there exists a unique self-adjoint operator associated with the resolvent formula and obtained an explicit wave function formula for N centers. The approach using this model to the scattering problem was addressed in reference [18]. Such a model is a generalization of the work in reference [19], where the Schrödinger equation for a relativistic point particle in an external one-dimensional δ-function potential was studied using dimensional regularization.

The physical regularization used in these models is consistent with the self-adjoint extension theory and the idea can also be used to study other versions of the Kronig-Penney model in condensed matter physics. Different forms of Kronig-Penney-type Hamiltonians can be found in the literature [20, 21]. To approach singular Hamiltonian, it is more convenient to apply von Neumann's theory of self-adjoint extensions [3, 22, 23]. In general, if we ignore the singularity, the resulting Hamiltonian is self-adjoint and positive definite [24], its spectrum is ℝ⁺ and there are no bound states. The situation changes if we consider the delta function because the singularity is physically equivalent to an extraction of a single point from the plane ℝ², which leads to the loss of the self-adjointness of the Hamiltonian. This has important consequences in the spectrum of the system [25]. However, the self-adjointness is necessary to have a unitary time evolution. So, we must guarantee that the Hamiltonian is self-adjoint, which here is done employing the self-adjoint extension of symmetric operators. With this approach, a new family of self-adjoint operators labeled by a real parameter is obtained.

The situation discussed above occurs, for instance, in the AB scattering of a spin-1/2 particle, where it is well-known that for all real values of the self-adjoint extension parameter, there is an additional scattering amplitude [6], which results from the interaction between the spin and the magnetic flux tube [26]. Moreover, there is one bound state solution with negative energy when this parameter is <0. This situation can be considered quite strange, however, it can be mathematically proved the existence of this negative eigenvalue [3, 5, 27–36]. It is interesting to comment that in reference [29], an equivalence between the renormalization and the self-adjoint extension is discussed.

In this paper, we review some elements of the self-adjoint extension theory which are necessary to address singular Hamiltonians in relativistic and non-relativistic quantum theory. As an application, we consider the model of a spin-1/2 particle with an anomalous magnetic moment in an AB potential in the cosmic string spacetime. As already mentioned above, in this model, a δ function potential arises in the equation of motion [4]. We derive the Dirac equation for this model and solve it for the scattering and bound states on the non-relativistic limit using the self-adjoint extension method. The main goal is to study the physical implications of both the cosmic string background and singularity on the properties of the system. Our application example is motivated by the importance of studying cosmic strings [37], which has been the usual framework for investigating the effects of localized curvature in physical systems. There is a significant number of articles in the literature that study the influence of topology on physical systems using the cosmic string as a background.

Recently, a detailed study to study geometric phase for an open system of a two-level atom interacting with a massless scalar field in the background spacetime of the cosmic string spacetime with torsion was proposed in reference [38]. The authors showed that the geometric phase depends not only on the inherent properties of the atom, but also on the topological properties of background spacetime. For this model, it was found that the correction to the geometric phase of the present system derives from a composite effect, which contains the cosmic string and screw dislocation associated with the curvature and torsion, respectively. The authors also showed that the phase depends on the initial state of this atom and, in particular, there is no geometric phase acquired for the atom if the initial state is prepared in the excited state. Another physical model of current interest that has several studies in cosmic string spacetime is the Dirac oscillator [39]. It is known that the Dirac oscillator is a kind of tensor coupling with a linear potential which leads to the simple harmonic oscillator with a strong spin-orbit coupling problem in the non-relativistic limit. The Dirac oscillator is an exactly soluble model and can be an excellent example in the context of many-particle models in relativistic and non-relativistic quantum mechanics [40]. In reference [41], it was studied the relativistic quantum dynamics of a Dirac oscillator subject to a linear interaction for spin-1/2 particles in a cosmic string spacetime. The authors showed in this model that the geometric and topological properties of these spacetimes lead to shifts in the energy spectrum and the wave-function. In reference [42], the self-adjoint extension method was used to study the effects of spin on the dynamics of a two-dimensional Dirac oscillator in the magnetic cosmic string background. For other important studies in the cosmic string spacetime, the reader may refer to the references [43–46] and in the context of non-relativistic quantum dynamics of a quantum particle constrained to move on a curved surface using da Costa's approach [47] to the references [48–50].

The rest of this work is organized as follows. In section 2 the theory of the self-adjoint extensions is presented and two different methods, both based on the self-adjoint extension, are discussed. In section 3 the Dirac equation that describes the motion of a spin-1/2 charged particle with an anomalous magnetic moment in the curved space is developed. The methods presented in the previous section are then applied to this system and the scattering and bound states scenarios are discussed. The scattering matrix and the expression for the bound state energy is presented. Finally, in the section 4 we present our conclusions.

2. The Self-Adjoint Extension Approach

In this section, we review some important concepts and results from the von-Neumann-Krein theory of self-adjoint extensions. Let A and B two operators. If the domain of A contains the domain of B, i.e., ${D}(A)\supseteq {D}(B)$, and in the domain of B the operators are equals, then we say that A is an extension of B. The domain of an operator A is called dense if for each vector ψ in this domain, there is a sequence ψ_n in such a way that ψ_n → ψ. If an operator A has a dense domain, the domain of its adjoint A^†, is the set of all vectors ψ for which there is a vector A^†ψ that satisfies

$\begin{array}{ll}(\varphi ,A^{†}\psi )=(A\varphi ,\psi ),& (1)\end{array}$

for all vectors $\varphi \in {D}(A)$. Equation (1) defines A^†ψ. On the other hand, an operator with dense domain A is symmetric if

$\begin{array}{ll}(\varphi ,A\psi )=(A\varphi ,\psi ),& (2)\end{array}$

for every ϕ and ψ in its domain. In this case A^†ψ is defined as A^†ψ = Aψ for all $\psi \in {D}(A)$, and A^† is said to be an extension of A. If A^† = A, then A is called self-adjoint or Hermitian. It is interesting to comment that in physics it is common to assume that Hermitian is the same as self-adjointness. However, they are different notions in mathematics literature and only the word Hermitian could be used for symmetric.

An important point here is that a symmetric operator can fail to be a self-adjoint operator. For A to be a self-adjoint operator it has to be symmetric, A = A^†, and the domains of the operator and its adjoint have to be equal as well, ${D}(A)={D}(A^{†})$. So, in the same way as a function needs a rule, a domain and a codomain to be defined, an operator needs not only its action but also its domain (Hilbert space) to be completely defined. Several traditional textbooks on quantum mechanics [51–54] do not mention the problems that could arise by the incorrect or incomplete definition of the operators. An exception being the textbook of the author Ballentine [55]. The mathematical framework of quantum mechanics is that of linear operators in Hilbert spaces and the problems and paradoxes that could arise come from the use of simplified rules described in many textbooks. As an example of this is the use of the theory if bounded operators to deal with unbounded operators [56].

2.1. The Weyl-Von Neumann's Theorem

Following the concept of self-adjoint extension, the question we want to answer is how many extensions, if any, are admitted by an operator. The answer to this question lies in the concept of deficiency index of an operator. Let A be a symmetric operator with domain ${D}(A)$ and the corresponding adjoint operator A^† with domain ${D}(A^{†})$. The deficiency subspaces ${{N}}_{\pm }$ are defined by [56]

$\begin{array}{ll}{{N}}_{\pm }=\left\{{\psi }_{\pm }\in {D}(A^{†}),A^{†}{\psi }_{\pm }=z_{\pm }{\psi }_{\pm },Im(z_{\pm })\gtrless 0\right\},& (3)\end{array}$

with dimensions $dim\left\{{{N}}_{\pm }\right\}=n_{\pm }$. The pair of non-negative integers (n₊, n₋) are called deficiency indices of A. The exact value of z_± is not important as long as z₊ (z₋) belongs to the upper (lower) half complex plane. For simplicity, it is chosen as z_± = ±iz₀, with z₀ an arbitrary positive real number, used for dimensional reasons. In this manner, to access the deficiency indices, all we have to do is to solve the eigenvalue equation

$\begin{array}{ll}{A}^{†}{\psi }_{\pm }=\pm i{z}_0{\psi }_{\pm },& (4)\end{array}$

and then count the number of linearly independent solutions that belong to the domain of the adjoint operator in the Hilbert space in question, i.e., those that are square integrable.

Theorem 1. (Weyl and Von Neumann [56]) Consider an operator A with deficiency index (n₊, n₋):

1. If n₊ = n₋, A is essentially self-adjoint;

2. If n₊ = n₋ = n ≥ 1, A posses an infinity number of self-adjoint extensions parameterized by a unitary matrix $U:{{N}}_{+}\to {{N}}_{-}$ of dimension n with n² real parameters;

3. If n₊ ≠ n₋, A does not admit a self-adjoint extension.

Therefore, the domain of A^† is

$\begin{array}{ll}{D}(A^{†})={D}(A)\oplus {{N}}_{+}\oplus {{N}}_{-}.& (5)\end{array}$

So, it is important to note that even for Hermitian operators, A = A^†, its domains might be different. In this manner, the self-adjoint extension essentially consists of extending the domain of A using the deficiency subspaces ${{N}}_{\pm }$ to match the domain of A^†.

Now that we have discussed some general concepts about the self-adjoint extension approach, we restrict our discussion to the specific case of singular Hamiltonian operators H in (2 + 1) dimensions. In these cases, the singularity is characterized by the presence of a two-dimensional δ function localized at the r = 0. It is well-known in the literature that these Hamiltonians are not self-adjoint and admit a one-parameter family of self-adjoint extension [22]. Thus, our main goal is to solve the time-independent Schrödinger equation

$\begin{array}{ll}H\psi =E\psi ,& (6)\end{array}$

with H the Hamiltonian, ψ the wave function and E the energy. To do so, we shall discuss two methods to characterize the family of self-adjoint extensions of H. In both methods, the delta function singularity is replaced by a boundary condition at the origin. In the first one, proposed by Bulla and Gesztesy (BG) in [57], the boundary condition is a mathematical limit allowing divergent solutions for the Hamiltonian H at isolated points, provided they remain square-integrable. In the second one, proposed by Kay and Studer (KS) in [58], the boundary condition is a match of the logarithmic derivatives of the zero-energy solutions for the regularized Hamiltonian and the solutions for the Hamiltonian H without the delta function plus a self-adjoint extension. As we shall show, the comparison between the results of the two methods allows us to express the self-adjoint extension parameter (a mathematical parameter that characterizes the self-adjoint extension) in terms of the physics of the problem.

2.2. The BG Method

Let us consider the radial singular Schrödinger operator in L²((0, ∞)) given by

$\begin{array}{ll}h=-\frac{d^2}{d{r}^2}+\frac{\ell (\ell -1)}{r^2}+\frac{\gamma }{r}+\frac{\beta }{r^a}+W,& (7)\end{array}$

with W ∈ L^∞((0, ∞)) real valued and 1/2 ≤ ℓ < 3/2, β, γ ∈ ℝ, 0 < a < 2. Bulla and Gesztesy showed that this operator, in the interval 1/2 ≤ ℓ < 3/2, is not self-adjoint having deficiency indices (1, 1). Thus admitting a one-parameter family of self-adjoint extensions. The following theorem characterizes all the self-adjoint extension of h.

Theorem 2. (Bulla and Gesztesy [3, 57]) All the self-adjoint extension h_ν of h can be characterized by

$\begin{array}{ll}{h}_{\nu }=-\frac{d^2}{d{r}^2}+\frac{\ell (\ell -1)}{r^2}+\frac{\gamma }{r}+\frac{\beta }{r^a}+W,& (8)\end{array}$

with domain

$\begin{array}{ll}{D}(h_{\nu })=\{g\in L^2((0,\infty ))|g,g^{\prime }\in A{C}_{\text{loc}}((0,\infty ));& (9)\end{array}$

$\begin{array}{ll}-g^{″}+\frac{\ell (\ell -1)}{r^2}g+\frac{\gamma }{r}g+\frac{\beta }{r^a}g\in L^2((0,\infty ))\}& (10)\end{array}$

with AC_loc((a, b)) denoting the set of locally absolutely continuous functions on ((a, b)) and the function g satisfies the boundary condition

$\begin{array}{ll}\nu g_{0,\ell }=g_{1,\ell },& (11)\end{array}$

and

$\begin{array}{ll}-\infty <\nu \le \infty ,\frac{1}{2}\le \ell <\frac{3}{2},\beta ,\gamma \in ℝ,0<a<2.& (12)\end{array}$

The boundary values in (11) are defined by

$\begin{array}{ll}{g}_{0,\ell }={\displaystyle \underset{r\to 0^{+}}{lim}}\frac{g(r)}{G_{\ell }^{(0)}(r)},& (13)\end{array}$

and

$\begin{array}{ll}{g}_{1,\ell }={\displaystyle \underset{r\to 0^{+}}{lim}}\frac{g(r)-g_{0,\ell }{G}_{\ell }^B(r)}{F_{\ell }^{(0)}(r)}.& (14)\end{array}$

The boundary condition g_{0, ℓ} = 0 (i.e., ν = ∞) represents the Friedrichs extension of h.

The functions $F_{\ell }^{(0)}(r)$ and $G_{\ell }^{(0)}(r)$ are given by

$\begin{array}{ll}{F}_{\ell }^{(0)}(r)=r^{\ell },& (15)\end{array}$

and

$\begin{array}{ll}{G}_{\ell }^{(0)}(r)=\{\begin{array}{ll}-r^{1/2}\ln (r),\hfill & \ell =\frac{1}{2},\hfill \\ \frac{r^{1-\ell }}{(2\ell -1)},\hfill & \frac{1}{2}<\ell <\frac{3}{2}.\hfill \end{array}& (16)\end{array}$

$G_{\ell }^B(r)$ denotes the asymptotic expansion of G_ℓ(r) for r → 0⁺ up to r^t, with t ≤ 2ℓ−1.

2.3. The KS Method

The authors Kay and Studer studied, in the context of self-adjoint extensions, the boundary conditions for singular Hamiltonians in conical spaces and fields around cosmic strings [58]. Among the studied problems, are the AB like problems in two dimensions.

The KS method starts by considering a regularization procedure for the point interaction at the origin. Thus, for the regularized Hamiltonian, where the point interaction is shifted from the origin by a finite very small radius r₀, the method is applied in the following manner [59]:

1. We temporally forget the point interaction at the origin substituting the singular Hamiltonian by the corresponding non-singular one;

2. We solve the Equation (4) for the deficiency spaces of the non-singular Hamiltonian;

3. The solutions obtained in the previous step are used to complete the space of solutions for the non-singular Hamiltonian;

4. In the last step, a boundary condition matching the logarithmic derivatives of the zero-energy solutions for the regularized Hamiltonian of step 1 and the general solutions obtained in step 3 is employed:

$\begin{array}{ll}\underset{r_0\to 0^{+}}{\lim }{r}_0\frac{{\dot{g}}_0}{g_0}{|}_{r=r_0}=\underset{r_0\to 0^{+}}{\lim }{r}_0\frac{{\dot{g}}_{\rho }}{g_{\rho }}{|}_{r=r_0}.& (17)\end{array}$

In the above equation, g_ρ are the solutions obtained in step 3 and g₀ are the zero-energy solutions (ġ = dg/dr).

Now that we have discussed the self-adjoint extension approach and the BG and KS methods, in what follows we exemplify the application of both methods to the problem of a spin-1/2 charged particle with an anomalous magnetic moment under the influence of an AB field in conical space.

3. The Dirac Equation for the AB System in the Conical Space

In this section, we shall obtain the Dirac equation to describe the motion of a spin-1/2 charged particle with mass M and anomalous magnetic moment μ_B interacting with an AB field in the cosmic string spacetime. The line element that describes this universe written in cylindrical coordinates is given by

$\begin{array}{ll}d{s}^2=d{t}^2-d{r}^2-{\alpha }^2{r}^{2}d{\phi }^2-d{z}^2,& (18)\end{array}$

with −∞ < (t, z) < ∞, r ≥ 0 and 0 ≤ φ ≤ 2π. The parameter α in the metric (18) is related to the linear mass density $\bar{m}$ of the cosmic string through the formula $\alpha =1-4\bar{m}$ and it stands for two situations:

• It describes the surface of a cone if 0 < α < 1. This is equivalent to removing a wedge angle of 2π(1 − α) and the defect presents a positive curvature.

• It describes the surface of an anticone or the figure of a saddle-like surface when α > 1. This situation corresponds to the addition of an excess angle of 2π(α − 1) and, in this case, the defect represents a negative curvature.

In this work, we shall discuss the case of a conical surface, so that 0 < α ≤ 1, with the equality corresponding to the flat space.

The metric in (18) can also be read as the Minkowski spacetime with a conic singularity at r = 0 [60]. Because of this characteristic, the only non-zero components of the curvature tensor is found to be

$\begin{array}{ll}{R}_{r,\phi }^{r,\phi }=\frac{1-\alpha }{4\alpha }{\delta }_2(\text{r}),& (19)\end{array}$

where δ₂(r) is the two-dimensional delta function in flat space. The conical singularity in the tensor (19) reveals that the curvature is concentrated on the cosmic string axis and in all other regions it is null.

Since the spacetime is not flat, we must take into account the spin connection in the Dirac equation. To implement this, we need to construct a frame which allows us to obtain the Dirac gamma matrices γ^μ in the Minkowskian spacetime (defined in terms of the local coordinates) in terms of global coordinates. This is done by using the tetrad base $e_{\mu }^{(a)}(x)$, which allows to contract the matrices γ^μ with the inverse tetrad $e_{(a)}^{\mu }(x)$ through the relation

$\begin{array}{ll}{\gamma }^{\mu }(x)=e_{(a)}^{\mu }(x){\gamma }^{(a)},& (20)\end{array}$

satisfying the generalized Clifford algebra

$\begin{array}{ll}\left\{{\gamma }^{\mu }(x),{\gamma }^{\nu }(x)\right\}=2g^{\mu \nu }(x),& (21)\end{array}$

with

$\begin{array}{ll}{g}_{\mu \nu }(x)=e_{\mu }^{(a)}(x)e_{\nu }^{(b)}(x){\eta }_{(a)(b)},& (22)\end{array}$

being the metric tensor of the spacetime in the presence of the background topological defect, where η_(a)(b) is the metric tensor of the flat space, and (μ, ν) = (0, 1, 2, 3) represent tensor indices while (a, b) = (0, 1, 2, 3) are tetrad indices. The tetrad and its inverse satisfy the following properties:

$\begin{array}{ll}{e}_{\mu }^{(a)}(x)e_{(b)}^{\mu }(x)={\delta }_{(b)}^{(a)}{e}_{(a)}^{\mu }(x)e_{\nu }^{(a)}(x)={\delta }_{\nu }^{\mu }.& (23)\end{array}$

The matrices γ^(a) = (γ⁽⁰⁾, γ⁽ⁱ⁾) in Equation (20) are the standard Dirac matrices in Minkowski spacetime, those representation is

$\begin{array}{ll}{\gamma }^{(0)}=\left(\begin{array}{cc}I& 0\\ 0& -I\end{array}\right),{\gamma }^{(i)}=\left(\begin{array}{cc}0& {\sigma }^i\\ -{\sigma }^i& 0\end{array}\right),(i=1,2,3),& (24)\end{array}$

where σⁱ = (σ¹, σ², σ³) are the standard Pauli matrices and I is the 2 × 2 identity matrix.

To write the generalized Dirac equation in the cosmic string background, we have to take into account the minimal and non-minimal couplings of the spinor to the electromagnetic field embedded in a classical gravitational field. The Dirac equation then reads

$\begin{array}{l}[i{\gamma }^{\mu }\left(x\right)\left({\partial }_{\mu }+{\Gamma }_{\mu }\left(x\right)\right)-e{\gamma }^{\mu }\left(x\right)A_{\mu }\left(x\right)\\ -\frac{a_e{\mu }_B}{2}{\sigma }^{\mu \nu }\left(x\right)F_{\mu \nu }\left(x\right)-M]\Psi \left(x\right)=0,& (25)\end{array}$

where e is the electric charge,

$\begin{array}{ll}{a}_e=\frac{g_e-2}{2}=0,00115965218091,& (26)\end{array}$

is the anomalous magnetic moment defined, with g_e being the electron's g-factor [61],

$\begin{array}{ll}{A}_{\mu }(x)=(A_0,-\text{A}),& (27)\end{array}$

is the 4-potential of the external electromagnetic field, with A being the vector potential and A₀ the scalar potential,

$\begin{array}{ll}{F}_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu },& (28)\end{array}$

is the electromagnetic field tensor whose components are given by

$\begin{array}{ll}\left(F_{0i},F_{ij}\right)=\left(E^i,{\epsilon }_{ijk}{B}^k\right),& (29)\end{array}$

and the operator

$\begin{array}{l}{\sigma }^{\mu \nu }(x)=\frac{i}{2}[e_{(a)}^{\mu }(x){\gamma }^{(a)},e_{(b)}^{\nu }(x){\gamma }^{(b)}]\\ =\frac{i}{2}\left[e_{(a)}^{\mu }{\gamma }^{(a)}{e}_{(b)}^{\nu }(x){\gamma }^{(b)}-e_{(b)}^{\nu }(x){\gamma }^{(b)}{e}_{(a)}^{\mu }(x){\gamma }^{(a)}\right],& (30)\end{array}$

those components are given by

$\begin{array}{ll}{\sigma }^{0i}=i{\alpha }^j=i\left(\begin{array}{cc}0& {\sigma }^i\\ {\sigma }^i& 0\end{array}\right),& (31)\end{array}$

$\begin{array}{ll}{\sigma }^{ij}=-{ϵ}_{ijk}{\Sigma }^k=-\left(\begin{array}{cc}{ϵ}_{ijk}{\sigma }^k& 0\\ 0& {ϵ}_{ijk}{\sigma }^k\end{array}\right),& (32)\end{array}$

where

$\begin{array}{ll}{\Sigma }^k=\left(\begin{array}{cc}{\sigma }^k& 0\\ 0& {\sigma }^k\end{array}\right)& (33)\end{array}$

is the spin operator. The spinor affine connection in Equation (25) is related with the tetrad fields as [62]

$\begin{array}{ll}{\Gamma }_{\mu }(x)=\frac{1}{8}{\omega }_{\mu (a)(b)}(x)\left[{\gamma }^{(a)},{\gamma }^{(b)}\right],& (34)\end{array}$

where ω_μ(a)(b) is the spin connection, which can be calculated from the relation

$\begin{array}{l}{\omega }_{\mu (a)(b)}(x)={\eta }_{(a)(c)}{e}_{\nu }^{(c)}(x)e_{(b)}^{\tau }(x){\Gamma }_{\tau \mu }^{\nu }\\ -{\eta }_{(a)(c)}{e}_{\nu }^{(c)}(x){\partial }_{\mu }{e}_{(b)}^{\nu }(x),& (35)\end{array}$

and ${\Gamma }_{\tau \mu }^{\nu }$ are the Christoffel symbols.

Now, we need of the tetrad fields to write the Dirac equation in curved space. For the cosmic string spacetime they are chosen to be [63]

$\begin{array}{lll}{e}_{\mu }^{(a)}& =& \left(\begin{array}{cccc}1& 0& 0& 0\\ 0& cos\phi & -\alpha rsin\phi & 0\\ 0& sin\phi & \alpha rcos\phi & 0\\ 0& 0& 0& 1\end{array}\right),\\ e_{(a)}^{\mu }& =& \left(\begin{array}{cccc}1& 0& 0& 0\\ 0& cos\phi & sin\phi & 0\\ 0& -sin\phi /\alpha r& cos\phi /\alpha r& 0\\ 0& 0& 0& 1\end{array}\right).& (36)\end{array}$

Using (36), the matrices γ^μ (x) in Equation (20) are written more explicitly as

$\begin{array}{ll}{\gamma }^0=\beta \equiv {\gamma }^t,& (37)\end{array}$

$\begin{array}{ll}{\gamma }^z\equiv {\gamma }^z,& (38)\end{array}$

$\begin{array}{ll}{\gamma }^1\equiv {\gamma }^r={\gamma }^{(2)}cos\phi +{\gamma }^{(2)}sin\phi ,& (39)\end{array}$

$\begin{array}{ll}{\gamma }^2\equiv \frac{{\gamma }^{\phi }}{\alpha r}=\frac{1}{\alpha r}\left(-{\gamma }^{(1)}sin\phi +{\gamma }^{(2)}cos\phi \right),& (40)\end{array}$

$\begin{array}{ll}{\gamma }^3\equiv {\gamma }^z.& (41)\end{array}$

The matrices (37)–(40) satisfy condition ${\nabla }_{\mu }{\gamma }^{\mu }=0$, which means that they are covariantly constant. The Pauli matrices σⁱ in Equation (31) have the following representation:

$\begin{array}{ll}{\sigma }^r=\left(\begin{array}{cc}0& e^{-i\phi }\\ e^{i\phi }& 0\end{array}\right),& (42)\end{array}$

$\begin{array}{ll}{\sigma }^{\phi }=\frac{1}{\alpha r}\left(\begin{array}{cc}0& -i{e}^{-i\phi }\\ i{e}^{i\phi }& 0\end{array}\right).& (43)\end{array}$

Using the basis tetrad (36), the affine connection (34) is found to be [64]

$\begin{array}{ll}\Gamma =(0,0,{\Gamma }_{\phi },0),& (44)\end{array}$

where

$\begin{array}{ll}{\Gamma }_{\phi }=\frac{1}{2}(1-\alpha ){\gamma }_{(1)}{\gamma }_{(2)}=-i\frac{(1-\alpha )}{2}{\sigma }^z,& (45)\end{array}$

arises as the only non-zero component.

For simplicity, let us assume that the particle interacts with the AB potential, which is generated by a solenoid along the z direction. Since the motion is translationally invariant along this direction, we require that p_z = z = 0 and, in Equation (29), we take Eⁱ = 0 for i = 1, 2, 3. Thus, the particle has a purely planar motion. Equation (25) takes the form

$\begin{array}{l}[-i{\partial }_0+\alpha \cdot \left[\frac{1}{i}({\nabla }_{\alpha }+\Gamma )-eA\right]\\ -a_e{\mu }_B{\gamma }^0\Sigma \cdot B+{\gamma }^{0}M]\Psi (x)=0.& (46)\end{array}$

It is well-known that, in the non-relativistic limit, the large energy M is the driving term in Equation (46). So, writing

$\begin{array}{ll}\text{Ψ}=e^{-iEt}\left(\begin{array}{c}\chi \\ \Phi \end{array}\right),& (47)\end{array}$

we obtain the coupled equations system

$\begin{array}{ll}\sigma \cdot \left[\frac{1}{i}({\nabla }_{\alpha }+\Gamma )-eA\right]\Phi =\left(i{\partial }_0+a_e{\mu }_B\sigma \cdot B\right)\chi , & (48)\end{array}$

$\begin{array}{ll}\sigma \cdot \left[\frac{1}{i}({\nabla }_{\alpha }+\Gamma )-eA\right]\chi \text{\hspace{0.17em}}=\left(i{\partial }_0-a_e{\mu }_B\sigma \cdot B+2M\right)\Phi .& (49)\end{array}$

On the right side of Equation (49), if we assume that 2M ≫ (i∂₀ − a_eμ_Bσ · B), we solve it as

$\begin{array}{ll}\Phi =\frac{1}{2M}\sigma \cdot \left[\frac{1}{i}(\nabla +\Gamma )-eA\right]\chi .& (50)\end{array}$

Substituting (50) into (48), we get

$\begin{array}{l}\frac{1}{2M}\sigma \cdot \left[\frac{1}{i}({\nabla }_{\alpha }+\Gamma )-eA\right]\sigma \cdot \left[\frac{1}{i}(\nabla +\Gamma )-eA\right]\chi \\ -a_e{\mu }_B\sigma \cdot B\chi =i{\partial }_0\chi .& (51)\end{array}$

Using the relation for Pauli's matrices

$\begin{array}{ll}(\sigma ·\text{a})(\sigma ·\text{b})=\text{a}·\text{b}+i\sigma ·(\text{a}\times \text{b}),& (52)\end{array}$

where a and b are arbitrary vectors, Equation (51) becomes

$\begin{array}{ll}\frac{1}{2M}{\left[\frac{1}{i}({\nabla }_{\alpha }+\Gamma )-eA\right]}^2\chi -\frac{e}{2M}\left(1+a_e\right)\sigma \cdot B\chi =i{\partial }_0\chi .& (53)\end{array}$

Now we need to define the field configuration. We consider the magnetic field generated by an infinity long cylindrical solenoid in the metric (18). Thus, in the Coulomb gauge, the vector potential reads

$\begin{array}{ll}eA=-\frac{e\Phi }{2\pi \alpha r}\widehat{\phi }=-\frac{\varphi }{\alpha r}\widehat{\phi },A_0=0,& (54)\end{array}$

and

$\begin{array}{ll}e\text{B}=-\frac{e\Phi }{2\pi \alpha }\frac{\delta (r)}{r}\widehat{\text{z}}=-\frac{\varphi }{\alpha }\frac{\delta (r)}{r}\widehat{\text{z}},& (55)\end{array}$

with ϕ = Φ/Φ₀ being the magnetic flux and Φ₀ = 2π/e is the quantum of magnetic flux. As we can observe, this magnetic field is singular at the origin. The presence of this singularity (a point interaction) in the Hamiltonian, demands that it must be treated by some kind of regularization or, more appropriately, by using the self-adjoint extension approach. We can note that χ in Equation (53) is an eigenfunction of σ^z, with eigenvalues s = ±1. In this way, we can write σ^zχ = ±χ = sχ. We can take the solutions in the form

$\begin{array}{ll}\chi (t,r,\phi )=e^{-iEt}\left(\begin{array}{c}{\chi }_{+}(r,\phi )\\ {\chi }_{-}(r,\phi )\end{array}\right)=e^{-iEt}{\chi }_s(r,\phi ).& (56)\end{array}$

Substituting (45), (54), (55), and (56) in Equation (53), we obtain

$\begin{array}{l}\frac{1}{2M}{\left[\frac{1}{i}{\nabla }_{\alpha }-\frac{(1-\alpha )}{2\alpha r}s\widehat{\phi }+\frac{\varphi }{\alpha r}\widehat{\phi }\right]}^2{\chi }_s+\frac{1}{2M}\frac{g_{e}s\varphi }{2\alpha }\frac{\delta (r)}{r}{\chi }_s\left(r,\phi \right)\\ =E{\chi }_s\left(r,\phi \right).\end{array}$

Therefore, the eigenvalues equation associated with Equation (25) is (k² = 2ME)

$\begin{array}{ll}H{\chi }_s=k^2{\chi }_s,& (58)\end{array}$

with

$\begin{array}{ll}H={\left[-i{\nabla }_{\alpha }-\frac{\left(1-\alpha \right)}{2\alpha r}s\widehat{\phi }+\frac{\varphi }{\alpha r}\widehat{\phi }\right]}^2+\frac{g_{e}s\varphi }{2\alpha }\frac{\delta (r)}{r}.& (59)\end{array}$

By expanding the above equation, we arrive at the Laplace-Beltrami operator in the curved space

$\begin{array}{ll}{\nabla }_{\alpha }^2=\frac{{\partial }^2}{\partial r^2}+\frac{1}{r}\frac{\partial }{\partial r}+\frac{1}{{\alpha }^2{r}^2}\frac{{\partial }^2}{\partial {\phi }^2}.& (60)\end{array}$

In the present system, the total angular momentum is the sum of the angular momentum and the spin, J = −i∂/∂φ + s/2. Since J commutes with H, we seek solutions of the form

$\begin{array}{ll}{\chi }_s={\displaystyle \sum _m}{\psi }_m(r)e^{im\phi },& (61)\end{array}$

with m = 0, ±1, ±2, ±3, … being the angular momentum quantum number and ψ_s(r) satisfies the differential equation

$\begin{array}{ll}h{\psi }_m(r)=k^2{\psi }_m(r),& (62)\end{array}$

with

$\begin{array}{ll}h=h_0+\lambda \frac{\delta (r)}{r},& (63)\end{array}$

and

$\begin{array}{ll}{h}_0=-\frac{d^2}{d{r}^2}-\frac{1}{r}\frac{d}{dr}+\frac{j^2}{r^2}.& (64)\end{array}$

The parameter j represents the effective angular momentum

$\begin{array}{ll}j=\frac{m+\varphi }{\alpha }-\frac{(1-\alpha )s}{2\alpha },& (65)\end{array}$

and

$\begin{array}{ll}\lambda =\frac{g_e\varphi s}{2\alpha }.& (66)\end{array}$

By observing equation (65), one can verify that the presence of the spin element in the model leads to the appearance of a δ function potential. The quantity λδ(r)/r in Equation (63) is interpreted as the interaction between the spin of the particle and the AB flux tube. As pointed out by Hagen [6, 7] in flat space (α = 1), this interaction affects the scattering phase shift. In this work, by using the self-adjoint extension approach, we shall confirm these results and show that this delta function also leads to bound states. This approach had to be adopted to deal with singular Hamiltonians in previous works as, for example, in the study of spin 1/2 AB system and cosmic strings [5, 65], in the Aharonov-Bohm-Coulomb problem [33, 34, 66, 67], and the study of the equivalence between the self-adjoint extension method and renormalization [29].

3.1. Application of the BG Method

In this section, we employ the KS method to find the S-matrix and from its poles we obtain an expression for the bound states. To apply the BG method, we need first transform the operator h₀ in (64) to compare with the form in Equation (7). This is accomplished by employing a similarity transformation by means of the unitary operator U : L²(ℝ⁺, rdr) → L²(ℝ⁺, dr), given by (Uξ)(r) = r^1/2ξ(r). Thus, the operator h₀ becomes

$\begin{array}{ll}{\tilde{h}}_0=U{H}_0{U}^{-1}=-\frac{d^2}{d{r}^2}+\left(j^2-\frac{1}{4}\right)\frac{1}{r^2},& (67)\end{array}$

and by comparing with (7) we must have γ = β = W = 0 and

$\begin{array}{ll}\ell (\ell -1)=j^2-\frac{1}{4}.& (68)\end{array}$

It is well-known that the radial operator h₀ is not essentially self-adjoint for ℓ(ℓ−1) < 3/4, otherwise it is essentially self-adjoint [22]. Therefore, using the above equation in this inequality, we have

$\begin{array}{ll}\left|j\right|<1.& (69)\end{array}$

Before we going to the application of Theorem 2, it is interesting to get a deeper understanding of the significance of the above equation for it informs us for which values of the angular momentum quantum number m the operator h₀ is not self-adjoint. From Equation (65), we see that these values are dependent on the magnetic quantum flux ϕ, the value of α and the spin parameter s. By employing the decomposition of the magnetic quantum flux as

$\begin{array}{ll}\varphi =N+\beta ,& (70)\end{array}$

with N being the largest integer contained in ϕ and

$\begin{array}{ll}0\le \beta <1,& (71)\end{array}$

the inequality in Equation (69), becomes

$\begin{array}{ll}{\pi }_{-}^{\text{AB}}(\alpha ,\beta )<m<{\pi }_{+}^{\text{AB}}(\alpha ,\beta ),& (72)\end{array}$

with

$\begin{array}{ll}{\pi }_{\pm }^{\text{AB}}(\alpha ,\beta )=\pm \alpha -(N+\beta )+\frac{(1-\alpha )s}{2}.& (73)\end{array}$

The planes ${\pi }_{\pm }^{\text{AB}}(\alpha ,\beta )$ delimit the region in which h₀ is not self-adjoint. Given the exact equivalence of the spin 1/2 AB and AC effects [68], Equation (73) should be compared with the corresponding planes obtained for the AC effect in the conical space. In reference [14] it was shown that the planes for the AC effect are given by¹

$\begin{array}{ll}{\pi }_{\pm }^{\text{AC}}(\alpha ,\beta )=\pm \alpha -s(N+\beta )+\frac{(1-\alpha )s}{2}.& (74)\end{array}$

Although the equations for the planes are very similar, there is an additional dependence on the spin parameter s in the AC effect. In Figure 1 we show the planes for AB (top panel) and AC (bottom panel) effects as a function of β and it is possible to see in the AB effect the s parameter changes the values of m in which h₀ is not self-adjoint and the planes are decreasing functions of β whatever the value of s while in the AC effect, besides of changing the values of m, it also controls the inclination of the planes (compare the figures at the bottom panel of Figure 1). We can have even more information about the affected m values (in the sense of which values of it h₀ is not self-adjoint) by looking at some specific values of α. Thus, in Figures 2, 3 we show cross sections of Figure 1 for s = −1 and s = +1, respectively. In Figures 2, 3 we can see that for s = −1 (s = +1) and α = 0.25 only for m = −N − 1 (m = −N) the operator h₀ is not self-adjoint. On the other hand, for α = 0.50 for both values of m = −N and m = −N − 1 the operator h₀ is not self-adjoint. In fact, the minimum value of α in which h₀ is not self-adjoint for both values of m is α_min = 1/3. Moreover, for α = 1 (flat space), the operator h₀ is not self-adjoint for both values of angular momentum for all range of β, which is a very well-known result [3, 69–71].

FIGURE 1

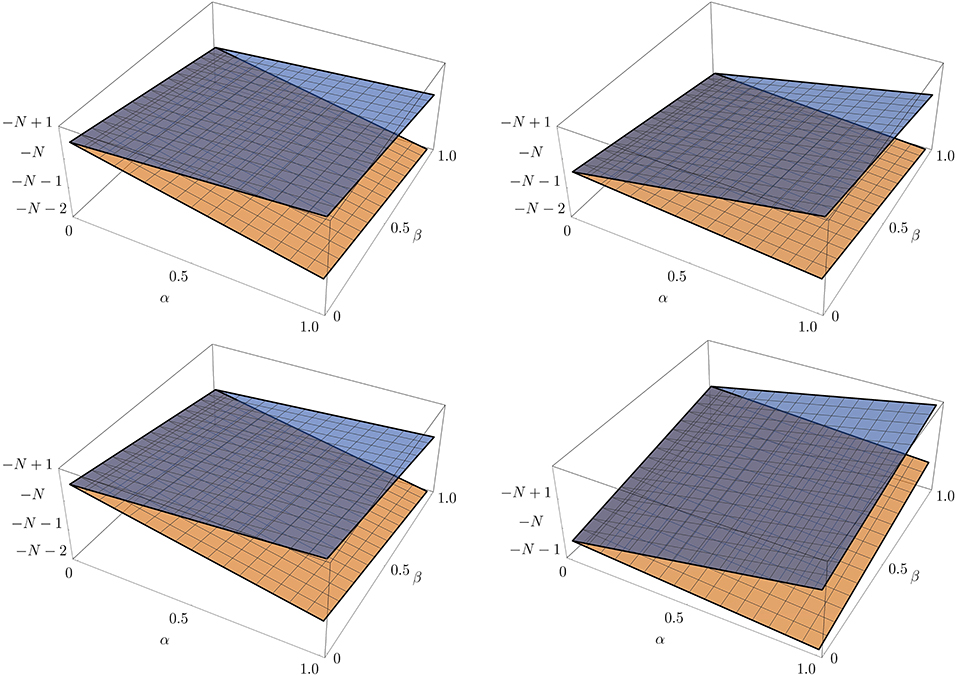
Figure 1. In this figure we show the graphs of the planes ${\pi }_{\pm }^{AB}(\alpha ,\beta )$ for the AB (top panel) and the planes ${\pi }_{\pm }^{AC}(\alpha ,\beta )$ for the AC (bottom panel) effects. The figures on the left are for s = −1 and on the right is for s = +1. The planes delimit the region where h₀ is not self-adjoint.

FIGURE 2

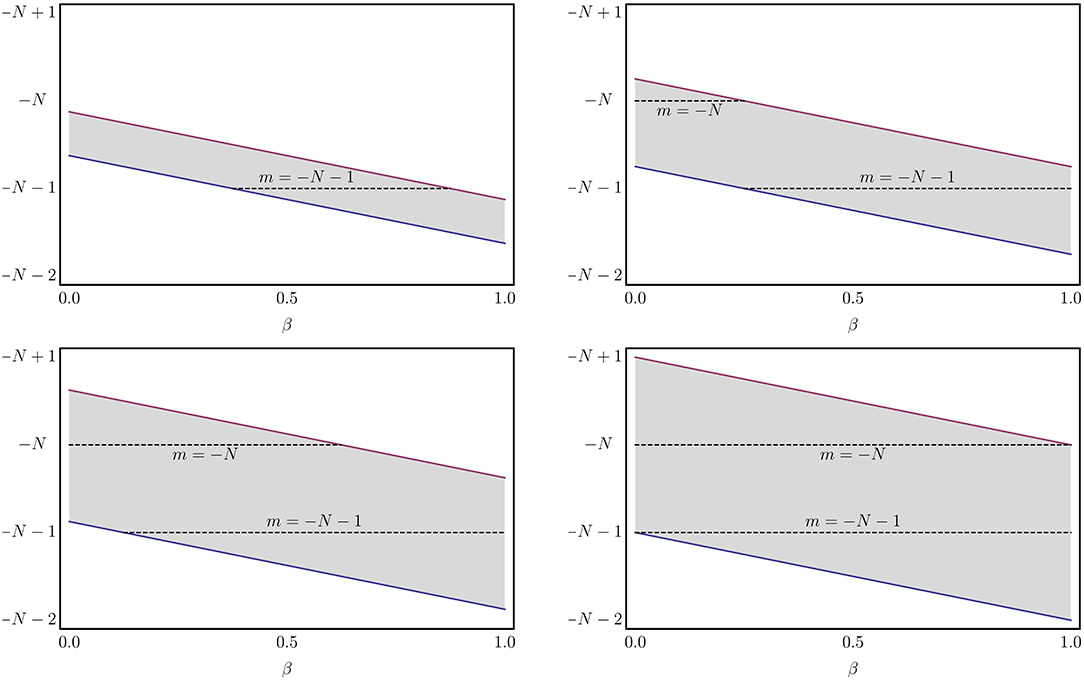
Figure 2. Cross sections of Figure 1 (top left panel) with s = −1 for: α = 0.25 (top left panel), α = 0.50 (top right panel), α = 0.75 (bottom left panel), and α = 1 (bottom right panel). The area of the stripe detached in the figure represents the region in which the operator h₀ is not self-adjoint. The dashed lines refer to the values of angular momentum quantum number.

FIGURE 3

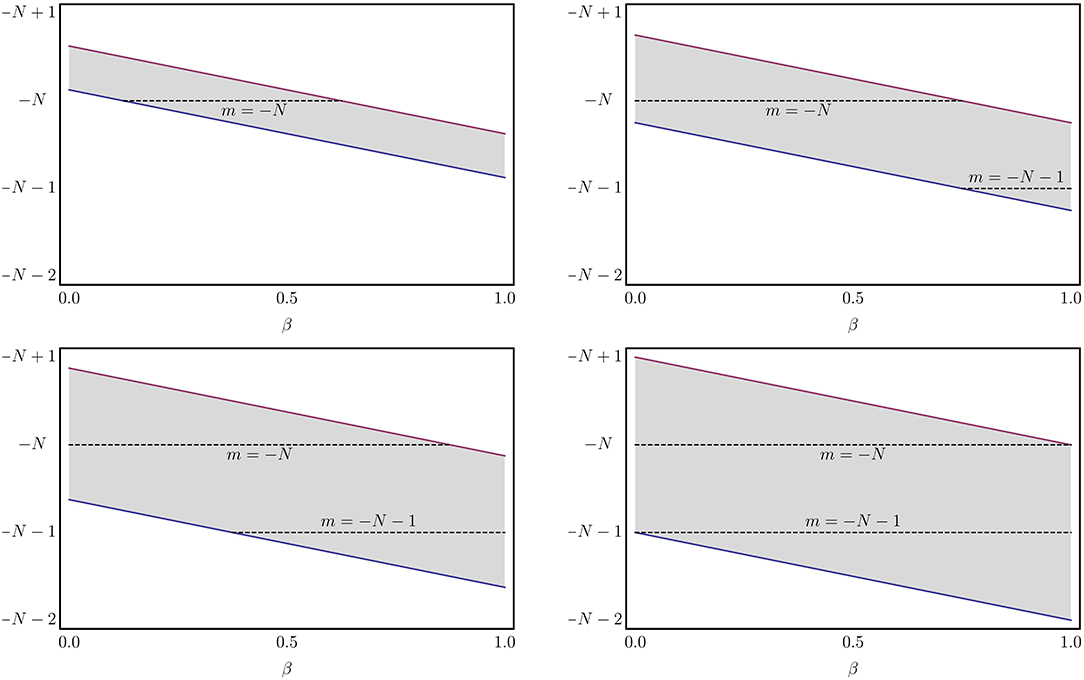
Figure 3. Cross sections of Figure 1 (top left panel) with s = +1 for: α = 0.25 (top left panel), α = 0.50 (top right panel), α = 0.75 (bottom left panel), and α = 1 (bottom right panel). The area of the stripe detached in the figure represents the region in which the operator h₀ is not self-adjoint. The dashed lines refer to the values of angular momentum quantum number.

Now that we have discussed in detail the significance of inequality |j| < 1, we can return to our main discussion. Thus, in the subspace where |j| < 1, we must apply Theorem 2, in such a way that all the self-adjoint extensions h_{0, ν} of h₀ are characterized by the boundary condition at the origin

$\begin{array}{ll}\nu {\psi }_{0,j}={\psi }_{1,j},& (75)\end{array}$

with −∞ < ν ≤ ∞, −1 < j < 1 and the boundary values are

$\begin{array}{l}{\psi }_{0,j}={\displaystyle \underset{r\to 0^{+}}{lim}}{r}^{\left|j\right|}{\psi }_m(r),\\ {\psi }_{1,j}={\displaystyle \underset{r\to 0^{+}}{lim}}\frac{1}{r^{\left|j\right|}}\left[{\psi }_m(r)-{\psi }_{0,j}\frac{1}{r^{\left|j\right|}}\right].\end{array}$

Physically, it turns out that we can interpret 1/ν as the scattering length of h_{0, ν} [3]. For ν = ∞ (the Friedrichs extension of h₀), we obtain the free Hamiltonian (the case describing spinless particles) with regular wave functions at the origin (ψ_m(0) = 0). This scenario is similar to imposing the Dirichlet boundary condition on the wave function and recovers the original result of Aharanov and Bohm [4]. On the other hand, if |ν| < ∞, h_{0, ν} characterizes a point interaction at r = 0 and the boundary condition permits a r^−|j| singularity in the wave functions at this point [72].

Now that we have a suitable boundary condition, we can return to Equation (62) and look for its solutions. Equation (62) is nothing more than the Bessel differential equation for r ≠ 0. Thus, the general solution for r ≠ 0 is given by

$\begin{array}{ll}{\psi }_m(r)=a_m{J}_{\left|j\right|}(kr)+b_m{J}_{-\left|j\right|}(kr),& (76)\end{array}$

where J_ν(z) is the Bessel function of fractional order and a_m and b_m are the coefficients corresponding to the contributions of the regular and irregular solutions at r = 0, respectively. By means of the boundary condition in Equation (75), we obtain a relation between a_m and b_m,

$\begin{array}{ll}{b}_m=-{\mu }_{\nu }{a}_m,& (77)\end{array}$

which is valid in the subspace |j| < 1. The term μ_ν is given by

$\begin{array}{ll}{\mu }_{\nu }=\frac{k^{2\left|j\right|}\Gamma \left(1-\left|j\right|\right)sin\left(\left|j\right|\pi \right)}{4^{\left|j\right|}\Gamma \left(1+\left|j\right|\right)\nu +k^{2\left|j\right|}\Gamma \left(1-\left|j\right|\right)cos\left(\left|j\right|\pi \right)},& (78)\end{array}$

where Γ(z) is the gamma function. In Equation (78) one can verify that μ_ν controls, through ν, the contribution of the irregular solution J_−|j| for the wave function. Thus, the solution in this subspace reads

$\begin{array}{ll}{\psi }_m(r)=a_m\left[J_{\left|j\right|}(kr)-{\mu }_{\nu }{J}_{-\left|j\right|}(kr)\right].& (79)\end{array}$

We can observe that for ν = ∞, we obtain μ_∞ = 0 and, in this case, there is no contribution of the irregular solution at the origin for the wave function. Consequently, in this case, the total wave function becomes

$\begin{array}{ll}\psi ={\displaystyle \sum _{m=-\infty }^{\infty }}{a}_m{J}_{\left|j\right|}(kr)e^{im\phi }.& (80)\end{array}$

The coefficient a_m in Equation (80) must be chosen in such a way that ψ represents a plane wave that is incident from the right. In this case, we find the following result:

$\begin{array}{ll}{a}_m=e^{-i\left|j\right|\pi /2}.& (81)\end{array}$

The scattering phase shift can be obtained from the asymptotic behavior of Equation (80). This leads to

$\begin{array}{ll}{\delta }_m=\frac{\pi }{2}(\left|m\right|-\left|j\right|).& (82)\end{array}$

This is the scattering phase shift of the AB effect in the cosmic string spacetime [26, 59]. It is important to mention that, for α = 1, it reduces to the phase shift for the usual AB effect in flat space ${\delta }_m^{AB}=\pi (\left|m\right|-|m+\varphi |)/2$ [4].

On the other hand, for |ν| < ∞, the contribution of the irregular solution changes the scattering phase shift to

$\begin{array}{ll}{\delta }_m^{\nu }={\delta }_m+arctan({\mu }_{\nu }).& (83)\end{array}$

Thus, from standard results for the S-matrix, one obtains

$\begin{array}{ll}{S}_m^{\nu }=e^{2i{\delta }_m^{\nu }}=e^{2i{\delta }_m}\left(\frac{1+i{\mu }_{\nu }}{1-i{\mu }_{\nu }}\right),& (84)\end{array}$

which is the expression for the S-matrix given in terms of phase shift. It can be seen in (84) that there is an additional scattering for any value of the self-adjoint extension parameter ν. By choosing ν = ∞, we find the S-matrix for the AB effect in the cosmic string spacetime, as it should be.

Having obtained the S-matrix, the bound state energies can be identified as the poles of it in the upper half of the complex k plane. To find them, we need to examine the zeros of the denominator in Equation (84), 1 − iμ_ν, with the replacement k → iκ_b with ${\kappa }_b=\sqrt{2M{E}_b}$. Therefore, for ν < 0, the bound state energy is given by

$\begin{array}{ll}{E}_b=-\frac{2}{M}{\left[-\nu \frac{\Gamma (1+\left|j\right|)}{\Gamma (1-\left|j\right|)}\right]}^{1/\left|j\right|}.& (85)\end{array}$

Thus, for a fixed negative value of the self-adjoint extension parameter ν, there is a single bound state and the value 2|ν|^1/|j|/M fixes the energy scale. The result in Equation (85) coincides with the bound state energy found in references [26, 59] for the AB effect in curved space and is similar that one found in contact interactions of anyons [73]. It is also possible to express the S-matrix in terms of the bound state energy. The result is seen to be

$\begin{array}{ll}{S}_m^{\nu }=e^{2i{\delta }_m}\left[\frac{e^{2i\pi \left|j\right|}-{({\kappa }_b/k)}^{2\left|j\right|}}{1-{({\kappa }_b/k)}^{2\left|j\right|}}\right].& (86)\end{array}$

It is important to comment that the above results for the scattering matrix and the bound state energy (for ν < 0) are valid only when |j| < 1. Moreover, all the results are dependent on a free parameter, the self-adjoint extension parameter ν. In what follows we shall show that by employing the KS method, we can find an expression relating the self-adjoint extension parameter with physical parameters of the system.

3.2. Application of the KS Method

In this section, we employ the KS approach to find the bound states for the Hamiltonian in Equation (63). Following the discussion in section 2.3, we temporarily forget the δ-function potential in h and substitute the problem in Equation (62) by the eigenvalue equation for h₀,

$\begin{array}{ll}{h}_0{\psi }_{\rho }=k^2{\psi }_{\rho },& (87)\end{array}$

plus self-adjoint extensions. Here, ψ_ρ is labeled by the parameter ρ of the self-adjoint extension, which is related to the behavior of the wave function at the origin. To turn h₀ into a self-adjoint operator its domain of definition has to be extended by the deficiency subspace, which is spanned by the solutions of the eigenvalue equation (cf. Equation 4)

$\begin{array}{ll}{h}_0^{†}{\psi }_{\pm }=\pm i{k}_0^2{\psi }_{\pm },& (88)\end{array}$

where $k_0^2\in ℝ$ is introduced for dimensional reasons. Since h₀ is Hermitian, $h_0^{†}=h_0$, the only square integrable functions which are solutions of Equation (88) are the modified Bessel functions of second kind,

$\begin{array}{ll}{\psi }_{\pm }=K_{\left|j\right|}(\sqrt{\mp i}{k}_{0}r),& (89)\end{array}$

with $Im\sqrt{\pm i}>0$. These functions are square integrable only in the range j ∈ (−1, 1), for which h₀ is not self-adjoint. The dimension of such deficiency subspace is thus (n₊, n₋) = (1, 1), in agreement with the results of the previous sections. In this manner, ${D}(h_{\rho ,0})$ in L²(ℝ⁺, rdr) is given by the set of functions [22]

$\begin{array}{ll}{\psi }_{\rho }(r)={\psi }_m(r)+C\left[K_{\left|j\right|}(\sqrt{-i}{k}_{0}r)+e^{i\rho }{K}_{\left|j\right|}(\sqrt{i}{k}_{0}r)\right],& (90)\end{array}$

where ψ_m(r), with ${\psi }_m(0)={\dot{\psi }}_m(0)=0$, is the regular wave function and the mathematical parameter ρ ∈ [0, 2π) represents a choice for the boundary condition. For different values of ρ, we have different domains for h₀. and the adequate boundary condition will be determined by the physical system [5, 35, 36, 48]. Thus, in this direction, we use a physically motivated regularization for the magnetic field. So, we replace the original potential vector of the AB flux tube by the following one [6–8, 68]

$\begin{array}{ll}eA=\{\begin{array}{ll}-\frac{\varphi }{\alpha r}\widehat{\phi },\hfill & r>r_0,\hfill \\ 0,\hfill & r<r_0.\hfill \end{array}& (91)\end{array}$

where r₀ is a length that defines the defect core radius [35, 58], which is a very small radius smaller than the Compton wave length λ_C of the electron [31]. So one makes the replacement

$\begin{array}{ll}\frac{\delta (r)}{r}\to \frac{\delta (r-r_0)}{r_0}.& (92)\end{array}$

This regularized form for the delta function allows us to determine an expression for ρ. To do so, we consider the zero-energy solutions ψ₀ and ψ_{ρ, 0} for h with the regularization in (92) and h₀, respectively,

$\begin{array}{ll}\left[-\frac{d^2}{d{r}^2}-\frac{1}{r}\frac{d}{dr}+\frac{j^2}{r^2}+\lambda \frac{\delta (r-r_0)}{r_0}\right]{\psi }_0=0,& (93)\end{array}$

$\begin{array}{ll}\left[-\frac{d^2}{d{r}^2}-\frac{1}{r}\frac{d}{dr}+\frac{j^2}{r^2}\right]{\psi }_{\rho ,0}=0.& (94)\end{array}$

The value of ρ is determined by the boundary condition

$\begin{array}{ll}{\underset{r_0\to 0^{+}}{\lim }{r}_0\frac{{\dot{\psi }}_0}{{\psi }_0}|}_{r=r_0}={\underset{r_0\to 0^{+}}{\lim }{r}_0\frac{{\dot{\psi }}_{\rho ,0}}{{\psi }_{\rho ,0}}|}_{r=r_0}.& (95)\end{array}$

The left-hand side of Equation (95) can be obtained by the direct integration of (93) from 0 to r₀. The result seems to be

$\begin{array}{ll}{\underset{r_0\to 0^{+}}{\lim }{r}_0\frac{{\dot{\psi }}_0}{{\psi }_0}|}_{r=r_0}=\lambda .& (96)\end{array}$

The right-hand side of Equation (95) is calculated as follows. First, we seek the solutions of the bound states for the Hamiltonian h₀. These solutions will allow us to obtain the solutions of the bound states for h. As before, for the bound state, we consider k as a pure imaginary quantity, k → iκ_b. So, we have

$\begin{array}{ll}\left[\frac{d^2}{d{r}^2}+\frac{1}{r}\frac{d}{dr}-\left(\frac{j^2}{r^2}+{\kappa }_b^2\right)\right]{\psi }_{\rho }(r)=0,& (97)\end{array}$

The solution for the above equation is the modified Bessel functions

$\begin{array}{ll}{\psi }_{\rho }(r)=K_{\left|j\right|}({\kappa }_{b}r).& (98)\end{array}$

Second, we observe that these solutions belong to ${D}(h_{\rho ,0})$, such that it is of the form (90) for some ρ selected from the physics of the problem. So, we substitute (98) into (90) and compute ${lim}_{r_0\to 0^{+}}{r}_0{\dot{\psi }}_{\rho }/{\psi }_{\rho }{|}_{r=r_0}$ by using the asymptotic representation for K_ν(z) in the limit z → 0, which is given by

$\begin{array}{ll}{K}_{\nu }(z)~\frac{\pi }{2sin(\pi \nu )}\left[\frac{z^{-\nu }}{2^{-\nu }\Gamma (1-\nu )}-\frac{z^{\nu }}{2^{\nu }\Gamma (1+\nu )}\right].& (99)\end{array}$

After a straightforward calculation, we have the relation

$\begin{array}{ll}{\underset{r_0\to 0^{+}}{\lim }{r}_0\frac{{\dot{\psi }}_{\rho ,0}}{{\psi }_{\rho ,0}}|}_{r=r_0}=\frac{|j|\left[r_0^{2|j|}\Gamma (1-|j|){({\kappa }_b/2)}^{|j|}+2^{|j|}\Gamma (1+|j|)\right]}{r_0^{2|j|}\Gamma (1-|j|){({\kappa }_b/2)}^{|j|}-2^{|j|}\Gamma (1+|j|)}=\lambda ,& (100)\end{array}$

where we used Equations (95) and (96). Then, solving the above equation for E_b, we find the sought bound state energy

$\begin{array}{ll}{E}_b=-\frac{2}{M{r}_0^2}{\left[\left(\frac{\lambda +\left|j\right|}{\lambda -\left|j\right|}\right)\frac{\Gamma (1+\left|j\right|)}{\Gamma (1-\left|j\right|)}\right]}^{1/\left|j\right|}.& (101)\end{array}$

Now, that we have the bound state energy obtained from BG and KS methods we can compare their results. Thus comparing (85) with (101) we have the following relation

$\begin{array}{ll}\nu =-\frac{1}{r_0^{2\left|j\right|}}\left(\frac{\lambda +\left|j\right|}{\lambda -\left|j\right|}\right).& (102)\end{array}$

So, we have obtained a relation between the self-adjoint extension parameter and physical parameters of the system.

4. Conclusions

In this work, we have discussed the self-adjoint extension approach to deal with singular Hamiltonians in (2 + 1) dimensions. Two different methods, both based on the self-adjoint extension approach were discussed in details. The BG and KS methods were applied to solve the problem of a spin-1/2 charged particle with an anomalous magnetic moment in the curved space. The presence of the spin gives rise to a point interaction, requiring the use of the self-adjoint extension approach to solving the problem. In the BG method, the S-matrix was determined and from its poles, one bound state energy expression was obtained. These results were obtained by imposing a suitable boundary condition and depend on the self-adjoint extension parameter, which can be identified as the inverse of the scattering length of the Hamiltonian. Nevertheless, from the mathematical point of view, this parameter is arbitrary. Then, by applying the KS method, an expression for the bound state energy for the same system was obtained, and it is given in terms of physical parameters of the system. Thus comparing the results from both methods a relation between the self-adjoint extension parameter and physical parameters was obtained.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

FA and ES conceived of the presented idea. VS and RC performed the computations. FA and ES verified the analytical methods. All authors discussed the results and contributed to the final manuscript.

Funding

This work was partially supported by the Brazilian agencies CNPq (Grants No. 313274/2017-7, No. 434134/3028-0, 427214/2016-5, and 303774/2016-9), Fundação Araucária (Grant No. 09/2017), FAPEMA (Grants No. 01852/14 and No. 01202/16). This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior-Brasil (CAPES)-Finance Code 001.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^There is a missprint in the signal of the term sN in π_±(α, β) in reference [14].

References

1. Case KM. Singular potentials. Phys Rev. (1950) 80:797.

Google Scholar

2. Kronig RL, Penney WG. Quantum mechanics of electrons in crystal lattices. Proc R Soc Lond A. (1931) 130:499.

Google Scholar

3. Albeverio S, Gesztesy F, Hoegh-Krohn R, Holden H. Solvable Models in Quantum Mechanics. 2nd ed. AMS Chelsea Publishing (2004). Available online at: http://books.google.com.br/books?id=cR6uhyqnpUQC

Google Scholar

4. Aharonov Y, Bohm D. Significance of electromagnetic potentials in the quantum theory. Phys Rev. (1959) 115:485.

Google Scholar

5. de Sousa Gerbert P. Fermions in an Aharonov-Bohm field and cosmic strings. Phys Rev D. (1989) 40:1346.

Google Scholar

6. Hagen CR. Aharonov-Bohm scattering of particles with spin. Phys Rev Lett. (1990) 64:503.

PubMed Abstract | Google Scholar

7. Hagen CR. Spin dependence of the Aharonov-Bohm effect. Int J Mod Phys A. (1991) 6:3119.

Google Scholar

8. Hagen CR. Effects of nongauge potentials on the spin-1/2 Aharonov-Bohm problem. Phys Rev D. (1993) 48:5935.

PubMed Abstract | Google Scholar

9. Hagen CR, Park DK. Relativistic Aharonov-Bohm-Coulomb problem. Ann Phys. (1996) 251:45.

Google Scholar

10. Geltman S. Bound states in delta function potentials. J Atomic Mol Opt Phys. (2011) 2011:4. doi: 10.1155/2011/573179

CrossRef Full Text | Google Scholar

11. Molina MI, Bustamante CA. The attractive nonlinear delta-function potential. Am J Phys. (2002) 70:67–70. doi: 10.1119/1.1417529

CrossRef Full Text | Google Scholar

12. Aharonov Y, Casher A. Topological quantum effects for neutral particles. Phys Rev Lett. (1984) 53:319–21.

Google Scholar

13. Shikakhwa MS, Al-Qaq E. The div E term does not change the Aharonov–Casher scattering cross section. J Phys A. (2010) 43:354008. doi: 10.1088/1751-8113/43/35/354008

CrossRef Full Text | Google Scholar

14. Andrade FM, Filgueiras C, Silva EO. Scattering and bound states of a spin-1/2 neutral particle in the cosmic string spacetime. Adv High Energy Phys. (2017) 2017:7. doi: 10.1155/2017/8934691

CrossRef Full Text | Google Scholar

15. Silva EO, Andrade FM, Filgueiras C, Belich H. On Aharonov-Casher bound states. Eur Phys J C. (2013) 73:2402. doi: 10.1140/epjc/s10052-013-2402-1

CrossRef Full Text | Google Scholar

16. Silvestro F, Fabio R, Stefano V. The spectrum of the SchrödingerHamiltonian for trapped particles in a cylinder with a topological defect perturbed by two attractive delta interactions. Int J Geom Methods Mod Phys. (2018) 15:1850135. doi: 10.1142/S0219887818501359

CrossRef Full Text | Google Scholar

17. Erman F, Gadella M, Uncu H. One-dimensional semirelativistic Hamiltonian with multiple Dirac delta potentials. Phys Rev D. (2017) 95:045004. doi: 10.1103/PhysRevD.95.045004

CrossRef Full Text | Google Scholar

18. Erman F, Gadella M, Uncu H. On scattering from the one-dimensional multiple Dirac delta potentials. Eur J Phys. (2018) 39:035403. doi: 10.1088/1361-6404/aaa8a3

CrossRef Full Text | Google Scholar

19. Al-Hashimi MH, Shalaby AM, Wiese UJ. Asymptotic freedom, dimensional transmutation, and an infrared conformal fixed point for the δ-function potential in one-dimensional relativistic quantum mechanics. Phys Rev D. (2014) 89:125023. doi: 10.1103/PhysRevD.89.125023

CrossRef Full Text | Google Scholar

20. Hughes RJ. Relativistic Kronig-Penney-type Hamiltonians. Integr Equ Oper Theory. (1998) 31:436–48. doi: 10.1007/BF01228101

CrossRef Full Text | Google Scholar

21. Bovier A, Ghez JM. Remarks on the spectral properties of tight-binding and Kronig-Penney models with substitution sequences. J Phys A. (1995) 28:2313–24.

Google Scholar

22. Reed M, Simon B. Methods of Modern Mathematical Physics. II. Fourier Analysis, Self-Adjointness. New York, NY; London: Academic Press (1975).

23. Akhiezer NI, Glazman IM. Theory of Linear Operators in Hilbert Space. New York, NY: Dover (1993).

Google Scholar

24. Kowalski K, Podlaski K, Rembieliński J. Quantum mechanics of a free particle on a plane with an extracted point. Phys Rev A. (2002) 66:032118. doi: 10.1103/PhysRevA.66.032118

CrossRef Full Text | Google Scholar

25. de Oliveira CR. Intermediate Spectral Theory and Quantum Dynamics. Basel; Boston, MA; Berlin: Birkhäuser Basel (2008).

Google Scholar

26. Andrade FM, Silva EO, Pereira M. Physical regularization for the spin-1/2 Aharonov-Bohm problem in conical space. Phys Rev D. (2012) 85:041701(R). doi: 10.1103/PhysRevD.85.041701

CrossRef Full Text | Google Scholar

27. Gesztesy F, Albeverio S, Hoegh-Krohn R, Holden H. Point interactions in two dimensions: Basic properties, approximations and applications to solid state physics. J Reine Angew Math. (1987) 380:87.

Google Scholar

28. de Sousa Gerbert P, Jackiw R. Classical and quantum scattering on a spinning cone. Commun Math Phys. (1989) 124:229.

Google Scholar

29. Jackiw RW. Diverse Topics in Theoretical and Mathematical Physics. Advanced Series in Mathematical Physics. Singapore: World Scientific (1995).

Google Scholar

30. Voropaev SA, Galtsov DV, Spasov DA. Bound states for fermions in the gauge Aharonov-Bohm field. Phys Lett B. (1991) 267:91–4.

Google Scholar

31. Bordag M, Voropaev S. Bound states of an electron in the field of the magnetic string. Phys Lett B. (1994) 333:238–44.

Google Scholar

32. Bordag M, Voropaev S. Charged particle with magnetic moment in the Aharonov-Bohm potential. J Phys A. (1993) 26:7637.

Google Scholar

33. Park DK, Oh JG. Self-adjoint extension approach to the spin-1/2 Aharonov-Bohm-Coulomb problem. Phys Rev D. (1994) 50:7715–20.

PubMed Abstract | Google Scholar

34. Park DK. Green's-function approach to two- and three-dimensional delta-function potentials and application to the spin-1/2 Aharonov-Bohm problem. J Math Phys. (1995) 36:5453.

Google Scholar

35. Filgueiras C, Moraes F. On the quantum dynamics of a point particle in conical space. Ann Phys. (2008) 323:3150–7. doi: 10.1016/j.aop.2008.08.002

CrossRef Full Text | Google Scholar

36. Filgueiras C, Silva EO, Oliveira W, Moraes F. The effect of singular potentials on the harmonic oscillator. Ann Phys. (2010) 325:2529. doi: 10.1016/j.aop.2010.05.012

CrossRef Full Text | Google Scholar

37. Vilenkin A, Shellard EPS. Cosmic Strings and Other Topological Defects. Canbridge: Cambridge University Pres (2000).

Google Scholar

38. Wang Z, Xu C. Discussion on the geometric phase for an open two-level system in the cosmic string spacetime with torsion. Europhys Lett. (2019) 126:50005. doi: 10.1209/0295-5075/126/50005

CrossRef Full Text | Google Scholar

39. Moshinsky M, Szczepaniak A. The Dirac oscillator. J Phys A. (1989) 22:L817.

Google Scholar

40. Sadurni E. The Dirac-Moshinsky oscillator: theory and applications. AIP Conf Proc. (2011) 1334:249–90. doi: 10.1063/1.3555484

CrossRef Full Text | Google Scholar

41. Hosseinpour M, Hassanabadi H, de Montigny M. The Dirac oscillator in a spinning cosmic string spacetime. Eur Phys J C. (2019) 79:311. doi: 10.1140/epjc/s10052-019-6830-4

CrossRef Full Text | Google Scholar

42. Andrade FM, Silva EO. Effects of spin on the dynamics of the 2D Dirac oscillator in the magnetic cosmic string background. Eur Phys J C. (2014) 74:3187. doi: 10.1140/epjc/s10052-014-3187-6

CrossRef Full Text | Google Scholar

43. Alford MG, Wilczek F. Aharonov-Bohm interaction of cosmic strings with matter. Phys Rev Lett. (1989) 62:1071–4.

PubMed Abstract | Google Scholar

44. Bakke K, Furtado C. Bound states for neutral particles in a rotating frame in the cosmic string spacetime. Phys Rev D. (2010) 82:084025. doi: 10.1103/PhysRevD.82.084025

CrossRef Full Text | Google Scholar

45. Filgueiras C, Moraes F. The bound-state Aharonov-Bohm effect around a cosmic string revisited. Phys Lett A. (2007) 361:13. doi: 10.1016/j.physleta.2006.09.030

CrossRef Full Text | Google Scholar

46. Frolov VP, Serebriany EM. Vacuum polarization in the gravitational field of a cosmic string. Phys Rev D. (1987) 35:3779–82.

PubMed Abstract | Google Scholar

47. da Costa RCT. Quantum mechanics of a constrained particle. Phys Rev A. (1981) 23:1982–7.

Google Scholar

48. Filgueiras C, Silva EO, Andrade FM. Nonrelativistic quantum dynamics on a cone with and without a constraining potential. J Math Phys. (2012) 53:122106. doi: 10.1063/1.4770048

CrossRef Full Text | Google Scholar

49. Silva EO, Ulhoa SC, Andrade FM, Filgueiras C, Amorin RGG. Quantum motion of a point particle in the presence of the Aharonov–Bohm potential in curved space. Ann Phys. (2015) 362:739. doi: 10.1016/j.aop.2015.09.011

CrossRef Full Text | Google Scholar

50. Andrade FM, Chumbes AR, Filgueiras C, Silva EO. Quantum motion of a point particle in the presence of the Aharonov-Bohm potential in curved space: viewpoint of scattering theory. arXiv:1608.00173 (2019).

Google Scholar

51. Sakurai JJ, Napolitano J. Modern Quantum Mechanics. 2nd ed. Boston, MA: Addison-Wesley (2011).

Google Scholar

52. Cohen-Tannoudji C, Diu B, Laloe F. Quantum Mechanics. John Wiley & Sons Inc (1977). Available online at: https://www.ebook.de/de/product/3236937/claude_cohen_tannoudji_bernard_diu_frank_laloe_quantum_mechanics_volume_1.html

Google Scholar

53. Shankar R. Principles of Quantum Mechanics. New York, NY: Springer (1994).

Google Scholar

54. Gasiorowicz S. Quantum Physics. John Wiley & Sons Inc (2003). Available online at: https://www.ebook.de/de/product/6374000/stephen_gasiorowicz_quantum_physics.html

Google Scholar

55. Ballentine Leslie E. Quantum Mechanics: A Modern Development. World Scientific (1998). Available online at: https://www.ebook.de/de/product/4350566/ballentine_leslie_e_quantum_mechanics_a_modern_development.html

Google Scholar

56. Bonneau G, Faraut J, Valent G. Self-adjoint extensions of operators and the teaching of quantum mechanics. Am J Phys. (2001) 69:322. doi: 10.1119/1.1328351

CrossRef Full Text | Google Scholar

57. Bulla W, Gesztesy F. Deficiency indices and singular boundary conditions in quantum mechanics. J Math Phys. (1985) 26:2520.

Google Scholar

58. Kay BS, Studer UM. Boundary conditions for quantum mechanics on cones and fields around cosmic strings. Commun Math Phys. (1991) 139:103.

Google Scholar

59. Andrade FM, Silva EO, Pereira M. On the spin-1/2 Aharonov-Bohm problem in conical space: bound states, scattering and helicity nonconservation. Ann Phys. (2013) 339:510–30. doi: 10.1016/j.aop.2013.10.001

CrossRef Full Text | Google Scholar

60. Sokolov DD, Starobinski AA. The structure of the curvature tensor at conical singularities. Sov Phys Dokl. (1977) 22:312.

Google Scholar

61. Mohr PJ, Newell DB, Taylor BN. CODATA recommended values of the fundamental physical constants: 2014. Rev Mod Phys. (2016) 88:035009. doi: 10.1103/RevModPhys.88.035009

CrossRef Full Text | Google Scholar

62. Pollock MD. On the Dirac equation in curved space-time. Acta Phys Pol B. (2010) 41:1827. Available online at: http://www.actaphys.uj.edu.pl/fulltext?series=Reg&vol=41&page=1827

Google Scholar

63. Bakke K, Nascimento JR, Furtado C. Geometric phase for a neutral particle in the presence of a topological defect. Phys Rev D. (2008) 78:064012. doi: 10.1103/PhysRevD.78.064012

CrossRef Full Text | Google Scholar

64. Lima DF, Andrade FM, Castro LB, Filgueiras C, Silva EO. On the 2D Dirac oscillator in the presence of vector and scalar potentials in the cosmic string spacetime in the context of spin and pseudospin symmetries. Eur Phys J C. (2019) 79:596. doi: 10.1140/epjc/s10052-019-7115-7

CrossRef Full Text | Google Scholar

65. Khalilov VR. Bound states of massive fermions in Aharonov-Bohm-like fields. Eur Phys J C. (2014) 74:2708. doi: 10.1140/epjc/s10052-013-2708-z

CrossRef Full Text | Google Scholar

66. Khalilov VR. Creation of planar charged fermions in Coulomb and Aharonov-Bohm potentials. Eur Phys J C. (2013) 73:2548. doi: 10.1140/epjc/s10052-013-2548-x

CrossRef Full Text | Google Scholar

67. Khalilov V, Mamsurov I. Scattering of a neutral fermion with anomalous magnetic moment by a charged straight thin thread. Theor Math Phys. (2009) 161:1503–12. doi: 10.1007/s11232-009-0137-9

CrossRef Full Text | Google Scholar

68. Hagen CR. Exact equivalence of spin-1/2 Aharonov-Bohm and Aharonov-Casher effects. Phys Rev Lett. (1990) 64:2347–9.

PubMed Abstract | Google Scholar

69. Adami R, Teta A. On the Aharonov–Bohm Hamiltonian. Lett Math Phys. (1998) 43:43–54.

Google Scholar

70. Dabrowski L, Stovicek P. Aharonov–Bohm effect with delta-type interaction. J Math Phys. (1998) 39:47–62.

Google Scholar

71. Ruijsenaars SNM. The Aharonov-Bohm effect and scattering theory. Ann Phys. (1983) 146:1.

Google Scholar

72. Hagen CR. Comment on “Relativistic Aharonov-Bohm effect in the presence of planar Coulomb potentials”. Phys Rev A. (2008) 77:036101. doi: 10.1103/PhysRevA.77.036101

CrossRef Full Text | Google Scholar

73. Manuel C, Tarrach R. Contact interactions of anyons. Phys Lett B. (1991) 268:222–6.

Google Scholar