- 1Dipartimento di Scienze e Metodi dell'Ingegneria, Università di Modena e Reggio Emilia, Modena, Italy
- 2Dipartimento di Scienze Matematiche, Politecnico di Torino, Turin, Italy
- 3Istituto Nazionale di Fisica Nucleare, Sezione di Torino, Turin, Italy
- 4Malaysia-Italy Centre of Excellence for Mathematical Sciences, Universiti Putra Malaysia, Seri Kembangan, Malaysia
- 5Dipartimento di Scienze Fisiche, Informatiche e Matematiche, Università di Modena e Reggio Emilia, Modena, Italy
Statistical mechanics harmonizes mechanical and thermodynamical quantities, via the notion of local thermodynamic equilibrium (LTE). In absence of external drivings, LTE becomes equilibrium tout court, and states are characterized by several thermodynamic quantities, each of which is associated with negligibly fluctuating microscopic properties. Under small driving and LTE, locally conserved quantities are transported as prescribed by linear hydrodynamic laws, in which the local material properties of the system are represented by the transport coefficients. In 1-dimensional systems, on the other hand, various anomalies are reported, such as the dependence of the heat conductivity on the global state, rather than on the local state. Such deductions, that rely on the existence of thermodynamic quantities like temperature and heat, are here interpreted within the framework of boundary driven 1-dimensional Lennard-Jones chains of N oscillators. It is found that these chains experience non-negligible O(N) lattice distortions, resulting in strongly inhomogeneous systems, and O(N) position fluctuations, that are in contrast with the requirements of LTE.
1. Introduction
In a seminal paper, Rieder, Lebowitz, and Lieb investigated the properties of chains of N harmonic oscillators, interacting at their ends with stochastic heat baths [1]. These authors proved that while energy flows from hot to cold baths, the kinetic temperature profile decreases exponentially in the direction of the hotter bath, rather than increasing, and in the bulk its slope vanishes as N grows. Thus, in case the kinetic temperature equals the thermodynamic temperature, heat flows against the direction of energy, in the bulk of such 1D systems. Were this a real fact, no steady state would be reached, because at the boundaries heat would flow in opposite directions and indefinitely accumulate. On the contrary, Rieder et al. [1] proves the existence of and explicitly expresses the steady state. Taken in Rieder et al. [1] as a paradox without explanation, this fact is now understood as related to the absence of phononic interactions in harmonic chains [2], and it reveals that, in harmonic chains, the kinetic temperature does not correspond to the thermodynamic temperature, or the energy flux does not represent a heat flux, or both.
Thermodynamically peculiar behaviors are realized in anharmonic chains as well. In particular, 1D chains of N oscillators without on-site potentials, and conserving momentum, generically enjoy anomalous transport, i.e., the divergence with N of the thermal conductivity, , where TR and TL are the temperatures at the two ends of a chain and 〈J〉 is the average heat flux [2–5]. On the other hand, evidence of normal transport in chains with asymmetric interactions, such as Lennard-Jones potentials, is reported in Zhong et al. [6] and Chen et al. [7]. Unexpected phenomena that seem to contradict the hydrodynanmic laws of transport, e.g., currents going against the density gradient, a phenomenon called “uphill diffusion,” can be observed in several experimental settings. In e.g., Colangeli et al. [8], the readers my find further references and a non-equilibrium model with phase transition exhibiting uphill diffusion, whose thermodynamic relevance is still under investigation.
The fact is that temperature and heat pertain to macroscopic objects with microscopic states corresponding to Local Thermodynamic Equilibrium (LTE); they cannot be directly identified with mechanical quantities such as kinetic energy and energy flux, Landau and Lifshitz [9], section 9 and Chibbaro et al. [10] chapters 3, 4, and 5. LTE is the essence of Thermodynamics: it can be viewed at once as the precondition for the existence of the thermodynamic fields, such as temperature and heat, and as the natural state of objects obeying the thermodynamic laws. The microscopic conditions under which LTE is expected to hold are extensively discussed in the literature, e.g., [11] section 15.1, [12] section 2.3, [13] section 3.3, [14] chapter 1. In short, LTE requires the existence of three well-separated time and space scales, so that: (1) a macroscopic object can be subdivided in mesoscopic cells that look like a point to macroscopic observers, while containing a large number of molecules; (2) boundary effects are negligible compared to bulk effects, so that the contributions of neighboring cells to the mass and energy of a given cell are inappreciable within a cell; (3) particle interactions allow the cells to thermalize (positions and velocities become respectively uniformly and Maxwell-Boltzmann distributed) within times that are mere instants on the macroscopic scale.
That macroscopic observables are not affected by microscopic fluctuations, despite the exceedingly disordered and energetic microscopic motions, is essential for mesoscopic quantities to be sufficiently stable that thermodynamic laws apply, e.g., Landau and Lifshitz [9], section 1 and 2. This is the case for a quantity that is spatially weakly inhomogeneous, when the number N of particles in a cell is large, and the molecular interactions randomize positions and momenta so that, for instance, the fluctuations of a quantity ϕ of size O(N) are order . The bulk of the cell then dominates in- and out-fluxes, and variations of ϕ are sufficiently slow on the mesoscopic scale.
Quantitatively, the space and time scales for which this description holds depend on the properties of the microscopic components of the systems of interest, [11–16]. However, the general rule is that fluctuations be negligible compared to the signal of interest; were e.g., position fluctuations large, two solids could kick each other, when placed at a short distance from each other. This, of course, is impossible in the thermodynamic realm (see also Exercise 4.5 in [17]).
Under the LTE condition, matter can be considered a continuum, obeying hydrodynamic laws, i.e., balance equations for locally conserved quantities, such as mass, momentum and energy [12, 18–20]. For small to moderate driving, they take a linear form, in which the local material properties are expressed by the linear transport coefficients. Locality implies that such coefficients do not depend on the conditions of the system far away from the considered region. The thermal conductivity of an iron bar at a given temperature at a given point in space does not depend on the conditions of the bar far from that region; cutting the bar in two, or joining it to another bar, without changing the local state, leaves unchanged its local properties.
Fluctuations remain of course present in systems made of particles; they are larger for larger systems, they may be observed [21, 22], and they play a major role in many circumstances (see e.g., [23, 24]). This motivates a considerable fraction of research in statistical physics, e.g.,[25, 26], concerning scales much smaller than the macroscopic ones, or occurring in low dimensional (1D and 2D) systems [4, 27–30]. In these phenomena, the linear transport coefficients do not always seem to exist [4], the robustness of the thermodynamic laws appear to be violated, and the behaviors appear to be strongly affected by boundary conditions and by all parameters that characterize a given object [7, 31–37]. It is also well-known that chains of oscillators behave more like some kind of (non-standard) fluids than like solids, because of the loss of crystalline structure, caused by cumulative position fluctuations [38]. Consequently, a fluid-like (possibly fluctuating) description has been adopted in a number of papers, cf. [39, 40].
In driven systems, the situation is problematic also because equipartition may be violated [41–43], the state of the system is model dependent, and the ergodic properties are partially understood [44, 45]. Hence, there is no universal agreement on the microscopic notion of temperature in non-equilibrium conditions [43, 46–51]. Further, a microscopic definition of heat flux requires a clear distinction between convection, i.e., energy transport due to macroscopic motions, and conduction, that is transport without macroscopic motions, cf. Chapter 4 of Zemansky and Dittman [52], and section III.2 and Chapter XI of De Groot et al. [18]. In 1D systems, this may not always be possible [53].
One interpretation of these facts is that LTE is violated in some situations, hence that thermodynamic concepts, such as heat and temperature, may be inappropriate [33, 34]. Another interpretation is that thermodynamic notions should be modified to treat small and strongly non-equilibrium systems (see e.g.,[46–49]). It is therefore interesting to investigate the validity and universality of the mechanical counterparts of thermodynamic quantities, in situations in which LTE is not expected to hold, and “anomalous” phenomena have been reported.
We address such questions considering chains of N Lennard-Jones oscillators interacting with deterministic baths at their ends, and without on-site potentials. We mainly focus on two quantities: the distortion of the equilibrium lattice and the fluctuations of the particles, whose position will be denoted by xi's. The former is the displacement of the average of xi with respect to its mechanical equilibrium value, while the latter is the standard deviation of xi. Our central findings are that:
• thermostats at different temperatures induce O(N) distortions of the equilibrium lattice, resulting in highly in-homogeneous chains;
• thermostats induce collective order O(N) fluctuations, i.e., “macroscopic” motions. Negligible incoherent vibrations typical of 3D equilibrium systems are thus replaced by kind of convective motions, even in chains bounded by still walls.
Note that these are two well distinct effects; the latter is crucial in our investigation, since it hinders thermodynamic properties, cf. section 3. Combined with the results of Rieder et al. [1] and further literature, e.g., [41, 46–50], this suggests that microscopic definitions appropriate for 3-dimensional equilibrium thermodynamic quantities, need extra scrutiny in 1D. As an example of the effects on observables of both O(N) lattice distortions and position fluctuations, we consider the notion of heat flux, J say, given by Equation (23) of Lepri et al. [2]. This confirms from a different standpoint conclusions reached in previous studies on the inapplicability of standard hydrodynamics [54, 55]. Note that Equation (23) of Lepri et al. [2] has been criticized as an incorrect expression for the “heat flow.” In fact, it would only reduce to the correct expression, e.g., Equation (3.8) of Spohn [12], (a) apart from a dimensional constant, (b) if the position in space could be identified with the position of one particle, and (c) if position fluctuations about the equilibrium lattice positions would be totally negligible. Such negligible fluctuations would at once satisfy one of the conditions for the validity of LTE, allow the particle position to play the role of a position in space, and make valid the periodic lattice assumption of Lepri et al. [2]. Therefore, this quantity suits us, in order to illustrate the effect of non-negligible fluctuations and of lattice distortions. We find that:
• J is not spatially uniform in steady states. Variations of J decrease if the baths temperature difference is reduced at constant N, but they do not if the mean temperature gradient is reduced increasing N at constant baths temperatures.
• Dividing J by the local mass density partially balances the lattice inhomogeneity and yields an approximately uniform quantity. This suggests that, although relevant, the lattice deformation is not the only reason for J to fail.
These observations should be combined with those of Giberti et al. [53] and Lepri et al. [55], according to which collective and molecular motions are correlated, making hard to disentangle convection from conduction. Whatever their motion, single particles push their neighbors, producing kinds of convective cascades. That difficulties do not ease when N grows, because of O(N) fluctuations and lattice distortions, explains why LTE, hence thermodynamic quantities, cannot be established in our 1D systems.
2. Chains of Lennard-Jones Oscillators
Consider a 1D chain of N identical moving particles of equal mass m, and positions xi, i = 1, …, N. Add two particles with fixed positions, x0 = 0 and xN + 1 = (N + 1)a, where a is the lattice spacing. Let nearest neighbors interact via the Lennard-Jones potential (LJ):
where r is the distance between nearest neighbors: r = |xi − xi−1| and ϵ > 0 is the depth of the potential well. Thus, xi = ai, with i = 0, …, N + 1, is a configuration of stable mechanical equilibrium for the system. We also consider interactions involving first and second nearest neighbors, with second potential given by [56, 57]:
where s = |xi − xi−2|. Further, we add two particles with fixed positions x−1 = − a and xN + 2 = (N + 2)a. With potential V = V1 + V2, the system has the usual stable mechanical equilibrium configuration xi = ai, i = −1, …, N + 2. The first and last moving particles are in contact with two Nosé-Hoover thermostats, at kinetic temperatures TL (on the left) and TR (on the right) and with relaxation times θL and θR. Introducing the forces
the equations of motion are given by:
with
in the case of nearest neighbors interaction. For first and second neighbors interactions, we have:
with
The hard-core nature of the LJ potentials preserves the order of particles: 0 < x1 < x2 < ··· < xN < (N + 1)a holds at all times, if it does at the initial time1.
For such systems, a form of single particle virial relation is often found to hold2. That fact is usually mentioned to identify the average kinetic energy of a given particle with the temperature Ti in position xi [2]:
Here, pi is the momentum of particle i, the angular brackets 〈·〉 denote time average, and Ti is called single particle kinetic temperature.
However, the validity of Equation (10) does not imply a Maxwell-Boltzmann distribution of velocities, corresponding to a thermodynamic temperature [53]. Indeed, for TL ≠ TR, the single particle kinetic temperature profile may take rather peculiar forms, compared to the linear thermodynamic temperature profiles in homogeneous solids when Fourier law holds. This is illustrated in great detail in the specialized literature, cf.[2–4, 34, 59–63] just to cite a few. Also, numerically simulated profiles of various kinds of 1D systems, appear to be sensitive to parameters such as the relaxation constants of the thermostats, the interaction parameters, the form of the boundaries etc. cf. e.g., [34]. This is not surprising, since many correlations persist in space and time in low dimensional systems, hindering the realization of LTE and leading to anomalous behaviors [33, 54, 55, 64–70]. As a further testimony of the complex behavior of 1D chains, we mention that heat conductivity may depend on details of the interaction potential such as its asymmetry; see [6, 7] in which evidence is given for normal conductivity in chains with LJ potential.
In the following sections, we report our results about systems with various numbers of particles N. The parameters defining the Lennard-Jones potentials are ϵ = 1 and a = 1, while the mass of the particles is m = 1. The relaxation times of the thermostats θL and θR are set to 1. The numerical integrator used is the fourth-order Runge-Kutta method with step size 10−3. The time averages are typically taken over O(108) − O(109) time steps in the stationary state.
3. Large Lattice Deformations and Fluctuations
The distinction between the different states of aggregation of matter is not strictly possible in 1D systems with short range interactions; one nevertheless realizes that our oscillators chains are more similar to (a kind of) compressible fluids than to solids [34, 54]. In particular, Lepri et al. [55] shows persistent correlations, O(N) dependence of relaxation times, and the failure of standard hydrodynamics, in non-driven LJ systems. Along similar lines of inquiry, we investigated two different effects in non-equilibrium conditions: the distortion of the equilibrium lattice and the size of the fluctuations of the particles.
For the first, we find that temperature differences at the boundaries of the chains induce “macroscopic” deformations of the periodic structure of the lattice; cf. Zhong et al. [6] for the influence of the asymmetry of the potential on such phenomenon. For all i, we obtain (〈xi 〉 − ia) ~ O(N), as shown in Figure 1, whose right panel plots the quantity as a function of N. Consequently, for sufficiently large N the system cannot be treated as a spatially homogeneous object.
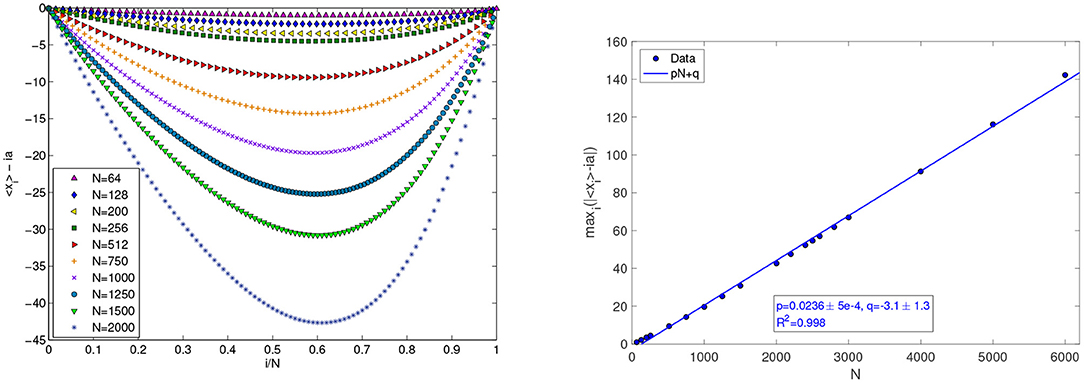
Figure 1. (Left) Plot of the displacement of the mean position of particle i from its mechanical equilibrium position, (〈xi 〉 − ia), for different values of N, for first and second neighbors interaction, when TL = 1 and TR = 10. The lattice is strongly distorted in presence of temperature differences. (Right) Linear fit of as a function of N ranging from 64 to 6000, for N > 400. The label of the particle corresponding to the maximum lattice distortion is fitted by imld = 0.6063N − 6.804 with R2 = 0.9997.
Our second observation, which concerns fluctuations, is that the presence of thermostats at different temperatures enhances the size of the vibrations, given by , of each particle i about its average position 〈xi〉. Such vibrations are order O(i1/2) in chains without thermostats with origin in i = 0 [38], which means that, for sufficiently large i, position fluctuations are incompatible with a crystal structure. In our framework, the length of chains is bounded, therefore the size of particle vibrations cannot indefinitely grow with particle index i: the vibrations are larger for particles in the bulk than for particles near the boundaries of the chains, see the left panel of Figure 2 More precisely, we find that for every particle i, the size of vibrations can be called “macroscopic”: . In the right panel of Figure 2 and in Figure 3, square root fits and linear fits are compared for N ranging from 64 to 6000. The square root fits are appropriate for small N, while at large N the linear fit takes over. The size of these vibrations appears even more striking observing that displacing by a large amount one of them, a whole collection of particles must be correspondingly displaced. Indeed, the repulsive part of the LJ potential does not allow particles' order to be modified, as noted also in Lepri et al. [55]. As observed e.g., in Giberti and Rondoni [34], this kind of constraint leads to long-range correlations, that necessarily develop while the O(N) fluctuations observed here take place. Concerning thermodynamics, they are in fact like the two sides of a coin: both long range correlations and large spatial fluctuations break locality, connecting mesoscopic cells over long distances. This violates the conditions for the validity of LTE, which require mesoscopic cells to be small independent equilibrium systems [14]. Absence of LTE in our systems was already noted e.g., Giberti et al. [53], in which non-Maxwellian velocities distributions were portrayed.
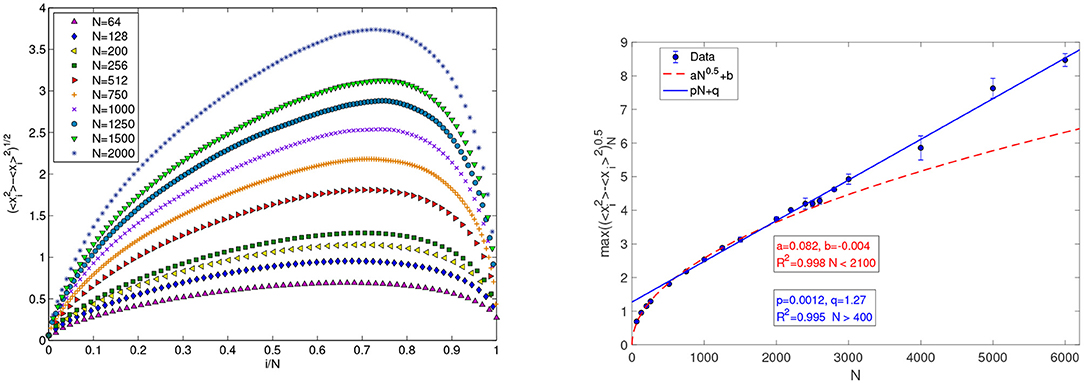
Figure 2. (Left) Standard deviations of the particles vibrations about their average position, in lattice vectors units, for the case of Figure 1. (Right) Dependence on N (ranging from 64 to 6000) of the maximum standard deviation together with a linear fit for N > 400 (continuous blue line) and one square root fit for lattices with N < 2100 (dashed red line). Growing linearly with N, collective vibrations look like convective motions. The label of the particle corresponding to the maximum fluctuation amplitude is fitted by imfa = 0.7398N − 6.75 with R2 = 0.9993.
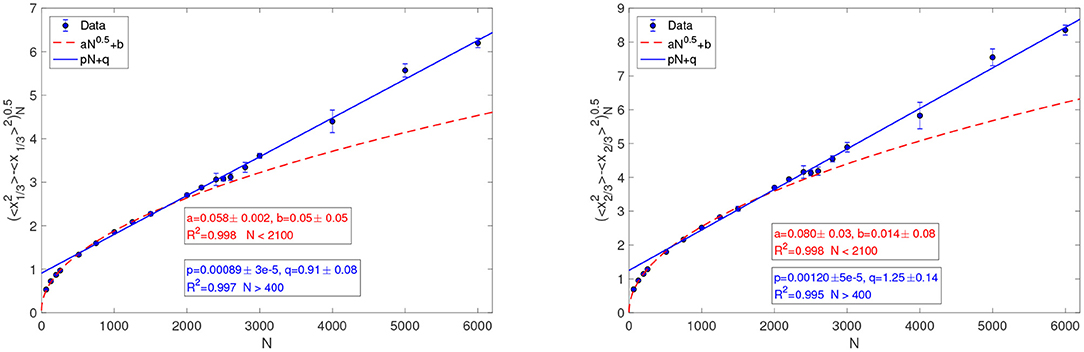
Figure 3. (Left) Dependence on N of the standard deviations of the vibrations of particles at 1/3 of the chain. (Right) Dependence on N of the standard deviations of the vibrations at 2/3 of the chain. In both cases, a square root and a linear fit are drawn. The square root fit holds at small N. At large N the linear fit takes over. In both panels N ranges from 64 to 6000. Particles motions look more like some kind of convection rather than like microscopic lattice vibrations.
As a result, the motion of particles about their average positions is not an irregular motion about fixed positions. In accord with the observations on persistent correlations, this motion looks like a kind of convection, although LTE and standard hydrodynamics do not hold [34, 39, 40, 54, 55]. It follows that, in these cases, energy transport cannot be directly related to “heat” flows.
The situation is different for TL = TR. Figure 4 shows that the lattice deformations are much smaller than the lattice spacing a, and can be neglected. The computed values of (〈xi 〉 − ia) practically vanish and do not depend on N. The standard deviation of the vibrations about the mean position is represented in the left panel of Figure 5 and it appears to be closer to than to O(N) as can be seen in the right panel of Figure 5. In this case, in which there is no net energy transport, the system also behaves more like a fluid than like a solid in sense closer to that of Peierls [38], although our results refers to a different situation.
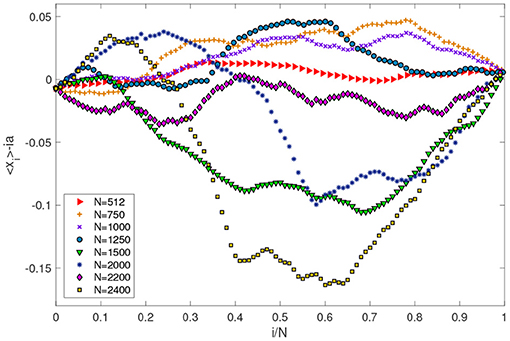
Figure 4. Equilibrium simulations. Plot of the displacement of the mean position of particle i from its mechanical equilibrium position, 〈xi 〉 − ia, for various values of N, for first and second neighbors interactions when TL = TR = 5. The deviations from the mechanical equilibrium are negligible.
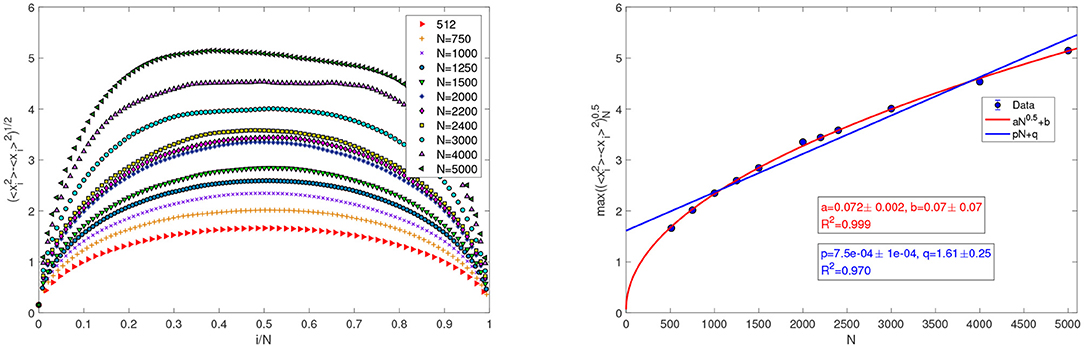
Figure 5. Equilibrium simulations (TL = TR = 5) for N ranging from 512 to 5000. (Left) Standard deviations of the particles vibrations about their average position (xi − 〈xi〉), in lattice vectors units. (Right) Dependence on N of the maximum standard deviation, together with linear and square root fits. This dependence on N should not be confused with the dependence on i of Peierls [38].
4. Energy Balance
In order to understand the effect of O(N) fluctuations and lattice distortions on LTE, we now consider, as an example, the “heat flux” Ji given by Equation (23) of Lepri et al. [2]. Note, exact expressions for the energy balance about single particles exist, e.g., Equation (17) of Lepri et al. [2]. Nevertheless, Ji, which had been presented as more accurate than Equation (17) of Lepri et al. [2], is here interesting because, in presence of LTE, it does correspond to a heat flux, apart from a dimensional constant, which is irrelevant for our investigation. Then, as the energy current flowing between neighboring particles labeled by i and i + 1 should not depend on i, the same should happen to the time average 〈Ji〉. In this section, we investigate whether this holds or not. A critical analysis of Equation (23) of Lepri et al. [2] as a heat flux is provided in Mejía-Monasterio et al. [71].
For the case of first and second nearest neighbors interactions, the expression given by Equation (23) of Lepri et al. [2] must be modified as follows:
where F1 and F2 are defined by Equation (3) and hi is the energy of the i-th particle.
The quantity Ji is only apparently “local” because it quantifies a flow through the position of particle i, and not through a fixed position in space. Moreover, it implicitly requires small position fluctuations and small lattice deformations, because Equation (11) is obtained through Fourier analysis for spatially homogeneous systems, in the limit of small wave vectors, [2, 28]. For instance, denoting by k the wave-vector, Equation (23) of Lepri et al. [2] follows from Equation (21) only if k(xn + 1 − xn) is small. On the contrary, in our cases, this quantity strongly varies in space and time, and average lattice distortions are of order O(N), cf. section 3. Therefore, one expects Ji to fail, and it is interesting to investigate how that is realized, varying the relevant model parameters.
For chains with nearest neighbors Lennard-Jones interactions [F2 ≡ 0 in Equation (11)], we find that while the steady state heat flow should not depend on position, the time average of Ji substantially changes with i, cf. Figure 6. To quantify this phenomenon, we introduce the relative variation of 〈Ji〉,
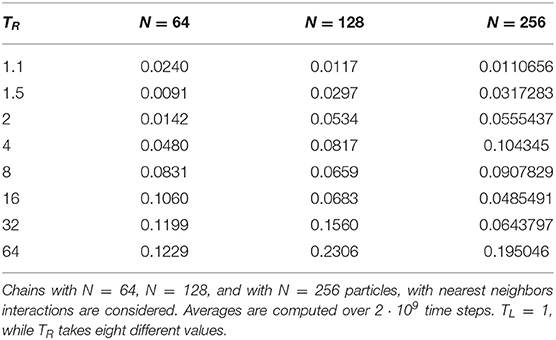
In Tables 1, 2, for average temperature gradients similar to those commonly found in the literature [62, 63, 72], we observe that δ tends to grow with the temperature gradient, at fixed N. In general, however, reducing the average gradient by increasing the system size, does not lead to smaller δ 3.
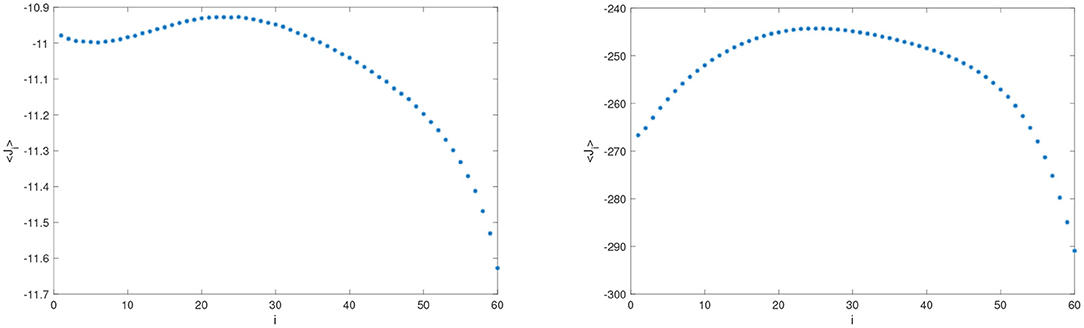
Figure 6. Chains with nearest neighbors Lennard-Jones interactions. (Left) Flux 〈Ji〉 computed according to Equation (11), for N = 64, TL = 1, TR = 4. (Right) 〈Ji〉 for N = 64, TL = 1, TR = 64.
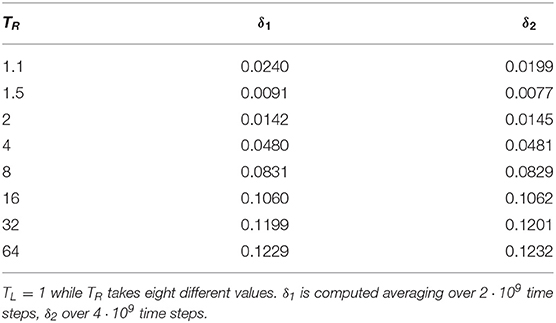
Table 1. Relative variation δ of the flux Ji for N = 64 particles with first and second nearest neighbors interactions.
We conclude that under our conditions the quantity Ji represents neither a heat nor an energy flow, and that this is not a consequence of the size of temperature gradients, but of the size of fluctuations. These increase with growing N, thus preventing LTE and standard hydrodynamics in the large N limit [34, 54, 55]. One may nevertheless ask whether the observed features of Ji are merely due to the deformation of the lattice, which invalidates the Fourier expansion of Lepri et al. [2]. One may thus take into account the lattice deformations and restore the correct units, normalizing Ji by the average distance between particles, as follows:
This quantity, that should not be taken as a correct alternative to the definition of heat flux, is indeed approximately constant as a function of i. This is shown in Figure 7, where results more stable than Ji as a function of i, thus indicating that the lattice inhomogeneity is one cause of error in Ji. However, the spurious fluctuations visible in Figure 7, reveal that lattice deformations are only one of the difficulties affecting Ji as a definition of heat flux.
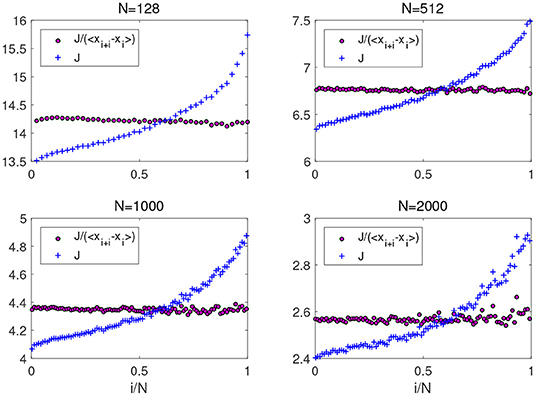
Figure 7. Normalized energy flux Jn (o) and the flux J (+) defined by Equation (11) for chains of different lengths (N = 128, 512, 1,000, 2,000) and with TL = 1 and TR = 10. Although Jn is not exactly constant, at large N it enjoys small fluctuations about a given average value.
5. Concluding Remarks
In this work we have presented numerical results on one 1D chains of Lennard-Jones oscillators, in contact with two Nosé-Hoover thermostats. Scrutinizing the behavior of mechanical quantities that are commonly considered in the specialized literature, we have investigated the fluctuations and lattice distortions, which are expected to prevent the onset of “thermodynamic” regimes [33, 34, 50, 55].
The thermodynamic behavior emerges from the collective behavior of very large assemblies of interacting particles, provided that two conditions are met: rapid (compared to observation time scales) decay of correlation and negligible boundary effects. These conditions often take place for 3D mesoscopic cells containing large numbers of properly interacting particles, but it is not obvious in 1D systems. Indeed, quoting Spohn: “The propagation of local equilibrium in time, if true, is a deep and highly non-obvious property of a system of many particles governed by Newton's equations of motion”, see [12] section 3.1.
In particular, we have observed that temperature differences at the boundaries produce O(N) deformations of the lattice, that result in strongly inhomogeneous systems, and O(N) position fluctuations that hinder LTE. In turn, we have observed that such O(N) effects imply that increasing N, and correspondingly decreasing “temperature gradient,” does not lead our systems any closer to thermodynamic systems. Consequently, as observed also elsewhere, standard hydrodynamics does not apply [34, 54, 55]. This must be taken into account when defining e.g., the heat conductivity, because its anomalies are necessarily related to the absence of LTE.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
This work is partially supported by Gruppo Nazionale per la Fisica Matematica (GNFM-INdAM). CG and CV acknowledge financial supports from Fondo di Ateneo per la Ricerca 2016 and Fondo di Ateneo per la Ricerca 2017- Università di Modena e Reggio Emilia. LR has been partially supported by Ministero dell'Istruzione dell'Università e della Ricerca (MIUR) grant Dipartimenti di Eccellenza 2018–2022.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors are grateful to Carlos Mejia-Monasterio for extensive discussions and enlightening remarks. The authors are grateful to Antonio Politi for very useful suggestions. Antonio Politi, in particular has suggested the normalization of the energy flux.
Footnotes
1. ^In some cases, we extended the Lennard-Jones interaction to the third nearest neighbors, preserving the equilibrium configuration xi = ia. The corresponding equations of motion and thermostats are the natural modification of the previous ones, hence are not reported here.
2. ^In Falasco et al. [58] a nonequilibrium mesoscopic version of the virial relation in given.
3. ^Actually, for mere energy flows, there is no reason to be bounded by small temperature gradients.
References
1. Rieder Z, Lebowitz JL, Lieb E. Properties of a harmonic crystal in a stationary nonequilibrium state. J Math Phys. (1967) 8:1073. doi: 10.1063/1.1705319
2. Lepri S, Livi R, Politi A. Thermal conduction in classical low-dimensional lattices. Phys Rep. (2003) 377:1–80. doi: 10.1016/S0370-1573(02)00558-6
3. Dhar A. Heat Transport in low-dimensional systems. Adv Phys. (2008) 57:457–537. doi: 10.1080/00018730802538522
4. Lepri S, editor. Thermal transport in low dimensions - From Statistical Physics to Nanoscale Heat Transfer. In: Lecture Notes in Physics, Vol. 921. Heidelberg: Springer (2016). p. 1–411.
5. Lepri S, Livi R, Politi A. Heat transport in low dimensions: introduction and phenomenology. In: Lepri S, editor. Thermal Transport in Low Dimensions - From Statistical Physics to Nanoscale Heat Transfer. Lecture Notes in Physics Vol. 921. Heidelberg: Springer (2016).
6. Zhong V, Zhang Y, Wang J, Zhao H. Normal heat conduction in one-dimensional momentum conserving lattices with asymmetric interactions. Phys Rev E. (2012) 85:060102(R). doi: 10.1103/PhysRevE.85.060102
7. Chen S, Zhang Y, Wang J, Zhao H. Key role of asymmetric interactions in low-dimensional heat transport. J Stat Mech. (2016) 2016:033205. doi: 10.1088/1742-5468/2016/03/033205
8. Colangeli M, Giardinà C, Giberti C, Vernia C. Nonequilibrium two-dimensional Ising model with stationary uphill diffusion. Phys Rev E. (2018) 97:030103(R). doi: 10.1103/PhysRevE.97.030103
9. Landau LD, Lifshitz EM. Statistical Physics. Volume 5 of Course of Theoretical Physics, Part 1. Oxford: Pergamon Press (1980). p. 544.
10. Chibbaro S, Rondoni L, Vulpiani A. Reductionism, Emergence and Levels of Reality. New York, NY: Springer Verlag (2014). p. 154.
11. Kondepudi D, Prigogine I. Modern Thermodynamics: From Heat Engines to Dissipative Structures. Chichester: John Wiley & Sons Ltd (1998). p. 486.
12. Spohn H. Large Scale Dynamics of Interacting Particles, Texts and Monographs in Physics. Heidelberg: Springer-Verlag (1991). p. 342.
13. Bellissard J. Coherent and dissipative transport in aperiodic solids: an overview. In: Garbaczewski P, Olkiewicz R, editors. Dynamics of Dissipation. Berlin: Springer Verlag (2002). p. 413–85.
14. Kreuzer HJ. Nonequilibrium Thermodynamics and Its Statistical Foundations. Oxford: Claredon Press (1981). p. 458.
15. Falcioni M, Palatella L, Pigolotti S, Rondoni L, Vulpiani A. Initial growth of Boltzmann entropy and chaos in a large assembly of weakly interacting systems. Physica A. (2007) 385:170–84. doi: 10.1016/j.physa.2007.06.036
16. Rondoni L, Pigolotti S. On Γ− and μ−space descriptions: Gibbs and Boltzmann entropies of symplectic coupled maps. Phys Scr. (2012) 86:058513. doi: 10.1088/0031-8949/86/05/058513
18. De Groot SR, Mazur P. Non-equilibrium Thermodynamics. New York, NY: Dover Publication (1984). p. 528.
19. Cohen EGD, Rondoni L. Note on phase space contraction and entropy production in thermostatted hamiltonian systems. Chaos. (1998) 8:357. doi: 10.1063/1.166317
20. Rondoni L, Cohen EGD. On some derivations of irreversible thermodynamics from dynamical systems theory. Physica D. (2002) 168–9:341–55. doi: 10.1016/S0167-2789(02)00522-5
21. Bonaldi M, Conti L, De Gregorio P, Rondoni L, Vedovato G, Vinante A, et al. Nonequilibrium steady-state fluctuations in actively cooled resonators. Phys Rev Lett. (2009) 103:010601. doi: 10.1103/PhysRevLett.103.010601
22. Conti L, Bonaldi M, Rondoni L. RareNoise: non-equilibrium effects in detectors of gravitational waves. Class Quantum Grav. (2010) 27:084032. doi: 10.1088/0264-9381/27/8/084032
23. Mishin Y. Thermodynamic theory of equilibrium fluctuations. Ann Phys. (2015) 363:48–97. doi: 10.1016/j.aop.2015.09.015
24. Hickman J, Mishin Y. Temperature fluctuations in canonical systems: insights from molecular dynamics simulations. Phys Rev B. (2016) 94:184311. doi: 10.1103/PhysRevB.94.184311
25. Seifert U. Stochastic thermodynamics, fluctuation theorems and molecular machines. Rep Prog Phys. (2012) 75:126001. doi: 10.1088/0034-4885/75/12/126001
26. Benenti G, Casati G, Saito K, Whitney RS. Fundamental aspects of steady-state conversion of heat to work at the nanoscale. Phys Rep. (2017) 694:1–124. doi: 10.1016/j.physrep.2017.05.008
27. Gao Z, Li N, Li B. Heat conduction and energy diffusion in momentum-conserving one-dimensional full-lattice ding-a-ling model. Phys Rev E. (2016) 93:022102. doi: 10.1103/PhysRevE.93.022102
28. Das SG, Dhar A, Narayan O. Heat conduction in the α - β Fermi-Pasta-Ulam chain. J Stat Phys. (2014) 154:204–13. doi: 10.1007/s10955-013-0871-0
29. Liu S, Hänggi P, Li N, Ren J, Li B. Anomalous heat diffusion. Phys Rev Lett. (2014) 112:040601. doi: 10.1103/PhysRevLett.112.040601
30. Wang J, Casati G. One dimensional self-organization and nonequilibrium phase transition in a Hamiltonian system. Phys Rev Lett. (2017) 118:040601. doi: 10.1103/PhysRevLett.118.040601
31. Chang CW, Okawa D, Garcia H, Majumdar A, Zettl A. Breakdown of Fourier's law in nanotube thermal conductors. Phys Rev Lett. (2008) 101:075903. doi: 10.1103/PhysRevLett.101.075903
32. Xu X, Pereira LF, Wang Y, Wu J, Zhang K, Zhao X, et al. Length-dependent thermal conductivity in suspended single-layer graphene. Nat Commun. (2014) 5:3689. doi: 10.1038/ncomms4689
33. Jepps OG, Rondoni L. Thermodynamics and complexity of simple transport phenomena. J Phys A. (2006) 39:1311–38. doi: 10.1088/0305-4470/39/6/007
34. Giberti C, Rondoni L. Anomalies and absence of local equilibrium, and universality, in one-dimensional particles systems. Phys Rev E. (2011) 83:041115. doi: 10.1103/PhysRevE.83.041115
35. Chen S, Zhang Y, Wang J, Zhao H. Diffusion of heat, energy, momentum and mass in one-dimensional systems. Phys Rev E. (2013) 87:032153. doi: 10.1103/PhysRevE.87.032153
36. Onorato M, Vozella L, Proment D, Lvov YV. Route to thermalization in the α-Fermi–Pasta–Ulam system. Proc Natl Acad Sci USA. (2015) 112:4208–13. doi: 10.1073/pnas.1404397112
37. Dhar A, Saito K. Heat conduction in the disordered Fermi-Pasta-Ulam chain. Phys Rev E. (2008) 78:061136. doi: 10.1103/PhysRevE.78.061136
38. Peierls R. Chapter 4: Melting in one, two and three dimensions. In: Surprises in Theoretical Physics, Princeton Series in Physics. Princeton, NJ: Princeton University Press (1979). p. 176.
39. Narayan O, Ramaswamy S. Anomalous heat conduction in one-dimensional momentum-conserving systems. Phys Rev Lett. (2002) 89:200601. doi: 10.1103/PhysRevLett.89.200601
40. Mai T, Narayan O. Universality of one-dimensional heat conductivity. Phys Rev E. (2006) 73:061202. doi: 10.1103/PhysRevE.73.061202
41. Conti L, De Gregorio P, Karapetyan G, Lazzaro C, Pegoraro M, Bonaldi M, et al. Effects of breaking vibrational energy equipartition on measurements of temperature in macroscopic oscillators subject to heat flux. J Stat Mech. (2013) 12:P12003. doi: 10.1088/1742-5468/2013/12/P12003
42. Ortiz de Zárate JM, Sengers JV. Hydrodynamic Fluctuations in Fluids and Fluid Mixtures. Amsterdam: Elsevier (2006). p. 320.
43. Puglisi A, Sarracino A, Vulpiani A. Temperature in and out of equilibrium: a review of concepts, tools and attempts. Phys Rep. (2017) 709–10:1–60. doi: 10.1016/j.physrep.2017.09.001
45. Evans DJ, Williams SR, Searles DJ, Rondoni L. On Typicality in Nonequilibrium Steady States. J Stat Phys. (2016) 164:842–57. doi: 10.1007/s10955-016-1563-3
46. Morriss GP, Rondoni L. Definition of temperature in equilibrium and nonequilibrium systems. Phys Rev E. (1999) 59:R5. doi: 10.1103/PhysRevE.59.R5
47. Casas-Vázquez J, Jou D. Temperature in non-equilibrium states: a review of open problems and current proposals. Rep Prog Phys. (2003) 66:1937–2023. doi: 10.1088/0034-4885/66/11/R03
48. Jou D, Restuccia L. Caloric and entropic temperatures in non-equilibrium steady states. Physica A. (2016) 460:246–53. doi: 10.1016/j.physa.2016.04.034
49. Cao X, He D. Interfacial thermal conduction and negative temperature jump in one-dimensional lattices. Phys Rev E. (2015) 92:032135. doi: 10.1103/PhysRevE.92.032135
50. Jou DJ, Casas-Vàzquez J, Lebon G. Extended Irreversible Thermodynamics. New York, NY: Springer-Verlag (2010). p. 463.
51. Criado-Sancho M, Jou D, Casas-Vázquez J. Nonequilibrium kinetic temperatures in flowing gases. Phys Lett A. (2006) 350:339–41. doi: 10.1016/j.physleta.2005.10.043
53. Giberti C, Rondoni L, Vernia C. Temperature and correlations in 1-dimensional systems. Eur Phys J Spec Top. (2019) 228:129. doi: 10.1140/epjst/e2019-800138-8
54. Hurtado PI. Breakdown of hydrodynamics in a simple one-dimensional fluid. Phys Rev Lett. (2006) 96:010601. doi: 10.1103/PhysRevLett.96.010601
55. Lepri S, Sandri P, Politi A. The one-dimensional Lennard-Jones system: collective fluctuations and breakdown of hydrodynamics. Eur Phys J B. (2005) 47:549–55. doi: 10.1140/epjb/e2005-00360-7
56. De Gregorio P, Rondoni L, Bonaldi M, Conti L. One-dimensional models and thermomechanical properties of solids. Phys Rev B. (2011) 84:224103. doi: 10.1103/PhysRevB.84.224103
57. Conti L, De Gregorio P, Bonaldi M, Borrielli A, Crivellari M, Karapetyan G, et al. Elasticity of mechanical oscillators in nonequilibrium steady states: experimental, numerical, and theoretical results. Phys Rev E. (2012) 85:066605. doi: 10.1103/PhysRevE.85.066605
58. Falasco G, Baldovin F, Kroy K, Baiesi M. Mesoscopic virial equation for nonequilibrium statistical mechanics. New J Phys. (2016) 18:093043. doi: 10.1088/1367-2630/18/9/093043
59. Delfini L, Lepri S, Livi R, Politi A. Self-consistent mode-coupling approach to one-dimensional heat transport. Phys Rev E. (2006) 73:060201(R). doi: 10.1103/PhysRevE.73.060201
60. Lepri S, Mejía-Monasterio C, Politi A. Nonequilibrium dynamics of a stochastic model of anomalous heat transport. J Phys A. (2010) 43:065002. doi: 10.1088/1751-8113/43/6/065002
61. Delfini L, Lepri S, Livi R, Mejía-Monasterio C, Politi A. Nonequilibrium dynamics of a stochastic model of anomalous heat transport: numerical analysis. J Phys A. (2010) 43:145001. doi: 10.1088/1751-8113/43/14/145001
62. Lepri S, Livi R, Politi A. Heat conduction in chains of nonlinear oscillators. Phys Rev Lett. (1997) 78:1896–9. doi: 10.1103/PhysRevLett.78.1896
63. Lepri S, Livi R, Politi A. Energy transport in anharmonic lattices close to and far from equilibrium. Physica D. (1998) 119:140–7. doi: 10.1016/S0167-2789(98)00076-1
64. Davie SJ, Jepps OG, Rondoni L, Reid JC, Searles DJ. Applicability of optimal protocols and the Jarzynski equality. Phys Scr. (2014) 89:048002. doi: 10.1088/0031-8949/89/04/048002
65. Jepps O, Bianca C, Rondoni L. Onset of diffusive behaviour in confined transport systems. Chaos. (2008) 18:013127. doi: 10.1063/1.2888759
66. Bianca C, Rondoni L. The nonequilibrium Ehrenfest gas: a chaotic model with flat obstacles? Chaos. (2009) 19:013121. doi: 10.1063/1.3085954
67. Salari L, Rondoni L, Giberti C, Klages R. A simple non-chaotic map generating subdiffusive, diffusive and superdiffusive dynamics. Chaos. (2015) 25:073113. doi: 10.1063/1.4926621
68. Spohn H. Nonlinear fluctuating hydrodynamics for anharmonic chains. J Stat Phys. (2014) 154:1191–227. doi: 10.1007/s10955-014-0933-y
69. Mendl CB, Spohn H. Dynamic correlators of Fermi-Pasta-Ulam chains and nonlinear fluctuating hydrodynamics. Phys Rev Lett. (2013) 111:230601. doi: 10.1103/PhysRevLett.111.230601
70. van Beijeren H. Exact results for anomalous transport in one-dimensional hamiltonian systems. Phys Rev Lett. (2012) 108:180801. doi: 10.1103/PhysRevLett.108.180601
71. Mejía-Monasterio C, Politi A. Rondoni L. Heat flux in one-dimesional systems. arXiv [preprint]. arXiv:1905.03326.
Keywords: chains of oscillators, local thermodynamic equilibrium, lattice distortion, macroscopic fluctuations, Lennard-Jones potential
Citation: Giberti C, Rondoni L and Vernia C (2019) O(N) Fluctuations and Lattice Distortions in 1-Dimensional Systems. Front. Phys. 7:180. doi: 10.3389/fphy.2019.00180
Received: 26 July 2019; Accepted: 23 October 2019;
Published: 12 November 2019.
Edited by:
Ralf Metzler, University of Potsdam, GermanyReviewed by:
Punyabrata Pradhan, S. N. Bose National Centre for Basic Sciences, IndiaHerbert Spohn, Technical University of Munich, Germany
Copyright © 2019 Giberti, Rondoni and Vernia. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Claudio Giberti, Y2xhdWRpby5naWJlcnRpQHVuaW1vcmUuaXQ=
†Present address: Lamberto Rondoni, Civil and Environmental Engineering Department, Princeton Environmental Institute, Princeton University, Princeton, NJ, United States
‡ORCID: Lamberto Rondoni orcid.org/0000-0002-4223-6279
 Claudio Giberti
Claudio Giberti Lamberto Rondoni
Lamberto Rondoni Cecilia Vernia
Cecilia Vernia