- Department of Chemical Engineering, University of Chemical Technology and Metallurgy, Sofia, Bulgaria
The heat transfer in living tissues is an evergreen problem in mathematical modeling with great practical importance starting from the Pennes equation postulation. This study focuses on concept in model building, the correct scaling of the bio-heat equation (one-dimensional) by appropriate choice of time and length scales, and consequently order of magnitude analysis of effects, as well as fractionalization approaches. Fractionalization by different constitutive approaches, leading to application of different fractional differential operators, modeling the finite speed of the heat wave, is one of the principle problems discussed in the study. The correct choice of the damping (relaxation) function of the heat flux is of primarily importance in the formulation of the bio-heat equation with memory. Moreover, this affects the consequent scaling, order of magnitude analysis and solutions.
Model building is the art of selecting those aspects of a process that are relevant to the question being asked - J.H Holland.
(Holland, JH (1995) Hidden Order.
Addison-Wesley, New York, USA.)
1. Introduction
All biological bodies live in space-depended temperature fields (environments), that is even in single organism there are no uniform temperatures of organs and tissues [1]. The non-uniformity of the temperature fields causes energy transfer between the organs (and tissues) with the perfused blood as wells at the body interface trough the skin [1].
Heat transfer in living tissues is a complex process and the mathematical modeling needs simplifications allowing to apply its methods. Hereafter, we will consider, in general, human bio-heat problems where the core body temperature is maintained at a level of 36–37°C. Cases related to organisms which body temperature varies as the external temperature changes (the so-called poikilothermic organisms [2]) are out of the scope of this work. In general, the heat exchange between a living body and the environment, taking place through the skin, involves mechanisms of conduction, convection,radiation and perspiration (consisting of separation and evaporation of sweat) [3, 4]. In medical applications, for instance, heat transfer procedures such as cryosurgery, radio-frequency and laser thermal ablations, thermal resections, ultrasound, etc. [5–7] need not only experimental data but also deep understanding of the basic mechanisms of heat transport and adequate mathematical modeling.
The human body temperature is affected by many factors, such as: environmental conditions, temperatures of media surrounding tissues, metabolism in muscles and blood circulation. We will briefly comment two heat transfer processes involved in the basic models discussed further in this work:
(i) Heat transfer through the skin (section 1.1), and
(ii) Blood circulation and its contribution to the overall heat exchange in the body (section 1.2). Moreover, basic steps in formalization of the heat fluxes due to different causes such as conduction, convection and metabolic heat generation are commented prior to the analysis of the bio-heat models (section 1.3).
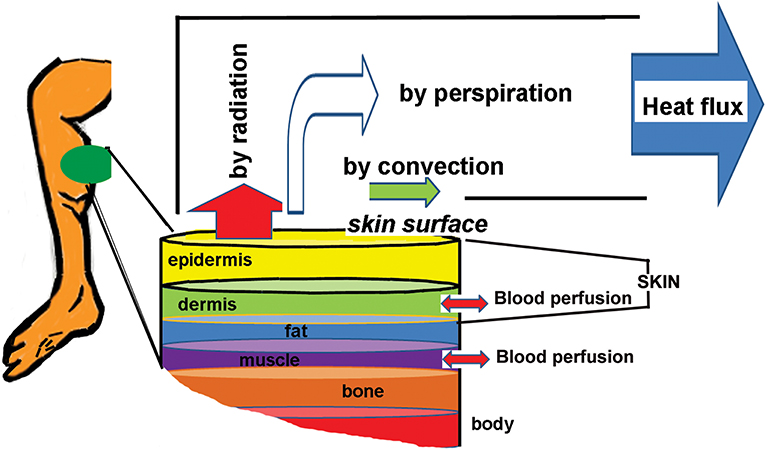
1.1. Heat Exchange Through the Skin
Skin is the largest single organ of the body [1] enabling protection from the surrounding environment and playing significant role in thermoregulation, sensory and host defense functions. The primary role of thermoregulation compromises heat generation, absorption, radiation, transmission and vaporization [1]. That is, the primary process occurring at the skin (and through the skin) is the thermal energy exchange with the environment. In humans the skin properties (structure and thickness) depend on the location and its function [1, 8]. The skin includes two layers epidermis and dermis [7, 9]. The former allows heat release by convection, radiation and perspiration (see Figure 1). In this context, the typical forearm skin temperature is about 31°C [7, 10] while the bone temperature is about 33°C. Hence, the increase in the temperature of a deep tissue requires higher temperatures to be imposed at the skin surface. The thermoregulation of the body, by help of the skin functions, is mainly by changing the blood flow rate in the micro-circulatory bed consisting of arterioles, arterial and vein capillaries, and venules [1]. In this context, an increase in the skin temperature to 42°C results in increased blood circulations (see below) in order to dissipate a portion of the thermal energy and to permit increase in the heat conduction mechanism through the deep tissue beneath [10, 11]. Last but not least, body fat affects strongly both the skin and deep tissue temperatures when the human body is at rest [11].
The common thermophysical parameters of the human skin are (collected from different sources) [1, 12–14]: density (ρ = 1.000 − 1.005[kg/m3]), heat conductivity (k = 0.5 − 0.628[W/mK]), heat capacity (c = 4.187 − 4.200[Jkg/K]). As it is shown by many authors (see data collected in [15]) the interior tissue temperature attains a constant value at a short distance from the surface, commonly this happens at a depth of 2–3 cm. Because of that in many studies the finite length of the tissue volume under consideration, commonly denoted as L, is within this range.
1.2. Blood Circulation and Heat Exchange at a Glance
Blood perfused tissues structures include layers of skin, fats, muscles and bones (see the schematic presentation vessels (see Figure 2A) (after [9]). Moreover, the blood circulation, trough the two principle sets of arteries and veins, is the principle mechanism in the body thermal regulation (see Figure 2B): Blood leaving the heart via the aorta (the largest blood vessel with a diameter of about 5000 μm is transported to the muscles through the arteries and the veins with diameters within the range of 300–1,000 μm: primary arteries with diameters of 100–300 μm are supplying blood to the secondary arteries 50–100 μm in diameter. Then, the blood is delivered to arterioles 20–40 μm connected to the smallest transport vessels, the capillaries [9]. The returning blood loop to the heart consists of veins.
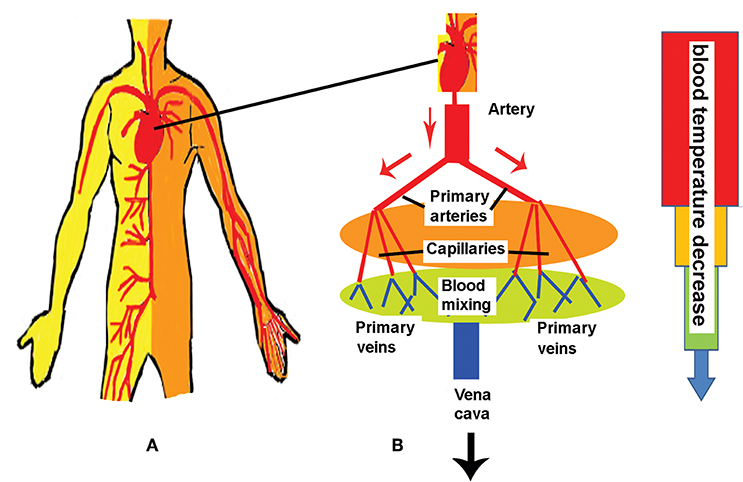
Figure 2. Schematic presentations of human body circulatory system (A) and blood temperature distributions through the vessels of the circulatory system (B). See comments in the text.
The blood is leaving the aorta (with a temperature Ta) practically does not exchange energy with the tissue up to the point where it enters the primary arteries where thermal equilibration with the surrounding tissue begins; this process completes before the points where the blood enters the arterioles and the capillaries. Further, the blood flow attains the temperature of the perfused tissue Tt and its value does not vary too much (if it is not mixed with other blood streams) [9]. The chilled blood from the peripheral tissues and the hot blood from the internal organs are mixed in the vena cava and the right atrium, and ventricle. The next heat transfer steps of the blood circulation are the pulmonary circulation and remixing in left heart chamber: this allows the blood to attain the temperature at which it left the heart at the beginning of its flow through the circulation system [9, 16].
The thermoregulation due to blood circulation and perfusion, in accordance with prevailing theories, is to maintain the body core temperature at a constant value required for the normal physiological functions [17]. Alternatively, the blood circulations should maintain the body energy balance and therefore the tissue temperatures are results, not the causes for the thermoregulation process [18, 19].
The common blood parameters involved in the bio-heat models are Torvi and Dale [12], Yamada et al. [13], and Askarizadeh and Ahmadikia [14]: temperature (), metabolic heat generation () perfusion rate (volumetric rate per unit tissue volume, i.e., ().
Note 1: Sometimes the blood perfusion rate is repressed as mass blood flux per unit mass of the tissue, that is [15]. The reader should take care what is the dimension used in a specific study, that mainly affects the nondimensalization procedures.
1.3. Bio-Heat Modeling Formalization
Analyzes of thermal energy balances in various biological tissues are multifaceted due to differences in tissue structures and functions. The relative importance of a certain heat transfer mechanism, the relevant time scale of the deposited energy and as well as differences in boundary and initial conditions strongly affect the energy balance [20]. In modeling, commonly simplifying assumptions are necessary thus making possible to model the basic properties of the thermal status of the organism (or its parts) and the effects of the boundary and initial conditions. The build-up of such models, in general, begins with application of the energy balance law over a control volume [20]
That is, the rate of heat gained is balanced by the heat stored and heat loss (by conduction or heat exchange with advanced fluids), and the rate of work W performed by the tissue [20]. Precisely, the heat gain (2) due to heat generated by unit tissue segment q(r, t) and heat energy storage (3) can be expressed as integral over the control volume V, namely
Further, we will restrict the heat transfer mechanisms to only conduction and convection in order to make clearer the following analyzes of the models, their scaling and consequently generated dimensionless groups, and the fractionalization when the thermal inertial should be taken into account. In bio-heat transfer problems the heat conduction mechanism is commonly modeled by the Fourier law when no inertia is taken into account, that is
where kt is the tissue heat conductivity with dimension [W/m · K], which is usually temperature-dependent; this transport coefficient strongly depends on the microscopic structures of the biological materials. In differential form the conduction component of the heat flux through the issue (per unit area) [W/m2] is
while the convection (perfusion) fluid-body term is
The heat transfer coefficient (fluid-solid surface) h [W/m2 · K] is dependent on the fluid velocity. In biological tissue the fluid-related heat transfer should be contributed to the blood perfusion and flow distribution due the heterogeneity of the living structures. Mathematically representing the blood perfusion component of the bio-heat thermal flux (through unit area of the tissue) qb [W/m2] the structure of the relationship is the same as in the case of heat transfer at the solid-fluid boundary (as in the case of simple blood flow in a cylindrical vessel commented in section 2.2). However, now the flux is proportional to the difference between the blood temperature in the artery (denoted as Tart or Ta) and the venous level temperature Tven, namely
The choice of this temperature difference is a matter of arguments as we will see in the sequel when model constructions will be discussed. However, at a glance, these are the only practically measurable temperatures when thermal sensors have to be introduced in the living organism, despite the physical models assumptions considering another temperature differences. However, it could be considered that in capillary beds the very slow blood flows attain complete thermal equilibria with the tissues; consequently the perfusion associated heat flux (7) could be approximated as
Hence, under such circumstances, the energy transfer by the blood stream, over the entire control volume, is (in original notations)
The result (9) is a not unconditional, despite the fact that it is frequently encountered in model formulations; in larger arteries it would be not valid due to strong blood mixing [20].
After considering the different heat transport mechanisms we may construct the balance of thermal energy (neglecting the work performed by the tissue) over an arbitrary volume element as
In one dimensional case and homogeneous distributed source of metabolic heat Qm we get
This is the standard form of the heat transfer through living organisms (tissues) or bio-heat transfer equation. We will discuss it components and assumptions behind, which may vary under circumstances imposed by the modeled object, as well the contribution of the transport mechanism involved by scaling and dimensional analysis. The study addresses three principle issues in bio-heat modeling:
(i) Models building concept,
(ii) Model scaling and nondimensalization and
(iii) Model fractionalization by involving fractional operators.
1.4. Motivation of This Study
Working in the modern direction of modeling involving fractional operators the author was intrigued by development of so-called fractional bio-heat models and how they are related to the classical ones such as Pennes's, Wulff's, Klinger's, Chen-Holmes' models, etc. [20, 21]. The literature search revealed that the dominating approach is to fractionalize formally the Pennes equation. Moreover, the correct solution of models either based on local or non-local operators needs correct scaling and nondimensalization. This formulates a special interest about the time and length scales, velocity scale and finally the dimensionless groups appearing as pre-factors in the modeling differential equations; as weighting factors and allowing to see the contributions of different physical effects accounted by the model of interest.
The classical models mentioned above are based on the continuum approach allowing easily to apply the local (integer-order) calculus and as fundamental base the Fourier law. Therefore, in all these models, parabolic by nature, the heat flux speed is infinite, which is unphysical. The flux damping in models involving local derivatives are based on extension of the Fourier law by applying first order approximation by Taylor series expansion; the Maxwell-Cattaneo and the Dual-phase-lag approaches resulting in hyperbolic models are commonly applied.
Therefore, the main motivation of this study is to revisit the existing bio-heat models, precisely thus considering blood perfused tissue, and to attempt representing them from a common basis thus allowing to see what are the links between them and how the modern trends, such as the fractional models should be correctly constructed. Therefore, to be precise, this study considers the following problems related to 1-D bio-heat transfer models:
(1) Basic concepts of model build-up and the relevant physical and mathematical assumptions.
(2) Scaling and nondimensalization, thus detecting the controlling dimensionless groups.
(3) Fractionalization: (a) Critical analysis of the existing fractional models, (b) A systematic approach based on fractional Taylor series expansion and the fading memory concept.
Analytic and numerical solutions of existing bio-heat transfer models are out of scope of this work, even though we will analyze them to some extent in the context of the three main directions declared above. Comprehensive analysis of analytical solutions of existing bio-heat models (integer-order) with/without flux damping are available in Xu et al. [1], Datta [16], Valvano [17], Orr and Eberhart [20], Charny [21], and Fan and Wang [22].
1.5. Aim and Paper Organization
The main focus of the article was formulated in the preceding sections of the Introduction considering skin properties (section 1.1), blood circulation in human body (section 1.2) and the general approach in construction of bio-heat models (section 1.3). Now after these initial words the following part of this article is organized in three main directions, with a common point of view, as follows:
1) Integer order models without flux damping (classical models of Pennes, Wulff, Klinger, Chen-Holmes, porous media concepts) in section 3. The models developed prior to that of Pennes are briefly presented in sections 2.1 and 2.2.
2) Integer order models with flux relaxation based on the Maxwell-Cattaneo and Dual-Phase-Lag approaches are discussed in section 5.
3) Bio-heat models with memory, that actually means heat flux damping modeled by fractional-order operators are especially analyzed in section 7.
4) A systematic approach in bio-heat heat conduction models is formulated in section 7.2 via application of two principle approaches: (a) Fractionalization via fractional Taylor series (section 8.1) developed in section 8, and (b) Fractionalization by application of the fading memory concept with different relaxation kernels (section 9).
For completeness of the exposition in this article, we will briefly present at the very beginning (section 2) some mechanistic ideas (models) that appeared in parallel to the continuum models forming the core of this study.
2. Formal Mechanistic Bio-heat Models
The mechanistic models presented briefly here have been developed by applying formal analogy between the blood vessels-tissue configurations and the design of the existing heat transfer equipments. This can be easily explained by the motivation to apply the existing knowledge, but at the same time this approach has inherent limitations which are obvious when more complex vascular architectures should be modeled. Two simple cases are commented: (a) Surface heat flux to the tissue by a convective blood flow streaming the blood-tissue interface, (b) Heat transfer between a cylindrical blood vessel of final length and the surrounding tissue.
2.1. Surface Heat Flux Model
Following the comprehensive analysis of Charny [21] the surface heat flux qs through tissue (per unit area At, that is qs has a dimension W/m2) and with missing flood flow is
where ωb is the volumetric blood flow to the tissue per unit volume of it, that is while the heat conductivity of the tissue with a thickness Lt is kt. Here, the first term in (12) is the thermal energy transported by the blood flow through the tissue layer of depth Lt and volume Vt = AtLt, while the second term is the Fourier law. This construction allows the effective thermal conductivity Keff to be determined by experimentally measured surface (at the skin) heat flux qs and temperature Ts, and the body core temperature Tb at a depth Lt. This formulation allows the effect of blood perfusion to be evaluated as an additional contribution to the dimensionless (relative) effective heat conductivity [21] using the tissue conductivity K0 in absence of blood perfusion as a reference scale. The value of Keff at large differences (Tb − Ts) does not vary thus corresponding to the maximum degree of vasoconstriction in the tissue [21]. In addition, the value of Lt was estimated by early physiological measurements at Lf = 2 cm [23] (see a comprehensive analysis in [21]).
The first term in (12) is related to macroscopic heat removal by a fluid flowing through the tissue (blood perfusion), while the second one is the heat transport by conduction mechanism. Now, in order to make more visible the contributions of each transport mechanism we transform the heat flux Equation (12) in two equivalent dimensionless forms, namely
The first form (13) defines the diffusion time scale of the blood as τb, while the second form (14) determines the heat diffusion time scale τt. Taking in to account that ωs has dimension [s−1] (see the definition above) the products ωbτb and ωbτt are dimensionless. Hence, this dimensionless presentation easily demonstrates the contribution of the blood perfusion to the total heat flux through the tissue.
2.2. Heat Exchanger Formalistic Models for Flow in Vessels
The models considered in this section are not the core of this article but prior to continue with more sophisticated continuum (section 3) and fractional models (section 7) we have to mentioned some mechanistic models, quite simplified, but related to well-known solutions of fluid-flow heat exchange in simple systems of tubes (modeling blood vessels).
The mechanistic tube flow models are analyzed by Chato [24, 25] using the facts that for individual blood vessels the capillaries are important for attaining the thermal equilibrium with the surrounding tissue: the smaller arteries and the veins have intensive heat transfer with the tissue, in contrast to the larger vessels affecting relatively little the heat exchange.
2.2.1. Heat Transfer From Blood Flowing in a Vessel
Following Chato [24, 25] the blood behaves as non-Newtonian yield stress medium (Casson fluid) with a constitutive equation
relating the shear stress τs, the yield stress τy and the yield-stress viscosity μ. In (15) V is the axial blood velocity, while y is the direction normal to the vessel wall.
For steady flow the relation of the mean Nusselt number Nu = hbD/kb based on the vessel diameter D is related to the Graetz number and can be approximated as
This approach invokes two principle questions [25]:
(1) At what distance from the entrance the blood-tissue will attain the equilibrium? That is, what is the heat transfer entrance length? This question was further discussed in construction of the more complex continuum model of Chen and Holmes (see section 3.4).
(2) What is the blood temperature in axial direction at a given length along the vessel wall?
Considering a simple model of concentric cylindrical vessel-surrounding tissue of final thickness R2 − R1 (see Figure 3), then applying what is well-known from every textbook on heat transfer, we have
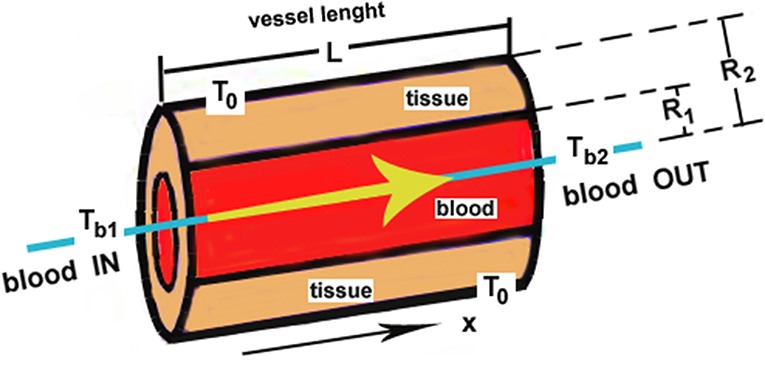
Figure 3. Mechanistic representations of single blood vessel-tissue heat transfer as a countercurrent energy exchange process: See the text about the studies in Chato [25].
Radial temperature distribution
Heat flux transferred to the tissue
where hb is the local heat transfer coefficient, while he is an effective heat transfer coefficient for the blood flow.
The axial temperature profile of the blood is simply modeled by one dimensional equation [25]
leading to exponential decaying temperature distribution along the x axis with a rate depending on Λx.
With these two examples we close this direction in the blood-tissue heat exchange since they are out of the scope of this study (the continuum based models). Extensive analysis of systems based on mechanical analogies are available in Charny [21] and Chato [24, 25].
3. Energy Balance Based Continuum Models (Starting by Pennes)
Modeling of the blood flow effect on bioheat in living tissues due the complex architecture of the vascular system has been developed in two distinct directions [26]:
(1) An approach considering the vascular system and as a system of rigid tubes protruding the tissues. With this point of view only large vessels are considered while the smaller ones are neglected thus reducing the order of complexity (similar approach was commented briefly in section 2.2).
(2) The second approach eliminates the vascular flow effects and uses continuum models incorporating in average the blood flow effects on the temperature over a control volume of the tissue.
The continuum approach allows, depending on the problem that should be modeled by an additional source term in the modeling equation; or defining effective transport coefficients such as the heat conductivity and the blood-tissue heat transfer coefficient. The most popular models are the Pennes model (see section 3.1) where the blood perfusion is modeled by a fluid-surface heat transfer term with a heat transfer coefficient dependent on the blood flow rate, and the Weinbaum-Jiji models (see section 3.5) with heat conductivity dependent on the vascular structure. These models will be analyzed here together with other continuum models since they provide a sufficient basis to develop two modeling trends accounting relaxation effects in bio-heat transfer, namely:
(a) Heat-wave models (section 5) with simple heat flux lagging (section 5.1), and dual-phase lag models (section 5.2), both of them employing local derivatives.
(b) Non-local models modeling the heat flux and temperature gradient damping (lagging) by fractional differential operators (sections 7 and 8.1).
3.1. The Model of Pennes
Pennes [27] formulated the oldest and the most studied mathematical model based on temperature profiles in limb (forearms) assuming maximum of temperature at the axis of symmetry, thus reasonably formulating the model equation in cylindrical coordinates, namely
assuming a uniform distribution of the metabolic heat generation Qm [W/m3] in the tissue layer, as well as uniform tissue heat conductivity kt. With a convective boundary condition at the skin surface (r = R)
The principle simplifying assumptions of the Pennes model are [4, 28]:
(a) Capillary bed equilibration: pre-arteriole heat transfer and pre-venule heat transfers are neglected. The only variable in the Pennes model is the tissue temperature.
(b) Isotropic blood flow in small capillaries, i.e., the blood flow direction is not considered.
(c) All blood vessels close to the capillary beds do not affect the heat exchange and the local vascular geometry is ignored.
(d) The blood reaches the capillary beds through the arterioles at deep body temperature (core temperature).
Actually, the Pennes model assumes that the arterial blood flow bathes the tissue at the same temperature everywhere in the limb cross section (see detailed comments in [21, 29]). This approach resembles the thermal problem of the longitudinal metal fin with constant cross section AF (and cross section perimeter PF), available in every textbook of heat transfer (see as good reference sources [30] and [31]), namely
where h is the heat convective transfer coefficient and T∞ equals the arterial blood temperature, as it is schematically illustrated in Figure 4 (Forearm-Fin analogy). This term in the Pennes' equation is a matter of arguments under different assumptions. In accordance with Wulff [32] the last term is not local in contrast to the other two (the time and space derivatives); this comment will appear in the criticism of the Wulff's continuum model [32] (see also [21, 29]) discussed further in this analysis. This standpoint would be true if the assumption of Pennes [27] about the thermal equilibrium between the tissue and venous blood is accepted. That is, if Tt (r, t) = Tb(ven) in this term is independent of the space coordinate x, then the last term in (3.6.1) is not local. However, if Tt (r, t) depends on the space coordinate r as TF (x, t) in the fin Equation (22) then this term is local: it is a distributed heat sink such as the distributed metabolic term Qm. Here, we can see the first contradiction in the Pennes equation formulation: in general the tissue temperature depends on both the space coordinate and time but the last cooling term it is assumed as space independent, even though actually it is; the source/sink term (termed also convective term) is homogeneously distributed along the x axis.
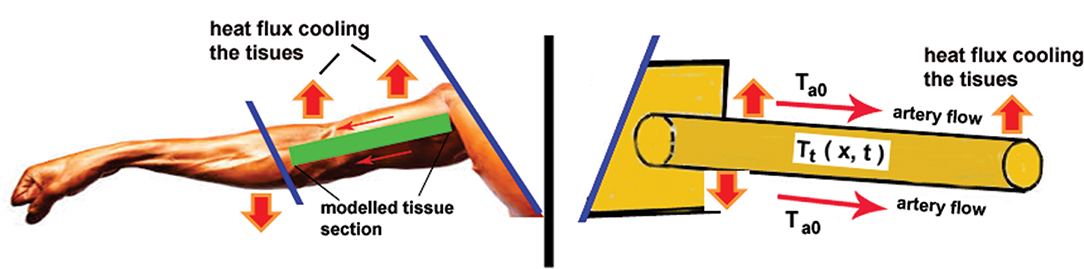
Figure 4. Forearm-Fin mechanical analogy of the logical construction used in the Pennes model. Present author conceived analogy and interpretations: see the explanations in the text.
The main deficiencies of the Pennes model can be briefly outlined as [28]:
(a) The thermal equilibration in the capillaries is a misconception since this process takes place in the pre-arteriole and post-venule vessels (with diameters within the range of 70–500 μ m).
(b) The blood flow spatial orientation is not taken into account, that is the countercurrent heat transfer between the artery-vein pairs is not considered, for example.
(c) The blood perfusion is overestimated since the arterial temperature changes continuously from the deep body temperature of the aorta to the secondary arteries and further to all branches of the system: (i) the pre-arteriole temperature is not equal to the body core temperature; (ii) The vein return temperature is not equal to the mean tissue temperature.
The nondimensalization of (22) yields
where the dimensionless variables are
The group is dimensionless and can be assumed as analog of the Biot number Bi. The product PFLF equals the total surface area of the fin; then with a dimension of length defines the characteristic length scale of the fin lF.
The solution of the Pennes model in radial coordinates [21] is
where I1 and I0 are modified Bessel functions
First, the parameter ap has a dimension [m−1] because it can be represented as , where ab is the thermal diffusivity of the blood. Taking into account that the dimension of ωb is [s−1] (volumetric blood flow rate per unit volume of the tissue) then the ratio (ωb/ab) has a dimension [1/m2]. Therefore, the products rap and Rap in (25) are dimensionless. Further, the ratio Qm/(ωbρbcb) has a dimension of temperature per second [K/s] since the dimension of ωb ((m3/s)/m3) is [s−1], as it was commented above.
The scaling of the boundary condition in (21) yields
where is the thermal Biot number representing the ratio of the heat transported to the tissue by convection to the heat transported through the tissue by conduction.
It is well-known that for very small Biot numbers (Bi < 1) the temperature gradients in the body (tissue) are negligible and the model of Pennes reduces to the lumped heat capacitance model, namely
or in a scaled version as
For example, the steady-state version of the Pennes equation in rectangular coordinates (1-D) is
and its solution is [21]
The Pennes equation was seriously criticized in consequent developed studies (see in the sequel), and we will stress the attention on this, but now we focus on nondimensalization and the physical meaning of the parameters in the solution (22). The principle shortcomings, in addition to the ones mentioned above, of the Pennes model can be outlined as:
(i) As mentioned above, the perfusion terms is assumed as that the tissue is bathed by the arterial flow, while the venous return from the distal part having an important effect on the tissue temperature is neglected.
(ii) The analysis of Shitzer and Kleiner [33] and Shitzer and Chato [34] reveals that the perfusion term may play a role of a sink in the warm core region of the tissue (precisely in the cylindrical limb model) and as source in the cooler peripheral area (see also analysis in [21, 29]. Further, with increase in the arterial bold flow, that is the increase in the perfusion rate, then the last term in the Pennes equation performs as a heat source in a large section of the living tissue [21]. Mathematically this means that the sign of the perfusion term should change (as source or as sink) depending on the location of the modeled tissue, a properties which is not encountered in the Pennes model.
(iii) The models do not consider the detailed structures of the vascular networks, especially the countercurrent arrangements as well as important anatomical characteristics of the blood circulatory system.
Despite these deficiencies the Pennes equation was extensively applied to model heat transfer in living tissues but mainly within body segments and with good very good agreements with experimental data. According to Charny [21] in most of cases the neglected heat transfer in the prearteriole and postvenule blood vessels of the circulatory systems can be used to explain discrepancies between the instrumental measurements and the data predicted by the Pennes model. We will meet again the Pennes model when problems related to its fractionalization will be discussed further in this article.
3.2. The Continuum Model of Wulff
The Wulff's approach [32] is a modeling of heat transfer through the tissue on a continuum basis and the main criticism is on the formulation of the perfusion terms. Actually, Wulff clearly states that Pennes' perfusion term is a global (integral term) that does not corresponds to the other terms (as derivatives) which are local derivatives. As mentioned earlier in this text, this is a matter of argument, but for better understanding what we mean, let us consider the basic idea of the Wulff's model. Following Wulff, since the blood is moving through the tissue it may remove or derive heat by convection in any directions but not only in the direction defined by of the local temperature gradient. Following this assumption, the convective energy transport through the tissue is Wulff [32] (see also [21, 29])
In (31) is the blood specific enthalpy formulated as
Further, ω is the solid angle across the control surface of the blood vessel, while Ω is the entire solid angle, and vh is the local mean apparent blood velocity. ΔHf is the specific enthalpy of the metabolic reaction. With these assumptions the energy flux at any point of the tissue is [32, 35]
Thus, the energy balance simply reads as
that in detailed form is [21, 29, 32]
The last term in right-hand side of (35) is equivalent to the metabolic heat source Qm. The main problem in application of the Wulff model is the determination of the local blood mass flux ρbvh [35].
Further, Wulff assumed that the blood temperature gradient in (35) equals the gradient of the temperature gradient of the environment surrounding the tissue and this step permits to assume that Tb = Tt (the same assumption as in the Pennes equation !). Hence (35), can be written in a more convenient form, namely
which can be also re-written (with -thermal diffusivity of the tissue) as
or in a more familiar form as 1–D convection-diffusion equation of heat transfer
3.2.1. Nondimensalization of the Wulff's Model
The nondimensalization of (37) or (38) with , , and (as well as assuming kt = kb) yields
The groups
are dimensionless.
Moreover, the Peclet number Pe = advective transport/diffusion transport is a weighting coefficient showing the contribution of the perfusion to the total heat transfer in the living tissue. For low Peclet numbers (low perfusion rates) the heat conduction transport mechanism dominates.
3.3. The Continuum Model of Klinger
The model of Klinger [36, 37] is similar to that of Wulff [32] and focuses on correct description of experimental data from thermal clearance experiments. In the Klinger's model the tissue temperature is related to the rate at which the deep tissue temperature changed during point source heating [38, 39]. Taking into account the critique of Perl [38, 39] to the Pennes model that the unidirectional blood flow was postulated while the naturally existing nonunidirectional blood flow, Klinger [40] formulated the main problems emerging in the implantation of the Pennes equation, and what should be improved, that is
K1) The solution envisages a microscopic (local) temperature, that is the temperature at each point of the tissue.
K2) The measuring devices have finite dimensions and in most of the cases larger than the length scale of the tissue of interest and consequently, the measured temperature is an average value and cannot be accepted as a local one, i.e., it is not local, but do not misunderstand it as a result of a memory based differential operator since all derivatives used in the integer-order models are local operators !
K3) The correction of the missing nonunidirectional blood flow in Pennes' model is corrected by introducing the concept of convection multipoles related upon the in vivo vascular anatomy, thus accounting not only the magnitude of the blood flow but also its direction [21, 36, 37]. The Klinger model is based on the assumption of constant tissue properties (kt, ρt and ct) and incompressibility of the blood flow (that is ∇ · vb = 0) and expressed as
In a dimensionless form (41) becomes [21, 36, 37]
Here v* denotes the blood velocity with respect to the characteristic velocity used in the formulation of the Peclet numberPe. In addition, is dimensionless Laplacian gradient operator based on a characteristic length scale L, while is the characteristic time (at is the tissue thermal diffusivity). As commented by Charny [21] this time characterization is equivalent to Fourier number of unity, that is when t = τ = L2/a. However, this is not true, as it possible to see from the preceding examples of nondimensalization of model equations. The main question arising here is: What is the definition of the characteristic length scale L? It should be determined arbitrary, that is depending on the region of the tissue considered and the experience of the modeler. It is noteworthy, to understand the main idea of this model, that Klinger introduced a dimensional velocity thus allowing the energy balance equation to presented as
Assuming the point heat source heating, the main idea in the studies of Klinger) is the replacement of the source term by a Dirac delta function (vanishing elsewhere but appearing at the position r1); this immediately invoked the Green function based solutions (41) [21, 36, 37, 41]. In accordance with Klinger, in all vascular arrangements studied, the multiple moment is directly proportional to the total volumetric blood flow rate through the vessels with repeating tissue element. The effects of the multipole moments depends on the ratio (λ/L); here L is the macroscopic length scale, while λ is the length of the side of cube over which the average tissue temperature is determined, and the nondimensional volume is (λ/L)3. Since (λ/L) < 1 the results of Klinger's modeling experiments is that the countercurrent flow effect on the tissue heat transfer is a second order effect.
Hence, the concept of averaging the temperature around a certain position leads to [40]:
K4) The effect of the blood convection on the average temperature can be represented as superposition of terms, each of which mirrors a particular properties of local symmetry of the vascular system.
K5) The order of magnitude of the convection effect decreases with increasing in the symmetry.
K6) The Peclet number used by Klinger [36] is defined as a ratio of two characteristic times: , where and (see the a comments after (refeq: Wulff-9) where Pe is defined as a ratio of the two heat fluxes (convection to conduction).
The model developed by Klinger is a serious contribution to bio-heat modeling since it address some important issues, among them [21, 36, 37, 40, 41]:
1) Since εb ≪ 1 [21] it follows that keff is practically independent of the blood flow, and consequently it is reasonable to accept keff ≈ ksolid tissue.
2) The Green function solution allows quantifying the vessel number density, blood perfusion rate and the vessel spatial construction. The principle outcome of this is that the temperature field are strongly influenced by the spatial geometry of the blood carrying vessels. More detailed analyzes are available elsewhere [21, 29].
3.4. The Model of Chen-Holmes
Chen and Holmes [42] have considered heat transfer applied in living tissue with hierarchical system of vessels with the continuum approach. The modeling technology is the same as in the models of Wulff and Klinger making energy balance of tissue-blood control volume. This physical hypothesis is based the existence of a large number of blood vessels in the tissue domain (volume) over which the energy balance is taken. As a rule, the characteristic length scale of this domain is much larger than the characteristic dimensions of the individual blood vessels, thus the continuum approach can be applied. Obviously, with this approach the blood flow through the small vessels protruding the tissue affects the definition of the effective heat transport coefficients such as tissue conductivity and the metabolic term. Hence, in terms of local mean temperature, the energy balance equation for both the tissue and vascular spaces are [21, 29, 42]:
In the solid tissue space
In the vascular space
where the last integral term is the contribution of the convective energy gain due to blood flow at velocity v across a surface area S. With help of (44) and (45) when dV (the bulk control volume) goes to zero the continuum energy balance of the tissue is
Note 2: The temperature under the integral sign in (47) is not simply equal to Ts in contrast to the assumption used by Wulff [32]. Moreover, the tissue temperature Tt is defined as
and since the ratio dVb/dV → 0 we get Tt → Ts.
Skipping details in the final formulation (see the analyzes in [21, 29] of the new equation) named Chen-Holmes bio-heat equation is
Referring to the effective heat conduction of the tissue we address the formulated conductivity enhancement by the blood flow through the tissue. Hence, the effective heat conduction flux qcond [the first term in the right-hand side of (50)] in the control volume of the perfused tissueδV is presented as
Here, the effective heat conductivity is defined as in a two-phase (solid-liquid) medium where the blood volumetric fraction is
Therefore, since εb ≪ 1 [21] it follows that keff is practically independent of the blood flow, and consequently it is reasonable to accept keff ≈ ksolid tissue. Further, using the porosity of the tissue εb where blood flows, the effective density, heat capacity and local mean tissue temperature are defined as [29, 42]
where the subscript b denotes blood.
3.4.1. Some Remarks on the Chen-Holmes Model
The Chen-Holmes final equations need some relevant sub-problems (of strong importance with respect to the physical background) to be commented briefly, that is:
Remark 1: The tissue temperature Ts can be replaced by the volume-weighted continuum temperature Tt as much as εb ≪ 1. Moreover, a perfusion term similar to that in the Pennes equation also emerges in the Chen-Holmes equation. However, this is a formal similarity, since the analysis performed by Chen and Holmes about the thermal equilibration lengths in various blood transporting vessels revealed that the velocities are proportional to power of 1/3 of the vessel radii. Hence, for larger vessels (such as aorta and large arteries, as well as vein) the thermal equilibria require equilibration lengths to have order of meters [21, 42]. Otherwise, in vessel compromising microcirculations (arterioles, venules and capillaries) the thermal equilibration lengths are of order of microns. Therefore, the Chen-Holmes model and the relevant analysis clearly contradict the Pennes formulation that all tissue-blood heat transfer occurs in the capillary bed.
Remark 2: In the context of the preceding remark, Chen and Holmes emphasis on the fact that the formal perfusion heat source (54) differs in its physics from the perfusion term in the model of Pennes. There two principle differences albeit the formal similarities, that is Charny [21] and Chen and Holmes [42]: (1) The coefficient is the total perfusion bleed-off to the tissue only from the microvessels past the j*th generation of branching. In contrast, the Pennes term ωb considers the bleed-off from all generations of vasculature. (2) The perfusion term of Chen-Holmes (54) is proportional to the departure difference which is different from (Ta0 − Tt) (see Equation 3.6.1). The difference between and Ta0−Tt can attain an order of 10 − 50 percents using as a base for comparison the thermal equilibration lengths of the large vessels.
Remark 3: Chen and Holmes accepted the idea of Wulff [32] that the blood temperature equals the solid tissue temperature everywhere in the control volume. This assumption allows the perfusion through the control volume to be presented by a conventional convection term −ρbcbvp · ∇Tt, where ρbcbvp is the blood mass flux through the control volume of the tissue.
Remark 4: The effective (perfusion) conductivity [see the second term in the right-hand sides of (49) and (50)] simplifies the analysis assuming that the conductivity kp is a vascular quantity, that is, it actually is related to the suggestion that the heat flux proportional to temperature gradient is normal to the differential surface area.
3.5. Weinbaum-Jiji Model
Weinbaum and Jiji [43–45] and Weinbaum et al. [46–49] developed a model starting from objections to the Pennes model addressing the missing directionality effects of the larger blood vessels on the blood-tissue-heat transfer. Additional critiques of Weinbaum and Jiji refereed to absence in the Pennes model characteristics describing the geometry of the vessel system, that is sizes, diameters, branching, etc. The series of studies began with the ideas presented in Weinbaum and Jiji [43].
The general step in the Weinbaum-Jiji model (WJM) is the modification of the Pennes equation with an effective thermal conductivity which is a function of the blood flow rate and the vessel architectures. This modification lays on the suggestion that small arteries and veins are parallel, thus the flow direction is countercurrent; hence, there are counterbalanced heating and cooling. The hypothesis is mainly applicable to intermediate skin layers (see comments in [21, 29]).
The governing equations for deep tissue layer are based on the vessel geometry and capillary bleed-off phenomena on a continuum basis. The continuity relationship related to the mass conservation in paired blood vessels is defined as . Here, s is the location along the length of the countercurrent network which differs from the distance x due to the inclination angle of the vessel pair with respect to the normal axis to the skin surface [21]. Further, ū is the bulk mean electricity in the blood vessel, while gb is the perfusion bleed-off per unit vessel surface area (the subscript b refers to blood).
Next, neglecting the axial heat conduction in arteries (with temperature Ta) and veins (with temperature Tv), the energy balances for the blood flows are
Here qa is the flux of heat loss through the artery wall, while qv is the heat gain by conduction (per unit length) into the vein through its wall; Ta and Tv are the blood bulk temperature in the arteries and the veins, respectively.
Further, the second term in (55) describes the heat loss from the artery due to perfusion, while in (56) the corresponding term is the gain from the atrial blood due to perfusion.
From (55) and (56), after substraction, it follows that
Applying the continuity equitation in the right-hand sides of these equations we get the heat fluxes, namely
Taking into account that only Ta and Tv exist in the definitions of the fluxes (58) it is impossible to determine the tissue temperature Tt. To overcome this problem, it was suggested a simplification that [44]
In addition, the authors suggested that the heat transfer through the tissue surrounding the vessels is dominated by heat conduction mechanism. As a consequence they assumed the simplification defined as
where σ is a shape factor related to the ratio of vessel spacing to the vessel diameter Ls/a.
After all these assumptions and simplifications the Weinbaum-Jiji equation [44] is
with Peclet number defined as
The Weinbaum-Jiji concept leads to a parabolic models with infinite speed of the heat flux. We will remember about this when the heat flux relation should be taken into account (in models with phase-lag and fractional models). Now, we stress the attention on some physical facts that might help us to understand the physics behind. As it is mentioned in Weinbaum et al. [46] the thermal relaxation of the blood in paired arteries and veins occurs through two principle mechanisms:
(a) An axial departure decay due to radial diffusion in blood vessels and the surrounding tissue,
(b) Countercurrent heat exchange when an arteries and veins are closely juxtaposed.
It is worthy to note that an important characteristic of the Weinbaum-Jiji model is its applicability to heat transfer in peripheral tissues only, where the basic assumptions used in its construction are valid. That is, the assumptions that the mean blood temperature (Ta + Tv)/2 equals the tissue temperature. In this models construction, the superposition used by Baish et al. [50] is used to validate the underlying assumptions.
The Weinbaum-Jiji simplified model based on parallel blood transporting vessels was commented thoroughly by Wissler [51] and some questionable assumptions, crucial for its derivation, were outlined, among them:
(a) The tissue and blood temperatures are related: therefore is not necessary the tissue temperature to be calculated as an arithmetic mean of the artery and venous temperatures (see Equation 59).
(b) The temperature at which the blood enters a large vessel is important because the thermal equilibration needs a certain distance along the vessel wall (see the assumptions of the Chen-Holmes model commented above).
(c) Obviously the tissue temperature will be intermediate between the arterial an venous blood temperatures but Equation (59) cast doubts about its general applicability.
(d) The assumed close thermal coupling between blood and tissue (the basis of the Weinbaum-Jiji simplified model-see Figure 5) leads to Equation (61) where the arterial blood departure is missing.
(e) Wissler commented that the first version of the Weinbaum-Jiji model (published in [47] and not commented here) is more realistic that the simplified one (61).
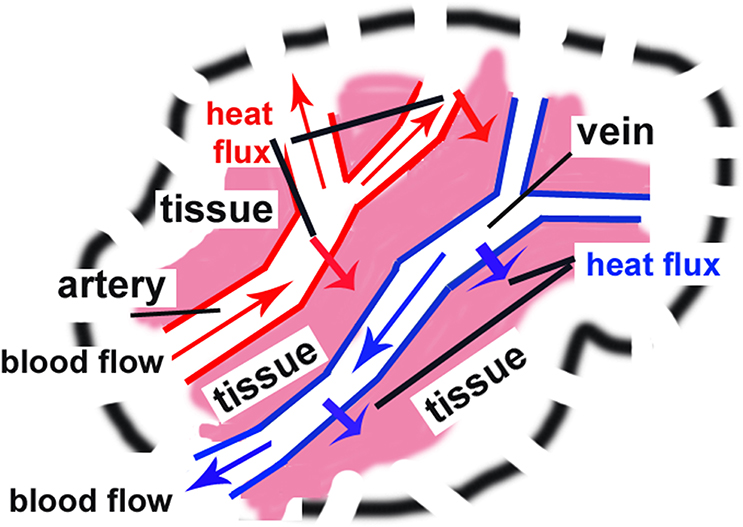
Figure 5. Blood bleed-off trough thermally significant parallel blood vessels only. See explanation in text about the works of Weinbaum et al. [46] and Nakayama et al. [52] and the ideas developed by Wissler [51]. Note: The area is subdivided by area of solid As and area of capillaries Ac.
For more details see Wissler [51] and the commented works of Weinbaum and Jiji [43–45] and Weinbaum et al. [46–49], the presentation in Chapter 10 of Jiji [28] as well as the analyzes in Charny [21] and Khanafer and Varfai [29].
3.6. Characteristic Length Scales of Temperature Distributions in Tissue
The temperature distributions in living tissues is related to number of spacial scales, which mainly are taken into account in the Chen-Holmes model (see Remark 1 in section 3.4.1). Let us stress the attention on some of them [53].
3.6.1. Range where the heat transfer is controlled by conduction
The Pennes equation , for instance defines the length scale
where at is the tissue thermal diffusivity, defined with assumptions that ρb ≈ ρt and cb ≈ ct. This length scale is associated with the time scale .
3.6.2. Length scale of the blood-tissue thermal equilibrium
Another, characteristic length scale Lv is considered as the mean distance in a single vessel where the arterial flow achieves thermal equilibrium the surrounding tissue when moving from the large arteries to the arterioles. This length scale, actually, equals the length scale LII characterizing the distance along vessel axis at which the blood and tissue become in thermal equilibrium. In accordance with [24, 46] the definition is
where Rv is the radius of vessel, dmean is the mean distance between vessels of the same length L; vb is the blood velocity (averaged over the vessel cross-section). Following Lubashevsky and Gafiychuk [53] and Witmore [54] commonly L ~ dmean an therefore taking into account that Lv ~ LII we get
since the total blood flow through the vessel is and consequently .
The value related to Lv directly affects the tissue thermal diffusivities [53]: typically , while and dmean/Rv ≈ 40. This yields length scales LD ≈ 0.6 cm. and Lv ≈ 0.3 cm, while the time scale τcond ≈ 3 min.
3.7. Some Comments on the Continuum Bio-Heat Models
The continuum models permit different features to be modeled but under correctly defined circumstances. Here we stress the attention on the comments of Crezee and Lagendijk [55] (even though they repeat some previous standpoints), among them:
(1) The basic problem is that the structure of vascularized tissues is too complex consisting of solid and fluid compartments with architecture that cannot be easily described and modeled. In the solid section the conduction is the dominant heat transfer mode while convection takes part in the fluid filled compartments. The vast number of small blood transporting vessels the modeler task to incorporate the role of all of them, down to singular capillaries, in the structures of mathematical models.
(2) Albeit the fact that it would be possible to require exact information on particular vascular geometry at micro-level, it becomes difficult to model it and the most important issue is that the results are unpractical despite the huge amounts of computing resources involved in the simulation process.
In the context of the previous comments, the adequate models should compromise between what we know and what is reasonable in the model build-up. Following this standpoint and looking at the modeling process pragmatically we may point out some comments on the existing continuum models, that is
(3) The first attempt of Pennes is criticized, as commented above, focusing on the basic assumption incorporated in the perfusion term: the blood enter the tissue with the arterial temperature and leave it with the averaged local temperature. From this, the main critical points are:
(a) the heat transfer related to the blood mass transport is neglected;
(b) the actual blood temperature entering a particular tissue compartment is not accounted for.
(c) the individual heat transfer processes of individual tissue such as cooling or heating are not incorporated in the model.
(d) the entire venous vessel architecture is neglected with the assumption that there is entrance lengths to attain thermal equilibria.
Despite these critical notes the Pennes model is widely popular due to its simple mathematical structure [56–61].
The models created after Pennes are based on effective transport coefficients, particularly on effective heat conductivity keff:
(4) The Wulff's model is the first incorporating such a transport coefficient by a substitution of the Pennes' perfusion term by the product ρbcbU · gradT, thus introducing the mean fluid velocity U as a variable. Actually, this is an attempt to create a model of heat transfer in living tissues, similar to the ones known from the convection heat transfer with unidirectional flow; but, the blood transport in tissues is not unidirectional.
(5) The models of Chen-Holmes and Weinbaum-Jiji also use keff, precisely an enhanced thermal conductivity (tensor). This approach requires details about every component in the vascularized structure, but assuming isotropy, for the sake of simplicity in modeling, the conductivity tensor reduces to scalar keff.
After these comments we may write the bio-heat transfer model in a generalized in the form proposed by Crezee and Lagendijk [55]
where keff and < fc ≤ 1 are phenomenological parameters.
Thus, repeating the Pennes construction, the generalized equation (65) is only an instructive heat balance model allowing on its basis particular bio-heat models to be developed: after successive procedures allowing to establish the model structures by direct averaging microscopic governing equations (see more comments in [53]).
At the end of this section we may conclude that creations of continuum based models of bio-heat transfer need serious preliminary analyzes of the particular tissue of interest and the associate blood transporting architectures of vessels.
4. Bio-heat Models Using the Porous Media Concept
All continuum models commented above, in their origins, start with criticisms of the flaws of the Pennes models and attempts to improve its deficiencies. As we saw each models is applicable to a particular type of living tissue and a generalization is hard to be attained. Alternatively, to the continuum models, a concept considering the matrix of tissue, arteries, veins and capillary vessels a porous medium with specific porosity variations, effective heat conductivities and heat dispersion by blood flow have been developed [21, 29, 52, 62–66]. Following this concept the thermal energy transfer between the blood flow and the tissue is modeled with the basic assumption of thermal non-equilibrium [29, 67–69] described by two energy equations for the blood phase and the solid phase [29], namely (in original notations)
Blood phase
Solid porous phase
Here 〈T〉b, 〈T〉s, , , hbs are local volume-averaged arterial blood temperature, local volume-averaged solid-tissue temperature, blood effective thermal conductivity tensors (for the blood and solid phases, respectively), and the interstitial convective heat transfer coefficient, correspondingly. Further, ε and 〈U〉b are the solid phase porosity and the blood velocity vector (all vectors are denoted as bold letters), accordingly. The locally averaged interstitial convective heat transfer coefficient hbs depends on the blood velocity and solid phase geometry; the heat transfer between the phases is proportional to the difference . 〈T〉b and 〈T〉s are locally averaged blood and solid tissue temperatures, while and the blood and solid tissue effective conductivity tensors (averaged), as mentioned above.
With the assumption of isotropic heat conduction the effective conductivities are
where denotes the thermal dispersion conductivity as a natural consequence of the already existing models of heat transfer in porous media [67, 68].
For tissues with small-sized blood vessels when ε << 1 the flowing blood is thermally equilibrated , then using (66) and (67) the following simplified model can be developed (in original notations)
The blood perfusion term in (69) corresponds to the ideas developed by Wulff [32], Charny [21], and Klinger [36, 37, 40, 41] in contrast to the Pennes model where a uniform blood perfusion ωρbcb(Ta,in − Tv,out) is assumed in the model construction.
4.1. Nakayama-Kuwahara Porous Medium Approach
The porous media concept in bio-heat transfer uses the volume averaging theory (VAT)[52, 65, 66], a technique well-established in the area of fluid-saturated porous media. Looking at the anatomy of the living tissues, three principle compartments can be identified: blood vessels, cells and interstitium (see Figure 6). For the sake of simplicity the volume averaging theory applicable to living tissues [52, 65, 66] considers only two regions: the vascular region and extravascular region (cells and interstitium). This approach considers the entire biological structure as a fluid-saturated porous medium through which the blood infiltrates. The extravascular region is regarded as a solid matrix (despite the fact that exatravascular liquid exists).
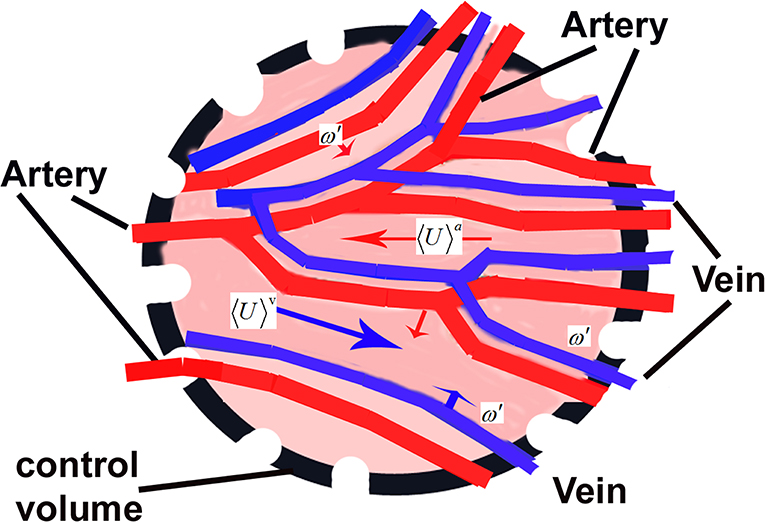
Figure 6. A schematic presentation of a control volume V in a tissue with blood supply through arteries and veins in parallel relevant to the studies of porous media approach.
The volume averaging needs the control volume V to be representative as characteristics but enough small in order to apply the tools of integer-order calculus. In such a case the volume averaging of certain variable ϕ is and therefore for the region occupied by the blood we have . The relationship between the two averaged values is 〈ϕ〉 = ε〈ϕ〉b, where ε = Vb/V defines the local porosity as a ratio of the volume of the fluid (blood) to the entire volume in the vascular space. In the dominating cases ε < 0.1 [65].
Further, considering the macroscopic governing equations of continuity, Navier-Stokes equation and the energy equation, the Nakayama-Kuwahara model consists of two energy equations based on VAT [52, 65, 66], namely (in original notations-take into account the summation notations)
Blood phase
where kdis(j, k) is the dispersion related heat conductivity [70]
The solid tissue phase
Equations (70) and (71) are correct for all cases of thermal non-equilibrium (for more details about their derivations we refer [65]). Now, the interesting part of this section is to see how these equations are related to the models discussed earlier and derived from a continuum point of view.
4.2. Relations of the Porous Media Concept to the Existing Continuum Models
4.2.1. Pennes Model in Porous Media Terms
In terms of (70) and (71) the Pennes model can be expressed as [52, 65]
where ωPennes is the mean blood perfusion rate; Ta0 is the mean branchial artery temperature Comparing to the solid phase energy equation (71) it is obvious that
where ab is the specific surface area contacting with the blood.
Assuming that for small vessels [65] it follows that
Hence, the Pennes perfusion rate is an effective value including the surface heat transfer [65]. The second term in (74) is a ratio of two components of the perfusion heat flux [see (73)]. Therefore the assumption for complete thermal equilibrium is valid when the Peclet number is too small (the diffusion transport dominates and the advection could be neglected).
4.2.2. Klinger and Wulff Models in Porous Media Terms
In terms of (70) and (71) the Klinger model is (in original notations)
Suggesting a thermal equilibrium, that is 〈T〉b = 〈T〉s [65] it follows from (70) and (71) that
Equation (76) reduces to the Klinger model (41) when the porosity (that is the ratio of vascular volume to the total volume) is sufficiently small. Further, when the blood flow is strong and the macroscopic diffusion transport can be neglected, then energy equation for the blood phase (70) becomes
It is easy to see that with the approximation (77) the energy equation for the solid phase (71) reduces to the Klinger equation (76). Hence, the condition the Peclet number to be sufficiently larger than unity (i.e., dominating convective transport with respect the negligible conduction heat transfer) leads to the Klinger model; the high Peclet number condition relates the Klinger model to the heat transport in large vessels.
5. Integer-Order Models With Relaxations (Hyperbolic Models)
The simplest model of heat conduction is based on the Fourier law assuming that the heat flux is related to the temperature gradient
via the heat conductivity k as a transport coefficient. This a reliable model confirmed by experiments, but there are serious limitations for its applications. Precisely (78), is an adequate model of the microscopic phenomenon of heat diffusion in cases when the length scales are much greater than the mean free path and the time scales are much greater then the thermal relaxation time (see the excellent comments in [71]). However, one unphysical outcome, such as with the diffusion models based on the Fick's law, is the infinite speed of temperature disturbances, that is the heat flux has no damping. Physically, temperature distribution is due to motion of particle carriers such as electrons and quanta such as photons [71] and reasonably the realistic picture is the thermal disturbances to propagate with finite speed.
The models of Pennes, Wulff, Klinger, Chen-Holmes and Nakayama are based on the Fourier law leading to parabolic equation with infinite speed of the heat flux. However, in real systems the flux propagates with finite speed. In metals, for example, the relaxation times are of orders from 10−8 to 10−14s [72–74], while in biological tissues the relaxation times are of order of 10–30 s [72–75]. In biological tissues, for example, in muscles under local strong heating the experiments reveal anisotropy in heat transport that cannot be explained by the Fourier law only [76–78]. This leads to formulation of thermal wave bio-heat models [79, 80] based on two main approaches:
(1) Maxwell-Cattaneo approach with heat flux time lag, known also as Single-Phase Lag (SPL) approach [81, 82].
(2) Double-Phase-Lag (DPL) approach with relaxations in both the heat flux and temperature gradient propagation [81–84].
Both approaches lead to hyperbolic equations with finite speeds of the solutions discussed in the sequel of this section.
5.1. Single-Phase Lag Heat Conduction (Maxwell-Cattaneo Approach)
5.1.1. Basic Approach in Modeling of Heat Flux Relaxation by SPL Approach
Considering the need of heat flux relaxation (damping) the simplest approach is to assume first order approximation (via Taylor series expansion) of the flux with respect to the time [81–84]. Hence,the extension of the Fourier law (see as an example [85]) as a model with a single time-lag of the flux is
According to this postulation the temperature gradient established at a point x at time t gives rise to a heat flux vector at x at a later time t + λq, that is there is time-shift between the heat flux and the temperature gradient. The heat flux relaxation time λq, called also a phase-lag parameter has been interpreted from different points of view [1]:
(i) from the framework of the second law of the irreversible thermodynamics [81, 86],
(ii) λq comes from the phase-lag shift between the heat flux vector and the temperature gradient [86] in high-rate responses;
(iii) λq is a constant representative for the interaction of different inner structural element of a material with the heat flux [73] and may take large values within the range (10−3 − 103s) [74].
By using the formal temporal translation (79) may be written in the equivalent delayed form [81]
Actually, SPL is a result of a first order Taylor expansion and this model is consistent with the Second law of Thermodynamics [87, 88].
Equations (79) and (80) are the forward and backward forms of SPL model, respectively [81]. For λq < 0 the role of cause and effect are exchanged in corresponding forward and backward forms [81].
Obviously, there are no restrictions to expand the flux (the forward SPL problem) with a truncated Taylor series of various orders. Thus, with second-order of Taylor expansion we have [81]
The divergence of (79) and by help of the energy balance (see Equation 84) yields a hyperbolic heat equation
The solution of (82) is a weakly-damped wave equation [71] where the temperature disturbance speed is .
Particularly, the first order approximation yields (79) which is equivalent to the constitutive equation with fading memory (see section 9)
The hyperbolic heat equation (82) can be regarded as a singular perturbation of the Fourier heat conduction model, recovered from (82) for λq → 0. This is a formal limit, as mentioned in [71] because any solution of (82) reduces to a solution of the Fourier heat conduction equation for λq → 0. This is a very sensitive situation since if λq cannot be considered as mathematically small the resulting solutions are unphysical (see detailed analysis in [71] and the comments in [89, 90]).
Similar interrelations between Taylor series expansions describing short-memory effects and integral constitutive equations with rapidly fading memory are widely encountered in other physical applications displaying memory effects such as viscoelasticity and electromagnetic wave propagation [81].
In the following parts of this section we will use the forward forms of SPL and DPL because only these versions are related to the existing time-fractional bio-heat models (section 6.2.1) as well to the systematic approach in equation fractionalizations (developed in section 7.2).
5.1.2. SPL (Heat-Wave) Model Without Blood Perfusion Relaxation
With (79) and applying the energy balance equation
we get a hyperbolic version of the Pennes model [22, 91] where both the blood perfusion term and the metabolic heat source are not affected by the thermal relaxation.
Hereafter, in this section, we will continue with the two-dimensional model of Bravo et. al.[92] in a dimensionless form, namely
where the dimensionless variables are defined as
In the model (86) the relaxation time is defined (as in the linear viscoelasticity [93–95] and heat waves [96, 97]) as a ratio of the thermal diffusivity a to the thermal velocity of propagation in the medium C. The relaxation time λq allows definition of the thermal version of the Deborah number as a ratio of λq to the characteristic time of the heat diffusion . Moreover, Φ is the dimensionless metabolic heat, despite the fact that the authors termed this terms as diffusive flux of energy.
The contribution of the blood perfusion (as in the model of Pennes) is weighted by the dimensionless factor σ = Lωb/at. Precisely, in [92] σ is presented as which actually is a ratio of the blood perfusion rate to a velocity scale (volume of fluid flow per volume of tissue) defined through the thermal diffusivity as without physical meaning). Comparing (85), (86), and (87) it is easy to see how the dimensionless groups can be defined.
In the context of dimensional consistency, let us look at Equation (85). The fist term in left-hand side has dimension s−1 (if we assume conditionally that T is dimensionless only for these comments), while the second and third terms are dimensionless since ωb in the prefactors has dimension s−1. The dimension of the first term in left-hand side is balanced by the dimension of first term in right-hand side (because at has a dimension m2s−1).
With the assumption to represent the solution as a sum of steady state θ0 and transient terms θt
the modeling dimensionless model and associated boundary conditions are
The Biot number at steady-state Bi0 is a measure of the thermal resistance of the tissue when the heat flux is imposed at its surface, while θair is the dimensionless temperature of the ambient air. In this context, the last term in (90) allows to be altered with small perturbation of the atmosphere, i.e., as in an air stream exhibiting a stochastic behavior. Hence, the model is oriented to modeling thermal reactions of living tissues when external fluid (air) with varying temperature is supplying or removing thermal energy from bodies. From the analyzes above, it becomes clear that this is a model oriented to bio-heat problems appearing close to the skin surface. Second, in this model construction, the blood perfusion is modeled as in the Pennes model without detailed analysis of the vascular architecture. Third, the definition of the Deborah number needs experimentally defined values of the thermal relaxation time of the tissue λ and the speed of thermal wave in the same medium.
The solutions performed in Bravo [92] with Biot number Bi0 less and almost equal to unity, indicate that they are related to cases with negligible thermal gradients inside the tissue. Furthermore, the range of variation in the Deborah number was chosen from DeT = 0 (this means classical Fourier law without flux lagging) up to DeT = 0.0013, that should mean fast thermal relaxation of the tissue. However, it is hard to judge these results since neither λ nor C are presented numerically in this work.
At the end, of this subsection, we may say that, actually, the only new element is the application of the SPL concept (Maxwell-Cattaneo approach) for heat flux relaxation. The definition of the Deborah number as it is done is not useful since by definition it should be a ratio of relaxation time λq to the current time t. Precisely, with a general definition of the time scale t0 we have for the left-hand side (after nondimensalization with respect to the temperature θ = T/Tc and the space coordinates)
Then, multiplying both sides of the dimensionless form of the equation by we get (86). Hence, the thermal Deborah number DeT defined in Bravo [92] is a ratio of the characteristic heat flux relaxation time to the characteristic thermal diffusion time. Now, making dimensionless both the nominator and denominator of DeT we get
Hence, the dimensionless prefactor DeT is a product of two dimensionless times (dimensionless numbers), that is DeT = DeFo.
We can see, that for small DeT, which is important when λq < < t0, the first term in the model (86) can be neglected while the parabolic term ∂θ/∂τ determines the model behavior with dominating diffusion and perfusion terms in the right-hand side of (86). This can be simply tested by dividing both sides of (86) by DeT. We have to stress the attention on the fact that the definition of DeT, which can be considered as a fixed value of the Fourier number Fo for t = λq, is by analogy, taking similarity of the relaxation process in viscoelastic transient flow, as mentioned above. It is not related to material flow, as mentioned in [92] since the heat conduction equation as (86) does not encounter a flow behavior of the material.
In the context of the SPL approach we have to mention the convolution form of the thermal flux damping (relaxation) with exponential memory kernel [96, 97], (related to 83), namely
which is erroneously represented as
following [98], thus destroying (violating) the memory effect (damping) in the flux relaxation model. The coefficient k in (94) should has a dimension [(W/m · K) · s]. It will be of a special interest further in this article when the fading memory formalism will be applied as a technique allowing correct fractionalization of model equations [see the SPL relationship (94) and the comments about (83)].
The Maxwell-Cattaneo approach was also used by Tang et al. [99] in solution of surface heating of biological tissues, that is excluding the perfusion effect from the problem. Well-performed analytical-numerical study of skin burn injury induced by radiation heating by 3-D model applying the Maxwell-Cattaneo approach was carried out by Dai et al. [100]; see also the results of Liu et al. [79].
5.1.3. Heat Wave Model With a Blood Perfusion Relaxation
The Maxwell-Cattaneo approach uses only the first order approximation of the heat flux (79) but as commented earlier there are no restrictions more terms of the Taylor series expansion to be involved [101] in the extension of the Fourier law, namely
Then, using the Pennes construction of the heat flux and its component (conduction, perfusion and metabolic source), and the external heating qr, we may write [101]
For the sake of simplicity of the analysis let us assume that qm = 0 and qr = 0. Then, following [101] let us consider only the temperature elevation θ = T(x, t) − T(x, 0) above the steady-state version of (97). In this case (subtracting (97) from the steady-state version) the resulting equation is
Assuming the traveling approach in solution of (98) (not presented here) Liu et al. [101] concluded in their analysis that the higher blood perfusion rate the higher frequency in osculation of the tissue temperature, an effect that cannot be accounted by the classical models of Pennes, Klinger, Wulff, and Chen-Holmes.
This is only an attempt in modeling the integer-order bio-heat transfer by application of the Maxwell-Cattaneo approach with a step ahead considering a relaxation of the blood perfusion term. No more studies in this direction cannot be detected in the literature, thus we stop comments on this approach. However, we will come back to this idea, in a different form, when the bio-heat models using fractional-differential operators will be used to model the finite speed of heat flux.
5.2. Dual-Phase-Lag Heat Conduction Concept
As an extension of the Maxwell-Cattaneo approach, which cannot work correctly when in the medium there are micro-structural interaction effects, the so-called Dual-Phase-Lag (DPL) was proposed by Tzou [84] (see also the analysis and solutions in [83, 102]) as
This construction of the heat flux-temperature gradient relationship can be easily understand if the Taylor series expansion is simultaneously applied to both sides of the Fourier law (see the beginning section 5), that is in terms of first order of approximations we get
In the DPL model (100) the relaxation times λq and λT can be interpreted as the periods arising from thermal inertia of the materials and the micro-structural interactions [1]. Especially λT (λq was discussed earlier) can be considered as heat diffusion with sharp wave front (the hyperbolic equations exhibit finite speed solutions) induced by the appearance of λq [83]. From (100) it follows that at any point of the heat conductor the heat flux vector at t + λq corresponds to a temperature gradient at time t + λT [1, 103].
The basic condition [84] (see also in [81]) is that both λq and λT are positive and the delay (the time-shift between λq and λT) should be also positive, that is
This condition allows to avoid violation of the common physical causality between ∂T/∂x and q [81]. In this context, if a temporal translation or is applied, then (99) can be presented as the SPL model with a time delay λd = λq − λT [81]. The stability of the DPL heat conduction models and the thermodynamic restrictions are analyzed in Fabrizio and Franchi [81], Quintanilla and Racke [103], Fabrizio and Lazzari [104], and Fabrizio et al. [105], but we skip these problems since they are out of the scope of this work.
It is noteworthy that when λq = λT the result of lagging disappears and we get a diffusion model of heat conduction [84]. For example, the experiments of Tang et al. [106] with IR irradiated tissue revealed that λq = 20 s and λT = 14 s (data obtained in the first 50 s of the tissue irradiation) and these data confirm the wave-like behavior of the heat transport [84].
Hence, by first and second order (or higher) approximations via Taylor series it is possible to construct different phase-lag heat conduction models with several relaxation times thus accounting for heat transport through materials with complex structures. Hereafter in this section, we will focus the attention only on simple phase-lag models (obtained by first order approximations). For more complex models of such a type we refer Xu et al. [1].
5.2.1. Dual-Phase Lag Bio-Heat Model
The approach used in (100) to model relaxations by mixed time-space derivative is well-known from the viscoelastic models [93–95] and was used also in construction of models with fractional derivatives [94, 95] (see further in this article).
Now, with the Pennes model [14] presented as
where Tb is the blood temperature in the artery, that is Tb − Ta0 in the Pennes' model. Then, expressing the heat flux as the second version of (100) we get [14]
with initial conditions T(x, 0) = T0 and T(x, 0) = 0 in accordance with the version of the model solved.
In (103) the product in the pre-factor of the second term in the left-hand side is completely dimensionless since the product λqωb is dimensionless.
Two simple examples of DPL model solutions are briefly presented next.
5.2.1.1. Constant flux as boundary condition to a tissue of final depth
With a boundary condition to a tissue with final depth L and introducing generalized time (t0), length (Lx), temperature (Tscale) and heat flux (qscale) scales (and order of magnitude analysis, as it was already done above) the following dimensionless variables can be defined as [14]
Hence, the dimensionless models is
with dimensionless initial and boundary conditions
The Laplace transform solution of (105), (106) in the s space is [14]
The time-domain solution needs inversion via the Bromwich integral but we will skip these huge expressions [14] since this is out of the scope of present work where model constructions and nondimensalizations are at issue.
Let us now see how the relaxation times and how their ratios control the contributions of different heat transfer effects, as terms, in the model equation. Dividing all terms in (105) by A we get
The ratio has order of magnitude of unity. Thus, the diffusion term in the right-hand side of (108) has a strong influence on heat transport (by heat conduction). Further, B/A = 1 + 1/Λq and for very small values of λq we have B/A >> 1, that is, there is a negligible inertia in the heat flux propagation; then the second term in the left-hand side of (108) dominates and determines a parabolic behavior of the model (while the first term can be neglected. Otherwise, for high values of Λq the model has strong hyperbolic behavior. In this case, the contribution of metabolic terms is low but cannot be neglected since this means eliminating of the metabolic heat from the model, which is unphysical.
5.2.1.2. Periodic surface heat flux
The boundary condition q = q0exp(iωt) and dimensionless variables
allow to express the governing energy equation as
with initial conditions
where E = τ1, F = 1 + Λ0τ1, G = Λ0 and H = τ1.
In the Laplace domain the solution of (110), (111) is
The simulations in Askarizadeh and Ahmadikia [14] used value of the surface heat flux (a value typical for the heat flux released by fire [107]).
5.2.2. Closing Briefs on the DPL Models
At the end of this section we have to refer to some additional studies applying the dual-phase-lag approach to modeling bio-heat problem. The dominating studies are on the Pennes model, among them: laser radiation heat supply to the tissue [108], temperature-dependent perfusion [109], skin heat transfer [14], pulsed IR irradiation [106], cryosurgery of lung cancer [110], laser heating [111, 112], interaction between tissue and a cryoprobe [113, 114], human head relaxation times [115]. The main idea of the DPL, that is the Taylor series expansions of the integer-order heat conduction equation, thus creating damping and heat wave behavior, is fruitfully used in fractionalization of bio-heat models (see section 8.4).
6. Fractional Bio-heat Equations: The State-of-the-Art in Model Formulations
This section is devoted to the existing fractional models of bio-heat transfer and the emphasis is on the technology of fractionalization, not on solution techniques. The correct model build-up, with correct application of both physical laws (and hypothesizes) and mathematical tools is of primary importance prior to attack the equations with simple or sophisticated solution techniques. With modern mathematical tools, either analytical or numerical any equation could be solved to greater extent. However, the principle question is: Does this equation is the adequate and correct model of what you need to represent in the mathematical space by it? We try to answer this question when analyzing the existing fractional versions of bio-heat equations.
6.1. Scaling and Nondimensalization of Fractional Operators
Before starting any analyzes of time-fractional bio-heat models we have to see how scaling and nondimensalizations have to carried out when time-fractional operators are used. The next section presents the common fractional operators used and the techniques of nondimensalization (based on the recent work [116]).
6.1.1. Time-Fractional Operators With Singular (Power-Law) Memory
We start with same definitions which will be useful in reading the following text even though they are available in many texts devoted to fractional modeling and textbooks [117]
6.1.1.1. Fractional integral
The Riemann-Liouville fractional integral of order α > 0 is a natural result of the Cauchy multiple integral the m-fold primitive of a function f(t) expressed as a single integral convolution for arbitrary positive number α > 0 [117]
The law of exponents for fractional integrals is:
The Laplace transform of the fractional integral through the convolution theorem yields
where LT[R(s) > 0], and F(s) = LT[f(t)] are Laplace transforms.
6.1.1.2. Riemann-Liouville time-fractional derivative
The Riemann-Liouville time-fractional derivative is defined as
6.1.1.3. Caputo time-fractional derivative
The Caputo derivative of a casual function f(t) is defined [117] as
For m = 1 we have the common definition
Caputo derivative of a constant is zero, i.e., [117]. Further, when f(0) = f′(0) = f″(0) = … = f(n)(0) = 0, then the Riemann-Liouville and the Caputo derivatives coincide.
Let us see the nondimensalization procedure to , which is uncommon in the existing literature [117] but is strongly related to the analysis of the existing fractional bio-heat models (see section 6.2). The Caputo derivative of the function U(t) is
Changing the variables as Y = U/U0 and , with U0 and TR as characteristic scales of the process, so that 0 < Y < 1, , yields: U = U0 ⇒ dU/dt = U0dY/dt ⇒ dU/dt = U0TR,
Further, the nondimensalization of (t − α)− α yields . Then, we get
If the nondimensalization is only with respect to the time, than we get
The result of nondimensalization can be easy attributed to the scale-invariant property of the power-law function used as memory kernel as commented in Hristov [116].
Alternatively, when the power law is expressed through the ratio (t/τ)− α where τ are the process relaxation time; the process time scale is TR. The introduction of the relaxation time leads to ταt−α and since τ = const. this is directly related to the scale invariance of the power-law function. With the nondimensalization procedure, as it was done above, we get
that is, an expression similar to (120),
Hence, we got a dimensionless scaling coefficient which could be considered as a weighting factor, too.
6.1.1.4. Caputo-Fabrizio fractional operator
The Caputo and Fabrizio [118] time-fractional operator with exponential kernel is defined as
where the normalizing function M(α) should obey the conditions M(0) = M(1) = 1, and is the operator Laplace transform.
From the definition (122) it follows that if f(t) = C = const., then , an expected results as in the classical Caputo derivative [117]. Analyzes of applications of the Caputo-Fabrizio operator are available in Hristov [96] and Hristov [119–121] and will skip reference quotations here.
The constitution of the Caputo-Fabrizio operator the stretched time is multiplied by a dimensional factor α/(1 − α) and therefore it should have a dimension of inverse time (t−1). Actually α is a dimensionless parameter and it is related to the relaxation time [119] via nondimensalization of the exponential relaxation kernel represented as exp[(t − s)/τ] [119–121] precisely nondimensalization of the exponential function, yields
where t0 is the characteristic time of the relaxation process.
The nondimensalization of the kernel preserves the meaning of the exponential memory function and avoids doubts about the definition of the fractional order α as Hristov [119] (see also the next comments).
Now, let us repeat the basic steps of nondimensalization of the convolution integral, as it was done in section 6.1.1.3. With Caputo-Fabrizio operator applied to a function U(t) and dimensionless variables we have defined as [116]
where TR is the characteristic time-scale of the process.
After nondimensalization we get [116]
and the Laplace transform is
When the nondimensalization is only with respect to the time by we get
Therefore, no additional prefactors emerge in front of the convolution integral unlike the case of the Caputo-derivative with a power-law kernel. This result can be attributed to the invariant properties of the exponential function used as memory kernel. The construction of Caputo-Fabrizio operator by definition, implicitly, contains a dimensionless kernel since it comes from the classical (exp − t/τ), which is dimensionless. Additional scaling inside the kernels such as (t/T) / (τ/T) does not change the ratio (exp − t/τ), but yields the product . Now, can be to be replaced by the ratio [α/(1 − α)] ∈ [0, ∞), where α ∈ [0, 1].
6.2. Existing Formally Fractionalized Versions: Analysis and Scaling
6.2.1. Ezzat's Models
Ezzat et al. [122, 123] considered the classical Maxwell-Cattaneo construction of the heat flux dependence on the temperature gradient q(x, t + τ) = −k∇T(x, t). Recall, that in the Maxwell-Cattaneo approach, a first order approximation (local expansion in a Taylor series) is used to reach the hyperbolic heat conduction equation (section 5.1). Mimicking this approach, Ezzat et al. [122, 123] applied fractional Taylor series expansion (of order α) (see section 8.1 for details about fractional Taylor series) with modified Riemann-Liouville derivatives of Jumarrie [124] [see the definition (130)] and the heat flux-temperature gradient was expressed as
where the Jumarries' fractional Taylor series are defined as [124]
through the modified Jummarie derivative (130)
The second version of (129) comes from the relationship Γ(1 + αk) = :(αk)!
Recall, that τα/α! should be equivalent to λq in the simple DPL model (79) and we may use the symbol . The dimension of is sα. The relationship (128) for α → 1 reduces to the integer-order Cattaneo construction (79) as mentioned above. Next, with the Fourier law construction (131) at hands, and taking the partial time-derivative of order α the result is (132)
Then, multiplying (132) by τα/α! both sides of (133) and applying (128) in the right-hand side, the final Ezzat's equation is
Actually, the Ezzat's equation is a result of a formal fractionalization of the Pennes' equation by fractional Taylor series (first order expansion) (about fractional Taylor series expansion see section 8.1) of the heat flux and accepting the concept of Wulff (see the preceding text) about the perfusion term (i.e., the reference temperature is the arterial blood temperature Ta). With the pre-factors τα/α! in both sides of (133) the equation is dimensionally consistent but why these pre-factors should exist and what they model are questions unanswered in the studies of Ezzat et al. [122, 123]. We will discuss this problem further in section 8.2.
The scaling by and the length, and time scales (Lx and t0) yields
Since the ratio (a = k/ρc is the thermal diffusivity of the tissue) has a dimension of inverse time [1/s] it follows that with a time scale we get the dimensionless relaxation time-delay (the term is in accordance with basic postulate of Cattaneo), or in other words a fractional Fourier number defined through τ, that is . Moreover, . Hence, the ratio in the Ezzat model (see (134) is
For α = 1 in (135) we get the integer-order relationship (93). In case of t0 = τ we get that and it follows from (135) that . This leads to simplified terms of the time-fractional derivatives in (134), that is
This result answers the question previously raised about appearance of the pre-factors in the Ezzat model (134). The answer is simple: incomplete nondimensalization of the model equation. In the above formula we did not use the correct expression of , omitting the dimensionless α!, only for the sake of simplicity. Actually, the left-hand-side of (128) can be presented as
, where the fractional relaxation time is .
Now, the problem remaining is the definition of the length scale Lx. From the general requirement all terms to have order of magnitude of unity and dimensionless pre-factors we get that (Q/ρcT0) is dimensionless. Hence, the length scale cannot be defined through the known parameters and it has to be taken from the experiments, depending on the precision of measurements. In this context, we have to remember that the magnitude of the time delay (relaxation time) of the tissue should be also determined from experiments parallel to adequate value of the fractional order α, thus recalling for accurate inverse problems taking into account their ill-posed natures.
6.2.2. Damor's Model
The model of Damor et al. [125] is a fractional version of the bio-heat equation by a simple replacement the time derivative with a fractional counterpart as Caputo derivative (order α ∈ (0, 1]) with singular (power-law) kernel and the spatial derivative by a Riesz-Feller fractional derivative of order β ∈ (0, 2], namely
where Wb and cb are related to the blood; the subscript t is related to the tissue, as in the model of Pennes.
With initial and boundary conditions (139)
Otherwise, for α = 1 and a Riemann-Liouville space derivative of order γ ∈ (0, 2] [see (141)] the formal fractionalization results in [126]
For β = 2 the model (138) reduces to [125]
With dimensionless variables [125]
equation (142) takes a dimensionless form, namely
with initial and boundary conditions
The dimensionless variables (143) reveal that the length and time scales are
The nondimensalization with the dimensionless variables (143) seems, to some extent, artificial (without explanations, performed in a typical mathematical manner without physical explanations). To be precise, if we use the generally defined length and time scales as (Lx and t0), and with classical dimensionless temperature θ = (T − Ta)/T0 or θ = T/T0 (in this case there is only a shift in the temperature scale origin), and applying the classical techniques of nondimensalization of differential equations we get from (142)
Now, dividing all terms by the prefactor of the time fractional derivative we get
Since at this moment all terms in (148), including the variable θ, should be of order of magnitude of unity and applying the order of magnitude analysis requirement we may obtain the length and time scales of the process. Hence, setting the pre-factor of the second term in the right-hand side we get the time scale . Further, from we have , where aα = kα/ρtct is the fractional thermal diffusivity of the tissue with a dimension [m2/sα]. Consequently, the requirement all prefactors of the dimensionless equation to be equal to 1 yields .
Therefore, the characteristic time and length scales depend on preliminary known process parameters and there is nothing magic in formulation of the dimensionless variables (143) (do not believe that they are formulated ad hoc). Moreover, since , consequently ηα defines the fractional Fourier number. . Thus, the time-fractional derivative in (144) can be expressed as
However, we refer the dimension of the fractional heat conductivity kα for correctness and physical relevance of the model. When we define the fraction thermal diffusivity aα = kα/ρtct it is obvious that it obeys the dimensional homogeneity of the time-fractional diffusion equation. Nevertheless, the problems is to the initial definition of kα. In the Damor's model this was not clarified and on this basis Ferras et al. [127] criticized it (see the next section 6.2.3). We may say briefly, that the crucial problem is the correct constitutive equation of the heat flux in terms of fractional integral with adequate memory function and we will discuss this problem at large further in this article.
6.2.3. Ferras et al. Model
Ferras et al. [127] adapted the Pennes equation by using timer-fractional Caputo derivative in the form
where
It is worth-mentioning that in this model a new parameter τ (this is not the past time in the fractional operator) was added to assure the dimensional consistency. Thus, this is the same step as in the approach of Ezzat commented above [see the operation transforming (132) into (133)] where the multiplication by τα/α! is applied.
It is worth noting that Ferras et al. [127] focused the attention on the fading memory approach following Gurtin [128] and Gurtin and Pipkin [128] where the non-locality of the heat flux is expressed by a convolution integral
With this step Ferras et al. [127] got a heat conduction equation with memory.
Note 3: However, we only mention at this point that the model (153) is not complete, as it should follow from the fading memory approach of Gurtin [128] and Gurtin and Pipkin [128], because the right-hand side of (153) is only the elastic part of the heat flux [97] (see also the analysis in [96]).
The next step of Ferras et al. [127] is the assumption that the memory kernel in (153) is a of power-law type, that resulted in
which, in fact, is that the heat flux is proportional to a Riemann-Liouville derivative of the temperature gradient. This is ad hoc formulation of a constitutive equation about heat flux, without any physical background, but in the sequel of this section we will see way this was done.
Then, with (154) the model (153) was transformed into
The result (154) is, in fact, the time-fractional diffusion equation where the thermal diffusivity aα should have a dimension [m2/sα]. Hence, we may see why (154) was constituted; the explanation is simple: to get an equation that we know how to solve.
Ferras et al. [127] raised a principle question about the construction of their model (150) by introducing the new parameter in the coefficients [see (151)] which physical meaning was difficult to be explained. Moreover, Ferras et al. [127] claimed that a new relationship between the heat flux and temperature gradient is established (153) and (154), which actually is not true since the fading memory approach of Gurtin and Pipkin [128] is incompletely used . We will explain these critical standpoints further in this article but now let us turn on last result of Ferras et al. [127]
defining in this way a “new fractional conductivity” .
Note 4: The approach of Ferras et al. [127] is very dubious because it uses only the pseudo-elastic part of the heat flux (see further the section devoted to fading memory concept) expressing it as a Riemann-Liouville derivative (154) that leads to a result which is a well-known, i.e., the time-fractional diffusion equation. Now, the principle question is: What would be the result is the Gurtin and Pipkin [128] approach is correctly applied ? This problem is discussed in the next section where a systematic approach in construction of bio-heat equation with memories involving time-fractional operators is drawn.
6.3. Briefs on the Existing Time-Fractional Bio-heat Models
Fractional models form a modern trend in modeling of transport processes with relaxations. In this context, the use of time-fractional derivatives in heat transfer model is a reasonable step since the integer-order models are related to infinite heat flux speed. However, formal replacement of integer-order derivatives by fractional counterparts (see the model of Damor), in general, is not a correct approach since it is not based on basic laws. Hence, striking the balance at the moment, the only correctly derived time-fractional bio-heat is that of Ezzat (136). The Ferras' model uses a completely different basis for fractionalization and we will comment it further in this text when the fading memory approach will be applied. Besides, the existing studies demonstrate only fractionalization techniques and model solutions but comparisons of the simulations outputs with experimental data are still missing.
7. Time-Fractional Bio-heat Models: A Systematic Approach
7.1. Short Preamble
After the analysis of the existing fractional versions of the bio-heat equations in the preceding section 6.2 we will try to draw some principle steps how fractional operators can be implemented in existing models. From the analysis of the continuum models it became clear that the main work how to account for the vascular geometries and the effects of either large or small blood transporting vessels was already done. At this moment we accept these models as granted and the focus is on the modeling technology accounting the fact that there is a heat flux damping when it propagates through the living tissue. We already saw how this could be done by the Maxwell-Cattaneo and the Dual-phase lag approaches. Now, we will use some ideas from them and will draw new ones toward correct formulation of heat transfer models applicable to living tissues. The principle model where we will test these approaches is the Pennes model due to its simplicity and taking into account that the already existing time-fractional bio-heat models are mainly based on it.
7.2. Fractionalization: Principle Directions
From the lessons learned we may suggest two principle directions in fractionalization of heat conduction models:
(A) By application of fractional Taylor series expansions concerning three examples:
(A1) Heat flux damping by application of the fractional Taylor series expansion (first order approximation).
(A2) Both heat flux and thermal gradient damping by application of the fractional Taylor series expansions (first order approximations).
(A3) Thermal gradient damping in a viscoelastic manner by applying time-fractional derivatives.
First of all, the fractional series expansions (first order approximations) will be discussed as an analog of the methods applied in integer-order models with relaxation (in section 8.2). All these methods use time-fractional derivatives with singular (power-law kernels).
(B) The fading memory concept in two versions:
(B1) Simple fading memory (SFM) and
(B2) Extended Fading Memory (EFM).
These two fading memory versions will be investigated with various relaxation kernels, some of them different from the common power-law. Now, we will investigate these ideas step-by-step.
8. Fractionalization by Series Expansions
8.1. Fractional Taylor Series: Necessary Information
With this short note we only explain what the fractional Taylor series expansion is meaning in the process of fractionalization of model equations, thus making the further discussions more readable.
Many authors suggested general forms of power series (we already commented an example with Jumarie's derivative), precisely Taylor series with fractional derivatives. Following Hardy [129] the Riemann general Taylor series is
where is the Riemann-Liouville Fractional integral of order k + r (see section 6.1.1.1).
Similarly, in 1931 Watanabe [130] developed the following expression [131]
with a residual term
where is Riemann-Liouville of order α + n.
A Taylor series expansion in terms of Riemann-Liouville fractional derivatives was proposed by Trujillo et al. [132]
with a residual terms
At the end, we refer to the work of Odibat and Shawagfeh [133] where a generalized Taylor series expansion in terms of Caputo derivative of order mα was proposed
more informatively, for the purposes of the following sections, we have
In terms of fractional relaxation times, we may write
where
and λαm has a dimension , where dimx is the dimension of x (time or length, depending on the physics of the modeled process).
Now, we will stop with definitions of fractional Taylor series since this is out of the scope of this work. We will concentrate the attention on the first-order approximations only, that is for m = 1. For more details and information we refer to El-Ajou et al. [131]. Hereafter in our discussion we may assume that the fractional Taylor series are based on Caputo derivative, if some other type is not especially specified. Recall, that in the above equations, x was used optionally and this is not the space coordinate used in the model. The relationships remain the same if we will use the time t instead x.
8.2. Heat Flux Damping by Fractional Taylor Series Expansion (Fractional SPL-Q)
This approach means application of the constitutive flux-gradient relationship in the form
without specification what type of fractional derivative is used (from the previous section it is easy to see that using only 2 terms for k = 0 and k = 1 we get similar results). When the Caputo derivative is used, then is defined by Equation (165).
Actually this a fractional version of the Maxwell-Cattaneo approach (see section 5) (which reduces to (79) for α = 1), an approach already used by Ezzat et al. [122, 123]. We already analyzed this model (see section 6.2.1) and therefore it will be more interesting to skip repetitions and explain the other ideas for fractionalizations. The case with α ≠ 1 is termed here Fractional SPL with respect to the heat flux, SPL-Q.
It is noteworthy to mention that this is the simplest way to achieve model fractionalization (excluding the formal replacement of the derivatives by fractional ones, which in many case results in unphysical models). However, there are no restrictions to apply high order approximation by of the heat flux as
Obviously, this will lead to more complex models with fractional derivatives of different orders. In this context, their applicability could be proved only by testing models to real data and answer sincerely to the question: What this flux damping approach will model and how it will improve the existing model to which it will be applied? Hence, we have an idea, and a guiding line how to perform it, but final formulations of the consequent models and solutions, and generally, answers to the emerging questions are not available yet. At this moment we have to take into account the comments at the end of section 5.1.1, precisely that λq should be mathematically small since if we like the model to be physically sound.
8.3. Thermal Gradient Damping by Fractional Taylor Series Expansions (Fractional SPL-T)
Alternatively to the approach used in section 8.2, we apply the fractional Taylor expansion to the temperature gradient only
where
with a dimension sβ. Then, the fractionalized heat flux is
or
The transport coefficient with a dimension (W/mK)sβ is a damping heat conduction (some times termed as elastic heat conduction) which has no effect when the memory kernel of ∂β/tβ goes to zero. For β = 1 in (170) and (171), we get the right-hand side of the integer-order DPL model. By analogy, we term this version of the fractional SPL, FSPL-T (fractional SPL with respect to the temperature gradient).
The approach demonstrated here can be applied by application of Taylor series expansions to either the time t, as it as done here, which corresponds to the assumption of a homogenous heat conductor, or with respect to the space coordinate x if the heat conduction is assumed as non-homogeneous in space (see such examples in [134, 135]).
8.4. Fractional Dual-Phase Lag Approach
This approach is a fractional version of the Dual-Phase Lag concept [83, 84, 102] and by analogy we will term it Fractional Dual-Phase Lag (FDPL) concept. The time-fractional version of the constitutive equation relating the heat flux and the temperature gradient is
Obviously, λq ≠ λT. In order to preserve the causality of the heat flux with respect to the temperature, we need λq > λT and λq − λT > 0. Consequently, the causality requirement mentioned above needs α < β, that is the flux should have stronger memory than the temperature gradient. There is no mandatory condition requiring α = β but the condition λq − λT > 0 remains. For α = β = 1 we get the integer order DPL model (section 5.2), and obviously we should have λq > λT. Further, the approach expressed by (166) could be applied to FDPL, but we will skip this point since a serious physical background to do that is missing, albeit the formal application of high order approximations by fractional Taylor series is a valid mathematical approach.
8.5. Thermal Gradient Damping in a Viscoelastic Manner
The idea for this damping of the heat flux (by high order time derivatives) comes from the viscoelastic models of non-Newtonian general second grade fluids where the relationship between the shear stress τshear(t) and strain εstrain(t) is presented as [93–95, 136]
Here μ is a fluid dynamic viscosity, while λe is the first normal stress modulus (analog to the heat conduction relaxation time in the expansions by Taylor series commented above [94, 136]
Alternatively, the second version of (173) leads to the governing integer-order equation of the unidirectional flow of a second grade fluid [93, 94, 136, 137], namely
where ν is fluid kinematic viscosity with dimension m2/s (analog of the thermal diffusivity a).
The last term in (175) is the same as in the integer order DPL model [see (99) or (100)].
To be precise, and for the sake of clarity of the following expression, we mention that from the basic relationship between the velocity u(x, t) and shear stress τfric (the flux of momentum in hydrodynamics
and the integer-order relationship
leading to (175) we actually have the SPL-T analog in the fluid flow.
The fractional version corresponding to (174) is
Therefore, using analogy between the fluid velocity field and the temperature field distribution in the body it is possible to formulate a constitutive relationship between the heat flux and temperature gradient as
Equation (179) is only the right-hand side of the Fractional Dual-Phase Lag model formulated above. For β = 1 we get the integer order DPL model (actually, only its half part related to the damping of the temperature gradient).
Then, with the energy balance relationship (without convection and volumetric heat sources: for the sake of simplicity in presentation of this fractionalization technique) we get
Fractional model
where λeT has a dimension sβ and therefore the product kλeT could be considered as a fractional (in time) heat conductivity kβ with a dimension (W/mK)sβ.
Integer-order model for β = 1
Further, applying this approach to the Pennes model we get
Actually, the fractionalization applied here is equivalent to the one-side approach (fractionalization only of the temperature gradient) demonstrated in section 8.3.
Note 5: We like to stress the attention on the last two versions of fractionalization where the damping effect is applied to the temperature gradient only (sections 8.3 and 8.5). At a glance, it would be a violation of the causalty between the heat flux and the temperature gradient. However, we have to mention that the Taylor series expansion and fractionalization of the viscoelastic manner are more philosophically related to the fading memory concept developed in the next section 9 and there is no violation of causality mentioned above.
8.6. Comments on Fractionalization by Taylor Series Expansions
Fractionalization of integer-order models by application of fractional Taylor series expansions (first-order approximation) is a feasible technique resulting in simple time-fractional equations. The techniques demonstrated in this section dealt only with models assuming homogenous tissues as heat conductors. Logically, the fractional Taylor series technique could be extended toward space-fractional models but this needs serious physical motivation and information about the non-homogeneity of the tissue of interest. Regarding the existing time fractional bio-heat models, only the Ezzat' equation (136) [through (128)] follows this approach correctly, despite the fact that the obsolete Jummarie fractional derivative is used. However, there are no obstacles the same approach to be applied with Taylor series based on the Caputo derivative (this will change only the pre-factors of the time-fractional terms). It might be expected that the approaches demonstrated in this section would be successfully applied for creation of new bio-heat models.
9. The Fading Memory Concept to Heat Conduction
9.1. Basic Principle of Fading Memory in Heat Conduction
The fading memory concept relating the flux j(x, t) to its gradient, for simple materials [128, 138–142], is modeled by the following integro-differential equation
as a manifestation of the Boltzmann linear superposition functional expressing the flux history [143] through the function of influence (memory kernel) R(t, τ). In (183) D0 and D′ are transport coefficients (diffusivities).
The appropriate history value problem is related to the hereditary integral in (183) [144]
allowing to give a function C(x, t) on (−∞ < t ≤ 0)
From (183) and (184) it follows that
Since C(x, t) is a causal function (vanishing for t < 0) and considered only for 0 < t < ∞ it follows that d(t) = ∇ · d(t) = 0, thus (185) can be rewritten as
Following Gurtin [128], Gurtin and Pipkin [128] the heat flux can be expressed in a shorter version by the hereditary integral only
which comes from (186) for D0 = 0. Hence we have two forms of the fading memory concept:
(B1) Simple fading memory concept expressed by (187).
(B2) Extended fading memory concept expressed by (186).
Let us now see how these two versions of the fading memory work in the heat conduction problem.
9.2. Simple Fading Memory Concept and Effect of the Kernel
As it was several times commented above the Fourier law trough the energy balance results in the simple parabolic heat conduction equation by the relationship
with infinite speed of the heat flux.
A damping function related to a finite speed of heat diffusion in rigid conductors was conceived by Cattaneo [145] by a generalization of the Fourier law through a linear superposition of the heat flux and its time history (with a time-delay s by a hereditary (memory) integral).
Now, the principle question is: What function R(x, t) should serve as adequate memory kernel? It is noteworthy to mention that the type of the relaxation function R(x, t) strongly depends on the reaction (response) of the material where the heat transport takes place. It was demonstrated in Hristov [116, 120], in the field of the linear viscoelasticity of materials, the relaxation response defines the type of the memory function in the hereditary integral. Hence, there is a freedom in choosing R(x, t), but this cannot be done voluntary since the physics should be taken into account. In the sequel we will see how the final form of the heat conduction equation depends on choice of R(x, t).
9.2.1. Exponential Kernel
For homogeneous rigid heat conductors the memory function R(x, t) is space-independent and can be represented, for instance, by the Jeffrey kernel [96, 97] as
where the relaxation time τ is finite, i.e., τ = const.
Then, the energy balance yields the Cattaneo equation
For t → ∞ the right-hand side is zero and no physical meaning comes from this. Here, the thermal diffusivity a2 is elastic thermal diffusivity relevant only to the fading memory term (see below the comments about (194). For τ → 0 the limit of the Cattaneo equation is the Fourier law.
The first order approximation of the heat flux, in τ yields [146] is
a technique already discussed in section 5.1
This leads to a first order differential equation [146]
The integration of (193) with help of (192) results in the Cattaneo equation, which is the simplest giving rise to finite speed of flux propagation. Further, continuing the integration and applying the energy balance we will get the classical telegraphic hyperbolic equation. However, now we look at results from a different viewpoint trying to interpret the constitutive equations involving hereditary integral from the position of fractional calculus.
9.2.2. Relaxation Function of Joseph and Preziosi
Considering the heat-wave nature of the conduction energy transfer Joseph and Preziosi [97] have considered a modified relaxation function replacing the exponential kernel in (189) by
, where δ(s) is Dirac delta function, while k1 and k2 are the effective thermal conductivity and the elastic conductivity, respectively. This constitutive equation defines the relaxation function in a way that matches exactly the philosophy of fading memory concept: the first term of RJP models the instantaneous (memory-less) reaction of the heat conductor, that is this corresponds to the Fourier law, while the second term corresponds to the flux damping effect and finite speed of propagation.
In this case the Fourier law leads to a flux defined as [97, 146]
Consequently, the conservation equation of the internal energy in the heat conductor [128] results in the Jeffrey-type integro-differential equation [146]
The second term in (196) goes to zero for large times, since the memory function fades and only the first term remains; despite this the time for existence of the second term is related to the finite heat flux speed (i.e., the flux is damped in time). Equation (196) corresponds to the extended fading memory concept with a simple exponential kernel, as it will be demonstrated in the sequel (see section 9.3.1).
Equation (196) can be expressed as [96] (see also the analysis in [119])
with a damping term controlled by the Caputo-Fabrizio operator (derivative) [118]
where M(α) is a normalization function such that M(0) = M(1) = 1.
9.2.3. Simple Power-Law Kernel
The exponential memory function (190) is a bonded kernel since for t → 0+ it approach unity. However, the power-law memory kernel tα−1/Γ(α) (with 0 < α <1) is unbounded at t → 0+ and time-scale invariant (the exponential function is not time scale invariant).
Now, constructing the shorter equation of the fading memory concept (187) with a power-law function we get
We can see that the right-hand side in (199) is the Riemann-Liouville fractional integral [117]. Hence, the heat flux gradient dq/dx is
Now, applying the energy balance equation we get
At this moment we may perform a small thought experiment. Let us suggest that the heat conduction is modeled by the Continuous Time Random Walk (CTRW) concept. Then, the right-hand side of (199) corresponds to this model and we get
Differentiation of (202) with respect to the time yields
The right-hand side of (203) is the core of the constitutive equation about the heat flux relaxation in the fractional model of Ferras et al. [127] (see Equation 154). Further, the suggestion of Ferras et al. [127] simply means that applying the heat balance we have to write
where and should be taken from the elastic part of Equation 201).
Therefore, the final result of the Ferras' constitutive equation should be
but not equation (154).
In this context, we can see, as it was mentioned earlier in section 6.2.3, that the quest to find something that is well-known and easily solvable may lead to use of wrong premises (the Ferras's et al. constitutive relationship heat flux-thermal gradient) violating basic thermodynamic principles such as the fading memory concept or naively applying it. We are aware about the commonly mentioned and published solutions of the time-fractional heat-wave equation [117] (the final result of Ferras et al. [127]) but applying it we need serious physical background. In the specific case of bio-heat models such physical reasons are still missing (or not published yet).
9.2.4. Extended Power-Law Kernel
Here, we suggest an extended power-law (EPL) memory kernel, by analogy of the extended exponential relaxation function (189) of Joseph and Preziosi [97], namely
With
we get
That is, the second term in (208) is the Riemann-Liouville fractional integral. The result (208) coincides with the one obtained by the extended fading memory concept and simple power-law kernel (see the next section 9.3.2).
Then, the heat conduction equation becomes
For large times, when the memory kernel goes to zero (209), reduces to the Fourier equation. The dimension of a1 is m2/s, while k1 has dimension [W/m · K], that is the same as in the Fourier law. The dimension of k2 (and a2) needs a special attention and this will be discussed in section 9.4.
9.3. Extended Fading Memory Concept and Effect of the Kernel
9.3.1. Exponential Kernel
With the general construction (186) and exponential kernel (190) we get
The result (210) matches (196) obtained with the simple fading memory concept and the extended exponential kernel (194).
9.3.2. Power-Law Kernel
The exponential memory function (190) is a bonded kernel since for t → 0+ it approach unity. However, the power-law memory kernel tα−1/Γ(α) (with 0 < α < 1) is unbounded at t → 0+ and time-scale invariant (the exponential function is not time scale invariant).
Constructing the basic equation of the fading memory concept (183) with a power-law function we get
The second term in (211) is the Riemann-Liouville fractional integral [117] and the heat flux gradient dq/dx is
Then, applying the energy balance equation we get
For large times, when the memory kernel vanishes, equation (213) reduces to the Fourier model.
9.4. On the Dimensionality in Constitutive Equations With Fading Memory Operators
The dimensions of the coefficients with temporal relaxations in both the fractional Taylor series and fading memory operators were mentioned several times, but now we like to stress the attention especially on this point. When the flux damping is modeled by either SPL or DPL in integer-order or fractional manner we have
the fading memory is incorporated in the construction of the fractional derivative. In this case the dimensionality of λq is [sα], thus the second term in (214) has a dimension of heat flux, that is (W/m2).
Similarly, when the temperature gradient is damped by SPL or DPL, we have
where kα has dimension of (W/m · K)sα, that is .
Alternatively, we may write
The term (1 + λT) is valid only during the short time relaxation defined by λT and has a temporal dimension defined by λT. Therefore, for times coinciding with the relaxation (damping) period (0 < t ≤ λT) the dimension of K is (W/m · K)sα in contrast to the long-time case (t > λT) when the dimension is (W/m · K). This is strongly related to the fact that the two terms in the right-side hand of (214) (the same in (215) are transient but:
(1) The local first term (with coefficient to k) is transient due the change in the boundary condition at t = 0, while
(2) The second one (with the memory) (with a lower terminal of the integral at t = 0 due to the causalty condition) is also transient but it is non-local and is related to the time history of the flux.
If the medium relaxation time is zero, that is an instantaneous reaction of the disturbed body is observed, this means that, for instance, with λT = λq we get K = k (see Equation 216). In this context, we may say something related to the heat conduction problem and the dimensionality of the coefficients involved.
In the classical heat conduction, since the time of Fourier, the dimension of the heat conductivity is time-independent and when a transient heat conductivity appears in constitutive equation with memory, this may cause ambiguities and cast doubts. The simple explanations are:
(a) The traditional time-independent conductivity occurs in problems when the transient processes are larger that the time duration of the action at the boundary (it is well-known that the Fourier heat conduction equation works only for large time, and fails for short times, as well as is thermodynamical inconsistent). That is, there is no need to know what is the relationship between the time of the action at the boundary, the total transient time of the process and the specific relaxation time (the accommodation time) of the materials, i.e., now knowledge about the process history is needed (memoryless process). Recall also the comments just after Equations (78) and (79).
(b) However, when the time duration of the action at the boundary is comparable with the material thermal relaxation time, then the damping of the heat flux should be taken into account and this is well described by a hereditary integral (a technique know since the time of Boltzmann [143]).
(c) Better understanding of the thoughts above, could be attained if we consider the heat transfer by conduction when the heat flux is related to the temperature gradient by the thermal diffusivity aT = k/ρcp. Then, we may write the well-known time-fractional heat-wave equation
where the dimensionality of is m2/sα, and the time fractional derivative is either from Riemann-Liouville or Caputo type.
From (217) it follows that of the heat balance equation is ∂T/∂t = −∂q/∂x then the heat flux should be related to the thermal gradient by the relation .
Hence, there is no contradiction with the classical heat condition, but only development of the existing knowledge. This is a simple example involving a time-fractional derivative, as a more familiar operator to the people working in fractional modeling, but the same philosophy remains when fractional integral of Riemann-Liouville type appears in application of the fading memory principle. Obviously, the physics of the heat flux relaxation should be correctly approximated by the type of the memory kernel and the definition of the temporal dimension of coefficient in front of the fractional integral.
This short section only marks the problem and comments issues relevant to the discussed topic since for many readers the appearance of time-fractional-dependent heat conductivity (or thermal diffusivity), for instance, will be quite unusual and heretic, or at least erroneous. For more studies and examples involving fractional (non-local problems) and fractal (local problems) dimensions we refer to Westerlund [147], Muslih and Baleanu [148], Ebaid et al. [149], Gomez-Aguilar et al. [150, 151], Dokoumetzidis and Macheras [152], and Liu [153].
10. Fading Memory Concept to Bio-heat Equations: Examples
Now, at the end of this long analysis we present two examples how the fading memory concept works in the formulation of bio-heat equations with memories.
10.1. Pennes' Equation With a Fading Memory
10.1.1. Extended Fading Memory Concept
Let us consider equation (22) in section 3.1. Assuming that the non-local perfusion term and the metabolic heat are not relaxing, and applying the fading memory principle we get
Now, applying different memory kernels R(t, τ) we may obtain equations in different forms with different fractional operators, but recall the choice of R(t, t) should be physically motivated. The application of the fading memory principle to the Pennes equation results in a nice-looking model, but it still retains its main deficiency: the already commented problems with the perfusion term.
10.1.2. Simple Fading Memory Concept
In this simple case there is no instantaneous heat flux component, that is first therm in (218) is zero. Then, we have
where is the thermal diffusivity with a dimension m2/sα. Hence, only the damping term remains. The relaxation function R(t, τ) strongly depends on the physical concept assumed in the heat conduction modeling, precisely what should be the heat conduction transfer mechanism. With the power-law kernel, for instance, as in (213), accepting the random walk concept, we get Riemann-Liouville integral and consequently the time-fractional heat-wave equation with a sink. It is easy to check different versions of (219) by change in the memory kernel, but this should be seriously motivated in regards what type of tissue will be considered and how the relaxation function is related to its real thermal behavior.
10.2. Wulff's Model With a Fading Memory
10.2.1. Extended Fading Memory Concept
Let us start with Wulff formulation of the heat flux (33) [21, 29, 32]. Applying the fading memory principle we have
Thus, the energy balance reads
which is the Wulff equation with a fading memory. The coefficients Kα and Kv depend on the type of the memory function used in the hereditary integrals. Applying different memory kernels (with strong physical motivation) equation (221) can be expressed in terms of different fractional operators. However, this draw new research lines which are out of the scope of this work.
11. Some Comments on the Fractionalization Approaches
Now, after the performed analyzes in sections 7 and 7.2 (and the related results in sections 8 and 9) we may draw some conclusions on feasibility of the fractionalization approaches and emerging problems, namely
(1) The simple replacement of time-derivatives in existing integer-order models by fractional counterparts, irrespective of the type of the memory kernels used is blind and erroneous approach without physical background.
(2) Fractionalization by fractional Taylor series expansion of both the heat flux and the temperature gradient is logical, mathematically correct and based on analogies already used in the Maxwell-Cattaneo approach resulting in the hyperbolic heat-wave model and in the Dual-Phase Lag (DPL) model.
(3) Fractionalization by additional mixed time-space derivative is useful approach based on analogies of the modeling equations of the non-Newtonian fluid flow (second order fluid) and the fact that lagging can be obtained by Taylor series (in time) expansion of the temperature gradient. The result is a simple equation with only one damping term in contrast the results of the preceding (point 1 and point 2) final models (see the model of Ezzat, for example).
(4) The fading memory approach is not restrictive in the initial step of fractionalization, as in the cases when fractional Taylor series are applied; it is based on rigorous thermodynamic principles and gives a freedom to apply different memory kernels depending on the experimentally exhibited responses (relaxation function) of the materials (tissues) where the heat conduction should be modeled. A good example is the Wulff models with a fading memory derived here since it demonstrates that both the heat diffusion (conduction) and the perfusion blood flux can exhibit relaxations (i.e., these fluxed have finite speeds of propagation). There are a lot attractive and challenging problems in this area that should be solved.
(5) The fractionalization problem discussed are oriented only to damping heat fluxes in the time domain, that is the tissues where the heat transfer should take place are assumed as homogenous. To some extent, the spacial non-homogeneity of the tissues are modeled by effective transport coefficients (such as in the models of Wulff, Klinger and Weinbaum-Jiji) thus facilitating the process of fractionalization. Space-fractional models are open problems [154] waiting correct build-ups with correct physical analyzes of the both the tissue structures and vascular architectures.
12. Final Comments
Finally, after the long route through the beautiful forest of bio-heat models we may say that the first goal of the analysis done is successfully attained. Precisely, a direct parallel between the existing integer-order models and the corresponding fractional versions was drawn. To some extent, the existing fractional bio-heat models are not systematically derived, excluding the attempt of Ezzat which falls into one of the systematic way how fractionalization could be done. Actually, the good understanding of the contributions of different terms of the discussed models needs nondimensalization since this allows to see the contributions of different processes involved in the heat transfer in tissues. This a standard procedure in mathematical modeling but sometimes the reported studies define the dimensionless variables ad hoc without deep physical analysis and consequent order of magnitude analysis. Last but not least, collecting dispersed studies in both bio-heat model formulations, their analyzes, solution and fractionalizations (if this is well motivated) is a difficult task. We hope the work done here and its results will serve as a good source of information and new ideas, and we may expect that the systematic approach in the formulation of the time-fractional models will draw more correct approaches, from mathematical and physical viewpoints, of course. The correct model formulation is of primary importance in mathematical modeling and this goal has a priority over calculation techniques.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Xu F, Lu TJ, Seffen KA, Ng EYK. Mathematical modelling of skin bioheat transfer Appl Mech Rev. (2009) 62:050801. doi: 10.1115/1.3124646
3. Gokul KC, Gurung DB, Adhikary PR. Effect of blood perfusion and metabolism in temperature distribution in human eye. Adv Appl Math Biosci. (2013) 4:13–23.
4. Nowakowska O, Bulinski Z. Mathematical modelling of heat transport in section of human arm. Comp Assist Meth Eng Sci. (2015) 22:347–63.
5. Hayes KW. Heat and cold in management of rheumatoid arthritis. Arthrit Care Res. (1994) 6:103–54.
7. Petrofsky JS, Lohman E III, Suh J, Garcia J, Anders A, Sutterfield C, et al. Determination of the conductive heat exchange of the skin in relation to environmental temperature. J Appl Res. (2006) 6:157–69.
9. Zolfaghari A, Maerefat M. Bioheat transfer. In: Marco Aurelio dos Santos Bernardes, editor. Developments in Heat Transfer Rijeka: IntechOpen (2011). doi: 10.5772/822
10. Petrofsky JS, Lind AR. The insulative power of body fat on deep muscle temperature and isometric endurance. J Appl Physiol. (1975) 39:639–42. doi: 10.1152/jappl.1975.39.4.639
11. Petrofsky JS, Lind AR. The relationship of body fat content to deep muscle temperature and isometric endurance in man. Clin Sci Mol Med. (1975) 48:405–12. doi: 10.1042/cs0480405
12. Torvi DA, Dale JD. A finite element model of skin subjected to a flash fire ASME J Bimech Eng. (1994) 116:250–5. doi: 10.1115/1.2895727
13. Yamada Y, Tien T, Ohta M. Theoretical analysis of temperature variation of biological tissue irradiated by light. ASME/JSME Ther Eng. Conf. (1995) 4:575–81.
14. Askarizadeh H, Ahmadikia H. Analytical analysis of the dual-phase-lag model of bioheat transfer equation during transient heating of skin tissue. Heat Mass Transf. (2014) 48:317–27. doi: 10.1007/s00231-014-1373-6
15. Kengne E, Sayde M, Lakhssasi A. Effect of convective term on temperature distribution in biological tissue. Eur Phys J Plus. (2013) 128:98. doi: 10.1140/epjp/i2013-13098-8
16. Datta A. Biological and Bioenviromental Heat and Mass Transfer. New York, NY: Marcel Dekker (2002).
17. Valvano JW. Bioheat transfer. In: Webster JG, editor. Encyclopedia of Medical Devices and Instrumentation, Vol. 1, 2nd ed. Hoboken, NJ: Wiley (2005). p. 188–97.
18. Chappuis P, Pittet P, Jequier E. Heat storage regulation in exercise during thermal transients. J Appl Physiol. (1976) 40:384–92. doi: 10.1152/jappl.1976.40.3.384
19. Webb P. The physiology of heat regulation. Am J Physiol. (1995) 268:R838–50. doi: 10.1152/ajpregu.1995.268.4.R838
20. Orr C-S, Eberhart RC. Overview of bioheat transfer. In: Welch AJ, van Gemert MJC, editors. Optical-Thermal Response of Laser-Irradiated Tissue. New York, NY: Plenum Press (1995). p. 367–84.
21. Charny CK. Mathematical model of bioheat transfer. Adv Heat Transf. (1992) 22:19–155. doi: 10.1016/S0065-2717(08)70344-7
22. Fan J, Wang L. Analytical theory of bioheat transport. J Appl Phys. (2011) 109:104702. doi: 10.1063/1.3580330
23. Baish JW, Foster KR, Ayyaswamy PS. Perfused phantom models of microwave irradiated issue. ASME J Biomech Eng. (1986) 108:239–45. doi: 10.1115/1.3138609
25. Chato JC. Fundamentals of bioheat transfer. In: Gautherie M, editor. Thermal Dosimetry and Treatment Planning. Heidelberg: Springer (1990). p. 1–56.
26. Zhu L, Schappeler T, Cordero-Tumangday C, Rosengard AJ. Thermal interaction between blood and tissue: development of a theoretical approach in predicting body departure during blood cooling/rewarming. In: Minkowycz WJ, SparrowEM, editors. Advances in Numerical Heat Transfer, Vol. 3. Boca Raton, FL: CRC Press, Taylor and Francis Group (2009). p. 197–219.
27. Pennes HH. Analysis of tissue and arterial blood temperatures in the resting forearm J Appl Phys. (1948) 1:93–122. doi: 10.1152/jappl.1948.1.2.93
29. Khanafer K, Varfai K. Synthesis of mathematical models representing bioheat transport. In: Minkowycz W, Sparrow E, Abraham J, editors. Advances in Numerical Heat Transfer, Vol. 3. CRC Press (2009). p. 1–28.
31. Aziz A, Kraus AD. Transient heat transfer in extended surfaces. Appl Mech Rev. (1995) 48:317–50. doi: 10.1115/1.3005105
32. Wulff W. The energy conservation equation for living tissues. IEEE Trans Biomed Eng. (1974) 21:494–5. doi: 10.1109/TBME.1974.324342
33. Shitzer A, Kleiner M. Thermal behavior of biological tissues- A General analysis Bull Math Biol. (1976) 38:369–86. doi: 10.1016/S0092-8240(76)80018-3
34. Shitzer A, Chato JC. Analytic solutions to the problem of transient heat in living tissue. ASME J Biomech Eng. (1978) 100:202–10. doi: 10.1115/1.3426211
35. Mincowycz WJ, Sparrow EM, Abraham JP. Advances in Numerical Heat Transfer. Boca Raton, FL: CRC Press (2009).
36. Klinger HG. Heat transfer in perfused biological tissue. I., General theory, Bull Math Biol. (1974) 36:403–15. doi: 10.1016/S0092-8240(74)80038-8
37. Klinger HG. Heat transfer in perfused biological tissue. I. The macroscopic temperature distribution. Bull Math Biol. (1976) 38:183–99. doi: 10.1007/BF02461434
38. Perl W. Heat and master distribution in body tissue and the determination of tissue bllodflow by local clearance methods. J Theor Biol. (1962) 2:201–3. doi: 10.1016/0022-5193(62)90025-5
39. Perl W, Hirsh RL. Local blood flow in kidney tissue by heat clearance measurements. J Theor Biol. (1966) 19:251–80. doi: 10.1016/0022-5193(66)90126-3
40. Klinger HG. The description of heat transfer in biological tissue. Ann N Y Acad Sci. (1980) 335:133–6. doi: 10.1111/j.1749-6632.1980.tb50741.x
41. Klinger HG. A simple solution of the non-stationary heat transport problem in capillarized biological tissue. Bull Math Biol. (1984) 46:879–89. doi: 10.1016/S0092-8240(84)80008-7
42. Chen MM, Holmes KR. Microvascular contributions in tissue heat transfer. Ann N Y Acad Sci. (1980) 335:137–50. doi: 10.1111/j.1749-6632.1980.tb50742.x
43. Weinbaum S, Jiji LM. A two phase theory for the influence of circulation on the heat transfer in surface tissue. In: Wells MK, editor. Advances in Bioengineering. New York, NY: ASME (1979). p. 179–82.
44. Weinbaum S, Jiji LM. A new simplified equation for the effect of blood flow on local average tissue temperature. ASME J Biomech Eng. (1985) 107:131–9. doi: 10.1115/1.3138533
45. Weinbaum S, Jiji LM. The matching if thermal fields surrounding countercurrent microvessels and the closure approximation in the Weinbaum-Jiji equation ASME J Biomech Eng. (1989) 111:271–5. doi: 10.1115/1.3168378
46. Weinbaum S, Jiji LM, Lemmons DE. Theory and experiment for the effect of vascular microstructure on the surface tissue heat transfer: part 1: anatomical foundation and model conceptualization. ASME J Biomech Eng. (1984) 106:321–30. doi: 10.1115/1.3138501
47. Weinbaum S, Jiji LM, Lemmons DE. Theory and experiment for the effect of vascular microstructure on the surface tissue heat transfer: part 2: model formulation and solution ASME J Biomech Eng. (1984) 106:331–41. doi: 10.1115/1.3138502
48. Song WJ, Weinbaum S, Jiji LM. A theoretical model for peripheral tissue heat transfer in living tissue using the bioheat equation of Weinbaum and Jiji. ASME J Biomech Eng. (1987) 109:72–8. doi: 10.1115/1.3138646
49. Song WJ, Weinbaum S, Jiji LM, Lemmons DE. A combined macro and microvascular model for whole limb heat transfer. ASME J Biomech Eng. (1987) 110:259–68. doi: 10.1115/1.3108440
50. Baish JW, Ayyaswamy PS, Foster KR. Small-scale temperature fluctuations in perfused tissues due to local hyperthermia. ASME J Biomech Eng. (1986) 108:246–50. doi: 10.1115/1.3138610
51. Wissler EH. Comments on the new bioheat equation proposed by Weinbaum and Jiji. ASME J Biomech Eng. (1987) 109:226–33. doi: 10.1115/1.3138673
52. Nakayama A, Sano Y, Yoshikawa K. A rigorous derivation of the bioheat equation for local tissue heat transfer based on a volume averaging theory. Heat Mass Transf. (2010) 46:739–46. doi: 10.1007/s00231-010-0619-1
53. Lubashevsky IA, Gafiychuk VV. Mathematical Description of Heat Transfer in Living Tissue. Lviv, VNTL Publishers (1999).
55. Crezee J, Lagendgijk JUW. Experimental verification of bioheat transfer theories: measurement of temperature profiles around large artificial vessels in perfused tissue. Phys Med Biol. (1990) 35:905–23. doi: 10.1088/0031-9155/35/7/007
56. Talaee MR, Kabiri A. Exact analytical solution of bioheat equation subjected to intensive moving heat source. J Mech Med Biol. (2017) 17:1750081. doi: 10.1142/S0219519417500816
57. Kengne E. Akhssasssi, bioheat transfer for one-dimensional spherical biological tissues. Math Biosci. (2015) 269:1–9. doi: 10.1016/j.mbs.2015.08.012
58. Liu KC. Thermal propagation analysis for living tissue with surface heating. Int J Therm Sci. (2008) 47:507–13. doi: 10.1016/j.ijthermalsci.2007.04.005
59. Shen W, Zhang J, Yang F. Modeling and numerical simulations of bioheat transfer and biomechanics in soft tissue. Math Comput Model. (2005) 41:1251–65. doi: 10.1016/j.mcm.2004.09.006
60. Lin M, Xu F, Lu TJ, Bai BF. A review of heat transfer in human tooth-Experimental characterization and mathematical modeling. Dental Mat. (2010) 26:501–13. doi: 10.1016/j.dental.2010.02.009
61. Deng ZS, Liu J. Analytical study on bioheat transfer problems with spatial or transient heating on skin surface or inside biological bodies. Trans ASME J Biomech Eng. (2002) 124:638–49. doi: 10.1115/1.1516810
62. Bejan A, Dincer I, Lorente S, Miguel A, Reis A. Porous and Complex Flow Structures in Modern Technologies. New York, NY: Springer-Verlag (1984).
63. Khaled ARA, Vafai K. The role of porous medium in modeling flow and heat transfer in biological tissues. Int J Heat Mass Trans. (2003) 46:4989–5003. doi: 10.1016/S0017-9310(03)00301-6
64. Khanafer K, Vafai K. The role of porous media in biomedical engineering as related to magnetic resonance imaging in drug delivery. Heat Mass Trans. (2006) 42:939–53. doi: 10.1007/s00231-006-0142-6
65. Nakayama A, Kuwahara F. A general bioheat transfer model based on the theory of porous media. Int J Heat Mass Trans. (2008) 51:3190–9. doi: 10.1016/j.ijheatmasstransfer.2007.05.030
66. Nakayama A, Kuwahara F, Liu W A general set of bioheat transfer equations based on the volume averaging theory. In Vafai K, editor. Porous Media, Applications in Biological Systems and Biotechnology. Boca Raton, FL: CRC Press (2010). p. 1–44. doi: 10.1201/9781420065428-2
67. Amiri A, Vafai K. Analysis of dispersion effects and nonthermal equilibrium, non-Darcian, variable porosity incompressible-flow through porous media. Int J Heat Mass Trans. (1994) 37:939–54. doi: 10.1016/0017-9310(94)90219-4
68. Amiri A, Vafai K. Transient analysis of incompressible flow through a packed bed Int J Heat Mass Trans. (1998) 41:4529–79. doi: 10.1016/S0017-9310(98)00120-3
69. Lee DY, Vafai K. Analytical characterization and conceptual assessment of solid and fluid temperature differentials in porous media. Int J Heat Mass Trans. (1999) 42:423–35. doi: 10.1016/S0017-9310(98)00185-9
70. Nakayama A, Kuwahara F, Hayashi T. Numerical modelling for three-dimensional heat and fluid flow through a bank of cylinders in yaw. J Fluid Mech. (2004) 498:139–59. doi: 10.1017/S0022112003006712
71. Fabrizio M, Giorgi C, Morro A. Modeling heat conduction via fractional derivatives Heat Mass Transf. (2017) 53:2785. doi: 10.1007/s00231-017-1985-8
72. Liu KC, Cheng PJ. Finite propagation of heat transfer in multilayer tissue. J Thermopphys Hear Transf. (2008) 22:775–82. doi: 10.2514/1.37267
73. Kaminski W. Hyperbolic heat conduction equation for materials with a nonhomogenous inner structure. J Heat Transf. (1990) 112:555–60. doi: 10.1115/1.2910422
75. Mitra K, Kumar S, Vedavarz A, Moalemi MK. Experimental evidence of hyperbolic heat conduction in processed meat. J Heat Transfer. (1995) 117:568–73. doi: 10.1115/1.2822615
76. Davidov EV, Lubashevsky IA, Milyaev IA, Musin RF. Nondiffusive heat transfer in muscle tissue. Preliminary results. arXiv: cond-mat/0102006. I(1). (2001).
77. Banerjee A, Ogale AA, das C, Mitra K, Subramanian C. Temperature distribution in different material due to short pulse laser. Heat Transf Eng. (2005) 26:41–9. doi: 10.1080/01457630591003754
78. Xu F, Lin M, Lu TJ. Modelling skin thermal pain sensation: role of non-Fourier thermal behaviour in transduction process of nociceptor Comp Biol Med. (2010) 40:478–86. doi: 10.1016/j.compbiomed.2010.03.002
79. Liu J, Chen X, Xu LX. New thermal wave aspects on burn evaluation of skin subjected to instantaneous heating. IEEE Trans Biomed Eng. (1999) 46:420–8. doi: 10.1109/10.752939
80. Yang WH. Thermal (Heat) shock biothermomechanical viewpoint. J Biomed Eng. (1993) 115:617–21. doi: 10.1115/1.2895549
81. Fabrizio M, Franchi F. Delayed thermal models: stability and thermodynamics. J Ther Stress. (2014) 37:160–73. doi: 10.1080/01495739.2013.839619
82. Cheng L, Xu M, Wang L. From Boltzmann transport equation to single-phase-lagging heat equation. Int J Heat Mass Transf. (2008) 51:6018–23. doi: 10.1016/j.ijheatmasstransfer.2008.04.004
83. Tzou DY. Experimental support for the lagging behaviour in heat propagation. J Thermophys Heat Transf. (1995) 9:686–93. doi: 10.2514/3.725
84. Tzou DY. Macro- to Microscale Heat Transfer: The Lagging Behaviour. Washington, DC: Taylor and Francis (1997).
85. Antaki PJ. Analysis of hyperbolic heat conduction in a semi-infinite slab with surface convection. Int J Heat Mass Transf. (1997) 40:3247–50. doi: 10.1016/S0017-9310(96)00351-1
86. Tzou DY. An engineering assessment to the relaxation time in thermal wave propagation. Int J Heat Mass Transf. (1993) 36:1845–51. doi: 10.1016/S0017-9310(05)80171-1
87. Fabrizio M, Morro A. Viscoelastic relaxation functions compatible with thermodynamics. J Elasticity. (1999) 19:63–75. doi: 10.1007/BF00041695
88. Fabrizio M, Morro A. Dissipativity and irreversibility of electromagnetic systems. Math Mod Meth Appl Sci. (2000) 10:217–46. doi: 10.1142/S0218202500000148
90. Jaisaardsuetrong J, Straughan B. Thermal waves in a rigid heat conductor Phys Lett A. (2007) 366:433–6. doi: 10.1016/j.physleta.2007.02.058
91. Kundu B, Dewanjee D. A new method for non-Fourier thermal response in single layer skin tissue. Case Stud. Ther Eng. (2015) 5:79–88. doi: 10.1016/j.csite.2015.02.001
92. Bravo ME, De Jesus Sanchez P, Vargas Aguilar RO, Chavez AE. Heat transfer in biological tissues. In: Klapp J, Chavarria GR, Ovando AM, Villa AL, editors. Selected Topics of Computational and Experimental Fluid Mechanics. Cham: Spinger International Publishing (2015). p. 313–20. doi: 10.1007/978-3-319-11487-3_21
93. Chen CI, Chen Ch K, Yang YT. Unsteady unidirectional flow of second grade fluid between the parallel plates with different given volume flow rate conditions. Appl Math Comput. (2003) 137:437–50. doi: 10.1016/S0096-3003(02)00149-2
94. Hristov J. Integral-balance solution to the stokes first problem of a viscoelastic generalized second grade fluid. Therm Sci. (2012) 16:395–410. doi: 10.2298/TSCI110401077H
95. Hristov J. A transient flow of a non-newtonian fluid modelled by a mixed time-space derivative: an improved integral-balance approach. In: Taş K, Baleanu D, Machado J, editors. Mathematical Methods in Engineering. Nonlinear Systems and Complexity, Vol. 24. Cham: Springer (2019). p. 153–74. doi: 10.1007/978-3-319-90972-1_11
96. Hristov J. Transient heat diffusion with a non-singular fading memory: from the cattaneo constitutive equation with Jeffrey's kernel to the Caputo-Fabrizio time-fractional derivative. Ther Sci. (2016) 20:765–70. doi: 10.2298/TSCI160112019H
98. Ozisik MN, Tzou DY. On the wave theory in heat conduction. J Heat Transf. (1994) 116:526–35. doi: 10.1115/1.2910903
99. Tang MM, Trujillo M, Lopez Molina JA, Rivera MJ, Berjan EJ. Modeling the heating of biological tissue on the hyperbolic transfer equation. Math Comput Model. (2009) 50:665–72. doi: 10.1016/j.mcm.2008.12.023
100. Dai W, Wang H, Jordan PM, Mickens RE, Bejan A. A mathematical model for skin burn injury induced by radiation heating. Int J Heat Mass Transf. (2008) 51:5497–510. doi: 10.1016/j.ijheatmasstransfer.2008.01.006
101. Liu J, Zhang X, Wang CC, Lu WQ, Ren Z. Generalized time delay bioheat equation and preliminary analysis on its wave nature. Chinese Sci. Bull. (1997) 42:289–92. doi: 10.1007/BF02882462
102. Tzou DY, Zhang YS. An analytical study on the fast-transient process in small scales. Int J Eng Sci. (1995) 33:1449–63. doi: 10.1016/0020-7225(94)00130-C
103. Quintanilla R, Racke R. A note on stability in dual-phase-lag heat conduction. Int J Heat Mass Transf. (2006) 49:1209–13. doi: 10.1016/j.ijheatmasstransfer.2005.10.016
104. Fabrizio M, Lazzari B. Stability and second law of thermodynamics in dual-phase-lag heat conduction. Int J Heat Mass Transf. (2014) 74:484–9. doi: 10.1016/j.ijheatmasstransfer.2014.02.027
105. Fabrizio M, Lazzari B, Tibullo V. Stability and thermodynamic restrictions for dual-phase-lag thermal model. J Non Equilib. Thermodyn. (2016) 42:243–52. doi: 10.1515/jnet-2016-0039
106. Tang DW, Araki N, Yamagishi N. Transient temperature responses in biological materials under pulsed IR irradiation. Heat Mass Transf. (2007) 43:579–85. doi: 10.1007/s00231-006-0125-7
107. Shih TC, Yuan P, Lin WL, Kou HS. Analytical analysis of the Pennes bioheat transfer equation with sinusoidal heat flux conditions on the skin surface. Med Eng Phys. (2007) 29:946–53. doi: 10.1016/j.medengphy.2006.10.008
108. Hooshmand P, Moradi A, Kherzry B. Bioheat transfer analysis of biological tissues by laser radiation. Int J Therm Sci. (2015) 90:214–23. doi: 10.1016/j.ijthermalsci.2014.12.004
109. Kengne E, Lakhssasi A. Analytico-numerical study of bio-heat transfer problems with temperature-dependent perfusion. Eur Phys J Plus. (2015) 130:89. doi: 10.1140/epjp/i2015-15089-1
110. Kumar A, Kumar S, Katiyar VK, Telles S. Dula phase lag bio-heat transfer during cryosurgery of lung cancer: comparison of three heat transfer models. J Ther Biol. (2017) 69:228–37. doi: 10.1016/j.jtherbio.2017.08.005
111. Zhou J, Zhang Y, Chen JK. An axisymmetric dual-phase lag bioheat model for laser heating of living tissues. Int J Term Sci. (2009) 48:1477–85. doi: 10.1016/j.ijthermalsci.2008.12.012
112. Zhou J, Zhang Y, Chen JK. Dual-phase lag effects on thermal damage to biological tissues caused by laser irradiation. Comput Biol Med. (2009) 39:286–93. doi: 10.1016/j.compbiomed.2009.01.002
113. Majchrzak E. Numerical solution of dual phase lag model of bioheat transfer using the general boundary element method. Comput Model Eng Sci. (2010) 69:43–60.
114. Mochnacki B, Majchrzak E. Numerical model of thermal interaction between cylindrical cryoprobe and biological tissue using the dual-phase lag equation. Int J Heat Mass Transf. (2017) 108:1–10. doi: 10.1016/j.ijheatmasstransfer.2016.11.103
115. Tullius TK, Bayazitoglu Y. Analysis of relaxation times on the human head using thermal wave model. Int J Heat Mass Transf. (2013) 67:1007–13. doi: 10.1016/j.ijheatmasstransfer.2013.08.097
116. Hristov J. Linear viscoelastic responses and constitutive equations in terms of fractional operators with non-singular kernels: pragmatic approach, memory kernel correspondence requirement and analyses. Eur Phys J Plus. (2019) 134:283. doi: 10.1140/epjp/i2019-12697-7
118. Caputo M, Fabrizio M. A new definition of fractional derivative without singular kernel. Progr Fract Differ Appl. (2015) 1:73–85.
119. Hristov J. Derivatives with non-singular kernels: from the Caputo-Fabrizio definition and beyond: appraising analysis with emphasis on diffusion models. In: Bhalekar S, editor. Frontiers in Fractional Calculus. Sharjah: Bentham Science Publishers (2017). p. 269–342. doi: 10.2174/9781681085999118010013
120. Hristov J. Response functions in linear viscoelastic constitutive equations and related fractional operators. Math Model Nat Phenom. (2019) 14:305. doi: 10.1051/mmnp/2018067
121. Hristov J. Linear viscoelastic responses: the Prony decomposition naturally leads into the Caputo-Fabrizio fractional operator. Front Phys. (2018) 6:135. doi: 10.3389/fphy.2018.00135
122. Ezzat MA, Al-Sowayan NS, Al-Muhiameed ZIA, Ezzat SM. Fractional modelling of Pennes' bioheat transfer equation. Heat Mass Transf. (2014) 50:907–14. doi: 10.1007/s00231-014-1300-x
123. Ezzat MA, El-Barry, Al-Sowayan NS. Tissue responses to fractional transfer heating with sinusoidal heat flux condition on skin surface. Anim Sci J. (2016) 10:1304–11. doi: 10.1111/asj.12568
124. Jumarrie GD. Derivation and solutions of some fractional Black-Sholes equations in coarse-grained space and time, applications of Merton's optimal portfolio. Comput Math Appl. (2010) 59:1142–64. doi: 10.1016/j.camwa.2009.05.015
125. Damor RS, Kumar S, Shukla AK. Solution of fractional bioheat equation in terms of Fox's H-function. SpingerPlus. (2016) 5:111. doi: 10.1186/s40064-016-1743-2
126. Damor RS, Kumar S, Shukla AK. Temperature distribution in living tissue with fractional bioheat model in thermal therapy. In: Patel H, Deheri G, Patel H, Mehta S, editors. Proceedings of the International Conference on Advances in Tribology and Engineering Systems. Lecture Notes in Mechanical Engineering. Springer India (2014). p. 493–8.
127. Ferras LL, Ford NJ, Morgado ML, Nóbrega JM, Regbelo MS. Fractional Pennes' bioheat eqaution: theoretical and numerical studies. Frac Cal Appl Anal. (2015) 18:10180–1106. doi: 10.1515/fca-2015-0062
128. Gurtin ME. A general theory of heat conduction with finite wave speed. Arch Rat Mech Anal. (1968) 31:113–26. doi: 10.1007/BF00281373
129. Hardy G. Riemann's form of Taylor series. J London Math Soc. (1945) 20:48–57. doi: 10.1112/jlms/s1-20.1.48
130. Watanabe Y. Notes on generalized derivatives of Riemann-Liouville and its application to Leibniz's formula. Tohoku Math J. (1931) 24:8–41.
131. El-Ajou A, Arqub OA, Al Zhour Z, Momani S. New results on fractional power series: theories and applications. Entropy. (2013) 15:5305–23. doi: 10.3390/e15125305
132. Trujillo J, Rivero M, Bonilla B. On a Riemann-Liouville generalized Taylor's formula J Math Anal Appl. (1999) 231:255–65. doi: 10.1006/jmaa.1998.6224
133. Odibat Z, Shawagfeh N. Generalized Taylor's formula. Appl Math Comput. (2007) 186:286–93. doi: 10.1016/j.amc.2006.07.102
134. Mehdinejadiani B, Jafari H, Baleanu D. Derivation of fractional Boussinesq equation for modelling unconfined groundwater. Eur Phys J. (2013) 222:1805–12. doi: 10.1140/epjst/e2013-01965-1
135. Mehdinejadiani B, Naseri AA, Jafari H, Chanbarzadeh A, Baleanu D. A mathematics model for simulation of a water table profile between two parallel subsurface drains using fractional derivatives. Comp Math Appl. (2013) 66:785–94. doi: 10.1016/j.camwa.2013.01.002
136. Kang J, Xu M. Exact solutions for unsteady unidirectional flows of a generalized second -order fluid through a rectangular conduit. Acta Mech Sin. (2009) 25:181–6. doi: 10.1007/s10409-008-0209-3
137. Bandelli R, Rajagopal KR. Start-up flows of second grade fluids in domains with one finite dimension. J Non-Linerar Mech. (1995) 30:817–39. doi: 10.1016/0020-7462(95)00035-6
138. Coleman B, Noll W. Foundations of linear Viscoelasticity. Rev Mod Phys. (1961) 33:239–49. doi: 10.1103/RevModPhys.33.239
139. Coleman B, Gurtin ME. Equipresence and constitutive equations for rigid heat conductors. Z Angew Math Phys. (1967) 18:188–208. doi: 10.1007/BF01596912
140. Nachlinger RR, Weeler L. A uniqueness theorem for rigid heat conductors with memory Q Appl Math. (1973) 31:267–73. doi: 10.1090/qam/436794
141. Nunciato JW. On heat conduction in materials with memory. Q Appl Math. (1971) 29:187–273. doi: 10.1090/qam/295683
142. Nunciato JW. On uniqueness in the linear theory of heat conduction with finite wave speds. SIAM J Appl Math. (1973) 25:1–4. doi: 10.1137/0125001
143. Boltzmann L. Zur Theorie der Elastischen Nachwirkung. Sitzungsber Akad Wiss. Wien Mathem Naturwiss. (1874) 70:275–300.
144. Miller RK. An integrodifferential equation for rigid heat conductors with memory. J Math Anal Appl. (1978) 66:313–32. doi: 10.1016/0022-247X(78)90234-2
145. Cattaneo C. On the conduction of heat (In Italian). Atti Sem Mat Fis Univ Modena. (1948) 3:83–101.
146. Araujo A, Ferreira JA, Oliveira P. The effect of memory terms in diffusion phenomena. J Comp Math. (2000) 24:191–102.
147. Westerlund S. Dead matter has memory? Phys Scrip. (1991) 43:174–9. doi: 10.1088/0031-8949/43/2/011
148. Muslih SI, Baleanu D. Fractional multipoles in fractional space. Nonlin Anal Real World Appl. (2007) 8:198–203. doi: 10.1016/j.nonrwa.2005.07.001
149. Ebaid A, Masaedeh B, El-Zahar E. A new fractional model for the falling body problem. Chin Phys Lett. (2012) 34:029201. doi: 10.1088/0256-307X/34/2/020201
150. Gomez-Aguilar JF, Rosales-Garcia JJ, Bernal-Alvarado JJ. Fractional mechanical oscillators. Rev Mex Fis. (2012) 58:348–52.
151. Gomez-Aguilar JF. Space-time fractional diffusion equation using a derivative with non-singular and regular kernel. Physica A. (2017) 465:562–72. doi: 10.1016/j.physa.2016.08.072
152. Dokoumetzidis A, Macheras P. Fractional kinetics in drug absorption and disposition processes. J Pharmacokinet Pharmacodyn. (2009) 3:165–78. doi: 10.1007/s10928-009-9116-x
153. Liu J. Preliminary survey on the mechanism of the wave-like behaviors of heat transfer in living tissues. Forsch. Ingenieurwesen. (2000) 66:1–10. doi: 10.1007/s100100000031
Keywords: bio-heat equation, model build-up, scaling, nondimensalization, fractionalization
Citation: Hristov J (2019) Bio-Heat Models Revisited: Concepts, Derivations, Nondimensalization and Fractionalization Approaches. Front. Phys. 7:189. doi: 10.3389/fphy.2019.00189
Received: 19 July 2019; Accepted: 30 October 2019;
Published: 21 November 2019.
Edited by:
Guo-Cheng Wu, Neijiang Normal University, ChinaReviewed by:
Pragya Shukla, Indian Institute of Technology Kharagpur, IndiaDimiter Prodanov, Interuniversity Microelectronics Centre (IMEC), Belgium
Copyright © 2019 Hristov. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jordan Hristov, am9yZGFuLmhyaXN0b3ZAbWFpbC5iZw==
 Jordan Hristov
Jordan Hristov