- 1Department of Electrical Engineering, University of Bojnord, Bojnord, Iran
- 2Department of Mathematics, Faculty of Arts and Sciences, Cankaya University, Ankara, Turkey
- 3Institute of Space Sciences, Magurele–Bucharest, Romania
- 4Department of Electrical and Computer Engineering, Hakim Sabzevari University, Sabzevar, Iran
- 5Department of Physics, College of Applied Sciences, Palestine Technical University, Tulkarm, Palestine
In this new work, the free motion of a coupled oscillator is investigated. First, a fully description of the system under study is formulated by considering its classical Lagrangian, and as a result, the classical Euler–Lagrange equations of motion are constructed. After this point, we extend the classical Lagrangian in fractional sense, and thus, the fractional Euler–Lagrange equations of motion are derived. In this new formulation, we consider a recently introduced fractional operator with Mittag–Leffler non-singular kernel. We also present an efficient numerical method for solving the latter equations in a proper manner. Due to this new powerful technique, we are able to obtain remarkable physical thinks; indeed, we indicate that the complex behavior of many physical systems is realistically demonstrated via the fractional calculus modeling. Finally, we report our numerical findings to verify the theoretical analysis.
1. Introduction
There are two main approaches in the classical mechanics to get the equations of motion for a dynamical system: Newtonian and Lagrangian. However, in the first approach, which is a force-based one, we encounter with some difficulties since all acting forces need to be set up while sometimes they are not clear. The second approach was invented by Joseph Louis Lagrange, a French Mathematician. This approach is considered as a useful technique to find the equations of motion for many kinds of physical processes [1]. During the past decade, the Lagrangian method has been used to solve some interesting systems such as Atwood's machine, coupled and spring pendulums, and many others.
The fractional calculus (FC) is a branch of mathematical analysis, which deals with the non-integer integral and derivative operators. The application of the FC has been extensively expanded in different fields of the basic and engineering sciences [2–9]. Over the past few decades, the classical mechanics has been extended by using the new aspects of the FC. In Riewe [10], the non-conservative Lagrangian systems were studied by Riewe using the concept of the FC. Indeed, the author employed the fractional-order derivatives to define conjugate momenta and formulated the fractional Hamilton equations. In Laskin [11], Laskin studied the path of Lévy flights by using a fractional path integral scheme. In Laskin [12], he also developed the fractional quantum mechanics and proved the hermiticity property of the Hamilton operator in fractional sense. Afterwards, the works by Riewe and Laskin were followed by many scientists and several interesting papers were published in this area [13–19]. According to these studies, the asymptotic behavior of many physical systems was explored by using the fractional Lagrangian (or the fractional Hamiltonian), which leads to the fractional Euler-Lagrange equations (FELEs) [20–22]. However, an important issue here is to solve these equations by an appropriate approximation method [23]. These techniques include the Adams-Bashforth-Moulton scheme [24], variational iteration method [25], Adomian decomposition method [26], and the Grünwald–Letnikov approximation [27].
According to the recent studies in the literature, the complex behavior of physical systems can be represented more precisely by the FC approach. However, some natural phenomena with nonlocal characteristic may not be described properly by the classical fractional derivatives (FDs) due to the appearance of singular kernel in the definition of these operators. Thus, an alternative analytical approach is needed to model and analyze the nonlocal dynamics in a proper manner. To solve this difficulty, a new type of the fractional operator with Mittag-Leffler (ML) kernel (ABC) was developed in Baleanu and Atangana [28] and applied to some practical cases [29]. Indeed, due to the presence of nonsingular kernel, this new definition shows a completely different property compared to the classical FDs, and hence, it can describe the nonlocal dynamics and capture different features of realistic systems more appropriately than the standard FC. Nevertheless, more practical cases should be examined via the ABC operator and some new and efficient numerical methods need to be designed to solve these fractional equations effectively. Motivated by the above discussion, the aim of this paper is to investigate the free motion of a coupled oscillator by using the newly introduced ABC fractional operator with ML kernel. We give a theoretical analysis to formulate the corresponding FELEs. Also, we provide an efficient numerical scheme to solve the aforementioned fractional equations effectively. In accordance with the obtained results, we conclude that a flexible model is provided by using the FC as the fractional order can be varied between 0 and 1. Due to this impressive feature, the new hidden aspects of the coupled oscillator system can be explored, which are not visible in the classic integer manner.
The rest of this paper is organized as follows. In section 2, some preliminary results regarding the fractional operators are given. Section 3 introduces the classical and fractional descriptions of the coupled oscillator. In section 4, an efficient numerical technique is proposed to solve the derived FELEs. In section 5, numerical simulations are presented, and finally, the paper is closed by some conclusions in the last section.
2. Preliminaries
This section gives some definitions and preliminaries regarding the fractional operator with ML kernel (ABC) [28]. For φ ∈ ℍ1(0, b), the (left) ABC fractional operator of order q ∈ (0, 1) is defined by
where S(q) denotes a normalization function with S(0) = S(1) = 1 and Eq(t) is the one–parameter ML function. The corresponding right fractional operator of order q ∈ (0, 1) is also expressed as
The integral operators associated with the definitions (1) and (2) are, respectively, described by
The following useful relations hold between the above–mentioned differential and integral operators
For more details and discussions, we refer the interested readers to Baleanu and Atangana [28] and Abdeljawad and Baleanu [30].
3. The Classical and Fractional Description
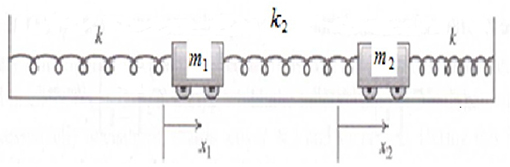
In this section, we consider a coupled oscillator system and provide a fully description of its dynamical equations both in the classical and fractional manner. For this purpose, we consider the physical system shown in Figure 1, which consists of two coupled carts with masses m1 and m2 attached to their respective walls by two identical springs (with force constant k) and to each other by another spring (with force constant k2). It is of interest to mention that in some books this system is known as the diatomic molecules.
Assuming that all springs are massless, we aim to obtain the classical Euler–Lagrange equations (CELEs) for the physical system under consideration. To this end, first we write the instantaneous kinetic and potential energies of the system, respectively, by the formulas
Then the classical Lagrangian Lc(t) is given in the form
Substituting the Lagrangian (9) into the CELEs (, i = 1, 2), we obtain
Now, we aim to derive the classical Hamiltonian equations (CHEs) of motion. For this purpose, first we introduce the following generalized momenta
Substituting Equations (9) and (12) into the Hamilton function H(t) = ẋ1(t)P1(t) + ẋ2(t)P2(t) − Lc(t), we provide
Then the CHEs of motion for the coupled oscillator are obtained from
which lead to the same results as the CELEs (10)–(11). Nevertheless, as it was pointed out in Agrawal [31], the theory of the calculus of variations cannot capture many laws of the natural phenomena; for example, the behavior of nonconservative systems cannot be described properly by the dynamical equations achieved in accordance with the traditional energy approach. On the other hand, the FC has overcome this limitation as it can characterize the behavior of many complex physical systems including hereditary properties. Accordingly, in the following, we investigate the fractional Lagrangian for the coupled oscillator in order to expose its new features. To this end, we modify the classical Lagrangian (9) according to the ABC operator defined by Equation (1)
Substituting Lf(t) from Equation (16) into the formula , i = 1, 2, yields the following FELEs
where , , and . As can be seen, the FELEs (17)–(18) are reduced to the CELEs (10)–(11) when q goes to 1.
Now, we are going to attain the fractional Hamiltonian equations (FHEs) of motion. To do so, we consider the fractional Hamilton function as follows
where P1, 1(t), P1, 2(t), P2, 1(t), and P2, 2(t) are the following generalized momenta
Thus, the fractional Hamilton function is obtained by substituting Equation (16) and (20) into Equation (19)
Accordingly, the FHEs of motion are concluded as follows
Here, it is notable that the FHEs (22)–(23) are the same as the previously derived FELEs (17)–(18) and reduced to the CELEs (10)–(11) as q → 1.
4. Numerical Method
In this section, we propose an efficient numerical technique to solve the FELEs (17)–(18) [or the FHEs (22)–(23)]. In order to this, we first define the new state variables and . Thus, the Equations (17)–(18) are rewritten as
Applying the definition of the left and right integral operators (3) and (4), we derive the following system of fractional integral equations
Now, we consider a uniform mesh on [0, b] with the time step size in which N is an arbitrary positive integer. Moreover, we represent the numerical approximation of xi(tj) and by xi, j and , respectively, where tj = 0 + jh (0 ≤ j ≤ N) is the time at node j. Applying the Euler method to discretize the convolution integrals in (25), we derive
where
By defining the augmented matrices AN, q and BN, q such as
the system of Equations (26)–(29) is combined in a compact form as follows
where
Rearranging Equation (32), we provide
where I is the (N + 1) × (N + 1) identity matrix and
Finally, we attain the following system of linear algebraic equations
which can be implemented easily by any linear solver. Note that the convergence of the fractional Euler method in the ABC sense was studied by Baleanu et al. [32] and the error bound was also reported. This verifies the validity of all numerical results provided in this paper. For more details on the stability and convergence analysis in this case, the interested reader can refer to Baleanu et al. [32].
5. Simulation Results and Discussion
In this section, we investigate the dynamical behavior of the FELEs of motion for the coupled oscillator expressed by Equations (17)–(18) considering different values of the fractional order q. To this aim, we take into account the following three cases for the physical system under study:
Case 1: A symmetric initial position. In this case, we consider the initial and terminal conditions as x1(0) = −x2(0) = 1 and , respectively. The other parameters are also assumed to be k = 2, k2 = 4, m1 = 3, m2 = 7, and q = 0.96, 0.965, 0.97, 0.975, 0.98, 0.985, 0.99, 0.995, 0.999. Simulation results for this case are shown in Figures 2, 3 as compared to the solution of the CELEs (10)–(11).
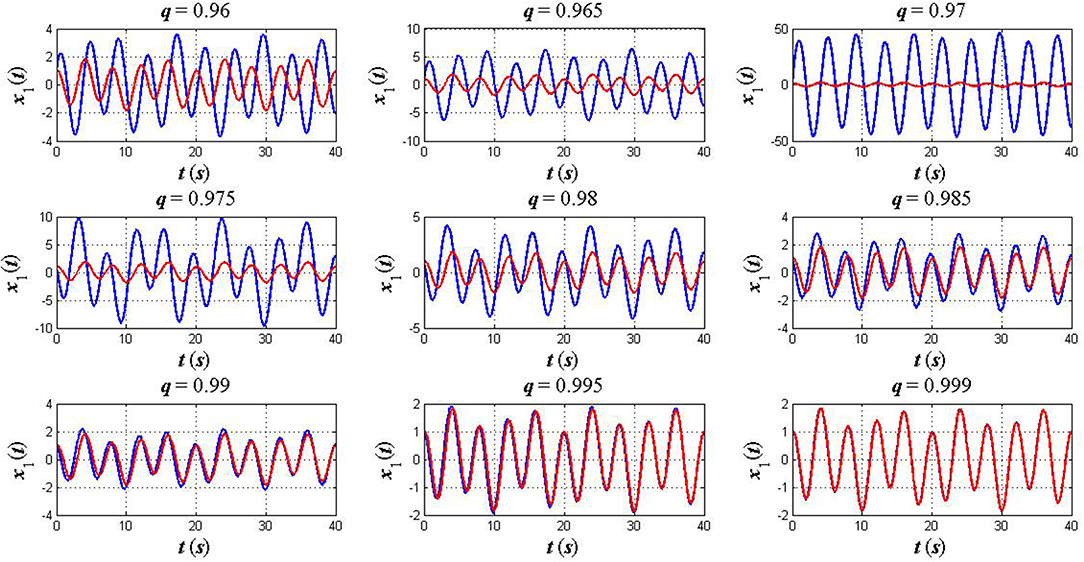
Figure 2. The plots of x1(t) in the fractional sense (blue) and classical sense (red): a symmetric initial position x1(0) = −x2(0) = 1.
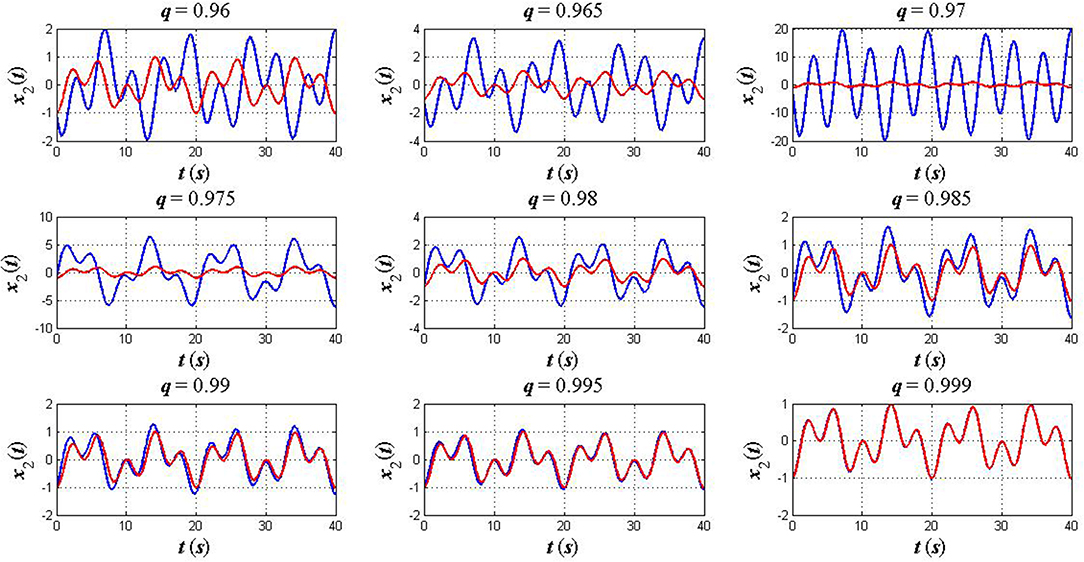
Figure 3. The plots of x2(t) in the fractional sense (blue) and classical sense (red): a symmetric initial position x1(0) = −x2(0) = 1.
Case 2: An anti–symmetric initial position. In this case, we take into account the initial condition as x1(0) = x2(0) = 1 while the terminal condition and other parameters take the same values as in the previous case. Simulation and comparative results for this case are depicted in Figures 4, 5.
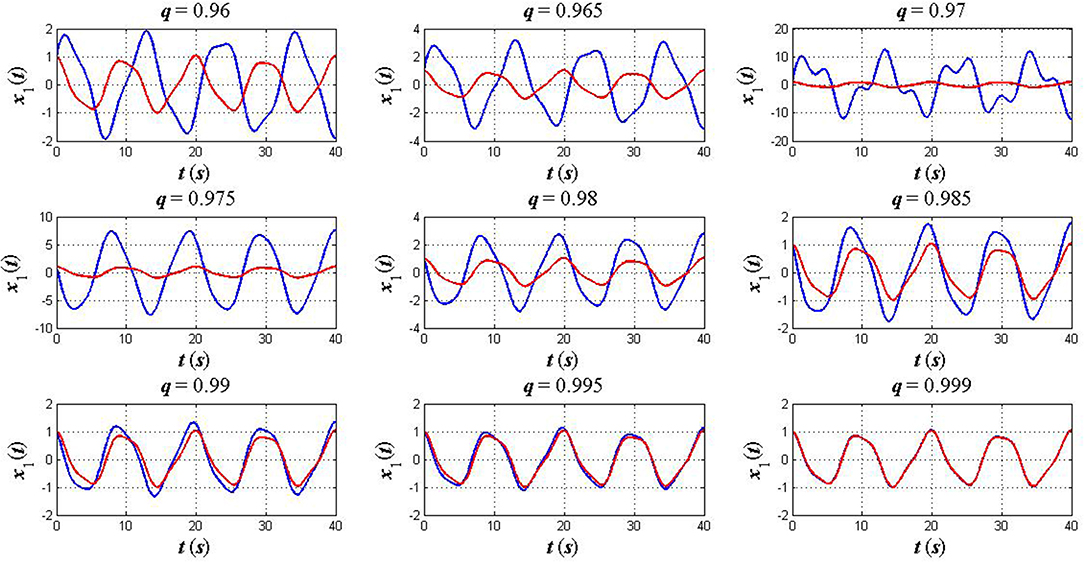
Figure 4. The plots of x1(t) in the fractional sense (blue) and classical sense (red): an anti–symmetric initial position x1(0) = x2(0) = 1.
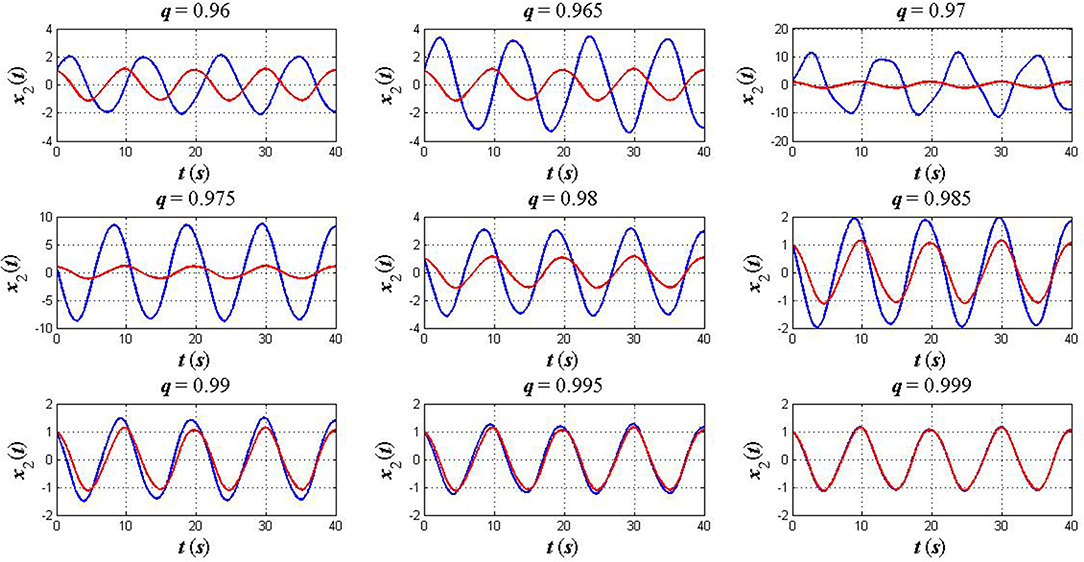
Figure 5. The plots of x2(t) in the fractional sense (blue) and classical sense (red): an anti–symmetric initial position x1(0) = x2(0) = 1.
Case 3: A weak coupled oscillator. Finally, we take into consideration a weak coupled oscillator in which k = 10 and k2 = 0.1 (k≫k2). The initial condition is also assumed to be x1(0) = 1, x2(0) = 0, and the other parameters remain unchanged as in the previous cases. Simulation results of the Euler–Lagrange equations for both fractional and classical cases are plotted in Figures 6, 7.
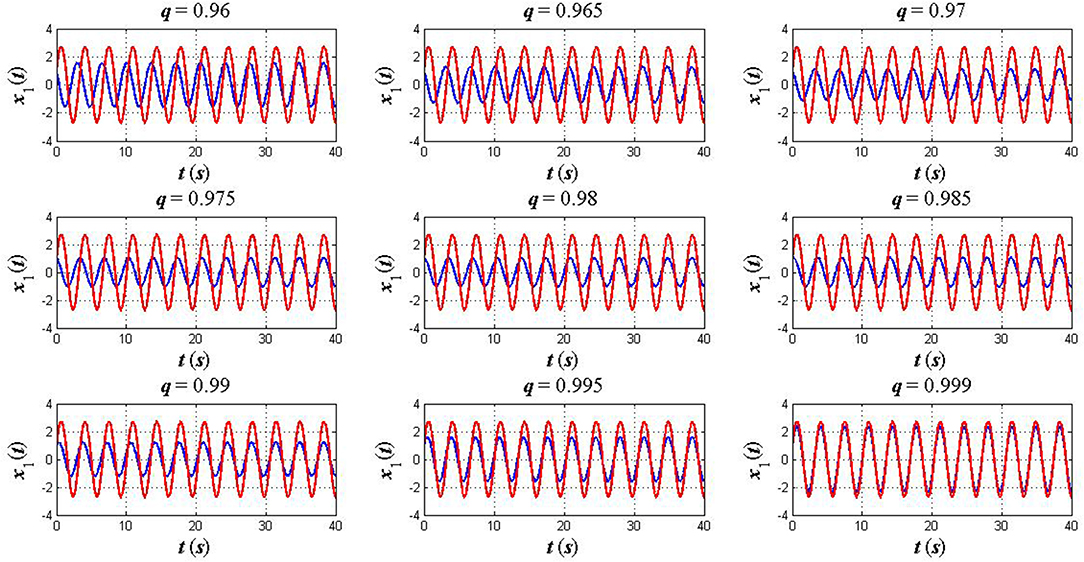
Figure 6. The plots of x1(t) in the fractional sense (blue) and classical sense (red): a weak coupled oscillator (k ≫ k2).
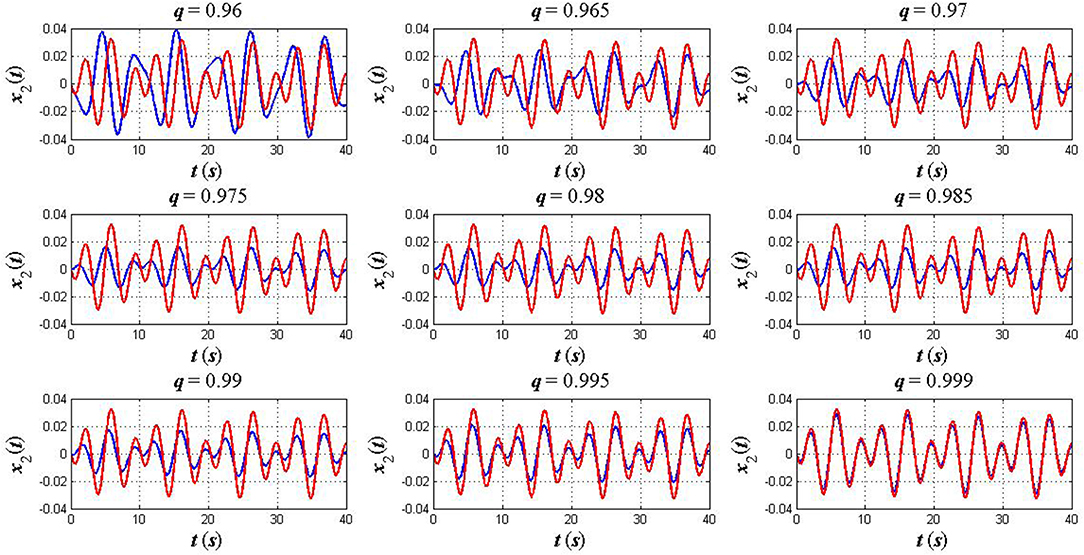
Figure 7. The plots of x2(t) in the fractional sense (blue) and classical sense (red): a weak coupled oscillator (k ≫ k2).
As can be seen from Figures 2–7, the numerical solution of the FELEs not only represents different asymptotic behaviors for different values of q but also tends to the solution of the CELEs as q goes to 1. This confirms that the FC provides a flexible model, which is able to extract hidden aspects of the physical system under study while this feature is unavailable when we use the ordinary time–derivatives.
6. Conclusions
This paper studied the concept of the FC to evaluate the equations of motion for a coupled oscillator. In this study, the classical and fractional Lagrangian were established, and then, the FELEs of motion were formulated including the recently introduced ABC operator with ML kernel. In order to solve the aforementioned equations numerically, an efficient approximation method was also suggested, which employed the Euler formula to discretize the convolution integral. Applying this powerful new technique, the FELEs for the considered problem were converted into a system of linear algebraic equations. Simulation results reported in Figures 2–7 indicated that the behavior of the FELEs varied with the fractional order q, and recovered the solution of the CELEs as q → 1. This verifies the advantage of the FC to provide a flexible model capable of extracting hidden aspects of the coupled oscillator system while this property is not available in the presence of ordinary time–derivatives.
Data Availability Statement
All datasets analyzed for this study are included in the article/supplementary material.
Author Contributions
All authors contributed equally to each part of this work. All authors read and approved the final manuscript.
Funding
DB was supported by the Scientific and Technological Research Council of Turkey (TÜBİTAK), Grant No: TBAG–117F473.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Greiner W. Classical Mechanics, Systems of Particles and Hamiltonian Dynamics. Berlin; Heidelberg: Springer–Verlag (2010).
2. Tariboon J, Ntouyas SK, Agarwal P. New concepts of fractional quantum calculus and applications to impulsive fractional q-difference equations. Adv Diff Equat. (2015) 2015:18. doi: 10.1186/s13662-014-0348-8
3. Hammouch Z, Mekkaoui T, Agarwal P. Optical solitons for the Calogero-Bogoyavlenskii-Schiff equation in (2 + 1) dimensions with time-fractional conformable derivative. Eur Phys J Plus. (2018) 133:248. doi: 10.1140/epjp/i2018-12096-8
4. Saad KM, Iyiola OS, Agarwal P. An effective homotopy analysis method to solve the cubic isothermal auto-catalytic chemical system. AIMS Math. (2018) 3:183–94. doi: 10.3934/Math.2018.1.183
5. Turalska M, West BJ. Fractional dynamics of individuals in complex networks. Front Phys. (2018) 6:110. doi: 10.3389/fphy.2018.00110
6. Jajarmi A, Hajipour M, Mohammadzadeh E, Baleanu D. A new approach for the nonlinear fractional optimal control problems with external persistent disturbances. J Franklin Instit. (2018) 335:3938–67. doi: 10.1016/j.jfranklin.2018.03.012
7. Hajipour M, Jajarmi A, Baleanu D, Sun HG. On an accurate discretization of a variable-order fractional reaction-diffusion equation. Commun Nonlin Sci Numer Simul. (2019) 69:119–33. doi: 10.1016/j.cnsns.2018.09.004
8. Yusuf A, Inc M, Aliyu AI, Baleanu D. Optical solitons possessing beta derivative of the Chen-Lee-Liu equation in optical fiber. Front Phys. (2019) 7:34. doi: 10.3389/fphy.2019.00034
9. Morales-Delgado VF, Gómez-Aguilar JF, Saad KM, Khan MA, Agarwal P. Analytic solution for oxygen diffusion from capillary to tissues involving external force effects: a fractional calculus approach. Phys A. (2019) 523:48–65. doi: 10.1016/j.physa.2019.02.018
10. Riewe F. Nonconservative Lagrangian and Hamiltonian mechanics. Phys Rev E. (1996) 53:1890–9. doi: 10.1103/PhysRevE.53.1890
11. Laskin N. Fractional quantum mechanics. Phys Rev E. (2000) 62:3135–45. doi: 10.1103/PhysRevE.62.3135
12. Laskin N. Fractional quantum mechanics. Phys Rev E. (2002) 66:056108. doi: 10.1103/PhysRevE.66.056108
13. Agila A, Baleanu D, Eid R, Irfanoglu B. A freely damped oscillating fractional dynamic system modeled by fractional Euler-Lagrange equations. J Vibrat Control. (2018) 24:1228–38. doi: 10.1177/1077546316685228
14. Almeida R, Morgado ML. The Euler-Lagrange and Legendre equations for functionals involving distributed-order fractional derivatives. Appl Math Comput. (2018) 331:394–403. doi: 10.1016/j.amc.2018.03.022
15. Baleanu D, Jajarmi A, Asad JH, Blaszczyk T. The motion of a bead sliding on a wire in fractional sense. Acta Phys Polon A. (2017) 131:1561–4. doi: 10.12693/APhysPolA.131.1561
16. Baleanu D, Asad JH, Jajarmi A. The fractional model of spring pendulum: new features within different kernels. Proc Roman Acad Ser A. (2018) 19:447–54. Available online at: https://acad.ro/sectii2002/proceedings/doc2018-3/05-Baleanu.pdf
17. Baleanu D, Asad JH, Jajarmi A. New aspects of the motion of a particle in a circular cavity. Proc Roman Acad Ser A. (2018) 19:361–7. Available online at: https://acad.ro/sectii2002/proceedings/doc2018-2/Art07Baleanu.pdf
18. Baleanu D, Jajarmi A, Asad JH. Classical and fractional aspects of two coupled pendulums. Roman Rep Phys. (2019) 71:103.
19. Baleanu D, Sajjadi SS, Jajarmi A, Asad JH. New features of the fractional Euler-Lagrange equations for a physical system within non-singular derivative operator. Eur Phys J Plus. (2019) 134:181. doi: 10.1140/epjp/i2019-12561-x
20. Chung WS. Fractional Newton mechanics with conformable fractional derivative. J Comput Appl Math. (2015) 290:150–8. doi: 10.1016/j.cam.2015.04.049
21. Baleanu D, Asad JH, Petras I. Numerical solution of the fractional Euler-Lagrange's equations of a thin elastica model. Nonlin Dyn. (2015) 81:97–102. doi: 10.1007/s11071-015-1975-7
22. Agila A, Baleanu D, Eid R, Irfanoglu R. Applications of the extended fractional Euler-Lagrange equations model to freely oscillating dynamical systems. Roman J Phys. (2016) 61:350–9. Available online at: http://www.nipne.ro/rjp/2016_61_3-4/RomJPhys.61.p350.pdf
23. Guezane-Lakoud A, Khaldi R. Solutions for a nonlinear fractional Euler Lagrange type equation. SeMA J. (2019) 76:195–202. doi: 10.1007/s40324-018-0170-4
24. Diethelm K, Ford NJ, Freed AD. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlin Dyn. (2002) 29:3–22. doi: 10.1023/A:1016592219341
25. Momani S, Odibat Z, Alawneh A. Variational iteration method for solving the space- and time-fractional KdV equation. Numer Methods Part Differ Equat. (2008) 24:262–71. doi: 10.1002/num.20247
26. Prakash A, Verma V. Numerical method for fractional model of Newell-Whitehead-Segel equation. Front Phys. (2019) 7:15. doi: 10.3389/fphy.2019.00015
27. Kilbas AA, Srivastava HM, Trujillo JJ. Theory and Applications of Fractional Differential Equations. Amsterdam: Elsevier (2006).
28. Baleanu D, Atangana A. New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. Therm Sci. (2016) 20:763–9. doi: 10.2298/TSCI160111018A
29. Tateishi AA, Ribeiro HV, Lenzi EK. The role of fractional time-derivative operators on anomalous diffusion. Front Phys. (2017) 5:52. doi: 10.3389/fphy.2017.00052
30. Abdeljawad T, Baleanu D. Integration by parts and its applications of a new nonlocal fractional derivative with Mittag–Leffler nonsingular kernel. J Nonlin Sci Appl. (2017) 10:1098–107. doi: 10.22436/jnsa.010.03.20
31. Agrawal OP. Formulation of Euler-Lagrange equations for fractional variational problems. J Math Anal Appl. (2002) 272:368–79. doi: 10.1016/S0022-247X(02)00180-4
Keywords: coupled oscillator, Euler–Lagrange equations, fractional derivative, nonsingular kernel, numerical method
Citation: Jajarmi A, Baleanu D, Sajjadi SS and Asad JH (2019) A New Feature of the Fractional Euler–Lagrange Equations for a Coupled Oscillator Using a Nonsingular Operator Approach. Front. Phys. 7:196. doi: 10.3389/fphy.2019.00196
Received: 26 March 2019; Accepted: 06 November 2019;
Published: 26 November 2019.
Edited by:
Carlo Cattani, Università degli Studi della Tuscia, ItalyReviewed by:
Zakia Hammouch, Moulay Ismail University, MoroccoPraveen Agarwal, Anand International College of Engineering, India
Haci Mehmet Baskonus, Harran University, Turkey
Copyright © 2019 Jajarmi, Baleanu, Sajjadi and Asad. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Amin Jajarmi, YS5qYWphcm1pQHViLmFjLmly
 Amin Jajarmi
Amin Jajarmi Dumitru Baleanu
Dumitru Baleanu Samaneh Sadat Sajjadi
Samaneh Sadat Sajjadi Jihad H. Asad
Jihad H. Asad