- 1Department of Engineering Science, Kermanshah University of Technology, Kermanshah, Iran
- 2Department of Mathematics, Faculty of Engineering and Natural Sciences, Bahçeşehir University, Istanbul, Turkey
- 3Department of Mathematics, Faculty of Arts and Sciences, Cankaya University, Ankara, Turkey
- 4Department of Medical Research, China Medical University Hospital, China Medical University, Taichung, Taiwan
- 5Institute of Space Sciences, Bucharest, Romania
This article introduces and applies new methods to determine the exact solutions of partial differential equations that will increase our understanding of the capabilities of applied models in real-world problems. With these new solutions, we can achieve remarkable advances in science and technology. This is the basic idea in this article. To accurately describe this, some exact solutions to the Gardner's equation are obtained with the help of two new analytical methods including the generalized exponential rational function method and a Jacobi elliptical solution finder method. A set of new exact solutions containing four parameters is reported. The results obtained in this paper are new solutions to this equation that have not been introduced in previous literature. Another advantage of these methods is the determination of the varied solutions involving various classes of functions, such as exponential, trigonometric, and elliptic Jacobian. The three-dimensional diagrams of some of these solutions are plotted with specific values for their existing parameters. By examining these graphs, the behavior of the solution to this equation will be revealed. Mathematica software was used to perform the computations and simulations. The suggested techniques can be used in other real-world models in science and engineering.
1. Introduction
It is difficult or impossible to determine the exact solution for many partial differential equations. In spite of these problems, in recent years a variety of efficient and practical methods have been proposed by mathematicians and physicists. Some of these methods are the exp-function method [1], the Darboux transformation [2], the Lie group analysis [3], the modified simple equation method [4], the homogeneous balance scheme [5], the sine-cosine method, and the tanh-coth method. Some new and effective attempts at determining solutions of partial differential equations can be found in [6–18].
The Gardner equation belongs to the category of integrable non-linear partial differential equations. The introduction of this equation is attributed to the famous mathematician Clifford Gardner in 1968 [19]. This equation can actually be generalized to the KdV equation. It is therefore sometimes referred to as the modified KdV equation. This equation is used in many areas of applications, such as hydrodynamics, plasma physics, and quantum field theory. This paper aims to employ two analytical methods to solve the following version of the integrable equation given by [20]
In this model, the dependent variable is u(x, t), and The independent variables x and t are the spatial and temporal variables, respectively. Abdul-Majid Wazwaz in [21] has obtained some multiple-soliton solutions for a variant of the equation called the Gardner-KP (GKP) equation. His approach is based on the Hirota's bilinear method. In [22] the authors have applied the mapping method to study the dynamics of solitary waves governed by Gardner's equation. This equation arises while studying the shallow water waves. The perturbed Gardner equation is also discussed in this article through the aid of He's semi-inverse variational approach. Very recently, a classification of Lie symmetries for the Gardner equation has been reported in [23]. They have also used the similarity transformation method to introduce the invariant solutions. Their solutions are of multisoliton, compacton, negaton, positon, and kink wave soliton types. Considering some suitable auxiliary dependent variables, the authors of [24, 25] have obtained some exact invariant solutions for the equation with non-local symmetries. By using the method of planar dynamical systems approach, in different parameter regions, the authors in [26] have constructed the bifurcation of phase portraits of a traveling wave system. The work of [27] presents the ill-posedness results for the initial value problem for the Gardner equation. In [28], a certain classification of single traveling wave solutions of the time-fraction Gardner equation is investigated. These forms of the Gardner equation can be utilized to model various physical phenomena, such as the non-linear propagation of ion acoustic waves in an unmagnetized plasma.
As can be seen, numerous numerical and analytical methods have been used to study this equation. That proves the importance of this equation. This is our main motivation for writing this article - to determine new solutions to this equation This paper is organized as follows. The analysis of the GERFM is outlined in section 2. The application of the method of solving (1) is presented in section 3. Also, to have a better insight into the resulting solutions, many numerical simulations are carried out in this section. Finally, some remarks are discussed in the last section.
2. The Analysis of the GERFM
The GERFM has recently been applied to solve many non-linear PDEs in some literature [29–31]. The successful use of this method in solving different sets of equations has made it an efficient method for solving partial equations. In order to gain insight into the method, let us have a quick review of the method. The steps to apply this method include the following.
1. Consider the following general non-linear PDE as
For two unknown constants of μ, ν, we define the new variables of ψ = ψ(ϰ) and ϰ = μx − νt. then, Equation (28) can be reformulated as a non-linear ODE as
2. Now, we take the solution Equation (29) into account for the following structure:
where
and ri, si(1 ≤ i ≤ 4), A0, Ak and Bk(1 ≤ k ≤ M) are unknown constants. Then, equating the two values of the amplitude, from (12) and (13), leads to the value of M.
3. Putting Equation (30) into Equation (29) and collecting all terms, the left-hand side of Equation (29) give us an algebraic equation P(Z1, Z2, Z3, Z4) = 0 in terms of for i = 1, …, 4. Zeroing each coefficient of P, we get a system of non-linear equations in terms of ri, si(1 ≤ i ≤ 4), and μ, l, A0, Ak and Bk(1 ≤ k ≤ M).
4. Any symbolic computation software can be utilized to solve this system to determine the values of ri, si(1 ≤ i ≤ 4), A0, Ak, and Bk(1 ≤ k ≤ M). Using these results will direct us to soliton solutions of the main non-linear PDE.
3. Application of the Method
Below, we present a detailed presentation of the solution of Equation (1). To this end, let us consider the following new definitions
where μ and ν are arbitrary unknown parameters. Utilizing the wave transformation (36) converts Equation (1) into the following single NODE:
Performing the integral with respect to ϰ and with c = 0, the last equation becomes
Then, equating the two values of 3M and M + 2, corresponding to and in Equation (8), leads to the value of M = 1. Using Equation (5) together with M = 1, we have
Proceeding as outlined in the second section and depending on the values of the parameters we obtain in the solitary wave solutions.
Set 1:
One obtains r = [−3, −1, 1, 1] along with s = [2, 0, 2, 0], so (5) turns to
In this case we obtain two exact solutions, as:
I.
Putting these values in Equations (10) and (37) yields a solitary wave solution for Equation (1) as:
where
II.
Putting these values in Equations (10) and (37) yields a solitary wave solution for Equation (1) as:
where
Set 2:
One obtains r = [−1, 3, 1, −1] along with s = [1, −1, 1, −1], so (5) turns to
In this case we obtain two exact solutions, as:
I.
Now, from Equations (13) and (37) we will reach to a solitary wave solution for Equation (1) as:
where
II.
Equations (13) and (37) for these values will introduce a solitary wave solution for Equation (1) as:
where
Set 3:
One obtains r = [3, 2, 1, 1] along with s = [1, 0, 1, 0], so (5) turns to
In this case we obtain an exact solution, as:
I.
Putting these values in Equations (16) and (37) yields a solitary wave solution for Equation (1) as:
where
Set 5:
One obtains r = [1, 1, 1, −1] along with s = [2, 0, 2, 0], so (5) turns to
In this case we obtain an exact solution, as:
I.
For these solutions in Equations (18) and (37) yields a solitary wave solution for Equation (1) as:
where
Set 6:
One obtains r = [−2−i, 2−i, −1, 1] along with s = [i, −i, i, −i], so (5) turns to
In this case we obtain an exact solution, as:
I.
Inserting these values in Equations (20) and (37) yields a solitary wave solution for Equation (1) as:
where
Set 7:
One obtains r = [−3, −1, 1, 1] along with s = [1, −1, 1, −1], so (5) turns to
In this case we obtain an exact solution, as:
I.
Putting these values in Equations (22) and (37) yields a solitary wave solution for Equation (1) as:
where
Set 8:
One obtains r = [1 + i, 1 − i, 1, 1] along with s = [i, −i, i, −i], so (5) turns to
In this case we obtain an exact solution, as:
I.
Using the above solutions in Equations (24) and (37) yields a solitary wave solution for Equation (1) as:
where
Set 9:
One obtains r = [−1, −2, 1, 1] along with s = [1, 0, 1, 0], so (5) turns to
In this case we obtain an exact solution, as:
I.
Inserting these values in Equations (26) and (37) yields a solitary wave solution for Equation (1) as:
where
It is worth mentioning that the necessary condition to establish the existence of the acquired solutions u1(x, t) − u10(x, t) is k3k4 < 0.
4. A Jacobi Elliptical Solutions Finder Method
In this part, we are going to obtain new exact soliton solutions to the equation under investigation, using a newly proposed method [32]. To this end, we will briefly review the steps of using the method.
1. The main purpose of this method is to solve an equation as follows:
2. Defining ϕ = ϕ(ϰ) and ϰ = μx − lt, Equation (28) is converted to
where μ and l are two constants.
3. At this point, the symbolic form of the Equation (29) can be formulated as follows:
where the values of constants A0, B0 and Ak, Bk(1 ≤ k ≤ 2N) are so that (30) is a solution to the Equation (29).
4. The value of N in Equation (30) is obtained using the balance principles and Θ(ϰ) satisfies the following non-linear ODE:
where hi(i = 0, 2, 4, 6) are real constants.
5. The solution of the Equation (31) should be as follows
where Φ(ϰ)2 + g > 0, and Φ(ϰ) is the solution of the Jacobian elliptic equation
and lj(j = 0, 2, 4) are constants need to be calculated, The relationships for f and g will also be as follows:
under the constraint condition
6. It is known that solutions of Equation (33) are in terms of Jacobi elliptic solutions. Inserting both (33) and (32) into Equation (30), one gets the optical solutions of Equation (28). It should be noted that by using the limits in Table 2, the Jacobian elliptic functions used in the solutions reduce to the known triangular functions.
5. The Application of the Method
In this section, to begin solving the equation, we first introduce the following new variables
Then we will consider the balancing principles in Equation (8). So, one gets N = 1. So, the Equation (30) can be rewritten as follows
The following results will be obtained using the method presented in section 4 of this article.
Set 11: We attain
Using No. 1 in Table 1 we have
provided that
The exact soliton solution to the equation will thus be determined as follows
where
Using No. 2 in Table 1 we have
provided that
The exact soliton solution to the equation will thus be determined as follows
where
Set 12: We attain
Using No. 1 in Table 1 we have
provided that
The exact soliton solution to the equation will thus be determined as follows
where
Using No. 4 in Table 1 we have
provided that
The exact soliton solution to the equation will thus be determined as follows
where
Using No. 7 in Table 1 we have
provided that
The exact soliton solution to the equation will thus be determined as follows
where
Set 13: We attain
Using No. 1 in Table 1 we have
provided that
The exact soliton solution to the equation will thus be determined as follows
where
Using No. 8 in Table 1 we have
provided that
The exact soliton solution to the equation will thus be determined as follows
where
Set 14: We attain
Using No. 1 in Table 1 we have
where provided that one of following conditions holds
The exact soliton solution to the equation will thus be determined as follows
where
Using No. 5 in Table 1 we have
where provided that one of following conditions holds
The exact soliton solution to the equation will thus be determined as follows
where
Likewise, other new families of solutions are obtained by following steps similar to the above using the following sets of parameters.
Set 15: We attain
Set 16: We attain
Set 17: We attain
As can be seen, many varied sets of soliton solutions to Gardner's equation will be obtained by applying this method. In the structure of these solutions, rational, hyperbolic, trigonometric, exponential and Jacobi elliptical functions are used. The correctness of all the obtained answers has been carefully examined. All of these soliton solutions are new findings presented for the first time in this article.
6. Graphical Representation
We aimed to find new solutions for a given problem in Equation (1), and these new solutions should be described graphically. Thus, we present a graphical representation of some obtained solutions with the help of Mathematica in Figures 1–9. From these plots, some interesting and important physics phenomena can be observed.
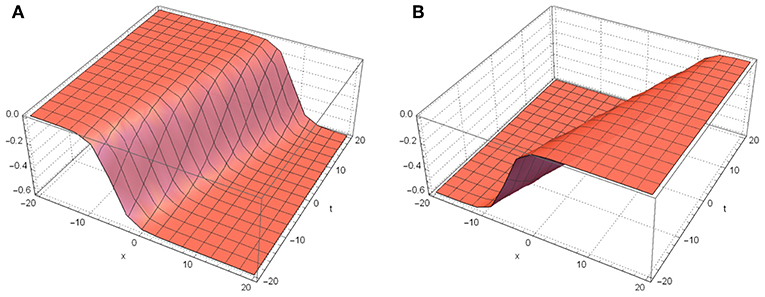
Figure 1. Dynamic behavior of u1(x, t), u2(x, t) for k2 = 1.2, k3 = 2, k4 = −2. (A) u1(x, t). (B) u2(x, t).
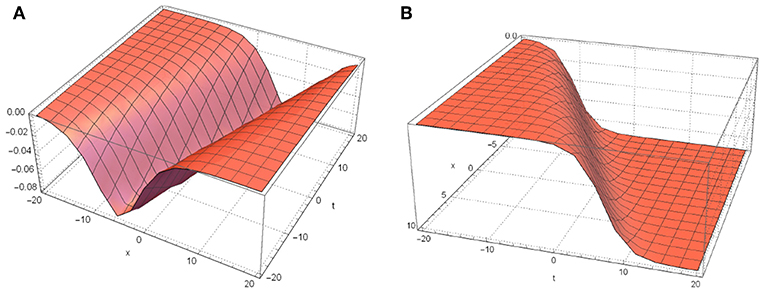
Figure 2. Dynamic behavior of u5(x, t), u8(x, t) for k2 = 1.2, k3 = 2, k4 = −2. (A) u5(x, t). (B) u8(x, t).
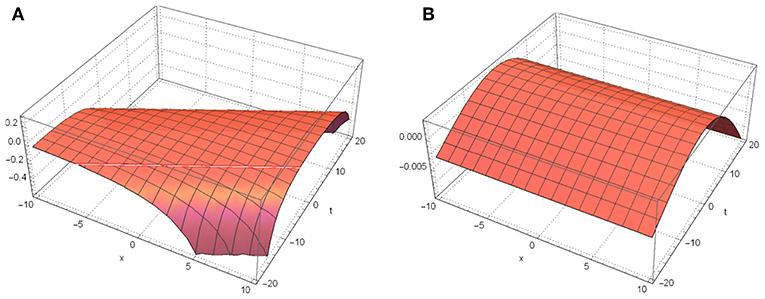
Figure 3. Dynamic behavior of u9(x, t), and u10(x, t) for k2 = 1.1, k3 = −1.2, k4 = 0.5. (A) u9(x, t). (B) u10(x, t).
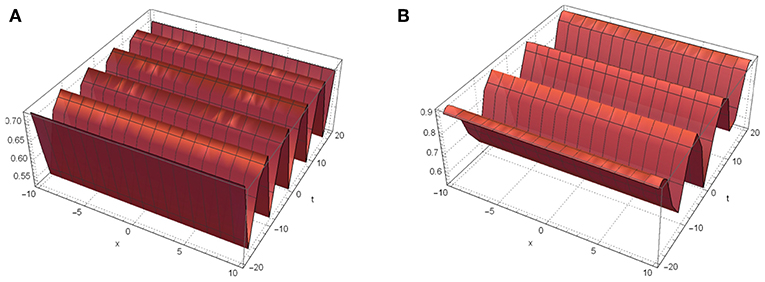
Figure 4. Dynamic behavior of |u11(x, t)| for k2 = 0.8, k3 = −0.5, k4 = 0.5., and α1 = 0.1. (A) m = 0.5 and . (B) m = 0.8 and .
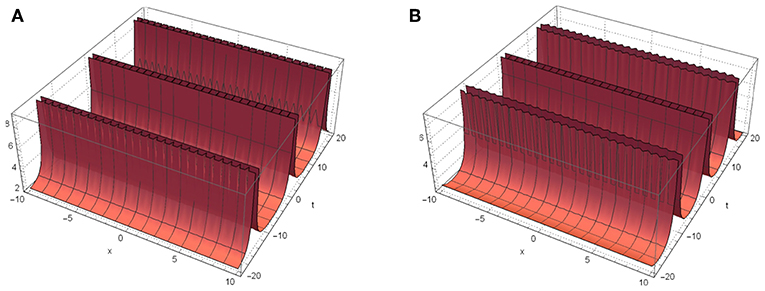
Figure 5. Dynamic behavior of |u12(x, t)| for k2 = 0.3, k3 = −0.1, k4 = 0.2. (A) m = 0.2 and . (B) m = 0.5 and .
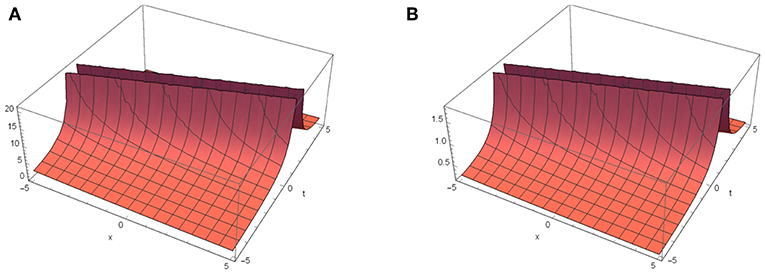
Figure 6. Dynamic behavior of |u15(x, t)| for k2 = 0.2, k3 = −0.9, k4 = 1. (A) m = 0.3 and . (B) m = 0.7 and .
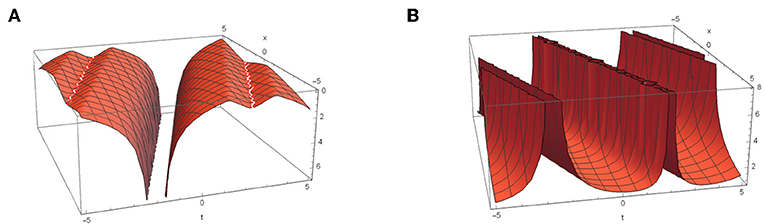
Figure 7. Dynamic behavior of |u16(x, t)| for k2 = 0.1, k3 = 0.7, k4 = −1.3, and α2 = 0.1, β1 = 1. (A) m = 0.1 and . (B) m = 0.9 and .
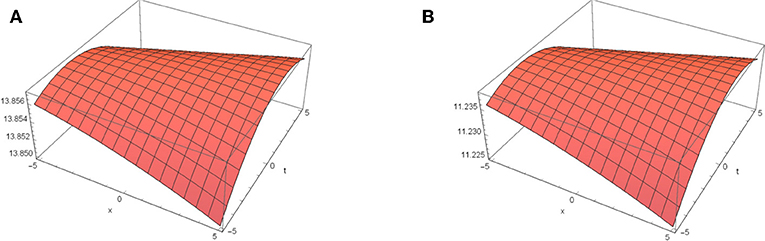
Figure 8. Dynamic behavior of |u18(x, t)| for k2 = 0.1, k3 = 0.7, k4 = −1.3, and β2 = 0.1, h6 = 1. (A) m = 0.3 and . (B) m = 0.8 and .
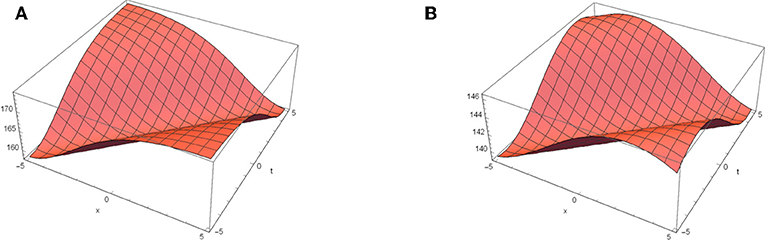
Figure 9. Dynamic behavior of |u19(x, t)| for k2 = 0.7, k3 = 0.4, k4 = −0.5, and β2 = h6 = 1. (A) m = 0.1 and . (B) m = 0.7 and .
7. Conclusion
In this manuscript, we have studied the Gardner equation with the help of two exact solution finder methods. A set of new exact solutions, including bright, kink, multi-soliton solutions, and singular solitons were found corresponding to four parameters, namely k1, k2, k3, and k4. The dynamic behavior of the acquired solutions was also demonstrated to deeply understand the features of the non-linear model. In order to better their properties, we have drawn some 3-D graphs. To the best of the authors knowledge, all the acquired results are novel findings, and cannot be found in the previous works. This result verifies the power of two suggested methods. The main advantages of the method are that they are very simple and quite efficient for the estimation of the optical solutions of PDES. Moreover, the proposed approaches represent efficient methodologies to investigate the exact solutions of the non-linear PDEs.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Funding
This work was supported by JMDC (100%.2019.FPHY.827).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Biazar J, Ayati Z. Extension of the Exp-function method for systems of two-dimensional Burgers equations. Comput Math Appl. (2009) 58:2103–6. doi: 10.1016/j.camwa.2009.03.003
2. Zhaqilao, Qiao Z. Darboux transformation and explicit solutions for two integrable equations. J Math Anal Appl. (2011) 380:794–806. doi: 10.1016/j.jmaa.2011.01.078
3. Yang S, Hua C. Lie symmetry reductions and exact solutions of a coupled KdV–Burgers equation. Appl Math Comput. (2014) 234:579–83. doi: 10.1016/j.amc.2014.01.044
4. Younis M. A new approach for the exact solutions of nonlinear equations of fractional order via modified simple equation method. Appl Math. (2014) 5:1927–32. doi: 10.4236/am.2014.513186
5. Wang M. Exact solutions for a compound KdV-Burgers equation. Phys Lett A. (1996) 213:279–87. doi: 10.1016/0375-9601(96)00103-x
6. Djilali S. Impact of prey herd shape on the predator-prey interaction. Chaos Solit Fract. (2019) 120:139–48. doi: 10.1016/j.chaos.2019.01.022
7. Djilali S, Bentout S. Spatiotemporal patterns in a diffusive predator-prey model with prey social behavior. Acta Appl Math. (2019). doi: 10.1007/s10440-019-00291-z. [Epub ahead of print].
8. Djilali S. Herd behavior in a predator–prey model with spatial diffusion: bifurcation analysis and Turing instability. J Appl Math Comput. (2017) 58:125–49. doi: 10.1007/s12190-017-1137-9
9. Djilali S, Touaoula TM, Miri SEH. A heroin epidemic model: very general non linear incidence, treat-age, and global stability. Acta Appl Math. (2017) 152:171–94. doi: 10.1007/s10440-017-0117-2
10. Goufo EFD, Kumar S, Mugisha SB. Similarities in a fifth-order evolution equation with and with no singular kernel. Chaos Solit Fract. (2020) 130:109467. doi: 10.1016/j.chaos.2019.109467
11. Odibat Z, Kumar S. A robust computational algorithm of homotopy asymptotic method for solving systems of fractional differential equations. J Comput Nonlin Dyn. (2019) 14:081004. doi: 10.1115/1.4043617
12. El-Ajou A, Oqielat MN, Al-Zhour Z, Kumar S, Momani S. Solitary solutions for time-fractional nonlinear dispersive PDEs in the sense of conformable fractional derivative. Chaos. (2019) 29:093102. doi: 10.1063/1.5100234
13. Cattani C, Rushchitskii YY. Cubically nonlinear elastic waves: wave equations and methods of analysis. Int Appl Mech. (2003) 39:1115–45. doi: 10.1023/b:inam.0000010366.48158.48
14. Yang AM, Zhang YZ, Cattani C, Xie GN, Rashidi MM, Zhou YJ, et al. Application of local fractional series expansion method to solve Klein-Gordon equations on cantor sets. Abstr Appl Anal. (2014) 2014:1–6. doi: 10.1155/2014/372741
15. Cattani C. Haar wavelet-based technique for sharp jumps classification. Math Comput Model. (2004) 39:255–78. doi: 10.1016/s0895-7177(04)90010-6
16. Cattani C. Harmonic wavelet solutions of the Schrodinger equation. Int J Fluid Mech Res. (2003) 30:463–72. doi: 10.1615/interjfluidmechres.v30.i5.10
17. Cattani C, Sulaiman TA, Baskonus HM, Bulut H. On the soliton solutions to the Nizhnik-Novikov-Veselov and the Drinfel'd-Sokolov systems. Opt Quant Electr. (2018) 50:138. doi: 10.1007/s11082-018-1406-3
18. Avazzadeh Z, Heydari MH, Cattani C. Legendre wavelets for fractional partial integro-differential viscoelastic equations with weakly singular kernels. Eur Phys J Plus. (2019) 134:368. doi: 10.1140/epjp/i2019-12743-6
19. Griffiths GW, Shiesser WE. Traveling Wave Analysis of Partial Differential Equations. Cambridge, MA: Elsevier (2012). doi: 10.1016/c2009-0-64536-0
20. Wazwaz AM. Soliton solutions for two three plus one dimensional non-integrable KdV-type equations. Math Comput Model. (2012) 55:1845–8. doi: 10.1016/j.mcm.2011.11.082
21. Wazwaz AM. Solitons and singular solitons for the Gardner–KP equation. Appl Math Comput. (2008) 204:162–9. doi: 10.1016/j.amc.2008.06.011
22. Krishnan EV, Triki H, Labidi M, Biswas A. A study of shallow water waves with Gardner's equation. Nonlin Dyn. (2011) 66:497–507. doi: 10.1007/s11071-010-9928-7
23. Kumar M, Tanwar DV. On Lie symmetries and invariant solutions of (2+1)–dimensional Gardner equation. Commun Nonlin Sci Numer Simul. (2019) 69:45–57. doi: 10.1016/j.cnsns.2018.09.009
24. Fei J, Cao W, Ma Z. Nonlocal symmetries and explicit solutions for the Gardner equation. Appl Math Comput. (2017) 314:293–8. doi: 10.1016/j.amc.2017.07.002
25. kai Liu Y, Li B. Nonlocal symmetry and exact solutions of the (2+1)-dimensional Gardner equation. Chin J Phys. (2016) 54:718–23. doi: 10.1016/j.cjph.2016.05.014
26. Betchewe G, Victor KK, Thomas BB, Crepin KT. New solutions of the Gardner equation: analytical and numerical analysis of its dynamical understanding. Appl Math Comput. (2013) 223:377–88. doi: 10.1016/j.amc.2013.08.028
27. Alejo MA. On the ill-posedness of the Gardner equation. J Math Anal Appl. (2012) 396:256–60. doi: 10.1016/j.jmaa.2012.06.018
28. Cao D. The classification of the single traveling wave solutions to the time-fraction Gardner equation. Chin J Phys. (2019) 59:379–92. doi: 10.1016/j.cjph.2019.03.003
29. Ghanbari B, Inc M. A new generalized exponential rational function method to find exact special solutions for the resonance nonlinear Schrödinger equation. Eur Phys J Plus. (2018) 133:142. doi: 10.1140/epjp/i2018-11984-1
30. Osman MS, Ghanbari B, Machado JAT. New complex waves in nonlinear optics based on the complex Ginzburg-Landau equation with Kerr law nonlinearity. Eur Phys J Plus. (2019) 134:20. doi: 10.1140/epjp/i2019-12442-4
31. Ghanbari B, Baleanu D, Qurashi MA. New exact solutions of the generalized Benjamin–Bona–Mahony equation. Symmetry. (2018) 11:20. doi: 10.3390/sym11010020
Keywords: soliton solutions, generalized exponential rational function method, analytical solutions, PDE, computational, solitons, Gardner's equation
Citation: Ghanbari B and Baleanu D (2019) New Solutions of Gardner's Equation Using Two Analytical Methods. Front. Phys. 7:202. doi: 10.3389/fphy.2019.00202
Received: 10 October 2019; Accepted: 13 November 2019;
Published: 06 December 2019.
Edited by:
Carlo Cattani, Università degli Studi della Tuscia, ItalyReviewed by:
Salih Djilali, University of Chlef, AlgeriaSunil Kumar, National Institute of Technology, Jamshedpur, India
Aliyu Isa Aliyu, Sun Yat-sen University, China
Copyright © 2019 Ghanbari and Baleanu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Behzad Ghanbari, Yi5naGFuYmFyeUB5YWhvby5jb20=
 Behzad Ghanbari
Behzad Ghanbari Dumitru Baleanu
Dumitru Baleanu