Computational and Physical Examination About the Aspects of Fluid Flow Between Two Coaxially Rotated Disks by Capitalizing Non-fourier Heat Flux Theory: Finite Difference Approach

Introduction

Rotational fluid flow generated by coaxial disks is one of the classical problems of fluid mechanics. In recent years, it has become a popular research area and has persuaded researchers due to magnificent theoretical and practical significance in engineering and applied sciences. Some important practical fields in which rotatory flow is capitalized are rotor–stator system, gas turbine engineering, air rotational cleaners, medical equipment, chemical engineering, and thermal power–generating systems. In view of its capitalization in various processes, researcher fraternity is examining such type of flows in current days. Inaugurated work on flow induced due to rotating disk is performed by Karman [1]. He introduced transformations and provided a mathematical framework for construction of ordinary differential systems of rotational flows from Navier Stokes theory. Cochran [2] also used these transformations to scrutinize rotating disk flow by using numerical integration scheme. Batchelor [3] validated that Karman transformation can be evenly used for fluid flow between two coaxial rotating disks. Rotating flow by two coaxial disks is primarily examined by Stewartson [4]. Chapple and Stokes [5] elucidated the flow features of fluid between two coaxially rotated disks. Mellor et al. [6] bestowed comprehensive treatment of fluid flow restricted between two coaxial infinite disks, one rotating, and other stationary. Thermal aspects of fluid between rotational disks were discussed by Arora and Stokes [7]. Interpretation of flow phenomenon between porous stationary disk and solid rotating disk was manipulated by Kumar et al. [8]. Xun et al. [9] considered rotating disk of variable thickness and adumbrated the flow features of Power law fluid. Hall effects on an unsteady MHD (magneto hydrodynamics) flow of viscous incompressible electrically conducting fluid between two rotating disks with non-coincident parallel axes embedded in a porous viscous medium were accorded by Das et al. [10]. Asgher et al. [11] conducted Lie group analysis on the thermal features of fluid manifested by rotating disks. Elmaboud et al. [12] discussed peristaltic flow induced by sinusoidal wave propagating with constant speed on the walls of two-dimensional infinite rotating channel by heeding semi-analytical solutions.

In the most recent couple of decades, researcher fraternity has shown fantastic energy in exploring the heat propagation by means of a wave mechanism rather than essentially by diffusion. Late studies affirm that this is not just a low-temperature phenomenon but heat transfer mechanism also occurs at high temperature through diffusion. Just about 200 years prior, thermal features in various circumstances and especially in flowing fluid environment were interpreted by Fourier law of heat conduction [13]. However, this law is inadequate in comprehending complete description about the heat exchange procedure among multiple connected surfaces in various conditions because of its disablement to fulfill the principle of causality. Later on, in 1948, Cattaneo [14] modified Fourier law by viewing the inadequateness generated by Fourier law of heat conduction and explored that this law explains the thermal attribute at low temperature because it generates parabolic heat equation in which initial disturbance are felt throughout the domain. After getting thorough analysis about Fourier law and viewing vector field aspect of heat flux, he included thermal relaxation time term to control generated thermal inertia, which is known as Maxwell-Cattaneo law. Afterward, Christov [15] proposed that objective time derivative instead of material time derivative is used for exact fulfillment of causality principle. He changed the time derivative in Maxwell-Cattaneo model by Oldryod upper convective derivative, which has successfully preserved the material invariant formulation and famously known as Cattaneo-Christov heat flux law. Cattaneo-Christov heat flux model has bounteous applications in engineering and modern industrial procedures like in skin burns and nanofluids, cooling of electronic devices, food technology, nuclear reactor cooling, power generation, heat exchangers, heat propagation in tissues, and so many. The uniqueness and stability of the solution for governing temperature equations by Cattaneo-Christov model in some initial and boundary value problems were proven by Straughan [16]. Additionally, steadiness of structure of Cattaneo-Christov heat flux model with uniqueness was revealed by Ciarletta and Straughan [17]. Tibullo and Zampoli [18] explicated the behavior of Cattaneo-Christov heat flux model in incompressible fluid flows. Aqsa [19] and Haddad [20] heeded numerical solution for thermal convection of an incompressible viscous fluid by obliging Cattaneo-Christov heat flux model. Mekheimer and Elmaboud [21] interpreted the aspects of temperature-dependent viscosity and thermal conductivity on peristaltic flow of a Newtonian fluid in a vertical asymmetric channel. Mekneimer [22] addressed heat transfer features of peristaltic couple stress fluid in asymmetric channel generated by wave with different phase and amplitudes. All of the abovementioned thought-provoking investigations have generated prodigious interest of researchers toward the analysis of flow in the presence of thermal aspects [23–26].

Transport procedures through porous space are commonly encountered in various chemical, mechanical, geophysical, electrochemical, and metallurgical routines. The theory about macroscopic movement of fluid in porous medium comprises differential equation that expresses linear relation between velocity and pressure gradient. Initially, Henry Darcy [27] (in 1856) presented a law to explicate the dynamic phenomenon in porous medium by working on the flow of sandy water through pebbles. Several technological processes depend on porous media theory, such as hydrology, oil exploration, solar collectors, porous insulations, packed beds, chromatography, heterogeneous catalysis, control of shear stresses at the seabed bottom, and oscillatory flow through seabed ripples. Darcy theory has promising applications in the field of biomedicine and the development of biological clogging and flow through tissues [28]. Granular material [29] where significant amount of pore structures exist has application in manufacturing, paper, ceramic products, and textiles. Taseer et al. [30] addressed the flow behavior of Maxwell nanofluid in porous medium by implementing zero mass flux condition. They capitalized on Darcy-Forchheimer law to depict the flow pattern. They found that porosity parameter mounts the magnitude of temperature and concentration of particles. Seddeek [31] probed convective heat transfer in fluid immersed in porous medium. Analytical results for Darcy flow was described by Jha and Kaurangini [32]. Aziz et al. [33] computed the traveling wave solution for the time-dependent viscoelastic fluid by way of a porous flat plate.

Magnetohydrodynamics is the study of the interaction between magnetic field and conductive fluid. The essence about magnetization is that the external magnetic field controls the turbulence in flow field. In addition, the magnetized flows differ from ordinary fluids because the generated current in the bulk fluid produces volumetric Lorentz force that extensively modifies the features. In recent years, magnetization and its impact on flow features have attained pervasive focus due to its extraordinary industrial applications, such as magnetized materials processes, manufacturing of glass, and MHD controlled electric generators. So the analysis of application of magnetic field has experienced great development and diversity. Andersson [34] performed exclusive study by manipulating electromagnet hydrodynamic waves mathematically. The stretched flow of two-dimensional Newtonian fluid under the effects of applied magnetic field was contemplated by Andersson [34]. Liu [35] extended the work of Andersson [34] and described the heat and mass transfer of MHD viscous fluid flow over stretching surface. He computed exact solution of the problem by following the procedure of Andersson [34]. The impact of normally impinging magnetic field on boundary layer flow of Newtonian fluid over permeable stretching sheet was analyzed by Kumaran et al. [36]. Yirga and Tesfay [37] developed the numerical simulations for MHD viscous fluid flow over non-linear stretching sheet. The fluid flow equations were solved via Keller-Box method, and variations in physical quantities were presented regarding different parametric conditions. Recently, Yasin et al. [38] simulated the problem of two-dimensional MHD viscous nanofluid flow over porous stretched sheet. The formulated equations were solved by implementing well-known shooting technique. Mabood et al. [39] developed the approximate analytic solution of MHD boundary layer fluid flow over exponentially stretching surface. Some of the literature regarding the mentioned aspects is accessed through the references [40–43].

Present disquisition is addressed to excogitate thermophysical features exhibited in viscous fluid flow between two coaxially rotating disks embedded in permeable medium by obliging Cattaneo-Christov heat flux law. According to author's knowledge and available literature survey, it is found that very concise work is done so far in this direction. Tremendous engineering and practical application generated by rotating disk flows make present analysis highly potential. The authors hope that this manuscript will serve as a reference study for future researches. The article is strategized in such a way that the literature assessment is presented in section Introduction, whereas the mathematical structuring is provided in section Mathematical Model. The explanation about the solution methodology is debated in section Numerical Procedure. Comprehensive analysis and interpretation of flow controlling parameters are disclosed in section Results and Discussion. Last, the outcome norms are listed in section Conclusions.

Mathematical Model

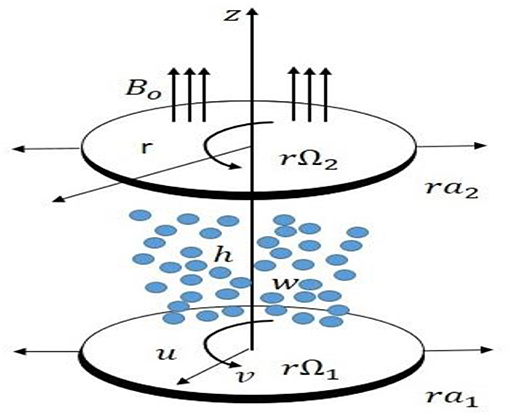
Consider a steady, incompressible flow of viscous fluid between two coaxially rotated disks. The lower disk is placed at z = 0, whereas the distance between the disks is h units. Lower and upper disks possess angular velocities Ω₁ and Ω₂, respectively, and a₁ and a₂ are corresponding stretching rates (Figure 1). Porous medium between disks is considered, and Cattaneo-Christov heat flux model is obliged to analyze thermal features of fluid flow model.

FIGURE 1

Figure 1. Physical configuration of the problem.

We have used cylindrical coordinates (r, θ, z) with velocity components $(\widehat{u},\widehat{v},\widehat{w})$ to the velocity profile and temperature equations as follows:

$\begin{array}{llll}\frac{\partial \widehat{u}}{\partial r}+\frac{\widehat{u}}{r}+\frac{\partial \widehat{w}}{\partial z}& =& 0,& (1)\end{array}$

$\begin{array}{l}\widehat{u}\frac{\partial \widehat{u}}{\partial r}+\widehat{w}\frac{\partial \widehat{u}}{\partial z}-\frac{{\widehat{v}}^2}{r}=-\frac{1}{\rho }\frac{\partial \widehat{p}}{\partial r}+\upsilon \left(\frac{{\partial }^2\widehat{u}}{\partial r^2}+\frac{1}{r}\frac{\partial \widehat{u}}{\partial r}+\frac{{\partial }^2\widehat{u}}{\partial z^2}-\frac{\widehat{u}}{r^2}\right)\\ -\frac{\sigma {\beta }_0^2}{\rho }\widehat{u}-\frac{\mu }{k_0}\widehat{u},& (2)\end{array}$

$\begin{array}{l}\widehat{u}\frac{\partial \widehat{v}}{\partial r}+\widehat{w}\frac{\partial \widehat{v}}{\partial z}+\frac{\widehat{u}\widehat{v}}{r}=\upsilon \left(\frac{{\partial }^2\widehat{v}}{\partial r^2}+\frac{1}{r}\frac{\partial \widehat{v}}{\partial r}+\frac{{\partial }^2\widehat{v}}{\partial z^2}-\frac{\widehat{v}}{r^2}\right)\\ -\frac{\sigma {\beta }_0^2}{\rho }\widehat{v}-\frac{\mu }{k_0}\widehat{v}& (3)\end{array}$

$\begin{array}{l}\widehat{u}\frac{\partial \widehat{w}}{\partial r}+\widehat{w}\frac{\partial \widehat{w}}{\partial z}=-\frac{1}{\rho }\frac{\partial \widehat{p}}{\partial z}+\upsilon \left(\frac{{\partial }^2\widehat{w}}{\partial r^2}+\frac{1}{r}\frac{\partial \widehat{w}}{\partial r}+\frac{{\partial }^2\widehat{w}}{\partial z^2}\right)\\ -\frac{\mu }{k_0}\widehat{w},& (4)\end{array}$

$\begin{array}{ll}\rho C_p\left(\widehat{u}\frac{\partial \widehat{T}}{\partial r}+\widehat{w}\frac{\partial \widehat{T}}{\partial z}\right)=-\nabla ·\vec{q},& (5)\end{array}$

with boundary conditions:

$\begin{array}{ll}\begin{array}{c}\widehat{u}=r{a}_1,\widehat{v}=r{\Omega }_1,\widehat{w}=0,\widehat{T}=\widehat{T_1}\text{ at }z=0,\\ \widehat{u}=r{a}_2,\widehat{v}=r{\Omega }_2,\widehat{w}=0,\widehat{T}=\widehat{T_2}\text{ at }z=h,\\ \end{array}& (6)\end{array}$

where Equations (3–5) are referred to Hayat et al. [25], also pressure is expressed as $\widehat{p},$ ${\widehat{T}}_1$ and ${\widehat{T}}_2$ are the temperatures of upper and lower disks, and flux of heat $\vec{q}$ satisfies:

$\begin{array}{ll}\overrightarrow{q}+\gamma \left(\frac{\partial \overrightarrow{q}}{\partial t}+V.\nabla \overrightarrow{q}-\overrightarrow{q}.\nabla V+(\nabla .V)\overrightarrow{q}\right)=-k\nabla \widehat{T},& (7)\end{array}$

where γ is the thermal relaxation parameter (It is defined as the parameter that controls the speed of heat waves produced within the system and makes them move with finite speed to follow the principle of causality), and k is the thermal conductivity. Now, we omit q from the Equations (5, 7) and obtain:

$\begin{array}{l}\left(\widehat{u}\frac{\partial \widehat{T}}{\partial r}+\widehat{w}\frac{\partial \widehat{T}}{\partial z}\right)=\frac{k}{\rho C_p}\left(\frac{{\partial }^2\widehat{T}}{\partial r^2}+\frac{1}{r}\frac{\partial \widehat{T}}{\partial r}+\frac{{\partial }^2\widehat{T}}{\partial z^2}\right)\\ -\gamma ({\widehat{u}}^2\frac{{\partial }^2\widehat{T}}{\partial r^2}+{\widehat{w}}^2\frac{{\partial }^2\widehat{T}}{\partial z^2}+2\widehat{u}\widehat{w}\frac{{\partial }^2\widehat{T}}{\partial r\partial z}\\ +\left(\widehat{u}\frac{\partial \widehat{u}}{\partial r}+\widehat{w}\frac{\partial \widehat{u}}{\partial z}\right)\frac{\partial \widehat{T}}{\partial r}+\left(\widehat{u}\frac{\partial \widehat{w}}{\partial r}+\widehat{w}\frac{\partial \widehat{w}}{\partial z}\right)\frac{\partial \widehat{T}}{\partial z}).& (8)\end{array}$

Equations (2–5) and Equation (8) are transformed into ordinary differential equations by obliging Von Karman transformations [1]:

$\begin{array}{r}\widehat{u}=r{\Omega }_1{f}^{\prime }(\zeta ),\widehat{v}=r{\Omega }_{1}g(\zeta ),\widehat{w}=-2h{\Omega }_{1}f(\zeta ),\\ \theta =\frac{\widehat{T}-{\widehat{T}}_2}{{\widehat{T}}_1-{\widehat{T}}_2},\\ \widehat{p}={\rho }_f{\Omega }_1{v}_f\left(P(\zeta )+\frac{1}{2}\frac{r^2}{h^2}ϵ\right),\zeta =\frac{z}{h}.& (9)\end{array}$

Mass conservation is identically satisfied, and Equations (2–4, 6, 8) take the following form:

$\begin{array}{ll}{f}^{‴}+Re\left(2f{f}^{″}-{f^{\prime }}^2+g^2-\frac{1}{\beta }{f}^{\prime }+M{f}^{\prime }\right)-ϵ=0,& (10)\end{array}$

$\begin{array}{ll}Re\left(2f^{\prime }g-2f{g}^{\prime }+\frac{1}{\beta }g+Mg\right)-g^{″}=0,& (11)\end{array}$

$\begin{array}{ll}{P}^{\prime }=Re\left(\frac{2}{\beta }f-4f{f}^{\prime }\right)-2f^{″},& (12)\end{array}$

$\begin{array}{ll}\frac{1}{Pr}{\theta }^{″}+2Ref{\theta }^{\prime }-4\lambda Re\left(f^2{\theta }^{″}+f{f}^{\prime }{\theta }^{\prime }\right)=0,& (13)\end{array}$

with

$\begin{array}{r}f(0)=0,f(1)=0,f^{\prime }(0)=A_{1,}{f}^{\prime }(1)=A_2,g(0)=1,\\ g(1)=\tau ,\theta (0)=1,\theta (1)=0,P(0)=0,& (14)\end{array}$

where

$\begin{array}{ll}\begin{array}{c}Re=\frac{{\Omega }_1{h}^2}{v_f},Pr=\frac{{\left(\rho C_p\right)}_f{v}_f}{k_f},\lambda =\gamma {\Omega }_1,\\ A_1=\frac{a_1}{{\Omega }_1},A_2=\frac{a_2}{{\Omega }_2},\tau =\frac{{\Omega }_2}{{\Omega }_1},\beta =\frac{k_0{\Omega }_1}{v},\\ \end{array}& (15)\end{array}$

where Re denotes Reynolds number, Pr is the Prandtl number, A₁ and A₂ are scaled stretching parameters, λ is the thermal relaxation, τ and β are rotational number and porosity parameter.

To make a simpler form of Equation (10), we removed ϵ.

$\begin{array}{ll}{f}^{(iv)}+Re\left(2f{f}^{‴}+2g{g}^{\prime }-\frac{1}{\beta }{f}^{″}-M{f}^{″}\right)=0.& (16)\end{array}$

The pressure parameter ϵ can be found by using Equations (10 and 14) as:

$\begin{array}{ll}ϵ=f^{″}(0)-Re\left({(f^{\prime }(0))}^2-{(g(0))}^2+\frac{1}{\beta }{f}^{\prime }(0)-M{f}^{\prime }(0)\right).& (17)\end{array}$

Equation (17) vanishes due to the given initial conditions in Equation (14).

The radial and tangential components of shear stress at lower disk are τ_zr and τ_zθ

$\begin{array}{r}{\tau }_{zr}=\mu \frac{\partial \widehat{u}}{\partial z}{\displaystyle {|}_{z=0}=\frac{\mu r{\Omega }_1{f}^{″}(0)}{h},{\tau }_{z\theta }=\mu \frac{\partial \widehat{v}}{\partial z}{|}_{z=0}}\\ =\frac{\mu r{\Omega }_1{g}^{\prime }(0)}{h}.& (18)\end{array}$

where τ_w is the total shear stress, which is defined as:

$\begin{array}{ll}{\tau }_w=\sqrt{{\tau }_{zr}^2+{\tau }_{z\theta }^2}.& (19)\end{array}$

C_f1 and C_f2 are the skin friction coefficients at lower and upper disks defined as:

$\begin{array}{ll}{C}_{f1}=\frac{{\tau }_w{|}_{z=0}}{\rho {(r{\Omega }_1)}^2}=\frac{1}{R{e}_r}{\left({(f^{″}(0))}^2+{(g^{\prime }(0))}^2\right)}^{1/2},& (20)\end{array}$

$\begin{array}{ll}{C}_{f2}=\frac{{\tau }_w{|}_{z=h}}{\rho {(r{\Omega }_1)}^2}=\frac{1}{R{e}_r}{\left({(f^{″}(1))}^2+{(g^{\prime }(1))}^2\right)}^{1/2},& (21)\end{array}$

where $R{e}_r=\frac{r{\Omega }_{1}h}{v}$ is the local Reynolds number.

Numerical Procedure

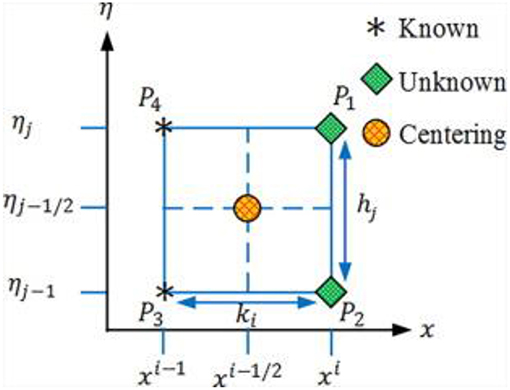
Manipulation of accurate solution is necessary for physical interpretation of current work. Initially, equations are modeled by using Karman approximation and afterward, we have attained an intricate system of ordinary differential Equations (10–13) along with boundary conditions in Equation (14). We have applied Keller-box scheme referred to [40, 44–46], that is, the implicit finite difference scheme. For the implementation of this technique, first, we have to transform it into a system of first-order equations and define new variables u(y, ζ), v(y, ζ),

$\begin{array}{r}w(y,\zeta ),s(y,\zeta ),t(y,\zeta )and\theta (y,\zeta )=q(y,\zeta )\text{ are}\\ f^{\prime }=u,u^{\prime }=v,v^{\prime }=w,g^{\prime }=s\text{ and }{q}^{\prime }=t,& (22)\end{array}$

and Equations (11–13, 16) are reduced to

$\begin{array}{ll}{s}^{\prime }-Re\left(2ug-2fs+Mg+\frac{1}{\beta }g\right)=0,& (23)\end{array}$

$\begin{array}{ll}{t}^{\prime }+2PrReft-4Pr\lambda Re\left(f^2{t}^{\prime }+fut\right)=0,& (24)\end{array}$

$\begin{array}{ll}{w}^{\prime }+Re\left(2fw+2gs-Mv-\frac{1}{\beta }v\right)=0.& (25)\end{array}$

Similarly, the boundary conditions are converted into the following forms

$\begin{array}{ll}\begin{array}{c}f(0)=0,u(0)=A_1,g(0)=1,q(0)=1,\\ f(1)=0,u(1)=A_2,g(1)=\tau ,q(1)=0.\\ \end{array}& (26)\end{array}$

Average and center difference gradients at the point of net derivatives are demarcated in Figure 2 and mathematically as below

$\begin{array}{l}{\eta }_o=0,{\eta }_k={\eta }_{k-1}+{\eta }_k,k=1,2,3,\dots ,k{\eta }_k={\eta }_{\infty }.\end{array}$

FIGURE 2

Figure 2. Schematic representation of domain.

Applying the Newton iteration f_k+1 = f_k+δf_k, for all dependent variables involved in linearized non-linear algebraic equations and substituting these expressions in non-linear equations and neglecting quadratic and higher order terms in δ, a linear tridiagonal system is presented as follows:

$\begin{array}{l}\delta f_k-\delta f_{k-1}-\frac{h_k}{2}\left(\delta u_k+\delta u_{k-1}\right)={\left(r_1\right)}_{k-\frac{1}{2}},\\ \delta u_k-\delta u_{k-1}-\frac{h_k}{2}\left(\delta v_k+\delta v_{k-1}\right)={\left(r_5\right)}_{k-\frac{1}{2}},\\ \delta v_k-\delta v_{k-1}-\frac{h_k}{2}\left(\delta w_k+\delta w_{k-1}\right)={\left(r_6\right)}_{k-\frac{1}{2}},\\ \delta g_k-\delta g_{k-1}-\frac{h_k}{2}\left(\delta s_k+\delta s_{k-1}\right)={\left(r_7\right)}_{k-\frac{1}{2}},\\ \delta q_k-\delta q_{k-1}-\frac{h_k}{2}\left(\delta t_k+\delta t_{k-1}\right)={\left(r_8\right)}_{k-\frac{1}{2}},\\ {\left(a_1\right)}_k\delta f_k+{\left(a_2\right)}_k\delta f_{k-1}+{\left(a_3\right)}_k\delta u_k\\ +{\left(a_4\right)}_k\delta u_{k-1}+{\left(a_5\right)}_k\delta g_k+{\left(a_6\right)}_k\delta g_{k-1}+{\left(a_7\right)}_k\delta s_k\\ +{\left(a_8\right)}_k\delta s_{k-1}={\left(r_2\right)}_{k-1/2},\\ {\left(b_1\right)}_k\delta f_k+{\left(b_2\right)}_k\delta f_{k-1}+{\left(b_3\right)}_k\delta u_k+{\left(b_4\right)}_k\delta u_{k-1}\\ +{\left(b_5\right)}_k\delta t_k+{\left(b_6\right)}_k\delta t_{k-1}={\left(r_3\right)}_{k-1/2},\\ {\left(c_1\right)}_k\delta f_k+{\left(c_2\right)}_k\delta f_{k-1}+{\left(c_3\right)}_k\delta v_k+{\left(c_4\right)}_k\delta v_{k-1}\\ +{\left(c_5\right)}_k\delta w_k+{\left(c_6\right)}_k\delta w_{k-1}+{\left(c_7\right)}_k\delta g_k+{\left(c_8\right)}_k\delta g_{k-1}\\ +{\left(c_7\right)}_k\delta s_k+{\left(c_8\right)}_k\delta s_{k-1}={\left(r_4\right)}_{k-1/2},\end{array}$

with boundary conditions are:

$\begin{array}{l}\begin{array}{c}\delta f_o=0,\delta u_o=A_1,\delta g_o=1,\delta q_o=1,\\ \delta f_k=0,\delta u_k=A_2,\delta g_k=\tau ,\delta q_k=1,\\ \end{array}\end{array}$

where

$\begin{array}{l}{\left(a_1\right)}_k={\left(a_2\right)}_k=hRe\left(s_{k-1/2}\right),\\ {\left(a_3\right)}_k={\left(a_4\right)}_k=hRe\left(g_{k-1/2}\right),\\ {\left(a_5\right)}_k={\left(a_6\right)}_k=hRe\left(u_{k-1/2}+\frac{1}{\beta }+M\right),\\ {\left(a_7\right)}_k=1+2hRe\left(f_{k-1/2}\right),\\ {\left(a_8\right)}_k=-1+2hRe\left(f_{k-1/2}\right),\\ {\left(b_1\right)}_k={\left(b_2\right)}_k=hRe\left(w_{k-1/2}\right),\\ {\left(b_3\right)}_k={\left(b_4\right)}_k=hRe\left(M+\frac{1}{\beta }\right),\\ {\left(b_5\right)}_k=1+2hRe\left(f_{k-1/2}\right),\\ {\left(b_6\right)}_k=-1+2hRe\left(f_{k-1/2}\right),\\ {\left(b_7\right)}_k={\left(b_8\right)}_k=2hRe\left(s_{k-1/2}\right),\\ {\left(b_9\right)}_k={\left(b_{10}\right)}_k=2hRe\left(g_{k-1/2}\right),\\ {\left(c_1\right)}_k={\left(c_2\right)}_k=2hRePr\left(t_{k-1/2}-2\lambda f_{k-1/2}\right),\\ {\left(c_3\right)}_k={\left(c_4\right)}_k=2hRePr\lambda \left(t_{k-1/2}\right)\left(f_{k-1/2}\right),\\ {\left(c_5\right)}_k=1+2hRePr(t_{k-1/2}-2\lambda {\left(f_{k-1/2}\right)}^2\\ +\left(u_{k-1/2}\right)\left(f_{k-1/2})\right),\\ {\left(c_6\right)}_k=-1+2hRePr(t_{k-1/2}-2\lambda {\left(f_{k-1/2}\right)}^2\\ +\left(u_{k-1/2}\right)\left(f_{k-1/2})\right),\end{array}$

and

$\begin{array}{l}{\left(r_1\right)}_k=f_{k-1}-f_k+h\left(u_{k-1/2}\right),\\ {\left(r_5\right)}_k=u_{k-1}-u_k+h\left(v_{k-1/2}\right),\\ {\left(r_6\right)}_k=v_{k-1}-v_k+h\left(w_{k-1/2}\right),\\ {\left(r_7\right)}_k=g_{k-1}-g_k+h\left(s_{k-1/2}\right),\\ {\left(r_8\right)}_k=q_{k-1}-q_k+h\left(t_{k-1/2}\right),\\ {\left(r_2\right)}_k=s_{k-1}-s_k+hRe(2u_{k-1/2}{g}_{k-1/2}-2f_{k-\frac{1}{2}}{s}_{k-\frac{1}{2}}\\ +\left(M+\frac{1}{\beta }\right)g_{k-1/2}\frac{1}{2}{s}_{k-\frac{1}{2}}),\\ {\left(r_3\right)}_k=w_{k-1}-w_k+hRe(2f_{k-1/2}{w}_{k-1/2}+2g_{k-1/2}{s}_{k-1/2},\\ -\left(M+\frac{1}{\beta }\right)v_{k-1/2})\\ {\left(r_4\right)}_k=t_{k-1}-t_k+hRePr(2f_{k-1/2}{t}_{k-1/2}-4\text{λ}(f_{k-1/2}{f}_{k-1/2}\\ +f_{k-1/2}{u}_{k-1/2}{t}_{k-1/2})).\end{array}$

Now, we consist the tridiagonal block matrices of given linearized equations in the form:

$\begin{array}{ll}\text{A}\delta =\text{r}& (27)\end{array}$

where

$\begin{array}{r}\left(\begin{array}{c}\begin{array}{lllllll}\left[A_1\right]\hfill & \left[C_1\right]\hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \left[B_1\right]\hfill & \left[A_2\right]\hfill & \hfill & \hfill & \hfill & \hfill & \hfill \\ \hfill & \hfill & \left[C_2\right]\hfill & \ddots \hfill & \ddots \hfill & \hfill & \hfill \\ \hfill & \hfill & \ddots \hfill & \ddots \hfill & \ddots \hfill & \hfill & \hfill \\ \hfill & \hfill & \ddots \hfill & \ddots \hfill & \left[B_{k-1}\right]\hfill & \hfill & \hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \left[A_{k-1}\right]\hfill & \left[C_{k-1}\right]\hfill \\ \hfill & \hfill & \hfill & \hfill & \hfill & \left[B_k\right]\hfill & \left[A_k\right]\hfill \end{array}\end{array}\right)\\ \left(\begin{array}{c}\begin{array}{l}\left[{\delta }_1\right]\hfill \\ \left[{\delta }_2\right]\hfill \\ ⋮\hfill \\ \left[{\delta }_{k-1}\right]\hfill \\ \hfill \\ \left[{\delta }_k\right]\hfill \end{array}\end{array}\right)=\left(\begin{array}{c}\begin{array}{l}\left[r_1\right]\hfill \\ \left[r_2\right]\hfill \\ ⋮\hfill \\ \left[r_{k-1}\right]\hfill \\ \hfill \\ \left[r_k\right]\hfill \end{array}\end{array}\right)& (28)\end{array}$

In Equation (28), the elements are defined as:

$\begin{array}{l}[A_1]=\left(\begin{array}{cccccccc}1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0\\ 0& -1& -e_k& 0& 0& 0& 0& 0\\ 0& 0& -1& -e_k& 0& 0& 0& 0\\ 0& 0& 0& 0& -1& -e_k& 0& 0\\ 0& 0& 0& 0& 0& 0& -1& -e_k\end{array}\right),e_k=\frac{1}{2}{h}_k\end{array}$

$\begin{array}{r}\left[{\alpha }_k\right]=\left(\begin{array}{cccccccc}1& -e_k& 0& 0& 0& 0& 0& 0\\ {\left(a_1\right)}_k& 0& {\left(a_3\right)}_k& {\left(a_5\right)}_k& {\left(a_7\right)}_k& {\left(a_9\right)}_k& 0& 0\\ {\left(b_1\right)}_k& {\left(b_3\right)}_k& 0& 0& {\left(b_5\right)}_k& {\left(b_7\right)}_k& 0& 0\\ {\left(c_1\right)}_k& {\left(c_3\right)}_k& 0& 0& 0& 0& 0& {\left(c_5\right)}_k\\ 0& -1& -e_k& 0& 0& 0& 0& 0\\ 0& 0& -1& -e_k& 0& 0& 0& 0\\ 0& 0& 0& 0& -1& -e_k& 0& 0\\ 0& 0& 0& 0& 0& 0& -1& -e_k\end{array}\right),\\ 2<k<K-1,\end{array}$

$\begin{array}{l}\left[{\alpha }_K\right]=\left(\begin{array}{cccccccc}1& -e_k& 0& 0& 0& 0& 0& 0\\ {\left(a_1\right)}_k& 0& {\left(a_3\right)}_k& {\left(a_5\right)}_k& {\left(a_7\right)}_k& {\left(a_9\right)}_k& 0& 0\\ {\left(b_1\right)}_k& {\left(b_3\right)}_k& 0& 0& {\left(b_5\right)}_k& {\left(b_7\right)}_k& 0& 0\\ {\left(c_1\right)}_k& {\left(c_3\right)}_k& 0& 0& 0& 0& 0& {\left(c_5\right)}_k\\ 1& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& 0\end{array}\right),\end{array}$

$\begin{array}{r}\left[{\beta }_k\right]=\left(\begin{array}{cccccccc}-1& -e_k& 0& 0& 0& 0& 0& 0\\ {\left(a_2\right)}_k& 0& {\left(a_4\right)}_k& {\left(a_6\right)}_k& {\left(a_8\right)}_k& {\left(a_{10}\right)}_k& 0& 0\\ {\left(b_2\right)}_k& {\left(b_4\right)}_k& 0& 0& {\left(b_6\right)}_k& {\left(b_8\right)}_k& 0& 0\\ {\left(c_2\right)}_k& {\left(c_4\right)}_k& 0& 0& 0& 0& 0& {\left(c_6\right)}_k\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right),\\ 2<k<K\end{array}$

$\begin{array}{l}\left[C_k\right]=\left(\begin{array}{cccccccc}0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& -e_k& 0& 0& 0& 0& 0\\ 0& 0& 1& -e_k& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& -e_k& 0& 0\\ 0& 0& 0& 0& 0& 0& 1& -e_k\end{array}\right),1<k<K-1,\end{array}$

$\begin{array}{c}\left[{\delta }_k\right]=\left(\begin{array}{c}\delta f_k\\ \delta u_k\\ \delta v_k\\ \delta w_k\\ \delta g_k\\ \delta s_k\\ \delta q_k\\ \delta t_k\end{array}\right),\left[r_k\right]=\left(\begin{array}{c}{\left(r_1\right)}_{k-(\frac{1}{2})}\\ {\left(r_2\right)}_{k-(\frac{1}{2})}\\ {\left(r_3\right)}_{k-(\frac{1}{2})}\\ {\left(r_4\right)}_{k-(\frac{1}{2})}\\ {\left(r_5\right)}_{k-(\frac{1}{2})}\\ {\left(r_6\right)}_{k-(\frac{1}{2})}\\ {\left(r_7\right)}_{k-(\frac{1}{2})}\\ {\left(r_8\right)}_{k-(\frac{1}{2})}\end{array}\right),1<k<K,\\ \text{A}=\text{LU},& (29)\end{array}$

These computations are repeated until some convergence criteria are satisfied.

Results and Discussion

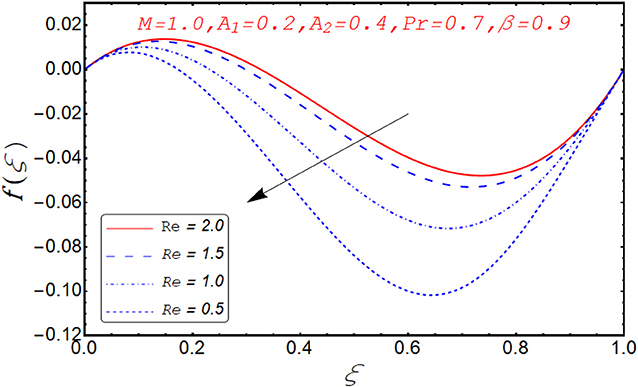
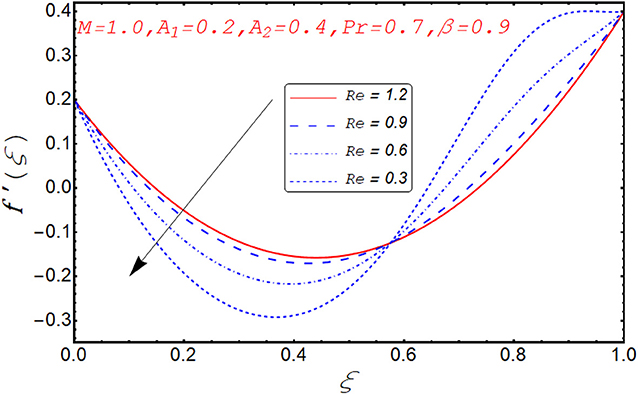
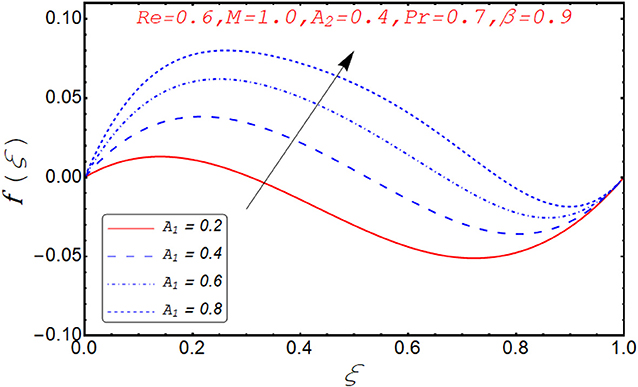
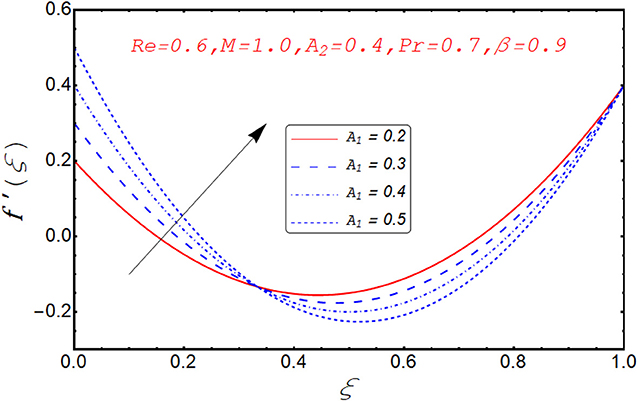
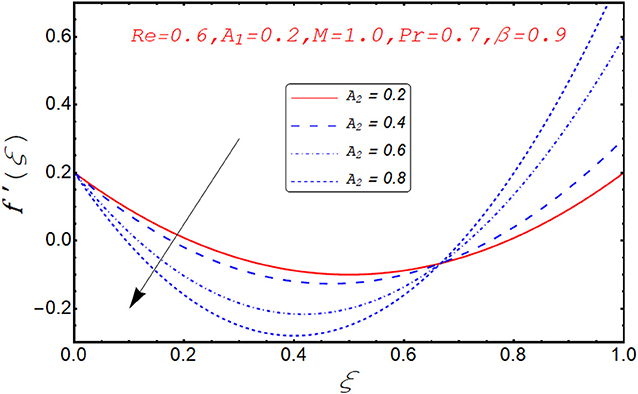
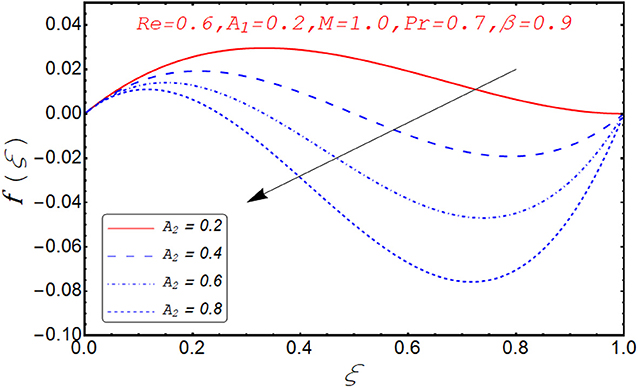
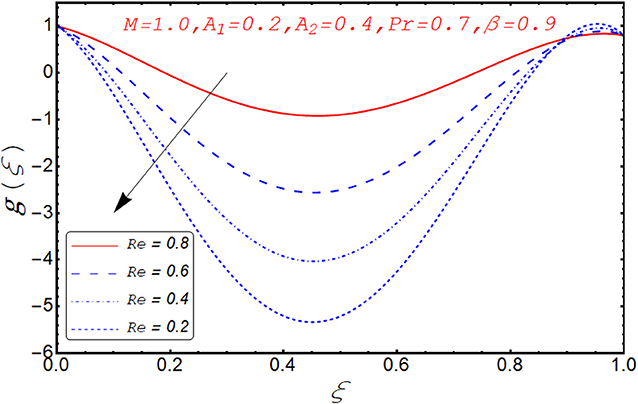
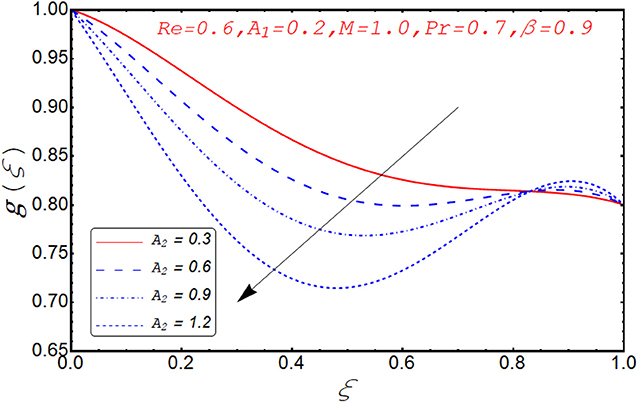
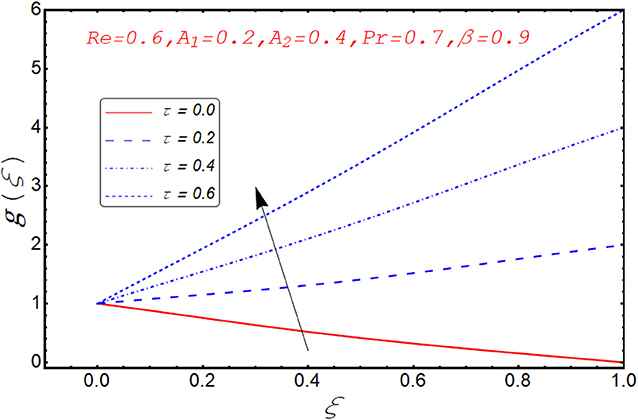
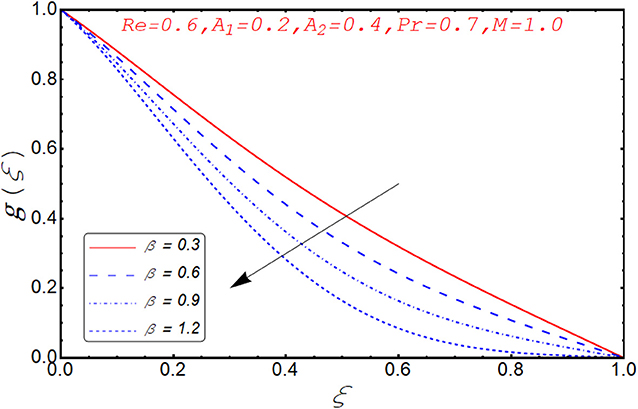
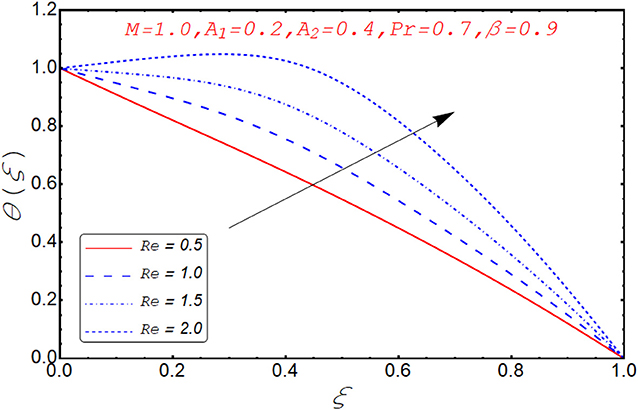
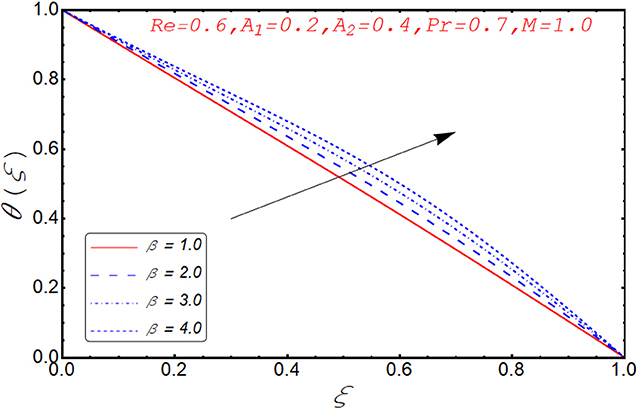
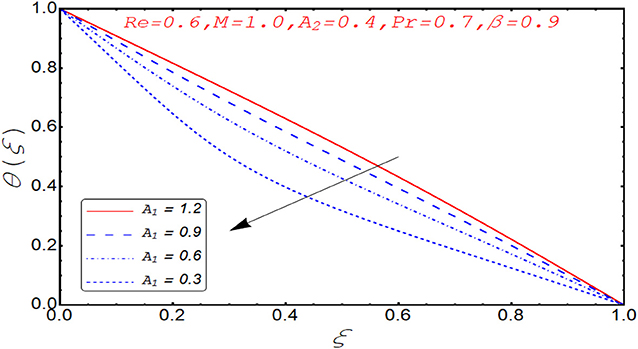
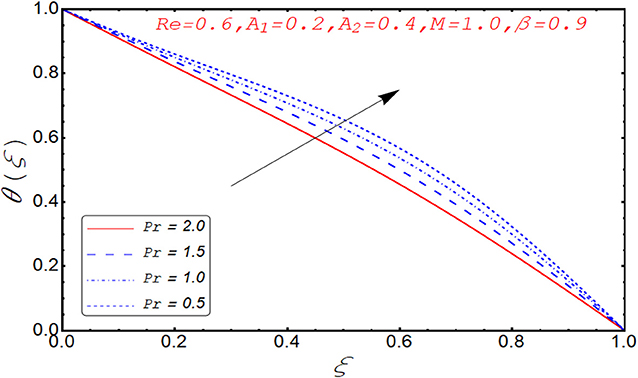
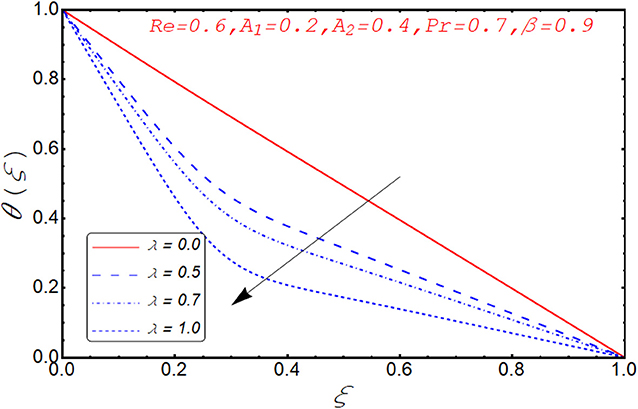
Current segment is dedicated to elucidate the numerical and graphical impact of velocity parameters involved and temperature profile and coefficient of skin friction. Variation in axial velocity against Reynolds number is adorned in Figure 3. It is found that axial velocity at lower disk decays with increment in Re. The reason behind this fact is that Re has direct relation with inertial forces. Therefore, with increase of Re, inertial effects dominate and cause the velocity of lower disk to decelerate. Figure 4 expresses the impact of Re on radial component of velocity. It is explored that with the increase of Re, velocity of lower disk diminishes and upper disk uplifts. It is seen from the picture that half of its portion from 0.0 to 0.6 represents velocity pattern of lower disk and from 0.6 to 1.0, it discloses radial velocity for upper plate. Impact of scaled stretching parameter on axial component of velocity at lower disk is exemplified in Figure 5. It is evidenced that with the increment of A₁, f(ξ) mounts at lower disk because stretching rate is decreasing continuously. Figure 6 is portrayed to manifest the variation in radial against A₁ velocity for lower and upper disks. It is found that radial component of velocity increases for the lower disk as compared to upper disk. This is due to the stretching rate of the lower disk that is continuously increasing and upper disk decrements. It is exhibited in Figure 7 that f′(ξ) decays with A₂ for lower disk and mounts in the case of upper disk. The justification behind this impact is that stretching rate of the upper disk is more than that of the lower disk. The behavior of axial velocity with stretching scaled parameter A₁of upper disk is depicted in Figure 8. For larger values of A₂, the axial velocity of fluid decrements near the upper disk and upsurging behavior is noticed at the lower disk. By increasing A₂, velocity magnitude along radial direction in the vicinity of the upper disk increases, so velocity along axial direction as an outcome depreciates. The impact of Re on tangential component of velocity g(ξ) is disclosed in Figure 9. It is fond that with increase of Re, g(ξ) suppresses. By increasing Re, inertial forces increase so more velocity is induced by the inertial forces. Behavior of tangential velocity g(ξ) against A₂ is stretched in Figure 10. It is found that g(ξ) decrements and f′(ξ) uplifts for A₂. With increase of A₂, stretching rate of the upper disk increases, and as an outcome, axial velocity increases and tangential velocity decreases. The variation in g(ξ) with rotational parameter is revealed in Figure 11. Positive attribute in g(ξ) is observed against τ. With the increase of rotational parameter τ, centrifugal force is induced, which as an outcome uplifts the tangential component of velocity. Curves investigating the aspects of β on tangential component of velocity are adorned in Figure 12. It is justified by the fact that momentum equation $\frac{1}{\beta }$ is a dimensionless parameter, so with the increase of β, momentum profile is tangential and its direction diminishes. Positive impact on thermal distribution against Re is observed in Figure 13. With increase of Re, viscous forces decrement and velocity of fluid particle increases. Thus, the temperature is defined as average motion of fluid molecules so thermal field molecules due to uplifts of movement of particles. The impact of θ(ξ) against β is anticipated and shown in Figure 14. Increase in thermal magnitude is observed if β is increased. Since increase in β raises the rotation of disks, by increasing the rotation of disk, more rotational motion in fluid is generated and as a consequence kinetic energy of fluid molecule increases. The increase in kinetic motion raises the temperature profile. Variation in thermal profile by varying A₁ in the range of (0.0 ≤ A₁ ≤ 1.5) is revealed in Figure 15. It is observed that temperature of fluid boosts against the values of A₁. As we increase the A₁, the stretching rate increases, the fluid particles between disks exceeds, and hence temperature boosts up. The impact of Prandtl number Pr on θ(ξ) is exhibited in Figure 16. It is found that thermal distribution decreases with Pr. This is due to the fact that Pr is the ratio of viscous diffusion to thermal diffusion. Thus, by increasing Pr, thermal diffusion decreases so temperature decreases. Figure 17 is adorned to study the impact of thermal relaxation parameter on thermal distribution. Declined attribute in temperature against thermal relaxation parameter λ is depicted. It is because of the fact that with the increase of λ, fluid particles will take more time to transfer heat to its neighboring particles, thus the temperature decreases.

FIGURE 3

Figure 3. Behavior of f(ξ) for different Re.

FIGURE 4

Figure 4. Behavior of f′(ξ) for different Re.

FIGURE 5

Figure 5. Behavior of f(ξ) for different A₁.

FIGURE 6

Figure 6. Behavior of f′(ξ) for different A1.

FIGURE 7

Figure 7. Behavior of f′(ξ) for different A₂.

FIGURE 8

Figure 8. Behavior of f(ξ) for different A₂.

FIGURE 9

Figure 9. Behavior of g(ξ) for different Re.

FIGURE 10

Figure 10. Behavior of g(ξ) for different A₂.

FIGURE 11

Figure 11. Behavior of g(ξ) for different τ.

FIGURE 12

Figure 12. Behavior of g(ξ) for different β.

FIGURE 13

Figure 13. Behavior of θ(ξ) for different Re.

FIGURE 14

Figure 14. Behavior of θ(ξ) for different β.

FIGURE 15

Figure 15. Behavior of θ(ξ) for different A₁.

FIGURE 16

Figure 16. Behavior of θ(ξ) for different Pr.

FIGURE 17

Figure 17. Behavior of θ(ξ) for different λ.

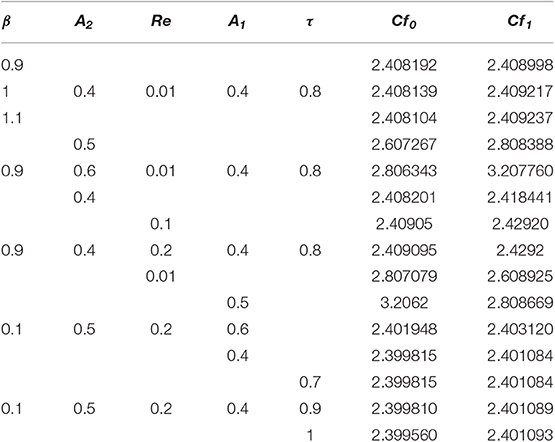
Table 1 numerically discloses the influence of porosity parameter β, stretching parameters A₁ and A₂, and Reynolds number Re. The skin friction coefficient increases for greater value of Re and stretching parameters A₁ and A₂, whereas it decreases for increasing values of porosity parameter β and rotating parameter τ at the upper and lower disks. Table 2 gives assurance of present work by constructing comparison with previously published literature for skin friction coefficient along radial and tangential components. Here, τ ≥ 0 shows the rotation of both disks in the same direction, τ ≤ 0 represents the direction of rotation of both disks in opposite direction, and τ = 0 means upper disk is fixed.

TABLE 1

Table 1. Influence of skin friction coefficient at wall of upper and lower disks.

TABLE 2

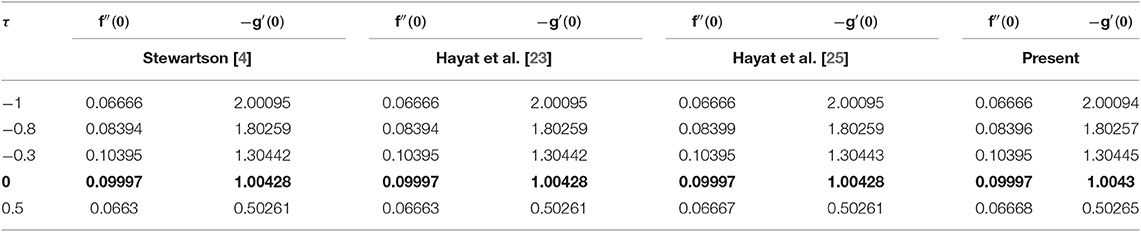
Table 2. Comparison of f″(0) and g′(0) with Stewartson [4], Hayat et al. [24], and Hayat et al. [25] when ϕ = A1 = A2 = 0 and Re = 1.

Conclusions

Current exertion is devoted to analyze the impact of Cattaneo-Christov heat flux theory on fluid flow between the two parallel rotating disks. Equations are modeled in the form of partial differential equations and then transformed into ordinary differential expressions. These ODE (ordinary differential equations) are tackled by Keller-box scheme. The key findings are summarized as follows:

• At the lower disk, the radial and axial velocity profile increases for maximum value of A1 while the same effects at upper disk for greater A₂.

• For rotational and stretching parameters, the tangential velocity profile increases at disk with variation of parameters.

• Thermal effects are reduced for both thermal relaxation and Prandtl number.

• The skin friction coefficient at both disks is less for greater value of rotational parameter.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at Majmaah University for funding this work under Project Number (RGP-2019-28).

References

1. Karman TV. Uber laminare and turbulente Reibung. Zeit Angew Math Mech. (1921) 1:233–52. doi: 10.1002/zamm.19210010401

CrossRef Full Text | Google Scholar

2. Cochran WG. The flow due to a rotating disk. Proc Cambridge Philos Soc. (1934) 30:365–75. doi: 10.1017/S0305004100012561

CrossRef Full Text | Google Scholar

3. Batchelor GK. Note on a class of solutions of the Navier-Stokes equations representing steady rotationally symmetric flow. The Quart J Mech App Maths. (1951) 4:29–41. doi: 10.1093/qjmam/4.1.29

CrossRef Full Text | Google Scholar

4. Stewartson K. On the flow between two rotating coaxial disks. Proc Combridge Philos Soc. (1951) 49:33–41.

Google Scholar

5. Chapple PJ, Stokes VK. On the Flow Between a Rotating and a Stationary Disk. Department Mechanics Enginerring, Princeton University, Report No. FLD (1952). p. 8.

Google Scholar

6. Mellor GL, Chapple PJ, Stokes VK. On the flow between a rotating and a stationary disk. J Fluid Mech. (1968) 31:95–112. doi: 10.1017/S0022112068000054

CrossRef Full Text | Google Scholar

7. Arora RC, Stokes VK. On the heat transfer between two rotating disks. Int J Heat Mass Transf. (1972) 15:2119–32. doi: 10.1016/0017-9310(72)90036-1

CrossRef Full Text | Google Scholar

8. Kumar SK, Tacher WI, Watson LT. Magnetohydrodynamic flow between a solid rotating disk and a porous stationary disk. Appl Math Model. (1989) 13:494–500. doi: 10.1016/0307-904X(89)90098-X

CrossRef Full Text | Google Scholar

9. Xun S, Zhao J, Zheng L, Chen X, Zhang X. Flow and heat transfer of Ostwald-de Waele fluid over a variable thickness rotating disk with index decreasing. Int J Heat Mass Transf . (2016) 103:1214–24. doi: 10.1016/j.ijheatmasstransfer.2016.08.066

CrossRef Full Text | Google Scholar

10. Das S, Maji SL, Guria M, Jana RN. Hall effects on unsteady MHD flow between two disks with non-coincident parallel axes of rotation. Int J Appl Mech Eng. (2010) 15:5–18. doi: 10.1007/s40010-012-0049-1

CrossRef Full Text | Google Scholar

11. Asgher S, Jalil M, Hussan M, Turkyimazoglu M. Lie group analysis of flow and heat transfer over a stretching rotating disk. Int J Heat Mass Transf. (2014) 69:140–6. doi: 10.1016/j.ijheatmasstransfer.2013.09.061

CrossRef Full Text | Google Scholar

12. Elmaboud YA, Abdelsalam SI, Mekheimer KS. Couple stress fluid flow in a rotating channel with peristalsis. J Hydrdynamics. (2018) 13:307–16. doi: 10.1007/s42241-018-0037-2

CrossRef Full Text | Google Scholar

13. Fourier JBJ. Theorie Analytique De La Chaleur. Paris: Chez Firmin Didot (1822).

Google Scholar

14. Cattaneo C. Sulla conduzionedelcalore. In: Atti del Seminario Maermatico e Fisico dell Universita di Modena e Reggio Emilia, Vol III. (1948). p. 83–101.

Google Scholar

15. Christov CI. On frame indifferent formulation of the Maxwell–Cattaneo model of finite-speed heat conduction. Mech Res Commun. (2009) 36:481–6. doi: 10.1016/j.mechrescom.2008.11.003

CrossRef Full Text | Google Scholar

16. Straughan B. Thermal convection with the Cattaneo–Christov model. Int J Heat Mass Transf. (2010) 53:95–8. doi: 10.1016/j.ijheatmasstransfer.2009.10.001

CrossRef Full Text | Google Scholar

17. Ciarletta M, Straughan B. Uniqueness and structural stability for the Cattaneo–Christov equations. Mech Res Commun. (2010) 37:445–7. doi: 10.1016/j.mechrescom.2010.06.002

CrossRef Full Text | Google Scholar

18. Tibullo V, Zampoli V. A uniqueness result for the Cattaneo–Christov heat conduction model applied to incompressible fluids. Mech Res Commun. (2011) 38:77–99. doi: 10.1016/j.mechrescom.2010.10.008

CrossRef Full Text | Google Scholar

19. Aqsa, Malik M, Imtiaz A, Awais M. Rheology of Burgers' model with Cattaneo-Christov heat flux in the presence of heat source/sink and magnetic field. Scientia Iranica. (2019) 26:323–30. doi: 10.24200/sci.2018.20165

CrossRef Full Text | Google Scholar

20. Haddad SAM. Thermal instability in Brinkman porous media with Cattaneo–Christov heat flux. Int J Heat Mass Transf. (2014) 68:659–68. doi: 10.1016/j.ijheatmasstransfer.2013.09.039

CrossRef Full Text | Google Scholar

21. Mekheimer KS, Elmaboud YA. Simultaneous effects of variable viscosity and thermal conductivity on peristaltic flow in a vertical asymmetric channel. Cand J Physc. (2014) 92:1541–55. doi: 10.1139/cjp-2013-0465

CrossRef Full Text | Google Scholar

22. Mekheimer KS. Thermal properties of couple-stress fluid flow in an asymmetric channel with peristalsis. J Heat Transf. (2013) 135:044502–1. doi: 10.1115/1.4023127

CrossRef Full Text | Google Scholar

23. Hayat T, Qayyum S, Imtiaz M, Alsaedi A. Impact of Cattaneo-Christov heat flux in Jeffrey fluid flow with homogeneous-heterogeneous reactions. PLoS ONE. (2017) 6:11201. doi: 10.1063/1.4942091

CrossRef Full Text | Google Scholar

24. Hayat T, Khan MI, Farooq M, Alsaedi A, Waqas M, Yasmeen T. Impact of Cattaneo-Christov heat flux model in flow of variable thermal conductivity fluid over a variable thicked surface. Int J Heat Mass Transf. (2016) 66:702–10. doi: 10.1016/j.ijheatmasstransfer.2016.04.016

CrossRef Full Text | Google Scholar

25. Hayat T, Qayyum S, Imtiaz M, Alsaedi A. Flow between two stretchable rotating disks with Cattaneo-Christov heat flux model. Results Phys. (2017) 126–33. doi: 10.1016/j.rinp.2016.12.007

CrossRef Full Text | Google Scholar

26. Mustafa M. Cattaneo-Christov heat flux model for rotating flow and heat transfer of upper-convected Maxwell fluid. AIP Adv. (2015) 5:047109. doi: 10.1063/1.4917306

CrossRef Full Text | Google Scholar

27. Darcy H. Les Fontaines Publiques de la Volle de Dijon. Paris: Vector Dalmont (1856).

Google Scholar

28. Khaled ARA, Vafai K. The role of porous media in modeling flow and heat transfer in biological tissues. Int J Heat Mass Transf. (2003) 46:4989–5003. doi: 10.1016/S0017-9310(03)00301-6

CrossRef Full Text | Google Scholar

29. Chen D, Mioshi H, Akai T, Yazawa Y. Colorless transparent fluorescence material: sintered porous glass containing rare-earth and transition-metal ions. Appl Phys Lett. (2005) 86:231–8. doi: 10.1063/1.1946897

CrossRef Full Text | Google Scholar

30. Muhammad T, Alsaedi A, Shahzad SA, Hayat T. A revised model for Darcy-Forchheimer flow of Maxwell nanofluid subject to convective boundary condition. Chin J Phys. (2017) 55:963–76. doi: 10.1016/j.cjph.2017.03.006

CrossRef Full Text | Google Scholar

31. Seddeek MA. Influence of viscous dissipation and thermophoresis on Darcy-Forchheimer mixed convection in a fluid saturated porous media. J Colloids Interface Sci. (2006) 293:137–42. doi: 10.1016/j.jcis.2005.06.039

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Jha BK, Kaurangini ML. Approximate analytical solutions for the non-linear Brinkman-Forchheimer-extended Darcy flow model. Appl Math. (2011) 21:1432–6. doi: 10.4236/am.2011.212202

CrossRef Full Text | Google Scholar

33. Aziz T, Mabood FM, Shahzad A. Travelling wave solutions for the unsteady flow of a third grade fluid induced due to impulsive motion of flat porous plate embedded in a porous medium. J Mech. (2017) 30:527–35. doi: 10.1017/jmech.2014.17

CrossRef Full Text | Google Scholar

34. Andersson HI. An exact solution of the Navier-Stokes equations for MHD flow. Acta Mech. (1995) 113:241–4. doi: 10.1007/BF01212646

CrossRef Full Text | Google Scholar

35. Liu IC. A note on heat and mass transfer for hydromagnetic flow over a stretching sheet. Int Comm Heat Mass Transf. (2005) 32:1075–84. doi: 10.1016/j.icheatmasstransfer.2005.02.003

CrossRef Full Text | Google Scholar

36. Kumaran V, Banerjee AK, Kumar AV, Vajravelu K. MHD flow past a stretching permeable sheet. Appl Math Comp. (2009) 210:26–32. doi: 10.1016/j.amc.2008.10.025

CrossRef Full Text | Google Scholar

37. Yirga Y, Tesfay D. Magnetohydrodynamic flow of viscous fluid over a non-linearly stretching sheet. Open Access Library J. (2014) 1:1–11. doi: 10.4236/oalib.1101030

CrossRef Full Text | Google Scholar

38. Yasin MHM, Ishak A, Pop I. MHD heat and mass transfer flow over a permeable stretching/shrinking sheet with radiation effect. J Magnet Mag Mater. (2016) 407:235–40. doi: 10.1016/j.jmmm.2016.01.087

CrossRef Full Text | Google Scholar

39. Mabood F, Khan WA, Ismail AIM. MHD flow over exponential radiating stretching sheet using homotopy analysis method. J King Saud Univ. (2017) 29:68–74. doi: 10.1016/j.jksues.2014.06.001

CrossRef Full Text | Google Scholar

40. Khalid A, Khan I, Khan A, Shafie S. Unsteady MHD free convection flow of Casson fluid past over an oscillating vertical plate embedded in a porous medium. Eng Sci Tech Int J. (2015) 18:307–19. doi: 10.1016/j.jestch.2014.12.006

CrossRef Full Text | Google Scholar

41. Abro KA, Khan I, Nisar KS. Novel technique of Atangana and Baleanu for heat dissipation in transmission line of electrical circuit. Chaos Solit Fractals. (2017) 129:40–5. doi: 10.1016/j.chaos.2019.08.001

CrossRef Full Text | Google Scholar

42. Saqib M, Ali F, Khan I, Sheikh NA, Aftab S, Jan SAA, et al. Exact solutions for free convection flow of generalized Jeffrey fluid: a Caputo-Fabrizio fractional model. Alex Eng J. (2017) 57:1849–58. doi: 10.1016/j.aej.2017.03.017

CrossRef Full Text | Google Scholar

43. Saqib M, Khan I, Shafie S. Natural convection channel flow of CMC-based CNTs nanofluid. Europ Phys J Plus. (2018) 133:549. doi: 10.1140/epjp/i2018-12340-3

CrossRef Full Text | Google Scholar

44. Keller HB, Cebeci T. Accurate numerical methods for boundary layer flows. II: two-dimensional turbulent flows. AIAA J. (1972) 10:1193–9. doi: 10.2514/3.50349

CrossRef Full Text | Google Scholar

45. Na TY. Computational Methods in Engineering Boundary Value Problem. Academic Press (1979).

Google Scholar

46. Cebeci T, Bradshaw P. Physical and Computational Aspects of Convective Heat Transfer. Springer (1984). doi: 10.1007/978-3-662-02411-9

CrossRef Full Text | Google Scholar

Nomenclature