Marangoni Driven Boundary Layer Flow of Carbon Nanotubes Toward a Riga Plate

1. Introduction

Marangoni boundary layer flow phenomena are characterized by gradients in surface tension due to variations in surfactant concentration, concentration of solute, and variations in temperature along the interface. In light of the enhanced significance of surface forces and greater interface extensions, Marangoni boundary layer flows become pertinent in microgravity and in earth gravity. On the other hand, for a duly defined sufficient large Reynolds number, Marangoni boundary layers are edge dissipative flows and form thin dissipative films near unrestricted surfaces [1]. These types of flows have widespread application in diverse fields of engineering and practical projects such as for stabilizing soap films, drying silicon wafers after wrap processing steps, growing crystals, spreading thin films, nucleating vapor bubbles, processing semiconductors, and welding and for use in packed distillation columns, falling film spectator, artificial rain, and materials science. In view of their importance, many researchers have studied and reported results for these types of flows. The first contribution to this research area was by Napolitano [2] during his survey of steady dissipative layers. Lin and Zheng [3] theoretically investigated the problem of Marangoni boundary layer flow and heat transfer of copper-water nanofluid over a porous medium disk. They concluded that the Marangoni parameter has a destabilizing effect on all the other parameters such as temperature, shear stress, velocity, and boundary layer velocity. Moreover, to achieve an analytical solution of the said model, they employed the Homotopy Analysis Method (HAM). Recently, Tiwari et al. [4] presented a mathematical model for electrically conducting Marangoni MHD flow saturated with carbon nanotubes (CNTs) as the nanoparticles in a base fluid over a porous medium. An analytical method was adopted to achieve a solution for this project. A similarity solution of Marangoni convection boundary layer flow, taking into account the impacts of gravitational and external pressure, has been studied by Zhang and Zheng [5]. They showed that flow and heat transfer phenomena were substantially affected by the Marangoni convection parameter and the Prandtl number. A numerical method was adopted by Mehdi et al. to investigate the influence of different nanoparticles on Marangoni convection boundary layer flow [6]. The study showed that some nanoparticles with low thermal conductivity have a greater amplification effect on heat transfer phenomena than other recommended particles. Sheikholeslami and Ganji [7] considered Marangoni boundary layer flow to investigate the effect of the magnetic field on various nanofluids. The results illustrated that a Lorentz force increase causes the velocity of nanofluid to decrease. Remeli et al. [8] investigated suction and injection in a nanofluid via Marangoni-driven boundary layer flow. The effect of the injection parameter is to decrease the velocity profile, while the suction parameter increases the velocity profile and delays the separation of the boundary layer. The effects of particle shape on Marangoni convection boundary layer flow of a nanofluid were addressed by Ellahi et al. [9]. They considered different types of nanoparticles, such as needle-shaped, disc-shaped, and sphere-shaped. They discussed the said flow model in the context of nanoparticles and found that with an increase in the volume fraction and size of the particles, the surface temperature gradient fluctuated correspondingly. The maximum heat transfer rate at the surface was found in the case of sphere-shaped particles. Further, numerous studies on Marangoni boundary layer flow of several types can be found in the literature [10–12].

The characteristic of nanofluid of tremendously intensifying heat transfer and thermal convection has led to its broad application in innumerable fields, such as in biomedical devices and in highly advanced technical contexts such as the cooling of microchips, nanodrug delivery, nuclear reactions and radiators, etc. To reconcile the issues associated with high-temperature mixtures and to improve thermal conductivity in practice, nanoparticles are soaked into a base fluid. Many contributions have been made to the literature on nanoparticles that disseminate in the base fluid to attain excellent thermal properties [13–15]. According to Tiwari et al. [16], the adding of nanoparticles within a base fluid alone is not enough. CNTs had a six-times improved thermal conductivity compared to other nanomaterials [17]. Through the enhancement of various models of CNTs, these tubes have a wide span of properties such as thermal and electronic [18]. Similarly, solid nanoparticles have higher conductivity than do liquids. Therefore, CNTs are a topic of interest for advanced technology due to their electrical and isolated structure. In recent years, different applications of CNTs [19–21] have been investigated to develop ideal materials ranging from ultra-strong fibers to field emission. These tubes have extensive uses and applications in various fields such as providing increased energy density for capacitors, modeling the structures of catalysts, detecting proteins that indicate the existence of oral cancer, for gas storage, for water purification devices, for detecting bacteria in drinking water, for minimizing the weight of coaxial cable in aerospace applications, for improving battery lifetime, as an extra powerful fiber, etc. In this regard, Hayat et al. [22] utilized carbon nanotubes in water flow under homogenous-heterogeneous reactions and with melting heat transfer effects. Two different types of CNTs, i.e., SWCNT and MWCNT, were incorporated in water for the flow model. It was found that, in comparison with other nanofluids, the minimum thermal resistance and maximum heat transfer was achieved when MWCNT was disseminated in the base fluid. Moreover, the surface thickness of carbon nanotubes with heat transfers in stagnation point flow was examined by Hayat et al. [23].

From the last few decades, many researchers have turned their attention toward the study of flow fields with different configurations. One of the new geometries devised by Gailitis and Lielausis [24] for weakly conducting fluids is the so-called Riga plate. The novelty of this plate is that it incorporates and imposes magnetic and electric fields, which properly instigates Lorentz forces parallel to the wall to constrain the flow of weakly conducting fluid. Avoiding boundary layer separation, it may be utilized as an efficient agent for submarine pressure drag, skin friction, and radiation. The related theory has important features and is employed in many areas such as engineering, geophysics, astrophysics, industrial procedures, and MHD generators. Pantokratoras et al. [25] addressed boundary layer flow based on a weakly conducting fluid passing through a Riga plate. Their analysis demonstrated that by keeping quality, suitable size of nanoparticles, and adjusting the magnitude of flow, aiding and opposing Lorentz force due to the Riga plate in order to control the skin friction. Magyari and Pantokratoras [26] carried out an investigation to extend the idea of opposing and aiding mixed convection flows through a Riga plate. Further, Pantokratoras [27] addressed Blasius and Sakiadis type flows over a Riga plate. Hayat et al. [28] explored the flow of nanofluid through a convectively heated Riga plate with variable thickness. The results demonstrated that for larger values of the modified Hartman number, the velocity distribution exhibited decreasing behavior. Shafiq et al. [29] analyzed the impact of radiation in stagnation point flow of Walters' B fluid through a Riga plate. Their observations indicated that due to enhancement of the strength of Newtonian heating, the temperature and surface heat transfer significantly increased. Theoretical and numerical discussion by Bhatti et al. has shown the effects of thermal radiation with EMD through a Riga plate [30]. Further, a Cattaneo-Christov model for third-grade nanofluid flow toward a Riga plate has been developed by Naseem et al. [31] by using a semi-analytical method, i.e., the optimal homotopy analysis method (OHAM). The proposed theory was adopted together with the newly esteemed zero nanoparticles mass flux condition to investigate mass and thermal diffusions. Thermal radiation and heat transfer phenomena play a central role in advanced technological systems through boundary layer flow. The important applications of this flow in the aforementioned fields can be seen in the literature [32–34]. Henceforth, in various flow fields, the importance of thermal radiation cannot be overlooked. Non-linear radiation and Joule heating in Marangoni mixed convection flow were demonstrated by Hayat et al. [35]. The impact of exponential temperature on radiation effects and particle shape was examined by Lin et al. by utilizing heat transfer of copper water-based nanofluid and Marangoni boundary layer flow [36]. Hayat et al. [37] reported the effect of Joule heating and thermal radiation in the flow of third-grade fluid over a radiative surface. They studied whether the presence of an electric field and the radiation parameter caused the temperature and velocity to increase. A revised model of second-grade nanofluid magnetohydrodynamic Falkner Skan flow was examined by Hayat et al. [38]. A few other interesting investigations are given in Ellahi et al. [39–44], Bhatti et al. [30, 45, 46], Ellahi and Riaz [47], and Waqas et al. [48].

The main intention of the present study is to interpret radiative Marangoni-driven boundary layer flow utilizing different types of CNTs (SWCNTs and MWCNTs) over a Riga plate. To the best of our knowledge, such a study does not yet exist in the literature. Suitable transformations are utilized to establish a non-linear system of equations. The homotopy analysis method (HAM) is utilized for convergent series solutions. The impacts of several influential parameters on the physical quantities of interest are analyzed through tables and graphs. The upcoming sections illustrate the mathematical model and explore the effects of the different physical parameters on the velocity and temperature profiles, respectively.

2. Mathematical Scheme of the Problem

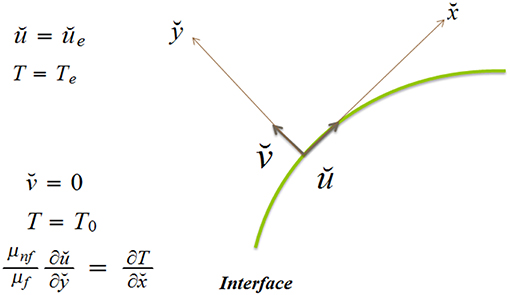
We consider Marangoni boundary layer flow of carbon-nanoliquids (SWCNTs and MWCNTs) toward a Riga surface along with radiation phenomenon. The Riga plate comprises a spanwise connected array of permanent magnets and irregular electrodes attached to a horizontal surface. Lorentz forces generated by the Riga plate and directed along the free stream are responsible for optimally controlling the proposed flow field. The base fluid, water, is packed with SWCNTs and MWCNTs. Further, the governing equations for the flow form may be expressed as (1–5):

$\begin{array}{ll}\frac{\partial \stackrel{⌣}{u}}{\partial \stackrel{⌣}{x}}+\frac{\partial \stackrel{⌣}{v}}{\partial \stackrel{⌣}{y}}=0,& (1)\end{array}$

$\begin{array}{l}\stackrel{⌣}{u}\frac{\partial \stackrel{⌣}{u}}{\partial \stackrel{⌣}{x}}+\stackrel{⌣}{v}\frac{\partial \stackrel{⌣}{u}}{\partial \stackrel{⌣}{y}}={\stackrel{⌣}{u}}_e\frac{d{\stackrel{⌣}{u}}_e}{d\stackrel{⌣}{x}}+\frac{{\mu }_{nf}}{{\rho }_{nf}}\frac{{\partial }^2\stackrel{⌣}{u}}{\partial {\stackrel{⌣}{y}}^2}+\frac{\pi M_0{J}_{0}Exp[-\frac{\pi }{b}\stackrel{⌣}{y}]}{8{\rho }_{nf}}\\ -g\stackrel{⌣}{\beta }(T-T_w),& (2)\end{array}$

$\begin{array}{l}\stackrel{⌣}{u}\frac{\partial T}{\partial \stackrel{⌣}{x}}+\stackrel{⌣}{v}\frac{\partial T}{\partial \stackrel{⌣}{y}}={\alpha }_{nf}\frac{{\partial }^{2}T}{\partial {\stackrel{⌣}{y}}^2}-\frac{1}{{(\rho c_p)}_{nf}}\frac{\partial q_r}{\partial \stackrel{⌣}{y}}\\ +\frac{\mu }{{(\rho c_p)}_{nf}}{\left(\frac{\partial \stackrel{⌣}{u}}{\partial \stackrel{⌣}{y}}\right)}^2,& (3)\end{array}$

and the boundary conditions are set as

$\begin{array}{l}\stackrel{⌣}{v}=0,T=T_0,\frac{{\mu }_{nf}}{{\mu }_f}\frac{\partial \stackrel{⌣}{u}}{\partial \stackrel{⌣}{y}}=\frac{\partial T}{\partial \stackrel{⌣}{x}}\text{ at }\stackrel{⌣}{y}=0,\\ \stackrel{⌣}{u}={\stackrel{⌣}{u}}_e,T=T_e\text{ at }\stackrel{⌣}{y}\to \infty .& (4)\end{array}$

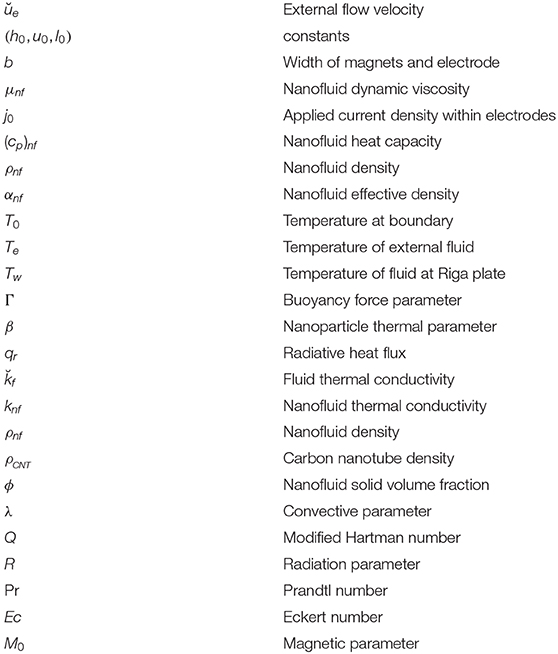
The velocity components in the $\stackrel{⌣}{x}$ and $\stackrel{⌣}{y}$ directions mentioned in the expressions are ŭ and $\stackrel{⌣}{v}$ , the fluid density is denoted by ρ, the velocity of external flow is ŭ_e(x), ρ_nf indicates the nanofluid density, μ_nf is the nanofluid dynamic viscosity, j₀ stands for the applied current density within the electrodes, M₀ is the magnetization of the permanent magnets, b indicates the width of the magnets and electrode, the constant temperature of the Riga plate is denoted by T_w where T_w > 0, K is the thermal conductivity, c_p represents the specific heat, μ is the dynamic viscosity, and T is the nanofluid temperature. The boundary temperature distribution is T₀(x), and (ρ_cp)nf is the nanofluid heat capacity. The nanofluid effective density is α_nf. The radiative heat flux q_r is defined as

$\begin{array}{ll}{q}_r=-\frac{4{\sigma }^{\ast }}{3k_1}\frac{\partial T^4}{\partial \breve{y}},& (5)\end{array}$

where σ^* is the Stefan-Boltzmann constant and k₁ is the mean absorption coefficient. Through Taylor's series, we have $T^4\cong 4T_e^{3}T-3T_e^4$, where T_e is the ambient temperature, and then energy equation now reduces to the following expression:

$\begin{array}{ll}{(\rho c_p)}_{nf}\left(\stackrel{⌣}{u}\frac{\partial T}{\partial \stackrel{⌣}{x}}+\stackrel{⌣}{v}\frac{\partial T}{\partial \stackrel{⌣}{y}}\right)=\left(\frac{16{\sigma }^{\ast }{T}_{\infty }^3}{3k_1}+K\right)\frac{{\partial }^{2}T}{\partial {\stackrel{⌣}{y}}^2}+\mu {\left(\frac{\partial \stackrel{⌣}{u}}{\partial \stackrel{⌣}{y}}\right)}^2.& (6)\end{array}$

Moreover, the mathematical properties of CNTs are demonstrated by the following Equation (19–22)

$\begin{array}{l}{\alpha }_{nf}=\frac{k_{nf}}{{(\rho c_p)}_{nf}},{\mu }_{nf}=\frac{{\mu }_f}{{(1-\varphi )}^{2.5}},{\stackrel{⌣}{v}}_{nf}=\frac{{\mu }_{nf}}{{\rho }_{nf}},\\ \frac{k_{nf}}{k_f}=\frac{2\varphi \frac{{\stackrel{⌣}{k}}_{CNT}}{k_{CNT}-k_f}\ln \frac{{\stackrel{⌣}{k}}_{CNT}+{\stackrel{⌣}{k}}_f}{2{\stackrel{⌣}{k}}_f}+(1-\varphi )}{2\varphi \frac{{\stackrel{⌣}{k}}_f}{k_{CNT}-k_f}\ln \frac{{\stackrel{⌣}{k}}_{CNT}+{\stackrel{⌣}{k}}_f}{2{\stackrel{⌣}{k}}_f}+(1-\varphi )},\\ {\rho }_{nf}={\rho }_f(1-\varphi )+{\rho }_s{(c_p)}_{CNT}\varphi ,& (7)\end{array}$

where ${\stackrel{⌣}{k}}_f$ is the fluid thermal conductivity, k_nf is the nanofluid thermal conductivity, the nanofluid solid volume fraction is ϕ, and μ_f is the fluid dynamic viscosity. $\frac{{\hat{\mu }}_{nf}}{{\hat{\mu }}_f}\frac{\partial u}{\partial y}{|}_{y=0}=\frac{\partial T}{\partial x}{|}_{y=0}$ denotes Marangoni condition at the interface. The linear relation of surface tension σ is given as:

$\begin{array}{ll}\sigma ={\sigma }_0\left[1-{\gamma }_1\left(T-T_e\right)\right],& (8)\end{array}$

where ${\gamma }_1=-\frac{1}{{\sigma }_0}\frac{\partial \sigma }{\partial T}>0$ represents the surface tension temperature coefficient, and σ₀ represents surface tension. The directions of the driving forces depend on the orientation of the temperature gradients in nanoliquids ∇T.

The similarity transformation is introduced:

$\begin{array}{l}u\left(x,y\right)=u_0{x}^{\left(2r-1\right)/3}{f}^{\prime }\left(\eta \right) ,\\ v\left(x,y\right)=\frac{1}{3}{u}_0{l}_0{x}^{\left(r-2\right)/3}\left[\left(2-r\right)\eta f^{\prime }\left(\eta \right)-\left(1+r\right)f\left(\eta \right)\right] ,\\ T\left(x,y\right)=T_e-h_0{x}^r\theta \left(\eta \right) ,\eta =x^{\left(r-2\right)/3}\frac{y}{l_0},& (9)\end{array}$

where h₀, u₀, and l₀ represent constants. The values of u₀ and l₀ take the following form when h₀ = 1:

$\begin{array}{ll}{u}_0={\left(\frac{3}{1+r}\right)}^{1/3}{r}^{2/3},l_0={\left(\frac{3}{1+r}\right)}^{1/3}{r}^{-1/3},& (10)\end{array}$

after the above-mentioned transformations, Equations (1)–(6) take the following form:

$\begin{array}{l}\frac{1}{{(1-\varphi )}^{2.5}(1-\varphi +\frac{{\rho }_{CNT}}{{\rho }_f}\varphi )}{f}^{\prime \prime \prime }+f{f}^{\prime \prime }-(\frac{2r-1}{1+r})[{(f^{\prime })}^2-1]\\ +\frac{3}{1+r}\lambda \theta (\eta )+\frac{3}{1+r}Q Exp[-c\eta ]=0,& (11)\end{array}$

$\begin{array}{l}\left(1+\frac{4}{3}R\right)\frac{\frac{k_{nf}}{k_f}}{[(1-\varphi )+\frac{{(\rho c_p)}_{CNT}}{{(\rho c_p)}_f}\varphi ]} {\theta }^{″}\\ -\frac{3}{1+r}\mathrm{Pr} \left[r{f}^{\prime }\theta -\frac{1+r}{3}f {\theta }^{\prime }\right]-\mathrm{Pr} Ec {(f″)}^2=0,& (12)\end{array}$

in which

$\begin{array}{ll}Q=\frac{\pi M_0{J}_0\stackrel{⌣}{x}}{8{\rho }_{nf}{\stackrel{⌣}{u}}_e^2},R=\frac{\text{4}{\sigma }^{\text{3}}{T}_{\infty }^{\text{3}}}{3k_{\mathrm{nf}}{k}^{\ast }},\mathrm{Pr}=\frac{c_p\mu }{k},Ec=\frac{{\stackrel{⌣}{u}}_e^{\text{2}}{\stackrel{⌣}{x}}^{\frac{\text{1}}{\text{3}}(r-\text{2})}}{\rho c_p^{\text{2}}{h}_{\text{0}}},& (13)\end{array}$

where Q denotes the modified Hartmann number, R represents the radiation parameter, Pr indicates the Prandtl number, and Ec symbolizes the Eckert number.

3. Solution Methodology

To find the series solution of the underlying problem, the Homotopy Analysis Method is adopted. Therefore, the auxiliary linear operators (${{I}}_f,{{I}}_{\theta }$) and the initial guess $(\left({\stackrel{⌣}{f}}_0,{\stackrel{⌣}{\theta }}_0\right))$ may be defined as:

$\begin{array}{ll}{\stackrel{⌣}{f}}_0(\eta )=\eta +{(1-\varphi )}^{2.5}(1-e^{-\eta }),{\stackrel{⌣}{\theta }}_0(\eta )=e^{-\eta },& (14)\end{array}$

$\begin{array}{ll}{{I}}_{\theta }(\stackrel{⌣}{\theta })=\frac{d^2\stackrel{⌣}{\theta }}{d{\eta }^2}-\stackrel{⌣}{\theta },{{I}}_f(\stackrel{⌣}{f})=\frac{d^3\stackrel{⌣}{f}}{d{\eta }^3}-\frac{d\stackrel{⌣}{f}}{d\eta },& (15)\end{array}$

$\begin{array}{l}{{I}}_f[K_1+K_{2}Exp(\eta )+K_{3}Exp(-\eta )]=0,\\ {{I}}_{\theta }[K_{4}Exp(\eta )+K_{5}Exp(-\eta )]=0,& (16)\end{array}$

where K_h (h = 1−5) are arbitrary constants.

The zeroth-order problem design is

$\begin{array}{ll}(1-\stackrel{⌣}{p}){{I}}_f[\stackrel{⌣}{f}(\eta ,\stackrel{⌣}{p})-{\stackrel{⌣}{f}}_0(\eta )]=\stackrel{⌣}{p}{\hslash }_f{ℳ}_f\left[\stackrel{⌣}{f}(\eta ,\stackrel{⌣}{p})\right],& (17)\end{array}$

$\begin{array}{l}{\frac{\partial \stackrel{⌣}{f}(\eta ;\stackrel{⌣}{p})}{\partial \eta }|}_{\eta =0}=0,{\frac{1}{{(1-\varphi )}^{2.5}}\frac{{\partial }^2\stackrel{⌣}{f}(\eta ;\stackrel{⌣}{p})}{\partial {\eta }^2}|}_{\eta =0}=-1,\\ {\frac{\partial \stackrel{⌣}{f}(\eta ;\stackrel{⌣}{p})}{\partial \eta }|}_{\eta \to \infty }=1,& (18)\end{array}$

$\begin{array}{ll}(1-\stackrel{⌣}{p}){{I}}_{\theta }[\stackrel{⌣}{\theta }(\eta ,\stackrel{⌣}{p})-{\stackrel{⌣}{\theta }}_0(\eta )]=\stackrel{⌣}{p}{\hslash }_{\theta }{ℳ}_{\theta }\left[\stackrel{⌣}{\theta }(\eta ,\stackrel{⌣}{p}),\stackrel{⌣}{f}(\eta ,\stackrel{⌣}{p})\right],& (19)\end{array}$

$\begin{array}{llll}\stackrel{⌣}{\theta }(\eta ;\stackrel{⌣}{p}){|}_{\eta =0}& =& 1,\stackrel{⌣}{\theta }(\eta ;\stackrel{⌣}{p}){|}_{\eta \to \infty }=0,& (20)\end{array}$

The non-linear operators are

$\begin{array}{l}{ℳ}_f\left[\stackrel{⌣}{f}(\eta ;\stackrel{⌣}{p})\right]=\frac{1}{{(1-\varphi )}^{2.5}[1-\varphi +\frac{{(\tilde{\rho }{c}_p)}_{CNT}}{{(\tilde{\rho }{c}_p)}_f}\varphi ]}\frac{{\partial }^3\stackrel{⌣}{f}(\eta ,\stackrel{⌣}{p})}{\partial {\eta }^3}\\ +\stackrel{⌣}{f}(\eta ,\stackrel{⌣}{p})\frac{{\partial }^2\stackrel{⌣}{f}(\eta ,\stackrel{⌣}{p})}{\partial {\eta }^2}-\frac{2r-1}{1+r}{\left(\frac{\partial \stackrel{⌣}{f}(\eta ,\stackrel{⌣}{p})}{\partial \eta }\right)}^2\\ +\frac{2r-1}{1+r}+\frac{3}{1+r}\lambda \theta (\eta )+\frac{3}{1+r}QExp[-c\eta ],\\ & (21)\end{array}$

$\begin{array}{l}{ℳ}_{\theta }\left[\stackrel{⌣}{f}\right(\eta ;\stackrel{⌣}{p}),\stackrel{⌣}{\theta }(\eta ;\stackrel{⌣}{p})]\\ =\left(1+\frac{4}{3}{R}_d\right)\frac{\frac{k_{nf}}{k_f}}{[1-\varphi +\frac{{(\tilde{\rho }{c}_p)}_{CNT} }{{(\tilde{\rho }{c}_p)}_f}\varphi ]}\frac{{\partial }^2\stackrel{⌣}{\theta }(\eta ,\stackrel{⌣}{p})}{\partial {\eta }^2}\\ -\frac{3}{1+r}\text{Pr}\left[r\frac{\partial \stackrel{⌣}{f}(\eta ,\stackrel{⌣}{p})}{\partial \eta }\stackrel{⌣}{\theta }(\eta ,\stackrel{⌣}{p})\right]\\ -\frac{3}{1+r}\text{Pr}\left[-\frac{1+r}{3}\stackrel{⌣}{f}(\eta ,\stackrel{⌣}{p})\frac{\partial \tilde{\theta }(\eta ,\stackrel{⌣}{p})}{\partial \eta }\right]\\ -\text{Pr} Ec {\left(\frac{{\partial }^2\stackrel{⌣}{f}(\eta ,\stackrel{⌣}{p})}{\partial {\eta }^2}\right)}^2,& (22)\end{array}$

where, $0\le \stackrel{⌣}{p}\le 1$and ℏ_f and ℏ_θ designate zero free auxiliary parameters.

The mth-order deformation problem is

$\begin{array}{ll}{{I}}_f\left[{\stackrel{⌣}{f}}_m(\eta )-{\stackrel{⌣}{\chi }}_m\stackrel{⌣}{f}(\eta )\right]={\hslash }_f{{P}}_m^{\stackrel{⌣}{f}}(\eta ),& (23)\end{array}$

$\begin{array}{l}\frac{{\partial }^2{\stackrel{⌣}{f}}_m(\eta ,\stackrel{⌣}{p})}{\partial {\eta }^2}{|}_{\eta =0}=0,\frac{\partial {\stackrel{⌣}{f}}_m(\eta ,\stackrel{⌣}{p})}{\partial \eta }{|}_{\eta \to \infty }=0,\\ {\stackrel{⌣}{f}}_m(\eta ;\stackrel{⌣}{p}){|}_{\eta =0}=0,& (24)\end{array}$

$\begin{array}{ll}{{I}}_{\theta }\left[{\stackrel{⌣}{\theta }}_m(\eta )-{\stackrel{⌣}{\chi }}_m{\stackrel{⌣}{\theta }}_{m-1}(\eta )\right]={\hslash }_{\theta }{{P}}_m^{\stackrel{⌣}{\theta }}(\eta ),& (25)\end{array}$

$\begin{array}{ll}{\stackrel{⌣}{\theta }}_m(\eta ;\stackrel{⌣}{p}){|}_{\eta =0}=0,{\stackrel{⌣}{\theta }}_m(\eta ;\stackrel{⌣}{p}){|}_{\eta \to \infty }=0,& (26)\end{array}$

$\begin{array}{l}{{P}}_m^{\stackrel{⌣}{f}}\left(\eta \right)=\frac{1}{{(1-\varphi )}^{2.5}[1-\varphi +\frac{{\rho }_{CNT}}{{\rho }_f}\varphi ]}{f}_{m-1}^{\prime \prime \prime }\left(\eta \right)\\ -{\displaystyle \sum _{k=0}^{m-1}{f}_{m-1-k}}{f}_k^{\prime \prime }-\frac{2r-1}{1+r}\left[{\displaystyle \sum _{k=0}^{m-1}{f}_k}{f}_{m-1-k}^{\prime }-\left(1-{\chi }_m\right)\right]\\ +\frac{3}{1+r}\lambda {\theta }_{m-1}(\eta )+\frac{3}{1+r}QExp[-c\eta ],& (27)\end{array}$

$\begin{array}{l}{{P}}_m^{\stackrel{⌣}{\theta }}(\eta )=\left(1+\frac{4}{3}{R}_d\right)\frac{\frac{{\stackrel{\sim }{k}}_{nf}}{k_f}}{[1-\varphi +\frac{{(\rho c_p)}_{CNT}}{{(\rho c_p)}_f}\varphi ]}{\theta }_{m-1}^{\prime \prime }(\eta )\\ -\frac{3}{1+r}\text{Pr}{\displaystyle \sum _{k=0}^{m-1}}[r{f}_k^{\prime }{\theta }_{m-1-k}-\frac{1+r}{3}{f}_{m-1-k}{\theta }_k^{\prime }]\\ -\text{Pr}Ec{\displaystyle \sum _{k=0}^{m-1}}{f}_{m-1-k}^{\prime }{f}_k^{\prime },& (28)\end{array}$

where

$\begin{array}{ll}{\stackrel{⌣}{\chi }}_m=\{\begin{array}{r}\hfill 0,m\le 1\\ \hfill 1,m>1\end{array}.& (29)\end{array}$

For $\stackrel{⌣}{p}=0$ and $\stackrel{⌣}{p}=1$, we have

$\begin{array}{ll}\stackrel{⌣}{f}(\eta ,0)={\stackrel{⌣}{f}}_0(\eta ),\stackrel{⌣}{f}(\eta ,1)=\stackrel{⌣}{f}(\eta ),& (30)\end{array}$

$\begin{array}{ll}\stackrel{⌣}{\theta }(\eta ,0)={\stackrel{⌣}{\theta }}_0(\eta ),\stackrel{⌣}{\theta }(\eta ,\text{1})=\stackrel{⌣}{\theta }(\eta ).& (31)\end{array}$

The solutions $\stackrel{⌣}{f}(\eta ;\stackrel{⌣}{p})$ and $\stackrel{⌣}{\theta }(\eta ;\stackrel{⌣}{p})$ vary from the primary solutions ${\stackrel{⌣}{f}}_0(\eta )$ and ${\stackrel{⌣}{\theta }}_0(\eta )$ to the final solutions $\stackrel{⌣}{f}(\eta )$ and $\stackrel{⌣}{\theta }(\eta )$, respectively, where $\stackrel{⌣}{p}$ differs from 0 to 1. The Taylor series expansion follows:

$\begin{array}{ll}\stackrel{⌣}{f}(\eta ,\stackrel{⌣}{p})={\stackrel{⌣}{f}}_0(\eta )+{\displaystyle \sum _{m=1}^{\infty }{\stackrel{⌣}{f}}_m}(\eta ){\stackrel{⌣}{p}}^m,{\stackrel{⌣}{f}}_m\left(\eta \right)=\frac{1}{m!}{\frac{{\partial }^m{\stackrel{⌣}{f}}_m(\eta ,\stackrel{⌣}{p})}{\partial {\stackrel{⌣}{p}}^m}|}_{\stackrel{⌣}{p}=0},& (32)\end{array}$

$\begin{array}{ll}\stackrel{⌣}{\theta }(\eta ,\stackrel{⌣}{p})={\stackrel{⌣}{\theta }}_0(\eta )+{\displaystyle \sum _{m=1}^{\infty }{\theta }_m}(\eta ){\stackrel{⌣}{p}}^m,{\stackrel{⌣}{\theta }}_m\left(\eta \right)=\frac{1}{m!}{\frac{{\partial }^m\stackrel{⌣}{\theta }(\eta ,\stackrel{⌣}{p})}{\partial {\stackrel{⌣}{p}}^m}|}_{\stackrel{⌣}{p}=0}.& (33)\end{array}$

The above series solutions converge if the auxiliary parameters are properly nominated. Therefore,

$\begin{array}{ll}\stackrel{⌣}{f}(\eta )={\stackrel{⌣}{f}}_0(\eta )+{\displaystyle \sum _{m=1}^{\infty }}{\stackrel{⌣}{f}}_m(\eta ),& (34)\end{array}$

$\begin{array}{ll}\stackrel{⌣}{\theta }(\eta )={\stackrel{⌣}{\theta }}_0(\eta )+{\displaystyle \sum _{m=1}^{\infty }}{\stackrel{⌣}{\theta }}_m(\eta ),& (35)\end{array}$

The general solutions $\left({\stackrel{⌣}{f}}_m,{\stackrel{⌣}{\theta }}_m\right)$ via special solutions $\left(f_m^{\times },{\theta }_m^{\times }\right)$ are

$\begin{array}{ll}{\stackrel{⌣}{f}}_m(\eta )=f_m^{\times }(\eta )+K_1+K_{2}Exp(\eta )+K_{3}Exp(-\eta ),& (36)\end{array}$

$\begin{array}{ll}{\stackrel{⌣}{\theta }}_m(\eta )={\theta }_m^{\times }(\eta )+K_{4}Exp(\eta )+K_{5}Exp(-\eta ),& (37)\end{array}$

where K_h (h = 1−5) are the elaborated constants.

4. Convergence of Series Solutions

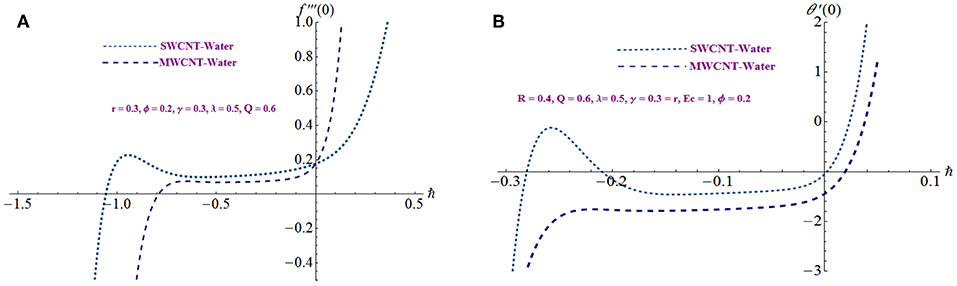
The convergence phenomenon of HAM solution is dependent on auxiliary parameters ℏ_f and ℏ_θ, which control and adjust the convergence of the derived series solution. Therefore, ℏ− curves are portrayed in Figures 2A,B for different values of the physical parameters in terms of SWCNT and MWCNT. The suitable values of these parameters ℏ_f and ℏ_θ are −0.78 ≤ ℏ_f < −0.19, −0.19 ≤ ℏ_θ < −0.03 for SWCNT and −0.66 ≤ ℏ_f < −0.1, −0.22 ≤ ℏ_θ < −0.01 for MWCNT.

5. Discussion

The major contribution of this section is to explore the physical influence of different dimensionless parameters on the velocity and temperature profiles. A physical sketch of the problem is given in Figure 1. The graphs in Figures 3–11 depict the results of the comprehensive analysis. We divide this section into three subsections for simplicity and clarity. In the first subsection, exploration is made of the physical impact of various parameters on the velocity profile. A discussion of the effects of the same parameters along with the radiation parameter on the temperature profile is given in the next subsection. The third subsection is based on the performance of the Nusselt number under the influence of different parameters.

FIGURE 1

Figure 1. Physical model of the problem.

FIGURE 2

Figure 2. (A) ℏ−curve for f^′′′(0). (B) ℏ−curve for θ′(0).

FIGURE 3

Figure 3. Significance of r on f′(η).

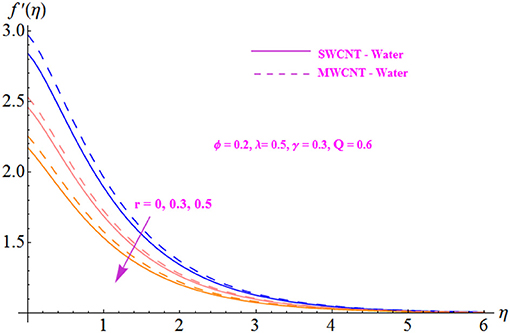
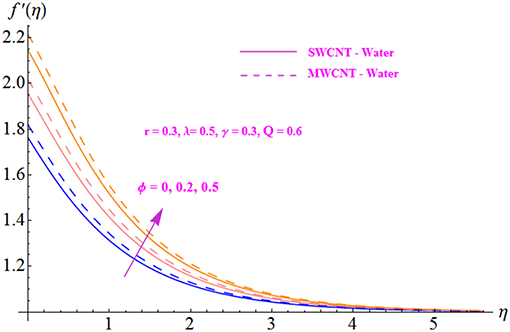
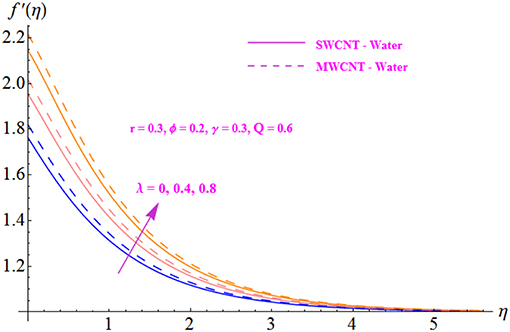
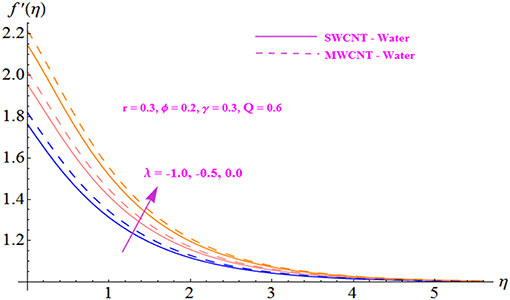
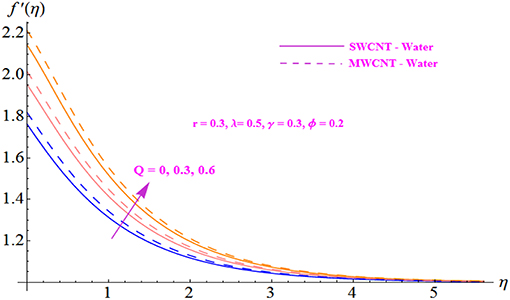
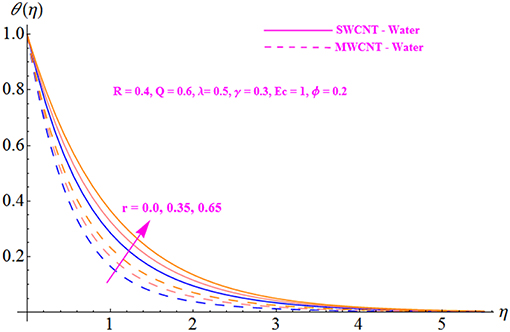
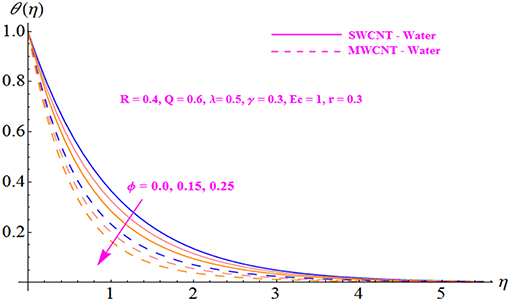
The impact of fluid parameter r on the velocity profile is illustrated in Figure 3 for both SWCNT and MWCNT. The velocity distribution is noted to decrease with the intensification of parameter r. Further, the velocity profile is seen to be higher in the case of MWCNT with a base fluid of water. Figure 4 is plotted to indicate the effect of the nanofluid solid volume fraction ϕ for both SWCNT and MWCNT. It is shown that the velocity distribution increases with the enhancement of the nanofluid volume fraction. In addition, a stronger response is seen with MWCNT than with SWCNT. This is due to the low density of MWCNT. Figures 5, 6 display the effects of variation in the convection parameter λ on the velocity profile in both opposing (λ <0) and assisting (λ > 0) flows. Under these circumstances, the velocity profile and the momentum boundary layer thickness exhibit increasing behavior with the buoyancy parameter for both SWCNT and MWCNT. Basically, the mixed convection may be defined as the ratio of buoyancy forces to inertial forces. The reason behind enhancement in the velocity of the fluid is the buoyancy force, which influences the inertial force, increasing the value of the mixed convection parameter. Moreover, MWCNT shows an increasing trend throughout the field in comparison to SWCNT. The effect of the Hartmann number Q on the velocity profile is shown in Figure 7 for both SWCNT and MWCNT. Physically, an increase in the modified Hartmann number increases the velocity field. The structure of the Hartmann number is the ratio of electromagnetic force to viscous force. Since the increasing phenomenon of the velocity profile is dependent on an increase in Q, this indicates development in the Lorentz force, which is generated by the presence of a magnetic field in the flow field and acts against the flow if the magnetic field is applied in the normal direction. The significance of the modified Hartmann number Q is exhibited in Figure 8 for both SWCNT and MWCNT. An increment in the Hartmann number correlates with a reduction in the temperature distribution.

FIGURE 4

Figure 4. Significance of ϕ on f′(η).

FIGURE 5

Figure 5. Significance of λ on f′(η).

FIGURE 6

Figure 6. Significance of λ on f′(η).

FIGURE 7

Figure 7. Significance of Q on f′(η).

FIGURE 8

Figure 8. Significance of Q on θ(η).

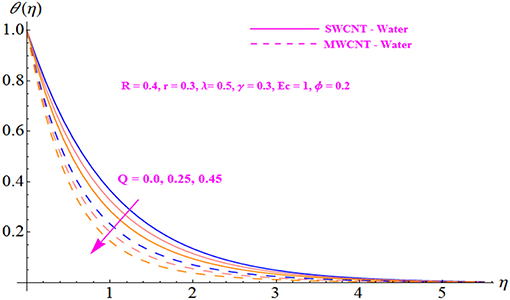
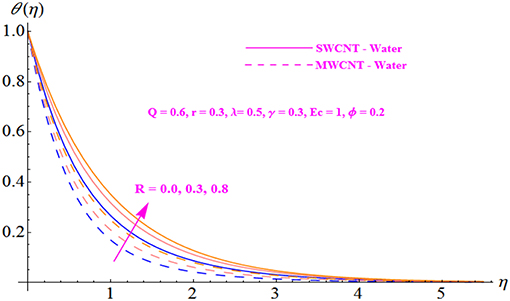
The effect of variation of radiative parameter R on temperature profile θ(η) is plotted in Figure 9 for both MWCNT and SWCNT. The behavior inferred from this figure is that there is an enhancement in temperature distribution and in the related boundary layer thickness due to the increment in R. Hence, the temperature profile is an increasing function of the radiative parameter. Hence, the enhancement in the temperature profile due to an increase in the radiative parameter causes a reduction in the absorption coefficient. Further, SWCNT shows a stronger response compared with MWCNT.

FIGURE 9

Figure 9. Significance of R on θ(η).

The physical effect of fluid parameter r on the velocity field is depicted in Figure 10 for both SWCNT and MWCNT. The velocity profile is noted to increase with escalation in parameter r. Figure 11 depicts the influence of the nanofluid solid volume fraction ϕ for both SWCNT and MWCNT. It is observed that with the augmentation of the nanofluid volume fraction, the velocity profile shows a reduction.

FIGURE 10

Figure 10. Significance of r on θ(η).

FIGURE 11

Figure 11. Significance of ϕ on θ(η).

Table 1 presents the thermophysical properties (density, specific heat, and thermal conductivity) of the base fluid (water) and carbon nanotubes (SWCNT and MWCNT). Table 2 shows that the series solutions are convergent up to four decimal places for the velocity profile at the 10th order of approximation for MWCNT and at the 20th order of approximation for SWCNT. Similarly, for the case of the temperature field, the 20th order of approximation for SWCNT and 15th order of approximation for MWCNT were observed for convergence. Further, Table 3 displays the behavior of the local Nusselt number for different values of physical parameters such as fluid parameter r, convection parameter λ, Hartman number Q, volume fraction ϕ, radiative parameter R , and parameter γ. The desired results were observed for both SWCNT and MWCNT. It is concluded that the Nusselt number shows decreasing behavior for larger values of r, λ, and ϕ in the cases of both SWCNT and MWCNT. On the other hand, the Nusselt number shows stronger behavior for larger values of Q, R , and γ for both SWCNT and MWCNT.

TABLE 1

Table 1. Thermophysical characteristics of base fluid and nanoparticles (SWCNT and MWCNT).

TABLE 2

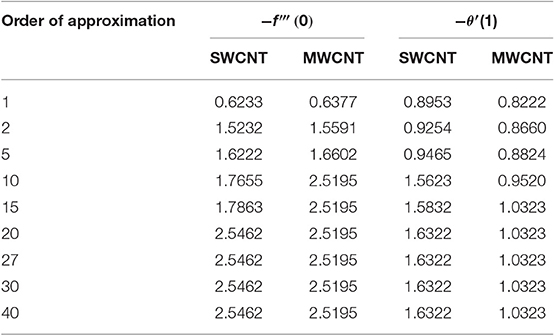
Table 2. Convergence of homotopy solutions when α = 0.01, β = 0.1, γ = 0.1, δ = 0.3, M = 0.1, Re = 2, Pr = 6.2, Ec = 0.1, and ℏ_f = ℏ_θ = −0.7.

TABLE 3

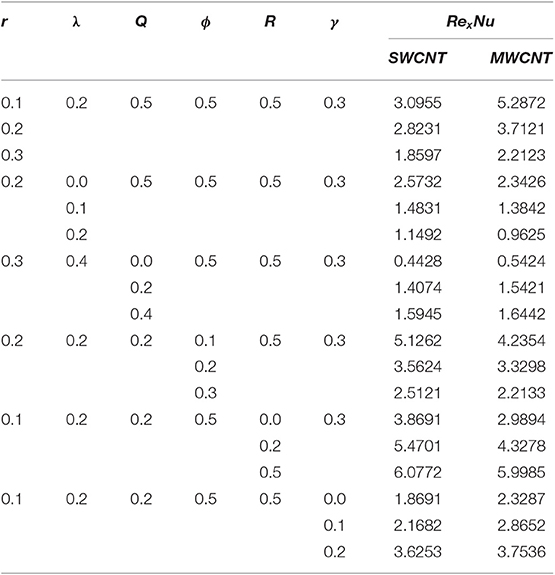
Table 3. Numerical values of the Nusselt number for both SWCNT and MWCNT at different values of other parameters.

6. Final Observation

The key points are as follows:

• Increment in the velocity profile is based on increases in the modified Hartmann number, buoyancy-assisting flow parameter, and solid volume fraction.

• The velocity profile for water-based MWCNT is higher than that for SWCNT for all of the discussed fluid parameters.

• Enhancement in parameter r results in a reduction in the velocity distribution.

• Augmentation in the temperature field is based on increment in the radiative parameter, whereas the Hartmann number, buoyancy-assisting flow parameter, and solid volume fraction have the opposite effect on the temperature profile to the radiative parameter.

• SWCNT shows excellent agreement with the temperature distribution than MWCNT for all proposed fluid parameters.

• For larger values of Q, R , and γ, the local Nusselt number increases for both SWCNT and MWCNT.

• The Nusselt number illustrates decreasing behavior for larger values of r, λ, and ϕ in the cases of SWCNT and MWCNT.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation, to any qualified researcher.

Author Contributions

AS formulated the problem. IZ solved the problem. TK computed the results. IK discussed the results with the conclusion. All authors contributed to writing the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors would like to extend their sincere appreciation to the Deanship of Scientific Research at King Saud University for its funding of this research through Researchers Supporting Project number (RSP-2019/33), King Saud University, Riyadh, Saudi Arabia. AS was supported by the Talented Young Scientist Program of Ministry of Science and Technology of China (Pakistan-19-007).

References

1. Pop I, Postelnicu A, Grosan T. Thermasolutal marangoni forced convection boundary layers. Meccanica. (2001) 36:555–71. doi: 10.1023/A:1017431224943

CrossRef Full Text | Google Scholar

2. Napolitano LG. Marangoni boundary layers. Mater Sci Space. (1979) 349–58.

Google Scholar

3. Lin Y, Zheng L. Marangoni boundary layer flow and heat transfer of copper-water nanofluid over a porous medium disk. AIP Adv. (2015) 5:107225. doi: 10.1063/1.4934932

CrossRef Full Text | Google Scholar

4. Tiwari AK, Raza F, Akhtar J. Mathematical model for Marangoni convection MHD flow of CNTs through a porous medium. J Adv Res Appl Sci. (2017) 4:216–22.

Google Scholar

5. Zhang Y, Zheng L. Similarity solutions of Marangoni convection boundary layer flow with gravity and external pressure. Chin J Chem Eng. (2014) 22:365–9. doi: 10.1016/S1004-9541(14)60040-9

CrossRef Full Text | Google Scholar

6. Mehdi M, Hosein M, Samareh R, Poor HM. Numerical study on the effects of Marangoni driven boundary layer flow for different nanoparticales with variable based fluids. J Int Acad Res Multidiscip. (2014) 2:2320–5083.

Google Scholar

7. Sheikholeslami M, Ganji DD. Influence of magnetic field on Cu Oe H2O nanofluid flow considering Marangoni boundary layer. Int J Hydr Energy. (2017) 42:821–9. doi: 10.1016/j.ijhydene.2016.09.121

CrossRef Full Text | Google Scholar

8. Remeli A, Arifin NM, Nazar R, Ismail F, Pop I. Marangoni-driven boundary layer flow in a nanofluid with suction and injection. World Appl Sci J. (2012) 17:21–6. doi: 10.1186/2251-7456-6-21

CrossRef Full Text | Google Scholar

9. Ellahi R, Zeeshan A, Hassan M. Particle shape effects on Marangoni convection boundary layer flow of a nanofluid. Int J Numer Methods Heat Fluid Flow. (2016) 26:2160–74. doi: 10.1108/HFF-11-2014-0348

CrossRef Full Text | Google Scholar

10. Christopher DM, Wang B. Prandtl number effects for Marangoni convection over a flat surface. Int J Ther Sci. (2001) 40:564–70. doi: 10.1016/S1290-0729(01)01244-3

CrossRef Full Text | Google Scholar

11. Mudhaf A, Chamkha AJ. Similarity solutions for MHD thermosolutal Marangoni convection over a flat surface in the presence of heat generation or absorption effects. Heat Mass Transf. (2005) 42:112–21. doi: 10.1007/s00231-004-0611-8

CrossRef Full Text | Google Scholar

12. Magyari E, Chamkha AJ. Exact analytical results for the thermosolutal MHD marangoni boundary layers. Int J Ther Sci. (2008) 47:848–57. doi: 10.1016/j.ijthermalsci.2007.07.004

CrossRef Full Text | Google Scholar

13. Hayat T, Qayyum S, Alsaedi A, Shafiq A. Inclined magnetic field and heat source/sink aspects in flow of nanofluid with nonlinear thermal radiation. Int J Heat Mass Transf. (2016) 103:99–107. doi: 10.1016/j.ijheatmasstransfer.2016.06.055

CrossRef Full Text | Google Scholar

14. Hayat T, Mumtaz M, Shafiq A, Alsaedi A. Stratified magnetohydrodynamic flow of tangent hyperbolic nanofluid induced by inclined sheet. Appl Math Mech. (2017) 38:271–88. doi: 10.1007/s10483-017-2168-9

CrossRef Full Text | Google Scholar

15. Shafiq A, Hammouch Z. Bioconvective MHD flow of tangent hyperbolic nanofluid with newtonian heating. Int J Mech Sci. (2017) 133:759–66. doi: 10.1016/j.ijmecsci.2017.07.048

CrossRef Full Text | Google Scholar

16. Khan A, Khan D, Khan I, Ali F, Karim F, Nisar KS. MHD flow of brinkman type H₂O-Cu, Ag, TiO₂ and Al₂O₃ nanofluids with chemical reaction and heat generation effects in a porous medium. J Magnet. (2019) 24:262–70. doi: 10.4283/JMAG.2019.24.2.262

CrossRef Full Text | Google Scholar

17. Murshd SMS, Leong KC, Yang C. Enhanced thermal conductivity of TiO2- Water based nanofluid. Int J Ther Sci. (2005) 4:367–73. doi: 10.1016/j.ijthermalsci.2004.12.005

CrossRef Full Text | Google Scholar

18. Oberlin A, Endo M, Koyama T. Filamentous growth of carbon though benzene decomposition. J Cryst Growth. (1976) 32:335–9. doi: 10.1016/0022-0248(76)90115-9

CrossRef Full Text | Google Scholar

19. Baughman RH, Zakhidov AA, Heer WA. Carbon nanotubes- the route toward applications. Science. (2002) 297:787–92. doi: 10.1126/science.1060928

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Ericson LM, Fan H, Peng H, Davis VA, Zhou W. Macroscopic neat single-walled carbon nanotube fibers. Science. (2004) 305:1447–50. doi: 10.1126/science.1101398

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Milne IW, Teo KB, Amaratunga GA, Legagneux P, Gangloff L, Schnell P. Carbon nanotubes as field emission sources. J Mat Chem. (2004) 14:933–43. doi: 10.1039/b314155c

CrossRef Full Text | Google Scholar

22. Hayat T, Hussain Z, Alsaedi A, Ahmad A. Heterogeneous-homogeneous reactions and melting heat transfer effects in flow with carbon nanotubes. J Mol Liquids. (2016) 220:200–7. doi: 10.1016/j.molliq.2016.04.012

CrossRef Full Text | Google Scholar

23. Hayat T, Khursheed M, Farooq M, Alsaedi A. Melting heat transfer in stagnation point flow of carbon nanotubes towards variable thickness surface. AIP Adv. (2016) 6:015214. doi: 10.1063/1.4940932

CrossRef Full Text | Google Scholar

24. Gailitis A, Lielausis O. On a possibility to reduce the hydrodynamic resistance of a plate in an electrolyte. Appl Magnetohydrodyn. (1961) 12:143–6.

Google Scholar

25. Pantokratoras A, Magyari E. EMHD free-convection boundary-layer flow from a Riga-plate. J Eng Math. (2009) 64:303–15. doi: 10.1007/s10665-008-9259-6

CrossRef Full Text | Google Scholar

26. Magyari E, Pantokratoras A. Aiding and opposing mixed convection flows over the Riga plate. Commun Nonlin Sci Numer Simulat. (2011) 16:3158–67. doi: 10.1016/j.cnsns.2010.12.003

CrossRef Full Text | Google Scholar

27. Pantokratoras A. The Blasius and Sakiadis flow along a Riga-plate. Prog Comput Fluid Dyn. (2011) 11:329–33. doi: 10.1504/PCFD.2011.042184

CrossRef Full Text | Google Scholar

28. Hayat T, Abbas M, Ayub M, Farooq M, Alsaedi A. Flow of nanofluid due to convectively heated Riga plate with variable thickness. J Mol Liquids. (2016) 222:854–62. doi: 10.1016/j.molliq.2016.07.111

CrossRef Full Text | Google Scholar

29. Shafiq A, Hammouch Z, Turab A. Impact of radiation in a stagnation point flow of Walters' B fluid towards a Riga plate. Ther Sci Eng Prog. (2017) 6:27–33. doi: 10.1016/j.tsep.2017.11.005

CrossRef Full Text | Google Scholar

30. Bhatti MM, Abbas T, Rashidi MM. Effects of thermal radiation and electromagnetohydrodynamics on viscous nanofluid through a Riga plate. Multidiscip Model Mater Struct. (2016) 12:605–18. doi: 10.1108/MMMS-07-2016-0029

CrossRef Full Text | Google Scholar

31. Naseem A, Shafiq A, Zhao L, Farooq MU. Analytical investigation of third grade nanofluidic flow over a Riga plate using Cattaneo-Christov model. Results Phys. (2018) 9:961–9. doi: 10.1016/j.rinp.2018.01.013

CrossRef Full Text | Google Scholar

32. Hayat T, Jabeen S, Shafiq A, Alsaedi A. Radiative squeezing flow of second grade fluid with convective boundary conditions. PLoS ONE. (2016) 11:e0152555. doi: 10.1371/journal.pone.0152555

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Sheikholeslamia M, Hayat T, Alsaedi A. MHD free convection of Al₂ O₃ –water nanofluid considering thermal radiation: a numerical study. Int J Heat Mass Transf. (2016) 96:513–24. doi: 10.1016/j.ijheatmasstransfer.2016.01.059

CrossRef Full Text | Google Scholar

34. Hayat T, Shehzad SA, Qasim M. Mixed convection flow of a micropolar fluid with radiation and chemical reaction. Int J Numer Methods Fluids. (2011) 67:1418–36. doi: 10.1002/fld.2424

CrossRef Full Text | Google Scholar

35. Hayat T, Shaheen U, Shafiq A, Alsaedi A, Asghar S. Marangoni mixed convection flow with Joule heating and nonlinear radiation. AIP Adv. (2015) 5:077140. doi: 10.1063/1.4927209

CrossRef Full Text | Google Scholar

36. Lin Y, Li B, Zheng L, Chen G. Particle shape and radiation effects on marangoni boundary layer flow and heat transfer of copper-water nanofluid driven by an exponential temperature. Powder Technol. (2016) 301:379–86. doi: 10.1016/j.powtec.2016.06.029

CrossRef Full Text | Google Scholar

37. Hayat T, Shafiq A, Alsaedi A. Effect of Joule heating and thermal radiation in flow of third-grade fluid over radiative surface. PLoS ONE. (2014) 9:e83153. doi: 10.1371/journal.pone.0083153

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Hayat T, Shafiq A, Imtiaz M, Alsaedi A. Impact of melting phenomenon in the Falkner-Skan wedge flow of second grade nanofluid: a revised model. J Mol Liquids. (2016) 215:664–70. doi: 10.1016/j.molliq.2016.01.004

CrossRef Full Text | Google Scholar

39. Ellahi R, Fetecau C, Sheikholeslami M. Recent advances in the application of differential equations in mechanical engineering problems. Math Prob Eng. (2018) 2018:1584920. doi: 10.1155/2018/1584920

CrossRef Full Text | Google Scholar

40. Ellahi R, Zeeshan A, Hussain F, Abbas T. Study of shiny film coating on multi-fluid flows of a rotating disk suspended with nano-sized silver and gold particles: a comparative analysis. Coatings. (2018) 8:422. doi: 10.3390/coatings8120422

CrossRef Full Text | Google Scholar

41. Ellahi R, Alamri SZ, Basit A, Majeed A. Effects of MHD and slip on heat transfer boundary layer flow over a moving plate based on specific entropy generation. J Taibah Univ Sci. (2018) 12:476–82. doi: 10.1080/16583655.2018.1483795

CrossRef Full Text | Google Scholar

42. Ellahi R, Riaz A, Abbasbandy S, Hayat T, Vafai K. A study on the mixed convection boundary layer flow and heat transfer over a vertical slender cylinder. Ther Sci. (2014) 18:1247–58. doi: 10.2298/TSCI110923097E

CrossRef Full Text | Google Scholar

43. Ellahi R, Tariq MH, Hassan M, Vafai K. On boundary layer magnetic flow of nano-Ferroliquid under the influence of low oscillating over stretchable rotating disk. J Mol Liquids. (2017) 229:339–45. doi: 10.1016/j.molliq.2016.12.073

CrossRef Full Text | Google Scholar

44. Ellahi R, Raza M, Akbar NS. Study of peristaltic flow of nanofluid with entropy generation in a porous medium. J Porous Media. (2017) 20:461–78. doi: 10.1615/JPorMedia.v20.i5.70

CrossRef Full Text | Google Scholar

45. Bhatti MM, Abbas MA, Rashidi MM. Entropy generation for peristaltic blood flow with casson model and consideration of magnetohydrodynamics effects. Walailak J Sci Technol. (2016) 14:451–61.

Google Scholar

46. Bhatti MM, Mishra SR, Abbas T, Rashidi MM. A mathematical model of MHD nanofluid flow having gyrotactic microorganisms with thermal radiation and chemical reaction effects. Neural Comput Appl. (2018) 30:1237–49. doi: 10.1007/s00521-016-2768-8

CrossRef Full Text | Google Scholar

47. Ellahi R, Riaz A. Analytical solutions for MHD flow in a third-grade fluid with variable viscosity. Math Comput Model. (2010) 52:1783–93. doi: 10.1016/j.mcm.2010.07.005

CrossRef Full Text | Google Scholar

48. Waqas H, Khan SU, Imran M, Bhatti MM. Thermally developed Falkner–Skan bioconvection flow of a magnetized nanofluid in the presence of a motile gyrotactic microorganism: Buongiorno's nanofluid model. Phys Script. (2019) 94:1–15. doi: 10.1088/1402-4896/ab2ddc

CrossRef Full Text | Google Scholar

Nomenclature