Local Nucleon-Nucleon and Three-Nucleon Interactions Within Chiral Effective Field Theory

1. Introduction

The last few decades have marked the emergence of the basic model of nuclear theory in which nuclear systems—particularly atomic nuclei and infinite nucleonic matter—can be described as a collection of point-like particles, the nucleons, interacting with each other in terms of two- and many-body effective interactions, and with external electroweak probes via effective current operators. This approach, in conjunction with a computational method of choice to solve the many-body Schrödinger equation, can then be used to study the structure and dynamics of nuclear systems in a fully microscopic way, which is commonly referred to as ab-initio calculations. Examples of such calculations are based on the no-core shell model (NCSM) [1, 2], the coupled cluster (CC) [3, 4] or hyperspherical harmonics (HH) [5] expansions, similarity renormalization group (SRG) approaches [6, 7], self-consistent Green's function techniques [8, 9], quantum Monte Carlo (QMC) methods [10], and nuclear lattice effective field theory (NLEFT) [11]. Although significant progress has been made in recent years, these ab-initio techniques remain challenging and their domain of applicability is, at present, limited to provide quantitative description of light and medium-mass nuclei [1, 4, 7–10, 12] and their reactions [13–16]. A special but related challenge is the development of microscopic models that include continuum couplings which are mandatory to describe, for instance, weakly bound nuclear systems [17, 18].

One might argue that nucleons are not the fundamental building blocks of the nuclear systems at hand, and that one should instead start from Quantum Chromodynamics (QCD). QCD provides the theoretical framework to describe strong interactions which governs the dynamics and properties of quarks and gluons. However, while strong interactions are weak and perturbative at high energies, i.e., short distances (asymptotic freedom), quarks are strongly interacting at low energies or long distances, of relevance for nuclear physics, which makes a non-perturbative treatment necessary. In addition, at these energies quarks are confined into colorless objects called hadrons (baryons, consisting of three quarks, e.g., the nucleon, and mesons consisting of a quark and an anti-quark, e.g., the pion). Hence, while QCD is responsible for the complex inter-nucleon forces in nuclear systems, which can be thought of as residual interactions among quarks, a description in terms of nucleon degrees of freedom is particularly valid at sufficiently low energies.

How the interactions among nucleons emerge from the fundamental theory, QCD, has kept nuclear theorists occupied for many decades. Since QCD is non-perturbative at low energies of interest in nuclear systems, one may try to solve QCD with brute computing power on a discretized Euclidean space-time lattice (known as lattice QCD) However, in spite of many advances [19–22], lattice QCD calculations are still limited to small nucleon numbers and/or large pion masses, and hence, at the present time, can only be used to address a limited set of representative key-issues.

As a consequence, most theoretical studies of nuclear systems have to resort to using the basic model of nuclear theory, i.e., assuming pointlike nucleons to be the relevant degrees of freedom instead of quarks. In this review, we will briefly introduce this basic model and discuss the current state-of-the-art for nuclear interactions, chiral effective field theory (EFT). We will then focus on a particular subclass of chiral EFT interactions, local chiral EFT interactions, intended for the use in QMC methods.

The review is structured as follows. In section 2, we discuss the general features of nuclear interactions starting with the phenomenological ones and moving to those obtained in chiral EFT. In section 3, we provide many details about the theoretical derivation of local interactions in both delta-full and delta-less chiral EFT, i.e., when explicitly including the delta resonance or not. In section 4, we briefly discuss finite cutoff and regulator artifacts that can appear in calculations with local interactions. Finally, in section 5, we report selected results for light and medium-mass nuclei and the equation of state of pure neutron matter using QMC methods.

2. Nuclear Hamiltonians

The basic model of nuclear theory assumes that a nuclear system can be described by a non-relativistic Hamiltonian that contains interactions among nucleons, i.e., protons and neutrons. The individual nucleons mostly interact via two-body (NN) interactions. However, nucleons can also interact via three-body (3N) and higher many-body interactions. The way these many-body interactions appear is 2-fold. First, nucleons are compound particles and, hence, treating them as point-like particles induces effective many-body interactions even if only two-quark interactions were to be considered. This is similar to describing tides on Earth, where the three-body system given by Earth, Moon, and Sun is relevant, even though gravity is only a two-body force. Second, since quarks themselves can have multi-quark interactions, this immediately leads to the appearance of “true” 3N forces among nucleons, where, for example, single quarks in each of the three nucleons interact with each other.

The resulting Hamiltonian can then be written as a sum of the non-relativistic one-body kinetic energy (${{T}}_i$), NN interactions between particle i and j (V_ij), 3N interactions between particle i, j, and k (V_ijk), and additional many-body interactions, and provides a good approximation for interacting nucleons in a given nuclear system:

$\begin{array}{ll}{H}={\displaystyle \sum _i}{{T}}_i+{\displaystyle \sum _{i<j}}{V}_{ij}+{\displaystyle \sum _{i<j<k}}{V}_{ijk}+\cdots .& (1)\end{array}$

There are indications that four-body interactions may contribute at the level of only ~100 keV in ⁴He [23] or pure neutron matter [24], and therefore are negligible compared to NN and 3N interactions. Hence, current formulations of the basic model do not typically include them (see e.g., [10]).

In order to derive two- and three-body nuclear forces, one has to take into account some general considerations, specify the theoretical framework in which such interactions are formulated, and the experimental inputs necessary to determine possible unknown parameters of the theory.

2.1. General Considerations for Nuclear Interactions

To accurately describe nuclear systems that are governed by QCD, nuclear interactions need to obey all the relevant symmetries of QCD. Hence, nuclear potentials need to have the following properties (we will focus on NN forces here, but the statements remain true for all parts of the interaction):

• V is hermitian, because the Hamiltonian is hermitian,

• V is symmetric under the permutation of identical particles, i.e., V_ij = V_ji,

• V is translationally and rotationally invariant,

• V is invariant under translations in time, i.e., time-independent,

• V is Lorentz invariant (for non-relativistic interactions this reduces to Galilean invariance),

• V is invariant under parity transformations and time reversal,

• V has to conserve baryon and lepton number,

• V has to be approximately isospin symmetric and charge independent,

• and V has to include the properties of spontaneously and explicitly broken chiral symmetry.

Chiral symmetry is a symmetry of the QCD Lagrangian with massless quarks under independent rotations of left- and right-handed quarks. Considering only u and d quarks, this symmetry can be written as SU(2)_L×SU(2)_R. This expression contains two symmetries: the first (vector) one represents isospin symmetry, i.e., symmetry under the exchange of u and d quarks, and the second (axial) one is the so-called chiral symmetry. These two symmetries imply degenerate fermions under isospin and spin-parity transformations. While isospin symmetry is approximately fulfilled in nature, i.e., the neutron and proton have similar masses, nucleons with spin 1/2⁺ and 1/2⁻ have very different masses (940 vs. 1,535 MeV). This signals that chiral symmetry is broken in nature.

In fact, chiral symmetry is broken 2-fold. First, it is broken spontaneously, leading to the formation of Goldstone bosons, that can be identified with the pions. Second, chiral symmetry is also explicitly broken by the finite quark masses, which leads to the pion being pseudo-Goldstone bosons with finite but small mass. In contrast, isospin symmetry remains a good symmetry, because the ratio (m_d − m_u)/Λ_QCD is very small, where m_u ≃ 2.4 MeV and m_d ≃ 4.8 MeV.

These symmetries only allow certain operator structures for nuclear interactions. Galilean invariance, for instance, implies that nuclear interactions depend only on relative momenta between two nucleons, p = p_i − p_j, while symmetry under parity transformations implies that nuclear interactions cannot be linear in p, and charge independence requires that the nuclear interactions can be written as

$\begin{array}{ll}V=V_{\mathbb{1}}·\mathbb{1}+V_{\mathit{\tau }}{\mathit{\tau }}_i·{\mathit{\tau }}_j,& (2)\end{array}$

and so on. In addition, the spin dependencies are included through operators like 1, σ_i · σ_j, spin-orbit interactions given by L · S with L = r × p, where r = r_i − r_j, or tensor interactions with the tensor operator $S_{ij}(\mathbf{\text{r}})={\mathit{\sigma }}_i·\widehat{\text{r}}{\mathit{\sigma }}_j·\widehat{\mathbf{\text{r}}}-{\mathit{\sigma }}_i·{\mathit{\sigma }}_j$. As a consequence, interactions typically have a spin-isospin operator structure given by

$\begin{array}{ll}{{O}}_V=\{\mathbb{1},{\mathit{\sigma }}_i·{\mathit{\sigma }}_j,\text{L}·\text{S},S_{ij}\}\times \{\mathbb{1},{\mathit{\tau }}_i·{\mathit{\tau }}_j\},& (3)\end{array}$

where the individual operators carry momentum-dependent functions consistent with all required symmetries.

2.2. Phenomenological Interactions

Historically, NN interactions were derived using phenomenological insight. They were characterized by a long-range component characterizing the interaction for inter-nucleon separations r ≳ 1/m_π, due to one-pion exchange (OPE) [25], and intermediate- and short-range components describing the interactions at 1 fm ≲ r ≲ 2 fm and r ≲ 1 fm, respectively. The intermediate- and short-range components were included to simulate intermediate-range attraction as well as short-range repulsion.

Up to the mid-1990's, nuclear interactions were based almost exclusively on meson-exchange phenomenology. Interactions of the mid-1990's [26–28] were constrained by fitting nucleon-nucleon (NN) elastic scattering data up to laboratory energies of 350 MeV, with χ²/datum ≃ 1 relative to the database available at the time [29]. Two well-known and still widely used examples in this class are the Argonne v₁₈ (AV18) [27] and CD-Bonn [28] interactions. These are so-called phenomenological interactions.

Already in the 1980's, accurate three-body calculations showed that contemporary NN interactions alone did not provide sufficient binding to reproduce experimental numbers for nuclei with nucleon number A = 3, ³H and ³He [30]. This realization was later on extended to the spectra (ground and low-lying excited states) of light p-shell nuclei, for instance, in calculations based on quantum Monte Carlo (QMC) methods [31] and in no-core shell-model (NCSM) studies [32]. Consequently, the basic model with only NN interactions fit to scattering data, without the inclusion of a three-nucleon (3N) interaction, was found to be unsatisfactory. However, because of the composite nature of the nucleon and, in particular, the dominant role of the Δ resonance, a spin-3/2, isospin-3/2 nucleon resonance, in pion-nucleon scattering, many-body interactions arise quite naturally in meson-exchange phenomenology.

For example, the Illinois 3N interaction [33] consists of a dominant two-pion exchange (TPE)—the Fujita-Miyazawa interaction [34]—and smaller multi-pion exchange components resulting from the excitation of intermediate Δ's. The most recent version, Illinois-7 (IL7) [35], also contains phenomenological isospin-dependent central terms. The parameters characterizing this 3N potential have been determined by fitting the low-lying spectra of nuclei in the mass range A = 3–10. The resulting AV18+IL7 Hamiltonian, generally utilized with QMC methods, then leads to predictions of 100 ground- and excited-state energies up to A=12, including the ¹²C ground- and Hoyle-state energies, in good agreement with the corresponding experimental values [10]. However, when used to compute the neutron-star equation of state, these interactions do not provide sufficient repulsion to guarantee the stability of the observed neutron stars with masses larger than two solar masses against gravitational collapse [36]. Thus, in the context of the phenomenological nuclear interactions, we do not have a Hamiltonian that can predict the properties of all nuclear systems, from NN scattering to dense nuclear and neutron matter.

Furthermore, high-precision phenomenological potentials suffer from several limitations, most notably the missing connection with the low-energy QCD, and hence, the absence of a guiding principle for the construction of interactions. As a consequence, phenomenological interactions do not provide rigorous schemes to consistently derive two- and three-body forces and compatible electroweak currents. In addition, there is no clear way to properly assess the theoretical uncertainty associated with the nuclear potentials and currents.

2.3. Chiral Effective Field Theory

These drawbacks were addressed when a new phase in the evolution of the basic model began in the early 1990's with the emergence of chiral effective field theory (EFT) [37–39].

Chiral EFT is a low-energy effective theory of QCD based on the choice of baryons as effective degrees of freedom: in chiral EFT one chooses pions and nucleons. At typical momenta in nuclei, $p~m_{\pi }~{O}(100\text{ MeV})$, this choice is accurate, because shorter-range structures, e.g., the quark substructure, or heavier meson exchanges, e.g., exchanges of the ρ-meson, are not resolved, and can be absorbed in short-range nucleon contact interactions. This separation of scales between typical momenta p and scales of the same order, i.e., the pion mass m_π ~ 140 MeV, and larger scales, e.g., the mass of the ρ, m_ρ ~ 770 MeV, can then be used to systematically derive an effective and most general scheme accommodating all possible interactions among the relevant degrees of freedom consistent with the symmetries of QCD. In some modern approaches, the choice of degrees of freedom also includes the Δ isobar (delta-full chiral EFT), because the Δ-nucleon mass splitting is only 300 MeV ~ 2m_π.

The starting point in chiral EFT is the most general Lagrangian in terms of the chosen degrees of freedom, which contains all allowed interaction mechanisms in accordance with the considerations in section 2.1. As a consequence, this Lagrangian contains an infinite number of terms and needs to be truncated using a given power-counting scheme. Most chiral interactions used in nuclear structure calculations are based on Weinberg power counting, which itself is based on naive dimensional analysis of interaction contributions. Within Weinberg power counting, the interactions are expanded in powers of the typical momentum p over the breakdown scale Λ_b, Q = p/Λ_b, where the breakdown scale denotes momenta at which the short distance structure becomes important and cannot be neglected and absorbed into contact interactions anymore (see [40–43] for recent review articles). It is worthwhile mentioning that alternative power-counting schemes have been also suggested as in Kaplan et al. [44, 45], Nogga et al. [46], Pavon Valderrama and Ruiz Arriola [47], Long and Yang [48], and van Kolck [49].

This expansion defines an order by order scheme, defined by the power ν of the expansion scale Q in each interaction contribution: leading order (LO) for ν = 0, next-to-leading order (NLO) for ν = 2, next-to-next-to-leading order (N²LO) for ν = 3 and so on. Similarly as for nuclear interactions, such a scheme can also be developed for electroweak currents. Therefore, chiral EFT provides a rigorous scheme to systematically construct many-body forces and consistent electroweak currents, and tools to estimate their uncertainties [50–55]. From this perspective, it can be justifiably argued that chiral EFT has put the basic model on a more fundamental basis, by providing a link between QCD with all its symmetries, and the strong and electroweak interactions in nuclei.

Figure 1 shows the state of the art of chiral contributions to the NN and 3N interactions in the delta-less and delta-full chiral EFT. Higher many-body forces, such as four-nucleon (4N) or five-nucleon (5N) interactions, can naturally also be derived within this framework [42], but they will not be discussed here. Nuclear forces in chiral EFT are separated into pion-exchange contributions and contact terms. Pion-exchange contributions represent the long- and intermediate-range parts of nuclear interactions and contain all chiral physics. Contact terms, on the other hand, encode the unresolved short-range physics and their strength is specified by unknown low-energy constants (LECs), that need to be adjusted to experimental data.

FIGURE 1

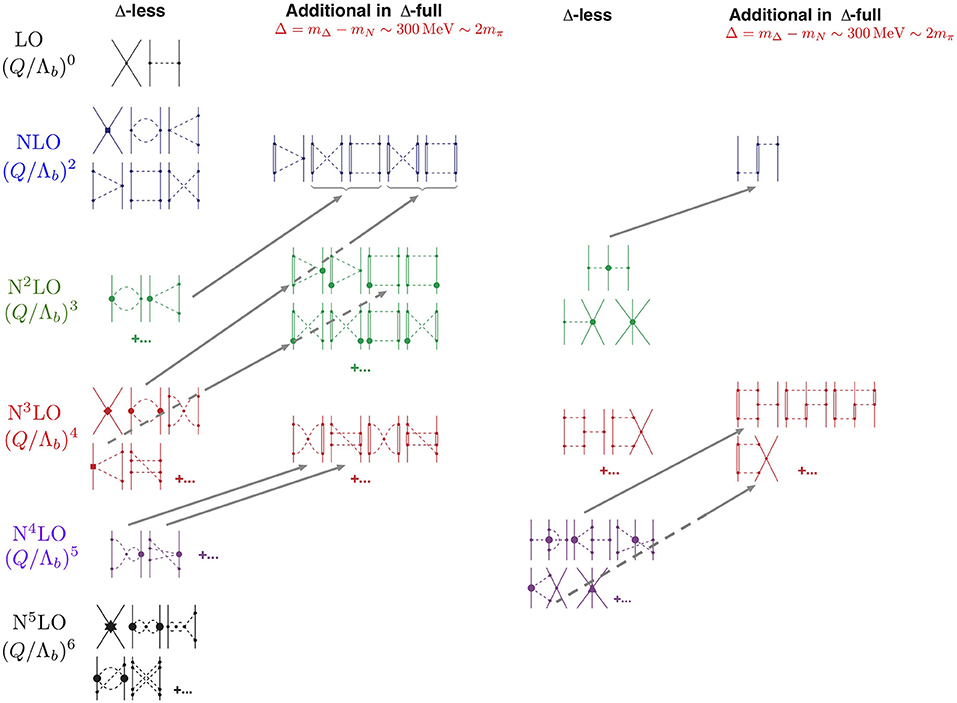
Figure 1. Chiral contributions to the NN and 3N interactions in the delta-less and delta-full chiral EFT based on Weinberg power counting. Solid lines represent nucleons, dashed lines represent pions, and double lines represent the Δ isobar. Gray arrows indicate the shift of individual contributions within the two power-counting schemes when explicit Δ's are accounted for. Figure adapted from Machleidt and Entem [41] and Machleidt and Sammarruca [42] under the Creative Commons CCBY license.

At LO, besides the already mentioned OPE potential, there are two NN contact terms with no momentum dependence that contribute only to the S-wave. They are identified by the four-nucleon-leg diagram with a momentum-independent vertex denoted by a small dot in the first row of Figure 1. The interaction at LO is a very simple approximation, but already takes into account some of the important features of the NN force. For instance, the OPE generates the tensor component of the nuclear force known to be crucial to properly describe the two-nucleon bound state (deuteron).

The leading NN two-pion-exchange (TPE) contributions appear at NLO. Diagrams involving virtual excitations of the Δ-isobars [56–59] also appear at NLO in the delta-full chiral-EFT approach. Most importantly, seven new momentum-dependent contact terms can be constructed at this order, which are denoted by the four-nucleon-leg graph with a solid square in the second row of Figure 1. These additional contact terms are important to correctly describe NN scattering in the S- and P-waves. More details about these contributions are presented in the next sections. Another important contribution at NLO is the leading 3N force, which can be described by the well-known Fujita-Miyazawa diagram [34], which involves intermediate excitation of the Δ-isobars between three nucleons. While this contribution has to be considered in the Δ-full approach, it can be shown that the net contribution of 3N forces vanishes in the delta-less chiral EFT [39, 49] at this order.

At next order, N²LO, the sub-leading NN TPE diagrams contain vertices (large solid dots) proportional to the so-called c_i coefficients. The values of these parameters can be obtained by pion-nucleon (πN) [60–67] or NN scattering data [41]. In the delta-less chiral EFT, these coefficients mimic the effect of the Δ-isobar (or some other meson resonances) through a mechanism known as resonance saturation. Hence, they are enhanced in magnitude and found to be “unnaturally” large. The explicit inclusion of the Δ isobar in the delta-full theory reduces the strength of the c_i's and promotes the corresponding contributions to a lower order (see gray arrows in Figure 1). As a consequence, the convergence of the expansion in the delta-full theory improves considerably at these orders. In the delta-full approach, additional sub-leading TPE contributions appear that have also been worked out at this order [60].

In addition to the NN sector, additional 3N diagrams appear at N²LO in both approaches. They involve a 3N TPE, a OPE-contact interaction, and a true 3N contact diagram. The 3N TPE potential also involves the c_i parameters already present in the TPE NN force. As in the case of the NN force, these contributions absorb the presence of the Δ-isobar in the delta-less approach, while some of their strength is promoted to lower order in the form of the already discussed Fujita-Miyazawa diagram in the delta-full approach. The OPE-contact and 3N contact diagrams include two purely three-body LECs that have to be adjusted to A ≥ 3 data. Finally, the are no additional diagrams due to Δ contributions to the 3N force at N2LO [68].

At higher orders, the number of contributions to the NN force dramatically increases. In Figure 1 only a few representative diagrams are displayed. For instance, at N³LO more TPE contributions occur—in both delta-less and delta-full chiral EFT—involving leading two-loop and relativistic corrections. In addition, leading three-pion (3π) exchange contributions arise at this order but they are found to be negligible. The main feature at N³LO is the presence of additional contact interactions represented by the four-nucleon-leg with a solid diamond. Since these interactions are ~ p⁴, p^′4, they have a relevant impact up to the D waves. Their full operator structure will be discussed in the next section. Additional complicated 3N diagrams appear at N³LO, as well as the first contributions to four-nucleon forces (4N). We will not discuss these diagrams here and refer the reader to Bernard et al. [69, 70] and Epelbaum [71, 72]. For additional contributions at N⁴LO and N⁵LO, we refer the interested reader to Entem et al. [73], Epelbaum et al. [74], Reinert et al. [75], and Entem et al. [76].

An important aspect of nuclear interactions (and currents) in the basic model is that they suffer from ultraviolet (UV) divergences which need to be removed by a proper regularization and renormalization procedure. There are two sources of UV divergences that require regularization: first, UV divergences appear in loop corrections, and second when solving the Schrödinger or Lippmann-Schwinger equations or when calculating matrix elements involving nuclear currents. Loop divergences can be treated via dimensional regularization (DR) or spectral-function regularization (SFR), where the latter is implemented through the inclusion of a finite cutoff in the spectral functions. To cure divergences when solving the Schrödinger or Lippmann-Schwinger equations, the nuclear potential is multiplied by regulator functions that remove large-momentum contributions above a chosen cutoff scale. The regularization of the potential (and current) operators is followed by a renormalization procedure, i.e., dependencies on the regularization scheme and cutoff are reabsorbed, order by order, by the LECs entering the potential (and currents).

Nucleon-nucleon scattering has been extensively studied in chiral EFT in the past two decades following the pioneering work by Weinberg [37–39] and Ordonez et al. [58]. In particular, NN potentials at N³LO in the chiral expansion are available since the early 2000's [77, 78] and have served as a basis for numerous ab initio calculations of nuclear structure and reactions. Recently, accurate and precise chiral EFT potentials up to fifth order in the chiral expansion, i.e., N⁴LO, have been developed [73–76], and provide an extremely accurate description of NN data bases up to laboratory energies of 300 MeV with a χ² per datum close to one. These databases have been provided by the Nijmegen group [26, 29], the VPI/GWU group [79], and more recently the Granada group [80–82]. In the standard optimization procedure, the NN potentials are first constrained through fits to neutron-proton (np) and proton-proton (pp) phase shifts, and then refined by minimizing the total χ² obtained from a direct comparison with the NN scattering data. However, new optimization schemes are being explored in Carlsson et al. [83] and Ekström et al. [84]. For instance, the optimization strategy of the N2LO_sat interaction of Ekström et al. [84] is based on a simultaneous fit of the two- and three-nucleon forces to low-energy NN data, the deuteron binding energy, and binding energies and charge radii of hydrogen, helium, carbon, and oxygen isotopes using consistent NN and 3N interactions at N²LO. However, despite the good description of properties of ¹⁶O and ⁴⁰Ca, the NN component of this interaction shows deficiencies in reproducing the pp and np scattering data even at very low energy.

Three-nucleon forces and their impact on nuclear structure and reactions has become an important frontier in nuclear physics, see Kalantar-Nayestanaki et al. [85] and Hammer et al. [86] for review articles. As shown in Figure 1, chiral contributions to the 3N interaction have been derived up to N4LO in the chiral expansion [69, 70, 87–89]. However, few- and many-nucleon calculations are, with very few exceptions, still limited to chiral 3N forces at N²LO. At this order, as we have mentioned above, 3N forces are characterized by the presence of two unknown LECs that have to be determined. The two LECs—namely c_D in the OPE-contact and c_E in the 3N contact interaction– have been constrained either by fitting exclusively strong-interaction observables [90–93] or by relying on a combination of strong- and weak-interaction observables [94–96]. This last approach is made possible by the relation between c_D in the OPE-contact interaction and the LEC in the NN contact axial current [94, 95, Schiavilla, private communication], established in chiral EFT [97]. This connection allows one to use nuclear properties governed by either strong or weak interactions to constrain simultaneously the 3N interaction and NN axial current.

As chiral EFT is a low-momentum expansion of nuclear interactions, many of the chiral interactions available in the literature are formulated in momentum space and have the feature of being strongly non-local in coordinate space. This makes them not well-suited for certain numerical algorithms, for example QMC methods. In this context, an interaction is local if it depends solely on the momentum transfer q = p − p′, which Fourier transforms to dependencies on r. However, interactions in momentum-space can also depend on the momentum scale k = (p′ + p)/2, which Fourier transform to derivatives in coordinate space. These k dependencies, and thus non-localities, come about because of (i) the specific functional choice made to regularize the momentum space potentials in terms of the two momentum scales p and p′, and (ii) contact interactions that explicitly depend on k.

QMC methods, for example variational (VMC) and Green's Function Monte Carlo (GFMC) [10, 98] techniques, provide reliable solutions of the many-body Schrödinger equation—presently for up to A = 12 nucleons—with full account of the complexity of the many-body, spin- and isospin-dependent correlations induced by nuclear interactions. The sampling of configuration space in VMC and GFMC simulations gives access to many important properties of light nuclei, such as spectra, form factors, transitions, low-energy scattering, and response functions. Auxiliary Field Diffusion Monte Carlo (AFDMC) [10, 98] uses Monte Carlo techniques to additionally sample the spin-isospin degrees of freedom, enabling studies of, for example, nuclei up to A = 16 [99, 100] and neutron matter [90, 91, 101–103, Piarulli et al., private communication] that is so critical to determining the structure of neutron stars. QMC simulations have surely proved to be very valuable in attacking many nuclear-structure problems over the last three decades but require local chiral interactions as input. Therefore, there is a need to develop local chiral interactions for the use in QMC methods in order combine these accurate many-body methods with systematic nuclear interactions and to test to what extent the chiral EFT framework impacts our knowledge of few- and many-body systems.

3. Local Hamiltonians

3.1. Local Two-Nucleon Interactions

A major thrust of our work is based on the theoretical derivation, optimization, and implementation of chiral interactions suitable for QMC methods. In recent years, local configuration-space chiral NN interactions have been derived by two groups [104–107]. In this section, we will introduce these two families of interactions, that are either derived in the delta-less [104, 105] or delta-full [106, 107] approach. We begin by introducing general features of both approaches and then describe the specifics. We will be stating general considerations in momentum-space, where q dependencies indicate local parts of interactions and k dependencies indicate non-localities, and then switch to coordinate-space where interactions are local if they only depend on the relative distance r = r_i − r_j. Fourier transformations connect interactions in momentum- and coordinate-space, with q and r being associated variables, while k leads to appearances of gradient terms.

As discussed before, nuclear interactions can generally be separated into different interaction channels depending on their operator structure. Obviously, chiral interactions can also be separated into long-range physics, mediated by pion-exchange interactions, and short-range physics, which is described by a set of operators consistent with all symmetries and accompanied by LECs adjusted to reproduce experimental data:

$\begin{array}{ll}V(\text{q},\text{k})=V_{\text{cont}}(\text{q},\text{k})+V_{\pi }(\text{q},\text{k}).& (4)\end{array}$

Each of these components can then be expanded in chiral order ν as discussed before:

$\begin{array}{ll}{V}_i={\displaystyle \sum _{\nu }}{V}_i^{(\nu )}=V_i^{(0)}+V_i^{(2)}+V_i^{(3)}+V_i^{(4)}+\dots .& (5)\end{array}$

At LO, ν = 0, both delta-less and delta-full chiral EFT have the same operator structure. At this order, only the leading contact interactions as well as the one-pion exchange (OPE) interaction contribute (see Figure 1). Generally, pion-exchange interaction can be written as

$\begin{array}{l}{V}_{\pi }=V_{C,\pi }+{\mathit{\tau }}_i·{\mathit{\tau }}_j{W}_C+(V_S+{\mathit{\tau }}_i·{\mathit{\tau }}_j{W}_S){\mathit{\sigma }}_i·{\mathit{\sigma }}_j\\ +(V_T+{\mathit{\tau }}_i·{\mathit{\tau }}_j{W}_T){\mathit{\sigma }}_i·\text{q }{\mathit{\sigma }}_j·\text{q}\\ +(V_{LS}+{\mathit{\tau }}_i·{\mathit{\tau }}_j{W}_{LS})i({\mathit{\sigma }}_i+{\mathit{\sigma }}_j)·\text{q}\times \text{k}\\ +(V_{\sigma L}+{\mathit{\tau }}_i·{\mathit{\tau }}_j{W}_{\sigma L}){\mathit{\sigma }}_i·\text{q}\times \text{k }{\mathit{\sigma }}_j·\text{q}\times \text{k},& (6)\end{array}$

with central, spin, tensor, spin-orbit and quadratic spin-orbit components, respectively. In the local chiral interactions discussed in this review, the spin-orbit and quadratic spin-orbit terms are not included as they are of higher order. The one-pion exchange interaction is given in momentum space as

$\begin{array}{ll}{V}_{\text{OPE}}^{(0)}(\text{q})=-\frac{g_A^2}{4f_{\pi }^2}\frac{{\mathit{\sigma }}_i·\text{q}{\mathit{\sigma }}_j·\mathbf{\text{q}}}{q^2+m_{\pi }^2}{\mathit{\tau }}_i·{\mathit{\tau }}_j,& (7)\end{array}$

where g_A, f_π = 92.4 MeV, and m_π denote the axial-vector coupling constant of the nucleon, the pion decay constant, and the pion mass, respectively. As a consequence, the OPE contributes to the W_T channel.

Including isospin-symmetry breaking effects induced by the mass difference between charged and neutral pions, the OPE interaction can be rewritten as

$\begin{array}{l}{V}_{\text{OPE}}^{(0)}(\text{q})=\left[v_{\sigma \tau }^{\pi ,\text{LO}}(q){\mathit{\sigma }}_i·{\mathit{\sigma }}_j+v_{t\tau }^{\pi ,\text{LO}}(q)S_{ij}(\text{q})\right]{\mathit{\tau }}_i·{\mathit{\tau }}_j\\ +\left[v_{\sigma T}^{\pi ,\text{LO}}(q){\mathit{\sigma }}_i·{\mathit{\sigma }}_j+v_{tT}^{\pi ,\text{LO}}(q)S_{ij}(\text{q})\right]T_{ij},& (8)\end{array}$

with the tensor operator S_ij(q) in momentum space, $S_{ij}(\text{q})=3{\mathit{\sigma }}_i·\text{q }{\mathit{\sigma }}_j·\text{q}-q^2{\mathit{\sigma }}_i·{\mathit{\sigma }}_j$, and the isotensor operator T_ij = 3τ_izτ_jz − τ_i · τ_j. Hence, when including isospin-symmetry breaking, the OPE adds to the W_S and W_T parts of Equation (6). The functions, $v_{\sigma \tau }^{\pi ,\text{LO}}(q)$, $v_{t\tau }^{\pi ,\text{LO}}(q)$, $v_{\sigma T}^{\pi ,\text{LO}}(q)$, and $v_{tT}^{\pi ,\text{LO}}(q)$ are defined as

$\begin{array}{l}{v}_{\sigma \tau }^{\pi ,\text{LO}}(q)=\frac{Y_0(q)+2Y_{+}(q)}{3},v_{t\tau }^{\pi ,\text{LO}}(q)=\frac{T_0(q)+2T_{+}(q)}{3},\\ v_{\sigma T}^{\pi ,\text{LO}}(q)=\frac{Y_0(q)-Y_{+}(q)}{3},v_{tT}^{\pi ,\text{LO}}(q)=\frac{T_0(q)-T_{+}(q)}{3},& (9)\end{array}$

with Y_α(q) and T_α(q) given by

$\begin{array}{ll}{Y}_{\alpha }(q)=-\frac{g_A^2}{3{(2f_{\pi })}^2}\frac{q^2}{q^2+m_{{\pi }_{\alpha }}^2},T_{\alpha }(q)=-\frac{g_A^2}{3{(2f_{\pi })}^2}\frac{1}{q^2+m_{{\pi }_{\alpha }}^2}.& (10)\end{array}$

Here, m_πα denotes the neutral (m_π0) and charged (m_π±) pion masses. When Fourier-transformed, the coordinate-space OPE is given by

$\begin{array}{l}{v}^{\pi ,\text{LO}}(\text{r})=\left[v_{\sigma \tau }^{\pi ,\text{LO}}(r){\mathit{\sigma }}_i·{\mathit{\sigma }}_j+v_{t\mathit{\tau }}^{\pi ,\text{LO}}(r)S_{ij}(\text{r})\right]{\mathit{\tau }}_i·{\mathit{\tau }}_j\\ +\left[v_{\sigma T}^{\pi ,\text{LO}}(r){\mathit{\sigma }}_i·{\mathit{\sigma }}_j+v_{tT}^{\pi ,\text{LO}}(r)S_{ij}\right]T_{ij}& (11)\end{array}$

where the individual functions can be obtained from Equation (9) with q → r and with the functions Y_α(r) and T_α(r) given by

$\begin{array}{ll}{Y}_{\alpha }(r)=\frac{g_A^2}{12\pi }\frac{m_{{\pi }_{\alpha }}^3}{{(2f_{\pi })}^2}\frac{e^{-x_{\alpha }}}{x_{\alpha }},T_{\alpha }(r)=Y_{\alpha }(r)\left(1+\frac{3}{x_{\alpha }}+\frac{3}{x_{\alpha }^2}\right).& (12)\end{array}$

Here, x_α = m_παr. Note that Equation (11) only holds in the case r > 0. In addition, upon Fourier transformation a δ-function appears, which has been dropped from Equation (11), because it can be reabsorbed in the short-range contact terms at LO, which we will discuss next.

The LO contact interactions are momentum-independent and can be described by the most general operator set allowed by all symmetries:

$\begin{array}{r}{V}_{\text{cont}}^{\text{LO}}(\text{q},\text{k})=V_{\text{cont}}^{\text{LO}}={\alpha }_1\mathbb{1}+{\alpha }_2{\mathit{\sigma }}_i·{\mathit{\sigma }}_j+{\alpha }_3{\mathit{\tau }}_i·{\mathit{\tau }}_j\\ +{\alpha }_4{\mathit{\sigma }}_i·{\mathit{\sigma }}_j{\mathit{\tau }}_i·{\mathit{\tau }}_j.& (13)\end{array}$

As these terms describe the interactions of nucleons, i.e., fermions, these interactions are used between anti-symmetrized wave functions. One can define the anti-symmetrized interaction $V_{\mathrm{\text{as}}}=1/2(V-{A}\left[V\right])$ by applying the anti-symmetrizer, given by

$\begin{array}{l}{A}\left[V(\text{q},\text{k})\right]=\frac{1}{4}(1+{\mathit{\sigma }}_i·{\mathit{\sigma }}_j)(1+{\mathit{\tau }}_i·{\mathit{\tau }}_j)\\ \times V\left(\text{q}\to -2\text{k},\text{k}\to -\frac{1}{2}\text{q}\right).& (14)\end{array}$

One then finds

$\begin{array}{l}{V}_{\text{cont,as}}^{\left(0\right)}=\frac{1}{2}\left(1-\frac{1}{4}(1+{\mathit{\sigma }}_i·{\mathit{\sigma }}_j)(1+{\mathit{\tau }}_i·{\mathit{\tau }}_j)\right)V_{\text{cont}}^{\left(0\right)}\\ =\left(\frac{3}{8}{\alpha }_1-\frac{3}{8}{\alpha }_2-\frac{3}{8}{\alpha }_3-\frac{9}{8}{\alpha }_4\right)\\ +\left(-\frac{1}{8}{\alpha }_1+\frac{5}{8}{\alpha }_2-\frac{3}{8}{\alpha }_3+\frac{3}{8}{\alpha }_4\right){\mathit{\sigma }}_i·{\mathit{\sigma }}_j\\ +\left(-\frac{1}{8}{\alpha }_1-\frac{3}{8}{\alpha }_2+\frac{5}{8}{\alpha }_3+\frac{3}{8}{\alpha }_4\right){\mathit{\tau }}_i·{\mathit{\tau }}_j\\ +\left(-\frac{1}{8}{\alpha }_1+\frac{1}{8}{\alpha }_2+\frac{1}{8}{\alpha }_3+\frac{3}{8}{\alpha }_4\right){\mathit{\sigma }}_i·{\mathit{\sigma }}_j{\mathit{\tau }}_i·{\mathit{\tau }}_j\\ ={\tilde{C}}_S+{\tilde{C}}_T{\mathit{\sigma }}_i·{\mathit{\sigma }}_j+\left(-\frac{2}{3}{\tilde{C}}_S-{\tilde{C}}_T\right){\mathit{\tau }}_i·{\mathit{\tau }}_j\\ +\left(-\frac{1}{3}{\tilde{C}}_S\right){\mathit{\sigma }}_i·{\mathit{\sigma }}_j{\mathit{\tau }}_i·{\mathit{\tau }}_j.& (15)\end{array}$

It follows immediately that only two out of these four couplings are linearly independent, describing the two possible S-wave scattering channels. The two commonly chosen LO contact operators are

$\begin{array}{ll}{V}_{\text{cont}}^{(0)}=C_S+C_T{\mathit{\sigma }}_i·{\mathit{\sigma }}_j,& (16)\end{array}$

but in principle any different two of the four contact interactions can be chosen and lead to the same physical description for fermionic systems. This is analogous to Fierz ambiguities and in the following we will call this freedom to choose operators Fierz rearrangement freedom.

Additionally, there are isospin breaking corrections to the LO contact interactions that have to be taken into account. These are due to different masses of u and d quarks, and account for differences in neutron-neutron (nn), np, and pp S-wave scattering lengths:

$\begin{array}{ll}{V}_{\text{cont},\text{ CIB}}(\text{r})=C_{\text{CIB}}\frac{1+4{\mathit{\tau }}_i^3{\mathit{\tau }}_j^3}{2}\frac{1-{\mathit{\sigma }}_i·{\mathit{\sigma }}_k}{4},& (17)\end{array}$

$\begin{array}{ll}{V}_{\text{cont},\text{ CSB}}(\text{r})=C_{\text{CSB}}({\mathit{\tau }}_i^3+{\mathit{\tau }}_j^3)\frac{1-{\mathit{\sigma }}_i·{\mathit{\sigma }}_k}{4}.& (18)\end{array}$

At higher orders, the description of the potential changes depending on the choice of delta-less or delta-full approach. In the following, we will describe both approaches as pursued by individual research groups.

3.1.1. Without Delta Isobars

At NLO in chiral EFT, additional momentum-dependent contact interactions as well as TPE interactions appear. For the TPE, we give the expressions within the spectral-function representation (SFR) as detailed in Epelbaum et al. [108], with spectral functions ρ_i and η_i:

$\begin{array}{ll}{V}_{C,\pi }(r)=\frac{1}{2{\pi }^{2}r}{\displaystyle {\int }_{2M_{\pi }}^{\tilde{\Lambda }}}d\mu \mu e^{-\mu r}{\rho }_C(\mu ),& (19)\end{array}$

$\begin{array}{ll}{V}_S(r)=-\frac{1}{6{\pi }^{2}r}{\displaystyle {\int }_{2M_{\pi }}^{\tilde{\Lambda }}}d\mu \mu e^{-\mu r}\left({\mu }^2{\rho }_T(\mu )-3{\rho }_S(\mu )\right),& (20)\end{array}$

$\begin{array}{ll}{V}_T(r)=-\frac{1}{6{\pi }^2{r}^3}{\displaystyle {\int }_{2M_{\pi }}^{\tilde{\Lambda }}}d\mu \mu e^{-\mu r}{\rho }_T(\mu )(3+3\mu r+{\mu }^2{r}^2).& (21)\end{array}$

Here, $\tilde{\Lambda }$ is the SFR cutoff. Similar expressions are valid for W_C, W_S, and W_T in terms of η_C, η_S, and η_T. The TPE spectral functions at NLO are given by Kaiser et al. [109]

$\begin{array}{ll}{\rho }_T^{(2)}(\mu )=\frac{1}{{\mu }^2}{\rho }_S^{(2)}(\mu )=\frac{3g_A^4}{128\pi f_{\pi }^4}\frac{\sqrt{{\mu }^2-4m_{\pi }^2}}{\mu },& (22)\end{array}$

$\begin{array}{l}{\eta }_C^{(2)}(\mu )=\frac{1}{768\pi f_{\pi }^4}\frac{\sqrt{{\mu }^2-4m_{\pi }^2}}{\mu }(4m_{\pi }^2(5g_A^4-4g_A^2-1)\\ -{\mu }^2(23g_A^4-10g_A^2-1)+\frac{48g_A^4{m}_{\pi }^4}{4m_{\pi }^2-{\mu }^2}).& (23)\end{array}$

For the NLO contact interactions, the most general set of operators is given by

$\begin{array}{l}{V}_{\text{cont}}^{\text{NLO}}(\text{q},\text{k})={\gamma }_1{q}^2+{\gamma }_2{q}^2{\mathit{\sigma }}_i·{\mathit{\sigma }}_j+{\gamma }_3{q}^2{\mathit{\tau }}_i·{\mathit{\tau }}_j+{\gamma }_4{q}^2{\mathit{\sigma }}_i·{\mathit{\sigma }}_j{\mathit{\tau }}_i·{\mathit{\tau }}_j\\ +{\gamma }_5{k}^2+{\gamma }_6{k}^2{\mathit{\sigma }}_i·{\mathit{\sigma }}_j+{\gamma }_7{k}^2{\mathit{\tau }}_i·{\mathit{\tau }}_j+{\gamma }_8{k}^2{\mathit{\sigma }}_i·{\mathit{\sigma }}_j{\mathit{\tau }}_i·{\mathit{\tau }}_j\\ +{\gamma }_9({\mathit{\sigma }}_i+{\mathit{\sigma }}_j)(\text{q }\times \text{ k})+{\gamma }_{10}({\mathit{\sigma }}_i+{\mathit{\sigma }}_j)(\text{q }\times \text{ k}){\mathit{\tau }}_i·{\mathit{\tau }}_j\\ +{\gamma }_{11}({\mathit{\sigma }}_i·\text{q})({\mathit{\sigma }}_j·\text{q})+{\gamma }_{12}({\mathit{\sigma }}_i·\text{q})({\mathit{\sigma }}_j·\text{q}){\mathit{\tau }}_i·{\mathit{\tau }}_j\\ +{\gamma }_{13}({\mathit{\sigma }}_i·\text{k})({\mathit{\sigma }}_j·\text{k})+{\gamma }_{14}({\mathit{\sigma }}_i·\text{k})({\mathit{\sigma }}_j·\text{k}){\mathit{\tau }}_i·{\mathit{\tau }}_j.& (24)\end{array}$

Using the same arguments as for the LO contact interactions, only 7 out of these 14 operators are linearly independent. To construct local interactions, one typically chooses the 6 local operators (proportional to γ₁-γ₄, γ₁₁, and γ₁₂) as well as the spin-orbit operator (proportional to γ₉):

$\begin{array}{l}{V}_{\text{cont}}^{(2)}=C_1{q}^2+C_2{q}^2{\mathit{\tau }}_i·{\mathit{\tau }}_j+\left(C_3{q}^2+C_4{q}^2{\mathit{\tau }}_i·{\mathit{\tau }}_j\right){\mathit{\sigma }}_i·{\mathit{\sigma }}_j+\\ +i\frac{C_5}{2}({\mathit{\sigma }}_i{\mathit{\sigma }}_j)·(\text{q }\times \text{ k})+C_6({\mathit{\sigma }}_i·\text{q})({\mathit{\sigma }}_j·\text{q})\\ +C_7({\mathit{\sigma }}_i·\text{q})({\mathit{\sigma }}_j·\text{q}){\mathit{\tau }}_i·{\mathit{\tau }}_j.& (25)\end{array}$

In coordinate space, this translates to

$\begin{array}{l}{V}_{\text{cont}}^{(2)}(\text{r})=-(C_1+C_2{\mathit{\tau }}_i·{\mathit{\tau }}_j)\Delta \delta (\text{r})-(C_3+C_4{\mathit{\tau }}_i·{\mathit{\tau }}_j){\mathit{\sigma }}_i·{\mathit{\sigma }}_j\Delta \delta (\text{r})\\ +\frac{C_5}{2}\frac{{\partial }_r\delta (\text{r})}{r}\text{L}·\text{S}+(C_6+C_7{\mathit{\tau }}_i·{\mathit{\tau }}_j)\\ \times \left[({\mathit{\sigma }}_i·\widehat{\text{r}})({\mathit{\sigma }}_j·\widehat{\text{r}})\left(\frac{{\partial }_r\delta (\text{r})}{r}-{\partial }_r^2\delta (\text{r})\right)-{\mathit{\sigma }}_i·{\mathit{\sigma }}_j\frac{{\partial }_r\delta (\text{r})}{r}\right].& (26)\end{array}$

At N²LO, the subleading TPE interactions appear. The spectral functions for these at N²LO read

$\begin{array}{ll}{\rho }_C^{(3)}(\mu )=-\frac{3g_A^2}{64\mu f_{\pi }^4}(2m_{\pi }^2-{\mu }^2)(2m_{\pi }^2(2c_1-c_3)+c_3{\mu }^2),& (27)\end{array}$

$\begin{array}{ll}{\eta }_T^{(3)}(\mu )=\frac{1}{{\mu }^2}{\eta }_S^{(3)}(\mu )=-\frac{g_A^2}{128\mu f_{\pi }^4}{c}_4(4m_{\pi }^2-{\mu }^2),& (28)\end{array}$

where the c_i denote the previously mentioned LECs of the subleading pion-nucleon vertices. For the N²LO TPE, one can solve Equations (19–21):

$\begin{array}{l}{W}_S^{(3)}(r)=\frac{g_A^2}{48{\pi }^2{f}_{\pi }^4}\frac{e^{-2x}}{r^6}{c}_4(1+x)(3+3x+2x^2)\\ -\frac{g_A^2}{384{\pi }^2{f}_{\pi }^4}\frac{e^{-y}}{r^6}{c}_4(24+24y+12y^2+4y^3+y^4\\ -4x^2(2+2y+y^2)),& (29)\end{array}$

$\begin{array}{l}{W}_T^{(3)}(r)=-\frac{g_A^2}{48{\pi }^2{f}_{\pi }^4}\frac{e^{-2x}}{r^6}{c}_4(1+x)(3+3x+x^2)\\ +\frac{g_A^2}{768{\pi }^2{f}_{\pi }^4}\frac{e^{-y}}{r^6}{c}_4(48+48y+24y^2+7y^3+y^4\hfill \\ -4x^2(8+5y+y^2)),\hfill & (30)\end{array}$

and

$\begin{array}{l}{V}_{C,\pi }^{(3)}(r)=\frac{3g_A^2}{32{\pi }^2{f}_{\pi }^4}\frac{e^{-2x}}{r^6}[2c_1{x}^2{(1+x)}^2+c_3(6+12x+10x^2\\ +4x^3+x^4)]-\frac{3g_A^2}{128{\pi }^2{f}_{\pi }^4}\frac{e^{-y}}{r^6}\left[4c_1{x}^2\right(2+y(2+y)-2x^2)\\ +c_3(24+y(24+12y+4y^2+y^3)-4x^2(2+2y\\ +y^2)+4x^4)],& (31)\end{array}$

where x ≡ m_πr and $y\equiv \tilde{\Lambda }r$.

The relativistic 1/m_N corrections, with m_N being the nucleon mass, have been omitted here since, in the counting employed here, they would appear at N³LO, provided the nucleon mass is counted according to $Q/m_N~Q^2/{\Lambda }_b^2$ as suggested in Weinberg [38].

The delta-less chiral EFT approach has been used to construct local interactions up to N²LO. At next higher order, N³LO, contact interactions cannot be written down in a purely local fashion, as only 8 out of 30 possible operators are local. A possible way forward is the definition of “maximally local” N³LO potentials, which has been pursued in the delta-full approach and will be discussed in the next section.

Finally, it is necessary to specify a regulator scheme. For the delta-less local interactions of Gezerlis et al. [104, 105], the following long- and short-range regulators are used:

$\begin{array}{ll}{f}_{\text{long}}(r)={\left(1-e^{-{\left(\frac{r}{R_0}\right)}^{n_1}}\right)}^{n_2},f_{\text{short}}(r)=\frac{n}{4\pi R_0^3\Gamma \left(\frac{3}{n}\right)}{e}^{-{\left(\frac{r}{R_0}\right)}^n}.& (32)\end{array}$

The long-range regulator multiplies each function Y(r), while the short-range regulator replaces all δ functions. The regulator functions depend on the cutoff scale R₀, that determines how long- and short-range physics are separated. For a smaller cutoff R₀ (i.e., for a larger momentum-space cutoff), the interactions is probed at shorter distances, and typically shows stronger short-range repulsion. We show the delta-less local chiral interactions in the ¹S₀ channel in Figure 2 for different values of the cutoff. Introducing a local regulator function leads to the appearance of regulator artifacts that brake Fierz-rearrangement freedom. We will address this topic in detail in section 4.1.

FIGURE 2

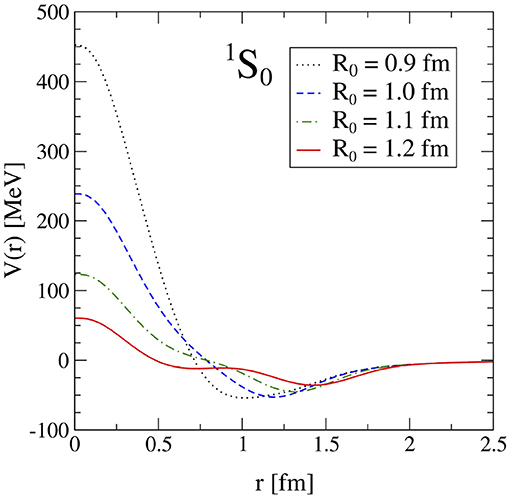
Figure 2. Local delta-less chiral potential in the ¹S₀ partial wave at N²LO. The smaller the coordinate-space cutoff R₀, the smaller is the short-range repulsive core. Figure taken from Gezerlis et al. [105] under the Creative Commons CCBY license.

3.1.2. With Delta Isobars

In the delta-full local chiral interactions, coordinate-space expressions for the TPE terms at NLO and N²LO are obtained by using the spectral function representation [108, 109] but with dimensional regularization (DR) [59]. This implies taking the cutoff $\tilde{\Lambda }$ in Equations (19–21) to infinity ($\tilde{\Lambda }\to \infty$). Consequently, the terms depending on the variable y in Equations (29–31) vanish. For the relevant radial functions involved in the one- and two-delta diagrams up to N²LO, we refer the interested reader to Appendix A (Supplementary Material). The singularities at the origin of the OPE and TPE components are regularized by cutoff functions of the form

$\begin{array}{ll}{f}_{\text{long}}^{\Delta }(r)=1-\frac{1}{{(r/R_{\text{L}})}^6{e}^{(r-R_{\text{L}})/a_{\text{L}}}+1},& (33)\end{array}$

where three values for the radius R_L are considered: R_L = (0.8, 1.0, 1.2) fm with the diffuseness a_L fixed at a_L = R_L/2 in each case.

Another difference between the delta-less and delta-full coordinate-space interactions lies in the operator structure of their short-range components. In the delta-full potentials, selected contact terms at N³LO are also retained in addition to the LO and NLO contributions given in Equations (16) and (26). The contact potential at order N3LO, $V_{\text{cont}}^{\text{N}3\text{LO}}(q,k)$, which involves four gradients acting on the nucleon fields, is expressed in terms of 15 independent operators [41] after considering the Fierz rearrangement freedom. Its standard parametrization, adopted in momentum-space potentials, is given by

$\begin{array}{l}{V}_{\text{cont}}^{\text{N3LO}}(q,k)={\tilde{D}}_1{q}^4+{\tilde{D}}_2{k}^4+{\tilde{D}}_3{q}^2{k}^2+{\tilde{D}}_4{\left(k\times q\right)}^2\\ +[{\tilde{D}}_5{q}^4+{\tilde{D}}_6{k}^4+{\tilde{D}}_7{q}^2{k}^2\\ +{\tilde{D}}_8{\left(k\times q\right)}^2]{\mathit{\sigma }}_i·{\mathit{\sigma }}_j+i({\tilde{D}}_9{q}^2+{\tilde{D}}_{10}{k}^2)S·\left(k\times q\right)\\ +({\tilde{D}}_{11}{q}^2+{\tilde{D}}_{12}{k}^2)S_{ij}(k)+({\tilde{D}}_{13}{q}^2+{\tilde{D}}_{14}{k}^2)S_{ij}(k)\\ +{\tilde{D}}_{15}[{\mathit{\sigma }}_i·(k\times q){\mathit{\sigma }}_j·(k\times q)].& (34)\end{array}$

However terms proportional to k² and k⁴ in those expressions, upon Fourier transformation, would lead to gradient operators in coordinate-space (p → −i∇ is the relative momentum operator), making the NN potential strongly non-local.

The number of non-localities can be reduced by reconsidering the Fierz rearrangement freedom. However, some of these non-local terms still persist at N³LO leading to the definition of “minimally non-local” contact interactions:

$\begin{array}{l}{V}_{\text{cont}}^{\text{N}3\text{LO}}(q,k)=D_1{q}^4+D_2{q}^4{\mathit{\tau }}_i·{\mathit{\tau }}_j+D_3{q}^4{\mathit{\sigma }}_i·{\mathit{\sigma }}_j+D_4{q}^4{\mathit{\sigma }}_i·{\mathit{\sigma }}_j{\mathit{\tau }}_i·{\mathit{\tau }}_j\\ +D_5{q}^2{S}_{ij}(\text{q})+D_6{q}^2{S}_{ij}(\text{q}){\mathit{\tau }}_i·{\mathit{\tau }}_j+i{D}_7{q}^2\text{S}·\left(\text{k }\times \text{ q}\right)\\ +i{D}_8{q}^2\text{S}·\left(\text{k }\times \text{ q}\right){\mathit{\tau }}_i·{\mathit{\tau }}_j+D_9{\left[\text{S}·\left(\text{k }\times \text{ q}\right)\right]}^2+D_{10}{\left(\text{k }\times \text{ q}\right)}^2\\ +D_{11}{\left(\text{k }\times \text{ q}\right)}^2{\mathit{\sigma }}_i·{\mathit{\sigma }}_j+D_{12}{q}^2{k}^2+D_{13}{q}^2{k}^2{\mathit{\sigma }}_i·{\mathit{\sigma }}_j\\ +D_{14}{k}^2{S}_{ij}(\text{q})+D_{15}{k}^2{S}_{ij}(\text{q}){\mathit{\tau }}_i·{\mathit{\tau }}_j.& (35)\end{array}$

In coordinate space, this reads as

$\begin{array}{l}{V}_{\text{cont}}^{(3)}(r)=\left[{\displaystyle \sum _{l=1}^{11}{v}_{\text{S}}^l}(r)O_{ij}^l\right]+\{v_{\text{S}}^p(r)+v_{\text{S}}^{p\sigma }(r){\mathit{\sigma }}_i·{\mathit{\sigma }}_j\\ +v_{\text{S}}^{pt}(r)S_{ij}(r)+v_{\text{S}}^{pt\tau }(r)S_{ij}(r){\mathit{\tau }}_i·{\mathit{\tau }}_j,p^2\},\hfill & (36)\end{array}$

where

$\begin{array}{l}{O}_{ij}^{l=1,\dots ,11}=\{1,{\mathit{\tau }}_i·{\mathit{\tau }}_j,{\mathit{\sigma }}_i·{\mathit{\sigma }}_j,{\mathit{\sigma }}_i·{\mathit{\sigma }}_j{\mathit{\tau }}_i·{\mathit{\tau }}_j,S_{ij},S_{ij}{\mathit{\tau }}_i·{\mathit{\tau }}_j,\\ L·S,L·S{\mathit{\tau }}_i·{\mathit{\tau }}_j,{(L·S)}^2,L^2,L^2{\mathit{\sigma }}_i·{\mathit{\sigma }}_j\},& (37)\end{array}$

referred to as c, τ, σ, στ, t, tτ for the first six operators, and b, bτ, bb, q, qσ for the remaining five operators. The four additional terms, denoted as p, pσ, pt, and ptτ, in the anti-commutator of Equation (36) are p²-dependent. For the definition of the radial functions $v_{\text{S}}^l(r)$ as well as those multiplying the p²-terms, we refer the reader to Appendix A.

A comment is now in order. The strict adherence to power counting would require the inclusion of additional one-loop as well as two-loop TPE and three-pion exchange contributions at N³LO. For the time being, these contributions have been neglected, since part of their strength is promoted at lower orders due to the inclusion of the Δ resonance, and some of the remaining diagrams are also known to be small (see e.g., [41]). Furthermore, it is the D_i LEC's at N³LO that are critical for a good reproduction of phase shifts in lower partial waves, particularly D-waves, and a good fit to the NN database. However, the consistency between the long- and short-range part at higher orders in the delta-full chiral EFT is work in progress.

The local versions of these “minimally non-local” NN potentials have been defined by dropping the terms proportional to p² in the anti-commutator when the optimization procedure for estimating the LECs is carried out [107]. In Piarulli et al. [107] we observed that the inclusion of the p²-dependent terms would have improved the fits to the database in the laboratory energy range up to 200 MeV only marginally. However, apart from the small improvement that the p²-dependent terms would bring to the total χ² in the fit to the NN scattering data, the effect of these terms on nuclear observables has not been studied.

Lastly, the delta-full local interactions contain additional isospin breaking terms at NLO. They are parameterized by the following operators

$\begin{array}{ll}{O}_{ij}^{l=12,\dots ,16}=\{{\tau }_i^z+{\tau }_j^z,T_{ij},{\mathit{\sigma }}_i·{\mathit{\sigma }}_j{T}_{ij},S_{ij}{T}_{ij},\text{L}·\text{S }{T}_{ij}\},& (38)\end{array}$

referred to as τz, T, σT, tT, bT. The radial functions multiplying these operators are also reported in Appendix A.

The short-range part of these potentials involve the local regulator given in Equation (32) with n = 2,

$\begin{array}{ll}{f}_{\text{short}}^{\Delta }(r)=\frac{1}{{\pi }^{3/2}{R}_{\text{S}}^3}{e}^{-{(r/R_{\text{S}})}^2},& (39)\end{array}$

where we consider, in combination with R_L = (0.8, 1.0, 1.2) fm, R_S = (0.6, 0.7, 0.8) fm, corresponding to typical momentum-space cutoffs Λ_S = 2/R_S ranging from about 660 MeV down to 500 MeV. Hereafter, we will denote the potential with cutoffs (R_L, R_S) = (1.2, 0.8) fm as model a, that with (1.0, 0.7) fm as model b, and that with (0.8, 0.6) fm as model c.

There are 26 LECs in the definition of the delta-full local interactions. Of these, 20 LECs describe the charge-independent part of the interaction: 2 at LO (Q⁰), 7 at NLO (Q²), and 11 at N³LO (Q⁴). The remaining 6 LECs describe its charge-dependent part: 2 at LO (one each from CIB and CSB), and 4 at NLO from CIB. The optimization procedure to fix these 26 LECs uses pp and np scattering data (including normalizations), as assembled in the Granada database [80], the NN scattering length, and the deuteron binding energy. The minimization of the χ² objective function with respect to the LECs is carried out with the Practical Optimization Using no Derivatives (for Squares) routine, POUNDerS [110]. For each of three different sets of cutoff radii (R_S, R_L), two classes of local interactions have been developed, which only differ in the range of laboratory energy over which the fits were carried out, either 0–125 MeV in class I or 0–200 MeV in class II. The χ²/datum achieved by the fits in class I (II) was ≲ 1.1(≲ 1.4) for a total of about 2,700 (3,700) data points. In the literature, we are referring to these NN interactions generically as the Norfolk potentials (NV2s), and designate those in class I as NV2-Ia, NV2-Ib, and NV2-Ic, and those in class II as NV2-IIa, NV2-IIb, and NV2-IIc.

The NV2 interactions were found to provide insufficient attraction in calculations of the ground-state energies of nuclei with A = 3–6 [107]. To remedy this and similar shortcomings, 3N interactions at N²LO have to be included in both approaches. This will be described in the next section.

3.2. Local Three-Nucleon Interactions

Three-nucleon forces are very important ingredients for the correct description of physical systems. They naturally appear within chiral EFT and are consistent with the NN sector. The exact description of the 3N interactions depends on the choice of delta-less vs. delta-full approach. In the following, we review 3N forces in both approaches.

3.2.1. Without Delta Isobars

In the delta-less chiral EFT approach, the leading 3N contributions appear at N²LO in the power counting. They an be separated into three topologies: (i) a long-range TPE interaction named V_C depending on the pion-nucleon LECs c₁, c₃, and c₄, that already appear in the NN sector, (ii) a one-pion-exchange–contact interaction V_D dependent on a new LEC c_D, and (iii) a 3N contact interaction V_E dependent in a new LEC c_E. The LECs c_D and c_E solely describe 3N physics and need to be adjusted to properties of A ≥ 3 systems. In momentum space, these interactions are defined as

$\begin{array}{ll}{V}_C=\frac{1}{2}{\left(\frac{g_A}{2f_{\pi }}\right)}^2{\displaystyle \sum _{\pi (ijk)}}\frac{{\mathit{\sigma }}_i·{\mathbf{\text{q}}}_i{\mathit{\sigma }}_k·{\mathbf{\text{q}}}_k}{(q_i^2+m_{\pi }^2)(q_k^2+m_{\pi }^2)}{F}_{ijk}^{\alpha \beta }{\mathit{\tau }}_i^{\alpha }{\mathit{\tau }}_k^{\beta },& (40)\end{array}$

$\begin{array}{ll}{V}_D=-\frac{g_A}{8f_{\pi }^2}\frac{c_D}{f_{\pi }^2{\Lambda }_{\chi }}{\displaystyle \sum _{\pi (ijk)}}\frac{{\mathit{\sigma }}_k·{\mathbf{\text{q}}}_k}{q_k^2+m_{\pi }^2}{\mathit{\sigma }}_i·{\mathbf{\text{q}}}_k{\mathit{\tau }}_i·{\mathit{\tau }}_k,& (41)\end{array}$

$\begin{array}{ll}{V}_E=\frac{c_E}{2f_{\pi }^4{\Lambda }_{\chi }}{\displaystyle \sum _{\pi (ijk)}}{\mathit{\tau }}_i·{\mathit{\tau }}_k,& (42)\end{array}$

where we sum over all permutations of the particles i, j, and k, where the first pion carries a momentum q_i from nucleon i to j, while the second pion carries q_k from j to k, and where $F_{ijk}^{\alpha \beta }$ is given by

$\begin{array}{l}{F}_{ijk}^{\alpha \beta }={\delta }^{\alpha \beta }\left[-\frac{4c_1{m}_{\pi }^2}{f_{\pi }^2}+\frac{2c_3}{f_{\pi }^2}{\mathbf{\text{q}}}_i·{\mathbf{\text{q}}}_k\right]\\ +{\displaystyle \sum _{\gamma }}\frac{c_4}{f_{\pi }^2}{\epsilon }^{\alpha \beta \gamma }{\mathit{\tau }}_j^{\gamma }{\mathit{\sigma }}_j·({\mathbf{\text{q}}}_i\times {\mathbf{\text{q}}}_k).& (43)\end{array}$

As one can easily see, all of these interactions are local, as long as local regulator functions are applied. To obtain expressions in coordinate space, these interactions have to be Fourier transformed. For the part of V_C proportional to c₁, we find

$\begin{array}{l}{V}_{C,c_1}^{ijk}=-\frac{c_1{m}_{\pi }^2{g}_A^2}{2f_{\pi }^4}{\displaystyle {\displaystyle \sum }_{\pi (ijk)}}{\mathit{\tau }}_i·{\mathit{\tau }}_k{\displaystyle \int }\frac{d^3{q}_i}{{(2\pi )}^3}\frac{{\mathit{\sigma }}_i·{\text{q}}_i}{q_i^2+m_{\pi }^2}{e}^{i{\text{q}}_i·{\text{r}}_{ij}}\\ {\displaystyle \int }\frac{d^3{q}_k}{{(2\pi )}^3}\frac{{\mathit{\sigma }}_k·{\text{q}}_k}{q_k^2+m_{\pi }^2}{e}^{i{\text{q}}_k·{\text{r}}_{kj}}.& (44)\end{array}$

This results in

$\begin{array}{l}{V}_{C,c_1}^{ijk}\\ =\frac{c_1{m}_{\pi }^6{g}_A^2}{2f_{\pi }^4{(4\pi )}^2}{\displaystyle \sum _{\pi (ijk)}}{\mathit{\tau }}_i·{\mathit{\tau }}_k{\mathit{\sigma }}_i·{\widehat{\text{r}}}_{ij}{\mathit{\sigma }}_k·{\widehat{\text{r}}}_{kj}U(r_{ij})Y(r_{ij})U(r_{kj})Y(r_{kj}),& (45)\end{array}$

where we have used

$\begin{array}{l}{\displaystyle \int }\frac{d^3{q}_i}{{(2\pi )}^3}\frac{{\mathit{\sigma }}_i·{\text{q}}_i}{q_i^2+m_{\pi }^2}{e}^{i{\text{q}}_i·{\text{r}}_{ij}}=-i{\sigma }_i^{\alpha }{\partial }^{\alpha }\frac{e^{-m_{\pi }{r}_{ij}}}{4\pi r_{ij}}\\ =i\frac{m_{\pi }^2}{4\pi }{\sigma }_i^{\alpha }{\widehat{r}}_{ij}^{\alpha }U(r_{ij})Y(r_{ij}),& (46)\end{array}$

and

$\begin{array}{ll}Y(r)=\frac{exp(-m_{\pi }·r)}{m_{\pi }r},U(r)=1+\frac{1}{m_{\pi }r}.& (47)\end{array}$

For the other parts of V_C we find

$\begin{array}{ll}{V}_{C,c_3}=\frac{g_A^2{m}_{\pi }^6{c}_3}{2304{\pi }^2{f}_{\pi }^4}{\displaystyle \sum _{\pi (ijk)}\{{\mathit{\tau }}_i·{\mathit{\tau }}_k,{\mathit{\tau }}_k·{\mathit{\tau }}_j\}\{{{X}}_{ik}(r_{ik}),{{X}}_{kj}(r_{kj})\}},& (48)\end{array}$

$\begin{array}{ll}{V}_{C,c_4}=-\frac{g_A^2{m}_{\pi }^6{c}_4}{4608{\pi }^2{f}_{\pi }^4}{\displaystyle \sum _{\pi (ijk)}}[{\mathit{\tau }}_i·{\mathit{\tau }}_k,{\mathit{\tau }}_k·{\mathit{\tau }}_j][{{X}}_{ik}({\text{r}}_{ik}),{{X}}_{kj}({\text{r}}_{kj})],& (49)\end{array}$

where

$\begin{array}{l}{{X}}_{ij}(\text{r})=X_{ij}(\text{r})-\frac{4\pi }{m_{\pi }^3}\delta (\text{r}){\mathit{\sigma }}_i·{\mathit{\sigma }}_j,\\ X_{ij}(\text{r})=\left(S_{ij}(\text{r})T(r)+{\mathit{\sigma }}_i·{\mathit{\sigma }}_{j}Y(r)\right),& (50)\end{array}$

and

$\begin{array}{ll}T(r)=\left(1+\frac{3}{m_{\pi }r}+\frac{3}{m_{\pi }^2{r}^2}\right)Y(r).& (51)\end{array}$

For the one-pion-exchange–contact part V_D we find

$\begin{array}{l}{V}_D^{ijk}=\frac{g_A}{24f_{\pi }^2}\frac{c_D}{f_{\pi }^2{\Lambda }_{\chi }}{\displaystyle \sum _{\pi (ijk)}{\mathit{\tau }}_i}·{\mathit{\tau }}_k[\frac{m_{\pi }^3}{4\pi }\delta ({\text{r}}_{ij})X_{ik}({\text{r}}_{kj})\\ -{\mathit{\sigma }}_i·{\mathit{\sigma }}_k\delta ({\text{r}}_{ij})\delta ({\text{r}}_{kj})],\hfill & (52)\end{array}$

and for the three-nucleon–contact interaction V_E we find

$\begin{array}{ll}{V}_E=\frac{c_E}{2f_{\pi }^4{\Lambda }_{\chi }}{\displaystyle \sum _{\pi (ijk)}}{\mathit{\tau }}_i·{\mathit{\tau }}_k\delta ({\text{r}}_{ij})\delta ({\text{r}}_{kj}).& (53)\end{array}$

To regularize these 3N topologies, we choose consistent regulators with the NN sector, i.e., we replace δ functions by f_short(r) and multiply Yukawa functions with f_long(r). The cutoff scale for 3N interactions does not necessarily have to be the same as for the NN sector, and we call it R_3N in the following.

To adjust the appearing 3N couplings to experimental data, one should select few-body observables that are uncorrelated. In the delta-less approach, these observables have been chosen to be the ⁴He binding energy and n-α scattering P wave phase shifts (see Figure 3), where we show parameter curves for the 3N LECs for different 3N cutoffs R_3N, chosen similar to R₀, and for different parameterizations that we will discuss in the next section. Stars in the parameter curves mark fits that also describe neutron-alpha scattering, shown in the right panel. For more details, see Lynn et al. [91].

FIGURE 3

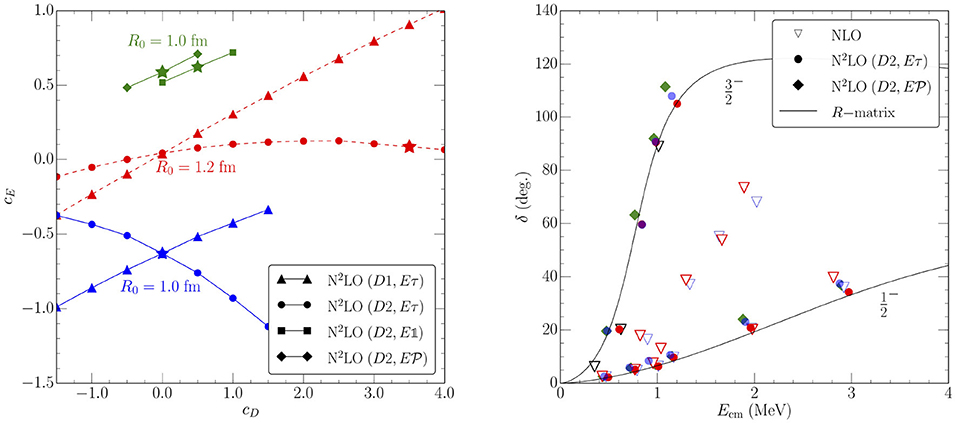
Figure 3. (Left) Parameter curves for the LECs c_D and c_E for the binding energy of ⁴He for different cutoffs and 3N parameterizations discussed in section 4. (Right) Reproduction of n-α P wave phase shifts at NLO and at N²LO for the parameter combinations marked by a star in the left panel. Figures taken from Lynn et al. [91] under the Creative Commons CCBY license.

3.2.2. With Delta Isobars

In the delta-full chiral EFT approach, the structure of the 3N force at N²LO is similar to the 3N force in the delta-less approach. We still have the three topologies V_C, V_D, and V_E at N²LO but, in addition, the well-known Fujita-Miyazawa interaction [34] (V_Δ), which in the delta-less approach is absorbed by V_C, appears already at NLO in the power counting. In momentum space, it reads as

$\begin{array}{l}{V}_{\Delta }^{ijk}=-\frac{g_A^2{h}_A^2}{16f_{\pi }^4}\frac{1}{m_{\Delta N}(q_i^2+m_{\pi }^2)(q_k^2+m_{\pi }^2)}\\ [{\mathit{\sigma }}_k·{\text{q}}_k{\text{ S}}_j^{†}·{\text{q}}_k{\text{ S}}_j·{\text{q}}_i{\mathit{\sigma }}_i·{\text{q}}_i{\mathit{\tau }}_k·{\text{T}}_j^{†}{\text{ T}}_j·{\mathit{\tau }}_i& (54)\end{array}$

$\begin{array}{ll}-{\mathit{\sigma }}_i·{\text{q}}_i{\text{ S}}_j^{†}·{\text{q}}_i{\text{ S}}_j·{\text{q}}_k{\mathit{\sigma }}_k·{\text{q}}_k{\mathit{\tau }}_i·T_j^{†}{\mathrm{ T}}_j·{\mathit{\tau }}_k],& (55)\end{array}$

where S, S^† and T, T^† are the transition spin and isospin operators: The operator S (T) converts a spin (isospin) 1/2 into a spin (isospin) 3/2 particle.

The configuration-space expression follows from

$\begin{array}{l}{V}_{\Delta }^{ijk}=-\frac{g_A^2{h}_A^2}{16·144{\pi }^2}\frac{m_{\pi }^6}{m_{\Delta N}{f}_{\pi }^4}\\ \left[X_{jk}^{II†}{X}_{ji}^{II}{\text{T}}_j^{†}·{\mathit{\tau }}_k{\text{T}}_j·{\mathit{\tau }}_i+X_{ji}^{II†}{X}_{jk}^{II}{\text{T}}_j^{†}·{\mathit{\tau }}_i{\text{T}}_j·{\mathit{\tau }}_k\right],& (56)\end{array}$

where the following definitions have been introduced:

$\begin{array}{ll}{X}_{ij}^{II}=T(r_{ij})S_{ij}^{II}+Y(r_{ij}){\text{S}}_i·{\mathit{\sigma }}_j,S_{ij}^{II}=3{\text{S}}_i·{\widehat{\text{r}}}_{ij}{\mathit{\sigma }}_j·{\widehat{\text{r}}}_{ij}-{\text{S}}_i·{\mathit{\sigma }}_j& (57)\end{array}$

and the dimensionless functions Y(r) and T(r) defined before. The term [⋯] in Equation (56) can be written as

$\begin{array}{l}[\cdots ]=\frac{1}{2}[\left(X_{jk}^{II†}{X}_{ji}^{II}+\text{h}.\text{c}.\right)\left(T_j^{†}·{\mathit{\tau }}_k{T}_j·{\mathit{\tau }}_i+\text{h}.\text{c}.\right)\\ +\left(X_{jk}^{II†}{X}_{ji}^{II}-\text{h}.\text{c}.\right)\left(T_j^{†}·{\mathit{\tau }}_k{T}_j·{\mathit{\tau }}_i-\text{h}.\text{c}.\right)],& (58)\end{array}$

and the transition-spin and transition-isospin operators can be eliminated using the identities

$\begin{array}{ll}{X}_{jk}^{II†}{X}_{ji}^{II}+\text{h}.\text{c}.=\frac{2}{3}\{X_{jk},X_{ji}\},& (59)\end{array}$

$\begin{array}{ll}{X}_{jk}^{II†}{X}_{ji}^{II}-\text{h}.\text{c}.=-\frac{1}{3}[X_{jk},X_{ji}],& (60)\end{array}$

$\begin{array}{ll}{\text{T}}_j^{†}·{\mathit{\tau }}_k{\text{T}}_j·{\mathit{\tau }}_i+\text{h}.\text{c}.=\frac{2}{3}\{{\mathit{\tau }}_j·{\mathit{\tau }}_k,{\mathit{\tau }}_j·{\mathit{\tau }}_i\},& (61)\end{array}$

$\begin{array}{ll}{\text{T}}_j^{†}·{\mathit{\tau }}_k{\text{T}}_j·{\mathit{\tau }}_i-\text{h}.\text{c}.=-\frac{1}{3}[{\mathit{\tau }}_j·{\mathit{\tau }}_k,{\mathit{\tau }}_j·{\mathit{\tau }}_i],& (62)\end{array}$

to obtain

$\begin{array}{l}{V}_{\Delta }^{ijk}=-\frac{g_A^2{h}_A^2}{72·144{\pi }^2}\frac{m_{\pi }^6}{m_{\Delta N}{f}_{\pi }^4}[\{X_{ij},X_{jk}\}\{{\mathit{\tau }}_i·{\mathit{\tau }}_j,{\mathit{\tau }}_j·{\mathit{\tau }}_k\}\\ +\frac{1}{4}[X_{ij},X_{jk}][{\mathit{\tau }}_i·{\mathit{\tau }}_j,{\mathit{\tau }}_j·{\mathit{\tau }}_k]],& (63)\end{array}$

where the function X_ij was defined in the previous section. In the definitions above, the δ(r)-function terms have been dropped.

In analogy to the 3N delta-less chiral EFT, we regularize the 3N contributions in the delta-full chiral EFT by replacing the δ functions with $f_{\text{short}}^{\Delta }(r)$ and multiplying the Yukawa functions with $f_{\text{long}}^{\Delta }(r)$. Note that the implementation of V_C and V_D in the delta-full chiral EFT does not retain the terms proportional to σ_i · σ_j in the definition of ${{X}}_{ik}$, in Equations (50) and (52). They can be reabsorbed in the redefinition of the short-range contact terms.

In the delta-full chiral EFT, two different sets for the values of c_D and c_E were obtained, leading to two different parametrization of the 3N interaction [93, 96]. In the first, these LECs were determined by simultaneously reproducing the experimental trinucleon ground-state energies and neutron-deuteron (nd) doublet scattering length, as shown in the left panel of Figure 4. In the second set, these c_D and c_E were constrained by fitting, in addition to the trinucleon energies, the empirical value of the Gamow-Teller matrix element in tritium β decay [96], see right panel of Figure 4. Because of the much reduced correlation between binding energies and the GT matrix element, the second fit procedure leads to a more robust determination of c_D and c_E then attained in the first one. Note that these observables have been calculated with hyperspherical-harmonics (HH) expansion methods [5] as described in Piarulli et al. [93], Gazit et al. [94], Marcucci et al. [95], and Baroni et al. [96].

FIGURE 4

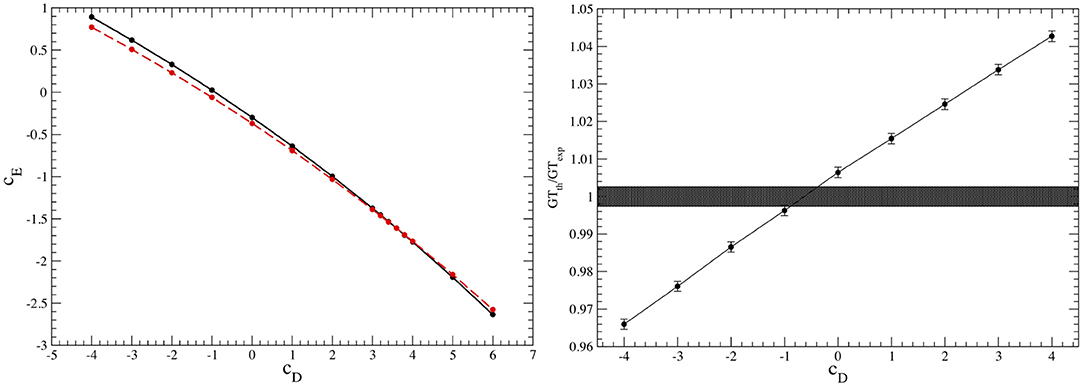
Figure 4. (Left) The c_D-c_E trajectories obtained by fitting the experimental trinucleon binding energies (solid line) and nd doublet scattering length (dashed line) (the intercept of these two lines gives the c_D and c_E values that reproduce these two observables simultaneously). Figure taken from Piarulli et al. [93] under the Creative Commons CCBY license. (Right) The calculated ratio GT_th/GT_exp as function of c_D (solid line; each point on his line reproduces the trinucleon binding energies). Figure taken from Baroni et al. [96] under the Creative Commons CCBY license.

4. Finite Cutoff and Regulator Artifacts

The derivations of local interactions in the last sections did not include any of the local regulator functions that necessarily have to be applied to the interactions to make them suitable for the use in nuclear many-body methods. Generally, when introducing a regulator function, terms beyond the order at which one is working are affected. Hence, the use of such regulator functions with finite values for the cutoff leads to the appearance of regulator artifacts, that might influence calculations of many-body observables. In this section, we will address the different regulator artifacts that can appear in calculations with local interactions.

4.1. Violation of Fierz-Rearrangement Freedom

The first regulator artifact for local interactions affects short-range operators. In previous sections we had shown how only half of the operators at each order are linearly independent due to their insertion between antisymmetric fermionic states (see e.g., Equation 15). However, this argument changes when a regulator function is applied. The discussion in this section will follow Huth et al. [111].

In general, a regulator function can depend on two momentum scales, f_R(q, k). Local regulators, on the other hand, only depend on q, f_{R, loc}(q). The derivation of Equation (15) remains valid if the regulator function commutes with the anti-symmetrizer and, hence, reduces to a simple pre-factor in Equation (15), i.e., when

$\begin{array}{ll}{f}_R(\text{q},\text{k})=f_R\left(-2\text{k},-\frac{1}{2}\text{q}\right).& (64)\end{array}$

We can immediately see, that a purely local regulator can never fulfill this condition while typical non-local regulators of the form [76–78, 83, 84]

$\begin{array}{ll}{f}_R(\text{p},{\text{p}}^{\prime })=exp\left[-{\left(\frac{\text{p}}{\Lambda }\right)}^{2n}\right]exp\left[-{\left(\frac{{\text{p}}^{\prime }}{\Lambda }\right)}^{2n}\right],& (65)\end{array}$

do. As a consequence,

$\begin{array}{l}{V}_{\text{cont,as}}^{(0,\text{loc})}=\frac{1}{2}\left(1-\frac{{{P}}^{\text{m}}}{4}(1+{\mathit{\sigma }}_i·{\mathit{\sigma }}_j)(1+{\mathit{\tau }}_i·{\mathit{\tau }}_j)\right)V_{\text{cont}}^{(0)}{f}_R(\text{q})\hfill \\ =\mathbb{1}\left(\frac{C_{\mathbb{1}}}{2}{f}_R(\text{q})-\frac{1}{8}(C_{\mathbb{1}}+3C_{\sigma }+3C_{\tau }+9C_{\sigma \tau })f_R(2\text{k})\right)\\ +{\mathit{\sigma }}_i·{\mathit{\sigma }}_j\left(\frac{C_{\sigma }}{2}{f}_R(\text{q})-\frac{1}{8}(C_{\mathbb{1}}-C_{\sigma }+3C_{\tau }-3C_{\sigma \tau })f_R(2\text{k})\right)\\ +{\mathit{\tau }}_i·{\mathit{\tau }}_j\left(\frac{C_{\tau }}{2}{f}_R(\text{q})-\frac{1}{8}(C_{\mathbb{1}}+3C_{\sigma }-C_{\tau }-3C_{\sigma \tau })f_R(2\text{k})\right)\\ +{\mathit{\sigma }}_i·{\mathit{\sigma }}_j{\mathit{\tau }}_i·{\mathit{\tau }}_j\left(\frac{C_{\sigma \tau }}{2}{f}_R(\text{q})-\frac{1}{8}(C_{\mathbb{1}}-C_{\sigma }-C_{\tau }+C_{\sigma \tau })f_R(2\text{k})\right),& (66)\end{array}$

and the Fierz-rearrangement freedom is violated. For general regulator functions as defined in the previous sections, this leads to

$\begin{array}{l}{V}_{\text{cont,as}}^{(0,\text{loc})}=({\tilde{C}}_S+{\tilde{C}}_T{\mathit{\sigma }}_i·{\mathit{\sigma }}_j+\left(-\frac{2}{3}{\tilde{C}}_S-{\tilde{C}}_T\right){\mathit{\tau }}_i·{\mathit{\tau }}_j\\ +\left(-\frac{1}{3}{\tilde{C}}_S\right){\mathit{\sigma }}_i·{\mathit{\sigma }}_j{\mathit{\tau }}_i·{\mathit{\tau }}_j)f_R(q)+V_{\text{corr}}^f(p·p^{\prime }),& (67)\end{array}$

where $V_{\mathrm{\text{corr}}}^f(\text{p}·{\text{p}}^{\prime })$ captures all the regulator artifacts that are of higher-order in the EFT. It depends on the functional form of the regulator and the cutoff value. One can also see, that the corrections can be angle-dependent, which leads to a mixing of different partial waves. As a consequence, when applying these regulators to a three-neutron system, for example, pure contact interactions, that otherwise would vanish due to the Pauli principle, start to contribute. This mixing of partial waves complicates the fitting procedure, increases theoretical uncertainties, and makes calculated observables dependent on the operator structure that was chosen.

In Figure 5 we show results for the ⁴He ground-state energy for different LO operator choices. As one can see, the ground-state energies can vary by ~10 MeV at LO, depending on the operator choice. However, when going to higher order and including subleading contact operators, regulator artifacts get partially absorbed and corrected. Then, only higher-order artifacts remain, which improves the situation considerably, as can be seen for the NLO results. In this case, the spread originating from different choices of LO operators reduces to ~4 MeV.

FIGURE 5

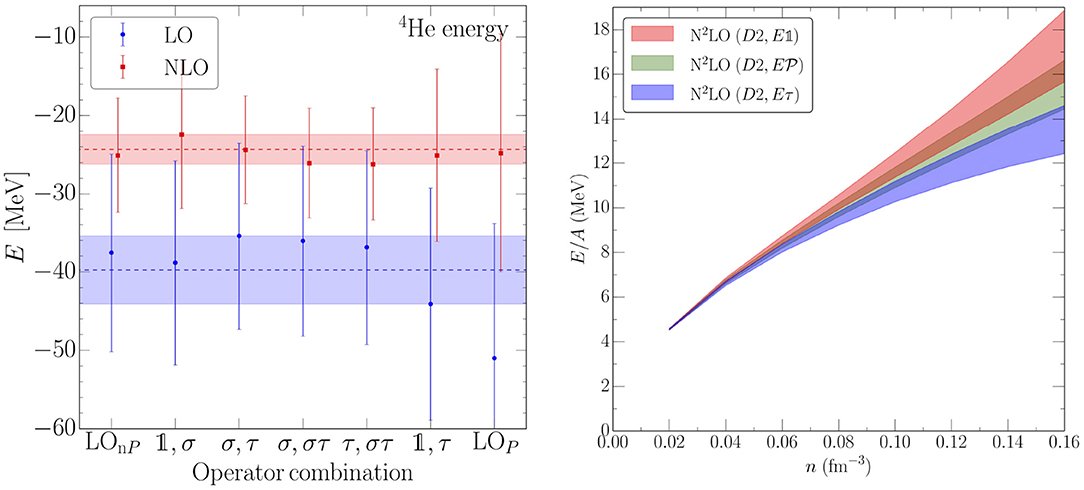
Figure 5. (Left) Ground-state energies of ⁴He at LO and NLO for different LO operator choices. Figure taken from Huth et al. [111] under the Creative Commons CCBY license. (Right) Regulator artifacts in pure neutron matter due to the violation of the Fierz rearrangement freedom for the 3N contact interactions. The three different bands correspond to three different operator choices, where the green band projects the 3N interaction on triples with S = 1/2 and T = 1/2. Figure taken from Lynn et al. [91] under the Creative Commons CCBY license.

A similar effect appears in the 3N sector, where the V_E contact interaction suffers from a similar violation of the Fierz freedom when local regulators are applied. While 3N forces are typically fit to symmetric systems where this dependence can then be approximately accounted for, in triples with S = 3/2 or T = 3/2 (where typically no 3N contact force can contribute due to the Pauli principle) regulator artifacts appear, and lead to a finite contribution from 3N contact interactions that depend on the operator choice. We show this behavior in Figure 5 in the right panel in the case of pure neutron matter, where all triples have T = 3/2. The three different bands explore three choices for the 3N contact operators. At nuclear saturation density, we find that the regulator artifacts introduce a spread of ~5 MeV. Unfortunately, higher-order correction terms only appear at N⁴LO and, to date, are not systematically included in any calculation.

Finally, we mention that the finite cutoff also introduces an ambiguity in the V_D term, that depends on the choice of the initial spin-isospin structure when Fourier transforming:

$\begin{array}{l}{V}_{D,1}^{ijk}=\frac{g_A}{24f_{\pi }^2}\frac{c_D}{f_{\pi }^2{\Lambda }_{\chi }}{\displaystyle \sum _{\pi (ijk)}{\mathit{\tau }}_i}·{\mathit{\tau }}_k[\frac{m_{\pi }^3}{4\pi }\delta (r_{ij})X_{ik}(r_{kj})\\ -{\mathit{\sigma }}_i·{\mathit{\sigma }}_k\delta (r_{ij})\delta (r_{kj})],\\ V_{D,2}^{ijk}=\frac{g_A}{24f_{\pi }^2}\frac{c_D}{f_{\pi }^2{\Lambda }_{\chi }}{\displaystyle \sum _{\pi (ijk)}{\mathit{\tau }}_i}·{\mathit{\tau }}_k[\frac{m_{\pi }^3}{4\pi }\delta (r_{ij})X_{ik}(r_{ik})\\ -{\mathit{\sigma }}_i·{\mathit{\sigma }}_k\delta (r_{ij})\delta (r_{ik})].& (68)\end{array}$

Both expressions are identical for true δ functions (infinite cutoff) but differ when a finite cutoff is applied.

4.2. Weaker Pion Exchanges

A second regulator artifact for local regulators affects the pion exchanges. In Tews et al. [90] it was shown that locally regulated pion exchanges lead to less 3N repulsion than non-locally regulated pion exchanges. At the Hartree-Fock level, for a typical cutoff of 2.5fm⁻¹, when applying non-local regulators ≈ 97% of the infinite cutoff result is recovered, while local regulators only recover ≈ 60%. To reproduce the momentum-space results, the cutoff has to be considerably increased.

Local regulators for pion exchanges have been investigated in detail in Dyhdalo et al. [112] in both the NN and 3N sector. The fact that the contribution due to pion exchanges is weaker for local than for non-local regulator functions is easy to understand in the Hartree-Fock approximation. At the Hartree-Fock level, there are both a direct and an exchange term. The momentum transfer q = p − p′ vanishes in the direct term because p = p′, but it is q = 2p in the exchange term because p = −p′. A typical local regulator of the form $exp\left(-{\left(\frac{q}{\Lambda }\right)}^n\right)$, thus, evaluates to 1 in the direct term, but to $exp\left(-{\left(\frac{p}{\Lambda /2}\right)}^n\right)$ in the exchange term. Therefore, compared to non-local regulators for which both terms are identical, $exp\left(-{\left(\frac{p}{\Lambda }\right)}^n\right)$, local regulators have a very different behavior. In particular, local regulators have an effectively lower cutoff in the exchange channel. In the Hartree-Fock approximation, where the direct term vanishes for spin-dependent interactions like pion exchanges, only the exchange term contributes and, hence, is weaker for local than for non-local regulators.

While the situation is more complicated when abandoning the Hartree-Fock approximation, this reasoning qualitatively remains valid and locally regulated pion exchanges are weaker than non-locally regulated pion exchanges.

5. Selected Results

In this section, we will briefly show the successes of Quantum Monte Carlo calculations with local chiral interactions for light atomic nuclei and infinite matter.

5.1. Light Nuclei

Local chiral interactions, both in the delta-less and delta-full approach, have been used to successfully describe properties of light nuclei using QMC methods. In Figure 6, we show GFMC results for ground- and excited states for nuclei up to ¹²C within the delta-full approach compared to experimental data. In addition, the results obtained with chiral EFT are compared to results with phenomenological interactions. The results clearly show that chiral interactions describe spectra of light nuclei with great success and are compatible to the accuracy of phenomenological interaction in these systems. In addition, we also show ground-state energies obtained in the AFDMC method for nuclei up to ¹⁶O for delta-less chiral interactions. Results are given at LO, NLO, and N²LO for two different 3N parameterizations to explore regulator artifacts. Again, chiral interactions agree well with experimental results, which are shown as green points.

FIGURE 6

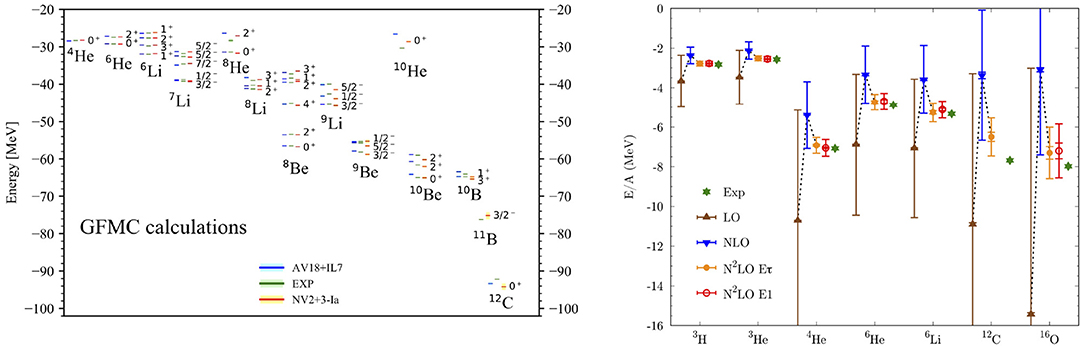
Figure 6. (Left) Spectra of light nuclei up to ¹²C obtained with GFMC with chiral interactions obtained in the delta-full approach (red) compared to experimental data (green) and GFMC calculations with phenomenological interactions (blue). Figure taken from Piarulli et al. [93] under the Creative Commons CCBY license. (Right) Ground-state energies for nuclei up to ¹⁶O at different orders in the chiral expansion for AFDMC calculations with local interactions in the delta-less approach. Reprinted from Lonardoni et al. [99] with permission from the American Physical Society.

In addition to energies, local chiral interactions describe charge radii well. In Figure 7, we present order-by-order AFDMC results for the charge radii of nuclei up to ¹⁶O, compared to experiment. Again, the description is accurate. In addition, as mentioned before, delta-less chiral interactions have been adjusted to reproduce neutron-alpha scattering phase shifts (see Figure 3). While NN interactions alone cannot reproduce the P wave splitting in this system (NLO calculations in Figure 3), chiral Hamiltonians at N²LO, including 3N interactions, reproduce the neutron-α P wave scattering phase shifts accurately.

FIGURE 7

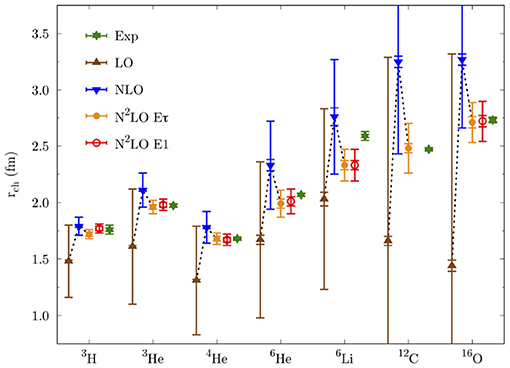
Figure 7. Same as Figure 6 (right) but for radii of nuclei up to ¹⁶O. Reprinted from Lonardoni et al. [99] with permission from the American Physical Society.

5.2. Infinite Matter

In addition to properties of atomic nuclei, local chiral interactions have been used to study infinite matter, and in particular, pure neutron matter. In the right panel of Figure 3, we have already shown results for the energy per particle of pure neutron matter. Results are shown for three Hamiltonians at N²LO, that explore the uncertainty due to regulator artifacts and the truncation of the chiral series. While uncertainties in pure neutron matter are enhanced due to the local regulator artifacts discussed before, indicated by the differences between the three bands, the resulting neutron-matter equation of state (EOS) is consistent with other ab initio determinations within uncertainties.

These calculations have been successfully used to study the EOS of neutron stars, and it has been found that the resulting equations of state are consistent with astrophysical observations of pulsar masses. The EOS have also been used to study gravitational waves from neutron-star mergers [102, 113, 114].

6. Conclusion and Outlook

The quest to understand properties of nuclear systems in terms of forces acting between the nucleons has been considered one of the most challenging efforts of nuclear theory. During the past quarter century, particular emphasis has been devoted to the systematic framework provided by chiral EFT. This approach allows for a consistent description of the two- and many-body interactions and ensuing many-body currents, and a quantification of the theoretical uncertainty due to the truncation error in the chiral expansion.

In this review, we have presented a comprehensive description of the two families of local chiral interactions that have been developed for the use in QMC methods: one within the delta-less and one within the delta-full approach. We provided many details about the theoretical derivation and optimization of these nuclear models addressing their similarities and differences. For completeness, we also presented selected QMC results for light nuclei and neutron matter. These results show that the combination of local chiral EFT interactions with powerful QMC many-body methods can accurately describe ground- and excited-state energies, radii of nuclei up to ¹⁶O, and n-α scattering, as well as the equation of state of neutron matter.

These local chiral interactions have also been used to calculate the distribution of nucleons in a nucleus in both momentum and coordinate space which are related to experimental observations [99, 100, 115, 116], in benchmark calculations of the energy per particle of pure neutron matter as a function of the baryon density [103] and in studies of neutrinoless double-beta decays [117].

In future, local chiral interactions will continue to serve as input for precise QMC methods to systematically study, for example, electroweak reactions, along the lines of Pastore et al. [118], Marcucci et al. [119], Lovato et al. [120, 121], Pastore et al. [122], Schiavilla et al. [123], and Pastore et al. [124] and infinite matter also at finite proton fractions.

Improvements to the interactions that reduce uncertainties due to the scheme and scale dependence of the interactions, e.g., the inclusion of higher orders in the chiral expansion in both the NN and 3N sectors, will provide exciting prospects and permit precision studies of many nuclear systems.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This work was supported by the US Department of Energy, Office of Science, Office of Nuclear Physics, under Contract DE-AC52-06NA25396 (IT), the FRIB Theory Alliance award DE-SC0013617 (MP), the Los Alamos National Laboratory (LANL) LDRD program, and the NUCLEI SciDAC and INCITE programs. Part of this research used resources of the Argonne Leadership Computing Facility at Argonne National Laboratory, the Los Alamos Open Supercomputing via the Institutional Computing (IC) program, and the National Energy Research Scientific Computing Center (NERSC), which was supported by the U.S. Department of Energy, Office of Science, under contract No. DE-AC02-05CH11231.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank our collaborators A. Baroni, J. Carlson, E. Epelbaum, S. Gandolfi, A. Gezerlis, L. Girlanda, K. Hebeler, L. Huth, A. Kievsky, D. Lonardoni, A. Lovato, J. E. Lynn, L. E. Marcucci, A. Nogga, S. Pastore, R. Schiavilla, K. E. Schmidt, A. Schwenk, M. Viviani, and R. B. Wiringa for their contributions to the studies presented in this work.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphy.2019.00245/full#supplementary-material

References

1. Barrett BR, Navratil P, Vary JP. Ab initio no core shell model. Prog Part Nucl Phys. (2013) 69:131–81. doi: 10.1016/j.ppnp.2012.10.003

CrossRef Full Text | Google Scholar

2. Jurgenson ED, Maris P, Furnstahl RJ, Navratil P, Ormand WE, Vary JP. Structure of p-shell nuclei using three-nucleon interactions evolved with the similarity renormalization group. Phys Rev. (2013) C87:054312. doi: 10.1103/PhysRevC.87.054312

CrossRef Full Text | Google Scholar

3. Hagen G, Papenbrock T, Ekström A, Wendt KA, Baardsen G, Gandolfi S, et al. Coupled-cluster calculations of nucleonic matter. Phys Rev. (2014) C89:014319. doi: 10.1103/PhysRevC.89.014319

CrossRef Full Text | Google Scholar

4. Hagen G, Papenbrock T, Hjorth-Jensen M, Dean DJ. Coupled-cluster computations of atomic nuclei. Rept Prog Phys. (2014) 77:096302. doi: 10.1088/0034-4885/77/9/096302

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Kievsky A, Rosati S, Viviani M, Marcucci LE, Girlanda L. A High-precision variational approach to three- and four-nucleon bound and zero-energy scattering states. J Phys. (2008) G35:063101. doi: 10.1088/0954-3899/35/6/063101

CrossRef Full Text | Google Scholar

6. Bogner SK, Furnstahl RJ, Schwenk A. From low-momentum interactions to nuclear structure. Prog Part Nucl Phys. (2010) 65:94–147. doi: 10.1016/j.ppnp.2010.03.001

CrossRef Full Text | Google Scholar

7. Hergert H, Bogner SK, Binder S, Calci A, Langhammer J, Roth R, et al. In-medium similarity renormalization group with chiral two- plus three-nucleon interactions. Phys Rev. (2013) C87:034307. doi: 10.1103/PhysRevC.87.034307

CrossRef Full Text | Google Scholar

8. Dickhoff WH, Barbieri C. Self-consistent Green's function method for nuclei and nuclear matter. Prog Part Nucl Phys. (2004) 52:377–496. doi: 10.1016/j.ppnp.2004.02.038

CrossRef Full Text | Google Scholar

9. Soma V, Barbieri C, Duguet T. Ab-initio Gorkov-Green's function calculations of open-shell nuclei. Phys Rev. (2013) C87:011303. doi: 10.1103/PhysRevC.87.011303

CrossRef Full Text | Google Scholar

10. Carlson J, Gandolfi S, Pederiva F, Pieper SC, Schiavilla R, Schmidt KE, et al. Quantum Monte Carlo methods for nuclear physics. Rev Mod Phys. (2015) 87:1067. doi: 10.1103/RevModPhys.87.1067

CrossRef Full Text | Google Scholar

11. Lähde TA, Epelbaum E, Krebs H, Lee D, Meißner UG, Rupak G. Lattice effective field theory for medium-mass nuclei. Phys Lett. (2014) B732:110–5. doi: 10.1016/j.physletb.2014.03.023

CrossRef Full Text | Google Scholar

12. Hagen G, Ekström A, Forssén C, Jansen GR, Nazarewicz W, Papenbrock T, et al. Neutron and weak-charge distributions of the ⁴⁸Ca nucleus. Nat Phys. (2015) 12:186–90. doi: 10.1038/nphys3529

CrossRef Full Text | Google Scholar

13. Lovato A, Gandolfi S, Carlson J, Pieper SC, Schiavilla R. Neutral weak current two-body contributions in inclusive scattering from ¹²C. Phys Rev Lett. (2014) 112:182502. doi: 10.1103/PhysRevLett.112.182502

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Lovato A, Rocco N, Schiavilla R. Muon capture in nuclei: an ab initio approach based on Green's function Monte Carlo methods. Phys Rev. (2019) C100:035502. doi: 10.1103/PhysRevC.100.035502

CrossRef Full Text | Google Scholar

15. Hupin G, Quaglioni S, Navrátil P. Unified description of ⁶Li structure and deuterium-⁴He dynamics with chiral two- and three-nucleon forces. Phys Rev Lett. (2015) 114:212502. doi: 10.1103/PhysRevLett.114.212502

CrossRef Full Text | Google Scholar

16. Elhatisari S, Lee D, Rupak G, Epelbaum E, Krebs H, Lähde TA, et al. Ab initio alpha-alpha scattering. Nature. (2015) 528:111. doi: 10.1038/nature16067

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Fossez K, Rotureau J, Michel N, Nazarewicz W. Continuum effects in neutron-drip-line oxygen isotopes. Phys Rev. (2017) C96:024308. doi: 10.1103/PhysRevC.96.024308

CrossRef Full Text | Google Scholar

18. Fossez K, Rotureau J, Nazarewicz W. Energy spectrum of neutron-rich helium isotopes: complex made simple. Phys Rev. (2018) C98:061302. doi: 10.1103/PhysRevC.98.061302

CrossRef Full Text | Google Scholar

19. Inoue T, Aoki S, Doi T, Hatsuda T, Ikeda Y, Ishii N, et al. Equation of state for nucleonic matter and its quark mass dependence from the nuclear force in lattice QCD. Phys Rev Lett. (2013) 111:112503. doi: 10.1103/PhysRevLett.111.112503

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Beane SR, Chang E, Cohen S, Detmold W, Lin HW, Orginos K, et al. Magnetic moments of light nuclei from lattice quantum chromodynamics. Phys Rev Lett. (2014) 113:252001. doi: 10.1103/PhysRevLett.113.252001

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Orginos K, Parreno A, Savage MJ, Beane SR, Chang E, Detmold W. Two nucleon systems at m_π~450 MeV from lattice QCD. Phys Rev. (2015) D92:114512. doi: 10.1103/PhysRevD.92.114512

CrossRef Full Text | Google Scholar

22. Savage MJ, Shanahan PE, Tiburzi BC, Wagman ML, Winter F, Beane SR, et al. Proton-proton fusion and tritium β decay from lattice quantum chromodynamics. Phys Rev Lett. (2017) 119:062002. doi: 10.1103/PhysRevLett.119.062002

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Rozpedzik D, Golak J, Skibinski R, Witala H, Glockle W, Epelbaum E, et al. A first estimation of chiral four-nucleon force effects in He-4. Acta Phys Polon. (2006) B37:2889–904.

Google Scholar

24. Krüger T, Tews I, Hebeler K, Schwenk A. Neutron matter from chiral effective field theory interactions. Phys Rev. (2013) C88:025802. doi: 10.1103/PhysRevC.88.025802

CrossRef Full Text | Google Scholar

25. Yukawa H. On the interaction of elementary particles I. Proc Phys Math Soc Jap. (1935) 17:48–57. doi: 10.1143/PTPS.1.1

CrossRef Full Text | Google Scholar

26. Stoks VGJ, Klomp RAM, Terheggen CPF, de Swart JJ. Construction of high quality NN potential models. Phys Rev. (1994) C49:2950–62. doi: 10.1103/PhysRevC.49.2950

CrossRef Full Text | Google Scholar

27. Wiringa RB, Stoks VGJ, Schiavilla R. An accurate nucleon-nucleon potential with charge independence breaking. Phys Rev. (1995) C51:38–51. doi: 10.1103/PhysRevC.51.38

CrossRef Full Text | Google Scholar

28. Machleidt R. The High precision, charge dependent Bonn nucleon-nucleon potential (CD-Bonn). Phys Rev. (2001) C63:024001. doi: 10.1103/PhysRevC.63.024001

CrossRef Full Text | Google Scholar

29. Stoks VGJ, Klomp RAM, Rentmeester MCM, de Swart JJ. Partial wave analaysis of all nucleon-nucleon scattering data below 350-MeV. Phys Rev. (1993) C48:792–815. doi: 10.1103/PhysRevC.48.792

CrossRef Full Text | Google Scholar

30. Friar JL, Gibson BF, Payne GL. Recent progress in understanding trinucleon properties. Ann Rev Nucl Part Sci. (1984) 34:403–33. doi: 10.1146/annurev.ns.34.120184.002155

CrossRef Full Text | Google Scholar

31. Pudliner BS, Pandharipande VR, Carlson J, Pieper SC, Wiringa RB. Quantum Monte Carlo calculations of nuclei with A < = 7. Phys Rev. (1997) C56:1720–50. doi: 10.1103/PhysRevC.56.1720

CrossRef Full Text | Google Scholar

32. Navratil P, Vary JP, Barrett BR. Large basis ab initio no-core shell model and its application to C-12. Phys Rev. (2000) C62:054311. doi: 10.1103/PhysRevC.62.054311

CrossRef Full Text | Google Scholar

33. Pieper SC, Pandharipande VR, Wiringa RB, Carlson J. Realistic models of pion exchange three nucleon interactions. Phys Rev. (2001) C64:014001. doi: 10.1103/PhysRevC.64.014001

CrossRef Full Text | Google Scholar

34. Fujita J, Miyazawa H. Pion theory of three-body forces. Prog Theor Phys. (1957) 17:360–5. doi: 10.1143/PTP.17.360

CrossRef Full Text | Google Scholar

35. Pieper SC. The Illinois extension to the Fujita-Miyazawa three-nucleon force. AIP Conf. Proc. (2008) 1011:143–52. doi: 10.1063/1.2932280

CrossRef Full Text | Google Scholar

36. Maris P, Vary JP, Gandolfi S, Carlson J, Pieper SC. Properties of trapped neutrons interacting with realistic nuclear Hamiltonians. Phys Rev. (2013) C87:054318. doi: 10.1103/PhysRevC.87.054318

CrossRef Full Text | Google Scholar

37. Weinberg S. Nuclear forces from chiral Lagrangians. Phys Lett. (1990) B251:288–92. doi: 10.1016/0370-2693(90)90938-3

CrossRef Full Text | Google Scholar

38. Weinberg S. Effective chiral Lagrangians for nucleon–pion interactions and nuclear forces. Nucl Phys. (1991) B363:3–18. doi: 10.1016/0550-3213(91)90231-L

CrossRef Full Text | Google Scholar

39. Weinberg S. Three body interactions among nucleons and pions. Phys Lett. (1992) B295:114–21. doi: 10.1016/0370-2693(92)90099-P

CrossRef Full Text | Google Scholar

40. Epelbaum E, Hammer HW, Meissner UG. Modern theory of nuclear forces. Rev Mod Phys. (2009) 81:1773–825. doi: 10.1103/RevModPhys.81.1773

CrossRef Full Text | Google Scholar

41. Machleidt R, Entem DR. Chiral effective field theory and nuclear forces. Phys Rept. (2011) 503:1–75. doi: 10.1016/j.physrep.2011.02.001

CrossRef Full Text | Google Scholar

42. Machleidt R, Sammarruca F. Chiral EFT based nuclear forces: achievements and challenges. Phys Scripta. (2016) 91:083007. doi: 10.1088/0031-8949/91/8/083007

CrossRef Full Text | Google Scholar

43. Machleidt R. Historical perspective and future prospects for nuclear interactions. Int J Mod Phys. (2017) E26:1730005. doi: 10.1142/S0218301317300053

CrossRef Full Text | Google Scholar

44. Kaplan DB, Savage MJ, Wise MB. A new expansion for nucleon-nucleon interactions. Phys Lett. (1998) B424:390–6. doi: 10.1016/S0370-2693(98)00210-X

CrossRef Full Text | Google Scholar

45. Kaplan DB, Savage MJ, Wise MB. Two nucleon systems from effective field theory. Nucl Phys. (1998) B534:329–55. doi: 10.1016/S0550-3213(98)00440-4

CrossRef Full Text | Google Scholar

46. Nogga A, Timmermans RGE, van Kolck U. Renormalization of one-pion exchange and power counting. Phys Rev. (2005) C72:054006. doi: 10.1103/PhysRevC.72.054006

CrossRef Full Text | Google Scholar

47. Pavon Valderrama M, Ruiz Arriola E. Renormalization of NN interaction with chiral two pion exchange potential. central phases and the deuteron. Phys Rev. (2006) C74:054001. doi: 10.1103/PhysRevC.74.054001

CrossRef Full Text | Google Scholar

48. Long B, Yang CJ. Renormalizing chiral nuclear forces: triplet channels. Phys Rev. (2012) C85:034002. doi: 10.1103/PhysRevC.85.034002

CrossRef Full Text | Google Scholar

49. van Kolck U. Few nucleon forces from chiral Lagrangians. Phys Rev. (1994) C49:2932–41. doi: 10.1103/PhysRevC.49.2932

CrossRef Full Text | Google Scholar

50. Furnstahl RJ, Phillips DR, Wesolowski S. A recipe for EFT uncertainty quantification in nuclear physics. J Phys. (2015) G42:034028. doi: 10.1088/0954-3899/42/3/034028

CrossRef Full Text | Google Scholar

51. Epelbaum E, Krebs H, Meißner UG. Improved chiral nucleon-nucleon potential up to next-to-next-to-next-to-leading order. Eur Phys J. (2015) A51:53. doi: 10.1140/epja/i2015-15053-8

CrossRef Full Text | Google Scholar

52. Furnstahl RJ, Klco N, Phillips DR, Wesolowski S. Quantifying truncation errors in effective field theory. Phys Rev. (2015) C92:024005. doi: 10.1103/PhysRevC.92.024005

CrossRef Full Text | Google Scholar

53. Wesolowski S, Klco N, Furnstahl RJ, Phillips DR, Thapaliya A. Bayesian parameter estimation for effective field theories. J Phys. (2016) G43:074001. doi: 10.1088/0954-3899/43/7/074001

CrossRef Full Text | Google Scholar

54. Melendez JA, Wesolowski S, Furnstahl RJ. Bayesian truncation errors in chiral effective field theory: nucleon-nucleon observables. Phys Rev. (2017) C96:024003. doi: 10.1103/PhysRevC.96.024003

CrossRef Full Text | Google Scholar

55. Wesolowski S, Furnstahl RJ, Melendez JA, Phillips DR. Exploring Bayesian parameter estimation for chiral effective field theory using nucleon-nucleon phase shifts. J Phys. (2019) 46:045102. doi: 10.1088/1361-6471/aaf5fc

CrossRef Full Text | Google Scholar

56. Ordonez C, Ray L, van Kolck U. Nucleon-nucleon potential from an effective chiral Lagrangian. Phys Rev Lett. (1994) 72:1982–5. doi: 10.1103/PhysRevLett.72.1982

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Ordonez C, van Kolck U. Chiral Lagrangians and nuclear forces. Phys Lett. (1992) B291:459–64. doi: 10.1016/0370-2693(92)91404-W

CrossRef Full Text | Google Scholar

58. Ordonez C, Ray L, van Kolck U. The two nucleon potential from chiral Lagrangians. Phys Rev. (1996) C53:2086–105. doi: 10.1103/PhysRevC.53.2086

CrossRef Full Text | Google Scholar

59. Kaiser N, Gerstendorfer S, Weise W. Peripheral NN scattering: role of delta excitation, correlated two pion and vector meson exchange. Nucl Phys. (1998) A637:395–420. doi: 10.1016/S0375-9474(98)00234-6

CrossRef Full Text | Google Scholar

60. Krebs H, Epelbaum E, Meissner UG. Nuclear forces with Delta-excitations up to next-to-next-to-leading order. I. Peripheral nucleon-nucleon waves. Eur Phys J. (2007) A32:127–37. doi: 10.1140/epja/i2007-10372-y

CrossRef Full Text | Google Scholar

61. Ditsche C, Hoferichter M, Kubis B, Meissner UG. Roy-Steiner equations for pion-nucleon scattering. JHEP. (2012) 6:43. doi: 10.1007/JHEP06(2012)043

CrossRef Full Text | Google Scholar

62. Hoferichter M, Ruiz de Elvira J, Kubis B, Meißner UG. High-precision determination of the Pion-nucleon σ term from Roy-Steiner equations. Phys Rev Lett. (2015) 115:092301. doi: 10.1103/PhysRevLett.115.092301

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Hoferichter M, Ruiz de Elvira J, Kubis B, Meißner UG. Roy–Steiner-equation analysis of pion–nucleon scattering. Phys Rept. (2016) 625:1–88. doi: 10.1016/j.physrep.2016.02.002

CrossRef Full Text | Google Scholar

64. Hoferichter M, Ruiz de Elvira J, Kubis B, Meißner UG. Matching pion-nucleon Roy-Steiner equations to chiral perturbation theory. Phys Rev Lett. (2015) 115:192301. doi: 10.1103/PhysRevLett.115.192301

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Siemens D, Bernard V, Epelbaum E, Gasparyan A, Krebs H, Meißner UG. Elastic pion-nucleon scattering in chiral perturbation theory: a fresh look. Phys Rev C. (2016) 94:014620. doi: 10.1103/PhysRevC.94.014620

CrossRef Full Text | Google Scholar

66. Siemens D, Ruiz de Elvira J, Epelbaum E, Hoferichter M, Krebs H, Kubis B, et al. Reconciling threshold and subthreshold expansions for Pion–nucleon scattering. Phys Lett. (2017) B770:27–34. doi: 10.1016/j.physletb.2017.04.039

CrossRef Full Text | Google Scholar

67. Yao DL, Siemens D, Bernard V, Epelbaum E, Gasparyan AM, Gegelia J, et al. Pion-nucleon scattering in covariant baryon chiral perturbation theory with explicit Delta resonances. JHEP. (2016) 5:38. doi: 10.1007/JHEP05(2016)038

CrossRef Full Text | Google Scholar

68. Epelbaum E, Krebs H, Meissner UG. Delta-excitations and the three-nucleon force. Nucl Phys. (2008) A806:65–78. doi: 10.1016/j.nuclphysa.2008.02.305

CrossRef Full Text | Google Scholar

69. Bernard V, Epelbaum E, Krebs H, Meissner UG. Subleading contributions to the chiral three-nucleon force. I. Long-range terms. Phys Rev. (2008) C77:064004. doi: 10.1103/PhysRevC.77.064004

CrossRef Full Text | Google Scholar

70. Bernard V, Epelbaum E, Krebs H, Meissner UG. Subleading contributions to the chiral three-nucleon force II: short-range terms and relativistic corrections. Phys Rev. (2011) C84:054001. doi: 10.1103/PhysRevC.84.054001

CrossRef Full Text | Google Scholar

71. Epelbaum E. Four-nucleon force in chiral effective field theory. Phys Lett. (2006) B639:456–61. doi: 10.1016/j.physletb.2006.06.046

CrossRef Full Text | Google Scholar

72. Epelbaum E. Four-nucleon force using the method of unitary transformation. Eur Phys J. (2007) A34:197–214. doi: 10.1140/epja/i2007-10496-0

CrossRef Full Text | Google Scholar

73. Entem DR, Kaiser N, Machleidt R, Nosyk Y. Dominant contributions to the nucleon-nucleon interaction at sixth order of chiral perturbation theory. Phys Rev. (2015) C92:064001. doi: 10.1103/PhysRevC.92.064001

CrossRef Full Text | Google Scholar

74. Epelbaum E, Krebs H, Meißner UG. Precision nucleon-nucleon potential at fifth order in the chiral expansion. Phys Rev Lett. (2015) 115:122301. doi: 10.1103/PhysRevLett.115.122301

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Reinert P, Krebs H, Epelbaum E. Semilocal momentum-space regularized chiral two-nucleon potentials up to fifth order. Eur Phys J. (2018) A54:86. doi: 10.1140/epja/i2018-12516-4

CrossRef Full Text | Google Scholar

76. Entem DR, Machleidt R, Nosyk Y. High-quality two-nucleon potentials up to fifth order of the chiral expansion. Phys Rev. (2017) C96:024004. doi: 10.1103/PhysRevC.96.024004

CrossRef Full Text | Google Scholar

77. Entem DR, Machleidt R. Accurate charge dependent nucleon-nucleon potential at fourth order of chiral perturbation theory. Phys Rev. (2003) C68:041001. doi: 10.1103/PhysRevC.68.041001

CrossRef Full Text | Google Scholar

78. Epelbaum E, Glockle W, Meissner UG. The two-nucleon system at next-to-next-to-next-to-leading order. Nucl Phys. (2005) A747:362–424. doi: 10.1016/j.nuclphysa.2004.09.107

CrossRef Full Text | Google Scholar

79. Arndt RA, Briscoe WJ, Strakovsky II, Workman RL. Updated analysis of NN elastic scattering to 3-GeV. Phys Rev. (2007) C76:025209. doi: 10.1103/PhysRevC.76.025209

CrossRef Full Text | Google Scholar

80. Navarro Pérez R, Amaro JE, Ruiz Arriola E. Coarse-grained potential analysis of neutron-proton and proton-proton scattering below the pion production threshold. Phys Rev. (2013) C88:064002. doi: 10.1103/PhysRevC.88.064002 [Erratum: Phys. Rev.C91,no.2,029901(2015)].

CrossRef Full Text | Google Scholar

81. Navarro Pérez R, Amaro JE, Ruiz Arriola E. Coarse grained NN potential with chiral two Pion exchange. Phys Rev. (2014) C89:024004. doi: 10.1103/PhysRevC.89.024004

CrossRef Full Text | Google Scholar

82. Navarro Perez R, Amaro JE, Ruiz Arriola E. Statistical error analysis for phenomenological nucleon-nucleon potentials. Phys Rev. (2014) C89:064006. doi: 10.1103/PhysRevC.89.064006

CrossRef Full Text | Google Scholar

83. Carlsson BD, Ekström A, Forssén C, Strömberg DF, Jansen GR, Lilja O, et al. Uncertainty analysis and order-by-order optimization of chiral nuclear interactions. Phys Rev. (2016) X6:011019. doi: 10.1103/PhysRevX.6.011019

CrossRef Full Text | Google Scholar

84. Ekström A, Jansen GR, Wendt KA, Hagen G, Papenbrock T, Carlsson BD, et al. Accurate nuclear radii and binding energies from a chiral interaction. Phys Rev. (2015) C91:051301. doi: 10.1103/PhysRevC.91.051301

CrossRef Full Text | Google Scholar

85. Kalantar-Nayestanaki N, Epelbaum E, Messchendorp JG, Nogga A. Signatures of three-nucleon interactions in few-nucleon systems. Rept Prog Phys. (2012) 75:016301. doi: 10.1088/0034-4885/75/1/016301

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Hammer HW, Nogga A, Schwenk A. Three-body forces: from cold atoms to nuclei. Rev Mod Phys. (2013) 85:197. doi: 10.1103/RevModPhys.85.197

CrossRef Full Text | Google Scholar

87. Krebs H, Gasparyan A, Epelbaum E. Chiral three-nucleon force at N⁴LO I: longest-range contributions. Phys Rev. (2012) C85:054006. doi: 10.1103/PhysRevC.85.054006

CrossRef Full Text | Google Scholar

88. Krebs H, Gasparyan A, Epelbaum E. Chiral three-nucleon force at N⁴LO II: intermediate-range contributions. Phys Rev. (2013) C87:054007. doi: 10.1103/PhysRevC.87.054007

CrossRef Full Text | Google Scholar

89. Girlanda L, Kievsky A, Viviani M. Subleading contributions to the three-nucleon contact interaction. Phys Rev. (2011) C84:014001. doi: 10.1103/PhysRevC.84.014001

CrossRef Full Text | Google Scholar

90. Tews I, Gandolfi S, Gezerlis A, Schwenk A. Quantum Monte Carlo calculations of neutron matter with chiral three-body forces. Phys Rev. (2016) C93:024305. doi: 10.1103/PhysRevC.93.024305

CrossRef Full Text | Google Scholar

91. Lynn JE, Tews I, Carlson J, Gandolfi S, Gezerlis A, Schmidt KE, et al. Chiral three-nucleon interactions in light nuclei, neutron-α scattering, and neutron matter. Phys Rev Lett. (2016) 116:062501. doi: 10.1103/PhysRevLett.116.062501

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Lynn JE, Tews I, Carlson J, Gandolfi S, Gezerlis A, Schmidt KE, et al. Quantum Monte Carlo calculations of light nuclei with local chiral two- and three-nucleon interactions. Phys Rev. (2017) C96:054007. doi: 10.1103/PhysRevC.96.054007

CrossRef Full Text | Google Scholar

93. Piarulli M, Baroni A, Girlanda L, Kievsky A, Lovato A, Lusk E, et al. Light-nuclei spectra from chiral dynamics. Phys Rev Lett. (2018) 120:052503. doi: 10.1103/PhysRevLett.120.052503

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Gazit D, Quaglioni S, Navratil P. Three-nucleon low-energy constants from the consistency of interactions and currents in chiral effective field theory. Phys Rev Lett. (2009) 103:102502. doi: 10.1103/PhysRevLett.103.102502

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Marcucci LE, Kievsky A, Rosati S, Schiavilla R, Viviani M. Chiral effective field theory predictions for muon capture on deuteron and ³He. Phys Rev Lett. (2012) 108:052502. doi: 10.1103/PhysRevLett.108.052502

CrossRef Full Text | Google Scholar

96. Baroni A, Schiavilla R, Marcucci LE, Girlanda L, Kievsky A, Lovato A, et al. Local chiral interactions, the tritium Gamow-Teller matrix element, and the three-nucleon contact term. Phys Rev. (2018) C98:044003. doi: 10.1103/PhysRevC.98.044003

CrossRef Full Text | Google Scholar

97. Gardestig A, Phillips DR. How low-energy weak reactions can constrain three-nucleon forces and the neutron-neutron scattering length. Phys Rev Lett. (2006) 96:232301. doi: 10.1103/PhysRevLett.96.232301

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Lynn JE, Tews I, Gandolfi S, Lovato A. Quantum Monte Carlo methods in nuclear physics: recent advances. Ann Rev Nucl Part Sci. (2019) 69:279–305. doi: 10.1146/annurev-nucl-101918-023600

CrossRef Full Text | Google Scholar

99. Lonardoni D, Gandolfi S, Lynn JE, Petrie C, Carlson J, Schmidt KE, et al. Auxiliary field diffusion Monte Carlo calculations of light and medium-mass nuclei with local chiral interactions. Phys Rev. (2018) C97:044318. doi: 10.1103/PhysRevC.97.044318

CrossRef Full Text | Google Scholar

100. Lonardoni D, Gandolfi S, Wang XB, Carlson J. Single- and two-nucleon momentum distributions for local chiral interactions. Phys Rev. (2018) C98:014322. doi: 10.1103/PhysRevC.98.014322

CrossRef Full Text | Google Scholar

101. Tews I, Carlson J, Gandolfi S, Reddy S. Constraining the speed of sound inside neutron stars with chiral effective field theory interactions and observations. Astrophys J. (2018) 860:149. doi: 10.3847/1538-4357/aac267

CrossRef Full Text | Google Scholar

102. Tews I, Margueron J, Reddy S. Critical examination of constraints on the equation of state of dense matter obtained from GW170817. Phys Rev. (2018) C98:045804. doi: 10.1103/PhysRevC.98.045804

CrossRef Full Text | Google Scholar

103. Piarulli M, Bombaci I, Logoteta D, Lovato A, Wiringa RB. Benchmark calculations of pure neutron matter with realistic nucleon-nucleon interactions. arXiv:1908.04426 [Preprint]. (2019). Available online at: https://arxiv.org/abs/1908.04426

Google Scholar

104. Gezerlis A, Tews I, Epelbaum E, Gandolfi S, Hebeler K, Nogga A, et al. Quantum Monte Carlo calculations with chiral effective field theory interactions. Phys Rev Lett. (2013) 111:032501. doi: 10.1103/PhysRevLett.111.032501

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Gezerlis A, Tews I, Epelbaum E, Freunek M, Gandolfi S, Hebeler K, et al. Local chiral effective field theory interactions and quantum Monte Carlo applications. Phys Rev. (2014) C90:054323. doi: 10.1103/PhysRevC.90.054323

CrossRef Full Text | Google Scholar

106. Piarulli M, Girlanda L, Schiavilla R, Navarro Pérez R, Amaro JE, Ruiz Arriola E. Minimally nonlocal nucleon-nucleon potentials with chiral two-pion exchange including Δ resonances. Phys Rev. (2015) C91:024003. doi: 10.1103/PhysRevC.91.024003

CrossRef Full Text | Google Scholar

107. Piarulli M, Girlanda L, Schiavilla R, Kievsky A, Lovato A, Marcucci LE, et al. Local chiral potentials with Δ-intermediate states and the structure of light nuclei. Phys Rev. (2016) C94:054007. doi: 10.1103/PhysRevC.94.054007

CrossRef Full Text | Google Scholar

108. Epelbaum E, Gloeckle W, Meissner UG. Improving the convergence of the chiral expansion for nuclear forces. 1. Peripheral phases. Eur Phys J. (2004) A19:125–37. doi: 10.1140/epja/i2003-10096-0

CrossRef Full Text | Google Scholar

109. Kaiser N, Brockmann R, Weise W. Peripheral nucleon-nucleon phase shifts and chiral symmetry. Nucl Phys. (1997) A625:758–88. doi: 10.1016/S0375-9474(97)00586-1

CrossRef Full Text | Google Scholar

110. Kortelainen M, Lesinski T, Moré J, Nazarewicz W, Sarich J, Schunck N, et al. Nuclear energy density optimization. Phys Rev C. (2010) 82:024313. doi: 10.1103/PhysRevC.82.024313

CrossRef Full Text | Google Scholar

111. Huth L, Tews I, Lynn JE, Schwenk A. Analyzing the Fierz rearrangement freedom for local chiral two-nucleon potentials. Phys Rev. (2017) C96:054003. doi: 10.1103/PhysRevC.96.054003

CrossRef Full Text | Google Scholar

112. Dyhdalo A, Furnstahl RJ, Hebeler K, Tews I. Regulator artifacts in uniform matter for chiral interactions. Phys Rev. (2016) C94:034001. doi: 10.1103/PhysRevC.94.034001

CrossRef Full Text | Google Scholar

113. Tews I, Margueron J, Reddy S. Confronting gravitational-wave observations with modern nuclear physics constraints. Eur Phys J. (2019) A55:97. doi: 10.1140/epja/i2019-12774-6

CrossRef Full Text | Google Scholar

114. Capano CD, Tews I, Brown SM, Margalit B, De S, Kumar S, et al. GW170817: stringent constraints on neutron-star radii from multimessenger observations and nuclear theory. arXiv:1908.10352. (2019).

Google Scholar

115. Cruz-Torres R, Lonardoni D, Weiss R, Barnea N, Higinbotham DW, Piasetzky E, et al. Scale and scheme independence and position-momentum equivalence of nuclear short-range correlations. arXiv:1907.03658. (2019).

Google Scholar

116. Lynn JE, Lonardoni D, Carlson J, Chen JW, Detmold W, Gandolfi S, et al. Ab initio short-range-correlation scaling factors from light to medium-mass nuclei. arXiv:1903.12587. (2019).

Google Scholar

117. Cirigliano V, Dekens W, De Vries J, Graesser ML, Mereghetti E, Pastore S, et al. A renormalized approach to neutrinoless double-beta decay. Phys Rev. (2019) 5:055504. doi: 10.1103/PhysRevC.100.055504

CrossRef Full Text | Google Scholar

118. Pastore S, Pieper SC, Schiavilla R, Wiringa RB. Quantum Monte Carlo calculations of electromagnetic moments and transitions in A ≤ 9 nuclei with meson-exchange currents derived from chiral effective field theory. Phys Rev. (2013) C87:035503. doi: 10.1103/PhysRevC.87.035503

CrossRef Full Text | Google Scholar

119. Marcucci LE, Gross F, Pena MT, Piarulli M, Schiavilla R, Sick I, et al. Electromagnetic structure of few-nucleon ground states. J Phys. (2016) G43:023002. doi: 10.1088/0954-3899/43/2/023002

CrossRef Full Text | Google Scholar

120. Lovato A, Gandolfi S, Carlson J, Pieper SC, Schiavilla R. Electromagnetic response of ¹²C: a first-principles calculation. Phys Rev Lett. (2016) 117:082501. doi: 10.1103/PhysRevLett.117.082501

CrossRef Full Text | Google Scholar

121. Lovato A, Gandolfi S, Carlson J, Lusk E, Pieper SC, Schiavilla R. Quantum Monte Carlo calculation of neutral-current ν−¹²C inclusive quasielastic scattering. Phys Rev. (2018) C97:022502. doi: 10.1103/PhysRevC.97.022502

CrossRef Full Text | Google Scholar

122. Pastore S, Baroni A, Carlson J, Gandolfi S, Pieper SC, Schiavilla R, et al. Quantum Monte Carlo calculations of weak transitions in A = 6−10 nuclei. Phys Rev. (2018) C97:022501. doi: 10.1103/PhysRevC.97.022501

CrossRef Full Text | Google Scholar

123. Schiavilla R, Baroni A, Pastore S, Piarulli M, Girlanda L, Kievsky A, et al. Local chiral interactions and magnetic structure of few-nucleon systems. Phys Rev. (2019) C99:034005. doi: 10.1103/PhysRevC.99.034005

CrossRef Full Text | Google Scholar

124. Pastore S, Carlson J, Gandolfi S, Schiavilla R, Wiringa RB. Quasielastic lepton scattering and back-to-back nucleons in the short-time approximation. arXiv:1909.06400 [Preprint]. (2019). Available online at: https://arxiv.org/abs/1909.06400

Google Scholar