Mini Review on Anomalous Diffusion by MRI: Potential Advantages, Pitfalls, Limitations, Nomenclature, and Correct Interpretation of Literature

Introduction

Diffusion magnetic resonance imaging (DMRI) is a consolidated radiation-free technology able to quantify in vivo features of water molecules' diffusion related to tissue microstructures [1]. The acquired diffusion-weighted images (DWI) are usually characterized by spatial resolution within the millimeter scale but are sensitized to the random motion of water molecules, providing an indirect measure of molecular displacement in the range of few tens micrometers (that is the intrinsic DMRI resolution). Conventional DMRI is based on normal (Brownian) diffusion, characterized by a Gaussian motion propagator (MP) for which the mean squared displacement (MSD) is linearly time dependent. Despite the great importance that DMRI has in medical diagnostics, being based on the Gaussian MP limits its potential in terms of intrinsic resolution, specificity, and sensitivity.

Indeed, biological tissues are structurally complex media with different length scales of intracellular and extracellular compartments, intricate microvasculature, submicroscopic traps, and barriers hindering water diffusion.

The normal diffusion of bulk water in tissues is not able to capture all these detailed microstructural features, providing non-local, diffusion measurement averaged on a length scale l_D approximately equal to the squared-root of the MSD of the diffusing particles.

However, all the aforementioned characteristics of biological tissues can be captured using an anomalous diffusion (AD) description of molecular diffusion in living systems that, unlike normal diffusion, has a non-Gaussian MP and its MSD is not linearly proportional to its diffusion time [2]. In particular, anomalous subdiffusion is the tendency of particles in a fluid to diffuse slower than normal diffusion due to random barriers and traps with heavy-tailed trap-time distribution, while anomalous superdiffusion is the behavior of particles that diffuse showing random walk with occasional very long steps in very short times [2].

AD is ubiquitously observed in biology: it can be due to macromolecular crowding in cytoplasmatic fluid of living cells [3], in cellular membranes [4–6] and extracellular space (ECS) [7], as shown by single-particle tracking (SPT) [8] and fluorescence-correlation spectroscopy (FCS) [9] techniques. Specifically, the cerebral ECS occupies ~20% of the total brain volume and includes all the space outside of neurons, glial cells and the interstitial space between cells. ECS has a well-connected foam-like structure and it is rich in heterogeneous ions accumulation, obstructions due to macromolecules, extracellular matrix binding sites and dead space microdomains that transiently entrap diffusing molecules in a dead-end [7, 10–12]. All these ECS features affect the diffusion of molecules such as dextran, smaller proteins, or little fluorophores showing anomalous subdiffusion. Therefore, we could expect such structural features to have a similar impact also on water diffusion.

The quantification of DMRI parameters related to AD could then provide higher sensitivity, resolution, and complementary information for improving the detection of early changes due to pathological conditions, compared to conventional metrics. For these reasons, in the last 10 years, some theoretical and experimental approaches have been proposed to account for and quantify AD by MRI. However, the methodologies used, the results and their interpretation have often aroused doubts, even questioning the fact that biological water in tissues can effectively diffuse with AD [13, 14]. To confuse further this scenario, some authors have used in a phenomenological way the stretched-exponential function to fit experimental DWI data that de facto is the function type predicted by the AD theory to quantify the superdiffusion and subdiffusion parameters. Lastly, different authors have assigned different nomenclatures to indicate the same stretching exponent, fueling the confusion that characterizes the literature of AD methods in MRI.

This mini-review is organized as follows. In the next section, we briefly introduce AD and the principal approaches for AD by MRI while, in section Transient-Anomalous Diffusion in Biological Systems, we indicate how to reconcile the theory and the established procedures of conventional DMRI with the advanced modality of tissue analysis provided by the AD. In section The Pseudo-superdiffusion, we describe the origin of the peculiar image contrast mechanism named pseudo-superdiffusion through which we provide, in section Literature Examination in the Light of the Pseudo-superdiffusion Mechanism, a new interpretation to results published by different authors, making order and clarity in the AD MRI literature. In section Conclusion, we draw our conclusions.

Ad by MRI: Mathematical and Physical Effective Approaches

AD is mathematically defined as the asymptotic power-law increase of the mean-squared displacement (MSD) as a function of the lag time t of diffusing particles: MSD = K_vt^v [15]. The sublinear increase with the exponent in the range 0 < v < 1 defines subdiffusion whereas the exponent in the range 1 < v < 2 regulates superdiffusion [15, 16]. Several theoretical models have been proposed to describe AD phenomenon, such as the continuous-time random walk (CTRW) model [15], the fractional motion (FM) model and others [3]. The adaptation of these models to DMRI experiments leads to fit experimental DW-data to functions containing stretched-exponentials. Two different approaches, based on CTRW framework, have emerged for quantifying parameters of AD by DMRI: a purely derived mathematical approach related to fractional derivatives [17, 18] and an effective approach mainly based on the physical phenomena [19, 20]. The mathematical approach, made use of stretched-exponential functions derived from fractional order differential operators in the Bloch-Torrey equation to quantify the subdiffusion and superdiffusion parameters, indicated as α and β, respectively. In particular, Magin et al. [17, 18] solved the fractional-derivative equations in space with the fractional-order time α = 1 and the fractional-order in space 0.5 < β < 1 and in time with 0 < α < 1 and β = 1. Successively, Mittag-Leffler type function [21], including both variable α and β were used [22, 23].

The effective physical approach takes into account AD by using two different functional forms to characterize subdiffusion and superdiffusion, quantified by two exponents α and μ = 2γ, respectively [19]. In particular, to investigate subdiffusive processes it is possible to assume the following asymptotic behavior for the Fourier Transform of AD MP [19]:

$\begin{array}{ll}W(k,t)\propto exp(-K_{\alpha }{k}^2{t}^{\alpha })\text{ when }{k}^2<<1/(K_{\alpha }{t}^{\alpha })& (1)\end{array}$

where k = 1/(2π)gδ⋎ with: g, the diffusion gradient strength, δ, the gradient-pulse width, ⋎ the nuclear gyromagnetic ratio and 0 < α < 1. Because the DW-signal is proportional to the Fourier-transform of the MP, AD parameters can be quantified by fitting the function W(k, t) to experimental DW-data. Clearly, to fit Equation (1) to the DW-signal, data must be collected by changing diffusion time t = Δ in a pulsed-field-gradient (PFG) acquisition sequence, as depicted in Figure 1. On the other hand, to quantify superdiffusive processes, it is possible to use the following function:

$\begin{array}{ll}W(k,t)\propto exp(-K^{2\gamma }{\left|k\right|}^{2\gamma }t)& (2)\end{array}$

where 1 < 2γ < 2. As k depends on g, the correct fit of Equation (2) to DW-signal requires data obtained by changing diffusion gradient strength g (Figure 1). It is very important to understand how to acquire the DW-signal (by changing g at fixed Δ or by changing Δ at fixed g) to disentangle and quantify subdiffusion or superdiffusion processes.

FIGURE 1

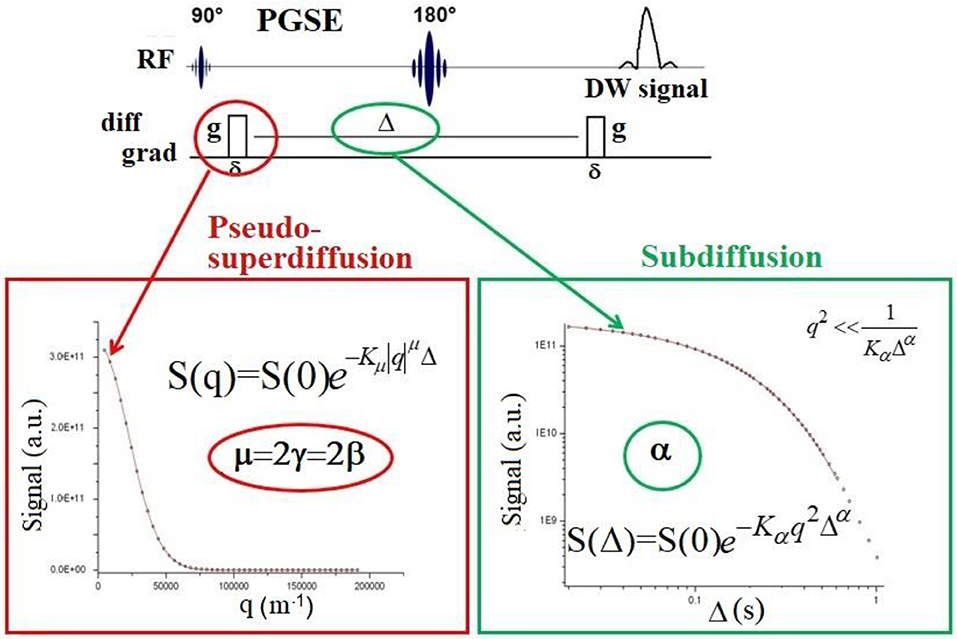
Figure 1. Schematic representation of the PGSE sequence at a given b-value, where δ is the diffusion gradient pulse width. By changing the gradient strength g at a fixed value of diffusion time Δ, the DW-signal decay must be fitted to the function displayed in red box, which is the correct signal representation describing superdiffusion processes. Please note that this function depends on q^μ, where q = (γgδ)1/2π and μ is the index that quantifies superdiffusion [15, 19] or the space derivative order. In literature, the μ index is also indicated as γ or β, where μ = 2γ = 2β. Conversely, by changing Δ value at a fixed g, the DW-signal decay must be fitted to the function displayed in green box, which depends on Δ^α, where the index α quantifies subdiffusion phenomena, or the time derivative order. It is important to pay attention to PFG acquisition modality and to the corresponding signal representation to fit data. The vast majority of clinical MRI scanners allow to acquire the DW-signal by varying the gradient strength only.

Indeed, clinical MRI scanners normally provide DW-images at varying g. Therefore, in principle, since there is no reason to find water superdiffusion in biological tissues, it would not be possible to quantify AD using conventional clinical scanners. However, in section The Pseudo-superdiffusion we report interesting results obtained by acquiring DW-signal at varying g and fitting Equation (2) to the data.

Some research groups have acquired DW-images at varying Δ, quantifying the subdiffusion in excised tissues [24, 25] and rat brain [26]. Other groups have collected data varying g while keeping Δ constant and varying Δ while keeping g constant to quantify subdiffusion and superdiffusion parameters by Mittag-Leffler type function [23, 27]. Since in a fractal-like system the subdiffusion is related to the fractal dimension d_f (d_f = 2/α), Özarslan et al. [26] quantified d_f in rat cerebellum. Other authors [28] failed to quantify d_f in the human brain because they acquired the DW-signal at varying g and fitted the stretched-exponential function reported in Equation (2) to the data. Therefore, they did not quantify subdiffusion, nor fractal dimension, although they obtained images of the human brain characterized by a new contrast compared to the conventional one provided by diffusion tensor imaging (DTI).

The incorrect use of the Mittag-Leffler function in AD MRI has generated questionable or unreliable results. Some authors have quantified both subdiffusion and superdiffusion parameters from data acquired at varying g fitted with the Mittag-Leffler function. In this way, the authors did not quantify the subdiffusion (because it is necessary to acquire DMRI by changing diffusion time) nor the correct value of the superdiffusion due to the simultaneous dependence of the Mittag-Leffler function on both α and β [29].

Another problem to deal with in AD MRI experiments using clinical scanners is related to the conditions of validity of the relations reported in Equations (1) and (2) and Magin et al. papers [17, 18], Ingo et al. papers [22, 23]. Equations (1) and (2) are valid when δ < < Δ (Figure 1), i.e., the diffusion-gradient pulse duration must be at least one order of magnitude shorter than the diffusion time. However, this condition is practically never satisfied in clinical scanners where the gradient pulse width of PFG is usually long. This scenario also influences the behavior of the DW-signal decay due to Gaussian diffusion, which is represented with a decreasing exponential function only when δ < < Δ [30, 31].

To overcome this drawback, Lin [32, 33] recently developed general expressions of PFG signal attenuation describing the AD NMR signal. Of particular interest is the general analytical expressions of PFG signal attenuation for AD that include the finite gradient pulse width effect, namely, the DW-signal attenuation during each gradient pulse application period [34, 35].

Transient-Anomalous Diffusion in Biological Systems

In physics literature, AD is defined to require the diffusion to be asymptotically anomalous. Considering the general AD relation: MSD ∞ K_vt^v, where MSD∞D(t)^*t with the anomalous exponent 0 < v < 1 that defines subdiffusion and 1 < v < 2 defining superdiffusion, the time dependent diffusion coefficient D(t) can be written as:

$\begin{array}{ll}\text{D}(\text{t})~{\text{t}}^{\text{v}-1}\text{o}\text{r},\text{D}(\text{t})~1/{\text{t}}^{1-\text{v}}& (3)\end{array}$

Using the above Equation (3) at long diffusion times, i.e., for t → ∞ we obtain D_∞ = 0 and D_∞ = ∞ for subdiffusion and superdiffusion behavior, respectively. Therefore, when we use AD in living systems, we collide with one of the fixed points of the diffusion in biological tissues: the existence of a diffusion coefficient D = D_∞ > 0, related to the tortuosity limit τ = (D₀/D_∞)^1/2 that assumes finite no zero values at long diffusion times [7, 13, 31, 36–38]. In other words, because of the central limit theorem, the diffusion is Gaussian at long diffusion times, with a finite effective diffusivity 0 < D_∞ ≤ D₀ [14].

However, a suitable infinite hierarchical structure (such as fractals) leads to AD at all times, i.e., diffusion asymptotically anomalous. On the other hand, finite hierarchies (such as three or four orders of magnitude microstructures from 0.1 to 50 μm) lead to AD that becomes normal diffusion at long times [39, 40]. Realistically, we find “transient-AD” in biological tissue, where AD exists between two crossover times (cr) (Figure 2) as experimentally showed by several works [3–11, 41]. As shown in Figure 2, for t < cr1, i.e., at very short diffusion times we find normal diffusion characterized by D = D₀, while for t > cr2, i.e., at long diffusion times, we still find normal diffusion, defined by a finite value of D = D_∞ ≤ D₀. Therefore, in the case of transient-subdiffusion, Equation (3) becomes [39]:

$\begin{array}{lll}\text{D}(\text{t})~{\text{D}}_0/(1+{\text{t}}^{1-\text{v}})& \text{with }0<v<1& \text{for t}\to 0\\ \text{D}(\text{t})~\text{D}\infty +1/{\text{t}}^{1-\text{v}}& \text{with }0<\text{v}<1& \text{for t}\to \infty & (4)\end{array}$

FIGURE 2

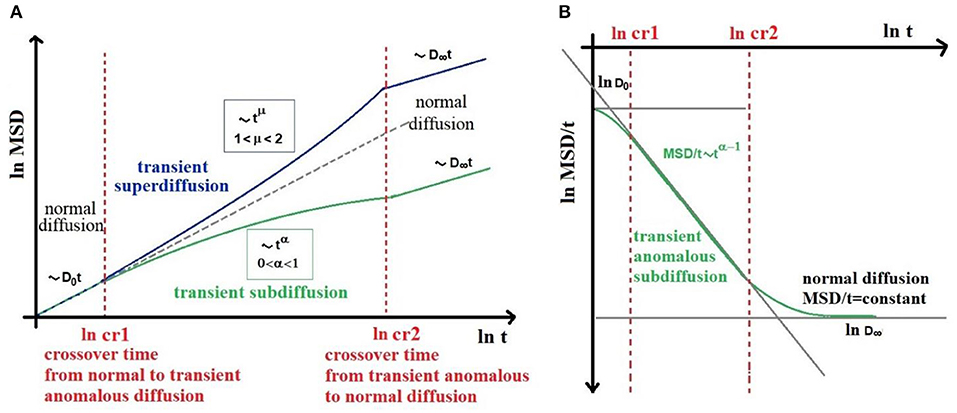
Figure 2. Schematic representation of MSD (A) and D(t) (B) behavior in high heterogeneous complex biological tissues, showing transient anomalous diffusion (AD). AD exists between two crossover times (cr1 and cr2). For t < cr1, i.e., at very short diffusion times we find normal diffusion characterized by D = D₀, while for t > cr2, i.e., at long diffusion times, we still find normal diffusion, defined by a finite value of D = D∞. The (cr1, cr2) time interval, must be long enough to include at least three orders of magnitude over time. As an example in AD MRI, the diffusion time Δ should run from 5 to 500 ms.

And in case of transient-superdiffusion:

$\begin{array}{lll}\text{D}(\text{t})~{\text{D}}_{\text{∞}}/(1+{\text{t}}^{1-\text{v}})& \text{with }1<\text{v}<2& \text{for t}\to \infty \\ \text{D}(\text{t})~{\text{D}}_0+1/{\text{t}}^{1-\text{v}}& \text{with }1<\text{v}<2& \text{for t}\to 0& (5)\end{array}$

The (cr1, cr2) time interval, which depends on microstructure investigated, must be long enough to include at least three orders of magnitude over time for defining a power-low. Therefore, it is preferable to use echo-stimulated types sequences (i.e., pulse-gradient stimulated-echo, PGSTE) to acquire DW-signal, since PGSTE allows to select a wider range of Δ values (Figure 1) compared to a pulse-gradient spin-echo (PGSE) sequence [31].

Transient-AD described with Equations (4) and (5), reconciles the advanced modality of tissue analysis provided by the AD with the theory and the established procedures of conventional DMRI [13, 30].

The Pseudo-Superdiffusion

Since our first works concerning AD by MRI, we showed a strong connection between magnetic susceptibility and AD image contrast [19, 24, 42] when data obtained by changing g in a PFG sequence were fitted with Equation (2). In particular, we obtained more details at the interface between different substances in AD MRI [42] and a strong negative correlation between the μ = 2γ parameter quantifying superdiffusion and the internal magnetic-field-gradient variance (Gi) arisen from the magnetic susceptibilities differences (Δχ) between water and polystyrene [19, 24]. Moreover, the dependence of γ on Δχ was stronger compared to that of the conventional apparent diffusion coefficient (ADC) on the same magnetic in-homogeneities. Building on our previous in vitro studies, we have recently demonstrated, using a clinical 3T MRI scanner, the utility of AD contrast in identifying key aspects of the composition (iron content, myelin density, and myelin distribution) and organization (tissue heterogeneity and tortuosity) in both cerebral white and gray matter [43]. Furthermore, we used this new AD image contrast based on γ maps, to obtain useful and complementary information (compared to that provided by DTI) about the early changing occurring in normal brain aging [44].

According to our experimental results, and considering the theory of AD, as well as the physical mechanisms underlying the MRI, we called the new AD image contrast “pseudo-superdiffusion,” as water molecules do not experience a real superdiffusion. In fact, no superdiffusion dynamics were predicted in phantoms comprised of packed polystyrene micro-beads in water, nor in the biological tissues that may eventually express subdiffusion. In practice, the γ parameter obtained with an effective physical approach is equal to the β parameter quantified by Magin through a mathematical approach. Therefore, β or γ are fractional exponents associated with intravoxel spatial heterogeneity related to the heterogeneous diffusion jump length. Water molecules can produce a variable displacement in each move, because of water multi-compartmentalization and local magnetic in-homogeneities (due to Δχ) at the interface between the different diffusion compartments. In particular, the coupling between diffusion gradients and Gi generated by Δχ, causes an irreversible signal loss and an unexpected signal refocusing that can be modeled as a pseudo-superdiffusion process. More in deep, local magnetic gradients impart a phase shift to the spins within a spatial region strictly close to interfaces. This Δχ-derived phase adds up to the phase shift given by the diffusion gradient pulse. When Gi and diffusion gradients are of the same order of magnitude, some spins contribute to increasing the DW signal attenuation; other spins (that can be very far from the first ones) acquire a phase shift that helps to increase the signal. Due to indistinguishable spins associated with water molecules, this scenario mimics a superdiffusion regime of water molecules, the signal of which disappears in one spot and appears in another one simulating long jumps of water molecules. This contrast mechanism increases the image sensitivity and resolution at the interfaces between different tissues [42, 43] and at sources of magnetic field inhomogeneities, such as iron accumulations in tissues [43, 44].

Literature Examination in the Light of the Pseudo-Superdiffusion Mechanism

Most of the papers concerning the measurement of AD parameters actually show the pseudo-superdiffusion measurement because the signal is acquired by changing g at a fixed value of Δ [43–49]. A careful examination of the maps shown in these papers reveals all the features of the pseudo-superdiffusion maps, namely: strong dependence on Δχ at the interfaces of different tissues; inverse correlation of voxels intensity with magnetic field in-homogeneities sources (iron and heavy metals deposits in the brain parenchyma), a better definition of density and orientation of the white matter tracts [47, 49].

Recently, a new elegant view of the formalism describing DMRI has been introduced [13, 30]. In particular, two complementary approaches have been highlighted for extracting information about the tissue microstructure from DW-signal: signal representations (or statistical model deriving from statistical quantum-mechanics) and tissue models [50]. Tissue models assume a priori picture of the underlying tissue while statistical models (such as DTI, diffusion kurtosis imaging, DKI, and AD imaging) aim at using mathematical representations of the empirical DW-signal without assumptions about the underlying tissue. Thus, they are applicable to any tissue type, but the estimated parameters lack specificity and therefore these methods need to be validated with complementary techniques such as SPT, FCS, and histology.

In the light of the considerations about the mechanism underpinning the pseudo-superdiffusion contrast, and taking into account DW-signal representation, it could be argued that most AD results (in particular those that seem most useful for future clinical applications) [43, 44, 46, 47, 49, 51, 52], do not concern the quantification of the actual AD process but rather the estimation of a new parameter γ (or β) introduced by the use of DW-signal representation describing superdiffusion. The biophysical mechanism underpinning the pseudo-superdiffusion contrast resides in the interaction between diffusion in multi-compartments of different dimensions and the Δχ at the interfaces between the different compartments. The multi-compartmentalization, if related to compartments characterized by length scale that covers at least three orders of magnitude, can contribute to the behavior of transient-AD of water in the tissues, but the Δχ heavily contribute to varying the effective length scale simulating a more obvious AD behavior. The suspicion is that only the Δχ in a heterogeneous tissue could be enough to “modeling” the DW-signal as an AD signal representation.

Conclusion

In this brief review, we addressed the transient-AD by MRI, starting from the assumption that transient-AD can exist in biological tissues, as demonstrated by the SPT and FCS experiments in living systems. We highlighted the two different modalities for quantifying subdiffusion and superdiffusion parameters. In biological tissues, we expect subdiffusion, not superdiffusion. However, most of the results found in the literature actually concern quantification of superdiffusion. As explained in sections The Pseudo-superdiffusion and Literature Examination in the Light of the Pseudo-superdiffusion Mechanism, this is not real superdiffusion, rather pseudo-superdiffusion due to the use of a superdiffusion signal representation. The biophysical origin of pseudo-superdiffusion depends on the multi-compartmentalization of water diffusion and on the presence of local magnetic in-homogeneities. The recent development of DW-signal representation of AD [32–35] should be used in order to investigate the role of the interplay between internal (background) and diffusion gradients, and to consider the effect of finite width of the diffusion gradient pulses. In conclusion, AD MRI is still in its early stages due to the no-flexible conventional acquisition modality of the clinical MRI, the lack of validation experiments (for example by using optical imaging) and the difficulties in a reliable signal representation.

Author Contributions

SC and MP conceived the original idea, planned the review, contributed to the interpretation of the literature, and read and approved the final manuscript. SC collected all the bibliography with the contribution of MP and wrote the manuscript.

Funding

This is part of ATTRACT that had received funding from the European Union's Horizon 2020 Research and Innovation Programme.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Jones DK. Diffusion MRI. New York, NY: Oxford University Press (2011).

Google Scholar

2. Klafter J, Sokolov IM. Anomalous diffusion spreads its wings. Phys World. (2005) 18:29–32. doi: 10.1088/2058-7058/18/8/33

CrossRef Full Text | Google Scholar

3. Hofling F, Franosch T. Anomalous transport in the crowded world of biological cells. Rep Prog Phys. (2013) 76:046602. doi: 10.1088/0034-4885/76/4/046602

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Saxton MJ, Jacobson K. Single-particle tracking: application to membrane dynamics. Anu Rev Biophys Biomol Struct. (1997) 26:373–99. doi: 10.1146/annurev.biophys.26.1.373

CrossRef Full Text | Google Scholar

5. Honigmann A, Muller V, Hell SW, Eggeling C. STED microscopy detects and quantifies liquid phase separation in lipid membranes using a new far-red emitting fluorescent phosphoglycerolipid analogue. Faraday Disc. (2013) 161:77–89. doi: 10.1039/C2FD20107K

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Weigel AV, Simon B, Tamkun MM, Krapf D. Ergodic and nonergodic processes coexist in the plasma membrane as observed by single-molecule tracking. Proc Natl Acad Sci USA. (2011) 108:6438–43. doi: 10.1073/pnas.1016325108

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Sykovà E, Nicholson C. Diffusion in brain extracellular space. Physiol Rev. (2008) 88:1277–340. doi: 10.1152/physrev.00027.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Manzo C, Garcia-Parajo MF. A review of progress in single particle tracking: from methods to biophysical insights. Rep Prog Phys. (2015) 78:124601. doi: 10.1088/0034-4885/78/12/124601

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Elson EL. Fluorescence correlation spectroscopy: past, present, future. Biophys J. (2011) 101:2855–70. doi: 10.1016/j.bpj.2011.11.012

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Nicholson C. Anomalous diffusion inspires anatomical insights. Biophys J. (2015) 108:2091–3. doi: 10.1016/j.bpj.2015.03.043

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Xiao F, Hrabe J, Hrabetova S. Anomalous extracellular diffusion in rat cerebellum. Biophys J. (2015) 108:2384–95. doi: 10.1016/j.bpj.2015.02.034

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Sherpa AD, Van De Nes P, Fanrong X, Weedon J, Hrabetova S. Gliotoxin-induced swelling of astrocytes hinders diffusion in brain extracellular space via formation of dead-space microdomains. Glia. (2014) 62:1053–65. doi: 10.1002/glia.22661

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Novikov DS, Kiselev VG, Jespersen SN. On modeling. Magn Reson Med. (2018) 79:3172–93. doi: 10.1002/mrm.27101

CrossRef Full Text | Google Scholar

14. Novikov DS, Fieremans E, Jespersen SN, Kiselev VG. Quantifying brain microstructure with diffusion MRI: theory and parameter estimation. NMR Biomed. (2018) 32:e3998. doi: 10.1002/nbm.3998

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Metzler R, Klafter J. The random walk's guide to anomalous diffusion: a fractional dynamics approach. Phys Rep. (2000) 339:1–77. doi: 10.1016/S0370-1573(00)00070-3

CrossRef Full Text | Google Scholar

16. Metzler R, Jeon JH, Cherstvy AG, Barkai E. Anomalous diffusion models and their properties: non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys Chem Chem Phys. (2014) 16:24128–64. doi: 10.1039/C4CP03465A

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Magin RL, Abdullah O, Baleanu D, Zhou XJ. Anomalous diffusion expressed through fractional order differential operators in the Bloch-Torrey equation. J Magn Reson. (2008) 190:255–70. doi: 10.1016/j.jmr.2007.11.007

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Magin RL. Fractional calculus models of complex dynamics in biological tissues. Comp Math Appl. (2010) 59:1586–93. doi: 10.1016/j.camwa.2009.08.039

CrossRef Full Text | Google Scholar

19. Palombo M, Gabrielli A, De Santis S, Cametti C, Ruocco G, Capuani S. Spatio-temporal anomalous diffusion in heterogeneous media by nuclear magnetic resonance. J Chem Phys. (2011) 135:034504. doi: 10.1063/1.3610367

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Palombo M, Gabrielli A, Servedio VDP, Ruocco G, Capuani S. Structural disorder and anomalous diffusion in random packing of spheres. Sci Rep. (2013) 3:2631. doi: 10.1038/srep02631

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Yu X, Zhang Y, Sun H, Zheng C. Time fractional derivative model with Mittag-Leffler function kernel for describing anomalous diffusion: analytical solution in bounded-domain and model comparison. Chaos Solitons Fractals. (2018) 115:306–12. doi: 10.1016/j.chaos.2018.08.026

CrossRef Full Text | Google Scholar

22. Magin RL, Ingo C, Colon-Perez L, Triplett W, Mareci TH. Characterization of anomalous diffusion in porous biological tissues using fractional order derivatives and entropy. Microporous Mesoporous Mater. (2013) 178:39–43. doi: 10.1016/j.micromeso.2013.02.054

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Ingo C, Magin RL, Colon-Perez L, Triplett W, Mareci TH. On random walks and entropy in diffusion-weighted magnetic resonance imaging studies of neural tissue. Magn Reson Med. (2014) 71:617–27. doi: 10.1002/mrm.24706

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Capuani S, Palombo M, Gabrielli A, Orlandi A, Maraviglia B, Pastore FS. Spatio-temporal anomalous diffusion imaging: results in controlled phantoms and in excised human meningiomas. Magn Reson Imaging. (2013) 31:359–65. doi: 10.1016/j.mri.2012.08.012

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Özarslan E, Basser PJ, Shepherd TM, Thelwall PE, Vemuri BC, Blackband SJ. Observation of anomalous diffusion in excised tissue by characterizing the diffusion-time dependence of the MR signal. J Magn Reson. (2006) 183:315–23. doi: 10.1016/j.jmr.2006.08.009

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Özarslan E, Shepherd TM, Koay CG, Blackband SJ, Basser PJ. Temporal scaling characteristics of diffusion as a new MRI contrast: findings in rat hippocampus. NeuroImage. (2012) 60:1380–93. doi: 10.1016/j.neuroimage.2012.01.105

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Fan Y, Gao JH. Fractional motion model for characterization of anomalous diffusion from NMR signals. Phys Rev E. (2015) 92:012707. doi: 10.1103/PhysRevE.92.012707

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Hall MG, Barrick TR. From diffusion-weighted MRI to anomalous diffusion imaging. Magn Reson Med. (2008) 59:447–55. doi: 10.1002/mrm.21453

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Karaman MM, Sui Y, Wang H, Magin RL, Li Y, Zhou XJ. Differentiating low- and high-grade pediatric brain tumors using a continuous-time random-walk diffusion model at high b-values. Magn Reson Med. (2016) 76:1149–57. doi: 10.1002/mrm.26012

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Kiselev VG. Fundamentals of diffusion MRI physics. NMR Biomed. (2017) 30:e3602. doi: 10.1002/nbm.3602

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Callaghan PT. Principles of Nuclear Magnetic Resonance Microscopy. New York, NY: Oxford University Press Inc. (1993).

Google Scholar

32. Lin G. General pulsed-field gradient signal attenuation expression based on a fractional integral modified-Bloch equation. Comm Nonl Sci Num Simul. (2018) 63:404–20. doi: 10.1016/j.cnsns.2018.04.008

CrossRef Full Text | Google Scholar

33. Lin G. General PFG signal attenuation expressions for anisotropic anomalous diffusion by modified-Bloch equations. Phys A Stat Mech Appl. (2018) 497:86–100. doi: 10.1016/j.physa.2018.01.008

CrossRef Full Text | Google Scholar

34. Lin G. Analyzing signal attenuation in PFG anomalous diffusion via a modified Gaussian phase distribution approximation based on fractal derivative model. Phys A Stat Mech Appl. (2017) 467:277–88. doi: 10.1016/j.physa.2016.10.036

CrossRef Full Text | Google Scholar

35. Lin G. Analysis of PFG anomalous diffusion via real-space and phase-space approaches. Mathematics. (2018) 6:17. doi: 10.3390/math6020017

CrossRef Full Text | Google Scholar

36. Zecca M, Vogt SJ, Connolly PRJ, May EF, Johns ML. NMR measurements of tortuosity in partially saturated porous media. Trans Porous Media. (2018) 125:271–88. doi: 10.1007/s11242-018-1118-y

CrossRef Full Text | Google Scholar

37. Fieremans E, Burcaw LM, Lee HH, Lemberskiy G, Veraart J, Novikov DS. In vivo observation and biophysical interpretation of time-dependent diffusion in human white matter. Neuroimage. (2016) 129:414–27. doi: 10.1016/j.neuroimage.2016.01.018

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Novikov DS, Jensen JH, Helpern JA, Fieremans E. Revealing mesoscopic structural universality with diffusion. Proc Natl Acad Sci USA. (2014) 111:5088–93. doi: 10.1073/pnas.1316944111

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Saxton MJ. A biological interpretation of transient anomalous subdiffusion. I Qualitative model. Biophys J. (2007) 92:1178–91. doi: 10.1529/biophysj.106.092619

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Bouchaud JP, Georges A. Anomalous diffusion in disordered media. Statistical mechanisms, models and physical applications. Phys Rep. (1990) 195:127–293. doi: 10.1016/0370-1573(90)90099-N

CrossRef Full Text | Google Scholar

41. Platani MI, Goldberg I, Lamond AI, Swedlow JR. Cajal body dynamics and association with chromatin are ATP-dependent. Nat Cell Biol. (2002) 4:502–8. doi: 10.1038/ncb809

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Palombo M, Gabrielli A, De Santis A, Capuani S. The γ parameter of the stretched-exponential model is influenced by internal gradients: validation in phantoms. J Magn Reson. (2012) 216:28–36. doi: 10.1016/j.jmr.2011.12.023

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Caporale A, Palombo M, Macaluso E, Guerreri M, Bozzali M, Capuani S. The γ-parameter of anomalous diffusion quantified in human brain by MRI depends on local magnetic susceptibility differences. Neuroimage. (2017) 147:619–31. doi: 10.1016/j.neuroimage.2016.12.051

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Guerreri M, Palombo M, Caporale A, Fasano F, Macaluso E, Bozzali M, et al. Age-related microstructural and physiological changes in normal brain measured by MRI γ-metrics derived from anomalous diffusion signal representation. Neuroimage. (2019) 188:654–67. doi: 10.1016/j.neuroimage.2018.12.044

PubMed Abstract | CrossRef Full Text | Google Scholar

45. De Santis S, Gabrielli A, Bozzali M, Maraviglia B, Macaluso E, Capuani S. Anisotropic anomalous diffusion assessed in the human brain by scalar invariant indice. Magn Reson Med. (2011) 65:1043–52. doi: 10.1002/mrm.22689

CrossRef Full Text | Google Scholar

46. Zhou XJ, Gao Q, Abdullah O, Magin RL. Studies of anomalous diffusion in the human brain using fractional order calculus. Magn Reson Med. (2010) 63:562–9. doi: 10.1002/mrm.22285

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Yu Q, Reutens D, Vegh V. Can anomalous diffusion models in magnetic resonance imaging be used to characterise white matter tissue microstructure? Neuroimage. (2018) 175:122–37. doi: 10.1016/j.neuroimage.2018.03.052

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Yu Q, Reutens D, O'Brien K, Vegh V. Tissue microstructure features derived from anomalous diffusion measurements in magnetic resonance imaging. Hum Brain Mapp. (2017) 38:1068–81. doi: 10.1002/hbm.23441

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Grinberg F, Farrher E, Ciobanu L, Geoffroy F, Le Bihan D, Shah NJ. (2014). Non-Gaussian diffusion imaging for enhanced contrast of brain tissue affected by ischemic stroke. PLoS ONE. (2014) 9:e89225. doi: 10.1371/journal.pone.0089225

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Jelescu IO, Budde MD. Design and validation of diffusion MRI models of white matter. Front Phys. (2017) 5:61. doi: 10.3389/fphy.2017.00061

CrossRef Full Text | Google Scholar

51. Xu B, Su L, Wang Z, Fan Y, Gong G, Zhu W, et al. Anomalous diffusion in cerebral glioma assessed using a fractional motion model. Magn Reson Med. (2017) 78:1944–9. doi: 10.1002/mrm.26581

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Sui Y, Wang H, Liu G, Damen FW, Wanamaker C, Li Y, et al. Differentiation of low-and high-grade pediatric brain tumors with high b-value diffusion-weighted MR imaging and a fractional order calculus model. Radiology. (2015) 277:489–96. doi: 10.1148/radiol.2015142156

PubMed Abstract | CrossRef Full Text | Google Scholar