Antiproton Physics

We review the physics of low-energy antiprotons, and its link with the nuclear forces. This includes: antinucleon scattering on nucleons and nuclei, antiprotonic atoms, and antinucleon-nucleon annihilation into mesons.

1. A Brief History

In 1932, the positron, the antiparticle of the electron, was discovered in cosmic rays and confirmed in the β⁺ decay of some radioactive nuclei (see e.g., the Nobel lecture by Anderson [1]). It was then reasonably anticipated that the proton also has an antiparticle, the antiproton¹. It was also suspected that the antiproton would be more difficult to produce and detect than positrons in cosmic rays. The Bevatron project (BeV, i.e., billion of electron-volts, was then a standard denomination for what is now GeV) was launched at Berkeley to reach an energy high-enough to produce antiprotons through the reaction

$\begin{array}{ll}p+A\to p+A+\overline{p}+p,& (1)\end{array}$

where A denotes the target nucleus. For A = p, this is a standard exercise in relativistic kinematics to demonstrate that the kinetic energy of the incoming proton should be higher than 6 m, where m is the proton mass, and c = 1. This threshold decreases if the target A is more massive. The Bevatron was completed in 1954, and the antiproton was discovered in 1955 by a team lead by Chamberlain and Segrè, who were awarded the Nobel prize in 1959².

Shortly after the antiproton, the antineutron, $\bar{n}$, was also discovered at Berkeley, and up to now, for any new elementary particle, the corresponding antiparticle has also been found. The discovery of the first anti-atom was well-advertised [2], but this was not the case for the earlier observation of the first antinucleus, antideuterium, because of a controversy between an European team [3] and its US competitors [4]. In experiments at very high energy, in particular collisions of heavy ions at STAR (Brookhaven) and ALICE (CERN), one routinely produces light antinuclei and even anti-hypernuclei (in which an antinucleon is replaced by an antihyperon $\bar{\Lambda }$) [5–7].

The matter-antimatter symmetry is almost perfect, except for a slight violation in the sector of weak interactions, which is nearly exactly compensated by a simultaneous violation of the left-right symmetry, i.e., the product PC of parity P and charge-conjugation C is only very marginally violated. Up to now, there is no indication of any violation of the product CPT, where T is the time-reversal operator: this implies that the proton and antiproton have the same mass, a property now checked to < 10⁻⁹ [8].

Many experiments have been carried out with low energy antiprotons, in particular at Brookhaven and CERN in the 60s and 70s, with interesting results, in particular for the physics of the mesons produced by annihilation. However, in these early experiments, the antiprotons were part of secondary beams containing many negatively-charged pions and kaons, and with a wide momentum spread.

In the 70s, Simon van der Meer, and his colleagues at CERN and elsewhere imagined and developed the method of stochastic cooling [9], which produces antiproton beams of high purity, sharp momentum resolution, and much higher intensity than in the previous devices. CERN transformed the fixed-target accelerator SpS into a proton-antiproton collider, Sp$\bar{\text{p}}$S, with the striking achievement of the discovery of the W^± and Z⁰, the intermediate bosons of the electro-weak interaction. A similar scheme was later adopted at Fermilab with higher energy and intensity, leading to many results, among which the discovery of the top quark.

As a side product of the experiments at the Sp$\bar{\text{p}}$S program, CERN built a low-energy facility, LEAR (Low-Energy Antiproton Ring) which operated from 1982 to 1996, and hosted several experiments on which we shall come back later. Today, the antiproton source of CERN is mainly devoted to experiments dealing with atomic physics and fundamental symmetries. In spite of several interesting proposals, no low-energy extension of the antiproton program was built at Fermilab.

As for the intermediate energies, at the beginning of the CERN cooled-antiproton program, a $\bar{p}$ beam was sent in the ISR accelerator to hit a thin hydrogen target. The experiment R704 got sharp peaks corresponding to some charmonium states, and in particular a first indication of the—then missing—P-wave singlet state h_c [10]. But ISR was to be closed, and in spite of a few more days of run, R704 was interrupted. The team moved to Fermilab, and charmonium physics with antiprotons was resumed with antiproton-proton collisions arranged in the accumulation device (experiments E760-E835) [11].

Today, the techniques of production of sharp antiproton beams is well-undercontrol. There are projects to perform strong-interaction physics with antiprotons at FAIR (Darmstadt) [12] and JPARC in Japan [13]. In the 80s, an ambitious extension of LEAR at higher energies, SuperLEAR [14], was proposed by Montanet et al., but was not approved by the CERN management. A major focus of SuperLEAR was charm physics. But more than 30 years later, this physics has been largely unveiled by beauty factories and high-energy hadron colliders.

Presently, the only running source of cooled antiprotons is the very low energy AD at CERN (Antiproton Decelerator) and its extension ELENA (Extra Low ENergy Antiproton) with the purpose of doing atomic-physics and high-precision tests of fundamental symmetries. Some further decelerating devices are envisaged for the gravitation experiments [15]. Of course, standard secondary antiproton beams are routinely produced, e.g., at KEK in Japan.

Note also that in devices making antiproton beams, a non-negligible fraction of antideuterium is produced, which could be cooled and stored. The intensity would be sufficient to perform strong-interaction measurements, but there is not yet any proposal for an experiment with an antideuterium beam.

We shall discuss along this review many results obtained at LEAR and elsewhere. Already the measurements made at Berkeley during the weeks following the discovery of the antiproton were remarkable. After more than 60 years, we realize today that they gave keys to the modern understanding of hadrons, but the correct interpretation was too far from the current wisdom of the 50s. Indeed, from the work by Fermi and Yang, on which more later, it was realized that one-pion exchange constitutes the long-range part of the antinucleon-nucleon interaction. The simplest model, just before the discovery of the antiproton, would be one-pion exchange supplemented by a very short-range annihilation. This would imply for the charge-exchange ($\bar{p}p\to \bar{n}n$), elastic ($\bar{p}p\to \bar{p}p$) and annihilation ($\bar{p}p\to \mathrm{\text{mesons}}$) cross-sections a hierarchy

$\begin{array}{ll}{\sigma }_{\text{ce}}>{\sigma }_{\text{el}}>{\sigma }_{\text{an}},& (2)\end{array}$

the first inequality resulting from straightforward isospin algebra. What was observed at Berkeley is just the opposite! And it took us years to admit and understand this pattern, which is a consequence of the composite character of the nucleon and antinucleon.

The era of LEAR and Sp$\bar{\text{p}}$S at CERN, and then the large $\bar{p}p$ collider of Fermilab will certainly be reminded as the culmination of antiproton physics. At very high energy, the trend is now more on pp rather than $\bar{p}p$ collision, due to the higher intensity of proton beams. Certainly very-low energy experiments will remain on the floor to probe the fundamental symmetries with higher and higher precision. The question is open on whether antiproton beams will be used for hadron physics, a field where electron beams and flavor factories already provide much information.

Of course, the role of antimatter in astrophysics is of the highest importance. Antiprotons and even antinuclei are seen in high-energy cosmic rays. The question is to estimate how many antinuclei are expected to be produced by standard cosmic rays, to estimate the rate of primary antinuclei (see e.g., [16, 17]). Some years ago, cosmological models were built [18] in which the same amount of matter and antimatter was created, with a separation of zones of matter and zones of antimatter. In modern cosmology, it is assumed that an asymmetry prevailed, so that, after annihilation, some matter survived.

This review is mainly devoted to the low-energy experiments with antinucleons. Needless to say that the literature is abundant, starting with dedicated workshops [19–24] and schools [25–28].

Because of the lack of space, some important subjects will not be discussed, in particular the ones related to fundamental symmetry: the inertial mass of the antiproton, its charge and magnetic moment, in comparison with the values for the proton; the detailed comparison of hydrogen and antihydrogen atoms; the gravitational properties of neutral atoms, such as antihydrogen, etc. We will mention only very briefly, in the section on antiprotonic atoms, the dramatically precise atomic physics made with the antiprotonic Helium.

2. From the Nucleon-Nucleon to the Antinucleon-Nucleon Interaction

In this section we outline the general theoretical framework: how to extrapolate our information on the nuclear forces to the antinucleon-nucleon system. We present the basics of the well-known G-parity rule, with a remark about the definition of antiparticle states.

2.1. The G-Parity Rule

In QED, the e⁻e⁻ → e⁻e⁻ and e⁺e⁻ → e⁺e⁻ amplitudes are related by crossing, but there is a long way from the region $\{s>4m_e^2,t<0\}$ to the one with $\{s<0,t>4m_e^2$ to attempt a reliable analytic extrapolation. Here, m_e is the electron mass and s and t the usual Mandelstam variables³. A more useful approach consists of comparing both reactions for the same values of s and t. The e⁻e⁻ → e⁻e⁻ amplitude can be decomposed into a even and odd part according to the C-conjugation in the t-channel, say

$\begin{array}{ll}{M}(e^{-}{e}^{-}\to e^{-}{e}^{-})={{M}}_{\text{even}}+{{M}}_{\text{odd}},& (3)\end{array}$

and the e⁺e⁻ → e⁺e⁻ amplitude for the same energy and transfer is given by

$\begin{array}{ll}{M}(e^{+}{e}^{-}\to e^{+}{e}^{-})={{M}}_{\text{even}}-{{M}}_{\text{odd}}.& (4)\end{array}$

The first term contains the exchange of an even number of photons, and the last one the exchange of an odd number. At lowest order, one retrieves the sign flip of the Coulomb potential. This rule remains valid to link pp → pp and $\bar{p}p\to \bar{p}p$ amplitudes: the exchange of a π⁰ with charge conjugation C = +1, is the same for both reactions, while the exchange of an ω meson (C = −1) flips sign.

Fermi and Yang [29] astutely combined this C-conjugation rule with isospin symmetry, allowing to include the exchange of charged mesons, as in the charge-exchange processes. Instead of comparing pp → pp to $\bar{p}p\to \bar{p}p$ or np → np to $\bar{n}p\to \bar{n}p$, the G-parity rule relates amplitudes of given isospin I. More precisely, if the nucleon-nucleon amplitude is decomposed as

$\begin{array}{ll}{{M}}^I(NN)={{M}}_{\text{G}=+1}+{{M}}_{\text{G}=\text{-}1},& (5)\end{array}$

according to the G-odd (pion, omega, …) or G-even (ρ, …) in the t-channel, then its $\bar{N}N$ counterpart reads

$\begin{array}{ll}{{M}}^I(\overline{N}N)={{M}}_{\text{G}=+1}-{{M}}_{\text{G}=\text{-}1}.& (6)\end{array}$

Note that there is sometimes some confusion between the C-conjugation and the G-parity rules, especially because there are two ways of defining the isospin doublet $\left\{\bar{n},\bar{p}\right\}$ (see Appendix: Isospin Conventions).

In current models of NN, the pion-exchange tail, the attraction due to isoscalar two-pion exchange, and the spin-dependent part of the ρ exchange are rather well-identified, and thus can be rather safely transcribed in the $\bar{N}N$ sector. Other terms, such as the central repulsion attributed to ω-exchange, might contain contributions carrying the opposite G-parity, hidden in the effective adjustment of the couplings. Thus, the translation toward $\bar{N}N$ might be biased.

2.2. Properties of the Long-Range Interaction

Some important consequences of the G-parity rule have been identified. First, the moderate attraction observed in NN, due to a partial cancellation of σ (or, say, the scalar-isoscalar part of two-pion exchange) and ω-exchanges, becomes a coherent attraction once ω-exchange flips sign. This led Fermi and Yang to question whether the mesons could be interpreted as bound states of a nucleon and an antinucleon. This idea has been regularly revisited, in particular at the time of bootstrap [30]. As stressed, e.g., in Ball et al. [31], this approach hardly accounts for the observed degeneracy of I = 0 and I = 1 mesons (for instance ω and ρ having about the same mass).

In the 70s, Shapiro et al., and others, suggested that baryon-antibaryon bound states were associated with new types of hadrons, with the name baryonium, or quasi-deuteron [32–34]. Similar speculations were made later for other hadron-hadron systems, for instance $D{\bar{D}}^{*}$, where D is a charmed meson $(\bar{c}q)$ of spin 0 and ${\bar{D}}^{*}$ an anticharmed meson $(\bar{c}q)$ of spin 1 [35]. Some candidates for baryonium were found in the late 70s, interpreted either as quasi-nuclear $\bar{N}N$ states à la Shapiro, or as exotic states in the quark model, and motivated the construction of the LEAR facility at CERN. Unfortunately, the baryonium states were not confirmed.

Another consequence of the G-parity rule is a dramatic change of the spin dependence of the interaction. At very low energy, the nucleon-nucleon interaction is dominated by the spin-spin and tensor contributions of the one-pion exchange. However, when the energy increases, or, equivalently, when one explores shorter distances, the main pattern is a pronounced spin-orbit interaction. It results from a coherent sum of the contributions of vector mesons and scalar mesons⁴. The tensor component of the NN interaction is known to play a crucial role: in most models, the ¹S₀ potential is stronger than the ³S₁ one, but in this latter partial wave⁵, the attraction is reinforced by S-D mixing. However, the effect of the tensor force remains moderate, with a percentage of D wave of about 5% for the deuteron.

In the case of the $\bar{N}N$ interaction, the most striking coherence occurs in the tensor potential, especially in the case of isospin I = 0 [36]. A scenario with dominant tensor forces is somewhat unusual, and leads to unexpected consequences, in particular a relaxation of the familiar hierarchy based on the hight of the centrifugal barrier. For instance, if one calculates the spectrum of bound states from the real part of the $\bar{N}N$ interaction, the ground-state is ^1,3P₀, and next a coherent superposition of ^1,3S₁ and ^1,3D₁, and so on. In a scattering process, there is no polarization if the tensor component is treated to first order, but polarization shows up at higher order. Thus, one needs more than polarization measurements⁶ to distinguish the dynamics with a moderate spin-orbit component from the dynamics with a very strong tensor component.

2.3. Appendix: Isospin Conventions

There are two possible conventions for writing the isospin states of antinucleons [37].

The natural choice is based on the charge conjugation operator C, namely $|{\overline{p}\rangle }_c=C|p\rangle$ and $|{\overline{n}\rangle }_c=C|n\rangle$. However, it transforms the two representation of SU(2) into a $\bar{2}$ which does not couple with the usual Clebsch-Gordan coefficients. For instance, the isospin I = 0 state of $\overline{N}N$ reads in this convention

$\begin{array}{ll}|I=0\rangle =\frac{|\overline{p}p{\rangle }_c+|\overline{n}n{\rangle }_c}{\sqrt{2}},& (7)\end{array}$

which anticipates the formula for an SU(3) singlet,

$\begin{array}{ll}|0\rangle =\frac{|\overline{u}u\rangle +|\overline{d}d\rangle +|\overline{s}s\rangle }{\sqrt{3}},& (8)\end{array}$

However, the $\bar{2}$ representation of SU(2) is equivalent to the 2 one, and it turns out convenient to perform the corresponding rotation, that is to say, define the states by the G-parity operator, namely (without subscript) $|\bar{p}\rangle =G|n\rangle$ and $|\bar{n}\rangle =G|p\rangle$. With this convention, the isospin singlet is written as.

$\begin{array}{ll}|I=0\rangle =\frac{|\overline{n}n\rangle -|\overline{p}p\rangle }{\sqrt{2}},& (9)\end{array}$

3. Baryonium

The occurrence of baryonium candidates in antiproton-induced reactions was a major subject of discussion in the late 70s and in the 80s and the main motivation to build new antiprotons beams and new detectors. The name “baryonium” suggests a baryon-antibaryon structure, as in the quasi-nuclear models. More generally “baryonium” denotes mesons that are preferentially coupled to the baryon-antibaryon channel, independently of any prejudice about their internal structure.

Nowadays, baryonium is almost dead, but interestingly, some of the innovative concepts and some unjustified approximations developed for baryonium are re-used in the current discussions about the new hidden-charm mesons XYZ and other exotic hadrons [38].

3.1. Experimental Candidates for Baryonium

For an early review on baryonium (see [39]). For an update, see the Particle Data Group [40]. In short: peaks have been seen in the integrated cross sections, or in the angular distribution (differential cross section) at given angle, or in some specific annihilation rates as a function of the energy. The most famous candidate was the S(1932), seen in several experiments [39]. The most striking candidate was the peak of mass 2.95 GeV/c² seen in $\bar{p}p{\pi }^{-}$ [41], with some weaker evidence for peaks at 2.0 and 2.2 GeV/c² in the $\bar{p}p$ subsystem, suggesting a sequential decay ${{B}}^{-}\to {B}+{\pi }^{-}$, where ${B}$ denotes a baryonium. Peaks were also seen in the inclusive photon and pion spectra of the annihilations $\bar{p}p\to \gamma X$ and $\bar{p}p\to \pi X$ at rest.

None of the experiments carried out at LEAR confirmed the existence of such peaks. However, some enhancements have been seen more recently in the $\bar{p}p$ mass distribution of the decay of heavy particles, such as $J/\psi \to \gamma \bar{p}p$, $B\to K\bar{p}p$, or $B\to D\bar{p}p$, see Ablikim et al. [42] and the notice on non $\bar{q}q$ mesons in Tanabashi et al. [40]. There is a debate about whether they correspond a baryonium states or just reveal a strong $\bar{p}p$ interaction in the final state (see e.g., the discussion in [43–45]). Also, as stressed by Amsler [46], the f₂(1565) is seen only in annihilation experiments, and thus could be a type of baryonium, ^1,3P₂ − ^1,3F₂ in the quasi-nuclear models. See the review on f₂(1565) in Tanabashi et al. [40].

3.2. The Quasi-Nuclear Model

Today, it is named “molecular” approach. The observation that the real part of the $\bar{N}N$ interaction is more attractive than its NN counterpart led Shapiro et al. [32], Dover et al. [33], and others, to predict the existence of deuteron-like $\bar{N}N$ bound states and resonances. Due to the pronounced spin-isospin dependence of the $\bar{N}N$ interaction, states with isospin I = 0 and natural parity were privileged in the predictions. The least one should say is that the role of annihilation was underestimated in most early studies. Attempts to include annihilation in the spectral problem have shown, indeed, that most structures created by the real potential are washed out when the absorptive part is switched on [47].

3.3. Duality

Duality is a very interesting concept developed in the 60s. For our purpose, the most important aspect is that in a hadronic reaction a + b → c + d, there is an equivalence between the t-channel dynamics, i.e., the exchanges schematically summarized as $\sum _{i}a+\bar{c}\to X_i\to \bar{b}+d$, and the low-energy resonances $\sum _{j}a+b\to Y_j\to c+d$. In practice, one approach is usually more efficient than the other, but a warning was set by duality against empirical superpositions of t-channel and s-channel contributions. For instance, $\bar{K}N$ scattering with strangeness S = −1 benefits the hyperons as s-channel resonances, and one also observes a coherent effect of the exchanged mesons. On the other hand, KN is exotic, and, indeed, has a much smaller cross-section. In KN, there should be destructive interferences among the t-channel exchanges.

Though invented before the quark model, duality is now better explained with the help of quark diagrams. Underneath is the Zweig rule, that suppresses the disconnected diagrams. See e.g., [48, 49] for an introduction to the Zweig rule, and refs. there. The case of $\bar{K}N$, or any other non-exotic meson-baryon scattering is shown in Figure 1. For the exotic KN channel the incoming antiquark is $\bar{s}$, and it cannot annihilate. So there is no possibility of forming a quark-antiquark meson in the t channel, nor a three-quark state in the s-channel. In a famous paper [50], Rosner pointed out that as meson-exchanges are permitted in nucleon-antinucleon scattering (or any baryon-antibaryon system with at least one quark matching an antiquark), there should be resonances in the s-channel: baryonium was born, and more generally a new family of hadrons. The corresponding quark diagram is shown in Figure 1. As stressed by Roy [49], duality suggests higher exotics.

FIGURE 1

Figure 1. Duality diagram for non-exotic meson-baryon (left) and baryon-antibaryon (right) scattering.

3.4. Baryonium in the Hadronic-String Picture

This concept of duality is illustrated in the hadronic-string picture, which, in turn, is supported by the strong-coupling limit of QCD (see e.g., the contribution by Rossi and Veneziano in [39]). A meson is described as a string linking a quark to an antiquark. A baryon contains three strings linking each of the three quarks to a junction, which acts as a sort of fourth component and tags the baryon number. The baryonium has a junction linked to the two quarks, and another junction linked to the two antiquarks (see Figure 2). The decay happens by string breaking and $q\bar{q}$, leading either to another baryonium and a meson, or to baryon-antibaryon pair. The decay into two mesons proceeds via the internal annihilation of the two junctions, and is suppressed.

FIGURE 2

Figure 2. String picture of a meson (left), a baryon (center), and a baryonium (right).

The baryonium of Jaffe was somewhat similar, with the string realized by the cigar-shape limit of the bag model [51]. Note that the suppression of the decay into mesons is due in this model to a centrifugal barrier, rather than to a topological selection rule. The orbitally excited mesons consist of a quark and an antiquark linked by a string, the excited baryons are the analogs with a quark and a diquark, and the baryonia involve a diquark and an antidiquark.

3.5. Color Chemistry

Chan et al.[52] pushed the speculations a little further in their “color chemistry.” They have baryonia with color $\bar{3}$ diquarks, which decay preferentially into a baryon-antibaryon pair rather than into mesons, also more exotic baryonia in which the diquark has color sextet. Then even the baryon-antibaryon decay is suppressed, and the state is expected to be rather narrow. This was a remarkable occurrence of the color degree of freedom in spectroscopy. However, there was no indication on how and why such diquark-antidiquark structure arises from the four-body dynamics.

3.6. Other Exotics?

The baryonium story is just an episode in the long saga of exotics, which includes the strangeness S = +1 “Z” baryons in the 60s, their revival under the name “light pentaquark” [40]. The so-called “molecular approach” hadrons was illustrated by the picture of the Δ resonance as πN by Chew and Low [53], and of the Λ(1405) as $\bar{K}N$ by Dalitz and Yan [54], with many further discussions and refinements.

As reminded, e.g., in Rossi and Veneziano [55], there is some analogy between the baryonium of the 70s and 80s and the recent XYZ spectroscopy. The XYZ are mesons with hidden heavy flavor that do not fit in the ordinary quarkonium spectroscopy [38]. One can replace “quasi-nuclear” by “molecular,” “baryon number” by “heavy flavor,” etc., to translate the concepts introduced for baryonium for use in the discussions about XYZ. The diquark clustering in the light sector is now replaced by an even more delicate assumption, namely cq or $\bar{c}\bar{q}$ clustering. While the X(3872) is very well-established, some other states either await confirmation or could be interpreted as mere threshold effects. Before the XYZ wave, it was suggested that baryon-antibaryon states could exist with strange or charmed hyperons. This spectroscopy is regularly revisited (see e.g., [56] and references therein).

4. Antinucleon-Nucleon Scattering

In this section, we give a brief survey of measurements of antinucleon-nucleon scattering and their interpretation, for some final states: $\bar{N}N$, $\bar{\Lambda }\Lambda$, and two pseudoscalars. Some emphasis is put on spin observables. It is stressed in other chapters of this book how useful were the measurements done with polarized targets and/or beams for our understanding of the NN interaction, leading to an almost unambiguous reconstruction of the NN amplitude. The interest in $\bar{N}N$ spin observables came at workshops held to prepare the LEAR experiments [19, 20, 22], and at the spin Conference held at Lausanne in 1980 [57]. A particular attention was paid to $p\bar{p}\to \bar{\Lambda }\Lambda$, but all the theoreticians failed in providing valuable guidance for the last measurements using a polarized target, as discussed below in section 4.7. However, Felix Culpa⁷, we learned how to better deal with the relationships and constraints among spin observables.

4.1. Integrated Cross Sections

As already mentioned, the integrated cross sections have been measured first at Berkeley, shortly after the discovery of the antiproton. More data have been taken in many experiments, mainly at the Brookhaven National Laboratory (BNL) and CERN, at various energies. The high-energy part, together with its proton-proton counter part, probes the Pomerantchuk theorem, Froissart bound and the possible onset of the odderon (see e.g., [58] and references therein).

As for the low-energy part, some values of the total cross section are shown in Figure 3, as measured by the PS172 collaboration [59]. It can be contrasted to the annihilation cross section of Figure 3, due to the PS173 collaboration [60]. When one compares the values at the same energy, one sees that annihilation is more than half the total cross section. Meanwhile, the integrated charge-exchange cross section is rather small (just a few mb).

FIGURE 3

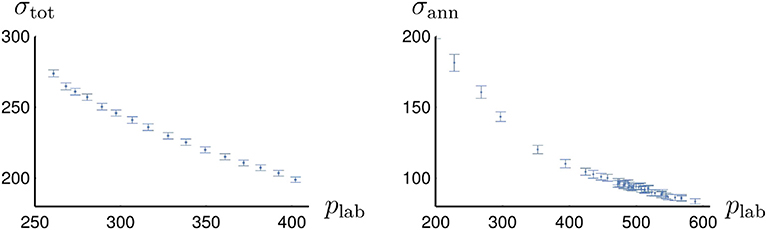
Figure 3. (Left) Total $\bar{p}p$ cross section (in mb), as measured by the PS172 collaboration at LEAR.lation. (Right) Annihilation $\bar{p}p$ cross section (in mb), as measured by the PS173 collaboration.

Let us stress once more that the hierarchy σ_ann > σ_el of the annihilation and elastic cross-sections is remarkable. One needs more than a full absorptive core. Somehow, the long-range attraction pulls the wave function toward the inner regions where annihilation takes place [61, 62].

4.2. Angular Distribution for Elastic and Charge-Exchange Reactions

The elastic scattering has been studied in several experiments, most recently at LEAR, in the experiments PS172, PS173, PS198, …An example of differential distribution is shown in Figure 4.

FIGURE 4

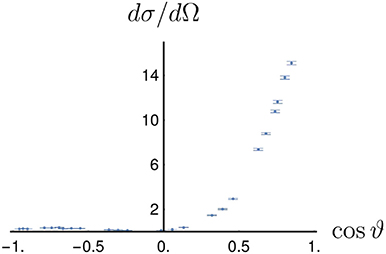
Figure 4. Angular distribution in elastic $\bar{p}p\to \bar{p}p$ scattering at 0.697 GeV/c, as measured by the PS198 collaboration [63].

The charge exchange scattering has been studied by the PS199-206 collaboration at LEAR. As discussed in one of the workshops on low-energy antiproton physics [19], charge exchange gives the opportunity to study the interplay between the long-range and short-range physics. An example of differential cross-section is shown in Figure 5, published in Ahmidouch et al. [65]. Clearly the distribution is far from flat. This illustrates the role of high partial waves. The amplitude for charge exchange corresponds to the isospin combination

$\begin{array}{ll}{M}(\overline{p}p\to \overline{n}n)\propto {{M}}_0-{{M}}_1,& (10)\end{array}$

The smallness of the integrated charge-exchange cross-section is due to a large cancellation in the low-partial waves. But in the high partial waves, there is a coherent superposition. In particular the one-pion exchange gets an isospin factor +1 for ${{M}}_1$, and a factor −3 for ${{M}}_0$.

FIGURE 5

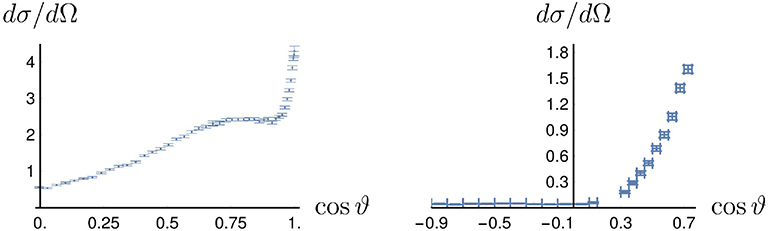
Figure 5. Angular distribution for the charge-exchange reaction $\bar{p}p\to \bar{n}n$ at incident momentum 0.601 Gev/c (left) and 1.083 GeV/c in the target frame [64]. Only the statistical error is shown here. Large systematic errors have to be added.

4.3. Antineutron Scattering

To access to pure isospin I = 1 scattering, data have been taken with antiproton beams and deuterium targets, but the subtraction of the $\bar{p}p$ contribution and accounting for the internal motion and shadowing effects is somewhat delicate. The OBELIX collaboration at CERN has done direct measurements with antineutrons [66]. For instance, the total $\bar{n}p$ cross-section has been measured between p_lab = 50 and 480 MeV/c [67]. The data are shown in Figure 6 together with a comparison with the $\bar{p}p$ analogs. There is obviously no pronounced isospin dependence. The same conclusion can be drawn for the $\bar{p}p$ and $\bar{n}p$ annihilation cross sections [68].

FIGURE 6

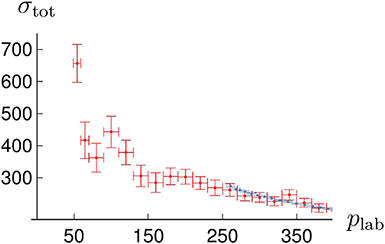
Figure 6. Total $\bar{n}p$ cross section (red), as measured by the PS201 collaboration, and comparison with the $\bar{p}p$ total cross-section (blue).

4.4. Spin Effects in Elastic and Charge-Exchange Scattering

A few measurements of spin effects in $\bar{N}N\to \bar{N}N$ were done before LEAR, mainly dealing with the analyzing power. Some further measurements were done at LEAR, with higher statistics and a wider angular range. An example of measurement by PS172 is shown in Figure 7: the analyzing power of $\bar{p}p\to \bar{p}p$ at 679 MeV/c [69]. One can see that the value of A_n is sizable, but not very large. It is compatible with either a moderate spin-orbit component of the interaction, or a rather strong tensor force acting at second order. PS172 also measured the depolarization parameter D_nn in $\bar{p}p\to \bar{p}p$. This parameter D_nn expresses the fraction of recoiling-proton polarization along the normal direction that is due to the polarization of the target. Thus, D_nn = 1 in absence of spin forces. PS172 obtained the interesting result D_nn = −0.169 ± 0.465 at cos ϑ = −0.169 for the momentum p_lab = 0.679 GeV/c [70]. The effect persists at higher momentum, as seen in Figure 8.

FIGURE 7

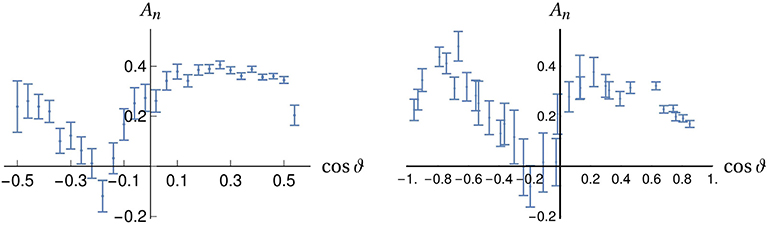
Figure 7. Analyzing power of $\bar{p}p\to \bar{p}p$ (left) at 672 MeV/c, as measured at LEAR by the PS172 collaboration [69], (right) at 697 MeV/c by the PS198 collaboration [63].

FIGURE 8

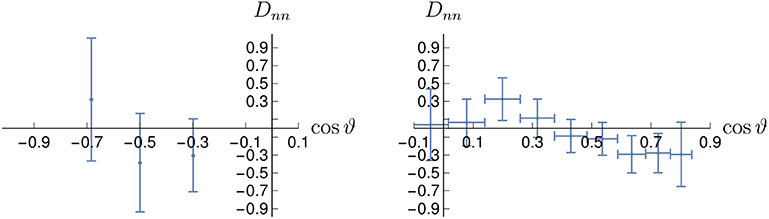
Figure 8. Transfer of polarization D_nn, in elastic $\bar{p}p$ scattering at p_lab = 1.089 GeV/c [70] (right) and in the charge exchange reaction at 0.875 GeV/c [72].

The charge-exchange reaction has been studied by the PS199-206 collaborations at LEAR (see e.g., [71, 72]). In Figure 8 is shown the depolarization parameter D_nn. The effect is clearly large. It is predicted that D_ℓℓ is even more pronounced, and interestingly, also K_ℓℓ, the transfer of polarization from the target to the antineutron. This means that one can produce polarized antineutrons by scattering antiprotons on a longitudinally polarized proton target.

4.5. Amplitude Analysis?

Decades of efforts have been necessary to achieve a reliable knowledge of the NN interaction at low energy, with experiments involving both a polarized beam and a polarized target. In the case of $\bar{N}N$, the task is more delicate, as the phase-shifts are complex even at very low energy, and there is no Pauli principle to remove every second partial wave. So, as we have much less observables available for $\bar{N}N$ than for NN, it is impossible to reconstruct the phase-shifts or the amplitudes: there are unavoidably several solutions with about the same χ², and one flips from one solution to another one when one adds or removes a set of data. This is why the fits by Timmermans et al. [73, 74] have been received with some skepticism [75, 76].

Clearly the measurements of analyzing power and depolarization at LEAR should have been pursued, as was proposed by some collaborations, but unfortunately not approved by the CERN management. Now, we badly miss the information that would be needed to reconstruct the $\bar{N}N$ interaction unambiguously, and estimate the possible ways to polarize antiprotons (spin filter, spin transfer).

4.6. Potential Models

For the use in studies of the protonium and antinucleon-nucleus systems, it is convenient to summarize the information about the “elementary” $\bar{N}N$ interaction in the form of an effective $\bar{N}N$ potential. Early attempts were made by Gourdin et al.[77], Bryan and Phillips [78] among others, and more recently by Kohno and Weise [79], and the Bonn-Jülich group [80–82]. Dover, Richard, and Sainio [62, 83, 84] used as long range potential V_LR the G-parity transformed of the Paris NN potential, regularized in a square-well manner, i.e., V_LR(r < r₀) = V_LR(r₀) with r₀ = 0.8fm, supplemented by a complex core to account for unknown short-range forces and for annihilation,

$\begin{array}{ll}{V}_{\text{SR}}(r)=-\frac{V_0+i{W}_0}{1+\text{exp}(-(r-R)/a)}.& (11)\end{array}$

The short-range interaction was taken as spin and isospin independent, for simplicity. A good fit of the data was achieved with two sets of parameters

$\begin{array}{llll}\text{model DR1}& R=0\text{ fm},\hfill & a=0.2\text{ fm}\hfill & V_0=21\text{ GeV},\hfill \\ \hfill & W_0=20\text{ GeV},\hfill & \hfill & \hfill \\ \text{model DR2}\hfill & R=0.8\text{ fm},\hfill & a=0.2\text{ fm},\hfill & V_0=0.5\text{ GeV},\hfill \\ \hfill & W_0=0.5\text{ GeV}.\hfill & \hfill & \hfill & (12)\end{array}$

In Timmers et al. [85], the annihilation part is not described by an optical model, but by two effective meson-meson channels. This probably gives a more realistic energy dependence. In some other models, the core contains some spin and isospin-dependent terms, but there are not enough data to constrain the fit. Some examples are given by the Paris group in El-Bennich et al. [86], and earlier attempts cited there. In Klempt et al. [87], a comparison is made of the successive versions of such a $\bar{N}N$ potential: the parameters change dramatically when the fit is adjusted to include a new measurement. The same pattern is observed for the latest iteration [86].

More recent models will be mentioned in section 8 devoted to the modern perspectives, namely an attempt to combine the quark model and meson-exchanges, or potentials derived in the framework of chiral effective theories.

4.7. Hyperon-Pair Production

The PS185 collaboration has measured in detail the reactions of the type $\bar{p}p\to ȲY^{\prime }$, where Y or Y′ is an hyperon. We shall concentrate here on the $\bar{\Lambda }\Lambda$ channel, which was commented on by many theorists (see e.g., [88]). In the last runs, a polarized hydrogen target was used. Thus, $\bar{p}p\to \bar{\Lambda }\Lambda$ interaction at low energy is known in great detail, and motivated new studies on the correlations among the spin observables, which are briefly summarized in Appendix: Constraints on Spin Observables.

The weak decay of the Λ (and $\bar{\Lambda })$ gives access to its polarization in the final state, and thus many results came from the first runs: the polarization P(Λ) and $P(\bar{\Lambda })$ (which were checked to be equal), and various spin correlations of the final state C_ij, where i or j denotes transverse, longitudinal, etc.⁸ In particular the combination of observables

$\begin{array}{ll}{F}_0=\frac{1}{4}(1+C_{xx}-C_{nn}+C_{\ell \ell }),& (13)\end{array}$

corresponds to the percentage of spin singlet, and was found to be compatible with zero within the error bars. Unfortunately, at least two explanations came:

• According to the quark model, the spin of Λ is carried by the s quark, with the light pair ud being in a state spin and isospin zero. The vanishing of the spin singlet fraction is due to the creation of the $s\bar{s}$ pair in a spin triplet to match the gluon in perturbative QCD or the prescription of the ³P₀ model, in which the created quark-antiquark pair has the quantum number 0⁺⁺.

• In the nuclear-physics type of approach, the reaction is mediated by K and K^* exchanges. This produces a coherence in some spin-triple amplitude, analogous to the strong tensor force in the isospin I = 0 of $\bar{N}N$. Hence, the triplet is favored.

It was then proposed to repeat the measurements on a polarized hydrogen target. This suggestion got support and was approved. In spite of a warning that longitudinal polarization might give larger effect, a transverse polarization was considered as an obvious choice, as it gives access to more observables. A detailed analysis of the latest PS185 are published in Bassalleck et al. and Paschke et al. [90, 91].

What retained attention was the somewhat emblematic D_nn which measures the transfer of normal polarization from p to Λ (in absence of spin effects, D_nn = 1). It was claimed that the transfer observable D_nn could distinguish among the different scenarios for the dynamics [92], with quark models favoring D_nn positive (except models making use of a polarized $s\bar{s}$ sea [93]), and meson-exchange D_nn < 0. When the result came with D_nn ~ 0, this was somewhat a disappointment. But in fact, it was realized [94, 95] that D_nn ~ 0 was a consequence of the earlier data! As reminded briefly in Appendix: Constraints on Spin Observables, there are indeed many constraints among the various spin observables of a given reaction. For instance, one can show that

$\begin{array}{ll}{C}_{\ell \ell }^2+D_{nn}^2\le 1.& (14)\end{array}$

This inequality, and other similar constraints, implied that D_nn had be small, just from data taken with an unpolarized target, while D_ℓℓ had a wider permitted range.

A sample of the PS185 results can be found in Figure 9.

FIGURE 9

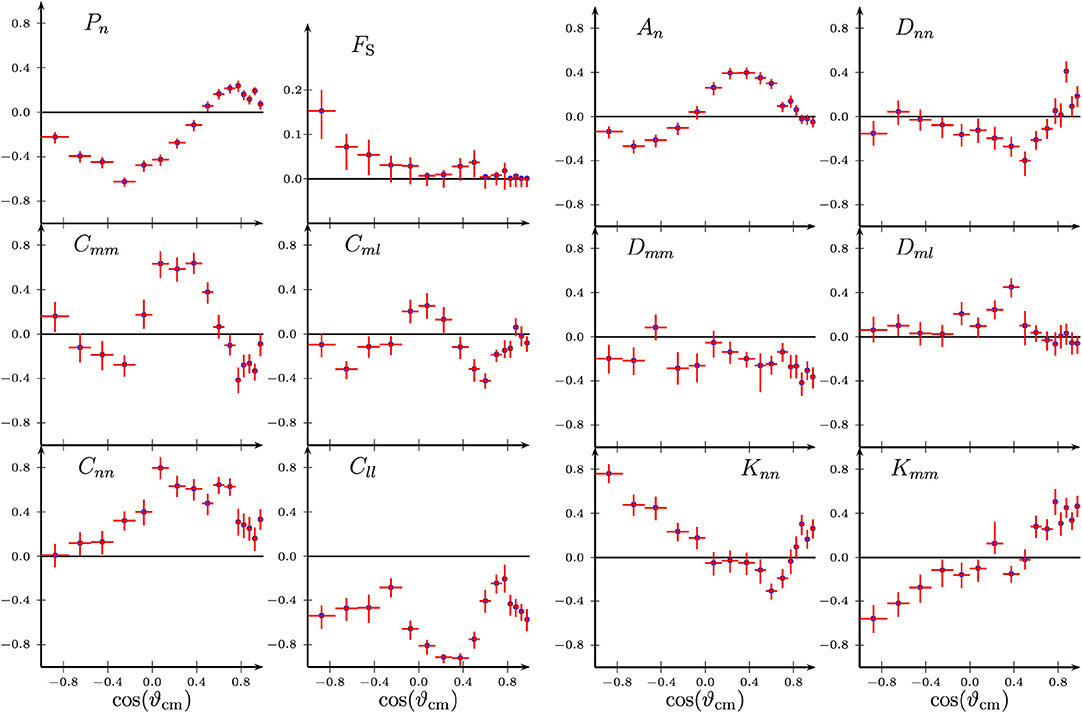
Figure 9. Some spin observables of the reaction $\bar{p}p\to \bar{\Lambda }\Lambda$. Reproduced from Artru et al. [95] with the permission from Physics Reports.

4.8. Spin Effects in Annihilation Into Two Pseudoscalar Mesons

The reactions $\bar{p}p\to {\pi }^{+}{\pi }^{-}$ (and to a lesser extent π⁰π⁰) and K⁺K⁻ were measured before LEAR. For instance, some results can be read in the proceedings of the Strasbourg conference in 1978 [96]. However, some adventurous analyses concluded to the existence of unnatural-parity broad resonances, the large-width sector of baryonium. Needless to say that such analyses with few or no spin observables, were flawed from the very beginning. The same methods, and sometimes the same authors, were responsible for the misleading indication in favor of the so-called Z baryons with strangeness S = +1, the ancestor of the late light pentaquark θ(1540).

The LEAR experiment PS172 remeasured these reactions with a polarized target. This gives access to the analyzing power A_n, the analog of the polarization in the crossed reactions, such as π⁻p → π⁻p. Remarkably, A_n is very large, in some wide ranges of energy and angle (see Figures 10, 11). There is a choice of amplitudes, actually the transversity amplitudes, such that

$\begin{array}{ll}{A}_n=\frac{|f{]}^2-|g{|}^2}{|f{]}^2+|g{|}^2},& (15)\end{array}$

In this notation, |A_n| ~ 1 requires one amplitude f or g to be dominant. This was understood from the coupled channel effects [97, 98]. Alternatively, one can argue that the initial state is made of partial waves ³(J − 1)_J and ³(J + 1)_J coupled by tensor forces. The amplitudes f and g correspond to the eigenstates of the tensor operator S₁₂ (see section 2), and the amplitude in which the tensor operator is strongly attractive tends to become dominant [99].

FIGURE 10

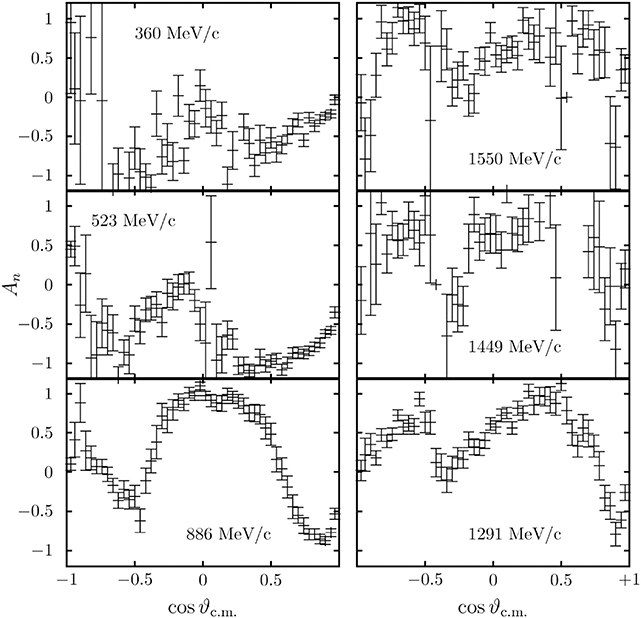
Figure 10. Some results on $\bar{p}p\to \pi \pi$ polarization at LEAR. Reproduced from Artru et al. [95] with the permission from Physics Reports.

FIGURE 11

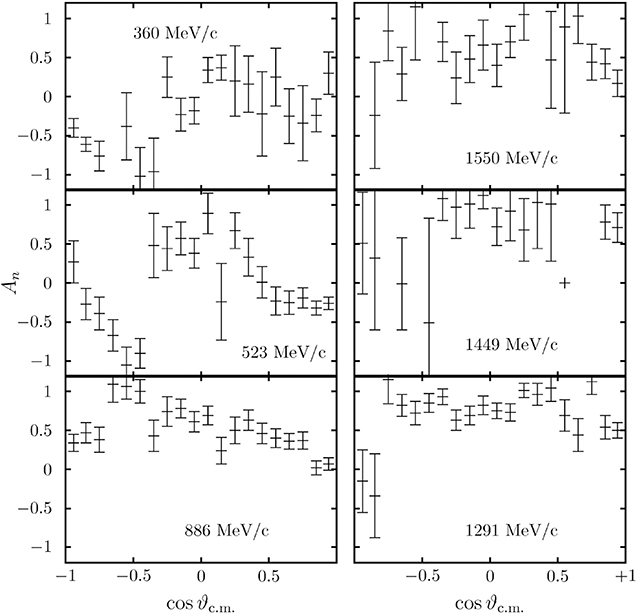
Figure 11. Some results on $\bar{p}p\to \bar{K}K$ polarization at LEAR. Reproduced from Artru et al. [95] with the permission from Physics Reports.

4.9. Appendix: Constraints on Spin Observables

A typical spin observable X is usually normalized such that −1 ≤ X ≤ + 1. But if one considers two normalized observables X and Y of the same reaction, several scenarios can occur:

• The entire square −1 ≤ X, Y ≤ +1 is allowed. Then the knowledge of X does not constrain Y.

• {X, Y} is restricted to a subdomain of the square. One often encounters the unit circle X² + Y² ≤ 1. In such case a large X implies a vanishing Y. This is what happens for D_nn vs. some of C_ij in $\bar{p}p\to \bar{\Lambda }\Lambda$. Another possibility is a triangle (see Figure 12).

FIGURE 12

Figure 12. Examples of constraints among spin observables: only the colored area is permitted.

For instance, in the simplest case of πN → πN (or its cross reaction as in Equation 15), there is a set of amplitudes such that the polarization (or the analyzing power), and the two independent transfer of polarization) are given by

$\begin{array}{ll}X=\frac{|f{]}^2-|g{|}^2}{|f{]}^2+|g{|}^2},Y=\frac{2\text{ Re}(f^{*}g)}{|f{]}^2+|g{|}^2},Z=\frac{2\text{ Im}(f^{*}g)}{|f{]}^2+|g{|}^2},& (16)\end{array}$

such that X² + Y² + Z² = 1 and thus X² + Y² ≤ 1. For reactions with two spin-1/2 particles, the algebra is somewhat more intricate [95].

At about the same time as the analysis of the PS172 and PS185 data, similar inequalities were derived for the spin-dependent parton distributions, in particular by the late Jacques Soffer, starting from the requirement of positivity. An unified presentation of the inequalities in the hadron-hadron and quark distribution sectors can be found in Artru et al. [95]. The domain allowed for three normalized observables X, Y, Z can be found in this reference, with sometimes rather amazing shapes for the frontier.

Perhaps a new strategy could emerge. Instead of either disregarding all spin measurements, or to cumulate all possible spin measurements in view of an elusive full reconstruction, one could advocate a stage by stage approach: measure first a few observables and look for which of the remaining are less constrained, i.e., keep the largest potential of non-redundant information.

5. Protonium

Exotic atoms provide a subtle investigation of the hadron-nucleon and hadron-nucleus interaction at zero energy. For a comprehensive review, see Deloff [100]. Let us consider (h⁻, A), where h⁻ is a negatively charged hadron, such as π⁻ or K⁻, and A a nucleus of charge +Z. One can calculate the energy levels $E_{n,\ell }^{(0)}$ by standard QED techniques, including finite volume, vacuum polarization, etc. The levels are shifted and broadened by the strong interactions, and it can be shown (most simply in potential models, but also in effective theories), that the complex shift is given by

$\begin{array}{ll}\delta E_{n,\ell }=E_{n,\ell }-E_{n,\ell }^{(0)}\simeq C_{n,\ell }{a}_{\ell },& (17)\end{array}$

where a_ℓ is the scattering length for ℓ = 0, volume for ℓ = 1, …of the strong hA interaction. C_n,ℓ is a know constant involving the reduced mass and the ℓ^th derivative of the radial wave function at the origin of the pure Coulomb problem. Experiments on protonium have been carried out before and after LEAR. For a summary, see e.g., Klempt et al. [68]. The latest results are:

• For the 1S level, the average shift and width are [101] δE(1S) = 712.5 ± 20.3 eV (to be compared with the Bohr energy E(1S) ≃ −12.5 keV), and Γ(1S) = 1054 ± 65 eV, with a tentative separation of the hyperfine level as δE(³S₁) = 785 ± 35 eV, Γ(³S₁) = 940 ± 80 eV, and δE(¹S₀) = 440 ± 75 eV, Γ(¹S₀) = 1200 ± 250 eV. The repulsive character is a consequence of the strong annihilation.

• For the 2P level, one can not distinguish among ¹P₁, SLJ3P1 and ³P₂, but this set of levels is clearly separated from the ³P₀ which receives a larger attractive shift, as predicted in potential models (see e.g., [84, 102]) and a larger width. More precisely [103], δE[2(³P₂, ³1P1, ³P₁)] ≃ 0, Γ[2(³P₂, ³1P1, ³P₁)] = 38 ± 9 meV, and δE[2³P₀] ≃ −139 ± 28 mEV, Γ[2³P₀] = 489 ± 30 meV. For the latter, the admixture of the $\bar{n}n$ component is crucial in the calculation, and the wave function at short distances is dominated by it isospin I = 0 component [104].

5.1. Quantum Mechanics of Exotic Atoms

Perturbation theory is valid if the energy shift is small as compared to the level spacing. However, a small shift does not mean that perturbation theory is applicable. For instance, a hard core of radius a added to the Coulomb interaction gives a small upward shift to the levels, as long as the core radius a remains small as compared to the Bohr radius R, but a naive application of ordinary perturbation theory will give an infinite correction! For a long-range interaction modified by a strong short-range term, the expansion parameters is the ratio of the ranges, instead of the coupling constant. At leading order, the energy shift is given by the formula of Deser et al. [105], and Trueman [106], which reads

$\begin{array}{ll}\delta E\simeq 4\pi |{\varphi }_{n\ell }(0){|}^2{a}_0,& (18)\end{array}$

where a₀ is the scattering length in the short-range potential alone, and ϕ_nℓ(0) the unperturbed wave function at zero separation. For a simple proof, see e.g., Klempt et al. [68]. The formula (18) and its generalization (17) look perturbative, because of the occurrence of the unperturbed wavefunction, but it is not, as the scattering length (volume, …) a_ℓ implies iterations of the short-range potential.

There are several improvements and generalizations to any superposition of a short-range and a long-range potential, the latter not necessarily Coulombic (see e.g., [107]). For instance, in the physics of cold atoms, one often considers systems experiencing some harmonic confinement and a short-range pairwise interaction.

5.2. Level Rearrangement

The approximation (18) implies that the scattering length a remains small as compared to the Bohr radius (or, say, the typical size of the unperturbed wave function). Zel'dovich [108], Shapiro [32], and others have studied what happens, when the attractive short-range potential becomes large enough to support a bound state on its own. Let the short-range attractive interaction be λV_SR, with λ > 0. When λ approaches and passes the critical value λ₀ for the first occurrence of binding in this potential, the whole Coulomb spectrum moves rapidly. The 1S state drops from the keV to the MeV range, the 2S level decreases rapidly and stabilizes in the region of the former 1S, etc. (see for instance, Figure 13). Other examples are given in Deloff and Combescure et al. [100, 107].

FIGURE 13

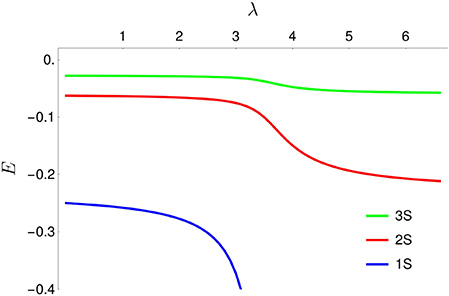
Figure 13. Rearrangement of levels: first three levels of the radial equation −u″(r) + V(r) u(r) = E u(r) with V(r) = − 1/r + λa²exp(−ar), here with a = 100 and λ variable.

It was then suggested that a weakly bound quasi-nuclear $\bar{N}N$ state will be revealed by large shifts in the atomic spectrum of protonium [32]. However, this rearrangement scenario holds for a single-channel real potential V_SR. In practice, the potential is complex, and the Coulomb spectrum is in the $\bar{p}p$ channel, and the putative baryonium in a state of pure isospin I = 0 or I = 1. Hence, the rearrangement pattern is more intricate.

5.3. Isospin Mixing

In many experiments dealing with “annihilation at rest,” protonium is the initial state before the transition $N\bar{N}\to$mesons. Hence the phenomenological analysis include parameters describing the protonium: S-wave vs. P-wave probability and isospin mixing. Consider, e.g., protonium in the ${}^1{\text{S}}_0$ state. In a potential model, its dynamics is given by

$\begin{array}{l}\hfill -u^{″}(r)/m+V_{11}u(r)+V_{12}v(r)-\frac{e^2}{r}u(r)=E_{1,0}u(r),\\ \hfill -v^{″}(r)/m+V_{22}v(r)+V_{21}u(r)+2\delta mu(r)=E_{1,0}v(r),& (19)\end{array}$

where δm is the mass difference between the proton and the neutron, and the strong (complex) potentials are the isospin combinations

$\begin{array}{ll}{V}_{11}=V_{22}=\frac{1}{2}(V_{I=0}+V_{I=1}),V_{12}=V_{21}=\frac{1}{2}(V_{I=0}-V_{I=1}).& (20)\end{array}$

The energy shift is well-approximated by neglecting the neutron-antineutron component, i.e., v(r) = 0. But at short distance, this component is crucial. In most current models, one isospin component is dominant, so that the protonium wave function is dominantly either I = 0 or I = 1 at short distances, where annihilation takes place. This influences much the pattern of branching ratios. For instance, Dover et al. [104] found in a typical potential model that the ³P₀ level consists of 95% of isospin I = 0 in the annihilation region. For ³P₁, the I = 1 dominates, with 87%. See references [104, 109, 110] for a detailed study of the role of the $\bar{n}n$ channel on the protonium levels and their annihilation.

5.4. Day-Snow-Sucher Effect

When a low-energy antiproton is sent on a gaseous or liquid hydrogen target, it is further slowed down by electromagnetic interaction, and is captured in a high orbit of the antiproton-proton system. The electrons are usually expelled during the capture and the subsequent decay of the antiproton toward lower orbits. The sequence favors circular orbits with ℓ = n − 1, in the usual notation. Annihilation is negligible for the high orbits, and becomes about 1% in 2P and, of course, 100% in 1S. This was already predicted in the classic paper by Kaufmann and Pilkuhn [111].

In a dense target, however, the compact $\bar{p}p$ atom travels inside the orbits of the ordinary atoms constituting the target, and experiences there an electric field which, by Stark effect, mixes the (ℓ = n − 1, n) level with states of same principal quantum number n and lower orbital momentum. Annihilation occurs from the states with the lowest ℓ. This is known as the Day-Snow-Sucher effect [112]. In practice, to extract the branching ratios and distinguish S-wave from P-wave annihilation, one studies the rates as a function of the target density.

5.5. Protonium Ion and Protonium Molecule

So far, the physics of hadronic atoms has been restricted to 2-body systems, such as $\bar{p}p$ or K⁻A. In fact, if one forgets about the experimental feasibility, there are many other possibilities. If one takes only the long-range Coulomb interaction, without electromagnetic annihilation nor strong interaction, many stable configurations exist, such as $\bar{p}pp$, the protonium ion, or $\bar{p}\bar{p}pp$, the heavy analog of the positronium molecule. Identifying these states and measuring the shift and width of the lowest level would be most interesting. Today this looks as science fiction, as it was the case when $\text{P}{\text{s}}_2=e^{+}{e}^{+}{e}^{-}{e}^{-}$ was suggested by Wheeler in 1945. But Ps₂ was eventually detected, in 2007.

6. The Antinucleon-Nucleus Interaction

6.1. Antinucleon-Nucleus Elastic Scattering

At the very beginning of LEAR, Garreta et al. [113, 114] measured the angular distribution of $\bar{p}$-A scattering, where A was ¹²C, ⁴⁰Ca or ²⁰⁸Pb. Some of their results are reproduced in Figure 14⁹. More energies and targets were later measured.

FIGURE 14

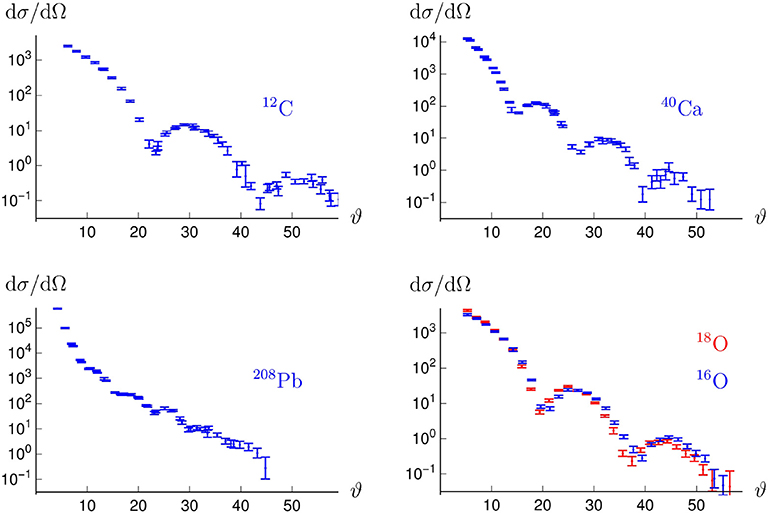
Figure 14. Angular distribution for $\bar{p}$ scattering on the nuclei ¹²C, ⁴⁰Ca, and ²⁰⁸Pb at kinetic energy $T_{\bar{p}}=180$ MeV, and on the two isotopes ¹⁶O and ¹⁶O [113, 114].

The results have been analyzed by Lemaire et al. in terms of phenomenological optical models [115], which were in turn derived by folding the elementary $\bar{N}N$ amplitudes with the nuclear density (see e.g., [116–118]).

In particular, a comparison of ¹⁶O and ¹⁸O isotopes (see Figure 14), reveals that there is very little isospin dependence of the $\bar{p}N$ interaction, when averaged on spins.

Other interesting measurements of the antinucleon-nucleus interaction have been carried out and analyzed by the PS179 and OBELIX (PS201) collaborations, with more nuanced conclusions about the isospin dependence of the interaction at very low energy (see, for instance [119, 120]).

6.2. Inelastic Scattering

It has been stressed that the inelastic scattering $\bar{p}A\to \bar{p}{A}^{*}$, where A is a known excitation of the nucleus A, could provide very valuable information on the spin-isospin dependence of the elementary $\bar{N}N$ amplitude, as the transfer of quantum numbers is identified. One can also envisage the charge-exchange reaction $\bar{p}A\to \bar{n}{B}^{(*)}$ (see, for instance [121]).

Some measurements were done by PS184, on ¹²C and ¹⁸O [122]. The angular distribution for $\overline{p}+{}^{12}\text{C}\to \overline{p}+{}^{12}\text{C}{}^{*}$ is given in Figure 15 for the case where ¹²C is the 3⁻ level at 9.6 MeV. In their analysis, the authors were able to distinguish among models that were equivalent for the $\bar{N}N$ data, but have some differences in the treatment of the short-range part of the interaction. This is confirmed by the analysis in references [121, 123]. Unfortunately, this program of inelastic antiproton-nucleus scattering was not thoroughly carried out.

FIGURE 15

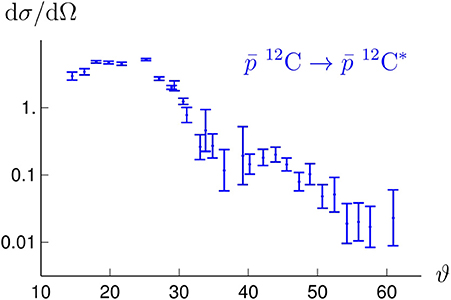
Figure 15. Angular distribution of the ¹²C$(\overline{p},\overline{p})$¹²C^* reaction for the 3⁻ excited state at 9.6 MeV [122]. The incident $\bar{p}$ has an energy of 179.7 MeV.

6.3. Antiprotonic Atoms

The physics is nearly the same as for protonium. A low energy antiproton sent toward a target consisting of atoms of nucleus ${}_Z{}^A\text{X}$, is decelerated by the electromagnetic interaction and captured in a high atomic orbit, and cascades down toward lower orbits. During this process, the electrons are expelled. The difference is that annihilation occurs before reaching the S or P levels, actually when the size of the orbit becomes comparable to the size of the nucleus. Again, the Day-Snow-Sucher mechanism can induce some Stark effect. Thus, precocious annihilation can happen, depending on the density of the target.

A review of the experimental data is provided in Batty et al. and Gotta [124, 125], where a comparison is made with pionic and kaonic atoms. The models developed to describe antiproton-nucleus scattering (see section 6.1) have been applied, and account rather well for the observed shifts. As for the purely phenomenological optical potentials V_opt, the most common parametrization is of the form

$\begin{array}{ll}2\mu V_{\text{opt}}=-4\pi \left(1+\frac{\mu }{m}\right)(b_{\text{R}}+i{b}_{\text{I}})\varrho (r),& (21)\end{array}$

where μ is the reduced mass of $\bar{p}$-A, m the mass of the nucleon, ϱ(r) the nuclear density and b_R + ib_i an effective scattering length.

More refined models, aiming at describing simultaneously the data on a variety of nuclei, are written as [124]

$\begin{array}{l}2\mu V_{\text{opt}}=-4\pi \left(1+\frac{\mu }{m}\right)(b_0[{\varrho }_n(r)+{\varrho }_p(r)]\\ +b_1[{\varrho }_n(r)-{\varrho }_p(r)]),\hfill & (22)\end{array}$

where the complex b_0,1 are the isospin-independent and isospin-dependent effective scattering lengths, respectively. Further refinements introduce in (22) a “P-wave” term ∇.α(r)∇, or terms proportional to the square of the density. Typical values are [124]

$\begin{array}{l}{b}_0=(2.7\pm 0.3)+i(3.1\pm +0.4)\text{ fm},\\ b_1=(1.2\pm 1.6)+i(1.6\pm +1.3)\text{ fm},\hfill & (23)\end{array}$

so that there is no firm evidence for a strong isospin dependence.

It is important to stress that the potential V_opt is probed mainly at the surface. Its value inside the nucleus hardly matters. The same property is seen in the low-energy heavy-ion collisions: what is important is the interaction at the point where the two ions come in contact.

6.4. Antiproton-Nucleus Dynamics

Modeling the antiproton-nucleus interaction has been done with various degrees of sophistication. We have seen in the last section that phenomenological (complex) potentials proportional to the nuclear density account for a wide body of data on antiprotonic atoms. A relativistic mean-field approach was attempted years ago by Bouyssy and Marcos [126] and revisited more recently [127]. Meanwhile, a Glauber approach has been formulated [128] and applied to the elastic and inelastic scattering of relativistic antiprotons.

There is a persisting interest in the domain of very low energies and possible bound states. For instance, Friedman et al. [129] analyzed the subtle interplay between the $\bar{N}N$ S- and P-waves when constructing the antiproton-nucleus potential. There has been also speculations about possible $\bar{p}-A$ states, in line with the studies on the molecular $\bar{N}N$ baryonium. For a recent update, see e.g., Hrtánková and Mareš [130].

One could also envisage to use antiprotons to probe the tail of the nuclear density for neutron-rich nuclei with a halo structure. For early references, see Bradamante et al. [27]. Recently, the PUMA proposal suggests an investigation by low-energy antiprotons of some unstable isotopes, for which the conventional probes have limitations [131].

6.5. Neutron-Antineutron Oscillations

In some theories of grand unification, the proton decay is suppressed, and one expects neutron-to-antineutron oscillations. An experimental search using free neutrons has been performed at Grenoble [132], with a limit of about ${\tau }_{n\bar{n}}\gtrsim 10^{-8}$ s for the oscillation period. Any new neutron source motivates new proposals of the same vein (see e.g., [133]).

An alternative is to use the bound neutrons of nuclei. The stability of, say, ¹⁶O, reflects as well the absence of decay of its protons as the lack of $n\to \bar{n}$ conversion with subsequent annihilation of the antineutron. It has been sometimes argued [134] that the phenomenon could be obscured in nuclei by uncontrolled medium corrections. However, the analysis shows that the neutrons oscillate mainly outside the nucleus, and the subsequent annihilation takes place at the surface, so that, fortunately, the medium corrections are small.

The peripheral character of the $n\bar{n}$ oscillations in nuclei explains why a simple picture (sometimes called closure approximation) does not work too well, with the neutron and the antineutron in a box feeling an average potential 〈V_n〉 or $\langle V_{\bar{n}}\rangle$, resulting in a simple 2 × 2 diagonalization. The true dynamics of $n\bar{n}$ oscillations relies on the tail of the neutron distribution, where n and $\bar{n}$ are almost free.

There are several approaches, see for instance [135]. The simplest is based on the Sternheimer equation, which gives the first order correction to the wave function without summing over unperturbed states. In a shell model with realistic neutron (reduced) radial wave functions u_nℓJ(r) with shell energy E_nℓJ, the induced $\bar{n}$ component is given by

$\begin{array}{ll}-\frac{{w^{″}}_{n\ell J}(r)}{\mu }+\frac{\ell (\ell +1)}{\mu r^2}+V_{\overline{n}}(r){w^{\prime }}_{n\ell J}(r)-E_{n\ell J}{w^{\prime }}_{n\ell J}(r)=\gamma u_{n\ell J}(r),& (24)\end{array}$

with μ the reduced mass of the $\bar{n}$-(A − 1) system, $V_{\bar{n}}$ the complex (optical) $\bar{n}$-(A − 1) potential, and $\gamma =1/{\tau }_{n\bar{n}}$ the strength of the transition. Once w_nℓJ is calculated, one can estimate the second-order correction to the energy, and in particular the width Γ_nℓJ of this shell

$\begin{array}{lll}{\Gamma }_{n\ell J}& =\hfill & -2{\displaystyle {\int }_0^{\infty }\text{ Im }}{V}_{\overline{n}}|w_{n\ell J}(r){|}^2\text{d}r=-2\gamma \hfill \\ \hfill & \hfill & {\displaystyle {\int }_0^{\infty }{u}_{n\ell J}}(r)\text{ Im }{w}_{n\ell J}(r)\text{d}r,\hfill & (25)\end{array}$

which scales as

$\begin{array}{ll}{\Gamma }_{n\ell J}\propto {\gamma }^2.& (26)\end{array}$

An averaging over the shells give a width per neutron Γ associated with a lifetime T

$\begin{array}{ll}T=T_r{\tau }_{n\overline{n}}^2,& (27)\end{array}$

where T_r is named either the “reduced lifetime” (in s⁻¹) or the “nuclear suppression factor.” The spatial distribution of the w_nℓJ and the integrands in (25), the relative contribution to Γ clearly indicate the peripheral character of the process. See e.g., Barrow et al. [136] for an application to a simulation in the forthcoming DUNE experiment, and refs. there to earlier estimates. Clearly, DUNE will provide the best limit for this phenomenon.

For the deuteron, an early calculation by Dover et al. [137] gave $T_r\simeq 2.5\times 10^{22}{\text{s}}^{-1}$. Oosterhof et al. [138], in an approach based on effective chiral theory (see section 8), found a value significantly smaller, $T_r\simeq 1.1\times 10^{22}{\text{s}}^{-1}$. However, their calculation has been revisited by Haidenbauer and Meißner [139], who got almost perfect agreement with Dover et al. For ⁴⁰Ar relevant for the DUNE experiment, the result of [136] is $T_r\simeq 5.6\times 10^{22}{\text{s}}^{-1}$.

7. Antinucleon Annihilation

7.1. General Considerations

$N\bar{N}$ annihilation is a rather fascinating process, in which the baryon and antibaryon structures disappear into mesons. The kinematics is favorable, with an initial center-of-mass energy of 2 GeV at rest and more in flight, allowing in principle up to more than a dozen of pions. Of course, the low mass of the pion is a special feature of light-quark physics. We notice, however, that the quark model predicts that $(QQQ)+(\bar{Q}\bar{Q}\bar{Q})>3(Q\bar{Q})$ [140], so that annihilation at rest remains possible in the limit where all quarks are heavy. The same quark models suggest that $(\bar{Q}\bar{Q}\bar{Q})+(qqq)<3(\bar{Q}q)$ if the mass ratio Q/q becomes large, so that, for instance, a triply-charmed antibaryon $(\bar{c}\bar{c}\bar{c})$ would not annihilate on an ordinary baryon.

One should acknowledge at the start of this section that there is no theory, nor even any model, that accounts for the many data accumulated on $\bar{N}N$ annihilation. Actually the literature is scattered across various subtopics, such a the overall strength and range of annihilation, the average multiplicity, the percentage of events with hidden-strangeness, the explanation of specific branching ratios, such as the one for $\bar{p}p\to \rho \pi$, the occurrence of new meson resonances, etc. We shall briefly survey each of these research themes.

7.2. Quantum Numbers

An initial $\bar{N}N$ state with isospin I, spin S, orbital momentum L and total angular momentum J has parity P = −(−1)^L and G-parity G = (−1)^I+L+S. If the system is neutral, its charge conjugation is C = (−1)^L+S. A summary of the quantum numbers for the S and P states is given in Table 1.

TABLE 1

Table 1. Quantum numbers of the S and P partial waves (PW) of the N̄ N system. The notation is ${}^{2I+1,2S+1}{L}_J$.

So, for a given initial state, some transitions are forbidden or allowed. The result for some important channels is shown in Table 2. In particular, producing two identical scalars or pseudoscalars requires an initial P-state.

TABLE 2

Table 2. Allowed decays from S and P-states into some two-meson final states.

The algebra of quantum numbers is not always trivial, especially if identical mesons are produced. For instance, the question was raised whether or not the ¹S₀ state of protonium with J^PC = 0⁻⁺ and I^G = 0 can lead to a final state made of four π⁰. An poll among colleagues gave an overwhelming majority of negative answers. But a transition, such as ¹S₀ → 4π⁰ is actually possible at the expense of several internal orbital excitations among the pions. For an elementary proof, see Klempt et al. [87], for a more mathematical analysis [141].

The best known case, already mentioned in section 1, deals with ππ. An S-wave π⁺π⁻ with a flat distribution, or a π⁰π⁰ system (necessarily with I = 0 and J even) requires an initial state ^1,3P₀. It has been observed to occur even in annihilation at rest on a dilute hydrogen target [142]. This is confirmed by a study of the J = 0 vs. J = 1 content of the ππ final state as a function of the density of the target, as already mentioned in section 5.4.

7.3. Global Picture of Annihilation

As already stressed, the main feature of annihilation is its large cross-section, which comes together with a suppression of the charge-exchange process. This is reinforced by the observation that even at rest, annihilation is not reduced to an S-wave phenomenon. This is hardly accommodated with a zero-range mechanism, such as baryon exchange. The baryon exchange, for say, annihilation into two mesons is directly inspired by electron exchange in e⁺e⁻ → γγ (see Figure 16). After iteration, the absorptive part of the $\bar{N}N$ interaction, in this old-fashioned picture, would be driven by diagrams, such as the one in Figure 16. Other contributions involve more than two mesons and crossed diagrams. As analyzed (e.g., [143, 144]), this corresponds to a very small range, practically a contact interaction. Not surprisingly, it was impossible to follow this prescription when building optical models to fit the observed cross-sections. Among the contributions, one may cite [62, 77–79]. Claims, such as Côté et al. [145], that it is possible to fit the cross sections with a short-range annihilation operator, are somewhat flawed by the use of very large strengths, wide form factors, and a momentum dependence of the optical potential that reinforce annihilation in L > 0 partial waves.

FIGURE 16

Figure 16. e⁺e⁻ annihilation into two photons (left), $\bar{N}N$ annihilation into two mesons (center) and its iteration contributing to the absorptive part of the $\bar{N}N$ amplitude.

In the 80s, another point of view started to prevail: annihilation should be understood at the quark level¹⁰. This picture was hardly accepted by a fraction of the community. An anecdote illustrates how hot was the debate. After a talk at the 1988 Mainz conference on antiproton physics, where I presented the quark rearrangement, Shapiro strongly objected. At this time, the questions and answers were recorded and printed in the proceedings. Here is the verbatim [148]: I.S. Shapiro (Lebedev) : The value of the annihilation range …is nota question for discussion. It is a general statement following from the analytical properties of the amplitudes in quantum field theory …. It does not matter how the annihilating objects are constructed from their constituents. It is only important that, in the scattering induced by annihilation, an energy of at least two baryons masses is transferred. J.M. Richard: First of all, for me, this is an important “question for discussion.” In fact, we agree completely in the case of “total annihilation,” for instance $\bar{N}N\to \varphi \varphi$. The important point is that [baryons and] mesons are composite, so, what we call “annihilation” is, in most cases, nothing but a soft rearrangement of the constituents, which does not have to be short range.

In the simplest quark scenario, the spatial dependence of “annihilation” comes from that this is not an actual annihilation similar to e⁺e⁻ → photons, in which the initial constituents disappear, but a mere rearrangement of the quarks, similar to the rearrangement of the atoms in some molecular collisions. This corresponds to the diagram of Figure 17. The amplitude for this process is 〈Ψ_f|H|Ψ_i〉, where H is the 6-quark Hamiltonian, Ψ_i the nucleon-antinucleon initial state, and Ψ_f the final state made of three mesons. See, for instance [149–151], for the details about the formalism. One gets already a good insight on the spatial distribution of annihilation within the quark-rearrangement model by considering the mere overlap 〈Ψ_f|Ψ_i〉 using simple oscillator wave functions. For the initial state, a set of Jacobi coordinates (here normalized to correspond to an unitary transformation)

$\begin{array}{lll}x=\frac{r_2-r_1}{\sqrt{2}},\hfill & \hfill y=\frac{2r_3-r_1-r_2}{\sqrt{6}},& \hfill z=\frac{r_1+r_2+r_3}{\sqrt{3}}\text{},\\ \hfill x^{\prime }=\frac{r_5-r_4}{\sqrt{2}},& \hfill y^{\prime }=\frac{2r_6-r_4-r_5}{\sqrt{6}},& \hfill z^{\prime }=\frac{r_4+r_5+r_6}{\sqrt{3}}\text{},& (28)\end{array}$

with the further change

$\begin{array}{ll}r=\frac{z^{\prime }-z}{\sqrt{2}},R=\frac{z+z^{\prime }}{\sqrt{2}},& (29)\end{array}$

which, to a factor, are the $\bar{N}N$ separation and the overall center of mass. The initial-state wave function is thus of the form

$\begin{array}{ll}{\Psi }_i={\left(\frac{\alpha }{\pi }\right)}^{\text{}3}\text{exp}\left[-(\alpha /2)(x^2+y^2+{x^{\prime }}^2+{y^{\prime }}^2)\right]\phi (r),& (30)\end{array}$

where φ denotes the $\bar{N}N$ wave function. Similarly for the final state, one can introduce the normalized Jacobi coordinates

$\begin{array}{lllllllllll}\hfill u_1& =\hfill & \frac{r_4-r_1}{\sqrt{2}},\hfill & \hfill & \hfill u_2& =\hfill & \frac{r_5-r_2}{\sqrt{2}},\hfill & \hfill & \hfill u_3& =\hfill & \frac{r_6-r_3}{\sqrt{2}},\hfill \\ v_1\hfill & =\hfill & \frac{r_1+r_4}{\sqrt{2}},\hfill & \hfill & \hfill v_2& =\hfill & \frac{r_2+r_5}{\sqrt{2}},\hfill & \hfill & \hfill v_3& =\hfill & \frac{r_3+r_6}{\sqrt{2}},\hfill \\ \hfill X& =\hfill & \frac{v_2-v_1}{\sqrt{2}},\hfill & \hfill & \hfill Y& =\hfill & \frac{2v_3-v_1-v_2}{\sqrt{6}},\text{}\hfill & \hfill & \hfill R& =\hfill & \frac{v_1+v_2+v_3}{\sqrt{3}},\hfill & (31)\end{array}$

and the wave function

$\begin{array}{ll}{\Psi }_f={\left(\frac{\beta }{\pi }\right)}^{\text{}9/4}\text{exp}\left[-(\beta /2)(u_1^2+u_2^2+u_3^2)\right]\Phi (X,Y).& (32)\end{array}$

Integrating for instance over x′ − x and y′ − y, one ends with

$\begin{array}{ll}{\Phi }_f^{*}(X,Y)\text{ exp}(-\beta r^2/2)\text{ exp}(-\alpha (X^2+Y^2)/2)\phi (r),& (33)\end{array}$

and after iteration, one gets a separable operator v(r)v(r′), where v(r) is proportional to exp(−βr²/2) and contains some energy-dependent factors [149, 151]. As expected, the operator is not local. There is an amazing exchange of roles: the size of the baryon, through the parameter α, governs the spatial spread of the three mesons, while the size the mesons becomes the range of the separable potential. Schematically speaking, the range of “annihilation” comes from the ability of the mesons to make a bridge, to pick up a quark in the baryon and an antiquark in the antibaryon.

FIGURE 17

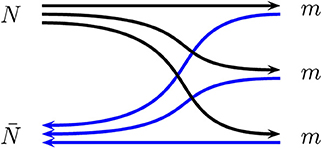
Figure 17. Rearrangement of the quarks and antiquarks from a baryon and an antibaryon to a set of three mesons.

Explicit calculations show that the rearrangement potential has about the required strength to account for the observed annihilation cross-sections. Of course, the model should be improved to include the unavoidable distortion of the initial- and final-state hadrons. Also one needs a certain amount of intrinsic quark-antiquark annihilation and creation to explain the production of strange mesons. This leads us to the discussion about the branching ratios.

7.4. Branching Ratios: Experimental Results

Dozens of final states are available for $\bar{N}N$ annihilation, even at rest. When the energy increases, some new channels become open. For instance, the ϕϕ channel was used to search for glueballs in the PS202 experiment [152]. However, most measurements have been performed at rest with essentially two complementary motivations. The first one was to detect new multi-pion resonances, and, indeed, several mesons have been either discovered or confirmed thanks to the antiproton-induced reactions. The second motivation was to identify some leading mechanisms for annihilation, and one should confess that the state of the art is not yet very convincing.

Several reviews contain a summary of the available branching ratios and a discussion on their interpretation (see e.g., [87, 153]). We shall not list all available results, but, instead, restrict ourselves to the main features or focus on some intriguing details. For instance:

• The average multiplicity is about 4 or 5. But in many cases, there is a formation of meson resonances, with their subsequent decay. In a rough survey, one can estimate that a very large fraction of the annihilation channels are compatible with the primary formation of two mesons which subsequently decay.

• In the case of a narrow resonance, one can distinguish the formation of a resonance from a background made of uncorrelated pions, e.g., ωπ from ππππ. In the case of broad resonances, e.g., ρπ vs. πππ, this is much more ambiguous.

• The amount of strangeness, in channels, such as $\bar{K}+K$, $\bar{K}+K^{*}$, $\bar{K}+K+\mathrm{\text{pions}}$, is about 5%.

• Charged states, such as $\bar{p}n$ or $\bar{n}p$ are pure isospin I = 1 initial state. In the case of $\bar{p}p$ annihilation at rest, the isospin is not known, except if deduced from the final state, like in the case of πη. Indeed, $\bar{p}p$ is the combination $(|I=0\rangle +|I=1\rangle )/\sqrt{2}$. But, at short distances, one of the components often prevails, at least in model calculations. In the particle basis, there is an admixture of $\bar{n}n$ component, which, depending on its relative sign, tends to make either a dominant I = 0, or I = 1. For instance, Kudryavtsev [154] analyzed the channels involving two pseudoscalars, and concluded that if protonium annihilation is assumed to originate from an equal mixture of I = 0 and I = 1, then annihilation is suppressed in one of the isospin channels, while a better understanding is achieved, if $\bar{p}p-\bar{n}n$ is accounted for.

7.5. Branching Ratios: Phenomenology

The simplest model, and most admired, is due to Vandermeulen [155]. It assumes a dominance of 2-body modes, say $\bar{N}N\to a+b$, where a and b are mesons or meson resonances, produced preferentially when the energy is slightly above the threshold $s_{ab}^{1/2}=m_a+m_b$. More precisely, the branching ratios are parameterized as

$\begin{array}{ll}f=C_{ab}p(\sqrt{s},m_a,m_b)\text{ exp}[-A(s-s_{ab})],& (34)\end{array}$

where A is an universal parameter, p the center-of-mass momentum and the constant C_ab assume only two values: C₀ for non-strange and C₁ for strange.

In the late 80s, following the work by Green and Niskanen [149, 150], and others, there were attempts to provide a detailed picture of the branching ratios, using quark-model wave functions supplemented by operators to create or annihilate quark-antiquark pairs. A precursor was the so-called ³P₀ model [156] introduced to describe decays, such as Δ → N + π.

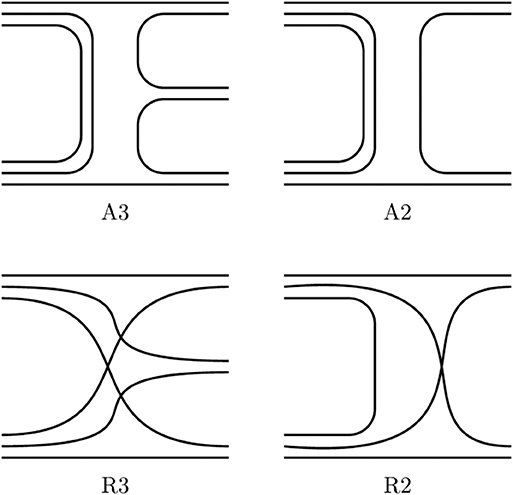
There has been attempts to understand the systematics of branching ratios at the quark level. We already mentioned some early papers [146, 147]. In the late 80s and in the 90s, several papers were published, based on a zoo of quark diagrams. Some of them are reproduced in Figure 18. The terminology adopted is An or Rn for annihilation or rearrangement into n mesons. Of course, they are not Feynman diagrams, but just a guidance for a quark model calculation with several assumptions to be specified. On the one had, the R3 diagram comes as the most “natural,” as it does not involve any change of the constituents. On the other hand, it was often advocated that planar diagrams should be dominant (see e.g., [157]). This opinion was, however, challenged by Pirner in his re-analysis the 1/N_c expansion, where N_c is the number of colors in QCD [158].

FIGURE 18

Figure 18. Some quark diagrams describing annihilation.

A key point is of course strangeness. The R3 diagram hardly produces kaons, except if extended as to include the sea quarks and antiquarks. On the other hand, the An diagrams tend to produce too often kaons, unless a controversial strangeness suppression factor is applied: at the vertex where a quark-antiquark pair is created, a factor f = 1 is applied for q = u, d and f ≪ 1 for q = s. This is an offending violation of the flavor SU(3)_F symmetry. For instance the decays $J/\psi \to p\bar{p}$ and $J/\psi \to \Lambda \bar{\Lambda }$ are nearly identical, especially once phase-space corrections are applied. The truth is that at low-energy, strangeness is dynamically suppressed by phase-space and a kind of tunneling effect [159]. This could have been implemented more properly in the analyses of the branching ratios. An energy-independent strangeness suppression factor is probably too crude.

Note that a simple phenomenology of quark diagrams is probably elusive. A diagram involving two primary mesons can lead to 4 or 5 pions after rescattering or the decay of a resonance. Also the An diagrams require a better overlap of the initial baryon and antibaryon, and thus are of shorter range than the Rn diagrams. So the relative importance can vary with the impact parameter and the incident energy.

7.6. Annihilation on Nuclei

There has been several studies of $\bar{N}$-A annihilation. In a typical scenario, a primary annihilation produces mesons, and some of them penetrate the nucleus, giving rise to a variety of phenomenons: pion production, nucleon emission, internal excitation, etc. (see e.g., [160]). Some detailed properties have been studied, for instance whether annihilation on nuclei produces less or more strange particles than annihilation on nucleons [161].

At very low energy, due to the large $\bar{N}N$ cross section, the primary annihilation takes place near the surface. It has been speculated that with medium-energy antiprotons, thanks to the larger momentum and the smaller cross section, the annihilation could sometimes take place near the center of the nucleus. Such rare annihilations with a high energy release (at least 2 GeV) and little pressure, would explore a sector of the properties of the nuclear medium somewhat complementary to the heavy-ion collisions (see e.g., [14, 162–164]).

Note the study of Pontecorvo reactions. In $\bar{N}N$ annihilation, at least two mesons have to be produced, to conserve energy and momentum. On a nucleus, there is the possibility of primary annihilation into n mesons, with n − 1 of them being absorbed by the remaining nucleons. An example is $\bar{p}NN\to \pi N$ or ϕn [165, 166]. This is somewhat related to the pionless decay of Λ in hypernuclei [167].

7.7. Remarkable Channels

Some annihilation channels have retained the attention:

• $p\bar{p}\to e^{+}{e}^{-}$ led to a measurement of the proton form factor in the time-like region. The reversed reaction $e^{+}{e}^{-}\to p\bar{p}$ was studied elsewhere, in particular at Frascati. For a general overview, see [168, 169], and for the results of the PS170 collaboration at CERN [170].

• We already mentioned the $\bar{p}p\to \mathrm{\text{charmonium}}\to \mathrm{\text{hadrons}}$, leading to a better measurement of the width of some charmonium states, and the first indication for the h_c, the ¹P₁ level of $c\bar{c}$ [10, 171]. In principle, while e⁺e⁻ → charmonium is restricted to the J^PC = 1⁻⁻ states, $\bar{p}p$ can match any partial wave. However, perturbative QCD suggests that the production is suppressed for some quantum numbers. It was thus a good surprise that η_c(1S) was seen in $\bar{p}p$, but the coupling turns out less favorable for η_c(2S) [11, 172].

• The overall amount of hidden-strangeness is about 5% [87]. This is remarkably small and is hardly accommodated in models where several incoming $q\bar{q}$ pairs are annihilated and several quark-antiquark pairs created. Note that the branching ratio for K⁺K⁻ is significantly larger for an initial S-wave than for P-wave [46]. This confirms the idea that annihilation diagrams are of shorter range than the rearrangement ones.

• $\bar{p}p\to K^0{\bar{K}}^0$ in the so-called CPLEAR experiment (PS195) [173] gave the opportunity to measure new parameters of the CP violation in the neutral K systems, a phenomenon first discovered at BNL in 1964 by Christenson, Cronin, Fitch, and Turlay¹¹. The CPLEAR experiment found evidence for a direct T-violation (time reversal).

• Precision measurements of the $\bar{p}p\to \gamma +X$ and $\bar{p}p\to \pi +X$ in search of bound baryonium, of which some indications were found before LEAR. The results of more intensive searches at LEAR were unfortunately negative (see e.g., [174]). When combined to the negative results of the scattering experiments, this was seen as the death sentence of baryonium. But, as mentioned in section 3, this opinion is now more mitigated, because of the $p\bar{p}$ enhancements observed in the decay of heavy particles.

• $\bar{p}p\to \rho \pi$ has intriguing properties. Amazingly, the same decay channel is also puzzling in charmonium decay, as the ratio of ψ(2S) → ρπ to J/ψ → ρπ differs significantly from its value for the other channels (see e.g., [175] and references therein). In the case of $\bar{p}p$ annihilation, the problem (see e.g., [46]), is that the production from ^1,3S₁ is much larger than from ^1,3S₀. Dover et al., for instance, concluded to the dominance of the A2 type of diagram [176], once the quark-antiquark creation operator is assumed to be given by the ³P₀ model [156]. But the A2 diagram tends to produce too often kaons!

• $\bar{p}N\to \bar{K}+X$, if occurring in a nucleus, monitors the production of heavy hypernuclei. It was a remarkable achievement of the LEAR experiment PS177 by Polikanov et al. to measure the lifetime of heavy hypernuclei (see e.g., [177]).

• $p\bar{p}\to {\pi }^{+}{\pi }^{-}$ and $p\bar{p}\to K^{+}{K}^{-}$ by PS172 revealed striking spin effects (see section 4.8).

• $p\bar{p}\to \varphi \varphi$ was used to search for glueballs (Experiment PS 202 “JETSET”) [152], with innovative detection techniques.

8. Modern Perspectives

So far in this review, the phenomenological interpretation was based either on the conventional meson-exchange picture or on the quark model for annihilation. The former was initiated in the 50s, and the latter in the 80s. Of course, it is not fully satisfactory to combine two different pictures, one for the short-range part, and another for the long-range, as the results are very sensitive to the assumptions for the matching of the two schemes. This is one of the many reasons why the quark-model description of the short-range nucleon-nucleon interaction has been abandoned, though it provided an interesting key for a simultaneous calculation of all baryon-baryon potentials. One way out that was explored consists of exchanging the mesons between quarks. Then the quark wave function generates a form factor. For $N\bar{N}$, a attempt was made by Entem and Fernández [102], with some phenomenological applications. In this paper, the annihilation potential is due to transition $q\bar{q}\to meson\to q\bar{q}$ or $q\bar{q}\to gluon\to q\bar{q}$. But this remains a rather hybrid picture and it was not further developed.

Somewhat earlier, in the 80s, interesting developments of the bag model have been proposed, where the nucleon is given a pion cloud that restores its interaction with other nucleons. This led to a solitonic picture, e.g., Skyrme-type of models for low-energy hadron physics [178]. A first application to $\bar{N}N$ was proposed by Zahed and Brown [179].

As seen in other chapters of this book, a real breakthrough was provided by the advent of effective chiral theories, with many successes, for instance in the description of the ππ interaction. For a general introduction, see e.g., the textbook by Donnelly et al. [180]. This approach was adopted by a large fraction of the nuclear-physics community, and, in particular, it was applied to the study of nuclear forces and nuclear structures. Chiral effective field theory led to very realistic potentials for the NN interaction, including the three-body forces and higher corrections in a consistent manner [181, 182]. Thus, the meson-exchange have been gradually forsaken.

In such modern NN potentials, one can identify the long-range part due to one-, two- or three-pion exchange, and apply the G-parity rule, to derive the corresponding long-range part of the $\bar{N}N$ potential. The short-range part of the NN interaction is determined empirically, by fixing the strength of a some constant terms which enter the interaction in this approach. This part cannot be translated as such to the $\bar{N}N$ sector. There exists for sure, analogous constant terms that describe the real part of the interaction. As for the annihilation part, there are two options. The first one consists of making the contact terms complex. This is the choice made by Chen et al. [183]. Another option that keeps unitarity more explicit is to introduce a few effective meson channels X_i and iterate, i.e., $\bar{N}N\to X\to \bar{N}N$, with the propagator of the mesonic channel X_i properly inserted [184]. Then some empirical constant terms enter now the transition potential $V(\bar{N}N\to X_i)$. A fit of the available data determines in principle the constants of the model [74]. The question remains whether the fit of the constant terms is unique, given the sparsity of spin observables. For a recent review on chiral effective theories applied to antiproton physics (see [76, 185]). The phenomenology will certainly extent beyond scattering data. One can already notice that the amplitude of Dai et al. [184], when properly folded with the nuclear density, provides with an optical potential that accounts fairly well for the scattering data, as seen in Figure 19 borrowed from Vorabbi et al. [186].

FIGURE 19

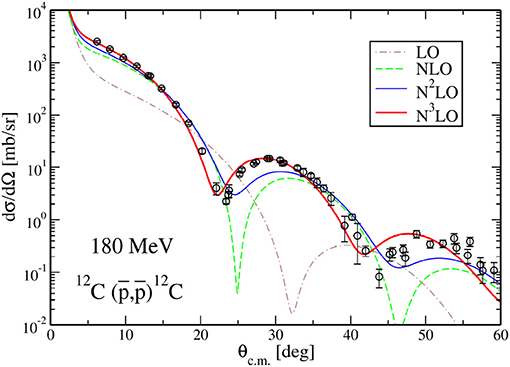
Figure 19. Differential cross-section for elastic $\bar{p}$ scattering on 12C at 180 MeV. The optical potential is computed from successive refinements in the effective theory. Reproduced from Vorabbi et al. [186] with the permission of the authors.

9. Outlook

The physics of low-energy antiprotons covers a variety of topics: fundamental symmetries, atomic physics, inter-hadronic forces, annihilation mechanisms, nuclear physics, etc.

New experiments are welcome or even needed to refine our understanding of this physics. For instance, a better measurement of the shift and width of the antiprotonic lines, and some more experiments on the scattering of antineutrons off nucleons or nuclei. We also insisted on the need for more measurements on $\bar{p}p$ scattering with a longitudinally or transversally polarized target.

Selected annihilation measurements could also be useful, from zero energy to well above the charm threshold, and again, the interest is 2-fold: access to new sectors of hadron spectroscopy, and test the mechanisms of annihilation. For this latter purpose, a through comparison of $\bar{N}N$- and ȲN-induced channels would be most useful, where Y denotes a hyperon.

The hottest sectors remain these linked to astrophysics: how antiprotons and light antinuclei are produced in high-energy cosmic ray? Is there a possibility in the early Universe of separating matter from antimatter before complete annihilation? Studying these questions require beforehand a good understanding of the antinucleon-nucleon and antinucleon-nucleus interaction.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I would like to thank many colleagues, in particular my collaborators, for several stimulating and entertaining discussions along the years about the physics of antiprotons, and also the editors of Frontiers in Physics for initiating this review, and their referees for constructive comments. Special acknowledgments are due to M. Asghar for remarks and suggestions.

Footnotes

1. ^The only doubt came from the magnetic moment of the proton, which is not what is expected for a particle obeying the Dirac equation.

2. ^The other collaborators were acknowledged in the Nobel lectures, but nevertheless Piccioni sued Chamberlain and Segrè in a court of California, which dismissed the suit on procedural grounds.

3. ^For a reaction 1 + 2 → 3 + 4, the Mandestam variables are given in terms of the energy-momentum quadrivectors as $s={({\tilde{p}}_1+{\tilde{p}}_2)}^2$, $t={({\tilde{p}}_3-{\tilde{p}}_1)}^2$ and $u={({\tilde{p}}_4-{\tilde{p}}_1)}^2$.

4. ^The origin is different, for vector mesons, this is a genuine spin-orbit effect, for scalar mesons, this is a consequence of Thomas precession, but the effect is the same in practice.

5. ^The notation is ${}^{2S+1}{L}_J$, as there is a single choice of isospin, and it will become ${}^{2I+1,2S+1}{L}_J$ for $\bar{N}N$.

6. ^Actually more than spin measurements along the normal $\widehat{n}$ to the scattering plane, such as the analyzing power A_n or the transfer D_nn or normal polarization.

7. ^“For God judged it better to bring good out of evil than not to permit any evil to exist,” Augustinus.

8. ^The data have been analyzed with the value of the decay parameter α of that time. The parameter α is defined, e.g., in the note “Baryon decay parameters” of Tanabashi et al. [40]. A recent measurement by the BESIII collaboration in Beijing gives a larger value of α [89]. This means that the Λ polarization would be about 17% smaller.

9. ^I thank Matteo Vorabbi for making available his retrieving of the data in a convenient electronic form.

10. ^Of course, the rearrangement was introduced much earlier, in particular by Stern, Rubinstein, Caroll, … [146, 147], but simply to calculate ratios of branching ratios, without any attempt to estimate the cross sections.

11. ^Happy BNL director, as his laboratory also hosted the experiment in which the Ω⁻ was discovered, the same year 1964.

References

1. Brink L, Ekspong G, Lundqvist S. Nobel Lectures Physics: Including Presentation Speeches and Laureates' Biographies. Singapore: World Scientific (1967). The first 3 volumes were published by North-Holland, Amsterdam.

2. Baur G, Boero G, Brauksiepe S, Buzzo A, Eyrich W, Geyer R, et al. Production of antihydrogen. Phys Lett B. (1996) 368:251–8. doi: 10.1016/0370-2693(96)00005-6

CrossRef Full Text | Google Scholar

3. Massam T, Muller T, Righini B, Schneegans M, Zichichi A. Experimental observation of antideuteron production. Nuovo Cim Ser. (1965) 39:10–4. doi: 10.1007/BF02814251

CrossRef Full Text | Google Scholar

4. Dorfan DE, Eades J, Lederman LM, Lee W, Ting CC. Observation of antideuterons. Phys Rev Lett. (1965) 14:1003–6. doi: 10.1103/PhysRevLett.14.1003

CrossRef Full Text | Google Scholar

5. Ma YG. Observation of antimatter nuclei at RHIC-STAR. J Phys Conf Ser. (2013) 420:012036. doi: 10.1088/1742-6596/420/1/012036

CrossRef Full Text | Google Scholar

6. Adam J, Adamczyk L, Adams JR, Adkins JK, Agakishiev G, Aggarwal MM, et al. Precise measurement of the mass difference and the binding energy of hypertriton and antihypertriton. arXiv [Preprint]. (2019) arXiv:1904.10520.

Google Scholar

7. Dönigus B. Highlights of the production of (anti-)(hyper-)nuclei and exotica with ALICE at the LHC. J Phys Conf Ser. (2019) 1271:012001. doi: 10.1088/1742-6596/1271/1/012001

CrossRef Full Text | Google Scholar

8. Hori M, Sótér A, Barna D, Dax A, Hayano R, Friedreich S, et al. Two-photon laser spectroscopy of antiprotonic helium and the antiproton-to-electron mass ratio. Nature. (2011) 475:484–8. doi: 10.1038/nature10260

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Mohl D. Stochastic cooling of particle beams. Lect Notes Phys. (2013) 866:1–139. doi: 10.1007/978-3-642-34979-9

CrossRef Full Text | Google Scholar

10. Baglin C, Baird SA, Bassompierre G, Borreani G, Brient JC, Broll C, et al. Charmonium spectroscopy by anti-proton annihilation with protons from an internal H₂ gas jet target. In: Nitti L, Preparata G, editors. International Europhysics Conference on High-Energy Physics, Bari, Laterza Bari (1985). p. 609.

Google Scholar

11. Patrignani C. E835 at FNAL: charmonium spectroscopy in anti-p p annihilations. AIP Conf Proc. (2004) 717:581–90. doi: 10.1063/1.1799766

CrossRef Full Text | Google Scholar

12. Augustin I, Gutbrod HH, Kramer D, Langanke K, Stocker H. New physics at the international facility for antiproton and ion research (FAIR) next to GSI. In: 4th International Conference on Fission and Properties of Neutron Rich nuclei (ICFN4), Sanibel Island, FL (2008). doi: 10.1142/9789812833433_0016

CrossRef Full Text | Google Scholar

13. Kumano S. Spin physics at J-PARC. Int J Mod Phys Conf Ser. (2016) 40:1660009. doi: 10.1142/S2010194516600090

CrossRef Full Text | Google Scholar

14. Dalpiaz P, Klapisch R, Lefevre P, Macri M, Montanet L, Mohl D, et al. Physics at SUPERLEAR. In: The Elementary Structure of Matter. Proceedings, Workshop, Les Houches (1987). p. 0414.

Google Scholar

15. Husson A, Lunney D. An antiproton deceleration device for the GBAR experiment at CERN. In: Proceedings, 12th International Conference on Low Energy Antiproton Physics (LEAP2016). Kanazawa (2019).

Google Scholar

16. Chardonnet P, Orloff J, Salati P. The production of antimatter in our galaxy. Phys Lett B. (1997) 409:313–20. doi: 10.1016/S0370-2693(97)00870-8

CrossRef Full Text | Google Scholar

17. Aguilar M, Ali Cavasonza L, Alpat B, Ambrosi G, Arruda L, Attig N, et al. Antiproton flux, antiproton-to-proton flux ratio, and properties of elementary particle fluxes in primary cosmic rays measured with the alpha magnetic spectrometer on the international space station. Phys Rev Lett. (2016) 117:091103. doi: 10.1103/PhysRevLett.117.091103

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Aly JJ, Caser S, Omnes R, Puget JL, Valladas G. The amount of matter in a matter-antimatter model of the universe. Astron Astrophys. (1974) 35:271.

Google Scholar

19. Gastaldi U, Klapisch R, editors. Physics at LEAR With Low-Energy Cooled Antiprotons, Proceedings of LEAR Workshop, Erice. New York, NY: Plenum (1984). doi: 10.1007/978-1-4684-8727-5

CrossRef Full Text | Google Scholar

20. Gastaldi U, Klapisch R, Richard JM, Trân Thanh Vân J, editors. Physics With Antiprotons at LEAR in the ACOL Era, Proceedings of 3th LEAR Workshop, Tignes. Gif-sur-Yvette: Frontières (1985).

Google Scholar

21. Charalambous S, Papastefanou C, Pavlopoulos P, editors. Anti-proton 86. Proceedings, 8th European Symposium on Nucleon Anti-nucleon Interactions, Thessaloniki. Singapore: World Scientific (1987).

Google Scholar

22. Amsler C, Backenstoss G, Klapisch R, Leluc C, Simon D, Tauscher L, editors. Physics at LEAR With Low Energy Antiprotons Proceedings of LEAR Workshop, Villars-sur-Ollon. Chur: Harwood (1988).

23. Amsler C, Urner D, editors. Physics at SuperLEAR, Proceedings of SuperLEAR Workshop, Zurich. Bristol: IOP (1992).

Google Scholar

24. Pinsky LS. A report on the first Fermilab workshop on antimatter physics at low energy. AIP Conf Proc. (1986) 150:515–9. doi: 10.1063/1.36123

CrossRef Full Text | Google Scholar

25. Bloch P, Pavlopoulos P, Klapisch R, editors. 1st International School of Physics With Low-Energy Antiprotons “Ettore Majorana” Fundamental Symmetries, Erice. New York, NY: Plenum (1987). doi: 10.1007/978-1-4684-5389-8

CrossRef Full Text

26. Gastaldi U, Klapisch R, Close F, editors. Spectroscopy of Light and Heavy Quarks. Proceedings, 2nd Course of the International School of Physics With Low-Energy Anti-protons, Erice (1989).

Google Scholar

27. Bradamante F, Richard JM, Klapisch R, editors. Proceedings, 3rd International School of Physics With Low-Energy Antiprotons “Ettore Majorana” Anti-proton–Nucleon and Anti-proton–Nucleus Interactions. New York, NY: Plenum (1990).

Google Scholar

28. Landua R, Klapisch R, Richard JM, editors. Proceedings, 4th International School of Physics With Low-Energy Antiprotons–Medium-Energy Anti-protons and the Quark–Gluon Structure of Hadrons. New York, NY: Plenum (1991).

Google Scholar

29. Fermi E, Yang CN. Are mesons elementary particles? Phys Rev. (1949) 76:1739–43. doi: 10.1103/PhysRev.76.1739

CrossRef Full Text | Google Scholar

30. Jacob MRM, Chew GF. Strong-Interaction Physics: a Lecture Note Volume. Frontiers in Physics. New York, NY: Benjamin (1964).

Google Scholar

31. Ball JS, Scotti A, Wong DY. O boson exchange model of NN and $N\bar{N}$ interaction. Phys Rev. (1966) 142:1000–12. doi: 10.1103/PhysRev.142.1000

CrossRef Full Text | Google Scholar

32. Shapiro IS. The physics of nucleon–antinucleon systems. Phys Rept. (1978) 35:129–85. doi: 10.1016/0370-1573(78)90190-4

CrossRef Full Text | Google Scholar

33. Buck WW, Dover CB, Richard JM. The interaction of nucleons with anti-nucleons. 1. General features of the $\bar{N}N$ spectrum in potential models. Ann Phys. (1979) 121:47. doi: 10.1016/0003-4916(79)90091-5

CrossRef Full Text | Google Scholar

34. Dover CB, Richard JM. The interaction of nucleons with anti-nucleons. 2. Narrow mesons near threshold: experiment and theory. Ann Phys. (1979) 121:70. doi: 10.1016/0003-4916(79)90092-7

CrossRef Full Text | Google Scholar

35. Törnqvist NA. From the deuteron to deusons, an analysis of deuteron–like meson meson bound states. Z Phys C. (1994) 61:525–37. doi: 10.1007/BF01413192

CrossRef Full Text | Google Scholar

36. Dover CB, Richard JM. Strong tensor forces and the possibility of high spin states in the nucleon-antinucleon system. Phys Rev D. (1978) 17:1770–7. doi: 10.1103/PhysRevD.17.1770

CrossRef Full Text | Google Scholar

37. Martin AD, Spearman TD. Elementary-Particle Theory. Amsterdam: North-Holland (1970).

Google Scholar

38. Brambilla N, Eidelman S, Hanhart C, Nefediev A, Shen CP, Thomas CE, et al. The XYZ states: experimental and theoretical status and perspectives. arXiv [Preprint]. (2019) arXiv:1907.07583.

Google Scholar

39. Montanet L, Rossi GC, Veneziano G. Baryonium physics. Phys Rept. (1980) 63:149–222. doi: 10.1016/0370-1573(80)90161-1

CrossRef Full Text | Google Scholar

40. Tanabashi M, Hagiwara K, Hikasa K, Nakamura K, Sumino Y, Takahashi F, et al. Review of particle physics. Phys Rev D. (2018) 98:030001. doi: 10.1103/PhysRevD.98.030001

CrossRef Full Text | Google Scholar

41. Evangelista C, Ghidini B, Palano A, Picciarelli V, Zitoa G, Mättig P, et al. Evidence for a narrow width boson of mass 2.95-GeV. Phys Lett B. (1977) 72:139–43. doi: 10.1016/0370-2693(77)90081-8

CrossRef Full Text | Google Scholar

42. Ablikim M, Achasov MN, An ZH, Bai JZ, Ferroli RB, Ban Y, et al. Spin-parity analysis of $p\bar{p}$ mass threshold structure in J/ψ and ψ′ radiative decays. Phys Rev Lett. (2012) 108:112003. doi: 10.1103/PhysRevLett.108.112003

CrossRef Full Text | Google Scholar

43. Loiseau B, Wycech S. Antiproton-proton channels in J/psi decays. Phys Rev C. (2005) 72:011001. doi: 10.1103/PhysRevC.72.011001

CrossRef Full Text | Google Scholar

44. Wycech S, Dedonder JP, Loiseau B. In search of baryonium. J Phys Conf Ser. (2012) 374:012002. doi: 10.1088/1742-6596/374/1/012002

CrossRef Full Text | Google Scholar

45. Kang XW, Haidenbauer J, Meißner UG. Near-threshold $\bar{p}p$ invariant mass spectrum measured in J/ψ and ψ′ decays. Phys Rev D. (2015) 91:074003. doi: 10.1103/PhysRevD.91.074003

CrossRef Full Text | Google Scholar

46. Amsler C. Nucleon-antinucleon annihilation at LEAR. In: Talk at the ECT^* Workshop on Antiproton Physics, Trento (2019).

Google Scholar

47. Myhrer F, Thomas A. The influence of absorption on possible nucleon-antinucleon resonances and bound states. Phys Lett B. (1976) 64:59–61. doi: 10.1016/0370-2693(76)90357-9

CrossRef Full Text | Google Scholar

48. Isgur N, Thacker HB. Origin of the Okubo-Zweig-Iizuka rule in QCD. Phys Rev D. (2001) 64:094507. doi: 10.1103/PhysRevD.64.094507

CrossRef Full Text | Google Scholar

49. Roy DP. History of exotic meson (four quark) and baryon (five quark) states. J Phys G. (2004) 30:R113. doi: 10.1088/0954-3899/30/3/R02

CrossRef Full Text | Google Scholar

50. Rosner JL. Possibility of baryon–anti-baryon enhancements with unusual quantum numbers. Phys Rev Lett. (1968) 21:950–2. doi: 10.1103/PhysRevLett.21.950

CrossRef Full Text | Google Scholar

51. Jaffe RL. $Q^2{\bar{Q}}^2$ resonances in the baryon–antibaryon system. Phys Rev D. (1978) 17:1444. doi: 10.1103/PhysRevD.17.1444

CrossRef Full Text | Google Scholar

52. Chan HM, Fukugita M, Hansson TH, Hoffman HJ, Konishi K, Hogaasen H, et al. Color chemistry: a study of metastable multiquark molecules. Phys Lett B. (1978) 76:634–40. doi: 10.1016/0370-2693(78)90872-9

CrossRef Full Text | Google Scholar

53. Chew GF, Low FE. Effective range approach to the low-energy p wave pion–nucleon interaction. Phys Rev. (1956) 101:1570–9. doi: 10.1103/PhysRev.101.1570

CrossRef Full Text | Google Scholar

54. Dalitz RH, Tuan SF. The phenomenological description of K-nucleon reaction processes. Ann Phys. (1960) 10:307–51. doi: 10.1016/0003-4916(60)90001-4

CrossRef Full Text | Google Scholar

55. Rossi G, Veneziano G. The string-junction picture of multiquark states: an update. JHEP. (2016) 6:041. doi: 10.1007/JHEP06(2016)041

CrossRef Full Text | Google Scholar

56. Maeda S, Yokota A, Hiyama E, Oka M, Liu Yr. Y_cN and Λ_cNN bound states in the potential model. JPS Conf Proc. (2017) 17:112006. doi: 10.7566/JPSCP.17.112006

CrossRef Full Text | Google Scholar

57. Joseph C, Soffer J, editors. Proceedings, International Symposium on High-Energy Physics with Polarized Beams and Polarized Targets, Vol. 38. Birkhaeuser. Basel: Birkhaeuser (1981). doi: 10.1007/978-3-0348-6301-8

CrossRef Full Text | Google Scholar

58. Martynov E, Nicolescu B. Evidence for maximality of strong interactions from LHC forward data. Phys Lett B. (2018) 786:207–11. doi: 10.1016/j.physletb.2018.09.049

CrossRef Full Text | Google Scholar

59. Bugg DV, Hall J, Clough AS, Shypit RL, Bos K, Kluyver JC, et al. $\bar{p}p$ Total cross sections below 420 MeV/c. Phys Lett B. (1987) 194:563–7. doi: 10.1016/0370-2693(87)90235-8

CrossRef Full Text | Google Scholar

60. Bruckner W, Cujec B, Döbbeling H, Dworschak K, Güttner F, Kneis H, et al. Measurements of the anti-proton–proton annihilation cross-section in the beam momentum range between 180-MeV/c and 600-MeV/c. Z Phys A. (1990) 335:217–29.

Google Scholar

61. Dalkarov OD, Myhrer F. A simple model for proton-anti-proton scattering at low-energies. Nuovo Cim A. (1977) 40:152. doi: 10.1007/BF02776782

CrossRef Full Text | Google Scholar

62. Dover CB, Richard JM. Elastic, charge exchange, and inelastic $\overline{p}p$ cross sections in the optical model. Phys Rev C. (1980) 21:1466–71. doi: 10.1103/PhysRevC.21.1466

CrossRef Full Text | Google Scholar

63. Bertini R, Costa M, Perrot F, Catz H, Chaumeaux A, Faivre JCl, et al. Full angular distribution of the analyzing power in $\bar{p}p$ elastic scattering at 697-MeV/c. Phys Lett B. (1989) 228:531–5. doi: 10.1016/0370-2693(89)90988-X

CrossRef Full Text | Google Scholar

64. Birsa R, Bradamante F, Bressan A, Dalla Torre-Colautti S, Giorgi M, Lamann M, et al. High precision measurement of the $\overline{p}p\to \overline{n}n$ charge exchange differential cross-section. Phys Lett B. (1994) 339:325–31. doi: 10.1016/S0370-2693(97)00685-0

CrossRef Full Text | Google Scholar

65. Ahmidouch A, Heer E, Hess R, Lechanoine-Leluc C, Mascarini Ch, Rapin D, et al. Charge exchange$\bar{p}p\to \bar{n}n$ differential cross-sections between 546 MeV/c and 1287 MeV/c. Phys Lett B. (1995) 364:116–20. doi: 10.1016/0370-2693(95)01348-7

CrossRef Full Text | Google Scholar

66. Marcello S. Five years of antineutron physics at LEAR. Nucl Phys A. (1999) 655:107–16. doi: 10.1016/S0375-9474(99)00187-6

CrossRef Full Text | Google Scholar

67. Iazzi F, Feliciello A, Agnello M, Astrua M, Botta E, Bressani T, et al. Antineutron proton total cross-section from 50 MeV/c to 400 MeV/c. Phys Lett B. (2000) 475:378–85. doi: 10.1016/S0370-2693(00)00086-1

CrossRef Full Text | Google Scholar

68. Klempt E, Bradamante F, Martin A, Richard JM. Antinucleon nucleon interaction at low energy: scattering and protonium. Phys Rept. (2002) 368:119–316. doi: 10.1016/S0370-1573(02)00144-8

CrossRef Full Text | Google Scholar

69. Kunne RA, Beard CI, Birsa R, Bos K, Bradamante F, Bugg DV, et al. Asymmetry in $\bar{p}p$ elastic scattering. Phys Lett B. (1988) 206:557–60. doi: 10.1016/0370-2693(88)91629-2

CrossRef Full Text | Google Scholar

70. Kunne RA, Beard CI, Birsa R, Bos K, Bradamante F, Bugg D, et al. First measurement of D_0n0n in $\bar{p}p$ elastic scattering. Phys Lett B. (1991) 261:191–6. doi: 10.1016/0370-2693(91)91349-Z

CrossRef Full Text | Google Scholar

71. Birsa R, Bradamante F, Dalla Torre S, Giorgi MA, Lamanna M, Martin A, et al. PS199: $\bar{p}p\to \bar{n}n$ spin physics at LEAR. In: Proceedings, 4th International School of Physics With Low-Energy Antiprotons–Medium-Energy Anti-protons and the Quark–Gluon Structure of Hadrons, Erice (1990). p. 195–201.

Google Scholar

72. Birsa R, Bradamante F, Bressan A, Dalla Torre-Colautti S, Giorgi M, Lamanna M, et al. First measurement of the depolarization parameter D_0n0n of the $\bar{p}p\to \bar{n}n$ charge exchange reaction. Phys Lett B. (1993) 302:517–22. doi: 10.1016/0370-2693(93)90436-L

CrossRef Full Text | Google Scholar

73. Timmermans R, Rijken TA, de Swart JJ. Anti-proton–proton partial wave analysis below 925-MeV/c. Phys Rev C. (1994) 50:48–73. doi: 10.1103/PhysRevC.50.48

CrossRef Full Text | Google Scholar

74. Zhou D, Timmermans RGE. Energy-dependent partial-wave analysis of all antiproton-proton scattering data below 925 MeV/c. Phys Rev C. (2012) 86:044003. doi: 10.1103/PhysRevC.86.044003

CrossRef Full Text | Google Scholar

75. Richard JM. Comment on ‘Antiproton proton partial wave analysis below 925 MeV/c'. Phys Rev C. (1995) 52:1143–4. doi: 10.1103/PhysRevC.52.1143

CrossRef Full Text | Google Scholar

76. [Dataset] Haidenbauer J, editor. Talk at the ECT^* Workshop on Antiproton Physics, Trento (2019). Available online at: https://indico.ectstar.eu/event/41/contributions/848/attachments/814/1048/Haidenbauer.pdf (accessed November 2019).

Google Scholar

77. Gourdin M, Jancovici B, Verlet L. On the nucleon-antinucleon interactions. Il Nuovo Cim. (1958) 8:485–96. doi: 10.1007/BF02828757

CrossRef Full Text | Google Scholar

78. Bryan RA, Phillips RJN. Nucleon anti-nucleon potential from single meson exchanges. Nucl Phys B. (1968) 5:201–19. doi: 10.1016/0550-3213(68)90125-9

CrossRef Full Text | Google Scholar

79. Kohno M, Weise W. Proton–anti-proton scattering and annihilation into two mesons. Nucl Phys A. (1986) 454:429–52. doi: 10.1016/0375-9474(86)90098-9

CrossRef Full Text | Google Scholar

80. Haidenbauer J, Hippchen T, Holinde K. The Bonn $N\bar{N}$ potential and the range of $N\bar{N}$ annihilation. Nucl Phys A. (1990) 508:329C–34C. doi: 10.1016/0375-9474(90)90493-6

CrossRef Full Text | Google Scholar

81. Hippchen T, Haidenbauer J, Holinde K, Mull V. Meson–baryon dynamics in the nucleon–antinucleon system. 1. The nucleon–antinucleon interaction. Phys Rev C. (1991) 44:1323–36. doi: 10.1103/PhysRevC.44.1323

CrossRef Full Text | Google Scholar

82. Mull V, Holinde K. Combined description of $\bar{N}N$ scattering and annihilation with a hadronic model. Phys Rev C. (1995) 51:2360–71. doi: 10.1103/PhysRevC.51.2360

PubMed Abstract | CrossRef Full Text | Google Scholar

83. Dover CB, Richard JM. Spin observables in low-energy nucleon anti-nucleon scattering. Phys Rev C. (1982) 25:1952–8. doi: 10.1103/PhysRevC.25.1952

CrossRef Full Text | Google Scholar

84. Richard JM, Sainio ME. Nuclear effects in protonium. Phys Lett B. (1982) 110B:349–52. doi: 10.1016/0370-2693(82)91270-9

CrossRef Full Text | Google Scholar

85. Timmers PH, van der Sanden WA, de Swart JJ. An antinucleon-nucleon potential. Phys Rev D. (1984) 29:1928. doi: 10.1103/PhysRevD.29.1928

CrossRef Full Text | Google Scholar

86. El-Bennich B, Lacombe M, Loiseau B, Wycech S. Paris $N\bar{N}$ potential constrained by recent antiprotonic-atom data and antineutron-proton total cross sections. Phys Rev C. (2009) 79:054001. doi: 10.1103/PhysRevC.79.054001

CrossRef Full Text | Google Scholar

87. Klempt E, Batty C, Richard JM. The antinucleon-nucleon interaction at low energy: annihilation dynamics. Phys Rept. (2005) 413:197–317. doi: 10.1016/j.physrep.2005.03.002

CrossRef Full Text | Google Scholar

88. Kohno M, Weise W. Anti-hyperon–hyperon production in low-energy anti-proton–proton reactions. Nucl Phys A. (1988) 479:433C–49C. doi: 10.1016/0375-9474(88)90454-X

CrossRef Full Text | Google Scholar

89. Ablikim M, Achasov MN, Ahmed S, Albrecht M, Alekseev M, Amoroso A, et al. Polarization and entanglement in baryon-antibaryon pair production in electron-positron annihilation. Nat Phys. 15 (2019) 631–634. doi: 10.1038/s41567-019-0494-8

CrossRef Full Text | Google Scholar

90. Bassalleck B, Berdoz A, Bradtke C, Bröders R, Bunker B, Dennert H, et al. Measurement of spin transfer observables in $\bar{p}p\to \bar{\Lambda }\Lambda$ at 1.637 GeV/c. Phys Rev Lett. (2002) 89:212302. doi: 10.1103/PhysRevLett.89.212302

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Paschke KD, Quinn B, Berdoz A, Franklin GB, Khaustov P, Meyer CA, et al. Experimental determination of the complete spin structure for $\bar{p}p\to \bar{\Lambda }\Lambda$ at 1.637 GeV/c. Phys Rev C. (2006) 74:015206. doi: 10.1103/PhysRevC.74.015206

CrossRef Full Text | Google Scholar

92. Haidenbauer J, Holinde K, Mull V, Speth J. Can one discriminate between meson exchange and quark–gluon transition mechanisms in the $\bar{p}p\to \bar{\Lambda }\Lambda$ process? Phys Lett B. (1992) 291:223–7. doi: 10.1016/0370-2693(92)91035-8

CrossRef Full Text | Google Scholar

93. Alberg MA, Ellis JR, Kharzeev D. The proton spin puzzle and depolarization in $\bar{p}p\to \bar{\Lambda }\Lambda$. Phys Lett B. (1995) 356:113–7. doi: 10.1016/0370-2693(95)00789-N

CrossRef Full Text | Google Scholar

94. Richard JM. Remarks about spin measurements in $\bar{p}\to \bar{\Lambda }\Lambda$. Phys Lett B. (1996) 369:358–61. doi: 10.1016/0370-2693(95)01598-1

CrossRef Full Text | Google Scholar

95. Artru X, Elchikh M, Richard JM, Soffer J, Teryaev OV. Spin observables and spin structure functions: inequalities and dynamics. Phys Rep. (2009) 470:1–92. doi: 10.1016/j.physrep.2008.09.004

CrossRef Full Text | Google Scholar

96. Fridman A, editor. 4th Antiproton Symposium, Proceedings of Antiproton Conference, Barr & Strasbourg. Paris: CNRS (1979).

Google Scholar

97. Liu GQ, Tabakin F. Coupled channels study of anti-proton proton reactions. Phys Rev C. (1990) 41:665–79. doi: 10.1103/PhysRevC.41.665

CrossRef Full Text | Google Scholar

98. Takeuchi S, Myhrer F, Kubodera K. Maximum asymmetry phenomena in $\bar{p}p\to {\pi }^{-}{\pi }^{+}$ and $\bar{p}p\to K^{-}{K}^{+}$ reactions. Nucl Phys A. (1993) 556:601–20. doi: 10.1016/0375-9474(93)90472-A

CrossRef Full Text | Google Scholar

99. Elchikh M, Richard JM. Meson exchange and nonlocality effects in proton anti-proton annihilation into two pseudoscalar mesons. Phys Rev C. (1993) 48:R17–20. doi: 10.1103/PhysRevC.48.R17

CrossRef Full Text | Google Scholar

100. Deloff A. Fundamentals in Hadronic Atom Theory. River Edge, NJ: World Scientific (2003). p. 352.

Google Scholar

101. Augsburger M, Anagnostopoulos D, Borchert G, Chatellard D, Egger JP, El-Khoury P, et al. Measurement of the strong interaction parameters in antiprotonic hydrogen and probable evidence for an interference with inner bremsstrahlung. Nucl Phys A (1999) 658:149–62. doi: 10.1016/S0375-9474(99)00352-8

CrossRef Full Text | Google Scholar

102. Entem DR, Fernandez F. The $N\bar{N}$ interaction in a constituent quark model: Baryonium states and protonium level shifts. Phys Rev C. (2006) 73:045214. doi: 10.1103/PhysRevC.73.045214

CrossRef Full Text | Google Scholar

103. Gotta D, Anagnostopoulos D, Augsburger M, Borchert G, Castelli C, Chatellard D, et al. Balmer α transitions in antiprotonic hydrogen and deuterium. Nucl Phys A. (1999) 660:283–321. doi: 10.1016/S0375-9474(99)00385-1

CrossRef Full Text | Google Scholar

104. Dover CB, Richard JM, Carbonell J. Isospin mixing in protonium and annihilation dynamics. Phys Rev C. (1991) 44:1281–8. doi: 10.1103/PhysRevC.44.1281

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Deser S, Goldberger ML, Baumann K, Thirring WE. Energy level displacements in pi mesonic atoms. Phys Rev. (1954) 96:774–6. doi: 10.1103/PhysRev.96.774

CrossRef Full Text | Google Scholar

106. Trueman TL. Energy level shifts in atomic states of strongly-interacting particles. Nucl Phys. (1961) 26:57–67. doi: 10.1016/0029-5582(61)90115-8

CrossRef Full Text | Google Scholar

107. Combescure M, Khare A, Raina A, Richard JM, Weydert C. Level rearrangement in exotic atoms and quantum dots. Int J Mod Phys B. (2007) 21:3765–81. doi: 10.1142/S0217979207037855

CrossRef Full Text | Google Scholar

108. Zel'dovich Y. Energy levels in a distorted coulomb field. Sov Phys Solid State. (1960) 1:1497.

Google Scholar

109. Carbonell J, Richard JM, Wycech S. On the relation between protonium level shifts and nucleon–anti-nucleon scattering amplitudes. Z Phys A. (1992) 343:325–29.

Google Scholar

110. Furui S, Strobel G, Faessler A, Vinh Mau R. The isospin mixing effect in $\bar{p}p$ annihilation at rest into π⁺π⁻ and $K\bar{K}$. Nucl Phys A. (1990) 516:643–61. doi: 10.1016/0375-9474(90)90132-6

CrossRef Full Text | Google Scholar

111. Kaufmann WB, Pilkuhn H. Black sphere model for the line widths of p state protonium. Phys Rev C. (1978) 17:215–8. doi: 10.1103/PhysRevC.17.215

CrossRef Full Text | Google Scholar

112. Day TB, Snow GA, Sucher J. High-orbital S-state capture of π-mesons by protons. Phys Rev. (1960) 118:864–6. doi: 10.1103/PhysRev.118.864

CrossRef Full Text | Google Scholar

113. Garreta D, Birien P, Bruge G, Chaumeaux A, Drake DM, Janouin S, et al. Elastic scattering of anti-protons from carbon, calcium and lead at 180-MeV. Phys Lett B. (1984) 149B:64–8. doi: 10.1016/0370-2693(84)91552-1

CrossRef Full Text | Google Scholar

114. Bruge G, Chaumeaux A, Birien P, Drake DM, Garreta D, Janouin S, et al. Comparative study of the elastic scattering of 178.4-MeV anti-protons by the ¹⁶O and ¹⁸O isotopes. Phys Lett B. (1986) 169:14–6. doi: 10.1016/0370-2693(86)90676-3

CrossRef Full Text | Google Scholar

115. Janouin S, Lemaire MC, Garreta D, Birien P, Bruge G, Drake DM, et al. Optical model analysis of anti-proton nucleus elastic scattering at 50-MeV and 180-MeV. Nucl Phys A. (1986) 451:541–61. doi: 10.1016/0375-9474(86)90291-5

CrossRef Full Text | Google Scholar

116. Adachi S, Von Geramb HV. Microscopic analysis of anti-proton–nucleus elastic scattering. Nucl Phys A. (1987) 470:461–76. doi: 10.1016/0375-9474(87)90581-1

CrossRef Full Text | Google Scholar

117. Suzuki T. Analysis of anti-proton nucleus scattering with the medium corrected optical potential. Nucl Phys A. (1985) 444:659–77. doi: 10.1016/0375-9474(85)90111-3

CrossRef Full Text | Google Scholar

118. Heiselberg H, Jensen AS, Miranda A, Oades GC, Richard JM. Microscopic calculation of anti-proton nucleus elastic scattering. Nucl Phys A. (1986) 451:562–80. doi: 10.1016/0375-9474(86)90292-7

CrossRef Full Text | Google Scholar

119. Balestra F, Bossolasco S, Bussa MP, Busso L, Ferrero L, Panzieri D, et al. Evidence of isospin effects in anti-proton–nucleus annihilation. Nucl Phys A. (1989) 491:572–86. doi: 10.1016/0375-9474(89)90518-6

CrossRef Full Text | Google Scholar

120. Botta E. Antineutron nucleus annihilation. Nucl Phys A. (2001) 692:39–46. doi: 10.1016/S0375-9474(01)01157-5

CrossRef Full Text | Google Scholar

121. Dover CB, Sainio ME, Walker GE. Antinucleon as a probe of nuclear spin and isospin excitations. Phys Rev C. (1983) 28:2368–73. doi: 10.1103/PhysRevC.28.2368

CrossRef Full Text | Google Scholar

122. Lemaire MC, Birien P, Bruge G, Drake DM, Garreta D, Janouin S, et al. Inelastic scattering of anti-protons from ¹²C and ¹⁸O at 50-MeV and 180-MeV. Nucl Phys A. (1986) 456:557–76. doi: 10.1016/0375-9474(86)90075-8

CrossRef Full Text | Google Scholar

123. Dover CB, Franey MA, Love WG, Sainio ME, Walker GE. Antinucleon nucleus inelastic scattering and the spin dependence of the $\bar{N}N$ annihilation potential. Phys Lett B. (1984) 143:45–9. doi: 10.1016/0370-2693(84)90801-3

CrossRef Full Text | Google Scholar

124. Batty CJ, Friedman E, Gal A. Strong interaction physics from hadronic atoms. Phys Rept. (1997) 287:385–445. doi: 10.1016/S0370-1573(97)00011-2

CrossRef Full Text | Google Scholar

125. Gotta D. Precision spectroscopy of light exotic atoms. Prog Part Nucl Phys. (2004) 52:133–95. doi: 10.1016/j.ppnp.2003.09.003

CrossRef Full Text | Google Scholar

126. Bouyssy A, Marcos S. Relativistic mean field approach to the scattering of antinucleons and nucleons by nuclei. Phys Lett B. (1982) 114:397–402. doi: 10.1016/0370-2693(82)90079-X

CrossRef Full Text | Google Scholar

127. Gaitanos T, Kaskulov M. Toward relativistic mean-field description of $\overline{\mathrm{\text{N}}}$-nucleus reactions. Nucl Phys A. (2015) 940:181–93. doi: 10.1016/j.nuclphysa.2015.04.006

CrossRef Full Text | Google Scholar

128. Larionov AB, Lenske H. Elastic scattering, polarization and absorption of relativistic antiprotons on nuclei. Nucl Phys A. (2017) 957:450–76. doi: 10.1016/j.nuclphysa.2016.10.006

CrossRef Full Text | Google Scholar

129. Friedman E, Gal A, Loiseau B, Wycech S. Antinucleonnucleus interaction near threshold from the Paris $\bar{N}N$ potential. Nucl Phys A. (2015) 943:101–16. doi: 10.1016/j.nuclphysa.2015.08.010

CrossRef Full Text | Google Scholar

130. Hrtánková J, Mareš J. Calculations of antiprotonnucleus quasi-bound states using the paris $\bar{n}n$ potential. Nucl Phys A. (2018) 969:45–59. doi: 10.1016/j.nuclphysa.2017.09.011

CrossRef Full Text | Google Scholar

131. Aumann T, Bartmann W, Bouvard A, Boine-Frankenheim O, Broche A, Butin F, et al. PUMA: Antiprotons and Radioactive Nuclei. Technical Report CERN-SPSC-2019-033. SPSC-P-361. Geneva: CERN (2019).

Google Scholar

132. Baldo-Ceolin M, Benetti P, Bitter T, Bobisut F, Calligarich E, Dolfini R, et al. A new experimental limit on neutron–anti-neutron oscillations. Z Phys C. (1994) 63:409–16. doi: 10.1007/BF01580321

CrossRef Full Text | Google Scholar

133. Theroine C. A neutron-antineutron oscillation experiment at the European spallation source. Nucl Part Phys Proc. (2016) 273–275:156–61. doi: 10.1016/j.nuclphysbps.2015.09.019

CrossRef Full Text | Google Scholar

134. Kabir PK. Limits on $n\bar{n}$ oscillations. Phys Rev Lett. (1983) 51:231. doi: 10.1103/PhysRevLett.51.231

CrossRef Full Text | Google Scholar

135. Alberico WM. Neutron antineutron oscillations: theory. In: Lepton and Baryon Number Violation in Particle Physics, Astrophysics and Cosmology. Proceedings, 1st International Symposium, Lepton-baryon'98, Trento (1998). p. 94–108.

Google Scholar

136. Barrow JL, Golubeva ES, Paryev E, Richard JM. Progress and simulations for intranuclear neutron–antineutron transformations in 4018Ar. arXiv [Preprint]. (2019) arXiv:1906.02833.

Google Scholar

137. Dover CB, Gal A, Richard JM. Neutron antineutron oscillations in nuclei. Phys Rev D. (1983) 27:1090–100. doi: 10.1103/PhysRevD.27.1090

CrossRef Full Text | Google Scholar

138. Oosterhof F, Long B, de Vries J, Timmermans RGE, van Kolck U. Baryon-number violation by two units and the deuteron lifetime. Phys Rev Lett. (2019) 122:172501. doi: 10.1103/PhysRevLett.122.172501

PubMed Abstract | CrossRef Full Text | Google Scholar

139. Haidenbauer J, Meißner UG. Neutron-antineutron oscillations in the deuteron studied with NN and $\bar{N}N$ interactions based on chiral effective field theory. arXiv [Preprint]. (2019) arXiv:1910.14423.

Google Scholar

140. Nussinov S, Lampert MA. QCD inequalities. Phys Rept. (2002) 362:193–301. doi: 10.1016/S0370-1573(01)00091-6

CrossRef Full Text | Google Scholar

141. Zupancic C. Decay of a spinless particle into four identical spinless bosons. Ann Phys. (1994) 235:245–317. doi: 10.1006/aphy.1994.1099

CrossRef Full Text | Google Scholar

142. Devons S, Kozlowski T, Nemethy P, Shapiro S, Horwitz N, Kalogeropoulos T, et al. Observation of $\bar{p}p\to 2{\pi }^0$ at rest: evidence concerning s state annihilation. Phys Rev Lett. (1971) 27:1614. doi: 10.1103/PhysRevLett.27.1614

CrossRef Full Text | Google Scholar

143. Lévy M. Range of proton-antiproton annihilation. Phys Rev Lett. (1960) 5:380–1. doi: 10.1103/PhysRevLett.5.380

CrossRef Full Text | Google Scholar

144. Martin A. Range of the nucleon-antinucleon annihilation potential. Phys Rev. (1961) 124:614–5. doi: 10.1103/PhysRev.124.614

CrossRef Full Text | Google Scholar

145. Côté J, Lacombe M, Loiseau B, Moussallam B, Mau RV. Nucleon-antinucleon optical potential. Phys Rev Lett. (1982) 48:1319–22. doi: 10.1103/PhysRevLett.48.1319

CrossRef Full Text | Google Scholar

146. Rubinstein HR, Stern H. Nucleon–antinucleon annihilation in the quark model. Phys Lett. (1966) 21:447–9. doi: 10.1016/0031-9163(66)90526-9

CrossRef Full Text | Google Scholar

147. Carroll JP. Extended quark-rearrangement model for proton-antiproton annihilation at rest. Phys Rev. (1969) 184:1793–802. doi: 10.1103/PhysRev.184.1793

CrossRef Full Text | Google Scholar

148. Kleinknecht K, Klempt E, editors. Proton Anti-proton Interactions and Fundamental Symmetries. Proceedings, 9th European Symposium, Vol. 8, Mainz (1989).

Google Scholar

149. Green AM, Niskanen JA. From phenomenological to microscopic descriptions of N$\overline{N}$ annihilation. Int Rev Nucl Phys. (1984) 1:569–700. doi: 10.1142/9789814415132_0007

CrossRef Full Text | Google Scholar

150. Green AM, Niskanen JA. Low-energy anti-proton physics in the early LEAR era. Prog Part Nucl Phys. (1987) 18:93–182. doi: 10.1016/0146-6410(87)90009-3

CrossRef Full Text | Google Scholar

151. Ihle G, Pirner HJ, Richard JM. s Wave nucleon–anti-nucleon interaction in the constituent quark model. Nucl Phys A. (1988) 485:481–508. doi: 10.1016/0375-9474(88)90549-0

CrossRef Full Text | Google Scholar

152. Eisenstein RA, Armenteros R, Bassi D, Birien P, Bock R, Busso A, et al. The JETSET experiment at LEAR. In: Proceedings, BNL Workshop on Glueballs, Hybrids, and Exotic Hadrons. Upton, NY: Brookhaven (1989). p. 636–42. doi: 10.1063/1.38092

CrossRef Full Text | Google Scholar

153. Amsler C, Myhrer F. Low-energy anti-proton physics. Ann Rev Nucl Part Sci. (1991) 41:219–67. doi: 10.1146/annurev.ns.41.120191.001251

CrossRef Full Text | Google Scholar

154. Kudryavtsev AE. Some comments on $\bar{n}p$ annihilation branching ratios into ππ, $\bar{K}K$ and πη channels. Phys Atom Nucl. (2000) 63:1969–72. doi: 10.1134/1.1335095

CrossRef Full Text | Google Scholar

155. Vandermeulen J. $N\bar{N}$ Annihilation creates two mesons. Z Phys C. (1988) 37:563–7. doi: 10.1007/BF01549715

CrossRef Full Text | Google Scholar

156. Le Yaouanc A, Oliver L, Pène O, Raynal JC. Hadron Transitions in the Quark Model. New York, NY: Gordon and Breach (1988).

Google Scholar

157. Genz H. The quark line rule in nucleon antinucleon annihilation. AIP Conf Proc. (1988) 176:405–10. doi: 10.1063/1.37745

CrossRef Full Text | Google Scholar

158. Pirner HJ. $N\bar{N}$ annihilation in the large N_c limit. Phys Lett B. (1988) 209:154–8. doi: 10.1016/0370-2693(88)90923-9

CrossRef Full Text | Google Scholar

159. Dosch HG, Gromes D. Flavor dependence of spontaneous pair creation. Z Phys C. (1987) 34:139. doi: 10.1007/BF01561125

CrossRef Full Text | Google Scholar

160. Cugnon J, Jasselette P, Vandermeulen J. Dynamics of the anti-p nucleus annihilation. In: Proceedings, 4th LEAR Workshop: Physics at LEAR With Low Energy Antiprotons, Villars (1996). p. 775–8.

Google Scholar

161. Cugnon J, Vandermeulen J. Double strangeness production in anti-proton annihilation on nuclei. Z Phys A. (1991) 338:349–56. doi: 10.1007/BF01288199

CrossRef Full Text | Google Scholar

162. Rafelski J. Deep anti-proton annihilations on nuclei. In: Proceedings, 3rd International School of Physics With Low-Energy Antiprotons “Ettore Majorana” Anti-proton–Nucleon and Anti-proton–Nucleus Interactions, Erice (1996). p. 231–9.

Google Scholar

163. Koch H. Hadron physics with antiprotons. Nucl Instrum Meth B. (2004) 214:50–5. doi: 10.1016/S0168-583X(03)01771-3

CrossRef Full Text | Google Scholar

164. Wiedner U. Hadron physics with PANDA. Hyperfine Interact. (2009) 194:219–23. doi: 10.1007/s10751-009-0075-9

CrossRef Full Text | Google Scholar

165. Chiba M, Fujitani T, Iwahori J, Kawaguti M, Kobayashi M, Kurokawa SI, et al. Pontecorvo reactions in antiproton annihilation at rest in deuterium to π⁰n, π⁰Δ⁰, ηn and ηΔ⁰. Phys Rev D. (1997) 55:2577–83. doi: 10.1103/PhysRevD.55.2577

CrossRef Full Text | Google Scholar

166. Gorchakov OE, Cerello P, Ableev VG, Prakhov SN, Rozhdestvensky AM, Sapozhnikov MG, et al. Measurement of the $\bar{p}d\to \varphi n$ Pontecorvo reaction for anti-proton annihilation at rest. Phys Lett B. (2002) 528:34–42. doi: 10.1016/S0370-2693(02)01175-9

CrossRef Full Text | Google Scholar

167. Alberico WM, Garbarino G. Weak decay of Λ hypernuclei. Phys Rept. (2002) 369:1–109. doi: 10.1016/S0370-1573(02)00199-0

CrossRef Full Text | Google Scholar

168. Denig A, Salme G. Nucleon electromagnetic form factors in the timelike region. Prog Part Nucl Phys. (2013) 68:113–57. doi: 10.1016/j.ppnp.2012.09.005

CrossRef Full Text | Google Scholar

169. Pacetti S, Baldini Ferroli R, Tomasi-Gustafsson E. Proton electromagnetic form factors: basic notions, present achievements and future perspectives. Phys Rept. (2015) 550–551:1–103. doi: 10.1016/j.physrep.2014.09.005

CrossRef Full Text | Google Scholar

170. Bardin G, Burgun G, Calabrese R, Capon G, Carlin R, Dalpiaz P, et al. Measurement of the proton electromagnetic form-factor near threshold in the timelike region. Phys Lett B. (1991) 255:149–54. doi: 10.1016/0370-2693(91)91157-Q

CrossRef Full Text | Google Scholar

171. Baglin C, Baird S, Bassompierre G, Borreani G, Brient JC, Broll C, et al. Search for the p wave singlet charmonium state in $\bar{p}p$ annihilations at the CERN intersecting storage rings. Phys Lett B. (1986) 171:135–41. doi: 10.1016/0370-2693(86)91013-0

CrossRef Full Text | Google Scholar

172. Ambrogiani M, Argirò S, Bagnasco S, Baldini W, Bettoni D, Borreani G, et al. Search for the ${\eta }_c^{\prime }(2^1{S}_0$) charmonium resonance. Phys Rev D. (2001) 64:052003. doi: 10.1103/PhysRevD.64.052003

CrossRef Full Text | Google Scholar

173. Gabathuler E, Pavlopoulos P. The CPLEAR experiment. Phys Rept. (2004) 403–404:303–21. doi: 10.1016/j.physrep.2004.08.020

CrossRef Full Text | Google Scholar

174. Hatzifotiadou D, Adiels L, Backenstoss G, Bergstrom I, Carius S, Charalambous S, et al. Some results of experiment PS182 at LEAR. In: Anti-proton 86. Proceedings, 8th European Symposium on Nucleon Anti-nucleon Interactions, Thessaloniki (1986). p. 199–204.

Google Scholar

175. Wang Q, Li G, Zhao Q. Open charm effects in the explanation of the long-standing ‘ρπ puzzle'. Phys Rev D. (2012) 85:074015. doi: 10.1103/PhysRevD.85.074015

CrossRef Full Text | Google Scholar

176. Dover CB, Fishbane PM, Furui S. Dynamical selection rules in $N\bar{N}$ annihilation. Phys Rev Lett. (1986) 57:1538–41. doi: 10.1103/PhysRevLett.57.1538

PubMed Abstract | CrossRef Full Text | Google Scholar

177. Nifenecker H. Fission of heavy hypernuclei. Prog Part Nucl Phys. (1993) 30:407–14. doi: 10.1016/0146-6410(93)90042-E

CrossRef Full Text | Google Scholar

178. Zahed I, Brown GE. The Skyrme model. Phys Rept. (1986) 142:1–102. doi: 10.1016/0370-1573(86)90142-0

CrossRef Full Text | Google Scholar

179. Zahed I, Brown GE. A nonperturbative description of $N\bar{N}$ annihilation. Z Phys A. Cambridge, (1990) 335:349–54.

Google Scholar

180. Donnelly TW, Formaggio JA, Holstein BR, Milner RG, Surrow B. Foundations of Nuclear and Particle Physics. Cambridge, UK: Cambridge University Press (2017).

Google Scholar

181. Machleidt R, Entem DR. Chiral effective field theory and nuclear forces. Phys Rept. (2011) 503:1–75. doi: 10.1016/j.physrep.2011.02.001

CrossRef Full Text | Google Scholar

182. Epelbaum E, Krebs H, Meißner UG. Improved chiral nucleon-nucleon potential up to next-to-next-to-next-to-leading order. Eur Phys J A. (2015) 51:53. doi: 10.1140/epja/i2015-15053-8

CrossRef Full Text | Google Scholar

183. Chen GY, Ma JP. $N\bar{N}$ scattering at NLO order in an effective theory. Phys Rev D. (2011) 83:094029. doi: 10.1103/PhysRevD.83.094029

CrossRef Full Text | Google Scholar

184. Dai LY, Haidenbauer J, Meißner UG. Antinucleon-nucleon interaction at next-to-next-to-next-to-leading order in chiral effective field theory. JHEP. (2017) 7:78. doi: 10.1007/JHEP07(2017)078

CrossRef Full Text | Google Scholar

185. Haidenbauer J. Antinucleon-nucleon interaction in chiral effective field theory. EPJ Web Conf. (2018) 181:01028. doi: 10.1051/epjconf/201818101028

CrossRef Full Text | Google Scholar

186. Vorabbi M, Gennari M, Finelli P, Giusti C, Navrátil P. Elastic antiproton-nucleus scattering from chiral forces. arXiv [Preprint]. (2019) arXiv:1906.11984.

Google Scholar