A Discrete Fracture Network Model With Stress-Driven Nucleation: Impact on Clustering, Connectivity, and Topology

Introduction

Fractures are ubiquitous structures controlling both flows and rock mechanical strength in geological environments. Modeling the fracture network is thus a key prerequisite of forecasting modeling in many industrial applications such as managing groundwater/petroleum resources, assessing risks associated with geotechnical constructions or deep waste disposal, among others. In most of the cases, fractures cannot be modeled deterministically, because they cannot be observed in three-dimensions with sufficient resolution at all scales. Hence, the modeling must be stochastic, which consists of generating a 3D fractured medium statistically equivalent to measures and observations. Discrete Fracture Network modeling is one of the most convenient and used of the stochastic methods; it describes fractured rocks as a population of individual fractures, whose parameters (size, shape, orientation, aperture, and position) are drawn from statistical probability distributions derived from observation maps (mainly 2D outcrop and tunnels, 1D fracture intensity along wells, or 3D geophysics imagery) and models [see [2, 3] for reviews]. In its simplest form, the model (which we will refer as the Poisson model) consists of positioning fractures at random in the generation volume with a given density, and of assigning other fracture parameters independently by bootstrapping the parameter distributions of observations [4–9]. The method is easy to implement, but it neglects most of the complexity of the underlying fracturing process, in particular the correlations induced by fracture-to-fracture mechanical interaction [10–12]. This so-called Poisson model is thus a crude representation of geological fractures that can lead to large discrepancy between modeled and natural network in terms of network topology [13, 14], having dramatical impact on the estimated hydrological and mechanical behavior of the fractured rock mass [15–17]. A way to improve the realism of DFN models is the use of genetic models, in which the fracture hierarchy reproduce correlations between their different geometrical attributes. Nevertheless, a full mechanical description of the fracturing process [18–20] is not feasible when dealing with dense networks made of fractures having sizes from centimeter to tens of kilometers. The broad range of natural fracture size distributions and their power-law nature [11, 21–23] suggest that all scales matters. This is even more important for industries such as nuclear deep waste disposal where small fractures may have an important role at the nearfield of the repository, whose footprint extends to several kilometers. Recent papers [1, 24] have proposed a genetic model of DFN, called “Universal Fracture Model” (UFM model), using simplified fracturing-relevant rules for nucleation, growth and arrest of fractures to draw complex and dense networks. With simple kinematic rules that mimic the main mechanical processes, the model produces fracture size distributions and fracture intersections that are consistent with observations [24]. It results in less connected networks than the Poisson model and changes in the network topology [25], which has been proven to have an impact on flow properties, particularly decreasing effective permeability and increasing flow channeling [26]. Nonetheless, the random positioning of new fractures (nuclei) in this model is still too simplified to reproduce spatial variability and clustering effect observed in natural fracture network patterns [11, 23]. Indeed, nucleation is a complex process both controlled by the repartition of flaws in the rock matrix such as grain boundaries, pores or cleavage plans [27–29] and the stress distributions that make nuclei active or not [30–32]. This problem can be addressed as a quenched disordered process where flaws are initially present in the system and activate as the system evolves [33, 34], or as an annealed disorder where nuclei positioning is directly a function of the system evolution [35]. In this paper, we aim to improve the UFM model by better reproducing the complex feedback-loop process between the propagation of fractures and the emergence of new ones. Our model is also based on the nucleation, growth, and arrest scheme, but we propose to condition the positioning of new nuclei to the mechanical perturbation induced by existing fractures in a timewise manner. This perturbation is modeled as the superposition of stress redistributions induced by each fracture loaded by an allegedly known remote stress field. Such a pseudo-mechanical model does not aim to catch all the complexity of fracture mechanical processes, but this first order approximation of fracture interactions at the network scale may already change dramatically the topology and connectivity of the DFN models. Since larger stress perturbations are expected in the vicinity of fractures, with an intensity that depends on fracture size, we expect the stress-driven nucleation in the timewise process of the UFM model to increase fracture spatial correlations. In order to highlight spatial correlations of the DFNs so generated, we compute fracture positions correlation dimension, fracture density variability, and fractures intersection matrix, and compare results with equivalent Poisson model.

The Model

The Discrete Fracture Network approach for modeling fractured rock masses refers to numerical models explicitly representing the geometry of each fractures forming the network. Generally, this geometry (positions, orientations, size…) is generated stochastically from data statistics. The simplest model considers fractures independent of each other; it will be referred to as the Poisson DFN model. The DFN model developed by Davy et al. [1] is based on basic mechanical concepts described in Davy et al. [24]. The fracturing process is divided in three main stages in a time-wise approach: nucleation, propagation and arrest of fractures. We first develop the model and how in its simplest form—i.e., with a Poisson distribution of nuclei—it controls the network size and intersection distributions. Then, we introduce a more complex nucleation model based on the stress perturbation of pre-existing fractures.

The Stress-Independent UFM Model

Nucleation is the fracture birth process, which is here defined by a nuclei size distribution p_N(l) (that can be a power-law, exponential, etc…) and a rate ṅ_N = dn_N/dt (with n_N the number of nuclei introduced in the system). Nuclei positions are assumed to be uniformly distributed in space here, we will refer to this model as the stress-independent UFM model.

Once created, fractures grow following a power law relationship to describe the crack tip velocity in the subcritical regime [36]:

$\begin{array}{l}v(l)=C{l}^a\end{array}$

with l the fracture length, C the growth rate and a the growth exponent. If not arrested, nuclei size increases non-linearly with time and becomes infinite for a finite time t_∞ dependent on the initial nuclei size and the parameters C and a. For constant nucleation rate and no fracture arrest, even if fractures grow, there is a stationary solution for the fracture size distribution [1]:

$\begin{array}{l}{n}_G(l)=\frac{{\dot{n}}_N}{C}{l}^{-a}\end{array}$

The arrest rule is assumed to reflect the mechanical interaction between fractures. In this model, we consider these interactions as a binary law where fractures can only abut on larger ones, but the reverse is not likely to occur. It results in a large proportion of T-shape intersections that are consistent with field observation, and in a quasi-universal self-similar fracture size distribution:

$\begin{array}{l}{n}_A(l)=D{\gamma }^D{l}^{-D+1}\end{array}$

with D the topological dimension associated to fracture centers, and γ a geometrical parameter dependent on fracture orientations. Small fractures are statistically freely growing with the size distribution n_G(l), while large fractures are statistically arrested and described by n_A(l). The model thus results in a two-power-law size distribution, where the transition size between n_G and n_A is both the scale at which the network is connected and the average size of fracture blocks. The two power-law distribution is obtained for modeling time t_∞, when first fractures become infinite. For larger times, the number of arrested fractures increases, and the transition size decreases. We refer the reader to Davy et al. [1] for further information.

Stress-Driven Nucleation

In this section, we further develop the stress-independent UFM model by making nucleation dependent on stress redistributions caused by existing fractures. For this, we introduce a stress field based probabilistic sampling of nuclei locations. The stress field evolves over the whole domain as the fracturing process. Considering the system to be linear elastic, which may not be the case for highly damaged materials, we define the stress field $\overline{\overline{\sigma }}(\overline{x},t)$ at any position $\overline{x}$ in the domain at time t as the superposition of the remote stress field $\overline{\overline{{\sigma }^{\infty }}}(t)$ plus the contribution of every fracture $\overline{\overline{{\sigma }_f}}(\overline{x},t)$:

$\begin{array}{l}\overline{\overline{\sigma }}(\overline{x},t)=\overline{\overline{{\sigma }^{\infty }}}(t)+{\displaystyle \sum _f}\overline{\overline{{\sigma }_f}}(\overline{x},t)\end{array}$

New nuclei are progressively introduced in the system following a probability field $\mathbb{P}(\overline{x},t)$ derived of this stress field:

$\begin{array}{l}\mathbb{P}\left(\overline{x},t\right)~{\left[{\sigma }_{VM}\left(\overline{x},t\right)\right]}^m\end{array}$

where ${\sigma }_{VM}(\overline{x},t)$ is the Von Mises stress [37] and m a parameter that quantifies the coupling between nucleation occurrence and stress (thereafter called the selectivity parameter). The Von Mises stress is a scalar invariant measure of the deviatoric stress intensity and a measure of the elastic strain energy of distortion stored in the matrix. We then generate a scalar stress-intensity field that will serve as a basis to construct a discrete probability distribution for nuclei position sampling, without using any strength criteria. This stress-driven nucleation process is thus defined as an annealed disorder process [35] where nuclei positioning is directly a function of the system evolution. The model then needs two more parameters: the remote stress field tensor $\overline{\overline{{\sigma }^{\infty }}}$ and the selectivity parameter m. The latter quantifies the influence of the stress field heterogeneity on nucleation. For large m, nuclei tend to concentrate in regions with high stress intensity. In the following, we will refer to this model as the stress-driven UFM model. The case m = 0, where the nucleation is uniformly distributed in space, corresponds to the stress-independent UFM model.

For numerical implementation of the model, we use the same basic assumptions as Davy et al. [1]: fractures are modeled as interacting growing disks in a time-wise process. At each time step Δt, $\stackrel{\bullet }{n_N}\Delta t$ nuclei are introduced in the cubic system. Those who are not intersecting any existing fractures are kept in the system and grow following equation [1], until they cross a larger fracture or reach an infinite size, that we set to be twice the system size. Nuclei are not allowed to intersect pre-existing fractures so that the available space for new nuclei and the effective nucleation rate decrease with simulation time. The stress perturbation associated to each fracture can be approximated using the 3D tensorial analytical solutions of Fabrikant [38] for uniformly loaded freely-slipping penny-shaped cracks, considering traction and/or shearing. If the system is under compression, then only the shearing part is considered. Each fracture is assumed to be uniformly loaded by the remote stress field and generate a stress perturbation that depends on the fracture size, the input remote stress field intensity, and their relative orientations. To fasten calculations, we do not calculate the interaction terms between fractures and set them to zero. Although these terms may be non-negligible when fractures get close with each other [39–41], in particular when the fracture density increases, we have estimated that this approximation is consistent with the degree of simplification used for the different stages of the model. A more elaborate version is under development.

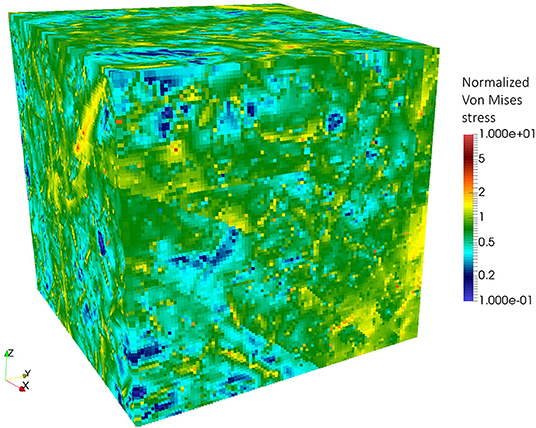
The stress field is computed over the whole domain, on a regular cartesian stress grid S_g of resolution r_stress. In order to obtain a dimensionless stress-intensity scalar field (Figure 1), each cell value is divided by the remote stress Von Mises value.

FIGURE 1

Figure 1. Stress-intensity field generated on a regular grid of size L = 1 and resolution r = 0.01.

For each nucleation step, a cell is chosen from a discrete probability sampling over the whole stress grid S_g, where the probability for each cell c is defined by:

$\begin{array}{l}P\left({\overline{x}}_c\right)=\frac{{\left[{\sigma }_{VM}\left(\overline{x_c}\right)\right]}^m}{{\sum }_{c^{\prime }}{{}_{\in }}_{S_g}{\left[{\sigma }_{VM}\left(\overline{x_{c^{\prime }}}\right)\right]}^m}\end{array}$

Once the nucleus cell has been determined, the nucleus center position is randomly taken inside this cell. The number of computations is directly related to the nucleation rate, the stress grid resolution, and the increasing number of fractures already present in the medium, which can be large. Since the addition of a single small nucleus does not affect the stress field at the system size, a single stress grid can be used for several nucleation steps n_step in order to accelerate computations. This heterogeneous probabilistic point process of nuclei positions constitutes an improvement of the stress-independent UFM model, while keeping constant nucleation rate.

Results

In this section, we focus on the spatial and topological analysis of fracture networks generated by this stress-driven UFM model. We analyze the evolution of the pattern complexity of this model with the selectivity parameter m, and compare the results with the stress-independent UFM (m = 0) and equivalent Poisson model (i.e., same population of fractures with random positions in the domain).

Numerical Simulations

For all models, we seed and let fractures grow in a domain of size L = 1 with a growth exponent a = 3, so that the power-law exponent of the dilute regime is −3, which is consistent with field data [24]. Nuclei appears in the system with a constant nucleation rate ṅ = 20, growth rate C = 1, and a size drawn from a narrow-ranged power-law distribution:

$\begin{array}{l}{p}_N\left(l\right)=\frac{\left(b-1\right)}{l_N}{\left(\frac{l}{l_N}\right)}^{-5}\end{array}$

l_N is the minimum nuclei size; its value has been set at 0.01 in order to cover two orders of magnitude in the resulting fracture size distribution. For each timestep Δt, we introduce n_step = 200 new nuclei. Nuclei intersecting existing fractures are rejected, the effective nucleation rate is thus decreasing with time, since the available space for new fractures to form is also decreasing. We stop simulations when the time is close to the t_∞(l_N), i.e., the time necessary for the smallest nuclei to become infinite [1]. Networks are generated for different values of selectivity parameters m = {0, 1, 2, 3, 4, 5} in order to quantify its impact on fracture clustering. The equivalent Poisson model is obtained by moving the fracture centers randomly in space, so that the size distribution remain identical but the correlations between fracture size and position are destroyed. We only show the Poisson model derived from the stress-independent UFM (m = 0). All stress-driven UFM are generated from the same constant and compressive remote stress field σ^∞, so that σ₁ = σ_xx = −4, σ₂ = σ_yy = −2, σ₃ = σ_zz = −1, and σ_xy = σ_xz = σ_yz = 0. The intensity and orientations of the principal stress components do not matter in this set of simulations since we consider that, for all generated DFNs, the orientation distribution is stress-decorrelated and is assumed uniform in order to minimize asymmetry due to the remote stress field. By doing so, we aim at focusing on the consequences of the stress field heterogeneity on spatial correlations only, but not on its spatialization. For this set of parameters, the simulation time for a stress-driven UFM model is about 60 times larger than for the stress-independent UFM model for which there is no stress. For all the models, we perform 50 realizations of each model for statistical analysis.

Figures 2A–C show 2D slices of generated three-dimensional Poisson, stress-independent UFM and stress-driven UFM (m = 3), respectively. Visually, the stress-driven nucleation process seems to increase the clustering effect of fractures positions. Simulations are stopped when t = t_∞(l_N), so that both the dilute and dense regime can be observed on the fracture size distribution (Figure 2D) and are consistent with equations [2] and [3], with a transitional length l_c = 0.15:

$\begin{array}{l}n(l)=\{\begin{array}{c}20.l^{-3}ifl<l_c\\ 3.l^{-4}ifl>l_c\end{array}\end{array}$

For all models, fracture size distributions are almost the same.

FIGURE 2

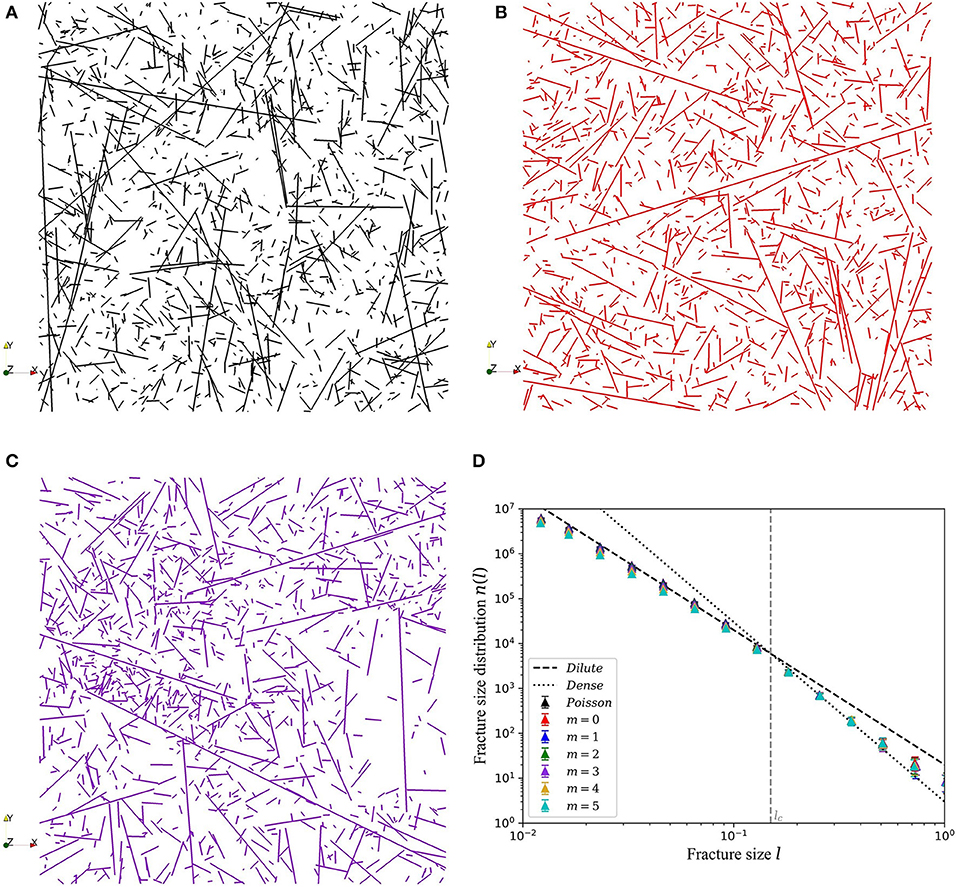
Figure 2. 2D slices of three-dimensional (A) Poisson, (B) stress-independent UFM (m = 0), and (C) stress-driven UFM (m = 3) models, and (D) associated size distributions (m ∈ [ 0, 5]).

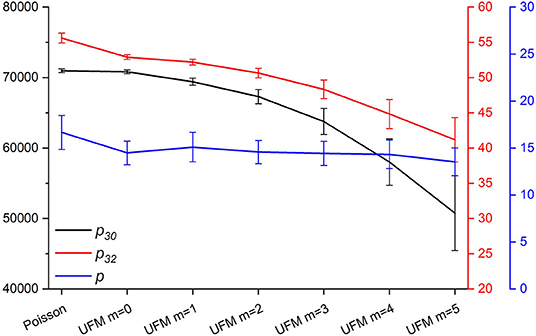
When increasing the selectivity parameter, new nuclei to form should be attracted to the tip of the largest existing fractures since the stress is high here, increasing the probability of rejection. Hence, for the same simulation time, the fracture density should decrease when increasing selectivity parameter m. We consider three-dimensional fracture densities here, such as defined by Dershowitz and Herda [42]: fracture number density p₃₀ (number of fractures per unit volume), fracture intensity p₃₂ (total fracture surface per unit volume), and percolation parameter p (total excluded volume around fractures per unit volume) that quantifies the network connectivity [43]. Considering the disk-shape assumption we made in our DFN models, we define these densities as:

$\begin{array}{l}{p}_{30}={\displaystyle \int n\left(l\right)\Pi \left(l,L\right)dl}\\ p_{32}=\frac{\pi }{4}{\displaystyle \int n\left(l\right)\Pi \left(l,L\right)l^{2}dl}\\ p=\frac{{\pi }^2}{8}{\displaystyle \int n\left(l\right)\Pi \left(l,L\right)l^{3}dl}\end{array}$

Π(l, L) is surface ratio of the fracture l included in the domain of size L. Figure 3 summarize the density statistics of the generated networks.

FIGURE 3

Figure 3. Fracture density statistics of generated networks in cubic systems of volume V = 1.

One can notice a decreasing of both p₃₀, p₃₂, and p with selectivity parameter m due the increasing number of rejected nuclei. Moreover, the fracture density of the stress-independent UFM model is slightly slower than its equivalent Poisson model, because both models are subjected to different finite size effects.

Impact on Clustering

The spatial organization and topology of fractures in a network may have dramatical impact on its connectivity and hydraulic behavior. Quantifying the fractures organization in DFN models and comparing with natural networks is a key challenge to qualify the relevance of simplified models. Natural fracture networks have shown complex clustered patterns [11, 44] that has consequences on connectivity [21, 45, 46].

Considering the multiscale nature of fractures, and thus of the subsequent stress fluctuations, we expect fractal correlations to develop in our model. The full multifractal spectrum of fracture organization may be quantified using the box-counting method [47], computing the number of boxes to cover the network at different scales. Nevertheless, this technique has be shown to be strongly affected by finite size effects [11, 23, 48]. We then compute the 2-point correlation integral (or correlation pair function) to describe the spatial correlations of fractures positions. This method gives the probability for two fractures to belong to the same cluster. For a population of N_f fractures, the associated correlation pair function is defined by:

$\begin{array}{l}{C}_2(r)=\frac{2.N(r)}{N_f.(N_f-1)}\end{array}$

with N(r) the number of points whose mutual distance is less than r [47]. For a large population of points, this quantity tends to scale a power-law $r^{D_2}$, where D₂ is the correlation dimension of fracture centers. The correlation dimension can thus be obtained by computing the slope of the correlation pair function in a log-log plot. Figure 4A shows the evolution of the correlation pair function and its derivative with scale r. This function is affected by finite-size and resolution effects when the mutual distance r tends to domain finite size and nuclei size, respectively. We calculate a correlation dimension D₂ in the interval [0.03, 0.08] that is not affected by size effects. Indeed, below the lower bound, the derivative of the correlation pair function increases dramatically because few fractures are so close to each other. This resolution effect is related to the no-intersecting assumption when introducing new nuclei in the UFM model. On the other hand, finite size effect due to the system size are already dramatic below the upper bound, as we should obtain a correlation dimension D₂ = 3, for the Poisson model. As expected, the correlation dimension of the 3D Poisson and stress-independent UFM models is D₂~3, which is consistent with a uniform distribution of fracture centers in space for both models. D₂ is smaller than 3 for the stress-driven UFM model and decreases when increasing the selectivity parameter m. For large values of m, nuclei concentrate in zones of high stress, mainly near the tips of the largest fractures, leading to a clustering of fractures. Figure 4B shows that correlations exist even at early simulation times. For large m values, the correlation dimension increases slightly with time, as the available space around fractures tips decreases.

FIGURE 4

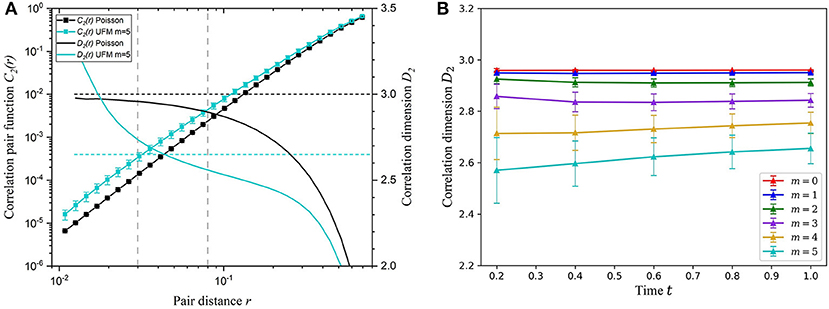
Figure 4. (A) Correlation pair function, and (B) correlation dimension analysis for the Poisson, stress-independent UFM, and stress-driven UFM models.

The correlation dimension of fracture centers indicates how much a fracture network occupies its underlying metric space. Nevertheless, two networks can have the same correlation dimension but very different patterns. In order to describe the texture associated to a network, we use the concept of lacunarity [49]. Fundamentally, lacunarity is a dimensionless representation of the variance to mean ratio [50] defined here as:

$\begin{array}{l}{\lambda }_M(s)={\left[\frac{{\sigma }_M(s)}{{\mu }_M(s)}\right]}^2\end{array}$

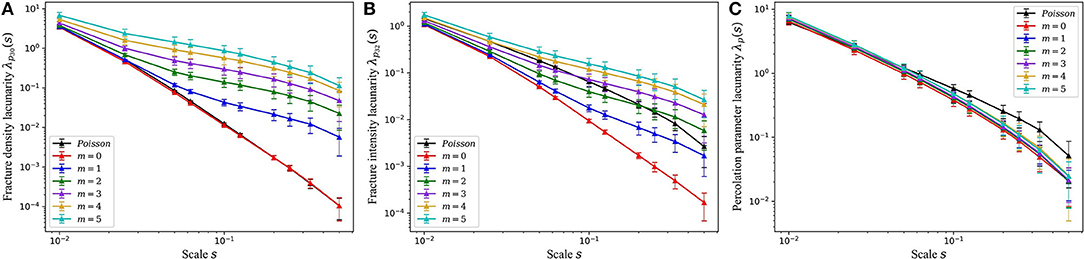
with σ_M(s) and μ_M(s) the standard deviation and mean of a measure M at scale s. For any density measure M, if λ_M(s) → 0, the pattern is perfectly homogeneous at scale s. Lacunarity is a scale dependent measure, whose analysis quantify the degree of clustering and anti-clustering [51], and potentially on different regimes [50, 52, 53], when analyzing lacunarity curves, showing λ_M(s) evolution with scale s. Lacunarity analysis can then be used to analyze textural heterogeneity of fracture densities [54]. For three-dimensional fracture networks, we can define various measures M quantifying fracture density as defined by Dershowitz and Herda [42], or in section Numerical Simulations.

Figure 5 shows the lacunarity curves of the three-dimensional fracture densities defined in section Numerical Simulations. As expected, the p₃₀ lacunarity curve is the same for the stress-independent UFM model and its equivalent Poisson model (because both follow a homogeneous Poisson point process) and scales ~ s⁻³. The p₃₀ lacunarity of the stress-driven UFM models are much larger and evolves differently with scale, which emphasizes that fracture center positions are correlated. They all follow a scaling As^−α, with A and α constant factors increasing with m. For fracture intensity p₃₂, the lacunarity of the stress-independent UFM model is smaller at all scales than that of the Poisson model. The p₃₂ lacunarity decreases faster with scale for the stress-independent UFM model than for Poisson model. This reflects a fracture density much more homogeneous in space at all scales for the stress-independent UFM than for the Poisson case. Indeed, the UFM rule (a fracture cannot cross a larger one) tends to produce an interconnected network of blocks of size of the order the transition scale l_c [1]. The p₃₂ lacunarity here quantifies the fracture position-size correlation induced by the UFM rule. The p₃₂ lacunarity increases at all scales with the selectivity parameter m for the stress-driven UFM models,. Even for small values of m, the shift in lacunarity with the stress-independent UFM case is important, which points out the impact of the clustering of fracture positions on density variability. The lacunarity associated to the percolation parameter is smaller for all UFM models than for Poisson model, meaning that the connectivity of the network is more homogeneous for UFM models. All percolation lacunarity curves are similar whatever the value of m, suggesting that the percolation parameter is more sensitive to the fracture position-size correlations induced by the UFM rule, than the fracture centers correlations.

FIGURE 5

Figure 5. Fracture density lacunarity curves for (A) p₃₀, (B) p₃₂, and (C) percolation parameters.

Consequences on Connectivity and Topology

Fracture correlation is likely changing the connectivity of the overall network. Maillot et al. [26] show that stress-independent UFM networks (which they refer as a “kinematic” model) have permeabilities 1.5–10 times smaller than the equivalent Poisson model, and a higher channeling (a higher portion of the total fracture surface where the flow is significant). Some studies [46, 55] show that, for networks with a power-law size distribution, the evolution of connectivity with scale is strongly dependent on the power-law exponent a and on the fractal dimension of fracture centers D₂. In our case, because fracture centers tend to concentrate in clusters around large fracture tips, the fracture interconnectivity may also increase. Increasing the connectivity between fractures should increase the backbone density, defined as the structure carrying flow in the network [56]. We here define the backbone by removing iteratively fractures having only one connection with the network or the boundary, keeping only the connected clusters without flow dead-ends. Figure 6 shows that the percentage of fractures in number and in total area (p₃₀ and p₃₂) involved in the backbone is smaller for any kind of UFM model (stress-independent or stress-driven) than for corresponding Poisson model. Moreover, for the UFM models, even if < 25% of fractures are part of the backbone, this represents more than 65% of the backbone surface, which shows that connectivity is mostly ensured by large structures [21, 45]. Finally, as the number of fractures involved in the backbone structure increases more than the total area with m, we can conclude that we tend to connect mostly small fractures to the backbone with this stress-driven nucleation process.

FIGURE 6

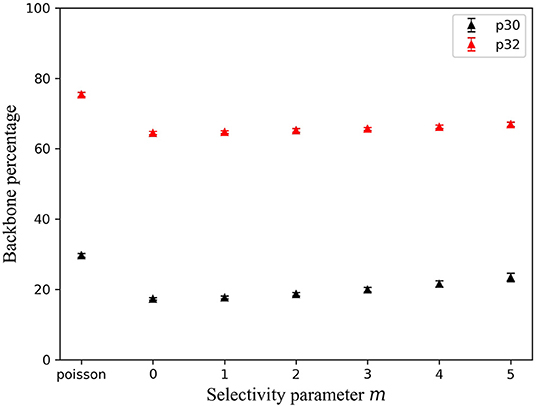
Figure 6. Evolution of backbone percentage with selectivity parameter m (m = Poisson refers to Poisson model).

The number of intersections per fracture is a good indicator of fracture connectivity. Maillot et al. [26] showed that the number of intersections per fracture is a function of fracture size for both Poisson and UFM models. Moreover, they showed that whatever the fracture size, the number of intersections is about two times lower for UFM model than for equivalent Poisson model. We here push further this topological analysis computing the fracture intersection matrix P_I so that for n_i and n_j fractures of size l_i and l_j, respectively, P_I[i, j] gives the number of fractures of size l_i intersecting fractures of size l_j, divided by n_in_j. Figures 7A–C show the mean intersection matrix for all generated Poisson, stress-independent UFM (m = 0), and stress-driven UFM (m = 5) models, respectively. As expected, in any case, the probability of intersection increases with fractures sizes. Figures 7D,E show the mean intersection matrix for stress-independent UFM (m = 0), and stress-driven UFM (m = 5) models, normalized by the mean equivalent Poisson's model intersection matrix, in order to highlight differences between UFM and Poisson models. Our analysis shows that the number of fractures intersections is smaller for UFM models than their equivalent Poisson. We can also notice that this number is much smaller for fractures of the same size, which is a consequence of the UFM rule assuming that a fracture cannot cross a larger one. Finally, Figure 7F shows the stress-dependent UFM (m = 5) model intersection matrix, normalized by the one of the stress-independent UFM (m = 0) model, showing that our stress-driven nucleation process tend to increase the connectivity of small fractures with the smallest and the largest fractures. Indeed, new fractures tend to develop at the tip of the largest existing fractures, increasing connectivity between both.

FIGURE 7

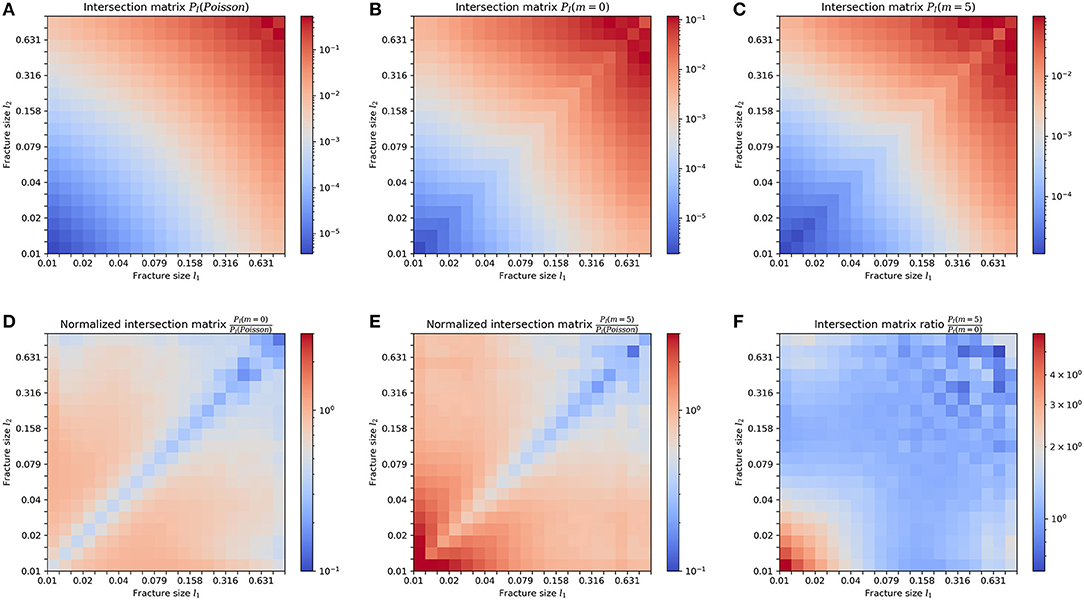
Figure 7. Intersection matrix for (A) Poisson, (B) stress-independent UFM, and (C) stress-driven UFM models. (D) Normalized intersection matrix $\frac{{\text{P}}_{\text{I}}(\text{m}=0)}{{\text{P}}_{\text{I}}(\text{P}oisson)}$ for the stress-independent UFM models, (E) Normalized intersection matrix $\frac{{\text{P}}_{\text{I}}(\text{m}=5)}{{\text{P}}_{\text{I}}(\text{P}oisson)}$ for the stress-driven UFM (m = 5) models, (F) Intersection matrix ratio $\frac{{\text{P}}_{\text{I}}(\text{m}=5)}{{\text{P}}_{\text{I}}(\text{m}=0)}$.

Conclusion

The genetic UFM model developed by Davy et al. [1], describing the fracturing process as a combination of simplified nucleation, growth and arrest laws, introduces a fracture size-position correlation in DFN modeling, that does not exist in equivalent Poisson model. It results in two distinct power-law fracture size distributions and a number of T-intersections that are consistent with field data [24]. Nevertheless, the model does not take into account the mechanical feedback loop between fracture growth and birth, therefore neglecting fracture-to-fracture positioning correlations. In this paper, we pushed further the model by improving the nucleation process, conditioning the position of newly created fractures by the stress perturbation induced by preexisting ones, in a timewise process. This stress perturbation is a function of fractures geometry (size and orientation), and the applied remote stress (orientation and intensity). This results in more correlated networks, showing fractal positioning, and a higher variability of fracture densities. We introduce a selectivity parameter m that quantifies the dependency of nucleation with the stress field. When nucleation is stress-independent (m = 0, uniform positions), we show that fracture density variability associated to UFM networks is much smaller than equivalent Poisson model. This means that the UFM rule, imposing that a fracture cannot cross a larger one, tends to organize networks into more homogeneous patterns than if fractures were positioned at random. Nonetheless, when nucleation is stress-driven (m ≠ 0), the higher m, the lower the correlation dimension of fracture positions, and the higher the spatial variability of fracture densities. This effect is dependent on the density measure, i.e., on the dependency of the density with fracture size. It is higher for the number of fractures per unit volume than for the percolation parameter. Moreover, our connectivity analysis brings up that the UFM rule tends to create a hierarchy between fractures, so that fractures of the same size order are less likely to cross one each other. The stress-driven nucleation process we propose tends to connect small fractures all together with the largest ones, that are responsible for the main stress perturbations. We also show that UFM models have lower percentage of fractures involved in the backbone than their equivalent Poisson model [26], whatever the selectivity parameter.

Finally, constraining fractures orientation according to the computed local stress field, in order to account for fracture position-orientation correlations, would constitute a huge improvement of the model. Once a full simplified mechanical description of the fracturing process is performed, this would allow us to perform real case studies, and compare our analysis results (clustering, connectivity…) between 2D numerical outcrops from generated DFNs, with real ones.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation, to any qualified researcher.

Author Contributions

EL, PD, CD, and RM conceived the idea of this study. EL and PD contributed in developing the model. EL ran network analysis and took the lead in writing manuscript. All authors provided critical feedback.

Funding

This work was funded by the CIFRE grant ITASCA Consultants SAS/ANRT (Association Nationale Recherche Technologie, France) 2016/1002, and partially supported by the Swedish Nuclear Fuel and Waste Management Co. (SKB).

Conflict of Interest

RM was employed by the company Svensk Kärnbränslehantering AB (SKB).

The authors declare that this study received funding from SKB. The funder had the following involvement with the study: formulation of some of the problems addressed and review of early drafts of the manuscript.

References

1. Davy P, Le Goc R, Darcel C. A model of fracture nucleation, growth and arrest, and consequences for fracture density and scaling. J Geophys Res. (2013) 118:1393–407. doi: 10.1002/jgrb.50120

CrossRef Full Text | Google Scholar

2. Jing L. A review of techniques, advances and outstanding issues in numerical modelling for rock mechanics and rock engineering. Int J Rock Mech Mining Sci. (2003) 40:283–353. doi: 10.1016/S1365-1609(03)00013-3

CrossRef Full Text | Google Scholar

3. Lei Q, Latham J-P, Tsang C-F. The use of discrete fracture networks for modelling coupled geomechanical and hydrological behaviour of fractured rocks. Comput Geotech. (2017) 85:151–76. doi: 10.1016/j.compgeo.2016.12.024

CrossRef Full Text | Google Scholar

4. Long J, Remer J, Wilson C, Witherspoon P. Porous media equivalents for networks of discontinuous fractures. Water Resour Res. (1982) 18:645–58. doi: 10.1029/WR018i003p00645

CrossRef Full Text | Google Scholar

5. Baecher GB. Statistical analysis of rock mass fracturing. J Int Assoc Math Geol. (1983) 15:329–48. doi: 10.1007/BF01036074

CrossRef Full Text | Google Scholar

6. Andersson J, Shapiro AM, Bear J. A stochastic model of a fractured rock conditioned by measured information. Water Resour Res. (1984) 20:79–88. doi: 10.1029/WR020i001p00079

CrossRef Full Text | Google Scholar

7. Endo H, Long J, Wilson C, Witherspoon P. A model for investigating mechanical transport in fracture networks. Water Resour Res. (1984) 20:1390–400. doi: 10.1029/WR020i010p01390

CrossRef Full Text | Google Scholar

8. Long J, Gilmour P, Witherspoon PA. A model for steady fluid flow in random three-dimensional networks of disc-shaped fractures. Water Resour Res. (1985) 21:1105–15. doi: 10.1029/WR021i008p01105

CrossRef Full Text | Google Scholar

9. Andersson J, Dverstorp B. Conditional simulations of fluid flow in three-dimensional networks of discrete fractures. Water Resour Res. (1987) 23:1876–86. doi: 10.1029/WR023i010p01876

CrossRef Full Text | Google Scholar

10. Ackermann RV, Schlische RW. Anticlustering of small normal faults around larger faults. Geology. (1997) 25:1127–30. doi: 10.1130/0091-7613(1997)025<1127:AOSNFA>2.3.CO;2

CrossRef Full Text | Google Scholar

11. Bonnet E, Bour O, Odling NE, Davy P, Main I, Cowie P, et al. Scaling of fracture systems in geological media. Rev Geophys. (2001) 39:347–83. doi: 10.1029/1999RG000074

CrossRef Full Text | Google Scholar

12. Du Bernard X, Labaume P, Darcel C, Davy P, Bour O. Cataclastic slip band distribution in normal fault damage zones, Nubian sandstones, Suez rift. J Geophys Res. (2002) 107:ETG 6-1–ETG 6-12. doi: 10.1029/2001JB000493

CrossRef Full Text | Google Scholar

13. Andresen CA, Hansen A, Le Goc R, Davy P, Hope SM. Topology of fracture networks. Front Phys. (2013) 1:7. doi: 10.3389/fphy.2013.00007

CrossRef Full Text | Google Scholar

14. Sanderson DJ, Nixon CW. The use of topology in fracture network characterization. J Struct Geol. (2015) 72:55–66. doi: 10.1016/j.jsg.2015.01.005

CrossRef Full Text | Google Scholar

15. Odling NE, Webman I. A “conductance” mesh approach to the permeability of natural and simulated fracture patterns. Water Resour Res. (1991) 27:2633–43. doi: 10.1029/91WR01382

CrossRef Full Text | Google Scholar

16. Berkowitz B, Hadad A. Fractal and multifractal measures of natural and synthetic fracture networks. J Geophys Res. (1997) 102:12205–18. doi: 10.1029/97JB00304

CrossRef Full Text | Google Scholar

17. Lei Q, Latham J-P, Xiang J, Tsang C-F, Lang P, Guo L. Effects of geomechanical changes on the validity of a discrete fracture network representation of a realistic two-dimensional fractured rock. Int J Rock Mech Mining Sci. (2014) 70:507–23. doi: 10.1016/j.ijrmms.2014.06.001

CrossRef Full Text | Google Scholar

18. Moës N, Dolbow J, Belytschko T. A finite element method for crack growth without remeshing. Int J Numer Methods Eng. (1999) 46:131–150. doi: 10.1002/(SICI)1097-0207(19990910)46:1<131::AID-NME726>3.0.CO;2-J

CrossRef Full Text | Google Scholar

19. Paluszny A, Matthäi SK. Numerical modeling of discrete multi-crack growth applied to pattern formation in geological brittle media. Int J Solids Struct. (2009) 46:3383–97. doi: 10.1016/j.ijsolstr.2009.05.007

CrossRef Full Text | Google Scholar

20. Paluszny A, Zimmerman RW. Numerical simulation of multiple 3D fracture propagation using arbitrary meshes. Comput Methods Appl Mech Eng. (2011) 200:953–66. doi: 10.1016/j.cma.2010.11.013

CrossRef Full Text | Google Scholar

21. Odling NE. Scaling and connectivity of joint systems in sandstones from western Norway. J Struct Geol. (1997) 19:1257–71. doi: 10.1016/S0191-8141(97)00041-2

CrossRef Full Text | Google Scholar

22. Bour O, Davy P. Clustering and size distributions of fault patterns: theory and measurements. Geophys Res Lett. (1999) 26:2001–4. doi: 10.1029/1999GL900419

CrossRef Full Text | Google Scholar

23. Bour O. A statistical scaling model for fracture network geometry, with validation on a multiscale mapping of a joint network (Hornelen Basin, Norway). J Geophys Res. (2002) 107:ETG 4-1–ETG 4-12. doi: 10.1029/2001JB000176

CrossRef Full Text | Google Scholar

24. Davy P, Le Goc R, Darcel C, Bour O, de Dreuzy JR, Munier R. A likely universal model of fracture scaling and its consequence for crustal hydromechanics. J Geophys Res. (2010) 115:B10411. doi: 10.1029/2009JB007043

CrossRef Full Text | Google Scholar

25. Hope SM, Davy P, Maillot J, Le Goc R, Hansen A. Topological impact of constrained fracture growth. Front Phys. (2015) 3:75. doi: 10.3389/fphy.2015.00075

CrossRef Full Text | Google Scholar

26. Maillot J, Davy P, Le Goc R, Darcel C, De Dreuzy J-R. Connectivity, permeability, and channeling in randomly distributed and kinematically defined discrete fracture network models. Water Resour Res. (2016) 52:8526–45. doi: 10.1002/2016WR018973

CrossRef Full Text | Google Scholar

27. Atkinson BK, Meredith PG. The theory of subcritical crack growth with applications to minerals and rocks. Fracture mechanics of rock. (1987) 2:111–66. doi: 10.1016/B978-0-12-066266-1.50009-0

CrossRef Full Text | Google Scholar

28. Engelder T. Joints and shear fractures in rock. Fract Mech Rock. (1987) 27–69. doi: 10.1016/B978-0-12-066266-1.50007-7

CrossRef Full Text | Google Scholar

29. Pollard DD, Aydin A. Progress in understanding jointing over the past century. Geol Soc Am Bull. (1988) 100:1181–204. doi: 10.1130/0016-7606(1988)100<1181:PIUJOT>2.3.CO;2

CrossRef Full Text | Google Scholar

30. Tapponnier P, Brace W. Development of stress-induced microcracks in Westerly granite. Int J Rock Mech Min Sci Geomech Abstr. (1976) 13:103–12. doi: 10.1016/0148-9062(76)91937-9

CrossRef Full Text | Google Scholar

31. Ingraffea AR. Theory of crack initiation and propagation in rock. Fract Mech Rock. (1987) 10:93–4. doi: 10.1016/B978-0-12-066266-1.50008-9

CrossRef Full Text | Google Scholar

32. Betekhtin V, Kadomtsev A. Evolution of microscopic cracks and pores in solids under loading. Phys Solid State. (2005) 47:825–31. doi: 10.1134/1.1924839

CrossRef Full Text | Google Scholar

33. Renshaw CE, Pollard DD. Numerical simulation of fracture set formation: a fracture mechanics model consistent with experimental observations. J Geophys Res. (1994) 99:9359–72. doi: 10.1029/94JB00139

CrossRef Full Text | Google Scholar

34. Olson JE. Predicting fracture swarms—The influence of subcritical crack growth and the crack-tip process zone on joint spacing in rock. Geol Soc Lond Spec Publ. (2004) 231:73–88. doi: 10.1144/GSL.SP.2004.231.01.05

CrossRef Full Text | Google Scholar

35. Bonneau F, Caumon G, Renard P. Impact of a stochastic sequential initiation of fractures on the spatial correlations and connectivity of discrete fracture networks. J Geophys Res. (2016) 121:5641–58. doi: 10.1002/2015JB012451

CrossRef Full Text | Google Scholar

36. Charles RJ. Dynamic fatigue of glass. J Appl Phys. (1958) 29:1657–62. doi: 10.1063/1.1723019

CrossRef Full Text | Google Scholar

37. Mises RV. Mechanik der festen Körper im plastisch-deformablen Zustand. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse. (1913) 1:582–92.

Google Scholar

38. Fabrikant VI. Complete solutions to some mixed boundary value problems in elasticity. Adv Appl Mech. (1989) 27:153–223. doi: 10.1016/S0065-2156(08)70196-0

CrossRef Full Text | Google Scholar

39. Kachanov M. Three-dimensional problems of strongly interacting arbitrarily located penny-shaped cracks. Int J Fract. (1989) 41:289–313. doi: 10.1007/BF00018861

CrossRef Full Text | Google Scholar

40. Kachanov M. On the problems of crack interactions and crack coalescence. Int J Fract. (2003) 120:537–43. doi: 10.1023/A:1025448314409

CrossRef Full Text | Google Scholar

41. Thomas RN, Paluszny A, Zimmerman RW. Quantification of fracture interaction using stress intensity factor variation maps. J Geophys Res. (2017) 122:7698–717. doi: 10.1002/2017JB014234

CrossRef Full Text | Google Scholar

42. Dershowitz WS, Herda HH. Interpretation of fracture spacing and intensity. In: The 33th US Symposium on Rock Mechanics (USRMS) Santa Fe, NM: American Rock Mechanics Association (1992).

Google Scholar

43. De Dreuzy JR, Davy P, Bour O. Percolation parameter and percolation-threshold estimates for three-dimensional random ellipses with widely scattered distributions of eccentricity and size. Phys Rev E. (2000) 62:5948–52. doi: 10.1103/PhysRevE.62.5948

CrossRef Full Text | Google Scholar

44. Davy P. On the frequency-length distribution of the San Andreas fault system. J Geophys Res. (1993) 98:12141–51. doi: 10.1029/93JB00372

CrossRef Full Text | Google Scholar

45. Bour O, Davy P. On the connectivity of three-dimensional fault networks. Water Resour Res. (1998) 34:2611–22. doi: 10.1029/98WR01861

CrossRef Full Text | Google Scholar

46. Darcel BO, Davy P, de Dreuzy JR. Connectivity properties of two-dimensional fracture networks with stochastic fractal correlation. Water Resour Res. (2003) 39:1272. doi: 10.1029/2002WR001628

CrossRef Full Text | Google Scholar

47. Hentschel H, Procaccia I. The infinite number of generalized dimensions of fractals and strange attractors. Phys D. (1983) 8:435–44. doi: 10.1016/0167-2789(83)90235-X

CrossRef Full Text | Google Scholar

48. Moein MJA, Valley B, Evans KF. Scaling of fracture patterns in three deep boreholes and implications for constraining fractal discrete fracture network models. Rock Mech Rock Eng. (2019) 52:1723–43. doi: 10.1007/s00603-019-1739-7

CrossRef Full Text | Google Scholar

49. Mandelbrot BB, Pignoni R. The Fractal Geometry of Nature. New York, NY: WH Freeman (1983). doi: 10.1119/1.13295

CrossRef Full Text | Google Scholar

50. Plotnick RE, Gardner RH, Hargrove WW, Prestegaard K, Perlmutter M. Lacunarity analysis: a general technique for the analysis of spatial patterns. Phys Rev E. (1996) 53:5461. doi: 10.1103/PhysRevE.53.5461

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Kaye BH. A Random Walk Through Fractal Dimensions. John Wiley & Sons (2008).

Google Scholar

52. Roy A, Perfect E, Dunne WM, Odling N, Kim J-W. Lacunarity analysis of fracture networks: evidence for scale-dependent clustering. J Struct Geol. (2010) 32:1444–9. doi: 10.1016/j.jsg.2010.08.010

CrossRef Full Text | Google Scholar

53. Roy A, Perfect E, Dunne WM, McKay LD. A technique for revealing scale-dependent patterns in fracture spacing data. J Geophys Res. (2014) 119:5979–86. doi: 10.1002/2013JB010647

CrossRef Full Text | Google Scholar

54. Lavoine E, Davy P, Darcel C, Le Goc R. On the density variability of poissonian discrete fracture networks, with application to power-law fracture size distributions. Adv Geosci. (2019) 49:77–83. doi: 10.5194/adgeo-49-77-2019

CrossRef Full Text | Google Scholar

55. Bour O, Davy P. Connectivity of random fault networks following a power law fault length distribution. Water Resour Res. (1997) 33:1567–83. doi: 10.1029/96WR00433

CrossRef Full Text | Google Scholar

56. Stauffer D, Aharony A. Introduction to Percolation Theory: Revised. 2nd Edition. CRC Press (2014).

Google Scholar