Hyperon-Nuclear Interactions From SU(3) Chiral Effective Field Theory

1. Introduction

Strangeness nuclear physics is an important topic of ongoing research, addressing for example scattering of baryons including strangeness, properties of hypernuclei, or strangeness in infinite nuclear matter and in neutron star matter. The theoretical foundation for such investigations are interaction potentials between nucleons and strange baryons such as the Λ hyperon.

Nuclear many-body systems are (mainly) governed by the strong interaction, described at the fundamental level by quantum chromodynamics (QCD). The elementary degrees of freedom of QCD are quarks and gluons. However, in the low-energy regime of QCD quarks and gluons are confined into colorless hadrons. This is the region where (hyper-)nuclear systems are formed. In this region QCD cannot be solved in a perturbative way. Lattice QCD is approaching this problem via large-scale numerical simulations: the (Euclidean) space-time is discretized and QCD is solved on a finite grid [1–4]. Since the seminal work of Weinberg [5, 6] chiral effective field theory (χEFT) has become a powerful tool for calculating systematically the strong interaction dynamics for low-energy hadronic processes [7–9]. Chiral EFTemploys the same symmetries and symmetry breaking patterns at low-energies as QCD, but it uses the proper degrees of freedom, namely hadrons instead of quarks and gluons. In combination with an appropriate expansion in small external momenta, the results can be improved systematically, by going to higher order in the power counting, and at the same time theoretical errors can be estimated. Furthermore, two- and three-baryon forces can be constructed in a consistent fashion. The unresolved short-distance dynamics is encoded in χEFT in contact terms, with a priori unknown low-energy constants (LECs).

The NN interaction is empirically known to very high precision. Corresponding two-nucleon potentials have been derived to high accuracy in phenomenological approaches [10–12]. Nowadays the systematic theory to construct nuclear forces is χEFT [13, 14]. (Note however that there are still debates about the Weinberg power counting schemes and how it is employed in practice [15–17]). In contrast, the YN interaction is presently not known in such detail. The scarce experimental data (about 35 data points for low-energy total cross sections) do not allow for a unique determination of the hyperon-nucleon interaction. The limited accuracy of the YN scattering data does not permit a unique phase shift analysis. However, at experimental facilities such as J-PARC in Japan or later at FAIR in Germany, a significant amount of beam time will be devoted to strangeness nuclear physics. Various phenomenological approaches have been employed to describe the YN interaction, in particular boson-exchange models [18–23] or quark models [24–26]. However, given the poor experimental data base, these interactions differ considerably from each other. Obviously there is a need for a more systematic investigation based on the underlying theory of the strong interaction, QCD. Some aspects of YN scattering and hyperon mass shifts in nuclear matter using EFT methods have been covered in Savage and Wise [27] and Korpa et al. [28]. The YN interaction has been investigated at leading order (LO) in SU(3) χEFT [29–31] by extending the very successful χEFT framework for the nucleonic sector [13, 14] to the strangeness sector. This work has been extended to next-to-leading order (NLO) in Petschauer and Kaiser [32], Haidenbauer et al. [33, 34] where an excellent description of the strangeness −1 sector has been achieved, comparable to most advanced phenomenological hyperon-nucleon interaction models. An extension to systems with more strangeness has been done in Haidenbauer et al. [35, 36] and Haidenbauer and Meißner [37]. Systems including decuplet baryons have been investigated in Haidenbauer et al. [38] at leading order in non-relativistic χEFT. Recently calculations within leading order covariant χEFT have been performed for YN interactions in the strangeness sector [39–43] with comparable results (see also [44]). It is worth to briefly discuss the differences between the covariant and the heavy-baryon approach. In the latter, due to the expansion in the inverse of the baryon masses, some terms are relegated to higher orders. Also, it can happen that the analytic structure is distorted in the strict heavy-baryon limit. This can easily be remedied by including the kinetic energy term in the baryon propagator [45]. In what follows, we will present results based on the heavy-baryon approach.

Numerous advanced few- and many-body techniques have been developed to employ such phenomenological or chiral interactions, in order to calculate the properties of nuclear systems with and without strangeness. For example, systems with three or four particles can be reliably treated by Faddeev-Yakubovsky theory [46–49], somewhat heavier (hyper)nuclei with approaches like the no-core-shell model [50–55]. In the nucleonic sector many-body approaches such as Quantum Monte Carlo calculations [56–58], or nuclear lattice simulations [59–61] have been successfully applied and can be extended to the strangeness sector. Furthermore, nuclear matter is well described by many-body perturbation theory with chiral low-momentum interactions [62–64]. Concerning Λ and Σ hyperons in nuclear matter, specific long-range processes related to two-pion exchange between hyperons and nucleons in the nuclear medium have been studied in Kaiser and Weise [65] and Kaiser [66]. Conventional Brueckner theory [67–69] at first order in the hole-line expansion, the so-called Bruecker-Hartree-Fock approximation, has been widely applied to calculations of hypernuclear matter [20, 24, 70, 71] employing phenomenological two-body potentials. This approach is also used in investigations of neutron star matter [72–74]. Recently, corresponding calculations of the properties of hyperons in nuclear matter have been also performed with chiral YN interaction potentials [37, 75, 76].

Employing the high precision NN interactions described above, even “simple” nuclear systems such as triton cannot be described satisfactorily with two-body interactions alone. The introduction of three-nucleon forces (3NF) substantially improves this situation [77–80] and also in the context of infinite nuclear matter 3NF are essential to achieve saturation of nuclear matter. These 3NF are introduced either phenomenologically, such as the families of Tuscon-Melbourne [81, 82], Brazilian [83], or Urbana-Illinois [84, 85] 3NF, or constructed according to the basic principles of χEFT [78, 86–94]. Within an EFT approach, 3NF arise naturally and consistently together with two-nucleon forces. Chiral three-nucleon forces are important in order to get saturation of nuclear matter from chiral low-momentum two-body interactions treated in many-body perturbation theory [63]. In the strangeness sectors the situation is similar: Three-baryon forces (3BF), especially the ΛNN interaction, seem to be important for a satisfactorily description of hypernuclei and hypernuclear matter [58, 95–103]. Especially in the context of neutron stars, 3BF are frequently discussed. The observation of two-solar-mass neutron stars [104, 105] sets strong constraints on the stiffness of the equation-of-state (EoS) of dense baryonic matter [106–110]. The analysis of recently observed gravitational wave signals from a two merging neutron stars [111, 112] provides further conditions, by constraining the tidal deformability of neutron star matter.

A naive introduction of Λ-hyperons as an additional baryonic degree of freedom would soften the EoS such that it is not possible to stabilize a two-solar-mass neutron star against gravitational collapse [113]. To solve this so-called hyperon puzzle, several ad-hoc mechanisms have so far been invoked, e.g., through vector meson exchange [114, 115], multi-Pomeron exchange [116] or a suitably adjusted repulsive ΛNN three-body interaction [117–119]. Clearly, a more systematic approach to the three-baryon interaction within χEFT is needed, to estimate whether the 3BF can provide the necessary repulsion and thus keep the equation-of-state sufficiently stiff. A first step in this direction was done in Petschauer et al. [120], where the leading 3BFs have been derived within SU(3) χEFT. The corresponding low-energy constants have been estimated by decuplet saturation in Petschauer et al. [121]. The effect of these estimated 3BF has been investigated in Petschauer et al. [121] and Kohno [122].

In this review article we present, on a basic level, the emergence of nuclear interactions in the strangeness sector from the perspective of (heavy-baryon) chiral effective field theory. After a brief introduction to SU(3) χEFT in section 2, we present how the interaction between hyperons and nucleons is derived at NLO from these basic principles for two-baryon interactions (section 3) and for three-baryon interactions (section 4). In section 5, applications of these potentials are briefly reviewed for YN scattering, infinite nuclear matter, hypernuclei, and neutron star matter.

2. SU(3) Chiral Effective Field Theory

An effective field theory (EFT) is a low-energy approximation to a more fundamental theory. Physical quantities can be calculated in terms of a low-energy expansion in powers of small energies and momenta over some characteristic large scale. The basic idea of an EFT is to include the relevant degrees of freedom explicitly, while heavier (frozen) degrees of freedom are integrated out. An effective Lagrangian is obtained by constructing the most general Lagrangian including the active degrees of freedom, that is consistent with the symmetries of the underlying fundamental theory [6]. At a given order in the expansion, the theory is characterized by a finite number of coupling constants, called low-energy constants (LECs). The LECs encode the unresolved short-distance dynamics and furthermore allow for an order-by-order renormalization of the theory. These constants are a priori unknown, but once determined from one experiment or from the underlying theory, predictions for physical observables can be made. However, due to the low-energy expansion and the truncation of degrees of freedom, an EFT has only a limited range of validity.

The underlying theory of chiral effective field theory is quantum chromodynamics. QCD is characterized by two important properties. For high energies the (running) coupling strength of QCD becomes weak, hence a perturbative approach in the high-energy regime of QCD is possible. This famous feature is called asymptotic freedom of QCD and originates from the non-Abelian structure of QCD. However, at low energies and momenta the coupling strength of QCD is of order one, and a perturbative approach is no longer possible. This is the region of non-perturbative QCD, in which we are interested in. Several strategies to approach this regime have been developed, such as lattice simulations, Dyson-Schwinger equations, QCD sum rules or chiral perturbation theory. The second important feature of QCD is the so-called color confinement: isolated quarks and gluons are not observed in nature, but only color-singlet objects. These color-neutral particles, the hadrons, are the active degrees of freedom in χEFT.

But already before QCD was established, the ideas of an effective field theory were used in the context of the strong interaction. In the 60's the Ward identities related to spontaneously broken chiral symmetry were explored by using current algebra methods (e.g., [123]). The group-theoretical foundations for constructing phenomenological Lagrangians in the presence of spontaneous symmetry breaking have been developed by Weinberg [5], Coleman et al. [124], and Callan et al. [125]. With Weinberg's seminal paper [6] it became clear how to systematically construct an EFT and generate loop corrections to tree level results. This method was improved later by Gasser and Leutwyler [7, 126]. A systematic introduction of nucleons as degrees of freedom was done by Gasser et al. [8]. They showed that a fully relativistic treatment of nucleons is problematic, as the nucleon mass does not vanish in the chiral limit and thus adds an extra scale. A solution for this problem was proposed by Jenkins and Manohar [127] by considering baryons as heavy static sources. This approach was further developed using a systematic path-integral framework in Bernard et al. [128]. The nucleon-nucleon interaction and related topics were considered by Weinberg [86]. Nowadays χEFT is used as a powerful tool for calculating systematically the strong interaction dynamics of hadronic processes, such as the accurate description of nuclear forces [13, 14].

In this section, we give a short introduction to the underlying symmetries of QCD and their breaking pattern. The basic concepts of χEFT are explained, especially the explicit degrees of freedom and the connection to the symmetries of QCD. We state in more detail how the chiral Lagrangian can be constructed from basic principles. However, it is beyond the scope of this work to give a detailed introduction to χEFT and QCD. Rather we will introduce only the concepts necessary for the derivation of hyperon-nuclear forces. We follow [9, 13, 14, 129–131] and refer the reader for more details to these references (and references therein).

2.1. Low-Energy Quantum Chromodynamics

Let us start the discussion with the QCD Lagrangian

$\begin{array}{ll}{{L}}_{\text{QCD}}={\displaystyle \sum _{f=u,d,s,c,b,t}}{\bar{q}}_f(\text{i}\cancel{D}-m_f)q_f-\frac{1}{4}{G}_{\mu \nu ,a}{G}_a^{\mu \nu },& (1)\end{array}$

with the six quark flavors f and the gluonic field-strength tensor G_{μν, a}(x). The gauge covariant derivative is defined by $D_{\mu }=𝟙{\partial }_{\mu }-\text{i}g{A}_{\mu }^a\frac{{\lambda }_a}{2}$, where $A_{\mu }^a(x)$ are the gluon fields and λ_a the Gell-Mann matrices. The QCD Lagrangian is symmetric under the local color gauge symmetry, under global Lorentz transformations, and the discrete symmetries parity, charge conjugation, and time reversal. In the following we will introduce the so-called chiral symmetry, an approximate global continuous symmetry of the QCD Lagrangian. The chiral symmetry is essential for chiral effective field theory. In view of the application to low energies, we divide the quarks into three light quarks u, d, s and three heavy quarks c, b, t, since the quark masses fulfill a hierarchical ordering:

$\begin{array}{ll}{m}_u,m_d,m_s\ll 1\text{ GeV}\le m_c,m_b,m_t.& (2)\end{array}$

At energies and momenta well below 1 GeV, the heavy quarks can be treated effectively as static. Therefore, the light quarks are the only active degrees of freedom of QCD for the low-energy region we are interested in. In the following we approximate the QCD Lagrangian by using only the three light quarks. Compared to characteristic hadronic scales, such as the nucleon mass (M_N ≈ 939 MeV), the light quark masses are small. Therefore, a good starting point for our discussion of low-energy QCD are massless quarks m_u = m_d = m_s = 0, which is referred to as the chiral limit. The QCD Lagrangian becomes in the chiral limit

$\begin{array}{ll}{{L}}_{\text{QCD}}^0={\displaystyle \sum _{f=u,d,s}}{\bar{q}}_f\text{i}\cancel{D}{q}_f-\frac{1}{4}{G}_{\mu \nu ,a}{G}_a^{\mu \nu }.& (3)\end{array}$

Now each quark field q_f(x) is decomposed into its chiral components

$\begin{array}{ll}{q}_{f,\text{L}}=P_{\text{L}}{q}_f,q_{f,\text{R}}=P_{\text{R}}{q}_f.& (4)\end{array}$

using the left- and right-handed projection operators

$\begin{array}{ll}{P}_{\text{L}}=\frac{1}{2}(1-{\gamma }_5),P_{\text{R}}=\frac{1}{2}(1+{\gamma }_5),& (5)\end{array}$

with the chirality matrix γ₅. These projectors are called left- and right-handed since in the chiral limit they project the free quark fields on helicity eigenstates, $\widehat{h}$ q_L,R = ± q_L,R, with $\widehat{h}=\overrightarrow{\sigma }·\overrightarrow{p}/\left|\overrightarrow{p}\right|$. For massless free fermions helicity is equal to chirality.

Collecting the three quark-flavor fields q = (q_u, q_d, q_s) and equivalently for the left and right handed components, we can express the QCD Lagrangian in the chiral limit as

$\begin{array}{ll}{{L}}_{\text{QCD}}^0={\bar{q}}_{\text{R}}\text{i}\cancel{D}{q}_{\text{R}}+{\bar{q}}_{\text{L}}\text{i}\cancel{D}{q}_{\text{L}}-\frac{1}{4}{G}_{\mu \nu ,a}{G}_a^{\mu \nu }.& (6)\end{array}$

Obviously the right- and left-handed components of the massless quarks are separated. The Lagrangian is invariant under a global transformation

$\begin{array}{ll}{q}_{\text{L}}\to L{q}_{\text{L}},q_{\text{R}}\to R{q}_{\text{R}},& (7)\end{array}$

with independent unitary 3 × 3 matrices L and R acting in flavor space. This means that ${{L}}_{\text{QCD}}^0$ possesses (at the classical, unquantized level) a global U(3)_L × U(3)_R symmetry, isomorphic to a global SU(3)_L × U(1)_L × SU(3)_R × U(1)_R symmetry. U(1)_L × U(1)_R are often rewritten into a vector and an axial-vector part U(1)_V × U(1)_A, named after the transformation behavior of the corresponding conserved currents under parity transformation. The flavor-singlet vector current originates from rotations of the left- and right-handed quark fields with the same phase (“V = L + R”) and the corresponding conserved charge is the baryon number. After quantization, the conservation of the flavor-singlet axial vector current, with transformations of left- an right-handed quark fields with opposite phase (“A = L − R”), gets broken due to the so-called Adler-Bell-Jackiw anomaly [132, 133]. The symmetry group SU(3)_L × SU(3)_R refers to the chiral symmetry. Similarly the conserved currents can be rewritten into flavor-octet vector and flavor-octet axial-vector currents, where the vector currents correspond to the diagonal subgroup SU(3)_V of SU(3)_L × SU(3)_R with L = R.

After the introduction of small non-vanishing quark masses, the quark mass term of the QCD Lagrangian Equation (1) can be expressed as

$\begin{array}{ll}{{L}}_M=-\bar{q}Mq=-({\bar{q}}_{\text{R}}M{q}_{\text{L}}+{\bar{q}}_{\text{L}}M{q}_{\text{R}}),& (8)\end{array}$

with the diagonal quark mass matrix M = diag(m_u, m_d, m_s). Left- and right-handed quark fields are mixed in ${L}$_M and the chiral symmetry is explicitly broken. The baryon number is still conserved, but the flavor-octet vector and axial-vector currents are no longer conserved. The axial-vector current is not conserved for any small quark masses. However, the flavor-octet vector current remains conserved, if the quark masses are equal, m_u = m_d = m_s, referred to as the (flavor) SU(3) limit.

Another crucial aspect of QCD is the so-called spontaneous chiral symmetry breaking. The chiral symmetry of the Lagrangian is not a symmetry of the ground state of the system, the QCD vacuum. The structure of the hadron spectrum allows to conclude that the chiral symmetry SU(3)_L × SU(3)_R is spontaneously broken to its vectorial subgroup SU(3)_V, the so-called Nambu-Goldstone realization of the chiral symmetry. The spontaneous breaking of chiral symmetry can be characterized by a non-vanishing chiral quark condensate $\langle \bar{q}q\rangle \ne 0$, i.e., the vacuum involves strong correlations of scalar quark-antiquark pairs.

The eight Goldstone bosons corresponding to the spontaneous symmetry breaking of the chiral symmetry are identified with the eight lightest hadrons, the pseudoscalar mesons (${\pi }^{\pm },{\pi }^0,K^{\pm },K^0,{\bar{K}}^0,\eta$). They are pseudoscalar particles, due to the parity transformation behavior of the flavor-octet axial-vector currents. The explicit chiral symmetry breaking due to non-vanishing quark masses leads to non-zero masses of the pseudoscalar mesons. However, there is a substantial mass gap, between the masses of the pseudoscalar mesons and the lightest hadrons of the remaining hadronic spectrum. For non-vanishing but equal quark masses, SU(3)_V remains a symmetry of the ground state. In this context SU(3)_V is often called the flavor group SU(3), which provides the basis for the classification of low-lying hadrons in multiplets. In the following we will consider the so-called isospin symmetric limit, with m_u = m_d ≠ m_s. The remaining symmetry is the SU(2) isospin symmetry. An essential feature of low-energy QCD is, that the pseudoscalar mesons interact weakly at low energies. This is a direct consequence of their Goldstone-boson nature. This feature allows for the construction of a low-energy effective field theory enabling a systematic expansion in small momenta and quark masses.

Let us introduce one more tool for the systematic development of χEFT called the external-field method. The chiral symmetry gives rise to so-called chiral Ward identities: relations between the divergence of Green functions that include a symmetry current (vector or axial-vector currents) to linear combinations of Green functions. Even if the symmetry is explicitly broken, Ward identities related to the symmetry breaking term exist. The chiral Ward identities do not rely on perturbation theory, but are also valid in the non-perturbative region of QCD. The external-field method is an elegant way to formally combine all chiral Ward identities in terms of invariance properties of a generating functional. Following the procedure of Gasser and Leutwyler [7, 126] we introduce (color neutral) external fields, s(x), p(x), v_μ(x), a_μ(x), of the form of Hermitian 3 × 3 matrices that couple to scalar, pseudoscalar, vector, and axial-vector currents of quarks:

$\begin{array}{l}{L}={{L}}_{\text{QCD}}^0+{{L}}_{\text{ext}}\\ ={{L}}_{\text{QCD}}^0+\bar{q}{\gamma }^{\mu }(v_{\mu }+{\gamma }_5{a}_{\mu })q-\bar{q}(s-\text{i }{\gamma }_{5}p)q.& (9)\end{array}$

All chiral Ward identities are encoded in the corresponding generating functional, if the global chiral symmetry SU(3)_L × SU(3)_R of ${{L}}_{\text{QCD}}^0$ is promoted to a local gauge symmetry of ${L}$ [134]. Since ${{L}}_{\text{QCD}}^0$ is only invariant under the global chiral symmetry, the external fields have to fulfill a suitable transformation behavior:

$\begin{array}{l}{v}_{\mu }+a_{\mu }\to R(v_{\mu }+a_{\mu })R^{†}+\text{i }R{\partial }_{\mu }{R}^{†},\\ v_{\mu }-a_{\mu }\to L(v_{\mu }-a_{\mu })L^{†}+\text{i }L{\partial }_{\mu }{L}^{†},\\ s+\text{i }p\to R(s+\text{i }p)L^{†},\\ s-\text{i }p\to L(s-\text{i }p)R^{†},& (10)\end{array}$

where L(x) and R(x) are (independent) space-time-dependent elements of SU(3)_L and SU(3)_R.

Furthermore, we still require the full Lagrangian ${L}$ to be invariant under P, C, and T. As the transformation properties of the quarks are well-known, the transformation behavior of the external fields can be determined and is displayed in Table 1. Time reversal symmetry is not considered explicitly, since it is automatically fulfilled due to the CPT theorem.

TABLE 1

Table 1. Transformation properties of the external fields under parity and charge conjugation.

Another central aspect of the external-field method is the addition of terms to the three-flavor QCD Lagrangian in the chiral limit, ${{L}}_{\text{QCD}}^0$. Non-vanishing current quark masses and therefore the explicit breaking of chiral symmetry can be included by setting the scalar field equal to the quark mass matrix, s(x) = M = diag(m_u, m_d, m_s). Similarly electroweak interactions can be introduced through appropriate external vector and axial vector fields. This feature is important, to systematically include explicit chiral symmetry breaking or couplings to electroweak gauge fields into the chiral effective Lagrangian.

2.2. Explicit Degrees of Freedom

In the low-energy regime of QCD, hadrons are the observable states. The active degrees of freedom of χEFT are identified as the pseudoscalar Goldstone-boson octet. The soft scale of the low-energy expansion is given by the small external momenta and the small masses of the pseudo-Goldstone bosons, while the large scale is a typical hadronic scale of about 1 GeV. The effective Lagrangian has to fulfill the same symmetry properties as QCD: invariance under Lorentz and parity transformations, charge conjugation and time reversal symmetry. Especially the chiral symmetry and its spontaneous symmetry breaking has to be incorporated. Using the external-field method, the same external fields v, a, s, p as in Equation (9), with the same transformation behavior, are included in the effective Lagrangian.

As the QCD vacuum is approximately invariant under the flavor symmetry group SU(3), one expects the hadrons to organize themselves in multiplets of irreducible representations of SU(3). The pseudoscalar mesons form an octet (cf. Figure 1). The members of the octet are characterized by the strangeness quantum number S and the third component I₃ of the isospin. The symbol η stands for the octet component (η₈). As an approximation we identify η₈ with the physical η, ignoring possible mixing with the singlet state η₁. For the lowest-lying baryons one finds an octet and a decuplet (see also Figure 1). In the following we summarize how these explicit degrees of freedom are included in the chiral Lagrangian in the standard non-linear realization of chiral symmetry [124, 125].

FIGURE 1

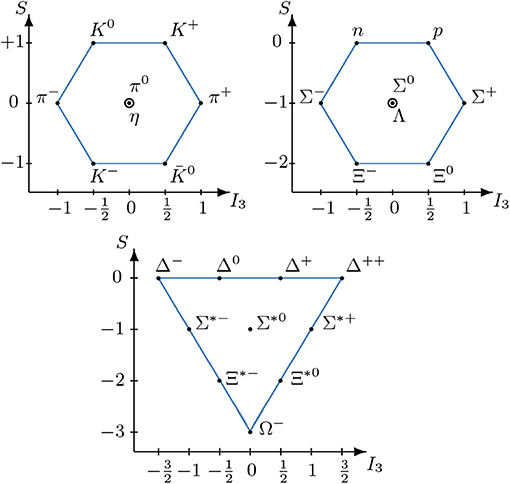
Figure 1. Pseudoscalar meson octet (J^P = 0⁻), baryon octet (J^P = 1/2⁺), and baryon decuplet (J^P = 3/2⁺).

The chiral symmetry group SU(3)_L × SU(3)_R is spontaneously broken to its diagonal subgroup SU(3)_V. Therefore, the Goldstone-boson octet should transform under SU(3)_L × SU(3)_R such that an irreducible 8-representation results for SU(3)_V. A convenient choice to describe the pseudoscalar mesons under these conditions is a unitary 3 × 3 matrix U(x) in flavor space, which fulfills

$\begin{array}{ll}{U}^{†}U=1,detU=1.& (11)\end{array}$

The transformation behavior under chiral symmetry reads

$\begin{array}{ll}U\to RU{L}^{†},& (12)\end{array}$

where L(x), R(x) are elements of SU(3)_L,R. An explicit parametrization of U(x) in terms of the pseudoscalar mesons is given by

$\begin{array}{ll}U(x)=exp\left[\text{i }\varphi (x)/f_0\right],& (13)\end{array}$

with the traceless Hermitian matrix

$\begin{array}{l}\varphi \left(x\right)={\displaystyle \sum _{a=1}^8}{\varphi }_a\left(x\right){\lambda }_a\\ =\left(\begin{array}{ccc}{\pi }^0+\frac{1}{\sqrt{3}}\eta & \sqrt{2}{\pi }^{+}& \sqrt{2}{K}^{+}\\ \sqrt{2}{\pi }^{-}& -{\pi }^0+\frac{1}{\sqrt{3}}\eta & \sqrt{2}{K}^0\\ \sqrt{2}{K}^{-}& \sqrt{2}{\bar{K}}^0& -\frac{2}{\sqrt{3}}\eta \end{array}\right).& (14)\end{array}$

The constant f₀ is the decay constant of the pseudoscalar Goldstone bosons in the chiral limit. For a transformation of the subgroup SU(3)_V with L = R = V, the meson matrix U transforms as

$\begin{array}{ll}U\to VU{V}^{†},& (15)\end{array}$

i.e., the mesons ϕ_a(x) transform in the adjoint (irreducible) 8-representation of SU(3). The parity transformation behavior of the pseudoscalar mesons is ${\varphi }_a(t,\overrightarrow{x})\stackrel{P}{\to }-{\varphi }_a(t,-\overrightarrow{x})$ or, equivalently, $U(t,\overrightarrow{x})\stackrel{P}{\to }{U}^{†}(t,-\overrightarrow{x})$. Under charge conjugation the particle fields are mapped to antiparticle fields, leading to $U\stackrel{C}{\to }{U}^{\top }$.

The octet baryons are described by Dirac spinor fields and represented in a traceless 3 × 3 matrix B(x) in flavor space,

$\begin{array}{l}B={\displaystyle \sum _{a=1}^8}\frac{B_a{\lambda }_a}{\sqrt{2}}\\ =\left(\begin{array}{ccc}\frac{1}{\sqrt{2}}{\Sigma }^0+\frac{1}{\sqrt{6}}\Lambda & {\Sigma }^{+}& p\\ {\Sigma }^{-}& -\frac{1}{\sqrt{2}}{\Sigma }^0+\frac{1}{\sqrt{6}}\Lambda & n\\ {\Xi }^{-}& {\Xi }^0& -\frac{2}{\sqrt{6}}\Lambda \end{array}\right).& (16)\end{array}$

We use the convenient [135] non-linear realization of chiral symmetry for the baryons, which lifts the well-known flavor transformations to the chiral symmetry group. The matrix B(x) transforms under the chiral symmetry group SU(3)_L × SU(3)_R as

$\begin{array}{ll}B\to KB{K}^{†},& (17)\end{array}$

with the SU(3)-valued compensator field

$\begin{array}{ll}K(L,R,U)=\sqrt{L{U}^{†}{R}^{†}}R\sqrt{U}.& (18)\end{array}$

Note that K(L, R, U) also depends on the meson matrix U. The square root of the meson matrix,

$\begin{array}{ll}u=\sqrt{U},& (19)\end{array}$

transforms as $u\to \sqrt{RU{L}^{†}}=Ru{K}^{†}=Ku{L}^{†}$. For transformations under the subgroup SU(3)_V the baryons transform as an octet, i.e., the adjoint representation of SU(3):

$\begin{array}{ll}B\to VB{V}^{†}.& (20)\end{array}$

The octet-baryon fields transform under parity and charge conjugation as $B_a(t,\overrightarrow{x})\stackrel{P}{\to }{\gamma }^0{B}_a(t,-\overrightarrow{x})$ and $B_{\alpha ,a}\stackrel{C}{\to }{C}_{\alpha \beta }{\bar{B}}_{\beta ,a}$ with the Dirac-spinor indices α, β, and with C = iγ²γ⁰.

A natural choice to represent the decuplet baryons is a totally symmetric three-index tensor T. It transforms under the chiral symmetry SU(3)_L × SU(3)_R as

$\begin{array}{ll}{T}_{abc}\to K_{ad}{K}_{be}{K}_{cf}{T}_{def},& (21)\end{array}$

with the compensator field K(L, R, U) of Equation (18). For an SU(3)_V transformation the decuplet fields transform as an irreducible representation of SU(3):

$\begin{array}{ll}{T}_{abc}\to V_{ad}{V}_{be}{V}_{cf}{T}_{def}.& (22)\end{array}$

The physical fields are assigned to the following components of the totally antisymmetric tensor:

$\begin{array}{l}{T}^{111}={\Delta }^{++},T^{112}=\frac{1}{\sqrt{3}}{\Delta }^{+},T^{122}=\frac{1}{\sqrt{3}}{\Delta }^0,T^{222}={\Delta }^{-},\\ T^{113}=\frac{1}{\sqrt{3}}{\Sigma }^{*+},T^{123}=\frac{1}{\sqrt{6}}{\Sigma }^{*0},T^{223}=\frac{1}{\sqrt{3}}{\Sigma }^{*-},\\ T^{133}=\frac{1}{\sqrt{3}}{\Xi }^{*0},T^{233}=\frac{1}{\sqrt{3}}{\Xi }^{*-},\\ T^{333}={\Omega }^{-}.& (23)\end{array}$

Since decuplet baryons are spin-3/2 particles, each component is expressed through Rarita-Schwinger fields. Within the scope of this article, decuplet baryons are only used for estimating LECs via decuplet resonance saturation. In that case it is sufficient to treat them in their non-relativistic form, where no complications with the Rarita-Schwinger formalism arise.

Now the representation of the explicit degrees of freedom and their transformation behavior are established. Together with the external fields the construction of the chiral effective Lagrangian is straightforward.

2.3. Construction of the Chiral Lagrangian

The chiral Lagrangian can be ordered according to the number of baryon fields:

$\begin{array}{ll}{{L}}_{\text{eff}}={{L}}_{\varphi }+{{L}}_B+{{L}}_{BB}+{{L}}_{BBB}+\dots ,& (24)\end{array}$

where ${L}$_ϕ denotes the purely mesonic part of the Lagrangian. Each part is organized in the number of small momenta (i.e., derivatives) or small meson masses, e.g.,

$\begin{array}{ll}{{L}}_{\varphi }={{L}}_{\varphi }^{(2)}+{{L}}_{\varphi }^{(4)}+{{L}}_{\varphi }^{(6)}+\dots .& (25)\end{array}$

${L}$_ϕ has been constructed to ${O}(q^6)$ in Fearing and Scherer [136] and Bijnens et al. [137]. The chiral Lagrangian for the baryon-number-one sector has been investigated in various works. The chiral effective pion-nucleon Lagrangian of order ${O}(q^4)$ has been constructed in Fettes et al. [138]. The three-flavor Lorentz invariant chiral meson-baryon Lagrangians ${L}$_B at order ${O}(q^2)$ and ${O}(q^3)$ have been first formulated in Krause [139] and were later completed in Oller et al. [140] and Frink and Meißner [141]. Concerning the nucleon-nucleon contact terms, the relativistically invariant contact Lagrangian at order ${O}(q^2)$ for two flavors (without any external fields) has been constructed in Girlanda et al. [142]. The baryon-baryon interaction Lagrangian ${L}$_BB has been considered up to NLO in Savage and Wise [27], Polinder et al. [29], and Petschauer and Kaiser [32]. Furthermore the leading three-baryon contact interaction Lagrangian ${L}$_BBB has been derived in Petschauer et al. [120].

We follow closely Petschauer and Kaiser [32] to summarize the basic procedure for constructing systematically the three-flavor chiral effective Lagrangian [124, 125] with the inclusion of external fields [7, 126]. The effective chiral Lagrangian has to fulfill all discrete and continuous symmetries of the strong interaction. Therefore, it has to be invariant under parity (P), charge conjugation (C), Hermitian conjugation (H), and the proper, orthochronous Lorentz transformations. Time reversal symmetry is then automatically fulfilled via the CPT theorem. Especially local chiral symmetry has to be fulfilled. A common way to construct the chiral Lagrangian is to define so-called building blocks, from which the effective Lagrangian can be determined as an invariant polynomial. Considering the chiral transformation properties, a convenient choice for the building blocks is

$\begin{array}{l}{u}_{\mu }=\text{i }\left[u^{†}({\partial }_{\mu }-\text{i }{r}_{\mu })u-u({\partial }_{\mu }-\text{i }{l}_{\mu })u^{†}\right],\\ {\chi }_{\pm }=u^{†}\chi u^{†}\pm u{\chi }^{†}u,\\ f_{\mu \nu }^{\pm }=u{f}_{\mu \nu }^{\text{L}}{u}^{†}\pm u^{†}{f}_{\mu \nu }^{\text{R}}u,& (26)\end{array}$

with the combination

$\begin{array}{ll}\chi =2B_0(s+\text{i }p),& (27)\end{array}$

containing the new parameter B₀ and the external scalar and pseudoscalar fields. One defines external field strength tensors by

$\begin{array}{l}{f}_{\mu \nu }^{\text{R}}={\partial }_{\mu }{r}_{\nu }-{\partial }_{\nu }{r}_{\mu }-\text{i }\left[r_{\mu },r_{\nu }\right],\\ f_{\mu \nu }^{\text{L}}={\partial }_{\mu }{l}_{\nu }-{\partial }_{\nu }{l}_{\mu }-\text{i }\left[l_{\mu },l_{\nu }\right],& (28)\end{array}$

where the fields

$\begin{array}{ll}{r}_{\mu }=v_{\mu }+a_{\mu },l_{\mu }=v_{\mu }-a_{\mu },& (29)\end{array}$

describe right handed and left handed external vector fields. In the absence of flavor singlet couplings one can assume 〈a_μ〉 = 〈v_μ〉 = 0, where 〈…〉 denotes the flavor trace. Therefore, the fields u_μ and $f_{\mu \nu }^{\pm }$ in Equation (26) are all traceless.

Using the transformation behavior of the pseudoscalar mesons and octet baryons in Equations (12) and (17), and the transformation properties of the external fields in Equation (10), one can determine the transformation behavior of the building blocks. All building blocks A, and therefore all products of these, transform according to the adjoint (octet) representation of SU(3), i.e., A → KAK^†. Note that traces of products of such building blocks are invariant under local chiral symmetry, since K^†K = 𝟙. The chiral covariant derivative of such a building block A is given by

$\begin{array}{ll}{D}_{\mu }A={\partial }_{\mu }A+\left[{\Gamma }_{\mu },A\right],& (30)\end{array}$

with the chiral connection

$\begin{array}{ll}{\Gamma }_{\mu }=\frac{1}{2}\left[u^{†}({\partial }_{\mu }-\text{i }{r}_{\mu })u+u({\partial }_{\mu }-\text{i }{l}_{\mu })u^{†}\right].& (31)\end{array}$

The covariant derivative transforms homogeneously under the chiral group as $D_{\mu }A\to K(D_{\mu }A)K^{†}$. The chiral covariant derivative of the baryon field B is given by Equation (30) as well.

A Lorentz-covariant power counting scheme has been introduced by Krause [139]. Due to the large baryon mass M₀ in the chiral limit, a time-derivative acting on a baryon field B cannot be counted as small. Only baryon three-momenta are small on typical chiral scales. This leads to the following counting rules for baryon fields and their covariant derivatives,

$\begin{array}{ll}B,\bar{B},D_{\mu }B~{O}(q^0),(\text{i}\cancel{D}-M_0)B~{O}(q).& (32)\end{array}$

The chiral dimension of the chiral building blocks and baryon bilinears $\bar{B}\Gamma B$ are given in Table 2. A covariant derivative acting on a building block (but not on B) raises the chiral dimension by one.

TABLE 2

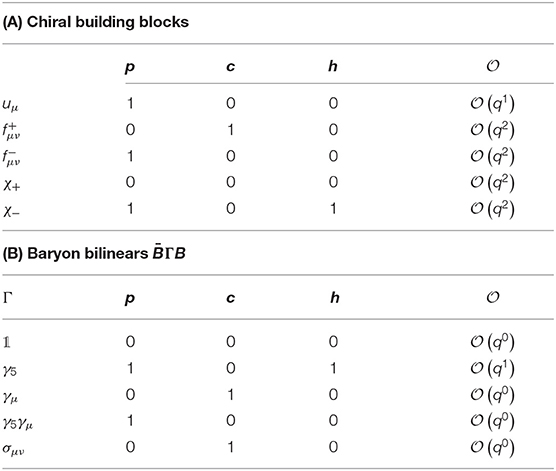
Table 2. Behavior under parity, charge conjugation, and Hermitian conjugation as well as the chiral dimensions of chiral building blocks and baryon bilinears $\bar{B}\Gamma B$ [140].

A building block A transforms under parity, charge conjugation and Hermitian conjugation as

$\begin{array}{ll}{A}^P={(-1)}^{p}A,A^C={(-1)}^c{A}^{\top },A^{†}={(-1)}^{h}A,& (33)\end{array}$

with the exponents (modulo two) p, c, h ∈ {0, 1} given in Table 2A, and ⊤ denotes the transpose of a (flavor) matrix. A sign change of the spatial argument, $(t,\overrightarrow{x})\to (t,-\overrightarrow{x})$, is implied in the fields in case of parity transformation P. Lorentz indices transform with the matrix ${P^{\mu }}_{\nu }=diag(+1,-1,-1,-1)$ under parity transformation, e.g., ${(u^{\mu })}^P={(-1)}^p{P^{\mu }}_{\nu }{u}^{\nu }$. The transformation behavior of commutators and anticommutators of two building blocks A₁, A₂ is the same as for building block and should therefore be used instead of simple products, e.g.,

$\begin{array}{l}{\left[A_1,A_2\right]}_{\pm }^C={(-1)}^{c_1+c_2}(A_1^{\top }{A}_2^{\top }\pm A_2^{\top }{A}_1^{\top })\\ =\pm {(-1)}^{c_1+c_2}{\left[A_1,A_2\right]}_{\pm }^{\top }.& (34)\end{array}$

The behavior under Hermitian conjugation is the same.

The basis elements of the Dirac algebra forming the baryon bilinears transform as

$\begin{array}{l}{\gamma }_0\Gamma {\gamma }_0={\left(-1\right)}^{p_{\Gamma }}\Gamma ,C^{-1}\Gamma C={\left(-1\right)}^{c_{\Gamma }}{\Gamma }^{\top },\\ {\gamma }_0{\Gamma }^{†}{\gamma }_0={\left(-1\right)}^{h_{\Gamma }}\Gamma ,& (35)\end{array}$

where the exponents p_Γ, c_Γ, h_Γ ∈ {0, 1} can be found in Table 2B. As before, Lorentz indices of baryon bilinears transform with the matrix ${P^{\mu }}_{\nu }$ under parity.

Due to the identity

$\begin{array}{ll}\left[D_{\mu },D_{\nu }\right]A=\frac{1}{4}\left[\left[u_{\mu },u_{\nu }\right],A\right]-\frac{\text{i }}{2}\left[f_{\mu \nu }^{+},A\right]& (36)\end{array}$

it is sufficient to use only totally symmetrized products of covariant derivatives, D^αβγ…A, for any building block A (or baryon field B). Moreover, because of the relation

$\begin{array}{ll}{D}_{\nu }{u}_{\mu }-D_{\mu }{u}_{\nu }=f_{\mu \nu }^{-},& (37)\end{array}$

only the symmetrized covariant derivative acting on u_μ need to be taken into account,

$\begin{array}{ll}{h}_{\mu \nu }=D_{\mu }{u}_{\nu }+D_{\nu }{u}_{\mu }.& (38)\end{array}$

Finally, the chiral effective Lagrangian can be constructed by taking traces (and products of traces) of different polynomials in the building blocks, so that they are invariant under chiral symmetry, Lorentz transformations, C and P.

2.3.1. Leading-Order Meson Lagrangian

As a first example, we show the leading-order purely mesonic Lagrangian. From the general construction principles discussed above, one obtains for the leading-order effective Lagrangian

$\begin{array}{ll}{{L}}_{\varphi }^{(2)}=\frac{f_0^2}{4}\langle u_{\mu }{u}^{\mu }+{\chi }_{+}\rangle .& (39)\end{array}$

Note that there is no contribution of order ${O}(q^0)$. This is consistent with the vanishing interaction of the Goldstone bosons in the chiral limit at zero momenta.

Before we continue with the meson-baryon interaction Lagrangian, let us elaborate on the leading chiral Lagrangian in the purely mesonic sector without external fields, but with non-vanishing quark masses in the isospin limit: v^μ(x) = a^μ(x) = p(x) = 0 and s(x) = M = diag(m, m, m_s). Inserting the definitions of the building blocks, Equation (39) becomes with these restrictions:

$\begin{array}{ll}{{L}}_{\varphi }^{(2)}=\frac{f_0^2}{4}\langle {\partial }_{\mu }U{\partial }^{\mu }{U}^{†}\rangle +\frac{1}{2}{B}_0{f}_0^2\langle M{U}^{†}+UM\rangle .& (40)\end{array}$

The physical decay constants f_π ≠ f_K ≠ f_η differ from the decay constant of the pseudoscalar Goldstone bosons in the chiral limit f₀ in terms of order (m, m_s): $f_{\varphi }=f_0\left\{1+{O}(m,m_s)\right\}$. The constant B₀ is related to the chiral quark condensate. Already from this leading-order Lagrangian famous relations such as the (reformulated) Gell-Mann–Oakes–Renner relations

$\begin{array}{l}{m}_{\pi }^2=2m{B}_0+{O}(m_q^2),\\ m_K^2=(m+m_s)B_0+{O}(m_q^2),\\ m_{\eta }^2=\frac{2}{3}(m+2m_s)B_0+{O}(m_q^2),& (41)\end{array}$

or the Gell-Mann–Okubo mass formula, $4m_K^2=3m_{\eta }^2+m_{\pi }^2$, can be derived systematically.

2.3.2. Leading-Order Meson-Baryon Interaction Lagrangian

The leading-order meson-baryon interaction Lagrangian ${{L}}_{\text{B}}^{(1)}$ is of order ${O}(q)$ and reads ¹

$\begin{array}{l}{{L}}_{\text{B}}^{(1)}=\langle \bar{B}(i\cancel{D}-M_{\text{B}})B\rangle +\frac{D}{2}\langle \bar{B}{\gamma }^{\mu }{\gamma }_5\{u_{\mu },B\}\rangle \\ +\frac{F}{2}\langle \bar{B}{\gamma }^{\mu }{\gamma }_5[u_{\mu },B]\rangle .& (42)\end{array}$

The constant M_B is the mass of the baryon octet in the chiral limit. The two new constants D and F are called axial-vector coupling constants. Their values can be obtained from semi-leptonic hyperon decays and are roughly D ≈ 0.8 and F ≈ 0.5 [143]. The sum of the two constants is related to the axial-vector coupling constant of nucleons, g_A = D + F = 1.27, obtained from neutron beta decay. At lowest order the pion-nucleon coupling constant g_πN is connected to the axial-vector coupling constant by the Goldberger-Treiman relation, g_πNf_π = g_AM_N. The covariant derivative in Equation (42) includes the field Γ_μ, which leads to a vertex between two octet baryons and two mesons, whereas the terms containing u_μ lead to a vertex between two octet baryons and one meson. Different octet-baryon masses appear first in ${{L}}_{\text{B}}^{(2)}$ due to explicit chiral symmetry breaking and renormalization and lead to corrections linear in the quark masses:

$\begin{array}{ll}{M}_i=M_{\text{B}}+{O}(m,m_s).& (43)\end{array}$

2.4. Weinberg Power Counting Scheme

As stated before, an effective field theory has an infinite number of terms in the effective Lagrangian and for a fixed process an infinite number of diagrams contribute. Therefore, it is crucial to have a power counting scheme, to assign the importance of a term. Then, to a certain order in the power counting, only a finite number of terms contribute and the observables can be calculated to a given accuracy.

First, let us discuss the power counting scheme of χEFT in the pure meson sector, i.e., only the pseudoscalar Goldstone bosons are explicit degrees of freedom. The chiral dimension ν of a Feynman diagram represents the order in the low-momentum expansion, ${(q/{\Lambda }_{\chi })}^{\nu }$. The symbol q is generic for a small external meson momentum or a small meson mass. The scale of chiral symmetry breaking Λ_χ is often estimated as 4πf_π ≈ 1 GeV or as the mass of the lowest-lying resonance, M_ρ ≈ 770 MeV. A simple dimensional analysis leads to the following expression for the chiral dimension of a connected Feynman diagram [6]:

$\begin{array}{ll}\nu =2+2L+{\displaystyle \sum _i}{v}_i{\Delta }_i,{\Delta }_i=d_i-2.& (44)\end{array}$

The number of Goldstone boson loops is denoted by L and v_i is the number of vertices with vertex dimension Δ_i. The symbol d_i stands for the number of derivatives or meson mass insertions at the vertex, i.e., the vertex originates from a term of the Lagrangian of the order ${O}(q^{d_i})$.

With the introduction of baryons in the chiral effective Lagrangian, the power counting is more complicated. The large baryon mass comes as an extra scale and destroys the one-to-one correspondence between the loop and the small momentum expansion. Jenkins and Manohar used methods from heavy-quark effective field theory to solve this problem [127]. Basically they considered baryons as heavy, static sources. This leads to a description of the baryons in the extreme non-relativistic limit with an expansion in powers of the inverse baryon mass, called heavy-baryon chiral perturbation theory.

Furthermore, in the two-baryon sector, additional features arise. Reducible Feynman diagrams are enhanced due to the presence of small kinetic energy denominators resulting from purely baryonic intermediate states. These graphs hint at the non-perturbative aspects in few-body problems, such as the existence of shallow bound states, and must be summed up to all orders. As suggested by Weinberg [86, 87], the baryons can be treated non-relativistically and the power counting scheme can be applied to an effective potential V, that contains only irreducible Feynman diagrams. Terms with the inverse baryon mass $M_{\text{B}}^{-1}$ may be counted as

$\begin{array}{ll}\frac{q}{M_{\text{B}}}\propto {\left(\frac{q}{{\Lambda }_{\chi }}\right)}^2.& (45)\end{array}$

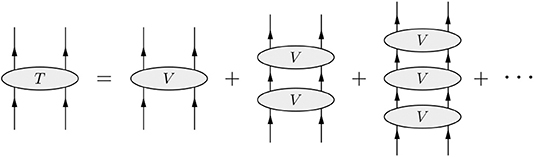
The resulting effective potential is the input for quantum mechanical few-body calculations. In case of the baryon-baryon interaction the effective potential is inserted into the Lippmann-Schwinger equation and solved for bound and scattering states. This is graphically shown in Figures 2, 3. The T-matrix is obtained from the infinite series of ladder diagrams with the effective potential V. In this way the omitted reducible diagrams are regained. In the many-body sector, e.g., Faddeev (or Yakubovsky) equations are typically solved within a coupled-channel approach. In a similar way reducible diagrams such as on the left-hand side of Figure 4, are generated automatically and are not part of the effective potential. One should distinguish such iterated two-body interactions, from irreducible three-baryon forces, as shown on the right-hand side of Figure 4.

FIGURE 2

Figure 2. Graphical representation of the Lippmann-Schwinger equation.

FIGURE 3

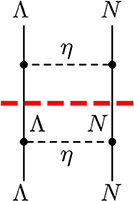
Figure 3. Example of a planar box diagram. It contains an reducible part equivalent to the iteration of two one-meson exchange diagrams, as generated by the Lippmann-Schwinger equation. Additionally it contains a genuine irreducible contribution that is part of the effective potential.

FIGURE 4

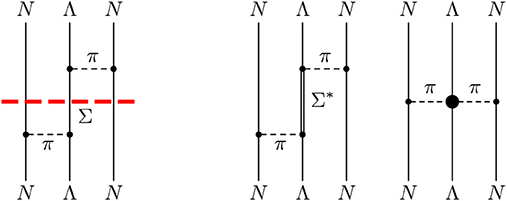
Figure 4. Examples for reducible (left) and irreducible (right) three-baryon interactions for ΛNN. The thick dashed line cuts the reducible diagram in two two-body interaction parts.

After these considerations, a consistent power counting scheme for the effective potential V is possible. The soft scale q in the low-momentum expansion ${(q/{\Lambda }_{\chi })}^{\nu }$ denotes now small external meson four-momenta, small external baryon three-momenta or the small meson masses. Naive dimensional analysis leads to the generalization of Equation (44):

$\begin{array}{ll}\nu =2-B+2L+{\displaystyle \sum _i}{v}_i{\Delta }_i,{\Delta }_i=d_i+\frac{1}{2}{b}_i-2,& (46)\end{array}$

where B is the number of external baryons and b_i is the number of internal baryon lines at the considered vertex. However, Equation (46) has an unwanted dependence on the baryon number, due to the normalization of baryon states. Such an effect can be avoided by assigning the chiral dimension to the transition operator instead of the matrix elements. This leads to the addition of 3B−6 to the formula for the chiral dimension, which leaves the B = 2 case unaltered, and one obtains (see for example [9, 13, 14, 130])

$\begin{array}{ll}\nu =-4+2B+2L+{\displaystyle \sum _i}{v}_i{\Delta }_i,{\Delta }_i=d_i+\frac{1}{2}{b}_i-2.& (47)\end{array}$

Following this scheme one arrives at the hierarchy of baryonic forces shown in Figure 5. The leading-order (ν = 0) potential is given by one-meson-exchange diagrams and non-derivative four-baryon contact terms. At next-to-leading order (ν = 2) higher order contact terms and two-meson-exchange diagrams with intermediate octet baryons contribute. Finally, at next-to-next-to-leading order (ν = 3) the three-baryon forces start to contribute. Diagrams that lead to mass and coupling constant renormalization are not shown.

FIGURE 5

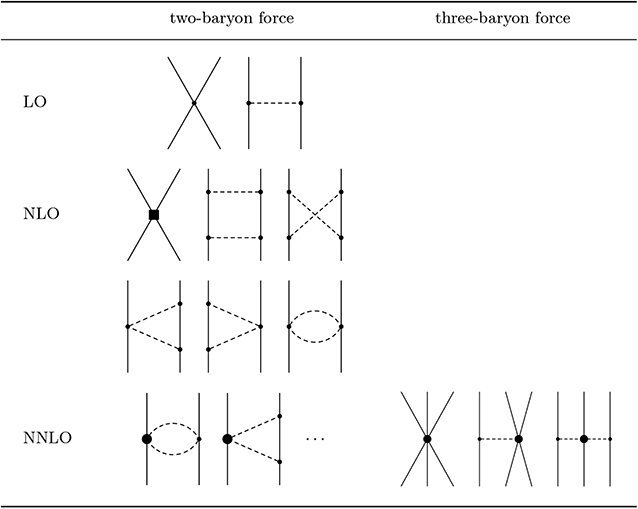
Figure 5. Hierarchy of baryonic forces. Solid lines are baryons, dashed lines are pseudoscalar mesons. Solid dots, filled circles, and squares denote vertices with Δ_i = 0, 1, and2, respectively.

3. Baryon-Baryon Interaction Potentials

This section is devoted to the baryon-baryon interaction potentials up to next-to-leading order, constructed from the diagrams shown in Figure 5. Contributions arise from contact interaction, one- and two-Goldstone-boson exchange. The constructed potentials serve not only as input for the description of baryon-baryon scattering, but are also basis for few- and many-body calculations. We give also a brief introduction to common meson-exchange models and the difference to interaction potentials from χEFT.

3.1. Baryon-Baryon Contact Terms

The chiral Lagrangian necessary for the contact vertices shown in Figure 6 can be constructed straightforwardly according to the principles outlined in section 2. For pure baryon-baryon scattering processes, no pseudoscalar mesons are involved in the contact vertices and almost all external fields can be dropped. Covariant derivatives D_μ reduce to ordinary derivatives ∂_μ. The only surviving external field is χ₊, which is responsible for the inclusion of quark masses into the chiral Lagrangian:

FIGURE 6

Figure 6. Leading-order and next-to-leading-order baryon-baryon contact vertices.

$\begin{array}{l}\frac{{\chi }_{+}}{2}=\chi =2B_0\left(\begin{array}{ccc}{m}_u& 0& 0\\ 0& m_d& 0\\ 0& 0& m_s\end{array}\right)\\ \approx \left(\begin{array}{ccc}{m}_{\pi }^2& 0& 0\\ 0& m_{\pi }^2& 0\\ 0& 0& 2m_K^2-m_{\pi }^2\end{array}\right),& (48)\end{array}$

where in the last step the Gell-Mann–Oakes–Renner relations, Equation (41), have been used. In flavor space the possible terms are of the schematic form

$\begin{array}{ll}\langle \bar{B}B\bar{B}B\rangle ,\langle \bar{B}\bar{B}BB\rangle ,\langle \bar{B}B\rangle \langle \bar{B}B\rangle ,\langle \bar{B}\bar{B}\rangle \langle BB\rangle ,& (49)\end{array}$

and terms where the field χ is inserted such as

$\begin{array}{ll}\langle \bar{B}\chi B\bar{B}B\rangle ,\langle \bar{B}B\chi \bar{B}B\rangle ,\langle \bar{B}\chi B\rangle \langle \bar{B}B\rangle ,\dots & (50)\end{array}$

where in both cases appropriate structures in Dirac space have to be inserted. For the case of the non-relativistic power counting it would also be sufficient, to insert the corresponding structures in spin-momentum space. The terms involving χ lead to explicit SU(3) symmetry breaking at NLO linear in the quark masses. A set of linearly independent Lagrangian terms up to ${O}(q^2)$ for pure baryon-baryon interaction in non-relativistic power counting can be found in Petschauer and Kaiser [32].

After a non-relativistic expansion up to ${O}(q^2)$ the four-baryon contact Lagrangian leads to potentials in spin and momentum space. A convenient operator basis is given by [29]:

$\begin{array}{l}{P}_1=𝟙,\\ P_2={\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2,\\ P_3=({\overrightarrow{\sigma }}_1·\overrightarrow{q})({\overrightarrow{\sigma }}_2·\overrightarrow{q})-\frac{1}{3}({\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2){\overrightarrow{q}}^2,\\ P_4=\frac{\text{i }}{2}({\overrightarrow{\sigma }}_1+{\overrightarrow{\sigma }}_2)·\overrightarrow{n},\\ P_5=({\overrightarrow{\sigma }}_1·\overrightarrow{n})({\overrightarrow{\sigma }}_2·\overrightarrow{n}),\\ P_6=\frac{\text{i }}{2}({\overrightarrow{\sigma }}_1-{\overrightarrow{\sigma }}_2)·\overrightarrow{n},\\ P_7=({\overrightarrow{\sigma }}_1·\overrightarrow{k})({\overrightarrow{\sigma }}_2·\overrightarrow{q})+({\overrightarrow{\sigma }}_1·\overrightarrow{q})({\overrightarrow{\sigma }}_2·\overrightarrow{k}),\\ P_8=({\overrightarrow{\sigma }}_1·\overrightarrow{k})({\overrightarrow{\sigma }}_2·\overrightarrow{q})-({\overrightarrow{\sigma }}_1·\overrightarrow{q})({\overrightarrow{\sigma }}_2·\overrightarrow{k}),& (51)\end{array}$

with ${\overrightarrow{\sigma }}_{1,2}$ the Pauli spin matrices and with the vectors

$\begin{array}{ll}\overrightarrow{k}=\frac{1}{2}({\overrightarrow{p}}_f+{\overrightarrow{p}}_i),\overrightarrow{q}={\overrightarrow{p}}_f-{\overrightarrow{p}}_i,\overrightarrow{n}={\overrightarrow{p}}_i\times {\overrightarrow{p}}_f.& (52)\end{array}$

The momenta ${\overrightarrow{p}}_f$ and ${\overrightarrow{p}}_i$ are the initial and final state momenta in the center-of-mass frame. In order to obtain the minimal set of Lagrangian terms in the non-relativistic power counting of Petschauer and Kaiser [32], the potentials have been decomposed into partial waves. The formulas for the partial wave projection of a general interaction $V=\sum _{j=1}^8{V}_j{P}_j$ can be found in the appendix of Polinder et al. [29]. For each partial wave one produces a non-square matrix which connects the Lagrangian constants with the different baryon-baryon channels. Lagrangian terms are considered as redundant if their omission does not lower the rank of this matrix. For the determination of the potential not only direct contributions have to be considered, but also additional structures from exchanged final state baryons, where the negative spin-exchange operator $-P^{(\sigma )}=-\frac{1}{2}(𝟙+{\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2)$ is applied. In the end 6 momentum-independent terms at LO contribute, and are therefore only visible in ¹S₀ and ³S₁ partial waves. At NLO 22 terms contribute that contain only baryon fields and derivatives, and are therefore SU(3) symmetric. The other 12 terms at NLO include the diagonal matrix χ and produce explicit SU(3) symmetry breaking.

In Table 3, the non-vanishing transitions projected onto partial waves in the isospin basis are shown (cf. [29–32]). The pertinent constants are redefined according to the relevant irreducible SU(3) representations. This comes about in the following way. Baryons form a flavor octet and the tensor product of two baryons decomposes into irreducible representations as follows:

$\begin{array}{ll}8\otimes 8={27}_s\oplus {10}_a\oplus {10}_a^{*}\oplus 8_s\oplus 8_a\oplus 1_s,& (53)\end{array}$

where the irreducible representations 27_s, 8_s, 1_s are symmetric and ${10}_a,{10}_a^{*},8_a$ are antisymmetric with respect to the exchange of both baryons. Due to the generalized Pauli principle, the symmetric flavor representations 27_s, 8_s, 1_s have to combine with the space-spin antisymmetric partial waves ¹S₀, ³P₀, ³P₁, ³P₂, … (L + S even). The antisymmetric flavor representations ${10}_a,{10}_a^{*},8_a$ combine with the space-spin symmetric partial waves ³S₁, ¹P₁, ³D₁ ↔ ³S₁, … (L + S odd). Transitions can only occur between equal irreducible representations. Hence, transitions between space-spin antisymmetric partial waves up to ${O}(q^2)$ involve the 15 constants ${\tilde{c}}_{{}^1{S}_0}^{27,8s,1}$, $c_{{}^1{S}_0}^{27,8s,1}$, $c_{{}^3{P}_0}^{27,8s,1}$, $c_{{}^3{P}_1}^{27,8s,1}$, and $c_{{}^3{P}_2}^{27,8s,1}$, whereas transitions between space-spin symmetric partial waves involve the 12 constants ${\tilde{c}}_{{}^3{S}_1}^{8a,10,10^{*}}$, $c_{{}^3{S}_1}^{8a,10,10^{*}}$, $c_{{}^1{P}_1}^{8a,10,10^{*}}$, and $c_{{}^3{D}_1{\text{-}}^3{S}_1}^{8a,10,10^{*}}$. The constants with a tilde denote leading-order constants, whereas the ones without tilde are at NLO. The spin singlet-triplet transitions ¹P₁ ↔ ³P₁ is perfectly allowed by SU(3) symmetry since it is related to transitions between the irreducible representations 8_a and 8_s. Such a transition originated from the antisymmetric spin-orbit operator P₆ and its Fierz-transformed counterpart P₈ and the single corresponding low-energy constant is denoted by c^8as. In case of the NN interaction such transitions are forbidden by isospin symmetry. The constants ${\tilde{c}}_{{}^1{S}_0}^{27,8s,1}$ and ${\tilde{c}}_{{}^3{S}_1}^{8a,10,10^{*}}$ fulfill the same SU(3) relations as the constants $c_{{}^1{S}_0}^{27,8s,1}$ and $c_{{}^3{S}_1}^{8a,10,10^{*}}$ in Table 3. SU(3) breaking terms linear in the quark masses appears only in the S-waves, ¹S₀, ³S₁, and are proportional $m_K^2-m_{\pi }^2$. The corresponding 12 constants are $c_{\chi }^{1,\dots ,12}$. The SU(3) symmetry relations in Table 3 can also be derived by group theoretical considerations [29, 144–146]. Clearly, for the SU(3)-breaking part this is not possible and these contributions have to be derived from the chiral Lagrangian.

TABLE 3

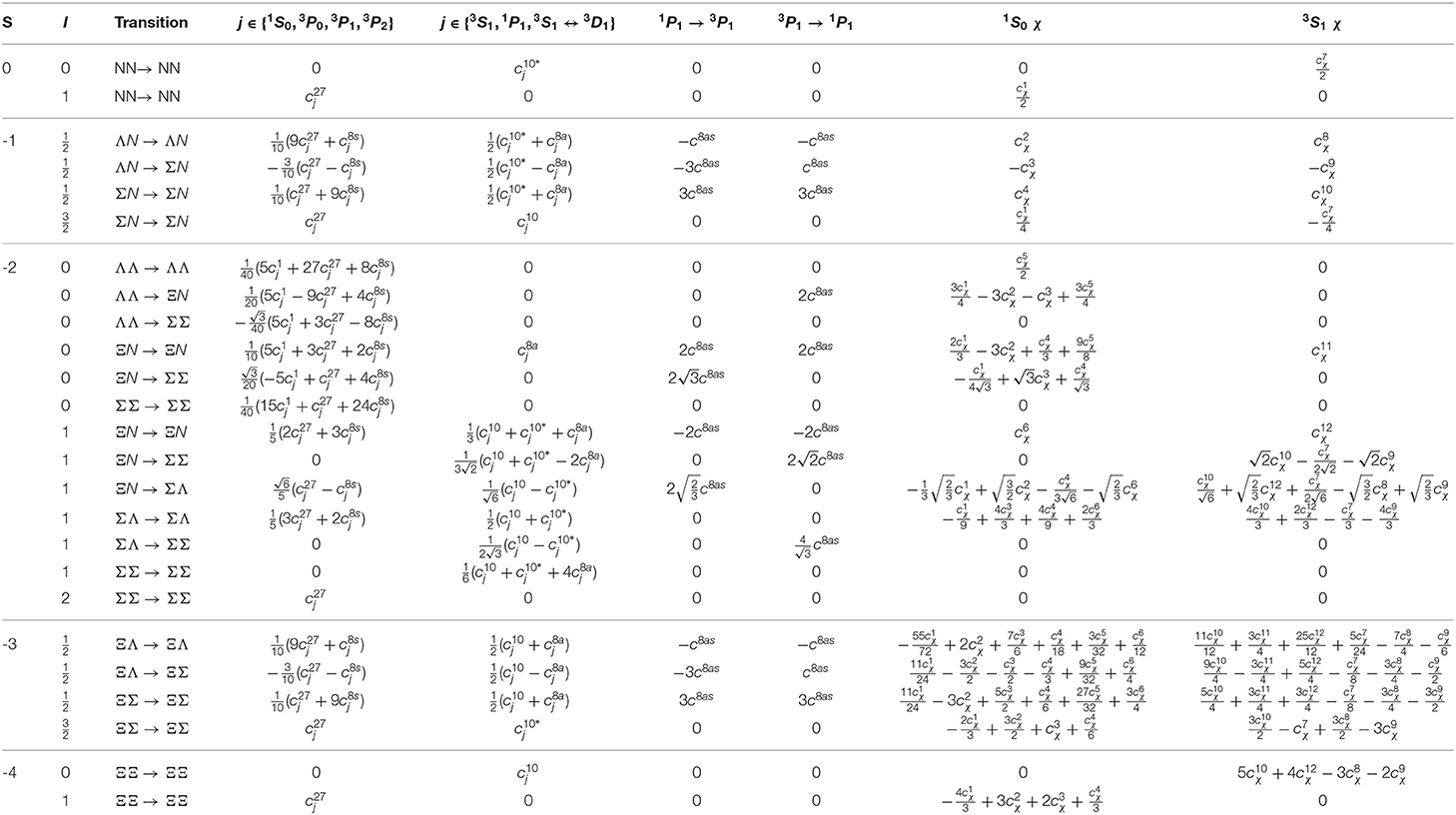
Table 3. SU(3) relations of pure baryon-baryon contact terms for non-vanishing partial waves up to ${O}(q^2)$ in non-relativistic power counting for channels described by strangeness S and total isospin I [32].

In order to obtain the complete partial-wave projected potentials, some entries in Table 3 have to be multiplied with additional momentum factors. The leading order constants ${\tilde{c}}_j^i$ receive no further factor. For the next-to-leading-order constants (without tilde and without χ) the contributions to the partial waves ¹S₀, ³S₁ have to be multiplied with a factor $p_i^2+p_f^2$. The contribution to the partial waves ¹S₀, ³S₁ from constants $c_{\chi }^j$ has to be multiplied with $(m_K^2-m_{\pi }^2)$. The partial waves ³P₀, ³P₁, ³P₂, ¹P₁, ¹P₁ ↔ ³P₁ get multiplied with the factor p_ip_f. The entries for ³S₁ → ³D₁ and ³D₁ → ³S₁ have to be multiplied with $p_i^2$ and $p_f^2$, respectively. For example, one obtains for the NN interaction in the ¹S₀ partial wave:

$\begin{array}{l}\langle NN{,}^1{S}_0|\widehat{V}|NN{,}^1{S}_0\rangle \\ ={\tilde{c}}_{{}^1{S}_0}^{27}+c_{{}^1{S}_0}^{27}(p_i^2+p_f^2)+\frac{1}{2}{c}_{\chi }^1(m_K^2-m_{\pi }^2),& (54)\end{array}$

or for the ΞN → ΣΣ interaction with total isospin I = 0 in the ¹P₁ → ³P₁ partial wave:

$\begin{array}{ll}\langle \sum \sum ,{}^{3}P{}_1|\widehat{V}|\Xi N,{}^{1}P{}_1\rangle =2\sqrt{3}{c}^{8as}{p}_i{p}_f.& (55)\end{array}$

When restricting to the NN channel the well-known two leading and seven next-to-leading order low-energy constants of Epelbaum et al. [147] are recovered, which contribute to the partial waves ¹S₀, ³S₁, ¹P₁, ³P₀, ³P₁, ³P₂, ³S₁ ↔ ³D₁.

Note, that the SU(3) relations in Table 3 are general relations that have to be fulfilled by the baryon-baryon potential in the SU(3) limit, i.e., m_π = m_K = m_η. This feature can be used as a check for the inclusion of the loop diagrams. Another feature is, that the SU(3) relations contain only a few constants in each partial wave. For example, in the ¹S₀ partial wave only the constants ${\tilde{c}}_{{}^1{S}_0}^{27}$, ${\tilde{c}}_{{}^1{S}_0}^{8s}$, ${\tilde{c}}_{{}^1{S}_0}^1$ are present. If these constants are fixed in some of the baryons channels, predictions for other channels can be made. This has, for instance, been used in Haidenbauer et al. [35], where the existence of ΣΣ, ΣΞ and ΞΞ bound states has been studied within SU(3) χEFT.

3.2. One- and Two-Meson-Exchange Contributions

In the last section, we have addressed the short-range part of the baryon-baryon interaction via contact terms. Let us now analyze the long- and mid-range part of the interaction, generated by one- and two-meson-exchange as determined in Haidenbauer et al. [33]. The contributing diagrams up to NLO are shown in Figure 5, which displays the hierarchy of baryonic forces.

The vertices, necessary for the construction of these diagrams stem from the leading-order meson-baryon interaction Lagrangian ${{L}}_{\text{B}}^{(1)}$ in Equation (42). The vertex between two baryons and one meson emerges from the part

$\begin{array}{l}\frac{D}{2}\langle \bar{B}{\gamma }^{\mu }{\gamma }_5\{u_{\mu },B\}\rangle +\frac{F}{2}\langle \bar{B}{\gamma }^{\mu }{\gamma }_5[u_{\mu },B]\rangle \\ =-\frac{1}{2f_0}{\displaystyle \sum _{i,j,k=1}^8}{N}_{B_i{B}_j{\varphi }_k}({\bar{B}}_i{\gamma }^{\mu }{\gamma }_5{B}_j)({\partial }_{\mu }{\varphi }_k)+{O}({\varphi }^3),& (56)\end{array}$

where we have used $u_{\mu }=-\frac{1}{f_0}{\partial }_{\mu }\varphi +{O}({\varphi }^3)$ and have rewritten the pertinent part of the Lagrangian in terms of the physical meson and baryon fields

$\begin{array}{l}{\varphi }_i\in \left\{{\pi }^0,{\pi }^{+},{\pi }^{-},K^{+},K^{-},K^0,{\bar{K}}^0,\eta \right\},\\ B_i\in \left\{n,p,{\Sigma }^0,{\Sigma }^{+},{\Sigma }^{-},\Lambda ,{\Xi }^0,{\Xi }^{-}\right\}.& (57)\end{array}$

The factors N_BiBjϕk are linear combinations of the axial vector coupling constants D and F with certain SU(3) coefficients. These factors vary for different combinations of the involved baryons and mesons and can be obtained easily by multiplying out the baryon and meson flavor matrices. In a similar way, we obtain the (Weinberg-Tomozawa) vertex between two baryons and two mesons from the covariant derivative in ${{L}}_{\text{B}}^{(1)}$, leading to

$\begin{array}{l}\langle \bar{B}\text{i }{\gamma }^{\mu }\left[{\Gamma }_{\mu },B\right]\rangle \\ =\frac{\text{i }}{8f_0^2}{\displaystyle \sum _{i,j,k,l=1}^8}{N}_{B_i{\varphi }_k{B}_j{\varphi }_l}({\bar{B}}_i{\gamma }^{\mu }{B}_j)({\varphi }_k{\partial }_{\mu }{\varphi }_l)+{O}({\varphi }^4),& (58)\end{array}$

where ${\Gamma }_{\mu }=\frac{1}{8f_0^2}\left[\varphi ,{\partial }_{\mu }\varphi \right]+{O}({\varphi }^4)$ was used.

The calculation of the baryon-baryon potentials is done in the center-of-mass frame and in the isospin limit m_u = m_d. To obtain the contribution of the Feynman diagrams to the non-relativistic potential, we perform an expansion in the inverse baryon mass 1/M_B. If loops are involved, the integrand is expanded before integrating over the loop momenta. This produces results that are equivalent to the usual heavy-baryon formalism. In the case of the two-meson-exchange diagrams at one-loop level, ultraviolet divergences are treated by dimensional regularization, which introduces a scale λ. In dimensional regularization divergences are isolated as terms proportional to

$\begin{array}{ll}R=\frac{2}{d-4}+{\gamma }_{\text{E}}-1-ln(4\pi ),& (59)\end{array}$

with d ≠ 4 the space-time dimension and the Euler-Mascheroni constant γ_E ≈ 0.5772. These terms can be absorbed by the contact terms.

According to Equations (56) and (58) the vertices have the same form for different combinations of baryons and mesons, just their prefactors change. Therefore, the one- and two-pseudoscalar-meson exchange potentials can be given by a master formula, where the proper masses of the exchanged mesons have to be inserted, and which has to be multiplied with an appropriate SU(3) factor N. In the following we will present the analytic formulas for the one- and two-meson-exchange diagrams, introduced in Haidenbauer et al. [33]. The pertinent SU(3) factors will be displayed next to the considered Feynman diagram (cf. Figure 7). The results will be given in terms of a central potential (V_C), a spin-spin potential $({\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2{V}_S)$ and a tensor-type potential $({\overrightarrow{\sigma }}_1·\overrightarrow{q}{\overrightarrow{\sigma }}_2·\overrightarrow{q}{V}_T)$. The momentum transfer is $q=|{\overrightarrow{p}}_f-{\overrightarrow{p}}_i|$, with ${\overrightarrow{p}}_i$ and ${\overrightarrow{p}}_f$ the initial and final state momenta in the center-of-mass frame.

FIGURE 7

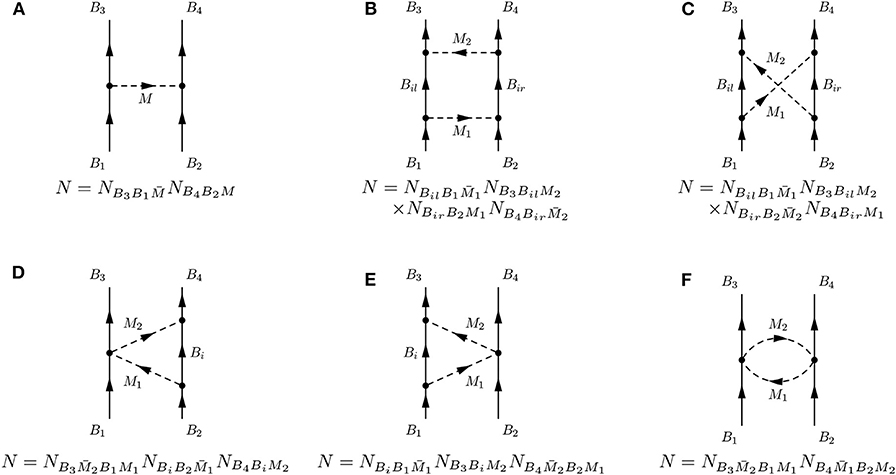
Figure 7. One- and two-meson-exchange contributions and corresponding SU(3) factors. (A) One-meson exchange, (B) planar box, (C) crossed box, (D) left triangle, (E) right triangle, and (F) football diagram.

Note that the presented results apply only to direct diagrams. This is for example the case for the leading-order one-eta exchange in the Λn interaction, i.e., for $\Lambda ({\overrightarrow{p}}_i)n(-{\overrightarrow{p}}_i)\underset{}{\overset{\eta }{\to }}\Lambda ({\overrightarrow{p}}_f)n(-{\overrightarrow{p}}_f)$. An example of a crossed diagram is the one-kaon exchange in the process $\Lambda ({\overrightarrow{p}}_i)n(-{\overrightarrow{p}}_i)\underset{}{\overset{K}{\to }}n(-{\overrightarrow{p}}_f)\Lambda ({\overrightarrow{p}}_f)$, where the nucleon and the hyperon in the final state are interchanged and strangeness is exchanged. In such cases, ${\overrightarrow{p}}_f$ is replaced by $-{\overrightarrow{p}}_f$ and the momentum transfer in the potentials is $q=|{\overrightarrow{p}}_f+{\overrightarrow{p}}_i|$. Due to the exchange of fermions in the final states a minus sign arises, and additionally the spin-exchange operator $P^{(\sigma )}=\frac{1}{2}(𝟙+{\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2)$ has to be applied. The remaining structure of the potentials stays the same (see also the discussion in section 4).

The leading-order contribution comes from the one-meson exchange diagram in Figure 7A. It contributes only to the tensor-type potential:

$\begin{array}{ll}{V}_{\text{T}}^{\text{ome}}(q)=-\frac{N}{4f_0^2}\frac{1}{q^2+m^2-\text{i}ϵ}.& (60)\end{array}$

The symbol $\bar{M}$ in the SU(3) coefficient N denotes the charge-conjugated meson of meson M in particle basis (e.g., π⁺ ↔ π⁻).

At next-to-leading order the two-meson exchange diagrams start to contribute. The planar box in Figure 7B contains an irreducible part and a reducible part coming from the iteration of the one-meson exchange to second order. Inserting the potential into the Lippmann-Schwinger equation generates the reducible part; it is therefore not part of the potential (see also section 2.4). The irreducible part is obtained from the residues at the poles of the meson propagators, disregarding the (far distant) poles of the baryon propagators. With the masses of the two exchanged mesons set to m₁ and m₂, the irreducible potentials can be written in closed analytical form,

$\begin{array}{l}{V}_{\text{irr},\text{\hspace{0.05em}C}}^{\text{planar box}}(q)=\frac{N}{3072{\pi }^2{f}_0^4}\{\frac{5}{3}{q}^2\\ +\frac{{\left(m_1^2-m_2^2\right)}^2}{q^2}+16\left(m_1^2+m_2^2\right)\\ +\left[23q^2+45\left(m_1^2+m_2^2\right)\right]\left(R+2\text{ln}\frac{\sqrt{m_1{m}_2}}{\lambda }\right)\\ +\frac{m_1^2-m_2^2}{q^4}[12q^4+{\left(m_1^2-m_2^2\right)}^2\\ -9q^2\left(m_1^2+m_2^2\right)]\text{ln}\frac{m_1}{m_2}\\ +\frac{2}{w^2\left(q\right)}[23q^4-\frac{{\left(m_1^2-m_2^2\right)}^4}{q^4}+56\left(m_1^2+m_2^2\right)q^2\\ +8\frac{m_1^2+m_2^2}{q^2}{\left(m_1^2-m_2^2\right)}^2\\ +2\left(21m_1^4+22m_1^2{m}_2^2+21m_2^4\right)]L\left(q\right)\},& (61)\end{array}$

$\begin{array}{l}{V}_{\text{irr},\text{\hspace{0.05em}T}}^{\text{planar box}}\left(q\right)=-\frac{1}{q^2}{V}_{\text{irr},\text{\hspace{0.05em}S}}^{\text{planar box}}(q)\\ =-\frac{N}{128{\pi }^2{f}_0^4}[L\left(q\right)-\frac{1}{2}-\frac{m_1^2-m_2^2}{2q^2}\text{ln}\frac{m_1}{m_2}\\ +\frac{R}{2}+\text{ln}\frac{\sqrt{m_1{m}_2}}{\lambda }]& (62)\end{array}$

where we have defined the functions

$\begin{array}{l}w(q)=\frac{1}{q}\sqrt{(q^2+{(m_1+m_2)}^2)(q^2+{(m_1-m_2)}^2)},\\ L(q)=\frac{w(q)}{2q}ln\frac{{\left[qw(q)+q^2\right]}^2-{(m_1^2-m_2^2)}^2}{4m_1{m}_2{q}^2}.& (63)\end{array}$

The relation between the spin-spin and tensor-type potential follows from the identity $({\overrightarrow{\sigma }}_1\times \overrightarrow{q})·({\overrightarrow{\sigma }}_2\times \overrightarrow{q})=q^2{\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2-({\overrightarrow{\sigma }}_1·\overrightarrow{q})({\overrightarrow{\sigma }}_2·\overrightarrow{q})$.

One should note that all potentials shown above are finite also in the limit q → 0. Terms proportional to 1/q² or 1/q⁴ are canceled by opposite terms in the functions L(q) and w(q) in the limit of small q. For numerical calculations it is advantageous to perform an expansion of the potentials in a power series for small q in order to implement directly this cancellation. For equal meson masses the expressions for the potentials reduce to the results in Kaiser et al. [148]. This is the case for the NN interaction of Epelbaum et al. [147, 149, 150] and Entem and Machleidt [151] based on χEFT, where only contributions from two-pion exchange need to be taken into account.

In actual applications of these potentials such as in Haidenbauer et al. [33], only the non-polynomial part of Equations (61) and (62) is taken into account, i.e., the pieces proportional to L(q) and to 1/q² and 1/q⁴. The polynomial part is equivalent to the LO and NLO contact terms and, therefore, does not need to be considered. The contributions proportional to the divergence R are likewise omitted. Their effect is absorbed by the contact terms or a renormalization of the coupling constants, see, e.g., the corresponding discussion in Appendix A of Epelbaum et al. [149] for the NN case.

These statements above apply also to the other contributions to the potential described below.

The crossed box diagrams in Figure 7C contribute to the central, spin-spin, and tensor-type potentials. The similar structure with some differences in the kinematics of the planar and crossed box diagram leads to relations between them. Obviously, the crossed box has no iterated part. The potentials of the crossed box are equal to the potentials of the irreducible part of the planar box, up to a sign in the central potential:

$\begin{array}{l}{V}_{\text{C}}^{\text{crossed box}}(q)=-V_{\text{C},\text{irr}}^{\text{planar box}}(q),\\ V_{\text{T}}^{\text{crossed box}}(q)=-\frac{1}{q^2}{V}_{\text{S}}^{\text{crossed box}}(q)=V_{\text{T},\text{irr}}^{\text{planar box}}(q).& (64)\end{array}$

The two triangle diagrams, Figures 7D,E, constitute potentials, that are of equal form with different SU(3) factors N. The corresponding central potential reads

$\begin{array}{l}{V}_{\text{C}}^{\text{triangle}}(q)=-\frac{N}{3072{\pi }^2{f}_0^4}\{-2\left(m_1^2+m_2^2\right)\\ +\frac{{\left(m_1^2-m_2^2\right)}^2}{q^2}-\frac{13}{3}{q}^2\\ +\left[8\left(m_1^2+m_2^2\right)-\frac{2{\left(m_1^2-m_2^2\right)}^2}{q^2}+10q^2\right]L\left(q\right)\\ +\frac{m_1^2-m_2^2}{q^4}\left[{\left(m_1^2-m_2^2\right)}^2-3\left(m_1^2+m_2^2\right)q^2\right]\text{ln}\frac{m_1}{m_2}\\ +\left[9\left(m_1^2+m_2^2\right)+5q^2\right]\left(R+2\text{ln}\frac{\sqrt{m_1{m}_2}}{\lambda }\right)\}.& (65)\end{array}$

The football diagrams in Figure 7F also contributes only to the central potential. One finds

$\begin{array}{l}{V}_{\text{C}}^{\text{football}}(q)=\frac{N}{3072{\pi }^2{f}_0^4}\{-2\left(m_1^2+m_2^2\right)\\ -\frac{{\left(m_1^2-m_2^2\right)}^2}{2q^2}-\frac{5}{6}{q}^2+w^2\left(q\right)L\left(q\right)\\ +\frac{1}{2}\left[3\left(m_1^2+m_2^2\right)+q^2\right]\left(R+2\text{ln}\frac{\sqrt{m_1{m}_2}}{\lambda }\right)\\ -\frac{m_1^2-m_2^2}{2q^4}\left[{\left(m_1^2-m_2^2\right)}^2+3\left(m_1^2+m_2^2\right)q^2\right]\ln \frac{m_1}{m_2}\}.& (66)\end{array}$

3.3. Meson-Exchange Models

Earlier investigations of the baryon-baryon interactions has been done within phenomenological meson-exchange potentials such as the Jülich [18, 19, 21], Nijmegen [20, 22, 23], or Ehime [152, 153] potentials. As we use two of them for comparison, we give a brief introduction to these type of models.

Conventional meson-exchange models of the YN interaction are usually also based on the assumption of SU(3) flavor symmetry for the occurring coupling constants, and in some cases even on the SU(6) symmetry of the quark model [18, 19]. In the derivation of the meson-exchange contributions one follows essentially the same procedure as outlined in section 3.2 for the case of pseudoscalar mesons. Besides the lowest pseudoscalar-meson multiplet also the exchanges of vector mesons (ρ, ω, K^*), of scalar mesons (σ (f₀(500)),…), or even of axial-vector mesons (a₁(1270),…) [22, 23] are included. The spin-space structure of the corresponding Lagrangians that enter into Equation (42) and subsequently into Equation (56) differ and, accordingly, the final expressions for the corresponding contributions to the YN interaction potentials differ too. Details can be found in Holzenkamp et al. [18] and Rijken et al. [20, 22]. We want to emphasize that even for pseudoscalar mesons the final result for the interaction potentials differs, in general, from the expression given in Equation (60). Contrary to the chiral EFT approach, recoil, and relativistic corrections are often kept in meson-exchange models because no power counting rules are applied. Moreover, in case of the Jülich potential pseudoscalar coupling is assumed for the meson-baryon interaction Lagrangian for the pseudoscalar mesons instead of the pseudovector coupling (Equation 42) dictated by chiral symmetry. Note that in some YN potentials of the Jülich group [18, 19] contributions from two-meson exchanges are included. The ESC08 and ESC16 potentials [22, 23] include likewise contributions from two-meson exchange, in particular, so-called meson-pair diagrams analog to the ones shown in Figures 7D–F.

The major conceptual difference between the various meson-exchange models consists in the treatment of the scalar-meson sector. This simply reflects the fact that, unlike for pseudoscalar and vector mesons, so far there is no general agreement about what are the actual members of the lowest lying scalar-meson SU(3) multiplet. Therefore, besides the question of the masses of the exchange particles it also remains unclear whether and how the relations for the coupling constants should be specified. As a consequence, different prescriptions for describing the scalar sector, whose contributions play a crucial role in any baryon-baryon interaction at intermediate ranges, were adopted by the various authors who published meson-exchange models of the YN interaction. For example, the Nijmegen group views this interaction as being generated by genuine scalar-meson exchange. In their models NSC97 [20] and ESC08 (ESC16) [22, 23] a scalar SU(3) nonet is exchanged—namely, two isospin-0 mesons [an ϵ(760) and the f₀(980)] an isospin-1 meson (a₀(980)) and an isospin-1/2 strange meson κ with a mass of 1,000 MeV. In the initial YN models of the Jülich group [18, 19] a σ (with a mass of ≈ 550 MeV) is included which is viewed as arising from correlated ππ exchange. In practice, however, the coupling strength of this fictitious σ to the baryons is treated as a free parameter and fitted to the data. In the latest meson-exchange YN potential presented by the Jülich group [21] a microscopic model of correlated ππ and $K\bar{K}$ exchange [154] is utilized to fix the contributions in the scalar-isoscalar (σ) and vector-isovector (ρ) channels.

Let us mention for completeness that meson-exchange models are typically equipped with phenomenological form factors in order to cut off the potential for large momenta (short distances). For example, in case of the YN models of the Jülich group the interaction is supplemented with form factors for each meson-baryon-baryon vertex (cf. [18, 19] for details). Those form factors are meant to take into account the extended hadron structure and are parameterized in the conventional monopole or dipole form. In case of the Nijmegen potentials a Gaussian form factor is used. In addition there is some additional sophisticated short-range phenomenology that controls the interaction at short distances [22, 23].

4. Three-Baryon Interaction Potentials

Three-nucleon forces are an essential ingredient for a proper description of nuclei and nuclear matter with low-momentum two-body interactions. Similarly, three-baryon forces, especially the ΛNN interaction, are expected to play an important role in nuclear systems with strangeness. Their introduction in calculations of light hypernuclei seems to be required. Furthermore, the introduction of 3BF is traded as a possible solution to the hyperon puzzle (see section 1). However, so far only phenomenological 3BF have been employed. In this section we present the leading irreducible three-baryon interactions from SU(3) chiral effective field theory as derived in Petschauer et al. [120]. We show the minimal effective Lagrangian required for the pertinent vertices. Furthermore the estimation of the corresponding LECs through decuplet saturation and an effective density-dependent two-baryon potential will be covered [121].

According to the power counting in Equation (47) the 3BF arise formally at NNLO in the chiral expansion, as can be seen from the hierarchy of baryonic forces in Figure 5. Three types of diagrams contribute: three-baryon contact terms, one-meson and two-meson exchange diagrams (cf. Figure 8). Note that a two-meson exchange diagram, such as in Figure 8, with a (leading order) Weinberg-Tomozawa vertex in the middle, would formally be a NLO contribution. However, as in the nucleonic sector, this contribution is kinematically suppressed due to the fact that the involved meson energies are differences of baryon kinetic energies. Anyway, parts of these NNLO contributions get promoted to NLO by the introduction of intermediate decuplet baryons, so that it becomes appropriate to use these three-body interactions together with the NLO two-body interaction of section 3. As already stated, the irreducible contributions to the chiral potential are presented. In contrast to typical phenomenological calculations, diagrams as on the left side of Figure 4 do not lead to a genuine three-body potential, but are an iteration of the two-baryon potential. Such diagrams will be incorporated automatically when solving, e.g., the Faddeev (or Yakubovsky) equations within a coupled-channel approach. The three-body potentials derived from SU(3) χEFT are expected to shed light on the effect of 3BFs in hypernuclear systems. Especially in calculations about light hypernuclei these potentials can be implemented within reliable few-body techniques [48, 49, 51, 52].

FIGURE 8

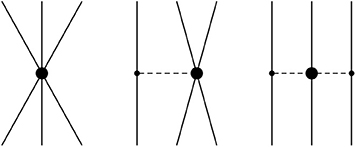
Figure 8. Leading three-baryon interactions: contact term, one-meson exchange, and two-meson exchange. Filled circles and solid dots denote vertices with Δ_i = 1 and Δ_i = 0, respectively.

4.1. Contact Interaction

In the following we consider the leading three-baryon contact interaction. Following the discussion in section 2.3 the corresponding Lagrangian can be constructed. The inclusion of external fields is not necessary, as we are interested in the purely baryonic contact term. One ends up with the following possible structures in flavor space [120]

$\begin{array}{l}\langle \bar{B}\bar{B}\bar{B}BBB\rangle ,\langle \bar{B}\bar{B}B\bar{B}BB\rangle ,\langle \bar{B}\bar{B}BB\bar{B}B\rangle ,\\ \langle \bar{B}B\bar{B}B\bar{B}B\rangle ,\langle \bar{B}\bar{B}BB\rangle \langle \bar{B}B\rangle ,\langle \bar{B}B\bar{B}B\rangle \langle \bar{B}B\rangle ,\\ \langle \bar{B}\bar{B}\bar{B}B\rangle \langle BB\rangle ,\langle \bar{B}\bar{B}\bar{B}\rangle \langle BBB\rangle ,\langle \bar{B}\bar{B}B\rangle \langle B\bar{B}B\rangle ,\\ \langle \bar{B}B\rangle \langle \bar{B}B\rangle \langle \bar{B}B\rangle ,\langle \bar{B}\bar{B}\rangle \langle \bar{B}B\rangle \langle BB\rangle ,& (67)\end{array}$

with possible Dirac structures

$\begin{array}{l}𝟙\otimes 𝟙\otimes 𝟙,𝟙\otimes {\gamma }_5{\gamma }^{\mu }\otimes {\gamma }_5{\gamma }_{\mu },{\gamma }_5{\gamma }^{\mu }\otimes 𝟙\otimes {\gamma }_5{\gamma }_{\mu },\\ {\gamma }_5{\gamma }^{\mu }\otimes {\gamma }_5{\gamma }_{\mu }\otimes 𝟙,{\gamma }_5{\gamma }_{\mu }\otimes \text{i }{\sigma }^{\mu \nu }\otimes {\gamma }_5{\gamma }_{\nu },& (68)\end{array}$

leading to the following operators in the three-body spin space

$\begin{array}{ll}𝟙,{\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2,{\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_3,{\overrightarrow{\sigma }}_2·{\overrightarrow{\sigma }}_3,\text{ i}{\overrightarrow{\sigma }}_1·({\overrightarrow{\sigma }}_2\times {\overrightarrow{\sigma }}_3).& (69)\end{array}$

All combinations of these possibilities leads to a (largely overcomplete) set of terms for the leading covariant Lagrangian. Note that in Petschauer et al. [120] the starting point is a covariant Lagrangian, but the minimal non-relativistic Lagrangian is the goal. Hence, only Dirac structures leading to independent (non-relativistic) spin operators are relevant.

Let us consider the process B₁B₂B₃ → B₄B₅B₆, where the B_i are baryons in the particle basis, $B_i\in \left\{n,p,\Lambda ,{\Sigma }^{+},{\Sigma }^0,{\Sigma }^{-},{\Xi }^0,{\Xi }^{-}\right\}$. The contact potential V has to be derived within a threefold spin space for this process. The operators in spin-space 1 is defined to act between the two-component Pauli spinors of B₁ and B₄. In the same way, spin-space 2 belongs to B₂ and B₅, and spin-space 3 to B₃ and B₆. For a fixed spin configuration the potential can be calculated from

$\begin{array}{ll}{{\chi }_{B_4}^{(1)}}^{†}{{\chi }_{B_5}^{(2)}}^{†}{{\chi }_{B_6}^{(3)}}^{†}V{\chi }_{B_1}^{(1)}{\chi }_{B_2}^{(2)}{\chi }_{B_3}^{(3)},& (70)\end{array}$

where the superscript of a spinor denotes the spin space and the subscript denotes the baryon to which the spinor belongs. The potential is obtained as V = −〈B₄B₅B₆| ${L}$ |B₁B₂B₃〉, where the contact Lagrangian ${L}$ has to be inserted, and the 36 Wick contractions need to be performed. The number 36 corresponds to the 3! × 3! possibilities to arrange the three initial and three final baryons into Dirac bilinears. One obtains six direct terms, where the baryon bilinears combine the baryon pairs 1–4, 2–5, and 3–6, as shown in Equation (70). For the other 30 Wick contractions, the resulting potential is not fitting to the form of Equation (70), because the wrong baryon pairs are connected in a separate spin space. Hence, an appropriate exchange of the spin wave functions in the final state has to be performed. This is achieved by multiplying the potential with the well-known spin-exchange operators $P_{ij}^{(\sigma )}=\frac{1}{2}(𝟙+{\overrightarrow{\sigma }}_i\cdot {\overrightarrow{\sigma }}_j)$. Furthermore, additional minus signs arise from the interchange of anti-commuting baryon fields. The full potential is then obtained by adding up all 36 contributions to the potential. One obtains a potential that fulfills automatically the generalized Pauli principle and that is fully anti-symmetrized.

In order to obtain a minimal set of Lagrangian terms of the final potential matrix have been eliminated until the rank of the final potential matrix (consisting of multiple Lagrangian terms and the spin structures in Equation 69) matches the number of terms in the Lagrangian. The minimal non-relativistic six-baryon contact Lagrangian is [120]

$\begin{array}{l}{L}=-C_1\langle {\overline{B}}_a{\overline{B}}_b{\overline{B}}_c{B}_a{B}_b{B}_c\rangle \\ +C_2\langle {\overline{B}}_a{\overline{B}}_b{B}_a{\overline{B}}_c{B}_b{B}_c\rangle \\ -C_3\langle {\overline{B}}_a{\overline{B}}_b{B}_a{B}_b{\overline{B}}_c{B}_c\rangle \\ +C_4\langle {\overline{B}}_a{B}_a{\overline{B}}_b{B}_b{\overline{B}}_c{B}_c\rangle \\ -C_5\langle {\overline{B}}_a{\overline{B}}_b{B}_a{B}_b\rangle \langle {\overline{B}}_c{B}_c\rangle \\ -C_6(\langle {\overline{B}}_a{\overline{B}}_b{\overline{B}}_c{B}_a{({\sigma }^{i}B)}_b{({\sigma }^{i}B)}_c\rangle \\ +\langle {\overline{B}}_c{\overline{B}}_b{\overline{B}}_a{({\sigma }^{i}B)}_c{({\sigma }^{i}B)}_b{B}_a\rangle )\\ +C_7(\langle {\overline{B}}_a{\overline{B}}_b{B}_a{\overline{B}}_c{({\sigma }^{i}B)}_b{({\sigma }^{i}B)}_c\rangle \\ +\langle {\overline{B}}_c{\overline{B}}_b{({\sigma }^{i}B)}_c{\overline{B}}_a{({\sigma }^{i}B)}_b{B}_a\rangle )\\ -C_8(\langle {\overline{B}}_a{\overline{B}}_b{B}_a{({\sigma }^{i}B)}_b{\overline{B}}_c{({\sigma }^{i}B)}_c\rangle \\ +\langle {\overline{B}}_b{\overline{B}}_a{({\sigma }^{i}B)}_b{B}_a{\overline{B}}_c{({\sigma }^{i}B)}_c\rangle )\\ +C_9\langle {\overline{B}}_a{B}_a{\overline{B}}_b{({\sigma }^{i}B)}_b{\overline{B}}_c{({\sigma }^{i}B)}_c\rangle \\ -C_{10}(\langle {\overline{B}}_a{\overline{B}}_b{B}_a{({\sigma }^{i}B)}_b\rangle \langle {\overline{B}}_c{({\sigma }^{i}B)}_c\rangle \\ +\langle {\overline{B}}_b{\overline{B}}_a{({\sigma }^{i}B)}_b{B}_a\rangle \langle {\overline{B}}_c{({\sigma }^{i}B)}_c\rangle )\\ -C_{11}\langle {\overline{B}}_a{\overline{B}}_b{\overline{B}}_c{({\sigma }^{i}B)}_a{B}_b{({\sigma }^{i}B)}_c\rangle \\ +C_{12}\langle {\overline{B}}_a{\overline{B}}_b{({\sigma }^{i}B)}_a{\overline{B}}_c{B}_b{({\sigma }^{i}B)}_c\rangle \\ -C_{13}\langle {\overline{B}}_a{\overline{B}}_b{({\sigma }^{i}B)}_a{({\sigma }^{i}B)}_b{\overline{B}}_c{B}_c\rangle \\ -C_{14}\langle {\overline{B}}_a{\overline{B}}_b{({\sigma }^{i}B)}_a{({\sigma }^{i}B)}_b\rangle \langle {\overline{B}}_c{B}_c\rangle \\ -\text{i }{ϵ}^{ijk}{C}_{15}\langle {\overline{B}}_a{\overline{B}}_b{\overline{B}}_c{({\sigma }^{i}B)}_a{({\sigma }^{j}B)}_b{({\sigma }^{k}B)}_c\rangle \\ +\text{i }{ϵ}^{ijk}{C}_{16}\langle {\overline{B}}_a{\overline{B}}_b{({\sigma }^{i}B)}_a{\overline{B}}_c{({\sigma }^{j}B)}_b{({\sigma }^{k}B)}_c\rangle \\ -\text{i }{ϵ}^{ijk}{C}_{17}\langle {\overline{B}}_a{\overline{B}}_b{({\sigma }^{i}B)}_a{({\sigma }^{j}B)}_b{\overline{B}}_c{({\sigma }^{k}B)}_c\rangle \\ +\text{i }{ϵ}^{ijk}{C}_{18}\langle {\overline{B}}_a{({\sigma }^{i}B)}_a{\overline{B}}_b{({\sigma }^{j}B)}_b{\overline{B}}_c{({\sigma }^{k}B)}_c\rangle ,& (71)\end{array}$

with vector indices i, j, k and two-component spinor indices a, b, c. In total 18 low-energy constants C₁…C₁₈ are present. The low-energy constant E of the six-nucleon contact term (cf. [78]) can be expressed through these LECs by E = 2(C₄ − C₉).

As in the two-body sector, group theoretical considerations can deliver valuable constrains on the resulting potentials. In flavor space the three octet baryons form the 512-dimensional tensor product 8⊗8⊗8, which decomposes into the following irreducible SU(3) representations

$\begin{array}{l}8\otimes 8\otimes 8=\\ 64\oplus {(35\oplus \overline{35})}_2\oplus {27}_6\oplus {(10\oplus \overline{10})}_4\oplus 8_8\oplus 1_2,& (72)\end{array}$

where the multiplicity of an irreducible representations is denoted by subscripts. In spin space one obtain for the product of three doublets

$\begin{array}{ll}2\otimes 2\otimes 2=2_2\oplus 4.& (73)\end{array}$

Transitions are only allowed between irreducible representations of the same type. Analogous to Dover and Feshbach [145] for the two-baryon sector, the contributions of different irreducible representations to three-baryon multiplets in Table 4 can be established. At leading order only transitions between S-waves are possible, since the potentials are momentum-independent. Due to the Pauli principle the totally symmetric spin-quartet 4 must combine with the totally antisymmetric part of 8⊗8⊗8 in flavor space,

$\begin{array}{ll}{\text{Alt}}_3(8)={56}_a={27}_a+{10}_a+{\overline{10}}_a+8_a+1_a.& (74)\end{array}$

It follows, that these totally antisymmetric irreducible representations are present only in states with total spin 3/2. The totally symmetric part of 8⊗8⊗8 leads to

$\begin{array}{ll}{\text{Sym}}_3(8)={120}_s={64}_s+{27}_s+{10}_s+{\overline{10}}_s+8_s+1_s.& (75)\end{array}$

However, the totally symmetric flavor part has no totally antisymmetric counterpart in spin space, hence these representations do not contribute to the potential. In Table 4, these restrictions obtained by the generalized Pauli principle have already be incorporated. The potentials of Petschauer et al. [120] (decomposed in isospin basis and partial waves) fulfill the restrictions of Table 4. For example the combination of LECs related to the representation $\overline{35}$ is present in the NNN interaction as well as in the Ξ Ξ Σ (−5, 2) interaction.

TABLE 4

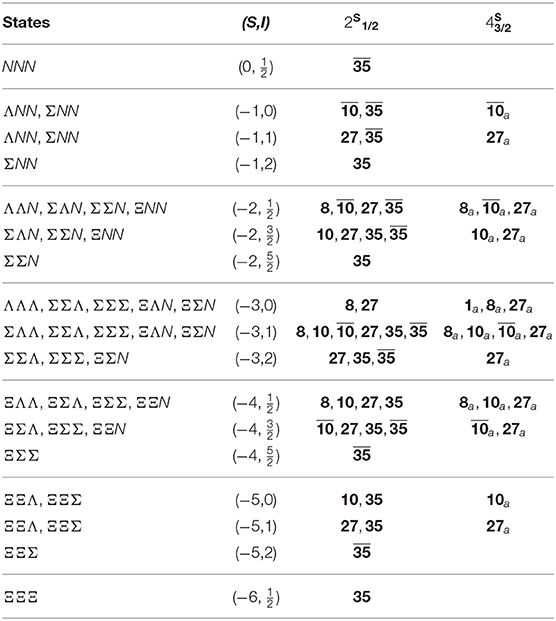
Table 4. Irreducible representations for three-baryon states with strangeness S and isospin I in partial waves |^2S+1L_J〉, with the total spin $S=\frac{1}{2},\frac{3}{2}$, the angular momentum L = 0, and the total angular momentum $J=\frac{1}{2},\frac{3}{2}$ [120].

4.2. One-Meson Exchange Component

The meson-baryon couplings in the one-meson exchange diagram of Figure 8 emerges from the leading-order chiral Lagrangian ${{L}}_{\text{B}}^{(1)}$ (see Equation 56). The other vertex involves four baryon fields and one pseudoscalar-meson field. In Petschauer et al. [120], an overcomplete set of terms for the corresponding Lagrangian has been constructed. In order to obtain the complete minimal Lagrangian from the overcomplete set of terms, the matrix elements of the process B₁B₂ → B₃B₄ϕ₁ has been considered in Petschauer et al. [120]. The corresponding spin operators in the potential are

$\begin{array}{ll}{\overrightarrow{\sigma }}_1·\overrightarrow{q},{\overrightarrow{\sigma }}_2·\overrightarrow{q},\text{ i}({\overrightarrow{\sigma }}_1\times {\overrightarrow{\sigma }}_2)·\overrightarrow{q},& (76)\end{array}$

where $\overrightarrow{q}$ denotes the momentum of the emitted meson. Redundant term are removed until the rank of the potential matrix formed by all transitions and spin operators matches the number of terms in the Lagrangian. One ends up with the minimal non-relativistic chiral Lagrangian

$\begin{array}{l}{L}=D_1/f_0\langle {\overline{B}}_a({\nabla }^i\varphi )B_a{\overline{B}}_b{({\sigma }^{i}B)}_b\rangle \\ +D_2/f_0(\langle {\overline{B}}_a{B}_a({\nabla }^i\varphi ){\overline{B}}_b{({\sigma }^{i}B)}_b\rangle \\ +\langle {\overline{B}}_a{B}_a{\overline{B}}_b{({\sigma }^{i}B)}_b({\nabla }^i\varphi )\rangle )\\ +D_3/f_0\langle {\overline{B}}_b({\nabla }^i\varphi ){({\sigma }^{i}B)}_b{\overline{B}}_a{B}_a\rangle \\ -D_4/f_0(\langle {\overline{B}}_a({\nabla }^i\varphi ){\overline{B}}_b{B}_a{({\sigma }^{i}B)}_b\rangle \\ +\langle {\overline{B}}_b{\overline{B}}_a{({\sigma }^{i}B)}_b({\nabla }^i\varphi )B_a\rangle )\\ -D_5/f_0(\langle {\overline{B}}_a{\overline{B}}_b({\nabla }^i\varphi )B_a{({\sigma }^{i}B)}_b\rangle \\ +\langle {\overline{B}}_b{\overline{B}}_a({\nabla }^i\varphi ){({\sigma }^{i}B)}_b{B}_a\rangle )\\ -D_6/f_0(\langle {\overline{B}}_b({\nabla }^i\varphi ){\overline{B}}_a{({\sigma }^{i}B)}_b{B}_a\rangle \\ +\langle {\overline{B}}_a{\overline{B}}_b{B}_a({\nabla }^i\varphi ){({\sigma }^{i}B)}_b\rangle )\\ -D_7/f_0(\langle {\overline{B}}_a{\overline{B}}_b{B}_a{({\sigma }^{i}B)}_b({\nabla }^i\varphi )\rangle \\ +\langle {\overline{B}}_b{\overline{B}}_a{({\sigma }^{i}B)}_b{B}_a({\nabla }^i\varphi )\rangle )\\ +D_8/f_0\langle {\overline{B}}_a({\nabla }^i\varphi )B_a\rangle \langle {\overline{B}}_b{({\sigma }^{i}B)}_b\rangle \\ +D_9/f_0\langle {\overline{B}}_a{B}_a({\nabla }^i\varphi )\rangle \langle {\overline{B}}_b{({\sigma }^{i}B)}_b\rangle \\ +D_{10}/f_0\langle {\overline{B}}_b({\nabla }^i\varphi ){({\sigma }^{i}B)}_b\rangle \langle {\overline{B}}_a{B}_a\rangle \\ +\text{i }{ϵ}^{ijk}{D}_{11}/f_0\langle {\overline{B}}_a{({\sigma }^{i}B)}_a({\nabla }^k\varphi ){\overline{B}}_b{({\sigma }^{j}B)}_b\rangle \\ -\text{i }{ϵ}^{ijk}{D}_{12}/f_0(\langle {\overline{B}}_a({\nabla }^k\varphi ){\overline{B}}_b{({\sigma }^{i}B)}_a{({\sigma }^{j}B)}_b\rangle \\ -\langle {\overline{B}}_b{\overline{B}}_a{({\sigma }^{j}B)}_b({\nabla }^k\varphi ){({\sigma }^{i}B)}_a\rangle )\\ -\text{i }{ϵ}^{ijk}{D}_{13}/f_0\langle {\overline{B}}_a{\overline{B}}_b({\nabla }^k\varphi ){({\sigma }^{i}B)}_a{({\sigma }^{j}B)}_b\rangle \\ -\text{i }{ϵ}^{ijk}{D}_{14}/f_0\langle {\overline{B}}_a{\overline{B}}_b{({\sigma }^{i}B)}_a{({\sigma }^{j}B)}_b({\nabla }^k\varphi )\rangle ,& (77)\end{array}$

with two-component spinor indices a and b and 3-vector indices i, j, and k. For all possible strangeness sectors S = −4…0 one obtains in total 14 low-energy constants D₁…D₁₄. The low-energy constant of the corresponding vertex in the nucleonic sector D is related to the LECs above by D = 4(D₁ − D₃ + D₈ − D₁₀).²

To obtain the 3BF one-meson-exchange diagram, the generic one-meson-exchange diagram in Figure 9A can be investigated. It involves the baryons i, j, k in the initial state, the baryons l, m, n in the final state and an exchanged meson ϕ. The contact vertex on the right is pictorially separated into two parts to indicate that baryon j–m and k–n are in the same bilinear. The spin spaces corresponding to the baryon bilinears are denoted by A, B, C.

FIGURE 9

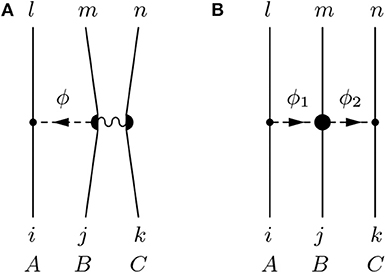
Figure 9. Generic meson-exchange diagrams. The wiggly line symbolized the four-baryon contact vertex, to illustrate the baryon bilinears. (A) Generic one-meson exchange diagram. (B) Generic two-meson exchange diagram.

On obtains a generic potential of the form

$\begin{array}{ll}V=\frac{1}{2f_0^2}\frac{{\overrightarrow{\sigma }}_A·{\overrightarrow{q}}_{li}}{{\overrightarrow{q}}_{li}^2+m_{\varphi }^2}{\displaystyle (N_1{\overrightarrow{\sigma }}_C·{\overrightarrow{q}}_{li}+N_2\text{i }({\overrightarrow{\sigma }}_B\times {\overrightarrow{\sigma }}_C)·{\overrightarrow{q}}_{li})},& (78)\end{array}$

with the momentum transfer ${\overrightarrow{q}}_{li}={\overrightarrow{p}}_l-{\overrightarrow{p}}_i$ carried by the exchanged meson. The constants N₁ and N₂ are linear combinations of low-energy constants.

The complete one-meson exchange three-baryon potential for the process B₁B₂B₃ → B₄B₅B₆ is finally obtained by summing up the 36 permutations of initial-state and final-state baryons for a fixed meson and by summing over all mesons $\varphi \in \left\{{\pi }^0,{\pi }^{+},{\pi }^{-},K^{+},K^{-},K^0,{\bar{K}}^0,\eta \right\}$. Additional minus signs arise from interchanging fermions and some diagrams need to be multiplied by spin exchange operators in order to be consistent with the form set up in Equation (70). As defined before, the baryons B₁, B₂, and B₃ belong to the spin-spaces 1, 2, and 3, respectively.

4.3. Two-Meson Exchange Component

The two-meson exchange diagram of Figure 8 includes the vertex arising from the Lagrangian in Equation (56). Furthermore the well-known ${O}(q^2)$ meson-baryon Lagrangian [139] is necessary. For the two-meson exchange diagram of Figure 8 we need in addition to the Lagrangian in Equation (56) the well-known ${O}(q^2)$ meson-baryon Lagrangian [139]. The relevant terms are [140]

$\begin{array}{l}{L}=b_D\langle \bar{B}\{{\chi }_{+},B\}\rangle +b_F\langle \bar{B}[{\chi }_{+},B]\rangle +b_0\langle \bar{B}B\rangle \langle {\chi }_{+}\rangle \\ +b_1\langle \bar{B}[u^{\mu },[u_{\mu },B]]\rangle +b_2\langle \bar{B}\{u^{\mu },\{u_{\mu },B\}\}\rangle \\ +b_3\langle \bar{B}\{u^{\mu },[u_{\mu },B]\}\rangle +b_4\langle \bar{B}B\rangle \langle u^{\mu }{u}_{\mu }\rangle \\ +\text{i }{d}_1\langle \bar{B}\{[u^{\mu },u^{\nu }],{\sigma }_{\mu \nu }B\}\rangle \\ +\text{i }{d}_2\langle \bar{B}[[u^{\mu },u^{\nu }],{\sigma }_{\mu \nu }B]\rangle \\ +\text{i }{d}_3\langle \bar{B}{u}^{\mu }\rangle \langle u^{\nu }{\sigma }_{\mu \nu }B\rangle ,& (79)\end{array}$

with $u_{\mu }=-\frac{1}{f_0}{\partial }_{\mu }\varphi +{O}({\varphi }^3)$ and ${\chi }_{+}=2\chi -\frac{1}{4f_0^2}\{\varphi ,\{\varphi ,\chi \}\}+{O}({\varphi }^4)$, where

$\begin{array}{ll}\chi =\left(\begin{array}{ccc}{m}_{\pi }^2& 0& 0\\ 0& m_{\pi }^2& 0\\ 0& 0& 2m_K^2-m_{\pi }^2\end{array}\right).& (80)\end{array}$

The terms proportional to b_D, b_F, b₀ break explicitly SU(3) flavor symmetry, because of different meson masses m_K ≠ m_π. The LECs of Equation (79) are related to the conventional LECs of the nucleonic sector by [155, 156]

$\begin{array}{l}{c}_1=\frac{1}{2}(2b_0+b_D+b_F),\\ c_3=b_1+b_2+b_3+2b_4,\\ c_4=4(d_1+d_2).& (81)\end{array}$

To obtain the potential of the two-meson exchange diagram of Figure 8, the generic diagram of Figure 9B can be considered. It includes the baryons i, j, k in the initial state, the baryons l, m, n in the final state, and two exchanged mesons ϕ₁ and ϕ₂. The spin spaces corresponding to the baryon bilinears are denoted by A, B, C and they are aligned with the three initial baryons. The momentum transfers carried by the virtual mesons are ${\overrightarrow{q}}_{li}={\overrightarrow{p}}_l-{\overrightarrow{p}}_i$ and ${\overrightarrow{q}}_{nk}={\overrightarrow{p}}_n-{\overrightarrow{p}}_k$. One obtains the generic transition amplitude

$\begin{array}{l}V=-\frac{1}{4f_0^4}\frac{{\overrightarrow{\sigma }}_A·{\overrightarrow{q}}_{li}{\overrightarrow{\sigma }}_C·{\overrightarrow{q}}_{nk}}{({\overrightarrow{q}}_{li}^2+m_{{\varphi }_1}^2)({\overrightarrow{q}}_{nk}^2+m_{{\varphi }_2}^2)}\\ \times (N_1^{\prime }+N_2^{\prime }{\overrightarrow{q}}_{li}·{\overrightarrow{q}}_{nk}+N_3^{\prime }\text{i }({\overrightarrow{q}}_{li}\times {\overrightarrow{q}}_{nk})·{\overrightarrow{\sigma }}_B),& (82)\end{array}$

with $N_i^{\prime }$ linear combinations of the low-energy constants of the three involved vertices. The complete three-body potential for a transition B₁B₂B₃ → B₄B₅B₆ can be calculated by summing up the contributions of all 18 distinguable Feynman diagrams and by summing over all possible exchanged mesons. If the baryon lines are not in the configuration 1–4, 2–5, and 3–6 additional (negative) spin-exchange operators have to be included.

4.4. ΛNN Three-Baryon Potentials

In order to give a concrete example the explicit expression for the ΛNN three-body potentials in spin-, isospin-, and momentum-space are presented for the contact interaction and one- and two-pion exchange contributions [120]. The potentials are calculated in the particle basis and afterwards rewritten into isospin operators.

The ΛNN contact interaction is described by the following potential

$\begin{array}{l}{V}_{\text{ct}}^{\Lambda NN}=C_1^{\prime }(𝟙-{\overrightarrow{\sigma }}_2·{\overrightarrow{\sigma }}_3)(3+{\overrightarrow{\tau }}_2·{\overrightarrow{\tau }}_3)\\ +C_2^{\prime }{\overrightarrow{\sigma }}_1·({\overrightarrow{\sigma }}_2+{\overrightarrow{\sigma }}_3)(𝟙-{\overrightarrow{\tau }}_2·{\overrightarrow{\tau }}_3)\\ +C_3^{\prime }(3+{\overrightarrow{\sigma }}_2·{\overrightarrow{\sigma }}_3)(𝟙-{\overrightarrow{\tau }}_2·{\overrightarrow{\tau }}_3),& (83)\end{array}$

where the primed constants are linear combinations of C₁…C₁₈ of Equation (71). The symbols $\overrightarrow{\sigma }$ and $\overrightarrow{\tau }$ denote the usual Pauli matrices in spin and isospin space. The constant $C_1^{\prime }$ appears only in the transition with total isospin I = 1. The constants $C_2^{\prime }$ and $C_3^{\prime }$ contribute for total isospin I = 0.

For the ΛNN one-pion exchange three-body potentials, various diagrams are absent due to the vanishing ΛΛπ-vertex, which is forbidden by isospin symmetry. One obtains the following potential

$\begin{array}{l}{V}_{\text{OPE}}^{\Lambda NN}=-\frac{g_A}{2f_0^2}\\ \times (\frac{{\overrightarrow{\sigma }}_2·{\overrightarrow{q}}_{52}}{{\overrightarrow{q}}_{52}^2+m_{\pi }^2}{\overrightarrow{\tau }}_2·{\overrightarrow{\tau }}_3[(D_1^{\prime }{\overrightarrow{\sigma }}_1+D_2^{\prime }{\overrightarrow{\sigma }}_3)·{\overrightarrow{q}}_{52}]\\ +\frac{{\overrightarrow{\sigma }}_3·{\overrightarrow{q}}_{63}}{{\overrightarrow{q}}_{63}^2+m_{\pi }^2}{\overrightarrow{\tau }}_2·{\overrightarrow{\tau }}_3[(D_1^{\prime }{\overrightarrow{\sigma }}_1+D_2^{\prime }{\overrightarrow{\sigma }}_2)·{\overrightarrow{q}}_{63}]\\ +P_{23}^{(\sigma )}{P}_{23}^{(\tau )}{P}_{13}^{(\sigma )}\frac{{\overrightarrow{\sigma }}_2·{\overrightarrow{q}}_{62}}{{\overrightarrow{q}}_{62}^2+m_{\pi }^2}{\overrightarrow{\tau }}_2·{\overrightarrow{\tau }}_3\\ \times [-\frac{D_1^{\prime }+D_2^{\prime }}{2}({\overrightarrow{\sigma }}_1+{\overrightarrow{\sigma }}_3)·{\overrightarrow{q}}_{62}\\ +\frac{D_1^{\prime }-D_2^{\prime }}{2}\text{i }({\overrightarrow{\sigma }}_3\times {\overrightarrow{\sigma }}_1)·{\overrightarrow{q}}_{62}]\\ +P_{23}^{(\sigma )}{P}_{23}^{(\tau )}{P}_{12}^{(\sigma )}\frac{{\overrightarrow{\sigma }}_3·{\overrightarrow{q}}_{53}}{{\overrightarrow{q}}_{53}^2+m_{\pi }^2}{\overrightarrow{\tau }}_2·{\overrightarrow{\tau }}_3\\ \times [-\frac{D_1^{\prime }+D_2^{\prime }}{2}({\overrightarrow{\sigma }}_1+{\overrightarrow{\sigma }}_2)·{\overrightarrow{q}}_{53}\\ -\frac{D_1^{\prime }-D_2^{\prime }}{2}\text{i }({\overrightarrow{\sigma }}_1\times {\overrightarrow{\sigma }}_2)·{\overrightarrow{q}}_{53}\left]\right),& (84)\end{array}$

with only two constants $D_1^{\prime }$ and $D_2^{\prime }$, which are linear combinations of the constants D₁…D₁₄. Exchange operators in spin space $P_{ij}^{(\sigma )}=\frac{1}{2}(𝟙+{\overrightarrow{\sigma }}_i·{\overrightarrow{\sigma }}_j)$ and in isospin space $P_{ij}^{(\tau )}=\frac{1}{2}(𝟙+{\overrightarrow{\tau }}_i·{\overrightarrow{\tau }}_j)$ have been introduced.

The ΛNN three-body interaction generated by two-pion exchange is given by

$\begin{array}{l}{V}_{\text{TPE}}^{\Lambda NN}=\frac{g_A^2}{3f_0^4}\frac{{\overrightarrow{\sigma }}_3·{\overrightarrow{q}}_{63}{\overrightarrow{\sigma }}_2·{\overrightarrow{q}}_{52}}{({\overrightarrow{q}}_{63}^2+m_{\pi }^2)({\overrightarrow{q}}_{52}^2+m_{\pi }^2)}{\overrightarrow{\tau }}_2·{\overrightarrow{\tau }}_3\\ \times (-(3b_0+b_D)m_{\pi }^2+(2b_2+3b_4){\overrightarrow{q}}_{63}·{\overrightarrow{q}}_{52})\\ -P_{23}^{(\sigma )}{P}_{23}^{(\tau )}\frac{g_A^2}{3f_0^4}\frac{{\overrightarrow{\sigma }}_3·{\overrightarrow{q}}_{53}{\overrightarrow{\sigma }}_2·{\overrightarrow{q}}_{62}}{({\overrightarrow{q}}_{53}^2+m_{\pi }^2)({\overrightarrow{q}}_{62}^2+m_{\pi }^2)}{\overrightarrow{\tau }}_2·{\overrightarrow{\tau }}_3\\ \times (-(3b_0+b_D)m_{\pi }^2+(2b_2+3b_4){\overrightarrow{q}}_{53}·{\overrightarrow{q}}_{62}).& (85)\end{array}$

Due to the vanishing of the ΛΛπ vertex, only those two diagrams contribute, where the (final and initial) Λ hyperon are attached to the central baryon line.

4.5. Three-Baryon Force Through Decuplet Saturation

Low-energy two- and three-body interactions derived from SU(2) χEFT are used consistently in combination with each other in nuclear few- and many-body calculations. The a priori unknown low-energy constants are fitted, for example, to NN scattering data and 3N observables such as 3-body binding energies [78]. Some of these LECs are, however, large compared to their order of magnitude as expected from the hierarchy of nuclear forces in Figure 5. This feature has its physical origin in strong couplings of the πN-system to the low-lying Δ(1232)-resonance. It is therefore, natural to include the Δ(1232)-isobar as an explicit degree of freedom in the chiral Lagrangian (cf. [157–159]). The small mass difference between nucleons and deltas (293 MeV) introduces a small scale, which can be included consistently in the chiral power counting scheme and the hierarchy of nuclear forces. The dominant parts of the three-nucleon interaction mediated by two-pion exchange at NNLO are then promoted to NLO through the delta contributions. The appearance of the inverse mass splitting explains the large numerical values of the corresponding LECs [13, 160].

In SU(3) χEFT the situation is similar. In systems with strangeness S = −1 like ΛNN, resonances such as the spin-3/2 Σ^*(1385)-resonance play a similar role as the Δ in the NNN system, as depicted in Figure 4 on the right side. The small decuplet-octet mass splitting (in the chiral limit), Δ: = M₁₀ − M₈, is counted together with external momenta and meson masses as ${O}(q)$ and thus parts of the NNLO three-baryon interaction are promoted to NLO by the explicit inclusion of the baryon decuplet, as illustrated in Figure 10. It is therefore likewise compelling to treat the three-baryon interaction together with the NLO hyperon-nucleon interaction of section 3. Note that in the nucleonic sector, only the two-pion exchange diagram with an intermediate Δ-isobar is allowed. Other diagrams are forbidden due to the Pauli principle, as we will show later. For three flavors more particles are involved and, in general, also the other diagrams (contact and one-meson exchange) with intermediate decuplet baryons in Figure 10 appear.

FIGURE 10

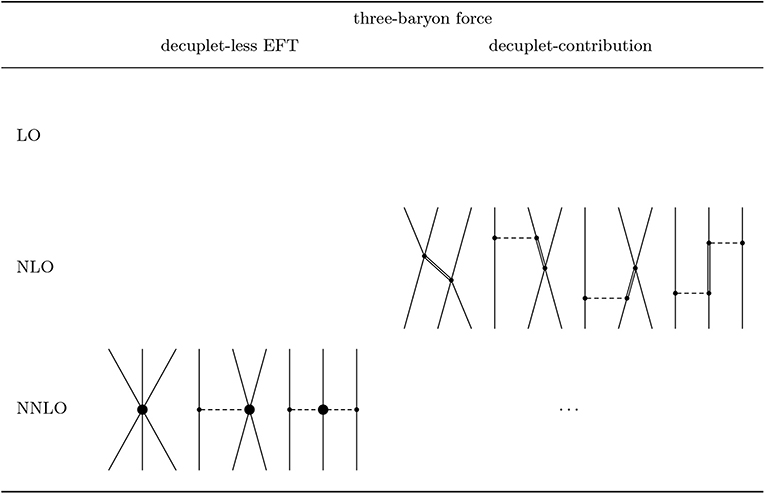
Figure 10. Hierarchy of three-baryon forces with explicit introduction of the baryon decuplet (represented by double lines).

The large number of unknown LECs presented in the previous subsections is related to the multitude of three-baryon multiplets, with strangeness ranging from 0 to −6. For selected processes only a small subset of these constants contributes as has been exemplified for the ΛNN three-body interaction. In this section we present the estimation of these LECs by resonance saturation as done in Petschauer et al. [121].

The leading-order non-relativistic interaction Lagrangian between octet and decuplet baryons (see, e.g., [161]) is

$\begin{array}{l}{L}=\frac{C}{f_0}{\displaystyle \sum _{a,b,c,d,e=1}^3}{ϵ}_{abc}({\bar{T}}_{ade}{\overrightarrow{S}}^{†}·\left(\overrightarrow{\nabla }{\varphi }_{db}\right)B_{ec}\hfill \\ \hfill +{\bar{B}}_{ce}\overrightarrow{S}·\left(\overrightarrow{\nabla }{\varphi }_{bd}\right)T_{ade}),& (86)\end{array}$

where the decuplet baryons are represented by the totally symmetric three-index tensor T (cf. Equation 23). At this order only a single LEC C appears. Typically the (large-N_c) value $C=\frac{3}{4}{g}_A\approx 1$ is used, as it leads to a decay width Γ(Δ → πN) = 110.6 MeV that is in good agreement with the empirical value of Γ(Δ → πN) = (115 ± 5) MeV [158]. The spin $\frac{1}{2}$ to $\frac{3}{2}$ transition operators $\overrightarrow{S}$ connect the two-component spinors of octet baryons with the four-component spinors of decuplet baryons (see e.g., [162]). In their explicit form they are given as 2 × 4 transition matrices

$\begin{array}{l}{S}_1=\left(\begin{array}{cccc}-\frac{1}{\sqrt{2}}& 0& \frac{1}{\sqrt{6}}& 0\\ 0& -\frac{1}{\sqrt{6}}& 0& \frac{1}{\sqrt{2}}\end{array}\right),\\ S_2=\left(\begin{array}{cccc}-\frac{i}{\sqrt{2}}& 0& -\frac{i}{\sqrt{6}}& 0\\ 0& -\frac{i}{\sqrt{6}}& 0& -\frac{i}{\sqrt{2}}\end{array}\right),\\ S_3=\left(\begin{array}{cccc}0& \sqrt{\frac{2}{3}}& 0& 0\\ 0& 0& \sqrt{\frac{2}{3}}& 0\end{array}\right).& (87)\end{array}$

These operators fulfill the relation $S_i{S_j}^{†}=\frac{1}{3}(2{\delta }_{ij}-\text{i}{ϵ}_{ijk}{\sigma }_k)$.

A non-relativistic B^*BBB Lagrangian with a minimal set of terms is given by [121]:

$\begin{array}{l}{L}=H_1{\displaystyle \sum _{\begin{array}{c}a,b,c,\\ d,e,f=1\end{array}}^3}{ϵ}_{abc}\left[\right({\bar{T}}_{ade}{\overrightarrow{S}}^{†}{B}_{db})·\left({\bar{B}}_{fc}\overrightarrow{\sigma }{B}_{ef}\right)\\ +\left({\bar{B}}_{bd}\overrightarrow{S}{T}_{ade}\right)·\left({\bar{B}}_{fe}\overrightarrow{\sigma }{B}_{cf}\right)]\\ +H_2{\displaystyle \sum _{\begin{array}{c}a,b,c,\\ d,e,f=1\end{array}}^3}{ϵ}_{abc}\left[\right({\bar{T}}_{ade}{\overrightarrow{S}}^{†}{B}_{fb})·\left({\bar{B}}_{dc}\overrightarrow{\sigma }{B}_{ef}\right)\\ +\left({\bar{B}}_{bf}\overrightarrow{S}{T}_{ade}\right)·\left({\bar{B}}_{fe}\overrightarrow{\sigma }{B}_{cd}\right)],& (88)\end{array}$

with the LECs H₁ and H₂. Again one can employ group theory to justify the number of two constants for a transition BB → B^*B. In flavor space the two initial octet baryons form the tensor product 8⊗8, and in spin space they form the product 2⊗2. These tensor products can be decomposed into irreducible representations:

$\begin{array}{l}8\otimes 8=\underset{\text{symmetric}}{\underbrace{27\oplus 8_s\oplus 1}}\oplus \underset{\text{antisymmetric}}{\underbrace{10\oplus 10^{\ast }\oplus 8_a}},\\ 2\otimes 2=1_a\oplus 3_s.& (89)\end{array}$

In the final state, having a decuplet and an octet baryon, the situation is similar:

$\begin{array}{l}10\otimes 8=35\oplus 27\oplus 10\oplus 8,\\ 4\otimes 2=3\oplus 5.& (90)\end{array}$

As seen in the previous sections, at leading order only S-wave transitions occur, as no momenta are involved. Transitions are only allowed between the same types of irreducible (flavor and spin) representations. Therefore, in spin space the representation 3 has to be chosen. Because of the Pauli principle in the initial state, the symmetric 3 in spin space combines with the antisymmetric representations 10, 10*, 8_a in flavor space. But only 10 and 8_a have a counterpart in the final state flavor space. This number of two allowed transitions matches the number of two LECs in the minimal Lagrangian. Another interesting observation can be made from Equations (89) and (90). For NN states only the representations 27 and 10^* can contribute, as can be seen, e.g., in Table 3. But these representations combine either with the wrong spin, or have no counterpart in the final state. Therefore, NN → ΔN transitions in S-waves are not allowed because of the Pauli principle.

Having the above two interaction types at hand, one can estimate the low-energy constants of the leading three-baryon interaction by decuplet saturation using the diagrams shown in Figure 10. At this order, where no loops are involved, one just needs to evaluate the diagrams with an intermediate decuplet baryon and the diagrams without decuplet baryons and compare them with each other.

In order to estimate the LECs of the six-baryon contact Lagrangian of Equation (71), one can consider the process B₁B₂B₃ → B₄B₅B₆ as depicted in Figure 11A. The left side of Figure 11A has already been introduced in the previous subsection and can be obtained by performing all 36 Wick contractions. For the diagrams on right side of Figure 11A the procedure is similar. After summing over all intermediate decuplet baryons B^*, the full three-body potential of all possible combinations of baryons on the left side of Figure 11A can be compared with the ones on the right side. In the end the 18 LECs of the six-baryon contact Lagrangian C₁, …, C₁₈ of Equation (71) can be expressed as linear combinations of the combinations $H_1^2$, $H_2^2$ and H₁H₂ and are proportional to the inverse average decuplet-octet baryon mass splitting 1/Δ [121].

FIGURE 11

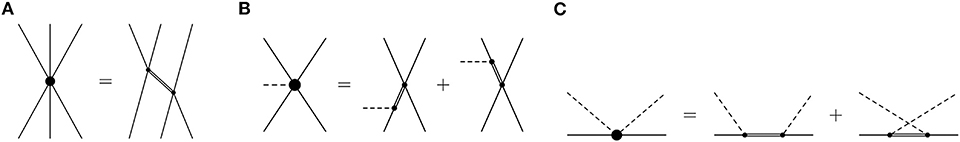
Figure 11. Saturation via decuplet resonances. (A) Saturation of the six-baryon contact interaction. (B) Saturation of the BB → BBϕ vertex. (C) Saturation of the NLO baryon-meson vertex.

Since we are at the leading order only tree-level diagrams are involved and we can estimate the LECs of the one-meson-exchange part of the three-baryon forces already on the level of the vertices, as depicted in Figure 11B. We consider the transition matrix elements of the process B₁B₂ → B₃B₄ϕ and start with the left side of Figure 11B. After doing all possible Wick contractions, summing over all intermediate decuplet baryons, and comparing the left side of Figure 11B with the right hand side for all combinations of baryons and mesons, the LECs can be estimated. The LECs of the minimal non-relativistic chiral Lagrangian for the four-baryon vertex including one meson of Equation (77) D₁, …, D₁₄ are then proportional to C/Δ and to linear combinations of H₁ and H₂ [121].

The last class of diagrams is the three-body interaction with two-meson exchange. As done for the one-meson exchange, the unknown LECs can be saturated directly on the level of the vertex and one can consider the process B₁ϕ₁ → B₂ϕ₂ as shown in Figure 11C. A direct comparison of the transition matrix elements for all combinations of baryons and mesons after summing over all intermediate decuplet baryons B^* leads to the following contributions to the LECs of the meson-baryon Lagrangian in Equation (79):

$\begin{array}{l}{b}_D=0,b_F=0,b_0=0,\\ b_1=\frac{7C^2}{36\Delta },b_2=\frac{C^2}{4\Delta },b_3=-\frac{C^2}{3\Delta },b_4=-\frac{C^2}{2\Delta },\\ d_1=\frac{C^2}{12\Delta },d_2=\frac{C^2}{36\Delta },d_3=-\frac{C^2}{6\Delta },& (91)\end{array}$

These findings are consistent with the Δ(1232) contribution to the LECs c₁, c₃, c₄ (see Equation 81) in the nucleonic sector [157, 160]:

$\begin{array}{ll}{c}_1=0,c_3=-2c_4=-\frac{g_A^2}{2\Delta }.& (92)\end{array}$

Employing the LECs obtained via decuplet saturation, the constants of the ΛNN interaction (contact interaction, one-pion and two-pion exchange) of section 4.4 can be evaluated:

$\begin{array}{l}{C}_1^{\prime }=C_3^{\prime }=\frac{{(H_1+3H_2)}^2}{72\Delta },C_2^{\prime }=0,\\ D_1^{\prime }=0,D_2^{\prime }=\frac{2C(H_1+3H_2)}{9\Delta },\\ 3b_0+b_D=0,2b_2+3b_4=-\frac{C^2}{\Delta }.& (93)\end{array}$

Obviously, the only unknown constant here is the combination $H^{\prime }=H_1+3H_2$. It is also interesting to see, that the (positive) sign of the constants $C_i^{\prime }$ for the contact interaction is already fixed, independently of the values of the two LECs H₁ and H₂.

4.6. Effective In-medium Two-Baryon Interaction

In this subsection we summarize how the effect of three-body force in the presence of a (hyper)nuclear medium can be incorporated in an effective baryon-baryon potential. In Holt et al. [163], the density-dependent corrections to the NN interaction have been calculated from the leading chiral three-nucleon forces. This work has been extended to the strangeness sector in Petschauer et al. [121]. In order to obtain an effective baryon-baryon interaction from the irreducible 3BFs in Figure 8, two baryon lines have been closed, which represents diagrammatically the sum over occupied states within the Fermi sea. Such a “medium insertion” is symbolized by short double lines on a baryon propagator. All types of diagrams arising this way are shown in Figure 12.

FIGURE 12

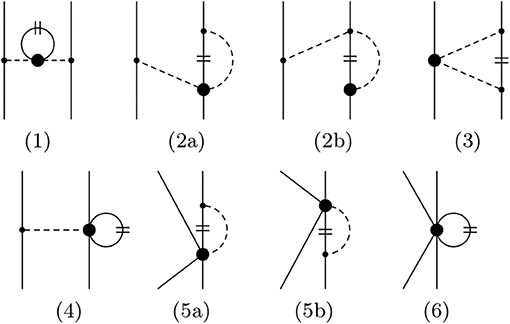
Figure 12. Effective two-baryon interaction from genuine three-baryon forces. Contributions arise from two-pion exchange (1), (2a), (2b), (3), one-pion exchange (4), (5a), (5b), and the contact interaction (6).

In Petschauer et al. [121], the calculation is restricted to the contact term and to the contributions from one- and two-pion exchange processes, as they are expected to be dominant. When computing the diagrams of Figure 8 the medium insertion corresponds to a factor $-2\pi \delta (k_0)\theta (k_f-|\overrightarrow{k}|)$. Furthermore, an additional minus sign comes from a closed fermion loop. The effective two-body interaction can also be calculated from the expressions for the three-baryon potentials of Petschauer et al. [120] via the relation

$\begin{array}{ll}{V}_{12}={\displaystyle \sum _B}{tr}_{{\sigma }_3}{\displaystyle {\int }_{\left|\overrightarrow{k}\right|\le k_f^B}}\frac{{\text{d}}^{3}k}{{(2\pi )}^3}{V}_{123},& (94)\end{array}$

where tr_σ3 denotes the spin trace over the third particle and where a summation over all baryon species B in the Fermi sea (with Fermi momentum $k_f^B$) is done.

As an example of such an effective interaction, we display the effective ΛN interaction in nuclear matter (with ρ_p ≠ ρ_n) derived in Petschauer et al. [121]. It is determined from two-pion-exchange, one-pion-exchange and contact ΛNN three-body forces. Only the expressions for the Λn potential are shown as the Λp potential can be obtained just by interchanging the Fermi momenta $k_f^p$ with $k_f^n$ (or the densities ρ_p with ρ_n) in the expressions for Λn. In the following formulas the sum over the contributions from the protons and neutrons in the Fermi sea is already employed. Furthermore, the values of the LECs are already estimated via decuplet saturation (see section 4.5). The topologies (1), (2a), and (2b) vanish here because of the non-existence of an isospin-symmetric ΛΛπ vertex. One obtains the density-dependent Λn potential in a nuclear medium

$\begin{array}{l}{V}_{\Lambda n}^{\text{med},\pi \pi }=\frac{C^2{g}_A^2}{12{\pi }^2{f}_0^4\Delta }\{\\ \frac{1}{4}[\frac{8}{3}(k_f^{n^3}+2k_f^{p^3})-4(q^2+2m^2){\tilde{\Gamma }}_0(p)-2q^2{\tilde{\Gamma }}_1(p)\\ +{(q^2+2m^2)}^2{\tilde{G}}_0(p,q)]\\ +\frac{\text{i }}{2}(\overrightarrow{q}\times \overrightarrow{p})·{\overrightarrow{\sigma }}_2(2{\tilde{\Gamma }}_0(p)+2{\tilde{\Gamma }}_1(p)\\ -(q^2+2m^2)({\tilde{G}}_0(p,q)+2{\tilde{G}}_1(p,q)))\},& (95)\end{array}$

$\begin{array}{ll}{V}_{\Lambda n}^{\text{med},\text{π}}=\frac{g_{A}C{H}^{\prime }}{54{\pi }^2{f}_0^2\Delta }(2({k_f^n}^3+2{k_f^p}^3)-3m^2{\tilde{\Gamma }}_0(p)),& (96)\end{array}$

$\begin{array}{ll}{V}_{\Lambda n}^{\text{med},\text{ct}}=\frac{{H{}^{\prime }}^2}{18\Delta }({\rho }_n+2{\rho }_p).& (97)\end{array}$

The different topologies related to two-pion exchange [(1), (2a), (2b), (3)] and one-pion exchange [(4), (5a), (5b)] have already been combined in V^med,ππ and V^med,π, respectively. The density and momentum dependent loop functions ${\tilde{\Gamma }}_i(p)$ and ${\tilde{G}}_i(p,q)$ can be found in Petschauer et al. [121]. The only spin-dependent term is the one proportional to ${\overrightarrow{\sigma }}_2=\frac{1}{2}({\overrightarrow{\sigma }}_1+{\overrightarrow{\sigma }}_2)-\frac{1}{2}({\overrightarrow{\sigma }}_1-{\overrightarrow{\sigma }}_2)$ and therefore one recognizes a symmetric and an antisymmetric spin-orbit potential of equal but opposite strength.

5. Applications

5.1. Hyperon-Nucleon and Hyperon-Hyperon Scattering

With the hyperon-nucleon potentials outlined in section 3 hyperon-nucleon scattering processes can be investigated. The very successful approach to the nucleon-nucleon interaction of Epelbaum et al. [147, 149, 150] within SU(2) χEFT, has been extended to the leading-order baryon-baryon interaction in Polinder et al. [29, 30] and Haidenbauer and Meißner [31] by the Bonn-Jülich group. In Haidenbauer et al. [33, 35, 36], this approach has been extended to next-to-leading order in SU(3) chiral effective field theory. As mentioned in section 2.4, the chiral power counting is applied to the potential, where only two-particle irreducible diagrams contribute. These potentials are then inserted into a regularized Lippmann-Schwinger equation to obtain the reaction amplitude (or T-matrix). In contrast to the NN interaction, the Lippmann-Schwinger equation for the YN interaction involves not only coupled partial waves, but also coupled two-baryon channels. The coupled-channel Lippmann-Schwinger equation in the particle basis reads after partial-wave decomposition (see also Figure 2)

$\begin{array}{l}{T}_{{\nu }^{″}{\nu }^{\prime }}^{{\rho }^{″}{\rho }^{\prime },J}(k^{″},k^{\prime };\sqrt{s})=V_{{\nu }^{″}{\nu }^{\prime }}^{{\rho }^{″}{\rho }^{\prime },J}(k^{″},k^{\prime })\\ +{\displaystyle \sum _{\rho ,\nu }}{\displaystyle {\int }_0^{\infty }}\frac{\text{d}k{k}^2}{{(2\pi )}^3}{V}_{{\nu }^{″}\nu }^{{\rho }^{″}\rho ,J}(k^{″},k)\\ \times \frac{2{\mu }_{\nu }}{k_{\nu }^2-k^2+\text{i}ϵ}{T}_{\nu {\nu }^{\prime }}^{\rho {\rho }^{\prime },J}(k,k^{\prime };\sqrt{s}),& (98)\end{array}$

where J denotes the conserved total angular momentum. The coupled two-particle channels (Λp, Σ⁺n, Σ⁰p, …) are labeled by ν, and the partial waves (¹S₀, ³P₀, …) by ρ. Furthermore, μ_ν is the reduced baryon mass in channel ν. In Haidenbauer et al. [33], a non-relativistic scattering equation has been chosen to ensure that the potential can also be applied consistently to Faddeev and Faddeev-Yakubovsky calculations in the few-body sector, and to (hyper-) nuclear matter calculations within the conventional Brueckner-Hartree-Fock formalism (see section 5.2). Nevertheless, the relativistic relation between the on-shell momentum k_ν and the center-of-mass energy has been used, $\sqrt{s}=\sqrt{M_{B_{1,\nu }}^2+k_{\nu }^2}+\sqrt{M_{B_{2,\nu }}^2+k_{\nu }^2}$, in order to get the two-particle thresholds at their correct positions. The physical baryon masses have been used in the Lippmann-Schwinger equation, which introduces some additional SU(3) symmetry breaking. Relativistic kinematics has also been used to relate the laboratory momentum p_lab of the hyperon to the center-of-mass energy $\sqrt{s}$. The Coulomb interaction has been implemented by the use of the Vincent-Phatak method [147, 164]. Similar to the nucleonic sector at NLO [147], a regulator function of the form $f_R(\Lambda )=exp\left[-({k{}^{\prime }}^4+k^4)/{\Lambda }^4\right]$ is employed to cut off the high-energy components of the potential. For higher orders in the chiral power counting, higher powers than 4 in the exponent of f_R have to be used. This ensures that the regulator introduces only contributions, that are beyond the given order. The cutoff Λ is varied in the range (500…700) MeV, i.e., comparable to what was used for the NN interaction in Epelbaum et al. [147]. The resulting bands represent the cutoff dependence, after readjusting the contact parameters, and thus could be viewed as a lower bound on the theoretical uncertainty. Recently, improved schemes to estimate the theoretical uncertainty were proposed and applied to the NN interaction [165–168]. Some illustrative results for YN scattering based on the method by Epelbaum et al. [166, 168] have been included in Haidenbauer et al. [34]. However, such schemes require higher orders than NLO in the chiral power counting if one wants to address questions like the convergence of the expansion.

The partial-wave contributions of the meson-exchange diagrams are obtained by employing the partial-wave decomposition formulas of Polinder et al. [29]. For further remarks on the employed approximations and the fitting strategy we refer the reader to Haidenbauer et al. [33]. As can be seen in Table 3, one gets for the YN contact terms five independent LO constants, acting in the S-waves, eight additional constants at NLO in the S-waves, and nine NLO constant acting in the P-waves. The contact terms represent the unresolved short-distance dynamics, and the corresponding low-energy constants are fitted to the “standard” set of 36 YN empirical data points [169–174]. The hypertriton ($\stackrel{3}{\Lambda }\text{H}$) binding energy has been chosen as a further input. It determines the relative strength of the spin-singlet and spin-triplet S-wave contributions of the Λp interaction. Due to the sparse and inaccurate experimental data, the obtained fit of the low-energy constants is not unique. For instance, the YN data can be described equally well with a repulsive or an attractive interaction in the ³S₁ partial wave of the ΣN interaction with isospin I = 3/2. However, recent calculations from lattice QCD [3, 4] suggest a repulsive ³S₁ phase shift in the ΣN I = 3/2 channel, hence the repulsive solution has been adopted. Furthermore, this is consistent with empirical information from Σ⁻-production on nuclei, which point to a repulsive Σ-nucleus potential (see also section 5.2).

In the following we present some of the results of Haidenbauer et al. [33]. For comparison, results of the Jülich '04 [21] and the Nijmegen [20] meson-exchange models are also shown in the figures. In Figure 13, the total cross sections as functions of p_lab for various YN interactions are presented. The experimental data is well reproduced at NLO. Especially the results in the Λp channel are in line with the data points (also at higher energies) and the energy dependence in the Σ⁺p channel is significantly improved at NLO. It is also interesting to note that the NLO results are now closer to the phenomenological Jülich '04 model than at LO. One expects the theoretical uncertainties to become smaller, when going to higher order in the chiral power counting. This is reflected in the fact, that the bands at NLO are considerably smaller than at LO. These bands represent only the cutoff dependence and therefore constitute a lower bound on the theoretical error.

FIGURE 13

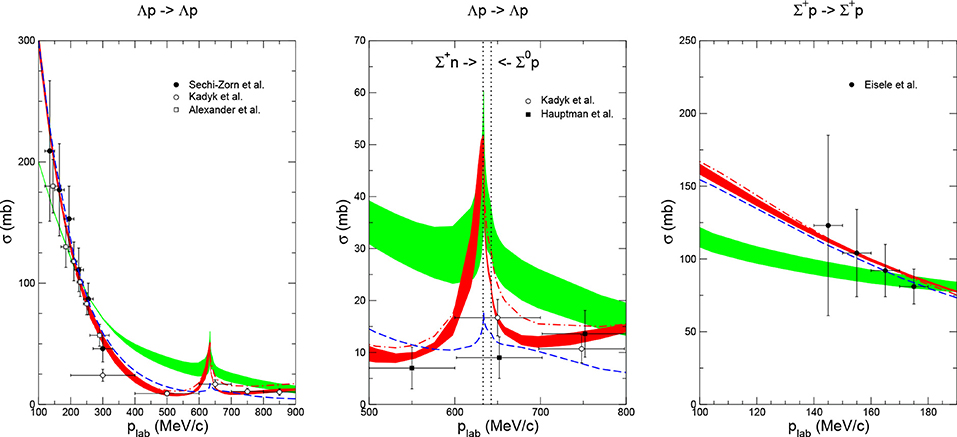
Figure 13. Total cross section σ as a function of p_lab. The red (dark) band shows the chiral EFT results to NLO for variations of the cutoff in the range Λ = (500…650) MeV [33], while the green (light) band are results to LO for Λ = (550…700) MeV [29]. The dashed curves are the result of the Jülich '04 meson-exchange potential [21], the dash-dotted curves of the Nijmegen NSC97f potential [20].

In Table 5, the scattering lengths and effective range parameters for the Λp and Σ⁺p interactions in the ¹S₀ and ³S₁ partial waves are given. Result for LO [29] and NLO χEFT [33], for the Jülich '04 model [21] and for the Nijmegen NSC97f potential [20] are shown. The NLO Λp scattering lengths are larger than for the LO calculation, and closer to the values obtained by the meson-exchange models. The triplet Σ⁺p scattering length is positive in the LO as well as the NLO calculation, which indicates a repulsive interaction in this channel. Also given in Table 5 is the hypertriton binding energy, calculated with the corresponding chiral potentials. As stated before, the hypertriton binding energy was part of the fitting procedure and values close to the experimental value could be achieved. The predictions for the $\stackrel{3}{\Lambda }H$ binding energy are based on the Faddeev equations in momentum space, as described in Nogga [49, 175]. Note that genuine (irreducible) three-baryon interactions were not included in this calculation. However, in the employed coupled-channel formalism, effects like the important Λ-Σ conversion process are naturally included. It is important to distinguish such iterated two-body interactions, from irreducible three-baryon forces, as exemplified in Figure 4.

TABLE 5

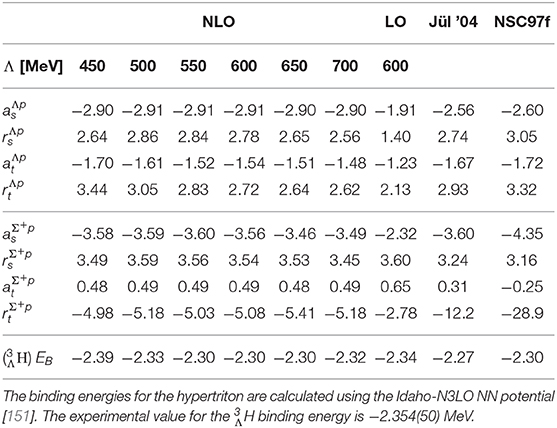
Table 5. The YN singlet (s) and triplet (t) scattering length a and effective range r (in fm) and the hypertriton binding energy E_B (in MeV) [33].

Predictions for S- and P-wave phase shifts δ as a function of p_lab for Λp and Σ⁺p scattering are shown in Figure 14. The ¹S₀ Λp phase shift from the NLO χEFT calculation is closer to the phenomenological Jülich '04 model than the LO result. It points to moderate attraction at low momenta and strong repulsion at higher momenta. At NLO the phase shift has a stronger downward bending at higher momenta compared to LO or the Jülich '04 model. As stated before, more repulsion at higher energies is a welcome feature in view of neutron star matter with Λ-hyperons as additional baryonic degree of freedom. The ³S₁ Λp phase shift, part of the S-matrix for the coupled ³S₁-³D₁ system, changes qualitatively from LO to NLO. The ³S₁ phase shift of the NLO interaction passes through 90° slightly below the ΣN threshold, which indicates the presence of an unstable bound state in the ΣN system. For the LO interaction and the Jülich '04 model no passing through 90° occurs and a cusp is predicted, that is caused by an inelastic virtual state in the ΣN system. These effects are also reflected by a strong increase of the Λp cross section close to the ΣN threshold (see Figure 13). The ³S₁ ΣN phase shift for the NLO interaction is moderately repulsive and comparable to the LO phase shift.

FIGURE 14

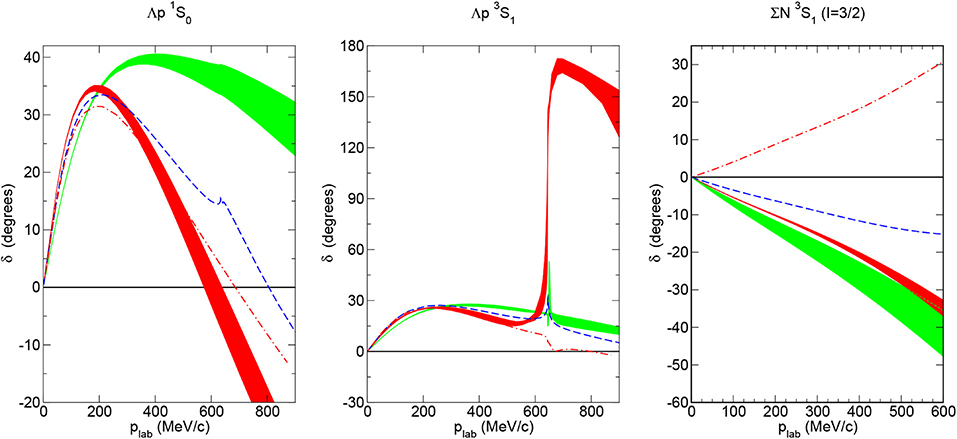
Figure 14. Various S- and P-wave phase shifts δ as a function of p_lab for the Λp and Σ⁺p interaction [33]. Same description of curves as in Figure 13.

Recently an alternative NLO χEFT potential for YN scattering has been presented [34]. In that work a different strategy for fixing the low-energy constants that determine the strength of the contact interactions is adopted. The objective of that exploration was to reduce the number of LECs that need to be fixed in a fit to the ΛN and ΣN data by inferring some of them from the NN sector via the underlying SU(3) symmetry (cf. section 3.1). Indeed, correlations between the LO and NLO LECs of the S-waves, i.e., between the $\tilde{c}$'s and c's, had been observed already in the initial YN study [33] and indicated that a unique determination of them by considering the existing ΛN and ΣN data alone is not possible. It may be not unexpected in view of those correlations, that the variant considered in Haidenbauer et al. [34] yields practically equivalent results for ΛN and ΣN scattering observables. However, it differs considerable in the strength of the ΛN → ΣN transition potential and that becomes manifest in applications to few- and many-body systems [34, 176].

There is very little empirical information about baryon-baryon systems with S = −2, i.e., about the interaction in the ΛΛ, ΣΣ, ΛΣ, and ΞN channels. Actually, all one can find in the literature [36] are a few values and upper bounds for the Ξ⁻p elastic and inelastic cross sections [177, 178]. In addition there are constraints on the strength of the ΛΛ interaction from the separation energy of the ${\Lambda }_{\Lambda }^6$He hypernucleus [179]. Furthermore estimates for the ΛΛ ¹S₀ scattering length exist from analyses of the ΛΛ invariant mass measured in the reaction ¹²C(K⁻, K⁺ΛΛX) [180] and of ΛΛ correlations measured in relativistic heavy-ion collisions [181].

Despite the rather poor experimental situation, it turned out that SU(3)-symmetry breaking contact terms that arise at NLO (see section 3.1), need to be taken into account when going from strangeness S = −1 to S = −2 in order to achieve agreement with the available measurements and upper bounds for the ΛΛ and ΞN cross sections [36]. This concerns, in particular, the LEC $c_{\chi }^1$ that appears in the ¹S₀ partial wave (cf. Equation 54). Actually, its value can be fixed by considering the pp and Σ⁺p systems, as shown in Haidenbauer et al. [35], and then employed in the ΛΛ system.

Selected results for the strangeness S = −2 sector are presented in Figure 15. Further results and a detailed description of the interactions can be found in Polinder et al. [30], Haidenbauer et al. [35, 36], and Haidenbauer and Meißner [37]. Interestingly, the results based on the LO interaction from Polinder et al. [30] (green/gray bands) are consistent with all empirical constraints. The cross sections at LO are basically genuine predictions that follow from SU(3) symmetry utilizing LECs fixed from a fit to the ΛN and ΣN data on the LO level. The ΛΛ ¹S₀ scattering length predicted by the NLO interaction is a_ΛΛ = −0.70···−0.62 fm [36]. These values are well within the range found in the aforementioned analyses which are a_ΛΛ = (−1.2 ± 0.6) fm [180] and −1.92 < a_ΛΛ < −0.50 fm [181], respectively. The values for the Ξ⁰p and Ξ⁰n S-wave scattering length are likewise small and typically in the order of ±0.3 ~ ±0.6 fm [36] and indicate that the ΞN interaction has to be relatively weak in order to be in accordance with the available empirical constraints. Indeed, the present results obtained in chiral EFT up to NLO imply that the published values and upper bounds for the Ξ⁻p elastic and inelastic cross sections [177, 178] practically rule out a somewhat stronger attractive ΞN force.

FIGURE 15

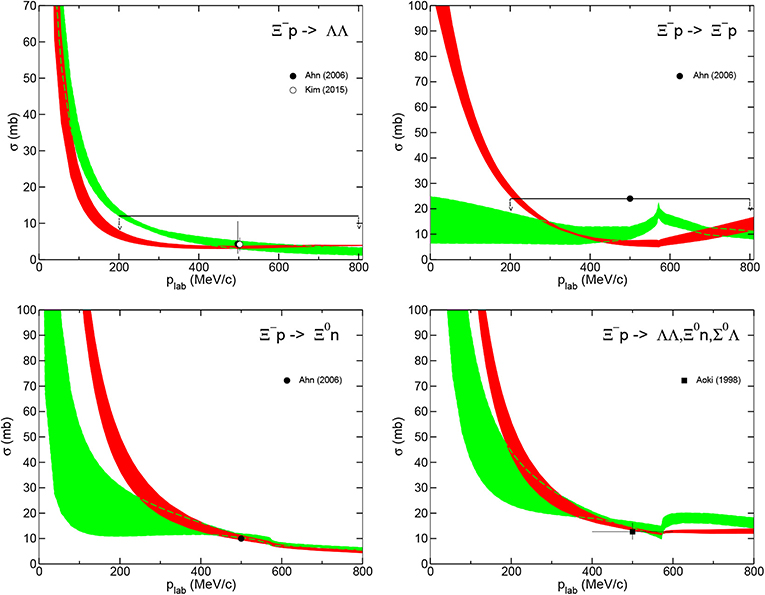
Figure 15. Ξ⁻p induced cross sections. The bands represent results at NLO (red/black) [36] and LO (green/gray) [30]. Experiments are from Ahn et al. [178], Kim et al. [unpublished data], and Aoki et al. [177]. Upper limits are indicated by arrows.

Also for ΞN scattering an alternative NLO χEFT potential has been presented recently [37]. Here the aim is to explore the possibility to establish a ΞN interaction that is still in line with all the experimental constraints for ΛΛ and ΞN scattering, but at the same time is somewhat more attractive. Recent experimental evidence for the existence of Ξ-hypernuclei [182] suggests that the in-medium interaction of the Ξ-hyperon should be moderately attractive [183].

5.2. Hyperons in Nuclear Matter

Experimental investigations of nuclear many-body systems including strange baryons, for instance, the spectroscopy of hypernuclei, provide important constraints on the underlying hyperon-nucleon interaction. The analysis of data for single Λ-hypernuclei over a wide range in mass number leads to the result, that the attractive Λ single-particle potential is about half as deep (≈ −28 MeV) as the one for nucleons [184, 185]. At the same time the Λ-nuclear spin-orbit interaction is found to be exceptionally weak [186, 187]. Recently, the repulsive nature of the Σ-nuclear potential has been experimentally established in Σ⁻-formation reactions on heavy nuclei [188]. Baryon-baryon potentials derived within χEFT as presented in section 3 are consistent with these observations [75, 76]. In this section we summarize results of hyperons in infinite homogeneous nuclear matter of Petschauer et al. [76] obtained by employing the interaction potentials from χEFT as microscopic input. The many-body problem is solved within first-order Brueckner theory. A detailed introduction can be found, e.g., in Day [69], Baldo [189], and Fetter and Walecka [190].

Brueckner theory is founded on the so-called Goldstone expansion, a linked-cluster perturbation series for the ground state energy of a fermionic many-body system. Let us consider a system of A identical fermions, described by the Hamiltonian

$\begin{array}{ll}H=T+V,& (99)\end{array}$

where T is the kinetic part and V corresponds to the two-body interaction. The goal is to calculate the ground state energy of this interacting A-body system. It is advantageous to introduced a so-called auxiliary potential, or single-particle potential, U. The Hamiltonian is then split into two parts

$\begin{array}{ll}H=(T+U)+(V-U)=H_0+H_1,& (100)\end{array}$

the unperturbed part H₀ and the perturbed part H₁. One expects the perturbed part to be small, if the single particle potential describes well the averaged effect of the medium on the particle. In fact, the proper introduction of the auxiliary potential is crucial for the convergence of Brueckner theory.

Conventional nucleon-nucleon potentials exhibit a strong short-range repulsion that leads to very large matrix elements. Hence, the Goldstone expansion in the form described above will not converge for such hard-core potentials. One way to approach this problem is the introduction of the so-called Brueckner reaction matrix, or G-matrix. The idea behind it is illustrated in Figure 16A. Instead of only using the simple interaction, an infinite number of diagrams with increasing number of interactions is summed up. This defines the G-matrix interaction, which is, in contrast to the bare potential, weak and of reasonable range. In a mathematical way, the reaction matrix is defined by the Bethe-Goldstone equation:

$\begin{array}{ll}G(\omega )=V+V\frac{Q}{\omega -H_0+\text{i}ϵ}G(\omega ),& (101)\end{array}$

with the so-called starting energy ω. The Pauli operator Q ensures, that the intermediate states are from outside the Fermi sea. As shown in Figure 16A, this equation represents a resummation of the ladder diagrams to all orders. The arising G-matrix interaction is an effective interaction of two particles in the presence of the medium. The medium effects come in solely through the Pauli operator and the energy denominator via the single-particle potentials. If we set the single-particle potentials to zero and omit the Pauli operator (Q = 1), we recover the usual Lippmann-Schwinger equation for two-body scattering in vacuum (see also Figure 2). This medium effect on the intermediate states is denoted by horizontal double lines in Figure 16A. An appropriate expansion using the G-matrix interaction instead of the bare potential is the so-called Brueckner-Bethe-Goldstone expansion, or hole-line expansion.

FIGURE 16

Figure 16. Graphical representation of the determination of the single-particle potential from the G-matrix interaction (B) and of the Bethe-Goldstone equation (A). The symbol ω_o.s denotes the on-shell starting energy.

Finally, the form of the auxiliary potential U needs to be chosen. This choice is important for the convergence of the hole-line expansion. Bethe et al. [191] showed for nuclear matter that important higher-order diagrams cancel each other if the auxiliary potential is taken as

$\begin{array}{ll}{U}_m=Re{\displaystyle \sum _{n\le A}}{\langle mn\left|G(\omega ={\omega }_{\text{o.s.}})\right|mn\rangle }_{{A}},& (102)\end{array}$

where the Brueckner reaction matrix is evaluated on-shell, i.e., the starting energy is equal to the energy of the two particles m, n in the initial state:

$\begin{array}{l}{\omega }_{\text{o.s.}}=E_1(k_1)+E_2(k_2),\\ E_{B_i}(k_i)=M_i+\frac{k_i^2}{2M_i}+Re{U}_i(k_i).& (103)\end{array}$

Pictorially Equation (102) means, that the single-particle potential can be obtained by taking the on-shell G-matrix interaction and by closing one of the baryon lines, as illustrated in Figure 16B. Note that this implies a non-trivial self-consistency problem. On the one hand, U is calculated from the G-matrix elements via Equation (102), and on the other hand the starting energy of the G-matrix elements depends on U through the single-particle energies E_i in Equation (103).

At the (leading) level of two hole-lines, called Brueckner-Hartree-Fock approximation (BHF), the total energy is given by

$\begin{array}{l}E={\displaystyle \sum _{n\le A}}\langle n\left|T\right|n\rangle +\frac{1}{2}{\displaystyle \sum _{m,n\le A}}{\langle mn\left|G\right|mn\rangle }_{{A}}\\ ={\displaystyle \sum _{n\le A}}\langle n\left|T\right|n\rangle +\frac{1}{2}{\displaystyle \sum _{n\le A}}\langle n\left|U\right|n\rangle ,& (104)\end{array}$

i.e., the ground-state energy E can be calculated directly after the single-particle potential has been determined.

The definition of U in Equation (102) applies only to occupied states within the Fermi sea. For intermediate-state energies above the Fermi sea, typically two choices for the single-particle potential are employed. In the so-called gap choice, the single-particle potential is given by Equation (102) for k ≤ k_F and set to zero for k > k_F, implying a “gap” (discontinuity) in the single-particle potential. Then only the free particle energies ($M+{\overrightarrow{p}}^2/2M$) of the intermediate states appear in the energy denominator of the Bethe-Goldstone equation (Equation 101) since the Pauli-blocking operator is zero for momenta below the Fermi momentum. In the so-called continuous choice Equation (102) is used for the whole momentum range, hence the single-particle potentials enter also into the energy denominator. In Song et al. [192], the equation of state in symmetric nuclear matter has been considered. It has been shown, that the result including three hole-lines is almost independent of the choice of the auxiliary potential. Furthermore, the two-hole line result with the continuous choice comes out closer to the three hole-line result, than the two-hole line calculation with the gap choice. Another advantage of the continuous choice for intermediate spectra is that it allows for a reliable determination of the single-particle potentials including their imaginary parts [70]. The results presented here employ the continuous choice.

In the following we present some results of Petschauer et al. [76] for the in-medium properties of hyperons, based on the YN interaction derived from SU(3) χEFT at NLO. The same potential V as in the Lippmann-Schwinger equation (Equation 98) for free scattering is used. However, as in Haidenbauer and Meißner [75] the contact term c^8as for the antisymmetric spin-orbit force in the YN interaction, allowing spin singlet-triplet transitions, has been fitted to the weak Λ-nuclear spin-orbit interaction [193, 194]. Additionally, for the ease of comparison, the G-matrix results obtained with two phenomenological YN potentials, namely of the Jülich '04 [21] and the Nijmegen NSC97f [20] meson-exchange models, are given. Note that, like the EFT potentials, these phenomenological YN interactions produce a bound hypertriton [49]. For more details about derivation and the commonly employed approximations, we refer the reader to Reuber et al. [19], Rijken et al. [20], Kohno et al. [24], Schulze et al. [70], Vidaña et al. [71].

Let us start with the properties of hyperons in symmetric nuclear matter. Figure 17 shows the momentum dependence of the real parts of the Λ single-particle potential. The values for the depth of the Λ single-particle potential U_Λ(k = 0) at saturation density, $k_F=1.35\text{ f}{\text{m}}^{-1}$, at NLO are between 27.0 and 28.3 MeV. In the Brueckner-Hartree-Fock approximation the binding energy of a hyperon in infinite nuclear matter is given by B_Y(∞) = − U_Y(k = 0). The results of the LO and NLO calculation are consistent with the empirical value of about U_Λ(0) ≈ −28 MeV [184, 185]. The phenomenological models (Jülich '04, Nijmegen NSC97f) lead to more attractive values of U_Λ(0) = (−35…−50) MeV, where the main difference is due to the contribution in the ³S₁ partial wave. In contrast to LO, at NLO the Λ single-particle potential at NLO turns to repulsion at fairly low momenta around k ≈ 2 fm⁻¹, which is also the case for the NSC97f potential.

FIGURE 17

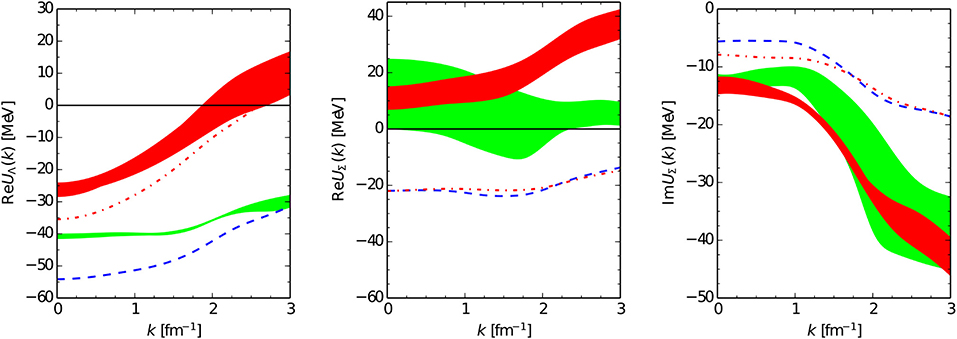
Figure 17. Momentum dependence of the real part of the single-particle potential of a Λ hyperon and of the real and imaginary parts of the single-particle potential of a Σ hyperon in isospin-symmetric nuclear matter at saturation density, $k_F=1.35\text{ f}{\text{m}}^{-1}$ [76]. The red band, green band, blue dashed curve, and red dash-dotted curve are for χEFT NLO, χEFT LO, the Jülich '04 model and the NSC97f model, respectively.

An important quantity of the interaction of hyperons with heavy nuclei is the strength of the Λ-nuclear spin-orbit coupling. It is experimentally well established [186, 187] that the Λ-nucleus spin-orbit force is very small. For the YN interaction of Haidenbauer and Meißner [75] it was indeed possible to tune the strength of the antisymmetric spin-orbit contact interaction (via the constant c^8as), generating a spin singlet-triplet mixing (¹P₁ ↔ ³P₁), in a way to achieve such a small nuclear spin-orbit potential.

Results for Σ hyperons in isospin-symmetric nuclear matter at saturation density are also displayed in Figure 17. Analyses of data on (π⁻, K⁺) spectra related to Σ⁻ formation in heavy nuclei lead to the observation, that the Σ-nuclear potential in symmetric nuclear matter is moderately repulsive [188]. The LO as well as the NLO results are consistent with this observation. Meson-exchange models often fail to produce such a repulsive Σ-nuclear potential. The imaginary part of the Σ-nuclear potential at saturation density is consistent with the empirical value of −16 MeV as extracted from Σ⁻-atom data [195]. The imaginary potential is mainly induced by the ΣN to ΛN conversion in nuclear matter. The bands representing the cutoff dependence of the chiral potentials, become smaller when going to higher order in the chiral expansion.

In Figure 18, the density dependence of the depth of the nuclear mean-field of Λ or Σ hyperons at rest (k = 0). In order to see the influence of the composition nuclear matter on the single-particle potentials, results for isospin-symmetric nuclear matter, asymmetric nuclear matter with ρ_p = 0.25ρ and pure neutron matter are shown. The single-particle potential of the Λ hyperon is almost independent of the composition of the nuclear medium, because of its isosinglet nature. Furthermore, it is attractive over the whole considered range of density 0.5 ≤ ρ/ρ₀ ≤ 1.5. In symmetric nuclear matter, the three Σ hyperons behave almost identical (up to small differences from the mass splittings). When introducing isospin asymmetry in the nuclear medium a splitting of the single-particle potentials occurs due to the strong isospin dependence of the ΣN interaction. The splittings among the Σ⁺, Σ⁰, and Σ⁻ potentials have a non-linear dependence on the isospin asymmetry which goes beyond the usual (linear) parametrization in terms of an isovector Lane potential [196].

FIGURE 18

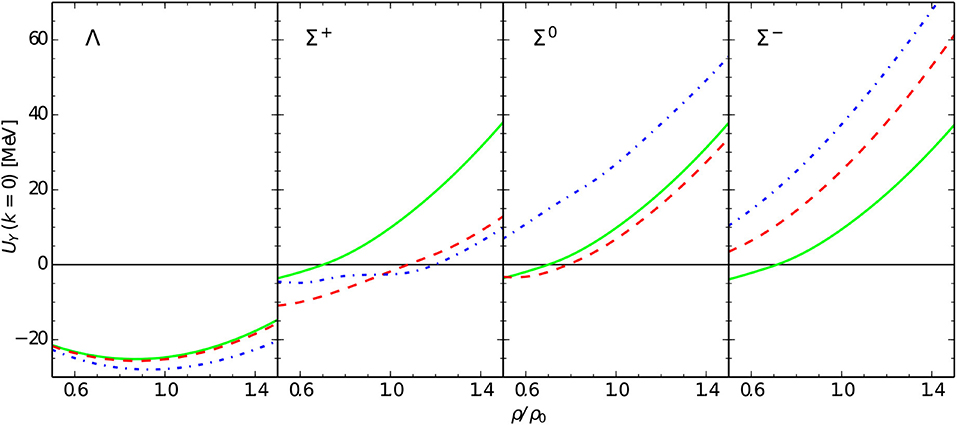
Figure 18. Density dependence of the hyperon single-particle potentials at k = 0 with different compositions of the nuclear matter, calculated in χEFT at NLO with a cutoff Λ = 600 MeV [76]. The green solid, red dashed and blue dash-dotted curves are for ρ_p = 0.5ρ, ρ_p = 0.25ρ, and ρ_p = 0, respectively.

Recently the in-medium properties of the Ξ have been investigated for ΞN potentials from χEFT [37]. For a more extensive discussion and further applications see Kohno [197].

5.3. Hypernuclei and Hyperons in Neutron Stars

The density-dependent single-particle potentials of hyperons interacting with nucleons in nuclear and neutron matter find their applications in several areas of high current interest: the physics of hypernuclei and the role played by hyperons in dense baryonic matter as it is realized in the core of neutron stars.

From hypernuclear spectroscopy, the deduced attractive strength of the phenomenological Λ-nuclear Woods-Saxon potential is U₀ ≃ −30 MeV at the nuclear center [183]. This provides an important constraint for U_Λ(k = 0) at ρ = ρ₀. The non-existence of bound Σ-hypernuclei, on the other hand, is consistent with the repulsive nature of the Σ-nuclear potential as shown in Figure 18. In this context effects of YNN three-body forces are a key issue. While their contributions at normal nuclear densities characteristic of hypernuclei are significant but modest, they play an increasingly important role when extrapolating to high baryon densities in neutron stars.

First calculations of hyperon-nuclear potentials based on chiral SU(3) EFT and using Brueckner theory have been reported in Haidenbauer et al. [176] and Kohno [122]. Further investigations of (finite) Λ hypernuclei utilizing the EFT interactions can be found in Haidenbauer and Vidana [198], based on the formalism described in Vidaña [199]. For even lighter hypernuclei, the interactions are also currently studied [200, 201]. Examples of three- and four-body results can be found in Haidenbauer et al. [34, 202] and Nogga [49, 175].

Here we give a brief survey of Λ-nuclear interactions for hypernuclei and extrapolations to high densities relevant to neutron stars, with special focus on the role of the (a priori unknown) contact terms of the ΛNN three-body force. Details can be found in Haidenbauer et al. [176]. Further extended work including explicit 3-body coupled channels (ΛNN ↔ ΣNN) in the Brueckner-Bethe-Goldstone equation is proceeding [203].

Results for the density dependence of the Λ single-particle potential are presented in Figure 19 for symmetric nuclear matter (Figure 19A) and for neutron matter (Figure 19B). Predictions from the chiral SU(3) EFT interactions (bands) are shown in comparison with those for meson-exchange YN models constructed by the Jülich [21] (dashed line) and Nijmegen [20] (dash-dotted line) groups. One observes an onset of repulsive effects around the saturation density of nuclear matter, i.e., ρ = ρ₀. The repulsion increases strongly as the density increases. Already around ρ ≈ 2ρ₀, U_Λ(0, ρ) turns over to net repulsion.

FIGURE 19

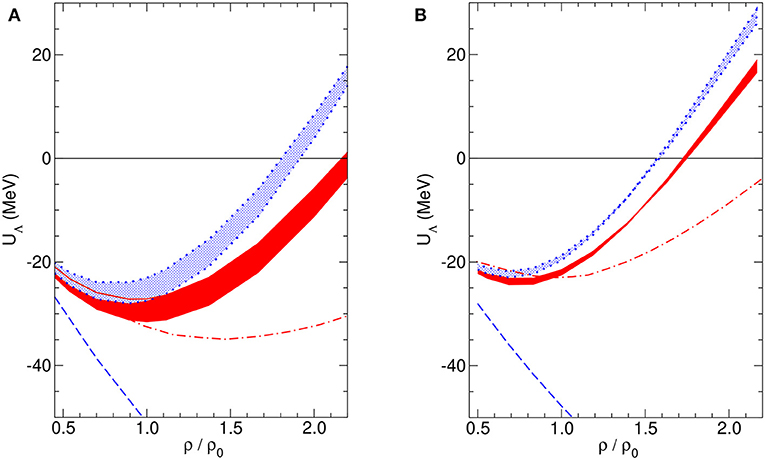
Figure 19. The Λ single-particle potential U_Λ(p_Λ = 0, ρ) as a function of ρ/ρ₀ in symmetric nuclear matter (A) and in neutron matter (B). The solid (red) band shows the chiral EFT results at NLO for cutoff variations Λ = 450−500 MeV. The dotted (blue) band includes the density-dependent ΛN-interaction derived from the ΛNN three-body force. The dashed curve is the result of the Jülich '04 meson-exchange model [21], the dash-dotted curve that of the Nijmegen NSC97f potential [20], taken from Yamamoto et al. [204].

Let us discuss possible implications for neutron stars. It should be clear that it is mandatory to include the ΛN–ΣN coupling in the pertinent calculations. This represents a challenging task since standard microscopic calculations without this coupling are already quite complex. However, without the ΛN–ΣN coupling, which has such a strong influence on the in-medium properties of hyperons, it will be difficult if not impossible to draw reliable conclusions.

The majority of YN-interactions employed so far in microscopic calculations of neutron stars have properties similar to those of the Jülich '04 model. In such calculations, hyperons start appearing in the core of neutron stars typically at relatively low densities around (2 − 3)ρ₀ [113, 119]. This causes the so-called hyperon puzzle: a strong softening of the equation-of-state, such that the maximum neutron star mass falls far below the constraint provided by the existence of several neutron stars with masses around 2M_⊙. Assume now that nature favors a scenario with a weak diagonal ΛN-interaction and a strong ΛN–ΣN coupling as predicted by SU(3) chiral EFT. The present study demonstrates that, in this case, the Λ single-particle potential U_Λ(k = 0, ρ) based on chiral EFT two-body interactions is already repulsive at densities ρ ~ (2 − 3)ρ₀. The one of the Σ-hyperon is likewise repulsive [35]. We thus expect that the appearance of hyperons in neutron stars will be shifted to much higher densities. In addition there is a repulsive density-dependent effective ΛN-interaction that arises within the same chiral EFT framework from the leading chiral YNN three-baryon forces. This enhances the aforementioned repulsive effect further. It makes the appearance of Λ-hyperons in neutron star matter energetically unfavorable. In summary, all these aspects taken together may well point to a solution of the hyperon puzzle in neutron stars without resorting to exotic mechanisms.

6. Conclusions

In this review we have presented the basics to derive the forces between octet baryons (N, Λ, Σ, Ξ) at next-to-leading order in SU(3) chiral effective field theory. The connection of SU(3) χEFT to quantum chromodynamics via the chiral symmetry and its symmetry breaking patterns, and the change of the degrees of freedom has been shown. The construction principles of the chiral effective Lagrangian and the external-field method have been presented and the Weinberg power-counting scheme has been introduced.

Within SU(3) χEFT the baryon-baryon interaction potentials have been considered at NLO. The effective baryon-baryon potentials include contributions from pure four-baryon contact terms, one-meson-exchange diagrams, and two-meson-exchange diagrams at one-loop level. The leading three-baryon forces, which formally start to contribute at NNLO, consist of a three-baryon contact interaction, a one-meson exchange and a two-meson exchange component. We have presented explicitly potentials for the ΛNN interaction in the spin and isospin basis. The emerging low-energy constants can be estimated via decuplet saturation, which leads to a promotion of some parts of the three-baryon forces to NLO. The expressions of the corresponding effective two-body potential in the nuclear medium has been presented.

In the second part of this review we have presented selected applications of these potentials. An excellent description of the available YN data has been achieved with χEFT, comparable to the most advanced phenomenological models. Furthermore, in studies of the properties of hyperons in isospin symmetric and asymmetric infinite nuclear matter, the chiral baryon-baryon potentials at NLO are consistent with the empirical knowledge about hyperon-nuclear single-particle potentials. The exceptionally weak Λ-nuclear spin-orbit force is found to be related to the contact term responsible for an antisymmetric spin-orbit interaction. Concerning hypernuclei and neutron stars promising results have been obtained and could point to a solution of the hyperon puzzle in neutron stars.

In summary, χEFT is an appropriate tool for constructing the interaction among baryons in a systematic way. It sets the framework for many promising applications in strangeness-nuclear physics.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This work was supported in part by the Deutsche Forschungsgemeinschaft (DFG) through the funds provided to the Sino-German Collaborative Research Center Symmetries and the Emergence of Structure in QCD (Grant No. TRR110), by the CAS President's International Fellowship Initiative (PIFI) (Grant No. 2018DM0034), and by the VolkswagenStiftung (Grant No. 93562).

Conflict of Interest

SP is employed by the company TNG Technology Consulting GmbH.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

1. ^Note that an overall plus sign in front of the constants D and F is chosen, consistent with the conventions in SU(2) χEFT [13].

2. ^This LEC D has not to be confused with the axial-vector coupling constant D in Equation (56).

References

1. Aoki S, Doi T, Hatsuda T, Ikeda Y, Inoue T, Ishii N, et al. Lattice quantum chromodynamical approach to nuclear physics. Prog Theor Exp Phys. (2012) 2012:01A105. doi: 10.1093/ptep/pts010

CrossRef Full Text | Google Scholar

2. Beane SR, Detmold W, Orginos K, Savage MJ. Nuclear physics from lattice QCD. Prog Part Nuclear Phys. (2011) 66:1–40. doi: 10.1016/j.ppnp.2010.08.002

CrossRef Full Text | Google Scholar

3. Beane SR, Chang E, Cohen SD, Detmold W, Lin HW, Luu TC, et al. Hyperon-nucleon interactions from quantum chromodynamics and the composition of dense nuclear matter. Phys Rev Lett. (2012) 109:172001. doi: 10.1103/PhysRevLett.109.172001

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Nemura H, Aoki S, Doi T, Gongyo S, Hatsuda T, Ikeda Y, et al. Baryon interactions from lattice QCD with physical masses— strangeness S = −1 sector —. EPJ Web Conf. (2018) 175:05030. doi: 10.1051/epjconf/201817505030

CrossRef Full Text | Google Scholar

5. Weinberg S. Nonlinear realizations of chiral symmetry. Phys Rev. (1968) 166:1568–77. doi: 10.1103/PhysRev.166.1568

CrossRef Full Text | Google Scholar

6. Weinberg S. Phenomenological lagrangians. Physica. (1979) 96A:327–40. doi: 10.1016/0378-4371(79)90223-1

CrossRef Full Text | Google Scholar

7. Gasser J, Leutwyler H. Chiral perturbation theory to one loop. Ann Phys. (1984) 158:142–210. doi: 10.1016/0003-4916(84)90242-2

CrossRef Full Text | Google Scholar

8. Gasser J, Sainio ME, Svarc A. Nucleons with chiral loops. Nucl Phys B. (1988) 307:779–853. doi: 10.1016/0550-3213(88)90108-3

CrossRef Full Text | Google Scholar

9. Bernard V, Kaiser N, Meißner UG. Chiral dynamics in nucleons and nuclei. Int J Modern Phys E. (1995) 4:193–344. doi: 10.1142/S0218301395000092

CrossRef Full Text | Google Scholar

10. Stoks VGJ, Klomp RAM, Terheggen CPF, de Swart JJ. Construction of high-quality NN potential models. Phys Rev C. (1994) 49:2950–62. doi: 10.1103/PhysRevC.49.2950

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Wiringa RB, Stoks VGJ, Schiavilla R. Accurate nucleon-nucleon potential with charge-independence breaking. Phys Rev C. (1995) 51:38–51. doi: 10.1103/PhysRevC.51.38

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Machleidt R. High-precision, charge-dependent Bonn nucleon-nucleon potential. Phys Rev C. (2001) 63:024001. doi: 10.1103/PhysRevC.63.024001

CrossRef Full Text | Google Scholar

13. Epelbaum E, Hammer HW, Meißner UG. Modern theory of nuclear forces. Rev Modern Phys. (2009) 81:1773–825. doi: 10.1103/RevModPhys.81.1773

CrossRef Full Text | Google Scholar

14. Machleidt R, Entem DR. Chiral effective field theory and nuclear forces. Phys Rep. (2011) 503:1–75. doi: 10.1016/j.physrep.2011.02.001

CrossRef Full Text | Google Scholar

15. Kaplan DB, Savage MJ, Wise MB. A new expansion for nucleon-nucleon interactions. Phys Lett. (1998) B424:390–6. doi: 10.1016/S0370-2693(98)00210-X

CrossRef Full Text | Google Scholar

16. Nogga A, Timmermans R, van Kolck U. Renormalization of one-pion exchange and power counting. Phys Rev. (2005) C72:054006. doi: 10.1103/PhysRevC.72.054006

CrossRef Full Text | Google Scholar

17. Epelbaum E, Meißner UG. On the renormalization of the one-pion exchange potential and the consistency of Weinberg‘s power counting. Few Body Syst. (2013) 54:2175–90. doi: 10.1007/s00601-012-0492-1

CrossRef Full Text | Google Scholar

18. Holzenkamp B, Holinde K, Speth J. A meson exchange model for the hyperon-nucleon interaction. Nucl Phys A. (1989) 500:485–528. doi: 10.1016/0375-9474(89)90223-6

CrossRef Full Text | Google Scholar

19. Reuber AG, Holinde K, Speth J. Meson-exchange hyperon-nucleon interactions in free scattering and nuclear matter. Nucl Phys A. (1994) 570:543–79. doi: 10.1016/0375-9474(94)90073-6

CrossRef Full Text | Google Scholar

20. Rijken TA, Stoks VGJ, Yamamoto Y. Soft-core hyperon-nucleon potentials. Phys Rev C. (1999) 59:21–40. doi: 10.1103/PhysRevC.59.21

CrossRef Full Text | Google Scholar

21. Haidenbauer J, Meißner UG. Jülich hyperon-nucleon model revisited. Phys Rev C. (2005) 72:044005. doi: 10.1103/PhysRevC.72.044005

CrossRef Full Text | Google Scholar

22. Rijken TA, Nagels MM, Yamamoto Y. Baryon-Baryon interactions. Prog Theor Phys Suppl. (2010) 185:14–71. doi: 10.1143/PTPS.185.14

CrossRef Full Text | Google Scholar

23. Nagels MM, Rijken TA, Yamamoto Y. Extended-soft-core baryon-baryon model ESC16. II. Hyperon-nucleon interactions. Phys Rev. (2019) C99:044003. doi: 10.1103/PhysRevC.99.044003

CrossRef Full Text | Google Scholar

24. Kohno M, Fujiwara Y, Fujita T, Nakamoto C, Suzuki Y. Hyperon single-particle potentials calculated from quark-model baryon-baryon interactions. Nucl Phys A. (2000) 674:229–45. doi: 10.1016/S0375-9474(00)00164-0

CrossRef Full Text | Google Scholar

25. Fujiwara Y, Suzuki Y, Nakamoto C. Baryon-baryon interactions in the SU(6) quark model and their applications to light nuclear systems. Prog Part Nucl Phys. (2007) 58:439–520. doi: 10.1016/j.ppnp.2006.08.001

CrossRef Full Text | Google Scholar

26. Garcilazo H, Fernandez-Carames T, Valcarce A. Lambda NN and sigma NN systems at threshold. Phys Rev. (2007) C75:034002. doi: 10.1103/PhysRevC.75.034002

CrossRef Full Text | Google Scholar

27. Savage MJ, Wise MB. Hyperon masses in nuclear matter. Phys Rev D. (1996) 53:349–54. doi: 10.1103/PhysRevD.53.349

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Korpa C, Dieperink A, Timmermans R. Hyperon-nucleon scattering and hyperon masses in the nuclear medium. Phys Rev. (2002) C65:015208. doi: 10.1103/PhysRevC.65.015208

CrossRef Full Text | Google Scholar

29. Polinder H, Haidenbauer J, Meißner UG. Hyperon-nucleon interactions - a chiral effective field theory approach. Nucl Phys A. (2006) 779:244–66. doi: 10.1016/j.nuclphysa.2006.09.006

CrossRef Full Text | Google Scholar

30. Polinder H, Haidenbauer J, Meißner UG. Strangeness S=-2 baryon-baryon interactions using chiral effective field theory. Phys Lett B. (2007) 653:29–37. doi: 10.1016/j.physletb.2007.07.045

CrossRef Full Text | Google Scholar

31. Haidenbauer J, Meißner UG. Predictions for the strangeness S=-3 and S=-4 baryon-baryon interactions in chiral effective field theory. Phys Lett B. (2010) 684:275–80. doi: 10.1016/j.physletb.2010.01.031

CrossRef Full Text | Google Scholar

32. Petschauer S, Kaiser N. Relativistic SU(3) chiral baryon-baryon Lagrangian up to order q**2. Nucl Phys A. (2013) 916:1–29. doi: 10.1016/j.nuclphysa.2013.07.010

CrossRef Full Text | Google Scholar

33. Haidenbauer J, Petschauer S, Kaiser N, Meißner UG, Nogga A, Weise W. Hyperon-nucleon interaction at next-to-leading order in chiral effective field theory. Nucl Phys A. (2013) 915:24–58. doi: 10.1016/j.nuclphysa.2013.06.008

CrossRef Full Text | Google Scholar

34. Haidenbauer J, Meißner U-G, Nogga A. Hyperon-nucleon interaction within chiral effective field theory revisited. arxiv:1906.11681 (2019).

Google Scholar

35. Haidenbauer J, Meißner UG, Petschauer S. Do Xi-Xi bound states exist? Eur Phys J A. (2015) 51:17. doi: 10.1140/epja/i2015-15017-0

CrossRef Full Text | Google Scholar

36. Haidenbauer J, Meißner UG, Petschauer S. Strangeness S=-2 baryon-baryon interaction at next-to-leading order in chiral effective field theory. Nucl Phys A. (2016) 954:273–93. doi: 10.1016/j.nuclphysa.2016.01.006

CrossRef Full Text | Google Scholar

37. Haidenbauer J, Meißner UG. In-medium properties of a XiN interaction derived from chiral effective field theory. Eur Phys J A. (2019) 55:23. doi: 10.1140/epja/i2019-12689-2

CrossRef Full Text | Google Scholar

38. Haidenbauer J, Petschauer S, Kaiser N, Meißner UG, Weise W. Scattering of decuplet baryons in chiral effective field theory. Eur Phys J C. (2017) 77:760. doi: 10.1140/epjc/s10052-017-5309-4

CrossRef Full Text | Google Scholar

39. Li KW, Ren XL, Geng LS, Long B. Strangeness S=-1 hyperon-nucleon scattering in covariant chiral effective field theory. Phys Rev D. (2016) 94:014029. doi: 10.1103/PhysRevD.94.014029

CrossRef Full Text | Google Scholar

40. Ren XL, Li KW, Geng LS, Long B, Ring P, Meng J. Leading order relativistic chiral nucleon-nucleon interaction. Chinese Phys C. (2018) 42:014103. doi: 10.1088/1674-1137/42/1/014103

CrossRef Full Text | Google Scholar

41. Li KW, Ren XL, Geng LS, Long BW. Leading order relativistic hyperon-nucleon interactions in chiral effective field theory. Chinese Phys C. (2018) 42:014105. doi: 10.1088/1674-1137/42/1/014105

CrossRef Full Text | Google Scholar

42. Song J, Li KW, Geng LS. Strangeness S=-1 hyperon-nucleon interactions: chiral effective field theory versus lattice QCD. Phys Rev C. (2018) 97:065201. doi: 10.1103/PhysRevC.97.065201

CrossRef Full Text | Google Scholar

43. Li K-W, Hyodo T, Geng L-S. Strangeness S = −2 baryon-baryon interactions in relativistic chiral effective field theory. Phys Rev. (2018) C98:065203. doi: 10.1103/PhysRevC.98.065203

CrossRef Full Text | Google Scholar

44. Ren XL, Epelbaum E, Gegelia J. Lambda-nucleon scattering in baryon chiral perturbation theory. arXiv:1911.05616 (2019).

Google Scholar

45. Bernard V, Kaiser N, Meißner UG, Schmidt A. Aspects of nucleon Compton scattering. Z Phys. (1994) A348:317. doi: 10.1007/BF01305891

CrossRef Full Text | Google Scholar

46. Miyagawa K, Glöckle W. Hypertriton calculation with meson theoretical nucleon-nucleon and hyperon nucleon interactions. Phys Rev. (1993) C48:2576–84. doi: 10.1103/PhysRevC.48.2576

CrossRef Full Text | Google Scholar

47. Miyagawa K, Kamada H, Glöckle W, Stoks VGJ. Properties of the bound Lambda (Sigma) N N system and hyperon nucleon interactions. Phys Rev. (1995) C51:2905–13. doi: 10.1103/PhysRevC.51.2905

CrossRef Full Text | Google Scholar

48. Nogga A, Kamada H, Glöckle W. The hypernuclei $\stackrel{4}{\Lambda }$ and $\stackrel{4}{\Lambda }$: challenges for modern hyperon-nucleon forces. Phys Rev Lett. (2002) 88:172501. doi: 10.1103/PhysRevLett.88.172501

CrossRef Full Text | Google Scholar

49. Nogga A. Light hypernuclei based on chiral interactions at next-to-leading order. Few Body Syst. (2014) 55:757–60. doi: 10.1007/s00601-014-0873-8

CrossRef Full Text | Google Scholar

50. Bogner SK, Furnstahl RJ, Schwenk A. From low-momentum interactions to nuclear structure. Prog Part Nucl Phys. (2010) 65:94–147. doi: 10.1016/j.ppnp.2010.03.001

CrossRef Full Text | Google Scholar

51. Wirth R, Gazda D, Navratil P, Calci A, Langhammer J, Roth R. Ab initio description of p-shell hypernuclei. Phys Rev Lett. (2014) 113:192502. doi: 10.1103/PhysRevLett.113.192502

PubMed Abstract | CrossRef Full Text | Google Scholar

52. Wirth R, Roth R. Induced hyperon-nucleon-nucleon interactions and the hyperon puzzle. Phys Rev Lett. (2016) 117:182501. doi: 10.1103/PhysRevLett.117.182501

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Wirth R, Gazda D, Navritil P, Roth R. Hypernuclear no-core shell model. Phys Rev C. (2018) 97:064315. doi: 10.1103/PhysRevC.97.064315

CrossRef Full Text | Google Scholar

54. Gazda D, Gal A. Ab initio Calculations of charge symmetry breaking in the A = 4 hypernuclei. Phys Rev Lett. (2016) 116:122501. doi: 10.1103/PhysRevLett.116.122501

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Gazda D, Gal A. Charge symmetry breaking in the A = 4 hypernuclei. Nucl Phys. (2016) A954:161–75. doi: 10.1016/j.nuclphysa.2016.05.015

CrossRef Full Text | Google Scholar

56. Gandolfi S, Pederiva F, Fantoni S, Schmidt KE. Quantum Monte Carlo calculations of symmetric nuclear matter. Phys Rev Lett. (2007) 98:102503. doi: 10.1103/PHYSREVLETT.98.102503

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Gandolfi S, Illarionov AY, Schmidt KE, Pederiva F, Fantoni S. Quantum Monte Carlo calculation of the equation of state of neutron matter. Phys Rev Lett. (2009) 79:054005. doi: 10.1103/PhysRevC.79.054005

CrossRef Full Text | Google Scholar

58. Lonardoni D, Pederiva F, Gandolfi S. Accurate determination of the interaction between Lambda hyperons and nucleons from auxiliary field diffusion Monte Carlo calculations. Phys Rev C. (2014) 89:014314. doi: 10.1103/PhysRevC.89.014314

CrossRef Full Text | Google Scholar

59. Borasoy B, Epelbaum E, Krebs H, Lee D, Meißner UG. Lattice simulations for light nuclei: chiral effective field theory at leading order. Eur Phys J A. (2007) 31:105–23. doi: 10.1140/epja/i2006-10154-1

CrossRef Full Text | Google Scholar

60. Epelbaum E, Krebs H, Lee D, Meißner UG. Ab initio calculation of the Hoyle state. Phys Rev Lett. (2011) 106:192501. doi: 10.1103/PhysRevLett.106.192501

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Lähde TA, Meißner UG. Nuclear lattice effective field theory. Lect Notes Phys. (2019) 957:1–396. doi: 10.1007/978-3-030-14189-9

CrossRef Full Text | Google Scholar

62. Holt JW, Kaiser N, Weise W. Nuclear chiral dynamics and thermodynamics. Prog Part Nucl Phys. (2013) 73:35–83. doi: 10.1016/j.ppnp.2013.08.001

CrossRef Full Text | Google Scholar

63. Coraggio L, Holt JW, Itaco N, Machleidt R, Marcucci LE, Sammarruca F. Nuclear-matter equation of state with consistent two- and three-body perturbative chiral interactions. Phys Rev C. (2014) 89:044321. doi: 10.1103/PhysRevC.89.044321

CrossRef Full Text | Google Scholar

64. Sammarruca F, Coraggio L, Holt JW, Itaco N, Machleidt R, Marcucci LE. Toward order-by-order calculations of the nuclear and neutron matter equations of state in chiral effective field theory. Phys Rev C. (2015) 91:054311. doi: 10.1103/PhysRevC.91.054311

CrossRef Full Text | Google Scholar

65. Kaiser N, Weise W. Chiral SU(3) dynamics and Lambda hyperons in the nuclear medium. Phys Rev C. (2005) 71:015203. doi: 10.1103/PhysRevC.71.015203

CrossRef Full Text | Google Scholar

66. Kaiser N. Chiral dynamics of Sigma hyperons in the nuclear medium. Phys Rev C. (2005) 71:068201. doi: 10.1103/PhysRevC.71.068201

CrossRef Full Text | Google Scholar

67. Brueckner K, Levinson CA, Mahmoud H. Two-body forces and nuclear saturation. I. Central forces. Phys Rev. (1954) 95:217–28. doi: 10.1103/PhysRev.95.217

CrossRef Full Text | Google Scholar

68. Brueckner K, Levinson CA. Approximate reduction of the many-body problem for strongly interacting particles to a problem of self-consistent fields. Phys Rev. (1955) 97:1344–52. doi: 10.1103/PhysRev.97.1344

CrossRef Full Text | Google Scholar

69. Day BD. Elements of the Brueckner-Goldstone theory of nuclear matter. Rev Modern Phys. (1967) 39:719–44. doi: 10.1103/RevModPhys.39.719

CrossRef Full Text | Google Scholar

70. Schulze HJ, Baldo M, Lombardo U, Cugnon J, Lejeune A. Hyperonic nuclear matter in Brueckner theory. Phys Rev C. (1998) 57:704–13. doi: 10.1103/PhysRevC.57.704

CrossRef Full Text | Google Scholar

71. Vidaña I, Polls A, Ramos A, Hjorth-Jensen M, Stoks VGJ. Strange nuclear matter within Brueckner-Hartree-Fock theory. Phys Rev C. (2000) 61:025802. doi: 10.1103/PhysRevC.61.025802

CrossRef Full Text | Google Scholar

72. Baldo M, Burgio GF, Schulze HJ. Hyperon stars in the Brueckner-Bethe-Goldstone theory. Phys Rev C. (2000) 61:055801. doi: 10.1103/PhysRevC.61.055801

CrossRef Full Text | Google Scholar

73. Schulze HJ, Polls A, Ramos A, Vidaña I. Maximum mass of neutron stars. Phys Rev C. (2006) 73:058801. doi: 10.1103/PhysRevC.73.058801

CrossRef Full Text | Google Scholar

74. Schulze HJ, Rijken TA. Maximum mass of hyperon stars with the Nijmegen ESC08 model. Phys Rev C. (2011) 84:035801. doi: 10.1103/PHYSREVC.84.035801

CrossRef Full Text | Google Scholar

75. Haidenbauer J, Meißner UG. A study of hyperons in nuclear matter based on chiral effective field theory. Nucl Phys A. (2015) 936:29–44. doi: 10.1016/j.nuclphysa.2015.01.005

CrossRef Full Text | Google Scholar

76. Petschauer S, Haidenbauer J, Kaiser N, Meißner UG, Weise W. Hyperons in nuclear matter from SU(3) chiral effective field theory. Eur Phys J A. (2016) 52:15. doi: 10.1140/epja/i2016-16015-4

CrossRef Full Text | Google Scholar

77. Pieper SC, Wiringa RB. Quantum Monte Carlo calculations of light nuclei. Annu Rev Nucl Part Sci. (2001) 51:53–90. doi: 10.1146/annurev.nucl.51.101701.132506

CrossRef Full Text | Google Scholar

78. Epelbaum E, Nogga A, Glöckle W, Kamada H, Meißner UG, Witala H. Three-nucleon forces from chiral effective field theory. Phys Rev C. (2002) 66:064001. doi: 10.1103/PhysRevC.66.064001

CrossRef Full Text | Google Scholar

79. Kalantar-Nayestanaki N, Epelbaum E, Messchendorp JG, Nogga A. Signatures of three-nucleon interactions in few-nucleon systems. Rept Prog Phys. (2012) 75:016301. doi: 10.1088/0034-4885/75/1/016301

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Hammer HW, Nogga A, Schwenk A. Three-body forces: from cold atoms to nuclei. Rev Mod Phys. (2013) 85:197. doi: 10.1103/RevModPhys.85.197

CrossRef Full Text | Google Scholar

81. McKellar BHJ, Rajaraman R. Three-body forces in nuclear matter. Phys Rev Lett. (1968) 21:450–3. doi: 10.1103/PhysRevLett.21.450

CrossRef Full Text | Google Scholar

82. Coon SA, Scadron MD, Barrett BR. The three-body force, off-shell πN scattering and binding energies in nuclear matter. Nucl Phys A. (1975) 242:467–80. doi: 10.1016/0375-9474(75)90109-8

CrossRef Full Text | Google Scholar

83. Coelho HT, Das TK, Robilotta MR. Two-pion-exchange three-nucleon force and the 3H and 3He nuclei. Phys Rev C. (1983) 28:1812–28. doi: 10.1103/PhysRevC.28.1812

CrossRef Full Text | Google Scholar

84. Pudliner BS, Pandharipande VR, Carlson J, Pieper SC, Wiringa RB. Quantum Monte Carlo calculations of nuclei with A ≤ 7. Phys Rev C. (1997) 56:1720–50. doi: 10.1103/PhysRevC.56.1720

CrossRef Full Text | Google Scholar

85. Pieper SC, Pandharipande VR, Wiringa RB, Carlson J. Realistic models of pion-exchange three-nucleon interactions. Phys Rev C. (2001) 64:014001. doi: 10.1103/PhysRevC.64.014001

CrossRef Full Text | Google Scholar

86. Weinberg S. Nuclear forces from chiral lagrangians. Phys Lett B. (1990) 251:288–92. doi: 10.1016/0370-2693(90)90938-3

CrossRef Full Text | Google Scholar

87. Weinberg S. Effective chiral lagrangians for nucleon-pion interactions and nuclear forces. Nucl Phys B. (1991) 363:3–18. doi: 10.1016/0550-3213(91)90231-L

CrossRef Full Text | Google Scholar

88. Weinberg S. Three-body interactions among nucleons and pions. Phys Lett B. (1992) 295:114–21. doi: 10.1016/0370-2693(92)90099-P

CrossRef Full Text | Google Scholar

89. van Kolck U. Few-nucleon forces from chiral Lagrangians. Phys Rev C. (1994) 49:2932–41. doi: 10.1103/PhysRevC.49.2932

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Ishikawa S, Robilotta MR. Two-pion exchange three-nucleon potential: O(q**4) chiral expansion. Phys Rev C. (2007) 76:014006. doi: 10.1103/PhysRevC.76.014006

CrossRef Full Text | Google Scholar

91. Bernard V, Epelbaum E, Krebs H, Meißner UG. Subleading contributions to the chiral three-nucleon force: Long-range terms. Phys Rev C. (2008) 77:064004. doi: 10.1103/PhysRevC.77.064004

CrossRef Full Text | Google Scholar

92. Bernard V, Epelbaum E, Krebs H, Meißner UG. Subleading contributions to the chiral three-nucleon force. II. Short-range terms and relativistic corrections. Phys Rev C. (2011) 84:054001. doi: 10.1103/PhysRevC.84.054001

CrossRef Full Text | Google Scholar

93. Krebs H, Gasparyan A, Epelbaum E. Chiral three-nucleon force at N⁴LO: longest-range contributions. Phys Rev C. (2012) 85:054006. doi: 10.1103/PhysRevC.85.054006

CrossRef Full Text | Google Scholar

94. Krebs H, Gasparyan A, Epelbaum E. Chiral three-nucleon force at N⁴LO. II. Intermediate-range contributions. Phys Rev C. (2013) 87:054007. doi: 10.1103/PhysRevC.87.054007

CrossRef Full Text | Google Scholar

95. Bhaduri RK, Loiseau BA, Nogami Y. Effect of three-body ΛNN long-range potential in nuclear matter. Nucl Phys B. (1967) 3:380–6. doi: 10.1016/0550-3213(67)90007-7

CrossRef Full Text | Google Scholar

96. Bhaduri RK, Loiseau BA, Nogami Y. Effects of three-body ΛNN forces in light hypernuclei. Ann Phys. (1967) 44:57–73. doi: 10.1016/0003-4916(67)90264-3

CrossRef Full Text | Google Scholar

97. Gal A, Soper JM, Dalitz RH. A shell-model analysis of Λ binding energies for the p-shell hypernuclei. I. Basic formulas and matrix elements for ΛN and ΛNN forces. Ann Phys. (1971) 63:53–126. doi: 10.1016/0003-4916(71)90297-1

CrossRef Full Text | Google Scholar

98. Gal A, Soper JM, Dalitz RH. A shell-model analysis of Λ binding energies for the p-shell hypernuclei II. Numerical fitting, interpretation, and hypernuclear predictions. Ann Phys. (1972) 72:445–88. doi: 10.1016/0003-4916(72)90222-9

CrossRef Full Text | Google Scholar

99. Gal A, Soper JM, Dalitz RH. A shell-model analysis of Λ binding energies for the p-shell hypernuclei III. Further analysis and predictions. Ann Phys. (1978) 113:79–97. doi: 10.1016/0003-4916(78)90250-6

CrossRef Full Text | Google Scholar

100. Bodmer AR, Usmani QN. Binding energies of the s-shell hypernuclei and the Λ well depth. Nucl Phys A. (1988) 477:621–51. doi: 10.1016/0375-9474(88)90410-1

CrossRef Full Text | Google Scholar

101. Usmani AA. Three-baryon Lambda N N potential. Phys Rev C. (1995) 52:1773–7. doi: 10.1103/PhysRevC.52.1773

CrossRef Full Text | Google Scholar

102. Lonardoni D, Gandolfi S, Pederiva F. Effects of the two-body and three-body hyperon-nucleon interactions in Λ hypernuclei. Phys Rev C. (2013) 87:041303. doi: 10.1103/PhysRevC.87.041303

CrossRef Full Text | Google Scholar

103. Logoteta D, Vidana I, Bombaci I. Impact of chiral hyperonic three-body forces on neutron stars. Eur Phys J. (2019) A55:207. doi: 10.1140/epja/i2019-12909-9

CrossRef Full Text | Google Scholar

104. Demorest PB, Pennucci TT, Ransom SM, Roberts MSE, Hessels JWT. A two-solar-mass neutron star measured using Shapiro delay. Nature. (2010) 467:1081–3. doi: 10.1038/nature09466

PubMed Abstract | CrossRef Full Text | Google Scholar

105. Antoniadis J, Freire PCC, Wex N, Tauris TM, Lynch RS, van Kerkwijk MH, et al. A massive pulsar in a compact relativistic binary. Science. (2013) 340:1233232. doi: 10.1126/science.1233232

PubMed Abstract | CrossRef Full Text | Google Scholar

106. Hebeler K, Lattimer JM, Pethick CJ, Schwenk A. Constraints on neutron star radii based on chiral effective field theory interactions. Phys Rev Lett. (2010) 105:161102. doi: 10.1103/PhysRevLett.105.161102

PubMed Abstract | CrossRef Full Text | Google Scholar

107. Hell T, Weise W. Dense baryonic matter: constraints from recent neutron star observations. Phys Rev C. (2014) 90:045801. doi: 10.1103/PhysRevC.90.045801

CrossRef Full Text | Google Scholar

108. Steiner AW, Lattimer JM, Brown EF. Neutron star radii, universal relations, and the role of prior distributions. arXiv:151007515 (2015). doi: 10.1140/epja/i2016-16018-1

CrossRef Full Text | Google Scholar

109. Vidaña I. Hyperons in neutron stars. J Phys Conf Ser. (2016) 668:012031. doi: 10.1088/1742-6596/668/1/012031

CrossRef Full Text | Google Scholar

110. Vidaña I. Hyperons: the strange ingredients of the nuclear equation of state. Proc R Soc Lond. (2018) A474:0145. doi: 10.1098/rspa.2018.0145

CrossRef Full Text | Google Scholar

111. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams C, et al. GW170817: observation of gravitational waves from a binary neutron star inspiral. Phys Rev Lett. (2017) 119:161101. doi: 10.1103/PhysRevLett.119.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

112. Abbott BP, Abbott R, Abbott TD, Acernese F, Ackley K, Adams T, et al. Multi-messenger observations of a binary neutron star merger. Astrophys J. (2017) 848:L12. doi: 10.3847/2041-8213/aa91c9

CrossRef Full Text | Google Scholar

113. Djapo H, Schaefer BJ, Wambach J. Appearance of hyperons in neutron stars. Phys Rev C. (2010) 81:035803. doi: 10.1103/PhysRevC.81.035803

CrossRef Full Text | Google Scholar

114. Weissenborn S, Chatterjee D, Schaffner-Bielich J. Hyperons and massive neutron stars: the role of hyperon potentials. Nucl Phys A. (2012) 881:62–77. doi: 10.1016/j.nuclphysa.2012.02.012

CrossRef Full Text | Google Scholar

115. Weissenborn S, Chatterjee D, Schaffner-Bielich J. Hyperons and massive neutron stars: vector repulsion and SU(3) symmetry. Phys Rev C. (2012) 85:065802. doi: 10.1103/PhysRevC.85.065802

CrossRef Full Text | Google Scholar

116. Yamamoto Y, Furumoto T, Yasutake N, Rijken TA. Hyperon mixing and universal many-body repulsion in neutron stars. Phys Rev C. (2014) 90:045805. doi: 10.1103/PhysRevC.90.045805

CrossRef Full Text | Google Scholar

117. Takatsuka T, Nishizaki S, Tamagaki R. Three-body force as an “Extra Repulsion” suggested from hyperon-mixed neutron stars. Prog Theor Phys Suppl. (2008) 174:80–3. doi: 10.1143/PTPS.174.80

CrossRef Full Text | Google Scholar

118. Vidaña I, Logoteta D, Providência C, Polls A, Bombaci I. Estimation of the effect of hyperonic three-body forces on the maximum mass of neutron stars. Europhys Lett. (2011) 94:11002. doi: 10.1209/0295-5075/94/11002

CrossRef Full Text | Google Scholar

119. Lonardoni D, Lovato A, Gandolfi S, Pederiva F. Hyperon puzzle: hints from quantum Monte Carlo calculations. Phys Rev Lett. (2015) 114:092301. doi: 10.1103/PhysRevLett.114.092301

PubMed Abstract | CrossRef Full Text | Google Scholar

120. Petschauer S, Kaiser N, Haidenbauer J, Meißner UG, Weise W. Leading three-baryon forces from SU(3) chiral effective field theory. Phys Rev C. (2016) 93:014001. doi: 10.1103/PhysRevC.93.014001

CrossRef Full Text | Google Scholar

121. Petschauer S, Haidenbauer J, Kaiser N, Meißner UG, Weise W. Density-dependent effective baryon-baryon interaction from chiral three-baryon forces. Nucl Phys A. (2017) 957:347–78. doi: 10.1016/j.nuclphysa.2016.09.010

CrossRef Full Text | Google Scholar

122. Kohno M. Single-particle potential of the Lambda hyperon in nuclear matter with chiral effective field theory NLO interactions including effects of YNN three-baryon interactions. Phys Rev C. (2018) 97:035206. doi: 10.1103/PhysRevC.97.035206

CrossRef Full Text | Google Scholar

123. Adler SL, Dashen RF. Current Algebras and Applications to Particle Physics. New York, NY: Benjamin (1968). Available online at: http://books.google.com/books?id=8OBEAAAAIAAJ

124. Coleman S, Wess J, Zumino B. Structure of phenomenological lagrangians. I. Phys Rev. (1969) 177:2239–47. doi: 10.1103/PhysRev.177.2239

CrossRef Full Text | Google Scholar

125. Callan CG, Coleman S, Wess J, Zumino B. Structure of phenomenological lagrangians. II. Phys Rev. (1969) 177:2247–50. doi: 10.1103/PhysRev.177.2247

CrossRef Full Text | Google Scholar

126. Gasser J, Leutwyler H. Chiral perturbation theory: expansions in the mass of the strange quark. Nucl Phys B. (1985) 250:465–516. doi: 10.1016/0550-3213(85)90492-4

CrossRef Full Text | Google Scholar

127. Jenkins E, Manohar AV. Baryon chiral perturbation theory using a heavy fermion lagrangian. Phys Lett B. (1991) 255:558–62. doi: 10.1016/0370-2693(91)90266-S

CrossRef Full Text | Google Scholar

128. Bernard V, Kaiser N, Kambor J, Meißner UG. Chiral structure of the nucleon. Nucl Phys. (1992) B388:315–45. doi: 10.1016/0550-3213(92)90615-I

CrossRef Full Text | Google Scholar

129. Thomas AW, Weise W. The Structure of the Nucleon. Berlin: Wiley-VCH Verlag (2001). Available online at: http://www.wiley-vch.de/publish/en/books/bySubjectPH00/ISBN3-527-40297-7/

Google Scholar

130. Scherer S, Schindler M. A primer for chiral perturbation theory. Lect Notes Phys. (2012) 830:1–338. doi: 10.1007/978-3-642-19254-8

CrossRef Full Text | Google Scholar

131. Petschauer S. Baryonic forces and hyperons in nuclear matter from SU(3) chiral effective field theory. Dissertation. Technische Universität München, München, Germany. (2016).

Google Scholar

132. Adler SL. Axial-vector vertex in spinor electrodynamics. Phys Rev. (1969) 177:2426–38. doi: 10.1103/PhysRev.177.2426

CrossRef Full Text | Google Scholar

133. Bell JS, Jackiw R. A PCAC puzzle: π⁰ → γγ in the σ-model. IL Nuovo Cimento A. (1969) 60:47–61. doi: 10.1007/BF02823296

CrossRef Full Text

134. Leutwyler H. On the foundations of chiral perturbation theory. Ann Phys. (1994) 235:165–203. doi: 10.1006/aphy.1994.1094

CrossRef Full Text | Google Scholar

135. Georgi H. Weak Interactions and Modern Particle Theory. Reading, MA: Benjamin; Cummings (1984).

Google Scholar

136. Fearing HW, Scherer S. Extension of the chiral perturbation theory meson Lagrangian to order p**6. Phys Rev D. (1996) 53:315–48. doi: 10.1103/PhysRevD.53.315

CrossRef Full Text | Google Scholar

137. Bijnens J, Colangelo G, Ecker G. The mesonic chiral lagrangian of order p**6. J High Energy Phys. (1999) 1999:020. doi: 10.1088/1126-6708/1999/02/020

CrossRef Full Text | Google Scholar

138. Fettes N, Meißner UG, Mojzis M, Steininger S. The chiral effective pion-nucleon lagrangian of order p**4. Ann Phys. (2000) 283:273–307. doi: 10.1006/aphy.2000.6059

CrossRef Full Text | Google Scholar

139. Krause A. Baryon matrix elements of the vector current in chiral perturbation theory. Helv Phys Acta. (1990) 63:3–70.

Google Scholar

140. Oller JA, Verbeni M, Prades J. Meson-baryon effective chiral Lagrangians to O(q**3). J High Energy Phys. (2006) 2006:079. doi: 10.1088/1126-6708/2006/09/079

CrossRef Full Text | Google Scholar

141. Frink M, Meißner UG. On the chiral effective meson-baryon Lagrangian at third order. Eur Phys J A. (2006) 29:255–60. doi: 10.1140/epja/i2006-10105-x

CrossRef Full Text | Google Scholar

142. Girlanda L, Pastore S, Schiavilla R, Viviani M. Relativity constraints on the two-nucleon contact interaction. Phys Rev C. (2010) 81:034005. doi: 10.1103/PhysRevC.81.034005

CrossRef Full Text | Google Scholar

143. Borasoy B. Baryon axial vector currents. Phys Rev D. (1999) 59:054021. doi: 10.1103/PhysRevD.59.054021

CrossRef Full Text | Google Scholar

144. Iwao S. Baryon-baryon interactions and unitary symmetry. IL Nuovo Cimento. (1964) 34:1167–83. doi: 10.1007/BF02748845

CrossRef Full Text | Google Scholar

145. Dover CB, Feshbach H. Unitary symmetry in baryon-baryon scattering. Ann Phys. (1990) 198:321–57. doi: 10.1016/0003-4916(90)90254-L

CrossRef Full Text | Google Scholar

146. Dover CB, Feshbach H. Unitary symmetry in baryon-baryon scattering, II. Ann Phys. (1992) 217:51–65. doi: 10.1016/0003-4916(92)90338-M

CrossRef Full Text | Google Scholar

147. Epelbaum E, Glöckle W, Meißner UG. The two-nucleon system at next-to-next-to-next-to-leading order. Nucl Phys A. (2005) 747:362–424. doi: 10.1016/j.nuclphysa.2004.09.107

CrossRef Full Text | Google Scholar

148. Kaiser N, Brockmann R, Weise W. Peripheral nucleon-nucleon phase shifts and chiral symmetry. Nucl Phys A. (1997) 625:758–88. doi: 10.1016/S0375-9474(97)00586-1

CrossRef Full Text | Google Scholar

149. Epelbaum E, Glöckle W, Meißner UG. Nuclear forces from chiral Lagrangians using the method of unitary transformation (I): formalism. Nucl Phys A. (1998) 637:107–34. doi: 10.1016/S0375-9474(98)00220-6

CrossRef Full Text | Google Scholar

150. Epelbaum E, Glöckle W, Meißner UG. Nuclear forces from chiral Lagrangians using the method of unitary transformation II: the two-nucleon system. Nucl Phys A. (2000) 671:295–331. doi: 10.1016/S0375-9474(99)00821-0

CrossRef Full Text | Google Scholar

151. Entem DR, Machleidt R. Accurate charge-dependent nucleon-nucleon potential at fourth order of chiral perturbation theory. Phys Rev C. (2003) 68:041001. doi: 10.1103/PhysRevC.68.041001

CrossRef Full Text | Google Scholar

152. Tominaga K, Ueda T, Yamaguchi M, Kijima N, Okamoto D, Miyagawa K, et al. A one-boson-exchange potential for Lambda N, Lambda Lambda and Xi N systems and hypernuclei. Nucl Phys. (1998) A642:483–505. doi: 10.1016/S0375-9474(98)00485-0

CrossRef Full Text | Google Scholar

153. Tominaga K, Ueda T. Effective one-boson-exchange potential for Lambda N and Sigma N systems and hypertriton. Nucl Phys. (2001) A693:731–54. doi: 10.1016/S0375-9474(01)00882-X

CrossRef Full Text | Google Scholar

154. Reuber A, Holinde K, Kim HC, Speth J. Correlated pi pi and K anti-K exchange in the baryon baryon interaction. Nucl Phys. (1996) A608:243–304. doi: 10.1016/0375-9474(96)00256-4

CrossRef Full Text | Google Scholar

155. Frink M, Meißner UG. Chiral extrapolations of baryon masses for unquenched three-flavor lattice simulations. J High Energy Phys. (2004) 407:28. doi: 10.1088/1126-6708/2004/07/028

CrossRef Full Text | Google Scholar

156. Mai M, Bruns P, Kubis B, Meißner UG. Aspects of meson-baryon scattering in three- and two-flavor chiral perturbation theory. Phys Rev D. (2009) 80:094006. doi: 10.1103/PhysRevD.80.094006

CrossRef Full Text | Google Scholar

157. Bernard V, Kaiser N, Meißner UG. Aspects of chiral pion-nucleon physics. Nucl Phys A. (1997) 615:483–500. doi: 10.1016/S0375-9474(97)00021-3

CrossRef Full Text | Google Scholar

158. Kaiser N, Gerstendörfer S, Weise W. Peripheral NN-scattering: role of delta-excitation, correlated two-pion and vector meson exchange. Nucl Phys. (1998) A637:395–420. doi: 10.1016/S0375-9474(98)00234-6

CrossRef Full Text | Google Scholar

159. Krebs H, Epelbaum E, Meißner UG. Nuclear forces with Δ excitations up to next-to-next-to-leading order, part I: peripheral nucleon-nucleon waves. Eur Phys J A. (2007) 32:127–37. doi: 10.1140/epja/i2007-10372-y

CrossRef Full Text | Google Scholar

160. Epelbaum E, Krebs H, Meißner UG. Δ-excitations and the three-nucleon force. Nucl Phys A. (2008) 806:65–78. doi: 10.1016/j.nuclphysa.2008.02.305

CrossRef Full Text | Google Scholar

161. Sasaki K, Oset E, Vacas M. Scalar ΛN and ΛΛ interaction in a chiral unitary approach. Phys Rev C. (2006) 74:064002. doi: 10.1103/PhysRevC.74.064002

CrossRef Full Text | Google Scholar

162. Ericson TEO, Weise W. Pions and Nuclei. Oxford: Clarendon Press (1988).

163. Holt JW, Kaiser N, Weise W. Density-dependent effective nucleon-nucleon interaction from chiral three-nucleon forces. Phys Rev C. (2010) 81:024002. doi: 10.1103/PhysRevC.81.024002

CrossRef Full Text | Google Scholar

164. Vincent CM, Phatak S. Accurate momentum-space method for scattering by nuclear and Coulomb potentials. Phys Rev C. (1974) 10:391–4. doi: 10.1103/PhysRevC.10.391

CrossRef Full Text | Google Scholar

165. Furnstahl RJ, Phillips DR, Wesolowski S. A recipe for EFT uncertainty quantification in nuclear physics. J Phys G. (2015) 42:034028. doi: 10.1088/0954-3899/42/3/034028

CrossRef Full Text | Google Scholar

166. Epelbaum E, Krebs H, Meißner UG. Improved chiral nucleon-nucleon potential up to next-to-next-to-next-to-leading order. Eur Phys J A. (2015) 51:53. doi: 10.1140/epja/i2015-15053-8

CrossRef Full Text | Google Scholar

167. Furnstahl RJ, Klco N, Phillips DR, Wesolowski S. Quantifying truncation errors in effective field theory. Phys Rev C. (2015) 92:024005. doi: 10.1103/PhysRevC.92.024005

CrossRef Full Text | Google Scholar

168. Binder S, Calci A, Epelbaum E, Furnstahl RJ, Golak J, Hebeler K, et al. Few-nucleon systems with state-of-the-art chiral nucleon-nucleon forces. Phys Rev C. (2016) 93:044002. doi: 10.1103/PhysRevC.93.044002

CrossRef Full Text | Google Scholar

169. Sechi-Zorn B, Kehoe B, Twitty J, Burnstein RA. Low-energy lambda-proton elastic scattering. Phys Rev. (1968) 175:1735–40. doi: 10.1103/PhysRev.175.1735

CrossRef Full Text | Google Scholar

170. Alexander G, Karshon U, Shapira A, Yekutieli G, Engelmann R, Filthuth H, et al. Study of the lambda-N system in low-energy lambda-p elastic scattering. Phys Rev. (1968) 173:1452–60. doi: 10.1103/PhysRev.173.1452

CrossRef Full Text | Google Scholar

171. Engelmann R, Filthuth H, Hepp V, Kluge E. Inelastic Σ⁻p-interactions at low momenta. Phys Lett. (1966) 21:587–9. doi: 10.1016/0031-9163(66)91310-2

CrossRef Full Text | Google Scholar

172. Eisele F, Filthuth H, Föhlisch W, Hepp V, Zech G. Elastic Σ^±p scattering at low energies. Phys Lett B. (1971) 37:204–6. doi: 10.1016/0370-2693(71)90053-0

CrossRef Full Text | Google Scholar

173. Hepp V, Schleich H. A new determination of the capture ratio $r_c=({\Sigma }^{-}p\to {\Sigma }^{0}n)/(({\Sigma }^{-}p\to {\Sigma }^{0}n)+({\Sigma }^{-}p\to {\Lambda }^{0}n))$, the Λ⁰-lifetime and Σ⁻Λ⁰ mass difference. Z Phys. (1968) 214:71–7. doi: 10.1007/BF01380085

CrossRef Full Text | Google Scholar

174. Stephen D. Ph.D. thesis, University of Massachsetts, unpublished (1970).

Google Scholar

175. Nogga A. Light hypernuclei based on chiral and phenomenological interactions. Nucl Phys A. (2013) 914:140–50. doi: 10.1016/j.nuclphysa.2013.02.053

CrossRef Full Text | Google Scholar

176. Haidenbauer J, Meißner UG, Kaiser N, Weise W. Lambda-nuclear interactions and hyperon puzzle in neutron stars. Eur Phys J A. (2017) 53:121. doi: 10.1140/epja/i2017-12316-4

CrossRef Full Text | Google Scholar

177. Aoki S, Asai S, Bahk SY, Chung SH, Funahashi H, Hahn CH, et al. Quasifree p(K-,K+)Xi- reaction in nuclear emulsion. Nucl Phys. (1998) A644:365–85. doi: 10.1016/S0375-9474(98)00596-X

CrossRef Full Text | Google Scholar

178. Ahn JK, Aoki S, Chung KS, Chung MS, Enyo H, Fukuda T, et al. Measurement of the Xi-p scattering cross sections at low energy. Phys Lett. (2006) B633:214–8.

Google Scholar

179. Takahashi H, Ahn JK, Akikawa H, Aoki S, Arai K, Bahk SY, et al. Observation of a (Lambda Lambda)He-6 double hypernucleus. Phys Rev Lett. (2001) 87:212502. doi: 10.1103/PhysRevLett.87.212502

CrossRef Full Text | Google Scholar

180. Gasparyan AM, Haidenbauer J, Hanhart C. Scattering lengths of strangeness S=-2 baryon-baryon interactions. Phys Rev. (2012) C85:015204. doi: 10.1103/PhysRevC.85.015204

CrossRef Full Text | Google Scholar

181. Ohnishi A, Morita K, Miyahara K, Hyodo T. Hadron? Hadron correlation and interaction from heavy? Ion collisions. Nucl Phys. (2016) A954:294–307. doi: 10.1016/j.nuclphysa.2016.05.010

CrossRef Full Text | Google Scholar

182. Nakazawa K, Endo Y, Fukunaga S, Hoshino K, Hwang SH, Imai K, et al. The first evidence of a deeply bound state of Xi--14N system. Prog Theor Exp Phys. (2015) 2015:033D02. doi: 10.1093/ptep/ptv008

CrossRef Full Text | Google Scholar

183. Gal A, Hungerford EV, Millener DJ. Strangeness in nuclear physics. Rev Mod Phys. (2016) 88:035004. doi: 10.1103/RevModPhys.88.035004

CrossRef Full Text | Google Scholar

184. Millener DJ, Dover CB, Gal A. Lambda-nucleus single-particle potentials. Phys Rev C. (1988) 38:2700–8. doi: 10.1103/PhysRevC.38.2700

PubMed Abstract | CrossRef Full Text | Google Scholar

185. Yamamoto Y, Bandō H, Zofka J. On the Lambda-hypernuclear single particle energies. Prog Theor Phys. (1988) 80:757–61. doi: 10.1143/PTP.80.757

CrossRef Full Text | Google Scholar

186. Ajimura S, Hayakawa H, Kishimoto T, Kohri H, Matsuoka K, Minami S, et al. Observation of spin-orbit splitting in lambda single-particle states. Phys Rev Lett. (2001) 86:4255–8. doi: 10.1103/PhysRevLett.86.4255

PubMed Abstract | CrossRef Full Text | Google Scholar

187. Akikawa H, Ajimura S, Chrien RE, Eugenio PM, Franklin GB, Franz J, et al. Hypernuclear fine structure in (Lambda*)Be-9. Phys Rev Lett. (2002) 88:082501. doi: 10.1103/PhysRevLett.88.082501

PubMed Abstract | CrossRef Full Text | Google Scholar

188. Friedman E, Gal A. In-medium nuclear interactions of low-energy hadrons. Phys Rep. (2007) 452:89–153. doi: 10.1016/j.physrep.2007.08.002

CrossRef Full Text | Google Scholar

189. Baldo M. Nuclear Methods and the Nuclear Equation of State, Vol. 8 of International Review of Nuclear Physics. World Scientific Publishing Co. Pte. Ltd. (1999). Available online at: http://ebooks.worldscinet.com/ISBN/9789812817501/9789812817501.html

Google Scholar

190. Fetter AL, Walecka JD. Quantum Theory of Many-Particle Systems. Dover Books on Physics. New York, NY: Dover Publications (2003).

Google Scholar

191. Bethe HA, Brandow BH, Petschek AG. Reference spectrum method for nuclear matter. Phys Rev. (1963) 129:225–64. doi: 10.1103/PhysRev.129.225

CrossRef Full Text | Google Scholar

192. Song HQ, Baldo M, Giansiracusa G, Lombardo U. Bethe-Brueckner-goldstone expansion in nuclear matter. Phys Rev Lett. (1998) 81:1584–7. doi: 10.1103/PhysRevLett.81.1584

CrossRef Full Text | Google Scholar

193. Gal A. Strangeness nuclear physics - 2010. Prog Theor Phys Suppl. (2010) 186:270–81. doi: 10.1143/PTPS.186.270

CrossRef Full Text | Google Scholar

194. Botta E, Bressani T, Garbarino G. Strangeness nuclear physics: a critical review on selected topics. Eur Phys J A. (2012) 48:41. doi: 10.1140/epja/i2012-12041-6

CrossRef Full Text | Google Scholar

195. Dover CB, Millener DJ, Gal A. On the production and spectroscopy of Sigma hypernuclei. Phys Rep. (1989) 184:1–97. doi: 10.1016/0370-1573(89)90105-1

CrossRef Full Text | Google Scholar

196. Dabrowski J. Isospin dependence of the single-particle potential of the Sigma hyperon in nuclear matter. Phys Rev C. (1999) 60:025205. doi: 10.1103/PhysRevC.60.025205

CrossRef Full Text | Google Scholar

197. Kohno M. Xi hyperons in the nuclear medium described by chiral NLO interactions. Phys Rev C. (2019) 100:024313. doi: 10.1103/PhysRevC.100.024313

CrossRef Full Text | Google Scholar

198. Haidenbauer J, Vidana I. Structure of single-Λ hypernuclei with chiral hyperon-nucleon potentials. arXiv: 1910.02695 (2019). doi: 10.1140/epja/s10050-020-00055-6

CrossRef Full Text | Google Scholar

199. Vidaña I. Single-particle spectral function of the Λ hyperon in finite nuclei. Nucl Phys. (2017) A958:48–70. doi: 10.1016/j.nuclphysa.2016.11.002

CrossRef Full Text | Google Scholar

200. Nogga A. Charge-symmetry breaking in light hypernuclei based on chiral and similarity renormalization group-evolved interactions. AIP Conf Proc. (2019) 2130:030004. doi: 10.1063/1.5118394

CrossRef Full Text | Google Scholar

201. Le H, Haidenbauer J, Meißner U-G, Nogga A. Implications of an increased Λ-separation energy of the hypertriton. Phys LettB. (2020) 801:135189. doi: 10.1016/j.physletb.2019.135189

CrossRef Full Text | Google Scholar

202. Haidenbauer J, Meißner UG, Nogga A, Polinder H. The hyperon-nucleon interaction: conventional versus effective field theory approach. Lect Notes Phys. (2007) 724:113–40. doi: 10.1007/978-3-540-72039-3_4

CrossRef Full Text | Google Scholar

203. Gerstung D, Kaiser N, Weise W. Hyperon-nucleon three-body forces and strangeness in neutron stars. arXiv: 2001.10563. (2020).

Google Scholar

204. Yamamoto Y, Nishizaki S, Takatsuka T. Single-particle potentials and effective masses of hyperons in hyperonic nuclear systems. Prog Theor Phys. (2000) 103:981–1000. doi: 10.1143/PTP.103.981

CrossRef Full Text | Google Scholar