- Department of Physics, Collaborative Innovation Center for Quantum Effects, and Key Laboratory of Low Dimensional Quantum Structures and Quantum Control of Ministry of Education, Hunan Normal University, Changsha, China
One of the major motivations for low-energy heavy-ion collision is the synthesis of superheavy nuclei. Based on the following two main aspects, various theoretical and experimental studies have been performed to explore the fusion dynamical process of superheavy nuclei production. The first reason is to elucidate and analyze the synthesis mechanism of superheavy nuclei; the other is to search the favorable incident energy and the best combination of projectile and target to produce new superheavy elements and isotopes of superheavy elements.
1. Introduction
The maximum mass and charge of a nucleus is a long-standing fundamental problem in nuclear physics [1, 2]. Pioneer studies have theoretically predicted the “island of stability” of superheavy nuclei (SHN). The macroscopic-microscopic models predicted 298Fl to be the double magic nucleus [3–7]. However, results of the self-consistent models showed that the closed shell of Z = 114 becomes weaker, and Z = 114 is replaced by Z = 120 or 126 [8–13].
The production process of superheavy nuclei is a very complicated dynamical problem [14]. Many theoretical models have been developed to explain the experimental data. On one hand, the synthesis mechanism of superheavy nuclei needs to be elucidated [15–21]. Different approaches are devoted to calculate and analyze the fusion probability and the distribution of quasifission fragments [15–41]. However, none of them has absolute advantage. On the other hand, in order to produce the new superheavy elements, or isotopes of superheavy elements, the favorable incident energy and the best combination of projectile and target should be evaluated.
The extended nuclear landscape allows us to investigate the nuclear structure of superheavy nuclei and the nuclear reaction mechanism. To search for the optimal condition of synthesis, the influence of the entrance channel [29, 42, 43] and the isospin of heavy colliding nuclei [44–46] on the evaporation residual cross section have been studied systematically in many works. The predictions of the possible way to synthesize the new superheavy elements Z = 119 and 120 have also been carried out [17, 47–52].
2. Experimental Progress
Producing superheavy nuclei in the laboratory is one of the major motivations of low-energy heavy-ion physics [1, 2, 53–55]. Over the past 30 years, great progress has been achieved for superheavy nuclei production in experimental studies [53–55]. The experimental trends α decay half-lives, and the evaporation residue cross sections of the superheavy nuclei show that the stability of superheavy nuclei increases as the neutron number approaches the closed neutron shell closure N = 184. However, the location of the “island of stability” has not been determined by experiment. Up until now, based on the fusion-evaporation reaction, the superheavy nuclei with charge numbers in the range of Z = 104118 have been synthesized successfully.
The superheavy elements Z = 107−112 was first synthesized by using the cold fusion reactions [1, 53, 54, 56, 57]. The excitation energy range of the formed compound nucleus was 10–18 MeV. The measurement of the evaporation residue cross section decreased dramatically from Z = 107 to Z = 113. Moreover, the final evaporated residual nuclei were extremely neutron deficient. Experiments of producing superheavy nuclei by cold fusion have been repeated and verified by other laboratories [54, 58, 59].
The 48Ca-induced hot-fusion reactions were used to synthesize Z = 112−118 superheavy nuclei in experiment [54, 55, 60]. From the measurement of evaporation residue cross sections, we found that there was no significant difference from Z = 112–118, and the values of the evaporation residual cross sections were all in the order of picobarn. Experiments based on hot fusion for synthesizing Z = 112 and 114–117 superheavy nuclei have been verified by other laboratories [60].
To search for the optimal condition of the superheavy nuclei production, various experiments have been performed to study the entrance channel effect on the evaporation residual cross section [61–65]. Recently, the isospin effect of the target nucleus on the evaporation residue cross section has been explored [66–68]. Some laboratories have also attempted to synthesize the Z = 119 and 120 superheavy elements by using hot fusion [69, 70].
Experimentally, the measurement of fusion probability is required to distinguish quasifission between fusion-fission and fast fission [71–76]. The experimental characteristics of the quasifission process are different from the fusion-fission process [77]. Therefore, it is important to distinguish the fusion and quasifission fragments for a better understanding of the fusion mechanism.
3. Theoretical Description of Fusion Reactions
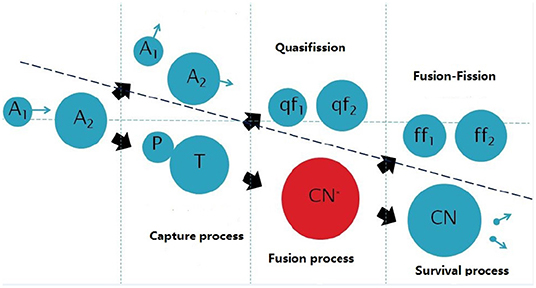
Theoretically, the synthesis process of superheavy nuclei can be divided into three stages [39]. A schematic diagram for this process is shown in Figure 1. The first stage is the capture process, which can be evaluated by the capture cross section. The second stage is that the dinuclear system evolves from the touching configuration to the formation of the compound nucleus, which can be evaluated by the fusion probability. The last stage is where the excited compound nucleus cools down through emitting neutrons or fission, and this can be evaluated by the survival probability. Finally, a very small evaporation residue cross section is obtained for the superheavy nuclei production. The evaporation residue cross section can be expressed as [39],
where Ec.m. is the incident energy in the center-of-mass frame.
3.1. Capture Cross Sections
For the low-energy heavy-ion collision, the capture cross section from the sub-barrier region to above the Coulomb barrier is an important issue for theoretical and experimental studies [78–83]. One of reasons is that the overall uncertainties in predicting superheavy nuclei production are associated with the calculations of capture cross sections [50, 84, 85].
The capture process is closely related to the nuclear structure of the interacting nuclei [86–97]. This is because the nucleus-nucleus potential contains nuclear structure information. To precisely describe the measurements of capture cross sections, the nucleus-nucleus interaction potential is the most important input quantity. In addition, the heavy-ion capture process is intimately linked to nuclear deformation [87, 88]. Thus, the nuclear deformation must be reliable to some extent.
Theoretically, the capture cross section is one of the important components in the synthesis of superheavy nuclei. The capture cross section have been explored extensively [82–84] from light to superheavy by averaging the penetration probability over barrier heights. Most of them have tested a number of experimental data of capture cross sections, however, these experimental data do not contain the capture cross sections of superheavy nuclei [84]. Therefore, it is very important to examine carefully the capture process for the study of the synthesis mechanism of superheavy nuclei.
Usually, the capture cross section σcap is mainly calculated with an empirical coupled-channel approach for the superheavy nuclei production [17, 44–52]. From a theoretical point of view, one of the powerful methods is to solve coupled-channels equations numerically. This may help us to understand the influence of the couplings between nuclear intrinsic degrees of freedom and the relative motion on capture cross sections.
Recently, the quantum diffusion approach [98–101] has also been used to calculate capture cross sections. This model takes into consideration the influence of fluctuations and dissipation effects on capture cross sections. The nuclear deformation effects and mutual orientations of the colliding nuclei are taken into account through using a double folding potential, and the influence of two neutrons transfer onto the sub-barrier capture through the change of the deformations of the colliding nuclei [100].
Another powerful theoretical tool is to calculate the capture cross section by the time-dependent Hartree Fock (TDHF) method. Recently, the pioneering work of studying capture cross section based on TDHF has been completed for the 40Ca+238U reaction [102]. In addition, Umar et al. found that the capture cross sections calculated by TDHF method agreed with the experimental data within 20% [103].
3.2. Fusion Dynamics
In order to explain the fusion dynamics process (the second stage), various theoretical approaches and models have been developed. The simplification can be made in different ways, and, as a result, we can obtain different theoretical pictures for the same real nuclear process. Some of the models can be roughly divided into two types. The first type is based on transport equations to describe the fusion dynamics process [15–41]. The second one is based on the time-dependent Hartree Fock method to describe the mainly experimental features in the process of fusion dynamics [104–115].
The first approach is that the multitude of degrees of freedom are decomposed into a dominating collective degree of freedom and other degrees (non-collective) of freedom. Therefore, the dissipative processes are introduced to account for the coupling between the collective motions and the intrinsic motions of the freedom of the system. Many models based on transport equations have been developed, and they assumed that the main characteristics of fusion dynamics process can be described by using the main collective degrees of freedom.
On the one hand, after eliminating the intrinsic motion, a stochastic equation can be derived theoretically. Many models adopted the Langevin forces (Langevin equation) to describe stochastic characteristics of the coupling between collective motions and intrinsic degrees of freedom. One can calculate a bundle of trajectories by solving a stochastic equation [16, 17, 28, 31, 35, 36].
On the other hand, through eliminating the intrinsic degrees of freedom, a diffusion equation can be derived theoretically to describe the distribution of collective degrees of freedom in the phase space [19–21, 27, 29, 29, 30, 32, 41–43, 46, 47, 49, 51, 116, 117]. Diffusion equations (the master equation, Smoluchowski equation, etc.,) may be used to describe the transport process of collective degrees of freedom in phase space.
The second approach is the time-dependent Hartree Fock method. The basic idea of this method is that the mean field produced by all nucleons not only determines the intrinsic motion of a single particle but also describes the evolution characteristics of collective degrees. TDHF calculations may be used to compute the ratio of fusion cross sections to capture cross sections. In addition, the TDHF method may be used to explore the effect of the orientation of the projectile and the target at the contact point, and the role of the nuclear shell structure and tensor force [104–115].
3.3. Fusion Mechanism
For the real fusion dynamics process, a theoretical model may be considered as a collection of theoretical assumptions. Up to now, there have been proposed fusion mechanisms that are incompatible with the compound nucleus formation. One assumption is that all the nucleons are immediately collectivized into one superdeformed mononucleus. Then, the dynamic evolution behavior of the superdeformed mononucleus can be described by the equation of motion or transport theory [15–17, 33, 34, 118]. The macroscopic dynamical model is the first model to describe the fusion mechanism based on the idea of forming one superdeformed mononucleus [15]. However, it encountered serious difficulties in attempts to describe evaporation residue cross sections for the synthesis of superheavy nuclei.
As the macroscopic dynamical models, the same approximations are used in the fluctuation-dissipation model [16, 118], the two-step model [17], and the fusion-by-diffusion model [33, 34]. But two significant improvements are taken into account for the description of the fusion-dynamics mechanism: shell effects in the calculation of the potential energy surface of the reaction system and statistical fluctuations in the interaction of colliding nuclei. These improvements permit one to describe the evaporation residue cross section of superheavy nuclei, the mass distribution of quasifission, and fusion-fission products [16, 17, 33, 34, 118, 119].
Another assumption is that two touching nuclei always keeps its own identity with their ground state characteristics and deformations (dinuclear system model) [19–21, 29], fusion is achieved by means of nucleon transfer. However, the real situation is due to strong Coulomb and nuclear interactions between projectile and target; the dinuclear system should be gradually deformed [30, 48]. This assumption has recently been improved upon. The coupling of the deformations evolution of project and target and the nucleon transfer has been studied numerically [120, 121]. The calculated results for the cold and hot fusion reactions by using the dinuclear system model match well with the available experimental data [20, 27, 29, 29, 30, 32, 41–43, 46, 47, 49, 51, 116, 117]. The fusion probability and the distribution of the quasifission fragments can be reasonably described based on the dinuclear system model [120–122].
A new fusion mechanism on compound nucleus formation was proposed by Zagrebaev [18]. The concept of a nucleon collectivization model assumes that two nuclei gradually lose their individualities through increasing the number of collectivized nucleons [18]; the reliability of the theoretical hypothesis needs further demonstration [123]. The nucleon collectivization model allows us to describe reasonably the fusion probability as well as the charge and mass distributions of the quasifission products [124].
3.4. Selection of Collective Degree and Calculation of Related Input Quantity in Transport or Diffusion Equations
To theoretically describe fusion dynamics and the mechanism based on transport equations as mentioned above, one needs to assume that several important degrees of freedoms can be used to describe the main characteristics of fusion dynamics process [15–21]. These important degrees of freedoms include the distance between the nuclear centers, the neutron and proton asymmetries of projectile-target combinations, deformations, and corresponding orientation effects, which influence the dynamics from touching the configuration to the compound nucleus.
Because equations of motion contain time derivatives up to the second order, there are three quantities in each equations of motion. The first quantity is the conservative potential. The second and third are the friction tensor (friction force) and the inertia tensor (inertia parameter), respectively. For the conservative potential, two different approaches have been taken into account to calculate the potential energy surface. The two assumptions of calculating potential energy surface are frozen density or sudden approximation [19–21] and the adiabatic approximation [15–18].
Recently, Diaz-Torres showed that the gradual transition of potential energy surface from the diabatic to the adiabatic should be more realistic for describing the fusion or quasifission [125, 126]. In addition, one needs to consider how the shell structure evolutes with excitation energy and deformation. The excitation energy dissipated from kinetic energy of relative motion makes the individual shell structure of nuclei become damped [127–131], and deformation tends to be spherical [132]. Thus, the dynamical potential energy surface has to be further studied. However, a small amount of research work has involved the shell correction energy employed in the fusion process being temperature dependent [133] and the potential energy surface from diabatic approximation to adiabatic approximation to describe the whole dynamic evolution process.
The dissipation tensor arises from the distinction between collective motion and intrinsic motion. The dissipation tensor accounts for the coupling between the collective degrees of freedom and other degrees (non-collective) of freedom. When equations of motion or stochastic equations are used to describe the dynamic process, the friction coefficients are mainly treated by the phenomenological approaches for the description of the fusion dynamics process [16, 124].
The inertial tensor describes the response of the system to small changes in the collective degrees of freedom. The macroscopic approach, macroscopic-microscopic approach, and microscopic approach are used to calculate the inertia tensor of the fission dynamics process [134–137]. However, in the low-energy heavy-ion collisions process, it seems that the proper calculation on inertial parameters has not been paid enough attention compared to the fission dynamics process. In the stochastic equation, the inertia parameter is calculated by the Werner-Wheeler approach [124, 127]. In the diffusion equation, the inertia parameter is treated as a reduced mass of relative motion [138]. From the theoretical point of view, the inertia parameters and friction coefficient of theoretical calculations have to match our understanding of the potential energy surface in the transport equations.
3.5. Survival Probabilities
The last important factor is the survival probability of the compound nucleus against fission in the deexcitation process. For exciting compound nuclei, there are two methods to describe the fission process: the statistical approach and the dynamical approach. Based on the statistical model, two different approaches are taken into account for the excitation energy dependent shell structure. The first one is to introduce the influence of excitation energy on the shell structure through the energy level density parameter [139]. The second one is to ensure the excitation energy-dependent shell effect is taken into account by the effective potential energy surface [140].
The uncertainty of survival probability calculation based on statistical model mainly comes from two aspects. On one hand, a number of approximations are adapted in the calculation of survival probability. One the other hand, the survival probabilities for the xn evaporation channels are very sensitive to the model input. The level densities, fission barriers, neutron-separation energies, as well as the transmission coefficients have to be known with sufficient accuracy. Only systematic calculations based on the same assumptions and parameters can help to confirm the validity and reliability of the theoretical approximations and input quantities [28, 117].
4. The Optimum Projectile-Target Combination and Bombarding Energy
4.1. Influence of Entrance Channel on ERCSs
Systematic studies of the existing experimental ERCSs are helpful to reveal reaction mechanisms. In addition, searching the optimal combination of the projectile and target and the range of the favorable beam energy is essential.
Some work systematically studies the influence of the neutron number of a target or projectile on the evaporation residue cross section [32, 36, 44–46]. Many researchers have found that the fusion probability and survival probability are sensitive to the neutron number of the target or projectile nuclei [32, 36, 44–46]. For 48Ca-induced hot fusion, the excess neutron of target nucleus is beneficial to the increase of the evaporation residue cross section of the synthesized superheavy nuclei [32, 45, 46].
Using a different combination of projectile and target to produce the same compound nucleus may help us to reveal the effect of the ground-state deformations, the reaction Q value, the asymmetry of charge and mass of target and projectile, and the Coulomb barrier on the evaporation residual cross section [33, 138, 141]. The results calculated by Liu et al. show that the Q value of reaction has a significant effect on the capture cross section and fusion probability [142].
4.2. The ERCS of Production Using Radioactive Beams
In order to investigate the possibility of neutron-rich superheavy nuclei production with radioactive beams, some calculations have been made [25, 116, 143, 144]. The evaporation residue cross section by using radioactive beams are comparable with a stable beam for some superheavy nuclei production [116, 143]. However, the choice of reaction channels is determined by the product of beam intensity and evaporation residue cross section [143].
The intensities of stable beams, in most of the cases, are significantly larger than those of the radioactive beams [143], and the results have shown that the calculated evaporation residue cross section based on stable beam is more favorable for the production of many superheavy nuclei [116, 143]. In addition, due to small evaporation residue cross sections and low radioactive beam intensities, the synthesis of higher charge number superheavy nuclei by using the neutron-rich radioactive beams seems impossible based on today's experimental conditions [116, 143].
4.3. Prediction ERCS Z = 119 and 120
By comparing evaporation residue cross sections for production Z = 119 and 120, we found that the calculations from different models were obviously different [17, 47–52, 124]. On one hand, the survival probability of the compound nucleus was very sensitive to the fission barrier. However, the difference in fission barriers of superheavy nuclei calculated by different models was obvious not only due to the absolute values but also the trends with charge number Z [2, 85]. On the other hand, due to different assumptions, the fusion probability calculated by different models was significantly different for synthesis Z = 119 and 120 [84].
According to our calculation and other theoretical predictions, almost all the models that predicted evaporation residue cross sections to produce superheavy new element Z = 119 are generally greater than those in producing Z = 120 [17, 47–52].
5. The Future
The synthesis of SHN in the laboratory has made great progress, and all the elements up to Z=118 have been synthesized successfully. However, the location of the island of stability has not been confirmed in experiments. Although many theoretical approaches were used to study the fusion mechanism, there are still many problems that have not been solved properly. In my opinion, the transport theory is the least developed one due to three factors: (i) the neck formation itself and the relationship between dynamic deformation and neck formation should be included to improve the theoretical description of fusion dynamic mechanism; (ii) the gradual transition of the potential energy surface from the diabatic approximation to the adiabatic approximation needs to be further explored; and (iii) the further study of inertia and damping coefficients to match our understanding of the potential energy surface in the transport equations should be performed.
6. Summary
The evaporation residue cross section of superheavy nuclei depends on three factors: the capture cross section σcap, the fusion probability PCN, and the survival probability Wsur. We found that the reasonable description of the capture cross section near the Coulomb barrier is very important. The coupled channel or TDHF can be better approached to calculate the value, especially for superheavy nuclei calculations.
I think the fusion probability PCN for producing superheavy nuclei is still not well understood. Not only the magnitude of the fusion probability PCN but also the dependence of PCN on the excitation energy and the entrance channel are lacking in clarity. The fusion mechanism must be further studied.
The uncertainty of survival probability calculation based on a statistical model mainly comes from theoretical approximations and input quantities. Systematic calculations based on the same assumptions and parameters can help to confirm the validity and reliability of the theoretical approximations and input quantities.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This work was supported by the National Natural Science Foundation of China (Grants 11705055) and Hunan Provincial Natural Science Foundation of China (2018JJ3324).
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Hofmann S, Münzenberg G. The discovery of the heaviest elements. Rev Mod Phys. (2000) 72:733. doi: 10.1103/RevModPhys.72.733
2. Giuliani SA, Matheson Z, Nazarewicz W, Olsen E, Reinhard PG, Sadhukhan J, et al. Colloquium: superheavy elements: oganesson and beyond. Rev Mod Phys. (2019) 91:011001. doi: 10.1103/RevModPhys.91.011001
3. Sobiczewski A, Gareev FA, Kalinkin BN. Closed shells for Z>82 and N>126 in a diffuse potential well. Phys Lett. (1966) 22:500. doi: 10.1016/0031-9163(66)91243-1
4. Mosel U, Greiner W. On the stability of superheavy nuclei against fission. Z Phys. (1969) 222:261. doi: 10.1007/BF01392125
5. Nilsson SG, Tsang CF, Sobiczewski A, Szymanski Z, Wycech S, Gustafson C, et al. On the nuclear structure and stability of heavy and superheavy elements. Nucl Phys A. (1969) 131:1. doi: 10.1016/0375-9474(69)90809-4
6. Moller P, Nix JR, Myers WD, Swiatecki WJ. Nuclear ground-state masses and deformations. At Data Nucl Data Tables. (1995) 59:185. doi: 10.1006/adnd.1995.1002
7. Smolańczuk R. Properties of the hypothetical spherical superheavy nuclei. Phys Rev C. (1997) 56:812. doi: 10.1103/PhysRevC.56.812
8. Decharge J, Berger JF, Dietrich K, Weiss MS. Superheavy and hyperheavy nuclei in the form of bubbles or semi-bubbles. Phys Lett B. (1999) 451:275–82. doi: 10.1016/s0370-2693(99)00225-7
9. Bender M, Nazarewicz W, Reinhard PG. Shell stabilization of super- and hyperheavy nuclei without magic gaps. Phys Lett B. (2001) 515:42–8. doi: 10.1016/S0370-2693(01)00863-2
10. Ring P. Relativistic mean field theory in finite nuclei. Prog Part Nucl Phys. (1996) 37:193–263. doi: 10.1016/0146-6410(96)00054-3
11. Meng J, Toki H, Zhou SG, Zhang SQ, Long WH, Geng LS. Relativistic continuum Hartree Bogoliubov theory for ground-state properties of exotic nuclei. Prog Part Nucl Phys. (2006) 57:470–563. doi: 10.1016/j.ppnp.2005.06.001
12. Li JJ, Long WH, Margueron J, Van Giai N. Superheavy magic structures in the relativistic HartreeCFockCBogoliubov approach. Phys Lett B. (2014) 732:169–73. doi: 10.1016/j.physletb.2014.03.031
13. Cwiok S, Dobaczewski J, Heenen PH, Magierski P, Nazarewicz W. Shell structure of the superheavy elements. Nucl Phys A. (1996) 611:211–46. doi: 10.1016/S0375-9474(96)00337-5
14. Swiatecki WJ. Three lectures on macroscopic aspects of nuclear dynamics. Prog Part Nucl Phys. (1980) 4:383. doi: 10.1016/0146-6410(80)90014-9
15. Swiatecki WJ. The dynamics of the fusion of two nuclei. Nucl Phys A. (1982) 376:275. doi: 10.1016/0375-9474(82)90065-3
16. Aritomo Y, Wada T, Ohta M, Abe Y. Fluctuation-dissipation model for synthesis of superheavy elements. Phys Rev C. (1999) 59:796. doi: 10.1103/PhysRevC.59.796
17. Shen CW, Abe Y, Boilley D, Kosenko G, Zhao EG. Isospin dependence of reactions 48Ca+243−251Bk. Int. J. Mod. Phys. E. (2008) 17:66. doi: 10.1142/S0218301308011768
18. Zagrebaev VI. Synthesis of superheavy nuclei: nucleon collectivization as a mechanism for compound nucleus formation. Phys Rev C. (2001) 64:034606. doi: 10.1103/PhysRevC.64.034606
19. Adamian GG, Antonenko NV, Scheid W, Volkov VV. Treatment of competition between complete fusion and quasifission in collisions of heavy nuclei. Nucl Phys A. (1997) 627:361. doi: 10.1016/S0375-9474(97)00605-2
20. Feng ZQ, Jin GM, Fu F, Li JQ. Production cross sections of superheavy nuclei based on dinuclear system model. Nucl Phys A. (2006) 771:50. doi: 10.1016/j.nuclphysa.2006.03.002
21. Diaz-Torres A, Adamian GG, Antonenko NV, Scheid W. Quasifission process in a transport model for a dinuclear system. Phys Rev C. (2001) 64:024604. doi: 10.1103/PhysRevC.64.024604
22. Zagrebaev V, Greiner W. Synthesis of superheavy nuclei: a search for new production reactions. Phys Rev C. (2008) 78:034610. doi: 10.1103/PhysRevC.78.034610
23. Smolańczuk R. Synthesis of transactinide nuclei in cold fusion reactions using radioactive beams. Phys Rev C. (2010) 81:067602. doi: 10.1103/PhysRevC.81.067602
24. Wang N, Tian J, Scheid W. Systematics of fusion probability in hot fusion reactions. Phys Rev C. (2011) 84:061601(R). doi: 10.1103/PhysRevC.84.061601
25. Wu ZH, Zhu L, Li F, Yu XB, Su J, Guo CC. Synthesis of neutron-rich superheavy nuclei with radioactive beams within the dinuclear system model. Phys Rev C. (2018) 97:064609. doi: 10.1103/PhysRevC.97.064609
26. Shen CW, Kosenko G, Abe Y. Two-step model of fusion for the synthesis of superheavy elements. Phys Rev C. (2002) 66:061602. doi: 10.1103/PhysRevC.66.061602
27. Wang N, Li JQ, Zhao EG. Orientation effects of deformed nuclei on the production of superheavy elements. Phys Rev C. (2008) 78:054607. doi: 10.1103/PhysRevC.78.054607
28. Siwek-Wilczyńska K, Cap T, Kowal M, Sobiczewski A, Wilczyński J. Predictions of the fusion-by-diffusion model for the synthesis cross sections of Z=114-120 elements based on macroscopic-microscopic fission barriers. Phys Rev C. (2012) 86:014611. doi: 10.1103/PhysRevC.86.014611
29. Nasirov AK, Giardina G, Mandaglio G, Manganaro M, Hanappe F, Heinz S, et al. Quasifission and fusion-fission in reactions with massive nuclei: Comparison of reactions leading to the Z = 120 element. Phys. Rev. C. (2009) 79:024606. doi: 10.1103/PhysRevC.79.024606
30. Bao XJ, Gao Y, Li JQ, Zhang HF. Influence of the nuclear dynamical deformation on production cross sections of superheavy nuclei. Phys Rev C. (2015) 91:011603(R). doi: 10.1103/PhysRevC.91.011603
31. Litnevsky VL, Pashkevich VV, Kosenko GI, Ivanyuk FA. Description of synthesis of super-heavy elements within the multidimensional stochastic model. Phys Rev C. (2014) 89:034626. doi: 10.1103/PhysRevC.89.034626
32. Adamian GG, Antonenko NV, Scheid W. Isotopic trends in the production of superheavy nuclei in cold fusion reactions. Phys Rev C. (2004) 69:011601. doi: 10.1103/PhysRevC.69.011601
33. Liu ZH, Bao JD. Isotopic dependence of the evaporation residue cross section in the synthesis of superheavy nuclei. Phys Rev C. (2007) 76:034604. doi: 10.1103/PhysRevC.76.034604
34. Liu ZH, Bao JD. Synthesis of superheavy element 120 via50Ti+ACf hot fusion reactions. Phys Rev C. (2009) 80:054608. doi: 10.1103/PhysRevC.80.054608
35. Zagrebaev VI, Karpov AV, Greiner W. Possibilities for synthesis of new isotopes of superheavy elements in fusion reactions. Phys Rev C. (2012) 85:014608. doi: 10.1103/PhysRevC.85.014608
36. Cap T, Wilczynska KS, Kowal M, Wilczynski J. Calculations of the cross sections for the synthesis of new 293-296118 isotopes in 249-252Cf(48Ca,xn) reactions. Phys Rev C. (2013) 88:037603. doi: 10.1103/PhysRevC.88.037603
37. Wang N, Zhao EG, Scheid W. Synthesis of superheavy nuclei with Z=118 in hot fusion reactions. Phys Rev C. (2014) 89:037601. doi: 10.1103/PhysRevC.89.037601
38. Li W, Wang N, Jia F, Xu H, Zuo W, Li JQ, et al. Fusion probability in heavy-ion collisions by a dinuclear-system model. J Phys G Nucl Phys. (2006) 32:1143. doi: 10.1209/epl/i2003-00622-0
39. Antonenko N, Cherepanov E, Nasirov A, Permjakov V, Volkov V. Competition between complete fusion and quasi-fission in reactions between massive nuclei. The fusion barrier. Phys Lett B. (1993) 319:425. doi: 10.1016/0370-2693(93)91746-A
40. Antonenko NV, Cherepanov EA, Nasirov AK, Permjakov VP, Volkov VV. Compound nucleus formation in reactions between massive nuclei: fusion barrier. Phys Rev C. (1995) 51:2635. doi: 10.1103/PhysRevC.51.2635
41. Huang MH, Gan ZG, Feng ZQ, Zhou XH, Li JQ. Neutron and proton diffusion in fusion reactions for the synthesis of superheavy nuclei. Chin Phys Lett. (2008) 25:1243. doi: 10.1088/0256-307X/25/4/022
42. Nasirov A, Fukushima A, Toyoshima Y, Aritomo Y, Muminov A, Kalandarov S, et al. The role of orientation of nucleus symmetry axis in fusion dynamics. Nucl Phys A. (2005) 759:342–69. doi: 10.1016/j.nuclphysa.2005.05.152
43. Hong J, Adamian GG, Antonenko NV. Possibilities of production of transfermium nuclei in charged-particle evaporation channels. Phys Rev C. (2016) 94:044606. doi: 10.1103/PhysRevC.94.044606
44. Feng ZQ, Jin GM, Li JQ, Scheid W. Formation of superheavy nuclei in cold fusion reactions. Phys Rev C. (2007) 76:044606. doi: 10.1103/PhysRevC.76.044606
45. Mandaglio G, Giardina G, Nasirov AK, Sobiczewski A. Investigation of the 48Ca+249-252Cf reactions synthesizing isotopes of the superheavy element 118. Phys Rev C. (2012) 86:064607. doi: 10.1103/PhysRevC.86.064607
46. Bao XJ, Gao Y, Li JQ, Zhang HF. Isotopic dependence of superheavy nuclear production in hot fusion reactions. Phys Rev C. (2015) 92:034612. doi: 10.1103/PhysRevC.92.034612
47. Liu ZH, Bao JD. Possibility to produce element 120 in the 54Cr+248 Cm hot fusion reaction. Phys Rev C. (2013) 87:034616. doi: 10.1103/PhysRevC.87.034616
48. Wang N, Zhao EG, Scheid W, Zhou SG. Theoretical study of the synthesis of superheavy nuclei with Z=119 and 120 in heavy-ion reactions with trans-uranium targets. Phys Rev C. (2012) 85:041601(R). doi: 10.1103/PhysRevC.85.041601
49. Zhu L, Xie WJ, Zhang FS. Production cross sections of superheavy elements Z=119 and 120 in hot fusion reactions. Phys Rev C. (2014) 89:024615. doi: 10.1103/PhysRevC.89.024615
50. Bao XJ, Guo SQ, Li JQ, Zhang HF. Influence of hexadecapole deformation on production cross sections of superheavy nuclei. J Phys G Nucl Part Phys. (2016) 43:125105. doi: 10.1088/0954-3899/43/12/125105
51. Huang MH, Zhang ZY, Gan ZG, Zhou XH, Li JQ, Scheid W. Dynamical deformation in heavy ion collisions and formation of superheavy nuclei. Phys Rev C. (2011) 84:064619. doi: 10.1103/PhysRevC.84.064619
52. Wang N, Liu M, Wu XZ. Modification of nuclear mass formula by considering isospin effects. Phys Rev C. (2010) 81:044322. doi: 10.1103/PhysRevC.81.044322
53. Hofmann S. Synthesis of superheavy elements by cold fusion. Radiochim Acta. (2011) 99:405. doi: 10.1524/ract.2011.1854
54. Kosuke M, Kouji M, Daiya K, Takahiro A, Sin-ichi G, Hiromitsu H, et al. Experiment on Synthesis of an Isotope 277112 by 208Pb+70Zn Reaction. J. Phys. Soc. Japan. (2007) 76:043201. doi: 10.1143/JPSJ.76.043201
55. Oganessian YT. Synthesis of the heaviest elements in 48Ca-induced reactions. Radiochim Acta. (2011) 99:429. doi: 10.1524/ract.2011.1860
56. Münzenberg G. Recent advances in the discovery of transuranium elements. Rep Prog Phys. (1988) 51:57. doi: 10.1088/0034-4885/51/1/002
58. Kosuke M, Kouji M, Daiya K, Takahiro A, Sin-ichi G, Hiromitsu H, et al. Experiment on the synthesis of element 113 in the reaction 209Bi(70Zn,n)278113. J Phys Soc Jpn. (2004) 73:2593. doi: 10.1143/JPSJ.73.2593
59. Morita K, Morimoto K, Kaji D, Haba H, Ozeki K, Kudou Y, et al. New result in the production and decay of an isotope, 278113, of the 113th Element. J Phys Soc Jpn. (2012) 81:103201. doi: 10.1143/JPSJ.81.103201
60. Oganessian YT, Utyonkov VK. Super-heavy element research. Rep Prog Phys. (2015) 78:036301. doi: 10.1088/0034-4885/78/3/036301
61. Dvorak J, Bruchle W, Dullmann Ch E, Dvorakova Z, Eberhardt K, Eichler R, et al. Cross section limits for the 248Cm(25Mg,4n-5n)268,269Hs reactions. Phys Rev C. (2009) 79:037602. doi: 10.1103/PhysRevC.79.037602
62. Graeger R, Ackermann D, Chelnokov M, Chepigin V, Dullmann Ch E, Dvorak J, et al. Experimental study of the 238U(36S,3-5n)269-271Hs reaction leading to the observation of 270 Hs. Phys Rev C. (2010) 8:061601(R). doi: 10.1103/PhysRevC.81.061601
63. Nishio K, Hofmann S, Heberger FP, Ackermann D, Antalic S, Aritomo Y, et al. Nuclear orientation in the reaction 34S+238U and synthesis of the new isotope 268 Hs. Phys Rev C. (2010) 82:024611. doi: 10.1103/PhysRevC.82.024611
64. Oganessian Yu Ts, Utyonkov VK, Abdullin FS, Dmitriev SN, Graeger R, Henderson RA, et al. Synthesis and study of decay properties of the doubly magic nucleus 270Hs in the 226Ra +48Ca reaction. Phys Rev C. (2013) 87:034605. doi: 10.1103/PhysRevC.87.034605
65. Dvorak J, Bruchle W, Chelnokov M, Dullmann Ch E, Dvorakova Z, Eberhardt K, et al. Observation of the 3n evaporation channel in the complete hot-fusion reaction 26Mg+248Cm leading to the new superheavy nuclide 271 Hs. Phys Rev Lett. (2008) 100:132503. doi: 10.1103/PhysRevLett.100.132503
66. Utyonkov VK, Brewer NT, Oganessian Yu Ts, Rykaczewski KP, Abdullin F Sh, Dmitriev SN, et al. Experiments on the synthesis of superheavy nuclei 284Fl and 285Fl in the 239,240Pu+48Ca reactions. Phys Rev C. (2015) 92:034609. doi: 10.1103/PhysRevC.92.034609
67. Brewer NT, Utyonkov VK, Rykaczewski KP, Oganessian Yu Ts, Abdullin F, Boll RA, et al. Search for the heaviest atomic nuclei among the products from reactions of mixed-Cf with a 48Ca beam. Phys Rev C. (2018) 98:024317. doi: 10.1103/PhysRevC.98.024317
68. Nishio K, Mitsuoka S, Nishinaka I, Makii H, Wakabayashi Y, Ikezoe H, et al. Fusion probabilities in the reactions40,48Ca+238U at energies around the Coulomb barrier. Phys Rev C. (2012) 86:034608. doi: 10.1103/PhysRevC.86.034608
69. Oganessian YT, Utyonkov VK, Lobanov Yu V, Abdullin F, Polyakov AN, Sagaidak RN, et al. Attempt to produce element 120 in the 244Pu+58Fe reaction. Phys Rev C. (2009) 79:024603. doi: 10.1103/PhysRevC.79.024603
71. Heusch B, Volant C, Freiesleben H, Chestnut RP, Hildenbrand KD, Puhlhofer F, et al. The reaction mechanism in the system132Xe+56Fe at 5.73 MeV/u: evidence for a new type of strongly damped collisions. Z Phys A. (1978) 288:391. doi: 10.1007/BF01417723
72. Toke J, Bock R, Dai GX, Gobbi A, Gralla S, Hildenbrand KD, et al. Quasi-fission — The mass-drift mode in heavy-ion reactions. Nucl Phys A. (1985) 440:327. doi: 10.1016/0375-9474(85)90344-6
73. du Rietz R, Williams E, Hinde DJ, Dasgupta M, Evers M, Lin CJ, et al. Mapping quasifission characteristics and timescales in heavy element formation reactions. Phys Rev C. (2013) 88:054618. doi: 10.1103/PhysRevC.88.054618
74. Itkis MG, Bogachev AA, Itkis IM, Kliman J, Knyazheva GN, Kondratiev NA, et al. The processes of fusion-fission and quasi-fission of superheavy nuclei. Nucl Phys A. (2007) 787:150c. doi: 10.1016/j.nuclphysa.2006.12.026
75. Itkis IM, Kozulin EM, Itkis MG, Knyazheva GN, Bogachev AA, Chernysheva EV, et al. Fission and quasifission modes in heavy-ion-induced reactions leading to the formation of Hs. Phys Rev C. (2011) 83:064613. doi: 10.1103/PhysRevC.83.064613
76. Kozulin EM, Knyazheva GN, Novikov KV, Itkis IM, Itkis MG, Dmitriev SN, et al. Fission and quasifission of composite systems with Z=108-120: transition from heavy-ion reactions involving S and Ca to Ti and Ni ions. Phys Rev C. (2014) 94:054613. doi: 10.1103/PhysRevC.94.054613
77. Banerjee K, Hinde DJ, Dasgupta M, Simpson EC, Jeung DY, Simenel C, et al. Mechanisms suppressing superheavy element yields in cold fusion reactions. Phys Rev Lett. (2019) 122:232503. doi: 10.1103/PhysRevLett.122.232503
78. Dasgupta M, Hinde DJ, Rowley N, Stefanini AM. Measuring barriers to fusion. Annu Rev Nucl Part Sci. (1998) 48:401. doi: 10.1146/annurev.nucl.48.1.401
79. Hagino K, Takigawa N. Subbarrier fusion reactions and many-particle quantum tunneling. Prog Theor Phys. (2012) 128:1061. doi: 10.1143/PTP.128.1061
80. Back BB, Esbensen H, Jiang CL, Rehm KE. Recent developments in heavy-ion fusion reactions. Rev Mod Phys. (2014) 86:317. doi: 10.1103/RevModPhys.86.317
81. Montagnoli G, Stefanini AM. Recent experimental results in sub- and near-barrier heavy-ion fusion reactions. Eur Phys J A. (2017) 53:169. doi: 10.1140/epja/i2017-12350-2
82. Wang N, Wu XZ, Li ZX, Liu M, Scheid W. Applications of Skyrme energy-density functional to fusion reactions for synthesis of superheavy nuclei. Phys Rev C. (2006) 74:044604. doi: 10.1103/PhysRevC.74.044604
83. Wang B, Wen K, Zhao WJ, Zhao EG, Zhou SG. Systematics of capture and fusion dynamics in heavy-ion collisions. At Data Nucl. Data Tables. (2017) 114:281. doi: 10.1016/j.adt.2016.06.003
84. Loveland W. An experimentalist's view of the uncertainties in understanding heavy element synthesis. Eur Phys J A. (2015) 51:120. doi: 10.1140/epja/i2015-15120-2
85. Bao XJ, Guo SQ, Zhang HF, Li JQ. Influence of proton shell closure on the evaporation residue cross sections of superheavy nuclei. J Phys G Nucl Part Phys. (2017) 44:045105. doi: 10.1088/1361-6471/aa53e8
86. Diaz-Torres A, Hinde DJ, Dasgupta M, Milburn GJ, Tostevin JA. Dissipative quantum dynamics in low-energy collisions of complex nuclei. Phys Rev C. (2008) 78:064604. doi: 10.1103/PhysRevC.78.064604
87. Sargsyan VV, Kanokov Z, Adamian GG, Antonenko NV, Scheid W. Capture process in nuclear reactions with a quantum master equation. Phys Rev C. (2009) 80:034606. doi: 10.1103/PhysRevC.80.034606
88. Sargsyan VV, Adamian GG, Antonenko NV, Scheid W, Zhang HQ. Effects of nuclear deformation and neutron transfer in capture processes, and fusion hindrance at deep sub-barrier energies. Phys Rev C. (2011) 84:064614. doi: 10.1103/PhysRevC.84.064614
89. Esbensen H, Stefanini AM. Influence of multiphonon excitations and transfer on the fusion of Ca+Zr. Phys Rev C. (2014) 89:044616. doi: 10.1103/PhysRevC.89.044616
90. Jiang CL, Rehm KE, Back BB, Esbensen H, Janssens VF, Stefanini AM, et al. Influence of heavy-ion transfer on fusion reactions. Phys Rev C. (2014) 89:051603(R). doi: 10.1103/PhysRevC.89.051603
91. Jia HM, Lin CJ, Yang F, Xu XX, Zhang HQ, Liu ZH, et al. Fusion of 32S+94Zr: further exploration of the effect of the positive Qxn value neutron transfer channels. Phys Rev C. (2014) 89:064605. doi: 10.1103/PhysRevC.89.064605
92. Rachkov VA, Karpov AV, Denikin AS, Zagrebaev VI. Examining the enhancement of sub-barrier fusion cross sections by neutron transfer with positive Q values. Phys Rev C. (2014) 90:014614. doi: 10.1103/PhysRevC.90.014614
93. Misicu S, Greiner W. Influence of hexadecupole deformation and role of orientation in capture reactions with 48Ca projectiles leading to superheavy nuclei. Phys Rev C. (2004) 69:054601. doi: 10.1103/PhysRevC.69.054601
94. Misicu S, Esbensen H. Hindrance of heavy-ion fusion due to nuclear incompressibility. Phys Rev Lett. (2006) 96:112701. doi: 10.1103/PhysRevLett.96.112701
95. Wong CY. Interaction Barrier in charged-particle nuclear reactions. Phys Rev Lett. (1973) 31:766. doi: 10.1103/PhysRevLett.31.766
96. Stokstad RG, Switkowski ZE, Dayras RA, Wieland RM. Measurements of fusion cross sections for heavy-ion systems at very low energies. Phys Rev Lett. (1976) 37:888. doi: 10.1103/PhysRevLett.37.888
97. Rowley N, Satchler GR, Stelson PH. On the “distribution of barriers” interpretation of heavy-ion fusion. Phys Lett B. (1991) 254:25. doi: 10.1016/0370-2693(91)90389-8
98. Sargsyan VV, Adamian GG, Antonenko NV, Scheid W. Peculiarities of the sub-barrier fusion with the quantum diffusion approach. Eur Phys J A. (2010) 45:125. doi: 10.1140/epja/i2010-10978-x
99. Sargsyan VV, Adamian GG, Antonenko NV, Scheid W, Zhang HQ. Sub-barrier capture with quantum diffusion approach: actinide-based reactions. Eur Phys J A. (2011) 47:38. doi: 10.1140/epja/i2011-11038-y
100. Sargsyan VV, Adamian GG, Antonenko NV, Scheid W, Zhang HQ. Role of neutron transfer in capture processes at sub-barrier energies. Phys Rev C. (2012) 85:024616. doi: 10.1103/PhysRevC.85.024616
101. Sargsyan VV, Adamian GG, Antonenko NV, Scheid W, Zhang HQ. Influence of neutron transfer in reactions with weakly and strongly bound nuclei on the sub-barrier capture process. Phys Rev C. (2012) 86:014602. doi: 10.1103/PhysRevC.86.014602
102. Wakhle A, Simenel C, Hinde DJ, Dasgupta M, Evers M, Luong DH, et al. Interplay between quantum shells and orientation in quasifission. Phys Rev Lett. (2014) 113:182502. doi: 10.1103/PhysRevLett.113.182502
103. Umar AS, Oberacker VE, Maruhn JA, Reinhard PG. Entrance channel dynamics of hot and cold fusion reactions leading to superheavy elements. Phys Rev C. (2010) 81:064607. doi: 10.1103/PhysRevC.81.064607
104. Simenel C, Hinde DJ, du Rietz R, Dasgupta M, Evers M, Lin CJ. Influence of entrance-channel magicity and isospin on quasi-fission. Phys Lett B. (2012) 710:607. doi: 10.1016/j.physletb.2012.03.063
105. Simenel C. Nuclear quantum many-body dynamics: from collective vibrations to heavy-ion collisions. Eur Phys J A. (2012) 48:152. doi: 10.1140/epja/i2012-12152-0
106. Oberacker VE, Umar AS, Simenel C. Energy dependence of potential barriers and its effect on fusion cross sections. Phys Rev C. (2014) 89:034611. doi: 10.1103/PhysRevC.89.034611
107. Umar AS, Oberacker VE, Simenel C. Shape evolution and collective dynamics of quasifission in the time-dependent Hartree-Fock approach. Phys Rev C. (2015) 92:024621. doi: 10.1103/PhysRevC.92.024621
108. Sekizawa K, Yabana K. Time-dependent Hartree-Fock calculations for multinucleon transfer and quasifission processes in the 64Ni+238U reaction. Phys Rev C. (2016) 93:054616. doi: 10.1103/PhysRevC.93.054616
109. Umar AS, Oberacker VE, Simenel C. Fusion and quasifission dynamics in the reactions 48Ca+249Bk and 50Ti+249Bk using a time-dependent Hartree-Fock approach. Phys Rev C. (2016) 94:024605. doi: 10.1103/PhysRevC.94.024605
110. Umar AS, Simenel C, Ye W. Transport properties of isospin asymmetric nuclear matter using the time-dependent Hartree-Fock method. Phys Rev C. (2017) 96:024625. doi: 10.1103/PhysRevC.96.024625
111. Sekizawa K. Enhanced nucleon transfer in tip collisions of 238U+124Sn. Phys Rev C. (2017) 96:041601(R). doi: 10.1103/PhysRevC.96.041601
112. Guo L, Simenel C, Shi L, Yu C. The role of tensor force in heavy-ion fusion dynamics. Phys Lett B. (2018) 782:401. doi: 10.1016/j.physletb.2018.05.066
113. Guo L, Godbey K, Umar AS. Influence of the tensor force on the microscopic heavy-ion interaction potential. Phys Rev C. (2018) 98:064607. doi: 10.1103/PhysRevC.98.064607
114. Simenel C, Umar AS. Heavy-ion collisions and fission dynamics with the time-dependent HartreeCFock theory and its extensions. Prog Part Nucl Phys. (2018) 103:19. doi: 10.1016/j.ppnp.2018.07.002
115. Godbey K, Umar AS, Simenel C. Deformed shell effects in Ca48+Bk249 quasifission fragments. Phys Rev C. (2019) 100:024610. doi: 10.1103/PhysRevC.100.024610
116. Bao XJ, Gao Y, Li JQ, Zhang HF. Theoretical study of the synthesis of superheavy nuclei using radioactive beams. Phys Rev C. (2015) 91:064612. doi: 10.1103/PhysRevC.91.064612
117. Bao XJ, Gao Y, Li JQ, Zhang HF. Influence of nuclear basic data on the calculation of production cross sections of superheavy nuclei. Phys Rev C. (2015) 92:014601. doi: 10.1103/PhysRevC.92.014601
118. Swiatecki WJ, Siwek-Wilczynska K, Wilczynski J. Fusion by diffusion. II. Synthesis of transfermium elements in cold fusion reactions. Phys Rev C. (2005) 71:014602. doi: 10.1103/PhysRevC.71.014602
119. Hagino K. Hot fusion reactions with deformed nuclei for synthesis of superheavy nuclei: an extension of the fusion-by-diffusion model. Phys Rev C. (2018) 98:014607. doi: 10.1103/PhysRevC.98.014607
120. Bao XJ, Guo SQ, Zhang HF, Li JQ. Dynamics of complete and incomplete fusion in heavy ion collisions. Phys Rev C. (2018) 97:024617. doi: 10.1103/PhysRevC.97.024617
121. Guo SQ, Gao Y, Li JQ, Zhang HF. Dynamical deformation in heavy ion reactions and the characteristics of quasifission products. Phys Rev C. (2017) 96:044622. doi: 10.1103/PhysRevC.96.044622
122. Adamian GG, Antonenko NV, Scheid W. Characteristics of quasifission products within the dinuclear system model. Phys Rev C. (2003) 68:034601. doi: 10.1103/PhysRevC.68.034601
123. Volkov VV. The mechanism of compound nucleus formation in complete fusion of two massive nuclei. Phys Atom Nuclei. (2003) 66:1065. doi: 10.1134/1.1586419
124. Zagrebaev VI, Greiner W. Cross sections for the production of superheavy nuclei. Nucl Phys A. (2015) 944:257–307. doi: 10.1016/j.nuclphysa.2015.02.010
125. Diaz-Torres A. Modeling of compound nucleus formation in the fusion of heavy nuclei. Phys Rev C. (2004) 69:021603(R). doi: 10.1103/PhysRevC.69.021603
126. Diaz-Torres A. Competition between fusion and quasifission in a heavy fusing system: diffusion of nuclear shapes through a dynamical collective potential energy landscape. Phys Rev C. (2006) 74:064601. doi: 10.1103/PhysRevC.74.064601
127. Aritomo Y. Analysis of dynamical processes using the mass distribution of fission fragments in heavy-ion reactions. Phys Rev C. (2009) 80:064604. doi: 10.1103/PhysRevC.80.064604
128. Bao XJ. Possibility to produce 293,295,296Og in the reactions 48Ca+249,250,251Cf. Phys Rev C. (2019) 100:011601(R). doi: 10.1103/PhysRevC.100.011601
129. Schmidtt KH, Morawekt W. The conditions for the synthesis of heavy nuclei. Rep Prog Phys. (1991) 54:949–1003. doi: 10.1088/0034-4885/54/7/002
130. Ivanyuk FA, Ishizuka C, Usang MD, Chiba S. Temperature dependence of shell corrections. Phys Rev C. (2018) 97:054331. doi: 10.1103/PhysRevC.97.054331
131. Zhu L, Wen PW, Lin CJ, Bao XJ, Su J, Li C, et al. Shell effects in a multinucleon transfer process. Phys Rev C. (2018) 97:044614. doi: 10.1103/PhysRevC.97.044614
132. Sauer G, Chandra H, Mosel U. Thermal properties of nuclei. Nucl Phys A. (1976) 264:221. doi: 10.1016/0375-9474(76)90429-2
133. Fröbrich P. On the dynamics of fission of hot nuclei. Nucl Phys A. (2007) 787:170c. doi: 10.1016/j.nuclphysa.2006.12.028
134. Brack M, Jens D, Jensen AS, Pauli HC, Strutinsky VM, Wong CY. Funny hills: the shell-correction approach to nuclear shell effects and its applications to the fission process. Rev Mod Phys. (1972) 44:320. doi: 10.1103/RevModPhys.44.320
135. Davies KTR, Sierk AJ, Nix JR. Effect of viscosity on the dynamics of fission. Phys Rev C. (1976) 13:2385. doi: 10.1103/PhysRevC.13.2385
136. Schunck N, Robledo LM. Microscopic theory of nuclear fission: a review. Rep Prog Phys. (2016) 79:116301. doi: 10.1088/0034-4885/79/11/116301
137. Schmidt KH, Jurado B. Review on the progress in nuclear fission-experimental methods and theoretical descriptions. Rep Prog Phys. (2018) 81:106301. doi: 10.1088/1361-6633/aacfa7
138. Bao XJ. Possibilities for synthesis of new neutron-deficient isotopes of superheavy nuclei. Chin Phys C. (2019) 43:054105. doi: 10.1088/1674-1137/43/5/054105
139. Ignatyuk AV, Smirenkin GN, Tishin AS. Yad Fiz. (1975) 21:485. [Sov. J. Nucl. Phys. (1975) 29:255].
141. Bao XJ, Guo SQ, Zhang HF, Li JQ. Influence of entrance channel on production cross sections of superheavy nuclei. Phys Rev C. (2017) 96:024610. doi: 10.1103/PhysRevC.96.024610
142. Liu ZH, Bao JD. Q-value effects on the production of superheavy nuclei. Phys Rev C. (2006) 74:057602. doi: 10.1103/PhysRevC.74.057602
143. Loveland W. Synthesis of transactinide nuclei using radioactive beams. Phys Rev C. (2007) 76:014612. doi: 10.1103/PhysRevC.76.014612
Keywords: low-energy heavy-ion collisions, superheavy nuclei production, fusion dynamics, transport theory, TDHF model
Citation: Bao XJ (2020) Fusion Dynamics of Low-Energy Heavy-Ion Collisions for Production of Superheavy Nuclei. Front. Phys. 8:14. doi: 10.3389/fphy.2020.00014
Received: 21 November 2019; Accepted: 16 January 2020;
Published: 28 February 2020.
Edited by:
Cedric Simenel, Australian National University, AustraliaReviewed by:
Sait Umar, Vanderbilt University, United StatesNikolai Antonenko, Joint Institute for Nuclear Research (JINR), Russia
Copyright © 2020 Bao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xiao Jun Bao, YmFveGlhb2p1bkBodW5udS5lZHUuY24=
 Xiao Jun Bao
Xiao Jun Bao