- 1Center for Computational Sciences, University of Tsukuba, Tsukuba, Japan
- 2Faculty of Pure and Applied Sciences, University of Tsukuba, Tsukuba, Japan
- 3RIKEN Nishina Center, Wako, Japan
Toward the microscopic theoretical description for large amplitude collective dynamics, we calculate the coefficients of inertial masses for low-energy nuclear reactions. Under the scheme of energy density functional, we apply the adiabatic self-consistent collective coordinate (ASCC) method, as well as the Inglis' cranking formula to calculate the inertias for the translational and the relative motions, in addition to those for the rotational motion. Taking the scattering between two α particles as an example, we investigate the impact of the time-odd components of the mean-field potential on the collective inertial masses. The ASCC method asymptotically reproduces the exact masses for both the relative and translational motions. On the other hand, the cranking formula fails to do so when the time-odd components exist.
1. Introduction
The time-dependent density functional theory (TDDFT) [1–5] is a general microscopic theoretical framework to study low-energy nuclear reactions. Based on the TDDFT, the mechanisms of nuclear collective dynamics have been extensively studied for decades. The linear approximation of TDDFT leads to the random-phase approximation (RPA) [5–7], which is capable of calculating nuclear response functions and providing us a unified description for both structural and dynamical properties. Despite the detailed microscopic information revealed by TDDFT, it has a difficulty in describing nuclear collective dynamics at low energy [5]. For instance, it cannot describe the sub-barrier fusion and spontaneous fission, due to its semiclassical nature [1, 5, 6].
The description of nuclear dynamics in terms of collective degrees of freedom has been explored in nuclear reaction theories. However, the derivation of the “macroscopic” reaction model based on the microscopic nuclear dynamics has been rarely studied in the past. For the theoretical description in terms of collective degrees of freedom, the collective inertial masses with respect to the collective coordinates are of paramount importance. One of the most commonly used methods to extract the collective mass coefficient is the Inglis' cranking formula [8–10], which can be derived based on the adiabatic perturbation theory.
It is well-known that the cranking formula has a problem that it fails to reproduce the total mass for the translational motion of the center of mass of a nucleus Ring and Schuck [6]. Therefore, it is highly desirable to replace the cranking mass by the one theoretically more advanced and justifiable. We believe that the adiabatic self-consistent collective coordinate (ASCC) method [11–14] suites for this purpose. The method, in the first place, aims at determining the canonical variables on the optimal collective subspace for description of a low-energy collective motion. The masses with respect to those collective coordinates can be extracted by solving a set of the ASCC equations. This method has been applied to many nuclear structure problems with large-amplitude nuclear dynamics with the Hamiltonian of the separable interactions [13–16]. Recently, by combining the imaginary-time evolution [17] and the finite amplitude method [18–21], we proposed a numerical method to solve the ASCC equations and to determine the optimal collective path for nuclear reaction [22]. At the same time, we obtain the collective inertial mass in a self-consistent manner. In this work, we calculate the collective masses for three modes of collective motion, the translational motion, the relative motion and rotational motion. We compare the ASCC results with those of the cranking formula.
Our calculations are under the scheme of energy density functional theory. In order to guarantee the Galilean symmetry during a collective motion, most of the energy density functionals must include densities that are odd with respect to the time reversal. Under the assumptions of the time-reversal symmetry, these terms vanish and therefore do not contribute to the time-even states, while they have non-zero values in situations of dynamical reactions. It has been found that the time-odd components play an important role in the inertia parameters for nuclear rotations [23, 24]. To investigate this problem in the context of reaction dynamics of light nuclei, we investigate the effects of time-odd terms on the different inertial masses, taking the α+α reaction as the simplest example.
This paper is organized as the following. In section 2, we recapitulate the formulation of the basic ASCC equations in the case of one-dimensional collective motion. We present the method of constructing the collective path and the coordinate transformation procedure to calculate the inertial mass parameter with respect to the relative coordinate. In section 3, we apply the method to the reaction system α+α↔8Be. We focus on the influence of the time-odd terms on both the relative and rotational inertias. Summary and concluding remarks are give in section 4.
2. Theoretical Framework
2.1. Formulation of ASCC Method
In this section, neglecting the paring correlation, we recapitulate the basic ASCC formulation, and introduce the numerical procedure of constructing the collective path and calculating the inertial mass. The details can be found in Wen and Nakatsukasa [22].
For simplicity, here we consider the collective motion described by only one collective coordinate q(t), which has a conjugate momentum p(t). We assume that the time-dependent mean-field states are parameterized by Slater determinants labeled as |ψ(p, q)〉. The energy of the system reads
which defines a classical collective Hamiltonian. In the ASCC method, the resulting collective path |ψ(p, q)〉 is determined so as to maximally be decoupled from other intrinsic degrees of freedom. The evolution of q(t) and p(t) obeys the canonical equations of motion with the classical Hamiltonian H(p, q).
In order to consider the adiabatic limit, we assume the momentum p is small and the states are expanded in powers of p about p = 0. The states |ψ(p, q)〉 are written as
where the generator is defined as . The conjugate is introduced as a generator for the infinitesimal translation in q, . and can be expressed in the form of one-body operator as
where i in the expression of is simply for convenience. They are locally defined at each coordinate q and will change their structure along the collective path. The particle (n ∈ p) and hole (j ∈ h) states are also defined with respect to the Slater determinant |ψ(q)〉.
In the adiabatic limit, expanding Equation (2) with respect to p up to second order, the invariance principle of the self-consistent collective coordinate (SCC) method [11] leads to the equations of the ASCC method [5, 12]. Neglecting the curvature terms, it reduces to somewhat simpler equation set:
with the inertial mass parameter M(q). The mass M(q) depends on the scale of the coordinate q. Thus, we can choose it to make M(q) = 1 without losing anything. The moving mean-field Hamiltonian and the potential V(q) are, respectively, defined as
Note that the collective path is given by |ψ(q), which represents the state |ψ(q, p) with p = 0. Equation (4) is similar to a constrained Hartee-Fock problem, however, the constraint operator depends on the coordinate q, which is self-consistently determined by the RPA-like Equations (5) and (6), called “moving RPA equations.” The conventional RPA forward and backward amplitude Xni(q) and Yni(q) can be regarded as the linear combination of and .
where the RPA eigenfrequency ω is related to the mass parameter and the second derivative of the potential
As a pair of canonical variables, a weak canonicity condition should be satisfied. This canonicity condition is automatically satisfied if the RPA normalization condition holds.
It should be noted that the ASCC method is applicable to systems with pairing correlations, in principle. However, in this paper, we neglect the pairing correlation to reduce the computational cost, and concentrate our discussion on effects of mean fields of particle-hole channels for the inertial masses. We present results for the α + α reaction in section 3, for which no level crossing at the Fermi surface is involved. Therefore, the pairing plays very little role in this particular case.
For superconducting systems, apart from the collective coordinate and momentum, an additional pair of canonical variables, the particle number and the conjugate gauge angle, are needed to label the nuclear state. Details of the formulation are give in Matsuo et al. [12] and Nakatsukasa et al. [5].
2.2. ASCC Collective Path and Inertial Mass
A change in the scale of the collective coordinate q results in a change in the collective mass M(q). Thus, in order to discuss the magnitude of the collective mass, we need to fix its scale. This is normally done by adopting an intuitive choice of the one-body time-even operator Ô. One of possible choices is the mass quadrupole operator . In the present study of nuclear scattering (nuclear fission), it is convenient to adopt the relative distance between two nuclei with the projectile mass number Apro and the target mass number Atar. Assuming that the center of mass of the two nuclei are on the x axis (y = z = 0),
where θ(x) is the step function, and x = xs is the artificially introduced section plane that divides the total space into two, each of which contains the nucleon number of Apro and Atar, respectively.
The operator has an evident physical meaning when the projectile and the target are far away to each other. When they touch each other, the distance between two nuclei is no longer a well-defined quantity, thus loses its significance. However, this is not a problem in the present microscopic formulation of the reaction model. We have determined the reaction path and the canonical variables (q, p), through the ASCC method. It is merely a coordinate transformation from q to R with a function R(q). The reaction dynamics do not depend on the choice of R, as far as the one-to-one correspondence between q and R is valid.
The coordinate transformation naturally leads to the transformation of the inertial mass from M(q) to M(R);
The calculation of the derivative dq/dR is straitforward, because the collective path |ψ(q) and the local generator of the coordinate q are obtained by solving the ASCC Equations (5) and (6).
The inertia mass parameter with respect to R or any other coordinate can be easily calculated with this formula.
We solve the moving RPA Equations (5) and (6) by taking advantage of the finite amplitude method (FAM) [18–21], especially the matrix FAM prescription [21]. To solve the ASCC Equations (4), (5), and (6) self-consistently and construct the collective path |ψ(q), we adopt the following procedures:
1. Prepare the Hartree-Fock ground state |ψ(q = 0) which can be either the two separated nuclei before fusion, or the ground state of the mother nucleus before fission.
2. Based on |ψ(q), solve the moving RPA Equations (5) and (6), to obtain and . First, we start with an approximation .
3. Solve the moving HF Equation (4) to calculate the state |ψ(q + δq) by imposing the condition
where we use the approximate relation, , to constrain the step size.
4. With this new state |ψ(q + δq), update the generators and by solving the moving RPA equations again. Then, with these updated generators, go back to the step 2.2. Repeat the steps 2.2 and 2.2 until the self-consistency is achieved at q + δq.
5. Then, regarding q + δq as q with an initial approximation , go to the step 2.2.
Carrying on this iterative procedure, we determine a series of states |ψ(0), |ψ(δq), |ψ(2δq), |ψ(3δq), ⋯ that form the ASCC collective path. Changing the sign of the right hand side of Equation (13), we can also construct the collective path toward the opposite direction {|ψ(−δq), |ψ(−2δq), ⋯ }. In this way, the collective path |ψ(q), the potential V(q), and the collective mass M(q) are determined self-consistently and no a priori assumption is used.
3. Applications
3.1. Solutions for the Translational Motion
First, we calculate the inertial mass for the translational motion, for which we know the exact value Am. The calculation is done in the three-dimensional coordinate space discretized in the square grid in a sphere with radius equal to 7 fm. The BKN energy density functional [25] is adopted in the present calculation.
The HF ground state is a trivial solution of Equations (4)–(6), on the collective path since it corresponds to the minimum of the potential surface, ∂V/∂q = 0. We calculate the translational inertia mass of the ground state of an alpha particle, and examine its grid size dependence. The left panel of Figure 1 shows the eigenfrequency ω in Equation (9) of the lowest several RPA states as a function of the mesh size of the grids. The three translational modes along x, y, z axis are degenerated and shown by the red dots, the absolute value of this eigenfrequency decreases and approaches zero as the mesh size becomes smaller. The value of the translational motion is significantly smaller than all the other collective modes. In the ideal case where the mesh size is sufficiently small, this value is expected to be zero. For other collective modes, the eigenfrequencies stay almost constant as functions of the mesh size. Due to the compact nature of alpha particle, except for the translational zero-modes, the lowest physical excitation mode is calculated to be about 20 MeV, which represents the monopole vibration.
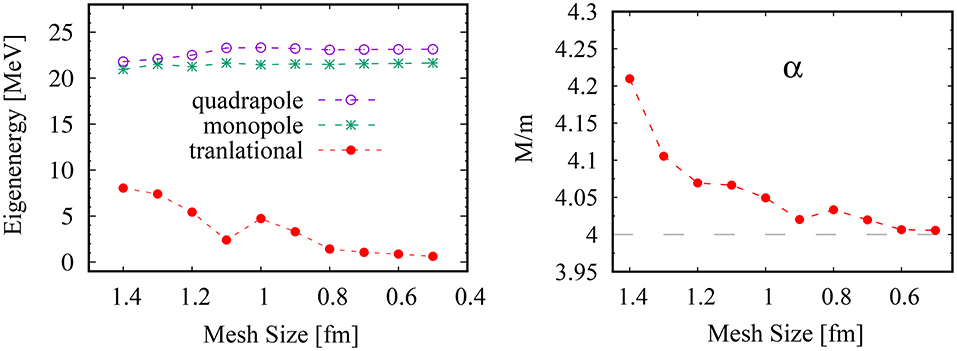
Figure 1. (Left panel) Calculated RPA eigenfrequencies based on the ground state of the alpha particle, as a function of mesh size. The red closed circles indicate the values for translational mode, while the green asterisks and purple open circles indicate those for monopole and quadrupole modes, respectively. (Right panel) Calculated translational mass M of a single alpha particle in units of nucleon's mass m, as a function of the mesh size. The calculated mass with respect to the y direction, perpendicular to the symmetry (x) axis, is shown. The one with respect to the x direction is presented in Figure 1 of Wen and Nakatsukasa [22].
Using Equation (11) we calculate the translational inertia mass of one alpha particle. The right panel of Figure 1 shows the result as a function of mesh size. As the mesh size decreases, the results approach to the value of 4 in the unit of nucleon mass, which is the exact total mass of the alpha particle. With the simple BKN energy density functional, this exact value for the translation is also obtained with the cranking mass formula of Inglis. However, it underestimates the exact total mass when the energy functional has a effective mass m*/m < 1. On the other hand, the ASCC mass for the translational motion is invariant and exact even with the effective mass. This is due to the Galilean symmetry of the energy density functional which inevitably contains the time-odd components. This will be discussed in section 3.4.
3.2. ASCC Reaction Path for α+α↔8Be
The numerical application of the ASCC method to determine a collective path for the nuclear fusion or fission reactions demands a substantial computational cost. Here, we present the result for the reaction path of α+α↔8Be, as the simplest example. It can be regarded as either the fusion path of two alpha particles or the fission path of 8Be. The model space is the three-dimensional grid space of the rectangular box of size 10 ×10 ×18 fm3 with mesh size equal to 1.0 fm. The standard BKN energy density functional is adopted.
Starting from the two ground states of α particle and carrying out the iterative procedure presented in section 2.2, we obtain a fusion path that connects the two well separated alpha particles to the ground state of 8Be. If we start the calculation from the ground state of 8Be, the same reaction path, that represents fission of 8Be, can be obtained. In the left four panels of Figure 2, we show the calculated density distribution of four different points on the obtained collective fusion path. The panel (a) shows the density distribution of two alpha particles at R = 6.90 fm, (d) shows that of the ground state of 8Be which corresponds to R = 3.55 fm. Those of (b) and (c) show those at R = 5.40 fm and 4.10 fm, respectively. The collective path smoothly evolves the separated two alpha particles into the ground state of 8Be.
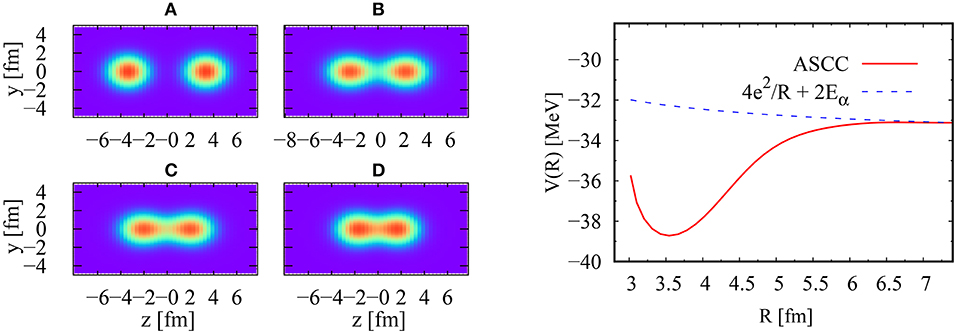
Figure 2. (Left panel) Calculated density distributions of four points on the ASCC collective fusion path α+α → 8Be. Inset (A) shows the density distribution of two well separated alpha particles at R = 6.90 fm, inset (D) is the ground state of 8Be at R = 3.55 fm. Inset (B,C) show the density distributions at R = 4.10 fm, 5.40 fm, respectively. Those on the y−z plane are plotted. (Right panel) Potential energy as a function of R shown by the red curve. The blue the dashed line is calculated as for reference.
The right panel of Figure 2 shows the potential energy along this collective path, as a function of R. The dashed cure shows the point Coulomb potential, 4e/R+2Eα, with the ground state energy of a single alpha particle Eα. With the BKN energy density functional, the 8Be is bound in the mean-field level. The ground state of 8Be is located in the potential minimum at R = 3.55 fm, while the Coulomb barrier top is at R = 6.50 fm. This ASCC collective path is self-consistently generated by the iterative procedure presented in section 2.2. The generators for the relative motion are microscopically given. Since the structure of the 8Be nucleus is very simple, this potential surface is actually similar to that of the constraint Hartree-Fock calculation.
3.3. Inertial Mass for α+α↔8Be
Upon the collective reaction path obtained, the inertial mass with respect to the relative distance R, MASCC(R), is calculated using Equation (11). In the asymptotic region, we expect the inertial mass to be identical to the reduced mass, μred = AproAtarm/(Apro + Atar), where m is the nucleon mass. For the current system α+α↔8Be, the value of μred is expected to be 2m.
The reduced mass μred is justifiable when two alpha particles are well separated. However, it loses its validity as two particles approach each other. A widely used approach to calculate inertial mass for nuclear collective motion is the “Constrained-Hartree-Fock-plus-cranking” (CHF+cranking) approach [26]. In this approach, the collective path is produced by the CHF calculation with a constraining operator Ô given by hand, and the inertial mass is calculated based on the cranking formula with respect to these CHF states. The formula for the cranking mass can be derived by the adiabatic perturbation [6]. In the present case of the one-dimensional motion, based on the states constructed by the CHF calculation with a given constraining operator Ô, the cranking formula reads [26]
where the single-particle states φμ and their energies eμ are defined with respect to hCHF(λ) = hHF[ρ] − λÔ,
We may use any operator Ô as a constraint, as far as it can generate the states with all the necessary values of . However, obviously the inertial mass M(R) depends on this choice, which is one of drawbacks of the CHF+cranking approach.
In most of the reaction models, the inertial mass with respect to R is assumed to be a constant value of μred. Our study reveales how the inertia changes as a function of R. In Figure 3, both the ASCC and the cranking masses are presented. For the cranking mass, since the CHF state needs to be prepared first. We calculate the CHF states in two ways with different constraining operators Ô; the mass quadrupole operator and the relative distance operator of Equation (10). The model space for both calculations are the same. As we can see from Figure 3, at large distance, both methods asymptotically reproduce the reduced mass of 2m, which is the exact value for the relative motion between two alpha particles. In the interior region where the two nuclei have merged into one system, these three masses give very different values. Generally the cranking mass is found to be larger than the ASCC mass, especially at around R = 4.7 fm where all the three masses develop a bump structure.
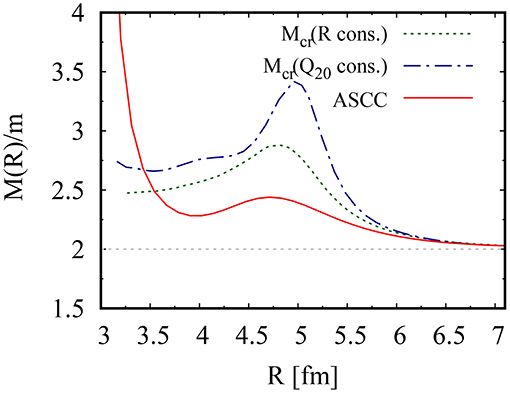
Figure 3. (Color online) Inertia masses MR for the reaction α+α↔8Be as a function of relative distance R. The solid (red) curve indicates the result of ASCC. The other curves show the cranking masses of Equation (14) calculated based on CHF states. The dotted (green) and dash-dotted (blue) lines indicate the results with constraints on and , respectively.
The difference between the ASCC and the cranking masses attributes to several factors. One is due to the fact that the cranking formula neglects residual fields induced by the density fluctuation. Another is that the constraining operators affect the single-particle energies eμ(R). We also note that the cranking masses obtained with different constraints give very different values. This is true even at the HF ground state (R = 3.55 fm), in which the single-particle states |φμ(R) and their single-particle energies eμ(R) are all identical to each other. This is because the derivative ∂/∂R gives different values, since the different constraint produces different states away from the HF ground state. This ambiguity exposes another drawback of the CHF+cranking approach, while the ASCC mass has an advantage that the collective coordinate as well as the wave functions are self-consistently calculated rather than artificially assumed.
3.4. Impact of Time-Odd Potential
All the results shown so far are obtained with the standard BKN energy density functional that has no derivative terms. Therefore, the nucleon's effective mass is identical to the bare nucleon mass. However, most of realistic effective interactions have effective mass smaller than the bare mass, typically m*/m ~ 0.7. In such cases, an improper treatment of the collective dynamics leads to a wrong answer for the collective inertial mass [27]. This change in the effective mass typically comes from the term ρτ in the Skyrme energy density functional, which should accompany the term −j2 to restore the Galilean symmetry [27, 28]. These terms are absent in the standard BKN functional.
To investigate the effect of the time-odd mean-field potential on the collective inertial mass, we add the term to the original BKN energy density functional. The modified BKN energy density functional reads,
where ρ(r), τ(r), and j(r) are the isoscalar density, the isoscalar kinetic density, and the isoscalar current density, respectively. In Equation (16), is the sum of the Yukawa and the Coulomb potentials [25].
The variation of the total energy with respect to the density (or equivalently single-particle wave functions) defines the single-particle (Hartree-Fock) Hamiltonian. In the present case, the single-particle Hamiltonian turns out to be
where the effective mass is now deviated from bare nucleon mass
For the time-even states, such as the ground state of even-even nuclei, the current density disappears, j = 0. Even though, these terms play an important role in the collective inertial mass. The parameter B3 ≠ 0 provides the effective mass and the time-odd effect. The rest of the parameters are the same as those in reference [25].
To examine the impact of the time-odd terms on the inertial mass, in Figure 4 we show M(R) calculated with and without the B3 term. When the time-odd terms are absent, B3 = 0, both the ASCC and the cranking formula reproduce the α+α reduced mass in the asymptotic limit (R → ∞). However, the cranking formula fails to do so with B3 ≠ 0. As the value of B3 increases, the asymptotic cranking mass decreases. This can be naively expected from the reduction of the effective mass from the bare mass. In contrast, the ASCC inertial mass converges to the correct reduced mass, no matter what B3 values are. This means that the ASCC method is capable of taking into account the time-odd effect and recovering the exact Galilean symmetry.
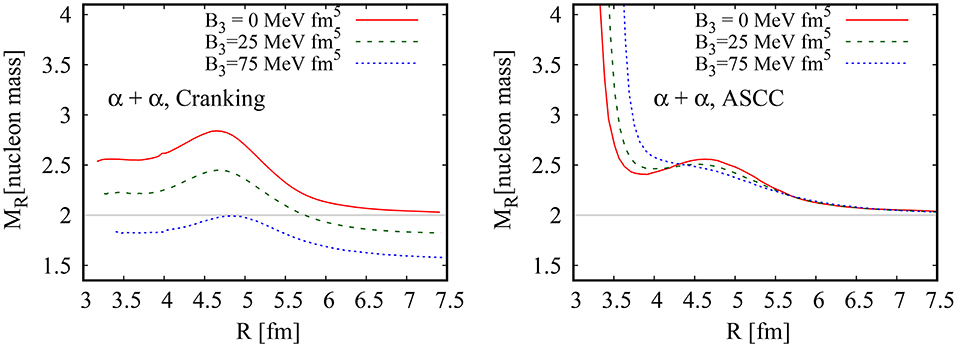
Figure 4. Relative inertial masses in the presence of time-odd mean-field potential for the reaction α+α↔8Be as a function of relative distance R. The results of the cranking masses are shown in the left panel and those of the ASCC method are shown in the right panel. The solid (red), dashed (green), and dotted (blue) curves show the results calculated with B3 = 0, 25, and 75 MeV fm5, respectively.
Another inertial mass indispensable in the collective Hamiltonian of nuclear reaction models is the rotational moments of inertia. The rotational motion is a Nambu-Goldstone (NG) mode. To calculate this, we utilize a method proposed in the reference [29], where the inertial masses of the NG modes are calculated from the zero-frequency linear response with the momentum operator of the NG modes. The formulation has been tested in the cases of translational and pairing rotational modes, showing high precision and efficiency. Based on the collective path obtained, we apply this technique to calculate the rotational moments of inertia.
In Figure 5, the calculated moments of inertias are presented. With B3 = 0, the moments of inertia calculated with the ASCC and with the cranking formula well agree with each other in the asymptotic region of large R. The value is equal to the point-mass approximation in which the point α particles are assumed at the center of mass of each α particle. However, when non-zero B3 comes in, the cranking mass formula can no longer reproduce this asymptotic value. Similar to the case of relative motion, as the value of B3 increases, the asymptotic moments of inertia decrease and deviate from the asymptotic value. In contrast, the ASCC method provides the moments of inertia almost invariant with respect to the B3 values. These results show again that, compared with the cranking formula, the ASCC method gives the collective inertial masses by properly taking into account the time-odd effects.
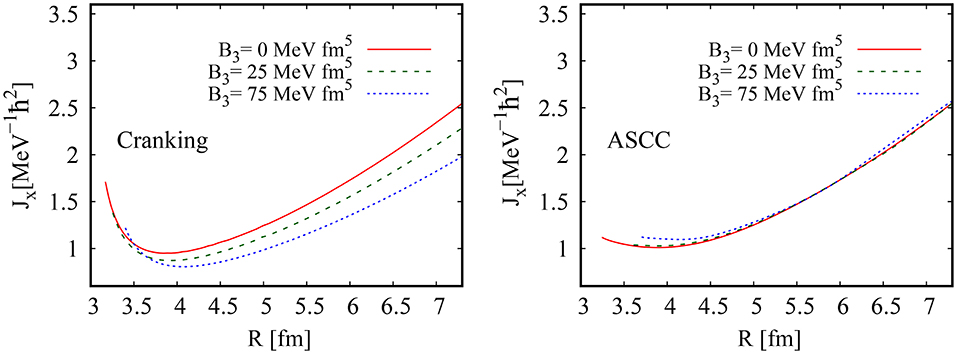
Figure 5. Rotational moments of inertias in the presence of time-odd mean-field potential for the system α+α as a function of relative distance R. The results of cranking formula are shown in the left panel and the results of ASCC are shown in the right panel. The solid (red), dashed (green), and dotted (blue) curves show the results calculated with B3 = 0, 25, 75 MeV fm5, respectively, as labeled in the figure.
4. Summary and Discussion
Based on the ASCC theory, we presented a method to determine the collective reaction path for the nuclear reaction as the large amplitude collective motion. This method is applied to the fusion/fission α+α↔8Be, using the BKN energy density functional. In the three-dimensional coordinate-space representation, the reaction path, the collective potential, as well as the inertial masses are self-consistently calculated. We compare the ASCC results with those of the CHF+cranking method. Since the reaction system is very simple, there is no significant difference between the calculated CHF reaction paths with different constraint operators. Despite of this similarity in the CHF states, the inertial masses calculated with the cranking formula turn out to sensitively depend on the choice of the constraint operator. The ASCC method is able to remove this ambiguity in the inertial mass, by taking into account the residual effects caused by the density fluctuation.
We add a term, which introduce the effective mass and time-odd mean fields, to the standard BKN energy density functional, to examine the effect of these terms on the inertial masses for both the relative and rotational motions. In the presence of time-odd term, the cranking formula fails to preserve the correct asymptotic values, while the validity of ASCC mass is not affected by the introduction of the effective mass. The time-odd mean-fields properly recover the Galilean symmetry, leading to the exact values of the asymptotic inertial mass. This is found to be true in both relative and rotational motions. With this property, we are quite confident that the ASCC method is promising to be applied to the modern nuclear energy density functionals, and make advanced microscopic theoretical analysis on various nuclear reaction models. Another important issue is the inclusion of the paring correlation, which may influence not only static but also dynamical nuclear properties. In order to keep the lowest-energy configuration during the collective motion, the pairing interaction is known to play a key role [30]. Therefore, we may expect significant impact on both the collective inertial masses and the reaction paths. To study the above issues are our future tasks.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
The numerical calculation was done by KW. The theoretical part of the work was contributed by TN. KW and TN collaborated to analyze the numerical results and wrote the paper.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported in part by JSPS KAKENHI Grant Nos. 19H05142 and 18H01209, and also by JSPS-NSFC Bilateral Program for Joint Research Project on Nuclear mass and life for unraveling mysteries of r-process. This research in part used computational resources provided through the HPCI System Research Project (Project ID: hp190031) and by Multidisciplinary Cooperative Research Program in Center for Computational Sciences, University of Tsukuba.
References
1. Negele JW. The mean-field theory of nuclear structure and dynamics. Rev Mod Phys. (1982) 54:913–1015. doi: 10.1103/RevModPhys.54.913
2. Simenel C. Nuclear quantum many-body dynamics. Eur Phys J A. (2012) 48:1–49. doi: 10.1140/epja/i2012-12152-0
3. Nakatsukasa T. Density functional approaches to collective phenomena in nuclei: time-dependent density functional theory for perturbative and non-perturbative nuclear dynamics. Prog Theor Exp Phys. (2012) 2012:01A207. doi: 10.1093/ptep/pts016
4. Maruhn JA, Reinhard PG, Stevenson PD, Umar AS. The TDHF code Sky3D. Comput Phys Commun. (2014) 185:2195–216. doi: 10.1016/j.cpc.2014.04.008
5. Nakatsukasa T, Matsuyanagi K, Matsuo M, Yabana K. Time-dependent density-functional description of nuclear dynamics. Rev Mod Phys. (2016) 88:045004. doi: 10.1103/RevModPhys.88.045004
8. Baranger M, Kumar K. Nuclear deformations in the pairing-plus-quadrupole model. Nucl Phys A. (1968) 110:490–528. doi: 10.1016/0375-9474(68)90370-9
9. Baranger M, Kumar K. Nuclear deformations in the pairing-plus-quadrupole model. Nucl Phys A. (1968) 122:241–72. doi: 10.1016/0375-9474(68)90044-4
10. Yuldashbaeva EK, Libert J, Quentin P, Girod M. Mass parameters for large amplitude collective motion: a perturbative microscopic approach. Phys Lett B. (1999) 461:1–8. doi: 10.1016/S0370-2693(99)00836-9
11. Marumori T, Maskawa T, Sakata F, Kuriyama A. Self-consistent collective-coordinate method for the large-amplitude nuclear collective motion. Prog Theor Phys. (1980) 64:1294. doi: 10.1143/PTP.64.1294
12. Matsuo M, Nakatsukasa T, Matsuyanagi K. Adiabatic selfconsistent collective coordinate method for large amplitude collective motion in nuclei with pairing correlations. Prog Theor Phys. (2000) 103:959–79. doi: 10.1143/PTP.103.959
13. Hinohara N, Nakatsukasa T, Matsuo M, Matsuyanagi K. Gauge-invariant formulation of the adiabatic self-consistent collective coordinate method. Prog Theor Phys. (2007) 117:451–78. doi: 10.1143/PTP.117.451
14. Hinohara N, Nakatsukasa T, Matsuo M, Matsuyanagi K. Microscopic description of oblate-prolate shape mixing in proton-rich Se isotopes. Phys Rev C. (2009) 80:014305. doi: 10.1103/PhysRevC.80.014305
15. Hinohara N, Li ZP, Nakatsukasa T, Nikšić T, Vretenar D. Effect of time-odd mean fields on inertial parameters of the quadrupole collective Hamiltonian. Phys Rev C. (2012) 85:024323. doi: 10.1103/PhysRevC.85.024323
16. Sato K, Hinohara N, Yoshida K, Nakatsukasa T, Matsuo M, Matsuyanagi K. Shape transition and fluctuations in neutron-rich Cr isotopes around N = 40. Phys Rev C. (2012) 86:024316. doi: 10.1103/PhysRevC.86.024316
17. Davies KTR, Flocard H, Krieger S, Weiss MS. Application of the imaginary time step method to the solution of the static Hartree-Fock problem. Nucl Phys A. (1980) 342:111–23. doi: 10.1016/0375-9474(80)90509-6
18. Nakatsukasa T, Inakura T, Yabana K. Finite amplitude method for the solution of the random-phase approximation. Phys Rev C. (2007) 76:024318. doi: 10.1103/PhysRevC.76.024318
19. Inakura T, Nakatsukasa T, Yabana K. Self-consistent calculation of nuclear photoabsorption cross sections: finite amplitude method with Skyrme functionals in the three-dimensional real space. Phys Rev C. (2009) 80:044301. doi: 10.1103/PhysRevC.80.044301
20. Avogadro P, Nakatsukasa T. Finite amplitude method for the quasiparticle random-phase approximation. Phys Rev C. (2011) 84:014314. doi: 10.1103/PhysRevC.84.014314
21. Avogadro P, Nakatsukasa T. Efficient calculation for the quasiparticle random-phase approximation matrix. Phys Rev C. (2013) 87:014331. doi: 10.1103/PhysRevC.87.014331
22. Wen K, Nakatsukasa T. Self-consistent collective coordinate for reaction path and inertial mass. Phys Rev C. (2016) 94:054618. doi: 10.1103/PhysRevC.94.054618
23. Egido JL, Borrajo M, Rodríguez TR. Collective and single-particle motion in beyond mean field approaches. Phys Rev Lett. (2016) 116:052502. doi: 10.1103/PhysRevLett.116.052502
24. Li ZP, Nikšić T, Ring P, Vretenar D, Yao JM, Meng J. Efficient method for computing the Thouless-Valatin inertia parameters. Phys Rev C. (2012) 86:034334. doi: 10.1103/PhysRevC.86.034334
25. Bonche P, Koonin S, Negele JW. One-dimensional nuclear dynamics in the time-dependent Hartree-Fock approximation. Phys Rev C. (1976) 13:1226–58. doi: 10.1103/PhysRevC.13.1226
26. Baran A, Sheikh JA, Dobaczewski J, Nazarewicz W, Staszczak A. Quadrupole collective inertia in nuclear fission: cranking approximation. Phys Rev C. (2011) 84:054321. doi: 10.1103/PhysRevC.84.054321
27. Thouless DJ, Valatin JG. Time-dependent Hartree-Fock equations and rotational states of nuclei. Nucl Phys. (1962) 31:211–30. doi: 10.1016/0029-5582(62)90741-1
29. Hinohara N. Collective inertia of the Nambu-Goldstone mode from linear response theory. Phys Rev C. (2015) 92:034321. doi: 10.1103/PhysRevC.92.034321
Keywords: nuclear reaction, inertial mass, nuclear fusion, nuclear collective dynamics, mass parameter
Citation: Wen K and Nakatsukasa T (2020) Collective Inertial Masses in Nuclear Reactions. Front. Phys. 8:16. doi: 10.3389/fphy.2020.00016
Received: 28 November 2019; Accepted: 20 January 2020;
Published: 05 February 2020.
Edited by:
Nicolas Schunck, Physical and Life Sciences Directorate, Lawrence Livermore National Laboratory, United StatesReviewed by:
Peter Ring, Technical University of Munich, GermanyLuis Robledo, Autonomous University of Madrid, Spain
Copyright © 2020 Wen and Nakatsukasa. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kai Wen, d2Vua2FpQG51Y2wucGgudHN1a3ViYS5hYy5qcA==
 Kai Wen
Kai Wen Takashi Nakatsukasa1,2,3
Takashi Nakatsukasa1,2,3