- Department of Physics, College of Physics and Optoelectronic Engineering, Shenzhen University, Shenzhen, China
Aiming to produce new neutron-rich nuclei at N = 126, the multi-nucleon transfer reactions 136Xe+194Ir, 208Pb are investigated by using the GRAZING model and the three-dimensional time-dependent Hartree-Fock (TDHF) approach. Deexcitation processes of the primary fragments are taken into account in both models. Comparison with the experimental data of 136Xe+208Pb at Ec.m. = 450 MeV indicates that the isotopic production cross sections around the entrance channel can be well reproduced by both models. The results of GRAZING indicate that 136Xe+194Ir is a promising candidate for producing new neutron-rich isotones with N = 126. The limitation of using TDHF to investigate multi-nucleon transfer reactions is also discussed.
1. Introduction
Neutron-rich nuclei are of great importance for understanding the astrophysical r-process [1]. For instance, those around the closed neutron shell N = 126 can provide information on the solar r-abundance distribution [2]. The neutron-rich radioactive isotopes can also be used as projectiles for synthesizing super-heavy nuclei which is one of the most interesting challenges in nuclear physics. However, new heavy neutron-rich nuclei out of limits of the present nuclear chart are hardly to be produced via traditional ways, such as fusion reactions with stable beams at low energies or fragmentation of heavy projectile at relativistic energies.
In recent years, theoretical predictions indicate that multi-nucleon transfer (MNT) reactions would be a possible route to produce heavy neutron-rich nuclei far away from the stability line [3, 4]. The experimental results of 136Xe + 198Pt at the incident energy of 8 MeV/nucleon [2] show that the production cross sections of neutron-rich nuclei with N = 126 are orders of magnitude larger than those obtained in fragmentation reaction of 208Pb (1 AGeV) + Be [5]. But in some other experiments of MNT reactions with stable beams such as 64Ni + 207Pb [6] and 136Xe + 208Pb [7, 8], no new neutron-rich nuclei is detected. Based on the N/Z equilibrium concept, theoretical predictions show that using neutron-rich radioactive beams can remarkably improve the production cross sections of neutron-rich isotopes along N = 126 [9, 10]. However, due to the fact that the experimental intensities of radioactive beams are orders of magnitude lower than stable beams, the advantage of using radioactive beams may be canceled. Opportunities will arise in the near future on the second generation radioactive beam facilities like the European EURISOL [11]. At the present time, to find an optimum stable projectile-target combination are highly appealed.
To describe MNT reactions, many theoretical models are developed. For example, the multidimensional Langevin model shows great success on predicting the isotopic production cross sections, even for those nuclei far away from projectile and target [3, 4, 12]. Semi-classical GRAZING model [13, 14] and the complex Wentzel-Kramers-Brillouin (CWKB) model [15] can well describe transfer process in peripheral collisions. In GRAZING model, the reactants move on classical trajectories in the combined field of Coulomb repulsion and nuclear surface-surface attraction. Surface modes of the colliding nuclei are taken into account. Independent single nucleon transfer between the projectile-like and target-like nuclei during the collision is governed by the quantum coupled equations [13, 14]. Neutron evaporation is considered for the excited primary fragments. The mass, charge, energy, and angular momentum distributions of the products produced in grazing collisions can be obtained. For details of GRAZING model and its applications (see, e.g., [16–19], and references therein). The dinuclear system model can reproduce the experimental data related with quasi-fission or deep-inelastic collisions [10, 20–23]. The improved quantum molecular dynamics (ImQMD) model [24–26] is capable of describing collisions from central to very peripheral regions on a microscopic basis, the widths of isotopic distributions can be reproduced in ImQMD since stochastic two-body collisions are taken into account [27–29]. The time-dependent Hartree-Fock (TDHF) theory shows success in describing few-nucleon transfer process [30–34]. Recently, the stochastic mean-field (SMF) approach beyond TDHF [35] has been proposed to investigate the damped MNT reaction 136Xe + 208Pb, the experimental broad mass distribution can be reproduced.
In this work, the GRAZING model and TDHF theory incorporating with GEMINI++1 [36] are adopted to investigate the production of neutron-rich nuclei in MNT reactions. The TDHF theory [37] is based on the independent particle picture and is a good approximation to the nuclear many-body problem. It is capable of describing low-energy heavy-ion reactions and provides insight on the average behavior of the dynamics. The state-of-art TDHF calculations are performed in a three-dimensional (3D) framework without any symmetry constraints due to the advances in computational power. It has been applied for investigations on various subjects, for instance, collective vibration [38, 39], fusion reaction [40, 41], fission dynamics [42–44], dissipation mechanism [45–48]. Recently, 3D TDHF is applied to MNT reactions [30–33, 49]. Fluctuation and dissipation can not be properly described in TDHF since two-body collisions and internucleon correlations are not included. Thus, widths of the mass or isotopic distributions in MNT reactions at incident energies above the Coulomb barrier are underestimated in TDHF. To consider these effects in TDHF is beyond the scope of this paper and further studied will be carried out in the future.
This paper is outlined as follows. In section 2, the TDHF approach and particle-number projection (PNP) method as well as the numerical details are introduced. In section 3, numerical results of the isotopic production cross sections in both GRAZING and TDHF approach are shown. Dynamical properties of the reactions are also discussed for TDHF. Finally, a summary is drawn in section 4.
2. Brief Introduction to TDHF Approach
In this section, we briefly introduce TDHF formalism, PNP method and the coupling to GEMINI++. Details of the TDHF theory can be found in, e.g., [50, 51], and references therein. In TDHF approach, time evolution for the single-particle states are described by a set of coupled non-linear equations
where ψα, ν(r, t) is the single-particle state and N is the total number of states. ĥ is the self-consistent mean-field Hamiltonian of single-particle motion and it is always related to Skyrme energy density functional (EDF) which depends on local densities [52]. We underline that there are no adjustable parameters in the TDHF approach. The uncertainty in TDHF calculations may arise from the uncertainty of fundamental nuclear properties, such as the distribution of shape deformation of the reactants in their ground states. This can be obtained by preparing reactants with deformation constraints. The above TDHF equations can be derived from the variation of the action [53]
where
is the correlated many-body wave function of the system and is given by a single Slater determinate.
In the present work, the 3D unrestricted TDHF code Sky3D [51] with Skyrme SLy5 parametrization [54] is adopted for both the static and dynamic calculations. The static HF calculations are performed on 32 × 32 × 32 Cartesian grids with 1.0 fm grid spacing in all three directions. In dynamical calculations, the meshes are extended to 70 × 32 × 70 with the same grid spacing in static HF. The projectile and target are initially placed at a separation distance of 24 fm and then boosted with the associated center-of-mass energy Ec.m. and the impact parameter b. The time step △t is set to be 0.2 fm/c and six-order Taylor series expansion is employed. The TDHF simulations are stopped when the separation distance of the primary fragments after collision reaches 30 fm. Since single-particle wave functions are partially exchanged between the projectile-like and target-like nuclei in the collision process, the outgoing states are not the eigenstates of the particle-number operators (Ẑ for protons and for neutrons) but superpositions of them. One can only get the expectation (mean) values of the charge and mass numbers for each fragment after collision. If one wants to get the distributions of proton or neutron numbers in one of the primary fragments, one should project the many-body states on good particle numbers by introducing the PNP operator [50, 55]
where q = n, p labels the nucleon species, and Nn means N neutrons while Np means Z protons. The subscript V denotes the region of coordinate space encompassing one of the primary fragments, and ΘV(r) = 1 if r ∈ subspace V and 0 elsewhere. The integral is performed with an M−point uniform discretion. For convergence, M is set to be 300.
The probability to find Nq particles in subspace V is then obtained accordingly. The cross section of primary fragment with neutron number N and charge number Z at a certain incident energy is
where P(N, Z; b) = P(N; b)P(Z; b) represents the probability to find N neutrons and Z protons at the impact parameter b; bmax is a cutoff impact parameter which depends on the incident energy and should be large enough to guarantee that most of the transfer cross sections are included. But it is not necessary to set bmax to be too large, because the transfer probability is extremely small and elastic collision dominates in very peripheral collisions. In this work, we set it to be 10 fm for 136Xe+208Pb at Ec.m. = 450 MeV and 13 fm for 136Xe+194Ir at Ec.m. = 720 MeV. b ranges from 0 to bmax with the interval Δb = 1 fm.
Deexcitation of the primary fragments are considered by using the statistical code GEMINI++ with default parameters [36, 56]. All possible sequential binary decay modes, from emission of nucleons and light particles through asymmetric to symmetric fission as well as the γ-emission are included in GEMINI++. The code needs information of a primary fragment including charge and mass number as well as the excitation energies and the angular momentum as the inputs. Detailed calculations of these quantities can be found in Jiang and Wang [34]. The deexcitation of a certain projectile-like fragment (PLF) or target-like fragment (TLF) should be repeated Mtrial times due to the statistical nature of GEMINI++. Here Mtrial = 1, 000 is used. The number of events in which final fragment with (Nfinal, Zfinal) is counted and denoted as M(Nfinal, Zfinal). Then the final production cross section is given as
Owing to the intrinsic stochastic nature of the Monte Carlo method employed in GEMINI++, Type A standard uncertainties for the isotopic production cross sections are calculated in the simplest case. The deexcitation process of a certain fragment is performed ten times repeatedly with Mtrial = 1, 000 for each time. Average values of σ(Nfinal, Zfinal) and the uncertainties can be obtained straightforwardly. We find the uncertainties are very small. For the sake of simplicity, the deexcitation process is performed only once with Mtrial = 1, 000 in this work.
3. Results and Discussions
136Xe + 208Pb is a candidate reaction for the production of neutron-rich nuclei at N = 126. The experiment at Ec.m. = 450 MeV was performed at Argonne in 2015 [8]. In Figure 1 we plot the calculated isotopic production cross sections of the PLFs in this reaction. The results of GRAZING are shown as blue solid lines while those of TDHF+GEMINI are presented as black dashed lines. The experimental data are shown for comparison. The production cross sections of the TLFs are also calculated but have already been published in another paper [34]. One can find that for Z = 51 − 53 and Z = 55 − 58, the magnitude of the peak values can be reproduced by TDHF+GEMINI. Whilst those for Z = 52, 53, 55, 56 can be reproduced by GRAZING. For Z = 54, the peak values are overestimated in both models. This is because the results of (quasi)elastic channels are not excluded in our calculations. One can also find that better predictions are obtained for proton pickup channels than stripping channels in both models. As the number of transferred nucleons increases, discrepancies between model predictions and the experimental data get larger. These isotopes far away from the entrance channel may be produced in strongly damped collisions. Such processes can not be well estimated by the two models: two-body collisions are not considered in TDHF [57, 58] while the GRAZING model only takes grazing collisions into account.
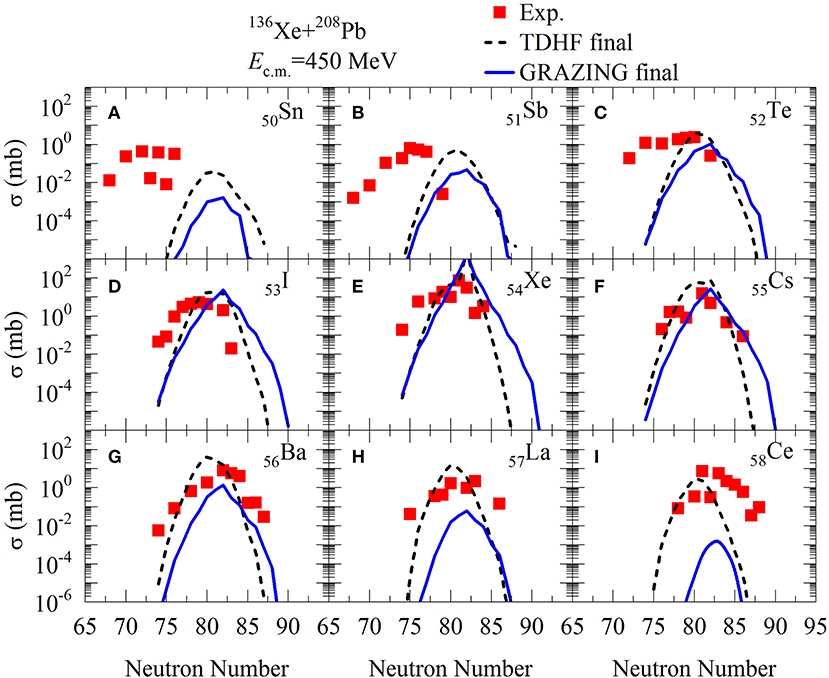
Figure 1. (Color online) Isotopic production cross sections of the PLFs for Z = 50–58 (A–I) in 136Xe + 208Pb at Ec.m. = 450 MeV. The results of GRAZING and TDHF+GEMINI are shown as blue solid and black dashed lines, respectively. The experimental data are taken from Barrett et al. [8] and shown as red solid squares.
However, no new neutron-rich nuclei were detected in 136Xe + 208Pb. The experiment results of 136Xe+198Pt at Ec.m. = 645 MeV [2] indicate that this reaction is a better candidate to produce neutron-rich nuclei with N = 126. Calculations of this reaction are performed by using both GRAZING and TDHF+GEMINI. Unfortunately, no neutron-rich nuclei with N = 126 is obtained in TDHF+GEMINI. The production cross sections of those nuclei predicted by GRAZING are given in Figure 2. Detailed discussions about the predictions of TDHF on this reaction will be reported elsewhere. At the end of this section, we will show some results of 136Xe + 194Ir given by TDHF+GEMINI and discuss the limits of TDHF approach on investigating MNT reactions when the incident energy is much above the Coulomb barrier. In the following, we concentrate on the predictions of GRAZING on neutron-rich nuclei with N = 126.
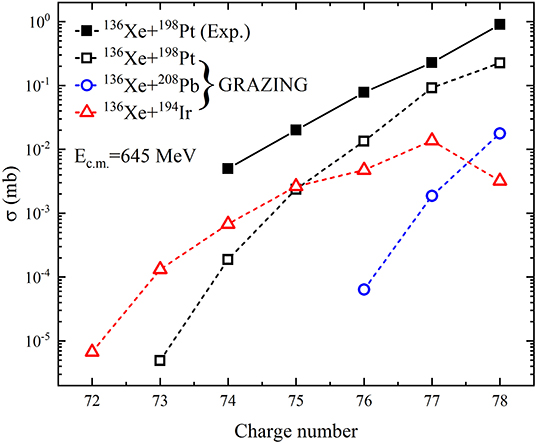
Figure 2. (Color online) Production cross sections of N = 126 isotones predicted by GRAZING in three different systems at Ec.m. = 645 MeV. The results of 136Xe + 208Pb, 198Pt, and 194Ir are presented as blue open circles, black open squares and red open triangles, respectively. The experimental data of 136Xe + 198Pt are taken from Watanabe et al. [2] and shown as black solid squares. The lines are drawn to guide the eye.
In order to find another optimum projectile-target combination for producing new exotic neutron-rich nuclei with stable reactants, we carry out a systematic study on 15 MNT reactions with projectile around 136Xe and target around 198Pt at various incident energies by using GRAZING. The results indicate that 136Xe + 194Ir is a surrogate reaction to produce neutron-rich nuclei around N = 126. The production cross sections of isotones with N = 126 in 136Xe + 194Ir are compared with those of 136Xe + 208Pb and 136Xe + 198Pt. The center-of-mass energy for all the three systems is set to be Ec.m. = 645 MeV (this energy is the same as the experiment of 136Xe + 198Pt [2], and we will show later that it is also an optimum energy for 136Xe + 194Ir). The simulation results are plotted in Figure 2 as open symbols. The experimental data of 136Xe + 198Pt taken from [2] are shown as black solid squares for comparison. One can first see that more N = 126 isotones with charge number Z ⩽ 78 can be produced in both 136Xe + 194Ir and 136Xe + 198Pt rather than 136Xe + 208Pb. Particularly, the system 136Xe + 194Ir has huge advantages for producing N = 126 isotones with Z ⩽ 74. Those nuclei are out of the limits of the present nuclear landscape and are of great interest for nuclear and astro-nuclear physics. One can also find that the experimental data are underestimated by GRAZING. This can be understood since only peripheral collisions are treated in GRAZING and those nuclei with large number of nucleon transferred are produced in damped collisions at small impact parameters.
To find an optimum incident energy to produce more neutron-rich nuclei with N = 126 in 136Xe + 194Ir, the production cross sections of N = 126 isotones with Z = 72 − 77 at various incident energies from Ec.m. = 1.07VB to 1.85VB (VB is the Bass barrier [59] and it is around 410 MeV for this reaction) are calculated by using GRAZING. The results are presented in Figure 3. It can be seen that very neutron-rich isotones with Z ⩽ 74 can not be produced if Elab/A ⩽ 5.5 MeV. The cross sections of all these isotones increase with the increasing incident energy when Elab/A < 6.5 MeV. However, when Elab/A is in the range of 7–9 MeV, plateau-like structures are observed for all the curves. This phenomenon indicates that the production cross sections of those nuclei are insensitive to the incident energy if 7 ⩽ Elab/A ⩽ 9 MeV.
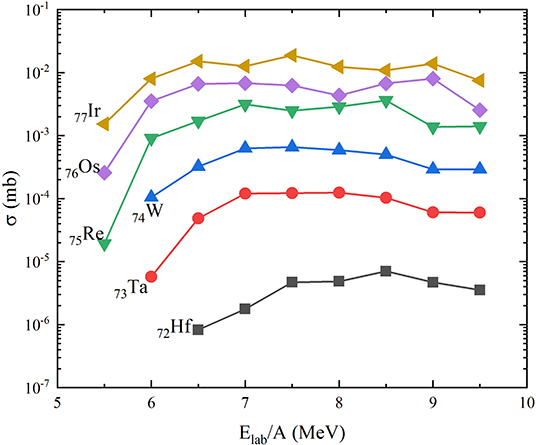
Figure 3. (Color online) Production cross sections of neutron-rich N = 126 isotones with Z = 72 − 77 in 136Xe + 194Ir as a function of the incident energy. The lines are drawn to guide the eye.
In Figure 4 we show the isotopic production cross sections of the TLFs with Z = 72 − 77 in 136Xe + 198Pt and 136Xe + 194Ir at Ec.m. = 645 MeV (Elab/A ≈ 8 MeV) as black dashed and red solid lines, respectively. It can be found that for nuclei on the proton-rich side, larger production cross sections are obtained in 136Xe + 194Ir. For isotopes with Z = 76 and 77, more neutron-rich ones are produced in 136Xe + 198Pt. Whilst for Z = 75 the two systems give comparable results for isotopes on the neutron-rich side. As Z decreases, the advantage to produce more neutron-rich nuclei arises in 136Xe + 194Ir. Note that the results of Z = 72 in 136Xe + 198Pt are not given by GRAZING. The above results of the two reactions are difficult to be understood through the N/Z equilibrium process because N/Z is around 1.52 for 136Xe and 194Ir while it is about 1.54 for 198Pt and 208Pb, respectively. It might be related with the Qgg value effect, where Qgg is the ground state-to-ground state Q value. Other quantum effect like shell effect might also play a role. Further studies should be carried out to check these discussions.
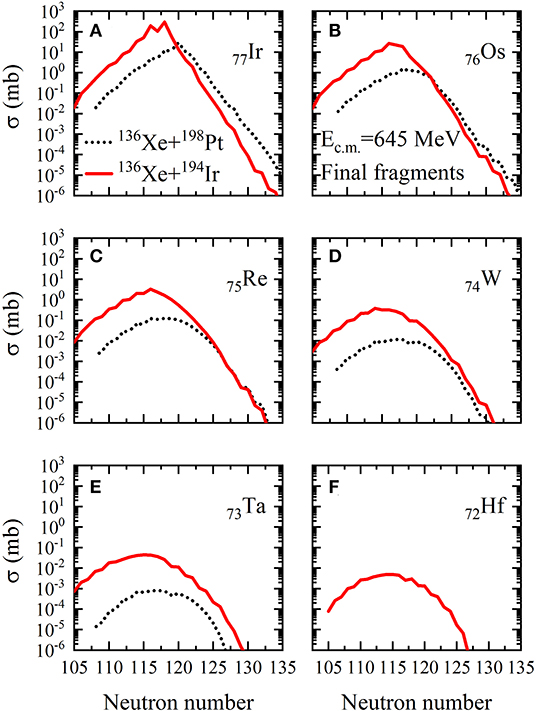
Figure 4. (Color online) Isotopic production cross sections of the TLFs with Z = 72 − 77 (A–F) in 136Xe + 198Pt and 136Xe + 194Ir at Ec.m. = 645 MeV, which are plotted as black dotted and red solid lines, respectively.
Finally, in Figure 5 we show the density contour plots of 136Xe + 194Ir at some special reaction stages in TDHF for two different initial configurations at Ec.m. = 720 MeV (Elab/A ≈ 9) and b = 6 fm. Isodensities at half the saturation density (ρ0/2 = 0.08 fm−3) is plotted as black solid lines. We should mention that in TDHF the projectile and target are both deformed in their ground states with β2 = 0.064 and 0.154, respectively. Since the deformation of 136Xe is very small, we only take into account the orientation effect of the deformed 194Ir at the beginning of the dynamical calculations. The two initial configurations are named “tip collision” (the symmetry axis of 194Ir is set parallel to the bombarding direction: z-axis) and “side collision” (the symmetry axis of 194Ir is set parallel to x-axis). It can be found that in both configurations, the composite system is strongly elongated before rupture of the neck. The primary fragments produced at the end of the dynamical calculations also have large deformations. Similar results are obtained for TDHF+GEMINI in 136Xe + 198Pt at Ec.m. = 645 MeV. Such large deformation in the exit channel makes the primary fragments have very large excitation energies. This leads to strong evaporation of nucleons in the deexcitation process. So no neutron-rich isotope with N = 126 is observed in TDHF+GEMINI for 136Xe + 194Ir and 136Xe + 198Pt reactions when the incident energy is much larger than the Coulomb barrier. It is well-known that mean-field model such as TDHF is suitable for low-energy reactions, however, the lack of two-body collisions limits the predictive power of TDHF on estimating the yields of MNT reactions when the incident energy is much above the barrier.
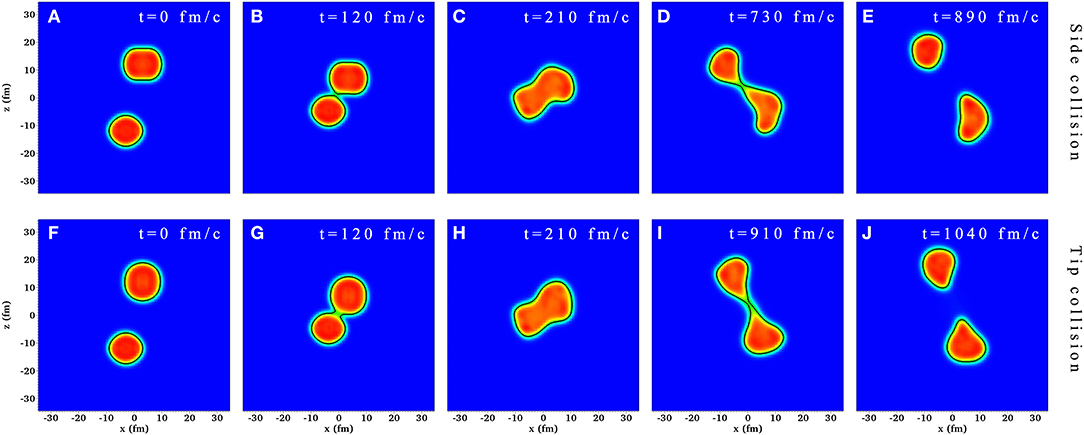
Figure 5. (Color online) Density contour plots of 136Xe + 194Ir for two different configurations (upper panels: “side collision” and lower panels: “tip collision”) at Ec.m. = 720 MeV and b = 6 fm. Five different reaction stages are given: (A,F) the initial stage at t = 0 fm/c, (B,G) the reactants just contact with each other, (C,H) the composite system has the most compact geometric shape, (D,I) the neck is going to rupture and (E,J) the end of the dynamical calculations. The isodensities of 0.08 fm−3 are shown as black solid lines.
4. Summary
Employing the semi-classic GRAZING model and the microscopic TDHF approach, we have investigated the MNT reactions of 136Xe + 194Ir, 208Pb. Neutron evaporation is considered in GRAZING while GEMINI++ is coupled with TDHF to deal with the deexcitation process. The calculated production cross sections of the PLFs for 136Xe + 208Pb at Ec.m. = 450 MeV are compared with the experimental data. The model predictions can well describe the yields of nuclei near the projectile. The predictions of GRAZING on 136Xe + 194Ir show that this reaction has the advantage to produce more neutron-rich nuclei with N = 126 compared with 136Xe + 198Pt. The latter one has been carried out at GANIL [2] and the results are inspiring. No new neutron-rich isotope is observed for these two reactions at energies much above the barrier in TDHF+GMINI which might be interpreted as the lack of two-body collisions in the mean-field theory. Further investigations on 136Xe + 194Ir by using other theoretical models with two-body collisions included, such as ImQMD, are in progress.
Data Availability Statement
All datasets generated for this study are included in the article/supplementary material.
Author Contributions
XJ performed numerical calculations. XJ and NW wrote the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China (Projects Nos. 11705118, 11647026, and 11475115) and Natural Science Foundation of SZU (grant no. 2016017).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
References
1. Grawe H, Langanke K, Martínez-Pinedo G. Nuclear structure and astrophysics. Rep Prog Phys. (2007) 70:1525. doi: 10.1088/0034-4885/70/9/R02
2. Watanabe YX, Kim YH, Jeong SC, Hirayama Y, Imai N, Ishiyama H, et al. Pathway for the production of neutron-rich isotopes around the N = 126 shell closure. Phys Rev Lett. (2015) 115:172503. doi: 10.1103/PhysRevLett.115.172503
3. Zagrebaev V, Greiner W. Production of new heavy isotopes in low-energy multinucleon transfer reactions. Phys Rev Lett. (2008) 101:122701. doi: 10.1103/PhysRevLett.101.122701
4. Zagrebaev VI, Greiner W. Production of heavy and superheavy neutron-rich nuclei in transfer reactions. Phys Rev C. (2011) 83:044618. doi: 10.1103/PhysRevC.83.044618
5. Kurtukian-Nieto T, Benlliure J, Schmidt KH, Audouin L, Becker F, Blank B, et al. Production cross sections of heavy neutron-rich nuclei approaching the nucleosynthesis r-process path around A = 195. Phys Rev C. (2014) 89:024616. doi: 10.1103/PhysRevC.89.024616
6. Beliuskina O, Heinz S, Zagrebaev V, Comas V, Heinz C, Hofmann S, et al. On the synthesis of neutron-rich isotopes along the N = 126 shell in multinucleon transfer reactions. Eur Phys J A. (2014) 50:161. doi: 10.1140/epja/i2014-14161-3
7. Kozulin EM, Vardaci E, Knyazheva GN, Bogachev AA, Dmitriev SN, Itkis IM, et al. Mass distributions of the system 136Xe+208Pb at laboratory energies around the Coulomb barrier: a candidate reaction for the production of neutron-rich nuclei at N = 126. Phys Rev C. (2012) 86:044611. doi: 10.1103/PhysRevC.86.044611
8. Barrett JS, Loveland W, Yanez R, Zhu S, Ayangeakaa AD, Carpenter MP, et al. 136Xe+208Pb reaction: a test of models of multinucleon transfer reactions. Phys Rev C. (2015) 91:064615. doi: 10.1103/PhysRevC.91.064615
9. Loveland W. Synthesis of transactinide nuclei using radioactive beams. Phys Rev C. (2007) 76:014612. doi: 10.1103/PhysRevC.76.014612
10. Zhu L, Su J, Xie WJ, Zhang FS. Theoretical study on production of heavy neutron-rich isotopes around the N=126 shell closure in radioactive beam induced transfer reactions. Phys Lett B. (2017) 767:437–42. doi: 10.1016/j.physletb.2017.01.082
11. Bonaccorso A, Prete G. EURISOL: an European Isotope Separation On-Line radioactive ion beam facility. J Phys Confer Ser. (2009) 168:012023. doi: 10.1088/1742-6596/168/1/012023
12. Karpov AV, Saiko VV. Modeling near-barrier collisions of heavy ions based on a Langevin-type approach. Phys Rev C. (2017) 96:024618. doi: 10.1103/PhysRevC.96.024618
13. Winther A. Grazing reactions in collisions between heavy nuclei. Nucl Phys A. (1994) 572:191–235.
14. Winther A. Dissipation, polarization and fluctuation in grazing heavy-ion collisions and the boundary to the chaotic regime. Nucl Phys A. (1995) 594:203–45.
15. Corradi L, Stefanini AM, Ackermann D, Beghini S, Montagnoli G, Petrache C, et al. Multinucleon transfer reactions in 32S+208Pb close to the Coulomb barrier. Phys Rev C. (1994) 49:R2875–9. doi: 10.1103/PhysRevC.49.R2875
16. Dasso CH, Pollarolo G, Winther A. Systematics of isotope production with radioactive beams. Phys Rev Lett. (1994) 73:1907–10. doi: 10.1103/PhysRevLett.73.1907
17. Corradi L, Pollarolo G, Szilner S. Multinucleon transfer processes in heavy-ion reactions. J Phys G Nucl Part Phys. (2009) 36:113101. doi: 10.1088/0954-3899/36/11/113101
18. Montanari D, Corradi L, Szilner S, Pollarolo G, Fioretto E, Montagnoli G, et al. Neutron pair transfer in 60Ni+116Sn far below the coulomb barrier. Phys Rev Lett. (2014) 113:052501. doi: 10.1103/PhysRevLett.113.052501
19. Wen P, Li C, Zhu L, Lin C, Zhang F. Mechanism of multinucleon transfer reaction based on the GRAZING model and DNS model. J Phys G Nucl Part Phys. (2017) 44:115101. doi: 10.1088/1361-6471/aa8b07
20. Penionzhkevich YE, Adamian GG, Antonenko NV. Towards neutron drip line via transfer-type reactions. Physics Lett B. (2005) 621:119–25. doi: 10.1016/j.physletb.2005.05.085
21. Adamian GG, Antonenko NV, Lukyanov SM, Penionzhkevich YE. Possibility of production of neutron-rich isotopes in transfer-type reactions at intermediate energies. Phys Rev C. (2008) 78:024613. doi: 10.1103/PhysRevC.78.024613
22. Feng ZQ. Production of neutron-rich isotopes around N = 126 in multinucleon transfer reactions. Phys Rev C. (2017) 95:024615. doi: 10.1103/PhysRevC.95.024615
23. Guo SQ, Bao XJ, Zhang HF, Li JQ, Wang N. Effect of dynamical deformation on the production distribution in multinucleon transfer reactions. Phys Rev C. (2019) 100:054616. doi: 10.1103/PhysRevC.100.054616
24. Wang N, Li Z, Wu X. Improved quantum molecular dynamics model and its applications to fusion reaction near barrier. Phys Rev C. (2002) 65:064608. doi: 10.1103/PhysRevC.65.064608
25. Wang N, Li Z, Wu X, Tian J, Zhang Y, Liu M. Further development of the improved quantum molecular dynamics model and its application to fusion reactions near the barrier. Phys Rev C. (2004) 69:034608. doi: 10.1103/PhysRevC.69.034608
26. Wang N, Guo L. New neutron-rich isotope production in 154Sm+160Gd. Phys Lett B. (2016) 760:236–41. doi: 10.1016/j.physletb.2016.06.073
27. Welsh T, Loveland W, Yanez R, Barrett JS, McCutchan EA, Sonzogni AA, et al. Modeling multi-nucleon transfer in symmetric collisions of massive nuclei. Phys Lett B. (2017) 771:119–24. doi: 10.1016/j.physletb.2017.05.044
28. Li C, Wen P, Li J, Zhang G, Li B, Xu X, et al. Production mechanism of new neutron-rich heavy nuclei in the Xe136+198Pt reaction. Phys Lett B. (2018) 776:278–83. doi: 10.1016/j.physletb.2017.11.060
29. Desai VV, Loveland W, McCaleb K, Yanez R, Lane G, Hota SS, et al. The 136Xe+198Pt reaction: A test of models of multi-nucleon transfer reactions. Phys Rev C. (2019) 99:044604. doi: 10.1103/PhysRevC.99.044604
30. Sekizawa K. Microscopic description of production cross sections including deexcitation effects. Phys Rev C. (2017) 96:014615. doi: 10.1103/PhysRevC.96.014615
31. Jiang X, Wang N. Production mechanism of neutron-rich nuclei around N=126 in the multi-nucleon transfer reaction 132Sn + 208Pb. Chinese Phys C. (2018) 42:104105. doi: 10.1088/1674-1137/42/10/104105
32. Sekizawa K. TDHF theory and its extensions for the multinucleon transfer reaction: a mini review. Front Phys. (2019) 7:20. doi: 10.3389/fphy.2019.00020
33. Wu Z, Guo L. Microscopic studies of production cross sections in multinucleon transfer reaction 58Ni+124Sn. Phys Rev C. (2019) 100:014612. doi: 10.1103/PhysRevC.100.014612
34. Jiang X, Wang N. Probing the production mechanism of neutron-rich nuclei in multinucleon transfer reactions. Phys Rev C. (2020) 101:014604. doi: 10.1103/PhysRevC.101.014604
35. Ayik S, Yilmaz B, Yilmaz O, Umar AS. Quantal diffusion approach for multinucleon transfers in Xe + Pb collisions. Phys Rev C. (2019) 100:014609. doi: 10.1103/PhysRevC.100.014609
36. Charity RJ. Systematic description of evaporation spectra for light and heavy compound nuclei. Phys Rev C. (2010) 82:014610. doi: 10.1103/PhysRevC.82.014610
37. Dirac PAM. Note on exchange phenomena in the Thomas atom. Math Proc Cambridge. (1930) 26:376–85.
38. Simenel C, Chomaz P. Nonlinear vibrations in nuclei. Phys Rev C. (2003) 68:024302. doi: 10.1103/PhysRevC.68.024302
39. Umar AS, Oberacker VE. Time-dependent response calculations of nuclear resonances. Phys Rev C. (2005) 71:034314. doi: 10.1103/PhysRevC.71.034314
40. Simenel C, Keser R, Umar AS, Oberacker VE. Microscopic study of 16O+16O fusion. Phys Rev C. (2013) 88:024617. doi: 10.1103/PhysRevC.88.024617
41. Jiang X, Maruhn JA, Yan S. Microscopic study of noncentral effects in heavy-ion fusion reactions with spherical nuclei. Phys Rev C. (2014) 90:064618. doi: 10.1103/PhysRevC.90.064618
42. Umar AS, Oberacker VE, Maruhn JA, Reinhard PG. Microscopic description of nuclear fission dynamics. J Phys G Nucl Part Phys. (2010) 37:064037. doi: 10.1088/0954-3899/37/6/064037
43. Goddard P, Stevenson P, Rios A. Fission dynamics within time-dependent Hartree-Fock: deformation-induced fission. Phys Rev C. (2015) 92:054610. doi: 10.1103/PhysRevC.92.054610
44. Simenel C, Umar AS. Formation and dynamics of fission fragments. Phys Rev C. (2014) 89:031601. doi: 10.1103/PhysRevC.89.031601
45. Maruhn JA, Reinhard PG, Stevenson PD, Strayer MR. Spin-excitation mechanisms in Skyrme-force time-dependent Hartree-Fock calculations. Phys Rev C. (2006) 74:027601. doi: 10.1103/PhysRevC.74.027601
46. Loebl N, Umar AS, Maruhn JA, Reinhard PG, Stevenson PD, Oberacker VE. Single-particle dissipation in a time-dependent Hartree-Fock approach studied from a phase-space perspective. Phys Rev C. (2012) 86:024608. doi: 10.1103/PhysRevC.86.024608
47. Guo L, Simenel C, Shi L, Yu C. The role of tensor force in heavy-ion fusion dynamics. Phys Lett B. (2018) 782:401–5. doi: 10.1016/j.physletb.2018.05.066
48. Wen K, Barton MC, Rios A, Stevenson PD. Two-body dissipation effect in nuclear fusion reactions. Phys Rev C. (2018) 98:014603. doi: 10.1103/PhysRevC.98.014603
49. Umar AS, Simenel C, Ye W. Transport properties of isospin asymmetric nuclear matter using the time-dependent Hartree-Fock method. Phys Rev C. (2017) 96:024625. doi: 10.1103/PhysRevC.96.024625
50. Bender M, Heenen PH, Reinhard PG. Self-consistent mean-field models for nuclear structure. Rev Mod Phys. (2003) 75:121–80. doi: 10.1103/RevModPhys.75.121
51. Maruhn JA, Reinhard PG, Stevenson PD, Umar AS. The {TDHF} code Sky3D. Comput Phys Commun. (2014) 185:2195–216. doi: 10.1016/j.cpc.2014.04.00
52. Vautherin D, Brink DM. Hartree-Fock calculations with Skyrme's interaction. I. Spherical nuclei. Phys Rev C. (1972) 5:626–47. doi: 10.1103/PhysRevC.5.626
53. Negele JW. The mean-field theory of nuclear structure and dynamics. Rev Mod Phys. (1982) 54:913–1015. doi: 10.1103/RevModPhys.54.913
54. Chabanat E, Bonche P, Haensel P, Meyer J, Schaeffer R. A Skyrme parametrization from subnuclear to neutron star densities Part II. Nuclei far from stabilities. Nucl Phys A. (1998) 635:231–56.
55. Simenel C. Particle transfer reactions with the time-dependent Hartree-Fock theory using a particle number projection technique. Phys Rev Lett. (2010) 105:192701. doi: 10.1103/PhysRevLett.105.192701
56. Mancusi D, Charity RJ, Cugnon J. Unified description of fission in fusion and spallation reactions. Phys Rev C. (2010) 82:044610. doi: 10.1103/PhysRevC.82.044610
57. Grangé P, Richert J, Wolschin G, Weidenmüller HA. Influence of a collision term on finite-size one-dimensional TDHF. Nucl Phys A. (1981) 356:260–8.
58. Goeke K, Reinhard PG. Time-Dependent Hartree-Fock and Beyond. Prog Theor Phys Suppl. (1983) 171:33–65.
Keywords: multi-nucleon transfer reactions, neutron-rich nuclei, GRAZING, TDHF, particle number projection
Citation: Jiang X and Wang N (2020) Predictions of New Neutron-Rich Isotopes at N = 126 in the Multinucleon Transfer Reaction 136Xe + 194Ir. Front. Phys. 8:38. doi: 10.3389/fphy.2020.00038
Received: 30 November 2019; Accepted: 06 February 2020;
Published: 26 February 2020.
Edited by:
Lu Guo, University of Chinese Academy of Sciences, ChinaReviewed by:
Andrea Celentano, National Institute of Nuclear Physics, Ministry of Education, Universities and Research, ItalyRosario Gianluca Pizzone, Laboratori Nazionali del Sud (INFN), Italy
Copyright © 2020 Jiang and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nan Wang, d2FuZ25hbkBzenUuZWR1LmNu
 Xiang Jiang
Xiang Jiang Nan Wang
Nan Wang