Applications of Time-Dependent Density-Matrix Approach

The equations of motion for reduced density matrices form a coupled chain known as the Bogoliubov-Born-Green-Kirkwood-Yvon (BBGKY) hierarchy. To close the coupled chain at the two-body level, approximations for a three-body density matrix with one-body and two-body density matrices are needed. The time-dependent density-matrix theory (TDDM) assumes that the three-body density matrix is given by the antisymmetrized products of the one-body and two-body density matrices. In this review the truncation schemes of the BBGKY hierarchy beyond TDDM are discussed and a formulation for the study of excited states which is derived from the time-dependent approach is explained. The truncation schemes and the formulation for excited states are applied to the Lipkin model and the Hubbard model to corroborate their validity. Two realistic applications of the TDDM approaches are also presented. One is the dipole and quadrupole excitations of ⁴⁰Ca and ⁴⁸Ca and the other the fusion reactions of ¹⁶O + ¹⁶O.

1. Introduction

The time-dependent Hartree-Fock theory (TDHF) is the basis of the mean-field theories such as the Hartree-Fock theory (HF) and the random-phase approximation (RPA): The HF ground state is given as a stationary solution of the TDHF equation and RPA can be formulated as the small amplitude limit of the TDHF equation. HF and RPA have extensively been used as standard theories to study nuclear structure problem [1]. Extensive TDHF simulations have also been performed for heavy-ion collisions [2, 3]. However, most experimental data suggest that beyond-mean field theories are required for a more realistic description of nuclear structure and reactions. In this paper an approach to extend the mean-field theories based on the equations of motion for reduced density matrices is reviewed. The equations of motion for reduced density matrices form a coupled chain known as the Bogoliubov-Born-Green-Kirkwood-Yvon (BBGKY) hierarchy [4] where the time evolution of an n-body density matrix depends on n-body and n+1-body density matrices. The advantage of such a time-dependent density-matrix approach (TDDMA) is that it is directly connected to TDHF in the lowest-level approximation: The truncation of the BBGKY hierarchy at the level of the one-body density matrix by approximating the two-body density matrix with the antisymmetrized product of the one-body density matrices gives TDHF. A beyond TDHF is obtained by the truncation of the BBGKY hierarchy at the two-body level and it needs approximations for the three-body density matrix. A few truncations schemes have been proposed. The simplest truncation scheme is to replace the three-body density matrix with the antisymmetrized products of the one-body and two-body density matrices, neglecting the correlated part of the three-body density matrix [the three-body correlation matrix (C₃)] [5, 6]. This truncation scheme has been called the time-dependent density-matrix theory (TDDM). TDDM has been applied to heavy-ion collisions [7–9] and collective excitations [6, 10–12]. A simplified TDDM called TDDM^P [13] where two-body correlations are consider only for a pair of time reversed single-particle (s.p.) states have also been employed to simulate heavy-ion collisions [13, 14]. It was found that TDDM sometimes overestimates ground-state correlations in a solvable model [15], gives unphysical s.p. occupation probabilities in dynamical simulations [16, 17] and causes divergent dynamical behaviors in highly excited and (or) strongly interacting cases [18, 19]. Obviously the problems originate in the neglect of C₃ and are related to the loss of N-representability [20] which refers to the properties of reduced density matrices derived from an N-body total wavefunction and is completely fulfilled only in the case of the untruncated BBGKY hierarchy. To remedy the difficulties of the naive truncation scheme in the description of ground states, an approximation for C₃ has been proposed based on perturbative consideration [21], where C₃ is given by the traced products of the correlated part of the two-body density matrix (C₂). This truncation scheme is referred to as TDDM1 hereafter. The correlation matrices C₂ and C₃ are also called the two-body and three-body cumulants and the above approximation for C₃ corresponds to taking the leading-order terms of the three-body cumulant [22, 23]. It has been demonstrated that TDDM1 improves the TDDM results for the ground states of model Hamiltonians [21, 23] and also ¹⁶O [24]. In the case of the Lipkin model [25], however, TDDM1 was found to overestimate C₃ in strongly interacting regions. There, another truncation scheme [26] where C₃ in TDDM1 is divided by a reduction factor was introduced. This truncation scheme is referred to as TDDM2. In this paper three truncation schemes TDDM, TDDM1 and TDDM2 are explained and their applications are presented.

The small amplitude limit of the TDDMA equations gives an extended RPA (ERPA) which is used for the study of excited states, as is the case of RPA which is formulated as the small amplitude limit of TDHF. RPA and ERPA are also formulated by using the equation of motion approach [27, 28]. ERPA consists of the coupled equations for the one-body and two-body amplitudes and include the effects of ground-state correlations through the fractional occupation probability n_α of a s.p. state α and C₂. ERPA is related to so far proposed beyond-RPA theories. When the coupling to the two-body amplitude is omitted, the ERPA equation for the one-body amplitude is the same as the self-consistent RPA (SCRPA) [29, 30] equation which includes both n_α and C₂. The neglect of C₂ in the SCRPA equation corresponds to the renormalized RPA (rRPA) [27, 28] which includes the ground-state correlation effect via n_α. When the HF ground state is assumed, the equations in ERPA are reduced to those in the second RPA (SRPA) [31]. If particle-hole correlations included in the two-body amplitudes were expressed by phonons, ERPA would be connected the particle-vibration coupling or quasiparticle-phonon models [32]. ERPA has been applied to solvable models [23, 33]. Realistic cases have also been studied in ERPA [34–36]. Main results of the ERPA applications are presented in this paper.

The TDDM truncation scheme has been used for simulations of heavy-ion collisions [7–9] where the TDDM equations are formulated by using the time-dependent s.p. states which obey a TDHF-like equation. The application of such a TDDM approach to the fusion reactions of ¹⁶O + ¹⁶O is also presented.

The paper is organized as follows: The equations of motion for the one-body and two-body density matrices formulated by using a time-independent s.p. basis are given in section 2 and the truncation schemes of the BBGKY hierarchy and the formulation of ERPA are discussed. The applications are made to two model Hamiltonians, the Lipkin model [25] and the one-dimensional Hubbard model [37] in section 2 and the obtained results are compared with the exact solutions. The ERPA results for the dipole and quadrupole excitations in ⁴⁰Ca and ⁴⁸Ca are presented in section 2 as realistic applications of ERPA. The TDDM formulation using a time-dependent s.p. basis and its application to the fusion reactions of ¹⁶O + ¹⁶O are given in section 3. Section 4 is devoted to summary and outlook.

2. Formulation in Time-Independent Single-Particle Basis

The TDDMA equations are formulated for an N fermion system described by the Hamiltonian H consisting of a one-body part t (the kinetic energy term) and a two-body interaction v

$\begin{array}{l}H={\displaystyle \sum _{\alpha {\alpha }^{\prime }}}\langle \alpha |t|{\alpha }^{\prime }\rangle a_{\alpha }^{+}{a}_{{\alpha }^{\prime }}+\frac{1}{2}{\displaystyle \sum _{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}}\langle \alpha \beta |v|{\alpha }^{\prime }{\beta }^{\prime }\rangle a_{\alpha }^{+}{a}_{\beta }^{+}{a}_{{\beta }^{\prime }}{a}_{{\alpha }^{\prime }},\end{array}$

where $a_{\alpha }^{+}$ and a_α are the creation and annihilation operators of a particle at a s.p. state α and the s.p. states are assumed time-independent.

2.1. Time-Dependent Density-Matrix Theory and Truncation Schemes

The TDDMA equations given in Tohyama and Schuck [21] are explained below. They consist of the coupled equations of motion for the one-body density matrix (the occupation matrix) $n_{\alpha {\alpha }^{\prime }}$ and the correlated part of the two-body density matrix $C_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}$ (C₂). These matrices are defined as

$\begin{array}{ll}{n}_{\alpha {\alpha }^{\prime }}(t)=\langle \Phi (t)|a_{{\alpha }^{\prime }}^{+}{a}_{\alpha }|\Phi (t)\rangle ,& (1)\end{array}$

$\begin{array}{ll}{C}_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}(t)={\rho }_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}(t)-{A}(n_{\alpha {\alpha }^{\prime }}(t)n_{\beta {\beta }^{\prime }}(t)),& (2)\end{array}$

where |Φ(t)〉 is the time-dependent total wavefunction |Φ(t)〉 = exp[−iHt]|Φ(t = 0)〉, ${\rho }_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}$ is the two-body density matrix (${\rho }_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}(t)=\langle \Phi (t)|a_{{\alpha }^{\prime }}^{+}{a}_{{\beta }^{\prime }}^{+}{a}_{\beta }{a}_{\alpha }|\Phi (t)\rangle$) and ${A}$ is an operator which properly antisymmetrizes $n_{\alpha {\alpha }^{\prime }}{n}_{\beta {\beta }^{\prime }}$ under the exchange of the s.p. indices such as α ↔ β and α′ ↔ β′. Units ℏ = 1 are used hereafter. The equations of motion for $n_{\alpha {\alpha }^{\prime }}$ and $C_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}$ are derived from

$\begin{array}{ll}i{\dot{n}}_{\alpha {\alpha }^{\prime }}=\langle \Phi (t)|[a_{{\alpha }^{\prime }}^{+}{a}_{\alpha },H]|\Phi (t)\rangle & (3)\end{array}$

$\begin{array}{ll}i{\stackrel{\bullet }{\rho }}_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}=\langle \Phi (t)|[a_{{\alpha }^{\prime }}^{+}{a}_{{\beta }^{\prime }}^{+}{a}_{\beta }{a}_{\alpha },H]|\Phi (t)\rangle ,& (4)\end{array}$

by evaluating the commutation relations. They are written as

$\begin{array}{l}i{\dot{n}}_{\alpha {\alpha }^{\prime }}={\displaystyle \sum _{\lambda }({ϵ}_{\alpha \lambda }{n}_{\lambda {\alpha }^{\prime }}-n_{\alpha \lambda }{ϵ}_{\lambda {\alpha }^{\prime }})}\\ +{\displaystyle \sum _{{\lambda }_1{\lambda }_2{\lambda }_3}[\langle \alpha {\lambda }_1|v|{\lambda }_2{\lambda }_3\rangle C_{{\lambda }_2{\lambda }_3{\alpha }^{\prime }{\lambda }_1}-C_{\alpha }{}_{{\lambda }_1{\lambda }_2{\lambda }_3}\langle {\lambda }_2{\lambda }_3|v|{\alpha }^{\prime }{\lambda }_1\rangle ],}& (5)\end{array}$

$\begin{array}{l}i{\dot{C}}_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}={\displaystyle \sum _{\lambda }(}{ϵ}_{\alpha \lambda }{C}_{\lambda \beta {\alpha }^{\prime }{\beta }^{\prime }}+{ϵ}_{\beta \lambda }{C}_{\alpha \lambda {\alpha }^{\prime }{\beta }^{\prime }}-{ϵ}_{\lambda {\alpha }^{\prime }}{C}_{\alpha \beta \lambda {\beta }^{\prime }}\\ -{ϵ}_{\lambda {\beta }^{\prime }}{C}_{\alpha \beta {\alpha }^{\prime }\lambda })+B_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}+P_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}+H_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}+T_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }},& (6)\end{array}$

where ${ϵ}_{\alpha {\alpha }^{\prime }}$ is the s.p. energy including the mean field and is given by

$\begin{array}{ll}{ϵ}_{\alpha {\alpha }^{\prime }}=\langle \alpha |t|{\alpha }^{\prime }\rangle +{\displaystyle \sum _{{\lambda }_1{\lambda }_2}}{\langle \alpha {\lambda }_1|v|{\alpha }^{\prime }{\lambda }_2\rangle }_A{n}_{{\lambda }_2{\lambda }_1}.& (7)\end{array}$

Here the subscript A means that the corresponding matrix is antisymmetrized. The term $B_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}$ in Equation (6) consists of only the occupation matrices and describes 2 particle (p) – 2 hole (h) and 2h–2p excitations, while $P_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}$ and $H_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}$ contain C₂ and express p–p (and h–h) and p–h correlations to infinite order, respectively [6]. The $T_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}$ term gives the coupling to the three-body correlation matrix (C₃)

$\begin{array}{l}{T}_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}=\text{}{\displaystyle \sum _{{\lambda }_1{\lambda }_2{\lambda }_3}[\langle \alpha {\lambda }_1|v|{\lambda }_2{\lambda }_3\rangle C_{{\lambda }_2{\lambda }_3\beta {\alpha }^{\prime }{\lambda }_1{\beta }^{\prime }}}\\ +\langle {\lambda }_1\beta |v|{\lambda }_2{\lambda }_3\rangle C_{{\lambda }_2{\lambda }_3\alpha {\alpha }^{\prime }{\lambda }_1{\beta }^{\prime }}\\ -\langle {\lambda }_1{\lambda }_2|v|{\alpha }^{\prime }{\lambda }_3\rangle C_{\alpha {\lambda }_3\beta {\lambda }_1{\lambda }_2{\beta }^{\prime }}-\langle {\lambda }_1{\lambda }_2|v|{\lambda }_3{\beta }^{\prime }\rangle C_{\alpha {\lambda }_3\beta {\lambda }_1{\lambda }_2{\alpha }^{\prime }}],& (8)\end{array}$

where $C_{\alpha \beta \gamma {\alpha }^{\prime }{\beta }^{\prime }{\gamma }^{\prime }}$ (C₃) is given by

$\begin{array}{ll}{C}_{\alpha \beta \gamma {\alpha }^{\prime }{\beta }^{\prime }{\gamma }^{\prime }}=\langle \Phi (t)|a_{{\alpha }^{\prime }}^{+}{a}_{{\beta }^{\prime }}^{+}{a}_{{\gamma }^{\prime }}^{+}{a}_{\gamma }{a}_{\beta }{a}_{\alpha }|\Phi (t)\rangle -{A}(n_{\alpha {\alpha }^{\prime }}{\rho }_{\beta \gamma {\beta }^{\prime }{\gamma }^{\prime }}).& (9)\end{array}$

Approximations for C₃ are needed to close the equations of motion within $n_{\alpha {\alpha }^{\prime }}$ and C₂. Three truncation schemes TDDM, TDDM1 and TDDM2 have been proposed. In TDDM, C₃ is simply omitted [5, 6]. In TDDM1, C₃ is given by [21]

$\begin{array}{ll}{C}_{{\text{p}}_1{\text{p}}_2{\text{h}}_1{\text{p}}_3{\text{p}}_4{\text{h}}_2}={\displaystyle \sum _{\text{h}}}{C}_{\text{h}{\text{h}}_1{\text{p}}_3{\text{p}}_4}{C}_{{\text{p}}_1{\text{p}}_2{\text{h}}_2\text{h}},& (10)\end{array}$

$\begin{array}{ll}{C}_{{\text{p}}_1{\text{h}}_1{\text{h}}_2{\text{p}}_2{\text{h}}_3{\text{h}}_4}={\displaystyle \sum _{\text{p}}}{C}_{{\text{h}}_1{\text{h}}_2{\text{p}}_2\text{p}}{C}_{{\text{p}}_1\text{p}{\text{h}}_3{\text{h}}_4},& (11)\end{array}$

where p and h refer to particle and hole states, respectively. These expressions were derived from perturbative consideration using the Coupled-Cluster-Doubles (CCD)-like ground state wavefunction [38]. In a time-independent density-matrix approach in quantum chemistry, known as the contracted Schr$\ddot{\text{o}}$dinger equation [20], Mazziotti [22] has proposed a method for constructing the three-body cumulant (C₃) with $n_{\alpha {\alpha }^{\prime }}$ and C₂. Equations (10) and (11) describe the leading-order terms in the three-body cumulant [23]. TDDM2 [26] is the most effective in the large N and strongly interacting limits of the Lipkin model and gives

$\begin{array}{ll}{C}_{{\text{p}}_1{\text{p}}_2{\text{h}}_1{\text{p}}_3{\text{p}}_4{\text{h}}_2}=\frac{1}{{N}}{\displaystyle \sum _{\text{h}}}{C}_{\text{h}{\text{h}}_1{\text{p}}_3{\text{p}}_4}{C}_{{\text{p}}_1{\text{p}}_2{\text{h}}_2\text{h}},& (12)\end{array}$

$\begin{array}{ll}{C}_{{\text{p}}_1{\text{h}}_1{\text{h}}_2{\text{p}}_2{\text{h}}_3{\text{h}}_4}=\frac{1}{{N}}{\displaystyle \sum _{\text{p}}}{C}_{{\text{h}}_1{\text{h}}_2{\text{p}}_2\text{p}}{C}_{{\text{p}}_1\text{p}{\text{h}}_3{\text{h}}_4},& (13)\end{array}$

where ${N}$ is

$\begin{array}{ll}{N}=1+\frac{1}{4}{\displaystyle \sum _{\text{p}{\text{p}}^{\prime }\text{h}{\text{h}}^{\prime }}}{C}_{\text{p}{\text{p}}^{\prime }\text{h}{\text{h}}^{\prime }}{C}_{\text{h}{\text{h}}^{\prime }\text{p}{\text{p}}^{\prime }}.& (14)\end{array}$

The factor ${N}$ was introduced to simulate many-body effects which reduce C₃ in large N systems and (or) strongly interacting regions of the Lipkin model. In the perturbative region where the second term on the right-hand side of Equation (26) is smaller than unity, ${N}$ has the meaning of the normalization factor of the total wavefunction.

The conservation of the total energy and total particle number is not affected by the truncation schemes for C₃ as long as its symmetry and anti-symmetry properties under the exchange of s.p. indices is respected. However, the trace relation between the one-body and two-body density matrices $n_{\alpha {\alpha }^{\prime }}=\sum _{\lambda }{\rho }_{\alpha \lambda {\alpha }^{\prime }\lambda }/(N-1)$ is not conserved when any approximation is made for C₃. This is an example of the loss of N-representability [20]. It was pointed out [21] that the fulfillment of the trace relation is drastically improved by going from TDDM to TDDM1. In an attempt to conserve the trace relation, Cassing and Pfitzner [39] proposed an approximation for C₃ which also contains quadratic terms of C₂. However, C₃ is not uniquely determined only by the requirement of the trace relation conservation. In contrast to TDDM1 their quadratic terms do not have the leading-order terms (Equations 10, 11) of the three-body cumulant [22, 23] and the dynamical effect of C₃ was found small in one-dimensional heavy-ion simulations [39]. C₃ in Reference [39] is not anti-symmetric under the exchange of s.p. indices, which may violate even the conservation of the trace relation as was pointed out by Gherega et al. [17]. There is another attempt [40] to conserve the trace relation, where the equation motion for C₃ was solved by truncating the BBGKY hierarchy at the three-body level. However, the application of such an approach was limited to model Hamiltonians [40].

2.2. Ground-State Calculation

The ground state in TDDMA is given as a stationary solution of the time-dependent equations (Equations 5, 6) which satisfies ${\dot{n}}_{\alpha {\alpha }^{\prime }}=0$ and $\dot{C}$₂ = 0. Two methods have been employed to obtain the stationary solution. One is the adiabatic method: Equations (5) and (6) are solved by starting from the HF configuration and gradually increasing the strength of the residual interaction such as $v(\overrightarrow{r}-\overrightarrow{r^{\prime }})\times t/T$. This method is based on the Gell-Mann-Low theorem [41] and has often been used to obtain approximate ground states with various time-dependent functionals [11, 13, 14, 42, 43]. To suppress oscillating components which come from the mixing of excited states, T must be much larger than the longest period in the system considered. The other method is a usual iterative gradient method which is useful to obtain a rigorously stationary solution. Since it involves matrix inversion, the application of the gradient method is limited to small systems: The gradient method has been employed to obtain the ground states of the Lipkin model [15] and the oxygen, calcium and tin isotopes [34–36] using several s.p. states around the Fermi level [34, 36] or the valence neutron s.p. states [35].

2.3. Excited-States Calculation

The formulation for excited states can be derived by either taking the small amplitude limit of the TDDM equations or using the equation of motion approach [1, 27]. Here the formulation based on the equation of motion approach is presented. Let us consider a generalized RPA operator with one-body and two-body sectors

$\begin{array}{ll}{{Q}}_{\mu }^{+}={\displaystyle \sum _{\lambda {\lambda }^{\prime }}}{x}_{\lambda {\lambda }^{\prime }}^{\mu }{a}_{\lambda }^{+}{a}_{{\lambda }^{\prime }}+{\displaystyle \sum _{{\lambda }_1{\lambda }_2{\lambda }_1^{\prime }{\lambda }_2^{\prime }}}{X}_{{\lambda }_1{\lambda }_2{\lambda }_1^{\prime }{\lambda }_2^{\prime }}^{\mu }{a}_{{\lambda }_1}^{+}{a}_{{\lambda }_2}^{+}{a}_{{\lambda }_2^{\prime }}{a}_{{\lambda }_1^{\prime }},& (15)\end{array}$

where there is no restriction on the s.p. indices: They can be both p and h. As usual with the equation of motion approach, the properties of the excitation operator ${{Q}}_{\mu }^{+}|{\Phi }_0\rangle =|{\Phi }_{\mu }\rangle$ and ${{Q}}_{\mu }|{\Phi }_0\rangle =0$ are assumed and the following equations of motion satisfied by exact states are taken into account

$\begin{array}{ll}\langle {\Phi }_0|[a_{\lambda }^{+}{a}_{{\lambda }^{\prime }},H]|{\Phi }_{\mu }\rangle ={\omega }_{\mu }{\Phi }_0|a_{\lambda }^{+}{a}_{{\lambda }^{\prime }}|{\Phi }_{\mu }\rangle & (16)\end{array}$

$\begin{array}{ll}\langle {\Phi }_0|[a_{{\lambda }_1}^{+}{a}_{{\lambda }_2}^{+}{a}_{{\lambda }_2^{\prime }}{a}_{{\lambda }_1^{\prime }},H]|{\Phi }_{\mu }\rangle ={\omega }_{\mu }\langle {\Phi }_0|a_{{\lambda }_1}^{+}{a}_{{\lambda }_2}^{+}{a}_{{\lambda }_2^{\prime }}{a}_{{\lambda }_1^{\prime }}|{\Phi }_{\mu }\rangle ,& (17)\end{array}$

where ω_μ is the excitation energy of an excited state |Φ_μ〉. The equations for $x_{\lambda {\lambda }^{\prime }}^{\mu }$ and $X_{{\lambda }_1{\lambda }_2{\lambda }_1^{\prime }{\lambda }_2^{\prime }}^{\mu }$ are obtained by inserting Equation (16) into the above equations. They are written in matrix form [15, 40]

$\begin{array}{ll}\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)\left(\begin{array}{c}{x}^{\mu }\\ X^{\mu }\end{array}\right)={\omega }_{\mu }\left(\begin{array}{cc}{S}_1& T_1\\ T_2& S_2\end{array}\right)\left(\begin{array}{c}{x}^{\mu }\\ X^{\mu }\end{array}\right).& (18)\end{array}$

The Hamiltonian matrices A, B, C and D are given by

$\begin{array}{ll}A(\alpha {\alpha }^{\prime }:\lambda {\lambda }^{\prime })=\langle {\Phi }_0|[[a_{{\alpha }^{\prime }}^{+}{a}_{\alpha },H],a_{\lambda }^{+}{a}_{{\lambda }^{\prime }}]|{\Phi }_0\rangle ,& (19)\end{array}$

$\begin{array}{l}B(\alpha {\alpha }^{\prime }:{\lambda }_1{\lambda }_2{\lambda }_1^{\prime }{\lambda }_2^{\prime })=C^{+}\\ =\langle {\Phi }_0|[[a_{{\alpha }^{\prime }}^{+}{a}_{\alpha },H],a_{{\lambda }_1}^{+}{a}_{{\lambda }_2}^{+}{a}_{{\lambda }_2^{\prime }}{a}_{{\lambda }_1^{\prime }}]|{\Phi }_0\rangle ,& (20)\end{array}$

$\begin{array}{ll}D(\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }:{\lambda }_1{\lambda }_2{\lambda }_1^{\prime }{\lambda }_2^{\prime })=\langle {\Phi }_0|[[a_{{\alpha }^{\prime }}^{+}{a}_{{\beta }^{\prime }}^{+}{a}_{\beta }{a}_{\alpha },H],a_{{\lambda }_1}^{+}{a}_{{\lambda }_2}^{+}{a}_{{\lambda }_2^{\prime }}{a}_{{\lambda }_1^{\prime }}]|{\Phi }_0\rangle .& (21)\end{array}$

The norm matrices S₁, T₁, T₂, and S₂ are given as

$\begin{array}{ll}{S}_1(\alpha {\alpha }^{\prime }:\lambda {\lambda }^{\prime })=\langle {\Phi }_0|[a_{{\alpha }^{\prime }}^{+}{a}_{\alpha },a_{\lambda }^{+}{a}_{{\lambda }^{\prime }}]|{\Phi }_0\rangle ,& (22)\end{array}$

$\begin{array}{ll}{T}_1(\alpha {\alpha }^{\prime }:{\lambda }_1{\lambda }_2{\lambda }_1^{\prime }{\lambda }_2^{\prime })=T_2^{+}=\langle {\Phi }_0|[a_{{\alpha }^{\prime }}^{+}{a}_{\alpha },a_{{\lambda }_1}^{+}{a}_{{\lambda }_2}^{+}{a}_{{\lambda }_2^{\prime }}{a}_{{\lambda }_1^{\prime }}]|{\Phi }_0\rangle ,& (23)\end{array}$

$\begin{array}{ll}{S}_2(\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }:{\lambda }_1{\lambda }_2{\lambda }_1^{\prime }{\lambda }_2^{\prime })=\langle {\Phi }_0|[a_{{\alpha }^{\prime }}^{+}{a}_{{\beta }^{\prime }}^{+}{a}_{\beta }{a}_{\alpha },a_{{\lambda }_1}^{+}{a}_{{\lambda }_2}^{+}{a}_{{\lambda }_2^{\prime }}{a}_{{\lambda }_1^{\prime }}]|{\Phi }_0\rangle .& (24)\end{array}$

These matrices are evaluated by assuming |Φ₀〉 to be the ground state in TDDMA. This means that the effects of ground-state correlations are included in the above matrices through $n_{\alpha {\alpha }^{\prime }}$ and C₂. All matrix elements in Equation (19) are given in Tohyama and Schuck [40]. The one-body sector of Equation (18), $A{x}^{\mu }={\omega }_{\mu }{S}_1{x}^{\mu }$, is explicitly shown below to explain how $n_{\alpha {\alpha }^{\prime }}$ and C₂ are included. The matrix S₁ is given by

$\begin{array}{ll}{S}_1(\alpha {\alpha }^{\prime }:\lambda {\lambda }^{\prime })=(n_{{\alpha }^{\prime }{\alpha }^{\prime }}-n_{\alpha \alpha }){\delta }_{\alpha \lambda }{\delta }_{{\alpha }^{\prime }{\lambda }^{\prime }}& (25)\end{array}$

and A by

$\begin{array}{l}A(\alpha {\alpha }^{\prime }:\lambda {\lambda }^{\prime })=({ϵ}_{\alpha }-{ϵ}_{{\alpha }^{\prime }})(n_{{\alpha }^{\prime }{\alpha }^{\prime }}-n_{\alpha \alpha }){\delta }_{\alpha \lambda }{\delta }_{{\alpha }^{\prime }{\lambda }^{\prime }}\\ +(n_{{\alpha }^{\prime }{\alpha }^{\prime }}-n_{\alpha \alpha })(n_{{\lambda }^{\prime }{\lambda }^{\prime }}-n_{\lambda \lambda }){\langle \alpha {\lambda }^{\prime }|v|{\alpha }^{\prime }\lambda \rangle }_A\\ -{\delta }_{{\alpha }^{\prime }{\lambda }^{\prime }}{\displaystyle \sum _{\gamma {\gamma }^{\prime }{\gamma }^{″}}}\langle \alpha \gamma |v|{\gamma }^{\prime }{\gamma }^{″}\rangle C_{{\gamma }^{\prime }{\gamma }^{″}\lambda \gamma }\\ -{\delta }_{\alpha \lambda }{\displaystyle \sum _{\gamma {\gamma }^{\prime }{\gamma }^{″}}}\langle \gamma {\gamma }^{\prime }|v|{\alpha }^{\prime }{\gamma }^{″}\rangle C_{{\lambda }^{\prime }{\gamma }^{″}\gamma {\gamma }^{\prime }}\\ +{\displaystyle \sum _{\gamma {\gamma }^{\prime }}}({\langle \alpha \gamma |v|\lambda {\gamma }^{\prime }\rangle }_A{C}_{{\lambda }^{\prime }{\gamma }^{\prime }{\alpha }^{\prime }\gamma }+{\langle {\lambda }^{\prime }\gamma |v|{\alpha }^{\prime }{\gamma }^{\prime }\rangle }_A{C}_{\alpha {\gamma }^{\prime }\lambda \gamma })\\ -{\displaystyle \sum _{\gamma {\gamma }^{\prime }}}(\langle \alpha {\lambda }^{\prime }|v|\gamma {\gamma }^{\prime }\rangle C_{\gamma {\gamma }^{\prime }{\alpha }^{\prime }\lambda }+\langle \gamma {\gamma }^{\prime }|v|{\alpha }^{\prime }\lambda \rangle C_{\alpha {\lambda }^{\prime }\gamma {\gamma }^{\prime }}),& (26)\end{array}$

where ${ϵ}_{\alpha {\alpha }^{\prime }}$ and $n_{\alpha {\alpha }^{\prime }}$ are assumed to be diagonal for simplicity. The first two terms on the right-hand side of Equation (22) are of the same form as the RPA and rRPA euqations, the next two terms with C₂ and the Kronecker delta ${\delta }_{\alpha {\alpha }^{\prime }}$ describe the self-energies of the α–α′ configurations due to ground-state correlations [29, 44], and the other terms with C₂ are interpreted as the vertex corrections [29, 44]. Equation (19) has the most general form of beyond RPA theories: It is reduced to SRPA when the ground-state correlations are neglected and the one-body sector of Equation (18) $A{x}^{\mu }={\omega }_{\mu }{S}_1{x}^{\mu }$ is formally the same as the equation in SCRPA. Equation (18) is referred to as the extended RPA (ERPA) hereafter.

Although ERPA has great advantages over other extended RPA theories, it is worth pointing out its limitations. The numbers of the matrix elements of C₂ and $X_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}^{\mu }$ increase rapidly with increasing number of the s.p. states. Therefore, truncation of the s.p. space is required in realistic applications. As shown below, basic effects of two-body correlations can be described with rather small s.p. space, however. The other limitation is concerned with hermiticity of D in Equation (18), which is related to the truncation of the BBGKY hierarchy. Equation (21) contains C₃ and it is approximated depending on the truncation scheme. Hermiticity of D which is guaranteed only when all the matrix elements of C₃ satisfy the stationary condition as those of $n_{\alpha {\alpha }^{\prime }}$ and C₂ do is not fulfilled [40] when any approximated is made for C₃. The non-hermiticity has not caused serious problems in the applications thus far considered, though. In the case of the Lipkin model, an attempt [40] to obtain Hermitian D was carried out by solving the equation of motion for C₃.

2.4. Applications

TDDMA's in the time-independent s.p. basis have been applied to model Hamiltonians [23, 33] to corroborate their validity: The Lipkin model [25] was used to compare three truncation schemes TDDM, TDDM1 and TDDM2. Comparison of ERPA with other beyond-RPA theories, rRPA, SCRPA and SRPA was performed for the one-dimensional Hubbard model [37]. As realistic applications of ERPA, the quadrupole excitations of oxygen isotopes [34], the low-lying quadrupole states in tin isotopes [35] and the dipole and quadrupole excitations of ⁴⁰Ca and ⁴⁸Ca [36] have been studied. In the following some of the results are presented.

2.4.1. Lipkin Model

The Lipkin model [25] has extensively been used to test theoretical models. It describes an N-fermions system with two N-fold degenerate levels. The upper (lower) levels have energies ϵ/2 (−ϵ/2) and quantum number p (−p) with p = 1, 2, …, N. The Hamiltonian is given by

$\begin{array}{ll}H=ϵJ_z+\frac{V}{2}(J_{+}^2+J_{-}^2),& (27)\end{array}$

where the operators are the followings

$\begin{array}{ll}{J}_z=\frac{1}{2}{\displaystyle \sum _{p=1}^N}(c_p^{+}{c}_p-{c_{-p}}^{+}{c}_{-p}),& (28)\end{array}$

$\begin{array}{ll}{J}_{+}=J_{-}^{+}={\displaystyle \sum _{p=1}^N}{c}_p^{+}{c}_{-p}.& (29)\end{array}$

For χ = |V|(N − 1)/ϵ ≤ 1 the HF ground state is given by $|\text{HF}\rangle ={\prod }_{p=1}^N{c}_{-p}^{+}|0\rangle$, where |0〉 is the true vacuum. For χ > 1 the lowest s.p. states are obtained by the transformation

$\begin{array}{ll}\left(\begin{array}{c}{a}_{-p}^{+}\\ a_p^{+}\end{array}\right)=\left(\begin{array}{cc}cos\alpha & sin\alpha \\ -sin\alpha & cos\alpha \end{array}\right)\left(\begin{array}{c}{c}_{-p}^{+}\\ c_p^{+}\end{array}\right),& (30)\end{array}$

where α satisfies cos2α = 1/χ. The HF ground state in this case is often called the “deformed” HF (DHF) state and is given by |DHF(α)〉= ${\displaystyle {\prod }_{P=1}^N{a}_{-p}^{+}}|0\rangle$.

The truncation schemes TDDM, TDDM1 and TDDM2 have been applied to the Lipkin model and it was found that the simplest scheme TDDM gives the exact solutions in the limits of large N and χ [45]. This is due to the unique property of the Lipkin model that the ground-state energy in DHF becomes exact in such limits [1]. The relation between the density-matrices in DHF and TDDM is discussed below. The occupation matrix in DHF is given by $n_{-p-p}={cos}^2\alpha$, $n_{pp}=1-n_{-p-p}={sin}^2\alpha$, and n_{p − p} = cosαsinα. The two-body and three-body density matrices in DHF are given by the above elements of the occupation matrix. For example the 2p–2h and ph–ph elements of the two-body density matrix are expressed as

$\begin{array}{l}{\rho }_{p{p}^{\prime }-p-p^{\prime }}=\langle \text{DHF}(\alpha )|c_{-p}^{+}{c}_{-p^{\prime }}^{+}{c}_{p^{\prime }}{c}_p|\text{DHF}(\alpha )\rangle \\ ={cos}^2\alpha {sin}^2\alpha =n_{p-p}{n}_{p^{\prime }-p^{\prime }}={\rho }_{p-p^{\prime }-p{p}^{\prime }}(p\ne p^{\prime }).& (31)\end{array}$

Similarly, the three-body density matrix is given by

$\begin{array}{ll}{\rho }_{p-p^{\prime }{p}^{″}p{p}^{\prime }-p^{″}}={cos}^2\alpha {sin}^4\alpha =n_{pp}{\rho }_{-p^{\prime }{p}^{″}{p}^{\prime }-p^{″}}.& (32)\end{array}$

This means that the correlated part ($C_{p-p^{\prime }{p}^{″}p{p}^{\prime }-p^{″}}$) of the three-body density matrix vanishes in DHF. The “spherical” total wavefunction |Ψ〉 in DHF which does not have the mixing of the p and −p states is given by the two DHF solutions as

$\begin{array}{ll}|\Psi \rangle =\frac{1}{\sqrt{2}}(|\text{DHF}(\alpha )\rangle +|\text{DHF}(-\alpha )\rangle ).& (33)\end{array}$

Since the overlap between |DHF(α)〉 and |DHF(−α)〉 is negligibly in the large χ and N limits, the three-body density matrix calculated with |Ψ〉 has also no correlated part. This is the reason why the results in TDDM approach the exact solutions in the large χ and N limits.

The ground-state energy E₀ calculated in TDDM (solid line) for N = 12 and 50 is presented respectively in Figures 1, 2 as a function of χ. The dashed and green (gray) lines denote the results in TDDM1 and TDDM2, respectively. In the case of N = 50 the results in TDDM2 are not displayed because they lie between the TDDM results and the exact values. The dotted and dot-dashed lines depict the results in HF and DHF (χ > 1) and the exact values, respectively. As seen in Figures 1, 2, the factor ${N}$ in Equations (12) and (13) plays a role in greatly reducing C₃, making TDDM2 almost equivalent to TDDM for N = 50. In the limits of large N and χ both TDDM and DHF results become close to the exact solutions. In the transitional region χ ≈ 1, however, TDDM1 and TDDM2 were found better than TDDM and DHF [45]. In the case of N = 12 this extends to χ ≈ 2 as seen in Figure 1.

FIGURE 1

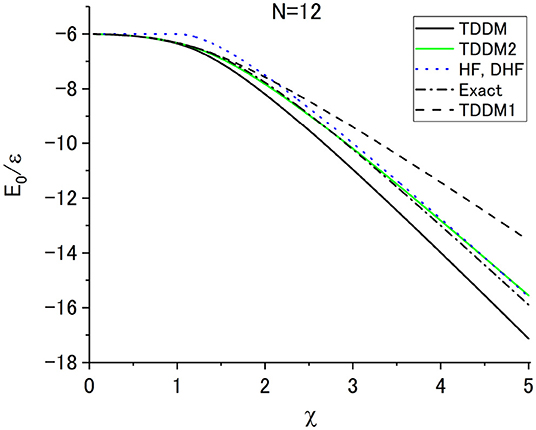
Figure 1. Ground-state energy in TDDM (solid line) as a function of χ = |V|(N − 1)/ϵ for N = 12. The results in TDDM1 where the three-body correlation matrix is given by Equations (10) and (11) are shown with the dashed line. The green (gray) line depicts the results in TDDM2 where the three-body correlation matrix is given by Equations (12) and (13). The results in HF and DHF(χ > 1) are depicted with the dotted line. The exact values are given by the dot-dashed line. Adapted from Tohyama and Schuck [45] with permission from Societ$\grave{\text{a}}$ Italiana di Fisica/Springer-Verlag GmbH Germany.

FIGURE 2

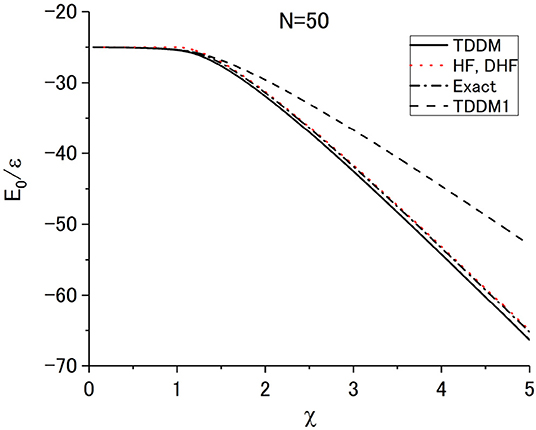
Figure 2. Ground-state energy in TDDM (solid line) as a function of χ for N = 50. The exact values are given with the dot-dashed line. The dashed line depicts the results in TDDM1. The results in TDDM2 lie between the TDDM results and the exact values and are not displayed here. The results in HF and DHF(χ > 1) are shown with the dotted line but cannot be distinguished from the exact values in the scale of the figure except for the region χ ≈ 1. Adapted from Tohyama and Schuck [45] with permission from Societ$\grave{\text{a}}$ Italiana di Fisica/Springer-Verlag GmbH Germany.

The excitation energies of the first and second excited states calculated from the small oscillations of the TDDM solutions (dots) are compared with the exact solutions (dot-dashed line) in Figures 3, 4 for N = 200 where TDDM is supposed to give the nearly exact ground state. The dotted lines in Figures 3, 4 depict the results in RPA and the “deformed” RPA (χ > 1) for the first excited state. In contrast to RPA and the deformed RPA TDDM reproduces the smoothly decreasing excitation energy of the first excited state with increasing interaction strength beyond χ = 1. Figure 4 shows that TDDM also gives good description of the second excited state. As seen in Figure 4, the excitation energies for the first excited state calculated in the deformed RPA become close to the exact values for the second excited state [1] with increasing χ. The excited states were also calculated for a small system with N = 4 by using the ground states in TDDM [15] and TDDM1 [23], and it was found that the TDDM1 ground state gives much better results.

FIGURE 3

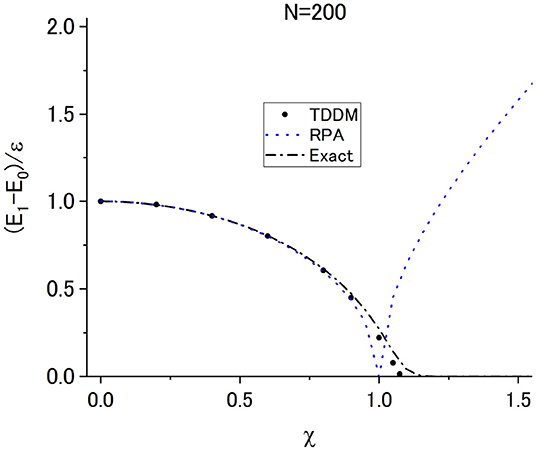
Figure 3. Excitation energy of the first excited state calculated in TDDM (dots) as a function of χ for N = 200. The exact values are shown with the dot-dashed line. The dotted line depicts the results in RPA. Adapted from Tohyama and Schuck [45] with permission from Societ$\grave{\text{a}}$ Italiana di Fisica/Springer-Verlag GmbH Germany.

FIGURE 4

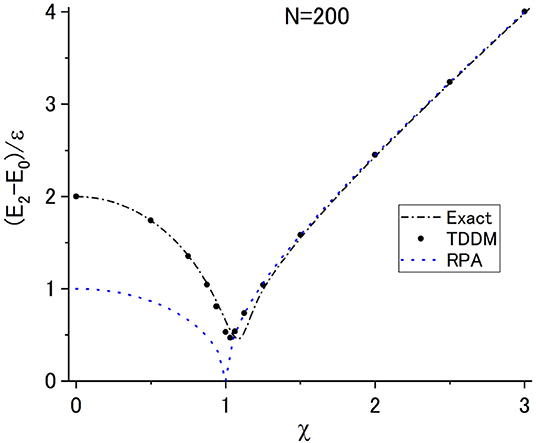
Figure 4. Same as Figure 3 but for the second excited state. The dotted line depicts the RPA results for the first excited state. Adapted from Tohyama and Schuck [45] with permission from Societ$\grave{\text{a}}$ Italiana di Fisica/Springer-Verlag GmbH Germany.

As was pointed out above, the fact that TDDM becomes exact in large N and χ limits is due to the unique feature of the Lipkin model that the mean-field theory DHF gives the exact solutions in such limits. In the transitional region χ ≈ 1 TDDM1 and TDDM2 give better description of the exact solutions than TDDM, and the applications to the ground states of other solvable models [23, 26] and ¹⁶O [24] also showed that TDDM1 largely improves TDDM whereas the improvement from TDDM1 to TDDM2 is not large [26]. Therefore, TDDM1 or TDDM2 may be a useful truncation scheme to be applied to realistic cases except for strongly interacting regions.

2.4.2. One-Dimensional Hubbard Model

ERPA based on the TDDM1 ground state has been applied to the one-dimensional (1-D) Hubbard model [37] to compare with other beyond RPA theories [33]. The Hubbard model is one of the most widespread models to investigate strong electron correlations and has often been used to corroborate the validity of beyond RPA theories [46]. In momentum space the Hamiltonian is given by [46]

$\begin{array}{ll}H={\displaystyle \sum _{k,\sigma }}{ϵ}_k{a}_{k,\sigma }^{+}{a}_{k,\sigma }+\frac{U}{2N}{\displaystyle \sum _{k,p,q,\sigma }}{a}_{k,\sigma }^{+}{a}_{k+q,\sigma }{a}_{p,-\sigma }^{+}{a}_{p-q,-\sigma },& (34)\end{array}$

where U is the matrix element of the on-site repulsive Coulomb interaction, σ spin projection and the s.p. energies are given by ϵ_α = −2t cos k_α with the nearest-neighbor hopping potential t. In the case of the six sites at half filling considered here, there are the following six wave numbers

$\begin{array}{l}{k}_1=0, k_2=\frac{\pi }{3}, k_3=-\frac{\pi }{3},\\ k_4=\frac{2\pi }{3}, k_5=-\frac{2\pi }{3}. k_6=-\pi .& (35)\end{array}$

The s.p. energies are ϵ₁ = −2t, ϵ₂ = ϵ₃ = −t, ϵ₄ = ϵ₅ = t, and ϵ₆ = 2t. In HF the lower states with ϵ₁, ϵ₂ and ϵ₃ are fully occupied by 6 particles.

The ground state energy calculated in TDDM1 (dots) with the adiabatic method is displayed in Figure 5 as a function of U/t. It was found [21] that TDDM1 gives much better ground states of this model Hamiltonian than TDDM and that the improvement from TDDM1 to TDDM2 is minor [26]. The exact values obtained in exact diagonalization approach are depicted with the solid line. The TDDM1 results agree well with the exact values. The occupation probabilities of the four s.p. states in TDDM1 (circles and squares) given in Figure 6 as functions of U/t also have reasonable agreement with the exact solutions (solid, dotted, dashed and dot-dashed lines). The deviation of the occupation probabilities from the HF values (n_αα = 1 or 0) exceeds 10% at U/t = 4.

FIGURE 5

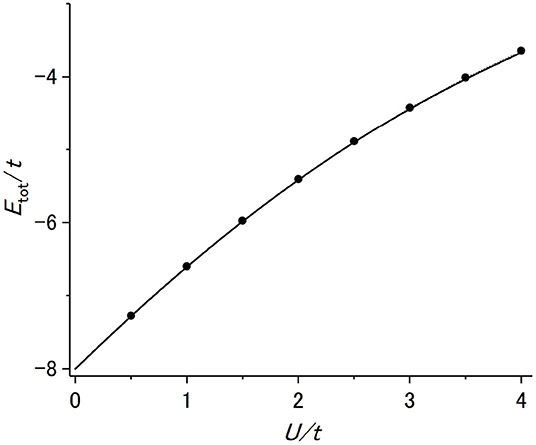
Figure 5. Ground-state energy E_tot calculated in TDDM1 (dots) as a function of U/t for N = 6 with half-filling. The exact solutions are displayed with the solid line. Adapted from Tohyama [33] under the Creative Commons CCBY license.

FIGURE 6

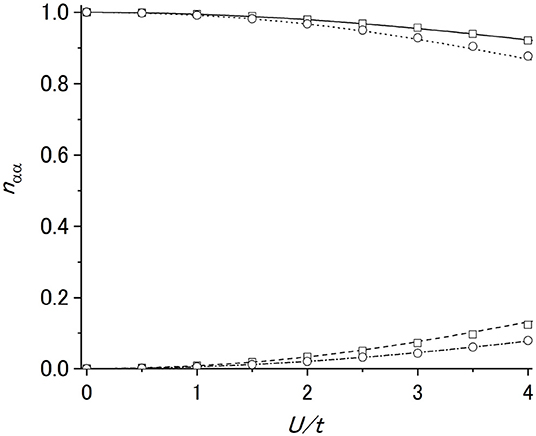
Figure 6. Occupation probability of each s.p. state calculated in TDDM1 (circles and squares) as a function of U/t. The exact solutions are depicted with the solid, dotted, dashed and dot-dashed lines. Adapted from Tohyama [33] under the Creative Commons CCBY license.

ERPA is compared with other beyond RPA theories for the spin mode with the momentum transfer q = π/3 which is excited mainly by the one-body operator $a_{k_4\uparrow }^{+}{a}_{k_2\uparrow }-a_{k_4\downarrow }^{+}{a}_{k_2\downarrow }$. Since the s.p. states are partially occupied, the h–h and p–p transitions such as k₁ → k₂ and k₆ → k₅ also contribute in rRPA, SCRPA and ERPA. In Figure 7 the excitation energies in ERPA (dots), RPA (open triangles), rRPA (filled triangles), SCRPA (squares) and SRPA (crosses) are shown as functions of U/t. The exact solutions are given with the solid line. The rRPA and SCRPA results are calculated with n_αα and $C_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}$ which are not self-consistently determined by the p–h and h–p amplitudes [28, 29] but given by the TDDM1 calculations. In the case of a repulsive interaction, the excitation energy of a spin mode where the s.p. transitions between spin-up states and spin-down states destructively interfere decreases with increasing U. The results in RPA agree rather well with the exact solutions. In rRPA there are two states below E/t < 2. The main components of the lower state at E/t ≈ 1 are the p–p and h–h transitions and the higher state consists of the p–h and h–p components. Thus in rRPA the configurations consisting of the p–p and h–h components appear as the lowest state as if it is a physical state. This indicates that it is not appropriate to include the ground-state correlation effects only through n_α. In SCRPA the states originating from the p–p and h–h transitions gain self energies and move to the high energy region (E/t > 10). This is because the terms in Equation (26) with C₂ are divided by the small values $n_{\text{pp}}-n_{{\text{p}}^{\prime }{\text{p}}^{\prime }}$ or $n_{\text{hh}}-n_{{\text{h}}^{\prime }{\text{h}}^{\prime }}$ when $A{x}^{\mu }=S_1{x}^{\mu }$ is solved. Thus in SCRPA the states consisting of the p–p and h–h components are energetically separated from the lowest state. The excitation energies of the lowest state calculated in SCRPA, however, exceed significantly the exact values. This is due to the neglect of the coupling to the two-body amplitudes. SRPA includes the coupling to the two-body amplitudes though the ground-state correlation effects are neglected. As shown in Figure 7 with the crosses, the coupling to the 2p–2h amplitudes considered in SRPA downwardly shift the RPA results with increasing U and SRPA collapses at U/t = 3.9. The results in ERPA have reasonable agreement with the exact solutions. The coupling to the two-body amplitudes included in ERPA plays a role in bringing down the results in SCRPA.

FIGURE 7

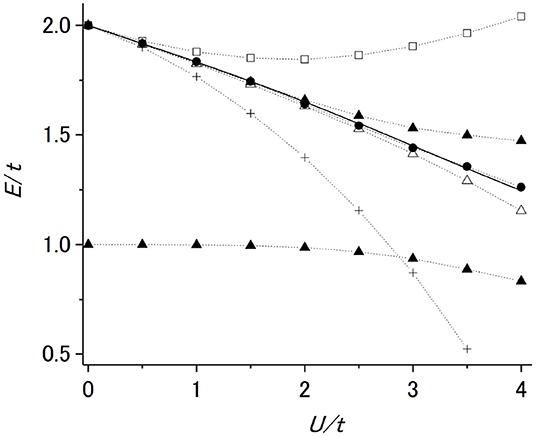
Figure 7. Excitation energy of the spin mode with momentum transfer q = π/3 as a function of U/t calculated in ERPA (dots). The results in RPA, rRPA, SCRPA, and SRPA are denoted with the open triangles, filled triangles, squares and crosses, respectively. The exact solutions are depicted with the solid line. Adapted from Tohyama [33] under the Creative Commons CCBY license.

From the application to the 1-D Hubbard model it was clarified that when the couping to the two-body amplitude is considered, the effects of ground-state correlations should also be included, and vice versa. Therefore, rRPA, SCRPA and SRPA which only include either the ground-state correlations effects or the coupling to the two-body amplitude cannot give satisfactory results.

2.4.3. Dipole and Quadrupole Excitations of ⁴⁰Ca and ⁴⁸Ca

In this subsection the applications of ERPA to the dipole excitation of ⁴⁸Ca and the quadrupole excitation of ⁴⁰Ca [36] are presented. It is demonstrated that the effects of ground-state correlations which are not fully incorporated in other beyond RPA theories play a significant role in the fragmentation of transition strengths.

Since the numbers of C₂ and $X_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}^{\mu }$ increase rapidly with the number of the s.p. states, rather sever truncation of the s.p. space is required in realistic applications. The occupation probability n_αα and C₂ were calculated within TDDM by using the truncated s.p. basis consisting of the 2s–1d and 1f–2p states, and only the 2p–2h and 2h–2p elements of C₂ were included to reduce the dimension size. It was pointed out in Reference [24] that TDDM with this truncation of C₂ gives as good results for the ground state of ¹⁶O as TDDM1 with all components of C₂. The Skyrme III force [47] was used to obtain the s.p. wavefunctions which satisfy a HF-like n_αα-dependent equation. In Pfitzner et al. [11] and Peter et al. [12] a fixed harmonic oscillator basis was chosen to facilitate the calculations of two-body matrix elements when the TDDM equations were applied to the study of giant resonances. A simplified interaction which contains only the t₀ and t₃ terms of the Skyrme III force was used as the residual interaction. The ground states were calculated with the iterative gradient method [15]. The one-body amplitudes $x_{\alpha {\alpha }^{\prime }}^{\mu }$ in Equation (18) were defined with a large number of s.p. states including those in the continuum to satisfy the energy-weighted sum rule: The continuum states were discretized by confining the wavefunctions in a sphere with radius 15 fm and all the s.p. states with ϵ_α ≤ 50 MeV and j_α ≤ 11/2ℏ were included. The residual interaction in Equation (18) was assumed to have the same form as that used in the ground-state calculations. Since the residual interaction differs from the effective interaction used in the calculation of the s.p. states, it is necessary to reduce the strength of the residual interaction. The reduction factors 0.66 and 0.69 for ⁴⁰Ca and ⁴⁸Ca, respectively, were determined so that the spurious mode corresponding to the center-of-mass motion has zero excitation energy in RPA. To reduce the number of the two-body amplitudes, only the 2p–2h and 2h–2p components of $X_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}^{\mu }$ were considered for the 2s–1d and 2p–1f states.

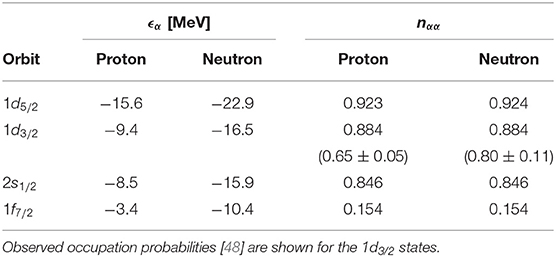
The occupation probabilities calculated in TDDM for ⁴⁰Ca and ⁴⁸Ca are given in Tables 1, 2, respectively. They deviate more than 10% from the HF values (n_αα=1 or 0) in ⁴⁰Ca. This indicates that the ground state of ⁴⁰Ca is highly correlated as an RPA study [49] and perturbative calculations [31, 50] have already shown. Since the occupation of the neutron 1f_7/2 state in ⁴⁸Ca blocks some 2p–2h excitations, the ground-state correlations are weaker in ⁴⁸Ca than in ⁴⁰Ca. As will be discussed below, the fractional occupation of the 2p–1f states plays an important role in the fragmentation of dipole and quadrupole transition strengths. Occupation probabilities deduced from ground-state-to-ground-state (p, d) and (e, e′p) reactions [48] are also shown for some s.p. states in Tables 1, 2 (values in parentheses). These values also strongly deviate from the HF value (n_α = 1). The TDDM results cannot be directly compared with these data, however. A more appropriate formalism such as the odd-particle number RPA [51] which deals with odd particle systems is needed to compare with experiment.

TABLE 1

Table 1. Single-particle energies ϵ_α and occupation probabilities n_αα calculated in TDDM for ⁴⁰Ca.

TABLE 2

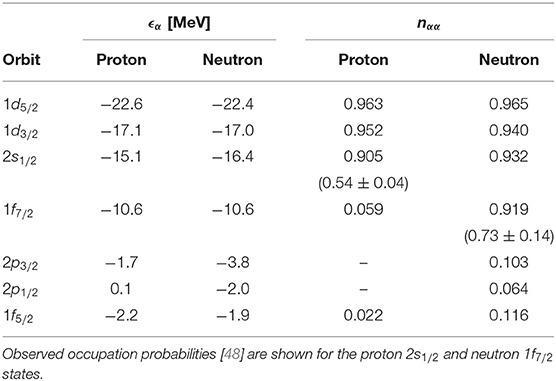
Table 2. Same as Table 1 but for ⁴⁸Ca.

The strength function for the isovector dipole excitation in ⁴⁸Ca calculated in ERPA (solid line) is displayed in Figure 8. The dotted and dot-dashed lines depict the results in RPA and SRPA, respectively. An artificial width Γ = 0.5 MeV is used to smooth the distributions. The strength distributions in Figure 8 exhaust about 90% of the energy-weighted-sum-rule (EWSR) value including the enhancement term given by the t₁ and t₂ parameters of the Skyrme III force. A better treatment of the residual interaction and the continuum states is required to fulfill the EWSR value. The sharp peak in RPA corresponds to the giant dipole resonance (GDR). GDR strongly couples to the 2p–2h states and it is damped both in SRPA and ERPA. The occupation of the neutron 1f_7/2 state in ⁴⁸Ca allows the 2p–2h states which include the neutron 1f_7/2 state as a hole state. Since these states have energies close to the energy of GDR, GDR is strongly damped due to the coupling to the 2p–2h states. The SRPA result in Figure 8 dose not show a strong downward shift of the dipole strength which has been reported in large scale SRPA calculations [53]. This is due to fact that a rather small number of the s.p. states are used to define the 2p–2h amplitudes. The peak position and width of GDR in ERPA are comparable with the experimental photo absorption cross section [52] as shown in the inset of Figure 8.

FIGURE 8

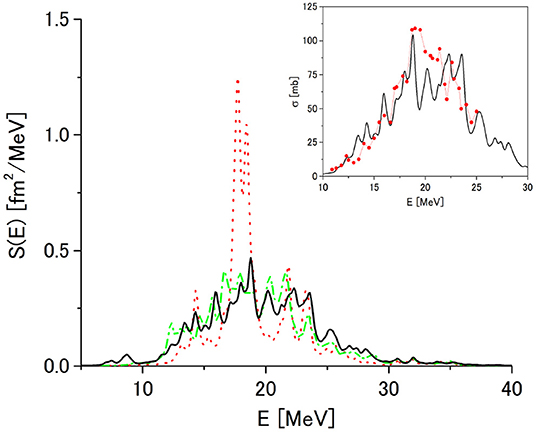
Figure 8. Strength functions calculated in RPA (dotted line), SRPA (dot-dashed line) and ERPA (solid line) for the isovector dipole excitation in ⁴⁸Ca. The distributions are smoothed with an artificial width Γ = 0.5 MeV. In the inset the photo absorption cross section in ERPA (solid line) is compared with experimental data [52] (dots). Readapted from Tohyama [36] under the Creative Commons CCBY license.

ERPA gives 7 states below 10 MeV, which are compared with experiment [54] in Figure 9. These states involve the transitions from the partially occupied neutron 2p_1/2, 2p_3/2 and 1f_5/2 states and the p–p transition components exhaust 15−39% of the transition amplitude (x^μ, X^μ). The summed strength below 10 MeV is 213 × 10⁻³e²fm², which somewhat overestimates the experimental value 61.5±7.8 × 10⁻³e²fm². SRPA gives two dipole states at 9.2 MeV and 9.3 MeV with the summed strength 21 × 10⁻³e²fm². The study of low-lying dipole strength distribution has been attracting strong interests and various theoretical approaches such as the large scale SRPA [55, 56] and the quasi-particle phonon coupling models [57, 58] have been successfully applied to calcium isotopes.

FIGURE 9

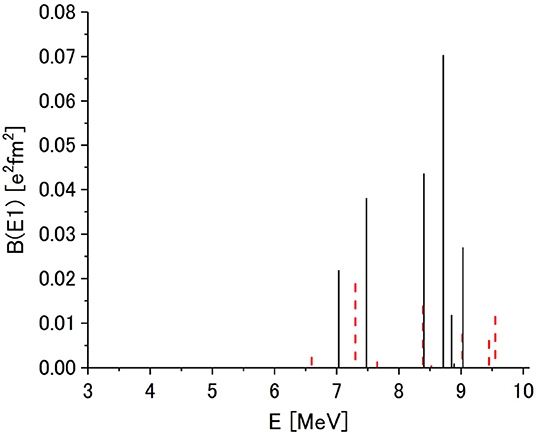
Figure 9. Distribution of B(E1) strength below 10 MeV calculated in ERPA for ⁴⁸Ca. Experimental data (dashed line) are taken from Hartmann et al. [54]. Adapted from Tohyama [36] under the Creative Commons CCBY license.

The strength function for the isoscalar quadrupole excitation in ⁴⁰Ca calculated in ERPA (solid line) is shown in Figure 10. The dotted and dot-dashed lines depict the results in RPA and SRPA, respectively. The distributions are smoothed with an artificial width Γ = 0.5 MeV. The energy-weighted sums of the strength distributions in Figure 10 exceed the EWSR value by about 10% due to the simple approximations for the residual interaction and the continuum states. The main peak in RPA corresponds to the giant quadrupole resonance (GQR). ERPA brings much larger fragmentation of the quadrupole strength than SRPA especially to the low energy region, indicating the importance of the ground-state correlations effects included in ERPA. The large fragmentation of the quadrupole strength is consistent with experiment [59, 60]. The p–p transitions allowed by the fractional occupation of the 1f_7/2 states and the coupling of the 2p–2h amplitudes to the h–h or p–p amplitudes through C₂ were found to play an important role in the large fragmentation of the quadrupole strength [34, 36]. The importance of the coupling of the one-body amplitude to C₂ in the fragmentation of GQR in ⁴⁰Ca was also pointed out by the 1p–1h⊗phonon configurations model [61, 62]. A large scale SRPA calculation [63] shows a downward shift of the quadrupole strength and larger fragmentation of GQR than the SRPA result in Figure 10. This difference again originates from the difference in the number of the 2p–2h configurations used. In the inset the ERPA strength distribution in the GQR region (lower part) is compared with the experimental data from (p, p′) experiments [59] (upper part). Although the peak position in ERPA corresponds to the experimental data, ERPA cannot describe the large fragmentation of GQR. The result of the large scale SRPA calculation [63] suggests the importance of higher configurations.

FIGURE 10

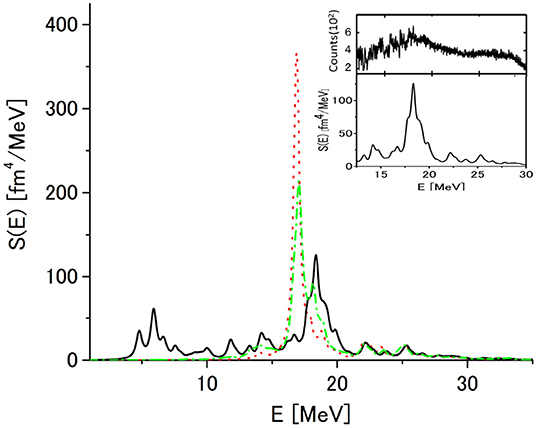
Figure 10. Strength functions calculated in RPA (dotted line), SRPA (dot-dashed line) and ERPA (solid line) for the isoscalor quadrupole excitation in ⁴⁰Ca. The distributions are smoothed with an artificial width Γ = 0.5 MeV. In the inset the ERPA strength distribution (lower part) is compared with the experimental data from (p, p′) experiments at E_p = 200 MeV and ${\theta }_{\text{Lab}}=11^{\bullet }$ [59] (upper part). Redapted from Tohyama [36] under the Creative Commons CCBY license.

There are 19 sates below 10 MeV in ERPA, which are compared with experiment [54] in Figure 11. The first 2⁺ state in ⁴⁰Ca cannot be described in RPA and ERPA because it mainly consists of 4p–4h states [64] as in the case of ¹⁶O [65]. The summed strength below 10 MeV is 166 e²fm⁴ in ERPA, which is about two thirds of the experimental value 263±46 e²fm⁴ where the first 2⁺ state is excluded.

FIGURE 11

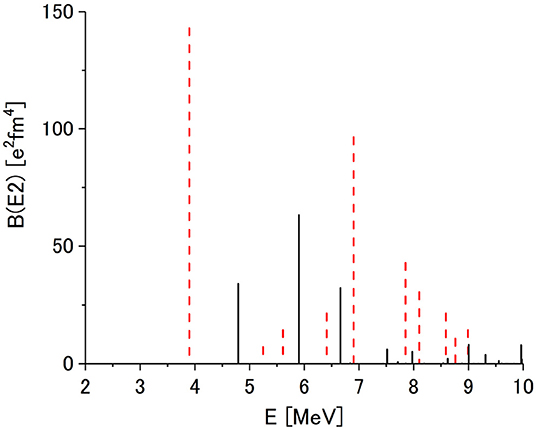
Figure 11. Distribution of B(E2) strength below 10 MeV for ⁴⁰Ca. Experimental data (dashed line) are taken from Hartmann et al. [54]. Adapted from Tohyama [36] under the Creative Commons CCBY license.

From the applications of ERPA to the dipole and quadrupole excitations of ⁴⁸Ca and ⁴⁰Ca it was clarified that the ground state correlation effects should be included to explain the large fragmentation of the dipole and quadrupole strengths in doubly-magic nuclei. The ground-state correlation effects in magic nuclei have extensively been studied for spin-isospin modes [31, 50, 66–68].

3. Formulation in Time-Dependent Single-Particle Basis

The first applications of the time-dependent density-matrix approach were based on the TDDM truncation scheme and the TDDM calculations [6, 7] were performed by using the time-dependent s.p. wavefunctions obtained from the then available TDHF code with axial symmetry and without spin-orbit force [69]. More advanced TDHF codes with spin-orbit force, unconstrained symmetry and improved effective interactions have been used to solve the TDDM equations [8, 13]. Since the calculation of the two-body matrix elements is time-consuming, a simpler approximation called TDDM^P [13, 14] has also been employed in heavy-ion collisions, where two-body correlations are considered only for a pair of time reversed s.p. states to reduce the number of matrix elements of C₂. The TDDM approaches based on the time-dependent s.p. basis have been applied to study the particle transfers in heavy-ion collisions [7], the fusion reactions [8, 9] and the damping of giant resonances at zero [6, 70, 71] and finite temperatures [10]. TDDM^P has been applied to the particle transfers in heavy-ion collisions [13] and the fusion reactions [14]. In the following the TDDM formulation in the time-dependent s.p. basis is given and the application to the fusion reactions of ¹⁶O + ¹⁶O is presented in some detail as an example.

3.1. TDDM Equations

The one-body density matrix ρ and the correlated part C₂ of the two-body density matrix ρ₂ are expanded with a finite number of time-dependent s.p. states ψ_α

$\begin{array}{ll}\rho (11^{\prime },t)={\displaystyle \sum _{\alpha {\alpha }^{\prime }}}{n}_{\alpha {\alpha }^{\prime }}(t){\psi }_{\alpha }(1,t){\psi }_{{\alpha }^{\prime }}^{*}(1^{\prime },t),& (36)\end{array}$

$\begin{array}{l}{C}_2(121^{\prime }{2}^{\prime },t)={\rho }_2-{A}(\rho \rho )\\ ={\displaystyle \sum _{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}}{C}_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}(t){\psi }_{\alpha }(1,t){\psi }_{\beta }(2,t){\psi }_{{\alpha }^{\prime }}^{*}(1^{\prime },t){\psi }_{{\beta }^{\prime }}^{*}(2^{\prime },t),& (37)\end{array}$

where the numbers denote space, spin and isospin coordinates. The equations of motion of TDDM in the time-dependent basis consist of the following three coupled equations [6]:

$\begin{array}{ll}i\frac{\partial }{\partial t}{\psi }_{\alpha }(1,t)=h(1,t){\psi }_{\alpha }(1,t),& (38)\end{array}$

$\begin{array}{ll}i{\dot{n}}_{\alpha {\alpha }^{\prime }}={\displaystyle \sum _{\beta \gamma \delta }}\left[\langle \alpha \beta |v|\gamma \delta \rangle C_{\gamma \delta {\alpha }^{\prime }\beta }-C_{\alpha \beta \gamma \delta }\langle \gamma \delta |v|{\alpha }^{\prime }\beta \rangle \right],& (39)\end{array}$

$\begin{array}{ll}i{Ċ}_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}=B_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}+P_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}+H_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }},& (40)\end{array}$

where h is the mean-field Hamiltonian given by ρ. When the time-dependent s.p. states are chosen, the terms with the s.p. energies on the right-hand side of Equations (5) and (6) are incorporated into the equation for the s.p. wavefunctions [6]. In TDDM^P [13, 14] $H_{\alpha \beta {\alpha }^{\prime }{\beta }^{\prime }}$ is neglected and two-body correlations are considered only for a pair of time reversed s.p. states.

3.2. Fusion Reactions of ¹⁶O + ¹⁶O

The fusion reactions of ¹⁶O + ¹⁶O studied in TDDM with the time-dependent s.p. basis are explained below. This work Tohyama and Umar [8] finally solved the longstanding problem of fusion window anomaly. Early TDHF calculations showed that the colliding heavy ions do not fuse in a small impact parameter region when incident energy is higher than a certain relatively low threshold value E_th [2]. This is known as the fusion window anomaly. Experimental search for the fusion window anomaly has found no evidence [72–75]. It was found that the inclusion of spin-orbit force introduced enough one-body dissipation to ¹⁶O + ¹⁶O collisions [76] because the degeneracy of the 1p_3/2 and 1p_1/2 states is lifted. It was also found [77] that the effects of two-body dissipation taken in TDDM resulted in the doubling of E_th without incorporating spin-orbit force. This is due to the inclusion of additional unoccupied s.p. states in TDDM. In Tohyama and Umar [8] the combined effects of spin-orbit force and two-body dissipation were studied for ¹⁶O + ¹⁶O. In this study the Skyrme II force (SKII) [78] was chosen as an effective interaction to calculate the s.p. wavefunctions since SKII has often been used in TDHF calculations [69]. The s.p. states were restricted to the 1s–1p and 2s–1d states and the simple force of the δ function form $v=v_0{\delta }^3(\overrightarrow{r}-\overrightarrow{r^{\prime }})$ with v₀ = −350 MeV·fm³ was used as the residual interaction to facilitate the calculation of the matrix elements. The threshold energy E_th was searched for four different calculation schemes for the head-on collisions of ¹⁶O + ¹⁶O: TDHF with and without spin-orbit force, and TDDM with and without spin-orbit force.

The obtained results for E_th in the center-of-mass (c.m.) frame are summarized in Table 3. The inclusion of either spin-orbit force or two-body dissipation dramatically increases E_th. However, two-body dissipation increases E_th only about 10 MeV when spin-orbit force is included. It was also found that the translational motion damps faster in TDDM than in TDHF [8] below E_c.m. = 69 MeV where the colliding system fuses both in TDHF and TDDM. The fusion reactions of ¹⁶O + ¹⁶O below E_th were also studied by Wen et al. [14] using the TDDM^P approach and a paring interaction as the residual interaction and it was found that extracted friction coefficients are enhanced by about 20% due to two-body dissipation.

TABLE 3

Table 3. Threshold energy E_th in the center-of-mass frame for the head-on collisions of ¹⁶O + ¹⁶O.

In the case of heavy-ion collisions the TDDM (and TDDM^P) equations ostensibly do not conserve the total energy because of the truncation of the s.p. space [7, 14]. Wen et al. [14] has proposed a method to recover the energy conservation within the truncated s.p. space.

4. Summary and Outlook

An approach which extends the time-dependent Hartree-Fock theory (TDHF) based on the equations of motion for reduced density matrices was presented. The equations of motions for reduced density matrices form a coupled chain known as the Bogoliubov-Born-Green-Kirkwood-Yvon (BBGKY) hierarchy. In this time-dependent density-matrix approach (TDDMA) the truncation of the BBGKY hierarchy is applied at the two-body level by approximating the correlated part of the three-body density matrix (C₃). TDDMA has great advantages that a correlated ground state is obtained as a stationary solution of the TDDMA equations and that the small amplitude limit of the TDDMA equations gives the most general form of beyond the random-phase approximation (RPA). TDDMA was applied to the Lipkin model to test the approximations for C₃. It was found that the simplest approximation where C₃ is neglected becomes exact in the limits of large number of particles and strong interaction. The extended RPA (ERPA) derived from the TDDMA equations was applied to the one-dimensional Hubbard model to compare with other beyond RPA theories. It was pointed out that when the effects of ground-state correlations are included, the coupling to the two-body amplitudes should also be considered, and vice versa. As the realistic applications of ERPA, the dipole and quadrupole excitations of ⁴⁰Ca and ⁴⁸Ca were studied. It was found that the effects of ground-state correlations play an important role in fragmenting the dipole and quadrupole strengths. The TDDMA study for the fusion reactions of ¹⁶O + ¹⁶O was also presented as an application of the TDDMA formulation with a time-dependent singe-particle basis. It was pointed out that the two-body dissipation plays a role in further damping the translational motion of ¹⁶O + ¹⁶O.

Although the obtained results indicate that TDDMA provides a promising beyond mean-field framework to include two-body correlation effects which are missing in TDHF, TDDMA has limitations and issues to be resolved. One limitation is the fact that the number of matrix elements of the two-body density matrix rapidly increases with increasing number of the s.p. states, which forces us to use small s.p. space around the Fermi level in realistic applications, though the obtained results show that basic effects of two-body correlations can be described with rather small s.p. space. In the realistic applications, simple residual interactions of the δ function form were used to facilitate the calculations of two-body matrix elements whereas the s.p. wavefunctions were obtained from the Skyrme interactions included in TDHF codes. The consistent treatment of the effective interactions is a subject to be addressed in TDDMA. Another point is the truncation scheme of the BBGKY hierarchy itself. In TDDMA the BBGKY hierarchy is truncated at the two-body level by making approximations for C₃. The truncation violates the properties of reduced density matrices which should be fulfilled if they are derived from an N-body total wavefunction. It was pointed out that the TDDM1 truncation scheme where C₃ is given by the traced products of the 2p–2h elements of the two-body correlation matrix largely improves the simple scheme where C₃ is neglected. However, the validity of TDDM1 cannot be simply extended to highly excited cases such as heavy-ion collisions. The study of the truncation schemes in such cases remains a difficult but interesting subject to be investigated.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Ring P, Schuck P. The Nuclear Many-Body Problem. Berlin: Springer-Verlag (2000).

Google Scholar

2. Davies KTR, Devi KRS, Koonin SE, Strayer MR. TDHF calculations of heavy-ion collisions. In: Bromley DA, editor. Treatise on Heavy Ion Science, Vol. 3. New York, NY: Plenum Press (1985).

Google Scholar

3. Sekizawa K. TDHF Theory and its extensions for the multinucleon transfer reaction: a mini review. Front Phys. (2019) 7:20. doi: 10.3389/fphy.2019.00020

CrossRef Full Text | Google Scholar

4. Bonitz M. Quantum Kinetic Theory, 2nd Edn. Berlin: Springer (2016). doi: 10.1007/978-3-319-24121-0

CrossRef Full Text | Google Scholar

5. Wang SJ, Cassing W. Explicit treatment of N-body correlations within a density-matrix formalism. Ann Phys. (1985) 159:328–50. doi: 10.1016/0003-4916(85)90116-2

CrossRef Full Text | Google Scholar

6. Gong M, Tohyama M. Application of a time-dependent density-matrix formalism. Z Phys A. (1990) 335:153–61. doi: 10.1007/BF01294470

CrossRef Full Text | Google Scholar

7. Gong M, Tohyama M, Randrup J. Time-dependent density matrix theory II. Mass dispersion in damped nuclear reactions. Z Phys A. (1990) 335:331–40. doi: 10.1007/BF01304712

CrossRef Full Text | Google Scholar

8. Tohyama M, Umar AS. Fusion window problem in time-dependent Hartree-Fock theory revisited. Phys Rev C. (2002) 65:037601. doi: 10.1103/PhysRevC.65.037601

CrossRef Full Text | Google Scholar

9. Tohyama M, Umar AS. Two-body dissipation effects on the synthesis of superheavy elements. Phys Rev C. (2016) 93:034607. doi: 10.1103/PhysRevC.93.034607

CrossRef Full Text | Google Scholar

10. De Blasio FV, Cassing W, Tohyama M, Bortignon PF, Broglia RA. Non-perturbative study of the damping of giant resonances in hot nuclei. Phys Rev Lett. (1992) 68:1663–6. doi: 10.1103/PhysRevLett.68.1663

CrossRef Full Text | Google Scholar

11. Pfitzner A, Cassing W, Peter A. Vibrations versus collisions and the iterative structure of two-body dynamics. Nucl Phys A. (1994) 577:753–72. doi: 10.1016/0375-9474(94)90943-1

CrossRef Full Text | Google Scholar

12. Peter A, Cassing W, Hauser JM, Pfitzner A. Microscopic analysis of two-body correlations in light nuclei. Nucl Phys A. (1994) 573:93–129. doi: 10.1016/0375-9474(94)90016-7

CrossRef Full Text | Google Scholar

13. Assiee M, Lacroix D. Probing neutron correlations through nuclear breakup. Phys Rev Lett. (2009) 102:202501. doi: 10.1103/PhysRevLett.102.202501

CrossRef Full Text | Google Scholar

14. Wen K, Barton MC, Rios A, Stevenson PD. Two-body dissipation in nuclear fusion reactions. Phys Rev C. (2018) 98:014603. doi: 10.1103/PhysRevC.98.014603

CrossRef Full Text | Google Scholar

15. Takahara S, Tohyama M, Schuck P. Extended RPA with ground-state correlations in a solvable model. Phys Rev C. (2004) 70:057307. doi: 10.1103/PhysRevC.70.057307

CrossRef Full Text | Google Scholar

16. Schmitt K-J, Reinhard P-G, Toepffer C. Truncation of time-dependent many-body theories. Z Phys A. (1990) 336:123–31. doi: 10.1007/BF01290612

CrossRef Full Text | Google Scholar

17. Gherega T, Krieg R, Reinhard P-G, Toepffer C. Dynamics of correlations in a solvable model. Nucl Phys A. (1993) 560:166–86. doi: 10.1016/0375-9474(93)90090-K

CrossRef Full Text | Google Scholar

18. Akbari A, Hashemi MJ, Rubio A, Nieminen RM, van Leeuwen R. Challenges in truncating the hierarchy of time-dependent reduced density matrices equations. Phys Rev B. (2012) 85:23512. doi: 10.1103/PhysRevB.85.235121

CrossRef Full Text | Google Scholar

19. Tohyama M. Time-dependent density-matrix approach to collective excitations of a quantum dot. J Phys Soc Jpn. (2012) 81:054707. doi: 10.1143/JPSJ.81.054707

CrossRef Full Text | Google Scholar

20. Coleman AJ, Yukalov VI. Reduced Density Matrices: Coulson's Challenge. Berlin: Springer-Verlag (2000). doi: 10.1007/978-3-642-58304-9

CrossRef Full Text | Google Scholar

21. Tohyama M, Schuck P. Truncation scheme of time-dependent density-matrix approach. Eur Phys J A. (2014) 50:77. doi: 10.1140/epja/i2014-14077-x

CrossRef Full Text | Google Scholar

22. Mazziotti DA. Pursuit of N-representability for the contracted Schrödinger equation through density-matrix reconstruction. Phys Rev A. (1999) 60:3618–26. doi: 10.1103/PhysRevA.60.3618

CrossRef Full Text | Google Scholar

23. Schuck P, Tohyama M. Progress in many-body theory with the equation of motion method: time-dependent density matrix meets self-consistent RPA and applications to solvable models. Phys Rev B. (2016) 93:165117. doi: 10.1103/PhysRevB.93.165117

CrossRef Full Text | Google Scholar

24. Tohyama M. New truncation scheme for a time-dependent density-matrix approach applied to the ground state of ¹6O. Phys Rev C. (2015) 91:017301. doi: 10.1103/PhysRevC.91.017301

CrossRef Full Text | Google Scholar

25. Lipkin HJ, Meshkov N, Glick AJ. Validity of many-body approximation methods for a solvable model: (I). Exact solutions and perturbation theory. Nucl Phys. (1965) 62:188–98. doi: 10.1016/0029-5582(65)90862-X

CrossRef Full Text | Google Scholar

26. Tohyama M, Schuck P. Truncation scheme of time-dependent density-matrix approach II. Eur Phys J A. (2017) 53:186. doi: 10.1140/epja/i2017-12377-3

CrossRef Full Text | Google Scholar

27. Rowe DJ. Equations-of-Motion method and the extended shell model. Rev Mod Phys. (1968) 40:153. doi: 10.1103/RevModPhys.40.153

CrossRef Full Text | Google Scholar

28. Rowe DJ. Methods for calculating ground-state correlations of vibrational nuclei. Phys Rev. (1968) 175:1283–92. doi: 10.1103/PhysRev.175.1283

CrossRef Full Text | Google Scholar

29. Schuck P, Ethofer S. Self-consistent (nuclear) phonons. Nucl Phys A. (1973) 212:269–86. doi: 10.1016/0375-9474(73)90563-0

CrossRef Full Text | Google Scholar

30. Dukelsky J, Schuck P. Towards a variational theory for RPA-like correlations and fluctuations. Nucl Phys A. (1990) 512:466–82. doi: 10.1016/0375-9474(90)90081-V

CrossRef Full Text | Google Scholar

31. Drożdż S, Nishizaki S, Speth J, Wambach J. The nuclear response within extended RPA theories. Phys Rep. (1990) 197:1–65. doi: 10.1016/0370-1573(90)90084-F

CrossRef Full Text | Google Scholar

32. Litvinova E, Schuck P. Toward an accurate strongly coupled many-body theory with in the equation-of-motion framework. arXiv[Preprint].arXiv:1908.05384.

Google Scholar

33. Tohyama M. Role of small-norm components in extended random-phase approximation. Prog Theor Exp Phys. (2017) 2017:093D06. doi: 10.1093/ptep/ptx128

CrossRef Full Text | Google Scholar

34. Tohyama M. Damping of collective states in an extended random-phase approximation with ground-state correlations. Phys Rev C. (2007) 75:044310. doi: 10.1103/PhysRevC.75.044310

CrossRef Full Text | Google Scholar

35. Tohyama M. Quadrupole excitation of tin isotopes in extended random-phase approximation. Prog Theor Phys. (2012) 127:1121–30. doi: 10.1143/PTP.127.1121

CrossRef Full Text | Google Scholar

36. Tohyama M. Effects of ground-state correlations on dipole and quadrupole excitations of ⁴0Ca and ⁴8Ca. Prog Theor Exp Phys. (2018) 2018:043D02. doi: 10.1093/ptep/pty035

CrossRef Full Text | Google Scholar

37. Hubbard J. Electron correlations in narrow energy bands. Proc Roy Soc (London). (1963) 276:238–57. doi: 10.1098/rspa.1963.0204

CrossRef Full Text | Google Scholar

38. Shavitt I, Bartlett RJ. Many-Body Methods in Chemistry and Physics. Cambridge: Cambridge University Press (2009). doi: 10.1017/CBO9780511596834

CrossRef Full Text | Google Scholar

39. Cassing W, Pfitzner A. Self-consistent truncation of the BBGKY hierarchy on the two-body level. Z Phys A. (1992) 342:161–7. doi: 10.1007/BF01288464

CrossRef Full Text | Google Scholar

40. Tohyama M, Schuck P. Extended random-phase approximation with three-body ground-state correlations. Eur Phys J A. (2008) 36:349–57. doi: 10.1140/epja/i2008-10596-3

CrossRef Full Text | Google Scholar

41. Gell-Mann M, Low F. Bound states in quantum field theory. Phys Rev. (1951) 84:350–4. doi: 10.1103/PhysRev.84.350

CrossRef Full Text | Google Scholar

42. Tohyama M. Stationary solution of a time dependent density matrix formalism. Prog Theor Phys. (1994) 92:905–8. doi: 10.1143/ptp/92.4.905

CrossRef Full Text | Google Scholar

43. Tohyama M. Mean-field approach to excitations of a trapped Bose-Einstein condensate gas at finite temperatures. Phys Rev A. (2005) 71:043613. doi: 10.1103/PhysRevA.71.043613

CrossRef Full Text | Google Scholar

44. Janssen D, Schuck P. On some aspects of selfconsistent RPA theory. Z Phys A. (1991) 339:43–50. doi: 10.1007/BF01282932

CrossRef Full Text | Google Scholar

45. Tohyama M, Schuck P. Truncation scheme of time-dependent density-matrix approach III. Eur Phys J A. (2019) 55:74. doi: 10.1140/epja/i2019-12746-x

CrossRef Full Text | Google Scholar

46. Jemaï M, Schuck P, Dukelsky J, Bennaceur R. Self-consistent random phase approximation: application to the Hubbard model for finite number of sites. Phys Rev B. (2005) 71:085115. doi: 10.1103/PhysRevB.71.085115

CrossRef Full Text | Google Scholar

47. Beiner M, Flocard H, Van Giai N, Quentin P. Nuclear ground-state properties and self-consistent calculations with the skyrme interaction: (I). Spherical description. Nucl Phys A. (1975) 238:29–69. doi: 10.1016/0375-9474(75)90338-3

CrossRef Full Text | Google Scholar

48. Lee J, Tostevin JA, Brown BA, Delaunay F, Lynch WG, Saelim MJ, et al. Reduced neutron spectroscopic factors when using potential geometries constrained by Hartree-Fock calculations. Phys Rev C. (2006) 73:044608. doi: 10.1103/PhysRevC.73.044608

CrossRef Full Text | Google Scholar

49. Agassi D, Gillet V, Lumbroso A. RPA description of the ground state of ¹2C, ¹6O, ⁴0Ca and ²08Pb. Nucl Phys A. (1969) 130:129–45. doi: 10.1016/0375-9474(69)90966-X

CrossRef Full Text | Google Scholar

50. Adachi S, Lipparini E, Nguyen van Giai. Gamow-Teller and M1 strengths in closed-shell nuclei. Nucl Phys A. (1985) 438:1–14. doi: 10.1016/0375-9474(85)90115-0

CrossRef Full Text | Google Scholar

51. Tohyama M, Schuck P. Odd particle number random-phase approximation and extensions: applications to particle and hole states around ¹6O. Phys Rev C. (2013) 87:044316. doi: 10.1103/PhysRevC.87.044316

CrossRef Full Text | Google Scholar

52. O'Keefe GJ, Thompson MN, Assafiri YI, Pywell RE. The photonuclear cross sections of ⁴8Ca. Nucl Phys A. (1987) 469:239–52. doi: 10.1016/0375-9474(87)90108-4

CrossRef Full Text | Google Scholar

53. Gambacurta D, Grasso M, Catara F. Collective nuclear excitations with Skyrme-second random-phase approximation. Phys Rev C. (2010) 81:054312. doi: 10.1103/PhysRevC.81.054312

CrossRef Full Text | Google Scholar

54. Hartmann T, Enders J, Mohr P, Vogt K, Volz S, Zilges A. Measurement of the dipole and electric quadrupole strength distributions up to 10 MeV in the doubly magic nuclei ⁴0Ca and ⁴8Ca. Phys Rev Lett. (2000) 85:274–7. doi: 10.1103/PhysRevLett.85.274

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Gambacurta D, Grasso M, Catara F. Low-lying dipole response in the stable ⁴0, 48Ca nuclei with the second random-phase approximation. Phys Rev C. (2011) 84:034301. doi: 10.1103/PhysRevC.84.034301

CrossRef Full Text | Google Scholar

56. Gambacurta D, Grasso M, Vasseur O. Electric dipole strength and dipole polarizability in ⁴8Ca within a fully self-consistent second random-phase approximation. Phys Lett B. (2018) 777:163–8. doi: 10.1016/j.physletb.2017.12.026

CrossRef Full Text | Google Scholar

57. Hartmann T, Babilon M, Kamerdzhiev S, Litvinova E, Savran D, Volz S, et al. Microscopic nature of the pygmy dipole resonance: the stable Ca isotopes. Phys Rev Lett. (2004) 93:192501. doi: 10.1103/PhysRevLett.93.192501

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Egorova I A, Litvinova E. Electric dipole response of neutron-rich calcium isotopes in relativistic quasiparticle time blocking approximation. Phys Rev C. (2016) 94:034322. doi: 10.1103/PhysRevC.94.034322

CrossRef Full Text | Google Scholar

59. Usman I, Buthelezia Z, Carterb J, Cooper GRJ, Fearickd RW, Förtsch SV, et al. Fine structure of the isoscalar giant quadrupole resonance in ⁴0Ca due to Landau damping? Phys Lett B. (2011) 698:191–5. doi: 10.1016/j.physletb.2011.03.015

CrossRef Full Text | Google Scholar

60. Diesener H, Helm U, Herbert G, Huck V, von Neumann-Cosel P, Rangacharyulu C, et al. Excitation and decay of giant resonances in the ⁴0Ca (e, e′x) reaction. Phys Rev Lett. (1994) 72:1994–7. doi: 10.1103/PhysRevLett.72.1994

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Kamerdzhiev S, Speth J, Tertychny G. Splitting of the isoscalar E2 giant resonance and evidence of low-lying E0 strength in ⁴0Ca. Phys Rev Lett. (1995) 74:3943–6. doi: 10.1103/PhysRevLett.74.3943

PubMed Abstract | CrossRef Full Text | Google Scholar

62. Kamerdzhiev S, Speth J, Tertychny G. Microscopic description of the E0, E2 and E1 giant resonances in ⁴0Ca, ⁴8Ca and ⁵6Ni. Nucl Phys A. (1997) 624:328–48. doi: 10.1016/S0375-9474(97)00315-1

CrossRef Full Text | Google Scholar

63. Vasseur O, Gambacurta D, Grasso M. Systematic study of giant quadrupole resonances with the subtracted second random-phase approximation: Beyond-mean-field centroids and fragmentation. Phys Rev C. (2018) 98:044313. doi: 10.1103/PhysRevC.98.044313

CrossRef Full Text | Google Scholar

64. Caurier E, Menéndez J, Nowacki F, Poves A. Coexistence of spherical states with deformed and superdeformed bands in doubly magic ⁴0Ca: a shell-model challenge. Phys Rev C. (2007) 75:054317. doi: 10.1103/PhysRevC.75.054317

CrossRef Full Text | Google Scholar

65. Zuker AP, Buck B, McGrory JB. Structure of O¹6. Phys Rev Lett. (1968) 21:39–43. doi: 10.1103/PhysRevLett.21.39

CrossRef Full Text | Google Scholar

66. Gross W, Meuer D, Richter A, Spamer E, Titze O, Knüpfer W. A strong magnetic dipole excitation in ⁴0Ca observed in high-resolution inelastic electron scattering and coherent spin-flip transitions due to cground-state correlations. Phys Lett B. (1979) 84:296–300. doi: 10.1016/0370-2693(79)90043-1

CrossRef Full Text | Google Scholar

67. Takayanagi K, Shimizu K, Arima A. A theoretical study of magnetic dipole transitions in ⁴8Ca. Nucl Phys A. (1988) 481:313–32. doi: 10.1016/0375-9474(88)90499-X

CrossRef Full Text | Google Scholar

68. Robin C, Litvinova E. Time-reversed particle-vibration loops and nuclear Gamow-Teller response. Phys Rev Lett. (2019) 123:202501. doi: 10.1103/PhysRevLett.123.202501

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Davies KTR, Koonin SE. Skyrme-force time-dependent Hartree-Fock calculations with axial symmetry. Phys Rev C. (1981) 23:2042–61. doi: 10.1103/PhysRevC.23.2042

CrossRef Full Text | Google Scholar

70. Tohyama M, Umar AS. Dipole resonances in oxygen isotopes in time-dependent density-matrix theory. Phys Lett B. (2001) 516:415–9. doi: 10.1016/S0370-2693(01)00925-X

CrossRef Full Text | Google Scholar

71. Tohyama M, Umar AS. Quadrupole resonances in unstable oxygen isotopes in time-dependent density-matrix formalism. Phys Lett B. (2002) 549:72–8. doi: 10.1016/S0370-2693(02)02885-X

CrossRef Full Text | Google Scholar

72. Lazzarini A, Doubre H, Lesko KT, Metag V, Seamster A, Vandenbosch R, et al. Search for a fusion L window in the ¹6O + ¹6O system at E_c.m. = 34 MeV. Phys Rev C. (1981) 24:309–12. doi: 10.1103/PhysRevC.24.309

CrossRef Full Text | Google Scholar

73. Kox S, Cole AJ, Ost R. Determination of limiting angular momenta for fusion from statistical-model fits to mass distributions of evaporation residues. Phys Rev Lett. (1980) 44:1204–6. doi: 10.1103/PhysRevLett.44.1204

CrossRef Full Text | Google Scholar

74. Szanto de Toledo A, Cormier TM, Herman M, Lin B, Stwertka PM, Coimbra MM, et al. Limiting angular momenta for light heavy-ion fusion at high energy. Phys Rev Lett. (1981) 47:1881–4. doi: 10.1103/PhysRevLett.47.1881

CrossRef Full Text | Google Scholar

75. Ikezoe H, Shikazono N, Tomita Y, Ideno K, Sugiyama Y, Takekoshi E, et al. Measurements of evaporation residues to investigate lower limiting angular momenta in fusion reactions. Nucl Phys A. (1986) 456:298–316. doi: 10.1016/0375-9474(86)90395-7

CrossRef Full Text | Google Scholar

76. Umar AS, Strayer MR, Reinhard P-G. Resolution of the fusion window anomaly in heavy-ion collisions. Phys Rev Lett. (1986) 56:2793–6. doi: 10.1103/PhysRevLett.56.2793

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Tohyama M. Application of quantum theory of particle collisions to ¹6O + ¹6O reactions. Phys Rev C. (1987) 36:187–92. doi: 10.1103/PhysRevC.36.187

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Vautherin D, Brink DM. Hartree-Fock calculations with Skyrme's interaction. I. Spherical nuclei. Phys Rev C. (1972) 5:626–47. doi: 10.1103/PhysRevC.5.626

CrossRef Full Text | Google Scholar