A Novel Investigation and Hidden Effects of MHD and Thermal Radiations in Viscous Dissipative Nanofluid Flow Models

Ahmed, Naveed; Adnan,; Khan, Umar; Mohyud-Din, Syed Tauseef; Khan, Ilyas; Murtaza, Rashid; Hussain, Iftikhar; Sherif, El-Sayed M.

doi:10.3389/fphy.2020.00075

ORIGINAL RESEARCH article

Front. Phys., 12 May 2020

Sec. Statistical and Computational Physics

Volume 8 - 2020 | https://doi.org/10.3389/fphy.2020.00075

This article is part of the Research Topic Recent Trends in Computational Fluid Dynamics View all 20 articles

A Novel Investigation and Hidden Effects of MHD and Thermal Radiations in Viscous Dissipative Nanofluid Flow Models

$\nNaveed Ahmed$ Naveed Ahmed¹

Adnan²

Umar Khan³

Syed Tauseef Mohyud-Din⁴

Ilyas Khan⁵^*

Rashid Murtaza²

Iftikhar Hussain²

El-Sayed M. Sherif^6,7

¹Department of Mathematics, Faculty of Sciences, HITEC University, Taxila, Pakistan
²Department of Mathematics, Mohi-ud-Din Islamic University, Nerian Sharif, Pakistan
³Department of Mathematics and Statistics, Hazara University, Mansehra, Pakistan
⁴Department of Mathematics, University of Multan, Multan, Pakistan
⁵Faculty of Mathematics and Statistics, Ton Duc Thang University, Ho Chi Minh City, Vietnam
⁶Center of Excellence for Research in Engineering Materials (CEREM), King Saud University, Riyadh, Saudi Arabia
⁷Electrochemistry and Corrosion Laboratory, Department of Physical Chemistry, National Research Centre, Cairo, Egypt

Hidden effects of MHD and thermal radiations for a viscous dissipative nanofluids (Al₂O₃ − H₂O and γAl₂O₃ − H₂O) are taken under consideration. The models are formulated by implementing the suitable similarity transformations. Then, two models are discussed mathematically by using RK scheme together with shooting method. The results for flow regimes, coefficient of skin friction, thermophysical characteristics, and heat transfer coefficient are pictured and discussed comprehensively by changing the pertinent flow parameters. It is observed that the nanofluids velocity increases abruptly for higher Hartree pressure gradient. For assisting flow situation, the velocity F′(η) increases and abrupt decreasing behavior is examined for opposing flow case. The composition of Al₂O₃ − H₂O, and γAl₂O₃ − H₂O becomes more dense for high volume fraction therefore, drops in the velocity field is noted. The temperature of Al₂O₃ − H₂O, and γAl₂O₃ − H₂O rises rapidly by varying opposing flow parameter γ < 0 and high volume fraction ϕ. Also, the temperature β(η) declines abruptly for parameter λ.

Introduction

The analysis of the host fluids saturated by various sort of nanoparticles over a wedge geometry is of the essential and interesting topic in fluid dynamics and heat transfer phenomena. Currently, the hidden effects of significant flow parameters like magnetic number, thermal radiation, and viscous dissipation for regular and nanofluids models becomes important.

The flow and entropy generation analysis in magnetized nanofluid by considering the impacts of porosity described in Ellahi et al. [1]. The study of effective dynamic viscosity in non-Newtonian fluids in porous medium reported in Eberhard et al. [2]. The analysis of Roselands heat flux over non-linear stretchable surface with slip flow conditions was examined in Majeed et al. [3].

Keeping in mind the importance and popularity of the wedge type flow, Falkner and Skan [4, 5] focused on this particular direction of fluid mechanics and presented earlier study. They analyzed the boundary layer model mathematically and extend the case for stretching walls of the wedge. The work of Falkner and Skan provided a new direction in the fluid dynamics. Rajagopal et al. [6] inspired by the work of Falkner and Skan [4, 5] and extended the boundary layer model for non-Newtonian fluid and found fascinating results. They analyzed the flow characteristics over a fixed wedge in the fluid. Later on, Lin et al. [7] inspired by the concept forced convection and extend the model by incorporating the various Prandtl values. Hartree [8] discussed the boundary layer model for approximate solutions and highlighted important results. Watanabe [9] and Watanabe and Pop [10] extended the Falkner Skan model by considering the phenomena of free and forced convection and explored the hidden effects on the flow characteristics, respectively. They presented the impacts of magnetic field, suction and injection in the flow field.

The porosity of the wedge walls affects the flow characteristics significantly. In the light of this fact, Koh and Hartnett [11] explored the results for skin friction and local coefficient of heat transfer and observed significant variations due to porosity parameter. Similarly, Kumari et al. [12] discussed the phenomena of mixed convection over a porous wedge. In 2003, Chamkha et al. [13] reported the radiative Falkner Skan flow and presented its characteristics over a semi-infinite domain. El-Dabe et al. [14] prolonged the Falkner Skan model for Casson fluid and treated the respective non-linear flow model numerically and incorporated the influences of magnetic field in the flow behavior and the heat transfer phenomena. The flow characteristics of Casson fluid over a symmetric wedge was presented by Mukhopadhyay et al. [15] in 2013. A novel analysis comprising the impacts of ohmic heating, applied magnetic field, and mixed convection on radiative flow over a stretchable wedge reported in Su et al. [16]. The alterations in the flow pattern of micropolar and Newtonian fluids over a wedge moving in the fluid and Viscoelastic fluid flow in the presence Lorentz force reported in Ishak et al. [17, 18] and Rashidi et al. [19], respectively.

Kandasamy et al. [20] prolonged the Falkner Skan flow by comprising the impacts of chemical reaction and found the results for suction or blowing on the radiative flow over a porous wedge. Hussanan et al. [21] highlighted the influences of Joule heating in the flow past over an oscillating plate. They also highlighted the alterations in the flow characteristics due to convective flow condition and resistive heat phenomena. A comprehensive analysis of Falkner Skan flow in the presence of velocity slip phenomena and applied Lorentz force described by Su et al. [22]. Recently, Ullah et al. [23] contributed the Falkner Skan model for non-Newtonian nature of the fluid.

A prominent fact that the regular fluids have less heat transfer characteristics. For many productions in various industries required considerable level of heat transfer and base liquids fail to provide such amount heat. However, researchers focused and thought to overcome this issue. Finally, a new class of the fluid developed and titled as Nanofluid. Basically, the nanofluid is a compound fluid composed by base liquid with the nanoparticles. These nanoparticles obtained from various metals and their oxides. In nanofluids, the volume fraction of the nanoparticles plays the role of back bone for the heat transfer enhancement. The development of the nanofluids reduces the problems and issues faced by the industrialist and engineers. Thus, the analysis of the nanofluids became an orbit for the researchers and engineers and explored new and fascinating characteristics of the nanofluids.

Recently, Rafique et al. [24] reported the numerical study of Casson nanofluid over an inclined surface and found the results for flow field. Impact of magnetic field by considering second slip flow condition on the flow Casson nanofluid explored by Majeed et al. [25]. In 2019, Bibi et al. [26] examined the flow model in the presence of convective boundary condition. The significant analysis for different sort of nanofluids under various flow conditions are examined in Saba et al. [27] and Srinivasacharya et al. [28].

The nanofluid models (Al₂O₃ − H₂O and γAl₂O₃ − H₂O) considering the phenomena of magnetic field, thermal radiation, and viscous dissipation is taken over a wedge geometry in the Cartesian coordinates. Two types of thermal conductivities are incorporated in the energy equation to enhance the heat transfer rate in Al₂O₃ − H₂O and γAl₂O₃ − H₂O nanofluids. The model is described in section Model Formulation and treated mathematically in section Mathematical Analysis. The fascinating role of magnetic field and thermal radiation in the flow regimes explored and explain in section Physical Interpretation of Results. The quantities related to engineering interest (Skin friction and local Nusselt number) are presented and analyzed for varying flow parameters. In the end, major effects of under consideration model are incorporated.

Model Formulation

Statement and Geometry

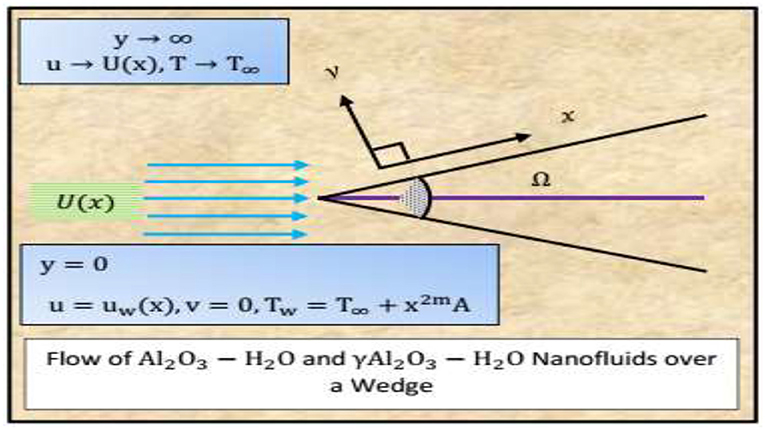
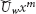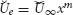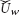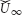Steady, laminar and viscous incompressible flow of H₂O saturated by Al₂O₃ and γAl₂O₃ nanoparticles is taken over a wedge. The effects of magnetic field and thermal radiation are taken into account. The velocity at the wedge surface is $ŭ_{w} =$ yes and at the free stream is yes and are functions of x. Here, yes and yes are constants at the surface and away from the surface. Furthermore, corresponding to wedge angle λ = Ω/π, the Hartree pressure parameter is λ = 2m/(m+1). Induced magnetic field produced due to the motion of Al₂O₃ − H₂O and γAl₂O₃ − H₂O nanofluids is neglected through the analysis. The temperature at the wedge surface is ${\hat{T}}_{w} = {\hat{T}}_{\infty} + A / x^{2 m}$ and is a function of x. The temperature at the surface and at the free stream is T_w and T_∞, respectively. The physical theme of the model comprising the role of Al₂O₃ and γAl₂O₃ nanoparticles is demonstrated in Figure 1 over a semi-infinite region.

FIGURE 1

Figure 1. Physical Theme of the Flow.

Governing Equations and Non-dimensionalization

In the light of above highlighted assumptions, the following is the model which govern the flow of nanofluids over a wedge [23, 28]:

\begin{array}{l} \frac{\partial \hat{u}}{\partial x} + \frac{\partial \hat{v}}{\partial y} = 0 & (1) \end{array}

yes

\begin{array}{l} \hat{u} \frac{\partial \hat{T}}{\partial x} + \hat{v} \frac{\partial \hat{T}}{\partial y} = \frac{{\hat{k}}_{n f}}{{(\hat{ρ} c_{p})}_{n f}} (\frac{\partial^{2} \hat{T}}{\partial y^{2}}) + \frac{1}{{(\hat{ρ} c_{p})}_{n f}} {(\frac{\partial \hat{u}}{\partial y})}^{2} \\ - \frac{16 σ^{*} T_{\infty}^{3}}{3 k {(\hat{ρ} C_{p})}_{n f}} (\frac{\partial^{2} \hat{T}}{\partial y^{2}}) & (3) \end{array}

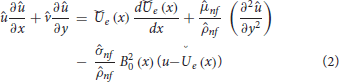
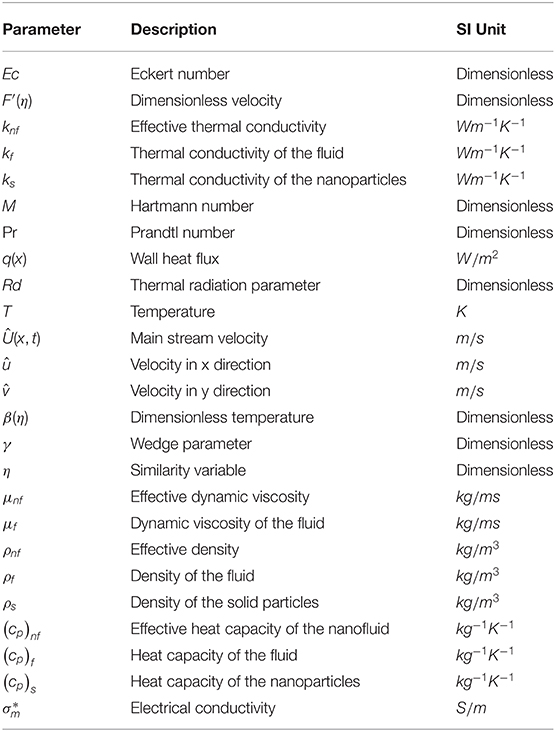
The law of conservation of mass, momentum and energy shown in Equations (1–3), respectively. The velocities in x and y directions are û and $\hat{v}$ , respectively. The velocity at the free stream, temperature, effective dynamic viscosity, density, electrical conductivity, thermal conductivity, and heat capacity are represented by yes , $\hat{T}$ , ${\hat{μ}}_{n f}$ , ${\hat{ρ}}_{n f}$ , ${\hat{σ}}_{n f}$ , ${\hat{k}}_{n f}$ , and (ρc_p)_nf, respectively. Mean absorption coefficient and Stefan Boltzmann constants are denoted by k and σ^*, respectively.

The conditions on the flow at the boundaries are defined as Ullah et al. [23]:

yes

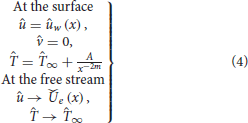
The similarity variables defined in the following way for the non-dimensionalization of the governing flow model [23]:

\begin{array}{l} \begin{matrix} \hat{u} = \frac{\partial \hat{ψ}}{\partial y} \\ \hat{v} = - \frac{\partial \hat{ψ}}{\partial x} \\ \hat{ψ} = \sqrt{\frac{2 ν_{f} x {\hat{U}}_{e} (x)}{(m + 1)}} F (η) \\ η = \sqrt{\frac{(m + 1) {\hat{U}}_{e} (x)}{2 ν_{f} x}} y \\ β (η) = \frac{\hat{T} - {\hat{T}}_{\infty}}{{\hat{T}}_{w} - {\hat{T}}_{\infty}} \end{matrix}} & (5) \end{array}

The following models are used to enhance the performance of the particular model [29]:

\begin{array}{l} {\hat{ρ}}_{n f} = {(1 - ϕ) + \frac{ϕ {\hat{ρ}}_{s}}{{\hat{ρ}}_{f}}} {\hat{ρ}}_{f} & (6) \end{array}

\begin{array}{l} \begin{matrix} {\hat{μ}}_{n f} = {\hat{μ}}_{f} {(1 - ϕ)}^{- 2.5} \\ {\hat{μ}}_{n f} = {\hat{μ}}_{f} (123 ϕ^{2} + 7.3 ϕ + 1) \end{matrix}} \\ For {Al}_{2} O_{3} - H_{2} O and γ {Al}_{2} O_{3} - H_{2} O, & (7) \end{array}

\begin{array}{l} {(\hat{ρ} c_{p})}_{n f} = {(1 - ϕ) + \frac{ϕ {(\hat{ρ} c_{p})}_{s}}{{(\hat{ρ} c_{p})}_{f}}} {(\hat{ρ} c_{p})}_{f} \\ \begin{array}{l} {\hat{k}}_{n f} = {\hat{k}}_{f} {\frac{{\hat{k}}_{s} + 2 {\hat{k}}_{f} - 2 ϕ ({\hat{k}}_{f} - {\hat{k}}_{s})}{{\hat{k}}_{s} + 2 {\hat{k}}_{f} + ϕ ({\hat{k}}_{f} - {\hat{k}}_{s})}} \\ {\hat{k}}_{n f} = {\hat{k}}_{f} (4.97 ϕ^{2} + 2.72 ϕ + 1) \end{array}} & (8) \end{array}

\begin{array}{l} For A l_{2} O_{3} - H_{2} O and γ A l_{2} O_{3} - H_{2} O & (9) \end{array}

\begin{array}{l} {\hat{σ}}_{n f} = {\hat{σ}}_{f} {1 + \frac{3 (\frac{{\hat{σ}}_{s}}{{\hat{σ}}_{f}} - 1) ϕ}{(\frac{{\hat{σ}}_{s}}{{\hat{σ}}_{f}} + 2) - (\frac{{\hat{σ}}_{s}}{{\hat{σ}}_{f}} - 1) ϕ}} . & (10) \end{array}

The particular values of thermophysical characteristics embedded in Equations (6–10) are given in Table 1.

TABLE 1

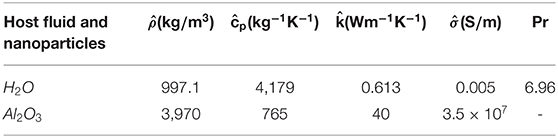
Table 1. Thermal and Physical Properties [29].

After performing the suitable differentiation and incorporating the effective nanofluids models given in Equations (6–10) in the dimensional model, the following two models of nanofluids are obtained:

Al₂O₃ − H₂O Model

\begin{array}{l} F^{‴} + \frac{1 - ϕ + \frac{ϕ {\hat{ρ}}_{s}}{{\hat{ρ}}_{f}}}{{(1 - ϕ)}^{- 2.5}} (F F^{″} + λ (1 - F^{'} 2)) \\ + \frac{{(1 - ϕ)}^{2.5}}{{(1 + \frac{3 (\frac{{\hat{σ}}_{s}}{{\hat{σ}}_{f}} - 1) ϕ}{(\frac{{\hat{σ}}_{s}}{{\hat{σ}}_{f}} + 2) - (\frac{{\hat{σ}}_{s}}{{\hat{σ}}_{f}} - 1) ϕ})}^{- 1}} M^{2} (1 - F^{'}) = 0, & (11) \end{array}

\begin{array}{l} [1 + \frac{R d}{\frac{{\hat{k}}_{s} + 2 {\hat{k}}_{f} - 2 ϕ ({\hat{k}}_{f} - {\hat{k}}_{s})}{{\hat{k}}_{s} + 2 {\hat{k}}_{f} + ϕ ({\hat{k}}_{f} - {\hat{k}}_{s})}}] β^{″} \\ + \frac{1}{\frac{{\hat{k}}_{s} + 2 {\hat{k}}_{f} - 2 ϕ ({\hat{k}}_{f} - {\hat{k}}_{s})}{{\hat{k}}_{s} + 2 {\hat{k}}_{f} + ϕ ({\hat{k}}_{f} - {\hat{k}}_{s})}} [\frac{(P r F β^{'} - 2 λ P r F^{'} β)}{{(1 - ϕ) + \frac{ϕ {(ρ c_{p})}_{s}}{{(ρ c_{p})}_{f}}}^{- 1}} + P r E c F^{″} 2] \\ = 0 . & (12) \end{array}

γAl₂O₃ − H₂O Model

\begin{array}{l} F^{‴} + \frac{(1 - ϕ + \frac{ϕ {\hat{ρ}}_{s}}{{\hat{ρ}}_{f}})}{123 ϕ^{2} + 7.3 ϕ + 1} (F F^{″} + λ (1 - F^{'} 2)) \\ + \frac{(1 + \frac{3 (\frac{{\hat{σ}}_{s}}{{\hat{σ}}_{f}} - 1) ϕ}{(\frac{{\hat{σ}}_{s}}{{\hat{σ}}_{f}} + 2) - (\frac{{\hat{σ}}_{s}}{{\hat{σ}}_{f}} - 1) ϕ})}{123 ϕ^{2} + 7.3 ϕ + 1} M^{2} (1 - F^{'}) = 0, & (13) \end{array}

\begin{array}{l} [1 + \frac{R d}{4.97 ϕ^{2} + 2.72 ϕ + 1}] β^{″} \\ + \frac{1}{4.97 ϕ^{2} + 2.72 ϕ + 1} [\frac{(P r F β^{'} - 2 λ P r F^{'} β)}{{(1 - ϕ) + \frac{ϕ {(\hat{ρ} c_{p})}_{s}}{{(\hat{ρ} c_{p})}_{f}}}^{- 1}} + P r E c F^{″} 2] \\ = 0 . & (14) \end{array}

The conditions at the boundaries at the surface and at the free stream are as under:

\begin{array}{l} \begin{matrix} A t t h e s u r f a c e η = 0 \\ F (η) = 0 \\ F^{'} (η) = γ \\ β (η) = 1 \\ A t t h e f r e e s u r f a c e η \to \infty \\ F^{'} (η) \to 1 \\ β (η) \to 0 \end{matrix}} & (15) \end{array}

The parameters embedded in the models are Eckert number,

yes

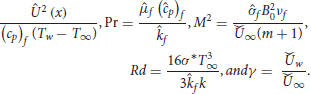
Quantities of Engineering Interest

Skin friction and local heat transfer phenomena are of great importance from engineering point of view. Mathematical dimensional expressions for these quantities are as under:

yes

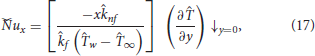
These expressions reduced in the following non-dimensional form by implementing the suitable differentiation and nanofluids models:

yes

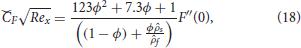
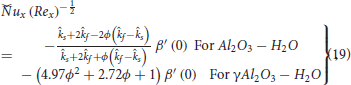
here, 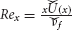yes is denotes the local Reynold number.

Mathematical Analysis

Shooting technique [30, 31] is adopted for the mathematical analysis of the particular nanofluids flow models. The reason behind this choice is the non-linearity (for instance see [32–40]) of the models over semi-infinite region. To initiate the technique, the following substitution are made:

\begin{array}{l} {\overset{︷}{y}}_{1} = F, {\overset{︷}{y}}_{2} = F^{'}, {\overset{︷}{y}}_{3} = F^{″}, {\overset{︷}{y}}_{4} = β, {\overset{︷}{y}}_{5} = β^{'} . & (20) \end{array}

Al₂O₃ − H₂O Model

The flow model Al₂O₃ − H₂O can be reduced into the following form:

\begin{array}{l} F^{‴} = - \frac{1 - ϕ + \frac{ϕ {\hat{ρ}}_{s}}{{\hat{ρ}}_{f}}}{{(1 - ϕ)}^{- 2.5}} (F F^{″} + λ (1 - F^{'} 2)) \\ - \frac{{(1 - ϕ)}^{2.5}}{{(1 + \frac{3 (\frac{{\hat{σ}}_{s}}{{\hat{σ}}_{f}} - 1) ϕ}{(\frac{{\hat{σ}}_{s}}{{\hat{σ}}_{f}} + 2) - (\frac{{\hat{σ}}_{s}}{{\hat{σ}}_{f}} - 1) ϕ})}^{- 1}} M^{2} (1 - F^{'}), & (21) \end{array}

\begin{array}{l} β^{″} = \frac{- 1}{1 + \frac{R d}{\frac{{\hat{k}}_{s} + 2 {\hat{k}}_{f} - 2 ϕ ({\hat{k}}_{f} - {\hat{k}}_{s})}{{\hat{k}}_{s} + 2 {\hat{k}}_{f} + ϕ ({\hat{k}}_{f} - {\hat{k}}_{s})}}} \\ [\frac{1}{\frac{{\hat{k}}_{s} + 2 {\hat{k}}_{f} - 2 ϕ ({\hat{k}}_{f} - {\hat{k}}_{s})}{{\hat{k}}_{s} + 2 {\hat{k}}_{f} + ϕ ({\hat{k}}_{f} - {\hat{k}}_{s})}} (\frac{(P r F β^{'} - 2 λ P r F^{'} β)}{{(1 - ϕ) + \frac{ϕ {(\hat{ρ} c_{p})}_{s}}{{(h a t ρ c_{p})}_{f}}}^{- 1}} + P r E c F^{″} 2)] . & (22) \end{array}

By implementing the transformations made in Equation (19), the system of Equations. (21, 22) transformed into the following initial value problem:

yes

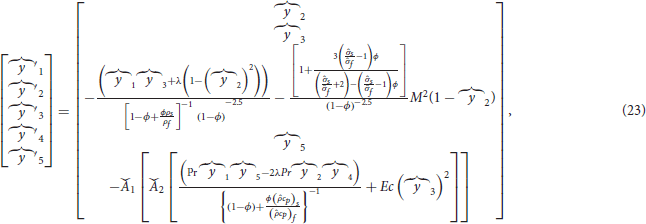
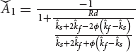
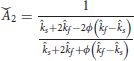
Where, yes

yes

and the set of conditions at η = 0 are as:

yes

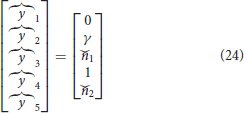
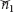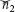Here, yes and yes are unknown and the accuracy is set as 10⁻⁶.

γAl₂O₃ − H₂O Model

The model γAl₂O₃ − H₂O reduced into the following pattern:

\begin{array}{l} F^{‴} = - \frac{(1 - ϕ + \frac{ϕ {\hat{ρ}}_{s}}{{\hat{ρ}}_{f}})}{123 ϕ^{2} + 7.3 ϕ + 1} (F F^{″} + λ (1 - F^{'} 2)) - \frac{(1 + \frac{3 (\frac{{\hat{σ}}_{s}}{{\hat{σ}}_{f}} - 1) ϕ}{(\frac{{\hat{σ}}_{s}}{{\hat{σ}}_{f}} + 2) - (\frac{{\hat{σ}}_{s}}{{\hat{σ}}_{f}} - 1) ϕ})}{123 ϕ^{2} + 7.3 ϕ + 1} M^{2} (1 - F^{'}), & (25) \end{array}

\begin{array}{l} β^{″} = \frac{- 1}{1 + \frac{R d}{4.97 ϕ^{2} + 2.72 ϕ + 1}} [\frac{1}{4.97 ϕ^{2} + 2.72 ϕ + 1} (\frac{(P r F β^{'} - 2 λ P r F^{'} β)}{{(1 - ϕ) + \frac{ϕ {(\hat{ρ} c_{p})}_{s}}{{(\hat{ρ} c_{p})}_{f}}}^{- 1}} + P r E c F^{″} 2)] . & (26) \end{array}

By using transformations, the following system is obtained:

yes

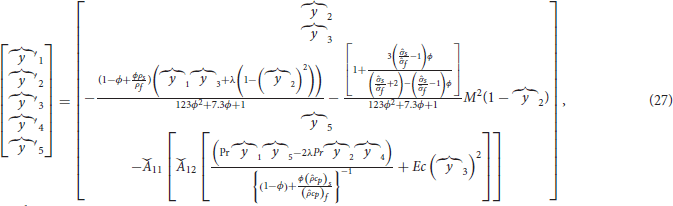
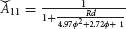
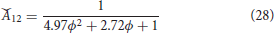
where, yes

yes

The initial conditions are same as in Equation (24).

Physical Interpretation of Results

The flow parameters like magnetic parameter, thermal radiation, and viscous dissipation play fascinating role in the flow regimes. The influences of afore mentioned flow parameters on the flow field explored graphically and discussed comprehensively in this section. Moreover, the results for the quantities of engineering interest are taken into account and discussed. The results plotted for two cases of the wedge according to the wedge movement. It is important to mention the cases of flow depending on the value of parameter γ. The wedge and fluid move in opposite direction for negative γ and move in alike direction for positive γ.

Velocity Field

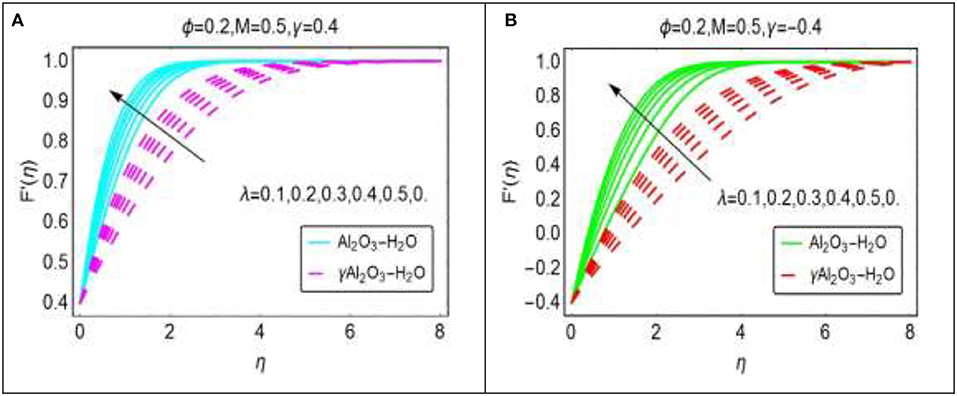
Figure 2 interprets the behavior of the nanofluids velocity (Al₂O₃ − H₂O and γAl₂O₃ − H₂O) for γ > 0 and γ < 0, respectively. From Figure 2A, it is obvious that the velocity increases when the wedge and the nanofluids move in alike way (γ > 0). The velocity of Al₂O₃ − H₂O nanofluids increases abruptly in comparison with γAl₂O₃ − H₂O nanofluid. The reason behind this is the difference between the effective models of dynamic viscosity for Al₂O₃ and γAl₂O₃. The nanofluid γAl₂O₃ − H₂O becomes more dense due to the dynamic viscosity containing high volume fraction of the nanoparticles and the momentum of the fluid drops. Due to drop in momentum, the velocity starts decreasing. Near the wedge surface, momentum of the nanofluids declines due to the friction between the wedge surface and the nanofluids. The effects of the pressure parameter are very prominent in the region 2 ≤ η ≤ 4. These effects are elaborated in Figure 2A. Figure 2B highlights the alterations in the nanofluids velocity for opposing case. The negative values of γ shows that the nanofluids and wedge move in opposite direction. For opposing case, the asymptotic region increases for γAl₂O₃ − H₂O nanofluid.

FIGURE 2

Figure 2. The effects of λ on dimensionless velocity F′(η) for (A) γ = 0.4, (B) γ = −0.4.

Figure 3 elaborates the alterations in the velocity F′(η) for varying wedge parameter γ. Due to altering wedge parameter, very interesting variations in the velocity field are observed. For assisting case γ > 0, the velocity upturns abruptly. When the nanofluids and wedge move in alike direction then the movement of wedge in the direction of nanofluids provide extra momentum to the nanofluids. Therefore, the velocity positively increases. In the vicinity of the wedge, the velocity increase abruptly for both sort of nanofluids. For Al₂O₃ − H₂O nanofluid, the velocity shows asymptotic behavior quickly in comparison with γAl₂O₃ − H₂O. These results are plotted in Figure 3A. Figure 3B shows that the velocity of the nanofluids drops very quickly over the domain of interest. The opposite movement of the wedge and the nanofluids cause the declines in the velocity profile. Due to the opposite movement, friction between the wedge surface and the nanofluids slow down the momentum of the nanofluids. Consequently, the velocity drops.

FIGURE 3

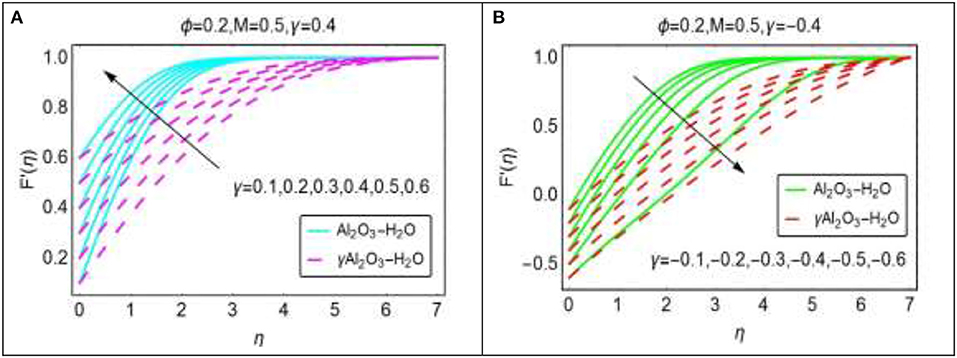
Figure 3. The effects of (A) γ positive, (B) γ negative on dimensionless ϕ on dimensionless velocity F′(η).

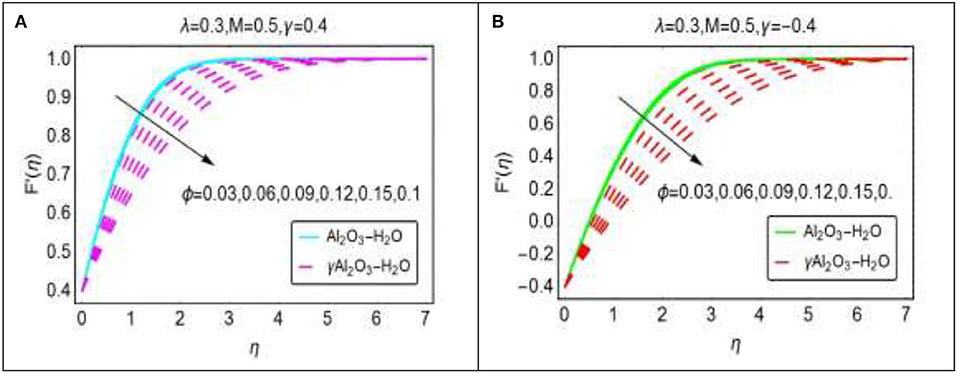
The volume fraction of the nanoparticles is very key ingredients which alters the nanofluid characteristics affectively. These effects are portrayed in Figures 4A,B for assisting and opposing case, respectively. The behavior of the velocity for assisting case elaborated in Figure 4A. For increasing ϕ, the nanofluids velocity drops rapidly. For γAl₂O₃ − H₂O, the prompt decrement in the velocity occurs due to high volume fraction incorporated in the dynamic viscosity. The velocity vanishes asymptotically beyond η ≥ 4. Figure 4B portrays the velocity profile for opposing flow case. For opposing flow, the velocity declines very abruptly in comparison with assisting flow. The opposite movement and high volume fraction of the nanoparticles opposes the opposes the motion. Therefore, the velocity rapidly drops and asymptotically vanishes beyond η ≥ 6.

FIGURE 4

Figure 4. The effects of ϕ on dimensionless velocity F′(η) for (A) γ = 0.4, (B) γ = −0.4.

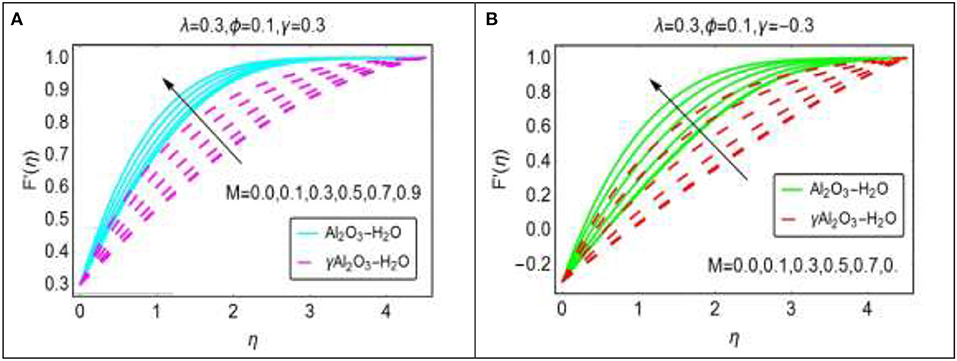
The influences in the velocity behavior by altering the magnetic parameter are depicted in Figure 5. From Figure 5A, it is observed that the velocity of the nanofluids F′(η) positively increases for assisting flow. Due to less dense composition of Al₂O₃ − H₂O nanofluid, the velocity profile increases promptly as compared to γAl₂O₃ − H₂O nanofluid. Similarly, for opposing case, the velocity field portrayed in Figure 5B. Figure 5B shows the prompt increasing behavior of the velocity for both sort of nanofluids. In the region 1 ≤ η ≤ 3.5, these effects of M on the velocity F′(η) are very rapid.

FIGURE 5

Figure 5. The effects of M on dimensionless velocity F′(η) for (A) γ = 0.3, (B) γ = −0.3.

Temperature Field

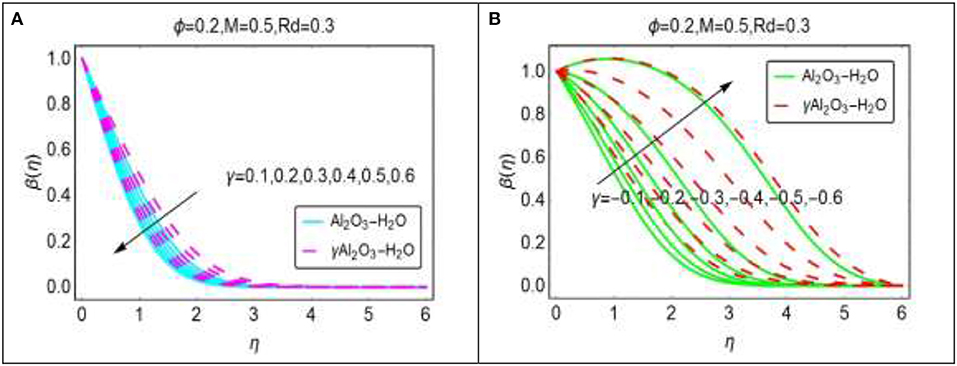
The alterations in temperature fields of Al₂O₃ − H₂O and γAl₂O₃ − H₂O nanofluids by varying the wedge parameter γ presented in Figure 6. Figure 6A shows that for assisting flow, the temperature β(η) drops. The drops in the temperature is due to the alike motion of the nanofluids and wedge. For Al₂O₃ − H₂O nanofluids, decreasing pattern of the temperature is quite rapid and prominent in the region 1 ≤ η ≤ 3. The temperature β(η) vanishes asymptotically at the free stream. An interesting impacts of γ are observed for opposing flow case. These alterations are depicted in Figure 6B. When the wedge moves in the opposite direction of the nanofluids, then due to the force of friction between the wedge surface and the molecules of the nanofluids heat produces which favors the temperature β(η). The temperature increases abruptly near the wedge. The reason is that the more friction between the molecules of the nanofluids and the wedge surface. For γAl₂O₃ − H₂O nanofluids, the temperature arises rapidly than Al₂O₃ − H₂O nanofluid.

FIGURE 6

Figure 6. The effects of (A) γ positive, (B) γ negative on dimensionless temperature β(η).

Figure 7 highlights the influences of pressure parameter λ on the temperature of Al₂O₃ − H₂O and γAl₂O₃ − H₂O nanofluids. The pressure parameter λ opposes the nanofluids temperature. For assisting flow, the temperature is decreasing function of λ and the decrement in Al₂O₃ − H₂O nanofluid is rapid. Due to high dynamic viscosity of γAl₂O₃ − H₂O nanofluid, the temperature drops slowly than Al₂O₃ − H₂O nanofluid. It is observed that the temperature vanishes at the thermal boundary layer which starts beyond η > 3. These influences are shown in Figure 7A. It is investigated that the opposite motion of the wedge and nanofluids reduces the temperature very rapidly. Due to opposite motion, the velocity of the momentum drops. Consequently, the velocity declines which cause the rapid decrement in the temperature. The role of λ on β(η) is very cleared. Moreover, for opposing case, thermal boundary layer increases and the temperature decreases beyond η > 5. This behavior of the temperature is portrays in Figure 7B.

FIGURE 7

Figure 7. The effects of λ on dimensionless temperature β(η) for (A) γ = 0.4, (B) γ = −0.4.

Figures 8–10 depicted the behavior of temperature β(η) for volumetric fraction ϕ, Eckert number Ec and thermal radiation parameter Rd, respectively. The temperature patterns for both assisting and opposing case are plotted.

FIGURE 8

Figure 8. The effects of ϕ on dimensionless temperature β(η) for (A) γ = 0.4, (B) γ = −0.4.

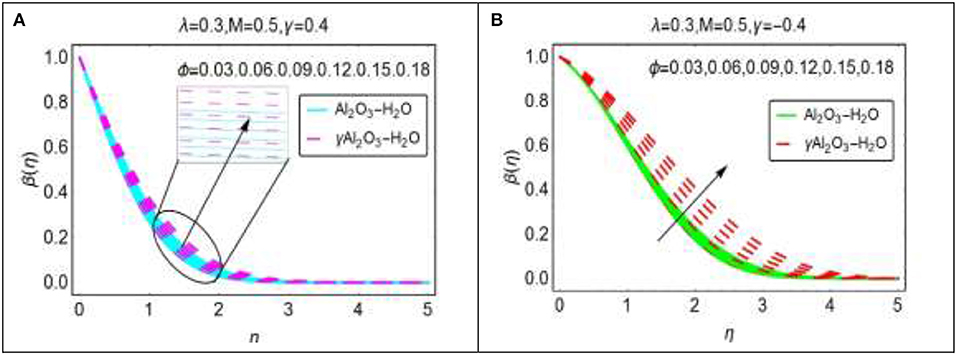
In the study of nanofluids, the importance of volume fraction cannot be neglected. The volume fraction alters the temperature effectively and plays vibrant role. The variations in the temperature for assisting and opposing flow due to altering ϕ are plotted in Figures 8A,B, respectively. From these, it is inspected that the volume fraction favors the temperature positively. For γ > 0, the increasing pattern of the temperature is quite slow than γ < 0. The main reason of this phenomena is the force of friction produces between the wedge surface and molecules of the nanofluids. For assisting case, thermal boundary layer decrease and in the case of opposing flow it starts increases and the temperature is vanishes beyond η > 3 and η > 4, respectively. For γAl₂O₃ − H₂O₃ the temperature β(η) increases very promptly due to the dynamic viscosities of Al₂O₃ − H₂O₃ and γAl₂O₃ − H₂O₃ nanofluids.

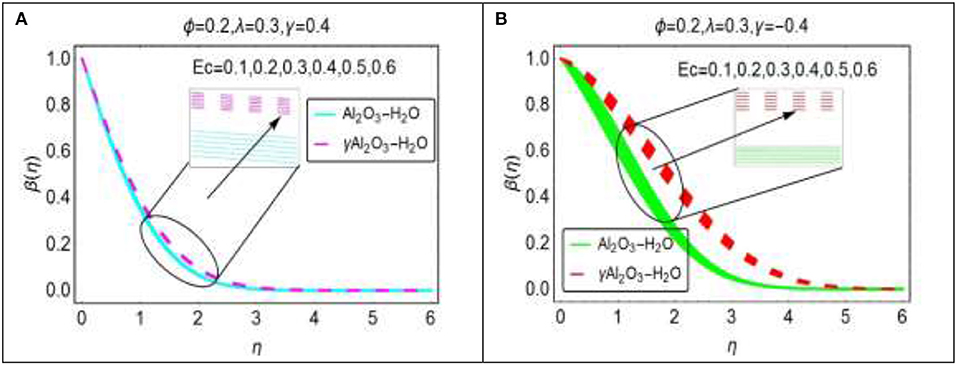
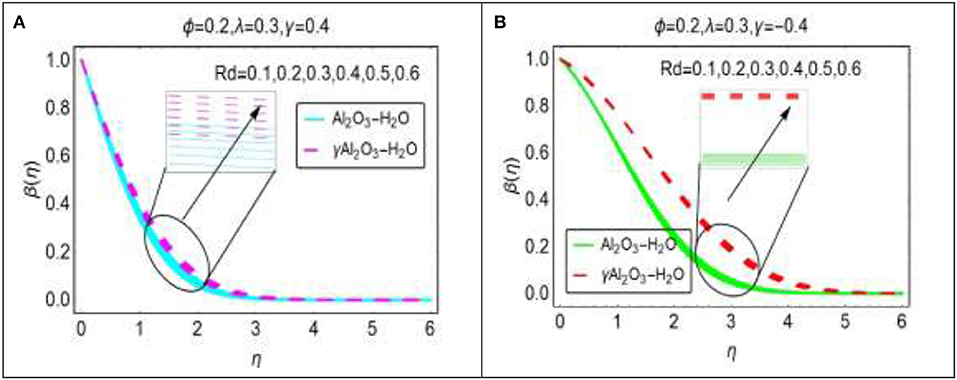
The effects of Eckert number which appears due to the viscous dissipation are plotted in Figures 9A,B for alike and opposing flow cases, respectively. The temperature varies almost inconsequentially for γ > 0 for both sort of nanofluids. On the other hand, it is inspected that for more dissipative nanofluids, the temperature β(η) arises rapidly. Thermal boundary layer decreases for Al₂O₃ − H₂O nanofluid and increases for γAl₂O₃ − H₂O nanofluid. From Figures 10A,B, it is obvious that thermal radiation parameter increases the nanofluids temperature for both the cases. For opposing case, the temperature β(η) arises quite rapid than alike flow case.

FIGURE 9

Figure 9. The effects of Ec on dimensionless temperature β(η) for (A) γ = 0.4, (B) γ = −0.4.

FIGURE 10

Figure 10. The effects of Rd on dimensionless temperature β(η) for (A) γ = 0.4, (B) γ = −0.4.

Skin Friction and Local Nusselt Number

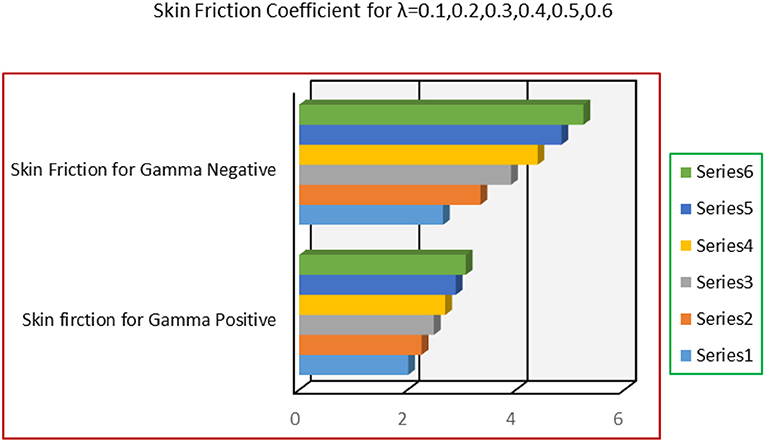
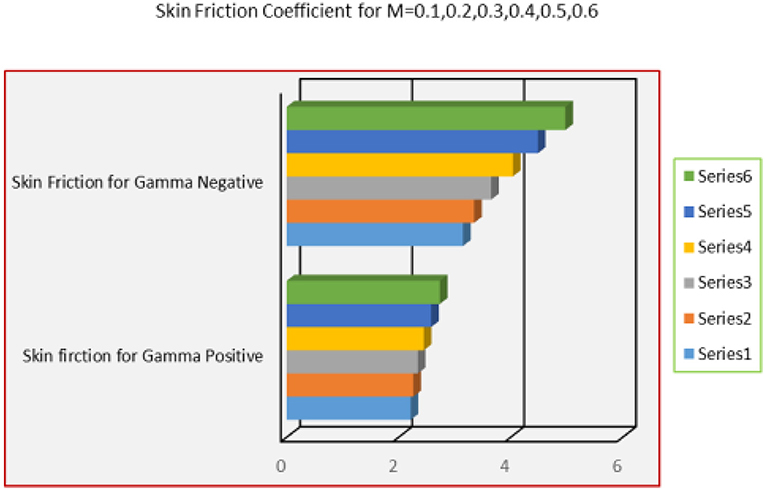
This subsection highlights the behavior of skin friction and local Nusselt number for different values of the flow parameters for assisting and opposing flow. It is observed that the skin friction is directly proportional to the pressure parameter λ. For opposing flow, skin friction increases slowly in comparison with opposing flow case. These are depicted in Figure 11. Figure 12 shows that the magnetic parameter M favors the skin friction for both assisting and opposing flows. For assisting case, it varies very slowly for assisting case while abrupt alterations are observed for opposing flow.

FIGURE 11

Figure 11. The effects of λ on skin friction coefficient.

FIGURE 12

Figure 12. The effects of M on skin friction coefficient.

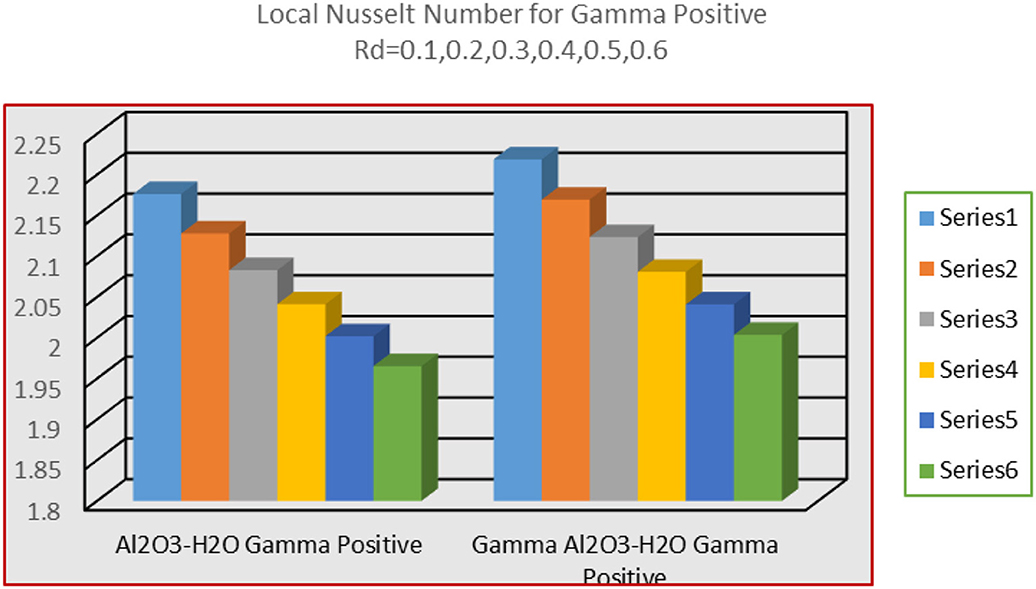
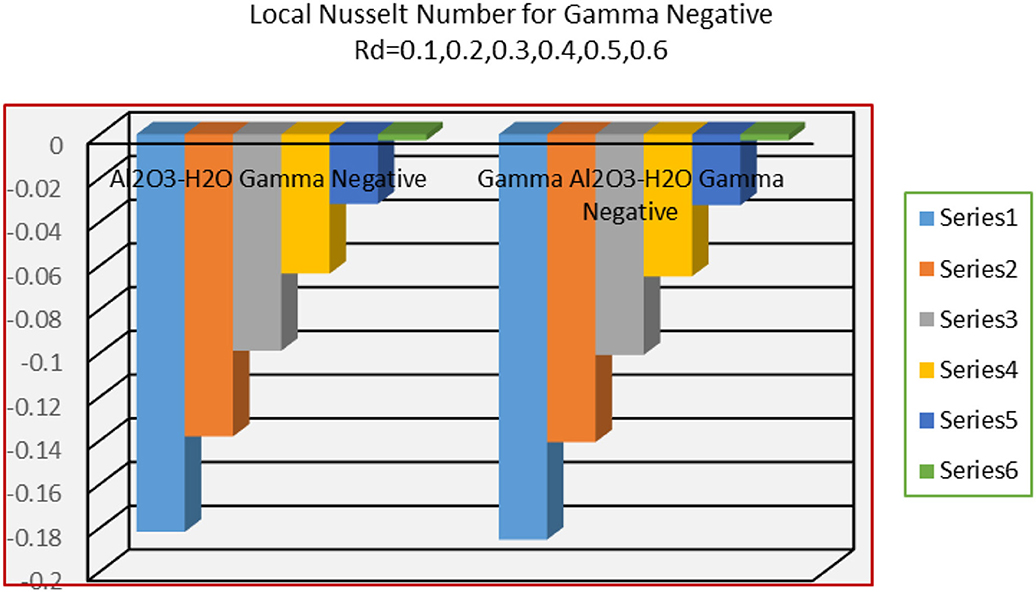
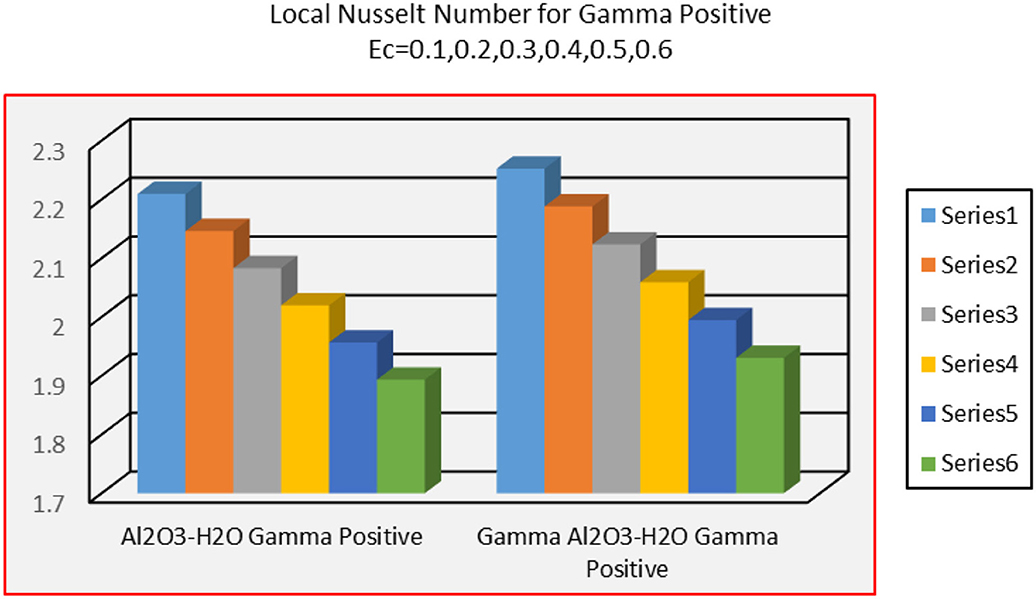
The alterations in local heat transfer coefficient (Nusselt number) for different parameters incorporating in Figures 13–15 for alike and opposing flow cases. It is observed that heat transfer decreases at the wedge surface for alike flow case for radiative flow. The heat transfers for γAl₂O₃ − H₂O nanofluids is rapidly drops than Al₂O₃ − H₂O nanofluids. On the other hand, decrement in the heat transfer is observed for opposing flow. The heat transfer drops abruptly for γAl₂O₃ − H₂O nanofluid. These variations are portrayed in Figure 14. Figure 15 depicts the influences of dissipation phenomena on the heat transfer. The heat transfer drops abruptly for more dissipative γAl₂O₃ − H₂O nanofluid and in Al₂O₃ − H₂O nanofluid, these effects are quite slow.

FIGURE 13

Figure 13. The effects of Rd on local Nusselt number (γ > 0).

FIGURE 14

Figure 14. The effects of Rd on local Nusselt number (γ < 0).

FIGURE 15

Figure 15. The effects of Ec on local Nusselt number (γ > 0).

Thermophysical Properties

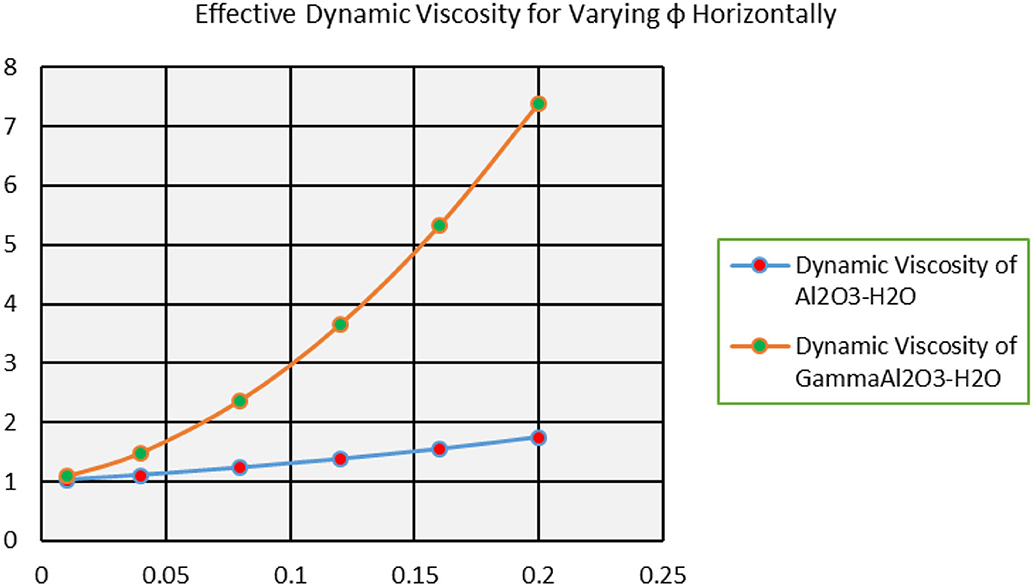
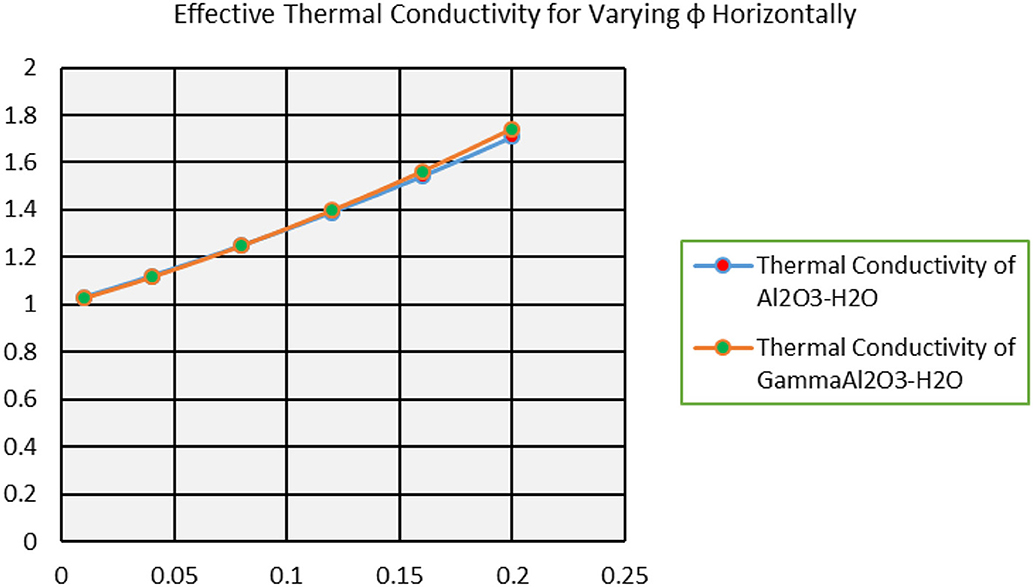
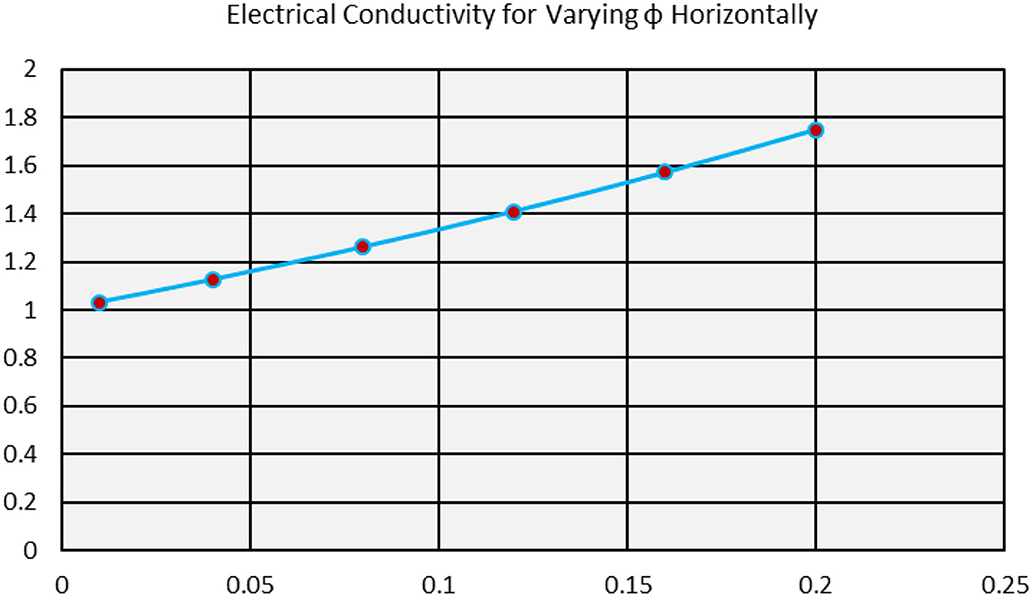
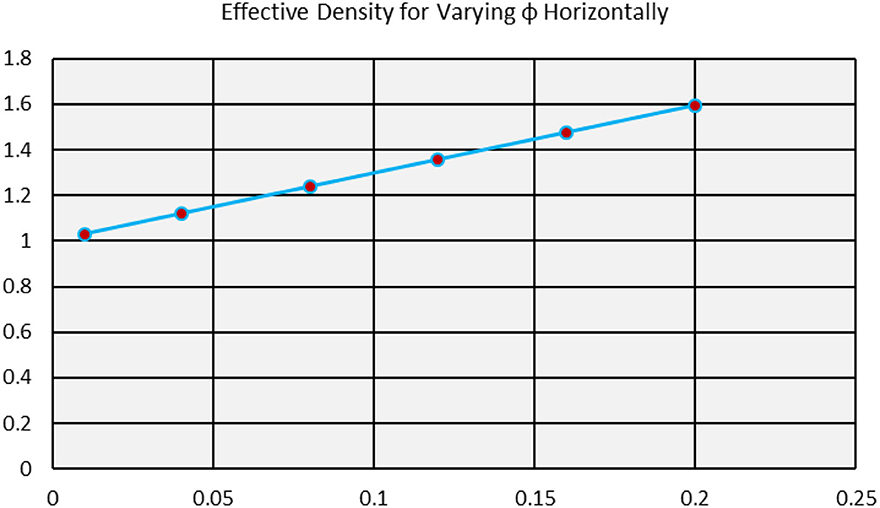
Thermophysical characteristics contribute vibrantly in the flow regimes of nanofluids. These properties effectively alter the nanofluid characteristics. The effects of volume fraction ϕ on the effective dynamic viscosity, thermal conductivity, electrical conductivity and density are plotted in Figures 16–19. From Figure 16, it is clear that the dynamic viscosity of γAl₂O₃ − H₂O increases exponentially. The for Al₂O₃ − H₂O nanofluids, these are very slow. Due to this improvement in the dynamic viscosity, the characteristics of the nanofluids affects. Similarly, thermal conductivity of γAl₂O₃ − H₂O nanofluid is quite rapid. However, no major difference between thermal conductivities of Al₂O₃ − H₂O and γAl₂O₃ − H₂O nanofluids is observed. Furthermore, electrical conductivity and density of the nanofluid arises by increasing the volume fraction in feasible domain. These are elaborated in Figures 18, 19, respectively.

FIGURE 16

Figure 16. The effects of ϕ on Effective Dynamic viscosity.

FIGURE 17

Figure 17. The effects of ϕ on Thermal conductivity.

FIGURE 18

Figure 18. The effects of ϕ on Electrical conductivity.

FIGURE 19

Figure 19. The effects of ϕ on Effective density.

Comparison With Scientific Literature

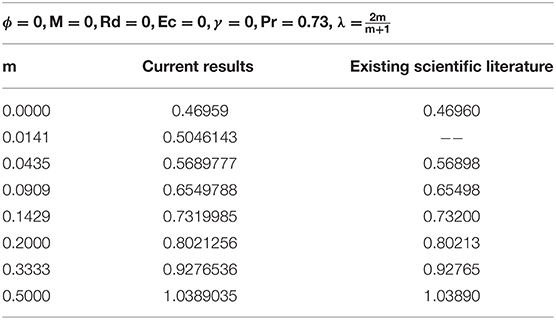
Table 2 elaborating the reliability of the presented results with existing scientific literature for F″(0). It is detected that by setting different physical parameters equal to zero, our results meets the existing scientific results in the literature that show the reliability of the presented physical results and applied numerical technique.

TABLE 2

Table 2. Reliability of the study by comparing with existing scientific literature for F″(0).

Conclusions

A novel radiative and dissipative study on Al₂O₃ − H₂O and γAl₂O₃ − H₂O nanofluids heat transfer model in the presence of applied magnetic field is considered over wedge. Two nanofluids models are obtained corresponding to two different sort of nanoparticles together with host liquid water. Then the models are treated mathematically by implementing RK scheme coupled with shooting method. Finally, the results for the flow regimes, heat transfer and thermophysical characteristics are plotted and found the following major outcomes:

i. The velocity of γAl₂O₃ − H₂O nanofluid increases for higher Hartree pressure gradient parameter.

ii. The assisting flow of nanofluid over wedge favors the velocity field F′(η) and the velocity drops for opposing flow.

iii. The velocity profile F′(η) drops for higher volume fraction factor ϕ of the nanoparticles.

iv. The temperature of the nanofluids arises for opposing flow.

v. The temperature β(η) arises for more dissipative and radiative nanofluids.

vi. The temperature field β(η) declines for higher Hartree pressure gradient parameter.

vii. The parameter λ and strength of magnetic field favors the skin friction coefficient.

viii. For more radiative and dissipative nanofluids, the heat transfer coefficient drops.

ix. Dynamic viscosity increases abruptly for γAl₂O₃ − H₂O than Al₂O₃ − H₂O nanofluid which alters the flow characteristics effectively.

x. Thermal and electrical conductivities increases by increasing the nanoparticles volume fraction ϕ.

xi. From comparison of presented results with existing scientific literature, it is observed that the presented physical results are valid.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

The formulation of the problem was done by UK, A and SM-D. Non-dimensionalization of the nanofluid models by using invertible transformations done by RM, IH, E-SS, and NA. Mathematical analysis and the graphical results plotted and discussed by SM-D and IK. The revision and editing was done by UK, E-SS, SM-D, and IK. All the authors have equal contributions.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Researchers Supporting Project number (RSP-2019/33), King Saud University, Riyadh, Saudi Arabia.

References

1. Ellahi R, Sait S, Shehzad S, Ayaz Z. A hybrid investigation on numerical and analytical solutions of electro-magnetohydrodynamics flow of nanofluid through porous media with entropy generation Int J Numer Methods Heat Fluid Flow. (2019) 30:834–54. doi: 10.1108/HFF-06-2019-0506

CrossRef Full Text | Google Scholar

2. Eberhard U, Seybold HJ, Floriancic M, Bertsch P, Martínez JJ, Andrade JJS, et al. Determination of the effective viscosity of non-newtonian fluids flowing through porous media. Front Phys. (2019) 7:71. doi: 10.3389/fphy.2019.00071

CrossRef Full Text | Google Scholar

3. Majeed A, Zeeshan A, Xu H, Kashif M, Masud U. Heat transfer analysis of magneto-eyring–powell fluid over a nonlinear stretching surface with multiple slip effects: application of roseland's heat flux. Can J Phys. (2019) 97:1253–61. doi: 10.1139/cjp-2018-0732

CrossRef Full Text | Google Scholar

4. Falkner VM, Skan SW. Some approximate solutions of the boundary layer equations. Philos Mag. (1931) 12:865–96.

Google Scholar

5. Falkner VM, Skan SW. Some approximate solutions of the boundary-layer for flow past a stretching boundary. SIAM J Appl Math. (1931) 49:1350–8. doi: 10.1137/0149081

CrossRef Full Text | Google Scholar

6. Rajagopal KR, Gupta AS, Na TY. A note on the falkner-skan flows of a non-newtonian fluid. Int J NonLin Mech. (1983) 18:313–20. doi: 10.1016/0020-7462(83)90028-8

CrossRef Full Text | Google Scholar

7. Lin HT, Lin LK. Similarity solutions for laminar forced convection heat transfer from wedges to fluids of any prandtl number. Int J Heat Mass Trans. (1987) 30:1111–8. doi: 10.1016/0017-9310(87)90041-X

CrossRef Full Text | Google Scholar

8. Hartree DH. On an equation occurring in falkner and skan's approximate treatment of the equations of the boundary layer. Proc Camb Phil Soc. (1973) 33:223–39. doi: 10.1017/S0305004100019575

CrossRef Full Text | Google Scholar

9. Watanabe T. Thermal boundary layer over wedge with uniform suction or injection in force flow. Acta Mech. (1990) 83:119–26. doi: 10.1007/BF01172973

CrossRef Full Text | Google Scholar

10. Watanabe T, Pop I. Magnetohydrodynamic free convection flow over a wedge in the presence of a transverse magnetic field. Int Com Heat Mass Trans. (1993) 20:871–81. doi: 10.1016/0735-1933(93)90040-3

CrossRef Full Text | Google Scholar

11. Koh JCY, Hartnett JP. Skin-friction and heat transfer for incompressible laminar flow over porous wedges with suction and variable wall temperature. Int J Heat Mass Trans. (1961) 2:185–98. doi: 10.1016/0017-9310(61)90088-6

CrossRef Full Text | Google Scholar

12. Kumari M, Takhar HS, Nath G. Mixed convection flow over a vertical wedge embedded in a highly porous medium. Heat Mass Trans. (2001) 37:139–46. doi: 10.1007/s002310000154

CrossRef Full Text | Google Scholar

13. Chamkha AJ, Mujtaba M, Quadri A, Issa C. Thermal radiation effects on MHD forced convection flow adjacent to a non-isothermal wedge in the presence of a heat source or sink. Heat Mass Trans. (2003) 39:305–12. doi: 10.1007/s00231-002-0353-4

CrossRef Full Text | Google Scholar

14. El-dabe NT, Ghaly AY, Rizkallah RR, Ewis KM. Numerical solution of MHD boundary layer flow of non-newtonian casson fluid on a moving wedge with heat and mass transfer and induced magnetic field. J Appl Math Phys. (2015) 3:649–63. doi: 10.4236/jamp.2015.36078

CrossRef Full Text | Google Scholar

15. Mukhopadhyay S, Mondal IC, Chamkha AJ. Casson fluid flow and heat transfer past a symmetric wedge. Heat Trans. Res. (2013) 42:665–75. doi: 10.1002/htj.21065

CrossRef Full Text | Google Scholar

16. Su X, Zheng L, Zhang X, Zhang J. MHD mixed convective heat transfer over a permeable stretching wedge with thermal radiation and ohmic heating. Chem Eng Sci. (2012) 78:1–8. doi: 10.1016/j.ces.2012.04.026

CrossRef Full Text | Google Scholar

17. Ishak A, Nazar R, Pop I. Falkner-Skan equation for flow past a moving wedge with suction or injection. J Appl Math Comp. (2007) 25:67–83. doi: 10.1007/BF02832339

CrossRef Full Text | Google Scholar

18. Ishak A, Nazar R, Pop I. Moving wedge and flat plate in a micropolar fluid. Int J Eng Sci. (2006) 44:1225–36. doi: 10.1016/j.ijengsci.2006.08.005

CrossRef Full Text | Google Scholar

19. Rashidi MM, Ali M, Freidoonimehr N, Rostami B, Hossain MA. Mixed convective heat transfer for MHD viscoelastic fluid flow over a porous wedge with thermal radiation. Adv Mechl Eng. (2014) 6:735939. doi: 10.1155/2014/735939

CrossRef Full Text | Google Scholar

20. Kandasamy R, Raji AWBM, Khamis AB. Efiects of chemical reaction, heat and mass transfer on boundary layer flow over a porous wedge with heat radiation in the presence of suction or injection. Theo Appl Mech. (2006) 33:123–48. doi: 10.2298/TAM0602123K

CrossRef Full Text | Google Scholar

21. Hussanan A, Anwar MI, Ali F, Khan I, Shafie S. Natural convection flow past an oscillating plate with newtonian heating. Heat Trans Res. (2014) 45:119–35. doi: 10.1615/HeatTransRes.2013006385

CrossRef Full Text | Google Scholar

22. Su X, Xiaohong L. Hall effect on MHD flow and heat transfer of nanofluids over a stretching wedge in the presence of velocity slip and joule heating. Cen Eur J Phys. (2013) 11:1694–703. doi: 10.2478/s11534-013-0331-0

CrossRef Full Text | Google Scholar

23. Ullah I, Khan I, Shafie S. Hydromagnetic falkner-skan flow of casson fluid past a moving wedge with heat transfer. Alex Eng J. (2016) 55:2139–48. doi: 10.1016/j.aej.2016.06.023

CrossRef Full Text | Google Scholar

24. Rafique K, Anwar MI, Misiran M, Khan I, Alharbi OS, Thounthong P, et al. Numerical solution of casson nanofluid flow over a non-linear inclined surface with soret and dufour effects by keller-box method. Front Phys. (2019) 7:139. doi: 10.3389/fphy.2019.00139

CrossRef Full Text | Google Scholar

25. Majeed A, Zeeshan A, Mahmood T, Rahman SU. Impact of magnetic field and second-order slip flow of casson liquid with heat transfer subject to suction/injection and convective boundary condition. J Mag. (2010) 24:181–89. doi: 10.4283/JMAG.2019.24.1.081

CrossRef Full Text | Google Scholar

26. Bibi M, Zeeshan A, Malik MY, Rehman KU. Numerical investigation of the unsteady solid-particle flow of a tangent hyperbolic fluid with variable thermal conductivity and convective boundary. Eur Phy J Plus. (2019) 137:298. doi: 10.1140/epjp/i2019-12651-9

CrossRef Full Text | Google Scholar

27. Saba F, Ahmed N, Khan U, Waheed A, Rafiq M, Mohyud-Din ST. Thermophysical analysis of water based (Cu–Al₂O₃) hybrid nanofluid in an asymmetric channel with dilating/squeezing walls considering different shapes of nanoparticles. Appl Sci. (2018) 8:1549. doi: 10.3390/app8091549

CrossRef Full Text | Google Scholar

28. Srinivasacharya D, Mendu U, Venumadhav K. MHD boundary layer flow of a nanofluid past a wedge. Proc Eng. (2015) 127:1064–70. doi: 10.1016/j.proeng.2015.11.463

CrossRef Full Text | Google Scholar

29. Rashidi MM, Ganesh NV, Hakeem AAK, Ganga B, Lorenzini G. Influences of an effective prandtl number model on nano boundary layer flow of gamma-Al₂O₃-H₂O and gamma-Al₂O₃-C₂H₆O₂ over a vertical stretching sheet. Int J Heat Mass Trans. (2016) 98:616–23. doi: 10.1016/j.ijheatmasstransfer.2016.03.006

CrossRef Full Text | Google Scholar

30. Khan U, Ahmed N, Mohyud-Din ST. Numerical investigation for three dimensional squeezing flow of nanofluid in a rotating channel with lower stretching wall suspended by carbon nanotubes. Appl Ther Eng. (2017) 113:1107–17. doi: 10.1016/j.applthermaleng.2016.11.104

CrossRef Full Text | Google Scholar

31. Khan JA, Mustafa M, Hayat T, Alsaedi A. On three-dimensional flow and heat transfer over a non-linearly stretching sheet: analytical and numerical solutions. PLoS ONE. (2014) 9:e107287. doi: 10.1371/journal.pone.0107287

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Yasutomi M. Thermodynamic mechanism of the density anomaly of liquid water. Front Phys. (2015) 3:8. doi: 10.3389/fphy.2015.00008

CrossRef Full Text | Google Scholar

33. Dhar A, Kundu A, Kundu A. Anomalous heat transport in one dimensional systems: a description using non-local fractional-type diffusion equation. Front Phys. (2019) 7:159. doi: 10.3389/fphy.2019.00159

CrossRef Full Text | Google Scholar

34. Hayat T, Nadeem S. Heat transfer enhancement with Ag–CuO/water hybrid nanofluid. Res Phys. (2017) 7:2317–24. doi: 10.1016/j.rinp.2017.06.034

CrossRef Full Text | Google Scholar

35. Alamri SZ, Khan AA, Azeez M, Ellahi R. Effects of mass transfer on MHD second grade fluid towards stretching cylinder: a novel perspective of cattaneo–christov heat flux model. Phys Lett A. (2019) 383:276–81. doi: 10.1016/j.physleta.2018.10.035

CrossRef Full Text | Google Scholar

36. Manjunatha S, Kuttan BA, Jayanthi S, Chamkha A, Gireesha BJ. Heat transfer enhancement in the boundary layer flow of hybrid nanofluids due to variable viscosity and natural convection. Heliyon. (2019) 5:e01469. doi: 10.1016/j.heliyon.2019.e01469

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Yasutomi M. Which shape characteristics of the intermolecular interaction of liquid water determine its compressibility? Front Phys. (2016) 4:21. doi: 10.3389/fphy.2016.00021

CrossRef Full Text | Google Scholar

38. Khan AA, Bukhari SR, Marin M, Ellahi R. Effects of chemical reactio on third-grade MHD fluid under the influence of heat and mass transfer with variable reactive index. Heat Trans Res. (2019) 50:1061–80. doi: 10.1615/HeatTransRes.2018028397

CrossRef Full Text | Google Scholar

39. Chamkha AJ, Dogonchi AS, Ganji DD. Magneto-hydrodynamic flow and heat transfer of a hybrid nanofluid in a rotating system among two surfaces in the presence of thermal radiation and joule heating. AIP Adv. (2019) 9:025103. doi: 10.1063/1.5086247

CrossRef Full Text | Google Scholar

40. Ellahi R, Sait SM, Shehzad N, Mobin N. Numerical simulation and mathematical modeling of electro-osmotic couette–poiseuille flow of MHD power-law nanofluid with entropy generation. Symmetry. (2019) 11:1038. doi: 10.3390/sym11081038

CrossRef Full Text | Google Scholar

Nomenclature

Keywords: wedge, host fluid, magnetic field, thermal radiation, viscous dissipation, γAl₂O₃ nanoparticles, RK scheme

Citation: Ahmed N, Adnan, Khan U, Mohyud-Din ST, Khan I, Murtaza R, Hussain I and Sherif E-SM (2020) A Novel Investigation and Hidden Effects of MHD and Thermal Radiations in Viscous Dissipative Nanofluid Flow Models. Front. Phys. 8:75. doi: 10.3389/fphy.2020.00075

Received: 04 October 2019; Accepted: 03 March 2020;
Published: 12 May 2020.

Edited by:

Ahmed Zeeshan, International Islamic University, Islamabad, Pakistan

Reviewed by:

Taseer Muhammad, King Khalid University, Saudi Arabia
Usman Masud, University of Engineering and Technology, Pakistan

Copyright © 2020 Ahmed, Adnan, Khan, Mohyud-Din, Khan, Murtaza, Hussain and Sherif. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.

*Correspondence: Ilyas Khan, aWx5YXNraGFuJiN4MDAwNDA7dGR0dS5lZHUudm4=

Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.

ORIGINAL RESEARCH article

A Novel Investigation and Hidden Effects of MHD and Thermal Radiations in Viscous Dissipative Nanofluid Flow Models

Introduction

Model Formulation

Statement and Geometry

Governing Equations and Non-dimensionalization

Al2O3 − H2O Model

γAl2O3 − H2O Model

Quantities of Engineering Interest

Mathematical Analysis

Al2O3 − H2O Model

γAl2O3 − H2O Model

Physical Interpretation of Results

Velocity Field

Temperature Field

Skin Friction and Local Nusselt Number

Thermophysical Properties

Comparison With Scientific Literature

Conclusions

Data Availability Statement

Author Contributions

Conflict of Interest

Acknowledgments

References

Nomenclature

Al₂O₃ − H₂O Model

γAl₂O₃ − H₂O Model

Al₂O₃ − H₂O Model

γAl₂O₃ − H₂O Model