Normal Aging: Alterations in Scalp EEG Using Broadband and Band-Resolved Topographic Maps

Given the majority of age-related diseases have been described as disconnection syndromes, understanding the functional connections of normal aging is of considerable importance. Here, an EEG-based scalp level analysis has been performed to identify the alterations in the synchronized brain regions in aged, compared to young persons. Two groups, aged and young subjects were studied, each consisting of 18 participants. First, conventionally extracted broadband topographic maps, also called microstate maps, were examined. The results showed an overall dominant alteration: a uniform decrease in synchronization of brain regions related to cognitive processing resources that was observed only when the maps C and D were characterized in temporal parameters. However, no remarkable change in the spatial distribution was found between the groups. This failure in identifying differences in the spatial distribution was hypothesized to be due to the presence of superimposed signals of several frequencies in the broadband signal that is used for the extraction of microstate maps. Second, spectrally resolved band-wise topographic maps, which we have shown, in a previous study, are able to detect spectral details associated with broadband microstates maps, were used to address this failure. The use of the instantaneous frequency concept is essential in the extraction of band-wise topographic maps, and represents a novelty compared to current studies. The method consists of three steps: (a) from EEG signal, the Empirical Mode Decomposition method is used to extract underlying oscillatory components; (b) these intrinsic oscillatory components are then amplitude demodulated and subjected to numerical equations for the calculation of instantaneous features, such as amplitude, and frequency; finally, (c) based on these instantaneous features, band-wise topographic maps are extracted. Here, as a first application to aging data, these band-wise topographic maps have shown the capability of capturing the age-related changes in both spatial distributions, and in temporal characterization. Spatially, the potential distribution in the aged and the young subject groups, respectively, showed differences, while, in temporal characterization, both increases and decreases were observed, suggesting the lengths of synchronized activities vary differentially, and in accordance with results from fMRI studies. These observed differences also support the dedifferentiation and compensation mechanisms.

Introduction

Numerous studies have shown age-related alterations in functional connectivity of brain regions while evaluating task-based performance as well as during rest, likely ensuing from a decline in cognitive performance. Intra and inter-networks changes in functional connectivity of resting-state networks have been recurrently reported [1]. The patterns of these alterations in functional connectivity are relatively complex i.e., both increases and decreases in number of connections have been found. For example, increase in anterior regions of DMN, subcortical and somatosensory/motor network, and decrease in posterior DMN regions, dorsal attention, and salience networks [2, 3]. In addition, the within-region functional connectivity in the somatosensory, and central visual areas, were found to be non-linearly related to aging, whereas other studies found results in contrast to the above mentioned [4].

In the literature, the complex nature of aging-related changes is based on two main hypotheses i.e., dedifferentiation and compensation. First, dedifferentiation is the term used to explain the loss of underlying functional resources required to perform the given task [5]. Biologically, it is referred to as the chain of processes affected by the deterioration of dopaminergic neuromodulation that result in a reduced specificity of involved cortical areas [6]. Second, the compensation hypothesis explains the involvement of newly recruited brain areas in a higher level of activity to overcome the decline in functional specificity [7]. The compensation process was first identified by Grady et al. [8] while investigating the performance metrics for memory tasks.

In recent years, research on brain changes related to aging increasingly relied on functional magnetic resonance imaging (fMRI). Numerous insights were provided e.g., key brain areas like the anterior cingulate cortex involved in emotional and cognitive processing has been found to be significantly affected by aging, even when its functional connections were investigated during rest [9]. Similarly, Roski et al. [10] found that the age-related resting-state functional connectivity alterations were correlated with behavioral changes. Despite advancements, in the existing literature, inconsistency of results in the aging-related resting-state functional connectivity alterations still persist [11]. Although fMRI data provide high spatial resolution, it has certain limitations. First, fMRI is primarily based on BOLD contrast which allows us to measure neuronal activity only indirectly, whereas non-neuronal factors such as metabolic rate and cerebral blood flow, influencing BOLD response, may hinder the correct assessment of aging-related functional connectivity alterations, aging being linked with several factors that include changes in dopaminergic neurotransmission [12], metabolism [13], alterations in brain structure [14], cerebral blood flow [15], and cognitive resources [16]. Second, due to low temporal resolution, fMRI is less efficient in the investigation of temporal dynamics of functional connectivity, and consequently, it is reasonable to mention that most of the existing aging studies assumed that functional connectivity is stationary during rest. However, a recent fMRI study by Chen et al. [11], inspired from the evidences in the studies of schizophrenia [17], cognition impairment [18], depression [19] and epilepsy [20], has examined the temporal dynamics of resting-state functional connectivity in young and elder subjects, and found it non-stationary. Moreover, they reported a decline in the modularization of dynamic functional connectivity in elderly subjects. Therefore, it is timely to further assess these observations with modalities providing a sufficiently high temporal resolution.

In EEG data analysis, several methods have been used to assess coupling and synchronizations among EEG signals [21]. However, one method, which has recently gained a wide interest of researchers aiming at assessing synchronization across signals, is capable of detecting short lived quasi stationary states. These EEG states are found useful to empirically analyze cognitive and sensory process [22]. Lehman et al. proposed this spatiotemporal method to keep track of quasi-stable neuronal processes at a fine resolution, and named it “Microstate analysis” [23]. In microstate analysis, short-lived functional states are referred to as microstates, which are topographic configurations representing the distribution of electric potential across the scalp [23]. An observation which made microstate analysis a strikingly influential tool for the assessment of neuronal activity in time domain was that the temporal sequence of these spatial maps is non-random, and does not change continuously. These topographic configurations are found to be stable for short duration before transiting abruptly into another. The average duration of microstate ranges from 40 to 120 ms [24]. These short-lived microstates are viewed as an electrophysiological signature of a global integrative process. A study by Lehmann et al. [25] in which microstate configurations and syntax were found significantly different for imagery, and abstract thoughts, respectively, is considered as a validation of their link with cognitive processes. In a clinical context, studies employing microstate analysis found substantial electrophysiological signatures for altered neuronal processes that differ between healthy controls and subjects with psychopathology [26], dementia [27], schizophrenia [28], and stroke [29], provide further evidence of their usefulness. Moreover, recent studies assessing resting state dynamics using simultaneous EEG and fMRI has shown that the imprints of abruptly changing short-lived states of brain calculated using multichannel electrode array are related to resting-state networks. The normative four states are reported to be associated with visual, verbal, interoceptive-autonomic processing and attention reorientation [30, 31]. On how the associations between dynamics of microstates derived from EEG at high temporal resolution and resting-state networks based on slow hemodynamic fluctuations are possible, Van De Ville et al. found that the temporal dynamics of microstates are scale-free dynamics over six dyadic cycles (256 ms-16 s), suggesting the same underlying neurophysiological phenomenon, and microstates being the probable candidate for electrophysiological signatures of slow fluctuations of brain activity as measured by methods relying on hemodynamics [32].

These considerations encouraged the present analysis to explicitly investigate aging-related resting-state alterations using microstate analysis. A related work in which microstates analysis was used to study developmental stages of brain was published in 2002 by Koenig et al. [33]. Temporal profiles of microstates were investigated in subjects aged 6–80 years. They found microstate temporal parameters differ as the brain develops, but mainly had focus on the investigation of developmental changes in the brain of age 6–16 years. However, without going into details, they suggested that the changes in the brains of subjects over 50 years of age are due to aging. In short, their study provided the preliminary evidence that microstates can capture age-related changes. With the knowledge and insights provided by the studies in the last decade, we believe that it is the need of the hour to investigate whether the altered neuronal signatures due to aging observed (if any) using the microstate analysis at scalp support the hypotheses derived from the evidence of existing fMRI studies that are dedifferentiation and compensation. We expect that age-related alterations will not only be found in temporal parameters of microstates but also in their spatial configurations. We have also applied our recently published method of band-wise topographic analysis as a new application to aging data. It has shown great promise to capture further details that are not identifiable with conventional microstate analysis.

Materials and Methods

Data and Pre-processing

Eyes closed resting-state EEG data were recorded in 36 healthy subjects equally divided into aged and young adults. The aged subjects group ranged between the ages of 62–85 years (mean age: 71.8 ± 5.6, 12 males), whereas, young subjects had age ranging from 19 to 31 years (mean age: 23.2 ± 4.1, 12 males). Scalp potentials were measured using Electrical Geodesics sensor net. No subject had a history of neurological disorders, head injuries causing loss of consciousness or mental illness. All subjects were right-handed, tested and confirmed by Edinburgh Manuality test. The acquisitions were performed at, and under the ethical guidelines of “Gabriele d'Annunzio” University of Chieti, after signed written informed consent. The subjects were instructed to close their eyes while staying conscious.

Data Analysis

The analysis has been performed for spatiotemporal assessment of the EEG data in two ways. First, the conventional microstate analysis was implemented using the well-established standardized procedure [34] over the whole bandwidth of the data i.e., 0.01–40 Hz. In this procedure, to start with, the standard deviation across channels also known as Global Field Potential (GFP) was calculated at each time point. It was calculated using the following formula

$\begin{array}{ll}GFP(t)=\sqrt{\frac{1}{N}\left({\sum }_{i=1}^N{(V_i(t)-V_m(t))}^2\right)}& (1)\end{array}$

where N is the number of channels, V_i(t) is the electric potential at the i_th electrode and V_m(t) represents the instantaneous mean potential across electrodes. The GFP(t) is the array representing standard deviations across channels for all data samples. Afterwards, from GFP(t) waveform, the time points of local maxima were extracted to find out the optimal set of microstate maps. The intuitions to only include time points with local maxima were that these instances have high signal-to-noise ratio and reduce the computational complexity of clustering algorithm [35]. Moreover, microstate maps are found to be stable at local maxima of GFP waveform and transitioning from one to another topographical map occurs at local minima [22]. Therefore, in next step, the potentials of all electrodes (topographic maps) at these local maxima time points are subjected to the K-means algorithm for clustering.

For an optimal selection of a number of microstates, the cluster size (number of microstates in the cluster) was varied from 2 to 7. The optimality criteria consisted of Cross Validation (CV)—a modified version of the predictive residual variance [34], and of Explained Variance (EV)—the fit percentage of segmented data. The EV and CV values were calculated for each cluster size. Based on statistical significance between consecutive EV and CV values over the cluster size range, the following two cases were used to define optimality. First, if the increase in EV value by increasing the cluster size is not found statistically significant while CV value increased statistically, previous cluster size is said to be optimum. Second, if, both, the increase in EV value and in CV value is significant, the statistical increase in CV value (i.e., the high probability of having different spatial patterns when clustering is repeated) is given priority and previous cluster size is chosen as optimum. Else, the statistical analysis is performed for the next consecutive cluster size. Based on the criteria, optimal microstates were calculated for individual subjects. For group microstates, these individual microstates were averaged based on minimal topographic dissimilarity [33] for both groups of young and aged subjects. Furthermore, these microstate maps explaining maximal variance were extracted after 300 iterations to minimize error due to stochastic processing. In summary, the step wise procedure for extraction of microstate maps is as follows

1. Calculate GFP waveform by computing standard deviation across electrodes for each time point.

2. Find time points where GFP waveform has local peaks.

3. Input topographic maps of EEG potential at time points found in step 2 to a clustering algorithm.

4. Pre-assign cluster size or set criteria for optimal selection of microstate maps.

5. Repeat clustering algorithm for multiple time (300 iterations performed commonly) to identify microstate maps explaining maximum variance present in the data.

The EEG data were segmented into a topographic sequence of extracted group averaged four microstates as shown in Figure 1.

FIGURE 1

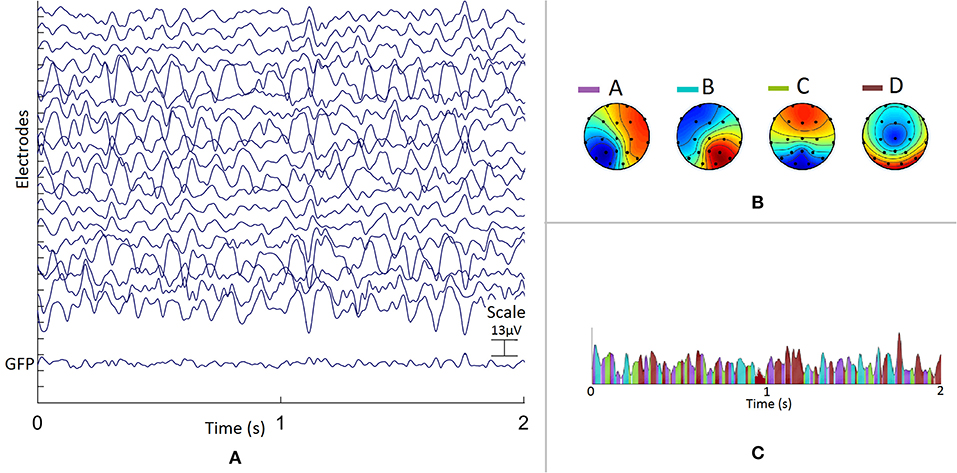
Figure 1. Example of a representative young subject, (A) 2 s epoch of EEG recorded during eyes closed resting state (average referenced) for each of the 19 EEG sensors. The Global Field Power (GFP), standard deviation of EEG across sensors, computed for each time point is shown at the bottom of EEG data. Four averaged microstates labeled a, b, c, d are presented in (B) in a color scale representing the normalized potentials on scalp. In (C) the EEG data is segmented using these microstates: intervals of stability of different microstates are shown in their respective colors.

Second, the conventional microstate analysis was extended to spectrally resolved topographic analysis using band-wise topographic maps [36]. This is to investigate the age-related spatial changes which are limited to a narrow band oscillations. The wide-band [0.01 Hz−40 Hz] EEG data is transformed into five fundamental EEG bands (delta (δ) = [0.01Hz–4Hz), theta (θ) = [4 Hz–8Hz), 191 alpha (α) = [8Hz–12Hz), beta (β) = [12Hz–30Hz), gamma (γ) >= 30 Hz) via time-frequency method with a concept of instantaneous frequencies. This means that the method, unlike traditional frequency analysis approaches, does not require few time periods to calculate the EEG power/energy in a particular frequency band, instead it calculates Instantaneous Frequencies (IFs) and Instantaneous Amplitudes (IAs) for each data time-point. In the method, first, the EEG data is decomposed into bands using the modified Hilbert Huang Transform proposed by Sandoval and Leon [37]. Where, intrinsic oscillations named Intrinsic Mode Functions (IMFs) present in the data are extracted using Complete Ensemble Empirical Mode Decomposition (CEEMD). The CEEMD is an improved version of Empirical Mode Decomposition (EMD) that reduces the “mode-mixing” problem and help in preserving the completeness property of the decomposition. Mode-mixing is named after the drawback of EMD that consists in the leakage of a single physical oscillation across several IMFs. Based on the inherited property of IMFs i.e., local orthogonality, their IFs and IAs are estimated at each time-point using “amplitude demodulation and numerical equations.” The data decomposed into IMFs can be represented as follows

$\begin{array}{ll}x(t)={{\displaystyle \sum }}_{n=1}^k{C}_n(t)+r(t)& (2)\end{array}$

where, ${\left\{C_i(t)\right\}}_{i=1}^k$ are the k decomposed IMFs of x(t) and r(t) is the residue. The process to extract IMFs is called sifting process [38]. The formulae to estimate their IFs and IAs are shown in (3) and (5) respectively:

$\begin{array}{ll}\widehat{w}(t)=d/dt\left[arg(\widehat{s}(t)+j\widehat{\sigma }(t))\right]& (3)\end{array}$

with $\widehat{w}(t)$ symbolizing IF estimated by calculating derivative $\frac{d}{dt}()$ of complex number in which real part $\widehat{s}(t)$ is an amplitude demodulated IMF (${\left\{C_i(t)\right\}}_{i=1}^k$) i.e., iteratively, dividing C(t) by its amplitude envelope until there are no oscillations in the envelope and the imaginary component $\widehat{\sigma }(\text{t})$ is calculated as in (3)

$\begin{array}{ll}\widehat{\sigma }(t)=-sgn\left[d/dt\widehat{s}(t)\right]\sqrt{1-{\widehat{s}}^2(t)}& (4)\end{array}$

where $\sqrt{1-{\widehat{s}}^2(t)}$, the magnitude of the imaginary component is calculated using Pythagorean Theorem in which the magnitude of the complex number is unity due to amplitude demodulation. The expression $-sgn\left[\frac{d}{dt}\widehat{s}(t)\right]$ estimates the sign of the imaginary component, or, in other words, it identifies +ve or –ve plane of the imaginary axis. It is calculated empirically i.e., if $\widehat{s}(t)$ is decreasing, the sign of imaginary component will be positive whereas a negative sign of the imaginary component is for increasing $\widehat{s}(t)$. Hence, reversing the sign (−sgn[]) of derivative $\frac{d}{dt}()$ of $\widehat{s}(t)$ will yield the sign of the imaginary component. While corresponding $\widehat{a}(t)$ is calculated by interpolating local maxima of respective IMF or simply by calculating the upper envelope as in (5):

$\begin{array}{ll}\widehat{a}(t)=interpolate({t_p,U}_p)& (5)\end{array}$

where, t_p are the times at which the local maxima occur and U_p is their magnitude (see details on these equations in [37]). The theoretical explanation along with the representation in algorithmic form can be found in our article in which the method was originally proposed [36]. That study also identifies the spectral details associated with wide-band microstates when the data is spectrally decomposed using the very method. Thus, based on an identified link between the band-wise topographic maps and conventional microstate maps, the use of the method in this study not only provides further insights to differences among distinct age groups but also a step forward in the effectiveness of its use in EEG analysis of synchronized activities. Interested readers are also referred to the studies [37, 38] for more details on method. However, a stepwise overview of procedure for calculation of band-wise topographic maps is as follows

1. Extract IMFs for a pre-processed signal as in equation 2 by employing CEEMD algorithm.

2. Calculate instantaneous frequencies (IFs) and instantaneous amplitudes (IAs) for each IMF and for all time-samples using equation 3 and 5, respectively.

3. Define frequency bands (e.g. δ, θ, α, β, and γ) and construct their amplitude-time-series based on above calculated IAs and IFs i.e., by assigning IA of given sample to the frequency band determined by IF of that sample. This is repeated for all IMFs and resultants are summed up in respective frequency bands to get single amplitude-time-series.

4. Above steps are repeated for all electrodes in a data individually.

5. After construction of band's amplitude time series, conventional microstate procedure as explained above is applied to get topographic maps for each band.

Optimality criterion is applied for each band's topographic maps to get final set of band-wise topographic maps.

The EEG data were spectrally transformed into five fundamental EEG bands based on the estimated IFs at each time point, providing the same temporal resolution as in the time domain EEG data. As will be shown below, the preserved timescale allowed us to analyze spatial patterns at each frequency band and to identify the differences between young and aged subjects that could not be captured by conventional microstate analysis due to the use of full band data. The procedure [34] for the extraction of topographic maps was then applied to each frequency band data and the same optimality criteria (mentioned above) for all band-wise topographic maps from both young and aged subjects group was used.

Moreover, the differences between the aged and young subjects in temporal dynamics of the topographic sequence are quantitatively analyzed for both conventional and band-wise topographic analysis using the following parameters:

- Mean-duration (MD): average stability time of each microstate.

- Frequency-of-occurrence (FO): average number of appearances of each microstate within a window size of 1 min.

- Coverage (Cov): the ratio of time covered by each microstate per total time.

- Transition-probability-matrix: the probability of each microstate transiting into other microstates e.g., transition probability of microstate A to microstate B symbolized by A → B. For example, in resting-state literature, it has been found that, on average, twelve transitions between microstates can occur in a second if the number of microstates is four.

In addition to these parameters, EV is also calculated to demonstrate the fit percentage of extracted microstate maps to the EEG data for both groups. Whereas, for spatial changes, the dissimilarity index has been calculated. The dissimilarity index represents the strength of spatial similarity, the value of which ranges from 0 to 2 with 0 representing the same spatial configuration with similar polarity and 2 for the same spatial configuration with inverted polarity. It should be noted that instead of strictly restricting the definition of similarity to these extremes, we used the range of 0–0.2 and 1.8–2 for similar and inverted polarity configuration, respectively, in our study to account for the variance induced due to averaging of maps across subjects (i.e., group averaged topographic maps).

Results

As mentioned in above section, the analysis is performed in two ways and their results highlighting the differences between two groups in respective analysis are presented in separate subsections below.

Differences Between Groups in the Conventional Microstate Analysis

Based on optimality criteria, for the conventional microstate analysis, four microstate maps are found to be optimal for both young and aged subject group. Four microstate maps are also found to be consistent with the normative and existing literature of microstate analysis. Based on resemblance in the topographic configurations of extracted microstate maps from both groups with the existing literature, standard labels of A, B, C, and D are assigned as shown in Figure 2. Note that these spatial configurations are prototypical representations of potential distribution across electrodes, ignoring polarity inversion (as polarity is not taken in to account: (1) when unique clusters for these potential distribution are being computed using clustering algorithm and (2) when spatial correlations are computed for back-fitting of these maps to the EEG data. The back-fitting is elaborated in Figure 1 where time series across electrodes presented in (a) are represented by topographic maps in (b) as a single time series of colored blocks in (c), whose amplitude is varied according to GFP waveform). The extracted microstate maps used to segment EEG data achieved Global Explained Variance (GEV) of 73.55 ± 3.7% for aged and 79.68 ± 4.1% for the young subjects group. The difference in GEVs is found statistically significant (independent t-test, p < 0.05). Moreover, an overall four microstate maps are also calculated by combining the data of both groups to investigate the need for separate microstate maps for longitudinal studies. The GEVs using overall microstate maps for both groups have decreased i.e., 71.64 ± 5.5% for aged and 78.72 ± 4.3% for the young subjects. Note that, although the differences in the explained variance between individual and combined microstate maps for each group are small, they are found statistical significant (independent t-test, p < 0.05).

FIGURE 2

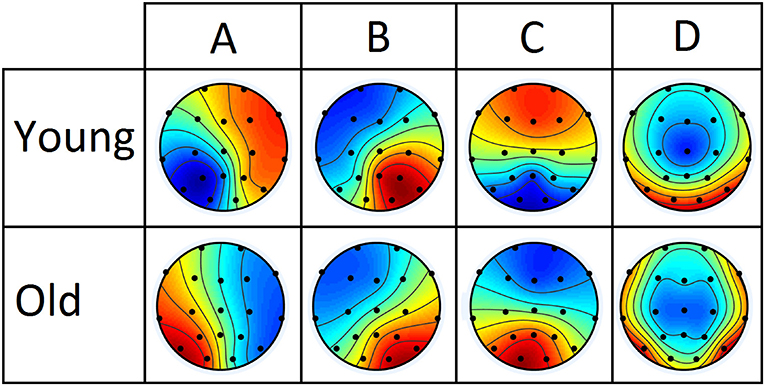
Figure 2. Four group-microstate maps extracted from young and aged datasets separately. The maps are labeled conventionally based on maximum resemblance.

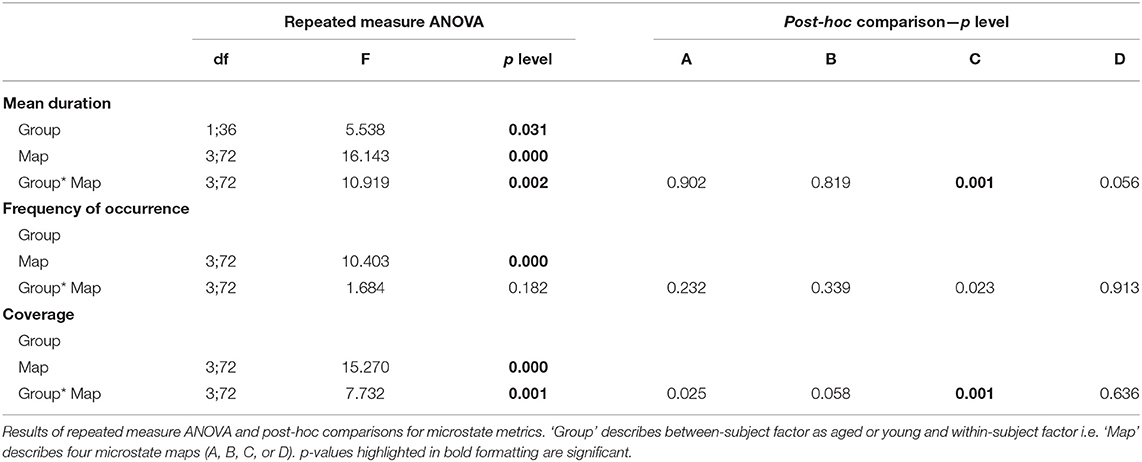
The repeated measures ANOVA (rmANOVA) has been separately (2 × 4) conducted for the three metrics that include duration, frequency of occurrence, and coverage. Each rmANOVA had one factor for groups (Aged, or Young) and one factor for microstate maps (A, B, C, or D). The difference in mean values for metrics presented in Figure 3 are found to be significant (p < 0.05) with the exception of the frequency of occurrence, as presented in Table 1. The significance found in the full model of mean duration and coverage is further tested using reduced models (post-hoc analyses), which revealed that the dynamics of microstate C are dependent on age-related changes and the mean values of metrics for microstate C decrease in aged compared to young subjects group (p < 0.0125, Bonferroni corrected independent t-test). The significance level p = 0.023 for microstate C is found in the frequency of occurrence metrics suggesting marginally significant difference. However, no relation has been found between age and dynamics of the rest of the microstate maps (A, B, or D) in all metrics (p > 0.02, independent t-test).

FIGURE 3

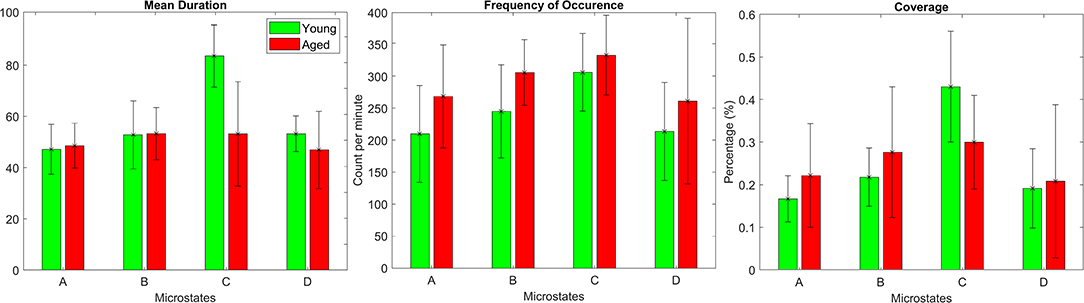
Figure 3. Bars representing average values of microstate metrics calculated for both aged (red) and young (green) subject groups to visualize within group differences for each group-microstate maps.

TABLE 1

Table 1. Statistical comparison of microstate temporal dynamics in aged and young subjects.

Additionally, the syntax analysis, i.e., analyzing the non-randomness or directional dominance in the microstate transitioning, probabilities for each transition pair (in total: twelve pairs, e.g., X↔Y represents two pairs that are X → Y and X←Y) of four microstates are calculated. Our analysis reports discernable patterns for aged and young subjects group i.e., directional dominance is always found opposite (i.e., for example, if aged subjects group has dominant transition from A to B, then young subjects group found having dominant transitions from B to A) for each pair as shown in Figure 4. However, this pattern was not statistically significant except for the transitions between microstates C and D (p < 0.0125, Bonferroni corrected independent t-test).

FIGURE 4

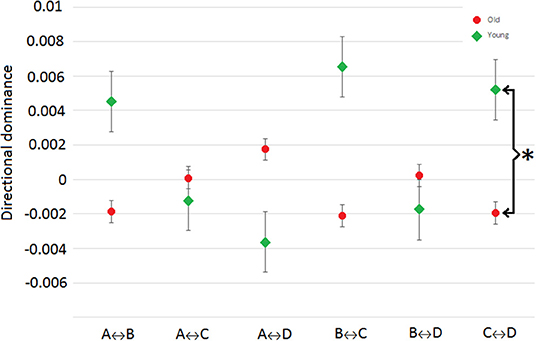
Figure 4. Directional predominance: difference between transition probabilities of each pair i.e., X↔Y = (X → Y)-(X←Y). The sign indicating dominant direction [+ve = (X → Y) and –ve = (X←Y)]. The values are averaged across subjects in respective groups. Asterisk is for significant differences (p < 0.0167) between groups.

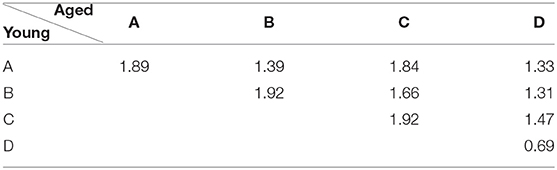
Apart from evaluation of age-related changes in the temporal parameters of conventional microstates, spatial changes across groups are also quantified using the dissimilarity index. The results are presented in Table 2. The results provide evidence that a change (if any) in spatial maps of scalp-level data can be detected effectively as in this case microstate map D found dissimilar across two groups while others are similar with inverted polarity.

TABLE 2

Table 2. Dissimilarity index among the group averaged microstates of young and aged subjects group.

Differences Between Groups in the Band-Wise Topographic Analysis

In this analysis, three topographic maps are found optimal for each band in both groups using the same optimal map selection procedure explained in conventional microstate analysis. The topographic maps of each band are presented in Figure 5. The segmentation of EEG data using these band-wise topographic maps yielded EV of 44.47 ± 3.4% in Delta, 49.15 ± 8.5% in Theta, 54.28 ± 7.3% in Alpha, 46.69 ± 6.7% in Beta, and 44.54 ± 5.5% in Gamma band for the young subjects group; While EV for the aged subjects group is: 61.52 ± 11.3% in Delta, 57.97 ± 9.7% in Theta, 56.79 ± 6.9% in Alpha, 56.48 ± 8.1% in Beta and 51.14 ± 6.5% in Gamma band. The difference in EVs in respective bands among groups has been found statistically significant (independent t-test, p < 0.01, Bonferroni corrected) for all bands except the alpha band.

FIGURE 5

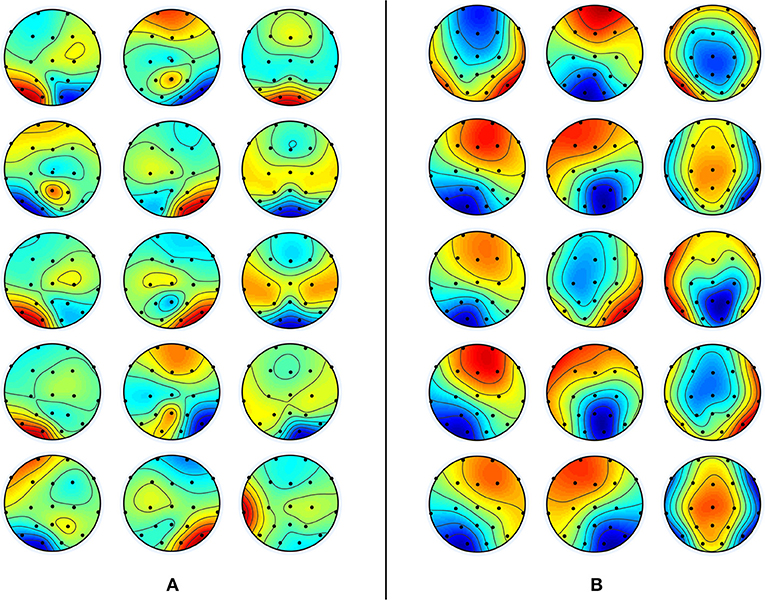
Figure 5. Band-wise group averaged topographic maps of young subject data in (A) and aged subject data in (B). From top to bottom are five frequency bands (δ, θ, α, β, and γ) with 3 maps for each band from left to right, labeled as D1, D2, D3 for delta, T1, T2, T3 for theta, A1, A2, A3 for alpha, B1, B2, B3 for beta, and G1, G2, G3 for gamma band. This sequence is the same for both panels.

Like conventional microstate analysis, the temporal dynamics of band-wise topographic segmentation are also analyzed. Same metrics: mean duration, frequency of occurrence, and coverage are calculated for all band maps i.e., D1, D2, D3 of the delta, T1, T2, T3 of theta, A1, A2, A3 of alpha, B1, B2, B3 of beta and G1, G2, G3 of gamma band. The results are presented in Figure 6. Statistical inferences for the changes among groups are drawn by conducting the repeated measures ANOVA (rmANOVA) separately (2 × 3) for these temporal metrics. Each rmANOVA had one factor for groups (Aged or Young) and one factor for band-wise topographic maps. In the full model i.e., Table 3A, the differences in the temporal characteristics of band-wise topographic segmentation have been found significant (p < 0.05) except for the theta band for the mean duration and for the beta band for the frequency of occurrence. To further analyze the relation found in the full model, post hoc analysis was performed (Table 3B) where, for every band-wise topographic map, at least one temporal metric is found significant (independent t-test, p < 0.0167, Bonferroni corrected).

FIGURE 6

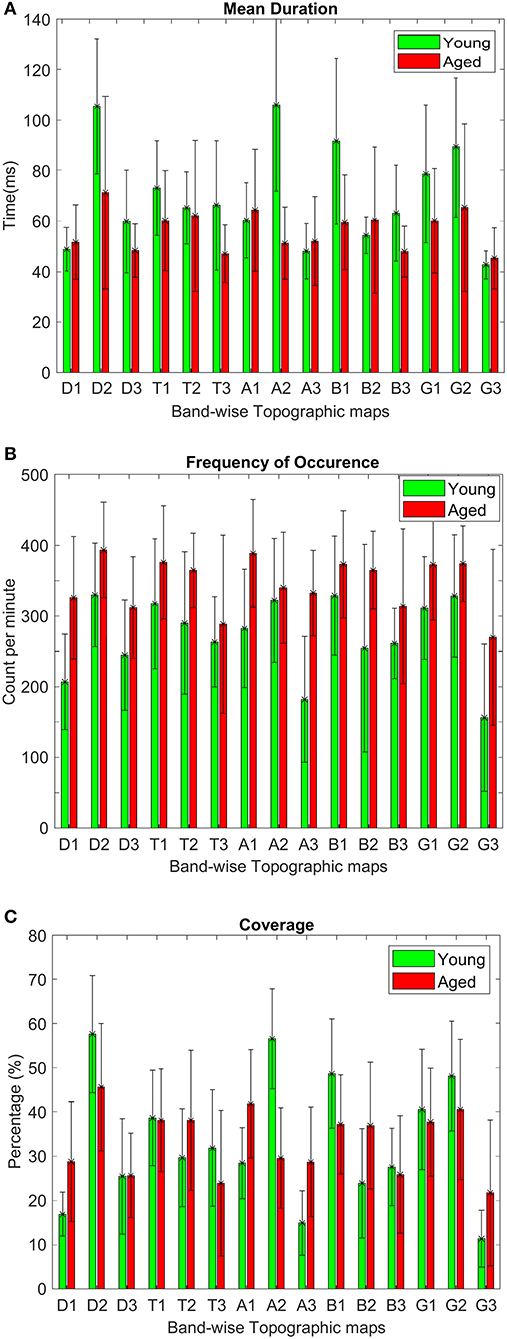
Figure 6. Average values along with standard deviations of microstate metrics: (A) mean duration, (B) frequency of occurrence, and (C) coverage, calculated for both aged and young subject groups to assess within-group differences for each grouped band-wise topographic map.

TABLE 3A

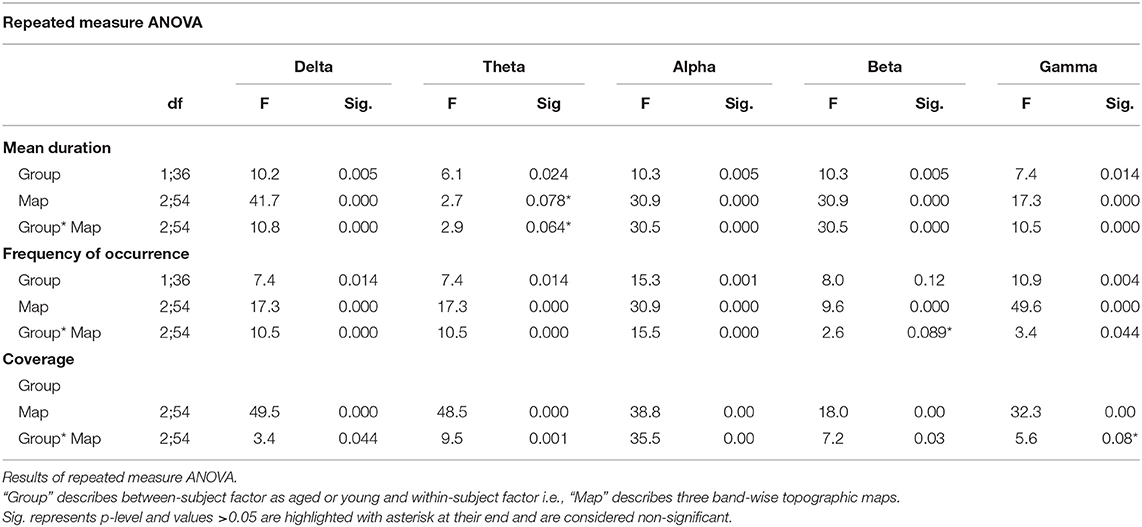
Table 3A. Statistical analysis of the temporal dynamics of band-wise topographic maps in aged and young subjects.

TABLE 3B

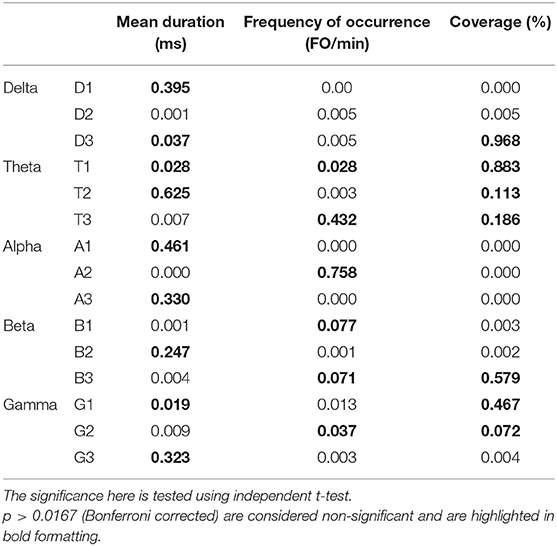
Table 3B. A post-hoc analysis of temporal dynamics of band-wise topographic maps in aged and young subjects.

In addition to the analysis of temporal dynamics, the dissimilarity index has been used to quantify the spatial changes between groups. The dissimilarity index has been calculated across the band-wise topographic maps to give us intra and inter-band similarities if there exist any between two groups. The results averaged across subjects are presented in Figure 7 which quantitatively confirms the visual observations of Figure 5 that narrow band topographies are not only unique with in the bands of same subject, but are also capable of capturing the differences across groups.

FIGURE 7

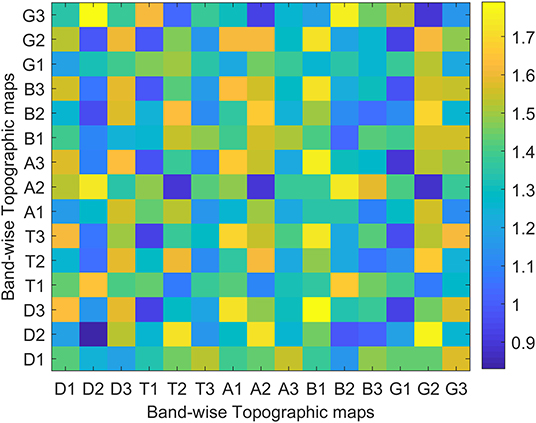
Figure 7. Intra and inter band dissimilarity Indices between topographic maps of young (x-axis) and aged (y-axis) subject groups.

Discussion

In this study, by means of band-wise microstate analysis, we have for the first time, to the best of our knowledge, observed age-related EEG differences in spectrally resolved, spatial domain, scalp EEG data. Conventional microstate analysis which constructs spatially synchronized topographies using the whole bandwidth of EEG data was also used. This conventional analysis served few purposes in the study. First, the extent to which age-related changes are identifiable using broad-band EEG data was still to be analyzed in detail. Second, this provided a reference for comparison of the band-wise topographic method which can be considered as a spectral extension of the former. Third, due to our recent study [36] identifying the link between band-wise topographic maps and conventional microstates, it allowed us to draw inferences and reasonably argue that the results observed using band-wise topographic maps could be linked with age related changes. Finally, on a similar note, to show how these observed results could possibly be related to the results of fMRI studies on normal aging i.e., dedifferentiation and compensation mechanisms. The interesting findings of this article are: (a) conventional microstate analysis was found to have limited effectiveness in identifying age-related changes compared to band-wise topographic analysis. That is, using the band-wise topographic method, the observed variations in temporal features could possibly represent the complex functional changes found in existing fMRI studies [4, 11], whereas conventional analysis failed in providing such details. (b) The relative increase or decrease in timing of synchronized activity between young and aged subject groups is observed at scalp level which among existing fMRI studies [4] has been well-reported. And, (c), the topographic maps of band-wise topographic analysis has shown spatial changes among groups which is unlike conventional microstate analysis. Here, the findings are discussed in the light of the results described above, along with new insights provided by the band-wise topographic method.

Differences Between Groups in the Conventional Microstate Analysis

A relevant work of Koenig et al. [33] in which they studied developmental stages with microstate analysis, using data of subjects between age of 6 and 80 years. They suggested that changes in microstate dynamics in subjects above 50 years of age could possibly be age-related changes. However, the focus of the study being on developmental stages they did not evaluate age-related changes in detail. Therefore, we started our analysis by assessing what insights can be provided by conventional microstates in this regard. In the present work, four microstates were found optimal for both datasets. The Global Explained Variance (GEV) was evaluated to find out whether representing both groups with grouped-averaged microstate maps (extracted after concatenating data of both groups), like in Koenig et al. [33], constitutes a sufficient model, or if, conversely, separating the two groups with distinct averaged microstate maps for each group, yields a more explanatory model. Results demonstrate a significant increase in the GEV values in each group when distinct microstates maps are used for distinct groups. Although the change in GEV is not large, it is statistically significant, and therefore encourages the use of separate microstate maps for aged and young subject groups, respectively (at least in this study). This is to avoid any segmentation bias that may hinder age-related changes. Therefore, we have used separate microstate maps for each group for further analysis. The extracted microstate maps are shown in Figure 2.

Temporal parameters of microstate analysis have their own neurophysiologic significance. The Mean Duration (MD) is representative of stability in underlying neuronal patterns, the Frequency of Occurrence (FO) is representative of propensity of specific neuronal generators to be activated in a given time-period, and coverage is interpreted as the amount of time neuronal generators remain dominant [29]. For example, Seitzman et al. [39] observed that the coverage and FO of microstate B has increased significantly when analyzing open-eyes data compared to closed-eyes data for same subject across 24 healthy young subjects (age: 21.1 ± 4.5 years). Note that microstate B has been previously linked with the visual system [40]. Similarly, a few other studies have also found alterations in the temporal parameters of other microstates, such as C and D [31, 41, 42]. Therefore, to investigate if there are any age-related alterations to these parameters, the above-mentioned metrics were calculated (results in Figure 3) for both groups, and rmANOVA (Table 1) was performed to search for an overall difference among the four microstate maps. The metrics MD and coverage have been found to be statistically different. Further investigation using post hoc analysis revealed that the differences in the respective metrics are mainly due to the decreases in microstate C in aged compared to young subjects. The decrease in microstate C in aged subjects group is not surprising considering its relation to the hemodynamic counterpart: It has been found positively correlated with the BOLD signals of the anterior cingulate cortex (ACC), right anterior insula, inferior frontal gyri and left claustrum [40]. These areas are also said to be roughly related to resting state network (RSN 6) in Mantini et al. work [43]. Several fMRI studies identified age-related decline in functional connectivity involving these regions. As in Damoiseaux et al. [2], decrease in connectivity involving most frontal and parietal brain regions has been found. The ACC which is related to working memory has been found to have decreased activations in elderly people [44]. Additionally, not only in fMRI studies, Kalpouzos et al. [45] suggested decline in metabolic activity at ACC and prefrontal cortex using Positron Emission Tomography. Similarly, structural changes i.e., gray matter volume in ACC along with parietal cortex, insula, and cerebellum has been found to be reduced in aged people [46]. Therefore, decrease in temporal parameters has been in-line with existing studies analyzing data of different modalities, and possibly this observed change is due to the attention deficiency and limited emotional, cognitive, and perceptual brain processing in normal aging.

Furthermore, we have also computed the syntax of microstate-based segmentation of EEG. The results in Figure 4 show that transitions in pairs is inverted between young and aged subjects but there is no statistically significant difference except for the pair of C↔D. This suggests an overall balance is maintained in connectivity patterns in both groups. The balance in elder people is suggested to be due to the compensatory mechanism which fulfills the need of any reduced activity in performing a given task [11]. Despite the differences in connectivity of several regions involved in deficiency due to normal aging, several fMRI studies have reported the compensatory mechanisms. This compensation-related activity has been formulated using three cognitive models as reported by Sala-Llonch et al. [4]. One of these models named “Hemispheric Asymmetry Reduction in Old Adults” informs about the compensatory activity arising from decline in lateralized pattern of activity in frontal region in elder people [47]. And, Britz et al. [40] reported that microstate D is related to the BOLD signal of ventral and right-lateralized dorsal areas of parietal and frontal cortex which are responsible for reorientation and switching of attention. Therefore, it is reasonable to assume that the significant change in the syntax of pair C↔D are due to the microstate D.

Besides inferring that the change in microstate D is due to compensatory activity, to further support the link of observed changes in our conventional microstate analysis with the dedifferentiation and compensatory mechanisms, we highlight that, in Figure 2, microstate D appears visually dissimilar between the groups in spatial configuration, a result that is also supported quantitatively by the dissimilarity index in Table 2. However, except for microstate D, no other microstate map shows such dissimilarity. This could be acceptable for microstates A and B, as they were found similar in their temporal parameters as well. But the spatial similarity of microstate C (even though its temporal parameters have shown significant alterations) across groups raised concern about the possibility of visualizing the spatial changes at scalp level that occurred locally in normal aging due to dedifferentiation and compensatory mechanisms as observed in fMRI studies at the cortical level. Having said that, it is also observed from the existing fMRI studies that the age-related changes are not straightforward, i.e., both increases and decreases are found which are in abidance to the results of dynamic balancing of connectivity patterns of both young and elder brains [11]. Based on these results, it can be deduced that for dedifferentiation and compensation mechanisms to be true, if there is a decrease in connectivity of a certain region, there should be a compensatory increase in connectivity involving other regions. However, detecting such mechanisms topographically with scalp-level data may well be tricky as in our analysis of conventional microstate analysis, and might require adding constraints or transformations to the scalp data to be resolved.

One possible reason which we thought of to help us solve this issue of observing age-related changes spatially at scalp-level analysis, was to spectrally decompose the data. The intuition behind is that we did not observe the age-related changes occurring in local brain areas could be due to the amalgamation of signals of different frequencies into one signal which will consequently describe only the prominent change even if multiple changes have occurred at different frequencies. In such a case, it would be reasonable to assume that the failure in capturing such changes could be due to the use of broad-bandwidth of the signal for the extraction of the conventional microstate maps. Therefore, we hypothesized that decomposing spectrally the EEG signals, and then evaluating the spatial patterns could capture the complex changes which are already known from fMRI studies. This brings forth the need to apply the band-wise topographic analysis to investigate differences between young and aged subjects.

Differences Between Groups in the Band-Wise Topographic Analysis

To strengthen our point of using separate microstate maps for young and aged subjects, EV has been calculated for band-wise topographic maps at each frequency band using EEG data. The statistically significant (p < 0.01) differences in EV values suggest age-related changes should be considered a factor while examining spatial synchronicity. As expected, there are more differences in temporal and spatial characterization of band-wise analysis compared to broad-band analysis between the two groups. For the temporal characterization of band-wise topographic analysis, the metrics analogous to those used in the conventional analysis, evaluating stability, occurrence, and percentage of existence over time, were used. The results presented in Figure 6 show a complex pattern of increase and decrease between groups. The rmANOVA (2 × 3) analysis (Table 3A) suggest a significant change between groups at each frequency band for each metric except for the theta band concerning MD, and for the beta band concerning FO. Further analysis (Post hoc: Table 3B) revealed that at least one metric is found to have statistically different values at each band between groups. The observed changes in temporal characteristics of band-wise topographic segmentation are in line with our hypothesis. That is, on one hand, in the temporal domain, both increases and decreases in MD are observed, however, the dynamic balance in synchronized activity across brain, which has been found in fMRI studies, is still maintained and can be noticed at scalp-level analysis. For example, the MD for A1 and A3 increased in aged compared to young subjects but a decrease in A2 compensate this. Similarly, other temporal parameters also adjusted themselves to maintain a dynamic balance.

On the other hand, in the spatial domain, from Figure 5, the spatial differences can also be visualized easily. The band-wise spatial maps of young subjects appear to be more localized than those of aged subjects. This spread in synchronized brain activity in the maps of aged subjects is not surprising because, in existing studies of fMRI data, increases in brain activity in aged subjects are reported, and these increases in activation have heterogeneous localization compared to young subjects [4]. At this point, we refrain from concluding that these spatial changes are a consequence of age-related dedifferentiation and compensation mechanisms, but the inferences that can be drawn from fMRI studies do highly support this notion. For example, a few studies also suggested that brain regions continue to reconfigure with age during rest to compensate for decline in other regions [48]. Moreover, the “Posterior-Anterior Shift with Aging (PASA),” experimentally proven model to describe age-related changes also support changes which include both increases and decreases in connected regions along with the changes in spatial patterns [49]. As in PASA, Davis et al., have described the dedifferentiation mechanism with the decline in posterior midline cortex combined with the compensatory mechanism of increased activity in medial frontal cortex. However, to be sure that the spatial changes observed in band-wise topographic maps are due to age-related changes, one has to reconstruct the underlying sources at the time of their occurrences by utilizing some forward/inverse modeling. But, to further add support to our opinion, we would like to take advantage of recently identified associations between band-wise topographic maps and conventional microstate maps in one of our works [36]. It says that conventional microstates maps could well be represented by the combination of any of these five band-wise topographic maps (one from each band). This means that a meta-process described by one microstate map can be spectrally resolved into five sub-processes, which are described by five band-wise topographic maps, one from each band. Thus, these observed spatial and temporal changes in band-wise topographic analysis can be linked to age-related changes observed in fMRI studies similar to the conventional microstate analysis in the above subsection. For example, in Javed et al. [36], band-wise topographies D2 and D3 are associated with conventional microstate C which is described above to be linked with ACC [40], and the ACC has been found to have decreased activations in elderly people [44]. Moreover, results of spatial dissimilarity index presented in Figure 7 show intra and inter band dissimilarities among groups. No two band-wise topographic maps are found similar, which is unlike conventional microstate maps. Therefore, it is reasonable to suggest that the failure in identifying the spatial changes among groups using conventional microstate maps is due to the amalgamation of signals of different frequencies into one signal of broad-bandwidth. However, being one of the very first studies using band-wise topographic maps to investigate dedifferentiation and compensation mechanism at scalp-level, these findings reveal new and interesting directions that require further assessments.

Conclusion and Future Work

One of the most frequently reported age-related factors is the change in cognitive and perceptual systems, which may consequently affect behavior. In turn, the majority of age-related diseases, including Alzheimer, which are related to these systems, are reported as disconnection syndromes. Therefore, the need to carry out this work lies in the importance of identifying the scalp-level electrophysiological correlates of fMRI findings. As it is believed that the results found via different modalities, more so with the one that directly measures neuronal potentials, and recent analysis tools, will be helpful in developing consensus over aging-related alterations; inching closer to the underlying mechanism which is still elusive, and consequently helping in limiting the differences between young and elder brain. In this work, we first showed that conventional microstate analysis can only identify the prominent changes in normal aging and is unable to detect complex changes. However, to conclude on results of conventional microstate analysis if one wants to use it for, let say, identification of any potential electrophysiological biomarkers of a given disease, we suggest using separate microstate maps for young and aged subject groups. Second, to get further insights, we applied our recently proposed band-wise topographic analysis which has shown more sensitivity in detecting the changes between the young and aged groups. However, we are constrained in drawing conclusions on their relevance since, to the best of our knowledge, this is the first study evaluating spectrally resolved spatial changes of aging. And unlike conventional microstate analysis where the corresponding resting state networks are known for each microstate map, a simultaneous study of EEG and fMRI is an imminent future prospect for band-wise topographic analysis to unfold its functional significance. Having said that, it is also important to mention that the band-wise topographic method has shown the glimpse of advancements that could converge the efforts of linking the results from different modalities to one another.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Ethics Statement

The studies involving human participants were reviewed and approved by Comitato di Bioetica Università Gabriele D'Annunzio, Chieti, Italy. The patients/participants provided their written informed consent to participate in this study.

Author Contributions

EJ with the supervision of CD contributed to design, implementation, and writing of the manuscript. PC and FZ collected and pre-processed data. PC provided technical assistance during implementation phase. All authors contributed to the analysis and discussed results.

Conflict of Interest

The authors declare that the research has been conducted independent of any financial or commercial interests.

References

1. Tomasi D, Volkow ND. Aging and functional brain networks. Mol Psychiatr. (2012) 17:471–558. doi: 10.1038/mp.2012.27

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Damoiseaux JS, Beckmann CF, Arigita EJ, Barkhof F, Scheltens P, Stam CJ, et al. Reduced resting-state brain activity in the ‘Default Network' in normal aging. Cereb Cortex. (2008) 18:1856–64. doi: 10.1093/cercor/bhm207

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Andrews-Hanna JR, Snyder AZ, Vincent JL, Lustig C, Head D, Raichle ME, et al. Disruption of large-scale brain systems in advanced aging. Neuron. (2007) 56:924–35. doi: 10.1016/j.neuron.2007.10.038

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Sala-Llonch R, Bartrés-Faz D, Junqu é C. Reorganization of brain networks in aging: a review of functional connectivity studies. Front Psychol. (2015) 6:663. doi: 10.3389/fpsyg.2015.00663

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Park DC, Polk TA, Park R, Minear M, Savage A, Smith MR. Aging reduces neural specialization in ventral visual cortex. Proc Natl Acad Sci USA. (2004) 101:13091–5. doi: 10.1073/pnas.0405148101

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Li SC, Lindenberger U, Sikström S. Aging cognition: from neuromodulation to representation. Trends Cognit Sci. (2001) 5:479–86. doi: 10.1016/S1364-6613(00)01769-1

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Turner GR, Spreng RN. Executive functions and neurocognitive aging: dissociable patterns of brain activity. Neurobiol Aging. (2012) 33:826.e1–826.e13. doi: 10.1016/j.neurobiolaging.2011.06.005

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Grady CL, Maisog JM, Horwitz B, Ungerleider LG, Mentis MJ, Salerno JA, et al. Age-related changes in cortical blood flow activation during visual processing of faces and location. J Neurosci. (1994) 14:1450–62. doi: 10.1523/JNEUROSCI.14-03-01450.1994

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Cao W, Luo C, Zhu B, Zhang D, Dong L, Gong J, et al. Resting-state functional connectivity in anterior cingulate cortex in normal aging. Front Aging Neurosci. (2014) 6:280. doi: 10.3389/fnagi.2014.00280

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Roski C, Caspers S, Langner R, Laird AR, Fox PT, Zilles K, et al. Adult age-dependent differences in resting-state connectivity within and between visual-attention and sensorimotor networks. Front Aging Neurosci. (2013) 5:67. doi: 10.3389/fnagi.2013.00067

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Chen Y, Wang W, Zhao X, Sha M, Liu Y, Zhang X, et al. Age-related decline in the variation of dynamic functional connectivity: a resting state analysis. Front Aging Neurosci. (2017) 9:203. doi: 10.3389/fnagi.2017.00203

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Bäckman L, Lindenberger U, Li SC, Nyberg L. Linking cognitive aging to alterations in dopamine neurotransmitter functioning: recent data and future avenues. Neurosci Biobehav Rev. (2010) 34:670–7. doi: 10.1016/j.neubiorev.2009.12.008

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Segobin S, La Joie R, Ritz L, Beaunieux H, Desgranges B, Chételat G, et al. FDG-PET contributions to the pathophysiology of memory impairment. Neuropsychol Rev. (2015) 25:326–55. doi: 10.1007/s11065-015-9297-6

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Salami A, Wåhlin A, Kaboodvand N, Lundquist A, Nyberg L. Longitudinal evidence for dissociation of anterior and posterior MTL resting-state connectivity in aging: links to perfusion and memory. Cereb Cortex. (2016) 26:3953–63. doi: 10.1093/cercor/bhw233

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Zarrinkoob L, Ambarki K, Wåhlin A, Birgander R, Eklund A, Malm J. Blood flow distribution in cerebral arteries. J Cereb Blood Flow Metabol. (2015) 35:648–54. doi: 10.1038/jcbfm.2014.241

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Nyberg L, Andersson M, Kauppi K, Lundquist A, Persson J, Pudas S, et al. Age-related and genetic modulation of frontal cortex efficiency. J Cogn Neurosci. (2014) 26:746–54. doi: 10.1162/jocn_a_00521

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Du Y, Pearlson GD, Yu Q, He H, Lin D, Sui J, et al. Interaction among subsystems within default mode network diminished in schizophrenia patients: a dynamic connectivity approach. Schizophr Res. (2016) 170:55–65. doi: 10.1016/j.schres.2015.11.021

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Wong WP, Hassed C, Chambers R, Coles J. The effects of mindfulness on persons with mild cognitive impairment: protocol for a mixed-methods longitudinal study. Front Aging Neurosci. (2016) 8:156. doi: 10.3389/fnagi.2016.00156

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Qin B, Zhou X, Michael KD, Liu Y, Whittington C, Cohen D, et al. Psychotherapy for depression in children and adolescents: study protocol for a systematic review and network meta-analysis. BMJ Open. (2015) 5:e005918. doi: 10.1136/bmjopen-2014-005918

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Liu S, Yu W, Lü Y. The causes of new-onset epilepsy and seizures in the elderly. Neuropsychiatr Disease Treat. (2016) 12:1425–34. doi: 10.2147/NDT.S107905

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Wen D, Zhou Y, Li X. A critical review: coupling and synchronization analysis methods of EEG signal with mild cognitive impairment. Front Aging Neurosci. (2015) 7:54. doi: 10.3389/fnagi.2015.00054

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Michel CM, Koenig T, Brandeis D, Gianotti LRR, Wackermann J. Electrical Neuroimaging. New York, NY: Cambridge University Press (2009).

Google Scholar

23. Lehmann D, Ozaki H, Pal I. EEG alpha map series: brain micro-states by space-oriented adaptive segmentation. Electroencephalogr Clin Neurophysiol. (1987) 67:271–88. doi: 10.1016/0013-4694(87)90025-3

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Khanna A, Pascual-Leone A, Michel CM, Farzan F. Microstates in resting-state EEG: current status and future directions. Neurosci Biobehav Rev. (2015) 49:105–13. doi: 10.1016/j.neubiorev.2014.12.010

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Lehmann D, Strik WK, Henggeler B, Koenig T, Koukkou M. Brain electric microstates and momentary conscious mind states as building blocks of spontaneous thinking: I. visual imagery and abstract thoughts. Int J Psychophysiol. (1998) 29:1–11. doi: 10.1016/S0167-8760(97)00098-6

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Fingelkurts AA, Fingelkurts AA, Bagnato S, Boccagni C, Galardi G. EEG oscillatory states as neuro-phenomenology of consciousness as revealed from patients in vegetative and minimally conscious states. Conscious Cogn. (2012) 21:149–69. doi: 10.1016/j.concog.2011.10.004

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Strik WK, Chiaramonti R, Muscas GC, Paganini M, Mueller TJ, Fallgatter AJ, et al. Decreased EEG microstate duration and anteriorisation of the brain electrical fields in mild and moderate dementia of the alzheimer type. Psychiatr Res Neuroimag. (1997) 75:183–91. doi: 10.1016/S0925-4927(97)00054-1

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Andreou C, Faber PL, Leicht G, Schoettle D, Polomac N, Hanganu-Opatz IL, et al. Resting-state connectivity in the prodromal phase of schizophrenia: insights from EEG microstates. Schizophren Res. (2014) 152:513–20. doi: 10.1016/j.schres.2013.12.008

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Zappasodi F, Croce P, Giordani A, Assenza G, Giannantoni NM, Profice P, et al. Prognostic value of EEG microstates in acute stroke. Brain Topogr. (2017) 30:698–710. doi: 10.1007/s10548-017-0572-0

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Schwab S, Koenig T, Morishima Y, Dierks T, Federspiel A, Jann K. Discovering frequency sensitive thalamic nuclei from EEG microstate informed resting state FMRI. NeuroImage. (2015) 118:368–75. doi: 10.1016/j.neuroimage.2015.06.001

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Milz P, Faber PL, Lehmann D, Koenig T, Kochi K, Pascual-Marqui RD. The functional significance of EEG microstates-associations with modalities of thinking. NeuroImage. (2016) 125:643–56. doi: 10.1016/j.neuroimage.2015.08.023

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Van de Ville D, Britz J, Michel CM. EEG microstate sequences in healthy humans at rest reveal scale-free dynamics. Proc Natl Acad Sci USA. (2010) 107:18179–84. doi: 10.1073/pnas.1007841107

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Koenig T, Prichep L, Lehmann D, Sosa PV, Braeker E, Kleinlogel H, et al. Millisecond by millisecond, year by year: normative EEG microstates and developmental stages. NeuroImage. (2002) 16:41–8. doi: 10.1006/nimg.2002.1070

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Brunet D, Murray MM, Michel CM. Spatiotemporal Analysis of Multichannel EEG: CARTOOL. Computational Intelligence and Neuroscience (2011).

PubMed Abstract | Google Scholar

35. Murray MM, Brunet D, Michel CM. Topographic ERP analyses: a step-by-step tutorial review. Brain Topogr. (2008) 20:249–64. doi: 10.1007/s10548-008-0054-5

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Javed E, Croce P, Zappasodi F, Gratta CD. Hilbert spectral analysis of EEG data reveals spectral dynamics associated with microstates. J Neurosci Methods. (2019) 325:108317. doi: 10.1016/j.jneumeth.2019.108317

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Sandoval S, De Leon PL. Theory of the hilbert spectrum. ArXiv. (2015) 1–61. Available online at: https://arxiv.org/abs/1504.07554v4

Google Scholar

38. Huang NE, Shen Z, Long SR, Wu MC, Shih HH, Zheng Q, et al. The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis. Proc Royal Soc Lond A. (1998) 495:903–95. doi: 10.1098/rspa.1998.0193

CrossRef Full Text | Google Scholar

39. Seitzman BA, Abell M, Bartley SC, Erickson MA, Bolbecker AR, Hetrick WP. Cognitive manipulation of brain electric microstates. NeuroImage. (2017) 146:533–43. doi: 10.1016/j.neuroimage.2016.10.002

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Britz J, Van De Ville D, Michel CM. BOLD correlates of EEG topography reveal rapid resting-state network dynamics. NeuroImage. (2010) 52:1162–70. doi: 10.1016/j.neuroimage.2010.02.052

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Katayama H, Gianotti LR, Isotani T, Faber PL, Sasada K, Kinoshita T, et al. Classes of multichannel EEG microstates in light and deep hypnotic conditions. Brain Topogr. (2007) 20:7–14. doi: 10.1007/s10548-007-0024-3

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Brodbeck V, Kuhn A, von Wegner F, Morzelewski A, Tagliazucchi E, Borisov S, et al. EEG microstates of wakefulness and NREM sleep. NeuroImage. (2012) 62:2129–39. doi: 10.1016/j.neuroimage.2012.05.060

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Mantini D, Perrucci MG, Del Gratta C, Romani GL, Corbetta M. Electrophysiological signatures of resting state networks in the human brain. Proc Natl Acad Sci USA. (2007) 104:13170–75. doi: 10.1073/pnas.0700668104

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Otsuka Y, Osaka N, Morishita M, Kondo H, Osaka M. Decreased activation of anterior cingulate cortex in the working memory of the elderly. NeuroReport. (2006) 17:1479–82. doi: 10.1097/01.wnr.0000236852.63092.9f

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Kalpouzos G, Chételat G, Baron JC, Landeau B, Mevel K, Godeau C, et al. Voxel-based mapping of brain gray matter volume and glucose metabolism profiles in normal aging. Neurobiol Aging. (2009) 30:112–24. doi: 10.1016/j.neurobiolaging.2007.05.019

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Good CD, Johnsrude IS, Ashburner J, Henson RN, Friston KJ, Frackowiak RS. A voxel-based morphometric study of ageing in 465 normal adult human brains. NeuroImage. (2001) 14:21–36. doi: 10.1006/nimg.2001.0786

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Cabeza R. Hemispheric asymmetry reduction in older adults: the HAROLD model. Psychol Aging. (2002) 17:85–100. doi: 10.1037/0882-7974.17.1.85

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Schaefer A, Margulies DS, Lohmann G, Gorgolewski KJ, Smallwood J, Kiebel SJ, et al. Dynamic network participation of functional connectivity hubs assessed by resting-state FMRI. Front Hum Neurosci. (2014) 8:195. doi: 10.3389/fnhum.2014.00195

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Davis SW, Dennis NA, Daselaar SM, Fleck MS, Cabeza R. Qué PASA? The posterior-anterior shift in aging. Cereb Cortex. (2008) 18:1201–9. doi: 10.1093/cercor/bhm155

PubMed Abstract | CrossRef Full Text | Google Scholar