Heterogeneous Solvent Dielectric Relaxation in Polymer Solutions of Water and Alcohols

Introduction

Water is the most abundant liquid on Earth and exhibits numerous peculiar properties. The supercooled state and the glassy state of water have been studied extensively [1]. Unfortunately, pure water is easily crystallized; hence, it is impossible to obtain water in a liquid state between 150 and 234 K (the so-called “no man's land”) [2]. To understand the phenomena in the no man's land, various types of systems that include water have been examined. The crystallization of water can be avoided by dissolving guest molecules in water [3–23]. Impregnating porous materials with water [24–35] can also prevent water's crystallization. These systems have been called soft and hard confinements, respectively. The physics of such systems involves not only the water but also the interaction between water and the guest molecules or the surface of the porous material.

One of the most intriguing and controversial aspects of the dynamics of water from its liquid state to its glassy state is the non-Arrhenius-Arrhenius (non-A-A) crossover [35–37]. This crossover has been discussed based on the observations of water dynamics over an extremely wide range of relaxation times and viscosities. The non-A-A crossover of water dynamics has been observed in various types of aqueous systems, such as aqueous solutions of alcohols, ethylene glycol (EG) oligomers, sugars, polymers, and protein and porous systems those contain water [3, 5–11, 35]. The temperature dependence of the relaxation process of water in these systems changes at a certain temperature, which is called the crossover temperature, T_c, in this paper. T_c has been observed in the temperature range of 160–260 K, depending on the kind of solute and water content. Below T_c, the relaxation process involves a temperature-independent apparent activation energy classified as the strong glass. Conversely, above T_c, the relaxation time, or viscosity shows a non-Arrhenius temperature dependence. The temperature dependence of the relaxation time of water increases with decreasing temperature; it shows Vogel–Fulcher–Tammann (VFT) temperature dependence [38–40]. In this case, the apparent activation energy of the relaxation process increases with decreasing temperature, which leads to the conclusion that the relaxation process is cooperative, and that the cooperativity of the molecular motion increases with decreasing temperature. The glass-forming materials whose apparent activation energy increases with decreasing temperature are called the fragile glasses [41]. For this reason, the non-A-A crossover of water dynamics has also been called the fragile–strong transition of water.

The non-A-A crossover has been generally observed for the Johari–Goldstein (JG) secondary β relaxation in glass-forming materials at T_g of the α-relaxation and also for the α-relaxation of faster components in dynamically asymmetric binary systems [42–44]. The dynamic crossover of the transport properties of glass-forming liquids has been actively discussed [45]. That study suggested the importance of the dynamic crossover temperature instead of the glass transition on single component glass-forming liquids. In this study, we discuss the role of the glass transition in the dynamic crossover of binary mixtures of a polymer and hydrogen-bonding solvents. In order to discuss the non-A-A crossover of water dynamics in a polymer matrix, in addition to the previous works, we performed broadband dielectric spectroscopy measurements of poly(vinylpyrrolidone)–water (PVP–water), PVP–propylene glycol (PG), PVP–EG, and PVP−1-propanol (PrOH) mixtures with 65 wt% of PVP in a wide frequency over a temperature range of 123–318 K. For the PVP–water mixture, three relaxation processes were observed simultaneously: the slowest process originated from the segmental chain motion of PVP (called the α-relaxation of PVP), the fastest process originated from the primary relaxation process of water (called the ν-process) [3], the relatively small relaxation process at a frequency between those of the α-relaxation of PVP and the ν-process. The temperature dependence of the relaxation time of the ν-process exhibits a non-A-A crossover at the glass transition temperature T_g,PVP of the α-relaxation of PVP. Conversely, the crossover of the relaxation process of alcohol at T_g,PVP in alcohol–PVP mixtures differs completely from that observed in the PVP–water mixture.

Experimental

The PVP used in this study was purchased from Sigma Aldrich and had a weight-averaged molecular weight M_w = 10,000 g/mol. The PG, EG, and PrOH were purchased from Wako Pure Chemical Industries, Ltd. The purities of the solvents (guaranteed reagent grade) were better than 99 % in those mass. Before use, the PVP was purified using an ion-transfer resin and then freeze-dried in a vacuum before being mixed with water or alcohols to reduce dc conductivity and electrode polarization (EP). The aqueous PVP solution was prepared with a PVP concentration C_PVP = 65 wt% in pure water with a conductivity of 18.2 MΩ cm (Milli-Q water) to avoid the crystallization of water. PVP solutions with PG, EG, and PrOH were also prepared with C_PVP = 65 wt%.

Dielectric measurements were carried out in the frequency range from 10 mHz to 3 GHz using an Alpha-A analyzer (Novocontrol, 10 mHz to 10 MHz), a precision impedance analyzer (IA; Agilent Technologies 4294A, 40 Hz to 110 MHz), and an impedance/material analyzer (IMA; Hewlett Packard 4291A, 1 MHz to 1.8 GHz, and Agilent Technologies E4991A, 1 MHz to 3 GHz). For the IA and IMA measurements, the temperature was controlled using a Kleemenko Cooler (Bio120; MMR Technologies) and a laboratory-made cooling system with liquid nitrogen, which allowed cooling from 153 to 298 K in steps of 5 K with an accuracy of ±0.1 K. For the Alpha-A analyzer measurement, the temperature was controlled using a Quatro cryosystem (Novocontrol) from 123 to 298 K in steps of 5 K with an accuracy of ±0.01 K. A coaxial cylindrical-cell-type electrode with an outer conductor with an inner diameter of 3.5 mm and an inner conductor with a diameter of 2.0 mm and a length of 2.0 mm (geometrical capacitance: 0.23 pF) was used for the IA and IMA measurements. A coaxial cylindrical-cell-type electrode with an outer conductor with an inner diameter of 24.0 mm and an inner conductor with a diameter of 19.0 mm (geometrical capacitance: 1.11 pF), an interdigitated electrode with 15 μm spacing between the electrodes (geometrical capacitance: 0.9 pF), and a parallel plates electrode with 0.1 mm spacing (geometrical capacitance: 28 pF) were used for the Alpha-A analyzer measurement. To determine T_g, differential scanning calorimetry (DSC) measurements were also carried out over a temperature range from 108 to 298 K, at a rate of 20 K/min using a DSC 7 (PerkinElmer).

Results

Figure 1 shows the real and imaginary parts of the complex permittivity of the 65 wt% PVP–PG mixture as a function of frequency. At 298 K, two relaxation steps appear clearly in the real part ε′: one around 100 Hz and the second around 100 MHz. A loss peak near 100 MHz appears in the imaginary part ε″, whereas no loss peak is visible at 100 Hz. The loss peak at 100 Hz is partly concealed by ionic contributions, namely, EP and dc conductivity. We also studied the two dielectric relaxation processes at 298 K in PVP solutions with water, alcohol, and chloroform and examined the origins in detail [3, 46–49]. The relaxation process observed above 100 MHz is the primary relaxation of the solvents. For comparison, the spectrum of pure PG at 298 K is shown as black dotted curves. The loss peak of the primary relaxation of PG slightly shifts to low frequency and the dielectric constant at around 1 MHz decreased from 29 to around 10 by adding PVP. The decrease of the dielectric constant is consistent with decreasing PG amount by adding PVP, i.e., 29 × (1–0.65) = 13. In contrast, the relaxation process below 10 MHz is caused by local chain fluctuations of PVP. In previous work, the effective dipole moment of the repeat unit of PVP was determined from the relaxation strength of the PVP process by using the Onsager equation, and the effects of the permittivity of solvents were estimated [49]. We confirm here that the effective dipole moments of the repeat unit of PVP obtained from all solutions were the same and corresponded to the repeat unit of PVP.

FIGURE 1

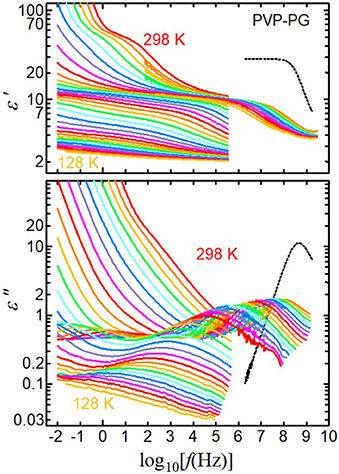
Figure 1. Real (ε′) and imaginary (ε″) parts of complex permittivity as a function of frequency for the 65 wt% PVP–PG mixture at 298–128 K in steps of 5 K. Black dotted curves are the spectra of pure PG at 298 K.

In addition to the studies at 298 K, we studied the dielectric constant of PVP solutions with chloroform and PG from the liquid state to the glassy state over a wide range of temperatures and frequencies [48, 50]. In these studies, the PVP-process observed at 298 K was the α-relaxation of PVP in solution, which is related to the glass transition of the solutions. Therefore, we call the relaxation process on the low-frequency side (around 100 Hz at 298 K in Figure 1) the α_PVP-process, whereas the relaxation process on the high-frequency side (around 100 MHz at 298 K in Figure 1) is called the h₁-process of the solvent.

As shown in Figure 1, the α_PVP- and h₁-processes shift to lower frequencies with decreasing temperature. Below 260 K, the α_PVP-process shifts to below our lowest detectable frequency; hence, only the h₁-process can be observed for temperatures below 260 K. On further decreasing the temperature, another relaxation process, which is not visible at higher temperatures, appears on the low-frequency side of the h₁-process. At 238 K and lower in the imaginary parts, two peaks are clearly visible, both of which originate from the solvent because the sum of their strengths is consistent with the strength of the single relaxation process of the solvent observed at higher temperatures, as shown in the real parts in Figure 1.

Figure 2 shows the dielectric losses at temperatures between 238 and 128 K, in which the additional processes of the solvents can be identified in the mixtures. At 238 K, the h₁-process appears in the MHz range. Above 238 K, the single relaxation process, h₁, of the solvents is visible in all PVP–alcohol mixtures. In addition to the h₁-process, one or two processes can be identified at lower temperatures in PVP–alcohol mixtures. We call the solvent processes at higher, medium, and lower frequencies h₁-, h₂-, and h₃-processes, respectively. For the PVP–water mixture, the loss peak of the ν-process retains its strength and simply shifts to lower frequency with decreasing temperature. In Figure 2, the dotted black curves with arrows show how the peaks shift as the temperature changes. The h₁- and h₂-processes appear for the PG solution, whereas the h₁-, h₂-, and h₃-processes appear for the PrOH solution.

FIGURE 2

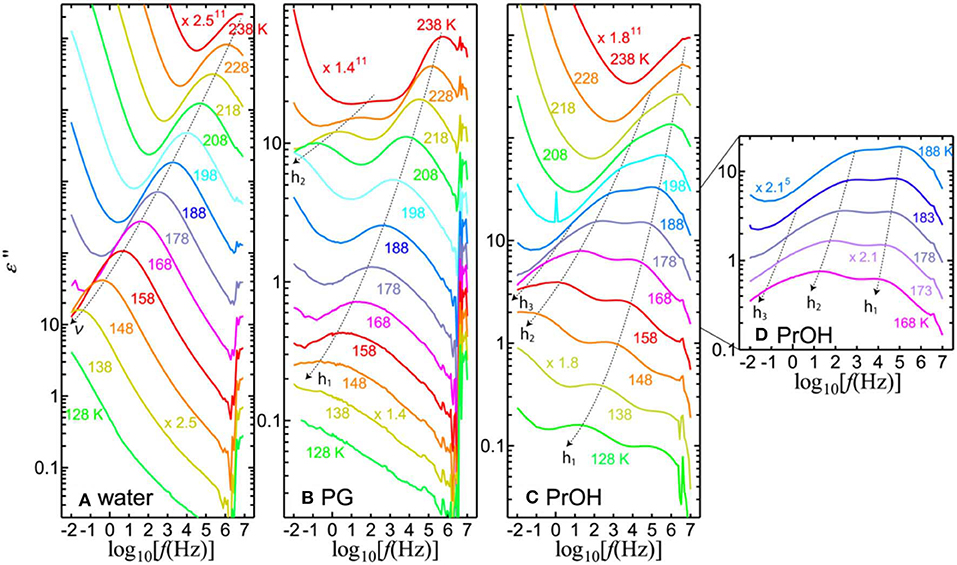
Figure 2. Imaginary part of permittivity for 65 wt% (A) PVP–water, (B) PVP–PG, and (C,D) PVP–PrOH mixtures as a function of frequency and for different temperatures in steps of 10 K except for panel (D), which is in step of 5 K. To clearly illustrate the solvent separation processes, the data are shifted vertically.

Although a loss peak was concealed by the large contribution of EP and dc conductivity, the real parts of dielectric permittivity of the PVP–water mixture show a small step that can be observed at a frequency range between the α_PVP-process and ν-process. To clearly illustrate this small step, Figure 3 shows frequency dependences of the real part of permittivity at various temperatures and frequency derivatives of the real part at 218 K. The frequency derivative of the real part has been known to correspond to the same profiles of dielectric loss. The small peak can be seen at the lower frequency side of the prominent peak of the ν-process of water at 218 K.

FIGURE 3

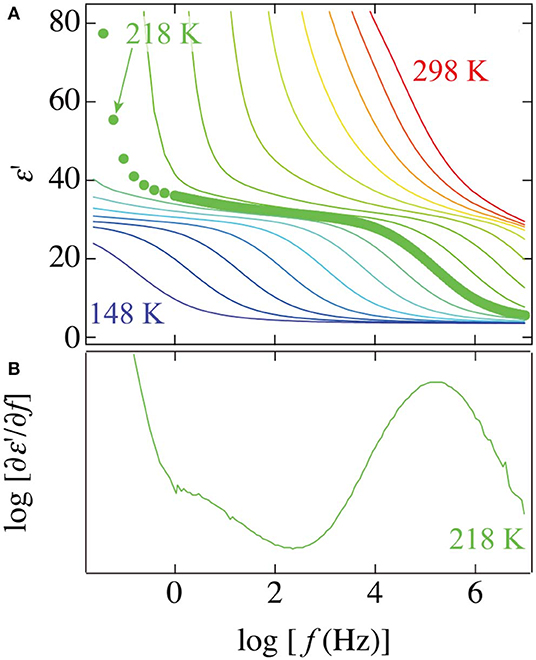
Figure 3. The frequency dependence of (A) the real part of permittivity at temperatures from 148 to 298 K in steps of 10 K and (B) the frequency derivative of the real part of permittivity at 218 K for the 65 wt% PVP–water mixture. Plots in the panel (A) indicate a spectrum at 218 K.

To characterize each process, we fit the data by the following equation:

$\begin{array}{l}{\epsilon }^{*}(\omega )={\epsilon }_{\infty }+{\sum }_{i=1}^3\frac{\Delta {\epsilon }_{{\text{h}}_i}}{1+{(j\omega {\tau }_{{\text{h}}_i})}^{{{\beta }_h}_i}}+\\ \Delta {\epsilon }_{\alpha }{\displaystyle {\int }_0^{\infty }}\left(-\frac{\text{d}\phi }{\text{d}t}\right)exp(-j\omega t)dt+\frac{{\epsilon }_{\text{EP}}}{1+{(j\omega {\tau }_{\text{EP}})}^{{\beta }_{\text{EP}}}}\\ -j\frac{\sigma }{{\epsilon }_0\omega }& (1)\end{array}$

with

$\begin{array}{l}\phi =exp\left[{-\left(\frac{t}{{\tau }_{\alpha }}\right)}^{{\beta }_{\text{KWW},\alpha }}\right].\end{array}$

Here ω is the angular frequency, j is the imaginary unit defined by j ² = −1, ε₀ is the permittivity of free space, ε_∞ is the high-frequency dielectric constant, σ is the dc conductivity, and β and β_KWW (0 < β, β_KWW ≤ 1) are the parameters indicating the broadness of the symmetric and asymmetric relaxation curves, respectively. The subscripts i = 1, 2, and 3 refer to h₁, h₂, and h₃ processes, respectively, whereas α denotes the α-relaxation process of PVP. This equation includes Cole–Cole relaxation functions [51] for the solvent-processes and EP contribution, one Kohlrausch–Williams–Watts relaxation function [52, 53] for the α_PVP-process, and a dc conductivity term. Although the α-process of the pure PG [54], EG [55], and PrOH [56] has an asymmetric peak shape, we used a symmetric Cole-Cole relaxation function to fit them. It is because that the loss peak of the solvent processes, especially that of the h₁-process, cannot be seen clearly to determine whether the loss peak is asymmetry or symmetry. Figure 4 shows the examples of relaxation processes determined using the curve fitting procedures of PVP-PG mixture at 283, 238, and 213 K.

FIGURE 4

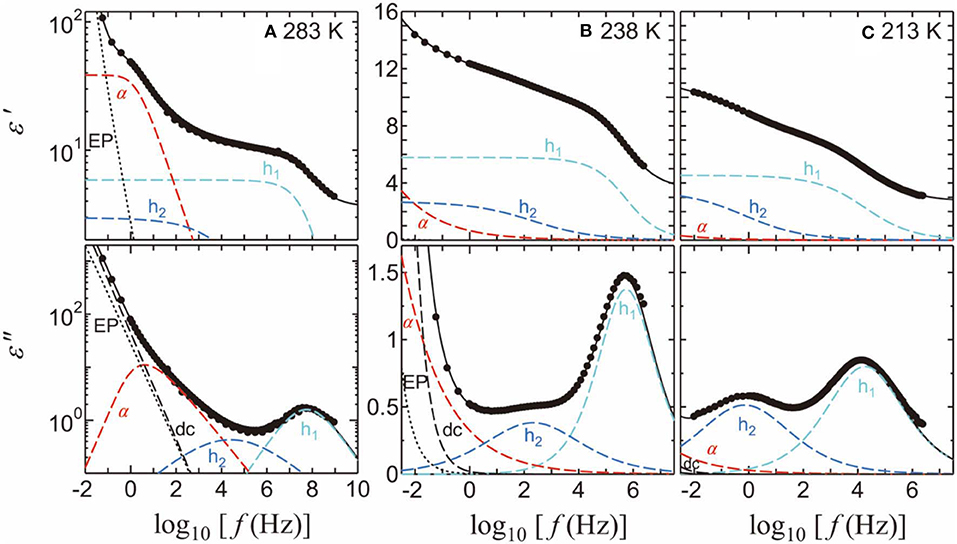
Figure 4. The fitting results and spectra for the 65 wt% PVP–PG mixture at (A) 283, (B) 238, and (C) 213 K. The solid black curves indicate the fitting results. The light-blue, blue, and red dashed curves indicate the h₁, h₂, and α-processes, respectively. The black dashed and dotted curves indicate dc conductivity and EP, respectively.

Figure 5 shows the relaxation time, τ, as a function of reciprocal temperature for PVP–water, –PG, –EG, and –PrOH mixtures. In this figure, red and blue symbols indicate α_PVP- and solvent (h₁-, h₂-, and h₃-) processes. Error bars indicate uncertainty of the fitting procedure as the maximum and minimum values of τ. The plots without error bars indicate that the uncertainty is smaller than the plot size. For comparison, τ of the pure solvents are plotted as gray solid symbols [56–58]. τ of α_PVP- and solvent (h₁-, h₂-, and h₃-) processes are fitted by the Vogel-Fulcher-Tammann (VFT) equation [38–40] and the Arrhenius equation, respectively. The VFT equation is τ=τ_VF∞exp(A/(T-T₀)), where τ_VF∞, A, and T₀ are empirical VFT parameters. The Arrhenius equation is τ=τ_Arr∞exp(ΔE/(RT)), where τ_Arr∞ is the preexponential factor, ΔE is the apparent molar activation energy, and R is the gas constant. The temperature at which the dielectric relaxation time τ reaches 100–1000 s can be defined as the glass-transition temperature T_g. In terms of a general treatment, we considered defining T_g here as the temperature at which τ = 100 s. The vertical dotted lines in Figure 5 show T_g for the α-relaxation process (T_g,PVP) for each solution. Moreover, the vertical dashed lines show T_g both h₂- and h₃-processes in each solution. Note that Figure 5 shows the results of DSC thermograms with the gray bands indicating possible T_g ranges. Moreover, for the PVP–PG and PVP–EG mixtures, DSC thermograms show two steps, at high-T and low-T sides, whereas PVP-water and PrOH mixtures show a single step that corresponds to the high-T side glass transition temperature in other mixtures. The results clearly show that T_g of the α_PVP-process obtained by BDS falls into the range of the high-T side T_g obtained by DSC, whereas for the PVP–PG and –EG mixtures, T_g of the slowest solvent process falls into the range of the low-T side T_g. Note that DSC measurements cannot detect the low-T side T_g for the PVP–water and PrOH mixtures. Steps in the DSC thermograms on the high-T side are placed at almost the same temperature range as that for all mixtures. The α_PVP-processes observed for all the mixtures are originated from the segmental motion of PVP, and this structural relaxation is related to the glass transition at the high-T side. On the other hand, the slowest process of solvent is related to the glass transition at the low-T side, which indicates that the slowest process of solvent can be interpreted to be the structural relaxation of the solvent.

FIGURE 5

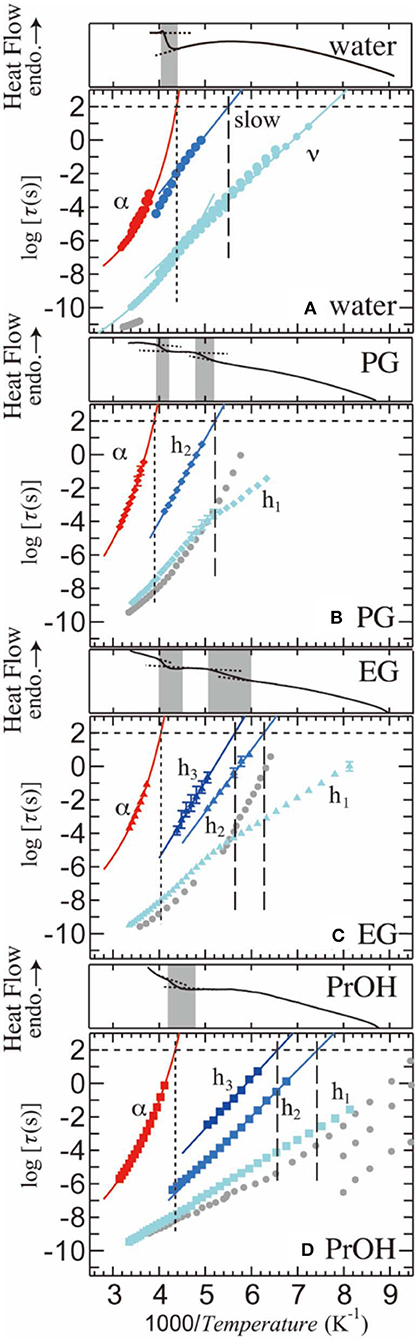
Figure 5. Relaxation time as a function of inverse temperature for the 65 wt% (A) PVP–water, (B) PVP–PG, (C) PVP–EG, and (D) PVP–PrOH mixtures. The corresponding DSC thermograms are also shown above each panel, with the gray ranges indicating the possible glass transition temperatures. Gray plots indicate the relaxation time of pure solvents [56–58]. Error bars indicate uncertainty of the fitting procedures. Plots without error bar have errors within the plot size. Multiple plots for the PVP–water mixture indicate measurements with different electrodes to characterize the additional small process.

Although Δε of the α_PVP-process monotonically increased with decreasing temperature, Δε of the solvent processes demonstrated a complicated temperature dependence. To demonstrate the Δε of the solvent processes and these relationships, Figures 6A,B show the reciprocal temperature dependence of Δε of the solvent processes and ratios of them. The ratios were obtained by Δε_k/Σ_kΔε_k where k corresponds to ν and slow in PVP–water mixture, h₁, h₂, and h₃ in PVP–alcohol mixtures at temperatures below T_g of α_PVP-process, i. e., Δε of the solvent process divided by the sum of Δε of the solvent processes. Therefore, ratios are calculated for limited temperature ranges which all solvent processes are observed. The error bars indicate errors of fitting procedure. Although the presence of relaxation process between α_PVP- and the primary (only at temperatures above T_gPVP)-process of solvent is for both PVP–alcohol mixtures and PVP–water mixture, the strength of the small process observed in the water mixture is less and the strength of the ν-process of water does not decrease and is almost constant. As shown in Figure 6B, the ratio for the small process of PVP–water mixture is temperature-independent, whereas the ratios of the h₂-processes in PVP–PG and –EG mixtures and h₃-processes in PVP–EG and PVP–PrOH mixtures depend on the temperature, which increases with decrease in temperature. Therefore, the primary process of water is considerably different from that of alcohols.

FIGURE 6

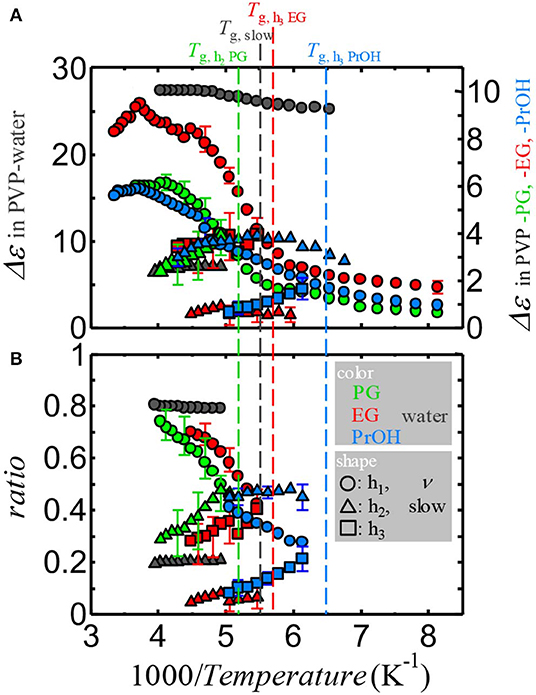
Figure 6. The reciprocal temperature dependence of (A) the relaxation strength of the solvent processes and (B) the ratio of the relaxation strength of the solvent processes divided by the summation of the relaxation strength of all solvent processes for each mixture. Black, green, red, and blue plots indicate the data for PVP–water, PVP–PG, PVP–EG, and PVP–PrOH mixtures, respectively. Vertical dashed lines indicate T_g of the slowest solvent process for each mixture. The error bars indicate errors of the fitting procedure.

Discussion

In the PVP–PG mixture, the h₁-process can be observed at a temperature above T_g,PVP. Above T_g,PVP, τ_h1 closes to the relaxation time of pure PG. Below T_g,PVP, the loss peak of the h₂-process can be visible. Moreover, the temperature dependence of τ_h1 does not undergo a non-A-A crossover at T_g,PVP. However, at T_g for the h₂-process (T_g,h2), the temperature dependence of τ_h1 exhibits a crossover. It is well known that the main relaxation process of pure PG exhibits an asymmetric loss peak with an excess wing at the high-frequency shoulder [54]. For an aged pure PG below its T_g, the excess wing has been confirmed to originate from the JG relaxation [54]. For PVP–PG mixtures with up to 50 wt% of PVP, the main PG process corresponds to the α-relaxation of PG. The relaxation time for the α-relaxation of PG increases with PVP concentration. Another secondary relaxation process has been recognized on the high-frequency side of the α-relaxation [50]. On the basis of a comparison between the relaxation times and the strength of the h₁- and h₂-process in the 65 wt% PVP–PG mixture and the α-relaxation of PG in PVP–PG mixtures with 50 wt% of PVP or less, the h₁-process above T_g,PVP mimics the α-relaxation of PG, whereas below T_g,PVP the h₂-process in the 65 wt% PVP mixture corresponds to the α-relaxation of PG. It is also consistent with the glass transition observed by DSC. For the 65 wt% PVP-PG mixture, the h₁-process at high temperatures does not continue to the α-relaxation, and the loss peak of the h₂-process (i.e., the α-relaxation of PG) can be clearly identified at a temperature below T_g,PVP. On the basis of a comparison between the h₁-process in the 65 wt% PVP–PG mixture below T_g,PVP and the secondary process on the high-frequency side of the α-relaxation of PG in PVP–PG mixtures with up to 50 wt% of PVP, the h₁-process below T_g,PVP corresponds to the secondary process of PG. This interpretation is consistent with the reciprocal temperature dependence of the ratio of the Δε that is shown in Figure 6B, i.e., the ratio of the Δε of the h₁- (h₂-) process decreases (increases) with decreasing temperature.

For the PVP–EG mixture, in addition to the α-relaxation of PVP, only the h₁-process can be recognized at temperatures above T_g,PVP. Below T_g,PVP, the loss peaks of the h₂-and h₃-processes can be observed. Moreover, the temperature dependence of τ_h1 exhibits no crossover at T_g,PVP. However, at T_g,h3, the temperature dependence of τ_h1 exhibits a crossover. The T_g,h3 has uncertainty caused by the relaxation time obtained from broad spectra of the h₃-process and the determination by the assumption of a linear extrapolation of the temperature dependence of τ_h3. Therefore, we regard the crossover of τ_h1 appears at T_g,h3. The temperature dependence of τ_h1 seems to show another weak crossover at T_g,h2, at which the slope below T_g,h2 is larger than that above T_g,h2. The change of the temperature dependence of τ_h1 at T_g,h2 is opposite compared to that at T_g,h3. This trend also appears τ_h1 for PVP-PG mixture below T_g,h2. Below T_g,h2 for PVP-PG mixture and at around T_g,h2 for PVP-EG mixture, the extremely broad spectra of the h₁-processes and the presence of the contributions of high frequency wing of the relaxation processes at lower frequency side seem to give rise to this crossover. These results imply that the h₁-process and h₃-processes correspond to the JG β relaxation and α-relaxation of EG. This is consistent with the reciprocal temperature dependence of the ratio of the Δε of the solvent processes that is shown in Figure 6B as having the same manner as those of the h₁- and h₂-processes in PVP–PG mixture. The existence of h₂-process in the PVP–EG mixture is somewhat peculiar and seems to be due to the mixture's dynamic heterogeneity. Details will be discussed in future works of the concentration dependence study. The h₁-process corresponds well with the main process of pure EG [46, 58] at temperatures above T_g,PVP.

For the PVP–PrOH mixture, in addition to the h₁-process, the loss peaks of the h₂- and h₃-processes can be observed below T_g,PVP. Above T_g,PVP, τ_h1 agrees with the relaxation time of pure PrOH. In contrast to the PVP–PG and EG mixtures, no crossover of τ_h1 appears in the PVP–PrOH mixture at T_g,h2 and T_g,h3. Even the reciprocal temperature dependence of τ_h1 of the PrOH–PVP mixture differs from that of the other PVP–alcohol mixtures. The reciprocal temperature dependence of the Δε of the h₁-process of the PVP–PrOH mixture shows similar behavior to that of other mixtures. Generally, the dielectric response of pure PrOH shows the so-called Debye process, which is attributed to the dynamics of a chain-like supermolecular structure composed of mono-alcohol molecules [59]. The h₁-process of the PVP–PrOH mixture at temperatures above T_g,PVP thus relates to the Debye process. According to our previous work that focused on the dielectric relaxation of the PVP-normal alcohol mixtures [47], the Debye process of pure PrOH smoothly connects to the h₁-process (in the previous study, it has been denoted as the h-process). Therefore, we considered that the h₁-process at temperatures above T_g,PVP seems to be related to the “modified” supermolecular structure of PrOH. A detailed discussion of the origin of the solvent processes in the PVP–PrOH mixture cannot be given because of the different origins of the h₁ processes in PVP–PrOH mixture and in the other PVP–alcohol mixtures. This point should be studied further in future investigations.

For the PVP–water mixture, Figure 5A clearly shows that the non-A-A crossover of the ν-process occurs at T_g,PVP, which is consistent with the results reported in Sasaki et al. [3] and also the results of Cerveny et al. [5]. The non-A-A crossover of the ν-process is mostly observed in various systems containing water. The activation energy E_a of water relaxation in the low-T Arrhenius region is nearly 50 kJ/mol, which is the universal value for supercooled water in aqueous mixtures [7, 35]. It is true that the PVP–water mixture shows an additional process (slow process) between the α_PVP-process and the primary process of the solvent (the ν-process) that can be found in the PVP–PG, PVP–EG, and PVP–PrOH mixtures, i.e., the h₂- and/or h₃-processes. However, the role of the slow process in the PVP–water mixture is much different from those of h₂- and/or h₃-processes in the PVP–alcohol mixtures, because the reciprocal temperature dependence of τ_h1 shows crossover at T_g of h₂- and/or h₃-processes, and τ_ν does not show crossover at the glass transition temperature of the slow process. In addition, the ratios of the Δε of the ν-process and the slow process are very different from those of the solvent processes in other mixtures. In addition, whereas the DSC thermograms for PVP-PG and -EG mixtures show two steps that correspond to the glass transition of the α_PVP- and h₂- or h₃-process, the DSC thermogram of PVP-water mixture shows a single step that corresponds to the α_PVP-process. This result suggests that the characteristic properties of the slow process are somewhat different from those of the structural relaxation of water. One possibility of the origin of the slow process is the JG β-process of PVP because τ of the slow process shows crossover at T_g,PVP. The origin of the slow process may yet be discovered with further investigation.

One major interpretation of the non-A-A crossover in water-containing systems is the freezing of the solute matrix at T_g [5, 16, 35, 60]. Above T_g, the solute molecules are mobile, and the relaxation time follows a VFT temperature dependence. The activation energy of solute relaxation, which is related to the cooperativity of the motion of solute molecules, increases with decreasing temperature. The change in the mobility of the solute matrix affects the mobility of confined water; hence, the relaxation time of water also exhibits a VFT temperature dependence. Below T_g, the matrix freezes, then the water environment no longer changes and the relaxation time of water exhibits an Arrhenius temperature dependence [35]. Below T_g, the fluctuation of solute molecules freezes not only for the PVP–water mixture but also for PVP–alcohol mixtures. If the freezing of the solute matrix is the origin of the non-A-A crossover of the solvent, then this must also appear in PVP–alcohol mixtures. Otherwise, the influence of the frozen matrix would differ between water and alcohols. In any case, the solute matrix freezes below T_g in all mixtures. Note that the freezing of the solute matrix does not always cause a non-A-A crossover. In addition, the confinement effect by the polymer chains should also exist even above T_g,PVP. Because of the relaxation time of the α-process of PVP is always several decades larger than those of alcohols and water, and the α-process is essentially frozen matrix even both above and below T_g,PVP. Therefore, the freezing of the solute matrix cannot be considered the origin of the non-A-A crossover.

Alternatively, even the non-A-A crossover may be interpreted by invoking the “finite size effect” for spatially confined molecular liquids [35]. Following the Adam–Gibbs theory [61], the size of the cooperative rearranging region (CRR) of the liquid increases with decreasing temperature. On decreasing the temperature, the CRR eventually reaches the size defined as the finite size, at which point the dynamic property of the liquid changes to an Arrhenius temperature dependence. This interpretation is based on the idea that the CRR size cannot exceed the given finite size. For the case of PVP solutions, according to this “finite size effect,” the finite size is determined by the freezing of the α_PVP-process. If this is true, then the h₁-process in the PVP–EG and PVP–PG solutions should exhibit a crossover at T_g,PVP. However, the h₁-processes in PVP–EG and PVP–PG solutions do not exhibit a non-A-A crossover at T_g,PVP, but rather at T_g of the h₂ and/or h₃-processes, indicating that the frozen matrix of the α_PVP-process does not serve as a template of confinement for the solvent processes. In addition, even if the τ_h1 crosses over at T_g,h2 instead of at T_g,PVP, the finite size effect cannot describe the discontinuity in the first derivative of the temperature dependence of τ_h1. When the CRR size reaches the given finite size, E_a should become fixed, which means that the first derivative of τ with respect to temperature related to the confined molecules should be continuous. However, this is not the case. For these reasons, the non-A-A crossover of the solvent dynamics in the mixtures cannot be described by the finite size effect.

One interpretation of the effect of matrix freezing is captured by the Coupling Model (CM). In general, glassy materials show two distinct relaxation processes: the structural α- and secondary β-processes. Currently, the origin of the α-process is understood to be a cooperative structural relaxation related to the glass transition. The secondary β-process has been characterized and classified [62]. The dynamics of molecules in glass formers of rigid molecules were investigated in the 1970s by Johari and Goldstein [63, 64]. The secondary relaxation found in rigid molecules with no internal degrees of freedom falls into the category of the JG β-process. The JG β-process cannot be assigned to any relaxation process involving the motion of an isolated part of a molecule. The temperature dependence of the relaxation time for the JG β-process, τ_JG, follows an Arrhenius temperature dependence at temperatures below the glass transition temperature, T_g,α, where the relaxation time of the α-process is 100–1,000 s. The Arrhenius temperature dependence of τ_JG does not continue at temperatures above T_g,α but changes to a VFT temperature dependence. The crossover of τ_JG can be understood as crossing a boundary of the system from equilibrium to nonequilibrium. CM has also been successfully applied to interpreting the relationship between the relaxation process of water and the α-relaxation observed in aqueous solutions [7]. According to CM description, it has been suggested that the JG β-process is the precursor of the cooperative α-process in analogy to the primitive relaxation of the CM. At temperatures far above T_g, a single relaxation process is observed in aqueous solutions of glycerol, EG oligomers, and fructose. At lower temperatures, the single relaxation process separates into two processes. The relaxation process with the smaller (larger) relaxation time originates from the local motion of water molecules (from the cooperative α-relaxation of solute and water molecules). In this case, the α-relaxation of water, and that of the solute do not appear individually. The relationship between water relaxation and α-relaxation mimics that of the JG β-process and the α-relaxation of various types of conventional glass formers. In other words, the relaxation process of water behaves like the JG β-process, which means that the water molecules in the mixtures move cooperatively with the solute molecules at low temperatures around T_g. For the PVP–water mixture, the relaxation of water (ν-process) behaves like the JG β-process because water molecules can move cooperatively with PVP, which is the origin of the α-relaxation. As a result, the structure, which fluctuates globally as the α-relaxation, behaves like a matrix for the local fluctuation of water.

In contrast, for the PVP–alcohol mixtures, the relaxation process of alcohol, which follows the h₁-process, does not exhibit a non-A-A crossover at T_g,PVP. The relaxation processes of the solvent are separated into a local motion (the h₁-process for the PVP–PG and PVP–EG mixtures and the h₂-process for the PVP–PrOH mixture) and an α-relaxation (the h₂-process for the PVP–PG mixture, the h₂ and h₃-processes for the PVP–EG mixture, and the h₃-process for the PVP–PrOH mixture) due to the presence of PVP. In this case, the α-relaxations originating from PVP and alcohol coexist. For PVP–PG and PVP–EG mixtures, the temperature dependence of τ_h1 changes at T_g,h2 and/or T_g,h3, which is lower than T_g,PVP. This indicates that the h₂- and/or h₃-process corresponds to the fluctuation of the matrix, and the freezing of the matrix affects the local h₁-process. Therefore, the temperature dependence of τ_h1 changes at T_g,h2 or T_g,h3. These results indicate that the h₁- and other solvent processes seem to correspond to the JG β-process and the structural α-relaxation of the solvent, respectively. For the relaxation process of water in the PVP–water mixture, the h₁-process in PVP–alcohol mixtures, and the JG β-process in conventional glass formers, the non-A-A crossover of the relaxation time of local motion initiated by the freezing of the matrix is universal.

Based on these results, the peculiarity of water is that the relaxation time of the cooperative motion of water is the same as that of the local chain motion of PVP, implying that water molecules cooperatively move with the PVP chains. For the PVP–alcohol mixtures, the α-relaxation of PVP and that of alcohol appear individually, which means that even alcohol molecules move cooperatively, and this appears as the α-relaxation of alcohol (i.e., an h₂- or h₃-process), although alcohol cannot move cooperatively with PVP chains. The separation of solvent relaxation in binary systems has not been generally observed, although it seems to be brought about by high polymer concentration, which is rarely measured. As seen for the PVP–PG mixtures with 50 wt% PVP and lower, the h₂-process does not appear on the low-frequency side of the h₁-process [50]. Two α-relaxations of PG h₂- and PVP- processes at temperatures far above T_g are observed continuously down to T_g, and both the PG h₂- and PVP- processes exhibit α-relaxation time with a VFT temperature dependence. In addition to the two α-relaxations, a secondary process can be observed on the high-frequency side of the α-relaxation of PG that corresponds to the h₁-process in the 65 wt% PVP–PG mixture.

Conclusion

This paper reports the dielectric relaxation processes observed in PVP mixtures with water and three types of alcohol. The results clearly show the uniqueness of water's relaxation process. We focused on comparing the relaxation processes of water with those of PG, because PG is a well-known glass former with a simple relaxation map and no crystallization. The presence of the single primary relaxation process of the solvent above T_g,PVP is common to all the solutions measured in this work. At T_g,PVP, the relaxation process of water exhibits a non-A-A crossover, whereas the observation of the multiple relaxation processes of the solvent is common to the three PVP–alcohol mixtures measured. From this point of view, the peculiarity of water is that the relaxation time of the cooperative motion of water is the same as that of the local chain motion of PVP, which means that water molecules move cooperatively with PVP chains. For the PVP–alcohol mixtures, the α-relaxations of PVP and that of alcohol appear individually. The multiple relaxation processes of alcohols remain veiled, and a better understanding of these mechanisms will require more detailed studies on the concentration dependence of the relaxation processes in alcohol–polymer mixtures.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

KS and NS conceived and designed the research and wrote the manuscript. KS, KB, MaT, and MF performed the experiments. KS, KB, MaT, MF, and NS analyzed the data. MiT and HK contributed to designing of the interdigitated electrode. All the others (RK and SY) have contributed to its evolution to the final form.

Funding

This study was partly supported by JSPS KAKENHI Grant Numbers 16K05522, 19K14679, 19J02028, and 17K06005 and by the MEXT-Supported Program for the Strategic Research Foundation at Private Universities, 2014–2018.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Debenedetti PG. Supercooled and glassy water. J Phys Condens Matter. (2003) 15:R1669–R1726. doi: 10.1088/0953-8984/15/45/R01

CrossRef Full Text | Google Scholar

2. Mishima O, Stanley HE. The relationship between liquid, supercooled and glassy water. Nature. (1998) 396:329–35. doi: 10.1038/24540

CrossRef Full Text | Google Scholar

3. Sasaki K, Matsui Y, Miyara M, Kita R, Shinyashiki N, Yagihara S. Glass transition and dynamics of the polymer and water in the poly (vinylpyrrolidone)–water mixtures studied by dielectric relaxation spectroscopy. J Phys Chem B. (2016) 120:6882–9. doi: 10.1021/acs.jpcb.6b05347

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Jansson H, Swenson J. The protein glass transition as measured by dielectric spectroscopy and differential scanning calorimetry. Biochim Biophys Acta. (2010) 1804:20–26. doi: 10.1016/j.bbapap.2009.06.026

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Cerveny S, Schwartz GA, Alegria A, Bergman R, Swenson J. Water dynamics in n-propylene glycol aqueous solutions. J Chem Phys. (2006) 124:194501. doi: 10.1063/1.2198206

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Sasaki K, Kita R, Shinyashiki N, Yagihara S. Glass transition of partially crystallized gelatin-water mixtures studied by broadband dielectric spectroscopy. J Chem Phys. (2014) 140:124506. doi: 10.1063/1.4869346

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Capaccioli S, Ngai KL, Shinyashiki N. The johari-goldstein β-relaxation of water. J Phys Chem B. (2007) 111:8197–209. doi: 10.1021/jp071857m

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Ngai KL, Capaccioli S, Shinyashiki N. The protein “glass” transition and the role of the solvent. J Phys Chem B. (2008) 112:3826–32. doi: 10.1021/jp710462e

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Sasaki K, Panagopoulou A, Kita R, Shinyashiki N, Yagihara S, Kyritsis A, et al. Dynamics of uncrystallized water, ice, and hydrated protein in partially crystallized gelatin-water mixtures studied by broadband dielectric spectroscopy. J Phys Chem B. (2017) 121:265–72. doi: 10.1021/acs.jpcb.6b04756

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Shinyashiki N, Shinohara M, Iwata Y, Goto T, Oyama M, Suzuki S, et al. The glass transition and dielectric secondary relaxation of fructose-water mixtures. J Phys Chem B. (2008) 112:15470–7. doi: 10.1021/jp807038r

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Shinyashiki N, Yamamoto W, Yokoyama A, Yoshinari T, Yagihara S, Kita R, et al. Glass transitions in aqueous solutions of protein (Bovine Serum Albumin). J Phys Chem B. (2009) 113:14448–56. doi: 10.1021/jp905511w

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Murata K, Tanaka H. Liquid-liquid transition without macroscopic phase separation in a water-glycerol mixture. Nat Mater. (2012) 11:436–43. doi: 10.1038/nmat3271

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Singh LP, Cerveny S, Alegria A, Colmenero J. Broadband dielectric spectroscopic, calorimetric, and FTIR-ATR investigations of D-arabinose aqueous solutions. Chemphyschem. (2011) 12:3624–33. doi: 10.1002/cphc.201100469

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Busselez R, Arbe A, Cerveny S, Capponi S, Colmenero J, Frick B. Component dynamics in polyvinylpyrrolidone concentrated aqueous solutions. J Chem Phys. (2012) 137:084902. doi: 10.1063/1.4746020

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Capponi S, Arbe A, Cerveny S, Busselez R, Frick B, Embs JP, et al. Quasielastic neutron scattering study of hydrogen motions in an aqueous poly(vinyl methyl ether) solution. J Chem Phys. (2011) 134:204906. doi: 10.1063/1.3592560

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Cerveny S, Alegria A, Colmenero J. Broadband dielectric investigation on poly(vinyl pyrrolidone) and its water mixtures. J Chem Phys. (2008) 128:044901. doi: 10.1063/1.2822332

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Cerveny S, Arrese-Igor S, Dolado JS, Gaitero JJ, Alegría A, Colmenero J. Effect of hydration on the dielectric properties of C-S-H Gel. J Chem Phys. (2011) 134:034509. doi: 10.1063/1.3521481

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Monasterio M, Jansson H, Gaitero JJ, Dolado JS, Cerveny S. Cause of the fragile-to-strong transition observed in water confined in C-S-H Gel. J Chem Phys. (2013) 139:164714. doi: 10.1063/1.4826638

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Pagnotta SE, Cerveny S, Alegria A, Colmenero J. Dielectric relaxations in ribose and deoxyribose supercooled water solutions. J Chem Phys. (2009) 131:085102. doi: 10.1063/1.3202215

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Singh LP, Cerveny S, Alegria A, Colmenero J. Dynamics of water in supercooled aqueous solutions of poly(propylene glycol) as studied by broadband dielectric spectroscopy and low-temperature FTIR-ATR spectroscopy. J Phys Chem B. (2011) 115:13817–27. doi: 10.1021/jp2073705

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Cerveny S, Combarro-Palacios I, Swenson J. Evidence of coupling between the motions of water and peptides. J Phys Chem Lett. (2016) 20:4093–8. doi: 10.1021/acs.jpclett.6b01864

CrossRef Full Text | Google Scholar

22. Cerveny S, Swenson J. Dynamics of supercooled water in a biological model system of the amino acid L-lysine. Phys Chem Chem Phys. (2014) 16:22382–90. doi: 10.1039/C4CP02487G

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Pagnotta SE, Cerveny S, Alegria A, Colmenero J. The dynamical behavior of hydrated glutathione: a model for protein-water interactions. Phys Chem Chem Phys. (2010) 12:10512–7. doi: 10.1039/c003493b

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Oguni M, Maruyama S, Wakabayashi K, Nagoe A. Glass transitions of ordinary and heavy water within silica-gel nanopores. Chem Asian J. (2007) 2:514–20. doi: 10.1002/asia.200600362

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Ryabov Y, Gutina A, Arkhipov V, Feldman Y. Dielectric relaxation of water absorbed in porous glass. J Phys Chem B. (2001) 105:1845–50. doi: 10.1021/jp0033061

CrossRef Full Text | Google Scholar

26. Cammarata M, Levantino M, Cupane A, Longo A, Martorana A, Bruni F. Structure and dynamics of water confined in silica hydrogels: x-ray scattering and dielectric spectroscopy studies. Eur Phys J E. (2003) 12:63–6. doi: 10.1140/epjed/e2003-01-016-2

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Frunza L, Kosslick H, Pitsch I, Frunza S, Schönhals A. Rotational fluctuations of water inside the nanopores of SBA-type molecular sieves. J Phys Chem B. (2005) 109:9154–59. doi: 10.1021/jp044503t

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Jansson H, Swenson J. Dynamics of water in molecular sieves by dielectric spectroscopy. Eur Phys J E. (2003) 12:51–4. doi: 10.1140/epjed/e2003-01-013-5

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Bergman R, Swenson J. Dynamics of supercooled water in confined geometry. Nature. (2000) 403:283–6. doi: 10.1038/35002027

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Sjöström J, Swenson J, Bergman R, Kittaka S. Investigating hydration dependence of dynamics of confined water: monolayer, hydration water and Maxwell–Wagner processes. J Chem Phys. (2008) 128:154503. doi: 10.1063/1.2902283

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Hedström J, Swenson J, Bergman R, Jansson H, Kittaka S. Does confined water exhibit a fragile-to-strong transition? Eur Phys J. (2007) 141:53–6. doi: 10.1140/epjst/e2007-00016-0

CrossRef Full Text | Google Scholar

32. Kinka M, Banys J, Macutkevic J, Pöppl A, Böhlmann W, Umamaheswari V, et al. Dielectric response of water confined in MCM-41 molecular sieve material. Phys Status Solidi B. (2005) 242:R100–2. doi: 10.1002/pssb.200541038

CrossRef Full Text | Google Scholar

33. Liu L, Chen SH, Faraone A, Yen CW, Mou CY. Pressure dependence of fragile-to-strong transition and a possible second critical point in supercooled confined water. Phys Rev Lett. (2005) 95:117802. doi: 10.1103/PhysRevLett.95.117802

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Hwang DW, Chu CC, Sinha AK, Hwang LP. Dynamics of supercooled water in various mesopore sizes. J Chem Phys. (2007) 126:044702. doi: 10.1063/1.2429065

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Cerveny S, Mallamace F, Swenson J, Vogel M, Xu L. Confined water as model of supercooled water. Chem Rev. (2016) 116:7608–25. doi: 10.1021/acs.chemrev.5b00609

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Doster W, Busch S, Gaspar AM, Appavou MS, Wuttke J, Scheer H. Dynamical transition of protein-hydration water. Phys Rev Lett. (2010) 104:098101. doi: 10.1103/PhysRevLett.104.098101

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Ito K, Moynihan C, Angell CA. Thermodynamic determination of fragility in liquids and a fragile-to-strong liquid transition in water. Nature. (1999) 398:492–95. doi: 10.1038/19042

CrossRef Full Text | Google Scholar

38. Vogel H. The law of the relation between the viscosity of liquids and the temperature. Phys Z. (1921) 22:645–6.

Google Scholar

39. Fulcher GS. Analysis of recent measurements of the viscosity of glasses. J Am Ceram Soc. (1925) 8:339–55. doi: 10.1111/j.1151-2916.1925.tb16731.x

CrossRef Full Text | Google Scholar

40. Tammann G. The dependence of viscosity upon the temperature of supercooled liquids. Z Anorg Allg Chem. (1926) 156:245–57.

41. Angell CA. Formation of glasses from liquids and biopolymers. Science. (1995) 267:1924–35. doi: 10.1126/science.267.5206.1924

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Pötzschner B, Mohamed F, Lichtinger A, Bock D, Rössler EA. Dynamics of asymmetric non-polymeric binary glass formers—A nuclear magnetic resonance and dielectric spectroscopy study. J Chem Phys. (2015) 143:154506 doi: 10.1063/1.4932981

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Blochowicz T, Schramm S, Lusceac S, Vogel M, Stühn B, Gutfreund P, et al. Signature of a type-A glass transition and intrinsic confinement effects in a binary glass-forming system. Phys Rev Lett. (2012) 109:035702 doi: 10.1103/PhysRevLett.109.035702

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Lorthioir C, Alegría A, Colmenero J. Out of equilibrium dynamics of poly(vinyl methyl ether) segments in miscible poly(styrene)-poly(vinyl methyl ether) blends. Phys Rev E Stat Nonlin Soft MatterPhys. (2003) 68:031805 doi: 10.1103/PhysRevE.68.031805

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Mallamace F, Branca C, Corsaro C, Leone N, Spooren J, Chen SH, et al. Transport properties of glass-forming liquids suggest that dynamic crossover temperature is as important as the glass transition temperature. Proc Natl Acad Sci USA. (2010) 107:22457–62. doi: 10.1073/pnas.1015340107

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Shinyashiki N, Sengwa RJ, Tsubotani S, Nakamura H, Sudo S, Yagihara S. Broadband dielectric study of dynamics of poly(vinyl pyrrolidone)-ethylene glycol oligomer blends. J Phys Chem A. (2006) 110:4953–7. doi: 10.1021/jp0605193

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Shinyashiki N, Imoto D, Yagihara S. Broadband dielectric study of dynamics of polymer and solvent in poly(vinyl pyrrolidone)/normal alcohol mixtures. J Phys Chem B. (2007) 111:2181–7. doi: 10.1021/jp065414e

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Shinyashiki N, Spanoudaki A, Yamamoto W, Nambu E, Yoneda K, Kyritsis A, et al. Segmental relaxation of hydrophilic poly (vinylpyrrolidone) in chloroform studied by broadband dielectric spectroscopy. Macromol. (2011) 44:2140–8. doi: 10.1021/ma102394s

CrossRef Full Text | Google Scholar

49. Shinyashiki N, Miyara M, Nakano S, Yamamoto W, Ueshima M, Imoto D, et al. Dielectric relaxation strength and magnitude of dipole moment of poly (vinyl pyrrolidone) in polar solutions. J Mol Liq. (2013) 181:110–4. doi: 10.1016/j.molliq.2013.02.020

CrossRef Full Text | Google Scholar

50. Spanoudaki A, Shinyashiki N, Kyritsis A, Pissis P. Dielectric spectroscopy on propylene glycol/poly (vinyl pyrrolidone) solutions: polymer and solvent dynamics in hydrogen-bonding systems. AIP Conf Proc. (2008) 982:125–30. doi: 10.1063/1.2897766

CrossRef Full Text | Google Scholar

51. Cole KS, Cole RH. Dispersion and absorption in dielectrics I. Alternating Current Characteristics. J Chem Phys. (1941) 9:341–51. doi: 10.1063/1.1750906

CrossRef Full Text | Google Scholar

52. Williams G, Watts DC. Non-Symmetrical dielectric relaxation behaviour arising from a simple empirical decay function. Trans Faraday Soc. (1970) 66:80–5. doi: 10.1039/tf9706600080

CrossRef Full Text | Google Scholar

53. Kohlrausch R. Theorie des elektrischen rückstandes in der leidener flasche. Ann Phys. (1854) 167:179–214 doi: 10.1002/andp.18541670203

CrossRef Full Text | Google Scholar

54. Ngai K, Lunkenheimer P, Leon C, Schneider U, Brand R, Loidl A. Nature and properties of the johari–goldstein β-relaxation in the equilibrium liquid state of a class of glass-formers. J Chem Phys. (2001) 115:1405–13. doi: 10.1063/1.1381054

CrossRef Full Text | Google Scholar

55. Kremer F, Huwe A, Arndt M, Behrens P, Schwieger W. How many molecules form a liquid? J Phys Condens Matter. (1999) 11:A175–88 doi: 10.1088/0953-8984/11/10A/013

CrossRef Full Text | Google Scholar

56. Gabriel J, Pabst F, Blochowicz T. Debye process and β-relaxation in 1-propanol probed by dielectric spectroscopy and depolarized dynamic light scattering. J Phys Chem B. (2017) 121:8847–53 doi: 10.1021/acs.jpcb.7b06134

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Buchner R, Barthel J, Stauber J. The dielectric relaxation of water between 0°C and 35°C. Chem Phys Lett. (1999) 306:57–63 doi: 10.1016/S0009-2614(99)00455-8

CrossRef Full Text | Google Scholar

58. Huwe A, Kremer F, Behrens P, Schwieger W. Molecular dynamics in confining space: from the single molecule to the liquid state. Phys Rev Lett. (1999) 82:2338 doi: 10.1103/PhysRevLett.82.2338

CrossRef Full Text | Google Scholar

59. Böhmer R, Gainaru C, Richert R. Structure and dynamics of monohydroxy alcohols-milestones towards their microscopic understanding, 100 years after Debye. Phys Rep. (2014) 545:125–95. doi: 10.1016/j.physrep.2014.07.005

CrossRef Full Text | Google Scholar

60. Cerveny S, Schwartz GA, Bergman R, Swenson J. Glass transition and relaxation processes in supercooled water. Phys Rev Lett. (2004) 93:245702. doi: 10.1103/PhysRevLett.93.245702

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Adam G, Gibbs J. H. On the temperature dependence of cooperative relaxation properties in glass-forming liquids. J Chem Phys. (1965) 43:139–46. doi: 10.1063/1.1696442

CrossRef Full Text | Google Scholar

62. Ngai K, Paluch M. Classification of secondary relaxation in glass-formers based on dynamic properties. J Chem Phys. (2004) 120:857–73. doi: 10.1063/1.1630295

PubMed Abstract | CrossRef Full Text | Google Scholar

63. Johari GP, Goldstein M. Viscous liquids and the glass transition. II. secondary relaxations in glasses of rigid molecules. J Chem Phys. (1970) 53:2372–88. doi: 10.1063/1.1674335

CrossRef Full Text | Google Scholar

64. Johari GP, Goldstein M. Viscous liquids and the glass transition. III. secondary relaxations in aliphatic alcohols and other nonrigid molecules. J Chem Phys. (1971) 55:4245–52. doi: 10.1063/1.1676742

CrossRef Full Text | Google Scholar