Implementing Chiral Three-Body Forces in Terms of Medium-Dependent Two-Body Forces

Three-nucleon (3N) forces are an indispensable ingredient for accurate few-body and many-body nuclear structure and reaction theory calculations. While the direct implementation of chiral 3N forces can be technically very challenging, a simpler approach is given by employing instead a medium-dependent NN interaction V_med that reflects the physics of three-body forces at the two-body normal-ordered approximation. We review the derivation and construction of V_med from the chiral 3N interaction at next-to-next-to-leading order (N2LO), consisting of a long-range 2π-exchange term, a mid-range 1π-exchange component, and a short-range contact-term. Several applications of V_med to the equation of state of cold nuclear and neutron matter, the nucleon single-particle potential in nuclear matter, and the nuclear quasiparticle interaction are discussed. We also explore differences in using local vs. non-local regulating functions on 3N forces and make direct comparisons to exact results at low order in perturbation theory expansions for the equation of state and single-particle potential. We end with a discussion and numerical calculation of the in-medium NN potential V_med from the next-to-next-to-next-to-leading order (N3LO) chiral 3N force, which consists of a series of long-range and short-range terms.

1. Introduction

Three-nucleon forces are essential to any microscopic description of nuclear many-body systems, from the structure and reactions of finite nuclei [1–4] to the equation of state and transport properties of dense matter encountered in core-collapse supernovae and neutron stars [2, 5–13]. Three-body forces have been shown to dramatically improve the saturation properties of nuclear matter [6, 7, 14], though there are still large uncertainties compared to the empirical saturation energy and density. Three-nucleon forces are now also routinely implemented in a number of ab initio many-body methods such as the no-core shell model [15], coupled-cluster theory [16, 17], self-consistent Green's function theory [18], the similarity renormalization group [19, 20], and quantum Monte Carlo [3] to study nuclear ground-state and excited states up to medium-mass nuclei. In particular, three-body forces have been shown to be especially relevant for understanding the properties of neutron-rich nuclei out to the drip line [16, 18, 21, 22].

In the past, it has been challenging [5] to obtain nuclear two- and three-body forces that simultaneously fit well the properties of finite nuclei and nuclear matter, but in recent years, much progress has been achieved within the framework of chiral effective field theory [23–27] to construct three-body forces consistent with the employed two-body force, all within a systematic power series expansion involving the ratio of the physical scale Q to the chiral symmetry breaking scale Λ_χ ~ 1 GeV. In chiral effective field theory with explicit nucleon and pion degrees of freedom only, three-nucleon forces appear first at third order in the chiral expansion ${(Q/{\Lambda }_{\chi })}^3$, or next-to-next-to-leading (N2LO) order. These leading contributions to the chiral three-nucleon force (3NF) are now routinely employed in nuclear structure and reaction theory calculations, but many-body contributions at N3LO [28–31] are expected to be important.

In the present work, we will review how to implement three-nucleon forces via medium-dependent two-body interactions [6, 7, 32] in nuclear many-body calculations of the equation of state, single-particle potential, and quasiparticle interaction. We will show that this approach provides an excellent approximation at first order in many-body perturbation theory by comparing to exact results from three-body forces. At higher orders in perturbation theory, the use of medium-dependent NN interactions fail to reproduce all topologies, however, residual three-body interactions have been shown [33] to give relatively small contributions (~ 1 MeV) to the nuclear equation of state at saturation density up to second order in perturbation theory. We also consider several commonly used high-momentum regulating functions for three-body forces and study their impact on the density-dependent interaction V_med. In particular, we find that local regulators introduce large artifacts compared to nonlocal regulators when the same value of the cutoff scale Λ is used in both cases.

2. From Three-Body Forces to Medium-Dependent Two-Body Forces

2.1. Chiral Three-Body Force at Next-to-Next-to-Leading Order

The nuclear Hamiltonian can generically be written in the form

$\begin{array}{ll}H={\displaystyle \sum _i}\frac{{\overrightarrow{p}}_i^2}{2M}+\frac{1}{2}{\displaystyle \sum _{ij}}{V}_{ij}+\frac{1}{6}{\displaystyle \sum _{ijk}}{V}_{ijk}+\cdots ,& (1)\end{array}$

where ${\overrightarrow{p}}_i$ is the momentum of nucleon i, V_ij represents the two-body interaction between particles i and j, and V_ijk represents the three-body interaction between particles i, j, k. Three-body forces emerge first at N2LO in the chiral expansion and comprise three different topologies represented diagrammatically in Figure 1. The two-pion-exchange three-body force (Figure 1A), consists of three terms proportional to the low-energy constants c₁, c₃, and c₄:

$\begin{array}{ll}{V}_{3N}^{(2\pi )}={\displaystyle \sum _{i\ne j\ne k}}\frac{g_A^2}{8f_{\pi }^4}\frac{{\overrightarrow{\sigma }}_i·{\overrightarrow{q}}_i{\overrightarrow{\sigma }}_j·{\overrightarrow{q}}_j}{({\overrightarrow{q_i}}^2+m_{\pi }^2)({\overrightarrow{q_j}}^2+m_{\pi }^2)}{F}_{ijk}^{\alpha \beta }{\tau }_i^{\alpha }{\tau }_j^{\beta },& (2)\end{array}$

where g_A = 1.29 is the axial coupling constant, m_π = 138 MeV is the average pion mass, f_π = 92.2 MeV is the pion decay constant, ${\overrightarrow{q}}_i={\overrightarrow{k}}_i^{\prime }-{\overrightarrow{k}}_i$ is the change in momentum of nucleon i (i.e., the momentum transfer), and the isospin tensor $F_{ijk}^{\alpha \beta }$ is defined by

$\begin{array}{ll}{F}_{ijk}^{\alpha \beta }={\delta }^{\alpha \beta }(-4c_1{m}_{\pi }^2+2c_3{\overrightarrow{q}}_i·{\overrightarrow{q}}_j)+c_4{ϵ}^{\alpha \beta \gamma }{\tau }_k^{\gamma }{\overrightarrow{\sigma }}_k·({\overrightarrow{q}}_i\times {\overrightarrow{q}}_j).& (3)\end{array}$

FIGURE 1

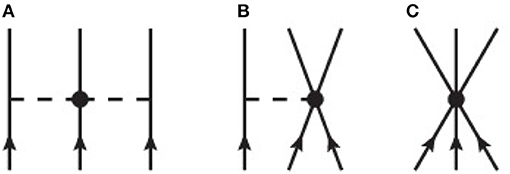
Figure 1. Diagrammatic contributions to the chiral three-nucleon force at next-to-next-to-leading order (N2LO) in the chiral expansion: (A) two-pion-exchange interaction, (B) one-pion-exchange interaction, and (C) contact interaction.

The three low-energy constants c₁, c₃, and c₄ can be fitted to empirical pion-nucleon [34, 35] or nucleon-nucleon [36, 37] scattering data.

The one-pion exchange term (Figure 1B), proportional to the low-energy constant c_D, has the form

$\begin{array}{ll}{V}_{3N}^{(1\pi )}=-{\displaystyle \sum _{i\ne j\ne k}}\frac{g_A{c}_D}{8f_{\pi }^4{\Lambda }_{\chi }}\frac{{\overrightarrow{\sigma }}_j·{\overrightarrow{q}}_j}{{\overrightarrow{q_j}}^2+m_{\pi }^2}{\overrightarrow{\sigma }}_i·{\overrightarrow{q}}_j{\overrightarrow{\tau }}_i·{\overrightarrow{\tau }}_j,& (4)\end{array}$

where the high-momentum scale is typically taken as Λ_χ = 700 MeV. The three-nucleon contact force (Figure 1C), proportional to c_E reads:

$\begin{array}{ll}{V}_{3N}^{(ct)}={\displaystyle \sum _{i\ne j\ne k}}\frac{c_E}{2f_{\pi }^4{\Lambda }_{\chi }}{\overrightarrow{\tau }}_i·{\overrightarrow{\tau }}_j.& (5)\end{array}$

There are several different experimental observables commonly used for fitting the low-energy constants c_D and c_E. Most approaches fit the binding energies of A = 3 nuclei together with one of the following observables: (a) the neutron-deuteron doublet scattering length [38, 39], (b) the radius of ⁴He [40], (c) the properties of light and medium-mass nuclei [41, 42], and (d) the triton lifetime [43, 44].

Since the three-nucleon force V_3N is symmetric under the interchange of particle labels, there are only three independent terms from the i, j, k permutations, which allows us to write V_3N = W₁ + W₂ + W₃. For instance, $W_1^{(ct)}=\frac{c_E}{f_{\pi }^4\Lambda }{\overrightarrow{\tau }}_2·{\overrightarrow{\tau }}_3$. The antisymmetrized three-body interaction ${\bar{V}}_{3N}$ can be written in terms of two-body antisymmetrization operators P_ij as follows:

$\begin{array}{ll}{\bar{V}}_{3N}=(1-P_{12})(1-P_{13}-P_{23})V_{3N},& (6)\end{array}$

where

$\begin{array}{ll}{P}_{ij}=\left(\frac{1+{\overrightarrow{\sigma }}_i·{\overrightarrow{\sigma }}_j}{2}\right)\left(\frac{1+{\overrightarrow{\tau }}_i·{\overrightarrow{\tau }}_j}{2}\right),{\overrightarrow{k}}_i\leftrightarrow {\overrightarrow{k}}_j·& (7)\end{array}$

2.2. Density-Dependent NN Interaction at Order N2LO

In second quantization, a three-body force V_3N can be written as

$\begin{array}{ll}{V}_{3N}=\frac{1}{36}{\displaystyle \sum _{123456}}\langle 123|{\bar{V}}_{3N}|456\rangle {\widehat{a}}_1^{†}{\widehat{a}}_2^{†}{\widehat{a}}_3^{†}{\widehat{a}}_6{\widehat{a}}_5{\widehat{a}}_4& (8)\end{array}$

where ${\bar{V}}_{3N}$ denotes the antisymmetrized three-body matrix element, and $a_i^{†}$ (a_i) are the usual creation (annihilation) operators associated with state |i〉. A medium-dependent two-body interaction can then be constructed by normal ordering the three-body force with respect to a convenient reference state, such as the ground state of the noninteracting many-body system, rather than the true vacuum as in Equation (8). Normal ordering with respect to the noninteracting ground state then produces a three-body force of the form

$\begin{array}{l}{V}_{3N}=\frac{1}{6}{\displaystyle \sum _{ijk}}\langle ijk|{\bar{V}}_{3N}|ijk\rangle +\frac{1}{2}{\displaystyle \sum _{ij14}}\langle ij1|{\bar{V}}_{3N}|ij4\rangle :{\widehat{a}}_1^{†}{\widehat{a}}_4:\\ +\frac{1}{4}{\displaystyle \sum _{i1245}}\langle i12|{\bar{V}}_{3N}|i45\rangle :{\widehat{a}}_1^{†}{\widehat{a}}_2^{†}{\widehat{a}}_5{\widehat{a}}_4:\\ +\frac{1}{36}{\displaystyle \sum _{123456}}\langle 123|{\bar{V}}_{3N}|456\rangle :{\widehat{a}}_1^{†}{\widehat{a}}_2^{†}{\widehat{a}}_3^{†}{\widehat{a}}_6{\widehat{a}}_5{\widehat{a}}_4:,& (9)\end{array}$

where $:{O}:$ denotes normal ordering of operator ${O}$. In practice the construction of the medium-dependent two-body force

$\begin{array}{ll}\frac{1}{4}{\displaystyle \sum _{i1245}}\langle i12|{\bar{V}}_{3N}|i45\rangle :{\widehat{a}}_1^{†}{\widehat{a}}_2^{†}{\widehat{a}}_5{\widehat{a}}_4:& (10)\end{array}$

then amounts to summing the third particle over the filled states in the noninteracting Fermi sea, involving spin and isospin summations as well as momentum integration:

$\begin{array}{ll}{\bar{V}}_{\text{med}}={\displaystyle \sum _{s_3{t}_3}}{\displaystyle \int \frac{d^3{k}_3}{{(2\pi )}^3}\theta (k_f-k_3)(1-P_{13}-P_{23})V_{3N},}& (11)\end{array}$

where k_f is the Fermi momentum and we have absorbed the particle exchange operator (1 − P₁₂) into the definition of the antisymmetrized medium-dependent NN interaction ${\bar{V}}_{\text{med}}$. In general, there are nine different diagrams that need to be evaluated independently: (1 − P₁₃ − P₂₃)(W₁ + W₂ + W₃), which correspond to different closings of one incoming and outgoing particle line.

As a simple example, we compute the density-dependent NN interaction arising from the three-body contact term at N2LO shown diagrammatically in Figure 2 (f). We begin by evaluating the spin and isospin traces in Equation (11):

$\begin{array}{l}T{r}_{{\sigma }_3{\tau }_3}{\displaystyle \left[(1-P_{13}-P_{23})({\overrightarrow{\tau }}_2·{\overrightarrow{\tau }}_3+{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_3+{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2)\right]}\\ =T{r}_{{\sigma }_3{\tau }_3}({\overrightarrow{\tau }}_2·{\overrightarrow{\tau }}_3+{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_3+{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2)-T{r}_{{\sigma }_3{\tau }_3}\\ {\displaystyle \left[\left(\frac{1+{\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_3}{2}\frac{1+{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_3}{2}\right)({\overrightarrow{\tau }}_2·{\overrightarrow{\tau }}_3+{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_3+{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2)\right]}\\ -T{r}_{{\sigma }_3{\tau }_3}{\displaystyle \left[\left(\frac{1+{\overrightarrow{\sigma }}_2·{\overrightarrow{\sigma }}_3}{2}\frac{1+{\overrightarrow{\tau }}_2·{\overrightarrow{\tau }}_3}{2}\right)({\overrightarrow{\tau }}_2·{\overrightarrow{\tau }}_3+{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_3+{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2)\right]}\\ =4{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2-\frac{1}{4}T{r}_{{\sigma }_3{\tau }_3}({\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2+({\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_3)({\overrightarrow{\tau }}_2·{\overrightarrow{\tau }}_3)+({\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_3)({\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_3))\\ -\frac{1}{4}T{r}_{{\sigma }_3{\tau }_3}({\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2+({\overrightarrow{\tau }}_2·{\overrightarrow{\tau }}_3)({\overrightarrow{\tau }}_2·{\overrightarrow{\tau }}_3)+({\overrightarrow{\tau }}_2·{\overrightarrow{\tau }}_3)({\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_3))\\ =2{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2-\frac{1}{2}(4{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2+12)=-6,& (12)\end{array}$

where we have used the well known properties of Pauli matrices: $Tr\overrightarrow{\sigma }=0$, Tr1 = 2, $T{r}_3({\overrightarrow{\tau }}_i·{\overrightarrow{\tau }}_3)({\overrightarrow{\tau }}_j·{\overrightarrow{\tau }}_3)=2{\overrightarrow{\tau }}_i·{\overrightarrow{\tau }}_j$, and ${\overrightarrow{\tau }}_i·{\overrightarrow{\tau }}_i=3$. The integration over filled momentum states is trivial:

$\begin{array}{ll}{\displaystyle \int \frac{d^3{k}_3}{{(2\pi )}^3}\theta (k_f-k_3)\frac{c_E}{f_{\pi }^4{\Lambda }_{\chi }}=\frac{1}{2{\pi }^2}\frac{k_f^3}{3}\frac{c_E}{f_{\pi }^4{\Lambda }_{\chi }},}& (13)\end{array}$

which gives a final result of

$\begin{array}{ll}{V}_{\text{med}}^{(ct)}=-\frac{c_E{k}_f^3}{{\pi }^2{f}_{\pi }^4{\Lambda }_{\chi }}.& (14)\end{array}$

FIGURE 2

Figure 2. Diagrammatic contributions to the density-dependent NN interaction derived from the N2LO chiral three-nucleon force: (A) one-pion-exchange propagator correction, (B) one-pion-exchange vertex correction, (C) Pauli-blocked two-pion exchange correction, (D) short-range one-pion-exchange vertex correction, (E) contact interaction vertex correction, and (F) two-body contact interaction.

This particularly simple three-body contact interaction gives rise to a momentum-independent effective two-body interaction. For the more complicated 1π- and 2π-exchange topologies, it is convenient to consider the on-shell scattering ($|\overrightarrow{p}|=|{\overrightarrow{p}}^{\prime }|$) of two nucleons in the center-of-mass frame: $N_1(\overrightarrow{p})+N_2(-\overrightarrow{p})\to N_1({\overrightarrow{p}}^{\prime })+N_2(-{\overrightarrow{p}}^{\prime })$. This assumption results in a medium-dependent 2N interaction with the same isospin and spin structures as the free-space 2N potential, which allows for a simple decomposition of V_med into partial-wave matrix elements as we show in section 4.1. In the more general case $N_1({\overrightarrow{p}}_1)+N_2({\overrightarrow{p}}_2)\to N_1({\overrightarrow{p}}_3)+N_2({\overrightarrow{p}}_4)$, the in-medium 2N interaction will contain operator structures depending on the center-of-mass momentum $\overrightarrow{P}={\overrightarrow{p}}_1+{\overrightarrow{p}}_2={\overrightarrow{p}}_3+{\overrightarrow{p}}_4$. Such contributions have been shown to be small in practice [45]. In the applications discussed below, higher-order perturbative contributions to the ground state energy and single-particle energies involve also off-shell matrix elements of the interaction $\langle {\overrightarrow{p}}^{\prime }|V|\overrightarrow{p}\rangle$, where $|\overrightarrow{p}|\ne |{\overrightarrow{p}}^{\prime }|$. In such cases we use as an approximation the substitution $p^2\to \frac{1}{2}(p^2+p^{\prime 2})$ in the formulas derived below. The resulting interaction can then be straightfowardly implemented into modern nuclear structure codes. We will explicitly test some of the approximations noted above by comparing exact results at low order in perturbation theory using the full three-body force to the results using instead the medium-dependent 2N interaction.

Note that in the above derivation of the density-dependent 2N interaction associated with $V_{3N}^{(ct)}$, we have not applied a high-momentum regulator, which would be necessary to eliminate the components of the nuclear interaction that lie beyond the breakdown scale of the effective field theory. In the case of nucleon-nucleon potentials, the cutoff scale is typically chosen Λ ≲ 700 MeV, beyond which the introduction of a new dynamical degree of freedom (the ρ meson with mass m_ρ = 770 MeV) would be required. On the other hand, in order to fit empirical nucleon-nucleon scattering phase shift data up to laboratory energies of E_lab = 350 MeV, the cutoff is normally chosen Λ ≳ 414 MeV (the relative momentum in the center-of-mass frame corresponding to E_lab = 350 MeV). In practice, it is found that relatively low values of the momentum-space cutoff Λ ≲ 500 MeV lead to perturbative nucleon-nucleon potentials, which are suitable for a wide range of methods to solve the quantum many-body problem. Such low-cutoff potentials, however, exhibit larger artifacts in calculations of the density-dependent ground state energy of nuclear matter and single-particle potential as we will discuss explicitly below. While the choice of cutoff scale is well motivated, the regulating function can take various forms. Traditionally, an exponential regulator in the incoming and outgoing relative momenta is chosen:

$\begin{array}{ll}f(p^{\prime },p)=exp\left[-{(p^{\prime }/\Lambda )}^{2n}-{(p/\Lambda )}^{2n}\right],& (15)\end{array}$

where $\overrightarrow{p}=\frac{1}{2}({\overrightarrow{p}}_1-{\overrightarrow{p}}_2)$ and ${\overrightarrow{p}}^{\prime }=\frac{1}{2}({\overrightarrow{p}}_3-{\overrightarrow{p}}_4)$ for the general two-body scattering process $N({\overrightarrow{p}}_1)+N({\overrightarrow{p}}_2)\to N({\overrightarrow{p}}_3)+N({\overrightarrow{p}}_4)$, and n is an integer chosen such that the regulator affects only high powers in the chiral expansion. More recently [27, 46], the pion-exchange components of the nucleon-nucleon interaction have been regularized in coordinate space according to

$\begin{array}{ll}{V}_{\pi }(\overrightarrow{r})\left[1-e^{-r^2/R^2}\right],& (16)\end{array}$

where 0.8fm ≤ R ≤ 1.2fm, while the contact terms in the nuclear potential were regularized according to Equation (15) above. In previous calculations [47, 48] of the medium-dependent 2N force V_med, we have imposed the nonlocal regulating function above only after the momentum-space integration over k₃ is performed. This choice led to simplified analytical expressions for the density-dependent NN interaction in cold nuclear matter. A three-body regulator that treats all particles symmetrically can be defined by [49]

$\begin{array}{ll}{W}_3\to W_{3}F(q_1,q_2)=W_{3}exp[-{(q_1/\Lambda )}^4-{(q_2/\Lambda )}^4],& (17)\end{array}$

where ${\overrightarrow{q}}_1={\overrightarrow{p}}_1^{\prime }-{\overrightarrow{p}}_1$ and ${\overrightarrow{q}}_2={\overrightarrow{p}}_2^{\prime }-{\overrightarrow{p}}_2$ are the momentum transfers for particles 1 and 2 in W₃. Analogous expressions hold for the contributions W₁ → W₁F(q₂, q₃) and W₂ → W₂F(q₁, q₃). This choice of regulating function leads to more complicated expressions for the density-dependent 2N interaction since now the regulator in general can involve the momentum k₃ over which we integrate. More importantly, the local regulator in Equation (17) leads to much stronger cutoff artifacts for the same choice of scale (Λ_loc = Λ_nonloc) as we will demonstrate in the following. Additional discussion regarding the role of cutoff artifacts on nuclear many-body calculations can be found in Dyhdalo et al. [50].

To start, when we employ the local regulator in Equation (17), we now find for the density-dependent NN interaction in isospin-symmetric nuclear matter:

$\begin{array}{l}{V}_{\text{med}}^{(ct)}=\frac{c_E}{2{\pi }^2{f}_{\pi }^4{\Lambda }_{\chi }}[\frac{4}{3}{k}_f^3{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2{F}^2(q^2,\Lambda )-2{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_{2}F(q^2,\Lambda ){\tilde{\Gamma }}_4(p)\\ -3{\Gamma }_4^{\prime }(p,q)],& (18)\end{array}$

where

$\begin{array}{ll}F(q^2,\Lambda )=e^{-q^4/{\Lambda }^4},& (19)\end{array}$

$\begin{array}{ll}{\tilde{\Gamma }}_4(p)={\displaystyle {\int }_0^{k_f}}dk{\displaystyle {\int }_{-1}^1}dx{k}^{2}F(p^2+k^2+2pkx,\Lambda ),& (20)\end{array}$

$\begin{array}{l}{\Gamma }_4^{\prime }(p,q)={\displaystyle {\int }_0^{k_f}d}k{\displaystyle {\int }_{-1}^{1}d}x{\displaystyle {\int }_0^{2\pi }d}\varphi \frac{k^2}{2\pi }F(p^2+k^2\\ +kx\sqrt{4p^2-q^2}+qk\sqrt{1-x^2}\cos \varphi ,\Lambda )\\ \times F(p^2+k^2+kx\sqrt{4p^2-q^2}-qk\sqrt{1-x^2}\cos \varphi ,\Lambda ).& (21)\end{array}$

In the limit of large Λ we find that F(q², Λ) → 1, ${\tilde{\Gamma }}_4(p)\to \frac{2k_f^3}{3}$, and ${\Gamma }_4^{\prime }(p,q)\to \frac{2k_f^3}{3}$. Thus, in this limit we clearly recover Equation (14).

Previously, for the in-medium pion self-energy correction (Figure 2A), with no regulator we found

$\begin{array}{ll}{V}_{NN}^{\text{med},1}=\frac{g_A^2{k}_f^3}{3{\pi }^2{f}_{\pi }^4}{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2\frac{{\overrightarrow{\sigma }}_1·\overrightarrow{q}{\overrightarrow{\sigma }}_2·\overrightarrow{q}}{{(m_{\pi }^2+q^2)}^2}(2c_1{m}_{\pi }^2+c_3{q}^2).& (22)\end{array}$

With the local regulator in Equation (17) we now find

$\begin{array}{ll}{V}_{NN}^{\text{med},1}=\frac{g_A^2{k}_f^3}{3{\pi }^2{f}_{\pi }^4}{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2\frac{{\overrightarrow{\sigma }}_1·\overrightarrow{q}{\overrightarrow{\sigma }}_2·\overrightarrow{q}}{{(m_{\pi }^2+q^2)}^2}(2c_1{m}_{\pi }^2+c_3{q}^2)F^2(q^2,\Lambda ).& (23)\end{array}$

Previously, for the Pauli-blocked vertex correction (Figure 2B), we found

$\begin{array}{l}{V}_{NN}^{\text{med},2}=\frac{g_A^2}{8{\pi }^2{f}_{\pi }^4}{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2\frac{{\overrightarrow{\sigma }}_1·\overrightarrow{q}{\overrightarrow{\sigma }}_2·\overrightarrow{q}}{m_{\pi }^2+q^2}\\ {\displaystyle (-4c_1{m}_{\pi }^2\left[{\Gamma }_0+{\Gamma }_1\right]-(c_3+c_4)\left[q^2({\Gamma }_0+2{\Gamma }_1+{\Gamma }_3)+4{\Gamma }_2\right]}\\ {\displaystyle +4c_4{\displaystyle [\frac{2}{3}{k}_f^3-m_{\pi }^2{\Gamma }_0]})}.& (24)\end{array}$

When the local regulators are employed, we now find that the p-dependent auxiliary functions Γ_i must be replaced by

$\begin{array}{ll}{\tilde{\Gamma }}_0(p)={\displaystyle {\int }_0^{k_f}}dk{\displaystyle {\int }_{-1}^1}dx\frac{k^2}{m_{\pi }^2+p^2+k^2+2pkx}F(p^2+k^2+2pkx,\Lambda ),& (25)\end{array}$

$\begin{array}{ll}{\tilde{\Gamma }}_1(p)={\displaystyle {\int }_0^{k_f}}dk{\displaystyle {\int }_{-1}^1}dx\frac{k^{3}x/p}{m_{\pi }^2+p^2+k^2+2pkx}F(p^2+k^2+2pkx,\Lambda ),& (26)\end{array}$

$\begin{array}{ll}{\tilde{\Gamma }}_2(p)={\displaystyle {\int }_0^{k_f}}dk{\displaystyle {\int }_{-1}^1}dx\frac{k^4(1-x^2)/2}{m_{\pi }^2+p^2+k^2+2pkx}F(p^2+k^2+2pkx,\Lambda ),& (27)\end{array}$

$\begin{array}{ll}{\tilde{\Gamma }}_3(p)={\displaystyle {\int }_0^{k_f}}dk{\displaystyle {\int }_{-1}^1}dx\frac{k^4(3x^2-1)/(2p^2)}{m_{\pi }^2+p^2+k^2+2pkx}F(p^2+k^2+2pkx,\Lambda ),& (28)\end{array}$

where the versions of these functions without the superscript tildes in Equation (24) can be obtained by setting Λ → ∞. In addition, the term $4c_4\left[\frac{2k_f^3}{3}\right]$ in $V_{NN}^{\text{med},2}$ must be replaced with the quantity

$\begin{array}{l}4c_4\left[\frac{2k_f^3}{3}\right]\to 4c_4{\displaystyle {\int }_0^{k_f}}dk{\displaystyle {\int }_{-1}^1}dx{k}^{2}F(p^2+k^2+2pkx,\Lambda )\\ \equiv 4c_4{\tilde{\Gamma }}_4(p).& (29)\end{array}$

Then the revised Pauli-blocked vertex correction has the form

$\begin{array}{l}{V}_{NN}^{\text{med},\text{2}}=\frac{g_A^2}{8{\pi }^2{f}_{\pi }^4}{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2\frac{{\overrightarrow{\sigma }}_1·\overrightarrow{q}{\overrightarrow{\sigma }}_2·\overrightarrow{q}}{m_{\pi }^2+q^2}(-4c_1{m}_{\pi }^2[{\tilde{\Gamma }}_0+{\tilde{\Gamma }}_1]\\ -(c_3+c_4)[q^2({\tilde{\Gamma }}_0+2{\tilde{\Gamma }}_1+{\tilde{\Gamma }}_3)+4{\tilde{\Gamma }}_2]\\ +4c_4\left[{\tilde{\Gamma }}_4-m_{\pi }^2{\tilde{\Gamma }}_0\right])F(q^2,\Lambda ).& (30)\end{array}$

Previously, we found for the Pauli-blocked two-pion-exchange interaction (Figure 2C),

$\begin{array}{l}{V}_{NN}^{\text{med},\text{3}}=\frac{g_A^2}{16{\pi }^2{f}_{\pi }^4}\{-12c_1{m}_{\pi }^2\left[2{\Gamma }_0-(2m_{\pi }^2+q^2)G_0\right]\\ -c_3[8k_f^3-12(2m_{\pi }^2+q^2){\Gamma }_0-6q^2{\Gamma }_1+3{(2m_{\pi }^2+q^2)}^2{G}_0]\\ +4c_4{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2({\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2{q}^2-{\overrightarrow{\sigma }}_1·\overrightarrow{q}{\overrightarrow{\sigma }}_2·\overrightarrow{q})G_2\\ -(3c_3+c_4{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2)i({\overrightarrow{\sigma }}_1+{\overrightarrow{\sigma }}_2)·(\overrightarrow{q}\times \overrightarrow{p})\\ \times [2{\Gamma }_0+2{\Gamma }_1-(2m_{\pi }^2+q^2)(G_0+2G_1)]\\ -12c_1{m}_{\pi }^{2}i({\overrightarrow{\sigma }}_1+{\overrightarrow{\sigma }}_2)·(\overrightarrow{q}\times \overrightarrow{p})[G_0+2G_1]\\ +4c_4{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2{\overrightarrow{\sigma }}_1·(\overrightarrow{q}\times \overrightarrow{p}){\overrightarrow{\sigma }}_2·(\overrightarrow{q}\times \overrightarrow{p})[G_0+4G_1+4G_3]\}.& (31)\end{array}$

When substituting in the local regulator functions we obtain

$\begin{array}{l}{V}_{NN}^{\text{med},\text{3}}=\frac{g_A^2}{16{\pi }^2{f}_{\pi }^4}\{-12c_1{m}_{\pi }^2\left[2{\Gamma }_0^{\prime }-(2m_{\pi }^2+q^2)G_0^{\prime }\right]\\ -c_3[12{\Gamma }_4^{\prime }-12(2m_{\pi }^2+q^2){\Gamma }_0^{\prime }-6q^2{\Gamma }_1^{\prime }\\ +3{(2m_{\pi }^2+q^2)}^2{G}_0^{\prime }]+4c_4{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2({\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2{q}^2-{\overrightarrow{\sigma }}_1·\overrightarrow{q}{\overrightarrow{\sigma }}_2·\overrightarrow{q})G_2^{\prime }\\ -(3c_3+c_4{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2)i({\overrightarrow{\sigma }}_1+{\overrightarrow{\sigma }}_2)·(\overrightarrow{q}\times \overrightarrow{p})\\ [2{\Gamma }_0^{\prime }+2{\Gamma }_1^{\prime }-(2m_{\pi }^2+q^2)(G_0^{\prime }+2G_1^{\prime })]\\ -12c_1{m}_{\pi }^{2}i({\overrightarrow{\sigma }}_1+{\overrightarrow{\sigma }}_2)·(\overrightarrow{q}\times \overrightarrow{p})[G_0^{\prime }+2G_1^{\prime }]\\ +4c_4{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2{\overrightarrow{\sigma }}_1·(\overrightarrow{q}\times \overrightarrow{p}){\overrightarrow{\sigma }}_2·(\overrightarrow{q}\times \overrightarrow{p})[G_0^{\prime }+4G_1^{\prime }+4G_3^{\prime }]\}.& (32)\end{array}$

In the above expressions we encounter the p- and q-dependent functions

$\begin{array}{l}{G}_{0,*,**}^{\prime }(p,q)={\displaystyle {\int }_0^{k_f}d}k{\displaystyle {\int }_{-1}^{1}d}x{\displaystyle {\int }_0^{2\pi }d}\varphi \frac{\{k^2,k^4,k^6\}/(2\pi )}{A^2-B^2{\cos }^2\varphi }\\ F(p^2+k^2+kx\sqrt{4p^2-q^2}+qk\sqrt{1-x^2}\cos \varphi ,\Lambda )\\ F(p^2+k^2+kx\sqrt{4p^2-q^2}\\ -qk\sqrt{1-x^2}\cos \varphi ,\Lambda ),& (33)\end{array}$

where $A=m_{\pi }^2+p^2+k^2+kx\sqrt{4p^2-q^2}$ and $B=qk\sqrt{1-x^2}$. In Equation (33), the functions G_{0, *, **}(p, q) are obtained from Equation (33) by substituting Λ → ∞. In addition we encounter the following p- and q-dependent functions

$\begin{array}{ll}{G}_1^{\prime }(p,q)=\frac{{\Gamma }_0^{\prime }-(m_{\pi }^2+p^2)G_0^{\prime }-G_{*}^{\prime }}{4p^2-q^2},& (34)\end{array}$

$\begin{array}{ll}{G}_{1*}^{\prime }(p,q)=\frac{3{\Gamma }_2^{\prime }+p^2{\Gamma }_3^{\prime }-(m_{\pi }^2+p^2)G_{*}^{\prime }-G_{**}^{\prime }}{4p^2-q^2},& (35)\end{array}$

$\begin{array}{ll}{G}_2^{\prime }(p,q)=(m_{\pi }^2+p^2)G_1^{\prime }+G_{*}^{\prime }+G_{1*}^{\prime },& (36)\end{array}$

$\begin{array}{ll}{G}_3^{\prime }(p,q)=\frac{\frac{1}{2}{\Gamma }_1^{\prime }-2(m_{\pi }^2+p^2)G_1^{\prime }-2G_{1*}^{\prime }-G_{*}^{\prime }}{4p^2-q^2},& (37)\end{array}$

where

$\begin{array}{l}{\Gamma }_0^{\prime }(p,q)={\displaystyle {\int }_0^{k_f}}dk{\displaystyle {\int }_{-1}^1}dx{\displaystyle {\int }_0^{2\pi }}d\varphi \\ \frac{k^2/(2\pi )}{m_{\pi }^2+p^2+k^2+kx\sqrt{4p^2-q^2}+qk\sqrt{1-x^2}cos\varphi }\\ \times F(p^2+k^2+kx\sqrt{4p^2-q^2}+qk\sqrt{1-x^2}cos\varphi ,\Lambda )\\ \times F(p^2+k^2+kx\sqrt{4p^2-q^2}-qk\sqrt{1-x^2}cos\varphi ,\Lambda ),& (38)\end{array}$

$\begin{array}{l}{\Gamma }_1^{\prime }(p,q)={\displaystyle {\int }_0^{k_f}}dk{\displaystyle {\int }_{-1}^1}dx{\displaystyle {\int }_0^{2\pi }}d\varphi \\ \frac{k^3\left[x\sqrt{4p^2-q^2}+q\sqrt{1-x^2}cos\varphi \right]/(4\pi p^2)}{m_{\pi }^2+p^2+k^2+kx\sqrt{4p^2-q^2}+qk\sqrt{1-x^2}cos\varphi }\\ \times F(p^2+k^2+kx\sqrt{4p^2-q^2}+qk\sqrt{1-x^2}cos\varphi ,\Lambda )\\ \times F(p^2+k^2+kx\sqrt{4p^2-q^2}-qk\sqrt{1-x^2}cos\varphi ,\Lambda ),& (39)\end{array}$

$\begin{array}{l}{\Gamma }_2^{\prime }(p,q)={\displaystyle {\int }_0^{k_f}}dk{\displaystyle {\int }_{-1}^1}dx{\displaystyle {\int }_0^{2\pi }}d\varphi \\ \frac{k^4{\displaystyle \left[4p^2-{\left(x\sqrt{4p^2-q^2}+q\sqrt{1-x^2}cos\varphi \right)}^2\right]}/(16\pi p^2)}{m_{\pi }^2+p^2+k^2+kx\sqrt{4p^2-q^2}+qk\sqrt{1-x^2}cos\varphi }\\ \times F(p^2+k^2+kx\sqrt{4p^2-q^2}+qk\sqrt{1-x^2}cos\varphi ,\Lambda )\\ \times F(p^2+k^2+kx\sqrt{4p^2-q^2}-qk\sqrt{1-x^2}cos\varphi ,\Lambda ),& (40)\end{array}$

$\begin{array}{l}{\Gamma }_3^{\prime }(p,q)={\displaystyle {\int }_0^{k_f}}dk{\displaystyle {\int }_{-1}^1}dx{\displaystyle {\int }_0^{2\pi }}d\varphi \\ \frac{k^4{\displaystyle \left[3{\left(x\sqrt{4p^2-q^2}+q\sqrt{1-x^2}cos\varphi \right)}^2-4p^2\right]}/(16\pi p^4)}{m_{\pi }^2+p^2+k^2+kx\sqrt{4p^2-q^2}+qk\sqrt{1-x^2}cos\varphi }\\ \times F(p^2+k^2+kx\sqrt{4p^2-q^2}+qk\sqrt{1-x^2}cos\varphi ,\Lambda )\\ \times F(p^2+k^2+kx\sqrt{4p^2-q^2}-qk\sqrt{1-x^2}cos\varphi ,\Lambda ),& (41)\end{array}$

Additionally, we have replaced the quantity $8k_f^3$ in Equation (21) with $12{\Gamma }_4^{\prime }$ defined in Equation (31). The term $8k_f^3$ in Equation (31) as well as all unprimed Γ and G functions can be obtained by setting Λ → ∞. For the c_D vertex correction to one-pion exchange (Figure 2D), we previously had

$\begin{array}{ll}{V}_{NN}^{\text{med},4}=-\frac{g_A{c}_D{k}_f^3}{12{\pi }^2{f}_{\pi }^4{\Lambda }_{\chi }}\frac{{\overrightarrow{\sigma }}_1·\overrightarrow{q}{\overrightarrow{\sigma }}_2·\overrightarrow{q}}{m_{\pi }^2+q^2}{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2.& (42)\end{array}$

Including the local regulators we find

$\begin{array}{ll}{V}_{NN}^{\text{med},4}=-\frac{g_A{c}_D}{8{\pi }^2{f}_{\pi }^4{\Lambda }_{\chi }}\frac{{\overrightarrow{\sigma }}_1·\overrightarrow{q}{\overrightarrow{\sigma }}_2·\overrightarrow{q}}{m_{\pi }^2+q^2}{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2\left(\frac{4}{3}{k}_f^{3}F(q^2,\Lambda )-{\Gamma }_4^{\prime }\right).& (43)\end{array}$

For the c_D vertex correction to the 2N contact term (Figure 2E), we previously had

$\begin{array}{l}{V}_{NN}^{\text{med},5}=\frac{g_A{c}_D}{16{\pi }^2{f}_{\pi }^4{\Lambda }_{\chi }}\{{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2[2{\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2{\Gamma }_2+({\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2(2p^2-\frac{q^2}{2})\\ +{\overrightarrow{\sigma }}_1·\overrightarrow{q}{\overrightarrow{\sigma }}_2·\overrightarrow{q}(1-\frac{2p^2}{q^2})-\frac{2}{q^2}{\overrightarrow{\sigma }}_1·(\overrightarrow{q}\times \overrightarrow{p}){\overrightarrow{\sigma }}_2·(\overrightarrow{q}\times \overrightarrow{p}))\\ ({\Gamma }_0+2{\Gamma }_1+{\Gamma }_3)]+4k_f^3-6m_{\pi }^2{\Gamma }_0\}.& (44)\end{array}$

Including the local regulators we obtain

$\begin{array}{l}{V}_{NN}^{\text{med},5}={\displaystyle \frac{g_A{c}_D}{16{\pi }^2{f}_{\pi }^4{\Lambda }_{\chi }}\{{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2[2{\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2{\tilde{\Gamma }}_2}\\ {\displaystyle +({\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2(2p^2-\frac{q^2}{2})}+{\overrightarrow{\sigma }}_1·\overrightarrow{q}{\overrightarrow{\sigma }}_2·\overrightarrow{q}(1-\frac{2p^2}{q^2})\\ {\displaystyle -\frac{2}{q^2}{\overrightarrow{\sigma }}_1·(\overrightarrow{q}\times \overrightarrow{p}){\overrightarrow{\sigma }}_2·(\overrightarrow{q}\times \overrightarrow{p}))}\\ {\displaystyle ({\tilde{\Gamma }}_0+2{\tilde{\Gamma }}_1+{\tilde{\Gamma }}_3)]+6{\tilde{\Gamma }}_4-6m_{\pi }^2{\tilde{\Gamma }}_0\}}F(q^2,\Lambda ).& (45)\end{array}$

We reiterate that the above expressions are obtained in the center-of-mass frame assuming on-shell scattering conditions. In all cases, the expressions for the in-medium 2N interaction above are well-behaved (no poles) and involve only elementary integrations.

3. Applications of Density-Dependent 2N Interactions to Nuclear Many-Body Systems

3.1. Equation of State of Cold Nuclear Matter

The equation of state of nuclear matter gives important insights into many properties of finite nuclei, including the volume and symmetry energy contributions to the binding energy in the semi-empirical mass formula, the saturated central density of medium-mass and heavy nuclei, as well as nuclear collective excitation modes and giant resonances. The equation of state is also essential for modeling neutron stars [51–59], including their birth in core-collapse supernovae, their radii as a function of mass, their tidal deformabilities in the presence of compact binary companions, and their moments of inertia. For relatively soft equations of state, the central densities of typical neutron stars with mass M ≃ 1.4M_⊙ reach n ≃ 3n₀ [60], where n₀ = 0.16 fm⁻³ is the nucleon number density in the saturated interior of heavy nuclei. At such densities, three-body forces give a large contribution to the pressure and are therefore critical for understanding neutron star structure.

The first-order perturbative contribution (Hartree-Fock approximation) to the ground state energy of isospin-symmetric nuclear matter is given by

$\begin{array}{ll}{E}_{2N}^{(1)}=\frac{1}{2}{\displaystyle \sum _{12}}\langle 12|{\bar{V}}_{2N}|12\rangle n_1{n}_2,& (46)\end{array}$

for the antisymmetrized two-body force ${\bar{V}}_{2N}$ and

$\begin{array}{ll}{E}_{3N}^{(1)}=\frac{1}{6}{\displaystyle \sum _{123}}\langle 123|{\bar{V}}_{3N}|123\rangle n_1{n}_2{n}_3,& (47)\end{array}$

for the antisymmetrized three-body force ${\bar{V}}_{3N}$. In the above equations, $n_i=\theta (k_f-|{\overrightarrow{k}}_i|)$ is the zero-temperature Fermi-Dirac distribution function with Fermi momentum k_f, and the sum is taken over the momentum, spin, and isospin of the occupied states in the Fermi sea.

In Figure 3, we show the density-dependence of the Hartree-Fock contribution to the ground state energy of isospin-symmetric nuclear matter from the N2LO chiral three-nucleon force in different approximations. As a representative example, we consider the low-energy constants c₁ = −0.81 GeV⁻¹, c₃ = −3.4 GeV⁻¹, c₄ = 3.4 GeV⁻¹, c_D = −0.24, and c_E = −0.106 obtained in Coraggio et al. [61] and associated with the N3LO NN chiral interaction with cutoff scale Λ = 450 MeV. We see that in all cases the first-order perturbative contribution from three-body forces in isospin-symmetric matter is strongly repulsive. The exact treatment of the Hartree-Fock contribution to the ground state energy arising from the N2LO three-nucleon force is shown in Figure 3 as the thick black line labeled “$V_{3N,\text{exact}}^{\Lambda \to \infty }$.” Employing instead the density-dependent NN interaction V_med with Λ → ∞ we obtain the contribution shown with the thin blue line and labeled “$V_{\text{med}}^{\Lambda \to \infty }$.” Note that in order to avoid triple-counting when the density-dependent NN interaction V_med is used in Equation (46), we must replace ${\bar{V}}_{2N}\to \frac{1}{3}{\bar{V}}_{\text{med}}$. From Figure 3, we observe that at the Hartree-Fock level the density-dependent NN interaction accurately reflects the physics encoded in the full three-body force. This is not a trivial observation since several approximations were employed to derive the density-dependent NN interaction from V_3N. In Figure 3, we see that the largest deviation in the two curves is only 1 MeV (or ≃ 3%) at n = 0.32 fm⁻³.

FIGURE 3

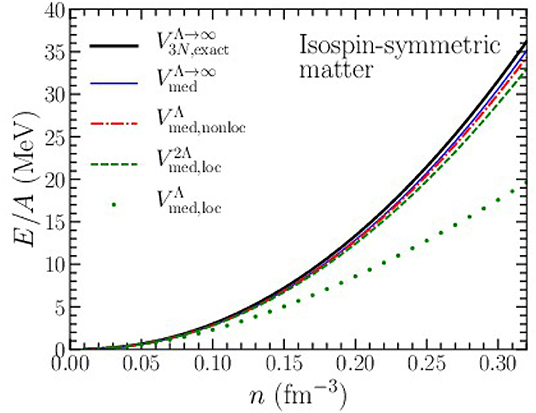
Figure 3. Hartree-Fock contribution to the ground-state energy of isospin-symmetric nuclear matter as a function of density due to the N2LO chiral three-nucleon force with cutoff scale Λ = 450 MeV.

Imposing the nonlocal regulator in Equation (15) leads to the red dot-dashed line labeled “$V_{\text{med},\text{nonloc}}^{\Lambda }$.” As expected, the presence of the momentum-space cutoff reduces the Hartree-Fock contribution to the ground-state energy, particularly at high densities. However, the cutoff artifacts introduced are rather small and amount to only 0.8 MeV (or ≃ 2%) relative to the result from $V_{\text{med}}^{\Lambda \to \infty }$ at n = 0.32 fm⁻³. We note that since the Hartree-Fock contribution to the ground state energy E/A is always finite and probes only the characteristic physical energy scale of the system, the differences between $V_{\text{med}}^{\Lambda \to \infty }$ and $V_{\text{med},\text{nonloc}}^{\Lambda }$ are true regulator artifacts. We next impose the local regulator in Equation (17), which is shown as the dotted green line in Figure 3 and labeled “$V_{\text{med},\text{loc}}^{\Lambda }$.” For this choice of regulator we find severe cutoff artifacts, even at low densities where one would expect the role of the regulating function to be minimal. For example, at n = 0.10 fm⁻³, there is a 19% relative error between $V_{\text{med}}^{\Lambda \to \infty }$ and $V_{\text{med},\text{loc}}^{\Lambda }$. From Equation (17), we expect the regulator to introduce corrections at order ${(Q/\Lambda )}^4~{(k_f/\Lambda )}^4$. The Fermi momentum at this density is k_f = 225 MeV, which for the Λ = 450 MeV chiral potential implies an error of ${(k_f/\Lambda )}^4\simeq 6\%$. One key difference between the non-local and local regulators of Equations (15) and (17) is that the relative momentum ranges from 0 < k < k_f while the momentum transfer ranges from 0 < q < 2k_f. Therefore, one naturally expects larger cutoff artifacts for the local regulating function in Equation (17). Indeed, when the value of the momentum-space cutoff is increased to 2Λ, as can be seen from the dashed green curve of Figure 3, the results from employing the local regulator are now comparable to those using the non-local regulator.

In Figure 4, we show the density-dependence of the Hartree-Fock contribution to the ground state energy of pure neutron matter from the N2LO chiral three-nucleon force in different approximations. Again we consider the low-energy constants c₁ = −0.81 GeV⁻¹, c₃ = −3.4 GeV⁻¹, c₄ = 3.4 GeV⁻¹, c_D = −0.24, and c_E = −0.106 associated with the N3LO NN chiral interaction with cutoff scale Λ = 450 MeV. However, in pure neutron matter the Hartree-Fock contribution from three-body forces is independent of c₄, c_D, and c_E. We show as the thick black line labeled “$V_{3N,\text{exact}}^{\Lambda \to \infty }$” in Figure 4, the Hartree-Fock contribution to the ground-state energy of pure neutron matter. Employing the density-dependent NN interaction V_med with Λ → ∞ we obtain the contribution shown with the thin blue line labeled “$V_{\text{med}}^{\Lambda \to \infty }$.” Again, at the Hartree-Fock level the density-dependent NN interaction very accurately reproduces the result from the full three-body force.

FIGURE 4

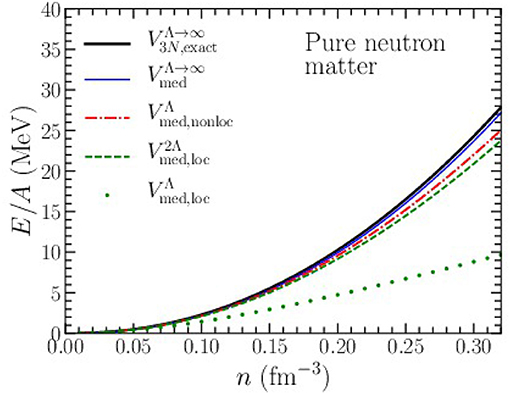
Figure 4. Hartree-Fock contribution to the ground-state energy of pure neutron matter as a function of density due to the N2LO chiral three-nucleon force with cutoff scale Λ = 450 MeV.

Inserting the nonlocal regulator in Equation (15) we find the red dot-dashed line labeled “$V_{\text{med},\text{nonloc}}^{\Lambda }$.” The non-local regulator preserves the property that none of the three-body force terms proportional to c₄, c_D, and c_E contribute to the ground-state energy of pure neutron matter. We find that the momentum-space cutoff reduces the Hartree-Fock contribution to the ground-state energy even more than that in isospin-symmetric nuclear matter. This is due to the larger neutron Fermi momentum (compared to the nucleon Fermi momentum in isospin-symmetric nuclear matter at the same density). The cutoff artifacts introduced are nevertheless relatively small and amount to 2 MeV at n = 0.32 fm⁻³. Finally, we impose the local regulator in Equation (17) to obtain the dotted green line labeled “$V_{\text{med},\text{loc}}^{\Lambda }$” in Figure 4. Again, the cutoff artifacts are very large. For example, at n = 0.10 fm⁻³, there is now a 34% relative error between $V_{\text{med}}^{\Lambda \to \infty }$ and V_{med, loc}. At this density, the maximum momentum transfer is q = 2k_f ≃ 570 MeV, which is clearly problematic for the chosen cutoff Λ = 450 MeV. In addition to larger artifacts, the local regulator also induces contributions to the density-dependent NN interaction in pure neutron matter that now depend on the low-energy constants c₄, c_D, and c_E. In the case of pure neutron matter, diagrams (d), (e), and (f) in Figure 2 produce $V_{NN}^{\text{med},4}=V_{NN}^{\text{med},5}=V_{NN}^{\text{med},6}=0$ with either the nonlocal regulator or no regulator at all. Instead, for the local regulator we find

$\begin{array}{ll}{V}_{NN}^{\text{med},4}=-\frac{g_A{c}_D}{8{\pi }^2{f}_{\pi }^4{\Lambda }_{\chi }}\frac{{\overrightarrow{\sigma }}_1·\overrightarrow{q}{\overrightarrow{\sigma }}_2·\overrightarrow{q}}{m_{\pi }^2+q^2}\left(\frac{2}{3}{k}_f^{3}F(q^2,\Lambda )-{\Gamma }_4^{\prime }\right),& (48)\end{array}$

which indeed vanishes when the local regulators are replaced by 1. For the c_D vertex correction to the 2N contact term with local regulators we obtain

$\begin{array}{l}{V}_{NN}^{\text{med},5}=\frac{g_A{c}_D}{16{\pi }^2{f}_{\pi }^4{\Lambda }_{\chi }}{\displaystyle \{2{\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2{\tilde{\Gamma }}_2+({\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2(2p^2-\frac{q^2}{2})}\\ +{\overrightarrow{\sigma }}_1·\overrightarrow{q}{\overrightarrow{\sigma }}_2·\overrightarrow{q}{\displaystyle (1-\frac{2p^2}{q^2})}\\ {\displaystyle -\frac{2}{q^2}{\overrightarrow{\sigma }}_1·(\overrightarrow{q}\times \overrightarrow{p}){\overrightarrow{\sigma }}_2·(\overrightarrow{q}\times \overrightarrow{p}))}({\tilde{\Gamma }}_0+2{\tilde{\Gamma }}_1+{\tilde{\Gamma }}_3)\\ {\displaystyle +2{\tilde{\Gamma }}_4-2m_{\pi }^2{\tilde{\Gamma }}_0\}}F(q^2,\Lambda ),& (49)\end{array}$

where ${\tilde{\Gamma }}_4(p)$ is defined in Equation (20). Finally, the three-body contact term with the local regulator leads to

$\begin{array}{l}{V}_{NN}^{\text{med},\text{6}}=\frac{c_E}{2{\pi }^2{f}_{\pi }^4{\Lambda }_{\chi }}[\frac{2}{3}{k}_f^3{F}^2(q^2,\Lambda )-2F(q^2,\Lambda ){\tilde{\Gamma }}_4(p)\\ -{\Gamma }_4^{\prime }(p,q)+\frac{4}{3}{k}_f^{3}F(q^2,\Lambda )].& (50)\end{array}$

Again, this term vanishes when the regulating functions are set to 1. These additional terms have been included in the present calculation of the dotted green line in Figure 4. Substituting Λ → 2Λ into the nonlocal regulator again reduces the cutoff artifacts, as seen in the dashed green curve of Figure 4.

The inclusion of three-body forces in the nuclear equation of state beyond the Hartree-Fock approximation remains challenging. While several recent works [33, 62] have computed the exact second-order contribution to the equation of state from three-body forces, the use of derived density-dependent two-body interactions allows for an approximate treatment up to third order in perturbation theory [61, 63]:

$\begin{array}{ll}{E}^{(2)}=-\frac{1}{4}{\displaystyle \sum _{1234}}|\langle 12|{\bar{V}}_{\text{eff}}|34\rangle {|}^2\frac{n_1{n}_2{\bar{n}}_3{\bar{n}}_4}{e_3+e_4-e_1-e_2},& (51)\end{array}$

$\begin{array}{l}{E}_{pp}^{(3)}=\frac{1}{8}{\displaystyle \sum _{123456}}\langle 12|{\bar{V}}_{\text{eff}}|34\rangle \langle 34|{\bar{V}}_{\text{eff}}|56\rangle \langle 56|{\bar{V}}_{\text{eff}}|12\rangle \\ \frac{n_1{n}_2{\bar{n}}_3{\bar{n}}_4{\bar{n}}_5{\bar{n}}_6}{(e_3+e_4-e_1-e_2)(e_5+e_6-e_1-e_2)},& (52)\end{array}$

$\begin{array}{l}{E}_{hh}^{(3)}=\frac{1}{8}{\displaystyle \sum _{123456}}\langle 12|{\bar{V}}_{\text{eff}}|34\rangle \langle 34|{\bar{V}}_{\text{eff}}|56\rangle \langle 56|{\bar{V}}_{\text{eff}}|12\rangle \\ \frac{{\bar{n}}_1{\bar{n}}_2{n}_3{n}_4{n}_5{n}_6}{(e_1+e_2-e_3-e_4)(e_1+e_2-e_5-e_6)},& (53)\end{array}$

$\begin{array}{l}{E}_{ph}^{(3)}=-{\displaystyle \sum _{123456}}\langle 12|{\bar{V}}_{\text{eff}}|34\rangle \langle 54|{\bar{V}}_{\text{eff}}|16\rangle \langle 36|{\bar{V}}_{\text{eff}}|52\rangle \\ \frac{n_1{n}_2{\bar{n}}_3{\bar{n}}_4{n}_5{\bar{n}}_6}{(e_3+e_4-e_1-e_2)(e_3+e_6-e_2-e_5)},& (54)\end{array}$

where ${\bar{n}}_j=1-n_j$ and V_eff = V_2N + V_med. The intermediate-state single-particle energies e_i in Equations (51)−(54) can be treated in several different approximations. In the simplest case, they are taken as the free-space energies: e(k) = k²/2M. More generally, they can be dressed with interaction lines [64] in which case e(k) = k²/2M + ℜΣ(e(k), k), where Σ(e(k), k) is the self-consistent energy- and momentum-dependent nucleon self energy.

Third-order diagrams [61] and fourth-order diagrams [33] are found to give rather small contributions (~ 2 MeV) to the equation of state up to n = 1.5n₀ for potentials with momentum-space cutoffs Λ ≃ 400−500 MeV. However, the intermediate-state energies in Equations (51)−(54) should be treated at least to second order [63] in a perturbative expansion of the self-energy. In Figure 5, we plot the equation of state of isospin-symmetric nuclear matter for several different choices of the cutoff scale Λ = 414, 450, 500 MeV (represented by red, blue, and green colors, respectively) and orders in many-body perturbation theory (denoted by the symbol). In all cases we employ an N3LO chiral nucleon-nucleon interaction with only the N2LO chiral three-body force with low-energy constants fitted to the binding energies of ³H and ³He as well as the beta-decay lifetime of ³H. For the density-dependent three-body force we use the nonlocal regulator in Equation (15). From Figures 3, 4, we see that the local regulator in Equation (17) would be highly constraining and only allow for a meaningful calculation of the nuclear equation of state below saturation density. In Figure 5, the dotted lines denote the inclusion of second-order ground-state energy diagrams (E⁽²⁾) with first-order self energies (Σ⁽¹⁾) for the intermediate-state propagators. The dashed lines denote the inclusion of second-order ground-state energy diagrams (E⁽²⁾) with second-order self energies (Σ⁽²⁾) for the intermediate-state propagators. From Figure 5, we see that the second-order self energy diagrams contribute 2−3 MeV to the ground state energy per particle for densities n ≥ 0.16 fm⁻³. Finally, the solid lines denote the inclusion of third-order ground-state energy diagrams [E⁽³⁾] with second-order self energies [Σ⁽²⁾] for the intermediate-state propagators. In general, the sum of all third-order diagrams gives a relatively small contribution to the equation of state around saturation density. However, below the critical density for the spinodal instability (n_c ≃ 0.08 fm⁻³) [65], denoted by the blue shaded region in Figure 5, the third-order diagrams give somewhat large effects due to the breakdown of perturbation theory. Nevertheless, the saturation of nuclear matter is robust and both the empirical saturation density and energy are within the uncertainties predicted from chiral nuclear forces. We note that the ground state energy from the N3LO-414 and N3LO-450 chiral potentials are very similar in all approximations. Both potentials are known to converge very rapidly in perturbation theory compared to the N3LO-500 potential [63], which may partly explain the similarity of their results.

FIGURE 5

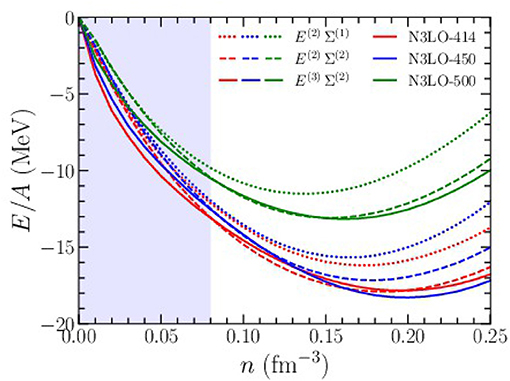
Figure 5. Equation of state of isospin-symmetric nuclear matter from chiral two- and three-body forces with different choices of the momentum-space cutoff Λ and at different orders in many-body perturbation theory. The label E⁽ⁱ⁾ denotes the i-th order in perturbation theory, and Σ⁽ⁿ⁾ denotes the n-th order treatment of the self-energy. The shaded region below n = 0.08 fm⁻³ represents the approximate location of the spinodal instability.

3.2. Nucleon-Nucleus Optical Potentials

The theoretical description of nucleon-nucleus scattering and reactions can be greatly simplified through the introduction of optical model potentials, which replace the complicated two- and many-body interactions between projectile and target with an average one-body potential. In many-body perturbation theory, the optical potential can be identified as the nucleon self-energy, which in general is complex, non-local, and energy dependent:

$\begin{array}{ll}V(\overrightarrow{r},{\overrightarrow{r}}^{\prime };E)=U(\overrightarrow{r},{\overrightarrow{r}}^{\prime };E)+iW(\overrightarrow{r},{\overrightarrow{r}}^{\prime };E).& (55)\end{array}$

While phenomenological optical potentials [66] are fitted to a great amount of differential elastic scattering, total cross section, and analyzing power data, microscopic optical potentials can be constructed from high-precision two-nucleon and three-nucleon forces [67–71]. In chiral effective field theory, three-nucleon forces in particular have been shown [64, 72] to give rise to an overall repulsive single-particle potential at all projectile energies that increases strongly with the density of the medium. Three-nucleon forces are therefore essential for an accurate description of nucleon-nucleus scattering at moderate energies where the projectile penetrates the target nucleus.

In the Hartree-Fock approximation, the contribution to the non-local (but energy-independent) nucleon self energy is given by

$\begin{array}{ll}{\Sigma }_{2N}^{(1)}(q)={\displaystyle \sum _1}\langle \overrightarrow{q}{\overrightarrow{h}}_{1}s{s}_{1}t{t}_1|{\bar{V}}_{2N}|\overrightarrow{q}{\overrightarrow{h}}_{1}s{s}_{1}t{t}_1\rangle n_1,& (56)\end{array}$

where ${\bar{V}}_{2N}$ denotes the antisymmetrized NN potential, $n_1=\theta (k_f-|{\overrightarrow{h}}_1|)$ is the zero-temperature Fermi-Dirac distribution function, and the sum is taken over the momentum, spin, and isospin of the intermediate hole state $|{\overrightarrow{h}}_1,s_1,t_1\rangle$. The Hartree-Fock contribution from three-body forces is given by

$\begin{array}{ll}{\Sigma }_{3N}^{(1)}(q)=\frac{1}{2}{\displaystyle \sum _{12}}\langle \overrightarrow{q}{\overrightarrow{h}}_1{\overrightarrow{h}}_2;s{s}_1{s}_2;t{t}_1{t}_2|{\bar{V}}_{3N}|\overrightarrow{q}{\overrightarrow{h}}_1{\overrightarrow{h}}_2;s{s}_1{s}_2;t{t}_1{t}_2\rangle n_1{n}_2,& (57)\end{array}$

where ${\bar{V}}_{3N}$ is the fully-antisymmetrized three-body interaction. We have computed the Hartree-Fock contribution to the single-particle energy exactly [64] from Equation (57) as well as from Equation (56) using the density-dependent NN interaction V_med. Note that in order to avoid double-counting we must replace ${\bar{V}}_{2N}\to \frac{1}{2}{\bar{V}}_{\text{med}}$ in Equation (56).

In Figure 6, we demonstrate the accuracy of using the density-dependent NN interaction in place of the full three-body force when computing the Hartree-Fock contribution to the nucleon self energy. Specifically, we plot the momentum-dependent nucleon self-energy (note that both the 2N and 3N Hartree-Fock contributions are real and energy independent) in isospin-symmetric nuclear matter at saturation density n₀. The thick black curve labeled “$V_{3N,\text{exact}}^{\Lambda }$” is the exact result without a high-momentum regulator. The thin blue curve labeled “$V_{\text{med}}^{\Lambda \to \infty }$” is obtained from the density-dependent NN interaction without regulator. We see that there is a systematic difference of 1 − 2 MeV (or about 5%) between the two results across all momenta. This difference represents the inherent error introduced through the approximations employed in constructing the density-dependent NN interaction. Except for this systematic reduction in the nucleon self energy, we see that overall V_med faithfully reproduces the exact Hartree-Fock self-energy across all momenta.

FIGURE 6

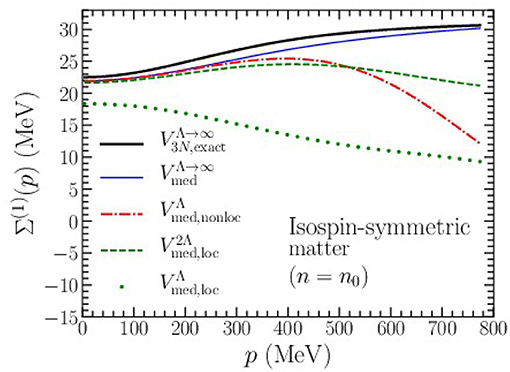
Figure 6. Hartree-Fock contribution to the nucleon self energy in symmetric nuclear matter at saturation density n₀ from the N2LO chiral three-nucleon force with cutoff scale Λ = 450 MeV. Results are shown for an exact treatment as well as from the density-dependent interaction V_med with different choices of regulating function (see text).

Introducing the non-local regulator in Equation (15) results in the red dash-dotted line of Figure 6. The artifacts associated with the nonlocal regulator grow rapidly for momenta beyond p ≃ 400 MeV and by p ≃ 600 MeV the three-nucleon force contribution to the self energy is reduced by ~25%. This corresponds to a lab energy of about E_lab ≃ 175 MeV [72] beyond which a description of nucleon-nucleus scattering in terms of chiral optical potentials becomes highly questionable. Introducing the local regulator in Equation (17) leads to the dotted green curve in Figure 6. We see that this regulator generates artifacts (of at least 15%) even for low-momentum particles in isospin-symmetric nuclear matter at saturation density. This is due to the already large nucleon Fermi momentum (k_f ≃ 270 MeV) in nuclear matter at this density. Finally, if we double the value of the momentum-space cutoff in the local regulating function, we find the results given by the dashed green curve in Figure 6. Again, this choice of cutoff leads to artifacts that are on par with those from the nonlocal regulator but which are noticeably smaller at the largest momenta considered.

In Figure 7, we plot the value of the Hartree-Fock single-particle potential at the Fermi momentum (p = k_f) from chiral three-body forces for densities up to n ≃ 2n₀. This contribution to the single-particle energy from the chiral 3NF grows approximately quadratically with the density. Again we find that the density-dependent NN interaction from the leading chiral three-nucleon force reproduces well the exact Hartree-Fock result. The artifacts introduced through the nonlocal regulator in Equation (15), the local regulator in Equation (17), and the local regulator with Λ_loc = 2Λ_nonloc follow the same trends already observed in the Hartree-Fock contribution to the equation of state.

FIGURE 7

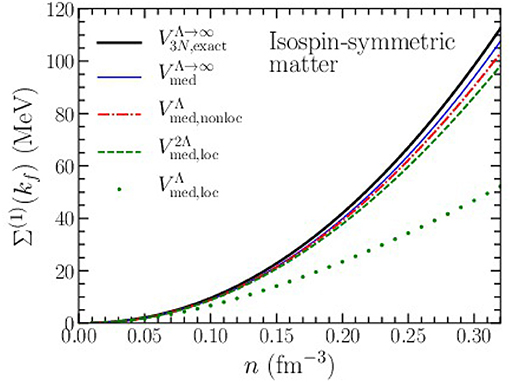
Figure 7. Hartree-Fock contribution to the nucleon self energy at the Fermi momentum (p = k_f) in symmetric nuclear matter as a function of density from the N2LO chiral three-nucleon force with cutoff scale Λ = 450 MeV. Results are shown for an exact treatment as well as from the density-dependent interaction V_med with different choices of regulating function (see text).

Recently, several works [64, 72] have included the second-order contributions to the nucleon self energy (both in isospin-symmetric and asymmetric nuclear matter):

$\begin{array}{ll}{\Sigma }_{2N}^{(2a)}(q,\omega )=\frac{1}{2}{\displaystyle \sum _{123}}\frac{|\langle {\overrightarrow{p}}_1{\overrightarrow{p}}_3{s}_1{s}_3{t}_1{t}_3|{\bar{V}}_{\text{eff}}|\overrightarrow{q}{\overrightarrow{h}}_{2}s{s}_{2}t{t}_2\rangle {|}^2}{\omega +e_2-e_1-e_3+i\eta }{\bar{n}}_1{n}_2{\bar{n}}_3& (58)\end{array}$

and

$\begin{array}{ll}{\Sigma }_{2N}^{(2b)}(q,\omega )=\frac{1}{2}{\displaystyle \sum _{123}}\frac{|\langle {\overrightarrow{h}}_1{\overrightarrow{h}}_3{s}_1{s}_3{t}_1{t}_3|{\bar{V}}_{\text{eff}}|\overrightarrow{q}{\overrightarrow{p}}_{2}s{s}_{2}t{t}_2\rangle {|}^2}{\omega +e_2-e_1-e_3-i\eta }{n}_1{\bar{n}}_2{n}_3,& (59)\end{array}$

with the antisymmetrized potential ${\bar{V}}_{\mathrm{\text{eff}}}={\bar{V}}_{2N}+{\bar{V}}_{\text{med}}$ that includes the density-dependent interaction from the N2LO chiral three-body force. The single-particle energies in Equations (58) and (59) are computed self-consistently according to

$\begin{array}{ll}e(q)=\frac{q^2}{2M}+R\Sigma (e(q),q).& (60)\end{array}$

Generically, Equations (58) and (59) give rise to complex and energy-dependent single-particle potentials. This allows for the construction of nucleon-nucleus optical potentials that have been shown [73] to reproduce well differential elastic scattering cross sections for proton projectiles on a range of calcium targets up to about E = 150 MeV.

The general form of phenomenological optical potentials for nucleon-nucleus scattering is given by

$\begin{array}{l}U(r,E)=V_V(r,E)+i{W}_V(r,E)+i{W}_D(r,E)+V_{SO}(r,E)\overrightarrow{\ell }·\overrightarrow{s}\\ +i{W}_{SO}(r,E)\overrightarrow{\ell }·\overrightarrow{s}+V_C(r),& (61)\end{array}$

consisting of a real volume term, an imaginary volume term, an imaginary surface term, a real spin-orbit term, an imaginary spin-orbit term, and finally a central Coulomb interaction. In Equation (61), $\overrightarrow{\ell }$ and $\overrightarrow{s}$ are the single-particle orbital angular momentum and spin angular momentum, respectively. To construct a microscopic nucleon-nucleus optical potential from the nuclear matter approach, one can employ the local density approximation (LDA):

$\begin{array}{ll}V(E;r)+iW(E;r)=V(E;k_f^p(r),k_f^n(r))+iW(E;k_f^p(r),k_f^n(r)),& (62)\end{array}$

where $k_f^p(r)$ and $k_f^n(r)$ are the local proton and neutron Fermi momenta. This approach can be improved by taking account of the finite range of the nuclear force through the improved local density approximation (ILDA):

$\begin{array}{ll}V{(E;r)}_{ILDA}={\displaystyle \frac{1}{{(t\sqrt{\pi })}^3}\int V(E;r^{\prime })e^{\frac{-|\overrightarrow{r}-{\overrightarrow{r}}^{\prime }{|}^2}{t^2}}{d}^3{r}^{\prime },}& (63)\end{array}$

which introduces an adjustable length scale t taken to be the typical range of the nuclear force. In previous works [73, 74], this Guassian smearing factor was chosen to be t ≃ 1.2 fm and varied in order to estimate the introduced theoretical uncertainties.

The ILDA approach starts by defining the isoscalar and isovector density distributions for a given target nucleus. In our previous works [73, 75], we have employed for this purpose Skyrme energy density functionals fitted to the equation of state of isospin-asymmetric nuclear matter [76] calculated from the same chiral two- and three-body forces used to compute the nucleon self energy in Equations (56)−(59). The Gaussian smearing factor t in the ILDA was chosen in the range 1.15fm ≤ t ≤ 1.25fm. The real part of the optical potential is found [73] to be in excellent agreement with that from phenomenological optical potentials [66], however, the microscopic imaginary part exhibits a surface peak that is too small and a volume contribution that grows too strongly with energy. This leads to larger total reaction cross sections [73] compared to phenomenology and experiment. This is in fact a general feature of the microscopic nuclear matter approach [77, 78] independent of the choice of nuclear potential, and previous works [74, 79] have attempted to mitigate this deficiency by introducing scaling factors for the imaginary part.

In Figure 8, we plot the differential elastic scattering cross sections for proton projectiles on ⁴⁰Ca and ⁴⁸Ca isotopes from microscopic optical potentials derived in chiral effective field theory. In this study we employ the N3LO nucleon-nucleon potential with momentum-space cutoff Λ = 450 MeV together with the density-dependent NN interaction using the nonlocal regulator in Equation (15). From Figure 8, we see that the predictions from chiral effective field theory (shown in blue) reproduce well the elastic scattering cross section data (red dots) from E = 25 to 45 MeV. The small uncertainty band associated with the blue curve is due entirely to variations in the ILDA Gaussian smearing factor. In some cases, the results from chiral nuclear optical potentials give better agreement with experiment than the Koning-Delaroche phenomenological optical potential (shown as the green dashed line in Figure 8). In contrast to semi-microscopic approaches [74, 79] that introduce energy-dependent scaling factors for the real and imaginary parts of the optical potential, our calculations are not fitted in any way to scattering data. Qualitatively similar results have been found [73] for proton energies as low as E ≃ 2 MeV and as high as E ≃ 160 MeV. Moreover, the construction of neutron-nucleus optical potentials is in progress [75] and preliminary results for differential elastic scattering cross sections are found to be of similar quality to the case of proton-nucleus scattering.

FIGURE 8

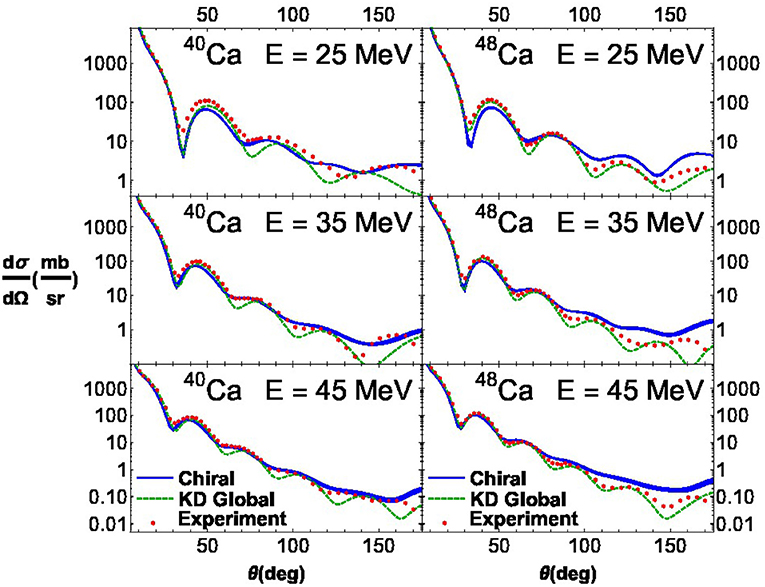
Figure 8. Differential elastic scattering cross sections for proton projectiles on ⁴⁰Ca and ⁴⁸Ca targets at the energies E = 25, 35, 45 MeV. The cross sections computed from microscopic chiral optical potentials including two- and three-body forces are shown as the blue band. The cross sections from the Koning-Delaroche “KD” phenomenological optical potential are given by the green dashed curves, and experimental data are shown by red circles.

3.3. Quasiparticle Interaction in Nuclear Matter

Landau's theory of normal Fermi liquids [80, 81] remains a valuable theoretical framework for understanding the excitations, response, and transport coefficients of nuclear many-body systems [82, 83]. Fermi liquid theory is based on the concept of quasiparticles, i.e., dressed single-particle excitations of a (potentially) strongly-interacting many-body system that retain key properties of the bare particles in the analogous non-interacting system. In this way, Fermi liquid theory allows for a convenient description of the low-energy excitations of the interacting system and in the context of the nuclear many-body problem helps justify the nuclear shell model and the independent-particle description of nuclei and nuclear matter. The theory is made quantitative through the introduction of the quasiparticle interaction ${F}$, defined as the second functional derivative of the energy with respect to the quasiparticle distribution function $n(\overrightarrow{p})$:

$\begin{array}{ll}E=E_0+{\displaystyle \sum _1}{e}_{{\overrightarrow{p}}_1}\delta n_{{\overrightarrow{p}}_1{s}_1{t}_1}+\frac{1}{2\Omega }{\displaystyle \sum _{12}}{F}({\overrightarrow{p}}_1{s}_1{t}_1;{\overrightarrow{p}}_2{s}_2{t}_2)\delta n_{{\overrightarrow{p}}_1{s}_1{t}_1}\delta n_{{\overrightarrow{p}}_2{s}_2{t}_2},& (64)\end{array}$

where E₀ is the ground state energy, Ω is a normalization volume, and $\delta n_{{\overrightarrow{p}}_i{s}_i{t}_i}$ is the change in occupation number of state i. In Equation (64), the quasiparticle interaction ${F}$ in momentum space has units fm², s_i labels the spin quantum number of quasiparticle i, and t_i labels the isospin quantum number. Enforcing the symmetries of the strong interaction and assuming that the quasiparticles lie exactly on the Fermi surface leads to the general form of the quasiparticle interaction:

$\begin{array}{ll}{F}({\overrightarrow{p}}_1,{\overrightarrow{p}}_2)={A}({\overrightarrow{p}}_1,{\overrightarrow{p}}_2)+{{A}}^{\prime }({\overrightarrow{p}}_1,{\overrightarrow{p}}_2){\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2,& (65)\end{array}$

where [84]

$\begin{array}{l}{A}({\overrightarrow{p}}_1,{\overrightarrow{p}}_2)=f({\overrightarrow{p}}_1,{\overrightarrow{p}}_2)+g({\overrightarrow{p}}_1,{\overrightarrow{p}}_2){\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2+h({\overrightarrow{p}}_1,{\overrightarrow{p}}_2)S_{12}(\widehat{p})\\ +k({\overrightarrow{p}}_1,{\overrightarrow{p}}_2)S_{12}(\widehat{P})+\ell ({\overrightarrow{p}}_1,{\overrightarrow{p}}_2)({\overrightarrow{\sigma }}_1\times {\overrightarrow{\sigma }}_2)·(\widehat{p}\times \widehat{P}),& (66)\end{array}$

and likewise for ${{A}}^{\prime }$ except with the replacement {f, g, h, k, ℓ} → {f′, g′, h′, k′, ℓ′}. The relative momentum is given by $\overrightarrow{p}={\overrightarrow{p}}_1-{\overrightarrow{p}}_2$, the center-of-mass momentum is defined by $\overrightarrow{P}={\overrightarrow{p}}_1+{\overrightarrow{p}}_2$, and the tensor operator has the form $S_{12}(\widehat{v})=3{\overrightarrow{\sigma }}_1·\widehat{v}{\overrightarrow{\sigma }}_2·\widehat{v}-{\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2$.

For two quasiparticle momenta on the Fermi surface ($|{\overrightarrow{p}}_1|=|{\overrightarrow{p}}_2|=k_f$), the scalar functions {f, g, h, k, ℓ, f′, g′, h′, k′, ℓ′} depend only the angle θ between and ${\overrightarrow{p}}_1$ and ${\overrightarrow{p}}_2$. The quasiparticle interaction can therefore be written in terms of Legendre polynomials:

$\begin{array}{l}f({\overrightarrow{p}}_1,{\overrightarrow{p}}_2)={\displaystyle \sum _{L=0}^{\infty }}{f}_L(k_f)P_L(\text{cos }\theta ),\\ f^{\prime }({\overrightarrow{p}}_1,{\overrightarrow{p}}_2)={\displaystyle \sum _{L=0}^{\infty }}{f}_L^{\prime }(k_f)P_L(\text{cos }\theta ),\\ \dots & (67)\end{array}$

where $cos\theta ={\widehat{p}}_1·{\widehat{p}}_2$, q = 2k_fsin(θ/2), and P = 2k_f cos (θ/2). The coefficients $f_L,f_L^{\prime },\dots$ are referred to as the Fermi liquid parameters. Dimensionless Fermi liquid parameters $F_L,F_L^{\prime },\dots$ can be defined by multiplying $f_L,f_L^{\prime },\dots$ by the density of states, e.g., for symmetric nuclear matter:

$\begin{array}{ll}{N}_0=2M^{*}{k}_f/{\pi }^2,& (68)\end{array}$

where M^* the effective nucleon mass.

Originally, Fermi liquid theory was treated as a phenomenological model [82] in which the lowest-order Fermi liquid parameters would be constrained by select experimental data. From the Brueckner-Goldstone linked diagram expansion for the ground-state energy [see e.g., Equations (46)−(54)], a diagrammatic expansion for the quasiparticle interaction in terms of the nuclear potential can be obtained [85] by performing functional derivatives with respect to the occupation probabilities. Up to second order in perturbation theory one obtains for a general two-body interaction V_2N:

$\begin{array}{ll}{{F}}_{2N}^{(1)}({\overrightarrow{p}}_1{s}_1{t}_1;{\overrightarrow{p}}_2{s}_2{t}_2)=\langle 12|{\bar{V}}_{2N}|12\rangle & (69)\end{array}$

$\begin{array}{ll}{{F}}_{2N}^{(2pp)}({\overrightarrow{p}}_1{s}_1{t}_1;{\overrightarrow{p}}_2{s}_2{t}_2)=\frac{1}{2}{\displaystyle \sum _{mn}}\frac{|\langle 12|{\bar{V}}_{2N}|mn\rangle {|}^2{\bar{n}}_m{\bar{n}}_n}{e_1+e_2-e_m-e_n}& (70)\end{array}$

$\begin{array}{ll}{{F}}_{2N}^{(2hh)}({\overrightarrow{p}}_1{s}_1{t}_1;{\overrightarrow{p}}_2{s}_2{t}_2)=\frac{1}{2}{\displaystyle \sum _{ij}}\frac{|\langle ij|{\bar{V}}_{2N}|12\rangle {|}^2{n}_i{n}_j}{e_i+e_j-e_1-e_2}& (71)\end{array}$

$\begin{array}{ll}{{F}}_{2N}^{(2ph)}({\overrightarrow{p}}_1{s}_1{t}_1;{\overrightarrow{p}}_2{s}_2{t}_2)=-2{\displaystyle \sum _{jn}}\frac{|\langle 1j|{\bar{V}}_{2N}|2n\rangle {|}^2{n}_j{\bar{n}}_n}{e_1+e_j-e_2-e_n},& (72)\end{array}$

which correspond, respectively to Figures 9A–D. The first-order contribution in Equation (69) is just the antisymmetrized two-body potential for two nucleons restricted to the Fermi surface. It contains only the four central terms f, f′, g, g′ as well as the two relative momentum tensor interactions h, h′. The second-order contributions in Equations (70)−(72) give rise generically to the center-of-mass tensor interactions k, k′, but only the particle-hole term Equation (72) can generate the cross-vector interactions l, l′ through the interference of a spin-orbit interaction with any other nonspin-orbit component in the bare nucleon-nucleon potential [86].

FIGURE 9

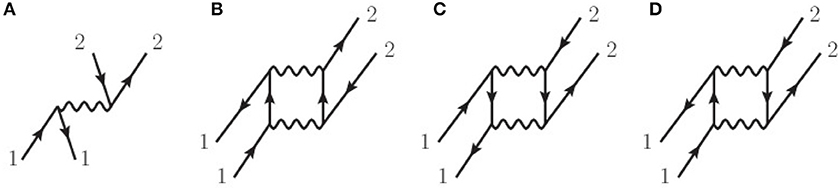
Figure 9. Diagrammatic contributions to the quasiparticle interaction up to second order in perturbation theory: (A) first-order contribution, (B) second-order particle-particle contribution, (C) second-order hole-hole contribution, and (D) second-order particle-hole contribution. Wavy lines denote the antisymmetrized nuclear interaction.

The expressions in Equations (69)−(72) can be decomposed into partial wave matrix elements of the bare nucleon-nucleon potential or the derived medium-dependent 2N interaction. In section 4.1 below, we give explicit expressions for the partial-wave matrix elements of the density-dependent 2N interaction derived from the N2LO [47] and N3LO [87, 88] chiral three-body force. To date, the contributions from the N2LO chiral three-body force have been included [86, 89, 90] exactly in the calculation of the quasiparticle interaction in isospin-symmetric nuclear matter and pure neutron matter. At first order in perturbation theory, the second functional derivative of Equation (47) leads to

$\begin{array}{ll}{{F}}_{3N}^{(1)}({\overrightarrow{p}}_1{s}_1{t}_1,{\overrightarrow{p}}_2{s}_2{t}_2)={\displaystyle \sum _i}{n}_i\langle i12|{\bar{V}}_{3N}|i12\rangle ,& (73)\end{array}$

where ${\bar{V}}_{3N}$ is the fully antisymmetrized three-body force. This is equivalent to the definition of the density-dependent NN interaction in Equation (11) but restricted by the kinematics of quasiparticles lying on the Fermi surface. Moreover, the use of the in-medium 2N interaction constructed assuming on-shell scattering in the center-of-mass frame is not appropriate [in particular, it would give no center-of-mass dependence at leading order in Equation (73)]. Explicit and exact expressions (in the absence of a momentum-space cutoff) for the Landau Fermi liquid parameters in Equations (65)−(67) from the N2LO chiral three-nucleon force have therefore been derived in Holt and Kaiser [90]. Only the higher-order perturbative contributions to the quasiparticle interaction (where medium effects are included through normal Pauli blocking of intermediate states) utilize the in-medium 2N interaction derived in the center-of-mass frame. In the following we highlight their qualitative significance on the different terms of the quasiparticle interaction.

In Figure 10, we plot the dimensionless Fermi liquid parameters associated with the L = 0, 1 Legendre polynomials (black and red dotted lines, respectively) in isospin-symmetric nuclear matter from the N2LO chiral three-body force as a function of the nucleon density (up to n = 0.4 fm⁻³). Although one may be skeptical of results from chiral effective field theory beyond n ≃ 2n₀, the Landau parameters must obey stability inequalities, e.g.,

$\begin{array}{ll}{Q}_L>-(2L+1),& (74)\end{array}$

where Q ∈ {F, F′, G, G′}, for the central components of the quasiparticle interaction. Therefore, we find it informative to speculate on the high-density behavior of the Landau parameters, since they might give hints toward possible instability mechanisms in dense matter. We note that complete stability conditions involving all spin-dependent interactions H, K, L (and H′, K′, L′) that couple to G (and G′) have not yet been worked out. To date only the effect of the relative tensor quasiparticle interaction has been considered [91]. We have found that in the presence of such Pomeranchuk instabilities, perturbation theory itself can be poorly behaved. For instance, in symmetric nuclear matter with density n ≲ n₀/2 (where F₀ < −1 and nuclear matter is unstable to density fluctuations), we have computed also the third-order particle-particle contributions to the Fermi liquid parameters and found that F₀ is of comparable size to the second-order particle-particle diagrams. For other Fermi liquid parameters, however, the third-order particle-particle contributions are generally small at low densities.

FIGURE 10

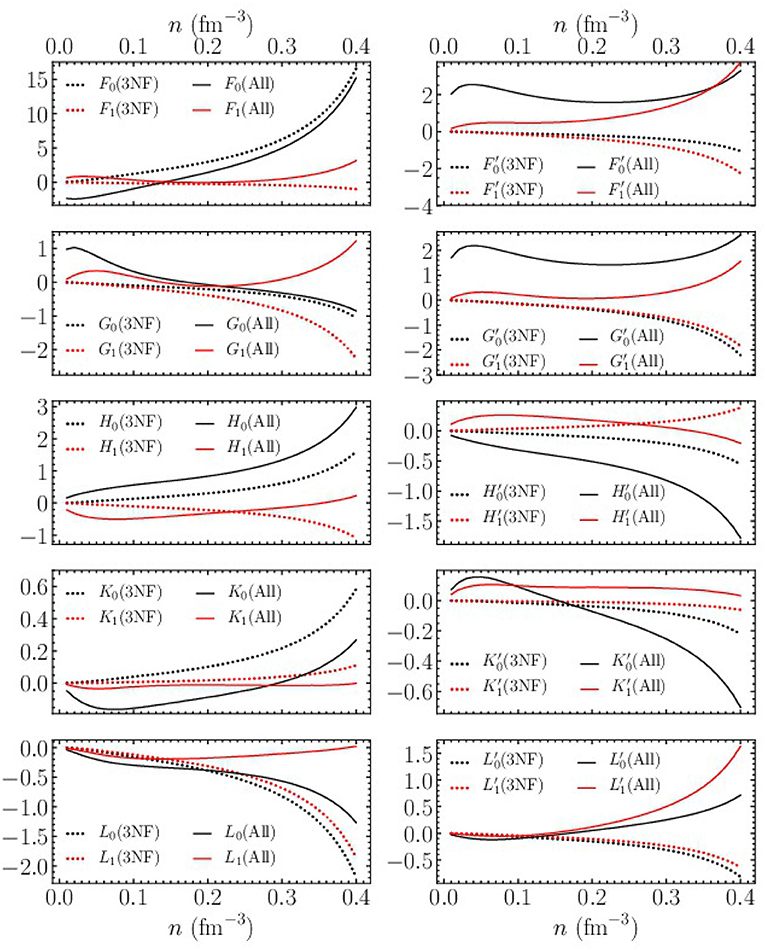
Figure 10. Density-dependent dimensionless Fermi liquid parameters in isospin-symmetric nuclear matter. Dotted lines symbolize the first-order perturbative contribution from three-body forces, while solid lines represent the sum of all second-order contributions including two- and three-body forces.

The dotted lines in Figure 10 are obtained from only the leading contribution due to three-body forces in Equation (73). The solid lines represent the Fermi liquid parameters obtained from the sum of two- and three-body forces up to second order in perturbation theory. For the second-order contributions in Equations (70)−(72) we have replaced the two-body interaction V_2N with V_2N + V_med, where V_2N is the N3LO-450 potential and V_med is the consistent density-dependent interaction constructed from the N2LO three-body force with nonlocal regulator. For several Fermi liquid parameters, we see that three-body forces provide the dominant contribution at high density. For instance, the strong increase in the F₀ Landau parameter (top left panel of Figure 10) as a function of density is a direct result of the first-order contribution from three-body forces. The nuclear matter incompressibility ${K}=9\partial P/\partial \rho$, where $P={\rho }^2\frac{\partial (E/A)}{\partial \rho }$, is related to the F₀ Landau parameter through

$\begin{array}{ll}{K}=\frac{3k_f^2}{M^{*}}(1+F_0),& (75)\end{array}$

where M^* is the nucleon effective mass, and therefore three-body forces play a central role in the saturation mechanism [7] of nuclear matter with chiral nuclear forces. On the other hand, in some cases three-body forces play only a minor role, such as for the Landau parameters F₁ and $F_0^{\prime }$. The former is related to the nucleon effective mass through

$\begin{array}{ll}\frac{M^{*}}{M}=1+\frac{F_1}{3},& (76)\end{array}$

and the latter is related to the nuclear isospin-asymmetry energy through

$\begin{array}{ll}{S}_2=\frac{k_f^2}{6M^{*}}(1+F_0^{\prime }),& (77)\end{array}$

where S₂ is defined as the first term in a power series expansion of the nuclear equation of state about the isospin-symmetric configuration:

$\begin{array}{ll}\frac{E}{A}(n,{\delta }_{np})=\frac{E}{A}(n,0)+S_2(n){\delta }_{np}^2+\cdots & (78)\end{array}$

with ${\delta }_{np}=\frac{n_n-n_p}{n_n+n_p}$.

In general, we see from Figure 10, that the noncentral components K and L of the quasiparticle interaction that depend explicitly on the center-of-mass momentum $\overrightarrow{P}$ are small at nuclear saturation density. However, several of the associated Fermi liquid parameters, such as $K_0^{\prime }$, L₀, and $L_1^{\prime }$ begin to grow rapidly for higher densities. Therefore, even though there has been little motivation to include such terms in modern energy density functionals fitted to the properties of finite nuclei, such novel interactions may become more relevant in applications related to neutron star physics. The full quasiparticle interaction in pure neutron matter has already been computed [86] with modern chiral two- and three-nucleon forces. One finds again an enhanced role of three-body forces on the incompressibility of pure neutron matter and therefore the stability of neutron stars against gravitational collapse. The more general case of the quasiparticle interaction in nuclear matter at arbitrary isospin-asymmetry is in progress.

4. Chiral Three-Nucleon Force at Next-to-Next-to-Next-to-Leading Order

Up to now we have considered only the chiral three-body force at N2LO. At order N3LO in the chiral power counting, additional three- and four-nucleon forces arise without any additional undetermined low-energy constants. However, except in the case of pure neutron matter, the inclusion of the N3LO three-body contributions requires a refitting of the three-body low-energy constants c_D and c_E. The N3LO three-body force is written schematically as

$\begin{array}{ll}{V}_{3N}^{(4)}=V_{1\pi -\text{cont}.}^{(4)}+V_{2\pi -\text{cont}.}^{(4)}+V_{1/M}^{(4)}+V_{2\pi }^{(4)}+V_{2\pi -1\pi }^{(4)}+V_{\text{ring}}^{(4)},& (79)\end{array}$

corresponding to the 1π − contact, 2π − contact, relativistic 1/M, 2π, 2π − 1π, and ring topologies, respectively. All contributions have been worked out and presented in Ishikawa and Robilotta [28] and Bernard et al. [29, 30]. Although we will not consider their specific effects in the present work, we note that the leading four-nucleon forces have been calculated in Epelbaum [31]. In deriving the density-dependent 2N interaction at N3LO, we take the expressions from Bernard et al. [29, 30] based on the method of unitary transformations.

The density-dependent 2N interaction from the short-range terms and relativistic corrections, shown diagrammatically in Figures 11A,B, was computed first in Kaiser and Niessner [87]. Results were derived in the absence of a regulating function depending explicitly on the value of the intermediate-state momentum k₃ in Equation (11). The resulting expressions for V_med obtained from the N3LO 3N force could therefore be simplified to analytical expressions involving at most a one-dimensional integration. In Kaiser and Niessner [87], it was found that the 1π-exchange contact topology proportional to the 2N low-energy constant C_T gives rise to a vanishing contribution to V_med in isospin-symmetric nuclear matter. The density-dependent 2N interaction derived from the long-range contributions to the N3LO three-body force, shown diagrammatically in Figures 11C–E, was calculated in Kaiser and Singh [88]. Again, the integration over the three-dimensional filled Fermi sphere could be performed up to at most one remaining integration. The formulas for the density-dependent NN interaction from the N3LO three-body force are quite lengthy, and we refer the reader to Kaiser and Niessner [87] and Kaiser and Singh [88] for additional details.

FIGURE 11

Figure 11. Schematic representation of the diagrammatic contributions to the chiral three-nucleon force at next-to-next-to-next-to-leading order (N3LO): (A) 1π-contact interaction, (B) 2π-contact interaction, (C) 2π interaction, (D) 2π-1π interaction, and (E) ring interaction.

4.1. Partial-Wave Decomposition

The analytical expressions for the medium-dependent 2N potential V_med obtained from the N3LO chiral three-body force [87, 88] can be conveniently understood by examining their attractive or repulsive effects in various partial waves. For comparison we will show also the lowest-order partial-wave contributions from the N2LO chiral three-body force, however, we note that the values of the three-body contact terms will need to be refitted in order to make a consistent comparison. In all cases, we choose the values c₁ = −0.81 GeV⁻¹, c₃ = −3.4 GeV⁻¹, c₄ = 3.4 GeV⁻¹, c_D = −0.24, and c_E = −0.106, which have been used in other calculations presented in this work. We recall that the low-energy constants c_D and c_E of the N2LO chiral 3N force are fitted (including the N3LO chiral 2N interaction with cutoff scale Λ = 450 MeV) to the binding energies of ³H and ³He as well as the beta-decay lifetime of ³H. Comparing to the values of c_D and c_E fitted in combination with the N2LO two-body force [see Table II of [12]], we do not expect qualitative differences in the results below coming from these two different choices in the chiral order. For the leading-order (LO) contact term C_T that appears in the 1π- and 2π-contact topologies, we use the value C_T = −2.46491 GeV⁻² from the N3LO-450 2N potential.

We follow the description in Erkelenz et al. [92] to obtain the diagonal momentum-space partial-wave matrix elements of the density-dependent NN interaction. With start with the form of a general nucleon-nucleon potential:

$\begin{array}{l}V(\overrightarrow{p},\overrightarrow{q})=V_C+{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2{W}_C+\left[V_S+{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2{W}_S\right]{\overrightarrow{\sigma }}_1·{\overrightarrow{\sigma }}_2\\ +\left[V_T+{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2{W}_T\right]{\overrightarrow{\sigma }}_1·\overrightarrow{q}{\overrightarrow{\sigma }}_2·\overrightarrow{q}\\ +\left[V_{SO}+{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2{W}_{SO}\right]i({\overrightarrow{\sigma }}_1+{\overrightarrow{\sigma }}_2)·(\overrightarrow{q}\times \overrightarrow{p})\\ +\left[V_Q+{\overrightarrow{\tau }}_1·{\overrightarrow{\tau }}_2{W}_Q\right]{\overrightarrow{\sigma }}_1·(\overrightarrow{q}\times \overrightarrow{p}){\overrightarrow{\sigma }}_2·(\overrightarrow{q}\times \overrightarrow{p}),& (80)\end{array}$

where the subscripts refer to the central (C), spin-spin (S), tensor (T), spin-orbit (SO), and quadratic spin orbit (Q) components, each with an isoscalar (V) and isovector (W) version. The diagonal (in momentum space) partial-wave matrix elements for different spin and orbital angular momentum channels are then given in terms of the functions U_K = V_K + (4I − 3)W_K, where K ∈ {C, S, T, SO, Q} and the total isospin quantum number takes the values I = 0, 1. Explicit expressions can be found in Holt et al. [47].

In Figure 12, we show the ¹S₀, ³S₁, ³D₁, ³S₁ – ³D₁ diagonal momentum-space matrix elements of V_med from the N2LO (blue circles) and N3LO (red diamonds) chiral three-nucleon force in isospin-symmetric nuclear matter at the density n = n₀. Note that we have multiplied the matrix elements by the nucleon mass M to obtain dimensions of [fm]. Interestingly, we observe that the total N3LO three-body force in these partial-wave channels is roughly equal in magnitude but opposite in sign compared to the N2LO three-body force. Whereas, the N2LO three-body force is largely repulsive in symmetric nuclear matter at saturation density, the N3LO three-body force is strongly attractive, except in the case of the coupled ³S₁ – ³D₁ tensor channel. One should keep in mind, however, that the low-energy constants c_D and c_E must be refitted after the introduction of the N3LO three-body force. One might expect from the above observations that the N2LO three-body force would be enhanced in order to offset the opposite behavior introduced from the N3LO three-body force in the lowest partial-wave channels.

FIGURE 12

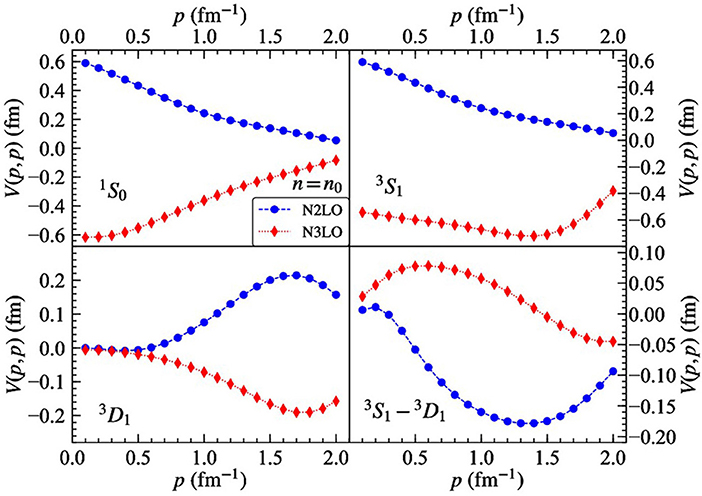
Figure 12. Diagonal momentum-space matrix elements of V_med associated with the total N2LO and N3LO three-body force in the ¹S₀ and ³S₁ – ³D₁ partial-wave channels at n = n₀ in isospin-symmetric nuclear matter.

In Figure 13, we show the ¹P₁, ³P₀, ³P₁, and ³P₂ diagonal momentum-space matrix elements of V_med from the N2LO (blue circles) and N3LO (red diamonds) chiral three-nucleon force in isospin-symmetric nuclear matter at the density n = n₀. In both the ¹P₁ and ³P₀ channels, the N2LO and N3LO contributions are approximately equal in magnitude but opposite in sign. In the ³P₁ channel, which is repulsive in the bare 2N potential, we see that the combination of N2LO and N3LO contributions enhances the repulsion. The ³P₂ channel, which is attractive in the free-space 2N potential, also receives repulsive contributions from the N2LO and N3LO in-medium interaction V_med. The feature that N3LO loop corrections are not small compared to N2LO tree contributions has been seen in several instances, e.g., in pion-nucleon scattering [93] as well as the three-nucleon force derivation [29] and its application [94]. The results presented in Figures 12, 13 are state of the art and may change if the effects of sub-sub-leading chiral 3N forces are included. For the 2π − 1π and ring topologies, the N4LO corrections are sizable and dominate in most cases over the nominally leading N3LO terms [95].

FIGURE 13

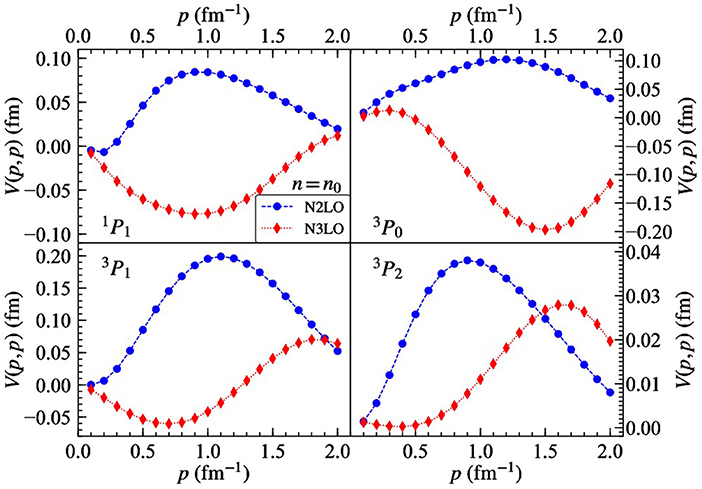
Figure 13. Diagonal momentum-space matrix elements of V_med associated with the total N2LO and N3LO three-body force in the ¹P₁, ³P₀, ³P₁, and ³P₂ partial-wave channels at n = n₀ in isospin-symmetric nuclear matter.

The long-range parts of the N3LO chiral three-body force are expected [96] to give larger contributions to the equation of state than the relativistic 1/M corrections and the 2π − contact topologies. Due to the large number of contributions to V_med at N3LO, we only show selected results for individual topologies. In Figure 14, we plot several of the dominant pion-ring contributions to the ¹S₀ partial-wave matrix elements for the density-dependent NN interaction derived from the N3LO chiral three-body force. We see that individual long-range contributions are large, but sizable cancelations lead to an overall reduced attractive ¹S₀ partial-wave channel at low momenta. In Figure 15, we plot several of the important 2π, 2π-1π, and ring topology contributions to the ³P₀ partial-wave matrix elements of the density-dependent NN interaction derived from the N3LO chiral three-body force. We again find large cancelations among individual terms, but the sum produces significant attraction in this partial-wave channel.

FIGURE 14

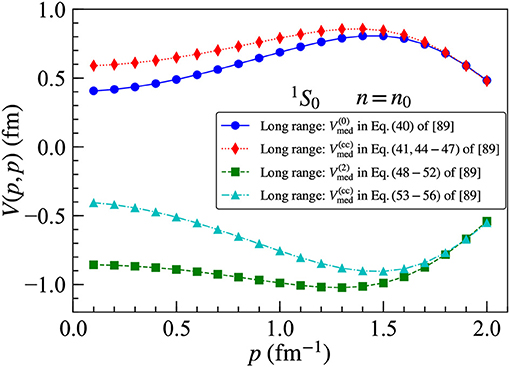
Figure 14. Diagonal momentum-space matrix elements of the N3LO three-body force for selected topologies in the ¹S₀ partial-wave channel at saturation density n₀ in isospin-symmetric nuclear matter.

FIGURE 15

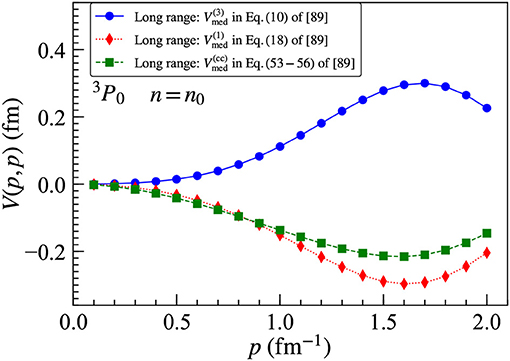
Figure 15. Diagonal momentum-space matrix elements of the N3LO three-body force for selected topologies in the ³P₀ partial-wave channel at saturation density n₀ in isospin-symmetric nuclear matter.

5. Summary and Conclusions

We have reviewed the construction and implementation of density-dependent two-body interactions from three-body forces at N2LO and N3LO in the chiral expansion. We showed that at leading order in many-body perturbation theory, the in-medium 2N interaction reproduces very well the exact contributions to the nuclear equation of state and nucleon self energy from the complete three-body force. The standard nonlocal high-momentum regulator used in our previous works leads to simpler analytical expressions for the density-dependent 2N interaction, consistency with the bare 2N potential, and relatively small artifacts in both the equation of state up to twice saturation density and the single-particle potential up to p ≃ 400 − 500 MeV at nuclear matter saturation density. Local 3N regulators with the same value of the cutoff, Λ_loc = Λ_nonloc, have been commonly used in previous studies of nuclear few-body systems, but these are shown to produce very large artifacts, even in the nuclear equation of state at saturation density. This could be remedied by choosing a local regulating function with Λ_loc = 2Λ_nonloc, which is well-motivated since the momentum transfer q can reach values twice as large as the relative momentum for two particles on the Fermi surface.

The use of medium-dependent two-body interactions has been shown to facilitate the implementation of three-body forces in higher-order perturbative calculations of the nuclear equation of state, single-particle potential, and quasiparticle interaction. In particular, nuclear matter was shown to saturate at the correct binding energy and density within theoretical uncertainties when computed up to third-order in perturbation theory. Moreover, microscopic nucleon-nucleus optical potentials derived from chiral two- and three-body forces have been shown to accurately predict proton elastic scattering cross sections on calcium isotopes up to projectile energies of E ≃ 150 MeV. The use of medium-dependent NN potentials derived from the N3LO chiral three-body force for calculations of the nuclear equation of state, single-particle potential, and quasiparticle interaction remain a topic of future research. As a first step, we have performed a partial-wave decomposition of V_med at N3LO in the chiral expansion and shown that the effective interaction is expected to be attractive in symmetric nuclear matter around saturation density.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

JH was primarily responsible for the preparation of the manuscript. JH, MK, and NK contributed to analytical derivations and their numerical implementation.

Funding

Work of JH was supported by the National Science Foundation under Grant No. PHY1652199 and by the U.S. Department of Energy National Nuclear Security Administration under Grant No. DE-NA0003841. The work of MK was supported in part by JSPS Grant-in-Aid for JSPS Research Fellow No. 18J15329. The work of NK has been supported in part by DFG and NSFC (CRC110).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Portions of this research were conducted with the advanced computing resources provided by Texas A&M High Performance Research Computing. This manuscript has been released as a Pre-Print at [97].

References

1. Hergert H, Bogner SK, Binder S, Calci A, Langhammer J, Roth R, et al. In-medium similarity renormalization group with chiral two- plus three-nucleon interactions. Phys Rev C. (2013) 87:034307. doi: 10.1103/PhysRevC.87.034307

CrossRef Full Text | Google Scholar

2. Hebeler K, Holt JD, Menendez J, Schwenk A. Nuclear forces and their impact on neutron-rich nuclei and neutron-rich matter. Annu Rev Nucl Part Sci. (2015) 65:457. doi: 10.1146/annurev-nucl-102313-025446

CrossRef Full Text | Google Scholar

3. Carlson J, Gandolfi S, Pederiva F, Pieper SC, Schiavilla R, Schmidt KE, et al. Quantum Monte Carlo methods for nuclear physics. Rev Mod Phys. (2015) 87:1067. doi: 10.1103/RevModPhys.87.1067

CrossRef Full Text | Google Scholar

4. Navratil P, Quaglioni S, Hupin G, Romero-Redondo C, Calci A. Unified ab initio approaches to nuclear structure and reactions. Phys Scripta. (2016) 91:053002. doi: 10.1088/0031-8949/91/5/053002

CrossRef Full Text | Google Scholar

5. Wiringa RB, Fiks V, Fabrocini A. Equation of state for dense nucleon matter. Phys Rev C. (1988) 38:1010. doi: 10.1103/PhysRevC.38.1010

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Baldo M, Bombaci I, Burgio GF. Microscopic nuclear equation of state with three-body forces and neutron star structure. Astron Astrophys. (1997) 328:274.

Google Scholar

7. Bogner SK, Schwenk A, Furnstahl RJ, Nogga A. Is nuclear matter perturbative with low-momentum interactions? Nucl Phys. (2005) A763:59. doi: 10.1016/j.nuclphysa.2005.08.024

CrossRef Full Text | Google Scholar

8. Coraggio L, Holt JW, Itaco N, Machleidt R, Sammarruca F. Reduced regulator dependence of neutron-matter predictions with perturbative chiral interactions. Phys Rev C. (2013) 87:014322. doi: 10.1103/PhysRevC.87.014322

CrossRef Full Text | Google Scholar

9. Gezerlis A, Tews I, Epelbaum E, Gandolfi S, Hebeler K, Nogga A, et al. Quantum Monte Carlo calculations with chiral effective field theory interactions. Phys Rev Lett. (2013) 111:032501. doi: 10.1103/PhysRevLett.111.032501

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Baardsen G, Ekström A, Hagen G, Hjorth-Jensen M. Coupled-Cluster studies of infinite nuclear matter. Phys Rev C. (2013) 88:054312. doi: 10.1103/PhysRevC.88.054312

CrossRef Full Text | Google Scholar

11. Carbone A, Rios A, Polls A. Correlated density-dependent chiral forces for infinite-matter calculations within the Green's function approach. Phys Rev C. (2014) 90:054322. doi: 10.1103/PhysRevC.90.054322

CrossRef Full Text | Google Scholar

12. Sammarruca F, Coraggio L, Holt JW, Itaco N, Machleidt R, Marcucci LE. Toward order-by-order calculations of the nuclear and neutron matter equations of state in chiral effective field theory. Phys Rev C. (2015) 91:054311. doi: 10.1103/PhysRevC.91.054311

CrossRef Full Text | Google Scholar

13. Drischler C, Carbone A, Hebeler K, Schwenk A. Neutron matter from chiral two- and three-nucleon calculations up to N3LO. Phys Rev C. (2016) 94:054307. doi: 10.1103/PhysRevC.94.054307

CrossRef Full Text | Google Scholar

14. Akmal A, Pandharipande VR, Ravenhall DG. Equation of state of nucleon matter and neutron star structure. Phys Rev C. (1998) 58:1804. doi: 10.1103/PhysRevC.58.1804

CrossRef Full Text | Google Scholar

15. Barrett BR, Navrátil P, Vary JP. Ab initio no core shell model. Prog Part Nucl Phys. (2013) 69:131. doi: 10.1016/j.ppnp.2012.10.003

CrossRef Full Text | Google Scholar

16. Hagen G, Hjorth-Jensen M, Jansen GR, Machleidt R, Papenbrock T. Evolution of shell structure in neutron-rich calcium isotopes. Phys Rev Lett. (2012) 109:032502. doi: 10.1103/PhysRevLett.109.032502

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Hagen G, Papenbrock T, Hjorth-Jensen M, Dean DJ. Coupled-cluster computations of atomic nuclei. Rept Prog Phys. (2014) 77:096302. doi: 10.1088/0034-4885/77/9/096302

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Somà V, Barbieri C, Duguet T. Ab-initio Gorkov-Green's function calculations of open-shell nuclei. Phys Rev C. (2013) 87:011303. doi: 10.1103/PhysRevC.87.011303

CrossRef Full Text | Google Scholar

19. Roth R, Langhammer J, Calci A, Binder S, Navrátil P. Similarity-transformed chiral NN+3N interactions for the ab initio description of 12-C and 16-O. Phys Rev Lett. (2011) 107:072501. doi: 10.1103/PhysRevLett.107.072501

CrossRef Full Text | Google Scholar

20. Stroberg SR, Bogner SK, Hergert H, Holt JD. Nonempirical interactions for the nuclear shell model: an update. Annu Rev Nucl Part Sci. (2019) 69:307. doi: 10.1146/annurev-nucl-101917-021120

CrossRef Full Text | Google Scholar

21. Otsuka T, Suzuki T, Holt JD, Schwenk A, Akaishi Y. Three-body forces and the limit of oxygen isotopes. Phys Rev Lett. (2010) 105:032501. doi: 10.1103/PhysRevLett.105.032501

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Hagen G, Hjorth-Jensen M, Jansen GR, Machleidt R, Papenbrock T. Continuum effects and three-nucleon forces in neutron-rich oxygen isotopes. Phys Rev Lett. (2012) 108:242501. doi: 10.1103/PhysRevLett.108.242501

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Weinberg S. Phenomenological lagrangians. Phys A. (1979) 96:327. doi: 10.1016/0378-4371(79)90223-1

CrossRef Full Text | Google Scholar

24. Epelbaum E, Hammer HW, Meißner UG. Modern theory of nuclear forces. Rev Mod Phys. (2009) 81:1773. doi: 10.1103/RevModPhys.81.1773

CrossRef Full Text | Google Scholar

25. Machleidt R, Entem DR. Chiral effective field theory and nuclear forces. Phys Rept. (2011) 503:1. doi: 10.1016/j.physrep.2011.02.001

CrossRef Full Text | Google Scholar

26. Entem DR, Machleidt R, Nosyk Y. High-quality two-nucleon potentials up to fifth order of the chiral expansion. Phys Rev C. (2017) 96:024004. doi: 10.1103/PhysRevC.96.024004

CrossRef Full Text | Google Scholar

27. Reinert P, Krebs H, Epelbaum E. Semilocal momentum-space regularized chiral two-nucleon potentials up to fifth order. Eur Phys J A. (2018) 54:86. doi: 10.1140/epja/i2018-12516-4

CrossRef Full Text | Google Scholar

28. Ishikawa S, Robilotta MR. Two-pion exchange three-nucleon potential: O(q⁴) chiral expansion. Phys Rev C. (2007) 76:102502. doi: 10.1103/PhysRevC.76.014006

CrossRef Full Text | Google Scholar

29. Bernard V, Epelbaum E, Krebs H, Meissner UG. Subleading contributions to the chiral three-nucleon force. I. Long-range terms. Phys Rev C. (2008) 77:064004. doi: 10.1103/PhysRevC.77.064004

CrossRef Full Text | Google Scholar

30. Bernard V, Epelbaum E, Krebs H, Meissner UG. Subleading contributions to the chiral three-nucleon force II: Short-range terms and relativistic corrections. Phys Rev C. (2011) 84:054001. doi: 10.1103/PhysRevC.84.054001

CrossRef Full Text | Google Scholar

31. Epelbaum E. Four-nucleon force in chiral effective field theory. Phys Lett. (2006) B639:456. doi: 10.1016/j.physletb.2006.06.046

CrossRef Full Text | Google Scholar

32. Hagen G, Papenbrock T, Dean DJ, Schwenk A, Nogga A, Włoch M, et al. Coupled-cluster theory for three-body Hamiltonians. Phys Rev C. (2007) 76:034302. doi: 10.1103/PhysRevC.76.034302

CrossRef Full Text | Google Scholar

33. Drischler C, Hebeler K, Schwenk A. Chiral interactions up to next-to-next-to-next-to-leading order and nuclear saturation. Phys Rev Lett. (2019) 122:042501. doi: 10.1103/PhysRevLett.122.042501

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Büttiker P, Meissner UG. Pion nucleon scattering inside the Mandelstam triangle. Nucl Phys. (2000) A668:97. doi: 10.1016/S0375-9474(99)00813-1

CrossRef Full Text | Google Scholar

35. Hoferichter M, Ruiz de Elvira J, Kubis B, Meißner UG. Matching pion-nucleon Roy-Steiner equations to chiral perturbation theory. Phys Rev Lett. (2015) 115:192301. doi: 10.1103/PhysRevLett.115.192301

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Rentmeester MCM, Timmermans RGE, de Swart JJ. Determination of the chiral coupling constants c(3) and c(4) in new pp and np partial wave analyses. Phys Rev C. (2003) 67:044001. doi: 10.1103/PhysRevC.67.044001

CrossRef Full Text | Google Scholar

37. Entem DR, Machleidt R. Accurate charge dependent nucleon nucleon potential at fourth order of chiral perturbation theory. Phys Rev C. (2003) 68:041001. doi: 10.1103/PhysRevC.68.041001

CrossRef Full Text | Google Scholar

38. Epelbaum E, Nogga A, Glöckle W, Kamada H, Meißner UG, Witała H. Three nucleon forces from chiral effective field theory. Phys Rev C. (2002) 66:064001. doi: 10.1103/PhysRevC.66.064001

CrossRef Full Text | Google Scholar

39. Piarulli M, Baroni A, Girlanda L, Kievsky A, Lovato A, Lusk E, et al. Light-nuclei spectra from chiral dynamics. Phys Rev Lett. (2018) 120:052503. doi: 10.1103/PhysRevLett.120.052503

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Hebeler K, Bogner SK, Furnstahl RJ, Nogga A, Schwenk A. Improved nuclear matter calculations from chiral low-momentum interactions. Phys Rev C. (2011) 83:031301. doi: 10.1103/PhysRevC.83.031301

CrossRef Full Text | Google Scholar

41. Navrátil P, Gueorguiev VG, Vary JP, Ormand WE, Nogga A. Structure of A=10-13 nuclei with two plus three-nucleon interactions from chiral effective field theory. Phys Rev Lett. (2007) 99:042501. doi: 10.1103/PhysRevLett.99.042501

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Ekström A, Jansen GR, Wendt KA, Hagen G, Papenbrock T, Carlsson BD, et al. Accurate nuclear radii and binding energies from a chiral interaction. Phys Rev C. (2015) 91:051301. doi: 10.1103/PhysRevC.91.051301

CrossRef Full Text | Google Scholar

43. Gardestig A, Phillips DR. How low-energy weak reactions can constrain three-nucleon forces and the neutron-neutron scattering length. Phys Rev Lett. (2006) 96:232301. doi: 10.1103/PhysRevLett.96.232301

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Gazit D, Quaglioni S, Navrátil P. Three-nucleon low-energy constants from the consistency of interactions and currents in chiral effective field theory. Phys Rev Lett. (2009) 103:102502. doi: 10.1103/PhysRevLett.103.102502

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Hebeler K, Schwenk A. Chiral three-nucleon forces and neutron matter. Phys Rev C. (2010) 82:014314. doi: 10.1103/PhysRevC.82.014314

CrossRef Full Text | Google Scholar

46. Epelbaum E, Krebs H, Meißner UG. Improved chiral nucleon-nucleon potential up to next-to-next-to-next-to-leading order. Eur Phys J A. (2015) 51:53. doi: 10.1140/epja/i2015-15053-8

CrossRef Full Text | Google Scholar

47. Holt JW, Kaiser N, Weise W. Density-dependent effective nucleon-nucleon interaction from chiral three-nucleon forces. Phys Rev C. (2010) 81:024002. doi: 10.1103/PhysRevC.81.024002

CrossRef Full Text | Google Scholar

48. Wellenhofer C, Holt JW, Kaiser N, Weise W. Nuclear thermodynamics from chiral low-momentum interactions. Phys Rev C. (2014) 89:064009. doi: 10.1103/PhysRevC.89.064009

CrossRef Full Text | Google Scholar

49. Navrátil P. Local three-nucleon interaction from chiral effective field theory. Few Body Syst. (2007) 41:117. doi: 10.1007/s00601-007-0193-3

CrossRef Full Text | Google Scholar

50. Dyhdalo A, Furnstahl RJ, Hebeler K, Tews I. Regulator artifacts in uniform matter for chiral interactions. Phys Rev C. (2016) 94:034001. doi: 10.1103/PhysRevC.94.034001

CrossRef Full Text | Google Scholar

51. Lattimer JM, Prakash M. Nuclear matter and its role in supernovae, neutron stars and compact object binary mergers. Phys Rept. (2000) 121:333–4. doi: 10.1016/S0370-1573(00)00019-3

CrossRef Full Text | Google Scholar

52. Steiner AW, Prakash M, Lattimer JM, Ellis PJ. Isospin asymmetry in nuclei and neutron stars. Phys Rept. (2005) 411:325–75. doi: 10.1016/j.physrep.2005.02.004

CrossRef Full Text | Google Scholar

53. Lattimer JM, Prakash M. Neutron star observations: prognosis for equation of state constraints. Phys Rept. (2007) 442:109–65. doi: 10.1016/j.physrep.2007.02.003

CrossRef Full Text | Google Scholar

54. Hebeler K, Lattimer JM, Pethick CJ, Schwenk A. Constraints on neutron star radii based on chiral effective field theory interactions. Phys Rev Lett. (2010) 105:161102. doi: 10.1103/PhysRevLett.105.161102

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Annala E, Gorda T, Kurkela A, Vuorinen A. Gravitational-wave constraints on the neutron-star-matter equation of state. Phys Rev Lett. (2018) 120:172703. doi: 10.1103/PhysRevLett.120.172703

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Most ER, Weih LR, Rezzolla L, Schaffner-Bielich J. New constraints on radii and tidal deformabilities of neutron stars from GW170817. Phys Rev Lett. (2018) 120:261103. doi: 10.1103/PhysRevLett.120.261103

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Lim Y, Holt JW. Neutron star tidal deformabilities constrained by nuclear theory and experiment. Phys Rev Lett. (2018) 121:062701. doi: 10.1103/PhysRevLett.121.062701

PubMed Abstract | CrossRef Full Text | Google Scholar

58. Landry P, Kumar B. Constraints on the moment of inertia of PSR J0737-3039A from GW170817. Astrophys J. (2018) 868:L22. doi: 10.3847/2041-8213/aaee76

CrossRef Full Text | Google Scholar

59. Lim Y, Holt JW, Stahulak RJ. Predicting the moment of inertia of pulsar J0737-3039A from Bayesian modeling of the nuclear equation of state. Phys Rev C. (2019) 100:035802. doi: 10.1103/PhysRevC.100.035802

CrossRef Full Text | Google Scholar

60. Lim Y, Holt JW. Bayesian modeling of the nuclear equation of state for neutron star tidal deformabilities and GW170817. Eur Phys J A. (2019) 55:209. doi: 10.1140/epja/i2019-12917-9

CrossRef Full Text | Google Scholar

61. Coraggio L, Holt JW, Itaco N, Machleidt R, Marcucci LE, Sammarruca F. Nuclear-matter equation of state with consistent two- and three-body perturbative chiral interactions. Phys Rev C. (2014) 89:044321. doi: 10.1103/PhysRevC.89.044321

CrossRef Full Text | Google Scholar

62. Kaiser N. Exact calculation of three-body contact interaction to second order. Eur J Phys A. (2012) 48:58. doi: 10.1140/epja/i2012-12058-9

CrossRef Full Text | Google Scholar

63. Holt JW, Kaiser N. Equation of state of nuclear and neutron matter at third-order in perturbation theory from chiral effective field theory. Phys Rev C. (2017) 95:034326. doi: 10.1103/PhysRevC.95.034326

CrossRef Full Text | Google Scholar

64. Holt JW, Kaiser N, Miller GA, Weise W. Microscopic optical potential from chiral nuclear forces. Phys Rev C. (2013) 88:024614. doi: 10.1103/PhysRevC.88.024614

CrossRef Full Text | Google Scholar

65. Wellenhofer C, Holt JW, Kaiser N. Thermodynamics of isospin-asymmetric nuclear matter from chiral effective field theory. Phys Rev C. (2015) 92:015801. doi: 10.1103/PhysRevC.92.015801

CrossRef Full Text | Google Scholar

66. Koning AJ, Delaroche JP. Local and global nucleon optical models from 1 keV to 200 MeV. Nucl Phys. (2003) A713:231. doi: 10.1016/S0375-9474(02)01321-0

CrossRef Full Text | Google Scholar

67. Jeukenne JP, Lejeune A, Mahaux C. Optical-model potential in finite nuclei from Reid's hard core interaction. Phys Rev C. (1977) 16:80. doi: 10.1103/PhysRevC.16.80

CrossRef Full Text | Google Scholar

68. Toyokawa M, Minomo K, Kohno M, Yahiro M. Roles of chiral three-nucleon forces in nucleon-nucleus scattering. J Phys G. (2015) 42:025104. doi: 10.1088/0954-3899/42/2/025104

CrossRef Full Text | Google Scholar

69. Vorabbi M, Finelli P, Giusti C. Theoretical optical potential derived from nucleon-nucleon chiral potentials. Phys Rev C. (2016) 93:034619. doi: 10.1103/PhysRevC.93.034619

CrossRef Full Text | Google Scholar

70. Rotureau J, Danielewicz P, Hagen G, Jansen GR, Nunes FM. Microscopic optical potentials for calcium isotopes. Phys Rev C. (2018) 98:044625. doi: 10.1103/PhysRevC.98.044625

CrossRef Full Text | Google Scholar

71. Idini A, Barbieri C, Navrátil P. Ab initio optical potentials and nucleon scattering on medium mass nuclei. Phys Rev Lett. (2019) 123:092501. doi: 10.1103/PhysRevLett.123.092501

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Holt JW, Kaiser N, Miller GA. Microscopic optical potential for exotic isotopes from chiral effective field theory. Phys Rev C. (2016) 93:064603. doi: 10.1103/PhysRevC.93.064603

CrossRef Full Text | Google Scholar

73. Whitehead TR, Lim Y, Holt JW. Proton elastic scattering on calcium isotopes from chiral nuclear optical potentials. Phys Rev C. (2019) 100:014601.

Google Scholar

74. Bauge E, Delaroche JP, Girod M. Semi-microscopic nucleon-nucleus spherical optical model for nuclei with A < 40 at energies up to 200 MeV. Phys Rev C. (1998) 58:1118. doi: 10.1103/PhysRevC.58.1118

CrossRef Full Text | Google Scholar

75. Whitehead TR, Lim Y, Holt JW. Neutron elastic scattering on calcium isotopes from chiral nuclear optical potentials. arXiv:1912.10043 (2019).

Google Scholar

76. Lim Y, Holt JW. Structure of neutron star crusts from new Skyrme effective interactions constrained by chiral effective field theory. Phys Rev C. (2017) 95:065805. doi: 10.1103/PhysRevC.95.065805

CrossRef Full Text | Google Scholar

77. Lagrange C, Lejeune A. Phenomenological and microscopic optical model analyses of the interaction of low-energy nucleons with Nb-93. Phys Rev C. (1982) 25:2278. doi: 10.1103/PhysRevC.25.2278

CrossRef Full Text | Google Scholar

78. Kohno M, Sprung DWL, Nagata S, Yamaguchi N. Incident energy dependence of the effective interaction and radius of the optical model potential. Phys Lett. (1984) B137:10–4. doi: 10.1016/0370-2693(84)91095-5

CrossRef Full Text | Google Scholar

79. Goriely S, Delaroche JP. The isovector imaginary neutron potential: a key ingredient for the r-process nucleosynthesis. Phys Lett. (2007) B653:178. doi: 10.1016/j.physletb.2007.07.046

CrossRef Full Text | Google Scholar

80. Landau LD. The theory of a Fermi liquid. Sov Phys JETP. (1957) 3:920.

Google Scholar

81. Landau LD. On the theory of the Fermi liquid. Sov Phys JETP. (1959) 8:70.

Google Scholar

82. Migdal AB, Larkin AI. A phenomenological approach to the theory of the nucleus. Sov Phys JETP. (1964) 18:717.

Google Scholar

83. Migdal AB. Theory of Finite Fermi Systems and Properties of Atomic Nuclei. New York, NY: Interscience (1967).

Google Scholar

84. Schwenk A, Friman B. Polarization contributions to the spin dependence of the effective interaction in neutron matter. Phys Rev Lett. (2004) 92:082501. doi: 10.1103/PhysRevLett.92.082501

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Brown GE. Landau, brueckner-bethe, and migdal theories of fermi systems. Rev Mod Phys. (1971) 43:1. doi: 10.1103/RevModPhys.43.1

CrossRef Full Text | Google Scholar

86. Holt JW, Kaiser N, Weise W. Chiral Fermi liquid approach to neutron matter. Phys Rev C. (2013) 87:014338. doi: 10.1103/PhysRevC.87.014338

CrossRef Full Text | Google Scholar

87. Kaiser N, Niessner V. Density-dependent NN interaction from subleading chiral 3N forces: short-range terms and relativistic corrections. Phys Rev C. (2018) 98:054002. doi: 10.1103/PhysRevC.98.054002

CrossRef Full Text | Google Scholar

88. Kaiser N, Singh B. Density-dependent NN interaction from subleading chiral three-nucleon forces: long-range terms. Phys Rev C. (2019) 100:014002. doi: 10.1103/PhysRevC.100.014002

CrossRef Full Text | Google Scholar

89. Holt JW, Kaiser N, Weise W. Quasiparticle interaction in nuclear matter with chiral three-nucleon forces. Nucl Phys. (2012) A876:61. doi: 10.1016/j.nuclphysa.2011.12.001

CrossRef Full Text | Google Scholar

90. Holt JW, Kaiser N, Whitehead TR. Tensor Fermi liquid parameters in nuclear matter from chiral effective field theory. Phys Rev C. (2018) 97:054325. doi: 10.1103/PhysRevC.97.054325

CrossRef Full Text | Google Scholar

91. Bäckman SO, Sjöberg O, Jackson AD. The role of tensor forces in Fermi liquid theory. Nucl Phys. (1979) A321:10. doi: 10.1016/0375-9474(79)90682-1

CrossRef Full Text | Google Scholar

92. Erkelenz K, Alzetta R, Holinde K. Momentum space calculations and helicity formalism in nuclear physics. Nucl Phys. (1971) A176:413. doi: 10.1016/0375-9474(71)90279-X

CrossRef Full Text | Google Scholar

93. Bernard V, Kaiser N, Meissner UG. Aspects of chiral pion-nucleon physics. Nucl Phys. (1997) A615:483. doi: 10.1016/S0375-9474(97)00021-3

CrossRef Full Text | Google Scholar

94. Golak J, Skibinski J, Topolnicki K, Witala H, Epelbaum E, Krebs H, et al. Low-energy neutron-deuteron reactions with N3LO chiral forces. Eur Phys J A. (2014) 50:177.

Google Scholar

95. Krebs H, Gasparyan A, Epelbaum E. Chiral three-nucleon force at N4LO II: intermediate-range contributions. Phys Rev C. (2013) 87:054007. doi: 10.1103/PhysRevC.87.054007

CrossRef Full Text | Google Scholar

96. Tews I, Krüger T, Hebeler K, Schwenk A. Neutron matter at next-to-next-to-next-to-leading order in chiral effective field theory. Phys Rev Lett. (2013) 110:032504. doi: 10.1103/PhysRevLett.110.032504

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Holt JW, Kawaguchi M, Kaiser N. Implementing chiral three-body forces in terms of medium-dependent two-body forces. arXiv:1912.06055. (2019).

Google Scholar