Studies on Nuclear Structure and Nuclear Dynamics Using Cb-TDHFB

1. Introduction

Our subject is the atomic nucleus which is a self-binding finite quantum many-body system composed of two kinds of particles (nucleon: proton and neutron). The nuclear system in which the nucleons are the primary degree of freedom has various aspects depending on its nucleon number and its energy. To describe the structure and the dynamics of the finite quantum many-body system from the degree of freedom of nucleon is the core aim of nuclear physics.

The existence of mean-field is a unique and essential property in the nucleus, which is supported by the nuclear magic numbers. The independent-particle model, like the Hartree-Fock (HF) approximation, is based on the mean-field aspect of the nucleus and expresses the many-body wave function in terms of the single-particle states. The HF is a useful method in the Fermi particle system, in which the anti-symmetrization of the single-particle wave functions are necessary to satisfy the Pauli principle. Furthermore, the pairing correlation is also an important nuclear aspect [1]. The ground-state properties of a nucleus with the pairing correlation is successfully described by the well-known theory [2] proposed by Bardeen-Cooper-Schrieffer (BCS) in the condensed matter physics.

The time-dependent (TD) mean-filed models, such as TD Hartree-Fock-Bogoliubov (TDHFB) theory [3], have been proposed with the aim at describing the nuclear structure and dynamics, taking account of the mean-field property as well as including the pairing correlations. However, the number of TDHFB applications is not so large. It is because huge computational costs are required in the TDHFB calculations. Hence, several methods have been proposed to solve the TDHFB equation, not in its full size but some approximate ways. The canonical-basis TDHFB (Cb-TDHFB) is one of such approximation methods [4] of solving the TDHFB equation. In this mini-review, we introduce the framework of the Cb-TDHFB, which is a feasible TD model dealing with nuclear pairing correlation, together with the results obtained by the Cb-TDHFB to demonstrate its possibilities.

2. Time-Dependent Mean-Field Models

In order to obtain to the Cb-TDHFB equations, we will briefly follow the naive derivation of TD Hartree-Fock (TDHF) and TDHFB equations, from time-dependent many-body Schrödinger equation (1). When a time-dependent many-body wave function is written as |Φ(t)〉, the time evolution of |Φ(t)〉 which obeys the many-body Schrödinger equation, is given by,

$\begin{array}{ll}|\Phi (t)\rangle =e^{-iHt/\sout{h}}|\Phi (0)\rangle .& (1)\end{array}$

Here the Hamiltonian H is assumed as the sum of a kinetic and a two-body interaction terms for the Fermion system, which is described by a Fermion creation and annihilation operators (c^†, c). The time-dependent density matrix ρ(t) and pairing tensor κ(t) are defined with the |Φ(t)〉 as ${\rho }_{ij}(t)\equiv \langle \Phi (t)|c_j^{†}{c}_i|\Phi (t)\rangle$ and κ_ij(t) ≡ 〈Φ(t)|c_jc_i|Φ(t)〉. The subscripts i, j mean the label of the particle states. The equations to describe the time-dependence of ρ(t) and κ(t) are written as follows, using Equation (1):

$\begin{array}{l}i\sout{h}\frac{\partial }{\partial t}{\rho }_{ij}(t)=\langle \Phi (t)|[c_j^{†}{c}_i,H]|\Phi (t)\rangle ,\\ i\sout{h}\frac{\partial }{\partial t}{\kappa }_{ij}(t)=\langle \Phi (t)|[c_j{c}_i,H]|\Phi (t)\rangle .& (2)\end{array}$

The TDHF (TDHFB) equation is derived by replacing |Φ(t)〉 in the Equation (2) with the HF state |Φ_HF(t)〉 (the HFB state |Φ_HFB(t)〉), respectively. The |Φ_HF(t)〉 is written as a single Slater-determinant composed of single-particle states ϕ_l. The number of the single-particle states in the HF state is usually the same as the particle number of the system. The |Φ_HFB(t)〉 is the vacuum of the quasi-particles whose creation and annihilation operators (β^†, β) are composed of particle operators (c^†, c) and the coefficient matrices U and V; ${\beta }_k^{†}\equiv \sum _{\alpha }{U}_{\alpha k}{c}_{\alpha }^{†}+V_{\alpha k}{c}_k$. The matrices U and V are the general form of the BCS factors and are defined under the normalization and the unitary condition. The number of the quasi-particle basis is infinite in principle.

2.1. Cb-TDHFB Equation

There was an attempt to develop a time-dependent method that incorporates the nuclear pair correlation without directly solving the TDHFB equation [6]. Blocki and Flocard [6] proposed the equation of motion for the canonical basis ϕ_l and their BCS factors u_l and v_l with a simple effective interaction and a very schematic pairing functional. In Cusson et al. [7], Scamps et al. [8], and Magierski et al. [9], the equation of motion is called TDHF+BCS which is essentially equivalent to the Cb-TDHFB. The difference between their formulation and the Cb-TDHFB is in the derivation of the basic set of equations. The equations in Blocki and Flocard [6] were derived from the time-dependent variational principle with constraint terms for the norm conservation of particle wave functions and the number conservation. The constraint for the norm conservation finally induces the phase term in the equation of motion of the canonical basis, which is written as ε_l in Blocki and Flocard [6]. The Cb-TDHFB equation is derived from the TDHFB equation with the canonical basis representation, in which the density matrix is diagonal. This is equivalent to replacing the HFB state by a state with the ordinary BCS form under an assumption for the functional form of the pair potential. In the Cb-TDHFB derivation, the phase term is naturally induced from the orthonormal property of the canonical basis. The phase term is essential to connect the canonical basis with pair probability κ_l [4] and to keep the total energy conservation in the time evolution. The Cb-TDHFB equations are composed of three types of differential equations with respect to the time of the canonical basis, the occupation provability ρ_l and the pair probability κ_l.

The BCS state can always be derived from the HFB state as a special solution, which is guaranteed by the Bloch-Messiah theorem. On the other hand, in the dynamical cases, the time dependence of the unitary transformation from HFB to BCS state is unclear on the way of time evolution. This leads to the fact that the canonical basis can not be guaranteed to keep their property in general. This is the most crucial key point in the formulation of the Cb-TDHFB derivation. The major factor that disturbs the canonical basis is the non-diagonal elements of pair potential Δ. Therefore, the assumption is introduced in the formulation of the Cb-TDHFB that the pair potential should be of the diagonal form: ${\Delta }_{l\bar{k}}\equiv -{\Delta }_k{\delta }_{kl}$, which is equal to the ordinary BCS approximation.

The number of canonical basis in the Cb-TDHFB equation is about twice the particle number at most, although it depends on the nucleus and the energy cutoff for the pairing channel. On the other hand, the TDHFB needs an infinite number of quasi-particle orbitals in principle. This property that the number of dynamical variables in the Cb-TDHFB is much smaller is a significant advantage of the Cb-TDHFB compared with the other time-dependent method which deals with pairing correlation. Therefore, the computational costs of the Cb-TDHFB and the TDHF applications are comparable, and it is computationally feasible to employ the three-dimensional (3D) representation of the orbitals: e.g., ϕ_l(r, t) = 〈r|ϕ_l(t)〉.

Here, let us mention two major concerns for the particle “gas” problem and the continuity equation in the Cb-TDHFB application. The gas problem is famous in the BCS treatment for the finite nuclear system, which is reported in previous studies [10, 11]. The problem is caused by the expression of the many-body wave function in the BCS approximation, which is well-checked and summarized by a recent study in Anguiano et al. [12] from the practical point of view. The single-particle states with the positive energy near the Fermi surface cause the unphysical particle gas. Because the initial state of the Cb-TDHFB is also HF+BCS state, we should avoid the nuclei near the drip-line.

In Scamps et al. [8], the problem of the continuity equation in the Cb-TDHFB calculation is studied relating with the particle transport phenomena. The Cb-TDHFB satisfies the conservation laws for the orthonormality of the canonical states, the average particle number, and the average total energy. The local density of HF+BCS and Cb-TDHFB is given by sum of $|v_l(t){|}^2|{\varphi }_l(r,t){|}^2$ in which the coefficients depend on time only. The separable expression of the density and the lack of the spatial degree of freedom in the occupation probability cause the unphysical density oscillation, which is the same reason as the particle gas problem and is unavoidable as long as the BCS expression is adopted. And the expression also causes the difficulty in describing the relative gauge angle between the superfluid nuclei in the collision reaction, which is well-explained in the supplemental material of Magierski et al. [9]. However, we know the source of the unphysical results, and we can find a method to address it. The frozen occupation approximation is suggested in Scamps et al. [8]. We should use the Cb-TDHFB as a feasible and beneficial tool while knowing the matters stated above.

2.2. Linear Response Calculation Using TD Mean-Field Model

There are many models to study nuclear excitation modes, such as the random phase approximation (RPA) or quasi-particle RPA (QRPA) formalism, which are the most used mean-field methods for nuclear excitation. The (Q)RPA formalism can be derived as the small-amplitude limit of the TDHF(B) method, which is the so-called linear response theory [3, 5]. The strength function calculated with the (Q)RPA can be reproduced by the TDHF(B) calculations of the small-amplitude oscillation.

The procedure to calculate the strength function is as follows [13–17]. (A) We prepare the initial states of the TD method and add a weak and instantaneous external field $V_{\text{ext}}(t)=-\eta \widehat{F}\delta (t)$ to them. The η stands for a strength of the external filed, and $\widehat{F}$ is an operator to excite the oscillations with a set of quantum numbers like multipolarity L, projection K, parity π, etc. The η should be small to guarantee the linearity throughout the numerical iteration, since we consider the linear response. In practice, the size of the η depends on the operator $\widehat{F}$. (B) We calculate the time-evolution of |Φ(t)〉 by using the time-dependent method and calculate the time-dependent expectation value of $\widehat{F}$: $f(t)\equiv \langle \Phi (t)|\widehat{F}|\Phi (t)\rangle$. After the calculation of |Φ(t)〉, the strength function $S(E;\widehat{F})$ can be obtained from the Fourier transformation of f(t).

Here, it is to be noted that some operators $\widehat{F}$ are related with the spurious mode of excitation. For instance, the operators isoscalar-compressional dipole and the quadrupole mode Q₂₁, induce the spurious modes of translational and rotational modes, respectively.

2.3. Collision Simulation by Means of TD Mean-Field Model

There have been many studies for the low-energy heavy-ion collisions by means of several types of TD mean-field models [18–25]. In the procedure to apply the TD mean-field models to the nuclear collision simulations, however, there is no essential difference among the models. The typical procedure for the collision simulation is as follows; (A) Set the wave functions of the target and the projectile to the positions with an impact parameter b, (B) Boost the wave functions with the incident energy E_in, (C) Calculate the time-evolution of the wave functions which are within the common mean-field.

The b and E_in are values when the relative distance between the two nuclei is infinite. Then, they must be changed due to the Coulomb field in the calculation space, which obeys the Rutherford's trajectory. This is realized by setting the initial wave functions at the positions where the interaction between projectile and target can be regarded as Coulomb force only. The frozen density approximation is well reasonable to indicate the initial positions. Indeed it is applied to the simple estimation of the Coulomb barrier [26–28]. When setting the wave functions for projectile and target to the initial positions, it is safe in practice to avoid the overlaps of them because the duplications cause complex interference in the phase of each other state.

3. Applications

3.1. Electric Dipole Excitation in the Linear Response Theory

In this and the next subsection, we show examples of the linear response calculations using the Cb-TDHFB. Following the procedure described in section 2.2, we investigate the strength functions for the electric dipole (E1) excitation of ytterbium-172 (¹⁷²Yb, Z=70). ¹⁷²Yb is an open-shell nucleus with the nuclear pairing correlation and has a prolate deformed shape in its ground state, which is calculated with SkM^* Skyrme parameter set.

The characteristic structure of the quadrupole deformed nucleus appears in the shape of the E1 strength function of ¹⁷²Yb in Figure 1I, in which two peaks corresponding to the K=0 and 1 modes appear. The photo-absorption cross-section of ¹⁷²Yb can be deduced from the strength function. The experimental data [29, 30] were well-reproduced by the cross section.

FIGURE 1

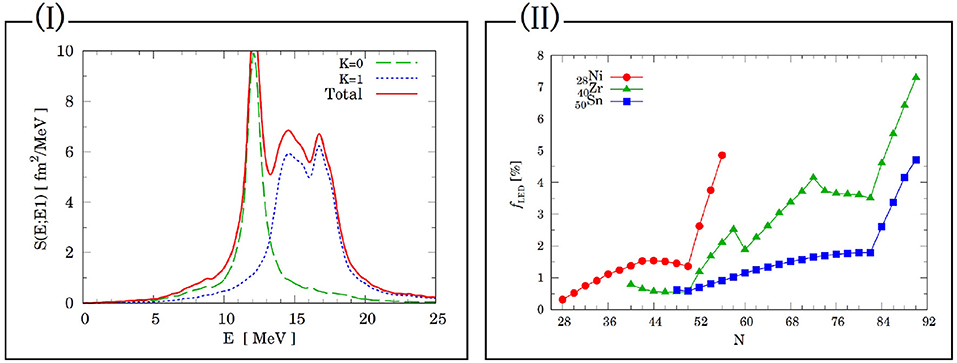
Figure 1. Example for linear response calculations: (I) E1 strength function of ¹⁷²Yb calculated by Cb-TDHFB with SkM^*, (II) Systematics of the LED ratio in the energy weighted sum rule for E1 of (circle) Ni, (triangle) Zr, and (square) Sn isotopes with respect to neutron number.

Furthermore, the strength function can be compared with the HFB+QRPA results shown in Figure 7 of Terasaki and Engel [31]. The peak positions of the strength functions are almost the same, although the small difference in the shapes of the peaks appears in the width and height of K = 0 mode. The results illustrate that the Cb-TDHFB works well in dealing with the pairing correlation at the small-amplitude limit.

The Cb-TDHFB calculations can be performed in the 3D Cartesian coordinate space, with a single-core computer and several hundred hours. The HFB+QRPA calculations had been performed in axial symmetric space using the many-core parallel computer (about 10,000 cores), which could be estimated from the proposal [32]. If we restrict ourselves only to the strength functions, the Cb-TDHFB can significantly reduce the computational cost compared with the other TDHFB methods, which is one of the practical benefits of using the Cb-TDHFB. Taking advantage of the benefit of the Cb-TDHFB, we can carry out the systematic study of the linear responses of a large number of nuclei on the nuclear chart. Here we note that the finite amplitude method (FAM) is also an effective method to calculate the excitation energies [33–36] within the (Q)RPA theory.

3.2. Systematic Study of E1 Excitation Modes

We have performed a systematic investigation of the E1 strength functions using the Cb-TDHFB represented in the 3D Cartesian coordinate [37]. The purpose of the systematic study was to clarify the excitation mechanism of low-energy dipole (LED) resonances, which have been called the pygmy dipole resonance (PDR). The PDR has been considered as the excited modes which is deeply connected with the characteristic structure of the neutron-rich nucleus [38, 39]. However, the systematic study showed that the PDR is not a unique excitation mode of the unstable nucleus, but can also be found in a stable nucleus, which suggests the PDR has a composite mechanism [37].

The comparison between the results of unstable heavy nuclei with and without a self-consistent residual interaction indicates that the PDR has the composite mechanism. The residual interaction can be excluded from the real-time calculation by using the single-particle Hamiltonian with the fixed density at the ground state. In the mechanism, there are the pure single-particle excitation mode and the decoupling modes from the giant dipole resonance. The decoupling modes might have a collective isoscalar character [37].

Figure 1II shows the neutron number dependence of the LED ratio f_LED of nickel, zirconium, and tin isotopes. The f_LED is defined as m₁(E_low)/m₁ where m₁(E_low) is the energy weighted sum of the E1 strength function up to the energy E_low=10 MeV, and m₁ is the value of the energy weighted sum rule of E1 mode. The panel shows the characteristic behavior of f_LED at the neutron numbers which correspond to the magic numbers (N = 28, 50, 82) of the spherical nuclei as well as those of the deformed nuclei (N = 60−74).

The systematic application of the Cb-TDHFB is carried out also for the quadrupole type excitations [40, 41], including modes with K = 0, 1, and 2. As mentioned in section 2.2, the quadrupole excitation with K = 1 induces the spurious mode. The authors in Scamps and Lacroix [41] employ an excellent practical method to avoid the spurious mode. The systematic study of the nuclear linear responses performed by using the TD method is significantly useful to prospect for understanding the nuclear structure of the broad range of nuclear mass number, although several techniques are necessary to extract physical quantities from the calculated data.

3.3. Fusion Reaction

The pairing effect on the large amplitude collective motion is one of the most exciting topics in nuclear physics. Many studies for nuclear collision and fission by using the mean-field models, including the pairing correlation, have been performed [7, 9, 42–50]. We performed the Cb-TDHFB and TDHF calculations for symmetric and asymmetric collisions; ²²O+²²O, ⁵²Ca+⁵²Ca, and ²²O+⁵²Ca, in Ebata and Nakatsukasa [46]. In Figure 2, we show examples of the simulations of the fusion reactions. Upper and lower panels show the snapshots of the time-evolutions of nucleon densities calculated by Cb-TDHFB and TDHF, respectively.

FIGURE 2

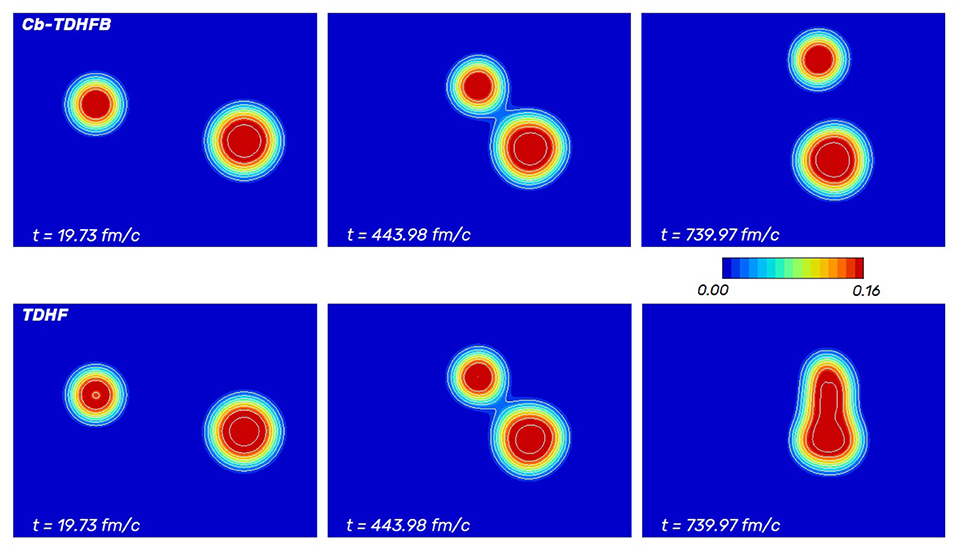
Figure 2. Time-evolution of nucleon density for the ²²O+⁵²Ca collision reactions which are calculated by (Upper panels) Cb-TDHFB and (Lower panels) TDHF. The calculations are performed with the parameters b=4.1 fm and E_in=35.6 MeV.

The Cb-TDHFB results indicate the repulsive effects of pairing correlation in the fusion reaction. The nuclear pairing correlation attractively acts in the ground state basically, although the discussions of the pairing role for the anti-halo effect have not yet converged [51–53]. The strength dependence of pairing correlation is reported for the fission reaction using full TDHFB calculations [50]. The pairing correlation might not be wholly clarified yet in the static and the dynamic processes.

4. Summary and Perspectives

We have introduced the studies using Cb-TDHFB [4] and the points to note for its applications. The problems due to the BCS treatment are pointed out: the particle gas and the continuity equation. The linear response study for E1 excitation of ¹⁷²Yb is simply explained, in which the comparisons between the strength functions obtained by HFB+QRPA and by Cb-TDHFB are mentioned, including the computational cost. The systematic studies with the strength function and the collision simulation for fusion reaction have also been shown to introduce the future possibilities of the Cb-TDHFB.

The TD mean-field study might be extended more and more in the future because there are large amounts of relevant regions that will be studied by using the TD mean-field model. The research for the large amplitude collective motion, such as fusion or fission, will especially increase, due to the continuous developments of nuclear theory and the numerical resource. The fusion and fission reactions are significantly important topics not only in nuclear physics but also in other fields: nuclear engineering, nuclear astrophysics.

Furthermore, the wave function in the TD mean-field model might be extended to the superposition of several wave functions such as the multi-Slater determinants, with the aim at expressing the stochastic phenomena [54–56]. There are upcoming trends of practical applications of the extended framework of mean-field among the recent researchers. At the same time, new effective interaction is demanded, just as the Skyrme interaction has been refined in the nuclear dynamics. Some new effective interactions have been suggested in Reinhard and Nazarewicz [57] and Bulgac et al. [58]. The feedback from many applications is necessary for the refinement and improvement of the effective interactions. The Cb-TDHFB application will be increasing to construct a next-generation mean-field model as one of the methods to treat nuclear pairing correlation.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I would like to express thanks to P. D. Stevenson, C. Simenel, D. Lacroix, L. Guo, and N. Schunk for giving an opportunity to write our works. This work was supported by Leading Initiative for Excellent Young Researchers, MEXT, Japan.

References

1. Bohr A, Mottelson BR, Pines D. Possible analogy between the excitation spectra of nuclei and those of the superconducting metallic state. Phys Rev. (1958) 110:936–8. doi: 10.1103/PhysRev.110.936

CrossRef Full Text | Google Scholar

2. Bardeen J, Cooper LN, Schrieffer JR. Theory of superconductivity. Phys Rev. (1957) 108:1175–204. doi: 10.1103/PhysRev.108.1175

CrossRef Full Text | Google Scholar

3. Jean-Paul B, Ripka G. Quantum Theory of Finite Systems. Cambridge: MIT Press (1986).

Google Scholar

4. Ebata S, Nakatsukasa T, Inakura T, Yoshida K, Hashimoto Y, Yabana K. Canonical-basis time-dependent Hartree-Fock-Bogoliubov theory and linear-response calculations. Phys Rev C. (2010) 82:034306. doi: 10.1103/PhysRevC.82.034306

CrossRef Full Text | Google Scholar

5. Ring P, Schuck P. The Nuclear Many-Body Problems. Berlin; Heidelberg: Springer Verlag (1980).

Google Scholar

6. Blocki J, Flocard H. Simple dynamical models including pairing residual interaction. Nuclear Phys A. (1976) 273:45–60.

Google Scholar

7. Cusson RY, Maruhn JA, Stocker H. Collision of ²³⁸U+²³⁸U using a three-dimensional TDHF−BCS model. Z Phys A Atoms Nuclei. (1980) 294:257–60. doi: 10.1007/BF01438163

CrossRef Full Text | Google Scholar

8. Scamps G, Lacroix D, Bertsch GF, Washiyama K. Pairing dynamics in particle transport. Phys Rev C. (2012) 85:034328. doi: 10.1103/PhysRevC.85.034328

CrossRef Full Text | Google Scholar

9. Magierski P, Sekizawa K, Wlazłowski G. Novel role of superfluidity in low-energy nuclear reactions. Phys Rev Lett. (2017) 119:042501. doi: 10.1103/PhysRevLett.119.042501

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Dobaczewski J, Flocard H, Treiner J. Hartree-Fock-Bogolyubov description of nuclei near the neutron-drip line. Nucl Phys A. (1984) 422:103–39.

Google Scholar

11. Dobaczewski J, Nazarewicz W, Werner TR, Berger JF, Chinn CR, Dechargé J. Mean-field description of ground-state properties of drip-line nuclei: pairing and continuum effects. Phys Rev C. (1996) 53:2809–40. doi: 10.1103/PhysRevC.53.2809

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Anguiano M, Lallena AM, Bernard R, Co' G. Neutron gas and pairing. Phys Rev C. (2019) 99:034302. doi: 10.1103/PhysRevC.99.034302

CrossRef Full Text | Google Scholar

13. Chinn CR, Umar AS, Vallieres M, Strayer MR. Mean field studies of exotic nuclei. Phys Rep. (1996) 264:107–21.

Google Scholar

14. Nakatsukasa T, Yabana K. 3D real-space calculation of the continuum response. Prog Theor Phys Suppl. (2002) 146:447–51. doi: 10.1143/PTPS.146.447

CrossRef Full Text | Google Scholar

15. Simenel C, Chomaz P. Nonlinear vibrations in nuclei. Phys Rev C. (2003) 68:024302. doi: 10.1103/PhysRevC.68.024302

CrossRef Full Text | Google Scholar

16. Nakatsukasa T, Yabana K. Linear response theory in the continuum for deformed nuclei: green's function vs time-dependent Hartree-Fock with the absorbing boundary condition. Phys Rev C. (2005) 71:024301. doi: 10.1103/PhysRevC.71.024301

CrossRef Full Text | Google Scholar

17. Maruhn JA, Reinhard PG, Stevenson PD, Stone JR, Strayer MR. Dipole giant resonances in deformed heavy nuclei. Phys Rev C. (2005) 71:064328. doi: 10.1103/PhysRevC.71.064328

CrossRef Full Text | Google Scholar

18. Bonche P, Koonin S, Negele JW. One-dimensional nuclear dynamics in the time-dependent Hartree-Fock approximation. Phys Rev C. (1976) 13:1226–58. doi: 10.1103/PhysRevC.13.1226

CrossRef Full Text | Google Scholar

19. Koonin SE, Davies KTR, Maruhn-Rezwani V, Feldmeier H, Krieger SJ, Negele JW. Time-dependent Hartree-Fock calculations for ¹⁶O + ¹⁶O and ⁴⁰Ca + ⁴⁰Ca reactions. Phys Rev C. (1977) 15:1359–74. doi: 10.1103/PhysRevC.15.1359

CrossRef Full Text | Google Scholar

20. Davies KTR, Feldmeier HT, Flocard H, Weiss MS. Comparisons of two- and three-dimensional time-dependent Hartree-Fock calculations of the reactions ¹⁶O + ¹⁶O and ⁴⁰Ca + ⁴⁰Ca. Phys Rev C. (1978) 18:2631–40. doi: 10.1103/PhysRevC.18.2631

CrossRef Full Text | Google Scholar

21. Davies KTR, Koonin SE. Skyrme-force time-dependent Hartree-Fock calculations with axial symmetry. Phys Rev C. (1981) 23:2042–61. doi: 10.1103/PhysRevC.23.2042

CrossRef Full Text | Google Scholar

22. Negele JW. The mean-field theory of nuclear structure and dynamics. Rev Mod Phys. (1982) 54:913–1015. doi: 10.1103/RevModPhys.54.913

CrossRef Full Text | Google Scholar

23. Kim KH, Otsuka T, Bonche P. Three-dimensional TDHF calculations for reactions of unstable nuclei. J Phys G Nucl Part Phys. (1997) 23:1267–73. doi: 10.1088/0954-3899/23/10/014

CrossRef Full Text | Google Scholar

24. Umar AS, Oberacker VE. Three-dimensional unrestricted time-dependent Hartree-Fock fusion calculations using the full Skyrme interaction. Phys Rev C. (2006) 73:054607. doi: 10.1103/PhysRevC.73.054607

CrossRef Full Text | Google Scholar

25. Maruhn JA, Reinhard PG, Stevenson PD, Umar AS. The TDHF code Sky3D. Comput Phys Commun. (2014) 185:2195–216. doi: 10.1016/j.cpc.2014.04.008

CrossRef Full Text | Google Scholar

26. Denisov VY, Norenberg W. Entrance channel potentials in the synthesis of the heaviest nuclei. Eur Phys J A. (2002) 15:375–88. doi: 10.1140/epja/i2002-10039-3

CrossRef Full Text | Google Scholar

27. Washiyama K, Lacroix D. Energy dependence of the nucleus-nucleus potential close to the Coulomb barrier. Phys Rev C. (2008) 78:024610. doi: 10.1103/PhysRevC.78.024610

CrossRef Full Text | Google Scholar

28. Washiyama K. Microscopic analysis of fusion hindrance in heavy nuclear systems. Phys Rev C. (2015) 91:064607. doi: 10.1103/PhysRevC.91.064607

CrossRef Full Text | Google Scholar

29. Goryachev AM, Zalesnyy GN. Photoneutron cross sections for Yb-170,171,172,173,174, and 176 in the region of giant resonance. Voprosy Teoreticheskoy i Yadernoy Fiziki (1976) 1976:42.

Google Scholar

30. Ebata S, Nakatsukasa T, Inakura T, Yoshida K, Hashimoto Y, Yabana K. Cb-TDHFB Calculations for Isovector Dipole Mode of Heavy Nucleus. RIKEN Accelerator Progress Report (2010). Available online at: http://www.nishina.riken.jp/researcher/APR/Document/ProgressReport_vol_44.pdf (accessed September 30, 2011).

Google Scholar

31. Terasaki J, Engel J. Self-consistent Skyrme quasiparticle random-phase approximation for use in axially symmetric nuclei of arbitrary mass. Phys Rev C. (2010) 82:034326. doi: 10.1103/PhysRevC.82.034326

CrossRef Full Text | Google Scholar

32. Engel J, Terasaki J. Systematics of Nuclear Surface Vibrations in Deformed Nuclei. Available online at: http://unedf.mps.ohio-state.edu/content/projects/engel_qra_teragrid_proposal.pdf (accessed Jun 18, 2010).

Google Scholar

33. Nakatsukasa T, Inakura T, Yabana K. Finite amplitude method for the solution of the random-phase approximation. Phys Rev C. (2007) 76:024318. doi: 10.1103/PhysRevC.76.024318

CrossRef Full Text | Google Scholar

34. Inakura T, Nakatsukasa T, Yabana K. Self-consistent calculation of nuclear photoabsorption cross sections: finite amplitude method with Skyrme functionals in the three-dimensional real space. Phys Rev C. (2009) 80:044301. doi: 10.1103/PhysRevC.80.044301

CrossRef Full Text | Google Scholar

35. Avogadro P, Nakatsukasa T. Finite amplitude method for the quasiparticle random-phase approximation. Phys Rev C. (2011) 84:014314. doi: 10.1103/PhysRevC.84.014314

CrossRef Full Text | Google Scholar

36. Washiyama K, Nakatsukasa T. Multipole modes of excitation in triaxially deformed superfluid nuclei. Phys Rev C. (2017) 96:041304. doi: 10.1103/PhysRevC.96.041304

CrossRef Full Text | Google Scholar

37. Ebata S, Nakatsukasa T, Inakura T. Systematic investigation of low-lying dipole modes using the canonical-basis time-dependent Hartree-Fock-Bogoliubov theory. Phys Rev C. (2014) 90:024303. doi: 10.1103/PhysRevC.90.024303

CrossRef Full Text | Google Scholar

38. Suzuki Y, Ikeda K, Sato H. New type of dipole vibration in nuclei. Prog Theor Phys. (1990) 83:180–4. doi: 10.1143/PTP.83.180

CrossRef Full Text | Google Scholar

39. Van Isacker P, Nagarajan MA, Warner DD. Effect of the neutron skin on collective states of nuclei. Phys Rev C. (1992) 45:R13–6. doi: 10.1103/PhysRevC.45.R13

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Scamps G, Lacroix D. Systematics of isovector and isoscalar giant quadrupole resonances in normal and superfluid spherical nuclei. Phys Rev C. (2013) 88:044310. doi: 10.1103/PhysRevC.88.044310

CrossRef Full Text | Google Scholar

41. Scamps G, Lacroix D. Systematic study of isovector and isoscalar giant quadrupole resonances in normal and superfluid deformed nuclei. Phys Rev C. (2014) 89:034314. doi: 10.1103/PhysRevC.89.034314

CrossRef Full Text | Google Scholar

42. Cusson RY, Meldner HW. Time-dependent Hartree-Fock-Bogoliubov calculations of heavy-element fusion and fission phenomena. Phys Rev Lett. (1979) 42:694–6. doi: 10.1103/PhysRevLett.42.694

CrossRef Full Text | Google Scholar

43. Mirea M. Time-dependent pairing equations for seniority-one nuclear systems. Phys Rev C. (2008) 78:044618. doi: 10.1103/PhysRevC.78.044618

CrossRef Full Text | Google Scholar

44. Mirea M. Energy partition in low energy fission. Phys Rev C. (2011) 83:054608. doi: 10.1103/PhysRevC.83.054608

CrossRef Full Text | Google Scholar

45. Ebata S. Simulation of heavy ion collision using a time-dependent density functional theory including nuclear superfluidity. J Phys. (2013) 454:012054. doi: 10.1088/1742-6596/454/1/012054

CrossRef Full Text | Google Scholar

46. Ebata S, Nakatsukasa T. Repulsive aspects of pairing correlation in nuclear fusion reaction. J Phys Soc Jpn. (2015) 6:020056. doi: 10.7566/JPSCP.6.020056

CrossRef Full Text | Google Scholar

47. Bulgac A, Magierski P, Roche KJ, Stetcu I. Induced fission of ²⁴⁰Pu within a real-time microscopic framework. Phys Rev Lett. (2016) 116:122504. doi: 10.1103/PhysRevLett.116.122504

CrossRef Full Text | Google Scholar

48. Hashimoto Y, Scamps G. Gauge angle dependence in time-dependent Hartree-Fock-Bogoliubov calculations of ²⁰O+²⁰O head-on collisions with the Gogny interaction. Phys Rev C. (2016) 94:014610. doi: 10.1103/PhysRevC.94.014610

CrossRef Full Text | Google Scholar

49. Scamps G, Simenel C. Impact of pear-shaped fission fragments on mass-asymmetric fission in actinides. Nature. (2018) 564:382–5. doi: 10.1038/s41586-018-0780-0

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Bulgac A, Jin S, Roche KJ, Schunck N, Stetcu I. Fission dynamics of ²⁴⁰Pu from saddle to scission and beyond. Phys Rev C. (2019) 100:034615. doi: 10.1103/PhysRevC.100.034615

CrossRef Full Text | Google Scholar

51. Bennaceur K, Dobaczewski J, Poszajczak M. Pairing anti-halo effect. Phys Lett B. (2000) 496:154–60. doi: 10.1016/S0370-2693(00)01292-2

CrossRef Full Text | Google Scholar

52. Zhang Y, Chen Y, Meng J, Ring P. Influence of pairing correlations on the radius of neutron-rich nuclei. Phys Rev C. (2017) 95:014316. doi: 10.1103/PhysRevC.95.014316

CrossRef Full Text | Google Scholar

53. Hagino K, Sagawa H. New concept for the pairing anti-halo effect as a localized wave packet of quasiparticles. Phys Rev C. (2017) 95:024304. doi: 10.1103/PhysRevC.95.024304

CrossRef Full Text | Google Scholar

54. Lacroix D, Ayik S. Stochastic quantum dynamics beyond mean field. Eur Phys J A. (2014) 50:95. doi: 10.1140/epja/i2014-14095-8

CrossRef Full Text | Google Scholar

55. Tanimura Y, Lacroix D, Ayik S. Microscopic phase-space exploration modeling of ²⁵⁸Fm Spontaneous Fission. Phys Rev Lett. (2017) 118:152501. doi: 10.1103/PhysRevLett.118.152501

CrossRef Full Text | Google Scholar

56. Simenel C, Umar AS. Heavy-ion collisions and fission dynamics with the time-dependent Hartree-Fock theory and its extensions. Prog Part Nucl Phys. (2018) 103:19–66. doi: 10.1016/j.ppnp.2018.07.002

CrossRef Full Text | Google Scholar

57. Reinhard PG, Nazarewicz W. Toward a global description of nuclear charge radii: exploring the Fayans energy density functional. Phys Rev C. (2017) 95:064328. doi: 10.1103/PhysRevC.95.064328

CrossRef Full Text | Google Scholar

58. Bulgac A, Forbes MM, Jin S, Perez RN, Schunck N. Minimal nuclear energy density functional. Phys Rev C. (2018) 97:044313. doi: 10.1103/PhysRevC.97.044313

CrossRef Full Text | Google Scholar