New Methods for the Steady-State Analysis of Complex Agent-Based Models

Among all tools used to understand collective human behavior, few tools have been as successful as agent-based models (ABMs). These models have been particularly effective at describing emergent social behavior, such as spatial segregation in neighborhoods or opinion polarization on social networks. ABMs are particularly common in the study of opinion and belief dynamics, being used by fields ranging from anthropology to statistical physics. These models, much like the social systems they describe, often do not have unique output variables, scales, or clear order parameters. This lack of clearly measurable emergent behavior makes such complex ABMs difficult to study, ultimately limiting their application to cases of empirical interest. In this paper, we introduce a series of approaches to analyze complex multidimensional ABMs, drawing from information theory and cluster analysis. We use these approaches to explore a multi-level agent-based model of ideological alignment introduced by Banisch and Olbrisch to extend Mäs and Flache's argument communication theory of bi-polarization. We use the tools introduced here to perform a thorough analysis of the model for small system sizes, identifying the convergence toward steady-state behavior, and describing the full spectrum of steady-state distributions produced by this model. Finally, we show how the approach we introduced can be easily adapted for larger implementations, as well as for other complex agent-based models of social behavior.

1. Introduction

Over the last decades, computational social science has risen as a strongly empirical discipline, drawing on data science methods to tackle high-dimensional large data sets that cannot be understood with simple analytical tools. This is particularly true in the study of public attention and public opinion dynamics: there are multiple studies looking at large-scale trends in Internet search queries, online petitions, and forums, as well as applying natural language processing methods to news articles and social media activity. It is now possible to quantify, to a degree, what people care about, and what they think of it.

This increasing availability of data on individual and public opinion calls for realistic, theory-informed models. Models of opinion change and belief dynamics have traditionally been studied by a large number of disciplines, including but not limited to economics [1–3], political science [4], sociology [5], anthropology [6], philosophy [7], and psychology [8] among others. There is also a tradition in statistical physics, dating back to the voter model [9–12], but also considering models such as the majority rule model [13], the Sznajd model [14], and a number of bounded confidence models [15]. Each model typically describes opinion change through a fixed strategy, where an agent might update their beliefs to more accurate values [16–18], or perhaps might seek conformity by following either the majority around them [13], or by copying the mean opinion [4]. The effects of social influence might vary with the distance between one's own opinion and the advocated one [19–21], on the details of how the new information is presented [22] or even to meta-information [23–25]. Opinion dynamics models often also take into account the structure of the social networks where agents are embedded. In these models, opinion formation is often described as a result of the combination of social structure and behavior, as agents in different parts of a social network will be exposed to different sources of information, while the social network itself might change over time, as agents choose to change their own connections according to the behavior and opinions of their neighbors [11, 26, 27].

Rather than producing an exhaustive list of models and modeling choices, this study aims to develop methods that allow for a thorough exploration of complex models. Many of the models presented above, much like the social systems they describe, have multiple output variables, often displaying divergent behavior in one coarse-graining scale while displaying convergent behavior in another. This makes such complex models hard to study, particularly as their application into questions of empirical interest requires expanding models to multidimensional landscapes and parameter spaces, where emergence and convergence are difficult to identify in first place.

With these problems in mind, in this paper we introduce a series of tools that provide a scalable way to explore the parameter space of complex agent-based models. As a case study, we use an multi-level opinion dynamics agent-based model which contains all of these features—no clear output variable, multidimensional parameter space and output space. We perform a thorough analysis of the model for small system sizes, and show how the same analysis could be performed for larger implementations of other complex models.

The agent-based model we use as a case study was originally introduced as a toy model of opinion polarization. In recent years, the spread of information on social networks has been described a driving force behind political polarization, through mechanisms of homophily leading to “filter bubbles” or “echo chambers” [11, 28, 29]. While a more robust body of evidence is needed to clarify the many roles of online social networks in political polarization, the role of homophily and social influence in the process of opinion polarization is already well-described by concepts such as the argument communication theory of bi-polarization, introduced by Mäs and Flache [30]. This theory proposes to account for the emergence of a bi-modal distribution in opinions through an amplification of small differences between individuals. It draws from the theory of informational influence, or persuasive argument theory [16–18], while assuming that homophily with respect to an individual's opinions [28, 31–34] will be the main factor behind communication and opinion change. As argued by Mäs and Flache, the cognitive-social bias of homophily is a sufficient mechanism to account for the emergence of a bimodal opinion distribution.

The simplicity of Mäs and Flache's theoretical model is also its limitation, in that it focuses on the emergence of polarization around a single issue, or a single pair of opposing issues on an axis. This limitation has been addressed by an extended computational model proposed by Banisch and Olbrich [35], who draw from structural theories of attitude dynamics [36–38] to make a distinction between individual beliefs held by an agent and their attitudes toward multiple issues. The relations between beliefs and attitudes are framed by Banisch and Olbrich as cognitive-evaluative maps shared by a population [39]. In their computational model, an individual's beliefs are encoded as a vector x of binary values, while their attitudes are represented as another vector y, this one with integer values, which depend on the belief vector but also on a cognitive-evaluative matrix C, through the linear equation y = C·x (in the notation used here). In the example shown in Figure 1A, a total of six beliefs determines an agent's attitude toward two issues. Each issue is affected positively by two issues, negatively by two others, and is not affected by the last two. This can be represented as a bipartite graph where every belief is connected to an opinion, which can be summarized by the adjacency matrix shown in Figure 1B. The separation between belief and attitude makes this network different from other network models of belief dynamics [40], where beliefs affect each influence each other directly. In this two-level model, in principle, unless two agents interact, one agent does not have access to another agent's beliefs—while the decision to interact might be based on attitudes only.

FIGURE 1

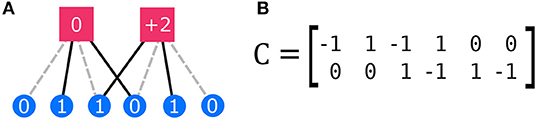
Figure 1. Representation of the agent cognitive-evaluative map, adapted from Banisch and Olbrich [35]. In this example, agents form attitudes on N = 2 different issues, represented by the squares in (A). Their attitudes are based on their beliefs M = 6 facts, represented as circles with ones indicating the presence of a belief and zeros indicating its absence. Beliefs may contribute positively (black solid lines), or negatively (gray dashed lines) to the attitudes, or may not contribute at all (no line). The mapping from beliefs to attitudes is summarized by the matrix C, shown in (B). Respectively, −1, 1, and 0 s represent positive, negative, and null contributions.

As described above, Banisch and Olbrich's model of ideological alignment is a multi-dimensional agent-based model which can exhibit emergent behavior in more than one level, posing an interesting challenge for current methods of analysis of ABMs. In the next sections, we explore the parameter space of this model by investigating the ensemble of all cognitive-evaluative maps for systems with small numbers of beliefs and attitudes. We then introduce different approaches to analyze the convergence of the model, as well as the range of steady-states it can produce. Finally, we argue how these approaches can easily be applied to other complex agent-based models of social behavior.

2. Methods

2.1. Multi-Level Agent Based Model

Following Banisch and Olbrich's model [35], we define the cognitive-evaluation matrix relating M beliefs to N issues as a N × M matrix C. We limit entries c_ij to values within {−1, 1, 0}, corresponding to the attitude toward an issue j being affected negatively, positively, or unaffected by a belief i. This implies a total of 3^MN possible cognitive-evaluative matrices. The exponential growth with M and N is a product of the combinatorial nature of the problem, since a priori the relation between a pair of beliefs i₁ and j₁ does not impose any constraint on the relation between any pair i₂ and j₂. Consequently, the number of possible C matrices quickly grows beyond what would be effectively enumerable. For M = 2, N = 2, there is a total of 3⁴ = 81 possible matrices, while for larger systems such as M = 10 beliefs affecting N = 3 issues, this number grows to 3³⁰ ≈ 2 × 10¹⁴. When considering the output of every agent based model, we take into account how multiple matrices might be equivalent under symmetry operations. These operations, which represent all permutations of an agent's beliefs and opinions (e.g., replacing belief i for belief j), result in a smaller set of isomorphic graphs connecting beliefs to opinions, thus mitigating the exponential growth described above. In this brief study, we focus on three case studies where a thorough study of the matrix ensemble is possible, once such symmetries are taken into consideration: namely M = 4,  N = 2 and M = 3,  N = 5.

For every matrix C in each matrix ensemble, we run a total of 20 simulations with different random seeds. For every random seed, we initialize 1,000 agents with random sets of beliefs, i.e., initializing their beliefs as random vectors x ∈ {0, 1}^M, and mapping them to y ∈ ℤ^N attitude vectors through y = C·x. We then iterate every simulation through 15,000 time steps, which we show is enough for model convergence. In every time step, for every agent a₁ in the model, we select another agent a₂ at random, measure the homophily between them, and if this homophily is above a given threshold, agent a₁ selects a random belief from a₂'s beliefs, and copies it. With 1,000 agents and 15,000 time steps, every simulation runs for a total of 15 × 10⁶ interactions between agents.

As described above, the similarity or homophily between agents can be measured in multiple ways. In this study, we define homophily as measured by one minus the normalized Manhattan distance between the attitudes of a pair of agents. The reasons for this choice are many. First, if the distance between agents were to be measured in belief space, i.e., according to their belief vectors only, the dynamics of the agent based model would be trivial: agents would move toward each other, aggregating in a few points in belief space, and no other kind of dynamics would be possible. In other words, agents would concentrate in a finite number of x ∈ {0, 1}^M points in belief space.

This kind of dynamics corresponds to a series of bounded confidence models in opinion dynamics, such as the ones introduced by Deffuant et al. [15] and by Krause and Stöckler [41] and Hegselmann and Krause [42], both of which were expanded by many following works [43–48]. In this category of models, for high enough homophily thresholds, agents might cluster in a few points, while for lower thresholds they would eventually all collapse into a single set of beliefs x, depending on the initial distribution of a agents in the opinion space, but not depending on the cognitive-evaluative matrix C. If one were to assume, for example, that every set of beliefs is equally likely a priori, thus defining the initial conditions of the simulation as a uniform distribution over {0, 1}^M, then every point in belief space would be equally likely to become the steady state of the system, upon a random perturbation to the uniform initial condition of the model. The corresponding dynamics in attitude space y ∈ ℤ^N would also be one of aggregation toward a few attitude vectors y, and the likelihood of convergence toward a specific attitude vector would be proportional to the fraction of x vectors that map to y through y = C·x. Other than that, unless the combination of a particular initial distribution over belief space and the right homophily threshold could allow to the formation of two clusters, measuring homophily as a function of belief homophily would only lead to the formation of homogeneous steady states where all agent have exactly the same opinions and beliefs.

Given that the dynamics induced by any distance metric in belief space will inevitably lead to agents aggregation in both belief and attitude space, what is left is to investigate the dynamics produced by metrics in attitude space. For this choice, if one were to use the Euclidean or L2 norm to measure the distance between attitude vectors y, for a given set of y₁ = (0, 0), y₂ = (1, 1), and y₃ = (0, 2), one would obtain dist(y₁, y₂) < dist(y₁, y₃). Were one to use the Manhattan or L1 norm, they would find dist(y₁, y₂) = dist(y₁, y₃). In the absence of reasons to argue that y₁ differs more from y₃ than from y₂, we will pick the simplest assumption, and use the Manhattan norm for simplicity.

2.2. Measuring Simulation Outputs

To test whether simulations with the same C matrix but initialized with different random seeds might produce different steady-state distributions, we first assess the variability within multiple runs of the same matrix, as shown in Figure 2. Since every run of the model produces 1,000 trajectories over a M-dimensional belief space and a N-dimensional opinion space, we represent the state of an individual run over time with a set of summary statistics: its centroid $y_{\mathrm{\text{centroid}}}\in {ℝ}^N$, its covariance matrix Σ_ij, and its maximum width in each of its principal axes, which can be identified by decomposing Σ_ij into its scaling and rotational components.

FIGURE 2

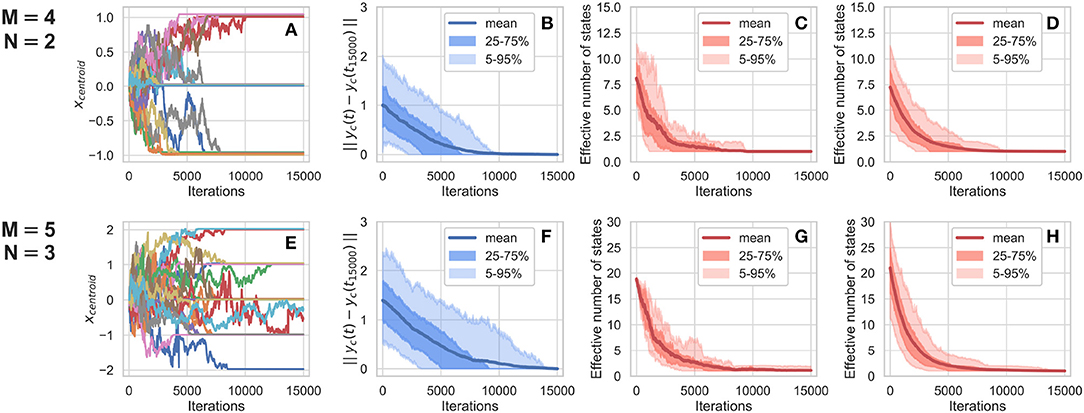
Figure 2. Multiple measures of model convergence. (A) Shows the trajectory of the centroid for 20 runs of the same M = 4,  N = 2 matrix, plotted for the first coordinate in attitude space, over time, reaching three possible values at t=15,000. (B) Shows the L1 distance between the centroid of every run at time t and the centroid of the same run at t=15,000, for all M = 4,  N = 2 matrices. (C) Shows the effective number of states over time, for 1,000 runs of the same M = 4,  N = 2 matrix, while (D) shows the effective number of states over time for runs of all M = 4,  N = 2 matrices. (E–H) Show the same analysis, for M = 5,  N = 3 matrices.

We measure the spread of agents over time for every run in two ways. First, we calculate the mean distance from the centroid of a simulation run at a given time step and the centroid of its steady state (i.e., its centroid after 15,000 steps). Second, we measure the effective number of states over time for each run. The effective number of states is a measure inspired in entropy-based measures of diversity, which have their origin in information theory [49, 50]. We define it as 2 to the power of the entropy of the distribution of agents over multiple states, as shown in Equation (1).

$\begin{array}{ll}\text{ENS(t)}=2^{-{\displaystyle {\sum }_i{p}_i}(t){\log }_2{p}_i(t)}& (1)\end{array}$

In Equation (1) above, the entropy term is summed over the proportion p_i(t) of agents occupying state y_i at time t, for all states y_i in attitude space. In essence, the effective number of states is a measure of the diversity of sets of attitudes taken by the agents in a run at a given point in time: in other words, of how their attitudes are divided between multiple simultaneous states (or sets of attitude values y), weighed according to how many agents adopt them at that point in time. This measure is highest when agents are evenly distributed across many states and lowest when they concentrated at a single state. In the social sciences, equivalent approaches have been used to describe the effective number of parties in a parliament [51], as well as the effective number of issues from a political agenda receiving public attention at the same time [52].

Finally, in addition to analyzing every simulation for every C matrix, we also cluster groups of steady-state distributions according to which points in attitude space are occupied at t=15,000 by a given run.

3. Results

In this section, we present the results of simulations for the three case studies mentioned above: M = 4,  N = 2 and M = 3,  N = 5. Unless specified, we use a distance threshold of β = 1. Unlike Banisch and Olbrich's study [35], which shows the results for a selected set of matrices that could produce a varied set of behaviors, we focus on the behavior emerging from the whole ensemble of matrices defined by a given (M, N) pair.

3.1. Studying Model Convergence

Figure 2 displays an analysis of convergence for this agent-based model, for system sizes of M = 4,  N = 2, and M = 5,  N = 3. In summary, it shows that different runs of the same matrix can produce different results, that convergence typically happens before t=15,000 steps, and that this convergence is usually to a single point in attitude space.

The figure compares the full ensembles of M = 4,  N = 2 and M = 5,  N = 3 matrices with the matrices C_{2 × 4} and C_{3 × 5} specified in Equation (2):

$\begin{array}{ll}{C}_{2\times 4}=\left[\begin{array}{cccc}-1& 0& 0& 1\\ 0& 1& 1& 0\end{array}\right]C_{3\times 5}=\left[\begin{array}{cccc}0& -1& 1& 1\\ 1& -1& 0& 1\\ 0& 0& -1& 0\end{array}\right]& (2)\end{array}$

The first point is illustrated by Figures 2A,E. Both panels show the trajectory of the first coordinate of the centroid of 20 different runs of the same C matrix. In plotting these time series, a small increment of 0.01 was added to the y-value of each run, to make visible the many horizontal lines that otherwise would be overlaid. The panels indicate that most centroids converge to a value before 15,000 steps, but that the value itself varies across runs. For this particular choice of C matrices, centroids stabilized at values of −1, 0, and +1 for C_{2 × 4}, and −2, −1, 0, +1, and +2 for C_{3 × 5}. The fact that the values of 2 and −2 are not observed for C_{2 × 4} and that neither 3 or −3 is observed for C_{3 × 5} is likely due to these specific maps. Still, the diversity of centroid values presented in both panels is enough to show the kind of behavior that would be erased if one were to average multiple runs for the same C matrix.

Naturally, displaying the results of a single pair of matrices is no argument for general convergence. The model convergence around 15,000 time steps for these (M, N) pairs is further presented in all other panels in Figure 2. Figures 2B,F show the L1 distance between the centroid of the distribution of agents in attitude space at time t and the same distribution at time t=15,000, averaged over all M = 4,  N = 2 and M = 5,  N = 3 matrices, respectively for each panel. Shaded areas represent the 25–75 and 5–95% intervals of the distribution of the distance to steady-state centroids, showing that the convergence observed at t=15,000 is not an average phenomenon, and also not unique to C_{2 × 4} and C_{3 × 5}, but rather that convergence is observed for both whole matrix ensembles.

The remaining panels show the evolution of the effective number of states over time, for 1,000 runs of C_{2 × 4} and C_{3 × 5} (Figures 2C,G) and for single runs of all matrices in that (M, N) pair (Figures 2D,H). The effective number of states, described in Equation (1), measures the diversity of points in attitude space occupied by the multiple agents in a model over time. In all panels, this effective number quickly converges to approximately 1.0, both on average and as a whole, as indicated by the shaded areas. This convergence implies that most runs ultimately lead to steady states occupying a single point in attitude space, for both M = 4,  N = 2 and M = 5,  N = 3 matrices.

3.2. Analyzing Steady States

In the previous section, we established that the model usually converges before 15,000 steps, that a typical run converges to a single point in attitude space, but that different runs of the same matrix might result in path-dependent symmetry breaking. In this section, we examine the range of steady-state distributions produced by multiple runs of this model for many C matrices, clustered according to which points in attitude space (i.e., which states) are occupied at t=15,000 by a given run.

The results of the clustered by steady-state distributions are shown in Figure 3 for 20 runs of every M = 5,  N = 3 matrix. Figure 3A shows a rank plot indicating the range of cluster sizes, i.e., the number of runs producing each steady-state distribution. As evidenced by the log-scale on the y axis, this is a long-tail distribution: most runs produce the same few steady-state distributions, while most steady states are only observed for 10 runs or less.

FIGURE 3

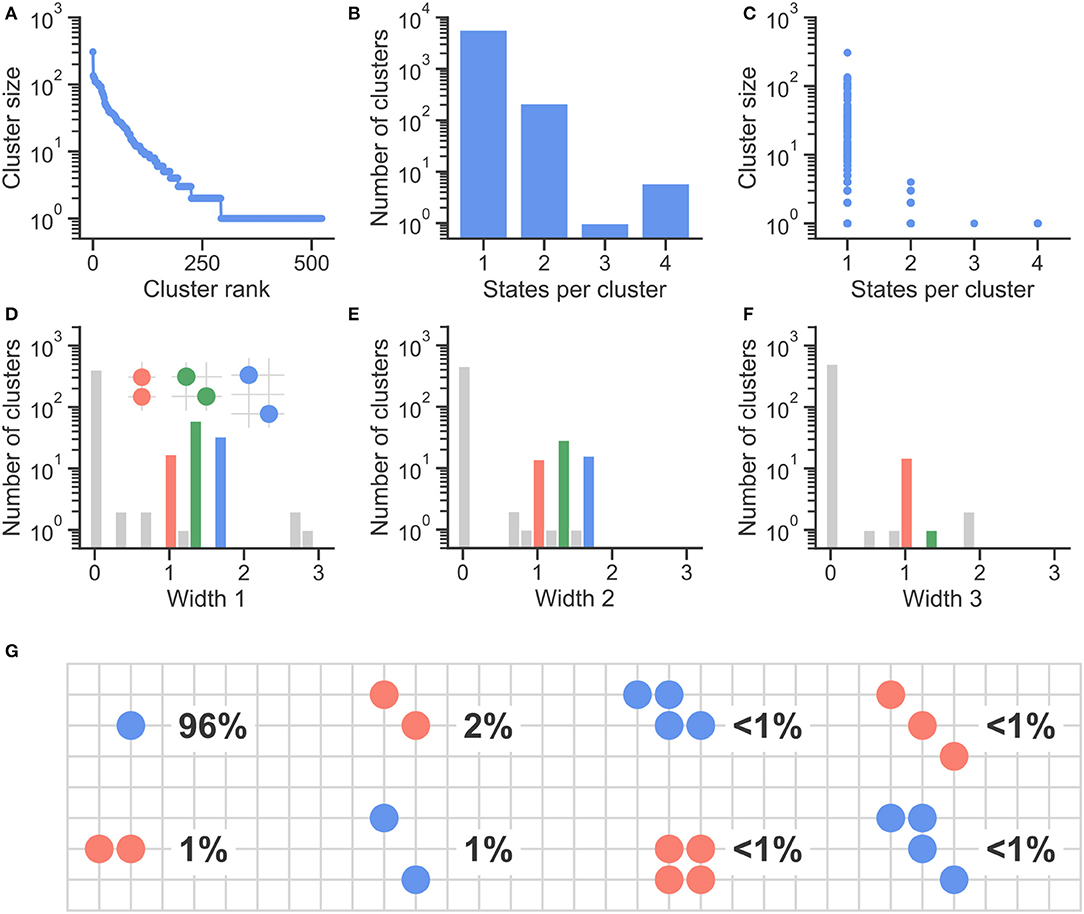
Figure 3. Examining all steady-state distributions for 20 runs of every M = 5,  N = 3 matrix. (A) Shows a rank plot indicating the range of cluster sizes, i.e., the number of runs producing each steady-state distribution. (B,C) Show a breakdown of the number of states (i.e., points in attitude space) per cluster: the number of clusters with a single state is over one order of magnitude above the number of clusters with two or more states, and those one-state steady states are also the ones corresponding to the largest number of runs, as shown in (C). (D–F) Count the number of clusters according to their width in each cluster's widest axis [Width 1, (D)], followed by its second and third widest axes [widths 2 and 3, (E,F), respectively]. In order, red, green, and blue bars indicate clusters with width 1, $\sqrt{2}$, and $\sqrt{3}$, as indicated by the insets in (D). (G) Shows the frequency of different steady-state distributions, when clustered only on their shape, but not on their position in attitude space.

From Figure 3B, we see that most steady-state clusters correspond to single states, while the number of clusters with two or more states is over an order of magnitude smaller. Figure 3C compares the number of states with the number of runs falling into each cluster, i.e., the cluster size: it shows that most large clusters are single-state clusters, followed by two-state clusters.

As indicated by the top three panels, most runs of this model result in a few single-state clusters, while wider steady-state distributions correspond to a small proportion of all resulting steady-states of the model, with many distributions corresponding to only a few model runs each. Figures 3D–F investigate this range of wider distributions, binning clusters according to their width in each cluster's principal axes, obtained by decomposing each their covariance matrices Σ_ij into scaling and rotational components. Principal components are shown in Figures 3D–F from most important to least important (namely, Widths 1, 2, and 3), with the height of every bar indicating the number of clusters with a particular width in each principal axis.

Figures 3D–F also show red, green, and blue bars. These bars indicate the number of steady-state clusters with particular widths, namely 1, $\sqrt{2}$, and $\sqrt{3}$. The high cluster count at these particular (Euclidean) distance values is a consequence of the discrete grid-like nature of the agent-based model, which produces steady states such as the ones indicated by the insets in Figure 3D, which have widths of 1, $\sqrt{2}$, and $\sqrt{3}$.

Finally, Figure 3G shows the frequency of different steady-state clusters, when grouped only regarding their shape, and therefore also aggregating over orientation and centroid position. It confirms what is indicated by the other six panels: the largest fraction of steady-state distributions is point-like, representing all 1,000 agents converging toward the same point in attitude space, a phenomenon which happens for 96% of all model runs, including C matrices with all kinds of symmetry and levels of interdependency between issues. Steady-state distributions two or more states together only take 4% of all runs of the model.

It is important to note that Figure 3G is a two-dimensional representation of a three-dimensional model. This is only possible because the frequency of three-dimensional steady states distribution is under 1%, which is comparable to the frequency of other two-dimensional steady states shown in the figure. This is in agreement with Figure 3F, which shows that <1% of all steady states have a non-zero width in their third main axis. In other words: zero-dimensional (point-like) steady states are by far the most common, corresponding to 96% of all model runs, followed by one-dimensional, two-dimensional and three-dimensional steady states, in order of decreasing frequency.

Finally, the reviewer might notice that steady-state distributions such as the bottom left in Figure 3G should not be absorbing states under the model with β = 1. Rather, given enough time, this distribution should converge to the point-like distribution on the top left of Figure 3G, which is an absorbing state. This 1% of all steady-state distributions likely corresponds to runs which are still in their transient state by t=15,000. Preliminary runs of (M = 10,  N = 2) and (M = 10,  N = 3) show a similar pattern: these system sizes tend to show polarized one-dimensional distributions for timescales longer than 15,000 time steps, only converging to absorbing states after over 50,000 time steps. In their paper, Banisch and Olbrich argue these transient distributions should become more empirically relevant as population sizes grow–we explore this point in more detail in the section 4.

4. Discussion

The aim of this article was to provide a good illustration of the complexity involved in studying an agent-based model of human behavior that is actually guided by social and cognitive psychology. The theoretical details and model choices made by Banisch and Olbrich [35] to model Mäs and Flache's argument communication theory of bi-polarization resulted in a model which is simple to define and to run, but which requires careful analysis, as its outputs are inherently multidimensional and dependent on a number of factors. It is this sort of system which often limits linear and analytical approaches, since the relevant part of the behavior happens at an emergent level. Through a complete enumeration of the M = 4,  N = 2 and M = 5,  N = 3 cognitive-evaluative matrices, we find that most runs of the model, for all cognitive-evaluative matrices, move toward a few steady-state distributions. We find that the clusters of steady-state distributions in attitude space corresponding to most runs are often pointwise steady-state distributions, where all agents converge toward the same vector y in attitude space. Steady states composed of two or more attitude states take over approximately 4% of all runs of the model, with distribution with 2 states being the most frequent.

Our analysis of small of Banisch and Olbrich's model for small M and N suggests that the most likely result after many iterations of the model is consensus, and that any deviation from consensus would hardly be described as “polarization.” These are, however, small systems: matrices with larger M and N allow for a larger spread of agents in attitude space, which allows for the emergence of distributions polarized along one axis. We observe that in preliminary runs of matrices with (M = 10,  N = 2) and (M = 10,  N = 3), which display one-dimensional distributions of agents in attitude space for longer than 15,000 time steps, only converging after over 50,000 time steps. This suggests that larger systems should take longer to converge, allowing for the sustained existence of social dynamics within transient population states. Distributions displayed during the transient period should be particularly relevant for larger population sizes, a point also made by Banisch and Araújo when talking more broadly about opinion dynamics models [47].

The main result of this work, beyond producing insights about small systems, is a methodological contribution. As described in more detail in section 2 this multi-level agent-based model does not have any clear output variables, nor a clear aggregation scale, order parameter or measurable outcome. Its emergent behavior is the product of countless interactions where agents update their beliefs and attitudes, but there is no clear metric assessing when such emergent behavior has happened, or even to tell apart the model transient from its steady state.

This paper introduced a number of approaches to address this problem: in Figure 2, after establishing that individual runs of the model for the same cognitive-evaluative matrix should not be averaged without losing significant information, we observe the distribution of agents in attitude space over time, plotting the distance between the agents' centroid over time and the final position of their centroid, as well as looking at the effective number of states of every run. This effective number of states, just like its equivalent measures from other multidimensional models of social behavior, takes an approach from information theory to quantify the diversity of states in the model. With these tools combined, we are able to establish model convergence around t=15,000 steps.

The analysis presented in Figure 3 presents further methods which can be applied to complex agent-based models: by using a combination of cluster analysis and PCA-like methods to establish the main directions of variation of all the steady states produced by 20 runs of the model for every M = 5,  N = 3. These states were then aggregated in multiple ways, leading to a thorough description of the full spectrum of outputs produced by this model.

The methods presented here open many doors for future research. Firstly, they allow for a more careful exploration of Banisch and Olbrich's model, at system sizes of empirical relevance. Moreover, the full enumeration approach used here might also be ideal—further research is needed to identify the correct ensembles of matrices to represent the mapping between opinions and attitudes. One might also want to consider the interplay of social network structures and cognitive-evaluative maps, as the separation between beliefs and attitudes might lead to stronger separation between agents in different parts of a network.

Most importantly, this work introduces a scalable way to explore the parameter space of complex agent-based models such as the one studied in this paper. Methods such as the effective number of states or the clustering by steady-state are most appropriate for models which resemble real-life social behavior, particularly the dynamics of beliefs, opinions and attitudes, where emergent phenomena are not static, easily measurable or even clearly defined—and where there usually is no order parameter that identifies different regimes of the model. Here we have introduced not an order parameter, but a set of analysis tools, which can bring more power and clarity to future complex models of social behavior.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

CC designed and performed the research as well as wrote the paper.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author would like to thank Sven Banisch for helpful discussions on the computational model, and the two reviewers for their very important feedback on previous iterations of this work.

References

1. Banarjee A. A simple model of herd behaviour. Q J Econ. (1992) 107:797–817.

Google Scholar

2. Golub B, Jackson MO. Using selection bias to explain the observed structure of internet diffusions. Proc Natl Acad Sci USA. (2010) 107:10833–6. doi: 10.1073/pnas.1000814107

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Golub B, Jackson MO. Naive learning in social networks and the wisdom of crowds. Am Econ J. (2010) 2:112–49. doi: 10.1257/mic.2.1.112

CrossRef Full Text | Google Scholar

4. Axelrod R. The dissemination of culture: a model with local convergence and global polarization. J Conflict Resol. (1997) 41:203–26. doi: 10.1177/0022002797041002001

CrossRef Full Text | Google Scholar

5. Friedkin NE, Johnsen EC. Social influence and opinions. J Math Sociol. (1990) 15:193–206. doi: 10.1080/0022250X.1990.9990069

CrossRef Full Text | Google Scholar

6. Boyd R, Richerson PJ. Why does culture increase human adaptability? Ethol Sociobiol. (1995) 16:125–43. doi: 10.1016/0162-3095(94)00073-G

CrossRef Full Text | Google Scholar

7. Van Benthem J, Van Eijck J, Kooi B. Logics of communication and change. Inform Comput. (2006) 204:1620–62. doi: 10.1016/j.ic.2006.04.006

CrossRef Full Text | Google Scholar

8. Nowak A, Szamrej J, Latané B. From private attitude to public opinion: a dynamic theory of social impact. Psychol Rev. (1990) 97:362. doi: 10.1037/0033-295X.97.3.362

CrossRef Full Text | Google Scholar

9. Clifford P, Sudbury A. A model for spatial conflict. Biometrika. (1973) 60:581–8. doi: 10.1093/biomet/60.3.581

CrossRef Full Text | Google Scholar

10. Holley RA, Liggett TM. Ergodic theorems for weakly interacting infinite systems and the voter model. Ann Probabil. (1975) 3:643–63. doi: 10.1214/aop/1176996306

CrossRef Full Text | Google Scholar

11. Fu F, Wang L. Coevolutionary dynamics of opinions and networks: from diversity to uniformity. Phys Rev E. (2008) 78:016104. doi: 10.1103/PhysRevE.78.016104

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Nardini C, Kozma B, Barrat A. Who's talking first? Consensus or lack thereof in coevolving opinion formation models. Phys Rev Lett. (2008) 100:158701. doi: 10.1103/PhysRevLett.100.158701

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Galam S. Minority opinion spreading in random geometry. Eur Phys J B-Condens Matter Complex Syst. (2002) 25:403–6. doi: 10.1140/epjb/e20020045

CrossRef Full Text | Google Scholar

14. Sznajd-Weron K, Sznajd J. Opinion evolution in closed community. Int J Modern Phys C. (2000) 11:1157–65. doi: 10.1142/S0129183100000936

CrossRef Full Text | Google Scholar

15. Deffuant G, Neau D, Amblard F, Weisbuch G. Mixing beliefs among interacting agents. Adv Complex Syst. (2000) 3:87–98. doi: 10.1142/S0219525900000078

CrossRef Full Text | Google Scholar

16. Burnstein E, Vinokur A. What a person thinks upon learning he has chosen differently from others: nice evidence for the persuasive-arguments explanation of choice shifts. J Exp Soc Psychol. (1975) 11:412–26. doi: 10.1016/0022-1031(75)90045-1

CrossRef Full Text | Google Scholar

17. Burnstein E, Vinokur A. Persuasive argumentation and social comparison as determinants of attitude polarization. J Exp Soc Psychol. (1977) 13:315–32. doi: 10.1016/0022-1031(77)90002-6

CrossRef Full Text | Google Scholar

18. Isenberg DJ. Group polarization: a critical review and meta-analysis. J Pers Soc Psychol. (1986) 50:1141. doi: 10.1037/0022-3514.50.6.1141

CrossRef Full Text | Google Scholar

19. Ewing TN. A study of certain factors involved in changes of opinion. J Soc Psychol. (1942) 16:63–88. doi: 10.1080/00224545.1942.9714105

CrossRef Full Text | Google Scholar

20. Darke PR, Chaiken S, Bohner G, Einwiller S, Erb HP, Hazlewood JD. Accuracy motivation, consensus information, and the law of large numbers: effects on attitude judgment in the absence of argumentation. Pers Soc Psychol Bull. (1998) 24:1205–15. doi: 10.1177/01461672982411007

CrossRef Full Text | Google Scholar

21. Kumkale GT, Albarracin D, Seignourel PJ. The effects of source credibility in the presence or absence of prior attitudes: implications for the design of persuasive communication campaigns. J Appl Soc Psychol. (2010) 40:1325–56. doi: 10.1111/j.1559-1816.2010.00620.x

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Yan Y, Liu J. Effects of media exemplars on the perception of social issues with pre-existing beliefs. J Mass Commun Q. (2016) 93:1026–49. doi: 10.1177/1077699016629374

CrossRef Full Text | Google Scholar

23. Fiedler K. Meta-cognitive myopia and the dilemmas of inductive-statistical inference. In: Ross B, editor Psychology of Learning and Motivation, Vol. 57. Cambridge: Elsevier (2012). p. 1–55.

Google Scholar

24. Tversky A, Kahneman D. Belief in the law of small numbers. Psychol Bull. (1971) 76:105. doi: 10.1037/h0031322

CrossRef Full Text | Google Scholar

25. Goldberg A, Stein SK. Beyond social contagion: associative diffusion and the emergence of cultural variation. Am Sociol Rev. (2018) 83:897–932. doi: 10.1177/0003122418797576

CrossRef Full Text | Google Scholar

26. Holme P, Newman ME. Nonequilibrium phase transition in the coevolution of networks and opinions. Phys Rev E. (2006) 74:056108. doi: 10.1103/PhysRevE.74.056108

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Zanette DH, Gil S. Opinion spreading and agent segregation on evolving networks. Phys D. (2006) 224:156–65. doi: 10.1016/j.physd.2006.09.010

CrossRef Full Text | Google Scholar

28. Bakshy E, Messing S, Adamic LA. Exposure to ideologically diverse news and opinion on Facebook. Science. (2015) 348:1130–2. doi: 10.1126/science.aaa1160

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Barberá P, Jost JT, Nagler J, Tucker JA, Bonneau R. Tweeting from left to right: is online political communication more than an echo chamber? Psychol Sci. (2015) 26:1531–42. doi: 10.1177/0956797615594620

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Mäs M, Flache A. Differentiation without distancing. Explaining BI-polarization of opinions without negative influence. PLoS ONE. (2013) 8:e74516. doi: 10.1371/journal.pone.0074516

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Byrne D. Interpersonal attraction and attitude similarity. J Abnorm Soc Psychol. (1961) 62:713. doi: 10.1037/h0044721

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Huston TL, Levinger G. Interpersonal attraction and relationships. Annu Rev Psychol. (1978) 29:115–56. doi: 10.1146/annurev.ps.29.020178.000555

PubMed Abstract | CrossRef Full Text | Google Scholar

33. McPherson M, Smith-Lovin L, Cook JM. Birds of a feather: homophily in social networks. Annu Rev Sociol. (2001) 27:415–44. doi: 10.1146/annurev.soc.27.1.415

CrossRef Full Text | Google Scholar

34. Wimmer A, Lewis K. Beyond and below racial homophily: ERG models of a friendship network documented on Facebook. Am J Sociol. (2010) 116:583–642. doi: 10.1086/653658

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Banisch S, Olbrich E. An argument communication model of polarization and ideological alignment. arXiv [preprint]. arXiv:180906134 (2018).

Google Scholar

36. Fishbein M, Raven BH. The AB scales: an operational definition of belief and attitude. Hum Relat. (1962) 15:35–44. doi: 10.1177/001872676201500104

CrossRef Full Text | Google Scholar

37. Fishbein M. An investigation of the relationships between beliefs about an object and the attitude toward that object. Hum Relat. (1963) 16:233–9. doi: 10.1177/001872676301600302

CrossRef Full Text | Google Scholar

38. Ajzen I. Nature and operation of attitudes. Annu Rev Psychol. (2001) 52:27–58. doi: 10.1146/annurev.psych.52.1.27

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Rosa H. Resonance: A Sociology of Our Relationship to the World. Hoboken, NJ: John Wiley & Sons (2019).

Google Scholar

40. Dalege J, Borsboom D, van Harreveld F, van den Berg H, Conner M, van der Maas HL. Toward a formalized account of attitudes: the Causal Attitude Network (CAN) model. Psychol Rev. (2016) 123:2–22. doi: 10.1037/a0039802

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Krause U, Stöckler M. Modellierung und Simulation von Dynamiken mit Vielen Interagierenden Akteuren. Bremen: Modus Universität (1997).

Google Scholar

42. Hegselmann R, Krause U. Opinion dynamics and bounded confidence models, analysis, and simulation. J Artif Soc Soc Simul. (2002) 5. Available online at: http://jasss.soc.surrey.ac.uk/5/3/2.html

Google Scholar

43. Deffuant G, Amblard F, Weisbuch G, Faure T. How can extremism prevail? A study based on the relative agreement interaction model. J Artif Soc Soc Simul. (2002) 5:1. Available online at:jasss.soc.surrey.ac.uk/5/4/1.html

Google Scholar

44. Weisbuch G, Deffuant G, Amblard F, Nadal JP. Meet, discuss, and segregate! Complexity (2002) 7:55–63. doi: 10.1002/cplx.10031

CrossRef Full Text | Google Scholar

45. Stauffer D, De Oliveira SMM, De Oliveira PMC, de Sá Martins JS. Biology, Sociology, Geology by Computational Physicists. Amsterdam: Elsevier (2006).

Google Scholar

46. Lorenz J. Continuous opinion dynamics under bounded confidence: a survey. Int J Modern Phys C. (2007) 18:1819–38. doi: 10.1142/S0129183107011789

CrossRef Full Text | Google Scholar

47. Banisch S, Araújo T, Louçã J. Opinion dynamics and communication networks. Adv Complex Syst. (2010) 13:95–111. doi: 10.1142/S0219525910002438

CrossRef Full Text | Google Scholar

48. Acemoglu D, Ozdaglar A. Opinion dynamics and learning in social networks. Dyn Games Appl. (2011) 1:3–49. doi: 10.1007/s13235-010-0004-1

CrossRef Full Text | Google Scholar

49. Shannon CE. A mathematical theory of communication. Bell Syst Tech J. (1948) 27:379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x

CrossRef Full Text | Google Scholar

50. Jost L. Entropy and diversity. Oikos. (2006) 113:363–75. doi: 10.1111/j.2006.0030-1299.14714.x

CrossRef Full Text | Google Scholar

51. Laakso M, Taagepera R. “Effective” number of parties: a measure with application to West Europe. Compar Polit Stud. (1979) 12:3–27. doi: 10.1177/001041407901200101

CrossRef Full Text | Google Scholar

52. Camargo CQ, Hale SA, John P, Margetts HZ. Volatility in the issue attention economy. arXiv [preprint]. arXiv:180809037. (2018).

Google Scholar